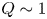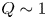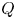1. Introduction
Building upon recent game-changing experimental breakthroughs in the operation of axisymmetric mirrors (Simonen Reference Simonen2016) and major advances in fusion technology (such as high-field magnets; Whyte et al. Reference Whyte, Minervini, LaBombard, Marmar, Bromberg and Greenwald2016), Egedal et al. (Reference Egedal, Endrizzi, Forest and Fowler2022) (henceforth Egedal22) have reminded us that for best-case scenarios of confinement, break-even conditions are accessible for neutral-beam injection (NBI) energies between 100 and 200 keV into a simple mirror if the mirror ratio is $\gtrsim$![]() 10. This is in stark contrast to the conclusion drawn in the late 1970s when it seemed clear that simple mirrors using non-axisymmetric yin-yang coils or baseball coils and limited to mirror ratios of order 2 would never reach break-even conditions.
10. This is in stark contrast to the conclusion drawn in the late 1970s when it seemed clear that simple mirrors using non-axisymmetric yin-yang coils or baseball coils and limited to mirror ratios of order 2 would never reach break-even conditions.
This paper continues to explore the confinement of high-field mirrors in search of an engineering design that can reach the break-even regime (see Fig. 1). We include realistic constraints and design considerations, and also address competing optimizations. These trade-offs include, for example, the consideration of high field at the cost of synchrotron radiation that cools the electrons and subsequently decreases the ion confinement time. Or the use of obliquely injected sloshing ions to stabilize the drift cyclotron loss cone (DCLC) instability at the cost of shorter particle confinement time, which is shown in figure 2). We also address temporal evolution with time-dependent Fokker–Planck solutions, demonstrating a path from low to high $\beta$![]() with realistic fuelling and heating. The Wisconsin High-temperature-superconductor Axisymmetric Mirror experiment (WHAM) described in a companion paper by Endrizzi et al. (Reference Endrizzi, Anderson, Brown, Egedal, Geiger, Harvey, Ialovega, Kirch, Peterson and Petrov2023) (henceforth Endrizzi23) is an axisymmetric mirror intended, like BEAM, to operate in the weakly collisional or classical mirror regime similar to the earlier generation of experiments (see figure 3) built to address physics risks before embarking on a BEAM. The WHAM will provide a technology development platform for mirror fusion and in particular the next step device sketched in this paper. Both WHAM and BEAM are assumed to operate in the classical mirror regime in which ion pitch angle scattering (rather than slowing of ions on electrons) governs confinement.
with realistic fuelling and heating. The Wisconsin High-temperature-superconductor Axisymmetric Mirror experiment (WHAM) described in a companion paper by Endrizzi et al. (Reference Endrizzi, Anderson, Brown, Egedal, Geiger, Harvey, Ialovega, Kirch, Peterson and Petrov2023) (henceforth Endrizzi23) is an axisymmetric mirror intended, like BEAM, to operate in the weakly collisional or classical mirror regime similar to the earlier generation of experiments (see figure 3) built to address physics risks before embarking on a BEAM. The WHAM will provide a technology development platform for mirror fusion and in particular the next step device sketched in this paper. Both WHAM and BEAM are assumed to operate in the classical mirror regime in which ion pitch angle scattering (rather than slowing of ions on electrons) governs confinement.

Figure 1. Conceptual layout of the BEAM device showing $45^{\circ }$![]() orientation of neutral-beam injectors (NBI), central plasma vessel (pink) surrounded by immersion blanket, principal superconducting magnets (purple) and end vessels with direct energy converters (DEC). The high-field mirror coils utilize high-temperature superconducting (HTS) magnets, while the larger lower-field magnets are conventional and lower-cost low-temperature superconducting magnets.
orientation of neutral-beam injectors (NBI), central plasma vessel (pink) surrounded by immersion blanket, principal superconducting magnets (purple) and end vessels with direct energy converters (DEC). The high-field mirror coils utilize high-temperature superconducting (HTS) magnets, while the larger lower-field magnets are conventional and lower-cost low-temperature superconducting magnets.

Figure 2. Fusion gain $Q$![]() for neutral-beam-driven classical mirror as a function of mirror ratio and NBI angle. Blue lines are results from Egedal22, and dotted red lines are an empirical fit to the simulation results, where $\theta _{\rm nbi}$
for neutral-beam-driven classical mirror as a function of mirror ratio and NBI angle. Blue lines are results from Egedal22, and dotted red lines are an empirical fit to the simulation results, where $\theta _{\rm nbi}$![]() is the injection angle, $\theta _{Rm}$
is the injection angle, $\theta _{Rm}$![]() is the loss cone pitch angle set by the mirror ratio and $\theta _{bw}$
is the loss cone pitch angle set by the mirror ratio and $\theta _{bw}$![]() is a 5$^\circ$
is a 5$^\circ$![]() beam half-width.
beam half-width.

Figure 3. The historical record of ion confinement time for simple mirror experiments as well as the predicted performance of WHAM (Endrizzi et al. Reference Endrizzi, Anderson, Brown, Egedal, Geiger, Harvey, Ialovega, Kirch, Peterson and Petrov2023) and BEAM compared with predictions by (1.1).
Axisymmetric mirrors are unstable to ideal magnetohydrodynamic (MHD) interchange modes that have fast growth rates of the order of an inverse ion bounce time, $\varGamma _{0} = L_p /v_{{\rm thi}}$![]() (Fowler Reference Fowler1981; Post Reference Post1987; Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011). Theory, experiments and simulations have shown that interchange modes with $m \geq 2$
(Fowler Reference Fowler1981; Post Reference Post1987; Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011). Theory, experiments and simulations have shown that interchange modes with $m \geq 2$![]() can be stabilized by two-fluid effects associated with finite Larmor radii (FLR) (Roberts & Taylor Reference Roberts and Taylor1962; Rosenbluth, Krall & Rostoker Reference Rosenbluth, Krall and Rostoker1962; Rosenbluth & Simon Reference Rosenbluth and Simon1965; Pearlstein Reference Pearlstein1966; Anikeev et al. Reference Anikeev, Bagryansky, Ivanov, Kuzmin and Salikova1992) of the NBI ions when the machine is long enough, and also that the global $m=1$
can be stabilized by two-fluid effects associated with finite Larmor radii (FLR) (Roberts & Taylor Reference Roberts and Taylor1962; Rosenbluth, Krall & Rostoker Reference Rosenbluth, Krall and Rostoker1962; Rosenbluth & Simon Reference Rosenbluth and Simon1965; Pearlstein Reference Pearlstein1966; Anikeev et al. Reference Anikeev, Bagryansky, Ivanov, Kuzmin and Salikova1992) of the NBI ions when the machine is long enough, and also that the global $m=1$![]() mode can be shear-flow-modified to saturate at a low amplitude when the shearing rate exceeds the growth rate by roughly a factor of 2 (Beklemishev et al. Reference Beklemishev, Bagryansky, Chaschin and Soldatkina2010; Bagryansky et al. Reference Bagryansky, Anikeev, Beklemishev, Donin, Ivanov, Korzhavina, Kovalenko, Kruglyakov, Lizunov and Maximov2011, Reference Bagryansky, Anikeev, Denisov, Gospodchikov, Ivanov, Lizunov, Kovalenko, Malygin, Maximov and Korobeinikova2015; Yakovlev et al. Reference Yakovlev, Shalashov, Gospodchikov, Maximov, Prikhodko, Savkin, Soldatkina, Solomakhin and Bagryansky2018; Soldatkina et al. Reference Soldatkina, Maximov, Prikhodko, Savkin, Skovorodin, Yakovlev and Bagryansky2020). Other stabilization mechanisms and techniques can also be used, as discussed in § 4.
mode can be shear-flow-modified to saturate at a low amplitude when the shearing rate exceeds the growth rate by roughly a factor of 2 (Beklemishev et al. Reference Beklemishev, Bagryansky, Chaschin and Soldatkina2010; Bagryansky et al. Reference Bagryansky, Anikeev, Beklemishev, Donin, Ivanov, Korzhavina, Kovalenko, Kruglyakov, Lizunov and Maximov2011, Reference Bagryansky, Anikeev, Denisov, Gospodchikov, Ivanov, Lizunov, Kovalenko, Malygin, Maximov and Korobeinikova2015; Yakovlev et al. Reference Yakovlev, Shalashov, Gospodchikov, Maximov, Prikhodko, Savkin, Soldatkina, Solomakhin and Bagryansky2018; Soldatkina et al. Reference Soldatkina, Maximov, Prikhodko, Savkin, Skovorodin, Yakovlev and Bagryansky2020). Other stabilization mechanisms and techniques can also be used, as discussed in § 4.
The development of axisymmetric MHD stable operation subsequently led to much higher electron temperatures ($\sim$![]() 1 keV) with the addition of modest amounts of electron cyclotron heating, and dispelled the myth that electrons are always ‘dead cold’ in mirrors. Separately, the recent development of high-temperature superconductor (HTS) magnets appropriate for fusion applications (Whyte et al. Reference Whyte, Minervini, LaBombard, Marmar, Bromberg and Greenwald2016; Whyte Reference Whyte2019) now allows for larger mirror ratios and better classical confinement, while axisymmetry precludes neoclassical radial transport effects.
1 keV) with the addition of modest amounts of electron cyclotron heating, and dispelled the myth that electrons are always ‘dead cold’ in mirrors. Separately, the recent development of high-temperature superconductor (HTS) magnets appropriate for fusion applications (Whyte et al. Reference Whyte, Minervini, LaBombard, Marmar, Bromberg and Greenwald2016; Whyte Reference Whyte2019) now allows for larger mirror ratios and better classical confinement, while axisymmetry precludes neoclassical radial transport effects.
This paper lays out performance predictions for a next step device (BEAM) that could take the mirror to near scientific break-even conditions and provide a useful blanket and materials testing facility. It is intended to be conceptual and provide a starting point for a more substantial optimization, now underway, of an engineering design for BEAM.
The principle extrapolation from prior mirror experiments to BEAM is a big step up in the injection energy of neutral beams. Previously, neutral beams in mirror experiments, including the gas dynamic trap as well as WHAM, are at an unfortunate injection energy of 25 keV. This energy is set by the requirement that the neutral beam be substantially attenuated by the small, low-density plasmas. As noted in Endrizzi23, injected ions at this energy are four times more likely to charge exchange with plasma ions than to be collisionally ionized, severely limiting the effectiveness of NBI for plasma fuelling. It also results in distribution functions peaked near the injection energy and pitch angle of the neutral beam itself.
An obvious advance would be to test mirror performance with TFTR/DIII-D/Asdex-U class neutral beams where the beams primarily fuel (rather than charge exchange) and the resulting beam distribution functions collisionally relax to classical mirror predictions. Nearly classical confinement in BEAM would also largely retire the risk in performance needed to embark on a tandem mirror for large-scale power production (Fowler, Moir & Simonen Reference Fowler, Moir and Simonen2017).
In this range of NBI energies, Fokker–Planck solutions such as FBIS (Egedal22; Killeen, Mirin & Rensink Reference Killeen, Mirin and Rensink1976) for classical mirror confinement have shown for nearly perpendicular injection and realistic $B(z)$![]() profiles
profiles
with a dimensionless $n_{20}$![]() in units of $10^{20}$
in units of $10^{20}$![]() m$^{-3}$
m$^{-3}$![]() , injection energy $E_b$
, injection energy $E_b$![]() normalized to 100 keV and $R_M$
normalized to 100 keV and $R_M$![]() the mirror ratio $B_{\max }/B_{\min }$
the mirror ratio $B_{\max }/B_{\min }$![]() . Incorporating an analytic deuterium–tritium fusion reactivity for ion energy between 100 and 200 keV, this confinement corresponds to a scientific fusion gain $Q_{{\rm sci}}$
. Incorporating an analytic deuterium–tritium fusion reactivity for ion energy between 100 and 200 keV, this confinement corresponds to a scientific fusion gain $Q_{{\rm sci}}$![]() given by
given by
Equation (1.2)Footnote 1 makes clear that for a next step mirror experiment to be capable of $Q\sim 1$![]() it should operate with $R_M\sim 10$
it should operate with $R_M\sim 10$![]() and use NBI energies near keV where fuelling and fusion optimize. Obliquely incident NBI is used to increase path length and create sloshing ions. This decreases the confinement (as shown in figure 2) due to the proximity of the injected ion to the loss cone in velocity space.
and use NBI energies near keV where fuelling and fusion optimize. Obliquely incident NBI is used to increase path length and create sloshing ions. This decreases the confinement (as shown in figure 2) due to the proximity of the injected ion to the loss cone in velocity space.
The small radial dimensions of prior mirror experiments (e.g. 0.20 m diameter in GDT) made the most energetic ions vulnerable to charge-exchange interactions with background gas, which led to additional energy losses from plasma. A higher-energy NBI-heated mirror must have much larger diameter, as well as denser plasma in order to ionize the neutral beam and have a well-defined energetic core region with classical confinement and a sufficiently thick edge region, protecting the core from recycled neutrals.
2. Size and magnetic field requirements for BEAM
In this section, the main physics issues driving size and cost of BEAM are considered, motivated by the question ‘What would be the minimum size and field to achieve $Q \sim 1$![]() in a simple mirror?’ The main requirements labelled (A) through (I) on BEAM are:
in a simple mirror?’ The main requirements labelled (A) through (I) on BEAM are:
(A) Minimum beam energy
The neutral-beam energy is chosen both to optimize the classical prediction of $Q$![]() ($E_{b,100\,{\rm keV}} = Q_\textrm {sci}^2 / (\log _{10} R_M )^2$
($E_{b,100\,{\rm keV}} = Q_\textrm {sci}^2 / (\log _{10} R_M )^2$![]() ), but also to ensure charge exchange losses do not dominate the energy balance, as discussed in Endrizzi23. We require that only 20 % of collisions are due to charge exchange, $\chi \equiv \sigma _{cx} / (\sigma _{cx} + \sigma _{i+e} )\leq 0.2$
), but also to ensure charge exchange losses do not dominate the energy balance, as discussed in Endrizzi23. We require that only 20 % of collisions are due to charge exchange, $\chi \equiv \sigma _{cx} / (\sigma _{cx} + \sigma _{i+e} )\leq 0.2$![]() , implying $E_b\geq 100$
, implying $E_b\geq 100$![]() keV. Conveniently, this is close to the optimal energy for $Q_{DT}$
keV. Conveniently, this is close to the optimal energy for $Q_{DT}$![]() and such beams are now available having been fully developed for tokamaks: TFTR-class (also ASDEX-U, DIII-D, KSTAR) NBIs at $E_b=100$
and such beams are now available having been fully developed for tokamaks: TFTR-class (also ASDEX-U, DIII-D, KSTAR) NBIs at $E_b=100$![]() keV.
keV.
(B) Maximum plasma pressure
The fast-ion pressure will be limited by the achievable $\beta \equiv 2 \mu _0 P/ B^2$![]() to values less than $\beta _c$
to values less than $\beta _c$![]() and the strength of the midplane magnetic field. In a typical axisymmetric mirror, $\beta _c$
and the strength of the midplane magnetic field. In a typical axisymmetric mirror, $\beta _c$![]() is set by interchange modes. GDT demonstrated techniques for mitigating this: the more deleterious higher $m$
is set by interchange modes. GDT demonstrated techniques for mitigating this: the more deleterious higher $m$![]() modes are stabilized by FLR and the global $m=1$
modes are stabilized by FLR and the global $m=1$![]() mode is stabilized by vortex biasing. In the absence of interchange, the next MHD pressure limit would likely be due to ballooning modes at a higher $\beta _c$
mode is stabilized by vortex biasing. In the absence of interchange, the next MHD pressure limit would likely be due to ballooning modes at a higher $\beta _c$![]() . However, GDT did not see ballooning modes even at $\beta \sim 0.6$
. However, GDT did not see ballooning modes even at $\beta \sim 0.6$![]() (Yakovlev et al. Reference Yakovlev, Shalashov, Gospodchikov, Maximov, Prikhodko, Savkin, Soldatkina, Solomakhin and Bagryansky2018).
(Yakovlev et al. Reference Yakovlev, Shalashov, Gospodchikov, Maximov, Prikhodko, Savkin, Soldatkina, Solomakhin and Bagryansky2018).
High $\beta$![]() may have significant positive impacts on confinement and stability by naturally enhancing the mirror ratio and providing access to wall-stabilized regimes. There may also be detrimental effects such as the loss of fast-ion and alpha-particle adiabaticity (Cohen et al. Reference Cohen, Rensink, Cutler and Mirin1978a; Endrizzi et al. Reference Endrizzi, Anderson, Brown, Egedal, Geiger, Harvey, Ialovega, Kirch, Peterson and Petrov2023) (see item (D) below). We choose a conservative limit of $\beta _c\sim 0.3$
may have significant positive impacts on confinement and stability by naturally enhancing the mirror ratio and providing access to wall-stabilized regimes. There may also be detrimental effects such as the loss of fast-ion and alpha-particle adiabaticity (Cohen et al. Reference Cohen, Rensink, Cutler and Mirin1978a; Endrizzi et al. Reference Endrizzi, Anderson, Brown, Egedal, Geiger, Harvey, Ialovega, Kirch, Peterson and Petrov2023) (see item (D) below). We choose a conservative limit of $\beta _c\sim 0.3$![]() while also noting higher values may be possible (GDT achieved $\beta _c\sim 0.6$
while also noting higher values may be possible (GDT achieved $\beta _c\sim 0.6$![]() ), acknowledging that the GDT vortex stabilization techniques have not yet been extended to the thermonuclear-grade parameters of a classical mirror when the confinement is much better. Further strategies for addressing axisymmetric MHD stability at powerplant scale are given in the next section.
), acknowledging that the GDT vortex stabilization techniques have not yet been extended to the thermonuclear-grade parameters of a classical mirror when the confinement is much better. Further strategies for addressing axisymmetric MHD stability at powerplant scale are given in the next section.
The plasma pressure of BEAM ($n T_i$![]() ) can be estimated from FBIS calculations that show $\langle E_i\rangle \equiv 3/2 T_i \sim E_b$
) can be estimated from FBIS calculations that show $\langle E_i\rangle \equiv 3/2 T_i \sim E_b$![]() and thus $T_i\equiv 2/3 E_b$
and thus $T_i\equiv 2/3 E_b$![]() . In practical units, $\beta \approx 3 n_{20} E_{b,100\,\textrm {keV}} / B_0^2$
. In practical units, $\beta \approx 3 n_{20} E_{b,100\,\textrm {keV}} / B_0^2$![]() with $B_0$
with $B_0$![]() in units of tesla, or equivalently the density $n_{20}$
in units of tesla, or equivalently the density $n_{20}$![]() in units of $10^{20}$
in units of $10^{20}$![]() m$^{-3}$
m$^{-3}$![]() will be limited to
will be limited to
(C) Minimum plasma radius
Given $\beta _c$![]() , the plasma size and density must also be large enough for sufficient ionization of the injected neutral beam as seen in figure 4. For the particular choice of 90 % absorption, this imposes a requirement of $n_{20} a_0 \geq 0.3E_{b,100\,\textrm {keV}}^{1/2}$
, the plasma size and density must also be large enough for sufficient ionization of the injected neutral beam as seen in figure 4. For the particular choice of 90 % absorption, this imposes a requirement of $n_{20} a_0 \geq 0.3E_{b,100\,\textrm {keV}}^{1/2}$![]() with $a_0$
with $a_0$![]() in metres, per fit to tabulated absorption data in figure 4. This constrains the radial dimension $a_0$
in metres, per fit to tabulated absorption data in figure 4. This constrains the radial dimension $a_0$![]() of the plasma:
of the plasma:

The scalings show clearly how the device size can be reduced as the midplane magnetic field is increased. If core fuelling by NBI is required, this may also impose an upper limit on plasma size as well.

Figure 4. FIDASIM computation study of neutral-beam ionization fraction for $45^{\circ }$![]() injection in a simple mirror (Geiger et al. Reference Geiger, Stagner, Heidbrink, Dux, Fischer, Fujiwara, Garcia, Jacobsen, van Vuuren and Karpushov2020). Left: neutral-beam ionization fraction at different energies including halo reionization of the charge exchange neutrals. Right: the empirical fits for different fractions ${\propto }\sqrt {E_b}$
injection in a simple mirror (Geiger et al. Reference Geiger, Stagner, Heidbrink, Dux, Fischer, Fujiwara, Garcia, Jacobsen, van Vuuren and Karpushov2020). Left: neutral-beam ionization fraction at different energies including halo reionization of the charge exchange neutrals. Right: the empirical fits for different fractions ${\propto }\sqrt {E_b}$![]() .
.
(D) Minimum dimensionless size
An alternative minimum plasma size is set by the number of ion gyroradii across the plasma and characterized by the dimensionless $N_\rho \equiv a_0 / \rho _i$![]() or its inverse $\rho ^\star = \rho _i/ a_0$
or its inverse $\rho ^\star = \rho _i/ a_0$![]() . Both kinetic stability and adiabaticity impose a size constraint of the form
. Both kinetic stability and adiabaticity impose a size constraint of the form
Fast ions and fusion alpha particles must remain adiabatic and confined. This requires that the plasma be large and the field strong enough that $L_B/\rho _i > 10$![]() everywhere, where $L_B$
everywhere, where $L_B$![]() represents the scale length of the magnetic field variation (either axial or radial). For the case of high $\beta$
represents the scale length of the magnetic field variation (either axial or radial). For the case of high $\beta$![]() the magnetic field will vary on the pressure gradient scale length leading to non-adiabatic behaviour (Cohen, Rowlands & Foote Reference Cohen, Rowlands and Foote1978b; Chernoshtanov Reference Chernoshtanov2022), although at large $\beta$
the magnetic field will vary on the pressure gradient scale length leading to non-adiabatic behaviour (Cohen, Rowlands & Foote Reference Cohen, Rowlands and Foote1978b; Chernoshtanov Reference Chernoshtanov2022), although at large $\beta$![]() radial gradients dominate. Assuming an edge pressure gradient scale length $L_{\boldsymbol {\nabla } p} \sim a_0/5$
radial gradients dominate. Assuming an edge pressure gradient scale length $L_{\boldsymbol {\nabla } p} \sim a_0/5$![]() , the magnetic radial gradient scale length $L_B$
, the magnetic radial gradient scale length $L_B$![]() is related by $L_B = L_{\boldsymbol {\nabla } p} / (1 - \sqrt {1-\beta } )$
is related by $L_B = L_{\boldsymbol {\nabla } p} / (1 - \sqrt {1-\beta } )$![]() .
.
For purposes of illustration, we will assume $N_\rho > 25$![]() as a design constraint. This sets an upper limit of $\beta < 3/4$
as a design constraint. This sets an upper limit of $\beta < 3/4$![]() from the adiabaticity constraint. In fact this would likely be above the MHD ballooning $\beta _c$
from the adiabaticity constraint. In fact this would likely be above the MHD ballooning $\beta _c$![]() limit and will be satisfied if (B) is satisfied. To fully optimize fusion power, the alpha particles must also be confined so that they can deposit their energy into the electrons, thereby reducing drag on the fast ions. This is a somewhat stricter limit on minimum size and field since $\rho _\alpha \sim 4 \rho _D$
limit and will be satisfied if (B) is satisfied. To fully optimize fusion power, the alpha particles must also be confined so that they can deposit their energy into the electrons, thereby reducing drag on the fast ions. This is a somewhat stricter limit on minimum size and field since $\rho _\alpha \sim 4 \rho _D$![]() .
.
A similar constraint arises from considerations of the DCLC and Alfvén ion cyclotron instabilities. These two instabilities have been studied extensively both theoretically (Baldwin Reference Baldwin1977) and experimentally (Ferron et al. Reference Ferron, Wong, Dimonte and Leikind1983) and occur due to the ambipolar hole in the ion distribution function that arises from the electrostatic potential drawing ions outward. Remarkably, these instabilities have been largely mitigated by use of ‘sloshing ions’ obliquely injected by neutral beams at energies larger than $10T_e$![]() . The resulting off-axis density peaking of the fast ions electrostatically confines a small fraction of warm ions in the ambipolar hole (see § 3.1 and Yushmanov Reference Yushmanov1966; Kesner Reference Kesner1973) providing a source of kinetic free energy that can couple to either electron drift waves or Alfvén waves. If the ambipolar hole is not filled, the DCLC can be also be minimized by making the plasma sufficiently large such that the density scale controlling the electron drift wave dispersion is large compared with the gyroradius: $L_n/\rho _i$
. The resulting off-axis density peaking of the fast ions electrostatically confines a small fraction of warm ions in the ambipolar hole (see § 3.1 and Yushmanov Reference Yushmanov1966; Kesner Reference Kesner1973) providing a source of kinetic free energy that can couple to either electron drift waves or Alfvén waves. If the ambipolar hole is not filled, the DCLC can be also be minimized by making the plasma sufficiently large such that the density scale controlling the electron drift wave dispersion is large compared with the gyroradius: $L_n/\rho _i$![]() should be of the order of 10 to 50, depending on density, magnetic field and warm ion density in the ambipolar hole.
should be of the order of 10 to 50, depending on density, magnetic field and warm ion density in the ambipolar hole.
Baldwin, Fowler and others equate $L_n$![]() and the radial size $a_0$
and the radial size $a_0$![]() and so this, too, becomes a constraint of the form $N_\rho > 10 \mbox { to } 50$
and so this, too, becomes a constraint of the form $N_\rho > 10 \mbox { to } 50$![]() . Further defining $N_{25} = N_\rho / 25$
. Further defining $N_{25} = N_\rho / 25$![]() , (2.3) can be translated into a constraint on the product of size and magnetic field:
, (2.3) can be translated into a constraint on the product of size and magnetic field:
and the DCLC might require $N_{25}$![]() between 1 and 2 if no sloshing ions are used. The BEAM scenario simulated below assumes the use of sloshing ions and therefore a conservative $N_{25}=1$
between 1 and 2 if no sloshing ions are used. The BEAM scenario simulated below assumes the use of sloshing ions and therefore a conservative $N_{25}=1$![]() seems adequate to ensure kinetic stability.
seems adequate to ensure kinetic stability.
The above relationships (2.1), (2.2) and (2.4) can now be algebraically solved to find a solution for size $a_0$![]() and the required magnetic field $B_0$
and the required magnetic field $B_0$![]() at the midplane in terms of the ion injection energy:
at the midplane in terms of the ion injection energy:
This gives the intuitive result that magnetic field must scale up with beam energy. The less intuitive inverse scaling of size with beam energy is due to the fact that with higher beam energy a larger magnetic field is required and for a constant $\beta _c$![]() this means higher density and therefore stopping power of the neutral beam.
this means higher density and therefore stopping power of the neutral beam.
(F) Minimum mirror ratio
The mirror ratio is somewhat arbitrarily chosen to be $R_M \sim 10$![]() although higher would be better. This brings $Q$
although higher would be better. This brings $Q$![]() close to 1 as documented in Egedal22. Large-bore magnet construction above 25 T, required for even higher mirror ratios, still seems too challenging. This dictates the field strength and warm bore size of the HTS mirror coils, in terms of the midplane field $B_0$
close to 1 as documented in Egedal22. Large-bore magnet construction above 25 T, required for even higher mirror ratios, still seems too challenging. This dictates the field strength and warm bore size of the HTS mirror coils, in terms of the midplane field $B_0$![]() and plasma radius $a_0$
and plasma radius $a_0$![]() :
:
The mirror ratio in the plasma core governing classical confinement $R_M$![]() is enhanced over the vacuum field by a factor of $1 / \sqrt {1 - \beta _c}$
is enhanced over the vacuum field by a factor of $1 / \sqrt {1 - \beta _c}$![]() which improves the overall confinement as $\beta _c$
which improves the overall confinement as $\beta _c$![]() increases (see top panels in figure 5) until adiabaticity limits particle confinement as already noted (Cohen et al. Reference Cohen, Rowlands and Foote1978b; Chernoshtanov Reference Chernoshtanov2022).
increases (see top panels in figure 5) until adiabaticity limits particle confinement as already noted (Cohen et al. Reference Cohen, Rowlands and Foote1978b; Chernoshtanov Reference Chernoshtanov2022).

Figure 5. Radial profiles of 100 keV neutral-beam-driven break-even scenarios, self-consistently modelling the equilibrium and neutral-beam fuelling using the Pleides, FIDASIM and FBIS codes. The three columns represent 45$^\circ$![]() injection, 45$^\circ$
injection, 45$^\circ$![]() injection without alpha-particle heating and 90$^\circ$
injection without alpha-particle heating and 90$^\circ$![]() injection. Here $Q_{\rm fuel}$
injection. Here $Q_{\rm fuel}$![]() is defined as the D–T fusion power divided by the absorbed power ignoring the shine-through losses.
is defined as the D–T fusion power divided by the absorbed power ignoring the shine-through losses.
For $Q_\textrm {sci}\sim 1$![]() , $\beta _c\sim 0.3$
, $\beta _c\sim 0.3$![]() , $B_0\sim 3$
, $B_0\sim 3$![]() and $R_M\sim 10$
and $R_M\sim 10$![]() the design point is essentially determined algebraically and shown in the table in figure 1, set at $a_0 = 0.3$
the design point is essentially determined algebraically and shown in the table in figure 1, set at $a_0 = 0.3$![]() m, $B_M\sim 25$
m, $B_M\sim 25$![]() T and $a_M\sim 10$
T and $a_M\sim 10$![]() cm, and this implies $n_{20}\sim 1$
cm, and this implies $n_{20}\sim 1$![]() .
.
(H) Minimum plasma length
The plasma must be long enough to stabilize $m\geq 2$![]() via FLR effects and to maintain fast-ion and alpha-particle adiabaticity. Ryutov et al. (Reference Ryutov, Berk, Cohen, Molvik and Simonen2011) provide the general criteria to stabilize mode numbers above $m$
via FLR effects and to maintain fast-ion and alpha-particle adiabaticity. Ryutov et al. (Reference Ryutov, Berk, Cohen, Molvik and Simonen2011) provide the general criteria to stabilize mode numbers above $m$![]() as
as
where
and this is strongly supported by experimental observations (Anikeev et al. Reference Anikeev, Bagryansky, Ivanov, Kuzmin and Salikova1992). Taking $m=2$![]() , this constraint becomes simply
, this constraint becomes simply
For our design point, $N_\rho \sim 25$![]() and $a_0\sim 0.3$
and $a_0\sim 0.3$![]() m; thus $L \geq 7.5$
m; thus $L \geq 7.5$![]() m.
m.
We note that the minimum volume is now also constrained:
and for BEAM, $V \sim 1\,{\rm m}^3$![]() .
.
(I) Minimum beam power
The overall power required by the NBI is now set by the fuelling rate $I_{b} = e n V / \tau _p$![]() required to maintain the density:
required to maintain the density:

and correspondingly

When $Q_{\rm sci} = P_{{\rm fus}}/P_{b} \approx 1$![]() , this expression also gives the fusion power.
, this expression also gives the fusion power.
3. Transport simulations
Given the zero-dimensional design of a break-even high-field simple mirror in the previous section and summarized in figure 1, we can now examine in more detail some of the properties of equilibria that arise when profile and other next order effects are included. We both use the semi-analytical FBIS model from Egedal22 and present results from the new CQL3D-m code.
First, the resulting steady-state (assumed) profiles from the FBIS code are shown in figure 5. This includes a self-consistent evolution of neutral-beam deposition including the effects of reionized halo neutrals generated by charge exchange described in Endrizzi23. In these simulations an ad hoc model for edge electron cooling (assumed to come from recycled neutrals or steep gradient induced transport) and extra electron heating from full slowing down of confined alpha particles are assumed.
Following the same procedure for computing the equilibrium as in Endrizzi23, the anisotropic force balance includes a self-consistent solution for the electrostatic ambipolar potential and therefore predicts the self-consistent $E\times B$![]() rotation profile. As intuitively would be expected, strong edge gradients of electron temperature and ion pressure seem likely to give ideal flows for vortex stabilization of the sort used by GDT naturally arise, without the need for biased limiters. This is a hallmark of the classical simple mirror: the electron temperature profile plays a major role in setting the plasma flows. This does not preclude the use of biased limiters to control the potential profile, but might relax the requirements on the power supplies and the complexity of anode rings. The impact of these flows on MHD stability are addressed further in the next section.
rotation profile. As intuitively would be expected, strong edge gradients of electron temperature and ion pressure seem likely to give ideal flows for vortex stabilization of the sort used by GDT naturally arise, without the need for biased limiters. This is a hallmark of the classical simple mirror: the electron temperature profile plays a major role in setting the plasma flows. This does not preclude the use of biased limiters to control the potential profile, but might relax the requirements on the power supplies and the complexity of anode rings. The impact of these flows on MHD stability are addressed further in the next section.
3.1. The CQL3D-m code
The above design strategy using the FBIS code employed several approximations including: the use of an incomplete collision operator which does not account for the anisotropic distribution functions, no radial variations of the distributions, no integrated neutral-beam deposition model, no radiation losses and intrinsically steady state. A design optimization for BEAM using the more complete CQL3D-m code (Harvey, Petrov & Forest Reference Harvey, Petrov and Forest2016; Petrov et al. Reference Petrov, Harvey, Forest and Anderson2023) is now beginning. This effort uses a mirror extension of the well-known and well-tested CQL3D toroidal geometry code (Harvey & McCoy Reference Harvey and McCoy1992). It aims to provide a more detailed and comprehensive classical modelling tool for axisymmetric mirrors in general, and for BEAM, compared with the alternative faster steady-state FBIS code.
In view of the bounce-average treatment in CQL3D-m, the model provides effectively a RZ-space two-dimensional (2-D)-velocity model. The neutral-beam deposition model including neutral-beam geometry and physics provides the 2-D-space ion and electron sources. The CQL3D-m code is run for ions and electrons, simultaneously, in a particle- and energy-conserving mode fully accounting for the effects of nonlinear Fokker–Planck Coulomb collisions, and a self-consistent parallel ambipolar electric field is iteratively computed at each time step, maintaining charge neutrality (Petrov et al. Reference Petrov, Harvey, Forest and Anderson2023). This enables the code to evolve time-dependently to a steady state, balancing particle and energy sources and sinks on each of a radial set of flux surfaces; it thus provides a complete classical solution for the ion and electron distribution functions in a mirror.
The top row of figure 6 shows the deuterium and electron distributions obtained at near steady state. The $f_T$![]() distribution is similar to $f_D$
distribution is similar to $f_D$![]() , scaled to lower velocity by the mass ratio. The bottom row of figure 6 gives the axial variation of plasma parameters near the plasma centre. For $f_D$
, scaled to lower velocity by the mass ratio. The bottom row of figure 6 gives the axial variation of plasma parameters near the plasma centre. For $f_D$![]() , note that the distribution has evolved from an initial Maxwellian to being more centred around the NBI energies indicated by the three peaks (full, half and one-third beam energy) along the $45^{\circ }$
, note that the distribution has evolved from an initial Maxwellian to being more centred around the NBI energies indicated by the three peaks (full, half and one-third beam energy) along the $45^{\circ }$![]() pitch angle. The distributions away from the midplane are obtained using the particle constants of motion, valid in the low-collisionality regime. This full evolution of the ion distributions to an entirely non-Maxwellian form is enabled with the self-consistent nonlinear collision operator (Killeen et al. Reference Killeen, Mirin and Rensink1976) in CQL3D-m. The energetic tail of the electron distribution in the magnetic loss cone (pitch angle less than the dashed line) is partially confined by the ambipolar potential, such that the electron and ion loss rates are kept equal consistent with Pastukhov (Reference Pastukhov1974). The resulting axial plasma densities, effective ion temperatures and the ambipolar potential are shown in the bottom row of figure 6, at simulation time 1.2 s. The peaking of the density at $Z/Z_{0}=0.6$
pitch angle. The distributions away from the midplane are obtained using the particle constants of motion, valid in the low-collisionality regime. This full evolution of the ion distributions to an entirely non-Maxwellian form is enabled with the self-consistent nonlinear collision operator (Killeen et al. Reference Killeen, Mirin and Rensink1976) in CQL3D-m. The energetic tail of the electron distribution in the magnetic loss cone (pitch angle less than the dashed line) is partially confined by the ambipolar potential, such that the electron and ion loss rates are kept equal consistent with Pastukhov (Reference Pastukhov1974). The resulting axial plasma densities, effective ion temperatures and the ambipolar potential are shown in the bottom row of figure 6, at simulation time 1.2 s. The peaking of the density at $Z/Z_{0}=0.6$![]() (where $Z=0$
(where $Z=0$![]() is at the midplane and $Z/Z_{0}=1$
is at the midplane and $Z/Z_{0}=1$![]() is at the right mirror coil) is near the bounce point for the $45^{\circ }$
is at the right mirror coil) is near the bounce point for the $45^{\circ }$![]() midplane ion injection. The variation of $T_\perp /T_\parallel (Z)$
midplane ion injection. The variation of $T_\perp /T_\parallel (Z)$![]() formed by the sloshing ions could impact microstability. The slight dip in $\varPhi (z)$
formed by the sloshing ions could impact microstability. The slight dip in $\varPhi (z)$![]() in the $Z/Z_0=0.0\unicode{x2013}0.6$
in the $Z/Z_0=0.0\unicode{x2013}0.6$![]() range, again formed by the sloshing ions, confines the ions at low velocity. As noted in the FBIS simulations shown in figure 5, the $45^{\circ }$
range, again formed by the sloshing ions, confines the ions at low velocity. As noted in the FBIS simulations shown in figure 5, the $45^{\circ }$![]() injection used here in CQL3D-m does not optimize the fusion gain. However, it may be needed to address kinetic instabilities by electrostatically trapping warm ions in the ambipolar hole.
injection used here in CQL3D-m does not optimize the fusion gain. However, it may be needed to address kinetic instabilities by electrostatically trapping warm ions in the ambipolar hole.

Figure 6. Results from CQL3D-m simulations of BEAM for 10 MW of $45^{\circ }$![]() incident neutral-beam power $E_b=100$
incident neutral-beam power $E_b=100$![]() keV split 70/30/10 in full/half/one-third energy components. Top left: the near-steady-state deuterium ion distribution function and the loss cone associated with just the magnetic field (dashed) and with the magnetic and electrostatic fields (solid). The ion distribution clearly has a confined warm ion species filling the low-velocity ambipolar hole. Top right: the electron distribution function and loss cones. Bottom row: profiles along the axis at $r=0$
keV split 70/30/10 in full/half/one-third energy components. Top left: the near-steady-state deuterium ion distribution function and the loss cone associated with just the magnetic field (dashed) and with the magnetic and electrostatic fields (solid). The ion distribution clearly has a confined warm ion species filling the low-velocity ambipolar hole. Top right: the electron distribution function and loss cones. Bottom row: profiles along the axis at $r=0$![]() .
.
The steady-state radial profiles of electron density, and ion and electron temperatures are shown in figure 7(a). The injection geometry of the 100 keV neutral beam is adjusted to provide a radially broad source, with 5 MW input power for each of D and T beams. On the right-hand side of the figure, the deposited neutral-beam power rises to near a steady-state value of 8.7 MW. Electron density settles at $8.0\times 10^{19}\,{\rm m}^{-3}$![]() . Power transfer from ions to electrons is 6.6 MW (separately tabulated), the remaining ion power being lost via charge exchange of ions and scattering into the loss cone.
. Power transfer from ions to electrons is 6.6 MW (separately tabulated), the remaining ion power being lost via charge exchange of ions and scattering into the loss cone.

Figure 7. Time-dependent CQL3D-m simulation with $45^{\circ }$![]() injection including synchrotron radiation for electron cooling but no alpha particle heating. (a) Radial profiles at $t=1.2$
injection including synchrotron radiation for electron cooling but no alpha particle heating. (a) Radial profiles at $t=1.2$![]() s. The temperatures are 2/3 of the average energies. (b) Evolution of plasma parameters from initial Maxwellian ions and electrons. As the density increases, up to 9.7 MW of neutral-beam power, from the input 10 MW, is absorbed. Central electron density is shown ($n_e$
s. The temperatures are 2/3 of the average energies. (b) Evolution of plasma parameters from initial Maxwellian ions and electrons. As the density increases, up to 9.7 MW of neutral-beam power, from the input 10 MW, is absorbed. Central electron density is shown ($n_e$![]() ). The value of $\beta$
). The value of $\beta$![]() increases to 0.2. Central $T_e$
increases to 0.2. Central $T_e$![]() increases to 6 keV. The D–T neutron power (6 MW) is 0.6 times the input neutral-beam power.
increases to 6 keV. The D–T neutron power (6 MW) is 0.6 times the input neutral-beam power.
Of the 6.6 MW of electron collisional heating by the ions, 2.0 MW is lost by synchrotron radiation (Brehmstrahlung is also included in the losses but is much less), and the remaining 4.6 MW passes into the loss cone. While high magnetic fields make the concept of BEAM possible, there is a trade-off as a high field increases the synchrotron emission $P_{{\rm synch}}\propto n T_e B^2$![]() , cooling the electrons. Somewhat off-setting this drop in $T_e$
, cooling the electrons. Somewhat off-setting this drop in $T_e$![]() , the collisional energy transfer from ions to electrons, proportional to $T_e^{-3/2}$
, the collisional energy transfer from ions to electrons, proportional to $T_e^{-3/2}$![]() , increases. The net result is that the neutron power is reduced by 10 % compared with the case where synchrotron radiation is omitted. This temperature reduction from synchrotron radiation is likely an over-prediction as CQL3D presently assumes the plasma is optically thin and all synchrotron radiation is lost. In reality, a substantial quantity of the synchrotron radiation emitted by the electrons will be reabsorbed.
, increases. The net result is that the neutron power is reduced by 10 % compared with the case where synchrotron radiation is omitted. This temperature reduction from synchrotron radiation is likely an over-prediction as CQL3D presently assumes the plasma is optically thin and all synchrotron radiation is lost. In reality, a substantial quantity of the synchrotron radiation emitted by the electrons will be reabsorbed.
The time evolutions of NBI power deposition, electron, $D+$![]() and $T+$
and $T+$![]() densities and effective temperatures are shown in figure 7(b); the near-stationary conditions being considered are met in around 1 s. The overall scientific gain $Q=P_{{\rm fus}}/P_{{\rm nbi},{\rm absorbed}}$
densities and effective temperatures are shown in figure 7(b); the near-stationary conditions being considered are met in around 1 s. The overall scientific gain $Q=P_{{\rm fus}}/P_{{\rm nbi},{\rm absorbed}}$![]() from the CQL3D-m simulation is $\sim$
from the CQL3D-m simulation is $\sim$![]() 0.75, to be compared with a value of 0.6, scaling results from FBIS. Future work will include alpha particle heating and synchrotron radiation reabsorption, increasing $Q$
0.75, to be compared with a value of 0.6, scaling results from FBIS. Future work will include alpha particle heating and synchrotron radiation reabsorption, increasing $Q$![]() somewhat.
somewhat.
4. Magnetohydrodynamic stability
The principal challenge in developing the axisymmetric mirror is, and has always been, stabilizing the ‘flute’ or ‘interchange’ mode first described by Rosenbluth & Longmire (Reference Rosenbluth and Longmire1957). Here we refer the reader to the recent review by Ryutov et al. (Reference Ryutov, Berk, Cohen, Molvik and Simonen2011) (henceforth Ryutov11) on techniques for stabilizing the flute modes in axisymmetric systems and adopt their notation.
The breakthrough results on the GDT used a combination of FLR stabilization of $m>1$![]() modes (see (C) above), enhanced good curvature at the expander (Mirnov & Ryutov Reference Mirnov and Ryutov1972; Bagryansky et al. Reference Bagryansky, Anikeev, Beklemishev, Donin, Ivanov, Korzhavina, Kovalenko, Kruglyakov, Lizunov and Maximov2011) and biased limiters and end rings to control plasma flow (Yakovlev et al. Reference Yakovlev, Shalashov, Gospodchikov, Maximov, Prikhodko, Savkin, Soldatkina, Solomakhin and Bagryansky2018). However, as discussed in what follows, sheared flow on BEAM may not be so easily influenced by biased limiters and end rings due to the vastly better predicted confinement of the classical mirror. Good confinement can limit the magnitude of the current flowing into and out of the end walls, reducing the ability of end walls to short out the polarization current of the flute modes and provide the torque to control the plasma flow. The remainder of this section describes a variety of paths to MHD stabilization.
modes (see (C) above), enhanced good curvature at the expander (Mirnov & Ryutov Reference Mirnov and Ryutov1972; Bagryansky et al. Reference Bagryansky, Anikeev, Beklemishev, Donin, Ivanov, Korzhavina, Kovalenko, Kruglyakov, Lizunov and Maximov2011) and biased limiters and end rings to control plasma flow (Yakovlev et al. Reference Yakovlev, Shalashov, Gospodchikov, Maximov, Prikhodko, Savkin, Soldatkina, Solomakhin and Bagryansky2018). However, as discussed in what follows, sheared flow on BEAM may not be so easily influenced by biased limiters and end rings due to the vastly better predicted confinement of the classical mirror. Good confinement can limit the magnitude of the current flowing into and out of the end walls, reducing the ability of end walls to short out the polarization current of the flute modes and provide the torque to control the plasma flow. The remainder of this section describes a variety of paths to MHD stabilization.
4.1. Sheared flow from natural diamagnetic drifts and ambipolar potential
For the $m=1$![]() mode, the most successful technique thus far has been to use a combination of good curvature expanders outside the plasma to reduce growth rates and sheared flow or ‘vortex’ stabilization to limit the amplitude of the $m=1$
mode, the most successful technique thus far has been to use a combination of good curvature expanders outside the plasma to reduce growth rates and sheared flow or ‘vortex’ stabilization to limit the amplitude of the $m=1$![]() instability which grows approximately on a time scale of
instability which grows approximately on a time scale of

Higher values of $m$![]() are stabilized by FLR effects as discussed above. To a first approximation, the stabilization condition is that a narrow edge region rotates around the ‘shifting’ central plasma at least once during a growth period giving ‘honey-stick’ confinement.
are stabilized by FLR effects as discussed above. To a first approximation, the stabilization condition is that a narrow edge region rotates around the ‘shifting’ central plasma at least once during a growth period giving ‘honey-stick’ confinement.
The ambipolar potential that maintains quasi-neutrality between the electron and ion densities provides a very natural mechanism for controlling the flow shear: with the ambipolar potential expected to be of order $5T_e$![]() to restrain electron losses, this naturally drives rotation and in principle can be controlled by additional targeted electron heating. Once the spatial profile of potential is determined along each flux surface, the radial electric field and axial rotational shear are also known.
to restrain electron losses, this naturally drives rotation and in principle can be controlled by additional targeted electron heating. Once the spatial profile of potential is determined along each flux surface, the radial electric field and axial rotational shear are also known.
Estimating the MHD interchange growth rate $\varGamma _{0} \approx V_{\textrm {thi}} / L_p$![]() (neglecting for now the FLR stabilization terms) and the natural $E \times B$
(neglecting for now the FLR stabilization terms) and the natural $E \times B$![]() rotation frequency $\omega _{E \times B} \equiv v_{E \times B}/a_0 \sim {5T_e}/{e a_0 B_0 \Delta r_{Te}}$
rotation frequency $\omega _{E \times B} \equiv v_{E \times B}/a_0 \sim {5T_e}/{e a_0 B_0 \Delta r_{Te}}$![]() , then assuming flat pressure and $T_e$
, then assuming flat pressure and $T_e$![]() profiles in the core with gradients localized to one fast-ion Larmor radius $\Delta r_{Te} \sim \rho _i$
profiles in the core with gradients localized to one fast-ion Larmor radius $\Delta r_{Te} \sim \rho _i$![]() at the edge, the stability condition based on edge rotation frequency exceeding $\varGamma _{0}$
at the edge, the stability condition based on edge rotation frequency exceeding $\varGamma _{0}$![]() becomes
becomes
This final constraint for BEAM would require $T_e/T_i \geq 2 / 5 \sqrt {10} = 0.13$![]() is satisfied by the $T_e/T_i = 0.15$
is satisfied by the $T_e/T_i = 0.15$![]() . Our scaling is somewhat more optimistic than given in equation (68) of Ryutov et al. (Reference Ryutov, Berk, Cohen, Molvik and Simonen2011) as we take credit for a narrower, edge-localized shear zone.
. Our scaling is somewhat more optimistic than given in equation (68) of Ryutov et al. (Reference Ryutov, Berk, Cohen, Molvik and Simonen2011) as we take credit for a narrower, edge-localized shear zone.
Axial shear, defined by $S_a = \partial \omega _{ExB} / \partial \ell$![]() , would also lead to twisting of the field-aligned perturbations with $m\neq 0$
, would also lead to twisting of the field-aligned perturbations with $m\neq 0$![]() azimuthal mode numbers and in principle can also suppress the growth of unstable modes if their growth rate $\varGamma _0$
azimuthal mode numbers and in principle can also suppress the growth of unstable modes if their growth rate $\varGamma _0$![]() is not too large:
is not too large:
For the collisionless mirror with very-high-field mirror regions, the maximum $E \times B$![]() rotation essentially drops from $5 T_e/ e \rho _i B$
rotation essentially drops from $5 T_e/ e \rho _i B$![]() to zero in the mirror throat and so this effect is comparable to (4.2) in magnitude. The rotation profiles predicted by FBIS and shown in figure 8 support this and also demonstrate the nearly equal importance of diamagnetic flows.
to zero in the mirror throat and so this effect is comparable to (4.2) in magnitude. The rotation profiles predicted by FBIS and shown in figure 8 support this and also demonstrate the nearly equal importance of diamagnetic flows.

Figure 8. Natural rotation profiles under the assumption of classical mirror confinement.
4.2. Effectiveness of line-tying
The effectiveness of line-tying for reducing growth rates and even stabilizing interchange modes has been studied extensively (Wickham Reference Wickham1982; Segal Reference Segal1983; Vandegrift & Good Reference Vandegrift and Good1986; Vandegrift Reference Vandegrift1989; Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011). Here, we quickly review the requirements for sufficient bipolar electrical conduction from the central plasma, through the mirror throat, to the end plates through the expander to short out the polarization current associated with the flute modes. This is ultimately set by a ‘sheath conductance’ $\varSigma$![]() that relates potential fluctuations associated with the flute mode to the parallel current density emitted from the end wall:
that relates potential fluctuations associated with the flute mode to the parallel current density emitted from the end wall:
For Boltzmann (and collisionless mirror) electrons deviating about ambipolarity,
with $U_0 = \sqrt {{2 E_i}/{m_i}}$![]() being the velocity of the escaping ions and intrinsically determined by the particle confinement and $C$
being the velocity of the escaping ions and intrinsically determined by the particle confinement and $C$![]() a constant of order 3.
a constant of order 3.
Ryutov defines a dimensionless line-tying parameter:
which should be larger than one to slow and possibly stabilize interchange. Here $\tau _0 = \varGamma _0^{-1}$![]() is the MHD growth time. Using the classical confinement time calculated from the Fokker–Planck equation, $\tau _{P} \sim 0.25 E_{b,{100\,\textrm {keV}}}^{3/2} \log _{10} R_M / n_{20}$
is the MHD growth time. Using the classical confinement time calculated from the Fokker–Planck equation, $\tau _{P} \sim 0.25 E_{b,{100\,\textrm {keV}}}^{3/2} \log _{10} R_M / n_{20}$![]() , and assuming $\tau _E \sim \tau _P$
, and assuming $\tau _E \sim \tau _P$![]() ,
,

For an $m=1$![]() mode with $k_\perp = m/a$
mode with $k_\perp = m/a$![]() this would reduce to
this would reduce to
where it has been assumed that $T_e\sim 1/10 \langle E_i\rangle$![]() . For BEAM conditions this would be a requirement that $N_\rho > 54$
. For BEAM conditions this would be a requirement that $N_\rho > 54$![]() . This can be hard to satisfy when the confinement time is long, the normalized plasma size $N_\rho$
. This can be hard to satisfy when the confinement time is long, the normalized plasma size $N_\rho$![]() small and the electron temperature high, which are the conditions of the core of BEAM. Ryutov notes that for a rigidly shifting $m=1$
small and the electron temperature high, which are the conditions of the core of BEAM. Ryutov notes that for a rigidly shifting $m=1$![]() mode, the line-tying at the edge may be much stronger than the simple analysis here.
mode, the line-tying at the edge may be much stronger than the simple analysis here.
4.3. Mantel stabilization
The large-diameter BEAM plasma would likely have a hot-ion classical mirror core where the electron temperature is high and also have a gas dynamic edge/mantel where $T_e$![]() is low due to stronger neutral cooling and lower fast-ion heating due to charge exchange and scrape-off losses (Segal Reference Segal1982, Reference Segal1983; Vandegrift & Good Reference Vandegrift and Good1986; Caponi, Cohen & Freis Reference Caponi, Cohen and Freis1987). In such a mantel, stabilization of the global $m=1$
is low due to stronger neutral cooling and lower fast-ion heating due to charge exchange and scrape-off losses (Segal Reference Segal1982, Reference Segal1983; Vandegrift & Good Reference Vandegrift and Good1986; Caponi, Cohen & Freis Reference Caponi, Cohen and Freis1987). In such a mantel, stabilization of the global $m=1$![]() via line-tying and biasing could be effective – a conjecture that can only be tested in a larger and higher-density plasma like BEAM. The benefits of this will ultimately depend upon on how much power is required to maintain this lossy plasma.
via line-tying and biasing could be effective – a conjecture that can only be tested in a larger and higher-density plasma like BEAM. The benefits of this will ultimately depend upon on how much power is required to maintain this lossy plasma.
The mantel scenarios would likely be further improved by use of an emissive cathode ring such as LaB$_6$![]() or refractory material with large secondary electron emission from ion impact for the outermost flux surfaces. Prior experiments on bench-scale plasmas have demonstrated this process (Fornaca, Kiwamoto & Rynn Reference Fornaca, Kiwamoto and Rynn1979; Good, Thompson & Rynn Reference Good, Thompson and Rynn1988). Such a ring limiter would tend to cool the plasma electrons but could also greatly enhance the ability of the edge plasma in the expanders to source parallel current and short out the divergence of $J_\perp$
or refractory material with large secondary electron emission from ion impact for the outermost flux surfaces. Prior experiments on bench-scale plasmas have demonstrated this process (Fornaca, Kiwamoto & Rynn Reference Fornaca, Kiwamoto and Rynn1979; Good, Thompson & Rynn Reference Good, Thompson and Rynn1988). Such a ring limiter would tend to cool the plasma electrons but could also greatly enhance the ability of the edge plasma in the expanders to source parallel current and short out the divergence of $J_\perp$![]() in the periphery.
in the periphery.
4.4. Wall stabilization at high $\beta$
It is likely that BEAM will incorporate a close-fitting conducting shell (or partial shell) to enhance stability at high $\beta$![]() as has been extensively studied theoretically (Pearlstein Reference Pearlstein1966; D'Ippolito, Myra & Ogden Reference D'Ippolito, Myra and Ogden1982; D'Ippolito & Myra Reference D'Ippolito and Myra1984; Kaiser & Pearlstein Reference Kaiser and Pearlstein1985; Kesner Reference Kesner1985; Cohen, Freis & Newcomb Reference Cohen, Freis and Newcomb1986; Caponi et al. Reference Caponi, Cohen and Freis1987; Beklemishev Reference Beklemishev2017; Kotelnikov et al. Reference Kotelnikov, Zeng, Prikhodko, Yakovlev, Zhang, Chen and Yu2022). Significant stabilization occurs when $\beta > 0.5$
as has been extensively studied theoretically (Pearlstein Reference Pearlstein1966; D'Ippolito, Myra & Ogden Reference D'Ippolito, Myra and Ogden1982; D'Ippolito & Myra Reference D'Ippolito and Myra1984; Kaiser & Pearlstein Reference Kaiser and Pearlstein1985; Kesner Reference Kesner1985; Cohen, Freis & Newcomb Reference Cohen, Freis and Newcomb1986; Caponi et al. Reference Caponi, Cohen and Freis1987; Beklemishev Reference Beklemishev2017; Kotelnikov et al. Reference Kotelnikov, Zeng, Prikhodko, Yakovlev, Zhang, Chen and Yu2022). Significant stabilization occurs when $\beta > 0.5$![]() and $r_w/a<1.2$
and $r_w/a<1.2$![]() (Kotelnikov et al. Reference Kotelnikov, Zeng, Prikhodko, Yakovlev, Zhang, Chen and Yu2022) and is especially effective when line-tying is also present. Finite wall resistivity will eventually result in resistive wall-mode instability on the time scale of magnetic diffusion to the wall. However, even if wall stabilization only slows down the instability growth rate, it can greatly improve dynamic stabilization techniques such as vortex and feedback stabilization. To our knowledge no experimental work has been done in the regime where wall stabilization would be effective, in part because a stable path from low to high $\beta$
(Kotelnikov et al. Reference Kotelnikov, Zeng, Prikhodko, Yakovlev, Zhang, Chen and Yu2022) and is especially effective when line-tying is also present. Finite wall resistivity will eventually result in resistive wall-mode instability on the time scale of magnetic diffusion to the wall. However, even if wall stabilization only slows down the instability growth rate, it can greatly improve dynamic stabilization techniques such as vortex and feedback stabilization. To our knowledge no experimental work has been done in the regime where wall stabilization would be effective, in part because a stable path from low to high $\beta$![]() may have been too great a stretch in the past.
may have been too great a stretch in the past.
4.5. Feedback stabilization
Another promising avenue is to take advantage of the enormous advances in high-speed/high-power amplifiers and digital signal processing made since the classical mirror experiments in the 1970s and 1980s, to actively control the instabilities, allowing the plasma to fly-by-wire. This requires sensitive and high-speed detection of unstable modes’ phase and amplitude and high-speedelectromagnetic actuators. The total response time of the feedback system needs to be considerably shorter than the perturbation's growth time and rotation velocity for energy-efficient feedback stabilization. The feedback actuators can take the form of azimuthally segmented and biased end rings (Prater Reference Prater1971; Kang, Lieberman & Sen Reference Kang, Lieberman and Sen1988; Lieberman & Wong Reference Lieberman and Wong2002; Be'ery, Seemann & Fisher Reference Be'ery, Seemann and Fisher2014; Be'ery & Seemann Reference Be'ery and Seemann2015) or magnetic saddle coils on the perimeter of the plasma that can band the static mirror magnetic field (Kogan, Be'ery & Seemann Reference Kogan, Be'ery and Seemann2016; Beklemishev Reference Beklemishev2017). A detailed design for a feedback-stabilized plasma with close-fitting conducting shells is underway to be tested on WHAM before being implemented on BEAM.
4.6. Rotating magnetic field stabilization
The application of rotating magnetic field perpendicular to the trap's axis with frequencies close to the ion-cyclotron frequency demonstrated stabilization of mirror-confined and field-reversed-configuration plasma in several experiments (Ferron et al. Reference Ferron, Goulding, Nelson, Intrator, Wang, Severn, Hershkowitz, Brouchous, Pew and Breun1987; Seemann, Be'ery & Fisher Reference Seemann, Be'ery and Fisher2018; Zhu et al. Reference Zhu, Shi, Yang, Zheng, Luo, Ying and Sun2019). The suggested stabilization mechanisms range from ponderomotive force to side-band coupling, diamagnetic pressure and electron current drive. While rotating magnetic field stabilization has been demonstrated in several medium-/low-temperature and medium-/low-strength magnetic fields, its scaling to high temperature and high field is a major question to be tested in BEAM.
The list above is not comprehensive. Ryutov11 and Simonen et al. (Reference Simonen, Cohen, Correll, Fowler, Post, Berk, Horton, Hooper, Fisch and Hassam2008) both provide a modern and more complete summary of techniques, many of which have not yet been evaluated for BEAM, including more complex cusp boundaries (Prater Reference Prater1971; Ferron et al. Reference Ferron, Wong, Dimonte and Leikind1983; Post et al. Reference Post, Brau, Casey, Coleman, Gerver and Golovato1989; Kotelnikov et al. Reference Kotelnikov, Ivanov, Yakovlev, Chen and Zeng2019), and the use of kinetic stabilizers (Post Reference Post2007).
5. $Q=1$ ?
?
The Fokker–Planck modelling of classical transport represents an upper bound to the confinement of a simple mirror. The 2-D self-consistent Fokker–Planck modelling of power deposition and parallel transport in § 3, while not yet complete, has essentially validated the zero design outlined in § 2. The conclusion is that with classical confinement at a modest $\beta \sim 0.3$![]() , the $Q_{\textrm {fuel}}\sim 1$
, the $Q_{\textrm {fuel}}\sim 1$![]() condition is marginally achievable with $45^{\circ }$
condition is marginally achievable with $45^{\circ }$![]() neutral beams, even with profile effects included. Increasing $\beta$
neutral beams, even with profile effects included. Increasing $\beta$![]() to values of 0.7 would require additional power but also increase the mirror ratio and confinement reaching $Q=1$
to values of 0.7 would require additional power but also increase the mirror ratio and confinement reaching $Q=1$![]() as noted by Fowler (Reference Fowler2022) and Beklemishev (Reference Beklemishev2016). We have not yet evaluated the extra energy inputs needed to maintain a mantel with poor confinement, feedback power or electron cyclotron heating power for profile control, all of which would be practically important.
as noted by Fowler (Reference Fowler2022) and Beklemishev (Reference Beklemishev2016). We have not yet evaluated the extra energy inputs needed to maintain a mantel with poor confinement, feedback power or electron cyclotron heating power for profile control, all of which would be practically important.
With the assumption that the plasma is able to be stabilized against MHD and kinetic instabilities, there may yet be additional energy losses as of yet uninvestigated. We would be irresponsible to ignore these as possibly additional loss mechanisms. For example, we have so far ignored the inherent classical perpendicular ion thermal conductivity. A simple estimate of $\chi _{\perp i}$![]() is
is
and for beam parameters, one has $\chi _{\perp i}\approx 0.0012\,{\textrm {m}^2}\,\textrm {s}^{-1}$![]() . The corresponding classical diffusion time of $\tau \sim {a_0^2}/{2\chi _{\perp i}} \sim 40$
. The corresponding classical diffusion time of $\tau \sim {a_0^2}/{2\chi _{\perp i}} \sim 40$![]() s is much longer than the parallel energy loss time and therefore unimportant.
s is much longer than the parallel energy loss time and therefore unimportant.
5.1. Drift wave turbulence
Almost no fusion-relevant experiment actually observes ‘classical confinement’ ($\chi \sim \rho ^2 \nu \sim {1}/{B^2 \sqrt {T}}$![]() ). Instead, above a certain temperature threshold, all closed field line toroidal plasmas experience what has historically been called ‘anomalous diffusion’ ($\chi \sim T/B$
). Instead, above a certain temperature threshold, all closed field line toroidal plasmas experience what has historically been called ‘anomalous diffusion’ ($\chi \sim T/B$![]() ), which has a weaker scaling with magnetic field strength, and gets worse instead of better with higher temperature. Very early plasma research characterized this empirically as Bohm diffusion:
), which has a weaker scaling with magnetic field strength, and gets worse instead of better with higher temperature. Very early plasma research characterized this empirically as Bohm diffusion:
assuming $T_e=T_i=T$![]() or
or
Today we understand the physical mechanism to be drift wave turbulence, and the nonlinear saturation of turbulent heat flux can be calculated from first principles, in the gyrokinetic limit ($\rho _* = \rho /a \to 0$![]() ). We note that either Bohm or gyro-Bohm have confinement time scalings, $\tau \equiv a^2 / 2 D_{\textrm {GB}}$
). We note that either Bohm or gyro-Bohm have confinement time scalings, $\tau \equiv a^2 / 2 D_{\textrm {GB}}$![]() , that would be very different from those of the classical mirror.
, that would be very different from those of the classical mirror.
Simple cylindrical plasmas with density and temperature gradients are typically unstable with respect to drift modes even in a straight (no curvature) magnetic field (Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2012, Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2013; Shi et al. Reference Shi, Hammett, Stoltzfus-Dueck and Hakim2017). Fortunately it is very plausible that a high-temperature axisymmetric mirror will not experience large radial transport from turbulence. First, it is well knownthat large ion orbits are weakly affected by turbulence because the FLR $(\rho \gg \lambda )$![]() averages over small-scalefluctuations. Even in the TFTR tokamak, it was observed that fusion alphas appeared to follow classical diffusion and this was attributed to FLR effects (Zweben et al. Reference Zweben, Arunasalam, Batha, Budny, Bush, Cauffman, Chang, Chang, Cheng and Darrow1997, Reference Zweben, Budny, Darrow, Medley, Nazikian, Stratton and Synakowski2000). Moreover, Doppler back-scattering measurements in a related field-reversed mirror configuration in Tri Alpha Energy's C2-W experiment recently showed the absence of ion-scale turbulence in a high-$\beta$
averages over small-scalefluctuations. Even in the TFTR tokamak, it was observed that fusion alphas appeared to follow classical diffusion and this was attributed to FLR effects (Zweben et al. Reference Zweben, Arunasalam, Batha, Budny, Bush, Cauffman, Chang, Chang, Cheng and Darrow1997, Reference Zweben, Budny, Darrow, Medley, Nazikian, Stratton and Synakowski2000). Moreover, Doppler back-scattering measurements in a related field-reversed mirror configuration in Tri Alpha Energy's C2-W experiment recently showed the absence of ion-scale turbulence in a high-$\beta$![]() plasma (Schmitz et al. Reference Schmitz, Ida, Kobayashi, Bader, Brezinsek, Evans, Funaba, Goto, Mitarai and Morisaki2016). This was also attributed to large ion orbits, and near-classical ion thermal confinement was obtained. This is particularly relevant for BEAM because the field-reversed configuration is embedded in an axisymmetric mirror.
plasma (Schmitz et al. Reference Schmitz, Ida, Kobayashi, Bader, Brezinsek, Evans, Funaba, Goto, Mitarai and Morisaki2016). This was also attributed to large ion orbits, and near-classical ion thermal confinement was obtained. This is particularly relevant for BEAM because the field-reversed configuration is embedded in an axisymmetric mirror.
Another observation from tokamaks is that the shearing flows can keep the turbulent diffusion well below the Bohm level (Bohm diffusion would be unacceptable) and under the right conditions this leads to neoclassical ion confinement (Levinton et al. Reference Levinton, Zarnstorff, Batha, Bell, Bell, Budny, Bush, Chang, Fredrickson and Janos1995; Lazarus et al. Reference Lazarus, Navratil, Greenfield, Strait, Austin, Burrell, Casper, Baker, DeBoo and Doyle1996; Miura and JT-60 Team Reference Miura2003). The three most widely studied variants of drift waves, in tokamaks, are the ion temperature gradient (ITG), the electron temperature gradient (ETG) and the trapped electron modes. Unstable drift waves have $k_\parallel \ll k_\perp$![]() with $k_\perp$
with $k_\perp$![]() approaching $\rho _i^{-1}$
approaching $\rho _i^{-1}$![]() for the ITG and trapped electron modes. In such a case, FLR effects would likely be quite beneficial for the mirror. We can also speculate that the high ratio of $\langle E_i\rangle /T_e$
for the ITG and trapped electron modes. In such a case, FLR effects would likely be quite beneficial for the mirror. We can also speculate that the high ratio of $\langle E_i\rangle /T_e$![]() expected in a BEAM device would be strongly stabilizing (especially for ITG modes), giving hope that ion thermal diffusivities would be unaffected.
expected in a BEAM device would be strongly stabilizing (especially for ITG modes), giving hope that ion thermal diffusivities would be unaffected.
Perhaps the most serious threat would come from the electron-scale ETG mode. Indeed, there has been some speculation in the tandem mirror context that critical gradient ETG would be the most likely drift wave for the long and uniform cylindrical central cell plasma (Horton et al. Reference Horton, Fu, Ivanov and Beklemishev2010; Fowler et al. Reference Fowler, Moir and Simonen2017) and affect the electron temperature. The ETG might be relatively unaffected by the sheared ion flow and FLR effects because the relative lengths for electron-scale turbulence are a square root mass ratio smaller. If ETG is present and on the electron scale, the turbulence may leave ion energy and particle transport unchanged, but reduce the electron temperature and therefore increasing the drag on the fast ions (Waltz, Candy & Fahey Reference Waltz, Candy and Fahey2007) similar to the role of synchrotron radiation.
Of course mirrors may have their own variants of drift-like modes beyond the tokamak variants, such as trapped particle modes (Scarmozzino, Sen & Navratil Reference Scarmozzino, Sen and Navratil1988; Gerver et al. Reference Gerver, Golovato, Irby, Kesner, Casey, Guss, Horne, Lane, Machuzak and Post1989) and convective cells (Navratil, Post & Ehrhardt Reference Navratil, Post and Ehrhardt1977; Kesner & Garnier Reference Kesner and Garnier2000). One can note that in GDT the cross-field diffusion did not play a significant role and that cross-field energy losses due to vortical electrostatic modes (convective cells) in the Gamma 10 device (Cho et al. Reference Cho, Higaki, Hirata, Hojo, Ichimura, Ishii, Islam, Itakura, Katanuma and Kohagura2005, Reference Cho, Kohagura, Numakura, Hirata, Higaki, Hojo, Ichimura, Ishii, Islam and Itakura2006) were entirely eliminated by control of the shear flow. Experimental evaluation of the cross-field transport caused by the drift-wave turbulence in the BEAM could be a very important contribution to both mirror reactors and general plasma physics.
5.2. Direct energy conversion
For useful energy generation it is often argued that $Q_{\textrm {sci}}$![]() needs to be much greater than 1. That may not be necessary, however, for the mirror because its geometry allows the plasma energy losses out of the ends to be directly recovered in an efficient manner. This can be an enormous advantage for fusion energy systems that can employ it (see Ribe (Reference Ribe1975) and more recently Wurzel & Hsu (Reference Wurzel and Hsu2022)). Appendix A introduces a direct energy converter (DEC)geometry that could be tested in BEAM and would be appropriate for an axisymmetric mirror. This potential is not fully captured by $Q_{\textrm {sci}} = P_{\textrm {fus}}/P_{\textrm {injected}}$
needs to be much greater than 1. That may not be necessary, however, for the mirror because its geometry allows the plasma energy losses out of the ends to be directly recovered in an efficient manner. This can be an enormous advantage for fusion energy systems that can employ it (see Ribe (Reference Ribe1975) and more recently Wurzel & Hsu (Reference Wurzel and Hsu2022)). Appendix A introduces a direct energy converter (DEC)geometry that could be tested in BEAM and would be appropriate for an axisymmetric mirror. This potential is not fully captured by $Q_{\textrm {sci}} = P_{\textrm {fus}}/P_{\textrm {injected}}$![]() or even the $Q_{\textrm {fuel}}={P_{\textrm {fus}}}/{P_{\textrm {absorbed}}}>1$
or even the $Q_{\textrm {fuel}}={P_{\textrm {fus}}}/{P_{\textrm {absorbed}}}>1$![]() metrics as put forth by Wurzel & Hsu (Reference Wurzel and Hsu2022).
metrics as put forth by Wurzel & Hsu (Reference Wurzel and Hsu2022).
The D–T fusion reaction considered on BEAM is
If a breeding blanket is included, there will also be additional power from breeding tritium from lithium (the majority of which is the exothermic $\textrm {Li}^6$![]() rather than the endothermic $\textrm {Li}^7$
rather than the endothermic $\textrm {Li}^7$![]() , even with natural lithium):
, even with natural lithium):
giving a total of 22.4 MeV per fusion reaction rather than the 17.6 MeV normally considered. Using this higher value for $P_{\textrm {fus}}$![]() has been the standard in the mirror literature (Killeen et al. Reference Killeen, Mirin and Rensink1976; Fowler Reference Fowler1981; Post Reference Post1987), boosting $Q$
has been the standard in the mirror literature (Killeen et al. Reference Killeen, Mirin and Rensink1976; Fowler Reference Fowler1981; Post Reference Post1987), boosting $Q$![]() by a factor of 1.27. Thus with this definition the CQL3D results (see figure 7) would reach $Q=1.27 Q_{\textrm {fuel}}$
by a factor of 1.27. Thus with this definition the CQL3D results (see figure 7) would reach $Q=1.27 Q_{\textrm {fuel}}$![]() .
.
For systems that can utilize DECs, a metric (other than $Q_{\textrm {fuel}}$![]() ) that emphasizes the importance of both energy recovery efficiency $\eta _{D}$
) that emphasizes the importance of both energy recovery efficiency $\eta _{D}$![]() and the heating system injection efficiency $\eta _I$
and the heating system injection efficiency $\eta _I$![]() is useful. Here $\eta _I$
is useful. Here $\eta _I$![]() is the efficiency of transforming electrical input power into power injected to the plasma, including inefficiencies both in the source power generation and also in the plasma deposition, and $\eta _D$
is the efficiency of transforming electrical input power into power injected to the plasma, including inefficiencies both in the source power generation and also in the plasma deposition, and $\eta _D$![]() measures the fraction of the out-flowing plasma losses directly converted into electrical power.
measures the fraction of the out-flowing plasma losses directly converted into electrical power.
For example, if process heat is chosen as an application, a quantity like a heat-pump coefficient of performance or Wurzel's wall-plug $Q_{\textrm {wp}}= P_{\textrm {heat}}/P_{\textrm {elec}}$![]() might be used (Wurzel & Hsu Reference Wurzel and Hsu2022). For a fusion system which utilizes only the high-quality heat from a blanket for process heat, this would be
might be used (Wurzel & Hsu Reference Wurzel and Hsu2022). For a fusion system which utilizes only the high-quality heat from a blanket for process heat, this would be
where the numerator represents the heat from the blanket and the denominator represents the electrical power input required from the grid to heat the plasma and operate the plant. $P_{\textrm {loss}}$![]() is power exhausted out of the ends of the mirror (noting that heating power can be offset by alpha particle heating), and the balance of plant power $P_{\textrm {bop}}$
is power exhausted out of the ends of the mirror (noting that heating power can be offset by alpha particle heating), and the balance of plant power $P_{\textrm {bop}}$![]() would be all the additional power needed to operate the auxiliary systems beyond the plasma heating systems including that for feedback stabilization. Net production of fusion energy in the form of heat for a given amount of input electrical power requires $Q_{\textrm {wp}} > 1$
would be all the additional power needed to operate the auxiliary systems beyond the plasma heating systems including that for feedback stabilization. Net production of fusion energy in the form of heat for a given amount of input electrical power requires $Q_{\textrm {wp}} > 1$![]() (Wurzel's ‘Kitty Hawk’ moment) or equivalently a requirement that
(Wurzel's ‘Kitty Hawk’ moment) or equivalently a requirement that
Using optimistic values of $\eta _{D}=\eta _I=0.8$![]() and $P_{\textrm {bop}}=0.1 P_{\textrm {loss}}$
and $P_{\textrm {bop}}=0.1 P_{\textrm {loss}}$![]() would only require $Q_{\textrm {fuel},\textrm {wp}}>0.4$
would only require $Q_{\textrm {fuel},\textrm {wp}}>0.4$![]() . This can also provide a fanciful path to net electricity generation if the high-temperature blanket heat is instead used to create electricity with an efficiency $\eta _E$
. This can also provide a fanciful path to net electricity generation if the high-temperature blanket heat is instead used to create electricity with an efficiency $\eta _E$![]() . This becomes a requirement that
. This becomes a requirement that
for net electricity. This can be easily related to Wurzel's $Q_{\textrm {eng}}$![]() by noting that $Q_{\textrm {eng}}= \eta _E Q_{\textrm {wp}} - 1$
by noting that $Q_{\textrm {eng}}= \eta _E Q_{\textrm {wp}} - 1$![]() . Assuming an advanced Brayton cycle efficiency of $\eta _E\sim 0.4$
. Assuming an advanced Brayton cycle efficiency of $\eta _E\sim 0.4$![]() generating net electricity would only require $Q_{\textrm {fuel},\textrm {elec}} > 0.85$
generating net electricity would only require $Q_{\textrm {fuel},\textrm {elec}} > 0.85$![]() to make $Q_{\textrm {eng}}> 0$
to make $Q_{\textrm {eng}}> 0$![]() .
.
6. Break-even axisymmetric mirror as a fusion volumetric neutron source (FVNS) for blanket and materials testing
The BEAM concept described here would be ideally suited to operate as a volumetric neutron source for materials and blanket testing – a critical step in the development path of the tandem mirror that follows, but also useful for developing blankets for stellarators and tokamaks.
A staged BEAM experimental programme might begin with demonstrating MHD stable operation and verifying the confinement properties of a classical mirror in deuterium during a short pulse (tens of seconds) and then move towards long pulse (one-hour pulse lengths) in a non-nuclear phase. This demonstration would motivate an upgrade to use tritium, requiring the addition of a blanket and neutron and gamma ray shielding of the HTS magnets. Alternatively, two devices, a nuclear and non-nuclear BEAM, could be considered. The non-nuclear BEAM focused on demonstrating plasma performance more quickly could have smaller bore magnets with lower capital cost and not require a tritium-qualified site. The assessment of cost savings versus time-line on risk reduction is on-going.
Tritium operation could also begin with short-pulse operation to test performance and then blankets could be added to begin a material and component testing facility. Here, we provide a low-resolution discussion of what BEAM's tritium fuel cycle and blanket might look like as a first step to assessing its utility as a FVNS.
6.1. Tritium inventory, throughput and consumption
Consideration of startup inventories, tritium consumption and tritium processing requirements is increasingly being noted as a critical path for fusion technology, requiring integral testing near-term experiments without using up the world's tritium supply (Abdou et al. Reference Abdou, Riva, Ying, Day, Loarte, Baylor, Humrickhouse, Fuerst and Cho2021). While a detailed fuel cycle analysis must be carried out, several observations are useful here to illustrate how a BEAM-scale device could be used to fill this mission need.
A NBI-driven BEAM, operated at steady state and generating 10 MW of fusion power, would have a consumption given by approximately
if operated with full availability; this would not break the world's tritium budget. Blanket technologies could be tested and tritium breeding ratios (TBRs) in the blanket would not need to be greater than 1 during this development phase.
Assuming half of the heating power is due to injection of 50 A of tritium at 100 keV, the required fuelling incident on the plasma can be estimated:
or about 5 g h$^{-1}$![]() in this design.
in this design.
The burn-up fraction of the injected tritium for the NBI-driven BEAM is
or about 1 %. This burn-up fraction can be used to estimate the required tritium throughput as a function of fusion power and relating it to the fuelling technique used. The fuelling efficiency $\eta _f = \varPhi _i/\varPhi _{f}$![]() of the current generation of positive NBI systems can be estimated from the ratio of the gas flow rate $\varPhi _f$
of the current generation of positive NBI systems can be estimated from the ratio of the gas flow rate $\varPhi _f$![]() into the plasma sources and neutralizers (e.g. the 2.5 MW ASDEX-U sources have gas flow rates of $\varPhi _f= 50$
into the plasma sources and neutralizers (e.g. the 2.5 MW ASDEX-U sources have gas flow rates of $\varPhi _f= 50$![]() mtorr l s$^{-1}$
mtorr l s$^{-1}$![]() (25 g h$^{-1}$
(25 g h$^{-1}$![]() )) to the tritium which ends up in the plasma after injection $\varPhi _i = I / e$
)) to the tritium which ends up in the plasma after injection $\varPhi _i = I / e$![]() and found to be about 20 % ($\eta _f\approx 0.2$
and found to be about 20 % ($\eta _f\approx 0.2$![]() ). The remainder of that flow is pumped away and needs to be processed, imposing a burden on the tritium reprocessing system and so
). The remainder of that flow is pumped away and needs to be processed, imposing a burden on the tritium reprocessing system and so
Limiting the tritium on-site inventory to less than 30 g would put BEAM in a category 3 tritium hazard facility according to the DOE Standard Hazard Categorization of DOE Nuclear Facilities DOE-STD-1027-2018, and potentially help in siting and licensing operation. From the estimates of tritium throughput from above, 30 g would allow operation for approximately 1 hour before regeneration (presumably the regeneration of the $2\times 10^6$![]() l s$^{-1}$
l s$^{-1}$![]() cryopanels in the NBI system). This is too stringent for a FVNS facility, especially if a tritium breeding blanket is included, but may be sufficient for a short-pulse-only experiment. Dual cryopanel systems would allow for steady-state operation if regenerated with a one-hour time scale but at the expense of increasing the required tritium inventory by a factor of 2 and the cost of a second pumping system. This approach likely has a very high technical readiness level (TRL). An alternative approach could make use of steady-state cryopanel technologies such as a snail pump (Foster Reference Foster1987; Baylor & Meitner Reference Baylor and Meitner2017) and/or development of direct internal recycling systems (Day & Giegerich Reference Day and Giegerich2013) such as metal foil pumps (Peters Reference Peters2020), which could have an enormous impact on reducing the required inventory. It is assumed that the plasma-facing components, probably tungsten, will operate hot to minimize tritium retention, but we recognize that a more thorough tritium analysis will be required.
cryopanels in the NBI system). This is too stringent for a FVNS facility, especially if a tritium breeding blanket is included, but may be sufficient for a short-pulse-only experiment. Dual cryopanel systems would allow for steady-state operation if regenerated with a one-hour time scale but at the expense of increasing the required tritium inventory by a factor of 2 and the cost of a second pumping system. This approach likely has a very high technical readiness level (TRL). An alternative approach could make use of steady-state cryopanel technologies such as a snail pump (Foster Reference Foster1987; Baylor & Meitner Reference Baylor and Meitner2017) and/or development of direct internal recycling systems (Day & Giegerich Reference Day and Giegerich2013) such as metal foil pumps (Peters Reference Peters2020), which could have an enormous impact on reducing the required inventory. It is assumed that the plasma-facing components, probably tungsten, will operate hot to minimize tritium retention, but we recognize that a more thorough tritium analysis will be required.
We note that operation of the NBIs with a 50–50 mixture of deuterium and tritium could greatly reduce the requirements on the tritium separation plant as it would only be needed at a rate needed to correct the mixture ratio. Existing technology such as cryogenic distillation and thermal cycling absorption process should be able satisfy this requirement (Ducret et al. Reference Ducret, Laquerbe, Ballanger, Steimetz, Porri, Verdin and Pelletier2002; Ana et al. Reference Ana, Niculescu, Bornea, Zamfirache and Draghia2018).
6.2. Power handling for DECs
The majority of the plasma losses for BEAM would be into the end cells and deposited on the DEC or other structure and it should be emphasized that the electrical energy collected by the DEC would reduce the dissipated heat loads.
Even without a DEC, the power levels are manageable (especially compared with toroidal systems) since the lost power can be expanded over a large area:
where $B_w$![]() is the magnetic field at the end plates and is assumed to be $\approx$
is the magnetic field at the end plates and is assumed to be $\approx$![]() 0.1 T. For a full-power BEAM at $Q\sim 1$
0.1 T. For a full-power BEAM at $Q\sim 1$![]() , the charged particle heat load to the end walls is only $q_{\textrm {pmi}}=0.7$
, the charged particle heat load to the end walls is only $q_{\textrm {pmi}}=0.7$![]() MW m$^{-2}$
MW m$^{-2}$![]() .
.
The ion energies are very high (unless slowed by electric fields with the DEC). At full energy, the implantation range of the escaping fast ions imposes the minimum thickness of the collecting material, e.g. ${\sim }650$![]() nm if Ta is used. Additionally, the effect of physical sputtering should be considered. For example, an incident flux of 50 A of tritium ions with the distribution shown in figure 9 would sputter off a layer of about 150 nm from 1 m$^2$
nm if Ta is used. Additionally, the effect of physical sputtering should be considered. For example, an incident flux of 50 A of tritium ions with the distribution shown in figure 9 would sputter off a layer of about 150 nm from 1 m$^2$![]() Ta surface during a 1 h pulse length or about 1 mm yr$^{-1}$
Ta surface during a 1 h pulse length or about 1 mm yr$^{-1}$![]() .
.

Figure 9. Spectrum of escaping fast ions from BEAM, noting the important role that sputtering and secondary emission can play from the end rings.
6.3. Magnet shielding and neutron wall load
The neutron wall load for a BEAM is a strong function of $\beta$![]() , but even modest $\beta$
, but even modest $\beta$![]() is sufficient to reach the >20 displacements per atom (DPA) needed for materials testing. The neutron wall load can be approximated by
is sufficient to reach the >20 displacements per atom (DPA) needed for materials testing. The neutron wall load can be approximated by

For $\beta _c\sim 0.3$![]() and $B_0\sim 3$
and $B_0\sim 3$![]() T, the neutron flux would be 1 MW m$^{-2}$
T, the neutron flux would be 1 MW m$^{-2}$![]() at the plasma edge. For ferric steels irradiated with D–T neutrons, one can assume that around 10 DPA will be obtained after one full-power year (FPY) of irradiation with a neutron wall load of 1 MW m$^{-2}$
at the plasma edge. For ferric steels irradiated with D–T neutrons, one can assume that around 10 DPA will be obtained after one full-power year (FPY) of irradiation with a neutron wall load of 1 MW m$^{-2}$![]() . For blanket testing, this will be more than adequate to demonstrate heat removal and tritium breeding. Increasing $\beta _c$
. For blanket testing, this will be more than adequate to demonstrate heat removal and tritium breeding. Increasing $\beta _c$![]() and $B_0$
and $B_0$![]() can increase wall load if higher fluxes are needed for materials testing. If maximizing neutron flux for material testing is not the objective, the vacuum vessel wall radius can be increased to extend the first-wall lifetime. The current limit of reduced-activation ferric/martensitic steel is about 20 DPA within a narrow operating temperature window, but there is reasonable hope that advanced materials such as oxide-dispersion-strengthened steels and castable nanostructured alloys can extend the operation envelope of structural materials (Zinkle et al. Reference Zinkle, Boutard, Hoelzer, Kimura, Lindau, Odette, Rieth, Tan and Tanigawa2017; Tan, Katoh & Snead Reference Tan, Katoh and Snead2018). A BEAM would offer an ideal neutron source to facilitate their development.
can increase wall load if higher fluxes are needed for materials testing. If maximizing neutron flux for material testing is not the objective, the vacuum vessel wall radius can be increased to extend the first-wall lifetime. The current limit of reduced-activation ferric/martensitic steel is about 20 DPA within a narrow operating temperature window, but there is reasonable hope that advanced materials such as oxide-dispersion-strengthened steels and castable nanostructured alloys can extend the operation envelope of structural materials (Zinkle et al. Reference Zinkle, Boutard, Hoelzer, Kimura, Lindau, Odette, Rieth, Tan and Tanigawa2017; Tan, Katoh & Snead Reference Tan, Katoh and Snead2018). A BEAM would offer an ideal neutron source to facilitate their development.
To test blankets for extended periods of time, the high-field magnets must be shielded against the damaging fast neutrons and to limit nuclear heating that must be balanced by cryogenics. This seems to impose a lifetime fast-neutron (>100 keV) fluence limit of around $3\times 10^{18}\,\textrm {cm}^{-2}$![]() on the magnets (Chudy et al. Reference Chudy, Eisterer, Weber, Veterníková, Sojak and Slugen2012; Prokopec et al. Reference Prokopec, Fischer, Weber and Eisterer2015; Fischer et al. Reference Fischer, Prokopec, Emhofer and Eisterer2018). This ultimately sets the size of the winding pack for the HTS magnets and their cost. Therefore, a high-performance fusion neutron shield must be designed to ensure the longevity of the HTS magnets. After evaluating a range of shielding materials, our neutronics analysis found water-cooled monolithic tungsten could satisfy the shielding requirements with a 0.5 m thick shield surrounding the HTS in the radial direction. Pure tungsten also has the highest technological readiness, but we note that the use of a W$_2$
on the magnets (Chudy et al. Reference Chudy, Eisterer, Weber, Veterníková, Sojak and Slugen2012; Prokopec et al. Reference Prokopec, Fischer, Weber and Eisterer2015; Fischer et al. Reference Fischer, Prokopec, Emhofer and Eisterer2018). This ultimately sets the size of the winding pack for the HTS magnets and their cost. Therefore, a high-performance fusion neutron shield must be designed to ensure the longevity of the HTS magnets. After evaluating a range of shielding materials, our neutronics analysis found water-cooled monolithic tungsten could satisfy the shielding requirements with a 0.5 m thick shield surrounding the HTS in the radial direction. Pure tungsten also has the highest technological readiness, but we note that the use of a W$_2$![]() B$_5$
B$_5$![]() shield could allow for smaller magnets (Windsor et al. Reference Windsor, Astbury, Davidson, McFadzean, Morgan, Wilson and Humphry-Baker2021)
shield could allow for smaller magnets (Windsor et al. Reference Windsor, Astbury, Davidson, McFadzean, Morgan, Wilson and Humphry-Baker2021)
The neutronics analysis for a BEAM blanket is described in Appendix B, focusing on the neutron wall load and the shielding of the HTS magnets using the OpenMC Monte-Carlo code (Romano et al. Reference Romano, Horelik, Herman, Nelson, Forget and Smith2015). The thermal hydraulics required to remove the heat has not yet been addressed. Tritium breeding ratios greater than 1 are achieved with a blanket of natural lithium metal and a layer of molten lead multiplier. The peak neutron fluxes at the vacuum vessel wall can exceed 1 MW m$^{-2}$![]() given 10 MW of D–T fusion power.
given 10 MW of D–T fusion power.
7. Technology gaps
Just as for all other fusion approaches, there are a number of scientific and technological developments which are necessary to realize a BEAM. On the scientific front, MHD stability on WHAM must be demonstrated with techniques applicable to BEAM, and modern theory and computational tools such as CQL3D-m, gyrokinetics and particle-in-cell codes must be used to optimize $Q$![]() and show that MHD, kinetic instabilities and perhaps even drift waves can be sufficiently well controlled. On the technology side, no one issue seems to be show-stopper at this stage, but must simply be advanced to higher TRLs. Some of these are shared with other fusion concepts (blankets and heating system) and might continue to progress independently of the mirror, but some are unique (such as direct energy conversion).
and show that MHD, kinetic instabilities and perhaps even drift waves can be sufficiently well controlled. On the technology side, no one issue seems to be show-stopper at this stage, but must simply be advanced to higher TRLs. Some of these are shared with other fusion concepts (blankets and heating system) and might continue to progress independently of the mirror, but some are unique (such as direct energy conversion).
The main technology development path items needing work are:
(a) Development of circular, planar high-field ($\sim$
 25 T) magnets and with a large enough bore ($\sim$
25 T) magnets and with a large enough bore ($\sim$ 1.5 m diameter) to accommodate a presumed tungsten shield.
1.5 m diameter) to accommodate a presumed tungsten shield.(b) Steady-state and efficient, tritium-compatible neutral-beam heating systems operating between 100 and 130 keV. This likely requires energy recovery (Blum et al. Reference Blum, Barr, Dexter, Fink, Moir and Wilcox1981; Barr, Moir & Hamilton Reference Barr, Moir and Hamilton1982; Fumelli, Jequier & Pamela Reference Fumelli, Jequier and Pamela1989) of un-neutralized ions and a cryopanel regeneration strategy. Operation with a mixture of tritium and deuterium could ease tritium reprocessing demands.
(c) Development of a modular, low-cost magnet system for shaping the 3–6 T magnetic field profile between the high-field end magnets.
(d) A materials solution to withstand the high-energy ion flux ($\sim$
 100 keV) exiting the machine as shown in figure 9 without sputtering.
100 keV) exiting the machine as shown in figure 9 without sputtering.(e) Tritium reprocessing at the level of 50 A (beyond the scope of this paper) and incorporation of direct internal recycling to reduce tritium inventory.
(f) A blanket solution capable of removing 10 MW of neutron energy with a tritium processing plant.
(g) Development of high-performance fast-neutron shields capable of attenuating fast-neutron flux by three orders of magnitude in less than 50 cm, while incorporating cooling to remove up to $1\,\textrm {W}\,\textrm {cm}^{-3}$
 of nuclear heat load. Generation of high-level radioactive waste from such a shield should also be avoided.
of nuclear heat load. Generation of high-level radioactive waste from such a shield should also be avoided.(h) A strategy for remote maintenance.
(i) Incorporation of direct energy conversion to further improve efficiency but also to dissipate fast-ion energy and reduce material damages of end ring collectors.
(j) As for all fusion energy systems, insulating materials feature significantly in many components including high-voltage neutral-beam insulators, dielectrics in radio-frequency systems and standoffs for biased limiters, direct energy conversion grids and also feedback actuators. Robust ceramics are needed (Hodgson & Shikama Reference Hodgson and Shikama2012).
8. Summary and conclusions
This paper, in a provocative spirit, has built the case that a break-even-class mirror experiment is within near-term reach given today's technologies. The particular case investigated above with the assumption of classical parallel transport has a scientific $Q$![]() slightly below 1 – it seems likely that a mirror ratio and geometry optimization $Q$
slightly below 1 – it seems likely that a mirror ratio and geometry optimization $Q$![]() could be made greater than one within the framework of idealized classical parallel transport.
could be made greater than one within the framework of idealized classical parallel transport.
A steady-state D–T BEAM would be in quantitatively new territory for several different metrics, all of which would be likely to improve performance. These are:
(i) The BEAM will operate with NBI systems which are efficient for fuelling plasma.
(ii) The BEAM will be opaque to recycled neutrals and correspondingly have a very low neutral density in the core thus reducing charge exchange losses for fast ions. Edge cooling by neutrals may also allow for a low-$T_e$
 line-tied mantel with a high-$T_e$
line-tied mantel with a high-$T_e$ core that is not line-tied (see mantel stabilization below).
core that is not line-tied (see mantel stabilization below).(iii) The large radial dimensions of the BEAM plasma and tightly focused ECH beams provide an opportunity for $T_e$
 profile control using high-frequency gyrotrons.
profile control using high-frequency gyrotrons.(iv) The large radial dimensions of BEAM compared to earlier generations of mirrors also implies many gyroradii across the plasma (large $N_\rho$
 ). This is favourable for DCLC as well as fast-ion adiabaticity.
). This is favourable for DCLC as well as fast-ion adiabaticity.(v) Owing to the larger radial size of the plasma the ratio of $r_w/a_p$
 can be of order unity, providing for improved conducting shell stabilization at high $\beta$
can be of order unity, providing for improved conducting shell stabilization at high $\beta$ .
.
We acknowledge that other sources of energy loss, e.g. drift waves, may ultimately play a role. Nonetheless, the utility of such a device as a FVNS, the application emphasized here, is clear even at the more modest values of $Q\leq 1$![]() . A preliminary neutronics analysis for a 10 MW neutron output (achievable with additional heating power even if $Q<1$
. A preliminary neutronics analysis for a 10 MW neutron output (achievable with additional heating power even if $Q<1$![]() ) has illustrated that such a FVNS could have both materials testing and blanket testing missions. We note that this same device (even at modest $Q$
) has illustrated that such a FVNS could have both materials testing and blanket testing missions. We note that this same device (even at modest $Q$![]() ) would be a central component of the development path needed for the tandem mirror and demonstrate the necessary conditions required of an end plug Fowler et al. (Reference Fowler, Moir and Simonen2017). Furthermore, there are numerous other applications for powerful fusion neutron sources such as recycling spent nuclear waste (Moir et al. Reference Moir, Martovetsky, Molvik, Ryutov and Simonen2012; Ruegsegger et al. Reference Ruegsegger, Moreno, Nyberg, Bohm, Wilson and Lindley2023) that are beyond the scope of this paper.
) would be a central component of the development path needed for the tandem mirror and demonstrate the necessary conditions required of an end plug Fowler et al. (Reference Fowler, Moir and Simonen2017). Furthermore, there are numerous other applications for powerful fusion neutron sources such as recycling spent nuclear waste (Moir et al. Reference Moir, Martovetsky, Molvik, Ryutov and Simonen2012; Ruegsegger et al. Reference Ruegsegger, Moreno, Nyberg, Bohm, Wilson and Lindley2023) that are beyond the scope of this paper.
Acknowledgements
The information, data or work presented herein was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), US Department of Energy, under Award Numbers DE-AR0001258 and DE-AR0001261, and US Department of Energy under Award Number DE-FG02-ER54744. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. For transparency of interests, the authors would like to state that J.K.A., C.B.F., K.F., B.L. and O.S. are co-founders of Realta Fusion. The authors would also like to thank Dmitri Ryutov and Ken Fowler for their helpful comments and support.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. An axisymmetric DEC for the mirror
Direct energy recovery has been experimentally demonstrated in a number of fusion technologies including: recapturing wasted energy from beams (Barr et al. Reference Barr, Moir and Hamilton1982), recovering electron beam energy in gyrotrons with depressed collectors (Kariya et al. Reference Kariya, Minami, Imai, Okada, Motoyoshi, Numakura, Nakashima, Idei, Onchi and Hanada2019), on the exhaust from real plasma experiments (Yasaka et al. Reference Yasaka, Kurumatani, Yamamoto, Takeno, Nakashima, Higashizono, Hirata, Cho, Tomita and Ishikawa2007) and with a variety of mechanisms (Barr et al. Reference Barr, Burleigh, Dexter, Moir and Smith1974; Gitomer & Krishnan Reference Gitomer and Krishnan1974; Forrester, Busnardo-Neto & Crow Reference Forrester, Busnardo-Neto and Crow1975; Gitomer Reference Gitomer1977). A DEC appropriate for an axisymmetric mirror is shown in figure 10. It builds upon a previously studied ‘Venetian blind’ concept (Moir & Barr Reference Moir and Barr1973; Barr et al. Reference Barr, Burleigh, Dexter, Moir and Smith1974; Moir, Barr & Miley Reference Moir, Barr and Miley1974; Barr, Moir & Kinney Reference Barr, Moir and Kinney1977) from above in important ways.

Figure 10. (a) Schematic of a DEC appropriate for an axisymmetric mirror. (b) Electron test particle trajectories in the electron screen. (c) Ion test particle trajectories, for energies equal to the potentials on the second, third and final stages. (d) Computer-aided design rendering.
Axisymmetric mirrors have large expansion chambers for several reasons: the field drop-off accelerates the ions through the mirror force (Moir & Barr Reference Moir and Barr1973), retains electrons via an ambipolar electric field (Soldatkina et al. Reference Soldatkina, Maximov, Prikhodko, Savkin, Skovorodin, Yakovlev and Bagryansky2020) and spreads out the power over a large area for dissipation. For the proposed DEC in BEAM, the field will drop from a maximum of 25 T to $\sim$![]() 0.1 T, with the plasma area expanding by the same factor of $\sim$
0.1 T, with the plasma area expanding by the same factor of $\sim$![]() 250. In BEAM, we anticipate that the escaping ion energies will be of order 100 keV but with a minimum energy set by the ambipolar potential drop of $5T_e$
250. In BEAM, we anticipate that the escaping ion energies will be of order 100 keV but with a minimum energy set by the ambipolar potential drop of $5T_e$![]() set by the electron temperature. An FBIS simulation of the distribution of energies is shown in figure 9.
set by the electron temperature. An FBIS simulation of the distribution of energies is shown in figure 9.
The first stage of the DEC proposed for BEAM will use concentric rings of a ferromagnetic material (e.g. iron) to concentrate the magnetic flux into electron-collecting anodes. The magnetic field in the iron will be near saturation. To fully screen electrons, all the magnetic flux must pass through the iron. Anticipating $B_{\textrm {vac}}\sim 0.1$![]() T and $B_{\textrm {sat}}\sim 2$
T and $B_{\textrm {sat}}\sim 2$![]() T, the ratio is $\sim$
T, the ratio is $\sim$![]() 1/20. For this case, the cross-sectional area of the iron can be roughly 1/20 of the area between rings and still concentrate all the flux into the iron rings.
1/20. For this case, the cross-sectional area of the iron can be roughly 1/20 of the area between rings and still concentrate all the flux into the iron rings.
In this electron-collecting region, the electrons are strongly magnetized with orbits that closely follow the magnetic field lines and are directed to the poles of the iron. Figure 10 shows a COMSOL simulation of the magnetic field in the vicinity of the iron rings together with representative electron (figure 10b) and ion (figure 10c) orbits. The characteristic ion Larmor radius $\rho ={mV_\perp }/{eB} =14\,\textrm {cm}\ \sqrt {E_{i,10\,\textrm {keV}}}/B_{\textrm {kG}}$![]() is enormous compared with dimensions ($d_1,d_2$
is enormous compared with dimensions ($d_1,d_2$![]() ) of the rings, and so the ions are only weakly affected by the magnetic field. The fraction of ions transmitted is due to the overall opacity of the grid, shown in figure 10 with $d_2/d_3$
) of the rings, and so the ions are only weakly affected by the magnetic field. The fraction of ions transmitted is due to the overall opacity of the grid, shown in figure 10 with $d_2/d_3$![]() of 0.1, for a transmission of 0.9. As in figure 1, a subsequent secondary electron suppressor element to prevent arcing to the first ion collecting grid may be needed.
of 0.1, for a transmission of 0.9. As in figure 1, a subsequent secondary electron suppressor element to prevent arcing to the first ion collecting grid may be needed.
This system of concentric ferromagnetic rings is an improvement over earlier designs as it allows for shear flow stabilization of the plasma. By independently biasing each electron-collecting ring at different potentials (requiring insulated electrical leads to each ring), the plasma potential could still be controlled in this configuration.
The ion-collecting grids rely on electric, not magnetic, fields established by the ion exhaust. The first ion-collecting grid potential is set to just below the energy of the least energetic ions (see figure 9). For the magnetic expander, this is a minimum of five times the electron temperature of potential drop from the plasma to the DEC, e.g. 88 kV as in the original ‘Venetian blind’ DEC of Moir & Barr (Reference Moir and Barr1973). The ions slow as they approach and then pass through with lower kinetic energy. This is followed by a second grid at an even more positive potential (e.g. 165 kV) that reflects some fraction of the ions back towards the first. The rings are echeloned at an angle such that the reflected ions have an orbit radially outward and are collected on the ion-collecting grids (figure 10c). The power generated is the collected current times the voltage on the grid, while the efficiency is limited by the extra kinetic energy dissipated by the ions impinging on the grid. Increasing the number of stages minimizes this wasted power (Moir & Barr Reference Moir and Barr1973).
The orientation of the ion-collecting rings, combined with the cumulative space charge of the ion beam, imparts a radial kick to the ion orbit and reflects them back towards the previous grid. The final design requires computing ion orbits, aligning the fins of the collectors with these orbits and spacing the fins to be opaque to the reflected ions. This will be solved with an iterative optimization process: beginning with the mirror ion exhaust distribution function, first calculating the space charge potentials of the pure ion beam beyond the electron screen, the trajectories of the ions, solving for the accumulated charge on each grid and updating the electric fields until a self-consistent solution is reached (as in Moir et al. Reference Moir, Barr and Miley1974).
The positively charged ions that strike the ion-collecting rings will recombine with electrons in the metallic surface and be released as neutral atoms to be pumped away in the end chambers. A low neutral density is critical to performance, as excess neutrals can lead to arcing between grids and charge exchange losses with the incoming ions. Vacuum pumping in the region surrounding the rings may be suitable but there may also be functional materials such as non-evaporable getters like tantalum. The gettering capacity of the tantalum wall interface can be regenerated with the flash heating of the material up to a temperature of 1100 K at which most of the trapped hydrogen isotopes will outgas.
The BEAM is fuelled by an injection current $I_b$![]() and the power lost out of the ends is approximated by $P_{\textrm {Loss}}=I_b\ E_b$
and the power lost out of the ends is approximated by $P_{\textrm {Loss}}=I_b\ E_b$![]() and split between the two ends. The space charge of the ion beam which passes through the electron collector sets limitations on the power/area that can be converted. The ion density at the convertor is related to the current carried and the area over which the beam is distributed:
and split between the two ends. The space charge of the ion beam which passes through the electron collector sets limitations on the power/area that can be converted. The ion density at the convertor is related to the current carried and the area over which the beam is distributed:
This space charge creates its own electric field which modifies the potential. The limit on current is ultimately linked to the accumulated voltages on and separation between the grids. The limit can be estimated as follows. The maximum current passing between two anodes is set by the well-known space-charge limit embodied in the Child–Langmuir law (Child Reference Child1911; Langmuir Reference Langmuir1913):

This space-charge limit sets the minimum area over which the lost current must be spread and therefore the maximum field strength in the expander at which the ring can be placed. For the example here, where $\Delta V \approx 80$![]() kV, assuming $L = 20$
kV, assuming $L = 20$![]() cm (set by breakdown voltages for the vacuum conditions) $J_{\max }=20$
cm (set by breakdown voltages for the vacuum conditions) $J_{\max }=20$![]() A m$^{-2}$
A m$^{-2}$![]() and so an expander area of several m$^2$
and so an expander area of several m$^2$![]() is adequate for $\sim$
is adequate for $\sim$![]() 50 A of current through each end.
50 A of current through each end.
As mentioned above, a low neutral density is critical to success of a DEC. While breakdown due to arcing is possible (and all electrode surfaces should be devoid of sharp corners that might encourage breakdown), more deleterious are losses due to charge exchange of fast ions with neutrals in the expander. The efficiency of the divertor would be reduced by a factor $\eta _{cx} = \exp (-Z / \lambda _{cx})$![]() , where $Z\sim 2$
, where $Z\sim 2$![]() m is the distance from the mirror to the divertor and $\lambda _{cx}= (\sigma n_o)^{-1}$
m is the distance from the mirror to the divertor and $\lambda _{cx}= (\sigma n_o)^{-1}$![]() is the mean free path for exhaust ions due to charge exchange with neutrals. Typical cross-sections for 10–100 keV deuterium ions with neutral deuterium are 10$^{-19}$
is the mean free path for exhaust ions due to charge exchange with neutrals. Typical cross-sections for 10–100 keV deuterium ions with neutral deuterium are 10$^{-19}$![]() –10$^{-21}$
–10$^{-21}$![]() m$^2$
m$^2$![]() . To maintain 95 % efficiency demands a neutral pressure below $8\,\mathrm {\mu }$
. To maintain 95 % efficiency demands a neutral pressure below $8\,\mathrm {\mu }$![]() torr (assuming $T\sim 300$
torr (assuming $T\sim 300$![]() K). This is regularly achieved even in low-performance plasma devices. The extra neutral pumping provided by the coating of the grids will ensure low charge exchange losses.
K). This is regularly achieved even in low-performance plasma devices. The extra neutral pumping provided by the coating of the grids will ensure low charge exchange losses.
Appendix B. Preliminary neutronics analysis for a prototype PbLi blanket
The OpenMC model transports fusion neutrons with source density proportional to ion density profile used by the Pleiades equilibrium, and a 10 MW of total D–T fusion power was assumed for the whole device. Continuous energy nuclear reaction cross-sections from the ENDF/B-VIII.0 library were used, and only half of the device was modelled with the use of a reflecting boundary condition at the midplane. Pure tungsten was chosen as the shielding material for the HTS magnets due to its excellent fast-neutron and gamma-ray attenuation characteristics and high TRL for manufacturing. A 15 % volume fraction of water is assumed to be necessary for cooling. With modest geometric optimization, it was possible to achieve ${<}1\,\textrm {mW}\,\textrm {cm}^{-3}$![]() of nuclear heating and ${<}3\times 10^{18}\,\textrm {n}\,{\textrm {cm}^{-2}}$
of nuclear heating and ${<}3\times 10^{18}\,\textrm {n}\,{\textrm {cm}^{-2}}$![]() fast-neutron fluence in the winding pack in 10 FPY (Prokopec et al. Reference Prokopec, Fischer, Weber and Eisterer2015; Fischer et al. Reference Fischer, Prokopec, Emhofer and Eisterer2018) with a warm magnet bore diameter of 1.5 m.
fast-neutron fluence in the winding pack in 10 FPY (Prokopec et al. Reference Prokopec, Fischer, Weber and Eisterer2015; Fischer et al. Reference Fischer, Prokopec, Emhofer and Eisterer2018) with a warm magnet bore diameter of 1.5 m.
It is possible that advanced neutron shielding materials (including tungsten borides, metal hydrides and tungsten carbide) could be used to reduce the magnet bore, lowering the cost and technical challenge. For example, spherical tokamak shielding studies have shown that if W$_2$![]() B$_5$
B$_5$![]() could be manufactured in large ($\sim$
could be manufactured in large ($\sim$![]() 100 ton) quantities, the neutron shielding could be reduced significantly (Windsor et al. Reference Windsor, Astbury, Davidson, McFadzean, Morgan, Wilson and Humphry-Baker2021).
100 ton) quantities, the neutron shielding could be reduced significantly (Windsor et al. Reference Windsor, Astbury, Davidson, McFadzean, Morgan, Wilson and Humphry-Baker2021).
For this study, a liquid immersion blanket design was chosen due to its simplicity and high TBR (the geometry is shown in figure 11) A number of blanket materials were modelled, and the best performing was a lithium blanket with a flowing layer of lead multiplier outside the vacuum vessel. Compared with a lead–lithium eutectic blanket, such a design concentrates the multiplier in the region with maximum fast-neutron flux and avoids parasitic epithermal neutron absorption deeper in the blanket. A maximum TBR of 1.27 was achieved with natural lithium without any blanket penetrations. With the addition of a single 60 cm diameter NBI duct at the midplane, figure 12(a) shows that neutron leakage through the beam duct increases the neutron flux at the central magnets. As a result of this leakage, a $7\,\%$![]() reduction in TBR was observed. The use of Li$^6$
reduction in TBR was observed. The use of Li$^6$![]() -enriched blankets can boost TBR further. However, there is no need for BEAM to be completely tritium self-sufficient as a FVNS facility. If run in steady state, we expect such a machine to provide up to $\sim$
-enriched blankets can boost TBR further. However, there is no need for BEAM to be completely tritium self-sufficient as a FVNS facility. If run in steady state, we expect such a machine to provide up to $\sim$![]() 14 DPA per FPY at the first wall, with a large testing volume of up to $5\,\textrm {m}^3$
14 DPA per FPY at the first wall, with a large testing volume of up to $5\,\textrm {m}^3$![]() available for irradiation of reactor-scale components. Figure 13 shows the profile of relevant neutronics parameters for the configuration described here.
available for irradiation of reactor-scale components. Figure 13 shows the profile of relevant neutronics parameters for the configuration described here.

Figure 11. A BEAM blanket geometry and neutron source parameters. (a) Iron-equivalent displacement damage rate, (b) neutron wall load and (c) model geometry description.

Figure 12. OpenMC blanket calculation results with 5 cm thick lead multiplier. (a,b) Fast-neutron flux with HTS magnet fluence limit of $3\times 10^{18}\,\textrm {n}\,{\textrm {cm}^{-2}}$![]() indicated by white and blue dashed lines at 10 and 1 FPY, respectively. (c) Nuclear heating power density. (d) Tritium breeding rate in blanket.
indicated by white and blue dashed lines at 10 and 1 FPY, respectively. (c) Nuclear heating power density. (d) Tritium breeding rate in blanket.

Figure 13. Neutronics parameters along first wall with 10 MW D–T neutron source. (a) Fast-neutron flux and iron-equivalent displacement damage rate in the material testing zone. (b) Wall load and nuclear heating power density.