Katabatic Snow Storms in Stable Atmospheric Conditions at Mizuho Station, Antarctica

Abstract

This paper describes the results of snow drift measurements made on a strong katabatic wind slope at Mizuho Station (70°42.6’S, 44°18.9’E; 2230 m above mean sea level) in East Antarctica. From the vertical profile of the mass flux of blowing snow up to 28 m above the snow surface under conditions of snow fall, the snow fall densitities have been estimated as asymptotes of the profile (Fohn 1980). Snow fall densities as asymptotes were estimated between 8x10^-6 and 8xl0^-5 kg/m³. Assuming a fall velocity of blowing snow particles as 0.5 m/s, above values correspond to values of the vertical flux of snow fall between 2x10^-3 and 1.5xl0^-1 mm/h.

Introduction

A study was made of the mass flux of a snow storm under conditions of strong katabatic wind accompanying a snow fall, on the basis of observation made in 1980 at Mizuho Station (70°42.6’S, 44°18.9’E; 2230 above mean sea level) in East Antarctica. This station is located about 250 km from the coast of the Antarctic continent (Figure 1). Snow storms occurring on a katabatic wind slope play an important role in snow redistribution on the ice sheet. Here we define a snow storm as the combination of blowing snow, drifting snow, and snow fall.

Fig. 1. Location map of Mizuho Station.

It is also important to separate the amount of snow Fall and the flux rates of drifting snow during a snow storm. Measurements of snow drift flux were made at eight heights above the snow surface (between 0.3-28 m), and snow fall densities have been estimated as asymptotes of vertical profiles of drift flux during snow storms.

Some of the snow drift measurements conducted in this area have been published already by Inoue and Fujino (1977), Narita (1978) and Kobayashi (1978); however, they had been almost exclusively concerned’ with snow drift on levels less than 10 m. This paper also describes some characteristics of horizontal visibility, height of blowing snow and atmospheric structures under strong wind condition with snow fall. Data of snow drift flux, and profiles of wind and air temperature have already been reported by Kobayashi and others (1983).

ATMOSPHERIC SURFACE LAYER UNDER SNOW STORMS

An aluminum tower 30 m in height was erected at Mizuho Station to measure vertical profiles of air temperature and mean wind speed in the atmospheric surface boundary layer (Mae and others 1981). To obtain the profiles, seven anemometers of the three-cup type and seven platinum resistance thermometers with stainless steel shelters were mounted on the arms of the tower, at the heights of 29.5, 15.5, 7.5, 3.5, 1.5, 1 and 0.5 m. Using these data, we calculated the Richardson number (Ri) and stability index (S), which are defined as follows:

(1)

(2)

where g is the acceleration of gravity, ϴ is the mean absolute potential temperature of the profile, Aø/△Z the vertical gradient of potential temperature, and Aø/△Z the vertical gradient of horizontal wind speed.

Figure 2 shows a typical wind speed profile in stable stratification above snow surface. Liljequist (1957) and Maki (1974) presented an equation of wind speed profile which is applicable to various stratifications ranging from slightly stable to super stable:

(3)

where Ur is the mean wind speed at the reference height, (ie here 30 m), Ua is the adiabatic component of wind speed corresponding to the logarithmic law of wind speed profile for neutral stability, and U _l , is the linear component of wind speed proportional to the height above the surface as shown in Figure 2. Now, k is assumed as follows:

Fig. 2. Typical wind speed profile under snow storm.

(4)

and relations between k and S are plotted in Figure 3. Values of k obtained at Mizuho Station were rather larger than values at Syowa Station reported by Maki (1974). The discrepancy between Mizuho Station and Syowa Station is thought to be caused by snow storms. However, this could not be proven.

Visibility

In Mizuho Station, horizontal visibility was observed using a series of fuel drums set at the distance of 0.05, 0.1, 0.2, 0.3, 0.5, 0.8, 1, 1.5 and 2 km. As shown in Figure 4, horizontal visibility decreased with increasing wind speed. The height of dense blown snow was observed visually using a 30 m high meterological tower. The relation between the horizontal visibility and the height of dense blown snow is plotted in Figure 5: horizontal visibility decreased up to the value of 100 m, then the height of dense blown snow rapidly increased; often the tower disappeared from sight.

Fig. 3. Relation between k(= U _l /U₃₀) and the stability index (S).

Fig. 4. Relation between horizontal visibility and wind speed.

Fig. 5. Relation between horizontal visibility and height of dense blown snow.

Vertical Distribution Of Drift Density Up To 28 M Height

Five collectors with 2 cm diameter inlet were mounted on 8 m high poles at heights of 0.3, 0.7, 1.3, 2.05 and 3.25 m, three collectors with 5 cm diameter inlet on a 30 m high meterological tower at 6.5, 14, and 28 m. Collecting efficiency of these collectors was 0.297. Some examples of vertical profile of drift density obtained at Mizuho Station are plotted in Figure 6B.

Fig. 6. schematic profile of drift density shown by Equation 10, and B: measured drift density profiles under conditions of snow fall.

As mentioned in the introduction, one objective of this study was to separate the amount of snow fall from the drift density of snow storm. According to Föhn (1980), snow fall densities have been estimated as asymptotes of the profile of blowing snow as shown in Figure 6A. As a result, the density of snow fall was estimated value between 1 x 10^-6 and 8 x 10^-5 kg/m^-3. A theoretical consideration of a turbulent diffusion equation will be discussed in the following section.

Discussion

To illustrate the profile of drift density under condition of snow fall, we consider next a turbulent diffusion equation. The basic equation of diffusion for steady state in the vertical direction is given by

(5)

where n ¡s drift density at height z, w is the apparent fall velocity of the snow particles, and K is the apparent diffusivity (eg Okubo 1975). Integrating Equation 5, the following linearized differential equation is obtained:

(6)

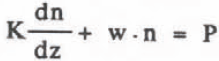
where P is the vertical flux of snow fall at the surface and defined as follows:

(7)

The general solution of equation 6 is

(8)

Let us now consider the following two conditions

First we assume, that K = KU*Z and P = o so that Equation 8 becomes

(9)

where n (Z₁),n (z₂) are drift densities at the heights z₁, z ₂ respectively, u* is friction velocity and K is the Von Karman constant. This equation was first published by Shiotani (1953), and has been used by many investigators; however, the equation cannot be used to discuss snow fall because P = 0.

Next, to discuss the contribution of snow fall, the following assumptions are made: K,w are constant and P ≠0, so that Equation 8 becomes

(10)

where n₀ is drift density at the surface. If w-n0>P>0, a profile of drift density under condition of snow fall is shown in Figure 6A. The asymptote of the profile in the z-direction approaches the snow fall density: , As indicated in the previous section, snow fall density has values between 1 x 10⁶ and 8 x 10^-5kg/m³. Here, if we assume that w is the fall velocity of snow particles, chosen according to Takahashi and others (1984) as 0.5 m/s, the value of snow fall density correspond to value of 0.002 and 0.14 mm/h.

Measurement of solid precipitation with any other kind of collector is a rather hopeless because of the effects of drifting snow and stormy winds. To compare the value obtained here with other, for example, mean precipitation obtained at Molodezhnaya Station had a maximum value of 0.24 mm/h in April between 1963 to 1965 (eg Schwerdtfeger 1970).