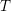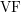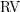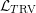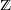1 Introduction
Towards the end of the introduction to [Reference Hrushovski and KazhdanHK06] three hopes for the future of the theory of motivic integration are mentioned. We propose to investigate one of them in a series of papers: additive invariants and integration in
![]() $o$
-minimal valued fields. A prototype of such valued fields is
$o$
-minimal valued fields. A prototype of such valued fields is
 $\unicode[STIX]{x211D}((t^{\unicode[STIX]{x211A}}))$
, the generalized power series field over
$\unicode[STIX]{x211D}((t^{\unicode[STIX]{x211A}}))$
, the generalized power series field over
![]() $\unicode[STIX]{x211D}$
with exponents in
$\unicode[STIX]{x211D}$
with exponents in
![]() $\unicode[STIX]{x211A}$
. One of the cornerstones of the methodology of [Reference Hrushovski and KazhdanHK06] is
$\unicode[STIX]{x211A}$
. One of the cornerstones of the methodology of [Reference Hrushovski and KazhdanHK06] is
![]() $C$
-minimality, which is the right analogue of
$C$
-minimality, which is the right analogue of
![]() $o$
-minimality for algebraically closed valued fields and other closely related structures that epitomizes the behavior of definable subsets of the affine line. It, of course, fails in an
$o$
-minimality for algebraically closed valued fields and other closely related structures that epitomizes the behavior of definable subsets of the affine line. It, of course, fails in an
![]() $o$
-minimal valued field, mainly due to the presence of a total ordering. Thus the construction we seek has to be carried out in a different framework, which affords a similar type of normal forms for definable subsets of the affine line, a special kind of weak
$o$
-minimal valued field, mainly due to the presence of a total ordering. Thus the construction we seek has to be carried out in a different framework, which affords a similar type of normal forms for definable subsets of the affine line, a special kind of weak
![]() $o$
-minimality; this framework is van den Dries and Lewenberg’s theory of
$o$
-minimality; this framework is van den Dries and Lewenberg’s theory of
![]() $T$
-convex valued fields [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97].
$T$
-convex valued fields [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97].
The reader is referred to the opening discussions in [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97] for a more detailed introduction to T-convexity and a summary of fundamental results. In those papers, how the valuation is expressed is somewhat inconsequential. In contrast, we shall work exclusively with a fixed two-sorted language
![]() ${\mathcal{L}}_{T\text{RV}}$
(see § 2.2 and Example 2.10 for a quick grasp of the central features of this language) since such a language is a part of the preliminary setup of any Hrushovski–Kazhdan style integration.
${\mathcal{L}}_{T\text{RV}}$
(see § 2.2 and Example 2.10 for a quick grasp of the central features of this language) since such a language is a part of the preliminary setup of any Hrushovski–Kazhdan style integration.
Throughout this paper, let
![]() $T$
be a complete power-bounded
$T$
be a complete power-bounded
![]() $o$
-minimal
$o$
-minimal
![]() ${\mathcal{L}}_{T\text{}}$
-theory extending the theory
${\mathcal{L}}_{T\text{}}$
-theory extending the theory
![]() $\text{RCF}_{\text{}}$
of real closed fields. For the real field
$\text{RCF}_{\text{}}$
of real closed fields. For the real field
![]() $\unicode[STIX]{x211D}$
, the condition of being power-bounded is the same as that of being polynomially bounded. However, for nonarchimedean real closed fields, the former condition is more general and is indeed more natural.
$\unicode[STIX]{x211D}$
, the condition of being power-bounded is the same as that of being polynomially bounded. However, for nonarchimedean real closed fields, the former condition is more general and is indeed more natural.
The language
![]() ${\mathcal{L}}_{T\text{}}$
extends the language
${\mathcal{L}}_{T\text{}}$
extends the language
 $\{{<},0,1,+,-,\times \}$
of ordered rings. Let
$\{{<},0,1,+,-,\times \}$
of ordered rings. Let
 ${\mathcal{R}}:=(R,<,\ldots )$
be a model of
${\mathcal{R}}:=(R,<,\ldots )$
be a model of
![]() $T$
. By definition, a T-convex subring
$T$
. By definition, a T-convex subring
![]() $\mathfrak{O}$
of
$\mathfrak{O}$
of
![]() ${\mathcal{R}}$
is a convex subring of
${\mathcal{R}}$
is a convex subring of
![]() ${\mathcal{R}}$
such that, for every definable (no parameters allowed) continuous function
${\mathcal{R}}$
such that, for every definable (no parameters allowed) continuous function
 $f:R\longrightarrow R$
, we have
$f:R\longrightarrow R$
, we have
 $f(\mathfrak{O})\subseteq \mathfrak{O}$
. The convexity of
$f(\mathfrak{O})\subseteq \mathfrak{O}$
. The convexity of
![]() $\mathfrak{O}$
implies that it is a valuation ring of
$\mathfrak{O}$
implies that it is a valuation ring of
![]() ${\mathcal{R}}$
. For instance, if
${\mathcal{R}}$
. For instance, if
![]() ${\mathcal{R}}$
is nonarchimedean and
${\mathcal{R}}$
is nonarchimedean and
![]() $\unicode[STIX]{x211D}\subseteq R$
then the convex hull of
$\unicode[STIX]{x211D}\subseteq R$
then the convex hull of
![]() $\unicode[STIX]{x211D}$
forms a valuation ring of
$\unicode[STIX]{x211D}$
forms a valuation ring of
![]() ${\mathcal{R}}$
and, accordingly, the infinitesimals form its maximal ideal. Such a convex hull is T-convex if no definable continuous function can grow so fast as to stretch the standard real numbers into infinity.
${\mathcal{R}}$
and, accordingly, the infinitesimals form its maximal ideal. Such a convex hull is T-convex if no definable continuous function can grow so fast as to stretch the standard real numbers into infinity.
Let
![]() $\mathfrak{O}$
be a proper
T-convex subring of
$\mathfrak{O}$
be a proper
T-convex subring of
![]() ${\mathcal{R}}$
. The theory
${\mathcal{R}}$
. The theory
![]() $T_{\text{convex}}$
of the pair
$T_{\text{convex}}$
of the pair
![]() $({\mathcal{R}},\mathfrak{O})$
, suitably axiomatized in the language
$({\mathcal{R}},\mathfrak{O})$
, suitably axiomatized in the language
![]() ${\mathcal{L}}_{\text{convex}}$
that expands
${\mathcal{L}}_{\text{convex}}$
that expands
![]() ${\mathcal{L}}_{T\text{}}$
with a new unary relation symbol, is complete, and if
${\mathcal{L}}_{T\text{}}$
with a new unary relation symbol, is complete, and if
![]() $T$
admits quantifier elimination and is universally axiomatizable then
$T$
admits quantifier elimination and is universally axiomatizable then
![]() $T_{\text{convex}}$
admits quantifier elimination as well.
$T_{\text{convex}}$
admits quantifier elimination as well.
Since
![]() $T$
is power-bounded, the definable subsets of
$T$
is power-bounded, the definable subsets of
![]() $R$
afford a type of normal form, a special kind of weak
$R$
afford a type of normal form, a special kind of weak
![]() $o$
-minimality (see [Reference Macpherson, Marker and SteinhornMMS00]), which we dub Holly normal form (since it was first studied by Holly in [Reference HollyHol95]); in a nutshell, every definable subset of
$o$
-minimality (see [Reference Macpherson, Marker and SteinhornMMS00]), which we dub Holly normal form (since it was first studied by Holly in [Reference HollyHol95]); in a nutshell, every definable subset of
![]() $R$
is a boolean combination of intervals and (valuative) discs. Clearly this is a natural generalization of
$R$
is a boolean combination of intervals and (valuative) discs. Clearly this is a natural generalization of
![]() $o$
-minimality in the presence of valuation. A number of desirable properties of definable sets in
$o$
-minimality in the presence of valuation. A number of desirable properties of definable sets in
![]() $R$
depend on the existence of such a normal form. For instance, every subset of
$R$
depend on the existence of such a normal form. For instance, every subset of
![]() $R$
defined by a principal type assumes one of the following four forms: a point, an open disc, a closed disc, and a half thin annulus, and, furthermore, these four forms are distinct in the sense that no definable bijection between any two of them is possible.
$R$
defined by a principal type assumes one of the following four forms: a point, an open disc, a closed disc, and a half thin annulus, and, furthermore, these four forms are distinct in the sense that no definable bijection between any two of them is possible.
Let
 $\operatorname{val}:R^{\times }\longrightarrow \unicode[STIX]{x1D6E4}$
be the valuation map induced by
$\operatorname{val}:R^{\times }\longrightarrow \unicode[STIX]{x1D6E4}$
be the valuation map induced by
![]() $\mathfrak{O}$
,
$\mathfrak{O}$
,
![]() $\Bbbk$
the corresponding residue field, and
$\Bbbk$
the corresponding residue field, and
 $\operatorname{res}:\mathfrak{O}\longrightarrow \Bbbk$
the residue map. There is a canonical way of turning
$\operatorname{res}:\mathfrak{O}\longrightarrow \Bbbk$
the residue map. There is a canonical way of turning
![]() $\Bbbk$
into a model of
$\Bbbk$
into a model of
![]() $T$
as well (see [Reference van den Dries and LewenbergVdDL95, Remark 2.16]). Let
$T$
as well (see [Reference van den Dries and LewenbergVdDL95, Remark 2.16]). Let
![]() $\mathfrak{M}$
be the maximal ideal of
$\mathfrak{M}$
be the maximal ideal of
![]() $\mathfrak{O}$
. Let
$\mathfrak{O}$
. Let
 $\text{RV}=R^{\times }/(1+\mathfrak{M})$
and
$\text{RV}=R^{\times }/(1+\mathfrak{M})$
and
 $\operatorname{rv}:R^{\times }\longrightarrow \text{RV}$
be the quotient map. Note that, for each
$\operatorname{rv}:R^{\times }\longrightarrow \text{RV}$
be the quotient map. Note that, for each
![]() $a\in R$
, the map
$a\in R$
, the map
![]() $\operatorname{val}$
is constant on the set
$\operatorname{val}$
is constant on the set
 $a+a\mathfrak{M}$
, and hence there is an induced map
$a+a\mathfrak{M}$
, and hence there is an induced map
 $\operatorname{vrv}:\text{RV}\longrightarrow \unicode[STIX]{x1D6E4}$
. The situation is illustrated in the following commutative diagram.
$\operatorname{vrv}:\text{RV}\longrightarrow \unicode[STIX]{x1D6E4}$
. The situation is illustrated in the following commutative diagram.

where the bottom sequence is exact. This structure may be expressed and axiomatized in a natural two-sorted first-order language
![]() ${\mathcal{L}}_{T\text{RV}}$
, in which
${\mathcal{L}}_{T\text{RV}}$
, in which
![]() $R$
is referred to as the
$R$
is referred to as the
![]() $\text{VF}$
-sort and
$\text{VF}$
-sort and
![]() $\text{RV}$
is taken as a new sort. Informally,
$\text{RV}$
is taken as a new sort. Informally,
![]() ${\mathcal{L}}_{T\text{RV}}$
is viewed as an extension of
${\mathcal{L}}_{T\text{RV}}$
is viewed as an extension of
![]() ${\mathcal{L}}_{\text{convex}}$
.
${\mathcal{L}}_{\text{convex}}$
.
We expand
![]() $({\mathcal{R}},\mathfrak{O})$
to an
$({\mathcal{R}},\mathfrak{O})$
to an
![]() ${\mathcal{L}}_{T\text{RV}}$
-structure. The main construction in this paper is carried out in such a setting. For concreteness, the reader is welcome to take
${\mathcal{L}}_{T\text{RV}}$
-structure. The main construction in this paper is carried out in such a setting. For concreteness, the reader is welcome to take
 $R=\unicode[STIX]{x211D}((t^{\unicode[STIX]{x211A}}))$
and
$R=\unicode[STIX]{x211D}((t^{\unicode[STIX]{x211A}}))$
and
 $\mathfrak{O}=\unicode[STIX]{x211D}\unicode[STIX]{x27E6}t^{\unicode[STIX]{x211A}}\unicode[STIX]{x27E7}$
in the remainder of this introduction (see Example 2.10 below for more on this generalized power series field).
$\mathfrak{O}=\unicode[STIX]{x211D}\unicode[STIX]{x27E6}t^{\unicode[STIX]{x211A}}\unicode[STIX]{x27E7}$
in the remainder of this introduction (see Example 2.10 below for more on this generalized power series field).
For a description of the ideas and the main results of the Hrushovski–Kazhdan style integration theory, we refer the reader to the original introduction in [Reference Hrushovski and KazhdanHK06] and also the introductions in [Reference YinYin11, Reference YinYin13b]. There is also a quite comprehensive introduction to the same material in [Reference Hrushovski and LoeserHL15] and, more importantly, a specialized version that relates the Hrushovski–Kazhdan style integration to the geometry and topology of Milnor fibers over the complex field. The method expounded there will be featured in a sequel to this paper as well. In fact, since much of the work below is closely modeled on that in [Reference Hrushovski and KazhdanHK06, Reference YinYin10, Reference YinYin11, Reference Hrushovski and LoeserHL15], the reader may simply substitute the term ‘theory of power-bounded
![]() $T$
-convex valued fields’ for ‘theory of algebraically closed valued fields’ or more generally ‘
$T$
-convex valued fields’ for ‘theory of algebraically closed valued fields’ or more generally ‘
![]() $V$
-minimal theories’ in those introductions and thereby acquire quite a good grip on what the results of this paper look like. For the reader’s convenience, however, we shall repeat some of the key points, perhaps with minor changes here and there.
$V$
-minimal theories’ in those introductions and thereby acquire quite a good grip on what the results of this paper look like. For the reader’s convenience, however, we shall repeat some of the key points, perhaps with minor changes here and there.
Let
![]() $\text{VF}_{\ast }$
and
$\text{VF}_{\ast }$
and
![]() $\text{RV}[\ast ]$
be two categories of definable sets that are respectively associated with the
$\text{RV}[\ast ]$
be two categories of definable sets that are respectively associated with the
![]() $\text{VF}$
-sort and the
$\text{VF}$
-sort and the
![]() $\text{RV}$
-sort as follows. In
$\text{RV}$
-sort as follows. In
![]() $\text{VF}_{\ast }$
, the objects are the definable subsets of cartesian products of the form
$\text{VF}_{\ast }$
, the objects are the definable subsets of cartesian products of the form
 $\text{VF}^{n}\times \text{RV}^{m}$
and the morphisms are the definable bijections. On the other hand, for technical reasons (particularly for keeping track of ambient dimensions),
$\text{VF}^{n}\times \text{RV}^{m}$
and the morphisms are the definable bijections. On the other hand, for technical reasons (particularly for keeping track of ambient dimensions),
![]() $\text{RV}[\ast ]$
is formulated in a somewhat complicated way and is hence equipped with a gradation by ambient dimensions (see Definition 4.4).
$\text{RV}[\ast ]$
is formulated in a somewhat complicated way and is hence equipped with a gradation by ambient dimensions (see Definition 4.4).
The Grothendieck semigroup of a category
![]() ${\mathcal{C}}$
, denoted by
${\mathcal{C}}$
, denoted by
![]() $\mathbf{K}_{+}{\mathcal{C}}$
, is the free semigroup generated by the isomorphism classes of
$\mathbf{K}_{+}{\mathcal{C}}$
, is the free semigroup generated by the isomorphism classes of
![]() ${\mathcal{C}}$
, subject to the usual scissor relation
${\mathcal{C}}$
, subject to the usual scissor relation
 $[A\smallsetminus B]+[B]=[A]$
, where
$[A\smallsetminus B]+[B]=[A]$
, where
![]() $[A]$
,
$[A]$
,
![]() $[B]$
denote the isomorphism classes of the objects
$[B]$
denote the isomorphism classes of the objects
![]() $A$
,
$A$
,
![]() $B$
and ‘
$B$
and ‘
![]() $\smallsetminus$
’ is a certain binary operation, usually just set subtraction. Sometimes
$\smallsetminus$
’ is a certain binary operation, usually just set subtraction. Sometimes
![]() ${\mathcal{C}}$
is also equipped with a binary operation (for example, cartesian product) that induces multiplication in
${\mathcal{C}}$
is also equipped with a binary operation (for example, cartesian product) that induces multiplication in
![]() $\mathbf{K}_{+}{\mathcal{C}}$
, in which case
$\mathbf{K}_{+}{\mathcal{C}}$
, in which case
![]() $\mathbf{K}_{+}{\mathcal{C}}$
becomes a (commutative) semiring. The formal groupification of
$\mathbf{K}_{+}{\mathcal{C}}$
becomes a (commutative) semiring. The formal groupification of
![]() $\mathbf{K}_{+}{\mathcal{C}}$
, which is then a ring, is denoted by
$\mathbf{K}_{+}{\mathcal{C}}$
, which is then a ring, is denoted by
![]() $\mathbf{K}\,{\mathcal{C}}$
.
$\mathbf{K}\,{\mathcal{C}}$
.
The main construction of the Hrushovski–Kazhdan integration theory is a canonical (that is, functorial in a suitable way) homomorphism from the Grothendieck semiring
 $\mathbf{K}_{+}\text{VF}_{\ast }$
of
$\mathbf{K}_{+}\text{VF}_{\ast }$
of
![]() $\text{VF}_{\ast }$
to the Grothendieck semiring
$\text{VF}_{\ast }$
to the Grothendieck semiring
 $\mathbf{K}_{+}\text{RV}[\ast ]$
of
$\mathbf{K}_{+}\text{RV}[\ast ]$
of
![]() $\text{RV}[\ast ]$
modulo a semiring congruence relation
$\text{RV}[\ast ]$
modulo a semiring congruence relation
![]() $\operatorname{I}_{\text{sp}}$
on the latter. In fact, it turns out to be an isomorphism. This construction has three main steps.
$\operatorname{I}_{\text{sp}}$
on the latter. In fact, it turns out to be an isomorphism. This construction has three main steps.
Step 1. We define a lifting map
![]() $\mathbb{L}$
from the set of objects of
$\mathbb{L}$
from the set of objects of
![]() $\text{RV}[\ast ]$
into the set of objects of
$\text{RV}[\ast ]$
into the set of objects of
![]() $\text{VF}_{\ast }$
(Definition 5.7). Next we single out a subclass of isomorphisms in
$\text{VF}_{\ast }$
(Definition 5.7). Next we single out a subclass of isomorphisms in
![]() $\text{VF}_{\ast }$
, which are called special bijections (Definition 5.2), and show that for any object
$\text{VF}_{\ast }$
, which are called special bijections (Definition 5.2), and show that for any object
![]() $A$
in
$A$
in
![]() $\text{VF}_{\ast }$
there is a special bijection
$\text{VF}_{\ast }$
there is a special bijection
![]() $T$
on
$T$
on
![]() $A$
and an object
$A$
and an object
![]() $\boldsymbol{U}$
in
$\boldsymbol{U}$
in
![]() $\text{RV}[\ast ]$
such that
$\text{RV}[\ast ]$
such that
![]() $T(A)$
is isomorphic to
$T(A)$
is isomorphic to
![]() $\mathbb{L}\boldsymbol{U}$
(Corollary 5.8). This implies that
$\mathbb{L}\boldsymbol{U}$
(Corollary 5.8). This implies that
![]() $\mathbb{L}$
is ‘essentially surjective’ on objects, meaning that it is surjective on isomorphism classes of
$\mathbb{L}$
is ‘essentially surjective’ on objects, meaning that it is surjective on isomorphism classes of
![]() $\text{VF}_{\ast }$
. For this result alone we do not have to limit our means to special bijections. However, in Step 3 below, special bijections become an essential ingredient in computing the semiring congruence relation
$\text{VF}_{\ast }$
. For this result alone we do not have to limit our means to special bijections. However, in Step 3 below, special bijections become an essential ingredient in computing the semiring congruence relation
![]() $\operatorname{I}_{\text{sp}}$
.
$\operatorname{I}_{\text{sp}}$
.
Step 2. We show that, for any two isomorphic objects
![]() $\boldsymbol{U}_{1}$
,
$\boldsymbol{U}_{1}$
,
![]() $\boldsymbol{U}_{2}$
of
$\boldsymbol{U}_{2}$
of
![]() $\text{RV}[\ast ]$
, their lifts
$\text{RV}[\ast ]$
, their lifts
 $\mathbb{L}\boldsymbol{U}_{1},\mathbb{L}\boldsymbol{U}_{2}$
in
$\mathbb{L}\boldsymbol{U}_{1},\mathbb{L}\boldsymbol{U}_{2}$
in
![]() $\text{VF}_{\ast }$
are isomorphic as well (Corollary 5.13). This implies that
$\text{VF}_{\ast }$
are isomorphic as well (Corollary 5.13). This implies that
![]() $\mathbb{L}$
induces a semiring homomorphism
$\mathbb{L}$
induces a semiring homomorphism
 $\mathbf{K}_{+}\text{RV}[\ast ]\longrightarrow \mathbf{K}_{+}\text{VF}_{\ast }$
, which is also denoted by
$\mathbf{K}_{+}\text{RV}[\ast ]\longrightarrow \mathbf{K}_{+}\text{VF}_{\ast }$
, which is also denoted by
![]() $\mathbb{L}$
. This homomorphism is surjective by Step 1 and hence, modulo the semiring congruence relation
$\mathbb{L}$
. This homomorphism is surjective by Step 1 and hence, modulo the semiring congruence relation
![]() $\operatorname{I}_{\text{sp}}$
(that is, the kernel of
$\operatorname{I}_{\text{sp}}$
(that is, the kernel of
![]() $\mathbb{L}$
), the inversion
$\mathbb{L}$
), the inversion
![]() $\int _{+}$
of the homomorphism
$\int _{+}$
of the homomorphism
![]() $\mathbb{L}$
is an isomorphism of semirings.
$\mathbb{L}$
is an isomorphism of semirings.
Step 3. A number of important properties of the classical integration can already be verified for
![]() $\int _{+}$
and hence, morally, this third step is not necessary. For applications, however, it is much more satisfying to have a precise description of the semiring congruence relation
$\int _{+}$
and hence, morally, this third step is not necessary. For applications, however, it is much more satisfying to have a precise description of the semiring congruence relation
![]() $\operatorname{I}_{\text{sp}}$
. The basic notion used in the description is that of a blowup of an object in
$\operatorname{I}_{\text{sp}}$
. The basic notion used in the description is that of a blowup of an object in
![]() $\text{RV}[\ast ]$
, which is essentially a restatement of the trivial fact that there is an additive translation from
$\text{RV}[\ast ]$
, which is essentially a restatement of the trivial fact that there is an additive translation from
![]() $1+\mathfrak{M}$
onto
$1+\mathfrak{M}$
onto
![]() $\mathfrak{M}$
(Definition 5.27). We then show that, for any two objects
$\mathfrak{M}$
(Definition 5.27). We then show that, for any two objects
![]() $\boldsymbol{U}_{1}$
,
$\boldsymbol{U}_{1}$
,
![]() $\boldsymbol{U}_{2}$
in
$\boldsymbol{U}_{2}$
in
![]() $\text{RV}[\ast ]$
, there are isomorphic blowups
$\text{RV}[\ast ]$
, there are isomorphic blowups
![]() $\boldsymbol{U}_{1}^{\flat }$
,
$\boldsymbol{U}_{1}^{\flat }$
,
![]() $\boldsymbol{U}_{2}^{\flat }$
of them if and only if
$\boldsymbol{U}_{2}^{\flat }$
of them if and only if
![]() $\mathbb{L}\boldsymbol{U}_{1}$
,
$\mathbb{L}\boldsymbol{U}_{1}$
,
![]() $\mathbb{L}\boldsymbol{U}_{2}$
are isomorphic (Proposition 5.39). The ‘if’ direction essentially contains a form of Fubini’s theorem and is the most technically involved part of the construction.
$\mathbb{L}\boldsymbol{U}_{2}$
are isomorphic (Proposition 5.39). The ‘if’ direction essentially contains a form of Fubini’s theorem and is the most technically involved part of the construction.
We call the semiring homomorphism
![]() $\int _{+}$
thus obtained a Grothendieck homomorphism. If the objects carry volume forms and the Jacobian transformation preserves the integral, that is, the change of variables formula holds, then it may be called a motivic integration; we will not consider this case here and postpone it to a future installment. When the semirings are formally groupified, this Grothendieck homomorphism is accordingly recast as a ring homomorphism, which is denoted by
$\int _{+}$
thus obtained a Grothendieck homomorphism. If the objects carry volume forms and the Jacobian transformation preserves the integral, that is, the change of variables formula holds, then it may be called a motivic integration; we will not consider this case here and postpone it to a future installment. When the semirings are formally groupified, this Grothendieck homomorphism is accordingly recast as a ring homomorphism, which is denoted by
![]() $\int$
and is understood as a (universal) additive invariant.
$\int$
and is understood as a (universal) additive invariant.
The structure of the Grothendieck ring
 $\mathbf{K}\,\text{RV}[\ast ]$
may be significantly elucidated. To wit, it can be expressed as a tensor product of two other Grothendieck rings
$\mathbf{K}\,\text{RV}[\ast ]$
may be significantly elucidated. To wit, it can be expressed as a tensor product of two other Grothendieck rings
 $\mathbf{K}\,\operatorname{RES}[\ast ]$
and
$\mathbf{K}\,\operatorname{RES}[\ast ]$
and
![]() $\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
, that is, there is an isomorphism of graded rings,
$\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
, that is, there is an isomorphism of graded rings,
 $$\begin{eqnarray}\mathbb{D}:\mathbf{K}\,\operatorname{RES}[\ast ]\otimes _{\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]}\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}\,\text{RV}[\ast ],\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{D}:\mathbf{K}\,\operatorname{RES}[\ast ]\otimes _{\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]}\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}\,\text{RV}[\ast ],\end{eqnarray}$$
where
![]() $\operatorname{RES}[\ast ]$
is essentially the category of definable sets in
$\operatorname{RES}[\ast ]$
is essentially the category of definable sets in
![]() $\unicode[STIX]{x211D}$
(as a model of the theory
$\unicode[STIX]{x211D}$
(as a model of the theory
![]() $T$
) and
$T$
) and
![]() $\unicode[STIX]{x1D6E4}[\ast ]$
is essentially the category of definable sets over
$\unicode[STIX]{x1D6E4}[\ast ]$
is essentially the category of definable sets over
![]() $\unicode[STIX]{x211A}$
(as an
$\unicode[STIX]{x211A}$
(as an
![]() $o$
-minimal group), both are graded by ambient dimension, and
$o$
-minimal group), both are graded by ambient dimension, and
![]() $\unicode[STIX]{x1D6E4}^{c}[\ast ]$
is the full subcategory of
$\unicode[STIX]{x1D6E4}^{c}[\ast ]$
is the full subcategory of
![]() $\unicode[STIX]{x1D6E4}[\ast ]$
of finite objects, whose Grothendieck ring admits a natural embedding into
$\unicode[STIX]{x1D6E4}[\ast ]$
of finite objects, whose Grothendieck ring admits a natural embedding into
 $\mathbf{K}\,\operatorname{RES}[\ast ]$
as well. This isomorphism results in various retractions from
$\mathbf{K}\,\operatorname{RES}[\ast ]$
as well. This isomorphism results in various retractions from
 $\mathbf{K}\,\text{RV}[\ast ]$
into
$\mathbf{K}\,\text{RV}[\ast ]$
into
 $\mathbf{K}\,\operatorname{RES}[\ast ]$
or
$\mathbf{K}\,\operatorname{RES}[\ast ]$
or
![]() $\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
and, when combined with the Grothendieck homomorphism
$\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
and, when combined with the Grothendieck homomorphism
![]() $\int$
and the two Euler characteristics in
$\int$
and the two Euler characteristics in
![]() $o$
-minimal groups (one is a truncated version of the other), yield a (generalized) Euler characteristic
$o$
-minimal groups (one is a truncated version of the other), yield a (generalized) Euler characteristic

which is actually an isomorphism, and two specializations to
![]() $\unicode[STIX]{x2124}$
,
$\unicode[STIX]{x2124}$
,

determined by the assignments
 $Y\longmapsto -1$
and
$Y\longmapsto -1$
and
 $Y\longmapsto 0$
or, equivalently,
$Y\longmapsto 0$
or, equivalently,
 $X\longmapsto 1$
and
$X\longmapsto 1$
and
 $X\longmapsto -1$
(see Proposition 4.24 and Theorem 5.41). We will demonstrate the significance of these two specializations, as opposed to only one, in a future paper that is dedicated to the study of generalized (real) Milnor fibers in the sense of [Reference Hrushovski and LoeserHL15].
$X\longmapsto -1$
(see Proposition 4.24 and Theorem 5.41). We will demonstrate the significance of these two specializations, as opposed to only one, in a future paper that is dedicated to the study of generalized (real) Milnor fibers in the sense of [Reference Hrushovski and LoeserHL15].
For certain purposes, the difference between model theory and algebraic geometry is somewhat easier to bridge if one works over the complex field, as is demonstrated in [Reference Hrushovski and LoeserHL15]; however, over the real field, although they do overlap significantly, the two worlds seem to diverge in their methods and ideas. Our results should be understood in the context of ‘
![]() $o$
-minimal geometry’ [Reference van den DriesVdD98, Reference van den Dries and MillerVdDM96] as opposed to real algebraic geometry. In general, the various Grothendieck rings considered in real algebraic geometry bring about lesser collapse of ‘algebraic data’ (since there are rather fewer morphisms in the background) and can yield much finer invariants, and hence are more faithful to the geometry in this regard, although the flip side of the story is that the invariants are often computationally intractable (especially when resolution of singularities is involved) and specializations are often needed in practice. For instance, the Grothendieck ring of real algebraic varieties may be specialized to
$o$
-minimal geometry’ [Reference van den DriesVdD98, Reference van den Dries and MillerVdDM96] as opposed to real algebraic geometry. In general, the various Grothendieck rings considered in real algebraic geometry bring about lesser collapse of ‘algebraic data’ (since there are rather fewer morphisms in the background) and can yield much finer invariants, and hence are more faithful to the geometry in this regard, although the flip side of the story is that the invariants are often computationally intractable (especially when resolution of singularities is involved) and specializations are often needed in practice. For instance, the Grothendieck ring of real algebraic varieties may be specialized to
![]() $\unicode[STIX]{x2124}[X]$
, which is called the virtual Poincaré polynomial (see [Reference McCrory and ParusińskiMP03]). Our method here does not seem to be suited for recovering invariants at this level, at least not directly.
$\unicode[STIX]{x2124}[X]$
, which is called the virtual Poincaré polynomial (see [Reference McCrory and ParusińskiMP03]). Our method here does not seem to be suited for recovering invariants at this level, at least not directly.
The role of
![]() $T$
-convexity in this paper cannot be overemphasized. However, it does not quite work if the exponential function is included in the theory
$T$
-convexity in this paper cannot be overemphasized. However, it does not quite work if the exponential function is included in the theory
![]() $T$
. It remains a worthy challenge to find a suitable framework in which the construction of this paper may be extended to that case.
$T$
. It remains a worthy challenge to find a suitable framework in which the construction of this paper may be extended to that case.
Much of the content of this paper is extracted from the preprint [Reference YinYin13a], which contains a more comprehensive study of T-convex valued fields. This auxiliary part of the theory we are developing may be regarded as a sequel to or a variation on the themes of the work in [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97]. It has become clear that some of the technicalities thereof may be of independent interest. For instance, the valuative or infinitesimal version of Lipschitz continuity plays a crucial role in proving the existence of Lipschitz stratifications in an arbitrary power-bounded
![]() $o$
-minimal field (this proof has been published in [Reference Halupczok and YinHY15] and the result cited there is Corollary 3.16).
$o$
-minimal field (this proof has been published in [Reference Halupczok and YinHY15] and the result cited there is Corollary 3.16).
Also, in a future paper, we will use the main result here to show that, in both the real and the complex cases, the Euler characteristic of the topological Milnor fiber coincides with that of the motivic Milnor fiber, avoiding the algebro-geometric machinery employed in [Reference Hrushovski and LoeserHL15, Remark 8.5.5].
2 Basic results in
 $T$
-convex valued fields
$T$
-convex valued fields
In this section, we first describe the two-sorted language
![]() ${\mathcal{L}}_{T\text{RV}}$
for
${\mathcal{L}}_{T\text{RV}}$
for
![]() $o$
-minimal valued fields and the
$o$
-minimal valued fields and the
![]() ${\mathcal{L}}_{T\text{RV}}$
-theory
${\mathcal{L}}_{T\text{RV}}$
-theory
![]() $\text{TCVF}$
. This theory is axiomatized. Then we show that
$\text{TCVF}$
. This theory is axiomatized. Then we show that
![]() $\text{TCVF}$
admits quantifier elimination. Some of the results in [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97] that are crucial for our construction are also translated into the present setting.
$\text{TCVF}$
admits quantifier elimination. Some of the results in [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97] that are crucial for our construction are also translated into the present setting.
2.1 Some notation
Recall from the introduction above that
![]() $T$
is a complete power-bounded
$T$
is a complete power-bounded
![]() $o$
-minimal
$o$
-minimal
![]() ${\mathcal{L}}_{T\text{}}$
-theory extending the theory
${\mathcal{L}}_{T\text{}}$
-theory extending the theory
![]() $\text{RCF}_{\text{}}$
of real closed fields.
$\text{RCF}_{\text{}}$
of real closed fields.
Convention 2.1. For the moment, by definable we mean definable with arbitrary parameters from the structure in question. But later (starting in § 3) we will abandon this practice and work with a fixed set of parameters. The reason for this change will be made abundantly clear when it happens.
Definition 2.2 (Power-bounded).
Suppose that
![]() ${\mathcal{R}}$
is an
${\mathcal{R}}$
is an
![]() $o$
-minimal real closed field. A power function in
$o$
-minimal real closed field. A power function in
![]() ${\mathcal{R}}$
is a definable endomorphism of the multiplicative group
${\mathcal{R}}$
is a definable endomorphism of the multiplicative group
![]() ${\mathcal{R}}^{+}$
. We say that
${\mathcal{R}}^{+}$
. We say that
![]() ${\mathcal{R}}$
is power-bounded if every definable function
${\mathcal{R}}$
is power-bounded if every definable function
 $f:{\mathcal{R}}\longrightarrow {\mathcal{R}}$
is eventually dominated by a power function, that is, there exists a power function
$f:{\mathcal{R}}\longrightarrow {\mathcal{R}}$
is eventually dominated by a power function, that is, there exists a power function
![]() $g$
such that
$g$
such that
 $|f(x)|\leqslant g(x)$
for all sufficiently large
$|f(x)|\leqslant g(x)$
for all sufficiently large
![]() $x$
. A complete
$x$
. A complete
![]() $o$
-minimal theory extending
$o$
-minimal theory extending
![]() $\text{RCF}_{\text{}}$
is power-bounded if all its models are.
$\text{RCF}_{\text{}}$
is power-bounded if all its models are.
All power functions in
![]() ${\mathcal{R}}$
may be understood as functions of the form
${\mathcal{R}}$
may be understood as functions of the form
 $x\longmapsto x^{\unicode[STIX]{x1D706}}$
, where
$x\longmapsto x^{\unicode[STIX]{x1D706}}$
, where
 $\unicode[STIX]{x1D706}=(d/dx)f(1)$
. The collection of all such
$\unicode[STIX]{x1D706}=(d/dx)f(1)$
. The collection of all such
![]() $\unicode[STIX]{x1D706}$
form a subfield called the field of exponents of
$\unicode[STIX]{x1D706}$
form a subfield called the field of exponents of
![]() ${\mathcal{R}}$
. We will quote the results on power-bounded structures directly from [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97] and hence do not need to know more about them other than things that have already been said. At any rate, a concise and lucid account of the essentials may be found in [Reference van den DriesVdD97, § 3].
${\mathcal{R}}$
. We will quote the results on power-bounded structures directly from [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97] and hence do not need to know more about them other than things that have already been said. At any rate, a concise and lucid account of the essentials may be found in [Reference van den DriesVdD97, § 3].
Remark 2.3 (Functional language).
We shall need a generality that is due to Lou van den Dries (private communication). It states that the theory
![]() $T$
can be reformulated in another language all of whose primitives, except the binary relation
$T$
can be reformulated in another language all of whose primitives, except the binary relation
![]() ${\leqslant}$
, are function symbols that are interpreted as continuous functions in all the models of
${\leqslant}$
, are function symbols that are interpreted as continuous functions in all the models of
![]() $T$
. Actually, for this to hold, we only need to assume that
$T$
. Actually, for this to hold, we only need to assume that
![]() $T$
is a complete
$T$
is a complete
![]() $o$
-minimal theory that extends
$o$
-minimal theory that extends
![]() $\text{RCF}_{\text{}}$
.
$\text{RCF}_{\text{}}$
.
More precisely, working in any model of
![]() $T$
, it can be shown that all definable sets are boolean combinations of sets of the form
$T$
, it can be shown that all definable sets are boolean combinations of sets of the form
 $f(x)=0$
or
$f(x)=0$
or
 $g(x)>0$
, where
$g(x)>0$
, where
![]() $f$
and
$f$
and
![]() $g$
are definable total continuous functions. In particular, this holds in the prime model
$g$
are definable total continuous functions. In particular, this holds in the prime model
![]() ${\mathcal{P}}$
of
${\mathcal{P}}$
of
![]() $T$
. Taking all definable total continuous functions in
$T$
. Taking all definable total continuous functions in
![]() ${\mathcal{P}}$
and the ordering
${\mathcal{P}}$
and the ordering
![]() ${<}$
as the primitives in a new language
${<}$
as the primitives in a new language
![]() ${\mathcal{L}}_{T^{\prime }\text{}}$
, we see that
${\mathcal{L}}_{T^{\prime }\text{}}$
, we see that
![]() $T$
can be reformulated as an equivalent
$T$
can be reformulated as an equivalent
![]() ${\mathcal{L}}_{T^{\prime }\text{}}$
-theory
${\mathcal{L}}_{T^{\prime }\text{}}$
-theory
![]() $T^{\prime }$
in the sense that the syntactic categories of
$T^{\prime }$
in the sense that the syntactic categories of
![]() $T$
and
$T$
and
![]() $T^{\prime }$
are naturally equivalent. In traditional but less general and more verbose model-theoretic jargon, this just says that if a model of
$T^{\prime }$
are naturally equivalent. In traditional but less general and more verbose model-theoretic jargon, this just says that if a model of
![]() $T$
is converted to a model of
$T$
is converted to a model of
![]() $T^{\prime }$
in the obvious way then the two models are bi-interpretable via the identity map, and vice versa.
$T^{\prime }$
in the obvious way then the two models are bi-interpretable via the identity map, and vice versa.
The theory
![]() $T^{\prime }$
also admits quantifier elimination, but it cannot be universally axiomatizable in
$T^{\prime }$
also admits quantifier elimination, but it cannot be universally axiomatizable in
![]() ${\mathcal{L}}_{T^{\prime }\text{}}$
. To see this, suppose for contradiction that it can be. Then, by the argument in the proof of [Reference van den Dries, Macintyre and MarkerVdDMM94, Corollary 2.15], every definable function
${\mathcal{L}}_{T^{\prime }\text{}}$
. To see this, suppose for contradiction that it can be. Then, by the argument in the proof of [Reference van den Dries, Macintyre and MarkerVdDMM94, Corollary 2.15], every definable function
![]() $f$
in a model of
$f$
in a model of
![]() $T^{\prime }$
, in particular, the multiplicative inverse, is given piecewise by terms. But all terms define total continuous functions. This means that, by
$T^{\prime }$
, in particular, the multiplicative inverse, is given piecewise by terms. But all terms define total continuous functions. This means that, by
![]() $o$
-minimality, multiplicative inverse near
$o$
-minimality, multiplicative inverse near
![]() $0$
is given by two total continuous functions, which is absurd.
$0$
is given by two total continuous functions, which is absurd.
Now, we may and do extend
![]() $T^{\prime }$
by definitions so that it is universally axiomatizable in the resulting language. Thus every substructure of a model of
$T^{\prime }$
by definitions so that it is universally axiomatizable in the resulting language. Thus every substructure of a model of
![]() $T^{\prime }$
is actually a model of
$T^{\prime }$
is actually a model of
![]() $T^{\prime }$
and, as such, is an elementary substructure. In fact, since
$T^{\prime }$
and, as such, is an elementary substructure. In fact, since
![]() $T^{\prime }$
has definable Skolem functions, we shall abuse notation slightly and redefine
$T^{\prime }$
has definable Skolem functions, we shall abuse notation slightly and redefine
![]() $T$
to be
$T$
to be
![]() $T^{\prime \text{df}}$
, where
$T^{\prime \text{df}}$
, where
![]() $T^{\prime \text{df}}$
is in effect a Skolemization of
$T^{\prime \text{df}}$
is in effect a Skolemization of
![]() $T^{\prime }$
(see [Reference van den Dries and LewenbergVdDL95, §§ 2.3–2.4] for further explanation). Note that the language of
$T^{\prime }$
(see [Reference van den Dries and LewenbergVdDL95, §§ 2.3–2.4] for further explanation). Note that the language of
![]() $T$
contains additional function symbols only and some of them must be interpreted in all models of
$T$
contains additional function symbols only and some of them must be interpreted in all models of
![]() $T$
as discontinuous functions for the reason given above.
$T$
as discontinuous functions for the reason given above.
To summarize, the main point is that
![]() $T$
admits quantifier elimination, is universally axiomatizable, is a definitional extension of
$T$
admits quantifier elimination, is universally axiomatizable, is a definitional extension of
![]() $T^{\prime }$
, and all the primitives of
$T^{\prime }$
, and all the primitives of
![]() ${\mathcal{L}}_{T^{\prime }\text{}}$
, except
${\mathcal{L}}_{T^{\prime }\text{}}$
, except
![]() ${\leqslant}$
, define continuous functions in all the models of
${\leqslant}$
, define continuous functions in all the models of
![]() $T^{\prime }$
.
$T^{\prime }$
.
The syntactical maneuver of passing through
![]() $T^{\prime }$
just described will only be used in Theorem 2.14 below, and it is not really necessary if one works with a concrete
$T^{\prime }$
just described will only be used in Theorem 2.14 below, and it is not really necessary if one works with a concrete
![]() $o$
-minimal extension of
$o$
-minimal extension of
![]() $\text{RCF}_{\text{}}$
such as
$\text{RCF}_{\text{}}$
such as
![]() $T_{\text{an}}$
defined in [Reference van den Dries, Macintyre and MarkerVdDMM94] (see also Example 2.10).
$T_{\text{an}}$
defined in [Reference van den Dries, Macintyre and MarkerVdDMM94] (see also Example 2.10).
We shall work with a sufficiently saturated model
 ${\mathcal{R}}:=(R,<,\ldots )$
of
${\mathcal{R}}:=(R,<,\ldots )$
of
![]() $T$
unless suggested otherwise. Its field of exponents is denoted by
$T$
unless suggested otherwise. Its field of exponents is denoted by
![]() $\unicode[STIX]{x1D542}$
.
$\unicode[STIX]{x1D542}$
.
Notation 2.4 (Coordinate projections).
For each
![]() $n\in \unicode[STIX]{x2115}$
, let
$n\in \unicode[STIX]{x2115}$
, let
![]() $[n]$
abbreviate the set
$[n]$
abbreviate the set
 $\{1,\ldots ,n\}$
. For any
$\{1,\ldots ,n\}$
. For any
![]() $E\subseteq [n]$
, we write
$E\subseteq [n]$
, we write
![]() $\operatorname{pr}_{E}(A)$
for the projection of
$\operatorname{pr}_{E}(A)$
for the projection of
![]() $A$
into the coordinates contained in
$A$
into the coordinates contained in
![]() $E$
. In practice, it is often more convenient to use simple standard descriptions as subscripts. For example, if
$E$
. In practice, it is often more convenient to use simple standard descriptions as subscripts. For example, if
![]() $E$
is a singleton
$E$
is a singleton
![]() $\{i\}$
then we shall always write
$\{i\}$
then we shall always write
![]() $E$
as
$E$
as
![]() $i$
and
$i$
and
 $\tilde{E}:=[n]\smallsetminus E$
as
$\tilde{E}:=[n]\smallsetminus E$
as
![]() $\tilde{i}$
; similarly, if
$\tilde{i}$
; similarly, if
![]() $E=[i]$
,
$E=[i]$
,
 $\{k:i\leqslant k\leqslant j\}$
,
$\{k:i\leqslant k\leqslant j\}$
,
 $\{k:i<k<j\}$
,
$\{k:i<k<j\}$
,
 $\{\text{all the coordinates in the sort }S\}$
, etc., then we may write
$\{\text{all the coordinates in the sort }S\}$
, etc., then we may write
![]() $\operatorname{pr}_{{\leqslant}i}$
,
$\operatorname{pr}_{{\leqslant}i}$
,
![]() $\operatorname{pr}_{[i,j]}$
,
$\operatorname{pr}_{[i,j]}$
,
![]() $\operatorname{pr}_{(i,j)}$
,
$\operatorname{pr}_{(i,j)}$
,
![]() $\operatorname{pr}_{S}$
, etc.; in particular,
$\operatorname{pr}_{S}$
, etc.; in particular,
![]() $A_{\text{VF}}$
and
$A_{\text{VF}}$
and
![]() $A_{\text{RV}}$
stand for the projections of
$A_{\text{RV}}$
stand for the projections of
![]() $A$
into the
$A$
into the
![]() $\text{VF}$
-sort and
$\text{VF}$
-sort and
![]() $\text{RV}$
-sort coordinates, respectively.
$\text{RV}$
-sort coordinates, respectively.
Unless otherwise specified, by writing
![]() $a\in A$
we shall mean that
$a\in A$
we shall mean that
![]() $a$
is a finite tuple of elements (or ‘points’) of
$a$
is a finite tuple of elements (or ‘points’) of
![]() $A$
, whose length, denoted by
$A$
, whose length, denoted by
![]() $\operatorname{lh}(a)$
, is not always indicated. If
$\operatorname{lh}(a)$
, is not always indicated. If
 $a=(a_{1},\ldots ,a_{n})$
then, for all
$a=(a_{1},\ldots ,a_{n})$
then, for all
 $1\leqslant i<j\leqslant n$
, following the notational scheme above,
$1\leqslant i<j\leqslant n$
, following the notational scheme above,
![]() $a_{i}$
,
$a_{i}$
,
![]() $a_{\tilde{i} }$
,
$a_{\tilde{i} }$
,
![]() $a_{{\leqslant}i}$
,
$a_{{\leqslant}i}$
,
![]() $a_{[i,j]}$
,
$a_{[i,j]}$
,
![]() $a_{[i,j)}$
, etc., are shorthand for the corresponding subtuples of
$a_{[i,j)}$
, etc., are shorthand for the corresponding subtuples of
![]() $a$
. We shall write
$a$
. We shall write
 $\{t\}\times A$
,
$\{t\}\times A$
,
![]() $\{t\}\cup A$
,
$\{t\}\cup A$
,
 $A\smallsetminus \{t\}$
, etc., simply as
$A\smallsetminus \{t\}$
, etc., simply as
![]() $t\times A$
,
$t\times A$
,
![]() $t\cup A$
,
$t\cup A$
,
![]() $A\smallsetminus t$
, etc., when no confusion can arise.
$A\smallsetminus t$
, etc., when no confusion can arise.
For
 $a\in \operatorname{pr}_{\tilde{E}}(A)$
, the fiber
$a\in \operatorname{pr}_{\tilde{E}}(A)$
, the fiber
 $\{b:(b,a)\in A\}\subseteq \operatorname{pr}_{E}(A)$
over
$\{b:(b,a)\in A\}\subseteq \operatorname{pr}_{E}(A)$
over
![]() $a$
is denoted by
$a$
is denoted by
![]() $A_{a}$
. Note that, in the discussion below, the distinction between the two sets
$A_{a}$
. Note that, in the discussion below, the distinction between the two sets
![]() $A_{a}$
and
$A_{a}$
and
![]() $A_{a}\times a$
is usually immaterial and hence they may and often shall be tacitly identified. In particular, given a function
$A_{a}\times a$
is usually immaterial and hence they may and often shall be tacitly identified. In particular, given a function
 $f:A\longrightarrow B$
and
$f:A\longrightarrow B$
and
![]() $b\in B$
, the pullback
$b\in B$
, the pullback
![]() $f^{-1}(b)$
is sometimes written as
$f^{-1}(b)$
is sometimes written as
![]() $A_{b}$
as well. This is a special case since functions are identified with their graphs. This notational scheme is especially useful when the function
$A_{b}$
as well. This is a special case since functions are identified with their graphs. This notational scheme is especially useful when the function
![]() $f$
has been clearly understood in the context and hence there is no need to spell it out all the time.
$f$
has been clearly understood in the context and hence there is no need to spell it out all the time.
Notation 2.5 (Subsets and substructures).
By a definable set we mean a definable subset in
![]() ${\mathcal{R}}$
, and by a subset in
${\mathcal{R}}$
, and by a subset in
![]() ${\mathcal{R}}$
we mean a subset in
${\mathcal{R}}$
we mean a subset in
![]() $R$
, by which we mean a subset of
$R$
, by which we mean a subset of
![]() $R^{n}$
for some
$R^{n}$
for some
![]() $n$
, unless indicated otherwise. Similarly for other structures or sets in place of
$n$
, unless indicated otherwise. Similarly for other structures or sets in place of
![]() ${\mathcal{R}}$
that have been clearly understood in the context.
${\mathcal{R}}$
that have been clearly understood in the context.
Often the ambient total ordering in
![]() ${\mathcal{R}}$
induces a total ordering on a definable set
${\mathcal{R}}$
induces a total ordering on a definable set
![]() $S$
of interest with a distinguished element
$S$
of interest with a distinguished element
![]() $e$
. Then it makes sense to speak of the positive and the negative parts of
$e$
. Then it makes sense to speak of the positive and the negative parts of
![]() $S$
relative to
$S$
relative to
![]() $e$
, which are denoted by
$e$
, which are denoted by
![]() $S^{+}$
and
$S^{+}$
and
![]() $S^{-}$
, respectively. Also write
$S^{-}$
, respectively. Also write
![]() $S_{e}^{+}$
for
$S_{e}^{+}$
for
![]() $S^{+}\cup e$
, etc. There may also be a natural absolute value map
$S^{+}\cup e$
, etc. There may also be a natural absolute value map
 $S\longrightarrow S_{e}^{+}$
, which is always denoted by
$S\longrightarrow S_{e}^{+}$
, which is always denoted by
![]() $|\cdot |$
; typically
$|\cdot |$
; typically
![]() $S$
is a sort and
$S$
is a sort and
 $S^{\times }:=S\smallsetminus e$
is equipped with a (multiplicatively written) group structure, in which case the absolute value map is usually given as a component of a (splitting) short exact sequence
$S^{\times }:=S\smallsetminus e$
is equipped with a (multiplicatively written) group structure, in which case the absolute value map is usually given as a component of a (splitting) short exact sequence
 $$\begin{eqnarray}\pm 1\longrightarrow S^{\times }\longrightarrow S^{+}\quad \text{or}\quad S^{+}\longrightarrow S^{\times }\longrightarrow \pm 1.\end{eqnarray}$$
$$\begin{eqnarray}\pm 1\longrightarrow S^{\times }\longrightarrow S^{+}\quad \text{or}\quad S^{+}\longrightarrow S^{\times }\longrightarrow \pm 1.\end{eqnarray}$$
Note that
![]() $e$
cannot be the identity element of
$e$
cannot be the identity element of
![]() $S^{\times }$
. We will also write
$S^{\times }$
. We will also write
![]() $A<e$
to mean that
$A<e$
to mean that
![]() $A\subseteq S$
and
$A\subseteq S$
and
![]() $a<e$
for all
$a<e$
for all
![]() $a\in A$
, etc. If
$a\in A$
, etc. If
![]() $\unicode[STIX]{x1D719}(x)$
is a formula then
$\unicode[STIX]{x1D719}(x)$
is a formula then
 $\unicode[STIX]{x1D719}(x)<e$
denotes the subset of
$\unicode[STIX]{x1D719}(x)<e$
denotes the subset of
![]() $S$
defined by the formula
$S$
defined by the formula
 $\unicode[STIX]{x1D719}(x)\wedge x<e$
.
$\unicode[STIX]{x1D719}(x)\wedge x<e$
.
Substructures of
![]() ${\mathcal{R}}$
are written as
${\mathcal{R}}$
are written as
![]() ${\mathcal{S}}\subseteq {\mathcal{R}}$
. As has been pointed out above, all substructures
${\mathcal{S}}\subseteq {\mathcal{R}}$
. As has been pointed out above, all substructures
![]() ${\mathcal{S}}$
of
${\mathcal{S}}$
of
![]() ${\mathcal{R}}$
are actually elementary substructures. If
${\mathcal{R}}$
are actually elementary substructures. If
 $A\subseteq {\mathcal{R}}^{n}$
is a set definable with parameters coming from
$A\subseteq {\mathcal{R}}^{n}$
is a set definable with parameters coming from
![]() ${\mathcal{S}}$
then
${\mathcal{S}}$
then
![]() $A({\mathcal{S}})$
is the subset in
$A({\mathcal{S}})$
is the subset in
![]() ${\mathcal{S}}$
defined by the same formula, that is,
${\mathcal{S}}$
defined by the same formula, that is,
 $A({\mathcal{S}})=A\cap {\mathcal{S}}^{n}$
. Given a substructure
$A({\mathcal{S}})=A\cap {\mathcal{S}}^{n}$
. Given a substructure
![]() ${\mathcal{S}}\subseteq {\mathcal{R}}$
and a set
${\mathcal{S}}\subseteq {\mathcal{R}}$
and a set
![]() $A\subseteq {\mathcal{R}}$
, the substructure generated by
$A\subseteq {\mathcal{R}}$
, the substructure generated by
![]() $A$
over
$A$
over
![]() ${\mathcal{S}}$
is denoted by
${\mathcal{S}}$
is denoted by
![]() $\langle {\mathcal{S}},A\rangle$
or
$\langle {\mathcal{S}},A\rangle$
or
![]() ${\mathcal{S}}\langle A\rangle$
. Clearly
${\mathcal{S}}\langle A\rangle$
. Clearly
![]() $\langle {\mathcal{S}},A\rangle$
is the definable closure of
$\langle {\mathcal{S}},A\rangle$
is the definable closure of
![]() $A$
over
$A$
over
![]() ${\mathcal{S}}$
. Later, we will expand
${\mathcal{S}}$
. Later, we will expand
![]() ${\mathcal{R}}$
and introduce more sorts and structures. In that situation we will write
${\mathcal{R}}$
and introduce more sorts and structures. In that situation we will write
![]() ${\mathcal{S}}\langle A\rangle _{T}$
or
${\mathcal{S}}\langle A\rangle _{T}$
or
![]() $\langle {\mathcal{S}},A\rangle _{T}$
to emphasize that this is the
$\langle {\mathcal{S}},A\rangle _{T}$
to emphasize that this is the
![]() ${\mathcal{L}}_{T\text{}}$
-substructure generated by
${\mathcal{L}}_{T\text{}}$
-substructure generated by
![]() $A$
over the
$A$
over the
![]() ${\mathcal{L}}_{T\text{}}$
-reduct of
${\mathcal{L}}_{T\text{}}$
-reduct of
![]() ${\mathcal{S}}$
.
${\mathcal{S}}$
.
Notation 2.6 (Topology).
The default topology on
![]() ${\mathcal{R}}$
is of course the order topology and the default topology on
${\mathcal{R}}$
is of course the order topology and the default topology on
![]() ${\mathcal{R}}^{n}$
is the corresponding product topology. Given a subset
${\mathcal{R}}^{n}$
is the corresponding product topology. Given a subset
![]() $S$
in
$S$
in
![]() ${\mathcal{R}}$
, we write
${\mathcal{R}}$
, we write
![]() $\operatorname{cl}(S)$
for its topological closure,
$\operatorname{cl}(S)$
for its topological closure,
![]() $\operatorname{int}(S)$
for its interior, and
$\operatorname{int}(S)$
for its interior, and
 $\unicode[STIX]{x2202}S:=\operatorname{cl}(S)\setminus S$
for its frontier (not to be confused with the boundary
$\unicode[STIX]{x2202}S:=\operatorname{cl}(S)\setminus S$
for its frontier (not to be confused with the boundary
 $\operatorname{cl}(S)\setminus \operatorname{int}(S)$
of
$\operatorname{cl}(S)\setminus \operatorname{int}(S)$
of
![]() $S$
, which is also sometimes denoted by
$S$
, which is also sometimes denoted by
![]() $\unicode[STIX]{x2202}S$
). The same topological discourse applies to a definable set if the ambient total ordering of
$\unicode[STIX]{x2202}S$
). The same topological discourse applies to a definable set if the ambient total ordering of
![]() ${\mathcal{R}}$
induces a total ordering on it.
${\mathcal{R}}$
induces a total ordering on it.
2.2 The theory
 $\text{TCVF}$
$\text{TCVF}$
The language
![]() ${\mathcal{L}}_{T\text{RV}}$
for
${\mathcal{L}}_{T\text{RV}}$
for
![]() $o$
-minimal valued fields (the theory
$o$
-minimal valued fields (the theory
![]() $T$
may vary, of course) has the following sorts and symbols.
$T$
may vary, of course) has the following sorts and symbols.
-
– A sort
 $\text{VF}$
, which uses the language
$\text{VF}$
, which uses the language
 ${\mathcal{L}}_{T\text{}}$
.
${\mathcal{L}}_{T\text{}}$
. -
– A sort
 $\text{RV}$
, whose basic language is that of groups, written multiplicatively as
$\text{RV}$
, whose basic language is that of groups, written multiplicatively as
 $\{1,\times ,^{-1}\}$
, together with a constant symbol
$\{1,\times ,^{-1}\}$
, together with a constant symbol
 $0_{\text{RV}}$
(for ease of notation, this will henceforth be written simply as
$0_{\text{RV}}$
(for ease of notation, this will henceforth be written simply as
 $0$
).
$0$
). -
– A unary predicate
 $\Bbbk ^{\times }$
in the
$\Bbbk ^{\times }$
in the
 $\text{RV}$
-sort. The union
$\text{RV}$
-sort. The union
 $\Bbbk ^{\times }\cup \{0\}$
is denoted by
$\Bbbk ^{\times }\cup \{0\}$
is denoted by
 $\Bbbk$
, which is more conveniently thought of as a sort and, as such, employs the language
$\Bbbk$
, which is more conveniently thought of as a sort and, as such, employs the language
 ${\mathcal{L}}_{T\text{}}$
as well, where the constant symbols
${\mathcal{L}}_{T\text{}}$
as well, where the constant symbols
 $0$
,
$0$
,
 $1$
are shared with the
$1$
are shared with the
 $\text{RV}$
-sort.
$\text{RV}$
-sort. -
– A binary relation symbol
 ${\leqslant}$
in the
${\leqslant}$
in the
 $\text{RV}$
-sort.
$\text{RV}$
-sort. -
– A function symbol
 $\operatorname{rv}:\text{VF}\longrightarrow \text{RV}_{0}$
.
$\operatorname{rv}:\text{VF}\longrightarrow \text{RV}_{0}$
.
We shall write
![]() $\text{RV}$
to mean the
$\text{RV}$
to mean the
![]() $\text{RV}$
-sort without the element
$\text{RV}$
-sort without the element
![]() $0$
, and
$0$
, and
![]() $\text{RV}_{0}$
otherwise, etc., although quite often the difference is immaterial.
$\text{RV}_{0}$
otherwise, etc., although quite often the difference is immaterial.
Definition 2.7. The axioms of the theory
![]() $\text{TCVF}_{\text{}}$
of
$\text{TCVF}_{\text{}}$
of
![]() $T$
-convex valued fields in the language
$T$
-convex valued fields in the language
![]() ${\mathcal{L}}_{T\text{RV}}$
are presented here informally. Many of these are clearly redundant as axioms, and we try to phrase some of them in such a way as to indicate so. The list also contains additional notation that will be used throughout the paper.
${\mathcal{L}}_{T\text{RV}}$
are presented here informally. Many of these are clearly redundant as axioms, and we try to phrase some of them in such a way as to indicate so. The list also contains additional notation that will be used throughout the paper.
-
(Ax. 1) The
 ${\mathcal{L}}_{T\text{}}$
-reduct of the
${\mathcal{L}}_{T\text{}}$
-reduct of the
 $\text{VF}$
-sort is a model of
$\text{VF}$
-sort is a model of
 $T$
.
$T$
.Recall from Notation 2.5 that
 $\text{VF}^{+}\subseteq \text{VF}$
is the subset of positive elements and
$\text{VF}^{+}\subseteq \text{VF}$
is the subset of positive elements and
 $\text{VF}^{-}\subseteq \text{VF}$
the subset of negative elements.
$\text{VF}^{-}\subseteq \text{VF}$
the subset of negative elements. -
(Ax. 2) The quadruple
 $(\text{RV},1,\times ,^{-1})$
forms an abelian group. Inversion is augmented by
$(\text{RV},1,\times ,^{-1})$
forms an abelian group. Inversion is augmented by
 $0^{-1}=0$
. Multiplication is augmented by
$0^{-1}=0$
. Multiplication is augmented by
 $t\times 0=0\times t=0$
for all
$t\times 0=0\times t=0$
for all
 $t\in \text{RV}$
. The map
$t\in \text{RV}$
. The map
 $\operatorname{rv}:\text{VF}^{\times }\longrightarrow \text{RV}$
is a surjective group homomorphism augmented by
$\operatorname{rv}:\text{VF}^{\times }\longrightarrow \text{RV}$
is a surjective group homomorphism augmented by
 $\operatorname{rv}(0)=0$
.
$\operatorname{rv}(0)=0$
. -
(Ax. 3) The binary relation
 ${\leqslant}$
is a total ordering on
${\leqslant}$
is a total ordering on
 $\text{RV}_{0}$
such that, for all
$\text{RV}_{0}$
such that, for all
 $t,t^{\prime }\in \text{RV}_{0}$
,
$t,t^{\prime }\in \text{RV}_{0}$
,
 $t<t^{\prime }$
if and only if
$t<t^{\prime }$
if and only if
 $\operatorname{rv}^{-1}(t)<\operatorname{rv}^{-1}(t^{\prime })$
.
$\operatorname{rv}^{-1}(t)<\operatorname{rv}^{-1}(t^{\prime })$
.The distinguished element
 $0\in \text{RV}_{0}$
is more aptly referred to as the middle element of
$0\in \text{RV}_{0}$
is more aptly referred to as the middle element of
 $\text{RV}_{0}$
. Clearly
$\text{RV}_{0}$
. Clearly
 $\text{RV}^{+}=\operatorname{rv}(\text{VF}^{+})$
and
$\text{RV}^{+}=\operatorname{rv}(\text{VF}^{+})$
and
 $\text{RV}^{-}=\operatorname{rv}(\text{VF}^{-})$
(see Notation 2.5). It follows from (Ax. 2) that
$\text{RV}^{-}=\operatorname{rv}(\text{VF}^{-})$
(see Notation 2.5). It follows from (Ax. 2) that
 $\text{RV}^{+}$
is an ordered convex subgroup of
$\text{RV}^{+}$
is an ordered convex subgroup of
 $\text{RV}$
and the quotient group
$\text{RV}$
and the quotient group
 $\text{RV}/\text{RV}^{+}$
is isomorphic to the group
$\text{RV}/\text{RV}^{+}$
is isomorphic to the group
 $\pm 1:=\operatorname{rv}(\pm 1)$
. This gives rise to an absolute value map on
$\pm 1:=\operatorname{rv}(\pm 1)$
. This gives rise to an absolute value map on
 $\text{RV}_{0}$
, which is compatible with the absolute value map on
$\text{RV}_{0}$
, which is compatible with the absolute value map on
 $\text{VF}$
in the sense that
$\text{VF}$
in the sense that
 $\operatorname{rv}(|a|)=|\text{rv}(a)|$
for all
$\operatorname{rv}(|a|)=|\text{rv}(a)|$
for all
 $a\in \text{VF}$
.
$a\in \text{VF}$
. -
(Ax. 4) The set
 $\Bbbk ^{\times }$
forms a nontrivial subgroup of
$\Bbbk ^{\times }$
forms a nontrivial subgroup of
 $\text{RV}$
and the set
$\text{RV}$
and the set
 $\Bbbk ^{+}=\Bbbk ^{\times }\cap \text{RV}^{+}$
forms a convex subgroup of
$\Bbbk ^{+}=\Bbbk ^{\times }\cap \text{RV}^{+}$
forms a convex subgroup of
 $\text{RV}^{+}$
.
$\text{RV}^{+}$
.The quotient groups
 $\text{RV}/\Bbbk ^{+}$
,
$\text{RV}/\Bbbk ^{+}$
,
 $\text{RV}^{+}/\Bbbk ^{+}$
are denoted by
$\text{RV}^{+}/\Bbbk ^{+}$
are denoted by
 $\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6E4}$
,
 $\unicode[STIX]{x1D6E4}^{+}$
and the corresponding quotient maps by
$\unicode[STIX]{x1D6E4}^{+}$
and the corresponding quotient maps by
 $\operatorname{vrv}$
,
$\operatorname{vrv}$
,
 $\operatorname{vrv}^{+}$
. Also set
$\operatorname{vrv}^{+}$
. Also set
 $\operatorname{vrv}(0)=0\in \unicode[STIX]{x1D6E4}_{0}$
. Since
$\operatorname{vrv}(0)=0\in \unicode[STIX]{x1D6E4}_{0}$
. Since
 $\Bbbk ^{+}$
is convex,
$\Bbbk ^{+}$
is convex,
 $\unicode[STIX]{x1D6E4}^{+}$
is an ordered group, where the induced ordering is also denoted by
$\unicode[STIX]{x1D6E4}^{+}$
is an ordered group, where the induced ordering is also denoted by
 ${\leqslant}$
, and the absolute value map on
${\leqslant}$
, and the absolute value map on
 $\text{RV}_{0}$
descends to
$\text{RV}_{0}$
descends to
 $\unicode[STIX]{x1D6E4}_{0}$
in the obvious sense.
$\unicode[STIX]{x1D6E4}_{0}$
in the obvious sense. -
(Ax. 5) Let
 ${\leqslant}^{-1}$
be the ordering on
${\leqslant}^{-1}$
be the ordering on
 $\unicode[STIX]{x1D6E4}_{0}^{+}$
inverse to
$\unicode[STIX]{x1D6E4}_{0}^{+}$
inverse to
 ${\leqslant}$
and
${\leqslant}$
and
 $|\unicode[STIX]{x1D6E4}|_{\infty }:=(\unicode[STIX]{x1D6E4}_{0}^{+},+,\leqslant ^{-1})$
the resulting additively written ordered abelian group with the top element
$|\unicode[STIX]{x1D6E4}|_{\infty }:=(\unicode[STIX]{x1D6E4}_{0}^{+},+,\leqslant ^{-1})$
the resulting additively written ordered abelian group with the top element
 $\infty$
. The compositionis a (nontrivial) valuation with respect to the ordering
$\infty$
. The compositionis a (nontrivial) valuation with respect to the ordering
 ${\leqslant}^{-1}$
, with valuation ring
${\leqslant}^{-1}$
, with valuation ring
 $\mathfrak{O}=\operatorname{rv}^{-1}(\text{RV}_{0}^{\circ })$
and maximal ideal
$\mathfrak{O}=\operatorname{rv}^{-1}(\text{RV}_{0}^{\circ })$
and maximal ideal
 $\mathfrak{M}=\operatorname{rv}^{-1}(\text{RV}_{0}^{\circ \circ })$
, where, denoting
$\mathfrak{M}=\operatorname{rv}^{-1}(\text{RV}_{0}^{\circ \circ })$
, where, denoting
 $\operatorname{vrv}^{+}\circ |\cdot |$
by
$\operatorname{vrv}^{+}\circ |\cdot |$
by
 $|\text{vrv}|$
,
$|\text{vrv}|$
,  $$\begin{eqnarray}\displaystyle \text{RV}_{0}^{\circ } & = & \displaystyle \{t\in \text{RV}:1\leqslant ^{-1}|\text{vrv}|(t)\},\nonumber\\ \displaystyle \text{RV}_{0}^{\circ \circ } & = & \displaystyle \{t\in \text{RV}:1{<}^{-1}|\text{vrv}|(t)\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{RV}_{0}^{\circ } & = & \displaystyle \{t\in \text{RV}:1\leqslant ^{-1}|\text{vrv}|(t)\},\nonumber\\ \displaystyle \text{RV}_{0}^{\circ \circ } & = & \displaystyle \{t\in \text{RV}:1{<}^{-1}|\text{vrv}|(t)\}.\nonumber\end{eqnarray}$$
-
(Ax. 6) The
 $\Bbbk$
-sort (recall that
$\Bbbk$
-sort (recall that
 $\Bbbk$
is informally referred to as a sort) is a model of
$\Bbbk$
is informally referred to as a sort) is a model of
 $T$
and, as a field, is the residue field of the valued field
$T$
and, as a field, is the residue field of the valued field
 $(\text{VF},\mathfrak{O})$
.
$(\text{VF},\mathfrak{O})$
.The natural quotient map
 $\mathfrak{O}\longrightarrow \Bbbk$
is denoted by
$\mathfrak{O}\longrightarrow \Bbbk$
is denoted by
 $\operatorname{res}$
. For notational convenience, we extend the domain of
$\operatorname{res}$
. For notational convenience, we extend the domain of
 $\operatorname{res}$
to
$\operatorname{res}$
to
 $\text{VF}$
by setting
$\text{VF}$
by setting
 $\operatorname{res}(a)=0$
for all
$\operatorname{res}(a)=0$
for all
 $a\in \text{VF}\smallsetminus \mathfrak{O}$
. The following function is also denoted by
$a\in \text{VF}\smallsetminus \mathfrak{O}$
. The following function is also denoted by
 $\operatorname{res}$
:
$\operatorname{res}$
:  $$\begin{eqnarray}\text{RV}\rightarrow ^{\operatorname{rv}^{-1}}\text{VF}\rightarrow ^{\operatorname{res}}\Bbbk .\end{eqnarray}$$
$$\begin{eqnarray}\text{RV}\rightarrow ^{\operatorname{rv}^{-1}}\text{VF}\rightarrow ^{\operatorname{res}}\Bbbk .\end{eqnarray}$$
-
(Ax. 7) (
 $T$
-convexity). Let
$T$
-convexity). Let
 $f:\text{VF}\longrightarrow \text{VF}$
be a continuous function defined by an
$f:\text{VF}\longrightarrow \text{VF}$
be a continuous function defined by an
 ${\mathcal{L}}_{T\text{}}$
-formula. Then
${\mathcal{L}}_{T\text{}}$
-formula. Then
 $f(\mathfrak{O})\subseteq \mathfrak{O}$
.
$f(\mathfrak{O})\subseteq \mathfrak{O}$
. -
(Ax. 8) Suppose that
 $\unicode[STIX]{x1D719}$
is an
$\unicode[STIX]{x1D719}$
is an
 ${\mathcal{L}}_{T\text{}}$
-formula that defines a continuous function
${\mathcal{L}}_{T\text{}}$
-formula that defines a continuous function
 $f:\text{VF}^{m}\longrightarrow \text{VF}$
. Then
$f:\text{VF}^{m}\longrightarrow \text{VF}$
. Then
 $\unicode[STIX]{x1D719}$
also defines a continuous function
$\unicode[STIX]{x1D719}$
also defines a continuous function
 $\overline{f}:\Bbbk ^{m}\longrightarrow \Bbbk$
. Moreover, for all
$\overline{f}:\Bbbk ^{m}\longrightarrow \Bbbk$
. Moreover, for all
 $a\in \mathfrak{O}^{m}$
, we have
$a\in \mathfrak{O}^{m}$
, we have
 $\operatorname{res}(f(a))=\overline{f}(\operatorname{res}(a))$
.
$\operatorname{res}(f(a))=\overline{f}(\operatorname{res}(a))$
.
By (Ax. 6) and Remark 2.3, (Ax. 8) can be simplified as: for all function symbols
![]() $f$
of
$f$
of
![]() ${\mathcal{L}}_{T^{\prime }\text{}}$
and all
${\mathcal{L}}_{T^{\prime }\text{}}$
and all
 $a\in \mathfrak{O}^{m}$
,
$a\in \mathfrak{O}^{m}$
,
 $\operatorname{res}(f(a))=\overline{f}(\operatorname{res}(a))$
. Then it is routine to check that, except for the surjectivity of the map
$\operatorname{res}(f(a))=\overline{f}(\operatorname{res}(a))$
. Then it is routine to check that, except for the surjectivity of the map
![]() $\operatorname{rv}$
and the nontriviality of the value group
$\operatorname{rv}$
and the nontriviality of the value group
![]() $|\unicode[STIX]{x1D6E4}|$
(this is an existential axiom and is actually expressed in (Ax. 4)),
$|\unicode[STIX]{x1D6E4}|$
(this is an existential axiom and is actually expressed in (Ax. 4)),
![]() $\text{TCVF}$
is also universally axiomatized.
$\text{TCVF}$
is also universally axiomatized.
Let
![]() ${\mathcal{S}}$
be a substructure of a model
${\mathcal{S}}$
be a substructure of a model
![]() ${\mathcal{M}}$
of
${\mathcal{M}}$
of
![]() $\text{TCVF}$
. We say that
$\text{TCVF}$
. We say that
![]() ${\mathcal{S}}$
is
${\mathcal{S}}$
is
![]() $\text{VF}$
-generated if
$\text{VF}$
-generated if
 $\text{RV}_{0}({\mathcal{S}})=\operatorname{rv}(\text{VF}({\mathcal{S}}))$
. Thus
$\text{RV}_{0}({\mathcal{S}})=\operatorname{rv}(\text{VF}({\mathcal{S}}))$
. Thus
![]() ${\mathcal{S}}$
is indeed a model of
${\mathcal{S}}$
is indeed a model of
![]() $\text{TCVF}$
if it is
$\text{TCVF}$
if it is
![]() $\text{VF}$
-generated and
$\text{VF}$
-generated and
![]() $\unicode[STIX]{x1D6E4}({\mathcal{S}})$
is nontrivial. At any rate,
$\unicode[STIX]{x1D6E4}({\mathcal{S}})$
is nontrivial. At any rate,
![]() $\text{VF}({\mathcal{S}})$
,
$\text{VF}({\mathcal{S}})$
,
 $\operatorname{res}(\text{VF}({\mathcal{S}}))$
, and
$\operatorname{res}(\text{VF}({\mathcal{S}}))$
, and
![]() $\Bbbk ({\mathcal{S}})$
are all models of
$\Bbbk ({\mathcal{S}})$
are all models of
![]() $T$
.
$T$
.
For
 $A\subseteq \text{VF}({\mathcal{M}})\cup \text{RV}({\mathcal{M}})$
, the substructure generated by
$A\subseteq \text{VF}({\mathcal{M}})\cup \text{RV}({\mathcal{M}})$
, the substructure generated by
![]() $A$
over
$A$
over
![]() ${\mathcal{S}}$
is denoted by
${\mathcal{S}}$
is denoted by
![]() $\langle {\mathcal{S}},A\rangle$
or
$\langle {\mathcal{S}},A\rangle$
or
![]() ${\mathcal{S}}\langle A\rangle$
. Clearly
${\mathcal{S}}\langle A\rangle$
. Clearly
 $\text{VF}(\langle {\mathcal{S}},A\rangle )=\langle {\mathcal{S}},A\rangle _{T}$
(see Notation 2.5).
$\text{VF}(\langle {\mathcal{S}},A\rangle )=\langle {\mathcal{S}},A\rangle _{T}$
(see Notation 2.5).
Remark 2.8. Although the behavior of the valuation map
![]() $|\text{val}|$
in the traditional sense is coded in
$|\text{val}|$
in the traditional sense is coded in
![]() $\text{TCVF}$
, we shall work with the signed valuation map, which is more natural in the present setting:
$\text{TCVF}$
, we shall work with the signed valuation map, which is more natural in the present setting:
 $$\begin{eqnarray}\operatorname{val}:\text{VF}\rightarrow ^{\operatorname{rv}}\operatorname{RV}_{0}\rightarrow ^{\operatorname{vrv}}\unicode[STIX]{x1D6E4}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{val}:\text{VF}\rightarrow ^{\operatorname{rv}}\operatorname{RV}_{0}\rightarrow ^{\operatorname{vrv}}\unicode[STIX]{x1D6E4}_{0},\end{eqnarray}$$
where the ordering
![]() ${\leqslant}$
on the signed value group
${\leqslant}$
on the signed value group
![]() $\unicode[STIX]{x1D6E4}_{0}$
no longer needs to be inverted. It is also tempting to use the ordering
$\unicode[STIX]{x1D6E4}_{0}$
no longer needs to be inverted. It is also tempting to use the ordering
![]() ${\leqslant}$
in the value group
${\leqslant}$
in the value group
![]() $|\unicode[STIX]{x1D6E4}|_{\infty }$
instead of its inverse, but this makes citing results in the literature a bit awkward. We shall actually abuse the notation and denote the ordering
$|\unicode[STIX]{x1D6E4}|_{\infty }$
instead of its inverse, but this makes citing results in the literature a bit awkward. We shall actually abuse the notation and denote the ordering
![]() ${\leqslant}^{-1}$
in
${\leqslant}^{-1}$
in
![]() $|\unicode[STIX]{x1D6E4}|_{\infty }$
also by
$|\unicode[STIX]{x1D6E4}|_{\infty }$
also by
![]() ${\leqslant}$
; this should not cause confusion since the ordering on
${\leqslant}$
; this should not cause confusion since the ordering on
![]() $\unicode[STIX]{x1D6E4}_{0}$
will rarely be used (we will indicate so explicitly when it is used).
$\unicode[STIX]{x1D6E4}_{0}$
will rarely be used (we will indicate so explicitly when it is used).
The axioms above guarantee that the ordered abelian group
![]() $\unicode[STIX]{x1D6E4}_{0}/\pm 1$
(here
$\unicode[STIX]{x1D6E4}_{0}/\pm 1$
(here
 $\operatorname{val}(\pm 1)$
is just written as
$\operatorname{val}(\pm 1)$
is just written as
![]() $\pm 1$
) with the bottom element
$\pm 1$
) with the bottom element
![]() $0$
is isomorphic to
$0$
is isomorphic to
![]() $|\unicode[STIX]{x1D6E4}|_{\infty }$
if either one of the orderings is inverted. So
$|\unicode[STIX]{x1D6E4}|_{\infty }$
if either one of the orderings is inverted. So
![]() $|\text{val}|$
may be thought of as the composition
$|\text{val}|$
may be thought of as the composition
 $\operatorname{val}/\pm 1:\text{VF}\longrightarrow \unicode[STIX]{x1D6E4}_{0}/\pm 1$
.
$\operatorname{val}/\pm 1:\text{VF}\longrightarrow \unicode[STIX]{x1D6E4}_{0}/\pm 1$
.
Convention 2.9. Semantically we shall treat the value group
![]() $\unicode[STIX]{x1D6E4}_{0}$
as an imaginary sort. However, syntactically any reference to
$\unicode[STIX]{x1D6E4}_{0}$
as an imaginary sort. However, syntactically any reference to
![]() $\unicode[STIX]{x1D6E4}_{0}$
may be eliminated in the usual way and we can still work with
$\unicode[STIX]{x1D6E4}_{0}$
may be eliminated in the usual way and we can still work with
![]() ${\mathcal{L}}_{T\text{RV}}$
-formulas for the same purpose.
${\mathcal{L}}_{T\text{RV}}$
-formulas for the same purpose.
Example 2.10. Here our main reference is [Reference van den Dries, Macintyre and MarkerVdDMM94]. A restricted analytic function
 $\unicode[STIX]{x211D}^{m}\longrightarrow \unicode[STIX]{x211D}$
is given on the cube
$\unicode[STIX]{x211D}^{m}\longrightarrow \unicode[STIX]{x211D}$
is given on the cube
![]() $[-1,1]^{n}$
by a power series in
$[-1,1]^{n}$
by a power series in
![]() $n$
variables over
$n$
variables over
![]() $\unicode[STIX]{x211D}$
that converges in a neighborhood of
$\unicode[STIX]{x211D}$
that converges in a neighborhood of
![]() $[-1,1]^{n}$
, and
$[-1,1]^{n}$
, and
![]() $0$
elsewhere. Let
$0$
elsewhere. Let
![]() ${\mathcal{L}}_{\text{an}}$
be the language that extends the language of ordered rings with a new function symbol for each restricted analytic function,
${\mathcal{L}}_{\text{an}}$
be the language that extends the language of ordered rings with a new function symbol for each restricted analytic function,
![]() $\unicode[STIX]{x211D}_{\text{an}}$
the real field with its natural
$\unicode[STIX]{x211D}_{\text{an}}$
the real field with its natural
![]() ${\mathcal{L}}_{\text{an}}$
-structure, and
${\mathcal{L}}_{\text{an}}$
-structure, and
![]() $T_{\text{an}}$
the
$T_{\text{an}}$
the
![]() ${\mathcal{L}}_{\text{an}}$
-theory of
${\mathcal{L}}_{\text{an}}$
-theory of
![]() $\unicode[STIX]{x211D}_{\text{an}}$
. Obviously
$\unicode[STIX]{x211D}_{\text{an}}$
. Obviously
![]() $T_{\text{an}}$
is polynomially bounded. More importantly, it is universally axiomatizable and admits quantifier elimination in a slightly enlarged language, and hence there is no longer any need to extend
$T_{\text{an}}$
is polynomially bounded. More importantly, it is universally axiomatizable and admits quantifier elimination in a slightly enlarged language, and hence there is no longer any need to extend
![]() $T_{\text{an}}$
by definitions as we have arranged in § 2.1. (This language is of course more natural than a brute force definitional extension that achieves the same thing, but we do not really care what it is.)
$T_{\text{an}}$
by definitions as we have arranged in § 2.1. (This language is of course more natural than a brute force definitional extension that achieves the same thing, but we do not really care what it is.)
A generalized power series with coefficients in the field
![]() $\unicode[STIX]{x211D}$
and exponents in the additive group
$\unicode[STIX]{x211D}$
and exponents in the additive group
![]() $\unicode[STIX]{x211A}$
is a formal sum
$\unicode[STIX]{x211A}$
is a formal sum
 $x=\sum _{q\in \unicode[STIX]{x211A}}a_{q}t^{q}$
such that its support
$x=\sum _{q\in \unicode[STIX]{x211A}}a_{q}t^{q}$
such that its support
 $\operatorname{supp}(x)=\{q\in \unicode[STIX]{x211A}:a_{q}\neq 0\}$
is well ordered. Let
$\operatorname{supp}(x)=\{q\in \unicode[STIX]{x211A}:a_{q}\neq 0\}$
is well ordered. Let
 $\unicode[STIX]{x211D}((t^{\unicode[STIX]{x211A}}))$
,
$\unicode[STIX]{x211D}((t^{\unicode[STIX]{x211A}}))$
,
![]() $K$
for short, be the set of all such series. Addition and multiplication in
$K$
for short, be the set of all such series. Addition and multiplication in
![]() $K$
are defined in the expected way, and this makes
$K$
are defined in the expected way, and this makes
![]() $K$
a field, generally referred to as a Hahn field. We consider
$K$
a field, generally referred to as a Hahn field. We consider
![]() $\unicode[STIX]{x211D}$
as a subfield of
$\unicode[STIX]{x211D}$
as a subfield of
![]() $K$
via the map
$K$
via the map
 $a\longmapsto at^{0}$
. The map
$a\longmapsto at^{0}$
. The map
 $K^{\times }\longrightarrow \unicode[STIX]{x211A}$
given by
$K^{\times }\longrightarrow \unicode[STIX]{x211A}$
given by
 $x\longmapsto \min \operatorname{supp}(x)$
is indeed a valuation. Its valuation ring
$x\longmapsto \min \operatorname{supp}(x)$
is indeed a valuation. Its valuation ring
![]() $\unicode[STIX]{x211D}\unicode[STIX]{x27E6}t^{\unicode[STIX]{x211A}}\unicode[STIX]{x27E7}$
,
$\unicode[STIX]{x211D}\unicode[STIX]{x27E6}t^{\unicode[STIX]{x211A}}\unicode[STIX]{x27E7}$
,
![]() $\mathfrak{O}$
for short, consists of those series
$\mathfrak{O}$
for short, consists of those series
![]() $x$
with
$x$
with
 $\min \operatorname{supp}(x)\geqslant 0$
and its maximal ideal
$\min \operatorname{supp}(x)\geqslant 0$
and its maximal ideal
![]() $\mathfrak{M}$
of those series
$\mathfrak{M}$
of those series
![]() $x$
with
$x$
with
 $\min \operatorname{supp}(x)>0$
. Its residue field admits a section onto
$\min \operatorname{supp}(x)>0$
. Its residue field admits a section onto
![]() $\unicode[STIX]{x211D}$
and hence is isomorphic to
$\unicode[STIX]{x211D}$
and hence is isomorphic to
![]() $\unicode[STIX]{x211D}$
. It is well known that
$\unicode[STIX]{x211D}$
. It is well known that
![]() $(K,\mathfrak{O})$
is a henselian valued field and
$(K,\mathfrak{O})$
is a henselian valued field and
![]() $K$
is real closed. Restricted analytic functions may be naturally interpreted in
$K$
is real closed. Restricted analytic functions may be naturally interpreted in
![]() $K$
. According to [Reference van den Dries, Macintyre and MarkerVdDMM94, Corollary 2.11], with its naturally induced ordering,
$K$
. According to [Reference van den Dries, Macintyre and MarkerVdDMM94, Corollary 2.11], with its naturally induced ordering,
![]() $K$
is indeed an elementary extension of
$K$
is indeed an elementary extension of
![]() $\unicode[STIX]{x211D}_{\text{an}}$
and hence a model of
$\unicode[STIX]{x211D}_{\text{an}}$
and hence a model of
![]() $T_{\text{an}}$
.
$T_{\text{an}}$
.
We turn
![]() $K$
into a model of
$K$
into a model of
![]() $\text{TCVF}$
, with signed valuation, as follows. First of all, set
$\text{TCVF}$
, with signed valuation, as follows. First of all, set
 $\text{RV}=K^{\times }/(1+\mathfrak{M})$
. Let
$\text{RV}=K^{\times }/(1+\mathfrak{M})$
. Let
 $\operatorname{rv}:K^{\times }\longrightarrow \text{RV}$
be the quotient map. The leading term of a series in
$\operatorname{rv}:K^{\times }\longrightarrow \text{RV}$
be the quotient map. The leading term of a series in
![]() $K^{\times }$
is its first term with nonzero coefficient. It is easy to see that two series
$K^{\times }$
is its first term with nonzero coefficient. It is easy to see that two series
![]() $x$
,
$x$
,
![]() $y$
have the same leading term if and only if
$y$
have the same leading term if and only if
 $\operatorname{rv}(x)=\operatorname{rv}(y)$
and hence
$\operatorname{rv}(x)=\operatorname{rv}(y)$
and hence
![]() $\text{RV}$
is isomorphic to the subgroup of
$\text{RV}$
is isomorphic to the subgroup of
![]() $K^{\times }$
consisting of all the leading terms. There is a natural isomorphism
$K^{\times }$
consisting of all the leading terms. There is a natural isomorphism
 $a_{q}t^{q}\longmapsto (q,a_{q})$
from this latter group of leading terms to the group
$a_{q}t^{q}\longmapsto (q,a_{q})$
from this latter group of leading terms to the group
 $\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{\times }$
, through which we may identify
$\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{\times }$
, through which we may identify
![]() $\text{RV}$
with
$\text{RV}$
with
 $\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{\times }$
. Since
$\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{\times }$
. Since
![]() $1+\mathfrak{M}$
is a convex subset of
$1+\mathfrak{M}$
is a convex subset of
![]() $K^{\times }$
, the total ordering on
$K^{\times }$
, the total ordering on
![]() $K^{\times }$
induces a total ordering
$K^{\times }$
induces a total ordering
![]() ${\leqslant}$
on
${\leqslant}$
on
![]() $\text{RV}$
. This ordering
$\text{RV}$
. This ordering
![]() ${\leqslant}$
is the same as the lexicographic ordering on
${\leqslant}$
is the same as the lexicographic ordering on
 $\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{+}$
or
$\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{+}$
or
 $\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{-}$
via the identification just made.
$\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{-}$
via the identification just made.
Let
![]() $\unicode[STIX]{x211D}^{+}$
be the multiplicative group of the positive reals and
$\unicode[STIX]{x211D}^{+}$
be the multiplicative group of the positive reals and
 $\text{RV}^{+}=\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{+}$
. Observe that
$\text{RV}^{+}=\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{+}$
. Observe that
![]() $\unicode[STIX]{x211D}^{+}$
is a convex subgroup of
$\unicode[STIX]{x211D}^{+}$
is a convex subgroup of
![]() $\text{RV}$
. The quotient group
$\text{RV}$
. The quotient group
 $\unicode[STIX]{x1D6E4}:=(\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{\times })/\unicode[STIX]{x211D}^{+}$
is naturally isomorphic to the subgroup
$\unicode[STIX]{x1D6E4}:=(\unicode[STIX]{x211A}\oplus \unicode[STIX]{x211D}^{\times })/\unicode[STIX]{x211D}^{+}$
is naturally isomorphic to the subgroup
 $\pm e^{\unicode[STIX]{x211A}}:=e^{\unicode[STIX]{x211A}}\cup -e^{\unicode[STIX]{x211A}}$
of
$\pm e^{\unicode[STIX]{x211A}}:=e^{\unicode[STIX]{x211A}}\cup -e^{\unicode[STIX]{x211A}}$
of
![]() $\unicode[STIX]{x211D}^{\times }$
so that
$\unicode[STIX]{x211D}^{\times }$
so that
![]() $\unicode[STIX]{x211A}$
is identified with
$\unicode[STIX]{x211A}$
is identified with
![]() $e^{\unicode[STIX]{x211A}}$
via the map
$e^{\unicode[STIX]{x211A}}$
via the map
 $q\longmapsto e^{q}$
. Adding a new symbol
$q\longmapsto e^{q}$
. Adding a new symbol
![]() $\infty$
to
$\infty$
to
![]() $\text{RV}$
, it is now routine to interpret
$\text{RV}$
, it is now routine to interpret
![]() $K$
as an
$K$
as an
![]() ${\mathcal{L}}_{T\text{RV}}$
-structure, with
${\mathcal{L}}_{T\text{RV}}$
-structure, with
 $T=T_{\text{an}}$
and the signed valuation given by
$T=T_{\text{an}}$
and the signed valuation given by
 $$\begin{eqnarray}x\longmapsto \operatorname{rv}(x)=(q,a_{q})\longmapsto \operatorname{sgn}(a_{q})e^{-q},\end{eqnarray}$$
$$\begin{eqnarray}x\longmapsto \operatorname{rv}(x)=(q,a_{q})\longmapsto \operatorname{sgn}(a_{q})e^{-q},\end{eqnarray}$$
where
![]() $\operatorname{sgn}(a_{q})$
is the sign of
$\operatorname{sgn}(a_{q})$
is the sign of
![]() $a_{q}$
. It is also a model of
$a_{q}$
. It is also a model of
![]() $\text{TCVF}$
: all the axioms are more or less immediately derivable from the valued field structure, except (Ax. 7), which holds since
$\text{TCVF}$
: all the axioms are more or less immediately derivable from the valued field structure, except (Ax. 7), which holds since
![]() $T_{\text{an}}$
is polynomially bounded, and (Ax. 8), which follows from [Reference van den Dries and LewenbergVdDL95, Proposition 2.20].
$T_{\text{an}}$
is polynomially bounded, and (Ax. 8), which follows from [Reference van den Dries and LewenbergVdDL95, Proposition 2.20].
2.3 Quantifier elimination
Recall from § 1 that
![]() $T_{\text{convex}}$
is the
$T_{\text{convex}}$
is the
![]() ${\mathcal{L}}_{\text{convex}}$
-theory of pairs
${\mathcal{L}}_{\text{convex}}$
-theory of pairs
![]() $({\mathcal{R}},\mathfrak{O})$
with
$({\mathcal{R}},\mathfrak{O})$
with
![]() ${\mathcal{R}}\models T$
and
${\mathcal{R}}\models T$
and
![]() $\mathfrak{O}$
a proper
$\mathfrak{O}$
a proper
![]() $T$
-convex subring. We may and shall view
$T$
-convex subring. We may and shall view
![]() $T_{\text{convex}}$
as the
$T_{\text{convex}}$
as the
![]() ${\mathcal{L}}_{\text{convex}}$
-reduct of
${\mathcal{L}}_{\text{convex}}$
-reduct of
![]() $\text{TCVF}$
.
$\text{TCVF}$
.
Theorem 2.11. The theory
![]() $T_{\text{convex}}$
admits quantifier elimination and is complete.
$T_{\text{convex}}$
admits quantifier elimination and is complete.
Proof. See [Reference van den Dries and LewenbergVdDL95, Theorem 3.10, Corollary 3.13]. ◻
That
![]() $\mathfrak{O}$
is a proper subring cannot be expressed by a universal axiom. Of course, we can always add a new constant symbol
$\mathfrak{O}$
is a proper subring cannot be expressed by a universal axiom. Of course, we can always add a new constant symbol
![]() $\imath$
to
$\imath$
to
![]() ${\mathcal{L}}_{\text{convex}}$
and an axiom ‘
${\mathcal{L}}_{\text{convex}}$
and an axiom ‘
![]() $\imath$
is in the maximal ideal’ to
$\imath$
is in the maximal ideal’ to
![]() $T_{\text{convex}}$
so that
$T_{\text{convex}}$
so that
![]() $T_{\text{convex}}$
may indeed be formulated as a universal theory. In that case, every substructure of a model of
$T_{\text{convex}}$
may indeed be formulated as a universal theory. In that case, every substructure of a model of
![]() $T_{\text{convex}}$
is a model of
$T_{\text{convex}}$
is a model of
![]() $T_{\text{convex}}$
and, moreover,
$T_{\text{convex}}$
and, moreover,
![]() $T_{\text{convex}}$
has definable Skolem functions given by
$T_{\text{convex}}$
has definable Skolem functions given by
![]() ${\mathcal{L}}_{T\text{}}(\imath )$
-terms (this is an easy consequence of our assumption on
${\mathcal{L}}_{T\text{}}(\imath )$
-terms (this is an easy consequence of our assumption on
![]() $T$
, quantifier elimination in
$T$
, quantifier elimination in
![]() $T_{\text{convex}}$
, and universality of
$T_{\text{convex}}$
, and universality of
![]() $T_{\text{convex}}$
, as in [Reference van den Dries, Macintyre and MarkerVdDMM94, Corollary 2.15]). We shall not implement this maneuver formally, even though the resulting properties may come in handy occasionally.
$T_{\text{convex}}$
, as in [Reference van den Dries, Macintyre and MarkerVdDMM94, Corollary 2.15]). We shall not implement this maneuver formally, even though the resulting properties may come in handy occasionally.
Remark 2.12. According to [Reference van den Dries and LewenbergVdDL95, Remark 2.16], there is a natural way to expand the residue field
![]() $\Bbbk$
of the
$\Bbbk$
of the
![]() $T_{\text{convex}}$
-model
$T_{\text{convex}}$
-model
![]() $({\mathcal{R}},\mathfrak{O})$
to a T-model as follows. Let
$({\mathcal{R}},\mathfrak{O})$
to a T-model as follows. Let
![]() ${\mathcal{R}}^{\prime }\subseteq \mathfrak{O}$
be a maximal subfield with respect to the property of being an elementary
${\mathcal{R}}^{\prime }\subseteq \mathfrak{O}$
be a maximal subfield with respect to the property of being an elementary
![]() ${\mathcal{L}}_{T\text{}}$
-substructure of
${\mathcal{L}}_{T\text{}}$
-substructure of
![]() ${\mathcal{R}}$
. It follows that
${\mathcal{R}}$
. It follows that
![]() ${\mathcal{R}}^{\prime }$
is isomorphic to
${\mathcal{R}}^{\prime }$
is isomorphic to
![]() $\Bbbk$
as fields via the residue map
$\Bbbk$
as fields via the residue map
![]() $\operatorname{res}$
. Then we can expand
$\operatorname{res}$
. Then we can expand
![]() $\Bbbk$
to a T-model so that the restriction
$\Bbbk$
to a T-model so that the restriction
 $\operatorname{res}\restriction {\mathcal{R}}^{\prime }$
becomes an isomorphism of
$\operatorname{res}\restriction {\mathcal{R}}^{\prime }$
becomes an isomorphism of
![]() ${\mathcal{L}}_{T\text{}}$
-structures. This expansion procedure does not depend on the choice of
${\mathcal{L}}_{T\text{}}$
-structures. This expansion procedure does not depend on the choice of
![]() ${\mathcal{R}}^{\prime }$
.
${\mathcal{R}}^{\prime }$
.
Proposition 2.13. Every
![]() $T_{\text{convex}}$
-model expands to a unique
$T_{\text{convex}}$
-model expands to a unique
![]() $\text{TCVF}$
-model up to isomorphism.
$\text{TCVF}$
-model up to isomorphism.
Proof. Let
![]() $({\mathcal{R}},\mathfrak{O})$
be a
$({\mathcal{R}},\mathfrak{O})$
be a
![]() $T_{\text{convex}}$
-model. It is enough to show that there is a canonical
$T_{\text{convex}}$
-model. It is enough to show that there is a canonical
![]() $\text{TCVF}$
-model expansion
$\text{TCVF}$
-model expansion
 $({\mathcal{R}},\operatorname{RV}_{0}({\mathcal{R}}))$
of
$({\mathcal{R}},\operatorname{RV}_{0}({\mathcal{R}}))$
of
![]() $({\mathcal{R}},\mathfrak{O})$
, where
$({\mathcal{R}},\mathfrak{O})$
, where
![]() ${\mathcal{R}}$
is the
${\mathcal{R}}$
is the
![]() $\text{VF}$
-sort, such that any other such expansion
$\text{VF}$
-sort, such that any other such expansion
 $({\mathcal{R}},\operatorname{RV}_{0})$
is isomorphic to it. This canonical expansion is constructed as follows.
$({\mathcal{R}},\operatorname{RV}_{0})$
is isomorphic to it. This canonical expansion is constructed as follows.
Let
![]() $\text{RV}({\mathcal{R}})$
be the quotient group
$\text{RV}({\mathcal{R}})$
be the quotient group
 ${\mathcal{R}}^{\times }/(1+\mathfrak{M})$
and
${\mathcal{R}}^{\times }/(1+\mathfrak{M})$
and
 $\operatorname{rv}:{\mathcal{R}}^{\times }\longrightarrow \text{RV}({\mathcal{R}})$
the quotient map. As in Example 2.10, it is routine to convert the pair
$\operatorname{rv}:{\mathcal{R}}^{\times }\longrightarrow \text{RV}({\mathcal{R}})$
the quotient map. As in Example 2.10, it is routine to convert the pair
 $({\mathcal{R}},\operatorname{RV}_{0}({\mathcal{R}}))$
into an
$({\mathcal{R}},\operatorname{RV}_{0}({\mathcal{R}}))$
into an
![]() ${\mathcal{L}}_{T\text{RV}}$
-structure and check that it satisfies all the axioms in Definition 2.7, where (Ax. 6) is implied by the construction just described above. We shall refer to the obvious bijection between
${\mathcal{L}}_{T\text{RV}}$
-structure and check that it satisfies all the axioms in Definition 2.7, where (Ax. 6) is implied by the construction just described above. We shall refer to the obvious bijection between
 $({\mathcal{R}},\operatorname{RV}_{0}({\mathcal{R}}))$
and
$({\mathcal{R}},\operatorname{RV}_{0}({\mathcal{R}}))$
and
 $({\mathcal{R}},\operatorname{RV}_{0})$
as the identity map. This map commutes with all the primitives of
$({\mathcal{R}},\operatorname{RV}_{0})$
as the identity map. This map commutes with all the primitives of
![]() ${\mathcal{L}}_{T\text{RV}}$
except, possibly, those in the
${\mathcal{L}}_{T\text{RV}}$
except, possibly, those in the
![]() $\Bbbk$
-sort. This is where the syntactical maneuver in Remark 2.3 comes in. Recall that all the functional primitives of
$\Bbbk$
-sort. This is where the syntactical maneuver in Remark 2.3 comes in. Recall that all the functional primitives of
![]() ${\mathcal{L}}_{T^{\prime }\text{}}$
define continuous functions in all the models of
${\mathcal{L}}_{T^{\prime }\text{}}$
define continuous functions in all the models of
![]() $T^{\prime }$
, and
$T^{\prime }$
, and
![]() $T$
is a definitional extension of
$T$
is a definitional extension of
![]() $T^{\prime }$
. It follows from (Ax. 8) that the identity map indeed induces an
$T^{\prime }$
. It follows from (Ax. 8) that the identity map indeed induces an
![]() ${\mathcal{L}}_{T\text{}}$
-isomorphism between the two
${\mathcal{L}}_{T\text{}}$
-isomorphism between the two
![]() $\Bbbk$
-sorts. Thus the two expansions are isomorphic.◻
$\Bbbk$
-sorts. Thus the two expansions are isomorphic.◻
Theorem 2.14. The theory
![]() $\text{TCVF}$
is complete.
$\text{TCVF}$
is complete.
Proof. By Proposition 2.13, every embedding between two
![]() $T_{\text{convex}}$
-models, which is necessarily elementary, expands uniquely to an
$T_{\text{convex}}$
-models, which is necessarily elementary, expands uniquely to an
![]() ${\mathcal{L}}_{T\text{RV}}$
-embedding between two
${\mathcal{L}}_{T\text{RV}}$
-embedding between two
![]() $\text{TCVF}$
-models. This latter embedding is indeed elementary since
$\text{TCVF}$
-models. This latter embedding is indeed elementary since
![]() $\text{TCVF}$
admits quantifier elimination, which will be shown below. It follows that the theory
$\text{TCVF}$
admits quantifier elimination, which will be shown below. It follows that the theory
![]() $\text{TCVF}$
is complete. But here we do not really need to go down that route. We can simply observe that, by the proof of Proposition 2.13,
$\text{TCVF}$
is complete. But here we do not really need to go down that route. We can simply observe that, by the proof of Proposition 2.13,
![]() $T_{\text{convex}}$
and
$T_{\text{convex}}$
and
![]() $\text{TCVF}$
are equivalent in the sense mentioned in Remark 2.3, and hence they are both complete if one of them is.◻
$\text{TCVF}$
are equivalent in the sense mentioned in Remark 2.3, and hence they are both complete if one of them is.◻
Convention 2.15. From now on, we shall work in the model
![]() ${\mathcal{R}}_{\operatorname{rv}}$
of
${\mathcal{R}}_{\operatorname{rv}}$
of
![]() $\text{TCVF}$
, which is the unique
$\text{TCVF}$
, which is the unique
![]() ${\mathcal{L}}_{T\text{RV}}$
-expansion of the sufficiently saturated
${\mathcal{L}}_{T\text{RV}}$
-expansion of the sufficiently saturated
![]() $T_{\text{convex}}$
-model
$T_{\text{convex}}$
-model
![]() $({\mathcal{R}},\mathfrak{O})$
. We shall write
$({\mathcal{R}},\mathfrak{O})$
. We shall write
 $\text{VF}({\mathcal{R}}_{\operatorname{rv}})$
simply as
$\text{VF}({\mathcal{R}}_{\operatorname{rv}})$
simply as
![]() $\text{VF}$
or
$\text{VF}$
or
![]() ${\mathcal{R}}$
, depending on the context,
${\mathcal{R}}$
, depending on the context,
 $\operatorname{RV}_{0}({\mathcal{R}}_{\operatorname{rv}})$
as
$\operatorname{RV}_{0}({\mathcal{R}}_{\operatorname{rv}})$
as
![]() $\text{RV}_{0}$
, etc. A subset in
$\text{RV}_{0}$
, etc. A subset in
![]() ${\mathcal{R}}_{\operatorname{rv}}$
may simply be referred to as a set.
${\mathcal{R}}_{\operatorname{rv}}$
may simply be referred to as a set.
When we work in the
![]() ${\mathcal{L}}_{T\text{}}$
-reduct
${\mathcal{L}}_{T\text{}}$
-reduct
![]() ${\mathcal{R}}$
of
${\mathcal{R}}$
of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
instead of
${\mathcal{R}}_{\operatorname{rv}}$
instead of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
, or just wish to emphasize that a set is definable in
${\mathcal{R}}_{\operatorname{rv}}$
, or just wish to emphasize that a set is definable in
![]() ${\mathcal{R}}$
instead of
${\mathcal{R}}$
instead of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
, the symbol ‘
${\mathcal{R}}_{\operatorname{rv}}$
, the symbol ‘
![]() ${\mathcal{L}}_{T\text{}}$
’ or ‘
${\mathcal{L}}_{T\text{}}$
’ or ‘
![]() $T$
’ will be inserted into the corresponding places in the terminology.
$T$
’ will be inserted into the corresponding places in the terminology.
Let
![]() ${\mathcal{S}}\subseteq {\mathcal{R}}$
be a small substructure and
${\mathcal{S}}\subseteq {\mathcal{R}}$
be a small substructure and
 $a,b\in {\mathcal{R}}\smallsetminus {\mathcal{S}}$
such that they make the same cut in (the ordering of)
$a,b\in {\mathcal{R}}\smallsetminus {\mathcal{S}}$
such that they make the same cut in (the ordering of)
![]() ${\mathcal{S}}$
. By
${\mathcal{S}}$
. By
![]() $o$
-minimality, there is an automorphism
$o$
-minimality, there is an automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() ${\mathcal{R}}$
over
${\mathcal{R}}$
over
![]() ${\mathcal{S}}$
such that
${\mathcal{S}}$
such that
 $\unicode[STIX]{x1D70E}(a)=b$
.
$\unicode[STIX]{x1D70E}(a)=b$
.
Recall that the field of exponents of
![]() ${\mathcal{R}}$
is denoted by
${\mathcal{R}}$
is denoted by
![]() $\unicode[STIX]{x1D542}$
.
$\unicode[STIX]{x1D542}$
.
Theorem 2.16. The theory
![]() $\text{TCVF}$
admits quantifier elimination.
$\text{TCVF}$
admits quantifier elimination.
Proof. We shall run the usual Shoenfield test for quantifier elimination. To that end, let
![]() ${\mathcal{M}}$
be a model of
${\mathcal{M}}$
be a model of
![]() $\text{TCVF}$
,
$\text{TCVF}$
,
![]() ${\mathcal{S}}$
a substructure of
${\mathcal{S}}$
a substructure of
![]() ${\mathcal{M}}$
, and
${\mathcal{M}}$
, and
 $\unicode[STIX]{x1D70E}:{\mathcal{S}}\longrightarrow {\mathcal{R}}_{\operatorname{rv}}$
an embedding. All we need to do is to extend
$\unicode[STIX]{x1D70E}:{\mathcal{S}}\longrightarrow {\mathcal{R}}_{\operatorname{rv}}$
an embedding. All we need to do is to extend
![]() $\unicode[STIX]{x1D70E}$
to an embedding
$\unicode[STIX]{x1D70E}$
to an embedding
 ${\mathcal{M}}\longrightarrow {\mathcal{R}}_{\operatorname{rv}}$
.
${\mathcal{M}}\longrightarrow {\mathcal{R}}_{\operatorname{rv}}$
.
The construction is more or less a variation of that in the proof of [Reference YinYin09, Theorem 3.10]. The strategy is to reduce the situation to Theorem 2.11. In the process of doing so, instead of the dimension inequality of the general theory of valued fields, the Wilkie inequality [Reference van den DriesVdD97, Corollary 5.6] is used (see [Reference van den Dries and LewenbergVdDL95, § 3.2] for the notion of ranks of
![]() $T$
-models). Note that, to use this inequality, we need to assume that
$T$
-models). Note that, to use this inequality, we need to assume that
![]() $T$
is power-bounded.
$T$
is power-bounded.
Let
 ${\mathcal{S}}_{\ast }=\langle \text{VF}({\mathcal{S}})\rangle$
and
${\mathcal{S}}_{\ast }=\langle \text{VF}({\mathcal{S}})\rangle$
and
 $t\in \text{RV}({\mathcal{S}})\smallsetminus \text{RV}({\mathcal{S}}_{\ast })$
. Note that if such a
$t\in \text{RV}({\mathcal{S}})\smallsetminus \text{RV}({\mathcal{S}}_{\ast })$
. Note that if such a
![]() $t$
does not exist then we have
$t$
does not exist then we have
![]() ${\mathcal{S}}={\mathcal{S}}_{\ast }$
and its
${\mathcal{S}}={\mathcal{S}}_{\ast }$
and its
![]() ${\mathcal{L}}_{\text{convex}}$
-reduct is an
${\mathcal{L}}_{\text{convex}}$
-reduct is an
![]() ${\mathcal{L}}_{\text{convex}}$
-substructure of the
${\mathcal{L}}_{\text{convex}}$
-substructure of the
![]() ${\mathcal{L}}_{\text{convex}}$
-reduct of
${\mathcal{L}}_{\text{convex}}$
-reduct of
![]() ${\mathcal{M}}$
, and hence an embedding as desired can be easily obtained by applying Theorem 2.11 and Proposition 2.13. Let
${\mathcal{M}}$
, and hence an embedding as desired can be easily obtained by applying Theorem 2.11 and Proposition 2.13. Let
 $a\in \text{VF}({\mathcal{M}})$
with
$a\in \text{VF}({\mathcal{M}})$
with
 $\operatorname{rv}(a)=t$
, and
$\operatorname{rv}(a)=t$
, and
![]() $b\in \text{VF}$
with
$b\in \text{VF}$
with
 $\operatorname{rv}(b)=\unicode[STIX]{x1D70E}(t)$
. Observe that, according to
$\operatorname{rv}(b)=\unicode[STIX]{x1D70E}(t)$
. Observe that, according to
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $a$
and
$a$
and
![]() $b$
must make the same cut in
$b$
must make the same cut in
![]() $\text{VF}({\mathcal{S}})$
and
$\text{VF}({\mathcal{S}})$
and
 $\text{VF}(\unicode[STIX]{x1D70E}({\mathcal{S}}))$
, respectively, and hence there is an
$\text{VF}(\unicode[STIX]{x1D70E}({\mathcal{S}}))$
, respectively, and hence there is an
![]() ${\mathcal{L}}_{T\text{}}$
-isomorphism
${\mathcal{L}}_{T\text{}}$
-isomorphism
 $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}:\langle {\mathcal{S}}_{\ast },a\rangle _{T}\longrightarrow \langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle _{T}\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}:\langle {\mathcal{S}}_{\ast },a\rangle _{T}\longrightarrow \langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle _{T}\end{eqnarray}$$
with
 $\bar{\unicode[STIX]{x1D70E}}(a)=b$
and
$\bar{\unicode[STIX]{x1D70E}}(a)=b$
and
 $\bar{\unicode[STIX]{x1D70E}}\restriction \text{VF}({\mathcal{S}})=\unicode[STIX]{x1D70E}\restriction \text{VF}({\mathcal{S}})$
. We shall show that
$\bar{\unicode[STIX]{x1D70E}}\restriction \text{VF}({\mathcal{S}})=\unicode[STIX]{x1D70E}\restriction \text{VF}({\mathcal{S}})$
. We shall show that
![]() $\bar{\unicode[STIX]{x1D70E}}$
expands to an isomorphism between
$\bar{\unicode[STIX]{x1D70E}}$
expands to an isomorphism between
![]() $\langle {\mathcal{S}}_{\ast },a\rangle$
and
$\langle {\mathcal{S}}_{\ast },a\rangle$
and
 $\langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle$
that is compatible with
$\langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle$
that is compatible with
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Case (1). There is an
 $a_{1}\in \langle {\mathcal{S}}_{\ast },a\rangle _{T}$
such that
$a_{1}\in \langle {\mathcal{S}}_{\ast },a\rangle _{T}$
such that
 $$\begin{eqnarray}|\mathfrak{O}({\mathcal{S}}_{\ast })|<a_{1}<|\text{VF}({\mathcal{S}}_{\ast })\smallsetminus \mathfrak{O}({\mathcal{S}}_{\ast })|.\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{O}({\mathcal{S}}_{\ast })|<a_{1}<|\text{VF}({\mathcal{S}}_{\ast })\smallsetminus \mathfrak{O}({\mathcal{S}}_{\ast })|.\end{eqnarray}$$
Set
 $|\unicode[STIX]{x1D6E4}|({\mathcal{S}}_{\ast })=G$
. Since
$|\unicode[STIX]{x1D6E4}|({\mathcal{S}}_{\ast })=G$
. Since
 $\mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
is
$\mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
is
![]() $T$
-convex, by [Reference van den DriesVdD97, Lemma 5.4] and [Reference van den Dries and LewenbergVdDL95, Remark 3.8],
$T$
-convex, by [Reference van den DriesVdD97, Lemma 5.4] and [Reference van den Dries and LewenbergVdDL95, Remark 3.8],
-
– either
 $a_{1}\in \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
and
$a_{1}\in \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
and
 $|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )=G$
or
$|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )=G$
or -
–
 $a_{1}\notin \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
and
$a_{1}\notin \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
and
 $|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )\cong G\oplus \unicode[STIX]{x1D542}$
.
$|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )\cong G\oplus \unicode[STIX]{x1D542}$
.
By the Wilkie inequality, if
 $$\begin{eqnarray}|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )\cong G\oplus \unicode[STIX]{x1D542}\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )\cong G\oplus \unicode[STIX]{x1D542}\end{eqnarray}$$
then
 $\Bbbk (\langle {\mathcal{S}}_{\ast },a\rangle )=\Bbbk ({\mathcal{S}}_{\ast })$
and hence
$\Bbbk (\langle {\mathcal{S}}_{\ast },a\rangle )=\Bbbk ({\mathcal{S}}_{\ast })$
and hence
 $|\text{vrv}|(t)\notin G$
, which implies
$|\text{vrv}|(t)\notin G$
, which implies
 $|\text{vrv}|(\unicode[STIX]{x1D70E}(t))\notin \unicode[STIX]{x1D70E}(G)$
; conversely, if
$|\text{vrv}|(\unicode[STIX]{x1D70E}(t))\notin \unicode[STIX]{x1D70E}(G)$
; conversely, if
 $$\begin{eqnarray}|\unicode[STIX]{x1D6E4}|(\langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle )\cong \unicode[STIX]{x1D70E}(G)\oplus \unicode[STIX]{x1D542}\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6E4}|(\langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle )\cong \unicode[STIX]{x1D70E}(G)\oplus \unicode[STIX]{x1D542}\end{eqnarray}$$
then
 $|\text{vrv}|(t)\notin G$
. Therefore
$|\text{vrv}|(t)\notin G$
. Therefore
 $$\begin{eqnarray}|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )\cong G\oplus \unicode[STIX]{x1D542}\quad \text{if and only if }|\unicode[STIX]{x1D6E4}|(\langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle )\cong \unicode[STIX]{x1D70E}(G)\oplus \unicode[STIX]{x1D542},\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )\cong G\oplus \unicode[STIX]{x1D542}\quad \text{if and only if }|\unicode[STIX]{x1D6E4}|(\langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle )\cong \unicode[STIX]{x1D70E}(G)\oplus \unicode[STIX]{x1D542},\end{eqnarray}$$
which, by [Reference van den Dries and LewenbergVdDL95, Remark 3.8], is equivalent to saying that
 $a_{1}\in \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
if and only if
$a_{1}\in \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
if and only if
 $\bar{\unicode[STIX]{x1D70E}}(a_{1})\in \mathfrak{O}(\langle \{({\mathcal{S}}_{\ast }),b\rangle )$
.
$\bar{\unicode[STIX]{x1D70E}}(a_{1})\in \mathfrak{O}(\langle \{({\mathcal{S}}_{\ast }),b\rangle )$
.
Subcase (1a).
 $a_{1}\in \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
. Subcase (1a) of the proof of [Reference van den Dries and LewenbergVdDL95, Theorem 3.10] shows that
$a_{1}\in \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
. Subcase (1a) of the proof of [Reference van den Dries and LewenbergVdDL95, Theorem 3.10] shows that
![]() $\bar{\unicode[STIX]{x1D70E}}$
expands to an
$\bar{\unicode[STIX]{x1D70E}}$
expands to an
![]() ${\mathcal{L}}_{\text{convex}}$
-isomorphism and hence to an
${\mathcal{L}}_{\text{convex}}$
-isomorphism and hence to an
![]() ${\mathcal{L}}_{T\text{RV}}$
-isomorphism, which is also denoted by
${\mathcal{L}}_{T\text{RV}}$
-isomorphism, which is also denoted by
![]() $\bar{\unicode[STIX]{x1D70E}}$
. Since
$\bar{\unicode[STIX]{x1D70E}}$
. Since
 $|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )=G$
, we may assume
$|\unicode[STIX]{x1D6E4}|(\langle {\mathcal{S}}_{\ast },a\rangle )=G$
, we may assume
 $t\in \Bbbk ({\mathcal{M}})$
. By the Wilkie inequality,
$t\in \Bbbk ({\mathcal{M}})$
. By the Wilkie inequality,
 $\Bbbk (\langle {\mathcal{S}}_{\ast },a\rangle )$
is precisely the
$\Bbbk (\langle {\mathcal{S}}_{\ast },a\rangle )$
is precisely the
![]() $T$
-model generated by
$T$
-model generated by
![]() $t$
over
$t$
over
![]() $\Bbbk ({\mathcal{S}}_{\ast })$
. So
$\Bbbk ({\mathcal{S}}_{\ast })$
. So
 $\text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle )=\langle \text{RV}({\mathcal{S}}_{\ast }),t\rangle$
and
$\text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle )=\langle \text{RV}({\mathcal{S}}_{\ast }),t\rangle$
and
 $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle )=\unicode[STIX]{x1D70E}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle ).\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle )=\unicode[STIX]{x1D70E}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle ).\end{eqnarray}$$
Subcase (1b).
 $a_{1}\notin \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
. As above, Subcase (1b) of the proof of [Reference van den Dries and LewenbergVdDL95, Theorem 3.10] shows that
$a_{1}\notin \mathfrak{O}(\langle {\mathcal{S}}_{\ast },a\rangle )$
. As above, Subcase (1b) of the proof of [Reference van den Dries and LewenbergVdDL95, Theorem 3.10] shows that
![]() $\bar{\unicode[STIX]{x1D70E}}$
expands to an
$\bar{\unicode[STIX]{x1D70E}}$
expands to an
![]() ${\mathcal{L}}_{T\text{RV}}$
-isomorphism and this time
${\mathcal{L}}_{T\text{RV}}$
-isomorphism and this time
 $\Bbbk (\langle {\mathcal{S}}_{\ast },a\rangle )=\Bbbk ({\mathcal{S}}_{\ast })$
. Again it is clear that
$\Bbbk (\langle {\mathcal{S}}_{\ast },a\rangle )=\Bbbk ({\mathcal{S}}_{\ast })$
. Again it is clear that
 $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle )=\unicode[STIX]{x1D70E}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle ).\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle )=\unicode[STIX]{x1D70E}\restriction \text{RV}(\langle {\mathcal{S}}_{\ast },a\rangle ).\end{eqnarray}$$
Case (2). Case (1) fails. Then there is also no
 $b_{1}\in \langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle _{T}$
such that
$b_{1}\in \langle \unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }),b\rangle _{T}$
such that
 $$\begin{eqnarray}|\mathfrak{O}(\unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }))|<b_{1}<|\text{VF}(\unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }))\smallsetminus \mathfrak{O}(\unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }))|.\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{O}(\unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }))|<b_{1}<|\text{VF}(\unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }))\smallsetminus \mathfrak{O}(\unicode[STIX]{x1D70E}({\mathcal{S}}_{\ast }))|.\end{eqnarray}$$
Using Case (2) of the proof of [Reference van den Dries and LewenbergVdDL95, Theorem 3.10], compatibility between
![]() $\bar{\unicode[STIX]{x1D70E}}$
and
$\bar{\unicode[STIX]{x1D70E}}$
and
![]() $\unicode[STIX]{x1D70E}$
may be deduced as in Case (1) above.
$\unicode[STIX]{x1D70E}$
may be deduced as in Case (1) above.
Iterating this procedure, we may assume
![]() ${\mathcal{S}}={\mathcal{S}}_{\ast }$
. The theorem follows.◻
${\mathcal{S}}={\mathcal{S}}_{\ast }$
. The theorem follows.◻
Corollary 2.17. For all sets
 $A\subseteq \text{VF}$
,
$A\subseteq \text{VF}$
,
![]() $\langle A\rangle$
is an elementary substructure of
$\langle A\rangle$
is an elementary substructure of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
if and only if
${\mathcal{R}}_{\operatorname{rv}}$
if and only if
![]() $\unicode[STIX]{x1D6E4}(\langle A\rangle )$
is nontrivial, that is,
$\unicode[STIX]{x1D6E4}(\langle A\rangle )$
is nontrivial, that is,
 $\unicode[STIX]{x1D6E4}(\langle A\rangle )\neq \pm 1$
.
$\unicode[STIX]{x1D6E4}(\langle A\rangle )\neq \pm 1$
.
Corollary 2.18. Every parametrically
![]() ${\mathcal{L}}_{T\text{RV}}$
-definable subset of
${\mathcal{L}}_{T\text{RV}}$
-definable subset of
![]() $\text{VF}^{n}$
is parametrically
$\text{VF}^{n}$
is parametrically
![]() ${\mathcal{L}}_{\text{convex}}$
-definable.
${\mathcal{L}}_{\text{convex}}$
-definable.
This corollary already follows from Proposition 2.13. It enables us to transfer results in the theory of
![]() $T$
-convex valued fields [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97] into our setting, which we shall do without further explanation.
$T$
-convex valued fields [Reference van den Dries and LewenbergVdDL95, Reference van den DriesVdD97] into our setting, which we shall do without further explanation.
We include here a couple of generalities on immediate isomorphisms. Their proofs are built on that of Theorem 2.16 and hence we shall skip some details.
Definition 2.19. Let
![]() ${\mathcal{M}}$
,
${\mathcal{M}}$
,
![]() ${\mathcal{N}}$
be substructures and
${\mathcal{N}}$
be substructures and
 $\unicode[STIX]{x1D70E}:{\mathcal{M}}\longrightarrow {\mathcal{N}}$
an
$\unicode[STIX]{x1D70E}:{\mathcal{M}}\longrightarrow {\mathcal{N}}$
an
![]() ${\mathcal{L}}_{T\text{RV}}$
-isomorphism. We say that
${\mathcal{L}}_{T\text{RV}}$
-isomorphism. We say that
![]() $\unicode[STIX]{x1D70E}$
is an immediate isomorphism if
$\unicode[STIX]{x1D70E}$
is an immediate isomorphism if
 $\unicode[STIX]{x1D70E}(t)=t$
for all
$\unicode[STIX]{x1D70E}(t)=t$
for all
 $t\in \text{RV}({\mathcal{M}})$
.
$t\in \text{RV}({\mathcal{M}})$
.
Note that if
![]() $\unicode[STIX]{x1D70E}$
is an immediate isomorphism then, ex post facto,
$\unicode[STIX]{x1D70E}$
is an immediate isomorphism then, ex post facto,
 $\text{RV}({\mathcal{M}})=\text{RV}({\mathcal{N}})$
.
$\text{RV}({\mathcal{M}})=\text{RV}({\mathcal{N}})$
.
Lemma 2.20. Every immediate isomorphism
 $\unicode[STIX]{x1D70E}:{\mathcal{M}}\longrightarrow {\mathcal{N}}$
can be extended to an immediate automorphism of
$\unicode[STIX]{x1D70E}:{\mathcal{M}}\longrightarrow {\mathcal{N}}$
can be extended to an immediate automorphism of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
.
${\mathcal{R}}_{\operatorname{rv}}$
.
Proof. Let
 ${\mathcal{M}}_{\ast }=\langle \text{VF}({\mathcal{M}})\rangle$
and
${\mathcal{M}}_{\ast }=\langle \text{VF}({\mathcal{M}})\rangle$
and
 ${\mathcal{N}}_{\ast }=\langle \text{VF}({\mathcal{N}})\rangle$
. Let
${\mathcal{N}}_{\ast }=\langle \text{VF}({\mathcal{N}})\rangle$
. Let
 $t\notin \text{RV}({\mathcal{M}}_{\ast })$
and
$t\notin \text{RV}({\mathcal{M}}_{\ast })$
and
 $a\in \operatorname{rv}^{-1}(t)$
. Since
$a\in \operatorname{rv}^{-1}(t)$
. Since
![]() $\unicode[STIX]{x1D70E}$
is immediate,
$\unicode[STIX]{x1D70E}$
is immediate,
![]() $a$
makes the same cut in
$a$
makes the same cut in
 $\text{VF}({\mathcal{M}})$
and
$\text{VF}({\mathcal{M}})$
and
![]() $\text{VF}({\mathcal{N}})$
according to
$\text{VF}({\mathcal{N}})$
according to
![]() $\unicode[STIX]{x1D70E}$
. By the proof of Theorem 2.16,
$\unicode[STIX]{x1D70E}$
. By the proof of Theorem 2.16,
![]() $\unicode[STIX]{x1D70E}$
may be extended to an immediate isomorphism
$\unicode[STIX]{x1D70E}$
may be extended to an immediate isomorphism
 $\langle {\mathcal{M}},a\rangle \longrightarrow \langle {\mathcal{N}},a\rangle$
. Iterating this procedure, we reach a stage where the assertion simply follows from Theorem 2.11.◻
$\langle {\mathcal{M}},a\rangle \longrightarrow \langle {\mathcal{N}},a\rangle$
. Iterating this procedure, we reach a stage where the assertion simply follows from Theorem 2.11.◻
We have something much stronger. For that, the following crucial property is needed.
Proposition 2.21 (Valuation property).
Let
![]() ${\mathcal{M}}$
be a
${\mathcal{M}}$
be a
![]() $\text{VF}$
-generated substructure and
$\text{VF}$
-generated substructure and
![]() $a\in \text{VF}$
. Suppose that
$a\in \text{VF}$
. Suppose that
 $\unicode[STIX]{x1D6E4}(\langle {\mathcal{M}},a\rangle )\neq \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. Then there is a
$\unicode[STIX]{x1D6E4}(\langle {\mathcal{M}},a\rangle )\neq \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. Then there is a
 $d\in \text{VF}({\mathcal{M}})$
such that
$d\in \text{VF}({\mathcal{M}})$
such that
 $\operatorname{val}(a-d)\notin \operatorname{val}({\mathcal{M}})$
.
$\operatorname{val}(a-d)\notin \operatorname{val}({\mathcal{M}})$
.
Proof. For the polynomially bounded case, see [Reference van den Dries and SpeisseggerVdDS00, Proposition 9.2] and the remark thereafter. Apparently this is established in full generality (power-bounded) in [Reference TyneTyn03], which is in a repository that is password-protected. ◻
Lemma 2.22. Let
 $\unicode[STIX]{x1D70E}:{\mathcal{M}}\longrightarrow {\mathcal{N}}$
be an immediate isomorphism. Let
$\unicode[STIX]{x1D70E}:{\mathcal{M}}\longrightarrow {\mathcal{N}}$
be an immediate isomorphism. Let
 $a\in \text{VF}\smallsetminus \text{VF}({\mathcal{M}})$
and
$a\in \text{VF}\smallsetminus \text{VF}({\mathcal{M}})$
and
 $b\in \text{VF}\smallsetminus \text{VF}({\mathcal{N}})$
such that
$b\in \text{VF}\smallsetminus \text{VF}({\mathcal{N}})$
such that
 $\operatorname{rv}(a-c)=\operatorname{rv}(b-\unicode[STIX]{x1D70E}(c))$
for all
$\operatorname{rv}(a-c)=\operatorname{rv}(b-\unicode[STIX]{x1D70E}(c))$
for all
 $c\in \text{VF}({\mathcal{M}})$
. Then
$c\in \text{VF}({\mathcal{M}})$
. Then
![]() $\unicode[STIX]{x1D70E}$
may be extended to an immediate isomorphism
$\unicode[STIX]{x1D70E}$
may be extended to an immediate isomorphism
 $\bar{\unicode[STIX]{x1D70E}}:\langle {\mathcal{M}},a\rangle \longrightarrow \langle {\mathcal{N}},b\rangle$
with
$\bar{\unicode[STIX]{x1D70E}}:\langle {\mathcal{M}},a\rangle \longrightarrow \langle {\mathcal{N}},b\rangle$
with
 $\bar{\unicode[STIX]{x1D70E}}(a)=b$
.
$\bar{\unicode[STIX]{x1D70E}}(a)=b$
.
Observe that, since every element of
 $\text{VF}(\langle {\mathcal{M}},a\rangle )=\langle {\mathcal{M}},a\rangle _{T}$
is of the form
$\text{VF}(\langle {\mathcal{M}},a\rangle )=\langle {\mathcal{M}},a\rangle _{T}$
is of the form
![]() $f(a,c)$
, where
$f(a,c)$
, where
 $c\in \text{VF}({\mathcal{M}})$
and
$c\in \text{VF}({\mathcal{M}})$
and
![]() $f$
is a function symbol of
$f$
is a function symbol of
![]() ${\mathcal{L}}_{T\text{}}$
, and similarly for
${\mathcal{L}}_{T\text{}}$
, and similarly for
![]() $\langle {\mathcal{N}},b\rangle$
, the lemma is equivalent to saying that
$\langle {\mathcal{N}},b\rangle$
, the lemma is equivalent to saying that
 $\operatorname{rv}(a-c)=\operatorname{rv}(b-\unicode[STIX]{x1D70E}(c))$
for all
$\operatorname{rv}(a-c)=\operatorname{rv}(b-\unicode[STIX]{x1D70E}(c))$
for all
 $c\in \text{VF}({\mathcal{M}})$
implies
$c\in \text{VF}({\mathcal{M}})$
implies
 $\operatorname{rv}(f(a,c))=\operatorname{rv}(f(b,\unicode[STIX]{x1D70E}(c)))$
for all
$\operatorname{rv}(f(a,c))=\operatorname{rv}(f(b,\unicode[STIX]{x1D70E}(c)))$
for all
 $c\in \text{VF}({\mathcal{M}})$
and all function symbols of
$c\in \text{VF}({\mathcal{M}})$
and all function symbols of
![]() ${\mathcal{L}}_{T\text{}}$
.
${\mathcal{L}}_{T\text{}}$
.
Proof. Without loss of generality, we may assume that
![]() ${\mathcal{M}}$
,
${\mathcal{M}}$
,
![]() ${\mathcal{N}}$
are
${\mathcal{N}}$
are
![]() $\text{VF}$
-generated. According to
$\text{VF}$
-generated. According to
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $a$
and
$a$
and
![]() $b$
must make the same cut respectively in
$b$
must make the same cut respectively in
 $\text{VF}({\mathcal{M}})$
and
$\text{VF}({\mathcal{M}})$
and
![]() $\text{VF}({\mathcal{N}})$
, and hence there is an
$\text{VF}({\mathcal{N}})$
, and hence there is an
![]() ${\mathcal{L}}_{T\text{}}$
-isomorphism
${\mathcal{L}}_{T\text{}}$
-isomorphism
 $\bar{\unicode[STIX]{x1D70E}}:\langle {\mathcal{M}},a\rangle _{T}\longrightarrow \langle {\mathcal{N}},b\rangle _{T}$
with
$\bar{\unicode[STIX]{x1D70E}}:\langle {\mathcal{M}},a\rangle _{T}\longrightarrow \langle {\mathcal{N}},b\rangle _{T}$
with
 $\bar{\unicode[STIX]{x1D70E}}(a)=b$
that extends
$\bar{\unicode[STIX]{x1D70E}}(a)=b$
that extends
 $\unicode[STIX]{x1D70E}\restriction \text{VF}({\mathcal{M}})$
. We shall first show that
$\unicode[STIX]{x1D70E}\restriction \text{VF}({\mathcal{M}})$
. We shall first show that
![]() $\bar{\unicode[STIX]{x1D70E}}$
expands to an
$\bar{\unicode[STIX]{x1D70E}}$
expands to an
![]() ${\mathcal{L}}_{T\text{RV}}$
-isomorphism. There are two cases to consider, corresponding to the two cases in the proof of Theorem 2.16.
${\mathcal{L}}_{T\text{RV}}$
-isomorphism. There are two cases to consider, corresponding to the two cases in the proof of Theorem 2.16.
Case (1). There is an
 $a^{\prime }\in \langle {\mathcal{M}},a\rangle _{T}$
such that
$a^{\prime }\in \langle {\mathcal{M}},a\rangle _{T}$
such that
 $$\begin{eqnarray}|\mathfrak{O}({\mathcal{M}})|<a^{\prime }<|\text{VF}({\mathcal{M}})\smallsetminus \mathfrak{O}({\mathcal{M}})|.\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{O}({\mathcal{M}})|<a^{\prime }<|\text{VF}({\mathcal{M}})\smallsetminus \mathfrak{O}({\mathcal{M}})|.\end{eqnarray}$$
Let
![]() $f$
be a function symbol of
$f$
be a function symbol of
![]() ${\mathcal{L}}_{T\text{}}$
and
${\mathcal{L}}_{T\text{}}$
and
 $c\in \text{VF}({\mathcal{M}})$
such that
$c\in \text{VF}({\mathcal{M}})$
such that
 $f(a,c)=a^{\prime }$
. Let
$f(a,c)=a^{\prime }$
. Let
 $b^{\prime }=\bar{\unicode[STIX]{x1D70E}}(f(a,c))$
. Then we also have
$b^{\prime }=\bar{\unicode[STIX]{x1D70E}}(f(a,c))$
. Then we also have
 $$\begin{eqnarray}|\mathfrak{O}({\mathcal{N}})|<b^{\prime }<|\text{VF}({\mathcal{N}})\smallsetminus \mathfrak{O}({\mathcal{N}})|.\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{O}({\mathcal{N}})|<b^{\prime }<|\text{VF}({\mathcal{N}})\smallsetminus \mathfrak{O}({\mathcal{N}})|.\end{eqnarray}$$
If
 $a^{\prime }\notin \mathfrak{O}(\langle {\mathcal{M}},a\rangle )$
then
$a^{\prime }\notin \mathfrak{O}(\langle {\mathcal{M}},a\rangle )$
then
 $\unicode[STIX]{x1D6E4}(\langle {\mathcal{M}},a\rangle )\neq \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. By the valuation property, there is a
$\unicode[STIX]{x1D6E4}(\langle {\mathcal{M}},a\rangle )\neq \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. By the valuation property, there is a
 $d\in \text{VF}({\mathcal{M}})$
such that
$d\in \text{VF}({\mathcal{M}})$
such that
 $\operatorname{val}(a-d)\notin \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. Then
$\operatorname{val}(a-d)\notin \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. Then
 $\operatorname{val}(b-\unicode[STIX]{x1D70E}(d))\notin \unicode[STIX]{x1D6E4}({\mathcal{N}})$
and hence, by the Wilkie inequality,
$\operatorname{val}(b-\unicode[STIX]{x1D70E}(d))\notin \unicode[STIX]{x1D6E4}({\mathcal{N}})$
and hence, by the Wilkie inequality,
 $\mathfrak{O}(\langle {\mathcal{N}},b\rangle )$
is the convex hull of
$\mathfrak{O}(\langle {\mathcal{N}},b\rangle )$
is the convex hull of
![]() $\mathfrak{O}({\mathcal{N}})$
in
$\mathfrak{O}({\mathcal{N}})$
in
![]() $\langle {\mathcal{N}},b\rangle _{T}$
. This implies
$\langle {\mathcal{N}},b\rangle _{T}$
. This implies
 $b^{\prime }\notin \mathfrak{O}(\langle {\mathcal{N}},b\rangle )$
. By symmetry and [Reference van den Dries and LewenbergVdDL95, Remark 3.8], we see that
$b^{\prime }\notin \mathfrak{O}(\langle {\mathcal{N}},b\rangle )$
. By symmetry and [Reference van den Dries and LewenbergVdDL95, Remark 3.8], we see that
 $a^{\prime }\in \mathfrak{O}(\langle {\mathcal{M}},a\rangle )$
if and only if
$a^{\prime }\in \mathfrak{O}(\langle {\mathcal{M}},a\rangle )$
if and only if
 $b^{\prime }\in \mathfrak{O}(\langle {\mathcal{N}},b\rangle )$
, and hence
$b^{\prime }\in \mathfrak{O}(\langle {\mathcal{N}},b\rangle )$
, and hence
 $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}(\mathfrak{O}(\langle {\mathcal{M}},a\rangle ))=\mathfrak{O}(\langle {\mathcal{N}},b\rangle ).\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}(\mathfrak{O}(\langle {\mathcal{M}},a\rangle ))=\mathfrak{O}(\langle {\mathcal{N}},b\rangle ).\end{eqnarray}$$
Case (2). Case (1) fails. We may proceed exactly as in Case (2) of the proof of Theorem 2.16.
This concludes our proof that
![]() $\bar{\unicode[STIX]{x1D70E}}$
expands to an
$\bar{\unicode[STIX]{x1D70E}}$
expands to an
![]() ${\mathcal{L}}_{T\text{RV}}$
-isomorphism.
${\mathcal{L}}_{T\text{RV}}$
-isomorphism.
Next, we show that
![]() $\bar{\unicode[STIX]{x1D70E}}$
is indeed immediate. If
$\bar{\unicode[STIX]{x1D70E}}$
is indeed immediate. If
 $\text{RV}(\langle {\mathcal{M}},a\rangle )\,=\,\text{RV}({\mathcal{M}})$
then also
$\text{RV}(\langle {\mathcal{M}},a\rangle )\,=\,\text{RV}({\mathcal{M}})$
then also
 $\text{RV}(\langle {\mathcal{N}},b\rangle )=\text{RV}({\mathcal{N}})$
, and there is nothing more to be done. So suppose
$\text{RV}(\langle {\mathcal{N}},b\rangle )=\text{RV}({\mathcal{N}})$
, and there is nothing more to be done. So suppose
 $\text{RV}(\langle {\mathcal{M}},a\rangle )\neq \text{RV}({\mathcal{M}})$
. We claim that there is a
$\text{RV}(\langle {\mathcal{M}},a\rangle )\neq \text{RV}({\mathcal{M}})$
. We claim that there is a
 $d\in \text{VF}({\mathcal{M}})$
such that
$d\in \text{VF}({\mathcal{M}})$
such that
 $\operatorname{rv}(a-d)\notin \text{RV}({\mathcal{M}})$
. We consider two (mutually exclusive) cases.
$\operatorname{rv}(a-d)\notin \text{RV}({\mathcal{M}})$
. We consider two (mutually exclusive) cases.
Case (1).
 $\unicode[STIX]{x1D6E4}(\langle {\mathcal{M}},a\rangle )\neq \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. Then the valuation property gives such a
$\unicode[STIX]{x1D6E4}(\langle {\mathcal{M}},a\rangle )\neq \unicode[STIX]{x1D6E4}({\mathcal{M}})$
. Then the valuation property gives such a
![]() $d$
directly.
$d$
directly.
Case (2).
 $\Bbbk (\langle {\mathcal{M}},a\rangle )\neq \Bbbk ({\mathcal{M}})$
. Let
$\Bbbk (\langle {\mathcal{M}},a\rangle )\neq \Bbbk ({\mathcal{M}})$
. Let
![]() $a^{\prime }$
be as above. Let
$a^{\prime }$
be as above. Let
![]() $\mathfrak{O}^{\prime }$
be the T-convex subring of
$\mathfrak{O}^{\prime }$
be the T-convex subring of
 $\text{VF}({\mathcal{M}})$
that does not contain
$\text{VF}({\mathcal{M}})$
that does not contain
![]() $a^{\prime }$
, that is,
$a^{\prime }$
, that is,
![]() $\mathfrak{O}^{\prime }$
is the convex hull of
$\mathfrak{O}^{\prime }$
is the convex hull of
![]() $\mathfrak{O}({\mathcal{M}})$
in
$\mathfrak{O}({\mathcal{M}})$
in
 $\langle {\mathcal{M}},a\rangle _{T}$
. Let
$\langle {\mathcal{M}},a\rangle _{T}$
. Let
![]() $\operatorname{val}^{\prime }$
,
$\operatorname{val}^{\prime }$
,
 $\unicode[STIX]{x1D6E4}^{\prime }(\langle {\mathcal{M}},a\rangle )$
be the corresponding signed valuation map and signed value group. Then the valuation property yields a
$\unicode[STIX]{x1D6E4}^{\prime }(\langle {\mathcal{M}},a\rangle )$
be the corresponding signed valuation map and signed value group. Then the valuation property yields a
 $d\in \text{VF}({\mathcal{M}})$
such that
$d\in \text{VF}({\mathcal{M}})$
such that
 $\operatorname{val}^{\prime }(a-d)\notin \unicode[STIX]{x1D6E4}^{\prime }({\mathcal{M}})$
. Since
$\operatorname{val}^{\prime }(a-d)\notin \unicode[STIX]{x1D6E4}^{\prime }({\mathcal{M}})$
. Since
 $$\begin{eqnarray}|\unicode[STIX]{x1D6E4}^{\prime }|(\langle {\mathcal{M}},a\rangle )\cong |\unicode[STIX]{x1D6E4}|({\mathcal{M}})\oplus \unicode[STIX]{x1D542},\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6E4}^{\prime }|(\langle {\mathcal{M}},a\rangle )\cong |\unicode[STIX]{x1D6E4}|({\mathcal{M}})\oplus \unicode[STIX]{x1D542},\end{eqnarray}$$
there is a
 $\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|({\mathcal{M}})$
such that (exactly) one of the following two relations holds:
$\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|({\mathcal{M}})$
such that (exactly) one of the following two relations holds:
 $$\begin{eqnarray}\displaystyle |\mathfrak{O}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|<|a-d| & {<} & \displaystyle |\text{VF}({\mathcal{M}})\smallsetminus \mathfrak{O}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|,\nonumber\\ \displaystyle |\mathfrak{M}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|<|a-d| & {<} & \displaystyle |\text{VF}({\mathcal{M}})\smallsetminus \mathfrak{M}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\mathfrak{O}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|<|a-d| & {<} & \displaystyle |\text{VF}({\mathcal{M}})\smallsetminus \mathfrak{O}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|,\nonumber\\ \displaystyle |\mathfrak{M}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|<|a-d| & {<} & \displaystyle |\text{VF}({\mathcal{M}})\smallsetminus \mathfrak{M}_{\unicode[STIX]{x1D6FE}}({\mathcal{M}})|,\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\mathfrak{O}_{\unicode[STIX]{x1D6FE}}=\{c\in \text{VF}:|\text{val}|(c)\geqslant \unicode[STIX]{x1D6FE}\}\quad \text{and}\quad \mathfrak{M}_{\unicode[STIX]{x1D6FE}}=\{c\in \text{VF}:|\text{val}|(c)>\unicode[STIX]{x1D6FE}\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{O}_{\unicode[STIX]{x1D6FE}}=\{c\in \text{VF}:|\text{val}|(c)\geqslant \unicode[STIX]{x1D6FE}\}\quad \text{and}\quad \mathfrak{M}_{\unicode[STIX]{x1D6FE}}=\{c\in \text{VF}:|\text{val}|(c)>\unicode[STIX]{x1D6FE}\}.\end{eqnarray}$$
It is not hard to see that, in either case,
 $\operatorname{rv}(a-d)\notin \text{RV}({\mathcal{M}})$
.
$\operatorname{rv}(a-d)\notin \text{RV}({\mathcal{M}})$
.
Since
 $\operatorname{rv}(a-d)=\operatorname{rv}(b-\unicode[STIX]{x1D70E}(d))=:t$
, by the Wilkie inequality,
$\operatorname{rv}(a-d)=\operatorname{rv}(b-\unicode[STIX]{x1D70E}(d))=:t$
, by the Wilkie inequality,
 $\text{RV}(\langle {\mathcal{M}},a\rangle )=\langle \text{RV}({\mathcal{M}}),t\rangle$
and hence
$\text{RV}(\langle {\mathcal{M}},a\rangle )=\langle \text{RV}({\mathcal{M}}),t\rangle$
and hence
![]() $\bar{\unicode[STIX]{x1D70E}}$
must be immediate.◻
$\bar{\unicode[STIX]{x1D70E}}$
must be immediate.◻
2.4 Fundamental structure of
 $T$
-convex valuation
$T$
-convex valuation
We review some fundamental facts concerning the valuation in
![]() ${\mathcal{R}}_{\operatorname{rv}}$
. Additional notation and terminology are also introduced.
${\mathcal{R}}_{\operatorname{rv}}$
. Additional notation and terminology are also introduced.
Recall [Reference van den DriesVdD97, Theorem A]: The structure of definable sets in the
![]() $\Bbbk$
-sort is precisely that given by the theory
$\Bbbk$
-sort is precisely that given by the theory
![]() $T$
.
$T$
.
Recall [Reference van den DriesVdD97, Theorem B]: The structure of definable sets in the (imaginary)
![]() $|\unicode[STIX]{x1D6E4}|$
-sort is precisely that given by the
$|\unicode[STIX]{x1D6E4}|$
-sort is precisely that given by the
![]() $o$
-minimal theory of nontrivially ordered vector spaces over
$o$
-minimal theory of nontrivially ordered vector spaces over
![]() $\unicode[STIX]{x1D542}$
. The structure of definable sets in the (imaginary)
$\unicode[STIX]{x1D542}$
. The structure of definable sets in the (imaginary)
![]() $\unicode[STIX]{x1D6E4}$
-sort is the same one modulo the sign. In particular, every definable function in the
$\unicode[STIX]{x1D6E4}$
-sort is the same one modulo the sign. In particular, every definable function in the
![]() $\unicode[STIX]{x1D6E4}$
-sort is definably piecewise
$\unicode[STIX]{x1D6E4}$
-sort is definably piecewise
![]() $\unicode[STIX]{x1D542}$
-linear modulo the sign.
$\unicode[STIX]{x1D542}$
-linear modulo the sign.
Lemma 2.23. If
 $f:\unicode[STIX]{x1D6E4}\longrightarrow \Bbbk$
is a definable function then
$f:\unicode[STIX]{x1D6E4}\longrightarrow \Bbbk$
is a definable function then
![]() $f(\Bbbk )$
is finite. Similarly, if
$f(\Bbbk )$
is finite. Similarly, if
 $g:\Bbbk \longrightarrow \unicode[STIX]{x1D6E4}$
is a definable function then
$g:\Bbbk \longrightarrow \unicode[STIX]{x1D6E4}$
is a definable function then
![]() $g(\unicode[STIX]{x1D6E4})$
is finite.
$g(\unicode[STIX]{x1D6E4})$
is finite.
Proof. See [Reference van den DriesVdD97, Proposition 5.8]. ◻
Note that [Reference van den DriesVdD97, Theorem B, Proposition 5.8] require that
![]() $T$
be power-bounded.
$T$
be power-bounded.
Notation 2.24. Recall Convention 2.9. There are two ways of treating an element
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
: as a point, when we study
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
: as a point, when we study
![]() $\unicode[STIX]{x1D6E4}$
as an independent structure (see Convention 2.9); or as a subset of
$\unicode[STIX]{x1D6E4}$
as an independent structure (see Convention 2.9); or as a subset of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
, when we need to remain in the realm of definable sets in
${\mathcal{R}}_{\operatorname{rv}}$
, when we need to remain in the realm of definable sets in
![]() ${\mathcal{R}}_{\operatorname{rv}}$
. The former perspective simplifies the notation but is of course dispensable.
${\mathcal{R}}_{\operatorname{rv}}$
. The former perspective simplifies the notation but is of course dispensable.
We shall write
![]() $\unicode[STIX]{x1D6FE}$
as
$\unicode[STIX]{x1D6FE}$
as
![]() $\unicode[STIX]{x1D6FE}^{\sharp }$
when we want to emphasize that it is the set
$\unicode[STIX]{x1D6FE}^{\sharp }$
when we want to emphasize that it is the set
 $\operatorname{vrv}^{-1}(\unicode[STIX]{x1D6FE})$
in
$\operatorname{vrv}^{-1}(\unicode[STIX]{x1D6FE})$
in
![]() ${\mathcal{R}}_{\operatorname{rv}}$
that is being considered. More generally, if
${\mathcal{R}}_{\operatorname{rv}}$
that is being considered. More generally, if
![]() $I$
is a set in
$I$
is a set in
![]() $\unicode[STIX]{x1D6E4}$
then we write
$\unicode[STIX]{x1D6E4}$
then we write
 $I^{\sharp }=\bigcup \{\unicode[STIX]{x1D6FE}^{\sharp }:\unicode[STIX]{x1D6FE}\in I\}$
. Similarly, if
$I^{\sharp }=\bigcup \{\unicode[STIX]{x1D6FE}^{\sharp }:\unicode[STIX]{x1D6FE}\in I\}$
. Similarly, if
![]() $U$
is a set in
$U$
is a set in
![]() $\text{RV}$
then
$\text{RV}$
then
![]() $U^{\sharp }$
stands for
$U^{\sharp }$
stands for
 $\bigcup \{\operatorname{rv}^{-1}(t):t\in U\}$
.
$\bigcup \{\operatorname{rv}^{-1}(t):t\in U\}$
.
Since
![]() $\text{TCVF}$
is a weakly
$\text{TCVF}$
is a weakly
![]() $o$
-minimal theory (see [Reference van den Dries and LewenbergVdDL95, Corollary 3.14] and Corollary 2.18), we can use the dimension theory of [Reference Macpherson, Marker and SteinhornMMS00, § 4] in
$o$
-minimal theory (see [Reference van den Dries and LewenbergVdDL95, Corollary 3.14] and Corollary 2.18), we can use the dimension theory of [Reference Macpherson, Marker and SteinhornMMS00, § 4] in
![]() ${\mathcal{R}}_{\operatorname{rv}}$
.
${\mathcal{R}}_{\operatorname{rv}}$
.
Definition 2.25. The
![]() $\text{VF}$
-dimension of a definable set
$\text{VF}$
-dimension of a definable set
![]() $A$
, denoted by
$A$
, denoted by
 $\dim _{\text{VF}}(A)$
, is the largest natural number
$\dim _{\text{VF}}(A)$
, is the largest natural number
![]() $k$
such that, possibly after re-indexing of the
$k$
such that, possibly after re-indexing of the
![]() $\text{VF}$
-coordinates,
$\text{VF}$
-coordinates,
 $\operatorname{pr}_{{\leqslant}k}(A_{t})$
has nonempty interior for some
$\operatorname{pr}_{{\leqslant}k}(A_{t})$
has nonempty interior for some
 $t\in A_{\text{RV}}$
.
$t\in A_{\text{RV}}$
.
For all substructures
![]() ${\mathcal{M}}$
and all
${\mathcal{M}}$
and all
![]() $a\in \text{VF}$
,
$a\in \text{VF}$
,
 $\text{VF}(\operatorname{dcl}_{{\mathcal{M}}}(a))=\langle {\mathcal{M}},a\rangle _{T}$
, where
$\text{VF}(\operatorname{dcl}_{{\mathcal{M}}}(a))=\langle {\mathcal{M}},a\rangle _{T}$
, where
 $\operatorname{dcl}_{{\mathcal{M}}}(a)$
is the definable closure of
$\operatorname{dcl}_{{\mathcal{M}}}(a)$
is the definable closure of
![]() $a$
over
$a$
over
![]() ${\mathcal{M}}$
. This implies that the exchange principle with respect to definable closure (or algebraic closure, which is the same thing since there is an ordering) holds in the
${\mathcal{M}}$
. This implies that the exchange principle with respect to definable closure (or algebraic closure, which is the same thing since there is an ordering) holds in the
![]() $\text{VF}$
-sort, because it holds for T-models. Therefore, by [Reference Macpherson, Marker and SteinhornMMS00, § 4.12], we may equivalently define
$\text{VF}$
-sort, because it holds for T-models. Therefore, by [Reference Macpherson, Marker and SteinhornMMS00, § 4.12], we may equivalently define
 $\dim _{\text{VF}}(A)$
to be the maximum of the algebraic dimensions of the fibers
$\dim _{\text{VF}}(A)$
to be the maximum of the algebraic dimensions of the fibers
![]() $A_{t}$
,
$A_{t}$
,
 $t\in A_{\text{RV}}$
.
$t\in A_{\text{RV}}$
.
Algebraic dimension is defined for (any sort of) any theory whose models have the exchange property with respect to algebraic closure, or more generally any suitable notion of closure. In the present setting, the algebraic dimension of a set
 $B\subseteq \text{VF}^{n}$
that is definable over a substructure
$B\subseteq \text{VF}^{n}$
that is definable over a substructure
![]() ${\mathcal{M}}$
is just the maximum of the ranks of the T-models
${\mathcal{M}}$
is just the maximum of the ranks of the T-models
 $\langle {\mathcal{M}},b\rangle _{T}$
,
$\langle {\mathcal{M}},b\rangle _{T}$
,
![]() $b\in B$
, relative to the T-model
$b\in B$
, relative to the T-model
 $\text{VF}({\mathcal{M}})$
(again, see [Reference van den Dries and LewenbergVdDL95, § 3.2] for the notion of ranks of
$\text{VF}({\mathcal{M}})$
(again, see [Reference van den Dries and LewenbergVdDL95, § 3.2] for the notion of ranks of
![]() $T$
-models). It can be shown that this does not depend on the choice of
$T$
-models). It can be shown that this does not depend on the choice of
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Yet another way to define this notion of
![]() $\text{VF}$
-dimension is to imitate [Reference YinYin10, Definiton 4.1], since we have the following lemma.
$\text{VF}$
-dimension is to imitate [Reference YinYin10, Definiton 4.1], since we have the following lemma.
Lemma 2.26. If
 $\dim _{\text{VF}}(A)=k$
then
$\dim _{\text{VF}}(A)=k$
then
![]() $k$
is the smallest number such that there is a definable injection
$k$
is the smallest number such that there is a definable injection
 $f:A\longrightarrow \text{VF}^{k}\times \text{RV}^{l}$
.
$f:A\longrightarrow \text{VF}^{k}\times \text{RV}^{l}$
.
Proof. This is immediate by a straightforward argument combining the exchange principle, Lemma 3.6 below, and compactness.
Alternatively, we may just quote [Reference Macpherson, Marker and SteinhornMMS00, Theorem 4.11]. ◻
Remark 2.27 (
 $\text{RV}$
-dimension and
$\text{RV}$
-dimension and
 $\unicode[STIX]{x1D6E4}$
-dimension).
$\unicode[STIX]{x1D6E4}$
-dimension).
It is routine to verify that the axioms concerning only the
![]() $\text{RV}$
-sort are all universal except for the one asserting that
$\text{RV}$
-sort are all universal except for the one asserting that
![]() $\Bbbk ^{\times }$
is a proper subgroup, which is existential. These axioms amount to a weakly
$\Bbbk ^{\times }$
is a proper subgroup, which is existential. These axioms amount to a weakly
![]() $o$
-minimal theory also and the exchange principle holds for this theory. Therefore, we can use the dimension theory of [Reference Macpherson, Marker and SteinhornMMS00, § 4] directly in the
$o$
-minimal theory also and the exchange principle holds for this theory. Therefore, we can use the dimension theory of [Reference Macpherson, Marker and SteinhornMMS00, § 4] directly in the
![]() $\text{RV}$
-sort as well. We call it the
$\text{RV}$
-sort as well. We call it the
![]() $\text{RV}$
-dimension and the corresponding operator is denoted by
$\text{RV}$
-dimension and the corresponding operator is denoted by
![]() $\dim _{\text{RV}}$
. Note that
$\dim _{\text{RV}}$
. Note that
![]() $\dim _{\text{RV}}$
does not depend on parameters (see [Reference Macpherson, Marker and SteinhornMMS00, § 4.12]) and agrees with the
$\dim _{\text{RV}}$
does not depend on parameters (see [Reference Macpherson, Marker and SteinhornMMS00, § 4.12]) and agrees with the
![]() $o$
-minimal dimension in the
$o$
-minimal dimension in the
![]() $\Bbbk$
-sort (see [Reference van den DriesVdD98, § 4.1]) whenever both are applicable.
$\Bbbk$
-sort (see [Reference van den DriesVdD98, § 4.1]) whenever both are applicable.
Similarly, we shall use the
![]() $o$
-minimal dimension in the
$o$
-minimal dimension in the
![]() $\unicode[STIX]{x1D6E4}$
-sort and call it the
$\unicode[STIX]{x1D6E4}$
-sort and call it the
![]() $\unicode[STIX]{x1D6E4}$
-dimension. The corresponding operator is denoted by
$\unicode[STIX]{x1D6E4}$
-dimension. The corresponding operator is denoted by
![]() $\dim _{\unicode[STIX]{x1D6E4}}$
.
$\dim _{\unicode[STIX]{x1D6E4}}$
.
Lemma 2.28. Let
 $U\subseteq \text{RV}^{n}$
be a definable set with
$U\subseteq \text{RV}^{n}$
be a definable set with
 $\dim _{\text{RV}}(U)=k$
. Then
$\dim _{\text{RV}}(U)=k$
. Then
 $\dim _{\text{RV}}(U_{\unicode[STIX]{x1D6FE}})=k$
for some
$\dim _{\text{RV}}(U_{\unicode[STIX]{x1D6FE}})=k$
for some
 $\unicode[STIX]{x1D6FE}\in \operatorname{vrv}(U)$
.
$\unicode[STIX]{x1D6FE}\in \operatorname{vrv}(U)$
.
Here
![]() $U_{\unicode[STIX]{x1D6FE}}$
denotes the pullback of
$U_{\unicode[STIX]{x1D6FE}}$
denotes the pullback of
![]() $\unicode[STIX]{x1D6FE}$
along the obvious function
$\unicode[STIX]{x1D6FE}$
along the obvious function
![]() $\operatorname{vrv}\restriction U$
, in line with the convention set in the last paragraph of Notation 2.4.
$\operatorname{vrv}\restriction U$
, in line with the convention set in the last paragraph of Notation 2.4.
Proof. By [Reference Macpherson, Marker and SteinhornMMS00, Theorem 4.11] we may assume
![]() $n=k$
. Then, for some
$n=k$
. Then, for some
 $\unicode[STIX]{x1D6FE}\in \operatorname{vrv}(U)$
,
$\unicode[STIX]{x1D6FE}\in \operatorname{vrv}(U)$
,
![]() $U_{\unicode[STIX]{x1D6FE}}$
contains an open subset of
$U_{\unicode[STIX]{x1D6FE}}$
contains an open subset of
![]() $\text{RV}^{n}$
. The lemma follows.◻
$\text{RV}^{n}$
. The lemma follows.◻
Lemma 2.29. Let
![]() $D\subseteq \unicode[STIX]{x1D6E4}^{n}$
be a definable set with
$D\subseteq \unicode[STIX]{x1D6E4}^{n}$
be a definable set with
 $\dim _{\unicode[STIX]{x1D6E4}}(D)=k$
. Then
$\dim _{\unicode[STIX]{x1D6E4}}(D)=k$
. Then
![]() $D^{\sharp }$
is definably bijective to a disjoint union of finitely many sets of the form
$D^{\sharp }$
is definably bijective to a disjoint union of finitely many sets of the form
 $(\Bbbk ^{+})^{n-k}\times {D^{\prime }}^{\sharp }$
, where
$(\Bbbk ^{+})^{n-k}\times {D^{\prime }}^{\sharp }$
, where
 $D^{\prime }\subseteq \unicode[STIX]{x1D6E4}^{k}$
.
$D^{\prime }\subseteq \unicode[STIX]{x1D6E4}^{k}$
.
Proof. Over a definable finite partition of
![]() $D$
, we may assume that
$D$
, we may assume that
 $D\subseteq (\unicode[STIX]{x1D6E4}^{+})^{n}$
and the restriction
$D\subseteq (\unicode[STIX]{x1D6E4}^{+})^{n}$
and the restriction
 $\operatorname{pr}_{{\leqslant}k}\restriction D$
is injective. It follows from [Reference van den DriesVdD97, Theorem B] that the induced function
$\operatorname{pr}_{{\leqslant}k}\restriction D$
is injective. It follows from [Reference van den DriesVdD97, Theorem B] that the induced function
 $f:D_{{\leqslant}k}\longrightarrow D_{{>}k}$
is piecewise
$f:D_{{\leqslant}k}\longrightarrow D_{{>}k}$
is piecewise
![]() $\unicode[STIX]{x1D542}$
-linear. Thus, for every
$\unicode[STIX]{x1D542}$
-linear. Thus, for every
 $\unicode[STIX]{x1D6FE}\in D_{{\leqslant}k}$
and every
$\unicode[STIX]{x1D6FE}\in D_{{\leqslant}k}$
and every
![]() $t\in \unicode[STIX]{x1D6FE}^{\sharp }$
there is a
$t\in \unicode[STIX]{x1D6FE}^{\sharp }$
there is a
![]() $t$
-definable point in
$t$
-definable point in
![]() $f(\unicode[STIX]{x1D6FE})^{\sharp }$
. The assertion follows.◻
$f(\unicode[STIX]{x1D6FE})^{\sharp }$
. The assertion follows.◻
Taking disjoint union of finitely many definable sets of course will introduce extra bookkeeping coordinates, but we shall suppress this in notation.
Remark 2.30 (
 $o$
-minimal sets in
$o$
-minimal sets in
 $\text{RV}$
).
$\text{RV}$
).
The theory of
![]() $o$
-minimality, in particular its terminologies and notions, may be applied to a set
$o$
-minimality, in particular its terminologies and notions, may be applied to a set
 $U\subseteq \text{RV}^{n}$
such that
$U\subseteq \text{RV}^{n}$
such that
![]() $\operatorname{vrv}(U)$
is a singleton or, more generally, is finite. For example, we shall say that
$\operatorname{vrv}(U)$
is a singleton or, more generally, is finite. For example, we shall say that
![]() $U$
is a cell if the multiplicative translation
$U$
is a cell if the multiplicative translation
 $U/u\subseteq (\Bbbk ^{+})^{n}$
of
$U/u\subseteq (\Bbbk ^{+})^{n}$
of
![]() $U$
by some
$U$
by some
![]() $u\in U$
is an
$u\in U$
is an
![]() $o$
-minimal cell (see [Reference van den DriesVdD98, § 3]); this definition does not depend on the choice of
$o$
-minimal cell (see [Reference van den DriesVdD98, § 3]); this definition does not depend on the choice of
![]() $u$
. Similarly, the
$u$
. Similarly, the
![]() $o$
-minimal Euler characteristic
$o$
-minimal Euler characteristic
![]() $\unicode[STIX]{x1D712}(U)$
of such a set
$\unicode[STIX]{x1D712}(U)$
of such a set
![]() $U$
is the
$U$
is the
![]() $o$
-minimal Euler characteristic of
$o$
-minimal Euler characteristic of
![]() $U/u$
(see [Reference van den DriesVdD98, § 4.2]). This definition may be extended to disjoint unions of finitely many (not necessarily disjoint) sets
$U/u$
(see [Reference van den DriesVdD98, § 4.2]). This definition may be extended to disjoint unions of finitely many (not necessarily disjoint) sets
 $U_{i}\subseteq \text{RV}^{n}\times \unicode[STIX]{x1D6E4}^{m}$
such that each
$U_{i}\subseteq \text{RV}^{n}\times \unicode[STIX]{x1D6E4}^{m}$
such that each
![]() $\operatorname{vrv}(U_{i})$
is finite.
$\operatorname{vrv}(U_{i})$
is finite.
Theorem 2.31. Let
![]() $U$
,
$U$
,
![]() $V$
be definable sets in
$V$
be definable sets in
![]() $\text{RV}$
with
$\text{RV}$
with
![]() $\operatorname{vrv}(U)$
,
$\operatorname{vrv}(U)$
,
![]() $\operatorname{vrv}(V)$
finite. Then there is a definable bijection between
$\operatorname{vrv}(V)$
finite. Then there is a definable bijection between
![]() $U$
and
$U$
and
![]() $V$
if and only if
$V$
if and only if
 $$\begin{eqnarray}\dim _{\text{RV}}(U)=\dim _{\text{RV}}(V)\quad \text{and}\quad \unicode[STIX]{x1D712}(U)=\unicode[STIX]{x1D712}(V).\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\text{RV}}(U)=\dim _{\text{RV}}(V)\quad \text{and}\quad \unicode[STIX]{x1D712}(U)=\unicode[STIX]{x1D712}(V).\end{eqnarray}$$
Proof. See [Reference van den DriesVdD98, § 8.2.11]. ◻
Definition 2.32 (Valuative discs).
A set
![]() $\mathfrak{b}\subseteq \text{VF}$
is an open disc if there is a
$\mathfrak{b}\subseteq \text{VF}$
is an open disc if there is a
![]() $\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|$
and a
$\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|$
and a
![]() $b\in \mathfrak{b}$
such that
$b\in \mathfrak{b}$
such that
![]() $a\in \mathfrak{b}$
if and only if
$a\in \mathfrak{b}$
if and only if
 $|\text{val}|(a-b)>\unicode[STIX]{x1D6FE}$
; it is a closed disc if
$|\text{val}|(a-b)>\unicode[STIX]{x1D6FE}$
; it is a closed disc if
![]() $a\in \mathfrak{b}$
if and only if
$a\in \mathfrak{b}$
if and only if
 $|\text{val}|(a-b)\geqslant \unicode[STIX]{x1D6FE}$
. The point
$|\text{val}|(a-b)\geqslant \unicode[STIX]{x1D6FE}$
. The point
![]() $b$
is a center of
$b$
is a center of
![]() $\mathfrak{b}$
. The value
$\mathfrak{b}$
. The value
![]() $\unicode[STIX]{x1D6FE}$
is the valuative radius or simply the radius of
$\unicode[STIX]{x1D6FE}$
is the valuative radius or simply the radius of
![]() $\mathfrak{b}$
, which is denoted by
$\mathfrak{b}$
, which is denoted by
![]() $\operatorname{rad}(\mathfrak{b})$
. A set of the form
$\operatorname{rad}(\mathfrak{b})$
. A set of the form
![]() $t^{\sharp }$
, where
$t^{\sharp }$
, where
![]() $t\in \text{RV}$
, is called an
$t\in \text{RV}$
, is called an
![]() $\text{RV}$
-disc (recall Notation 2.24).
$\text{RV}$
-disc (recall Notation 2.24).
A closed disc with a maximal open subdisc removed is called a thin annulus.
A set
 $\mathfrak{p}\subseteq \text{VF}^{n}\times \text{RV}_{0}^{m}$
of the form
$\mathfrak{p}\subseteq \text{VF}^{n}\times \text{RV}_{0}^{m}$
of the form
 $(\prod _{i\leqslant n}\mathfrak{b}_{i})\times t$
is an (open, closed,
$(\prod _{i\leqslant n}\mathfrak{b}_{i})\times t$
is an (open, closed,
![]() $\text{RV}$
-) polydisc, where each
$\text{RV}$
-) polydisc, where each
![]() $\mathfrak{b}_{i}$
is an (open, closed,
$\mathfrak{b}_{i}$
is an (open, closed,
![]() $\text{RV}$
-) disc. The polyradius
$\text{RV}$
-) disc. The polyradius
![]() $\operatorname{rad}(\mathfrak{p})$
of
$\operatorname{rad}(\mathfrak{p})$
of
![]() $\mathfrak{p}$
is the tuple
$\mathfrak{p}$
is the tuple
 $(\operatorname{rad}(\mathfrak{b}_{1}),\ldots ,\operatorname{rad}(\mathfrak{b}_{n}))$
, whereas the radius of
$(\operatorname{rad}(\mathfrak{b}_{1}),\ldots ,\operatorname{rad}(\mathfrak{b}_{n}))$
, whereas the radius of
![]() $\mathfrak{p}$
is
$\mathfrak{p}$
is
 $\min \operatorname{rad}(\mathfrak{p})$
. If all the discs
$\min \operatorname{rad}(\mathfrak{p})$
. If all the discs
![]() $\mathfrak{b}_{i}$
are of the same valuative radius then
$\mathfrak{b}_{i}$
are of the same valuative radius then
![]() $\mathfrak{p}$
is referred to as a ball.
$\mathfrak{p}$
is referred to as a ball.
The open and the closed polydiscs centered at a point
 $a\in \text{VF}^{n}$
with polyradius
$a\in \text{VF}^{n}$
with polyradius
 $\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|^{n}$
are denoted by
$\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|^{n}$
are denoted by
![]() $\mathfrak{o}(a,\unicode[STIX]{x1D6FE})$
and
$\mathfrak{o}(a,\unicode[STIX]{x1D6FE})$
and
![]() $\mathfrak{c}(a,\unicode[STIX]{x1D6FE})$
, respectively.
$\mathfrak{c}(a,\unicode[STIX]{x1D6FE})$
, respectively.
The
![]() $\text{RV}$
-hull of a set
$\text{RV}$
-hull of a set
![]() $A$
, denoted by
$A$
, denoted by
 $\operatorname{RVH}(A)$
, is the union of all the
$\operatorname{RVH}(A)$
, is the union of all the
![]() $\text{RV}$
-polydiscs whose intersections with
$\text{RV}$
-polydiscs whose intersections with
![]() $A$
are nonempty. If
$A$
are nonempty. If
![]() $A$
equals
$A$
equals
 $\operatorname{RVH}(A)$
then
$\operatorname{RVH}(A)$
then
![]() $A$
is called an
$A$
is called an
![]() $\text{RV}$
-pullback.
$\text{RV}$
-pullback.
The map
![]() $|\text{val}|$
is constant on a disc if and only if it does not contain
$|\text{val}|$
is constant on a disc if and only if it does not contain
![]() $0$
if and only it is contained in an
$0$
if and only it is contained in an
![]() $\text{RV}$
-disc. If two discs have nonempty intersection then one of them contains the other. Many such elementary facts about discs will be used throughout the rest of the paper without further explanation.
$\text{RV}$
-disc. If two discs have nonempty intersection then one of them contains the other. Many such elementary facts about discs will be used throughout the rest of the paper without further explanation.
Notation 2.33 (The definable sort
 $\operatorname{DC}$
of discs).
$\operatorname{DC}$
of discs).
At times it will be more convenient to work in the traditional expansion
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\text{eq}}$
of
${\mathcal{R}}_{\operatorname{rv}}^{\text{eq}}$
of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
by all definable sorts. However, for our purpose, a much simpler expansion
${\mathcal{R}}_{\operatorname{rv}}$
by all definable sorts. However, for our purpose, a much simpler expansion
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
suffices. This expansion has only one additional sort
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
suffices. This expansion has only one additional sort
![]() $\operatorname{DC}$
that contains, as elements, all the open and closed discs (since each point in
$\operatorname{DC}$
that contains, as elements, all the open and closed discs (since each point in
![]() $\text{VF}$
may be regarded as a closed disc of valuative radius
$\text{VF}$
may be regarded as a closed disc of valuative radius
![]() $\infty$
, for convenience, we may and occasionally do think of
$\infty$
, for convenience, we may and occasionally do think of
![]() $\text{VF}$
as a subset of
$\text{VF}$
as a subset of
![]() $\operatorname{DC}$
). Heuristically, we may think of a disc that is properly contained in an
$\operatorname{DC}$
). Heuristically, we may think of a disc that is properly contained in an
![]() $\text{RV}$
-disc as a ‘thickened’ point of certain stature in
$\text{RV}$
-disc as a ‘thickened’ point of certain stature in
![]() $\text{VF}$
. For each
$\text{VF}$
. For each
![]() $\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|$
, there are two additional cross-sort maps
$\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|$
, there are two additional cross-sort maps
 $\text{VF}\longrightarrow \operatorname{DC}$
in
$\text{VF}\longrightarrow \operatorname{DC}$
in
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
; one sends
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
; one sends
![]() $a$
to the open disc, the other to the closed disc, of radius
$a$
to the open disc, the other to the closed disc, of radius
![]() $\unicode[STIX]{x1D6FE}$
that contains
$\unicode[STIX]{x1D6FE}$
that contains
![]() $a$
.
$a$
.
The expansion
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
can help reduce the technical complexity of our discussion. However, as is the case with the imaginary
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
can help reduce the technical complexity of our discussion. However, as is the case with the imaginary
![]() $\unicode[STIX]{x1D6E4}$
-sort, it is conceptually inessential since, for the purpose of this paper, all allusions to discs as (imaginary) elements may be eliminated in favor of objects already definable in
$\unicode[STIX]{x1D6E4}$
-sort, it is conceptually inessential since, for the purpose of this paper, all allusions to discs as (imaginary) elements may be eliminated in favor of objects already definable in
![]() ${\mathcal{R}}_{\operatorname{rv}}$
.
${\mathcal{R}}_{\operatorname{rv}}$
.
Whether parameters in
![]() $\operatorname{DC}$
are used or not shall be indicated explicitly, if it is necessary. Note that it is redundant to include in
$\operatorname{DC}$
are used or not shall be indicated explicitly, if it is necessary. Note that it is redundant to include in
![]() $\operatorname{DC}$
discs centered at
$\operatorname{DC}$
discs centered at
![]() $0$
, since they may be identified with their valuative radii.
$0$
, since they may be identified with their valuative radii.
For a disc
![]() $\mathfrak{a}\subseteq \text{VF}$
, the corresponding imaginary element in
$\mathfrak{a}\subseteq \text{VF}$
, the corresponding imaginary element in
![]() $\operatorname{DC}$
is denoted by
$\operatorname{DC}$
is denoted by
![]() $\ulcorner \mathfrak{a}\urcorner$
when notational distinction makes the discussion more streamlined;
$\ulcorner \mathfrak{a}\urcorner$
when notational distinction makes the discussion more streamlined;
![]() $\ulcorner \mathfrak{a}\urcorner$
may be heuristically thought of as the ‘name’ of
$\ulcorner \mathfrak{a}\urcorner$
may be heuristically thought of as the ‘name’ of
![]() $\mathfrak{a}$
. Conversely, a set
$\mathfrak{a}$
. Conversely, a set
 $D\subseteq \operatorname{DC}$
is often identified with the set
$D\subseteq \operatorname{DC}$
is often identified with the set
 $\{\mathfrak{a}:\ulcorner \mathfrak{a}\urcorner \in D\}$
, in which case
$\{\mathfrak{a}:\ulcorner \mathfrak{a}\urcorner \in D\}$
, in which case
![]() $\bigcup D$
denotes a subset of
$\bigcup D$
denotes a subset of
![]() $\text{VF}$
.
$\text{VF}$
.
Notation 2.34. For each
![]() $\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|$
, let
$\unicode[STIX]{x1D6FE}\in |\unicode[STIX]{x1D6E4}|$
, let
![]() $\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
and
$\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
and
![]() $\mathfrak{O}_{\unicode[STIX]{x1D6FE}}$
be the open and closed discs around
$\mathfrak{O}_{\unicode[STIX]{x1D6FE}}$
be the open and closed discs around
![]() $0$
with radius
$0$
with radius
![]() $\unicode[STIX]{x1D6FE}$
, respectively. Assume
$\unicode[STIX]{x1D6FE}$
, respectively. Assume
![]() $\unicode[STIX]{x1D6FE}\geqslant 0$
. Let
$\unicode[STIX]{x1D6FE}\geqslant 0$
. Let
 $\text{RV}_{\unicode[STIX]{x1D6FE}}=\text{VF}^{\times }/(1+\mathfrak{M}_{\unicode[STIX]{x1D6FE}})$
, which is a subset of
$\text{RV}_{\unicode[STIX]{x1D6FE}}=\text{VF}^{\times }/(1+\mathfrak{M}_{\unicode[STIX]{x1D6FE}})$
, which is a subset of
![]() $\operatorname{DC}$
. It is an abelian group and also inherits an ordering from
$\operatorname{DC}$
. It is an abelian group and also inherits an ordering from
![]() $\text{VF}^{\times }$
. The canonical map
$\text{VF}^{\times }$
. The canonical map
 $\text{VF}^{\times }\longrightarrow \text{RV}_{\unicode[STIX]{x1D6FE}}$
is denoted by
$\text{VF}^{\times }\longrightarrow \text{RV}_{\unicode[STIX]{x1D6FE}}$
is denoted by
![]() $\operatorname{rv}_{\unicode[STIX]{x1D6FE}}$
and is augmented by
$\operatorname{rv}_{\unicode[STIX]{x1D6FE}}$
and is augmented by
 $\operatorname{rv}_{\unicode[STIX]{x1D6FE}}(0)=0$
.
$\operatorname{rv}_{\unicode[STIX]{x1D6FE}}(0)=0$
.
If
 $\ulcorner \mathfrak{b}\urcorner \in \operatorname{DC}$
,
$\ulcorner \mathfrak{b}\urcorner \in \operatorname{DC}$
,
![]() $b\in \mathfrak{b}$
, and
$b\in \mathfrak{b}$
, and
 $\operatorname{rad}(\mathfrak{b})\leqslant |\text{val}|(b)+\unicode[STIX]{x1D6FE}$
then
$\operatorname{rad}(\mathfrak{b})\leqslant |\text{val}|(b)+\unicode[STIX]{x1D6FE}$
then
![]() $\mathfrak{b}$
is a union of discs of the form
$\mathfrak{b}$
is a union of discs of the form
 $\operatorname{rv}_{\unicode[STIX]{x1D6FE}}^{-1}(\ulcorner \mathfrak{a}\urcorner )$
. In this case, we shall abuse the notation slightly and write
$\operatorname{rv}_{\unicode[STIX]{x1D6FE}}^{-1}(\ulcorner \mathfrak{a}\urcorner )$
. In this case, we shall abuse the notation slightly and write
![]() $\ulcorner \mathfrak{a}\urcorner \in \mathfrak{b}$
,
$\ulcorner \mathfrak{a}\urcorner \in \mathfrak{b}$
,
 $\mathfrak{b}\subseteq \text{RV}_{\unicode[STIX]{x1D6FE}}$
, etc.
$\mathfrak{b}\subseteq \text{RV}_{\unicode[STIX]{x1D6FE}}$
, etc.
For each
 $\ulcorner \mathfrak{a}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}}$
, let
$\ulcorner \mathfrak{a}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}}$
, let
 $\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\subseteq \text{RV}_{\unicode[STIX]{x1D6FE}}$
be the
$\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\subseteq \text{RV}_{\unicode[STIX]{x1D6FE}}$
be the
![]() $\ulcorner \mathfrak{a}\urcorner$
-definable subset such that
$\ulcorner \mathfrak{a}\urcorner$
-definable subset such that
 $\operatorname{rv}_{\unicode[STIX]{x1D6FE}}^{-1}(\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner ))$
forms the smallest closed disc containing
$\operatorname{rv}_{\unicode[STIX]{x1D6FE}}^{-1}(\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner ))$
forms the smallest closed disc containing
![]() $\mathfrak{a}$
. Set
$\mathfrak{a}$
. Set
 $$\begin{eqnarray}\displaystyle \operatorname{Tor}^{\times }(\ulcorner \mathfrak{a}\urcorner ) & = & \displaystyle \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\smallsetminus \ulcorner \mathfrak{a}\urcorner ,\nonumber\\ \displaystyle \operatorname{Tor}^{+}(\ulcorner \mathfrak{a}\urcorner ) & = & \displaystyle \{t\in \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner ):t>\ulcorner \mathfrak{a}\urcorner \},\nonumber\\ \displaystyle \operatorname{Tor}^{-}(\ulcorner \mathfrak{a}\urcorner ) & = & \displaystyle \{t\in \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner ):t<\ulcorner \mathfrak{a}\urcorner \}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Tor}^{\times }(\ulcorner \mathfrak{a}\urcorner ) & = & \displaystyle \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\smallsetminus \ulcorner \mathfrak{a}\urcorner ,\nonumber\\ \displaystyle \operatorname{Tor}^{+}(\ulcorner \mathfrak{a}\urcorner ) & = & \displaystyle \{t\in \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner ):t>\ulcorner \mathfrak{a}\urcorner \},\nonumber\\ \displaystyle \operatorname{Tor}^{-}(\ulcorner \mathfrak{a}\urcorner ) & = & \displaystyle \{t\in \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner ):t<\ulcorner \mathfrak{a}\urcorner \}.\nonumber\end{eqnarray}$$
If
 $\ulcorner \mathfrak{a}\urcorner =(\ulcorner \mathfrak{a}_{1}\urcorner ,\ldots ,\ulcorner \mathfrak{a}_{n}\urcorner )$
with
$\ulcorner \mathfrak{a}\urcorner =(\ulcorner \mathfrak{a}_{1}\urcorner ,\ldots ,\ulcorner \mathfrak{a}_{n}\urcorner )$
with
 $\ulcorner \mathfrak{a}_{i}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}_{i}}$
then
$\ulcorner \mathfrak{a}_{i}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}_{i}}$
then
 $\prod _{i}\operatorname{Tor}(\ulcorner \mathfrak{a}_{i}\urcorner )$
is simply written as
$\prod _{i}\operatorname{Tor}(\ulcorner \mathfrak{a}_{i}\urcorner )$
is simply written as
 $\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
; similarly for
$\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
; similarly for
 $\operatorname{Tor}^{\times }(\ulcorner \mathfrak{a}\urcorner )$
,
$\operatorname{Tor}^{\times }(\ulcorner \mathfrak{a}\urcorner )$
,
 $\operatorname{Tor}^{+}(\ulcorner \mathfrak{a}\urcorner )$
, etc.
$\operatorname{Tor}^{+}(\ulcorner \mathfrak{a}\urcorner )$
, etc.
If
![]() $\unicode[STIX]{x1D6FE}=0$
then we may, for all purposes, identify
$\unicode[STIX]{x1D6FE}=0$
then we may, for all purposes, identify
 $\operatorname{Tor}^{\times }(\ulcorner \mathfrak{a}\urcorner )$
,
$\operatorname{Tor}^{\times }(\ulcorner \mathfrak{a}\urcorner )$
,
 $\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
, etc., with
$\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
, etc., with
 $\operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC}):=|\text{vrv}|^{-1}(\unicode[STIX]{x1D6FC})\subseteq \text{RV}$
,
$\operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC}):=|\text{vrv}|^{-1}(\unicode[STIX]{x1D6FC})\subseteq \text{RV}$
,
 $\operatorname{Tor}(\unicode[STIX]{x1D6FC}):=\operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})\cup \{0\}$
, etc., where
$\operatorname{Tor}(\unicode[STIX]{x1D6FC}):=\operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})\cup \{0\}$
, etc., where
 $\unicode[STIX]{x1D6FC}=\operatorname{rad}(\mathfrak{a})$
.
$\unicode[STIX]{x1D6FC}=\operatorname{rad}(\mathfrak{a})$
.
Remark 2.35 (
 $\Bbbk$
-torsors).
$\Bbbk$
-torsors).
Let
 $\ulcorner \mathfrak{a}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}}$
and
$\ulcorner \mathfrak{a}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}}$
and
 $\unicode[STIX]{x1D6FC}=\operatorname{rad}(\mathfrak{a})$
. Since, via additive translation by
$\unicode[STIX]{x1D6FC}=\operatorname{rad}(\mathfrak{a})$
. Since, via additive translation by
![]() $\ulcorner \mathfrak{a}\urcorner$
, there is a canonical
$\ulcorner \mathfrak{a}\urcorner$
, there is a canonical
![]() $\ulcorner \mathfrak{a}\urcorner$
-definable order-preserving bijection
$\ulcorner \mathfrak{a}\urcorner$
-definable order-preserving bijection
 $$\begin{eqnarray}\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner }:\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\longrightarrow \operatorname{Tor}(\unicode[STIX]{x1D6FC}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner }:\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\longrightarrow \operatorname{Tor}(\unicode[STIX]{x1D6FC}),\end{eqnarray}$$
we see that
![]() $\ulcorner \mathfrak{a}\urcorner$
-definable subsets of
$\ulcorner \mathfrak{a}\urcorner$
-definable subsets of
 $\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )^{n}$
naturally correspond to those of
$\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )^{n}$
naturally correspond to those of
 $\operatorname{Tor}(\unicode[STIX]{x1D6FC})^{n}$
. If there is an
$\operatorname{Tor}(\unicode[STIX]{x1D6FC})^{n}$
. If there is an
![]() $\ulcorner \mathfrak{a}\urcorner$
-definable
$\ulcorner \mathfrak{a}\urcorner$
-definable
 $t\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})$
then, via multiplicative translation by
$t\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})$
then, via multiplicative translation by
![]() $t$
, this correspondence may be extended to
$t$
, this correspondence may be extended to
![]() $\ulcorner \mathfrak{a}\urcorner$
-definable subsets of
$\ulcorner \mathfrak{a}\urcorner$
-definable subsets of
 $\operatorname{Tor}(0)^{n}=\Bbbk ^{n}$
. More generally, for any
$\operatorname{Tor}(0)^{n}=\Bbbk ^{n}$
. More generally, for any
 $t\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})$
, the induced bijection
$t\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})$
, the induced bijection
 $\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\longrightarrow \Bbbk$
is denoted by
$\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\longrightarrow \Bbbk$
is denoted by
![]() $\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner ,t}$
. Consequently,
$\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner ,t}$
. Consequently,
 $\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
may be viewed as a
$\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
may be viewed as a
![]() $\Bbbk$
-torsor and, as such, is equipped with much of the structure of
$\Bbbk$
-torsor and, as such, is equipped with much of the structure of
![]() $\Bbbk$
.
$\Bbbk$
.
Definition 2.36 (Derivation between
 $\Bbbk$
-torsors).
$\Bbbk$
-torsors).
Let
![]() $\ulcorner \mathfrak{a}\urcorner$
,
$\ulcorner \mathfrak{a}\urcorner$
,
![]() $\unicode[STIX]{x1D6FC}$
be as above. Let
$\unicode[STIX]{x1D6FC}$
be as above. Let
 $\ulcorner \mathfrak{b}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FF}}$
and
$\ulcorner \mathfrak{b}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FF}}$
and
 $\unicode[STIX]{x1D6FD}=\operatorname{rad}(\mathfrak{b})$
. Let
$\unicode[STIX]{x1D6FD}=\operatorname{rad}(\mathfrak{b})$
. Let
 $f:\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\longrightarrow \operatorname{Tor}(\ulcorner \mathfrak{b}\urcorner )$
be a function. We define the derivative
$f:\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\longrightarrow \operatorname{Tor}(\ulcorner \mathfrak{b}\urcorner )$
be a function. We define the derivative
 $(d/dx)f$
of
$(d/dx)f$
of
![]() $f$
at any point
$f$
at any point
 $\ulcorner \mathfrak{d}\urcorner \in \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
as follows. Choose any
$\ulcorner \mathfrak{d}\urcorner \in \operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )$
as follows. Choose any
 $t\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})$
and any
$t\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FC})$
and any
 $s\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FD})$
. Consider the function
$s\in \operatorname{Tor}^{\times }(\unicode[STIX]{x1D6FD})$
. Consider the function
 $$\begin{eqnarray}f_{\ulcorner \mathfrak{a}\urcorner ,\ulcorner \mathfrak{b}\urcorner ,t,s}:\Bbbk \rightarrow ^{\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner ,t}^{-1}}\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\rightarrow ^{f}\operatorname{Tor}(\ulcorner \mathfrak{b}\urcorner )\rightarrow ^{\operatorname{Aff}_{\ulcorner \mathfrak{b}\urcorner ,s}}\Bbbk .\end{eqnarray}$$
$$\begin{eqnarray}f_{\ulcorner \mathfrak{a}\urcorner ,\ulcorner \mathfrak{b}\urcorner ,t,s}:\Bbbk \rightarrow ^{\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner ,t}^{-1}}\operatorname{Tor}(\ulcorner \mathfrak{a}\urcorner )\rightarrow ^{f}\operatorname{Tor}(\ulcorner \mathfrak{b}\urcorner )\rightarrow ^{\operatorname{Aff}_{\ulcorner \mathfrak{b}\urcorner ,s}}\Bbbk .\end{eqnarray}$$
Put
 $r=\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner ,t}(\ulcorner \mathfrak{d}\urcorner )$
and suppose that
$r=\operatorname{Aff}_{\ulcorner \mathfrak{a}\urcorner ,t}(\ulcorner \mathfrak{d}\urcorner )$
and suppose that
 $(d/dx)f_{\ulcorner \mathfrak{a}\urcorner ,\ulcorner \mathfrak{b}\urcorner ,t,s}(r)\in \Bbbk$
exists. Then we set
$(d/dx)f_{\ulcorner \mathfrak{a}\urcorner ,\ulcorner \mathfrak{b}\urcorner ,t,s}(r)\in \Bbbk$
exists. Then we set
 $$\begin{eqnarray}\frac{d}{dx}f(\ulcorner \mathfrak{d}\urcorner )=st^{-1}\frac{d}{dx}f_{\ulcorner \mathfrak{a}\urcorner ,\ulcorner \mathfrak{b}\urcorner ,t,s}(r)\in \operatorname{Tor}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{d}{dx}f(\ulcorner \mathfrak{d}\urcorner )=st^{-1}\frac{d}{dx}f_{\ulcorner \mathfrak{a}\urcorner ,\ulcorner \mathfrak{b}\urcorner ,t,s}(r)\in \operatorname{Tor}(\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
It is routine to check that this construction does not depend on the choice of
![]() $\ulcorner \mathfrak{a}\urcorner$
,
$\ulcorner \mathfrak{a}\urcorner$
,
![]() $\ulcorner \mathfrak{b}\urcorner$
,
$\ulcorner \mathfrak{b}\urcorner$
,
![]() $t$
,
$t$
,
![]() $s$
and hence the derivative
$s$
and hence the derivative
 $(d/dx)f(\ulcorner \mathfrak{d}\urcorner )$
is well defined.
$(d/dx)f(\ulcorner \mathfrak{d}\urcorner )$
is well defined.
Definition 2.37 (
 $\operatorname{val}$
-intervals).
$\operatorname{val}$
-intervals).
Let
![]() $\mathfrak{a}$
,
$\mathfrak{a}$
,
![]() $\mathfrak{b}$
be discs, not necessarily disjoint. The subset
$\mathfrak{b}$
be discs, not necessarily disjoint. The subset
 $\mathfrak{a}<x<\mathfrak{b}$
of
$\mathfrak{a}<x<\mathfrak{b}$
of
![]() $\text{VF}$
, if it is not empty, is called an open
$\text{VF}$
, if it is not empty, is called an open
![]() $\operatorname{val}$
-interval and is denoted by
$\operatorname{val}$
-interval and is denoted by
![]() $(\mathfrak{a},\mathfrak{b})$
, whereas the subset
$(\mathfrak{a},\mathfrak{b})$
, whereas the subset
 $$\begin{eqnarray}\{a\in \text{VF}:\exists x\in \mathfrak{a},y\in \mathfrak{b}\;(x\leqslant a\leqslant y)\},\end{eqnarray}$$
$$\begin{eqnarray}\{a\in \text{VF}:\exists x\in \mathfrak{a},y\in \mathfrak{b}\;(x\leqslant a\leqslant y)\},\end{eqnarray}$$
if it is not empty, is called a closed
![]() $\operatorname{val}$
-interval and is denoted by
$\operatorname{val}$
-interval and is denoted by
![]() $[\mathfrak{a},\mathfrak{b}]$
. The other
$[\mathfrak{a},\mathfrak{b}]$
. The other
![]() $\operatorname{val}$
-intervals
$\operatorname{val}$
-intervals
![]() $[\mathfrak{a},\mathfrak{b})$
,
$[\mathfrak{a},\mathfrak{b})$
,
 $(-\infty ,\mathfrak{b}]$
, etc., are defined in the obvious way, where
$(-\infty ,\mathfrak{b}]$
, etc., are defined in the obvious way, where
 $(-\infty ,\mathfrak{b}]$
is a closed (or half-closed)
$(-\infty ,\mathfrak{b}]$
is a closed (or half-closed)
![]() $\operatorname{val}$
-interval that is unbounded from below.
$\operatorname{val}$
-interval that is unbounded from below.
Let
![]() $A$
be such a
$A$
be such a
![]() $\operatorname{val}$
-interval. The discs
$\operatorname{val}$
-interval. The discs
![]() $\mathfrak{a}$
,
$\mathfrak{a}$
,
![]() $\mathfrak{b}$
are called the end-discs of
$\mathfrak{b}$
are called the end-discs of
![]() $A$
. If
$A$
. If
![]() $\mathfrak{a}$
,
$\mathfrak{a}$
,
![]() $\mathfrak{b}$
are both points in
$\mathfrak{b}$
are both points in
![]() $\text{VF}$
then of course we just say that
$\text{VF}$
then of course we just say that
![]() $A$
is an interval, and if
$A$
is an interval, and if
![]() $\mathfrak{a}$
,
$\mathfrak{a}$
,
![]() $\mathfrak{b}$
are both
$\mathfrak{b}$
are both
![]() $\text{RV}$
-discs then we say that
$\text{RV}$
-discs then we say that
![]() $A$
is an
$A$
is an
![]() $\text{RV}$
-interval. If
$\text{RV}$
-interval. If
![]() $A$
is of the form
$A$
is of the form
![]() $(\mathfrak{a},\mathfrak{b}]$
or
$(\mathfrak{a},\mathfrak{b}]$
or
![]() $[\mathfrak{b},\mathfrak{a})$
, where
$[\mathfrak{b},\mathfrak{a})$
, where
![]() $\mathfrak{a}$
is an open disc and
$\mathfrak{a}$
is an open disc and
![]() $\mathfrak{b}$
is the smallest closed disc containing
$\mathfrak{b}$
is the smallest closed disc containing
![]() $\mathfrak{a}$
, then
$\mathfrak{a}$
, then
![]() $A$
is called a half thin annulus and the radius of
$A$
is called a half thin annulus and the radius of
![]() $A$
is
$A$
is
![]() $\operatorname{rad}(\mathfrak{b})$
.
$\operatorname{rad}(\mathfrak{b})$
.
Two
![]() $\operatorname{val}$
-intervals are disconnected if their union is not a
$\operatorname{val}$
-intervals are disconnected if their union is not a
![]() $\operatorname{val}$
-interval.
$\operatorname{val}$
-interval.
Obviously the open
![]() $\operatorname{val}$
-interval
$\operatorname{val}$
-interval
![]() $(\mathfrak{a},\mathfrak{b})$
is empty if
$(\mathfrak{a},\mathfrak{b})$
is empty if
![]() $\mathfrak{a}$
,
$\mathfrak{a}$
,
![]() $\mathfrak{b}$
are not disjoint. Equally obvious is that a
$\mathfrak{b}$
are not disjoint. Equally obvious is that a
![]() $\operatorname{val}$
-interval is definable over some substructure
$\operatorname{val}$
-interval is definable over some substructure
![]() ${\mathcal{S}}$
if and only if its end-discs are definable over
${\mathcal{S}}$
if and only if its end-discs are definable over
![]() ${\mathcal{S}}$
.
${\mathcal{S}}$
.
Remark 2.38 (Holly normal form).
By the valuation property Proposition 2.21 and [Reference van den DriesVdD97, Proposition 7.6], we have an important tool called Holly normal form [Reference HollyHol95, Theorem 4.8] (HNF); that is, every definable subset of
![]() $\text{VF}$
is a unique union of finitely many definable pairwise disconnected
$\text{VF}$
is a unique union of finitely many definable pairwise disconnected
![]() $\operatorname{val}$
-intervals. This is obviously a generalization of the
$\operatorname{val}$
-intervals. This is obviously a generalization of the
![]() $o$
-minimal condition.
$o$
-minimal condition.
3 Definable sets in
 $\text{VF}$
$\text{VF}$
From here on, we shall work with a fixed small substructure
![]() ${\mathcal{S}}$
of
${\mathcal{S}}$
of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
, also occasionally of
${\mathcal{R}}_{\operatorname{rv}}$
, also occasionally of
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
(primarily in this section). The conceptual reason for this move is that the Grothendieck rings in our main construction below change their meaning if the set of parameters changes. In particular, allowing all parameters trivializes the whole construction somewhat. For instance, every definable set will contain a definable point. Consequently, all Galois actions on the classes of finite definable sets are killed off, and this is highly undesirable for motivic integration in algebraically closed valued fields. Admittedly, this problem is not as severe in our setting. Anyway, we follow the practice in [Reference Hrushovski and KazhdanHK06].
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
(primarily in this section). The conceptual reason for this move is that the Grothendieck rings in our main construction below change their meaning if the set of parameters changes. In particular, allowing all parameters trivializes the whole construction somewhat. For instance, every definable set will contain a definable point. Consequently, all Galois actions on the classes of finite definable sets are killed off, and this is highly undesirable for motivic integration in algebraically closed valued fields. Admittedly, this problem is not as severe in our setting. Anyway, we follow the practice in [Reference Hrushovski and KazhdanHK06].
Note that
![]() ${\mathcal{S}}$
is regarded as a part of the language now and hence, contrary to the usual convention in the model-theoretic literature, ‘
${\mathcal{S}}$
is regarded as a part of the language now and hence, contrary to the usual convention in the model-theoretic literature, ‘
![]() $\emptyset$
-definable’ or ‘definable’ only means ‘
$\emptyset$
-definable’ or ‘definable’ only means ‘
![]() ${\mathcal{S}}$
-definable’ instead of ‘parametrically definable’ if no other qualifications are given. To simplify the notation, we shall not mention
${\mathcal{S}}$
-definable’ instead of ‘parametrically definable’ if no other qualifications are given. To simplify the notation, we shall not mention
![]() ${\mathcal{S}}$
and its extensions in context if no confusion can arise. For example, the definable closure operator
${\mathcal{S}}$
and its extensions in context if no confusion can arise. For example, the definable closure operator
![]() $\operatorname{dcl}_{{\mathcal{S}}}$
, etc., will simply be written as
$\operatorname{dcl}_{{\mathcal{S}}}$
, etc., will simply be written as
![]() $\operatorname{dcl}$
, etc.
$\operatorname{dcl}$
, etc.
For the moment we do not require that
![]() ${\mathcal{S}}$
be
${\mathcal{S}}$
be
![]() $\text{VF}$
-generated or
$\text{VF}$
-generated or
![]() $\unicode[STIX]{x1D6E4}({\mathcal{S}})$
be nontrivial. When we work in
$\unicode[STIX]{x1D6E4}({\mathcal{S}})$
be nontrivial. When we work in
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
(either by introducing parameters of the form
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
(either by introducing parameters of the form
![]() $\ulcorner \mathfrak{a}\urcorner$
or the phrase ‘in
$\ulcorner \mathfrak{a}\urcorner$
or the phrase ‘in
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
’) the substructure
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
’) the substructure
![]() ${\mathcal{S}}$
may contain names for discs that may or may not be definable from
${\mathcal{S}}$
may contain names for discs that may or may not be definable from
 $\text{VF}({\mathcal{S}})\cup \text{RV}({\mathcal{S}})$
.
$\text{VF}({\mathcal{S}})\cup \text{RV}({\mathcal{S}})$
.
3.1 Definable functions and atomic open discs
The structural analysis of definable sets in
![]() $\text{VF}$
below is, for the most part, of a rather technical nature. One highlight is Corollary 3.16. It is a crucial ingredient of the proof in [Reference Halupczok and YinHY15] that all definable closed sets in an arbitrary power-bounded
$\text{VF}$
below is, for the most part, of a rather technical nature. One highlight is Corollary 3.16. It is a crucial ingredient of the proof in [Reference Halupczok and YinHY15] that all definable closed sets in an arbitrary power-bounded
![]() $o$
-minimal field admit Lipschitz stratification.
$o$
-minimal field admit Lipschitz stratification.
Convention 3.1. Since apart from
![]() ${\leqslant}$
the language
${\leqslant}$
the language
![]() ${\mathcal{L}}_{T\text{}}$
only has function symbols, we may and shall assume that, in any
${\mathcal{L}}_{T\text{}}$
only has function symbols, we may and shall assume that, in any
![]() ${\mathcal{L}}_{T\text{RV}}$
-formula, every
${\mathcal{L}}_{T\text{RV}}$
-formula, every
![]() ${\mathcal{L}}_{T\text{}}$
-term occurs in the scope of an instance of the function symbol
${\mathcal{L}}_{T\text{}}$
-term occurs in the scope of an instance of the function symbol
![]() $\operatorname{rv}$
. For example, if
$\operatorname{rv}$
. For example, if
![]() $f(x)$
,
$f(x)$
,
![]() $g(x)$
are
$g(x)$
are
![]() ${\mathcal{L}}_{T\text{}}$
-terms then the formula
${\mathcal{L}}_{T\text{}}$
-terms then the formula
 $f(x)<g(x)$
is equivalent to
$f(x)<g(x)$
is equivalent to
 $\operatorname{rv}(f(x)-g(x))<0$
. The
$\operatorname{rv}(f(x)-g(x))<0$
. The
![]() ${\mathcal{L}}_{T\text{}}$
-term
${\mathcal{L}}_{T\text{}}$
-term
![]() $f(x)$
in
$f(x)$
in
 $\operatorname{rv}(f(x))$
shall be referred to as a top
$\operatorname{rv}(f(x))$
shall be referred to as a top
![]() ${\mathcal{L}}_{T\text{}}$
-term.
${\mathcal{L}}_{T\text{}}$
-term.
We begin by studying definable functions between various regions of the structure.
Lemma 3.2. Let
 $f:\mathfrak{O}\longrightarrow \text{VF}$
be a definable function. Then for some
$f:\mathfrak{O}\longrightarrow \text{VF}$
be a definable function. Then for some
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{0}$
and
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{0}$
and
![]() $a\in \mathfrak{O}$
we have
$a\in \mathfrak{O}$
we have
 $\operatorname{val}(f(b))=\unicode[STIX]{x1D6FE}$
for all
$\operatorname{val}(f(b))=\unicode[STIX]{x1D6FE}$
for all
![]() $b>a$
in
$b>a$
in
![]() $\mathfrak{O}$
.
$\mathfrak{O}$
.
Proof. See [Reference van den DriesVdD97, Proposition 4.2]. ◻
Note that this is false if
![]() $T$
is not power-bounded.
$T$
is not power-bounded.
A definable function
![]() $f$
is quasi-
$f$
is quasi-
![]() ${\mathcal{L}}_{T\text{}}$
-definable if it is a restriction of an
${\mathcal{L}}_{T\text{}}$
-definable if it is a restriction of an
![]() ${\mathcal{L}}_{T\text{}}$
-definable function (with parameters in
${\mathcal{L}}_{T\text{}}$
-definable function (with parameters in
![]() $\text{VF}({\mathcal{S}})$
, of course).
$\text{VF}({\mathcal{S}})$
, of course).
Lemma 3.3. Every definable function
 $f:\text{VF}^{n}\longrightarrow \text{VF}$
is piecewise quasi-
$f:\text{VF}^{n}\longrightarrow \text{VF}$
is piecewise quasi-
![]() ${\mathcal{L}}_{T\text{}}$
-definable; that is, there are a definable finite partition
${\mathcal{L}}_{T\text{}}$
-definable; that is, there are a definable finite partition
![]() $A_{i}$
of
$A_{i}$
of
![]() $\text{VF}^{n}$
and
$\text{VF}^{n}$
and
![]() ${\mathcal{L}}_{T\text{}}$
-definable functions
${\mathcal{L}}_{T\text{}}$
-definable functions
 $f_{i}:\text{VF}^{n}\longrightarrow \text{VF}$
such that
$f_{i}:\text{VF}^{n}\longrightarrow \text{VF}$
such that
 $f\restriction A_{i}=f_{i}\restriction A_{i}$
for all
$f\restriction A_{i}=f_{i}\restriction A_{i}$
for all
![]() $i$
.
$i$
.
Proof. By compactness, this is immediately reduced to the case
![]() $n=1$
. In that case, let
$n=1$
. In that case, let
![]() $\unicode[STIX]{x1D719}(x,y)$
be a quantifier-free formula that defines
$\unicode[STIX]{x1D719}(x,y)$
be a quantifier-free formula that defines
![]() $f$
. Let
$f$
. Let
![]() $\unicode[STIX]{x1D70F}_{i}(x,y)$
enumerate the top
$\unicode[STIX]{x1D70F}_{i}(x,y)$
enumerate the top
![]() ${\mathcal{L}}_{T\text{}}$
-terms in
${\mathcal{L}}_{T\text{}}$
-terms in
![]() $\unicode[STIX]{x1D719}(x,y)$
. For each
$\unicode[STIX]{x1D719}(x,y)$
. For each
![]() $a\in \text{VF}$
and each
$a\in \text{VF}$
and each
![]() $t_{i}(a,y)$
, let
$t_{i}(a,y)$
, let
 $B_{a,i}\subseteq \text{VF}$
be the characteristic finite subset of the function
$B_{a,i}\subseteq \text{VF}$
be the characteristic finite subset of the function
![]() $t_{i}(a,y)$
given by
$t_{i}(a,y)$
given by
![]() $o$
-minimal monotonicity (see [Reference van den DriesVdD98, § 3.1]). It is not difficult to see that if
$o$
-minimal monotonicity (see [Reference van den DriesVdD98, § 3.1]). It is not difficult to see that if
 $f(a)\notin \bigcup _{i}B_{a,i}$
then there would be a
$f(a)\notin \bigcup _{i}B_{a,i}$
then there would be a
 $b\neq f(a)$
such that
$b\neq f(a)$
such that
 $$\begin{eqnarray}\operatorname{rv}(\unicode[STIX]{x1D70F}_{i}(a,b))=\operatorname{rv}(\unicode[STIX]{x1D70F}_{i}(a,f(a)))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rv}(\unicode[STIX]{x1D70F}_{i}(a,b))=\operatorname{rv}(\unicode[STIX]{x1D70F}_{i}(a,f(a)))\end{eqnarray}$$
for all
![]() $i$
and hence
$i$
and hence
![]() $\unicode[STIX]{x1D719}(a,b)$
holds, which is impossible since
$\unicode[STIX]{x1D719}(a,b)$
holds, which is impossible since
![]() $f$
is a function. The lemma follows.◻
$f$
is a function. The lemma follows.◻
This lemma is just a variation of [Reference van den DriesVdD97, Lemma 2.6].
Corollary 3.4 (Monotonicity).
Let
 $A\subseteq \text{VF}$
and
$A\subseteq \text{VF}$
and
 $f:A\longrightarrow \text{VF}$
be a definable function. Then there is a definable finite partition of
$f:A\longrightarrow \text{VF}$
be a definable function. Then there is a definable finite partition of
![]() $A$
into
$A$
into
![]() $\operatorname{val}$
-intervals
$\operatorname{val}$
-intervals
![]() $A_{i}$
such that every
$A_{i}$
such that every
![]() $f\restriction A_{i}$
is quasi-
$f\restriction A_{i}$
is quasi-
![]() ${\mathcal{L}}_{T\text{}}$
-definable, continuous, and monotone (constant or strictly increasing or strictly decreasing). Consequently, each
${\mathcal{L}}_{T\text{}}$
-definable, continuous, and monotone (constant or strictly increasing or strictly decreasing). Consequently, each
![]() $f(A_{i})$
is a
$f(A_{i})$
is a
![]() $\operatorname{val}$
-interval.
$\operatorname{val}$
-interval.
Proof. This is immediate by Lemma 3.3,
![]() $o$
-minimal monotonicity, and HNF.◻
$o$
-minimal monotonicity, and HNF.◻
This corollary is a version of [Reference van den DriesVdD97, Corollary 2.8], slightly finer due to the presence of HNF.
Corollary 3.5. For the function
![]() $f$
in Corollary 3.4, there is a definable function
$f$
in Corollary 3.4, there is a definable function
 $\unicode[STIX]{x1D70B}:A\longrightarrow \text{RV}^{2}$
such that, for each
$\unicode[STIX]{x1D70B}:A\longrightarrow \text{RV}^{2}$
such that, for each
 $t\in \text{RV}^{2}$
,
$t\in \text{RV}^{2}$
,
![]() $f\restriction A_{t}$
is either constant or injective.
$f\restriction A_{t}$
is either constant or injective.
Proof. This follows easily from monotonicity. Also, the proof of [Reference YinYin09, Lemma 4.11] still works. ◻
Lemma 3.6. Given a tuple
 $t=(t_{1},\ldots ,t_{n})\in \text{RV}$
, if
$t=(t_{1},\ldots ,t_{n})\in \text{RV}$
, if
![]() $a\in \text{VF}$
is
$a\in \text{VF}$
is
![]() $t$
-definable then
$t$
-definable then
![]() $a$
is definable. Similarly, for
$a$
is definable. Similarly, for
 $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n})\in \unicode[STIX]{x1D6E4}$
, if
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n})\in \unicode[STIX]{x1D6E4}$
, if
![]() $t\in \text{RV}$
is
$t\in \text{RV}$
is
![]() $\unicode[STIX]{x1D6FE}$
-definable then
$\unicode[STIX]{x1D6FE}$
-definable then
![]() $t$
is definable.
$t$
is definable.
Proof. The first assertion follows directly from Lemma 3.3. It can also be easily seen through an induction on
![]() $n$
with the trivial base case
$n$
with the trivial base case
![]() $n=0$
. For any
$n=0$
. For any
![]() $b\in t_{n}^{\sharp }$
, by the inductive hypothesis, we have
$b\in t_{n}^{\sharp }$
, by the inductive hypothesis, we have
 $a\in \text{VF}(\langle b\rangle )$
. If
$a\in \text{VF}(\langle b\rangle )$
. If
![]() $a$
were not definable then, by the exchange principle, we would have
$a$
were not definable then, by the exchange principle, we would have
 $b\in \text{VF}(\langle a\rangle )$
and hence
$b\in \text{VF}(\langle a\rangle )$
and hence
 $t_{n}^{\sharp }\subseteq \text{VF}(\langle a\rangle )$
, which is impossible. The second assertion is similar, using the exchange principle in the
$t_{n}^{\sharp }\subseteq \text{VF}(\langle a\rangle )$
, which is impossible. The second assertion is similar, using the exchange principle in the
![]() $\text{RV}$
-sort (see Remark 2.27).◻
$\text{RV}$
-sort (see Remark 2.27).◻
Corollary 3.7. Let
 $U\subseteq \text{RV}^{m}$
be a definable set and
$U\subseteq \text{RV}^{m}$
be a definable set and
 $f:U\longrightarrow \text{VF}^{n}$
a definable function. Then
$f:U\longrightarrow \text{VF}^{n}$
a definable function. Then
![]() $f(U)$
is finite.
$f(U)$
is finite.
Proof. We may assume
![]() $n=1$
. Then this is immediate by Lemma 3.6 and compactness.◻
$n=1$
. Then this is immediate by Lemma 3.6 and compactness.◻
There is a more general version of Lemma 3.6 that involves parameters in the
![]() $\operatorname{DC}$
-sort.
$\operatorname{DC}$
-sort.
Lemma 3.8. Let
 $\ulcorner \mathfrak{a}\urcorner =(\ulcorner \mathfrak{a}_{1}\urcorner ,\ldots ,\ulcorner \mathfrak{a}_{n}\urcorner )\in \operatorname{DC}^{n}$
. If
$\ulcorner \mathfrak{a}\urcorner =(\ulcorner \mathfrak{a}_{1}\urcorner ,\ldots ,\ulcorner \mathfrak{a}_{n}\urcorner )\in \operatorname{DC}^{n}$
. If
![]() $a\in \text{VF}$
is
$a\in \text{VF}$
is
![]() $\ulcorner \mathfrak{a}\urcorner$
-definable then
$\ulcorner \mathfrak{a}\urcorner$
-definable then
![]() $a$
is definable.
$a$
is definable.
Proof. We proceed by induction on
![]() $n$
. Let
$n$
. Let
![]() $b\in \mathfrak{a}_{n}$
and
$b\in \mathfrak{a}_{n}$
and
![]() $t\in \text{RV}$
such that
$t\in \text{RV}$
such that
 $|\text{vrv}|(t)=\operatorname{rad}(\mathfrak{a}_{n})$
. Then
$|\text{vrv}|(t)=\operatorname{rad}(\mathfrak{a}_{n})$
. Then
![]() $a$
is
$a$
is
 $(\ulcorner \mathfrak{a}_{1}\urcorner ,\ldots ,\ulcorner \mathfrak{a}_{n-1}\urcorner ,t,b)$
-definable. By the inductive hypothesis and Lemma 3.6, we have
$(\ulcorner \mathfrak{a}_{1}\urcorner ,\ldots ,\ulcorner \mathfrak{a}_{n-1}\urcorner ,t,b)$
-definable. By the inductive hypothesis and Lemma 3.6, we have
 $a\in \text{VF}(\langle b\rangle )$
. If
$a\in \text{VF}(\langle b\rangle )$
. If
![]() $a$
were not definable then we would have
$a$
were not definable then we would have
 $b\in \text{VF}(\langle a\rangle )$
and hence
$b\in \text{VF}(\langle a\rangle )$
and hence
 $\mathfrak{a}_{n}\subseteq \text{VF}(\langle a\rangle )$
, which is impossible unless
$\mathfrak{a}_{n}\subseteq \text{VF}(\langle a\rangle )$
, which is impossible unless
![]() $\mathfrak{a}_{n}$
is a definable point in
$\mathfrak{a}_{n}$
is a definable point in
![]() $\text{VF}$
.◻
$\text{VF}$
.◻
Lemma 3.9. In
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
![]() $\mathfrak{a}\subseteq \text{VF}$
be a definable open disc and
$\mathfrak{a}\subseteq \text{VF}$
be a definable open disc and
 $f:\mathfrak{a}\longrightarrow \Bbbk$
a definable nonconstant function. Then there is a definable proper subdisc
$f:\mathfrak{a}\longrightarrow \Bbbk$
a definable nonconstant function. Then there is a definable proper subdisc
![]() $\mathfrak{b}\subseteq \mathfrak{a}$
such that
$\mathfrak{b}\subseteq \mathfrak{a}$
such that
 $f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b})$
is constant.
$f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b})$
is constant.
Proof. If
![]() $\mathfrak{b}_{1}$
and
$\mathfrak{b}_{1}$
and
![]() $\mathfrak{b}_{2}$
are two proper subdiscs of
$\mathfrak{b}_{2}$
are two proper subdiscs of
![]() $\mathfrak{a}$
such that
$\mathfrak{a}$
such that
 $f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b}_{1})$
and
$f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b}_{1})$
and
 $f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b}_{2})$
are both constant then
$f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b}_{2})$
are both constant then
![]() $\mathfrak{b}_{1}$
and
$\mathfrak{b}_{1}$
and
![]() $\mathfrak{b}_{2}$
must be concentric, that is,
$\mathfrak{b}_{2}$
must be concentric, that is,
 $\mathfrak{b}_{1}\cap \mathfrak{b}_{2}\neq \emptyset$
, for otherwise
$\mathfrak{b}_{1}\cap \mathfrak{b}_{2}\neq \emptyset$
, for otherwise
![]() $f$
would be constant. Therefore, it is enough to show that
$f$
would be constant. Therefore, it is enough to show that
 $f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b})$
is constant for some proper subdisc
$f\restriction (\mathfrak{a}\smallsetminus \mathfrak{b})$
is constant for some proper subdisc
![]() $\mathfrak{b}\subseteq \mathfrak{a}$
. To that end, without loss of generality, we may assume that
$\mathfrak{b}\subseteq \mathfrak{a}$
. To that end, without loss of generality, we may assume that
![]() $\mathfrak{a}$
is centered at
$\mathfrak{a}$
is centered at
![]() $0$
. For each
$0$
. For each
 $\unicode[STIX]{x1D6FE}\in \operatorname{val}(\mathfrak{a})\subseteq \unicode[STIX]{x1D6E4}$
, by [Reference van den DriesVdD97, Theorem A] and
$\unicode[STIX]{x1D6FE}\in \operatorname{val}(\mathfrak{a})\subseteq \unicode[STIX]{x1D6E4}$
, by [Reference van den DriesVdD97, Theorem A] and
![]() $o$
-minimality,
$o$
-minimality,
 $f(\operatorname{val}^{-1}(\unicode[STIX]{x1D6FE}))$
contains a
$f(\operatorname{val}^{-1}(\unicode[STIX]{x1D6FE}))$
contains a
![]() $\unicode[STIX]{x1D6FE}$
-definable element
$\unicode[STIX]{x1D6FE}$
-definable element
![]() $t_{\unicode[STIX]{x1D6FE}}\in \Bbbk$
. By weak
$t_{\unicode[STIX]{x1D6FE}}\in \Bbbk$
. By weak
![]() $o$
-minimality,
$o$
-minimality,
 $f(\operatorname{val}^{-1}(\unicode[STIX]{x1D6FE}))=t_{\unicode[STIX]{x1D6FE}}$
for all but finitely many
$f(\operatorname{val}^{-1}(\unicode[STIX]{x1D6FE}))=t_{\unicode[STIX]{x1D6FE}}$
for all but finitely many
 $\unicode[STIX]{x1D6FE}\in \operatorname{val}(\mathfrak{a})$
. Let
$\unicode[STIX]{x1D6FE}\in \operatorname{val}(\mathfrak{a})$
. Let
 $g:\operatorname{val}(\mathfrak{a})\longrightarrow \Bbbk$
be the definable function given by
$g:\operatorname{val}(\mathfrak{a})\longrightarrow \Bbbk$
be the definable function given by
 $\unicode[STIX]{x1D6FE}\longrightarrow t_{\unicode[STIX]{x1D6FE}}$
. By Lemma 2.23, the image of
$\unicode[STIX]{x1D6FE}\longrightarrow t_{\unicode[STIX]{x1D6FE}}$
. By Lemma 2.23, the image of
![]() $g$
is finite. The assertion follows.◻
$g$
is finite. The assertion follows.◻
Alternatively, we may simply quote [Reference MaříkováMař11, Theorem 1.2].
Definition 3.10. Let
![]() $D$
be a set of parameters. We say that a (not necessarily definable) nonempty set
$D$
be a set of parameters. We say that a (not necessarily definable) nonempty set
![]() $A$
generates a (complete)
$A$
generates a (complete)
![]() $D$
-type if, for every
$D$
-type if, for every
![]() $D$
-definable set
$D$
-definable set
![]() $B$
, either
$B$
, either
![]() $A\subseteq B$
or
$A\subseteq B$
or
 $A\cap B=\emptyset$
. In that case,
$A\cap B=\emptyset$
. In that case,
![]() $A$
is
$A$
is
![]() $D$
-type-definable if no set properly contains
$D$
-type-definable if no set properly contains
![]() $A$
and also generates a
$A$
and also generates a
![]() $D$
-type. If
$D$
-type. If
![]() $A$
is
$A$
is
![]() $D$
-definable and generates a
$D$
-definable and generates a
![]() $D$
-type, or equivalently, if
$D$
-type, or equivalently, if
![]() $A$
is both
$A$
is both
![]() $D$
-definable and
$D$
-definable and
![]() $D$
-type-definable then we say that
$D$
-type-definable then we say that
![]() $A$
is
$A$
is
![]() $D$
-atomic or atomic over
$D$
-atomic or atomic over
![]() $D$
.
$D$
.
We simply say ‘atomic’ when
![]() $D=\emptyset$
.
$D=\emptyset$
.
In the literature, a type could be a partial type and hence a type-definable set may have nontrivial intersection with a definable set. In this paper, since partial types do not play a role, we shall not carry the superfluous qualifier ‘complete’ in our terminology.
Remark 3.11 (Taxonomy of atomic sets).
It is not hard to see that, by HNF, if
![]() $\mathfrak{i}\subseteq \text{VF}$
is atomic then
$\mathfrak{i}\subseteq \text{VF}$
is atomic then
![]() $\mathfrak{i}$
must be a
$\mathfrak{i}$
must be a
![]() $\operatorname{val}$
-interval. In fact, there are only four possibilities for
$\operatorname{val}$
-interval. In fact, there are only four possibilities for
![]() $\mathfrak{i}$
: a point, an open disc, a closed disc, and a half thin annulus. There are no ‘meaningful’ relations between them (see Lemma 3.34).
$\mathfrak{i}$
: a point, an open disc, a closed disc, and a half thin annulus. There are no ‘meaningful’ relations between them (see Lemma 3.34).
Lemma 3.12. In
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
![]() $\mathfrak{a}$
be an atomic set. Then
$\mathfrak{a}$
be an atomic set. Then
![]() $\mathfrak{a}$
remains
$\mathfrak{a}$
remains
![]() $\unicode[STIX]{x1D6FE}$
-atomic for all
$\unicode[STIX]{x1D6FE}$
-atomic for all
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. Moreover, if
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. Moreover, if
 $\mathfrak{a}\subseteq \text{VF}^{n}$
is an open polydisc then it remains
$\mathfrak{a}\subseteq \text{VF}^{n}$
is an open polydisc then it remains
![]() $\ulcorner \mathfrak{a}\urcorner$
-atomic.
$\ulcorner \mathfrak{a}\urcorner$
-atomic.
Proof. The first assertion is a direct consequence of definable choice in the
![]() $\unicode[STIX]{x1D6E4}$
-sort. For the second assertion, let
$\unicode[STIX]{x1D6E4}$
-sort. For the second assertion, let
 $\unicode[STIX]{x1D6FE}=\operatorname{rad}(\mathfrak{a})$
. If
$\unicode[STIX]{x1D6FE}=\operatorname{rad}(\mathfrak{a})$
. If
![]() $\mathfrak{a}$
were not
$\mathfrak{a}$
were not
![]() $\ulcorner \mathfrak{a}\urcorner$
-atomic then, by compactness, there would be a
$\ulcorner \mathfrak{a}\urcorner$
-atomic then, by compactness, there would be a
![]() $\unicode[STIX]{x1D6FE}$
-definable subset
$\unicode[STIX]{x1D6FE}$
-definable subset
 $A\subseteq \text{VF}^{n}$
such that
$A\subseteq \text{VF}^{n}$
such that
![]() $A\cap \mathfrak{a}$
is nonempty and, for all open polydiscs
$A\cap \mathfrak{a}$
is nonempty and, for all open polydiscs
![]() $\mathfrak{b}$
with
$\mathfrak{b}$
with
 $\unicode[STIX]{x1D6FE}=\operatorname{rad}(\mathfrak{b})$
, if
$\unicode[STIX]{x1D6FE}=\operatorname{rad}(\mathfrak{b})$
, if
![]() $A\,\cap \,\mathfrak{b}$
is nonempty then it is a proper subset of
$A\,\cap \,\mathfrak{b}$
is nonempty then it is a proper subset of
![]() $\mathfrak{b}$
; this contradicts the first assertion that
$\mathfrak{b}$
; this contradicts the first assertion that
![]() $\mathfrak{a}$
is
$\mathfrak{a}$
is
![]() $\unicode[STIX]{x1D6FE}$
-atomic.◻
$\unicode[STIX]{x1D6FE}$
-atomic.◻
Recall from [Reference Macpherson, Marker and SteinhornMMS00, Definition 4.5] the notion of a cell in a weakly
![]() $o$
-minimal structure. In our setting, it is easy to see that, by HNF, we may require that the images of the bounding functions
$o$
-minimal structure. In our setting, it is easy to see that, by HNF, we may require that the images of the bounding functions
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
of a cell
$f_{2}$
of a cell
 $(f_{1},f_{2})_{A}$
in the
$(f_{1},f_{2})_{A}$
in the
![]() $\text{VF}$
-sort be contained in
$\text{VF}$
-sort be contained in
![]() $\operatorname{DC}$
; cell decomposition [Reference Macpherson, Marker and SteinhornMMS00, Theorem 4.6] holds accordingly. Cells are in general not invariant under coordinate permutations; however, by cell decomposition, an atomic subset of
$\operatorname{DC}$
; cell decomposition [Reference Macpherson, Marker and SteinhornMMS00, Theorem 4.6] holds accordingly. Cells are in general not invariant under coordinate permutations; however, by cell decomposition, an atomic subset of
![]() $\text{VF}^{n}$
must be a cell and must remain so under coordinate permutations.
$\text{VF}^{n}$
must be a cell and must remain so under coordinate permutations.
Lemma 3.13. In
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
 $\mathfrak{a}\subseteq \text{VF}^{n}$
be an atomic open polydisc and
$\mathfrak{a}\subseteq \text{VF}^{n}$
be an atomic open polydisc and
 $f:\mathfrak{a}\longrightarrow \text{VF}$
a definable function. If
$f:\mathfrak{a}\longrightarrow \text{VF}$
a definable function. If
![]() $f$
is not constant then
$f$
is not constant then
![]() $f(\mathfrak{a})$
is an (atomic) open disc; in particular,
$f(\mathfrak{a})$
is an (atomic) open disc; in particular,
 $\operatorname{rv}\restriction f(\mathfrak{a})$
is always constant.
$\operatorname{rv}\restriction f(\mathfrak{a})$
is always constant.
Proof. By atomicity,
![]() $f(\mathfrak{a})$
must be an atomic
$f(\mathfrak{a})$
must be an atomic
![]() $\operatorname{val}$
-interval. We proceed by induction on
$\operatorname{val}$
-interval. We proceed by induction on
![]() $n$
. For the base case
$n$
. For the base case
![]() $n=1$
, suppose for contradiction that
$n=1$
, suppose for contradiction that
![]() $f(\mathfrak{a})$
is a closed disc (other than a point) or a half thin annulus. By monotonicity, we may assume that
$f(\mathfrak{a})$
is a closed disc (other than a point) or a half thin annulus. By monotonicity, we may assume that
![]() $f(\mathfrak{a})$
is, say, strictly increasing. Then
$f(\mathfrak{a})$
is, say, strictly increasing. Then
![]() $f^{-1}$
violates Lemma 3.2, contradiction.
$f^{-1}$
violates Lemma 3.2, contradiction.
For the case
![]() $n>1$
, suppose for contradiction again that
$n>1$
, suppose for contradiction again that
![]() $f(\mathfrak{a})$
is a closed disc or a half thin annulus. By the inductive hypothesis, for every
$f(\mathfrak{a})$
is a closed disc or a half thin annulus. By the inductive hypothesis, for every
 $a\in \operatorname{pr}_{1}(\mathfrak{a})$
there is a maximal open subdisc
$a\in \operatorname{pr}_{1}(\mathfrak{a})$
there is a maximal open subdisc
 $\mathfrak{b}_{a}\subseteq f(\mathfrak{a})$
that contains
$\mathfrak{b}_{a}\subseteq f(\mathfrak{a})$
that contains
![]() $f(\mathfrak{a}_{a})$
, similarly for every
$f(\mathfrak{a}_{a})$
, similarly for every
 $a\in \operatorname{pr}_{{>}1}(\mathfrak{a})$
. It follows that
$a\in \operatorname{pr}_{{>}1}(\mathfrak{a})$
. It follows that
![]() $f(\mathfrak{a})$
is actually contained in a maximal open subdisc of
$f(\mathfrak{a})$
is actually contained in a maximal open subdisc of
![]() $f(\mathfrak{a})$
, which is absurd.◻
$f(\mathfrak{a})$
, which is absurd.◻
Corollary 3.14. Let
 $f:\text{VF}^{n}\longrightarrow \text{VF}$
be a definable function and
$f:\text{VF}^{n}\longrightarrow \text{VF}$
be a definable function and
 $\mathfrak{a}\subseteq \text{VF}^{n}$
an open polydisc. If
$\mathfrak{a}\subseteq \text{VF}^{n}$
an open polydisc. If
 $(\operatorname{rv}\circ f)\restriction \mathfrak{a}$
is not constant then there is an
$(\operatorname{rv}\circ f)\restriction \mathfrak{a}$
is not constant then there is an
![]() $\ulcorner \mathfrak{a}\urcorner$
-definable nonempty proper subset of
$\ulcorner \mathfrak{a}\urcorner$
-definable nonempty proper subset of
![]() $\mathfrak{a}$
.
$\mathfrak{a}$
.
The following result is a strengthening of Lemma 3.12.
Lemma 3.15. Let
 $B\subseteq \text{VF}^{n}$
be
$B\subseteq \text{VF}^{n}$
be
![]() ${\mathcal{L}}_{T\text{}}$
-type-definable and
${\mathcal{L}}_{T\text{}}$
-type-definable and
 $\mathfrak{a}=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n}\subseteq B$
an open polydisc. Then, for all
$\mathfrak{a}=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n}\subseteq B$
an open polydisc. Then, for all
 $a=(a_{1},\ldots ,a_{n})$
and
$a=(a_{1},\ldots ,a_{n})$
and
 $b=(b_{1},\ldots ,b_{n})$
in
$b=(b_{1},\ldots ,b_{n})$
in
![]() $\mathfrak{a}$
, there is an immediate automorphism
$\mathfrak{a}$
, there is an immediate automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
with
${\mathcal{R}}_{\operatorname{rv}}$
with
 $\unicode[STIX]{x1D70E}(a)=b$
. Consequently,
$\unicode[STIX]{x1D70E}(a)=b$
. Consequently,
![]() $\mathfrak{a}$
is
$\mathfrak{a}$
is
![]() $(\ulcorner \mathfrak{a}\urcorner ,t)$
-atomic for all
$(\ulcorner \mathfrak{a}\urcorner ,t)$
-atomic for all
![]() $t\in \text{RV}$
.
$t\in \text{RV}$
.
Proof. To see that the first assertion implies the second, suppose for contradiction that there is an
![]() $(\ulcorner \mathfrak{a}\urcorner ,t)$
-definable nonempty proper subset
$(\ulcorner \mathfrak{a}\urcorner ,t)$
-definable nonempty proper subset
![]() $A\subseteq \mathfrak{a}$
. Let
$A\subseteq \mathfrak{a}$
. Let
![]() $a\in A$
,
$a\in A$
,
 $b\in \mathfrak{a}\smallsetminus A$
, and
$b\in \mathfrak{a}\smallsetminus A$
, and
![]() $\unicode[STIX]{x1D70E}$
be an immediate automorphism of
$\unicode[STIX]{x1D70E}$
be an immediate automorphism of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
with
${\mathcal{R}}_{\operatorname{rv}}$
with
 $\unicode[STIX]{x1D70E}(a)=b$
. Then
$\unicode[STIX]{x1D70E}(a)=b$
. Then
![]() $\unicode[STIX]{x1D70E}$
is also an immediate automorphism of
$\unicode[STIX]{x1D70E}$
is also an immediate automorphism of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
over
${\mathcal{R}}_{\operatorname{rv}}$
over
![]() $\langle \ulcorner \mathfrak{a}\urcorner ,t\rangle$
, contradicting the assumption that
$\langle \ulcorner \mathfrak{a}\urcorner ,t\rangle$
, contradicting the assumption that
![]() $A$
is
$A$
is
![]() $(\ulcorner \mathfrak{a}\urcorner ,t)$
-definable.
$(\ulcorner \mathfrak{a}\urcorner ,t)$
-definable.
For the first assertion, by Lemma 2.20, it is enough to show that there is an immediate isomorphism
 $\unicode[STIX]{x1D70E}:\langle a\rangle \longrightarrow \langle b\rangle$
sending
$\unicode[STIX]{x1D70E}:\langle a\rangle \longrightarrow \langle b\rangle$
sending
![]() $a$
to
$a$
to
![]() $b$
. Write
$b$
. Write
 $$\begin{eqnarray}\mathfrak{a}^{\prime }=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n-1},\quad a^{\prime }=(a_{1},\ldots ,a_{n-1}),\quad b^{\prime }=(b_{1},\ldots ,b_{n-1}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{a}^{\prime }=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n-1},\quad a^{\prime }=(a_{1},\ldots ,a_{n-1}),\quad b^{\prime }=(b_{1},\ldots ,b_{n-1}).\end{eqnarray}$$
Then, by induction on
![]() $n$
and Lemma 2.22, it is enough to show that, for any immediate isomorphism
$n$
and Lemma 2.22, it is enough to show that, for any immediate isomorphism
 $\unicode[STIX]{x1D70E}^{\prime }:\langle a^{\prime }\rangle \longrightarrow \langle b^{\prime }\rangle$
sending
$\unicode[STIX]{x1D70E}^{\prime }:\langle a^{\prime }\rangle \longrightarrow \langle b^{\prime }\rangle$
sending
![]() $a^{\prime }$
to
$a^{\prime }$
to
![]() $b^{\prime }$
and any
$b^{\prime }$
and any
![]() ${\mathcal{L}}_{T\text{}}$
-definable function
${\mathcal{L}}_{T\text{}}$
-definable function
 $f:\text{VF}^{n-1}\longrightarrow \text{VF}$
,
$f:\text{VF}^{n-1}\longrightarrow \text{VF}$
,
 $$\begin{eqnarray}\operatorname{rv}(a_{n}-f(a^{\prime }))=\operatorname{rv}(b_{n}-\unicode[STIX]{x1D70E}^{\prime }(f(a^{\prime }))).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rv}(a_{n}-f(a^{\prime }))=\operatorname{rv}(b_{n}-\unicode[STIX]{x1D70E}^{\prime }(f(a^{\prime }))).\end{eqnarray}$$
This is clear for the base case
![]() $n=1$
, since
$n=1$
, since
![]() $\mathfrak{a}$
must be disjoint from
$\mathfrak{a}$
must be disjoint from
![]() $\text{VF}({\mathcal{S}})$
. For the case
$\text{VF}({\mathcal{S}})$
. For the case
![]() $n>1$
, we choose an immediate automorphism of
$n>1$
, we choose an immediate automorphism of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
extending
${\mathcal{R}}_{\operatorname{rv}}$
extending
![]() $\unicode[STIX]{x1D70E}^{\prime }$
, which is still denoted by
$\unicode[STIX]{x1D70E}^{\prime }$
, which is still denoted by
![]() $\unicode[STIX]{x1D70E}^{\prime }$
; this is possible by Lemma 2.20. By the inductive hypothesis and Lemma 3.13,
$\unicode[STIX]{x1D70E}^{\prime }$
; this is possible by Lemma 2.20. By the inductive hypothesis and Lemma 3.13,
 $f(\mathfrak{a}^{\prime })=f(\unicode[STIX]{x1D70E}^{\prime }(\mathfrak{a}^{\prime }))=\unicode[STIX]{x1D70E}^{\prime }(f(\mathfrak{a}^{\prime }))$
is either a point or an open disc. Since
$f(\mathfrak{a}^{\prime })=f(\unicode[STIX]{x1D70E}^{\prime }(\mathfrak{a}^{\prime }))=\unicode[STIX]{x1D70E}^{\prime }(f(\mathfrak{a}^{\prime }))$
is either a point or an open disc. Since
![]() $B$
is
$B$
is
![]() ${\mathcal{L}}_{T\text{}}$
-type-definable, it follows that
${\mathcal{L}}_{T\text{}}$
-type-definable, it follows that
![]() $f(\mathfrak{a}^{\prime })$
must be disjoint from
$f(\mathfrak{a}^{\prime })$
must be disjoint from
![]() $\mathfrak{a}_{n}$
and hence the desired condition is satisfied.◻
$\mathfrak{a}_{n}$
and hence the desired condition is satisfied.◻
Corollary 3.16. Let
 $A\subseteq \text{VF}^{n}$
and
$A\subseteq \text{VF}^{n}$
and
 $f:A\longrightarrow \text{VF}$
be an
$f:A\longrightarrow \text{VF}$
be an
![]() ${\mathcal{L}}_{T\text{}}$
-definable function. Then there is an
${\mathcal{L}}_{T\text{}}$
-definable function. Then there is an
![]() ${\mathcal{L}}_{T\text{}}$
-definable finite partition
${\mathcal{L}}_{T\text{}}$
-definable finite partition
![]() $A_{i}$
of
$A_{i}$
of
![]() $A$
such that, for all
$A$
such that, for all
![]() $i$
, if
$i$
, if
![]() $\mathfrak{a}\subseteq A_{i}$
is an open polydisc then
$\mathfrak{a}\subseteq A_{i}$
is an open polydisc then
 $\operatorname{rv}\restriction f(\mathfrak{a})$
is constant and
$\operatorname{rv}\restriction f(\mathfrak{a})$
is constant and
![]() $f(\mathfrak{a})$
is either a point or an open disc.
$f(\mathfrak{a})$
is either a point or an open disc.
Proof. For
![]() $a\in A$
, let
$a\in A$
, let
 $D_{a}\subseteq A$
be the
$D_{a}\subseteq A$
be the
![]() ${\mathcal{L}}_{T\text{}}$
-type-definable subset containing
${\mathcal{L}}_{T\text{}}$
-type-definable subset containing
![]() $a$
. By Lemma 3.15, every open polydisc
$a$
. By Lemma 3.15, every open polydisc
![]() $\mathfrak{a}\subseteq D_{a}$
is
$\mathfrak{a}\subseteq D_{a}$
is
![]() $\ulcorner \mathfrak{a}\urcorner$
-atomic and hence, by Lemma 3.13, the assertion holds for
$\ulcorner \mathfrak{a}\urcorner$
-atomic and hence, by Lemma 3.13, the assertion holds for
![]() $\mathfrak{a}$
. Then, by compactness, the assertion must hold in a definable subset
$\mathfrak{a}$
. Then, by compactness, the assertion must hold in a definable subset
 $A_{a}\subseteq A$
that contains
$A_{a}\subseteq A$
that contains
![]() $a$
; by compactness again, it holds in finitely many definable subsets
$a$
; by compactness again, it holds in finitely many definable subsets
 $A_{1},\ldots ,A_{m}$
of
$A_{1},\ldots ,A_{m}$
of
![]() $A$
with
$A$
with
 $\bigcup _{i}A_{i}=A$
. Then the partition of
$\bigcup _{i}A_{i}=A$
. Then the partition of
![]() $A$
generated by
$A$
generated by
 $A_{1},\ldots ,A_{m}$
is as desired.◻
$A_{1},\ldots ,A_{m}$
is as desired.◻
Remark 3.17. Clearly the conclusion of Corollary 3.16 still holds if we replace ‘
![]() ${\mathcal{L}}_{T\text{}}$
-definable’ with ‘definable’ everywhere therein. Moreover, its proof works almost verbatim in all situations where we want to partition an
${\mathcal{L}}_{T\text{}}$
-definable’ with ‘definable’ everywhere therein. Moreover, its proof works almost verbatim in all situations where we want to partition an
![]() ${\mathcal{L}}_{T\text{}}$
-definable set
${\mathcal{L}}_{T\text{}}$
-definable set
 $A\subseteq \text{VF}^{n}$
into finitely many
$A\subseteq \text{VF}^{n}$
into finitely many
![]() ${\mathcal{L}}_{T\text{}}$
-definable pieces
${\mathcal{L}}_{T\text{}}$
-definable pieces
![]() $A_{i}$
such that certain definable property, not necessarily
$A_{i}$
such that certain definable property, not necessarily
![]() ${\mathcal{L}}_{T\text{}}$
-definable, holds on every open polydisc (or other imaginary elements) contained in
${\mathcal{L}}_{T\text{}}$
-definable, holds on every open polydisc (or other imaginary elements) contained in
![]() $A_{i}$
.
$A_{i}$
.
The next lemma is a variation of Lemma 3.15.
Lemma 3.18. Let
 $\mathfrak{a}\subseteq \text{VF}^{n}$
be an
$\mathfrak{a}\subseteq \text{VF}^{n}$
be an
![]() $\ulcorner \mathfrak{a}\urcorner$
-atomic open polydisc. Let
$\ulcorner \mathfrak{a}\urcorner$
-atomic open polydisc. Let
 $e\in \text{VF}^{\times }$
with
$e\in \text{VF}^{\times }$
with
 $|\text{val}|(e)\gg 0$
(here
$|\text{val}|(e)\gg 0$
(here
![]() $\gg$
stands for ‘sufficiently larger than’). Then
$\gg$
stands for ‘sufficiently larger than’). Then
![]() $\mathfrak{a}$
is
$\mathfrak{a}$
is
![]() $(\ulcorner \mathfrak{a}\urcorner ,e)$
-atomic.
$(\ulcorner \mathfrak{a}\urcorner ,e)$
-atomic.
Proof. The argument is somewhat similar to that in the proof of Lemma 3.15. We proceed by induction on
![]() $n$
. Write
$n$
. Write
 $\mathfrak{a}=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n}$
and
$\mathfrak{a}=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n}$
and
 $\mathfrak{a}^{\prime }=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n-1}$
. Let
$\mathfrak{a}^{\prime }=\mathfrak{a}_{1}\times \cdots \times \mathfrak{a}_{n-1}$
. Let
![]() $(a^{\prime },a_{n})$
and
$(a^{\prime },a_{n})$
and
![]() $(b^{\prime },b_{n})$
be two points in
$(b^{\prime },b_{n})$
be two points in
![]() $\mathfrak{a}^{\prime }\times \mathfrak{a}_{n}$
. By the inductive hypothesis and Lemma 3.15, there is an immediate isomorphism
$\mathfrak{a}^{\prime }\times \mathfrak{a}_{n}$
. By the inductive hypothesis and Lemma 3.15, there is an immediate isomorphism
 $\unicode[STIX]{x1D70E}^{\prime }:\langle a^{\prime },e\rangle \longrightarrow \langle b^{\prime },e\rangle$
with
$\unicode[STIX]{x1D70E}^{\prime }:\langle a^{\prime },e\rangle \longrightarrow \langle b^{\prime },e\rangle$
with
 $\unicode[STIX]{x1D70E}^{\prime }(e)=e$
and
$\unicode[STIX]{x1D70E}^{\prime }(e)=e$
and
 $\unicode[STIX]{x1D70E}^{\prime }(a^{\prime })=b^{\prime }$
. Thus, it is enough to show that, for all
$\unicode[STIX]{x1D70E}^{\prime }(a^{\prime })=b^{\prime }$
. Thus, it is enough to show that, for all
![]() ${\mathcal{L}}_{T\text{}}$
-definable function
${\mathcal{L}}_{T\text{}}$
-definable function
 $f:\text{VF}^{n}\longrightarrow \text{VF}$
,
$f:\text{VF}^{n}\longrightarrow \text{VF}$
,
 $$\begin{eqnarray}\operatorname{rv}(a_{n}-f(e,a^{\prime }))=\operatorname{rv}(b_{n}-\unicode[STIX]{x1D70E}^{\prime }(f(e,a^{\prime }))).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rv}(a_{n}-f(e,a^{\prime }))=\operatorname{rv}(b_{n}-\unicode[STIX]{x1D70E}^{\prime }(f(e,a^{\prime }))).\end{eqnarray}$$
Suppose for contradiction that we can always find an
 $e\in \text{VF}^{\times }$
that is arbitrarily close to
$e\in \text{VF}^{\times }$
that is arbitrarily close to
![]() $0$
such that
$0$
such that
 $f(e,\mathfrak{a}^{\prime })\cap \mathfrak{a}_{n}\neq \emptyset$
(this must hold for some such
$f(e,\mathfrak{a}^{\prime })\cap \mathfrak{a}_{n}\neq \emptyset$
(this must hold for some such
![]() $f$
, for otherwise we are already done by compactness); more precisely, by weak
$f$
, for otherwise we are already done by compactness); more precisely, by weak
![]() $o$
-minimality, without loss of generality, there is an open interval
$o$
-minimality, without loss of generality, there is an open interval
 $(0,\unicode[STIX]{x1D716})\subseteq \text{VF}^{+}$
such that
$(0,\unicode[STIX]{x1D716})\subseteq \text{VF}^{+}$
such that
 $f(e,\mathfrak{a}^{\prime })\cap \mathfrak{a}_{n}\neq \emptyset$
for all
$f(e,\mathfrak{a}^{\prime })\cap \mathfrak{a}_{n}\neq \emptyset$
for all
 $e\in (0,\unicode[STIX]{x1D716})$
.
$e\in (0,\unicode[STIX]{x1D716})$
.
For each
![]() $a^{\prime }\in \mathfrak{a}^{\prime }$
, let
$a^{\prime }\in \mathfrak{a}^{\prime }$
, let
![]() $f_{a^{\prime }}$
be the
$f_{a^{\prime }}$
be the
![]() $a^{\prime }$
-
$a^{\prime }$
-
![]() ${\mathcal{L}}_{T\text{}}$
-definable function on
${\mathcal{L}}_{T\text{}}$
-definable function on
![]() $\text{VF}^{+}$
given by
$\text{VF}^{+}$
given by
 $b\longmapsto f(b,a^{\prime })$
. By
$b\longmapsto f(b,a^{\prime })$
. By
![]() $o$
-minimal monotonicity, there is an
$o$
-minimal monotonicity, there is an
![]() $\ulcorner \mathfrak{a}^{\prime }\urcorner$
-definable function
$\ulcorner \mathfrak{a}^{\prime }\urcorner$
-definable function
 $l:\mathfrak{a}^{\prime }\longrightarrow \text{VF}^{+}$
such that
$l:\mathfrak{a}^{\prime }\longrightarrow \text{VF}^{+}$
such that
 $f_{a^{\prime }}^{\ast }:=f_{a^{\prime }}\restriction A_{a^{\prime }}$
is continuously monotone (of the same kind) for all
$f_{a^{\prime }}^{\ast }:=f_{a^{\prime }}\restriction A_{a^{\prime }}$
is continuously monotone (of the same kind) for all
![]() $a^{\prime }\in \mathfrak{a}^{\prime }$
, where
$a^{\prime }\in \mathfrak{a}^{\prime }$
, where
 $A_{a^{\prime }}:=(0,l(a^{\prime }))$
. By Lemma 3.13,
$A_{a^{\prime }}:=(0,l(a^{\prime }))$
. By Lemma 3.13,
![]() $l(\mathfrak{a}^{\prime })$
is either a point or an open disc. Thus the
$l(\mathfrak{a}^{\prime })$
is either a point or an open disc. Thus the
![]() $\operatorname{val}$
-interval
$\operatorname{val}$
-interval
 $(0,l(\mathfrak{a}^{\prime }))$
is nonempty, which implies that
$(0,l(\mathfrak{a}^{\prime }))$
is nonempty, which implies that
 $f_{a^{\prime }}^{\ast }(e)\in \mathfrak{a}_{n}$
for some
$f_{a^{\prime }}^{\ast }(e)\in \mathfrak{a}_{n}$
for some
![]() $a^{\prime }\in \mathfrak{a}^{\prime }$
and some
$a^{\prime }\in \mathfrak{a}^{\prime }$
and some
![]() $e\in A_{a^{\prime }}$
. In that case, we must have that, for all
$e\in A_{a^{\prime }}$
. In that case, we must have that, for all
![]() $a^{\prime }\in \mathfrak{a}^{\prime }$
,
$a^{\prime }\in \mathfrak{a}^{\prime }$
,
 $\mathfrak{a}_{n}\subseteq f_{a^{\prime }}^{\ast }(A_{a^{\prime }})$
and hence
$\mathfrak{a}_{n}\subseteq f_{a^{\prime }}^{\ast }(A_{a^{\prime }})$
and hence
![]() $f_{a^{\prime }}^{\ast }$
is bijective. By
$f_{a^{\prime }}^{\ast }$
is bijective. By
![]() $o$
-minimality in the
$o$
-minimality in the
![]() $\unicode[STIX]{x1D6E4}$
-sort,
$\unicode[STIX]{x1D6E4}$
-sort,
 $|\text{val}|((f_{a^{\prime }}^{\ast })^{-1}(\mathfrak{a}_{n}))$
has to be a singleton, say,
$|\text{val}|((f_{a^{\prime }}^{\ast })^{-1}(\mathfrak{a}_{n}))$
has to be a singleton, say,
![]() $\unicode[STIX]{x1D6FD}_{a^{\prime }}$
; in fact, the function given by
$\unicode[STIX]{x1D6FD}_{a^{\prime }}$
; in fact, the function given by
 $a^{\prime }\longmapsto \unicode[STIX]{x1D6FD}_{a^{\prime }}$
has to be constant, and hence we may write
$a^{\prime }\longmapsto \unicode[STIX]{x1D6FD}_{a^{\prime }}$
has to be constant, and hence we may write
![]() $\unicode[STIX]{x1D6FD}_{a^{\prime }}$
as
$\unicode[STIX]{x1D6FD}_{a^{\prime }}$
as
![]() $\unicode[STIX]{x1D6FD}$
. It follows that, for all
$\unicode[STIX]{x1D6FD}$
. It follows that, for all
 $e\in \text{VF}^{+}$
with
$e\in \text{VF}^{+}$
with
 $|\text{val}|(e)>\unicode[STIX]{x1D6FD}$
,
$|\text{val}|(e)>\unicode[STIX]{x1D6FD}$
,
 $f(e,\mathfrak{a}^{\prime })\cap \mathfrak{a}_{n}=\emptyset$
, contradiction.◻
$f(e,\mathfrak{a}^{\prime })\cap \mathfrak{a}_{n}=\emptyset$
, contradiction.◻
Next we come to the issue of finding definable points in definable sets. As we have mentioned above, this is a trivial issue if the space of parameters is not fixed.
Lemma 3.19. The substructure
![]() ${\mathcal{S}}$
is definably closed.
${\mathcal{S}}$
is definably closed.
Proof. By Lemma 3.6, we have
 $\text{VF}(\operatorname{dcl}({\mathcal{S}}))=\text{VF}({\mathcal{S}})$
. Suppose that
$\text{VF}(\operatorname{dcl}({\mathcal{S}}))=\text{VF}({\mathcal{S}})$
. Suppose that
![]() $t\in \text{RV}$
is definable. By the first sentence of Remark 2.27, if
$t\in \text{RV}$
is definable. By the first sentence of Remark 2.27, if
 $\operatorname{vrv}(\text{RV}({\mathcal{S}}))$
is nontrivial then
$\operatorname{vrv}(\text{RV}({\mathcal{S}}))$
is nontrivial then
![]() $\text{RV}({\mathcal{S}})$
is a model of the reduct of
$\text{RV}({\mathcal{S}})$
is a model of the reduct of
![]() $\text{TCVF}$
to the
$\text{TCVF}$
to the
![]() $\text{RV}$
-sort and hence, by quantifier elimination, is an elementary substructure of
$\text{RV}$
-sort and hence, by quantifier elimination, is an elementary substructure of
![]() $\text{RV}$
, which implies
$\text{RV}$
, which implies
 $t\in \text{RV}({\mathcal{S}})$
. On the other hand, if
$t\in \text{RV}({\mathcal{S}})$
. On the other hand, if
 $\operatorname{vrv}(\text{RV}({\mathcal{S}}))$
is trivial then
$\operatorname{vrv}(\text{RV}({\mathcal{S}}))$
is trivial then
 $\text{RV}({\mathcal{S}})=\Bbbk ({\mathcal{S}})$
and it is not hard, though a bit tedious, to check, using quantifier elimination again, that
$\text{RV}({\mathcal{S}})=\Bbbk ({\mathcal{S}})$
and it is not hard, though a bit tedious, to check, using quantifier elimination again, that
 $t\in \Bbbk ({\mathcal{S}})$
.◻
$t\in \Bbbk ({\mathcal{S}})$
.◻
If
![]() ${\mathcal{S}}$
is
${\mathcal{S}}$
is
![]() $\text{VF}$
-generated and
$\text{VF}$
-generated and
![]() $\unicode[STIX]{x1D6E4}({\mathcal{S}})$
is nontrivial then
$\unicode[STIX]{x1D6E4}({\mathcal{S}})$
is nontrivial then
![]() ${\mathcal{S}}$
is an elementary substructure, and hence every definable set contains a definable point. This, of course, fails if
${\mathcal{S}}$
is an elementary substructure, and hence every definable set contains a definable point. This, of course, fails if
![]() ${\mathcal{S}}$
carries extra
${\mathcal{S}}$
carries extra
![]() $\text{RV}$
-data, by the above lemma. However, we do have the following result.
$\text{RV}$
-data, by the above lemma. However, we do have the following result.
Lemma 3.20. Every definable closed disc
![]() $\mathfrak{b}$
contains a definable point.
$\mathfrak{b}$
contains a definable point.
Proof. Suppose for contradiction that
![]() $\mathfrak{b}$
does not contain a definable point. Since
$\mathfrak{b}$
does not contain a definable point. Since
![]() ${\mathcal{R}}_{\operatorname{rv}}$
is sufficiently saturated, there is an open disc
${\mathcal{R}}_{\operatorname{rv}}$
is sufficiently saturated, there is an open disc
![]() $\mathfrak{a}$
that is disjoint from
$\mathfrak{a}$
that is disjoint from
![]() $\text{VF}({\mathcal{S}})$
and properly contains
$\text{VF}({\mathcal{S}})$
and properly contains
![]() $\mathfrak{b}$
. Let
$\mathfrak{b}$
. Let
 $a\in \mathfrak{a}\smallsetminus \mathfrak{b}$
and
$a\in \mathfrak{a}\smallsetminus \mathfrak{b}$
and
![]() $b\in \mathfrak{b}$
. Clearly
$b\in \mathfrak{b}$
. Clearly
 $\operatorname{rv}(c-b)=\operatorname{rv}(c-a)$
for all
$\operatorname{rv}(c-b)=\operatorname{rv}(c-a)$
for all
 $c\in \text{VF}({\mathcal{S}})$
. As in the proof of Lemma 3.15, there is an immediate automorphism
$c\in \text{VF}({\mathcal{S}})$
. As in the proof of Lemma 3.15, there is an immediate automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() ${\mathcal{R}}_{\operatorname{rv}}$
such that
${\mathcal{R}}_{\operatorname{rv}}$
such that
 $\unicode[STIX]{x1D70E}(a)=b$
. This means that
$\unicode[STIX]{x1D70E}(a)=b$
. This means that
![]() $\mathfrak{b}$
is not definable, which is a contradiction.◻
$\mathfrak{b}$
is not definable, which is a contradiction.◻
Notice that the argument above does not work if
![]() $\mathfrak{b}$
is an open disc.
$\mathfrak{b}$
is an open disc.
Corollary 3.21. Let
![]() $\mathfrak{a}\subseteq \text{VF}$
be a disc and
$\mathfrak{a}\subseteq \text{VF}$
be a disc and
![]() $A$
a definable subset of
$A$
a definable subset of
![]() $\text{VF}$
. If
$\text{VF}$
. If
![]() $\mathfrak{a}\cap A$
is a nonempty proper subset of
$\mathfrak{a}\cap A$
is a nonempty proper subset of
![]() $\mathfrak{a}$
then
$\mathfrak{a}$
then
![]() $\mathfrak{a}$
contains a definable point.
$\mathfrak{a}$
contains a definable point.
Proof. It is not hard to see that, by HNF, if
![]() $\mathfrak{a}\cap A$
is a nonempty proper subset of
$\mathfrak{a}\cap A$
is a nonempty proper subset of
![]() $\mathfrak{a}$
then
$\mathfrak{a}$
then
![]() $\mathfrak{a}$
contains a definable closed disc, and hence the claim is immediate by Lemma 3.20.◻
$\mathfrak{a}$
contains a definable closed disc, and hence the claim is immediate by Lemma 3.20.◻
Lemma 3.22. Let
 $A\subseteq \text{VF}$
be a definable set that contains infinitely many open discs of radius
$A\subseteq \text{VF}$
be a definable set that contains infinitely many open discs of radius
![]() $\unicode[STIX]{x1D6FD}$
. Then one of these discs
$\unicode[STIX]{x1D6FD}$
. Then one of these discs
![]() $\mathfrak{a}$
is
$\mathfrak{a}$
is
![]() $(\ulcorner \mathfrak{a}\urcorner ,\unicode[STIX]{x1D6FD})$
-atomic.
$(\ulcorner \mathfrak{a}\urcorner ,\unicode[STIX]{x1D6FD})$
-atomic.
Proof. By Lemmas 3.12 and 3.15, it is enough to show that some open disc
![]() $\mathfrak{a}\subseteq A$
of radius
$\mathfrak{a}\subseteq A$
of radius
![]() $\unicode[STIX]{x1D6FD}$
is contained in a type-definable set. Suppose for contradiction that this is not the case. By Corollary 3.21 and HNF, for every definable set
$\unicode[STIX]{x1D6FD}$
is contained in a type-definable set. Suppose for contradiction that this is not the case. By Corollary 3.21 and HNF, for every definable set
![]() $B\subseteq A$
, we have either
$B\subseteq A$
, we have either
 $\mathfrak{a}\cap B=\emptyset$
or
$\mathfrak{a}\cap B=\emptyset$
or
![]() $\mathfrak{a}\subseteq B$
for all but finitely many such open discs
$\mathfrak{a}\subseteq B$
for all but finitely many such open discs
![]() $\mathfrak{a}\subseteq A$
. Passing to
$\mathfrak{a}\subseteq A$
. Passing to
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
and applying compactness (with the parameter
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
and applying compactness (with the parameter
![]() $\unicode[STIX]{x1D6FD}$
), the claim follows.◻
$\unicode[STIX]{x1D6FD}$
), the claim follows.◻
3.2 Contracting from
 $\text{VF}$
to
$\text{VF}$
to
 $\text{RV}$
$\text{RV}$
We can relate definable sets in
![]() $\text{VF}$
to those in
$\text{VF}$
to those in
![]() $\text{RV}$
, specifically,
$\text{RV}$
, specifically,
![]() $\text{RV}$
-pullbacks, through a procedure called contraction. But a more comprehensive study of the latter will be postponed to the next section.
$\text{RV}$
-pullbacks, through a procedure called contraction. But a more comprehensive study of the latter will be postponed to the next section.
Definition 3.23 (Disc-to-disc).
Let
![]() $A$
,
$A$
,
![]() $B$
be two subsets of
$B$
be two subsets of
![]() $\text{VF}$
and
$\text{VF}$
and
 $f:A\longrightarrow B$
a bijection. We say that
$f:A\longrightarrow B$
a bijection. We say that
![]() $f$
is concentric if, for all open discs
$f$
is concentric if, for all open discs
![]() $\mathfrak{a}\subseteq A$
,
$\mathfrak{a}\subseteq A$
,
![]() $f(\mathfrak{a})$
is also an open disc; if both
$f(\mathfrak{a})$
is also an open disc; if both
![]() $f$
and
$f$
and
![]() $f^{-1}$
are concentric then
$f^{-1}$
are concentric then
![]() $f$
has the disc-to-disc property (dtdp).
$f$
has the disc-to-disc property (dtdp).
More generally, let
 $f:A\longrightarrow B$
be a bijection between two sets
$f:A\longrightarrow B$
be a bijection between two sets
![]() $A$
and
$A$
and
![]() $B$
, each with exactly one
$B$
, each with exactly one
![]() $\text{VF}$
-coordinate. For each
$\text{VF}$
-coordinate. For each
 $(t,s)\in f_{\text{RV}}$
, let
$(t,s)\in f_{\text{RV}}$
, let
 $f_{t,s}=f\cap (\text{VF}^{2}\times (t,s))$
, which is called a
$f_{t,s}=f\cap (\text{VF}^{2}\times (t,s))$
, which is called a
![]() $\text{VF}$
-fiber of
$\text{VF}$
-fiber of
![]() $f$
. We say that
$f$
. We say that
![]() $f$
has dtdp if every
$f$
has dtdp if every
![]() $\text{VF}$
-fiber of
$\text{VF}$
-fiber of
![]() $f$
has dtdp.
$f$
has dtdp.
We are somewhat justified in not specifying ‘open disc’ in the terminology since if
![]() $f$
has dtdp then, for all open discs
$f$
has dtdp then, for all open discs
![]() $\mathfrak{a}\subseteq A$
and all closed discs
$\mathfrak{a}\subseteq A$
and all closed discs
![]() $\mathfrak{c}\subseteq \mathfrak{a}$
,
$\mathfrak{c}\subseteq \mathfrak{a}$
,
![]() $f(\mathfrak{c})$
is also a closed disc. In fact, this latter property is stronger: if
$f(\mathfrak{c})$
is also a closed disc. In fact, this latter property is stronger: if
![]() $f(\mathfrak{c})$
is a closed disc for all closed discs
$f(\mathfrak{c})$
is a closed disc for all closed discs
![]() $\mathfrak{c}\subseteq A$
then
$\mathfrak{c}\subseteq A$
then
![]() $f$
has dtdp. But we shall only be concerned with open discs, so we ask for it directly.
$f$
has dtdp. But we shall only be concerned with open discs, so we ask for it directly.
Lemma 3.24. Let
 $f:A\longrightarrow B$
be a definable bijection between two sets
$f:A\longrightarrow B$
be a definable bijection between two sets
![]() $A$
and
$A$
and
![]() $B$
, each with exactly one
$B$
, each with exactly one
![]() $\text{VF}$
-coordinate. Then there is a definable finite partition
$\text{VF}$
-coordinate. Then there is a definable finite partition
![]() $A_{i}$
of
$A_{i}$
of
![]() $A$
such that each
$A$
such that each
![]() $f\restriction A_{i}$
has dtdp.
$f\restriction A_{i}$
has dtdp.
Proof. By compactness, we may simply assume that
![]() $A$
and
$A$
and
![]() $B$
are subsets of
$B$
are subsets of
![]() $\text{VF}$
. Then we may proceed exactly as in the proof of Corollary 3.16, using Lemmas 3.13 and 3.15 (see also Remark 3.17).◻
$\text{VF}$
. Then we may proceed exactly as in the proof of Corollary 3.16, using Lemmas 3.13 and 3.15 (see also Remark 3.17).◻
Definition 3.25. Let
![]() $A$
be a subset of
$A$
be a subset of
![]() $\text{VF}^{n}$
. The
$\text{VF}^{n}$
. The
![]() $\text{RV}$
-boundary of
$\text{RV}$
-boundary of
![]() $A$
, denoted by
$A$
, denoted by
![]() $\unicode[STIX]{x2202}_{\text{RV}}A$
, is the definable subset of
$\unicode[STIX]{x2202}_{\text{RV}}A$
, is the definable subset of
![]() $\operatorname{rv}(A)$
such that
$\operatorname{rv}(A)$
such that
 $t\in \unicode[STIX]{x2202}_{\text{RV}}A$
if and only if
$t\in \unicode[STIX]{x2202}_{\text{RV}}A$
if and only if
![]() $t^{\sharp }\cap A$
is a proper nonempty subset of
$t^{\sharp }\cap A$
is a proper nonempty subset of
![]() $t^{\sharp }$
. The definable set
$t^{\sharp }$
. The definable set
 $\operatorname{rv}(A)\smallsetminus \unicode[STIX]{x2202}_{\text{RV}}A$
, denoted by
$\operatorname{rv}(A)\smallsetminus \unicode[STIX]{x2202}_{\text{RV}}A$
, denoted by
 $\operatorname{int}_{\text{RV}}(A)$
, is called the
$\operatorname{int}_{\text{RV}}(A)$
, is called the
![]() $\text{RV}$
-interior of
$\text{RV}$
-interior of
![]() $A$
.
$A$
.
Obviously,
 $A\subseteq \text{VF}^{n}$
is an
$A\subseteq \text{VF}^{n}$
is an
![]() $\text{RV}$
-pullback if and only if
$\text{RV}$
-pullback if and only if
![]() $\unicode[STIX]{x2202}_{\text{RV}}A$
is empty. Note that
$\unicode[STIX]{x2202}_{\text{RV}}A$
is empty. Note that
![]() $\unicode[STIX]{x2202}_{\text{RV}}A$
is in general different from the topological boundary
$\unicode[STIX]{x2202}_{\text{RV}}A$
is in general different from the topological boundary
 $\unicode[STIX]{x2202}(\operatorname{rv}(A))$
of
$\unicode[STIX]{x2202}(\operatorname{rv}(A))$
of
![]() $\operatorname{rv}(A)$
in
$\operatorname{rv}(A)$
in
![]() $\text{RV}^{n}$
and neither one of them includes the other.
$\text{RV}^{n}$
and neither one of them includes the other.
Lemma 3.26. Let
![]() $A$
be a definable subset of
$A$
be a definable subset of
![]() $\text{VF}^{n}$
. Then
$\text{VF}^{n}$
. Then
 $\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}A)<n$
.
$\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}A)<n$
.
Proof. We do induction on
![]() $n$
. The base case
$n$
. The base case
![]() $n=1$
follows immediately from HNF.
$n=1$
follows immediately from HNF.
We proceed to the inductive step. Since
![]() $\unicode[STIX]{x2202}_{\text{RV}}A_{a}$
is finite for every
$\unicode[STIX]{x2202}_{\text{RV}}A_{a}$
is finite for every
![]() $i\in [n]$
and every
$i\in [n]$
and every
 $a\in \operatorname{pr}_{\tilde{i} }(A)$
, by Corollary 3.21 and compactness, there are a definable finite partition
$a\in \operatorname{pr}_{\tilde{i} }(A)$
, by Corollary 3.21 and compactness, there are a definable finite partition
![]() $A_{ij}$
of
$A_{ij}$
of
![]() $\operatorname{pr}_{\tilde{i} }(A)$
and, for each
$\operatorname{pr}_{\tilde{i} }(A)$
and, for each
![]() $A_{ij}$
, finitely many definable functions
$A_{ij}$
, finitely many definable functions
 $f_{ijk}:A_{ij}\longrightarrow \text{VF}$
such that
$f_{ijk}:A_{ij}\longrightarrow \text{VF}$
such that
 $$\begin{eqnarray}\mathop{\bigcup }_{k}\operatorname{rv}(f_{ijk}(a))=\unicode[STIX]{x2202}_{\text{RV}}A_{a}\quad \text{for all }a\in A_{ij}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{k}\operatorname{rv}(f_{ijk}(a))=\unicode[STIX]{x2202}_{\text{RV}}A_{a}\quad \text{for all }a\in A_{ij}.\end{eqnarray}$$
By Corollary 3.16, we may assume that if
 $t^{\sharp }\subseteq A_{ij}$
then the restriction
$t^{\sharp }\subseteq A_{ij}$
then the restriction
 $\operatorname{rv}\restriction f_{ijk}(t^{\sharp })$
is constant. Hence each
$\operatorname{rv}\restriction f_{ijk}(t^{\sharp })$
is constant. Hence each
![]() $f_{ijk}$
induces a definable function
$f_{ijk}$
induces a definable function
 $C_{ijk}:\operatorname{int}_{\text{RV}}(A_{ij})\longrightarrow \operatorname{RV}_{0}$
. Let
$C_{ijk}:\operatorname{int}_{\text{RV}}(A_{ij})\longrightarrow \operatorname{RV}_{0}$
. Let
 $$\begin{eqnarray}C=\mathop{\bigcup }_{i,j,k}C_{ijk}\quad \text{and}\quad B=\mathop{\bigcup }_{i,j}\mathop{\bigcup }_{t\in \unicode[STIX]{x2202}_{\text{RV}}A_{ij}}\operatorname{rv}(A)_{t}.\end{eqnarray}$$
$$\begin{eqnarray}C=\mathop{\bigcup }_{i,j,k}C_{ijk}\quad \text{and}\quad B=\mathop{\bigcup }_{i,j}\mathop{\bigcup }_{t\in \unicode[STIX]{x2202}_{\text{RV}}A_{ij}}\operatorname{rv}(A)_{t}.\end{eqnarray}$$
Obviously
 $\dim _{\text{RV}}(C)<n$
. By the inductive hypothesis, for all
$\dim _{\text{RV}}(C)<n$
. By the inductive hypothesis, for all
![]() $A_{ij}$
we have
$A_{ij}$
we have
 $\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}A_{ij})<n-1$
. Thus
$\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}A_{ij})<n-1$
. Thus
 $\dim _{\text{RV}}(B)<n$
. Since
$\dim _{\text{RV}}(B)<n$
. Since
 $\unicode[STIX]{x2202}_{\text{RV}}A\subseteq B\cup C$
, the claim follows.◻
$\unicode[STIX]{x2202}_{\text{RV}}A\subseteq B\cup C$
, the claim follows.◻
For
 $(a,t)\in \text{VF}^{n}\times \text{RV}_{0}^{m}$
, we write
$(a,t)\in \text{VF}^{n}\times \text{RV}_{0}^{m}$
, we write
![]() $\operatorname{rv}(a,t)$
to mean
$\operatorname{rv}(a,t)$
to mean
 $(\operatorname{rv}(a),t)$
, and similarly for other maps.
$(\operatorname{rv}(a),t)$
, and similarly for other maps.
Definition 3.27 (Contractions).
A function
 $f:A\longrightarrow B$
is
$f:A\longrightarrow B$
is
![]() $\operatorname{rv}$
-contractible if there is a (necessarily unique) function
$\operatorname{rv}$
-contractible if there is a (necessarily unique) function
 $f_{\downarrow }:\operatorname{rv}(A)\longrightarrow \operatorname{rv}(B)$
, called the
$f_{\downarrow }:\operatorname{rv}(A)\longrightarrow \operatorname{rv}(B)$
, called the
![]() $\operatorname{rv}$
-contraction of
$\operatorname{rv}$
-contraction of
![]() $f$
, such that
$f$
, such that
 $$\begin{eqnarray}(\operatorname{rv}\restriction B)\circ f=f_{\downarrow }\circ (\operatorname{rv}\restriction A).\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{rv}\restriction B)\circ f=f_{\downarrow }\circ (\operatorname{rv}\restriction A).\end{eqnarray}$$
Similarly, it is
![]() $\operatorname{res}$
-contractible (respectively,
$\operatorname{res}$
-contractible (respectively,
![]() $\operatorname{val}$
-contractible) if the same holds in terms of
$\operatorname{val}$
-contractible) if the same holds in terms of
![]() $\operatorname{res}$
(respectively,
$\operatorname{res}$
(respectively,
![]() $\operatorname{val}$
or
$\operatorname{val}$
or
![]() $\operatorname{vrv}$
, depending on the coordinates) instead of
$\operatorname{vrv}$
, depending on the coordinates) instead of
![]() $\operatorname{rv}$
.
$\operatorname{rv}$
.
The subscripts in these contractions will be written as
![]() $\downarrow _{\operatorname{rv}}$
,
$\downarrow _{\operatorname{rv}}$
,
![]() $\downarrow _{\operatorname{res}}$
, etc., if they occur in the same context and therefore need to be distinguished from one another notationally.
$\downarrow _{\operatorname{res}}$
, etc., if they occur in the same context and therefore need to be distinguished from one another notationally.
Lemma 3.28. For every definable function
 $f:\text{VF}^{n}\longrightarrow \text{VF}$
there is a definable set
$f:\text{VF}^{n}\longrightarrow \text{VF}$
there is a definable set
 $U\subseteq \text{RV}^{n}$
with
$U\subseteq \text{RV}^{n}$
with
 $\dim _{\text{RV}}(U)<n$
such that
$\dim _{\text{RV}}(U)<n$
such that
 $f\restriction (\text{VF}^{n}\smallsetminus U^{\sharp })$
is
$f\restriction (\text{VF}^{n}\smallsetminus U^{\sharp })$
is
![]() $\operatorname{rv}$
-contractible.
$\operatorname{rv}$
-contractible.
Proof. By Corollary 3.14, for any
 $t\in \text{RV}^{n}$
, if
$t\in \text{RV}^{n}$
, if
 $\operatorname{rv}(f(t^{\sharp }))$
is not a singleton then
$\operatorname{rv}(f(t^{\sharp }))$
is not a singleton then
![]() $t^{\sharp }$
has a
$t^{\sharp }$
has a
![]() $t$
-definable proper subset. By compactness, there is a definable subset
$t$
-definable proper subset. By compactness, there is a definable subset
 $A\subseteq \text{VF}^{n}$
such that
$A\subseteq \text{VF}^{n}$
such that
 $t\in \unicode[STIX]{x2202}_{\text{RV}}A$
if and only if
$t\in \unicode[STIX]{x2202}_{\text{RV}}A$
if and only if
 $\operatorname{rv}(f(t^{\sharp }))$
is not a singleton. So the assertion follows from Lemma 3.26.◻
$\operatorname{rv}(f(t^{\sharp }))$
is not a singleton. So the assertion follows from Lemma 3.26.◻
For any definable set
![]() $A$
, a property holds almost everywhere in
$A$
, a property holds almost everywhere in
![]() $A$
or for almost every point in
$A$
or for almost every point in
![]() $A$
if it holds away from a definable subset of
$A$
if it holds away from a definable subset of
![]() $A$
of a smaller
$A$
of a smaller
![]() $\text{VF}$
-dimension. This terminology will also be used with respect to other notions of dimension.
$\text{VF}$
-dimension. This terminology will also be used with respect to other notions of dimension.
Remark 3.29 (Regular points).
Let
 $f:\text{VF}^{n}\longrightarrow \text{VF}^{m}$
be a definable function. By Lemma 3.3 and
$f:\text{VF}^{n}\longrightarrow \text{VF}^{m}$
be a definable function. By Lemma 3.3 and
![]() $o$
-minimal differentiability,
$o$
-minimal differentiability,
![]() $f$
is
$f$
is
![]() $C^{p}$
almost everywhere for all
$C^{p}$
almost everywhere for all
![]() $p$
(see [Reference van den DriesVdD98, § 7.3]). For each
$p$
(see [Reference van den DriesVdD98, § 7.3]). For each
![]() $p$
, let
$p$
, let
 $\operatorname{reg}^{p}(f)\subseteq \text{VF}^{n}$
be the definable subset of regular
$\operatorname{reg}^{p}(f)\subseteq \text{VF}^{n}$
be the definable subset of regular
![]() $C^{p}$
-points of
$C^{p}$
-points of
![]() $f$
. If
$f$
. If
![]() $p=0$
then we write
$p=0$
then we write
![]() $\operatorname{reg}(f)$
, which is simply the subset of the regular points of
$\operatorname{reg}(f)$
, which is simply the subset of the regular points of
![]() $f$
.
$f$
.
Assume
![]() $n=m$
. If
$n=m$
. If
 $a\in \operatorname{reg}(f)$
and
$a\in \operatorname{reg}(f)$
and
![]() $f$
is
$f$
is
![]() $C^{1}$
in a neighborhood of
$C^{1}$
in a neighborhood of
![]() $a$
then
$a$
then
![]() $\operatorname{reg}^{1}(f)$
contains a neighborhood of
$\operatorname{reg}^{1}(f)$
contains a neighborhood of
![]() $a$
on which the sign of the Jacobian of
$a$
on which the sign of the Jacobian of
![]() $f$
, which is denoted by
$f$
, which is denoted by
 $\operatorname{Jcb}_{\text{VF}}f$
, is constant. If
$\operatorname{Jcb}_{\text{VF}}f$
, is constant. If
![]() $f$
is locally injective on a definable open subset
$f$
is locally injective on a definable open subset
 $A\subseteq \text{VF}^{n}$
then
$A\subseteq \text{VF}^{n}$
then
![]() $f$
is regular almost everywhere in
$f$
is regular almost everywhere in
![]() $A$
and hence, for all
$A$
and hence, for all
![]() $p$
,
$p$
,
 $\dim _{\text{VF}}(A\smallsetminus \operatorname{reg}^{p}(f))<n$
.
$\dim _{\text{VF}}(A\smallsetminus \operatorname{reg}^{p}(f))<n$
.
By [Reference van den DriesVdD97, Theorem A], the situation is quite similar if
![]() $f$
is a (parametrically) definable function of the form
$f$
is a (parametrically) definable function of the form
 $\operatorname{Tor}(\unicode[STIX]{x1D6FC})^{n}\longrightarrow \operatorname{Tor}(\unicode[STIX]{x1D6FD})^{m}$
,
$\operatorname{Tor}(\unicode[STIX]{x1D6FC})^{n}\longrightarrow \operatorname{Tor}(\unicode[STIX]{x1D6FD})^{m}$
,
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in |\unicode[STIX]{x1D6E4}|$
, and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in |\unicode[STIX]{x1D6E4}|$
, and
![]() $\dim _{\text{VF}}$
is replaced by
$\dim _{\text{VF}}$
is replaced by
![]() $\dim _{\text{RV}}$
, in particular, if
$\dim _{\text{RV}}$
, in particular, if
![]() $f$
is such a function from
$f$
is such a function from
![]() $\Bbbk ^{n}$
into
$\Bbbk ^{n}$
into
![]() $\Bbbk ^{m}$
, or more generally, from
$\Bbbk ^{m}$
, or more generally, from
![]() $\operatorname{Tor}(u)$
into
$\operatorname{Tor}(u)$
into
![]() $\operatorname{Tor}(v)$
, where
$\operatorname{Tor}(v)$
, where
 $u\in \text{RV}_{\unicode[STIX]{x1D6FC}}^{n}$
and
$u\in \text{RV}_{\unicode[STIX]{x1D6FC}}^{n}$
and
 $v\in \text{RV}_{\unicode[STIX]{x1D6FD}}^{m}$
(see Notation 2.35 and Definition 2.36).
$v\in \text{RV}_{\unicode[STIX]{x1D6FD}}^{m}$
(see Notation 2.35 and Definition 2.36).
Remark 3.30 (
 $\operatorname{rv}$
-contraction of univariate functions).
$\operatorname{rv}$
-contraction of univariate functions).
Suppose that
![]() $f$
is a definable function from
$f$
is a definable function from
![]() $\mathfrak{O}^{\times }$
into
$\mathfrak{O}^{\times }$
into
![]() $\mathfrak{O}$
. By monotonicity, there are a definable finite set
$\mathfrak{O}$
. By monotonicity, there are a definable finite set
 $B\subseteq \mathfrak{O}^{\times }$
and a definable finite partition of
$B\subseteq \mathfrak{O}^{\times }$
and a definable finite partition of
 $A:=\mathfrak{O}^{\times }\smallsetminus B$
into infinite
$A:=\mathfrak{O}^{\times }\smallsetminus B$
into infinite
![]() $\operatorname{val}$
-intervals
$\operatorname{val}$
-intervals
![]() $A_{i}$
such that both
$A_{i}$
such that both
![]() $f$
and
$f$
and
 $(d/dx)f$
are quasi-
$(d/dx)f$
are quasi-
![]() ${\mathcal{L}}_{T\text{}}$
-definable, continuous, and monotone on each
${\mathcal{L}}_{T\text{}}$
-definable, continuous, and monotone on each
![]() $A_{i}$
. If
$A_{i}$
. If
![]() $\operatorname{rv}(A_{i})$
is not a singleton then let
$\operatorname{rv}(A_{i})$
is not a singleton then let
![]() $U_{i}\subseteq \Bbbk$
be the largest open interval contained in
$U_{i}\subseteq \Bbbk$
be the largest open interval contained in
![]() $\operatorname{rv}(A_{i})$
. Let
$\operatorname{rv}(A_{i})$
. Let
 $$\begin{eqnarray}A_{i}^{\ast }=U_{i}^{\sharp },\quad U=\mathop{\bigcup }_{i}U_{i},\quad A^{\ast }=U^{\sharp },\quad f^{\ast }=f\restriction A^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}A_{i}^{\ast }=U_{i}^{\sharp },\quad U=\mathop{\bigcup }_{i}U_{i},\quad A^{\ast }=U^{\sharp },\quad f^{\ast }=f\restriction A^{\ast }.\end{eqnarray}$$
By Lemma 3.28, we may refine the partition such that both
![]() $f^{\ast }$
and
$f^{\ast }$
and
 $(d/dx)f^{\ast }$
are
$(d/dx)f^{\ast }$
are
![]() $\operatorname{rv}$
-contractible. By Lemma 2.23,
$\operatorname{rv}$
-contractible. By Lemma 2.23,
 $\operatorname{val}\restriction f^{\ast }(A_{i}^{\ast })$
and
$\operatorname{val}\restriction f^{\ast }(A_{i}^{\ast })$
and
 $\operatorname{val}\restriction (d/dx)f^{\ast }(A_{i}^{\ast })$
must be constant, say
$\operatorname{val}\restriction (d/dx)f^{\ast }(A_{i}^{\ast })$
must be constant, say
![]() $\unicode[STIX]{x1D6FC}_{i}$
and
$\unicode[STIX]{x1D6FC}_{i}$
and
![]() $\unicode[STIX]{x1D6FD}_{i}$
, respectively. So it makes sense to speak of
$\unicode[STIX]{x1D6FD}_{i}$
, respectively. So it makes sense to speak of
 $(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }$
on each
$(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }$
on each
![]() $U_{i}$
, which a priori is not the same as
$U_{i}$
, which a priori is not the same as
 $((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}$
. Deleting finitely many points from
$((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}$
. Deleting finitely many points from
![]() $U$
if necessary, we assume that
$U$
if necessary, we assume that
![]() $f_{\downarrow _{\operatorname{rv}}}^{\ast }$
,
$f_{\downarrow _{\operatorname{rv}}}^{\ast }$
,
 $((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}$
, and
$((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}$
, and
 $(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }$
are all continuous monotone functions on each
$(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }$
are all continuous monotone functions on each
![]() $U_{i}$
.
$U_{i}$
.
We claim that
 $|\unicode[STIX]{x1D6FD}_{i}|=|\unicode[STIX]{x1D6FC}_{i}|$
unless
$|\unicode[STIX]{x1D6FD}_{i}|=|\unicode[STIX]{x1D6FC}_{i}|$
unless
 $f_{\downarrow _{\operatorname{rv}}}^{\ast }\restriction U_{i}$
is constant. Suppose for contradiction that
$f_{\downarrow _{\operatorname{rv}}}^{\ast }\restriction U_{i}$
is constant. Suppose for contradiction that
 $f_{\downarrow _{\operatorname{rv}}}^{\ast }\restriction U_{i}$
is not constant and
$f_{\downarrow _{\operatorname{rv}}}^{\ast }\restriction U_{i}$
is not constant and
 $|\unicode[STIX]{x1D6FD}_{i}|\neq |\unicode[STIX]{x1D6FC}_{i}|$
. First examine the case
$|\unicode[STIX]{x1D6FD}_{i}|\neq |\unicode[STIX]{x1D6FC}_{i}|$
. First examine the case
 $|\unicode[STIX]{x1D6FD}_{i}|<|\unicode[STIX]{x1D6FC}_{i}|$
. A moment of reflection shows that then
$|\unicode[STIX]{x1D6FD}_{i}|<|\unicode[STIX]{x1D6FC}_{i}|$
. A moment of reflection shows that then
![]() $f^{\ast }\restriction A_{i}^{\ast }$
would increase or decrease too fast to confine
$f^{\ast }\restriction A_{i}^{\ast }$
would increase or decrease too fast to confine
![]() $f^{\ast }(A_{i}^{\ast })$
in
$f^{\ast }(A_{i}^{\ast })$
in
 $\operatorname{val}^{-1}(\unicode[STIX]{x1D6FC}_{i})$
. Dually, if
$\operatorname{val}^{-1}(\unicode[STIX]{x1D6FC}_{i})$
. Dually, if
 $|\unicode[STIX]{x1D6FD}_{i}|>|\unicode[STIX]{x1D6FC}_{i}|$
then
$|\unicode[STIX]{x1D6FD}_{i}|>|\unicode[STIX]{x1D6FC}_{i}|$
then
![]() $f^{\ast }\restriction A_{i}^{\ast }$
would increase or decrease too slowly to make
$f^{\ast }\restriction A_{i}^{\ast }$
would increase or decrease too slowly to make
 $f_{\downarrow _{\operatorname{rv}}}^{\ast }(U_{i})$
contain more than one point. In either case, we have reached a contradiction. Actually, a similar estimate shows that if
$f_{\downarrow _{\operatorname{rv}}}^{\ast }(U_{i})$
contain more than one point. In either case, we have reached a contradiction. Actually, a similar estimate shows that if
 $|\unicode[STIX]{x1D6FD}_{i}|=|\unicode[STIX]{x1D6FC}_{i}|<\infty$
then
$|\unicode[STIX]{x1D6FD}_{i}|=|\unicode[STIX]{x1D6FC}_{i}|<\infty$
then
 $f_{\downarrow _{\operatorname{rv}}}^{\ast }\restriction U_{i}$
cannot be constant.
$f_{\downarrow _{\operatorname{rv}}}^{\ast }\restriction U_{i}$
cannot be constant.
Finally, we show that
 $|\unicode[STIX]{x1D6FD}_{i}|=|\unicode[STIX]{x1D6FC}_{i}|$
implies
$|\unicode[STIX]{x1D6FD}_{i}|=|\unicode[STIX]{x1D6FC}_{i}|$
implies
 $((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}=(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }$
on
$((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}=(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }$
on
![]() $U_{i}$
(note that if
$U_{i}$
(note that if
 $|\unicode[STIX]{x1D6FD}_{i}|>|\unicode[STIX]{x1D6FC}_{i}|$
then
$|\unicode[STIX]{x1D6FD}_{i}|>|\unicode[STIX]{x1D6FC}_{i}|$
then
 $(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }=0$
). Suppose for contradiction that, say,
$(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }=0$
). Suppose for contradiction that, say,
 $$\begin{eqnarray}\biggl(\frac{d}{dx}f^{\ast }\biggr)_{\downarrow _{\operatorname{rv}}}(\operatorname{rv}(a))>\frac{d}{dx}f_{\downarrow _{\operatorname{rv}}}^{\ast }(\operatorname{rv}(a))>0\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{d}{dx}f^{\ast }\biggr)_{\downarrow _{\operatorname{rv}}}(\operatorname{rv}(a))>\frac{d}{dx}f_{\downarrow _{\operatorname{rv}}}^{\ast }(\operatorname{rv}(a))>0\end{eqnarray}$$
for some
![]() $a\in A_{i}^{\ast }$
. Then there is an open interval
$a\in A_{i}^{\ast }$
. Then there is an open interval
![]() $I\subseteq U_{i}$
containing
$I\subseteq U_{i}$
containing
![]() $\operatorname{rv}(a)$
such that
$\operatorname{rv}(a)$
such that
 $((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}(I)>(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }(I)$
. It follows that
$((d/dx)f^{\ast })_{\downarrow _{\operatorname{rv}}}(I)>(d/dx)f_{\downarrow _{\operatorname{rv}}}^{\ast }(I)$
. It follows that
![]() $f_{\downarrow _{\operatorname{rv}}}^{\ast }(I)$
is properly contained in
$f_{\downarrow _{\operatorname{rv}}}^{\ast }(I)$
is properly contained in
 $\operatorname{rv}(f^{\ast }(I^{\sharp }))=f_{\downarrow _{\operatorname{rv}}}^{\ast }(I)$
, which is absurd. The other cases are similar.
$\operatorname{rv}(f^{\ast }(I^{\sharp }))=f_{\downarrow _{\operatorname{rv}}}^{\ast }(I)$
, which is absurd. The other cases are similar.
The higher-order multivariate version is more complicated to state than to prove.
Lemma 3.31. Let
 $A\subseteq (\mathfrak{O}^{\times })^{n}$
be a definable
$A\subseteq (\mathfrak{O}^{\times })^{n}$
be a definable
![]() $\text{RV}$
-pullback with
$\text{RV}$
-pullback with
 $\dim _{\text{RV}}(\operatorname{rv}(A))=n$
and
$\dim _{\text{RV}}(\operatorname{rv}(A))=n$
and
 $f:A\longrightarrow \mathfrak{O}$
a definable function. Let
$f:A\longrightarrow \mathfrak{O}$
a definable function. Let
![]() $p\in \unicode[STIX]{x2115}^{n}$
be a multi-index of order
$p\in \unicode[STIX]{x2115}^{n}$
be a multi-index of order
![]() $|p|=d$
and
$|p|=d$
and
![]() $k\in \unicode[STIX]{x2115}$
with
$k\in \unicode[STIX]{x2115}$
with
![]() $k\gg d$
. Suppose that
$k\gg d$
. Suppose that
![]() $f$
is
$f$
is
![]() $C^{k}$
and, for all
$C^{k}$
and, for all
![]() $q\leqslant p$
,
$q\leqslant p$
,
 $(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f$
is
$(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f$
is
![]() $\operatorname{rv}$
-contractible and its contraction
$\operatorname{rv}$
-contractible and its contraction
 $((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f)_{\downarrow _{\operatorname{rv}}}$
is also
$((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f)_{\downarrow _{\operatorname{rv}}}$
is also
![]() $C^{k}$
. Then there is a definable set
$C^{k}$
. Then there is a definable set
 $V\subseteq \operatorname{rv}(A)$
with
$V\subseteq \operatorname{rv}(A)$
with
 $\dim _{\text{RV}}(V)<n$
and
$\dim _{\text{RV}}(V)<n$
and
 $U:=\operatorname{rv}(A)\smallsetminus V$
open such that, for all
$U:=\operatorname{rv}(A)\smallsetminus V$
open such that, for all
![]() $a\in U^{\sharp }$
and all
$a\in U^{\sharp }$
and all
 $q^{\prime }<q\leqslant p$
with
$q^{\prime }<q\leqslant p$
with
 $|q^{\prime }|+1=q$
, exactly one of the following two conditions holds:
$|q^{\prime }|+1=q$
, exactly one of the following two conditions holds:
-
– either
 $(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f(a)=0$
or
$(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f(a)=0$
or
 $|\text{val}|((\unicode[STIX]{x2202}^{q^{\prime }}/\unicode[STIX]{x2202}x^{q^{\prime }})f(a))<|\text{val}|((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f(a))$
,
$|\text{val}|((\unicode[STIX]{x2202}^{q^{\prime }}/\unicode[STIX]{x2202}x^{q^{\prime }})f(a))<|\text{val}|((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f(a))$
, -
–
 $((\unicode[STIX]{x2202}^{q-q^{\prime }}/\unicode[STIX]{x2202}x^{q-q^{\prime }})(\unicode[STIX]{x2202}^{q^{\prime }}/\unicode[STIX]{x2202}x^{q^{\prime }})f)_{\downarrow _{\operatorname{rv}}}(\operatorname{rv}(a))=(\unicode[STIX]{x2202}^{q-q^{\prime }}/\unicode[STIX]{x2202}x^{q-q^{\prime }})((\unicode[STIX]{x2202}^{q^{\prime }}/\unicode[STIX]{x2202}x^{q^{\prime }})f)_{\downarrow _{\operatorname{rv}}}(\operatorname{rv}(a))\neq 0$
.
$((\unicode[STIX]{x2202}^{q-q^{\prime }}/\unicode[STIX]{x2202}x^{q-q^{\prime }})(\unicode[STIX]{x2202}^{q^{\prime }}/\unicode[STIX]{x2202}x^{q^{\prime }})f)_{\downarrow _{\operatorname{rv}}}(\operatorname{rv}(a))=(\unicode[STIX]{x2202}^{q-q^{\prime }}/\unicode[STIX]{x2202}x^{q-q^{\prime }})((\unicode[STIX]{x2202}^{q^{\prime }}/\unicode[STIX]{x2202}x^{q^{\prime }})f)_{\downarrow _{\operatorname{rv}}}(\operatorname{rv}(a))\neq 0$
.
If the first condition never occurs then, for all
![]() $q\leqslant p$
, we actually have
$q\leqslant p$
, we actually have
 $((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f)_{\downarrow _{\operatorname{rv}}}=(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f_{\downarrow _{\operatorname{rv}}}$
on
$((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f)_{\downarrow _{\operatorname{rv}}}=(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f_{\downarrow _{\operatorname{rv}}}$
on
![]() $U$
. At any rate, for all
$U$
. At any rate, for all
![]() $q\leqslant p$
, we have
$q\leqslant p$
, we have
 $((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f)_{\downarrow _{\operatorname{res}}}=(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f_{\downarrow _{\operatorname{res}}}$
on
$((\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f)_{\downarrow _{\operatorname{res}}}=(\unicode[STIX]{x2202}^{q}/\unicode[STIX]{x2202}x^{q})f_{\downarrow _{\operatorname{res}}}$
on
![]() $U$
.
$U$
.
Proof. First observe that, by induction on
![]() $d$
, it is enough to consider the case
$d$
, it is enough to consider the case
![]() $d=1$
and
$d=1$
and
 $p=(0,\ldots ,0,1)$
. For each
$p=(0,\ldots ,0,1)$
. For each
 $a\in \operatorname{pr}_{{<}n}(A)$
, by the discussion in Remark 3.30, there is an
$a\in \operatorname{pr}_{{<}n}(A)$
, by the discussion in Remark 3.30, there is an
![]() $a$
-definable finite set
$a$
-definable finite set
![]() $V_{a}$
of
$V_{a}$
of
 $\operatorname{rv}(A)_{\operatorname{rv}(a)}$
such that the assertion holds for the restriction
$\operatorname{rv}(A)_{\operatorname{rv}(a)}$
such that the assertion holds for the restriction
 $f\restriction (A_{a}\smallsetminus V_{a}^{\sharp })$
. Let
$f\restriction (A_{a}\smallsetminus V_{a}^{\sharp })$
. Let
 $A^{\ast }=\bigcup _{a\in \operatorname{pr}_{{<}n}(A)}V_{a}^{\sharp }\subseteq A$
. By Lemma 3.26,
$A^{\ast }=\bigcup _{a\in \operatorname{pr}_{{<}n}(A)}V_{a}^{\sharp }\subseteq A$
. By Lemma 3.26,
 $\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}A^{\ast })<n$
and hence
$\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}A^{\ast })<n$
and hence
 $\dim _{\text{RV}}(\operatorname{rv}(A^{\ast }))<n$
. Therefore, by Lemma 3.28, there is a definable open set
$\dim _{\text{RV}}(\operatorname{rv}(A^{\ast }))<n$
. Therefore, by Lemma 3.28, there is a definable open set
 $U\subseteq \operatorname{int}(\operatorname{rv}(A)\smallsetminus \operatorname{rv}(A^{\ast }))$
that is as desired.◻
$U\subseteq \operatorname{int}(\operatorname{rv}(A)\smallsetminus \operatorname{rv}(A^{\ast }))$
that is as desired.◻
Suppose that
 $f=(f_{1},\ldots ,f_{m}):A\longrightarrow \mathfrak{O}$
is a sequence of definable
$f=(f_{1},\ldots ,f_{m}):A\longrightarrow \mathfrak{O}$
is a sequence of definable
![]() $\operatorname{res}$
-contractible functions, where the set
$\operatorname{res}$
-contractible functions, where the set
![]() $A$
is as in Lemma 3.31. Let
$A$
is as in Lemma 3.31. Let
 $P(x_{1},\ldots ,x_{m})$
be a partial differential operator with definable
$P(x_{1},\ldots ,x_{m})$
be a partial differential operator with definable
![]() $\operatorname{res}$
-contractible coefficients
$\operatorname{res}$
-contractible coefficients
 $a_{i}:A\longrightarrow \mathfrak{O}$
, and
$a_{i}:A\longrightarrow \mathfrak{O}$
, and
 $P_{\downarrow _{\operatorname{res}}}(x_{1},\ldots ,x_{m})$
the corresponding operator with
$P_{\downarrow _{\operatorname{res}}}(x_{1},\ldots ,x_{m})$
the corresponding operator with
![]() $\operatorname{res}$
-contracted coefficients
$\operatorname{res}$
-contracted coefficients
 $a_{i\downarrow _{\operatorname{res}}}:\operatorname{res}(A)\longrightarrow \Bbbk$
. Note that both
$a_{i\downarrow _{\operatorname{res}}}:\operatorname{res}(A)\longrightarrow \Bbbk$
. Note that both
 $P(f):A\longrightarrow \mathfrak{O}$
and
$P(f):A\longrightarrow \mathfrak{O}$
and
 $P_{\downarrow _{\operatorname{res}}}(f_{\downarrow _{\operatorname{res}}}):\operatorname{res}(A)\longrightarrow \Bbbk$
are defined almost everywhere. By Lemma 3.31, such an operator
$P_{\downarrow _{\operatorname{res}}}(f_{\downarrow _{\operatorname{res}}}):\operatorname{res}(A)\longrightarrow \Bbbk$
are defined almost everywhere. By Lemma 3.31, such an operator
![]() $P$
almost commutes with
$P$
almost commutes with
![]() $\operatorname{res}$
.
$\operatorname{res}$
.
Corollary 3.32. For almost all
 $t\in \operatorname{rv}(A)$
and all
$t\in \operatorname{rv}(A)$
and all
![]() $a\in t^{\sharp }$
,
$a\in t^{\sharp }$
,
 $$\begin{eqnarray}\operatorname{res}(P(f)(a))=P_{\downarrow _{\operatorname{res}}}(f_{\downarrow _{\operatorname{res}}})(\operatorname{res}(a)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{res}(P(f)(a))=P_{\downarrow _{\operatorname{res}}}(f_{\downarrow _{\operatorname{res}}})(\operatorname{res}(a)).\end{eqnarray}$$
Corollary 3.33. Let
![]() $U$
,
$U$
,
![]() $V$
be definably connected subsets of
$V$
be definably connected subsets of
![]() $(\Bbbk ^{+})^{n}$
and
$(\Bbbk ^{+})^{n}$
and
 $f:U^{\sharp }\longrightarrow V^{\sharp }$
a definable
$f:U^{\sharp }\longrightarrow V^{\sharp }$
a definable
![]() $\operatorname{res}$
-contractible function. Suppose that
$\operatorname{res}$
-contractible function. Suppose that
 $f_{\downarrow _{\operatorname{res}}}:U\longrightarrow V$
is continuous and locally injective. Then there is a definable subset
$f_{\downarrow _{\operatorname{res}}}:U\longrightarrow V$
is continuous and locally injective. Then there is a definable subset
 $U^{\ast }\subseteq U$
of
$U^{\ast }\subseteq U$
of
![]() $\text{RV}$
-dimension less than
$\text{RV}$
-dimension less than
![]() $n$
such that the sign of
$n$
such that the sign of
 $\operatorname{Jcb}_{\text{VF}}f$
is constant on
$\operatorname{Jcb}_{\text{VF}}f$
is constant on
 $(U\smallsetminus U^{\ast })^{\sharp }$
.
$(U\smallsetminus U^{\ast })^{\sharp }$
.
Proof. This follows immediately from Corollary 3.32 and [Reference Peterzil and StarchenkoPS07, Theorem 3.2]. ◻
Lemma 3.34. In
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
![]() $\mathfrak{a}\subseteq \text{VF}$
be an atomic subset and
$\mathfrak{a}\subseteq \text{VF}$
be an atomic subset and
 $f:\mathfrak{a}\longrightarrow \text{VF}$
a definable injection. Then
$f:\mathfrak{a}\longrightarrow \text{VF}$
a definable injection. Then
![]() $\mathfrak{a}$
and
$\mathfrak{a}$
and
![]() $f(\mathfrak{a})$
must be of the same one of the four possible forms (see Remark 3.11).
$f(\mathfrak{a})$
must be of the same one of the four possible forms (see Remark 3.11).
Proof. This is trivial if
![]() $\mathfrak{a}$
is a point. The case of
$\mathfrak{a}$
is a point. The case of
![]() $\mathfrak{a}$
being an open disc is covered by Lemma 3.13. So we only need to show that if
$\mathfrak{a}$
being an open disc is covered by Lemma 3.13. So we only need to show that if
![]() $\mathfrak{a}$
is a closed disc then
$\mathfrak{a}$
is a closed disc then
![]() $f(\mathfrak{a})$
cannot be a half thin annulus. We shall give two proofs. The first one works only when
$f(\mathfrak{a})$
cannot be a half thin annulus. We shall give two proofs. The first one works only when
![]() $T$
is polynomially bounded, but is more intuitive and much simpler.
$T$
is polynomially bounded, but is more intuitive and much simpler.
Suppose that
![]() $T$
is polynomially bounded. Suppose for contradiction that
$T$
is polynomially bounded. Suppose for contradiction that
![]() $\ulcorner \mathfrak{a}\urcorner$
is of the form
$\ulcorner \mathfrak{a}\urcorner$
is of the form
 $\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
for some
$\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
for some
 $\ulcorner \mathfrak{m}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}}$
and
$\ulcorner \mathfrak{m}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FE}}$
and
![]() $\ulcorner f(\mathfrak{a})\urcorner$
is of the form
$\ulcorner f(\mathfrak{a})\urcorner$
is of the form
 $\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
for some
$\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
for some
 $\ulcorner \mathfrak{n}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FF}}$
. By Lemma 3.24 and monotonicity,
$\ulcorner \mathfrak{n}\urcorner \in \text{RV}_{\unicode[STIX]{x1D6FF}}$
. By Lemma 3.24 and monotonicity,
![]() $f$
induces an increasing (or decreasing, which can be handled similarly) bijection
$f$
induces an increasing (or decreasing, which can be handled similarly) bijection
 $f_{\downarrow }:\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )\longrightarrow \operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
. In fact, for all
$f_{\downarrow }:\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )\longrightarrow \operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
. In fact, for all
![]() $p\in \unicode[STIX]{x2115}$
,
$p\in \unicode[STIX]{x2115}$
,
 $$\begin{eqnarray}\frac{d^{p}}{dx^{p}}f_{\downarrow }:\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )\longrightarrow \operatorname{Tor}^{+}(\unicode[STIX]{x1D6FF}-p\unicode[STIX]{x1D6FE})\end{eqnarray}$$
$$\begin{eqnarray}\frac{d^{p}}{dx^{p}}f_{\downarrow }:\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )\longrightarrow \operatorname{Tor}^{+}(\unicode[STIX]{x1D6FF}-p\unicode[STIX]{x1D6FE})\end{eqnarray}$$
cannot be constant and hence must be continuous, surjective, and increasing. Using additional parameters, we can translate
![]() $f_{\downarrow }$
into a function
$f_{\downarrow }$
into a function
 $\Bbbk \longrightarrow \Bbbk ^{+}$
and this function cannot be polynomially bounded by elementary differential calculus, which is a contradiction.
$\Bbbk \longrightarrow \Bbbk ^{+}$
and this function cannot be polynomially bounded by elementary differential calculus, which is a contradiction.
We move on to the second proof. The argument is essentially the same as that in the proof of [Reference Hrushovski and KazhdanHK06, Lemma 3.45].
Consider the group
 $$\begin{eqnarray}G:=\operatorname{Aut}(\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )/\Bbbk )\leqslant \operatorname{Aut}({\mathcal{R}}_{\operatorname{rv}}^{\bullet }/\Bbbk ).\end{eqnarray}$$
$$\begin{eqnarray}G:=\operatorname{Aut}(\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )/\Bbbk )\leqslant \operatorname{Aut}({\mathcal{R}}_{\operatorname{rv}}^{\bullet }/\Bbbk ).\end{eqnarray}$$
Suppose for contradiction that
![]() $G$
is finite. Since every
$G$
is finite. Since every
![]() $G$
-orbit is finite, every point in
$G$
-orbit is finite, every point in
 $\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
is
$\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
is
![]() $\Bbbk$
-definable. It follows that there exists a nonconstant definable function
$\Bbbk$
-definable. It follows that there exists a nonconstant definable function
 $\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )\longrightarrow \Bbbk$
. But this is not possible since
$\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )\longrightarrow \Bbbk$
. But this is not possible since
![]() $\mathfrak{a}$
is atomic.
$\mathfrak{a}$
is atomic.
Let
![]() $\unicode[STIX]{x1D6EC}$
be the group of affine transformations of
$\unicode[STIX]{x1D6EC}$
be the group of affine transformations of
![]() $\Bbbk$
, that is,
$\Bbbk$
, that is,
 $\unicode[STIX]{x1D6EC}=\Bbbk ^{\times }\ltimes \Bbbk$
, where the first factor is the multiplicative group of
$\unicode[STIX]{x1D6EC}=\Bbbk ^{\times }\ltimes \Bbbk$
, where the first factor is the multiplicative group of
![]() $\Bbbk$
and the second the additive group of
$\Bbbk$
and the second the additive group of
![]() $\Bbbk$
. Every automorphism in
$\Bbbk$
. Every automorphism in
![]() $G$
is a
$G$
is a
![]() $\Bbbk$
-affine transformation of
$\Bbbk$
-affine transformation of
 $\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
, and hence
$\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
, and hence
![]() $G$
is a subgroup of
$G$
is a subgroup of
![]() $\unicode[STIX]{x1D6EC}$
. For each
$\unicode[STIX]{x1D6EC}$
. For each
![]() $\Bbbk$
-definable relation
$\Bbbk$
-definable relation
![]() $\unicode[STIX]{x1D719}$
on
$\unicode[STIX]{x1D719}$
on
 $\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
, let
$\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
, let
 $G_{\unicode[STIX]{x1D719}}\subseteq \unicode[STIX]{x1D6EC}$
be the definable subgroup of
$G_{\unicode[STIX]{x1D719}}\subseteq \unicode[STIX]{x1D6EC}$
be the definable subgroup of
![]() $\Bbbk$
-affine transformations that preserve
$\Bbbk$
-affine transformations that preserve
![]() $\unicode[STIX]{x1D719}$
. So
$\unicode[STIX]{x1D719}$
. So
 $G=\bigcap _{\unicode[STIX]{x1D719}}G_{\unicode[STIX]{x1D719}}$
. Since there is no infinite descending chain of definable subgroups of
$G=\bigcap _{\unicode[STIX]{x1D719}}G_{\unicode[STIX]{x1D719}}$
. Since there is no infinite descending chain of definable subgroups of
![]() $\unicode[STIX]{x1D6EC}$
, we see that
$\unicode[STIX]{x1D6EC}$
, we see that
![]() $G$
is actually an infinite definable group. Then we may choose two nontrivial automorphisms
$G$
is actually an infinite definable group. Then we may choose two nontrivial automorphisms
 $g,g^{\prime }\in G$
whose fixed points are distinct. It follows that the commutator of
$g,g^{\prime }\in G$
whose fixed points are distinct. It follows that the commutator of
![]() $g$
,
$g$
,
![]() $g^{\prime }$
is a translation and hence, by
$g^{\prime }$
is a translation and hence, by
![]() $o$
-minimality,
$o$
-minimality,
![]() $G$
contains all the translations, that is,
$G$
contains all the translations, that is,
![]() $\Bbbk \leqslant G$
.
$\Bbbk \leqslant G$
.
By a similar argument, every automorphism in
 $H:=\operatorname{Aut}(\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )/\Bbbk )$
is a
$H:=\operatorname{Aut}(\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )/\Bbbk )$
is a
![]() $\Bbbk$
-linear transformation of
$\Bbbk$
-linear transformation of
 $\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
, and hence
$\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
, and hence
 $H=\Bbbk ^{+}\leqslant \Bbbk ^{\times }$
.
$H=\Bbbk ^{+}\leqslant \Bbbk ^{\times }$
.
Now any definable bijection between
 $\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
and
$\operatorname{Tor}(\ulcorner \mathfrak{m}\urcorner )$
and
 $\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
would induce a definable group isomorphism
$\operatorname{Tor}^{+}(\ulcorner \mathfrak{n}\urcorner )$
would induce a definable group isomorphism
 $\Bbbk \longrightarrow \Bbbk ^{+}$
, that is, an exponential function, which of course contradicts the assumption that
$\Bbbk \longrightarrow \Bbbk ^{+}$
, that is, an exponential function, which of course contradicts the assumption that
![]() $T$
is power-bounded.◻
$T$
is power-bounded.◻
Definition 3.35 (
 $\operatorname{val}$
-affine and
$\operatorname{val}$
-affine and
 $\operatorname{rv}$
-affine).
$\operatorname{rv}$
-affine).
Let
![]() $\mathfrak{a}$
be an open disc and
$\mathfrak{a}$
be an open disc and
 $f:\mathfrak{a}\longrightarrow \text{VF}$
an injection. We say that
$f:\mathfrak{a}\longrightarrow \text{VF}$
an injection. We say that
![]() $f$
is
$f$
is
![]() $\operatorname{val}$
-affine if there is a (necessarily unique)
$\operatorname{val}$
-affine if there is a (necessarily unique)
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, called the shift of
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, called the shift of
![]() $f$
, such that, for all
$f$
, such that, for all
 $a,a^{\prime }\in \mathfrak{a}$
,
$a,a^{\prime }\in \mathfrak{a}$
,
 $$\begin{eqnarray}|\text{val}|(f(a)-f(a^{\prime }))=\unicode[STIX]{x1D6FE}+|\text{val}|(a-a^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}|\text{val}|(f(a)-f(a^{\prime }))=\unicode[STIX]{x1D6FE}+|\text{val}|(a-a^{\prime }).\end{eqnarray}$$
We say that
![]() $f$
is
$f$
is
![]() $\operatorname{rv}$
-affine if there is a (necessarily unique)
$\operatorname{rv}$
-affine if there is a (necessarily unique)
![]() $t\in \text{RV}$
, called the slope of
$t\in \text{RV}$
, called the slope of
![]() $f$
, such that, for all
$f$
, such that, for all
 $a,a^{\prime }\in \mathfrak{a}$
,
$a,a^{\prime }\in \mathfrak{a}$
,
 $$\begin{eqnarray}\operatorname{rv}(f(a)-f(a^{\prime }))=t\operatorname{rv}(a-a^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rv}(f(a)-f(a^{\prime }))=t\operatorname{rv}(a-a^{\prime }).\end{eqnarray}$$
Obviously
![]() $\operatorname{rv}$
-affine implies
$\operatorname{rv}$
-affine implies
![]() $\operatorname{val}$
-affine. With the extra structure afforded by the total ordering, we can reproduce (an analogue of) [Reference YinYin11, Lemma 3.18] with a somewhat simpler proof.
$\operatorname{val}$
-affine. With the extra structure afforded by the total ordering, we can reproduce (an analogue of) [Reference YinYin11, Lemma 3.18] with a somewhat simpler proof.
Lemma 3.36. In
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
, let
 $f:\mathfrak{a}\longrightarrow \mathfrak{b}$
be a definable bijection between two atomic open discs. Then
$f:\mathfrak{a}\longrightarrow \mathfrak{b}$
be a definable bijection between two atomic open discs. Then
![]() $f$
is
$f$
is
![]() $\operatorname{rv}$
-affine and hence
$\operatorname{rv}$
-affine and hence
![]() $\operatorname{val}$
-affine with respect to
$\operatorname{val}$
-affine with respect to
 $\operatorname{rad}(\mathfrak{b})-\operatorname{rad}(\mathfrak{a})$
.
$\operatorname{rad}(\mathfrak{b})-\operatorname{rad}(\mathfrak{a})$
.
Proof. Since
![]() $f$
has dtdp by Lemma 3.24, for all
$f$
has dtdp by Lemma 3.24, for all
 $\operatorname{rad}(\mathfrak{a})<\unicode[STIX]{x1D6FF}$
and all
$\operatorname{rad}(\mathfrak{a})<\unicode[STIX]{x1D6FF}$
and all
 $$\begin{eqnarray}\mathfrak{d}:=\operatorname{Tor}(\ulcorner \mathfrak{c}\urcorner )\subseteq \operatorname{rv}_{\unicode[STIX]{x1D6FF}-|\text{val}|(\mathfrak{a})}(\mathfrak{a}),\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{d}:=\operatorname{Tor}(\ulcorner \mathfrak{c}\urcorner )\subseteq \operatorname{rv}_{\unicode[STIX]{x1D6FF}-|\text{val}|(\mathfrak{a})}(\mathfrak{a}),\end{eqnarray}$$
it induces a
![]() $\ulcorner \mathfrak{d}\urcorner$
-definable
$\ulcorner \mathfrak{d}\urcorner$
-definable
![]() $C^{1}$
function
$C^{1}$
function
 $f_{\ulcorner \mathfrak{d}\urcorner }:\mathfrak{d}\longrightarrow \operatorname{Tor}(\ulcorner f(\mathfrak{c})\urcorner )$
. The codomain of its derivative
$f_{\ulcorner \mathfrak{d}\urcorner }:\mathfrak{d}\longrightarrow \operatorname{Tor}(\ulcorner f(\mathfrak{c})\urcorner )$
. The codomain of its derivative
 $(d/dx)f_{\ulcorner \mathfrak{d}\urcorner }$
can be narrowed down to either
$(d/dx)f_{\ulcorner \mathfrak{d}\urcorner }$
can be narrowed down to either
 $\operatorname{Tor}^{+}(\unicode[STIX]{x1D716}-\unicode[STIX]{x1D6FF})$
or
$\operatorname{Tor}^{+}(\unicode[STIX]{x1D716}-\unicode[STIX]{x1D6FF})$
or
 $\operatorname{Tor}^{-}(\unicode[STIX]{x1D716}-\unicode[STIX]{x1D6FF})$
, where
$\operatorname{Tor}^{-}(\unicode[STIX]{x1D716}-\unicode[STIX]{x1D6FF})$
, where
 $\unicode[STIX]{x1D716}=\operatorname{rad}(f(\mathfrak{c}))$
. By Lemma 3.13, there is a
$\unicode[STIX]{x1D716}=\operatorname{rad}(f(\mathfrak{c}))$
. By Lemma 3.13, there is a
![]() $t\in \text{RV}$
such that
$t\in \text{RV}$
such that
 $(d/dx)f(\mathfrak{a})\subseteq t^{\sharp }$
. By Lemma 3.12,
$(d/dx)f(\mathfrak{a})\subseteq t^{\sharp }$
. By Lemma 3.12,
![]() $\mathfrak{a}$
remains atomic over
$\mathfrak{a}$
remains atomic over
![]() $\unicode[STIX]{x1D6FF}$
. Then, by (an accordingly modified version of) Remark 3.30, we must have that, for all
$\unicode[STIX]{x1D6FF}$
. Then, by (an accordingly modified version of) Remark 3.30, we must have that, for all
![]() $\mathfrak{d}$
as above, all
$\mathfrak{d}$
as above, all
![]() $\ulcorner \mathfrak{c}\urcorner \in \mathfrak{d}$
, and all
$\ulcorner \mathfrak{c}\urcorner \in \mathfrak{d}$
, and all
![]() $a\in \mathfrak{c}$
,
$a\in \mathfrak{c}$
,
 $$\begin{eqnarray}\frac{d}{dx}f_{\ulcorner \mathfrak{d}\urcorner }(\ulcorner \mathfrak{c}\urcorner )=\operatorname{rv}\biggl(\frac{d}{dx}f(a)\biggr)=t,\end{eqnarray}$$
$$\begin{eqnarray}\frac{d}{dx}f_{\ulcorner \mathfrak{d}\urcorner }(\ulcorner \mathfrak{c}\urcorner )=\operatorname{rv}\biggl(\frac{d}{dx}f(a)\biggr)=t,\end{eqnarray}$$
and hence
 $$\begin{eqnarray}\operatorname{Aff}_{\ulcorner f(\mathfrak{c})\urcorner }\circ f_{\ulcorner \mathfrak{d}\urcorner }\circ \operatorname{Aff}_{\ulcorner \mathfrak{c}\urcorner }^{-1}:\operatorname{Tor}(\unicode[STIX]{x1D6FF})\longrightarrow \operatorname{Tor}(\unicode[STIX]{x1D716})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Aff}_{\ulcorner f(\mathfrak{c})\urcorner }\circ f_{\ulcorner \mathfrak{d}\urcorner }\circ \operatorname{Aff}_{\ulcorner \mathfrak{c}\urcorner }^{-1}:\operatorname{Tor}(\unicode[STIX]{x1D6FF})\longrightarrow \operatorname{Tor}(\unicode[STIX]{x1D716})\end{eqnarray}$$
is a linear function given by
 $u\longmapsto tu$
(see Definition 2.36 for the notation). It follows that, for
$u\longmapsto tu$
(see Definition 2.36 for the notation). It follows that, for
-
–
 $a$
and
$a$
and
 $a^{\prime }$
in
$a^{\prime }$
in
 $\mathfrak{a}$
,
$\mathfrak{a}$
, -
–
 $\mathfrak{d}$
the smallest closed disc containing
$\mathfrak{d}$
the smallest closed disc containing
 $a$
and
$a$
and
 $a^{\prime }$
,
$a^{\prime }$
, -
–
 $\mathfrak{c}$
and
$\mathfrak{c}$
and
 $\mathfrak{c}^{\prime }$
the maximal open subdiscs of
$\mathfrak{c}^{\prime }$
the maximal open subdiscs of
 $\mathfrak{d}$
containing
$\mathfrak{d}$
containing
 $a$
and
$a$
and
 $a^{\prime }$
, respectively,
$a^{\prime }$
, respectively,
we have
 $$\begin{eqnarray}\operatorname{rv}(f(a)-f(a^{\prime }))=\operatorname{rv}(f(\mathfrak{c})-f(\mathfrak{c}^{\prime }))=t\operatorname{rv}(\mathfrak{c}-\mathfrak{c}^{\prime })=t\operatorname{rv}(a-a^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rv}(f(a)-f(a^{\prime }))=\operatorname{rv}(f(\mathfrak{c})-f(\mathfrak{c}^{\prime }))=t\operatorname{rv}(\mathfrak{c}-\mathfrak{c}^{\prime })=t\operatorname{rv}(a-a^{\prime }).\end{eqnarray}$$
That is,
![]() $f$
is
$f$
is
![]() $\operatorname{rv}$
-affine. Moreover, it is clear from dtdp that
$\operatorname{rv}$
-affine. Moreover, it is clear from dtdp that
 $|\text{vrv}|(t)=\operatorname{rad}(\mathfrak{b})-\operatorname{rad}(\mathfrak{a})$
.◻
$|\text{vrv}|(t)=\operatorname{rad}(\mathfrak{b})-\operatorname{rad}(\mathfrak{a})$
.◻
4 Grothendieck semirings
In this section, we define various categories of definable sets and explore the relations between their Grothendieck semirings. The first main result is that the Grothendieck semiring
 $\mathbf{K}_{+}\text{RV}[\ast ]$
of the
$\mathbf{K}_{+}\text{RV}[\ast ]$
of the
![]() $\text{RV}$
-category
$\text{RV}$
-category
![]() $\text{RV}[\ast ]$
can be naturally expressed as a tensor product of the Grothendieck semirings of two of its full subcategories
$\text{RV}[\ast ]$
can be naturally expressed as a tensor product of the Grothendieck semirings of two of its full subcategories
![]() $\operatorname{RES}[\ast ]$
and
$\operatorname{RES}[\ast ]$
and
![]() $\unicode[STIX]{x1D6E4}[\ast ]$
. The second main result is that there is a natural surjective semiring homomorphism from
$\unicode[STIX]{x1D6E4}[\ast ]$
. The second main result is that there is a natural surjective semiring homomorphism from
 $\mathbf{K}_{+}\text{RV}[\ast ]$
onto the Grothendieck semiring
$\mathbf{K}_{+}\text{RV}[\ast ]$
onto the Grothendieck semiring
 $\mathbf{K}_{+}\text{VF}_{\ast }$
of the
$\mathbf{K}_{+}\text{VF}_{\ast }$
of the
![]() $\text{VF}$
-category
$\text{VF}$
-category
![]() $\text{VF}_{\ast }$
.
$\text{VF}_{\ast }$
.
Hypothesis 4.1. By (the proof of) Lemma 3.19, every definable set in
![]() $\text{RV}$
contains a definable point if and only if
$\text{RV}$
contains a definable point if and only if
 $\unicode[STIX]{x1D6E4}({\mathcal{S}})\neq \pm 1$
. Thus, from now on, we shall assume that
$\unicode[STIX]{x1D6E4}({\mathcal{S}})\neq \pm 1$
. Thus, from now on, we shall assume that
![]() $\unicode[STIX]{x1D6E4}({\mathcal{S}})$
is nontrivial.
$\unicode[STIX]{x1D6E4}({\mathcal{S}})$
is nontrivial.
4.1 The categories of definable sets
As in Definition 3.23, an
![]() $\text{RV}$
-fiber of a definable set
$\text{RV}$
-fiber of a definable set
![]() $A$
is a set of the form
$A$
is a set of the form
![]() $A_{a}$
, where
$A_{a}$
, where
 $a\in A_{\text{VF}}$
. The
$a\in A_{\text{VF}}$
. The
![]() $\text{RV}$
-fiber dimension of
$\text{RV}$
-fiber dimension of
![]() $A$
is the maximum of the
$A$
is the maximum of the
![]() $\text{RV}$
-dimensions of its
$\text{RV}$
-dimensions of its
![]() $\text{RV}$
-fibers and is denoted by
$\text{RV}$
-fibers and is denoted by
 $\dim _{\text{RV}}^{\operatorname{fib}}(A)$
.
$\dim _{\text{RV}}^{\operatorname{fib}}(A)$
.
Lemma 4.2. Suppose that
 $f:A\longrightarrow A^{\prime }$
is a definable bijection. Then
$f:A\longrightarrow A^{\prime }$
is a definable bijection. Then
 $\dim _{\text{RV}}^{\operatorname{fib}}(A)=\dim _{\text{RV}}^{\operatorname{fib}}(A^{\prime })$
.
$\dim _{\text{RV}}^{\operatorname{fib}}(A)=\dim _{\text{RV}}^{\operatorname{fib}}(A^{\prime })$
.
Proof. Let
 $\dim _{\text{RV}}^{\operatorname{fib}}(A)=k$
and
$\dim _{\text{RV}}^{\operatorname{fib}}(A)=k$
and
 $\dim _{\text{RV}}^{\operatorname{fib}}(A^{\prime })=k^{\prime }$
. For each
$\dim _{\text{RV}}^{\operatorname{fib}}(A^{\prime })=k^{\prime }$
. For each
 $a\in \operatorname{pr}_{\text{VF}}(A)$
, let
$a\in \operatorname{pr}_{\text{VF}}(A)$
, let
 $h_{a}:A_{a}\longrightarrow A_{\text{VF}}^{\prime }$
be the
$h_{a}:A_{a}\longrightarrow A_{\text{VF}}^{\prime }$
be the
![]() $a$
-definable function induced by
$a$
-definable function induced by
![]() $f$
and
$f$
and
![]() $\operatorname{pr}_{\text{VF}}$
. By Corollary 3.7, the image of
$\operatorname{pr}_{\text{VF}}$
. By Corollary 3.7, the image of
![]() $h_{a}$
is finite. It follows that
$h_{a}$
is finite. It follows that
![]() $k\leqslant k^{\prime }$
. Symmetrically we also have
$k\leqslant k^{\prime }$
. Symmetrically we also have
![]() $k\geqslant k^{\prime }$
and hence
$k\geqslant k^{\prime }$
and hence
![]() $k=k^{\prime }$
.◻
$k=k^{\prime }$
.◻
Definition 4.3 (
 $\text{VF}$
-categories).
$\text{VF}$
-categories).
The objects of the category
![]() $\text{VF}[k]$
are the definable sets of
$\text{VF}[k]$
are the definable sets of
![]() $\text{VF}$
-dimension less than or equal to
$\text{VF}$
-dimension less than or equal to
![]() $k$
and
$k$
and
![]() $\text{RV}$
-fiber dimension
$\text{RV}$
-fiber dimension
![]() $0$
(that is, all the
$0$
(that is, all the
![]() $\text{RV}$
-fibers are finite). Any definable bijection between two such objects is a morphism of
$\text{RV}$
-fibers are finite). Any definable bijection between two such objects is a morphism of
![]() $\text{VF}[k]$
. Set
$\text{VF}[k]$
. Set
 $\text{VF}_{\ast }=\bigcup _{k}\text{VF}[k]$
.
$\text{VF}_{\ast }=\bigcup _{k}\text{VF}[k]$
.
Definition 4.4 (
 $\text{RV}$
-categories).
$\text{RV}$
-categories).
The objects of the category
![]() $\text{RV}[k]$
are the pairs
$\text{RV}[k]$
are the pairs
![]() $(U,f)$
with
$(U,f)$
with
![]() $U$
a definable set in
$U$
a definable set in
![]() $\operatorname{RV}_{0}$
and
$\operatorname{RV}_{0}$
and
 $f:U\longrightarrow \text{RV}^{k}$
a definable finite-to-one function. Given two such objects
$f:U\longrightarrow \text{RV}^{k}$
a definable finite-to-one function. Given two such objects
![]() $(U,f)$
,
$(U,f)$
,
![]() $(V,g)$
, any definable bijection
$(V,g)$
, any definable bijection
 $F:U\longrightarrow V$
is a morphism of
$F:U\longrightarrow V$
is a morphism of
![]() $\text{RV}[k]$
.
$\text{RV}[k]$
.
Set
 $\text{RV}[{\leqslant}k]=\bigoplus _{i\leqslant k}\text{RV}[i]$
and
$\text{RV}[{\leqslant}k]=\bigoplus _{i\leqslant k}\text{RV}[i]$
and
 $\text{RV}[\ast ]=\bigoplus _{k}\text{RV}[k]$
; similarly for the other categories below.
$\text{RV}[\ast ]=\bigoplus _{k}\text{RV}[k]$
; similarly for the other categories below.
Notation 4.5. We emphasize that if
![]() $(U,f)$
is an object of
$(U,f)$
is an object of
![]() $\text{RV}[k]$
then
$\text{RV}[k]$
then
![]() $f(U)$
is a subset of
$f(U)$
is a subset of
![]() $\text{RV}^{k}$
instead of
$\text{RV}^{k}$
instead of
![]() $\text{RV}_{0}^{k}$
, while
$\text{RV}_{0}^{k}$
, while
![]() $0$
can occur in any coordinate of
$0$
can occur in any coordinate of
![]() $U$
. An object of
$U$
. An object of
![]() $\text{RV}[\ast ]$
of the form
$\text{RV}[\ast ]$
of the form
![]() $(U,\operatorname{id})$
is often written as
$(U,\operatorname{id})$
is often written as
![]() $U$
.
$U$
.
More generally, if
 $f:U\longrightarrow \text{RV}_{0}^{k}$
is a definable finite-to-one function then
$f:U\longrightarrow \text{RV}_{0}^{k}$
is a definable finite-to-one function then
![]() $(U,f)$
denotes the obvious object of
$(U,f)$
denotes the obvious object of
![]() $\text{RV}[{\leqslant}k]$
. Often
$\text{RV}[{\leqslant}k]$
. Often
![]() $f$
will be a coordinate projection (every object in
$f$
will be a coordinate projection (every object in
![]() $\text{RV}[\ast ]$
is isomorphic to an object of this form). In that case,
$\text{RV}[\ast ]$
is isomorphic to an object of this form). In that case,
 $(U,\operatorname{pr}_{{\leqslant}k})$
is simply denoted by
$(U,\operatorname{pr}_{{\leqslant}k})$
is simply denoted by
![]() $U_{{\leqslant}k}$
and its class in
$U_{{\leqslant}k}$
and its class in
 $\mathbf{K}_{+}\text{RV}[k]$
by
$\mathbf{K}_{+}\text{RV}[k]$
by
![]() $[U]_{{\leqslant}k}$
, etc.
$[U]_{{\leqslant}k}$
, etc.
Remark 4.6. Alternatively, we could allow only injections instead of finite-to-one functions in defining the objects of
![]() $\text{RV}[k]$
. As far as the Grothendieck semigroup
$\text{RV}[k]$
. As far as the Grothendieck semigroup
 $\mathbf{K}_{+}\text{RV}[k]$
is concerned, this is not more restrictive in our setting since for any
$\mathbf{K}_{+}\text{RV}[k]$
is concerned, this is not more restrictive in our setting since for any
 $\boldsymbol{U}:=(U,f)\in \text{RV}[k]$
there is a definable finite partition
$\boldsymbol{U}:=(U,f)\in \text{RV}[k]$
there is a definable finite partition
 $\boldsymbol{U}_{i}:=(U_{i},f_{i})$
of
$\boldsymbol{U}_{i}:=(U_{i},f_{i})$
of
![]() $\boldsymbol{U}$
, in other words,
$\boldsymbol{U}$
, in other words,
 $[\boldsymbol{U}]=\sum _{i}[\boldsymbol{U}_{i}]$
in
$[\boldsymbol{U}]=\sum _{i}[\boldsymbol{U}_{i}]$
in
 $\mathbf{K}_{+}\text{RV}[k]$
, such that each
$\mathbf{K}_{+}\text{RV}[k]$
, such that each
![]() $f_{i}$
is injective. It is technically more convenient to work with finite-to-one functions, though (for instance, we can take finite disjoint unions).
$f_{i}$
is injective. It is technically more convenient to work with finite-to-one functions, though (for instance, we can take finite disjoint unions).
In the above definitions and other similar ones below, all morphisms are actually isomorphisms and hence the categories are all groupoids. For the cases
![]() $k=0$
, the reader should interpret things such as
$k=0$
, the reader should interpret things such as
![]() $\text{RV}^{0}$
and how they interact with other things in a natural way. For instance,
$\text{RV}^{0}$
and how they interact with other things in a natural way. For instance,
![]() $\text{RV}^{0}$
may be treated as the empty tuple. So the categories
$\text{RV}^{0}$
may be treated as the empty tuple. So the categories
![]() $\text{VF}[0]$
,
$\text{VF}[0]$
,
![]() $\text{RV}[0]$
are equivalent.
$\text{RV}[0]$
are equivalent.
About the position of ‘
![]() $\ast$
’ in the notation: ‘
$\ast$
’ in the notation: ‘
![]() $\text{VF}_{\ast }$
’ suggests that the category is filtrated and ‘
$\text{VF}_{\ast }$
’ suggests that the category is filtrated and ‘
![]() $\text{RV}[\ast ]$
’ suggests that the category is graded.
$\text{RV}[\ast ]$
’ suggests that the category is graded.
Definition 4.7 (
 $\operatorname{RES}$
-categories).
$\operatorname{RES}$
-categories).
The category
![]() $\operatorname{RES}[k]$
is the full subcategory of
$\operatorname{RES}[k]$
is the full subcategory of
![]() $\text{RV}[k]$
such that
$\text{RV}[k]$
such that
 $(U,f)\in \operatorname{RES}[k]$
if and only if
$(U,f)\in \operatorname{RES}[k]$
if and only if
![]() $\operatorname{vrv}(U)$
is finite.
$\operatorname{vrv}(U)$
is finite.
Remark 4.8 (Explicit description of
 $\mathbf{K}_{+}\operatorname{RES}[k]$
).
$\mathbf{K}_{+}\operatorname{RES}[k]$
).
Let
![]() $\operatorname{RES}$
be the category whose objects are the definable sets
$\operatorname{RES}$
be the category whose objects are the definable sets
![]() $U$
in
$U$
in
![]() $\operatorname{RV}_{0}$
with
$\operatorname{RV}_{0}$
with
![]() $\operatorname{vrv}(U)$
finite and whose morphisms are the definable bijections. The obvious forgetful functor
$\operatorname{vrv}(U)$
finite and whose morphisms are the definable bijections. The obvious forgetful functor
 $\operatorname{RES}[\ast ]\longrightarrow \operatorname{RES}$
induces a surjective semiring homomorphism
$\operatorname{RES}[\ast ]\longrightarrow \operatorname{RES}$
induces a surjective semiring homomorphism
 $\mathbf{K}_{+}\operatorname{RES}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}$
, which is clearly not injective.
$\mathbf{K}_{+}\operatorname{RES}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}$
, which is clearly not injective.
The semiring
 $\mathbf{K}_{+}\operatorname{RES}$
is actually generated by isomorphism classes
$\mathbf{K}_{+}\operatorname{RES}$
is actually generated by isomorphism classes
![]() $[U]$
with
$[U]$
with
![]() $U$
a set in
$U$
a set in
![]() $\Bbbk ^{+}$
. By Theorem 2.31, we have the following explicit description of
$\Bbbk ^{+}$
. By Theorem 2.31, we have the following explicit description of
 $\mathbf{K}_{+}\operatorname{RES}$
. Its underlying set is
$\mathbf{K}_{+}\operatorname{RES}$
. Its underlying set is
 $(0\times \unicode[STIX]{x2115})\cup (\unicode[STIX]{x2115}^{+}\times \unicode[STIX]{x2124})$
. For all
$(0\times \unicode[STIX]{x2115})\cup (\unicode[STIX]{x2115}^{+}\times \unicode[STIX]{x2124})$
. For all
 $(a,b),(c,d)\in \mathbf{K}_{+}\operatorname{RES}$
,
$(a,b),(c,d)\in \mathbf{K}_{+}\operatorname{RES}$
,
 $$\begin{eqnarray}(a,b)+(c,d)=(\max \{a,c\},b+d),\quad (a,b)\times (c,d)=(a+c,b\times d).\end{eqnarray}$$
$$\begin{eqnarray}(a,b)+(c,d)=(\max \{a,c\},b+d),\quad (a,b)\times (c,d)=(a+c,b\times d).\end{eqnarray}$$
By the computation in [Reference Kageyama and FujitaKF06], the dimensional part is lost in the groupification
![]() $\mathbf{K}\,\operatorname{RES}$
of
$\mathbf{K}\,\operatorname{RES}$
of
 $\mathbf{K}_{+}\operatorname{RES}$
, that is,
$\mathbf{K}_{+}\operatorname{RES}$
, that is,
 $\mathbf{K}\,\operatorname{RES}=\unicode[STIX]{x2124}$
, which is of course much simpler than
$\mathbf{K}\,\operatorname{RES}=\unicode[STIX]{x2124}$
, which is of course much simpler than
 $\mathbf{K}_{+}\operatorname{RES}$
. However, following the philosophy of [Reference Hrushovski and KazhdanHK06], we shall work with Grothendieck semirings whenever possible.
$\mathbf{K}_{+}\operatorname{RES}$
. However, following the philosophy of [Reference Hrushovski and KazhdanHK06], we shall work with Grothendieck semirings whenever possible.
By Lemma 2.23, if
 $(U,f)\in \operatorname{RES}[\ast ]$
then
$(U,f)\in \operatorname{RES}[\ast ]$
then
 $\operatorname{vrv}(f(U))$
is finite as well. Therefore the semiring
$\operatorname{vrv}(f(U))$
is finite as well. Therefore the semiring
 $\mathbf{K}_{+}\operatorname{RES}[\ast ]$
is generated by isomorphism classes
$\mathbf{K}_{+}\operatorname{RES}[\ast ]$
is generated by isomorphism classes
![]() $[(U,f)]$
with
$[(U,f)]$
with
![]() $f$
a bijection between two sets in
$f$
a bijection between two sets in
![]() $\Bbbk ^{+}$
. As above, each
$\Bbbk ^{+}$
. As above, each
 $\mathbf{K}_{+}\operatorname{RES}[k]$
may be described explicitly as well. The semigroup
$\mathbf{K}_{+}\operatorname{RES}[k]$
may be described explicitly as well. The semigroup
 $\mathbf{K}_{+}\operatorname{RES}[0]$
is canonically isomorphic to the semiring
$\mathbf{K}_{+}\operatorname{RES}[0]$
is canonically isomorphic to the semiring
 $(0,0)\times \unicode[STIX]{x2115}$
. For
$(0,0)\times \unicode[STIX]{x2115}$
. For
![]() $k>0$
, the underlying set of
$k>0$
, the underlying set of
 $\mathbf{K}_{+}\operatorname{RES}[k]$
is
$\mathbf{K}_{+}\operatorname{RES}[k]$
is
 $\bigcup _{0\leqslant i\leqslant k}((k,i)\times \unicode[STIX]{x2124})$
, and its semigroup operation is given by
$\bigcup _{0\leqslant i\leqslant k}((k,i)\times \unicode[STIX]{x2124})$
, and its semigroup operation is given by
 $$\begin{eqnarray}(k,i,a)+(k,i^{\prime },a^{\prime })=(k,\max \{i,i^{\prime }\},a+a^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}(k,i,a)+(k,i^{\prime },a^{\prime })=(k,\max \{i,i^{\prime }\},a+a^{\prime }).\end{eqnarray}$$
Moreover, multiplication in
 $\mathbf{K}_{+}\operatorname{RES}[\ast ]$
is given by
$\mathbf{K}_{+}\operatorname{RES}[\ast ]$
is given by
 $$\begin{eqnarray}(k,i,a)\times (l,j,b)=(k+l,i+j,a\times b).\end{eqnarray}$$
$$\begin{eqnarray}(k,i,a)\times (l,j,b)=(k+l,i+j,a\times b).\end{eqnarray}$$
Definition 4.9 (
 $\unicode[STIX]{x1D6E4}$
-categories).
$\unicode[STIX]{x1D6E4}$
-categories).
The objects of the category
![]() $\unicode[STIX]{x1D6E4}[k]$
are the finite disjoint unions of definable subsets of
$\unicode[STIX]{x1D6E4}[k]$
are the finite disjoint unions of definable subsets of
![]() $\unicode[STIX]{x1D6E4}^{k}$
. Any definable bijection between two such objects is a morphism of
$\unicode[STIX]{x1D6E4}^{k}$
. Any definable bijection between two such objects is a morphism of
![]() $\unicode[STIX]{x1D6E4}[k]$
. The category
$\unicode[STIX]{x1D6E4}[k]$
. The category
![]() $\unicode[STIX]{x1D6E4}^{c}[k]$
is the full subcategory of
$\unicode[STIX]{x1D6E4}^{c}[k]$
is the full subcategory of
![]() $\unicode[STIX]{x1D6E4}[k]$
such that
$\unicode[STIX]{x1D6E4}[k]$
such that
 $I\in \unicode[STIX]{x1D6E4}^{c}[k]$
if and only if
$I\in \unicode[STIX]{x1D6E4}^{c}[k]$
if and only if
![]() $I$
is finite.
$I$
is finite.
Clearly
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[k]$
is naturally isomorphic to
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[k]$
is naturally isomorphic to
![]() $\unicode[STIX]{x2115}$
for all
$\unicode[STIX]{x2115}$
for all
![]() $k$
and hence
$k$
and hence
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\cong \unicode[STIX]{x2115}[X]$
.
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\cong \unicode[STIX]{x2115}[X]$
.
Notation 4.10. We introduce the following shorthand for distinguished elements in the various Grothendieck semigroups and their groupifications (and closely related constructions):
 $$\begin{eqnarray}\displaystyle & \mathbf{1}_{\Bbbk }=[\{1\}]\in \mathbf{K}_{+}\operatorname{RES}[0],\quad [1]=[(\{1\},\operatorname{id})]\in \mathbf{K}_{+}\operatorname{RES}[1], & \displaystyle \nonumber\\ \displaystyle & [\boldsymbol{T}]=[(\Bbbk ^{+},\operatorname{id})]\in \mathbf{K}_{+}\operatorname{RES}[1],\quad [\boldsymbol{A}]=2[\boldsymbol{T}]+[1]\in \mathbf{K}_{+}\operatorname{RES}[1], & \displaystyle \nonumber\\ \displaystyle & \mathbf{1}_{\unicode[STIX]{x1D6E4}}=[\unicode[STIX]{x1D6E4}^{0}]\in \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[0],\quad [e]=[\{1\}]\in \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[1],\quad [\boldsymbol{H}]=[(0,1)]\in \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[1], & \displaystyle \nonumber\\ \displaystyle & [\boldsymbol{P}]=[(\text{RV}^{\circ \circ },\operatorname{id})]-[1]\in \mathbf{K}\,\text{RV}[1]. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathbf{1}_{\Bbbk }=[\{1\}]\in \mathbf{K}_{+}\operatorname{RES}[0],\quad [1]=[(\{1\},\operatorname{id})]\in \mathbf{K}_{+}\operatorname{RES}[1], & \displaystyle \nonumber\\ \displaystyle & [\boldsymbol{T}]=[(\Bbbk ^{+},\operatorname{id})]\in \mathbf{K}_{+}\operatorname{RES}[1],\quad [\boldsymbol{A}]=2[\boldsymbol{T}]+[1]\in \mathbf{K}_{+}\operatorname{RES}[1], & \displaystyle \nonumber\\ \displaystyle & \mathbf{1}_{\unicode[STIX]{x1D6E4}}=[\unicode[STIX]{x1D6E4}^{0}]\in \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[0],\quad [e]=[\{1\}]\in \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[1],\quad [\boldsymbol{H}]=[(0,1)]\in \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[1], & \displaystyle \nonumber\\ \displaystyle & [\boldsymbol{P}]=[(\text{RV}^{\circ \circ },\operatorname{id})]-[1]\in \mathbf{K}\,\text{RV}[1]. & \displaystyle \nonumber\end{eqnarray}$$
Here
 $\text{RV}^{\circ \circ }=\text{RV}_{0}^{\circ \circ }\smallsetminus 0$
. Note that the interval
$\text{RV}^{\circ \circ }=\text{RV}_{0}^{\circ \circ }\smallsetminus 0$
. Note that the interval
![]() $\boldsymbol{H}$
is formed in the signed value group
$\boldsymbol{H}$
is formed in the signed value group
![]() $\unicode[STIX]{x1D6E4}$
, whose ordering is inverse to that of the value group
$\unicode[STIX]{x1D6E4}$
, whose ordering is inverse to that of the value group
![]() $|\unicode[STIX]{x1D6E4}|_{\infty }$
(recall Remark 2.8). The interval
$|\unicode[STIX]{x1D6E4}|_{\infty }$
(recall Remark 2.8). The interval
 $(1,\infty )\subseteq \unicode[STIX]{x1D6E4}$
is denoted by
$(1,\infty )\subseteq \unicode[STIX]{x1D6E4}$
is denoted by
![]() $\boldsymbol{H}^{-1}$
.
$\boldsymbol{H}^{-1}$
.
As in [Reference Hrushovski and KazhdanHK06], the elements
![]() $[\boldsymbol{P}]$
and
$[\boldsymbol{P}]$
and
 $\mathbf{1}_{\Bbbk }+[\boldsymbol{P}]$
in
$\mathbf{1}_{\Bbbk }+[\boldsymbol{P}]$
in
 $\mathbf{K}\,\text{RV}[\ast ]$
play special roles in the main construction (see Propositions 5.39 and the remarks thereafter).
$\mathbf{K}\,\text{RV}[\ast ]$
play special roles in the main construction (see Propositions 5.39 and the remarks thereafter).
The following lemma is a generality proven elsewhere. It is only needed to prove Lemma 4.12.
Lemma 4.11. Let
![]() $K$
be an integral domain and
$K$
be an integral domain and
![]() $M$
a torsion-free
$M$
a torsion-free
![]() $K$
-module; the latter is viewed as the main sort of a first-order structure of some expansion of the usual
$K$
-module; the latter is viewed as the main sort of a first-order structure of some expansion of the usual
![]() $K$
-module language. Let
$K$
-module language. Let
![]() $\mathfrak{F}$
be a class of definable functions in the sort
$\mathfrak{F}$
be a class of definable functions in the sort
![]() $M$
such that
$M$
such that
-
– all the identity functions are in
 $\mathfrak{F}$
,
$\mathfrak{F}$
, -
– all the functions in
 $\mathfrak{F}$
are definably piecewise
$\mathfrak{F}$
are definably piecewise
 $K$
-linear, that is, they are definably piecewise of the form
$K$
-linear, that is, they are definably piecewise of the form
 $x\longmapsto Mx+c$
, where
$x\longmapsto Mx+c$
, where
 $M$
is a matrix with entries in
$M$
is a matrix with entries in
 $K$
and
$K$
and
 $c$
is a definable point,
$c$
is a definable point, -
–
 $\mathfrak{F}$
is closed under composition, inversion, composition with
$\mathfrak{F}$
is closed under composition, inversion, composition with
 $\operatorname{GL}(K)$
-transformations (
$\operatorname{GL}(K)$
-transformations (
 $K$
-linear functions with invertible matrices), and composition with coordinate projections.
$K$
-linear functions with invertible matrices), and composition with coordinate projections.
If
 $g:D\longrightarrow E$
is a bijection in
$g:D\longrightarrow E$
is a bijection in
![]() $\mathfrak{F}$
, where
$\mathfrak{F}$
, where
 $D,E\subseteq M^{n}$
, then
$D,E\subseteq M^{n}$
, then
![]() $g$
is definably a piecewise
$g$
is definably a piecewise
 $\operatorname{GL}_{n}(K)$
-transformation.
$\operatorname{GL}_{n}(K)$
-transformation.
Proof. See [Reference YinYin13b, Lemma 2.29]. ◻
Lemma 4.12. Let
![]() $g$
be a
$g$
be a
![]() $\unicode[STIX]{x1D6E4}[k]$
-morphism. Then
$\unicode[STIX]{x1D6E4}[k]$
-morphism. Then
![]() $g$
is definably a piecewise
$g$
is definably a piecewise
 $\operatorname{GL}_{k}(\unicode[STIX]{x1D542})$
-transformation modulo the sign, that is, a piecewise
$\operatorname{GL}_{k}(\unicode[STIX]{x1D542})$
-transformation modulo the sign, that is, a piecewise
 $\operatorname{GL}_{k}(\unicode[STIX]{x1D542})\times \unicode[STIX]{x2124}_{2}$
-transformation. Consequently,
$\operatorname{GL}_{k}(\unicode[STIX]{x1D542})\times \unicode[STIX]{x2124}_{2}$
-transformation. Consequently,
![]() $g$
is a
$g$
is a
![]() $\operatorname{vrv}$
-contraction (recall Definition 3.27).
$\operatorname{vrv}$
-contraction (recall Definition 3.27).
Proof. For the first claim, it is routine to check that Lemma 4.11 is applicable to the class of definable functions in the
![]() $|\unicode[STIX]{x1D6E4}|$
-sort. The second claim follows from the fact that the natural actions of
$|\unicode[STIX]{x1D6E4}|$
-sort. The second claim follows from the fact that the natural actions of
 $\operatorname{GL}_{k}(\unicode[STIX]{x1D542})$
on
$\operatorname{GL}_{k}(\unicode[STIX]{x1D542})$
on
![]() $(\text{RV}^{+})^{k}$
and
$(\text{RV}^{+})^{k}$
and
![]() $(\unicode[STIX]{x1D6E4}^{+})^{k}$
commute with the map
$(\unicode[STIX]{x1D6E4}^{+})^{k}$
commute with the map
![]() $\operatorname{vrv}$
.◻
$\operatorname{vrv}$
.◻
Remark 4.13. In [Reference Hrushovski and KazhdanHK06],
![]() $\unicode[STIX]{x1D6E4}[k]$
-morphisms are by definition piecewise
$\unicode[STIX]{x1D6E4}[k]$
-morphisms are by definition piecewise
 $\operatorname{GL}_{k}(\unicode[STIX]{x2124})$
-transformations. This is because, in the setting there, the
$\operatorname{GL}_{k}(\unicode[STIX]{x2124})$
-transformations. This is because, in the setting there, the
![]() $\operatorname{vrv}$
-contractions are precisely the piecewise
$\operatorname{vrv}$
-contractions are precisely the piecewise
 $\operatorname{GL}_{k}(\unicode[STIX]{x2124})$
-transformations, which form a proper subclass of definable bijections in the
$\operatorname{GL}_{k}(\unicode[STIX]{x2124})$
-transformations, which form a proper subclass of definable bijections in the
![]() $\unicode[STIX]{x1D6E4}$
-sort, which in general are piecewise
$\unicode[STIX]{x1D6E4}$
-sort, which in general are piecewise
 $\operatorname{GL}_{k}(\unicode[STIX]{x211A})$
-transformations.
$\operatorname{GL}_{k}(\unicode[STIX]{x211A})$
-transformations.
Lemma 4.14. For all
 $I\in \unicode[STIX]{x1D6E4}[k]$
there are finitely many definable sets
$I\in \unicode[STIX]{x1D6E4}[k]$
there are finitely many definable sets
 $H_{i}\subseteq \unicode[STIX]{x1D6E4}^{n_{i}}$
with
$H_{i}\subseteq \unicode[STIX]{x1D6E4}^{n_{i}}$
with
 $\dim _{\unicode[STIX]{x1D6E4}}(H_{i})=n_{i}\leqslant k$
such that
$\dim _{\unicode[STIX]{x1D6E4}}(H_{i})=n_{i}\leqslant k$
such that
 $[I]=\sum _{i}[H_{i}][e]^{k-n_{i}}$
in
$[I]=\sum _{i}[H_{i}][e]^{k-n_{i}}$
in
![]() $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[k]$
.
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[k]$
.
Proof. We do induction on
![]() $k$
. The base case
$k$
. The base case
![]() $k=0$
is trivial. For the inductive step
$k=0$
is trivial. For the inductive step
![]() $k>0$
, the claim is also trivial if
$k>0$
, the claim is also trivial if
 $\dim _{\unicode[STIX]{x1D6E4}}(I)=k$
; so let us assume that
$\dim _{\unicode[STIX]{x1D6E4}}(I)=k$
; so let us assume that
 $\dim _{\unicode[STIX]{x1D6E4}}(I)<k$
. By [Reference van den DriesVdD97, Theorem B], we may partition
$\dim _{\unicode[STIX]{x1D6E4}}(I)<k$
. By [Reference van den DriesVdD97, Theorem B], we may partition
![]() $I$
into finitely many definable pieces
$I$
into finitely many definable pieces
![]() $I_{i}$
such that each
$I_{i}$
such that each
![]() $I_{i}$
is the graph of a definable function
$I_{i}$
is the graph of a definable function
 $I_{i}^{\prime }\longrightarrow \unicode[STIX]{x1D6E4}$
, where
$I_{i}^{\prime }\longrightarrow \unicode[STIX]{x1D6E4}$
, where
 $I_{i}^{\prime }\in \unicode[STIX]{x1D6E4}[k-1]$
. So the claim simply follows from the inductive hypothesis.◻
$I_{i}^{\prime }\in \unicode[STIX]{x1D6E4}[k-1]$
. So the claim simply follows from the inductive hypothesis.◻
Remark 4.15. There is a natural map
 $\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \text{RV}[\ast ]$
given by
$\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \text{RV}[\ast ]$
given by
 $I\longmapsto \boldsymbol{I}:=(I^{\sharp },\operatorname{id})$
(see Notation 2.24). By Lemma 4.12, this map induces a homomorphism
$I\longmapsto \boldsymbol{I}:=(I^{\sharp },\operatorname{id})$
(see Notation 2.24). By Lemma 4.12, this map induces a homomorphism
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]$
of graded semirings. By [Reference van den DriesVdD97, Theorem A] and Theorem 2.31, this homomorphism restricts to an injective homomorphism
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]$
of graded semirings. By [Reference van den DriesVdD97, Theorem A] and Theorem 2.31, this homomorphism restricts to an injective homomorphism
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}[\ast ]$
of graded semirings. There is also a similar semiring homomorphism
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}[\ast ]$
of graded semirings. There is also a similar semiring homomorphism
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}$
, but it is not injective.
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}$
, but it is not injective.
Question 4.16. Is the homomorphism
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]$
above injective?
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]$
above injective?
Now, the map from
 $\mathbf{K}_{+}\operatorname{RES}[\ast ]\times \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]$
to
$\mathbf{K}_{+}\operatorname{RES}[\ast ]\times \mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]$
to
 $\mathbf{K}_{+}\text{RV}[\ast ]$
naturally determined by the assignment
$\mathbf{K}_{+}\text{RV}[\ast ]$
naturally determined by the assignment
 $$\begin{eqnarray}([(U,f)],[I])\longmapsto [(U\times I^{\sharp },f\times \operatorname{id})]\end{eqnarray}$$
$$\begin{eqnarray}([(U,f)],[I])\longmapsto [(U\times I^{\sharp },f\times \operatorname{id})]\end{eqnarray}$$
is well defined and is clearly
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-bilinear. Hence it induces a
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-bilinear. Hence it induces a
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-linear map
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-linear map
 $$\begin{eqnarray}\mathbb{D}:\mathbf{K}_{+}\operatorname{RES}[\ast ]\otimes _{\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]}\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ],\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{D}:\mathbf{K}_{+}\operatorname{RES}[\ast ]\otimes _{\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]}\mathbf{K}_{+}\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ],\end{eqnarray}$$
which is a homomorphism of graded semirings. We shall abbreviate ‘
 $\otimes _{\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]}$
’ as ‘
$\otimes _{\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]}$
’ as ‘
![]() $\otimes$
’ below. Note that, by the universal mapping property, groupifying a tensor product in the category of
$\otimes$
’ below. Note that, by the universal mapping property, groupifying a tensor product in the category of
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-semimodules is the same, up to isomorphism, as taking the corresponding tensor product in the category of
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-semimodules is the same, up to isomorphism, as taking the corresponding tensor product in the category of
![]() $\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-modules. We will show that
$\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]$
-modules. We will show that
![]() $\mathbb{D}$
is indeed an isomorphism of graded semirings.
$\mathbb{D}$
is indeed an isomorphism of graded semirings.
4.2 The tensor expression
Heuristically,
![]() $\text{RV}$
may be viewed as a union of infinitely many one-dimensional vector spaces over
$\text{RV}$
may be viewed as a union of infinitely many one-dimensional vector spaces over
![]() $\Bbbk$
. Weak
$\Bbbk$
. Weak
![]() $o$
-minimality states that every definable subset of
$o$
-minimality states that every definable subset of
![]() $\text{RV}$
is nontrivial only within finitely many such one-dimensional spaces. The tensor expression of
$\text{RV}$
is nontrivial only within finitely many such one-dimensional spaces. The tensor expression of
 $\mathbf{K}_{+}\text{RV}[\ast ]$
we seek may be thought of as a generalization of this phenomenon to all definable sets in
$\mathbf{K}_{+}\text{RV}[\ast ]$
we seek may be thought of as a generalization of this phenomenon to all definable sets in
![]() $\text{RV}$
.
$\text{RV}$
.
Lemma 4.17. Let
 $A\subseteq \text{RV}^{k}\times \unicode[STIX]{x1D6E4}^{l}$
be an
$A\subseteq \text{RV}^{k}\times \unicode[STIX]{x1D6E4}^{l}$
be an
![]() $\unicode[STIX]{x1D6FC}$
-definable set, where
$\unicode[STIX]{x1D6FC}$
-definable set, where
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}$
. Set
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}$
. Set
 $\operatorname{pr}_{{\leqslant}k}(A)=U$
and suppose that
$\operatorname{pr}_{{\leqslant}k}(A)=U$
and suppose that
![]() $\operatorname{vrv}(U)$
is finite. Then there is an
$\operatorname{vrv}(U)$
is finite. Then there is an
![]() $\unicode[STIX]{x1D6FC}$
-definable finite partition
$\unicode[STIX]{x1D6FC}$
-definable finite partition
![]() $U_{i}$
of
$U_{i}$
of
![]() $U$
such that, for each
$U$
such that, for each
![]() $i$
and all
$i$
and all
 $t,t^{\prime }\in U_{i}$
, we have
$t,t^{\prime }\in U_{i}$
, we have
 $A_{t}=A_{t^{\prime }}$
.
$A_{t}=A_{t^{\prime }}$
.
Proof. By stable embeddedness, for every
![]() $t\in U$
,
$t\in U$
,
![]() $A_{t}$
is
$A_{t}$
is
 $(\operatorname{vrv}(t),\unicode[STIX]{x1D6FC})$
-definable in the
$(\operatorname{vrv}(t),\unicode[STIX]{x1D6FC})$
-definable in the
![]() $\unicode[STIX]{x1D6E4}$
-sort alone. Since
$\unicode[STIX]{x1D6E4}$
-sort alone. Since
![]() $\operatorname{vrv}(U)$
is finite, the assertion simply follows from compactness.◻
$\operatorname{vrv}(U)$
is finite, the assertion simply follows from compactness.◻
Lemma 4.18. Let
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
 $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{m})$
be finite tuples in
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{m})$
be finite tuples in
![]() $\unicode[STIX]{x1D6E4}$
. If there is a
$\unicode[STIX]{x1D6E4}$
. If there is a
![]() $\unicode[STIX]{x1D6FD}$
-definable nonempty proper subset of
$\unicode[STIX]{x1D6FD}$
-definable nonempty proper subset of
![]() $\unicode[STIX]{x1D6FE}^{\sharp }$
then, for some
$\unicode[STIX]{x1D6FE}^{\sharp }$
then, for some
![]() $\unicode[STIX]{x1D6FE}_{i}$
and every
$\unicode[STIX]{x1D6FE}_{i}$
and every
![]() $t\in \unicode[STIX]{x1D6FE}_{\tilde{i} }^{\sharp }$
,
$t\in \unicode[STIX]{x1D6FE}_{\tilde{i} }^{\sharp }$
,
![]() $\unicode[STIX]{x1D6FE}_{i}^{\sharp }$
contains a
$\unicode[STIX]{x1D6FE}_{i}^{\sharp }$
contains a
![]() $t$
-definable point. Consequently, if
$t$
-definable point. Consequently, if
![]() $U$
is such a subset of
$U$
is such a subset of
![]() $\unicode[STIX]{x1D6FE}^{\sharp }$
then either
$\unicode[STIX]{x1D6FE}^{\sharp }$
then either
![]() $U$
contains a definable point or there exists a subtuple
$U$
contains a definable point or there exists a subtuple
![]() $\unicode[STIX]{x1D6FE}_{\ast }\subseteq \unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}_{\ast }\subseteq \unicode[STIX]{x1D6FE}$
such that
 $\operatorname{pr}_{\unicode[STIX]{x1D6FE}_{\ast }}(U)=\unicode[STIX]{x1D6FE}_{\ast }^{\sharp }$
, where
$\operatorname{pr}_{\unicode[STIX]{x1D6FE}_{\ast }}(U)=\unicode[STIX]{x1D6FE}_{\ast }^{\sharp }$
, where
![]() $\operatorname{pr}_{\unicode[STIX]{x1D6FE}_{\ast }}$
denotes the obvious coordinate projection, and there is a
$\operatorname{pr}_{\unicode[STIX]{x1D6FE}_{\ast }}$
denotes the obvious coordinate projection, and there is a
![]() $\unicode[STIX]{x1D6FD}$
-definable function from
$\unicode[STIX]{x1D6FD}$
-definable function from
![]() $\unicode[STIX]{x1D6FE}_{\ast }^{\sharp }$
into
$\unicode[STIX]{x1D6FE}_{\ast }^{\sharp }$
into
 $(\unicode[STIX]{x1D6FE}\smallsetminus \unicode[STIX]{x1D6FE}_{\ast })^{\sharp }$
.
$(\unicode[STIX]{x1D6FE}\smallsetminus \unicode[STIX]{x1D6FE}_{\ast })^{\sharp }$
.
Proof. For the first claim we do induction on
![]() $m$
. The base case
$m$
. The base case
![]() $m=1$
simply follows from
$m=1$
simply follows from
![]() $o$
-minimality in the
$o$
-minimality in the
![]() $\Bbbk$
-sort and Lemma 3.6. For the inductive step
$\Bbbk$
-sort and Lemma 3.6. For the inductive step
![]() $m>1$
, let
$m>1$
, let
![]() $U$
be a
$U$
be a
![]() $\unicode[STIX]{x1D6FD}$
-definable nonempty proper subset of
$\unicode[STIX]{x1D6FD}$
-definable nonempty proper subset of
![]() $\unicode[STIX]{x1D6FE}^{\sharp }$
. By the inductive hypothesis, we may assume
$\unicode[STIX]{x1D6FE}^{\sharp }$
. By the inductive hypothesis, we may assume
 $$\begin{eqnarray}\{t\in \operatorname{pr}_{{>}1}(U):U_{t}\neq \unicode[STIX]{x1D6FE}_{1}^{\sharp }\}=\unicode[STIX]{x1D6FE}_{{>}1}^{\sharp }.\end{eqnarray}$$
$$\begin{eqnarray}\{t\in \operatorname{pr}_{{>}1}(U):U_{t}\neq \unicode[STIX]{x1D6FE}_{1}^{\sharp }\}=\unicode[STIX]{x1D6FE}_{{>}1}^{\sharp }.\end{eqnarray}$$
Then
![]() $\unicode[STIX]{x1D6FE}_{1}$
is as desired.
$\unicode[STIX]{x1D6FE}_{1}$
is as desired.
The second claim follows easily from the first. ◻
Lemma 4.19. Let
 $U\subseteq \text{RV}^{m}$
be a definable set. Then there are finitely many definable sets of the form
$U\subseteq \text{RV}^{m}$
be a definable set. Then there are finitely many definable sets of the form
 $V_{i}\times D_{i}\subseteq (\Bbbk ^{+})^{k_{i}}\times \unicode[STIX]{x1D6E4}^{l_{i}}$
such that
$V_{i}\times D_{i}\subseteq (\Bbbk ^{+})^{k_{i}}\times \unicode[STIX]{x1D6E4}^{l_{i}}$
such that
 $k_{i}+l_{i}=m$
for all
$k_{i}+l_{i}=m$
for all
![]() $i$
and
$i$
and
 $[U]=\sum _{i}[V_{i}\times D_{i}^{\sharp }]$
in
$[U]=\sum _{i}[V_{i}\times D_{i}^{\sharp }]$
in
 $\mathbf{K}_{+}\text{RV}[\ast ]$
.
$\mathbf{K}_{+}\text{RV}[\ast ]$
.
Proof. The case
![]() $m=1$
is an immediate consequence of weak
$m=1$
is an immediate consequence of weak
![]() $o$
-minimality in the
$o$
-minimality in the
![]() $\text{RV}$
-sort. For the case
$\text{RV}$
-sort. For the case
![]() $m>1$
, by Lemma 4.18, compactness, and a routine induction on
$m>1$
, by Lemma 4.18, compactness, and a routine induction on
![]() $m$
, over a definable finite partition of
$m$
, over a definable finite partition of
![]() $U$
, we may assume that
$U$
, we may assume that
![]() $U$
is a union of sets of the form
$U$
is a union of sets of the form
![]() $t\times \unicode[STIX]{x1D6FE}^{\sharp }$
, where
$t\times \unicode[STIX]{x1D6FE}^{\sharp }$
, where
 $t\in (\Bbbk ^{+})^{k}$
,
$t\in (\Bbbk ^{+})^{k}$
,
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}^{l}$
, and
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}^{l}$
, and
 $k+l=m$
. Then the assertion follows from Lemma 4.17.◻
$k+l=m$
. Then the assertion follows from Lemma 4.17.◻
Let
![]() $Q$
be a set of parameters in
$Q$
be a set of parameters in
![]() ${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
. We say that a
${\mathcal{R}}_{\operatorname{rv}}^{\bullet }$
. We say that a
![]() $Q$
-definable set
$Q$
-definable set
![]() $I\subseteq \unicode[STIX]{x1D6E4}^{m}$
is
$I\subseteq \unicode[STIX]{x1D6E4}^{m}$
is
![]() $Q$
-reducible if
$Q$
-reducible if
![]() $I^{\sharp }$
is
$I^{\sharp }$
is
![]() $Q$
-definably bijective to
$Q$
-definably bijective to
![]() $\Bbbk ^{+}\times I_{\tilde{i} }^{\sharp }$
, where
$\Bbbk ^{+}\times I_{\tilde{i} }^{\sharp }$
, where
![]() $i\in [m]$
and
$i\in [m]$
and
 $I_{\tilde{i} }=\operatorname{pr}_{\tilde{i} }(I)$
. For every
$I_{\tilde{i} }=\operatorname{pr}_{\tilde{i} }(I)$
. For every
 $t\in (\Bbbk ^{+})^{n}$
and every
$t\in (\Bbbk ^{+})^{n}$
and every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}^{m}$
,
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}^{m}$
,
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $(t,\unicode[STIX]{x1D6FC})$
-reducible if and only if, by Lemma 4.18, there is a
$(t,\unicode[STIX]{x1D6FC})$
-reducible if and only if, by Lemma 4.18, there is a
![]() $(t,\unicode[STIX]{x1D6FC})$
-definable nonempty proper subset of
$(t,\unicode[STIX]{x1D6FC})$
-definable nonempty proper subset of
![]() $\unicode[STIX]{x1D6FC}^{\sharp }$
if and only if, by Lemma 4.18 again, there is an
$\unicode[STIX]{x1D6FC}^{\sharp }$
if and only if, by Lemma 4.18 again, there is an
![]() $\unicode[STIX]{x1D6FC}$
-definable set
$\unicode[STIX]{x1D6FC}$
-definable set
 $U\subseteq (\Bbbk ^{+})^{n}$
containing
$U\subseteq (\Bbbk ^{+})^{n}$
containing
![]() $t$
such that
$t$
such that
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $(u,\unicode[STIX]{x1D6FC})$
-reducible for every
$(u,\unicode[STIX]{x1D6FC})$
-reducible for every
![]() $u\in U$
if and only if, by
$u\in U$
if and only if, by
![]() $o$
-minimality in the
$o$
-minimality in the
![]() $\Bbbk$
-sort and Lemma 3.6,
$\Bbbk$
-sort and Lemma 3.6,
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $\unicode[STIX]{x1D6FC}$
-reducible.
$\unicode[STIX]{x1D6FC}$
-reducible.
We say that a definable set
![]() $A$
in
$A$
in
![]() $\text{RV}$
is
$\text{RV}$
is
![]() $\unicode[STIX]{x1D6E4}$
-tamped of height
$\unicode[STIX]{x1D6E4}$
-tamped of height
![]() $l$
if there are
$l$
if there are
 $U\in \operatorname{RES}[k]$
and
$U\in \operatorname{RES}[k]$
and
![]() $I\in \unicode[STIX]{x1D6E4}[l]$
with
$I\in \unicode[STIX]{x1D6E4}[l]$
with
 $\dim _{\unicode[STIX]{x1D6E4}}(I)=l$
such that
$\dim _{\unicode[STIX]{x1D6E4}}(I)=l$
such that
 $A=U\times I^{\sharp }$
. In that case, there is only one way to write
$A=U\times I^{\sharp }$
. In that case, there is only one way to write
![]() $A$
as such a product, and if
$A$
as such a product, and if
 $B=V\times J^{\sharp }\subseteq A$
is also
$B=V\times J^{\sharp }\subseteq A$
is also
![]() $\unicode[STIX]{x1D6E4}$
-tamped then the coordinates occupied by
$\unicode[STIX]{x1D6E4}$
-tamped then the coordinates occupied by
![]() $J^{\sharp }$
are also occupied by
$J^{\sharp }$
are also occupied by
![]() $I^{\sharp }$
, in particular,
$I^{\sharp }$
, in particular,
 $\dim _{\unicode[STIX]{x1D6E4}}(J)=l$
if and only if
$\dim _{\unicode[STIX]{x1D6E4}}(J)=l$
if and only if
![]() $V\subseteq U$
and
$V\subseteq U$
and
![]() $J\subseteq I$
.
$J\subseteq I$
.
Lemma 4.20. Let
 $A=U\times I^{\sharp }$
,
$A=U\times I^{\sharp }$
,
 $B=V\times J^{\sharp }$
be
$B=V\times J^{\sharp }$
be
![]() $\unicode[STIX]{x1D6E4}$
-tamped sets of the same height
$\unicode[STIX]{x1D6E4}$
-tamped sets of the same height
![]() $l$
, where
$l$
, where
![]() $U$
,
$U$
,
![]() $V$
are sets in
$V$
are sets in
![]() $\Bbbk ^{+}$
. Let
$\Bbbk ^{+}$
. Let
![]() $f$
be a definable bijection whose domain contains
$f$
be a definable bijection whose domain contains
![]() $A$
and whose range contains
$A$
and whose range contains
![]() $B$
. Suppose that
$B$
. Suppose that
 $B\smallsetminus f(A)$
,
$B\smallsetminus f(A)$
,
 $A\smallsetminus f^{-1}(B)$
do not have
$A\smallsetminus f^{-1}(B)$
do not have
![]() $\unicode[STIX]{x1D6E4}$
-tamped subsets of height
$\unicode[STIX]{x1D6E4}$
-tamped subsets of height
![]() $l$
. Then there are finitely many
$l$
. Then there are finitely many
![]() $\unicode[STIX]{x1D6E4}$
-tamped sets
$\unicode[STIX]{x1D6E4}$
-tamped sets
 $A_{i}=U_{i}\times I_{i}^{\sharp }\subseteq U\times I^{\sharp }$
and
$A_{i}=U_{i}\times I_{i}^{\sharp }\subseteq U\times I^{\sharp }$
and
 $B_{i}=V_{i}\times J_{i}^{\sharp }\subseteq V\times J^{\sharp }$
such that
$B_{i}=V_{i}\times J_{i}^{\sharp }\subseteq V\times J^{\sharp }$
such that
-
–
 $A\smallsetminus \bigcup _{i}A_{i}$
and
$A\smallsetminus \bigcup _{i}A_{i}$
and
 $B\smallsetminus \bigcup _{i}B_{i}$
do not have
$B\smallsetminus \bigcup _{i}B_{i}$
do not have
 $\unicode[STIX]{x1D6E4}$
-tamped subsets of height
$\unicode[STIX]{x1D6E4}$
-tamped subsets of height
 $l$
,
$l$
, -
– each restriction
 $f\restriction A_{i}$
is of the form
$f\restriction A_{i}$
is of the form
 $p_{i}\times q_{i}$
, where
$p_{i}\times q_{i}$
, where
 $p_{i}:U_{i}\longrightarrow V_{i}$
,
$p_{i}:U_{i}\longrightarrow V_{i}$
,
 $q_{i}:I_{i}^{\sharp }\longrightarrow J_{i}^{\sharp }$
are bijections and the latter
$q_{i}:I_{i}^{\sharp }\longrightarrow J_{i}^{\sharp }$
are bijections and the latter
 $\operatorname{vrv}$
-contracts to a
$\operatorname{vrv}$
-contracts to a
 $\unicode[STIX]{x1D6E4}[\ast ]$
-morphism
$\unicode[STIX]{x1D6E4}[\ast ]$
-morphism
 $q_{i\downarrow }:I_{i}\longrightarrow J_{i}$
.
$q_{i\downarrow }:I_{i}\longrightarrow J_{i}$
.
Let
 $t\times \unicode[STIX]{x1D6FC}^{\sharp }\subseteq A$
. If
$t\times \unicode[STIX]{x1D6FC}^{\sharp }\subseteq A$
. If
 $t\times \unicode[STIX]{x1D6FC}^{\sharp }\subseteq A\smallsetminus f^{-1}(B)$
then, by Lemma 4.17, it is contained in a definable set
$t\times \unicode[STIX]{x1D6FC}^{\sharp }\subseteq A\smallsetminus f^{-1}(B)$
then, by Lemma 4.17, it is contained in a definable set
 $U^{\prime }\times {I^{\prime }}^{\sharp }\subseteq A\smallsetminus f^{-1}(B)$
with
$U^{\prime }\times {I^{\prime }}^{\sharp }\subseteq A\smallsetminus f^{-1}(B)$
with
![]() $U^{\prime }\subseteq U$
and
$U^{\prime }\subseteq U$
and
![]() $I^{\prime }\subseteq I$
. Since
$I^{\prime }\subseteq I$
. Since
 $A\smallsetminus f^{-1}(B)$
does not have
$A\smallsetminus f^{-1}(B)$
does not have
![]() $\unicode[STIX]{x1D6E4}$
-tamped subsets of height
$\unicode[STIX]{x1D6E4}$
-tamped subsets of height
![]() $l$
, we must have
$l$
, we must have
 $\dim _{\unicode[STIX]{x1D6E4}}(I^{\prime })<l$
. It follows from (the proof of) Lemma 2.29 that
$\dim _{\unicode[STIX]{x1D6E4}}(I^{\prime })<l$
. It follows from (the proof of) Lemma 2.29 that
![]() $I^{\prime }$
is piecewise reducible, which implies that
$I^{\prime }$
is piecewise reducible, which implies that
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $\unicode[STIX]{x1D6FC}$
-reducible. At any rate, if
$\unicode[STIX]{x1D6FC}$
-reducible. At any rate, if
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $(t,\unicode[STIX]{x1D6FC})$
-reducible then
$(t,\unicode[STIX]{x1D6FC})$
-reducible then
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $\unicode[STIX]{x1D6FC}$
-reducible and hence there is a reducible subset of
$\unicode[STIX]{x1D6FC}$
-reducible and hence there is a reducible subset of
![]() $I$
that contains
$I$
that contains
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Proof. Remove all the reducible subsets of
![]() $I$
from
$I$
from
![]() $I$
and call the resulting set
$I$
and call the resulting set
![]() $\bar{I}$
; similarly for
$\bar{I}$
; similarly for
![]() $\bar{J}$
. Then, for all
$\bar{J}$
. Then, for all
![]() $t\in U$
and all
$t\in U$
and all
![]() $\unicode[STIX]{x1D6FC}\in \bar{I}$
,
$\unicode[STIX]{x1D6FC}\in \bar{I}$
,
 $f(t\times \unicode[STIX]{x1D6FC}^{\sharp })$
must be contained in a set of the form
$f(t\times \unicode[STIX]{x1D6FC}^{\sharp })$
must be contained in a set of the form
![]() $s\times \unicode[STIX]{x1D6FD}^{\sharp }$
, for otherwise it would have a
$s\times \unicode[STIX]{x1D6FD}^{\sharp }$
, for otherwise it would have a
![]() $(t,\unicode[STIX]{x1D6FC})$
-definable nonempty proper subset and hence would be
$(t,\unicode[STIX]{x1D6FC})$
-definable nonempty proper subset and hence would be
![]() $(t,\unicode[STIX]{x1D6FC})$
-reducible. In fact,
$(t,\unicode[STIX]{x1D6FC})$
-reducible. In fact,
 $f(t\times \unicode[STIX]{x1D6FC}^{\sharp })=s\times \unicode[STIX]{x1D6FD}^{\sharp }$
, for otherwise
$f(t\times \unicode[STIX]{x1D6FC}^{\sharp })=s\times \unicode[STIX]{x1D6FD}^{\sharp }$
, for otherwise
![]() $\unicode[STIX]{x1D6FD}$
is
$\unicode[STIX]{x1D6FD}$
is
![]() $(t,\unicode[STIX]{x1D6FC})$
-reducible and hence, by
$(t,\unicode[STIX]{x1D6FC})$
-reducible and hence, by
![]() $o$
-minimality in the
$o$
-minimality in the
![]() $\Bbbk$
-sort and the assumption
$\Bbbk$
-sort and the assumption
 $\dim _{\unicode[STIX]{x1D6E4}}(I)=\dim _{\unicode[STIX]{x1D6E4}}(J)=l$
, a
$\dim _{\unicode[STIX]{x1D6E4}}(I)=\dim _{\unicode[STIX]{x1D6E4}}(J)=l$
, a
![]() $(t,\unicode[STIX]{x1D6FC})$
-definable subset of
$(t,\unicode[STIX]{x1D6FC})$
-definable subset of
![]() $\unicode[STIX]{x1D6FC}^{\sharp }$
can be easily constructed. For the same reason, we must actually have
$\unicode[STIX]{x1D6FC}^{\sharp }$
can be easily constructed. For the same reason, we must actually have
![]() $\unicode[STIX]{x1D6FD}\in \bar{J}$
. It follows that
$\unicode[STIX]{x1D6FD}\in \bar{J}$
. It follows that
 $f(U\times \bar{I}^{\sharp })=V\times \bar{J}^{\sharp }$
. Then, by compactness, there are finitely many reducible subsets
$f(U\times \bar{I}^{\sharp })=V\times \bar{J}^{\sharp }$
. Then, by compactness, there are finitely many reducible subsets
![]() $I_{i}$
of
$I_{i}$
of
![]() $I$
such that, for all
$I$
such that, for all
![]() $t\in U$
and all
$t\in U$
and all
 $\unicode[STIX]{x1D6FC}\in I_{\ast }=I\smallsetminus \bigcup _{i}I_{i}$
,
$\unicode[STIX]{x1D6FC}\in I_{\ast }=I\smallsetminus \bigcup _{i}I_{i}$
,
 $f(t\times \unicode[STIX]{x1D6FC}^{\sharp })=s\times \unicode[STIX]{x1D6FD}^{\sharp }$
for some
$f(t\times \unicode[STIX]{x1D6FC}^{\sharp })=s\times \unicode[STIX]{x1D6FD}^{\sharp }$
for some
![]() $s\in V$
and
$s\in V$
and
![]() $\unicode[STIX]{x1D6FD}\in J$
. Applying Lemma 4.17 to (the graph of) the function on
$\unicode[STIX]{x1D6FD}\in J$
. Applying Lemma 4.17 to (the graph of) the function on
![]() $U\times I_{\ast }$
induced by
$U\times I_{\ast }$
induced by
![]() $f$
, the lemma follows.◻
$f$
, the lemma follows.◻
Proposition 4.21.
![]() $\mathbb{D}$
is an isomorphism of graded semirings.
$\mathbb{D}$
is an isomorphism of graded semirings.
Proof. Surjectivity of
![]() $\mathbb{D}$
follows immediately from Lemma 4.19. For injectivity, let
$\mathbb{D}$
follows immediately from Lemma 4.19. For injectivity, let
 $\boldsymbol{U}_{i}\,:=\,(U_{i},f_{i})$
,
$\boldsymbol{U}_{i}\,:=\,(U_{i},f_{i})$
,
 $\boldsymbol{V}_{j}:=(V_{j},g_{j})$
be objects in
$\boldsymbol{V}_{j}:=(V_{j},g_{j})$
be objects in
![]() $\operatorname{RES}[\ast ]$
and
$\operatorname{RES}[\ast ]$
and
![]() $I_{i}$
,
$I_{i}$
,
![]() $J_{j}$
objects in
$J_{j}$
objects in
![]() $\unicode[STIX]{x1D6E4}[\ast ]$
such that
$\unicode[STIX]{x1D6E4}[\ast ]$
such that
 $\mathbb{D}([\boldsymbol{U}_{i}]\,\otimes \,[I_{i}])$
,
$\mathbb{D}([\boldsymbol{U}_{i}]\,\otimes \,[I_{i}])$
,
 $\mathbb{D}([\boldsymbol{V}_{j}]\,\otimes \,[J_{j}])$
are objects in
$\mathbb{D}([\boldsymbol{V}_{j}]\,\otimes \,[J_{j}])$
are objects in
 $\mathbf{K}_{+}\text{RV}[l]$
for all
$\mathbf{K}_{+}\text{RV}[l]$
for all
![]() $i$
,
$i$
,
![]() $j$
. Set
$j$
. Set
 $$\begin{eqnarray}M_{i}=U_{i}\times I_{i}^{\sharp },\quad N_{i}=V_{j}\times J_{j}^{\sharp },\quad M=\mathop{\uplus }_{i}M_{i},\quad N=\mathop{\uplus }_{j}N_{j}.\end{eqnarray}$$
$$\begin{eqnarray}M_{i}=U_{i}\times I_{i}^{\sharp },\quad N_{i}=V_{j}\times J_{j}^{\sharp },\quad M=\mathop{\uplus }_{i}M_{i},\quad N=\mathop{\uplus }_{j}N_{j}.\end{eqnarray}$$
Suppose that there is a definable bijection
 $f:M\longrightarrow N$
. We need to show
$f:M\longrightarrow N$
. We need to show
 $$\begin{eqnarray}\mathop{\sum }_{i}[\boldsymbol{U}_{i}]\otimes [I_{i}]=\mathop{\sum }_{j}[\boldsymbol{V}_{j}]\otimes [J_{j}].\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i}[\boldsymbol{U}_{i}]\otimes [I_{i}]=\mathop{\sum }_{j}[\boldsymbol{V}_{j}]\otimes [J_{j}].\end{eqnarray}$$
By Lemma 2.29, we may assume that all
![]() $M_{i}$
,
$M_{i}$
,
![]() $N_{j}$
are
$N_{j}$
are
![]() $\unicode[STIX]{x1D6E4}$
-tamped. By
$\unicode[STIX]{x1D6E4}$
-tamped. By
![]() $o$
-minimal cell decomposition, without changing the sums, we may assume that each
$o$
-minimal cell decomposition, without changing the sums, we may assume that each
![]() $U_{i}$
is a disjoint union of finitely many copies of
$U_{i}$
is a disjoint union of finitely many copies of
![]() $(\Bbbk ^{+})^{i}$
and thereby re-index
$(\Bbbk ^{+})^{i}$
and thereby re-index
![]() $M_{i}$
more informatively as
$M_{i}$
more informatively as
 $M_{i,m}=U_{i}\times I_{m}^{\sharp }$
, where
$M_{i,m}=U_{i}\times I_{m}^{\sharp }$
, where
![]() $I_{m}$
is an object in
$I_{m}$
is an object in
![]() $\unicode[STIX]{x1D6E4}[m]$
; similarly each
$\unicode[STIX]{x1D6E4}[m]$
; similarly each
![]() $N_{j}$
is re-indexed as
$N_{j}$
is re-indexed as
![]() $N_{j,n}$
. By Lemma 2.28, the respective maximums of the numbers
$N_{j,n}$
. By Lemma 2.28, the respective maximums of the numbers
![]() $i+m$
,
$i+m$
,
![]() $j+n$
are the
$j+n$
are the
![]() $\text{RV}$
-dimensions of
$\text{RV}$
-dimensions of
![]() $M$
,
$M$
,
![]() $N$
and hence must be equal; they are denoted by
$N$
and hence must be equal; they are denoted by
![]() $p$
. Let
$p$
. Let
![]() $q$
be the largest
$q$
be the largest
![]() $m$
such that
$m$
such that
 $i+m=p$
for some
$i+m=p$
for some
![]() $M_{i,m}$
and
$M_{i,m}$
and
![]() $q^{\prime }$
the largest
$q^{\prime }$
the largest
![]() $n$
such that
$n$
such that
 $j+n=p$
for some
$j+n=p$
for some
![]() $N_{j,n}$
. It is not hard to see that we may arrange
$N_{j,n}$
. It is not hard to see that we may arrange
![]() $q=q^{\prime }$
.
$q=q^{\prime }$
.
We now proceed by induction on
![]() $q$
. The base case
$q$
. The base case
![]() $q=0$
is rather trivial. For the inductive step, by Lemma 4.20, we see that certain products contained in
$q=0$
is rather trivial. For the inductive step, by Lemma 4.20, we see that certain products contained in
![]() $M_{p-q,q}$
,
$M_{p-q,q}$
,
![]() $N_{p-q,q}$
give rise to the same sum and the inductive hypothesis may be applied to the remaining portions.◻
$N_{p-q,q}$
give rise to the same sum and the inductive hypothesis may be applied to the remaining portions.◻
We may view
![]() $\unicode[STIX]{x1D6E4}$
as a double cover of
$\unicode[STIX]{x1D6E4}$
as a double cover of
![]() $|\unicode[STIX]{x1D6E4}|$
via the identification
$|\unicode[STIX]{x1D6E4}|$
via the identification
 $\unicode[STIX]{x1D6E4}/\pm 1=|\unicode[STIX]{x1D6E4}|$
. Consequently, we can associate two Euler characteristics
$\unicode[STIX]{x1D6E4}/\pm 1=|\unicode[STIX]{x1D6E4}|$
. Consequently, we can associate two Euler characteristics
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}$
,
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}$
,
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}$
with the
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}$
with the
![]() $\unicode[STIX]{x1D6E4}$
-sort, induced by those on
$\unicode[STIX]{x1D6E4}$
-sort, induced by those on
![]() $|\unicode[STIX]{x1D6E4}|$
(see [Reference Kageyama and FujitaKF06] and also [Reference Hrushovski and KazhdanHK06, § 9]). They are distinguished by
$|\unicode[STIX]{x1D6E4}|$
(see [Reference Kageyama and FujitaKF06] and also [Reference Hrushovski and KazhdanHK06, § 9]). They are distinguished by
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}(\boldsymbol{H})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}(\boldsymbol{H}^{-1})=-1\quad \text{and}\quad \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}(\boldsymbol{H})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}(\boldsymbol{H}^{-1})=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}(\boldsymbol{H})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}(\boldsymbol{H}^{-1})=-1\quad \text{and}\quad \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}(\boldsymbol{H})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}(\boldsymbol{H}^{-1})=0.\end{eqnarray}$$
Similarly, there is an Euler characteristic
![]() $\unicode[STIX]{x1D712}_{\Bbbk }$
associated with the
$\unicode[STIX]{x1D712}_{\Bbbk }$
associated with the
![]() $\Bbbk$
-sort (there is only one). We shall denote all of these Euler characteristics simply by
$\Bbbk$
-sort (there is only one). We shall denote all of these Euler characteristics simply by
![]() $\unicode[STIX]{x1D712}$
if no confusion can arise. Using these
$\unicode[STIX]{x1D712}$
if no confusion can arise. Using these
![]() $\unicode[STIX]{x1D712}$
and the groupification of
$\unicode[STIX]{x1D712}$
and the groupification of
![]() $\mathbb{D}$
(also denoted by
$\mathbb{D}$
(also denoted by
![]() $\mathbb{D}$
), we can construct various retractions from the Grothendieck ring
$\mathbb{D}$
), we can construct various retractions from the Grothendieck ring
 $\mathbf{K}\,\text{RV}[\ast ]$
to (certain localizations of) the Grothendieck rings
$\mathbf{K}\,\text{RV}[\ast ]$
to (certain localizations of) the Grothendieck rings
 $\mathbf{K}\,\operatorname{RES}[\ast ]$
and
$\mathbf{K}\,\operatorname{RES}[\ast ]$
and
![]() $\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
.
$\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
.
Lemma 4.22. The Euler characteristics naturally induce three graded ring homomorphisms:
 $$\begin{eqnarray}{\mathcal{E}}_{\Bbbk }:\mathbf{K}\,\operatorname{RES}[\ast ]\longrightarrow \unicode[STIX]{x2124}[X]\quad \text{and}\quad {\mathcal{E}}_{\unicode[STIX]{x1D6E4},g},{\mathcal{E}}_{\unicode[STIX]{x1D6E4},b}:\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \unicode[STIX]{x2124}[X].\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{\Bbbk }:\mathbf{K}\,\operatorname{RES}[\ast ]\longrightarrow \unicode[STIX]{x2124}[X]\quad \text{and}\quad {\mathcal{E}}_{\unicode[STIX]{x1D6E4},g},{\mathcal{E}}_{\unicode[STIX]{x1D6E4},b}:\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]\longrightarrow \unicode[STIX]{x2124}[X].\end{eqnarray}$$
Proof. For
 $U\in \operatorname{RES}[k]$
and
$U\in \operatorname{RES}[k]$
and
 $I\in \unicode[STIX]{x1D6E4}[k]$
, we set
$I\in \unicode[STIX]{x1D6E4}[k]$
, we set
 ${\mathcal{E}}_{\Bbbk ,k}([U])=\unicode[STIX]{x1D712}(U)$
(see Remark 2.30) and
${\mathcal{E}}_{\Bbbk ,k}([U])=\unicode[STIX]{x1D712}(U)$
(see Remark 2.30) and
 ${\mathcal{E}}_{\unicode[STIX]{x1D6E4},k}([I])=\unicode[STIX]{x1D712}(I)$
. These maps are well defined and induce graded ring homomorphisms
${\mathcal{E}}_{\unicode[STIX]{x1D6E4},k}([I])=\unicode[STIX]{x1D712}(I)$
. These maps are well defined and induce graded ring homomorphisms
 ${\mathcal{E}}_{\Bbbk }:=\sum _{k}{\mathcal{E}}_{\Bbbk ,k}X^{k}$
and
${\mathcal{E}}_{\Bbbk }:=\sum _{k}{\mathcal{E}}_{\Bbbk ,k}X^{k}$
and
 ${\mathcal{E}}_{\unicode[STIX]{x1D6E4}}:=\sum _{k}{\mathcal{E}}_{\unicode[STIX]{x1D6E4},k}X^{k}$
as desired.◻
${\mathcal{E}}_{\unicode[STIX]{x1D6E4}}:=\sum _{k}{\mathcal{E}}_{\unicode[STIX]{x1D6E4},k}X^{k}$
as desired.◻
By the computation in [Reference Kageyama and FujitaKF06],
![]() $\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
is canonically isomorphic to the graded ring
$\mathbf{K}\,\unicode[STIX]{x1D6E4}[\ast ]$
is canonically isomorphic to the graded ring
 $$\begin{eqnarray}\unicode[STIX]{x2124}[X,Y^{(2)}]:=\unicode[STIX]{x2124}\oplus \bigoplus _{i\geqslant 1}(\unicode[STIX]{x2124}[Y]/(Y^{2}+Y))X^{i},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2124}[X,Y^{(2)}]:=\unicode[STIX]{x2124}\oplus \bigoplus _{i\geqslant 1}(\unicode[STIX]{x2124}[Y]/(Y^{2}+Y))X^{i},\end{eqnarray}$$
where
![]() $YX$
represents the class
$YX$
represents the class
 $[\boldsymbol{H}]=[\boldsymbol{H}^{-1}]$
in
$[\boldsymbol{H}]=[\boldsymbol{H}^{-1}]$
in
![]() $\mathbf{K}\,\unicode[STIX]{x1D6E4}[1]$
. Thus
$\mathbf{K}\,\unicode[STIX]{x1D6E4}[1]$
. Thus
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D6E4},g}$
,
${\mathcal{E}}_{\unicode[STIX]{x1D6E4},g}$
,
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D6E4},b}$
are also given by
${\mathcal{E}}_{\unicode[STIX]{x1D6E4},b}$
are also given by

Remark 4.23 (Explicit description of
 $\mathbf{K}\,\text{RV}[\ast ]$
).
$\mathbf{K}\,\text{RV}[\ast ]$
).
Of course,
![]() ${\mathcal{E}}_{\Bbbk }$
is actually an isomorphism. The homomorphism
${\mathcal{E}}_{\Bbbk }$
is actually an isomorphism. The homomorphism
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}[\ast ]$
in Remark 4.15 and
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \mathbf{K}_{+}\operatorname{RES}[\ast ]$
in Remark 4.15 and
![]() ${\mathcal{E}}_{\Bbbk }$
then induce an isomorphism
${\mathcal{E}}_{\Bbbk }$
then induce an isomorphism
 ${\mathcal{E}}_{\Bbbk ^{c}}:\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \unicode[STIX]{x2124}[X]$
. But this isomorphism is different from the groupification
${\mathcal{E}}_{\Bbbk ^{c}}:\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]\longrightarrow \unicode[STIX]{x2124}[X]$
. But this isomorphism is different from the groupification
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D6E4}^{c}}$
of the canonical isomorphism
${\mathcal{E}}_{\unicode[STIX]{x1D6E4}^{c}}$
of the canonical isomorphism
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\cong \mathbf{K}_{+}\unicode[STIX]{x2115}[\ast ]$
. This latter isomorphism
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]\cong \mathbf{K}_{+}\unicode[STIX]{x2115}[\ast ]$
. This latter isomorphism
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D6E4}^{c}}$
is also induced by
${\mathcal{E}}_{\unicode[STIX]{x1D6E4}^{c}}$
is also induced by
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D6E4},g}$
,
${\mathcal{E}}_{\unicode[STIX]{x1D6E4},g}$
,
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D6E4},b}$
(the two homomorphisms agree on
${\mathcal{E}}_{\unicode[STIX]{x1D6E4},b}$
(the two homomorphisms agree on
![]() $\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]$
). They are distinguished by
$\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]$
). They are distinguished by
 ${\mathcal{E}}_{\Bbbk ^{c}}([e])=-X$
and
${\mathcal{E}}_{\Bbbk ^{c}}([e])=-X$
and
 ${\mathcal{E}}_{\unicode[STIX]{x1D6E4}^{c}}([e])=X$
. We have a commutative diagram
${\mathcal{E}}_{\unicode[STIX]{x1D6E4}^{c}}([e])=X$
. We have a commutative diagram

where
![]() $\unicode[STIX]{x1D70F}$
is the involution determined by
$\unicode[STIX]{x1D70F}$
is the involution determined by
 $X\longmapsto -X$
. The graded ring
$X\longmapsto -X$
. The graded ring
 $$\begin{eqnarray}\unicode[STIX]{x2124}[X]\otimes _{\unicode[STIX]{x2124}[X]}\unicode[STIX]{x2124}[X,Y^{(2)}]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2124}[X]\otimes _{\unicode[STIX]{x2124}[X]}\unicode[STIX]{x2124}[X,Y^{(2)}]\end{eqnarray}$$
may be identified with
 $\unicode[STIX]{x2124}[X,Y^{(2)}]$
via the isomorphism given by
$\unicode[STIX]{x2124}[X,Y^{(2)}]$
via the isomorphism given by
 $x\otimes y\longmapsto \unicode[STIX]{x1D70F}(x)y$
. Consequently, by Proposition 4.21, there is a graded ring isomorphism
$x\otimes y\longmapsto \unicode[STIX]{x1D70F}(x)y$
. Consequently, by Proposition 4.21, there is a graded ring isomorphism
 $$\begin{eqnarray}\mathbf{K}\,\text{RV}[\ast ]\rightarrow ^{{\sim}}\unicode[STIX]{x2124}[X,Y^{(2)}]\quad \text{with }\pmb{{\it 1}}_{\mathbb{ k}}+[\boldsymbol{P}]\longmapsto 1+2YX+X.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{K}\,\text{RV}[\ast ]\rightarrow ^{{\sim}}\unicode[STIX]{x2124}[X,Y^{(2)}]\quad \text{with }\pmb{{\it 1}}_{\mathbb{ k}}+[\boldsymbol{P}]\longmapsto 1+2YX+X.\end{eqnarray}$$
Setting
 $$\begin{eqnarray}\unicode[STIX]{x2124}^{(2)}[X]=\unicode[STIX]{x2124}[X,Y^{(2)}]/(1+2YX+X),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2124}^{(2)}[X]=\unicode[STIX]{x2124}[X,Y^{(2)}]/(1+2YX+X),\end{eqnarray}$$
we see that there is a canonical ring isomorphism
 $$\begin{eqnarray}\mathbb{E}_{\unicode[STIX]{x1D6E4}}:\mathbf{K}\,\text{RV}[\ast ]/(\mathbf{1}_{\Bbbk }+[\boldsymbol{P}])\rightarrow ^{{\sim}}\unicode[STIX]{x2124}^{(2)}[X].\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{\unicode[STIX]{x1D6E4}}:\mathbf{K}\,\text{RV}[\ast ]/(\mathbf{1}_{\Bbbk }+[\boldsymbol{P}])\rightarrow ^{{\sim}}\unicode[STIX]{x2124}^{(2)}[X].\end{eqnarray}$$
There are exactly two ring homomorphisms
 $\unicode[STIX]{x2124}^{(2)}[X]\longrightarrow \unicode[STIX]{x2124}$
determined by the assignments
$\unicode[STIX]{x2124}^{(2)}[X]\longrightarrow \unicode[STIX]{x2124}$
determined by the assignments
 $Y\longmapsto -1$
and
$Y\longmapsto -1$
and
 $Y\longmapsto 0$
or, equivalently,
$Y\longmapsto 0$
or, equivalently,
 $X\longmapsto 1$
and
$X\longmapsto 1$
and
 $X\longmapsto -1$
. Combining these with
$X\longmapsto -1$
. Combining these with
![]() $\mathbb{E}_{\unicode[STIX]{x1D6E4}}$
, we see that there are exactly two ring homomorphisms
$\mathbb{E}_{\unicode[STIX]{x1D6E4}}$
, we see that there are exactly two ring homomorphisms
 $$\begin{eqnarray}\mathbb{E}_{\unicode[STIX]{x1D6E4},g},\mathbb{E}_{\unicode[STIX]{x1D6E4},b}:\mathbf{K}\,\text{RV}[\ast ]/(\mathbf{1}_{\Bbbk }+[\boldsymbol{P}])\longrightarrow \unicode[STIX]{x2124}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{\unicode[STIX]{x1D6E4},g},\mathbb{E}_{\unicode[STIX]{x1D6E4},b}:\mathbf{K}\,\text{RV}[\ast ]/(\mathbf{1}_{\Bbbk }+[\boldsymbol{P}])\longrightarrow \unicode[STIX]{x2124}.\end{eqnarray}$$
Proposition 4.24. There are two ring homomorphisms
 $$\begin{eqnarray}\mathbb{E}_{\Bbbk ,g}:\mathbf{K}\,\text{RV}[\ast ]\longrightarrow \mathbf{K}\,\operatorname{RES}[\ast ][[\boldsymbol{A}]^{-1}]\quad \text{and}\quad \mathbb{E}_{\mathbb{ k},b}:\mathbf{K}\,\text{RV}[\ast ]\longrightarrow \mathbf{K}\,\operatorname{RES}[\ast ][[1]^{-1}]\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{\Bbbk ,g}:\mathbf{K}\,\text{RV}[\ast ]\longrightarrow \mathbf{K}\,\operatorname{RES}[\ast ][[\boldsymbol{A}]^{-1}]\quad \text{and}\quad \mathbb{E}_{\mathbb{ k},b}:\mathbf{K}\,\text{RV}[\ast ]\longrightarrow \mathbf{K}\,\operatorname{RES}[\ast ][[1]^{-1}]\end{eqnarray}$$
such that
-
– their ranges are precisely the zeroth graded pieces of their respective codomains,
-
–
 $\mathbf{1}_{\Bbbk }+[\boldsymbol{P}]$
vanishes under both of them,
$\mathbf{1}_{\Bbbk }+[\boldsymbol{P}]$
vanishes under both of them, -
– for all
 $x\in \mathbf{K}\,\operatorname{RES}[k]$
,
$x\in \mathbf{K}\,\operatorname{RES}[k]$
,
 $\mathbb{E}_{\Bbbk ,g}(x)=x[\boldsymbol{A}]^{-k}$
and
$\mathbb{E}_{\Bbbk ,g}(x)=x[\boldsymbol{A}]^{-k}$
and
 $\mathbb{E}_{\Bbbk ,b}(x)=x[1]^{-k}$
.
$\mathbb{E}_{\Bbbk ,b}(x)=x[1]^{-k}$
.
Proof. We first define, for each
![]() $n$
, a homomorphism
$n$
, a homomorphism
 $$\begin{eqnarray}\mathbb{E}_{g,n}:\mathbf{K}\,\text{RV}[n]\longrightarrow \mathbf{K}\,\operatorname{RES}[n]\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{g,n}:\mathbf{K}\,\text{RV}[n]\longrightarrow \mathbf{K}\,\operatorname{RES}[n]\end{eqnarray}$$
as follows. By Proposition 4.21, there is an isomorphism
 $$\begin{eqnarray}\mathbb{D}_{n}:\bigoplus _{i+j=n}\mathbf{K}\,\operatorname{RES}[i]\otimes \mathbf{K}\,\unicode[STIX]{x1D6E4}[j]\rightarrow ^{{\sim}}\mathbf{K}\,\text{RV}[n].\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{D}_{n}:\bigoplus _{i+j=n}\mathbf{K}\,\operatorname{RES}[i]\otimes \mathbf{K}\,\unicode[STIX]{x1D6E4}[j]\rightarrow ^{{\sim}}\mathbf{K}\,\text{RV}[n].\end{eqnarray}$$
Let the group homomorphism
 ${\mathcal{E}}_{g,j}:\mathbf{K}\,\unicode[STIX]{x1D6E4}[j]\longrightarrow \unicode[STIX]{x2124}$
be defined as in Lemma 4.22, using
${\mathcal{E}}_{g,j}:\mathbf{K}\,\unicode[STIX]{x1D6E4}[j]\longrightarrow \unicode[STIX]{x2124}$
be defined as in Lemma 4.22, using
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}$
. Let
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}$
. Let
 $$\begin{eqnarray}E_{g}^{i,j}:\mathbf{K}\,\operatorname{RES}[i]\otimes \mathbf{K}\,\unicode[STIX]{x1D6E4}[j]\longrightarrow \mathbf{K}\,\operatorname{RES}[i+j]\end{eqnarray}$$
$$\begin{eqnarray}E_{g}^{i,j}:\mathbf{K}\,\operatorname{RES}[i]\otimes \mathbf{K}\,\unicode[STIX]{x1D6E4}[j]\longrightarrow \mathbf{K}\,\operatorname{RES}[i+j]\end{eqnarray}$$
be the group homomorphism determined by
 $x\otimes y\longmapsto {\mathcal{E}}_{g,j}(y)x[\boldsymbol{T}]^{j}$
. Let
$x\otimes y\longmapsto {\mathcal{E}}_{g,j}(y)x[\boldsymbol{T}]^{j}$
. Let
 $$\begin{eqnarray}E_{g,n}=\mathop{\sum }_{i+j=n}E_{g}^{i,j}\quad \text{and}\quad \mathbb{E}_{g,n}=E_{g,n}\circ \mathbb{D}_{n}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}E_{g,n}=\mathop{\sum }_{i+j=n}E_{g}^{i,j}\quad \text{and}\quad \mathbb{E}_{g,n}=E_{g,n}\circ \mathbb{D}_{n}^{-1}.\end{eqnarray}$$
Note that, due to the presence of the tensor
![]() $\otimes _{\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]}$
and the replacement of
$\otimes _{\mathbf{K}\,\unicode[STIX]{x1D6E4}^{c}[\ast ]}$
and the replacement of
![]() $y$
with
$y$
with
 ${\mathcal{E}}_{g,j}(y)[\boldsymbol{T}]^{j}$
, there is this issue of compatibility between the various components of
${\mathcal{E}}_{g,j}(y)[\boldsymbol{T}]^{j}$
, there is this issue of compatibility between the various components of
![]() $E_{g,n}$
. In our setting, this is easily resolved since all definable bijections are allowed in
$E_{g,n}$
. In our setting, this is easily resolved since all definable bijections are allowed in
![]() $\unicode[STIX]{x1D6E4}[\ast ]$
and hence
$\unicode[STIX]{x1D6E4}[\ast ]$
and hence
 $\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
is generated by isomorphism classes of the form
$\mathbf{K}_{+}\unicode[STIX]{x1D6E4}^{c}[\ast ]$
is generated by isomorphism classes of the form
![]() $[e]^{k}$
. In the setting of [Reference Hrushovski and KazhdanHK06], however, one has to pass to a quotient ring to achieve compatibility (see Remark 4.13 and also [Reference Hrushovski and LoeserHL15, § 2.5]).
$[e]^{k}$
. In the setting of [Reference Hrushovski and KazhdanHK06], however, one has to pass to a quotient ring to achieve compatibility (see Remark 4.13 and also [Reference Hrushovski and LoeserHL15, § 2.5]).
Now, it is straightforward to check the equality
 $$\begin{eqnarray}\mathbb{E}_{g,n}(x)\mathbb{E}_{g,m}(y)=\mathbb{E}_{g,n+m}(xy).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{g,n}(x)\mathbb{E}_{g,m}(y)=\mathbb{E}_{g,n+m}(xy).\end{eqnarray}$$
The group homomorphisms
 $\unicode[STIX]{x1D70F}_{m,k}:\mathbf{K}\,\operatorname{RES}[m]\longrightarrow \mathbf{K}\,\operatorname{RES}[m+k]$
given by
$\unicode[STIX]{x1D70F}_{m,k}:\mathbf{K}\,\operatorname{RES}[m]\longrightarrow \mathbf{K}\,\operatorname{RES}[m+k]$
given by
 $x\longmapsto x[\boldsymbol{A}]^{k}$
determine a colimit system, and the group homomorphisms
$x\longmapsto x[\boldsymbol{A}]^{k}$
determine a colimit system, and the group homomorphisms
 $$\begin{eqnarray}\mathbb{E}_{g,\leqslant n}:=\mathop{\sum }_{m\leqslant n}\unicode[STIX]{x1D70F}_{m,n-m}\circ \mathbb{E}_{g,m}:\mathbf{K}\,\text{RV}[{\leqslant}n]\longrightarrow \mathbf{K}\,\operatorname{RES}[n]\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{g,\leqslant n}:=\mathop{\sum }_{m\leqslant n}\unicode[STIX]{x1D70F}_{m,n-m}\circ \mathbb{E}_{g,m}:\mathbf{K}\,\text{RV}[{\leqslant}n]\longrightarrow \mathbf{K}\,\operatorname{RES}[n]\end{eqnarray}$$
determine a homomorphism of colimit systems. Hence we have a ring homomorphism:
 $$\begin{eqnarray}\underset{n}{\text{colim}}\,\mathbb{E}_{g,\leqslant n}:\mathbf{K}\,\text{RV}[\ast ]\longrightarrow \underset{\unicode[STIX]{x1D70F}_{n,k}}{\text{colim}}\,\mathbf{K}\,\operatorname{RES}[n].\end{eqnarray}$$
$$\begin{eqnarray}\underset{n}{\text{colim}}\,\mathbb{E}_{g,\leqslant n}:\mathbf{K}\,\text{RV}[\ast ]\longrightarrow \underset{\unicode[STIX]{x1D70F}_{n,k}}{\text{colim}}\,\mathbf{K}\,\operatorname{RES}[n].\end{eqnarray}$$
For all
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
 $$\begin{eqnarray}\mathbb{E}_{g,\leqslant n}(\mathbf{1}_{\Bbbk }+[\boldsymbol{P}])=[\boldsymbol{A}]^{n}-2[\boldsymbol{T}][\boldsymbol{A}]^{n-1}-[1][\boldsymbol{A}]^{n-1}=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{g,\leqslant n}(\mathbf{1}_{\Bbbk }+[\boldsymbol{P}])=[\boldsymbol{A}]^{n}-2[\boldsymbol{T}][\boldsymbol{A}]^{n-1}-[1][\boldsymbol{A}]^{n-1}=0.\end{eqnarray}$$
This yields the desired homomorphism
![]() $\mathbb{E}_{\Bbbk ,g}$
since the colimit in question can be embedded into the zeroth graded piece of
$\mathbb{E}_{\Bbbk ,g}$
since the colimit in question can be embedded into the zeroth graded piece of
 $\mathbf{K}\,\operatorname{RES}[\ast ][[\boldsymbol{A}]^{-1}]$
.
$\mathbf{K}\,\operatorname{RES}[\ast ][[\boldsymbol{A}]^{-1}]$
.
The construction of
![]() $\mathbb{E}_{\Bbbk ,b}$
is completely analogous, with
$\mathbb{E}_{\Bbbk ,b}$
is completely analogous, with
![]() $[\boldsymbol{A}]$
replaced by
$[\boldsymbol{A}]$
replaced by
![]() $[1]$
and
$[1]$
and
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}$
by
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},g}$
by
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}$
.◻
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6E4},b}$
.◻
Since the zeroth graded pieces of both
 $\mathbf{K}\,\operatorname{RES}[\ast ][[\boldsymbol{A}]^{-1}]$
and
$\mathbf{K}\,\operatorname{RES}[\ast ][[\boldsymbol{A}]^{-1}]$
and
 $\mathbf{K}\,\operatorname{RES}[\ast ][[1]^{-1}]$
are canonically isomorphic to
$\mathbf{K}\,\operatorname{RES}[\ast ][[1]^{-1}]$
are canonically isomorphic to
![]() $\unicode[STIX]{x2124}$
, the homomorphisms
$\unicode[STIX]{x2124}$
, the homomorphisms
![]() $\mathbb{E}_{\Bbbk ,g}$
,
$\mathbb{E}_{\Bbbk ,g}$
,
![]() $\mathbb{E}_{\Bbbk ,b}$
are just the homomorphisms
$\mathbb{E}_{\Bbbk ,b}$
are just the homomorphisms
![]() $\mathbb{E}_{\unicode[STIX]{x1D6E4},g}$
,
$\mathbb{E}_{\unicode[STIX]{x1D6E4},g}$
,
![]() $\mathbb{E}_{\unicode[STIX]{x1D6E4},b}$
in Remark 4.23; more precisely,
$\mathbb{E}_{\unicode[STIX]{x1D6E4},b}$
in Remark 4.23; more precisely,
 $\mathbb{E}_{\Bbbk ,g}=\mathbb{E}_{\unicode[STIX]{x1D6E4},g}$
and
$\mathbb{E}_{\Bbbk ,g}=\mathbb{E}_{\unicode[STIX]{x1D6E4},g}$
and
 $\mathbb{E}_{\Bbbk ,b}=\mathbb{E}_{\unicode[STIX]{x1D6E4},b}$
.
$\mathbb{E}_{\Bbbk ,b}=\mathbb{E}_{\unicode[STIX]{x1D6E4},b}$
.
5 Generalized Euler characteristic
From here on, our discussion will be of an increasingly formal nature. Many statements are exact copies of those in [Reference YinYin10, Reference YinYin11, Reference YinYin13b] and often the same proofs work, provided that the auxiliary results are replaced by the corresponding ones obtained above. For the reader’s convenience, we will write down all the details.
5.1 Special bijections
Our first task is to connect
 $\mathbf{K}_{+}\text{VF}_{\ast }$
with
$\mathbf{K}_{+}\text{VF}_{\ast }$
with
 $\mathbf{K}_{+}\text{RV}[\ast ]$
, or more precisely, to establish a surjective homomorphism
$\mathbf{K}_{+}\text{RV}[\ast ]$
, or more precisely, to establish a surjective homomorphism
 $\mathbf{K}_{+}\text{RV}[\ast ]\longrightarrow \mathbf{K}_{+}\text{VF}_{\ast }$
. Notice the direction of the arrow. The main instrument in this endeavor is special bijections.
$\mathbf{K}_{+}\text{RV}[\ast ]\longrightarrow \mathbf{K}_{+}\text{VF}_{\ast }$
. Notice the direction of the arrow. The main instrument in this endeavor is special bijections.
Convention 5.1. We reiterate [Reference YinYin13b, Convention 2.32] here, with a different terminology, since this trivial-looking convention is actually quite crucial for understanding the discussion below, especially the parts that involve special bijections. For any set
![]() $A$
, let
$A$
, let
 $$\begin{eqnarray}\mathbf{c}(A)=\{(a,\operatorname{rv}(a),t):(a,t)\in A\text{ and }a\in \operatorname{pr}_{\text{VF}}(A)\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{c}(A)=\{(a,\operatorname{rv}(a),t):(a,t)\in A\text{ and }a\in \operatorname{pr}_{\text{VF}}(A)\}.\end{eqnarray}$$
The natural bijection
 $\mathbf{c}:A\longrightarrow \mathbf{c}(A)$
is called the regularization of
$\mathbf{c}:A\longrightarrow \mathbf{c}(A)$
is called the regularization of
![]() $A$
. We shall tacitly substitute
$A$
. We shall tacitly substitute
![]() $\mathbf{c}(A)$
for
$\mathbf{c}(A)$
for
![]() $A$
if it is necessary or is just more convenient. Whether this substitution has been performed or not should be clear in context (or rather, it is always performed).
$A$
if it is necessary or is just more convenient. Whether this substitution has been performed or not should be clear in context (or rather, it is always performed).
Definition 5.2 (Special bijections).
Let
![]() $A$
be a (regularized) definable set whose first coordinate is a
$A$
be a (regularized) definable set whose first coordinate is a
![]() $\text{VF}$
-coordinate (of course nothing is special about the first
$\text{VF}$
-coordinate (of course nothing is special about the first
![]() $\text{VF}$
-coordinate, we choose it simply for ease of notation). Let
$\text{VF}$
-coordinate, we choose it simply for ease of notation). Let
 $C\subseteq \operatorname{RVH}(A)$
be an
$C\subseteq \operatorname{RVH}(A)$
be an
![]() $\text{RV}$
-pullback (see Definition 2.32) and
$\text{RV}$
-pullback (see Definition 2.32) and
 $$\begin{eqnarray}\unicode[STIX]{x1D706}:\operatorname{pr}_{{>}1}(C\cap A)\longrightarrow \text{VF}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}:\operatorname{pr}_{{>}1}(C\cap A)\longrightarrow \text{VF}\end{eqnarray}$$
a definable function whose graph is contained in
![]() $C$
. Recall Notation 2.34. Let
$C$
. Recall Notation 2.34. Let
 $$\begin{eqnarray}C^{\sharp }=\mathop{\bigcup }_{x\in \operatorname{pr}_{{>}1}(C)}\mathfrak{M}_{|\text{vrv}|(\operatorname{pr}_{1}(x_{\text{RV}}))}\times x\quad \text{and}\quad \operatorname{RVH}(A)^{\sharp }=C^{\sharp }\uplus (\operatorname{RVH}(A)\smallsetminus C),\end{eqnarray}$$
$$\begin{eqnarray}C^{\sharp }=\mathop{\bigcup }_{x\in \operatorname{pr}_{{>}1}(C)}\mathfrak{M}_{|\text{vrv}|(\operatorname{pr}_{1}(x_{\text{RV}}))}\times x\quad \text{and}\quad \operatorname{RVH}(A)^{\sharp }=C^{\sharp }\uplus (\operatorname{RVH}(A)\smallsetminus C),\end{eqnarray}$$
where
 $x_{\text{RV}}=\operatorname{pr}_{\text{RV}}(x)$
. The centripetal transformation
$x_{\text{RV}}=\operatorname{pr}_{\text{RV}}(x)$
. The centripetal transformation
 $\unicode[STIX]{x1D702}:A\longrightarrow \operatorname{RVH}(A)^{\sharp }$
with respect to
$\unicode[STIX]{x1D702}:A\longrightarrow \operatorname{RVH}(A)^{\sharp }$
with respect to
![]() $\unicode[STIX]{x1D706}$
is defined by
$\unicode[STIX]{x1D706}$
is defined by
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D702}(a,x)=(a-\unicode[STIX]{x1D706}(x),x)\quad & \text{on }C\cap A,\\ \unicode[STIX]{x1D702}=\operatorname{id}\quad & \text{on }A\smallsetminus C.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D702}(a,x)=(a-\unicode[STIX]{x1D706}(x),x)\quad & \text{on }C\cap A,\\ \unicode[STIX]{x1D702}=\operatorname{id}\quad & \text{on }A\smallsetminus C.\end{array}\right.\end{eqnarray}$$
Note that
![]() $\unicode[STIX]{x1D702}$
is injective. The inverse of
$\unicode[STIX]{x1D702}$
is injective. The inverse of
![]() $\unicode[STIX]{x1D702}$
is naturally called the centrifugal transformation with respect to
$\unicode[STIX]{x1D702}$
is naturally called the centrifugal transformation with respect to
![]() $\unicode[STIX]{x1D706}$
. The function
$\unicode[STIX]{x1D706}$
. The function
![]() $\unicode[STIX]{x1D706}$
is referred to as the focus of
$\unicode[STIX]{x1D706}$
is referred to as the focus of
![]() $\unicode[STIX]{x1D702}$
and the
$\unicode[STIX]{x1D702}$
and the
![]() $\text{RV}$
-pullback
$\text{RV}$
-pullback
![]() $C$
as the locus of
$C$
as the locus of
![]() $\unicode[STIX]{x1D706}$
(or
$\unicode[STIX]{x1D706}$
(or
![]() $\unicode[STIX]{x1D702}$
).
$\unicode[STIX]{x1D702}$
).
A special bijection
![]() $T$
on
$T$
on
![]() $A$
is an alternating composition of centripetal transformations and regularizations. By Convention 5.1, we shall only display the centripetal transformations in such a composition. The length of such a special bijection
$A$
is an alternating composition of centripetal transformations and regularizations. By Convention 5.1, we shall only display the centripetal transformations in such a composition. The length of such a special bijection
![]() $T$
, denoted by
$T$
, denoted by
![]() $\operatorname{lh}(T)$
, is the number of centripetal transformations in
$\operatorname{lh}(T)$
, is the number of centripetal transformations in
![]() $T$
. The range of
$T$
. The range of
![]() $T$
is sometimes denoted by
$T$
is sometimes denoted by
![]() $A^{\flat }$
.
$A^{\flat }$
.
For functions between sets that have only one
![]() $\text{VF}$
-coordinate, composing with special bijections on the right and inverses of special bijections on the left obviously preserves dtdp.
$\text{VF}$
-coordinate, composing with special bijections on the right and inverses of special bijections on the left obviously preserves dtdp.
Lemma 5.3. Let
![]() $T$
be a special bijection on
$T$
be a special bijection on
 $A\subseteq \text{VF}\times \text{RV}^{m}$
such that
$A\subseteq \text{VF}\times \text{RV}^{m}$
such that
![]() $A^{\flat }$
is an
$A^{\flat }$
is an
![]() $\text{RV}$
-pullback. Then there is a definable function
$\text{RV}$
-pullback. Then there is a definable function
 $\unicode[STIX]{x1D716}:\operatorname{pr}_{\text{RV}}(A^{\flat })\longrightarrow \text{VF}$
such that, for every
$\unicode[STIX]{x1D716}:\operatorname{pr}_{\text{RV}}(A^{\flat })\longrightarrow \text{VF}$
such that, for every
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
 $\mathfrak{p}=t^{\sharp }\times s\subseteq A^{\flat }$
,
$\mathfrak{p}=t^{\sharp }\times s\subseteq A^{\flat }$
,
 $(T^{-1}(\mathfrak{p}))_{\text{VF}}=t^{\sharp }+\unicode[STIX]{x1D716}(s)$
.
$(T^{-1}(\mathfrak{p}))_{\text{VF}}=t^{\sharp }+\unicode[STIX]{x1D716}(s)$
.
Proof. It is clear that
![]() $\mathfrak{p}$
is the image of an open polydisc
$\mathfrak{p}$
is the image of an open polydisc
 $\mathfrak{a}\times r\subseteq A$
. Let
$\mathfrak{a}\times r\subseteq A$
. Let
![]() $T^{\prime }$
be
$T^{\prime }$
be
![]() $T$
with the last centripetal transformation deleted. Then
$T$
with the last centripetal transformation deleted. Then
 $T^{\prime }(\mathfrak{a}\times r)$
is also an open polydisc
$T^{\prime }(\mathfrak{a}\times r)$
is also an open polydisc
![]() $\mathfrak{a}^{\prime }\times r^{\prime }$
. The range of the focus map of
$\mathfrak{a}^{\prime }\times r^{\prime }$
. The range of the focus map of
![]() $\unicode[STIX]{x1D702}_{n}$
contains a point in the smallest closed disc containing
$\unicode[STIX]{x1D702}_{n}$
contains a point in the smallest closed disc containing
![]() $\mathfrak{a}^{\prime }$
. This point can be transported back by the previous focus maps to a point in the smallest closed disc containing
$\mathfrak{a}^{\prime }$
. This point can be transported back by the previous focus maps to a point in the smallest closed disc containing
![]() $\mathfrak{a}$
. The lemma follows easily from this observation.◻
$\mathfrak{a}$
. The lemma follows easily from this observation.◻
Note that, since
 $\operatorname{dom}(\unicode[STIX]{x1D716})\subseteq \text{RV}^{l}$
for some
$\operatorname{dom}(\unicode[STIX]{x1D716})\subseteq \text{RV}^{l}$
for some
![]() $l$
, by Corollary 3.7,
$l$
, by Corollary 3.7,
![]() $\operatorname{ran}(\unicode[STIX]{x1D716})$
is actually finite.
$\operatorname{ran}(\unicode[STIX]{x1D716})$
is actually finite.
A definable set
![]() $A$
is called a deformed
$A$
is called a deformed
![]() $\text{RV}$
-pullback if there is a special bijection
$\text{RV}$
-pullback if there is a special bijection
![]() $T$
on
$T$
on
![]() $A$
such that
$A$
such that
![]() $A^{\flat }$
is an
$A^{\flat }$
is an
![]() $\text{RV}$
-pullback.
$\text{RV}$
-pullback.
Lemma 5.4. Every definable set
 $A\subseteq \text{VF}\times \text{RV}^{m}$
is a deformed
$A\subseteq \text{VF}\times \text{RV}^{m}$
is a deformed
![]() $\text{RV}$
-pullback.
$\text{RV}$
-pullback.
Proof. By compactness and HNF this is immediately reduced to the situation where
 $A\subseteq \text{VF}$
is contained in an
$A\subseteq \text{VF}$
is contained in an
![]() $\text{RV}$
-disc and is a
$\text{RV}$
-disc and is a
![]() $\operatorname{val}$
-interval with end-discs
$\operatorname{val}$
-interval with end-discs
![]() $\mathfrak{a}$
,
$\mathfrak{a}$
,
![]() $\mathfrak{b}$
. This may be further divided into several cases according to whether
$\mathfrak{b}$
. This may be further divided into several cases according to whether
![]() $\mathfrak{a}$
,
$\mathfrak{a}$
,
![]() $\mathfrak{b}$
are open or closed discs and whether the ends of
$\mathfrak{b}$
are open or closed discs and whether the ends of
![]() $A$
are open or closed. In each of these cases, Lemma 3.20 is applied in much the same way as its counterpart is applied in the proof of [Reference YinYin09, Lemma 4.26]. It is a tedious exercise and is left to the reader.◻
$A$
are open or closed. In each of these cases, Lemma 3.20 is applied in much the same way as its counterpart is applied in the proof of [Reference YinYin09, Lemma 4.26]. It is a tedious exercise and is left to the reader.◻
The following result is an analogue of [Reference YinYin10, Theorem 5.4] (see also [Reference YinYin13b, Theorem 4.25]).
Theorem 5.5. Let
 $F(x)=F(x_{1},\ldots ,x_{n})$
be an
$F(x)=F(x_{1},\ldots ,x_{n})$
be an
![]() ${\mathcal{L}}_{T\text{}}$
-term. Let
${\mathcal{L}}_{T\text{}}$
-term. Let
 $u\in \text{RV}^{n}$
and
$u\in \text{RV}^{n}$
and
 $R:u^{\sharp }\longrightarrow A$
be a special bijection. Then there is a special bijection
$R:u^{\sharp }\longrightarrow A$
be a special bijection. Then there is a special bijection
 $T:A\longrightarrow A^{\flat }$
such that
$T:A\longrightarrow A^{\flat }$
such that
 $F\circ R^{-1}\circ T^{-1}$
is
$F\circ R^{-1}\circ T^{-1}$
is
![]() $\operatorname{rv}$
-contractible. In a commutative diagram,
$\operatorname{rv}$
-contractible. In a commutative diagram,

Proof. First observe that if the assertion holds for one
![]() ${\mathcal{L}}_{T\text{}}$
-term then it holds simultaneously for any finite number of
${\mathcal{L}}_{T\text{}}$
-term then it holds simultaneously for any finite number of
![]() ${\mathcal{L}}_{T\text{}}$
-terms, since
${\mathcal{L}}_{T\text{}}$
-terms, since
![]() $\operatorname{rv}$
-contractibility is preserved by further special bijections on
$\operatorname{rv}$
-contractibility is preserved by further special bijections on
![]() $A^{\flat }$
. We do induction on
$A^{\flat }$
. We do induction on
![]() $n$
. For the base case
$n$
. For the base case
![]() $n=1$
, by Corollary 3.16 and Remark 3.17, there is a definable finite partition
$n=1$
, by Corollary 3.16 and Remark 3.17, there is a definable finite partition
![]() $B_{i}$
of
$B_{i}$
of
![]() $u^{\sharp }$
such that, for all
$u^{\sharp }$
such that, for all
![]() $i$
, if
$i$
, if
![]() $\mathfrak{a}\subseteq B_{i}$
is an open disc then
$\mathfrak{a}\subseteq B_{i}$
is an open disc then
 $\operatorname{rv}\restriction F(\mathfrak{a})$
is constant. By consecutive applications of Lemma 5.4, we obtain a special bijection
$\operatorname{rv}\restriction F(\mathfrak{a})$
is constant. By consecutive applications of Lemma 5.4, we obtain a special bijection
![]() $T$
on
$T$
on
![]() $A$
such that each
$A$
such that each
 $(T\circ R)(B_{i})$
is an
$(T\circ R)(B_{i})$
is an
![]() $\text{RV}$
-pullback. Clearly
$\text{RV}$
-pullback. Clearly
![]() $T$
is as required.
$T$
is as required.
For the inductive step, we may concentrate on a single
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
 $\mathfrak{p}=v^{\sharp }\times (v,r)\subseteq A$
. Let
$\mathfrak{p}=v^{\sharp }\times (v,r)\subseteq A$
. Let
![]() $\unicode[STIX]{x1D719}(x,y)$
be a quantifier-free formula that defines the function
$\unicode[STIX]{x1D719}(x,y)$
be a quantifier-free formula that defines the function
![]() $\operatorname{rv}\circ f$
. Recall Convention 3.1. Let
$\operatorname{rv}\circ f$
. Recall Convention 3.1. Let
![]() $G_{i}(x)$
enumerate the top
$G_{i}(x)$
enumerate the top
![]() ${\mathcal{L}}_{T\text{}}$
-terms of
${\mathcal{L}}_{T\text{}}$
-terms of
![]() $\unicode[STIX]{x1D719}$
. For
$\unicode[STIX]{x1D719}$
. For
![]() $a\in v_{1}^{\sharp }$
, write
$a\in v_{1}^{\sharp }$
, write
 $G_{i,a}=G_{i}(a,x_{2},\ldots ,x_{n})$
. By the inductive hypothesis, there is a special bijection
$G_{i,a}=G_{i}(a,x_{2},\ldots ,x_{n})$
. By the inductive hypothesis, there is a special bijection
![]() $R_{a}$
on
$R_{a}$
on
 $(v_{2},\ldots ,v_{n})^{\sharp }$
such that every
$(v_{2},\ldots ,v_{n})^{\sharp }$
such that every
 $G_{i,a}\circ R_{a}^{-1}$
is
$G_{i,a}\circ R_{a}^{-1}$
is
![]() $\operatorname{rv}$
-contractible. Let
$\operatorname{rv}$
-contractible. Let
![]() $U_{k,a}$
enumerate the loci of the components of
$U_{k,a}$
enumerate the loci of the components of
![]() $R_{a}$
and
$R_{a}$
and
![]() $\unicode[STIX]{x1D706}_{k,a}$
the corresponding focus maps. By compactness,
$\unicode[STIX]{x1D706}_{k,a}$
the corresponding focus maps. By compactness,
-
– for each
 $i$
, there is a quantifier-free formula
$i$
, there is a quantifier-free formula
 $\unicode[STIX]{x1D713}_{i}$
such that
$\unicode[STIX]{x1D713}_{i}$
such that
 $\unicode[STIX]{x1D713}_{i}(a)$
defines
$\unicode[STIX]{x1D713}_{i}(a)$
defines
 $(G_{i,a}\circ R_{a}^{-1})_{\downarrow }$
,
$(G_{i,a}\circ R_{a}^{-1})_{\downarrow }$
, -
– there is a quantifier-free formula
 $\unicode[STIX]{x1D703}$
such that
$\unicode[STIX]{x1D703}$
such that
 $\unicode[STIX]{x1D703}(a)$
determines the sequence
$\unicode[STIX]{x1D703}(a)$
determines the sequence
 $\operatorname{rv}(U_{k,a})$
and the
$\operatorname{rv}(U_{k,a})$
and the
 $\text{VF}$
-coordinates targeted by
$\text{VF}$
-coordinates targeted by
 $\unicode[STIX]{x1D706}_{k,a}$
.
$\unicode[STIX]{x1D706}_{k,a}$
.
Let
![]() $H_{j}(x_{1})$
enumerate the top
$H_{j}(x_{1})$
enumerate the top
![]() ${\mathcal{L}}_{T\text{}}$
-terms of the formulas
${\mathcal{L}}_{T\text{}}$
-terms of the formulas
![]() $\unicode[STIX]{x1D713}_{i}$
,
$\unicode[STIX]{x1D713}_{i}$
,
![]() $\unicode[STIX]{x1D703}$
. Applying the inductive hypothesis again, we obtain a special bijection
$\unicode[STIX]{x1D703}$
. Applying the inductive hypothesis again, we obtain a special bijection
![]() $T_{1}$
on
$T_{1}$
on
![]() $v_{1}^{\sharp }$
such that every
$v_{1}^{\sharp }$
such that every
 $H_{j}\,\circ \,T_{1}^{-1}$
is
$H_{j}\,\circ \,T_{1}^{-1}$
is
![]() $\operatorname{rv}$
-contractible. This means that, for every
$\operatorname{rv}$
-contractible. This means that, for every
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
 $\mathfrak{q}\subseteq T_{1}(v_{1}^{\sharp })$
and all
$\mathfrak{q}\subseteq T_{1}(v_{1}^{\sharp })$
and all
 $a_{1},a_{2}\in T_{1}^{-1}(\mathfrak{q})$
,
$a_{1},a_{2}\in T_{1}^{-1}(\mathfrak{q})$
,
-
– the formulas
 $\unicode[STIX]{x1D713}_{i}(a_{1})$
,
$\unicode[STIX]{x1D713}_{i}(a_{1})$
,
 $\unicode[STIX]{x1D713}_{i}(a_{2})$
define the same
$\unicode[STIX]{x1D713}_{i}(a_{2})$
define the same
 $\operatorname{rv}$
-contraction,
$\operatorname{rv}$
-contraction, -
– the special bijections
 $R_{a_{1}}$
,
$R_{a_{1}}$
,
 $R_{a_{2}}$
may be glued together in the obvious sense to form one special bijection on
$R_{a_{2}}$
may be glued together in the obvious sense to form one special bijection on
 $\{a_{1},a_{2}\}\times (v_{2},\ldots ,v_{n})^{\sharp }$
.
$\{a_{1},a_{2}\}\times (v_{2},\ldots ,v_{n})^{\sharp }$
.
Consequently,
![]() $T_{1}$
and
$T_{1}$
and
![]() $R_{a}$
naturally induce a special bijection
$R_{a}$
naturally induce a special bijection
![]() $T$
on
$T$
on
![]() $\mathfrak{p}$
such that every
$\mathfrak{p}$
such that every
 $G_{i}\circ T^{-1}$
is
$G_{i}\circ T^{-1}$
is
![]() $\operatorname{rv}$
-contractible. This implies that
$\operatorname{rv}$
-contractible. This implies that
 $F\circ R^{-1}\circ T^{-1}$
is
$F\circ R^{-1}\circ T^{-1}$
is
![]() $\operatorname{rv}$
-contractible and hence
$\operatorname{rv}$
-contractible and hence
![]() $T$
is as required.◻
$T$
is as required.◻
Corollary 5.6. Let
 $A\subseteq \text{VF}^{n}$
be a definable set and
$A\subseteq \text{VF}^{n}$
be a definable set and
 $f:A\longrightarrow \text{RV}^{m}$
a definable function. Then there is a special bijection
$f:A\longrightarrow \text{RV}^{m}$
a definable function. Then there is a special bijection
![]() $T$
on
$T$
on
![]() $A$
such that
$A$
such that
![]() $A^{\flat }$
is an
$A^{\flat }$
is an
![]() $\text{RV}$
-pullback and the function
$\text{RV}$
-pullback and the function
![]() $f\circ T^{-1}$
is
$f\circ T^{-1}$
is
![]() $\operatorname{rv}$
-contractible.
$\operatorname{rv}$
-contractible.
Proof. By compactness, we may assume that
![]() $A$
is contained in an
$A$
is contained in an
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $\mathfrak{p}$
. Let
$\mathfrak{p}$
. Let
![]() $\unicode[STIX]{x1D719}$
be a quantifier-free formula that defines
$\unicode[STIX]{x1D719}$
be a quantifier-free formula that defines
![]() $f$
. Let
$f$
. Let
![]() $F_{i}(x,y)$
enumerate the top
$F_{i}(x,y)$
enumerate the top
![]() ${\mathcal{L}}_{T\text{}}$
-terms of
${\mathcal{L}}_{T\text{}}$
-terms of
![]() $\unicode[STIX]{x1D719}$
. For
$\unicode[STIX]{x1D719}$
. For
 $s\in \text{RV}^{m}$
, let
$s\in \text{RV}^{m}$
, let
 $F_{i,s}=F_{i}(x,s)$
. By Theorem 5.5, there is a special bijection
$F_{i,s}=F_{i}(x,s)$
. By Theorem 5.5, there is a special bijection
![]() $T$
on
$T$
on
![]() $\mathfrak{p}$
such that each function
$\mathfrak{p}$
such that each function
 $F_{i,s}\circ T^{-1}$
is contractible. This means that, for each
$F_{i,s}\circ T^{-1}$
is contractible. This means that, for each
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
 $\mathfrak{q}\subseteq T(\mathfrak{p})$
,
$\mathfrak{q}\subseteq T(\mathfrak{p})$
,
-
– either
 $T^{-1}(\mathfrak{q})\subseteq A$
or
$T^{-1}(\mathfrak{q})\subseteq A$
or
 $T^{-1}(\mathfrak{q})\cap A=\emptyset$
,
$T^{-1}(\mathfrak{q})\cap A=\emptyset$
, -
– if
 $T^{-1}(\mathfrak{q})\subseteq A$
then
$T^{-1}(\mathfrak{q})\subseteq A$
then
 $(f\circ T^{-1})(\mathfrak{q})$
is a singleton.
$(f\circ T^{-1})(\mathfrak{q})$
is a singleton.
So
![]() $T\restriction A$
is as required.◻
$T\restriction A$
is as required.◻
Definition 5.7 (Lifting maps).
Let
![]() $U$
be a set in
$U$
be a set in
![]() $\text{RV}$
and
$\text{RV}$
and
 $f:U\longrightarrow \text{RV}^{k}$
a function. Let
$f:U\longrightarrow \text{RV}^{k}$
a function. Let
![]() $U_{f}$
stand for the set
$U_{f}$
stand for the set
 $\bigcup \{f(u)^{\sharp }\times u:u\in U\}$
. The
$\bigcup \{f(u)^{\sharp }\times u:u\in U\}$
. The
![]() $k$
th lifting map
$k$
th lifting map
 $$\begin{eqnarray}\mathbb{L}_{k}:\text{RV}[k]\longrightarrow \text{VF}[k]\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{L}_{k}:\text{RV}[k]\longrightarrow \text{VF}[k]\end{eqnarray}$$
is given by
 $(U,f)\longmapsto U_{f}$
. The map
$(U,f)\longmapsto U_{f}$
. The map
 $\mathbb{L}_{{\leqslant}k}:\text{RV}[{\leqslant}k]\longrightarrow \text{VF}[k]$
is given by
$\mathbb{L}_{{\leqslant}k}:\text{RV}[{\leqslant}k]\longrightarrow \text{VF}[k]$
is given by
 $\bigoplus _{i}\boldsymbol{U}_{i}\longmapsto \uplus _{i}\mathbb{L}_{i}\boldsymbol{U}_{i}$
. Set
$\bigoplus _{i}\boldsymbol{U}_{i}\longmapsto \uplus _{i}\mathbb{L}_{i}\boldsymbol{U}_{i}$
. Set
 $\mathbb{L}=\bigcup _{k}\mathbb{L}_{{\leqslant}k}$
.
$\mathbb{L}=\bigcup _{k}\mathbb{L}_{{\leqslant}k}$
.
Corollary 5.8. Every definable set
 $A\subseteq \text{VF}^{n}\times \text{RV}^{m}$
is a deformed
$A\subseteq \text{VF}^{n}\times \text{RV}^{m}$
is a deformed
![]() $\text{RV}$
-pullback. In particular, if
$\text{RV}$
-pullback. In particular, if
 $A\in \text{VF}_{\ast }$
then there are a
$A\in \text{VF}_{\ast }$
then there are a
 $\boldsymbol{U}\in \text{RV}[{\leqslant}n]$
and a special bijection from
$\boldsymbol{U}\in \text{RV}[{\leqslant}n]$
and a special bijection from
![]() $A$
onto
$A$
onto
 $\mathbb{L}_{{\leqslant}n}(\boldsymbol{U})$
.
$\mathbb{L}_{{\leqslant}n}(\boldsymbol{U})$
.
Proof. For the first assertion, by compactness, we may assume
 $A\subseteq \text{VF}^{n}$
. Then it is a special case of Corollary 5.6. The second assertion follows from Lemma 4.2.◻
$A\subseteq \text{VF}^{n}$
. Then it is a special case of Corollary 5.6. The second assertion follows from Lemma 4.2.◻
Definition 5.9 (Lifts).
Let
 $F:(U,f)\longrightarrow (V,g)$
be an
$F:(U,f)\longrightarrow (V,g)$
be an
![]() $\text{RV}[k]$
-morphism. Then
$\text{RV}[k]$
-morphism. Then
![]() $F$
induces a definable finite-to-finite correspondence
$F$
induces a definable finite-to-finite correspondence
 $F^{\dagger }\subseteq f(U)\times g(V)$
. Since
$F^{\dagger }\subseteq f(U)\times g(V)$
. Since
![]() $F^{\dagger }$
can be decomposed into finitely many definable bijections, we assume for simplicity that
$F^{\dagger }$
can be decomposed into finitely many definable bijections, we assume for simplicity that
![]() $F^{\dagger }$
is itself a bijection. Let
$F^{\dagger }$
is itself a bijection. Let
 $F^{\sharp }:f(U)^{\sharp }\longrightarrow g(V)^{\sharp }$
be a definable bijection that
$F^{\sharp }:f(U)^{\sharp }\longrightarrow g(V)^{\sharp }$
be a definable bijection that
![]() $\operatorname{rv}$
-contracts to
$\operatorname{rv}$
-contracts to
![]() $F^{\dagger }$
. Then
$F^{\dagger }$
. Then
![]() $F^{\sharp }$
is called a lift of
$F^{\sharp }$
is called a lift of
![]() $F$
. By Convention 5.1, we shall think of
$F$
. By Convention 5.1, we shall think of
![]() $F^{\sharp }$
as a definable bijection
$F^{\sharp }$
as a definable bijection
 $\mathbb{L}(U,f)\longrightarrow \mathbb{L}(V,g)$
that
$\mathbb{L}(U,f)\longrightarrow \mathbb{L}(V,g)$
that
![]() $\operatorname{rv}$
-contracts to
$\operatorname{rv}$
-contracts to
![]() $F^{\dagger }$
.
$F^{\dagger }$
.
Lemma 5.10. Let
 $f:A\longrightarrow B$
be a definable bijection between two sets that have exactly one
$f:A\longrightarrow B$
be a definable bijection between two sets that have exactly one
![]() $\text{VF}$
-coordinate each. Then there are special bijections
$\text{VF}$
-coordinate each. Then there are special bijections
 $T_{A}:A\longrightarrow A^{\flat }$
,
$T_{A}:A\longrightarrow A^{\flat }$
,
 $T_{B}:B\longrightarrow B^{\flat }$
such that
$T_{B}:B\longrightarrow B^{\flat }$
such that
![]() $A^{\flat }$
,
$A^{\flat }$
,
![]() $B^{\flat }$
are
$B^{\flat }$
are
![]() $\text{RV}$
-pullbacks and
$\text{RV}$
-pullbacks and
![]() $f_{\downarrow }^{\flat }$
is bijective in the following commutative diagram.
$f_{\downarrow }^{\flat }$
is bijective in the following commutative diagram.

Thus, if
 $A,B\in \text{VF}_{\ast }$
then
$A,B\in \text{VF}_{\ast }$
then
![]() $f^{\flat }$
is a lift of
$f^{\flat }$
is a lift of
![]() $f_{\downarrow }^{\flat }$
, where the latter is regarded as an
$f_{\downarrow }^{\flat }$
, where the latter is regarded as an
![]() $\text{RV}[1]$
-morphism between
$\text{RV}[1]$
-morphism between
![]() $\operatorname{rv}(A^{\flat })_{1}$
and
$\operatorname{rv}(A^{\flat })_{1}$
and
![]() $\operatorname{rv}(B^{\flat })_{1}$
(recall Notation 4.5).
$\operatorname{rv}(B^{\flat })_{1}$
(recall Notation 4.5).
Proof. By Corollaries 5.6, 5.8, and Lemma 3.24, we may assume that
![]() $A$
,
$A$
,
![]() $B$
are
$B$
are
![]() $\text{RV}$
-pullbacks,
$\text{RV}$
-pullbacks,
![]() $f$
is
$f$
is
![]() $\operatorname{rv}$
-contractible and has dtdp, and there is a special bijection
$\operatorname{rv}$
-contractible and has dtdp, and there is a special bijection
 $T_{B}:B\longrightarrow B^{\flat }$
such that
$T_{B}:B\longrightarrow B^{\flat }$
such that
 $(T_{B}\circ f)^{-1}$
is
$(T_{B}\circ f)^{-1}$
is
![]() $\operatorname{rv}$
-contractible. Let
$\operatorname{rv}$
-contractible. Let
 $T_{B}=\unicode[STIX]{x1D702}_{n}\circ \cdots \circ \unicode[STIX]{x1D702}_{1}$
, where each
$T_{B}=\unicode[STIX]{x1D702}_{n}\circ \cdots \circ \unicode[STIX]{x1D702}_{1}$
, where each
![]() $\unicode[STIX]{x1D702}_{i}$
is a centripetal transformation (and regularization maps are not displayed). Then it is enough to construct a special bijection
$\unicode[STIX]{x1D702}_{i}$
is a centripetal transformation (and regularization maps are not displayed). Then it is enough to construct a special bijection
 $T_{A}=\unicode[STIX]{x1D701}_{n}\circ \cdots \circ \unicode[STIX]{x1D701}_{1}$
on
$T_{A}=\unicode[STIX]{x1D701}_{n}\circ \cdots \circ \unicode[STIX]{x1D701}_{1}$
on
![]() $A$
such that, for each
$A$
such that, for each
![]() $i$
, both
$i$
, both
 $f_{i}:=T_{B,i}\circ f\circ T_{A,i}^{-1}$
and
$f_{i}:=T_{B,i}\circ f\circ T_{A,i}^{-1}$
and
 $T_{A,i}\circ (T_{B}\circ f)^{-1}$
are
$T_{A,i}\circ (T_{B}\circ f)^{-1}$
are
![]() $\operatorname{rv}$
-contractible, where
$\operatorname{rv}$
-contractible, where
 $T_{B,i}=\unicode[STIX]{x1D702}_{i}\circ \cdots \circ \unicode[STIX]{x1D702}_{1}$
and
$T_{B,i}=\unicode[STIX]{x1D702}_{i}\circ \cdots \circ \unicode[STIX]{x1D702}_{1}$
and
 $T_{A,i}=\unicode[STIX]{x1D701}_{i}\circ \cdots \circ \unicode[STIX]{x1D701}_{1}$
.
$T_{A,i}=\unicode[STIX]{x1D701}_{i}\circ \cdots \circ \unicode[STIX]{x1D701}_{1}$
.
To that end, suppose that
![]() $\unicode[STIX]{x1D701}_{i}$
has been constructed for each
$\unicode[STIX]{x1D701}_{i}$
has been constructed for each
 $i\leqslant k<n$
. Let
$i\leqslant k<n$
. Let
 $A_{k}=T_{A,k}(A)$
and
$A_{k}=T_{A,k}(A)$
and
 $B_{k}=T_{B,k}(B)$
. Let
$B_{k}=T_{B,k}(B)$
. Let
 $D\subseteq B_{k}$
be the locus of
$D\subseteq B_{k}$
be the locus of
![]() $\unicode[STIX]{x1D702}_{k+1}$
and
$\unicode[STIX]{x1D702}_{k+1}$
and
![]() $\unicode[STIX]{x1D706}$
the corresponding focus map. Since
$\unicode[STIX]{x1D706}$
the corresponding focus map. Since
![]() $f_{k}$
is
$f_{k}$
is
![]() $\operatorname{rv}$
-contractible and has dtdp, each
$\operatorname{rv}$
-contractible and has dtdp, each
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $\mathfrak{p}\subseteq B_{k}$
is a union of disjoint sets of the form
$\mathfrak{p}\subseteq B_{k}$
is a union of disjoint sets of the form
![]() $f_{k}(\mathfrak{q})$
, where
$f_{k}(\mathfrak{q})$
, where
![]() $\mathfrak{q}\subseteq A_{k}$
is an
$\mathfrak{q}\subseteq A_{k}$
is an
![]() $\text{RV}$
-polydisc. For each
$\text{RV}$
-polydisc. For each
 $t=(t_{1},t_{\tilde{1}})\in \operatorname{dom}(\unicode[STIX]{x1D706})$
, let
$t=(t_{1},t_{\tilde{1}})\in \operatorname{dom}(\unicode[STIX]{x1D706})$
, let
![]() $O_{t}$
be the set of those
$O_{t}$
be the set of those
![]() $\text{RV}$
-polydiscs
$\text{RV}$
-polydiscs
![]() $\mathfrak{q}\subseteq A_{k}$
such that
$\mathfrak{q}\subseteq A_{k}$
such that
 $f_{k}(\mathfrak{q})\subseteq t_{1}^{\sharp }\times t$
. Let
$f_{k}(\mathfrak{q})\subseteq t_{1}^{\sharp }\times t$
. Let
-
–
 $\mathfrak{q}_{t}\in O_{t}$
be the
$\mathfrak{q}_{t}\in O_{t}$
be the
 $\text{RV}$
-polydisc with
$\text{RV}$
-polydisc with
 $(\unicode[STIX]{x1D706}(t),t)\in \mathfrak{o}_{t}:=f_{k}(\mathfrak{q}_{t})$
,
$(\unicode[STIX]{x1D706}(t),t)\in \mathfrak{o}_{t}:=f_{k}(\mathfrak{q}_{t})$
, -
–
 $C=\bigcup _{t\in \operatorname{dom}(\unicode[STIX]{x1D706})}\mathfrak{q}_{t}\subseteq A_{k}$
and
$C=\bigcup _{t\in \operatorname{dom}(\unicode[STIX]{x1D706})}\mathfrak{q}_{t}\subseteq A_{k}$
and
 $a_{t}=f_{k}^{-1}(\unicode[STIX]{x1D706}(t),t)\in \mathfrak{q}_{t}$
,
$a_{t}=f_{k}^{-1}(\unicode[STIX]{x1D706}(t),t)\in \mathfrak{q}_{t}$
, -
–
 $\unicode[STIX]{x1D705}:\operatorname{pr}_{{>}1}(C)\longrightarrow \text{VF}$
the corresponding focus map given by
$\unicode[STIX]{x1D705}:\operatorname{pr}_{{>}1}(C)\longrightarrow \text{VF}$
the corresponding focus map given by
 $\operatorname{pr}_{{>}1}(\mathfrak{q}_{t})\longmapsto \operatorname{pr}_{1}(a_{t})$
,
$\operatorname{pr}_{{>}1}(\mathfrak{q}_{t})\longmapsto \operatorname{pr}_{1}(a_{t})$
, -
–
 $\unicode[STIX]{x1D701}_{k+1}$
the centripetal transformation determined by
$\unicode[STIX]{x1D701}_{k+1}$
the centripetal transformation determined by
 $C$
and
$C$
and
 $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
For each
 $t\in \operatorname{dom}(\unicode[STIX]{x1D706})$
,
$t\in \operatorname{dom}(\unicode[STIX]{x1D706})$
,
![]() $f_{k+1}$
restricts to a bijection between the
$f_{k+1}$
restricts to a bijection between the
![]() $\text{RV}$
-pullbacks
$\text{RV}$
-pullbacks
 $\unicode[STIX]{x1D701}_{k+1}(\mathfrak{q}_{t})$
and
$\unicode[STIX]{x1D701}_{k+1}(\mathfrak{q}_{t})$
and
 $\unicode[STIX]{x1D702}_{k+1}(\mathfrak{o}_{t})$
that is
$\unicode[STIX]{x1D702}_{k+1}(\mathfrak{o}_{t})$
that is
![]() $\operatorname{rv}$
-contractible in both ways and, for any
$\operatorname{rv}$
-contractible in both ways and, for any
![]() $\mathfrak{q}\in O_{t}$
with
$\mathfrak{q}\in O_{t}$
with
![]() $\mathfrak{q}\neq \mathfrak{q}_{t}$
,
$\mathfrak{q}\neq \mathfrak{q}_{t}$
,
![]() $f_{k+1}(\mathfrak{q})$
is an open polydisc contained in an
$f_{k+1}(\mathfrak{q})$
is an open polydisc contained in an
![]() $\text{RV}$
-polydisc. So
$\text{RV}$
-polydisc. So
![]() $f_{k+1}$
is
$f_{k+1}$
is
![]() $\operatorname{rv}$
-contractible.
$\operatorname{rv}$
-contractible.
On the other hand, it is clear that, for any
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $\mathfrak{p}\subseteq B^{\flat }$
,
$\mathfrak{p}\subseteq B^{\flat }$
,
 $T_{A,k}\circ (T_{B}\circ f)^{-1}(\mathfrak{p})$
does not contain any
$T_{A,k}\circ (T_{B}\circ f)^{-1}(\mathfrak{p})$
does not contain any
![]() $a_{t}$
and hence, by the construction of
$a_{t}$
and hence, by the construction of
![]() $T_{A,k}$
,
$T_{A,k}$
,
 $T_{A,k+1}\circ (T_{B}\circ f)^{-1}$
is
$T_{A,k+1}\circ (T_{B}\circ f)^{-1}$
is
![]() $\operatorname{rv}$
-contractible.◻
$\operatorname{rv}$
-contractible.◻
Hypothesis 5.11. The following lemma is used directly only once in Corollary 5.13. It should have been presented right after Definition 3.27. We place it here because this is the first place in this paper (in fact, one of only two places, the other being Lemma 5.35) where we need to assume that every definable
![]() $\text{RV}$
-disc contains a definable point. The easiest way to guarantee this is to assume that
$\text{RV}$
-disc contains a definable point. The easiest way to guarantee this is to assume that
![]() ${\mathcal{S}}$
is
${\mathcal{S}}$
is
![]() $\text{VF}$
-generated, which, together with Hypothesis 4.1, implies that it is a model of
$\text{VF}$
-generated, which, together with Hypothesis 4.1, implies that it is a model of
![]() $\text{TCVF}$
and is indeed an elementary substructure (so every definable set contains a definable point). This assumption will be in effect throughout the rest of the paper.
$\text{TCVF}$
and is indeed an elementary substructure (so every definable set contains a definable point). This assumption will be in effect throughout the rest of the paper.
Lemma 5.12. Every definable bijection
 $f:U\longrightarrow V$
between two subsets of
$f:U\longrightarrow V$
between two subsets of
![]() $\text{RV}^{k}$
can be lifted, that is, there is a definable bijection
$\text{RV}^{k}$
can be lifted, that is, there is a definable bijection
 $f^{\sharp }:U^{\sharp }\longrightarrow V^{\sharp }$
that
$f^{\sharp }:U^{\sharp }\longrightarrow V^{\sharp }$
that
![]() $\operatorname{rv}$
-contracts to
$\operatorname{rv}$
-contracts to
![]() $f$
.
$f$
.
Proof. We do induction on
 $n=\dim _{\text{RV}}(U)=\dim _{\text{RV}}(V)$
. If
$n=\dim _{\text{RV}}(U)=\dim _{\text{RV}}(V)$
. If
![]() $n=0$
then
$n=0$
then
![]() $U$
is finite and hence, for every
$U$
is finite and hence, for every
![]() $u\in U$
, the
$u\in U$
, the
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $u^{\sharp }$
contains a definable point, similarly for
$u^{\sharp }$
contains a definable point, similarly for
![]() $V$
, in which case how to construct an
$V$
, in which case how to construct an
![]() $f^{\sharp }$
as desired is obvious.
$f^{\sharp }$
as desired is obvious.
For the inductive step, by weak
![]() $o$
-minimality in the
$o$
-minimality in the
![]() $\text{RV}$
-sort, there are definable finite partitions
$\text{RV}$
-sort, there are definable finite partitions
![]() $U_{i}$
,
$U_{i}$
,
![]() $V_{i}$
of
$V_{i}$
of
![]() $U$
,
$U$
,
![]() $V$
and injective coordinate projections
$V$
and injective coordinate projections
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{i}:U_{i}\longrightarrow \text{RV}^{k_{i}},\quad \unicode[STIX]{x1D70B}_{i}^{\prime }:V_{i}\longrightarrow \text{RV}^{k_{i}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{i}:U_{i}\longrightarrow \text{RV}^{k_{i}},\quad \unicode[STIX]{x1D70B}_{i}^{\prime }:V_{i}\longrightarrow \text{RV}^{k_{i}},\end{eqnarray}$$
where
 $\dim _{\text{RV}}(U_{i})=\dim _{\text{RV}}(V_{i})=k_{i}$
; the obvious bijection
$\dim _{\text{RV}}(U_{i})=\dim _{\text{RV}}(V_{i})=k_{i}$
; the obvious bijection
 $\unicode[STIX]{x1D70B}_{i}(U_{i})\longrightarrow \unicode[STIX]{x1D70B}_{i}^{\prime }(V_{i})$
induced by
$\unicode[STIX]{x1D70B}_{i}(U_{i})\longrightarrow \unicode[STIX]{x1D70B}_{i}^{\prime }(V_{i})$
induced by
![]() $f$
is denoted by
$f$
is denoted by
![]() $f_{i}$
. Observe that if every
$f_{i}$
. Observe that if every
![]() $f_{i}$
can be lifted as desired then, by the construction in the base case above,
$f_{i}$
can be lifted as desired then, by the construction in the base case above,
![]() $F$
can be lifted as desired as well. Therefore, without loss of generality, we may assume
$F$
can be lifted as desired as well. Therefore, without loss of generality, we may assume
![]() $k=n$
. For
$k=n$
. For
![]() $u\in U$
and
$u\in U$
and
![]() $a\in u^{\sharp }$
, the
$a\in u^{\sharp }$
, the
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $f(u)^{\sharp }$
contains an
$f(u)^{\sharp }$
contains an
![]() $a$
-definable point and hence, by compactness, there is a definable function
$a$
-definable point and hence, by compactness, there is a definable function
 $f^{\sharp }:U^{\sharp }\longrightarrow V^{\sharp }$
that
$f^{\sharp }:U^{\sharp }\longrightarrow V^{\sharp }$
that
![]() $\operatorname{rv}$
-contracts to
$\operatorname{rv}$
-contracts to
![]() $f$
. By Lemma 3.26,
$f$
. By Lemma 3.26,
 $\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}f^{\sharp }(U^{\sharp }))<n$
and hence, by the inductive hypothesis, we may assume that
$\dim _{\text{RV}}(\unicode[STIX]{x2202}_{\text{RV}}f^{\sharp }(U^{\sharp }))<n$
and hence, by the inductive hypothesis, we may assume that
![]() $f^{\sharp }$
is surjective. Then there is a definable function
$f^{\sharp }$
is surjective. Then there is a definable function
 $g:V^{\sharp }\longrightarrow U^{\sharp }$
such that
$g:V^{\sharp }\longrightarrow U^{\sharp }$
such that
 $f^{\sharp }(g(b))=b$
for all
$f^{\sharp }(g(b))=b$
for all
![]() $b\in V^{\sharp }$
. By Lemma 3.26 and the inductive hypothesis again, we may further assume that
$b\in V^{\sharp }$
. By Lemma 3.26 and the inductive hypothesis again, we may further assume that
![]() $g$
is also a surjection, which just means that
$g$
is also a surjection, which just means that
![]() $f^{\sharp }$
is a bijection as desired.◻
$f^{\sharp }$
is a bijection as desired.◻
The following corollary is an analogue of [Reference Hrushovski and KazhdanHK06, Proposition 6.1].
Corollary 5.13. For every
![]() $\text{RV}[k]$
-morphism
$\text{RV}[k]$
-morphism
 $F:(U,f)\longrightarrow (V,g)$
there is a
$F:(U,f)\longrightarrow (V,g)$
there is a
![]() $\text{VF}[k]$
-morphism
$\text{VF}[k]$
-morphism
![]() $F^{\sharp }$
that lifts
$F^{\sharp }$
that lifts
![]() $F$
.
$F$
.
Proof. As in Definition 5.9, we may assume that the finite-to-finite correspondence
![]() $F^{\dagger }$
is actually a bijection. Then this is immediate by Lemma 5.12.◻
$F^{\dagger }$
is actually a bijection. Then this is immediate by Lemma 5.12.◻
Corollary 5.14. The lifting map
![]() $\mathbb{L}_{{\leqslant}k}$
induces a surjective homomorphism, which is sometimes simply denoted by
$\mathbb{L}_{{\leqslant}k}$
induces a surjective homomorphism, which is sometimes simply denoted by
![]() $\mathbb{L}$
, between the Grothendieck semigroups
$\mathbb{L}$
, between the Grothendieck semigroups
 $$\begin{eqnarray}\mathbf{K}_{+}\text{RV}[{\leqslant}k]{\twoheadrightarrow}\mathbf{K}_{+}\text{VF}[k].\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{K}_{+}\text{RV}[{\leqslant}k]{\twoheadrightarrow}\mathbf{K}_{+}\text{VF}[k].\end{eqnarray}$$
5.2
 $2$
-cells
$2$
-cells
The remaining object of this section is to identify the kernels of the semigroup homomorphisms
![]() $\mathbb{L}$
in Corollary 5.14 and thereby complete the construction of the universal additive invariant. We begin with a discussion of the issue of
$\mathbb{L}$
in Corollary 5.14 and thereby complete the construction of the universal additive invariant. We begin with a discussion of the issue of
![]() $2$
-cells, as in [Reference YinYin11, § 4].
$2$
-cells, as in [Reference YinYin11, § 4].
The notion of a
![]() $2$
-cell, which corresponds to that of a bicell in [Reference Cluckers and LoeserCL08], may look strange and is, perhaps, only of technical interest. It arises when we try to prove some analogue of Fubini’s theorem, such as Lemma 5.38 below. The difficulty is that, although the interaction between
$2$
-cell, which corresponds to that of a bicell in [Reference Cluckers and LoeserCL08], may look strange and is, perhaps, only of technical interest. It arises when we try to prove some analogue of Fubini’s theorem, such as Lemma 5.38 below. The difficulty is that, although the interaction between
![]() $\operatorname{rv}$
-contractions and special bijections for definable sets of
$\operatorname{rv}$
-contractions and special bijections for definable sets of
![]() $\text{VF}$
-dimension
$\text{VF}$
-dimension
![]() $1$
is in a sense ‘functorial’ (see Lemma 5.10), we are unable to extend the construction to higher
$1$
is in a sense ‘functorial’ (see Lemma 5.10), we are unable to extend the construction to higher
![]() $\text{VF}$
-dimensions. This is the concern of [Reference Hrushovski and KazhdanHK06, Question 7.9]. It has also occurred in [Reference Cluckers and LoeserCL08] and actually may be traced back to the construction of the
$\text{VF}$
-dimensions. This is the concern of [Reference Hrushovski and KazhdanHK06, Question 7.9]. It has also occurred in [Reference Cluckers and LoeserCL08] and actually may be traced back to the construction of the
![]() $o$
-minimal Euler characteristic in [Reference van den DriesVdD98]; see [Reference Cluckers and LoeserCL08, § 1.7].
$o$
-minimal Euler characteristic in [Reference van den DriesVdD98]; see [Reference Cluckers and LoeserCL08, § 1.7].
Anyway, in this situation, a natural strategy for
![]() $\operatorname{rv}$
-contracting the isomorphism class of a definable set of higher
$\operatorname{rv}$
-contracting the isomorphism class of a definable set of higher
![]() $\text{VF}$
-dimension is to apply the result for
$\text{VF}$
-dimension is to apply the result for
![]() $\text{VF}$
-dimension
$\text{VF}$
-dimension
![]() $1$
parametrically and proceed with one
$1$
parametrically and proceed with one
![]() $\text{VF}$
-coordinate at a time. As in the classical theory of integration, this strategy requires some form of Fubini’s theorem: for a well-behaved integration (or additive invariant in our case), an integral should yield the same value when it is evaluated along different orders of the variables. By induction, this problem is immediately reduced to the case of two variables. A
$\text{VF}$
-coordinate at a time. As in the classical theory of integration, this strategy requires some form of Fubini’s theorem: for a well-behaved integration (or additive invariant in our case), an integral should yield the same value when it is evaluated along different orders of the variables. By induction, this problem is immediately reduced to the case of two variables. A
![]() $2$
-cell is a definable subset of
$2$
-cell is a definable subset of
![]() $\text{VF}^{2}$
with certain symmetrical (or ‘linear’ in the sense described in Remark 5.18 below) internal structure that satisfies this Fubini-type requirement. Now the idea is that, if we can find a definable partition for every definable set such that each piece is a
$\text{VF}^{2}$
with certain symmetrical (or ‘linear’ in the sense described in Remark 5.18 below) internal structure that satisfies this Fubini-type requirement. Now the idea is that, if we can find a definable partition for every definable set such that each piece is a
![]() $2$
-cell indexed by some
$2$
-cell indexed by some
![]() $\text{RV}$
-sort parameters, then, by compactness, every definable set satisfies the Fubini-type requirement. This kind of partition is achieved in Lemma 5.20.
$\text{RV}$
-sort parameters, then, by compactness, every definable set satisfies the Fubini-type requirement. This kind of partition is achieved in Lemma 5.20.
Lemma 5.15. Let
 $f:A\longrightarrow B$
be a definable bijection between two subsets of
$f:A\longrightarrow B$
be a definable bijection between two subsets of
![]() $\text{VF}$
. Then there is a special bijection
$\text{VF}$
. Then there is a special bijection
![]() $T$
on
$T$
on
![]() $A$
such that
$A$
such that
![]() $A^{\flat }$
is an
$A^{\flat }$
is an
![]() $\text{RV}$
-pullback and, for each
$\text{RV}$
-pullback and, for each
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $\mathfrak{p}\subseteq A^{\flat }$
,
$\mathfrak{p}\subseteq A^{\flat }$
,
 $f\restriction T^{-1}(\mathfrak{p})$
is
$f\restriction T^{-1}(\mathfrak{p})$
is
![]() $\operatorname{rv}$
-affine.
$\operatorname{rv}$
-affine.
Proof. By Lemma 3.36 and compactness, for all but finitely many
![]() $a\in A$
there is an
$a\in A$
there is an
![]() $a$
-definable
$a$
-definable
![]() $\unicode[STIX]{x1D6FF}_{a}\in |\unicode[STIX]{x1D6E4}|$
such that
$\unicode[STIX]{x1D6FF}_{a}\in |\unicode[STIX]{x1D6E4}|$
such that
 $f\restriction \mathfrak{o}(a,\unicode[STIX]{x1D6FF}_{a})$
is
$f\restriction \mathfrak{o}(a,\unicode[STIX]{x1D6FF}_{a})$
is
![]() $\operatorname{rv}$
-affine. Without loss of generality, we may assume that, for all
$\operatorname{rv}$
-affine. Without loss of generality, we may assume that, for all
![]() $a\in A$
,
$a\in A$
,
![]() $\unicode[STIX]{x1D6FF}_{a}$
exists and is the least element that satisfies this condition. Let
$\unicode[STIX]{x1D6FF}_{a}$
exists and is the least element that satisfies this condition. Let
 $g:A\longrightarrow |\unicode[STIX]{x1D6E4}|$
be the definable function given by
$g:A\longrightarrow |\unicode[STIX]{x1D6E4}|$
be the definable function given by
 $a\longmapsto \unicode[STIX]{x1D6FF}_{a}$
. By Corollary 5.6, there is a special bijection
$a\longmapsto \unicode[STIX]{x1D6FF}_{a}$
. By Corollary 5.6, there is a special bijection
![]() $T$
on
$T$
on
![]() $A$
such that
$A$
such that
![]() $A^{\flat }$
is an
$A^{\flat }$
is an
![]() $\text{RV}$
-pullback and, for all
$\text{RV}$
-pullback and, for all
![]() $\text{RV}$
-polydiscs
$\text{RV}$
-polydiscs
![]() $\mathfrak{p}\subseteq A^{\flat }$
,
$\mathfrak{p}\subseteq A^{\flat }$
,
 $(g\circ T^{-1})\restriction \mathfrak{p}$
is constant. By Lemmas 3.22 and 3.36, we must have
$(g\circ T^{-1})\restriction \mathfrak{p}$
is constant. By Lemmas 3.22 and 3.36, we must have
 $(g\circ T^{-1})(\mathfrak{p})\leqslant \operatorname{rad}(\mathfrak{p})$
, for otherwise the choice of
$(g\circ T^{-1})(\mathfrak{p})\leqslant \operatorname{rad}(\mathfrak{p})$
, for otherwise the choice of
![]() $\unicode[STIX]{x1D6FF}_{a}$
is violated for some
$\unicode[STIX]{x1D6FF}_{a}$
is violated for some
 $a\in T^{-1}(\mathfrak{p})$
. So
$a\in T^{-1}(\mathfrak{p})$
. So
![]() $T$
is as required.◻
$T$
is as required.◻
Lemma 5.16. Let
 $A\subseteq \text{VF}^{2}$
be a definable set such that
$A\subseteq \text{VF}^{2}$
be a definable set such that
 $\mathfrak{a}_{1}:=\operatorname{pr}_{1}(A)$
and
$\mathfrak{a}_{1}:=\operatorname{pr}_{1}(A)$
and
 $\mathfrak{a}_{2}:=\operatorname{pr}_{2}(A)$
are open discs. Suppose that there is a definable bijection
$\mathfrak{a}_{2}:=\operatorname{pr}_{2}(A)$
are open discs. Suppose that there is a definable bijection
 $f:\mathfrak{a}_{1}\longrightarrow \mathfrak{a}_{2}$
that has dtdp and, for each
$f:\mathfrak{a}_{1}\longrightarrow \mathfrak{a}_{2}$
that has dtdp and, for each
![]() $a\in \mathfrak{a}_{1}$
, there is a
$a\in \mathfrak{a}_{1}$
, there is a
 $t_{a}\in \operatorname{RV}_{0}$
with
$t_{a}\in \operatorname{RV}_{0}$
with
 $A_{a}=t_{a}^{\sharp }+f(a)$
. Then there is a special bijection
$A_{a}=t_{a}^{\sharp }+f(a)$
. Then there is a special bijection
![]() $T$
on
$T$
on
![]() $\mathfrak{a}_{1}$
such that
$\mathfrak{a}_{1}$
such that
![]() $\mathfrak{a}_{1}^{\flat }$
is an
$\mathfrak{a}_{1}^{\flat }$
is an
![]() $\text{RV}$
-pullback and, for each
$\text{RV}$
-pullback and, for each
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $\mathfrak{p}\subseteq \mathfrak{a}_{1}^{\flat }$
,
$\mathfrak{p}\subseteq \mathfrak{a}_{1}^{\flat }$
,
![]() $\operatorname{rv}$
is constant on the set
$\operatorname{rv}$
is constant on the set
 $$\begin{eqnarray}\{a-f^{-1}(b):a\in T^{-1}(\mathfrak{p})\text{ and }b\in A_{a}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{a-f^{-1}(b):a\in T^{-1}(\mathfrak{p})\text{ and }b\in A_{a}\}.\end{eqnarray}$$
Proof. For each
![]() $a\in \mathfrak{a}_{1}$
, let
$a\in \mathfrak{a}_{1}$
, let
![]() $\mathfrak{b}_{a}$
be the smallest closed disc that contains
$\mathfrak{b}_{a}$
be the smallest closed disc that contains
![]() $A_{a}$
. Since
$A_{a}$
. Since
 $A_{a}-f(a)=t_{a}^{\sharp }$
, we have
$A_{a}-f(a)=t_{a}^{\sharp }$
, we have
 $f(a)\in \mathfrak{b}_{a}$
but
$f(a)\in \mathfrak{b}_{a}$
but
 $f(a)\notin A_{a}$
if
$f(a)\notin A_{a}$
if
![]() $t_{a}\neq 0$
. Hence
$t_{a}\neq 0$
. Hence
 $a\notin f^{-1}(A_{a})$
if
$a\notin f^{-1}(A_{a})$
if
![]() $t_{a}\neq 0$
and
$t_{a}\neq 0$
and
 $\{a\}=f^{-1}(A_{a})$
if
$\{a\}=f^{-1}(A_{a})$
if
![]() $t_{a}=0$
. Since
$t_{a}=0$
. Since
 $f^{-1}(A_{a})$
is a disc or a point, in either case, the function on
$f^{-1}(A_{a})$
is a disc or a point, in either case, the function on
 $f^{-1}(A_{a})$
given by
$f^{-1}(A_{a})$
given by
 $b\longmapsto \operatorname{rv}(a-b)$
is constant. The function
$b\longmapsto \operatorname{rv}(a-b)$
is constant. The function
 $h:\mathfrak{a}_{1}\longrightarrow \operatorname{RV}_{0}$
given by
$h:\mathfrak{a}_{1}\longrightarrow \operatorname{RV}_{0}$
given by
 $a\longmapsto \operatorname{rv}(a-f^{-1}(A_{a}))$
is definable. Now we apply Corollary 5.6 as in the proof of Lemma 5.15. The lemma follows.◻
$a\longmapsto \operatorname{rv}(a-f^{-1}(A_{a}))$
is definable. Now we apply Corollary 5.6 as in the proof of Lemma 5.15. The lemma follows.◻
Definition 5.17. Let
![]() $A$
,
$A$
,
![]() $\mathfrak{a}_{1}$
,
$\mathfrak{a}_{1}$
,
![]() $\mathfrak{a}_{2}$
, and
$\mathfrak{a}_{2}$
, and
![]() $f$
be as in Lemma 5.16. We say that
$f$
be as in Lemma 5.16. We say that
![]() $f$
is balanced in
$f$
is balanced in
![]() $A$
if
$A$
if
![]() $f$
is actually
$f$
is actually
![]() $\operatorname{rv}$
-affine and there are
$\operatorname{rv}$
-affine and there are
 $t_{1},t_{2}\in \operatorname{RV}_{0}$
, called the paradigms of
$t_{1},t_{2}\in \operatorname{RV}_{0}$
, called the paradigms of
![]() $f$
, such that, for every
$f$
, such that, for every
![]() $a\in \mathfrak{a}_{1}$
,
$a\in \mathfrak{a}_{1}$
,
 $$\begin{eqnarray}A_{a}=t_{2}^{\sharp }+f(a)\quad \text{and}\quad f^{-1}(A_{a})=a-t_{1}^{\sharp }.\end{eqnarray}$$
$$\begin{eqnarray}A_{a}=t_{2}^{\sharp }+f(a)\quad \text{and}\quad f^{-1}(A_{a})=a-t_{1}^{\sharp }.\end{eqnarray}$$
Remark 5.18. Suppose that
![]() $f$
is balanced in
$f$
is balanced in
![]() $A$
with paradigms
$A$
with paradigms
![]() $t_{1}$
,
$t_{1}$
,
![]() $t_{2}$
. If one of the paradigms is
$t_{2}$
. If one of the paradigms is
![]() $0$
then the other one must be
$0$
then the other one must be
![]() $0$
. In this case
$0$
. In this case
![]() $A$
is just the (graph of the) bijection
$A$
is just the (graph of the) bijection
![]() $f$
itself.
$f$
itself.
Assume that
![]() $t_{1}$
,
$t_{1}$
,
![]() $t_{2}$
are nonzero. Let
$t_{2}$
are nonzero. Let
![]() $\mathfrak{B}_{1}$
,
$\mathfrak{B}_{1}$
,
![]() $\mathfrak{B}_{2}$
be, respectively, the sets of closed subdiscs of
$\mathfrak{B}_{2}$
be, respectively, the sets of closed subdiscs of
![]() $\mathfrak{a}_{1}$
,
$\mathfrak{a}_{1}$
,
![]() $\mathfrak{a}_{2}$
of radii
$\mathfrak{a}_{2}$
of radii
 $|\!\operatorname{vrv}(t_{1})|$
,
$|\!\operatorname{vrv}(t_{1})|$
,
 $|\!\operatorname{vrv}(t_{2})|$
. Let
$|\!\operatorname{vrv}(t_{2})|$
. Let
 $a_{1}\in \mathfrak{b}_{1}\in \mathfrak{B}_{1}$
and
$a_{1}\in \mathfrak{b}_{1}\in \mathfrak{B}_{1}$
and
![]() $\mathfrak{o}_{1}$
be the maximal open subdisc of
$\mathfrak{o}_{1}$
be the maximal open subdisc of
![]() $\mathfrak{b}_{1}$
containing
$\mathfrak{b}_{1}$
containing
![]() $a_{1}$
. Let
$a_{1}$
. Let
 $\mathfrak{b}_{2}\in \mathfrak{B}_{2}$
be the smallest closed disc containing the open disc
$\mathfrak{b}_{2}\in \mathfrak{B}_{2}$
be the smallest closed disc containing the open disc
 $\mathfrak{o}_{2}:=A_{a_{1}}$
. Then, for all
$\mathfrak{o}_{2}:=A_{a_{1}}$
. Then, for all
![]() $a_{2}\in \mathfrak{o}_{2}$
, we have
$a_{2}\in \mathfrak{o}_{2}$
, we have
 $$\begin{eqnarray}\mathfrak{o}_{2}=t_{2}^{\sharp }+f(\mathfrak{o}_{1})=A_{a_{1}}\quad \text{and}\quad A_{a_{2}}=f^{-1}(\mathfrak{o}_{2})+t_{1}^{\sharp }=\mathfrak{o}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{o}_{2}=t_{2}^{\sharp }+f(\mathfrak{o}_{1})=A_{a_{1}}\quad \text{and}\quad A_{a_{2}}=f^{-1}(\mathfrak{o}_{2})+t_{1}^{\sharp }=\mathfrak{o}_{1}.\end{eqnarray}$$
This internal symmetry of
![]() $A$
is illustrated by the following diagram.
$A$
is illustrated by the following diagram.

Since
![]() $f$
is
$f$
is
![]() $\operatorname{rv}$
-affine, we see that its slope must be
$\operatorname{rv}$
-affine, we see that its slope must be
![]() $-t_{2}/t_{1}$
(recall Definition 3.35).
$-t_{2}/t_{1}$
(recall Definition 3.35).
If we think of
![]() $\mathfrak{b}_{1}$
,
$\mathfrak{b}_{1}$
,
![]() $\mathfrak{b}_{2}$
as
$\mathfrak{b}_{2}$
as
 $\operatorname{Tor}(\ulcorner \mathfrak{o}_{1}\urcorner )$
,
$\operatorname{Tor}(\ulcorner \mathfrak{o}_{1}\urcorner )$
,
 $\operatorname{Tor}(\ulcorner \mathfrak{o}_{2}\urcorner )$
then the set
$\operatorname{Tor}(\ulcorner \mathfrak{o}_{2}\urcorner )$
then the set
 $A\cap (\mathfrak{b}_{1}\times \mathfrak{b}_{2})$
may be thought of as the ‘line’ in
$A\cap (\mathfrak{b}_{1}\times \mathfrak{b}_{2})$
may be thought of as the ‘line’ in
 $\operatorname{Tor}(\ulcorner \mathfrak{o}_{1}\urcorner )\times \operatorname{Tor}(\ulcorner \mathfrak{o}_{2}\urcorner )$
given by the equation
$\operatorname{Tor}(\ulcorner \mathfrak{o}_{1}\urcorner )\times \operatorname{Tor}(\ulcorner \mathfrak{o}_{2}\urcorner )$
given by the equation
 $$\begin{eqnarray}x_{2}=-\frac{t_{2}}{t_{1}}(x_{1}-\ulcorner \mathfrak{o}_{1}\urcorner )+(\ulcorner \mathfrak{o}_{2}\urcorner -t_{2}).\end{eqnarray}$$
$$\begin{eqnarray}x_{2}=-\frac{t_{2}}{t_{1}}(x_{1}-\ulcorner \mathfrak{o}_{1}\urcorner )+(\ulcorner \mathfrak{o}_{2}\urcorner -t_{2}).\end{eqnarray}$$
Thus, by Lemma 5.10, the obvious bijection between
 $\operatorname{pr}_{1}(A)\times t_{2}^{\sharp }$
and
$\operatorname{pr}_{1}(A)\times t_{2}^{\sharp }$
and
 $t_{1}^{\sharp }\times \operatorname{pr}_{2}(A)$
is the lift of an
$t_{1}^{\sharp }\times \operatorname{pr}_{2}(A)$
is the lift of an
![]() $\text{RV}[{\leqslant}2]$
-morphism modulo special bijections; see Lemma 5.25 below for details. The slope of
$\text{RV}[{\leqslant}2]$
-morphism modulo special bijections; see Lemma 5.25 below for details. The slope of
![]() $f$
will play a more important role when volume forms are introduced into the categories (in a sequel).
$f$
will play a more important role when volume forms are introduced into the categories (in a sequel).
Definition 5.19 (
 $2$
-cell).
$2$
-cell).
We say that a set
![]() $A$
is a 1-cell if it is either an open disc contained in a single
$A$
is a 1-cell if it is either an open disc contained in a single
![]() $\text{RV}$
-disc or a point in
$\text{RV}$
-disc or a point in
![]() $\text{VF}$
. We say that
$\text{VF}$
. We say that
![]() $A$
is a 2-cell if
$A$
is a 2-cell if
-
(i)
 $A$
is a subset of
$A$
is a subset of
 $\text{VF}^{2}$
contained in a single
$\text{VF}^{2}$
contained in a single
 $\text{RV}$
-polydisc and
$\text{RV}$
-polydisc and
 $\operatorname{pr}_{1}(A)$
is a
$\operatorname{pr}_{1}(A)$
is a
 $1$
-cell,
$1$
-cell, -
(ii) there is a function
 $\unicode[STIX]{x1D716}:\operatorname{pr}_{1}(A)\longrightarrow \text{VF}$
and a
$\unicode[STIX]{x1D716}:\operatorname{pr}_{1}(A)\longrightarrow \text{VF}$
and a
 $t\in \text{RV}$
such that, for every
$t\in \text{RV}$
such that, for every
 $a\in \operatorname{pr}_{1}(A)$
,
$a\in \operatorname{pr}_{1}(A)$
,
 $A_{a}=t^{\sharp }+\unicode[STIX]{x1D716}(a)$
,
$A_{a}=t^{\sharp }+\unicode[STIX]{x1D716}(a)$
, -
(iii) one of the following three possibilities occurs:
-
(a)
 $\unicode[STIX]{x1D716}$
is constant,
$\unicode[STIX]{x1D716}$
is constant, -
(b)
 $\unicode[STIX]{x1D716}$
is injective, has dtdp, and
$\unicode[STIX]{x1D716}$
is injective, has dtdp, and
 $\operatorname{rad}(\unicode[STIX]{x1D716}(\operatorname{pr}_{1}(A)))\geqslant |\text{vrv}(t)|$
,
$\operatorname{rad}(\unicode[STIX]{x1D716}(\operatorname{pr}_{1}(A)))\geqslant |\text{vrv}(t)|$
, -
(c)
 $\unicode[STIX]{x1D716}$
is balanced in
$\unicode[STIX]{x1D716}$
is balanced in
 $A$
.
$A$
.
-
The function
![]() $\unicode[STIX]{x1D716}$
is called the positioning function of
$\unicode[STIX]{x1D716}$
is called the positioning function of
![]() $A$
and the element
$A$
and the element
![]() $t$
the paradigm of
$t$
the paradigm of
![]() $A$
.
$A$
.
More generally, a set
![]() $A$
with exactly one
$A$
with exactly one
![]() $\text{VF}$
-coordinate is a
$\text{VF}$
-coordinate is a
![]() $1$
-cell if, for each
$1$
-cell if, for each
 $t\in \operatorname{pr}_{{>}1}(A)$
,
$t\in \operatorname{pr}_{{>}1}(A)$
,
![]() $A_{t}$
is a
$A_{t}$
is a
![]() $1$
-cell in the above sense; the parameterized version of the notion of a
$1$
-cell in the above sense; the parameterized version of the notion of a
![]() $2$
-cell is formulated in the same way.
$2$
-cell is formulated in the same way.
A
![]() $2$
-cell is definable if all the relevant ingredients are definable. Naturally we will only be concerned with definable
$2$
-cell is definable if all the relevant ingredients are definable. Naturally we will only be concerned with definable
![]() $2$
-cells. Notice that Corollary 5.8 implies that for every definable set
$2$
-cells. Notice that Corollary 5.8 implies that for every definable set
![]() $A$
with exactly one
$A$
with exactly one
![]() $\text{VF}$
-coordinate there is a definable function
$\text{VF}$
-coordinate there is a definable function
 $\unicode[STIX]{x1D70B}:A\longrightarrow \text{RV}^{l}$
such that every fiber
$\unicode[STIX]{x1D70B}:A\longrightarrow \text{RV}^{l}$
such that every fiber
![]() $A_{s}$
is a
$A_{s}$
is a
![]() $1$
-cell. This should be understood as
$1$
-cell. This should be understood as
![]() $1$
-cell decomposition and the next lemma as
$1$
-cell decomposition and the next lemma as
![]() $2$
-cell decomposition.
$2$
-cell decomposition.
Lemma 5.20 (
 $2$
-cell decomposition).
$2$
-cell decomposition).
For every definable set
 $A\subseteq \text{VF}^{2}$
there is a definable function
$A\subseteq \text{VF}^{2}$
there is a definable function
 $\unicode[STIX]{x1D70B}:A\longrightarrow \text{RV}^{m}$
such that every fiber
$\unicode[STIX]{x1D70B}:A\longrightarrow \text{RV}^{m}$
such that every fiber
![]() $A_{s}$
is an
$A_{s}$
is an
![]() $s$
-definable
$s$
-definable
![]() $2$
-cell.
$2$
-cell.
Proof. By compactness, we may assume that
![]() $A$
is contained in a single
$A$
is contained in a single
![]() $\text{RV}$
-polydisc. For each
$\text{RV}$
-polydisc. For each
 $a\in \operatorname{pr}_{1}(A)$
, by Corollary 5.8, there is an
$a\in \operatorname{pr}_{1}(A)$
, by Corollary 5.8, there is an
![]() $a$
-definable special bijection
$a$
-definable special bijection
![]() $T_{a}$
on
$T_{a}$
on
![]() $A_{a}$
such that
$A_{a}$
such that
![]() $A_{a}^{\flat }$
is an
$A_{a}^{\flat }$
is an
![]() $\text{RV}$
-pullback. By Lemma 5.3, there is an
$\text{RV}$
-pullback. By Lemma 5.3, there is an
![]() $a$
-definable function
$a$
-definable function
 $\unicode[STIX]{x1D716}_{a}:(A_{a}^{\flat })_{\text{RV}}\longrightarrow \text{VF}$
such that, for every
$\unicode[STIX]{x1D716}_{a}:(A_{a}^{\flat })_{\text{RV}}\longrightarrow \text{VF}$
such that, for every
 $(t,s)\in (A_{a}^{\flat })_{\text{RV}}$
, we have
$(t,s)\in (A_{a}^{\flat })_{\text{RV}}$
, we have
 $$\begin{eqnarray}T_{a}^{-1}(t^{\sharp }\times (t,s))=t^{\sharp }+\unicode[STIX]{x1D716}_{a}(t,s).\end{eqnarray}$$
$$\begin{eqnarray}T_{a}^{-1}(t^{\sharp }\times (t,s))=t^{\sharp }+\unicode[STIX]{x1D716}_{a}(t,s).\end{eqnarray}$$
By compactness, we may glue these functions together, that is, there is a definable set
 $C\subseteq \operatorname{pr}_{1}(A)\times \text{RV}^{l}$
and a definable function
$C\subseteq \operatorname{pr}_{1}(A)\times \text{RV}^{l}$
and a definable function
 $\unicode[STIX]{x1D716}:C\longrightarrow \text{VF}$
such that, for every
$\unicode[STIX]{x1D716}:C\longrightarrow \text{VF}$
such that, for every
 $a\in \operatorname{pr}_{1}(A)$
,
$a\in \operatorname{pr}_{1}(A)$
,
 $C_{a}=(A_{a}^{\flat })_{\text{RV}}$
and
$C_{a}=(A_{a}^{\flat })_{\text{RV}}$
and
 $\unicode[STIX]{x1D716}\restriction C_{a}=\unicode[STIX]{x1D716}_{a}$
. For
$\unicode[STIX]{x1D716}\restriction C_{a}=\unicode[STIX]{x1D716}_{a}$
. For
 $(t,s)\in C_{\text{RV}}$
, write
$(t,s)\in C_{\text{RV}}$
, write
 $\unicode[STIX]{x1D716}_{(t,s)}=\unicode[STIX]{x1D716}\restriction C_{(t,s)}$
. By Corollary 3.5 and compactness, we are reduced to the case that each
$\unicode[STIX]{x1D716}_{(t,s)}=\unicode[STIX]{x1D716}\restriction C_{(t,s)}$
. By Corollary 3.5 and compactness, we are reduced to the case that each
![]() $\unicode[STIX]{x1D716}_{(t,s)}$
is either constant or injective. If no
$\unicode[STIX]{x1D716}_{(t,s)}$
is either constant or injective. If no
![]() $\unicode[STIX]{x1D716}_{(t,s)}$
is injective then we can finish by applying Corollary 5.8 to each
$\unicode[STIX]{x1D716}_{(t,s)}$
is injective then we can finish by applying Corollary 5.8 to each
![]() $C_{(t,s)}$
and then compactness.
$C_{(t,s)}$
and then compactness.
Suppose that some
![]() $\unicode[STIX]{x1D716}_{(t,s)}$
is injective. Then, by Lemmas 3.24 and 5.15, we are reduced to the case that
$\unicode[STIX]{x1D716}_{(t,s)}$
is injective. Then, by Lemmas 3.24 and 5.15, we are reduced to the case that
![]() $C_{(t,s)}$
is an open disc and
$C_{(t,s)}$
is an open disc and
![]() $\unicode[STIX]{x1D716}_{(t,s)}$
is
$\unicode[STIX]{x1D716}_{(t,s)}$
is
![]() $\operatorname{rv}$
-affine and has dtdp. Write
$\operatorname{rv}$
-affine and has dtdp. Write
 $\mathfrak{b}_{(t,s)}=\operatorname{ran}(\unicode[STIX]{x1D716}_{(t,s)})$
. If
$\mathfrak{b}_{(t,s)}=\operatorname{ran}(\unicode[STIX]{x1D716}_{(t,s)})$
. If
 $\operatorname{rad}(\mathfrak{b}_{(t,s)})\geqslant |\text{vrv}|(t)$
then
$\operatorname{rad}(\mathfrak{b}_{(t,s)})\geqslant |\text{vrv}|(t)$
then
![]() $\unicode[STIX]{x1D716}_{(t,s)}$
satisfies condition (iii(b)) in Definition 5.19. So let us suppose
$\unicode[STIX]{x1D716}_{(t,s)}$
satisfies condition (iii(b)) in Definition 5.19. So let us suppose
 $\operatorname{rad}(\mathfrak{b}_{(t,s)})<|\text{vrv}|(t)$
. Then
$\operatorname{rad}(\mathfrak{b}_{(t,s)})<|\text{vrv}|(t)$
. Then
 $$\begin{eqnarray}\mathfrak{b}_{(t,s)}=\mathop{\bigcup }_{a\in C_{(t,s)}}(t^{\sharp }+\unicode[STIX]{x1D716}_{(t,s)}(a)).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{b}_{(t,s)}=\mathop{\bigcup }_{a\in C_{(t,s)}}(t^{\sharp }+\unicode[STIX]{x1D716}_{(t,s)}(a)).\end{eqnarray}$$
By Lemma 5.16, we are further reduced to the case that there is an
![]() $r\in \text{RV}$
such that, for every
$r\in \text{RV}$
such that, for every
 $a\in C_{(t,s)}$
,
$a\in C_{(t,s)}$
,
 $$\begin{eqnarray}\operatorname{rv}(a-\unicode[STIX]{x1D716}_{(t,s)}^{-1}(t^{\sharp }+\unicode[STIX]{x1D716}_{(t,s)}(a)))=r\quad \text{and hence }\unicode[STIX]{x1D716}_{(t,s)}^{-1}(t^{\sharp }+\unicode[STIX]{x1D716}_{(t,s)}(a))=a-r^{\sharp }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rv}(a-\unicode[STIX]{x1D716}_{(t,s)}^{-1}(t^{\sharp }+\unicode[STIX]{x1D716}_{(t,s)}(a)))=r\quad \text{and hence }\unicode[STIX]{x1D716}_{(t,s)}^{-1}(t^{\sharp }+\unicode[STIX]{x1D716}_{(t,s)}(a))=a-r^{\sharp }.\end{eqnarray}$$
So, in this case,
![]() $\unicode[STIX]{x1D716}_{(t,s)}$
is balanced. Now we are done by compactness.◻
$\unicode[STIX]{x1D716}_{(t,s)}$
is balanced. Now we are done by compactness.◻
To extend Lemma 5.10 to all definable bijections, we need not only
![]() $2$
-cell decomposition but also the following notions.
$2$
-cell decomposition but also the following notions.
Let
 $A\subseteq \text{VF}^{n}\times \text{RV}^{m}$
,
$A\subseteq \text{VF}^{n}\times \text{RV}^{m}$
,
 $B\subseteq \text{VF}^{n}\times \text{RV}^{m^{\prime }}$
, and
$B\subseteq \text{VF}^{n}\times \text{RV}^{m^{\prime }}$
, and
 $f:A\longrightarrow B$
be a definable bijection.
$f:A\longrightarrow B$
be a definable bijection.
Definition 5.21. We say that
![]() $f$
is relatively unary or, more precisely, relatively unary in the ith
$f$
is relatively unary or, more precisely, relatively unary in the ith
![]() $\text{VF}$
-coordinate, if
$\text{VF}$
-coordinate, if
 $(\operatorname{pr}_{\tilde{i} }\circ f)(x)=\operatorname{pr}_{\tilde{i} }(x)$
for all
$(\operatorname{pr}_{\tilde{i} }\circ f)(x)=\operatorname{pr}_{\tilde{i} }(x)$
for all
![]() $x\in A$
, where
$x\in A$
, where
![]() $i\in [n]$
. If
$i\in [n]$
. If
![]() $f\restriction A_{y}$
is also a special bijection for every
$f\restriction A_{y}$
is also a special bijection for every
 $y\in \operatorname{pr}_{\tilde{i} }(A)$
then we say that
$y\in \operatorname{pr}_{\tilde{i} }(A)$
then we say that
![]() $f$
is relatively special in the ith
$f$
is relatively special in the ith
![]() $\text{VF}$
-coordinate.
$\text{VF}$
-coordinate.
Obviously the inverse of a relatively unary bijection is a relatively unary bijection. Also note that every special bijection on
![]() $A$
is a composition of relatively special bijections.
$A$
is a composition of relatively special bijections.
Choose an
![]() $i\in [n]$
. By Corollary 5.8 and compactness, there is a bijection
$i\in [n]$
. By Corollary 5.8 and compactness, there is a bijection
![]() $T_{i}$
on
$T_{i}$
on
![]() $A$
, relatively special in the
$A$
, relatively special in the
![]() $i$
th
$i$
th
![]() $\text{VF}$
-coordinate, such that
$\text{VF}$
-coordinate, such that
![]() $T_{i}(A_{a})$
is an
$T_{i}(A_{a})$
is an
![]() $\text{RV}$
-pullback for every
$\text{RV}$
-pullback for every
 $a\in \operatorname{pr}_{\tilde{i} }(A)$
. Note that
$a\in \operatorname{pr}_{\tilde{i} }(A)$
. Note that
![]() $T_{i}$
is not necessarily a special bijection on
$T_{i}$
is not necessarily a special bijection on
![]() $A$
, since the special bijections in the
$A$
, since the special bijections in the
![]() $i$
th
$i$
th
![]() $\text{VF}$
-coordinate for distinct
$\text{VF}$
-coordinate for distinct
 $a,a^{\prime }\in \operatorname{pr}_{\tilde{i} }(A)$
with
$a,a^{\prime }\in \operatorname{pr}_{\tilde{i} }(A)$
with
 $\operatorname{rv}(a)=\operatorname{rv}(a^{\prime })$
may not even be of the same length. Let
$\operatorname{rv}(a)=\operatorname{rv}(a^{\prime })$
may not even be of the same length. Let
 $$\begin{eqnarray}A_{i}=\mathop{\bigcup }_{a\in \operatorname{pr}_{\tilde{i} }(A)}a\times (T_{i}(A_{a}))_{\text{RV}}\subseteq \text{VF}^{n-1}\times \text{RV}^{m_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}A_{i}=\mathop{\bigcup }_{a\in \operatorname{pr}_{\tilde{i} }(A)}a\times (T_{i}(A_{a}))_{\text{RV}}\subseteq \text{VF}^{n-1}\times \text{RV}^{m_{i}}.\end{eqnarray}$$
Write
 $\hat{T}_{i}:A\longrightarrow A_{i}$
for the function naturally induced by
$\hat{T}_{i}:A\longrightarrow A_{i}$
for the function naturally induced by
![]() $T_{i}$
. For any
$T_{i}$
. For any
 $j\in [n-1]$
, we repeat the above procedure on
$j\in [n-1]$
, we repeat the above procedure on
![]() $A_{i}$
with respect to the
$A_{i}$
with respect to the
![]() $j$
th
$j$
th
![]() $\text{VF}$
-coordinate and thereby obtain a set
$\text{VF}$
-coordinate and thereby obtain a set
 $A_{j}\subseteq \text{VF}^{n-2}\times \text{RV}^{m_{j}}$
and a function
$A_{j}\subseteq \text{VF}^{n-2}\times \text{RV}^{m_{j}}$
and a function
 $\hat{T}_{j}:A_{i}\longrightarrow A_{j}$
. The relatively special bijection on
$\hat{T}_{j}:A_{i}\longrightarrow A_{j}$
. The relatively special bijection on
![]() $T_{i}(A)$
induced by
$T_{i}(A)$
induced by
![]() $\hat{T}_{j}$
is denoted by
$\hat{T}_{j}$
is denoted by
![]() $T_{j}$
. Continuing thus, we obtain a sequence of bijections
$T_{j}$
. Continuing thus, we obtain a sequence of bijections
 $T_{\unicode[STIX]{x1D70E}(1)},\ldots ,T_{\unicode[STIX]{x1D70E}(n)}$
and a corresponding function
$T_{\unicode[STIX]{x1D70E}(1)},\ldots ,T_{\unicode[STIX]{x1D70E}(n)}$
and a corresponding function
 $\hat{T}_{\unicode[STIX]{x1D70E}}:A\longrightarrow \text{RV}^{l}$
, where
$\hat{T}_{\unicode[STIX]{x1D70E}}:A\longrightarrow \text{RV}^{l}$
, where
![]() $\unicode[STIX]{x1D70E}$
is the permutation of
$\unicode[STIX]{x1D70E}$
is the permutation of
![]() $[n]$
in question. The composition
$[n]$
in question. The composition
 $T_{\unicode[STIX]{x1D70E}(n)}\circ \cdots \circ T_{\unicode[STIX]{x1D70E}(1)}$
, which is referred to as the lift of
$T_{\unicode[STIX]{x1D70E}(n)}\circ \cdots \circ T_{\unicode[STIX]{x1D70E}(1)}$
, which is referred to as the lift of
![]() $\hat{T}_{\unicode[STIX]{x1D70E}}$
, is denoted by
$\hat{T}_{\unicode[STIX]{x1D70E}}$
, is denoted by
![]() $T_{\unicode[STIX]{x1D70E}}$
.
$T_{\unicode[STIX]{x1D70E}}$
.
Definition 5.22. Suppose that there is a
 $k\in 0\cup [m]$
such that
$k\in 0\cup [m]$
such that
 $(A_{a})_{{\leqslant}k}\in \text{RV}[k]$
for every
$(A_{a})_{{\leqslant}k}\in \text{RV}[k]$
for every
 $a\in A_{\text{VF}}$
. In particular, if
$a\in A_{\text{VF}}$
. In particular, if
![]() $k=0$
then
$k=0$
then
 $A\in \text{VF}_{\ast }$
. By Lemma 4.2,
$A\in \text{VF}_{\ast }$
. By Lemma 4.2,
 $\hat{T}_{\unicode[STIX]{x1D70E}}(A)_{{\leqslant}n+k}$
is an object of
$\hat{T}_{\unicode[STIX]{x1D70E}}(A)_{{\leqslant}n+k}$
is an object of
 $\text{RV}[{\leqslant}l+k]$
, where
$\text{RV}[{\leqslant}l+k]$
, where
 $\dim _{\text{VF}}(A)=l$
. The function
$\dim _{\text{VF}}(A)=l$
. The function
![]() $\hat{T}_{\unicode[STIX]{x1D70E}}$
(or the object
$\hat{T}_{\unicode[STIX]{x1D70E}}$
(or the object
 $\hat{T}_{\unicode[STIX]{x1D70E}}(A)_{{\leqslant}n+k}$
) is referred to as a standard contraction of the set
$\hat{T}_{\unicode[STIX]{x1D70E}}(A)_{{\leqslant}n+k}$
) is referred to as a standard contraction of the set
![]() $A$
with the head start
$A$
with the head start
![]() $k$
.
$k$
.
The head start of a standard contraction is usually implicit. In fact, it is always
![]() $0$
except in Lemma 5.36, and can be circumvented even there. This seemingly needless gadget only serves to make the above definition more streamlined: if
$0$
except in Lemma 5.36, and can be circumvented even there. This seemingly needless gadget only serves to make the above definition more streamlined: if
 $A\in \text{VF}_{\ast }$
then the intermediate steps of a standard contraction of
$A\in \text{VF}_{\ast }$
then the intermediate steps of a standard contraction of
![]() $A$
may or may not result in objects of
$A$
may or may not result in objects of
![]() $\text{VF}_{\ast }$
and hence the definition cannot be formulated entirely within
$\text{VF}_{\ast }$
and hence the definition cannot be formulated entirely within
![]() $\text{VF}_{\ast }$
.
$\text{VF}_{\ast }$
.
Remark 5.23. In Lemma 5.10, clearly
![]() $\operatorname{rv}(A^{\flat })$
,
$\operatorname{rv}(A^{\flat })$
,
![]() $\operatorname{rv}(B^{\flat })$
are standard contractions of
$\operatorname{rv}(B^{\flat })$
are standard contractions of
![]() $A$
,
$A$
,
![]() $B$
. Indeed, if
$B$
. Indeed, if
 $A,B\in \text{VF}_{\ast }$
then
$A,B\in \text{VF}_{\ast }$
then
 $[\operatorname{rv}(A^{\flat })]_{{\leqslant}1}=[\operatorname{rv}(B^{\flat })]_{{\leqslant}1}$
.
$[\operatorname{rv}(A^{\flat })]_{{\leqslant}1}=[\operatorname{rv}(B^{\flat })]_{{\leqslant}1}$
.
Lemma 5.24. There is a definable finite partition
![]() $A_{i}$
of
$A_{i}$
of
![]() $A$
such that each
$A$
such that each
![]() $f\restriction A_{i}$
is a composition of relatively unary bijections.
$f\restriction A_{i}$
is a composition of relatively unary bijections.
Proof. This is an easy consequence of weak
![]() $o$
-minimality. In more detail, for each
$o$
-minimality. In more detail, for each
 $a\in \operatorname{pr}_{{<}n}(A)$
there are an
$a\in \operatorname{pr}_{{<}n}(A)$
there are an
![]() $a$
-definable finite partition
$a$
-definable finite partition
![]() $A_{ai}$
of
$A_{ai}$
of
![]() $A_{a}$
and injective coordinate projections
$A_{a}$
and injective coordinate projections
 $\unicode[STIX]{x1D70B}_{i}:f(A_{ai})\longrightarrow \text{VF}\times \text{RV}^{m^{\prime }}$
. Therefore, by compactness, there are a definable finite partition
$\unicode[STIX]{x1D70B}_{i}:f(A_{ai})\longrightarrow \text{VF}\times \text{RV}^{m^{\prime }}$
. Therefore, by compactness, there are a definable finite partition
![]() $A_{i}$
of
$A_{i}$
of
![]() $A$
, definable injections
$A$
, definable injections
 $f_{i}:A_{i}\longrightarrow \text{VF}^{n}\times \text{RV}^{m^{\prime }}$
, and
$f_{i}:A_{i}\longrightarrow \text{VF}^{n}\times \text{RV}^{m^{\prime }}$
, and
![]() $j_{i}\in [n]$
such that, for all
$j_{i}\in [n]$
such that, for all
![]() $x\in A_{i}$
,
$x\in A_{i}$
,
 $$\begin{eqnarray}\operatorname{pr}_{{<}n}(x)=\operatorname{pr}_{{<}n}(f_{i}(x))\quad \text{and}\quad \operatorname{pr}_{n\cup [m^{\prime }]}(f_{i}(x))=\operatorname{pr}_{j_{i}\cup [m^{\prime }]}(f(x)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{pr}_{{<}n}(x)=\operatorname{pr}_{{<}n}(f_{i}(x))\quad \text{and}\quad \operatorname{pr}_{n\cup [m^{\prime }]}(f_{i}(x))=\operatorname{pr}_{j_{i}\cup [m^{\prime }]}(f(x)).\end{eqnarray}$$
The claim now follows from compactness and an obvious induction on
![]() $n$
.◻
$n$
.◻
For the next two lemmas, let
![]() $12$
and
$12$
and
![]() $21$
denote the permutations of
$21$
denote the permutations of
![]() $[2]$
.
$[2]$
.
Lemma 5.25. Let
 $A\subseteq \text{VF}^{2}$
be a definable
$A\subseteq \text{VF}^{2}$
be a definable
![]() $2$
-cell. Then there are standard contractions
$2$
-cell. Then there are standard contractions
![]() $\hat{T}_{12}$
,
$\hat{T}_{12}$
,
![]() $\hat{R}_{21}$
of
$\hat{R}_{21}$
of
![]() $A$
such that
$A$
such that
 $[\hat{T}_{12}(A)]_{{\leqslant}2}=[\hat{R}_{21}(A)]_{{\leqslant}2}$
.
$[\hat{T}_{12}(A)]_{{\leqslant}2}=[\hat{R}_{21}(A)]_{{\leqslant}2}$
.
Proof. Let
![]() $\unicode[STIX]{x1D716}$
be the positioning function of
$\unicode[STIX]{x1D716}$
be the positioning function of
![]() $A$
and
$A$
and
 $t\in \text{RV}_{0}$
the paradigm of
$t\in \text{RV}_{0}$
the paradigm of
![]() $A$
. If
$A$
. If
![]() $t=0$
then
$t=0$
then
![]() $A$
is (the graph of) the function
$A$
is (the graph of) the function
 $\unicode[STIX]{x1D716}:\operatorname{pr}_{1}(A)\longrightarrow \operatorname{pr}_{2}(A)$
, which is either a constant function or a bijection. In the former case, since
$\unicode[STIX]{x1D716}:\operatorname{pr}_{1}(A)\longrightarrow \operatorname{pr}_{2}(A)$
, which is either a constant function or a bijection. In the former case, since
![]() $A$
is essentially just an open ball, the lemma simply follows from Corollary 5.8. In the latter case, there are relatively special bijections
$A$
is essentially just an open ball, the lemma simply follows from Corollary 5.8. In the latter case, there are relatively special bijections
![]() $T_{2}$
,
$T_{2}$
,
![]() $R_{1}$
on
$R_{1}$
on
![]() $A$
in the coordinates
$A$
in the coordinates
![]() $2$
,
$2$
,
![]() $1$
such that
$1$
such that
 $$\begin{eqnarray}T_{2}(A)=\operatorname{pr}_{1}(A)\times 0\times 0\quad \text{and}\quad R_{1}(A)=0\times \operatorname{pr}_{2}(A)\times 0.\end{eqnarray}$$
$$\begin{eqnarray}T_{2}(A)=\operatorname{pr}_{1}(A)\times 0\times 0\quad \text{and}\quad R_{1}(A)=0\times \operatorname{pr}_{2}(A)\times 0.\end{eqnarray}$$
So the lemma follows from Remark 5.23. For the rest of the proof we assume
![]() $t\neq 0$
.
$t\neq 0$
.
If
![]() $\unicode[STIX]{x1D716}$
is not balanced in
$\unicode[STIX]{x1D716}$
is not balanced in
![]() $A$
then
$A$
then
 $A=\operatorname{pr}_{1}(A)\times \operatorname{pr}_{2}(A)$
is an open polydisc. By Corollary 5.8, there are special bijections
$A=\operatorname{pr}_{1}(A)\times \operatorname{pr}_{2}(A)$
is an open polydisc. By Corollary 5.8, there are special bijections
![]() $T_{1}$
,
$T_{1}$
,
![]() $T_{2}$
on
$T_{2}$
on
![]() $\operatorname{pr}_{1}(A)$
,
$\operatorname{pr}_{1}(A)$
,
![]() $\operatorname{pr}_{2}(A)$
such that
$\operatorname{pr}_{2}(A)$
such that
![]() $\operatorname{pr}_{1}(A)^{\flat }$
,
$\operatorname{pr}_{1}(A)^{\flat }$
,
![]() $\operatorname{pr}_{2}(A)^{\flat }$
are
$\operatorname{pr}_{2}(A)^{\flat }$
are
![]() $\text{RV}$
-pullbacks. In this case the standard contractions determined by
$\text{RV}$
-pullbacks. In this case the standard contractions determined by
![]() $(T_{1},T_{2})$
and
$(T_{1},T_{2})$
and
![]() $(T_{2},T_{1})$
are essentially the same.
$(T_{2},T_{1})$
are essentially the same.
Suppose that
![]() $\unicode[STIX]{x1D716}$
is balanced in
$\unicode[STIX]{x1D716}$
is balanced in
![]() $A$
. Let
$A$
. Let
![]() $r$
be the other paradigm of
$r$
be the other paradigm of
![]() $\unicode[STIX]{x1D716}$
. Recall that
$\unicode[STIX]{x1D716}$
. Recall that
 $\unicode[STIX]{x1D716}:\operatorname{pr}_{1}(A)\longrightarrow \operatorname{pr}_{2}(A)$
is again a bijection. Let
$\unicode[STIX]{x1D716}:\operatorname{pr}_{1}(A)\longrightarrow \operatorname{pr}_{2}(A)$
is again a bijection. Let
![]() $T_{2}$
be the relatively special bijection on
$T_{2}$
be the relatively special bijection on
![]() $A$
in the coordinate
$A$
in the coordinate
![]() $2$
given by
$2$
given by
 $(a,b)\longmapsto (a,b-\unicode[STIX]{x1D716}(a))$
and
$(a,b)\longmapsto (a,b-\unicode[STIX]{x1D716}(a))$
and
![]() $R_{1}$
the relatively special bijection on
$R_{1}$
the relatively special bijection on
![]() $A$
in the coordinate
$A$
in the coordinate
![]() $1$
given by
$1$
given by
 $(a,b)\longmapsto (a-\unicode[STIX]{x1D716}^{-1}(b),b)$
, where
$(a,b)\longmapsto (a-\unicode[STIX]{x1D716}^{-1}(b),b)$
, where
 $(a,b)\in A$
. Clearly
$(a,b)\in A$
. Clearly
 $$\begin{eqnarray}T_{2}(A)=\operatorname{pr}_{1}(A)\times t^{\sharp }\times t\quad \text{and}\quad R_{1}(A)=r^{\sharp }\times \operatorname{pr}_{2}(A)\times r.\end{eqnarray}$$
$$\begin{eqnarray}T_{2}(A)=\operatorname{pr}_{1}(A)\times t^{\sharp }\times t\quad \text{and}\quad R_{1}(A)=r^{\sharp }\times \operatorname{pr}_{2}(A)\times r.\end{eqnarray}$$
So, again, the lemma follows from Remark 5.23. ◻
Lemma 5.26. Let
 $A\subseteq \text{VF}^{2}\times \text{RV}^{m}$
be an object in
$A\subseteq \text{VF}^{2}\times \text{RV}^{m}$
be an object in
![]() $\text{VF}_{\ast }$
. Then there are a definable injection
$\text{VF}_{\ast }$
. Then there are a definable injection
 $f:A\longrightarrow \text{VF}^{2}\times \text{RV}^{l}$
, relatively unary in both coordinates, and standard contractions
$f:A\longrightarrow \text{VF}^{2}\times \text{RV}^{l}$
, relatively unary in both coordinates, and standard contractions
![]() $\hat{T}_{12}$
,
$\hat{T}_{12}$
,
![]() $\hat{R}_{21}$
of
$\hat{R}_{21}$
of
![]() $f(A)$
such that
$f(A)$
such that
 $[\hat{T}_{12}(f(A))]_{{\leqslant}2}=[\hat{R}_{21}(f(A))]_{{\leqslant}2}$
.
$[\hat{T}_{12}(f(A))]_{{\leqslant}2}=[\hat{R}_{21}(f(A))]_{{\leqslant}2}$
.
Proof. By Lemma 5.20 and compactness, there is a definable function
 $f:A\longrightarrow \text{VF}^{2}\times \text{RV}^{l}$
such that
$f:A\longrightarrow \text{VF}^{2}\times \text{RV}^{l}$
such that
![]() $f(A)$
is a
$f(A)$
is a
![]() $2$
-cell and, for each
$2$
-cell and, for each
 $(a,t)\in A$
,
$(a,t)\in A$
,
 $f(a,t)=(a,t,s)$
for some
$f(a,t)=(a,t,s)$
for some
 $s\in \text{RV}^{l-m}$
. By Lemma 5.25 and compactness, there are standard contractions
$s\in \text{RV}^{l-m}$
. By Lemma 5.25 and compactness, there are standard contractions
![]() $\hat{T}_{12}$
,
$\hat{T}_{12}$
,
![]() $\hat{R}_{21}$
of
$\hat{R}_{21}$
of
![]() $f(A)$
into
$f(A)$
into
![]() $\text{RV}^{k+l}$
such that the diagram
$\text{RV}^{k+l}$
such that the diagram

commutes and
![]() $F$
is an
$F$
is an
![]() $\text{RV}[{\leqslant}2]$
-morphism
$\text{RV}[{\leqslant}2]$
-morphism
 $\hat{T}_{12}(f(A))_{{\leqslant}2}\longrightarrow \hat{R}_{21}(f(A))_{{\leqslant}2}$
.◻
$\hat{T}_{12}(f(A))_{{\leqslant}2}\longrightarrow \hat{R}_{21}(f(A))_{{\leqslant}2}$
.◻
5.3 Blowups and the main theorems
The central notion for understanding the kernels of the semigroup homomorphisms
![]() $\mathbb{L}$
is that of a blowup.
$\mathbb{L}$
is that of a blowup.
Definition 5.27 (Blowups).
Let
 $\boldsymbol{U}=(U,f)\in \text{RV}[k]$
, where
$\boldsymbol{U}=(U,f)\in \text{RV}[k]$
, where
![]() $k>0$
, such that, for some
$k>0$
, such that, for some
![]() $j\leqslant k$
, the restriction
$j\leqslant k$
, the restriction
 $\operatorname{pr}_{\tilde{j}}\restriction f(U)$
is finite-to-one. Write
$\operatorname{pr}_{\tilde{j}}\restriction f(U)$
is finite-to-one. Write
 $f=(f_{1},\ldots ,f_{k})$
. The elementary blowup of
$f=(f_{1},\ldots ,f_{k})$
. The elementary blowup of
![]() $\boldsymbol{U}$
in the
$\boldsymbol{U}$
in the
![]() $j$
th coordinate is the pair
$j$
th coordinate is the pair
 $\boldsymbol{U}^{\flat }=(U^{\flat },f^{\flat })$
, where
$\boldsymbol{U}^{\flat }=(U^{\flat },f^{\flat })$
, where
 $U^{\flat }=U\times \text{RV}_{0}^{\circ \circ }$
and, for every
$U^{\flat }=U\times \text{RV}_{0}^{\circ \circ }$
and, for every
 $(t,s)\in U^{\flat }$
,
$(t,s)\in U^{\flat }$
,
 $$\begin{eqnarray}f_{i}^{\flat }(t,s)=f_{i}(t)\quad \text{for }i\neq j\quad \text{and}\quad f_{j}^{\flat }(t,s)=sf_{j}(t).\end{eqnarray}$$
$$\begin{eqnarray}f_{i}^{\flat }(t,s)=f_{i}(t)\quad \text{for }i\neq j\quad \text{and}\quad f_{j}^{\flat }(t,s)=sf_{j}(t).\end{eqnarray}$$
Note that
![]() $\boldsymbol{U}^{\flat }$
is an object in
$\boldsymbol{U}^{\flat }$
is an object in
![]() $\text{RV}[{\leqslant}k]$
(actually in
$\text{RV}[{\leqslant}k]$
(actually in
 $\text{RV}[k-1]\oplus \text{RV}[k]$
) because
$\text{RV}[k-1]\oplus \text{RV}[k]$
) because
 $f_{j}^{\flat }(t,0)=0$
.
$f_{j}^{\flat }(t,0)=0$
.
Let
 $\boldsymbol{V}=(V,g)\in \text{RV}[k]$
and
$\boldsymbol{V}=(V,g)\in \text{RV}[k]$
and
![]() $C\subseteq V$
be a definable set. Suppose that
$C\subseteq V$
be a definable set. Suppose that
 $F:\boldsymbol{U}\longrightarrow \boldsymbol{C}$
is an
$F:\boldsymbol{U}\longrightarrow \boldsymbol{C}$
is an
![]() $\text{RV}[k]$
-morphism, where
$\text{RV}[k]$
-morphism, where
 $\boldsymbol{C}=(C,g\restriction C)\in \text{RV}[k]$
. Then
$\boldsymbol{C}=(C,g\restriction C)\in \text{RV}[k]$
. Then
 $$\begin{eqnarray}\boldsymbol{U}^{\flat }\uplus (V\smallsetminus C,g\restriction (V\smallsetminus C))\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{U}^{\flat }\uplus (V\smallsetminus C,g\restriction (V\smallsetminus C))\end{eqnarray}$$
is a blowup of
![]() $\boldsymbol{V}$
via
$\boldsymbol{V}$
via
![]() $F$
, denoted by
$F$
, denoted by
![]() $\boldsymbol{V}_{F}^{\flat }$
. The subscript
$\boldsymbol{V}_{F}^{\flat }$
. The subscript
![]() $F$
is usually dropped in context if there is no danger of confusion. The object
$F$
is usually dropped in context if there is no danger of confusion. The object
![]() $\boldsymbol{C}$
(or the set
$\boldsymbol{C}$
(or the set
![]() $C$
) is referred to as the locus of
$C$
) is referred to as the locus of
![]() $\boldsymbol{V}_{F}^{\flat }$
.
$\boldsymbol{V}_{F}^{\flat }$
.
A blowup of length
![]() $n$
is a composition of
$n$
is a composition of
![]() $n$
blowups.
$n$
blowups.
Remark 5.28. In an elementary blowup, the condition that the coordinate of interest is definably dependent (the coordinate projection is finite-to-one) on the other ones is needed so that the resulting objects stay in
![]() $\text{RV}[{\leqslant}k]$
. In the setting of [Reference Hrushovski and KazhdanHK06], this condition is also needed for matching blowups with special bijections, since otherwise we would not be able to use (a generalization of) Hensel’s lemma to find enough centers of
$\text{RV}[{\leqslant}k]$
. In the setting of [Reference Hrushovski and KazhdanHK06], this condition is also needed for matching blowups with special bijections, since otherwise we would not be able to use (a generalization of) Hensel’s lemma to find enough centers of
![]() $\text{RV}$
-discs to construct focus maps. In our setting, Lemma 5.12 plays the role of Hensel’s lemma, which is more powerful, and hence ‘algebraicity’ is no longer needed for this purpose (see Lemma 5.35).
$\text{RV}$
-discs to construct focus maps. In our setting, Lemma 5.12 plays the role of Hensel’s lemma, which is more powerful, and hence ‘algebraicity’ is no longer needed for this purpose (see Lemma 5.35).
If there is an elementary blowup of
 $(U,f)\in \text{RV}[k]$
then, a posteriori,
$(U,f)\in \text{RV}[k]$
then, a posteriori,
 $\dim _{\text{RV}}(f(U))<k$
. Also, there is at most one elementary blowup of
$\dim _{\text{RV}}(f(U))<k$
. Also, there is at most one elementary blowup of
![]() $(U,f)$
with respect to any coordinate of
$(U,f)$
with respect to any coordinate of
![]() $f(U)$
. We should have included the coordinate that is blown up as a part of the data. However, in context, either this is clear or it does not need to be spelled out, and we shall suppress mention of it below for ease of notation.
$f(U)$
. We should have included the coordinate that is blown up as a part of the data. However, in context, either this is clear or it does not need to be spelled out, and we shall suppress mention of it below for ease of notation.
Lemma 5.29. Let
 $\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}k]$
such that
$\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}k]$
such that
 $[\boldsymbol{U}]=[\boldsymbol{V}]$
in
$[\boldsymbol{U}]=[\boldsymbol{V}]$
in
 $\mathbf{K}_{+}\text{RV}[{\leqslant}k]$
. Let
$\mathbf{K}_{+}\text{RV}[{\leqslant}k]$
. Let
![]() $\boldsymbol{U}_{1}$
,
$\boldsymbol{U}_{1}$
,
![]() $\boldsymbol{V}_{1}$
be blowups of
$\boldsymbol{V}_{1}$
be blowups of
![]() $\boldsymbol{U}$
,
$\boldsymbol{U}$
,
![]() $\boldsymbol{V}$
of lengths
$\boldsymbol{V}$
of lengths
![]() $m$
,
$m$
,
![]() $n$
, respectively. Then there are blowups
$n$
, respectively. Then there are blowups
![]() $\boldsymbol{U}_{2}$
,
$\boldsymbol{U}_{2}$
,
![]() $\boldsymbol{V}_{2}$
of
$\boldsymbol{V}_{2}$
of
![]() $\boldsymbol{U}_{1}$
,
$\boldsymbol{U}_{1}$
,
![]() $\boldsymbol{V}_{1}$
of lengths
$\boldsymbol{V}_{1}$
of lengths
![]() $n$
,
$n$
,
![]() $m$
, respectively, such that
$m$
, respectively, such that
 $[\boldsymbol{U}_{2}]=[\boldsymbol{V}_{2}]$
.
$[\boldsymbol{U}_{2}]=[\boldsymbol{V}_{2}]$
.
Proof. Fix an isomorphism
 $I:\boldsymbol{U}\longrightarrow \boldsymbol{V}$
. We do induction on the sum
$I:\boldsymbol{U}\longrightarrow \boldsymbol{V}$
. We do induction on the sum
 $l=m+n$
. For the base case
$l=m+n$
. For the base case
![]() $l=1$
, without loss of generality, we may assume
$l=1$
, without loss of generality, we may assume
![]() $n=0$
. Let
$n=0$
. Let
![]() $C$
be the blowup locus of
$C$
be the blowup locus of
![]() $\boldsymbol{U}_{1}$
. Clearly
$\boldsymbol{U}_{1}$
. Clearly
![]() $\boldsymbol{V}$
may be blown up by using the same elementary blowup as
$\boldsymbol{V}$
may be blown up by using the same elementary blowup as
![]() $\boldsymbol{U}_{1}$
, where the blowup locus is changed to
$\boldsymbol{U}_{1}$
, where the blowup locus is changed to
![]() $I(C)$
, and the resulting blowup is as required.
$I(C)$
, and the resulting blowup is as required.

We proceed to the inductive step. How the isomorphic blowups are constructed is illustrated above. Write
 $\boldsymbol{U}=(U,f)$
and
$\boldsymbol{U}=(U,f)$
and
 $\boldsymbol{V}=(V,g)$
. Let
$\boldsymbol{V}=(V,g)$
. Let
![]() $\boldsymbol{U}^{\flat }$
,
$\boldsymbol{U}^{\flat }$
,
![]() $\boldsymbol{V}^{\flat }$
be the first blowups in
$\boldsymbol{V}^{\flat }$
be the first blowups in
![]() $\boldsymbol{U}_{1}$
,
$\boldsymbol{U}_{1}$
,
![]() $\boldsymbol{V}_{1}$
and
$\boldsymbol{V}_{1}$
and
![]() $C$
,
$C$
,
![]() $D$
their blowup loci, respectively. Let
$D$
their blowup loci, respectively. Let
![]() $\boldsymbol{U}^{\prime \flat }$
,
$\boldsymbol{U}^{\prime \flat }$
,
![]() $\boldsymbol{V}^{\prime \flat }$
be the corresponding elementary blowups contained in
$\boldsymbol{V}^{\prime \flat }$
be the corresponding elementary blowups contained in
![]() $\boldsymbol{U}^{\flat }$
,
$\boldsymbol{U}^{\flat }$
,
![]() $\boldsymbol{V}^{\flat }$
. If, say,
$\boldsymbol{V}^{\flat }$
. If, say,
![]() $n=0$
, then by the argument in the base case
$n=0$
, then by the argument in the base case
![]() $\boldsymbol{V}$
may be blown up to an object that is isomorphic to
$\boldsymbol{V}$
may be blown up to an object that is isomorphic to
![]() $\boldsymbol{U}^{\flat }$
and hence the inductive hypothesis may be applied. So assume
$\boldsymbol{U}^{\flat }$
and hence the inductive hypothesis may be applied. So assume
 $m,n>0$
. Let
$m,n>0$
. Let
 $A=C\cap I^{-1}(D)$
and
$A=C\cap I^{-1}(D)$
and
 $B=I(C)\cap D$
. Since
$B=I(C)\cap D$
. Since
 $(A,f\restriction A)$
and
$(A,f\restriction A)$
and
 $(B,g\restriction B)$
are isomorphic, the blowups of
$(B,g\restriction B)$
are isomorphic, the blowups of
![]() $\boldsymbol{U}^{\prime }$
,
$\boldsymbol{U}^{\prime }$
,
![]() $\boldsymbol{V}^{\prime }$
with the loci
$\boldsymbol{V}^{\prime }$
with the loci
 $(A,f\restriction A)$
and
$(A,f\restriction A)$
and
 $(B,g\restriction B)$
are isomorphic. Then, it is not hard to see that the blowup
$(B,g\restriction B)$
are isomorphic. Then, it is not hard to see that the blowup
![]() $\boldsymbol{U}^{\flat \flat }$
of
$\boldsymbol{U}^{\flat \flat }$
of
![]() $\boldsymbol{U}^{\flat }$
using the locus
$\boldsymbol{U}^{\flat }$
using the locus
 $I^{-1}(D)\smallsetminus C$
and its corresponding blowup of
$I^{-1}(D)\smallsetminus C$
and its corresponding blowup of
![]() $\boldsymbol{V}^{\prime }$
and the blowup
$\boldsymbol{V}^{\prime }$
and the blowup
![]() $\boldsymbol{V}^{\flat \flat }$
of
$\boldsymbol{V}^{\flat \flat }$
of
![]() $\boldsymbol{V}^{\flat }$
using the locus
$\boldsymbol{V}^{\flat }$
using the locus
 $I(C)\smallsetminus D$
and its corresponding blowup of
$I(C)\smallsetminus D$
and its corresponding blowup of
![]() $\boldsymbol{U}^{\prime }$
are isomorphic.
$\boldsymbol{U}^{\prime }$
are isomorphic.
Applying the inductive hypothesis to the blowups
![]() $\boldsymbol{U}^{\flat \flat }$
,
$\boldsymbol{U}^{\flat \flat }$
,
![]() $\boldsymbol{U}_{1}$
of
$\boldsymbol{U}_{1}$
of
![]() $\boldsymbol{U}^{\flat }$
, we obtain a blowup
$\boldsymbol{U}^{\flat }$
, we obtain a blowup
![]() $\boldsymbol{U}^{\flat 3}$
of
$\boldsymbol{U}^{\flat 3}$
of
![]() $\boldsymbol{U}^{\flat \flat }$
of length
$\boldsymbol{U}^{\flat \flat }$
of length
![]() $m-1$
and a blowup
$m-1$
and a blowup
![]() $\boldsymbol{U}_{1}^{\flat }$
of
$\boldsymbol{U}_{1}^{\flat }$
of
![]() $\boldsymbol{U}_{1}$
of length
$\boldsymbol{U}_{1}$
of length
![]() $1$
such that they are isomorphic. Similarly, we obtain a blowup
$1$
such that they are isomorphic. Similarly, we obtain a blowup
![]() $\boldsymbol{V}^{\flat 3}$
of
$\boldsymbol{V}^{\flat 3}$
of
![]() $\boldsymbol{V}^{\flat \flat }$
of length
$\boldsymbol{V}^{\flat \flat }$
of length
![]() $n-1$
and a blowup
$n-1$
and a blowup
![]() $\boldsymbol{V}_{1}^{\flat }$
of
$\boldsymbol{V}_{1}^{\flat }$
of
![]() $\boldsymbol{V}_{1}$
of length
$\boldsymbol{V}_{1}$
of length
![]() $1$
such that they are isomorphic. Applying the inductive hypothesis again to the blowups
$1$
such that they are isomorphic. Applying the inductive hypothesis again to the blowups
![]() $\boldsymbol{U}^{\flat 3}$
,
$\boldsymbol{U}^{\flat 3}$
,
![]() $\boldsymbol{V}^{\flat 3}$
of
$\boldsymbol{V}^{\flat 3}$
of
![]() $\boldsymbol{U}^{\flat \flat }$
,
$\boldsymbol{U}^{\flat \flat }$
,
![]() $\boldsymbol{V}^{\flat \flat }$
, we obtain a blowup
$\boldsymbol{V}^{\flat \flat }$
, we obtain a blowup
![]() $\boldsymbol{U}^{\flat 4}$
of
$\boldsymbol{U}^{\flat 4}$
of
![]() $\boldsymbol{U}^{\flat 3}$
of length
$\boldsymbol{U}^{\flat 3}$
of length
![]() $n-1$
and a blowup
$n-1$
and a blowup
![]() $\boldsymbol{V}^{\flat 4}$
of
$\boldsymbol{V}^{\flat 4}$
of
![]() $\boldsymbol{V}^{\flat 3}$
of length
$\boldsymbol{V}^{\flat 3}$
of length
![]() $m-1$
such that they are isomorphic. Finally, applying the inductive hypothesis to the blowups
$m-1$
such that they are isomorphic. Finally, applying the inductive hypothesis to the blowups
![]() $\boldsymbol{U}^{\flat 4}$
,
$\boldsymbol{U}^{\flat 4}$
,
![]() $\boldsymbol{U}_{1}^{\flat }$
of
$\boldsymbol{U}_{1}^{\flat }$
of
![]() $\boldsymbol{U}^{\flat 3}$
,
$\boldsymbol{U}^{\flat 3}$
,
![]() $\boldsymbol{U}_{1}^{\flat }$
and the blowups
$\boldsymbol{U}_{1}^{\flat }$
and the blowups
![]() $\boldsymbol{V}^{\flat 4}$
,
$\boldsymbol{V}^{\flat 4}$
,
![]() $\boldsymbol{V}_{1}^{\flat }$
of
$\boldsymbol{V}_{1}^{\flat }$
of
![]() $\boldsymbol{V}^{\flat 3}$
,
$\boldsymbol{V}^{\flat 3}$
,
![]() $\boldsymbol{V}_{1}^{\flat }$
, we obtain a blowup
$\boldsymbol{V}_{1}^{\flat }$
, we obtain a blowup
![]() $\boldsymbol{U}_{2}$
of
$\boldsymbol{U}_{2}$
of
![]() $\boldsymbol{U}_{1}^{\flat }$
of length
$\boldsymbol{U}_{1}^{\flat }$
of length
![]() $n-1$
and a blowup
$n-1$
and a blowup
![]() $\boldsymbol{V}_{2}$
of
$\boldsymbol{V}_{2}$
of
![]() $\boldsymbol{V}_{1}^{\flat }$
of length
$\boldsymbol{V}_{1}^{\flat }$
of length
![]() $m-1$
such that
$m-1$
such that
![]() $\boldsymbol{U}^{\flat 4}$
,
$\boldsymbol{U}^{\flat 4}$
,
![]() $\boldsymbol{U}_{2}$
,
$\boldsymbol{U}_{2}$
,
![]() $\boldsymbol{V}^{\flat 4}$
, and
$\boldsymbol{V}^{\flat 4}$
, and
![]() $\boldsymbol{V}_{2}$
are all isomorphic. So
$\boldsymbol{V}_{2}$
are all isomorphic. So
![]() $\boldsymbol{U}_{2}$
,
$\boldsymbol{U}_{2}$
,
![]() $\boldsymbol{V}_{2}$
are as desired.◻
$\boldsymbol{V}_{2}$
are as desired.◻
Corollary 5.30. Let
 $[\boldsymbol{U}]=[\boldsymbol{U}^{\prime }]$
and
$[\boldsymbol{U}]=[\boldsymbol{U}^{\prime }]$
and
 $[\boldsymbol{V}]=[\boldsymbol{V}^{\prime }]$
in
$[\boldsymbol{V}]=[\boldsymbol{V}^{\prime }]$
in
 $\mathbf{K}_{+}\text{RV}[{\leqslant}k]$
. If there are isomorphic blowups of
$\mathbf{K}_{+}\text{RV}[{\leqslant}k]$
. If there are isomorphic blowups of
![]() $\boldsymbol{U}$
,
$\boldsymbol{U}$
,
![]() $\boldsymbol{V}$
then there are isomorphic blowups of
$\boldsymbol{V}$
then there are isomorphic blowups of
![]() $\boldsymbol{U}^{\prime }$
,
$\boldsymbol{U}^{\prime }$
,
![]() $\boldsymbol{V}^{\prime }$
.
$\boldsymbol{V}^{\prime }$
.
Definition 5.31. Let
![]() $\operatorname{I}_{\text{sp}}[k]$
be the set of pairs
$\operatorname{I}_{\text{sp}}[k]$
be the set of pairs
![]() $(\boldsymbol{U},\boldsymbol{V})$
of objects of
$(\boldsymbol{U},\boldsymbol{V})$
of objects of
![]() $\text{RV}[{\leqslant}k]$
such that there exist isomorphic blowups
$\text{RV}[{\leqslant}k]$
such that there exist isomorphic blowups
![]() $\boldsymbol{U}^{\flat }$
,
$\boldsymbol{U}^{\flat }$
,
![]() $\boldsymbol{V}^{\flat }$
. Set
$\boldsymbol{V}^{\flat }$
. Set
 $\operatorname{I}_{\text{sp}}[\ast ]=\bigcup _{k}\operatorname{I}_{\text{sp}}[k]$
.
$\operatorname{I}_{\text{sp}}[\ast ]=\bigcup _{k}\operatorname{I}_{\text{sp}}[k]$
.
We will just write
![]() $\operatorname{I}_{\text{sp}}$
for all these sets when there is no danger of confusion. By Corollary 5.30,
$\operatorname{I}_{\text{sp}}$
for all these sets when there is no danger of confusion. By Corollary 5.30,
![]() $\operatorname{I}_{\text{sp}}$
may be regarded as a binary relation on isomorphism classes.
$\operatorname{I}_{\text{sp}}$
may be regarded as a binary relation on isomorphism classes.
Lemma 5.32.
![]() $\operatorname{I}_{\text{sp}}[k]$
is a semigroup congruence relation and
$\operatorname{I}_{\text{sp}}[k]$
is a semigroup congruence relation and
![]() $\operatorname{I}_{\text{sp}}[\ast ]$
is a semiring congruence relation.
$\operatorname{I}_{\text{sp}}[\ast ]$
is a semiring congruence relation.
Proof. Clearly
![]() $\operatorname{I}_{\text{sp}}[k]$
is reflexive and symmetric. If
$\operatorname{I}_{\text{sp}}[k]$
is reflexive and symmetric. If
 $([\boldsymbol{U}_{1}],[\boldsymbol{U}_{2}])$
,
$([\boldsymbol{U}_{1}],[\boldsymbol{U}_{2}])$
,
 $([\boldsymbol{U}_{2}],[\boldsymbol{U}_{3}])$
are in
$([\boldsymbol{U}_{2}],[\boldsymbol{U}_{3}])$
are in
![]() $\operatorname{I}_{\text{sp}}[k]$
then, by Lemma 5.29, there are blowups
$\operatorname{I}_{\text{sp}}[k]$
then, by Lemma 5.29, there are blowups
![]() $\boldsymbol{U}_{1}^{\flat }$
of
$\boldsymbol{U}_{1}^{\flat }$
of
![]() $\boldsymbol{U}_{1}$
,
$\boldsymbol{U}_{1}$
,
![]() $\boldsymbol{U}_{2}^{\flat 1}$
and
$\boldsymbol{U}_{2}^{\flat 1}$
and
![]() $\boldsymbol{U}_{2}^{\flat 2}$
of
$\boldsymbol{U}_{2}^{\flat 2}$
of
![]() $\boldsymbol{U}_{2}$
, and
$\boldsymbol{U}_{2}$
, and
![]() $\boldsymbol{U}_{3}^{\flat }$
of
$\boldsymbol{U}_{3}^{\flat }$
of
![]() $\boldsymbol{U}_{3}$
such that they are all isomorphic. So
$\boldsymbol{U}_{3}$
such that they are all isomorphic. So
![]() $\operatorname{I}_{\text{sp}}[k]$
is transitive and hence is an equivalence relation. For any
$\operatorname{I}_{\text{sp}}[k]$
is transitive and hence is an equivalence relation. For any
 $[\boldsymbol{W}]\in \mathbf{K}_{+}\text{RV}[l]$
, the following are easily checked:
$[\boldsymbol{W}]\in \mathbf{K}_{+}\text{RV}[l]$
, the following are easily checked:
 $$\begin{eqnarray}([\boldsymbol{U}_{1}\uplus \boldsymbol{W}],[\boldsymbol{U}_{2}\uplus \boldsymbol{W}])\in \operatorname{I}_{\text{sp}},\quad ([\boldsymbol{U}_{1}\times \boldsymbol{W}],[\boldsymbol{U}_{2}\times \boldsymbol{W}])\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([\boldsymbol{U}_{1}\uplus \boldsymbol{W}],[\boldsymbol{U}_{2}\uplus \boldsymbol{W}])\in \operatorname{I}_{\text{sp}},\quad ([\boldsymbol{U}_{1}\times \boldsymbol{W}],[\boldsymbol{U}_{2}\times \boldsymbol{W}])\in \text{I}_{\text{sp}}.\end{eqnarray}$$
These yield the desired congruence relations. ◻
Let
 $\boldsymbol{U}=(U,f)$
be an object of
$\boldsymbol{U}=(U,f)$
be an object of
![]() $\text{RV}[k]$
and
$\text{RV}[k]$
and
![]() $T$
a special bijection on
$T$
a special bijection on
![]() $\mathbb{L}\boldsymbol{U}$
. The set
$\mathbb{L}\boldsymbol{U}$
. The set
 $(T(\mathbb{L}\boldsymbol{U}))_{\text{RV}}$
is simply denoted by
$(T(\mathbb{L}\boldsymbol{U}))_{\text{RV}}$
is simply denoted by
![]() $U_{T}$
and the object
$U_{T}$
and the object
 $(U_{T})_{{\leqslant}k}\in \text{RV}[{\leqslant}k]$
by
$(U_{T})_{{\leqslant}k}\in \text{RV}[{\leqslant}k]$
by
![]() $\boldsymbol{U}_{T}$
.
$\boldsymbol{U}_{T}$
.
Lemma 5.33. The object
![]() $\boldsymbol{U}_{T}$
is isomorphic to a blowup of
$\boldsymbol{U}_{T}$
is isomorphic to a blowup of
![]() $\boldsymbol{U}$
of the same length as
$\boldsymbol{U}$
of the same length as
![]() $T$
.
$T$
.
Proof. By induction on the length
![]() $\operatorname{lh}(T)$
of
$\operatorname{lh}(T)$
of
![]() $T$
and Lemma 5.29, this is immediately reduced to the case
$T$
and Lemma 5.29, this is immediately reduced to the case
 $\operatorname{lh}(T)=1$
. For that case, let
$\operatorname{lh}(T)=1$
. For that case, let
![]() $\unicode[STIX]{x1D706}$
be the focus map of
$\unicode[STIX]{x1D706}$
be the focus map of
![]() $T$
. Without loss of generality, we may assume that the locus of
$T$
. Without loss of generality, we may assume that the locus of
![]() $\unicode[STIX]{x1D706}$
is
$\unicode[STIX]{x1D706}$
is
![]() $\mathbb{L}\boldsymbol{U}$
. Then it is clear how to construct an (elementary) blowup of
$\mathbb{L}\boldsymbol{U}$
. Then it is clear how to construct an (elementary) blowup of
![]() $\boldsymbol{U}$
as desired.◻
$\boldsymbol{U}$
as desired.◻
Lemma 5.34. Suppose that
 $[A]=[B]$
in
$[A]=[B]$
in
 $\mathbf{K}_{+}\text{VF}[1]$
and
$\mathbf{K}_{+}\text{VF}[1]$
and
 $\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}1]$
are two standard contractions of
$\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}1]$
are two standard contractions of
![]() $A$
,
$A$
,
![]() $B$
, respectively. Then
$B$
, respectively. Then
 $([\boldsymbol{U}],[\boldsymbol{V}])\in \operatorname{I}_{\text{sp}}$
.
$([\boldsymbol{U}],[\boldsymbol{V}])\in \operatorname{I}_{\text{sp}}$
.
Proof. By Lemma 5.10, there are special bijections
![]() $T$
,
$T$
,
![]() $R$
on
$R$
on
![]() $\mathbb{L}\boldsymbol{U}$
,
$\mathbb{L}\boldsymbol{U}$
,
![]() $\mathbb{L}\boldsymbol{V}$
such that
$\mathbb{L}\boldsymbol{V}$
such that
![]() $\boldsymbol{U}_{T}$
,
$\boldsymbol{U}_{T}$
,
![]() $\boldsymbol{V}_{R}$
are isomorphic. So the assertion follows from Lemma 5.33.◻
$\boldsymbol{V}_{R}$
are isomorphic. So the assertion follows from Lemma 5.33.◻
Lemma 5.35. Let
![]() $\boldsymbol{U}^{\flat }$
be a blowup of
$\boldsymbol{U}^{\flat }$
be a blowup of
 $\boldsymbol{U}=(U,f)\in \text{RV}[{\leqslant}k]$
of length
$\boldsymbol{U}=(U,f)\in \text{RV}[{\leqslant}k]$
of length
![]() $l$
. Then
$l$
. Then
![]() $\mathbb{L}\boldsymbol{U}^{\flat }$
is isomorphic to
$\mathbb{L}\boldsymbol{U}^{\flat }$
is isomorphic to
![]() $\mathbb{L}\boldsymbol{U}$
.
$\mathbb{L}\boldsymbol{U}$
.
Proof. By induction on
![]() $l$
this is immediately reduced to the case
$l$
this is immediately reduced to the case
![]() $l=1$
. For that case, without loss of generality, we may assume that
$l=1$
. For that case, without loss of generality, we may assume that
 $\operatorname{pr}_{\tilde{1}}\restriction f(U)$
is injective and
$\operatorname{pr}_{\tilde{1}}\restriction f(U)$
is injective and
![]() $\boldsymbol{U}^{\flat }$
is an elementary blowup in the first coordinate. So it is enough to show that there is a focus map into the first coordinate with locus
$\boldsymbol{U}^{\flat }$
is an elementary blowup in the first coordinate. So it is enough to show that there is a focus map into the first coordinate with locus
![]() $f(U)^{\sharp }$
. This is guaranteed by Hypothesis 5.11.◻
$f(U)^{\sharp }$
. This is guaranteed by Hypothesis 5.11.◻
Lemma 5.36. Let
![]() $A^{\prime }$
,
$A^{\prime }$
,
![]() $A^{\prime \prime }$
be definable sets with
$A^{\prime \prime }$
be definable sets with
 $A_{\text{VF}}^{\prime }=A_{\text{VF}}^{\prime \prime }=:A\subseteq \text{VF}^{n}$
. Suppose that there is a
$A_{\text{VF}}^{\prime }=A_{\text{VF}}^{\prime \prime }=:A\subseteq \text{VF}^{n}$
. Suppose that there is a
![]() $k\in \unicode[STIX]{x2115}$
such that, for every
$k\in \unicode[STIX]{x2115}$
such that, for every
![]() $a\in A$
,
$a\in A$
,
 $([A_{a}^{\prime }]_{{\leqslant}k},[A_{a}^{\prime \prime }]_{{\leqslant}k})\in \operatorname{I}_{\text{sp}}$
. Let
$([A_{a}^{\prime }]_{{\leqslant}k},[A_{a}^{\prime \prime }]_{{\leqslant}k})\in \operatorname{I}_{\text{sp}}$
. Let
![]() $\hat{T}_{\unicode[STIX]{x1D70E}}$
,
$\hat{T}_{\unicode[STIX]{x1D70E}}$
,
![]() $\hat{R}_{\unicode[STIX]{x1D70E}}$
be respectively standard contractions of
$\hat{R}_{\unicode[STIX]{x1D70E}}$
be respectively standard contractions of
![]() $A^{\prime }$
,
$A^{\prime }$
,
![]() $A^{\prime \prime }$
. Then
$A^{\prime \prime }$
. Then
 $$\begin{eqnarray}([\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })]_{{\leqslant}n+k},[\hat{R}_{\unicode[STIX]{x1D70E}}(A^{\prime \prime })]_{{\leqslant}n+k})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })]_{{\leqslant}n+k},[\hat{R}_{\unicode[STIX]{x1D70E}}(A^{\prime \prime })]_{{\leqslant}n+k})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
Note that the condition
 $([A_{a}^{\prime }]_{{\leqslant}k},[A_{a}^{\prime \prime }]_{{\leqslant}k})\in \operatorname{I}_{\text{sp}}$
makes sense only over the substructure
$([A_{a}^{\prime }]_{{\leqslant}k},[A_{a}^{\prime \prime }]_{{\leqslant}k})\in \operatorname{I}_{\text{sp}}$
makes sense only over the substructure
![]() ${\mathcal{S}}\langle a\rangle$
.
${\mathcal{S}}\langle a\rangle$
.
Proof. By induction on
![]() $n$
this is immediately reduced to the case
$n$
this is immediately reduced to the case
![]() $n=1$
. So assume
$n=1$
. So assume
 $A\subseteq \text{VF}$
. Let
$A\subseteq \text{VF}$
. Let
![]() $\unicode[STIX]{x1D719}^{\prime }$
,
$\unicode[STIX]{x1D719}^{\prime }$
,
![]() $\unicode[STIX]{x1D719}^{\prime \prime }$
be quantifier-free formulas that define
$\unicode[STIX]{x1D719}^{\prime \prime }$
be quantifier-free formulas that define
![]() $A^{\prime }$
,
$A^{\prime }$
,
![]() $A^{\prime \prime }$
, respectively. Let
$A^{\prime \prime }$
, respectively. Let
![]() $\unicode[STIX]{x1D703}$
be a quantifier-free formula such that, for every
$\unicode[STIX]{x1D703}$
be a quantifier-free formula such that, for every
![]() $a\in A$
,
$a\in A$
,
![]() $\unicode[STIX]{x1D703}(a)$
defines the necessary data (two blowups and an
$\unicode[STIX]{x1D703}(a)$
defines the necessary data (two blowups and an
![]() $\text{RV}[\ast ]$
-morphism) that witness the condition
$\text{RV}[\ast ]$
-morphism) that witness the condition
 $([A_{a}^{\prime }]_{{\leqslant}k},[A_{a}^{\prime \prime }]_{{\leqslant}k})\in \operatorname{I}_{\text{sp}}$
. Applying Corollary 5.6 to the top
$([A_{a}^{\prime }]_{{\leqslant}k},[A_{a}^{\prime \prime }]_{{\leqslant}k})\in \operatorname{I}_{\text{sp}}$
. Applying Corollary 5.6 to the top
![]() ${\mathcal{L}}_{T\text{}}$
-terms of
${\mathcal{L}}_{T\text{}}$
-terms of
![]() $\unicode[STIX]{x1D719}^{\prime }$
,
$\unicode[STIX]{x1D719}^{\prime }$
,
![]() $\unicode[STIX]{x1D719}^{\prime \prime }$
, and
$\unicode[STIX]{x1D719}^{\prime \prime }$
, and
![]() $\unicode[STIX]{x1D703}$
, we obtain a special bijection
$\unicode[STIX]{x1D703}$
, we obtain a special bijection
 $F:A\longrightarrow A^{\flat }$
such that
$F:A\longrightarrow A^{\flat }$
such that
![]() $A^{\flat }$
is an
$A^{\flat }$
is an
![]() $\text{RV}$
-pullback and, for all
$\text{RV}$
-pullback and, for all
![]() $\text{RV}$
-polydiscs
$\text{RV}$
-polydiscs
![]() $\mathfrak{p}\subseteq A^{\flat }$
and all
$\mathfrak{p}\subseteq A^{\flat }$
and all
 $a_{1},a_{2}\in F^{-1}(\mathfrak{p})$
,
$a_{1},a_{2}\in F^{-1}(\mathfrak{p})$
,
-
–
 $A_{a_{1}}^{\prime }=A_{a_{2}}^{\prime }$
and
$A_{a_{1}}^{\prime }=A_{a_{2}}^{\prime }$
and
 $A_{a_{1}}^{\prime \prime }=A_{a_{2}}^{\prime \prime }$
,
$A_{a_{1}}^{\prime \prime }=A_{a_{2}}^{\prime \prime }$
, -
–
 $\unicode[STIX]{x1D703}(a_{1})$
and
$\unicode[STIX]{x1D703}(a_{1})$
and
 $\unicode[STIX]{x1D703}(a_{2})$
define the same data.
$\unicode[STIX]{x1D703}(a_{2})$
define the same data.
The second item implies that the data defined by
![]() $\unicode[STIX]{x1D703}$
over
$\unicode[STIX]{x1D703}$
over
![]() $F^{-1}(\mathfrak{p})$
is actually
$F^{-1}(\mathfrak{p})$
is actually
![]() $\operatorname{rv}(\mathfrak{p})$
-definable.
$\operatorname{rv}(\mathfrak{p})$
-definable.
Let
 $B^{\prime }=\bigcup _{a\in A}F(a)\times A_{a}^{\prime }$
, and similarly for
$B^{\prime }=\bigcup _{a\in A}F(a)\times A_{a}^{\prime }$
, and similarly for
![]() $B^{\prime \prime }$
. Note that
$B^{\prime \prime }$
. Note that
![]() $B^{\prime }$
,
$B^{\prime }$
,
![]() $B^{\prime \prime }$
are obtained through special bijections on
$B^{\prime \prime }$
are obtained through special bijections on
![]() $A^{\prime }$
,
$A^{\prime }$
,
![]() $A^{\prime \prime }$
. For all
$A^{\prime \prime }$
. For all
 $t\in A_{\text{RV}}^{\prime }$
,
$t\in A_{\text{RV}}^{\prime }$
,
![]() $B_{t}^{\prime }$
is an
$B_{t}^{\prime }$
is an
![]() $\text{RV}$
-pullback that is
$\text{RV}$
-pullback that is
![]() $t$
-definably bijective to the
$t$
-definably bijective to the
![]() $\text{RV}$
-pullback
$\text{RV}$
-pullback
![]() $T_{\unicode[STIX]{x1D70E}}(A^{\prime })_{t}$
. By Lemma 5.34, we have, for all
$T_{\unicode[STIX]{x1D70E}}(A^{\prime })_{t}$
. By Lemma 5.34, we have, for all
 $t\in A_{\text{RV}}^{\prime }$
,
$t\in A_{\text{RV}}^{\prime }$
,
 $$\begin{eqnarray}([(B_{\text{RV}}^{\prime })_{t}]_{1},[\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })_{t}]_{1})\in \operatorname{I}_{\text{sp}}\end{eqnarray}$$
$$\begin{eqnarray}([(B_{\text{RV}}^{\prime })_{t}]_{1},[\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })_{t}]_{1})\in \operatorname{I}_{\text{sp}}\end{eqnarray}$$
and hence, by compactness,
 $$\begin{eqnarray}([B_{\text{RV}}^{\prime }]_{{\leqslant}k+1},[\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })]_{{\leqslant}k+1})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([B_{\text{RV}}^{\prime }]_{{\leqslant}k+1},[\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })]_{{\leqslant}k+1})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
The same holds for
![]() $B^{\prime \prime }$
and
$B^{\prime \prime }$
and
![]() $\hat{R}_{\unicode[STIX]{x1D70E}}(A^{\prime \prime })$
. On the other hand, by the second item above, for every
$\hat{R}_{\unicode[STIX]{x1D70E}}(A^{\prime \prime })$
. On the other hand, by the second item above, for every
![]() $\text{RV}$
-polydisc
$\text{RV}$
-polydisc
![]() $\mathfrak{p}\subseteq A^{\flat }$
, we have
$\mathfrak{p}\subseteq A^{\flat }$
, we have
 $((B_{\text{RV}}^{\prime })_{\operatorname{rv}(\mathfrak{p})},(B_{\text{RV}}^{\prime \prime })_{\operatorname{rv}(\mathfrak{p})})\in \operatorname{I}_{\text{sp}}$
and hence, by compactness,
$((B_{\text{RV}}^{\prime })_{\operatorname{rv}(\mathfrak{p})},(B_{\text{RV}}^{\prime \prime })_{\operatorname{rv}(\mathfrak{p})})\in \operatorname{I}_{\text{sp}}$
and hence, by compactness,
 $$\begin{eqnarray}([B_{\text{RV}}^{\prime }]_{{\leqslant}k+1},[B_{\text{RV}}^{\prime \prime }]_{{\leqslant}k+1})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([B_{\text{RV}}^{\prime }]_{{\leqslant}k+1},[B_{\text{RV}}^{\prime \prime }]_{{\leqslant}k+1})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
Since
![]() $\operatorname{I}_{\text{sp}}$
is a congruence relation, the lemma follows.◻
$\operatorname{I}_{\text{sp}}$
is a congruence relation, the lemma follows.◻
Corollary 5.37. Let
 $A^{\prime },A^{\prime \prime }\in \text{VF}_{\ast }$
with exactly
$A^{\prime },A^{\prime \prime }\in \text{VF}_{\ast }$
with exactly
![]() $n$
$n$
![]() $\text{VF}$
-coordinates each and
$\text{VF}$
-coordinates each and
 $f:A^{\prime }\longrightarrow A^{\prime \prime }$
be a relatively unary bijection in the
$f:A^{\prime }\longrightarrow A^{\prime \prime }$
be a relatively unary bijection in the
![]() $i$
th coordinate. Then for any permutation
$i$
th coordinate. Then for any permutation
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $[n]$
with
$[n]$
with
 $\unicode[STIX]{x1D70E}(1)=i$
and any standard contractions
$\unicode[STIX]{x1D70E}(1)=i$
and any standard contractions
![]() $\hat{T}_{\unicode[STIX]{x1D70E}}$
,
$\hat{T}_{\unicode[STIX]{x1D70E}}$
,
![]() $\hat{R}_{\unicode[STIX]{x1D70E}}$
of
$\hat{R}_{\unicode[STIX]{x1D70E}}$
of
![]() $A^{\prime }$
,
$A^{\prime }$
,
![]() $A^{\prime \prime }$
,
$A^{\prime \prime }$
,
 $$\begin{eqnarray}([\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })]_{{\leqslant}n},[\hat{R}_{\unicode[STIX]{x1D70E}}(A^{\prime \prime })]_{{\leqslant}n})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([\hat{T}_{\unicode[STIX]{x1D70E}}(A^{\prime })]_{{\leqslant}n},[\hat{R}_{\unicode[STIX]{x1D70E}}(A^{\prime \prime })]_{{\leqslant}n})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
The following lemma is essentially a version of Fubini’s theorem (see also Theorem 5.42 below).
Lemma 5.38. Let
 $A\in \text{VF}_{\ast }$
with exactly
$A\in \text{VF}_{\ast }$
with exactly
![]() $n$
$n$
![]() $\text{VF}$
-coordinates. Suppose that
$\text{VF}$
-coordinates. Suppose that
 $i,j\in [n]$
are distinct and
$i,j\in [n]$
are distinct and
![]() $\unicode[STIX]{x1D70E}_{1}$
,
$\unicode[STIX]{x1D70E}_{1}$
,
![]() $\unicode[STIX]{x1D70E}_{2}$
are permutations of
$\unicode[STIX]{x1D70E}_{2}$
are permutations of
![]() $[n]$
such that
$[n]$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(1)=\unicode[STIX]{x1D70E}_{2}(2)=i,\quad \unicode[STIX]{x1D70E}_{1}(2)=\unicode[STIX]{x1D70E}_{2}(1)=j,\quad \unicode[STIX]{x1D70E}_{1}\restriction \{3,\ldots ,n\}=\unicode[STIX]{x1D70E}_{2}\restriction \{3,\ldots ,n\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(1)=\unicode[STIX]{x1D70E}_{2}(2)=i,\quad \unicode[STIX]{x1D70E}_{1}(2)=\unicode[STIX]{x1D70E}_{2}(1)=j,\quad \unicode[STIX]{x1D70E}_{1}\restriction \{3,\ldots ,n\}=\unicode[STIX]{x1D70E}_{2}\restriction \{3,\ldots ,n\}.\end{eqnarray}$$
Then, for any standard contractions
![]() $\hat{T}_{\unicode[STIX]{x1D70E}_{1}}$
,
$\hat{T}_{\unicode[STIX]{x1D70E}_{1}}$
,
![]() $\hat{T}_{\unicode[STIX]{x1D70E}_{2}}$
of
$\hat{T}_{\unicode[STIX]{x1D70E}_{2}}$
of
![]() $A$
,
$A$
,
 $$\begin{eqnarray}([\hat{T}_{\unicode[STIX]{x1D70E}_{1}}(A)]_{{\leqslant}n},[\hat{T}_{\unicode[STIX]{x1D70E}_{2}}(A)]_{{\leqslant}n})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([\hat{T}_{\unicode[STIX]{x1D70E}_{1}}(A)]_{{\leqslant}n},[\hat{T}_{\unicode[STIX]{x1D70E}_{2}}(A)]_{{\leqslant}n})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
Proof. Let
![]() $ij$
,
$ij$
,
![]() $ji$
denote the permutations of
$ji$
denote the permutations of
 $E:=\{i,j\}$
. By compactness and Lemma 5.36, it is enough to show that, for any
$E:=\{i,j\}$
. By compactness and Lemma 5.36, it is enough to show that, for any
 $a\in \operatorname{pr}_{\tilde{E}}(A)$
and any standard contractions
$a\in \operatorname{pr}_{\tilde{E}}(A)$
and any standard contractions
![]() $\hat{T}_{ij}$
,
$\hat{T}_{ij}$
,
![]() $\hat{T}_{ji}$
of
$\hat{T}_{ji}$
of
![]() $A_{a}$
,
$A_{a}$
,
 $$\begin{eqnarray}([\hat{T}_{ij}(A_{a})]_{{\leqslant}2},[\hat{T}_{ji}(A_{a})]_{{\leqslant}2})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([\hat{T}_{ij}(A_{a})]_{{\leqslant}2},[\hat{T}_{ji}(A_{a})]_{{\leqslant}2})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
To that end, fix an
 $a\in \operatorname{pr}_{\tilde{E}}(A)$
. By Lemma 5.26, there are a definable bijection
$a\in \operatorname{pr}_{\tilde{E}}(A)$
. By Lemma 5.26, there are a definable bijection
![]() $f$
on
$f$
on
![]() $A_{a}$
that is relatively unary in both
$A_{a}$
that is relatively unary in both
![]() $\text{VF}$
-coordinates and standard contractions
$\text{VF}$
-coordinates and standard contractions
![]() $\hat{R}_{ij}$
,
$\hat{R}_{ij}$
,
![]() $\hat{R}_{ji}$
of
$\hat{R}_{ji}$
of
![]() $f(A_{a})$
such that
$f(A_{a})$
such that
 $$\begin{eqnarray}[\hat{R}_{ij}(f(A_{a}))]_{{\leqslant}2}=[\hat{R}_{ji}(f(A_{a}))]_{{\leqslant}2}.\end{eqnarray}$$
$$\begin{eqnarray}[\hat{R}_{ij}(f(A_{a}))]_{{\leqslant}2}=[\hat{R}_{ji}(f(A_{a}))]_{{\leqslant}2}.\end{eqnarray}$$
So the desired property follows from Corollary 5.37. ◻
The following proposition is the culmination of the preceding technicalities; it identifies the congruence relation
![]() $\operatorname{I}_{\text{sp}}$
with that induced by
$\operatorname{I}_{\text{sp}}$
with that induced by
![]() $\mathbb{L}$
.
$\mathbb{L}$
.
Proposition 5.39. For
 $\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}k]$
,
$\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}k]$
,
 $$\begin{eqnarray}[\mathbb{L}\boldsymbol{U}]=[\mathbb{L}\boldsymbol{V}]\quad \text{if and only if }([\boldsymbol{U}],[\boldsymbol{V}])\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}[\mathbb{L}\boldsymbol{U}]=[\mathbb{L}\boldsymbol{V}]\quad \text{if and only if }([\boldsymbol{U}],[\boldsymbol{V}])\in \text{I}_{\text{sp}}.\end{eqnarray}$$
Proof. The ‘if’ direction simply follows from Lemma 5.35 and Corollary 5.14.
For the ‘only if’ direction, we show a stronger claim: if
 $[A]=[B]$
in
$[A]=[B]$
in
 $\mathbf{K}_{+}\text{VF}_{\ast }$
and
$\mathbf{K}_{+}\text{VF}_{\ast }$
and
 $\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}k]$
are two standard contractions of
$\boldsymbol{U},\boldsymbol{V}\in \text{RV}[{\leqslant}k]$
are two standard contractions of
![]() $A$
,
$A$
,
![]() $B$
then
$B$
then
 $([\boldsymbol{U}],[\boldsymbol{V}])\in \operatorname{I}_{\text{sp}}$
. We do induction on
$([\boldsymbol{U}],[\boldsymbol{V}])\in \operatorname{I}_{\text{sp}}$
. We do induction on
![]() $k$
. The base case
$k$
. The base case
![]() $k=1$
is of course Lemma 5.34.
$k=1$
is of course Lemma 5.34.
For the inductive step, suppose that
 $F:\mathbb{L}\boldsymbol{U}\longrightarrow \mathbb{L}\boldsymbol{V}$
is a definable bijection. By Lemma 5.24, there is a partition of
$F:\mathbb{L}\boldsymbol{U}\longrightarrow \mathbb{L}\boldsymbol{V}$
is a definable bijection. By Lemma 5.24, there is a partition of
![]() $\mathbb{L}\boldsymbol{U}$
into definable sets
$\mathbb{L}\boldsymbol{U}$
into definable sets
 $A_{1},\ldots ,A_{n}$
such that each restriction
$A_{1},\ldots ,A_{n}$
such that each restriction
 $F_{i}=F\restriction A_{i}$
is a composition of relatively unary bijections. Applying Corollary 5.6 as before, we obtain two special bijections
$F_{i}=F\restriction A_{i}$
is a composition of relatively unary bijections. Applying Corollary 5.6 as before, we obtain two special bijections
![]() $T$
,
$T$
,
![]() $R$
on
$R$
on
![]() $\mathbb{L}\boldsymbol{U}$
,
$\mathbb{L}\boldsymbol{U}$
,
![]() $\mathbb{L}\boldsymbol{V}$
such that
$\mathbb{L}\boldsymbol{V}$
such that
![]() $T(A_{i})$
,
$T(A_{i})$
,
 $(R\circ F)(A_{i})$
is an
$(R\circ F)(A_{i})$
is an
![]() $\text{RV}$
-pullback for each
$\text{RV}$
-pullback for each
![]() $i$
. By Lemma 5.33, it is enough to show that, for each
$i$
. By Lemma 5.33, it is enough to show that, for each
![]() $i$
, there are standard contractions
$i$
, there are standard contractions
![]() $\hat{T}_{\unicode[STIX]{x1D70E}}$
,
$\hat{T}_{\unicode[STIX]{x1D70E}}$
,
![]() $\hat{R}_{\unicode[STIX]{x1D70F}}$
of
$\hat{R}_{\unicode[STIX]{x1D70F}}$
of
![]() $T(A_{i})$
,
$T(A_{i})$
,
 $(R\circ F)(A_{i})$
such that
$(R\circ F)(A_{i})$
such that
 $$\begin{eqnarray}([(\hat{T}_{\unicode[STIX]{x1D70E}}\circ T)(A_{i})]_{{\leqslant}k},[(\hat{R}_{\unicode[STIX]{x1D70F}}\circ R\circ F)(A_{i})]_{{\leqslant}k})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}([(\hat{T}_{\unicode[STIX]{x1D70E}}\circ T)(A_{i})]_{{\leqslant}k},[(\hat{R}_{\unicode[STIX]{x1D70F}}\circ R\circ F)(A_{i})]_{{\leqslant}k})\in \text{I}_{\text{sp}}.\end{eqnarray}$$
To that end, first note that each
 $(R\circ F\circ T^{-1})\restriction T(A_{i})$
is a composition of relatively unary bijections, say
$(R\circ F\circ T^{-1})\restriction T(A_{i})$
is a composition of relatively unary bijections, say
 $$\begin{eqnarray}T(A_{i})=B_{1}\rightarrow ^{G_{1}}B_{2}\cdots B_{l}\rightarrow ^{G_{l}}B_{l+1}=(R\circ F)(A_{i}).\end{eqnarray}$$
$$\begin{eqnarray}T(A_{i})=B_{1}\rightarrow ^{G_{1}}B_{2}\cdots B_{l}\rightarrow ^{G_{l}}B_{l+1}=(R\circ F)(A_{i}).\end{eqnarray}$$
For each
 $j\leqslant l-2$
, we can choose five standard contractions,
$j\leqslant l-2$
, we can choose five standard contractions,
 $$\begin{eqnarray}[U_{j}]_{{\leqslant}k},\quad [U_{j+1}]_{{\leqslant}k},\quad [U_{j+1}^{\prime }]_{{\leqslant}k},\quad [U_{j+1}^{\prime \prime }]_{{\leqslant}k},\quad [U_{j+2}]_{{\leqslant}k},\end{eqnarray}$$
$$\begin{eqnarray}[U_{j}]_{{\leqslant}k},\quad [U_{j+1}]_{{\leqslant}k},\quad [U_{j+1}^{\prime }]_{{\leqslant}k},\quad [U_{j+1}^{\prime \prime }]_{{\leqslant}k},\quad [U_{j+2}]_{{\leqslant}k},\end{eqnarray}$$
of
![]() $B_{j}$
,
$B_{j}$
,
![]() $B_{j+1}$
,
$B_{j+1}$
,
![]() $B_{j+1}$
,
$B_{j+1}$
,
![]() $B_{j+1}$
,
$B_{j+1}$
,
![]() $B_{j+2}$
with the permutations
$B_{j+2}$
with the permutations
![]() $\unicode[STIX]{x1D70E}_{j}$
,
$\unicode[STIX]{x1D70E}_{j}$
,
![]() $\unicode[STIX]{x1D70E}_{j+1}$
,
$\unicode[STIX]{x1D70E}_{j+1}$
,
![]() $\unicode[STIX]{x1D70E}_{j+1}^{\prime }$
,
$\unicode[STIX]{x1D70E}_{j+1}^{\prime }$
,
![]() $\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }$
,
$\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }$
,
![]() $\unicode[STIX]{x1D70E}_{j+2}$
of
$\unicode[STIX]{x1D70E}_{j+2}$
of
![]() $[k]$
, respectively, such that
$[k]$
, respectively, such that
-
–
 $\unicode[STIX]{x1D70E}_{j+1}(1)$
and
$\unicode[STIX]{x1D70E}_{j+1}(1)$
and
 $\unicode[STIX]{x1D70E}_{j+1}(2)$
are the
$\unicode[STIX]{x1D70E}_{j+1}(2)$
are the
 $\text{VF}$
-coordinates targeted by
$\text{VF}$
-coordinates targeted by
 $G_{j}$
and
$G_{j}$
and
 $G_{j+1}$
, respectively,
$G_{j+1}$
, respectively, -
–
 $\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }(1)$
and
$\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }(1)$
and
 $\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }(2)$
are the
$\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }(2)$
are the
 $\text{VF}$
-coordinates targeted by
$\text{VF}$
-coordinates targeted by
 $G_{j+1}$
and
$G_{j+1}$
and
 $G_{j+2}$
, respectively,
$G_{j+2}$
, respectively, -
–
 $\unicode[STIX]{x1D70E}_{j}=\unicode[STIX]{x1D70E}_{j+1}$
,
$\unicode[STIX]{x1D70E}_{j}=\unicode[STIX]{x1D70E}_{j+1}$
,
 $\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }=\unicode[STIX]{x1D70E}_{j+2}$
, and
$\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }=\unicode[STIX]{x1D70E}_{j+2}$
, and
 $\unicode[STIX]{x1D70E}_{j+1}^{\prime }(1)=\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }(1)$
,
$\unicode[STIX]{x1D70E}_{j+1}^{\prime }(1)=\unicode[STIX]{x1D70E}_{j+1}^{\prime \prime }(1)$
, -
– the relation between
 $\unicode[STIX]{x1D70E}_{j+1}$
and
$\unicode[STIX]{x1D70E}_{j+1}$
and
 $\unicode[STIX]{x1D70E}_{j+1}^{\prime }$
is as described in Lemma 5.38.
$\unicode[STIX]{x1D70E}_{j+1}^{\prime }$
is as described in Lemma 5.38.
By Corollary 5.37 and Lemma 5.38, all the adjacent pairs of these standard contractions are
![]() $\operatorname{I}_{\text{sp}}$
-congruent, except
$\operatorname{I}_{\text{sp}}$
-congruent, except
 $([U_{j+1}^{\prime }]_{{\leqslant}k},[U_{j+1}^{\prime \prime }]_{{\leqslant}k})$
. Since we can choose
$([U_{j+1}^{\prime }]_{{\leqslant}k},[U_{j+1}^{\prime \prime }]_{{\leqslant}k})$
. Since we can choose
 $[U_{j+1}^{\prime }]_{{\leqslant}k}$
,
$[U_{j+1}^{\prime }]_{{\leqslant}k}$
,
 $[U_{j+1}^{\prime \prime }]_{{\leqslant}k}$
so that they start with the same contraction in the first targeted
$[U_{j+1}^{\prime \prime }]_{{\leqslant}k}$
so that they start with the same contraction in the first targeted
![]() $\text{VF}$
-coordinate of
$\text{VF}$
-coordinate of
![]() $B_{j+1}$
, the resulting sets from this step are the same. So, applying the inductive hypothesis in each fiber over the just contracted coordinate, we see that this last pair is also
$B_{j+1}$
, the resulting sets from this step are the same. So, applying the inductive hypothesis in each fiber over the just contracted coordinate, we see that this last pair is also
![]() $\operatorname{I}_{\text{sp}}$
-congruent. This completes the ‘only if’ direction.◻
$\operatorname{I}_{\text{sp}}$
-congruent. This completes the ‘only if’ direction.◻
This proposition shows that the semiring congruence relation on
 $\mathbf{K}_{+}\text{RV}[\ast ]$
induced by
$\mathbf{K}_{+}\text{RV}[\ast ]$
induced by
![]() $\mathbb{L}$
is generated by the pair
$\mathbb{L}$
is generated by the pair
 $([1],\mathbf{1}_{\Bbbk }+[(\text{RV}^{\circ \circ },\operatorname{id})])$
and hence its corresponding ideal in the graded ring
$([1],\mathbf{1}_{\Bbbk }+[(\text{RV}^{\circ \circ },\operatorname{id})])$
and hence its corresponding ideal in the graded ring
 $\mathbf{K}\,\text{RV}[\ast ]$
is generated by the element
$\mathbf{K}\,\text{RV}[\ast ]$
is generated by the element
 $\mathbf{1}_{\Bbbk }+[\boldsymbol{P}]$
(see Notation 4.10 and Remark 4.15).
$\mathbf{1}_{\Bbbk }+[\boldsymbol{P}]$
(see Notation 4.10 and Remark 4.15).
Theorem 5.40. For each
![]() $k\geqslant 0$
there is a canonical isomorphism of Grothendieck semigroups
$k\geqslant 0$
there is a canonical isomorphism of Grothendieck semigroups
 $$\begin{eqnarray}\int _{+}:\mathbf{K}_{+}\text{VF}[k]\longrightarrow \mathbf{K}_{+}\text{RV}[{\leqslant}k]/\operatorname{I}_{\text{sp}}\end{eqnarray}$$
$$\begin{eqnarray}\int _{+}:\mathbf{K}_{+}\text{VF}[k]\longrightarrow \mathbf{K}_{+}\text{RV}[{\leqslant}k]/\operatorname{I}_{\text{sp}}\end{eqnarray}$$
such that
 $$\begin{eqnarray}\int _{+}[A]=[\boldsymbol{U}]/\operatorname{I}_{\text{sp}}\quad \text{if and only if }[A]=[\mathbb{L}\boldsymbol{U}].\end{eqnarray}$$
$$\begin{eqnarray}\int _{+}[A]=[\boldsymbol{U}]/\operatorname{I}_{\text{sp}}\quad \text{if and only if }[A]=[\mathbb{L}\boldsymbol{U}].\end{eqnarray}$$
Putting these together, we obtain a canonical isomorphism of Grothendieck semirings
 $$\begin{eqnarray}\int _{+}:\mathbf{K}_{+}\text{VF}_{\ast }\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]/\text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{+}:\mathbf{K}_{+}\text{VF}_{\ast }\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]/\text{I}_{\text{sp}}.\end{eqnarray}$$
Theorem 5.41. The Grothendieck semiring isomorphism
![]() $\int _{+}$
naturally induces a ring isomorphism,
$\int _{+}$
naturally induces a ring isomorphism,

and two ring homomorphisms onto
![]() $\unicode[STIX]{x2124}$
,
$\unicode[STIX]{x2124}$
,

Let
![]() $F$
be a definable set with
$F$
be a definable set with
 $A:=F_{\text{VF}}\subseteq \text{VF}^{n}$
. Then
$A:=F_{\text{VF}}\subseteq \text{VF}^{n}$
. Then
![]() $F$
may be viewed as a representative of a definable function
$F$
may be viewed as a representative of a definable function
 $\boldsymbol{F}:A\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]/\operatorname{I}_{\text{sp}}$
given by
$\boldsymbol{F}:A\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]/\operatorname{I}_{\text{sp}}$
given by
 $a\longmapsto [F_{a}]/\operatorname{I}_{\text{sp}}$
. Note that the class
$a\longmapsto [F_{a}]/\operatorname{I}_{\text{sp}}$
. Note that the class
![]() $[F_{a}]$
depends on the parameter
$[F_{a}]$
depends on the parameter
![]() $a$
and hence can only be guaranteed to lie in the semiring
$a$
and hence can only be guaranteed to lie in the semiring
 $\mathbf{K}_{+}\text{RV}[\ast ]$
constructed over
$\mathbf{K}_{+}\text{RV}[\ast ]$
constructed over
![]() ${\mathcal{S}}\langle a\rangle$
instead of
${\mathcal{S}}\langle a\rangle$
instead of
![]() ${\mathcal{S}}$
, but we abuse the notation. Similarly, for distinct
${\mathcal{S}}$
, but we abuse the notation. Similarly, for distinct
 $a,a^{\prime }\in A$
, there is a priori no way to compare
$a,a^{\prime }\in A$
, there is a priori no way to compare
![]() $[F_{a}]$
and
$[F_{a}]$
and
![]() $[F_{a^{\prime }}]$
unless we work over the substructure
$[F_{a^{\prime }}]$
unless we work over the substructure
![]() ${\mathcal{S}}\langle a,a^{\prime }\rangle$
; given another definable set
${\mathcal{S}}\langle a,a^{\prime }\rangle$
; given another definable set
![]() $G$
with
$G$
with
 $A=G_{\text{VF}}$
, the corresponding definable function
$A=G_{\text{VF}}$
, the corresponding definable function
![]() $\boldsymbol{G}$
is the same as
$\boldsymbol{G}$
is the same as
![]() $\boldsymbol{F}$
if
$\boldsymbol{F}$
if
 $\boldsymbol{G}(a)=\boldsymbol{F}(a)$
over
$\boldsymbol{G}(a)=\boldsymbol{F}(a)$
over
![]() ${\mathcal{S}}\langle a\rangle$
for all
${\mathcal{S}}\langle a\rangle$
for all
![]() $a\in A$
. The set of all such functions is denoted by
$a\in A$
. The set of all such functions is denoted by
 $\text{FN}_{+}(A)$
, which is a semimodule over
$\text{FN}_{+}(A)$
, which is a semimodule over
 $\mathbf{K}_{+}\text{RV}[\ast ]/\operatorname{I}_{\text{sp}}$
. Let
$\mathbf{K}_{+}\text{RV}[\ast ]/\operatorname{I}_{\text{sp}}$
. Let
![]() $E\subseteq [n]$
be a nonempty set. Then, for each
$E\subseteq [n]$
be a nonempty set. Then, for each
 $a\in \operatorname{pr}_{E}(A)$
, the definable function in
$a\in \operatorname{pr}_{E}(A)$
, the definable function in
 $\text{FN}_{+}(A_{a})$
represented by
$\text{FN}_{+}(A_{a})$
represented by
![]() $F_{a}$
is denoted by
$F_{a}$
is denoted by
![]() $\boldsymbol{F}_{a}$
.
$\boldsymbol{F}_{a}$
.
Let
 $\mathbb{L}F=\bigcup _{a\in A}a\times F_{a}^{\sharp }$
and then set
$\mathbb{L}F=\bigcup _{a\in A}a\times F_{a}^{\sharp }$
and then set
 $\int _{+A}\boldsymbol{F}=\int _{+}[\mathbb{L}F]$
, which, by Proposition 5.39 and compactness, does not depend on the representative
$\int _{+A}\boldsymbol{F}=\int _{+}[\mathbb{L}F]$
, which, by Proposition 5.39 and compactness, does not depend on the representative
![]() $F$
. Thus there is a canonical homomorphism of semimodules:
$F$
. Thus there is a canonical homomorphism of semimodules:
 $$\begin{eqnarray}\int _{+A}:\text{FN}_{+}(A)\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]/\text{I}_{\text{sp}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{+A}:\text{FN}_{+}(A)\longrightarrow \mathbf{K}_{+}\text{RV}[\ast ]/\text{I}_{\text{sp}}.\end{eqnarray}$$
Theorem 5.42. For all
 $\boldsymbol{F}\in \text{FN}_{+}(A)$
and all nonempty sets
$\boldsymbol{F}\in \text{FN}_{+}(A)$
and all nonempty sets
 $E,E^{\prime }\subseteq [n]$
,
$E,E^{\prime }\subseteq [n]$
,
 $$\begin{eqnarray}\int _{+a\in \operatorname{pr}_{E}(A)}\int _{+A_{a}}\boldsymbol{F}_{a}=\int _{+a\in \operatorname{pr}_{E^{\prime }}(A)}\int _{+A_{a}}\boldsymbol{F}_{a}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{+a\in \operatorname{pr}_{E}(A)}\int _{+A_{a}}\boldsymbol{F}_{a}=\int _{+a\in \operatorname{pr}_{E^{\prime }}(A)}\int _{+A_{a}}\boldsymbol{F}_{a}.\end{eqnarray}$$
Proof. This is clear since both sides equal
![]() $\int _{+A}\boldsymbol{F}$
.◻
$\int _{+A}\boldsymbol{F}$
.◻