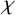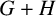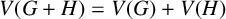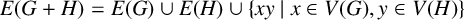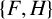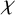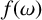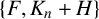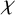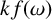1. Introduction
Throughout this paper, all graphs have finite vertex sets and no loops or parallel edges. We follow [Reference Bondy and Murty1] for undefined notation and terminology.
We say that a graph G contains a graph H if some induced subgraph of G is isomorphic to H. A graph is H-free if it does not contain H. When
![]() $\mathcal {H}$
is a set of graphs, G is
$\mathcal {H}$
is a set of graphs, G is
![]() $\mathcal {H}$
-free if G contains no graph of
$\mathcal {H}$
-free if G contains no graph of
![]() $\mathcal {H}$
. A class of graphs
$\mathcal {H}$
. A class of graphs
![]() $\mathcal {G}$
is called hereditary if every induced subgraph of any graph in
$\mathcal {G}$
is called hereditary if every induced subgraph of any graph in
![]() $\mathcal {G}$
also belongs to
$\mathcal {G}$
also belongs to
![]() $\mathcal {G}$
. One important and well-studied class of hereditary graphs is the family of
$\mathcal {G}$
. One important and well-studied class of hereditary graphs is the family of
![]() $\mathcal {H}$
-free graphs.
$\mathcal {H}$
-free graphs.
Let G be a graph and X be a subset of
![]() $V(G)$
. We use
$V(G)$
. We use
![]() $G[X]$
to denote the subgraph of G induced by X, and call X a clique (independent set) if
$G[X]$
to denote the subgraph of G induced by X, and call X a clique (independent set) if
![]() $G[X]$
is a complete graph. The clique number
$G[X]$
is a complete graph. The clique number
![]() $\omega (G)$
of G is the maximum size taken over all cliques of G (we sometimes simply write
$\omega (G)$
of G is the maximum size taken over all cliques of G (we sometimes simply write
![]() $\omega (X)$
for
$\omega (X)$
for
![]() $\omega (G[X])$
). If
$\omega (G[X])$
). If
![]() $v\in V(G)$
, we denote the set of neighbours of a vertex v by
$v\in V(G)$
, we denote the set of neighbours of a vertex v by
![]() $N(v)$
or
$N(v)$
or
![]() $N_G(v)$
. For
$N_G(v)$
. For
![]() $X\subseteq V(G)$
, let
$X\subseteq V(G)$
, let
(We omit the subscript G if there is no ambiguity.)
Let G and H be two vertex disjoint graphs. The union
![]() $G\cup H$
is the graph with vertex set
$G\cup H$
is the graph with vertex set
![]() $V(G)\cup V(H)$
and edge set
$V(G)\cup V(H)$
and edge set
![]() $E(G)\cup E(H)$
. The join
$E(G)\cup E(H)$
. The join
![]() $G+H$
is the graph with
$G+H$
is the graph with
![]() $V(G+H)=V(G)+V(H)$
and
$V(G+H)=V(G)+V(H)$
and
![]() $E(G+H)=E(G)\cup E(H)\cup \{xy \mid x\in V(G), y\in V(H)\}$
.
$E(G+H)=E(G)\cup E(H)\cup \{xy \mid x\in V(G), y\in V(H)\}$
.
For a graph G,
![]() $\chi (G)$
denotes the chromatic number of G (we sometimes simply write
$\chi (G)$
denotes the chromatic number of G (we sometimes simply write
![]() $\chi (X)$
for
$\chi (X)$
for
![]() $\chi (G[X])$
). Erdős [Reference Erdős9] showed that for any n, there exists a triangle-free graph with chromatic number at least n. Hence, in general, there exists no function of
$\chi (G[X])$
). Erdős [Reference Erdős9] showed that for any n, there exists a triangle-free graph with chromatic number at least n. Hence, in general, there exists no function of
![]() $\omega (G)$
that gives an upper bound on
$\omega (G)$
that gives an upper bound on
![]() $\chi (G)$
for all graphs G. We denote by
$\chi (G)$
for all graphs G. We denote by
![]() $\mathbb {N}$
the set of all positive integers. A class of graphs
$\mathbb {N}$
the set of all positive integers. A class of graphs
![]() $\mathcal {G}$
is said to be
$\mathcal {G}$
is said to be
![]() $\chi $
-bounded if there is a function
$\chi $
-bounded if there is a function
![]() $f:\mathbb {N}\to \mathbb {N}$
(called a
$f:\mathbb {N}\to \mathbb {N}$
(called a
![]() $\chi $
-binding function) such that
$\chi $
-binding function) such that
![]() $\chi (G)\leq f(\omega (G))$
for every graph
$\chi (G)\leq f(\omega (G))$
for every graph
![]() $G\in \mathcal {G}$
; and the class is polynomially
$G\in \mathcal {G}$
; and the class is polynomially
![]() $\chi $
-bounded if f can be taken to be a polynomial.
$\chi $
-bounded if f can be taken to be a polynomial.
A graph G is perfect if
![]() $\chi (H)=\omega (H)$
for each induced subgraph H of G. Perfect graphs are a well-known hereditary
$\chi (H)=\omega (H)$
for each induced subgraph H of G. Perfect graphs are a well-known hereditary
![]() $\chi $
-bounded graph class, that is, a class of graphs for which the identity function is a
$\chi $
-bounded graph class, that is, a class of graphs for which the identity function is a
![]() $\chi $
-binding function. A hole in a graph is an induced subgraph which is a cycle of length at least four, and a hole is even or odd according to whether its length is even or odd. An antihole of a graph G is an induced subgraph of G whose complement graph is a cycle of length at least four. Chudnovsky et al. [Reference Chudnovsky, Robertson, Seymour and Thomas4] characterised perfect graphs as the class of
$\chi $
-binding function. A hole in a graph is an induced subgraph which is a cycle of length at least four, and a hole is even or odd according to whether its length is even or odd. An antihole of a graph G is an induced subgraph of G whose complement graph is a cycle of length at least four. Chudnovsky et al. [Reference Chudnovsky, Robertson, Seymour and Thomas4] characterised perfect graphs as the class of
![]() $\{\text {odd hole, odd antihole}\}$
-free graphs, a result known as the strong perfect graph theorem.
$\{\text {odd hole, odd antihole}\}$
-free graphs, a result known as the strong perfect graph theorem.
One important research direction in the area of
![]() $\chi $
-boundedness is to determine graph families
$\chi $
-boundedness is to determine graph families
![]() $\mathcal {H}$
such that the class of
$\mathcal {H}$
such that the class of
![]() $\mathcal {H}$
-free graphs is
$\mathcal {H}$
-free graphs is
![]() $\chi $
-bounded, as well as finding the smallest possible
$\chi $
-bounded, as well as finding the smallest possible
![]() $\chi $
-binding function for such a hereditary class of graphs. Gyárfás [Reference Gyárfás15] and Sumner [Reference Sumner and Chartrand32] independently reported the following conjecture.
$\chi $
-binding function for such a hereditary class of graphs. Gyárfás [Reference Gyárfás15] and Sumner [Reference Sumner and Chartrand32] independently reported the following conjecture.
Conjecture 1.1 [Reference Gyárfás15, Reference Sumner and Chartrand32]
For every forest F, the class of F-free graphs is
![]() $\chi $
-bounded.
$\chi $
-bounded.
This conjecture remains open in general, though it has been proved for some very restricted trees (see, for example, [Reference Chudnovsky, Scott and Seymour5, Reference Gyárfás15–Reference Kierstead and Zhu18, Reference Scott23, Reference Scott and Seymour25]).
For any positive integer t, we use
![]() $P_t$
to denote a t-vertex path. It is known that
$P_t$
to denote a t-vertex path. It is known that
![]() $P_3$
-free graphs are disjoint unions of complete graphs and
$P_3$
-free graphs are disjoint unions of complete graphs and
![]() $P_4$
-free graphs are perfect [Reference Seinsche31]. From [Reference Gravier, Hoàng and Maffray14] (see also [Reference Esperet, Lemoine, Maffray and Morel13]), every
$P_4$
-free graphs are perfect [Reference Seinsche31]. From [Reference Gravier, Hoàng and Maffray14] (see also [Reference Esperet, Lemoine, Maffray and Morel13]), every
![]() $P_5$
-free graph G with
$P_5$
-free graph G with
![]() $\omega (G)\geq 3$
satisfies
$\omega (G)\geq 3$
satisfies
![]() $\chi (G) \leq 5\cdot 3^{\omega (G)-3}$
, and a recent result of Scott et al. [Reference Scott, Seymour and Spirkl30] states that every
$\chi (G) \leq 5\cdot 3^{\omega (G)-3}$
, and a recent result of Scott et al. [Reference Scott, Seymour and Spirkl30] states that every
![]() $P_5$
-free graph G satisfies
$P_5$
-free graph G satisfies
![]() ${\chi (G) \leq \omega (G)^{\log _2\omega (G)}}$
. In general, Gyárfás [Reference Gyárfás15] showed that
${\chi (G) \leq \omega (G)^{\log _2\omega (G)}}$
. In general, Gyárfás [Reference Gyárfás15] showed that
![]() $\chi (G) \leq (t-1)^{\omega (G)-1}$
for all
$\chi (G) \leq (t-1)^{\omega (G)-1}$
for all
![]() $P_t$
-free graphs. This upper bound was improved to
$P_t$
-free graphs. This upper bound was improved to
![]() $\chi (G) \leq (t-2)^{\omega (G)-1}$
in [Reference Gravier, Hoàng and Maffray14].
$\chi (G) \leq (t-2)^{\omega (G)-1}$
in [Reference Gravier, Hoàng and Maffray14].
To support Conjecture 1.1, one approach is to continuously expand the known graph classes which are
![]() $\chi $
-bounded. We state three recent results of Chudnovsky et al. [Reference Chudnovsky, Scott, Seymour and Spirkl6], Wu and Xu [Reference Wu and Xu34], and Schiermeyer and Randerath [Reference Schiermeyer and Randerath22].
$\chi $
-bounded. We state three recent results of Chudnovsky et al. [Reference Chudnovsky, Scott, Seymour and Spirkl6], Wu and Xu [Reference Wu and Xu34], and Schiermeyer and Randerath [Reference Schiermeyer and Randerath22].
Theorem 1.2 [Reference Chudnovsky, Scott, Seymour and Spirkl6, Theorem 1.3]
Let F be a forest. If F-free graphs are polynomially
![]() $\chi $
-bounded, then
$\chi $
-bounded, then
![]() $\{F\cup P_4\}$
-free graphs are polynomially
$\{F\cup P_4\}$
-free graphs are polynomially
![]() $\chi $
-bounded.
$\chi $
-bounded.
Theorem 1.3 [Reference Wu and Xu34, Theorem 1.1]
Let H be a connected graph or the union of a connected graph and an isolated vertex with
![]() $|V(H)|\ge 3$
, and let G be a connected
$|V(H)|\ge 3$
, and let G be a connected
![]() $\{P_5,K_1+H\}$
-free graph. If
$\{P_5,K_1+H\}$
-free graph. If
![]() $\{P_5,H\}$
-free graphs have a
$\{P_5,H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $f(\omega )$
, then
$f(\omega )$
, then
![]() $\{P_5, K_1+H\}$
-free graphs have a
$\{P_5, K_1+H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $kf(\omega )$
for some constant k.
$kf(\omega )$
for some constant k.
Theorem 1.4 [Reference Schiermeyer and Randerath22, Theorem 33]
Let G be a
![]() $\{P_k, \text {gem}\}$
-free graph for
$\{P_k, \text {gem}\}$
-free graph for
![]() $k\ge 4$
with clique number
$k\ge 4$
with clique number
![]() $\omega (G)\ge 2$
. Then,
$\omega (G)\ge 2$
. Then,
![]() $\chi (G)\le (k-2)(\omega (G)-1)$
.
$\chi (G)\le (k-2)(\omega (G)-1)$
.
We refer to a graph that contains at least one vertex as a nonnull graph. Using the idea of [Reference Schiermeyer and Randerath22, Theorem 33], we generalise the results of Wu and Xu [Reference Wu and Xu34], and Schiermeyer and Randerath [Reference Schiermeyer and Randerath22].
Theorem 1.5. For any finite linear forest F and any nonnull graph H, if
![]() $\{F, H\}$
-free graphs have a
$\{F, H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $f(\omega )$
, then
$f(\omega )$
, then
![]() $\{F, K_n+H\}$
-free graphs have a
$\{F, K_n+H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $kf(\omega )$
for some constant k.
$kf(\omega )$
for some constant k.
We derive Theorem 1.5 from the following theorem.
Theorem 1.6. For any integers
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $t \geq 4$
, if H is a nonnull graph and
$t \geq 4$
, if H is a nonnull graph and
![]() $\{P_t, H\}$
-free graphs have a
$\{P_t, H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $f(\omega )$
, then
$f(\omega )$
, then
![]() $\{P_t, K_n+H\}$
-free graphs have a
$\{P_t, K_n+H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $(t-2)^{n+1}f(\omega )$
.
$(t-2)^{n+1}f(\omega )$
.
2. The main proof
The aim of this section is to prove Theorems 1.6 and 1.5. Following a proof idea in [Reference Schiermeyer and Randerath22], we first establish a lemma which generalises a result of Schiermeyer and Randerath [Reference Schiermeyer and Randerath22].
Lemma 2.1. Let
![]() $t \geq 4$
be an integer and G be a
$t \geq 4$
be an integer and G be a
![]() $P_t$
-free graph with
$P_t$
-free graph with
![]() $\omega (G)\geq 2$
. If there exists a function
$\omega (G)\geq 2$
. If there exists a function
![]() $\phi :\mathbb {N}\to \mathbb {N}$
such that
$\phi :\mathbb {N}\to \mathbb {N}$
such that
![]() $\phi (x)\geq x$
and
$\phi (x)\geq x$
and
![]() $\chi (N(v)) \leq \phi (\omega (G)-1)$
for every vertex v of G, then
$\chi (N(v)) \leq \phi (\omega (G)-1)$
for every vertex v of G, then
![]() $\chi (G)\leq (t-2)\phi (\omega (G)-1)$
.
$\chi (G)\leq (t-2)\phi (\omega (G)-1)$
.
Proof. We proceed by induction on t. It is known that
![]() $P_4$
-free graphs are perfect. Therefore,
$P_4$
-free graphs are perfect. Therefore,
![]() $\chi (G)=\omega (G)\leq 2\omega (G)-2\leq 2 \phi (\omega (G)-1)$
if
$\chi (G)=\omega (G)\leq 2\omega (G)-2\leq 2 \phi (\omega (G)-1)$
if
![]() $t=4$
. Now, for some fixed
$t=4$
. Now, for some fixed
![]() ${t\ge 4}$
, suppose that
${t\ge 4}$
, suppose that
![]() $(t-2)\phi (\omega (G)-1)$
is a
$(t-2)\phi (\omega (G)-1)$
is a
![]() $\chi $
-binding function for all
$\chi $
-binding function for all
![]() $P_t$
-free graphs G. We will prove Lemma 2.1 holds for all
$P_t$
-free graphs G. We will prove Lemma 2.1 holds for all
![]() $P_{t+1}$
-free graphs to complete our proof.
$P_{t+1}$
-free graphs to complete our proof.
Let G be a
![]() $P_{t+1}$
-free graph. Without loss of generality, G is connected. Assuming that
$P_{t+1}$
-free graph. Without loss of generality, G is connected. Assuming that
![]() $\chi (G)> ((t+1)-2) \phi (\omega (G)-1)$
, we shall reach a contradiction by constructing an induced
$\chi (G)> ((t+1)-2) \phi (\omega (G)-1)$
, we shall reach a contradiction by constructing an induced
![]() $(t+1)$
-vertex path
$(t+1)$
-vertex path
![]() $P_{t+1}$
in G.
$P_{t+1}$
in G.
We define sets
![]() $V(G_i)\subseteq V(G_{i-1})\subseteq \cdots \subseteq V(G_1)=V(G)$
and vertices
$V(G_i)\subseteq V(G_{i-1})\subseteq \cdots \subseteq V(G_1)=V(G)$
and vertices
![]() $v_1\in V(G_1), v_2\in V(G_2), \ldots , v_i\in V(G_i)$
for all i satisfying
$v_1\in V(G_1), v_2\in V(G_2), \ldots , v_i\in V(G_i)$
for all i satisfying
![]() $1\leq i\leq t-1$
with the following properties:
$1\leq i\leq t-1$
with the following properties:
-
(1)
 $G_i$
is a connected subgraph of G;
$G_i$
is a connected subgraph of G; -
(2)
 $\chi (G_i)>(t-i)\phi (\omega (G)-1)$
; and
$\chi (G_i)>(t-i)\phi (\omega (G)-1)$
; and -
(3) if
 $1\leq j<i$
and
$1\leq j<i$
and
 $v\in V(G_i)$
, then
$v\in V(G_i)$
, then
 $v_jv$
is an edge of G if and only if
$v_jv$
is an edge of G if and only if
 $j=i-1$
and
$j=i-1$
and
 $v=v_i$
.
$v=v_i$
.
Notice that
![]() $G_1=G$
and
$G_1=G$
and
![]() $\chi (G_1)>(t-1)\phi (\omega (G)-1)$
as we have assumed. Let
$\chi (G_1)>(t-1)\phi (\omega (G)-1)$
as we have assumed. Let
![]() $v_1$
be any vertex of
$v_1$
be any vertex of
![]() $G_1$
. Assume that
$G_1$
. Assume that
![]() $G_1,G_2, \ldots ,G_i$
and
$G_1,G_2, \ldots ,G_i$
and
![]() $v_1, v_2, \ldots , v_i$
are already defined for some
$v_1, v_2, \ldots , v_i$
are already defined for some
![]() $i\leq t-1$
; moreover, properties (1)–(3) are satisfied. Define
$i\leq t-1$
; moreover, properties (1)–(3) are satisfied. Define
![]() $G_{i+1}$
and
$G_{i+1}$
and
![]() $v_{i+1}$
as follows. Let A denote the set of neighbours of
$v_{i+1}$
as follows. Let A denote the set of neighbours of
![]() $v_i$
in
$v_i$
in
![]() $G_i$
. Let
$G_i$
. Let
The graph
![]() $G[A]$
satisfies
$G[A]$
satisfies
![]() $\omega (A)\leq \omega (G)-1$
. Otherwise, adding
$\omega (A)\leq \omega (G)-1$
. Otherwise, adding
![]() $v_i$
would give a clique of cardinality
$v_i$
would give a clique of cardinality
![]() $\omega (G)+1$
. Furthermore, since
$\omega (G)+1$
. Furthermore, since
![]() $A=N_{G_i}(v_i)$
,
$A=N_{G_i}(v_i)$
,
Suppose first that
![]() $B\neq \emptyset $
. Then,
$B\neq \emptyset $
. Then,
![]() $\chi (G_i)\leq \chi (A)+ \chi (B)$
. It follows that
$\chi (G_i)\leq \chi (A)+ \chi (B)$
. It follows that
 $$ \begin{align*} \chi(B) \geq \chi(G_i)-\chi(A) &> ((t+1)-1-i)\phi(\omega(G)-1)-\phi(\omega(G)- 1) \\ &=(t-(i + 1))\phi(\omega(G)- 1), \end{align*} $$
$$ \begin{align*} \chi(B) \geq \chi(G_i)-\chi(A) &> ((t+1)-1-i)\phi(\omega(G)-1)-\phi(\omega(G)- 1) \\ &=(t-(i + 1))\phi(\omega(G)- 1), \end{align*} $$
which allows us to choose a connected component H of
![]() $G[B]$
satisfying
$G[B]$
satisfying
![]() ${\chi (H)> (t-(i + 1))\phi (\omega (G)- 1)}$
. Since
${\chi (H)> (t-(i + 1))\phi (\omega (G)- 1)}$
. Since
![]() $G_i$
is connected by property (1), there exists a vertex
$G_i$
is connected by property (1), there exists a vertex
![]() $v_{i+1}\in A$
such that
$v_{i+1}\in A$
such that
![]() $V(H)\cup \{v_{i+1}\}$
induces a connected subgraph which we choose as
$V(H)\cup \{v_{i+1}\}$
induces a connected subgraph which we choose as
![]() $G_{i+1}$
. Now it is easy to check that
$G_{i+1}$
. Now it is easy to check that
![]() $G_1,G_2, \ldots ,G_{i+1}$
and
$G_1,G_2, \ldots ,G_{i+1}$
and
![]() $v_1, v_2, \ldots , v_{i+1}$
satisfy the requirements in properties (1)–(3).
$v_1, v_2, \ldots , v_{i+1}$
satisfy the requirements in properties (1)–(3).
Suppose now that
![]() $B=\emptyset $
. Then
$B=\emptyset $
. Then
![]() $\chi (G_i)\leq \phi (\omega (G)- 1)$
, which in turn implies that
$\chi (G_i)\leq \phi (\omega (G)- 1)$
, which in turn implies that
![]() ${(t-i)\phi (\omega (G)- 1) < \chi (G_i)\leq \phi (\omega (G)- 1)}$
. It follows that
${(t-i)\phi (\omega (G)- 1) < \chi (G_i)\leq \phi (\omega (G)- 1)}$
. It follows that
![]() $i=t$
.
$i=t$
.
Since
![]() $A\neq \emptyset $
by properties (1) and (2) of
$A\neq \emptyset $
by properties (1) and (2) of
![]() $G_i$
,
$G_i$
,
![]() $v_{t+1}$
can be defined as any vertex of A, that is to say,
$v_{t+1}$
can be defined as any vertex of A, that is to say,
![]() $G[\{v_1,v_2,\ldots ,v_{t+1}\}]$
is an induced
$G[\{v_1,v_2,\ldots ,v_{t+1}\}]$
is an induced
![]() $(t+1)$
-vertex path
$(t+1)$
-vertex path
![]() $P_{t+1}$
in G, which is a contradiction. This completes the proof of Lemma 2.1.
$P_{t+1}$
in G, which is a contradiction. This completes the proof of Lemma 2.1.
Proof of Theorem 1.6
We proceed by induction on n. For a fixed integer
![]() $t\ge 4$
, since
$t\ge 4$
, since
![]() $\{P_t, H\}$
-free graphs have a
$\{P_t, H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $f(\omega )$
, Theorem 1.6 holds when
$f(\omega )$
, Theorem 1.6 holds when
![]() $n=0$
. We may assume that
$n=0$
. We may assume that
![]() $\{P_t, K_{n-1}+H\}$
-free graphs have a
$\{P_t, K_{n-1}+H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() ${(t-2)^nf(\omega )}$
. Now, let G be a
${(t-2)^nf(\omega )}$
. Now, let G be a
![]() $\{P_t, K_{n}+H\}$
-free graph. Since G is
$\{P_t, K_{n}+H\}$
-free graph. Since G is
![]() $\{P_t, K_{n}+H\}$
-free,
$\{P_t, K_{n}+H\}$
-free,
![]() $G[N(v)]$
is
$G[N(v)]$
is
![]() $\{P_t, K_{n-1}+H\}$
-free for every vertex v of G. Therefore, there exists a function
$\{P_t, K_{n-1}+H\}$
-free for every vertex v of G. Therefore, there exists a function
![]() $(t-2)^nf:\mathbb {N}\to \mathbb {N}$
such that
$(t-2)^nf:\mathbb {N}\to \mathbb {N}$
such that
![]() $(t-2)^nf(x)\geq x$
and
$(t-2)^nf(x)\geq x$
and
![]() ${\chi (N(v)) \leq (t-2)^nf(\omega (G)-1)}$
for every vertex v of G. By Lemma 2.1,
${\chi (N(v)) \leq (t-2)^nf(\omega (G)-1)}$
for every vertex v of G. By Lemma 2.1,
![]() $\chi (G)\leq (t-2)(t-2)^nf(\omega (G)-1)= (t-2)^{n+1}f(\omega (G)-1).$
This proves Theorem 1.6.
$\chi (G)\leq (t-2)(t-2)^nf(\omega (G)-1)= (t-2)^{n+1}f(\omega (G)-1).$
This proves Theorem 1.6.
Using Theorem 1.6 as the induction base, we next prove Theorem 1.5 by induction on the number of paths contained in F.
Proof of Theorem 1.5
With the same arguments as in Theorem 1.6, it suffices to prove that
![]() $\{F, K_1+H\}$
-free graphs have a
$\{F, K_1+H\}$
-free graphs have a
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $kf(\omega )$
for some constant k.
$kf(\omega )$
for some constant k.
Let G be an
![]() $\{F, K_1+H\}$
-free graph. Since F is a finite linear forest, we may assume that F consists of m vertex disjoint paths. We proceed by induction on m. If
$\{F, K_1+H\}$
-free graph. Since F is a finite linear forest, we may assume that F consists of m vertex disjoint paths. We proceed by induction on m. If
![]() $m=1$
, by Theorem 1.6, we are done. Suppose Theorem 1.5 holds for any positive integer
$m=1$
, by Theorem 1.6, we are done. Suppose Theorem 1.5 holds for any positive integer
![]() $m'<m$
. Choose any path in F such that this path is a component of F, say P. Consequently, we assume that
$m'<m$
. Choose any path in F such that this path is a component of F, say P. Consequently, we assume that
![]() $|V(P)|=h$
.
$|V(P)|=h$
.
For each vertex
![]() $v\in V(P)$
, the graph
$v\in V(P)$
, the graph
![]() $G[N(v)]$
is
$G[N(v)]$
is
![]() $\{F, H\}$
-free and thus
$\{F, H\}$
-free and thus
![]() ${\chi (N(v))\le f(\omega (G))}$
. So,
${\chi (N(v))\le f(\omega (G))}$
. So,
![]() $\chi (N(V(P)))\le hf(\omega (G))$
. By the induction hypothesis, there exists an integer
$\chi (N(V(P)))\le hf(\omega (G))$
. By the induction hypothesis, there exists an integer
![]() $k'$
such that
$k'$
such that
![]() ${\chi (G\setminus (V(P)\cup N(V(P))))\le k'f(\omega (G))}$
. Therefore,
${\chi (G\setminus (V(P)\cup N(V(P))))\le k'f(\omega (G))}$
. Therefore,
![]() $\chi (G)\le (k'+h)f(\omega (G))$
. This proves Theorem 1.5.
$\chi (G)\le (k'+h)f(\omega (G))$
. This proves Theorem 1.5.
3. Remarks
In most cases, proofs of
![]() $\chi $
-boundedness give fairly fast-growing functions, so it is interesting to ask: when do we get the stronger property of polynomial
$\chi $
-boundedness give fairly fast-growing functions, so it is interesting to ask: when do we get the stronger property of polynomial
![]() $\chi $
-boundedness? A provocative conjecture of Esperet [Reference Esperet12] asserted that every
$\chi $
-boundedness? A provocative conjecture of Esperet [Reference Esperet12] asserted that every
![]() $\chi $
-bounded hereditary class is polynomially
$\chi $
-bounded hereditary class is polynomially
![]() $\chi $
-bounded, but this was recently disproved by Briański et al. [Reference Briański, Davies and Walczak2]. So the question now is: which hereditary classes are polynomially
$\chi $
-bounded, but this was recently disproved by Briański et al. [Reference Briański, Davies and Walczak2]. So the question now is: which hereditary classes are polynomially
![]() $\chi $
-bounded? For any tree T, perhaps every T-free graph is polynomially
$\chi $
-bounded? For any tree T, perhaps every T-free graph is polynomially
![]() $\chi $
-bounded. Scott et al. [Reference Scott, Seymour and Spirkl28] proved that if T contains no
$\chi $
-bounded. Scott et al. [Reference Scott, Seymour and Spirkl28] proved that if T contains no
![]() $P_5$
, then every T-free graph is polynomially
$P_5$
, then every T-free graph is polynomially
![]() $\chi $
-bounded. We refer to [Reference Chudnovsky, Scott, Seymour and Spirkl6, Reference Chudnovsky, Scott, Seymour and Spirkl7, Reference Liu, Schroeder, Wang and Yu19, Reference Scott and Seymour26–Reference Scott, Seymour and Spirkl30] for some recent results and to [Reference Randerath and Schiermeyer20, Reference Schiermeyer and Randerath22, Reference Scott and Seymour24] for some surveys about topics related to
$\chi $
-bounded. We refer to [Reference Chudnovsky, Scott, Seymour and Spirkl6, Reference Chudnovsky, Scott, Seymour and Spirkl7, Reference Liu, Schroeder, Wang and Yu19, Reference Scott and Seymour26–Reference Scott, Seymour and Spirkl30] for some recent results and to [Reference Randerath and Schiermeyer20, Reference Schiermeyer and Randerath22, Reference Scott and Seymour24] for some surveys about topics related to
![]() $\chi $
-boundedness.
$\chi $
-boundedness.
Actually, if a
![]() $\chi $
-binding function is polynomial, it has another very important consequence. Graph classes with polynomial
$\chi $
-binding function is polynomial, it has another very important consequence. Graph classes with polynomial
![]() $\chi $
-binding functions satisfy the Erdős–Hajnal conjecture [Reference Erdős and Hajnal10, Reference Erdős and Hajnal11].
$\chi $
-binding functions satisfy the Erdős–Hajnal conjecture [Reference Erdős and Hajnal10, Reference Erdős and Hajnal11].
Conjecture 3.1 (Erdős–Hajnal conjecture)
For every graph H, there exists some
![]() $\epsilon>0$
such that each H-free graph G has a clique or an independent set of size at least
$\epsilon>0$
such that each H-free graph G has a clique or an independent set of size at least
![]() $|G|^\epsilon $
.
$|G|^\epsilon $
.
The problem of finding a polynomial
![]() $\chi $
-binding function for the class of
$\chi $
-binding function for the class of
![]() $P_5$
-free graphs is still open, and the problem is open even for the class of
$P_5$
-free graphs is still open, and the problem is open even for the class of
![]() $\{P_5,C_5\}$
-free graphs (mentioned in [Reference Char and Karthick3]). The best known result is an exponential upper bound,
$\{P_5,C_5\}$
-free graphs (mentioned in [Reference Char and Karthick3]). The best known result is an exponential upper bound,
![]() $2^{\omega (G)-1}$
, due to Chudnovsky and Sivaraman [Reference Chudnovsky and Sivaraman8]). The following well-known problem is proposed by Schiermeyer [Reference Schiermeyer21].
$2^{\omega (G)-1}$
, due to Chudnovsky and Sivaraman [Reference Chudnovsky and Sivaraman8]). The following well-known problem is proposed by Schiermeyer [Reference Schiermeyer21].
Problem 3.2 [Reference Schiermeyer21]
Are there polynomial functions
![]() $f_{p_k}$
for
$f_{p_k}$
for
![]() $k\ge 5$
such that
$k\ge 5$
such that
![]() ${\chi (G)\le f_{p_k}(\omega (G))}$
for every
${\chi (G)\le f_{p_k}(\omega (G))}$
for every
![]() $P_k$
-free graph G?
$P_k$
-free graph G?
According to Theorem 1.6, we can directly derive the following result.
Theorem 3.3. For any integers
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $t \geq 4$
, if H is a nonnull graph and
$t \geq 4$
, if H is a nonnull graph and
![]() $\{P_t, H\}$
-free graphs have a polynomial
$\{P_t, H\}$
-free graphs have a polynomial
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $f(\omega )$
, then
$f(\omega )$
, then
![]() $\{P_t, K_n+H\}$
-free graphs have a polynomial
$\{P_t, K_n+H\}$
-free graphs have a polynomial
![]() $\chi $
-binding function
$\chi $
-binding function
![]() $(t-2)^{n+1}f(\omega )$
.
$(t-2)^{n+1}f(\omega )$
.
Theorem 3.3 has some interesting corollaries. We use
![]() $M_s$
to denote the disjoint union of s edges. A friendship graph
$M_s$
to denote the disjoint union of s edges. A friendship graph
![]() $F_s$
is the graph
$F_s$
is the graph
![]() $K_1+M_s$
(see Figure 1). We give a polynomial
$K_1+M_s$
(see Figure 1). We give a polynomial
![]() $\chi $
-binding function for
$\chi $
-binding function for
![]() $\{P_t, K_n+F_s\}$
-free graphs. We first introduce the following result of Wagon [Reference Wagon33].
$\{P_t, K_n+F_s\}$
-free graphs. We first introduce the following result of Wagon [Reference Wagon33].

Figure 1 Graph
![]() $F_2$
.
$F_2$
.
Lemma 3.4 [Reference Wagon33]
For every
![]() $s\in \mathbb {N}$
, every
$s\in \mathbb {N}$
, every
![]() $M_s$
-free graph G satisfies
$M_s$
-free graph G satisfies
![]() $\chi (G)\leq \omega (G)^{2s-2}$
.
$\chi (G)\leq \omega (G)^{2s-2}$
.
Then we have the following corollary of Theorem 3.3.
Corollary 3.5. Let
![]() $n\ge 0,s\geq 1$
and
$n\ge 0,s\geq 1$
and
![]() $t \geq 4$
be integers. Let G be a
$t \geq 4$
be integers. Let G be a
![]() $\{P_t, K_n+F_s\}$
-free graph. Then
$\{P_t, K_n+F_s\}$
-free graph. Then
![]() $\chi (G)\leq (t-2)^{n+1}(\omega (G)-1)^{2s-2}$
.
$\chi (G)\leq (t-2)^{n+1}(\omega (G)-1)^{2s-2}$
.
Proof. Let H be a
![]() $\{P_t, F_s\}$
-free graph and
$\{P_t, F_s\}$
-free graph and
![]() $\phi (x)=x^{2s-2}$
. Since H is
$\phi (x)=x^{2s-2}$
. Since H is
![]() $F_s$
-free,
$F_s$
-free,
![]() $H[N(v)]$
is
$H[N(v)]$
is
![]() $M_s$
-free for any vertex v of H; moreover,
$M_s$
-free for any vertex v of H; moreover,
![]() $\omega (H[N(v)])\leq \omega (H)-1$
. From Lemma 3.4,
$\omega (H[N(v)])\leq \omega (H)-1$
. From Lemma 3.4,
for every vertex v of H. Therefore, from Lemma 2.1,
By Theorem 1.6,
![]() $\chi (G)\leq (t-2)^{n+1}(\omega (G)-1)^{2s-2} $
if G is a
$\chi (G)\leq (t-2)^{n+1}(\omega (G)-1)^{2s-2} $
if G is a
![]() $\{P_t, K_n+F_s\}$
-free graph. This completes the proof of Corollary 3.5.
$\{P_t, K_n+F_s\}$
-free graph. This completes the proof of Corollary 3.5.