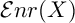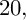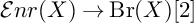1 Introduction
Let S be a complex Enriques surface, and let
![]() $\pi \colon X\to S$
be its K3 étale double cover. J.-L. Colliot-Thélène asked whether the induced map of Brauer groups
$\pi \colon X\to S$
be its K3 étale double cover. J.-L. Colliot-Thélène asked whether the induced map of Brauer groups
![]() $\pi ^*\colon \mathrm {{Br}}(S)\simeq {\mathbb Z}/2\to \mathrm {{Br}}(X)$
is injective or zeroFootnote
1
. Beauville has given a necessary and sufficient condition for the injectivity of
$\pi ^*\colon \mathrm {{Br}}(S)\simeq {\mathbb Z}/2\to \mathrm {{Br}}(X)$
is injective or zeroFootnote
1
. Beauville has given a necessary and sufficient condition for the injectivity of
![]() $\pi ^*$
[Reference BeauvilleB, Cor. 5.7] and showed that the Enriques surfaces S for which this map is zero form a countable union of hypersurfaces in the moduli space of Enriques surfaces [Reference BeauvilleB, Cor. 6.5]. Enriques surfaces with injective
$\pi ^*$
[Reference BeauvilleB, Cor. 5.7] and showed that the Enriques surfaces S for which this map is zero form a countable union of hypersurfaces in the moduli space of Enriques surfaces [Reference BeauvilleB, Cor. 6.5]. Enriques surfaces with injective
![]() $\pi ^*$
are used in explicit constructions of Enriques surfaces over
$\pi ^*$
are used in explicit constructions of Enriques surfaces over
![]() ${\mathbb Q}$
for which the Brauer–Manin obstruction fails to control weak approximation [Reference Harari and SkorobogatovHS1] and the Hasse principle [Reference Várilly-Alvarado and VirayVV]). Enriques surfaces over
${\mathbb Q}$
for which the Brauer–Manin obstruction fails to control weak approximation [Reference Harari and SkorobogatovHS1] and the Hasse principle [Reference Várilly-Alvarado and VirayVV]). Enriques surfaces over
![]() ${\mathbb Q}$
such that the map
${\mathbb Q}$
such that the map
![]() $\pi ^*$
is zero have been constructed in [Reference Hulek and SchüttHS2, Reference Garbagnati and SchüttGS].
$\pi ^*$
is zero have been constructed in [Reference Hulek and SchüttHS2, Reference Garbagnati and SchüttGS].
From a different perspective, one can start with a K3 surface X and consider the set
![]() $\mathcal F(X)\subset \mathrm {Aut}(X)$
of fixed point free involutions
$\mathcal F(X)\subset \mathrm {Aut}(X)$
of fixed point free involutions
![]() $\sigma \colon X\to X$
, which are precisely the involutions such that the quotient
$\sigma \colon X\to X$
, which are precisely the involutions such that the quotient
![]() $X/\sigma $
is an Enriques surface.
$X/\sigma $
is an Enriques surface.
In this paper, we are interested in the map
which sends
![]() $\sigma \in \mathcal F(X)$
to
$\sigma \in \mathcal F(X)$
to
![]() $\pi ^*(b_S)$
, where
$\pi ^*(b_S)$
, where
![]() $\pi \colon X\to X/\sigma =S$
is the quotient morphism, and
$\pi \colon X\to X/\sigma =S$
is the quotient morphism, and
![]() $b_S$
is the unique nonzero element of
$b_S$
is the unique nonzero element of
![]() $\mathrm {{Br}}(S)$
. A combination of results of Beauville and of Keum and Ohashi show that
$\mathrm {{Br}}(S)$
. A combination of results of Beauville and of Keum and Ohashi show that
![]() $\mathrm {{Im}}(\Phi _X)$
depends only on the isomorphism class of the transcendental lattice
$\mathrm {{Im}}(\Phi _X)$
depends only on the isomorphism class of the transcendental lattice
![]() $T(X)$
of X (see Corollary 2.6). A description of all lattices
$T(X)$
of X (see Corollary 2.6). A description of all lattices
![]() $T(X)$
such that
$T(X)$
such that
![]() ${\mathcal F}(X)\neq \emptyset $
can be found in [Reference Brandhorst, Sonel and VenianiBSV, Th. 1.6].
${\mathcal F}(X)\neq \emptyset $
can be found in [Reference Brandhorst, Sonel and VenianiBSV, Th. 1.6].
Let
![]() ${\mathcal Enr}(X)$
be the set of Enriques quotients of X, considered up to isomorphism of varieties. Equivalently,
${\mathcal Enr}(X)$
be the set of Enriques quotients of X, considered up to isomorphism of varieties. Equivalently,
![]() ${\mathcal Enr}(X)$
is the set of conjugacy classes of
${\mathcal Enr}(X)$
is the set of conjugacy classes of
![]() $\mathrm {Aut}(X)$
contained in
$\mathrm {Aut}(X)$
contained in
![]() $\mathcal F(X)$
(see [Reference OhashiO1, Prop. 2.1]). Ohashi proved that the set
$\mathcal F(X)$
(see [Reference OhashiO1, Prop. 2.1]). Ohashi proved that the set
![]() ${\mathcal Enr}(X)$
is always finite [Reference OhashiO1, Cor. 0.4] although its size is not bounded [Reference OhashiO1, Th. 0.1]. The map
${\mathcal Enr}(X)$
is always finite [Reference OhashiO1, Cor. 0.4] although its size is not bounded [Reference OhashiO1, Th. 0.1]. The map
![]() $\Phi _X$
is
$\Phi _X$
is
![]() $\mathrm { Aut}(X)$
-equivariant, where
$\mathrm { Aut}(X)$
-equivariant, where
![]() $\mathrm {Aut}(X)$
acts on
$\mathrm {Aut}(X)$
acts on
![]() $\mathcal F(X)$
by conjugation, so
$\mathcal F(X)$
by conjugation, so
![]() $\Phi _X$
descends to a map
$\Phi _X$
descends to a map
The action of
![]() $\mathrm {Aut}(X)$
on
$\mathrm {Aut}(X)$
on
![]() $\mathrm {{Br}}(X)[2]$
factors through the action of the group of Hodge isometries of the integral Hodge structure on
$\mathrm {{Br}}(X)[2]$
factors through the action of the group of Hodge isometries of the integral Hodge structure on
![]() $T(X)$
, so when
$T(X)$
, so when
![]() $\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
the action of
$\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
the action of
![]() $\mathrm {Aut}(X)$
on
$\mathrm {Aut}(X)$
on
![]() $\mathrm {{Br}}(X)[2]$
is trivial. In such a generic situation,
$\mathrm {{Br}}(X)[2]$
is trivial. In such a generic situation,
![]() $\varphi _X$
is a map
$\varphi _X$
is a map
![]() ${\mathcal Enr}(X) \to \mathrm {{Br}}(X)[2]$
. In this case, the set
${\mathcal Enr}(X) \to \mathrm {{Br}}(X)[2]$
. In this case, the set
![]() ${\mathcal Enr}(X)$
depends only on the isomorphism class of the lattice
${\mathcal Enr}(X)$
depends only on the isomorphism class of the lattice
![]() $T(X)$
(see the discussion after Theorem 2.5).
$T(X)$
(see the discussion after Theorem 2.5).
Examples show that the set
![]() ${\mathcal Enr}(X)$
can be empty or very large, so in general
${\mathcal Enr}(X)$
can be empty or very large, so in general
![]() $\varphi _X$
is neither surjective nor injective. A very general Enriques surface S (corresponding to the points of the moduli space outside a countable union of hypersurfaces) is the unique Enriques quotient of its K3 cover X; by Beauville, in this case,
$\varphi _X$
is neither surjective nor injective. A very general Enriques surface S (corresponding to the points of the moduli space outside a countable union of hypersurfaces) is the unique Enriques quotient of its K3 cover X; by Beauville, in this case,
![]() $\varphi _X({\mathcal Enr}(X))$
is a certain nonzero element of
$\varphi _X({\mathcal Enr}(X))$
is a certain nonzero element of
![]() $\mathrm {{Br}}(X)[2]$
.
$\mathrm {{Br}}(X)[2]$
.
The aim of this paper is to clarify the structure of
![]() $\Phi _X$
and
$\Phi _X$
and
![]() $\varphi _X$
in some favourable situations. Keum [Reference KeumK, Th. 2] proved that every Kummer surface is a double cover of some Enriques surface. His method can be used to prove the following.
$\varphi _X$
in some favourable situations. Keum [Reference KeumK, Th. 2] proved that every Kummer surface is a double cover of some Enriques surface. His method can be used to prove the following.
Theorem A. Let X be a Kummer surface. Then, for every
![]() $\alpha \in \mathrm {{Br}}(X)$
of order
$\alpha \in \mathrm {{Br}}(X)$
of order
![]() $2,$
there is an Enriques quotient
$2,$
there is an Enriques quotient
![]() $\pi _S\colon X\to S$
such that
$\pi _S\colon X\to S$
such that
![]() $\alpha =\pi _S^*(b_S)$
.
$\alpha =\pi _S^*(b_S)$
.
In other words, for Kummer surfaces, the set
![]() $\mathrm {{Br}}(X)[2]\setminus \{0\}$
is contained in the image of
$\mathrm {{Br}}(X)[2]\setminus \{0\}$
is contained in the image of
![]() $\Phi _X$
. As a kind of partial converse, in Corollary 2.7, we show that if X is a K3 surface such that the abelian group
$\Phi _X$
. As a kind of partial converse, in Corollary 2.7, we show that if X is a K3 surface such that the abelian group
![]() $\mathrm {{Br}}(X)[2]$
is generated by the image of
$\mathrm {{Br}}(X)[2]$
is generated by the image of
![]() $\Phi _X$
, then the transcendental lattice of X is divisible by 2 as an even lattice. We do not know if there exist Kummer surfaces such that
$\Phi _X$
, then the transcendental lattice of X is divisible by 2 as an even lattice. We do not know if there exist Kummer surfaces such that
![]() $\Phi _X^{-1}(0)$
is non-empty. At the end of §2, we give examples of non-Kummer K3 surfaces such that
$\Phi _X^{-1}(0)$
is non-empty. At the end of §2, we give examples of non-Kummer K3 surfaces such that
![]() $\mathrm {{Im}}(\Phi _X)=\{0\}$
.
$\mathrm {{Im}}(\Phi _X)=\{0\}$
.
In two generic cases, Ohashi classified all Enriques quotients of a given K3 surface. Combining Theorem A with his results [Reference OhashiO1, Th. 4.1], [Reference OhashiO2, Th. 1.1] we obtain the following corollary.
Corollary B. Let X be the Kummer surface attached to any of the following abelian surfaces:
-
(i) a product of two non-isogenous elliptic curves;
-
(ii) the Jacobian J of a curve of genus
 $2$
such that
$2$
such that
 $\mathrm {NS\,}(J)\cong {\mathbb Z}$
.
$\mathrm {NS\,}(J)\cong {\mathbb Z}$
.
Then
![]() $\varphi _X$
is a bijection between
$\varphi _X$
is a bijection between
![]() ${\mathcal Enr}(X)$
and
${\mathcal Enr}(X)$
and
![]() $\mathrm {{Br}}(X)[2]\setminus \{0\}$
.
$\mathrm {{Br}}(X)[2]\setminus \{0\}$
.
For some K3 surfaces of maximal Picard rank, the following result gives information about the fibers of
![]() $\varphi _X$
. Its proof uses a certain Galois action on
$\varphi _X$
. Its proof uses a certain Galois action on
![]() $\mathrm {{Br}}(X)[2]$
constructed by the second named author in [Reference ValloniV].
$\mathrm {{Br}}(X)[2]$
constructed by the second named author in [Reference ValloniV].
Theorem C. Let X be a K3 surface of Picard rank
![]() $20$
. Let
$20$
. Let
![]() $E={\mathbb Q}(\sqrt {-d})$
, where d is the discriminant of the transcendental lattice
$E={\mathbb Q}(\sqrt {-d})$
, where d is the discriminant of the transcendental lattice
![]() $T(X)$
. Assume that
$T(X)$
. Assume that
![]() $\mathrm {{End}}_{\mathrm {Hdg}} (T(X))$
is the ring of integers
$\mathrm {{End}}_{\mathrm {Hdg}} (T(X))$
is the ring of integers
![]() ${\mathcal O}_E\subset E$
and, moreover,
${\mathcal O}_E\subset E$
and, moreover,
![]() $2$
is inert in E and
$2$
is inert in E and
![]() $E \neq {\mathbb Q}(\sqrt {-3})$
. Then
$E \neq {\mathbb Q}(\sqrt {-3})$
. Then
![]() $\mathrm {Aut}_{\mathrm {Hdg}} (T(X))=\{\pm 1\}$
and the fibers of
$\mathrm {Aut}_{\mathrm {Hdg}} (T(X))=\{\pm 1\}$
and the fibers of
![]() $\varphi _X\colon {\mathcal Enr}(X) \to \mathrm {{Br}}(X)[2]$
above the nonzero points have the same cardinality.
$\varphi _X\colon {\mathcal Enr}(X) \to \mathrm {{Br}}(X)[2]$
above the nonzero points have the same cardinality.
The conditions in Theorem C are easy to check. Let
 $$ \begin{align*} \left(\begin{array}{cc} 2a&b\\b&2c\end{array}\right) \end{align*} $$
$$ \begin{align*} \left(\begin{array}{cc} 2a&b\\b&2c\end{array}\right) \end{align*} $$
be the Gram matrix of
![]() $T(X)$
, where
$T(X)$
, where
![]() $a,b,c\in {\mathbb Z}$
, so that
$a,b,c\in {\mathbb Z}$
, so that
![]() $-d=b^2-4ac<0$
. Write
$-d=b^2-4ac<0$
. Write
![]() $-d=f^2D$
, where
$-d=f^2D$
, where
![]() $f\in {\mathbb Z}$
and D is the discriminant of E. By [Reference ValloniV, Th. 3.2] we have
$f\in {\mathbb Z}$
and D is the discriminant of E. By [Reference ValloniV, Th. 3.2] we have
![]() $\mathrm {{End}}_{\mathrm {Hdg}} (T(X))={\mathcal O}_E$
if and only if
$\mathrm {{End}}_{\mathrm {Hdg}} (T(X))={\mathcal O}_E$
if and only if
![]() $f=\mathrm {gcd}(a,b,c)$
. Next,
$f=\mathrm {gcd}(a,b,c)$
. Next,
![]() $2$
is inert in E if and only if
$2$
is inert in E if and only if
![]() $D\equiv 5 \bmod 8$
. If f is odd, so that
$D\equiv 5 \bmod 8$
. If f is odd, so that
![]() $-d\equiv 5 \bmod 8$
, we have
$-d\equiv 5 \bmod 8$
, we have
![]() ${\mathcal Enr}(X)=\emptyset $
by [Reference Shimada and VenianiS], so in this case, the fibers of
${\mathcal Enr}(X)=\emptyset $
by [Reference Shimada and VenianiS], so in this case, the fibers of
![]() $\varphi _X$
are empty. Using Theorem A, it is easy to see that for each
$\varphi _X$
are empty. Using Theorem A, it is easy to see that for each
![]() $D\equiv 5 \bmod 8$
,
$D\equiv 5 \bmod 8$
,
![]() $D\neq -3$
, there are infinitely many pairwise non-isomorphic K3 surfaces of Picard rank
$D\neq -3$
, there are infinitely many pairwise non-isomorphic K3 surfaces of Picard rank
![]() $20$
with complex multiplication by
$20$
with complex multiplication by
![]() ${\mathcal O}_{{\mathbb Q}(\sqrt {D})}$
such that the fibers of
${\mathcal O}_{{\mathbb Q}(\sqrt {D})}$
such that the fibers of
![]() $\varphi _X$
above the nonzero points of
$\varphi _X$
above the nonzero points of
![]() $\mathrm {{Br}}(X)[2]$
have the same positive number of elements.
$\mathrm {{Br}}(X)[2]$
have the same positive number of elements.
It would be interesting to describe the K3 surfaces X such that
![]() $\Phi _X$
is surjective onto
$\Phi _X$
is surjective onto
![]() $\mathrm {{Br}}(X)[2]$
or onto
$\mathrm {{Br}}(X)[2]$
or onto
![]() $\mathrm {{Br}}(X)[2]\setminus \{0\}$
. In this direction, we have the following result, whose proof uses Nikulin’s theory of lattices [Reference NikulinN] and surjectivity of the period map for K3 surfaces.
$\mathrm {{Br}}(X)[2]\setminus \{0\}$
. In this direction, we have the following result, whose proof uses Nikulin’s theory of lattices [Reference NikulinN] and surjectivity of the period map for K3 surfaces.
Theorem D. Let X be a K3 surface such that
![]() $\mathrm {{rk}}(\mathrm {NS\,}(X))\geq 12$
. Then there exist infinitely many K3 surfaces Y such that:
$\mathrm {{rk}}(\mathrm {NS\,}(X))\geq 12$
. Then there exist infinitely many K3 surfaces Y such that:
-
(1)
 $T(X)_{\mathbb Q} \cong T(Y)_{\mathbb Q}$
as polarized Hodge structures.
$T(X)_{\mathbb Q} \cong T(Y)_{\mathbb Q}$
as polarized Hodge structures. -
(2) The discriminants of
 $T(Y)$
are pairwise different.
$T(Y)$
are pairwise different. -
(3) There is a natural isomorphism
 $\mathrm {{Br}}(X)[2]\cong \mathrm {{Br}}(Y)[2]$
under which
$\mathrm {{Br}}(X)[2]\cong \mathrm {{Br}}(Y)[2]$
under which  $$ \begin{align*} \mathrm{{Im}}(\Phi_X)\setminus\{0\}=\mathrm{{Im}}(\Phi_Y)\setminus\{0\}. \end{align*} $$
$$ \begin{align*} \mathrm{{Im}}(\Phi_X)\setminus\{0\}=\mathrm{{Im}}(\Phi_Y)\setminus\{0\}. \end{align*} $$
We recall results of Beauville, Keum, and Ohashi, and then prove some useful lemmas in §2. Theorem A and Corollary B are proved in §3, Theorem C is proved in §4, and Theorem D in §5.
2 Lattices and the topology of Enriques quotients
A lattice L is a free finitely generated abelian group with a non-degenerate integral symmetric bilinear form. Write
![]() $L(2)$
for the same group with the form
$L(2)$
for the same group with the form
![]() $2(x.y)$
.
$2(x.y)$
.
For a lattice L, we denote by
![]() $A_L=L^*/L$
the discriminant group of L. If L is even, then
$A_L=L^*/L$
the discriminant group of L. If L is even, then
![]() $q_L\colon A_L\to {\mathbb Q}/2{\mathbb Z}$
is the associated quadratic form.
$q_L\colon A_L\to {\mathbb Q}/2{\mathbb Z}$
is the associated quadratic form.
If
![]() $L\subset M$
are lattices, we denote by
$L\subset M$
are lattices, we denote by
![]() $L^{\perp }_M$
the orthogonal complement to L in M. It is clear that
$L^{\perp }_M$
the orthogonal complement to L in M. It is clear that
![]() $L^{\perp }_M$
is a primitive sublattice of M.
$L^{\perp }_M$
is a primitive sublattice of M.
Let
![]() $\mathrm {U}$
be the hyperbolic plane. Write
$\mathrm {U}$
be the hyperbolic plane. Write
![]() $\mathrm {U}={\mathbb Z} e\oplus {\mathbb Z} f$
, where
$\mathrm {U}={\mathbb Z} e\oplus {\mathbb Z} f$
, where
![]() $(e^2)=(f^2)=0$
,
$(e^2)=(f^2)=0$
,
![]() $(e.f)=1$
. We denote by
$(e.f)=1$
. We denote by
![]() $\mathrm {E}_8$
the negative-definite, even, unimodular lattice of the root system
$\mathrm {E}_8$
the negative-definite, even, unimodular lattice of the root system
![]() $\mathrm { E}_8$
. Write
$\mathrm { E}_8$
. Write
Here,
![]() $\Lambda $
is the K3 lattice. Let
$\Lambda $
is the K3 lattice. Let
![]() $\iota \colon \Lambda \to \Lambda $
be the involution permuting two copies of
$\iota \colon \Lambda \to \Lambda $
be the involution permuting two copies of
![]() $\mathrm {E}_8\oplus \mathrm {U}$
, and acting as
$\mathrm {E}_8\oplus \mathrm {U}$
, and acting as
![]() $-1$
on the third copy of
$-1$
on the third copy of
![]() $\mathrm {U}$
. Then
$\mathrm {U}$
. Then
![]() $\Lambda ^+\cong M$
and
$\Lambda ^+\cong M$
and
![]() $\Lambda ^-\cong N$
, where
$\Lambda ^-\cong N$
, where
![]() $\Lambda ^{\pm }$
is the
$\Lambda ^{\pm }$
is the
![]() $\pm 1$
-eigenspace of
$\pm 1$
-eigenspace of
![]() $\iota $
. By [Reference HuybrechtsH2, (vii) on p. 305], for any Enriques quotient
$\iota $
. By [Reference HuybrechtsH2, (vii) on p. 305], for any Enriques quotient
![]() $\pi _S\colon X\to S=X/\sigma $
, the induced map
$\pi _S\colon X\to S=X/\sigma $
, the induced map
can be identified with the composition
Here, the fixed point free involution
![]() $\sigma \colon X\to X$
induces the involution
$\sigma \colon X\to X$
induces the involution
![]() $\iota $
on
$\iota $
on
![]() $\Lambda $
.
$\Lambda $
.
The lattice N has a canonical character
![]() $N\to {\mathbb Z}/2$
which will play a crucial role in what follows.
$N\to {\mathbb Z}/2$
which will play a crucial role in what follows.
Lemma 2.1. The homomorphism
![]() $\varepsilon \colon N\to {\mathbb Z}/2$
given by
$\varepsilon \colon N\to {\mathbb Z}/2$
given by
![]() $\varepsilon (x):=\big (x.(e+f)\big )\bmod 2$
, where e and f are standard generators of
$\varepsilon (x):=\big (x.(e+f)\big )\bmod 2$
, where e and f are standard generators of
![]() $\mathrm {U}\subset N$
, does not depend on the embedding of lattices
$\mathrm {U}\subset N$
, does not depend on the embedding of lattices
![]() $\mathrm {U}\hookrightarrow N$
. Hence,
$\mathrm {U}\hookrightarrow N$
. Hence,
![]() $\alpha ^*(\varepsilon )=\varepsilon $
for any
$\alpha ^*(\varepsilon )=\varepsilon $
for any
![]() $\alpha \in \mathrm {Aut}(N)$
.
$\alpha \in \mathrm {Aut}(N)$
.
Proof. Let
![]() $e',f'$
be standard generators of
$e',f'$
be standard generators of
![]() $\mathrm {U}$
embedded in N. Write
$\mathrm {U}$
embedded in N. Write
![]() $e'=ae+bf+u$
,
$e'=ae+bf+u$
,
![]() $f'=ce+df+w$
, where
$f'=ce+df+w$
, where
![]() $a,b,c,d\in {\mathbb Z}$
and
$a,b,c,d\in {\mathbb Z}$
and
![]() $u,w\in \mathrm {U}(2)\oplus \mathrm { E}_8(2)$
. We have
$u,w\in \mathrm {U}(2)\oplus \mathrm { E}_8(2)$
. We have
![]() $2ab+(u^2)=2cd+(w^2)=0$
and
$2ab+(u^2)=2cd+(w^2)=0$
and
![]() $ad+bc+(u.w)=1$
. Since
$ad+bc+(u.w)=1$
. Since
![]() $(u^2)$
and
$(u^2)$
and
![]() $(w^2)$
are divisible by 4, and
$(w^2)$
are divisible by 4, and
![]() $(u.w)$
is even, we see that
$(u.w)$
is even, we see that
![]() $ab$
is even,
$ab$
is even,
![]() $cd$
is even, and
$cd$
is even, and
![]() $ad+bc$
is odd. It follows that either
$ad+bc$
is odd. It follows that either
![]() $a,d$
are odd and
$a,d$
are odd and
![]() $b,c$
are even, or
$b,c$
are even, or
![]() $a,d$
are even and
$a,d$
are even and
![]() $b,c$
are odd. In both cases,
$b,c$
are odd. In both cases,
![]() $e'+f'$
equals
$e'+f'$
equals
![]() $e+f$
modulo
$e+f$
modulo
![]() $2 \mathrm {U} \oplus \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
, hence the result.
$2 \mathrm {U} \oplus \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
, hence the result.
Lemma 2.2. If
![]() $x\in N$
is such that
$x\in N$
is such that
![]() $(x^2)\equiv 2\bmod 4$
, then
$(x^2)\equiv 2\bmod 4$
, then
![]() $\varepsilon (x)=0$
.
$\varepsilon (x)=0$
.
Proof. Write
![]() $x=ae+bf+u$
, where
$x=ae+bf+u$
, where
![]() $a,b\in {\mathbb Z}$
and
$a,b\in {\mathbb Z}$
and
![]() $u\in \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
. Then a and b are both odd, hence
$u\in \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
. Then a and b are both odd, hence
![]() $\varepsilon (x)\equiv a+b\equiv 0\bmod 2$
.
$\varepsilon (x)\equiv a+b\equiv 0\bmod 2$
.
Lemma 2.3. Let L be a sublattice of N. If the restriction of
![]() $\varepsilon \colon N\to {\mathbb Z}/2$
to L is nonzero, then
$\varepsilon \colon N\to {\mathbb Z}/2$
to L is nonzero, then
![]() $L^{\perp }_N=L'(2)$
for some even lattice
$L^{\perp }_N=L'(2)$
for some even lattice
![]() $L'$
.
$L'$
.
Proof. Suppose
![]() $\varepsilon (x)\neq 0$
for some
$\varepsilon (x)\neq 0$
for some
![]() $x\in L$
. Writing
$x\in L$
. Writing
![]() $x=ae+bf+u$
, where
$x=ae+bf+u$
, where
![]() $a,b\in {\mathbb Z}$
and
$a,b\in {\mathbb Z}$
and
![]() $u\in \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
, we see that a and b have opposite pairity. If
$u\in \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
, we see that a and b have opposite pairity. If
![]() $y=ce+df+w \in L^{\perp }_N$
, where
$y=ce+df+w \in L^{\perp }_N$
, where
![]() $c,d\in {\mathbb Z}$
and
$c,d\in {\mathbb Z}$
and
![]() $w\in \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
, then
$w\in \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
, then
![]() $ad+bc$
is even, which implies that either c or d is even. Then
$ad+bc$
is even, which implies that either c or d is even. Then
![]() $(y^2)=2cd +(w^2)$
is divisible by
$(y^2)=2cd +(w^2)$
is divisible by
![]() $4$
, hence
$4$
, hence
![]() $L^{\perp }_N=L'(2)$
for some even lattice
$L^{\perp }_N=L'(2)$
for some even lattice
![]() $L'$
.
$L'$
.
The importance of the character
![]() $\varepsilon \colon N\to {\mathbb Z}/2$
has been revealed by Beauville. Namely, let
$\varepsilon \colon N\to {\mathbb Z}/2$
has been revealed by Beauville. Namely, let
![]() $\pi _S\colon X\to S=X/\sigma $
be an Enriques quotient of a K3 surface X. Let
$\pi _S\colon X\to S=X/\sigma $
be an Enriques quotient of a K3 surface X. Let
![]() $T(X)\subset \Lambda $
be the transcendental lattice of X. Recall the canonical isomorphism
$T(X)\subset \Lambda $
be the transcendental lattice of X. Recall the canonical isomorphism
(see [Reference Colliot-Thélène and SkorobogatovCS, (5.5) on p. 130, p. 142]). It is well known that the involution
![]() $\sigma $
is not symplectic [Reference HuybrechtsH2, Cor. 15.1.5 and (ii) on p. 356], so it acts on
$\sigma $
is not symplectic [Reference HuybrechtsH2, Cor. 15.1.5 and (ii) on p. 356], so it acts on
![]() $\mathrm {H}^0(X,\Omega ^2_X)$
as
$\mathrm {H}^0(X,\Omega ^2_X)$
as
![]() $-1$
. Therefore,
$-1$
. Therefore,
![]() $\sigma ^*=\iota $
acts on
$\sigma ^*=\iota $
acts on
![]() $T(X)$
as
$T(X)$
as
![]() $-1$
, so
$-1$
, so
![]() $T(X)\subset N$
.
$T(X)\subset N$
.
Theorem 2.4 (Beauville).
Let
![]() $\pi _S\colon X\to S$
be an Enriques quotient of a K3 surface X. Then
$\pi _S\colon X\to S$
be an Enriques quotient of a K3 surface X. Then
![]() $\pi _S^*(b_S)\in \mathrm {{Br}}(X)[2]$
is the restriction of
$\pi _S^*(b_S)\in \mathrm {{Br}}(X)[2]$
is the restriction of
![]() $\varepsilon \colon N\to {\mathbb Z}/2$
to
$\varepsilon \colon N\to {\mathbb Z}/2$
to
![]() $T(X)$
.
$T(X)$
.
Proof. See [Reference BeauvilleB, Prop s. 3.4 and 5.3].
An embedding
![]() $T(X)\subset N$
coming from an Enriques quotient of X is clearly primitive. The orthogonal complement
$T(X)\subset N$
coming from an Enriques quotient of X is clearly primitive. The orthogonal complement
![]() $T(X)^{\perp }_N\subset N$
contains no
$T(X)^{\perp }_N\subset N$
contains no
![]() $(-2)$
-elements x, because by Riemann–Roch either x or
$(-2)$
-elements x, because by Riemann–Roch either x or
![]() $-x$
is effective, but
$-x$
is effective, but
![]() $\sigma ^*$
preserves effectivity. In fact, these are the only conditions. Horikawa’s theorem on the surjectivity of the period map for Enriques surfaces [Reference HorikawaH1] leads to the following result. See [Reference KeumK, Th. 1], which was extended in [Reference OhashiO2, Prop. 2.1].
$\sigma ^*$
preserves effectivity. In fact, these are the only conditions. Horikawa’s theorem on the surjectivity of the period map for Enriques surfaces [Reference HorikawaH1] leads to the following result. See [Reference KeumK, Th. 1], which was extended in [Reference OhashiO2, Prop. 2.1].
Theorem 2.5 (Keum, Ohashi).
Let X be a K3 surface. Associating to an Enriques quotient of X a primitive embedding
![]() $T(X)\subset N$
defines a bijection between
$T(X)\subset N$
defines a bijection between
![]() ${\mathcal Enr}(X)$
and the set of equivalence classes of primitive embeddings of
${\mathcal Enr}(X)$
and the set of equivalence classes of primitive embeddings of
![]() $T(X)$
into N without
$T(X)$
into N without
![]() $(-2)$
-elements in the orthogonal complement. Here the embeddings
$(-2)$
-elements in the orthogonal complement. Here the embeddings
![]() $i_1$
and
$i_1$
and
![]() $i_2$
are equivalent if there is an automorphism
$i_2$
are equivalent if there is an automorphism
![]() $\tilde \phi $
of the lattice N and a
$\tilde \phi $
of the lattice N and a
![]() $\phi \in \mathrm {Aut}_{\mathrm {Hdg}}(T(X))$
such that
$\phi \in \mathrm {Aut}_{\mathrm {Hdg}}(T(X))$
such that
![]() $i_2\circ \phi =\tilde \phi \circ i_1$
.
$i_2\circ \phi =\tilde \phi \circ i_1$
.
If
![]() $\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
(which holds, e.g., when the Picard number of X is odd), the set
$\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
(which holds, e.g., when the Picard number of X is odd), the set
![]() $\mathcal Enr(X)$
depends only on the lattice
$\mathcal Enr(X)$
depends only on the lattice
![]() $T(X)$
.
$T(X)$
.
Corollary 2.6. For any K3 surface
![]() $X,$
the following statements hold.
$X,$
the following statements hold.
-
(i)
 $\mathrm {{Im}}(\Phi _X)\setminus \{0\}$
is the set of nonzero
$\mathrm {{Im}}(\Phi _X)\setminus \{0\}$
is the set of nonzero
 $\alpha \in \mathrm {{Br}}(X)[2]\cong \mathrm {{Hom}}(T(X),{\mathbb Z}/2)$
, for which there exists a primitive embedding
$\alpha \in \mathrm {{Br}}(X)[2]\cong \mathrm {{Hom}}(T(X),{\mathbb Z}/2)$
, for which there exists a primitive embedding
 $i\colon T(X)\hookrightarrow N$
such that
$i\colon T(X)\hookrightarrow N$
such that
 $\alpha =i^*(\varepsilon )$
.
$\alpha =i^*(\varepsilon )$
. -
(ii)
 $0\in \mathrm {{Im}}(\Phi _X)$
if and only if there exists a primitive embedding
$0\in \mathrm {{Im}}(\Phi _X)$
if and only if there exists a primitive embedding
 $i\colon T(X)\hookrightarrow N$
without
$i\colon T(X)\hookrightarrow N$
without
 $(-2)$
-elements in the orthogonal complement such that
$(-2)$
-elements in the orthogonal complement such that
 $i^*(\varepsilon )=0$
.
$i^*(\varepsilon )=0$
. -
(iii) If
 $x\in T(X)$
is such that
$x\in T(X)$
is such that
 $(x^2)\equiv 2\bmod 4$
, then
$(x^2)\equiv 2\bmod 4$
, then
 $\alpha (x)=0$
for any
$\alpha (x)=0$
for any
 $\alpha \in \mathrm {{Im}}(\Phi _X)$
.
$\alpha \in \mathrm {{Im}}(\Phi _X)$
.
Proof. Parts (i) and (ii) formally follow from Theorems 2.4 and 2.5 and Lemma 2.3. In particular, Lemma 2.3 implies that
![]() $i(T(X))^{\perp }_N$
does not contain
$i(T(X))^{\perp }_N$
does not contain
![]() $(-2)$
-classes. Part (iii) follows from Lemma 2.2.
$(-2)$
-classes. Part (iii) follows from Lemma 2.2.
Corollary 2.7. If X is a K3 surface such that the abelian group
![]() $\mathrm {{Br}}(X)[2]$
is generated by the image of
$\mathrm {{Br}}(X)[2]$
is generated by the image of
![]() $\Phi _X$
, then there is an even lattice
$\Phi _X$
, then there is an even lattice
![]() $T'$
such that
$T'$
such that
![]() $T(X)\cong T'(2)$
.
$T(X)\cong T'(2)$
.
Proof. It is enough to show that for every
![]() $x\in T(X)$
we have
$x\in T(X)$
we have
![]() $(x^2)\equiv 0\bmod 4$
. Suppose that there is an element
$(x^2)\equiv 0\bmod 4$
. Suppose that there is an element
![]() $y\in T(X)$
such that
$y\in T(X)$
such that
![]() $(y^2)\equiv 2\bmod 4$
. Then y is not divisible by 2 in
$(y^2)\equiv 2\bmod 4$
. Then y is not divisible by 2 in
![]() $T(X)$
. By Corollary 2.6(iii), the nonzero class of y in
$T(X)$
. By Corollary 2.6(iii), the nonzero class of y in
![]() $T(X)/2T(X)$
is in the kernel of every
$T(X)/2T(X)$
is in the kernel of every
![]() $\alpha \in \mathrm {{Im}}(\Phi _X)$
. Thus
$\alpha \in \mathrm {{Im}}(\Phi _X)$
. Thus
![]() $\mathrm {{Im}}(\Phi _X)$
is contained in a proper subgroup of
$\mathrm {{Im}}(\Phi _X)$
is contained in a proper subgroup of
![]() $\mathrm {{Br}}(X)[2]$
.
$\mathrm {{Br}}(X)[2]$
.
Corollary 2.8. Let X be a K3 surface such that
![]() $T(X)$
has a basis
$T(X)$
has a basis
![]() $e_1,\ldots ,e_n$
with
$e_1,\ldots ,e_n$
with
![]() $(e_i^2)\equiv 2 \bmod 4$
for
$(e_i^2)\equiv 2 \bmod 4$
for
![]() $i=1,\ldots ,n$
. Then either
$i=1,\ldots ,n$
. Then either
![]() $\mathcal Enr(X)=\emptyset $
or
$\mathcal Enr(X)=\emptyset $
or
![]() $\mathrm {{Im}}(\Phi _X)=\{0\}$
.
$\mathrm {{Im}}(\Phi _X)=\{0\}$
.
Proof. Suppose that a nonzero
![]() $\alpha \in \mathrm {{Hom}}(T(X),{\mathbb Z}/2)$
is in the image of
$\alpha \in \mathrm {{Hom}}(T(X),{\mathbb Z}/2)$
is in the image of
![]() $\Phi _X$
. By Theorem 2.4, there is a primitive embedding
$\Phi _X$
. By Theorem 2.4, there is a primitive embedding
![]() $i\colon T(X)\to N$
such that
$i\colon T(X)\to N$
such that
![]() $i^*(\varepsilon )=\alpha $
. By Lemma 2.2, we have
$i^*(\varepsilon )=\alpha $
. By Lemma 2.2, we have
![]() $\alpha (e_i)=0$
for
$\alpha (e_i)=0$
for
![]() $i=1,\ldots ,n$
, hence
$i=1,\ldots ,n$
, hence
![]() $\alpha (T(X))=0$
which is a contradiction.
$\alpha (T(X))=0$
which is a contradiction.
This can be used to give examples of K3 surfaces X such that
![]() $\mathrm {{Im}}(\Phi _X)=\{0\}$
. For example, one can take the K3 surface X of Picard rank 20 with transcendental lattice
$\mathrm {{Im}}(\Phi _X)=\{0\}$
. For example, one can take the K3 surface X of Picard rank 20 with transcendental lattice
 $$ \begin{align*} \left(\begin{array}{cc}2&0\\ 0&2c\end{array}\right) \end{align*} $$
$$ \begin{align*} \left(\begin{array}{cc}2&0\\ 0&2c\end{array}\right) \end{align*} $$
with
![]() $c=3, 5, 7$
. Indeed, by [Reference SertözSV, Table 3.1] in these cases, we have
$c=3, 5, 7$
. Indeed, by [Reference SertözSV, Table 3.1] in these cases, we have
![]() $|\mathcal Enr(X)|=1$
.
$|\mathcal Enr(X)|=1$
.
3 Kummer surfaces
Proof of Theorem A
By Corollary 2.6(i), it is enough to construct, for any nonzero
![]() $\alpha \in \mathrm {{Hom}}(T(X),{\mathbb Z}/2)$
, a primitive embedding
$\alpha \in \mathrm {{Hom}}(T(X),{\mathbb Z}/2)$
, a primitive embedding
![]() $i\colon T(X)\hookrightarrow N=\mathrm {U}\oplus \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
such that
$i\colon T(X)\hookrightarrow N=\mathrm {U}\oplus \mathrm {U}(2)\oplus \mathrm {E}_8(2)$
such that
![]() $\varepsilon (x)=\alpha (x)$
for any
$\varepsilon (x)=\alpha (x)$
for any
![]() $x\in T(X)$
. We use Morrison’s classification of transcendental lattices of Kummer surfaces (see [Reference HuybrechtsH2, Cor. 14.3.20]). For each of them, Keum [Reference KeumK, pp. 106–108] constructed a primitive embedding into N; we follow the same strategy to construct all
$x\in T(X)$
. We use Morrison’s classification of transcendental lattices of Kummer surfaces (see [Reference HuybrechtsH2, Cor. 14.3.20]). For each of them, Keum [Reference KeumK, pp. 106–108] constructed a primitive embedding into N; we follow the same strategy to construct all
![]() $2^n-1$
embeddings, where
$2^n-1$
embeddings, where
![]() $n=\mathrm {{rk}}(T(X))$
. We keep the notation of [Reference KeumK], in particular,
$n=\mathrm {{rk}}(T(X))$
. We keep the notation of [Reference KeumK], in particular,
![]() $e,f$
is a standard basis of
$e,f$
is a standard basis of
![]() $\mathrm {U}$
and
$\mathrm {U}$
and
![]() $h,k$
is a standard basis of
$h,k$
is a standard basis of
![]() $\mathrm {U}(2)$
. We denote by
$\mathrm {U}(2)$
. We denote by
![]() $\rho $
the Picard rank of X.
$\rho $
the Picard rank of X.
In the proof below, we shall use the following particular case of a result of Nikulin.
Lemma 3.1. Any even negative-definite lattice of rank at most
![]() $4$
has a primitive embedding in
$4$
has a primitive embedding in
![]() $\mathrm {E}_8$
.
$\mathrm {E}_8$
.
Proof. This follows from [Reference NikulinN, Th. 1.12.4] using the fact that
![]() $\mathrm {E}_8$
is a unique even unimodular negative-definite lattice of rank 8.
$\mathrm {E}_8$
is a unique even unimodular negative-definite lattice of rank 8.
 $\rho =20$
$\rho =20$
In this case, the lattice
![]() $T={\mathbb Z} x\oplus {\mathbb Z} y$
is positive-definite with Gram matrix
$T={\mathbb Z} x\oplus {\mathbb Z} y$
is positive-definite with Gram matrix
 $$ \begin{align*} \left(\begin{array}{cc}4a&2b\\2b&4c \end{array}\right),\end{align*} $$
$$ \begin{align*} \left(\begin{array}{cc}4a&2b\\2b&4c \end{array}\right),\end{align*} $$
where
![]() $a,b,c\in {\mathbb Z}$
. The three primitive embeddings can be given by sending
$a,b,c\in {\mathbb Z}$
. The three primitive embeddings can be given by sending
![]() $x,y$
to the following two elements of N:
$x,y$
to the following two elements of N:
 $\rho =19$
$\rho =19$
Now T has signature
![]() $(2,1)$
. We can choose an integral basis
$(2,1)$
. We can choose an integral basis
![]() $x,y,t$
of T so that the Gram matrix is
$x,y,t$
of T so that the Gram matrix is
 $$ \begin{align*}\left(\begin{array}{ccc}4a&2d&2l\\2d&4b&2m\\2l&2m&4c \end{array}\right),\end{align*} $$
$$ \begin{align*}\left(\begin{array}{ccc}4a&2d&2l\\2d&4b&2m\\2l&2m&4c \end{array}\right),\end{align*} $$
where
![]() $a,b,c,d,l,m\in {\mathbb Z}$
and
$a,b,c,d,l,m\in {\mathbb Z}$
and
![]() $a,b,c<0$
. The embeddings we need to construct are numbered by the nonzero vectors
$a,b,c<0$
. The embeddings we need to construct are numbered by the nonzero vectors
![]() $(v_1,v_2,v_3)\in ({\mathbb F}_2)^3$
given by evaluating
$(v_1,v_2,v_3)\in ({\mathbb F}_2)^3$
given by evaluating
![]() $\varepsilon $
on the images of
$\varepsilon $
on the images of
![]() $x,y,t$
in this order. By symmetry it is enough to construct embeddings labeled
$x,y,t$
in this order. By symmetry it is enough to construct embeddings labeled
![]() $(1,0,0)$
,
$(1,0,0)$
,
![]() $(1,1,0)$
, and
$(1,1,0)$
, and
![]() $(1,1,1)$
. The first two can be given by sending
$(1,1,1)$
. The first two can be given by sending
![]() $x,y,t$
to the following three elements of N, where w is a primitive element of
$x,y,t$
to the following three elements of N, where w is a primitive element of
![]() $\mathrm {E}_8(2)$
such that
$\mathrm {E}_8(2)$
such that
![]() $(w^2)=4c$
:
$(w^2)=4c$
:
Next, we deal with
![]() $(1,1,1)$
. Without loss of generality, we can assume
$(1,1,1)$
. Without loss of generality, we can assume
![]() $m>0$
. Take
$m>0$
. Take
where
![]() ${\mathbb Z} w'\oplus {\mathbb Z} w$
is a primitive sublattice of
${\mathbb Z} w'\oplus {\mathbb Z} w$
is a primitive sublattice of
![]() $\mathrm {E}_8(2)$
such that
$\mathrm {E}_8(2)$
such that
![]() $(w^{\prime 2})=4b-4m<0$
,
$(w^{\prime 2})=4b-4m<0$
,
![]() $(w^2)=4c<0$
,
$(w^2)=4c<0$
,
![]() $(w'.w)=0$
.
$(w'.w)=0$
.
 $\rho =18$
$\rho =18$
Here, the lattice T is the orthogonal direct sum of
![]() ${\mathbb Z} x\oplus {\mathbb Z} y$
with signature
${\mathbb Z} x\oplus {\mathbb Z} y$
with signature
![]() $(1,1)$
and Gram matrix
$(1,1)$
and Gram matrix
 $$ \begin{align*} \left(\begin{array}{cc}4a&2b\\2b&4c\end{array}\right) \end{align*} $$
$$ \begin{align*} \left(\begin{array}{cc}4a&2b\\2b&4c\end{array}\right) \end{align*} $$
and
![]() $\mathrm {U}(2)={\mathbb Z} r\oplus {\mathbb Z} s$
. Without loss of generality, we assume that
$\mathrm {U}(2)={\mathbb Z} r\oplus {\mathbb Z} s$
. Without loss of generality, we assume that
![]() $a,c<0$
and
$a,c<0$
and
![]() $b>0$
. Let w and u be primitive vectors of
$b>0$
. Let w and u be primitive vectors of
![]() $\mathrm {E}_8(2)$
such that
$\mathrm {E}_8(2)$
such that
![]() $(w^2)=4c<0$
and
$(w^2)=4c<0$
and
![]() $(u^2)=4(a-b+c)<0$
. We label the embeddings in the same way as above. Up to exchanging the roles of x and y, and of r and s, it is enough to construct embeddings with the following labels:
$(u^2)=4(a-b+c)<0$
. We label the embeddings in the same way as above. Up to exchanging the roles of x and y, and of r and s, it is enough to construct embeddings with the following labels:
Let us first construct primitive embeddings with labels
![]() $(1,0,0,0)$
and
$(1,0,0,0)$
and
![]() $(1,1,0,0)$
by taking the direct sum of a primitive embedding
$(1,1,0,0)$
by taking the direct sum of a primitive embedding
![]() ${\mathbb Z} x\oplus {\mathbb Z} y$
into
${\mathbb Z} x\oplus {\mathbb Z} y$
into
![]() $\mathrm { U}\oplus \mathrm {E}_8(2)$
and the identity embedding
$\mathrm { U}\oplus \mathrm {E}_8(2)$
and the identity embedding
![]() $\mathrm {U}(2)\tilde \longrightarrow \mathrm {U}(2)$
. We send
$\mathrm {U}(2)\tilde \longrightarrow \mathrm {U}(2)$
. We send
![]() $x,y$
to
$x,y$
to
The embedding with label
![]() $(1,0,1,0)$
can be obtained by sending
$(1,0,1,0)$
can be obtained by sending
![]() $x,y,r,s$
to
$x,y,r,s$
to
For
![]() $(0,0,1,0)$
, we take
$(0,0,1,0)$
, we take
![]() $(h+w_1,bk+w_2,e,2e+2f+w_3)$
, where
$(h+w_1,bk+w_2,e,2e+2f+w_3)$
, where
![]() ${\mathbb Z} w_1\oplus {\mathbb Z} w_2\oplus {\mathbb Z} w_3$
is a primitive sublattice of
${\mathbb Z} w_1\oplus {\mathbb Z} w_2\oplus {\mathbb Z} w_3$
is a primitive sublattice of
![]() $\mathrm {E}_8(2)$
with diagonal Gram matrix such that
$\mathrm {E}_8(2)$
with diagonal Gram matrix such that
![]() $(w_1^2)=4a<0$
,
$(w_1^2)=4a<0$
,
![]() $(w_2^2)=4c<0$
,
$(w_2^2)=4c<0$
,
![]() $(w_3^2)=-8$
.
$(w_3^2)=-8$
.
For
![]() $(0,0,1,1)$
, we take
$(0,0,1,1)$
, we take
![]() $(h+w_1,bk+w_2,e,e+2f+w_3)$
, where
$(h+w_1,bk+w_2,e,e+2f+w_3)$
, where
![]() ${\mathbb Z} w_1\oplus {\mathbb Z} w_2\oplus {\mathbb Z} w_3$
is a primitive sublattice of
${\mathbb Z} w_1\oplus {\mathbb Z} w_2\oplus {\mathbb Z} w_3$
is a primitive sublattice of
![]() $\mathrm {E}_8(2)$
with diagonal Gram matrix such that
$\mathrm {E}_8(2)$
with diagonal Gram matrix such that
![]() $(w_1^2)=4a<0$
,
$(w_1^2)=4a<0$
,
![]() $(w_2^2)=4c<0$
,
$(w_2^2)=4c<0$
,
![]() $(w_3^2)=-4$
.
$(w_3^2)=-4$
.
For
![]() $(1,1,1,0)$
, we take
$(1,1,1,0)$
, we take
![]() $(e+2af-ak,e+(2b-2a)f+(a-b)k+u,e+h,k)$
.
$(e+2af-ak,e+(2b-2a)f+(a-b)k+u,e+h,k)$
.
For
![]() $(1,0,1,1)$
, we take
$(1,0,1,1)$
, we take
![]() $(e+2af-ak,2bf-bk+w,e+h,e+k+h+w')$
, where
$(e+2af-ak,2bf-bk+w,e+h,e+k+h+w')$
, where
![]() ${\mathbb Z} w\oplus {\mathbb Z} w'$
is a primitive sublattice of
${\mathbb Z} w\oplus {\mathbb Z} w'$
is a primitive sublattice of
![]() $\mathrm {E}_8(2)$
such that
$\mathrm {E}_8(2)$
such that
![]() $(w^2)=4c<0$
,
$(w^2)=4c<0$
,
![]() $(w^{\prime 2})=-4$
,
$(w^{\prime 2})=-4$
,
![]() $(w.w')=0$
.
$(w.w')=0$
.
For
![]() $(1,1,1,1)$
, we take
$(1,1,1,1)$
, we take
![]() $(e+2af-ak,e+(2b-2a)f+(a-b)k+u,e+h,e+k+h+w')$
, where
$(e+2af-ak,e+(2b-2a)f+(a-b)k+u,e+h,e+k+h+w')$
, where
![]() ${\mathbb Z} u\oplus {\mathbb Z} w'$
is a primitive sublattice of
${\mathbb Z} u\oplus {\mathbb Z} w'$
is a primitive sublattice of
![]() $\mathrm {E}_8(2)$
such that
$\mathrm {E}_8(2)$
such that
![]() $(u^2)=4(a-b+c)<0$
,
$(u^2)=4(a-b+c)<0$
,
![]() $(w^{\prime 2})=-4$
,
$(w^{\prime 2})=-4$
,
![]() $(u.w')=0$
.
$(u.w')=0$
.
 $\rho =17$
$\rho =17$
Here, we have
![]() $T=\mathrm {U}(2)\oplus \mathrm {U}(2)\oplus (-4m)$
, where
$T=\mathrm {U}(2)\oplus \mathrm {U}(2)\oplus (-4m)$
, where
![]() $m\geq 1$
. A standard basis is
$m\geq 1$
. A standard basis is
![]() $\{x,y,x',y',t\}$
. Up to swapping the two copies of
$\{x,y,x',y',t\}$
. Up to swapping the two copies of
![]() $\mathrm {U}(2)$
and swapping the elements of a standard basis of each
$\mathrm {U}(2)$
and swapping the elements of a standard basis of each
![]() $\mathrm {U}(2)$
it is enough to construct embeddings with the following labels:
$\mathrm {U}(2)$
it is enough to construct embeddings with the following labels:
The first five embeddings are obtained as direct sums of a primitive embedding of
![]() $\mathrm {U}(2)\oplus (-4m)$
into
$\mathrm {U}(2)\oplus (-4m)$
into
![]() $\mathrm {U}\oplus \mathrm {E}_8(2)$
and the identity embedding
$\mathrm {U}\oplus \mathrm {E}_8(2)$
and the identity embedding
![]() $\mathrm { U}(2)\tilde \longrightarrow \mathrm {U}(2)$
. The respective primitive embeddings of
$\mathrm { U}(2)\tilde \longrightarrow \mathrm {U}(2)$
. The respective primitive embeddings of
![]() $\mathrm {U}(2)\oplus (-4m)$
into
$\mathrm {U}(2)\oplus (-4m)$
into
![]() $\mathrm {U}\oplus \mathrm {E}_8(2)$
are given by sending
$\mathrm {U}\oplus \mathrm {E}_8(2)$
are given by sending
![]() $x,y,t$
to the following triples:
$x,y,t$
to the following triples:
Here,
![]() ${\mathbb Z} u_i\oplus {\mathbb Z} v_i$
is a primitive sublattice of
${\mathbb Z} u_i\oplus {\mathbb Z} v_i$
is a primitive sublattice of
![]() $\mathrm {E}_8(2)$
such that:
$\mathrm {E}_8(2)$
such that:
![]() $(u_1^2)=-8$
,
$(u_1^2)=-8$
,
![]() $(v_1^2)=-4m$
,
$(v_1^2)=-4m$
,
![]() $(u_1.v_1)=0$
;
$(u_1.v_1)=0$
;
![]() $(u_2^2)=-4$
,
$(u_2^2)=-4$
,
![]() $(v_2^2)=-4m$
,
$(v_2^2)=-4m$
,
![]() $(u_2.v_2)=0$
;
$(u_2.v_2)=0$
;
![]() $(u_3^2)=-8$
,
$(u_3^2)=-8$
,
![]() $(v_3^2)=-4m$
,
$(v_3^2)=-4m$
,
![]() $(u_3.v_3)=-2$
;
$(u_3.v_3)=-2$
;
![]() $(u_4^2)=-4$
,
$(u_4^2)=-4$
,
![]() $(v_4^2)=-4m$
,
$(v_4^2)=-4m$
,
![]() $(u_4.v_4)=-2$
.
$(u_4.v_4)=-2$
.
The embedding labeled
![]() $(0,0,0,0,1)$
can be obtained by sending
$(0,0,0,0,1)$
can be obtained by sending
![]() $x,y,t$
to
$x,y,t$
to
where
![]() $w_0,w_1,w_2$
generate a primitive sublattice of
$w_0,w_1,w_2$
generate a primitive sublattice of
![]() $\mathrm {E}_8(2)$
with Gram matrix
$\mathrm {E}_8(2)$
with Gram matrix
 $$ \begin{align*} \left(\begin{array}{ccc}-8&-6&-2\\-6&-8&-2\\-2&-2&-4m \end{array}\right). \end{align*} $$
$$ \begin{align*} \left(\begin{array}{ccc}-8&-6&-2\\-6&-8&-2\\-2&-2&-4m \end{array}\right). \end{align*} $$
Indeed, this matrix is negative-definite.
To construct the last six embeddings, we exhibit the images of
![]() $x,y,x',y',t$
. In the case of
$x,y,x',y',t$
. In the case of
![]() $(1,1,1,1,0)$
, we consider
$(1,1,1,1,0)$
, we consider
where
![]() $w_0,w_1,w_2$
generate a primitive sublattice of
$w_0,w_1,w_2$
generate a primitive sublattice of
![]() $\mathrm {E}_8(2)$
with diagonal Gram matrix such that
$\mathrm {E}_8(2)$
with diagonal Gram matrix such that
![]() $(w_0^2)=(w_1^2)=-4$
and
$(w_0^2)=(w_1^2)=-4$
and
![]() $(w_2^2)=-4m$
.
$(w_2^2)=-4m$
.
In the case of
![]() $(1,1,1,1,1)$
, we take
$(1,1,1,1,1)$
, we take
where
![]() $w_0,w_1,w_2$
generate a primitive sublattice of
$w_0,w_1,w_2$
generate a primitive sublattice of
![]() $\mathrm {E}_8(2)$
with the negative-definite Gram matrix
$\mathrm {E}_8(2)$
with the negative-definite Gram matrix
 $$ \begin{align*} \left(\begin{array}{ccc}-4&0&-2\\0&-4&0\\-2&0&-4m \end{array}\right). \end{align*} $$
$$ \begin{align*} \left(\begin{array}{ccc}-4&0&-2\\0&-4&0\\-2&0&-4m \end{array}\right). \end{align*} $$
In the case of
![]() $(1,0,1,0,0)$
, we take
$(1,0,1,0,0)$
, we take
![]() $(e,2f+k,e-h,-k,w)$
, where w is a primitive element of
$(e,2f+k,e-h,-k,w)$
, where w is a primitive element of
![]() $\mathrm {E}_8(2)$
with
$\mathrm {E}_8(2)$
with
![]() $(w^2)=-4m$
.
$(w^2)=-4m$
.
For
![]() $(1,1,1,0,0)$
, we take
$(1,1,1,0,0)$
, we take
![]() $(e,e+2f+k+u_2,e-h,-k,v_2)$
.
$(e,e+2f+k+u_2,e-h,-k,v_2)$
.
For
![]() $(1,1,1,0,1)$
, we take
$(1,1,1,0,1)$
, we take
![]() $(e,e+2f+k+u_4,e-h,-k,e+v_4)$
.
$(e,e+2f+k+u_4,e-h,-k,e+v_4)$
.
For
![]() $(1,0,1,0,1)$
, we take
$(1,0,1,0,1)$
, we take
![]() $(e,2e+2f+k+u_3,e-h,-k,e+v_3)$
.
$(e,2e+2f+k+u_3,e-h,-k,e+v_3)$
.
Proof of Corollary B
(i) Let
![]() $E_1$
and
$E_1$
and
![]() $E_2$
be non-isogenous elliptic curves, and let
$E_2$
be non-isogenous elliptic curves, and let
![]() $X=\mathrm {Kum}(E_1\times E_2)$
. By [Reference OhashiO1, §4], we have
$X=\mathrm {Kum}(E_1\times E_2)$
. By [Reference OhashiO1, §4], we have
![]() $\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
and
$\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
and
![]() $|\mathcal Enr(X)|=15$
. (The 15 Enriques involutions can be described geometrically as the Lieberman involutions and the Kondo–Mukai involutions.) We have
$|\mathcal Enr(X)|=15$
. (The 15 Enriques involutions can be described geometrically as the Lieberman involutions and the Kondo–Mukai involutions.) We have
![]() $\mathrm {{rk}}(T(X))=4$
, hence
$\mathrm {{rk}}(T(X))=4$
, hence
![]() $|\mathrm {{Br}}(X)[2]\setminus \{0\}|=15$
.
$|\mathrm {{Br}}(X)[2]\setminus \{0\}|=15$
.
(ii) Let C be a smooth projective curve of genus 2 such that
![]() $\mathrm {NS\,}(\mathrm {Jac}(C))\cong {\mathbb Z}$
. Let
$\mathrm {NS\,}(\mathrm {Jac}(C))\cong {\mathbb Z}$
. Let
![]() $X=\mathrm {Kum}(\mathrm {Jac}(C))$
. Condition
$X=\mathrm {Kum}(\mathrm {Jac}(C))$
. Condition
![]() $\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
is satisfied since the Picard rank of X is odd. Ohashi [Reference OhashiO2] shows that
$\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
is satisfied since the Picard rank of X is odd. Ohashi [Reference OhashiO2] shows that
![]() $|\mathcal Enr(X)|=31$
and describes these 31 involutions geometrically. In this case
$|\mathcal Enr(X)|=31$
and describes these 31 involutions geometrically. In this case
![]() $\mathrm {{rk}}(T(X))=5$
, so
$\mathrm {{rk}}(T(X))=5$
, so
![]() $|\mathrm {{Br}}(X)[2]\setminus \{0\}|=31$
.
$|\mathrm {{Br}}(X)[2]\setminus \{0\}|=31$
.
Taking into account (i) and (ii), Corollary B follows from Theorem A since a surjective map of finite sets of the same cardinality is a bijection.
4 Singular K3 surfaces
K3 surfaces over
 $\overline {\mathbb Q}$
$\overline {\mathbb Q}$
For a variety X over
![]() $\overline {\mathbb Q}$
and an element
$\overline {\mathbb Q}$
and an element
![]() $g \in \mathrm {{Gal}}(\overline {\mathbb Q}/{\mathbb Q})$
, we define
$g \in \mathrm {{Gal}}(\overline {\mathbb Q}/{\mathbb Q})$
, we define
![]() $X^g=X\times _{\overline {\mathbb Q}, g}\overline {\mathbb Q}$
. Then, we have a morphism
$X^g=X\times _{\overline {\mathbb Q}, g}\overline {\mathbb Q}$
. Then, we have a morphism
![]() $g\colon X\to X^g$
making the following diagram commutative:
$g\colon X\to X^g$
making the following diagram commutative:

Here, the vertical arrows are structure morphisms. A morphism of
![]() $\overline {\mathbb Q}$
-varieties
$\overline {\mathbb Q}$
-varieties
![]() $\phi \colon X\to Y$
gives rise to a morphism of
$\phi \colon X\to Y$
gives rise to a morphism of
![]() $\overline {\mathbb Q}$
-varieties
$\overline {\mathbb Q}$
-varieties
![]() $\phi ^g=g\phi g^{-1}\colon X^g\to Y^g$
.
$\phi ^g=g\phi g^{-1}\colon X^g\to Y^g$
.
Let
![]() $K\subset \overline {\mathbb Q}$
be a subfield, and let
$K\subset \overline {\mathbb Q}$
be a subfield, and let
![]() $G_K=\mathrm {{Gal}}(\overline {\mathbb Q}/K)$
.
$G_K=\mathrm {{Gal}}(\overline {\mathbb Q}/K)$
.
Definition 4.1. Let X be a variety over
![]() $\overline {\mathbb Q}$
.
$\overline {\mathbb Q}$
.
-
(i) The field of moduli of X over K is the subfield
 $K(X)\subset \overline {\mathbb Q}$
fixed by the group
$K(X)\subset \overline {\mathbb Q}$
fixed by the group
 $\{g\in G_K | X\cong X^g \}$
.
$\{g\in G_K | X\cong X^g \}$
. -
(ii) Let
 $B \subset \mathrm {{Br}}(X)$
be a finite subgroup. The field of moduli of the pair
$B \subset \mathrm {{Br}}(X)$
be a finite subgroup. The field of moduli of the pair
 $(X, B)$
over K is the subfield
$(X, B)$
over K is the subfield
 $K(X,B)\subset \overline {\mathbb Q}$
fixed by the group
$K(X,B)\subset \overline {\mathbb Q}$
fixed by the group  $$ \begin{align*}\{g\in G_K| \exists \, \text{an isomorphism} \, f \colon X^g\rightarrow X \, \text{such that} \, (g^* \circ f^*)|_B= \mathrm{id}_B \}.\end{align*} $$
$$ \begin{align*}\{g\in G_K| \exists \, \text{an isomorphism} \, f \colon X^g\rightarrow X \, \text{such that} \, (g^* \circ f^*)|_B= \mathrm{id}_B \}.\end{align*} $$
Let us fix an embedding
![]() $\overline {\mathbb Q}\subset {\mathbb C}$
. For a K3 surface X over
$\overline {\mathbb Q}\subset {\mathbb C}$
. For a K3 surface X over
![]() $\overline {\mathbb Q}$
we write
$\overline {\mathbb Q}$
we write
![]() $T(X)$
for the transcendental lattice of
$T(X)$
for the transcendental lattice of
![]() $X_{\mathbb C}$
. One has natural isomorphisms ([Reference Colliot-Thélène and SkorobogatovCS, Prop. 5.2.3 and p. 142])
$X_{\mathbb C}$
. One has natural isomorphisms ([Reference Colliot-Thélène and SkorobogatovCS, Prop. 5.2.3 and p. 142])
Remark 4.2. Let X be a K3 surface over
![]() $\overline {\mathbb Q}$
of Picard rank at least
$\overline {\mathbb Q}$
of Picard rank at least
![]() $12$
. According to [Reference ValloniV, Rem. 6.1(2), p. 32] a Hodge isometry
$12$
. According to [Reference ValloniV, Rem. 6.1(2), p. 32] a Hodge isometry
![]() $h \colon T(X^g) \tilde \rightarrow T(X)$
exists if and only if
$h \colon T(X^g) \tilde \rightarrow T(X)$
exists if and only if
![]() $X \cong X^g$
. It follows that in this case
$X \cong X^g$
. It follows that in this case
![]() $K(X,B)$
is the fixed field of the group
$K(X,B)$
is the fixed field of the group
For a K3 surface over
![]() $\overline {\mathbb Q}$
, we have
$\overline {\mathbb Q}$
, we have
![]() $\mathrm {Aut}(X)=\mathrm {Aut}(X_{\mathbb C})$
, since
$\mathrm {Aut}(X)=\mathrm {Aut}(X_{\mathbb C})$
, since
![]() $Aut_{X/\overline {\mathbb Q}}$
is a discrete group scheme. Hence, the set of conjugacy classes of fixed point free involutions
$Aut_{X/\overline {\mathbb Q}}$
is a discrete group scheme. Hence, the set of conjugacy classes of fixed point free involutions
![]() $\mathcal Enr(X)\subset \mathrm {Aut}(X)$
coincides with
$\mathcal Enr(X)\subset \mathrm {Aut}(X)$
coincides with
![]() $\mathcal Enr(X_{\mathbb C})$
.
$\mathcal Enr(X_{\mathbb C})$
.
Proposition 4.3. Let X be a K3 surface over
![]() $\overline {\mathbb Q}$
such that
$\overline {\mathbb Q}$
such that
![]() $\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
. The Galois group
$\mathrm {Aut}_{\mathrm {Hdg}}(T(X))=\{\pm 1\}$
. The Galois group
![]() $G_{K(X)}$
acts naturally on
$G_{K(X)}$
acts naturally on
![]() ${\mathcal Enr}(X)$
and on
${\mathcal Enr}(X)$
and on
![]() $\mathrm {{Br}}(X)[2]$
so that the map
$\mathrm {{Br}}(X)[2]$
so that the map
![]() $\varphi _X\colon {\mathcal Enr}(X) \to \mathrm {{Br}}(X)[2]$
is
$\varphi _X\colon {\mathcal Enr}(X) \to \mathrm {{Br}}(X)[2]$
is
![]() $G_{K(X)}$
-equivariant.
$G_{K(X)}$
-equivariant.
Proof. Write
![]() $K := K(X)$
. We use
$K := K(X)$
. We use
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
to denote arbitrary elements of
$\tau $
to denote arbitrary elements of
![]() $G_K$
. By Definition 4.1(i), we can find an isomorphism
$G_K$
. By Definition 4.1(i), we can find an isomorphism
![]() $f_{\sigma ,\tau } \colon X^{\sigma } \tilde \longrightarrow X^{\tau }$
.
$f_{\sigma ,\tau } \colon X^{\sigma } \tilde \longrightarrow X^{\tau }$
.
Let us denote the conjugacy class of
![]() $\psi \in \mathrm {Aut}(X)$
by
$\psi \in \mathrm {Aut}(X)$
by
![]() $[\psi ]$
.
$[\psi ]$
.
A fixed point free involution
![]() $\iota \colon X\to X$
gives rise to a fixed point free involution
$\iota \colon X\to X$
gives rise to a fixed point free involution
![]() $\iota ^{\sigma }=\sigma \iota \sigma ^{-1}\colon X^{\sigma }\rightarrow X^{\sigma }$
, and one has
$\iota ^{\sigma }=\sigma \iota \sigma ^{-1}\colon X^{\sigma }\rightarrow X^{\sigma }$
, and one has
![]() $(\iota ^{\sigma })^{\tau }=\iota ^{\tau \sigma }$
. We define an action of
$(\iota ^{\sigma })^{\tau }=\iota ^{\tau \sigma }$
. We define an action of
![]() $G_K$
on
$G_K$
on
![]() ${\mathcal Enr}(X)$
by making
${\mathcal Enr}(X)$
by making
![]() $\sigma $
send
$\sigma $
send
![]() $[\iota ]$
to
$[\iota ]$
to
![]() $[f_{1,\sigma }^{-1}\iota ^{\sigma } f_{1,\sigma }]$
. This class depends neither on the choice of
$[f_{1,\sigma }^{-1}\iota ^{\sigma } f_{1,\sigma }]$
. This class depends neither on the choice of
![]() $\iota $
in its conjugacy class, nor on the choice of
$\iota $
in its conjugacy class, nor on the choice of
![]() $f_{1,\sigma }$
. We have
$f_{1,\sigma }$
. We have
because
![]() $f_{1,\tau \sigma }$
and
$f_{1,\tau \sigma }$
and
![]() $f_{1,\sigma }^{\tau } f_{1,\tau }$
are both isomorphisms
$f_{1,\sigma }^{\tau } f_{1,\tau }$
are both isomorphisms
![]() $X\tilde \longrightarrow X^{\tau \sigma }$
, so replacing one of them by the other does not change the conjugacy class.
$X\tilde \longrightarrow X^{\tau \sigma }$
, so replacing one of them by the other does not change the conjugacy class.
Let us now define an action of
![]() $G_K$
on
$G_K$
on
![]() $\mathrm {{Br}}(X)[2]$
by making
$\mathrm {{Br}}(X)[2]$
by making
![]() $\sigma \in G_{K}$
act as
$\sigma \in G_{K}$
act as
![]() $f_{1,\sigma }^*(\sigma ^{-1})^*$
which is induced by
$f_{1,\sigma }^*(\sigma ^{-1})^*$
which is induced by
![]() $\sigma ^{-1}f_{1,\sigma }\colon X\to X^{\sigma }\to X$
. This action on
$\sigma ^{-1}f_{1,\sigma }\colon X\to X^{\sigma }\to X$
. This action on
![]() $\mathrm {{Br}}(X)[2]$
does not depend on the choice of
$\mathrm {{Br}}(X)[2]$
does not depend on the choice of
![]() $f_{1,\sigma }$
. Indeed,
$f_{1,\sigma }$
. Indeed,
![]() $f_{1,\sigma }$
is well defined up to an automorphism of X, but the action of
$f_{1,\sigma }$
is well defined up to an automorphism of X, but the action of
![]() $\mathrm {Aut}(X)$
on
$\mathrm {Aut}(X)$
on
![]() $\mathrm {{Br}}(X)[2]$
factors through the action of
$\mathrm {{Br}}(X)[2]$
factors through the action of
![]() $\mathrm {Aut}_{\mathrm { Hdg}}(T(X))$
. The latter group is
$\mathrm {Aut}_{\mathrm { Hdg}}(T(X))$
. The latter group is
![]() $\{\pm 1\}$
by assumption, so
$\{\pm 1\}$
by assumption, so
![]() $\mathrm {Aut}(X)$
acts on
$\mathrm {Aut}(X)$
acts on
![]() $\mathrm {{Br}}(X)[2]$
trivially. The map
$\mathrm {{Br}}(X)[2]$
trivially. The map
![]() $(f_{1,\sigma })^{\tau }=\tau f_{1,\sigma }\tau ^{-1}$
is an isomorphism
$(f_{1,\sigma })^{\tau }=\tau f_{1,\sigma }\tau ^{-1}$
is an isomorphism
![]() $X^{\tau }\tilde \longrightarrow X^{\tau \sigma }$
, hence
$X^{\tau }\tilde \longrightarrow X^{\tau \sigma }$
, hence
![]() $(f_{1,\sigma })^{\tau } f_{1,\tau }$
is an isomorphism
$(f_{1,\sigma })^{\tau } f_{1,\tau }$
is an isomorphism
![]() $X\to X^{\tau \sigma }$
, so for the purpose of calculating the induced action of
$X\to X^{\tau \sigma }$
, so for the purpose of calculating the induced action of
![]() $\mathrm {{Br}}(X)[2]$
, we can replace it with
$\mathrm {{Br}}(X)[2]$
, we can replace it with
![]() $f_{1,\tau \sigma }$
. This shows that sending
$f_{1,\tau \sigma }$
. This shows that sending
![]() $\sigma \in G_{K}$
to the map induced on
$\sigma \in G_{K}$
to the map induced on
![]() $\mathrm {{Br}}(X)[2]$
by
$\mathrm {{Br}}(X)[2]$
by
![]() $\sigma ^{-1}f_{1,\sigma }$
is indeed an action.
$\sigma ^{-1}f_{1,\sigma }$
is indeed an action.
We have a commutative diagram

where the vertical maps are quotients by the respective fixed point free involutions. Thus the image of the nonzero element of
![]() $\mathrm {{Br}}(X/\iota )$
in
$\mathrm {{Br}}(X/\iota )$
in
![]() $\mathrm {{Br}}(X)[2]$
followed by the action of
$\mathrm {{Br}}(X)[2]$
followed by the action of
![]() $\sigma $
on
$\sigma $
on
![]() $\mathrm {{Br}}(X)[2]$
is the same as the image of the nonzero element of
$\mathrm {{Br}}(X)[2]$
is the same as the image of the nonzero element of
![]() $\mathrm {{Br}}(X/(f_{1,\sigma }^{-1}\iota ^{\sigma } f_{1,\sigma }))$
in
$\mathrm {{Br}}(X/(f_{1,\sigma }^{-1}\iota ^{\sigma } f_{1,\sigma }))$
in
![]() $\mathrm {{Br}}(X)[2]$
. This proves that
$\mathrm {{Br}}(X)[2]$
. This proves that
![]() $\varphi _X$
is
$\varphi _X$
is
![]() $G_{K}$
-equivariant.
$G_{K}$
-equivariant.
Moduli fields of singular K3 surfaces
Let X be a singular K3 surface, that is, a K3 surface of maximal Picard rank
![]() $20$
. It is well known that every singular K3 surface is defined over
$20$
. It is well known that every singular K3 surface is defined over
![]() $\overline {\mathbb Q}$
and has complex multiplication by the imaginary quadratic field
$\overline {\mathbb Q}$
and has complex multiplication by the imaginary quadratic field
![]() $E = \mathrm {{End}}_{\mathrm {Hdg}} (T(X)_{\mathbb Q})$
. Assume that
$E = \mathrm {{End}}_{\mathrm {Hdg}} (T(X)_{\mathbb Q})$
. Assume that
![]() $\mathrm {{End}}_{\mathrm {Hdg}}(T(X))$
is the ring of integers
$\mathrm {{End}}_{\mathrm {Hdg}}(T(X))$
is the ring of integers
![]() $\mathcal {O}_E\subset E$
. In this situation, the results of [Reference ValloniV] give explicit descriptions of the moduli fields
$\mathcal {O}_E\subset E$
. In this situation, the results of [Reference ValloniV] give explicit descriptions of the moduli fields
![]() $E(X)$
and
$E(X)$
and
![]() $E(X, \mathrm {{Br}}(X)[n])$
which we now recall.
$E(X, \mathrm {{Br}}(X)[n])$
which we now recall.
The group
![]() $\mathrm {{Br}}(X)\cong \mathrm {{Hom}}(T(X),{\mathbb Q}/{\mathbb Z})$
is naturally an
$\mathrm {{Br}}(X)\cong \mathrm {{Hom}}(T(X),{\mathbb Q}/{\mathbb Z})$
is naturally an
![]() $\mathcal {O}_E$
-module. Let
$\mathcal {O}_E$
-module. Let
![]() $K_n/E$
be the ray class field of E with modulus
$K_n/E$
be the ray class field of E with modulus
![]() $n\mathcal {O}_E,$
and let
$n\mathcal {O}_E,$
and let
![]() $\mathrm {Cl}_n(E) \cong \mathrm {Gal}(K_n/E)$
. The complex conjugation c acts on
$\mathrm {Cl}_n(E) \cong \mathrm {Gal}(K_n/E)$
. The complex conjugation c acts on
![]() $\mathrm {Cl}_n(E)$
. Let
$\mathrm {Cl}_n(E)$
. Let
![]() $\mathrm {Cl}_n(E)^c$
be the c-invariant subgroup of
$\mathrm {Cl}_n(E)^c$
be the c-invariant subgroup of
![]() $\mathrm {Cl}_n(E)$
. Define
$\mathrm {Cl}_n(E)$
. Define
![]() $\widetilde {K}_n \subset K_n$
as the fixed field of
$\widetilde {K}_n \subset K_n$
as the fixed field of
![]() $\mathrm {Cl}_n(E)^c$
, so that
$\mathrm {Cl}_n(E)^c$
, so that
![]() $\mathrm {Gal}(\widetilde {K}_n/E) \cong \mathrm {Cl}_n(E)/ \mathrm {Cl}_n(E)^c$
. Note that
$\mathrm {Gal}(\widetilde {K}_n/E) \cong \mathrm {Cl}_n(E)/ \mathrm {Cl}_n(E)^c$
. Note that
![]() $K_1$
is the Hilbert class field of E and
$K_1$
is the Hilbert class field of E and
![]() $\mathrm {Cl}_1(E) = \mathrm {Cl}(E)$
is the usual class group. The complex conjugation c acts on
$\mathrm {Cl}_1(E) = \mathrm {Cl}(E)$
is the usual class group. The complex conjugation c acts on
![]() $\mathrm {Cl}(E)$
as
$\mathrm {Cl}(E)$
as
![]() $-1$
.
$-1$
.
Theorem 4.4. Let X be a singular K3 surface. Then
![]() $\widetilde {K}_n=E(X, \mathrm {{Br}}(X)[n])$
.
$\widetilde {K}_n=E(X, \mathrm {{Br}}(X)[n])$
.
Proof. See [Reference ValloniV, Th. 11.2 and Rem. 9.2 on p. 41].
In particular, we have
![]() $\widetilde {K}_1=E(X)$
. If n divides m, then
$\widetilde {K}_1=E(X)$
. If n divides m, then
![]() $\widetilde {K}_n \subset \widetilde {K}_m$
.
$\widetilde {K}_n \subset \widetilde {K}_m$
.
Proof of Theorem C
The assumptions of Theorem C imply that
![]() $\mathrm {Aut}_{\mathrm {Hdg}}(T(X))={\mathcal O}_E^{\times }=\{\pm 1\}$
, so we can apply Proposition 4.3. Let
$\mathrm {Aut}_{\mathrm {Hdg}}(T(X))={\mathcal O}_E^{\times }=\{\pm 1\}$
, so we can apply Proposition 4.3. Let
![]() $\rho $
be the representation of
$\rho $
be the representation of
![]() $G_{\widetilde {K}_1}$
in
$G_{\widetilde {K}_1}$
in
![]() $\mathrm {{Br}}(X)[2] \cong ({\mathbb Z}/2)^2$
constructed in the proof of Proposition 4.3. It is enough to show that under our assumptions one has
$\mathrm {{Br}}(X)[2] \cong ({\mathbb Z}/2)^2$
constructed in the proof of Proposition 4.3. It is enough to show that under our assumptions one has
![]() $|\rho (G_{\widetilde {K}_1})| = 3$
. Then
$|\rho (G_{\widetilde {K}_1})| = 3$
. Then
![]() $G_{\widetilde {K}_1}$
acts transitively on
$G_{\widetilde {K}_1}$
acts transitively on
![]() $\mathrm {{Br}}(X)[2]\setminus \{0\}$
, so in view of the
$\mathrm {{Br}}(X)[2]\setminus \{0\}$
, so in view of the
![]() $G_{\widetilde {K}_1}$
-equivariance established in Proposition 4.3 this will imply Theorem C. By Theorem 4.4, we need to prove that
$G_{\widetilde {K}_1}$
-equivariance established in Proposition 4.3 this will imply Theorem C. By Theorem 4.4, we need to prove that
![]() $[\widetilde K_2:\widetilde K_1]=3$
.
$[\widetilde K_2:\widetilde K_1]=3$
.
The following exact sequence describes the ray class group
![]() $\mathrm {Cl}_2(E)$
:
$\mathrm {Cl}_2(E)$
:
 $$ \begin{align*} 0 \rightarrow \frac{\mathcal{O}_E^{\times}}{\{ x \in \mathcal{O}_E^{\times} | x \equiv 1 \, \mathrm{mod} \, 2 \}} \rightarrow (\mathcal{O}_E/2)^{\times} \rightarrow \mathrm{Cl}_2(E) \rightarrow \mathrm{Cl}(E) \rightarrow 0. \end{align*} $$
$$ \begin{align*} 0 \rightarrow \frac{\mathcal{O}_E^{\times}}{\{ x \in \mathcal{O}_E^{\times} | x \equiv 1 \, \mathrm{mod} \, 2 \}} \rightarrow (\mathcal{O}_E/2)^{\times} \rightarrow \mathrm{Cl}_2(E) \rightarrow \mathrm{Cl}(E) \rightarrow 0. \end{align*} $$
Under our assumptions, we have
![]() $\mathcal {O}_E^{\times } =\{ x \in \mathcal {O}_E^{\times } | x \equiv 1 \, \mathrm {mod} \, 2 \} = \{ \pm 1 \}$
. Since
$\mathcal {O}_E^{\times } =\{ x \in \mathcal {O}_E^{\times } | x \equiv 1 \, \mathrm {mod} \, 2 \} = \{ \pm 1 \}$
. Since
![]() $2$
is inert in E, we have
$2$
is inert in E, we have
![]() $\mathcal {O}_E / 2 \cong \mathbb {F}_4$
, and thus the sequence above becomes
$\mathcal {O}_E / 2 \cong \mathbb {F}_4$
, and thus the sequence above becomes
This is a sequence of G-modules, where
![]() $G = \{1, c \}$
. We have
$G = \{1, c \}$
. We have
![]() $({\mathbb F}_4^{\times })^c =\{1\}$
and
$({\mathbb F}_4^{\times })^c =\{1\}$
and
![]() $\mathrm {H}^1(G, \mathbb {F}_4^{\times }) = 0$
, and hence
$\mathrm {H}^1(G, \mathbb {F}_4^{\times }) = 0$
, and hence
![]() $\mathrm {Cl}_2(E)^c = \mathrm {Cl}(E)^c$
. From this, we obtain the exact sequence
$\mathrm {Cl}_2(E)^c = \mathrm {Cl}(E)^c$
. From this, we obtain the exact sequence
Thus,
![]() $[\widetilde K_2:\widetilde K_1]=3$
, as required.
$[\widetilde K_2:\widetilde K_1]=3$
, as required.
Remark 4.5. When
![]() $2$
is split, a similar argument shows that the
$2$
is split, a similar argument shows that the
![]() $G_{\widetilde {K}_1}$
-action on
$G_{\widetilde {K}_1}$
-action on
![]() $\mathrm {{Br}}(X)[2]$
is trivial.
$\mathrm {{Br}}(X)[2]$
is trivial.
5 Constructing Enriques involutions
For a finite abelian group
![]() $G,$
we write
$G,$
we write
![]() $\ell (G)$
for the minimal number of generators of G. For a prime p we denote by
$\ell (G)$
for the minimal number of generators of G. For a prime p we denote by
![]() $G_p$
the p-primary subgroup of G. Recall that for a lattice L we write
$G_p$
the p-primary subgroup of G. Recall that for a lattice L we write
![]() $A_L=L^*/L$
for the discriminant group of L. When L is even, we denote by
$A_L=L^*/L$
for the discriminant group of L. When L is even, we denote by
![]() $q_L\colon A_L\to {\mathbb Q}/2{\mathbb Z}$
the finite quadratic form of L.
$q_L\colon A_L\to {\mathbb Q}/2{\mathbb Z}$
the finite quadratic form of L.
We need to recall fundamental results of Nikulin about the existence of lattices and their primitive embeddings.
Let
![]() $q \colon A \rightarrow {\mathbb Q} / 2 {\mathbb Z}$
be a finite quadratic form. The signature
$q \colon A \rightarrow {\mathbb Q} / 2 {\mathbb Z}$
be a finite quadratic form. The signature
![]() $\mathrm {sign}(q) \in {\mathbb Z} / 8 {\mathbb Z}$
of q is defined as
$\mathrm {sign}(q) \in {\mathbb Z} / 8 {\mathbb Z}$
of q is defined as
![]() $(t_+ - t_-) \bmod 8$
, where
$(t_+ - t_-) \bmod 8$
, where
![]() $(t_+, t_-)$
is the signature of any even lattice whose discriminant form is isomorphic to
$(t_+, t_-)$
is the signature of any even lattice whose discriminant form is isomorphic to
![]() $(A,q)$
(such a lattice always exists and, moreover, this notion is well-defined). One also has
$(A,q)$
(such a lattice always exists and, moreover, this notion is well-defined). One also has
Write
![]() $A = \bigoplus _p A_p$
, where p ranges over the prime numbers. Then one has quadratic forms
$A = \bigoplus _p A_p$
, where p ranges over the prime numbers. Then one has quadratic forms
![]() $q_p \colon A_p \rightarrow {\mathbb Q}_p / {\mathbb Z}_p$
when p is odd and
$q_p \colon A_p \rightarrow {\mathbb Q}_p / {\mathbb Z}_p$
when p is odd and
![]() $q_2 \colon A_2 \rightarrow {\mathbb Q}_2/ 2 {\mathbb Z}_2$
when
$q_2 \colon A_2 \rightarrow {\mathbb Q}_2/ 2 {\mathbb Z}_2$
when
![]() $p=2$
. It is clear that q is the orthogonal direct sum of the forms
$p=2$
. It is clear that q is the orthogonal direct sum of the forms
![]() $q_p$
.
$q_p$
.
For an odd prime p, a finite abelian p-group
![]() $A_p$
, and a quadratic form
$A_p$
, and a quadratic form
![]() $q_p\colon A_p\to {\mathbb Q}_p/{\mathbb Z}_p$
, Nikulin [Reference NikulinN, Th. 1.9.1] showed that there is a unique
$q_p\colon A_p\to {\mathbb Q}_p/{\mathbb Z}_p$
, Nikulin [Reference NikulinN, Th. 1.9.1] showed that there is a unique
![]() ${\mathbb Z}_p$
-lattice
${\mathbb Z}_p$
-lattice
![]() $K(q_p)$
of rank
$K(q_p)$
of rank
![]() $\ell (A_p)$
whose quadratic form is isomorphic to
$\ell (A_p)$
whose quadratic form is isomorphic to
![]() $q_p$
.
$q_p$
.
When
![]() $p=2$
, the same result of Nikulin says the following. Let
$p=2$
, the same result of Nikulin says the following. Let
![]() $q^{(2)}_{\theta } (2)$
be the discriminant quadratic form of the rank one
$q^{(2)}_{\theta } (2)$
be the discriminant quadratic form of the rank one
![]() ${\mathbb Z}_2$
-lattice
${\mathbb Z}_2$
-lattice
![]() $(2 \theta )$
, where
$(2 \theta )$
, where
![]() $\theta \in {\mathbb Z}_2^{\times }$
. For a finite abelian 2-group
$\theta \in {\mathbb Z}_2^{\times }$
. For a finite abelian 2-group
![]() $A_2$
and a quadratic form
$A_2$
and a quadratic form
![]() $q_2\colon A_2\to {\mathbb Q}_2/2{\mathbb Z}_2$
we have the following alternative. If
$q_2\colon A_2\to {\mathbb Q}_2/2{\mathbb Z}_2$
we have the following alternative. If
![]() $q_2$
splits as an orthogonal direct sum
$q_2$
splits as an orthogonal direct sum
![]() $q_2=q^{(2)}_{\theta } (2) \oplus q^{\prime }_2$
, then there are precisely two even
$q_2=q^{(2)}_{\theta } (2) \oplus q^{\prime }_2$
, then there are precisely two even
![]() ${\mathbb Z}_2$
-lattices of rank
${\mathbb Z}_2$
-lattices of rank
![]() $\ell (A_2)$
whose quadratic form is isomorphic to
$\ell (A_2)$
whose quadratic form is isomorphic to
![]() $q_2$
. If such a splitting of
$q_2$
. If such a splitting of
![]() $q_2$
does not exist, there is a unique
$q_2$
does not exist, there is a unique
![]() ${\mathbb Z}_2$
-lattice
${\mathbb Z}_2$
-lattice
![]() $K(q_2)$
of rank
$K(q_2)$
of rank
![]() $\ell (A_2)$
whose quadratic form is isomorphic to
$\ell (A_2)$
whose quadratic form is isomorphic to
![]() $q_2$
. The following result is [Reference NikulinN, Th. 1.10.1].
$q_2$
. The following result is [Reference NikulinN, Th. 1.10.1].
Theorem 5.1 (Nikulin).
An even lattice with signature
![]() $(t_+, t_-)$
and quadratic form
$(t_+, t_-)$
and quadratic form
![]() $q\colon A\to {\mathbb Q}/2{\mathbb Z}$
exists if and only if the following conditions are satisfied:
$q\colon A\to {\mathbb Q}/2{\mathbb Z}$
exists if and only if the following conditions are satisfied:
-
(1)
 $t_+ - t_- \equiv \mathrm {sign}(q) \mod 8$
;
$t_+ - t_- \equiv \mathrm {sign}(q) \mod 8$
; -
(2)
 $t_+, t_- \geq 0$
and
$t_+, t_- \geq 0$
and
 $t_+ + t_- \geq \ell (A)$
;
$t_+ + t_- \geq \ell (A)$
; -
(3)
 $(-1)^{t_-} |A_p| \equiv \mathrm {discr} K(q_p) \bmod {\mathbb Z}_p^{\times 2}$
for the odd primes p such that
$(-1)^{t_-} |A_p| \equiv \mathrm {discr} K(q_p) \bmod {\mathbb Z}_p^{\times 2}$
for the odd primes p such that
 $t_+ + t_- = \ell (A_p)$
;
$t_+ + t_- = \ell (A_p)$
; -
(4)
 $|A_2| \equiv \pm \mathrm {discr} K(q_2) \bmod {\mathbb Z}_2^{\times 2}$
if
$|A_2| \equiv \pm \mathrm {discr} K(q_2) \bmod {\mathbb Z}_2^{\times 2}$
if
 $t_+ + t_- = \ell (A_2)$
and
$t_+ + t_- = \ell (A_2)$
and
 $q_2 \neq q_{\theta }^{(2)}(2) \oplus q_2'$
for any
$q_2 \neq q_{\theta }^{(2)}(2) \oplus q_2'$
for any
 $\theta $
and
$\theta $
and
 $q_2'$
.
$q_2'$
.
The following result is a consequence of [Reference NikulinN, Prop. 1.15.1] where we took into account that N is the unique lattice of signature
![]() $(2,10)$
whose quadratic form is isomorphic to
$(2,10)$
whose quadratic form is isomorphic to
![]() $q_N$
(see [Reference NikulinN, Cor. 1.13.4].
$q_N$
(see [Reference NikulinN, Cor. 1.13.4].
Theorem 5.2 (Nikulin).
Let L be an even lattice with signature
![]() $(2_+, k_-)$
and quadratic form
$(2_+, k_-)$
and quadratic form
![]() $q_L\colon A_L\to {\mathbb Q}/2{\mathbb Z}$
. The existence of a primitive embedding
$q_L\colon A_L\to {\mathbb Q}/2{\mathbb Z}$
. The existence of a primitive embedding
![]() $L \hookrightarrow N$
is equivalent to the existence of the following data:
$L \hookrightarrow N$
is equivalent to the existence of the following data:
-
• subgroups
 $H_L \subset A_L$
and
$H_L \subset A_L$
and
 $H_N \subset A_N$
;
$H_N \subset A_N$
; -
• an isomorphism of finite quadratic forms
 $\gamma \colon (H_L,q_L|_{H_L}) \xrightarrow {\sim } (H_N,q_N|_{H_N})$
;
$\gamma \colon (H_L,q_L|_{H_L}) \xrightarrow {\sim } (H_N,q_N|_{H_N})$
; -
• an even negative-definite lattice K of rank
 $10-k$
;
$10-k$
; -
• an isomorphism of finite quadratic forms
 $\delta $
from
$\delta $
from
 $(A_K,-q_K)$
to the restriction of
$(A_K,-q_K)$
to the restriction of
 $q_L\oplus -q_N$
to
$q_L\oplus -q_N$
to
 $\Gamma _{\gamma }^{\perp } / \Gamma _{\gamma }$
, where the isotropic subgroup
$\Gamma _{\gamma }^{\perp } / \Gamma _{\gamma }$
, where the isotropic subgroup
 $\Gamma _{\gamma }\subset A_L\oplus A_N$
is the graph of
$\Gamma _{\gamma }\subset A_L\oplus A_N$
is the graph of
 $\gamma $
in
$\gamma $
in
 $H_L\oplus H_N\subset A_L\oplus A_N$
.
$H_L\oplus H_N\subset A_L\oplus A_N$
.
Moreover, if
![]() $i \colon L \hookrightarrow N$
is a primitive embedding associated to
$i \colon L \hookrightarrow N$
is a primitive embedding associated to
![]() $(H_L, H_N, \gamma, K, \delta )$
, then
$(H_L, H_N, \gamma, K, \delta )$
, then
![]() $K \cong i(L)^{\perp }$
.
$K \cong i(L)^{\perp }$
.
Remark 5.3.
-
(1) If
 $f \colon \widetilde {K} \to K$
is an isomorphism of lattices and
$f \colon \widetilde {K} \to K$
is an isomorphism of lattices and
 $\bar {f} \colon A_{\widetilde {K}} \to A_K$
is the induced isomorphism, then the primitive embeddings
$\bar {f} \colon A_{\widetilde {K}} \to A_K$
is the induced isomorphism, then the primitive embeddings
 $L\hookrightarrow N$
associated to
$L\hookrightarrow N$
associated to
 $(H_L, H_N, \gamma , K, \delta )$
and to
$(H_L, H_N, \gamma , K, \delta )$
and to
 $(H_L, H_N, \gamma , \widetilde {K},\delta \circ \bar {f})$
are isomorphic.
$(H_L, H_N, \gamma , \widetilde {K},\delta \circ \bar {f})$
are isomorphic. -
(2) An analog of Theorem 5.2 gives the conditions for the existence of a primitive embedding of
 $L\otimes {\mathbb Z}_p$
into
$L\otimes {\mathbb Z}_p$
into
 $N\otimes {\mathbb Z}_p$
, for any prime p. The analog of (1) also holds in this context.
$N\otimes {\mathbb Z}_p$
, for any prime p. The analog of (1) also holds in this context.
Definition 5.4. Let L be a lattice such that
![]() $0<\mathrm {{rk}}(L) \leq 10$
. We say that a sublattice
$0<\mathrm {{rk}}(L) \leq 10$
. We say that a sublattice
![]() $L' \subset L$
of finite index satisfies condition
$L' \subset L$
of finite index satisfies condition
![]() $(*)$
if
$(*)$
if
and for each prime p not dividing
![]() $ 2\mathrm {discr}(L),$
we have
$ 2\mathrm {discr}(L),$
we have
![]() $\ell (A_{L',p}) < 12 - \mathrm {{rk}}(L')$
.
$\ell (A_{L',p}) < 12 - \mathrm {{rk}}(L')$
.
Proposition 5.5. Any lattice L such that
![]() $0<\mathrm {{rk}}(L) \leq 10$
contains infinitely many distinct sublattices
$0<\mathrm {{rk}}(L) \leq 10$
contains infinitely many distinct sublattices
![]() $L'\subset L$
satisfying condition
$L'\subset L$
satisfying condition
![]() $(*)$
.
$(*)$
.
Proof. Let p be any odd prime not dividing
![]() $\mathrm {discr}(L)$
. As is well known (see, e.g., [Reference NikulinN, Cor. 1.9.3]), the unimodular p-adic lattice
$\mathrm {discr}(L)$
. As is well known (see, e.g., [Reference NikulinN, Cor. 1.9.3]), the unimodular p-adic lattice
![]() $L\otimes {\mathbb Z}_p$
has an orthogonal
$L\otimes {\mathbb Z}_p$
has an orthogonal
![]() ${\mathbb Z}_p$
-basis
${\mathbb Z}_p$
-basis
![]() $v_1,\ldots ,v_n$
such that
$v_1,\ldots ,v_n$
such that
![]() $(v_i^2)\in {\mathbb Z}_p^{\times }$
for
$(v_i^2)\in {\mathbb Z}_p^{\times }$
for
![]() $i=1,\ldots , n$
. The images of
$i=1,\ldots , n$
. The images of
![]() $v_1,\ldots ,v_n$
in
$v_1,\ldots ,v_n$
in
![]() $(L\otimes {\mathbb Z}_p)/p\cong L/p$
form a basis of this
$(L\otimes {\mathbb Z}_p)/p\cong L/p$
form a basis of this
![]() ${\mathbb F}_p$
-vector space. Let
${\mathbb F}_p$
-vector space. Let
![]() $L'\subset L$
be the inverse image of the hyperplane spanned by the images of
$L'\subset L$
be the inverse image of the hyperplane spanned by the images of
![]() $v_2,\ldots ,v_n$
. Thus
$v_2,\ldots ,v_n$
. Thus
![]() $[L:L']=p$
, so that
$[L:L']=p$
, so that
![]() $\mathrm {discr}(L')=p^2\mathrm {discr}(L)$
. Since p does not divide
$\mathrm {discr}(L')=p^2\mathrm {discr}(L)$
. Since p does not divide
![]() $\mathrm { discr}(L)$
, we have a canonical isomorphism
$\mathrm { discr}(L)$
, we have a canonical isomorphism
![]() $A_{L'}\cong A_L\oplus A_{L',p}$
. It is enough to check that
$A_{L'}\cong A_L\oplus A_{L',p}$
. It is enough to check that
![]() $\ell (A_{L',p})=1$
, which says that
$\ell (A_{L',p})=1$
, which says that
![]() $A_{L',p}$
is cyclic. It is clear that
$A_{L',p}$
is cyclic. It is clear that
![]() $A_{L',p}\cong A_{L'\otimes {\mathbb Z}_p}$
, so it is enough to prove that
$A_{L',p}\cong A_{L'\otimes {\mathbb Z}_p}$
, so it is enough to prove that
![]() $\mathrm {{Hom}}_{{\mathbb Z}_p}(L'\otimes {\mathbb Z}_p,{\mathbb Z}_p)/(L'\otimes {\mathbb Z}_p)\cong {\mathbb Z}/p^2$
. The
$\mathrm {{Hom}}_{{\mathbb Z}_p}(L'\otimes {\mathbb Z}_p,{\mathbb Z}_p)/(L'\otimes {\mathbb Z}_p)\cong {\mathbb Z}/p^2$
. The
![]() ${\mathbb Z}_p$
-module
${\mathbb Z}_p$
-module
![]() $L'\otimes {\mathbb Z}_p$
is freely generated by
$L'\otimes {\mathbb Z}_p$
is freely generated by
![]() $pv_1,v_2,\ldots ,v_n$
, hence the
$pv_1,v_2,\ldots ,v_n$
, hence the
![]() ${\mathbb Z}_p$
-module
${\mathbb Z}_p$
-module
![]() $\mathrm {{Hom}}_{{\mathbb Z}_p}(L'\otimes {\mathbb Z}_p,{\mathbb Z}_p)\subset L'\otimes {\mathbb Q}_p$
is freely generated by
$\mathrm {{Hom}}_{{\mathbb Z}_p}(L'\otimes {\mathbb Z}_p,{\mathbb Z}_p)\subset L'\otimes {\mathbb Q}_p$
is freely generated by
![]() $p^{-1}v_1,v_2,\ldots ,v_n$
, which implies the result.
$p^{-1}v_1,v_2,\ldots ,v_n$
, which implies the result.
Condition
![]() $(*)$
implies that
$(*)$
implies that
![]() $[L \colon L']$
is odd, and hence the inclusion
$[L \colon L']$
is odd, and hence the inclusion
![]() $L' \subset L$
induces a natural isomorphism
$L' \subset L$
induces a natural isomorphism
Recall that for a primitive embedding
![]() $i\colon L\hookrightarrow N$
we denote by
$i\colon L\hookrightarrow N$
we denote by
![]() $i^*(\varepsilon )$
the precomposition of the character
$i^*(\varepsilon )$
the precomposition of the character
![]() $\varepsilon \colon N\to {\mathbb Z}/2$
with i.
$\varepsilon \colon N\to {\mathbb Z}/2$
with i.
Theorem 5.6. Let
![]() $L' \subset L$
be an inclusion of even lattices of signature
$L' \subset L$
be an inclusion of even lattices of signature
![]() $(2_+, k_-)$
, where
$(2_+, k_-)$
, where
![]() $0\leq k\leq 8$
. Then we have the following statements.
$0\leq k\leq 8$
. Then we have the following statements.
-
(a) If
 $L' \subset L$
satisfies condition
$L' \subset L$
satisfies condition
 $(*)$
, then for any primitive embedding
$(*)$
, then for any primitive embedding
 $i\colon L\hookrightarrow N$
with
$i\colon L\hookrightarrow N$
with
 $i^*(\varepsilon )\neq 0$
there exists a primitive embedding
$i^*(\varepsilon )\neq 0$
there exists a primitive embedding
 $i'\colon L'\hookrightarrow N$
such that
$i'\colon L'\hookrightarrow N$
such that
 $i^{\prime *}(\varepsilon )=i^*(\varepsilon )$
under the identification (2).
$i^{\prime *}(\varepsilon )=i^*(\varepsilon )$
under the identification (2). -
(b) If
 $[L \colon L']$
is odd, then for any primitive embedding
$[L \colon L']$
is odd, then for any primitive embedding
 $i'\colon L'\hookrightarrow N$
with
$i'\colon L'\hookrightarrow N$
with
 $i^{\prime *}(\varepsilon )\neq 0$
there exists a primitive embedding
$i^{\prime *}(\varepsilon )\neq 0$
there exists a primitive embedding
 $i\colon L\hookrightarrow N$
such that
$i\colon L\hookrightarrow N$
such that
 $i^{\prime *}(\varepsilon )=i^*(\varepsilon )$
under the identification (2).
$i^{\prime *}(\varepsilon )=i^*(\varepsilon )$
under the identification (2).
Proof. (a) Let
![]() $i\colon L\hookrightarrow N$
be a primitive embedding such that
$i\colon L\hookrightarrow N$
be a primitive embedding such that
![]() $i^*(\varepsilon )\neq 0$
. Then
$i^*(\varepsilon )\neq 0$
. Then
![]() $K:=i(L)^{\perp }_N$
is an even negative-definite lattice of rank
$K:=i(L)^{\perp }_N$
is an even negative-definite lattice of rank
![]() $10-k$
. By Theorem 5.2, the embedding i corresponds to some datum
$10-k$
. By Theorem 5.2, the embedding i corresponds to some datum
![]() $(H_L, H_N, \gamma , K, \delta )$
.
$(H_L, H_N, \gamma , K, \delta )$
.
Since
![]() $L' \subset L$
satisfies condition
$L' \subset L$
satisfies condition
![]() $(*)$
, the index
$(*)$
, the index
![]() $[L:L']$
is coprime to
$[L:L']$
is coprime to
![]() $|A_L|$
, hence
$|A_L|$
, hence
![]() $A_{L'}$
canonically isomorphic to
$A_{L'}$
canonically isomorphic to
![]() $A_L \oplus A_{\mathrm {new}}$
, where
$A_L \oplus A_{\mathrm {new}}$
, where
![]() $|A_{\mathrm {new}}|=[L:L']^2$
. Then
$|A_{\mathrm {new}}|=[L:L']^2$
. Then
![]() $q_{L'}$
is an orthogonal direct sum
$q_{L'}$
is an orthogonal direct sum
![]() $q_{L'}\cong q_L\oplus q_{\mathrm {new}}$
, where
$q_{L'}\cong q_L\oplus q_{\mathrm {new}}$
, where
![]() $q_{\mathrm {new}}$
is a quadratic form on
$q_{\mathrm {new}}$
is a quadratic form on
![]() $A_{\mathrm {new}}$
.
$A_{\mathrm {new}}$
.
We claim that there is a negative-definite lattice
![]() $K'$
of rank
$K'$
of rank
![]() $10 - k$
such that
$10 - k$
such that
![]() $A_{K'}\cong A_K \oplus A_{\mathrm {new}}$
and
$A_{K'}\cong A_K \oplus A_{\mathrm {new}}$
and
![]() $q_{K'}\cong q_K\oplus -q_{\mathrm {new}}$
. Since
$q_{K'}\cong q_K\oplus -q_{\mathrm {new}}$
. Since
![]() $L'$
is a sublattice of L of finite index and
$L'$
is a sublattice of L of finite index and
![]() $\mathrm {{rk}}(K)=10-k$
, we have
$\mathrm {{rk}}(K)=10-k$
, we have
Since
![]() $q_{L'}\cong q_L \oplus q_{\mathrm {new}}$
, we have that
$q_{L'}\cong q_L \oplus q_{\mathrm {new}}$
, we have that
![]() $\mathrm {sign}(q_{L'}) = \mathrm {sign}(q_{L}) + \mathrm {sign}(q_{\mathrm {new}})$
by (1). Thus
$\mathrm {sign}(q_{L'}) = \mathrm {sign}(q_{L}) + \mathrm {sign}(q_{\mathrm {new}})$
by (1). Thus
![]() $\mathrm {sign}(q_{\mathrm {new}}) \equiv 0 \bmod 8$
, which implies property (1) of Theorem 5.1.
$\mathrm {sign}(q_{\mathrm {new}}) \equiv 0 \bmod 8$
, which implies property (1) of Theorem 5.1.
By condition
![]() $(*)$
, we know that
$(*)$
, we know that
![]() $|A_{\mathrm {new}}|$
is odd and coprime to
$|A_{\mathrm {new}}|$
is odd and coprime to
![]() $|A_L|$
. For any odd prime p, the
$|A_L|$
. For any odd prime p, the
![]() ${\mathbb Z}_p$
-lattices
${\mathbb Z}_p$
-lattices
![]() $L \otimes {\mathbb Z}_p$
and
$L \otimes {\mathbb Z}_p$
and
![]() $K \otimes {\mathbb Z}_p$
are orthogonal complements of each other in the unimodular
$K \otimes {\mathbb Z}_p$
are orthogonal complements of each other in the unimodular
![]() ${\mathbb Z}_p$
-lattice
${\mathbb Z}_p$
-lattice
![]() $N \otimes {\mathbb Z}_p$
, hence
$N \otimes {\mathbb Z}_p$
, hence
![]() $|A_{L,p}|=|A_{K,p}|$
. Thus,
$|A_{L,p}|=|A_{K,p}|$
. Thus,
![]() $|A_K|$
and
$|A_K|$
and
![]() $|A_{\mathrm {new}}|$
are coprime. This implies
$|A_{\mathrm {new}}|$
are coprime. This implies
since
![]() $\ell (A_K)\leq \mathrm {{rk}}(K)=10-k$
and
$\ell (A_K)\leq \mathrm {{rk}}(K)=10-k$
and
![]() $\ell (A_{\mathrm {new}})\leq \ell (A_{L'})< 12-\mathrm {{rk}}(L)$
by condition
$\ell (A_{\mathrm {new}})\leq \ell (A_{L'})< 12-\mathrm {{rk}}(L)$
by condition
![]() $(*)$
. Thus, property (2) of Theorem 5.1 also holds.
$(*)$
. Thus, property (2) of Theorem 5.1 also holds.
We now check properties (3) and (4) taking into account the coprimality of
![]() $|A_K|$
and
$|A_K|$
and
![]() $|A_{\mathrm {new}}|$
. If p divides
$|A_{\mathrm {new}}|$
. If p divides
![]() $|A_K|$
, then (3) and (4) hold because they hold for
$|A_K|$
, then (3) and (4) hold because they hold for
![]() $A_K$
. If p divides
$A_K$
. If p divides
![]() $|A_{\mathrm {new}}|$
, then
$|A_{\mathrm {new}}|$
, then
![]() $\ell ( A_{\mathrm {new}}) < \mathrm {{rk}}(K')$
by condition
$\ell ( A_{\mathrm {new}}) < \mathrm {{rk}}(K')$
by condition
![]() $(*)$
, so there is nothing to check.
$(*)$
, so there is nothing to check.
Theorem 5.1 now implies the existence of
![]() $K'$
with required properties.
$K'$
with required properties.
Let us construct a datum defining the desired primitive embedding
![]() $L' \hookrightarrow N$
. Since
$L' \hookrightarrow N$
. Since
![]() $2A_N=0$
, we have
$2A_N=0$
, we have
![]() $2H_N=0$
and thus
$2H_N=0$
and thus
![]() $2H_L=0$
, so that
$2H_L=0$
, so that
![]() $H_L \subset A_{L,2}$
. In view of the canonical isomorphism
$H_L \subset A_{L,2}$
. In view of the canonical isomorphism
![]() $A_{L,2} \cong A_{L',2}$
, we can keep the same
$A_{L,2} \cong A_{L',2}$
, we can keep the same
![]() $H_{L'}=H_L$
,
$H_{L'}=H_L$
,
![]() $H_N$
and
$H_N$
and
![]() $\gamma '=\gamma $
as the first three entries of our datum.
$\gamma '=\gamma $
as the first three entries of our datum.
Recall that
![]() $A_{L'}\cong A_L \oplus A_{\mathrm {new}}$
. We have
$A_{L'}\cong A_L \oplus A_{\mathrm {new}}$
. We have
hence
![]() $\Gamma _{\gamma '}^{\perp } / \Gamma _{\gamma '} = \Gamma _{\gamma }^{\perp } / \Gamma _{\gamma }\oplus A_{\mathrm {new}} \cong A_K \oplus A_{\mathrm {new}}$
. The restriction of
$\Gamma _{\gamma '}^{\perp } / \Gamma _{\gamma '} = \Gamma _{\gamma }^{\perp } / \Gamma _{\gamma }\oplus A_{\mathrm {new}} \cong A_K \oplus A_{\mathrm {new}}$
. The restriction of
to
![]() $\Gamma _{\gamma '}^{\perp } / \Gamma _{\gamma '}$
is isomorphic to
$\Gamma _{\gamma '}^{\perp } / \Gamma _{\gamma '}$
is isomorphic to
![]() $-q_K\oplus q_{\mathrm {new}}$
via the isomorphism
$-q_K\oplus q_{\mathrm {new}}$
via the isomorphism
![]() $\delta ':=(\delta , \mathrm {id})$
.
$\delta ':=(\delta , \mathrm {id})$
.
Take a negative-definite lattice
![]() $K'$
of rank
$K'$
of rank
![]() $10 - k$
as above, that is, such that
$10 - k$
as above, that is, such that
![]() $A_{K'}\cong A_K \oplus A_{\mathrm {new}}$
and
$A_{K'}\cong A_K \oplus A_{\mathrm {new}}$
and
![]() $q_{K'}\cong q_K\oplus -q_{\mathrm {new}}$
. Let
$q_{K'}\cong q_K\oplus -q_{\mathrm {new}}$
. Let
![]() $i'\colon L'\hookrightarrow N$
be a primitive embedding associated to the datum
$i'\colon L'\hookrightarrow N$
be a primitive embedding associated to the datum
![]() $(H_{L'}, H_{N}, \gamma ', K', \delta ')$
.
$(H_{L'}, H_{N}, \gamma ', K', \delta ')$
.
To prove that
![]() $i^{\prime *}(\varepsilon )=i(\varepsilon )$
under the natural identification (2), it is enough to show that the induced embeddings of
$i^{\prime *}(\varepsilon )=i(\varepsilon )$
under the natural identification (2), it is enough to show that the induced embeddings of
![]() ${\mathbb Z}_2$
-lattices
${\mathbb Z}_2$
-lattices
![]() $i_2\colon L\otimes {\mathbb Z}_2\hookrightarrow N\otimes {\mathbb Z}_2$
and
$i_2\colon L\otimes {\mathbb Z}_2\hookrightarrow N\otimes {\mathbb Z}_2$
and
![]() $i^{\prime }_2\colon L'\otimes {\mathbb Z}_2\hookrightarrow N\otimes {\mathbb Z}_2$
are isomorphic.
$i^{\prime }_2\colon L'\otimes {\mathbb Z}_2\hookrightarrow N\otimes {\mathbb Z}_2$
are isomorphic.
First, we claim that
![]() $K \otimes {\mathbb Z}_2$
and
$K \otimes {\mathbb Z}_2$
and
![]() $K' \otimes {\mathbb Z}_2$
are isomorphic
$K' \otimes {\mathbb Z}_2$
are isomorphic
![]() ${\mathbb Z}_2$
-lattices. Since K and
${\mathbb Z}_2$
-lattices. Since K and
![]() $K'$
are negative-definite of the same rank, and
$K'$
are negative-definite of the same rank, and
![]() $|A_{K'}| = |A_K| \cdot |A_{\mathrm {new}}|$
, we have
$|A_{K'}| = |A_K| \cdot |A_{\mathrm {new}}|$
, we have
![]() $\mathrm {discr}(K')= \mathrm {discr}(K)\cdot |A_{\mathrm {new}}|$
. Since
$\mathrm {discr}(K')= \mathrm {discr}(K)\cdot |A_{\mathrm {new}}|$
. Since
![]() $|A_{\mathrm {new}}|$
is a square of an odd integer, the even
$|A_{\mathrm {new}}|$
is a square of an odd integer, the even
![]() $2$
-adic lattices
$2$
-adic lattices
![]() $K \otimes {\mathbb Z}_2$
and
$K \otimes {\mathbb Z}_2$
and
![]() $K' \otimes {\mathbb Z}_2$
have the same rank, the same discriminant form, and the same discriminant modulo
$K' \otimes {\mathbb Z}_2$
have the same rank, the same discriminant form, and the same discriminant modulo
![]() ${\mathbb Z}_2^{\times 2}$
. This implies that the
${\mathbb Z}_2^{\times 2}$
. This implies that the
![]() ${\mathbb Z}_2$
-lattices
${\mathbb Z}_2$
-lattices
![]() $K \otimes {\mathbb Z}_2$
and
$K \otimes {\mathbb Z}_2$
and
![]() $K' \otimes {\mathbb Z}_2$
are isomorphic (see [Reference NikulinNik79, Cor. 1.9.3]).
$K' \otimes {\mathbb Z}_2$
are isomorphic (see [Reference NikulinNik79, Cor. 1.9.3]).
It remains to show that after tensoring with
![]() ${\mathbb Z}_2$
the data
${\mathbb Z}_2$
the data
![]() $(H_{L}, H_{N}, \gamma , K, \delta )$
and
$(H_{L}, H_{N}, \gamma , K, \delta )$
and
![]() $(H_{L'}, H_{N}, \gamma ', K', \delta ')$
give rise to isomorphic embeddings of
$(H_{L'}, H_{N}, \gamma ', K', \delta ')$
give rise to isomorphic embeddings of
![]() $L' \otimes {\mathbb Z}_2 \cong L \otimes {\mathbb Z}_2$
into
$L' \otimes {\mathbb Z}_2 \cong L \otimes {\mathbb Z}_2$
into
![]() $N\otimes {\mathbb Z}_2$
. The first three entries of each datum are the same. By Remark 5.3, it is enough to find an isomorphism of
$N\otimes {\mathbb Z}_2$
. The first three entries of each datum are the same. By Remark 5.3, it is enough to find an isomorphism of
![]() ${\mathbb Z}_2$
-lattices
${\mathbb Z}_2$
-lattices
![]() $f \colon K' \otimes {\mathbb Z}_2 \rightarrow K \otimes {\mathbb Z}_2$
such that
$f \colon K' \otimes {\mathbb Z}_2 \rightarrow K \otimes {\mathbb Z}_2$
such that
![]() $\delta ^{\prime }_2 =\delta _2 \circ \bar {f}$
. The existence of such an f follows from [Reference NikulinN, Th. 1.9.5]. This concludes the proof of (a).
$\delta ^{\prime }_2 =\delta _2 \circ \bar {f}$
. The existence of such an f follows from [Reference NikulinN, Th. 1.9.5]. This concludes the proof of (a).
(b) Write
![]() $A := A_L = A_2 \oplus A_{\mathrm {odd}}$
, where
$A := A_L = A_2 \oplus A_{\mathrm {odd}}$
, where
![]() $A_2$
is the 2-primary subgroup of A. Similarly, write
$A_2$
is the 2-primary subgroup of A. Similarly, write
![]() $A' := A_{L'} = A^{\prime }_2 \oplus A^{\prime }_{\mathrm {odd}}$
. It is clear that
$A' := A_{L'} = A^{\prime }_2 \oplus A^{\prime }_{\mathrm {odd}}$
. It is clear that
![]() $A_2\cong A^{\prime }_2$
. Then
$A_2\cong A^{\prime }_2$
. Then
![]() $q_{L'}$
is an orthogonal direct sum of quadratic forms
$q_{L'}$
is an orthogonal direct sum of quadratic forms
![]() $q_{L,2}$
on
$q_{L,2}$
on
![]() $A_2$
and
$A_2$
and
![]() $q_{\mathrm {odd}}$
on
$q_{\mathrm {odd}}$
on
![]() $A^{\prime }_{\mathrm {odd}}$
.
$A^{\prime }_{\mathrm {odd}}$
.
The overlattice L of
![]() $L'$
defines an isotropic subgroup
$L'$
defines an isotropic subgroup
![]() $I \subset A'$
, where
$I \subset A'$
, where
![]() $|I|=[L:L']$
, so that
$|I|=[L:L']$
, so that
![]() $q_L$
is the quadratic form induced by
$q_L$
is the quadratic form induced by
![]() $q_{L'}$
on
$q_{L'}$
on
![]() $A= I^{\perp }/I$
. Since
$A= I^{\perp }/I$
. Since
![]() $[L \colon L']$
is odd by assumption, we have
$[L \colon L']$
is odd by assumption, we have
![]() $I \subset A^{\prime }_{\mathrm {odd}}$
. Thus
$I \subset A^{\prime }_{\mathrm {odd}}$
. Thus
![]() $I^{\perp } = A_2 \oplus I^{\perp }_{\mathrm {odd}}$
, where
$I^{\perp } = A_2 \oplus I^{\perp }_{\mathrm {odd}}$
, where
![]() $I^{\perp }_{\mathrm {odd}}=I^{\perp }\cap A^{\prime }_{\mathrm {odd}}$
. This shows that
$I^{\perp }_{\mathrm {odd}}=I^{\perp }\cap A^{\prime }_{\mathrm {odd}}$
. This shows that
![]() $A= A_2 \oplus (I^{\perp }_{\mathrm {odd}}/I)$
.
$A= A_2 \oplus (I^{\perp }_{\mathrm {odd}}/I)$
.
Let
![]() $i'\colon L'\hookrightarrow N$
be a primitive embedding such that
$i'\colon L'\hookrightarrow N$
be a primitive embedding such that
![]() $i^{\prime *}(\varepsilon )\neq 0$
. Then
$i^{\prime *}(\varepsilon )\neq 0$
. Then
![]() $K':=i(L')^{\perp }_N$
is an even negative-definite lattice of rank
$K':=i(L')^{\perp }_N$
is an even negative-definite lattice of rank
![]() $10-k$
. Let
$10-k$
. Let
![]() $(H_{L'}, H_N, \gamma ', K', \delta ')$
be a datum associated to
$(H_{L'}, H_N, \gamma ', K', \delta ')$
be a datum associated to
![]() $i'\colon L'\hookrightarrow N$
as in Theorem 5.2. In particular,
$i'\colon L'\hookrightarrow N$
as in Theorem 5.2. In particular,
![]() $\delta '$
is an isomorphism of
$\delta '$
is an isomorphism of
![]() $-q_{K'}$
with the restriction of
$-q_{K'}$
with the restriction of
![]() $q_{L'}\oplus -q_N$
to
$q_{L'}\oplus -q_N$
to
![]() $\Gamma _{\gamma '}^{\perp } / \Gamma _{\gamma '}$
. Since
$\Gamma _{\gamma '}^{\perp } / \Gamma _{\gamma '}$
. Since
![]() $2A_N=0$
, we have
$2A_N=0$
, we have
![]() $2H_{L'}=0$
, so that
$2H_{L'}=0$
, so that
![]() $H_{L'} \subset A^{\prime }_2=A_2$
. Hence
$H_{L'} \subset A^{\prime }_2=A_2$
. Hence
![]() $\Gamma _{\gamma '} \subset A_2\oplus A_N \subset A' \oplus A_N$
and thus
$\Gamma _{\gamma '} \subset A_2\oplus A_N \subset A' \oplus A_N$
and thus
![]() $\Gamma _{\gamma '}^{\perp } = (\Gamma _{\gamma '}^{\perp })_2 \oplus A^{\prime }_{\mathrm {odd}}$
, where
$\Gamma _{\gamma '}^{\perp } = (\Gamma _{\gamma '}^{\perp })_2 \oplus A^{\prime }_{\mathrm {odd}}$
, where
![]() $(\Gamma _{\gamma '}^{\perp })_2=\Gamma _{\gamma '}^{\perp }\cap (A_2 \oplus A_N)$
. This shows that
$(\Gamma _{\gamma '}^{\perp })_2=\Gamma _{\gamma '}^{\perp }\cap (A_2 \oplus A_N)$
. This shows that
![]() $\delta '$
identifies the finite quadratic form
$\delta '$
identifies the finite quadratic form
![]() $-q_{K'}$
on
$-q_{K'}$
on
![]() $A_{K'}$
with the restriction of
$A_{K'}$
with the restriction of
![]() $(q_{L,2}\oplus -q_N)\oplus q_{\mathrm {odd}}$
to
$(q_{L,2}\oplus -q_N)\oplus q_{\mathrm {odd}}$
to
![]() $\big ((\Gamma _{\gamma '}^{\perp }\big )_2/\Gamma _{\gamma '}) \oplus A^{\prime }_{\mathrm {odd}}$
.
$\big ((\Gamma _{\gamma '}^{\perp }\big )_2/\Gamma _{\gamma '}) \oplus A^{\prime }_{\mathrm {odd}}$
.
The isotropic subgroup
![]() $I \subset A^{\prime }_{\mathrm {odd}}$
gives rise, via
$I \subset A^{\prime }_{\mathrm {odd}}$
gives rise, via
![]() $\delta '$
, to an isotropic subgroup in
$\delta '$
, to an isotropic subgroup in
![]() $A_{K'}$
. The latter defines an overlattice
$A_{K'}$
. The latter defines an overlattice
![]() $K' \subset K$
with
$K' \subset K$
with
![]() $[K:K']=[L:L']$
, so that
$[K:K']=[L:L']$
, so that
![]() $\delta '$
induces an isomorphism
$\delta '$
induces an isomorphism
![]() $\delta $
of the quadratic form
$\delta $
of the quadratic form
![]() $-q_K$
on
$-q_K$
on
![]() $A_K$
with the restriction of
$A_K$
with the restriction of
![]() $(q_{L,2}\oplus -q_N)\oplus q_{\mathrm {odd}}$
to
$(q_{L,2}\oplus -q_N)\oplus q_{\mathrm {odd}}$
to
![]() $\big ( (\Gamma _{\gamma '}^{\perp })_2/\Gamma _{\gamma '}\big )\oplus (I^{\perp }_{\mathrm {odd}}/I)$
. Let
$\big ( (\Gamma _{\gamma '}^{\perp })_2/\Gamma _{\gamma '}\big )\oplus (I^{\perp }_{\mathrm {odd}}/I)$
. Let
![]() $i\colon L\hookrightarrow N$
be a primitive embedding associated to the datum
$i\colon L\hookrightarrow N$
be a primitive embedding associated to the datum
![]() $(H_{L}, H_N, \gamma , K, \delta )$
, where
$(H_{L}, H_N, \gamma , K, \delta )$
, where
![]() $H_L=H_{L'}$
and
$H_L=H_{L'}$
and
![]() $\gamma =\gamma '$
.
$\gamma =\gamma '$
.
To complete the proof of (b), it remains to show that i and
![]() $i'$
induce isomorphic embeddings of
$i'$
induce isomorphic embeddings of
![]() ${\mathbb Z}_2$
-lattices. This is proved by the same arguments as in (a).
${\mathbb Z}_2$
-lattices. This is proved by the same arguments as in (a).
Corollary 5.7. Let L be an even lattice of signature
![]() $(2_+, k_-)$
, where
$(2_+, k_-)$
, where
![]() $0\leq k\leq 8$
. Write
$0\leq k\leq 8$
. Write
![]() ${\mathcal S}(L)$
for the set of nonzero homomorphisms
${\mathcal S}(L)$
for the set of nonzero homomorphisms
![]() $\alpha \colon L\to {\mathbb Z}/2$
such that there is a primitive embedding
$\alpha \colon L\to {\mathbb Z}/2$
such that there is a primitive embedding
![]() $i\colon L\hookrightarrow N$
with
$i\colon L\hookrightarrow N$
with
![]() $\alpha =i^*(\varepsilon )$
. Let
$\alpha =i^*(\varepsilon )$
. Let
![]() $L'$
be a sublattice of L that satisfies condition
$L'$
be a sublattice of L that satisfies condition
![]() $(*)$
. Then, under the natural identification
$(*)$
. Then, under the natural identification
![]() $\mathrm {{Hom}}(L,{\mathbb Z}/2) \cong \mathrm {{Hom}}(L', {\mathbb Z}/2)$
, we have
$\mathrm {{Hom}}(L,{\mathbb Z}/2) \cong \mathrm {{Hom}}(L', {\mathbb Z}/2)$
, we have
![]() ${\mathcal S}(L)={\mathcal S}(L')$
.
${\mathcal S}(L)={\mathcal S}(L')$
.
Proof. Part (a) of Theorem 5.6 implies
![]() ${\mathcal S}(L)\subset {\mathcal S}(L')$
, whereas part (b) implies
${\mathcal S}(L)\subset {\mathcal S}(L')$
, whereas part (b) implies
![]() ${\mathcal S}(L')\subset {\mathcal S}(L)$
since
${\mathcal S}(L')\subset {\mathcal S}(L)$
since
![]() $[L:L']$
is odd.
$[L:L']$
is odd.
Proof of Theorem D
By Proposition 5.5, there are infinitely many sublattices
![]() $T \subset T(X)$
with pairwise different discriminants that satisfy condition
$T \subset T(X)$
with pairwise different discriminants that satisfy condition
![]() $(*)$
. Endow T with the Hodge structure coming from
$(*)$
. Endow T with the Hodge structure coming from
![]() $T(X)$
. Since
$T(X)$
. Since
![]() $\mathrm {{rk}}(T) \leq 10$
, by [Reference NikulinN, Th. 1.14.4], there exists a unique primitive embedding of the lattice T into the K3 lattice
$\mathrm {{rk}}(T) \leq 10$
, by [Reference NikulinN, Th. 1.14.4], there exists a unique primitive embedding of the lattice T into the K3 lattice
![]() $\Lambda $
. We equip
$\Lambda $
. We equip
![]() $\Lambda $
with the Hodge structure induced by the Hodge structure on T so that
$\Lambda $
with the Hodge structure induced by the Hodge structure on T so that
![]() $T^{\perp }_{\Lambda }\subset \Lambda ^{(1,1)}$
. By the surjectivity of the period map, there is a K3 surface Y together with a Hodge isometry between
$T^{\perp }_{\Lambda }\subset \Lambda ^{(1,1)}$
. By the surjectivity of the period map, there is a K3 surface Y together with a Hodge isometry between
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathrm {H}^2(Y,{\mathbb Z})$
. The transcendental lattice
$\mathrm {H}^2(Y,{\mathbb Z})$
. The transcendental lattice
![]() $T(Y)$
is the orthogonal complement to
$T(Y)$
is the orthogonal complement to
![]() $\mathrm {H}^2(Y,{\mathbb Z})^{(1,1)}$
, hence
$\mathrm {H}^2(Y,{\mathbb Z})^{(1,1)}$
, hence
![]() $T(Y)\cong T$
.
$T(Y)\cong T$
.
Applying Corollary 5.7 with
![]() $L=T(X)$
, we obtain
$L=T(X)$
, we obtain
![]() ${\mathcal S}(T(X))={\mathcal S}(T(Y))$
. Now Corollary 2.6(i) (whose proof uses Lemma 2.3) gives
${\mathcal S}(T(X))={\mathcal S}(T(Y))$
. Now Corollary 2.6(i) (whose proof uses Lemma 2.3) gives
![]() $\mathrm {{Im}}(\Phi _X)\setminus \{0\}=\mathrm {{Im}}(\Phi _Y)\setminus \{0\}$
.
$\mathrm {{Im}}(\Phi _X)\setminus \{0\}=\mathrm {{Im}}(\Phi _Y)\setminus \{0\}$
.
Acknowledgments
This note was written while A.N.S. was a fellow of FRIAS, University of Freiburg. He is grateful to FRIAS for hospitality and excellent working conditions. We would like to thank the referee for careful reading of the paper and helpful suggestions.