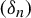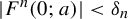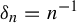1 Introduction
1.1 Regular and non-regular parameters
Given a real parameter a, we let
![]() $x \mapsto 1-ax^2 = F(x;a)$
denote the corresponding real quadratic map. We will study the recurrent behaviour of the critical point
$x \mapsto 1-ax^2 = F(x;a)$
denote the corresponding real quadratic map. We will study the recurrent behaviour of the critical point
![]() $x = 0$
when the parameter belongs to the interval
$x = 0$
when the parameter belongs to the interval
![]() $[1, 2]$
. For such a choice of parameter, there exists an invariant interval
$[1, 2]$
. For such a choice of parameter, there exists an invariant interval
![]() $I_a \subset [-1,1]$
, that is,
$I_a \subset [-1,1]$
, that is,
containing the critical point
![]() $x = 0$
. The parameter interval is naturally divided into a regular
$x = 0$
. The parameter interval is naturally divided into a regular
![]() $(\mathcal{R})$
and non-regular
$(\mathcal{R})$
and non-regular
![]() $(\mathcal{N}\mathcal{R})$
part
$(\mathcal{N}\mathcal{R})$
part
with
![]() $a \in \mathcal{R}$
being such that
$a \in \mathcal{R}$
being such that
![]() $x \mapsto 1-ax^2$
has an attracting cycle, and
$x \mapsto 1-ax^2$
has an attracting cycle, and
![]() $\mathcal{N}\mathcal{R} = [1,2] \smallsetminus \mathcal{R}$
. These two sets turn out to be intertwined in an intricate manner, and this has led to an extensive study of the real quadratic family. We briefly mention some of the more fundamental results and refer to [Reference LyubichLyu00b] for an overview.
$\mathcal{N}\mathcal{R} = [1,2] \smallsetminus \mathcal{R}$
. These two sets turn out to be intertwined in an intricate manner, and this has led to an extensive study of the real quadratic family. We briefly mention some of the more fundamental results and refer to [Reference LyubichLyu00b] for an overview.
The regular maps are, from a dynamic point of view, well behaved, with almost every point, including the critical point, tending to the attracting cycle. This set of parameters, which with an application of the inverse function theorem is seen to be open, constitutes a large portion of
![]() $[1,2]$
. The celebrated genericity result, known as the real Fatou conjecture, was settled independently by Graczyk and Świątek [Reference Graczyk and ŚwiatekGS97] and Lyubich [Reference LyubichLyu97]:
$[1,2]$
. The celebrated genericity result, known as the real Fatou conjecture, was settled independently by Graczyk and Świątek [Reference Graczyk and ŚwiatekGS97] and Lyubich [Reference LyubichLyu97]:
![]() $\operatorname {\mathrm {\mathcal {R}}}$
is (open and) dense. This has later been extended to real polynomials of arbitrary degree by Kozlovski, Shen and van Strien [Reference Kozlovski, Shen and van StrienKSvS07], solving the second part of the eleventh problem of Smale [Reference SmaleSma98]. The corresponding result for complex quadratic maps, the Fatou conjecture, is still to this day open.
$\operatorname {\mathrm {\mathcal {R}}}$
is (open and) dense. This has later been extended to real polynomials of arbitrary degree by Kozlovski, Shen and van Strien [Reference Kozlovski, Shen and van StrienKSvS07], solving the second part of the eleventh problem of Smale [Reference SmaleSma98]. The corresponding result for complex quadratic maps, the Fatou conjecture, is still to this day open.
The non-regular maps, in contrast to the regular ones, exhibit chaotic behaviour. In [Reference JakobsonJak81], Jakobson showed the abundance of stochastic maps, proving that the set of parameters
![]() $a \in \mathcal {S}$
for which the corresponding quadratic map has an absolutely continuous (with respect to Lebesgue) invariant measure (a.c.i.m), is of positive Lebesgue measure. This showed that, from a probabilistic point of view, non-regular maps are not negligible: for a regular map, any (finite) a.c.i.m is necessarily singular with respect to Lebesgue measure.
$a \in \mathcal {S}$
for which the corresponding quadratic map has an absolutely continuous (with respect to Lebesgue) invariant measure (a.c.i.m), is of positive Lebesgue measure. This showed that, from a probabilistic point of view, non-regular maps are not negligible: for a regular map, any (finite) a.c.i.m is necessarily singular with respect to Lebesgue measure.
Chaotic dynamics is often associated with the notion of sensitive dependence on initial conditions. A compelling way to capture this property was introduced by Collet and Eckmann in [Reference Collet and EckmannCE80] where they studied certain maps of the interval having expansion along the critical orbit, proving the abundance of chaotic behaviour. This condition is now known as the Collet–Eckmann condition and, for a real quadratic map, it states that
Focusing on this condition, Benedicks and Carleson gave, in their seminal papers [BC85, BC91], another proof of Jakobson’s theorem by proving the stronger result that the set
![]() $\operatorname {\mathrm {\mathcal {C}\mathcal {E}}}$
of Collet–Eckmann parameters is of positive measure. As a matter of fact, subexponential increase of the derivative along the critical orbit is enough to imply the existence of an a.c.i.m, but the stronger Collet–Eckmann condition implies, and is sometimes equivalent to, ergodic properties such as exponential decay of correlations [Reference Keller and NowickiKN92, Reference Nowicki and SandsNS98, Reference YoungYou92] and stochastic stability [Reference Baladi and VianaBV96]. For a survey on the role of the Collet–Eckmann condition in one-dimensional dynamics, we refer to [Reference Świa̧tekŚ01].
$\operatorname {\mathrm {\mathcal {C}\mathcal {E}}}$
of Collet–Eckmann parameters is of positive measure. As a matter of fact, subexponential increase of the derivative along the critical orbit is enough to imply the existence of an a.c.i.m, but the stronger Collet–Eckmann condition implies, and is sometimes equivalent to, ergodic properties such as exponential decay of correlations [Reference Keller and NowickiKN92, Reference Nowicki and SandsNS98, Reference YoungYou92] and stochastic stability [Reference Baladi and VianaBV96]. For a survey on the role of the Collet–Eckmann condition in one-dimensional dynamics, we refer to [Reference Świa̧tekŚ01].
Further investigating the stochastic behaviour of non-regular maps, supported by the results in [Reference LyubichLyu00a, Reference Martens and NowickiMN00], Lyubich [Reference LyubichLyu02] established the following famous dichotomy: almost all real quadratic maps are either regular or stochastic. Thus, it turned out that the stochastic behaviour described by Jakobson is in fact typical for a non-regular map. In [Reference Avila and MoreiraAM05], Avila and Moreira later proved the strong result that expansion along the critical orbit is no exception either: almost all non-regular maps are Collet–Eckmann. Thus, a typical non-regular map has excellent ergodic properties.
1.2 Recurrence and Theorem A
In this paper, we will study recurrence of the critical orbit to the critical point for a typical non-regular (stochastic, Collet–Eckmann) real quadratic map. For this reason, we introduce the following set.
Definition 1.1. (Recurrence set)
Given a sequence
![]() $(\delta _n)_{n = 1}^\infty $
of real numbers, we define the recurrence set as
$(\delta _n)_{n = 1}^\infty $
of real numbers, we define the recurrence set as
In [Reference Avila and MoreiraAM05], Avila and Moreira also established the following recurrence result, proving a conjecture by Sinai: for almost every non-regular parameter a,
Another way to state this result is as follows: for almost every non-regular parameter a, the set of n such that
![]() $\vert F^n(0;a) \vert < n^{-\theta }$
is finite if
$\vert F^n(0;a) \vert < n^{-\theta }$
is finite if
![]() $\theta> 1$
and infinite if
$\theta> 1$
and infinite if
![]() $\theta < 1$
. In terms of the above defined recurrence set, this result translates to
$\theta < 1$
. In terms of the above defined recurrence set, this result translates to
 $$ \begin{align*} \operatorname{\mathrm{\operatorname{Leb}}} \Lambda( n^{-\theta}) = \begin{cases} \operatorname{\mathrm{\operatorname{Leb}}} \operatorname{\mathrm{\mathcal{N}\mathcal{R}}} &\mbox{if}\ \theta> 1,\\ 0 &\mbox{if}\ \theta < 1. \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\operatorname{Leb}}} \Lambda( n^{-\theta}) = \begin{cases} \operatorname{\mathrm{\operatorname{Leb}}} \operatorname{\mathrm{\mathcal{N}\mathcal{R}}} &\mbox{if}\ \theta> 1,\\ 0 &\mbox{if}\ \theta < 1. \end{cases} \end{align*} $$
In [Reference Gao and ShenGS14], as a special case, a new proof of the positive measure case in the above stated result was obtained, together with a new proof that almost every non-regular map is Collet–Eckmann. In this paper, we will give a new proof of the measure zero case. In particular, we will fill in the missing case of
![]() $\theta = 1$
, and thus complete the picture of polynomial recurrence. Our result will be restricted to the following class of recurrence rates.
$\theta = 1$
, and thus complete the picture of polynomial recurrence. Our result will be restricted to the following class of recurrence rates.
Definition 1.2. A non-increasing sequence
![]() $(\delta _n)$
of positive real numbers is called admissible if there exists a constant
$(\delta _n)$
of positive real numbers is called admissible if there exists a constant
![]() $0 \leq \overline {e} < \infty $
and an integer
$0 \leq \overline {e} < \infty $
and an integer
![]() $N \geq 1$
, such that
$N \geq 1$
, such that
The following is the main result of this paper.
Theorem A. There exists
![]() $\tau \in (0,1)$
such that if
$\tau \in (0,1)$
such that if
![]() $(\delta _n)$
is admissible and
$(\delta _n)$
is admissible and
then
![]() $\operatorname {\mathrm {\operatorname {Leb}}} (\Lambda (\delta _n) \cap \operatorname {\mathrm {\mathcal {C}\mathcal {E}}}) = 0$
.
$\operatorname {\mathrm {\operatorname {Leb}}} (\Lambda (\delta _n) \cap \operatorname {\mathrm {\mathcal {C}\mathcal {E}}}) = 0$
.
Here,
![]() $\log ^*$
denotes to so-called iterated logarithm, which is defined recursively as
$\log ^*$
denotes to so-called iterated logarithm, which is defined recursively as
 $$ \begin{align*} \log^* x = \begin{cases} 0 &\mbox{if}\ x \leq 1, \\ 1 + \log^* \log x &\mbox{if}\ x> 1. \end{cases} \end{align*} $$
$$ \begin{align*} \log^* x = \begin{cases} 0 &\mbox{if}\ x \leq 1, \\ 1 + \log^* \log x &\mbox{if}\ x> 1. \end{cases} \end{align*} $$
That is,
![]() $\log ^* x$
is the number of times one has to iteratively apply the logarithm to x for the result to be less than or equal to
$\log ^* x$
is the number of times one has to iteratively apply the logarithm to x for the result to be less than or equal to
![]() $1$
. In particular,
$1$
. In particular,
![]() $\log ^*$
grows slower than
$\log ^*$
grows slower than
![]() $\log _j = \log \circ \log _{j-1}$
for any
$\log _j = \log \circ \log _{j-1}$
for any
![]() $j \geq 1$
.
$j \geq 1$
.
Theorem A, together with the fact that almost every non-regular real quadratic map is Collet–Eckmann, clearly implies the following.
Corollary 1.3.
![]() $\operatorname {\mathrm {\operatorname {Leb}}} \Lambda (n^{-1}) = 0$
.
$\operatorname {\mathrm {\operatorname {Leb}}} \Lambda (n^{-1}) = 0$
.
Remark 1.4. In fact, one can conclude the stronger statement
At this moment, we do not get any result for when
![]() $\delta _n = 1/(n \log n)$
and this would be interesting to investigate further.
$\delta _n = 1/(n \log n)$
and this would be interesting to investigate further.
One of the key points in the proof of Theorem A is the introduction of unbounded distortion estimates; this differs from the classical Benedicks–Carleson techniques.
2 Reduction and outline of proof
2.1 Some definitions and Theorem B
We reduce the proof of Theorem A to that of Theorem B stated below. For this, we begin with some suitable definitions.
It will be convenient to explicitly express the constant in the Collet–Eckmann condition of equation (1) and, for this reason, we agree on the following definition.
Definition 2.1. Given
![]() $\gamma , C>0$
, we call a parameter
$\gamma , C>0$
, we call a parameter
![]() $a (\gamma ,C)$
-Collet–Eckmann if
$a (\gamma ,C)$
-Collet–Eckmann if
The set of all
![]() $(\gamma ,C)$
-Collet–Eckmann parameters is denoted
$(\gamma ,C)$
-Collet–Eckmann parameters is denoted
![]() $\operatorname {\mathrm {\mathcal {C}\mathcal {E}}}(\gamma ,C)$
.
$\operatorname {\mathrm {\mathcal {C}\mathcal {E}}}(\gamma ,C)$
.
Our parameter exclusion will be carried out on intervals centred at Collet–Eckmann parameters satisfying the following recurrence assumption.
Definition 2.2. A Collet–Eckmann parameter a is said to have polynomial recurrence (PR) if there exist constants
![]() $K=K(a)> 0$
and
$K=K(a)> 0$
and
![]() $\sigma = \sigma (a) \geq 0$
such that
$\sigma = \sigma (a) \geq 0$
such that
The set of all PR-parameters is denoted
![]() $\operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
.
$\operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
.
Finally, we consider parameters for which the corresponding quadratic maps satisfy the reversed recurrence condition after some fixed time
![]() $N \geq 1$
:
$N \geq 1$
:
Clearly, we have that
Theorem A will be deduced from the following theorem.
Theorem B. There exists
![]() $\tau \in (0,1)$
such that if
$\tau \in (0,1)$
such that if
![]() $(\delta _n)$
is admissible and
$(\delta _n)$
is admissible and
then for all
![]() $N \geq 1$
,
$N \geq 1$
,
![]() $\gamma> 0$
,
$\gamma> 0$
,
![]() $C> 0$
, and for all
$C> 0$
, and for all
![]() $a \in \mathcal {P}\mathcal {R}$
, there exists an interval
$a \in \mathcal {P}\mathcal {R}$
, there exists an interval
![]() $\omega _a$
centred at a such that
$\omega _a$
centred at a such that
2.2 Proof of Theorem A
Using Theorem B, Theorem A is proved by a standard covering argument. Since
![]() $\omega _a$
is centred at a, so is the smaller interval
$\omega _a$
is centred at a, so is the smaller interval
![]() $\omega _a' = \omega _a/5$
. By Vitali’s covering lemma, there exists a countable collection
$\omega _a' = \omega _a/5$
. By Vitali’s covering lemma, there exists a countable collection
![]() $(a_j)$
of PR-parameters such that
$(a_j)$
of PR-parameters such that
 $$ \begin{align*} \operatorname{\mathrm{\mathcal{P}\mathcal{R}}} \subset \bigcup_{a \in \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}} \omega'_a \subset \bigcup_{j = 1}^\infty \omega_{a_j}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\mathcal{P}\mathcal{R}}} \subset \bigcup_{a \in \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}} \omega'_a \subset \bigcup_{j = 1}^\infty \omega_{a_j}. \end{align*} $$
It now follows directly that
 $$ \begin{align*} \operatorname{\mathrm{\operatorname{Leb}}}(\Lambda_N(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma,C) \cap \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}) \leq \sum_{j=1}^\infty \operatorname{\mathrm{\operatorname{Leb}}}(\Lambda_N(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma,C) \cap \omega_{a_j}) = 0, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\operatorname{Leb}}}(\Lambda_N(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma,C) \cap \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}) \leq \sum_{j=1}^\infty \operatorname{\mathrm{\operatorname{Leb}}}(\Lambda_N(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma,C) \cap \omega_{a_j}) = 0, \end{align*} $$
and therefore
 $$ \begin{align*} \operatorname{\mathrm{\operatorname{Leb}}} (\Lambda(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}} \cap \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}) &\leq \sum_{N,k,l \geq 1} \operatorname{\mathrm{\operatorname{Leb}}}(\Lambda_N(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(k^{-1}\log 2,l^{-1}) \cap \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}) \\ &= 0. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\operatorname{Leb}}} (\Lambda(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}} \cap \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}) &\leq \sum_{N,k,l \geq 1} \operatorname{\mathrm{\operatorname{Leb}}}(\Lambda_N(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(k^{-1}\log 2,l^{-1}) \cap \operatorname{\mathrm{\mathcal{P}\mathcal{R}}}) \\ &= 0. \end{align*} $$
Finally, we notice that
![]() $\Lambda (\delta _n) \cap \operatorname {\mathrm {\mathcal {C}\mathcal {E}}} \subset \operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
; indeed, this is clearly the case since
$\Lambda (\delta _n) \cap \operatorname {\mathrm {\mathcal {C}\mathcal {E}}} \subset \operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
; indeed, this is clearly the case since
![]() $(\delta _n)$
is assumed to be admissible.
$(\delta _n)$
is assumed to be admissible.
Remark 2.3. With the introduction of the set
![]() $\operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
, we are avoiding the use of previous recurrence results (e.g. Avila–Moreira) to prove Theorem A, by (a priori) allowing
$\operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
, we are avoiding the use of previous recurrence results (e.g. Avila–Moreira) to prove Theorem A, by (a priori) allowing
![]() $\operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
to be a set of measure zero. In either case, the statement of Theorem A is true.
$\operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
to be a set of measure zero. In either case, the statement of Theorem A is true.
2.3 Outline of proof of Theorem B
The proof of Theorem B will rely on the classical parameter exclusion techniques developed by Benedicks and Carleson [Reference Benedicks and CarlesonBC85, Reference Benedicks and CarlesonBC91], complemented with more recent results. In particular, we allow for perturbation around a parameter in a more general position than
![]() $a=2$
. In contrast to the usual application of these techniques, our goal here is the show that what remains after excluding parameters is a set of zero Lebesgue measure. One of the key points in our approach is the introduction of unbounded distortion estimates.
$a=2$
. In contrast to the usual application of these techniques, our goal here is the show that what remains after excluding parameters is a set of zero Lebesgue measure. One of the key points in our approach is the introduction of unbounded distortion estimates.
We will carefully study the returns of the critical orbit, simultaneously for maps corresponding to parameters in a suitable interval
![]() $\omega \subset [1,2]$
, to a small and fixed interval
$\omega \subset [1,2]$
, to a small and fixed interval
![]() $(-\delta ,\delta ) = (-e^{-\Delta },e^{-\Delta })$
. These returns to
$(-\delta ,\delta ) = (-e^{-\Delta },e^{-\Delta })$
. These returns to
![]() $(-\delta ,\delta )$
will be classified as either inessential, essential, escape, or complete. Per definition of a complete return, we return close enough to
$(-\delta ,\delta )$
will be classified as either inessential, essential, escape, or complete. Per definition of a complete return, we return close enough to
![]() $x = 0$
to be able to remove a large portion of
$x = 0$
to be able to remove a large portion of
![]() $(-\delta _n,\delta _n)$
in phase space. To estimate what is removed in parameter space, we need distortion estimates. This will be achieved by (i) enforcing a
$(-\delta _n,\delta _n)$
in phase space. To estimate what is removed in parameter space, we need distortion estimates. This will be achieved by (i) enforcing a
![]() $(\gamma ,C)$
-Collet–Eckmann condition and (ii) continuously making suitable partitions in phase space:
$(\gamma ,C)$
-Collet–Eckmann condition and (ii) continuously making suitable partitions in phase space:
![]() $(-\delta ,\delta )$
is subdivided into partition elements
$(-\delta ,\delta )$
is subdivided into partition elements
![]() $I_r = (e^{-r-1},e^{-r})$
for
$I_r = (e^{-r-1},e^{-r})$
for
![]() $r>0$
, and
$r>0$
, and
![]() $I_r = -I_{-r}$
for
$I_r = -I_{-r}$
for
![]() $r < 0$
. Furthermore, each
$r < 0$
. Furthermore, each
![]() $I_r$
is subdivided into
$I_r$
is subdivided into
![]() $r^2$
smaller intervals
$r^2$
smaller intervals
![]() $I_{rl} \subset I_r$
, of equal length
$I_{rl} \subset I_r$
, of equal length
![]() $\vert I_r\vert /r^2$
. After partitioning, we consider iterations of each partition element individually, and the proof of Theorem B will be one by induction.
$\vert I_r\vert /r^2$
. After partitioning, we consider iterations of each partition element individually, and the proof of Theorem B will be one by induction.
We make a few comments on the summability condition appearing in the statement of Theorems A and B. To prove our result, we need to estimate how much is removed at a complete return, but also how long it takes from one complete return to the next. The factor
![]() $\tau ^{(\log ^* n)^3}$
is connected to the estimate of what is removed at complete returns and, more specifically, it is connected to distortion; as will be seen, our distortion estimates are unbounded. The factor
$\tau ^{(\log ^* n)^3}$
is connected to the estimate of what is removed at complete returns and, more specifically, it is connected to distortion; as will be seen, our distortion estimates are unbounded. The factor
![]() $(\log n)^{-1}$
is directly connected to the time between two complete returns: if n is the index of a complete return, it will take
$(\log n)^{-1}$
is directly connected to the time between two complete returns: if n is the index of a complete return, it will take
![]() $\lesssim \log n$
iterations until we reach the next complete return.
$\lesssim \log n$
iterations until we reach the next complete return.
In the next section, we prove a couple of preliminary lemmas and confirm the existence of a suitable start-up interval
![]() $\omega _a$
centred at
$\omega _a$
centred at
![]() $a \in \operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
, for which the parameter exclusion will be carried out. After that, the induction step will be proved and an estimate for the measure of
$a \in \operatorname {\mathrm {\mathcal {P}\mathcal {R}}}$
, for which the parameter exclusion will be carried out. After that, the induction step will be proved and an estimate for the measure of
![]() $\Lambda _N(\delta _n) \cap \operatorname {\mathrm {\mathcal {C}\mathcal {E}}}(\gamma , C) \cap \omega _a$
will be given.
$\Lambda _N(\delta _n) \cap \operatorname {\mathrm {\mathcal {C}\mathcal {E}}}(\gamma , C) \cap \omega _a$
will be given.
3 Preliminary lemmas
In this section, we establish three important lemmas that will be used in the induction step. These are derived from Lemmas 2.6, 2.10, and 3.1 in [Reference AspenbergAsp21], respectively, where they are proved in the more general setting of a complex rational map.
3.1 Outside expansion lemma
The first result we will need is the following version of the classical Mañé hyperbolicity theorem (see [Reference de Melo and van StriendMvS93], for instance).
Lemma 3.1. (Outside expansion)
Given a Collet–Eckmann parameter
![]() $a_0$
, there exist constants
$a_0$
, there exist constants
![]() $\gamma _M,C_M> 0$
such that, for all
$\gamma _M,C_M> 0$
such that, for all
![]() $\delta> 0$
sufficiently small, there is a constant
$\delta> 0$
sufficiently small, there is a constant
![]() $\epsilon _M = \epsilon _M(\delta )> 0$
such that, for all
$\epsilon _M = \epsilon _M(\delta )> 0$
such that, for all
![]() $a \in (a_0 - \epsilon _M,a_0 + \epsilon _M)$
, if
$a \in (a_0 - \epsilon _M,a_0 + \epsilon _M)$
, if
then
Furthermore, if we also have that
![]() $F^n(x;a) \in (-2\delta ,2\delta )$
, then
$F^n(x;a) \in (-2\delta ,2\delta )$
, then
A similar lemma for the quadratic family can be found in [Reference Baladi, Benedicks and SchnellmannBBS15, Reference TsujiiTsu93], for instance. The version stated here allows for
![]() $\delta $
-independence at a more shallow return to the interval
$\delta $
-independence at a more shallow return to the interval
![]() $(-2\delta ,2\delta )$
. To get this kind of annular result constitutes a minor modification of Lemma 4.1 in [Reference TsujiiTsu93]. We refer to Lemma 2.6 in [Reference AspenbergAsp21] and the proof therein, however, for a proof of the above result. This proof is based on Przytycki’s telescope lemma (see [Reference PrzytyckiPrz90] and also [Reference Przytycki, Rivera-Letelier and SmirnovPRLS03]). In contrast to the techniques in [Reference TsujiiTsu93], in the case of the quadratic family, no recurrence assumption is needed.
$(-2\delta ,2\delta )$
. To get this kind of annular result constitutes a minor modification of Lemma 4.1 in [Reference TsujiiTsu93]. We refer to Lemma 2.6 in [Reference AspenbergAsp21] and the proof therein, however, for a proof of the above result. This proof is based on Przytycki’s telescope lemma (see [Reference PrzytyckiPrz90] and also [Reference Przytycki, Rivera-Letelier and SmirnovPRLS03]). In contrast to the techniques in [Reference TsujiiTsu93], in the case of the quadratic family, no recurrence assumption is needed.
3.2 Phase-parameter distortion
If
![]() $t \mapsto F(x;a+t)$
is a family of (analytic) perturbations of
$t \mapsto F(x;a+t)$
is a family of (analytic) perturbations of
![]() $(x;a) \mapsto F(x;a)$
at a, we may expand each such perturbation as
$(x;a) \mapsto F(x;a)$
at a, we may expand each such perturbation as
and it is easy to verify that
 $$ \begin{align*} \frac{\partial_a F^n(x;a)}{\partial_x F^{n-1}(F(x;a);a)} = \frac{\partial_a F^{n-1}(x;a)}{\partial_x F^{n-2}(F(x;a);a)} + \frac{\partial_a F(F^{n-1}(x;a);a)}{\partial_x F^{n-1}(F(x;a);a)}. \end{align*} $$
$$ \begin{align*} \frac{\partial_a F^n(x;a)}{\partial_x F^{n-1}(F(x;a);a)} = \frac{\partial_a F^{n-1}(x;a)}{\partial_x F^{n-2}(F(x;a);a)} + \frac{\partial_a F(F^{n-1}(x;a);a)}{\partial_x F^{n-1}(F(x;a);a)}. \end{align*} $$
Our concern is with the quadratic family
![]() $x \mapsto 1-ax^2 = F(x;a)$
, with a being the parameter value. In particular, we are interested in the critical orbit of each such member and, to this end, we introduce the functions
$x \mapsto 1-ax^2 = F(x;a)$
, with a being the parameter value. In particular, we are interested in the critical orbit of each such member and, to this end, we introduce the functions
![]() $a \mapsto \xi _j(a) = F^j(0;a)$
for
$a \mapsto \xi _j(a) = F^j(0;a)$
for
![]() $j \geq 0$
. In view of our notation and the above relationship, we see that
$j \geq 0$
. In view of our notation and the above relationship, we see that
 $$ \begin{align*} \frac{\partial_a F^n(0;a)}{\partial_x F^{n-1}(1;a)} = \sum_{k=0}^{n-1} \frac{\partial_aF(\xi_k(a);a)}{\partial_x F^k(1;a)}. \end{align*} $$
$$ \begin{align*} \frac{\partial_a F^n(0;a)}{\partial_x F^{n-1}(1;a)} = \sum_{k=0}^{n-1} \frac{\partial_aF(\xi_k(a);a)}{\partial_x F^k(1;a)}. \end{align*} $$
Throughout the proof of Theorem B, it will be of importance to be able to compare phase and parameter derivatives. Under the assumption of exponential increase of the phase derivative along the critical orbit, this can be done, as is formulated in the following lemma. The proof is that of Lemma 2.10 in [Reference AspenbergAsp21].
Lemma 3.2. (Phase-parameter distortion)
Let
![]() $a_0$
be
$a_0$
be
![]() $(\gamma _0,C_0)$
-Collet–Eckmann,
$(\gamma _0,C_0)$
-Collet–Eckmann,
![]() $\gamma _T \in (0,\gamma _0)$
,
$\gamma _T \in (0,\gamma _0)$
,
![]() $C_T \in (0,C_0)$
, and
$C_T \in (0,C_0)$
, and
![]() $A \in (0,1)$
. There exist
$A \in (0,1)$
. There exist
![]() $T, N_T, \epsilon _T> 0$
such that if
$T, N_T, \epsilon _T> 0$
such that if
![]() $a \in (a_0-\epsilon _T,a_0 + \epsilon _T)$
satisfies
$a \in (a_0-\epsilon _T,a_0 + \epsilon _T)$
satisfies
for some
![]() $n-1 \geq N_T$
, then
$n-1 \geq N_T$
, then
 $$ \begin{align*} (1-A)T \leq \bigg\vert \frac{\partial_a F^n(0;a)}{\partial_x F^{n-1} (1;a)} \bigg\vert \leq (1+A)T. \end{align*} $$
$$ \begin{align*} (1-A)T \leq \bigg\vert \frac{\partial_a F^n(0;a)}{\partial_x F^{n-1} (1;a)} \bigg\vert \leq (1+A)T. \end{align*} $$
Proof. According to Theorem 3 in [Reference TsujiiTsu00] (see also Theorem 1 in [Reference LevinLev14]),
 $$ \begin{align*} \lim_{j \to \infty} \frac{\partial_a F^j(0;a_0)}{\partial_x F^{j-1}(1;a_0)} = \sum_{k=0}^\infty \frac{\partial_a F(\xi_k(a_0);a_0)}{\partial_x F^k(1;a_0)} = T \in \mathbb{R}_{>0}. \end{align*} $$
$$ \begin{align*} \lim_{j \to \infty} \frac{\partial_a F^j(0;a_0)}{\partial_x F^{j-1}(1;a_0)} = \sum_{k=0}^\infty \frac{\partial_a F(\xi_k(a_0);a_0)}{\partial_x F^k(1;a_0)} = T \in \mathbb{R}_{>0}. \end{align*} $$
Let
![]() $N_T> 0$
be large enough so that
$N_T> 0$
be large enough so that
 $$ \begin{align*} \bigg\vert \sum_{k=N_T}^\infty \frac{\partial_a F(\xi_k(a_0);a_0)}{\partial_x F^k(1;a_0)} \bigg\vert \leq \sum_{k=N_T}^\infty \frac{1}{C_0 e^{\gamma_0 k}} \leq \sum_{k=N_T}^\infty \frac{1}{C_T e^{\gamma_T k}} \leq \frac{1}{3}A T. \end{align*} $$
$$ \begin{align*} \bigg\vert \sum_{k=N_T}^\infty \frac{\partial_a F(\xi_k(a_0);a_0)}{\partial_x F^k(1;a_0)} \bigg\vert \leq \sum_{k=N_T}^\infty \frac{1}{C_0 e^{\gamma_0 k}} \leq \sum_{k=N_T}^\infty \frac{1}{C_T e^{\gamma_T k}} \leq \frac{1}{3}A T. \end{align*} $$
Since
![]() $a \mapsto \partial _a F(\xi _k(a);a)/\partial _x F^k(1;a)$
is continuous, there exists
$a \mapsto \partial _a F(\xi _k(a);a)/\partial _x F^k(1;a)$
is continuous, there exists
![]() $\epsilon _T> 0$
such that given
$\epsilon _T> 0$
such that given
![]() $a \in (a_0-\epsilon _T,a_0+\epsilon _T)$
,
$a \in (a_0-\epsilon _T,a_0+\epsilon _T)$
,
 $$ \begin{align*} \bigg\vert \sum_{k=0}^{N_T-1} \frac{\partial_a F(\xi_k(a);a)}{\partial_x F(1;a)} - T \bigg\vert \leq \frac{1}{2}A T. \end{align*} $$
$$ \begin{align*} \bigg\vert \sum_{k=0}^{N_T-1} \frac{\partial_a F(\xi_k(a);a)}{\partial_x F(1;a)} - T \bigg\vert \leq \frac{1}{2}A T. \end{align*} $$
Assuming
![]() $x \mapsto 1-ax^2$
to be
$x \mapsto 1-ax^2$
to be
![]() $(\gamma _T,C_T)$
-Collet–Eckmann up to time
$(\gamma _T,C_T)$
-Collet–Eckmann up to time
![]() $n> N_T$
, the result now follows since
$n> N_T$
, the result now follows since
 $$ \begin{align*} \bigg\vert \sum_{k=0}^n \frac{\partial_a F(\xi_k(a);a)}{\partial_x F^k(1;a)} - T \bigg\vert \leq AT.\\[-4pc] \end{align*} $$
$$ \begin{align*} \bigg\vert \sum_{k=0}^n \frac{\partial_a F(\xi_k(a);a)}{\partial_x F^k(1;a)} - T \bigg\vert \leq AT.\\[-4pc] \end{align*} $$
Remark 3.3. The quotient
![]() $(1+A)/(1-A) = D_A$
can be chosen arbitrarily close to
$(1+A)/(1-A) = D_A$
can be chosen arbitrarily close to
![]() $1$
by increasing
$1$
by increasing
![]() $N_T$
and decreasing
$N_T$
and decreasing
![]() $\epsilon _T$
.
$\epsilon _T$
.
3.3 Start-up lemma
With the above two lemmas, we now prove the existence of a suitable interval in parameter space on which the parameter exclusion will be carried out.
Given an admissible sequence
![]() $(\delta _n)$
, let
$(\delta _n)$
, let
![]() $N_A$
be the integer in Definition 1.2. Fix
$N_A$
be the integer in Definition 1.2. Fix
![]() $N_B \geq 1, \gamma _B> 0$
, and
$N_B \geq 1, \gamma _B> 0$
, and
![]() $C_B> 0$
, and let
$C_B> 0$
, and let
![]() $a_0$
be a PR-parameter satisfying a
$a_0$
be a PR-parameter satisfying a
![]() $(\gamma _0,C_0)$
-Collet–Eckmann condition. In Lemma 3.2, we make the choice
$(\gamma _0,C_0)$
-Collet–Eckmann condition. In Lemma 3.2, we make the choice
Furthermore, let
and let
![]() $m_{-1} = \max (N_A,N_B,N_T)$
.
$m_{-1} = \max (N_A,N_B,N_T)$
.
Lemma 3.4. (Start-up lemma)
There exist an interval
![]() $\omega _0 = (a_0-\epsilon ,a_0 + \epsilon )$
, an integer
$\omega _0 = (a_0-\epsilon ,a_0 + \epsilon )$
, an integer
![]() $m_0 \geq m_{-1}$
, and a constant
$m_0 \geq m_{-1}$
, and a constant
![]() $S = \epsilon _1 \delta $
such that the following hold.
$S = \epsilon _1 \delta $
such that the following hold.
-
(i)
 $\xi _{m_0} : \omega _0 \to [-1,1]$
is injective, and
$\xi _{m_0} : \omega _0 \to [-1,1]$
is injective, and  $$ \begin{align*} \vert \xi_{m_0}(\omega_0)\vert \geq \begin{cases} e^{-r}/r^2 &\mbox{if}\ \xi_{m_0}(\omega_0) \cap I_r \neq \emptyset, \\ S &\mbox{if}\ \xi_{m_0}\cap(-\delta,\delta) = \emptyset.\end{cases} \end{align*} $$
$$ \begin{align*} \vert \xi_{m_0}(\omega_0)\vert \geq \begin{cases} e^{-r}/r^2 &\mbox{if}\ \xi_{m_0}(\omega_0) \cap I_r \neq \emptyset, \\ S &\mbox{if}\ \xi_{m_0}\cap(-\delta,\delta) = \emptyset.\end{cases} \end{align*} $$
-
(ii) Each
 $a \in \omega _0$
is
$a \in \omega _0$
is
 $(\gamma ,C)$
-Collet–Eckmann up to time
$(\gamma ,C)$
-Collet–Eckmann up to time
 $m_0$
:
$m_0$
:  $$ \begin{align*} \vert \partial_x F^j(1;a) \vert \geq Ce^{\gamma j} \quad (j=0,1,\ldots,m_0-1). \end{align*} $$
$$ \begin{align*} \vert \partial_x F^j(1;a) \vert \geq Ce^{\gamma j} \quad (j=0,1,\ldots,m_0-1). \end{align*} $$
-
(iii) Each
 $a \in \omega _0$
enjoys polynomial recurrence up to time
$a \in \omega _0$
enjoys polynomial recurrence up to time
 $m_0$
: there exist absolute constants
$m_0$
: there exist absolute constants
 $K> 0$
and
$K> 0$
and
 $\sigma \geq 0$
such that, for
$\sigma \geq 0$
such that, for
 $a \in \omega _0$
,
$a \in \omega _0$
,  $$ \begin{align*} \vert \xi_j(a) \vert \geq \frac{K}{j^\sigma} \quad (j = 1,2,\ldots,m_0-1). \end{align*} $$
$$ \begin{align*} \vert \xi_j(a) \vert \geq \frac{K}{j^\sigma} \quad (j = 1,2,\ldots,m_0-1). \end{align*} $$
Proof. Given
![]() $x,y \in \xi _{j}(\omega _0)$
,
$x,y \in \xi _{j}(\omega _0)$
,
![]() $j \geq 1$
, consider the following distance condition:
$j \geq 1$
, consider the following distance condition:
 $$ \begin{align} \vert x - y \vert \leq \begin{cases} e^{-r}/r^2 &\mbox{if}\ \xi_{j}(\omega_0) \cap I_r \neq \emptyset, \\ S = \epsilon_1 \delta &\mbox{if}\ \xi_{j}(\omega_0) \cap (-\delta,\delta) = \emptyset. \end{cases} \end{align} $$
$$ \begin{align} \vert x - y \vert \leq \begin{cases} e^{-r}/r^2 &\mbox{if}\ \xi_{j}(\omega_0) \cap I_r \neq \emptyset, \\ S = \epsilon_1 \delta &\mbox{if}\ \xi_{j}(\omega_0) \cap (-\delta,\delta) = \emptyset. \end{cases} \end{align} $$
By making
![]() $\epsilon $
smaller, we may assume that equation (2) is satisfied up to time
$\epsilon $
smaller, we may assume that equation (2) is satisfied up to time
![]() $m_{-1}$
. Moreover, we make sure that
$m_{-1}$
. Moreover, we make sure that
![]() $\epsilon $
is small enough to comply with Lemma 3.2. Whenever equation (2) is satisfied, phase derivatives are comparable as follows:
$\epsilon $
is small enough to comply with Lemma 3.2. Whenever equation (2) is satisfied, phase derivatives are comparable as follows:
 $$ \begin{align} \frac{1}{C_1} \leq \bigg\vert \frac{\partial_x F(x;a)}{\partial_x F(y;b)} \bigg\vert \leq C_1, \end{align} $$
$$ \begin{align} \frac{1}{C_1} \leq \bigg\vert \frac{\partial_x F(x;a)}{\partial_x F(y;b)} \bigg\vert \leq C_1, \end{align} $$
with
![]() $C_1> 1$
a constant. This can be seen through the following estimate:
$C_1> 1$
a constant. This can be seen through the following estimate:
 $$ \begin{align*} \bigg\vert \frac{\partial_x F(x;a)}{\partial_x F(y;b)}\bigg\vert = \bigg\vert \frac{-2ax}{-2by} \bigg\vert \leq \frac{a_0 + \epsilon}{a_0-\epsilon}\bigg(\bigg\vert \frac{x-y}{y} \bigg\vert + 1\bigg). \end{align*} $$
$$ \begin{align*} \bigg\vert \frac{\partial_x F(x;a)}{\partial_x F(y;b)}\bigg\vert = \bigg\vert \frac{-2ax}{-2by} \bigg\vert \leq \frac{a_0 + \epsilon}{a_0-\epsilon}\bigg(\bigg\vert \frac{x-y}{y} \bigg\vert + 1\bigg). \end{align*} $$
If we are outside
![]() $(-\delta ,\delta )$
, then
$(-\delta ,\delta )$
, then
 $$ \begin{align*} \bigg\vert \frac{x-y}{y} \bigg\vert \leq \frac{S}{\delta} = \epsilon_1, \end{align*} $$
$$ \begin{align*} \bigg\vert \frac{x-y}{y} \bigg\vert \leq \frac{S}{\delta} = \epsilon_1, \end{align*} $$
and if we are hitting
![]() $I_r$
with largest possible r,
$I_r$
with largest possible r,
 $$ \begin{align*} \bigg\vert \frac{x-y}{y} \bigg\vert \leq \frac{e^{-r}}{r^2}\frac{1}{e^{-(r+1)}} = \frac{e}{r^2} \leq \frac{e}{\Delta^2}. \end{align*} $$
$$ \begin{align*} \bigg\vert \frac{x-y}{y} \bigg\vert \leq \frac{e^{-r}}{r^2}\frac{1}{e^{-(r+1)}} = \frac{e}{r^2} \leq \frac{e}{\Delta^2}. \end{align*} $$
By making sure that
![]() $\epsilon $
,
$\epsilon $
,
![]() $\epsilon _1$
, and
$\epsilon _1$
, and
![]() $\delta $
are small enough,
$\delta $
are small enough,
![]() $C_1$
can be made as close to
$C_1$
can be made as close to
![]() $1$
as we want. In particular, we make
$1$
as we want. In particular, we make
![]() $C_1$
close enough to
$C_1$
close enough to
![]() $1$
so that
$1$
so that
As long as the distance condition in equation (2) is satisfied, we will have good expansion along the critical orbits. Indeed, by equations (3) and (4), it follows that, given
![]() $a \in \omega _0$
,
$a \in \omega _0$
,
 $$ \begin{align*} \vert \partial_x F^j(1;a) \vert &\geq C_1^{-j}\vert \partial_x F^j(1;a_0) \vert \\ &\geq C_1^{-j}C_0 e^{\gamma_0 j} \\ &\geq C e^{\gamma j} \quad (j \geq 0\ \text{such that equation}\ (2)\ \text{is satisfied}). \end{align*} $$
$$ \begin{align*} \vert \partial_x F^j(1;a) \vert &\geq C_1^{-j}\vert \partial_x F^j(1;a_0) \vert \\ &\geq C_1^{-j}C_0 e^{\gamma_0 j} \\ &\geq C e^{\gamma j} \quad (j \geq 0\ \text{such that equation}\ (2)\ \text{is satisfied}). \end{align*} $$
This tells us that, during the time for which equation (2) is satisfied, each
![]() $a \in \omega _0$
is
$a \in \omega _0$
is
![]() $(\gamma ,C)$
-Collet–Eckmann. In particular, since
$(\gamma ,C)$
-Collet–Eckmann. In particular, since
![]() $\gamma> \gamma _T$
and
$\gamma> \gamma _T$
and
![]() $C> C_T$
, we can apply Lemma 3.2 and, together with the mean value theorem, we have that
$C> C_T$
, we can apply Lemma 3.2 and, together with the mean value theorem, we have that
 $$ \begin{align*} \vert \xi_{j}(\omega_0)\vert &= \vert \partial_a F^j(0;a') \vert \vert \omega_0 \vert \\ &\geq (1-A)T \vert \partial_x F^{j-1}(1;a') \vert \vert \omega_0\vert \\ &\geq (1-A)T C e^{\gamma (j-1)} \vert \omega_0 \vert. \end{align*} $$
$$ \begin{align*} \vert \xi_{j}(\omega_0)\vert &= \vert \partial_a F^j(0;a') \vert \vert \omega_0 \vert \\ &\geq (1-A)T \vert \partial_x F^{j-1}(1;a') \vert \vert \omega_0\vert \\ &\geq (1-A)T C e^{\gamma (j-1)} \vert \omega_0 \vert. \end{align*} $$
Our interval is thus expanding, and we let
![]() $m_0 = j$
, with
$m_0 = j$
, with
![]() $j \geq m_{-1}$
the smallest integer for which equation (2) is no longer satisfied. This proves statements (i) and (ii).
$j \geq m_{-1}$
the smallest integer for which equation (2) is no longer satisfied. This proves statements (i) and (ii).
To prove statement (iii), let
![]() $K_0> 0$
and
$K_0> 0$
and
![]() $\sigma _0 \geq 0$
be the constants associated to
$\sigma _0 \geq 0$
be the constants associated to
![]() $a_0$
for which
$a_0$
for which
In view of equation (2), when we hit
![]() $(-\delta ,\delta )$
at some time
$(-\delta ,\delta )$
at some time
![]() $j < m_0$
,
$j < m_0$
,
Here, r is such that
and therefore, given
![]() $\delta $
small enough,
$\delta $
small enough,
 $$ \begin{align*} \vert \xi_j(a) \vert \geq \vert \xi_j(a_0) \vert \bigg(1 - \frac{e}{\Delta^2} \bigg) \geq \frac{K_0/2}{j^{\sigma_0}} \quad (j = 1,2,\ldots,m_0-1).\\[-3.6pc] \end{align*} $$
$$ \begin{align*} \vert \xi_j(a) \vert \geq \vert \xi_j(a_0) \vert \bigg(1 - \frac{e}{\Delta^2} \bigg) \geq \frac{K_0/2}{j^{\sigma_0}} \quad (j = 1,2,\ldots,m_0-1).\\[-3.6pc] \end{align*} $$
Remark 3.5. By making
![]() $\delta $
small enough so that
$\delta $
small enough so that
![]() $1/\Delta ^2 < \epsilon _1$
, S will be larger than any partition element
$1/\Delta ^2 < \epsilon _1$
, S will be larger than any partition element
![]() $I_{rl} \subset (-\delta ,\delta )$
. This S is usually referred to as the large scale.
$I_{rl} \subset (-\delta ,\delta )$
. This S is usually referred to as the large scale.
Since
![]() $\Lambda _{N_B}(\delta _n) \subset \Lambda _{m_0}(\delta _n)$
, Theorem B follows if
$\Lambda _{N_B}(\delta _n) \subset \Lambda _{m_0}(\delta _n)$
, Theorem B follows if
4 Induction step
4.1 Initial iterates
Let
![]() $\omega _0 = \Delta _0$
be the start-up interval obtained in Lemma 3.4. Iterating this interval under
$\omega _0 = \Delta _0$
be the start-up interval obtained in Lemma 3.4. Iterating this interval under
![]() $\xi $
and successively excluding parameters that do not satisfy the recurrence condition, or the Collet–Eckmann condition, we will inductively define a nested sequence
$\xi $
and successively excluding parameters that do not satisfy the recurrence condition, or the Collet–Eckmann condition, we will inductively define a nested sequence
![]() $\Delta _0 \supset \Delta _1 \supset \cdots \supset \Delta _k \supset \cdots $
of sets of parameters satisfying
$\Delta _0 \supset \Delta _1 \supset \cdots \supset \Delta _k \supset \cdots $
of sets of parameters satisfying
 $$ \begin{align*} \Lambda_{m_0}(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma_B,C_B) \cap \omega_0 \subset \Delta_\infty = \bigcap_{k = 0}^\infty \Delta_k, \end{align*} $$
$$ \begin{align*} \Lambda_{m_0}(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma_B,C_B) \cap \omega_0 \subset \Delta_\infty = \bigcap_{k = 0}^\infty \Delta_k, \end{align*} $$
and our goal is to estimate the Lebesgue measure of
![]() $\Delta _\infty $
. This will require a careful analysis of the so-called returns to
$\Delta _\infty $
. This will require a careful analysis of the so-called returns to
![]() $(-\delta ,\delta )$
, and we will distinguish between four types of returns: inessential, essential, escape, and complete. At the
$(-\delta ,\delta )$
, and we will distinguish between four types of returns: inessential, essential, escape, and complete. At the
![]() $k\text {th}$
complete return, we will be in the position of excluding parameters and form the partition that will make up the set
$k\text {th}$
complete return, we will be in the position of excluding parameters and form the partition that will make up the set
![]() $\Delta _k$
. Below, we will describe the iterations from the
$\Delta _k$
. Below, we will describe the iterations from the
![]() $k\text {th}$
complete return to the
$k\text {th}$
complete return to the
![]() $(k+1)\text {th}$
complete return, and hence the forming of
$(k+1)\text {th}$
complete return, and hence the forming of
![]() $\Delta _{k+1}$
. Before indicating the partition and giving a definition of the different returns, we begin by considering the first initial iterates of
$\Delta _{k+1}$
. Before indicating the partition and giving a definition of the different returns, we begin by considering the first initial iterates of
![]() $\xi _{m_0}(\omega _0)$
.
$\xi _{m_0}(\omega _0)$
.
If
![]() $\xi _{m_0}(\omega _0) \cap (-\delta ,\delta ) \neq \emptyset $
, then we have reached a return and we proceed accordingly as is described below. If this is not the case, then we are in the situation
$\xi _{m_0}(\omega _0) \cap (-\delta ,\delta ) \neq \emptyset $
, then we have reached a return and we proceed accordingly as is described below. If this is not the case, then we are in the situation
with S larger than any partition element
![]() $I_{rl} \subset (-\delta ,\delta )$
(see Remark 3.5). Since the length of the image is bounded from below, there is an integer
$I_{rl} \subset (-\delta ,\delta )$
(see Remark 3.5). Since the length of the image is bounded from below, there is an integer
![]() $n^* = n^*(S)$
such that, for some smallest
$n^* = n^*(S)$
such that, for some smallest
![]() $n \leq n^*$
, we have
$n \leq n^*$
, we have
In this case,
![]() $m_0 + n$
is the index of the first return. We claim that if
$m_0 + n$
is the index of the first return. We claim that if
![]() $m_0$
is large enough, we can assume a good derivative up to time
$m_0$
is large enough, we can assume a good derivative up to time
![]() $m_0 + n$
. To realize this, consider for
$m_0 + n$
. To realize this, consider for
![]() $j < n$
the distortion quotient
$j < n$
the distortion quotient
 $$ \begin{align*} \bigg\vert\frac{\partial_x F^{m_0+j}(1;a)}{\partial_x F^{m_0+j}(1;b)} \bigg\vert = \bigg\vert\frac{\partial_x F^{m_0-1}(1;a)}{\partial_x F^{m_0-1}(1;b)} \bigg\vert \bigg\vert\frac{\partial_x F^{j+1}(\xi_{m_0}(a);a)}{\partial_x F^{j+1}(\xi_{m_0}(b);b)} \bigg\vert. \end{align*} $$
$$ \begin{align*} \bigg\vert\frac{\partial_x F^{m_0+j}(1;a)}{\partial_x F^{m_0+j}(1;b)} \bigg\vert = \bigg\vert\frac{\partial_x F^{m_0-1}(1;a)}{\partial_x F^{m_0-1}(1;b)} \bigg\vert \bigg\vert\frac{\partial_x F^{j+1}(\xi_{m_0}(a);a)}{\partial_x F^{j+1}(\xi_{m_0}(b);b)} \bigg\vert. \end{align*} $$
Since the distance conditions in equation (2) are satisfied up to time
![]() $m_0 - 1$
, the first factor in the above right-hand side is bounded from above by the constant
$m_0 - 1$
, the first factor in the above right-hand side is bounded from above by the constant
![]() $C_1^{m_0-1}$
, with
$C_1^{m_0-1}$
, with
![]() $C_1> 1$
being very close to
$C_1> 1$
being very close to
![]() $1$
(see equation (3)). Furthermore, since
$1$
(see equation (3)). Furthermore, since
![]() $j < n < n^*(S)$
, and since we, by assumption, are iterating outside
$j < n < n^*(S)$
, and since we, by assumption, are iterating outside
![]() $(-\delta ,\delta )$
, the second factor in the above right-hand side is bounded from above by some positive constant
$(-\delta ,\delta )$
, the second factor in the above right-hand side is bounded from above by some positive constant
![]() $C_{S,\delta }$
dependent on S and
$C_{S,\delta }$
dependent on S and
![]() $\delta $
.
$\delta $
.
If there is no parameter
![]() $a' \in \omega _0$
such that
$a' \in \omega _0$
such that
![]() $\vert \partial _x F^{m_0+j}(1;a') \vert \geq C_B e^{\gamma _B(m_0 + j)}$
, then we have already reached our desired result. If, however, there is such a parameter
$\vert \partial _x F^{m_0+j}(1;a') \vert \geq C_B e^{\gamma _B(m_0 + j)}$
, then we have already reached our desired result. If, however, there is such a parameter
![]() $a'$
, then for all
$a'$
, then for all
![]() $a \in \omega _0$
, it follows from the above distortion estimate and our choice of
$a \in \omega _0$
, it follows from the above distortion estimate and our choice of
![]() $\gamma $
that
$\gamma $
that
 $$ \begin{align*} \vert \partial_x F^{m_0+j}(1;a) \vert \geq \frac{C_B e^{\gamma_B (m_0+j)}}{C_1^{m_0-1}C_{S,\delta}} \geq Ce^{\gamma(m_0+j)}, \end{align*} $$
$$ \begin{align*} \vert \partial_x F^{m_0+j}(1;a) \vert \geq \frac{C_B e^{\gamma_B (m_0+j)}}{C_1^{m_0-1}C_{S,\delta}} \geq Ce^{\gamma(m_0+j)}, \end{align*} $$
provided
![]() $m_0$
is large enough. We conclude that
$m_0$
is large enough. We conclude that
In the case where we have to iterate
![]() $\xi _{m_0}(\omega _0)$
further to hit
$\xi _{m_0}(\omega _0)$
further to hit
![]() $(-\delta ,\delta )$
, we still let
$(-\delta ,\delta )$
, we still let
![]() $m_0$
denote the index of the first return.
$m_0$
denote the index of the first return.
4.2 The partition
At the
![]() $(k+1)\text {th}$
step in our process of excluding parameters,
$(k+1)\text {th}$
step in our process of excluding parameters,
![]() $\Delta _k$
consists of disjoint intervals
$\Delta _k$
consists of disjoint intervals
![]() $\omega _k^{rl}$
, and for each such interval, there is an associated time
$\omega _k^{rl}$
, and for each such interval, there is an associated time
![]() $m_k^{rl}$
for which either
$m_k^{rl}$
for which either
![]() $\xi _{m_k^{rl}}(\omega _k^{rl}) = I_{rl} \subset (-4\delta ,4\delta )$
or
$\xi _{m_k^{rl}}(\omega _k^{rl}) = I_{rl} \subset (-4\delta ,4\delta )$
or
![]() $\xi _{m_k^{rl}}(\omega _k^{rl})$
is mapped onto
$\xi _{m_k^{rl}}(\omega _k^{rl})$
is mapped onto
![]() $\pm (\delta ,x)$
, with
$\pm (\delta ,x)$
, with
![]() $\vert x-\delta \vert \geq 3\delta $
. We iterate each such interval individually and let
$\vert x-\delta \vert \geq 3\delta $
. We iterate each such interval individually and let
![]() $m_{k+1}^{rl}$
be the time for which
$m_{k+1}^{rl}$
be the time for which
![]() $\xi _{m_{k+1}^{rl}}(\omega _k^{rl})$
hits deep enough for us to be able to remove a significant portion of
$\xi _{m_{k+1}^{rl}}(\omega _k^{rl})$
hits deep enough for us to be able to remove a significant portion of
![]() $(-\delta _{m_{k+1}^{rl}},\delta _{m_{k+1}^{rl}})$
in phase space, and let
$(-\delta _{m_{k+1}^{rl}},\delta _{m_{k+1}^{rl}})$
in phase space, and let
![]() $E_k^{rl}$
denote the corresponding set that is removed in parameter space. We now form the set
$E_k^{rl}$
denote the corresponding set that is removed in parameter space. We now form the set
![]() $\hat {\omega }_k^{rl} \subset \Delta _{k+1}$
and make the partition
$\hat {\omega }_k^{rl} \subset \Delta _{k+1}$
and make the partition
 $$ \begin{align*} \hat{\omega}_k^{rl} = \omega_k^{rl} \smallsetminus E_k^{rl} = \bigg( \bigcup_{r',l'} \omega_{k+1}^{r'l'} \bigg) \cup T_{k+1} = N_{k+1} \cup T_{k+1}. \end{align*} $$
$$ \begin{align*} \hat{\omega}_k^{rl} = \omega_k^{rl} \smallsetminus E_k^{rl} = \bigg( \bigcup_{r',l'} \omega_{k+1}^{r'l'} \bigg) \cup T_{k+1} = N_{k+1} \cup T_{k+1}. \end{align*} $$
Here, each
![]() $\omega _{k+1}^{r'l'} \subset N_{k+1}$
is such that
$\omega _{k+1}^{r'l'} \subset N_{k+1}$
is such that
![]() $\xi _{m_{k+1}^{rl}}(\omega _{k+1}^{r'l'}) = I_{r'l'} \subset (-4\delta ,4\delta )$
, and
$\xi _{m_{k+1}^{rl}}(\omega _{k+1}^{r'l'}) = I_{r'l'} \subset (-4\delta ,4\delta )$
, and
![]() $T_{k+1}$
consists of (at most) two intervals whose image under
$T_{k+1}$
consists of (at most) two intervals whose image under
![]() $\xi _{m_{k+1}^{rl}}$
is
$\xi _{m_{k+1}^{rl}}$
is
![]() $\pm (\delta ,x)$
, with
$\pm (\delta ,x)$
, with
![]() $\vert x-\delta \vert \geq 3 \delta $
.
$\vert x-\delta \vert \geq 3 \delta $
.
Remark 4.1. At most four intervals
![]() $\omega _{k+1}^{r'l'} \subset N_{k+1}$
will be mapped onto an interval slightly larger than
$\omega _{k+1}^{r'l'} \subset N_{k+1}$
will be mapped onto an interval slightly larger than
![]() $I_{r'l'}$
, that is,
$I_{r'l'}$
, that is,
with
![]() $I_{r'l'}$
and
$I_{r'l'}$
and
![]() $I_{r"l"}$
adjacent partition elements.
$I_{r"l"}$
adjacent partition elements.
Remark 4.2. At essential returns and escape returns we will, if possible, make a partial partition. To these partitioned parameter intervals, we associate a complete return time even though nothing is removed at these times. This is described in more detail in §§4.8 and 4.9.
Remark 4.3. Notice that our way of partitioning differs slightly from the original one considered in [Reference Benedicks and CarlesonBC85], since here we do not continue to iterate what is mapped outside of
![]() $(-\delta ,\delta )$
, but instead stop and make a partition.
$(-\delta ,\delta )$
, but instead stop and make a partition.
4.3 The different returns to
 $(-\delta ,\delta )$
$(-\delta ,\delta )$
At time
![]() $m_{k+1}^{rl}$
, we say that
$m_{k+1}^{rl}$
, we say that
![]() $\omega _k^{rl}$
has reached the
$\omega _k^{rl}$
has reached the
![]() $(k+1)\text {th}$
complete return to
$(k+1)\text {th}$
complete return to
![]() $(-\delta ,\delta )$
. In between the two complete returns of index
$(-\delta ,\delta )$
. In between the two complete returns of index
![]() $m_{k}^{rl}$
and
$m_{k}^{rl}$
and
![]() $m_{k+1}^{rl}$
, we might have returns which are not complete. Given a return at time
$m_{k+1}^{rl}$
, we might have returns which are not complete. Given a return at time
![]() $n> m_k^{rl}$
, we classify it as follows.
$n> m_k^{rl}$
, we classify it as follows.
-
(i) If
 $\xi _n(\omega _k^{rl}) \subset I_{r'l'} \cup I_{r"l"}$
, with
$\xi _n(\omega _k^{rl}) \subset I_{r'l'} \cup I_{r"l"}$
, with
 $I_{r'l'}$
and
$I_{r'l'}$
and
 $I_{r"l"}$
adjacent partition elements (
$I_{r"l"}$
adjacent partition elements (
 $r' \geq r"$
), and if
$r' \geq r"$
), and if
 $\vert \xi _n(\omega _k^{rl}) \vert < \vert I_{r'l'}\vert $
, we call this an inessential return. The interval
$\vert \xi _n(\omega _k^{rl}) \vert < \vert I_{r'l'}\vert $
, we call this an inessential return. The interval
 $I_{r'l'}\cup I_{r"l"}$
is called the host interval.
$I_{r'l'}\cup I_{r"l"}$
is called the host interval. -
(ii) If the return is not inessential, it is called an essential return. The outer most partition element
 $I_r$
contained in the image is called the essential interval.
$I_r$
contained in the image is called the essential interval. -
(iii) If
 $\xi _n(\omega _k^{rl}) \cap (-\delta ,\delta ) \neq \emptyset $
and
$\xi _n(\omega _k^{rl}) \cap (-\delta ,\delta ) \neq \emptyset $
and
 $\vert \xi _n(\omega _k^{rl}) \smallsetminus (-\delta ,\delta ) \vert \geq 3\delta $
, we call this an escape return. The interval
$\vert \xi _n(\omega _k^{rl}) \smallsetminus (-\delta ,\delta ) \vert \geq 3\delta $
, we call this an escape return. The interval
 $\xi _n(\omega _k^{rl}) \smallsetminus (-\delta ,\delta )$
is called the escape interval.
$\xi _n(\omega _k^{rl}) \smallsetminus (-\delta ,\delta )$
is called the escape interval. -
(iv) Finally, if a return satisfies
 $\xi _n(\omega _k^{rl}) \cap (-\delta _n/3,\delta _n/3) \neq \emptyset $
, it is called a complete return.
$\xi _n(\omega _k^{rl}) \cap (-\delta _n/3,\delta _n/3) \neq \emptyset $
, it is called a complete return.
We use these terms exclusively, that is, an inessential return is not essential, an essential return is not an escape, and an escape return is not complete.
Given
![]() $\omega _k^{rl} \subset \Delta _k$
, we want to find an upper bound for the index of the next complete return. In the worst case scenario, we encounter all of the above kinds of returns, in the order
$\omega _k^{rl} \subset \Delta _k$
, we want to find an upper bound for the index of the next complete return. In the worst case scenario, we encounter all of the above kinds of returns, in the order
Given such behaviour, we show below that there is an absolute constant
![]() $\kappa>0$
such that the index of the
$\kappa>0$
such that the index of the
![]() $(k+1){\text {th}}$
complete return satisfies
$(k+1){\text {th}}$
complete return satisfies
![]() $m_{k+1}^{rl} \leq m_k^{rl} + \kappa \log m_k^{rl}$
.
$m_{k+1}^{rl} \leq m_k^{rl} + \kappa \log m_k^{rl}$
.
4.4 Induction assumptions
Up until the start time
![]() $m_0$
, we do not want to assume anything regarding recurrence with respect to our recurrence rate
$m_0$
, we do not want to assume anything regarding recurrence with respect to our recurrence rate
![]() $(\delta _n)$
. Since the perturbation is made around a PR-parameter
$(\delta _n)$
. Since the perturbation is made around a PR-parameter
![]() $a_0$
, we do however have the following polynomial recurrence to rely on (Lemma 3.4).
$a_0$
, we do however have the following polynomial recurrence to rely on (Lemma 3.4).
-
(PR)
 $\vert F^j(0;a) \vert \geq K/j^\sigma $
for all
$\vert F^j(0;a) \vert \geq K/j^\sigma $
for all
 $a \in \omega ^{rl}_k$
and
$a \in \omega ^{rl}_k$
and
 $j = 1,2,\ldots ,m_0-1$
.
$j = 1,2,\ldots ,m_0-1$
.
After
![]() $m_0$
we start excluding parameters according to the following basic assumption.
$m_0$
we start excluding parameters according to the following basic assumption.
-
(BA)
 $\vert F^j(0;a) \vert \geq \delta _j/3$
for all
$\vert F^j(0;a) \vert \geq \delta _j/3$
for all
 $a \in \omega _k^{rl}$
and
$a \in \omega _k^{rl}$
and
 $j = m_0,m_0+1,\ldots ,m_k^{rl}$
.
$j = m_0,m_0+1,\ldots ,m_k^{rl}$
.
Since our sequence
![]() $\delta _j$
is assumed to be admissible, we will frequently use the fact that
$\delta _j$
is assumed to be admissible, we will frequently use the fact that
![]() $\delta _j/3 \geq 1/(3j^{\overline {e}})$
.
$\delta _j/3 \geq 1/(3j^{\overline {e}})$
.
From equation (5), we know that every
![]() $a \in \omega ^{rl}_k$
is
$a \in \omega ^{rl}_k$
is
![]() $(\gamma ,C)$
-Collet–Eckmann up to time
$(\gamma ,C)$
-Collet–Eckmann up to time
![]() $m_0$
, and this condition is strong enough to ensure phase-parameter distortion (Lemma 3.2). We will continue to assume this condition at complete returns, but in between two complete returns, we will allow the exponent to drop slightly due to the loss of derivative when returning close to the critical point
$m_0$
, and this condition is strong enough to ensure phase-parameter distortion (Lemma 3.2). We will continue to assume this condition at complete returns, but in between two complete returns, we will allow the exponent to drop slightly due to the loss of derivative when returning close to the critical point
![]() $x = 0$
. We define the basic exponent conditions as follows.
$x = 0$
. We define the basic exponent conditions as follows.
-
(BE)(1)
 $\vert \partial _x F^{m_k^{rl}-1}(1;a) \vert \geq C e^{\gamma (m_k^{rl}-1)}$
for all
$\vert \partial _x F^{m_k^{rl}-1}(1;a) \vert \geq C e^{\gamma (m_k^{rl}-1)}$
for all
 $a \in \omega ^{rl}_k $
.
$a \in \omega ^{rl}_k $
. -
(BE)(2)
 $\vert \partial _x F^j(1;a) \vert \geq C e^{(\gamma /3) j}$
for all
$\vert \partial _x F^j(1;a) \vert \geq C e^{(\gamma /3) j}$
for all
 $a \in \omega ^{rl}_k$
and
$a \in \omega ^{rl}_k$
and
 $j = 0,1,\ldots ,m_k^{rl}-1$
.
$j = 0,1,\ldots ,m_k^{rl}-1$
.
Assuming (BA) and (BE)(1,2) for
![]() $a \in \omega _k^{rl} \subset \Delta _k$
, we will prove it for
$a \in \omega _k^{rl} \subset \Delta _k$
, we will prove it for
![]() $a' \in \omega _{k+1}^{r'l'} \subset \Delta _{k+1} \subset \Delta _k$
. Before considering the iteration of
$a' \in \omega _{k+1}^{r'l'} \subset \Delta _{k+1} \subset \Delta _k$
. Before considering the iteration of
![]() $\omega _k^{rl}$
, we define the bound period and the free period, and prove some useful lemmas connected to them. For technical reasons, these lemmas will be proved using the following weaker assumption on the derivative. Given a time
$\omega _k^{rl}$
, we define the bound period and the free period, and prove some useful lemmas connected to them. For technical reasons, these lemmas will be proved using the following weaker assumption on the derivative. Given a time
![]() $n \geq m^{rl}_k$
, we consider the following condition.
$n \geq m^{rl}_k$
, we consider the following condition.
-
(BE)(3)
 $\vert \partial _x F^j(1;a) \vert \geq C e^{(\gamma /9)j}$
for all
$\vert \partial _x F^j(1;a) \vert \geq C e^{(\gamma /9)j}$
for all
 $a \in \omega _k^{rl}$
and
$a \in \omega _k^{rl}$
and
 $j = 0,1,\ldots ,n-1$
.
$j = 0,1,\ldots ,n-1$
.
Notice that
![]() $\gamma /9> \gamma _T$
and hence we will be able to apply Lemma 3.2 at all times.
$\gamma /9> \gamma _T$
and hence we will be able to apply Lemma 3.2 at all times.
To rid ourselves of cumbersome notation, we drop the indices from this point on and write
![]() $\omega = \omega _k^{rl}$
and
$\omega = \omega _k^{rl}$
and
![]() $m = m_k^{rl}$
.
$m = m_k^{rl}$
.
4.5 The bound and free periods
Assuming we are in the situation of a return for which
![]() $\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1} \subset (-4\delta ,4\delta )$
, we are relatively close to the critical point, and therefore the next iterates
$\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1} \subset (-4\delta ,4\delta )$
, we are relatively close to the critical point, and therefore the next iterates
![]() $\xi _{n+j}(\omega )$
will closely resemble those of
$\xi _{n+j}(\omega )$
will closely resemble those of
![]() $\xi _j(\omega )$
. We quantify this and define the bound period associated to this return as the maximal p such that
$\xi _j(\omega )$
. We quantify this and define the bound period associated to this return as the maximal p such that
-
(BC)
 $\vert \xi _\nu (a) - F^\nu (\eta ;a) \vert \leq \vert \xi _\nu (a) \vert /(10\nu ^2)$
for
$\vert \xi _\nu (a) - F^\nu (\eta ;a) \vert \leq \vert \xi _\nu (a) \vert /(10\nu ^2)$
for
 $\nu = 1,2,\ldots ,p$
$\nu = 1,2,\ldots ,p$
holds for all
![]() $a \in \omega $
and all
$a \in \omega $
and all
![]() $\eta \in (0,e^{-\vert r-1\vert })$
. We refer to (BC) as the binding condition.
$\eta \in (0,e^{-\vert r-1\vert })$
. We refer to (BC) as the binding condition.
Remark 4.4. In the proof of Lemma 4.12, we will refer to pointwise binding, meaning that for a given parameter a, we associate a bound period
![]() $p = p(a)$
according to when (BC) breaks for this specific parameter. We notice that the conclusions of Lemmas 4.5 and 4.6 below are still true if we only consider iterations of one specific parameter.
$p = p(a)$
according to when (BC) breaks for this specific parameter. We notice that the conclusions of Lemmas 4.5 and 4.6 below are still true if we only consider iterations of one specific parameter.
The bound period is of central importance and we establish some results connected to it (compare with [Reference Benedicks and CarlesonBC85]). An important fact is that during this period, the derivatives are comparable in the following sense.
Lemma 4.5. (Bound distortion)
Let n be the index of a return for which
![]() $\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
, and let p be the bound period. Then, for all
$\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
, and let p be the bound period. Then, for all
![]() $a \in \omega $
and
$a \in \omega $
and
![]() $\eta \in (0,e^{-\vert r-1\vert })$
,
$\eta \in (0,e^{-\vert r-1\vert })$
,
 $$ \begin{align*} \frac{1}{2} \leq \bigg\vert \frac{\partial_x F^j(1-a\eta^2;a)}{\partial_xF^j(1;a)} \bigg\vert \leq 2 \quad (j = 1,2,\ldots,p). \end{align*} $$
$$ \begin{align*} \frac{1}{2} \leq \bigg\vert \frac{\partial_x F^j(1-a\eta^2;a)}{\partial_xF^j(1;a)} \bigg\vert \leq 2 \quad (j = 1,2,\ldots,p). \end{align*} $$
Proof. It is enough to prove that
 $$ \begin{align} \bigg \vert \frac{\partial_x F^j(1-a\eta^2;a)}{\partial_x F^j(1;a)} - 1 \bigg\vert \leq \frac{1}{2}. \end{align} $$
$$ \begin{align} \bigg \vert \frac{\partial_x F^j(1-a\eta^2;a)}{\partial_x F^j(1;a)} - 1 \bigg\vert \leq \frac{1}{2}. \end{align} $$
The quotient can be expressed as
 $$ \begin{align*} \frac{\partial_x F^j(1-a\eta^2;a)}{\partial_x F^j(1;a)} = \prod_{\nu=1}^j \bigg( \frac{F^\nu(\eta;a) - \xi_\nu(a)}{\xi_\nu(a)} + 1\bigg), \end{align*} $$
$$ \begin{align*} \frac{\partial_x F^j(1-a\eta^2;a)}{\partial_x F^j(1;a)} = \prod_{\nu=1}^j \bigg( \frac{F^\nu(\eta;a) - \xi_\nu(a)}{\xi_\nu(a)} + 1\bigg), \end{align*} $$
and applying the elementary inequality
 $$ \begin{align*} \bigg\vert \prod_{\nu = 1}^j (u_n + 1) - 1\bigg\vert \leq \exp \bigg(\sum_{\nu=1}^j \vert u_n \vert \bigg) -1, \end{align*} $$
$$ \begin{align*} \bigg\vert \prod_{\nu = 1}^j (u_n + 1) - 1\bigg\vert \leq \exp \bigg(\sum_{\nu=1}^j \vert u_n \vert \bigg) -1, \end{align*} $$
valid for complex
![]() $u_n$
, equation (6) now follows since
$u_n$
, equation (6) now follows since
 $$ \begin{align*} \sum_{\nu = 1}^j \frac{\vert F^\nu(\eta;a) - \xi_\nu(a)\vert}{\vert \xi_\nu(a) \vert} \leq \frac{1}{10}\sum_{\nu=1}^j \frac{1}{\nu^2} \leq \log \frac{3}{2}.\\[-3.8pc] \end{align*} $$
$$ \begin{align*} \sum_{\nu = 1}^j \frac{\vert F^\nu(\eta;a) - \xi_\nu(a)\vert}{\vert \xi_\nu(a) \vert} \leq \frac{1}{10}\sum_{\nu=1}^j \frac{1}{\nu^2} \leq \log \frac{3}{2}.\\[-3.8pc] \end{align*} $$
The next result gives us an estimate of the length of the bound period. As will be seen, if (BA) and (BE)(3) are assumed up to time
![]() $n \geq m = m_k^{rl}$
, the bound period is never longer than n, and we are therefore allowed to use the induction assumptions during this period. In particular, in view of the above distortion result and (BE)(3), we inherit expansion along the critical orbit during the bound period; making sure
$n \geq m = m_k^{rl}$
, the bound period is never longer than n, and we are therefore allowed to use the induction assumptions during this period. In particular, in view of the above distortion result and (BE)(3), we inherit expansion along the critical orbit during the bound period; making sure
![]() $m_0$
is large enough, and using (BA) together with the assumption that
$m_0$
is large enough, and using (BA) together with the assumption that
![]() $(\delta _n)$
is admissible, we have
$(\delta _n)$
is admissible, we have
 $$ \begin{align} \vert \partial_x F^{n + j}(1;a) \vert &= 2a \vert \xi_n(a) \vert \vert \partial_x F^{n-1}(1;a) \vert \vert \partial_x F^j(1-a\xi_n(a)^2;a) \vert \nonumber \\ &\geq \frac{2}{3n^{\overline{e}}} C^2e^{(\gamma/9)(n+j-1)} \nonumber \\ &= \frac{2}{3}C^2 e^{-\gamma/9} \exp\bigg\{ \bigg(\frac{\gamma}{9} - \frac{\overline{e}\log n}{n+j}\bigg)(n+j)\bigg\} \nonumber \\ &\geq C_T e^{\gamma_T (n+j)} \quad (j = 0,1,\ldots,p). \end{align} $$
$$ \begin{align} \vert \partial_x F^{n + j}(1;a) \vert &= 2a \vert \xi_n(a) \vert \vert \partial_x F^{n-1}(1;a) \vert \vert \partial_x F^j(1-a\xi_n(a)^2;a) \vert \nonumber \\ &\geq \frac{2}{3n^{\overline{e}}} C^2e^{(\gamma/9)(n+j-1)} \nonumber \\ &= \frac{2}{3}C^2 e^{-\gamma/9} \exp\bigg\{ \bigg(\frac{\gamma}{9} - \frac{\overline{e}\log n}{n+j}\bigg)(n+j)\bigg\} \nonumber \\ &\geq C_T e^{\gamma_T (n+j)} \quad (j = 0,1,\ldots,p). \end{align} $$
This above estimate is an a priori one, and will allow us to use Lemma 3.2 in the proof of Lemma 4.10.
Lemma 4.6. (Bound length)
Let n be the index of a return such that
![]() $\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
, and suppose that (BA) and (BE)(3) are satisfied up to time n. Then there exists a constant
$\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
, and suppose that (BA) and (BE)(3) are satisfied up to time n. Then there exists a constant
![]() $\kappa _1> 0$
such that the corresponding bound period satisfies
$\kappa _1> 0$
such that the corresponding bound period satisfies
Proof. By the mean value theorem and Lemma 4.5, we have that
 $$ \begin{align} \vert \xi_j(a) - F^j(\eta;a) \vert &= \vert F^{j - 1}(1;a) - F^{j-1}(1-a\eta^2;a) \vert \nonumber \\ &= a\eta^2 \vert \partial_x F^{j-1}(1-a\eta^{\prime2};a)\vert \\ &\geq \frac{a\eta^2}{2} \vert \partial_x F^{j-1}(1;a) \vert, \nonumber \end{align} $$
$$ \begin{align} \vert \xi_j(a) - F^j(\eta;a) \vert &= \vert F^{j - 1}(1;a) - F^{j-1}(1-a\eta^2;a) \vert \nonumber \\ &= a\eta^2 \vert \partial_x F^{j-1}(1-a\eta^{\prime2};a)\vert \\ &\geq \frac{a\eta^2}{2} \vert \partial_x F^{j-1}(1;a) \vert, \nonumber \end{align} $$
as long as
![]() $j \leq p$
. (Here,
$j \leq p$
. (Here,
![]() $0 < \eta ' < \eta $
.) Furthermore, as long as we also have
$0 < \eta ' < \eta $
.) Furthermore, as long as we also have
![]() $j \leq (\log n)^2$
, say, we can use the induction assumptions: using (BE)(3), we find that
$j \leq (\log n)^2$
, say, we can use the induction assumptions: using (BE)(3), we find that
 $$ \begin{align*} \frac{1}{2} e^{-2(r+1)} C e^{(\gamma/9)(j-1)} \leq \frac{a\eta^2}{2} \vert \partial_x F^{j-1}(1;a)\vert \leq \frac{\vert \xi_j(a)\vert}{10j^2} \leq 1. \end{align*} $$
$$ \begin{align*} \frac{1}{2} e^{-2(r+1)} C e^{(\gamma/9)(j-1)} \leq \frac{a\eta^2}{2} \vert \partial_x F^{j-1}(1;a)\vert \leq \frac{\vert \xi_j(a)\vert}{10j^2} \leq 1. \end{align*} $$
Taking the logarithm, using (BA), and making sure that
![]() $m_0$
is large enough, we therefore have
$m_0$
is large enough, we therefore have
as long as
![]() $j \leq p$
and
$j \leq p$
and
![]() $j \leq (\log n)^2$
. This tells us that
$j \leq (\log n)^2$
. This tells us that
![]() $j \leq p$
must break before
$j \leq p$
must break before
![]() $j \leq (\log n)^2$
; in particular, there is a constant
$j \leq (\log n)^2$
; in particular, there is a constant
![]() $\kappa _1> 0$
such that
$\kappa _1> 0$
such that
![]() $p \leq \kappa _1 r$
.
$p \leq \kappa _1 r$
.
For the lower bound, consider
![]() $j = p+1$
and the equality in equation (9). With
$j = p+1$
and the equality in equation (9). With
![]() $a \in \omega $
being the parameter for which the inequality in the binding condition is reversed, using Lemma 4.5, we find that
$a \in \omega $
being the parameter for which the inequality in the binding condition is reversed, using Lemma 4.5, we find that
Using the upper bound for p, we know that (BA) (or (PR)) is valid at time
![]() $p+1$
, and hence
$p+1$
, and hence
where
![]() $\hat {e} = \max (\overline {e},\sigma )$
. Therefore,
$\hat {e} = \max (\overline {e},\sigma )$
. Therefore,
 $$ \begin{align*} \frac{1}{30(p+1)^{2 + \hat{e}}} \leq 4 e^{-2r}4^p, \end{align*} $$
$$ \begin{align*} \frac{1}{30(p+1)^{2 + \hat{e}}} \leq 4 e^{-2r}4^p, \end{align*} $$
and taking the logarithm proves the lower bound.
Remark 4.7. Notice that the lower bound is true without assuming the upper bound (which in our proof requires (BE)(3) at time n) as long as we assume (BA) to hold at time
![]() $p+1$
.
$p+1$
.
The next result will concern the growth of
![]() $\xi _n(\omega )$
during the bound period.
$\xi _n(\omega )$
during the bound period.
Lemma 4.8. (Bound growth)
Let n be the index of a return such that
![]() $\xi _n(\omega ) \subset I$
with
$\xi _n(\omega ) \subset I$
with
![]() $I_{rl} \subset I \subset I_{r+1} \cup I_r \cup I_{r-1}$
, and suppose that (BA) and (BE)(3) are satisfied up to time n. Then there exists a constant
$I_{rl} \subset I \subset I_{r+1} \cup I_r \cup I_{r-1}$
, and suppose that (BA) and (BE)(3) are satisfied up to time n. Then there exists a constant
![]() $\kappa _2> 0$
such that
$\kappa _2> 0$
such that
Proof. Denote
![]() $\Omega = \xi _{n+p+1}(\omega ) $
and notice that for any two given parameters
$\Omega = \xi _{n+p+1}(\omega ) $
and notice that for any two given parameters
![]() $a,b \in \omega $
, we have
$a,b \in \omega $
, we have
 $$ \begin{align} \vert \Omega \vert &\geq \vert F^{n + p + 1}(0;a) - F^{n + p + 1}(0;b) \vert \nonumber \\ &= \vert F^{p + 1}(\xi_{n}(a);a) - F^{p + 1}(\xi_{n}(b);b) \vert \nonumber \\ &\geq \vert F^{p+1}(\xi_{n}(a);a) - F^{p+1}(\xi_{n}(b);a) \vert \nonumber \\ &\quad - \vert F^{p+1}(\xi_{n}(b);a) - F^{p+1}(\xi_{n}(b);b)\vert. \end{align} $$
$$ \begin{align} \vert \Omega \vert &\geq \vert F^{n + p + 1}(0;a) - F^{n + p + 1}(0;b) \vert \nonumber \\ &= \vert F^{p + 1}(\xi_{n}(a);a) - F^{p + 1}(\xi_{n}(b);b) \vert \nonumber \\ &\geq \vert F^{p+1}(\xi_{n}(a);a) - F^{p+1}(\xi_{n}(b);a) \vert \nonumber \\ &\quad - \vert F^{p+1}(\xi_{n}(b);a) - F^{p+1}(\xi_{n}(b);b)\vert. \end{align} $$
Due to the exponential increase of the phase derivative along the critical orbit, the dependence on the parameters is inessential in the following sense:
To realize this, first notice that we have the following (somewhat crude) estimate for the parameter derivative:
Indeed,
![]() $\vert \partial _a F(x;a) \vert \leq 1 < 5$
, and by induction,
$\vert \partial _a F(x;a) \vert \leq 1 < 5$
, and by induction,
 $$ \begin{align*} \vert \partial_a F^{j+1}(x;a)\vert &= \vert \partial_a (1-aF^j(x;a)^2) \vert \\ &= \vert -F^j(x;a)^2 - 2aF^j(x;a)\partial_a F^j(x;a) \vert \\ &\leq 1 + 4\cdot5^j \\ &\leq 5^{j+1}. \end{align*} $$
$$ \begin{align*} \vert \partial_a F^{j+1}(x;a)\vert &= \vert \partial_a (1-aF^j(x;a)^2) \vert \\ &= \vert -F^j(x;a)^2 - 2aF^j(x;a)\partial_a F^j(x;a) \vert \\ &\leq 1 + 4\cdot5^j \\ &\leq 5^{j+1}. \end{align*} $$
Using the mean value theorem twice, Lemma 3.2, and (BE)(3), we find that
In view of equation (8) and (BA), making
![]() $m_0$
larger if needed, the inequality in equation (11) can be achieved.
$m_0$
larger if needed, the inequality in equation (11) can be achieved.
Assume now that at time
![]() $p+1$
, (BC) is broken for parameter a, and let b be an endpoint of
$p+1$
, (BC) is broken for parameter a, and let b be an endpoint of
![]() $\omega $
such that
$\omega $
such that
Continuing the estimate of
![]() $\vert \Omega \vert $
, using equation (11), we find that
$\vert \Omega \vert $
, using equation (11), we find that
 $$ \begin{align} \vert \Omega \vert &\geq \vert F^{p}(1-a\xi_{n}(a)^2;a) - F^{p}(1-a\xi_{n}(b)^2;a)\vert \nonumber \\ &\quad - \vert F^{p+1}(\xi_{n}(b);a) - F^{p+1}(\xi_{n}(b);b)\vert \nonumber \\ &\geq (a \vert \xi_{n}(a) + \xi_{n}(b)\vert \vert \partial_x F^{p}(1-a\xi_{n}(a')^2;a)\vert - 2e^{-(\gamma /18)n}) \frac{\vert \xi_n(\omega) \vert}{2} \nonumber \\ &\geq (2ae^{-r}\vert \partial_xF^{p}(1-a\xi_{n}(a')^2;a) \vert - 2e^{-(\gamma /18)n} ) \frac{\vert \xi_n(\omega)\vert}{2}. \end{align} $$
$$ \begin{align} \vert \Omega \vert &\geq \vert F^{p}(1-a\xi_{n}(a)^2;a) - F^{p}(1-a\xi_{n}(b)^2;a)\vert \nonumber \\ &\quad - \vert F^{p+1}(\xi_{n}(b);a) - F^{p+1}(\xi_{n}(b);b)\vert \nonumber \\ &\geq (a \vert \xi_{n}(a) + \xi_{n}(b)\vert \vert \partial_x F^{p}(1-a\xi_{n}(a')^2;a)\vert - 2e^{-(\gamma /18)n}) \frac{\vert \xi_n(\omega) \vert}{2} \nonumber \\ &\geq (2ae^{-r}\vert \partial_xF^{p}(1-a\xi_{n}(a')^2;a) \vert - 2e^{-(\gamma /18)n} ) \frac{\vert \xi_n(\omega)\vert}{2}. \end{align} $$
Using Lemma 4.5 twice and the equality in equation (9) (with
![]() $p+1$
instead of p) together with (BC) (now reversed inequality), we continue the estimate in equation (12) to find that
$p+1$
instead of p) together with (BC) (now reversed inequality), we continue the estimate in equation (12) to find that
 $$ \begin{align} \vert \Omega \vert &\geq \bigg( 2ae^{-r}\frac{1}{4 a\eta^2}\frac{\vert \xi_{p+1} (a) \vert}{10(p+1)^2} - 2e^{-(\gamma/18)n} \bigg) \frac{\vert \xi_n(\omega)\vert}{2} \nonumber \\ &\geq \bigg( e^r \frac{\vert \xi_{p+1}(a) \vert}{20 (p+1)^2} - 2e^{-(\gamma/18)n} \bigg) \frac{\vert \xi_n(\omega)\vert}{2}. \end{align} $$
$$ \begin{align} \vert \Omega \vert &\geq \bigg( 2ae^{-r}\frac{1}{4 a\eta^2}\frac{\vert \xi_{p+1} (a) \vert}{10(p+1)^2} - 2e^{-(\gamma/18)n} \bigg) \frac{\vert \xi_n(\omega)\vert}{2} \nonumber \\ &\geq \bigg( e^r \frac{\vert \xi_{p+1}(a) \vert}{20 (p+1)^2} - 2e^{-(\gamma/18)n} \bigg) \frac{\vert \xi_n(\omega)\vert}{2}. \end{align} $$
In either case of
![]() $p \leq m_0$
or
$p \leq m_0$
or
![]() $p> m_0$
, we have that (using (BA), (PR), and the assumption that our recurrence rate is admissible)
$p> m_0$
, we have that (using (BA), (PR), and the assumption that our recurrence rate is admissible)
where
![]() $\hat {e} = \max (\overline {e},\sigma )$
. We can make sure that the second term in the parenthesis in equation (13) is always less than a fraction, say
$\hat {e} = \max (\overline {e},\sigma )$
. We can make sure that the second term in the parenthesis in equation (13) is always less than a fraction, say
![]() $1/2$
, of the first term and therefore, using (BC), equation (8), and that
$1/2$
, of the first term and therefore, using (BC), equation (8), and that
![]() $e^r \geq 1/(2r^2 \vert I \vert )$
, we finish the estimate as follows:
$e^r \geq 1/(2r^2 \vert I \vert )$
, we finish the estimate as follows:
 $$ \begin{align} \vert \Omega \vert &\geq \frac{K}{240}\frac{1}{(p+1)^{2+\hat{e}}} \vert \xi_n(\omega)\vert e^r \nonumber \\ &\geq \frac{K}{480}\frac{1}{r^2 (p+1)^{2 + \hat{e}}} \frac{\vert \xi_n(\omega) \vert}{\vert I \vert}\nonumber \\ &\geq \frac{K}{480 (2\kappa_1)^{2+\hat{e}}}\frac{1}{r^{4+\hat{e}}} \frac{\vert \xi_n(\omega) \vert}{\vert I \vert} \nonumber \\ &\geq \frac{1}{r^{\kappa_2}} \frac{\vert \xi_n(\omega) \vert}{\vert I \vert}, \end{align} $$
$$ \begin{align} \vert \Omega \vert &\geq \frac{K}{240}\frac{1}{(p+1)^{2+\hat{e}}} \vert \xi_n(\omega)\vert e^r \nonumber \\ &\geq \frac{K}{480}\frac{1}{r^2 (p+1)^{2 + \hat{e}}} \frac{\vert \xi_n(\omega) \vert}{\vert I \vert}\nonumber \\ &\geq \frac{K}{480 (2\kappa_1)^{2+\hat{e}}}\frac{1}{r^{4+\hat{e}}} \frac{\vert \xi_n(\omega) \vert}{\vert I \vert} \nonumber \\ &\geq \frac{1}{r^{\kappa_2}} \frac{\vert \xi_n(\omega) \vert}{\vert I \vert}, \end{align} $$
where we can choose
![]() $\kappa _2 = 5 + \hat {e}$
as long as
$\kappa _2 = 5 + \hat {e}$
as long as
![]() $\delta $
is sufficiently small.
$\delta $
is sufficiently small.
Remark 4.9. Using the lower bound for p, the upper bound
can be proved similarly.
This finishes the analysis of the bound period, and we continue with describing the free period. A free period will always follow a bound period, and during this period, we will be iterating outside
![]() $(-\delta ,\delta )$
. We let L denote the length of this period, that is, L is the smallest integer for which
$(-\delta ,\delta )$
. We let L denote the length of this period, that is, L is the smallest integer for which
The following lemma gives an upper bound for the length of the free period, following the bound period of a complete return or an essential return.
Lemma 4.10. (Free length)
Let
![]() $\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
with n being the index of a complete return or an essential return, and suppose that (BA) and (BE)(3) are satisfied up to time n. Let p be the associated bound period and let L be the free period. Then there exists a constant
$\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
with n being the index of a complete return or an essential return, and suppose that (BA) and (BE)(3) are satisfied up to time n. Let p be the associated bound period and let L be the free period. Then there exists a constant
![]() $\kappa _3> 0$
such that
$\kappa _3> 0$
such that
Proof. Assuming
![]() $j \leq L$
and
$j \leq L$
and
![]() $j \leq (\log n)^2$
, similar calculations as in the proof of Lemma 4.8 gives us parameter independence (see equation (11) and notice that from equation (7), we are allowed to apply Lemma 3.2); using Lemmas 4.8 and 3.1, we find that
$j \leq (\log n)^2$
, similar calculations as in the proof of Lemma 4.8 gives us parameter independence (see equation (11) and notice that from equation (7), we are allowed to apply Lemma 3.2); using Lemmas 4.8 and 3.1, we find that
Taking the logarithm, using (BA), and making sure that
![]() $m_0$
is large enough, we therefore have
$m_0$
is large enough, we therefore have
as long as
![]() $j \leq L$
and
$j \leq L$
and
![]() $j \leq (\log n)^2$
. This tells us that
$j \leq (\log n)^2$
. This tells us that
![]() $j \leq L$
must break before
$j \leq L$
must break before
![]() $j \leq (\log n)^2$
; in particular, there is a constant
$j \leq (\log n)^2$
; in particular, there is a constant
![]() $\kappa _3> 0$
such that
$\kappa _3> 0$
such that
![]() $L \leq \kappa _3 r$
.
$L \leq \kappa _3 r$
.
Remark 4.11. If the return
![]() $\xi _{n+p+L}(\omega )$
is inessential or essential, then there is no
$\xi _{n+p+L}(\omega )$
is inessential or essential, then there is no
![]() $\delta $
-dependence in the growth factor; more generally, if the prerequisites of Lemma 4.8 are satisfied, then
$\delta $
-dependence in the growth factor; more generally, if the prerequisites of Lemma 4.8 are satisfied, then
Before considering iterations of
![]() $\omega = \omega _k^{rl} \subset \Delta _k$
from
$\omega = \omega _k^{rl} \subset \Delta _k$
from
![]() $m = m_k^{rl}$
to
$m = m_k^{rl}$
to
![]() $m_{k+1}^{rl}$
, we make the following observation that as long as (BA) is assumed in a time window
$m_{k+1}^{rl}$
, we make the following observation that as long as (BA) is assumed in a time window
![]() $[n,2n]$
, the derivative will not drop too much.
$[n,2n]$
, the derivative will not drop too much.
Lemma 4.12. Suppose that a is a parameter such that
with
![]() $\gamma ' \geq \gamma /3$
. Then, if (BA) is satisfied up to time
$\gamma ' \geq \gamma /3$
. Then, if (BA) is satisfied up to time
![]() $2n$
, we have
$2n$
, we have
In other words, if (BA) and (BE)(1) [(BE)(2)] are satisfied up to time n, then (BE)(2) [(BE)(3)] is satisfied up to time
![]() $2n$
, as long as (BA) is.
$2n$
, as long as (BA) is.
Proof. The proof is based on the fact that we trivially have no loss of derivative during the bound and free periods. Indeed, suppose
![]() $\xi _{n'}(a) \sim e^{-r}$
, with
$\xi _{n'}(a) \sim e^{-r}$
, with
![]() $n' \geq n$
, and let p be the bound period (here we use pointwise binding, see Remark 4.4) and L the free period. Moreover, we assume that
$n' \geq n$
, and let p be the bound period (here we use pointwise binding, see Remark 4.4) and L the free period. Moreover, we assume that
![]() $n' + p + L < 2n$
; in particular, this implies
$n' + p + L < 2n$
; in particular, this implies
![]() $p < n$
and we can use equation (15) during this period. Introducing
$p < n$
and we can use equation (15) during this period. Introducing
![]() $D_p = \vert \partial _x F^p(1;a) \vert $
and using similar calculations as in Lemma 4.8 (e.g. the equality in equation (9) and reversed inequality in (BC)), we find that
$D_p = \vert \partial _x F^p(1;a) \vert $
and using similar calculations as in Lemma 4.8 (e.g. the equality in equation (9) and reversed inequality in (BC)), we find that
where we used (BA) (or (PR)). Since
![]() $p < n$
, we are free to use equation (15) and therefore, the above inequalities yield
$p < n$
, we are free to use equation (15) and therefore, the above inequalities yield
 $$ \begin{align*} e^{-r} D_p \gtrsim D_p^{1/2} \frac{1}{\sqrt{(p+1)^{2 + \hat{e}}}} \gtrsim \frac{e^{(\gamma'/2)p}}{\sqrt{(p+1)^{2 + \hat{e}}}} \geq C_M^{-1}, \end{align*} $$
$$ \begin{align*} e^{-r} D_p \gtrsim D_p^{1/2} \frac{1}{\sqrt{(p+1)^{2 + \hat{e}}}} \gtrsim \frac{e^{(\gamma'/2)p}}{\sqrt{(p+1)^{2 + \hat{e}}}} \geq C_M^{-1}, \end{align*} $$
provided
![]() $\delta $
is small enough. Here, in the last inequality, we used the lower bound in equation (8) (see Remark 4.7). Assuming
$\delta $
is small enough. Here, in the last inequality, we used the lower bound in equation (8) (see Remark 4.7). Assuming
![]() $\xi _{n'+p+L}(a)$
is a return (and that
$\xi _{n'+p+L}(a)$
is a return (and that
![]() $n'+p+ L < 2n$
), we therefore have
$n'+p+ L < 2n$
), we therefore have
 $$ \begin{align*} \vert \partial_x F^{p+L}(\xi_{n'}(a);a) \vert &\geq 2a\vert \xi_{n'}(a) \vert \vert \partial_x F^p(1-a\xi_{n'}(a)^2;a) \vert \vert \partial_x F^{L-1}(\xi_{n'+p+1}(a);a)\vert \\ &\gtrsim e^{-r} D_p C_M e^{\gamma_M(L-1)} \\ &\geq 1. \end{align*} $$
$$ \begin{align*} \vert \partial_x F^{p+L}(\xi_{n'}(a);a) \vert &\geq 2a\vert \xi_{n'}(a) \vert \vert \partial_x F^p(1-a\xi_{n'}(a)^2;a) \vert \vert \partial_x F^{L-1}(\xi_{n'+p+1}(a);a)\vert \\ &\gtrsim e^{-r} D_p C_M e^{\gamma_M(L-1)} \\ &\geq 1. \end{align*} $$
We conclude that the combination of a return, a bound period, and a free period does not decrease the derivative.
Let us now follow a parameter a satisfying equation (15) and (BA) up to time
![]() $2n$
. If the iterates
$2n$
. If the iterates
![]() $\xi _{n+j}(a)$
are always outside
$\xi _{n+j}(a)$
are always outside
![]() $(-\delta ,\delta )$
, then
$(-\delta ,\delta )$
, then
 $$ \begin{align*} \vert \partial_x F^{n+j}(1;a) \vert &= \vert \partial_x F^{n-1}(1;a) \vert \vert \partial_x F^{j+1}(\xi_n(a);a) \vert \\ &\geq Ce^{\gamma'(n-1)} \delta C_M e^{\gamma_M(j+1)} \\ &\geq Ce^{(\gamma'/3)(n+j)} \delta C_M e^{(2\gamma'/3)(n+j)} \\ &\geq Ce^{(\gamma'/3)(n+j)} \quad (j = 0,1,\ldots,n-1), \end{align*} $$
$$ \begin{align*} \vert \partial_x F^{n+j}(1;a) \vert &= \vert \partial_x F^{n-1}(1;a) \vert \vert \partial_x F^{j+1}(\xi_n(a);a) \vert \\ &\geq Ce^{\gamma'(n-1)} \delta C_M e^{\gamma_M(j+1)} \\ &\geq Ce^{(\gamma'/3)(n+j)} \delta C_M e^{(2\gamma'/3)(n+j)} \\ &\geq Ce^{(\gamma'/3)(n+j)} \quad (j = 0,1,\ldots,n-1), \end{align*} $$
provided
![]() $m_0$
is big enough.
$m_0$
is big enough.
Otherwise, the worst case is if we have a short free period followed by a return, a bound period, a free period, and so on, and which ends with a return together with a short bound period. In this case, using the above argument, the estimate is as follows:
 $$ \begin{align*} \vert \partial_x F^{n+j}(1;a) \vert &\geq \vert \partial_x F^{n-1}(1;a) \vert \cdot C_M \cdot 1 \cdot 1 \cdots 1 \cdot 2a\vert \xi_{n+j}(a) \vert \cdot C \\ &\geq Ce^{\gamma'(n-1)} C_M C 2a \frac{\delta_{n+j}}{3} \\ &\geq Ce^{(\gamma'/3)(n+j)} C_M C \frac{2}{3a} e^{(\gamma'/3)n - \overline{e}\log(2n)} \\ &\geq Ce^{(\gamma'/3)(n+j)} \quad (j = 0,1,\ldots,n-1), \end{align*} $$
$$ \begin{align*} \vert \partial_x F^{n+j}(1;a) \vert &\geq \vert \partial_x F^{n-1}(1;a) \vert \cdot C_M \cdot 1 \cdot 1 \cdots 1 \cdot 2a\vert \xi_{n+j}(a) \vert \cdot C \\ &\geq Ce^{\gamma'(n-1)} C_M C 2a \frac{\delta_{n+j}}{3} \\ &\geq Ce^{(\gamma'/3)(n+j)} C_M C \frac{2}{3a} e^{(\gamma'/3)n - \overline{e}\log(2n)} \\ &\geq Ce^{(\gamma'/3)(n+j)} \quad (j = 0,1,\ldots,n-1), \end{align*} $$
provided
![]() $m_0$
is big enough. This proves the lemma.
$m_0$
is big enough. This proves the lemma.
4.6 From the
 $k\text {th}$
complete return to the first inessential return
$k\text {th}$
complete return to the first inessential return
If
![]() $\omega \subset T_k$
, then we have already reached an escape situation and proceed accordingly as is described below in the section about escape. We therefore assume
$\omega \subset T_k$
, then we have already reached an escape situation and proceed accordingly as is described below in the section about escape. We therefore assume
![]() $\omega \subset N_k$
and
$\omega \subset N_k$
and
![]() $\xi _m(\omega ) = I_{r_0l} \subset (-4\delta ,4\delta )$
.
$\xi _m(\omega ) = I_{r_0l} \subset (-4\delta ,4\delta )$
.
If it happens that for some
![]() $j \leq p$
,
$j \leq p$
,
then we stop and consider this return complete. If not, we notice that
![]() $\xi _{m+p}(\omega )$
can not be a return, unless it is escape or complete; indeed, we would otherwise have
$\xi _{m+p}(\omega )$
can not be a return, unless it is escape or complete; indeed, we would otherwise have
![]() $\vert \xi _{m+p+1}(\omega ) \vert < \vert \xi _{m+p}(\omega )\vert $
, due to the fact that we return close to the critical point, and thus contradict the definition of the bound period. We therefore assume that
$\vert \xi _{m+p+1}(\omega ) \vert < \vert \xi _{m+p}(\omega )\vert $
, due to the fact that we return close to the critical point, and thus contradict the definition of the bound period. We therefore assume that
![]() $\xi _{m+p}(\omega )$
does not intersect
$\xi _{m+p}(\omega )$
does not intersect
![]() $(-\delta ,\delta )$
.
$(-\delta ,\delta )$
.
Up until the next return, we will therefore experience an orbit outside of
![]() $(-\delta ,\delta )$
, that is, we will be in a free period. After the free period, our return is either inessential, essential, escape, or complete. In the next section, we consider the situation of an inessential return.
$(-\delta ,\delta )$
, that is, we will be in a free period. After the free period, our return is either inessential, essential, escape, or complete. In the next section, we consider the situation of an inessential return.
4.7 From the first inessential return to the first essential return
Let
![]() $i_1 = m + p_0 + L_0$
denote the index of the first inessential return to
$i_1 = m + p_0 + L_0$
denote the index of the first inessential return to
![]() $(-\delta ,\delta )$
. We will keep iterating
$(-\delta ,\delta )$
. We will keep iterating
![]() $\xi _{i_1}(\omega )$
until we once again return. If this next return is again inessential, we denote its index by
$\xi _{i_1}(\omega )$
until we once again return. If this next return is again inessential, we denote its index by
![]() $i_2 = i_1 + p_1 + L_1$
, where
$i_2 = i_1 + p_1 + L_1$
, where
![]() $p_1$
and
$p_1$
and
![]() $L_1$
are the associated bound period and free period, respectively. Continuing like this, let
$L_1$
are the associated bound period and free period, respectively. Continuing like this, let
![]() $i_j$
be the index of the
$i_j$
be the index of the
![]() $j\text {th}$
inessential return.
$j\text {th}$
inessential return.
The following lemma gives an upper bound for the total time spent doing inessential returns (compare with Lemma 2.3 in [Reference Benedicks and CarlesonBC91]).
Lemma 4.13. (Inessential length)
Let
![]() $\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
with n being the index of a complete return or an essential return, and suppose that (BA) and (BE)(2) are satisfied up to time n. Then there exists a constant
$\xi _n(\omega ) \subset I_{r+1} \cup I_r \cup I_{r-1}$
with n being the index of a complete return or an essential return, and suppose that (BA) and (BE)(2) are satisfied up to time n. Then there exists a constant
![]() $\kappa _4> 0$
such that the total time o spent doing inessential returns satisfies
$\kappa _4> 0$
such that the total time o spent doing inessential returns satisfies
Proof. Let
![]() $i_1 = n + p + L$
be the index of the first inessential return, that is,
$i_1 = n + p + L$
be the index of the first inessential return, that is,
![]() $\xi _{i_1}(\omega ) \subset I_{r_1}$
, with
$\xi _{i_1}(\omega ) \subset I_{r_1}$
, with
![]() $I_{r_1}$
being the host interval. From Lemmas 4.6 and 4.10, together with (BA), we have that
$I_{r_1}$
being the host interval. From Lemmas 4.6 and 4.10, together with (BA), we have that
provided
![]() $m_0$
is large enough. We can therefore apply Lemma 4.12 and conclude that (BE)(3) is satisfied at time
$m_0$
is large enough. We can therefore apply Lemma 4.12 and conclude that (BE)(3) is satisfied at time
![]() $i_1$
. To this first inessential return, we associate a bound period of length
$i_1$
. To this first inessential return, we associate a bound period of length
![]() $p_1$
(satisfying
$p_1$
(satisfying
![]() $p_1 \leq \kappa _1 r_1$
due to the fact that (BE)(3) is satisfied at time
$p_1 \leq \kappa _1 r_1$
due to the fact that (BE)(3) is satisfied at time
![]() $i_1$
) and a free period of length
$i_1$
) and a free period of length
![]() $L_1$
. We let
$L_1$
. We let
![]() $i_2 = i_1 + p_1 + L_1$
denote the index of the second inessential return. Continuing like this, we denote by
$i_2 = i_1 + p_1 + L_1$
denote the index of the second inessential return. Continuing like this, we denote by
![]() $i_j = i_{j-1} + p_{j-1} + L_{j-1}$
the index of the
$i_j = i_{j-1} + p_{j-1} + L_{j-1}$
the index of the
![]() $j\text {th}$
inessential return. With
$j\text {th}$
inessential return. With
![]() $o_j$
denoting the total time spent doing inessential returns up to time
$o_j$
denoting the total time spent doing inessential returns up to time
![]() $i_j$
, we have that
$i_j$
, we have that
![]() $o_j = i_{j} - i_1 = \sum _{k = 1}^{j-1} (p_k + L_k)$
. Suppose that the return with index
$o_j = i_{j} - i_1 = \sum _{k = 1}^{j-1} (p_k + L_k)$
. Suppose that the return with index
![]() $i_s$
is the first that is not inessential. We estimate
$i_s$
is the first that is not inessential. We estimate
![]() $o = o_s$
as follows. Suppose that
$o = o_s$
as follows. Suppose that
![]() $o_j$
is as above and that
$o_j$
is as above and that
![]() $p_k \leq \kappa _1 r_k$
for
$p_k \leq \kappa _1 r_k$
for
![]() $k = 1,2,\ldots ,j-1$
. Using Remark 4.11, we find that
$k = 1,2,\ldots ,j-1$
. Using Remark 4.11, we find that
 $$ \begin{align} \frac{\vert \xi_{i_{k+1}}(\omega)\vert}{\vert \xi_{i_k}(\omega)\vert} \geq \frac{C_M e^{\gamma_M (L_k-1)}}{2 r_k^{\kappa_2}\vert I_{r_k}\vert} \geq \frac{C_M}{2} \frac{e^{\gamma_M (L_k-1) + r_k}}{r_k^{\kappa_2}}, \end{align} $$
$$ \begin{align} \frac{\vert \xi_{i_{k+1}}(\omega)\vert}{\vert \xi_{i_k}(\omega)\vert} \geq \frac{C_M e^{\gamma_M (L_k-1)}}{2 r_k^{\kappa_2}\vert I_{r_k}\vert} \geq \frac{C_M}{2} \frac{e^{\gamma_M (L_k-1) + r_k}}{r_k^{\kappa_2}}, \end{align} $$
and therefore,
 $$ \begin{align} 2 \geq \vert \xi_{i_j}(\omega) \vert = \vert \xi_{i_1}(\omega)\vert \prod_{k=1}^{j-1} \frac{\vert \xi_{i_{k+1}}(\omega)\vert}{\vert \xi_{i_k}(\omega) \vert} \geq \frac{\delta C_Me^{\gamma_M}}{2 r^{\kappa_2}} \prod_{k=1}^{j-1} \frac{C_M}{2} \frac{e^{\gamma_M (L_k-1) + r_k}}{r_k^{\kappa_2}}. \end{align} $$
$$ \begin{align} 2 \geq \vert \xi_{i_j}(\omega) \vert = \vert \xi_{i_1}(\omega)\vert \prod_{k=1}^{j-1} \frac{\vert \xi_{i_{k+1}}(\omega)\vert}{\vert \xi_{i_k}(\omega) \vert} \geq \frac{\delta C_Me^{\gamma_M}}{2 r^{\kappa_2}} \prod_{k=1}^{j-1} \frac{C_M}{2} \frac{e^{\gamma_M (L_k-1) + r_k}}{r_k^{\kappa_2}}. \end{align} $$
Here, the
![]() $\delta $
is added to make sure that the estimate also holds for the last free orbit, when the return can be escape or complete. This gives us a rather poor estimate, but since
$\delta $
is added to make sure that the estimate also holds for the last free orbit, when the return can be escape or complete. This gives us a rather poor estimate, but since
![]() $p \lesssim r$
, it is good enough.
$p \lesssim r$
, it is good enough.
Taking the logarithm of equation (17), we find that
 $$ \begin{align*} \sum_{k=1}^{j-1} (\log C_M - \log 2 + \gamma_M (L_k-1) + r_k - \kappa_2 \log r_k ) \leq \kappa_2 \log r + \Delta + \operatorname{const.} \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{j-1} (\log C_M - \log 2 + \gamma_M (L_k-1) + r_k - \kappa_2 \log r_k ) \leq \kappa_2 \log r + \Delta + \operatorname{const.} \end{align*} $$
Provided
![]() $\delta $
is small enough, we have
$\delta $
is small enough, we have
![]() $r_k \geq 4\kappa _2 \log r_k$
and
$r_k \geq 4\kappa _2 \log r_k$
and
![]() $r_k \geq -\log \delta> -2(\log C_M + \gamma _M + \log 2)$
. Therefore, using
$r_k \geq -\log \delta> -2(\log C_M + \gamma _M + \log 2)$
. Therefore, using
![]() $p_k \leq \kappa _1 r_k$
, we find that
$p_k \leq \kappa _1 r_k$
, we find that
 $$ \begin{align*} o_j = i_j - i_1 = \sum_{k=1}^{j-1}( p_k + L_k ) \leq \kappa_4 r, \end{align*} $$
$$ \begin{align*} o_j = i_j - i_1 = \sum_{k=1}^{j-1}( p_k + L_k ) \leq \kappa_4 r, \end{align*} $$
with
![]() $\kappa _4$
being an absolute constant. In particular,
$\kappa _4$
being an absolute constant. In particular,
and therefore (BE)(3) is still valid at time
![]() $i_j$
. Consequently, the associated bound period satisfies
$i_j$
. Consequently, the associated bound period satisfies
![]() $p_j \leq \kappa _1 r_j$
, and the above argument can therefore be repeated. With this, we conclude that
$p_j \leq \kappa _1 r_j$
, and the above argument can therefore be repeated. With this, we conclude that
![]() $o_s \leq \kappa _4 r$
.
$o_s \leq \kappa _4 r$
.
We proceed in the next section with describing the situation if our return is assumed to be essential.
4.8 From the first essential return to the first escape return
With
![]() $n_1$
denoting the index of the first essential return, we are in the following situation:
$n_1$
denoting the index of the first essential return, we are in the following situation:
 $$ \begin{align*} &\xi_{n_1}(\omega) \cap I_{rl} \neq \emptyset, \quad \vert \xi_{n_1}(\omega)\vert \geq \vert I_{rl}\vert,\\ &\text{and}\quad \xi_{n_1}(\omega) \subset (-4\delta,4\delta) \smallsetminus (-\delta_{n_1}/3,\delta_{n_1}/3) \end{align*} $$
$$ \begin{align*} &\xi_{n_1}(\omega) \cap I_{rl} \neq \emptyset, \quad \vert \xi_{n_1}(\omega)\vert \geq \vert I_{rl}\vert,\\ &\text{and}\quad \xi_{n_1}(\omega) \subset (-4\delta,4\delta) \smallsetminus (-\delta_{n_1}/3,\delta_{n_1}/3) \end{align*} $$
for some
![]() $r,l$
. At this point, to not lose too much distortion, we will make a partition of as much as possible, and keep iterating what is left. That is, we will consider iterations of larger partition elements
$r,l$
. At this point, to not lose too much distortion, we will make a partition of as much as possible, and keep iterating what is left. That is, we will consider iterations of larger partition elements
![]() $I_r = (e^{-r-1},e^{-r}) \subset (-4\delta ,4\delta )$
, and we establish an upper bound for the number of essential returns needed to reach an escape return or a complete return.
$I_r = (e^{-r-1},e^{-r}) \subset (-4\delta ,4\delta )$
, and we establish an upper bound for the number of essential returns needed to reach an escape return or a complete return.
Let
![]() $\Omega _1 = \xi _{n_1}(\omega )$
and let
$\Omega _1 = \xi _{n_1}(\omega )$
and let
![]() $I_1 = I_{r_1} \subset \Omega _1$
for smallest such
$I_1 = I_{r_1} \subset \Omega _1$
for smallest such
![]() $r_1$
. (In fact, we extend
$r_1$
. (In fact, we extend
![]() $I_1$
to the closest endpoint of
$I_1$
to the closest endpoint of
![]() $\Omega _1$
, and therefore have
$\Omega _1$
, and therefore have
![]() $I_1 \subset I_{r_1} \cup I_{r_1-1}$
.) If there is no such r, we instead let
$I_1 \subset I_{r_1} \cup I_{r_1-1}$
.) If there is no such r, we instead let
![]() $I_1 = \Omega _1$
. Moreover, let
$I_1 = \Omega _1$
. Moreover, let
![]() $\omega ^1$
be the interval in parameter space for which
$\omega ^1$
be the interval in parameter space for which
![]() $\xi _{n_1}(\omega ^1) = I_{1}$
. The interval
$\xi _{n_1}(\omega ^1) = I_{1}$
. The interval
![]() $I_1$
is referred to as the essential interval, and this is the interval we will iterate. If
$I_1$
is referred to as the essential interval, and this is the interval we will iterate. If
![]() $\hat {\omega } = \omega \smallsetminus \omega ^1$
is non-empty, we make a partition
$\hat {\omega } = \omega \smallsetminus \omega ^1$
is non-empty, we make a partition
where each
![]() $\omega ^{rl}$
is such that
$\omega ^{rl}$
is such that
![]() $I_{rl} \subset \xi _{n_1}(\omega ^{rl}) = I_{rl}\cup I_{r'l'} \subset (-4\delta ,4\delta )$
. (If there is not enough left for a partition, we extend
$I_{rl} \subset \xi _{n_1}(\omega ^{rl}) = I_{rl}\cup I_{r'l'} \subset (-4\delta ,4\delta )$
. (If there is not enough left for a partition, we extend
![]() $I_1$
further so that
$I_1$
further so that
![]() $I_1 \subset I_{r_1+1}\cup I_{r_1} \cup I_{r_1-1}$
.) Notice that, since the intervals
$I_1 \subset I_{r_1+1}\cup I_{r_1} \cup I_{r_1-1}$
.) Notice that, since the intervals
![]() $I_r$
are dyadic, the proportion of what remains after partitioning satisfies
$I_r$
are dyadic, the proportion of what remains after partitioning satisfies
We associate for each partitioned parameter interval
![]() $\omega ^{rl}$
the complete return time
$\omega ^{rl}$
the complete return time
![]() $n_1$
(even though nothing is removed from these intervals). From the conclusions made in the previous sections, we know that
$n_1$
(even though nothing is removed from these intervals). From the conclusions made in the previous sections, we know that
provided
![]() $m_0$
is large enough. In particular, Lemma 4.12 tells us that (BE)(2) is satisfied up to time
$m_0$
is large enough. In particular, Lemma 4.12 tells us that (BE)(2) is satisfied up to time
![]() $n_1$
for all
$n_1$
for all
![]() $a \in \omega $
. At this step, to make sure that (BE)(1) is satisfied for our partitioned parameter intervals
$a \in \omega $
. At this step, to make sure that (BE)(1) is satisfied for our partitioned parameter intervals
![]() $\omega ^{rl} \subset \Delta _{k+1}$
, we make the following rule (compare with the initial iterates at the beginning of the induction step). If there is no
$\omega ^{rl} \subset \Delta _{k+1}$
, we make the following rule (compare with the initial iterates at the beginning of the induction step). If there is no
![]() $a' \in \omega $
such that
$a' \in \omega $
such that
then we remove the entire interval. If there is such a parameter, however, using Lemma 5.1, we have that
 $$ \begin{align*} \vert \partial_x F^{n_1 - 1}(1;a) \vert &\geq D_1^{-(\log^* m)^2} \vert \partial_x F^{n_1-1}(1;a')\vert \\ &\geq C_B \exp\bigg\{ \bigg(\gamma_B - \frac{(\log^* m)^2}{n_1-1}\log D_1 \bigg)(n_1-1) \bigg\} \\ &\geq Ce^{\gamma(n_1-1)}, \end{align*} $$
$$ \begin{align*} \vert \partial_x F^{n_1 - 1}(1;a) \vert &\geq D_1^{-(\log^* m)^2} \vert \partial_x F^{n_1-1}(1;a')\vert \\ &\geq C_B \exp\bigg\{ \bigg(\gamma_B - \frac{(\log^* m)^2}{n_1-1}\log D_1 \bigg)(n_1-1) \bigg\} \\ &\geq Ce^{\gamma(n_1-1)}, \end{align*} $$
provided
![]() $m_0$
is large enough.
$m_0$
is large enough.
With the above rules applied at each essential return to come, we now describe the iterations. Since
![]() $\xi _{m}(\omega ) = I_{r_0l}$
, using Lemma 4.8, we know that the length of
$\xi _{m}(\omega ) = I_{r_0l}$
, using Lemma 4.8, we know that the length of
![]() $\Omega _1$
satisfies
$\Omega _1$
satisfies
 $$ \begin{align*} \vert \Omega_1 \vert \geq \frac{C_M e^{\gamma_M}}{2}\frac{1}{r_0^{\kappa_2}} \geq \frac{1}{r_0^{\kappa_2 + 1}}. \end{align*} $$
$$ \begin{align*} \vert \Omega_1 \vert \geq \frac{C_M e^{\gamma_M}}{2}\frac{1}{r_0^{\kappa_2}} \geq \frac{1}{r_0^{\kappa_2 + 1}}. \end{align*} $$
Notice that since
![]() $e^{-r_1+1} \geq \vert \Omega _1 \vert $
, we have that
$e^{-r_1+1} \geq \vert \Omega _1 \vert $
, we have that
![]() $r_1 \leq 2\kappa _2 \log r_0$
. Iterating
$r_1 \leq 2\kappa _2 \log r_0$
. Iterating
![]() $I_{1}$
with the same rules as before, we will eventually reach a second non-inessential return, and if this return is essential, we denote its index by
$I_{1}$
with the same rules as before, we will eventually reach a second non-inessential return, and if this return is essential, we denote its index by
![]() $n_2$
. This index constitutes the addition of a bound period, a free period, and an inessential period:
$n_2$
. This index constitutes the addition of a bound period, a free period, and an inessential period:
![]() $n_2 = n_1 + p_1 + L_1 + o_1$
. Similarly as before, we let
$n_2 = n_1 + p_1 + L_1 + o_1$
. Similarly as before, we let
![]() $\Omega _2 = \xi _{n_2}(\omega ^1)$
, and let
$\Omega _2 = \xi _{n_2}(\omega ^1)$
, and let
![]() $I_{2} \subset \Omega _2$
denote the essential interval of
$I_{2} \subset \Omega _2$
denote the essential interval of
![]() $\Omega _2$
. Let
$\Omega _2$
. Let
![]() $\omega ^2 \subset \omega ^1$
be such that
$\omega ^2 \subset \omega ^1$
be such that
![]() $\xi _{n_2}(\omega ^2) = I_{2}$
, and make a complete partition of
$\xi _{n_2}(\omega ^2) = I_{2}$
, and make a complete partition of
![]() $\omega ^1 \smallsetminus \omega ^2$
. By applying Lemma 4.8 again, we find that
$\omega ^1 \smallsetminus \omega ^2$
. By applying Lemma 4.8 again, we find that
 $$ \begin{align*} \vert \Omega_2 \vert \geq \frac{1}{r_1^{\kappa_2 + 1}} \geq \frac{1}{(2\kappa_2 \log r_0)^{\kappa_2 + 1}}. \end{align*} $$
$$ \begin{align*} \vert \Omega_2 \vert \geq \frac{1}{r_1^{\kappa_2 + 1}} \geq \frac{1}{(2\kappa_2 \log r_0)^{\kappa_2 + 1}}. \end{align*} $$
If we have yet to reach an escape return or a complete return, let
![]() $n_j$
be the index of the
$n_j$
be the index of the
![]() $j\text {th}$
essential return, and realize that we are in the following situation:
$j\text {th}$
essential return, and realize that we are in the following situation:
 $$ \begin{align} \xi_{n_j}(\omega^j) = I_j \subset \Omega_j = \xi_{n_j}(\omega^{j-1})\quad \text{and} \quad \vert \Omega_j \vert \geq \frac{1}{r_{j-1}^{\kappa_2 + 1}}. \end{align} $$
$$ \begin{align} \xi_{n_j}(\omega^j) = I_j \subset \Omega_j = \xi_{n_j}(\omega^{j-1})\quad \text{and} \quad \vert \Omega_j \vert \geq \frac{1}{r_{j-1}^{\kappa_2 + 1}}. \end{align} $$
Introducing the function
![]() $r \mapsto 2\kappa _2 \log r = \varphi (r)$
, we see from the above that
$r \mapsto 2\kappa _2 \log r = \varphi (r)$
, we see from the above that
![]() $r_j \leq \varphi ^j(r_0)$
. The orbit
$r_j \leq \varphi ^j(r_0)$
. The orbit
![]() $\varphi ^j(r_0)$
will tend to the attracting fixed point
$\varphi ^j(r_0)$
will tend to the attracting fixed point
![]() $\hat {r} = -2\kappa _2 W(-1/(2\kappa _2))$
, where W is the Lambert W function. The following simple lemma gives an upper bound for the number of essential returns needed to reach an escape return or a complete return.
$\hat {r} = -2\kappa _2 W(-1/(2\kappa _2))$
, where W is the Lambert W function. The following simple lemma gives an upper bound for the number of essential returns needed to reach an escape return or a complete return.
Lemma 4.14. Let
![]() $\varphi (r) = 2\kappa _2 \log r$
, and let
$\varphi (r) = 2\kappa _2 \log r$
, and let
![]() $s = s(r)$
be the integer defined by
$s = s(r)$
be the integer defined by
Then,
Proof. Using the fact that
![]() $3 \leq 2\kappa _2 \leq \log _j r$
, for
$3 \leq 2\kappa _2 \leq \log _j r$
, for
![]() $j = 0,1,\ldots , s-1$
, it is straightforward to check that
$j = 0,1,\ldots , s-1$
, it is straightforward to check that
Therefore,
Given
![]() $s = s(r_0)$
as in the above lemma, we have that
$s = s(r_0)$
as in the above lemma, we have that
![]() $r_s \leq \varphi ^s(r_0) \leq 12\kappa _2^2$
. By making sure
$r_s \leq \varphi ^s(r_0) \leq 12\kappa _2^2$
. By making sure
![]() $\delta $
is small enough, we therefore conclude that
$\delta $
is small enough, we therefore conclude that
 $$ \begin{align*} \vert \Omega_{s+1} \vert \geq \frac{1}{(12\kappa_2^2)^{\kappa_2 + 1}} \geq 4\delta. \end{align*} $$
$$ \begin{align*} \vert \Omega_{s+1} \vert \geq \frac{1}{(12\kappa_2^2)^{\kappa_2 + 1}} \geq 4\delta. \end{align*} $$
To express s in terms of
![]() $r_0$
, we introduce the so-called iterated logarithm, which is defined recursively as
$r_0$
, we introduce the so-called iterated logarithm, which is defined recursively as
 $$ \begin{align*} \log^* x = \begin{cases} 0 &\mbox{if}\ x \leq 1, \\ 1 + \log^* \log x &\mbox{if}\ x> 1. \end{cases} \end{align*} $$
$$ \begin{align*} \log^* x = \begin{cases} 0 &\mbox{if}\ x \leq 1, \\ 1 + \log^* \log x &\mbox{if}\ x> 1. \end{cases} \end{align*} $$
That is,
![]() $\log ^* x$
is the number of times one has to apply to logarithm to x for the result to be less than or equal to one.
$\log ^* x$
is the number of times one has to apply to logarithm to x for the result to be less than or equal to one.
Since s satisfies
![]() $\log _s r_0 \leq 2\kappa _2 \leq \log _{s-1} r_0$
and since
$\log _s r_0 \leq 2\kappa _2 \leq \log _{s-1} r_0$
and since
![]() $2\kappa _2> 1$
, we have
$2\kappa _2> 1$
, we have
We finish by giving an upper bound for the index of the first escape return (or
![]() $(k+1){\text {th}}$
complete return), that is, we wish to estimate
$(k+1){\text {th}}$
complete return), that is, we wish to estimate
 $$ \begin{align*} n_{s+1} = m + \sum_{j=0}^{s} (p_j + L_j + o_j).\end{align*} $$
$$ \begin{align*} n_{s+1} = m + \sum_{j=0}^{s} (p_j + L_j + o_j).\end{align*} $$
From Lemmas 4.6, 4.10, and 4.13, we have that
Together with the inequalities
![]() $r_j \leq \varphi ^j(r_0)$
and equation (20), we find that
$r_j \leq \varphi ^j(r_0)$
and equation (20), we find that
 $$ \begin{align*} \sum_{j=0}^{s}( p_j + L_j + o_j) &\lesssim r_0 + \sum_{j=1}^{s} \varphi^j(r_0) \\ &\lesssim r_0 + \sum_{j=1}^{s} \log_j r_0 \\ &\lesssim r_0. \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{s}( p_j + L_j + o_j) &\lesssim r_0 + \sum_{j=1}^{s} \varphi^j(r_0) \\ &\lesssim r_0 + \sum_{j=1}^{s} \log_j r_0 \\ &\lesssim r_0. \end{align*} $$
Using (BA), we conclude that
![]() $n_{s+1} - m \lesssim \log m$
, provided
$n_{s+1} - m \lesssim \log m$
, provided
![]() $m_0$
is large enough.
$m_0$
is large enough.
4.9 From the first escape return to the
 $(k+1)\text {th}$
complete return
$(k+1)\text {th}$
complete return
Keeping the notation from the previous section,
![]() $\Omega _{s+1} = \xi _{n_{s+1}}(\omega ^s)$
is the first escape return, satisfying
$\Omega _{s+1} = \xi _{n_{s+1}}(\omega ^s)$
is the first escape return, satisfying
 $$ \begin{align*} \Omega_{s+1} \cap (-\delta,&\delta) \neq \emptyset, \quad \Omega_{s+1} \cap (-\delta_{n_s}/3,\delta_{n_s}/3) = \emptyset \\ &\kern-2pt\text{and} \quad \vert \Omega_{s+1} \smallsetminus (-\delta,\delta) \vert \geq 3\delta. \end{align*} $$
$$ \begin{align*} \Omega_{s+1} \cap (-\delta,&\delta) \neq \emptyset, \quad \Omega_{s+1} \cap (-\delta_{n_s}/3,\delta_{n_s}/3) = \emptyset \\ &\kern-2pt\text{and} \quad \vert \Omega_{s+1} \smallsetminus (-\delta,\delta) \vert \geq 3\delta. \end{align*} $$
We will keep iterating
![]() $\omega ^s$
until we get a complete return, and we show below that this must happen within finite (uniform) time. To not run into problems with distortion, we will, as in the case of essential returns, whenever possible make a partition of everything that is mapped inside of
$\omega ^s$
until we get a complete return, and we show below that this must happen within finite (uniform) time. To not run into problems with distortion, we will, as in the case of essential returns, whenever possible make a partition of everything that is mapped inside of
![]() $(-\delta ,\delta )$
, and the corresponding parameter intervals will be a part of
$(-\delta ,\delta )$
, and the corresponding parameter intervals will be a part of
![]() $\Delta _{k+1}$
; that is, at time
$\Delta _{k+1}$
; that is, at time
![]() $n_{s+1+j} = n_{s+1}+j$
let
$n_{s+1+j} = n_{s+1}+j$
let
![]() $I_{s+1+j} = \Omega _{s+1+j} \smallsetminus (\Omega _{s+1+j} \cap (-\delta ,\delta ))$
, let
$I_{s+1+j} = \Omega _{s+1+j} \smallsetminus (\Omega _{s+1+j} \cap (-\delta ,\delta ))$
, let
![]() $\omega ^{s+1+j}$
be such that
$\omega ^{s+1+j}$
be such that
![]() $\xi _{n_{s+1+j}}(\omega ^{s+1+j}) = I_{s+1+j}$
, and make a partition of
$\xi _{n_{s+1+j}}(\omega ^{s+1+j}) = I_{s+1+j}$
, and make a partition of
![]() $\omega ^{s+j}\smallsetminus \omega ^{s+1+j}$
. As in the case of essential returns, we associate to each partitioned parameter interval the complete time
$\omega ^{s+j}\smallsetminus \omega ^{s+1+j}$
. As in the case of essential returns, we associate to each partitioned parameter interval the complete time
![]() $n_{s+1+j}$
and, as before, we make sure that at these times, (BE)(1) is satisfied.
$n_{s+1+j}$
and, as before, we make sure that at these times, (BE)(1) is satisfied.
Let
![]() $\omega _e = \omega _L \cup \omega _M \cup \omega _R$
be the disjoint union of parameter intervals for which
$\omega _e = \omega _L \cup \omega _M \cup \omega _R$
be the disjoint union of parameter intervals for which
Clearly, it is enough to show that
![]() $\omega _e$
reaches a complete return within finite time. Let
$\omega _e$
reaches a complete return within finite time. Let
![]() $t_*$
be the smallest integer for which
$t_*$
be the smallest integer for which
If
![]() $\delta $
is small enough, and if
$\delta $
is small enough, and if
![]() $\vert \omega _0 \vert = 2\epsilon $
is small enough, we can make sure that
$\vert \omega _0 \vert = 2\epsilon $
is small enough, we can make sure that
Suppose that, for some
![]() $j \geq t_*$
,
$j \geq t_*$
,
![]() $\xi _{n_{s+1+j}}(\omega _e) \cap (-\delta ,\delta ) \neq \emptyset $
, and that this return is not complete. Assuming that
$\xi _{n_{s+1+j}}(\omega _e) \cap (-\delta ,\delta ) \neq \emptyset $
, and that this return is not complete. Assuming that
![]() $\omega _L$
returns, we can not have
$\omega _L$
returns, we can not have
![]() $\xi _{n_{s+1+j}}(\omega _L) \subset (-2\delta ,2\delta )$
. Indeed, if this was the case, then (using Lemma 3.1 and parameter independence)
$\xi _{n_{s+1+j}}(\omega _L) \subset (-2\delta ,2\delta )$
. Indeed, if this was the case, then (using Lemma 3.1 and parameter independence)
which contradicts the return not being complete. We conclude that after partitioning what is mapped inside of
![]() $(-\delta ,\delta )$
, what is left is of size at least
$(-\delta ,\delta )$
, what is left is of size at least
![]() $\delta $
, and we are back to the original setting. In particular,
$\delta $
, and we are back to the original setting. In particular,
![]() $\omega _M$
did not return to
$\omega _M$
did not return to
![]() $(-\delta ,\delta )$
. Repeating this argument,
$(-\delta ,\delta )$
. Repeating this argument,
![]() $\omega _L$
and
$\omega _L$
and
![]() $\omega _R$
will return, but
$\omega _R$
will return, but
![]() $\omega _M$
will stay outside of
$\omega _M$
will stay outside of
![]() $(-\delta ,\delta )$
. (Here, we abuse the notation: if
$(-\delta ,\delta )$
. (Here, we abuse the notation: if
![]() $\omega _L$
returns, we update it so that it maps onto
$\omega _L$
returns, we update it so that it maps onto
![]() $(\delta ,2\delta )$
, and similarly if
$(\delta ,2\delta )$
, and similarly if
![]() $\omega _R$
returns.) Due to Lemma 3.1, we therefore have
$\omega _R$
returns.) Due to Lemma 3.1, we therefore have
and clearly we must reach a complete return after
![]() $j = t$
iterations, with
$j = t$
iterations, with
With this, we conclude that if
![]() $m_0$
is large enough, then there exists a constant
$m_0$
is large enough, then there exists a constant
![]() $\kappa> 0$
such that
$\kappa> 0$
such that
We finish by estimating how much of
![]() $\Omega _{s+1+j}$
is being partitioned at each iteration. By definition of an escape return, we have that
$\Omega _{s+1+j}$
is being partitioned at each iteration. By definition of an escape return, we have that
![]() $\vert \Omega _{s+1}\vert \geq 3\delta $
, and since it takes a long time for
$\vert \Omega _{s+1}\vert \geq 3\delta $
, and since it takes a long time for
![]() $\omega _e$
to return, the following estimate is valid:
$\omega _e$
to return, the following estimate is valid:
 $$ \begin{align} \frac{\vert I_{s+1+j} \vert}{\vert \Omega_{s+1+j} \vert} \geq \frac{\vert \Omega_{s+1+j} \vert - \delta}{\vert \Omega_{s+1+j} \vert } \geq 1 -\frac{1}{3} = \frac{2}{3}. \end{align} $$
$$ \begin{align} \frac{\vert I_{s+1+j} \vert}{\vert \Omega_{s+1+j} \vert} \geq \frac{\vert \Omega_{s+1+j} \vert - \delta}{\vert \Omega_{s+1+j} \vert } \geq 1 -\frac{1}{3} = \frac{2}{3}. \end{align} $$
4.10 Parameter exclusion
We are finally in the position to estimate how much of
![]() $\omega $
is being removed at the next complete return. Up until the first free return, nothing is removed (unless we have a bound return, for which we either remove nothing, or remove enough to consider the return complete). Let E be what is removed in parameter space, and write
$\omega $
is being removed at the next complete return. Up until the first free return, nothing is removed (unless we have a bound return, for which we either remove nothing, or remove enough to consider the return complete). Let E be what is removed in parameter space, and write
![]() $\omega = \omega ^0$
. Taking into account what we partition in between
$\omega = \omega ^0$
. Taking into account what we partition in between
![]() $m_k$
and
$m_k$
and
![]() $m_{k+1}$
, we have that
$m_{k+1}$
, we have that
 $$ \begin{align*} \frac{\vert E \vert}{\vert \omega^0 \vert} = \frac{\vert E \vert}{\vert \omega^{s+t} \vert} \prod_{\nu = 0}^{t-1} \frac{\vert \omega^{s+1+\nu}\vert}{\vert \omega^{s+\nu}\vert} \prod_{\nu=0}^{s-1} \frac{\vert \omega^{1 + \nu}\vert}{\vert \omega^\nu \vert}. \end{align*} $$
$$ \begin{align*} \frac{\vert E \vert}{\vert \omega^0 \vert} = \frac{\vert E \vert}{\vert \omega^{s+t} \vert} \prod_{\nu = 0}^{t-1} \frac{\vert \omega^{s+1+\nu}\vert}{\vert \omega^{s+\nu}\vert} \prod_{\nu=0}^{s-1} \frac{\vert \omega^{1 + \nu}\vert}{\vert \omega^\nu \vert}. \end{align*} $$
Using the the mean value theorem, we find that for each factor in the above expression,
 $$ \begin{align*} \frac{\vert \omega^j\vert}{\vert \omega^{j-1}\vert} &= \frac{\vert a_j - b_j \vert}{\vert a_{j-1} - b_{j-1} \vert} \\ &= \frac{\vert a_j - b_j \vert}{\vert \xi_{n_j}(a_j) - \xi_{n_j}(b_j)\vert} \frac{\vert \xi_{n_j}(a_{j-1}) - \xi_{n_j}(b_{j-1})\vert}{\vert a_{j-1} - b_{j-1}\vert} \frac{\vert \xi_{n_j}(a_j) - \xi_{n_j}(b_j)\vert}{\vert \xi_{n_j}(a_{j-1}) - \xi_{n_j}(b_{j-1})\vert} \\ &= \frac{1}{\vert \partial_a \xi_{n_j}(c_j)\vert} \vert \partial_a \xi_{n_j}(c_{j-1})\vert \frac{\vert I_{j}\vert}{\vert \Omega_j \vert} \\ &= \frac{\vert \partial_x F^{n_j-1}(1;c_j)\vert}{\vert \partial_a \xi_{n_j}(c_j)\vert} \frac{\vert \partial_a \xi_{n_j}(c_{j-1})\vert}{\vert \partial_x F^{n_j-1}(1;c_{j-1})\vert} \frac{\vert \partial_x F^{n_j-1}(1;c_{j-1})\vert}{\vert \partial_x F^{n_j-1}(1;c_j)\vert} \frac{\vert I_{j}\vert}{\vert \Omega_j \vert}. \end{align*} $$
$$ \begin{align*} \frac{\vert \omega^j\vert}{\vert \omega^{j-1}\vert} &= \frac{\vert a_j - b_j \vert}{\vert a_{j-1} - b_{j-1} \vert} \\ &= \frac{\vert a_j - b_j \vert}{\vert \xi_{n_j}(a_j) - \xi_{n_j}(b_j)\vert} \frac{\vert \xi_{n_j}(a_{j-1}) - \xi_{n_j}(b_{j-1})\vert}{\vert a_{j-1} - b_{j-1}\vert} \frac{\vert \xi_{n_j}(a_j) - \xi_{n_j}(b_j)\vert}{\vert \xi_{n_j}(a_{j-1}) - \xi_{n_j}(b_{j-1})\vert} \\ &= \frac{1}{\vert \partial_a \xi_{n_j}(c_j)\vert} \vert \partial_a \xi_{n_j}(c_{j-1})\vert \frac{\vert I_{j}\vert}{\vert \Omega_j \vert} \\ &= \frac{\vert \partial_x F^{n_j-1}(1;c_j)\vert}{\vert \partial_a \xi_{n_j}(c_j)\vert} \frac{\vert \partial_a \xi_{n_j}(c_{j-1})\vert}{\vert \partial_x F^{n_j-1}(1;c_{j-1})\vert} \frac{\vert \partial_x F^{n_j-1}(1;c_{j-1})\vert}{\vert \partial_x F^{n_j-1}(1;c_j)\vert} \frac{\vert I_{j}\vert}{\vert \Omega_j \vert}. \end{align*} $$
Making use of Lemmas 3.2 and 5.1, we find that
 $$ \begin{align*} \frac{\vert \omega^j \vert}{\vert \omega^{j-1}\vert} : \frac{\vert I_{j} \vert}{\vert \Omega_j \vert} \sim D_A D_1^{(\log^* m_k)^2}, \end{align*} $$
$$ \begin{align*} \frac{\vert \omega^j \vert}{\vert \omega^{j-1}\vert} : \frac{\vert I_{j} \vert}{\vert \Omega_j \vert} \sim D_A D_1^{(\log^* m_k)^2}, \end{align*} $$
and therefore, using equations (21), (18), and (23), there is, provided
![]() $m_0$
is large enough, an absolute constant
$m_0$
is large enough, an absolute constant
![]() $0 < \tau < 1$
such that
$0 < \tau < 1$
such that
 $$ \begin{align*} \frac{\vert E \vert}{\vert \omega^0 \vert} \geq \frac{(\delta_{m_{k+1}}/3)}{1}\bigg(\frac{1}{3}D_A^{-1} D_1^{-(\log^* m_k)^2}\bigg)^{t + \log^* m_k} \geq \delta_{m_{k+1}}\tau^{(\log^* m_{k+1})^3}. \end{align*} $$
$$ \begin{align*} \frac{\vert E \vert}{\vert \omega^0 \vert} \geq \frac{(\delta_{m_{k+1}}/3)}{1}\bigg(\frac{1}{3}D_A^{-1} D_1^{-(\log^* m_k)^2}\bigg)^{t + \log^* m_k} \geq \delta_{m_{k+1}}\tau^{(\log^* m_{k+1})^3}. \end{align*} $$
In particular, for the remaining interval
![]() $\hat {\omega } = \omega \smallsetminus E$
, we have that
$\hat {\omega } = \omega \smallsetminus E$
, we have that
5 Main distortion lemma
Before giving a proof of Theorem B, we give a proof of the very important distortion lemma that, together with Lemma 3.2, allow us to restore the derivative and to estimate what is removed in parameter space at the
![]() $(k+1)\text {th}$
complete return. The proof is similar to that of Lemma 5 in [Reference Benedicks and CarlesonBC85], with the main difference being how we proceed at essential returns. As will be seen, our estimate is unbounded.
$(k+1)\text {th}$
complete return. The proof is similar to that of Lemma 5 in [Reference Benedicks and CarlesonBC85], with the main difference being how we proceed at essential returns. As will be seen, our estimate is unbounded.
If not otherwise stated, the notation is consistent with that of the induction step. Recall that
with
![]() $\omega _k \subset N_k$
being mapped onto some
$\omega _k \subset N_k$
being mapped onto some
![]() $I_{rl} \subset (-4\delta ,4\delta )$
, and
$I_{rl} \subset (-4\delta ,4\delta )$
, and
![]() $\omega _k \subset T_k$
being mapped onto an interval
$\omega _k \subset T_k$
being mapped onto an interval
![]() $\pm (\delta ,x)$
with
$\pm (\delta ,x)$
with
![]() $\vert x-\delta \vert \geq 3\delta $
. Moreover, we let
$\vert x-\delta \vert \geq 3\delta $
. Moreover, we let
![]() $m_{k+1}(a,b)$
denote the largest time for which parameters
$m_{k+1}(a,b)$
denote the largest time for which parameters
![]() $a,b \in \omega _k$
belong to the same parameter interval
$a,b \in \omega _k$
belong to the same parameter interval
![]() $\omega _k^j \subset \omega _k$
, e.g. if
$\omega _k^j \subset \omega _k$
, e.g. if
![]() $a,b \in \omega _k^j$
, then
$a,b \in \omega _k^j$
, then
![]() $m_{k+1}(a,b) \geq n_{j+1}$
.
$m_{k+1}(a,b) \geq n_{j+1}$
.
Lemma 5.1. (Main distortion lemma)
Let
![]() $\omega _k \subset \Delta _k$
and let
$\omega _k \subset \Delta _k$
and let
![]() $m_k$
be the index of the
$m_k$
be the index of the
![]() $k\text {th}$
complete return. There exists a constant
$k\text {th}$
complete return. There exists a constant
![]() $D_1> 1$
such that, for
$D_1> 1$
such that, for
![]() $a,b \in \omega _k$
and
$a,b \in \omega _k$
and
![]() $j < m_{k+1} = m_{k+1}(a,b)$
,
$j < m_{k+1} = m_{k+1}(a,b)$
,
 $$ \begin{align*} \frac{\vert \partial_x F^j(1;a)\vert}{\vert \partial_x F^j(1;b)\vert} \leq D_1^{(\log^* m_k)^2}. \end{align*} $$
$$ \begin{align*} \frac{\vert \partial_x F^j(1;a)\vert}{\vert \partial_x F^j(1;b)\vert} \leq D_1^{(\log^* m_k)^2}. \end{align*} $$
Proof. Using the chain rule and the elementary inequality
![]() $x+1 \leq e^x$
, we have
$x+1 \leq e^x$
, we have
 $$ \begin{align*} \frac{\vert \partial_x F^j(1;a)\vert}{\vert \partial_x F^j(1;b)\vert} &= \prod_{\nu= 0}^{j-1} \frac{\vert \partial_x F(F^\nu(1;a);a) \vert}{\vert \partial_x F(F^\nu(1;b);b) \vert} \\ &= \bigg(\frac{a}{b}\bigg)^j \prod_{\nu =1}^j \frac{\vert \xi_\nu(a) \vert}{\vert \xi_\nu(b)\vert} \\ &\leq \bigg( \frac{a}{b} \bigg)^j \prod_{\nu=1}^j \bigg(\frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b)\vert} + 1\bigg) \\ &\leq \bigg(\frac{a}{b}\bigg)^j \exp\bigg(\sum_{\nu=1}^j \frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b) \vert}\bigg). \end{align*} $$
$$ \begin{align*} \frac{\vert \partial_x F^j(1;a)\vert}{\vert \partial_x F^j(1;b)\vert} &= \prod_{\nu= 0}^{j-1} \frac{\vert \partial_x F(F^\nu(1;a);a) \vert}{\vert \partial_x F(F^\nu(1;b);b) \vert} \\ &= \bigg(\frac{a}{b}\bigg)^j \prod_{\nu =1}^j \frac{\vert \xi_\nu(a) \vert}{\vert \xi_\nu(b)\vert} \\ &\leq \bigg( \frac{a}{b} \bigg)^j \prod_{\nu=1}^j \bigg(\frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b)\vert} + 1\bigg) \\ &\leq \bigg(\frac{a}{b}\bigg)^j \exp\bigg(\sum_{\nu=1}^j \frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b) \vert}\bigg). \end{align*} $$
We claim that the first factor in the above expression can be made arbitrarily close to
![]() $1$
. To see this, notice that
$1$
. To see this, notice that
 $$ \begin{align*} \bigg(\frac{a}{b}\bigg)^j \leq (1 + \vert \omega_k \vert )^j. \end{align*} $$
$$ \begin{align*} \bigg(\frac{a}{b}\bigg)^j \leq (1 + \vert \omega_k \vert )^j. \end{align*} $$
Using (BE)(1) and Lemma 3.2, we have that
![]() $\vert \omega _k\vert \lesssim e^{-\gamma m_k}$
, and for
$\vert \omega _k\vert \lesssim e^{-\gamma m_k}$
, and for
![]() $m_0$
large enough, we have from equation (22) that
$m_0$
large enough, we have from equation (22) that
![]() $j < m_{k+1} \leq m_k + \kappa \log m_k \leq 2 m_k$
; therefore,
$j < m_{k+1} \leq m_k + \kappa \log m_k \leq 2 m_k$
; therefore,
Since
making
![]() $m_0$
larger if needed proves the claim. It is therefore enough to only consider the sum
$m_0$
larger if needed proves the claim. It is therefore enough to only consider the sum
 $$ \begin{align*} \Sigma = \sum_{\nu = 1}^{m_{k+1} -1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert}. \end{align*} $$
$$ \begin{align*} \Sigma = \sum_{\nu = 1}^{m_{k+1} -1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert}. \end{align*} $$
With
![]() $m_k^* \leq m_{k+1}$
being the last index of a return, that is,
$m_k^* \leq m_{k+1}$
being the last index of a return, that is,
![]() $\xi _{m_{k^*}}(\omega _k) \subset I_{r_k^*} \subset (-4\delta ,4\delta )$
, we divide
$\xi _{m_{k^*}}(\omega _k) \subset I_{r_k^*} \subset (-4\delta ,4\delta )$
, we divide
![]() $\Sigma $
as
$\Sigma $
as
 $$ \begin{align*} \Sigma = \sum_{\nu = 1}^{m_k^*-1} + \sum_{\nu = m_k^*}^{m_{k+1}-1} = \Sigma_1 + \Sigma_2, \end{align*} $$
$$ \begin{align*} \Sigma = \sum_{\nu = 1}^{m_k^*-1} + \sum_{\nu = m_k^*}^{m_{k+1}-1} = \Sigma_1 + \Sigma_2, \end{align*} $$
and begin with estimating
![]() $\Sigma _1$
.
$\Sigma _1$
.
The history of
![]() $\omega _k$
will be that of
$\omega _k$
will be that of
![]() $\omega _0, \omega _1,\ldots ,\omega _{k-1}$
. Let
$\omega _0, \omega _1,\ldots ,\omega _{k-1}$
. Let
![]() $\{t_j\}_{j=0}^N$
be all the inessential, essential, escape, and complete returns. We further divide
$\{t_j\}_{j=0}^N$
be all the inessential, essential, escape, and complete returns. We further divide
![]() $\Sigma _1$
as
$\Sigma _1$
as
 $$ \begin{align*} \sum_{\nu = 1}^{m_k^*-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} = \sum_{j=0}^{N-1}\sum_{\nu = t_j}^{t_{j+1}-1}\frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b)\vert} = \sum_{j=0}^{N-1} S_j. \end{align*} $$
$$ \begin{align*} \sum_{\nu = 1}^{m_k^*-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} = \sum_{j=0}^{N-1}\sum_{\nu = t_j}^{t_{j+1}-1}\frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b)\vert} = \sum_{j=0}^{N-1} S_j. \end{align*} $$
The contribution to
![]() $S_j$
from the bound period is
$S_j$
from the bound period is
 $$ \begin{align*} \sum_{\nu=0}^{p_j} \frac{\vert \xi_{t_j+\nu}(a) - \xi_{t_j + \nu}(b)\vert}{\vert \xi_{t_j+\nu}(b)\vert} \lesssim \frac{\vert \xi_{t_j}(\omega)\vert}{\vert \xi_{t_j}(b) \vert} + \frac{\vert \xi_{t_j}(\omega) \vert}{\vert \xi_{t_j}(b)\vert}\sum_{\nu=1}^{p_j}\frac{e^{-2r_j} \vert \partial_xF^{\nu-1}(1;a)\vert}{\vert \xi_\nu(b) \vert}. \end{align*} $$
$$ \begin{align*} \sum_{\nu=0}^{p_j} \frac{\vert \xi_{t_j+\nu}(a) - \xi_{t_j + \nu}(b)\vert}{\vert \xi_{t_j+\nu}(b)\vert} \lesssim \frac{\vert \xi_{t_j}(\omega)\vert}{\vert \xi_{t_j}(b) \vert} + \frac{\vert \xi_{t_j}(\omega) \vert}{\vert \xi_{t_j}(b)\vert}\sum_{\nu=1}^{p_j}\frac{e^{-2r_j} \vert \partial_xF^{\nu-1}(1;a)\vert}{\vert \xi_\nu(b) \vert}. \end{align*} $$
Let
![]() $\iota = (\kappa _1 \log 4)^{-1}$
and further divide the sum in the above right-hand side as
$\iota = (\kappa _1 \log 4)^{-1}$
and further divide the sum in the above right-hand side as
 $$ \begin{align*} \sum_{\nu=1}^{\iota p_j} + \sum_{\nu = \iota p_j + 1}^{p_j}. \end{align*} $$
$$ \begin{align*} \sum_{\nu=1}^{\iota p_j} + \sum_{\nu = \iota p_j + 1}^{p_j}. \end{align*} $$
To estimate the first sum, we use the inequalities
![]() $\vert \partial _x F^\nu \vert \leq 4^\nu $
and
$\vert \partial _x F^\nu \vert \leq 4^\nu $
and
![]() $\vert \xi _\nu (b) \vert \geq \delta _\nu /3 \gtrsim \nu ^{-\overline {e}}$
, and that
$\vert \xi _\nu (b) \vert \geq \delta _\nu /3 \gtrsim \nu ^{-\overline {e}}$
, and that
![]() $p_j \leq \kappa _1 r_j$
, to find that
$p_j \leq \kappa _1 r_j$
, to find that
 $$ \begin{align*} \sum_{\nu=1}^{\iota p_j} \frac{e^{-2r_j} \vert\partial_xF^{\nu-1}(1;a)\vert}{\vert \xi_\nu(b)\vert} &\lesssim e^{-2r_j}\sum_{\nu=1}^{\iota p_j} 4^\nu \nu^{\overline{e}} \\ &\lesssim e^{-2 r_j} 4^{\iota p_j}p_j^{\overline{e}} \\ &\lesssim \frac{r_j^{\overline{e}}}{e^{r_j}}. \end{align*} $$
$$ \begin{align*} \sum_{\nu=1}^{\iota p_j} \frac{e^{-2r_j} \vert\partial_xF^{\nu-1}(1;a)\vert}{\vert \xi_\nu(b)\vert} &\lesssim e^{-2r_j}\sum_{\nu=1}^{\iota p_j} 4^\nu \nu^{\overline{e}} \\ &\lesssim e^{-2 r_j} 4^{\iota p_j}p_j^{\overline{e}} \\ &\lesssim \frac{r_j^{\overline{e}}}{e^{r_j}}. \end{align*} $$
To estimate the second sum, we use (BC) and the equality in equation (9), and find that
 $$ \begin{align*} \sum_{\nu = \iota p_j + 1}^{p_j} \frac{e^{-2r_j} \vert \partial_x F^{\nu-1}(1;a)\vert}{\vert \xi_\nu(b)\vert} \lesssim \frac{1}{r_j^2}. \end{align*} $$
$$ \begin{align*} \sum_{\nu = \iota p_j + 1}^{p_j} \frac{e^{-2r_j} \vert \partial_x F^{\nu-1}(1;a)\vert}{\vert \xi_\nu(b)\vert} \lesssim \frac{1}{r_j^2}. \end{align*} $$
Therefore, the contribution from the bound period adds up to
 $$ \begin{align*} \sum_{\nu = t_j}^{t_j+p_j} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b) \vert} &\lesssim \frac{\vert \xi_{t_j}(\omega) \vert}{\vert \xi_{t_j}(b) \vert} + \frac{\vert \xi_{t_j}(\omega)\vert}{\vert \xi_{t_j}(b)\vert}\bigg(\frac{1}{r_j^2} + \frac{r_j^{\overline{e}}}{e^{r_j}}\bigg) \\ &\lesssim \frac{\vert \xi_{t_j}(\omega) \vert}{\vert \xi_{t_j}(b)\vert}. \end{align*} $$
$$ \begin{align*} \sum_{\nu = t_j}^{t_j+p_j} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b) \vert} &\lesssim \frac{\vert \xi_{t_j}(\omega) \vert}{\vert \xi_{t_j}(b) \vert} + \frac{\vert \xi_{t_j}(\omega)\vert}{\vert \xi_{t_j}(b)\vert}\bigg(\frac{1}{r_j^2} + \frac{r_j^{\overline{e}}}{e^{r_j}}\bigg) \\ &\lesssim \frac{\vert \xi_{t_j}(\omega) \vert}{\vert \xi_{t_j}(b)\vert}. \end{align*} $$
After the bound period and up to time
![]() $t_{j+1}$
, we have a free period of length
$t_{j+1}$
, we have a free period of length
![]() $L_j$
during which we have exponential increase of the derivative. We wish to estimate
$L_j$
during which we have exponential increase of the derivative. We wish to estimate
 $$ \begin{align*} \sum_{\nu = t_j + p_j + 1}^{t_{j+1}-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} = \sum_{\nu = 1}^{L_j-1} \frac{\vert \xi_{t_j+p_j + \nu}(a) - \xi_{t_j+p_j + \nu}(b) \vert}{\vert \xi_{t_j+p_j + \nu}(b)\vert}. \end{align*} $$
$$ \begin{align*} \sum_{\nu = t_j + p_j + 1}^{t_{j+1}-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} = \sum_{\nu = 1}^{L_j-1} \frac{\vert \xi_{t_j+p_j + \nu}(a) - \xi_{t_j+p_j + \nu}(b) \vert}{\vert \xi_{t_j+p_j + \nu}(b)\vert}. \end{align*} $$
Using the mean value theorem, parameter independence, and Lemma 3.1, we have that for
![]() $1 \leq \nu \leq L_j-1$
,
$1 \leq \nu \leq L_j-1$
,
 $$ \begin{align*} \vert \xi_{t_{j+1}}(a) - \xi_{t_{j+1}}(b)\vert &= \vert \xi_{t_j+p_j+L_j}(a) - \xi_{t_j + p_j + L_j}(b)\vert \\ &\simeq \vert F^{L_j-\nu}(\xi_{t_j+p_j+\nu}(a);a) - F^{L_j -\nu}(\xi_{t_j+p_j+\nu}(b);a)\vert \\ &= \vert \partial_x F^{L_j-\nu}(\xi_{t_j+p_j+\nu}(a');a)\vert \vert \xi_{t_j+p_j+\nu}(a) - \xi_{t_j+p_j+\nu}(b)\vert \\ &\gtrsim e^{\gamma_M (L_j-\nu)}\vert \xi_{t_j+p_j+\nu}(a) - \xi_{t_j+p_j+\nu}(b)\vert, \end{align*} $$
$$ \begin{align*} \vert \xi_{t_{j+1}}(a) - \xi_{t_{j+1}}(b)\vert &= \vert \xi_{t_j+p_j+L_j}(a) - \xi_{t_j + p_j + L_j}(b)\vert \\ &\simeq \vert F^{L_j-\nu}(\xi_{t_j+p_j+\nu}(a);a) - F^{L_j -\nu}(\xi_{t_j+p_j+\nu}(b);a)\vert \\ &= \vert \partial_x F^{L_j-\nu}(\xi_{t_j+p_j+\nu}(a');a)\vert \vert \xi_{t_j+p_j+\nu}(a) - \xi_{t_j+p_j+\nu}(b)\vert \\ &\gtrsim e^{\gamma_M (L_j-\nu)}\vert \xi_{t_j+p_j+\nu}(a) - \xi_{t_j+p_j+\nu}(b)\vert, \end{align*} $$
and therefore,
provided
![]() $\xi _{t_{j+1}}(\omega )$
does not belong to an escape interval. If
$\xi _{t_{j+1}}(\omega )$
does not belong to an escape interval. If
![]() $\xi _{t_{j+1}}(\omega )$
belongs to an escape interval, then we simply extend the above estimate to
$\xi _{t_{j+1}}(\omega )$
belongs to an escape interval, then we simply extend the above estimate to
![]() $t_{j+2}, t_{j+3},\ldots ,$
until we end up inside some
$t_{j+2}, t_{j+3},\ldots ,$
until we end up inside some
![]() $I_{rl} \subset (-4\delta ,4\delta )$
(which will eventually happen, per definition of
$I_{rl} \subset (-4\delta ,4\delta )$
(which will eventually happen, per definition of
![]() $m_k^*$
). Hence, we may disregard escape returns, and see them as an extended free period.
$m_k^*$
). Hence, we may disregard escape returns, and see them as an extended free period.
Since
![]() $\vert \xi _{t_{j+1}}(b) \vert \leq \vert \xi _{t_j+p_j+\nu }(b) \vert $
for
$\vert \xi _{t_{j+1}}(b) \vert \leq \vert \xi _{t_j+p_j+\nu }(b) \vert $
for
![]() $1 \leq \nu \leq L_j-1$
, it follows from the above inequality that
$1 \leq \nu \leq L_j-1$
, it follows from the above inequality that
 $$ \begin{align*} \sum_{\nu=1}^{L_j-1} \frac{\vert \xi_{t_j+p_j+\nu}(a) - \xi_{t_j+p_j+\nu}(b)\vert}{\vert \xi_{t_j+p_j+\nu}(b)\vert} &\leq \frac{\vert \xi_{t_{j+1}}(a) - \xi_{t_{j+1}}(b)\vert}{\vert \xi_{t_{j+1}}(b)\vert}\sum_{\nu=1}^{L_j -1} e^{-\gamma_M (L_j-\nu)} \\ &\lesssim \frac{\vert \xi_{t_{j+1}}(a) - \xi_{t_{j+1}}(b)\vert}{\vert \xi_{t_{j+1}}(b) \vert}, \end{align*} $$
$$ \begin{align*} \sum_{\nu=1}^{L_j-1} \frac{\vert \xi_{t_j+p_j+\nu}(a) - \xi_{t_j+p_j+\nu}(b)\vert}{\vert \xi_{t_j+p_j+\nu}(b)\vert} &\leq \frac{\vert \xi_{t_{j+1}}(a) - \xi_{t_{j+1}}(b)\vert}{\vert \xi_{t_{j+1}}(b)\vert}\sum_{\nu=1}^{L_j -1} e^{-\gamma_M (L_j-\nu)} \\ &\lesssim \frac{\vert \xi_{t_{j+1}}(a) - \xi_{t_{j+1}}(b)\vert}{\vert \xi_{t_{j+1}}(b) \vert}, \end{align*} $$
thus the contribution from the free period is absorbed in
![]() $S_{j+1}$
.
$S_{j+1}$
.
What is left is to give an estimate of
 $$ \begin{align*} \sum_{\nu = m_0}^{m_k^*-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} \lesssim \sum_{j=0}^N \frac{\vert \xi_{t_j}(\omega)\vert}{\vert \xi_{t_j}(b)\vert} \lesssim \sum_{j=0}^N \frac{\vert \xi_{t_j}(\omega)\vert}{\vert I_{r_j}\vert}, \end{align*} $$
$$ \begin{align*} \sum_{\nu = m_0}^{m_k^*-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} \lesssim \sum_{j=0}^N \frac{\vert \xi_{t_j}(\omega)\vert}{\vert \xi_{t_j}(b)\vert} \lesssim \sum_{j=0}^N \frac{\vert \xi_{t_j}(\omega)\vert}{\vert I_{r_j}\vert}, \end{align*} $$
where, with the above argument,
![]() $\{t_j\}_{j=0}^N$
are now considered to be indices of inessential, essential, and complete returns only. Because of the rapid growth rate, we will see that among the returns to the same interval, only the last return will be significant. From Lemma 4.8, we have that
$\{t_j\}_{j=0}^N$
are now considered to be indices of inessential, essential, and complete returns only. Because of the rapid growth rate, we will see that among the returns to the same interval, only the last return will be significant. From Lemma 4.8, we have that
![]() $\vert \xi _{t_j+1}(\omega ) \vert \gtrsim (e^{r_j}/r_j^{\kappa _2}) \vert \xi _{t_j}(\omega ) \vert \gg 2 \vert \xi _{t_j}(\omega )\vert $
, and hence with
$\vert \xi _{t_j+1}(\omega ) \vert \gtrsim (e^{r_j}/r_j^{\kappa _2}) \vert \xi _{t_j}(\omega ) \vert \gg 2 \vert \xi _{t_j}(\omega )\vert $
, and hence with
![]() $J(\nu )$
the last j for which
$J(\nu )$
the last j for which
![]() $r_j = \nu $
,
$r_j = \nu $
,
 $$ \begin{align*} \sum_{j=0}^N \frac{\vert \xi_{t_j}(\omega)\vert}{\vert I_{r_j}\vert} = \sum_{\nu \in \{r_j\}} \frac{1}{\vert I_\nu\vert} \sum_{r_j = \nu} \vert \xi_{t_j}(\omega)\vert \lesssim \sum_{\nu \in \{r_j\}} \frac{\vert \xi_{t_{J(\nu)}}(\omega) \vert}{\vert I_{\nu}\vert}. \end{align*} $$
$$ \begin{align*} \sum_{j=0}^N \frac{\vert \xi_{t_j}(\omega)\vert}{\vert I_{r_j}\vert} = \sum_{\nu \in \{r_j\}} \frac{1}{\vert I_\nu\vert} \sum_{r_j = \nu} \vert \xi_{t_j}(\omega)\vert \lesssim \sum_{\nu \in \{r_j\}} \frac{\vert \xi_{t_{J(\nu)}}(\omega) \vert}{\vert I_{\nu}\vert}. \end{align*} $$
If
![]() $t_{J(\nu )}$
is the index of an inessential return, then
$t_{J(\nu )}$
is the index of an inessential return, then
![]() $\vert \xi _{t_{J(\nu )}}(\omega _k) \vert / \vert I_\nu \vert \lesssim \nu ^{-2}$
, and therefore the contribution from the inessential returns to the above left most sum is bound by some small constant. It is therefore enough to only consider the contribution from essential returns and complete returns. To estimate this contribution, we may assume that
$\vert \xi _{t_{J(\nu )}}(\omega _k) \vert / \vert I_\nu \vert \lesssim \nu ^{-2}$
, and therefore the contribution from the inessential returns to the above left most sum is bound by some small constant. It is therefore enough to only consider the contribution from essential returns and complete returns. To estimate this contribution, we may assume that
![]() $m_k^* \geq m_k$
, and that
$m_k^* \geq m_k$
, and that
![]() $\xi _{m_k}(\omega ) = I_{r_k l}$
. Moreover, we assume that
$\xi _{m_k}(\omega ) = I_{r_k l}$
. Moreover, we assume that
![]() $\xi _{m_j}(\omega ) = I_{r_j l}$
for all j.
$\xi _{m_j}(\omega ) = I_{r_j l}$
for all j.
With
![]() $n_{j,0} = m_j$
being the index of the
$n_{j,0} = m_j$
being the index of the
![]() $j\text {th}$
complete return, and
$j\text {th}$
complete return, and
![]() $n_{j,\nu } \in (m_j,m_{j+1})$
being the index of the
$n_{j,\nu } \in (m_j,m_{j+1})$
being the index of the
![]() $\nu \text {th}$
essential return for which
$\nu \text {th}$
essential return for which
![]() $\xi _{n_{j,\nu }}(\omega ) \subset I_{r_{j,\nu }}$
, we write
$\xi _{n_{j,\nu }}(\omega ) \subset I_{r_{j,\nu }}$
, we write
 $$ \begin{align*} \sum_{\nu \in \{r_j\}} \frac{\vert \xi_{t_{J(\nu)}}(\omega)\vert}{\vert I_\nu\vert} \lesssim \sum_{j = 0}^{k} \sum_{\nu = 0}^{\nu_j} \frac{\vert \xi_{n_{j,\nu}}(\omega) \vert}{\vert I_{r_{j,\nu}} \vert} = \sum_{j=0}^{k} S_{m_j}. \end{align*} $$
$$ \begin{align*} \sum_{\nu \in \{r_j\}} \frac{\vert \xi_{t_{J(\nu)}}(\omega)\vert}{\vert I_\nu\vert} \lesssim \sum_{j = 0}^{k} \sum_{\nu = 0}^{\nu_j} \frac{\vert \xi_{n_{j,\nu}}(\omega) \vert}{\vert I_{r_{j,\nu}} \vert} = \sum_{j=0}^{k} S_{m_j}. \end{align*} $$
For the last partial sum, we use the trivial estimate
![]() $S_{m_k} \leq \log ^* m_k$
. To estimate
$S_{m_k} \leq \log ^* m_k$
. To estimate
![]() $S_{m_j}$
for
$S_{m_j}$
for
![]() $j \neq k$
, we realize that between any two free returns
$j \neq k$
, we realize that between any two free returns
![]() $n_{j,\nu }$
and
$n_{j,\nu }$
and
![]() $n_{j,\nu +1}$
, the distortion is uniformly bound by some constant
$n_{j,\nu +1}$
, the distortion is uniformly bound by some constant
![]() $C_1> 1$
. Therefore,
$C_1> 1$
. Therefore,
 $$ \begin{align*} \frac{\vert \xi_{n_{k-1,\nu_{k-1}-j}}(\omega)\vert}{\vert I_{r_{k-1,\nu_{k-1}-j}} \vert} \leq \frac{C_1^j}{r_k^2}, \end{align*} $$
$$ \begin{align*} \frac{\vert \xi_{n_{k-1,\nu_{k-1}-j}}(\omega)\vert}{\vert I_{r_{k-1,\nu_{k-1}-j}} \vert} \leq \frac{C_1^j}{r_k^2}, \end{align*} $$
and consequently, since
![]() $\nu _j \leq \log ^* r_j$
(see equation (21)),
$\nu _j \leq \log ^* r_j$
(see equation (21)),
 $$ \begin{align*} S_{m_{k-1}} \leq \frac{C_2^{\log^* r_{k-1}}}{r_k^2} \end{align*} $$
$$ \begin{align*} S_{m_{k-1}} \leq \frac{C_2^{\log^* r_{k-1}}}{r_k^2} \end{align*} $$
for some uniform constant
![]() $C_2> 1$
. Continuing like this, we find that
$C_2> 1$
. Continuing like this, we find that
 $$ \begin{align*} S_{m_{k-j}} &\leq \frac{C_2^{\log^* r_{k-j}}C_2^{\log^* r_{k-j+1}} \ldots C_2^{\log^* r_{k-1}}}{r_{k-j+1}^2 r_{k-j+2}^2 \ldots r_k^2} \\ &\leq \frac{C_2^{\log^*{r_{k-j}}}}{r_{k-j+1}^{3/2} r_{k-j+2}^{3/2} \ldots r_{k}^2}, \end{align*} $$
$$ \begin{align*} S_{m_{k-j}} &\leq \frac{C_2^{\log^* r_{k-j}}C_2^{\log^* r_{k-j+1}} \ldots C_2^{\log^* r_{k-1}}}{r_{k-j+1}^2 r_{k-j+2}^2 \ldots r_k^2} \\ &\leq \frac{C_2^{\log^*{r_{k-j}}}}{r_{k-j+1}^{3/2} r_{k-j+2}^{3/2} \ldots r_{k}^2}, \end{align*} $$
where we, in the last inequality, used the (very crude) estimate
Let us call the estimate of
![]() $S_{m_{k-j}}$
good if
$S_{m_{k-j}}$
good if
![]() $C_2^{\log ^* r_{k-j}} \leq r_{k-j+1}$
. For such
$C_2^{\log ^* r_{k-j}} \leq r_{k-j+1}$
. For such
![]() $S_{m_{k-j}}$
, we clearly have
$S_{m_{k-j}}$
, we clearly have
Let
![]() $j_1 \geq 1$
be the smallest integer for which
$j_1 \geq 1$
be the smallest integer for which
![]() $S_{m_{k-j_1}}$
is not good, that is,
$S_{m_{k-j_1}}$
is not good, that is,
We call this the first bad estimate, and for the contribution from
![]() $S_{m_{k-j_1}}$
to the distortion, we instead use the trivial estimate
$S_{m_{k-j_1}}$
to the distortion, we instead use the trivial estimate
Suppose that
![]() $j_2> j_1$
is the next integer for which
$j_2> j_1$
is the next integer for which
If it turns out that
then
and we still call this estimate good. If not, then
and
![]() $j_2$
is the index of the second bad estimate. Continuing like this, we get a number s of bad estimates and an associated sequence
$j_2$
is the index of the second bad estimate. Continuing like this, we get a number s of bad estimates and an associated sequence
![]() $R_i = r_{k-j_i}$
satisfying
$R_i = r_{k-j_i}$
satisfying
 $$ \begin{align*} \log^* R_1 &\geq (\log C_2)^{-1} \log \Delta, \\ \log^* R_2 &\geq (\log C_2)^{-1} \log R_1, \\ &\vdots \\ \log^* R_s &\geq (\log C_2)^{-1} \log R_{s-1}. \end{align*} $$
$$ \begin{align*} \log^* R_1 &\geq (\log C_2)^{-1} \log \Delta, \\ \log^* R_2 &\geq (\log C_2)^{-1} \log R_1, \\ &\vdots \\ \log^* R_s &\geq (\log C_2)^{-1} \log R_{s-1}. \end{align*} $$
This sequence grows incredibly fast, and its not difficult to convince oneself that
 $$ \begin{align*} R_s \gg \underbrace{e^{e^{.^{.^{.^{e}}}}}}_{s\ \text{copies of}\ e}. \end{align*} $$
$$ \begin{align*} R_s \gg \underbrace{e^{e^{.^{.^{.^{e}}}}}}_{s\ \text{copies of}\ e}. \end{align*} $$
In particular, since
![]() $R_s \leq m_k$
, we find that
$R_s \leq m_k$
, we find that
We conclude that
 $$ \begin{align*} \bigg(\sum_{\text{good}} + \sum_{\text{bad}}\bigg) S_{m_j} &\leq \sum_{j=1}^\infty \frac{1}{\Delta^{j/2}} + s \log^* m_k \\ &\lesssim (\log^* m_k)^2, \end{align*} $$
$$ \begin{align*} \bigg(\sum_{\text{good}} + \sum_{\text{bad}}\bigg) S_{m_j} &\leq \sum_{j=1}^\infty \frac{1}{\Delta^{j/2}} + s \log^* m_k \\ &\lesssim (\log^* m_k)^2, \end{align*} $$
and hence
 $$ \begin{align*} \sum_{\nu = 1}^{m_k^*-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} \lesssim (\log^* m_k)^2. \end{align*} $$
$$ \begin{align*} \sum_{\nu = 1}^{m_k^*-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b)\vert}{\vert \xi_\nu(b)\vert} \lesssim (\log^* m_k)^2. \end{align*} $$
From
![]() $m_{k^*}$
to
$m_{k^*}$
to
![]() $m_{k+1} - 1$
, the assumption is that we only experience an orbit outside
$m_{k+1} - 1$
, the assumption is that we only experience an orbit outside
![]() $(-\delta ,\delta )$
. By a similar estimate as equation (25), we find that for
$(-\delta ,\delta )$
. By a similar estimate as equation (25), we find that for
![]() $\nu \geq 1$
,
$\nu \geq 1$
,
and therefore
 $$ \begin{align*} \sum_{\nu = m_k^*}^{m_{k+1}-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b) \vert} \lesssim 1 + \frac{1}{\delta^2} \leq (\log^* m_k)^2, \end{align*} $$
$$ \begin{align*} \sum_{\nu = m_k^*}^{m_{k+1}-1} \frac{\vert \xi_\nu(a) - \xi_\nu(b) \vert}{\vert \xi_\nu(b) \vert} \lesssim 1 + \frac{1}{\delta^2} \leq (\log^* m_k)^2, \end{align*} $$
provided
![]() $m_0$
is large enough. This proves the lemma.
$m_0$
is large enough. This proves the lemma.
6 Proof of Theorem B
Returning to the more cumbersome notation used in the beginning of the induction step, let
![]() $\omega _k^{rl} \subset \Delta _k$
. We claim that a similar inequality as equation (24) is still true if we replace
$\omega _k^{rl} \subset \Delta _k$
. We claim that a similar inequality as equation (24) is still true if we replace
![]() $\hat {\omega }$
and
$\hat {\omega }$
and
![]() $\omega $
with
$\omega $
with
![]() $\Delta _{k+1}$
and
$\Delta _{k+1}$
and
![]() $\Delta _k$
, respectively. To realize this, write
$\Delta _k$
, respectively. To realize this, write
![]() $\Delta _{k+1}$
as the disjoint union
$\Delta _{k+1}$
as the disjoint union
With
![]() $m_0$
being the start time, consider the sequence of integers defined by the equality
$m_0$
being the start time, consider the sequence of integers defined by the equality
where
![]() $\lceil x \rceil $
denotes the smallest integer satisfying
$\lceil x \rceil $
denotes the smallest integer satisfying
![]() $x \leq \lceil x \rceil $
. By induction, using equation (22),
$x \leq \lceil x \rceil $
. By induction, using equation (22),
Hence, the sequence
![]() $(m_k)$
dominates every other sequence
$(m_k)$
dominates every other sequence
![]() $(m_k^{rl})$
, and therefore it follows from equation (24) that
$(m_k^{rl})$
, and therefore it follows from equation (24) that
 $$ \begin{align*} \vert \Delta_{k+1} \vert &= \sum \vert \hat{\omega}_k^{rl} \vert \\ &= \sum \vert \omega_k^{rl} \vert (1-\delta_{m_{k+1}^{rl}} \tau^{(\log^*m_{k+1}^{rl})^3}) \\ &\leq \bigg(\sum \vert \omega_k^{rl} \vert \bigg) (1-\delta_{m_{k+1}}\tau^{(\log^* m_{k+1})^3}) \\ &= \vert \Delta_k \vert (1-\delta_{m_{k+1}}\tau^{(\log^* m_{k+1})^3}). \end{align*} $$
$$ \begin{align*} \vert \Delta_{k+1} \vert &= \sum \vert \hat{\omega}_k^{rl} \vert \\ &= \sum \vert \omega_k^{rl} \vert (1-\delta_{m_{k+1}^{rl}} \tau^{(\log^*m_{k+1}^{rl})^3}) \\ &\leq \bigg(\sum \vert \omega_k^{rl} \vert \bigg) (1-\delta_{m_{k+1}}\tau^{(\log^* m_{k+1})^3}) \\ &= \vert \Delta_k \vert (1-\delta_{m_{k+1}}\tau^{(\log^* m_{k+1})^3}). \end{align*} $$
By construction,
 $$ \begin{align*} \Lambda_{m_0}(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma_B,C_B) \cap \omega_0 \subset \Delta_\infty = \bigcap_{k=0}^\infty \Delta_k, \end{align*} $$
$$ \begin{align*} \Lambda_{m_0}(\delta_n) \cap \operatorname{\mathrm{\mathcal{C}\mathcal{E}}}(\gamma_B,C_B) \cap \omega_0 \subset \Delta_\infty = \bigcap_{k=0}^\infty \Delta_k, \end{align*} $$
and therefore, to prove Theorem B, it is sufficient to show that
 $$ \begin{align*} \prod_{k=0}^\infty(1-\delta_{m_k}\tau^{(\log^* m_{k})^3}) = 0. \end{align*} $$
$$ \begin{align*} \prod_{k=0}^\infty(1-\delta_{m_k}\tau^{(\log^* m_{k})^3}) = 0. \end{align*} $$
By standard theory of infinite products, this is the case if and only if
 $$ \begin{align*} \sum_{k = 0}^\infty \delta_{m_k}\tau^{(\log^* m_k)^3} = \infty. \end{align*} $$
$$ \begin{align*} \sum_{k = 0}^\infty \delta_{m_k}\tau^{(\log^* m_k)^3} = \infty. \end{align*} $$
To evaluate the above sum, we make use of the following classical result, due to Schlömilch [Reference SchlömilchSchl73] (see also [Reference KnoopKno56], for instance).
Proposition 6.1. (Schlömilch condensation test)
Let
![]() $q_0 < q_1 < q_2 \ldots $
be a strictly increasing sequence of positive integers such that there exists a positive real number
$q_0 < q_1 < q_2 \ldots $
be a strictly increasing sequence of positive integers such that there exists a positive real number
![]() $\alpha $
such that
$\alpha $
such that
Then, for a non-increasing sequence
![]() $a_n$
of positive non-negative real numbers,
$a_n$
of positive non-negative real numbers,
 $$ \begin{align*} \sum_{n = 0}^\infty a_n = \infty \quad \text{if and only if}\quad \sum_{k=0}^\infty (q_{k+1} -q_k)a_{q_k} = \infty. \end{align*} $$
$$ \begin{align*} \sum_{n = 0}^\infty a_n = \infty \quad \text{if and only if}\quad \sum_{k=0}^\infty (q_{k+1} -q_k)a_{q_k} = \infty. \end{align*} $$
Proof. We have
 $$ \begin{align*} (q_{k+1}-q_k) a_{q_{k+1}} \leq \sum_{n=0}^{q_{k+1} - q_k -1} a_{q_k + n} \leq (q_{k+1}-q_k) a_{q_k}, \end{align*} $$
$$ \begin{align*} (q_{k+1}-q_k) a_{q_{k+1}} \leq \sum_{n=0}^{q_{k+1} - q_k -1} a_{q_k + n} \leq (q_{k+1}-q_k) a_{q_k}, \end{align*} $$
and therefore,
 $$ \begin{align*} \alpha^{-1}\sum_{k=0}^\infty (q_{k+2}-q_{k+1}) a_{q_{k+1}} \leq \sum_{n = q_0}^\infty a_n \leq \sum_{k=0}^\infty (q_{k+1} - q_k) a_{q_k}.\\[-3.8pc] \end{align*} $$
$$ \begin{align*} \alpha^{-1}\sum_{k=0}^\infty (q_{k+2}-q_{k+1}) a_{q_{k+1}} \leq \sum_{n = q_0}^\infty a_n \leq \sum_{k=0}^\infty (q_{k+1} - q_k) a_{q_k}.\\[-3.8pc] \end{align*} $$
Since
![]() $m_{k+1} - m_k \sim \log m_k$
is only dependent on
$m_{k+1} - m_k \sim \log m_k$
is only dependent on
![]() $m_k$
, we can easily apply the above result in a backwards manner. Indeed, we have that
$m_k$
, we can easily apply the above result in a backwards manner. Indeed, we have that
 $$ \begin{align*} \frac{m_{k+1} - m_k}{m_{k} - m_{k-1}} &\leq \frac{\kappa \log m_k + 1}{\kappa \log m_{k-1}} \\ &\leq \frac{\kappa \log (m_{k-1} + \kappa\log m_{k-1} + 1) + 1}{\kappa \log m_{k-1}} \\ &\leq 1 + \frac{\operatorname{const.}}{\log m_0} \quad (k \geq 0), \end{align*} $$
$$ \begin{align*} \frac{m_{k+1} - m_k}{m_{k} - m_{k-1}} &\leq \frac{\kappa \log m_k + 1}{\kappa \log m_{k-1}} \\ &\leq \frac{\kappa \log (m_{k-1} + \kappa\log m_{k-1} + 1) + 1}{\kappa \log m_{k-1}} \\ &\leq 1 + \frac{\operatorname{const.}}{\log m_0} \quad (k \geq 0), \end{align*} $$
and therefore with
![]() $q_k = m_k$
and
$q_k = m_k$
and
![]() $a_n = \delta _n \tau ^{(\log ^* n)^3}/\log n$
, the preconditions of Schlömilch's test are satisfied. We conclude that
$a_n = \delta _n \tau ^{(\log ^* n)^3}/\log n$
, the preconditions of Schlömilch's test are satisfied. We conclude that
 $$ \begin{align*} \sum_{n = m_0}^\infty \frac{\delta_n}{\log n}\tau^{(\log^*n)^3} = \infty \end{align*} $$
$$ \begin{align*} \sum_{n = m_0}^\infty \frac{\delta_n}{\log n}\tau^{(\log^*n)^3} = \infty \end{align*} $$
if and only if
 $$ \begin{align*} \sum_{k=0}^\infty (m_{k+1} - m_k)\frac{\delta_{m_k}}{\log m_k} \tau^{(\log^* m_k)^3} \sim \sum_{k=0}^\infty \delta_{m_k} \tau^{(\log^* m_k)^3} = \infty. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^\infty (m_{k+1} - m_k)\frac{\delta_{m_k}}{\log m_k} \tau^{(\log^* m_k)^3} \sim \sum_{k=0}^\infty \delta_{m_k} \tau^{(\log^* m_k)^3} = \infty. \end{align*} $$
This proves Theorem B.
Acknowledgements
This project has been carried out under supervision of Magnus Aspenberg as part of my doctoral thesis. I am very grateful to Magnus for proposing this problem, for his support, and for many valuable discussions and ideas. I express gratitude to my co-supervisor Tomas Persson for helpful comments and remarks. I would also like to thank Viviane Baladi for communicating useful references, and I thank Michael Benedicks for interesting discussions. Finally, I thank the referee whose careful reading and comments helped improve the manuscript.