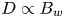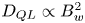1. Introduction
Resonant electron interactions with whistler-mode waves are one of the main drivers of electron pitch-angle scattering and acceleration in various space plasma systems, e.g. solar flares (Bespalov, Zaitsev & Stepanov Reference Bespalov, Zaitsev and Stepanov1991; Filatov & Melnikov Reference Filatov and Melnikov2017; Melnikov & Filatov Reference Melnikov and Filatov2020), solar wind (Tong et al. Reference Tong, Vasko, Artemyev, Bale and Mozer2019; Cattell et al. Reference Cattell, Short, Breneman and Grul2020, Reference Cattell, Short, Breneman, Halekas, Whittesley, Larson, Kasper, Stevens, Case and Moncuquet2021; Mozer et al. Reference Mozer, Bonnell, Halekas, Rahmati, Schum and Vasko2021), shock waves (Hull et al. Reference Hull, Muschietti, Oka, Larson, Mozer, Chaston, Bonnell and Hospodarsky2012; Wilson et al. Reference Wilson, Koval, Szabo, Breneman, Cattell, Goetz, Kellogg, Kersten, Kasper and Maruca2013; Oka et al. Reference Oka, Wilson III, Phan, Hull, Amano, Hoshino, Argall, Le Contel, Agapitov and Gershman2017; Page et al. Reference Page, Vasko, Artemyev and Bale2021), planetary radiation belts (Li et al. Reference Li, Ma, Shen, Zhang, Mauk, Clark, Allegrini, Kurth, Hospodarsky and Hue2021; Menietti et al. Reference Menietti, Averkamp, Kurth, Imai, Faden, Hospodarsky, Santolik, Clark, Allegrini and Elliott2021; Thorne et al. Reference Thorne, Bortnik, Li and Ma2021) and magnetic reconnection regions (Le Contel et al. Reference Le Contel, Roux, Jacquey, Robert, Berthomier, Chust, Grison, Angelopoulos, Sibeck and Chaston2009; Breuillard et al. Reference Breuillard, Le Contel, Retino, Chasapis, Chust, Mirioni, Graham, Wilder, Cohen and Vaivads2016; Zhang et al. Reference Zhang, Angelopoulos, Artemyev and Liu2018a). The basic theoretical framework for description of such interactions is the quasi-linear model (Drummond & Pines Reference Drummond and Pines1962; Vedenov, Velikhov & Sagdeev Reference Vedenov, Velikhov and Sagdeev1962; Andronov & Trakhtengerts Reference Andronov and Trakhtengerts1964; Kennel & Engelmann Reference Kennel and Engelmann1966) that is based on the assumption of weak perturbation of particle dynamics by each single resonance. This assumption reduces the Vlasov equation to the Fokker–Planck diffusion equation (Drummond & Pines Reference Drummond and Pines1962; Vedenov et al. Reference Vedenov, Velikhov and Sagdeev1962) where the main characteristics of wave–particle resonant interactions are diffusion rates. The requirement of a weak perturbation of particle trajectories for a single resonance is equivalent to the requirement that each individual wave–particle resonant interaction should not last for a long time (so particle energy/pitch-angle change for a single resonance is sufficiently small), and there are several mechanisms responsible for particle escape from the resonance.
The original quasi-linear diffusion model assumes the broad spectrum of waves resonating with charged particles (Drummond & Pines Reference Drummond and Pines1962; Vedenov et al. Reference Vedenov, Velikhov and Sagdeev1962), when the resonance width in velocity space $\Delta v_R$![]() is equal to the difference of resonance $v_R$
is equal to the difference of resonance $v_R$![]() velocity (determined for the cyclotron resonant conditions) and wave group velocity $v_g=\partial \omega /\partial k$
velocity (determined for the cyclotron resonant conditions) and wave group velocity $v_g=\partial \omega /\partial k$![]() (where $\omega$
(where $\omega$![]() and $k$
and $k$![]() are wave frequency and wavenumber). The estimate for the resonance width can be derived from the condition that a change of the resonant particle velocity, $\Delta v_R \sim |v_R-v_g|\Delta k/k$
are wave frequency and wavenumber). The estimate for the resonance width can be derived from the condition that a change of the resonant particle velocity, $\Delta v_R \sim |v_R-v_g|\Delta k/k$![]() , will remove the particle from the cyclotron resonance (Karpman Reference Karpman1974). The small factor $\Delta k/k$
, will remove the particle from the cyclotron resonance (Karpman Reference Karpman1974). The small factor $\Delta k/k$![]() is determined by the wave spectrum width in wavenumber space, $\Delta k$
is determined by the wave spectrum width in wavenumber space, $\Delta k$![]() . This mechanism determines the shortness of an individual resonance and justifies the applicability of the diffusion approximation for modelling the dynamics of the charged particle ensemble (Karpman Reference Karpman1974; Le Queau & Roux Reference Le Queau and Roux1987; Shapiro & Sagdeev Reference Shapiro and Sagdeev1997). This description works well for low-amplitude whistler-mode waves resonating with electrons in homogeneous systems (without spatial gradients of the background plasma and magnetic field), e.g. in the solar wind (see review by Verscharen et al. (Reference Verscharen, Chandran, Boella, Halekas, Innocenti, Jagarlamudi, Micera, Pierrard, Štverák and Vasko2022) and references therein).
. This mechanism determines the shortness of an individual resonance and justifies the applicability of the diffusion approximation for modelling the dynamics of the charged particle ensemble (Karpman Reference Karpman1974; Le Queau & Roux Reference Le Queau and Roux1987; Shapiro & Sagdeev Reference Shapiro and Sagdeev1997). This description works well for low-amplitude whistler-mode waves resonating with electrons in homogeneous systems (without spatial gradients of the background plasma and magnetic field), e.g. in the solar wind (see review by Verscharen et al. (Reference Verscharen, Chandran, Boella, Halekas, Innocenti, Jagarlamudi, Micera, Pierrard, Štverák and Vasko2022) and references therein).
The assumption of background magnetic field homogeneity, however, does not work for many space plasma systems. Resonant electron scattering by whistler-mode waves is often observed in magnetic field traps, regions with a spatially localized minimum of the magnetic field magnitude, where charged particles can be trapped and bouncing. Important examples of such traps are the radiation belt dipole field (Lyons & Williams Reference Lyons and Williams1984; Schulz & Lanzerotti Reference Schulz and Lanzerotti1974) and magnetic holes generated by compressional perturbations on a bow shock (Oka et al. Reference Oka, Otsuka, Matsukiyo, Wilson, Argall, Amano, Phan, Hoshino, Le Contel and Gershman2019; Hull et al. Reference Hull, Muschietti, Le Contel, Dorelli and Lindqvist2020; Yao et al. Reference Yao, Shi, Zong, Degeling, Guo, Li, Li, Tian, Zhang and Yao2021). Bouncing within magnetic traps, electrons periodically resonate with whistler-mode waves, and the resonance width for cyclotron resonance in an inhomogeneous field is determined from the condition that a change of the resonant particle velocity (due to the field spatial gradient) $\Delta v_R \sim |\partial v_R/\partial s|/k$![]() will remove the particle from the cyclotron resonance (Trakhtengerts & Rycroft Reference Trakhtengerts and Rycroft2008). If $\Delta v_R$
will remove the particle from the cyclotron resonance (Trakhtengerts & Rycroft Reference Trakhtengerts and Rycroft2008). If $\Delta v_R$![]() is finite, the quasi-linear diffusion model works even for monochromatic waves ($\Delta k \to 0$
is finite, the quasi-linear diffusion model works even for monochromatic waves ($\Delta k \to 0$![]() ) resonating with electrons in magnetic traps (Karpman & Shklyar Reference Karpman and Shklyar1977; Albert Reference Albert2001, Reference Albert2010; Shklyar Reference Shklyar2021). Thus, the only condition required for the application of the quasi-linear diffusion model is that the mirror force due to the background magnetic field gradient should be stronger than the Lorentz force of the wave field (Karpman Reference Karpman1974).
) resonating with electrons in magnetic traps (Karpman & Shklyar Reference Karpman and Shklyar1977; Albert Reference Albert2001, Reference Albert2010; Shklyar Reference Shklyar2021). Thus, the only condition required for the application of the quasi-linear diffusion model is that the mirror force due to the background magnetic field gradient should be stronger than the Lorentz force of the wave field (Karpman Reference Karpman1974).
The small wave intensity approximation, however, is often violated for whistler-mode waves observed in the highly unstable plasma of shock waves (Zhang et al. Reference Zhang, Matsumoto, Kojima and Omura1999; Artemyev et al. Reference Artemyev, Shi, Liu, Zhang, Vasko and Angelopoulos2022) and plasma injections (Zhang et al. Reference Zhang, Thorne, Artemyev, Mourenas, Angelopoulos, Bortnik, Kletzing, Kurth and Hospodarsky2018b, Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019). Such intense waves may resonate with electrons in a nonlinear regime, including effects of phase trapping and phase bunching (e.g. Nunn Reference Nunn1971, Reference Nunn1974; Karpman, Istomin & Shklyar Reference Karpman, Istomin and Shklyar1974; Inan, Bell & Helliwell Reference Inan, Bell and Helliwell1978). Although phase bunching is a strongly nonlinear effect (Albert Reference Albert1993; Bortnik, Thorne & Inan Reference Bortnik, Thorne and Inan2008), due to the smallness of the electron energy and pitch-angle changes in a single resonant phase bunching, it can be incorporated as a drift term into the Fokker–Planck equation (see discussion in Artemyev et al. (Reference Artemyev, Vasiliev, Mourenas, Agapitov and Krasnoselskikh2014), Gan et al. (Reference Gan, Li, Ma, Albert, Artemyev and Bortnik2020) and Allanson et al. (Reference Allanson, Watt, Allison and Ratcliffe2021)). Changes of electron energy and pitch angle due to phase trapping are comparable with the initial energies/pitch angles (Omura, Furuya & Summers Reference Omura, Furuya and Summers2007; Summers & Omura Reference Summers and Omura2007), and thus it is not clear how to include this effect into the Fokker–Planck equation. Several approaches with different integral operators describing the phase trapping contribution to the electron flux dynamics have been proposed (e.g. Omura et al. Reference Omura, Miyashita, Yoshikawa, Summers, Hikishima, Ebihara and Kubota2015; Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev and Mourenas2018b; Vainchtein et al. Reference Vainchtein, Zhang, Artemyev, Mourenas, Angelopoulos and Thorne2018; Hsieh, Kubota & Omura Reference Hsieh, Kubota and Omura2020), but the evaluation of such operators is computationally expensive and significantly changes the Fokker–Planck equation. Thus, it is important and practically useful to propose an approach for incorporation of nonlinear effects without significantly altering models based on the Fokker–Planck equation.
The principal possibility for such an approach has been proposed in Solovev & Shkliar (Reference Solovev and Shkliar1986): namely, the total contribution of trapping and bunching may compensate each other. This idea has been reinvestigated in Mourenas et al. (Reference Mourenas, Zhang, Artemyev, Angelopoulos, Thorne, Bortnik, Neishtadt and Vasiliev2018), where effects of wave modulations were taken into account. Spacecraft observations (e.g. Oka et al. Reference Oka, Otsuka, Matsukiyo, Wilson, Argall, Amano, Phan, Hoshino, Le Contel and Gershman2019; Zhang et al. Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019, Reference Zhang, Mourenas, Artemyev, Angelopoulos, Kurth, Kletzing and Hospodarsky2020b; Foster, Erickson & Omura Reference Foster, Erickson and Omura2021; Artemyev et al. Reference Artemyev, Shi, Liu, Zhang, Vasko and Angelopoulos2022) and numerical simulations (e.g. Nunn & Omura Reference Nunn and Omura2012; Katoh & Omura Reference Katoh and Omura2016; Demekhov, Taubenschuss & Santolık Reference Demekhov, Taubenschuss and Santolık2017; Tao et al. Reference Tao, Zonca, Chen and Wu2020; Zhang et al. Reference Zhang, Demekhov, Katoh, Nunn, Tao, Mourenas, Omura, Artemyev and Angelopoulos2021) show that intense whistler-mode waves mostly propagate in a form of short, modulated wave packets. Typical wave packets include only a few wave periods (see figure 1), which can be an effect of sideband instability of wave generation (Nunn Reference Nunn1986) or overlapping of several waves with close wave frequencies (Zhang et al. Reference Zhang, Mourenas, Artemyev, Angelopoulos, Kurth, Kletzing and Hospodarsky2020b; Nunn et al. Reference Nunn, Zhang, Mourenas and Artemyev2021). Such modulation reduces the efficiency of phase trapping (Tao et al. Reference Tao, Bortnik, Thorne, Albert and Li2012b, Reference Tao, Bortnik, Albert, Thorne and Li2013), and can make the net effect of electron resonant interactions with waves more diffusive (Zhang et al. Reference Zhang, Agapitov, Artemyev, Mourenas, Angelopoulos, Kurth, Bonnell and Hospodarsky2020a; Allanson et al. Reference Allanson, Watt, Ratcliffe, Allison, Meredith, Bentley, Ross and Glauert2020, Reference Allanson, Watt, Allison and Ratcliffe2021; Gan et al. Reference Gan, Li, Ma, Albert, Artemyev and Bortnik2020; An, Wu & Tao Reference An, Wu and Tao2022; Mourenas et al. Reference Mourenas, Zhang, Nunn, Artemyev, Angelopoulos, Tsai and Wilkins2022). Thus, the derivation of diffusion rates is the main question for theoretical description of such regime of wave–particle interaction.

Figure 1. Examples of typical wave packets of whistler-mode waves captured by THEMIS spacecraft (Angelopoulos Reference Angelopoulos2008) in the Earth bow shock (a), foreshock transient (b), outer radiation belt (c) and plasma injection region (d). These events are picked up from statistics published in Artemyev et al. (Reference Artemyev, Shi, Liu, Zhang, Vasko and Angelopoulos2022), Shi et al. (Reference Shi, Liu, Angelopoulos and Zhang2020), Zhang et al. (Reference Zhang, Thorne, Artemyev, Mourenas, Angelopoulos, Bortnik, Kletzing, Kurth and Hospodarsky2018b) and Zhang et al. (Reference Zhang, Angelopoulos, Artemyev and Liu2018a).
In this paper, we propose an approach for the evaluation of diffusion rates including nonlinear effects for intense, but strongly modulated waves. First, in § 2 we describe the concept of the diffusion coefficient model. Then, in § 3 we provide the basic model equations for the diffusion rate and evaluate diffusion rates for arbitrary wave intensity. Finally, in § 4 we show the contribution of nonlinear effects to diffusion rates averaged over wave intensity distributions and discuss the obtained results.
2. Basic concept
To propose the approach for the evaluation of such diffusion rates, let us illustrate the wave modulation effect on nonlinear wave–particle interactions. We consider electrons bouncing in a magnetic trap modelled by a curvature-free dipole field (Bell Reference Bell1984) and their resonant interaction with a monochromatic and intense whistler-mode wave. To evaluate a set of test particle trajectories resonating once with whistler-mode waves, we use the approximation of a monochromatic field-aligned wave. The wave field distribution along the magnetic field lines and the concept of description of wave packets are taken from Mourenas et al. (Reference Mourenas, Zhang, Nunn, Artemyev, Angelopoulos, Tsai and Wilkins2022). We start with the Hamiltonian of a relativistic electron (rest mass is $m_e$![]() and charge is $-e$
and charge is $-e$![]() ) bouncing in a magnetic trap and interacting with a field-aligned whistler-mode wave:
) bouncing in a magnetic trap and interacting with a field-aligned whistler-mode wave:
where ${\boldsymbol p}$![]() is a canonical momentum and ${\boldsymbol A}$
is a canonical momentum and ${\boldsymbol A}$![]() is a vector potential that can be derived from ${\boldsymbol B} = \boldsymbol {\nabla }\times {\boldsymbol A}$
is a vector potential that can be derived from ${\boldsymbol B} = \boldsymbol {\nabla }\times {\boldsymbol A}$![]() with ${\boldsymbol B} = {\boldsymbol B}_0 + {\boldsymbol B}_w$
with ${\boldsymbol B} = {\boldsymbol B}_0 + {\boldsymbol B}_w$![]() . Here ${\boldsymbol B}_0$
. Here ${\boldsymbol B}_0$![]() is the background magnetic field of Earth's dipole and ${\boldsymbol B}_w$
is the background magnetic field of Earth's dipole and ${\boldsymbol B}_w$![]() describes the wave field. As the electron gyroradius is significantly smaller than the dipole magnetic field line curvature, $\sim LR_E$
describes the wave field. As the electron gyroradius is significantly smaller than the dipole magnetic field line curvature, $\sim LR_E$![]() where $R_E$
where $R_E$![]() is Earth's radius and $L$
is Earth's radius and $L$![]() -shell, we consider a curvature-free magnetic field with a pair $(z, p_z)$
-shell, we consider a curvature-free magnetic field with a pair $(z, p_z)$![]() of Cartesian coordinates and momentum playing a role of field-aligned coordinate and momentum $(s,p_{\parallel })$
of Cartesian coordinates and momentum playing a role of field-aligned coordinate and momentum $(s,p_{\parallel })$![]() (see Bell Reference Bell1984). The equatorial magnetic field is determined by a dipole model, $B_0(0)\propto L^{-3}$
(see Bell Reference Bell1984). The equatorial magnetic field is determined by a dipole model, $B_0(0)\propto L^{-3}$![]() . To define a $B_0(z)$
. To define a $B_0(z)$![]() function, we introduce a geomagnetic latitude $\lambda$
function, we introduce a geomagnetic latitude $\lambda$![]() :
:

The smallness of electron gyroradius allows us to write ${\boldsymbol A}_0=x\tilde {B}_0(z) {\boldsymbol e}_y$![]() (${\boldsymbol B}_0 = \boldsymbol {\nabla }\times {\boldsymbol A}_0$
(${\boldsymbol B}_0 = \boldsymbol {\nabla }\times {\boldsymbol A}_0$![]() ), where ${\boldsymbol e}_{r_i}$
), where ${\boldsymbol e}_{r_i}$![]() is the unit vector along the $r_i$
is the unit vector along the $r_i$![]() axis, $r_i = (x, y, z)$
axis, $r_i = (x, y, z)$![]() , and $x$
, and $x$![]() is the cross-field coordinate. As the magnetic field ${\boldsymbol B}_0$
is the cross-field coordinate. As the magnetic field ${\boldsymbol B}_0$![]() is mainly oriented along the $z$
is mainly oriented along the $z$![]() axis, we use the approximation $\tilde {B}_0(z) \approx B_0(z)$
axis, we use the approximation $\tilde {B}_0(z) \approx B_0(z)$![]() . To derive the equation for the wave vector potential ${\boldsymbol A}_w$
. To derive the equation for the wave vector potential ${\boldsymbol A}_w$![]() , we introduce the wave phase $\phi$
, we introduce the wave phase $\phi$![]() and define the magnetic vector ${\boldsymbol B}_w$
and define the magnetic vector ${\boldsymbol B}_w$![]() as $B_w {\boldsymbol e}_x \cos \phi - B_w {\boldsymbol e}_y \sin \phi$
as $B_w {\boldsymbol e}_x \cos \phi - B_w {\boldsymbol e}_y \sin \phi$![]() . Note that $B_w$
. Note that $B_w$![]() may be a function of $z$
may be a function of $z$![]() (or/and $\phi$
(or/and $\phi$![]() ), but for the following derivations we assume that $|{\rm d}B_w/{\rm d}z| \ll |(\partial \phi /\partial z)B_w|$
), but for the following derivations we assume that $|{\rm d}B_w/{\rm d}z| \ll |(\partial \phi /\partial z)B_w|$![]() . The wave frequency $\omega$
. The wave frequency $\omega$![]() and the wave vector ${\boldsymbol k}$
and the wave vector ${\boldsymbol k}$![]() are defined by equations $\omega = -\partial \phi /\partial t$
are defined by equations $\omega = -\partial \phi /\partial t$![]() and ${\boldsymbol k} = \boldsymbol {\nabla } \phi \approx (\partial \phi /\partial z) {\boldsymbol e}_z$
and ${\boldsymbol k} = \boldsymbol {\nabla } \phi \approx (\partial \phi /\partial z) {\boldsymbol e}_z$![]() for field-aligned waves. We consider $\omega ={\rm const.}$
for field-aligned waves. We consider $\omega ={\rm const.}$![]() and determine ${\boldsymbol k}$
and determine ${\boldsymbol k}$![]() from a cold plasma dispersion: $k c / \varOmega _{pe} = ( \varOmega _{ce}/\omega - 1)^{-{1}/{2}}$
from a cold plasma dispersion: $k c / \varOmega _{pe} = ( \varOmega _{ce}/\omega - 1)^{-{1}/{2}}$![]() , where $\varOmega _{pe} = \sqrt {4 {\rm \pi}n_e e^2 / m_e}$
, where $\varOmega _{pe} = \sqrt {4 {\rm \pi}n_e e^2 / m_e}$![]() is the plasma frequency and $\varOmega _{ce} = e B_0 / m_e c$
is the plasma frequency and $\varOmega _{ce} = e B_0 / m_e c$![]() is the cyclotron frequency (Stix Reference Stix1962). Therefore, ${\boldsymbol A}_w\approx B_w {\boldsymbol e}_x \cos \phi / k - B_w {\boldsymbol e}_y \sin \phi / k$
is the cyclotron frequency (Stix Reference Stix1962). Therefore, ${\boldsymbol A}_w\approx B_w {\boldsymbol e}_x \cos \phi / k - B_w {\boldsymbol e}_y \sin \phi / k$![]() and Hamiltonian (2.1) can be presented as
and Hamiltonian (2.1) can be presented as

This Hamiltonian does not depend on $y$![]() , and thus canonical momentum $p_y$
, and thus canonical momentum $p_y$![]() is a constant: $\dot {p}_y = -\partial H/\partial y = 0$
is a constant: $\dot {p}_y = -\partial H/\partial y = 0$![]() . Without loss of generality, we can set $p_y = 0$
. Without loss of generality, we can set $p_y = 0$![]() .
.
In the absence of a wave, this Hamiltonian describes fast $(x,p_x)$![]() oscillations and slow $(z,p_z)$
oscillations and slow $(z,p_z)$![]() oscillations. Thus, we can introduce an adiabatic invariant $I_x=(2{\rm \pi} )^{-1}\oint \,{{{\rm d} x} p_x}$
oscillations. Thus, we can introduce an adiabatic invariant $I_x=(2{\rm \pi} )^{-1}\oint \,{{{\rm d} x} p_x}$![]() as an area surrounded by a closed trajectory in the $(x,p_x)$
as an area surrounded by a closed trajectory in the $(x,p_x)$![]() plane (Landau & Lifshitz Reference Landau and Lifshitz1988):
plane (Landau & Lifshitz Reference Landau and Lifshitz1988):

with

We consider the canonical transformation $(x, p_x) \to (\psi, I_x)$![]() given by a generating function $F_2(x, I_x)=(2{\rm \pi} )^{-1}\int \,{{{\rm d} x} p_x}$
given by a generating function $F_2(x, I_x)=(2{\rm \pi} )^{-1}\int \,{{{\rm d} x} p_x}$![]() (Landau & Lifshitz Reference Landau and Lifshitz1988):
(Landau & Lifshitz Reference Landau and Lifshitz1988):

The corresponding variable transformations are

Thus, equations for $x$![]() and $p_x$
and $p_x$![]() are
are
A new equation for $\varGamma = H / m_e c^2$![]() in terms of variables $(z, p_z)$
in terms of variables $(z, p_z)$![]() and $(\psi, I_x)$
and $(\psi, I_x)$![]() can be written as
can be written as

The Hamiltonian $H=m_ec^2\varGamma$![]() describes the dynamics of two pairs of conjugated variables, $(z, p_z)$
describes the dynamics of two pairs of conjugated variables, $(z, p_z)$![]() and $(\psi, I_x)$
and $(\psi, I_x)$![]() . The system of Hamiltonian equations can be solved with respect to these variables and time $t$
. The system of Hamiltonian equations can be solved with respect to these variables and time $t$![]() . The general approach consists of expanding $H$
. The general approach consists of expanding $H$![]() over $B_w/B_0$
over $B_w/B_0$![]() , keeping only the linear $\sim B_w/B_0$
, keeping only the linear $\sim B_w/B_0$![]() term:
term:

We introduce the wave modulation through the $B_w$![]() dependence on the wave phase $\phi$
dependence on the wave phase $\phi$![]() ($B_w(\phi )$
($B_w(\phi )$![]() periodicity mimics effect if multiple wave packets):
periodicity mimics effect if multiple wave packets):
where $B_m$![]() is the peak wave amplitude, $l$
is the peak wave amplitude, $l$![]() defines the number of wave oscillations (periods) within one wave packet and $h$
defines the number of wave oscillations (periods) within one wave packet and $h$![]() controls the intensity of modulations. The effective wave amplitude $B_{{\rm eff}}$
controls the intensity of modulations. The effective wave amplitude $B_{{\rm eff}}$![]() can be determined by averaging $B_w$
can be determined by averaging $B_w$![]() over the period of modulations:
over the period of modulations:
where ${\rm I}_n(z)$![]() is the modified Bessel function of the first kind. The average intensity of the plane wave with $B_w = B_{{\rm eff}} = {\rm const.}$
is the modified Bessel function of the first kind. The average intensity of the plane wave with $B_w = B_{{\rm eff}} = {\rm const.}$![]() equals the intensity of the modulated wave with $B_w$
equals the intensity of the modulated wave with $B_w$![]() given by (2.11). Thus, to describe the electron diffusion theoretically, the approximation $B_w \approx B_{{\rm eff}} = {\rm const.}$
given by (2.11). Thus, to describe the electron diffusion theoretically, the approximation $B_w \approx B_{{\rm eff}} = {\rm const.}$![]() can be used. However, this assumption neglects nonlinear effects and, therefore, to determine whether the theory is applicable, we perform numerical simulations of modulated waves. Parameter $h$
can be used. However, this assumption neglects nonlinear effects and, therefore, to determine whether the theory is applicable, we perform numerical simulations of modulated waves. Parameter $h$![]() in (2.11) determines the depth of the modulation: at $h \to \infty$
in (2.11) determines the depth of the modulation: at $h \to \infty$![]() and $l\to \infty$
and $l\to \infty$![]() the wave packet reduces to a plane wave. Parameter $l$
the wave packet reduces to a plane wave. Parameter $l$![]() determines the wave packet size with typical values $l\in [10,30]$
determines the wave packet size with typical values $l\in [10,30]$![]() (see Zhang et al. Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019, Reference Zhang, Demekhov, Katoh, Nunn, Tao, Mourenas, Omura, Artemyev and Angelopoulos2021). For numerical simulations we use $h=1$
(see Zhang et al. Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019, Reference Zhang, Demekhov, Katoh, Nunn, Tao, Mourenas, Omura, Artemyev and Angelopoulos2021). For numerical simulations we use $h=1$![]() and $l=20$
and $l=20$![]() . Note that these parameters well satisfy the condition $|{\rm d}B_w/{\rm d}z| \ll |(\partial \phi /\partial z)B_w|$
. Note that these parameters well satisfy the condition $|{\rm d}B_w/{\rm d}z| \ll |(\partial \phi /\partial z)B_w|$![]() , because ${\rm d}B_w/{\rm d}z=(\partial \phi /\partial z) ({\rm d}B_w/{\rm d}\phi )$
, because ${\rm d}B_w/{\rm d}z=(\partial \phi /\partial z) ({\rm d}B_w/{\rm d}\phi )$![]() and $({\rm d}B_w/{\rm d}\phi )B_w^{-1}\sim h/l \ll 1$
and $({\rm d}B_w/{\rm d}\phi )B_w^{-1}\sim h/l \ll 1$![]() .
.
We consider particles having the same initial energy $E_0$![]() and pitch angle $\alpha _0$
and pitch angle $\alpha _0$![]() , but random wave phase $\phi$
, but random wave phase $\phi$![]() and gyrophase $\psi$
and gyrophase $\psi$![]() . Figure 2 shows typical examples of electron resonance interactions with whistler-mode waves obtained by a numerical integration of Hamiltonian equations: diffusive electron scattering by low-amplitude wave (figure 2a), nonlinear resonant interactions with intense coherent wave (figure 2b) and nonlinear resonant interactions with well-modulated intense wave (figure 2c). The resonant interaction occurs once per simulation interval (half of the bounce period), i.e. there is only one point along the unperturbed particle trajectory where the resonant condition $\dot {\phi } + \dot {\psi } = 0$
. Figure 2 shows typical examples of electron resonance interactions with whistler-mode waves obtained by a numerical integration of Hamiltonian equations: diffusive electron scattering by low-amplitude wave (figure 2a), nonlinear resonant interactions with intense coherent wave (figure 2b) and nonlinear resonant interactions with well-modulated intense wave (figure 2c). The resonant interaction occurs once per simulation interval (half of the bounce period), i.e. there is only one point along the unperturbed particle trajectory where the resonant condition $\dot {\phi } + \dot {\psi } = 0$![]() is satisfied. The diffusive scattering is characterized by a symmetric (relative to zero) distribution of energy changes, and thus this process should be described by a diffusion rate $\sim \langle (\Delta E)^2\rangle$
is satisfied. The diffusive scattering is characterized by a symmetric (relative to zero) distribution of energy changes, and thus this process should be described by a diffusion rate $\sim \langle (\Delta E)^2\rangle$![]() . The nonlinear resonances with an intense coherent wave are characterized by a small population changing the energy significantly ($\Delta E>0$
. The nonlinear resonances with an intense coherent wave are characterized by a small population changing the energy significantly ($\Delta E>0$![]() , the phase trapping effect) and a large population with a small energy change, but almost identical for all particles ($\Delta E<0$
, the phase trapping effect) and a large population with a small energy change, but almost identical for all particles ($\Delta E<0$![]() , the phase bunching effect). Thus, nonlinear resonances with a coherent wave should be described separately for trapped and bunched particle populations, and due to the large energy change of the trapped population it is not thought to be possible to include this into the Fokker–Planck equation (see Hsieh & Omura Reference Hsieh and Omura2017a,Reference Hsieh and Omurab; Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev, Zhang, Mourenas and Vainchtein2021b; Zhang et al. Reference Zhang, Artemyev, Angelopoulos, Tsai, Wilkins, Kasahara, Mourenas, Yokota, Keika and Hori2022). The nonlinear resonances with modulated waves are characterized by: (i) an increase of probability for the $\Delta E>0$
, the phase bunching effect). Thus, nonlinear resonances with a coherent wave should be described separately for trapped and bunched particle populations, and due to the large energy change of the trapped population it is not thought to be possible to include this into the Fokker–Planck equation (see Hsieh & Omura Reference Hsieh and Omura2017a,Reference Hsieh and Omurab; Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev, Zhang, Mourenas and Vainchtein2021b; Zhang et al. Reference Zhang, Artemyev, Angelopoulos, Tsai, Wilkins, Kasahara, Mourenas, Yokota, Keika and Hori2022). The nonlinear resonances with modulated waves are characterized by: (i) an increase of probability for the $\Delta E>0$![]() changes; (ii) but also with a decrease in size of $|\Delta E|$
changes; (ii) but also with a decrease in size of $|\Delta E|$![]() itself; and (iii) further a randomization of energy change for this population. Thus, for modulated waves, the resonant wave–particle interaction is closer to diffusive scattering (Tao et al. Reference Tao, Bortnik, Albert, Thorne and Li2013; Zhang et al. Reference Zhang, Agapitov, Artemyev, Mourenas, Angelopoulos, Kurth, Bonnell and Hospodarsky2020a; An et al. Reference An, Wu and Tao2022; Mourenas et al. Reference Mourenas, Zhang, Nunn, Artemyev, Angelopoulos, Tsai and Wilkins2022).
itself; and (iii) further a randomization of energy change for this population. Thus, for modulated waves, the resonant wave–particle interaction is closer to diffusive scattering (Tao et al. Reference Tao, Bortnik, Albert, Thorne and Li2013; Zhang et al. Reference Zhang, Agapitov, Artemyev, Mourenas, Angelopoulos, Kurth, Bonnell and Hospodarsky2020a; An et al. Reference An, Wu and Tao2022; Mourenas et al. Reference Mourenas, Zhang, Nunn, Artemyev, Angelopoulos, Tsai and Wilkins2022).

Figure 2. A set of trajectories obtained by the numerical integration of Hamiltonian equations for a system (2.10a,b). Results are shown for (a) low-amplitude wave with diffusive scattering, (b) coherent high-amplitude wave with trapping and bunching and (c) modulated high-amplitude wave with diffusive-like scattering. System parameters are: electron energy $E_0=100$![]() keV, equatorial pitch angle $\alpha _0 = 40^\circ$
keV, equatorial pitch angle $\alpha _0 = 40^\circ$![]() , number of particles $N = 100$
, number of particles $N = 100$![]() , wave amplitude $B_w = 5$
, wave amplitude $B_w = 5$![]() pT (a), $B_w = 500$
pT (a), $B_w = 500$![]() pT (b,c). System parameters correspond to $L\text {-shell} = 6$
pT (b,c). System parameters correspond to $L\text {-shell} = 6$![]() , whistler-mode waves with frequency equal to $0.35$
, whistler-mode waves with frequency equal to $0.35$![]() of the electron cyclotron frequency at the equator, and the constant plasma frequency equal to $10$
of the electron cyclotron frequency at the equator, and the constant plasma frequency equal to $10$![]() times the electron cyclotron frequency at the equator.
times the electron cyclotron frequency at the equator.
In Figure 3 we show how wave intensity and wave modulation control the efficiency of the nonlinear interactions. Figure 3(a–c) shows distributions of energy changes $\Delta E$![]() depending on the normalized wave amplitude $\varepsilon =B_w/B_{0}(0)$
depending on the normalized wave amplitude $\varepsilon =B_w/B_{0}(0)$![]() . Below $\varepsilon \sim 10^{-4}$
. Below $\varepsilon \sim 10^{-4}$![]() –$10^{-3}$
–$10^{-3}$![]() , the resonant interaction is diffusive with a symmetric $\Delta E$
, the resonant interaction is diffusive with a symmetric $\Delta E$![]() distribution and $\langle {(\Delta E)^2}\rangle ^{1/2}$
distribution and $\langle {(\Delta E)^2}\rangle ^{1/2}$![]() linearly growing with $\varepsilon$
linearly growing with $\varepsilon$![]() . This dependence $\langle {(\Delta E)^2}\rangle ^{1/2}\propto \varepsilon$
. This dependence $\langle {(\Delta E)^2}\rangle ^{1/2}\propto \varepsilon$![]() demonstrates the applicability of the unperturbed trajectory approximation, a core assumption of the quasi-linear diffusion theory (Tao et al. Reference Tao, Bortnik, Albert, Liu and Thorne2011, Reference Tao, Bortnik, Albert and Thorne2012a; Allanson et al. Reference Allanson, Watt, Ratcliffe, Allison, Meredith, Bentley, Ross and Glauert2020). After the wave amplitude reaches a certain threshold (depending on the electron energy, pitch angle and system characteristics; see Omura et al. Reference Omura, Matsumoto, Nunn and Rycroft1991; Shklyar & Matsumoto Reference Shklyar and Matsumoto2009), the resonant interaction becomes nonlinear with a clear formation of a population of trapped electrons (a separate group of large positive $\Delta E$
demonstrates the applicability of the unperturbed trajectory approximation, a core assumption of the quasi-linear diffusion theory (Tao et al. Reference Tao, Bortnik, Albert, Liu and Thorne2011, Reference Tao, Bortnik, Albert and Thorne2012a; Allanson et al. Reference Allanson, Watt, Ratcliffe, Allison, Meredith, Bentley, Ross and Glauert2020). After the wave amplitude reaches a certain threshold (depending on the electron energy, pitch angle and system characteristics; see Omura et al. Reference Omura, Matsumoto, Nunn and Rycroft1991; Shklyar & Matsumoto Reference Shklyar and Matsumoto2009), the resonant interaction becomes nonlinear with a clear formation of a population of trapped electrons (a separate group of large positive $\Delta E$![]() in figure 3a–c) and a highly asymmetric $\Delta E$
in figure 3a–c) and a highly asymmetric $\Delta E$![]() distribution (most of the electrons experience phase bunching and form a large maximum at $\Delta E<0$
distribution (most of the electrons experience phase bunching and form a large maximum at $\Delta E<0$![]() ). For such nonlinear resonant interactions the $\Delta E$
). For such nonlinear resonant interactions the $\Delta E$![]() distribution with phase-trapped and phase-bunched populations cannot be characterized by a diffusion $\langle {(\Delta E)^2}\rangle$
distribution with phase-trapped and phase-bunched populations cannot be characterized by a diffusion $\langle {(\Delta E)^2}\rangle$![]() only, and thus it is not known how to include this regime of resonant interactions into the Fokker–Planck equation.
only, and thus it is not known how to include this regime of resonant interactions into the Fokker–Planck equation.

Figure 3. Distributions of the energy change $\Delta E$![]() for different $B_{{\rm eff}}$
for different $B_{{\rm eff}}$![]() with $h=1$
with $h=1$![]() and $l=20$
and $l=20$![]() for coherent (a–c) and modulated (d–f) waves with $\Delta E \propto B_w$
for coherent (a–c) and modulated (d–f) waves with $\Delta E \propto B_w$![]() fitting (black dashed lines) and with $\langle {(\Delta E)^2}\rangle ^{1/2}$
fitting (black dashed lines) and with $\langle {(\Delta E)^2}\rangle ^{1/2}$![]() profiles (black dots): (a,d) $E_0 = 100$
profiles (black dots): (a,d) $E_0 = 100$![]() keV, $\alpha _0 = 40^{\circ }$
keV, $\alpha _0 = 40^{\circ }$![]() ; (b,e) $E_0 = 100$
; (b,e) $E_0 = 100$![]() keV, $\alpha _0 = 60^{\circ }$
keV, $\alpha _0 = 60^{\circ }$![]() ; (c, f) $E_0 = 300$
; (c, f) $E_0 = 300$![]() keV, $\alpha _0 = 60^{\circ }$
keV, $\alpha _0 = 60^{\circ }$![]() . For each $B_w$
. For each $B_w$![]() we use $10^4$
we use $10^4$![]() trajectories to evaluate the $\Delta E$
trajectories to evaluate the $\Delta E$![]() distribution, each particle resonates with the wave only once and $\Delta E$
distribution, each particle resonates with the wave only once and $\Delta E$![]() is the energy change for a single resonance, initial particle phases and wave phases are random and thus for a modulated case the actual wave amplitude is different for different particles having the same energy/pitch angle. For each $B_{{\rm eff}}$
is the energy change for a single resonance, initial particle phases and wave phases are random and thus for a modulated case the actual wave amplitude is different for different particles having the same energy/pitch angle. For each $B_{{\rm eff}}$![]() the $\Delta E$
the $\Delta E$![]() distribution is normalized to one. System parameters correspond to $L\text {-shell} = 6$
distribution is normalized to one. System parameters correspond to $L\text {-shell} = 6$![]() , whistler-mode waves with frequency equal to $0.35$
, whistler-mode waves with frequency equal to $0.35$![]() of the electron cyclotron frequency at the equator, and the constant plasma frequency equal to $10$
of the electron cyclotron frequency at the equator, and the constant plasma frequency equal to $10$![]() times the electron cyclotron frequency at the equator.
times the electron cyclotron frequency at the equator.
Figure 3(d–f) shows $\Delta E$![]() distributions as a function of wave amplitude for strongly modulated waves. For small wave intensity, $\varepsilon <10^{-4}$
distributions as a function of wave amplitude for strongly modulated waves. For small wave intensity, $\varepsilon <10^{-4}$![]() , there is the same diffusive regime of wave–particle resonant interactions as for non-modulated waves: a symmetric $\Delta E$
, there is the same diffusive regime of wave–particle resonant interactions as for non-modulated waves: a symmetric $\Delta E$![]() distribution with $\langle {(\Delta E)^2}\rangle ^{1/2}\propto \varepsilon$
distribution with $\langle {(\Delta E)^2}\rangle ^{1/2}\propto \varepsilon$![]() . With amplitude increasing, the regime of wave–particle resonant interaction changes. However, the wave modulation does not allow strong trapping acceleration (there is no population with large positive $\Delta E$
. With amplitude increasing, the regime of wave–particle resonant interaction changes. However, the wave modulation does not allow strong trapping acceleration (there is no population with large positive $\Delta E$![]() ), but increases the number of trapped particles (the populations of particles with $\Delta E>0$
), but increases the number of trapped particles (the populations of particles with $\Delta E>0$![]() and with $\Delta E<0$
and with $\Delta E<0$![]() are comparable even for $\varepsilon >10^{-3}$
are comparable even for $\varepsilon >10^{-3}$![]() ). Thus, for intense modulated waves, the $\Delta E$
). Thus, for intense modulated waves, the $\Delta E$![]() distribution remains almost symmetric and can be characterized by $\langle {(\Delta E)^2}\rangle$
distribution remains almost symmetric and can be characterized by $\langle {(\Delta E)^2}\rangle$![]() . Despite such a symmetric $\Delta E$
. Despite such a symmetric $\Delta E$![]() distribution, the resonant interaction for large $\varepsilon$
distribution, the resonant interaction for large $\varepsilon$![]() is nonlinear, and the wave field alters electron dynamics in the resonance. This results in inapplicability of the unperturbed trajectory approximation, and thus $\langle {(\Delta E)^2}\rangle ^{1/2}\propto \varepsilon ^A$
is nonlinear, and the wave field alters electron dynamics in the resonance. This results in inapplicability of the unperturbed trajectory approximation, and thus $\langle {(\Delta E)^2}\rangle ^{1/2}\propto \varepsilon ^A$![]() with $A<1$
with $A<1$![]() . Therefore, for intense modulated waves we deal with diffusion of resonant electrons, but it is not a quasi-linear diffusion. In this study, we aim to derive the diffusion coefficient $\sim \langle {(\Delta E)^2}\rangle$
. Therefore, for intense modulated waves we deal with diffusion of resonant electrons, but it is not a quasi-linear diffusion. In this study, we aim to derive the diffusion coefficient $\sim \langle {(\Delta E)^2}\rangle$![]() as a function of $\varepsilon$
as a function of $\varepsilon$![]() for a wide $\varepsilon$
for a wide $\varepsilon$![]() range. Figure 3(d–f) shows that $\langle {(\Delta E)^2}\rangle$
range. Figure 3(d–f) shows that $\langle {(\Delta E)^2}\rangle$![]() for small $\varepsilon$
for small $\varepsilon$![]() should be similar to that for the quasi-linear diffusion (see also Albert Reference Albert2010), whereas for large $\varepsilon$
should be similar to that for the quasi-linear diffusion (see also Albert Reference Albert2010), whereas for large $\varepsilon$![]() the dispersion $\langle {(\Delta E)^2}\rangle$
the dispersion $\langle {(\Delta E)^2}\rangle$![]() should be about $\langle {\Delta E}\rangle ^2$
should be about $\langle {\Delta E}\rangle ^2$![]() of the phase-bunched particle population. We have checked this assumption with an analytical approach, which we further introduce.
of the phase-bunched particle population. We have checked this assumption with an analytical approach, which we further introduce.
3. The diffusion coefficient model for an arbitrary wave intensity
The Hamiltonian $H=m_ec^2\gamma$![]() with $\gamma$
with $\gamma$![]() given by (2.9) determines the electron dynamics. For this Hamiltonian system, we derive an analytical approximation for the energy change $\Delta E = m_e c^2 \Delta \gamma$
given by (2.9) determines the electron dynamics. For this Hamiltonian system, we derive an analytical approximation for the energy change $\Delta E = m_e c^2 \Delta \gamma$![]() due to a single resonant interaction. Such a change depends on the initial electron energy and pitch angle, and on the initial phase $\phi +\psi$
due to a single resonant interaction. Such a change depends on the initial electron energy and pitch angle, and on the initial phase $\phi +\psi$![]() . Thus, we finally aim to find a mean value $V_\gamma =\langle \Delta \gamma \rangle$
. Thus, we finally aim to find a mean value $V_\gamma =\langle \Delta \gamma \rangle$![]() and variance $D_{\gamma \gamma }=\langle (\Delta \gamma )^2 \rangle$
and variance $D_{\gamma \gamma }=\langle (\Delta \gamma )^2 \rangle$![]() with the averaging over initial phases.
with the averaging over initial phases.
To derive the $\Delta \gamma$![]() equation for $H=m_ec^2\gamma$
equation for $H=m_ec^2\gamma$![]() , we follow the approach from Neishtadt & Vasiliev (Reference Neishtadt and Vasiliev2006) and Artemyev et al. (Reference Artemyev, Neishtadt, Vainchtein, Vasiliev, Vasko and Zelenyi2018a) for the perturbation theory application to a resonant system containing a phase and a small wave amplitude, $B_w / B_0 \ll 1$
, we follow the approach from Neishtadt & Vasiliev (Reference Neishtadt and Vasiliev2006) and Artemyev et al. (Reference Artemyev, Neishtadt, Vainchtein, Vasiliev, Vasko and Zelenyi2018a) for the perturbation theory application to a resonant system containing a phase and a small wave amplitude, $B_w / B_0 \ll 1$![]() (more precisely, $\varepsilon = B_w / B_0(0) \ll 1$
(more precisely, $\varepsilon = B_w / B_0(0) \ll 1$![]() ). For analytical consideration we assume that $B_w$
). For analytical consideration we assume that $B_w$![]() is a constant or a function of the magnetic latitude with spatial gradient much weaker than wave phase gradients $\partial \phi /\partial s=k$
is a constant or a function of the magnetic latitude with spatial gradient much weaker than wave phase gradients $\partial \phi /\partial s=k$![]() .
.
The Hamiltonian from (2.10a,b) is time-dependent as $\phi = \phi (t)$![]() . To find the invariant equation, we define a generation function of the second kind $F_2(s, \psi, P_z, I)$
. To find the invariant equation, we define a generation function of the second kind $F_2(s, \psi, P_z, I)$![]() for $(s, p_z, \psi, I_x) \to (\tilde {z}, P_z, \zeta, I)$
for $(s, p_z, \psi, I_x) \to (\tilde {z}, P_z, \zeta, I)$![]() :
:

As a result, a modified Hamiltonian ${\mathcal {H}}$![]() is
is

Note that $\partial _t {\mathcal {H}} = 0$![]() . Thus, in the zeroth order of $\varepsilon$
. Thus, in the zeroth order of $\varepsilon$![]() the first invariant of this system can be written as
the first invariant of this system can be written as
Without a wave perturbation, $I$![]() is invariant ($I = \textrm {const.}$
is invariant ($I = \textrm {const.}$![]() ) by its definition, and $\gamma$
) by its definition, and $\gamma$![]() has a constant value, considering (3.3). Thus, all derivatives of those variables are first-order terms of $\varepsilon$
has a constant value, considering (3.3). Thus, all derivatives of those variables are first-order terms of $\varepsilon$![]() or higher. Resonant wave–particle interactions change the particle energy $E = m_e c^2 \gamma$
or higher. Resonant wave–particle interactions change the particle energy $E = m_e c^2 \gamma$![]() : $\gamma _0 \to \gamma _0 + \Delta \gamma$
: $\gamma _0 \to \gamma _0 + \Delta \gamma$![]() , where $\gamma _0$
, where $\gamma _0$![]() is the initial Lorentz factor (at $t = 0$
is the initial Lorentz factor (at $t = 0$![]() ). The resonance equation can be written as $\dot {\zeta } = \partial {\mathcal {H}}/\partial I = 0$
). The resonance equation can be written as $\dot {\zeta } = \partial {\mathcal {H}}/\partial I = 0$![]() . This equation characterizes the dynamics of the system near the resonance point and, considering (3.2), can be written as (subscript $R$
. This equation characterizes the dynamics of the system near the resonance point and, considering (3.2), can be written as (subscript $R$![]() means that the function is evaluated at resonance)
means that the function is evaluated at resonance)
The Hamiltonian ${\mathcal {H}}$![]() has to be expanded near the resonance point $\dot {\zeta } = 0$
has to be expanded near the resonance point $\dot {\zeta } = 0$![]() with values $\gamma _R = \gamma _0 + O(\varepsilon )$
with values $\gamma _R = \gamma _0 + O(\varepsilon )$![]() , $I_R = I_0 + O(\varepsilon )$
, $I_R = I_0 + O(\varepsilon )$![]() :
:

where
Thus, the final form of ${\mathcal {H}}$![]() is
is

The second term of ${\mathcal {H}}$![]() from (3.7) is an analogue of the kinetic energy of the particle motion near the resonance, with $I - I_R$
from (3.7) is an analogue of the kinetic energy of the particle motion near the resonance, with $I - I_R$![]() being the canonical momentum and $g$
being the canonical momentum and $g$![]() playing the role of mass. Thus, we introduce a generating function of the third kind $F_3(\tilde {z}, \tilde {\zeta }, P_z, I)$
playing the role of mass. Thus, we introduce a generating function of the third kind $F_3(\tilde {z}, \tilde {\zeta }, P_z, I)$![]() for $(z, P_z, \zeta, I) \to (\tilde {z}, \tilde {P}_z, \tilde {\zeta }, P_{\zeta })$
for $(z, P_z, \zeta, I) \to (\tilde {z}, \tilde {P}_z, \tilde {\zeta }, P_{\zeta })$![]() :
:

As $I$![]() is an invariant in the unperturbed system, $\partial _{P_z} I_R \sim \varepsilon$
is an invariant in the unperturbed system, $\partial _{P_z} I_R \sim \varepsilon$![]() and $\partial _{\tilde {z}} I_R \sim \varepsilon$
and $\partial _{\tilde {z}} I_R \sim \varepsilon$![]() . This means that the first term of the Hamiltonian ${\mathcal {H}}$
. This means that the first term of the Hamiltonian ${\mathcal {H}}$![]() can be expanded with respect to $\varepsilon$
can be expanded with respect to $\varepsilon$![]() :
:

Substituting the expanded form of ${\mathcal {H}}_R$![]() into (3.7), we obtain two separate parts of the Hamiltonian ${\mathcal {H}}={\mathcal {H}}_R+{\mathcal {H}}_\zeta$
into (3.7), we obtain two separate parts of the Hamiltonian ${\mathcal {H}}={\mathcal {H}}_R+{\mathcal {H}}_\zeta$![]() , ${\mathcal {H}}_R = m_e c^2 \gamma _R - \omega I_R$
, ${\mathcal {H}}_R = m_e c^2 \gamma _R - \omega I_R$![]() with canonical variables $(\tilde {z}, \tilde {P}_z, \zeta, P_{\zeta })$
with canonical variables $(\tilde {z}, \tilde {P}_z, \zeta, P_{\zeta })$![]() :
:
Hamiltonian ${\mathcal {H}}_R$![]() describes $(\tilde {z}, \tilde {P}_z)\approx (z, P_z)$
describes $(\tilde {z}, \tilde {P}_z)\approx (z, P_z)$![]() dynamics in the resonance, and this Hamiltonian does not depend on the fast phase $\zeta$
dynamics in the resonance, and this Hamiltonian does not depend on the fast phase $\zeta$![]() . Hamiltonian ${\mathcal {H}}_{\zeta }$
. Hamiltonian ${\mathcal {H}}_{\zeta }$![]() is a $\zeta$
is a $\zeta$![]() -dependent pendulum Hamiltonian that describes fast phase and conjugated momentum dynamics around the resonance. Coefficients of Hamiltonian ${\mathcal {H}}_\zeta$
-dependent pendulum Hamiltonian that describes fast phase and conjugated momentum dynamics around the resonance. Coefficients of Hamiltonian ${\mathcal {H}}_\zeta$![]() depend on $(\tilde {z}, \tilde {P}_z)$
depend on $(\tilde {z}, \tilde {P}_z)$![]() and slowly change along the resonant trajectory.
and slowly change along the resonant trajectory.
In the Hamiltonian ${\mathcal {H}}_\zeta$![]() , an effective potential energy, ${\mathcal {H}}_\zeta -P_\zeta ^2/2g$
, an effective potential energy, ${\mathcal {H}}_\zeta -P_\zeta ^2/2g$![]() , contains two terms: the first term $\sim \{{\mathcal {H}}_R,I_R\}_{\tilde {z}, \tilde {P}_z}$
, contains two terms: the first term $\sim \{{\mathcal {H}}_R,I_R\}_{\tilde {z}, \tilde {P}_z}$![]() describes the impact of the background magnetic field gradient and the second term $\sim B_w$
describes the impact of the background magnetic field gradient and the second term $\sim B_w$![]() describes the effect of the wave's field. The important system parameter is the ratio of magnitudes of these two terms:
describes the effect of the wave's field. The important system parameter is the ratio of magnitudes of these two terms:
Taking into account ${\mathcal {H}}_R=m_ec^2\gamma _R-\omega I_R$![]() , we can rewrite the Poisson bracket:
, we can rewrite the Poisson bracket:
where $\gamma _R$![]() and $I_R$
and $I_R$![]() are given by (3.2) and (3.4a,b). Combining these equations, we obtain (subscript $R$
are given by (3.2) and (3.4a,b). Combining these equations, we obtain (subscript $R$![]() is omitted in equations below)
is omitted in equations below)

Therefore, the Poisson bracket $\{\cdots \} = \{\cdots \}_{s,P_{\parallel }}$![]() can be rewritten as
can be rewritten as

To determine $\partial _z [ \ln ({\omega }/{k c}) ]$![]() we use the cold plasma approximation, $k c / \omega = (\varOmega _{pe} / \omega ) ( \varOmega _{ce}/\omega - 1)^{-{1}/{2}}$
we use the cold plasma approximation, $k c / \omega = (\varOmega _{pe} / \omega ) ( \varOmega _{ce}/\omega - 1)^{-{1}/{2}}$![]() , with constant plasma frequency $\varOmega _{pe}$
, with constant plasma frequency $\varOmega _{pe}$![]() . Therefore, for partial derivatives in $\{ \gamma, I \}$
. Therefore, for partial derivatives in $\{ \gamma, I \}$![]() we can write
we can write

and

Having $\{ \gamma, I \}$![]() , we can determine $a$
, we can determine $a$![]() from (3.11) at the resonance. As we show, this is the main parameter controlling the energy change due to the resonant wave–particle interaction.
from (3.11) at the resonance. As we show, this is the main parameter controlling the energy change due to the resonant wave–particle interaction.
To write an equation for the resonant energy change, $\Delta \gamma$![]() , we use the invariant from (3.3):
, we use the invariant from (3.3):

where $\varOmega _{ce,R}=eB_{0,R}/m_ec$![]() and $B_{0,R}$
and $B_{0,R}$![]() is defined at the resonant $z=z(t_R)$
is defined at the resonant $z=z(t_R)$![]() for given initial energy and pitch angle. For $\dot \zeta$
for given initial energy and pitch angle. For $\dot \zeta$![]() we use the Hamiltonian equation $\dot \zeta =\partial {\mathcal {H}}_\zeta /\partial P_\zeta$
we use the Hamiltonian equation $\dot \zeta =\partial {\mathcal {H}}_\zeta /\partial P_\zeta$![]() . The resonance is defined by $\dot {\zeta } = P_{\zeta } / g = 0$
. The resonance is defined by $\dot {\zeta } = P_{\zeta } / g = 0$![]() with the solution $\zeta _R$
with the solution $\zeta _R$![]() according to $\zeta _R + a\cos \zeta _R=\xi$
according to $\zeta _R + a\cos \zeta _R=\xi$![]() with the resonant energy $\xi = {\mathcal {H}}_\zeta / \{ {\mathcal {H}}_R, I_R \}$
with the resonant energy $\xi = {\mathcal {H}}_\zeta / \{ {\mathcal {H}}_R, I_R \}$![]() . Thus, (3.17) can be written as
. Thus, (3.17) can be written as

Figure 4(a) shows the $f(a,\xi )$![]() function. This function is periodic with period $2{\rm \pi}$
function. This function is periodic with period $2{\rm \pi}$![]() for $\xi$
for $\xi$![]() (this can be shown analytically; see Appendix A).
(this can be shown analytically; see Appendix A).

Figure 4. (a) Profiles of $f(a,\xi )$![]() for three $a$
for three $a$![]() values. (b) Profiles of $\langle f(a,\xi )\rangle _{\xi }$
values. (b) Profiles of $\langle f(a,\xi )\rangle _{\xi }$![]() and $\langle (f(a,\xi ))^2\rangle _{\xi }$
and $\langle (f(a,\xi ))^2\rangle _{\xi }$![]() .
.
The value of $\xi$![]() varies with the initial conditions, i.e. with wave phase $\phi$
varies with the initial conditions, i.e. with wave phase $\phi$![]() , gyrophase $\psi$
, gyrophase $\psi$![]() and electron position on the trajectory in $(s,P_\parallel )$
and electron position on the trajectory in $(s,P_\parallel )$![]() plane far from the resonance. Assuming a uniform distribution of these parameters, we numerically integrate an ensemble of trajectories as determined by (2.10a,b), and so determine the probability function for $\xi$
plane far from the resonance. Assuming a uniform distribution of these parameters, we numerically integrate an ensemble of trajectories as determined by (2.10a,b), and so determine the probability function for $\xi$![]() . Figure 5 shows such distributions of $\xi$
. Figure 5 shows such distributions of $\xi$![]() for three sets of the system parameters. These distributions are very close to uniform distributions with $\xi \in [0,2{\rm \pi} ]$
for three sets of the system parameters. These distributions are very close to uniform distributions with $\xi \in [0,2{\rm \pi} ]$![]() , which suggests that averaging over initial parameters $\phi$
, which suggests that averaging over initial parameters $\phi$![]() , $\psi$
, $\psi$![]() and $s$
and $s$![]() can be substituted with averaging over $\xi$
can be substituted with averaging over $\xi$![]() with constant weights (see also discussion in Itin, Neishtadt & Vasiliev (Reference Itin, Neishtadt and Vasiliev2000) and Albert et al. (Reference Albert, Artemyev, Li, Gan and Ma2022)):
with constant weights (see also discussion in Itin, Neishtadt & Vasiliev (Reference Itin, Neishtadt and Vasiliev2000) and Albert et al. (Reference Albert, Artemyev, Li, Gan and Ma2022)):

where $\varPi$![]() is the parametric range ($3D$
is the parametric range ($3D$![]() uniform distribution) and $\xi _0 = \xi _0(a)$
uniform distribution) and $\xi _0 = \xi _0(a)$![]() determines the case when the integral diverges near the resonance point (see Appendix A). Thus, the equation for the variance $D_{\gamma \gamma }$
determines the case when the integral diverges near the resonance point (see Appendix A). Thus, the equation for the variance $D_{\gamma \gamma }$![]() can be written as
can be written as
where $D_{\gamma \gamma }$![]() can be considered as a diffusion rate for a unit time interval between two resonant interactions (the actual diffusion rate is the ratio of $\langle D_{\gamma \gamma } \rangle$
can be considered as a diffusion rate for a unit time interval between two resonant interactions (the actual diffusion rate is the ratio of $\langle D_{\gamma \gamma } \rangle$![]() and a fraction of electron bounce period).
and a fraction of electron bounce period).

Figure 5. Probability distributions of $\xi$![]() for $10^5$
for $10^5$![]() trajectories and (a) $E_0 = 100$
trajectories and (a) $E_0 = 100$![]() keV, $\alpha _0 = 40^{\circ }$
keV, $\alpha _0 = 40^{\circ }$![]() , $B_w = 50$
, $B_w = 50$![]() pT, (b) $E_0 = 100$
pT, (b) $E_0 = 100$![]() keV, $\alpha _0 = 40^{\circ }$
keV, $\alpha _0 = 40^{\circ }$![]() , $B_w = 500$
, $B_w = 500$![]() pT, (c) $E_0 = 300$
pT, (c) $E_0 = 300$![]() keV, $\alpha _0 = 60^{\circ }$
keV, $\alpha _0 = 60^{\circ }$![]() , $B_w = 500$
, $B_w = 500$![]() pT.
pT.
The function $f(a,\xi )$![]() determines the difference of the diffusion coefficient $\sim D_{\gamma \gamma }$
determines the difference of the diffusion coefficient $\sim D_{\gamma \gamma }$![]() and the quasi-linear model. For the case of $a \ll 1$
and the quasi-linear model. For the case of $a \ll 1$![]() , $D_{\gamma \gamma }$
, $D_{\gamma \gamma }$![]() asymptotically tends to the quasi-linear equation $D_{\gamma \gamma } = \langle (\Delta \gamma )^2 \rangle \sim (B_w / B_0)^2$
asymptotically tends to the quasi-linear equation $D_{\gamma \gamma } = \langle (\Delta \gamma )^2 \rangle \sim (B_w / B_0)^2$![]() (Albert Reference Albert2010). To verify that, we have to expand $f(a,\xi )$
(Albert Reference Albert2010). To verify that, we have to expand $f(a,\xi )$![]() in a Taylor series:
in a Taylor series:

and thus $D_{\gamma \gamma } \propto (B_w/B_0)\langle f^2(a,\xi ) \rangle _{\xi } \propto (B_w/B_0)^2$![]() , because $a\propto B_w/B_0$
, because $a\propto B_w/B_0$![]() (see (3.11)).
(see (3.11)).
Figure 4(b) shows that there are two $a$![]() ranges with different wave–particle resonant effects: for $a<1$
ranges with different wave–particle resonant effects: for $a<1$![]() the mean value of $\langle f(a,\xi ) \rangle _{\xi }$
the mean value of $\langle f(a,\xi ) \rangle _{\xi }$![]() equals zero and there is only a particle diffusion $\propto a \langle f^2(a,\xi ) \rangle _{\xi }$
equals zero and there is only a particle diffusion $\propto a \langle f^2(a,\xi ) \rangle _{\xi }$![]() , whereas for $a>1$
, whereas for $a>1$![]() there is a non-zero negative $\langle f(a,\xi ) \rangle _{\xi }$
there is a non-zero negative $\langle f(a,\xi ) \rangle _{\xi }$![]() . The diffusion $\propto a \langle f^2(a,\xi ) \rangle _{\xi }$
. The diffusion $\propto a \langle f^2(a,\xi ) \rangle _{\xi }$![]() has a local maximum at $a\approx 1.0392$
has a local maximum at $a\approx 1.0392$![]() , a local minimum at $a\approx 1.5923$
, a local minimum at $a\approx 1.5923$![]() and then increases with $a$
and then increases with $a$![]() as $\propto a$
as $\propto a$![]() . The mean value $\langle f(a,\xi ) \rangle _{\xi }$
. The mean value $\langle f(a,\xi ) \rangle _{\xi }$![]() has an asymptote $4 \sqrt {2} / {\rm \pi}$
has an asymptote $4 \sqrt {2} / {\rm \pi}$![]() for $a\gg 1$
for $a\gg 1$![]() . There is an important property of $f(a,\xi )$
. There is an important property of $f(a,\xi )$![]() : $\langle f^2(a,\xi ) \rangle _{\xi }-\langle f(a,\xi ) \rangle _{\xi }^2 \to 0$
: $\langle f^2(a,\xi ) \rangle _{\xi }-\langle f(a,\xi ) \rangle _{\xi }^2 \to 0$![]() for $a\to \infty$
for $a\to \infty$![]() (see Appendix A for details). This property defines the behaviour of the diffusion rate $\propto a\langle f^2(a,\xi ) \rangle _{\xi }$
(see Appendix A for details). This property defines the behaviour of the diffusion rate $\propto a\langle f^2(a,\xi ) \rangle _{\xi }$![]() for $a\gg 1$
for $a\gg 1$![]() .
.
As shown in figure 3, the strong wave modulation should result in a symmetric distribution of $\Delta \gamma$![]() with a zero mean value and with the dispersion $\langle (\Delta \gamma )^2 \rangle$
with a zero mean value and with the dispersion $\langle (\Delta \gamma )^2 \rangle$![]() about $\langle (\Delta \gamma )^2 \rangle _{\xi }$
about $\langle (\Delta \gamma )^2 \rangle _{\xi }$![]() where $\xi$
where $\xi$![]() averaging is performed for population of phase-bunched particles (i.e. particles with $\Delta \gamma <0$
averaging is performed for population of phase-bunched particles (i.e. particles with $\Delta \gamma <0$![]() ). Therefore, for such strongly modulated waves, we consider $\langle (\Delta \gamma )^2 \rangle _{\xi }$
). Therefore, for such strongly modulated waves, we consider $\langle (\Delta \gamma )^2 \rangle _{\xi }$![]() as a diffusion rate for both $a<1$
as a diffusion rate for both $a<1$![]() and $a>1$
and $a>1$![]() parametric ranges. Figure 6 shows $\langle (\Delta \gamma )^2 \rangle _{\xi }$
parametric ranges. Figure 6 shows $\langle (\Delta \gamma )^2 \rangle _{\xi }$![]() distributions in energy and pitch-angle space for three typical wave intensities. Electrons of lower energy/higher pitch angle resonate with waves closer to the equatorial plane, where $a$
distributions in energy and pitch-angle space for three typical wave intensities. Electrons of lower energy/higher pitch angle resonate with waves closer to the equatorial plane, where $a$![]() is large because $\{ \gamma _R, I_R \}_{s, P_{\parallel }} \propto \partial \varOmega _{ce}/\partial s$
is large because $\{ \gamma _R, I_R \}_{s, P_{\parallel }} \propto \partial \varOmega _{ce}/\partial s$![]() and tends to zero around the equator.
and tends to zero around the equator.

Figure 6. Two-dimensional energy/pitch-angle maps of $(E_0,\alpha _{0})$![]() for (a) $B_w = 100$
for (a) $B_w = 100$![]() pT, (b) $B_w = 500$
pT, (b) $B_w = 500$![]() pT and (c) $B_w = 1000$
pT and (c) $B_w = 1000$![]() pT. Black curve shows $a=1$
pT. Black curve shows $a=1$![]() .
.
4. Discussion and conclusions
In this study, we derive the diffusion rate for electrons resonantly interacting with intense whistler-mode waves. Although such intense waves may resonate with electrons nonlinearly, the efficiency of this interaction would be significantly reduced by wave modulation (Zhang et al. Reference Zhang, Agapitov, Artemyev, Mourenas, Angelopoulos, Kurth, Bonnell and Hospodarsky2020a; Tao et al. Reference Tao, Bortnik, Thorne, Albert and Li2012b; Allanson et al. Reference Allanson, Watt, Allison and Ratcliffe2021; An et al. Reference An, Wu and Tao2022; Gan et al. Reference Gan, Li, Ma, Albert, Artemyev and Bortnik2020, Reference Gan, Li, Ma, Artemyev and Albert2022). Indeed, most of the intense whistler-mode waves that are observed in space plasma systems (like Earth's radiation belts, bow shock, foreshock transients and plasma injections) are presented in the form of short well-modulated wave packets (see examples in figure 1 and references in the figure caption).
Using test particle simulations, we show that such modulation will reduce the difference between energy changes of phase trapping and phase bunching electrons, and make the energy change distribution more symmetric (see figure 3). In the limit of total symmetrization of energy change distribution (extremely modulated wave packets), the main (and the only one) characteristic of electron resonant scattering will be the diffusion rate describing the dispersion of this distribution. Such a diffusion rate can be evaluated analytically: the dispersion of the energy changes $\langle (\Delta \gamma )^2\rangle _\xi$![]() tends to $\langle \Delta \gamma \rangle _\xi ^2$
tends to $\langle \Delta \gamma \rangle _\xi ^2$![]() for large wave amplitudes. That is to say, $\langle (\Delta \gamma )^2\rangle _\xi \to \langle \Delta \gamma \rangle _\xi ^2 \propto B_w$
for large wave amplitudes. That is to say, $\langle (\Delta \gamma )^2\rangle _\xi \to \langle \Delta \gamma \rangle _\xi ^2 \propto B_w$![]() for $a\gg 1$
for $a\gg 1$![]() (i.e. when wave amplitude is sufficiently large).
(i.e. when wave amplitude is sufficiently large).
Using this theoretical result, we can calculate the ratio of such a nonlinear diffusion rate and the quasi-linear rate, $\langle (\Delta \gamma )^2\rangle _\xi ^{QL} \sim B_w^2$![]() . We can extrapolate to the large-wave-amplitude limit using a renormalization:
. We can extrapolate to the large-wave-amplitude limit using a renormalization:
where $B_{w,\min }$![]() corresponds to the $a\ll 1$
corresponds to the $a\ll 1$![]() limit. The ratio $\langle (\Delta \gamma )^2\rangle _\xi /\langle (\Delta \gamma )^2\rangle _\xi ^{QL}$
limit. The ratio $\langle (\Delta \gamma )^2\rangle _\xi /\langle (\Delta \gamma )^2\rangle _\xi ^{QL}$![]() should show how quasi-linear diffusion models overestimate the diffusion rates for intense waves, because such models scale $\langle (\Delta \gamma )^2\rangle _\xi ^{QL}$
should show how quasi-linear diffusion models overestimate the diffusion rates for intense waves, because such models scale $\langle (\Delta \gamma )^2\rangle _\xi ^{QL}$![]() with wave intensity $B_w^2$
with wave intensity $B_w^2$![]() . Both the numerator and the denominator of this ratio should be weighted with the actual distribution of observed wave intensities, ${\mathcal {F}}(B_w/B_0)$
. Both the numerator and the denominator of this ratio should be weighted with the actual distribution of observed wave intensities, ${\mathcal {F}}(B_w/B_0)$![]() , and we use two distributions of whistler-mode wave packets collected in the inner magnetosphere.
, and we use two distributions of whistler-mode wave packets collected in the inner magnetosphere.
Figure 7(a) shows two examples of ${\mathcal {F}}(B_w/B_0)$![]() : the main difference between these distributions is in the definition of wave packets used in the two statistics (see details in Zhang et al. (Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019, Reference Zhang, Mourenas, Artemyev, Angelopoulos, Kurth, Kletzing and Hospodarsky2020b)). Using these distributions, we plot the ratio $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon }$
: the main difference between these distributions is in the definition of wave packets used in the two statistics (see details in Zhang et al. (Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019, Reference Zhang, Mourenas, Artemyev, Angelopoulos, Kurth, Kletzing and Hospodarsky2020b)). Using these distributions, we plot the ratio $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon }$![]() as a function of energy and pitch angle in figure 7(b,c). The region with $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon } \approx 1$
as a function of energy and pitch angle in figure 7(b,c). The region with $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon } \approx 1$![]() corresponds to the dominant contribution of waves with insufficiently large wave amplitude, where $a<1$
corresponds to the dominant contribution of waves with insufficiently large wave amplitude, where $a<1$![]() for most part of $\varepsilon$
for most part of $\varepsilon$![]() , and the diffusion rate is $\langle (\Delta \gamma )^2\rangle _{\xi } \propto B_w^2$
, and the diffusion rate is $\langle (\Delta \gamma )^2\rangle _{\xi } \propto B_w^2$![]() . The region with $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon } < 1$
. The region with $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon } < 1$![]() corresponds to the dominant contribution of high-intensity waves, where $a>1$
corresponds to the dominant contribution of high-intensity waves, where $a>1$![]() for a significant fraction of the ${\mathcal {F}}(B_w/B_0)$
for a significant fraction of the ${\mathcal {F}}(B_w/B_0)$![]() distribution, and the diffusion rate $\langle (\Delta \gamma )^2\rangle _{\xi } \propto B_w$
distribution, and the diffusion rate $\langle (\Delta \gamma )^2\rangle _{\xi } \propto B_w$![]() . Note that electrons of smaller energy/larger pitch angle resonate with waves closer to the equator, where $a<1$
. Note that electrons of smaller energy/larger pitch angle resonate with waves closer to the equator, where $a<1$![]() for the larger part of the ${\mathcal {F}}(B_w/B_0)$
for the larger part of the ${\mathcal {F}}(B_w/B_0)$![]() distribution.
distribution.

Figure 7. (a) Probability distribution functions ${\mathcal {F}}(B_w/B_0)$![]() of whistler-mode wave intensities from Zhang et al. (Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019) (blue) and Zhang et al. (Reference Zhang, Mourenas, Artemyev, Angelopoulos, Kurth, Kletzing and Hospodarsky2020b) (red). (b,c) Two-dimensional distributions of $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon }$
of whistler-mode wave intensities from Zhang et al. (Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019) (blue) and Zhang et al. (Reference Zhang, Mourenas, Artemyev, Angelopoulos, Kurth, Kletzing and Hospodarsky2020b) (red). (b,c) Two-dimensional distributions of $\langle \langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \rangle _{\varepsilon }$![]() in $(E_0,\alpha _{0})$
in $(E_0,\alpha _{0})$![]() space for the two ${\mathcal {F}}(B_w/B_0)$
space for the two ${\mathcal {F}}(B_w/B_0)$![]() distributions from (a).
distributions from (a).
Figure 7(b,c) demonstrates clearly that the quasi-linear diffusion model significantly overestimates the real diffusion of electrons of smaller energy/larger pitch angle. Note that a similar effect of diffusion rate reduction relative to the quasi-linear theory predictions has been obtained for broadband waves (see Tao et al. Reference Tao, Bortnik, Albert, Liu and Thorne2011, Reference Tao, Bortnik, Albert and Thorne2012a). This overestimation will be stronger for active geomagnetic conditions with higher wave intensity (Meredith et al. Reference Meredith, Horne, Thorne and Anderson2003, Reference Meredith, Horne, Sicard-Piet, Boscher, Yearby, Li and Thorne2012; Agapitov et al. Reference Agapitov, Artemyev, Krasnoselskikh, Khotyaintsev, Mourenas, Breuillard, Balikhin and Rolland2013, Reference Agapitov, Mourenas, Artemyev, Mozer, Hospodarsky, Bonnell and Krasnoselskikh2018), because $\langle (\Delta \gamma )^2\rangle _{\xi }/\langle (\Delta \gamma )^2\rangle _{\xi }^{QL} \propto 1/B_{w}$![]() . Figure 7(b,c) is plotted under the assumption that there is no net contribution of nonlinear resonant phase bunching and phase trapping effects, and that all wave–particle interactions can be solely described by diffusion because the wave field is dominated by well-modulated short wave packets. The opposite assumption consists of a dominant role of phase trapping and phase bunching effects of electron resonant interactions with coherent long wave packets. For long-term electron dynamics, such effects also can be fitted by diffusion, but the diffusion rate will be much larger than the quasi-linear one (Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev and Mourenas2021a).
. Figure 7(b,c) is plotted under the assumption that there is no net contribution of nonlinear resonant phase bunching and phase trapping effects, and that all wave–particle interactions can be solely described by diffusion because the wave field is dominated by well-modulated short wave packets. The opposite assumption consists of a dominant role of phase trapping and phase bunching effects of electron resonant interactions with coherent long wave packets. For long-term electron dynamics, such effects also can be fitted by diffusion, but the diffusion rate will be much larger than the quasi-linear one (Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev and Mourenas2021a).
The schematic of figure 8 generalizes both regimes of wave–particle resonant interactions for large-amplitude waves: $\langle (\Delta \gamma )^2\rangle _{\xi } \propto B_{w}$![]() for well-modulated short wave packets and $\langle (\Delta \gamma )^2\rangle _{\xi } \propto B_{w}^{1/2}$
for well-modulated short wave packets and $\langle (\Delta \gamma )^2\rangle _{\xi } \propto B_{w}^{1/2}$![]() for highly coherent long wave packets. For Earth's radiation belts, the quasi-linear simulations of long-term electron flux dynamics generally describe observed electron fluxes with a reasonable tuning of the averaged wave intensity (e.g. Thorne et al. Reference Thorne, Li, Ni, Ma, Bortnik, Chen, Baker, Spence, Reeves and Henderson2013; Li et al. Reference Li, Thorne, Ma, Ni, Bortnik, Baker, Spence, Reeves, Kanekal and Green2014; Drozdov et al. Reference Drozdov, Shprits, Orlova, Kellerman, Subbotin, Baker, Spence and Reeves2015; Ma et al. Reference Ma, Li, Bortnik, Thorne, Chu, Ozeke, Reeves, Kletzing, Kurth and Hospodarsky2018; Allison et al. Reference Allison, Shprits, Zhelavskaya, Wang and Smirnov2021). This will not be possible if either of the two limiting cases shown in figure 8 would work. Therefore, we conclude that wave–particle resonant interactions include both diffusion by short wave packets and nonlinear phase trapping/bunching by rare long wave packets, and a fine balance of these two regimes results in electron diffusion that can be mimicked by the quasi-linear diffusion models. However, for each specific event, such mimicking would require a proper tuning of wave intensity. This underlines the importance of investigations of nonlinear resonant interactions for accurate inclusion of the net effects of phase trapping and phase bunching into wave–particle interaction models.
for highly coherent long wave packets. For Earth's radiation belts, the quasi-linear simulations of long-term electron flux dynamics generally describe observed electron fluxes with a reasonable tuning of the averaged wave intensity (e.g. Thorne et al. Reference Thorne, Li, Ni, Ma, Bortnik, Chen, Baker, Spence, Reeves and Henderson2013; Li et al. Reference Li, Thorne, Ma, Ni, Bortnik, Baker, Spence, Reeves, Kanekal and Green2014; Drozdov et al. Reference Drozdov, Shprits, Orlova, Kellerman, Subbotin, Baker, Spence and Reeves2015; Ma et al. Reference Ma, Li, Bortnik, Thorne, Chu, Ozeke, Reeves, Kletzing, Kurth and Hospodarsky2018; Allison et al. Reference Allison, Shprits, Zhelavskaya, Wang and Smirnov2021). This will not be possible if either of the two limiting cases shown in figure 8 would work. Therefore, we conclude that wave–particle resonant interactions include both diffusion by short wave packets and nonlinear phase trapping/bunching by rare long wave packets, and a fine balance of these two regimes results in electron diffusion that can be mimicked by the quasi-linear diffusion models. However, for each specific event, such mimicking would require a proper tuning of wave intensity. This underlines the importance of investigations of nonlinear resonant interactions for accurate inclusion of the net effects of phase trapping and phase bunching into wave–particle interaction models.

Figure 8. A schematic view of diffusion rate scaling with wave amplitude normalized to the amplitude threshold for nonlinear resonant interactions, $B_w^{*}$![]() . Quasi-linear diffusion rate $D_{QL}\propto B_w^2$
. Quasi-linear diffusion rate $D_{QL}\propto B_w^2$![]() works only for $B_w/B_w^{*}<1$
works only for $B_w/B_w^{*}<1$![]() . For $B_w/B_w^{*}>1$
. For $B_w/B_w^{*}>1$![]() and incoherent waves should work $D\propto B_w$
and incoherent waves should work $D\propto B_w$![]() , whereas for coherent waves should work $D_{NL}\propto \sqrt {B_w}$
, whereas for coherent waves should work $D_{NL}\propto \sqrt {B_w}$![]() (see Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev and Mourenas2021a).
(see Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev and Mourenas2021a).
5. Summary
We have derived the diffusion rate for relativistic electron scattering by intense whistler-mode waves of arbitrary amplitude. This diffusion rate repeats the $D\propto B_w^2$![]() scaling of the quasi-linear diffusion rate $D_{QL}$
scaling of the quasi-linear diffusion rate $D_{QL}$![]() for small amplitudes, and tends to $D\propto B_w$
for small amplitudes, and tends to $D\propto B_w$![]() scaling for amplitudes exceeding the threshold of nonlinear wave–particle interactions. Therefore, under the assumption of the absence of main nonlinear resonant effects (phase trapping and phase bunching) due to low wave coherence, the quasi-linear diffusion model will overestimate the diffusion rate for large amplitudes, because $D/D_{QL}\propto B_w^{-1}$
scaling for amplitudes exceeding the threshold of nonlinear wave–particle interactions. Therefore, under the assumption of the absence of main nonlinear resonant effects (phase trapping and phase bunching) due to low wave coherence, the quasi-linear diffusion model will overestimate the diffusion rate for large amplitudes, because $D/D_{QL}\propto B_w^{-1}$![]() . This result demonstrates that the extrapolation of quasi-linear diffusion models should not work for high wave amplitudes, whereas the approximation of the total destruction of nonlinear resonant effects (phase trapping and phase bunching) due to low wave coherence/strong wave modulation will underestimate the rates of electron flux dynamics. Thus, for accurate inclusion of statistics of high wave amplitudes into electron flux models, we must account for the contribution of nonlinear resonant effects.
. This result demonstrates that the extrapolation of quasi-linear diffusion models should not work for high wave amplitudes, whereas the approximation of the total destruction of nonlinear resonant effects (phase trapping and phase bunching) due to low wave coherence/strong wave modulation will underestimate the rates of electron flux dynamics. Thus, for accurate inclusion of statistics of high wave amplitudes into electron flux models, we must account for the contribution of nonlinear resonant effects.
Acknowledgements
Editor Dmitri Uzdensky thanks the referees for their advice in evaluating this article.
Funding
V.A.F., P.I.S. and A.A.P. acknowledge support from the Russian Science Foundation through grant no. 19-12-00313 covering the theoretical part of this work. A.V.A. and X.-J.Z. acknowledge support from NASA HGI 80NSSC22K0522 covering spacecraft data analysis. O.A. gratefully acknowledges financial support from the University of Exeter, and also from the United Kingdom Research and Innovation (UKRI) Natural Environment Research Council (NERC) Independent Research Fellowship NE/V013963/1.
Declaration of interests
The authors report no conflict of interest.
Appendix A.
This appendix is devoted to the investigation of the properties of $f(a,\xi )$![]() :
:
Considering that $\xi$![]() is a uniformly distributed random variable (see figure 5), we determine the mean value $\langle f(a,\xi ) \rangle _{\xi }$
is a uniformly distributed random variable (see figure 5), we determine the mean value $\langle f(a,\xi ) \rangle _{\xi }$![]() and the mean square value $\langle f^2(a,\xi ) \rangle _{\xi }$
and the mean square value $\langle f^2(a,\xi ) \rangle _{\xi }$![]() .
.
First, let us discuss the convergence of $f(a,\xi )$![]() integral. At $\zeta \to -\infty$
integral. At $\zeta \to -\infty$![]() , the function $\sin \zeta / \sqrt {\xi -\zeta -a \cos \zeta }$
, the function $\sin \zeta / \sqrt {\xi -\zeta -a \cos \zeta }$![]() tends to $\sin \zeta / \sqrt {|\zeta |}$
tends to $\sin \zeta / \sqrt {|\zeta |}$![]() , corresponding to the Fresnel integral, and therefore the integral converges. At $\zeta \to \zeta _R$
, corresponding to the Fresnel integral, and therefore the integral converges. At $\zeta \to \zeta _R$![]() , the convergence depends on the behaviour of $\xi -\zeta -a \cos \zeta$
, the convergence depends on the behaviour of $\xi -\zeta -a \cos \zeta$![]() . We introduce $\zeta = \zeta _R - \delta \zeta$
. We introduce $\zeta = \zeta _R - \delta \zeta$![]() and consider $\delta \zeta$
and consider $\delta \zeta$![]() to be sufficiently small:
to be sufficiently small:

If $1 - a \sin \zeta _R \neq 0$![]() , the integral converges near $\zeta _R$
, the integral converges near $\zeta _R$![]() as $\delta \zeta ^{-1/2}$
as $\delta \zeta ^{-1/2}$![]() . The equation $1 - a \sin \zeta _R = 0$
. The equation $1 - a \sin \zeta _R = 0$![]() determines cases when $f(a,\xi )$
determines cases when $f(a,\xi )$![]() has an infinite value. Thus, these points have to be excluded from the averaging procedure. By definition, $\zeta _R$
has an infinite value. Thus, these points have to be excluded from the averaging procedure. By definition, $\zeta _R$![]() has to be the only solution of $\xi -\zeta -a\cos \zeta =0$
has to be the only solution of $\xi -\zeta -a\cos \zeta =0$![]() on the interval of integration. Therefore, we expect $\zeta _R$
on the interval of integration. Therefore, we expect $\zeta _R$![]() to satisfy the equation $\zeta _R=\arcsin ({1}/{a}) + 2{\rm \pi} n$
to satisfy the equation $\zeta _R=\arcsin ({1}/{a}) + 2{\rm \pi} n$![]() , where $n\in \mathbb {Z}$
, where $n\in \mathbb {Z}$![]() . Values of $\xi$
. Values of $\xi$![]() , corresponding to the diverging cases (noted as $\xi _0$
, corresponding to the diverging cases (noted as $\xi _0$![]() ), can be simply determined from the following system of equations:
), can be simply determined from the following system of equations:

In the case of $a < 1$![]() , there is no solution and the interval of integration for $\xi$
, there is no solution and the interval of integration for $\xi$![]() can be performed, i.e. $\xi \in ({\rm \pi} /2, 5 {\rm \pi}/2)$
can be performed, i.e. $\xi \in ({\rm \pi} /2, 5 {\rm \pi}/2)$![]() (we take $\xi _0(a<1) \equiv \lim _{a \to 1^+} \xi _0(a) = {\rm \pi}/2$
(we take $\xi _0(a<1) \equiv \lim _{a \to 1^+} \xi _0(a) = {\rm \pi}/2$![]() ). For $a\geqslant 1$
). For $a\geqslant 1$![]() , this system has infinitely many solutions, separated by $2{\rm \pi}$
, this system has infinitely many solutions, separated by $2{\rm \pi}$![]() . The function $f(a,\xi )$
. The function $f(a,\xi )$![]() is periodic with period $2{\rm \pi}$
is periodic with period $2{\rm \pi}$![]() for $\xi$
for $\xi$![]() :
:

Thus, without loss of generality, we consider only one value of $\xi _0$![]() and the corresponding phase $\zeta _0$
and the corresponding phase $\zeta _0$![]() . As a result, the mean value $\langle f(a,\xi ) \rangle _{\xi }$
. As a result, the mean value $\langle f(a,\xi ) \rangle _{\xi }$![]() and the mean square value $\langle f^2(a,\xi ) \rangle _{\xi }$
and the mean square value $\langle f^2(a,\xi ) \rangle _{\xi }$![]() can be defined as
can be defined as


To proceed, it is necessary to determine $\zeta _R$![]() as a function of $\xi$
as a function of $\xi$![]() on the interval $(\xi _0, \xi _0 + 2{\rm \pi} )$
on the interval $(\xi _0, \xi _0 + 2{\rm \pi} )$![]() :
:

Thus, $\zeta _R$![]() is bounded on the interval $(\zeta _m, \zeta _0 + 2{\rm \pi} )$
is bounded on the interval $(\zeta _m, \zeta _0 + 2{\rm \pi} )$![]() and is monotonic on it, considering the equation for $\partial _{\xi } \zeta _R$
and is monotonic on it, considering the equation for $\partial _{\xi } \zeta _R$![]() . This implies that the integral interval can be expanded (Neishtadt Reference Neishtadt1999; Artemyev et al. Reference Artemyev, Neishtadt, Vainchtein, Vasiliev, Vasko and Zelenyi2018a; Albert et al. Reference Albert, Artemyev, Li, Gan and Ma2022):
. This implies that the integral interval can be expanded (Neishtadt Reference Neishtadt1999; Artemyev et al. Reference Artemyev, Neishtadt, Vainchtein, Vasiliev, Vasko and Zelenyi2018a; Albert et al. Reference Albert, Artemyev, Li, Gan and Ma2022):

The integral from (A8) does not have any singularities on the interval of integration and, thus, can be easily computed. To neglect the dependency on $\zeta _m$![]() , an integral in a complex plane can be introduced:
, an integral in a complex plane can be introduced:

Additionally, (A8) determines $\langle f(a,\xi ) \rangle _{\xi }$![]() for $a < 1$
for $a < 1$![]() : $\langle f(a,\xi ) \rangle _{\xi } = 0$
: $\langle f(a,\xi ) \rangle _{\xi } = 0$![]() as $\zeta _m = \zeta _0$
as $\zeta _m = \zeta _0$![]() . For $a\to \infty$
. For $a\to \infty$![]() , we get
, we get

Figure 9 shows that the asymptote $a \gg 1$![]() is the same for $\langle f^2(a,\xi ) \rangle _{\xi }$
is the same for $\langle f^2(a,\xi ) \rangle _{\xi }$![]() and $\langle f(a,\xi ) \rangle _{\xi }^2$
and $\langle f(a,\xi ) \rangle _{\xi }^2$![]() functions and, considering (A10), $\lim _{a \to \infty } \langle f^2(a,\xi ) \rangle _{\xi } = {32}/{{\rm \pi} ^2}$
functions and, considering (A10), $\lim _{a \to \infty } \langle f^2(a,\xi ) \rangle _{\xi } = {32}/{{\rm \pi} ^2}$![]() .
.

Figure 9. Comparison between $\langle f^2(a,\xi ) \rangle _{\xi }$![]() and $\langle f(a,\xi ) \rangle _{\xi }^2$
and $\langle f(a,\xi ) \rangle _{\xi }^2$![]() as functions of $a$
as functions of $a$![]() .
.