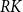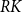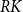1. Introduction
The rapid proliferation of robotization and automation over the past two decades is considered one of the most pressing challenges for the future of workers and their societal integration (e.g., Ford, Reference Ford2015; West, Reference West2018; Susskind, Reference Susskind2020). Among the major concerns voiced at academic, policy, and political levels is the potential escalation of income inequality among various types of workers.
While this concern echoes the computerization process of the late twentieth century, the advent of artificial intelligence, digital technologies, and robotics in the labor market introduces unique features. This has prompted expressions such as “Is this time different?” (e.g., Mokyr et al. 2015; Furman, Reference Furman2016; Estlund, Reference Estlund2021). Some scholars even advocate for robot taxation (Costinot & Werning, Reference Costinot and Werning2020; Guerreiro et al. Reference Guerreiro, Rebelo and Teles2022).Footnote 1
In general, the widespread increase in the utilization of skilled labor/workers (hereinafter referred to as
![]() $S$
), relative to unskilled labor/workers (hereinafter referred to as
$S$
), relative to unskilled labor/workers (hereinafter referred to as
![]() $U$
), is well documented. For instance, the average hours worked by
$U$
), is well documented. For instance, the average hours worked by
![]() $S$
increased by 6% in OECD countries during the 1995–2005 period, while hours worked by
$S$
increased by 6% in OECD countries during the 1995–2005 period, while hours worked by
![]() $U$
in the same period dropped by 7%. Moreover, the skilled-to-unskilled labor ratio has been growing in the World Input-Output Database, WIOD, (Timmer et al. Reference Timmer, Dietzenbacher, Los, Stehrer and De Vries2015) countries according to Battisti et al. (Reference Battisti, Gatto and Parmeter2022).
$U$
in the same period dropped by 7%. Moreover, the skilled-to-unskilled labor ratio has been growing in the World Input-Output Database, WIOD, (Timmer et al. Reference Timmer, Dietzenbacher, Los, Stehrer and De Vries2015) countries according to Battisti et al. (Reference Battisti, Gatto and Parmeter2022).
From a theoretical perspective, various frameworks have addressed this phenomenon. The “race between technology and education” framework, pioneered by Tinbergen, (Reference Tinbergen1974) and further explored by Goldin & Katz (Reference Goldin and Katz2009), Acemoglu & Autor (Reference Acemoglu and Autor2011), Autor et al. (2020), among many others, highlights the natural replacement of routine and repetitive tasks by technology, while more abstract duties requiring higher education are inherently more complementary. Griliches (Reference Griliches1969) discusses how the introduction of new technologies in production could lead to adjustments in the relative demand for different labor skills, which, in turn, are reflected in their relative wages. In a dynamic general equilibrium model incorporating investments in both robots and traditional capital, Berg et al. (Reference Berg, Buffie and Zanna2018) state that automation can have positive effects on growth while increasing income inequality. Similarly, Moll et al. (2021) argue that automation may exacerbate inequality in a model linking technology to personal income and wealth distribution. In the same vein, the growth model of “directed technical change”Footnote
2
proposed by Hémous & Olsen (Reference Hémous and Olsen2022) suggests that machines complement
![]() $S$
and replace
$S$
and replace
![]() $U$
, thereby intensifying wage disparities through stagnating wages for
$U$
, thereby intensifying wage disparities through stagnating wages for
![]() $U$
.
$U$
.
The contributions to understanding the divergent impact of technological progress on different types of workers have been primarily focused on two strands of literature, driven by the well-known challenge of jointly identifying technological progress and the elasticity of substitution (EoS) in production functions with both technical progress and possibility of substitution among inputs, like the generalized constant elasticity of substitution (CES) of David & Van de Klundert (Reference David and Van de Klundert1965) — a problem pioneered by Diamond et al. (Reference Diamond, McFadden and Rodriguez1978).
A substantial body of work centers on skill-biased technical change, SBTC, (Katz & Murphy, Reference Katz and Murphy1992) and the more recent routine-biased technical change, RBTC, (Autor et al. 2003). In the latter framework, the “hollowing out” effect of automation leads to the disappearance of jobs requiring a well-defined set of repetitive tasks, typically assigned to middle-skilled workers.Footnote 3 A documented “polarization process” from the 1980s reveals employment gradually clustering at the tails of the occupational skill distribution (see, for instance, Acemoglu & Autor, Reference Acemoglu and Autor2011). For instance, Jaimovich et al. (2021) illustrate how the likelihood of working in routine occupations decreased by roughly 16% between the pre-polarization and post-polarization eras.
Within the broader literature on the asymmetric effects of technological progress, this paper hones in on the specific aspect of robotization, examining the extent of complementarity/substitutability between an original measure of robotic capital (hereinafter referred to as
![]() $RK$
), derived from data on installed industrial robots, and workers at different skill levels.
$RK$
), derived from data on installed industrial robots, and workers at different skill levels.
The alternative approach investigates varying degrees of substitutability of skills with (general) capital, as seen in works such as Griliches (Reference Griliches1969), Fallon & Layard (Reference Fallon and Layard1975), Duffy et al. (Reference Duffy, Papageorgiou and Perez-Sebastian2004), and Henderson (Reference Henderson2009).Footnote
4
In this respect, empirical analysis generally supports the “capital-skill complementarity” hypothesis (i.e., between capital and
![]() $S$
).
$S$
).
However, a further body of literature has emerged investigating the complementarity hypothesis with specific types of capital. For instance, Krusell et al. (Reference Krusell, Ohanian, Ríos-Rull and Violante2000) disaggregate capital into structures and equipment, finding the latter to be less substitutable with
![]() $S$
. In a similar vein, focusing on developing economies, Raveh & Reshef (Reference Raveh and Reshef2016) find that only R&D capital is complementary to
$S$
. In a similar vein, focusing on developing economies, Raveh & Reshef (Reference Raveh and Reshef2016) find that only R&D capital is complementary to
![]() $S$
, while less innovative capital is complementary to
$S$
, while less innovative capital is complementary to
![]() $U$
. Likewise, Taniguchi & Yamada (Reference Taniguchi and Yamada2022) and Eden & Gaggl (Reference Eden and Gaggl2018) report similar results for ICT capital in a panel of OECD countries and the US, respectively. Moreover, Caselli & Manning (Reference Caselli and Manning2019) demonstrate how, under the assumption of a reduction in the relative price of investment goods driven by technological progress, capital return can drop, thereby generating higher returns for labor.
$U$
. Likewise, Taniguchi & Yamada (Reference Taniguchi and Yamada2022) and Eden & Gaggl (Reference Eden and Gaggl2018) report similar results for ICT capital in a panel of OECD countries and the US, respectively. Moreover, Caselli & Manning (Reference Caselli and Manning2019) demonstrate how, under the assumption of a reduction in the relative price of investment goods driven by technological progress, capital return can drop, thereby generating higher returns for labor.
Our study aligns with the aforementioned literature strand by focusing on industrial robotization. While the extant contributions typically emphasize “robot density” (often measured as the ratio of the number of robots to hours worked or employment) and its differential impact on various workers, our paper engages in a formal analysis of the EoS. Specifically, this study represents the first attempt, to the best of our knowledge, to measure the extent of complementarity/substitutability between an original measure of
![]() $RK$
and workers at different skill levels. By focusing on this aspect, we contribute to understanding how different types of labor interact with advanced forms of capital in the production process. Consequently, our work falls within the strand of literature that examines the substitutability between production factors, specifically robotic capital versus skilled and unskilled workers.
$RK$
and workers at different skill levels. By focusing on this aspect, we contribute to understanding how different types of labor interact with advanced forms of capital in the production process. Consequently, our work falls within the strand of literature that examines the substitutability between production factors, specifically robotic capital versus skilled and unskilled workers.
Our empirical approach enables us to estimate EoS patterns between RK and S on one hand (denoted as
![]() $\sigma _{RK,S}$
), and between RK and U on the other (denoted as
$\sigma _{RK,S}$
), and between RK and U on the other (denoted as
![]() $\sigma _{RK,U}$
). This provides us with the capacity to draw conclusions regarding the impact of the robotization process on the
$\sigma _{RK,U}$
). This provides us with the capacity to draw conclusions regarding the impact of the robotization process on the
![]() $\frac{S}{U}$
. In addition, it sheds light on whether the sign of such impact aligns with the previously documented country-sector tendency of increasing the
$\frac{S}{U}$
. In addition, it sheds light on whether the sign of such impact aligns with the previously documented country-sector tendency of increasing the
![]() $\frac{S}{U}$
or deviates from it.
$\frac{S}{U}$
or deviates from it.
The primary analysis leverages information on installed industrial robots, sourced from the International Federation of Robotics (IFR), which is integrated with WIOD data. This integration allows us to construct a country-sector-year measure of
![]() $RK$
covering 35 countries and 17 industries over the period 1995–2009. According to this measure, the share of
$RK$
covering 35 countries and 17 industries over the period 1995–2009. According to this measure, the share of
![]() $RK$
has increased by approximately 40% during the years under investigation.
$RK$
has increased by approximately 40% during the years under investigation.
The country-sector-year measure of
![]() $RK$
is then utilized, in conjunction with corresponding WIOD information on labor skills, to estimate the dynamics of the country-sector patterns of
$RK$
is then utilized, in conjunction with corresponding WIOD information on labor skills, to estimate the dynamics of the country-sector patterns of
![]() $\sigma _{RK,S}$
and
$\sigma _{RK,S}$
and
![]() $\sigma _{RK,U}$
from 1995 to 2009. While this would be a challenging task in a parametric setup, we rely on recent advances in nonparametric analysis, particularly using local polynomial estimation. Such an approach allows for direct pairwise comparison between the two elasticities at the country-sector level throughout the entire period under consideration. This provides us with the ability to study the extent to which the “RK-Skill complementarity” hypothesis, positing that robotization is more complementary (less substitutive) to
$\sigma _{RK,U}$
from 1995 to 2009. While this would be a challenging task in a parametric setup, we rely on recent advances in nonparametric analysis, particularly using local polynomial estimation. Such an approach allows for direct pairwise comparison between the two elasticities at the country-sector level throughout the entire period under consideration. This provides us with the ability to study the extent to which the “RK-Skill complementarity” hypothesis, positing that robotization is more complementary (less substitutive) to
![]() $S$
(i.e.,
$S$
(i.e.,
![]() $\sigma _{RK,U} \gt \sigma _{RK,S}$
) is supported by the data. In so doing, we add to the ongoing debate on whether robotization contributes to or opposes the documented upward dynamics in
$\sigma _{RK,U} \gt \sigma _{RK,S}$
) is supported by the data. In so doing, we add to the ongoing debate on whether robotization contributes to or opposes the documented upward dynamics in
![]() $\frac{S}{U}$
over the last decades.
$\frac{S}{U}$
over the last decades.
Overall, our results support the “RK-Skill complementarity” hypothesis.Footnote
5
Specifically, we demonstrate that: i) robotic capital exhibits
![]() $\sigma _{RK,S} \lt \sigma _{RK,U}$
on average; ii) this tendency strengthened over the first decade of the 2000s; iii) the increase has been more pronounced in OECD than in Non-OECD countries (where the increase mainly occurred through a reduction in
$\sigma _{RK,S} \lt \sigma _{RK,U}$
on average; ii) this tendency strengthened over the first decade of the 2000s; iii) the increase has been more pronounced in OECD than in Non-OECD countries (where the increase mainly occurred through a reduction in
![]() $\sigma _{RK,S}$
), and in Manufacturing compared to Non-Manufacturing industries. In general, the dynamics of complementarity appears heterogeneous throughout the period under consideration. At the end of the ’00s, evidence against “RK-Skill complementarity” is still found in 28% of cases (down from 50% in the second half of the ’90s). This indicates a consistent pattern of greater relative substitutability of
$\sigma _{RK,S}$
), and in Manufacturing compared to Non-Manufacturing industries. In general, the dynamics of complementarity appears heterogeneous throughout the period under consideration. At the end of the ’00s, evidence against “RK-Skill complementarity” is still found in 28% of cases (down from 50% in the second half of the ’90s). This indicates a consistent pattern of greater relative substitutability of
![]() $U$
with respect to
$U$
with respect to
![]() $RK$
.
$RK$
.
The exposition unfolds as follows. Section 2 briefly illustrates the data and our
![]() $RK$
measure. Section 3 sets up the empirical framework. Section 4 reports our analysis and discusses the main results. Section 5 presents robustness checks and a broad validation exercise, mainly focused on comparisons with parametric estimates, also addressing the role played by price and productivity dimensions in determining the estimated EoS patterns. Finally, Section 6 concludes.
$RK$
measure. Section 3 sets up the empirical framework. Section 4 reports our analysis and discusses the main results. Section 5 presents robustness checks and a broad validation exercise, mainly focused on comparisons with parametric estimates, also addressing the role played by price and productivity dimensions in determining the estimated EoS patterns. Finally, Section 6 concludes.
2. Data
Our analysis builds upon an integration of data on robots, sourced from International Federation of Robotics (2005, 2019), with information on worker types, capital assets and value-added, provided by WIOD (2015).Footnote
6
The IFR-WIOD merged dataset is used to obtain a measure of
![]() $RK$
(total capital is decomposed into its robotic and non-robotic components) covering 35 countries and 17 industries spanning the period 1995–2009 (8,217 observations), due to the missing information and/or coverage at 2-digit level on skill groups in the new WIOD releases, as well as the unavailability of original industrial robot prices for a number of economies (i.e., different from the US).
$RK$
(total capital is decomposed into its robotic and non-robotic components) covering 35 countries and 17 industries spanning the period 1995–2009 (8,217 observations), due to the missing information and/or coverage at 2-digit level on skill groups in the new WIOD releases, as well as the unavailability of original industrial robot prices for a number of economies (i.e., different from the US).
For data consistency, we also merge International Federation of Robotics (2019) with information collected from EU KLEMS (2009), obtaining a smaller dataset of 2,843 observations (15 countries, 17 industries, 1994–2005) which, however, allows us to decompose capital accumulation into four, instead of two, components: robotic, non-robotic, ICT, and other capital (the detailed coverage is reported in Section C of the Appendix).
Differently from the past automation/robotization literature that uses a “robot density” variable, relying on crude stocks of robots (weighted by workers), our main indicator of interest is a novel
![]() $RK$
value, which is specifically designed to be used within the framework of production function estimations, and built upon two main elements: the prices and stock of industrial robots. It is obtained as follows (see Graetz & Michaels (Reference Graetz and Michaels2018), for a similar methodology). As for the industrial robots, information on the number of operating robots and deliveries (i.e., newly installed robots in the year) is retrieved from “World Robotics: Industrial Robots and Service Robots” (International Federation of Robotics, 2019), and used to compute the robot stock at time
$RK$
value, which is specifically designed to be used within the framework of production function estimations, and built upon two main elements: the prices and stock of industrial robots. It is obtained as follows (see Graetz & Michaels (Reference Graetz and Michaels2018), for a similar methodology). As for the industrial robots, information on the number of operating robots and deliveries (i.e., newly installed robots in the year) is retrieved from “World Robotics: Industrial Robots and Service Robots” (International Federation of Robotics, 2019), and used to compute the robot stock at time
![]() $t$
, for each country-sector pair, through the perpetual inventory method assuming a depreciation rate of 10 percent.Footnote
7
Specifically, we calculate
$t$
, for each country-sector pair, through the perpetual inventory method assuming a depreciation rate of 10 percent.Footnote
7
Specifically, we calculate
![]() $R^{S}_{ci,t}=R^{D}_{ci,t}+(1-\delta )R^{S}_{ci,t-1}$
, where
$R^{S}_{ci,t}=R^{D}_{ci,t}+(1-\delta )R^{S}_{ci,t-1}$
, where
![]() $c$
,
$c$
,
![]() $i$
, and
$i$
, and
![]() $t$
represent country, industry, and year, respectively;
$t$
represent country, industry, and year, respectively;
![]() $R^{S}$
and
$R^{S}$
and
![]() $R^{D}$
denote, respectively, the stock and deliveries of robots, whereas
$R^{D}$
denote, respectively, the stock and deliveries of robots, whereas
![]() $\delta$
is the depreciation rate. Consequently,
$\delta$
is the depreciation rate. Consequently,
![]() $RK$
, is obtained as:
$RK$
, is obtained as:
where
![]() $D^K$
is the (total) capital deflator, drawn from WIOD (2015) or EU KLEMS (2009), and
$D^K$
is the (total) capital deflator, drawn from WIOD (2015) or EU KLEMS (2009), and
![]() $R^{P}$
represents the (country-specific) average unit price of industrial robots, which has been manually collected from several annual IFR reports.Footnote
8
It is worth noting that IFR provides robot prices (in current thousand dollars) only for Japan, US, Germany, Italy, Republic of Korea, United Kingdom and France for a limited number of years. The procedure to define and assign the most appropriate robot price for the other economies in our samples follows a criterion of geographical and economic proximity. Specifically, robot prices for economies with missing data are imputed relying on the average available price of countries within the same continent. The detailed description of this procedure is reported in Section A of the Appendix. While this approach may be more suitable for OECD countries, it is important to acknowledge that: i) these countries constitute the majority of our sample, and ii) the nonparametric estimation framework employs the ratio of production function derivatives, effectively smoothing the potential measurement errors by weighting the EoS numerator (i.e., the
$R^{P}$
represents the (country-specific) average unit price of industrial robots, which has been manually collected from several annual IFR reports.Footnote
8
It is worth noting that IFR provides robot prices (in current thousand dollars) only for Japan, US, Germany, Italy, Republic of Korea, United Kingdom and France for a limited number of years. The procedure to define and assign the most appropriate robot price for the other economies in our samples follows a criterion of geographical and economic proximity. Specifically, robot prices for economies with missing data are imputed relying on the average available price of countries within the same continent. The detailed description of this procedure is reported in Section A of the Appendix. While this approach may be more suitable for OECD countries, it is important to acknowledge that: i) these countries constitute the majority of our sample, and ii) the nonparametric estimation framework employs the ratio of production function derivatives, effectively smoothing the potential measurement errors by weighting the EoS numerator (i.e., the
![]() $S$
set) in relation to the denominator (i.e., the
$S$
set) in relation to the denominator (i.e., the
![]() $U$
set).
$U$
set).
Furthermore, from WIOD (2015), we draw data on: Total capital (
![]() $TotK$
), allowing us to obtain non-
$TotK$
), allowing us to obtain non-
![]() $RK$
as
$RK$
as
![]() $NRK_{ci,t}=TotK_{ci,t}-RK_{ci,t}$
, as well as information on high- (i.e.,
$NRK_{ci,t}=TotK_{ci,t}-RK_{ci,t}$
, as well as information on high- (i.e.,
![]() $S$
), medium- and low-skilled workers (i.e.,
$S$
), medium- and low-skilled workers (i.e.,
![]() $U$
), expressed in terms of hours worked, hourly wages, hours and income shares, depending on the specific estimated models.Footnote
9
Ultimately, from EU KLEMS (2009), we also collect information on ICT capital,
$U$
), expressed in terms of hours worked, hourly wages, hours and income shares, depending on the specific estimated models.Footnote
9
Ultimately, from EU KLEMS (2009), we also collect information on ICT capital,
![]() $IK$
, which allows us to calculate the “other” capital stock as
$IK$
, which allows us to calculate the “other” capital stock as
![]() $OK_{ci,t}=TotK_{ci,t}-RK_{ci,t}-IK_{ci,t}$
.
$OK_{ci,t}=TotK_{ci,t}-RK_{ci,t}-IK_{ci,t}$
.
![]() $RK$
and all variables used throughout the empirical analysis are expressed in real terms, as PPP-adjusted 2005 international dollars, using the PPP conversion factor from Inklaar & Timmer (Reference Inklaar and Timmer2014). Detailed descriptive statistics are reported in Section D of the Appendix.
$RK$
and all variables used throughout the empirical analysis are expressed in real terms, as PPP-adjusted 2005 international dollars, using the PPP conversion factor from Inklaar & Timmer (Reference Inklaar and Timmer2014). Detailed descriptive statistics are reported in Section D of the Appendix.
2.1 Robotic capital penetration
Similarly to what happened for the diffusion of computers in the ’80s and early ’90s (see, for instance, Brynjolfsson, Reference Brynjolfsson1993), the spread of robots occurs through increasing quantities and decreasing prices. This is evident in Figure 1, which reports the evolution of number of robots (panel (a)) and robot prices (panel (b)) in the US (the only country for which IFR provides a longer time-series on prices), also in relative terms with respect to employees (panel (c)) and wages (panel (d)), respectively. In particular, the measure reported in panel (b) of Figure 1, basically an indicator of “robot density,” points to a 90% increase, alongside with a decrease of approximately 80% in the unit price of robots, relative to the price of labor (i.e., average wages, in panel (d)), during the years 1995–2009.

Figure 1. Robot diffusion, 1995–2009 and 1995–2018, USA.
Elaboration on IFR and WIOD data.
In Figure 2, we compare the time evolution of our
![]() $RK$
variable with that of other forms of capital (including
$RK$
variable with that of other forms of capital (including
![]() $IK$
,
$IK$
,
![]() $OK$
and
$OK$
and
![]() $TotK$
), provided by EU KLEMS (2009) for a subset of countries and up to year 2005. With the exception of ICT capital (
$TotK$
), provided by EU KLEMS (2009) for a subset of countries and up to year 2005. With the exception of ICT capital (
![]() $IK$
, which does not include robots),Footnote
10
the trend of
$IK$
, which does not include robots),Footnote
10
the trend of
![]() $RK$
has been much more pronounced than
$RK$
has been much more pronounced than
![]() $OK$
and
$OK$
and
![]() $TotK$
.Footnote
11
This provides a clear picture about the strength of penetration of automation and digital technologies within the production process. However, Figure 3 shows how the average share of
$TotK$
.Footnote
11
This provides a clear picture about the strength of penetration of automation and digital technologies within the production process. However, Figure 3 shows how the average share of
![]() $RK$
(with respect to total capital) in the period is in general quite low: about 2.5–3% in Japan, Spain, Italy and Germany, and particularly in wood products, electronics, and transport equipment industries (labeled as
$RK$
(with respect to total capital) in the period is in general quite low: about 2.5–3% in Japan, Spain, Italy and Germany, and particularly in wood products, electronics, and transport equipment industries (labeled as
![]() $Wo$
,
$Wo$
,
![]() $El$
and
$El$
and
![]() $Tr$
, respectively).Footnote
12
In any case, this does not diminish the relevance our analysis, whose focus is on the type of patterns followed by the extent of complementarity/substitutability between robots and different types of labor over the period under consideration, in order to shed light on the expected sign of the labor impact of robotization, in perspective.
$Tr$
, respectively).Footnote
12
In any case, this does not diminish the relevance our analysis, whose focus is on the type of patterns followed by the extent of complementarity/substitutability between robots and different types of labor over the period under consideration, in order to shed light on the expected sign of the labor impact of robotization, in perspective.

Figure 2. Evolution of robotic capital and other forms of capital: % growth rates, 1994–2005 (1994 = 1).
Elaboration on IFR and EUKLEMS data.

Figure 3. Share of robotic capital (% of total capital) in the more robotized countries and industries, 1995–2009, average values.
Elaboration on IFR and EU KLEMS data.
In this respect, it is noteworthy that, despite a lower reported
![]() $RK$
share for the US compared to many other developed countries over the 1994–2005 period, a dramatic expansion in this indicator (growing by more than four times) is observed in the US economy from 2006 to 2018. This was presumably due to a halving of the average unit price of robots (see panel (c) in Figure 1). Since the share of
$RK$
share for the US compared to many other developed countries over the 1994–2005 period, a dramatic expansion in this indicator (growing by more than four times) is observed in the US economy from 2006 to 2018. This was presumably due to a halving of the average unit price of robots (see panel (c) in Figure 1). Since the share of
![]() $RK$
has recorded an average value of about 1% (with peaks of 3% in the computer, electronics, and optical industry, and 5% in the transport equipment sector), while for
$RK$
has recorded an average value of about 1% (with peaks of 3% in the computer, electronics, and optical industry, and 5% in the transport equipment sector), while for
![]() $IK$
(whose price level declined by about 40%) an average share of approximately 8% is documented, data (available upon request) point to a 8:1 proportion between
$IK$
(whose price level declined by about 40%) an average share of approximately 8% is documented, data (available upon request) point to a 8:1 proportion between
![]() $IK$
and
$IK$
and
![]() $RK$
growth in the US. This is also evident in Figure E1 in the Appendix, reporting the evolution of our
$RK$
growth in the US. This is also evident in Figure E1 in the Appendix, reporting the evolution of our
![]() $RK$
measure for a subset of countries and sectors.
$RK$
measure for a subset of countries and sectors.
3. Estimation strategy
To assess the skill complementarity of
![]() $RK$
, we estimate the (country-sector-year)
$RK$
, we estimate the (country-sector-year)
![]() $\sigma _{RK,S}$
on the one hand, and
$\sigma _{RK,S}$
on the one hand, and
![]() $\sigma _{RK,U}$
, on the other hand; this allows us to compare the dynamics of the two elasticities from the second half of ’90s to the end of ’00s, relying on our IFR-WIOD dataset. As a measure of the “degree of curvature” of the isoquant, the EoS between two factors embodies information on how technically easy is to substitute a factor by another. In carrying out the empirical analysis, we use the recently developed local polynomial estimation (Li & Racine, Reference Li and Racine2007; Hall & Racine, Reference Hall and Racine2015), in the spirit of Henderson (Reference Henderson2009), who applied these techniques in the evaluation of capital-skill complementarity from a cross-country perspective. Particularly, we consider the following framework (see Battisti et al., (Reference Battisti, Gatto and Parmeter2022), for an application to two factors production function estimation):
$\sigma _{RK,U}$
, on the other hand; this allows us to compare the dynamics of the two elasticities from the second half of ’90s to the end of ’00s, relying on our IFR-WIOD dataset. As a measure of the “degree of curvature” of the isoquant, the EoS between two factors embodies information on how technically easy is to substitute a factor by another. In carrying out the empirical analysis, we use the recently developed local polynomial estimation (Li & Racine, Reference Li and Racine2007; Hall & Racine, Reference Hall and Racine2015), in the spirit of Henderson (Reference Henderson2009), who applied these techniques in the evaluation of capital-skill complementarity from a cross-country perspective. Particularly, we consider the following framework (see Battisti et al., (Reference Battisti, Gatto and Parmeter2022), for an application to two factors production function estimation):
where discrete variables
![]() $d_{ci}$
and
$d_{ci}$
and
![]() $d_{t}$
represent, respectively, a country-sector effect and a time effect. The advantage of following this approach is twofold. First, incorporating these effects within a parametric setting would quickly reduce degrees of freedom. Conversely, in a nonparametric framework, we can employ smoothing techniques across both time and sectors to leverage neighboring cells for localized information (see Li & Racine, Reference Li and Racine2007). Second, it enables us to avoid making any assumptions in terms of the functional specification of the production technology.Footnote
13
$d_{t}$
represent, respectively, a country-sector effect and a time effect. The advantage of following this approach is twofold. First, incorporating these effects within a parametric setting would quickly reduce degrees of freedom. Conversely, in a nonparametric framework, we can employ smoothing techniques across both time and sectors to leverage neighboring cells for localized information (see Li & Racine, Reference Li and Racine2007). Second, it enables us to avoid making any assumptions in terms of the functional specification of the production technology.Footnote
13
Equation (1) is estimated using local polynomial least squares (LPLS). Common examples include local constant and local linear. However, our primary focus in this context is less on directly estimating
![]() $m(\cdot )$
and more on the estimation of various orders of derivatives of the function (i.e., the first and second order). Therefore, we employ a higher-order polynomial to directly estimate the derivatives of interest. Specifically, we make use of a local quadratic estimation with data-driven bandwidth selection. Considering that we are estimating derivatives of an unknown smooth function, the data-driven bandwidths are adjusted to account for the optimal rate difference, as suggested by Henderson et al. (Reference Henderson, Kumbhakar, Li and Parmeter2015) (see Section B of the Appendix for methodological details).
$m(\cdot )$
and more on the estimation of various orders of derivatives of the function (i.e., the first and second order). Therefore, we employ a higher-order polynomial to directly estimate the derivatives of interest. Specifically, we make use of a local quadratic estimation with data-driven bandwidth selection. Considering that we are estimating derivatives of an unknown smooth function, the data-driven bandwidths are adjusted to account for the optimal rate difference, as suggested by Henderson et al. (Reference Henderson, Kumbhakar, Li and Parmeter2015) (see Section B of the Appendix for methodological details).
Among possible EoS specifications, we rely on the “Morishima EoS,” which can be viewed as a multifactor extension of the Hicks EoS (Blackorby & Russell, Reference Blackorby and Russell1981). In a two-input context, the Hicks EoS measures the percentage change in the factor ratio associated with a 1% change in the marginal rate of technical substitution (i.e., the marginal productivity ratio) between the two inputs. The Morishima multifactor extension is defined, for any two inputs, at given values of output and keeping constant the EoS with respect to all the other production factors. The higher the value, the higher is the substitutability between the two inputs. While two inputs are said to be substitutes when the estimated values are positive and complements when values are negative (i.e., if
![]() $\sigma^{RK,U}\lt 0$
, the amount of
$\sigma^{RK,U}\lt 0$
, the amount of
![]() $U$
will grow more than proportionally to
$U$
will grow more than proportionally to
![]() $RK$
as a consequence of an increase in the marginal productivity of
$RK$
as a consequence of an increase in the marginal productivity of
![]() $RK$
), we are mainly concerned with the inequality between
$RK$
), we are mainly concerned with the inequality between
![]() $\sigma^{RK,S}$
and
$\sigma^{RK,S}$
and
![]() $\sigma ^{RK,U}$
: whenever
$\sigma ^{RK,U}$
: whenever
![]() $\widehat{\sigma }_{RK,S}\lt \widehat{\sigma }_{RK,U}$
, we conclude that
$\widehat{\sigma }_{RK,S}\lt \widehat{\sigma }_{RK,U}$
, we conclude that
![]() $RK$
is more likely to substitute for
$RK$
is more likely to substitute for
![]() $U$
than for
$U$
than for
![]() $S$
or, alternatively, more likely to complement with
$S$
or, alternatively, more likely to complement with
![]() $S$
than with
$S$
than with
![]() $U$
, depending on whether the estimated elasticities are positive or negative — i.e., “RK-Skill complementarity.” This circumstance results in an increasing
$U$
, depending on whether the estimated elasticities are positive or negative — i.e., “RK-Skill complementarity.” This circumstance results in an increasing
![]() $\frac{S}{U}$
ratio, but, not necessarily a decreasing amount of
$\frac{S}{U}$
ratio, but, not necessarily a decreasing amount of
![]() $U$
, at given levels of
$U$
, at given levels of
![]() $S$
and
$S$
and
![]() $Y$
.
$Y$
.
Formally, the EoS between input
![]() $q$
and
$q$
and
![]() $l$
for the multiple-input production technology in equation (1) is defined as
$l$
for the multiple-input production technology in equation (1) is defined as
where
![]() $x_q$
and
$x_q$
and
![]() $x_l$
denote the used quantities of inputs
$x_l$
denote the used quantities of inputs
![]() $q$
and
$q$
and
![]() $l$
;
$l$
;
![]() $m_l$
and
$m_l$
and
![]() $m_q$
are the first partial derivatives of
$m_q$
are the first partial derivatives of
![]() $m$
with respect to
$m$
with respect to
![]() $q$
and
$q$
and
![]() $l$
;
$l$
;
![]() $|H|$
represents the determinant of the bordered Hessian matrix;
$|H|$
represents the determinant of the bordered Hessian matrix;
![]() $H_{ql}$
is the cofactor of the element
$H_{ql}$
is the cofactor of the element
![]() $m_{ql}$
in
$m_{ql}$
in
![]() $H$
, with
$H$
, with
![]() $m_{ql}$
indicating the cross-partial derivative of
$m_{ql}$
indicating the cross-partial derivative of
![]() $m$
.
$m$
.
A well-known problem in a parametric equivalent of a production function estimation like Equation (1), dating back to Marschak & Andrews (Reference Marschak and Andrews1944), is the “simultaneity” between the choice concerning the amount of inputs and the (unknown to the econometrician but known to the firm when the decision is made) productivity (or technological) component of the production function. While simultaneity poses a challenge in firm-level estimation, its nature at an aggregate level (i.e., country-sector) is less straightforward to discern — in terms of how firm knowledge of productivity affecting input choices may be analogously applied to the behavior of the entire industry to which it belongs. This is tantamount to stating that the diverse fixed effects in nonparametric estimation entirely capture productivity heterogeneity at the sector level. Equivalently, it assumes that any productivity innovations are observed subsequent to input decisions (at the sector level), thereby ensuring no correlation with input decisions.Footnote 14 Moreover, within this setup, the EoS is derived through estimating “relative” gradients. Any potential simultaneity bias, if present, would impact both the numerator and denominator, effectively canceling out when ratios are taken. However, we also recognize that the presence of endogeneity bias is serious and so we must interpret our results with caution. Future research in this area could assess the impact of endogeneity bias through productivity shocks and the adoption of robotic capital, similar to the large literature on firm-level productivity (Olley and Pakes, Reference Olley and Pakes1996; Ackerberg, Caves and Frazier, Reference Ackerberg, Caves and Frazer2015; Gandhi, Navarro and Rivers, Reference Gandhi, Navarro and Rivers2020, etc.).
4. Results
In Figure 4, we show the kernel densities of estimated median
![]() $\sigma _{RK,S}$
and
$\sigma _{RK,S}$
and
![]() $\sigma _{RK,U}$
, by country and by industry. We cut 10 percent of observations on the tails of the overall distribution to exclude potential outliers (subsequent analysis is based on such distribution).Footnote
15
As can be observed, in both panels, the distribution of
$\sigma _{RK,U}$
, by country and by industry. We cut 10 percent of observations on the tails of the overall distribution to exclude potential outliers (subsequent analysis is based on such distribution).Footnote
15
As can be observed, in both panels, the distribution of
![]() $\sigma _{RK,S}$
— the solid line — is located to the left, with respect to that of
$\sigma _{RK,S}$
— the solid line — is located to the left, with respect to that of
![]() $\sigma _{RK,U}$
, pointing to (relative) overall higher complementarity (or lower substitutability) between
$\sigma _{RK,U}$
, pointing to (relative) overall higher complementarity (or lower substitutability) between
![]() $RK$
and
$RK$
and
![]() $S$
. Ultimately, we find that in approximately 60% of cases,
$S$
. Ultimately, we find that in approximately 60% of cases,
![]() $\sigma _{RK,S}$
is lower than
$\sigma _{RK,S}$
is lower than
![]() $\sigma _{RK,U}$
In this regard, Figure E2 in the Appendix reports the distribution of both
$\sigma _{RK,U}$
In this regard, Figure E2 in the Appendix reports the distribution of both
![]() $\sigma _{RK,S}$
and
$\sigma _{RK,S}$
and
![]() $\sigma _{RK,U}$
values over the entire sample.
$\sigma _{RK,U}$
values over the entire sample.

Figure 4. Kernel distribution of the estimated median Morishima EoS, 1995–2009.
Ideally, we would like to test that
![]() $\sigma _{RK,S}$
is lower than
$\sigma _{RK,S}$
is lower than
![]() $\sigma _{RK,U}$
for all observations. This entails the hypothesis:
$\sigma _{RK,U}$
for all observations. This entails the hypothesis:
against the alternative that
where
![]() $X$
here is the complete vector of inputs. This is a difficult testing problem as it requires a comparison of each pair of estimates of EoS of a rather complex nonparametric object. To our knowledge, a general one-sided test of nonparametrically estimated objects does not yet exist. It is common in tests of, say, statistical significance or correct functional form that a weighted test statistic is deployed to eliminate the random denominator that arises with nonparametrically constructed obejcts. However, our situation here is much more difficult as the ‘denominator’ of
$X$
here is the complete vector of inputs. This is a difficult testing problem as it requires a comparison of each pair of estimates of EoS of a rather complex nonparametric object. To our knowledge, a general one-sided test of nonparametrically estimated objects does not yet exist. It is common in tests of, say, statistical significance or correct functional form that a weighted test statistic is deployed to eliminate the random denominator that arises with nonparametrically constructed obejcts. However, our situation here is much more difficult as the ‘denominator’ of
![]() $\sigma _{RK,S}$
(or its difference with
$\sigma _{RK,S}$
(or its difference with
![]() $\sigma _{RK,U}$
) is not obvious or known.
$\sigma _{RK,U}$
) is not obvious or known.
To address this testing challenge, we employ a two-pronged approach: a Kolmogorov–Smirnov (KS) test of first-order stochastic dominance and a graphical analysis of the EoS dynamics over time. The KS test examines whether the probability of observing a given level of
![]() $\sigma _{RK,S}$
is higher than an equally sized value of
$\sigma _{RK,S}$
is higher than an equally sized value of
![]() $\sigma _{RK,U}$
. While not ideal, it provides a step toward establishing that
$\sigma _{RK,U}$
. While not ideal, it provides a step toward establishing that
![]() $RK$
is more substitutable with
$RK$
is more substitutable with
![]() $U$
than with
$U$
than with
![]() $S$
labor. We apply such a test to the entire period and three distinct sub-periods (1995–1999, 2000–2004, 2005–2009). The results reveal an evolving pattern: for the full period and the latter two sub-periods, we fail to reject the null hypothesis that
$S$
labor. We apply such a test to the entire period and three distinct sub-periods (1995–1999, 2000–2004, 2005–2009). The results reveal an evolving pattern: for the full period and the latter two sub-periods, we fail to reject the null hypothesis that
![]() $\sigma _{RK,U}$
first-order stochastically dominates
$\sigma _{RK,U}$
first-order stochastically dominates
![]() $\sigma _{RK,S}$
(
$\sigma _{RK,S}$
(
![]() $p$
-values of 0.4212, 0.6603, and 1, respectively). However, for the initial sub-period (1995–1999), we reject the null hypothesis (
$p$
-values of 0.4212, 0.6603, and 1, respectively). However, for the initial sub-period (1995–1999), we reject the null hypothesis (
![]() $p$
-value of 1.649e-06).
$p$
-value of 1.649e-06).
To complement the statistical analysis, we exploit our nonparametric estimates to visually examine the EoS dynamics. Figure 5 presents the (normalized) cumulative distribution functions (CDFs) of the two EoS for the three aforementioned sub-periods: at the beginning (1995–1999), in the middle (2000–2004), and at the end of the period (2005–2009). Additionally, the last panel displays the distribution of the difference between
![]() $\sigma _{RK,S}$
and
$\sigma _{RK,S}$
and
![]() $\sigma _{RK,U}$
across these three periods.Footnote
16
The graphical analysis corroborates and extends the insights from the KS test. In fact, the overall trend suggests that the relationship between the two distributions has evolved substantially over time: initially, they intersected, indicating a lack of clear dominance. However, toward the end of the period, the distribution of
$\sigma _{RK,U}$
across these three periods.Footnote
16
The graphical analysis corroborates and extends the insights from the KS test. In fact, the overall trend suggests that the relationship between the two distributions has evolved substantially over time: initially, they intersected, indicating a lack of clear dominance. However, toward the end of the period, the distribution of
![]() $\sigma _{RK,U}$
exhibits a higher mean and lower variance compared to
$\sigma _{RK,U}$
exhibits a higher mean and lower variance compared to
![]() $\sigma _{RK,S}$
, consistent with the failure to reject stochastic dominance in later periods.
$\sigma _{RK,S}$
, consistent with the failure to reject stochastic dominance in later periods.
To sum up, this dual approach offers evidence of an increasing tendency for
![]() $RK$
to be more substitutable with
$RK$
to be more substitutable with
![]() $U$
than with
$U$
than with
![]() $S$
labor over the studied period, particularly after 2000.
$S$
labor over the studied period, particularly after 2000.

Figure 5. EoS normalized cumulative distribution: time dynamics.
This trend is confirmed by the evolution of the share of cases in which
![]() $\widehat{\sigma }_{RK,U}\gt \widehat{\sigma }_{RK,S}$
: 50% in the period 1995–1999, 60% over the years 2000–2004, and 72% in the period 2005–2009%.Footnote
17
$\widehat{\sigma }_{RK,U}\gt \widehat{\sigma }_{RK,S}$
: 50% in the period 1995–1999, 60% over the years 2000–2004, and 72% in the period 2005–2009%.Footnote
17
Global trends are reported in Figure 6.Footnote 18 Quite interestingly, we observe that the two EoS exhibit a tendency to cross at the end of the 1990s and diverge in the early 2000s, with an inversion at the end of the period.

Figure 6. EoS estimated patterns, 1995–2009, normalized median values.
To delve more into the country-sector dimension of this aspect, Figures 7 and 8 report some disaggregated patterns. Namely, Figure 7 shows how the overall tendency in Figure 6 differently mirrors OECD and Non-OECD evolutions. In particular, while in the OECD countries the widening gap between
![]() $\sigma _{RK,U}$
and
$\sigma _{RK,U}$
and
![]() $\sigma _{RK,S}$
is driven by a substantial increase in the former, we document an important reduction in
$\sigma _{RK,S}$
is driven by a substantial increase in the former, we document an important reduction in
![]() $\sigma _{RK,S}$
in Non-OECD countries, with a higher complementarity between
$\sigma _{RK,S}$
in Non-OECD countries, with a higher complementarity between
![]() $RK$
and
$RK$
and
![]() $S$
detected (i.e.,
$S$
detected (i.e.,
![]() $\sigma _{RK,S} \lt 0$
), especially at the end of the period. Within the OECD group, European countries’ patterns look very similar to the US, in terms of timing of sign change of the difference between
$\sigma _{RK,S} \lt 0$
), especially at the end of the period. Within the OECD group, European countries’ patterns look very similar to the US, in terms of timing of sign change of the difference between
![]() $\sigma _{RK,U}$
and
$\sigma _{RK,U}$
and
![]() $\sigma _{RK,S}$
.
$\sigma _{RK,S}$
.

Figure 7. EoS estimated patterns in selected (groups of) countries, 1995–2009, normalized median values.

Figure 8. EoS estimated patterns in selected (groups of) sectors, 1995–2009, normalized median values.
At the sectoral level (see Figure 8), the divergence in Manufacturing started before and seems to last longer, compared to Non-Manufacturing. The two sectors more interested by the robotization process (transport equipment and electrical and optical equipment industries, according to our
![]() $RK$
measure) display different trajectories: unskilled are less complementary than skilled since the beginning of the period (i.e.,
$RK$
measure) display different trajectories: unskilled are less complementary than skilled since the beginning of the period (i.e.,
![]() $\sigma _{RK,U}$
always stands above
$\sigma _{RK,U}$
always stands above
![]() $\sigma _{RK,S}$
), with an increasing trend in the whole first decade of 2000 (without reversal) in electrical and optical equipment sector; the initial situation was opposite in the transport equipment industry.
$\sigma _{RK,S}$
), with an increasing trend in the whole first decade of 2000 (without reversal) in electrical and optical equipment sector; the initial situation was opposite in the transport equipment industry.
The above dynamics are not surprising. In fact, as pointed out by Autor (Reference Autor2015), the years at the turn of the new millennium coincided with a dramatic drop for those workers employed in “production” and occupied as “operators/laborers” — the most vulnerable to robotization and included, throughout our empirical analysis, within the
![]() $U$
category. Moreover, such a pattern retraces the evidence uncovered by Koch et al. (Reference Koch, Manuylov and Smolka2021) in Spain, where robot adoption increased rapidly after 1998. Finally, Acemoglu and Restrepo (Reference Acemoglu and Restrepo2020) argue that the distinct impact of robots from other technologies started to appear after the 1990s. By and large, this phenomenon may be interpreted as a hint of an increasingly higher relative complementarity of
$U$
category. Moreover, such a pattern retraces the evidence uncovered by Koch et al. (Reference Koch, Manuylov and Smolka2021) in Spain, where robot adoption increased rapidly after 1998. Finally, Acemoglu and Restrepo (Reference Acemoglu and Restrepo2020) argue that the distinct impact of robots from other technologies started to appear after the 1990s. By and large, this phenomenon may be interpreted as a hint of an increasingly higher relative complementarity of
![]() $ S$
during the process of development (and of robotization).
$ S$
during the process of development (and of robotization).
4.1 Statistical Inference
Given the highly nonlinear nature of our estimated EoS, an asymptotic variance is unlikely to be of empirical value. Rather, we rely on a nonparametric bootstrap to construct standard errors for each of our EoS estimates. To do this, we use a two-point wild bootstrap procedure with 500 replications (see, Battisti et al. (Reference Battisti, Gatto and Parmeter2022), for details on bootstrapping in this framework). We keep the bandwidths fixed across the replications to reduce noise stemming from the estimation of the smoothing parameters.
In our benchmark analysis, conducted over
![]() $7,504$
Footnote
19
country-sector pairs, we find:
$7,504$
Footnote
19
country-sector pairs, we find:
-
• about 37% of estimates for
 $\sigma _{RK,S}$
are statistically significant at least at the 10% level;
$\sigma _{RK,S}$
are statistically significant at least at the 10% level; -
• about 45% of estimates for
 $\sigma _{RK,U}$
are statistically significant at least at the 10% level.Footnote
20
$\sigma _{RK,U}$
are statistically significant at least at the 10% level.Footnote
20
Although these values may appear prima-facie low, the nonparametric point estimates cannot be simply compared with the statistical significance of coefficients estimated via OLS (a mean estimator). A more proper comparison within similar works (such as, Henderson (Reference Henderson2009), who examined the capital-skill complementarity from a cross-country perspective, with a single type of capital and no sector controls), reveals a much higher share of statistically significant nonparametric EoS estimates in our case. In fact, the present analysis relies on a sample mainly containing OECD and/or developed economies, observed over a shorter time span, and is broken down by sector. Further, we detect that the proportion of statistically and economically significant EoS estimates increases when we consider observations with nonzero
![]() $RK$
. Specifically, this share peaks to nearly 70% when focusing on these observations, implying a higher confidence in estimations for developed countries as opposed to emerging economies, which utilize a much lower stock of
$RK$
. Specifically, this share peaks to nearly 70% when focusing on these observations, implying a higher confidence in estimations for developed countries as opposed to emerging economies, which utilize a much lower stock of
![]() $RK$
.
$RK$
.
5. Robustness and broad validation
5.1 Different depreciation rates and different types of capital
The robustness of our results is first of all checked by changing the depreciation rate used in the construction of our
![]() $RK$
stock. As a further investigation, we repeat our analysis replacing our
$RK$
stock. As a further investigation, we repeat our analysis replacing our
![]() $RK$
measure with total capital in order to understand to what extent our findings can be thought of to be driven by the estimation methodology.Footnote
21
Table 1 synthesizes all the above checks focusing on some country classifications, the two major industries in terms of
$RK$
measure with total capital in order to understand to what extent our findings can be thought of to be driven by the estimation methodology.Footnote
21
Table 1 synthesizes all the above checks focusing on some country classifications, the two major industries in terms of
![]() $RK$
intensity, as well as years at the beginning, in the middle and at the end of the period. Benchmark results (i.e., when
$RK$
intensity, as well as years at the beginning, in the middle and at the end of the period. Benchmark results (i.e., when
![]() $RK$
is calculated assuming
$RK$
is calculated assuming
![]() $\delta = 10\%$
) are reported in the first two columns to ease comparison. In the vast majority of cases, the hypothesis of a relatively lower (higher) substitutability (complementarity) between
$\delta = 10\%$
) are reported in the first two columns to ease comparison. In the vast majority of cases, the hypothesis of a relatively lower (higher) substitutability (complementarity) between
![]() $RK$
and
$RK$
and
![]() $S$
, as well as between
$S$
, as well as between
![]() $TotK$
and
$TotK$
and
![]() $S$
, seems consistent with the data.
$S$
, seems consistent with the data.
Table 1. Estimated EoS: different depreciation rates and different types of capital. Median values

Notes: Time and country-by-sector fixed effects included. The cases in which the “RK-Skill complementarity” and capital-skill complementarity hypotheses holds true are reported in bold.
Anglo-saxons: Australia, United Kingdom, USA. Asian: Indonesia, India, Japan, Republic of Korea, Turkey.
Europe: Austria, Belgium, Bulgaria, Czech Republic, Germany, Denmark, Spain, Estonia, Finland, France, Greece, Hungary, Ireland, Italy, Lithuania, Latvia, Malta, Netherlands, Poland, Portugal, Romania, Russia, Slovak Republic, Slovenia, Sweden.
Non-Europe: Australia, Brazil, Indonesia, India, Japan, Republic of Korea, Turkey, USA.
OECD: Belgium, Denmark, Germany, France, Netherlands, Sweden, Finland, Austria, Greece, Spain, Italy, Portugal, Ireland, United Kingdom, Czech Republic, Estonia, Hungary, Lithuania, Latvia, Poland, Slovak Republic, Slovenia, Turkey, Australia, Japan, Republic of Korea, USA. Non-OECD: Bulgaria, Brazil, Indonesia, India, Malta, Romania, Russia.
Finally, a key result of our analysis is the unraveling of a diverging pattern driven by increasing
![]() $\sigma _{RK,U}$
in the first decade of 2000 in the OECD country-group (see Figure 7). One might wonder whether such tendency can be a some mechanical consequence of
$\sigma _{RK,U}$
in the first decade of 2000 in the OECD country-group (see Figure 7). One might wonder whether such tendency can be a some mechanical consequence of
![]() $RK$
accumulation. To check whether this is the case, we re-estimate the OECD trend using
$RK$
accumulation. To check whether this is the case, we re-estimate the OECD trend using
![]() $IK$
, relying on the EU KLEMS (2009) sample, in place of
$IK$
, relying on the EU KLEMS (2009) sample, in place of
![]() $RK$
(that is estimating
$RK$
(that is estimating
![]() $\sigma _{IK,S}$
and
$\sigma _{IK,S}$
and
![]() $\sigma _{IK,U}$
instead of
$\sigma _{IK,U}$
instead of
![]() $\sigma _{RK,S}$
and
$\sigma _{RK,S}$
and
![]() $\sigma _{RK,U}$
). In so doing, we exploit the remarkable growth of ICT capital displayed in Figure 2. Since this type of capital does not include robots, a different dynamics can be expected. Indeed, Figure 9 reports decreasing substitutability with respect to both
$\sigma _{RK,U}$
). In so doing, we exploit the remarkable growth of ICT capital displayed in Figure 2. Since this type of capital does not include robots, a different dynamics can be expected. Indeed, Figure 9 reports decreasing substitutability with respect to both
![]() $ S$
and
$ S$
and
![]() $U$
, with the former steadily and steeply decreasing over the whole period, with an acceleration in the first decade of the century. This seems to be in line with previous “ICT capital-skill complementarity” studies such as Eden & Gaggl (Reference Eden and Gaggl2018) and Taniguchi & Yamada (Reference Taniguchi and Yamada2022), providing a further broad validation of our nonparametric framework with respect to more traditional parametric settings.
$U$
, with the former steadily and steeply decreasing over the whole period, with an acceleration in the first decade of the century. This seems to be in line with previous “ICT capital-skill complementarity” studies such as Eden & Gaggl (Reference Eden and Gaggl2018) and Taniguchi & Yamada (Reference Taniguchi and Yamada2022), providing a further broad validation of our nonparametric framework with respect to more traditional parametric settings.

Figure 9. Estimated patterns of
![]() $\sigma _{IK,S}$
and
$\sigma _{IK,S}$
and
![]() $\sigma _{IK,U}$
, OECD, 1994–2005.
$\sigma _{IK,U}$
, OECD, 1994–2005.
5.2 Price and productivity effects
In principle, the above patterns can be driven by two order of forces. First, decreasing robot prices, coupled with non-decreasing skill premia, might induce a more intense use of robots — that is, robot prices might have fallen, relative to
![]() $U$
’s wage, more than
$U$
’s wage, more than
![]() $S$
’s wage did (i.e., a price effect). Second, the relative increase in robots usage might be pushed by robots’ increased ability to perform manual and/or routine tasks (i.e., a productivity effect).
$S$
’s wage did (i.e., a price effect). Second, the relative increase in robots usage might be pushed by robots’ increased ability to perform manual and/or routine tasks (i.e., a productivity effect).
The first force relies on the assumption that
![]() $ U$
(and their manual tasks) are easier to replace and can be linked to the directed technical change hypothesis (Acemoglu, 2002). The second effect can be intended as an equivalent of Moore’s Law applied to
$ U$
(and their manual tasks) are easier to replace and can be linked to the directed technical change hypothesis (Acemoglu, 2002). The second effect can be intended as an equivalent of Moore’s Law applied to
![]() $RK$
, so that even without an increasing diffusion, new robots could be able to perform more tasks than previous ones.Footnote
22
$RK$
, so that even without an increasing diffusion, new robots could be able to perform more tasks than previous ones.Footnote
22
Graphical inspection seems to suggest that both effects have been at work. As for the price effect, the declining medium-run trend of robot prices, relative to the (un)skill premium (the
![]() $U/S$
wage gap) in Figure 10 provides a first, strong incentive to replace
$U/S$
wage gap) in Figure 10 provides a first, strong incentive to replace
![]() $U$
with robots.
$U$
with robots.

Figure 10. Evolution of robot price over unskilled/skilled wage ratio, US and Japan, 1995–2009.
Additionally, the marginal product of
![]() $RK$
sharply increased over the same years, as we document in Figure 11; thus, also the productivity effect might have triggered the substitutability process.
$RK$
sharply increased over the same years, as we document in Figure 11; thus, also the productivity effect might have triggered the substitutability process.

Figure 11. Evolution of marginal product of robotic capital, 1995–2009.
To more formally inquire into these relationships, we regress the (nonparametrically) estimated EoS on two proxies for the price and productivity effects.Footnote 23
where
![]() $x = \left \lbrace (RK,S) \text{ or } (RK,U)\right \rbrace$
;
$x = \left \lbrace (RK,S) \text{ or } (RK,U)\right \rbrace$
;
![]() $W_S$
and
$W_S$
and
![]() $W_U$
are the wage of
$W_U$
are the wage of
![]() $ S$
and
$ S$
and
![]() $U$
, respectively;
$U$
, respectively;
![]() $\widehat{MP}^{RK}=$
denotes the estimated marginal product of
$\widehat{MP}^{RK}=$
denotes the estimated marginal product of
![]() $RK$
;
$RK$
;
![]() $j$
is the country-sector index. Estimation of this regression is straighforward, however, we have nonparametrically generated regressors on both sides of the equation (see Mammen, Rothe and Scheinle, Reference Mammen, Rothe and Schienle2012, Chu, Reference Chu2023). This necessitates use of bootstrapping to construct appropriate standard errors.
$j$
is the country-sector index. Estimation of this regression is straighforward, however, we have nonparametrically generated regressors on both sides of the equation (see Mammen, Rothe and Scheinle, Reference Mammen, Rothe and Schienle2012, Chu, Reference Chu2023). This necessitates use of bootstrapping to construct appropriate standard errors.
It is worth noting that we interpret this relationship as a simple correlation, due to the lack of exogenous sources of variation. Therefore, we cannot claim any causal effect in this exercise, given the presence of reverse causality between EoS and prices/productivity.Footnote
24
A statistically significant negative (positive)
![]() $\hat{\beta }$
, when
$\hat{\beta }$
, when
![]() $\widehat{\sigma }_{RK,S}$
(
$\widehat{\sigma }_{RK,S}$
(
![]() $\widehat{\sigma }_{RK,U}$
) is used as dependent variable, would suggest the price (i.e.,
$\widehat{\sigma }_{RK,U}$
) is used as dependent variable, would suggest the price (i.e.,
![]() $\beta _1$
) and/or the productivity (i.e.,
$\beta _1$
) and/or the productivity (i.e.,
![]() $\beta _2$
) to play a role.
$\beta _2$
) to play a role.
Results in Table 2 show that the estimated partial correlations have the expected signs, that is, negative (positive) in the left (right) panels, implying higher complementarity of
![]() $ S$
(substitutability of
$ S$
(substitutability of
![]() $ U$
), with increasing relative costs of
$ U$
), with increasing relative costs of
![]() $ U$
and higher marginal product of
$ U$
and higher marginal product of
![]() $RK$
. By including country—, industry— and time-controls, the magnitude is reinforced and the statistical significance of the estimated coefficients is unaltered. These findings turn out to be robust when
$RK$
. By including country—, industry— and time-controls, the magnitude is reinforced and the statistical significance of the estimated coefficients is unaltered. These findings turn out to be robust when
![]() $RK$
is computed using different depreciation rates.
$RK$
is computed using different depreciation rates.
Table 2. Price and productivity effects (Eq. 3)

Notes: *
![]() $p\lt 0.10$
,**
$p\lt 0.10$
,**
![]() $p\lt 0.05$
, ***
$p\lt 0.05$
, ***
![]() $p\lt 0.01$
. Bootstrapped standard errors in parentheses.
$p\lt 0.01$
. Bootstrapped standard errors in parentheses.
6. Conclusions
The growing concerns stemming from the extensive use of automation in production are prompting scholars to seek a better understanding of its implications for the labor market. Additionally, the pressure from international shocks necessitating a complete rethinking of the production process is fueling a heated debate on whether robots and other forms of automation will favor skilled workers (
![]() $S$
) at the expense of unskilled labor (
$S$
) at the expense of unskilled labor (
![]() $U$
).
$U$
).
In this paper, we contribute to the debate by investigating the extent of complementarity and substitutability in the productive processes between robotic capital (
![]() $RK$
) and workers of different skill levels (high-skilled versus medium-low-skilled).
$RK$
) and workers of different skill levels (high-skilled versus medium-low-skilled).
We estimate country-sector Elasticity of Substitution (EoS) patterns between
![]() $RK$
and labor inputs. The main results of the analysis can be summarized as follows:
$RK$
and labor inputs. The main results of the analysis can be summarized as follows:
-
• Overall evidence of “RK-skill complementarity,” with
 $\sigma _{RK,S} \lt \sigma _{RK,U}$
, suggesting that
$\sigma _{RK,S} \lt \sigma _{RK,U}$
, suggesting that
 $RK$
deepening proceeds hand in hand with increasing labor ratios (i.e.,
$RK$
deepening proceeds hand in hand with increasing labor ratios (i.e.,
 $\frac{S}{U}$
). However, it is not always the case that robotization results in shrinking
$\frac{S}{U}$
). However, it is not always the case that robotization results in shrinking
 $U$
and/or
$U$
and/or
 $S$
.
$S$
. -
• A certain degree of heterogeneity at the country-sector level.
-
• The dynamic pattern of elasticities shows as the difference between
 $\sigma _{RK,U}$
and
$\sigma _{RK,U}$
and
 $\sigma _{RK,S}$
has grown substantially over the first decade of 2000 (indeed, while often lower than
$\sigma _{RK,S}$
has grown substantially over the first decade of 2000 (indeed, while often lower than
 $\sigma _{RK,S}$
at the beginning,
$\sigma _{RK,S}$
at the beginning,
 $\sigma _{RK,U}$
ends up being much higher in 2009).
$\sigma _{RK,U}$
ends up being much higher in 2009). -
• Both the difference and its increase over the period have been more pronounced in OECD than in non-OECD countries (where the increase is mainly driven by shrinking
 $\sigma _{RK,S}$
) and in Manufacturing with respect to Non-Manufacturing.
$\sigma _{RK,S}$
) and in Manufacturing with respect to Non-Manufacturing.
A possible explanation for the existence of a turning point at the end of the ’90s, in which the two estimated EoS cross each other with the
![]() $\sigma _{RK,U}$
growing more than the
$\sigma _{RK,U}$
growing more than the
![]() $\sigma _{RK,S}$
, can be associated with the fact that robots have increased their ability to reproduce complex tasks.
$\sigma _{RK,S}$
, can be associated with the fact that robots have increased their ability to reproduce complex tasks.
By and large, the contribution to increasing the
![]() $\frac{S}{U}$
ratio raises issues linked to unemployment and/or wage pressures for vulnerable segments of the labor market. In this respect, policymakers face numerous challenges. By shedding light on understanding the labor market asymmetries associated with the ongoing process of technological change, especially in manufacturing industries of advanced and transition economies, our study highlights how, if, on the one hand, industrial robots, as a subset of the broader category of automation technologies, turn out to be a powerful engine of economic growth, on the other hand, they appear to be associated with intensifying inequalities that, far from being trivial in terms of sign and intensity, follow strongly different patterns across countries and sectors.
$\frac{S}{U}$
ratio raises issues linked to unemployment and/or wage pressures for vulnerable segments of the labor market. In this respect, policymakers face numerous challenges. By shedding light on understanding the labor market asymmetries associated with the ongoing process of technological change, especially in manufacturing industries of advanced and transition economies, our study highlights how, if, on the one hand, industrial robots, as a subset of the broader category of automation technologies, turn out to be a powerful engine of economic growth, on the other hand, they appear to be associated with intensifying inequalities that, far from being trivial in terms of sign and intensity, follow strongly different patterns across countries and sectors.
We end here by noting there are many directions in which we could extend our analysis further. First, developing a formal test for size of skill bias through the EoS holds great empirical promise. Second, investigating the price of
![]() $RK$
and its impact on the analysis would provide an excellent robustness check. We have only investigated country-sector pairs with available information, including those completed through an imputation process, which obviously limits our coverage. Collecting and obtaining data for more countries-sectors (and years) would be an important upgrade. Third, our approach here effectively dealt with human capital stocks by moving middle-skilled workers into the
$RK$
and its impact on the analysis would provide an excellent robustness check. We have only investigated country-sector pairs with available information, including those completed through an imputation process, which obviously limits our coverage. Collecting and obtaining data for more countries-sectors (and years) would be an important upgrade. Third, our approach here effectively dealt with human capital stocks by moving middle-skilled workers into the
![]() $U$
group. This made our analysis much easier but also blurs the lines of the skill level of many workers. It would be worthwhile to consider a three skill level model and determine how robust our results are.
$U$
group. This made our analysis much easier but also blurs the lines of the skill level of many workers. It would be worthwhile to consider a three skill level model and determine how robust our results are.
Acknowledgements
We are grateful to David Andolfatto, Rosario Crinó, Joseph Zeira, and the participants in the “North American Productivity Workshop XI” (NAPW XI, 2020), the Research Centre for Economic Analysis “3rd Warsaw Money-Macro-Finance Conference” (RCEA, 2021), the “II Biannual Workshop: Technological Change, Health, Inequality and Data for Policy Evaluation” (LABOR, 2022), the International Centre for Economic Analysis “Future of Work” Conference (ICEA, 2022), the “XXII AISSEC Scientific Conference” and the 2023 ISGEP Workshop on “Firms, Trade and Productivity” at “G. d’Annunzio” University of Chieti-Pescara, the “64th Annal Conference of the Italian Economic Association” (Gran Sasso Science Institute, 2023), and the “Economics Seminar Series” (Universities of Bergamo and Palermo, 2022) for many useful comments and suggestions. The usual caveat applies.
Financial support
Michele Battisti and Massimo Del Gatto gratefully acknowledge financial support from the Fondo per il Programma Nazionale di Ricerca e Progetti di Rilevante Interesse Nazionale (PRIN) 2022 of the Ministry of University and Research of Italy (grant number 2022FLBY7J - D53D23006480006).
Appendix
A. RK construction: retrieving the unit price of robots
Information on average unit price of robots, needed to obtain our RK measure, is retrieved from different IFR reports. In particular, prices are computed as the ratio of the turnover of total robot systems to the number of robots delivered in a specific country. Unfortunately, IFR provides series of industrial robot prices (in current, thousand dollars) for a few countries only (see, for instance, International Federation of Robotics (2005). Specifically, unit prices are available for: Japan, US, Germany, Republic of Korea, United Kingdom and France, from 1995 to 2008. For Italy, robot prices are available from 1995 to 2006.
To define the average unit price of robots in the remaining countries, we proceed as follows. For Italy, the 2007 and 2008 prices are computed using the average growth rate of the countries for which we have original data. For all the other countries, we relied upon geographical proximity, economic proximity and trade relationships. In particular:
-
• European countries are assigned the average robot prices of Germany, United Kingdom, France and Italy;
-
• American countries are assigned US robot prices;
-
Asian countries (plus Australia) are assigned the average robot prices of Japan and Republic of Korea.
In order to obtain the 1995 and 2009 prices, data are smoothed using uniformly weighted moving averages, with 1 lagged term, 1 forward term and the current observation in the filter.
B. The empirical methodology in details
Local polynomial least squares estimation. Nonparametric kernel methods have the ability to alleviate many of the restrictive assumptions made in classical parametric frameworks (the use of CES for example). Consider the canonical nonparametric regression model:
where
![]() $y_i$
is our response (in this case output growth),
$y_i$
is our response (in this case output growth),
![]() $x_i$
is a vector of
$x_i$
is a vector of
![]() $q$
regressors,
$q$
regressors,
![]() $\varepsilon _i$
is the additive (mean zero) random disturbance and
$\varepsilon _i$
is the additive (mean zero) random disturbance and
![]() $m\left ( \cdot \right )$
is an unknown smooth function. Here,
$m\left ( \cdot \right )$
is an unknown smooth function. Here,
![]() $m\left ( \cdot \right )$
is interpreted as the conditional mean of
$m\left ( \cdot \right )$
is interpreted as the conditional mean of
![]() $y$
given
$y$
given
![]() $x$
; in a traditional linear in parameters setting it is implicitly assumed that
$x$
; in a traditional linear in parameters setting it is implicitly assumed that
![]() $E\left ( y_{i}|x_{i}\right ) =\alpha +\beta x_{i}$
.
$E\left ( y_{i}|x_{i}\right ) =\alpha +\beta x_{i}$
.
Popular estimation approaches for estimating the conditional mean in (B.1) are local-constant and local-linear least-squares (LCLS and LLLS, respectively) regression. The intuition behind these estimators is that they construct a weighted average of
![]() $y_{i}$
based on the location of the covariates. These weights are dictated by kernels. The “local” determination is controlled through a user defined parameter known as the bandwidth.
$y_{i}$
based on the location of the covariates. These weights are dictated by kernels. The “local” determination is controlled through a user defined parameter known as the bandwidth.
One benefit of LLLS over LCLS is that the slope of the conditional mean is also estimated directly. This is important for our setting as we are not interested directly in the conditional mean of growth, but in the slope of the relationship in various dimensions that will allow us to measure “RK-skill complementarity.” In fact, because we are interested in second derivatives and cross partials, we need more advanced local smoothing methods to recover these gradients. For this, we turn to LPLS.
To describe LPLS, we note that we can approximate
![]() $m$
around
$m$
around
![]() $x_0$
as:
$x_0$
as:
where
 \begin{align*} \mathbf{j} =& \left ( j_1,\ldots, j_d\right ), \qquad \mathbf{j}! = j_1! \times \ldots \times j_d!, \qquad \vert \mathbf{j} \vert = \sum _{k =1}^d j_k,\\ (x_i - x_0)^{\mathbf{j}} =& (x_{1i} - x_{10})^{j_1} \times \ldots \times (x_{di} - x_{d0})^{j_d},\\ \sum _{0 \leq \vert \mathbf{j} \vert \leq \rho } =& \underset{j_1 + \ldots + j_d = \vert \mathbf{j} \vert }{\sum _{k =0}^{\rho } \sum _{j_1 = 0}^k \ldots \sum _{j_d = 0}^k}, \end{align*}
\begin{align*} \mathbf{j} =& \left ( j_1,\ldots, j_d\right ), \qquad \mathbf{j}! = j_1! \times \ldots \times j_d!, \qquad \vert \mathbf{j} \vert = \sum _{k =1}^d j_k,\\ (x_i - x_0)^{\mathbf{j}} =& (x_{1i} - x_{10})^{j_1} \times \ldots \times (x_{di} - x_{d0})^{j_d},\\ \sum _{0 \leq \vert \mathbf{j} \vert \leq \rho } =& \underset{j_1 + \ldots + j_d = \vert \mathbf{j} \vert }{\sum _{k =0}^{\rho } \sum _{j_1 = 0}^k \ldots \sum _{j_d = 0}^k}, \end{align*}
and
 \begin{equation*} (D^{(\mathbf {j})}m)(x_0) = \frac {\partial ^{\mathbf {j}} m(x_0)}{\partial x^{j_1}_{10} \ldots \partial x^{j_d}_{d0}}. \end{equation*}
\begin{equation*} (D^{(\mathbf {j})}m)(x_0) = \frac {\partial ^{\mathbf {j}} m(x_0)}{\partial x^{j_1}_{10} \ldots \partial x^{j_d}_{d0}}. \end{equation*}
Notice that in this formulation, we can allow for an arbitrary order of polynomial for each different component in
![]() $x$
. From here we are interested in the solution to the weighted least squares problem
$x$
. From here we are interested in the solution to the weighted least squares problem
 \begin{equation} \frac{1}{nh} \sum _{i=1}^n \left [y_i - \sum _{\ell =0}^L \beta _\ell x_{\ell i}-x_{s0})^{j} \right ]^2 \mathcal{K}\left (\frac{x_i-x}{h} \right ) \end{equation}
\begin{equation} \frac{1}{nh} \sum _{i=1}^n \left [y_i - \sum _{\ell =0}^L \beta _\ell x_{\ell i}-x_{s0})^{j} \right ]^2 \mathcal{K}\left (\frac{x_i-x}{h} \right ) \end{equation}
in which
![]() $\mathcal{K}(\cdot )$
is a product kernel function and
$\mathcal{K}(\cdot )$
is a product kernel function and
![]() $h$
is a bandwidth vector. In this setup,
$h$
is a bandwidth vector. In this setup,
![]() $\beta _\ell$
denotes the partial derivative of order
$\beta _\ell$
denotes the partial derivative of order
![]() $j$
for coefficient
$j$
for coefficient
![]() $k$
with respect to component
$k$
with respect to component
![]() $s$
.
$s$
.
Define
![]() $\widetilde{x}_{si} \equiv \left ((x_{si} - x_s)^1,(x_{si} - x_s)^2,\ldots, (x_{si} - x_s)^{p_s} \right )$
and
$\widetilde{x}_{si} \equiv \left ((x_{si} - x_s)^1,(x_{si} - x_s)^2,\ldots, (x_{si} - x_s)^{p_s} \right )$
and
![]() $\widetilde{Z}_i \equiv \left (\widetilde{x}_{1i},\widetilde{x}_{2i},\ldots, \widetilde{x}_{Si} \right )$
. Then, for
$\widetilde{Z}_i \equiv \left (\widetilde{x}_{1i},\widetilde{x}_{2i},\ldots, \widetilde{x}_{Si} \right )$
. Then, for
![]() $\widetilde{X}_i \equiv \displaystyle \binom{X_i}{\widetilde{x}_i \otimes x_i}'$
, we seek the
$\widetilde{X}_i \equiv \displaystyle \binom{X_i}{\widetilde{x}_i \otimes x_i}'$
, we seek the
![]() $(L+1) \times (\sum p_s + 1)$
estimator
$(L+1) \times (\sum p_s + 1)$
estimator
![]() $\widehat{\delta }$
given by
$\widehat{\delta }$
given by
Note that our estimates of the functions
![]() $\beta _\ell (z)$
are recovered by
$\beta _\ell (z)$
are recovered by
![]() $\widehat{\beta }_\ell (z) = e_1 \widehat{\delta }$
for
$\widehat{\beta }_\ell (z) = e_1 \widehat{\delta }$
for
![]() $e_1$
being a
$e_1$
being a
![]() $(L+1) \times (\sum p_s + 1)$
-dimensioned vector with the first
$(L+1) \times (\sum p_s + 1)$
-dimensioned vector with the first
![]() $L+1$
elements being unity and the remaining
$L+1$
elements being unity and the remaining
![]() $(L+1) \times \sum p_s$
elements being zero.
$(L+1) \times \sum p_s$
elements being zero.
To make our estimator operational in a mixed data setting, we follow Racine & Li (Reference Racine and Li2004) and deploy the generalized product kernel function for
![]() $\mathcal{K}(\cdot )$
.
$\mathcal{K}(\cdot )$
.
 \begin{equation} \mathcal{K}(\cdot ) = \prod _{c=1}^{S_c} k^c\left (\frac{x_{i}^c - x^c}{h_c} \right ) \prod _{u=1}^{S_u} k^u(x_{i}^u - x^u; h_u) \prod _{o=1}^{S_o} k^o(x_{i}^o - x^o; h_o) \end{equation}
\begin{equation} \mathcal{K}(\cdot ) = \prod _{c=1}^{S_c} k^c\left (\frac{x_{i}^c - x^c}{h_c} \right ) \prod _{u=1}^{S_u} k^u(x_{i}^u - x^u; h_u) \prod _{o=1}^{S_o} k^o(x_{i}^o - x^o; h_o) \end{equation}
in which
 \begin{equation} k^c\left (\frac{x_{i}^c - x^c}{h_c} \right ) = \frac{1}{\sqrt{2 \pi }} \mbox{exp}\left [\frac{1}{2} \left (\frac{x_{i}^c - x^c}{h_c} \right )^2 \right ] \end{equation}
\begin{equation} k^c\left (\frac{x_{i}^c - x^c}{h_c} \right ) = \frac{1}{\sqrt{2 \pi }} \mbox{exp}\left [\frac{1}{2} \left (\frac{x_{i}^c - x^c}{h_c} \right )^2 \right ] \end{equation}
is a univariate Gaussian kernel function used for each of the
![]() $S_{c}$
continuous variables in
$S_{c}$
continuous variables in
![]() $x_{i}$
,
$x_{i}$
,
 \begin{equation} k^u(x_{i}^u - x^u; h_u) = \left \{ \begin{array}{ll} 1 & \mbox{if } x_{i}^u - x^u = 0\\ h_u & \mbox{if } x_{i}^u - x^u \neq 0.\end{array} \right . \end{equation}
\begin{equation} k^u(x_{i}^u - x^u; h_u) = \left \{ \begin{array}{ll} 1 & \mbox{if } x_{i}^u - x^u = 0\\ h_u & \mbox{if } x_{i}^u - x^u \neq 0.\end{array} \right . \end{equation}
is a univariate discrete kernel function used for each of the
![]() $S_u$
unordered discrete variables in
$S_u$
unordered discrete variables in
![]() $x_{i}$
, and
$x_{i}$
, and
 \begin{equation} k^o (x_{i}^o - x^o; h_o) = \left \{ \begin{array}{ll} 1 & \mbox{if } x_{i}^o - x^o = 0\\ h_o^{|x_{i}^o - x^o|} & \mbox{if } x_{i}^o - x^o \neq 0.\end{array} \right . \end{equation}
\begin{equation} k^o (x_{i}^o - x^o; h_o) = \left \{ \begin{array}{ll} 1 & \mbox{if } x_{i}^o - x^o = 0\\ h_o^{|x_{i}^o - x^o|} & \mbox{if } x_{i}^o - x^o \neq 0.\end{array} \right . \end{equation}
is a univariate discrete kernel function used for each of the
![]() $S_o$
ordered discrete variables in
$S_o$
ordered discrete variables in
![]() $x_{i}$
(Li & Racine, Reference Li and Racine2007). In the above product kernel setup,
$x_{i}$
(Li & Racine, Reference Li and Racine2007). In the above product kernel setup,
![]() $h_c$
is a
$h_c$
is a
![]() $S_c$
-dimensioned vector of bandwidths for the continuous variables and
$S_c$
-dimensioned vector of bandwidths for the continuous variables and
![]() $h_u$
and
$h_u$
and
![]() $h_o$
are
$h_o$
are
![]() $S_u$
- and
$S_u$
- and
![]() $S_o$
-dimensioned vectors of unordered and ordered discrete variable bandwidths.
$S_o$
-dimensioned vectors of unordered and ordered discrete variable bandwidths.
Since we are concerned with the class of second derivatives, we engage in local-cubic (
![]() $p=3$
) estimation. We deploy least-squares cross-validation (LSCV) to estimate the respective bandwidths. Specifically, LSCV selects bandwidths which minimize
$p=3$
) estimation. We deploy least-squares cross-validation (LSCV) to estimate the respective bandwidths. Specifically, LSCV selects bandwidths which minimize
where
![]() $\widehat{m}_{-i}(x_i)$
is the leave-one-out estimator of
$\widehat{m}_{-i}(x_i)$
is the leave-one-out estimator of
![]() $m(\cdot )$
. The idea of the leave-one-out estimator is that the conditional mean of
$m(\cdot )$
. The idea of the leave-one-out estimator is that the conditional mean of
![]() $y_i$
is estimated without using the observation with the most information,
$y_i$
is estimated without using the observation with the most information,
![]() $x_i$
. In this way, the bandwidths are selected so that the surrounding observations are providing as much information as possible to assist with smoothing.
$x_i$
. In this way, the bandwidths are selected so that the surrounding observations are providing as much information as possible to assist with smoothing.
C. Countries and industries covered
Table C1. List of WIOD and EU KLEMS countries

Table C2. List of industries

Notes: Industries codes are ISIC Rev. 3.1.
D. Descriptive statistics (tables)
Table D1a. IFR-WIOD dataset: main variables’ average by country

Source: Authors’ calculations based on International Federation of Robotics (2019) and WIOD (2015). *
![]() $R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
$R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
Table D1b. IFR-WIOD dataset: main variables’ average by industry

Source: Authors’ calculations based on International Federation of Robotics (2019) and WIOD (2015). *
![]() $R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
$R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
Table D2a. IFR-EU KLEMS dataset: main variables’ average by country

Source: Authors’ calculations based on International Federation of Robotics (2019) and EU KLEMS (2009). *
![]() $R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
$R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
Table D2b. IFR-EU KLEMS dataset: main variables’ average by industry

Source: Authors’ calculations based on International Federation of Robotics (2019) and EU KLEMS (2009). *
![]() $R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
$R^S$
(i.e., the robot stock) is obtained through Perpetual Inventory method and expressed in quantity (number of robots); this explains the presence of non-integer values.
E. Additional figures

Figure E1. Robotic capital evolution in selected WIOD countries and industries 1995–2009.

Figure E2. Kernel distribution of the estimated morishima EoS, 1995–2009.
F. Comparison with parametric estimates
For the sake of completeness, we carry out an EoS analysis adopting a parametric approach in order to highlight key differences with our nonparametric setup, on the one hand, and to contrast results (to the extent it is possible), on the other. Indeed, the type of analysis that we can perform in a parametric setting is limited from a number of perspectives. First, being our benchmark approach observation-specific, we are not able to have an equivalent direct estimate of EoS in a parametric setup. Second, since marginal productivity can hardly be estimated at the country-sector-year level using parametric methods, the EoS analysis usually proceeds by proxying the marginal rate of technical substitution with the factor price ratio under the implicit assumption that input markets are perfectly competitive. Our nonparametric approach allows us to completely avoid this, being based on marginal productivity comparison. Third, a functional specification of the production technology is required under the parametric approach; estimation usually relies on a CES nested in Cobb–Douglas specification (e.g., (Krusell et al. Reference Krusell, Ohanian, Ríos-Rull and Violante2000; Duffy et al. Reference Duffy, Papageorgiou and Perez-Sebastian2004; Eden & Gaggl, Reference Eden and Gaggl2018)).
In light of this, a standard formulation incorporating distinct kinds of capital and derive different substitutability degrees among factor inputs is offered by the Cobb–Douglas production function (removing subscripts for countries, industry and time to ease notation) over
![]() $NRK$
, assumed as neutral, with respect to skill types, and a CES technology over non-neutral
$NRK$
, assumed as neutral, with respect to skill types, and a CES technology over non-neutral
![]() $RK$
,
$RK$
,
![]() $S$
and
$S$
and
![]() $U$
:
$U$
:
 \begin{align} Y=NRK^\alpha \left [ \beta \: Q^{\sigma } + (1-\beta ) \: U^{\sigma } \right ] ^{\frac{1-\alpha }{\sigma }} \\ \text{with} \; Q=\left [ \gamma \: RK^\rho + \left ( 1 - \gamma \right ) \: S^\rho )\right ] ^{\frac{1}{\rho }}, \nonumber \end{align}
\begin{align} Y=NRK^\alpha \left [ \beta \: Q^{\sigma } + (1-\beta ) \: U^{\sigma } \right ] ^{\frac{1-\alpha }{\sigma }} \\ \text{with} \; Q=\left [ \gamma \: RK^\rho + \left ( 1 - \gamma \right ) \: S^\rho )\right ] ^{\frac{1}{\rho }}, \nonumber \end{align}
where
![]() $Y$
represents aggregate output;
$Y$
represents aggregate output;
![]() $\beta$
and
$\beta$
and
![]() $\gamma$
are distribution parameters;
$\gamma$
are distribution parameters;
![]() $\rho$
and
$\rho$
and
![]() $\sigma$
govern the elasticity of substitution between
$\sigma$
govern the elasticity of substitution between
![]() $RK$
and
$RK$
and
![]() $S$
, and between the composite input (
$S$
, and between the composite input (
![]() $Q$
, encompassing
$Q$
, encompassing
![]() $RK$
and
$RK$
and
![]() $S$
) and
$S$
) and
![]() $U$
, respectively.Footnote
25
Throughout the empirical analysis,
$U$
, respectively.Footnote
25
Throughout the empirical analysis,
![]() $ U$
includes medium- and low-skilled workers.
$ U$
includes medium- and low-skilled workers.
As can be observed, direct pairwise comparison between
![]() $\sigma _{RK,S}$
and
$\sigma _{RK,S}$
and
![]() $\sigma _{RK,U}$
is not possible in the parametric setup, which can only focus on comparing
$\sigma _{RK,U}$
is not possible in the parametric setup, which can only focus on comparing
![]() $\sigma _{RK,S}$
with the EoS, with respect to
$\sigma _{RK,S}$
with the EoS, with respect to
![]() $U$
, of the inputs bundle
$U$
, of the inputs bundle
![]() $Q$
(i.e.,
$Q$
(i.e.,
![]() $\sigma _{Q,U}$
). Indeed, assuming that the markets for inputs are competitive, the first-order conditions of profit-maximizing and price-taking firms imply (simultaneously) estimating the following system of equations:
$\sigma _{Q,U}$
). Indeed, assuming that the markets for inputs are competitive, the first-order conditions of profit-maximizing and price-taking firms imply (simultaneously) estimating the following system of equations:
 \begin{equation} \ln \left (\frac{\theta ^{RK}_{ci,t}}{\theta ^{S}_{ci,t}}\right )=\ln \left (\frac{\gamma }{1 - \gamma }\right )+\rho \ln \left (\frac{RK_{ci,t}}{S_{ci,t}}\right )+\epsilon _{ci,t} \end{equation}
\begin{equation} \ln \left (\frac{\theta ^{RK}_{ci,t}}{\theta ^{S}_{ci,t}}\right )=\ln \left (\frac{\gamma }{1 - \gamma }\right )+\rho \ln \left (\frac{RK_{ci,t}}{S_{ci,t}}\right )+\epsilon _{ci,t} \end{equation}
 \begin{equation} \ln \left (\frac{\theta ^{U}_{ci,t}}{\theta ^{Q}_{ci,t}}\right )=\ln \left (\frac{\beta }{1 - \beta }\right )+\sigma \ln \left (\frac{U_{ci,t}}{Q_{ci,t}}\right )+\mu _{ci,t} \end{equation}
\begin{equation} \ln \left (\frac{\theta ^{U}_{ci,t}}{\theta ^{Q}_{ci,t}}\right )=\ln \left (\frac{\beta }{1 - \beta }\right )+\sigma \ln \left (\frac{U_{ci,t}}{Q_{ci,t}}\right )+\mu _{ci,t} \end{equation}
where
![]() $c$
,
$c$
,
![]() $i$
and
$i$
and
![]() $t$
represent country, industry and time, respectively;
$t$
represent country, industry and time, respectively;
![]() $\theta ^R$
,
$\theta ^R$
,
![]() $\theta ^S$
,
$\theta ^S$
,
![]() $\theta ^U$
and
$\theta ^U$
and
![]() $\theta ^Q$
denote the income shares of
$\theta ^Q$
denote the income shares of
![]() $RK$
,
$RK$
,
![]() $S$
,
$S$
,
![]() $U$
and
$U$
and
![]() $Q$
, respectively, while
$Q$
, respectively, while
![]() $\epsilon$
and
$\epsilon$
and
![]() $\mu$
are the error terms, allowed to be correlated across equations. EoS between
$\mu$
are the error terms, allowed to be correlated across equations. EoS between
![]() $RK$
and
$RK$
and
![]() $S$
,
$S$
,
![]() $\left .1\right /\left (1-\rho \right )$
, is derived by equation (F.2), while EoS between the composite factor and
$\left .1\right /\left (1-\rho \right )$
, is derived by equation (F.2), while EoS between the composite factor and
![]() $U$
,
$U$
,
![]() $\left .1\right /\left (1-\sigma \right )$
, is identified from equation (F.3).
$\left .1\right /\left (1-\sigma \right )$
, is identified from equation (F.3).
Table F1. EoS, parametric estimates

Notes: *
![]() $p\lt 0.10$
,**
$p\lt 0.10$
,**
![]() $p\lt 0.05$
, ***
$p\lt 0.05$
, ***
![]() $p\lt 0.01$
. Standard errors in parentheses. All the models are simultaneously estimated using GMM estimation techniques, with lagged values of input factors as instrumental variables and HAC robust standard errors.
$p\lt 0.01$
. Standard errors in parentheses. All the models are simultaneously estimated using GMM estimation techniques, with lagged values of input factors as instrumental variables and HAC robust standard errors.
Table F2. Robustness checks: EoS, parametric estimates. Different
![]() $RK$
depreciation rates
$RK$
depreciation rates

Notes: *
![]() $p\lt 0.10$
,**
$p\lt 0.10$
,**
![]() $p\lt 0.05$
, ***
$p\lt 0.05$
, ***
![]() $p\lt 0.01$
. Standard errors in parentheses. All the models are simultaneously estimated using GMM estimation techniques, with lagged values of input factors as instrumental variables and HAC robust standard errors.
$p\lt 0.01$
. Standard errors in parentheses. All the models are simultaneously estimated using GMM estimation techniques, with lagged values of input factors as instrumental variables and HAC robust standard errors.
Complementarity between
![]() $RK$
and
$RK$
and
![]() $ S$
can be said to exist iff:
$ S$
can be said to exist iff:
Estimation is conducted using GMM, treating all the input factors as endogenous and exploiting their second and third lagged values as instruments. Table F1 reports the results of our benchmark parametric estimates.Footnote
26
In this respect, our findings provide broad evidence in favor of complementarity between
![]() $RK$
and
$RK$
and
![]() $S$
. Specifically, the procedure points to this direction when applied to both the IFR-WIOD and the IFR-EU KLEMS datasets, where the EoS between the
$S$
. Specifically, the procedure points to this direction when applied to both the IFR-WIOD and the IFR-EU KLEMS datasets, where the EoS between the
![]() $RK$
and
$RK$
and
![]() $S$
,
$S$
,
![]() $\left .1\right /\left (1-\rho \right )$
, is lower than between the
$\left .1\right /\left (1-\rho \right )$
, is lower than between the
![]() $\left [RK-S\right ]$
composite and
$\left [RK-S\right ]$
composite and
![]() $U$
,
$U$
,
![]() $\left .1\right /\left (1-\sigma \right )$
, which implies
$\left .1\right /\left (1-\sigma \right )$
, which implies
![]() $\sigma \gt \rho$
.
$\sigma \gt \rho$
.
The sensitivity of the estimates presented in Table F1 is assessed, in line with suggestions by Graetz & Michaels (Reference Graetz and Michaels2018), to different constructions of the
![]() $RK$
stock, using both 5 and 15 percent depreciation rates. The corresponding results are presented in Table F2. In both cases, our main findings remain unchanged, thus providing substantial confirmation of the presence higher complementarity between
$RK$
stock, using both 5 and 15 percent depreciation rates. The corresponding results are presented in Table F2. In both cases, our main findings remain unchanged, thus providing substantial confirmation of the presence higher complementarity between
![]() $RK$
and
$RK$
and
![]() $S$
.
$S$
.