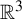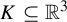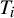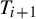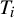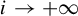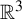1 Introduction
This paper lies at the intersection of geometric topology and topological dynamics. We focus on the class of toroidal sets, which are those compact subsets
![]() $K \subseteq \mathbb {R}^3$
that have a neighbourhood basis of solid tori. They are a natural generalization of the well-known cellular sets of geometric topology, which are those that have a neighbourhood basis of cells. Toroidal sets encompass objects such as n-adic solenoids, generalized solenoids (where the winding number n of each torus inside the previous need not be constant), knotted solenoids (where the construction begins with a knotted torus), classical knots, and some wild knots such as those constructed by taking an infinite connected sum of tame knots.
$K \subseteq \mathbb {R}^3$
that have a neighbourhood basis of solid tori. They are a natural generalization of the well-known cellular sets of geometric topology, which are those that have a neighbourhood basis of cells. Toroidal sets encompass objects such as n-adic solenoids, generalized solenoids (where the winding number n of each torus inside the previous need not be constant), knotted solenoids (where the construction begins with a knotted torus), classical knots, and some wild knots such as those constructed by taking an infinite connected sum of tame knots.
We are interested in the problem of characterizing what toroidal sets
![]() $K \subseteq \mathbb {R}^3$
can be realized as an attractor for a flow or a homeomorphism of
$K \subseteq \mathbb {R}^3$
can be realized as an attractor for a flow or a homeomorphism of
![]() $\mathbb {R}^3$
or, since this problem is much too difficult, at least of showing that certain toroidal sets cannot be so realized. By an attractor we mean a compact invariant set
$\mathbb {R}^3$
or, since this problem is much too difficult, at least of showing that certain toroidal sets cannot be so realized. By an attractor we mean a compact invariant set
![]() $K \subseteq \mathbb {R}^3$
which is stable in the sense of Lyapunov and attracts all points in some neighbourhood U of K. The latter condition means that the forward orbit of any point in U eventually enters any prescribed neighbourhood of K, and the stability condition then implies that this property actually holds for any compact subset of U, rather than just points. Precise definitions and a detailed discussion are given at the beginning of §7.
$K \subseteq \mathbb {R}^3$
which is stable in the sense of Lyapunov and attracts all points in some neighbourhood U of K. The latter condition means that the forward orbit of any point in U eventually enters any prescribed neighbourhood of K, and the stability condition then implies that this property actually holds for any compact subset of U, rather than just points. Precise definitions and a detailed discussion are given at the beginning of §7.
The motivation for this ‘realization problem’ is the well-known fact that attractors can have a very complicated structure. Heuristically, obtaining topological obstructions which prevent a compactum from being an attractor provides ‘upper bounds’ on the complexity of attractors. Realizability problems of this sort have been studied in many different contexts and accordingly with different techniques: attractors for topological flows [Reference Bhatia and Szegő3, Reference Garay11, Reference Günther and Segal15, Reference Sánchez-Gabites28, Reference Sanjurjo31], for analytic flows [Reference Jiménez and Llibre18, Reference Jiménez and Peralta-Salas19], critical sets rather than attractors [Reference Grayson and Pugh12, Reference Norton and Pugh24, Reference Souto33], attractors for homeomorphisms [Reference Günther14, Reference Kato20, Reference Ortega and Sánchez-Gabites25, Reference Sánchez-Gabites29, Reference Sánchez-Gabites30], or iterated function systems instead of single homeomorphisms [Reference Crovisier and Rams6, Reference Duvall and Husch8].
Perhaps we should mention that we always consider K as a given subset of
![]() $\mathbb {R}^3$
and not in the abstract; that is, we do not consider whether there is an embedding of K in some suitable Euclidean space where it can be realized as an attractor. These two problems are very different in nature, since in the first the way K sits in
$\mathbb {R}^3$
and not in the abstract; that is, we do not consider whether there is an embedding of K in some suitable Euclidean space where it can be realized as an attractor. These two problems are very different in nature, since in the first the way K sits in
![]() $\mathbb {R}^3$
is crucial whereas in the second only the topological properties of K may play a role. Thus, for example, Williams, in his work on expanding attractors, obtains a very general realizability result for solenoids [Reference Williams34, Theorem B, p. 171] which would appear to be in conflict with our Corollary 7.3; however, Williams’s results are concerned with the realizability problem in the abstract.
$\mathbb {R}^3$
is crucial whereas in the second only the topological properties of K may play a role. Thus, for example, Williams, in his work on expanding attractors, obtains a very general realizability result for solenoids [Reference Williams34, Theorem B, p. 171] which would appear to be in conflict with our Corollary 7.3; however, Williams’s results are concerned with the realizability problem in the abstract.
A toroidal set K can be expressed as an intersection of nested solid tori. Since these tori can be knotted and wind inside each other, it seems reasonable to think that K itself may have some sort of knottedness and some amount of winding ‘in itself’. As it turns out, both phenomena have implications for the realization problem and so we need to develop tools to formalize and analyse them. The first one was already addressed in an earlier paper [Reference Barge and Sánchez-Gabites2] by defining the genus
![]() $g(K)$
of a toroidal set K as a generalization of the classical genus of a knot. Namely,
$g(K)$
of a toroidal set K as a generalization of the classical genus of a knot. Namely,
![]() $g(K)$
is the smallest
$g(K)$
is the smallest
![]() $g = 0,1,\ldots ,+\infty $
such that K has arbitrarily close neighbourhoods which are solid tori whose core curves, thought of as classical knots, have genus bounded above by g. A toroidal set which can be realized as an attractor must have a finite genus, and so this provides a first obstruction for the realization problem.
$g = 0,1,\ldots ,+\infty $
such that K has arbitrarily close neighbourhoods which are solid tori whose core curves, thought of as classical knots, have genus bounded above by g. A toroidal set which can be realized as an attractor must have a finite genus, and so this provides a first obstruction for the realization problem.
In this paper we introduce the self-geometric index
![]() $\mathcal {N}(K)$
of a toroidal set K to describe the winding of K in itself mentioned above. Since measuring winding algebraically would essentially reproduce the Čech cohomology of the toroidal set we turn to another measure of winding which was first introduced by Schubert [Reference Schubert32, §9] under the name ‘order’. Consider a simple closed curve
$\mathcal {N}(K)$
of a toroidal set K to describe the winding of K in itself mentioned above. Since measuring winding algebraically would essentially reproduce the Čech cohomology of the toroidal set we turn to another measure of winding which was first introduced by Schubert [Reference Schubert32, §9] under the name ‘order’. Consider a simple closed curve
![]() $\gamma $
contained in the interior of a solid torus T. The geometric index of
$\gamma $
contained in the interior of a solid torus T. The geometric index of
![]() $\gamma $
with respect to T is defined as the minimum number of points of intersection of
$\gamma $
with respect to T is defined as the minimum number of points of intersection of
![]() $\gamma $
with any meridional disk D of T. Now, if
$\gamma $
with any meridional disk D of T. Now, if
![]() $T_2$
is a solid torus contained in the interior of another solid torus
$T_2$
is a solid torus contained in the interior of another solid torus
![]() $T_1$
, the geometric index of
$T_1$
, the geometric index of
![]() $T_2$
with respect to
$T_2$
with respect to
![]() $T_1$
is defined as the geometric index of any core curve of
$T_1$
is defined as the geometric index of any core curve of
![]() $T_2$
with respect to
$T_2$
with respect to
![]() $T_1$
. We denote this index by
$T_1$
. We denote this index by
![]() $N(T_2,T_1)$
following the notation used in [Reference Andrist, Garity, Repovš and Wright1]. Now let the toroidal set K be written as the intersection of a nested sequence
$N(T_2,T_1)$
following the notation used in [Reference Andrist, Garity, Repovš and Wright1]. Now let the toroidal set K be written as the intersection of a nested sequence
![]() $\{T_j\}$
of solid tori. One may attempt to define the self-geometric index of K as some sort of limit of the sequence
$\{T_j\}$
of solid tori. One may attempt to define the self-geometric index of K as some sort of limit of the sequence
![]() $N(T_{j+1},T_j)$
. This runs into difficulties since the limit depends on the sequence
$N(T_{j+1},T_j)$
. This runs into difficulties since the limit depends on the sequence
![]() $\{T_j\}$
, and so a subtler approach is needed. The self-geometric index of a toroidal set K will turn out to be a subgroup
$\{T_j\}$
, and so a subtler approach is needed. The self-geometric index of a toroidal set K will turn out to be a subgroup
![]() $\mathcal {N}(K)$
of the (additive) group of the real numbers. In certain cases
$\mathcal {N}(K)$
of the (additive) group of the real numbers. In certain cases
![]() $\mathcal {N}(K)$
behaves essentially as an integer number n, and we will then say that
$\mathcal {N}(K)$
behaves essentially as an integer number n, and we will then say that
![]() $\mathcal {N}(K)$
is ‘number-like’ and write
$\mathcal {N}(K)$
is ‘number-like’ and write
![]() $\mathcal {N}(K) \sim n$
. For example,
$\mathcal {N}(K) \sim n$
. For example,
![]() $\mathcal {N}(K) \sim n$
for an n-adic solenoid, and
$\mathcal {N}(K) \sim n$
for an n-adic solenoid, and
![]() $\mathcal {N}(K) \sim 1$
precisely when
$\mathcal {N}(K) \sim 1$
precisely when
![]() $\mathcal {N}(K) = \mathbb {Z}$
. All this is made precise in §4 after some preparatory work in §3.
$\mathcal {N}(K) = \mathbb {Z}$
. All this is made precise in §4 after some preparatory work in §3.
With these definitions we can now state our main results about the realization problem for toroidal sets. We start with the case of flows.
Theorem A. A toroidal set
![]() $K \subseteq \mathbb {R}^3$
can be realized as an attractor for a flow if and only if its genus is finite and
$K \subseteq \mathbb {R}^3$
can be realized as an attractor for a flow if and only if its genus is finite and
![]() $\mathcal {N}(K) \sim 1$
.
$\mathcal {N}(K) \sim 1$
.
The realization problem for homeomorphisms is much more complicated than that for flows, and in fact to our knowledge it has only been completely solved when K is either a cellular subset of
![]() $\mathbb {R}^n$
or a compact subset of a
$\mathbb {R}^n$
or a compact subset of a
![]() $2$
-manifold. The case of toroidal sets is no exception, and in this paper we obtain the following partial result.
$2$
-manifold. The case of toroidal sets is no exception, and in this paper we obtain the following partial result.
Theorem B. Let K be a toroidal set that is an attractor for a homeomorphism f of
![]() $\mathbb {R}^3$
. Then
$\mathbb {R}^3$
. Then
![]() $\mathcal {N}(K)$
is number-like. Moreover,
$\mathcal {N}(K)$
is number-like. Moreover,
![]() $\mathcal {N}(K) \sim 1$
if and only if K can be realized as an attractor for a flow.
$\mathcal {N}(K) \sim 1$
if and only if K can be realized as an attractor for a flow.
The main application of this theorem is in showing that certain toroidal sets cannot be realized as attractors for homeomorphisms. By combining some technical results in §5 with Theorem B we obtain the following result (p. 7) which guarantees the existence of many toroidal sets which are unknotted, have a prescribed cohomology, and cannot be realized as attractors.
Theorem C. Let H be a feasible group. There exists an uncountable family
![]() $\{K_{\alpha }\}$
of toroidal sets such that:
$\{K_{\alpha }\}$
of toroidal sets such that:
-
(i) none of the
 $K_{\alpha }$
can be realized as an attractor for a homeomorphism of
$K_{\alpha }$
can be realized as an attractor for a homeomorphism of
 $\mathbb {R}^3$
;
$\mathbb {R}^3$
; -
(ii) the
 $K_{\alpha }$
are pairwise different (that is, not ambient homeomorphic);
$K_{\alpha }$
are pairwise different (that is, not ambient homeomorphic); -
(iii) each
 $K_{\alpha }$
is unknotted;
$K_{\alpha }$
is unknotted; -
(iv) each
 $K_{\alpha }$
has H as its first Čech cohomology group.
$K_{\alpha }$
has H as its first Čech cohomology group.
The feasibility condition on H is explained in §5 and is unrelated to dynamics: it just ensures that H can be realized as the cohomology of some toroidal set.
As another illustration of Theorem B we consider the case of generalized knotted solenoids. Such a solenoid K is the intersection of a nested sequence of solid tori
![]() $\{T_j\}$
such that each
$\{T_j\}$
such that each
![]() $T_{j+1}$
winds monotonically (that is, without turning back)
$T_{j+1}$
winds monotonically (that is, without turning back)
![]() $n_j$
times inside the previous
$n_j$
times inside the previous
![]() $T_j$
and the thickness of the
$T_j$
and the thickness of the
![]() $T_j$
tends to
$T_j$
tends to
![]() $0$
as j increases. To avoid degenerate cases we require
$0$
as j increases. To avoid degenerate cases we require
![]() $n_j> 1$
for each j, and if all the
$n_j> 1$
for each j, and if all the
![]() $n_j = n$
then we say that K is an n-adic solenoid. Notice that by choosing
$n_j = n$
then we say that K is an n-adic solenoid. Notice that by choosing
![]() $T_1$
to be knotted one obtains a knotted solenoid. Then one can prove the following (Corollary 7.3).
$T_1$
to be knotted one obtains a knotted solenoid. Then one can prove the following (Corollary 7.3).
Corollary. If a generalized solenoid
![]() $K \subseteq \mathbb {R}^3$
can be realized as an attractor for a homeomorphism of
$K \subseteq \mathbb {R}^3$
can be realized as an attractor for a homeomorphism of
![]() $\mathbb {R}^3$
, then it must be an unknotted n-adic solenoid for some n.
$\mathbb {R}^3$
, then it must be an unknotted n-adic solenoid for some n.
The assumption that K be realized as an attractor for a homeomorphism defined on the whole of
![]() $\mathbb {R}^3$
is crucial in our results. If homeomorphisms defined only on subsets of
$\mathbb {R}^3$
is crucial in our results. If homeomorphisms defined only on subsets of
![]() $\mathbb {R}^3$
are allowed, counterexamples to Theorem B can be found (see, for instance, the first stage of the construction of the example in [Reference Grines, Laudenbach and Pochinka13, §5]). If phase spaces other than
$\mathbb {R}^3$
are allowed, counterexamples to Theorem B can be found (see, for instance, the first stage of the construction of the example in [Reference Grines, Laudenbach and Pochinka13, §5]). If phase spaces other than
![]() $\mathbb {R}^3$
are allowed, then the corollary above is false since knotted n-adic solenoids can indeed be realized as attractors (see, for instance, [Reference Jiang, Ni and Wang17]). Similarly, if the condition
$\mathbb {R}^3$
are allowed, then the corollary above is false since knotted n-adic solenoids can indeed be realized as attractors (see, for instance, [Reference Jiang, Ni and Wang17]). Similarly, if the condition
![]() $n_j> 1$
is omitted then the corollary is again false: any polyhedral or smooth knot then qualifies as a generalized knotted solenoid and can be easily realized as an attractor, even for a flow.
$n_j> 1$
is omitted then the corollary is again false: any polyhedral or smooth knot then qualifies as a generalized knotted solenoid and can be easily realized as an attractor, even for a flow.
The paper is organized as follows. In §2 we recall some definitions and provide some bibliographic references. Section 3 discusses some simple algebra needed for the definition of the self-geometric index in §4. The contents of §§5 and 6 are of a more technical nature and are required in the proof of the main results stated above. These are proved in §7. Finally, §8 contains some concluding remarks and questions.
2 Background definitions
A toroidal set is a compact set
![]() $K \subseteq \mathbb {R}^3$
that is not cellular and has a neighbourhood basis comprised of solid tori. In this paper we will always assume that sets other than toroidal sets are polyhedral (toroidal sets, in general, can have a very complicated structure). For maps we adopt the opposite convention: they will never be assumed to be piecewise linear unless explicitly stated otherwise. A taming result of Moise ensures that a toroidal set has a neighbourhood basis of polyhedral solid tori (see [Reference Barge and Sánchez-Gabites2, p. 5]). We say that two solid tori
$K \subseteq \mathbb {R}^3$
that is not cellular and has a neighbourhood basis comprised of solid tori. In this paper we will always assume that sets other than toroidal sets are polyhedral (toroidal sets, in general, can have a very complicated structure). For maps we adopt the opposite convention: they will never be assumed to be piecewise linear unless explicitly stated otherwise. A taming result of Moise ensures that a toroidal set has a neighbourhood basis of polyhedral solid tori (see [Reference Barge and Sánchez-Gabites2, p. 5]). We say that two solid tori
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are nested if
$T_2$
are nested if
![]() $T_2$
is contained in the interior of
$T_2$
is contained in the interior of
![]() $T_1$
. Here the word ‘interior’ may be taken in the topological sense or in the manifold sense: both agree by the invariance of domain theorem. A standard basis for a toroidal set K is a sequence of (polyhedral) nested solid tori
$T_1$
. Here the word ‘interior’ may be taken in the topological sense or in the manifold sense: both agree by the invariance of domain theorem. A standard basis for a toroidal set K is a sequence of (polyhedral) nested solid tori
![]() $\{T_j\}$
whose intersection is K.
$\{T_j\}$
whose intersection is K.
A framing of a solid torus
![]() $T \subseteq \mathbb {R}^3$
is a particular piecewise linear homeomorphism
$T \subseteq \mathbb {R}^3$
is a particular piecewise linear homeomorphism
![]() $f : \mathbb {D}^2 \times \mathbb {S}^1 \longrightarrow T$
, where
$f : \mathbb {D}^2 \times \mathbb {S}^1 \longrightarrow T$
, where
![]() $\mathbb {D}^2$
is a closed
$\mathbb {D}^2$
is a closed
![]() $2$
-disk. A core curve of T is a curve
$2$
-disk. A core curve of T is a curve
![]() $\gamma $
of the form
$\gamma $
of the form
![]() $f(0 \times \mathbb {S}^1)$
for some framing f. Notice that
$f(0 \times \mathbb {S}^1)$
for some framing f. Notice that
![]() $\gamma $
lies in the interior of T and T is a regular neighbourhood of
$\gamma $
lies in the interior of T and T is a regular neighbourhood of
![]() $\gamma $
(recall our convention about the polyhedral nature of sets unless otherwise explicitly stated). Core curves are not unique, but any two core curves are related by an isotopy of T that is the identity on
$\gamma $
(recall our convention about the polyhedral nature of sets unless otherwise explicitly stated). Core curves are not unique, but any two core curves are related by an isotopy of T that is the identity on
![]() $\partial T$
. A meridian of T is a curve of the form
$\partial T$
. A meridian of T is a curve of the form
![]() $f(\partial \mathbb {D}^2 \times *)$
for some framing of T (here
$f(\partial \mathbb {D}^2 \times *)$
for some framing of T (here
![]() $*$
denotes any point in
$*$
denotes any point in
![]() $\mathbb {S}^1$
). Alternatively, meridians can be characterized as those simple closed curves in
$\mathbb {S}^1$
). Alternatively, meridians can be characterized as those simple closed curves in
![]() $\partial T$
which bound a disk in T but not in
$\partial T$
which bound a disk in T but not in
![]() $\partial T$
. A meridional disk of T is a disk
$\partial T$
. A meridional disk of T is a disk
![]() $D \subseteq T$
that is properly embedded (that is,
$D \subseteq T$
that is properly embedded (that is,
![]() $D \cap \partial T = \partial D$
) and whose boundary
$D \cap \partial T = \partial D$
) and whose boundary
![]() $\partial D$
is a meridian of T.
$\partial D$
is a meridian of T.
Consider a pair of nested solid tori
![]() $T_2 \subseteq T_1$
. The geometric index of
$T_2 \subseteq T_1$
. The geometric index of
![]() $T_2$
in
$T_2$
in
![]() $T_1$
is the minimum number of points of intersection of a core curve
$T_1$
is the minimum number of points of intersection of a core curve
![]() $\gamma $
of
$\gamma $
of
![]() $T_2$
with any meridional disk D of
$T_2$
with any meridional disk D of
![]() $T_1$
. The minimum is taken over all meridional disks that intersect
$T_1$
. The minimum is taken over all meridional disks that intersect
![]() $\gamma $
transversely, so that
$\gamma $
transversely, so that
![]() $D \cap \gamma $
consists of finitely many points. Since any two core curves of
$D \cap \gamma $
consists of finitely many points. Since any two core curves of
![]() $T_2$
are related by an isotopy of
$T_2$
are related by an isotopy of
![]() $T_2$
that is the identity on
$T_2$
that is the identity on
![]() $\partial T_2$
and can therefore be extended to an isotopy of
$\partial T_2$
and can therefore be extended to an isotopy of
![]() $T_1$
, it follows that this definition is independent of the particular core curve
$T_1$
, it follows that this definition is independent of the particular core curve
![]() $\gamma $
. The geometric index is multiplicative: if
$\gamma $
. The geometric index is multiplicative: if
![]() $T_3 \subseteq T_2 \subseteq T_1$
are three nested solid tori, then
$T_3 \subseteq T_2 \subseteq T_1$
are three nested solid tori, then
![]() $N(T_3,T_1) = N(T_3,T_2) \cdot N(T_2,T_1)$
(see [Reference Schubert32, Satz 3, p. 175]). We will make extensive use of this property.
$N(T_3,T_1) = N(T_3,T_2) \cdot N(T_2,T_1)$
(see [Reference Schubert32, Satz 3, p. 175]). We will make extensive use of this property.
Suppose
![]() $T_2 \subseteq T_1$
and
$T_2 \subseteq T_1$
and
![]() $T^{\prime }_2 \subseteq T^{\prime }_1$
are two pairs of nested solid tori. It is clear from the definition of the geometric index that if there exists a piecewise linear homeomorphism between the pairs
$T^{\prime }_2 \subseteq T^{\prime }_1$
are two pairs of nested solid tori. It is clear from the definition of the geometric index that if there exists a piecewise linear homeomorphism between the pairs
![]() $(T_1,T_2)$
and
$(T_1,T_2)$
and
![]() $(T^{\prime }_1,T^{\prime }_2)$
then the geometric indices
$(T^{\prime }_1,T^{\prime }_2)$
then the geometric indices
![]() $N(T_2,T_1)$
and
$N(T_2,T_1)$
and
![]() $N(T^{\prime }_2,T^{\prime }_1)$
are equal. We will need a slightly stronger statement, however, which is given in Lemma 2.1 below. We have opted for a quick, if not particularly neat, proof.
$N(T^{\prime }_2,T^{\prime }_1)$
are equal. We will need a slightly stronger statement, however, which is given in Lemma 2.1 below. We have opted for a quick, if not particularly neat, proof.
Lemma 2.1. Suppose that
![]() $f : (T_1,T_2) \longrightarrow (T^{\prime }_1,T^{\prime }_2)$
is a homeomorphism between two pairs of nested polyhedral tori. Assume that f is piecewise linear on
$f : (T_1,T_2) \longrightarrow (T^{\prime }_1,T^{\prime }_2)$
is a homeomorphism between two pairs of nested polyhedral tori. Assume that f is piecewise linear on
![]() $T_1 - \text {int}\ T_2$
. Then the geometric indices of the two pairs are equal.
$T_1 - \text {int}\ T_2$
. Then the geometric indices of the two pairs are equal.
Proof. By an approximation theorem of Bing (see, for instance, [Reference Bing4, Theorem 4, p. 149]) there exists a piecewise linear homeomorphism
![]() $f' : T_1 \longrightarrow T^{\prime }_1$
which coincides with f on
$f' : T_1 \longrightarrow T^{\prime }_1$
which coincides with f on
![]() $T_1 - \text {int}\ T_2$
. In particular, it sends
$T_1 - \text {int}\ T_2$
. In particular, it sends
![]() $T_2$
onto
$T_2$
onto
![]() $T^{\prime }_2$
and therefore provides a piecewise linear homeomorphism from
$T^{\prime }_2$
and therefore provides a piecewise linear homeomorphism from
![]() $(T_1,T_2)$
onto
$(T_1,T_2)$
onto
![]() $(T^{\prime }_1,T^{\prime }_2)$
. The result follows.
$(T^{\prime }_1,T^{\prime }_2)$
. The result follows.
A natural way of constructing toroidal sets is, of course, by taking a nested sequence of tori
![]() $\{T_j\}$
and letting
$\{T_j\}$
and letting
![]() $K := \bigcap _{j \geq 0} T_j$
. Although such a K certainly has a neighbourhood basis of solid tori, to guarantee that K is a toroidal set we must also make sure that it is not cellular. The following proposition provides an easy criterion to check this in terms of the geometric index.
$K := \bigcap _{j \geq 0} T_j$
. Although such a K certainly has a neighbourhood basis of solid tori, to guarantee that K is a toroidal set we must also make sure that it is not cellular. The following proposition provides an easy criterion to check this in terms of the geometric index.
Proposition 2.2. Let K be defined as the intersection of a nested sequence of solid tori
![]() $\{T_j\}$
. Then K is cellular if and only if
$\{T_j\}$
. Then K is cellular if and only if
![]() $N(T_{j+1},T_j) = 0$
for infinitely many j.
$N(T_{j+1},T_j) = 0$
for infinitely many j.
For the proof we make use of the following fact: if
![]() $T_2 \subseteq T_1$
is a nested pair of solid tori, then
$T_2 \subseteq T_1$
is a nested pair of solid tori, then
![]() $N(T_2,T_1) = 0$
if and only if
$N(T_2,T_1) = 0$
if and only if
![]() $T_2$
is contained in a
$T_2$
is contained in a
![]() $3$
-cell B inside T. This should be intuitively clear, and a very sketchy argument will be given in the proof of the proposition. A formal proof can be found in [Reference Schubert32, Satz 1, p. 171].
$3$
-cell B inside T. This should be intuitively clear, and a very sketchy argument will be given in the proof of the proposition. A formal proof can be found in [Reference Schubert32, Satz 1, p. 171].
Proof Proof of Proposition 2.2
Assume first that K is cellular. Choose any
![]() $T_{j_0}$
. Since K is cellular, it has a neighbourhood B which is a
$T_{j_0}$
. Since K is cellular, it has a neighbourhood B which is a
![]() $3$
-cell contained in
$3$
-cell contained in
![]() $\text {int}\ T_{j_0}$
. In turn, take
$\text {int}\ T_{j_0}$
. In turn, take
![]() $j_1$
such that
$j_1$
such that
![]() $T_{j_1} \subseteq \text {int}\ B$
. Shrink the cell B by an ambient isotopy of
$T_{j_1} \subseteq \text {int}\ B$
. Shrink the cell B by an ambient isotopy of
![]() $T_{j_0}$
(relative to
$T_{j_0}$
(relative to
![]() $\partial T_{j_0}$
) until it becomes extremely small. It is then clear that there is a meridional disk D of
$\partial T_{j_0}$
) until it becomes extremely small. It is then clear that there is a meridional disk D of
![]() $T_{j_0}$
that is disjoint from the shrunken cell. Carrying D along with the reverse isotopy, one obtains a meridional disk of
$T_{j_0}$
that is disjoint from the shrunken cell. Carrying D along with the reverse isotopy, one obtains a meridional disk of
![]() $T_{j_0}$
that is disjoint from the original cell B, and consequently also from
$T_{j_0}$
that is disjoint from the original cell B, and consequently also from
![]() $T_{j_1}$
. Thus the geometric index of
$T_{j_1}$
. Thus the geometric index of
![]() $T_{j_1}$
in
$T_{j_1}$
in
![]() $T_{j_0}$
is
$T_{j_0}$
is
![]() $0$
. The multiplicativity of the index then implies that
$0$
. The multiplicativity of the index then implies that
![]() $N(T_{j+1},T_j) = 0$
for some
$N(T_{j+1},T_j) = 0$
for some
![]() $j_0 \leq j < j_1$
.
$j_0 \leq j < j_1$
.
Conversely, assume that
![]() $N(T_{j+1},T_j) = 0$
for infinitely many j. Choose any
$N(T_{j+1},T_j) = 0$
for infinitely many j. Choose any
![]() $T_{j_0}$
and pick
$T_{j_0}$
and pick
![]() $j \geq j_0$
such that
$j \geq j_0$
such that
![]() $N(T_{j+1},T_j) = 0$
. Then
$N(T_{j+1},T_j) = 0$
. Then
![]() $N(T_{j+1},T_{j_0}) = 0$
too by the multiplicative property of the geometric index. This means that there exists a meridional disk D of
$N(T_{j+1},T_{j_0}) = 0$
too by the multiplicative property of the geometric index. This means that there exists a meridional disk D of
![]() $T_{j_0}$
such that
$T_{j_0}$
such that
![]() $T_{j+1}$
is disjoint from D. Thickening D to a regular neighbourhood (relative to
$T_{j+1}$
is disjoint from D. Thickening D to a regular neighbourhood (relative to
![]() $\partial T_{j_0}$
) small enough that it is still disjoint from
$\partial T_{j_0}$
) small enough that it is still disjoint from
![]() $T_{j+1}$
and then removing its interior from
$T_{j+1}$
and then removing its interior from
![]() $T_{j_0}$
produces a polyhedral
$T_{j_0}$
produces a polyhedral
![]() $3$
-cell B contained in
$3$
-cell B contained in
![]() $T_{j_0}$
. Thus K has a neighbourhood basis of
$T_{j_0}$
. Thus K has a neighbourhood basis of
![]() $3$
-cells and is therefore cellular.
$3$
-cells and is therefore cellular.
Warning. Whenever we construct a toroidal set as an intersection of a sequence of nested tori we will never check explicitly that it is not cellular, since this will always be a direct consequence of the above proposition.
Consider once more a nested pair of solid tori
![]() $T_2 \subseteq T_1$
. The inclusion induces a map
$T_2 \subseteq T_1$
. The inclusion induces a map
![]() $H^1(T_1;\mathbb {Z}) \longrightarrow H^1(T_2;\mathbb {Z})$
which, after identifying each of the cohomology groups with
$H^1(T_1;\mathbb {Z}) \longrightarrow H^1(T_2;\mathbb {Z})$
which, after identifying each of the cohomology groups with
![]() $\mathbb {Z}$
with an appropriate orientation, simply becomes multiplication by a non-negative integer
$\mathbb {Z}$
with an appropriate orientation, simply becomes multiplication by a non-negative integer
![]() $w \geq 0$
. This is usually called the winding number of
$w \geq 0$
. This is usually called the winding number of
![]() $T_2$
inside
$T_2$
inside
![]() $T_1$
. It is not difficult to see that, if D is any meridional disk of
$T_1$
. It is not difficult to see that, if D is any meridional disk of
![]() $T_1$
and
$T_1$
and
![]() $\gamma $
is a core curve of
$\gamma $
is a core curve of
![]() $T_2$
transverse to D, then w is the (absolute value of the) number of intersections of
$T_2$
transverse to D, then w is the (absolute value of the) number of intersections of
![]() $\gamma $
with D counted with sign according to the sense in which
$\gamma $
with D counted with sign according to the sense in which
![]() $\gamma $
crosses D. In particular, choosing D to minimize the number of points of intersection with
$\gamma $
crosses D. In particular, choosing D to minimize the number of points of intersection with
![]() $\gamma $
, one has that
$\gamma $
, one has that
![]() $w \leq N(T_2,T_1)$
and also that w and
$w \leq N(T_2,T_1)$
and also that w and
![]() $N(T_2,T_1)$
have the same parity.
$N(T_2,T_1)$
have the same parity.
The (Čech) cohomology of toroidal sets will play a role in this paper, so we now devote a few lines to its description. Let
![]() $\{T_j\}$
be a standard basis for a toroidal set K. By the continuity property of Čech cohomology,
$\{T_j\}$
be a standard basis for a toroidal set K. By the continuity property of Čech cohomology,
![]() $\check {H}^q(K;\mathbb {Z})$
is the direct limit of the direct sequence
$\check {H}^q(K;\mathbb {Z})$
is the direct limit of the direct sequence
![]() $\check {H}^q(T_j;\mathbb {Z}) \longrightarrow \check {H}^q(T_{j+1};\mathbb {Z})$
, where the arrows are induced by the inclusions
$\check {H}^q(T_j;\mathbb {Z}) \longrightarrow \check {H}^q(T_{j+1};\mathbb {Z})$
, where the arrows are induced by the inclusions
![]() $T_{j+1} \subseteq T_j$
. In degrees
$T_{j+1} \subseteq T_j$
. In degrees
![]() $q \geq 2$
clearly
$q \geq 2$
clearly
![]() $\check {H}^q(K;\mathbb {Z}) = 0$
. In degree
$\check {H}^q(K;\mathbb {Z}) = 0$
. In degree
![]() $q = 1$
, and according to the discussion in the previous paragraph, each of these arrows can be identified with
$q = 1$
, and according to the discussion in the previous paragraph, each of these arrows can be identified with
![]() $\mathbb {Z} \stackrel {\cdot w_j}{\longrightarrow } \mathbb {Z}$
, where
$\mathbb {Z} \stackrel {\cdot w_j}{\longrightarrow } \mathbb {Z}$
, where
![]() $w_j$
is the winding number of
$w_j$
is the winding number of
![]() $T_{j+1}$
inside
$T_{j+1}$
inside
![]() $T_j$
. It is very easy to check (or see a proof in [Reference Barge and Sánchez-Gabites2, Proposition 1.6]) that there are three mutually exclusive possibilities for
$T_j$
. It is very easy to check (or see a proof in [Reference Barge and Sánchez-Gabites2, Proposition 1.6]) that there are three mutually exclusive possibilities for
![]() $\check {H}^1(K;\mathbb {Z})$
.
$\check {H}^1(K;\mathbb {Z})$
.
-
(i) If infinitely many of the
 $w_j$
vanish, then
$w_j$
vanish, then
 $\check {H}^1(K;\mathbb {Z}) = 0$
. We then say that K is trivial.
$\check {H}^1(K;\mathbb {Z}) = 0$
. We then say that K is trivial. -
(ii) If
 $w_j = 1$
from some j onwards, then
$w_j = 1$
from some j onwards, then
 $\check {H}^1(K;\mathbb {Z}) = \mathbb {Z}$
.
$\check {H}^1(K;\mathbb {Z}) = \mathbb {Z}$
. -
(iii) Otherwise
 $\check {H}^1(K;\mathbb {Z})$
is not finitely generated.
$\check {H}^1(K;\mathbb {Z})$
is not finitely generated.
3 Some algebraic preliminaries
We shall begin with some very simple algebra. Given a sequence of non-negative integers
![]() $\{m_j\}_{j \geq 1}$
, consider the direct sequence
$\{m_j\}_{j \geq 1}$
, consider the direct sequence
where each arrow is multiplication by
![]() $m_j$
. Denote by G the direct limit of this sequence. The following mutually exclusive alternatives hold.
$m_j$
. Denote by G the direct limit of this sequence. The following mutually exclusive alternatives hold.
-
(i)
 $G = 0$
if and only if
$G = 0$
if and only if
 $m_j = 0$
for infinitely many j.
$m_j = 0$
for infinitely many j. -
(ii)
 $G = \mathbb {Z}$
if and only if
$G = \mathbb {Z}$
if and only if
 $m_j = 1$
from some j onwards.
$m_j = 1$
from some j onwards. -
(iii) Otherwise G is not finitely generated.
Let p be a prime number. If every element in G is divisible by p we then say that p divides G, or that p is a prime factor of G, and write
![]() $p | G$
. The following proposition provides an alternative characterization of this notion. The proof is extremely simple but we include it for completeness.
$p | G$
. The following proposition provides an alternative characterization of this notion. The proof is extremely simple but we include it for completeness.
Proposition 3.1. With the above notation,
![]() $p | G$
if and only if p divides infinitely many of the
$p | G$
if and only if p divides infinitely many of the
![]() $m_j$
.
$m_j$
.
Proof. It will be convenient to attach a subscript
![]() $(j)$
to each copy of
$(j)$
to each copy of
![]() $\mathbb {Z}$
in (1) to distinguish them. We choose the notation so that the arrows read
$\mathbb {Z}$
in (1) to distinguish them. We choose the notation so that the arrows read
![]() . Any element
. Any element
![]() $z \in G$
is represented by some
$z \in G$
is represented by some
![]() $z_{(j_0)} \in \mathbb {Z}_{(j_0)}$
. Of course, z is also represented by any of its successive images
$z_{(j_0)} \in \mathbb {Z}_{(j_0)}$
. Of course, z is also represented by any of its successive images
![]() $z_{(j)} \in \mathbb {Z}_{(j)}$
along the sequence. The relation between
$z_{(j)} \in \mathbb {Z}_{(j)}$
along the sequence. The relation between
![]() $z_{(j_0)}$
and
$z_{(j_0)}$
and
![]() $z_{(j)}$
is just
$z_{(j)}$
is just
Suppose first that p divides infinitely many of the
![]() $m_j$
. Let z be represented by
$m_j$
. Let z be represented by
![]() $z_{(j_0)} \in \mathbb {Z}_{(j_0)}$
. Our assumption implies that there exists
$z_{(j_0)} \in \mathbb {Z}_{(j_0)}$
. Our assumption implies that there exists
![]() $j \geq j_0$
such that
$j \geq j_0$
such that
![]() $p | m_j$
. From (2) we see that
$p | m_j$
. From (2) we see that
![]() $p | z_{(j+1)}$
, and then
$p | z_{(j+1)}$
, and then
![]() $z^{\prime }_{(j+1)} := z_{(j+1)}/p \in \mathbb {Z}_{(j+1)}$
represents an element
$z^{\prime }_{(j+1)} := z_{(j+1)}/p \in \mathbb {Z}_{(j+1)}$
represents an element
![]() $z' \in G$
such that
$z' \in G$
such that
![]() $pz' = z$
.
$pz' = z$
.
Conversely, assume every element in G is divisible by p. Fix
![]() $j_0$
and consider the element
$j_0$
and consider the element
![]() $z \in G$
represented by
$z \in G$
represented by
![]() $z_{(j_0)} = 1 \in \mathbb {Z}_{(j_0)}$
. By assumption there exists
$z_{(j_0)} = 1 \in \mathbb {Z}_{(j_0)}$
. By assumption there exists
![]() $z' \in G$
such that
$z' \in G$
such that
![]() $pz' = z$
. Then for big enough j we must have
$pz' = z$
. Then for big enough j we must have
![]() $pz^{\prime }_{(j)} = z_{(j)}$
, so in particular
$pz^{\prime }_{(j)} = z_{(j)}$
, so in particular
![]() $p | z_{(j)}$
. But then from (2) we see that p divides some
$p | z_{(j)}$
. But then from (2) we see that p divides some
![]() $m_k$
with
$m_k$
with
![]() $j_0 \leq k < j$
. Since
$j_0 \leq k < j$
. Since
![]() $j_0$
was arbitrary, it follows that p divides infinitely many of the
$j_0$
was arbitrary, it follows that p divides infinitely many of the
![]() $m_j$
.
$m_j$
.
Using the proposition, one can easily see that G may not have any prime factors at all or, at the other extreme, it may have infinitely many of them. In fact, it is easy to produce groups G having any prescribed set P of prime numbers as prime divisors.
Example 3.2. Given any set P of prime numbers, there exists a group G whose prime divisors are precisely the elements of P. For instance:
-
(i) when
 $P = \emptyset $
choose
$P = \emptyset $
choose
 $m_j$
to be the jth prime number;
$m_j$
to be the jth prime number; -
(ii) when P is finite choose all the
 $m_j$
to be equal to m, the product of all the elements in P;
$m_j$
to be equal to m, the product of all the elements in P; -
(iii) when P is infinite, let
 $\{p_k\}$
be an enumeration of its elements and choose
$\{p_k\}$
be an enumeration of its elements and choose
 $m_j := p_1 \cdot \,\cdots \,\cdot p_j$
.
$m_j := p_1 \cdot \,\cdots \,\cdot p_j$
.
If all the
![]() $m_j$
are equal to some number
$m_j$
are equal to some number
![]() $m \geq 1$
for big enough j we will say that G is number-like
Footnote
†
. It is well known that G can then be identified with the m-adic rationals; that is, the subgroup of
$m \geq 1$
for big enough j we will say that G is number-like
Footnote
†
. It is well known that G can then be identified with the m-adic rationals; that is, the subgroup of
![]() $\mathbb {Q}$
that consists of numbers of the form
$\mathbb {Q}$
that consists of numbers of the form
![]() with
with
![]() $z \in \mathbb {Z}$
and k a non-negative integer. This subgroup is usually denoted by
$z \in \mathbb {Z}$
and k a non-negative integer. This subgroup is usually denoted by
![]() . We will now show that the prime divisors of a number-like G determine it completely.
. We will now show that the prime divisors of a number-like G determine it completely.
Proposition 3.3. Let G be number-like. Then it has finitely many prime divisors
![]() $p_1, \ldots , p_r$
and
$p_1, \ldots , p_r$
and
![]() .
.
Proof. Since G is number-like, it is the direct limit of (1) with
![]() $m_j = m \geq 1$
for large enough j. Then by Proposition 3.1 the prime divisors of G are exactly the prime divisors of m (in the sense of ordinary arithmetic). In particular, G has finitely many prime divisors (and it has none exactly when
$m_j = m \geq 1$
for large enough j. Then by Proposition 3.1 the prime divisors of G are exactly the prime divisors of m (in the sense of ordinary arithmetic). In particular, G has finitely many prime divisors (and it has none exactly when
![]() $m = 1$
, or equivalently when
$m = 1$
, or equivalently when
![]() $G = \mathbb {Z}$
). Write
$G = \mathbb {Z}$
). Write
![]() $m = p_1^{n_1}\!\cdot \,\cdots \,\cdot {p_r}^{n_r}$
for appropriate exponents
$m = p_1^{n_1}\!\cdot \,\cdots \,\cdot {p_r}^{n_r}$
for appropriate exponents
![]() $n_i \geq 1$
. Also, set
$n_i \geq 1$
. Also, set
![]() $m_0 := p_1 \cdot \,\cdots \,\cdot p_r$
for brevity. Notice that
$m_0 := p_1 \cdot \,\cdots \,\cdot p_r$
for brevity. Notice that
![]() $m_0 | m$
.
$m_0 | m$
.
Now we prove that
. Since G can be identified with the subgroup of m-adic rationals, we only need to show that the m-adic rationals are the same as the
![]() $m_0$
-adic rationals. First, every
$m_0$
-adic rationals. First, every
![]() $m_0$
-adic rational can be written as an m-adic rational as follows:
$m_0$
-adic rational can be written as an m-adic rational as follows:

because
![]() $m_0 | m$
. To prove that every m-adic rational is an
$m_0 | m$
. To prove that every m-adic rational is an
![]() $m_0$
-adic rational we first perform the following computation. Letting
$m_0$
-adic rational we first perform the following computation. Letting
![]() $n = \max \ n_i$
, we can write m as follows:
$n = \max \ n_i$
, we can write m as follows:
 $$ \begin{align*} m = p_1^{n_1} \cdot\,\cdots\,\cdot {p_r}^{n_r} = \frac{(p_1 \cdot\,\cdots\,\cdot p_r)^n}{p_1^{n-n_1} \cdot\,\cdots\,\cdot p_r^{n-n_r}} = \frac{m_0^n}{m'} \end{align*} $$
$$ \begin{align*} m = p_1^{n_1} \cdot\,\cdots\,\cdot {p_r}^{n_r} = \frac{(p_1 \cdot\,\cdots\,\cdot p_r)^n}{p_1^{n-n_1} \cdot\,\cdots\,\cdot p_r^{n-n_r}} = \frac{m_0^n}{m'} \end{align*} $$
where
![]() $m' = p_1^{n-n_1} \cdot \,\cdots \,\cdot p_r^{n-n_r} \in \mathbb {Z}$
because of the definition of n. Then any m-adic rational can be expressed as
$m' = p_1^{n-n_1} \cdot \,\cdots \,\cdot p_r^{n-n_r} \in \mathbb {Z}$
because of the definition of n. Then any m-adic rational can be expressed as

We thus see that when G is number-like it conveys exactly the same information as the number
![]() $p_1 \cdot \,\cdots \,\cdot p_r$
. Hopefully this justifies our terminology. We shall sometimes write
$p_1 \cdot \,\cdots \,\cdot p_r$
. Hopefully this justifies our terminology. We shall sometimes write
![]() $G \sim p_1 \cdot \,\cdots \,\cdot p_r$
. As mentioned in the proof of the proposition, a somewhat degenerate case is
$G \sim p_1 \cdot \,\cdots \,\cdot p_r$
. As mentioned in the proof of the proposition, a somewhat degenerate case is
![]() $G = \mathbb {Z}$
, which is indeed number-like but has no prime factors. We shall then write
$G = \mathbb {Z}$
, which is indeed number-like but has no prime factors. We shall then write
![]() $G \sim 1$
. Notice that
$G \sim 1$
. Notice that
![]() $\mathbb {Z}$
is the only number-like G that does not have any prime factors.
$\mathbb {Z}$
is the only number-like G that does not have any prime factors.
We conclude this section with a very simple observation. There are two manipulations that can be performed on (1) which clearly do not alter its limit G. The first is just removing a finite number of terms from the beginning of the sequence. The second involves organizing the arrows in (1) into groups of
![]() $k_1,k_2,\ldots $
consecutive arrows and replacing each group with a single arrow which is the composition of all the arrows in the group, obtaining the direct sequence
$k_1,k_2,\ldots $
consecutive arrows and replacing each group with a single arrow which is the composition of all the arrows in the group, obtaining the direct sequence
These two operations allow the sequence (1) to be put in a somewhat canonical form that is sometimes convenient.
Lemma 3.4. Given any group G represented as the direct limit of (1) we may assume that the
![]() $\{m_j\}$
are in one of the mutually exclusive forms.
$\{m_j\}$
are in one of the mutually exclusive forms.
-
(i) All the
 $m_j = 0$
, in which case
$m_j = 0$
, in which case
 $G = 0$
.
$G = 0$
. -
(ii) All the
 $m_j = 1$
, in which case
$m_j = 1$
, in which case
 $G = \mathbb {Z}$
.
$G = \mathbb {Z}$
. -
(iii) All the
 $m_j \geq 2$
, in which case G is not finitely generated.
$m_j \geq 2$
, in which case G is not finitely generated.
Proof. (i) If infinitely many of the
![]() $m_j$
are zero, then by grouping the arrows in such a way that each group contains at least one zero arrow we may assume that
$m_j$
are zero, then by grouping the arrows in such a way that each group contains at least one zero arrow we may assume that
![]() $m_j = 0$
for all j. Clearly then
$m_j = 0$
for all j. Clearly then
![]() $G = 0$
.
$G = 0$
.
(ii) If (i) does not hold, then only finitely many of the
![]() $m_j$
are zero. We may discard them and assume directly that
$m_j$
are zero. We may discard them and assume directly that
![]() $m_j \geq 1$
for every j. If only finitely many of the
$m_j \geq 1$
for every j. If only finitely many of the
![]() $m_j$
satisfy
$m_j$
satisfy
![]() $m_j \geq 2$
then we may also discard them and obtain
$m_j \geq 2$
then we may also discard them and obtain
![]() $m_j = 1$
for every j. Clearly then
$m_j = 1$
for every j. Clearly then
![]() $G = \mathbb {Z}$
.
$G = \mathbb {Z}$
.
(iii) If (i) and (ii) do not hold, then infinitely many of the
![]() $m_j$
satisfy
$m_j$
satisfy
![]() $m_j \geq 2$
(and
$m_j \geq 2$
(and
![]() $m_j \geq 1$
for every j). Then by grouping the arrows in (1) in such a way that each group contains at least one element equal to or greater than
$m_j \geq 1$
for every j). Then by grouping the arrows in (1) in such a way that each group contains at least one element equal to or greater than
![]() $2$
we may assume that
$2$
we may assume that
![]() $m_j \geq 2$
for every j. It is then very easy to see that G is not finitely generated (the argument is essentially the same as in [Reference Barge and Sánchez-Gabites2, Proposition 1.6]).
$m_j \geq 2$
for every j. It is then very easy to see that G is not finitely generated (the argument is essentially the same as in [Reference Barge and Sánchez-Gabites2, Proposition 1.6]).
4 The self-index of a toroidal set
Let K be a toroidal set and let
![]() $\{T_j\}$
be a standard basis for K. Denote by
$\{T_j\}$
be a standard basis for K. Denote by
![]() $N_j$
the geometric index of
$N_j$
the geometric index of
![]() $T_{j+1}$
inside
$T_{j+1}$
inside
![]() $T_j$
and consider the direct sequence
$T_j$
and consider the direct sequence
Proposition 4.1. The direct limit of
![]() $\mathcal {N}\{T_j\}$
is independent of the basis
$\mathcal {N}\{T_j\}$
is independent of the basis
![]() $\{T_j\}$
chosen to compute it.
$\{T_j\}$
chosen to compute it.
Proof. First let us show that replacing
![]() $\{T_j\}$
with a subsequence
$\{T_j\}$
with a subsequence
![]() $\{T_{j_k}\}$
leaves the direct limit of
$\{T_{j_k}\}$
leaves the direct limit of
![]() $\mathcal {N}\{T_j\}$
unchanged. The multiplicativity of the geometric index ensures that
$\mathcal {N}\{T_j\}$
unchanged. The multiplicativity of the geometric index ensures that
and similarly for the following
![]() $j_k$
. Thus the sequence
$j_k$
. Thus the sequence
![]() $\mathcal {N}\{T_{j_k}\}$
associated to
$\mathcal {N}\{T_{j_k}\}$
associated to
![]() $\{T_{j_k}\}$
is precisely
$\{T_{j_k}\}$
is precisely
This can be obtained from the original
![]() $\mathcal {N}\{T_j\}$
by removing the first
$\mathcal {N}\{T_j\}$
by removing the first
![]() $j_1-1$
terms and then grouping the remaining arrows into the blocks
$j_1-1$
terms and then grouping the remaining arrows into the blocks
![]() $N_{j_k} \cdot \,\cdots \,\cdot N_{j_{k+1}-1}$
. These two manipulations do not alter the direct limit of the original sequence, and so
$N_{j_k} \cdot \,\cdots \,\cdot N_{j_{k+1}-1}$
. These two manipulations do not alter the direct limit of the original sequence, and so
![]() $\mathcal {N}\{T_j\}$
and
$\mathcal {N}\{T_j\}$
and
![]() $\mathcal {N}\{T_{j_k}\}$
have the same direct limit, as claimed above.
$\mathcal {N}\{T_{j_k}\}$
have the same direct limit, as claimed above.
Now let
![]() $\{T^{\prime }_j\}$
be another standard basis for K. We want to show that the direct limits of
$\{T^{\prime }_j\}$
be another standard basis for K. We want to show that the direct limits of
![]() $\mathcal {N}\{T_j\}$
and
$\mathcal {N}\{T_j\}$
and
![]() $\mathcal {N}\{T^{\prime }_j\}$
coincide. After passing to suitable subsequences of
$\mathcal {N}\{T^{\prime }_j\}$
coincide. After passing to suitable subsequences of
![]() $\{T_j\}$
and
$\{T_j\}$
and
![]() $\{T^{\prime }_j\}$
we may assume that
$\{T^{\prime }_j\}$
we may assume that
![]() $T_j \supseteq T^{\prime }_j \supseteq T_{j+1}$
for every j. By the previous paragraph there is no loss of generality in doing this. As before, we use the notation
$T_j \supseteq T^{\prime }_j \supseteq T_{j+1}$
for every j. By the previous paragraph there is no loss of generality in doing this. As before, we use the notation
![]() $N_j = N(T_{j+1},T_j)$
and
$N_j = N(T_{j+1},T_j)$
and
![]() $N^{\prime }_j = N(T^{\prime }_{j+1},T^{\prime }_j)$
. Also, set
$N^{\prime }_j = N(T^{\prime }_{j+1},T^{\prime }_j)$
. Also, set
The multiplicative property of the geometric index ensures that
![]() $N_j = M_j M^{\prime }_j$
and
$N_j = M_j M^{\prime }_j$
and
![]() $N^{\prime }_j = M^{\prime }_j M_{j+1}$
. Consider the direct sequence
$N^{\prime }_j = M^{\prime }_j M_{j+1}$
. Consider the direct sequence
Grouping the arrows in pairs yields the sequence
which is precisely
![]() $\mathcal {N}\{T_j\}$
, whereas discarding the first arrow and grouping the remaining ones in pairs yields the sequence
$\mathcal {N}\{T_j\}$
, whereas discarding the first arrow and grouping the remaining ones in pairs yields the sequence
which is precisely
![]() $\mathcal {N}\{T^{\prime }_j\}$
. It follows that the direct limit of all three sequences is the same, and so in particular
$\mathcal {N}\{T^{\prime }_j\}$
. It follows that the direct limit of all three sequences is the same, and so in particular
![]() $\mathcal {N}\{T_j\}$
and
$\mathcal {N}\{T_j\}$
and
![]() $\mathcal {N}\{T^{\prime }_j\}$
have the same direct limit, as was to be shown.
$\mathcal {N}\{T^{\prime }_j\}$
have the same direct limit, as was to be shown.
The proposition justifies the correctness of the following definition.
Definition 4.2. Given a toroidal set K, its self-geometric index (or self-index for brevity) is the direct limit of the direct sequence
![]() $\mathcal {N}\{T_j\}$
for any standard basis
$\mathcal {N}\{T_j\}$
for any standard basis
![]() $\{T_j\}$
of K. We denote the self-index by
$\{T_j\}$
of K. We denote the self-index by
![]() $\mathcal {N}(K)$
.
$\mathcal {N}(K)$
.
Since a toroidal set is not cellular by definition, it follows from Proposition 2.2 that
![]() $N_j \geq 1$
for sufficiently large j. Thus
$N_j \geq 1$
for sufficiently large j. Thus
![]() $\mathcal {N}(K) \neq 0$
and
$\mathcal {N}(K) \neq 0$
and
![]() $\mathcal {N}(K)$
is either
$\mathcal {N}(K)$
is either
![]() $\mathbb {Z}$
or not finitely generated. The case
$\mathbb {Z}$
or not finitely generated. The case
![]() $\mathcal {N}(K) = \mathbb {Z}$
, or
$\mathcal {N}(K) = \mathbb {Z}$
, or
![]() $\mathcal {N}(K) \sim 1$
in our notational convention, is interesting enough to single out.
$\mathcal {N}(K) \sim 1$
in our notational convention, is interesting enough to single out.
Proposition 4.3. Let
![]() $K \subseteq \mathbb {R}^3$
be a toroidal set. The following three statements are equivalent.
$K \subseteq \mathbb {R}^3$
be a toroidal set. The following three statements are equivalent.
-
(i)
 $\mathcal {N}(K) \sim 1$
.
$\mathcal {N}(K) \sim 1$
. -
(ii)
 $N(T_{j+1},T_j) = 1$
for large enough j for some standard basis
$N(T_{j+1},T_j) = 1$
for large enough j for some standard basis
 $\{T_j\}$
for K.
$\{T_j\}$
for K. -
(iii)
 $N(T_{j+1},T_j) = 1$
for large enough j for any standard basis
$N(T_{j+1},T_j) = 1$
for large enough j for any standard basis
 $\{T_j\}$
for K.
$\{T_j\}$
for K.
Moreover, if any of these conditions holds then
![]() $\check {H}^1(K;\mathbb {Z}) = \mathbb {Z}$
.
$\check {H}^1(K;\mathbb {Z}) = \mathbb {Z}$
.
Proof. Notice that
![]() $\mathcal {N}(K) = \mathbb {Z}$
occurs precisely when
$\mathcal {N}(K) = \mathbb {Z}$
occurs precisely when
![]() $N_j = N(T_{j+1},T_j) = 1$
for large j, so this condition must be independent of the basis
$N_j = N(T_{j+1},T_j) = 1$
for large j, so this condition must be independent of the basis
![]() $\{T_j\}$
since the same is true of
$\{T_j\}$
since the same is true of
![]() $\mathcal {N}(K)$
by Proposition 4.1. This establishes the equivalence of (i), (ii) and (iii). Denote by
$\mathcal {N}(K)$
by Proposition 4.1. This establishes the equivalence of (i), (ii) and (iii). Denote by
![]() $w_j$
the winding number of
$w_j$
the winding number of
![]() $T_{j+1}$
inside
$T_{j+1}$
inside
![]() $T_j$
. Recall that
$T_j$
. Recall that
![]() $w_j$
and
$w_j$
and
![]() $N_j$
have the same parity and also
$N_j$
have the same parity and also
![]() $w_j \leq N_j$
. These two conditions (together with
$w_j \leq N_j$
. These two conditions (together with
![]() $N_j = 1$
) force
$N_j = 1$
) force
![]() $w_j = 1$
, and so
$w_j = 1$
, and so
![]() $\check {H}^1(K;\mathbb {Z}) = \mathbb {Z}$
.
$\check {H}^1(K;\mathbb {Z}) = \mathbb {Z}$
.
Mimicking the definitions of the previous section, we say that a prime p divides
![]() $\mathcal {N}(K)$
if every element in
$\mathcal {N}(K)$
if every element in
![]() $\mathcal {N}(K)$
is divisible by p or, more operationally and as a consequence of Proposition 3.1, if
$\mathcal {N}(K)$
is divisible by p or, more operationally and as a consequence of Proposition 3.1, if
![]() $p|N(T_{j+1},T_j)$
for infinitely many j.
$p|N(T_{j+1},T_j)$
for infinitely many j.
Example 4.4. Recall from the Introduction that a (possibly knotted) generalized solenoid is a toroidal set K defined as the intersection of nested solid tori
![]() $\{T_j\}$
such that each
$\{T_j\}$
such that each
![]() $T_{j+1}$
winds monotonically
$T_{j+1}$
winds monotonically
![]() $n_j$
times inside the previous
$n_j$
times inside the previous
![]() $T_j$
and the thickness of the
$T_j$
and the thickness of the
![]() $T_j$
tends to
$T_j$
tends to
![]() $0$
as j increases. We require
$0$
as j increases. We require
![]() $n_j> 1$
for each j. The monotonicity condition implies that
$n_j> 1$
for each j. The monotonicity condition implies that
![]() $N(T_{j+1},T_j) = n_j$
for every j, and so
$N(T_{j+1},T_j) = n_j$
for every j, and so
![]() $\mathcal {N}(K) \not \sim 1$
and
$\mathcal {N}(K) \not \sim 1$
and
![]() $p | \mathcal {N}(K)$
if and only if p is a prime factor of infinitely many of the
$p | \mathcal {N}(K)$
if and only if p is a prime factor of infinitely many of the
![]() $n_j$
. Depending on our choice of the
$n_j$
. Depending on our choice of the
![]() $n_j$
we may find several scenarios.
$n_j$
we may find several scenarios.
-
(i) If K is an n-adic solenoid (
 $n_j = n$
for every j) then
$n_j = n$
for every j) then
 $\mathcal {N}(K)$
is number-like and the prime divisors of
$\mathcal {N}(K)$
is number-like and the prime divisors of
 $\mathcal {N}(K)$
are precisely the prime divisors of n (in the ordinary sense of elementary arithmetic).
$\mathcal {N}(K)$
are precisely the prime divisors of n (in the ordinary sense of elementary arithmetic). -
(ii) One may pick the
 $n_j$
in such a way that each prime p appears as a factor of infinitely many of them (for instance, by taking
$n_j$
in such a way that each prime p appears as a factor of infinitely many of them (for instance, by taking
 $n_j = j!$
). Then every prime divides
$n_j = j!$
). Then every prime divides
 $\mathcal {N}(K)$
.
$\mathcal {N}(K)$
. -
(iii) At the other extreme, one may choose the
 $n_j$
in such a way that no prime p is a factor of infinitely many of them, for instance by letting all the
$n_j$
in such a way that no prime p is a factor of infinitely many of them, for instance by letting all the
 $n_j$
be pairwise prime to each other. Then
$n_j$
be pairwise prime to each other. Then
 $\mathcal {N}(K)$
has no prime divisors.
$\mathcal {N}(K)$
has no prime divisors.
We conclude this section with a very simple remark concerning generalized solenoids. The monotonicity condition on the tori
![]() $\{T_j\}$
implies that the geometric index and the winding number of each pair of consecutive tori both coincide. In particular, the direct sequences that arise when computing the self-index of a generalized solenoid and its Čech cohomology in degree
$\{T_j\}$
implies that the geometric index and the winding number of each pair of consecutive tori both coincide. In particular, the direct sequences that arise when computing the self-index of a generalized solenoid and its Čech cohomology in degree
![]() $1$
are the same and so their direct limits coincide; that is,
$1$
are the same and so their direct limits coincide; that is,
![]() $\mathcal {N} = \check {H}^1$
. Moreover, since generalized solenoids are topologically characterized by their Čech cohomology (see, for instance, the argument in [Reference McCord22, p. 198]), we have the following remark.
$\mathcal {N} = \check {H}^1$
. Moreover, since generalized solenoids are topologically characterized by their Čech cohomology (see, for instance, the argument in [Reference McCord22, p. 198]), we have the following remark.
Remark 4.5. Let K and
![]() $K'$
be two generalized solenoids. Then K is homeomorphic to
$K'$
be two generalized solenoids. Then K is homeomorphic to
![]() $K'$
if and only if their self-indices
$K'$
if and only if their self-indices
![]() $\mathcal {N}(K)$
and
$\mathcal {N}(K)$
and
![]() $\mathcal {N}(K')$
are isomorphic (as groups).
$\mathcal {N}(K')$
are isomorphic (as groups).
5 Elementary properties of the self-index
In this section we discuss some elementary properties of the self-index. We begin by considering the status of the prime
![]() $p = 2$
as a factor of
$p = 2$
as a factor of
![]() $\mathcal {N}(K)$
, which turns out to be somewhat special.
$\mathcal {N}(K)$
, which turns out to be somewhat special.
Proposition 5.1. The prime
![]() $p = 2$
is a factor of
$p = 2$
is a factor of
![]() $\mathcal {N}(K)$
if and only if every element in
$\mathcal {N}(K)$
if and only if every element in
![]() $\check {H}^1(K;\mathbb {Z})$
is divisible by
$\check {H}^1(K;\mathbb {Z})$
is divisible by
![]() $2$
. In particular, having
$2$
. In particular, having
![]() $p = 2$
as a prime factor of
$p = 2$
as a prime factor of
![]() $\mathcal {N}(K)$
is a topological property of toroidal sets.
$\mathcal {N}(K)$
is a topological property of toroidal sets.
Proof. Let
![]() $\{T_j\}$
be a standard basis for K and denote by
$\{T_j\}$
be a standard basis for K and denote by
![]() $w_j$
and
$w_j$
and
![]() $N_j$
the winding number and the geometric index of each
$N_j$
the winding number and the geometric index of each
![]() $T_{j+1}$
inside
$T_{j+1}$
inside
![]() $T_j$
, respectively. By the continuity property of Čech cohomology
$T_j$
, respectively. By the continuity property of Čech cohomology
![]() $\check {H}^1(K;\mathbb {Z})$
is the direct limit of the direct sequence
$\check {H}^1(K;\mathbb {Z})$
is the direct limit of the direct sequence
whereas
![]() $\mathcal {N}(K)$
is by definition the direct limit of
$\mathcal {N}(K)$
is by definition the direct limit of
Since the geometric index and the winding number both have the same parity,
![]() $p = 2$
divides infinitely many of the
$p = 2$
divides infinitely many of the
![]() $w_j$
if and only if it divides infinitely many of the
$w_j$
if and only if it divides infinitely many of the
![]() $N_j$
. The result follows from the characterization of Proposition 3.1.
$N_j$
. The result follows from the characterization of Proposition 3.1.
The next property we consider is the invariance of the self-index under (local) ambient homeomorphisms. It seems reasonable to expect it to hold, but there is a slight technical subtlety: since Definition 4.2 involves neighbourhood bases that consist of polyhedral tori (for the geometric index to be defined), it is clear that the self-index is invariant under piecewise linear homeomorphisms, but not necessarily under arbitrary ones. To prove this in general we will need to make use of the deep result that any homeomorphism of a
![]() $3$
-manifold can be approximated arbitrarily closely by a piecewise linear one.
$3$
-manifold can be approximated arbitrarily closely by a piecewise linear one.
Proposition 5.2. Let K and
![]() $K'$
be toroidal sets in
$K'$
be toroidal sets in
![]() $\mathbb {R}^3$
. Suppose that
$\mathbb {R}^3$
. Suppose that
![]() $f : O \longrightarrow f(O)$
is a homeomorphism defined on an open neighbourhood O of K and
$f : O \longrightarrow f(O)$
is a homeomorphism defined on an open neighbourhood O of K and
![]() $f(K) = K'$
. Then
$f(K) = K'$
. Then
![]() $\mathcal {N}(K)$
and
$\mathcal {N}(K)$
and
![]() $\mathcal {N}(K')$
are equal.
$\mathcal {N}(K')$
are equal.
Proof. By the invariance of domain theorem f is an open map and
![]() $O' := f(O)$
is a neighbourhood of
$O' := f(O)$
is a neighbourhood of
![]() $K'$
. Consider the open
$K'$
. Consider the open
![]() $3$
-manifolds
$3$
-manifolds
![]() $O-K$
and
$O-K$
and
![]() $O' - K'$
. These are homeomorphic via f. Let
$O' - K'$
. These are homeomorphic via f. Let
![]() $\phi : O - K \longrightarrow (0,+\infty )$
be defined by
$\phi : O - K \longrightarrow (0,+\infty )$
be defined by
![]() $\phi (p) := \text {d}(p,K)$
, where
$\phi (p) := \text {d}(p,K)$
, where
![]() $\text {d}$
denotes the usual distance. Clearly
$\text {d}$
denotes the usual distance. Clearly
![]() $\phi $
is bounded away from
$\phi $
is bounded away from
![]() $0$
on every compact subset of
$0$
on every compact subset of
![]() $O - K$
, and then [Reference Moise23, Theorem 1, p. 253] guarantees that there exists a piecewise linear homeomorphism
$O - K$
, and then [Reference Moise23, Theorem 1, p. 253] guarantees that there exists a piecewise linear homeomorphism
![]() $g : O - K \longrightarrow O' - K'$
such that
$g : O - K \longrightarrow O' - K'$
such that
![]() $\text {d}(f(p),g(p)) < \phi (p)$
for every
$\text {d}(f(p),g(p)) < \phi (p)$
for every
![]() $p \in O - K$
. Extend g to all of O by defining
$p \in O - K$
. Extend g to all of O by defining
![]() $g(p) := f(p)$
for
$g(p) := f(p)$
for
![]() $p \in K$
. It is straightforward to check that this extension provides a continuous bijection from O to
$p \in K$
. It is straightforward to check that this extension provides a continuous bijection from O to
![]() $O'$
, which is therefore a homeomorphism by the invariance of domain theorem.
$O'$
, which is therefore a homeomorphism by the invariance of domain theorem.
Now let
![]() $\{T_j\}$
be a standard basis for K with all
$\{T_j\}$
be a standard basis for K with all
![]() $T_j$
contained in O. Define
$T_j$
contained in O. Define
![]() $T^{\prime }_j := g(T_j)$
. These clearly form a standard basis for
$T^{\prime }_j := g(T_j)$
. These clearly form a standard basis for
![]() $K'$
because g is a homeomorphism. Moreover, by construction g provides homeomorphisms of pairs
$K'$
because g is a homeomorphism. Moreover, by construction g provides homeomorphisms of pairs
![]() $g : (T_j,T_{j+1}) \longrightarrow (T^{\prime }_j,T^{\prime }_{j+1})$
which are piecewise linear on
$g : (T_j,T_{j+1}) \longrightarrow (T^{\prime }_j,T^{\prime }_{j+1})$
which are piecewise linear on
![]() $T_j - \text {int}\ T_{j+1}$
. Thus by Lemma 2.1 the geometric indices
$T_j - \text {int}\ T_{j+1}$
. Thus by Lemma 2.1 the geometric indices
![]() $N(T_{j+1},T_j)$
and
$N(T_{j+1},T_j)$
and
![]() $N(T^{\prime }_{j+1},T^{\prime }_j)$
are equal. The equality
$N(T^{\prime }_{j+1},T^{\prime }_j)$
are equal. The equality
![]() $\mathcal {N}(K) = \mathcal {N}(K')$
then follows from Proposition 4.1.
$\mathcal {N}(K) = \mathcal {N}(K')$
then follows from Proposition 4.1.
We conclude this section by investigating the relation between the cohomology of a toroidal set and its self-index. Essentially we shall see that, besides the relation between these two magnitudes afforded by Propositions 4.3 and 5.1, they are independent variables. This we do by showing how to construct toroidal sets K that have a prescribed cohomology group H (in degree
![]() $1$
) and whose self-index is some prescribed group N. Of course H and N cannot be entirely arbitrary since they must be the direct limit of a direct sequence of the form (1). Let us say that a group is feasible if it has this form. Also, the fact that toroidal sets cannot be cellular requires that
$1$
) and whose self-index is some prescribed group N. Of course H and N cannot be entirely arbitrary since they must be the direct limit of a direct sequence of the form (1). Let us say that a group is feasible if it has this form. Also, the fact that toroidal sets cannot be cellular requires that
![]() $N \neq 0$
by Proposition 2.2. Finally, and as a consequence of Propositions 4.3 and 5.1, if the variables H and N are to be realized as the cohomology and self-index of a toroidal set they must satisfy the following two compatibility conditions.
$N \neq 0$
by Proposition 2.2. Finally, and as a consequence of Propositions 4.3 and 5.1, if the variables H and N are to be realized as the cohomology and self-index of a toroidal set they must satisfy the following two compatibility conditions.
-
(C1)
 $2 | H$
if and only if
$2 | H$
if and only if
 $2 | N$
.
$2 | N$
. -
(C2) If
 $N \sim 1$
then
$N \sim 1$
then
 $H \sim 1$
.
$H \sim 1$
.
Theorem 5.3. Let H and N be feasible groups. Suppose that
![]() $N \neq 0$
, and H and N satisfy the above compatibility conditions. Then there exists a toroidal set K such that
$N \neq 0$
, and H and N satisfy the above compatibility conditions. Then there exists a toroidal set K such that
![]() $\check {H}^1(K;\mathbb {Z}) = H$
and
$\check {H}^1(K;\mathbb {Z}) = H$
and
![]() $\mathcal {N}(K) = N$
. Moreover, K is unknotted.
$\mathcal {N}(K) = N$
. Moreover, K is unknotted.
We recall that a toroidal set is unknotted if it has a neighbourhood basis of unknotted solid tori. A consequence of Theorem 5.3 and Example 3.2 is that if P is any set of prime numbers that satisfies the consistency condition
![]() $2 \in P \Leftrightarrow 2 | \check {H}^1(K;\mathbb {Z})$
, there exists a toroidal set K such that the prime divisors of
$2 \in P \Leftrightarrow 2 | \check {H}^1(K;\mathbb {Z})$
, there exists a toroidal set K such that the prime divisors of
![]() $\mathcal {N}(K)$
are precisely the elements of P.
$\mathcal {N}(K)$
are precisely the elements of P.
To prove the theorem we need an auxiliary lemma which provides the key to the construction.
Lemma 5.4. Let w and k be a pair of non-negative integers. Denote by
![]() $V_0 \subseteq \mathbb {R}^3$
the standard unknotted solid torus. Then there exists an unknotted solid torus
$V_0 \subseteq \mathbb {R}^3$
the standard unknotted solid torus. Then there exists an unknotted solid torus
![]() $V_1 \subseteq \text {int}\ V_0$
such that the winding number of
$V_1 \subseteq \text {int}\ V_0$
such that the winding number of
![]() $V_1$
inside
$V_1$
inside
![]() $V_0$
is w and the geometric index
$V_0$
is w and the geometric index
![]() $N(V_1,V_0)=w+2k$
.
$N(V_1,V_0)=w+2k$
.
Proof. To prove the lemma it suffices to find an unknotted simple closed curve
![]() $\gamma $
in
$\gamma $
in
![]() $\text {int}\ V_0$
such that its winding number and geometric index in
$\text {int}\ V_0$
such that its winding number and geometric index in
![]() $V_0$
are w and
$V_0$
are w and
![]() $w + 2k$
respectively, since then any regular neighbourhood
$w + 2k$
respectively, since then any regular neighbourhood
![]() $V_1$
of
$V_1$
of
![]() $\gamma $
contained in
$\gamma $
contained in
![]() $\text { int}\ V_0$
will fulfil our requirements.
$\text { int}\ V_0$
will fulfil our requirements.
Figure 1(a) shows a view of
![]() $V_0$
from the top and, contained in its interior, two groups of oriented simple closed curves. The outermost group, labeled (1), consists of w curves
$V_0$
from the top and, contained in its interior, two groups of oriented simple closed curves. The outermost group, labeled (1), consists of w curves
![]() $\gamma _1,\ldots ,\gamma _w$
that wind monotonically once around
$\gamma _1,\ldots ,\gamma _w$
that wind monotonically once around
![]() $V_0$
. The innermost group (2) consists of k curves
$V_0$
. The innermost group (2) consists of k curves
![]() $\gamma _{w+1},\ldots ,\gamma _{w+k}$
which we call Whitehead curves because they are patterned after one of the components of the Whitehead link. All the curves in the first group have the same orientation. The Whitehead curves have alternating orientations, chosen in such a way that the outermost strand of the outermost Whitehead curve runs parallel to the innermost curve of group (1).
$\gamma _{w+1},\ldots ,\gamma _{w+k}$
which we call Whitehead curves because they are patterned after one of the components of the Whitehead link. All the curves in the first group have the same orientation. The Whitehead curves have alternating orientations, chosen in such a way that the outermost strand of the outermost Whitehead curve runs parallel to the innermost curve of group (1).

Figure 1 The construction for Lemma 5.4.
Let
![]() $\gamma $
be the result of taking the (oriented) connected sum of all the
$\gamma $
be the result of taking the (oriented) connected sum of all the
![]() $\gamma _j$
arranged as shown in Figure 1(b). The choice of orientations ensures that in performing the connected sum of each curve with the adjacent one we include a twist rather than having a turning point where
$\gamma _j$
arranged as shown in Figure 1(b). The choice of orientations ensures that in performing the connected sum of each curve with the adjacent one we include a twist rather than having a turning point where
![]() $\gamma $
would double back over.
$\gamma $
would double back over.
Since each
![]() $\gamma _j$
is the unknot, the same is true of
$\gamma _j$
is the unknot, the same is true of
![]() $\gamma $
. It is also clear from the construction that each
$\gamma $
. It is also clear from the construction that each
![]() $\gamma _j$
with
$\gamma _j$
with
![]() $j \leq w$
has winding number
$j \leq w$
has winding number
![]() $1$
in
$1$
in
![]() $V_0$
while each
$V_0$
while each
![]() $\gamma _j$
with
$\gamma _j$
with
![]() $j>w$
has winding number
$j>w$
has winding number
![]() $0$
, so that
$0$
, so that
![]() $\gamma $
has winding number w in
$\gamma $
has winding number w in
![]() $V_0$
. It only remains to check that the geometric index of
$V_0$
. It only remains to check that the geometric index of
![]() $\gamma $
in
$\gamma $
in
![]() $V_0$
is precisely
$V_0$
is precisely
![]() $2k+w$
. To see this we apply a technique of Andrist et al. [Reference Andrist, Garity, Repovš and Wright1]. The dotted radial lines in Figure 1(b) represent two meridional disks which decompose the solid torus
$2k+w$
. To see this we apply a technique of Andrist et al. [Reference Andrist, Garity, Repovš and Wright1]. The dotted radial lines in Figure 1(b) represent two meridional disks which decompose the solid torus
![]() $V_0$
into two sectors
$V_0$
into two sectors
![]() $C_1$
and
$C_1$
and
![]() $C_2$
, where
$C_2$
, where
![]() $C_1$
is shaded light grey. Sectors of this form are called chambers in [Reference Andrist, Garity, Repovš and Wright1]. For
$C_1$
is shaded light grey. Sectors of this form are called chambers in [Reference Andrist, Garity, Repovš and Wright1]. For
![]() $1 \leq j \leq w$
the intersection
$1 \leq j \leq w$
the intersection
![]() $\gamma _j \cap C_1$
just consists of an arc that runs from one of the meridional disks to the other without turning back over. Arcs of this form are called spanning arcs. For
$\gamma _j \cap C_1$
just consists of an arc that runs from one of the meridional disks to the other without turning back over. Arcs of this form are called spanning arcs. For
![]() $w+1 \leq j \leq w+k$
the intersection
$w+1 \leq j \leq w+k$
the intersection
![]() $\gamma _j \cap C_1$
consists of a pair of linked arcs; these are called Whitehead clasps (see [Reference Andrist, Garity, Repovš and Wright1, Figure 5(b), p. 9]). The intersection of every
$\gamma _j \cap C_1$
consists of a pair of linked arcs; these are called Whitehead clasps (see [Reference Andrist, Garity, Repovš and Wright1, Figure 5(b), p. 9]). The intersection of every
![]() $\gamma _j$
with the chamber
$\gamma _j$
with the chamber
![]() $C_2$
just consists of one or two spanning arcs. In this situation [Reference Andrist, Garity, Repovš and Wright1, Corollary 4.6, p. 237] ensures that the geometric index
$C_2$
just consists of one or two spanning arcs. In this situation [Reference Andrist, Garity, Repovš and Wright1, Corollary 4.6, p. 237] ensures that the geometric index
![]() $N(\gamma ,V_0)=w+2k$
.
$N(\gamma ,V_0)=w+2k$
.
Proof Proof of Theorem 5.3
Since H and N are feasible, both can be written as direct limits of the form
where the
![]() $\{w_j\}$
and
$\{w_j\}$
and
![]() $\{n_j\}$
are as described in Lemma 3.4. Of the cases considered there we must have
$\{n_j\}$
are as described in Lemma 3.4. Of the cases considered there we must have
![]() $n_j \geq 1$
for all j because
$n_j \geq 1$
for all j because
![]() $N \neq 0$
by assumption.
$N \neq 0$
by assumption.
Claim. We can assume that all the
![]() $w_j$
and
$w_j$
and
![]() $n_j$
have the same parity.
$n_j$
have the same parity.
To check this suppose first that
![]() $ 2 | H$
. By Proposition 3.1 we see that
$ 2 | H$
. By Proposition 3.1 we see that
![]() $w_j$
must be even for infinitely many j, and by grouping the
$w_j$
must be even for infinitely many j, and by grouping the
![]() $w_j$
into blocks each of which contains at least an even arrow we may assume that all the
$w_j$
into blocks each of which contains at least an even arrow we may assume that all the
![]() $w_j$
are even. By the consistency condition of the theorem
$w_j$
are even. By the consistency condition of the theorem
![]() $2 | N$
too, and by the same argument we may take
$2 | N$
too, and by the same argument we may take
![]() $n_j$
to be even for all j. A similar reasoning applies when
$n_j$
to be even for all j. A similar reasoning applies when
![]() $2 \not | H$
(this time discarding a finite number of the
$2 \not | H$
(this time discarding a finite number of the
![]() $w_j$
and
$w_j$
and
![]() $n_j$
instead of grouping arrows as before), and in that case we may take all the
$n_j$
instead of grouping arrows as before), and in that case we may take all the
![]() $w_j$
and
$w_j$
and
![]() $n_j$
to be odd. Summing up, we can assume without loss of generality that all the
$n_j$
to be odd. Summing up, we can assume without loss of generality that all the
![]() $w_j$
and
$w_j$
and
![]() $n_j$
have the same parity.
$n_j$
have the same parity.
Claim. We can assume that
![]() $w_j \leq n_j$
for every j.
$w_j \leq n_j$
for every j.
In the case
![]() $N \sim 1$
the compatibility condition (C2) requires
$N \sim 1$
the compatibility condition (C2) requires
![]() $H \sim 1$
and so
$H \sim 1$
and so
![]() $w_j = n_j = 1$
for large enough j. Let us assume then that
$w_j = n_j = 1$
for large enough j. Let us assume then that
![]() $N \not \sim 1$
. Then according to Lemma 3.4 we must have
$N \not \sim 1$
. Then according to Lemma 3.4 we must have
![]() $n_j \geq 2$
for every j. Now consider
$n_j \geq 2$
for every j. Now consider
![]() $w_1$
. Since
$w_1$
. Since
![]() $n_j \geq 2$
for every j, by taking a product
$n_j \geq 2$
for every j, by taking a product
![]() $n_1\!\cdot \,\cdots \,\cdot n_{k_1}$
for sufficiently large
$n_1\!\cdot \,\cdots \,\cdot n_{k_1}$
for sufficiently large
![]() $k_1$
we can achieve
$k_1$
we can achieve
![]() $w_1 \leq n_1 \cdot \,\cdots \,\cdot n_{k_1}$
. Similarly, taking
$w_1 \leq n_1 \cdot \,\cdots \,\cdot n_{k_1}$
. Similarly, taking
![]() $k_2> k_1$
big enough we can achieve
$k_2> k_1$
big enough we can achieve
![]() $w_2 \leq n_{k_1+1} \cdot \,\cdots \,\cdot n_{k_2}$
, and so on. That is, by grouping the arrows in the defining sequence for N we can certainly assume that
$w_2 \leq n_{k_1+1} \cdot \,\cdots \,\cdot n_{k_2}$
, and so on. That is, by grouping the arrows in the defining sequence for N we can certainly assume that
![]() $w_j \leq n_j$
for every j. Notice that this does not change the parity of the
$w_j \leq n_j$
for every j. Notice that this does not change the parity of the
![]() $n_j$
.
$n_j$
.
Our choice of the
![]() $w_j$
and
$w_j$
and
![]() $n_j$
ensures that the equation
$n_j$
ensures that the equation
![]() $2k_j + w_j = n_j$
has an integer solution
$2k_j + w_j = n_j$
has an integer solution
![]() $k_j \geq 1$
for each j. Then by Lemma 5.4 we may construct a nested sequence of unknotted solid tori
$k_j \geq 1$
for each j. Then by Lemma 5.4 we may construct a nested sequence of unknotted solid tori
![]() $\{T_j\}$
such that the winding number and the geometric index of
$\{T_j\}$
such that the winding number and the geometric index of
![]() $T_{j+1}$
inside
$T_{j+1}$
inside
![]() $T_j$
are precisely
$T_j$
are precisely
![]() $w_j$
and
$w_j$
and
![]() $n_j$
, respectively. Let
$n_j$
, respectively. Let
![]() $K := \bigcap _{j \geq 0} T_j$
. Proposition 2.2 shows that K is not cellular; hence, it is a toroidal set. It is clear that K is unknotted and has
$K := \bigcap _{j \geq 0} T_j$
. Proposition 2.2 shows that K is not cellular; hence, it is a toroidal set. It is clear that K is unknotted and has
![]() $\check {H}^1(K;\mathbb {Z}) = H$
and
$\check {H}^1(K;\mathbb {Z}) = H$
and
![]() $\mathcal {N}(K) = N$
as required.
$\mathcal {N}(K) = N$
as required.
6 Weak tameness of toroidal sets
In this section we characterize weakly tame toroidal sets. A compact set
![]() $K \subseteq \mathbb {R}^3$
is called weakly tame if there exists a compact polyhedron
$K \subseteq \mathbb {R}^3$
is called weakly tame if there exists a compact polyhedron
![]() $P \subseteq \mathbb {R}^3$
such that
$P \subseteq \mathbb {R}^3$
such that
![]() $\mathbb {R}^3 - K$
and
$\mathbb {R}^3 - K$
and
![]() $\mathbb {R}^3 - P$
are homeomorphic. For example, cellular sets are weakly tame because they are point-like: their complement is homeomorphic to the complement of a point. Every tame set (that is, a set that can be carried onto a polyhedron by an ambient homeomorphism) is also weakly tame, but the converse is not generally true. For example, there is an arc in
$\mathbb {R}^3 - P$
are homeomorphic. For example, cellular sets are weakly tame because they are point-like: their complement is homeomorphic to the complement of a point. Every tame set (that is, a set that can be carried onto a polyhedron by an ambient homeomorphism) is also weakly tame, but the converse is not generally true. For example, there is an arc in
![]() $\mathbb {R}^3$
(see [Reference Moise23, pp. 137–138]) which is not tame but is weakly tame because its complement is homeomorphic to the complement of a point.
$\mathbb {R}^3$
(see [Reference Moise23, pp. 137–138]) which is not tame but is weakly tame because its complement is homeomorphic to the complement of a point.
To formulate our results we need to recall a definition (see [Reference Barge and Sánchez-Gabites2]) which generalizes the classical notion of the genus of a knot to toroidal sets. First define the genus
![]() $g(T)$
of a solid torus T as the genus of a core curve of T (this definition is correct because core curves are unique up to isotopy). Then for a toroidal set
$g(T)$
of a solid torus T as the genus of a core curve of T (this definition is correct because core curves are unique up to isotopy). Then for a toroidal set
![]() $K \subseteq \mathbb {R}^3$
define its genus
$K \subseteq \mathbb {R}^3$
define its genus
![]() $g(K)$
as the minimum
$g(K)$
as the minimum
![]() $g = 0,1,\ldots , +\infty $
such that K has arbitrarily small neighbourhoods that are solid tori of genus less than or equal to g. Notice that if K has finite genus then it has a standard basis
$g = 0,1,\ldots , +\infty $
such that K has arbitrarily small neighbourhoods that are solid tori of genus less than or equal to g. Notice that if K has finite genus then it has a standard basis
![]() $\{T_j\}$
such that
$\{T_j\}$
such that
![]() $g(T_j) = g(K)$
for every j. By contrast, if K has infinite genus then
$g(T_j) = g(K)$
for every j. By contrast, if K has infinite genus then
![]() $\lim _{j \rightarrow +\infty } g(T_j) = +\infty $
for any such basis. Also, a toroidal set K has genus
$\lim _{j \rightarrow +\infty } g(T_j) = +\infty $
for any such basis. Also, a toroidal set K has genus
![]() $0$
if and only if it has a neighbourhood basis of solid tori
$0$
if and only if it has a neighbourhood basis of solid tori
![]() $\{T_j\}$
of genus
$\{T_j\}$
of genus
![]() $0$
, which means that they are all unknotted. This is precisely what we called unknotted toroidal sets earlier. For information about knot theory we refer the reader to the books by Burde and Zieschang [Reference Burde and Zieschang5], Lickorish [Reference Lickorish21] or Rolfsen [Reference Rolfsen26].
$0$
, which means that they are all unknotted. This is precisely what we called unknotted toroidal sets earlier. For information about knot theory we refer the reader to the books by Burde and Zieschang [Reference Burde and Zieschang5], Lickorish [Reference Lickorish21] or Rolfsen [Reference Rolfsen26].
The main theorem in this section is as follows.
Theorem 6.1. Let
![]() $K \subseteq \mathbb {R}^3$
be a toroidal set. Then K is weakly tame if and only if the genus of K is finite and
$K \subseteq \mathbb {R}^3$
be a toroidal set. Then K is weakly tame if and only if the genus of K is finite and
![]() $\mathcal {N}(K) \sim 1$
.
$\mathcal {N}(K) \sim 1$
.
In fact, when the genus of K is strictly positive, the condition
![]() $\mathcal {N}(K) \sim 1$
can be replaced with a weaker one.
$\mathcal {N}(K) \sim 1$
can be replaced with a weaker one.
Theorem 6.2. Let
![]() $K \subseteq \mathbb {R}^3$
be a toroidal set with positive genus. Then K is weakly tame if and only if the genus of K is finite and K is non-trivial.
$K \subseteq \mathbb {R}^3$
be a toroidal set with positive genus. Then K is weakly tame if and only if the genus of K is finite and K is non-trivial.
Example 6.3. None of the (unknotted) generalized solenoids of Example 4.4 satisfies
![]() $\mathcal {N} \sim 1$
; thus, none of them is weakly tame.
$\mathcal {N} \sim 1$
; thus, none of them is weakly tame.
We devote the rest of this section to proving Theorems 6.1 and 6.2. This requires some work. We begin with a criterion that allows one to recognize when a toroidal set is weakly tame in terms of any one of its standard neighbourhood bases. We recall that two nested tori
![]() $T_2 \subseteq T_1$
are concentric if there exists a homeomorphism
$T_2 \subseteq T_1$
are concentric if there exists a homeomorphism
![]() $g : T_1 - \text {int}\ T_2 \longrightarrow (\partial T_1) \times [0,1]$
such that for every
$g : T_1 - \text {int}\ T_2 \longrightarrow (\partial T_1) \times [0,1]$
such that for every
![]() $p \in \partial T_1$
one has
$p \in \partial T_1$
one has
![]() $g(p) = (p,0) \in (\partial T_1) \times [0,1]$
.
$g(p) = (p,0) \in (\partial T_1) \times [0,1]$
.
Proposition 6.4. Let
![]() $K \subseteq \mathbb {R}^3$
be a toroidal set. Then the following assertions are equivalent.
$K \subseteq \mathbb {R}^3$
be a toroidal set. Then the following assertions are equivalent.
-
(i) K is weakly tame.
-
(ii) There exists a standard basis
 $\{T_j\}$
for K such that
$\{T_j\}$
for K such that
 $T_{j+1}$
and
$T_{j+1}$
and
 $T_j$
are concentric for all j.
$T_j$
are concentric for all j. -
(iii) For any standard basis
 $\{T_j\}$
for K there exists
$\{T_j\}$
for K there exists
 $j_0$
such that
$j_0$
such that
 $T_{j+1}$
and
$T_{j+1}$
and
 $T_j$
are concentric for all
$T_j$
are concentric for all
 $j \geq j_0$
.
$j \geq j_0$
.
Proof. (i)
![]() $\Rightarrow $
(ii) By assumption there exists a homeomorphism
$\Rightarrow $
(ii) By assumption there exists a homeomorphism
![]() $h : \mathbb {R}^3 - P \longrightarrow \mathbb {R}^3 - K$
for some compact polyhedron P. We may assume without loss of generality that h is piecewise linear [Reference Moise23, Theorem 2, p. 253]. Notice that
$h : \mathbb {R}^3 - P \longrightarrow \mathbb {R}^3 - K$
for some compact polyhedron P. We may assume without loss of generality that h is piecewise linear [Reference Moise23, Theorem 2, p. 253]. Notice that
where the first and last equalities follow from Alexander duality. This shows (setting
![]() $q = 0$
) that P must be connected and
$q = 0$
) that P must be connected and
![]() $\check {H}^q(P;\mathbb {Z}) = 0$
for
$\check {H}^q(P;\mathbb {Z}) = 0$
for
![]() $q \geq 2$
. For
$q \geq 2$
. For
![]() $q = 1$
we argue as follows. The only possibilities for
$q = 1$
we argue as follows. The only possibilities for
![]() $\check {H}^1(K;\mathbb {Z})$
are either
$\check {H}^1(K;\mathbb {Z})$
are either
![]() $0$
,
$0$
,
![]() $\mathbb {Z}$
, or a non-finitely generated group. Since compact polyhedra have finitely generated cohomology, it follows that
$\mathbb {Z}$
, or a non-finitely generated group. Since compact polyhedra have finitely generated cohomology, it follows that
![]() $H^1(P;\mathbb {Z})$
is either
$H^1(P;\mathbb {Z})$
is either
![]() $0$
or
$0$
or
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Claim.
h admits an extension to a homeomorphism
![]() $\hat {h} : \mathbb {S}^3 - P \longrightarrow \mathbb {S}^3 - K$
.
$\hat {h} : \mathbb {S}^3 - P \longrightarrow \mathbb {S}^3 - K$
.
Proof of claim
Let
![]() $B \subseteq \mathbb {R}^3$
be a closed
$B \subseteq \mathbb {R}^3$
be a closed
![]() $3$
-ball so big that it contains P in its interior and denote by S its boundary
$3$
-ball so big that it contains P in its interior and denote by S its boundary
![]() $2$
-sphere. Clearly
$2$
-sphere. Clearly
![]() $\mathbb {R}^3 - S$
has two connected components: an unbounded one U (which is the complement of B) and a bounded one
$\mathbb {R}^3 - S$
has two connected components: an unbounded one U (which is the complement of B) and a bounded one
![]() $\text {int}\ B$
. Let us examine the connected components of
$\text {int}\ B$
. Let us examine the connected components of
![]() $(\mathbb {R}^3 - P) - S$
. Since P has zero cohomology in degree
$(\mathbb {R}^3 - P) - S$
. Since P has zero cohomology in degree
![]() $2$
, it does not disconnect any connected open set that contains it (this follows from Alexander’s duality). Writing
$2$
, it does not disconnect any connected open set that contains it (this follows from Alexander’s duality). Writing
![]() $(\mathbb {R}^3 - P) - S = U \cup ((\text {int}\ B) - P)$
thus exhibits
$(\mathbb {R}^3 - P) - S = U \cup ((\text {int}\ B) - P)$
thus exhibits
![]() $(\mathbb {R}^3 - P) - S$
as the disjoint union of two connected sets, which are therefore its connected components. Notice that both have non-zero homology in dimension
$(\mathbb {R}^3 - P) - S$
as the disjoint union of two connected sets, which are therefore its connected components. Notice that both have non-zero homology in dimension
![]() $2$
: the first one because it is just homeomorphic to
$2$
: the first one because it is just homeomorphic to
![]() $\mathbb {S}^2 \times \mathbb {R}$
by construction; the second one because it is the result of removing a non-empty compact set from the interior of an open set with trivial homology (formally, this follows again from an application of Alexander’s duality).
$\mathbb {S}^2 \times \mathbb {R}$
by construction; the second one because it is the result of removing a non-empty compact set from the interior of an open set with trivial homology (formally, this follows again from an application of Alexander’s duality).
Since the
![]() $2$
-sphere S is contained in
$2$
-sphere S is contained in
![]() $\mathbb {R}^3 - P$
we may transform it via h to obtain another
$\mathbb {R}^3 - P$
we may transform it via h to obtain another
![]() $2$
-sphere
$2$
-sphere
![]() $S' := h(S)$
. By the polyhedral Schönflies theorem [Reference Moise23, Theorem 12, p. 122],
$S' := h(S)$
. By the polyhedral Schönflies theorem [Reference Moise23, Theorem 12, p. 122],
![]() $S'$
bounds a closed
$S'$
bounds a closed
![]() $3$
-ball
$3$
-ball
![]() $B'$
in
$B'$
in
![]() $\mathbb {R}^3$
. Notice that we do not know a priori whether K is contained in this ball; this is precisely what we want to prove now. Denote
$\mathbb {R}^3$
. Notice that we do not know a priori whether K is contained in this ball; this is precisely what we want to prove now. Denote
![]() $U' := \mathbb {R}^3 - B'$
. The same reasoning as used in the previous paragraph, but now taking into account that K may be contained in
$U' := \mathbb {R}^3 - B'$
. The same reasoning as used in the previous paragraph, but now taking into account that K may be contained in
![]() $U'$
or in
$U'$
or in
![]() $B'$
, leads to the conclusion that the connected components of
$B'$
, leads to the conclusion that the connected components of
![]() $(\mathbb {R}^3 - K) - S'$
are either
$(\mathbb {R}^3 - K) - S'$
are either
or
We mentioned earlier that both components of
![]() $(\mathbb {R}^3 - P) - S$
have non-zero homology in dimension
$(\mathbb {R}^3 - P) - S$
have non-zero homology in dimension
![]() $2$
, so the same must be true of the components of
$2$
, so the same must be true of the components of
![]() $(\mathbb {R}^3 - K) - S'$
because the two spaces are homeomorphic under h. This rules out the first alternative above, because
$(\mathbb {R}^3 - K) - S'$
because the two spaces are homeomorphic under h. This rules out the first alternative above, because
![]() $\text {int}\ B'$
has trivial homology. Thus it must be the case that
$\text {int}\ B'$
has trivial homology. Thus it must be the case that
![]() $K \subseteq \text {int}\ B'$
and the components of
$K \subseteq \text {int}\ B'$
and the components of
![]() $(\mathbb {R}^3 - K)-S'$
are precisely
$(\mathbb {R}^3 - K)-S'$
are precisely
![]() $U'$
and
$U'$
and
![]() $(\text {int}\ B') - K$
. Now, there are two possibilities for how h matches the components of
$(\text {int}\ B') - K$
. Now, there are two possibilities for how h matches the components of
![]() $(\mathbb {R}^3 - P)-S$
and
$(\mathbb {R}^3 - P)-S$
and
![]() $(\mathbb {R}^3 - K)-S'$
. Either we have
$(\mathbb {R}^3 - K)-S'$
. Either we have
or we have
However, the second alternative is not possible. From
![]() $h(U) = (\text {int}\ B') - K$
we would get
$h(U) = (\text {int}\ B') - K$
we would get
![]() $h(U \cup S) = B' - K$
, and this would extend to a homeomorphism between the one-point compactifications of
$h(U \cup S) = B' - K$
, and this would extend to a homeomorphism between the one-point compactifications of
![]() $U \cup S$
and
$U \cup S$
and
![]() $B' - K$
. That of
$B' - K$
. That of
![]() $U \cup S$
is just a
$U \cup S$
is just a
![]() $3$
-ball, whereas the one-point compactification of
$3$
-ball, whereas the one-point compactification of
![]() $B' - K$
can be thought of as
$B' - K$
can be thought of as
![]() $B'/K$
with
$B'/K$
with
![]() $[K]$
acting as the point at infinity. But then
$[K]$
acting as the point at infinity. But then
![]() $B'/K$
is a
$B'/K$
is a
![]() $3$
-ball, which implies that K is pointlike and by [Reference Daverman and Venema7, Proposition 2.4.5, p. 61] that K is actually cellular, contradicting the definition of a toroidal set. We are left with
$3$
-ball, which implies that K is pointlike and by [Reference Daverman and Venema7, Proposition 2.4.5, p. 61] that K is actually cellular, contradicting the definition of a toroidal set. We are left with
![]() $h(U) = U'$
. Then
$h(U) = U'$
. Then
![]() $h(U \cup S) = U' \cup S$
and this can be extended to the point at infinity to yield the required
$h(U \cup S) = U' \cup S$
and this can be extended to the point at infinity to yield the required
![]() $\hat {h}$
. This concludes the proof of the claim.
$\hat {h}$
. This concludes the proof of the claim.
Let N be a regular neighbourhood of P and define
![]() $T := \hat {h}(N - P) \cup K$
. Clearly T contains K. In fact, the following claim holds.
$T := \hat {h}(N - P) \cup K$
. Clearly T contains K. In fact, the following claim holds.
Claim.
T is a compact manifold that is a neighbourhood of K. Moreover, T is connected and
![]() $\partial T$
is either a
$\partial T$
is either a
![]() $2$
-sphere or a
$2$
-sphere or a
![]() $2$
-torus.
$2$
-torus.
Proof of claim
Begin by writing
![]() $\mathbb {S}^3 = (\mathbb {S}^3 - N) \uplus (N - P) \uplus P$
, where
$\mathbb {S}^3 = (\mathbb {S}^3 - N) \uplus (N - P) \uplus P$
, where
![]() $\uplus $
means a union of disjoint sets. Then we see that
$\uplus $
means a union of disjoint sets. Then we see that
![]() $\mathbb {S}^3 = \hat {h}(\mathbb {S}^3 - N) \uplus \hat {h}(N - P) \uplus K = \hat {h}(\mathbb {S}^3 - N) \uplus T$
, and this gives the convenient relation
$\mathbb {S}^3 = \hat {h}(\mathbb {S}^3 - N) \uplus \hat {h}(N - P) \uplus K = \hat {h}(\mathbb {S}^3 - N) \uplus T$
, and this gives the convenient relation
![]() $\mathbb {S}^3 - T = \hat {h}(\mathbb {S}^3 - N)$
.
$\mathbb {S}^3 - T = \hat {h}(\mathbb {S}^3 - N)$
.
To prove that T is a neighbourhood of K, suppose the contrary. Then there exists a sequence
![]() $\{q_n\}$
in
$\{q_n\}$
in
![]() $\mathbb {S}^3 - T$
that converges to some point in K. The sequence
$\mathbb {S}^3 - T$
that converges to some point in K. The sequence
![]() $\{p_n := \hat {h}^{-1}(q_n)\}$
is then contained in
$\{p_n := \hat {h}^{-1}(q_n)\}$
is then contained in
![]() $\hat {h}^{-1}(\mathbb {S}^3 - T) = \mathbb {S}^3 - N$
, and so after passing to a subsequence we may assume that it converges to some point
$\hat {h}^{-1}(\mathbb {S}^3 - T) = \mathbb {S}^3 - N$
, and so after passing to a subsequence we may assume that it converges to some point
![]() $p \in \overline {\mathbb {S}^3 - N} = \mathbb {S}^3 - \text {int}\ N$
. But this set is still contained in the domain of
$p \in \overline {\mathbb {S}^3 - N} = \mathbb {S}^3 - \text {int}\ N$
. But this set is still contained in the domain of
![]() $\hat {h}$
, and so
$\hat {h}$
, and so
![]() $q_n = \hat {h}(p_n)$
would converge to
$q_n = \hat {h}(p_n)$
would converge to
![]() $\hat {h}(p)$
, which is not possible because
$\hat {h}(p)$
, which is not possible because
![]() $\{q_n\}$
does not converge in
$\{q_n\}$
does not converge in
![]() $\mathbb {S}^3 - K$
.
$\mathbb {S}^3 - K$
.
Writing
![]() $T = (T - K) \cup \text {int}\ T$
exhibits it as the union of two open (in T) sets. The first is a
$T = (T - K) \cup \text {int}\ T$
exhibits it as the union of two open (in T) sets. The first is a
![]() $3$
-manifold with boundary because it is homeomorphic to
$3$
-manifold with boundary because it is homeomorphic to
![]() $N - P$
via
$N - P$
via
![]() $\hat {h}^{-1}$
by definition, whereas the second is a
$\hat {h}^{-1}$
by definition, whereas the second is a
![]() $3$
-manifold without boundary because it is open in
$3$
-manifold without boundary because it is open in
![]() $\mathbb {S}^3$
. Thus T is a compact
$\mathbb {S}^3$
. Thus T is a compact
![]() $3$
-manifold with boundary. Resorting again to Alexander’s duality and bearing in mind that
$3$
-manifold with boundary. Resorting again to Alexander’s duality and bearing in mind that
![]() $\mathbb {S}^3 - T$
and
$\mathbb {S}^3 - T$
and
![]() $\mathbb {S}^3 - N$
are homeomorphic via
$\mathbb {S}^3 - N$
are homeomorphic via
![]() $\hat {h}$
, we have
$\hat {h}$
, we have
where in the last step we have used that N is a regular neighbourhood of P and so collapses onto it. Recalling the computation of the cohomology of P at the beginning of this proof, we conclude that T is connected, has vanishing cohomology in degrees
![]() $q \geq 2$
, and has cohomology either
$q \geq 2$
, and has cohomology either
![]() $0$
or
$0$
or
![]() $\mathbb {Z}$
in dimension
$\mathbb {Z}$
in dimension
![]() $q = 1$
. A routine argument using the Poincaré–Lefschetz duality then shows that
$q = 1$
. A routine argument using the Poincaré–Lefschetz duality then shows that
![]() $\partial T$
is either a
$\partial T$
is either a
![]() $2$
-sphere or a
$2$
-sphere or a
![]() $2$
-torus.
$2$
-torus.
Now we repeat the same construction not just for a single N, but for a neighbourhood basis of P comprised of nested regular neighbourhoods
![]() $N_j$
. As before, denote by
$N_j$
. As before, denote by
![]() $T_j = \hat {h}(N_j - P) \cup K$
the corresponding neighbourhoods of K. Since the sets
$T_j = \hat {h}(N_j - P) \cup K$
the corresponding neighbourhoods of K. Since the sets
![]() $\mathbb {S}^3 - N_j$
clearly form an ascending sequence whose union is
$\mathbb {S}^3 - N_j$
clearly form an ascending sequence whose union is
![]() $\mathbb {S}^3 - P$
, the sets
$\mathbb {S}^3 - P$
, the sets
![]() $\hat {h}(\mathbb {S}^3 - N_j)$
also form an ascending sequence whose union is
$\hat {h}(\mathbb {S}^3 - N_j)$
also form an ascending sequence whose union is
![]() $\hat {h}(\mathbb {S}^3 - P) = \mathbb {S}^3 - K$
. It then follows from the expression
$\hat {h}(\mathbb {S}^3 - P) = \mathbb {S}^3 - K$
. It then follows from the expression
![]() $\mathbb {S}^3 - T_j = \hat {h}(\mathbb {S}^3 - N_j)$
obtained above that the
$\mathbb {S}^3 - T_j = \hat {h}(\mathbb {S}^3 - N_j)$
obtained above that the
![]() $T_j$
form a decreasing sequence whose intersection is K. Thus
$T_j$
form a decreasing sequence whose intersection is K. Thus
![]() $\{T_j\}$
is a nested neighbourhood basis of K comprised of compact, connected manifolds.
$\{T_j\}$
is a nested neighbourhood basis of K comprised of compact, connected manifolds.
We established earlier that
![]() $\partial T_j$
is either a
$\partial T_j$
is either a
![]() $2$
-sphere or a
$2$
-sphere or a
![]() $2$
-torus. In the first case, the Schönflies theorem for polyhedral spheres implies that
$2$
-torus. In the first case, the Schönflies theorem for polyhedral spheres implies that
![]() $T_j$
is a
$T_j$
is a
![]() $3$
-ball. If this occurs for infinitely many indices j then K would be cellular, which contradicts the definition of a toroidal set. Thus we may assume without loss of generality that all the
$3$
-ball. If this occurs for infinitely many indices j then K would be cellular, which contradicts the definition of a toroidal set. Thus we may assume without loss of generality that all the
![]() $\partial T_j$
are
$\partial T_j$
are
![]() $2$
-tori. Consider any one
$2$
-tori. Consider any one
![]() $T_{j_0}$
. Since K is toroidal, it has a neighbourhood T which is a solid torus contained in the interior of
$T_{j_0}$
. Since K is toroidal, it has a neighbourhood T which is a solid torus contained in the interior of
![]() $T_{j_0}$
. Choose
$T_{j_0}$
. Choose
![]() $j_1> j_0$
so that
$j_1> j_0$
so that
![]() $T_{j_1} \subseteq \text {int}\ T$
. Observe that
$T_{j_1} \subseteq \text {int}\ T$
. Observe that
![]() $T_{j_0} - \text {int}\ T_{j_1}$
is homeomorphic via h to
$T_{j_0} - \text {int}\ T_{j_1}$
is homeomorphic via h to
![]() $N_{j_0} - \text {int}\ N_{j_1}$
, which is in turn homeomorphic to
$N_{j_0} - \text {int}\ N_{j_1}$
, which is in turn homeomorphic to
![]() $(\partial N_{j_0}) \times [0,1]$
by the annulus theorem for regular neighbourhoods [Reference Rourke and Sanderson27, Corollary 3.18, p. 35]. Pulling back this homeomorphism via h shows that
$(\partial N_{j_0}) \times [0,1]$
by the annulus theorem for regular neighbourhoods [Reference Rourke and Sanderson27, Corollary 3.18, p. 35]. Pulling back this homeomorphism via h shows that
![]() $T_{j_0} - \text {int}\ T_{j_1}$
is also homeomorphic to
$T_{j_0} - \text {int}\ T_{j_1}$
is also homeomorphic to
![]() $(\partial T_{j_0}) \times [0,1]$
. A direct application of a concentricity theorem of Edwards [Reference Edwards9, Theorem 2, p. 419] then ensures that T is concentric with both
$(\partial T_{j_0}) \times [0,1]$
. A direct application of a concentricity theorem of Edwards [Reference Edwards9, Theorem 2, p. 419] then ensures that T is concentric with both
![]() $T_{j_0}$
and
$T_{j_0}$
and
![]() $T_{j_1}$
, so in particular all three of them are homeomorphic; hence, they are all (concentric) solid tori. Thus
$T_{j_1}$
, so in particular all three of them are homeomorphic; hence, they are all (concentric) solid tori. Thus
![]() $\{T_j\}$
is the required neighbourhood basis of K.
$\{T_j\}$
is the required neighbourhood basis of K.
(ii)
![]() $\Rightarrow $
(iii) Let
$\Rightarrow $
(iii) Let
![]() $\{T_j\}$
and
$\{T_j\}$
and
![]() $\{T^{\prime }_k\}$
be two neighbourhood bases of K comprised of nested solid tori. Assume that the
$\{T^{\prime }_k\}$
be two neighbourhood bases of K comprised of nested solid tori. Assume that the
![]() $T_j$
are all concentric. Choose
$T_j$
are all concentric. Choose
![]() $k_0$
big enough so that
$k_0$
big enough so that
![]() $T^{\prime }_{k_0} \subseteq \text {int}\ T_1$
. Pick any
$T^{\prime }_{k_0} \subseteq \text {int}\ T_1$
. Pick any
![]() $k_1> k_0$
and finally let j be big enough so that
$k_1> k_0$
and finally let j be big enough so that
![]() $T_{j} \subseteq \text {int}\ T^{\prime }_{k_1}$
. Thus we have the nested tori
$T_{j} \subseteq \text {int}\ T^{\prime }_{k_1}$
. Thus we have the nested tori
![]() $T_{j} \subseteq T^{\prime }_{k_1} \subseteq T^{\prime }_{k_0} \subseteq T_1$
. Since
$T_{j} \subseteq T^{\prime }_{k_1} \subseteq T^{\prime }_{k_0} \subseteq T_1$
. Since
![]() $T_1$
and
$T_1$
and
![]() $T_{j}$
are concentric by assumption, the concentricity theorem of Edwards mentioned in the previous paragraph ensures that
$T_{j}$
are concentric by assumption, the concentricity theorem of Edwards mentioned in the previous paragraph ensures that
![]() $T^{\prime }_{k_0}$
is concentric with both
$T^{\prime }_{k_0}$
is concentric with both
![]() $T_1$
and
$T_1$
and
![]() $T_j$
. Then again the same theorem, this time applied to
$T_j$
. Then again the same theorem, this time applied to
![]() $T_j \subseteq T^{\prime }_{k_1} \subseteq T^{\prime }_{k_0}$
, ensures that
$T_j \subseteq T^{\prime }_{k_1} \subseteq T^{\prime }_{k_0}$
, ensures that
![]() $T^{\prime }_{k_1}$
is concentric with
$T^{\prime }_{k_1}$
is concentric with
![]() $T^{\prime }_{k_0}$
. Thus the
$T^{\prime }_{k_0}$
. Thus the
![]() $\{T^{\prime }_k\}$
are all concentric for
$\{T^{\prime }_k\}$
are all concentric for
![]() $k \geq k_0$
.
$k \geq k_0$
.
(iii)
![]() $\Rightarrow $
(i) Let
$\Rightarrow $
(i) Let
![]() $\{T_j\}$
be a standard basis for K comprised of concentric tori. Denote by
$\{T_j\}$
be a standard basis for K comprised of concentric tori. Denote by
![]() $R_j$
each region
$R_j$
each region
![]() $T_j - \text {int}\ T_{j+1}$
, so that
$T_j - \text {int}\ T_{j+1}$
, so that
![]() $T_1 - K = \bigcup R_j$
. Since the
$T_1 - K = \bigcup R_j$
. Since the
![]() $\{T_j\}$
are concentric, each
$\{T_j\}$
are concentric, each
![]() $R_j$
is homeomorphic to
$R_j$
is homeomorphic to
![]() $(\partial T_j) \times [j,j+1]$
via some homeomorphism
$(\partial T_j) \times [j,j+1]$
via some homeomorphism
![]() $h_j$
such that
$h_j$
such that
![]() $h_j(p,j) = p$
for every
$h_j(p,j) = p$
for every
![]() $p \in \partial T_j$
. It is then easy to modify the
$p \in \partial T_j$
. It is then easy to modify the
![]() $h_j$
in such a way that they can all be pasted together to yield a homeomorphism from
$h_j$
in such a way that they can all be pasted together to yield a homeomorphism from
![]() $\bigcup R_j$
onto
$\bigcup R_j$
onto
![]() $(\partial T_1) \times [1,+\infty )$
. (See the proof of implication (ii)
$(\partial T_1) \times [1,+\infty )$
. (See the proof of implication (ii)
![]() $\Rightarrow $
(i) in [Reference Barge and Sánchez-Gabites2, Theorem 3.11, p. 18] for more details.) The latter is, in turn, homeomorphic to
$\Rightarrow $
(i) in [Reference Barge and Sánchez-Gabites2, Theorem 3.11, p. 18] for more details.) The latter is, in turn, homeomorphic to
![]() $T_1 - \gamma $
, where
$T_1 - \gamma $
, where
![]() $\gamma $
is a core curve of
$\gamma $
is a core curve of
![]() $T_1$
. Thus we have obtained a homeomorphism
$T_1$
. Thus we have obtained a homeomorphism
![]() $T_1 - K \cong T_1 - \gamma $
that is the identity on
$T_1 - K \cong T_1 - \gamma $
that is the identity on
![]() $\partial T_1$
. Extending this by the identity to all of
$\partial T_1$
. Extending this by the identity to all of
![]() $\mathbb {R}^3$
yields a homeomorphism between
$\mathbb {R}^3$
yields a homeomorphism between
![]() $\mathbb {R}^3 - K$
and
$\mathbb {R}^3 - K$
and
![]() $\mathbb {R}^3 - \gamma $
, where
$\mathbb {R}^3 - \gamma $
, where
![]() $\gamma $
is a polyhedral simple closed curve. This shows that K is weakly tame.
$\gamma $
is a polyhedral simple closed curve. This shows that K is weakly tame.
Remark 6.5. Since a polyhedral simple closed curve is perhaps the simplest example of a toroidal set, it would also seem reasonable to define a toroidal set to be weakly tame if its complement is homeomorphic to the complement of such a curve, rather than to the complement of an arbitrary polyhedron P. It follows from the proof of (iii)
![]() $\Rightarrow $
(i) in the preceding proposition that both definitions are equivalent.
$\Rightarrow $
(i) in the preceding proposition that both definitions are equivalent.
The proof of Theorem 6.1 is now very simple.
Proof Proof of Theorem 6.1
Suppose first K is weakly tame. Then it has a standard basis of concentric tori
![]() $\{T_j\}$
by Proposition 6.4. Clearly concentric tori have the same genus and the geometric index
$\{T_j\}$
by Proposition 6.4. Clearly concentric tori have the same genus and the geometric index
![]() $N(T_{j+1},T_j)$
is
$N(T_{j+1},T_j)$
is
![]() $1$
. It follows that
$1$
. It follows that
![]() $g(K) < +\infty $
(by definition) and
$g(K) < +\infty $
(by definition) and
![]() $\mathcal {N}(K) \sim 1$
by Proposition 4.1.
$\mathcal {N}(K) \sim 1$
by Proposition 4.1.
Now suppose
![]() $g(K) < +\infty $
and
$g(K) < +\infty $
and
![]() $\mathcal {N}(K) \sim 1$
. By the definition of the genus of a toroidal set there exists a standard basis
$\mathcal {N}(K) \sim 1$
. By the definition of the genus of a toroidal set there exists a standard basis
![]() $\{T_j\}$
for K such that
$\{T_j\}$
for K such that
![]() $g(T_j) = g(K)$
for every j. Also, the assumption that
$g(T_j) = g(K)$
for every j. Also, the assumption that
![]() $\mathcal {N}(K) \sim 1$
implies, by Proposition 4.3, that
$\mathcal {N}(K) \sim 1$
implies, by Proposition 4.3, that
![]() $N(T_{j+1},T_j) = 1$
for large enough j. This condition on the geometric index entails (see [Reference Schubert32, Satz 2, p. 171]) that the core curve of
$N(T_{j+1},T_j) = 1$
for large enough j. This condition on the geometric index entails (see [Reference Schubert32, Satz 2, p. 171]) that the core curve of
![]() $T_{j+1}$
is the connected sum of the core curve of
$T_{j+1}$
is the connected sum of the core curve of
![]() $T_j$
with some other knot
$T_j$
with some other knot
![]() $\gamma _j$
. But, since the genera of
$\gamma _j$
. But, since the genera of
![]() $T_j$
and
$T_j$
and
![]() $T_{j+1}$
are equal and genus is additive under connected sums, it follows that the genus of
$T_{j+1}$
are equal and genus is additive under connected sums, it follows that the genus of
![]() $\gamma _j$
must be
$\gamma _j$
must be
![]() $0$
. Therefore the core curves of
$0$
. Therefore the core curves of
![]() $T_j$
and
$T_j$
and
![]() $T_{j+1}$
are equivalently knotted. A result of Edwards [Reference Edwards, Gordon and Kirby10, Theorem 3, p. 4] then implies that
$T_{j+1}$
are equivalently knotted. A result of Edwards [Reference Edwards, Gordon and Kirby10, Theorem 3, p. 4] then implies that
![]() $T_j$
and
$T_j$
and
![]() $T_{j+1}$
are concentric. Hence K is weakly tame by Proposition 6.4.
$T_{j+1}$
are concentric. Hence K is weakly tame by Proposition 6.4.
As for Theorem 6.2, we require still another previous lemma.
Lemma 6.6. Let
![]() $T_2 \subseteq T_1$
be a nested pair of solid tori. Assume that:
$T_2 \subseteq T_1$
be a nested pair of solid tori. Assume that:
-
(i) the winding number w of
 $T_2$
inside
$T_2$
inside
 $T_1$
is positive;
$T_1$
is positive; -
(ii) the genera g of
 $T_1$
and
$T_1$
and
 $T_2$
are equal and positive.
$T_2$
are equal and positive.
Then
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are concentric.
$T_2$
are concentric.
Before proving the lemma, recall that a spine of a polyhedral manifold N is a polyhedron
![]() $P \subseteq \text {int}\ N$
such that N collapses onto P, which we denote by
$P \subseteq \text {int}\ N$
such that N collapses onto P, which we denote by
![]() $N \searrow P$
as customary. We will need the following result of Hudson and Zeeman (see [Reference Hudson and Zeeman16, Corollary 5, p. 727]): if P and
$N \searrow P$
as customary. We will need the following result of Hudson and Zeeman (see [Reference Hudson and Zeeman16, Corollary 5, p. 727]): if P and
![]() $P'$
are two polyhedra in
$P'$
are two polyhedra in
![]() $\text {int}\ N$
that are related by a sequence of collapses and expansions in N (but not necessarily in
$\text {int}\ N$
that are related by a sequence of collapses and expansions in N (but not necessarily in
![]() $\text {int}\ N$
) then P is a spine of N if and only if
$\text {int}\ N$
) then P is a spine of N if and only if
![]() $P'$
is a spine of N. In our case N will always be a neighbourhood of P in the ambient
$P'$
is a spine of N. In our case N will always be a neighbourhood of P in the ambient
![]() $3$
-manifold (so in particular its interior as a manifold coincides with its topological interior), and then saying that P is a spine of N is equivalent to saying that N is a regular neighbourhood of P (see [Reference Rourke and Sanderson27, Corollary 3.30, p. 41]).
$3$
-manifold (so in particular its interior as a manifold coincides with its topological interior), and then saying that P is a spine of N is equivalent to saying that N is a regular neighbourhood of P (see [Reference Rourke and Sanderson27, Corollary 3.30, p. 41]).
Proof Proof of Lemma 6.6
Let
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
be core curves for
$\gamma _2$
be core curves for
![]() $T_1$
and
$T_1$
and
![]() $T_2$
, respectively. Let also
$T_2$
, respectively. Let also
![]() $\unicode{x3bb} _1 \subseteq \partial T_1$
be a longitude of
$\unicode{x3bb} _1 \subseteq \partial T_1$
be a longitude of
![]() $T_1$
.
$T_1$
.
Claim. It suffices to show that
![]() $\gamma _2$
and
$\gamma _2$
and
![]() $\unicode{x3bb} _1$
cobound an annulus in
$\unicode{x3bb} _1$
cobound an annulus in
![]() $T_1$
.
$T_1$
.
Proof of claim
Let
![]() $A'$
be the annulus cobounded by
$A'$
be the annulus cobounded by
![]() $\gamma _2$
and
$\gamma _2$
and
![]() $\unicode{x3bb} _1$
in
$\unicode{x3bb} _1$
in
![]() $T_1$
, and denote by A an annulus cobounded by
$T_1$
, and denote by A an annulus cobounded by
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\unicode{x3bb} _1$
in
$\unicode{x3bb} _1$
in
![]() $T_1$
(this always exists). Any annulus collapses onto each one of its boundary curves. Thus we may write
$T_1$
(this always exists). Any annulus collapses onto each one of its boundary curves. Thus we may write
![]() $\gamma _1 \nearrow A \searrow \unicode{x3bb} _1 \nearrow A' \searrow \gamma _2$
within
$\gamma _1 \nearrow A \searrow \unicode{x3bb} _1 \nearrow A' \searrow \gamma _2$
within
![]() $T_1$
, and since
$T_1$
, and since
![]() $\gamma _1$
is a spine of
$\gamma _1$
is a spine of
![]() $T_1$
, the result of Hudson and Zeeman mentioned earlier implies that
$T_1$
, the result of Hudson and Zeeman mentioned earlier implies that
![]() $\gamma _2$
is a spine of
$\gamma _2$
is a spine of
![]() $T_1$
. This means that
$T_1$
. This means that
![]() $T_1$
is a regular neighbourhood of
$T_1$
is a regular neighbourhood of
![]() $\gamma _2$
in
$\gamma _2$
in
![]() $\mathbb {R}^3$
and, since
$\mathbb {R}^3$
and, since
![]() $T_2$
is also a regular neighbourhood of
$T_2$
is also a regular neighbourhood of
![]() $\gamma _2$
(the latter being a core for
$\gamma _2$
(the latter being a core for
![]() $T_2$
), the regular neighbourhood annulus theorem (see, for instance, [Reference Hudson and Zeeman16, Corollary 1, p. 725] or [Reference Rourke and Sanderson27, Corollary 3.18, p. 36]) guarantees that
$T_2$
), the regular neighbourhood annulus theorem (see, for instance, [Reference Hudson and Zeeman16, Corollary 1, p. 725] or [Reference Rourke and Sanderson27, Corollary 3.18, p. 36]) guarantees that
![]() $T_2$
and
$T_2$
and
![]() $T_1$
are concentric. This proves the claim.
$T_1$
are concentric. This proves the claim.
Now we shall show
![]() $\gamma _2$
and
$\gamma _2$
and
![]() $\unicode{x3bb} _1$
indeed cobound an annulus in
$\unicode{x3bb} _1$
indeed cobound an annulus in
![]() $T_1$
. This follows from an examination of the proof of Schubert’s relation between the genus of a satellite knot and its companion as given, for example, in the book by Burde and Zieschang [Reference Burde and Zieschang5]. In our setting
$T_1$
. This follows from an examination of the proof of Schubert’s relation between the genus of a satellite knot and its companion as given, for example, in the book by Burde and Zieschang [Reference Burde and Zieschang5]. In our setting
![]() $\gamma _2$
is a satellite of
$\gamma _2$
is a satellite of
![]() $\gamma _1$
and the relation just mentioned reads
$\gamma _1$
and the relation just mentioned reads
![]() $g(T_2) \geq w \cdot g(T_1) + g'$
, where
$g(T_2) \geq w \cdot g(T_1) + g'$
, where
![]() $g'$
is the genus of the pattern of
$g'$
is the genus of the pattern of
![]() $T_2$
inside
$T_2$
inside
![]() $T_1$
. By assumption
$T_1$
. By assumption
![]() $g(T_1) = g(T_2) = g> 0$
and (since
$g(T_1) = g(T_2) = g> 0$
and (since
![]() $g' \geq 0$
and
$g' \geq 0$
and
![]() $w \geq 1$
), this inequality implies
$w \geq 1$
), this inequality implies
![]() $w = 1$
.
$w = 1$
.
Let S be a Seifert surface of minimal genus that spans
![]() $\gamma _2$
. Without loss of generality we may assume that S is transversal to
$\gamma _2$
. Without loss of generality we may assume that S is transversal to
![]() $\partial T_1$
. Let
$\partial T_1$
. Let
![]() $S_i$
and
$S_i$
and
![]() $S_o$
be the parts of S that lie inside and outside
$S_o$
be the parts of S that lie inside and outside
![]() $T_1$
, respectively; that is,
$T_1$
, respectively; that is,
![]() $S_i := S \cap T_1$
and
$S_i := S \cap T_1$
and
![]() $S_o := S \cap \overline {(\mathbb {R}^3 - T_1)}$
. Both of these are (a priori, possibly non-connected) orientable surfaces with boundary. We may choose (see [Reference Burde and Zieschang5, Lemma 2.11, p. 21]) S so that: (i) it intersects
$S_o := S \cap \overline {(\mathbb {R}^3 - T_1)}$
. Both of these are (a priori, possibly non-connected) orientable surfaces with boundary. We may choose (see [Reference Burde and Zieschang5, Lemma 2.11, p. 21]) S so that: (i) it intersects
![]() $\partial T_1$
transversally in a longitude
$\partial T_1$
transversally in a longitude
![]() $\unicode{x3bb} _1$
; and (ii)
$\unicode{x3bb} _1$
; and (ii)
![]() $S_o$
consists of a single connected component (whose boundary is, therefore, precisely
$S_o$
consists of a single connected component (whose boundary is, therefore, precisely
![]() $\unicode{x3bb} _1$
).
$\unicode{x3bb} _1$
).
Since
![]() $\unicode{x3bb} _1$
is a longitude of
$\unicode{x3bb} _1$
is a longitude of
![]() $T_1$
, it cobounds an annulus in
$T_1$
, it cobounds an annulus in
![]() $T_1$
with its core curve
$T_1$
with its core curve
![]() $\gamma _1$
. The union of this annulus and
$\gamma _1$
. The union of this annulus and
![]() $S_o$
produces a Seifert surface for
$S_o$
produces a Seifert surface for
![]() $\gamma _1$
whose genus is the same as that of
$\gamma _1$
whose genus is the same as that of
![]() $S_o$
. Thus the genus of
$S_o$
. Thus the genus of
![]() $S_o$
is greater than or equal to the genus of
$S_o$
is greater than or equal to the genus of
![]() $\gamma _1$
, namely g. In terms of the Euler characteristic,
$\gamma _1$
, namely g. In terms of the Euler characteristic,
![]() $\chi (S_o) \leq 1 - 2g$
.
$\chi (S_o) \leq 1 - 2g$
.
Recall that S was a minimal Seifert surface for
![]() $\gamma _2$
, which also has genus g by assumption. Thus we have
$\gamma _2$
, which also has genus g by assumption. Thus we have
![]() $\chi (S) = 1-2g$
. Then from
$\chi (S) = 1-2g$
. Then from
![]() $\chi (S) = \chi (S_i) + \chi (S_o)$
and the inequality of the previous paragraph we get
$\chi (S) = \chi (S_i) + \chi (S_o)$
and the inequality of the previous paragraph we get
![]() $\chi (S_i) \geq 0$
. Since
$\chi (S_i) \geq 0$
. Since
![]() $S_i$
arose by cutting the connected surface S along
$S_i$
arose by cutting the connected surface S along
![]() $\partial T_1$
, the boundary of each component of
$\partial T_1$
, the boundary of each component of
![]() $S_i$
must have a non-empty intersection with
$S_i$
must have a non-empty intersection with
![]() $\partial T_1$
. But, since
$\partial T_1$
. But, since
![]() $S \cap \partial T_1$
consists of the single curve
$S \cap \partial T_1$
consists of the single curve
![]() $\unicode{x3bb} _1$
, it follows that
$\unicode{x3bb} _1$
, it follows that
![]() $S_i$
is actually connected and its boundary has precisely two components; namely
$S_i$
is actually connected and its boundary has precisely two components; namely
![]() $\gamma _2$
and
$\gamma _2$
and
![]() $\unicode{x3bb} _1$
. The only connected, orientable surface with two boundary components and non-negative Euler characteristic is the annulus. Thus
$\unicode{x3bb} _1$
. The only connected, orientable surface with two boundary components and non-negative Euler characteristic is the annulus. Thus
![]() $S_i$
is the required annulus that cobounds
$S_i$
is the required annulus that cobounds
![]() $\gamma _2$
and the longitude
$\gamma _2$
and the longitude
![]() $\unicode{x3bb} _1$
in
$\unicode{x3bb} _1$
in
![]() $T_1$
.
$T_1$
.
Proof Proof of Theorem 6.2
It follows from the definition of the genus that K has a standard basis
![]() $\{T_j\}$
such that
$\{T_j\}$
such that
![]() $g(T_j) = g(K)$
for all j. Denote by
$g(T_j) = g(K)$
for all j. Denote by
![]() $w_j$
the winding number of
$w_j$
the winding number of
![]() $T_{j+1}$
inside
$T_{j+1}$
inside
![]() $T_j$
. Since
$T_j$
. Since
![]() $\check {H}^1(K;\mathbb {Z}) \neq 0$
by assumption, we must have
$\check {H}^1(K;\mathbb {Z}) \neq 0$
by assumption, we must have
![]() $w_j> 0$
for big enough j. It then follows from Lemma 6.6 that all the pairs
$w_j> 0$
for big enough j. It then follows from Lemma 6.6 that all the pairs
![]() $(T_j,T_{j+1})$
are concentric from some j onwards. Finally, Proposition 6.4 implies that K is weakly tame.
$(T_j,T_{j+1})$
are concentric from some j onwards. Finally, Proposition 6.4 implies that K is weakly tame.
Conversely, if K is weakly tame then by Theorem 6.1 its genus is finite. Also, it has a neighbourhood basis of concentric tori by Proposition 6.4 and therefore clearly
![]() $\mathcal {N}(K) \sim 1$
(or use Proposition 4.3).
$\mathcal {N}(K) \sim 1$
(or use Proposition 4.3).
7 Applications to the realizability problem
We finally turn to the realizability problem for toroidal sets, and we begin by recalling some definitions from topological dynamics. We state them for the discrete case, but the case of flows is completely analogous. Let f be a homeomorphism of
![]() $\mathbb {R}^3$
. An attractor (sometimes called asymptotically stable) for f is a compact invariant set
$\mathbb {R}^3$
. An attractor (sometimes called asymptotically stable) for f is a compact invariant set
![]() $K \subseteq \mathbb {R}^3$
which is stable in the sense of Lyapunov and attracts all points in some neighbourhood U of K. Explicitly, these conditions have the following meanings.
$K \subseteq \mathbb {R}^3$
which is stable in the sense of Lyapunov and attracts all points in some neighbourhood U of K. Explicitly, these conditions have the following meanings.
-
(i) K is invariant:
 $f(K) = K$
.
$f(K) = K$
. -
(ii) K attracts points in U: for every neighbourhood V of K and every
 $p \in U$
there exists
$p \in U$
there exists
 $n_0 \in \mathbb {N}$
such that
$n_0 \in \mathbb {N}$
such that
 $f^n(p) \in V$
for every
$f^n(p) \in V$
for every
 $n \geq n_0$
.
$n \geq n_0$
. -
(iii) K is Lyapunov stable: for every neighbourhood V of K there exists another neighbourhood
 $V_0$
of K such that
$V_0$
of K such that
 $f^n(V_0) \subseteq V$
for every
$f^n(V_0) \subseteq V$
for every
 $n \geq 0$
.
$n \geq 0$
.
The maximal neighbourhood U with property (ii) is called the basin of attraction of K and is an open invariant subset of
![]() $\mathbb {R}^3$
. We denote it by
$\mathbb {R}^3$
. We denote it by
![]() $\mathcal {A}(K)$
.
$\mathcal {A}(K)$
.
The conjunction of (ii) and (iii) implies that K not only attracts points in
![]() $\mathcal {A}(K)$
but also neighbourhoods of points and in fact compacta P of the basin of attraction. This is fairly easy to check. Consider first a point
$\mathcal {A}(K)$
but also neighbourhoods of points and in fact compacta P of the basin of attraction. This is fairly easy to check. Consider first a point
![]() $p \in \mathcal {A}(K)$
. Given a neighbourhood V of K, by (iii) we may find another neighbourhood
$p \in \mathcal {A}(K)$
. Given a neighbourhood V of K, by (iii) we may find another neighbourhood
![]() $V_0$
of K such that
$V_0$
of K such that
![]() $f^n(V_0) \subseteq V$
for every
$f^n(V_0) \subseteq V$
for every
![]() $n \geq 0$
. In turn by (ii) there exists
$n \geq 0$
. In turn by (ii) there exists
![]() $n_0 \in \mathbb {N}$
such that
$n_0 \in \mathbb {N}$
such that
![]() $f^{n_0}(p) \in \text {int}\ V_0$
and, since
$f^{n_0}(p) \in \text {int}\ V_0$
and, since
![]() $f^{n_0}$
is continuous, there exists a neighbourhood
$f^{n_0}$
is continuous, there exists a neighbourhood
![]() $W_p$
of p such that
$W_p$
of p such that
![]() $f^{n_0}(W_p) \subseteq V_0$
. Then
$f^{n_0}(W_p) \subseteq V_0$
. Then
![]() $f^n(W_p) \subseteq f^{n-n_0}(V_0) \subseteq V$
for every
$f^n(W_p) \subseteq f^{n-n_0}(V_0) \subseteq V$
for every
![]() $n \geq n_0$
, which is a condition analogous to (ii) but now for the neighbourhood
$n \geq n_0$
, which is a condition analogous to (ii) but now for the neighbourhood
![]() $W_p$
of p instead of p alone. Now let P be a compact subset of
$W_p$
of p instead of p alone. Now let P be a compact subset of
![]() $\mathcal {A}(K)$
. Covering it with a finite number of the
$\mathcal {A}(K)$
. Covering it with a finite number of the
![]() $W_p$
and choosing
$W_p$
and choosing
![]() $n_0$
to be the maximum of the
$n_0$
to be the maximum of the
![]() $n_0$
s associated to these
$n_0$
s associated to these
![]() $W_p$
, one sees that
$W_p$
, one sees that
![]() $f^n(P) \subseteq V$
for
$f^n(P) \subseteq V$
for
![]() $n \geq n_0$
. Thus K attracts compact subsets of
$n \geq n_0$
. Thus K attracts compact subsets of
![]() $\mathcal {A}(K)$
. (Actually in our case, where the phase space is locally compact, attracting compact subsets of
$\mathcal {A}(K)$
. (Actually in our case, where the phase space is locally compact, attracting compact subsets of
![]() $\mathcal {A}(K)$
is equivalent to the attractor being stable in the sense of Lyapunov.) It is this geometric property of f that we will make essential use of. For attractors that are not stable our results do not hold true in general.
$\mathcal {A}(K)$
is equivalent to the attractor being stable in the sense of Lyapunov.) It is this geometric property of f that we will make essential use of. For attractors that are not stable our results do not hold true in general.
The realization problems for flows and homeomorphisms are not equivalent, with the former being much easier than the latter. The reason is that the flow near an attractor is parallelizable, which entails that if U is an appropriate neighbourhood of the attractor K then
![]() $U - K$
has the structure of a Cartesian product
$U - K$
has the structure of a Cartesian product
![]() $\Sigma \times \mathbb {R}$
where
$\Sigma \times \mathbb {R}$
where
![]() $\Sigma $
arises dynamically as a section of the flow in
$\Sigma $
arises dynamically as a section of the flow in
![]() $\mathcal {A}(K) - K$
. The converse is also true: if K is a compactum having a neighbourhood U such that
$\mathcal {A}(K) - K$
. The converse is also true: if K is a compactum having a neighbourhood U such that
![]() $U - K$
has such a product structure, then it can be realized as an attractor for a flow. In
$U - K$
has such a product structure, then it can be realized as an attractor for a flow. In
![]() $3$
-manifolds this can be exploited to show that a compactum K can be realized as an attractor for a flow if and only if it is weakly tame [Reference Sánchez-Gabites28, Theorem 11, p. 6169], which combined with Theorem 6.1 leads to our first result in §1.
$3$
-manifolds this can be exploited to show that a compactum K can be realized as an attractor for a flow if and only if it is weakly tame [Reference Sánchez-Gabites28, Theorem 11, p. 6169], which combined with Theorem 6.1 leads to our first result in §1.
Theorem A. A toroidal set
![]() $K \subseteq \mathbb {R}^3$
can be realized as an attractor for a flow if and only if its genus is finite and
$K \subseteq \mathbb {R}^3$
can be realized as an attractor for a flow if and only if its genus is finite and
![]() $\mathcal {N}(K) \sim 1$
.
$\mathcal {N}(K) \sim 1$
.
Using this we may be more explicit about the claim made above that the realization problems for flows and homeomorphisms are not equivalent, since we can easily exhibit examples of toroidal sets that are attractors for homeomorphisms but cannot be realized as attractors for flows. For example, an n-adic solenoid K is one of the most paradigmatic attractors for a homeomorphism but it cannot be realized as an attractor for a flow since
![]() $\mathcal {N}(K) \not \sim 1$
(the prime divisors of
$\mathcal {N}(K) \not \sim 1$
(the prime divisors of
![]() $\mathcal {N}(K)$
are the prime divisors of n by Example 4.4). As another example, consider an unknotted solid torus
$\mathcal {N}(K)$
are the prime divisors of n by Example 4.4). As another example, consider an unknotted solid torus
![]() $V_0 \subseteq \mathbb {R}^3$
and let
$V_0 \subseteq \mathbb {R}^3$
and let
![]() $f : \mathbb {R}^3 \longrightarrow \mathbb {R}^3$
be a homeomorphism such that the solid torus
$f : \mathbb {R}^3 \longrightarrow \mathbb {R}^3$
be a homeomorphism such that the solid torus
![]() $f(V_0)$
lies inside the interior of
$f(V_0)$
lies inside the interior of
![]() $V_0$
in the pattern of a Whitehead curve (the innermost curve in Figure 1(a)). The positively invariant set
$V_0$
in the pattern of a Whitehead curve (the innermost curve in Figure 1(a)). The positively invariant set
![]() $V_0$
contains the attractor
$V_0$
contains the attractor
![]() $K := \bigcap _{j \geq 0} f^j(V_0)$
, which is a classical object in geometric topology called the Whitehead continuum. The tori
$K := \bigcap _{j \geq 0} f^j(V_0)$
, which is a classical object in geometric topology called the Whitehead continuum. The tori
![]() $T_j := f^j(T)$
form a neighbourhood basis for K and, since
$T_j := f^j(T)$
form a neighbourhood basis for K and, since
![]() $N(T_{j+1},T_j) = 2$
for each j, one has that
$N(T_{j+1},T_j) = 2$
for each j, one has that
![]() $2|\mathcal {N}(K)$
. Thus
$2|\mathcal {N}(K)$
. Thus
![]() $\mathcal {N}(K) \not \sim 1$
and therefore K cannot be realized as an attractor for a flow.
$\mathcal {N}(K) \not \sim 1$
and therefore K cannot be realized as an attractor for a flow.
For the rest of this section we concentrate on the realizability of toroidal sets as attractors for homeomorphisms. The usefulness of the self-index in this problem stems from the following theorem.
Theorem B. Let K be a toroidal set that is an attractor for a homeomorphism f of
![]() $\mathbb {R}^3$
. Then
$\mathbb {R}^3$
. Then
![]() $\mathcal {N}(K)$
is number-like. Moreover,
$\mathcal {N}(K)$
is number-like. Moreover,
![]() $\mathcal {N}(K) \sim 1$
if and only if K can be realized as an attractor for a flow.
$\mathcal {N}(K) \sim 1$
if and only if K can be realized as an attractor for a flow.
Before proving the theorem we include some corollaries. The following two characterize what toroidal sets can be realized as attractors for two wide families of sets: (i) non-trivial toroidal sets with positive genus; and (ii) toroidal sets with no prime factors in
![]() $\mathcal {N}(K)$
. Both corollaries combine Theorem B with the result that an attracting toroidal set must have a finite genus (see [Reference Barge and Sánchez-Gabites2, Theorem 3.1, p. 13]).
$\mathcal {N}(K)$
. Both corollaries combine Theorem B with the result that an attracting toroidal set must have a finite genus (see [Reference Barge and Sánchez-Gabites2, Theorem 3.1, p. 13]).
Corollary 7.1. Let
![]() $K \subseteq \mathbb {R}^3$
be a non-trivial toroidal set with positive genus. Then K can be realized as an attractor for a homeomorphism if and only if its genus is finite.
$K \subseteq \mathbb {R}^3$
be a non-trivial toroidal set with positive genus. Then K can be realized as an attractor for a homeomorphism if and only if its genus is finite.
Proof. As just mentioned, it is known that toroidal attractors have finite genus; therefore, only
![]() $(\Leftarrow )$
needs proof. By Theorem 6.2 the condition that K is non-trivial and has a positive and finite genus implies that it is weakly tame. Then it can be realized as an attractor for a flow and also for a homeomorphism (namely, the time-
$(\Leftarrow )$
needs proof. By Theorem 6.2 the condition that K is non-trivial and has a positive and finite genus implies that it is weakly tame. Then it can be realized as an attractor for a flow and also for a homeomorphism (namely, the time-
![]() $1$
map of the flow).
$1$
map of the flow).
Corollary 7.2. Let
![]() $K \subseteq \mathbb {R}^3$
be a toroidal set such that
$K \subseteq \mathbb {R}^3$
be a toroidal set such that
![]() $\mathcal {N}(K)$
has no prime factors. Then K can be realized as an attractor for a homeomorphism if and only if its genus is finite and
$\mathcal {N}(K)$
has no prime factors. Then K can be realized as an attractor for a homeomorphism if and only if its genus is finite and
![]() $\mathcal {N}(K) \sim 1$
.
$\mathcal {N}(K) \sim 1$
.
Proof. If K is an attractor for a homeomorphism, then
![]() $\mathcal {N}(K)$
is number-like. Since it does not have prime divisors, it must be
$\mathcal {N}(K)$
is number-like. Since it does not have prime divisors, it must be
![]() $\mathcal {N}(K) \sim 1$
. Conversely, if the genus of K is finite and
$\mathcal {N}(K) \sim 1$
. Conversely, if the genus of K is finite and
![]() $\mathcal {N}(K) \sim 1$
then K is weakly tame by Theorem 6.2. Therefore it can be realized as an attractor for a flow and hence also for a homeomorphism.
$\mathcal {N}(K) \sim 1$
then K is weakly tame by Theorem 6.2. Therefore it can be realized as an attractor for a flow and hence also for a homeomorphism.
A result of Günther [Reference Günther14, Theorem 1, p. 653] shows that a generalized solenoid constructed in the manner described in Example 4.4(iii) cannot be realized as an attractor of a homeomorphism (in fact, of an arbitrary continuous map) of
![]() $\mathbb {R}^3$
. Our next corollary sharpens this.
$\mathbb {R}^3$
. Our next corollary sharpens this.
Corollary 7.3. If a generalized solenoid can be realized as an attractor for a homeomorphism, then it must be an unknotted n-adic solenoid for some n.
Proof. Let K be a generalized solenoid that is an attractor for a homeomorphism. The fact that K is unknotted is a consequence of [Reference Barge and Sánchez-Gabites2, Theorem 2.9(ii)]. Also, by Theorem B the self-index of K is number-like; say
![]() $\mathcal {N}(K) \sim n$
for some n. The self-index of an n-adic solenoid
$\mathcal {N}(K) \sim n$
for some n. The self-index of an n-adic solenoid
![]() $K'$
also satisfies
$K'$
also satisfies
![]() $\mathcal {N}(K') \sim n$
, so by Proposition 3.3 the groups
$\mathcal {N}(K') \sim n$
, so by Proposition 3.3 the groups
![]() $\mathcal {N}(K)$
and
$\mathcal {N}(K)$
and
![]() $\mathcal {N}(K')$
are isomorphic. Then Remark 4.5 implies that K and the n-adic solenoid
$\mathcal {N}(K')$
are isomorphic. Then Remark 4.5 implies that K and the n-adic solenoid
![]() $K'$
are homeomorphic.
$K'$
are homeomorphic.
Now suppose
![]() $K \subseteq \mathbb {R}^3$
is a non-trivial toroidal set. Let T be a neighbourhood of K that is a solid torus and such that the inclusion
$K \subseteq \mathbb {R}^3$
is a non-trivial toroidal set. Let T be a neighbourhood of K that is a solid torus and such that the inclusion
![]() $K \subseteq T$
induces a non-zero map in cohomology (this happens as soon as T is sufficiently close to K). Let
$K \subseteq T$
induces a non-zero map in cohomology (this happens as soon as T is sufficiently close to K). Let
![]() $e : T \longrightarrow \mathbb {R}^3$
be an embedding such that
$e : T \longrightarrow \mathbb {R}^3$
be an embedding such that
![]() $e(T)$
is non-trivially knotted. Then we say that
$e(T)$
is non-trivially knotted. Then we say that
![]() $K' := e(K)$
is the result of knotting K via the embedding e. Informally speaking, the following corollary shows that the chances of a set being realizable as an attractor only decrease under this knotting construction, and in fact only attractors for flows survive it.
$K' := e(K)$
is the result of knotting K via the embedding e. Informally speaking, the following corollary shows that the chances of a set being realizable as an attractor only decrease under this knotting construction, and in fact only attractors for flows survive it.
Corollary 7.4. Let
![]() $K \subseteq \mathbb {R}^3$
be a non-trivial toroidal set and let
$K \subseteq \mathbb {R}^3$
be a non-trivial toroidal set and let
![]() $K'$
be the result of knotting it as just described. Then the following assertions are equivalent.
$K'$
be the result of knotting it as just described. Then the following assertions are equivalent.
-
(i) K can be realized as an attractor for a flow.
-
(ii)
 $K'$
can be realized as an attractor for a flow.
$K'$
can be realized as an attractor for a flow. -
(iii)
 $K'$
can be realized as an attractor for a homeomorphism.
$K'$
can be realized as an attractor for a homeomorphism.
Proof. (i)
![]() $\Rightarrow $
(ii) Suppose K can be realized as an attractor for a flow. Then it is weakly tame, and so it has a neighbourhood basis of concentric tori. Since the knotting embedding e can be used to copy this basis (perhaps after discarding a finite number of initial neighbourhoods) onto a neighbourhood basis of
$\Rightarrow $
(ii) Suppose K can be realized as an attractor for a flow. Then it is weakly tame, and so it has a neighbourhood basis of concentric tori. Since the knotting embedding e can be used to copy this basis (perhaps after discarding a finite number of initial neighbourhoods) onto a neighbourhood basis of
![]() $K'$
and concentricity is clearly preserved by such copying, it follows that
$K'$
and concentricity is clearly preserved by such copying, it follows that
![]() $K'$
is also weakly tame. Thus it can be realized as an attractor for a flow.
$K'$
is also weakly tame. Thus it can be realized as an attractor for a flow.
(ii)
![]() $\Rightarrow $
(iii) is trivial.
$\Rightarrow $
(iii) is trivial.
(iii)
![]() $\Rightarrow $
(i) Suppose that
$\Rightarrow $
(i) Suppose that
![]() $K'$
is realizable as an attractor for a homeomorphism. Then we have that
$K'$
is realizable as an attractor for a homeomorphism. Then we have that
![]() $\mathcal {N}(K')$
is number-like by Theorem B. The genus of
$\mathcal {N}(K')$
is number-like by Theorem B. The genus of
![]() $K'$
is positive: if
$K'$
is positive: if
![]() $K'$
were unknotted, then
$K'$
were unknotted, then
![]() $e(T)$
should also be unknotted [Reference Barge and Sánchez-Gabites2, Proposition 2.10, p. 10], but it is not by construction. It is also finite because
$e(T)$
should also be unknotted [Reference Barge and Sánchez-Gabites2, Proposition 2.10, p. 10], but it is not by construction. It is also finite because
![]() $K'$
can be realized as an attractor. Since the cohomology of K and
$K'$
can be realized as an attractor. Since the cohomology of K and
![]() $K'$
is the same (non-trivial) it follows from Theorem 6.2 that
$K'$
is the same (non-trivial) it follows from Theorem 6.2 that
![]() $K'$
is weakly tame. Then the argument of the previous paragraph run in the reverse shows that K is also weakly tame and therefore realizable as an attractor for a flow.
$K'$
is weakly tame. Then the argument of the previous paragraph run in the reverse shows that K is also weakly tame and therefore realizable as an attractor for a flow.
As the last result we prove Theorem C from §1, which shows that there exist plenty of unknotted toroidal sets that cannot be realized as attractors. We will discuss briefly in the next section whether this can be extended to toroidal sets with positive genus.
Theorem C. Let H be a feasible group. There exists an uncountable family
![]() $\{K_{\alpha }\}$
of toroidal sets such that:
$\{K_{\alpha }\}$
of toroidal sets such that:
-
(i) none of the
 $K_{\alpha }$
can be realized as an attractor for a homeomorphism of
$K_{\alpha }$
can be realized as an attractor for a homeomorphism of
 $\mathbb {R}^3$
;
$\mathbb {R}^3$
; -
(ii) the
 $K_{\alpha }$
are pairwise different (that is, not ambient homeomorphic);
$K_{\alpha }$
are pairwise different (that is, not ambient homeomorphic); -
(iii) each
 $K_{\alpha }$
is unknotted;
$K_{\alpha }$
is unknotted; -
(iv) each
 $K_{\alpha }$
has H as its first Čech cohomology group.
$K_{\alpha }$
has H as its first Čech cohomology group.
Proof. We prove the result in the case when no element in H is divisible by
![]() $2$
. The other case (when every element in H is divisible by
$2$
. The other case (when every element in H is divisible by
![]() $2$
) is completely analogous. Let the family
$2$
) is completely analogous. Let the family
![]() $\{P_{\alpha }\}$
run over all infinite sets
$\{P_{\alpha }\}$
run over all infinite sets
![]() $P_{\alpha }$
of prime numbers such that
$P_{\alpha }$
of prime numbers such that
![]() $2 \not \in P_{\alpha }$
. Evidently
$2 \not \in P_{\alpha }$
. Evidently
![]() $\{P_{\alpha }\}$
is an uncountable family. By Theorem 5.3 for each
$\{P_{\alpha }\}$
is an uncountable family. By Theorem 5.3 for each
![]() $\alpha $
there exists an unknotted toroidal set
$\alpha $
there exists an unknotted toroidal set
![]() $K_{\alpha }$
such that
$K_{\alpha }$
such that
![]() $\check {H}^1(K_{\alpha };\mathbb {Z}) = H$
and the prime divisors of
$\check {H}^1(K_{\alpha };\mathbb {Z}) = H$
and the prime divisors of
![]() $\mathcal {N}(K_{\alpha })$
are precisely the elements of
$\mathcal {N}(K_{\alpha })$
are precisely the elements of
![]() $P_{\alpha }$
. Since each
$P_{\alpha }$
. Since each
![]() $P_{\alpha }$
is infinite, it follows that
$P_{\alpha }$
is infinite, it follows that
![]() $\mathcal {N}(K_{\alpha })$
is not number-like and then from Theorem B we conclude that no
$\mathcal {N}(K_{\alpha })$
is not number-like and then from Theorem B we conclude that no
![]() $K_{\alpha }$
can be realized as an attractor for a homeomorphism of
$K_{\alpha }$
can be realized as an attractor for a homeomorphism of
![]() $\mathbb {R}^3$
. Finally, since
$\mathbb {R}^3$
. Finally, since
![]() $P_{\alpha } \neq P_{\beta }$
for
$P_{\alpha } \neq P_{\beta }$
for
![]() $\alpha \neq \beta $
, by Proposition 5.2 the toroidal sets
$\alpha \neq \beta $
, by Proposition 5.2 the toroidal sets
![]() $K_{\alpha }$
and
$K_{\alpha }$
and
![]() $K_{\beta }$
cannot be ambient homeomorphic (not even locally ambient homeomorphic).
$K_{\beta }$
cannot be ambient homeomorphic (not even locally ambient homeomorphic).
We turn to the proof of Theorem B. Since the self-index is defined in terms of polyhedral solid tori, it is convenient to be able to replace the purely topological situation of the theorem with a piecewise linear one. This is accomplished by the following lemma.
Lemma 7.5. Let
![]() $K \subseteq \mathbb {R}^3$
be an attractor for a homeomorphism f of
$K \subseteq \mathbb {R}^3$
be an attractor for a homeomorphism f of
![]() $\mathbb {R}^3$
. Then K can be realized as an attractor for a homeomorphism of
$\mathbb {R}^3$
. Then K can be realized as an attractor for a homeomorphism of
![]() $\mathbb {R}^3$
that is piecewise linear on
$\mathbb {R}^3$
that is piecewise linear on
![]() $\mathbb {R}^3 - K$
.
$\mathbb {R}^3 - K$
.
In the proof of the lemma we will use the following notation: if
![]() $A \subseteq \mathbb {R}^3$
is a compact set and
$A \subseteq \mathbb {R}^3$
is a compact set and
![]() $\phi> 0$
is a positive number, we write
$\phi> 0$
is a positive number, we write
![]() $A + \phi $
to denote the set of points whose distance to A is less than or equal to
$A + \phi $
to denote the set of points whose distance to A is less than or equal to
![]() $\phi $
. Obviously
$\phi $
. Obviously
![]() $A + \phi $
is also a compact set.
$A + \phi $
is also a compact set.
Proof Proof of Lemma 7.5
Since K is a stable attractor, it has a compact neighbourhood P contained in its basin of attraction and such that
![]() $f(P)$
is contained in the interior of P. Define
$f(P)$
is contained in the interior of P. Define
![]() $P_k := f^k(P)$
for
$P_k := f^k(P)$
for
![]() $k \geq 0$
. These sets form a decreasing neighbourhood basis for K. Also, since each
$k \geq 0$
. These sets form a decreasing neighbourhood basis for K. Also, since each
![]() $P_{k+1}$
is contained in the interior of
$P_{k+1}$
is contained in the interior of
![]() $P_k$
, there exists a positive number
$P_k$
, there exists a positive number
![]() $\phi _k> 0$
such that
$\phi _k> 0$
such that
![]() $P_{k+1} + \phi _k \subseteq P_k$
. Clearly the
$P_{k+1} + \phi _k \subseteq P_k$
. Clearly the
![]() $\phi _k$
can be chosen so that the sequence
$\phi _k$
can be chosen so that the sequence
![]() $\{\phi _k\}$
is strictly decreasing and converges to
$\{\phi _k\}$
is strictly decreasing and converges to
![]() $0$
.
$0$
.
Let
![]() $U := \mathbb {R}^3 - K$
. Notice that U is the union of the sets
$U := \mathbb {R}^3 - K$
. Notice that U is the union of the sets
![]() $(P_k - P_{k+1})$
together with
$(P_k - P_{k+1})$
together with
![]() $\mathbb {R}^3 - P_0$
. Define a (non-continuous) mapping
$\mathbb {R}^3 - P_0$
. Define a (non-continuous) mapping
![]() $\phi $
on U by
$\phi $
on U by
 $$ \begin{align*}\phi(p) := \left\{ \begin{array}{@{}ll} \phi_1 \quad &\text{if } p \in \mathbb{R}^3 - P_0, \\ \phi_{k+1} \quad & \text{if } p \in P_k - P_{k+1} \ (k \geq 0). \end{array} \right.\end{align*} $$
$$ \begin{align*}\phi(p) := \left\{ \begin{array}{@{}ll} \phi_1 \quad &\text{if } p \in \mathbb{R}^3 - P_0, \\ \phi_{k+1} \quad & \text{if } p \in P_k - P_{k+1} \ (k \geq 0). \end{array} \right.\end{align*} $$
It is easy to check (using that
![]() $\{\phi _k\}$
is a decreasing sequence) that
$\{\phi _k\}$
is a decreasing sequence) that
![]() $\phi |_{\mathbb {R}^3 - P_k}$
is bounded below by
$\phi |_{\mathbb {R}^3 - P_k}$
is bounded below by
![]() $\phi _{k+1}$
. Since every compact subset of U is contained in a set of the form
$\phi _{k+1}$
. Since every compact subset of U is contained in a set of the form
![]() $\mathbb {R}^3 - P_k$
, it follows that
$\mathbb {R}^3 - P_k$
, it follows that
![]() $\phi $
is bounded away from
$\phi $
is bounded away from
![]() $0$
on every compact subset of U. Thus
$0$
on every compact subset of U. Thus
![]() $\phi $
is strictly positive in the sense of Moise [Reference Moise23, p. 46]. The map
$\phi $
is strictly positive in the sense of Moise [Reference Moise23, p. 46]. The map
![]() $f^2$
is a homeomorphism of U, and by the same approximation theorem that we invoked in the proof of Proposition 5.2 (namely [Reference Moise23, Theorem 1, p. 253]) there exists a piecewise linear homeomorphism g of U that is a
$f^2$
is a homeomorphism of U, and by the same approximation theorem that we invoked in the proof of Proposition 5.2 (namely [Reference Moise23, Theorem 1, p. 253]) there exists a piecewise linear homeomorphism g of U that is a
![]() $\phi $
-approximation of
$\phi $
-approximation of
![]() $f^2$
; that is, such that
$f^2$
; that is, such that
![]() $\text {d}(f^2(p),g(p)) < \phi (p)$
for every
$\text {d}(f^2(p),g(p)) < \phi (p)$
for every
![]() $p \in U$
.
$p \in U$
.
Extend g to a map
![]() $\hat {g}$
on all of
$\hat {g}$
on all of
![]() $\mathbb {R}^3$
by defining
$\mathbb {R}^3$
by defining
![]() $\hat {g} = f^2$
on K (and of course
$\hat {g} = f^2$
on K (and of course
![]() $\hat {g} = g$
on U). Clearly
$\hat {g} = g$
on U). Clearly
![]() $\hat {g}$
is a bijection of
$\hat {g}$
is a bijection of
![]() $\mathbb {R}^3$
and it is continuous on U. We claim that
$\mathbb {R}^3$
and it is continuous on U. We claim that
![]() $\hat {g}$
is also continuous on each
$\hat {g}$
is also continuous on each
![]() $p \in K$
. To check this pick
$p \in K$
. To check this pick
![]() $p \in K$
and a sequence
$p \in K$
and a sequence
![]() $\{p_n\}$
in U converging to p. By definition
$\{p_n\}$
in U converging to p. By definition
![]() $\hat {g}(p) = f^2(p)$
and
$\hat {g}(p) = f^2(p)$
and
![]() $\hat {g}(p_n) = g(p_n)$
, so we may write
$\hat {g}(p_n) = g(p_n)$
, so we may write
 $$ \begin{align*}\text{d}(\hat{g}(p),\hat{g}(p_n)) &= \text{d}(f^2(p),g(p_n)) \leq \text{d}(f^2(p),f^2(p_n))\\ &\quad + \text{d}(f^2(p_n),g(p_n)) < \text{d}(f^2(p),f^2(p_n)) + \phi(p_n)\end{align*} $$
$$ \begin{align*}\text{d}(\hat{g}(p),\hat{g}(p_n)) &= \text{d}(f^2(p),g(p_n)) \leq \text{d}(f^2(p),f^2(p_n))\\ &\quad + \text{d}(f^2(p_n),g(p_n)) < \text{d}(f^2(p),f^2(p_n)) + \phi(p_n)\end{align*} $$
where in the last step we have used that g is a
![]() $\phi $
-approximation to
$\phi $
-approximation to
![]() $f^2$
on U. Now notice that
$f^2$
on U. Now notice that
![]() $\{p_n\}$
eventually enters every
$\{p_n\}$
eventually enters every
![]() $P_k$
and so
$P_k$
and so
![]() $\phi (p_n)$
eventually becomes less than or equal to
$\phi (p_n)$
eventually becomes less than or equal to
![]() $\phi _{k+1}$
(we are again using the fact that
$\phi _{k+1}$
(we are again using the fact that
![]() $\{\phi _k\}$
is decreasing). Thus
$\{\phi _k\}$
is decreasing). Thus
![]() $\{\phi (p_n)\}$
converges to
$\{\phi (p_n)\}$
converges to
![]() $0$
because the
$0$
because the
![]() $\{\phi _k\}$
were chosen to converge to
$\{\phi _k\}$
were chosen to converge to
![]() $0$
. Similarly
$0$
. Similarly
![]() $\text {d}(f^2(p),f^2(p_n))$
converges to
$\text {d}(f^2(p),f^2(p_n))$
converges to
![]() $0$
because
$0$
because
![]() $f^2$
is continuous. Hence the distance between
$f^2$
is continuous. Hence the distance between
![]() $\hat {g}(p)$
and
$\hat {g}(p)$
and
![]() $\hat {g}(p_n)$
converges to
$\hat {g}(p_n)$
converges to
![]() $0$
and so
$0$
and so
![]() $\hat {g}$
is continuous at p. In sum,
$\hat {g}$
is continuous at p. In sum,
![]() $\hat {g}$
is a continuous bijection of
$\hat {g}$
is a continuous bijection of
![]() $\mathbb {R}^3$
and therefore (by the invariance of domain theorem) it is a homeomorphism. Evidently it is piecewise linear on
$\mathbb {R}^3$
and therefore (by the invariance of domain theorem) it is a homeomorphism. Evidently it is piecewise linear on
![]() $\mathbb {R}^3 - K$
by construction.
$\mathbb {R}^3 - K$
by construction.
To prove the lemma it only remains to show that K is an attractor for
![]() $\hat {g}$
. Since g is a
$\hat {g}$
. Since g is a
![]() $\phi $
-approximation to
$\phi $
-approximation to
![]() $f^2$
and
$f^2$
and
![]() $\phi |_{P_k - K} \leq \phi _{k+1}$
, we have
$\phi |_{P_k - K} \leq \phi _{k+1}$
, we have
![]() $g(P_k - K) \subseteq f^2(P_k - K) + \phi _{k+1}$
. Using
$g(P_k - K) \subseteq f^2(P_k - K) + \phi _{k+1}$
. Using
![]() $f^2(P_k) = P_{k+2}$
, we may then write
$f^2(P_k) = P_{k+2}$
, we may then write
Consequently
![]() $\hat {g}(P_k)$
, which is the union of
$\hat {g}(P_k)$
, which is the union of
![]() $g(P_k - K)$
and
$g(P_k - K)$
and
![]() $\hat {g}(K) = f^2(K) = K$
, is also contained in
$\hat {g}(K) = f^2(K) = K$
, is also contained in
![]() $P_{k+1}$
. It follows that K is an attractor for
$P_{k+1}$
. It follows that K is an attractor for
![]() $\hat {g}$
.
$\hat {g}$
.
Proof Proof of Theorem B
By Lemma 7.5 we may assume that the homeomorphism f which realizes K as an attractor is piecewise linear on
![]() $\mathbb {R}^3 - K$
. Denote by
$\mathbb {R}^3 - K$
. Denote by
![]() $\mathcal {A}(K)$
the basin of attraction of K. Since K is toroidal, it has a neighbourhood T that is a polyhedral solid torus contained in
$\mathcal {A}(K)$
the basin of attraction of K. Since K is toroidal, it has a neighbourhood T that is a polyhedral solid torus contained in
![]() $\mathcal {A}(K)$
. Let n be a sufficiently high iterate of f so that
$\mathcal {A}(K)$
. Let n be a sufficiently high iterate of f so that
![]() $f^n(T)$
is contained in the interior of T and define
$f^n(T)$
is contained in the interior of T and define
![]() $T_j := f^{n j}(T)$
for
$T_j := f^{n j}(T)$
for
![]() $j \geq 0$
. These
$j \geq 0$
. These
![]() $\{T_j\}$
form a nested family of polyhedral solid tori that provide a neighbourhood basis for K.
$\{T_j\}$
form a nested family of polyhedral solid tori that provide a neighbourhood basis for K.
Now consider any pair
![]() $T_{j+1} \subseteq T_j$
. The map
$T_{j+1} \subseteq T_j$
. The map
![]() $f^{nj}$
provides a homeomorphism from the pair
$f^{nj}$
provides a homeomorphism from the pair
![]() $(T_0,T_1)$
onto the pair
$(T_0,T_1)$
onto the pair
![]() $(T_j,T_{j+1})$
which is piecewise linear on
$(T_j,T_{j+1})$
which is piecewise linear on
![]() $T_0 - \text {int}\ T_1$
. Thus by Lemma 2.1 we have that
$T_0 - \text {int}\ T_1$
. Thus by Lemma 2.1 we have that
![]() $N(T_{j+1},T_j) = N(T_1,T_0)$
. It then follows from Proposition 4.1 that
$N(T_{j+1},T_j) = N(T_1,T_0)$
. It then follows from Proposition 4.1 that
![]() $\mathcal {N}(K)$
is number-like.
$\mathcal {N}(K)$
is number-like.
To conclude the proof observe that K has finite genus because all the
![]() $T_j$
are ambient homeomorphic to each other and therefore have the same genus, and then Theorem 6.1 shows that
$T_j$
are ambient homeomorphic to each other and therefore have the same genus, and then Theorem 6.1 shows that
![]() $\mathcal {N}(K) \sim 1$
if and only if K is weakly tame. But the latter is equivalent to K being realizable as an attractor for a flow.
$\mathcal {N}(K) \sim 1$
if and only if K is weakly tame. But the latter is equivalent to K being realizable as an attractor for a flow.
An alternative (and somewhat more elementary) argument for the last paragraph of the proof above can be obtained by resorting to [Reference Barge and Sánchez-Gabites2, Theorem 3.11, p.19], where it is shown that a toroidal set can be realized as an attractor for a flow if and only if it has a neighbourhood basis of concentric solid tori. This is equivalent to requiring that K be weakly tame by Proposition 6.4.
8 Concluding remarks
In this final section we briefly discuss some loose ends.
8.1 Topological invariance of the self-index
One of the properties of the self-index is its invariance under ambient homeomorphisms (or in fact, under homeomorphisms of a neighbourhood of the toroidal set). There is no reason to expect that two homeomorphic but not ambient homeomorphic toroidal sets should have the same self-index; that is, that the self-index should be a topological invariant of toroidal sets. However, we do not know how to construct an example that illustrates this. Also, Proposition 5.1 does show that having
![]() $2$
as a prime factor of the self-index is indeed a topological invariant. This prompts the question of whether the self-index enjoys some subtler sort of topological invariance property, perhaps involving only its prime factors or its number-like nature.
$2$
as a prime factor of the self-index is indeed a topological invariant. This prompts the question of whether the self-index enjoys some subtler sort of topological invariance property, perhaps involving only its prime factors or its number-like nature.
8.2 Dependence relations between Čech cohomology, the self-index and the genus
We now have three magnitudes associated to a toroidal set K: its Čech cohomology
![]() $\check {H}$
, its self-index
$\check {H}$
, its self-index
![]() $\mathcal {N}$
, and its genus g. We already showed that
$\mathcal {N}$
, and its genus g. We already showed that
![]() $\check {H}$
and
$\check {H}$
and
![]() $\mathcal {N}$
are essentially independent magnitudes beyond the elementary constraints between them discussed before Theorem 5.3. Something similar occurs for
$\mathcal {N}$
are essentially independent magnitudes beyond the elementary constraints between them discussed before Theorem 5.3. Something similar occurs for
![]() $\check {H}$
and g. Theorems 6.1 and 6.2 entail that if a toroidal set has cohomology
$\check {H}$
and g. Theorems 6.1 and 6.2 entail that if a toroidal set has cohomology
![]() $\check {H} \neq 0$
and genus
$\check {H} \neq 0$
and genus
![]() $0 < g < +\infty $
, then its self-index must be
$0 < g < +\infty $
, then its self-index must be
![]() $\mathcal {N} \sim 1$
and therefore
$\mathcal {N} \sim 1$
and therefore
![]() $\check {H} \sim 1$
by Proposition 4.3. Beyond this condition, they are independent: ordinary knots provide examples of a toroidal set having
$\check {H} \sim 1$
by Proposition 4.3. Beyond this condition, they are independent: ordinary knots provide examples of a toroidal set having
![]() $\check {H} \sim 1$
and a prescribed positive and finite genus, and solenoids provide examples of toroidal sets having a prescribed cohomology and
$\check {H} \sim 1$
and a prescribed positive and finite genus, and solenoids provide examples of toroidal sets having a prescribed cohomology and
![]() $0$
(if unknotted) or infinite (if knotted) genus. However, the interaction between g and
$0$
(if unknotted) or infinite (if knotted) genus. However, the interaction between g and
![]() $\mathcal {N}$
is much more complicated, and in fact we do not know whether there exist toroidal sets with a prescribed genus
$\mathcal {N}$
is much more complicated, and in fact we do not know whether there exist toroidal sets with a prescribed genus
![]() $0 < g < +\infty $
and a prescribed self-index N.
$0 < g < +\infty $
and a prescribed self-index N.
A partial result in this direction is afforded by the following theorem, which uses a variation on the technique of Theorem 5.3.
Theorem 8.1. Let
![]() $N \neq 0$
be a feasible group such that
$N \neq 0$
be a feasible group such that
![]() $2 | N$
. Then there exists a toroidal set K such that
$2 | N$
. Then there exists a toroidal set K such that
![]() $\mathcal {N}(K) = N$
and
$\mathcal {N}(K) = N$
and
![]() $g(K) = 1$
.
$g(K) = 1$
.
The requirement that
![]() $2 | N$
is necessary, otherwise
$2 | N$
is necessary, otherwise
![]() $\check {H} \neq 0$
and by Theorems 6.1 and 6.2 we would have that
$\check {H} \neq 0$
and by Theorems 6.1 and 6.2 we would have that
![]() $\mathcal {N} \sim 1$
, while in general N is arbitrary.
$\mathcal {N} \sim 1$
, while in general N is arbitrary.
Proof Proof of Theorem 8.1
Write N in the form
Since
![]() $2|N$
, arguing as in the proof of Theorem 5.3, we may assume that all the
$2|N$
, arguing as in the proof of Theorem 5.3, we may assume that all the
![]() $n_j$
are even; moreover, since
$n_j$
are even; moreover, since
![]() $N \neq 0$
we may also assume
$N \neq 0$
we may also assume
![]() $n_j \geq 2$
for every j (see Lemma 3.4).
$n_j \geq 2$
for every j (see Lemma 3.4).
We construct the required toroidal set as the intersection of a nested family of tori
![]() $\{T_j\}$
as follows. Let V be the standard unknotted torus in
$\{T_j\}$
as follows. Let V be the standard unknotted torus in
![]() $\mathbb {R}^3$
and let
$\mathbb {R}^3$
and let
![]() $W \subseteq \text {int}\ V$
be another solid torus arranged as a Whitehead curve (that is, as the innermost curve in Figure 1(a)). Now start with a torus
$W \subseteq \text {int}\ V$
be another solid torus arranged as a Whitehead curve (that is, as the innermost curve in Figure 1(a)). Now start with a torus
![]() $T_1 \subseteq \mathbb {R}^3$
knotted in a non-trivial way. Let
$T_1 \subseteq \mathbb {R}^3$
knotted in a non-trivial way. Let
![]() $W_1 \subseteq \text {int}\ T_1$
be another solid torus which lies inside
$W_1 \subseteq \text {int}\ T_1$
be another solid torus which lies inside
![]() $T_1$
according to the pattern
$T_1$
according to the pattern
![]() $(V,W)$
. Now let
$(V,W)$
. Now let
![]() $T_2 \subseteq \text {int}\ W_1$
be a third solid torus that winds monotonically
$T_2 \subseteq \text {int}\ W_1$
be a third solid torus that winds monotonically
![]() $n_1/2$
times inside
$n_1/2$
times inside
![]() $W_1$
(as in the generalized solenoids). Let again
$W_1$
(as in the generalized solenoids). Let again
![]() $W_2 \subseteq \text {int}\ T_2$
be a solid torus which lies inside
$W_2 \subseteq \text {int}\ T_2$
be a solid torus which lies inside
![]() $T_2$
in the pattern
$T_2$
in the pattern
![]() $(V,W)$
and then let
$(V,W)$
and then let
![]() $T_3 \subseteq \text {int}\ W_2$
wind monotonically
$T_3 \subseteq \text {int}\ W_2$
wind monotonically
![]() $n_2/2$
times inside
$n_2/2$
times inside
![]() $W_2$
. Continue in this fashion and define
$W_2$
. Continue in this fashion and define
![]() $K := \bigcap _j T_j$
. Notice that both
$K := \bigcap _j T_j$
. Notice that both
![]() $\{T_j\}$
and
$\{T_j\}$
and
![]() $\{W_j\}$
are standard bases for K.
$\{W_j\}$
are standard bases for K.
Since the winding number of W inside V is
![]() $0$
, the same is true of every pair
$0$
, the same is true of every pair
![]() $W_j \subseteq T_j$
. Thus
$W_j \subseteq T_j$
. Thus
![]() $\check {H}^1(K;\mathbb {Z}) = 0$
. Notice that
$\check {H}^1(K;\mathbb {Z}) = 0$
. Notice that
![]() $N(T_{j+1},T_j) = N(T_{j+1},W_j) \cdot N(W_j,T_j) = (n_j/2) \cdot 2 = n_j$
by construction. This implies that K is indeed a toroidal set (because it is not cellular by Proposition 4.1) and also that
$N(T_{j+1},T_j) = N(T_{j+1},W_j) \cdot N(W_j,T_j) = (n_j/2) \cdot 2 = n_j$
by construction. This implies that K is indeed a toroidal set (because it is not cellular by Proposition 4.1) and also that
![]() $\mathcal {N}(K) = N$
by Proposition 4.1.
$\mathcal {N}(K) = N$
by Proposition 4.1.
Finally, we show that
![]() $g(K) = 1$
. This is very similar to the proof that the Whitehead double of a knot has genus
$g(K) = 1$
. This is very similar to the proof that the Whitehead double of a knot has genus
![]() $1$
. First, since the core curve of W bounds a Seifert surface of genus
$1$
. First, since the core curve of W bounds a Seifert surface of genus
![]() $1$
inside the torus V, each
$1$
inside the torus V, each
![]() $W_j$
also bounds a Seifert surface of genus
$W_j$
also bounds a Seifert surface of genus
![]() $1$
and therefore
$1$
and therefore
![]() $g(K) \leq 1$
because the
$g(K) \leq 1$
because the
![]() $W_j$
form a neighbourhood basis of K. To prove that
$W_j$
form a neighbourhood basis of K. To prove that
![]() $g(K)> 0$
, suppose to the contrary that K were unknotted. Then K would have a neighbourhood basis of unknotted tori, and in particular we could interpolate an unknotted torus U between
$g(K)> 0$
, suppose to the contrary that K were unknotted. Then K would have a neighbourhood basis of unknotted tori, and in particular we could interpolate an unknotted torus U between
![]() $T_1$
and
$T_1$
and
![]() $T_j$
for some big enough j. Then
$T_j$
for some big enough j. Then
![]() $N(T_j,T_1) = N(T_j,U) \cdot N(U,T_1)$
and, since
$N(T_j,T_1) = N(T_j,U) \cdot N(U,T_1)$
and, since
![]() $N(T_j,T_1) = N(T_j,T_{j-1}) \cdot \,\cdots \,\cdot N(T_2,T_1) = n_{j-1} \cdot \,\cdots \,\cdot n_1 \neq 0$
by the computations of the previous paragraph,
$N(T_j,T_1) = N(T_j,T_{j-1}) \cdot \,\cdots \,\cdot N(T_2,T_1) = n_{j-1} \cdot \,\cdots \,\cdot n_1 \neq 0$
by the computations of the previous paragraph,
![]() $N(U,T_1)$
is also non-zero. In particular, U is a satellite of
$N(U,T_1)$
is also non-zero. In particular, U is a satellite of
![]() $T_1$
, but this is impossible: the unknot cannot be a satellite of a non-trivial knot (see [Reference Burde and Zieschang5, Remark before Proposition 3.12, p. 39] or [Reference Rolfsen26, Corollary 10, p. 113]).
$T_1$
, but this is impossible: the unknot cannot be a satellite of a non-trivial knot (see [Reference Burde and Zieschang5, Remark before Proposition 3.12, p. 39] or [Reference Rolfsen26, Corollary 10, p. 113]).
8.3 A remark about the construction of homeomorphisms with a prescribed attractor
The self-index (and the genus) are very useful as obstructions for the realizability of a toroidal set as an attractor, but no so much as complete characterizations. This is due to the fact that even in the presence of the most convenient geometric hypotheses, defining a homeomorphism that realizes a given set K as an attractor is very difficult. Very roughly speaking, the main difference between the case of flows and homeomorphisms stems from the fact that a flow can be ‘slowed down’ near any prescribed set. Thus, if one has already defined a flow near K in such a way that it carries points towards K (using whatever geometric assumptions are available), then one can gradually slow it down and make it stationary on K. For homeomorphisms there is no possibility of doing this last step and therefore even if the homeomorphism behaves in a promising manner near K (again, moving points towards K), it is very difficult to ensure that it does not ‘overshoot’ K. This, for instance, explains that the proof of Corollaries 7.1 and 7.2 proceeds by showing that the toroidal sets are actually attractors for a flow. It is an open problem to find constructions of homeomorphisms that realize sets as attractors without proceeding through flows.
Acknowledgements
The authors are partially supported by the Spanish Ministerio de Ciencia, Innovación y Universidades (grant PGC2018-098321-B-I00). The second author is funded by the Ramón y Cajal programme (RYC2018-025843-I). The authors would like to thank the anonymous referees for their helpful suggestions, which have hopefully improved the readability of the paper.