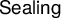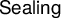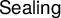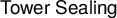1. Introduction
Soon after Cohen discovered forcing and established the consistency of the failure of the
![]() $\mathsf {Continuum\ Hypothesis\ (CH)}$
with
$\mathsf {Continuum\ Hypothesis\ (CH)}$
with
![]() $\mathsf {ZFC}$
, thus establishing the independence of
$\mathsf {ZFC}$
, thus establishing the independence of
![]() $\mathsf {CH}$
from
$\mathsf {CH}$
from
![]() $\mathsf {ZFC}$
,Footnote 1 many natural and useful set theoretic principles have been discovered to remove independence from set theory. Perhaps the two best known ones are
$\mathsf {ZFC}$
,Footnote 1 many natural and useful set theoretic principles have been discovered to remove independence from set theory. Perhaps the two best known ones are
![]() $\mathsf {Shoenfield's\ Absoluteness\ Theorem}$
and
$\mathsf {Shoenfield's\ Absoluteness\ Theorem}$
and
![]() $\mathsf {Martin's\ Axiom}$
.
$\mathsf {Martin's\ Axiom}$
.
As is well known,
![]() $\mathsf {Shoenfield's\ Absoluteness\ Theorem}$
, proved in [Reference Shoenfield45], asserts that there cannot be any independence result expressible as a
$\mathsf {Shoenfield's\ Absoluteness\ Theorem}$
, proved in [Reference Shoenfield45], asserts that there cannot be any independence result expressible as a
![]() $\Sigma ^1_2$
fact. In the language of real analysis,
$\Sigma ^1_2$
fact. In the language of real analysis,
![]() $\Sigma ^1_2$
sets of reals are projections of co-analytic sets.Footnote 2 Shoenfield’s theorem says that a co-analytic set is empty if and only if its natural interpretations in all generic extensions are empty.Footnote 3 What is so wonderful about
$\Sigma ^1_2$
sets of reals are projections of co-analytic sets.Footnote 2 Shoenfield’s theorem says that a co-analytic set is empty if and only if its natural interpretations in all generic extensions are empty.Footnote 3 What is so wonderful about
![]() $\mathsf {Shoenfield's\ Absoluteness}$
$\mathsf {Shoenfield's\ Absoluteness}$
![]() $\mathsf {Theorem}$
is that it is a theorem of
$\mathsf {Theorem}$
is that it is a theorem of
![]() $\mathsf {ZFC}$
. We will discuss
$\mathsf {ZFC}$
. We will discuss
![]() $\mathsf {Martin's\ Axiom}$
and its generalization later on.
$\mathsf {Martin's\ Axiom}$
and its generalization later on.
The goal of this paper is to establish an equiconsistency result between one Shoenfield-type generic absoluteness principle known as
![]() $\mathsf {Sealing}$
and a determinacy axiom that we abbreviated as
$\mathsf {Sealing}$
and a determinacy axiom that we abbreviated as
![]() $\mathsf {LSA-over-uB}$
.
$\mathsf {LSA-over-uB}$
.
![]() $\mathsf {LSA}$
stands for the Largest-Suslin-Axiom. To state the main theorem, we need a few definitions.
$\mathsf {LSA}$
stands for the Largest-Suslin-Axiom. To state the main theorem, we need a few definitions.
A set of reals is universally Baire if all of its continuous preimages in topological spaces have the property of Baire. Let
![]() $\Gamma ^{\infty }$
be the collection of universally Baire sets.Footnote 4 Given a generic g, we let
$\Gamma ^{\infty }$
be the collection of universally Baire sets.Footnote 4 Given a generic g, we let
![]() $\Gamma ^{\infty }_g=_{def}(\Gamma ^{\infty })^{V[g]}$
and
$\Gamma ^{\infty }_g=_{def}(\Gamma ^{\infty })^{V[g]}$
and
![]() ${\mathbb {R}}_g=_{def}{\mathbb {R}}^{V[g]}$
.
${\mathbb {R}}_g=_{def}{\mathbb {R}}^{V[g]}$
.
![]() ${\wp }(X)$
is the powerset of X.
${\wp }(X)$
is the powerset of X.
![]() $\mathsf {AD}$
stands for the
$\mathsf {AD}$
stands for the
![]() $\mathsf {Axiom\ of\ Determinacy}$
, and
$\mathsf {Axiom\ of\ Determinacy}$
, and
![]() $\mathsf {AD}^+$
is a strengthening of
$\mathsf {AD}^+$
is a strengthening of
![]() $\mathsf {AD}$
due to Woodin. The reader can ignore the
$\mathsf {AD}$
due to Woodin. The reader can ignore the
![]() $+$
or can consult [Reference Woodin61, Definition 9.6].
$+$
or can consult [Reference Woodin61, Definition 9.6].
Motivated by Woodin’s
![]() $\mathsf {Sealing\ Theorem}$
([Reference Larson23, Theorem 3.4.17] and [Reference Woodin60, Sealing Theorem]), we define
$\mathsf {Sealing\ Theorem}$
([Reference Larson23, Theorem 3.4.17] and [Reference Woodin60, Sealing Theorem]), we define
![]() $\mathsf {Sealing}$
, a key notion in this paper. We say
$\mathsf {Sealing}$
, a key notion in this paper. We say
![]() $V[g], V[h]$
are two successive generic extensions (of V) if
$V[g], V[h]$
are two successive generic extensions (of V) if
![]() $g, h$
are V-generic and
$g, h$
are V-generic and
![]() $V[g]\subseteq V[h]$
.
$V[g]\subseteq V[h]$
.
Definition 1.1.
![]() $\mathsf {Sealing}$
is the conjunction of the following statements.
$\mathsf {Sealing}$
is the conjunction of the following statements.
-
1. For every set generic g,
 $L(\Gamma ^{\infty }_g, \mathbb {R}_g){\vDash } \mathsf {AD}^+$
and
$L(\Gamma ^{\infty }_g, \mathbb {R}_g){\vDash } \mathsf {AD}^+$
and
 ${\wp }({\mathbb {R}}_g)\cap L(\Gamma ^{\infty }_g, \mathbb {R}_g)=\Gamma ^{\infty }_g$
.
${\wp }({\mathbb {R}}_g)\cap L(\Gamma ^{\infty }_g, \mathbb {R}_g)=\Gamma ^{\infty }_g$
. -
2. For every two successive set generic extensions
 $V[g]\subseteq V[h]$
, there is an elementary embedding
$V[g]\subseteq V[h]$
, there is an elementary embedding  $$ \begin{align*} j: L(\Gamma^{\infty}_g, \mathbb{R}_g)\rightarrow L(\Gamma^{\infty}_h, \mathbb{R}_h) \end{align*} $$
$$ \begin{align*} j: L(\Gamma^{\infty}_g, \mathbb{R}_g)\rightarrow L(\Gamma^{\infty}_h, \mathbb{R}_h) \end{align*} $$
such that for every
![]() $A\in \Gamma ^{\infty }_g$
,
$A\in \Gamma ^{\infty }_g$
,
![]() $j(A)=A_h$
.Footnote 5
$j(A)=A_h$
.Footnote 5
To introduce
![]() $\mathsf {LSA-over-uB}$
, we first need to introduce the
$\mathsf {LSA-over-uB}$
, we first need to introduce the
![]() $\mathsf {Largest\ Suslin\ Axiom}$
$\mathsf {Largest\ Suslin\ Axiom}$
![]() $(\mathsf {LSA})$
. A cardinal
$(\mathsf {LSA})$
. A cardinal
![]() ${\kappa }$
is
${\kappa }$
is
![]() $\mathsf {OD}$
-inaccessible if for every
$\mathsf {OD}$
-inaccessible if for every
![]() ${\alpha }<{\kappa }$
, there is no surjection
${\alpha }<{\kappa }$
, there is no surjection
![]() $f: {\wp }({\alpha })\rightarrow {\kappa }$
that is definable from ordinal parameters. A set of reals
$f: {\wp }({\alpha })\rightarrow {\kappa }$
that is definable from ordinal parameters. A set of reals
![]() $A\subseteq {\mathbb {R}}$
is
$A\subseteq {\mathbb {R}}$
is
![]() ${\kappa }$
-Suslin if for some tree T on
${\kappa }$
-Suslin if for some tree T on
![]() ${\kappa }$
,
${\kappa }$
,
![]() $A=p[T]$
.Footnote 6 A set A is Suslin if it is
$A=p[T]$
.Footnote 6 A set A is Suslin if it is
![]() $\kappa $
-Suslin for some
$\kappa $
-Suslin for some
![]() $\kappa $
; A is co-Suslin if its complement
$\kappa $
; A is co-Suslin if its complement
![]() $\mathbb {R}\backslash A$
is Suslin. A set A is Suslin, co-Suslin if both A and its complement are Suslin. A cardinal
$\mathbb {R}\backslash A$
is Suslin. A set A is Suslin, co-Suslin if both A and its complement are Suslin. A cardinal
![]() ${\kappa }$
is a Suslin cardinal if there is a set of reals A such that A is
${\kappa }$
is a Suslin cardinal if there is a set of reals A such that A is
![]() ${\kappa }$
-Suslin but A is not
${\kappa }$
-Suslin but A is not
![]() ${\lambda }$
-Suslin for any
${\lambda }$
-Suslin for any
![]() ${\lambda }<{\kappa }$
. Suslin cardinals play an important role in the study of models of determinacy as can be seen by just flipping through the Cabal Seminar Volumes ([Reference Kechris, Martin and Moschovakis15], [Reference Kechris, Martin and Steel16], [Reference Kechris, Löwe and Steel17], [Reference Kechris, Löwe and Steel18], [Reference Kechris, Löwe and Steel19], [Reference Kechris, Martin and Moschovakis20], [Reference Kechris and Moschovakis21]).
${\lambda }<{\kappa }$
. Suslin cardinals play an important role in the study of models of determinacy as can be seen by just flipping through the Cabal Seminar Volumes ([Reference Kechris, Martin and Moschovakis15], [Reference Kechris, Martin and Steel16], [Reference Kechris, Löwe and Steel17], [Reference Kechris, Löwe and Steel18], [Reference Kechris, Löwe and Steel19], [Reference Kechris, Martin and Moschovakis20], [Reference Kechris and Moschovakis21]).
The
![]() $\mathsf {Largest\ Suslin\ Axiom}$
was introduced by Woodin in [Reference Woodin61, Remark 9.28]. The terminology is due to the first author. Here is the definition.
$\mathsf {Largest\ Suslin\ Axiom}$
was introduced by Woodin in [Reference Woodin61, Remark 9.28]. The terminology is due to the first author. Here is the definition.
Definition 1.2. The
![]() $\mathsf {Largest\ Suslin\ Axiom}$
, abbreviated as
$\mathsf {Largest\ Suslin\ Axiom}$
, abbreviated as
![]() $\mathsf {LSA}$
, is the conjunction of the following statements:
$\mathsf {LSA}$
, is the conjunction of the following statements:
-
1.
 $\mathsf {AD}^+$
.
$\mathsf {AD}^+$
. -
2. There is a largest Suslin cardinal.
-
3. The largest Suslin cardinal is
 $\mathsf {OD}$
-inaccessible.
$\mathsf {OD}$
-inaccessible.
In the hierarchy of determinacy axioms, which one may appropriately call the
![]() $\mathsf {Solovay\ Hierarchy}$
,Footnote 7
$\mathsf {Solovay\ Hierarchy}$
,Footnote 7
![]() $\mathsf {LSA}$
is an anomaly as it belongs to the successor stage of the
$\mathsf {LSA}$
is an anomaly as it belongs to the successor stage of the
![]() $\mathsf {Solovay\ Hierarchy}$
but does not conform to the general norms of the successor stages of the
$\mathsf {Solovay\ Hierarchy}$
but does not conform to the general norms of the successor stages of the
![]() $\mathsf {Solovay\ Hierarchy}$
. Prior to [Reference Sargsyan and Trang38],
$\mathsf {Solovay\ Hierarchy}$
. Prior to [Reference Sargsyan and Trang38],
![]() $\mathsf {LSA}$
was not known to be consistent. In [Reference Sargsyan and Trang38], the first author showed that it is consistent relative to a Woodin cardinal that is a limit of Woodin cardinals. Nowadays, the axiom plays a key role in many aspects of inner model theory and features prominently in Woodin’s
$\mathsf {LSA}$
was not known to be consistent. In [Reference Sargsyan and Trang38], the first author showed that it is consistent relative to a Woodin cardinal that is a limit of Woodin cardinals. Nowadays, the axiom plays a key role in many aspects of inner model theory and features prominently in Woodin’s
![]() $\mathsf {Ultimate\ L}$
framework (see [Reference Woodin62, Definition 7.14] and Axiom I and Axiom II on page 97 of [Reference Woodin62]).Footnote 8
$\mathsf {Ultimate\ L}$
framework (see [Reference Woodin62, Definition 7.14] and Axiom I and Axiom II on page 97 of [Reference Woodin62]).Footnote 8
Definition 1.3. Let
![]() $\mathsf {LSA-over-uB}$
be the statement: For all V-generic g, in
$\mathsf {LSA-over-uB}$
be the statement: For all V-generic g, in
![]() $V[g]$
, there is
$V[g]$
, there is
![]() $A\subseteq {\mathbb {R}}_g$
such that
$A\subseteq {\mathbb {R}}_g$
such that
![]() $L(A, {\mathbb {R}}_g){\vDash } \mathsf {LSA}$
and
$L(A, {\mathbb {R}}_g){\vDash } \mathsf {LSA}$
and
![]() $\Gamma ^{\infty }_g$
is the Suslin co-Suslin sets of
$\Gamma ^{\infty }_g$
is the Suslin co-Suslin sets of
![]() $L(A, {\mathbb {R}}_g)$
.
$L(A, {\mathbb {R}}_g)$
.
The following is our main theorem. We say that
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are equiconsistent over theory T if there is a model of
$\psi $
are equiconsistent over theory T if there is a model of
![]() $T\cup \{\phi \}$
if and only if there is a model of
$T\cup \{\phi \}$
if and only if there is a model of
![]() $T\cup \{\psi \}$
.
$T\cup \{\psi \}$
.
Theorem 1.4.
![]() $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
are equiconsistent over the theory ‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’.
$\mathsf {LSA-over-uB}$
are equiconsistent over the theory ‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’.
In Theorem 1.4, ‘
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are equiconsistent’ is used in the following stronger sense: there is a well-founded model of
$T_2$
are equiconsistent’ is used in the following stronger sense: there is a well-founded model of
![]() $T_1$
if and only if there is a well-founded model of
$T_1$
if and only if there is a well-founded model of
![]() $T_2$
.
$T_2$
.
Remark 1.5. It is our intention to consider
![]() $\mathsf {Sealing}$
under large cardinals. The reason for doing this is that universally Baire sets do not in general behave nicely when there are no large cardinals in the universe. One may choose to drop clause 1 from the definition of
$\mathsf {Sealing}$
under large cardinals. The reason for doing this is that universally Baire sets do not in general behave nicely when there are no large cardinals in the universe. One may choose to drop clause 1 from the definition of
![]() $\mathsf {Sealing}$
. Call the resulting principle
$\mathsf {Sealing}$
. Call the resulting principle
![]() $\mathsf {Weak\ Sealing}$
. If there is an inaccessible cardinal
$\mathsf {Weak\ Sealing}$
. If there is an inaccessible cardinal
![]() ${\kappa }$
which is a limit of Woodin cardinals and strong cardinals, then
${\kappa }$
which is a limit of Woodin cardinals and strong cardinals, then
![]() $\mathsf {Weak\ Sealing}$
implies
$\mathsf {Weak\ Sealing}$
implies
![]() $\mathsf {Sealing}$
. This is because one may arrange so that
$\mathsf {Sealing}$
. This is because one may arrange so that
![]() $\Gamma ^{\infty }$
is the derived model after Levy collapsing
$\Gamma ^{\infty }$
is the derived model after Levy collapsing
![]() ${\kappa }$
to be
${\kappa }$
to be
![]() $\omega _1$
(see Theorem 1.10). We do not know the consistency strength of
$\omega _1$
(see Theorem 1.10). We do not know the consistency strength of
![]() $\mathsf {Weak\ Sealing}$
or
$\mathsf {Weak\ Sealing}$
or
![]() $\mathsf {Sealing}$
in the absence of large cardinals. But one gets that
$\mathsf {Sealing}$
in the absence of large cardinals. But one gets that
![]() $\mathsf {Weak\ Sealing}$
and
$\mathsf {Weak\ Sealing}$
and
![]() $\mathsf {Sealing}$
are equiconsistent over the large cardinal hypothesis in Theorem 1.4.
$\mathsf {Sealing}$
are equiconsistent over the large cardinal hypothesis in Theorem 1.4.
Based on the above theorems, it is very tempting to conjecture that
![]() $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
are equivalent over ‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’. However, [Reference Sargsyan and Trang41] shows that this conjecture is false. The following variation of
$\mathsf {LSA-over-uB}$
are equivalent over ‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’. However, [Reference Sargsyan and Trang41] shows that this conjecture is false. The following variation of
![]() $\mathsf {Sealing}$
, called
$\mathsf {Sealing}$
, called
![]() $\mathsf {Tower\ Sealing}$
, is also isolated by Woodin.
$\mathsf {Tower\ Sealing}$
, is also isolated by Woodin.
Definition 1.6.
![]() $\mathsf {Tower\ Sealing}$
is the conjunction of the following:
$\mathsf {Tower\ Sealing}$
is the conjunction of the following:
-
1. For any set generic g,
 $L(\Gamma ^{\infty }_g) {\vDash } \mathsf {AD}^+$
, and
$L(\Gamma ^{\infty }_g) {\vDash } \mathsf {AD}^+$
, and
 $\Gamma ^{\infty }_g = {\wp }(\mathbb {R})\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
.
$\Gamma ^{\infty }_g = {\wp }(\mathbb {R})\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
. -
2. For any set generic g, in
 $V[g]$
, suppose
$V[g]$
, suppose
 $\delta $
is Woodin. Whenever G is
$\delta $
is Woodin. Whenever G is
 $V[g]$
-generic for either the
$V[g]$
-generic for either the
 $\mathbb {P}_{<\delta }$
-stationary tower or the
$\mathbb {P}_{<\delta }$
-stationary tower or the
 $\mathbb {Q}_{<\delta }$
-stationary tower at
$\mathbb {Q}_{<\delta }$
-stationary tower at
 $\delta $
, then where
$\delta $
, then where $$ \begin{align*} j(\Gamma^{\infty}_g) = \Gamma^{\infty}_{g*G}, \end{align*} $$
$$ \begin{align*} j(\Gamma^{\infty}_g) = \Gamma^{\infty}_{g*G}, \end{align*} $$
 $j: V[g] \rightarrow M \subset V[g*G]$
is the generic elementary embedding given by G.
$j: V[g] \rightarrow M \subset V[g*G]$
is the generic elementary embedding given by G.
Theorem 1.7.
![]() $\mathsf {Tower\ Sealing}$
and
$\mathsf {Tower\ Sealing}$
and
![]() $\mathsf {Sealing}$
are equiconsistent over ‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’.
$\mathsf {Sealing}$
are equiconsistent over ‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’.
Remark 1.8.
-
1. The proof of Theorems 1.4 and 1.7 shows that over the large cardinal assumption stated in Theorem 1.4,
 $\mathsf {LSA-over-uB}$
and
$\mathsf {LSA-over-uB}$
and
 $\mathsf {Sealing}$
are equiconsistent relative to the following consequence of
$\mathsf {Sealing}$
are equiconsistent relative to the following consequence of
 $\mathsf {Sealing}$
and of
$\mathsf {Sealing}$
and of
 $\mathsf {Tower\ Sealing}$
(cf. Proposition 4.1):
$\mathsf {Tower\ Sealing}$
(cf. Proposition 4.1): $\mathsf {Sealing}^{-}$
: ‘for any set generic g,
$\mathsf {Sealing}^{-}$
: ‘for any set generic g,
 $\Gamma ^{\infty }_g = {\wp }(\mathbb {R})\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
and there is no
$\Gamma ^{\infty }_g = {\wp }(\mathbb {R})\cap L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
and there is no
 $\omega _1$
-sequence of distinct reals in
$\omega _1$
-sequence of distinct reals in
 $L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
’.
$L(\Gamma ^{\infty }_g,\mathbb {R}_g)$
’. -
2. As mentioned above, [Reference Sargsyan and Trang41] shows that
 $\mathsf {LSA-over-UB}$
is not equivalent to
$\mathsf {LSA-over-UB}$
is not equivalent to
 $\mathsf {Sealing}$
(over some large cardinal theory). However, the equivalence of
$\mathsf {Sealing}$
(over some large cardinal theory). However, the equivalence of
 $\mathsf {Sealing}$
,
$\mathsf {Sealing}$
,
 $\mathsf {Tower\ Sealing}$
, other weak forms of these theories may still hold (over the large cardinal theory of Theorem 1.4). See Conjecture 13.4.
$\mathsf {Tower\ Sealing}$
, other weak forms of these theories may still hold (over the large cardinal theory of Theorem 1.4). See Conjecture 13.4. -
3. Woodin has observed that assuming a proper class of Woodin cardinals which are limits of strong cardinals,
 $\mathsf {Tower\ Sealing}$
implies
$\mathsf {Tower\ Sealing}$
implies
 $\mathsf {Sealing}$
.
$\mathsf {Sealing}$
.
Before giving the proof, in the next few sections, we will explain the context of Theorem 1.4.
Generic Absoluteness
As was mentioned in the opening paragraph, the discovery of forcing almost immediately initiated the study of removing independence phenomenon from set theory. Large cardinals were used to establish a plethora of results that generalize
![]() $\mathsf {Shoenfield's\ Absoluteness\ Theorem}$
to more complex formulas than
$\mathsf {Shoenfield's\ Absoluteness\ Theorem}$
to more complex formulas than
![]() $\Sigma ^1_2$
. In another direction, new axioms were discovered that imply what is forced is already true. These axioms are called forcing axioms, and
$\Sigma ^1_2$
. In another direction, new axioms were discovered that imply what is forced is already true. These axioms are called forcing axioms, and
![]() $\mathsf {Martin's\ Axiom}$
is the first one.
$\mathsf {Martin's\ Axiom}$
is the first one.
Forcing axioms assert that analogues of the
![]() $\mathsf {Baire\ Category\ Theorem}$
hold for any collection of
$\mathsf {Baire\ Category\ Theorem}$
hold for any collection of
![]() $\aleph _1$
-dense sets. A consequence of this is that the
$\aleph _1$
-dense sets. A consequence of this is that the
![]() $\aleph _1$
-fragment of the generic object added by the relevant forcing notion exists as a set in the ground model, implying that what is forced by the
$\aleph _1$
-fragment of the generic object added by the relevant forcing notion exists as a set in the ground model, implying that what is forced by the
![]() $\aleph _1$
-fragment of the generic is already true in the ground model.
$\aleph _1$
-fragment of the generic is already true in the ground model.
![]() $\mathsf {Martin's\ Axiom}$
and its generalizations do not follow from
$\mathsf {Martin's\ Axiom}$
and its generalizations do not follow from
![]() $\mathsf {ZFC}$
. Many axioms of this type have been introduced and extensively studied. Perhaps the best known ones are
$\mathsf {ZFC}$
. Many axioms of this type have been introduced and extensively studied. Perhaps the best known ones are
![]() $\mathsf {Martin's\ Axiom}$
([Reference Martin and Solovay24]), the
$\mathsf {Martin's\ Axiom}$
([Reference Martin and Solovay24]), the
![]() $\mathsf {Proper\ Forcing\ Axiom}$
(
$\mathsf {Proper\ Forcing\ Axiom}$
(
![]() $\mathsf {PFA}$
, see [Reference Baumgartner3]) and
$\mathsf {PFA}$
, see [Reference Baumgartner3]) and
![]() $\mathsf {Martin's\ Maximum}$
(see [Reference Foreman, Magidor and Shelah7]).
$\mathsf {Martin's\ Maximum}$
(see [Reference Foreman, Magidor and Shelah7]).
The general set theoretic theme described above is known as generic absoluteness. The interested reader can consult [Reference Audrito and Viale2], [Reference Foreman, Magidor and Shelah7], [Reference Foreman, Magidor and Shelah8], [Reference Hauser9], [Reference Larson23], [Reference Steel54], [Reference Todorcevic56], [Reference Viale58], [Reference Wilson59], [Reference Woodin61] and the references appearing in those papers. We will not be dealing with forcing axioms in this paper, but
![]() $\mathsf {PFA}$
will be used for illustrative purposes.
$\mathsf {PFA}$
will be used for illustrative purposes.
The largest class of sets of reals for which a Shoenfield-type generic absoluteness can hold is the collection of the universally Baire sets. We will explain this claim below. The story begins with the fact that the universally Baire sets have canonical interpretations in all generic extensions, and in a sense, they are the only ones that have this property. The next paragraph describes exactly how this happens. The proofs appear in [Reference Feng, Magidor and Woodin6], [Reference Larson23] and [Reference Steel47].
In [Reference Feng, Magidor and Woodin6], it was shown by Feng, Magidor and Woodin that a set of reals A is universally Baire if and only if for each uncountable cardinal
![]() ${\kappa }$
, there are trees T and S on
${\kappa }$
, there are trees T and S on
![]() ${\kappa }$
such that
${\kappa }$
such that
![]() $p[T]=A$
and in all set generic extensions
$p[T]=A$
and in all set generic extensions
![]() $V[g]$
of V obtained by a poset of size
$V[g]$
of V obtained by a poset of size
![]() $<{\kappa }$
,
$<{\kappa }$
,
![]() $V[g]{\vDash } p[T]={\mathbb {R}}-p[S]$
. The canonical interpretation of A in
$V[g]{\vDash } p[T]={\mathbb {R}}-p[S]$
. The canonical interpretation of A in
![]() $V[g]$
is just
$V[g]$
is just
![]() $A_g=_{def}(p[T])^{V[g]}$
, where T is chosen on a
$A_g=_{def}(p[T])^{V[g]}$
, where T is chosen on a
![]() $\kappa $
that is bigger than the size of the poset that adds g. It is not hard to show, using the absoluteness of well-foundedness, that
$\kappa $
that is bigger than the size of the poset that adds g. It is not hard to show, using the absoluteness of well-foundedness, that
![]() $A_g$
is independent of the choice of
$A_g$
is independent of the choice of
![]() $(T, S)$
.
$(T, S)$
.
Woodin showed that if A is a universally Baire set of reals and the universe has a class of Woodin cardinals, then the theory of
![]() $L(A, {\mathbb {R}})$
cannot be changed. He achieved this by showing that if there is a class of Woodin cardinals, then for any universally Baire set A and any two successive set generic extensions
$L(A, {\mathbb {R}})$
cannot be changed. He achieved this by showing that if there is a class of Woodin cardinals, then for any universally Baire set A and any two successive set generic extensions
![]() $V[g]\subseteq V[h]$
, there is an elementary embedding
$V[g]\subseteq V[h]$
, there is an elementary embedding
![]() $j:L(A_g, {\mathbb {R}}_g)\rightarrow L(A_h, {\mathbb {R}}_h)$
.Footnote 9
$j:L(A_g, {\mathbb {R}}_g)\rightarrow L(A_h, {\mathbb {R}}_h)$
.Footnote 9
Moreover, if sufficient generic absoluteness is true about a set of reals, then that set is universally Baire. More precisely, suppose
![]() $\phi $
is a property of reals. Let
$\phi $
is a property of reals. Let
![]() $A_{\phi }$
be the set of reals defined by
$A_{\phi }$
be the set of reals defined by
![]() $\phi $
. If sufficiently many statements about
$\phi $
. If sufficiently many statements about
![]() $A_{\phi }$
are generically absolute, then it is because
$A_{\phi }$
are generically absolute, then it is because
![]() $A_{\phi }$
is universally Baire (see the
$A_{\phi }$
is universally Baire (see the
![]() $\mathsf {Tree\ Production\ Lemma}$
in [Reference Larson23] or in [Reference Steel47]).Footnote 10 Thus, the next place to look for absoluteness is the set of all universally Baire sets.
$\mathsf {Tree\ Production\ Lemma}$
in [Reference Larson23] or in [Reference Steel47]).Footnote 10 Thus, the next place to look for absoluteness is the set of all universally Baire sets.
Is it possible that there is no independence result about the set of universally Baire sets?
![]() $\mathsf {Sealing}$
, introduced in the preamble of this paper, is the formal version of the English sentence asserting that much like individual universally Baire sets, much like integers, the theory of universally Baire sets is immune to forcing. It is stated in the spirit of Woodin’s aforementioned theorem for the individual universally Baire sets.
$\mathsf {Sealing}$
, introduced in the preamble of this paper, is the formal version of the English sentence asserting that much like individual universally Baire sets, much like integers, the theory of universally Baire sets is immune to forcing. It is stated in the spirit of Woodin’s aforementioned theorem for the individual universally Baire sets.
Although the definition of
![]() $\mathsf {Sealing}$
is very natural and its statement is seemingly benign,
$\mathsf {Sealing}$
is very natural and its statement is seemingly benign,
![]() $\mathsf {Sealing}$
has drastic consequences on the
$\mathsf {Sealing}$
has drastic consequences on the
![]() $\mathsf {Inner\ Model\ Program}$
, which is one of the oldest set theoretic projects and is also the next set theoretical theme that we introduce.
$\mathsf {Inner\ Model\ Program}$
, which is one of the oldest set theoretic projects and is also the next set theoretical theme that we introduce.
The Inner Model Program and The Inner Model Problem
The goal of the Inner Model Program (
![]() $\mathsf {IMP}$
) is to build canonical L-like inner models with large cardinals. The problem of building a canonical inner model for a large cardinal axiom
$\mathsf {IMP}$
) is to build canonical L-like inner models with large cardinals. The problem of building a canonical inner model for a large cardinal axiom
![]() $\phi $
is known as the
$\phi $
is known as the
![]() $\mathsf {Inner\ Model\ Problem}$
(
$\mathsf {Inner\ Model\ Problem}$
(
![]() $\mathsf {IMPr}$
) for
$\mathsf {IMPr}$
) for
![]() $\phi $
. There are several expository articles written about
$\phi $
. There are several expository articles written about
![]() $\mathsf {IMP}$
and
$\mathsf {IMP}$
and
![]() $\mathsf {IMPr}$
. The reader who wants to learn more can consult [Reference Jensen12], [Reference Sargsyan32], [Reference Schimmerling42].
$\mathsf {IMPr}$
. The reader who wants to learn more can consult [Reference Jensen12], [Reference Sargsyan32], [Reference Schimmerling42].
In [Reference Neeman31], Neeman, assuming the existence of a Woodin cardinal that is a limit of Woodin cardinals, solved the
![]() $\mathsf {IMPr}$
for a Woodin cardinal that is a limit of Woodin cardinals and for large cardinals somewhat beyond. Neeman’s result is the best current result on
$\mathsf {IMPr}$
for a Woodin cardinal that is a limit of Woodin cardinals and for large cardinals somewhat beyond. Neeman’s result is the best current result on
![]() $\mathsf {IMPr}$
. However, this is only a tiny fragment of the large cardinal paradise, and also, its solution is specific to the hypothesis (we will discuss this point more).
$\mathsf {IMPr}$
. However, this is only a tiny fragment of the large cardinal paradise, and also, its solution is specific to the hypothesis (we will discuss this point more).
Dramatically,
![]() $\mathsf {Sealing}$
implies that
$\mathsf {Sealing}$
implies that
![]() $\mathsf {IMP}$
, as is known today, cannot succeed as if
$\mathsf {IMP}$
, as is known today, cannot succeed as if
![]() ${\mathcal {M}}$
is a model that conforms to the norms of modern inner model theory and has some very basic closure properties; then
${\mathcal {M}}$
is a model that conforms to the norms of modern inner model theory and has some very basic closure properties; then
![]() ${\mathcal {M}}{\vDash }$
‘there is a well-ordering of reals in
${\mathcal {M}}{\vDash }$
‘there is a well-ordering of reals in
![]() $L(\Gamma ^{\infty }, {\mathbb {R}})$
’. As
$L(\Gamma ^{\infty }, {\mathbb {R}})$
’. As
![]() $\mathsf {AD}$
implies the reals cannot be well ordered,
$\mathsf {AD}$
implies the reals cannot be well ordered,
![]() ${\mathcal {M}}$
cannot satisfy
${\mathcal {M}}$
cannot satisfy
![]() $\mathsf {Sealing}$
. Thus, we must have the following.Footnote 11
$\mathsf {Sealing}$
. Thus, we must have the following.Footnote 11
Sealing Dichotomy
Either no large cardinal theory implies
![]() $\mathsf {Sealing}$
or the
$\mathsf {Sealing}$
or the
![]() $\mathsf {Inner\ Model\ Problem}$
for some large cardinal cannot have a solution conforming to the modern norms.
$\mathsf {Inner\ Model\ Problem}$
for some large cardinal cannot have a solution conforming to the modern norms.
Intriguingly, Woodin, assuming the existence of a supercompact cardinal and a class of Woodin cardinals, has shown that
![]() $\mathsf {Sealing}$
holds after collapsing the powerset of the powerset of a supercompact cardinal to be countable (for a proof, see [Reference Larson23, Theorem 3.4.17]). Because we are collapsing the supercompact to be countable, it seems that Woodin’s result does not imply that
$\mathsf {Sealing}$
holds after collapsing the powerset of the powerset of a supercompact cardinal to be countable (for a proof, see [Reference Larson23, Theorem 3.4.17]). Because we are collapsing the supercompact to be countable, it seems that Woodin’s result does not imply that
![]() $\mathsf {Sealing}$
has dramatic effect on
$\mathsf {Sealing}$
has dramatic effect on
![]() $\mathsf {IMP}$
, or at least this impact cannot be seen in the large cardinal region below supercompact cardinals, which is known as the short extender region.
$\mathsf {IMP}$
, or at least this impact cannot be seen in the large cardinal region below supercompact cardinals, which is known as the short extender region.
As part of proving Theorem 1.4 and Theorem 1.7, we will establish the following.
Theorem 1.9.
![]() $\mathsf {Sealing}$
is consistent relative to a Woodin cardinal that is a limit of Woodin cardinals. So is
$\mathsf {Sealing}$
is consistent relative to a Woodin cardinal that is a limit of Woodin cardinals. So is
![]() $\mathsf {Tower\ Sealing}$
.
$\mathsf {Tower\ Sealing}$
.
One consequence of Theorem 1.9 is that
![]() $\mathsf {Sealing}$
is within the short extender region. Although Theorem 1.9 does not illustrate the impact of
$\mathsf {Sealing}$
is within the short extender region. Although Theorem 1.9 does not illustrate the impact of
![]() $\mathsf {Sealing}$
, its exact impact on
$\mathsf {Sealing}$
, its exact impact on
![]() $\mathsf {IMP}$
in the short extender region can also be precisely stated. But to do this, we will need extenders.
$\mathsf {IMP}$
in the short extender region can also be precisely stated. But to do this, we will need extenders.
Extender detour
Before we go on, let us take a minute to introduce extenders, which are natural generalization of ultrafilters. In fact, extenders are just a coherent sequence of ultrafilters. As was mentioned above, the goal of
![]() $\mathsf {IMP}$
is to build canonical L-like inner models for large cardinals. The current methodology is that such models should be constructed in Gödel’s sense from extenders, the very objects whose existence large cardinal axioms assert. Perhaps the best way to introduce extenders is via the elementary embeddings that they induce.
$\mathsf {IMP}$
is to build canonical L-like inner models for large cardinals. The current methodology is that such models should be constructed in Gödel’s sense from extenders, the very objects whose existence large cardinal axioms assert. Perhaps the best way to introduce extenders is via the elementary embeddings that they induce.
Suppose M and N are two transitive models of set theory and
![]() $j:M\rightarrow N$
is a nontrivial elementary embedding. Let
$j:M\rightarrow N$
is a nontrivial elementary embedding. Let
![]() $\kappa =\mathrm {crit }(j)$
and let
$\kappa =\mathrm {crit }(j)$
and let
![]() ${\lambda }\in [{\kappa }, j({\kappa }))$
be any ordinal. Set
${\lambda }\in [{\kappa }, j({\kappa }))$
be any ordinal. Set
![]() $E_j$
is called the
$E_j$
is called the
![]() $({\kappa }, {\lambda })$
-extender derived from j.
$({\kappa }, {\lambda })$
-extender derived from j.
![]() $E_j$
is really an M-extender as it measures the sets in M. As with more familiar ultrafilters, one can define extenders abstractly without using the parent embedding j and then show that each extender, via an ultrapower construction, gives rise to an embedding. Given a
$E_j$
is really an M-extender as it measures the sets in M. As with more familiar ultrafilters, one can define extenders abstractly without using the parent embedding j and then show that each extender, via an ultrapower construction, gives rise to an embedding. Given a
![]() $({\kappa }, {\lambda })$
-extender E over M, we let
$({\kappa }, {\lambda })$
-extender E over M, we let
![]() $\pi _E: M\rightarrow Ult(M, E)$
be the ultrapower embedding. A computation that involves chasing the definitions shows that E is the extender derived from
$\pi _E: M\rightarrow Ult(M, E)$
be the ultrapower embedding. A computation that involves chasing the definitions shows that E is the extender derived from
![]() $\pi _E$
. Similar computations also show that
$\pi _E$
. Similar computations also show that
![]() ${\kappa }=\mathrm {crit }(\pi _E)$
and
${\kappa }=\mathrm {crit }(\pi _E)$
and
![]() $\pi _E({\kappa })\geq {\lambda }$
. It is customary to write
$\pi _E({\kappa })\geq {\lambda }$
. It is customary to write
![]() $\mathrm {crit }(E)$
for
$\mathrm {crit }(E)$
for
![]() ${\kappa }$
and
${\kappa }$
and
![]() $lh(E)={\lambda }$
.Footnote 12 It is also not hard to see that for each
$lh(E)={\lambda }$
.Footnote 12 It is also not hard to see that for each
![]() $a\in [{\lambda }]^{<\omega }$
,
$a\in [{\lambda }]^{<\omega }$
,
![]() $E_a$
is an ultrafilter concentrating on
$E_a$
is an ultrafilter concentrating on
![]() $[{\kappa }]^{\vert {a}\vert }$
, and that if
$[{\kappa }]^{\vert {a}\vert }$
, and that if
![]() $a\subseteq b$
, then
$a\subseteq b$
, then
![]() $E_b$
naturally projects to
$E_b$
naturally projects to
![]() $E_a$
.
$E_a$
.
The motivation behind extenders is the fact that extenders capture more of the universe in the ultrapower than one can achieve via the usual ultrapower construction. In particular, under large cardinal assumptions, one can have
![]() $({\kappa }, {\lambda })$
-extender E such that
$({\kappa }, {\lambda })$
-extender E such that
![]() $V_{\lambda }\subseteq Ult(V, E)$
. Because of this, all large cardinal notions below superstrong cardinals can be captured by extenders.
$V_{\lambda }\subseteq Ult(V, E)$
. Because of this, all large cardinal notions below superstrong cardinals can be captured by extenders.
The extenders as we defined them above are called short extenders, where shortness refers to the fact that all of its ultrafilters concentrate on its critical point. Large cardinal notions such as supercompactness and hugeness cannot be captured by such short extenders as embeddings witnessing supercompactness give rise to measures that do not concentrate on the critical point of the embedding. However, one can capture these large cardinal notions by using the so-called long extenders. We do not need them in this paper, and so we will not dwell on them.
The large cardinal region that can be captured by short extenders is the region of superstrong cardinals. A cardinal
![]() ${\kappa }$
is called superstrong if there is an embedding
${\kappa }$
is called superstrong if there is an embedding
![]() $j:V\rightarrow M$
with
$j:V\rightarrow M$
with
![]() $\mathrm {crit }(j)={\kappa }$
and
$\mathrm {crit }(j)={\kappa }$
and
![]() $V_{j({\kappa })}\subseteq M$
. Superstrong cardinals are close to the optimal cardinal notions that can be expressed via short extenders.
$V_{j({\kappa })}\subseteq M$
. Superstrong cardinals are close to the optimal cardinal notions that can be expressed via short extenders.
Currently, to solve
![]() $\mathsf {IMPr}$
for a large cardinal, one attempts to build a model of the form
$\mathsf {IMPr}$
for a large cardinal, one attempts to build a model of the form
![]() $L[\vec {E}]$
, where
$L[\vec {E}]$
, where
![]() $\vec {E}$
is a carefully chosen sequence of extenders. The reader interested in learning more about what
$\vec {E}$
is a carefully chosen sequence of extenders. The reader interested in learning more about what
![]() $L[\vec {E}]$
should be can consult [Reference Steel53]. This ends our detour.
$L[\vec {E}]$
should be can consult [Reference Steel53]. This ends our detour.
The Core Model Induction
What is a solution to the
![]() $\mathsf {IMPr}$
for a given large cardinal? In the short extender region,
$\mathsf {IMPr}$
for a given large cardinal? In the short extender region,
![]() $\mathsf {IMPr}$
for a large cardinal notion, such as superstrong cardinals, has a somewhat precise meaning. One is essentially asked to build a model of the form
$\mathsf {IMPr}$
for a large cardinal notion, such as superstrong cardinals, has a somewhat precise meaning. One is essentially asked to build a model of the form
![]() $L[\vec {E}]$
which has a superstrong cardinal and
$L[\vec {E}]$
which has a superstrong cardinal and
![]() $\vec {E}$
is a fine extender sequence as defined in [Reference Steel53, Definition 2.4]. However, one may do this construction under many different hypotheses.
$\vec {E}$
is a fine extender sequence as defined in [Reference Steel53, Definition 2.4]. However, one may do this construction under many different hypotheses.
As was mentioned above, Neeman solved the
![]() $\mathsf {IMPr}$
for a Woodin cardinal that is a limit of Woodin cardinals assuming the existence of such a cardinal. One very plausible precise interpretation of
$\mathsf {IMPr}$
for a Woodin cardinal that is a limit of Woodin cardinals assuming the existence of such a cardinal. One very plausible precise interpretation of
![]() $\mathsf {IMPr}$
is exactly in this sense. Namely, given a large cardinal axiom
$\mathsf {IMPr}$
is exactly in this sense. Namely, given a large cardinal axiom
![]() $\phi $
, assuming large cardinals that are possibly stronger than
$\phi $
, assuming large cardinals that are possibly stronger than
![]() $\phi $
, build an
$\phi $
, build an
![]() ${\mathcal {M}}=L[\vec {E}]$
such that
${\mathcal {M}}=L[\vec {E}]$
such that
![]() ${\mathcal {M}}{\vDash } \exists {\kappa } \phi ({\kappa })$
.
${\mathcal {M}}{\vDash } \exists {\kappa } \phi ({\kappa })$
.
Our interpretation of
![]() $\mathsf {IMPr}$
is influenced by John Steel’s view on Gödel’s Program (see [Reference Steel54]). In a nutshell, the idea is to develop a theory that connects various foundational frameworks, such as Forcing Axioms, Large Cardinals and Determinacy Axioms, with one another.Footnote 13 In this view,
$\mathsf {IMPr}$
is influenced by John Steel’s view on Gödel’s Program (see [Reference Steel54]). In a nutshell, the idea is to develop a theory that connects various foundational frameworks, such as Forcing Axioms, Large Cardinals and Determinacy Axioms, with one another.Footnote 13 In this view,
![]() $\mathsf {IMPr}$
is the bridge between all of these natural frameworks, and
$\mathsf {IMPr}$
is the bridge between all of these natural frameworks, and
![]() $\mathsf {IMPr}$
needs to be solved under a variety of hypotheses, such as
$\mathsf {IMPr}$
needs to be solved under a variety of hypotheses, such as
![]() $\mathsf {PFA}$
or failure of Jensen’s
$\mathsf {PFA}$
or failure of Jensen’s
![]() $\square $
principles. Our primary tool for solving
$\square $
principles. Our primary tool for solving
![]() $\mathsf {IMPr}$
in large cardinal-free contexts is the
$\mathsf {IMPr}$
in large cardinal-free contexts is the
![]() $\mathsf {Core\ Model\ Induction}$
(
$\mathsf {Core\ Model\ Induction}$
(
![]() $\mathsf {CMI}$
), which is a technique invented by Woodin and developed by many set theorists during the past 20–25 years.Footnote 14
$\mathsf {CMI}$
), which is a technique invented by Woodin and developed by many set theorists during the past 20–25 years.Footnote 14
In the earlier days,
![]() $\mathsf {CMI}$
was perceived as an inductive method for proving determinacy in models such as
$\mathsf {CMI}$
was perceived as an inductive method for proving determinacy in models such as
![]() $L(\mathbb {R})$
. The goal was to prove that
$L(\mathbb {R})$
. The goal was to prove that
![]() $L_{\alpha }({\mathbb {R}}){\vDash } \mathsf {AD}$
by induction on
$L_{\alpha }({\mathbb {R}}){\vDash } \mathsf {AD}$
by induction on
![]() ${\alpha }$
. In those earlier days, which is approximately the period 1995–2010, the method worked by establishing intricate connections between large cardinals, universally Baire sets and determinacy.Footnote 15 The fundamental work done by Jensen, Neeman, Martin, Mitchell, Steel and Woodin were, and still are, at the heart of current developments of
${\alpha }$
. In those earlier days, which is approximately the period 1995–2010, the method worked by establishing intricate connections between large cardinals, universally Baire sets and determinacy.Footnote 15 The fundamental work done by Jensen, Neeman, Martin, Mitchell, Steel and Woodin were, and still are, at the heart of current developments of
![]() $\mathsf {CMI}$
. The following is a non-exhaustive list of influential papers: most papers in the Cabal Seminar Volumes that discuss scales or playful universes ([Reference Kechris, Martin and Moschovakis15], [Reference Kechris, Martin and Steel16], [Reference Kechris, Löwe and Steel17], [Reference Kechris, Löwe and Steel18], [Reference Kechris, Löwe and Steel19], [Reference Kechris, Martin and Moschovakis20], [Reference Kechris and Moschovakis21]), [Reference Jensen11], [Reference Martin and Steel25], [Reference Martin and Steel26], [Reference Mitchell and Steel28], [Reference Neeman30], [Reference Steel49]. Several fundamental papers were written implicitly developing this view of
$\mathsf {CMI}$
. The following is a non-exhaustive list of influential papers: most papers in the Cabal Seminar Volumes that discuss scales or playful universes ([Reference Kechris, Martin and Moschovakis15], [Reference Kechris, Martin and Steel16], [Reference Kechris, Löwe and Steel17], [Reference Kechris, Löwe and Steel18], [Reference Kechris, Löwe and Steel19], [Reference Kechris, Martin and Moschovakis20], [Reference Kechris and Moschovakis21]), [Reference Jensen11], [Reference Martin and Steel25], [Reference Martin and Steel26], [Reference Mitchell and Steel28], [Reference Neeman30], [Reference Steel49]. Several fundamental papers were written implicitly developing this view of
![]() $\mathsf {CMI}$
. For example, the reader can consult [Reference O’Neal Ketchersid22], [Reference Steel46] and [Reference Steel and Schindler48]. As
$\mathsf {CMI}$
. For example, the reader can consult [Reference O’Neal Ketchersid22], [Reference Steel46] and [Reference Steel and Schindler48]. As
![]() $\mathsf {CMI}$
evolved, it became more of a tool for deriving maximal determinacy models from non-large cardinal hypotheses.
$\mathsf {CMI}$
evolved, it became more of a tool for deriving maximal determinacy models from non-large cardinal hypotheses.
In a seminal work, Woodin has developed a technique for deriving determinacy models from large cardinals. The theorem is known as the
![]() $\mathsf {Derived\ Model\ Theorem}$
. A typical situation works as follows. Suppose
$\mathsf {Derived\ Model\ Theorem}$
. A typical situation works as follows. Suppose
![]() ${\lambda }$
is a limit of Woodin cardinals and
${\lambda }$
is a limit of Woodin cardinals and
![]() $g\subseteq Coll(\omega , <{\lambda })$
is generic. Let
$g\subseteq Coll(\omega , <{\lambda })$
is generic. Let
![]() ${\mathbb {R}}^*=\cup _{{\alpha }<{\lambda }}{\mathbb {R}}^{V[g\cap Coll(\omega , {\alpha })]}$
. Working in
${\mathbb {R}}^*=\cup _{{\alpha }<{\lambda }}{\mathbb {R}}^{V[g\cap Coll(\omega , {\alpha })]}$
. Working in
![]() $V(\mathbb {R}^*)$
,Footnote 16 let
$V(\mathbb {R}^*)$
,Footnote 16 let
![]() $\Gamma =\{A\subseteq {\mathbb {R}}: L(A, {\mathbb {R}}){\vDash } \mathsf {AD}\}$
. Then we have the following.
$\Gamma =\{A\subseteq {\mathbb {R}}: L(A, {\mathbb {R}}){\vDash } \mathsf {AD}\}$
. Then we have the following.
Theorem 1.10 (Woodin, [Reference Steel47])
![]() $L(\Gamma , {\mathbb {R}}){\vDash } \mathsf {AD}$
.
$L(\Gamma , {\mathbb {R}}){\vDash } \mathsf {AD}$
.
In Woodin’s theorem,
![]() $\Gamma $
is maximal as there are no more (strongly) determined sets in the universe that are not in
$\Gamma $
is maximal as there are no more (strongly) determined sets in the universe that are not in
![]() $\Gamma $
. If one assumes that
$\Gamma $
. If one assumes that
![]() ${\lambda }$
is a limit of strong cardinals, then
${\lambda }$
is a limit of strong cardinals, then
![]() $\Gamma $
above is just
$\Gamma $
above is just
![]() $(\Gamma ^{\infty })^{V({\mathbb {R}}^*)}$
.
$(\Gamma ^{\infty })^{V({\mathbb {R}}^*)}$
.
The aim of
![]() $\mathsf {CMI}$
is to do the same for other natural set theoretic frameworks, such as forcing axioms and combinatorial statements. Suppose T is a natural set theoretic framework and
$\mathsf {CMI}$
is to do the same for other natural set theoretic frameworks, such as forcing axioms and combinatorial statements. Suppose T is a natural set theoretic framework and
![]() $V{\vDash } T$
. Let
$V{\vDash } T$
. Let
![]() $\kappa $
be an uncountable cardinal. One way to perceive
$\kappa $
be an uncountable cardinal. One way to perceive
![]() $\mathsf {CMI}$
is the following.
$\mathsf {CMI}$
is the following.
(
![]() $\mathsf {CMI}$
at
$\mathsf {CMI}$
at
![]() ${\kappa }$
) Saying that one is doing
${\kappa }$
) Saying that one is doing
![]() $\mathsf {Core\ Model\ Induction}$
at
$\mathsf {Core\ Model\ Induction}$
at
![]() ${\kappa }$
means that for some
${\kappa }$
means that for some
![]() $g\subseteq Coll(\omega , {\kappa })$
Footnote 17, in
$g\subseteq Coll(\omega , {\kappa })$
Footnote 17, in
![]() $V[g]$
, one is proving that
$V[g]$
, one is proving that
![]() $L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \mathsf {AD}^+$
.
$L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \mathsf {AD}^+$
.
(
![]() $\mathsf {CMI}$
below
$\mathsf {CMI}$
below
![]() ${\kappa }$
) Saying that one is doing
${\kappa }$
) Saying that one is doing
![]() $\mathsf {Core\ Model\ Induction}$
below
$\mathsf {Core\ Model\ Induction}$
below
![]() ${\kappa }$
means that for some
${\kappa }$
means that for some
![]() $g\subseteq Coll(\omega , <{\kappa })$
Footnote 18, in
$g\subseteq Coll(\omega , <{\kappa })$
Footnote 18, in
![]() $V[g]$
, one is proving that
$V[g]$
, one is proving that
![]() $L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \mathsf {AD}^+$
.
$L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \mathsf {AD}^+$
.
In both cases, the aim might be less ambitious. It might be that one’s goal is to just produce
![]() $\Gamma \subseteq \Gamma ^{\infty }$
such that
$\Gamma \subseteq \Gamma ^{\infty }$
such that
![]() $L(\Gamma , {\mathbb {R}})$
is a determinacy model with desired properties.
$L(\Gamma , {\mathbb {R}})$
is a determinacy model with desired properties.
![]() $\mathsf {CMI}$
can even help proving versions of the
$\mathsf {CMI}$
can even help proving versions of the
![]() $\mathsf {Derived\ Model\ Theorem}$
. Here is an example. We use the setup introduced for stating the
$\mathsf {Derived\ Model\ Theorem}$
. Here is an example. We use the setup introduced for stating the
![]() $\mathsf {Derived\ Model\ Theorem}$
(Theorem 1.10). Suppose
$\mathsf {Derived\ Model\ Theorem}$
(Theorem 1.10). Suppose
![]() $A\in V({\mathbb {R}}^*)$
is a set of reals such that for some
$A\in V({\mathbb {R}}^*)$
is a set of reals such that for some
![]() ${\alpha }<{\lambda }$
, there is a
${\alpha }<{\lambda }$
, there is a
![]() $<{\lambda }$
-universally Baire set
$<{\lambda }$
-universally Baire set
![]() $B\in V[g\cap Coll(\omega , {\alpha })]$
such that
$B\in V[g\cap Coll(\omega , {\alpha })]$
such that
![]() $A=B_g$
. The tools developed during the earlier period of
$A=B_g$
. The tools developed during the earlier period of
![]() $\mathsf {CMI}$
can be used to show that
$\mathsf {CMI}$
can be used to show that
![]() $L(A, {\mathbb {R}}^*){\vDash } \mathsf {AD}$
. The point here is just that
$L(A, {\mathbb {R}}^*){\vDash } \mathsf {AD}$
. The point here is just that
![]() $\mathsf {CMI}$
is the most general method for proving derived model types of results. In the
$\mathsf {CMI}$
is the most general method for proving derived model types of results. In the
![]() $\mathsf {Derived\ Model\ Theorem}$
, the presence of large cardinals makes
$\mathsf {Derived\ Model\ Theorem}$
, the presence of large cardinals makes
![]() $\mathsf {CMI}$
unnecessary, but in other cases, it is the only method we currently have. One can also attempt to prove the full
$\mathsf {CMI}$
unnecessary, but in other cases, it is the only method we currently have. One can also attempt to prove the full
![]() $\mathsf {Derived\ Model\ Theorem}$
via
$\mathsf {Derived\ Model\ Theorem}$
via
![]() $\mathsf {CMI}$
, but this seems harder, and some of the main technical difficulties associated with other non-large cardinal frameworks resurface.
$\mathsf {CMI}$
, but this seems harder, and some of the main technical difficulties associated with other non-large cardinal frameworks resurface.
The goal, however, is not to just derive a determinacy model from natural set theoretic frameworks but to establish that the determinacy model has the same set theoretic complexity as V has.
Let M be the maximal model of determinacy derived from V. One naturalFootnote 19 way of saying that M has the same complexity as V is by saying that the large cardinal complexity of V is reflected into M, and one particularly elegant way of saying this is to say that
![]() ${\mathrm {HOD}}^M$
, the universe of the hereditarily ordinal definable sets of M, acquires these large cardinals. A typical conjecture that we can now state in this language is as follows.
${\mathrm {HOD}}^M$
, the universe of the hereditarily ordinal definable sets of M, acquires these large cardinals. A typical conjecture that we can now state in this language is as follows.
Conjecture 1.11. Assume the
![]() $\mathsf {Proper\ Forcing\ Axiom}$
and suppose
$\mathsf {Proper\ Forcing\ Axiom}$
and suppose
![]() ${\kappa }\geq \omega _2$
. Let
${\kappa }\geq \omega _2$
. Let
![]() $g\subseteq Coll(\omega , {\kappa })$
. Then
$g\subseteq Coll(\omega , {\kappa })$
. Then
![]() ${\mathrm {HOD}}^{L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)}{\vDash }$
‘there is a superstrong cardinal’.
${\mathrm {HOD}}^{L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)}{\vDash }$
‘there is a superstrong cardinal’.
A less ambitious conjecture would be that
![]() $\mathsf {PFA}$
implies that whenever
$\mathsf {PFA}$
implies that whenever
![]() $g\subseteq Coll(\omega , {\kappa })$
is V-generic, there is a set of reals
$g\subseteq Coll(\omega , {\kappa })$
is V-generic, there is a set of reals
![]() $A\in \Gamma ^{\infty }_g$
such that
$A\in \Gamma ^{\infty }_g$
such that
![]() ${\mathrm {HOD}}^{L(A, {\mathbb {R}}_g)}{\vDash }$
‘there is a superstrong cardinal’. However, we believe that the stronger conjecture is also true. One can change
${\mathrm {HOD}}^{L(A, {\mathbb {R}}_g)}{\vDash }$
‘there is a superstrong cardinal’. However, we believe that the stronger conjecture is also true. One can change
![]() $\mathsf {PFA}$
to any other natural framework that is expected to be stronger than superstrong cardinals.Footnote 20 As we brought up
$\mathsf {PFA}$
to any other natural framework that is expected to be stronger than superstrong cardinals.Footnote 20 As we brought up
![]() ${\mathrm {HOD}}$
, it is perhaps important to discuss its use in
${\mathrm {HOD}}$
, it is perhaps important to discuss its use in
![]() $\mathsf {CMI}$
.
$\mathsf {CMI}$
.
HOD analysis and covering
Conjecture 1.11 is a product of many decades of work that goes back to the UCLA’s Cabal Seminar, where the study of playful universes originates (see, for example, [Reference Becker and Moschovakis4] and [Reference Moschovakis29]). Our attempt is to avoid a historical introduction to the subject, and so we will avoid the long history of studying
![]() ${\mathrm {HOD}}$
and its playful inner models assuming determinacy.
${\mathrm {HOD}}$
and its playful inner models assuming determinacy.
Nowadays, we know that
![]() ${\mathrm {HOD}}$
of many models satisfying
${\mathrm {HOD}}$
of many models satisfying
![]() $\mathsf {AD}$
is an L-like model carrying many large cardinals,Footnote 21 and the problem of showing that
$\mathsf {AD}$
is an L-like model carrying many large cardinals,Footnote 21 and the problem of showing that
![]() ${\mathrm {HOD}}$
of every model of
${\mathrm {HOD}}$
of every model of
![]() $\mathsf {AD}$
is an L-like model is one of the central open problems of descriptive inner model theory (see [Reference Sargsyan32] and [Reference Steel55]).
$\mathsf {AD}$
is an L-like model is one of the central open problems of descriptive inner model theory (see [Reference Sargsyan32] and [Reference Steel55]).
The current methodology for proving that
![]() ${\mathrm {HOD}}^{L(\Gamma ^{\infty }, {\mathbb {R}})}$
has the desired large cardinals is via a failure of a certain covering principle involving
${\mathrm {HOD}}^{L(\Gamma ^{\infty }, {\mathbb {R}})}$
has the desired large cardinals is via a failure of a certain covering principle involving
![]() ${\mathrm {HOD}}^{L(\Gamma ^{\infty }, {\mathbb {R}})}$
. Recall that under determinacy,
${\mathrm {HOD}}^{L(\Gamma ^{\infty }, {\mathbb {R}})}$
. Recall that under determinacy,
![]() $\Theta $
is defined to be the least ordinal that is not a surjective image of the reals. Set
$\Theta $
is defined to be the least ordinal that is not a surjective image of the reals. Set
![]() ${\mathcal { H}}^-={\mathrm {HOD}}^{L(\Gamma ^{\infty }, {\mathbb {R}})}|\Theta $
.
${\mathcal { H}}^-={\mathrm {HOD}}^{L(\Gamma ^{\infty }, {\mathbb {R}})}|\Theta $
.
To define the aforementioned covering principle, we first need to extend
![]() ${\mathcal { H}}^-$
to a model
${\mathcal { H}}^-$
to a model
![]() ${\mathcal { H}}$
in which
${\mathcal { H}}$
in which
![]() $\Theta $
is the largest cardinal. This is a standard construction in inner model theory. We simply let
$\Theta $
is the largest cardinal. This is a standard construction in inner model theory. We simply let
![]() ${\mathcal { H}}$
be the union of all hod mice extending
${\mathcal { H}}$
be the union of all hod mice extending
![]() ${\mathcal { H}}$
whose countable submodels have iteration strategies in
${\mathcal { H}}$
whose countable submodels have iteration strategies in
![]() $L(\Gamma ^{\infty }, {\mathbb {R}})$
. This sentence perhaps means little to a general reader. It turns out, however, that in many situations, it is possible to describe
$L(\Gamma ^{\infty }, {\mathbb {R}})$
. This sentence perhaps means little to a general reader. It turns out, however, that in many situations, it is possible to describe
![]() ${\mathcal { H}}$
without any reference to inner model theoretic objects.
${\mathcal { H}}$
without any reference to inner model theoretic objects.
Here is one such example. Suppose
![]() ${\kappa }$
is a measurable cardinal which is a limit of strong cardinals and suppose we are doing
${\kappa }$
is a measurable cardinal which is a limit of strong cardinals and suppose we are doing
![]() $\mathsf {CMI}$
below
$\mathsf {CMI}$
below
![]() ${\kappa }$
. Let
${\kappa }$
. Let
![]() $g\subseteq Coll(\omega , <{\kappa })$
be our generic. We also make the assumption that all sets of reals produced by the
$g\subseteq Coll(\omega , <{\kappa })$
be our generic. We also make the assumption that all sets of reals produced by the
![]() $\mathsf {CMI}$
below
$\mathsf {CMI}$
below
![]() $\kappa $
are universally Baire.Footnote 22 Let
$\kappa $
are universally Baire.Footnote 22 Let
![]() $j:V\rightarrow M$
be any embedding with
$j:V\rightarrow M$
be any embedding with
![]() $\mathrm {crit }(j)={\kappa }$
. We furthermore assume that we have succeeded in showing that
$\mathrm {crit }(j)={\kappa }$
. We furthermore assume that we have succeeded in showing that
![]() $\sup (j[\Theta ])<j(\Theta )$
.Footnote 23 Setting
$\sup (j[\Theta ])<j(\Theta )$
.Footnote 23 Setting
![]() $\nu =\sup (j[\Theta ])$
, let
$\nu =\sup (j[\Theta ])$
, let
![]() $\mathcal {C}({\mathcal { H}}^-)$
be the set of all
$\mathcal {C}({\mathcal { H}}^-)$
be the set of all
![]() $A\subseteq \Theta $
such that
$A\subseteq \Theta $
such that
![]() $j(A)\cap \nu \in j({\mathcal { H}}^-)$
. Then
$j(A)\cap \nu \in j({\mathcal { H}}^-)$
. Then
![]() ${\mathcal { H}}$
is the transitive model extending
${\mathcal { H}}$
is the transitive model extending
![]() ${\mathcal { H}}^-$
that is coded by the elements of
${\mathcal { H}}^-$
that is coded by the elements of
![]() $\mathcal {C}({\mathcal { H}}^-)$
.Footnote 24
$\mathcal {C}({\mathcal { H}}^-)$
.Footnote 24
At any rate, one can simply regard
![]() ${\mathcal { H}}$
as a canonical one-cardinal extension of
${\mathcal { H}}$
as a canonical one-cardinal extension of
![]() ${\mathcal { H}}^-$
. In fact, that
${\mathcal { H}}^-$
. In fact, that
![]() ${\mathcal { H}}$
is a canonical extension of
${\mathcal { H}}$
is a canonical extension of
![]() ${\mathcal { H}}^-$
is the central point. The next paragraph explains this.
${\mathcal { H}}^-$
is the central point. The next paragraph explains this.
Continuing with the above scenario, let now
![]() $h\subseteq Coll(\omega , \kappa )$
be
$h\subseteq Coll(\omega , \kappa )$
be
![]() $V[g]$
-generic.Footnote 25 Because
$V[g]$
-generic.Footnote 25 Because
![]() $\vert {V_{\kappa }\vert }={\kappa }$
, we have that
$\vert {V_{\kappa }\vert }={\kappa }$
, we have that
![]() ${\vert {\mathcal { H}}^-\vert }^{V[g*h]}=\aleph _0$
and
${\vert {\mathcal { H}}^-\vert }^{V[g*h]}=\aleph _0$
and
![]() ${\vert {\mathcal { H}}\vert }^{V[g*h]}\leq \aleph _1$
. Letting
${\vert {\mathcal { H}}\vert }^{V[g*h]}\leq \aleph _1$
. Letting
![]() $\eta =Ord\cap {\mathcal { H}}$
,
$\eta =Ord\cap {\mathcal { H}}$
,
Assuming
![]() $\mathsf {Sealing}$
, we get that
$\mathsf {Sealing}$
, we get that
![]() $\eta <\omega _1$
as under
$\eta <\omega _1$
as under
![]() $\mathsf {Sealing}$
,
$\mathsf {Sealing}$
,
![]() $L(\Gamma ^{\infty }_{g*h}, {\mathbb {R}}_{g*h}){\vDash } \mathsf {AD}$
, and under
$L(\Gamma ^{\infty }_{g*h}, {\mathbb {R}}_{g*h}){\vDash } \mathsf {AD}$
, and under
![]() $\mathsf {AD}$
, there is no
$\mathsf {AD}$
, there is no
![]() $\omega _1$
-sequence of reals. Therefore, in V,
$\omega _1$
-sequence of reals. Therefore, in V,
![]() $\eta <\kappa ^+$
as we have that
$\eta <\kappa ^+$
as we have that
![]() $(\kappa ^+)^V=\omega _1^{V[g*h]}$
. Letting now
$(\kappa ^+)^V=\omega _1^{V[g*h]}$
. Letting now
![]() $\mathsf {UB-Covering:} \ {\mathrm cf}^V(Ord\cap {\mathcal { H}})\geq {\kappa }$
,
$\mathsf {UB-Covering:} \ {\mathrm cf}^V(Ord\cap {\mathcal { H}})\geq {\kappa }$
,
![]() $\mathsf {Sealing}$
implies that
$\mathsf {Sealing}$
implies that
![]() $\mathsf {UB-Covering}$
fails at measurable cardinals that are limits of strong cardinals. A similar argument can be carried out by only assuming that
$\mathsf {UB-Covering}$
fails at measurable cardinals that are limits of strong cardinals. A similar argument can be carried out by only assuming that
![]() ${\kappa }$
is a singular strong limit cardinal.Footnote 26
${\kappa }$
is a singular strong limit cardinal.Footnote 26
All other sufficiently strong frameworks also imply that the
![]() $\mathsf {UB-Covering}$
fails but for different reasons. One particular reason is that
$\mathsf {UB-Covering}$
fails but for different reasons. One particular reason is that
![]() $\mathsf {UB-Covering}$
implies that Jensen’s
$\mathsf {UB-Covering}$
implies that Jensen’s
![]() $\square _{\kappa }$
holds at singular cardinal
$\square _{\kappa }$
holds at singular cardinal
![]() $\kappa $
, while a celebrated theorem of Todorcevic says that under
$\kappa $
, while a celebrated theorem of Todorcevic says that under
![]() $\mathsf {PFA}$
,
$\mathsf {PFA}$
,
![]() $\square _{\kappa }$
has to fail for all
$\square _{\kappa }$
has to fail for all
![]() ${\kappa }\geq \omega _2$
.
${\kappa }\geq \omega _2$
.
The argument that has been used to show that
![]() ${\mathcal { H}}$
has large cardinals proceeds as follows. Pick a target large cardinal
${\mathcal { H}}$
has large cardinals proceeds as follows. Pick a target large cardinal
![]() $\phi $
, which for technical reasons we assume is a
$\phi $
, which for technical reasons we assume is a
![]() $\Sigma _2$
-formula. Assume
$\Sigma _2$
-formula. Assume
![]() ${\mathcal { H}}{\vDash } \forall \gamma \neg \phi (\gamma )$
. Thus far, in all applications of the
${\mathcal { H}}{\vDash } \forall \gamma \neg \phi (\gamma )$
. Thus far, in all applications of the
![]() $\mathsf {CMI}$
, the facts that
$\mathsf {CMI}$
, the facts that
![]() $\phi \mathsf {\ -\ Minimality}: \ {\mathcal { H}}{\vDash } \forall \gamma \neg \phi (\gamma )$
$\phi \mathsf {\ -\ Minimality}: \ {\mathcal { H}}{\vDash } \forall \gamma \neg \phi (\gamma )$
and
![]() $\neg \ \mathsf {UB-Covering}$
: cf
$\neg \ \mathsf {UB-Covering}$
: cf
![]() $^V({{\mathcal { H}}\cap Ord})<{\kappa }$
$^V({{\mathcal { H}}\cap Ord})<{\kappa }$
hold have been used to prove that there is a universally Baire set not in
![]() $\Gamma ^{\infty }_g$
where
$\Gamma ^{\infty }_g$
where
![]() $g\subseteq Coll(\omega , {\kappa })$
or
$g\subseteq Coll(\omega , {\kappa })$
or
![]() $g\subseteq Coll(\omega , <{\kappa })$
(depending where we do
$g\subseteq Coll(\omega , <{\kappa })$
(depending where we do
![]() $\mathsf {CMI}$
), which is obviously a contradiction.
$\mathsf {CMI}$
), which is obviously a contradiction.
Because of the work done in the first 15 years of the 2000s, it seemed as though this is a general pattern that will persist through the short extender region. That is, for any
![]() $\phi $
that is in the short extender region, either
$\phi $
that is in the short extender region, either
![]() $\phi \mathsf {\ -\ Minimality}$
must fail or
$\phi \mathsf {\ -\ Minimality}$
must fail or
![]() $\mathsf {UB-Covering}$
must hold. The main way Theorem 1.9 affects
$\mathsf {UB-Covering}$
must hold. The main way Theorem 1.9 affects
![]() $\mathsf {IMPr}$
in the short extender region is by implying that this prevalent view is false.
Footnote 27
$\mathsf {IMPr}$
in the short extender region is by implying that this prevalent view is false.
Footnote 27
Almost all existing literature on
![]() $\mathsf {CMI}$
uses the argument outlined above in one way or another. The interested reader can consult [Reference Adolf1], [Reference Sargsyan34], [Reference Sargsyan and Trang38], [Reference Sargsyan and Trang39], [Reference Steel46], [Reference Trang57], [Reference Zhu63].
$\mathsf {CMI}$
uses the argument outlined above in one way or another. The interested reader can consult [Reference Adolf1], [Reference Sargsyan34], [Reference Sargsyan and Trang38], [Reference Sargsyan and Trang39], [Reference Steel46], [Reference Trang57], [Reference Zhu63].
The future of
 $\mathsf {CMI}$
$\mathsf {CMI}$
In the authors’ view,
![]() $\mathsf {CMI}$
should be viewed as a technique for proving that a certain type of covering holds rather than a technique for showing that
$\mathsf {CMI}$
should be viewed as a technique for proving that a certain type of covering holds rather than a technique for showing that
![]() ${\mathrm {HOD}}$
has large cardinals. The latter should be the corollary, not the goal. The type of covering that we have in mind is the following. We state it in the short extender region, and we use
${\mathrm {HOD}}$
has large cardinals. The latter should be the corollary, not the goal. The type of covering that we have in mind is the following. We state it in the short extender region, and we use
![]() $\mathsf {NLE}$
Footnote 28 of [Reference Steel55] to state that we are in the short extender region.
$\mathsf {NLE}$
Footnote 28 of [Reference Steel55] to state that we are in the short extender region.
Conjecture 1.12. Assume
![]() $\mathsf {NLE}$
and suppose there are unboundedly many Woodin cardinals and strong cardinals. Let
$\mathsf {NLE}$
and suppose there are unboundedly many Woodin cardinals and strong cardinals. Let
![]() $\kappa $
be a limit of Woodin cardinals and strong cardinals such that either
$\kappa $
be a limit of Woodin cardinals and strong cardinals such that either
![]() ${\kappa }$
is a measurable cardinal or has cofinality
${\kappa }$
is a measurable cardinal or has cofinality
![]() $\omega $
. Then there is a transitive model M of
$\omega $
. Then there is a transitive model M of
![]() $\mathsf {ZFC-Powerset}$
such that
$\mathsf {ZFC-Powerset}$
such that
-
1.
 $Ord\cap M= {\kappa }^+$
,
$Ord\cap M= {\kappa }^+$
, -
2. M has a largest cardinal
 $\nu $
,
$\nu $
, -
3. for any V-generic
 $g\subseteq Coll(\omega , <{\kappa })$
, letting
$g\subseteq Coll(\omega , <{\kappa })$
, letting
 $\mathbb {R}^* = \bigcup _{\alpha <{\kappa }} \mathbb {R}^{V[g\cap Coll(\omega ,\alpha )]}$
, in
$\mathbb {R}^* = \bigcup _{\alpha <{\kappa }} \mathbb {R}^{V[g\cap Coll(\omega ,\alpha )]}$
, in
 $V({\mathbb {R}}^*)$
,
$V({\mathbb {R}}^*)$
,  $$ \begin{align*} L(M, \bigcup_{{\alpha}<\nu}(M|{\alpha})^\omega, \Gamma^{\infty}, {\mathbb{R}}^*){\vDash} \mathsf{AD}. \end{align*} $$
$$ \begin{align*} L(M, \bigcup_{{\alpha}<\nu}(M|{\alpha})^\omega, \Gamma^{\infty}, {\mathbb{R}}^*){\vDash} \mathsf{AD}. \end{align*} $$
-
4. If in addition there is no inner model with a subcompact cardinal, then
 $M{\vDash } \square _{\nu }$
.
$M{\vDash } \square _{\nu }$
.
In [Reference Sargsyan36], the first author showed that Conjecture 1.12 holds in hod mice. Assuming V is a hod mouse and keeping the notation of Conjecture 1.12, M is simply the direct limit of all iterates of
![]() $V|\kappa ^+$
that are below
$V|\kappa ^+$
that are below
![]() $\kappa $
and have a countable length in
$\kappa $
and have a countable length in
![]() $V[g]$
.
$V[g]$
.
With more work, the conjecture can also be stated without assuming the large cardinals. We do not believe that the conjecture is true in the long extender region because of the following general argument. Assume
![]() ${\kappa }$
is an indestructible supercompact cardinal and suppose the conclusion of the conjecture holds at
${\kappa }$
is an indestructible supercompact cardinal and suppose the conclusion of the conjecture holds at
![]() ${\kappa }$
. Let
${\kappa }$
. Let
![]() $g\subseteq Coll({\kappa }, {\kappa }^+)$
be V-generic. Then presumably if M satisfies the conclusion of Conjecture 1.12, then
$g\subseteq Coll({\kappa }, {\kappa }^+)$
be V-generic. Then presumably if M satisfies the conclusion of Conjecture 1.12, then
![]() $M^V=M^{V[g]}$
. The confidence that this is true comes from the fact that we expect that any M satisfying clause 3 must have an absolute definition. Because
$M^V=M^{V[g]}$
. The confidence that this is true comes from the fact that we expect that any M satisfying clause 3 must have an absolute definition. Because
![]() ${\kappa }$
is still a supercompact in
${\kappa }$
is still a supercompact in
![]() $V[g]$
, clause 1 has to fail.
$V[g]$
, clause 1 has to fail.
We believe that proving Conjecture 1.12 should become the goal of
![]() $\mathsf {CMI}$
. To prove it, one has to develop techniques for building third- order canonical objects, objects that are canonical subsets of
$\mathsf {CMI}$
. To prove it, one has to develop techniques for building third- order canonical objects, objects that are canonical subsets of
![]() $\Gamma ^{\infty }$
.
$\Gamma ^{\infty }$
.
One possible source of such objects is described in forthcoming [Reference Sargsyan and Trang40]. There, the authors introduced the notion of Z-hod pairs and developed their basic theory. We should also note that even in this paper, to prove Theorem 1.4, we build objects that resemble objects that are of third order. We build our third-order objects more or less according to the current conventions following [Reference Sargsyan and Trang38]. What we meant above is that we believe that to get to superstrongs entirely, new kinds of canonical objects need to be constructed. The reader can read more about such speculations in [Reference Sargsyan36].
The abstract claimed that Theorem 1.4 is the ultimate equiconsistency proved via
![]() $\mathsf {CMI}$
. This does not mean that there are no other equiconsistencies in the region of
$\mathsf {CMI}$
. This does not mean that there are no other equiconsistencies in the region of
![]() $\mathsf {LSA}$
. All it means is that to go beyond, one has to start thinking of
$\mathsf {LSA}$
. All it means is that to go beyond, one has to start thinking of
![]() $\mathsf {CMI}$
as a method of building third-order objects.
$\mathsf {CMI}$
as a method of building third-order objects.
The authors view Theorem 1.4 as a natural accumulation point in the development of their understanding of
![]() $\mathsf {CMI}$
and the way it is used to translate set theoretic strength between natural set theoretic frameworks – namely, between forcing axioms, large cardinals, determinacy and other frameworks. It has been proven by arriving at it via a 15-year-long-process of trying to understand
$\mathsf {CMI}$
and the way it is used to translate set theoretic strength between natural set theoretic frameworks – namely, between forcing axioms, large cardinals, determinacy and other frameworks. It has been proven by arriving at it via a 15-year-long-process of trying to understand
![]() $\mathsf {CMI}$
. Because of this, we feel that it is a theorem proven by the entire community rather than by the authors. We especially thank Hugh Woodin and John Steel for their influential ideas throughout the first 25 years of the
$\mathsf {CMI}$
. Because of this, we feel that it is a theorem proven by the entire community rather than by the authors. We especially thank Hugh Woodin and John Steel for their influential ideas throughout the first 25 years of the
![]() $\mathsf {Core\ Model\ Induction}$
.
$\mathsf {Core\ Model\ Induction}$
.
The history of Theorem 1.4 is as follows. The first author, in [Reference Sargsyan33], stated a conjecture that in his view captured the ideas of the first 15 years of the 2000s – namely, that
![]() $\phi \mathsf {\ -\ Minimality}$
and
$\phi \mathsf {\ -\ Minimality}$
and
![]() $\neg \ \mathsf {UB-Covering}$
cannot coexist in the short extender region. Unfortunately, very soon after finishing that paper, he realized that the covering conjecture of that paper has to fail in the region of
$\neg \ \mathsf {UB-Covering}$
cannot coexist in the short extender region. Unfortunately, very soon after finishing that paper, he realized that the covering conjecture of that paper has to fail in the region of
![]() $\mathsf {LSA}$
.Footnote 29 However, no easily quotable theorem was proven by him. It was not until fall of 2018 when the second author was visiting the first author, that they realized that Theorem 1.4 says exactly that
$\mathsf {LSA}$
.Footnote 29 However, no easily quotable theorem was proven by him. It was not until fall of 2018 when the second author was visiting the first author, that they realized that Theorem 1.4 says exactly that
![]() $\phi \mathsf {\ -\ Minimality}$
and
$\phi \mathsf {\ -\ Minimality}$
and
![]() $\neg \ \mathsf {UB-Covering}$
can coexist in the short extender region.
$\neg \ \mathsf {UB-Covering}$
can coexist in the short extender region.
2. An overview of the fine structure of the minimal
 $\mathsf {LSA}$
-hod mouse and excellent hybrid mice
$\mathsf {LSA}$
-hod mouse and excellent hybrid mice
As was mentioned above, the proof of Theorem 1.4 is an accumulation of many ideas developed in the last 20 years. We will try to develop enough of the required background in general terms so that a reader familiar with the terminology of descriptive inner model theory can follow the arguments. The main technical machinery used in the proof is developed more carefully in [Reference Sargsyan and Trang38]. In the next few sections, we will write an introduction to this technical machinery intended for set theorists who are familiar with [Reference Sargsyan32].
We say that M is a minimal model of
![]() $\mathsf {LSA}$
if
$\mathsf {LSA}$
if
-
1.
 $M{\vDash } \mathsf {LSA}$
,
$M{\vDash } \mathsf {LSA}$
, -
2.
 $M=L(A, \mathbb {R})$
for some
$M=L(A, \mathbb {R})$
for some
 $A\subseteq \mathbb {R}$
, and
$A\subseteq \mathbb {R}$
, and -
3. for any
 $B\in {\wp }(\mathbb {R})\cap M$
such that
$B\in {\wp }(\mathbb {R})\cap M$
such that
 $w(B)<w(A)$
,
$w(B)<w(A)$
,
 $L(B,\mathbb {R}){\vDash } \neg \mathsf {LSA}$
.
$L(B,\mathbb {R}){\vDash } \neg \mathsf {LSA}$
.
It makes sense to talk about ‘the’ minimal model of
![]() $\mathsf {LSA}$
. When we say M is the minimal model of
$\mathsf {LSA}$
. When we say M is the minimal model of
![]() $\mathsf {LSA}$
, we mean that M is a minimal model of
$\mathsf {LSA}$
, we mean that M is a minimal model of
![]() $\mathsf {LSA}$
and
$\mathsf {LSA}$
and
![]() $Ord, {\mathbb {R}}\subseteq M$
. Clearly from the prospective of a minimal model of
$Ord, {\mathbb {R}}\subseteq M$
. Clearly from the prospective of a minimal model of
![]() $\mathsf {LSA}$
, the universe is the minimal model of
$\mathsf {LSA}$
, the universe is the minimal model of
![]() $\mathsf {LSA}$
. The proof of [Reference Sargsyan and Trang38, Theorem 10.3.1] implies that there is a unique minimal model of
$\mathsf {LSA}$
. The proof of [Reference Sargsyan and Trang38, Theorem 10.3.1] implies that there is a unique minimal model of
![]() $\mathsf {LSA}$
such that
$\mathsf {LSA}$
such that
![]() $Ord, {\mathbb {R}}\subseteq M$
.Footnote 30 This unique minimal model of
$Ord, {\mathbb {R}}\subseteq M$
.Footnote 30 This unique minimal model of
![]() $\mathsf {LSA}$
is the minimal model of
$\mathsf {LSA}$
is the minimal model of
![]() $\mathsf {LSA}$
.
$\mathsf {LSA}$
.
One of the main contributions of [Reference Sargsyan and Trang38] is the detailed description of
![]() $V_{\Theta }^{\mathrm {HOD}}$
assuming that the universe is the minimal model of
$V_{\Theta }^{\mathrm {HOD}}$
assuming that the universe is the minimal model of
![]() $\mathsf {LSA}$
. The early chapters of [Reference Sargsyan and Trang38] deal with what is commonly referred to as the
$\mathsf {LSA}$
. The early chapters of [Reference Sargsyan and Trang38] deal with what is commonly referred to as the
![]() ${\mathrm {HOD}}$
analysis. These early chapters introduce the notion of a short-tree-strategy mouse, which is the most important technical notion studied by [Reference Sargsyan and Trang38]. To motivate the need for this concept, we first recall some of the other aspects of the
${\mathrm {HOD}}$
analysis. These early chapters introduce the notion of a short-tree-strategy mouse, which is the most important technical notion studied by [Reference Sargsyan and Trang38]. To motivate the need for this concept, we first recall some of the other aspects of the
![]() ${\mathrm {HOD}}$
analysis.
${\mathrm {HOD}}$
analysis.
Recall the
![]() $\mathsf {Solovay\ Sequence}$
(for example, see [Reference Sargsyan34, Definition 0.9] or [Reference Woodin61, Definition 9.23]). Recall that
$\mathsf {Solovay\ Sequence}$
(for example, see [Reference Sargsyan34, Definition 0.9] or [Reference Woodin61, Definition 9.23]). Recall that
![]() $\Theta $
is the least ordinal that is not a surjective image of the reals. The
$\Theta $
is the least ordinal that is not a surjective image of the reals. The
![]() $\mathsf {Solovay\ Sequence}$
is a way of measuring the complexity of the surjections that can be used to map the reals onto the ordinals below
$\mathsf {Solovay\ Sequence}$
is a way of measuring the complexity of the surjections that can be used to map the reals onto the ordinals below
![]() $\Theta $
. Assuming
$\Theta $
. Assuming
![]() $\mathsf {AD}$
, let
$\mathsf {AD}$
, let
![]() $(\theta _{\alpha }: {\alpha }\leq \Omega )$
be a closed in
$(\theta _{\alpha }: {\alpha }\leq \Omega )$
be a closed in
![]() $\Theta $
sequence of ordinals such that
$\Theta $
sequence of ordinals such that
-
1.
 $\theta _0$
is the least ordinal
$\theta _0$
is the least ordinal
 $\eta $
such that
$\eta $
such that
 $\mathbb {R}$
cannot be mapped surjectively onto
$\mathbb {R}$
cannot be mapped surjectively onto
 $\eta $
via an ordinal definable function,
$\eta $
via an ordinal definable function, -
2. for
 ${\alpha }+1\leq \Omega $
, fixing a set of reals A such that A has Wadge rank
${\alpha }+1\leq \Omega $
, fixing a set of reals A such that A has Wadge rank
 $\theta _{\alpha }$
,
$\theta _{\alpha }$
,
 $\theta _{{\alpha }+1}$
is the least ordinal
$\theta _{{\alpha }+1}$
is the least ordinal
 $\eta $
such that
$\eta $
such that
 $\mathbb {R}$
cannot be mapped surjectively onto
$\mathbb {R}$
cannot be mapped surjectively onto
 $\eta $
via a function that is ordinal definable from A,
$\eta $
via a function that is ordinal definable from A, -
3. for limit ordinal
 ${\lambda }\leq \Omega $
,
${\lambda }\leq \Omega $
,
 $\theta _{\lambda }=\sup _{{\alpha }<{\lambda }}\theta _{\alpha }$
, and
$\theta _{\lambda }=\sup _{{\alpha }<{\lambda }}\theta _{\alpha }$
, and -
4.
 $\Omega $
is least such that
$\Omega $
is least such that
 $\theta _{\Omega }=\Theta $
.
$\theta _{\Omega }=\Theta $
.
It follows from the definition of
![]() $\mathsf {LSA}$
(Definition 1.2) that if
$\mathsf {LSA}$
(Definition 1.2) that if
![]() ${\kappa }$
is the largest Suslin cardinal, then it is a member of the
${\kappa }$
is the largest Suslin cardinal, then it is a member of the
![]() $\mathsf {Solovay\ Sequence}$
. It is not hard to show that
$\mathsf {Solovay\ Sequence}$
. It is not hard to show that
![]() $\mathsf {LSA}$
is a much stronger axiom than
$\mathsf {LSA}$
is a much stronger axiom than
![]() $\mathsf {AD}_{\mathbb {R}}+ \text {`}\Theta $
is regular’. Under
$\mathsf {AD}_{\mathbb {R}}+ \text {`}\Theta $
is regular’. Under
![]() $\mathsf {LSA}$
, letting
$\mathsf {LSA}$
, letting
![]() ${\kappa }$
be the largest Suslin cardinal, there is an
${\kappa }$
be the largest Suslin cardinal, there is an
![]() $\omega $
-club
$\omega $
-club
![]() $C\subseteq {\kappa }$
such that for every
$C\subseteq {\kappa }$
such that for every
![]() ${\lambda }\in C$
,
${\lambda }\in C$
,
![]() $L(\Gamma _{\lambda }, \mathbb {R}){\vDash } \text {`}\mathsf {AD}_{\mathbb {R}} + {\lambda }=\Theta +\Theta $
is regular’, where
$L(\Gamma _{\lambda }, \mathbb {R}){\vDash } \text {`}\mathsf {AD}_{\mathbb {R}} + {\lambda }=\Theta +\Theta $
is regular’, where
![]() $\Gamma _{\lambda }=\{A\subseteq \mathbb {R}: w(A)<{\lambda }\}$
.Footnote 31
$\Gamma _{\lambda }=\{A\subseteq \mathbb {R}: w(A)<{\lambda }\}$
.Footnote 31
Assume now that V is the minimal model of
![]() $\mathsf {LSA}$
. It follows from the work done in [Reference Sargsyan and Trang38] that for every
$\mathsf {LSA}$
. It follows from the work done in [Reference Sargsyan and Trang38] that for every
![]() $\kappa $
that is a member of the
$\kappa $
that is a member of the
![]() $\mathsf {Solovay\ Sequence}$
but is not the largest Suslin cardinal there is a hod pair
$\mathsf {Solovay\ Sequence}$
but is not the largest Suslin cardinal there is a hod pair
![]() $({\mathcal {P}}, \Sigma )$
such that
$({\mathcal {P}}, \Sigma )$
such that
-
1. the Wadge rank of
 $\Sigma $
(or rather the set of reals coding
$\Sigma $
(or rather the set of reals coding
 $\Sigma $
) is
$\Sigma $
) is
 $\geq {\kappa }$
and
$\geq {\kappa }$
and -
2. for some
 $\eta \in {\mathcal {P}}$
, letting
$\eta \in {\mathcal {P}}$
, letting
 ${\mathcal {M}}_{\infty }({\mathcal {P}}, \Sigma )$
be the direct limit of all countable
${\mathcal {M}}_{\infty }({\mathcal {P}}, \Sigma )$
be the direct limit of all countable
 $\Sigma $
-iterates
$\Sigma $
-iterates
 ${\mathcal {Q}}$
of
${\mathcal {Q}}$
of
 ${\mathcal {P}}$
such that the iteration embedding
${\mathcal {P}}$
such that the iteration embedding
 $\pi ^\Sigma _{{\mathcal {P}}, {\mathcal {Q}}}$
is defined and letting
$\pi ^\Sigma _{{\mathcal {P}}, {\mathcal {Q}}}$
is defined and letting
 $\pi ^\Sigma _{{\mathcal {P}}, \infty }:{\mathcal {P}}\rightarrow {\mathcal {M}}_{\infty }({\mathcal {P}}, \Sigma )$
be the iteration map, then
$\pi ^\Sigma _{{\mathcal {P}}, \infty }:{\mathcal {P}}\rightarrow {\mathcal {M}}_{\infty }({\mathcal {P}}, \Sigma )$
be the iteration map, then
 $V_{\kappa }^{\mathrm {HOD}}$
is the universe of
$V_{\kappa }^{\mathrm {HOD}}$
is the universe of
 ${\mathcal {M}}_{\infty }({\mathcal {P}}, \Sigma )|\pi ^\Sigma _{{\mathcal {P}}, \infty }(\eta )$
.Footnote 32
${\mathcal {M}}_{\infty }({\mathcal {P}}, \Sigma )|\pi ^\Sigma _{{\mathcal {P}}, \infty }(\eta )$
.Footnote 32
A technical reformulation of the above fact appears as [Reference Sargsyan and Trang38, Theorem 7.2.2].
The situation, however, is drastically different for the largest Suslin cardinal. Let
![]() ${\kappa }$
be the largest Suslin cardinal. The inner model theoretic object that has Wadge rank
${\kappa }$
be the largest Suslin cardinal. The inner model theoretic object that has Wadge rank
![]() $ {\kappa }$
cannot be an iteration strategy. This is because if
$ {\kappa }$
cannot be an iteration strategy. This is because if
![]() $\Sigma $
is an iteration strategy with nice properties like hull condensation,Footnote 33 then assuming
$\Sigma $
is an iteration strategy with nice properties like hull condensation,Footnote 33 then assuming
![]() $\mathsf {AD}$
holds in
$\mathsf {AD}$
holds in
![]() $L(\Sigma , {\mathbb {R}})$
,
$L(\Sigma , {\mathbb {R}})$
,
![]() $L(\Sigma , {\mathbb {R}}){\vDash } \text {`}{\mathcal {M}}_1^{\#, \Sigma }$
exists and is
$L(\Sigma , {\mathbb {R}}){\vDash } \text {`}{\mathcal {M}}_1^{\#, \Sigma }$
exists and is
![]() $\omega _1$
-iterable’.Footnote 34 This then easily implies that
$\omega _1$
-iterable’.Footnote 34 This then easily implies that
![]() $\Sigma $
is both Suslin and co-Suslin. It then follows that no nice iteration strategy can have Wadge rank
$\Sigma $
is both Suslin and co-Suslin. It then follows that no nice iteration strategy can have Wadge rank
![]() $\geq {\kappa }$
, as any such strategy is both Suslin and co-Suslin.Footnote 35
$\geq {\kappa }$
, as any such strategy is both Suslin and co-Suslin.Footnote 35
The inner model theoretic object that has Wadge rank
![]() $ {\kappa }$
is a short-tree strategy, which is a partial iteration strategy. Suppose
$ {\kappa }$
is a short-tree strategy, which is a partial iteration strategy. Suppose
![]() ${\mathcal {P}}$
is any iterable structure and
${\mathcal {P}}$
is any iterable structure and
![]() $\Sigma $
is its iteration strategy. Suppose
$\Sigma $
is its iteration strategy. Suppose
![]() ${\delta }$
is a Woodin cardinal of
${\delta }$
is a Woodin cardinal of
![]() ${\mathcal {P}}$
. Given
${\mathcal {P}}$
. Given
![]() ${\mathcal {T}}\in dom(\Sigma )$
that is based on
${\mathcal {T}}\in dom(\Sigma )$
that is based on
![]() ${\mathcal {P}}|{\delta }$
, we say that
${\mathcal {P}}|{\delta }$
, we say that
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\Sigma $
-short if letting
$\Sigma $
-short if letting
![]() $\Sigma ({\mathcal {T}})=b$
, either the iteration map
$\Sigma ({\mathcal {T}})=b$
, either the iteration map
![]() $\pi ^{\mathcal {T}}_b$
is undefined or
$\pi ^{\mathcal {T}}_b$
is undefined or
![]() $\pi ^{\mathcal {T}}_b({\delta })>{\delta }({\mathcal {T}})$
. If
$\pi ^{\mathcal {T}}_b({\delta })>{\delta }({\mathcal {T}})$
. If
![]() ${\mathcal {T}}$
is not
${\mathcal {T}}$
is not
![]() $\Sigma $
-short, then we say that it is
$\Sigma $
-short, then we say that it is
![]() $\Sigma $
-maximal. We then set
$\Sigma $
-maximal. We then set
![]() $\Sigma ^{stc}$
be the fragment of
$\Sigma ^{stc}$
be the fragment of
![]() $\Sigma $
that acts on short trees.
$\Sigma $
that acts on short trees.
Following [Reference Sargsyan and Trang38, Definition 3.1.4], we make the following definition.
Definition 2.1. Suppose
![]() ${\mathcal {T}}$
is a normal iteration tree of limit length. We then let
${\mathcal {T}}$
is a normal iteration tree of limit length. We then let
In the language of the above definition, the convention used in [Reference Sargsyan and Trang38] is the following:
![]() $\Sigma ^{stc}({\mathcal {T}})=b$
if and only if
$\Sigma ^{stc}({\mathcal {T}})=b$
if and only if
-
1.
 ${\mathcal {T}}$
is
${\mathcal {T}}$
is
 $\Sigma $
-short and
$\Sigma $
-short and
 $\Sigma ({\mathcal {T}})=b$
, or
$\Sigma ({\mathcal {T}})=b$
, or -
2.
 ${\mathcal {T}}$
is
${\mathcal {T}}$
is
 $\Sigma $
-maximal and
$\Sigma $
-maximal and
 $b={\mathrm m}^+({\mathcal {T}})$
.
$b={\mathrm m}^+({\mathcal {T}})$
.
Thus,
![]() $\Sigma ^{stc}$
tells us the branch of a
$\Sigma ^{stc}$
tells us the branch of a
![]() $\Sigma $
-short tree or the last model of a
$\Sigma $
-short tree or the last model of a
![]() $\Sigma $
-maximal tree.
$\Sigma $
-maximal tree.
The reader can perhaps imagine many ways of defining the notion of short-tree strategy without a reference to an actual strategy. The convention that we adopt in this paper is the following. If
![]() $\Lambda $
is a short-tree strategy for
$\Lambda $
is a short-tree strategy for
![]() ${\mathcal {P}}$
, then we will require that
${\mathcal {P}}$
, then we will require that
-
1. for some
 ${\mathcal {P}}$
-cardinal
${\mathcal {P}}$
-cardinal
 ${\delta }$
,
${\delta }$
,
 ${\mathcal {P}}=({\mathcal {P}}|{\delta })^\#$
and
${\mathcal {P}}=({\mathcal {P}}|{\delta })^\#$
and
 ${\mathcal {P}}{\vDash } \text {`}{\delta }$
is a Woodin cardinal’,
${\mathcal {P}}{\vDash } \text {`}{\delta }$
is a Woodin cardinal’, -
2. if
 ${\delta }$
is as above and
${\delta }$
is as above and
 $\nu $
is the least
$\nu $
is the least
 $<{\delta }$
-strong cardinal of
$<{\delta }$
-strong cardinal of
 ${\mathcal {P}}$
, then
${\mathcal {P}}$
, then
 ${\mathcal {P}}{\vDash } \text {`}\nu $
is a limit of Woodin cardinals’,
${\mathcal {P}}{\vDash } \text {`}\nu $
is a limit of Woodin cardinals’, -
3. given an iteration tree
 ${\mathcal {T}}\in dom(\Lambda )$
,
${\mathcal {T}}\in dom(\Lambda )$
,
 $\Lambda ({\mathcal {T}})$
is either a cofinal well-founded branch of
$\Lambda ({\mathcal {T}})$
is either a cofinal well-founded branch of
 ${\mathcal {T}}$
or is equal to
${\mathcal {T}}$
or is equal to
 ${\mathrm m}^+({\mathcal {T}})$
,
${\mathrm m}^+({\mathcal {T}})$
, -
4. for all iteration trees
 ${\mathcal {T}}\in dom(\Lambda )$
, if
${\mathcal {T}}\in dom(\Lambda )$
, if
 $\Lambda ({\mathcal {T}})$
is a branch b, then
$\Lambda ({\mathcal {T}})$
is a branch b, then
 $\pi ^{\mathcal {T}}_b({\delta })>{\delta }({\mathcal {T}})$
,
$\pi ^{\mathcal {T}}_b({\delta })>{\delta }({\mathcal {T}})$
, -
5. for all iteration trees
 ${\mathcal {T}}\in dom(\Lambda )$
, if
${\mathcal {T}}\in dom(\Lambda )$
, if
 $\Lambda ({\mathcal {T}})$
is a model, then
$\Lambda ({\mathcal {T}})$
is a model, then
 ${\mathrm m}^+({\mathcal {T}}){\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’.
${\mathrm m}^+({\mathcal {T}}){\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’.
If a hod mouse
![]() ${\mathcal {P}}$
has properties 1 and 2 above, then we say that
${\mathcal {P}}$
has properties 1 and 2 above, then we say that
![]() ${\mathcal {P}}$
is of
${\mathcal {P}}$
is of
![]() $\#$
-lsa type. [Reference Sargsyan and Trang38, Definition 2.7.3] introduces other types of LSA hod premice.
$\#$
-lsa type. [Reference Sargsyan and Trang38, Definition 2.7.3] introduces other types of LSA hod premice.
The set of reals that has Wadge rank
![]() ${\kappa }$
is some short-tree strategy
${\kappa }$
is some short-tree strategy
![]() $\Lambda $
. The hod mouse
$\Lambda $
. The hod mouse
![]() ${\mathcal {P}}$
that
${\mathcal {P}}$
that
![]() $\Lambda $
iterates has a unique Woodin cardinal
$\Lambda $
iterates has a unique Woodin cardinal
![]() ${\delta }$
such that if
${\delta }$
such that if
![]() $\nu <{\delta }$
is the least cardinal that is
$\nu <{\delta }$
is the least cardinal that is
![]() $<{\delta }$
-strong in
$<{\delta }$
-strong in
![]() ${\mathcal {P}}$
, then
${\mathcal {P}}$
, then
![]() ${\mathcal {P}}{\vDash } \text {`}\nu $
is a limit of Woodin cardinals’. The aforementioned Woodin cardinal
${\mathcal {P}}{\vDash } \text {`}\nu $
is a limit of Woodin cardinals’. The aforementioned Woodin cardinal
![]() ${\delta }$
is also the largest Woodin cardinal of
${\delta }$
is also the largest Woodin cardinal of
![]() ${\mathcal {P}}$
. This fact is proven in [Reference Sargsyan and Trang38] (for example, see [Reference Sargsyan and Trang38, Theorem 7.2.2] and [Reference Sargsyan and Trang38, Chapter 8]). There is yet another way that the
${\mathcal {P}}$
. This fact is proven in [Reference Sargsyan and Trang38] (for example, see [Reference Sargsyan and Trang38, Theorem 7.2.2] and [Reference Sargsyan and Trang38, Chapter 8]). There is yet another way that the
![]() $\mathsf {LSA}$
stages of the
$\mathsf {LSA}$
stages of the
![]() $\mathsf {Solovay\ Sequence}$
are different from other points.
$\mathsf {Solovay\ Sequence}$
are different from other points.
We continue assuming that V is the minimal model of
![]() $\mathsf {LSA}$
. If
$\mathsf {LSA}$
. If
![]() $\Sigma $
is a strategy of a hod mouse with nice properties, then ordinal definability with respect to
$\Sigma $
is a strategy of a hod mouse with nice properties, then ordinal definability with respect to
![]() $\Sigma $
is captured by
$\Sigma $
is captured by
![]() $\Sigma $
-mice. More precisely, [Reference Sargsyan and Trang38, Theorem 10.2.1] implies that if x and y are reals, then x is ordinal definable from y using
$\Sigma $
-mice. More precisely, [Reference Sargsyan and Trang38, Theorem 10.2.1] implies that if x and y are reals, then x is ordinal definable from y using
![]() $\Sigma $
as a parameter if and only if there is a
$\Sigma $
as a parameter if and only if there is a
![]() $\Sigma $
-mouse
$\Sigma $
-mouse
![]() ${\mathcal {M}}$
over y
Footnote 36 such that
${\mathcal {M}}$
over y
Footnote 36 such that
![]() $x\in {\mathcal {M}}$
.
$x\in {\mathcal {M}}$
.
[Reference Sargsyan and Trang38, Theorem 10.2.1] also implies that the same conclusion is true for short-tree strategies. Namely, if
![]() $\Lambda $
is a short-tree strategy, then for x and y reals, x is ordinal definable from y using
$\Lambda $
is a short-tree strategy, then for x and y reals, x is ordinal definable from y using
![]() $\Lambda $
as a parameter if and only if there is a
$\Lambda $
as a parameter if and only if there is a
![]() $\Lambda $
-mouse
$\Lambda $
-mouse
![]() ${\mathcal {M}}$
over y such that
${\mathcal {M}}$
over y such that
![]() $x\in {\mathcal {M}}$
. Theorems of this sort are known as
$x\in {\mathcal {M}}$
. Theorems of this sort are known as
![]() $\mathsf {Mouse\ Capturing}$
theorems. Such theorems are very important when analyzing models of determinacy using inner model theoretic tools.
$\mathsf {Mouse\ Capturing}$
theorems. Such theorems are very important when analyzing models of determinacy using inner model theoretic tools.
For a strategy
![]() $\Sigma $
, the concept of a
$\Sigma $
, the concept of a
![]() $\Sigma $
-mouse has appeared in many places. The reader can consult [Reference Sargsyan34, Definition 1.20], but the notion probably was first mentioned in [Reference Steel46] and was finally fully developed in [Reference Schlutzenberg and Trang43].
$\Sigma $
-mouse has appeared in many places. The reader can consult [Reference Sargsyan34, Definition 1.20], but the notion probably was first mentioned in [Reference Steel46] and was finally fully developed in [Reference Schlutzenberg and Trang43].
A
![]() $\Sigma $
-mouse
$\Sigma $
-mouse
![]() ${\mathcal {M}}$
, besides having an extender sequence, also has a predicate that indexes the strategy. The idea, which is due to Woodin, is that the strategy predicate should index the branch of the least tree that has not yet been indexed.
${\mathcal {M}}$
, besides having an extender sequence, also has a predicate that indexes the strategy. The idea, which is due to Woodin, is that the strategy predicate should index the branch of the least tree that has not yet been indexed.
Unfortunately, this idea does not quite work for
![]() $\Lambda $
-mice where
$\Lambda $
-mice where
![]() $\Lambda $
is a short-tree strategy. In the next subsection, we will explain the solution presented in [Reference Sargsyan and Trang38].
$\Lambda $
is a short-tree strategy. In the next subsection, we will explain the solution presented in [Reference Sargsyan and Trang38].
2.1. Short-tree-strategy mice
We are assuming that V is the minimal model of
![]() $\mathsf {LSA}$
. Suppose
$\mathsf {LSA}$
. Suppose
![]() $\Lambda $
is a short-tree strategy for a hod mouse
$\Lambda $
is a short-tree strategy for a hod mouse
![]() ${\mathcal {P}}$
. We let
${\mathcal {P}}$
. We let
![]() ${\delta }$
be the largest Woodin cardinal of
${\delta }$
be the largest Woodin cardinal of
![]() ${\mathcal {P}}$
. Thus,
${\mathcal {P}}$
. Thus,
![]() ${\mathcal {P}}=({\mathcal {P}}|{\delta })^\#$
. In this subsection, we would like to convince the reader that the concept of
${\mathcal {P}}=({\mathcal {P}}|{\delta })^\#$
. In this subsection, we would like to convince the reader that the concept of
![]() $\Lambda $
-mouse, while much more involved, behaves very similarly to the concept of a
$\Lambda $
-mouse, while much more involved, behaves very similarly to the concept of a
![]() $\Sigma $
-mouse where
$\Sigma $
-mouse where
![]() $\Sigma $
is an iteration strategy.
$\Sigma $
is an iteration strategy.
In general, when introducing any notion of a mouse, one has to keep in mind the procedures that allow us to build such mice. Formally speaking, many notions of
![]() $\Lambda $
-mice might make perfect sense, but when we factor into it the constructions that are supposed to produce such mice, we run into a key issue.
$\Lambda $
-mice might make perfect sense, but when we factor into it the constructions that are supposed to produce such mice, we run into a key issue.
In any construction that produces some sort of mouse (e.g.,
![]() $K^c$
-constructions, fully backgrounded constructions, etc.), there are stages where one has to consider certain kinds of Skolem hulls, or as inner model theorists call them, fine structural cores. The reader can view these cores as some carefuly defined Skolem hulls. To illustrate the aformentioned problem, imagine we do have some notion of
$K^c$
-constructions, fully backgrounded constructions, etc.), there are stages where one has to consider certain kinds of Skolem hulls, or as inner model theorists call them, fine structural cores. The reader can view these cores as some carefuly defined Skolem hulls. To illustrate the aformentioned problem, imagine we do have some notion of
![]() $\Lambda $
-mice and let us try to run a construction that will produce such mice. Suppose
$\Lambda $
-mice and let us try to run a construction that will produce such mice. Suppose
![]() ${\mathcal {T}}$
is a tree according to
${\mathcal {T}}$
is a tree according to
![]() $\Lambda $
that appears in this construction. Having a notion of a
$\Lambda $
that appears in this construction. Having a notion of a
![]() $\Lambda $
-mouse means that we have a prescription for deciding whether
$\Lambda $
-mouse means that we have a prescription for deciding whether
![]() $\Lambda ({\mathcal {T}})$
should be indexed in the strategy predicate or not.
$\Lambda ({\mathcal {T}})$
should be indexed in the strategy predicate or not.
Suppose
![]() ${\mathcal {T}}$
is a
${\mathcal {T}}$
is a
![]() $\Lambda $
-maximal tree. It is hard to see exactly what one can index so that the strategy predicate remembers that
$\Lambda $
-maximal tree. It is hard to see exactly what one can index so that the strategy predicate remembers that
![]() ${\mathcal {T}}$
is maximal. And this ‘remembering’ is the issue. Imagine that at a later stage, we have a Skolem hull
${\mathcal {T}}$
is maximal. And this ‘remembering’ is the issue. Imagine that at a later stage, we have a Skolem hull
![]() $\pi : {\mathcal {M}}\rightarrow {\mathcal {N}}$
of our current stage such that
$\pi : {\mathcal {M}}\rightarrow {\mathcal {N}}$
of our current stage such that
![]() ${\mathcal {T}}\in rng(\pi )$
. It is possible that
${\mathcal {T}}\in rng(\pi )$
. It is possible that
![]() ${\mathcal {U}}=_{def}\pi ^{-1}({\mathcal {T}})$
is
${\mathcal {U}}=_{def}\pi ^{-1}({\mathcal {T}})$
is
![]() $\Lambda $
-short. If we have indexed X in our strategy that proves
$\Lambda $
-short. If we have indexed X in our strategy that proves
![]() $\Lambda $
-maximality of
$\Lambda $
-maximality of
![]() ${\mathcal {T}}$
, then
${\mathcal {T}}$
, then
![]() $\pi ^{-1}(X)$
now can no longer prove that
$\pi ^{-1}(X)$
now can no longer prove that
![]() ${\mathcal {U}}$
is
${\mathcal {U}}$
is
![]() $\Lambda $
-maximal. Thus, the notion of
$\Lambda $
-maximal. Thus, the notion of
![]() $\Lambda $
-mouse cannot be first order.
$\Lambda $
-mouse cannot be first order.
The solution is simply not to index anything for
![]() $\Lambda $
-maximal trees. This does not quite solve the problem as the above situation implies that nothing should be indexed for many
$\Lambda $
-maximal trees. This does not quite solve the problem as the above situation implies that nothing should be indexed for many
![]() $\Lambda $
-short trees as well. To solve this problem, we will only index the branches of some
$\Lambda $
-short trees as well. To solve this problem, we will only index the branches of some
![]() $\Lambda $
-short trees, those that we can locally prove are
$\Lambda $
-short trees, those that we can locally prove are
![]() $\Lambda $
-short. We explain this below in more details.
$\Lambda $
-short. We explain this below in more details.
Fix an lsa type hod premouse
![]() ${\mathcal {P}}$
and let
${\mathcal {P}}$
and let
![]() $\Lambda $
be its short-tree strategy. Let
$\Lambda $
be its short-tree strategy. Let
![]() ${\delta }$
be the largest Woodin cardinal of
${\delta }$
be the largest Woodin cardinal of
![]() ${\mathcal {P}}$
and
${\mathcal {P}}$
and
![]() $\nu $
be the least
$\nu $
be the least
![]() $<{\delta }$
-strong of
$<{\delta }$
-strong of
![]() ${\mathcal {P}}$
. To explain the exact prescription that we use to index
${\mathcal {P}}$
. To explain the exact prescription that we use to index
![]() $\Lambda $
, we explain some properties of the models that have already been constructed according to this indexing scheme. Suppose
$\Lambda $
, we explain some properties of the models that have already been constructed according to this indexing scheme. Suppose
![]() ${\mathcal {M}}$
is a
${\mathcal {M}}$
is a
![]() $\Lambda $
-premouse.
$\Lambda $
-premouse.
Call
![]() ${\mathcal {T}}\in {\mathcal {M}}$
universally short (
${\mathcal {T}}\in {\mathcal {M}}$
universally short (
![]() $\mathsf {uvs}$
) if
$\mathsf {uvs}$
) if
![]() ${\mathcal {T}}$
is obviously short (see [Reference Sargsyan and Trang38, Definition 3.3.2]). For instance, it can be that the
${\mathcal {T}}$
is obviously short (see [Reference Sargsyan and Trang38, Definition 3.3.2]). For instance, it can be that the
![]() $\#$
-operator provides a
$\#$
-operator provides a
![]() ${\mathcal {Q}}$
-structure and determines a branch c of
${\mathcal {Q}}$
-structure and determines a branch c of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() ${\mathcal {Q}}(c, {\mathcal {T}})$
Footnote 37 exists and
${\mathcal {Q}}(c, {\mathcal {T}})$
Footnote 37 exists and
![]() ${\mathcal {Q}}(c, {\mathcal {T}})\unlhd {\mathrm m}^+({\mathcal {T}})$
. Another way that a tree can be obviously short is that there could be a model
${\mathcal {Q}}(c, {\mathcal {T}})\unlhd {\mathrm m}^+({\mathcal {T}})$
. Another way that a tree can be obviously short is that there could be a model
![]() ${\mathcal {Q}}$
in
${\mathcal {Q}}$
in
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() $\pi ^{\mathcal {T}}_{{\mathcal {P}}, {\mathcal {Q}}}:{\mathcal {P}}\rightarrow {\mathcal {Q}}$
is defined and the portion of
$\pi ^{\mathcal {T}}_{{\mathcal {P}}, {\mathcal {Q}}}:{\mathcal {P}}\rightarrow {\mathcal {Q}}$
is defined and the portion of
![]() ${\mathcal {T}}$
that comes after
${\mathcal {T}}$
that comes after
![]() ${\mathcal {Q}}$
is based on
${\mathcal {Q}}$
is based on
![]() ${\mathcal {Q}}^b$
. Here,
${\mathcal {Q}}^b$
. Here,
![]() ${\mathcal {Q}}^b$
is defined as
${\mathcal {Q}}^b$
is defined as
![]() ${\mathcal {Q}}|(\kappa ^+)^{\mathcal {Q}}$
, where
${\mathcal {Q}}|(\kappa ^+)^{\mathcal {Q}}$
, where
![]() $\kappa $
is the supremum of the Woodin cardinals below the largest Woodin of
$\kappa $
is the supremum of the Woodin cardinals below the largest Woodin of
![]() ${\mathcal {Q}}$
. The reader should keep in mind that there is a formula
${\mathcal {Q}}$
. The reader should keep in mind that there is a formula
![]() $\zeta $
in the language of
$\zeta $
in the language of
![]() $\Lambda $
-premice such that for any
$\Lambda $
-premice such that for any
![]() $\Lambda $
-premouse
$\Lambda $
-premouse
![]() ${\mathcal {M}}$
and for any iteration tree
${\mathcal {M}}$
and for any iteration tree
![]() ${\mathcal {T}}\in {\mathcal {M}}$
,
${\mathcal {T}}\in {\mathcal {M}}$
,
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\mathsf {uvs}$
if and only if
$\mathsf {uvs}$
if and only if
![]() ${\mathcal {M}}{\vDash } \zeta [{\mathcal {T}}]$
.
${\mathcal {M}}{\vDash } \zeta [{\mathcal {T}}]$
.
Unfortunately, there can be trees that are not universally short (
![]() $\mathsf {nuvs}$
). Suppose then
$\mathsf {nuvs}$
). Suppose then
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\mathsf {nuvs}$
. In this case, whether we index
$\mathsf {nuvs}$
. In this case, whether we index
![]() $\Lambda ({\mathcal {T}})$
or not depends on whether we can find a
$\Lambda ({\mathcal {T}})$
or not depends on whether we can find a
![]() ${\mathcal {Q}}$
-structure that can be authenticated to be the correct one. There can be many ways to certify a
${\mathcal {Q}}$
-structure that can be authenticated to be the correct one. There can be many ways to certify a
![]() ${\mathcal {Q}}$
-structure, and [Reference Sargsyan and Trang38] provides one such method. An interested reader can consult [Reference Sargsyan and Trang38, Chapter 3.7]. Notice that because
${\mathcal {Q}}$
-structure, and [Reference Sargsyan and Trang38] provides one such method. An interested reader can consult [Reference Sargsyan and Trang38, Chapter 3.7]. Notice that because
![]() ${\mathcal {P}}$
has only one Woodin cardinal, not being able to find a
${\mathcal {P}}$
has only one Woodin cardinal, not being able to find a
![]() ${\mathcal {Q}}$
-structure is equivalent to the tree being maximal. Thus, in a nutshell, the solution proposed by [Reference Sargsyan and Trang38] is that we index only branches that are given by internally authenticated
${\mathcal {Q}}$
-structure is equivalent to the tree being maximal. Thus, in a nutshell, the solution proposed by [Reference Sargsyan and Trang38] is that we index only branches that are given by internally authenticated
![]() ${\mathcal {Q}}$
-structures.
${\mathcal {Q}}$
-structures.
Suppose now that we have the above Skolem hull situation – namely, that we have
![]() $\pi :{\mathcal {M}}\rightarrow {\mathcal {N}}$
and
$\pi :{\mathcal {M}}\rightarrow {\mathcal {N}}$
and
![]() ${\mathcal {T}}$
in
${\mathcal {T}}$
in
![]() ${\mathcal {N}}$
that is
${\mathcal {N}}$
that is
![]() $\Lambda $
-maximal but
$\Lambda $
-maximal but
![]() $\pi ^{-1}({\mathcal {T}})$
is short. There is no more indexing problem. The reason is that in order to index
$\pi ^{-1}({\mathcal {T}})$
is short. There is no more indexing problem. The reason is that in order to index
![]() $\Lambda (\pi ^{-1}({\mathcal {T}}))$
in
$\Lambda (\pi ^{-1}({\mathcal {T}}))$
in
![]() ${\mathcal {M}}$
, we need to find an authenticated
${\mathcal {M}}$
, we need to find an authenticated
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() $\pi ^{-1}({\mathcal {T}})$
. The authentication process is first order, and so if
$\pi ^{-1}({\mathcal {T}})$
. The authentication process is first order, and so if
![]() ${\mathcal {N}}$
does not have such an authenticated
${\mathcal {N}}$
does not have such an authenticated
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() ${\mathcal {T}}$
, then
${\mathcal {T}}$
, then
![]() ${\mathcal {M}}$
cannot have such an authenticated
${\mathcal {M}}$
cannot have such an authenticated
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() $\pi ^{-1}({\mathcal {T}})$
.
$\pi ^{-1}({\mathcal {T}})$
.
The reader of this paper does not need to know the exact way the authentication procedure works. However, the reader should keep in mind that the authentication procedure is internal to the mouse. More precisely, the following holds:
Internal Definability of Authentication: there is a formula
![]() $\phi $
in the appropriate language such that whenever
$\phi $
in the appropriate language such that whenever
![]() $({\mathcal {P}}, \Lambda )$
is as above and
$({\mathcal {P}}, \Lambda )$
is as above and
![]() ${\mathcal {M}}$
is a
${\mathcal {M}}$
is a
![]() $\Lambda $
-mouse over some set X such that
$\Lambda $
-mouse over some set X such that
![]() ${\mathcal {P}}\in X$
, for any iteration tree
${\mathcal {P}}\in X$
, for any iteration tree
![]() ${\mathcal {T}}\in {\mathcal {M}}$
,
${\mathcal {T}}\in {\mathcal {M}}$
,
![]() ${\mathcal {M}}{\vDash } \phi [{\mathcal {T}}]$
if and only if
${\mathcal {M}}{\vDash } \phi [{\mathcal {T}}]$
if and only if
![]() ${\mathcal {T}}\in dom(\Lambda )$
,
${\mathcal {T}}\in dom(\Lambda )$
,
![]() ${\mathcal {T}}$
is short and
${\mathcal {T}}$
is short and
![]() $\Lambda ({\mathcal {T}})\in {\mathcal {M}}$
.
$\Lambda ({\mathcal {T}})\in {\mathcal {M}}$
.
We again note that the Internal Definability of Authentication (IDA) is only shown to be true for the minimal model of
![]() $\mathsf {LSA}$
. In general, IDA cannot be true as there can be short trees without
$\mathsf {LSA}$
. In general, IDA cannot be true as there can be short trees without
![]() ${\mathcal {Q}}$
-structures. The authors have recently discovered another short-tree indexing scheme that can work in all cases but has some weaknesses compared to the one introduced in [Reference Sargsyan and Trang38].
${\mathcal {Q}}$
-structures. The authors have recently discovered another short-tree indexing scheme that can work in all cases but has some weaknesses compared to the one introduced in [Reference Sargsyan and Trang38].
Using the notation in [Reference Sargsyan and Trang38], recall that
![]() ${\mathcal {P}}^b$
is the ‘bottom part’ of
${\mathcal {P}}^b$
is the ‘bottom part’ of
![]() ${\mathcal {P}}$
(i.e.,
${\mathcal {P}}$
(i.e.,
![]() ${\mathcal {P}}^b = {\mathcal {P}}|(\nu ^+)^{{\mathcal {P}}}$
, where
${\mathcal {P}}^b = {\mathcal {P}}|(\nu ^+)^{{\mathcal {P}}}$
, where
![]() $\nu $
is the supremum of the Woodin cardinals below the top Woodin of
$\nu $
is the supremum of the Woodin cardinals below the top Woodin of
![]() ${\mathcal {P}}$
).
${\mathcal {P}}$
).
We now describe another key feature of the indexing scheme of [Reference Sargsyan and Trang38] that is of importance here. We say
![]() $\Sigma $
is a low-level component of
$\Sigma $
is a low-level component of
![]() $\Lambda $
if there is a tree
$\Lambda $
if there is a tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {P}}$
according to
${\mathcal {P}}$
according to
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\pi ^{{\mathcal {T}}, b}$
existsFootnote 38 (
$\pi ^{{\mathcal {T}}, b}$
existsFootnote 38 (
![]() ${\mathcal {T}}$
may be
${\mathcal {T}}$
may be
![]() $\emptyset $
) and for some
$\emptyset $
) and for some
![]() ${\mathcal {R}}\unlhd \pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)$
,
${\mathcal {R}}\unlhd \pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)$
,
![]() $\Sigma =\Lambda _{\mathcal {R}}$
. Let
$\Sigma =\Lambda _{\mathcal {R}}$
. Let
![]() $LLC(\Lambda )$
be the set of
$LLC(\Lambda )$
be the set of
![]() $\Sigma $
that are low-level components of
$\Sigma $
that are low-level components of
![]() $\Lambda $
. What is shown in [Reference Sargsyan and Trang38] is that
$\Lambda $
. What is shown in [Reference Sargsyan and Trang38] is that
![]() $\Lambda $
is determined by
$\Lambda $
is determined by
![]() $LLC(\Lambda )$
in a strong sense.
$LLC(\Lambda )$
in a strong sense.
Given a transitive model M of a fragment of
![]() $\mathsf {ZFC}$
such that
$\mathsf {ZFC}$
such that
![]() ${\mathcal {P}}\in M$
, we say M is closed under
${\mathcal {P}}\in M$
, we say M is closed under
![]() $LLC(\Lambda )$
if whenever
$LLC(\Lambda )$
if whenever
![]() ${\mathcal {T}}\in M$
is a tree according to
${\mathcal {T}}\in M$
is a tree according to
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists,
$\pi ^{{\mathcal {T}}, b}$
exists,
![]() $\Lambda _{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)}$
has a universally Baire representation over M. More precisely, whenever
$\Lambda _{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)}$
has a universally Baire representation over M. More precisely, whenever
![]() $g\subseteq Coll(\omega , \pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b))$
is M-generic, for every M-cardinal
$g\subseteq Coll(\omega , \pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b))$
is M-generic, for every M-cardinal
![]() ${\lambda }$
, there are trees
${\lambda }$
, there are trees
![]() $T, S\in M[g]$
on
$T, S\in M[g]$
on
![]() ${\lambda }$
such that
${\lambda }$
such that
![]() $M[g]{\vDash } \text {`}(T, S)$
are
$M[g]{\vDash } \text {`}(T, S)$
are
![]() $<{\lambda }$
-complementing’ and for all
$<{\lambda }$
-complementing’ and for all
![]() $<{\lambda }$
-generics h,
$<{\lambda }$
-generics h,
![]() $(p[T])^{M[g*h]}=Code(\Lambda _{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)})\cap M[g*h]$
. Here,
$(p[T])^{M[g*h]}=Code(\Lambda _{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)})\cap M[g*h]$
. Here,
![]() $Code(\Phi )$
is the set of reals coding
$Code(\Phi )$
is the set of reals coding
![]() $\Phi $
(with respect to a fixed coding of elements of
$\Phi $
(with respect to a fixed coding of elements of
![]() $HC$
by reals).
$HC$
by reals).
It is shown in [Reference Sargsyan and Trang38] that if, assuming
![]() $\mathsf {AD}^+$
,
$\mathsf {AD}^+$
,
![]() $(M, \Sigma )$
is such that
$(M, \Sigma )$
is such that
-
1. M is a countable model of a fragment of
 $\mathsf {ZFC}$
,
$\mathsf {ZFC}$
, -
2. M has a class of Woodin cardinals,
-
3.
 $\Sigma $
is an
$\Sigma $
is an
 $\omega _1$
-iteration strategy for M and
$\omega _1$
-iteration strategy for M and -
4. whenever
 $i:M\rightarrow N$
is an iteration via
$i:M\rightarrow N$
is an iteration via
 $\Sigma $
, N is closed under
$\Sigma $
, N is closed under
 $LLC(\Lambda )$
,
$LLC(\Lambda )$
,
then there is a formula
![]() $\psi $
such that whenever g is M-generic, for any
$\psi $
such that whenever g is M-generic, for any
![]() ${\mathcal {T}}\in M[g]$
,
${\mathcal {T}}\in M[g]$
,
The interested reader can consult Chapters 5, 6 and 8 of [Reference Sargsyan and Trang38].
The reason we explained the above is to give the reader some confidence that defining a short-tree strategy
![]() $\Lambda $
for a hod premose
$\Lambda $
for a hod premose
![]() ${\mathcal {P}}$
is equivalent to describing the set
${\mathcal {P}}$
is equivalent to describing the set
![]() $LLC(\Lambda )$
. This fact is the reason that the indexing schema of [Reference Sargsyan and Trang38] works in the following sense.
$LLC(\Lambda )$
. This fact is the reason that the indexing schema of [Reference Sargsyan and Trang38] works in the following sense.
Being able to define short-tree-strategy mice is one thing; proving that they are useful is another. Usually what needs to be shown are the following two key statements. We let
![]() $\phi _{sts}$
be the formula that is mentioned in the Internal Definability of Authentication.
$\phi _{sts}$
be the formula that is mentioned in the Internal Definability of Authentication.
The Eventual Authentication. Suppose
![]() $({\mathcal {P}}, \Lambda )$
is as above and
$({\mathcal {P}}, \Lambda )$
is as above and
![]() ${\mathcal {M}}$
is a sound
${\mathcal {M}}$
is a sound
![]() $\Lambda $
-mouse over some set X such that
$\Lambda $
-mouse over some set X such that
![]() ${\mathcal {P}}\in X$
and
${\mathcal {P}}\in X$
and
![]() ${\mathcal {M}}$
projects to X. Suppose
${\mathcal {M}}$
projects to X. Suppose
![]() ${\mathcal {T}}\in {\mathcal {M}}$
is according to
${\mathcal {T}}\in {\mathcal {M}}$
is according to
![]() $\Lambda $
and is
$\Lambda $
and is
![]() $\Lambda $
-short. Suppose further that
$\Lambda $
-short. Suppose further that
![]() ${\mathcal {M}}{\vDash } \neg \phi _{sts}[{\mathcal {T}}]$
. Then there is a sound
${\mathcal {M}}{\vDash } \neg \phi _{sts}[{\mathcal {T}}]$
. Then there is a sound
![]() $\Lambda $
-mouse
$\Lambda $
-mouse
![]() ${\mathcal {N}}$
over X such that
${\mathcal {N}}$
over X such that
![]() ${\mathcal {M}}\unlhd {\mathcal {N}}$
and
${\mathcal {M}}\unlhd {\mathcal {N}}$
and
![]() ${\mathcal {N}}{\vDash } \phi _{sts}[{\mathcal {T}}]$
.Footnote 39
${\mathcal {N}}{\vDash } \phi _{sts}[{\mathcal {T}}]$
.Footnote 39
Mouse Capturing for
![]() $\Lambda $
: Suppose
$\Lambda $
: Suppose
![]() $({\mathcal {P}}, \Lambda )$
is as above. Then for any
$({\mathcal {P}}, \Lambda )$
is as above. Then for any
![]() $x\in \mathbb {R}$
that codes
$x\in \mathbb {R}$
that codes
![]() ${\mathcal {P}}$
and any
${\mathcal {P}}$
and any
![]() $y\in \mathbb {R}$
, y is ordinal definable from x and
$y\in \mathbb {R}$
, y is ordinal definable from x and
![]() $\Lambda $
if and only if there is a
$\Lambda $
if and only if there is a
![]() $\Lambda $
-mouse
$\Lambda $
-mouse
![]() ${\mathcal {M}}$
over x such that
${\mathcal {M}}$
over x such that
![]() $y\in {\mathcal {M}}$
.
$y\in {\mathcal {M}}$
.
Both The Eventual Authentication and Mouse Capturing for
![]() $\Lambda $
are proven in [Reference Sargsyan and Trang38] (see [Reference Sargsyan and Trang38, Chapter 8, Lemma 8.1.3, Lemma 8.1.5] and [Reference Sargsyan and Trang38, Theorem 10.2.1]).
$\Lambda $
are proven in [Reference Sargsyan and Trang38] (see [Reference Sargsyan and Trang38, Chapter 8, Lemma 8.1.3, Lemma 8.1.5] and [Reference Sargsyan and Trang38, Theorem 10.2.1]).
The next subsection discusses the
![]() ${\mathcal {Q}}$
-structure authentication process mentioned above.
${\mathcal {Q}}$
-structure authentication process mentioned above.
2.2. The authentication method
Suppose
![]() ${\mathcal {P}}$
is a
${\mathcal {P}}$
is a
![]() $\#$
-lsa type hod premouse. Recall from the previous subsections that this means that
$\#$
-lsa type hod premouse. Recall from the previous subsections that this means that
![]() ${\mathcal {P}}$
has a largest Woodin cardinal
${\mathcal {P}}$
has a largest Woodin cardinal
![]() ${\delta }$
such that
${\delta }$
such that
![]() ${\mathcal {P}}=({\mathcal {P}}|{\delta })^\#$
and the least
${\mathcal {P}}=({\mathcal {P}}|{\delta })^\#$
and the least
![]() $<{\delta }$
-strong cardinal of
$<{\delta }$
-strong cardinal of
![]() ${\mathcal {P}}$
is a limit of Woodin cardinals. We let
${\mathcal {P}}$
is a limit of Woodin cardinals. We let
![]() ${\delta }^{\mathcal {P}}$
be the largest Woodin cardinal of
${\delta }^{\mathcal {P}}$
be the largest Woodin cardinal of
![]() ${\mathcal {P}}$
and
${\mathcal {P}}$
and
![]() ${\kappa }^{\mathcal {P}}$
be the least
${\kappa }^{\mathcal {P}}$
be the least
![]() $<{\delta }^{\mathcal {P}}$
-strong cardinal of
$<{\delta }^{\mathcal {P}}$
-strong cardinal of
![]() ${\mathcal {P}}$
. We shall also require that
${\mathcal {P}}$
. We shall also require that
![]() ${\mathcal {P}}$
is tame, meaning that for any
${\mathcal {P}}$
is tame, meaning that for any
![]() $\nu <{\delta }^{\mathcal {P}}$
, if
$\nu <{\delta }^{\mathcal {P}}$
, if
![]() $({\mathcal {P}}|\nu )^\#$
is of lsa type and
$({\mathcal {P}}|\nu )^\#$
is of lsa type and
![]() ${\mathcal {M}}{\trianglelefteq } {\mathcal {P}}$
is the largest such that
${\mathcal {M}}{\trianglelefteq } {\mathcal {P}}$
is the largest such that
![]() ${\mathcal {M}}{\vDash } \text {`}\nu $
is a Woodin cardinal’, then
${\mathcal {M}}{\vDash } \text {`}\nu $
is a Woodin cardinal’, then
![]() $\nu $
is not overlapped in
$\nu $
is not overlapped in
![]() ${\mathcal {M}}$
.Footnote 40
${\mathcal {M}}$
.Footnote 40
Our goal here is to explain the
![]() ${\mathcal {Q}}$
-structure authentication procedure employed by [Reference Sargsyan and Trang38]. Recall our discussion of
${\mathcal {Q}}$
-structure authentication procedure employed by [Reference Sargsyan and Trang38]. Recall our discussion of
![]() $\mathsf {uvs}$
and
$\mathsf {uvs}$
and
![]() $\mathsf {nuvs}$
trees. The
$\mathsf {nuvs}$
trees. The
![]() ${\mathcal {Q}}$
-structure authentication procedure applies to only
${\mathcal {Q}}$
-structure authentication procedure applies to only
![]() $\mathsf {nuvs}$
trees – trees that are not obviously short.
$\mathsf {nuvs}$
trees – trees that are not obviously short.
[Reference Sargsyan and Trang38, Chapters 3.6-3.9] develop the aforementioned authentication procedure. [Reference Sargsyan and Trang38, Definition 3.8.9, 3.8.16, 3.8.17] introduce the sts indexing scheme. For illustrative purposes, it is better to think of the indexing scheme introduced there as a hierarchy of indexing schemes indexed by ordinals. Naturally, this hierarchy is defined by induction. For illustrative purposes we call
![]() ${\gamma }$
th level of the hierarchy
${\gamma }$
th level of the hierarchy
![]() $sts_{\gamma }$
. Thus,
$sts_{\gamma }$
. Thus,
![]() $sts_{\gamma }({\mathcal {P}})$
is the set of all sts premice that are based on
$sts_{\gamma }({\mathcal {P}})$
is the set of all sts premice that are based on
![]() ${\mathcal {P}}$
(i.e., their short-tree-strategy predicate describes a short-tree strategy for
${\mathcal {P}}$
(i.e., their short-tree-strategy predicate describes a short-tree strategy for
![]() ${\mathcal {P}}$
) and have rank
${\mathcal {P}}$
) and have rank
![]() $\leq {\gamma }$
.
$\leq {\gamma }$
.
To begin the induction, we let
![]() $sts_0({\mathcal {P}})$
be the set of all sts premice that do not index a branch for any
$sts_0({\mathcal {P}})$
be the set of all sts premice that do not index a branch for any
![]() $\mathsf {nuvs}$
tree. More precisely, if
$\mathsf {nuvs}$
tree. More precisely, if
![]() ${\mathcal {M}}\in sts_0({\mathcal {P}})$
and
${\mathcal {M}}\in sts_0({\mathcal {P}})$
and
![]() ${\mathcal {T}}\in dom(S^{\mathcal {M}})$
, then if
${\mathcal {T}}\in dom(S^{\mathcal {M}})$
, then if
![]() $S^{\mathcal {M}}({\mathcal {T}})$
is defined, then
$S^{\mathcal {M}}({\mathcal {T}})$
is defined, then
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\mathsf {uvs}$
.
$\mathsf {uvs}$
.
Below and elsewhere,
![]() $S^{\mathcal {M}}$
is the strategy predicate of
$S^{\mathcal {M}}$
is the strategy predicate of
![]() ${\mathcal {M}}$
. Given
${\mathcal {M}}$
. Given
![]() $sts_{{\alpha }}({\mathcal {P}})$
, we let
$sts_{{\alpha }}({\mathcal {P}})$
, we let
![]() $sts_{{\alpha }+1}({\mathcal {P}})$
be the set of all sts premice that index branches of those
$sts_{{\alpha }+1}({\mathcal {P}})$
be the set of all sts premice that index branches of those
![]() $\mathsf {nuvs}$
trees that have a
$\mathsf {nuvs}$
trees that have a
![]() ${\mathcal {Q}}$
-structure in
${\mathcal {Q}}$
-structure in
![]() $sts_{\alpha }({\mathcal {P}})$
. More precisely, suppose
$sts_{\alpha }({\mathcal {P}})$
. More precisely, suppose
![]() ${\mathcal {M}}\in sts_{{\alpha }+1}({\mathcal {P}})$
and
${\mathcal {M}}\in sts_{{\alpha }+1}({\mathcal {P}})$
and
![]() ${\mathcal {T}}\in dom(S^{\mathcal {M}})$
and
${\mathcal {T}}\in dom(S^{\mathcal {M}})$
and
![]() $S^{\mathcal {M}}({\mathcal {T}})$
is defined. Then either
$S^{\mathcal {M}}({\mathcal {T}})$
is defined. Then either
-
1.
 ${\mathcal {T}}$
is
${\mathcal {T}}$
is
 $\mathsf {uvs}$
or
$\mathsf {uvs}$
or -
2.
 ${\mathcal {T}}$
is
${\mathcal {T}}$
is
 $\mathsf {nuvs}$
and there is
$\mathsf {nuvs}$
and there is
 ${\mathcal {Q}}\in {\mathcal {M}}$
such that
${\mathcal {Q}}\in {\mathcal {M}}$
such that
 ${\mathcal {M}}{\vDash } \text {`}{\mathcal {Q}}\in sts_{\alpha }({\mathcal {P}})'$
,
${\mathcal {M}}{\vDash } \text {`}{\mathcal {Q}}\in sts_{\alpha }({\mathcal {P}})'$
,
 ${\mathrm m}^+({\mathcal {T}}){\trianglelefteq }{\mathcal {Q}}$
,
${\mathrm m}^+({\mathcal {T}}){\trianglelefteq }{\mathcal {Q}}$
,
 ${\mathcal {Q}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ but
${\mathcal {Q}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ but
 ${\delta }({\mathcal {T}})$
is not a Woodin cardinal with respect to some function definable over
${\delta }({\mathcal {T}})$
is not a Woodin cardinal with respect to some function definable over
 ${\mathcal {Q}}$
Footnote 41 and there is a cofinal branch b of
${\mathcal {Q}}$
Footnote 41 and there is a cofinal branch b of
 ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
 ${\mathcal {Q}}{\trianglelefteq } {\mathcal {M}}^{\mathcal {T}}_b$
.
${\mathcal {Q}}{\trianglelefteq } {\mathcal {M}}^{\mathcal {T}}_b$
.
When
![]() ${\mathcal {Q}}$
exhibits the properties listed in clause 2, we say that
${\mathcal {Q}}$
exhibits the properties listed in clause 2, we say that
![]() ${\mathcal {Q}}$
is a
${\mathcal {Q}}$
is a
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() ${\mathcal {T}}$
. It follows from the zipper argument of [Reference Martin and Steel25, Theorem 2.2] that for each
${\mathcal {T}}$
. It follows from the zipper argument of [Reference Martin and Steel25, Theorem 2.2] that for each
![]() ${\mathcal {Q}}$
-structure
${\mathcal {Q}}$
-structure
![]() ${\mathcal {Q}}$
, there is at most one branch b with properties described in clause 2 above. However, there is nothing that we have said so far that guarantees the uniqueness of the
${\mathcal {Q}}$
, there is at most one branch b with properties described in clause 2 above. However, there is nothing that we have said so far that guarantees the uniqueness of the
![]() ${\mathcal {Q}}$
-structure itself. The uniqueness is usually a consequence of iterability and comparison (see [Reference Steel53, Theorem 3.11]).Footnote 42 Thus, to make the definition of
${\mathcal {Q}}$
-structure itself. The uniqueness is usually a consequence of iterability and comparison (see [Reference Steel53, Theorem 3.11]).Footnote 42 Thus, to make the definition of
![]() $sts_{{\alpha }+1}$
complete, we need to impose an iterability condition on
$sts_{{\alpha }+1}$
complete, we need to impose an iterability condition on
![]() ${\mathcal {Q}}$
.
${\mathcal {Q}}$
.
The exact iterability condition that one needs is stated as clause 5 of [Reference Sargsyan and Trang38, Definition 3.8.9]. This clause may seem technical, but there are good reasons for it. For the purposes of identifying a unique branch b saying that
![]() ${\mathcal {Q}}$
in clause 2 is sufficiently iterable in
${\mathcal {Q}}$
in clause 2 is sufficiently iterable in
![]() ${\mathcal {M}}$
would have sufficed. However, recall the statement of the Internal Definability of Authentication. The problem is that when we require that an
${\mathcal {M}}$
would have sufficed. However, recall the statement of the Internal Definability of Authentication. The problem is that when we require that an
![]() ${\mathcal {M}}$
as above is a
${\mathcal {M}}$
as above is a
![]() $\Lambda $
-premouse, we in addition must say that the branch b that the
$\Lambda $
-premouse, we in addition must say that the branch b that the
![]() ${\mathcal {Q}}$
-structure
${\mathcal {Q}}$
-structure
![]() ${\mathcal {Q}}$
defines is the exact same branch that
${\mathcal {Q}}$
defines is the exact same branch that
![]() $\Lambda $
picks. To guarantee this, we need to impose a condition on
$\Lambda $
picks. To guarantee this, we need to impose a condition on
![]() ${\mathcal {Q}}$
such that
${\mathcal {Q}}$
such that
![]() ${\mathcal {Q}}$
will be iterable not just in
${\mathcal {Q}}$
will be iterable not just in
![]() ${\mathcal {M}}$
but in V. The easiest way of doing this is to say that
${\mathcal {M}}$
but in V. The easiest way of doing this is to say that
![]() ${\mathcal {Q}}$
has an iteration strategy in some derived model as then, using genericity iterations (see [Reference Steel53, Chapter 7.2]), we can extend such a strategy for
${\mathcal {Q}}$
has an iteration strategy in some derived model as then, using genericity iterations (see [Reference Steel53, Chapter 7.2]), we can extend such a strategy for
![]() ${\mathcal {Q}}$
to a strategy that acts on iterations in V.
${\mathcal {Q}}$
to a strategy that acts on iterations in V.
For limit
![]() ${\alpha }$
,
${\alpha }$
,
![]() $sts_{\alpha }({\mathcal {P}})$
is essentially
$sts_{\alpha }({\mathcal {P}})$
is essentially
![]() $\bigcup _{{\beta }<{\alpha }}sts_{\beta }({\mathcal {P}})$
. What has been left unexplained is the kind of strategy that the
$\bigcup _{{\beta }<{\alpha }}sts_{\beta }({\mathcal {P}})$
. What has been left unexplained is the kind of strategy that the
![]() ${\mathcal {Q}}$
-structure
${\mathcal {Q}}$
-structure
![]() ${\mathcal {Q}}$
must have in some derived model. Let
${\mathcal {Q}}$
must have in some derived model. Let
![]() $\Sigma $
be this strategy. If
$\Sigma $
be this strategy. If
![]() ${\mathcal {M}}\in sts_{\alpha }({\mathcal {P}})$
is a
${\mathcal {M}}\in sts_{\alpha }({\mathcal {P}})$
is a
![]() $\Lambda $
-mouse, then
$\Lambda $
-mouse, then
![]() ${\mathcal {Q}}$
must be a
${\mathcal {Q}}$
must be a
![]() $\Lambda _{{\mathrm m}^+({\mathcal {T}})}$
-mouse over
$\Lambda _{{\mathrm m}^+({\mathcal {T}})}$
-mouse over
![]() ${\mathrm m}^+({\mathcal {T}})$
. Thus, our next challenge is to find a first-order way of guaranteeing that
${\mathrm m}^+({\mathcal {T}})$
. Thus, our next challenge is to find a first-order way of guaranteeing that
![]() $\Sigma $
-iterates of
$\Sigma $
-iterates of
![]() ${\mathcal {Q}}$
are
${\mathcal {Q}}$
are
![]() $\Lambda _{{\mathrm m}^+({\mathcal {T}})}$
-mice, even those iterates that we will obtain after blowing up
$\Lambda _{{\mathrm m}^+({\mathcal {T}})}$
-mice, even those iterates that we will obtain after blowing up
![]() $\Sigma $
via genericity iterations.
$\Sigma $
via genericity iterations.
The solution that is employed in [Reference Sargsyan and Trang38] is that if
![]() ${\mathcal {R}}$
is a
${\mathcal {R}}$
is a
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {Q}}$
and
${\mathcal {Q}}$
and
![]() ${\mathcal {U}}\in dom(S^{\mathcal {R}})$
, then
${\mathcal {U}}\in dom(S^{\mathcal {R}})$
, then
![]() ${\mathcal {U}}$
itself is authenticated by the extenders of
${\mathcal {U}}$
itself is authenticated by the extenders of
![]() ${\mathcal {M}}$
. Below, we refer to this certification as tree certification. This is again a rather technical notion, but the following essentially illustrates the situation.
${\mathcal {M}}$
. Below, we refer to this certification as tree certification. This is again a rather technical notion, but the following essentially illustrates the situation.
Let us suppose
![]() ${\mathcal {R}}={\mathcal {Q}}$
and
${\mathcal {R}}={\mathcal {Q}}$
and
![]() ${\mathcal {U}}\in dom(S^{\mathcal {Q}})$
. The indexing scheme of [Reference Sargsyan and Trang38] does not index all trees in
${\mathcal {U}}\in dom(S^{\mathcal {Q}})$
. The indexing scheme of [Reference Sargsyan and Trang38] does not index all trees in
![]() ${\mathcal {P}}$
. In other words,
${\mathcal {P}}$
. In other words,
![]() $S^{\mathcal {M}}$
is never total.
$S^{\mathcal {M}}$
is never total.
![]() $dom(S^{\mathcal {M}})$
consists of trees that are built via a comparison procedure that iterates
$dom(S^{\mathcal {M}})$
consists of trees that are built via a comparison procedure that iterates
![]() ${\mathcal {P}}$
to a background construction of
${\mathcal {P}}$
to a background construction of
![]() ${\mathcal {M}}$
. Set
${\mathcal {M}}$
. Set
![]() ${\mathcal {N}}={\mathrm m}^+({\mathcal {U}})$
. One requirement is that
${\mathcal {N}}={\mathrm m}^+({\mathcal {U}})$
. One requirement is that
![]() ${\mathcal {N}}$
also iterates to one such background construction to which
${\mathcal {N}}$
also iterates to one such background construction to which
![]() ${\mathcal {P}}$
also iterates. Let
${\mathcal {P}}$
also iterates. Let
![]() ${\mathcal {S}}$
be this common background construction and suppose
${\mathcal {S}}$
be this common background construction and suppose
![]() ${\alpha }+1<lh({\mathcal {U}})$
is such that
${\alpha }+1<lh({\mathcal {U}})$
is such that
![]() ${\alpha }$
is a limit ordinal. First, assume
${\alpha }$
is a limit ordinal. First, assume
![]() ${\mathcal {U}}{\restriction } {\alpha }$
is
${\mathcal {U}}{\restriction } {\alpha }$
is
![]() $\mathsf {uvs}$
. What is shown in [Reference Sargsyan and Trang38] is that knowing the branch of
$\mathsf {uvs}$
. What is shown in [Reference Sargsyan and Trang38] is that knowing the branch of
![]() ${\mathcal {P}}$
-to-
${\mathcal {P}}$
-to-
![]() ${\mathcal {S}}$
tree, there is a first-order procedure that identifies the branch of
${\mathcal {S}}$
tree, there is a first-order procedure that identifies the branch of
![]() ${\mathcal {U}}{\restriction } {\alpha }$
, and that procedure is the tree certification procedure applied to
${\mathcal {U}}{\restriction } {\alpha }$
, and that procedure is the tree certification procedure applied to
![]() ${\mathcal {U}}{\restriction } {\alpha }$
.
${\mathcal {U}}{\restriction } {\alpha }$
.
Suppose next that
![]() ${\mathcal {U}}{\restriction } {\alpha }$
is
${\mathcal {U}}{\restriction } {\alpha }$
is
![]() $\mathsf {nuvs}$
. Then because
$\mathsf {nuvs}$
. Then because
![]() ${\alpha }+1<lh({\mathcal {U}})$
,
${\alpha }+1<lh({\mathcal {U}})$
,
![]() ${\mathcal {U}}{\restriction } {\alpha }$
must be short and the branch chosen for it in
${\mathcal {U}}{\restriction } {\alpha }$
must be short and the branch chosen for it in
![]() ${\mathcal {Q}}$
must have a
${\mathcal {Q}}$
must have a
![]() ${\mathcal {Q}}$
-structure
${\mathcal {Q}}$
-structure
![]() ${\mathcal {Q}}_1$
, which is itself an sts mouse. We have that
${\mathcal {Q}}_1$
, which is itself an sts mouse. We have that
![]() ${\mathcal {Q}}_1\in {\mathcal {Q}}$
and
${\mathcal {Q}}_1\in {\mathcal {Q}}$
and
![]() ${\mathcal {Q}}_1$
must have the same certification in
${\mathcal {Q}}_1$
must have the same certification in
![]() ${\mathcal {Q}}$
that
${\mathcal {Q}}$
that
![]() ${\mathcal {Q}}$
has in
${\mathcal {Q}}$
has in
![]() ${\mathcal {M}}$
. Again, the
${\mathcal {M}}$
. Again, the
![]() $\mathsf {nuvs}$
trees in
$\mathsf {nuvs}$
trees in
![]() ${\mathcal {Q}}_1$
have a tree certification in
${\mathcal {Q}}_1$
have a tree certification in
![]() ${\mathcal {Q}}$
according to the above procedure. The
${\mathcal {Q}}$
according to the above procedure. The
![]() $\mathsf {uvs}$
ones produce another
$\mathsf {uvs}$
ones produce another
![]() ${\mathcal {Q}}_2\in {\mathcal {Q}}_1$
. Because we cannot have an infinite descent, the definition of tree certification is meaningful.
${\mathcal {Q}}_2\in {\mathcal {Q}}_1$
. Because we cannot have an infinite descent, the definition of tree certification is meaningful.
Remark 2.2. It is sometimes convenient to think of a short-tree strategy as one having two components: the branch component and the model component. Given a short-tree strategy
![]() $\Lambda $
, we let
$\Lambda $
, we let
![]() $b(\Lambda )$
be the set of those trees
$b(\Lambda )$
be the set of those trees
![]() ${\mathcal {T}}\in dom(\Lambda )$
such that
${\mathcal {T}}\in dom(\Lambda )$
such that
![]() $\Lambda ({\mathcal {T}})$
is a branch of
$\Lambda ({\mathcal {T}})$
is a branch of
![]() ${\mathcal {T}}$
, and we let
${\mathcal {T}}$
, and we let
![]() $m(\Lambda )$
be the set of those trees
$m(\Lambda )$
be the set of those trees
![]() ${\mathcal {T}}\in dom(\Lambda )$
such that
${\mathcal {T}}\in dom(\Lambda )$
such that
![]() $\Lambda ({\mathcal {T}})$
is a model.
$\Lambda ({\mathcal {T}})$
is a model.
The convention adopted in this paper is that if
![]() ${\mathcal {T}}\in m(\Lambda )$
, then
${\mathcal {T}}\in m(\Lambda )$
, then
![]() $\Lambda ({\mathcal {T}})={\mathrm m}^+({\mathcal {T}})$
Footnote 43. Thus, if
$\Lambda ({\mathcal {T}})={\mathrm m}^+({\mathcal {T}})$
Footnote 43. Thus, if
![]() ${\mathcal {M}}$
is an sts premouse, then
${\mathcal {M}}$
is an sts premouse, then
![]() $S^{\mathcal {M}}$
is a short-tree strategy in the above sense (i.e., for
$S^{\mathcal {M}}$
is a short-tree strategy in the above sense (i.e., for
![]() ${\mathcal {T}}\not \in b(S^{\mathcal {M}})$
,
${\mathcal {T}}\not \in b(S^{\mathcal {M}})$
,
![]() $S^{\mathcal {M}}({\mathcal {T}})$
is simply left undefined).
$S^{\mathcal {M}}({\mathcal {T}})$
is simply left undefined).
This ends our discussion of sts premice. Of course, a lot has been left out, and the mathematical details are unfortunately excruciating, but we hope that the reader has gained some level of intuition to proceed with the paper.
In the next subsection, we will deal with one of the most important aspects of hod mice – namely, the generic interpretability of iteration strategies.
2.3. Generic interpretability
There are several situations when one has to be careful when discussing sts premice and
![]() $\Lambda $
-premice in general. First, for an iteration strategy
$\Lambda $
-premice in general. First, for an iteration strategy
![]() $\Sigma $
,
$\Sigma $
,
![]() ${\mathcal {M}}_1^{\#, \Sigma }$
makes complete sense. It is the minimal active
${\mathcal {M}}_1^{\#, \Sigma }$
makes complete sense. It is the minimal active
![]() $\Sigma $
-mouse with a Woodin cardinal. For short-tree strategy
$\Sigma $
-mouse with a Woodin cardinal. For short-tree strategy
![]() $\Lambda $
, the situation is somewhat different. The expression ‘
$\Lambda $
, the situation is somewhat different. The expression ‘
![]() ${\mathcal {M}}_1^{\#, \Lambda }$
is the minimal active
${\mathcal {M}}_1^{\#, \Lambda }$
is the minimal active
![]() $\Lambda $
-mouse with a Woodin cardinal’ does not say much as we do not say how closed
$\Lambda $
-mouse with a Woodin cardinal’ does not say much as we do not say how closed
![]() ${\mathcal {M}}_1^{\#, \Lambda }$
must be. One must also add statements of the form ‘in which all
${\mathcal {M}}_1^{\#, \Lambda }$
must be. One must also add statements of the form ‘in which all
![]() $\Lambda $
-short trees are indexed’. This is because it could be that
$\Lambda $
-short trees are indexed’. This is because it could be that
![]() $\Lambda $
-premouse
$\Lambda $
-premouse
![]() ${\mathcal {M}}$
is active and has a Woodin cardinal but there is a
${\mathcal {M}}$
is active and has a Woodin cardinal but there is a
![]() $\Lambda $
-short tree
$\Lambda $
-short tree
![]() ${\mathcal {T}}\in {\mathcal {M}}$
that has not yet been indexed in
${\mathcal {T}}\in {\mathcal {M}}$
that has not yet been indexed in
![]() ${\mathcal {M}}$
(see The Eventual Certification above). In particular, without extra assumptions, it may be the case that given a
${\mathcal {M}}$
(see The Eventual Certification above). In particular, without extra assumptions, it may be the case that given a
![]() $\Lambda $
-sts mouse
$\Lambda $
-sts mouse
![]() ${\mathcal {M}}{\vDash } \mathsf {ZFC}$
,
${\mathcal {M}}{\vDash } \mathsf {ZFC}$
,
![]() $\Lambda {\restriction } {\mathcal {M}}$
is not definable over
$\Lambda {\restriction } {\mathcal {M}}$
is not definable over
![]() ${\mathcal {M}}$
. Clearly, such definability holds for many strategy mice.
${\mathcal {M}}$
. Clearly, such definability holds for many strategy mice.
The above issue becomes somewhat of a problem when dealing with generic interpretability, which is the statement that the internal strategy predicate can be uniquely extended onto generic extensions. For ordinary strategy mice, generic interpretability is, in general, easier to prove. For short-tree-strategy mice, the situation is somewhat parallel to the above anomaly. Suppose
![]() ${\mathcal {M}}$
is a
${\mathcal {M}}$
is a
![]() $\Lambda $
-mouse where
$\Lambda $
-mouse where
![]() $\Lambda $
is a short-tree strategy and suppose g is
$\Lambda $
is a short-tree strategy and suppose g is
![]() ${\mathcal {M}}$
-generic. In general, we cannot hope to prove that
${\mathcal {M}}$
-generic. In general, we cannot hope to prove that
![]() $\Lambda {\restriction } {\mathcal {M}}[g]$
is definable over
$\Lambda {\restriction } {\mathcal {M}}[g]$
is definable over
![]() ${\mathcal {M}}[g]$
. In this subsection, we introduce some properties of short-tree strategies that allow us to prove generic interpretability, albeit in a somewhat weaker sense.
${\mathcal {M}}[g]$
. In this subsection, we introduce some properties of short-tree strategies that allow us to prove generic interpretability, albeit in a somewhat weaker sense.
The most important concept that is behind most arguments of [Reference Sargsyan and Trang38] is the concept of branch condensation (see [Reference Sargsyan and Trang38, Chapter 4.9]). It is very possible that the concept of full normalization introduced in [Reference Steel55] can be used instead of branch condensation to obtain a greater generality. In fact, the authors have recently discovered a new notion of a short-tree-strategy mouse utilizing full normalization.
Branch condensation implies generic interpretability. The following is our generic interpretability theorem, which is essentially [Reference Sargsyan and Trang38, Theorem 6.1.5]. The aforementioned theorem is stated for strategies with branch condensation that are associated with a pointclass
![]() $\Gamma $
. Here, we need strategies whose association with pointclasses is a consequence of some abstract properties that it has, not something explicitly assumed about them. Such strategies can be obtained working inside a model of determinacy. The specific properties that we need are the following properties:
$\Gamma $
. Here, we need strategies whose association with pointclasses is a consequence of some abstract properties that it has, not something explicitly assumed about them. Such strategies can be obtained working inside a model of determinacy. The specific properties that we need are the following properties:
-
1. hull condensation,
-
2. strong branch condensation,
-
3. branch condensation for pull-backs.
The meaning of clause 3 above is as follows. Suppose
![]() $({\mathcal {P}}, \Lambda )$
is an sts hod pair.
$({\mathcal {P}}, \Lambda )$
is an sts hod pair.
![]() $\Lambda $
has branch condensation for pullbacks if whenever
$\Lambda $
has branch condensation for pullbacks if whenever
![]() $\xi \in {\mathcal {P}}$
is a limit of Woodin cardinals of
$\xi \in {\mathcal {P}}$
is a limit of Woodin cardinals of
![]() ${\mathcal {P}}$
such that
${\mathcal {P}}$
such that
![]() ${\mathcal {P}}{\vDash } \text {`}{\mathrm cf}(\xi )=\omega '$
and
${\mathcal {P}}{\vDash } \text {`}{\mathrm cf}(\xi )=\omega '$
and
![]() $\pi :{\mathcal {Q}}\rightarrow {\mathcal {P}}|\xi $
is elementary, the
$\pi :{\mathcal {Q}}\rightarrow {\mathcal {P}}|\xi $
is elementary, the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Lambda _{{\mathcal {P}}|\xi }$
has branch condensation. For more on branch condensation, the reader may consult [Reference Sargsyan and Trang38, Chapter 4.9].
$\Lambda _{{\mathcal {P}}|\xi }$
has branch condensation. For more on branch condensation, the reader may consult [Reference Sargsyan and Trang38, Chapter 4.9].
Definition 2.3. We say that a short-tree strategy is splendid if it satisfies the above 3 properties.
Clause 3 above implies that the pullback of splendid strategies are splendid.Footnote 44 It might help to consult Remark 2.2 before reading the next theorem.
Theorem 2.4. Suppose
![]() ${\mathcal {P}}$
is an lsa type hod premouse and
${\mathcal {P}}$
is an lsa type hod premouse and
![]() $\Lambda $
is a splendid short-tree strategy for
$\Lambda $
is a splendid short-tree strategy for
![]() ${\mathcal {P}}$
. Suppose
${\mathcal {P}}$
. Suppose
![]() ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
![]() $\Lambda $
-premouse satisfying
$\Lambda $
-premouse satisfying
![]() $\mathsf {ZFC}$
and that
$\mathsf {ZFC}$
and that
![]() ${\mathcal {N}}$
has unboundedly many Woodin cardinals. Then for any
${\mathcal {N}}$
has unboundedly many Woodin cardinals. Then for any
![]() ${\mathcal {N}}$
-generic g,
${\mathcal {N}}$
-generic g,
![]() $\Psi =_{def}S^{\mathcal {N}}$
has a unique extension
$\Psi =_{def}S^{\mathcal {N}}$
has a unique extension
![]() $\Psi ^g\subseteq {\mathcal {N}}[g]$
that is definable from
$\Psi ^g\subseteq {\mathcal {N}}[g]$
that is definable from
![]() $\Psi $
over
$\Psi $
over
![]() ${\mathcal {N}}[g]$
and
${\mathcal {N}}[g]$
and
![]() $b(\Psi ^g)\subseteq b(\Lambda ){\restriction } {\mathcal {N}}[g]$
.
$b(\Psi ^g)\subseteq b(\Lambda ){\restriction } {\mathcal {N}}[g]$
.
Our Theorem 2.4 is weaker than [Reference Sargsyan and Trang38, Theorem 6.1.4]. The conclusion of the aforementioned theorem is that
![]() $\Psi ^g=\Lambda {\restriction } {\mathcal {N}}[g]$
. However, in [Reference Sargsyan and Trang38, Theorem 6.1.4],
$\Psi ^g=\Lambda {\restriction } {\mathcal {N}}[g]$
. However, in [Reference Sargsyan and Trang38, Theorem 6.1.4],
![]() ${\mathcal {N}}$
satisfies a strong iterability hypothesis. Without this iterability hypothesis,
${\mathcal {N}}$
satisfies a strong iterability hypothesis. Without this iterability hypothesis,
![]() $b(\Psi ^g)\subseteq b(\Lambda ){\restriction } {\mathcal {N}}[g]$
is all the proof that [Reference Sargsyan and Trang38, Theorem 6.1.4] gives.
$b(\Psi ^g)\subseteq b(\Lambda ){\restriction } {\mathcal {N}}[g]$
is all the proof that [Reference Sargsyan and Trang38, Theorem 6.1.4] gives.
In the next subsection, we will introduce a type of short-tree-strategy mouse that we will use to establish Theorem 1.4.
2.4. Excellent hod premice
Our proof of Theorem 1.4 is an example of how one can translate set theoretic strength from one set of principles to another set of principles by using inner model theoretic objects as intermediaries. Below, we introduce the notion of an excellent hybrid premouse. We will then use this notion to show that both
![]() $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
hold in a generic extension of an excellent hybrid premouse. Conversely, we will show that in any model of either
$\mathsf {LSA-over-uB}$
hold in a generic extension of an excellent hybrid premouse. Conversely, we will show that in any model of either
![]() $\mathsf {Sealing}$
or
$\mathsf {Sealing}$
or
![]() $\mathsf {LSA-over-uB}$
, there is an excellent hybrid premouse. We start by introducing some terminology and then introduce the excellent hybrid premice.
$\mathsf {LSA-over-uB}$
, there is an excellent hybrid premouse. We start by introducing some terminology and then introduce the excellent hybrid premice.
Remark 2.5. Below and elsewhere, when discussing iterability, we usually mean with respect to the extender sequence of the structures in consideration. Sometimes our definitions will be stated with no reference to such an extender sequence, but these definitions will always be applied in contexts where there is a distinguished extender sequence.
To state our generic interpretability results, we need to introduce a form of self-iterability – namely, window-based self-iterability. We say that
![]() $[\nu , {\delta }]$
is a window if there are no Woodin cardinals in the interval
$[\nu , {\delta }]$
is a window if there are no Woodin cardinals in the interval
![]() $(\nu , {\delta })$
. Given a window w, we let
$(\nu , {\delta })$
. Given a window w, we let
![]() $\nu ^w$
and
$\nu ^w$
and
![]() ${\delta }^w$
be such that
${\delta }^w$
be such that
![]() $w=[\nu ^w, {\delta }^w]$
. We say that a window w is above
$w=[\nu ^w, {\delta }^w]$
. We say that a window w is above
![]() ${\kappa }$
if
${\kappa }$
if
![]() $\nu ^w\geq {\kappa }$
. We say that a window w is not overlapped if there is no
$\nu ^w\geq {\kappa }$
. We say that a window w is not overlapped if there is no
![]() $\nu ^w$
-strong cardinal. We say w is maximal if
$\nu ^w$
-strong cardinal. We say w is maximal if
![]() $\nu ^w=\sup \{{\alpha }+1: {\alpha }<\nu ^w$
is a Woodin cardinal
$\nu ^w=\sup \{{\alpha }+1: {\alpha }<\nu ^w$
is a Woodin cardinal
![]() $\}$
and
$\}$
and
![]() ${\delta }^w$
is a Woodin cardinal.
${\delta }^w$
is a Woodin cardinal.
Window-Based Self-Iterability. Suppose
![]() ${\kappa }$
is a cardinal. We say
${\kappa }$
is a cardinal. We say
![]() $\mathsf {WBSI}$
holds at
$\mathsf {WBSI}$
holds at
![]() ${\kappa }$
if for any window w that is above
${\kappa }$
if for any window w that is above
![]() ${\kappa }$
and for any successor cardinal
${\kappa }$
and for any successor cardinal
![]() $\eta \in (\nu ^w, {\delta }^w)$
, setting
$\eta \in (\nu ^w, {\delta }^w)$
, setting
![]() $Q= H_{\eta ^+}$
, Q has an
$Q= H_{\eta ^+}$
, Q has an
![]() $Ord$
-iteration strategy
$Ord$
-iteration strategy
![]() $\Sigma $
which acts on iterations that only use extenders with critical points
$\Sigma $
which acts on iterations that only use extenders with critical points
![]() $>\nu ^w$
.
$>\nu ^w$
.
One usually says that Q is
![]() $Ord$
-iterable above
$Ord$
-iterable above
![]() $\nu ^w$
to mean exactly what is written above.
$\nu ^w$
to mean exactly what is written above.
Definition 2.6. We let
![]() $T_0$
be the conjunction of the following statements.
$T_0$
be the conjunction of the following statements.
-
1.
 $\mathsf {ZFC}$
.
$\mathsf {ZFC}$
. -
2. There are unboundedly many Woodin cardinals.
-
3. The class of measurable cardinals is stationary.
-
4. No measurable cardinal that is a limit of Woodin cardinals carries a normal ultrafilter concentrating on the set of measurable cardinals.
When we write
![]() $M{\vDash } T_0$
and M has a distinguished extender sequence, then we make the tacit assumption that the large cardinals and specific ultrafilters mentioned in Definition 2.6 are witnessed by extenders on the sequence of M.
$M{\vDash } T_0$
and M has a distinguished extender sequence, then we make the tacit assumption that the large cardinals and specific ultrafilters mentioned in Definition 2.6 are witnessed by extenders on the sequence of M.
Definition 2.7. Suppose
![]() ${\mathcal {P}}$
is hybrid premouse. We say that
${\mathcal {P}}$
is hybrid premouse. We say that
![]() ${\mathcal {P}}$
is almost excellent if
${\mathcal {P}}$
is almost excellent if
-
1.
 ${\mathcal {P}}{\vDash } T_0$
.
${\mathcal {P}}{\vDash } T_0$
. -
2. There is a Woodin cardinal
 ${\delta }$
of
${\delta }$
of
 ${\mathcal {P}}$
such that
${\mathcal {P}}$
such that
 ${\mathcal {P}}{\vDash } \text {`}{\mathcal {P}}_0=_{def}({\mathcal {P}}|{\delta })^{\#}$
is a hod premouse of
${\mathcal {P}}{\vDash } \text {`}{\mathcal {P}}_0=_{def}({\mathcal {P}}|{\delta })^{\#}$
is a hod premouse of
 $\#$
-lsa type’,
$\#$
-lsa type’,
 ${\mathcal {P}}$
is an sts premouse based on
${\mathcal {P}}$
is an sts premouse based on
 ${\mathcal {P}}_0$
and
${\mathcal {P}}_0$
and
 ${\mathcal {P}}{\vDash } \text {`}S^{\mathcal {P}}$
, which is a short-tree strategy for
${\mathcal {P}}{\vDash } \text {`}S^{\mathcal {P}}$
, which is a short-tree strategy for
 ${\mathcal {P}}_0$
, is splendid’.
${\mathcal {P}}_0$
, is splendid’. -
3. Given any
 $\tau <{\delta }^{{\mathcal {P}}_0}$
such that
$\tau <{\delta }^{{\mathcal {P}}_0}$
such that
 $({\mathcal {P}}_0|\tau )^{\#}$
is of
$({\mathcal {P}}_0|\tau )^{\#}$
is of
 $\#$
-lsa type, there is
$\#$
-lsa type, there is
 ${\mathcal {M}}{\trianglelefteq } {\mathcal {P}}$
such that
${\mathcal {M}}{\trianglelefteq } {\mathcal {P}}$
such that
 $\tau $
is a cutpoint of
$\tau $
is a cutpoint of
 ${\mathcal {M}}$
and
${\mathcal {M}}$
and
 ${\mathcal {M}}{\vDash } \text {`}\tau $
is not a Woodin cardinal’.
${\mathcal {M}}{\vDash } \text {`}\tau $
is not a Woodin cardinal’.We say that
 ${\mathcal {P}}$
is excellent if in addition to the above clauses,
${\mathcal {P}}$
is excellent if in addition to the above clauses,
 ${\mathcal {P}}$
satisfies the following:
${\mathcal {P}}$
satisfies the following: -
4. Letting
 ${\delta }$
be as in clause 2,
${\delta }$
be as in clause 2,
 ${\mathcal {P}}{\vDash } \text {`}\mathsf {WBSI}$
holds at
${\mathcal {P}}{\vDash } \text {`}\mathsf {WBSI}$
holds at
 ${\delta }$
’.
${\delta }$
’.
If
![]() ${\mathcal {P}}$
is excellent, then we let
${\mathcal {P}}$
is excellent, then we let
![]() ${\delta }^{\mathcal {P}}$
be the
${\delta }^{\mathcal {P}}$
be the
![]() ${\delta }$
of clause 2 above and
${\delta }$
of clause 2 above and
![]() ${\mathcal {P}}_0=(({\mathcal {P}}|{\delta }^{\mathcal {P}})^\#)^{\mathcal {P}}$
.
${\mathcal {P}}_0=(({\mathcal {P}}|{\delta }^{\mathcal {P}})^\#)^{\mathcal {P}}$
.
Remark 2.8. In the previous subsection, we were mainly concerned with the structure of hod mice associated with the minimal model of
![]() $\mathsf {LSA}$
. An excellent hybrid premouse is beyond the minimal model of
$\mathsf {LSA}$
. An excellent hybrid premouse is beyond the minimal model of
![]() $\mathsf {LSA}$
. Indeed, the arguments used in the proofs of [Reference Sargsyan and Trang38, Lemma 8.1.10 and Theorem 8.2.6] apply to show that if
$\mathsf {LSA}$
. Indeed, the arguments used in the proofs of [Reference Sargsyan and Trang38, Lemma 8.1.10 and Theorem 8.2.6] apply to show that if
![]() ${\mathcal {P}}$
is excellent and
${\mathcal {P}}$
is excellent and
![]() ${\lambda }>{\delta }^{\mathcal {P}}$
is a limit of Woodin cardinals of
${\lambda }>{\delta }^{\mathcal {P}}$
is a limit of Woodin cardinals of
![]() ${\mathcal {P}}$
, then the (new) derived model at
${\mathcal {P}}$
, then the (new) derived model at
![]() ${\lambda }$
is a model of
${\lambda }$
is a model of
![]() $\mathsf {LSA}$
. It follows from a standard Skolem hull argument and the derived model theorem that there is
$\mathsf {LSA}$
. It follows from a standard Skolem hull argument and the derived model theorem that there is
![]() $A\in {\wp }({\mathbb {R}}^{\mathcal {P}})\cap {\mathcal {P}}$
such that
$A\in {\wp }({\mathbb {R}}^{\mathcal {P}})\cap {\mathcal {P}}$
such that
![]() $L(A, {\mathbb {R}}^{\mathcal {P}}){\vDash } \mathsf {LSA}$
.
$L(A, {\mathbb {R}}^{\mathcal {P}}){\vDash } \mathsf {LSA}$
.
Nevertheless, everything that we have said in the previous subsection about short-tree strategies and sts mice carries over to the level of excellent hybrid mice. The methods of [Reference Sargsyan and Trang38] work through the tame Footnote 45 hod mice. The authors recently have discovered a new sts indexing scheme that works for arbitrary hod mice. This work is not relevant to the current work as the indexing of [Reference Sargsyan and Trang38] just carries over verbatim.
For the rest of this paper, we assume the following minimality hypothesis
![]() $\neg (\dagger )$
, where
$\neg (\dagger )$
, where
![]() $(\dagger ):$
In some generic extension, there is a (possibly class-sized) excellent hybrid premouse.
$(\dagger ):$
In some generic extension, there is a (possibly class-sized) excellent hybrid premouse.
We will periodically remind the reader of this. One consequence of this assumption is the following fact, which roughly says that all local non-Woodin cardinals of a hod premouse (or hybrid premouse) are witnessed by
![]() ${\mathcal {Q}}$
-structures which are initial segments of the model and are tame. It also shows that if
${\mathcal {Q}}$
-structures which are initial segments of the model and are tame. It also shows that if
![]() ${\mathcal {P}}$
is a hod mouse such that there is an lsa initial segment
${\mathcal {P}}$
is a hod mouse such that there is an lsa initial segment
![]() ${\mathcal {P}}_0$
of
${\mathcal {P}}_0$
of
![]() ${\mathcal {P}}$
and there is a Woodin cardinal
${\mathcal {P}}$
and there is a Woodin cardinal
![]() $\delta> o({\mathcal {P}}_0)$
inside
$\delta> o({\mathcal {P}}_0)$
inside
![]() ${\mathcal {P}}$
, then we can construct an excellent hybrid premouse in
${\mathcal {P}}$
, then we can construct an excellent hybrid premouse in
![]() ${\mathcal {P}}$
by essentially performing a fully backgrounded sts construction in
${\mathcal {P}}$
by essentially performing a fully backgrounded sts construction in
![]() ${\mathcal {P}}|\delta $
above
${\mathcal {P}}|\delta $
above
![]() ${\mathcal {P}}_0$
(with respect to the short-tree component of
${\mathcal {P}}_0$
(with respect to the short-tree component of
![]() ${\mathcal {P}}_0$
).
${\mathcal {P}}_0$
).
Proposition 2.9 (
 $\neg (\dagger )$
)
$\neg (\dagger )$
)
Suppose
![]() ${\mathcal {P}}$
is a hod premouse. Let
${\mathcal {P}}$
is a hod premouse. Let
![]() $\kappa $
be a measurable limit of Woodin cardinals of
$\kappa $
be a measurable limit of Woodin cardinals of
![]() ${\mathcal {P}}$
and let
${\mathcal {P}}$
and let
![]() $\xi \leq o^{\mathcal {P}}(\kappa )$
. Suppose
$\xi \leq o^{\mathcal {P}}(\kappa )$
. Suppose
![]() $({\mathcal {P}}|\xi )^\#{\vDash } \text {`}\xi $
is a Woodin cardinal’ but either
$({\mathcal {P}}|\xi )^\#{\vDash } \text {`}\xi $
is a Woodin cardinal’ but either
![]() $\xi $
is not the largest Woodin cardinal of
$\xi $
is not the largest Woodin cardinal of
![]() ${\mathcal {P}}$
or
${\mathcal {P}}$
or
![]() $\xi <o^{\mathcal {P}}(\kappa )$
. Then there is
$\xi <o^{\mathcal {P}}(\kappa )$
. Then there is
![]() ${\mathcal {M}}{\trianglelefteq } {\mathcal {P}}$
such that
${\mathcal {M}}{\trianglelefteq } {\mathcal {P}}$
such that
![]() $\xi $
is a cutpoint in
$\xi $
is a cutpoint in
![]() ${\mathcal {M}}$
,
${\mathcal {M}}$
,
![]() $\rho ({\mathcal {M}})\leq \xi $
and
$\rho ({\mathcal {M}})\leq \xi $
and
![]() ${\mathcal {M}}{\vDash } \text {`}\xi $
is not a Woodin cardinal’.
${\mathcal {M}}{\vDash } \text {`}\xi $
is not a Woodin cardinal’.
Proof. Towards a contradiction, assume that there is no such
![]() ${\mathcal {M}}$
. Suppose first that
${\mathcal {M}}$
. Suppose first that
![]() $\xi $
is a Woodin cardinal of
$\xi $
is a Woodin cardinal of
![]() ${\mathcal {P}}$
. It must then be a cutpoint cardinal as otherwise we easily get an excellent hybrid premouse by performing a fully backgrounded construction inside
${\mathcal {P}}$
. It must then be a cutpoint cardinal as otherwise we easily get an excellent hybrid premouse by performing a fully backgrounded construction inside
![]() ${\mathcal {P}}|\kappa $
with respect to the short-tree component of
${\mathcal {P}}|\kappa $
with respect to the short-tree component of
![]() ${\mathcal {P}}_0$
, where
${\mathcal {P}}_0$
, where
![]() ${\mathcal {P}}_0$
is an lsa hod initial segment of
${\mathcal {P}}_0$
is an lsa hod initial segment of
![]() ${\mathcal {P}}|\kappa $
. The existence of
${\mathcal {P}}|\kappa $
. The existence of
![]() ${\mathcal {P}}_0$
follows from the fact that
${\mathcal {P}}_0$
follows from the fact that
![]() $({\mathcal {P}}|\xi )^\sharp $
is an lsa initial segment of
$({\mathcal {P}}|\xi )^\sharp $
is an lsa initial segment of
![]() ${\mathcal {P}}$
and
${\mathcal {P}}$
and
![]() $\xi < o^{\mathcal {P}}(\kappa )$
.
$\xi < o^{\mathcal {P}}(\kappa )$
.
It then follows that there is a Woodin cardinal
![]() $\zeta $
of
$\zeta $
of
![]() ${\mathcal {P}}$
above
${\mathcal {P}}$
above
![]() $\xi $
. Now we can use [Reference Sargsyan and Trang38, Lemma 8.1.4] to build an excellent hybrid premouse via a backgrounded construction of
$\xi $
. Now we can use [Reference Sargsyan and Trang38, Lemma 8.1.4] to build an excellent hybrid premouse via a backgrounded construction of
![]() ${\mathcal {P}}|\zeta $
as above (with respect to the short-tree component of
${\mathcal {P}}|\zeta $
as above (with respect to the short-tree component of
![]() $({\mathcal {P}}|\xi )^\sharp $
).
$({\mathcal {P}}|\xi )^\sharp $
).
Suppose next that
![]() $\xi $
is not a Woodin cardinal. Because no
$\xi $
is not a Woodin cardinal. Because no
![]() ${\mathcal {M}}$
as above exists, it follows that
${\mathcal {M}}$
as above exists, it follows that
![]() $\xi <o^{\mathcal {P}}(\kappa )$
. We can now repeat the above steps in
$\xi <o^{\mathcal {P}}(\kappa )$
. We can now repeat the above steps in
![]() $Ult({\mathcal {P}}, E)$
where E is the least extender overlapping
$Ult({\mathcal {P}}, E)$
where E is the least extender overlapping
![]() $\xi $
.
$\xi $
.
There are a few important facts that we will need about excellent hybrid premice that one can prove by using more or less standard ideas, and that in one form or another have appeared in [Reference Sargsyan and Trang38]. We will use the next subsection recording some of these facts.
2.5. More on self-iterability
Here, we prove that window-based strategy acts on the entire model. The main theorem that we would like to prove is the following.
Theorem 2.10. Suppose
![]() ${\mathcal {P}}$
is an excellent hybrid premouse, w is a maximal window of
${\mathcal {P}}$
is an excellent hybrid premouse, w is a maximal window of
![]() ${\mathcal {P}}$
above
${\mathcal {P}}$
above
![]() ${\delta }^{\mathcal {P}}$
and
${\delta }^{\mathcal {P}}$
and
![]() $\eta \in [\nu ^w, {\delta }^w)$
is a regular cardinal. Let
$\eta \in [\nu ^w, {\delta }^w)$
is a regular cardinal. Let
![]() $\Sigma $
be the
$\Sigma $
be the
![]() $Ord$
-strategy of
$Ord$
-strategy of
![]() ${\mathcal {Q}}={\mathcal {P}}|\eta $
that acts on iterations that are above
${\mathcal {Q}}={\mathcal {P}}|\eta $
that acts on iterations that are above
![]() $\nu ^w$
. Let g be
$\nu ^w$
. Let g be
![]() ${\mathcal {P}}$
-generic for some poset
${\mathcal {P}}$
-generic for some poset
![]() $\mathbb {P}\in {\mathcal {P}}$
. Then
$\mathbb {P}\in {\mathcal {P}}$
. Then
![]() $\Sigma $
has a unique extension
$\Sigma $
has a unique extension
![]() $\Sigma ^g$
definable over
$\Sigma ^g$
definable over
![]() ${\mathcal {P}}[g]$
such that in
${\mathcal {P}}[g]$
such that in
![]() ${\mathcal {P}}[g]$
,
${\mathcal {P}}[g]$
,
![]() $\Sigma ^g$
is an
$\Sigma ^g$
is an
![]() $Ord$
-iteration strategy for
$Ord$
-iteration strategy for
![]() ${\mathcal {P}}$
that acts on iterations that are based on
${\mathcal {P}}$
that acts on iterations that are based on
![]() ${\mathcal {Q}}$
and are above
${\mathcal {Q}}$
and are above
![]() $\nu ^w$
.
$\nu ^w$
.
The proof will be presented as a sequence of lemmas. First we make a few observations. Suppose
![]() ${\mathcal {P}}$
is excellent and for some
${\mathcal {P}}$
is excellent and for some
![]() ${\mathcal {P}}$
-cardinal
${\mathcal {P}}$
-cardinal
![]() $\xi>{\delta }^{\mathcal {P}}$
is a limit of Woodin cardinals of
$\xi>{\delta }^{\mathcal {P}}$
is a limit of Woodin cardinals of
![]() ${\mathcal {P}}$
,
${\mathcal {P}}$
,
![]() $\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
is an elementary embedding in
$\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
is an elementary embedding in
![]() ${\mathcal {P}}$
such that
${\mathcal {P}}$
such that
![]() ${\mathcal {N}}$
is countable. It follows that
${\mathcal {N}}$
is countable. It follows that
![]() $\eta =_{def}\sup (\pi [{\delta }^{\mathcal {N}}])<{\delta }^{\mathcal {P}}$
, and therefore, letting
$\eta =_{def}\sup (\pi [{\delta }^{\mathcal {N}}])<{\delta }^{\mathcal {P}}$
, and therefore, letting
![]() $\Lambda =(\pi $
-pullback of
$\Lambda =(\pi $
-pullback of
![]() $S^{\mathcal {P}}$
),
$S^{\mathcal {P}}$
),
(O1)
![]() ${\mathcal {P}}{\vDash } \text {`}\Lambda ^{stc}$
is a splendid
${\mathcal {P}}{\vDash } \text {`}\Lambda ^{stc}$
is a splendid
![]() $Ord$
-strategy for
$Ord$
-strategy for
![]() ${\mathcal {N}}_0^{\prime }$
,Footnote 46
${\mathcal {N}}_0^{\prime }$
,Footnote 46
(O2)
![]() ${\mathcal {P}}{\vDash } \text {"}{\mathcal {N}}$
is a
${\mathcal {P}}{\vDash } \text {"}{\mathcal {N}}$
is a
![]() $\Lambda ^{stc}$
-premouse.Footnote 47
$\Lambda ^{stc}$
-premouse.Footnote 47
(O3) in
![]() ${\mathcal {P}}$
, Theorem 2.4 applies to
${\mathcal {P}}$
, Theorem 2.4 applies to
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() $\Lambda $
.
$\Lambda $
.
(O4) if
![]() $i:{\mathcal {N}}\rightarrow {\mathcal {N}}_1$
is such that
$i:{\mathcal {N}}\rightarrow {\mathcal {N}}_1$
is such that
![]() $\mathrm {crit }(i)>{\delta }^{\mathcal {N}}$
, and for some
$\mathrm {crit }(i)>{\delta }^{\mathcal {N}}$
, and for some
![]() $\sigma :{\mathcal {N}}_1\rightarrow {\mathcal {P}}|\xi $
,
$\sigma :{\mathcal {N}}_1\rightarrow {\mathcal {P}}|\xi $
,
![]() $\pi =\sigma \circ i$
, then
$\pi =\sigma \circ i$
, then
![]() ${\mathcal {N}}_1$
is a
${\mathcal {N}}_1$
is a
![]() $\Lambda ^{stc}$
-premouse.
$\Lambda ^{stc}$
-premouse.
(O4) will be key in many arguments in this paper, but often we will ignore stating it for the sake of succinctness. In each case, however, the reader can easily find the realizable embeddings. The reason (O4) is important is that without, it we cannot really prove any self-iterability results, as if iterating
![]() ${\mathcal {N}}$
above destroyed the fact that the resulting premouse is a
${\mathcal {N}}$
above destroyed the fact that the resulting premouse is a
![]() $\Lambda ^{stc}$
-premouse. Then we could not find the relevant
$\Lambda ^{stc}$
-premouse. Then we could not find the relevant
![]() ${\mathcal {Q}}$
-structures using
${\mathcal {Q}}$
-structures using
![]() $\Lambda $
or comparison techniques.
$\Lambda $
or comparison techniques.
Lemma 2.11. Suppose
![]() ${\mathcal {P}}$
is an excellent hybrid premouse, w is a maximal window of
${\mathcal {P}}$
is an excellent hybrid premouse, w is a maximal window of
![]() ${\mathcal {P}}$
above
${\mathcal {P}}$
above
![]() ${\delta }^{\mathcal {P}}$
and
${\delta }^{\mathcal {P}}$
and
![]() $\eta \in [\nu ^w, {\delta }^w)$
is a regular cardinal. Let
$\eta \in [\nu ^w, {\delta }^w)$
is a regular cardinal. Let
![]() $\Sigma $
be the
$\Sigma $
be the
![]() $Ord$
-strategy of
$Ord$
-strategy of
![]() ${\mathcal {Q}}={\mathcal {P}}|\eta $
that acts on iterations that are above
${\mathcal {Q}}={\mathcal {P}}|\eta $
that acts on iterations that are above
![]() $\nu ^w$
. Then
$\nu ^w$
. Then
![]() $\Sigma $
is an
$\Sigma $
is an
![]() $Ord$
-iteration strategy for
$Ord$
-iteration strategy for
![]() ${\mathcal {P}}$
that acts on iterations that are based on
${\mathcal {P}}$
that acts on iterations that are based on
![]() ${\mathcal {Q}}$
and are above
${\mathcal {Q}}$
and are above
![]() $\nu ^w$
.
$\nu ^w$
.
Proof. We set
![]() $V={\mathcal {P}}$
. Suppose
$V={\mathcal {P}}$
. Suppose
![]() ${\mathcal {T}}$
is an iteration tree on
${\mathcal {T}}$
is an iteration tree on
![]() ${\mathcal {Q}}$
according to
${\mathcal {Q}}$
according to
![]() $\Sigma $
. We can then naturally regard
$\Sigma $
. We can then naturally regard
![]() ${\mathcal {T}}$
as a tree on
${\mathcal {T}}$
as a tree on
![]() ${\mathcal {P}}$
. We claim that all the models of this tree are well founded. Towards a contradiction, assume not. Fix an inaccessible
${\mathcal {P}}$
. We claim that all the models of this tree are well founded. Towards a contradiction, assume not. Fix an inaccessible
![]() $\xi>{\delta }^w$
such that when regarding
$\xi>{\delta }^w$
such that when regarding
![]() ${\mathcal {T}}$
as a tree on
${\mathcal {T}}$
as a tree on
![]() ${\mathcal {P}}|\xi $
, some model of it is ill founded. Let
${\mathcal {P}}|\xi $
, some model of it is ill founded. Let
![]() ${\mathcal {T}}^+$
be the result of applying
${\mathcal {T}}^+$
be the result of applying
![]() ${\mathcal {T}}$
to
${\mathcal {T}}$
to
![]() ${\mathcal {P}}|\xi $
, and let
${\mathcal {P}}|\xi $
, and let
![]() $\pi : {\mathcal {M}}\rightarrow {\mathcal {P}}|\xi $
be such that
$\pi : {\mathcal {M}}\rightarrow {\mathcal {P}}|\xi $
be such that
-
1.
 $w, {\mathcal {T}}^+ \in rng(\pi )$
,
$w, {\mathcal {T}}^+ \in rng(\pi )$
, -
2.
 ${\vert {\mathcal {M}}\vert }=\eta $
, and
${\vert {\mathcal {M}}\vert }=\eta $
, and -
3.
 $\mathrm {crit }(\pi )>\eta $
.
$\mathrm {crit }(\pi )>\eta $
.
Let
![]() ${\mathcal {U}}=\pi ^{-1}({\mathcal {T}})$
and
${\mathcal {U}}=\pi ^{-1}({\mathcal {T}})$
and
![]() ${\mathcal {U}}^+=\pi ^{-1}({\mathcal {T}}^+)$
. We thus have that some model of
${\mathcal {U}}^+=\pi ^{-1}({\mathcal {T}}^+)$
. We thus have that some model of
![]() ${\mathcal {U}}^+$
is ill founded.
${\mathcal {U}}^+$
is ill founded.
Let
![]() ${\mathcal {R}}={\mathcal {P}}|\eta ^+$
and let
${\mathcal {R}}={\mathcal {P}}|\eta ^+$
and let
![]() ${\mathcal {U}}^{\mathcal {R}}$
be the result of applying
${\mathcal {U}}^{\mathcal {R}}$
be the result of applying
![]() ${\mathcal {U}}$
to
${\mathcal {U}}$
to
![]() ${\mathcal {R}}$
. Notice that
${\mathcal {R}}$
. Notice that
![]() ${\mathcal {M}}\in {\mathcal {R}}$
. Because
${\mathcal {M}}\in {\mathcal {R}}$
. Because
![]() ${\mathcal {P}}$
has no Woodin cardinals in the interval
${\mathcal {P}}$
has no Woodin cardinals in the interval
![]() $(\nu ^w, \eta ^+)$
, we have that
$(\nu ^w, \eta ^+)$
, we have that
![]() ${\mathcal {U}}^{\mathcal {R}}$
is according to any
${\mathcal {U}}^{\mathcal {R}}$
is according to any
![]() $Ord$
-strategy of
$Ord$
-strategy of
![]() ${\mathcal {R}}$
. Thus,
${\mathcal {R}}$
. Thus,
![]() ${\mathcal {U}}^{\mathcal {R}}$
only has well-founded models. It is not hard to show, however, that for each
${\mathcal {U}}^{\mathcal {R}}$
only has well-founded models. It is not hard to show, however, that for each
![]() ${\alpha }<lh({\mathcal {U}})$
, if
${\alpha }<lh({\mathcal {U}})$
, if
![]() $[0, {\alpha }]_{\mathcal {U}}\cap \mathcal {D}^{\mathcal {U}}=\emptyset $
, then there is an elementary embedding
$[0, {\alpha }]_{\mathcal {U}}\cap \mathcal {D}^{\mathcal {U}}=\emptyset $
, then there is an elementary embedding
![]() $\sigma _{\alpha }:{\mathcal {M}}_{\alpha }^{{\mathcal {U}}^+}\rightarrow \pi ^{{\mathcal {U}}^{\mathcal {R}}}_{0, {\alpha }}({\mathcal {M}})$
. In the case
$\sigma _{\alpha }:{\mathcal {M}}_{\alpha }^{{\mathcal {U}}^+}\rightarrow \pi ^{{\mathcal {U}}^{\mathcal {R}}}_{0, {\alpha }}({\mathcal {M}})$
. In the case
![]() $[0, {\alpha }]_{\mathcal {U}}\cap \mathcal {D}^{\mathcal {U}}\not =\emptyset $
,
$[0, {\alpha }]_{\mathcal {U}}\cap \mathcal {D}^{\mathcal {U}}\not =\emptyset $
,
![]() ${\mathcal {M}}_{\alpha }^{{\mathcal {U}}^+}={\mathcal {M}}_{\alpha }^{\mathcal {U}}={\mathcal {M}}_{\alpha }^{{\mathcal {U}}^{\mathcal {R}}}$
.
${\mathcal {M}}_{\alpha }^{{\mathcal {U}}^+}={\mathcal {M}}_{\alpha }^{\mathcal {U}}={\mathcal {M}}_{\alpha }^{{\mathcal {U}}^{\mathcal {R}}}$
.
In fact, more is true.
Lemma 2.12. Suppose
![]() ${\mathcal {P}}$
is an excellent hybrid premouse, w is a maximal window of
${\mathcal {P}}$
is an excellent hybrid premouse, w is a maximal window of
![]() ${\mathcal {P}}$
above
${\mathcal {P}}$
above
![]() ${\delta }^{\mathcal {P}}$
and
${\delta }^{\mathcal {P}}$
and
![]() $\eta \in [\nu ^w, {\delta }^w)$
is a regular cardinal. Let
$\eta \in [\nu ^w, {\delta }^w)$
is a regular cardinal. Let
![]() $\Sigma $
be the
$\Sigma $
be the
![]() $Ord$
-strategy of
$Ord$
-strategy of
![]() ${\mathcal {Q}}={\mathcal {P}}|\eta $
that acts on iterations that are above
${\mathcal {Q}}={\mathcal {P}}|\eta $
that acts on iterations that are above
![]() $\nu ^w$
. Let
$\nu ^w$
. Let
![]() $\mathbb {P}\in {\mathcal {P}}$
be a poset and
$\mathbb {P}\in {\mathcal {P}}$
be a poset and
![]() $g\subseteq \mathbb {P}$
be
$g\subseteq \mathbb {P}$
be
![]() ${\mathcal {P}}$
-generic. Then
${\mathcal {P}}$
-generic. Then
![]() $\Sigma $
has a unique extension
$\Sigma $
has a unique extension
![]() $\Sigma ^g$
definable over
$\Sigma ^g$
definable over
![]() ${\mathcal {P}}[g]$
such that in
${\mathcal {P}}[g]$
such that in
![]() ${\mathcal {P}}[g]$
,
${\mathcal {P}}[g]$
,
![]() $\Sigma ^g$
is an
$\Sigma ^g$
is an
![]() $Ord$
-iteration strategy for
$Ord$
-iteration strategy for
![]() ${\mathcal {Q}}$
acting on iterations that are above
${\mathcal {Q}}$
acting on iterations that are above
![]() $\nu ^w$
.
$\nu ^w$
.
Moreover, in
![]() ${\mathcal {P}}[g]$
,
${\mathcal {P}}[g]$
,
![]() $\Sigma ^g$
can be regarded as an
$\Sigma ^g$
can be regarded as an
![]() $Ord$
-iteration strategy for
$Ord$
-iteration strategy for
![]() ${\mathcal {P}}$
that acts on iterations that are based on
${\mathcal {P}}$
that acts on iterations that are based on
![]() ${\mathcal {Q}}$
and are above
${\mathcal {Q}}$
and are above
![]() $\nu ^w$
.Footnote 48
$\nu ^w$
.Footnote 48
Proof. The proof is by now a standard argument in descriptive inner model theory. It has appeared in several publications. For example, the reader can consult the proof of [Reference Sargsyan34, Lemma 3.9 and Theorem 3.10] or [Reference Sargsyan37, Proposition 1.4-1.7]. We will only give an outline of the proof.
Fix
![]() $\zeta $
such that
$\zeta $
such that
![]() $\mathbb {P}\in {\mathcal {P}}|\zeta $
. Fix now a maximal window v such that
$\mathbb {P}\in {\mathcal {P}}|\zeta $
. Fix now a maximal window v such that
![]() $\nu ^v>\max (\zeta , \nu ^w)$
. Let
$\nu ^v>\max (\zeta , \nu ^w)$
. Let
![]() $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\Omega )$
be the output of the fully background
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\Omega )$
be the output of the fully background
![]() $S^{\mathcal {P}}$
-construction done over
$S^{\mathcal {P}}$
-construction done over
![]() ${\mathcal {P}}|\nu ^w$
with critical point
${\mathcal {P}}|\nu ^w$
with critical point
![]() $>\nu ^v$
. Because
$>\nu ^v$
. Because
![]() $\Sigma $
is an
$\Sigma $
is an
![]() $Ord$
-strategy, we must have a
$Ord$
-strategy, we must have a
![]() $\xi <\Omega $
such that
$\xi <\Omega $
such that
![]() ${\mathcal {N}}_{\xi }$
is a normal iterate of
${\mathcal {N}}_{\xi }$
is a normal iterate of
![]() ${\mathcal {Q}}$
via an iteration
${\mathcal {Q}}$
via an iteration
![]() ${\mathcal {T}}$
that is according to
${\mathcal {T}}$
that is according to
![]() $\Sigma $
and is such that the iteration embedding
$\Sigma $
and is such that the iteration embedding
![]() $\pi ^{\mathcal {T}}:{\mathcal {Q}}\rightarrow {\mathcal {N}}_{\xi }$
is defined.Footnote 49
$\pi ^{\mathcal {T}}:{\mathcal {Q}}\rightarrow {\mathcal {N}}_{\xi }$
is defined.Footnote 49
Assume now that we have determined that an iteration
![]() ${\mathcal {U}}\in {\mathcal {P}}|\nu ^v[g]$
of
${\mathcal {U}}\in {\mathcal {P}}|\nu ^v[g]$
of
![]() ${\mathcal {Q}}$
is according to
${\mathcal {Q}}$
is according to
![]() $\Sigma ^g$
and has limit length. For simplicity, let us assume
$\Sigma ^g$
and has limit length. For simplicity, let us assume
![]() ${\mathcal {U}}$
has no drops. We want to describe
${\mathcal {U}}$
has no drops. We want to describe
![]() $\Sigma ^g({\mathcal {U}})$
. Set
$\Sigma ^g({\mathcal {U}})$
. Set
![]() $\Sigma ^g({\mathcal {U}})=b$
if and only if there is
$\Sigma ^g({\mathcal {U}})=b$
if and only if there is
![]() $\sigma :{\mathcal {M}}^{\mathcal {U}}_b\rightarrow {\mathcal {N}}_{\xi }$
such that
$\sigma :{\mathcal {M}}^{\mathcal {U}}_b\rightarrow {\mathcal {N}}_{\xi }$
such that
![]() $\pi ^{\mathcal {T}}=\sigma \circ \pi ^{\mathcal {U}}_b$
. To show that this works, we need to show that there is a unique branch b with the desired property. Such a branch b is called
$\pi ^{\mathcal {T}}=\sigma \circ \pi ^{\mathcal {U}}_b$
. To show that this works, we need to show that there is a unique branch b with the desired property. Such a branch b is called
![]() $\pi ^{\mathcal {T}}$
-realizable.
$\pi ^{\mathcal {T}}$
-realizable.
Towards a contradiction, assume that either there is no such branch or there are two. Let
![]() ${\lambda }=(({\delta }^v)^{+2})^{\mathcal {P}}$
. Let now
${\lambda }=(({\delta }^v)^{+2})^{\mathcal {P}}$
. Let now
![]() $\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|{\lambda }$
be a pointwise definable countable hull of
$\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|{\lambda }$
be a pointwise definable countable hull of
![]() ${\mathcal {P}}|{\lambda }$
. It follows that we can find a maximal window u of
${\mathcal {P}}|{\lambda }$
. It follows that we can find a maximal window u of
![]() ${\mathcal {N}}$
, an
${\mathcal {N}}$
, an
![]() ${\mathcal {N}}$
-regular cardinal
${\mathcal {N}}$
-regular cardinal
![]() $\zeta \in (\nu ^u, {\delta }^u)$
, a partial ordering
$\zeta \in (\nu ^u, {\delta }^u)$
, a partial ordering
![]() $\mathbb {Q}\in {\mathcal {N}}$
and a maximal window z of
$\mathbb {Q}\in {\mathcal {N}}$
and a maximal window z of
![]() ${\mathcal {N}}$
such that
${\mathcal {N}}$
such that
-
1.
 $\mathbb {Q}\in {\mathcal {N}}|\nu ^z$
,
$\mathbb {Q}\in {\mathcal {N}}|\nu ^z$
, -
2. for some
 ${\mathcal {W}}$
that is a model appearing in the fully backgrounded construction of
${\mathcal {W}}$
that is a model appearing in the fully backgrounded construction of
 ${\mathcal {N}}|{\delta }^z$
done over
${\mathcal {N}}|{\delta }^z$
done over
 ${\mathcal {N}}|\nu ^u$
with respect to
${\mathcal {N}}|\nu ^u$
with respect to
 $S^{\mathcal {N}}$
using extenders with critical points
$S^{\mathcal {N}}$
using extenders with critical points
 $>\nu ^z$
, there is an iteration
$>\nu ^z$
, there is an iteration
 ${\mathcal { K}}\in {\mathcal {N}}$
on
${\mathcal { K}}\in {\mathcal {N}}$
on
 ${\mathcal {R}}=_{def}{\mathcal {N}}|\zeta $
with last model
${\mathcal {R}}=_{def}{\mathcal {N}}|\zeta $
with last model
 ${\mathcal {W}}$
such that
${\mathcal {W}}$
such that
 $\pi ^{\mathcal { K}}$
is defined,
$\pi ^{\mathcal { K}}$
is defined, -
3. some condition
 $q\in \mathbb {Q}$
forces that whenever
$q\in \mathbb {Q}$
forces that whenever
 $h\subseteq \mathbb {Q}$
is
$h\subseteq \mathbb {Q}$
is
 ${\mathcal {N}}$
-generic, there is an iteration
${\mathcal {N}}$
-generic, there is an iteration
 ${\mathcal {X}}\in ({\mathcal {N}}|\nu ^z)[h]$
of
${\mathcal {X}}\in ({\mathcal {N}}|\nu ^z)[h]$
of
 ${\mathcal {R}}$
with no drops such that either there is no
${\mathcal {R}}$
with no drops such that either there is no
 $\pi ^{\mathcal { K}}$
-realizable branch or there are at least two
$\pi ^{\mathcal { K}}$
-realizable branch or there are at least two
 $\pi ^{\mathcal { K}}$
-realizable branches.
$\pi ^{\mathcal { K}}$
-realizable branches.
Let
![]() $h\in {\mathcal {P}}$
be
$h\in {\mathcal {P}}$
be
![]() ${\mathcal {N}}$
-generic for
${\mathcal {N}}$
-generic for
![]() $\mathbb {Q}$
. Let
$\mathbb {Q}$
. Let
![]() ${\mathcal {X}}\in ({\mathcal {N}}|\nu ^z)[h]$
be as in clause 3 above. Because
${\mathcal {X}}\in ({\mathcal {N}}|\nu ^z)[h]$
be as in clause 3 above. Because
![]() $\pi ({\mathcal {R}})$
is fully iterable in
$\pi ({\mathcal {R}})$
is fully iterable in
![]() ${\mathcal {P}}$
above
${\mathcal {P}}$
above
![]() $\pi (\nu ^u)$
, we have that
$\pi (\nu ^u)$
, we have that
![]() ${\mathcal {R}}$
is fully iterable in
${\mathcal {R}}$
is fully iterable in
![]() ${\mathcal {P}}$
above
${\mathcal {P}}$
above
![]() $\nu ^u$
. Let b be the branch of
$\nu ^u$
. Let b be the branch of
![]() ${\mathcal {X}}$
according to the strategy of
${\mathcal {X}}$
according to the strategy of
![]() ${\mathcal {R}}$
that is obtained as the
${\mathcal {R}}$
that is obtained as the
![]() $\pi $
-pullback of the strategy of
$\pi $
-pullback of the strategy of
![]() $\pi ({\mathcal {R}})$
(recall that
$\pi ({\mathcal {R}})$
(recall that
![]() $\pi ({\mathcal {R}})$
is iterable as a
$\pi ({\mathcal {R}})$
is iterable as a
![]() $S^{\mathcal {P}}$
-mouse). Because
$S^{\mathcal {P}}$
-mouse). Because
![]() ${\mathcal {R}}$
has no Woodin cardinals above
${\mathcal {R}}$
has no Woodin cardinals above
![]() $\nu ^u$
, we have a largest
$\nu ^u$
, we have a largest
![]() ${\mathcal {S}}{\trianglelefteq } {\mathcal {M}}^{\mathcal {X}}_b$
such that
${\mathcal {S}}{\trianglelefteq } {\mathcal {M}}^{\mathcal {X}}_b$
such that
![]() ${\mathcal {S}}{\vDash } \text {`}{\delta }({\mathcal {X}})$
is a Woodin cardinal’ but
${\mathcal {S}}{\vDash } \text {`}{\delta }({\mathcal {X}})$
is a Woodin cardinal’ but
![]() $rud({\mathcal {S}}){\vDash } \text {`}{\delta }^{\mathcal {X}}$
is not a Woodin cardinal’.
$rud({\mathcal {S}}){\vDash } \text {`}{\delta }^{\mathcal {X}}$
is not a Woodin cardinal’.
We claim that
Claim.
![]() ${\mathcal {S}}\in {\mathcal {N}}[h]$
.
${\mathcal {S}}\in {\mathcal {N}}[h]$
.
Proof. To see this, as
![]() ${\mathcal {N}}$
is closed under
${\mathcal {N}}$
is closed under
![]() $\#$
, we can assume that
$\#$
, we can assume that
![]() ${\mathrm m}^+({\mathcal {X}}){\vDash } \text {`}{\delta }({\mathcal {X}})$
is a Woodin cardinal’. Let
${\mathrm m}^+({\mathcal {X}}){\vDash } \text {`}{\delta }({\mathcal {X}})$
is a Woodin cardinal’. Let
![]() ${\mathcal {V}}={\mathrm m}^+({\mathcal {X}})$
. We now compare
${\mathcal {V}}={\mathrm m}^+({\mathcal {X}})$
. We now compare
![]() ${\mathcal {V}}$
with the construction producing
${\mathcal {V}}$
with the construction producing
![]() ${\mathcal {W}}$
. As
${\mathcal {W}}$
. As
![]() ${\mathcal {W}}$
has no Woodin cardinals above
${\mathcal {W}}$
has no Woodin cardinals above
![]() $\nu ^u$
, we get that there are models
$\nu ^u$
, we get that there are models
![]() ${\mathcal {V}}^*{\trianglelefteq } {\mathcal {V}}^{**}$
appearing on the construction producing
${\mathcal {V}}^*{\trianglelefteq } {\mathcal {V}}^{**}$
appearing on the construction producing
![]() ${\mathcal {W}}$
, a tree
${\mathcal {W}}$
, a tree
![]() ${\mathcal {Y}}$
on
${\mathcal {Y}}$
on
![]() ${\mathcal {V}}$
and a branch c of
${\mathcal {V}}$
and a branch c of
![]() ${\mathcal {Y}}$
such that
${\mathcal {Y}}$
such that
![]() ${\mathcal {V}}^*={\mathcal {M}}^{\mathcal {Y}}_c$
and
${\mathcal {V}}^*={\mathcal {M}}^{\mathcal {Y}}_c$
and
![]() ${\mathcal {V}}^{**}$
is the least model appearing on the construction producing
${\mathcal {V}}^{**}$
is the least model appearing on the construction producing
![]() ${\mathcal {W}}$
such that
${\mathcal {W}}$
such that
![]() ${\mathcal {V}}^{**}{\vDash } \text {`}\pi ^{\mathcal {Y}}_c({\delta }({\mathcal {X}}))$
is a Woodin cardinal’ but
${\mathcal {V}}^{**}{\vDash } \text {`}\pi ^{\mathcal {Y}}_c({\delta }({\mathcal {X}}))$
is a Woodin cardinal’ but
![]() $rud({\mathcal {V}}^{**}){\vDash } \text {`}\pi ^{\mathcal {Y}}_c({\delta }({\mathcal {X}}))$
is not a Woodin cardinal’. It follows that
$rud({\mathcal {V}}^{**}){\vDash } \text {`}\pi ^{\mathcal {Y}}_c({\delta }({\mathcal {X}}))$
is not a Woodin cardinal’. It follows that
![]() ${\mathcal {S}}=Hull_n^{{\mathcal {V}}^{**}}(\{p\}\cup rng(\pi ^{\mathcal {Y}}_c))$
, where n is the fine structural level at which a counterexample to Woodiness of
${\mathcal {S}}=Hull_n^{{\mathcal {V}}^{**}}(\{p\}\cup rng(\pi ^{\mathcal {Y}}_c))$
, where n is the fine structural level at which a counterexample to Woodiness of
![]() ${\delta }({\mathcal {X}})$
can be defined over
${\delta }({\mathcal {X}})$
can be defined over
![]() ${\mathcal {S}}$
and p is the n-th standard parameter of
${\mathcal {S}}$
and p is the n-th standard parameter of
![]() ${\mathcal {V}}^{**}$
. Because
${\mathcal {V}}^{**}$
. Because
![]() ${\mathcal {V}}^{**}, {\mathcal {Y}}, c\in {\mathcal {N}}[h]$
, we have that
${\mathcal {V}}^{**}, {\mathcal {Y}}, c\in {\mathcal {N}}[h]$
, we have that
![]() ${\mathcal {S}}\in {\mathcal {N}}[h]$
.
${\mathcal {S}}\in {\mathcal {N}}[h]$
.
It now follows that
![]() $b\in {\mathcal {N}}[h]$
, and as
$b\in {\mathcal {N}}[h]$
, and as
![]() ${\mathcal {N}}$
is pointwise definable, we must have that b is
${\mathcal {N}}$
is pointwise definable, we must have that b is
![]() $\pi ^{\mathcal { K}}$
-realizable in
$\pi ^{\mathcal { K}}$
-realizable in
![]() ${\mathcal {N}}[h]$
(notice that the argument from the above paragraph implies that
${\mathcal {N}}[h]$
(notice that the argument from the above paragraph implies that
![]() ${\mathcal {M}}^{\mathcal {X}}_b$
iterates to
${\mathcal {M}}^{\mathcal {X}}_b$
iterates to
![]() ${\mathcal {W}}$
). If d is another
${\mathcal {W}}$
). If d is another
![]() $\pi ^{\mathcal { K}}$
-realizable branch in
$\pi ^{\mathcal { K}}$
-realizable branch in
![]() ${\mathcal {N}}[h]$
(or in
${\mathcal {N}}[h]$
(or in
![]() ${\mathcal {P}}$
), then as both
${\mathcal {P}}$
), then as both
![]() ${\mathcal {M}}^{\mathcal {X}}_b$
and
${\mathcal {M}}^{\mathcal {X}}_b$
and
![]() ${\mathcal {M}}^{\mathcal {X}}_d$
are iterable as
${\mathcal {M}}^{\mathcal {X}}_d$
are iterable as
![]() $S^{\mathcal {N}}$
-mice, we have that
$S^{\mathcal {N}}$
-mice, we have that
![]() ${\mathcal {M}}^{\mathcal {X}}_b={\mathcal {M}}^{\mathcal {X}}_d$
. This is a contradiction as
${\mathcal {M}}^{\mathcal {X}}_b={\mathcal {M}}^{\mathcal {X}}_d$
. This is a contradiction as
![]() ${\delta }({\mathcal {X}})$
is not Woodin in either
${\delta }({\mathcal {X}})$
is not Woodin in either
![]() ${\mathcal {M}}^{\mathcal {X}}_b$
or
${\mathcal {M}}^{\mathcal {X}}_b$
or
![]() ${\mathcal {M}}^{\mathcal {X}}_d$
.
${\mathcal {M}}^{\mathcal {X}}_d$
.
In the case
![]() ${\mathcal {U}}$
has drops, the argument is very similar to the proof of the claim above. In this case, we cannot hope to find a realizable branch, but we can find the appropriate
${\mathcal {U}}$
has drops, the argument is very similar to the proof of the claim above. In this case, we cannot hope to find a realizable branch, but we can find the appropriate
![]() ${\mathcal {Q}}$
-structure using the proof of the claim.
${\mathcal {Q}}$
-structure using the proof of the claim.
Putting the proofs of Lemma 2.11 and Lemma 2.12 together, we obtain the proof of Theorem 2.10.
The proof of Theorem 2.10.
We outline the proof. We use the notation introduced in Theorem 2.10. Let
![]() $\xi $
be a
$\xi $
be a
![]() ${\mathcal {P}}$
-inaccessible limit of
${\mathcal {P}}$
-inaccessible limit of
![]() ${\mathcal {P}}$
-Woodin cardinals and such that
${\mathcal {P}}$
-Woodin cardinals and such that
![]() $\mathbb {P}\in {\mathcal {P}}|\xi $
, and let
$\mathbb {P}\in {\mathcal {P}}|\xi $
, and let
![]() $\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
be such that
$\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
be such that
![]() ${\vert {\mathcal {N}}\vert }=\eta $
,
${\vert {\mathcal {N}}\vert }=\eta $
,
![]() $\mathrm {crit }(\pi )>\eta $
and
$\mathrm {crit }(\pi )>\eta $
and
![]() $\mathbb {P}\in rng(\pi )$
. Let
$\mathbb {P}\in rng(\pi )$
. Let
![]() $\mathbb {Q}=\pi ^{-1}(\mathbb {P})$
. Let h be
$\mathbb {Q}=\pi ^{-1}(\mathbb {P})$
. Let h be
![]() ${\mathcal {P}}$
-generic for
${\mathcal {P}}$
-generic for
![]() $\mathbb {Q}$
. Notice now that Lemma 2.12 applies both in
$\mathbb {Q}$
. Notice now that Lemma 2.12 applies both in
![]() ${\mathcal {N}}[h]$
and
${\mathcal {N}}[h]$
and
![]() ${\mathcal {P}}[h]$
. Moreover, the proof of Lemma 2.12 shows that
${\mathcal {P}}[h]$
. Moreover, the proof of Lemma 2.12 shows that
(1)
![]() $(\Sigma ^h)^{{\mathcal {P}}[h]}{\restriction } ({\mathcal {N}}[h])=(\Sigma ^h)^{{\mathcal {N}}[h]}$
.
$(\Sigma ^h)^{{\mathcal {P}}[h]}{\restriction } ({\mathcal {N}}[h])=(\Sigma ^h)^{{\mathcal {N}}[h]}$
.
To see (1), notice that as
![]() ${\mathcal {Q}}$
has no Woodin cardinals, both
${\mathcal {Q}}$
has no Woodin cardinals, both
![]() $(\Sigma ^h)^{{\mathcal {P}}[h]}$
and
$(\Sigma ^h)^{{\mathcal {P}}[h]}$
and
![]() $(\Sigma ^h)^{{\mathcal {N}}[h]}$
are guided by
$(\Sigma ^h)^{{\mathcal {N}}[h]}$
are guided by
![]() ${\mathcal {Q}}$
-structures. To see that (1) holds, we need to show that both
${\mathcal {Q}}$
-structures. To see that (1) holds, we need to show that both
![]() $(\Sigma ^h)^{{\mathcal {P}}[h]}$
and
$(\Sigma ^h)^{{\mathcal {P}}[h]}$
and
![]() $(\Sigma ^h)^{{\mathcal {N}}[h]}$
pick the same
$(\Sigma ^h)^{{\mathcal {N}}[h]}$
pick the same
![]() ${\mathcal {Q}}$
-structures, and this would follow if we show that the
${\mathcal {Q}}$
-structures, and this would follow if we show that the
![]() ${\mathcal {Q}}$
-structures picked by
${\mathcal {Q}}$
-structures picked by
![]() $(\Sigma ^h)^{{\mathcal {N}}[h]}$
are iterable in
$(\Sigma ^h)^{{\mathcal {N}}[h]}$
are iterable in
![]() ${\mathcal {P}}[h]$
. To see this, we have to recall our definition of
${\mathcal {P}}[h]$
. To see this, we have to recall our definition of
![]() $(\Sigma ^h)^{{\mathcal {N}}[h]}$
. The iterability of any
$(\Sigma ^h)^{{\mathcal {N}}[h]}$
. The iterability of any
![]() ${\mathcal {Q}}$
-structure picked by
${\mathcal {Q}}$
-structure picked by
![]() $(\Sigma ^h)^{{\mathcal {N}}[h]}$
is reduced to iterabilty of
$(\Sigma ^h)^{{\mathcal {N}}[h]}$
is reduced to iterabilty of
![]() ${\mathcal {N}}$
in some non-maximal window
${\mathcal {N}}$
in some non-maximal window
![]() $u^{\mathcal {N}}$
. The iterability of this window is reduced to the iterability of
$u^{\mathcal {N}}$
. The iterability of this window is reduced to the iterability of
![]() ${\mathcal {P}}$
in some non-maximal window
${\mathcal {P}}$
in some non-maximal window
![]() $\pi (u^{\mathcal {N}})$
, and according to Lemma 2.12, this last iterability holds.
$\pi (u^{\mathcal {N}})$
, and according to Lemma 2.12, this last iterability holds.
Finally, notice that if we let
![]() ${\mathcal {Q}}^+={\mathcal {P}}|(\eta ^+)^{\mathcal {P}}$
and
${\mathcal {Q}}^+={\mathcal {P}}|(\eta ^+)^{\mathcal {P}}$
and
![]() $\Lambda ^h$
be the strategy of
$\Lambda ^h$
be the strategy of
![]() ${\mathcal {Q}}^+$
given by Lemma 2.12,
${\mathcal {Q}}^+$
given by Lemma 2.12,
![]() $\Lambda ^h_{\mathcal {Q}}=\Sigma ^h$
(again this is simply because they both are
$\Lambda ^h_{\mathcal {Q}}=\Sigma ^h$
(again this is simply because they both are
![]() ${\mathcal {Q}}$
-structure guided strategies). It now just remains to repeat the argument from Lemma 2.11. Given any tree
${\mathcal {Q}}$
-structure guided strategies). It now just remains to repeat the argument from Lemma 2.11. Given any tree
![]() ${\mathcal {T}}\in {\mathcal {N}}[h]$
according to
${\mathcal {T}}\in {\mathcal {N}}[h]$
according to
![]() $\Sigma ^h$
such that
$\Sigma ^h$
such that
![]() $\pi ^{\mathcal {T}}$
exists,
$\pi ^{\mathcal {T}}$
exists,
![]() $\pi ^{\mathcal {T}}$
can be applied to
$\pi ^{\mathcal {T}}$
can be applied to
![]() ${\mathcal {Q}}^+$
and hence to
${\mathcal {Q}}^+$
and hence to
![]() ${\mathcal {N}}$
. This finishes the proof of Theorem 2.10.
${\mathcal {N}}$
. This finishes the proof of Theorem 2.10.
![]() $\Box $
$\Box $
2.6. Iterability of countable hulls
Here, we would like to prove that countable hulls of an excellent hybrid premouse have iteration strategies. The reason for doing this is to show that if
![]() ${\mathcal {P}}$
is an excellent hybrid premouse and g is
${\mathcal {P}}$
is an excellent hybrid premouse and g is
![]() ${\mathcal {P}}$
-generic, then any universally Baire set A in
${\mathcal {P}}$
-generic, then any universally Baire set A in
![]() ${\mathcal {P}}[g]$
is reducible to some iteration strategy which is Wadge below
${\mathcal {P}}[g]$
is reducible to some iteration strategy which is Wadge below
![]() $S^{\mathcal {P}}$
. We will use this to show that
$S^{\mathcal {P}}$
. We will use this to show that
![]() $\mathsf {Sealing}$
holds in a generic extension of an excellent hybrid premouse (see Theorem 3.1).
$\mathsf {Sealing}$
holds in a generic extension of an excellent hybrid premouse (see Theorem 3.1).
Proposition 2.13. Suppose
![]() ${\mathcal {P}}$
is an excellent hybrid premouse and
${\mathcal {P}}$
is an excellent hybrid premouse and
![]() $(w_i: i<\omega )$
are infinitely many consecutive windows of
$(w_i: i<\omega )$
are infinitely many consecutive windows of
![]() ${\mathcal {P}}$
. Set
${\mathcal {P}}$
. Set
![]() $\xi =\sup _{i<\omega }{\delta }^{w_i}$
. Suppose
$\xi =\sup _{i<\omega }{\delta }^{w_i}$
. Suppose
![]() $\mathbb {P}\in {\mathcal {P}}|\nu ^{w_0}$
is a poset and
$\mathbb {P}\in {\mathcal {P}}|\nu ^{w_0}$
is a poset and
![]() $g\subseteq \mathbb {P}$
is
$g\subseteq \mathbb {P}$
is
![]() ${\mathcal {P}}$
-generic. Working in
${\mathcal {P}}$
-generic. Working in
![]() ${\mathcal {P}}[g]$
, let
${\mathcal {P}}[g]$
, let
![]() $\pi : {\mathcal {N}}\rightarrow {\mathcal {P}}|(\xi ^+)^{\mathcal {P}}[g]$
be a countable transitive hull. Then in
$\pi : {\mathcal {N}}\rightarrow {\mathcal {P}}|(\xi ^+)^{\mathcal {P}}[g]$
be a countable transitive hull. Then in
![]() ${\mathcal {P}}[g]$
,
${\mathcal {P}}[g]$
,
![]() ${\mathcal {N}}$
has a
${\mathcal {N}}$
has a
![]() $\nu ^{w_0}$
-strategy
$\nu ^{w_0}$
-strategy
![]() $\Sigma $
that acts on nondropping trees that are based on the interval
$\Sigma $
that acts on nondropping trees that are based on the interval
![]() $[\pi ^{-1}(\nu ^{w_0}), \pi ^{-1}(\xi )]$
.
$[\pi ^{-1}(\nu ^{w_0}), \pi ^{-1}(\xi )]$
.
Proof. Set
![]() $u_i=\pi ^{-1}(w_i)$
and
$u_i=\pi ^{-1}(w_i)$
and
![]() $\zeta =\pi ^{-1}(\xi )$
. Our intention is to lift trees from
$\zeta =\pi ^{-1}(\xi )$
. Our intention is to lift trees from
![]() ${\mathcal {N}}$
to
${\mathcal {N}}$
to
![]() ${\mathcal {P}}$
and use
${\mathcal {P}}$
and use
![]() ${\mathcal {P}}$
’s strategy. However, as
${\mathcal {P}}$
’s strategy. However, as
![]() ${\mathcal {P}}$
-moves, we lose Theorem 2.10; it is now only applicable inside the iterate of
${\mathcal {P}}$
-moves, we lose Theorem 2.10; it is now only applicable inside the iterate of
![]() ${\mathcal {P}}$
. To deal with this issue, we will use Neeman’s ‘realizable maps are generic’ theorem (see [Reference Neeman31, Theorem 4.9.1]). That it applies is a consequence of the fact that the strategy of
${\mathcal {P}}$
. To deal with this issue, we will use Neeman’s ‘realizable maps are generic’ theorem (see [Reference Neeman31, Theorem 4.9.1]). That it applies is a consequence of the fact that the strategy of
![]() ${\mathcal {P}}$
we have described in Theorem 2.10 is unique; thus, the lifted-up trees from
${\mathcal {P}}$
we have described in Theorem 2.10 is unique; thus, the lifted-up trees from
![]() ${\mathcal {N}}$
to
${\mathcal {N}}$
to
![]() ${\mathcal {P}}$
pick unique branches (this is a consequence of Steel’s result that UBH holds in mice – see [Reference Steel51, Theorem 3.3] – but can also be proved using methods of Theorem 2.10). One last wrinkle is to notice that when lifting trees from
${\mathcal {P}}$
pick unique branches (this is a consequence of Steel’s result that UBH holds in mice – see [Reference Steel51, Theorem 3.3] – but can also be proved using methods of Theorem 2.10). One last wrinkle is to notice that when lifting trees from
![]() ${\mathcal {N}}$
to
${\mathcal {N}}$
to
![]() ${\mathcal {P}}$
, Theorem 2.10 applies. This is because for each i,
${\mathcal {P}}$
, Theorem 2.10 applies. This is because for each i,
![]() $\sup (\pi [{\delta }^{u_i}])<{\delta }^{w_i}$
.
$\sup (\pi [{\delta }^{u_i}])<{\delta }^{w_i}$
.
We now describe our intended strategy for
![]() ${\mathcal {N}}$
. We call this strategy
${\mathcal {N}}$
. We call this strategy
![]() $\Lambda $
. Notice that if
$\Lambda $
. Notice that if
![]() ${\mathcal {T}}$
is a normal iteration of
${\mathcal {T}}$
is a normal iteration of
![]() ${\mathcal {N}}$
based on the interval
${\mathcal {N}}$
based on the interval
![]() $[\nu ^{u_0}, \zeta ]$
, then
$[\nu ^{u_0}, \zeta ]$
, then
![]() ${\mathcal {T}}$
can be reorganized as a stack of
${\mathcal {T}}$
can be reorganized as a stack of
![]() $\omega $
-iterations
$\omega $
-iterations
![]() $({\mathcal {T}}_i, {\mathcal {N}}_i: i<\omega )$
, where
$({\mathcal {T}}_i, {\mathcal {N}}_i: i<\omega )$
, where
![]() ${\mathcal {N}}_0={\mathcal {N}}$
,
${\mathcal {N}}_0={\mathcal {N}}$
,
![]() ${\mathcal {N}}_{i+1}$
is the last model of
${\mathcal {N}}_{i+1}$
is the last model of
![]() ${\mathcal {T}}_i$
and
${\mathcal {T}}_i$
and
![]() ${\mathcal {T}}_{i+1}$
is the largest initial segment of
${\mathcal {T}}_{i+1}$
is the largest initial segment of
![]() ${\mathcal {T}}_{\geq {\mathcal {N}}_i}$
that is based on the window
${\mathcal {T}}_{\geq {\mathcal {N}}_i}$
that is based on the window
![]() $\pi ^{{\mathcal {T}}_{\leq {\mathcal {N}}_i}}(u_{i+1})$
.
$\pi ^{{\mathcal {T}}_{\leq {\mathcal {N}}_i}}(u_{i+1})$
.
Suppose then
![]() ${\mathcal {T}}=({\mathcal {T}}_i, {\mathcal {N}}_i: i<\omega )$
is a normal nondropping iteration of
${\mathcal {T}}=({\mathcal {T}}_i, {\mathcal {N}}_i: i<\omega )$
is a normal nondropping iteration of
![]() ${\mathcal {N}}$
based on
${\mathcal {N}}$
based on
![]() $[\nu ^{u_0}, \zeta ]$
. We say
$[\nu ^{u_0}, \zeta ]$
. We say
![]() ${\mathcal {T}}$
is according to
${\mathcal {T}}$
is according to
![]() $\Lambda $
if and only if there is an iteration
$\Lambda $
if and only if there is an iteration
![]() ${\mathcal {U}}=({\mathcal {U}}_i, {\mathcal {P}}_i: i<\omega )$
of
${\mathcal {U}}=({\mathcal {U}}_i, {\mathcal {P}}_i: i<\omega )$
of
![]() ${\mathcal {P}}$
and embeddings
${\mathcal {P}}$
and embeddings
![]() $\pi _i:{\mathcal {N}}_i\rightarrow {\mathcal {P}}_i$
such that
$\pi _i:{\mathcal {N}}_i\rightarrow {\mathcal {P}}_i$
such that
-
1.
 ${\mathcal {P}}_0={\mathcal {P}}$
,
${\mathcal {P}}_0={\mathcal {P}}$
, -
2.
 ${\mathcal {U}}_i=\pi _i{\mathcal {T}}_i$
for each
${\mathcal {U}}_i=\pi _i{\mathcal {T}}_i$
for each
 $i<\omega $
,
$i<\omega $
, -
3.
 ${\mathcal {P}}_{i+1}$
is the last model of
${\mathcal {P}}_{i+1}$
is the last model of
 ${\mathcal {U}}_i$
for each
${\mathcal {U}}_i$
for each
 $i<\omega $
,
$i<\omega $
, -
4. for
 $i<\omega $
, letting
$i<\omega $
, letting
 $s_i=\pi ^{\mathcal {T}}_{{\mathcal {N}}, {\mathcal {N}}_i}(u_i)$
,
$s_i=\pi ^{\mathcal {T}}_{{\mathcal {N}}, {\mathcal {N}}_i}(u_i)$
,
 ${\lambda }_i=\sup (\pi _i[{\delta }^{s_i}])$
and
${\lambda }_i=\sup (\pi _i[{\delta }^{s_i}])$
and
 ${\mathcal {Q}}_i={\mathcal {P}}_i|({\lambda }_i^+)^{{\mathcal {P}}_i}$
,
${\mathcal {Q}}_i={\mathcal {P}}_i|({\lambda }_i^+)^{{\mathcal {P}}_i}$
,
 ${\mathcal {P}}_i[g][\pi _i]{\vDash } \text {`}{\mathcal {U}}_i$
is according to the strategy (as described in Lemma 2.12) of
${\mathcal {P}}_i[g][\pi _i]{\vDash } \text {`}{\mathcal {U}}_i$
is according to the strategy (as described in Lemma 2.12) of
 ${\mathcal {Q}}_i$
’.Footnote 50
${\mathcal {Q}}_i$
’.Footnote 50
The reader can now use Theorem 2.10 and Neeman’s aforementioned result to show that
![]() ${\mathcal {N}}$
has a
${\mathcal {N}}$
has a
![]() $\nu ^{w_0}$
-iteration strategy. The main point is that for any
$\nu ^{w_0}$
-iteration strategy. The main point is that for any
![]() ${\mathcal {P}}[g]$
-generic
${\mathcal {P}}[g]$
-generic
![]() $G \subseteq Coll(\omega ,{\mathcal {T}})$
, in
$G \subseteq Coll(\omega ,{\mathcal {T}})$
, in
![]() ${\mathcal {P}}[g][G]$
,
${\mathcal {P}}[g][G]$
,
![]() ${\mathcal {T}}$
is countable, so we can find generics
${\mathcal {T}}$
is countable, so we can find generics
![]() $g_i$
for each i such that
$g_i$
for each i such that
![]() $\pi _i\in {\mathcal {P}}_i[g][g_i]$
. Furthermore,
$\pi _i\in {\mathcal {P}}_i[g][g_i]$
. Furthermore,
![]() ${\mathcal {Q}}_i$
’s strategy is unique and uniquely extends to all generic extensions of
${\mathcal {Q}}_i$
’s strategy is unique and uniquely extends to all generic extensions of
![]() ${\mathcal {P}}_i$
, so the procedure described above can be carried out in
${\mathcal {P}}_i$
, so the procedure described above can be carried out in
![]() ${\mathcal {P}}[g]$
using the forcing relation of
${\mathcal {P}}[g]$
using the forcing relation of
![]() $Coll(\omega , {\mathcal {T}})$
.
$Coll(\omega , {\mathcal {T}})$
.
2.7. A revised authentication method
Suppose
![]() ${\mathcal {P}}$
is an excellent hybrid premouse. Let g be
${\mathcal {P}}$
is an excellent hybrid premouse. Let g be
![]() ${\mathcal {P}}$
-generic. We would like to know if
${\mathcal {P}}$
-generic. We would like to know if
![]() $S^{\mathcal {P}}$
has a canonical interpretation in
$S^{\mathcal {P}}$
has a canonical interpretation in
![]() ${\mathcal {P}}[g]$
. That this is possible follows from Theorem 2.4. Perhaps consulting Remark 2.2 will be helpful. However, to make these notions more precise, we will need to dig deeper into the proof of Theorem 2.4 and understand how the definition of
${\mathcal {P}}[g]$
. That this is possible follows from Theorem 2.4. Perhaps consulting Remark 2.2 will be helpful. However, to make these notions more precise, we will need to dig deeper into the proof of Theorem 2.4 and understand how the definition of
![]() $\Psi ^g$
works. For this, we will need to understand expressions such as
$\Psi ^g$
works. For this, we will need to understand expressions such as
![]() $\text {`}{\mathcal {Q}}$
is an authenticated sts premouse’. The intended meaning of ‘authenticated’ is the one used in the proof of [Reference Sargsyan and Trang38, Theorem 6.1.5]. More specifically, the interested reader should consult [Reference Sargsyan and Trang38, Definition 3.7.3, 3.7.4, 6.2.1 and 6.2.2]. Here, we will briefly explain the meaning of the expression and state a useful consequence of it that equates this notion to the standard notion of being constructed by fully backgrounded constructions (see Remark 2.16). The new key concepts are
$\text {`}{\mathcal {Q}}$
is an authenticated sts premouse’. The intended meaning of ‘authenticated’ is the one used in the proof of [Reference Sargsyan and Trang38, Theorem 6.1.5]. More specifically, the interested reader should consult [Reference Sargsyan and Trang38, Definition 3.7.3, 3.7.4, 6.2.1 and 6.2.2]. Here, we will briefly explain the meaning of the expression and state a useful consequence of it that equates this notion to the standard notion of being constructed by fully backgrounded constructions (see Remark 2.16). The new key concepts are
![]() $({\mathcal {P}}, \Sigma , X)$
-authenticated hybrid premouse and
$({\mathcal {P}}, \Sigma , X)$
-authenticated hybrid premouse and
![]() $({\mathcal {P}}, \Sigma , X)$
-authenticated iteration. The essence of these two notions are as follows.
$({\mathcal {P}}, \Sigma , X)$
-authenticated iteration. The essence of these two notions are as follows.
Definition 2.14 (Authenticated hod premouse)
Suppose
![]() $({\mathcal {P}}, \Sigma )$
is an sts pair,
$({\mathcal {P}}, \Sigma )$
is an sts pair,
![]() $X\subseteq {\mathcal {P}}^b$
and
$X\subseteq {\mathcal {P}}^b$
and
![]() ${\mathcal {R}}$
is a hod premouse. We say
${\mathcal {R}}$
is a hod premouse. We say
![]() ${\mathcal {R}}$
is
${\mathcal {R}}$
is
![]() $({\mathcal {P}}, \Sigma , X)$
-authenticated if there are
$({\mathcal {P}}, \Sigma , X)$
-authenticated if there are
(e1) a
![]() $\Sigma $
-iterate
$\Sigma $
-iterate
![]() ${\mathcal {S}}$
of
${\mathcal {S}}$
of
![]() ${\mathcal {P}}$
such that the iteration embedding
${\mathcal {P}}$
such that the iteration embedding
![]() $\pi :{\mathcal {P}}\rightarrow {\mathcal {S}}$
exists and
$\pi :{\mathcal {P}}\rightarrow {\mathcal {S}}$
exists and
(e2) an iteration
![]() ${\mathcal {U}}$
of
${\mathcal {U}}$
of
![]() ${\mathcal {R}}$
with last model some
${\mathcal {R}}$
with last model some
![]() ${\mathcal {S}}^b||\xi $
.
${\mathcal {S}}^b||\xi $
.
The iteration
![]() ${\mathcal {U}}$
is constructed using information given by
${\mathcal {U}}$
is constructed using information given by
![]() $\pi [X]$
. More precisely, for each maximal window w of
$\pi [X]$
. More precisely, for each maximal window w of
![]() ${\mathcal {S}}^b$
, consider
${\mathcal {S}}^b$
, consider
It is required that for each limit
![]() ${\alpha }<lh({\mathcal {U}})$
, if
${\alpha }<lh({\mathcal {U}})$
, if
![]() $c=[0, {\alpha }]_{\mathcal {U}}$
, then one of the following two conditions holds:
$c=[0, {\alpha }]_{\mathcal {U}}$
, then one of the following two conditions holds:
(C1)
![]() ${\mathcal {S}}{\vDash } \text {`}{\delta }({\mathcal {U}}{\restriction } {\alpha })$
is not a Woodin cardinal’,
${\mathcal {S}}{\vDash } \text {`}{\delta }({\mathcal {U}}{\restriction } {\alpha })$
is not a Woodin cardinal’,
![]() ${\mathcal {Q}}(c, {\mathcal {U}}{\restriction } {\alpha })$
exists and
${\mathcal {Q}}(c, {\mathcal {U}}{\restriction } {\alpha })$
exists and
![]() ${\mathcal {Q}}(c, {\mathcal {U}}{\restriction } {\alpha }){\trianglelefteq } {\mathcal {S}}$
.
${\mathcal {Q}}(c, {\mathcal {U}}{\restriction } {\alpha }){\trianglelefteq } {\mathcal {S}}$
.
(C2)
![]() ${\mathcal {S}}{\vDash } \text {`}{\delta }({\mathcal {U}}{\restriction } {\alpha })$
is a Woodin cardinal’ and letting w be the maximal window of
${\mathcal {S}}{\vDash } \text {`}{\delta }({\mathcal {U}}{\restriction } {\alpha })$
is a Woodin cardinal’ and letting w be the maximal window of
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() ${\delta }^w={\delta }({\mathcal {U}}{\restriction } {\alpha })$
,
${\delta }^w={\delta }({\mathcal {U}}{\restriction } {\alpha })$
,
![]() $s(\pi , X, w)\subseteq rng(\pi ^{{\mathcal {U}}{\restriction } {\alpha }}_c)$
.
$s(\pi , X, w)\subseteq rng(\pi ^{{\mathcal {U}}{\restriction } {\alpha }}_c)$
.
Usually, X is chosen in a way that for each window w of
![]() ${\mathcal {S}}$
,
${\mathcal {S}}$
,
![]() $\sup (s(\pi , X, w))={\delta }^w$
. For such X, conditions (C1) and (C2) completely determine
$\sup (s(\pi , X, w))={\delta }^w$
. For such X, conditions (C1) and (C2) completely determine
![]() ${\mathcal {U}}$
.
${\mathcal {U}}$
.
Given a hod premouse
![]() ${\mathcal {P}}$
of lsa type, a set
${\mathcal {P}}$
of lsa type, a set
![]() $X\subseteq {\mathcal {P}}^b$
and a set
$X\subseteq {\mathcal {P}}^b$
and a set
![]() $\Gamma $
consisting of iterations of
$\Gamma $
consisting of iterations of
![]() ${\mathcal {P}}$
we can similarly define
${\mathcal {P}}$
we can similarly define
![]() $({\mathcal {P}}, \Gamma , X)$
-authenticated hod premice.
$({\mathcal {P}}, \Gamma , X)$
-authenticated hod premice.
Definition 2.15 (Authenticated iteration)
Suppose
![]() ${\mathcal {R}}$
is a
${\mathcal {R}}$
is a
![]() $({\mathcal {P}}, \Sigma , X)$
authenticated hybrid premouse and
$({\mathcal {P}}, \Sigma , X)$
authenticated hybrid premouse and
![]() ${\mathcal {W}}$
is an iteration of
${\mathcal {W}}$
is an iteration of
![]() ${\mathcal {R}}$
. We say
${\mathcal {R}}$
. We say
![]() ${\mathcal {W}}$
is
${\mathcal {W}}$
is
![]() $({\mathcal {P}}, \Sigma , X)$
-authenticated if there is a triple
$({\mathcal {P}}, \Sigma , X)$
-authenticated if there is a triple
![]() $({\mathcal {S}}, {\mathcal {U}}, \xi )$
$({\mathcal {S}}, {\mathcal {U}}, \xi )$
![]() $({\mathcal {P}}, \Sigma , X)$
-authenticating
$({\mathcal {P}}, \Sigma , X)$
-authenticating
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $\pi ^{\mathcal {U}}$
-exists and
$\pi ^{\mathcal {U}}$
-exists and
![]() ${\mathcal {W}}$
is according to
${\mathcal {W}}$
is according to
![]() $\pi ^{\mathcal {U}}$
-pullback of
$\pi ^{\mathcal {U}}$
-pullback of
![]() $\Sigma _{{\mathcal {S}}||\xi }$
.
$\Sigma _{{\mathcal {S}}||\xi }$
.
Suppose now that
![]() ${\mathcal {M}}$
is an sts premouse based on
${\mathcal {M}}$
is an sts premouse based on
![]() ${\mathcal {P}}$
and g is
${\mathcal {P}}$
and g is
![]() ${\mathcal {M}}$
-generic for a poset in
${\mathcal {M}}$
-generic for a poset in
![]() ${\mathcal {M}}|\zeta $
. Suppose
${\mathcal {M}}|\zeta $
. Suppose
![]() ${\mathcal {R}}\in {\mathcal {M}}|\zeta [g]$
is an lsa type hod premouse such that
${\mathcal {R}}\in {\mathcal {M}}|\zeta [g]$
is an lsa type hod premouse such that
![]() ${\mathcal {R}}^b$
is
${\mathcal {R}}^b$
is
![]() $({\mathcal {P}}, {\mathcal {S}}^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated and
$({\mathcal {P}}, {\mathcal {S}}^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated and
![]() ${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^\#$
. In
${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^\#$
. In
![]() ${\mathcal {M}}[g]$
, we can build an sts premouse
${\mathcal {M}}[g]$
, we can build an sts premouse
![]() ${\mathcal {W}}$
based on
${\mathcal {W}}$
based on
![]() ${\mathcal {R}}$
using
${\mathcal {R}}$
using
![]() $({\mathcal {P}}, S^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated iterations. This means that whenever
$({\mathcal {P}}, S^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated iterations. This means that whenever
![]() ${\mathcal {U}}$
is an iteration indexed in
${\mathcal {U}}$
is an iteration indexed in
![]() ${\mathcal {W}}$
,
${\mathcal {W}}$
,
![]() ${\alpha }<lh({\mathcal {U}})$
is a limit ordinal such that
${\alpha }<lh({\mathcal {U}})$
is a limit ordinal such that
![]() $\pi ^{{\mathcal {U}}{\restriction } {\alpha }, b}$
exists and
$\pi ^{{\mathcal {U}}{\restriction } {\alpha }, b}$
exists and
![]() ${\mathcal {X}}$
is the longest initial segment of
${\mathcal {X}}$
is the longest initial segment of
![]() ${\mathcal {U}}_{\geq {\alpha }}$
that is based on
${\mathcal {U}}_{\geq {\alpha }}$
that is based on
![]() ${\mathcal {V}}=_{def}({\mathcal {M}}_{\alpha }^{\mathcal {U}})^b$
; then both
${\mathcal {V}}=_{def}({\mathcal {M}}_{\alpha }^{\mathcal {U}})^b$
; then both
![]() ${\mathcal {V}}$
and
${\mathcal {V}}$
and
![]() ${\mathcal {X}}$
are
${\mathcal {X}}$
are
![]() $({\mathcal {P}}, S^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated. In addition to the above, we also require that if
$({\mathcal {P}}, S^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated. In addition to the above, we also require that if
![]() ${\mathcal {Q}}$
is a
${\mathcal {Q}}$
is a
![]() ${\mathcal {Q}}$
-structure for some
${\mathcal {Q}}$
-structure for some
![]() $\mathsf {nuvs}$
tree in
$\mathsf {nuvs}$
tree in
![]() ${\mathcal {W}}$
that has been authenticated by
${\mathcal {W}}$
that has been authenticated by
![]() ${\mathcal {W}}$
via the authentication procedure used in sts premice, then any iteration indexed in
${\mathcal {W}}$
via the authentication procedure used in sts premice, then any iteration indexed in
![]() ${\mathcal {Q}}$
is
${\mathcal {Q}}$
is
![]() $({\mathcal {P}}, {\mathcal {P}}^b, S^{\mathcal {M}})$
-authenticated. Moreover, the same holds for all iterates of
$({\mathcal {P}}, {\mathcal {P}}^b, S^{\mathcal {M}})$
-authenticated. Moreover, the same holds for all iterates of
![]() ${\mathcal {Q}}$
via the strategy witnessing that
${\mathcal {Q}}$
via the strategy witnessing that
![]() ${\mathcal {Q}}$
is authenticated in
${\mathcal {Q}}$
is authenticated in
![]() ${\mathcal {W}}$
.
${\mathcal {W}}$
.
It is important to keep in mind that the above construction may fail simply because some non-
![]() $({\mathcal {P}}, S^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated object has been constructed. Also, the same construction can be done using
$({\mathcal {P}}, S^{\mathcal {M}}, {\mathcal {P}}^b)$
-authenticated object has been constructed. Also, the same construction can be done using
![]() $({\mathcal {P}}, S^{\mathcal {M}}, X)$
-authenticated objects where
$({\mathcal {P}}, S^{\mathcal {M}}, X)$
-authenticated objects where
![]() $X\subseteq {\mathcal {P}}^b$
.
$X\subseteq {\mathcal {P}}^b$
.
Remark 2.16. Suppose now that
![]() ${\mathcal {M}}$
is an sts premouse based on
${\mathcal {M}}$
is an sts premouse based on
![]() ${\mathcal {P}}$
and g is
${\mathcal {P}}$
and g is
![]() ${\mathcal {M}}$
-generic for a poset in
${\mathcal {M}}$
-generic for a poset in
![]() ${\mathcal {M}}|\zeta $
. Suppose
${\mathcal {M}}|\zeta $
. Suppose
![]() ${\mathcal {R}}\in {\mathcal {M}}|\zeta [g]$
is an lsa type hod premouse such that
${\mathcal {R}}\in {\mathcal {M}}|\zeta [g]$
is an lsa type hod premouse such that
![]() ${\mathcal {R}}^b$
is
${\mathcal {R}}^b$
is
![]() $({\mathcal {P}}, {\mathcal {P}}^b, S^{\mathcal {M}})$
-authenticated and
$({\mathcal {P}}, {\mathcal {P}}^b, S^{\mathcal {M}})$
-authenticated and
![]() ${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^\#$
. Suppose
${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^\#$
. Suppose
![]() ${\mathcal {M}}$
has a Woodin cardinal
${\mathcal {M}}$
has a Woodin cardinal
![]() ${\delta }$
above
${\delta }$
above
![]() $\zeta $
. To say that an sts premouse
$\zeta $
. To say that an sts premouse
![]() ${\mathcal {Q}}$
over
${\mathcal {Q}}$
over
![]() ${\mathcal {R}}$
is
${\mathcal {R}}$
is
![]() $({\mathcal {P}}, {\mathcal {P}}^b, S^{\mathcal {M}})$
-authenticated is equivalent to saying that
$({\mathcal {P}}, {\mathcal {P}}^b, S^{\mathcal {M}})$
-authenticated is equivalent to saying that
![]() ${\mathcal {Q}}{\trianglelefteq } {\mathcal {W}}$
, where
${\mathcal {Q}}{\trianglelefteq } {\mathcal {W}}$
, where
![]() ${\mathcal {W}}$
is a model in the
${\mathcal {W}}$
is a model in the
![]() $({\mathcal {M}},{\mathcal {P}}^b)$
-authenticated fully backgrounded construction described in [Reference Sargsyan and Trang38, Definition 6.2.2].
$({\mathcal {M}},{\mathcal {P}}^b)$
-authenticated fully backgrounded construction described in [Reference Sargsyan and Trang38, Definition 6.2.2].
The reader may be wondering why it is enough to only authenticate the lower-level iterations. The reason is that in many situations, the lower-level strategies define the entire short-tree strategy. This point was explained in Section 2.1.
The construction mentioned in Remark 2.16 is called the
![]() $({\mathcal {P}}, X, S^{\mathcal {M}})$
-authenticated hod pair construction over
$({\mathcal {P}}, X, S^{\mathcal {M}})$
-authenticated hod pair construction over
![]() ${\mathcal {R}}$
. The details of everything that we have said above appears in [Reference Sargsyan and Trang38, Chapter 6.2]. The reader may choose to consult [Reference Sargsyan and Trang38, Definition 6.2.2].
${\mathcal {R}}$
. The details of everything that we have said above appears in [Reference Sargsyan and Trang38, Chapter 6.2]. The reader may choose to consult [Reference Sargsyan and Trang38, Definition 6.2.2].
2.8. Generic interpretability
In this portion of the current section, we would like to outline the proof of generic interpretability. As was mentioned before, generic interpretability is somewhat tricky for short-tree strategies. This is because given a
![]() $\Lambda $
-sts premouse
$\Lambda $
-sts premouse
![]() ${\mathcal {N}}$
and a tree
${\mathcal {N}}$
and a tree
![]() ${\mathcal {T}}\in {\mathcal {N}}[h]$
,
${\mathcal {T}}\in {\mathcal {N}}[h]$
,
![]() ${\mathcal {T}}$
may be short, but
${\mathcal {T}}$
may be short, but
![]() ${\mathcal {N}}[h]$
may not be able to find the branch of
${\mathcal {N}}[h]$
may not be able to find the branch of
![]() ${\mathcal {T}}$
that is according to
${\mathcal {T}}$
that is according to
![]() $\Lambda $
, as this branch might have a
$\Lambda $
, as this branch might have a
![]() ${\mathcal {Q}}$
-structure that is more complex than
${\mathcal {Q}}$
-structure that is more complex than
![]() ${\mathcal {N}}$
.
${\mathcal {N}}$
.
Suppose
![]() ${\mathcal {P}}$
is an excellent hybrid premouse. For the purposes of this paper, we say that
${\mathcal {P}}$
is an excellent hybrid premouse. For the purposes of this paper, we say that
![]() ${\mathcal {P}}$
satisfies weak generic interpretability if for every poset
${\mathcal {P}}$
satisfies weak generic interpretability if for every poset
![]() $\mathbb {P}\in {\mathcal {P}}$
and for every
$\mathbb {P}\in {\mathcal {P}}$
and for every
![]() ${\mathcal {P}}$
-generic
${\mathcal {P}}$
-generic
![]() $g\subseteq \mathbb {P}$
, there is an sts strategy
$g\subseteq \mathbb {P}$
, there is an sts strategy
![]() $\Lambda $
for
$\Lambda $
for
![]() ${\mathcal {P}}_0$
Footnote 51 that is definable (with parameters) over
${\mathcal {P}}_0$
Footnote 51 that is definable (with parameters) over
![]() ${\mathcal {P}}[g]$
such that for every tree
${\mathcal {P}}[g]$
such that for every tree
![]() ${\mathcal {T}}\in dom(\Lambda )$
,
${\mathcal {T}}\in dom(\Lambda )$
,
-
1. if
 ${\mathcal {T}}$
is
${\mathcal {T}}$
is
 $\mathsf {uvs}$
, then letting
$\mathsf {uvs}$
, then letting
 $\Lambda ({\mathcal {T}})=c$
, either
$\Lambda ({\mathcal {T}})=c$
, either-
(a) for some node
 ${\mathcal {R}}$
of
${\mathcal {R}}$
of
 ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
 $\pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
is defined,
$\pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
is defined,
 ${\mathcal {T}}_{\geq {\mathcal {R}}}$
is a tree on
${\mathcal {T}}_{\geq {\mathcal {R}}}$
is a tree on
 ${\mathcal {R}}^b$
and
${\mathcal {R}}^b$
and
 ${\mathcal {T}}^\frown \{c\}$
is
${\mathcal {T}}^\frown \{c\}$
is
 $({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated, or
$({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated, or -
(b) for some node
 ${\mathcal {R}}$
of
${\mathcal {R}}$
of
 ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
 $\pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
is defined,
$\pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
is defined,
 ${\mathcal {T}}_{\geq {\mathcal {R}}}$
is a tree on
${\mathcal {T}}_{\geq {\mathcal {R}}}$
is a tree on
 ${\mathcal {R}}^b$
that is above
${\mathcal {R}}^b$
that is above
 $Ord\cap {\mathcal {R}}^b$
,
$Ord\cap {\mathcal {R}}^b$
,
 ${\mathcal {Q}}(c, {\mathcal {T}})$
exists and
${\mathcal {Q}}(c, {\mathcal {T}})$
exists and
 ${\mathcal {Q}}(c, {\mathcal {T}}){\trianglelefteq } {\mathrm m}^+({\mathcal {T}})$
,
${\mathcal {Q}}(c, {\mathcal {T}}){\trianglelefteq } {\mathrm m}^+({\mathcal {T}})$
,
-
-
2. if
 ${\mathcal {T}}$
is
${\mathcal {T}}$
is
 $\mathsf {nuvs}$
, then letting
$\mathsf {nuvs}$
, then letting
 $c=\Lambda ({\mathcal {T}})$
, c is a cofinal branch if and only if
$c=\Lambda ({\mathcal {T}})$
, c is a cofinal branch if and only if
 ${\mathcal {Q}}(c, {\mathcal {T}})$
exists and
${\mathcal {Q}}(c, {\mathcal {T}})$
exists and
 ${\mathcal {T}}^\frown \{c\}$
is
${\mathcal {T}}^\frown \{c\}$
is
 $({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated.
$({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated.
Proposition 2.17. Suppose
![]() ${\mathcal {P}}$
is an excellent hybrid premouse. Then
${\mathcal {P}}$
is an excellent hybrid premouse. Then
![]() ${\mathcal {P}}$
satisfies weak generic interpretability.
${\mathcal {P}}$
satisfies weak generic interpretability.
Proof. We outline the proof, as the proof is very much like the proof of [Reference Sargsyan and Trang38, Theorem 6.1.5]. Let g be
![]() ${\mathcal {P}}$
-generic. The definition of
${\mathcal {P}}$
-generic. The definition of
![]() $\Lambda $
essentially repeats the above clauses. We first consider trees that are
$\Lambda $
essentially repeats the above clauses. We first consider trees that are
![]() $\mathsf {uvs}$
.
$\mathsf {uvs}$
.
Suppose
![]() ${\mathcal {T}}$
is an
${\mathcal {T}}$
is an
![]() $\mathsf {uvs}$
tree according to
$\mathsf {uvs}$
tree according to
![]() $\Lambda $
, and suppose that for some node
$\Lambda $
, and suppose that for some node
![]() ${\mathcal {R}}$
on
${\mathcal {R}}$
on
![]() ${\mathcal {T}}$
,
${\mathcal {T}}$
,
![]() $\pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
exists and
$\pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
exists and
![]() ${\mathcal {T}}_{\geq {\mathcal {R}}}$
is a tree based on
${\mathcal {T}}_{\geq {\mathcal {R}}}$
is a tree based on
![]() ${\mathcal {R}}^b$
. Because
${\mathcal {R}}^b$
. Because
![]() ${\mathcal {T}}$
is according to
${\mathcal {T}}$
is according to
![]() $\Lambda $
, we may assume that
$\Lambda $
, we may assume that
![]() ${\mathcal {R}}$
is
${\mathcal {R}}$
is
![]() $({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated. Thus, we can fix a window w of
$({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated. Thus, we can fix a window w of
![]() ${\mathcal {P}}$
such that g is
${\mathcal {P}}$
such that g is
![]() $<\nu ^w$
-generic over
$<\nu ^w$
-generic over
![]() ${\mathcal {P}}$
, and letting
${\mathcal {P}}$
, and letting
![]() ${\mathcal {W}}$
be the iterate of
${\mathcal {W}}$
be the iterate of
![]() ${\mathcal {P}}_0$
constructed by the fully backgrounded hod pair construction of
${\mathcal {P}}_0$
constructed by the fully backgrounded hod pair construction of
![]() ${\mathcal {P}}|{\delta }^w$
using extenders with critical point
${\mathcal {P}}|{\delta }^w$
using extenders with critical point
![]() $>\nu ^w$
, we can find an embedding
$>\nu ^w$
, we can find an embedding
![]() $\sigma :{\mathcal {R}}^b\rightarrow {\mathcal {W}}^b$
such that
$\sigma :{\mathcal {R}}^b\rightarrow {\mathcal {W}}^b$
such that
(a)
![]() $\pi ^{{\mathcal {U}}, b}=\sigma \circ \pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
, where
$\pi ^{{\mathcal {U}}, b}=\sigma \circ \pi ^{{\mathcal {T}}_{\leq {\mathcal {R}}}, b}$
, where
![]() ${\mathcal {U}}$
is the
${\mathcal {U}}$
is the
![]() ${\mathcal {P}}_0$
-to-
${\mathcal {P}}_0$
-to-
![]() ${\mathcal {W}}$
tree according to
${\mathcal {W}}$
tree according to
![]() $S^{\mathcal {P}}$
and
$S^{\mathcal {P}}$
and
(b)
![]() ${\mathcal {T}}_{\geq {\mathcal {R}}}$
is according to the
${\mathcal {T}}_{\geq {\mathcal {R}}}$
is according to the
![]() $\sigma $
-pullback of
$\sigma $
-pullback of
![]() $S^{\mathcal {P}}_{{\mathcal {W}}^b}$
.
$S^{\mathcal {P}}_{{\mathcal {W}}^b}$
.
Letting c be the branch according to the strategy as in (b), we have that
![]() ${\mathcal {T}}^\frown \{c\}$
is
${\mathcal {T}}^\frown \{c\}$
is
![]() $({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated. Moreover, there is only one such branch c. To see this, we need to reflect.
$({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated. Moreover, there is only one such branch c. To see this, we need to reflect.
Let
![]() $\xi $
be large and let
$\xi $
be large and let
![]() $\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
be a countable hull. Fix an
$\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
be a countable hull. Fix an
![]() ${\mathcal {N}}$
-generic
${\mathcal {N}}$
-generic
![]() $h\in {\mathcal {P}}$
. Let
$h\in {\mathcal {P}}$
. Let
![]() ${\mathcal {U}}\in {\mathcal {N}}[h]$
be an
${\mathcal {U}}\in {\mathcal {N}}[h]$
be an
![]() $\mathsf {uvs}$
tree on
$\mathsf {uvs}$
tree on
![]() ${\mathcal {N}}_0$
such that for some node
${\mathcal {N}}_0$
such that for some node
![]() ${\mathcal {S}}$
on
${\mathcal {S}}$
on
![]() ${\mathcal {U}}$
with the property that
${\mathcal {U}}$
with the property that
![]() $\pi ^{{\mathcal {U}}, b}$
exists,
$\pi ^{{\mathcal {U}}, b}$
exists,
![]() ${\mathcal {U}}_{\geq {\mathcal {S}}}$
is a normal tree on
${\mathcal {U}}_{\geq {\mathcal {S}}}$
is a normal tree on
![]() ${\mathcal {S}}^b$
, and moreover,
${\mathcal {S}}^b$
, and moreover,
![]() ${\mathcal {U}}$
is
${\mathcal {U}}$
is
![]() $({\mathcal {N}}_0, {\mathcal {N}}_0^b, S^{\mathcal {N}})$
-authenticated in
$({\mathcal {N}}_0, {\mathcal {N}}_0^b, S^{\mathcal {N}})$
-authenticated in
![]() ${\mathcal {N}}[h]$
. Suppose now that there are two distinct branches c and d obtained in the above manner. We can then fix
${\mathcal {N}}[h]$
. Suppose now that there are two distinct branches c and d obtained in the above manner. We can then fix
![]() ${\mathcal {N}}$
-windows
${\mathcal {N}}$
-windows
![]() $u_1, u_2$
that play the role of w above and build
$u_1, u_2$
that play the role of w above and build
![]() ${\mathcal { K}}_1$
and
${\mathcal { K}}_1$
and
![]() ${\mathcal { K}}_2$
, the equivalents of
${\mathcal { K}}_2$
, the equivalents of
![]() ${\mathcal {W}}$
above, inside
${\mathcal {W}}$
above, inside
![]() ${\mathcal {N}}|{\delta }^{u_1}$
and
${\mathcal {N}}|{\delta }^{u_1}$
and
![]() ${\mathcal {N}}|{\delta }^{u_2}$
. For
${\mathcal {N}}|{\delta }^{u_2}$
. For
![]() $i\leq 2$
, we have maps
$i\leq 2$
, we have maps
![]() $m_i:{\mathcal {S}}^b\rightarrow {\mathcal { K}}^b_i$
and
$m_i:{\mathcal {S}}^b\rightarrow {\mathcal { K}}^b_i$
and
![]() $S^{\mathcal {N}}$
-iteration maps
$S^{\mathcal {N}}$
-iteration maps
![]() $\tau _i:{\mathcal {N}}_0^b\rightarrow {\mathcal { K}}^b_i$
such that
$\tau _i:{\mathcal {N}}_0^b\rightarrow {\mathcal { K}}^b_i$
such that
![]() $\tau _i=m_i\circ \pi ^{{\mathcal {U}}_{\leq {\mathcal {S}}}, b}$
. Let
$\tau _i=m_i\circ \pi ^{{\mathcal {U}}_{\leq {\mathcal {S}}}, b}$
. Let
![]() $\tau _i: {\mathcal { K}}^b_i \rightarrow \mathcal {Y}$
be the comparison map using strategies
$\tau _i: {\mathcal { K}}^b_i \rightarrow \mathcal {Y}$
be the comparison map using strategies
![]() $(S^{\mathcal {N}})_{{\mathcal { K}}^b_i}$
. Then, for
$(S^{\mathcal {N}})_{{\mathcal { K}}^b_i}$
. Then, for
![]() $i\in \{c,d\}$
, there is an embedding
$i\in \{c,d\}$
, there is an embedding
![]() ${\lambda }_i: {\mathcal {M}}^{\mathcal {U}}_i \rightarrow \mathcal {Y}$
that factors into the iteration map from
${\lambda }_i: {\mathcal {M}}^{\mathcal {U}}_i \rightarrow \mathcal {Y}$
that factors into the iteration map from
![]() ${\mathcal {N}}_0^b$
to
${\mathcal {N}}_0^b$
to
![]() $\mathcal {Y}$
. It is then easy to see, using branch condensation of
$\mathcal {Y}$
. It is then easy to see, using branch condensation of
![]() $S^{\mathcal {P}}$
and its
$S^{\mathcal {P}}$
and its
![]() $\pi $
-pullback, that
$\pi $
-pullback, that
![]() $c = d$
.
$c = d$
.
The rest of the argument is very similar. For example, we outline the proof of clause 2 in the definition of weak generic interpretability. Suppose
![]() ${\mathcal {T}}\in {\mathcal {P}}[g]$
is
${\mathcal {T}}\in {\mathcal {P}}[g]$
is
![]() $\mathsf {nuvs}$
and
$\mathsf {nuvs}$
and
![]() ${\mathcal {Q}}$
is a
${\mathcal {Q}}$
is a
![]() $({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated
$({\mathcal {P}}_0, {\mathcal {P}}_0^b, S^{\mathcal {P}})$
-authenticated
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() ${\mathcal {T}}$
. We want to see that there is a cofinal well-founded branch
${\mathcal {T}}$
. We want to see that there is a cofinal well-founded branch
![]() $c\in {\mathcal {P}}[g]$
such that
$c\in {\mathcal {P}}[g]$
such that
![]() ${\mathcal {Q}}(c, {\mathcal {T}})={\mathcal {Q}}$
. As above, instead of working with
${\mathcal {Q}}(c, {\mathcal {T}})={\mathcal {Q}}$
. As above, instead of working with
![]() ${\mathcal {P}}$
, we can work with a reflection. Thus, we assume that
${\mathcal {P}}$
, we can work with a reflection. Thus, we assume that
![]() $\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
is a countable elementary embedding,
$\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi $
is a countable elementary embedding,
![]() $h\in {\mathcal {P}}$
is
$h\in {\mathcal {P}}$
is
![]() ${\mathcal {N}}$
-generic and
${\mathcal {N}}$
-generic and
![]() ${\mathcal {T}}, {\mathcal {Q}}\in {\mathcal {N}}[h]$
. Moreover, we can assume that
${\mathcal {T}}, {\mathcal {Q}}\in {\mathcal {N}}[h]$
. Moreover, we can assume that
![]() ${\mathcal {N}}$
is pointwise definable. Let
${\mathcal {N}}$
is pointwise definable. Let
![]() $\Psi $
be the
$\Psi $
be the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $S^{\mathcal {P}}$
. As
$S^{\mathcal {P}}$
. As
![]() ${\mathcal {Q}}$
is
${\mathcal {Q}}$
is
![]() $({\mathcal {N}}_0, {\mathcal {N}}_0^b, S^{\mathcal {N}})$
-authenticated, it follows from Theorem 2.13 that
$({\mathcal {N}}_0, {\mathcal {N}}_0^b, S^{\mathcal {N}})$
-authenticated, it follows from Theorem 2.13 that
![]() ${\mathcal {Q}}$
has an iteration strategy as a
${\mathcal {Q}}$
has an iteration strategy as a
![]() $\Psi _{{\mathrm m}^+({\mathcal {T}})}$
-sts premouse. Let c be the branch of
$\Psi _{{\mathrm m}^+({\mathcal {T}})}$
-sts premouse. Let c be the branch of
![]() ${\mathcal {T}}$
according to
${\mathcal {T}}$
according to
![]() $\Psi $
. As
$\Psi $
. As
![]() ${\mathcal {N}}$
is pointwise definable, we have that
${\mathcal {N}}$
is pointwise definable, we have that
![]() ${\mathcal {Q}}(c, {\mathcal {T}})$
-exists, and hence,
${\mathcal {Q}}(c, {\mathcal {T}})$
-exists, and hence,
![]() ${\mathcal {Q}}(c, {\mathcal {T}})={\mathcal {Q}}$
.
${\mathcal {Q}}(c, {\mathcal {T}})={\mathcal {Q}}$
.
Next, we show that the low-level strategies are, in fact, universally Baire. However, Proposition 2.21 shows that
![]() $S^{\mathcal {P}}$
itself does not have a universally Baire representation.
$S^{\mathcal {P}}$
itself does not have a universally Baire representation.
Proposition 2.18. Suppose
![]() ${\mathcal {P}}$
is excellent, g is
${\mathcal {P}}$
is excellent, g is
![]() ${\mathcal {P}}$
-generic and
${\mathcal {P}}$
-generic and
![]() $\Sigma $
is the generic interpretation of
$\Sigma $
is the generic interpretation of
![]() $S^{\mathcal {P}}$
onto
$S^{\mathcal {P}}$
onto
![]() ${\mathcal {P}}[g]$
. Let
${\mathcal {P}}[g]$
. Let
![]() ${\mathcal {T}}\in {\mathcal {P}}[g]$
be an iteration tree on
${\mathcal {T}}\in {\mathcal {P}}[g]$
be an iteration tree on
![]() ${\mathcal {P}}$
of length
${\mathcal {P}}$
of length
![]() $<\omega _1^{{\mathcal {P}}[g]}$
such that
$<\omega _1^{{\mathcal {P}}[g]}$
such that
![]() $\pi ^{{\mathcal {T}}, b}$
-exists. Set
$\pi ^{{\mathcal {T}}, b}$
-exists. Set
![]() ${\mathcal {R}}=\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)$
. Then
${\mathcal {R}}=\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)$
. Then
![]() $(\Sigma _{\mathcal {R}}{\restriction } HC^{{\mathcal {P}}[g]})\in \Gamma ^{\infty }_g$
. Moreover, for any
$(\Sigma _{\mathcal {R}}{\restriction } HC^{{\mathcal {P}}[g]})\in \Gamma ^{\infty }_g$
. Moreover, for any
![]() ${\mathcal {P}}$
-cardinal
${\mathcal {P}}$
-cardinal
![]() $\eta $
, there are
$\eta $
, there are
![]() $\eta $
-complementing trees
$\eta $
-complementing trees
![]() $T, S\in {\mathcal {P}}[g]$
such that for all posets
$T, S\in {\mathcal {P}}[g]$
such that for all posets
![]() $\mathbb {Q}\in {\mathcal {P}}[g]$
such that
$\mathbb {Q}\in {\mathcal {P}}[g]$
such that
![]() ${\vert {\mathbb {Q}}\vert }^{{\mathcal {P}}[g]}<\eta $
and for all
${\vert {\mathbb {Q}}\vert }^{{\mathcal {P}}[g]}<\eta $
and for all
![]() ${\mathcal {P}}[g]$
-generic
${\mathcal {P}}[g]$
-generic
![]() $h\subseteq \mathbb {Q}$
,
$h\subseteq \mathbb {Q}$
,
Proof. We again outline the proof as the proof uses standard ideas. Let w be a maximal window of
![]() ${\mathcal {P}}$
such that g is generic for a poset in
${\mathcal {P}}$
such that g is generic for a poset in
![]() ${\mathcal {P}}|\nu ^w$
. We now outline the construction producing
${\mathcal {P}}|\nu ^w$
. We now outline the construction producing
![]() $\nu ^w$
-complementing trees
$\nu ^w$
-complementing trees
![]() $(T, S)$
as in the statement of the proposition.
$(T, S)$
as in the statement of the proposition.
Let
![]() ${\mathcal {S}}$
be the model appearing on the hod pair construction of
${\mathcal {S}}$
be the model appearing on the hod pair construction of
![]() ${\mathcal {P}}|{\delta }^w$
in which extenders used have critical points
${\mathcal {P}}|{\delta }^w$
in which extenders used have critical points
![]() $>\nu ^w$
and to which
$>\nu ^w$
and to which
![]() ${\mathcal {R}}$
normally iterates via
${\mathcal {R}}$
normally iterates via
![]() $\Sigma _{\mathcal {R}}$
. Let
$\Sigma _{\mathcal {R}}$
. Let
![]() $i: {\mathcal {R}}\rightarrow {\mathcal {S}}$
be the iteration embedding. What we need to show is that club many hulls of
$i: {\mathcal {R}}\rightarrow {\mathcal {S}}$
be the iteration embedding. What we need to show is that club many hulls of
![]() ${\mathcal {P}}[g]$
are correct about
${\mathcal {P}}[g]$
are correct about
![]() $\Sigma _{\mathcal {R}}$
, where we take
$\Sigma _{\mathcal {R}}$
, where we take
![]() $\Sigma _{\mathcal {R}}$
to be defined as i-pullback of the strategy of
$\Sigma _{\mathcal {R}}$
to be defined as i-pullback of the strategy of
![]() ${\mathcal {S}}$
that
${\mathcal {S}}$
that
![]() ${\mathcal {S}}$
inherits from
${\mathcal {S}}$
inherits from
![]() ${\mathcal {P}}$
(see Theorem 2.12). That this works follows from the fact that the strategy of
${\mathcal {P}}$
(see Theorem 2.12). That this works follows from the fact that the strategy of
![]() ${\mathcal {S}}$
has hull condensation. Let
${\mathcal {S}}$
has hull condensation. Let
![]() $\Psi $
be the strategy of
$\Psi $
be the strategy of
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
More precisely, let
![]() $\phi (x, {\mathcal {R}}, {\mathcal {S}}, i)$
be the formula that says ‘
$\phi (x, {\mathcal {R}}, {\mathcal {S}}, i)$
be the formula that says ‘
![]() $x\in {\mathbb {R}}$
codes an iteration of
$x\in {\mathbb {R}}$
codes an iteration of
![]() ${\mathcal {R}}$
that is according to the i-pullback of
${\mathcal {R}}$
that is according to the i-pullback of
![]() $\Psi $
’. Clearly,
$\Psi $
’. Clearly,
![]() $\phi $
defines
$\phi $
defines
![]() $\Sigma _{\mathcal {R}}{\restriction } HC^{{\mathcal {P}}[g]}$
. Let now
$\Sigma _{\mathcal {R}}{\restriction } HC^{{\mathcal {P}}[g]}$
. Let now
![]() $\xi $
be large and
$\xi $
be large and
![]() $\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi [g]$
be countable such that
$\pi :{\mathcal {N}}\rightarrow {\mathcal {P}}|\xi [g]$
be countable such that
![]() ${\mathcal {R}}, (i, {\mathcal {S}})\in rng(\pi )$
. Let
${\mathcal {R}}, (i, {\mathcal {S}})\in rng(\pi )$
. Let
![]() $\Phi =\pi ^{-1}(\Psi )$
and
$\Phi =\pi ^{-1}(\Psi )$
and
![]() $j=\pi ^{-1}(i)$
. Let
$j=\pi ^{-1}(i)$
. Let
![]() $h\in {\mathcal {P}}[g]$
be a
$h\in {\mathcal {P}}[g]$
be a
![]() $<\pi ^{-1}(\nu ^w)$
-generic over
$<\pi ^{-1}(\nu ^w)$
-generic over
![]() ${\mathcal {N}}$
and let
${\mathcal {N}}$
and let
![]() ${\mathcal {U}}\in {\mathcal {N}}[g]$
be a tree on
${\mathcal {U}}\in {\mathcal {N}}[g]$
be a tree on
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
Suppose first that
![]() ${\mathcal {N}}[h]{\vDash } \text {`}j{\mathcal {U}}$
is according to the strategy of
${\mathcal {N}}[h]{\vDash } \text {`}j{\mathcal {U}}$
is according to the strategy of
![]() $\Phi ^h$
’. Because
$\Phi ^h$
’. Because
![]() $\Phi ^h$
is the
$\Phi ^h$
is the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Psi $
, we have that
$\Psi $
, we have that
![]() $i{\mathcal {U}}=\pi (j{\mathcal {U}})$
is according to
$i{\mathcal {U}}=\pi (j{\mathcal {U}})$
is according to
![]() $\Psi $
. Hence,
$\Psi $
. Hence,
![]() ${\mathcal {U}}$
is according to
${\mathcal {U}}$
is according to
![]() $\Sigma _{\mathcal {R}}$
.
$\Sigma _{\mathcal {R}}$
.
Next, suppose that
![]() ${\mathcal {U}}$
is according to
${\mathcal {U}}$
is according to
![]() $\Sigma _{\mathcal {R}}$
. It then follows by the above reasoning that
$\Sigma _{\mathcal {R}}$
. It then follows by the above reasoning that
![]() ${\mathcal {N}}[h]{\vDash } \text {`}j{\mathcal {U}}$
is according to the strategy of
${\mathcal {N}}[h]{\vDash } \text {`}j{\mathcal {U}}$
is according to the strategy of
![]() $\Phi ^h$
’. This finishes the proof that
$\Phi ^h$
’. This finishes the proof that
![]() $\Sigma _{\mathcal {R}}$
has a uB representation. The rest of the proposition follows from the fact that the formula
$\Sigma _{\mathcal {R}}$
has a uB representation. The rest of the proposition follows from the fact that the formula
![]() $\phi $
above defines
$\phi $
above defines
![]() $\Sigma _{\mathcal {R}}$
in all
$\Sigma _{\mathcal {R}}$
in all
![]() $<\nu ^w$
-generic extensions of
$<\nu ^w$
-generic extensions of
![]() ${\mathcal {P}}[g]$
. Such calculations were carried out more carefully in [Reference Sargsyan34] and also in [Reference Sargsyan37]. In particular, the reader may wish to consult [Reference Sargsyan37, Proposition 1.4].
${\mathcal {P}}[g]$
. Such calculations were carried out more carefully in [Reference Sargsyan34] and also in [Reference Sargsyan37]. In particular, the reader may wish to consult [Reference Sargsyan37, Proposition 1.4].
2.9. Fully backgrounded constructions inside excellent hybrid premice
Given an excellent hybrid premouse
![]() ${\mathcal {P}}$
, we would eventually like to show that collapsing
${\mathcal {P}}$
, we would eventually like to show that collapsing
![]() $(({\delta }^{\mathcal {P}})^+)^{\mathcal {P}}$
to be countable forces both
$(({\delta }^{\mathcal {P}})^+)^{\mathcal {P}}$
to be countable forces both
![]() $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
. Such an analysis of generic extensions of fine structural models usually requires some kind of reconstructibility property, which guarantees that the model can somehow see versions of itself inside it. In this subsection, we would like to establish some such facts about excellent hybrid premice. Proposition 2.19 is a key proposition that we will need in this paper. Recall the definition of
$\mathsf {LSA-over-uB}$
. Such an analysis of generic extensions of fine structural models usually requires some kind of reconstructibility property, which guarantees that the model can somehow see versions of itself inside it. In this subsection, we would like to establish some such facts about excellent hybrid premice. Proposition 2.19 is a key proposition that we will need in this paper. Recall the definition of
![]() ${\mathcal {P}}_0$
from Definition 2.7.
${\mathcal {P}}_0$
from Definition 2.7.
Proposition 2.19. Suppose
![]() ${\mathcal {P}}$
is excellent and g is
${\mathcal {P}}$
is excellent and g is
![]() ${\mathcal {P}}$
-generic. Let
${\mathcal {P}}$
-generic. Let
![]() $\Sigma $
be the generic interpretation of
$\Sigma $
be the generic interpretation of
![]() $S^{\mathcal {P}}$
onto
$S^{\mathcal {P}}$
onto
![]() ${\mathcal {P}}[g]$
and suppose
${\mathcal {P}}[g]$
and suppose
![]() ${\mathcal {R}}$
is a
${\mathcal {R}}$
is a
![]() $\Sigma $
-maximal iterate of
$\Sigma $
-maximal iterate of
![]() ${\mathcal {P}}_0$
. Let w be a maximal window of
${\mathcal {P}}_0$
. Let w be a maximal window of
![]() ${\mathcal {P}}$
such that w is above
${\mathcal {P}}$
such that w is above
![]() ${\delta }^{\mathcal {P}}$
, g is generic for a poset in
${\delta }^{\mathcal {P}}$
, g is generic for a poset in
![]() ${\mathcal {P}}|\nu ^w$
and
${\mathcal {P}}|\nu ^w$
and
![]() ${\mathcal {R}}\in {\mathcal {P}}|\nu ^w[g]$
. Let
${\mathcal {R}}\in {\mathcal {P}}|\nu ^w[g]$
. Let
![]() $\xi <{\delta }^{{\mathcal {R}}^b}$
be a Woodin cardinal of
$\xi <{\delta }^{{\mathcal {R}}^b}$
be a Woodin cardinal of
![]() ${\mathcal {R}}$
. Suppose
${\mathcal {R}}$
. Suppose
![]() ${\mathcal {N}}_0$
is the output of the fully backgrounded hod pair construction of
${\mathcal {N}}_0$
is the output of the fully backgrounded hod pair construction of
![]() ${\mathcal {P}}|{\delta }^w[g]$
done relative to
${\mathcal {P}}|{\delta }^w[g]$
done relative to
![]() $\Sigma _{{\mathcal {R}}|\xi }$
and over
$\Sigma _{{\mathcal {R}}|\xi }$
and over
![]() ${\mathcal {R}}|\xi $
and using extenders with critical points
${\mathcal {R}}|\xi $
and using extenders with critical points
![]() $>\nu ^w$
. Then
$>\nu ^w$
. Then
![]() $Ord\cap {\mathcal {N}}_0={\delta }^w$
.
$Ord\cap {\mathcal {N}}_0={\delta }^w$
.
Proof. Towards a contradiction, suppose that
![]() $\eta =_{def}Ord\cap {\mathcal {N}}_0<{\delta }^w$
. We will now work towards showing that
$\eta =_{def}Ord\cap {\mathcal {N}}_0<{\delta }^w$
. We will now work towards showing that
![]() $\eta $
is a Woodin cardinal of
$\eta $
is a Woodin cardinal of
![]() ${\mathcal {P}}$
. As
${\mathcal {P}}$
. As
![]() $\eta \in (\nu ^w, {\delta }^w)$
, this is clearly a contradiction. Suppose then
$\eta \in (\nu ^w, {\delta }^w)$
, this is clearly a contradiction. Suppose then
![]() $\eta $
is not a Woodin cardinal of
$\eta $
is not a Woodin cardinal of
![]() ${\mathcal {P}}$
. As
${\mathcal {P}}$
. As
![]() ${\mathcal {P}}$
has no Woodin cardinals in the interval
${\mathcal {P}}$
has no Woodin cardinals in the interval
![]() $(\nu ^w, {\delta }^w)$
, we must have that there is a
$(\nu ^w, {\delta }^w)$
, we must have that there is a
![]() $\Sigma $
-mouse
$\Sigma $
-mouse
![]() ${\mathcal {P}}|\eta {\trianglelefteq } {\mathcal {Q}}{\trianglelefteq } {\mathcal {P}}$
such that
${\mathcal {P}}|\eta {\trianglelefteq } {\mathcal {Q}}{\trianglelefteq } {\mathcal {P}}$
such that
![]() $\eta $
is a cutpoint of
$\eta $
is a cutpoint of
![]() ${\mathcal {Q}}$
,
${\mathcal {Q}}$
,
![]() ${\mathcal {Q}}{\vDash } \text {`}\eta $
is a Woodin cardinal’ but
${\mathcal {Q}}{\vDash } \text {`}\eta $
is a Woodin cardinal’ but
![]() $\eta $
is not Woodin relative to functions definable over
$\eta $
is not Woodin relative to functions definable over
![]() ${\mathcal {Q}}$
. Unfortunately,
${\mathcal {Q}}$
. Unfortunately,
![]() ${\mathcal {Q}}$
cannot be translated into a
${\mathcal {Q}}$
cannot be translated into a
![]() $\Sigma _{{\mathcal {N}}_0}$
-mouse, but we can rebuild it in a sufficiently rich model extending
$\Sigma _{{\mathcal {N}}_0}$
-mouse, but we can rebuild it in a sufficiently rich model extending
![]() ${\mathcal {N}}_0$
.
${\mathcal {N}}_0$
.
Let
![]() ${\mathcal {N}}$
be the output of a fully backgrounded construction of
${\mathcal {N}}$
be the output of a fully backgrounded construction of
![]() ${\mathcal {P}}|{\delta }^w[g]$
done with respect to
${\mathcal {P}}|{\delta }^w[g]$
done with respect to
![]() $\Sigma _{{\mathcal {N}}_0}$
and over
$\Sigma _{{\mathcal {N}}_0}$
and over
![]() ${\mathcal {N}}_0$
using extenders with critical point
${\mathcal {N}}_0$
using extenders with critical point
![]() $>\eta $
. As
$>\eta $
. As
![]() ${\mathcal {N}}_0$
is a
${\mathcal {N}}_0$
is a
![]() $\Sigma $
-maximal iterate of
$\Sigma $
-maximal iterate of
![]() ${\mathcal {P}}_0$
,Footnote 52 we have that
${\mathcal {P}}_0$
,Footnote 52 we have that
![]() ${\mathcal {N}}{\vDash } \text {`}\eta $
is a Woodin cardinal’. We now want to rebuild
${\mathcal {N}}{\vDash } \text {`}\eta $
is a Woodin cardinal’. We now want to rebuild
![]() ${\mathcal {Q}}$
inside
${\mathcal {Q}}$
inside
![]() ${\mathcal {N}}[{\mathcal {P}}|\eta ]$
. The idea here goes back to [Reference Sargsyan and Trang38, Theorem 8.1.13] (for instance, the construction of
${\mathcal {N}}[{\mathcal {P}}|\eta ]$
. The idea here goes back to [Reference Sargsyan and Trang38, Theorem 8.1.13] (for instance, the construction of
![]() ${\mathcal {N}}_2$
in the proof of the aforementioned theorem). Notice that if p is the
${\mathcal {N}}_2$
in the proof of the aforementioned theorem). Notice that if p is the
![]() ${\mathcal {P}}_0$
-to-
${\mathcal {P}}_0$
-to-
![]() ${\mathcal {N}}_0$
-iteration,Footnote 53 then
${\mathcal {N}}_0$
-iteration,Footnote 53 then
![]() $\pi ^{p, b}$
exists and
$\pi ^{p, b}$
exists and
![]() $\pi ^{p, b}\in {\mathcal {N}}[{\mathcal {P}}|\eta ]$
. Let
$\pi ^{p, b}\in {\mathcal {N}}[{\mathcal {P}}|\eta ]$
. Let
![]() $X=\pi ^{p, b}[{\mathcal {P}}_0^b]$
. Working inside
$X=\pi ^{p, b}[{\mathcal {P}}_0^b]$
. Working inside
![]() ${\mathcal {N}}[{\mathcal {P}}|\eta ]$
, we can build a
${\mathcal {N}}[{\mathcal {P}}|\eta ]$
, we can build a
![]() $\Sigma $
-premouse over
$\Sigma $
-premouse over
![]() ${\mathcal {P}}|\eta $
via a fully backgrounded
${\mathcal {P}}|\eta $
via a fully backgrounded
![]() $({\mathcal {N}}_0, X, S^{\mathcal {N}})$
-authenticated construction. In this construction, we only use extenders with critical point
$({\mathcal {N}}_0, X, S^{\mathcal {N}})$
-authenticated construction. In this construction, we only use extenders with critical point
![]() $>\eta $
. Let
$>\eta $
. Let
![]() ${\mathcal {W}}$
be the output of this construction. As
${\mathcal {W}}$
be the output of this construction. As
![]() ${\mathcal {W}}$
is universal, we have that
${\mathcal {W}}$
is universal, we have that
![]() ${\mathcal {Q}}{\trianglelefteq } {\mathcal {W}}$
. Thus,
${\mathcal {Q}}{\trianglelefteq } {\mathcal {W}}$
. Thus,
![]() ${\mathcal {N}}[{\mathcal {P}}|\eta ]{\vDash } \text {`}\eta $
is not a Woodin cardinal’.
${\mathcal {N}}[{\mathcal {P}}|\eta ]{\vDash } \text {`}\eta $
is not a Woodin cardinal’.
However, standard arguments show that
![]() ${\mathcal {N}}[{\mathcal {P}}|\eta ]{\vDash } \text {`}\eta $
is a Woodin cardinal’. Indeed, let
${\mathcal {N}}[{\mathcal {P}}|\eta ]{\vDash } \text {`}\eta $
is a Woodin cardinal’. Indeed, let
![]() $f:\eta \rightarrow \eta $
be a function in
$f:\eta \rightarrow \eta $
be a function in
![]() ${\mathcal {N}}[{\mathcal {P}}|\eta ]$
. Because
${\mathcal {N}}[{\mathcal {P}}|\eta ]$
. Because
![]() ${\mathcal {P}}|\eta $
is added by an
${\mathcal {P}}|\eta $
is added by an
![]() $\eta $
-cc poset, we can find
$\eta $
-cc poset, we can find
![]() $g\in {\mathcal {N}}$
such that for every
$g\in {\mathcal {N}}$
such that for every
![]() ${\alpha }<\eta $
,
${\alpha }<\eta $
,
![]() $f({\alpha })<g({\alpha })$
. Let
$f({\alpha })<g({\alpha })$
. Let
![]() $E\in \vec {E}^{{\mathcal {N}}_0}$
be any extender witnessing Woodiness for g and such that
$E\in \vec {E}^{{\mathcal {N}}_0}$
be any extender witnessing Woodiness for g and such that
![]() ${\mathcal {N}}{\vDash } \text {`}\nu _E$
is a measurable cardinal’. Thus,
${\mathcal {N}}{\vDash } \text {`}\nu _E$
is a measurable cardinal’. Thus,
![]() $\pi ^{{\mathcal {N}}_0}_E(g)(\kappa )<\nu _E$
, where
$\pi ^{{\mathcal {N}}_0}_E(g)(\kappa )<\nu _E$
, where
![]() $\kappa $
is the critical point of E. Let F be the resurrection of E. We must have that
$\kappa $
is the critical point of E. Let F be the resurrection of E. We must have that
![]() $\pi ^{\mathcal {P}}_F(f)(\kappa )<\nu _E$
. Thus,
$\pi ^{\mathcal {P}}_F(f)(\kappa )<\nu _E$
. Thus,
![]() $F{\restriction } \nu _E\in {\mathcal {P}}|\eta $
is an extender witnessing Woodinness for f in
$F{\restriction } \nu _E\in {\mathcal {P}}|\eta $
is an extender witnessing Woodinness for f in
![]() ${\mathcal {P}}|\eta $
and hence in
${\mathcal {P}}|\eta $
and hence in
![]() ${\mathcal {N}}[{\mathcal {P}}|\eta ]$
.
${\mathcal {N}}[{\mathcal {P}}|\eta ]$
.
Using Proposition 2.19, we can now prove that
![]() $S^{\mathcal {P}}$
itself is not a universally Baire set. Its proof requires a few more facts from [Reference Sargsyan and Trang38], which we now review. Given an lsa type pair
$S^{\mathcal {P}}$
itself is not a universally Baire set. Its proof requires a few more facts from [Reference Sargsyan and Trang38], which we now review. Given an lsa type pair
![]() $({\mathcal {P}}, \Sigma )$
, following [Reference Sargsyan and Trang38, Definition 3.3.9], we let
$({\mathcal {P}}, \Sigma )$
, following [Reference Sargsyan and Trang38, Definition 3.3.9], we let
![]() $\Gamma ^b({\mathcal {P}}, \Sigma )$
be the set of all
$\Gamma ^b({\mathcal {P}}, \Sigma )$
be the set of all
![]() $A\subseteq {\mathbb {R}}$
such that for some countable iteration
$A\subseteq {\mathbb {R}}$
such that for some countable iteration
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists, A is Wadge reducible to
$\pi ^{{\mathcal {T}}, b}$
exists, A is Wadge reducible to
![]() $\Sigma _{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)}$
. The following comparison theorem is essentially [Reference Sargsyan and Trang38, Theorem 4.13.1].
$\Sigma _{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}^b)}$
. The following comparison theorem is essentially [Reference Sargsyan and Trang38, Theorem 4.13.1].
Theorem 2.20. Assume
![]() $\mathsf {AD}^+$
and suppose
$\mathsf {AD}^+$
and suppose
![]() $({\mathcal {P}}, \Sigma )$
and
$({\mathcal {P}}, \Sigma )$
and
![]() $({\mathcal {Q}}, \Lambda )$
are two lsa type hod pairs such that
$({\mathcal {Q}}, \Lambda )$
are two lsa type hod pairs such that
![]() $\Gamma ^b({\mathcal {P}}, \Sigma )=\Gamma ^b({\mathcal {Q}}, \Lambda )$
and both
$\Gamma ^b({\mathcal {P}}, \Sigma )=\Gamma ^b({\mathcal {Q}}, \Lambda )$
and both
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Lambda $
are splendid. Then there is an lsa type hod pair
$\Lambda $
are splendid. Then there is an lsa type hod pair
![]() $({\mathcal {R}}, \Psi )$
such that
$({\mathcal {R}}, \Psi )$
such that
![]() ${\mathcal {R}}$
is a
${\mathcal {R}}$
is a
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {P}}$
and a
${\mathcal {P}}$
and a
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal {Q}}$
and
${\mathcal {Q}}$
and
![]() $\Sigma _{\mathcal {R}}=\Psi =\Lambda _{\mathcal {R}}$
.
$\Sigma _{\mathcal {R}}=\Psi =\Lambda _{\mathcal {R}}$
.
Proposition 2.21. Suppose
![]() ${\mathcal {P}}$
is excellent and g is
${\mathcal {P}}$
is excellent and g is
![]() ${\mathcal {P}}$
-generic. Let
${\mathcal {P}}$
-generic. Let
![]() $\Sigma $
be the generic interpretation of
$\Sigma $
be the generic interpretation of
![]() $S^{\mathcal {P}}$
onto
$S^{\mathcal {P}}$
onto
![]() ${\mathcal {P}}[g]$
. Then
${\mathcal {P}}[g]$
. Then
![]() ${\mathcal {P}}[g] \vDash \Sigma \notin \Gamma ^{\infty }$
.
${\mathcal {P}}[g] \vDash \Sigma \notin \Gamma ^{\infty }$
.
Proof. Towards a contradiction, suppose that
![]() ${\mathcal {P}}[g]{\vDash } \Sigma ^g \in \Gamma ^{\infty }$
. Let
${\mathcal {P}}[g]{\vDash } \Sigma ^g \in \Gamma ^{\infty }$
. Let
![]() $(w_i: i<\omega )$
be a sequence of successive windows of
$(w_i: i<\omega )$
be a sequence of successive windows of
![]() ${\mathcal {P}}$
such that g is generic over a poset in
${\mathcal {P}}$
such that g is generic over a poset in
![]() ${\mathcal {P}}|\nu ^{w_0}$
. Set
${\mathcal {P}}|\nu ^{w_0}$
. Set
![]() ${\delta }_i={\delta }^{w_i}$
.
${\delta }_i={\delta }^{w_i}$
.
For each i, let
![]() ${\mathcal {P}}_i$
be the
${\mathcal {P}}_i$
be the
![]() $S^{\mathcal {P}}$
-iterateFootnote 54 built via the fully backgrounded hod pair construction of
$S^{\mathcal {P}}$
-iterateFootnote 54 built via the fully backgrounded hod pair construction of
![]() ${\mathcal {P}}|{\delta }_i$
using extenders with critical points
${\mathcal {P}}|{\delta }_i$
using extenders with critical points
![]() $>\nu _i^{w_i}$
. It follows from Proposition 2.19 that
$>\nu _i^{w_i}$
. It follows from Proposition 2.19 that
(1)
![]() ${\delta }^{{\mathcal {P}}_i}={\delta }_i$
, i.e.,
${\delta }^{{\mathcal {P}}_i}={\delta }_i$
, i.e.,
![]() ${\delta }_i$
is the largest Woodin cardinal of
${\delta }_i$
is the largest Woodin cardinal of
![]() ${\mathcal {P}}_i$
.
${\mathcal {P}}_i$
.
Fix now
![]() $k\subseteq Coll(\omega , <{\delta }_{\omega })$
generic over
$k\subseteq Coll(\omega , <{\delta }_{\omega })$
generic over
![]() ${\mathcal {P}}[g]$
, where
${\mathcal {P}}[g]$
, where
![]() ${\delta }_{\omega }=\sup _{i<\omega }{\delta }_i$
. Recall next that Steel showed that if there are unboundedly many Woodin cardinals, then every universally Baire set has a universally Baire scale (see [Reference Steel47, Theorem 4.3]).Footnote 55 Let now W be the derived model of
${\delta }_{\omega }=\sup _{i<\omega }{\delta }_i$
. Recall next that Steel showed that if there are unboundedly many Woodin cardinals, then every universally Baire set has a universally Baire scale (see [Reference Steel47, Theorem 4.3]).Footnote 55 Let now W be the derived model of
![]() ${\mathcal {P}}$
as computed in
${\mathcal {P}}$
as computed in
![]() ${\mathcal {P}}[m]$
where
${\mathcal {P}}[m]$
where
![]() $m=g*k$
. It follows that
$m=g*k$
. It follows that
(2) the canonical set of reals coding
![]() $\Sigma ^m{\restriction } HC^W$
Footnote 56 has a scale in W.
$\Sigma ^m{\restriction } HC^W$
Footnote 56 has a scale in W.
This paragraph will be using Theorem 2.20 and the notation introduced there. Working inside W, let
![]() $\Gamma =\Gamma ^b({\mathcal {P}}_0, \Sigma ^m)$
. Thus,
$\Gamma =\Gamma ^b({\mathcal {P}}_0, \Sigma ^m)$
. Thus,
![]() $\Gamma $
is the set of reals that are generated by the low-level-components of
$\Gamma $
is the set of reals that are generated by the low-level-components of
![]() $\Sigma ^m$
. More precisely,
$\Sigma ^m$
. More precisely,
![]() $A\in \Gamma $
if there is an iteration
$A\in \Gamma $
if there is an iteration
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {P}}_0$
according to
${\mathcal {P}}_0$
according to
![]() $\Sigma ^m$
such that
$\Sigma ^m$
such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists and A is Wadge below
$\pi ^{{\mathcal {T}}, b}$
exists and A is Wadge below
![]() $\Sigma ^m_{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}_0^b)}$
. As
$\Sigma ^m_{\pi ^{{\mathcal {T}}, b}({\mathcal {P}}_0^b)}$
. As
![]() $\Sigma ^m{\restriction } HC^W$
is Suslin, co-Suslin in W, we must have a hod pair
$\Sigma ^m{\restriction } HC^W$
is Suslin, co-Suslin in W, we must have a hod pair
![]() $({\mathcal {S}}, \Lambda )\in W$
such that
$({\mathcal {S}}, \Lambda )\in W$
such that
![]() $\Gamma ^b({\mathcal {S}}, \Lambda )=\Gamma $
(this follows from the Generation of Mouse Full Pointclasses; see [Reference Sargsyan and Trang38, Theorem 10.1.2]). We can further assume that
$\Gamma ^b({\mathcal {S}}, \Lambda )=\Gamma $
(this follows from the Generation of Mouse Full Pointclasses; see [Reference Sargsyan and Trang38, Theorem 10.1.2]). We can further assume that
![]() ${\mathcal {S}}$
is a
${\mathcal {S}}$
is a
![]() $\Sigma ^m$
-iterate of
$\Sigma ^m$
-iterate of
![]() ${\mathcal {P}}_0$
and
${\mathcal {P}}_0$
and
![]() $\Lambda ^{stc}=\Sigma ^m_{{\mathcal {S}}}{\restriction } HC^W$
(this extra possibility follows from Theorem 2.20).
$\Lambda ^{stc}=\Sigma ^m_{{\mathcal {S}}}{\restriction } HC^W$
(this extra possibility follows from Theorem 2.20).
Fix now
![]() $i<\omega $
such that letting
$i<\omega $
such that letting
![]() $n=k\cap Coll(\omega , {\delta }_i)$
,
$n=k\cap Coll(\omega , {\delta }_i)$
,
![]() ${\mathcal {P}}[g*n]$
has a uB representation of
${\mathcal {P}}[g*n]$
has a uB representation of
![]() $\Lambda $
. It now follows that since
$\Lambda $
. It now follows that since
(3)
![]() ${\mathcal {P}}_{i+1}$
is a
${\mathcal {P}}_{i+1}$
is a
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
(4) letting
![]() $l:{\mathcal {S}}\rightarrow {\mathcal {P}}_{i+1}$
be the iteration embedding,
$l:{\mathcal {S}}\rightarrow {\mathcal {P}}_{i+1}$
be the iteration embedding,
![]() $l[{\delta }^{\mathcal {S}}]$
is cofinal in
$l[{\delta }^{\mathcal {S}}]$
is cofinal in
![]() ${\delta }^{{\mathcal {P}}_{i+1}}$
,
${\delta }^{{\mathcal {P}}_{i+1}}$
,
we have
This directly contradicts (1).
2.10. Constructing an iterate via fully backgrounded constructions
Suppose
![]() ${\mathcal {M}}$
is strategy-hybrid
${\mathcal {M}}$
is strategy-hybrid
![]() $\eta $
-iterable mouse such that
$\eta $
-iterable mouse such that
![]() ${\mathcal {M}}\in V_{\eta }$
,
${\mathcal {M}}\in V_{\eta }$
,
![]() $\eta $
is an inaccessible cardinal and
$\eta $
is an inaccessible cardinal and
![]() ${\mathcal {M}}$
has an
${\mathcal {M}}$
has an
![]() $\eta $
-strategy with hull condensation. Thus,
$\eta $
-strategy with hull condensation. Thus,
![]() ${\mathcal {M}}$
has an extender sequence
${\mathcal {M}}$
has an extender sequence
![]() $\vec {E}$
and a strategy predicate
$\vec {E}$
and a strategy predicate
![]() $S^{\mathcal {M}}$
, which can be a strategy of
$S^{\mathcal {M}}$
, which can be a strategy of
![]() ${\mathcal {M}}$
itself (as in hod mice) or a strategy of some
${\mathcal {M}}$
itself (as in hod mice) or a strategy of some
![]() ${\mathcal {N}}\in {\mathcal {M}}$
. We want to build an iterate
${\mathcal {N}}\in {\mathcal {M}}$
. We want to build an iterate
![]() ${\mathcal {X}}$
of
${\mathcal {X}}$
of
![]() ${\mathcal {M}}$
such that the extenders of
${\mathcal {M}}$
such that the extenders of
![]() ${\mathcal {X}}$
are all fully backgrounded. Here, we describe this construction.
${\mathcal {X}}$
are all fully backgrounded. Here, we describe this construction.
We say
![]() $({\mathcal {V}}_{\xi }, {\mathcal {W}}_{\xi }, {\mathcal {T}}_{\xi }, {\mathcal {X}}_{\xi }: \xi <\iota )$
are the models and iterations of the fully backgrounded
$({\mathcal {V}}_{\xi }, {\mathcal {W}}_{\xi }, {\mathcal {T}}_{\xi }, {\mathcal {X}}_{\xi }: \xi <\iota )$
are the models and iterations of the fully backgrounded
![]() $({\mathcal {M}}, \Sigma )$
-iterate-construction of
$({\mathcal {M}}, \Sigma )$
-iterate-construction of
![]() $V_{\eta }$
if the following conditions are satisfied with
$V_{\eta }$
if the following conditions are satisfied with
![]() ${\alpha }_{\xi }=Ord\cap {\mathcal {V}}_{\xi }$
.
${\alpha }_{\xi }=Ord\cap {\mathcal {V}}_{\xi }$
.
-
1.
 ${\mathcal {V}}_0={\mathcal {W}}_0=J_0^{\mathcal {M}}$
.
${\mathcal {V}}_0={\mathcal {W}}_0=J_0^{\mathcal {M}}$
. -
2. For every
 $\xi <\iota $
,
$\xi <\iota $
,
 ${\mathcal {V}}_{\xi }={\mathcal {W}}_{\xi }|{\alpha }_{\xi }$
.
${\mathcal {V}}_{\xi }={\mathcal {W}}_{\xi }|{\alpha }_{\xi }$
. -
3. For
 $\xi <\iota $
,
$\xi <\iota $
,
 ${\mathcal {T}}_{\xi }$
is an iteration of
${\mathcal {T}}_{\xi }$
is an iteration of
 ${\mathcal {M}}$
according to
${\mathcal {M}}$
according to
 $\Sigma $
with last model
$\Sigma $
with last model
 ${\mathcal {X}}_{\xi }$
such that
${\mathcal {X}}_{\xi }$
such that
 ${\mathcal {V}}_{\xi }={\mathcal {X}}_{\xi }|{\alpha }_{\xi }$
and the generators of
${\mathcal {V}}_{\xi }={\mathcal {X}}_{\xi }|{\alpha }_{\xi }$
and the generators of
 ${\mathcal {T}}_{\xi }$
are contained in
${\mathcal {T}}_{\xi }$
are contained in
 ${\alpha }_{\xi }$
.Footnote 57
${\alpha }_{\xi }$
.Footnote 57 -
4. For
 $\xi <\iota $
, if
$\xi <\iota $
, if
 ${\alpha }_{\xi }\in dom(\vec {E}^{{\mathcal {X}}_{\xi }})\cup dom(S^{{\mathcal {X}}_{\xi }})$
, then
${\alpha }_{\xi }\in dom(\vec {E}^{{\mathcal {X}}_{\xi }})\cup dom(S^{{\mathcal {X}}_{\xi }})$
, then
 ${\mathcal {W}}_{\xi }= {\mathcal {X}}_{\xi }||{\alpha }_{\xi }$
.
${\mathcal {W}}_{\xi }= {\mathcal {X}}_{\xi }||{\alpha }_{\xi }$
. -
5. For
 $\xi <\iota $
, if
$\xi <\iota $
, if
 ${\alpha }_{\xi }\not \in (dom(\vec {E}^{{\mathcal {X}}_{\xi }})\cup dom(S^{{\mathcal {X}}_{\xi }}))$
and
${\alpha }_{\xi }\not \in (dom(\vec {E}^{{\mathcal {X}}_{\xi }})\cup dom(S^{{\mathcal {X}}_{\xi }}))$
and
 ${\mathcal {V}}_{\xi }\not ={\mathcal {X}}_{\xi }$
, then
${\mathcal {V}}_{\xi }\not ={\mathcal {X}}_{\xi }$
, then
 ${\mathcal {W}}_{\xi }=J_1({\mathcal {V}}_{\xi })$
.
${\mathcal {W}}_{\xi }=J_1({\mathcal {V}}_{\xi })$
. -
6. For
 $\xi <\iota $
, if there is a total extender
$\xi <\iota $
, if there is a total extender
 $F\in V_{\eta }$
such that then
$F\in V_{\eta }$
such that then $$ \begin{align*} \pi_F(({\mathcal{V}}_{\zeta}, {\mathcal{W}}_{\zeta}, {\mathcal{T}}_{\zeta}, {\mathcal{X}}_{\zeta}: \zeta<\xi)){\restriction} \xi=({\mathcal{V}}_{\zeta}, {\mathcal{W}}_{\zeta}, {\mathcal{T}}_{\zeta}, {\mathcal{X}}_{\zeta}: \zeta<\xi), \end{align*} $$
$$ \begin{align*} \pi_F(({\mathcal{V}}_{\zeta}, {\mathcal{W}}_{\zeta}, {\mathcal{T}}_{\zeta}, {\mathcal{X}}_{\zeta}: \zeta<\xi)){\restriction} \xi=({\mathcal{V}}_{\zeta}, {\mathcal{W}}_{\zeta}, {\mathcal{T}}_{\zeta}, {\mathcal{X}}_{\zeta}: \zeta<\xi), \end{align*} $$
 $F\cap {\mathcal {V}}_{\xi }=E_{{\alpha }_{\xi }}^{{\mathcal {X}}_{\xi }}$
. It follows that
$F\cap {\mathcal {V}}_{\xi }=E_{{\alpha }_{\xi }}^{{\mathcal {X}}_{\xi }}$
. It follows that
 ${\mathcal {W}}_{\xi }=({\mathcal {V}}_{\xi }, E_{{\alpha }_{\xi }}^{{\mathcal {X}}_{\xi }})$
.
${\mathcal {W}}_{\xi }=({\mathcal {V}}_{\xi }, E_{{\alpha }_{\xi }}^{{\mathcal {X}}_{\xi }})$
.
-
7. For
 $\xi +1<\iota $
,
$\xi +1<\iota $
,
 ${\mathcal {V}}_{\xi +1}=\mathcal {C}({\mathcal {W}}_{\xi })$
.
${\mathcal {V}}_{\xi +1}=\mathcal {C}({\mathcal {W}}_{\xi })$
. -
8. If
 $\xi <\iota $
is limit, then
$\xi <\iota $
is limit, then
 ${\mathcal {W}}_{\xi }=liminf_{\zeta \rightarrow \xi }{\mathcal {W}}_{\zeta }$
and
${\mathcal {W}}_{\xi }=liminf_{\zeta \rightarrow \xi }{\mathcal {W}}_{\zeta }$
and
 ${\mathcal {V}}_{\xi }=C({\mathcal {W}}_{\xi })$
. More precisely, given
${\mathcal {V}}_{\xi }=C({\mathcal {W}}_{\xi })$
. More precisely, given
 ${\mathcal {W}}_{\xi }|\kappa $
,
${\mathcal {W}}_{\xi }|\kappa $
,
 ${\mathcal {W}}_{\xi }|(\kappa ^+)^{{\mathcal {W}}_{\xi }}$
is the eventual value of
${\mathcal {W}}_{\xi }|(\kappa ^+)^{{\mathcal {W}}_{\xi }}$
is the eventual value of
 ${\mathcal {W}}_{\zeta }|(\kappa ^+)^{{\mathcal {W}}_{\zeta }}$
.
${\mathcal {W}}_{\zeta }|(\kappa ^+)^{{\mathcal {W}}_{\zeta }}$
.
We then let
![]() $\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta )$
be the models and iterations of the above construction. We can vary this construction in two ways. The first way is that fixing some
$\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta )$
be the models and iterations of the above construction. We can vary this construction in two ways. The first way is that fixing some
![]() ${\lambda }<\eta $
, we can require that the extender F in clause 6 has critical point
${\lambda }<\eta $
, we can require that the extender F in clause 6 has critical point
![]() $>{\lambda }$
. This amounts to backgrounding extenders via total extenders that have critical points
$>{\lambda }$
. This amounts to backgrounding extenders via total extenders that have critical points
![]() $>{\lambda }$
. The second way is that we may choose to start the construction with any initial segment of
$>{\lambda }$
. The second way is that we may choose to start the construction with any initial segment of
![]() ${\mathcal {M}}$
. More precisely, given a cardinal cutpoint
${\mathcal {M}}$
. More precisely, given a cardinal cutpoint
![]() $\nu $
of
$\nu $
of
![]() ${\mathcal {M}}$
, we can start by setting
${\mathcal {M}}$
, we can start by setting
![]() ${\mathcal {V}}_0={\mathcal {M}}|\nu $
.
${\mathcal {V}}_0={\mathcal {M}}|\nu $
.
Thus, by saying that
![]() $({\mathcal {V}}_{\xi }, {\mathcal {W}}_{\xi }, {\mathcal {T}}_{\xi }, {\mathcal {X}}_{\xi }: \xi <\iota )$
are the models and iterations of the
$({\mathcal {V}}_{\xi }, {\mathcal {W}}_{\xi }, {\mathcal {T}}_{\xi }, {\mathcal {X}}_{\xi }: \xi <\iota )$
are the models and iterations of the
![]() $\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
, we mean that the sequence is built as above but starting with
$\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
, we mean that the sequence is built as above but starting with
![]() ${\mathcal {M}}|\nu $
and using backgrounded extenders that have critical points
${\mathcal {M}}|\nu $
and using backgrounded extenders that have critical points
![]() $>{\lambda }$
.
$>{\lambda }$
.
![]() $\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
can break without reaching its eventual goal. We say
$\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
can break without reaching its eventual goal. We say
is successful if one of the following conditions holds.
-
1.
 $\iota =\xi +1$
,
$\iota =\xi +1$
,
 $\pi ^{{\mathcal {T}}_{\xi }}$
exists and either
$\pi ^{{\mathcal {T}}_{\xi }}$
exists and either
 ${\mathcal {V}}_{\xi }={\mathcal {X}}_{\xi }$
or
${\mathcal {V}}_{\xi }={\mathcal {X}}_{\xi }$
or
 ${\mathcal {W}}_{\xi }={\mathcal {X}}_{\xi }$
,
${\mathcal {W}}_{\xi }={\mathcal {X}}_{\xi }$
, -
2.
 $\iota $
is a limit ordinal and
$\iota $
is a limit ordinal and
 $liminf_{\xi \rightarrow \iota }{\mathcal {V}}_{\xi }$
is the last model of a normal
$liminf_{\xi \rightarrow \iota }{\mathcal {V}}_{\xi }$
is the last model of a normal
 $\Sigma $
-iteration
$\Sigma $
-iteration
 ${\mathcal {T}}$
of
${\mathcal {T}}$
of
 ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
 $\pi ^{\mathcal {T}}$
exists.
$\pi ^{\mathcal {T}}$
exists.
If
![]() $\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
is successful, then we say
$\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
is successful, then we say
![]() ${\mathcal {N}}$
is its output if it is the iterate of
${\mathcal {N}}$
is its output if it is the iterate of
![]() ${\mathcal {M}}$
described above.
${\mathcal {M}}$
described above.
The following is the main theorem that we will need from this section. We say E is a strictly short extender if its generators are bounded below
![]() $\pi _E(\mathrm {crit }(E))$
. We say
$\pi _E(\mathrm {crit }(E))$
. We say
![]() ${\mathcal {M}}$
is strictly short if all of its extenders are strictly short.
${\mathcal {M}}$
is strictly short if all of its extenders are strictly short.
Theorem 2.22. Suppose
![]() $({\mathcal {M}}, \Sigma )$
and
$({\mathcal {M}}, \Sigma )$
and
![]() $\eta $
are as above and in addition to the above data,
$\eta $
are as above and in addition to the above data,
![]() $\eta $
is a Woodin cardinal and
$\eta $
is a Woodin cardinal and
![]() ${\mathcal {M}}$
is strictly short. Suppose
${\mathcal {M}}$
is strictly short. Suppose
![]() ${\lambda }<\eta $
and
${\lambda }<\eta $
and
![]() $\nu $
is a cutpoint cardinal of
$\nu $
is a cutpoint cardinal of
![]() ${\mathcal {M}}$
. Then
${\mathcal {M}}$
. Then
![]() $\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
is successful.
$\mathsf {FBIC}({\mathcal {M}}, \Sigma , \eta , {\lambda }, \nu )$
is successful.
The proof is a standard combination of universality (see [Reference Steel52, Lemma 11.1]) and stationarity (see [Reference Schlutzenberg and Trang44, Lemma 3.23]) of fully backgrounded constructions.
3. An upper bound for
 $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
 $\mathsf {LSA-over-uB}$
$\mathsf {LSA-over-uB}$
The goal of this section is to prove Theorem 3.1. It reduces
![]() $\mathsf {Sealing}$
,
$\mathsf {Sealing}$
,
![]() $\mathsf {Tower\ Sealing}$
and
$\mathsf {Tower\ Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
to a large cardinal theory. This essentially constitutes one half of Theorem 1.4 and Theorem 1.7.
$\mathsf {LSA-over-uB}$
to a large cardinal theory. This essentially constitutes one half of Theorem 1.4 and Theorem 1.7.
Theorem 3.1. Suppose
![]() ${\mathcal {P}}$
is excellent and
${\mathcal {P}}$
is excellent and
![]() $g\subseteq Coll(\omega , {\delta }^{\mathcal {P}})$
is
$g\subseteq Coll(\omega , {\delta }^{\mathcal {P}})$
is
![]() ${\mathcal {P}}$
-generic. Then both
${\mathcal {P}}$
-generic. Then both
![]() $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
hold in
$\mathsf {LSA-over-uB}$
hold in
![]() ${\mathcal {P}}[g]$
.
${\mathcal {P}}[g]$
.
We start the proof of Theorem 3.1. Let
![]() ${\mathcal {P}}$
be excellent (see Definition 2.7). Set
${\mathcal {P}}$
be excellent (see Definition 2.7). Set
![]() ${\delta }_0={\delta }^{\mathcal {P}}$
and let
${\delta }_0={\delta }^{\mathcal {P}}$
and let
![]() $g\subseteq Coll(\omega ,\delta _0)$
be
$g\subseteq Coll(\omega ,\delta _0)$
be
![]() ${\mathcal {P}}$
-generic. We first show that
${\mathcal {P}}$
-generic. We first show that
![]() $\mathsf {Sealing}$
holds in
$\mathsf {Sealing}$
holds in
![]() ${\mathcal {P}}[g]$
. Let
${\mathcal {P}}[g]$
. Let
![]() ${\mathcal {P}}_0=_{def}({\mathcal {P}}|{\delta }_0)^{\#}$
. We write
${\mathcal {P}}_0=_{def}({\mathcal {P}}|{\delta }_0)^{\#}$
. We write
![]() ${\mathcal {P}} = (|{\mathcal {P}}|,\in , \mathbb {E}^{\mathcal {P}}, S^{\mathcal {P}})$
, where
${\mathcal {P}} = (|{\mathcal {P}}|,\in , \mathbb {E}^{\mathcal {P}}, S^{\mathcal {P}})$
, where
![]() $\mathbb {E}^{\mathcal {P}}$
is the extender sequence of
$\mathbb {E}^{\mathcal {P}}$
is the extender sequence of
![]() ${\mathcal {P}}$
and
${\mathcal {P}}$
and
![]() $S^{\mathcal {P}}$
is the predicate coding the short-tree strategy of
$S^{\mathcal {P}}$
is the predicate coding the short-tree strategy of
![]() ${\mathcal {P}}_0$
in
${\mathcal {P}}_0$
in
![]() ${\mathcal {P}}$
. Thus,
${\mathcal {P}}$
. Thus,
![]() ${\mathcal {P}}$
above
${\mathcal {P}}$
above
![]() ${\delta }_0$
is a short-tree-strategy premouse over
${\delta }_0$
is a short-tree-strategy premouse over
![]() ${\mathcal {P}}_0$
.
${\mathcal {P}}_0$
.
Let
![]() $\Sigma ^-$
be this short-tree strategy. It follows from Proposition 2.17 that for any
$\Sigma ^-$
be this short-tree strategy. It follows from Proposition 2.17 that for any
![]() ${\mathcal {P}}[g]$
-generic h,
${\mathcal {P}}[g]$
-generic h,
![]() $\Sigma ^-$
has a canonical extension
$\Sigma ^-$
has a canonical extension
![]() $\Sigma ^h$
in
$\Sigma ^h$
in
![]() ${\mathcal {P}}[g*h]$
Footnote 58. Let then
${\mathcal {P}}[g*h]$
Footnote 58. Let then
![]() $\Sigma $
be the extension of
$\Sigma $
be the extension of
![]() $\Sigma ^-$
in
$\Sigma ^-$
in
![]() ${\mathcal {P}}[g]$
.
${\mathcal {P}}[g]$
.
3.1. An upper bound for
 $\mathsf {Sealing}$
$\mathsf {Sealing}$
Let h be
![]() ${\mathcal {P}}[g]$
-generic. Working in
${\mathcal {P}}[g]$
-generic. Working in
![]() ${\mathcal {P}}[g][h]$
, let
${\mathcal {P}}[g][h]$
, let
![]() $\Delta ^h=\Gamma ^b({\mathcal {P}}_0, \Sigma )$
. Equivalently,
$\Delta ^h=\Gamma ^b({\mathcal {P}}_0, \Sigma )$
. Equivalently,
![]() $\Delta ^h$
is the set of reals
$\Delta ^h$
is the set of reals
![]() $A\subseteq {\mathbb {R}}^{{\mathcal {P}}[g*h]}$
such that for some countable tree
$A\subseteq {\mathbb {R}}^{{\mathcal {P}}[g*h]}$
such that for some countable tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {P}}_0$
with last model
${\mathcal {P}}_0$
with last model
![]() ${\mathcal {Q}}$
such that
${\mathcal {Q}}$
such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists,
$\pi ^{{\mathcal {T}}, b}$
exists,
![]() $A\in L(\Sigma ^h_{{\mathcal {Q}}^b}, {\mathbb {R}}^{{\mathcal {P}}[g*h]})$
. It follows from Proposition 2.18 that if
$A\in L(\Sigma ^h_{{\mathcal {Q}}^b}, {\mathbb {R}}^{{\mathcal {P}}[g*h]})$
. It follows from Proposition 2.18 that if
![]() ${\mathcal {Q}}$
is as above, then
${\mathcal {Q}}$
is as above, then
![]() $\Sigma ^h_{{\mathcal {Q}}^b}\in \Gamma ^{\infty }_{g*h}$
.
$\Sigma ^h_{{\mathcal {Q}}^b}\in \Gamma ^{\infty }_{g*h}$
.
Lemma 3.2.
![]() $\Gamma ^{\infty }_{g*h}=\Delta ^h$
.
$\Gamma ^{\infty }_{g*h}=\Delta ^h$
.
Proof. It follows from Proposition 2.18 that
![]() $\Delta ^h\subseteq \Gamma ^{\infty }_{g*h}$
. Fix
$\Delta ^h\subseteq \Gamma ^{\infty }_{g*h}$
. Fix
![]() $A\subseteq {\mathbb {R}}^{{\mathcal {P}}[g*h]}$
that is a universally Baire set in
$A\subseteq {\mathbb {R}}^{{\mathcal {P}}[g*h]}$
that is a universally Baire set in
![]() ${\mathcal {P}}[g*h]$
. Work in
${\mathcal {P}}[g*h]$
. Work in
![]() ${\mathcal {P}}[g*h]$
and suppose
${\mathcal {P}}[g*h]$
and suppose
![]() $A\not \in \Delta ^h$
. Because there is a proper class of Woodin cardinals, any two universally Baire sets are Wadge comparable. Since
$A\not \in \Delta ^h$
. Because there is a proper class of Woodin cardinals, any two universally Baire sets are Wadge comparable. Since
![]() $\Delta ^h\cup \{A\}\subseteq \Gamma ^{\infty }_{g*h}$
and
$\Delta ^h\cup \{A\}\subseteq \Gamma ^{\infty }_{g*h}$
and
![]() $A\not \in \Delta ^h$
, we have that
$A\not \in \Delta ^h$
, we have that
![]() $\Delta ^h\subseteq L(A, {\mathbb {R}}_{g*h})$
. Recall that by a result of Steel ([Reference Steel47, Theorem 4.3]), A is Suslin, co-Suslin in
$\Delta ^h\subseteq L(A, {\mathbb {R}}_{g*h})$
. Recall that by a result of Steel ([Reference Steel47, Theorem 4.3]), A is Suslin, co-Suslin in
![]() $\Gamma ^{\infty }_{g*h}$
. Hence, we can assume, without losing generality, that in
$\Gamma ^{\infty }_{g*h}$
. Hence, we can assume, without losing generality, that in
![]() $L(A, {\mathbb {R}}_{g*h})$
, there are Suslin, co-Suslin sets beyond
$L(A, {\mathbb {R}}_{g*h})$
, there are Suslin, co-Suslin sets beyond
![]() $\Delta ^h$
.
$\Delta ^h$
.
It follows from [Reference Sargsyan and Trang38, Theorem 10.1.1] that there is a lsa-type hod pair
![]() $({\mathcal {S}}, \Lambda )\in \Gamma ^{\infty }_{g*h}$
such that
$({\mathcal {S}}, \Lambda )\in \Gamma ^{\infty }_{g*h}$
such that
![]() $\Gamma ^b({\mathcal {S}}, \Lambda )=\Delta ^h$
. Just like in the proof of Proposition 2.21, we can assume that
$\Gamma ^b({\mathcal {S}}, \Lambda )=\Delta ^h$
. Just like in the proof of Proposition 2.21, we can assume that
![]() ${\mathcal {S}}$
is a
${\mathcal {S}}$
is a
![]() $\Sigma ^h$
-iterate of
$\Sigma ^h$
-iterate of
![]() ${\mathcal {P}}_0$
and
${\mathcal {P}}_0$
and
![]() $\Lambda ^{stc}=\Sigma ^h_{\mathcal {S}}$
. It then follows that
$\Lambda ^{stc}=\Sigma ^h_{\mathcal {S}}$
. It then follows that
![]() $\Sigma ^h\in \Gamma ^{\infty }_{g*h}$
, contradicting Proposition 2.21.
$\Sigma ^h\in \Gamma ^{\infty }_{g*h}$
, contradicting Proposition 2.21.
By the results of [Reference Sargsyan and Trang38, Section 8.1] (specifically, [Reference Sargsyan and Trang38, Theorem 8.1.1 clause 4]), we get that in
![]() ${\mathcal {P}}[g*h]$
,
${\mathcal {P}}[g*h]$
,
The lemma and (1) immediately give us clause (1) of
![]() $\mathsf {Sealing}$
. For clause (2), let h be
$\mathsf {Sealing}$
. For clause (2), let h be
![]() ${\mathcal {P}}[g]$
-generic and k be
${\mathcal {P}}[g]$
-generic and k be
![]() ${\mathcal {P}}[g*h]$
-generic. We want to show that there is an elementary embedding
${\mathcal {P}}[g*h]$
-generic. We want to show that there is an elementary embedding
such that for every
![]() $A\in \Delta ^h$
,
$A\in \Delta ^h$
,
![]() $j(A)$
is the canonical extension of A in
$j(A)$
is the canonical extension of A in
![]() ${\mathcal {P}}[g*h*k]$
. This will be accomplished in Lemma 3.4. The next lemma provides a key step in the construction of the desired elementary embedding. It does so by realizing
${\mathcal {P}}[g*h*k]$
. This will be accomplished in Lemma 3.4. The next lemma provides a key step in the construction of the desired elementary embedding. It does so by realizing
![]() $L(\Delta ^h, {\mathbb {R}}_{g*h})$
as a derived model of an iterate of
$L(\Delta ^h, {\mathbb {R}}_{g*h})$
as a derived model of an iterate of
![]() ${\mathcal {P}}_0$
.
${\mathcal {P}}_0$
.
Recall from [Reference Sargsyan and Trang38, Definition 2.7.2] that if
![]() ${\mathcal {S}}$
is a hod premouse of limit type (including lsa type), then
${\mathcal {S}}$
is a hod premouse of limit type (including lsa type), then
![]() ${\delta }^{{\mathcal {S}}^b}$
is the supremum of the Woodin cardinals of
${\delta }^{{\mathcal {S}}^b}$
is the supremum of the Woodin cardinals of
![]() ${\mathcal {S}}^b$
. In general, the reader may wish to review some of the notation concerning hod premice; the relevant notation can be found in [Reference Sargsyan and Trang38, Chapter 2 and 3]. The Key Phenomenon stated before [Reference Sargsyan and Trang38, Definition 2.7.8] might also be useful.
${\mathcal {S}}^b$
. In general, the reader may wish to review some of the notation concerning hod premice; the relevant notation can be found in [Reference Sargsyan and Trang38, Chapter 2 and 3]. The Key Phenomenon stated before [Reference Sargsyan and Trang38, Definition 2.7.8] might also be useful.
Lemma 3.3. Suppose
![]() $\mathbb {P}\in {\mathcal {P}}[g]$
is a poset and
$\mathbb {P}\in {\mathcal {P}}[g]$
is a poset and
![]() $m\subseteq \mathbb {P}$
is
$m\subseteq \mathbb {P}$
is
![]() ${\mathcal {P}}[g]$
-generic. Suppose further that in
${\mathcal {P}}[g]$
-generic. Suppose further that in
![]() ${\mathcal {P}}[g*m]$
,
${\mathcal {P}}[g*m]$
,
![]() ${\mathcal {S}}$
is a countable
${\mathcal {S}}$
is a countable
![]() $\Sigma ^m$
-iterate of
$\Sigma ^m$
-iterate of
![]() ${\mathcal {P}}_0$
such that the
${\mathcal {P}}_0$
such that the
![]() ${\mathcal {P}}_0$
-to-
${\mathcal {P}}_0$
-to-
![]() ${\mathcal {S}}$
iteration embedding exists. Suppose
${\mathcal {S}}$
iteration embedding exists. Suppose
![]() ${\kappa }<{\delta }^{{\mathcal {S}}^b}$
is a Woodin cardinal of
${\kappa }<{\delta }^{{\mathcal {S}}^b}$
is a Woodin cardinal of
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
![]() $A\in \Gamma ^{\infty }_{g*m}$
(in
$A\in \Gamma ^{\infty }_{g*m}$
(in
![]() ${\mathcal {P}}[g*m]$
). Then in
${\mathcal {P}}[g*m]$
). Then in
![]() ${\mathcal {P}}[g*m]$
, there is a countable
${\mathcal {P}}[g*m]$
, there is a countable
![]() $\Sigma ^m_{\mathcal {S}}$
-iterate
$\Sigma ^m_{\mathcal {S}}$
-iterate
![]() ${\mathcal {W}}$
of
${\mathcal {W}}$
of
![]() ${\mathcal {S}}$
such that the
${\mathcal {S}}$
such that the
![]() ${\mathcal {S}}$
-to-
${\mathcal {S}}$
-to-
![]() ${\mathcal {W}}$
iteration embedding exists, the
${\mathcal {W}}$
iteration embedding exists, the
![]() ${\mathcal {S}}$
-to-
${\mathcal {S}}$
-to-
![]() ${\mathcal {W}}$
iteration is above
${\mathcal {W}}$
iteration is above
![]() ${\kappa }$
and A is Wadge below
${\kappa }$
and A is Wadge below
![]() $\Sigma ^m_{{\mathcal {W}}^b}$
.
$\Sigma ^m_{{\mathcal {W}}^b}$
.
Proof. The lemma follows from Proposition 2.19. Indeed, let w be a window of
![]() ${\mathcal {P}}$
such that
${\mathcal {P}}$
such that
![]() $g*m$
is generic for a poset in
$g*m$
is generic for a poset in
![]() ${\mathcal {P}}|\nu ^w$
. Let
${\mathcal {P}}|\nu ^w$
. Let
![]() ${\mathcal {N}}_0$
be the output of
${\mathcal {N}}_0$
be the output of
![]() $\mathsf {FBIC}({\mathcal {S}}, \Sigma ^m, {\delta }^w, \nu ^w, {\kappa })$
(see Theorem 2.22). Thus,
$\mathsf {FBIC}({\mathcal {S}}, \Sigma ^m, {\delta }^w, \nu ^w, {\kappa })$
(see Theorem 2.22). Thus,
![]() ${\mathcal {N}}_0$
is a
${\mathcal {N}}_0$
is a
![]() $\Sigma ^m$
-iterate of
$\Sigma ^m$
-iterate of
![]() ${\mathcal {S}}$
above
${\mathcal {S}}$
above
![]() ${\kappa }$
, and all of its extenders with critical point
${\kappa }$
, and all of its extenders with critical point
![]() $>{\kappa }$
have, in
$>{\kappa }$
have, in
![]() ${\mathcal {P}}[g*h]$
, full background certificates whose critical points are strictly greater than
${\mathcal {P}}[g*h]$
, full background certificates whose critical points are strictly greater than
![]() $\nu ^w$
. We also have that
$\nu ^w$
. We also have that
(A)
![]() $Ord\cap {\mathcal {N}}_0={\delta }^w$
(see Proposition 2.19).
$Ord\cap {\mathcal {N}}_0={\delta }^w$
(see Proposition 2.19).
Working inside
![]() ${\mathcal {N}}_0$
, let
${\mathcal {N}}_0$
, let
![]() ${\mathcal {N}}$
be the output of the hod pair construction of
${\mathcal {N}}$
be the output of the hod pair construction of
![]() ${\mathcal {N}}_0$
done using extenders with critical point
${\mathcal {N}}_0$
done using extenders with critical point
![]() $>{\delta }^{{\mathcal {N}}_0^b}$
.
$>{\delta }^{{\mathcal {N}}_0^b}$
.
It follows from Lemma 3.2 that there is a countable iteration p of
![]() ${\mathcal {P}}_0$
according to
${\mathcal {P}}_0$
according to
![]() $\Sigma ^m$
such that
$\Sigma ^m$
such that
![]() $\pi ^{p, b}$
exists and letting
$\pi ^{p, b}$
exists and letting
![]() ${\mathcal {R}}=\pi ^{p, b}({\mathcal {P}}_0^b)$
, A is Wadge below
${\mathcal {R}}=\pi ^{p, b}({\mathcal {P}}_0^b)$
, A is Wadge below
![]() $\Sigma ^m_{{\mathcal {R}}}$
. Fix such a
$\Sigma ^m_{{\mathcal {R}}}$
. Fix such a
![]() $(p, {\mathcal {R}})$
. We now claim that
$(p, {\mathcal {R}})$
. We now claim that
Claim. for some
![]() $\xi <{\delta }^{{\mathcal {N}}^b}$
,
$\xi <{\delta }^{{\mathcal {N}}^b}$
,
![]() ${\mathcal {N}}|\xi $
is a
${\mathcal {N}}|\xi $
is a
![]() $\Sigma ^m_{\mathcal {R}}$
-iterate of
$\Sigma ^m_{\mathcal {R}}$
-iterate of
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
Proof. To see this, we compare
![]() ${\mathcal {R}}$
with the construction producing
${\mathcal {R}}$
with the construction producing
![]() ${\mathcal {N}}$
. We need to see that
${\mathcal {N}}$
. We need to see that
![]() ${\mathcal {R}}$
can be compared with
${\mathcal {R}}$
can be compared with
![]() ${\mathcal {N}}$
. There are two ways such a comparison could go wrong.
${\mathcal {N}}$
. There are two ways such a comparison could go wrong.
-
1.
 ${\mathcal {N}}$
and
${\mathcal {N}}$
and
 ${\mathcal {R}}$
are not full with respect to the same
${\mathcal {R}}$
are not full with respect to the same
 $Lp$
-operator. More precisely, for some normal
$Lp$
-operator. More precisely, for some normal
 $\Sigma ^m_{\mathcal {R}}$
-iteration
$\Sigma ^m_{\mathcal {R}}$
-iteration
 ${\mathcal {T}}$
of limit length letting
${\mathcal {T}}$
of limit length letting
 $b=\Sigma ^m_{\mathcal {R}}({\mathcal {T}})$
, either
$b=\Sigma ^m_{\mathcal {R}}({\mathcal {T}})$
, either-
(a)
 ${\mathcal {M}}^{\mathcal {T}}_b{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ and
${\mathcal {M}}^{\mathcal {T}}_b{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ and
 ${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’ or
${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’ or -
(b)
 ${\mathcal {M}}^{\mathcal {T}}_b{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’ and
${\mathcal {M}}^{\mathcal {T}}_b{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’ and
 ${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal.
${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal.
-
-
2. A strategy disagreement is reached. More precisely, for some normal
 $\Sigma ^m_{\mathcal {R}}$
-iteration
$\Sigma ^m_{\mathcal {R}}$
-iteration
 ${\mathcal {T}}$
with last model
${\mathcal {T}}$
with last model
 ${\mathcal {R}}^*$
and some
${\mathcal {R}}^*$
and some
 $\xi $
which is a Woodin cardinal of
$\xi $
which is a Woodin cardinal of
 ${\mathcal {R}}^*$
,
${\mathcal {R}}^*$
,
 ${\mathcal {R}}^*|\xi ={\mathcal {N}}|\xi $
yet
${\mathcal {R}}^*|\xi ={\mathcal {N}}|\xi $
yet
 $S^{\mathcal {N}}_{{\mathcal {R}}^*|\xi }\not = \Sigma ^m_{{\mathcal {R}}^*|\xi }$
.
$S^{\mathcal {N}}_{{\mathcal {R}}^*|\xi }\not = \Sigma ^m_{{\mathcal {R}}^*|\xi }$
.
It is easier to argue that case 2 cannot happen. This essentially follows from [Reference Sargsyan and Trang38, Theorem 4.13.2]. Because
![]() ${\mathcal {N}}$
is backgrounded via extenders whose critical points are
${\mathcal {N}}$
is backgrounded via extenders whose critical points are
![]() $>{\delta }^{{\mathcal {N}}_0^b}$
, the fragment of
$>{\delta }^{{\mathcal {N}}_0^b}$
, the fragment of
![]() $\Sigma ^m_{{\mathcal {N}}_0}$
, we need to compute the strategy of
$\Sigma ^m_{{\mathcal {N}}_0}$
, we need to compute the strategy of
![]() ${\mathcal {N}}|\xi $
as the fragment that acts on nondropping trees that are above
${\mathcal {N}}|\xi $
as the fragment that acts on nondropping trees that are above
![]() ${\delta }^{{\mathcal {N}}_0^b}$
and are based on
${\delta }^{{\mathcal {N}}_0^b}$
and are based on
![]() ${\mathcal {N}}_0|\zeta $
. Then [Reference Sargsyan and Trang38, Theorem 4.13.2] implies that this fragment of
${\mathcal {N}}_0|\zeta $
. Then [Reference Sargsyan and Trang38, Theorem 4.13.2] implies that this fragment of
![]() $\Sigma ^m_{{\mathcal {N}}_0}$
is induced by the unique strategy of
$\Sigma ^m_{{\mathcal {N}}_0}$
is induced by the unique strategy of
![]() ${\mathcal {P}}|\zeta $
. The same strategy of
${\mathcal {P}}|\zeta $
. The same strategy of
![]() ${\mathcal {P}}|\zeta $
also induces
${\mathcal {P}}|\zeta $
also induces
![]() $\Sigma ^m_{{\mathcal {R}}^*|\xi }$
. Therefore, clause 2 cannot happen.
$\Sigma ^m_{{\mathcal {R}}^*|\xi }$
. Therefore, clause 2 cannot happen.
We now show that clause 1 also cannot happen. Suppose
![]() $\xi <{\delta }^{{\mathcal {N}}^b}$
is a limit of Woodin cardinals or is a Woodin cardinal. Let
$\xi <{\delta }^{{\mathcal {N}}^b}$
is a limit of Woodin cardinals or is a Woodin cardinal. Let
![]() $\zeta =o^{\mathcal {N}}(\xi )$
, the Mitchell order of
$\zeta =o^{\mathcal {N}}(\xi )$
, the Mitchell order of
![]() $\xi $
, and let
$\xi $
, and let
![]() ${\mathcal {T}}$
be a normal tree on
${\mathcal {T}}$
be a normal tree on
![]() ${\mathcal {R}}$
with last model
${\mathcal {R}}$
with last model
![]() ${\mathcal {W}}$
such that
${\mathcal {W}}$
such that
![]() ${\mathcal {W}}|\zeta ={\mathcal {N}}|\zeta $
and the generators of
${\mathcal {W}}|\zeta ={\mathcal {N}}|\zeta $
and the generators of
![]() ${\mathcal {T}}$
are contained in
${\mathcal {T}}$
are contained in
![]() $\zeta $
. Furthermore, assume that
$\zeta $
. Furthermore, assume that
![]() $\zeta $
is a cutpoint in
$\zeta $
is a cutpoint in
![]() ${\mathcal {W}}$
. Let
${\mathcal {W}}$
. Let
![]() $\nu $
be the least Woodin cardinal of
$\nu $
be the least Woodin cardinal of
![]() ${\mathcal {W}}$
above
${\mathcal {W}}$
above
![]() $\zeta $
and let
$\zeta $
and let
![]() $\tau $
be the least Woodin cardinal of
$\tau $
be the least Woodin cardinal of
![]() ${\mathcal {N}}$
above
${\mathcal {N}}$
above
![]() $\zeta $
. It is enough to show that whenever
$\zeta $
. It is enough to show that whenever
![]() $({\mathcal {T}}, {\mathcal {W}}, \xi , \zeta , \nu , \tau )$
are as above, then
$({\mathcal {T}}, {\mathcal {W}}, \xi , \zeta , \nu , \tau )$
are as above, then
![]() ${\mathcal {W}}|\nu $
normally iterates via
${\mathcal {W}}|\nu $
normally iterates via
![]() $\Sigma ^m_{{\mathcal {W}}|\nu }$
to
$\Sigma ^m_{{\mathcal {W}}|\nu }$
to
![]() ${\mathcal {N}}|\tau $
.
${\mathcal {N}}|\tau $
.
To see this, it is enough to show that if
![]() ${\mathcal {U}}$
is a normal tree on
${\mathcal {U}}$
is a normal tree on
![]() ${\mathcal {W}}|\nu $
of limit length and
${\mathcal {W}}|\nu $
of limit length and
![]() ${\mathrm m}({\mathcal {U}}){\trianglelefteq } {\mathcal {N}}|\tau $
, then setting
${\mathrm m}({\mathcal {U}}){\trianglelefteq } {\mathcal {N}}|\tau $
, then setting
![]() $b=\Sigma ^m_{{\mathcal {W}}}({\mathcal {U}})$
, either
$b=\Sigma ^m_{{\mathcal {W}}}({\mathcal {U}})$
, either
-
1.
 ${\delta }({\mathcal {U}})<\tau $
and
${\delta }({\mathcal {U}})<\tau $
and
 ${\mathcal {Q}}(b, {\mathcal {U}})$
exists and
${\mathcal {Q}}(b, {\mathcal {U}})$
exists and
 ${\mathcal {Q}}(b, {\mathcal {U}}){\trianglelefteq } {\mathcal {N}}|\tau $
or
${\mathcal {Q}}(b, {\mathcal {U}}){\trianglelefteq } {\mathcal {N}}|\tau $
or -
2.
 ${\delta }({\mathcal {U}})=\tau $
and
${\delta }({\mathcal {U}})=\tau $
and
 $\pi ^{\mathcal {U}}_b(\nu )=\tau $
.
$\pi ^{\mathcal {U}}_b(\nu )=\tau $
.
To see the above, fix
![]() ${\mathcal {U}}$
and b as above. Suppose first that
${\mathcal {U}}$
and b as above. Suppose first that
![]() ${\delta }({\mathcal {U}})<\tau $
. Let
${\delta }({\mathcal {U}})<\tau $
. Let
![]() ${\mathcal {Q}}{\trianglelefteq } {\mathcal {N}}|\tau $
be largest such that
${\mathcal {Q}}{\trianglelefteq } {\mathcal {N}}|\tau $
be largest such that
![]() ${\mathcal {Q}}{\vDash } \text {`}{\delta }({\mathcal {U}})$
is a Woodin cardinal’. Then, as
${\mathcal {Q}}{\vDash } \text {`}{\delta }({\mathcal {U}})$
is a Woodin cardinal’. Then, as
![]() $\Sigma ^m$
is fullness preserving,
$\Sigma ^m$
is fullness preserving,
![]() ${\mathcal {Q}}{\trianglelefteq } {\mathcal {M}}^{\mathcal {U}}_b$
.
${\mathcal {Q}}{\trianglelefteq } {\mathcal {M}}^{\mathcal {U}}_b$
.
Suppose then
![]() ${\delta }({\mathcal {U}})=\tau $
. If
${\delta }({\mathcal {U}})=\tau $
. If
![]() $\pi ^{\mathcal {U}}_b(\nu )>\tau $
, then
$\pi ^{\mathcal {U}}_b(\nu )>\tau $
, then
![]() ${\mathcal {Q}}(b, {\mathcal {U}})$
-exists and is
${\mathcal {Q}}(b, {\mathcal {U}})$
-exists and is
![]() $Ord$
-iterable inside
$Ord$
-iterable inside
![]() ${\mathcal {P}}[g*m]$
. Working inside
${\mathcal {P}}[g*m]$
. Working inside
![]() ${\mathcal {N}}$
, let
${\mathcal {N}}$
, let
![]() ${\mathcal { K}}$
be the output of the fully backgrounded construction of
${\mathcal { K}}$
be the output of the fully backgrounded construction of
![]() ${\mathcal {N}}$
done with respect to
${\mathcal {N}}$
done with respect to
![]() $S^{\mathcal {N}}_{{\mathcal {N}}|\tau }$
over
$S^{\mathcal {N}}_{{\mathcal {N}}|\tau }$
over
![]() ${\mathcal {N}}|\tau $
and using extenders with critical point
${\mathcal {N}}|\tau $
and using extenders with critical point
![]() $>{\delta }^{{\mathcal {N}}^b}$
. Because
$>{\delta }^{{\mathcal {N}}^b}$
. Because
![]() ${\mathcal { K}}$
is universal, we must have that
${\mathcal { K}}$
is universal, we must have that
![]() ${\mathcal {Q}}({\beta }, {\mathcal {U}}){\trianglelefteq } {\mathcal { K}}$
. Thus,
${\mathcal {Q}}({\beta }, {\mathcal {U}}){\trianglelefteq } {\mathcal { K}}$
. Thus,
![]() ${\mathcal { K}}{\vDash } \text {`}\tau $
is not a Woodin cardinal’, which implies that
${\mathcal { K}}{\vDash } \text {`}\tau $
is not a Woodin cardinal’, which implies that
![]() ${\mathcal {N}}{\vDash } \text {`}\tau $
is not a Woodin cardinal’.
${\mathcal {N}}{\vDash } \text {`}\tau $
is not a Woodin cardinal’.
Let now
![]() ${\mathcal {Y}}^*$
be a normal tree on
${\mathcal {Y}}^*$
be a normal tree on
![]() ${\mathcal {S}}$
according to
${\mathcal {S}}$
according to
![]() $\Sigma ^m_{\mathcal {S}}$
whose last model is
$\Sigma ^m_{\mathcal {S}}$
whose last model is
![]() ${\mathcal {N}}_0$
. Let
${\mathcal {N}}_0$
. Let
![]() $\eta \in ({\delta }^{{\mathcal {N}}_0^b}, {\delta }^w)$
be such that
$\eta \in ({\delta }^{{\mathcal {N}}_0^b}, {\delta }^w)$
be such that
![]() ${\mathcal {R}}$
iterates to the hod pair construction of
${\mathcal {R}}$
iterates to the hod pair construction of
![]() ${\mathcal {N}}_0|\eta $
. Let
${\mathcal {N}}_0|\eta $
. Let
![]() $E\in \vec {E}^{{\mathcal {N}}_0}$
be such that
$E\in \vec {E}^{{\mathcal {N}}_0}$
be such that
![]() $\mathrm {crit }(E)={\delta }^{{\mathcal {N}}_0^b}$
and
$\mathrm {crit }(E)={\delta }^{{\mathcal {N}}_0^b}$
and
![]() $lh(E)>\eta $
(the existence of such an E follows from (A) above). Let
$lh(E)>\eta $
(the existence of such an E follows from (A) above). Let
![]() ${\alpha }<lh({\mathcal {Y}}^*)$
be the least such that
${\alpha }<lh({\mathcal {Y}}^*)$
be the least such that
![]() $E\in {\mathcal {M}}_{\alpha }^{{\mathcal {Y}}^*}$
and set
$E\in {\mathcal {M}}_{\alpha }^{{\mathcal {Y}}^*}$
and set
![]() ${\mathcal {Y}}^{**}={\mathcal {Y}}^*{\restriction } {\alpha }+1$
. Finally, set
${\mathcal {Y}}^{**}={\mathcal {Y}}^*{\restriction } {\alpha }+1$
. Finally, set
![]() ${\mathcal {Y}}={\mathcal {Y}}^{**\frown } \{E\}$
. Notice that if
${\mathcal {Y}}={\mathcal {Y}}^{**\frown } \{E\}$
. Notice that if
![]() ${\mathcal {V}}$
is the last model of
${\mathcal {V}}$
is the last model of
![]() ${\mathcal {Y}}$
, then
${\mathcal {Y}}$
, then
![]() $\pi ^{\mathcal {Y}}$
-exists.
$\pi ^{\mathcal {Y}}$
-exists.
To finish the proof of the lemma, we need to take a countable Skolem hull of
![]() ${\mathcal {P}}|{\lambda }[g*m]$
, where
${\mathcal {P}}|{\lambda }[g*m]$
, where
![]() ${\lambda }=(({\delta }^w)^+)^{\mathcal {P}}$
. Let
${\lambda }=(({\delta }^w)^+)^{\mathcal {P}}$
. Let
![]() $\pi :{\mathcal {M}}\rightarrow {\mathcal {P}}|{\lambda }[g*m]$
be a countable Skolem hull of
$\pi :{\mathcal {M}}\rightarrow {\mathcal {P}}|{\lambda }[g*m]$
be a countable Skolem hull of
![]() ${\mathcal {P}}|{\lambda }[g*m]$
such that
${\mathcal {P}}|{\lambda }[g*m]$
such that
![]() ${\mathcal {R}}, {\mathcal {N}}, {\mathcal {Y}} \in rng(\pi )$
. Let
${\mathcal {R}}, {\mathcal {N}}, {\mathcal {Y}} \in rng(\pi )$
. Let
![]() ${\mathcal {X}}=\pi ^{-1}({\mathcal {Y}})$
and let
${\mathcal {X}}=\pi ^{-1}({\mathcal {Y}})$
and let
![]() ${\mathcal {W}}$
be the last model of
${\mathcal {W}}$
be the last model of
![]() ${\mathcal {X}}$
. By elementarity,
${\mathcal {X}}$
. By elementarity,
![]() ${\mathcal {X}}={\mathcal {X}}^{*\frown }\{ F\}$
and
${\mathcal {X}}={\mathcal {X}}^{*\frown }\{ F\}$
and
![]() ${\mathcal {R}}$
normally iterates via
${\mathcal {R}}$
normally iterates via
![]() $\Sigma ^m_{\mathcal {R}}$
to a hod pair construction of
$\Sigma ^m_{\mathcal {R}}$
to a hod pair construction of
![]() ${\mathcal {W}}|lh(F)$
. It follows now that
${\mathcal {W}}|lh(F)$
. It follows now that
![]() $\Sigma ^m_{{\mathcal {W}}^b}$
is Wadge above
$\Sigma ^m_{{\mathcal {W}}^b}$
is Wadge above
![]() $\Sigma ^m_{\mathcal {R}}$
and hence Wadge above A. Therefore,
$\Sigma ^m_{\mathcal {R}}$
and hence Wadge above A. Therefore,
![]() ${\mathcal {X}}$
is as desired.
${\mathcal {X}}$
is as desired.
Lemma 3.4. There is an elementary embedding
such that for each
![]() $A\in \Delta ^h$
,
$A\in \Delta ^h$
,
![]() $j(A)=A^k$
, the interpretation of A in
$j(A)=A^k$
, the interpretation of A in
![]() ${\mathcal {P}}[g*h*k]$
.
${\mathcal {P}}[g*h*k]$
.
Proof. Let
![]() $W_1=L(\Delta ^h,\mathbb {R}^{{\mathcal {P}}[g*h]})$
and
$W_1=L(\Delta ^h,\mathbb {R}^{{\mathcal {P}}[g*h]})$
and
![]() $W_2=L(\Delta ^{h*k},\mathbb {R}^{{\mathcal {P}}[g*h*k]})$
. Let C be the set of inaccessible cardinals of
$W_2=L(\Delta ^{h*k},\mathbb {R}^{{\mathcal {P}}[g*h*k]})$
. Let C be the set of inaccessible cardinals of
![]() ${\mathcal {P}}[g*h*k]$
. Because we have a class of Woodin cardinals, it follows that
${\mathcal {P}}[g*h*k]$
. Because we have a class of Woodin cardinals, it follows that
![]() $(\Delta ^h)^\#$
exists. Moreover, for
$(\Delta ^h)^\#$
exists. Moreover, for
![]() $\Gamma \subseteq {\wp }({\mathbb {R}})$
, assuming
$\Gamma \subseteq {\wp }({\mathbb {R}})$
, assuming
![]() $\Gamma ^\#$
exists, any set in
$\Gamma ^\#$
exists, any set in
![]() $L(\Gamma ,{\mathbb {R}})$
is definable from a set in
$L(\Gamma ,{\mathbb {R}})$
is definable from a set in
![]() $\Gamma $
, a real and a finite sequence of indiscernibles. It is then enough to show that
$\Gamma $
, a real and a finite sequence of indiscernibles. It is then enough to show that
(*) if
![]() $s=({\alpha }_0, ..., {\alpha }_n)\in C^{<\omega }$
,
$s=({\alpha }_0, ..., {\alpha }_n)\in C^{<\omega }$
,
![]() $A\in \Delta ^h$
,
$A\in \Delta ^h$
,
![]() $x\in {\mathbb {R}}_{g*h}$
and
$x\in {\mathbb {R}}_{g*h}$
and
![]() $\phi $
is a formula, then
$\phi $
is a formula, then
Indeed, we first show that (*) induces an elementary
![]() $j:W_1\rightarrow W_2$
as desired. Let Y be the set of a that are definable over
$j:W_1\rightarrow W_2$
as desired. Let Y be the set of a that are definable over
![]() $L(\Delta ^{h*k}, {\mathbb {R}}_{g*h*k})$
from a member of
$L(\Delta ^{h*k}, {\mathbb {R}}_{g*h*k})$
from a member of
![]() $C^{<\omega }$
, a set of the form
$C^{<\omega }$
, a set of the form
![]() $A^k$
for some
$A^k$
for some
![]() $A\in \Delta ^h$
and a real
$A\in \Delta ^h$
and a real
![]() $x\in {\mathbb {R}}_{g*h}$
. Notice that (*) implies that
$x\in {\mathbb {R}}_{g*h}$
. Notice that (*) implies that
Claim 1.
Y is elementary in
![]() $L(\Delta ^{h*k}, {\mathbb {R}}_{g*h*k})$
.
$L(\Delta ^{h*k}, {\mathbb {R}}_{g*h*k})$
.
Proof. We show that Y is
![]() $\Sigma _1$
-elementary. The general case follows from Tarski-Vaught criteria. To see this, fix
$\Sigma _1$
-elementary. The general case follows from Tarski-Vaught criteria. To see this, fix
![]() $a\in Y$
and let
$a\in Y$
and let
![]() $\phi $
be a
$\phi $
be a
![]() $\Sigma _1$
formula. Suppose that
$\Sigma _1$
formula. Suppose that
Fix a term t,
![]() $s\in C^{<\omega }$
, a set of the form
$s\in C^{<\omega }$
, a set of the form
![]() $A^k$
, where
$A^k$
, where
![]() $A\in \Delta ^h$
and
$A\in \Delta ^h$
and
![]() $x\in {\mathbb {R}}_{g*h}$
such that
$x\in {\mathbb {R}}_{g*h}$
such that
![]() $a=t^{W_2}[s, A^k, x]$
. It then follows from (*) that if
$a=t^{W_2}[s, A^k, x]$
. It then follows from (*) that if
![]() $b=t^{W_1}[s, A, x]$
,
$b=t^{W_1}[s, A, x]$
,
![]() $W_1{\vDash } \phi [b]$
. Let
$W_1{\vDash } \phi [b]$
. Let
![]() $\phi =\exists u \psi (u, v)$
. Fix a term
$\phi =\exists u \psi (u, v)$
. Fix a term
![]() $t_1$
,
$t_1$
,
![]() $s_1\in C^{<\omega }$
,
$s_1\in C^{<\omega }$
,
![]() $B\in \Delta ^h$
and
$B\in \Delta ^h$
and
![]() $y\in {\mathbb {R}}_{g*h}$
such that setting
$y\in {\mathbb {R}}_{g*h}$
such that setting
![]() $c=t^{W_1}_1[s_1, B, y]$
,
$c=t^{W_1}_1[s_1, B, y]$
,
![]() $W_1{\vDash } \psi [c, b]$
. Therefore, (*) implies that if
$W_1{\vDash } \psi [c, b]$
. Therefore, (*) implies that if
![]() $d=t^{W_2}[s_1, B^k, y]$
, then
$d=t^{W_2}[s_1, B^k, y]$
, then
![]() $W_2{\vDash } \psi [d, a]$
. As
$W_2{\vDash } \psi [d, a]$
. As
![]() $d\in Y$
, we have
$d\in Y$
, we have
![]() $Y{\vDash } \phi [a]$
.
$Y{\vDash } \phi [a]$
.
Let now N be the transitive collapse of Y. It is enough to show that
![]() $N=W_1$
. This easily follows from (*) and the proof of the claim. For example, let us show that
$N=W_1$
. This easily follows from (*) and the proof of the claim. For example, let us show that
![]() ${\mathbb {R}}^N={\mathbb {R}}^{W_1}$
. Fix
${\mathbb {R}}^N={\mathbb {R}}^{W_1}$
. Fix
![]() $x\in {\mathbb {R}}^N$
. Let t be a term,
$x\in {\mathbb {R}}^N$
. Let t be a term,
![]() $s\in C^{<\omega }$
,
$s\in C^{<\omega }$
,
![]() $A\in \Delta ^h$
and
$A\in \Delta ^h$
and
![]() $a\in {\mathbb {R}}^{W_1}$
such that
$a\in {\mathbb {R}}^{W_1}$
such that
![]() $x=t^{W_2}[s, A^k, a]$
. Letting
$x=t^{W_2}[s, A^k, a]$
. Letting
![]() $y=t^{W_1}[s, A, a]$
, it is easy to see that
$y=t^{W_1}[s, A, a]$
, it is easy to see that
![]() $x=y$
. We now let
$x=y$
. We now let
![]() $j:W_1\rightarrow W_2$
be the inverse of the transitive collapse of Y. Clearly, j is elementary and
$j:W_1\rightarrow W_2$
be the inverse of the transitive collapse of Y. Clearly, j is elementary and
![]() $j(A)=A^k$
for
$j(A)=A^k$
for
![]() $A\in \Delta ^h$
.
$A\in \Delta ^h$
.
By a similar reduction, using the definition of
![]() $\Delta ^h$
and
$\Delta ^h$
and
![]() $\Delta ^{h*k}$
, it is enough to show that (**) holds where
$\Delta ^{h*k}$
, it is enough to show that (**) holds where
(**) if
![]() $s=({\alpha }_0, ..., {\alpha }_n)\in C^{<\omega }$
,
$s=({\alpha }_0, ..., {\alpha }_n)\in C^{<\omega }$
,
![]() ${\mathcal {T}}$
is a countable iteration of
${\mathcal {T}}$
is a countable iteration of
![]() ${\mathcal {P}}_0$
according to
${\mathcal {P}}_0$
according to
![]() $\Sigma ^h$
such that
$\Sigma ^h$
such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists,
$\pi ^{{\mathcal {T}}, b}$
exists,
![]() ${\mathcal {R}}=\pi ^{{\mathcal {T}}, b}({\mathcal {P}}_0^b)$
,
${\mathcal {R}}=\pi ^{{\mathcal {T}}, b}({\mathcal {P}}_0^b)$
,
![]() $x\in {\mathbb {R}}_{g*h}$
and
$x\in {\mathbb {R}}_{g*h}$
and
![]() $\phi $
is a formula, then
$\phi $
is a formula, then
To show (**), let
![]() $s\in C^{<\omega }$
,
$s\in C^{<\omega }$
,
![]() ${\mathcal {T}}$
be a countable iteration of
${\mathcal {T}}$
be a countable iteration of
![]() ${\mathcal {P}}_0$
according to
${\mathcal {P}}_0$
according to
![]() $\Sigma ^h$
such that
$\Sigma ^h$
such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists,
$\pi ^{{\mathcal {T}}, b}$
exists,
![]() ${\mathcal {R}}=\pi ^{{\mathcal {T}}, b}({\mathcal {P}}_0^b)$
,
${\mathcal {R}}=\pi ^{{\mathcal {T}}, b}({\mathcal {P}}_0^b)$
,
![]() $x\in {\mathbb {R}}_{g*h}$
and
$x\in {\mathbb {R}}_{g*h}$
and
![]() $\phi $
be a formula such that
$\phi $
be a formula such that
![]() $W_1{\vDash } \phi [\Sigma ^h_{\mathcal {R}}, x, s]$
. Notice that without losing generality, we can assume that
$W_1{\vDash } \phi [\Sigma ^h_{\mathcal {R}}, x, s]$
. Notice that without losing generality, we can assume that
![]() $\pi ^{\mathcal {T}}$
exists, as otherwise we can work with a shorter initial segment of
$\pi ^{\mathcal {T}}$
exists, as otherwise we can work with a shorter initial segment of
![]() ${\mathcal {T}}$
that produces the same bottom part
${\mathcal {T}}$
that produces the same bottom part
![]() ${\mathcal {R}}$
. Let
${\mathcal {R}}$
. Let
![]() ${\mathcal {S}}^*$
be the last model of
${\mathcal {S}}^*$
be the last model of
![]() ${\mathcal {T}}$
and let
${\mathcal {T}}$
and let
![]() ${\mathcal {S}}^{**}$
be the ultrapower of
${\mathcal {S}}^{**}$
be the ultrapower of
![]() ${\mathcal {S}}^*$
by the least extender on the sequence of
${\mathcal {S}}^*$
by the least extender on the sequence of
![]() ${\mathcal {S}}^*$
with the critical point
${\mathcal {S}}^*$
with the critical point
![]() ${\delta }^{{\mathcal {R}}}$
. Let
${\delta }^{{\mathcal {R}}}$
. Let
![]() $\iota $
be the least Woodin of
$\iota $
be the least Woodin of
![]() ${\mathcal {S}}^{**}$
that is
${\mathcal {S}}^{**}$
that is
![]() $>{\delta }^{\mathcal {R}}$
. Let
$>{\delta }^{\mathcal {R}}$
. Let
![]() ${\mathcal {W}}$
be the
${\mathcal {W}}$
be the
![]() $\Sigma ^h$
-iterate of
$\Sigma ^h$
-iterate of
![]() ${\mathcal {S}}^{**}$
that is obtained via an x-genericity iteration done in the window
${\mathcal {S}}^{**}$
that is obtained via an x-genericity iteration done in the window
![]() $({\delta }^{\mathcal {R}}, \iota )$
.
$({\delta }^{\mathcal {R}}, \iota )$
.
We would now like to see that
![]() $W_2{\vDash } \phi [\Sigma ^{h*k}_{\mathcal {R}}, x, s]$
. The idea is to realize
$W_2{\vDash } \phi [\Sigma ^{h*k}_{\mathcal {R}}, x, s]$
. The idea is to realize
![]() $W_1$
and
$W_1$
and
![]() $W_2$
, respectively, as a derived model of
$W_2$
, respectively, as a derived model of
![]() ${\mathcal {W}}$
. Given a transitive model of set theory M with
${\mathcal {W}}$
. Given a transitive model of set theory M with
![]() ${\lambda }$
a limit of Woodin cardinals of M, we let
${\lambda }$
a limit of Woodin cardinals of M, we let
![]() $D(M, {\lambda })$
be the derived model at
$D(M, {\lambda })$
be the derived model at
![]() ${\lambda }$
as computed by some symmetric collapse of
${\lambda }$
as computed by some symmetric collapse of
![]() ${\lambda }$
. While
${\lambda }$
. While
![]() $D(M, {\lambda })$
depends on this generic, its theory does not. Thus, expressions like
$D(M, {\lambda })$
depends on this generic, its theory does not. Thus, expressions like
![]() $D(M, {\lambda }){\vDash } \psi $
have an
$D(M, {\lambda }){\vDash } \psi $
have an
![]() $\mathsf {uvs}$
meaning. If
$\mathsf {uvs}$
meaning. If
![]() $u\subseteq Coll(\omega , <{\lambda })$
is the generic, then
$u\subseteq Coll(\omega , <{\lambda })$
is the generic, then
![]() $D({\mathcal {M}}, {\lambda }, u)$
is the derived model computed using u.Footnote 59
$D({\mathcal {M}}, {\lambda }, u)$
is the derived model computed using u.Footnote 59
To finish the proof, we will need a way of realizing
![]() $W_1$
as a derived model of an iterate of
$W_1$
as a derived model of an iterate of
![]() ${\mathcal {W}}$
that is obtained by iterating above
${\mathcal {W}}$
that is obtained by iterating above
![]() $\xi $
, where
$\xi $
, where
![]() $\xi $
is the least Woodin cardinal of
$\xi $
is the least Woodin cardinal of
![]() ${\mathcal {W}}$
above
${\mathcal {W}}$
above
![]() $\delta ^{\mathcal {R}}$
. The same construction will also realize
$\delta ^{\mathcal {R}}$
. The same construction will also realize
![]() $W_2$
as a derived model of a
$W_2$
as a derived model of a
![]() ${\mathcal {W}}$
’s iterate. Let
${\mathcal {W}}$
’s iterate. Let
![]() $l\subseteq Coll(\omega , \Gamma ^{\infty }_{g*h})$
be
$l\subseteq Coll(\omega , \Gamma ^{\infty }_{g*h})$
be
![]() ${\mathcal {P}}[g*h]$
-generic. Working in
${\mathcal {P}}[g*h]$
-generic. Working in
![]() ${\mathcal {P}}[g*h*l]$
, let
${\mathcal {P}}[g*h*l]$
, let
![]() $(A_i: i<\omega )$
be a generic enumeration of
$(A_i: i<\omega )$
be a generic enumeration of
![]() $\Gamma ^{\infty }_{g*h}$
and let
$\Gamma ^{\infty }_{g*h}$
and let
![]() $(x_i: i<\omega )$
be a generic enumeration of
$(x_i: i<\omega )$
be a generic enumeration of
![]() ${\mathbb {R}}_{g*h}$
.
${\mathbb {R}}_{g*h}$
.
(1) There is sequence
![]() $({\mathcal {W}}_i, p_i^*, p_i: i<\omega ) \in {\mathcal {P}}[g*h*l]$
such that
$({\mathcal {W}}_i, p_i^*, p_i: i<\omega ) \in {\mathcal {P}}[g*h*l]$
such that
-
1. for each
 $n<\omega $
,
$n<\omega $
,
 $({\mathcal {W}}_i, p_i^*, p_i: i\leq n)\in HC^{{\mathcal {P}}[g*h]}$
,
$({\mathcal {W}}_i, p_i^*, p_i: i\leq n)\in HC^{{\mathcal {P}}[g*h]}$
, -
2.
 ${\mathcal {W}}_0={\mathcal {W}}$
,
${\mathcal {W}}_0={\mathcal {W}}$
, -
3. letting
 $E_i\in \vec {E}^{{\mathcal {W}}_i}$
be the Mitchell order 0 measure on
$E_i\in \vec {E}^{{\mathcal {W}}_i}$
be the Mitchell order 0 measure on
 ${\delta }^{{\mathcal {W}}_i^b}$
and
${\delta }^{{\mathcal {W}}_i^b}$
and
 ${\mathcal {M}}_i=Ult({\mathcal {W}}_i, E_i)$
,Footnote 60
${\mathcal {M}}_i=Ult({\mathcal {W}}_i, E_i)$
,Footnote 60
 $p_i^*$
is an iteration of
$p_i^*$
is an iteration of
 ${\mathcal {M}}_i$
according to
${\mathcal {M}}_i$
according to
 $\Sigma ^h_{{\mathcal {M}}_i}$
that is above
$\Sigma ^h_{{\mathcal {M}}_i}$
that is above
 ${\delta }^{{\mathcal {W}}_i^b}$
, has a last model
${\delta }^{{\mathcal {W}}_i^b}$
, has a last model
 ${\mathcal {N}}_i$
and is such that
${\mathcal {N}}_i$
and is such that
 $\pi ^{p_i^*}$
exists and for some
$\pi ^{p_i^*}$
exists and for some
 $\nu _i<{\delta }^{{\mathcal {N}}_i^b}$
a Woodin cardinal of
$\nu _i<{\delta }^{{\mathcal {N}}_i^b}$
a Woodin cardinal of
 ${\mathcal {N}}_{i}$
,
${\mathcal {N}}_{i}$
,
 $A_i<_w \Sigma ^h_{{\mathcal {N}}_i|\nu _i}$
,
$A_i<_w \Sigma ^h_{{\mathcal {N}}_i|\nu _i}$
, -
4. fixing some
 $\nu _i$
as above and letting
$\nu _i$
as above and letting
 $\xi $
be the least Woodin cardinal of
$\xi $
be the least Woodin cardinal of
 ${\mathcal {N}}_i$
that is
${\mathcal {N}}_i$
that is
 $>\nu _i$
,
$>\nu _i$
,
 ${\mathcal {W}}_{i+1}$
is the
${\mathcal {W}}_{i+1}$
is the
 $\Sigma ^h_{{\mathcal {N}}_i}$
-iterate of
$\Sigma ^h_{{\mathcal {N}}_i}$
-iterate of
 ${\mathcal {N}}_i$
that is above
${\mathcal {N}}_i$
that is above
 $\nu _i$
and makes
$\nu _i$
and makes
 $x_i$
generic at the image of
$x_i$
generic at the image of
 $\xi $
;
$\xi $
;
 $p_i$
is the corresponding iteration.
$p_i$
is the corresponding iteration.
The proof of (1) is a straightforward application of Lemma 3.3. Let
![]() $\pi _{i, j}:{\mathcal {W}}_i\rightarrow {\mathcal {W}}_j$
be the iteration embedding and let
$\pi _{i, j}:{\mathcal {W}}_i\rightarrow {\mathcal {W}}_j$
be the iteration embedding and let
![]() ${\mathcal {W}}_{\omega }$
be the direct limit of
${\mathcal {W}}_{\omega }$
be the direct limit of
![]() $({\mathcal {W}}_i, \pi _{i, j}: i<j<\omega )$
. It follows that for some
$({\mathcal {W}}_i, \pi _{i, j}: i<j<\omega )$
. It follows that for some
![]() $u\subseteq Coll(\omega , <{\delta }^{{\mathcal {W}}_{\omega }^b})$
-generic,
$u\subseteq Coll(\omega , <{\delta }^{{\mathcal {W}}_{\omega }^b})$
-generic,
(2)
![]() ${\mathbb {R}}^{{\mathcal {W}}_{\omega }[u]}={\mathbb {R}}_{g*h}$
and
${\mathbb {R}}^{{\mathcal {W}}_{\omega }[u]}={\mathbb {R}}_{g*h}$
and
![]() $\Gamma ^{\infty }_{g*h}={\wp }({\mathbb {R}}_{g*h})\cap D({\mathcal {W}}_{\omega }, {\delta }^{{\mathcal {W}}_{\omega }^b}, u)$
, and hence,
$\Gamma ^{\infty }_{g*h}={\wp }({\mathbb {R}}_{g*h})\cap D({\mathcal {W}}_{\omega }, {\delta }^{{\mathcal {W}}_{\omega }^b}, u)$
, and hence,
(3)
![]() $W_1=D({\mathcal {W}}_{\omega }, {\delta }^{{\mathcal {W}}_{\omega }^b}, u)$
$W_1=D({\mathcal {W}}_{\omega }, {\delta }^{{\mathcal {W}}_{\omega }^b}, u)$
Letting S stand for the strategy predicate and t be the sequence of the first n indiscernibles of
![]() ${\mathcal {W}}|{\delta }^{{\mathcal {W}}^b}$
, we thus get by our assumption
${\mathcal {W}}|{\delta }^{{\mathcal {W}}^b}$
, we thus get by our assumption
![]() $W_1{\vDash } \phi [\Sigma ^h_{\mathcal {R}}, x, s]$
and by elementarity that
$W_1{\vDash } \phi [\Sigma ^h_{\mathcal {R}}, x, s]$
and by elementarity that
(4)
![]() $D({\mathcal {W}}[x], {\delta }^{{\mathcal {S}}^b}){\vDash } \phi [S^{\mathcal {W}}_{\mathcal {R}}, x, t]$
.
$D({\mathcal {W}}[x], {\delta }^{{\mathcal {S}}^b}){\vDash } \phi [S^{\mathcal {W}}_{\mathcal {R}}, x, t]$
.
The same construction that gives (3) also gives
![]() ${\mathcal {N}}_{\omega }$
and v such that
${\mathcal {N}}_{\omega }$
and v such that
(5)
![]() ${\mathcal {N}}_{\omega }$
is a
${\mathcal {N}}_{\omega }$
is a
![]() $\Sigma ^{h*k}$
-iterate of
$\Sigma ^{h*k}$
-iterate of
![]() ${\mathcal {W}}$
above
${\mathcal {W}}$
above
![]() $\xi $
,
$\xi $
,
![]() $v\subseteq Coll(\omega , <{\delta }^{{\mathcal {N}}_{\omega }^b})$
is generic and
$v\subseteq Coll(\omega , <{\delta }^{{\mathcal {N}}_{\omega }^b})$
is generic and
![]() $D({\mathcal {N}}_{\omega }, {\delta }^{{\mathcal {N}}_{\omega }^b}, v)=W_2$
.
$D({\mathcal {N}}_{\omega }, {\delta }^{{\mathcal {N}}_{\omega }^b}, v)=W_2$
.
Thus,
![]() $W_2{\vDash } \phi [\Sigma ^{h*k}_{\mathcal {R}}, x, t_1]$
, where
$W_2{\vDash } \phi [\Sigma ^{h*k}_{\mathcal {R}}, x, t_1]$
, where
![]() $t_1$
is the image of t in
$t_1$
is the image of t in
![]() ${\mathcal {N}}_{\omega }$
. By indiscernability, we get that
${\mathcal {N}}_{\omega }$
. By indiscernability, we get that
![]() $W_2{\vDash } \phi [\Sigma ^{h*k}_{\mathcal {R}}, x, s]$
.
$W_2{\vDash } \phi [\Sigma ^{h*k}_{\mathcal {R}}, x, s]$
.
3.2. An upper bound for
 $\mathsf {LSA-over-uB}$
$\mathsf {LSA-over-uB}$
Let
![]() $({\mathcal {P}}_0,\Sigma ^-), {\mathcal {P}}, \Sigma , g$
be as before (see right after Theorem 3.1). Now we show
$({\mathcal {P}}_0,\Sigma ^-), {\mathcal {P}}, \Sigma , g$
be as before (see right after Theorem 3.1). Now we show
![]() $\mathsf {LSA-over-uB}$
is satisfied in
$\mathsf {LSA-over-uB}$
is satisfied in
![]() ${\mathcal {P}}[g]$
. Fix a poset
${\mathcal {P}}[g]$
. Fix a poset
![]() $\mathbb {P}\in P[g]$
and let
$\mathbb {P}\in P[g]$
and let
![]() $h\subseteq \mathbb {P}$
be
$h\subseteq \mathbb {P}$
be
![]() ${\mathcal {P}}[g]$
-generic. We will show that
${\mathcal {P}}[g]$
-generic. We will show that
-
1.
 $L(\Sigma ^{g*h}, {\mathbb {R}}_{g*h}){\vDash } \mathsf {LSA}$
and
$L(\Sigma ^{g*h}, {\mathbb {R}}_{g*h}){\vDash } \mathsf {LSA}$
and -
2.
 $\Gamma ^{\infty }_{g*h}$
is the Suslin co-Suslin sets of
$\Gamma ^{\infty }_{g*h}$
is the Suslin co-Suslin sets of
 $L(\Sigma ^{g*h}, {\mathbb {R}}_{g*h})$
.
$L(\Sigma ^{g*h}, {\mathbb {R}}_{g*h})$
.
Clause 2 above is an immediate consequence of clause 1 and the results of the previous section.
We now show clause 1. Let
![]() $(\gamma _i : i<\omega )$
be the first
$(\gamma _i : i<\omega )$
be the first
![]() $\omega $
Woodin cardinals of
$\omega $
Woodin cardinals of
![]() ${\mathcal {P}}[g*h]$
and
${\mathcal {P}}[g*h]$
and
![]() $\gamma = sup_{i<\omega } \gamma _i$
. Let
$\gamma = sup_{i<\omega } \gamma _i$
. Let
![]() $w_i$
be the corresponding consecutive windows determined by the
$w_i$
be the corresponding consecutive windows determined by the
![]() $\gamma _i$
’s. Write
$\gamma _i$
’s. Write
![]() $\Lambda $
for
$\Lambda $
for
![]() $\Sigma ^{h}$
, the canonical interpretation of
$\Sigma ^{h}$
, the canonical interpretation of
![]() $\Sigma $
in
$\Sigma $
in
![]() $P[g*h]$
. In
$P[g*h]$
. In
![]() ${\mathcal {P}}[g*h]$
, let
${\mathcal {P}}[g*h]$
, let
be elementary and such that
![]() ${\mathcal {M}}$
is countable and
${\mathcal {M}}$
is countable and
![]() $\mathrm {crit }(\pi )> {\delta }_0$
. For each i, let
$\mathrm {crit }(\pi )> {\delta }_0$
. For each i, let
![]() $\delta _i = \pi ^{-1}(\gamma _i)$
, and
$\delta _i = \pi ^{-1}(\gamma _i)$
, and
![]() $\lambda = \sup _{i<\omega } \delta _i$
. Note that because
$\lambda = \sup _{i<\omega } \delta _i$
. Note that because
![]() $\mathrm {crit }(\pi )> {\delta }_0$
,
$\mathrm {crit }(\pi )> {\delta }_0$
,
![]() ${\mathcal {M}}|{\lambda }$
is closed under
${\mathcal {M}}|{\lambda }$
is closed under
![]() $\Lambda $
, and
$\Lambda $
, and
![]() $\lambda $
is the supremum of the Woodin cardinals of
$\lambda $
is the supremum of the Woodin cardinals of
![]() ${\mathcal {M}}$
. It follows from Proposition 2.13 that
${\mathcal {M}}$
. It follows from Proposition 2.13 that
![]() ${\mathcal {M}}$
has a
${\mathcal {M}}$
has a
![]() $\nu ^{w_0}$
-strategy acting on nondropping trees based on the interval
$\nu ^{w_0}$
-strategy acting on nondropping trees based on the interval
![]() $[\pi ^{-1}(\nu ^{w_0}), \lambda )$
in
$[\pi ^{-1}(\nu ^{w_0}), \lambda )$
in
![]() ${\mathcal {P}}[g*h]$
; call this strategy
${\mathcal {P}}[g*h]$
; call this strategy
![]() $\Psi $
.
$\Psi $
.
Let
![]() $k\subseteq Coll(\omega , <\lambda )$
be
$k\subseteq Coll(\omega , <\lambda )$
be
![]() ${\mathcal {M}}$
-generic. Let
${\mathcal {M}}$
-generic. Let
![]() $\mathbb {R}^*_k = \bigcup _{\xi <\lambda } \mathbb {R}^{{\mathcal {M}}[k|\xi ]}$
and recall the ‘new’ derived model of
$\mathbb {R}^*_k = \bigcup _{\xi <\lambda } \mathbb {R}^{{\mathcal {M}}[k|\xi ]}$
and recall the ‘new’ derived model of
![]() ${\mathcal {M}}$
at
${\mathcal {M}}$
at
![]() $\lambda $
$\lambda $
By Woodin’s derived model theorem, cf. [Reference Steel47],
![]() $D^+({\mathcal {M}},{\lambda },k){\vDash } \mathsf {AD}^+$
. Again, the theory of
$D^+({\mathcal {M}},{\lambda },k){\vDash } \mathsf {AD}^+$
. Again, the theory of
![]() $D^+({\mathcal {M}},\lambda ,k)$
does not depend on k. When we reason about the theory of the new derived model without concerning about any particular generic, we write
$D^+({\mathcal {M}},\lambda ,k)$
does not depend on k. When we reason about the theory of the new derived model without concerning about any particular generic, we write
![]() $D^+({\mathcal {M}},\lambda )$
. Recall that we set
$D^+({\mathcal {M}},\lambda )$
. Recall that we set
![]() $\Lambda =\Sigma ^h$
.
$\Lambda =\Sigma ^h$
.
Proposition 3.5.
![]() $\Lambda \cap {\mathcal {M}}(\mathbb {R}^*_k)\in D^+({\mathcal {M}}, {\lambda })$
. Furthermore, in
$\Lambda \cap {\mathcal {M}}(\mathbb {R}^*_k)\in D^+({\mathcal {M}}, {\lambda })$
. Furthermore, in
![]() $D^+({\mathcal {M}},{\lambda })$
,
$D^+({\mathcal {M}},{\lambda })$
,
![]() $L(\Lambda ,\mathbb {R})\vDash \mathsf {LSA}$
.
$L(\Lambda ,\mathbb {R})\vDash \mathsf {LSA}$
.
Proof. First, note that there is a term
![]() $\tau \in {\mathcal {M}}$
such that
$\tau \in {\mathcal {M}}$
such that
![]() $({\mathcal {M}},\Psi ,\tau )$
term captures
$({\mathcal {M}},\Psi ,\tau )$
term captures
![]() $\Sigma ^{h}$
. More precisely, letting
$\Sigma ^{h}$
. More precisely, letting
![]() $i:{\mathcal {M}} \rightarrow {\mathcal {N}}$
be an iteration map according to
$i:{\mathcal {M}} \rightarrow {\mathcal {N}}$
be an iteration map according to
![]() $\Psi $
, let l be a
$\Psi $
, let l be a
![]() $<i(\lambda )$
-generic over
$<i(\lambda )$
-generic over
![]() ${\mathcal {N}}$
. Then
${\mathcal {N}}$
. Then
![]() $Code(\Sigma ^{h})\cap {\mathcal {N}}[l] = i(\tau )_{l}$
; this follows from results in Section 2 (cf. Proposition 2.17). To see that in
$Code(\Sigma ^{h})\cap {\mathcal {N}}[l] = i(\tau )_{l}$
; this follows from results in Section 2 (cf. Proposition 2.17). To see that in
![]() ${\mathcal {M}}(\mathbb {R}^*_k)$
,
${\mathcal {M}}(\mathbb {R}^*_k)$
,
![]() $L(\Lambda ,\mathbb {R}) {\vDash } \mathsf {AD}$
; suppose not. Let x be a real and A be the least
$L(\Lambda ,\mathbb {R}) {\vDash } \mathsf {AD}$
; suppose not. Let x be a real and A be the least
![]() $OD(\Lambda ,x)$
counterexample to
$OD(\Lambda ,x)$
counterexample to
![]() $\mathsf {AD}$
in
$\mathsf {AD}$
in
![]() $L(\Lambda ,\mathbb {R})$
. Also, by minimizing the ordinal parameters, we may assume A is definable from x and
$L(\Lambda ,\mathbb {R})$
. Also, by minimizing the ordinal parameters, we may assume A is definable from x and
![]() $\Lambda $
in
$\Lambda $
in
![]() $L(\Lambda ,\mathbb {R})$
. Using the term
$L(\Lambda ,\mathbb {R})$
. Using the term
![]() $\tau $
for
$\tau $
for
![]() $\Lambda $
, we can easily define a term
$\Lambda $
, we can easily define a term
![]() $\sigma $
over
$\sigma $
over
![]() ${\mathcal {M}}[x]$
such that
${\mathcal {M}}[x]$
such that
![]() $({\mathcal {M}}[x],\Psi ,\sigma )$
term captures A.Footnote 61 Applying Neeman’s theorem (cf. [Reference Neeman30]), we get that A is determined. Finally, let
$({\mathcal {M}}[x],\Psi ,\sigma )$
term captures A.Footnote 61 Applying Neeman’s theorem (cf. [Reference Neeman30]), we get that A is determined. Finally, let
![]() $i:{\mathcal {M}}[x]\rightarrow {\mathcal {N}}$
be a
$i:{\mathcal {M}}[x]\rightarrow {\mathcal {N}}$
be a
![]() $\mathbb {R}^{{\mathcal {P}}[g*h]}$
-genericity iteration according to
$\mathbb {R}^{{\mathcal {P}}[g*h]}$
-genericity iteration according to
![]() $\Psi $
.Footnote 62 By the argument just given, in
$\Psi $
.Footnote 62 By the argument just given, in
![]() ${\mathcal {N}}(\mathbb {R}_{g*h})$
, A is determined. So
${\mathcal {N}}(\mathbb {R}_{g*h})$
, A is determined. So
![]() ${\mathcal {M}}(\mathbb {R}^*_k){\vDash } \sigma _k$
is determined. Contradiction.
${\mathcal {M}}(\mathbb {R}^*_k){\vDash } \sigma _k$
is determined. Contradiction.
If
![]() $\mathsf {LSA}$
fails in
$\mathsf {LSA}$
fails in
![]() $L(\Lambda ,\mathbb {R})$
, then
$L(\Lambda ,\mathbb {R})$
, then
![]() $\Lambda $
is Suslin co-Suslin in
$\Lambda $
is Suslin co-Suslin in
![]() $D^+({\mathcal {M}},\lambda )$
, and the argument in Proposition 2.21 gives a contradiction. The point is that in
$D^+({\mathcal {M}},\lambda )$
, and the argument in Proposition 2.21 gives a contradiction. The point is that in
![]() $D^+({\mathcal {M}},{\lambda })$
, the Wadge ordinal of
$D^+({\mathcal {M}},{\lambda })$
, the Wadge ordinal of
![]() $\Gamma ^b({\mathcal {P}}_0,\Lambda )$
is a limit of Suslin cardinals, and the failure of
$\Gamma ^b({\mathcal {P}}_0,\Lambda )$
is a limit of Suslin cardinals, and the failure of
![]() $\mathsf {LSA}$
means that there is a larger Suslin cardinal above the Wadge ordinalFootnote 63 of
$\mathsf {LSA}$
means that there is a larger Suslin cardinal above the Wadge ordinalFootnote 63 of
![]() $\Gamma ^b({\mathcal {P}}_0,\Lambda )$
. So
$\Gamma ^b({\mathcal {P}}_0,\Lambda )$
. So
![]() $\Lambda $
is Suslin co-Suslin in
$\Lambda $
is Suslin co-Suslin in
![]() $D^+({\mathcal {M}},\lambda )$
. Now we can run the argument in Proposition 2.21 to obtain a contradiction. Hence, in
$D^+({\mathcal {M}},\lambda )$
. Now we can run the argument in Proposition 2.21 to obtain a contradiction. Hence, in
![]() $D^+({\mathcal {M}},\lambda )$
,
$D^+({\mathcal {M}},\lambda )$
,
Now perform a
![]() $\mathbb {R}^{{\mathcal {P}}[g*h]}$
-genericity iteration according to
$\mathbb {R}^{{\mathcal {P}}[g*h]}$
-genericity iteration according to
![]() $\Psi $
at
$\Psi $
at
![]() $\lambda $
. More precisely, there is an iteration
$\lambda $
. More precisely, there is an iteration
![]() $i:{\mathcal {M}}\rightarrow {\mathcal {N}}$
according to
$i:{\mathcal {M}}\rightarrow {\mathcal {N}}$
according to
![]() $\Psi $
such that letting
$\Psi $
such that letting
![]() $l \subseteq Coll(\omega , < i(\lambda ))$
be
$l \subseteq Coll(\omega , < i(\lambda ))$
be
![]() ${\mathcal {N}}$
-generic, letting
${\mathcal {N}}$
-generic, letting
![]() $\mathbb {R}^*_{l} = \bigcup _{\xi <i(\lambda )}\mathbb {R}^{{\mathcal {N}}[l|\xi ]}$
, we get
$\mathbb {R}^*_{l} = \bigcup _{\xi <i(\lambda )}\mathbb {R}^{{\mathcal {N}}[l|\xi ]}$
, we get
and
Hence, by (2),
This completes the proof of clause 1 above and also the proof of
![]() $\mathsf {LSA-over-uB}$
in
$\mathsf {LSA-over-uB}$
in
![]() ${\mathcal {P}}[g]$
.
${\mathcal {P}}[g]$
.
3.3. An upper bound for
 $\mathsf {Tower\ Sealing}$
$\mathsf {Tower\ Sealing}$
Let
![]() $({\mathcal {P}}_0,\Sigma ^-), {\mathcal {P}}, \Sigma , g$
be as before (see right after Theorem 3.1). We prove clause (2) of
$({\mathcal {P}}_0,\Sigma ^-), {\mathcal {P}}, \Sigma , g$
be as before (see right after Theorem 3.1). We prove clause (2) of
![]() $\mathsf {Tower\ Sealing}$
holds in
$\mathsf {Tower\ Sealing}$
holds in
![]() ${\mathcal {P}}[g]$
. Clause (1) has already been established by the previous sections. Let
${\mathcal {P}}[g]$
. Clause (1) has already been established by the previous sections. Let
![]() $\mathbb {P}\in {\mathcal {P}}[g]$
be any poset,
$\mathbb {P}\in {\mathcal {P}}[g]$
be any poset,
![]() $h\subseteq \mathbb {P}$
be a
$h\subseteq \mathbb {P}$
be a
![]() ${\mathcal {P}}[g]$
-generic and let
${\mathcal {P}}[g]$
-generic and let
![]() $\delta $
be Woodin in
$\delta $
be Woodin in
![]() ${\mathcal {P}}[g*h] =_{def} W$
. Let
${\mathcal {P}}[g*h] =_{def} W$
. Let
![]() $G\subseteq \mathbb {Q}_{<\delta }$
be W-generic (the argument for
$G\subseteq \mathbb {Q}_{<\delta }$
be W-generic (the argument for
![]() $\mathbb {P}_{<\delta }$
is the same) and
$\mathbb {P}_{<\delta }$
is the same) and
![]() $j: W\rightarrow M \subset W[G]$
be the generic elementary embedding induced by G.Footnote 64
$j: W\rightarrow M \subset W[G]$
be the generic elementary embedding induced by G.Footnote 64
Let
![]() $\Lambda $
be the canonical interpretation of
$\Lambda $
be the canonical interpretation of
![]() $\Sigma ^-$
in W and
$\Sigma ^-$
in W and
![]() $\Lambda ^G$
be the canonical interpretation of
$\Lambda ^G$
be the canonical interpretation of
![]() $\Lambda $
in
$\Lambda $
in
![]() $W[G]$
(considered as the short-tree strategy of
$W[G]$
(considered as the short-tree strategy of
![]() ${\mathcal {P}}_0$
acting on countable trees). Now, by the fact that M is closed under countable sequences in
${\mathcal {P}}_0$
acting on countable trees). Now, by the fact that M is closed under countable sequences in
![]() $W[G]$
and the way
$W[G]$
and the way
![]() $\Lambda ^G$
is defined (using generic interpretability),
$\Lambda ^G$
is defined (using generic interpretability),
Here is the outline of the argument. Let
![]() ${\mathcal {T}}$
be countable and according to both
${\mathcal {T}}$
be countable and according to both
![]() $j(\Lambda )$
and
$j(\Lambda )$
and
![]() $\Lambda ^G$
. Note that
$\Lambda ^G$
. Note that
![]() ${\mathcal {T}}\in M$
. Suppose
${\mathcal {T}}\in M$
. Suppose
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\mathsf {nuvs}$
(the case
$\mathsf {nuvs}$
(the case
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\mathsf {uvs}$
is similar). One gets that in
$\mathsf {uvs}$
is similar). One gets that in
![]() $W[G]$
,
$W[G]$
,
![]() ${\mathcal {Q}}(\Lambda ^G({\mathcal {T}}),{\mathcal {T}})$
exists and is authenticated by
${\mathcal {Q}}(\Lambda ^G({\mathcal {T}}),{\mathcal {T}})$
exists and is authenticated by
![]() $\vec {C}$
, a fully backgrounded authenticated construction in W where extenders have critical point
$\vec {C}$
, a fully backgrounded authenticated construction in W where extenders have critical point
![]() $> \delta $
; note that we can take
$> \delta $
; note that we can take
![]() $\vec {C}\in W$
. This implies that
$\vec {C}\in W$
. This implies that
![]() ${\mathcal {Q}}(\Lambda ^G({\mathcal {T}}),{\mathcal {T}})$
is authenticated by
${\mathcal {Q}}(\Lambda ^G({\mathcal {T}}),{\mathcal {T}})$
is authenticated by
![]() $j(\vec {C})\in M$
;
$j(\vec {C})\in M$
;
![]() ${\mathcal {Q}}(j(\Lambda )({\mathcal {T}}),{\mathcal {T}})$
is also authenticated by
${\mathcal {Q}}(j(\Lambda )({\mathcal {T}}),{\mathcal {T}})$
is also authenticated by
![]() $j(\vec {C})$
in M. The details are very similar to the proof of Proposition 2.17. So
$j(\vec {C})$
in M. The details are very similar to the proof of Proposition 2.17. So
![]() $j(\Lambda )({\mathcal {T}}) = \Lambda ^G({\mathcal {T}})$
. Hence,
$j(\Lambda )({\mathcal {T}}) = \Lambda ^G({\mathcal {T}})$
. Hence,
![]() $\Lambda ^G\in M$
.
$\Lambda ^G\in M$
.
By Lemma 3.2,
By elementarity, the fact that
![]() $(\Gamma ^{\infty })^W = \Gamma ^b({\mathcal {P}}_0,\Lambda )$
, 3, and Lemma 3.2,
$(\Gamma ^{\infty })^W = \Gamma ^b({\mathcal {P}}_0,\Lambda )$
, 3, and Lemma 3.2,
So indeed,
![]() $(\Gamma ^{\infty })^{W[G]}= j((\Gamma ^{\infty })^W)$
as desired.
$(\Gamma ^{\infty })^{W[G]}= j((\Gamma ^{\infty })^W)$
as desired.
Remark 3.6. Another proof of clause (2) of
![]() $\mathsf {Tower\ Sealing}$
is the following. We give a sketch: by results of [Reference Sargsyan and Trang38],
$\mathsf {Tower\ Sealing}$
is the following. We give a sketch: by results of [Reference Sargsyan and Trang38],
![]() $\Lambda ^G\in L(\pi ^b_{{\mathcal {P}}_0,\infty }[{\mathcal {P}}_0], \mathcal {H},(\Gamma ^{\infty })^{W[G]})$
. Here, working in
$\Lambda ^G\in L(\pi ^b_{{\mathcal {P}}_0,\infty }[{\mathcal {P}}_0], \mathcal {H},(\Gamma ^{\infty })^{W[G]})$
. Here, working in
![]() $W[G]$
, let
$W[G]$
, let
![]() $\mathcal {H}^-$
be the direct limit of hod pairs
$\mathcal {H}^-$
be the direct limit of hod pairs
![]() $({\mathcal {R}},\Delta )\in L(\Gamma ^{\infty })$
such that in
$({\mathcal {R}},\Delta )\in L(\Gamma ^{\infty })$
such that in
![]() $ L(\Gamma ^{\infty })$
,
$ L(\Gamma ^{\infty })$
,
![]() $\Delta $
is fullness preserving and has hull and branch condensation.
$\Delta $
is fullness preserving and has hull and branch condensation.
![]() $|\mathcal {H}^-| = V^{HOD}_{\Theta }$
in
$|\mathcal {H}^-| = V^{HOD}_{\Theta }$
in
![]() $L(\Gamma ^{\infty })$
. Let
$L(\Gamma ^{\infty })$
. Let
![]() $\mathcal {H} = \bigcup \{{\mathcal {M}} : \mathcal {H}^- \lhd {\mathcal {M}}, {\mathcal {M}} \textrm { be a sound, hybrid } \textrm {countably iterable premouse such that } \rho _{\omega }({\mathcal {M}})\leq o(\mathcal {H}^-)\}$
. For each
$\mathcal {H} = \bigcup \{{\mathcal {M}} : \mathcal {H}^- \lhd {\mathcal {M}}, {\mathcal {M}} \textrm { be a sound, hybrid } \textrm {countably iterable premouse such that } \rho _{\omega }({\mathcal {M}})\leq o(\mathcal {H}^-)\}$
. For each
![]() ${\mathcal {M}}\lhd \mathcal {H}$
as above, for every
${\mathcal {M}}\lhd \mathcal {H}$
as above, for every
![]() ${\mathcal {N}}$
countably transitive such that
${\mathcal {N}}$
countably transitive such that
![]() ${\mathcal {N}}$
is embeddable into
${\mathcal {N}}$
is embeddable into
![]() ${\mathcal {M}}$
,
${\mathcal {M}}$
,
![]() ${\mathcal {N}}$
has an
${\mathcal {N}}$
has an
![]() $\omega _1$
-strategy in
$\omega _1$
-strategy in
![]() $L(\Gamma ^{\infty })$
.
$L(\Gamma ^{\infty })$
.
If
![]() $(\Gamma ^{\infty })^{W[G]}\neq j((\Gamma ^{\infty })^W)$
, then suppose the former is a strict Wadge initial segment of the latter (the other case is handled similarly). So the model
$(\Gamma ^{\infty })^{W[G]}\neq j((\Gamma ^{\infty })^W)$
, then suppose the former is a strict Wadge initial segment of the latter (the other case is handled similarly). So the model
as M is closed under
![]() $\omega $
-sequences in
$\omega $
-sequences in
![]() $W[G]$
. In fact, we get that
$W[G]$
. In fact, we get that
![]() $\Lambda ^G \in j((\Gamma ^{\infty })^W)$
. By Generation of Mouse Full Pointclasses (applied in
$\Lambda ^G \in j((\Gamma ^{\infty })^W)$
. By Generation of Mouse Full Pointclasses (applied in
![]() $L(j((\Gamma ^{\infty })^W))$
and a comparison argument as in Lemma 2.21, there is a (maximal)
$L(j((\Gamma ^{\infty })^W))$
and a comparison argument as in Lemma 2.21, there is a (maximal)
![]() $\Lambda ^G$
-iterate
$\Lambda ^G$
-iterate
![]() ${\mathcal {S}}$
of
${\mathcal {S}}$
of
![]() ${\mathcal {P}}_0$
such that
${\mathcal {P}}_0$
such that
![]() ${\mathcal {S}}$
has an iteration strategy
${\mathcal {S}}$
has an iteration strategy
![]() $\Psi $
such that
$\Psi $
such that
-
○
 $\Psi ^{stc} = (\Lambda ^G)_{\mathcal {S}}$
,
$\Psi ^{stc} = (\Lambda ^G)_{\mathcal {S}}$
, -
○
 $\Gamma ^b({\mathcal {S}},\Psi ) = \Gamma ({\mathcal {P}}_0,\Lambda ^G)$
,
$\Gamma ^b({\mathcal {S}},\Psi ) = \Gamma ({\mathcal {P}}_0,\Lambda ^G)$
, -
○
 $\Psi \in j((\Gamma ^{\infty })^W)$
.
$\Psi \in j((\Gamma ^{\infty })^W)$
.
By elementarity, the existence of
![]() ${\mathcal {S}},\Psi $
holds in
${\mathcal {S}},\Psi $
holds in
![]() $L((\Gamma ^{\infty })^W)$
. This contradicts the fact that
$L((\Gamma ^{\infty })^W)$
. This contradicts the fact that
![]() $j(\Lambda )\notin (\Gamma ^{\infty })^W$
.
$j(\Lambda )\notin (\Gamma ^{\infty })^W$
.
4. Basic core model induction
The notation introduced in the section will be used throughout this paper. It will be wise to refer back to this section for clarifications. From this point on, the paper is devoted to proving that both
![]() $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
imply the existence of a (possibly class size) excellent hybrid premouse. As we have already shown that a forcing extension of an excellent hybrid premouse satisfies both
$\mathsf {LSA-over-uB}$
imply the existence of a (possibly class size) excellent hybrid premouse. As we have already shown that a forcing extension of an excellent hybrid premouse satisfies both
![]() $\mathsf {Sealing}$
and
$\mathsf {Sealing}$
and
![]() $\mathsf {LSA-over-uB}$
, this will complete the proof of Theorem 1.4.
$\mathsf {LSA-over-uB}$
, this will complete the proof of Theorem 1.4.
We will accomplish our goal by considering
![]() ${\mathrm {HOD}}$
of
${\mathrm {HOD}}$
of
![]() $L(\Gamma ^{\infty }, {\mathbb {R}})$
and showing that, in some sense, it reaches an excellent hybrid premouse. Our first step towards this goal is to show that
$L(\Gamma ^{\infty }, {\mathbb {R}})$
and showing that, in some sense, it reaches an excellent hybrid premouse. Our first step towards this goal is to show that
![]() $\Theta $
is a limit point of the Solovay sequence of
$\Theta $
is a limit point of the Solovay sequence of
![]() $L(\Gamma ^{\infty }, {\mathbb {R}})$
.
$L(\Gamma ^{\infty }, {\mathbb {R}})$
.
Proposition 4.1. Assume there are unboundedly many Woodin cardinals. Furthermore, assume either
![]() $\mathsf {Sealing}$
, or
$\mathsf {Sealing}$
, or
![]() $\mathsf {Tower\ Sealing}$
, or
$\mathsf {Tower\ Sealing}$
, or
![]() $\mathsf {LSA-over-uB}$
. Then for all set generic g, the following holds in
$\mathsf {LSA-over-uB}$
. Then for all set generic g, the following holds in
![]() $V[g]$
:
$V[g]$
:
-
1.
 ${\wp }({\mathbb {R}})\cap L(\Gamma ^{\infty }, {\mathbb {R}})=\Gamma ^{\infty }$
,
${\wp }({\mathbb {R}})\cap L(\Gamma ^{\infty }, {\mathbb {R}})=\Gamma ^{\infty }$
, -
2.
 $L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \mathsf {AD}_{\mathbb {R}}$
.
$L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \mathsf {AD}_{\mathbb {R}}$
.
Proof. Towards a contradiction, assume that
![]() $L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \neg \mathsf {AD}_{\mathbb {R}}$
. By a result of Steel ([Reference Steel47, Theorem 4.3]), every set in
$L(\Gamma ^{\infty }, {\mathbb {R}}){\vDash } \neg \mathsf {AD}_{\mathbb {R}}$
. By a result of Steel ([Reference Steel47, Theorem 4.3]), every set in
![]() $\Gamma ^{\infty }$
has a scale in
$\Gamma ^{\infty }$
has a scale in
![]() $\Gamma ^{\infty }$
. Notice then that clause 1 implies clause 2. This is because given clause 1,
$\Gamma ^{\infty }$
. Notice then that clause 1 implies clause 2. This is because given clause 1,
![]() $L(\Gamma ^{\infty }, {\mathbb {R}})$
satisfies that every set has a scale, and therefore, it satisfies
$L(\Gamma ^{\infty }, {\mathbb {R}})$
satisfies that every set has a scale, and therefore, it satisfies
![]() $\mathsf {AD}_{\mathbb {R}}$
.Footnote 65
$\mathsf {AD}_{\mathbb {R}}$
.Footnote 65
It is then enough to show that clause 1 holds. It trivially follows from
![]() $\mathsf {Sealing}$
or
$\mathsf {Sealing}$
or
![]() $\mathsf {Tower\ Sealing}$
. To see that it also follows from
$\mathsf {Tower\ Sealing}$
. To see that it also follows from
![]() $\mathsf {LSA-over-uB}$
, fix a set
$\mathsf {LSA-over-uB}$
, fix a set
![]() $A\subseteq {\mathbb {R}}$
such that
$A\subseteq {\mathbb {R}}$
such that
![]() $\Gamma ^{\infty }$
is the set of Suslin, co-Suslin sets of
$\Gamma ^{\infty }$
is the set of Suslin, co-Suslin sets of
![]() $L(A, {\mathbb {R}})$
and
$L(A, {\mathbb {R}})$
and
![]() $L(A, {\mathbb {R}}){\vDash } \mathsf {LSA}$
. It now follows that if
$L(A, {\mathbb {R}}){\vDash } \mathsf {LSA}$
. It now follows that if
![]() ${\kappa }$
is the largest Suslin cardinal of
${\kappa }$
is the largest Suslin cardinal of
![]() $L(A, {\mathbb {R}})$
, then, in
$L(A, {\mathbb {R}})$
, then, in
![]() $L(A, {\mathbb {R}})$
,
$L(A, {\mathbb {R}})$
,
![]() $\Gamma ^{\infty }$
is the set of reals whose Wadge rank is
$\Gamma ^{\infty }$
is the set of reals whose Wadge rank is
![]() $<{\kappa }$
. Since
$<{\kappa }$
. Since
![]() $\kappa $
is on the Solovay sequence of
$\kappa $
is on the Solovay sequence of
![]() $L(A,\mathbb {R})$
,
$L(A,\mathbb {R})$
,
![]() $\Gamma ^{\infty } = L(\Gamma ^{\infty })\cap {\wp }(\mathbb {R})$
. Therefore, clause 1 follows.
$\Gamma ^{\infty } = L(\Gamma ^{\infty })\cap {\wp }(\mathbb {R})$
. Therefore, clause 1 follows.
For the rest of this paper, we write
![]() $\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
to mean that clause 1 and 2 above hold in all generic extensions.
$\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
to mean that clause 1 and 2 above hold in all generic extensions.
![]() $\Omega $
here is a reference to Woodin’s
$\Omega $
here is a reference to Woodin’s
![]() $\Omega $
-logic. We develop the notations below under
$\Omega $
-logic. We develop the notations below under
![]() $\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{\mathbb {R}}$
.
$\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{\mathbb {R}}$
.
Suppose
![]() $\mu $
is a cardinal. Let
$\mu $
is a cardinal. Let
![]() $g\subset Col(\omega ,<\mu )$
be V-generic. Working in V, we say that a pair
$g\subset Col(\omega ,<\mu )$
be V-generic. Working in V, we say that a pair
![]() $({\mathcal {M}},\Sigma )$
is a hod pair at
$({\mathcal {M}},\Sigma )$
is a hod pair at
![]() $\mu $
if
$\mu $
if
-
1.
 ${\mathcal {M}}\in V_{\mu }$
,
${\mathcal {M}}\in V_{\mu }$
, -
2.
 $\Sigma $
is a
$\Sigma $
is a
 $(\mu ,\mu )$
-iteration strategy of
$(\mu ,\mu )$
-iteration strategy of
 ${\mathcal {M}}$
that is in
${\mathcal {M}}$
that is in
 $\Gamma ^{\infty }$
in
$\Gamma ^{\infty }$
in
 $V^{Coll(\omega ,|{\mathcal {M}}|)}$
and is positional, commuting and has branch condensation, and
$V^{Coll(\omega ,|{\mathcal {M}}|)}$
and is positional, commuting and has branch condensation, and -
3.
 $\Sigma $
is fullness preserving with respect to mice with
$\Sigma $
is fullness preserving with respect to mice with
 $\Gamma ^{\infty }$
-iteration strategy.
$\Gamma ^{\infty }$
-iteration strategy.
Let
![]() $\mathcal {F}$
be the set of hod pairs at
$\mathcal {F}$
be the set of hod pairs at
![]() $\mu $
. It is shown in [Reference Sargsyan and Trang38] that hod mice at
$\mu $
. It is shown in [Reference Sargsyan and Trang38] that hod mice at
![]() $\mu $
can be compared (see [Reference Sargsyan and Trang38, Chapter 4.6 and 4.10].). More precisely, given any two hod pairs
$\mu $
can be compared (see [Reference Sargsyan and Trang38, Chapter 4.6 and 4.10].). More precisely, given any two hod pairs
![]() $({\mathcal {M}}, \Sigma )$
and
$({\mathcal {M}}, \Sigma )$
and
![]() $({\mathcal {N}}, \Lambda )$
in
$({\mathcal {N}}, \Lambda )$
in
![]() $\mathcal {F}$
, there is a hod pair
$\mathcal {F}$
, there is a hod pair
![]() $({\mathcal {S}}, \Psi )\in \mathcal {F}$
such that for some
$({\mathcal {S}}, \Psi )\in \mathcal {F}$
such that for some
![]() ${\mathcal {M}}^*\unlhd _{hod} {\mathcal {S}}$
and
${\mathcal {M}}^*\unlhd _{hod} {\mathcal {S}}$
and
![]() ${\mathcal {N}}^*\unlhd _{hod} {\mathcal {S}}$
,
${\mathcal {N}}^*\unlhd _{hod} {\mathcal {S}}$
,
-
1.
 ${\mathcal {M}}^*$
is a
${\mathcal {M}}^*$
is a
 $\Sigma $
-iterate of
$\Sigma $
-iterate of
 ${\mathcal {M}}$
such that the main branch of
${\mathcal {M}}$
such that the main branch of
 ${\mathcal {M}}$
-to-
${\mathcal {M}}$
-to-
 ${\mathcal {M}}^*$
iteration does not drop,
${\mathcal {M}}^*$
iteration does not drop, -
2.
 ${\mathcal {N}}^*$
is a
${\mathcal {N}}^*$
is a
 $\Lambda $
-iterate of
$\Lambda $
-iterate of
 ${\mathcal {N}}$
such that the main branch of
${\mathcal {N}}$
such that the main branch of
 ${\mathcal {N}}$
-to-
${\mathcal {N}}$
-to-
 ${\mathcal {N}}^*$
iteration does not drop,
${\mathcal {N}}^*$
iteration does not drop, -
3.
 $\Sigma _{{\mathcal {M}}^*}=\Psi _{{\mathcal {M}}^*}$
and
$\Sigma _{{\mathcal {M}}^*}=\Psi _{{\mathcal {M}}^*}$
and
 $\Lambda _{{\mathcal {N}}^*}=\Psi _{{\mathcal {N}}^*}$
and
$\Lambda _{{\mathcal {N}}^*}=\Psi _{{\mathcal {N}}^*}$
and -
4. either
 ${\mathcal {S}}={\mathcal {M}}^*$
or
${\mathcal {S}}={\mathcal {M}}^*$
or
 ${\mathcal {S}}={\mathcal {N}}^*$
.
${\mathcal {S}}={\mathcal {N}}^*$
.
Working in
![]() $V[g]$
, let
$V[g]$
, let
![]() $\mathcal {F}^+$
be the set of all hod pairs
$\mathcal {F}^+$
be the set of all hod pairs
![]() $({\mathcal {M}},\Sigma )$
such that
$({\mathcal {M}},\Sigma )$
such that
![]() ${\mathcal {M}}$
is countable and
${\mathcal {M}}$
is countable and
![]() $\Sigma $
is an
$\Sigma $
is an
![]() $(\omega _1,\omega _1+1)$
-strategy of
$(\omega _1,\omega _1+1)$
-strategy of
![]() ${\mathcal {M}}$
that is
${\mathcal {M}}$
that is
![]() $\Gamma ^{\infty }$
-fullness preserving, positional, commuting, has branch condensation,Footnote 66 and
$\Gamma ^{\infty }$
-fullness preserving, positional, commuting, has branch condensation,Footnote 66 and
![]() $\Sigma {\restriction } \mathrm {HC}\in \Gamma ^{\infty }$
.
$\Sigma {\restriction } \mathrm {HC}\in \Gamma ^{\infty }$
.
Because any two hod pairs in
![]() $\mathcal {F}^+$
can be compared,
$\mathcal {F}^+$
can be compared,
![]() $\mathcal {F}$
covers
$\mathcal {F}$
covers
![]() $\mathcal {F}^+$
. More precisely, for each hod pair
$\mathcal {F}^+$
. More precisely, for each hod pair
![]() $({\mathcal {M}}, \Sigma )\in \mathcal {F}^+$
, there is
$({\mathcal {M}}, \Sigma )\in \mathcal {F}^+$
, there is
![]() $\Sigma $
-iterate
$\Sigma $
-iterate
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
such that the
${\mathcal {M}}$
such that the
![]() ${\mathcal {M}}$
-to-
${\mathcal {M}}$
-to-
![]() ${\mathcal {N}}$
iteration does not drop on its main branch,
${\mathcal {N}}$
iteration does not drop on its main branch,
![]() $(\Sigma _{\mathcal {N}}{\restriction } V)\in V$
and
$(\Sigma _{\mathcal {N}}{\restriction } V)\in V$
and
![]() $\Sigma _{\mathcal {N}}$
is the unique extension of
$\Sigma _{\mathcal {N}}$
is the unique extension of
![]() $(\Sigma _{\mathcal {N}}{\restriction } V)$
to
$(\Sigma _{\mathcal {N}}{\restriction } V)$
to
![]() $V[g]$
.
$V[g]$
.
Given any hod pair
![]() $({\mathcal {M}}, \Sigma )$
, let
$({\mathcal {M}}, \Sigma )$
, let
![]() $I({\mathcal {M}}, \Sigma )$
be the set of iterates
$I({\mathcal {M}}, \Sigma )$
be the set of iterates
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
by
${\mathcal {M}}$
by
![]() $\Sigma $
such that the main branch of
$\Sigma $
such that the main branch of
![]() ${\mathcal {M}}$
-to-
${\mathcal {M}}$
-to-
![]() ${\mathcal {N}}$
does not drop. Let
${\mathcal {N}}$
does not drop. Let
![]() $X\subseteq I({\mathcal {M}}, \Sigma )$
be a directed set (i.e., if
$X\subseteq I({\mathcal {M}}, \Sigma )$
be a directed set (i.e., if
![]() ${\mathcal {N}}, {\mathcal {P}}\in X$
, then there is
${\mathcal {N}}, {\mathcal {P}}\in X$
, then there is
![]() ${\mathcal {R}}\in X$
such that
${\mathcal {R}}\in X$
such that
![]() ${\mathcal {R}}$
is a
${\mathcal {R}}$
is a
![]() $\Sigma _{\mathcal {N}}$
-iterate of
$\Sigma _{\mathcal {N}}$
-iterate of
![]() ${\mathcal {N}}$
and a
${\mathcal {N}}$
and a
![]() $\Sigma _{\mathcal {P}}$
-iterate of
$\Sigma _{\mathcal {P}}$
-iterate of
![]() ${\mathcal {R}}$
). We then let
${\mathcal {R}}$
). We then let
![]() ${\mathcal {M}}_{\infty }({\mathcal {M}}, \Sigma , X)$
be the direct limit of all iterates of
${\mathcal {M}}_{\infty }({\mathcal {M}}, \Sigma , X)$
be the direct limit of all iterates of
![]() ${\mathcal {M}}$
by
${\mathcal {M}}$
by
![]() $\Sigma $
that are in X. Usually, X will be clear from context and we will omit it.
$\Sigma $
that are in X. Usually, X will be clear from context and we will omit it.
Working in
![]() $V[g]$
, let
$V[g]$
, let
![]() $\mathbb {R}_g = \mathbb {R}^{V[g]}$
. Let
$\mathbb {R}_g = \mathbb {R}^{V[g]}$
. Let
![]() $\mathcal {H}^{-}$
be the direct limit of hod pairs in
$\mathcal {H}^{-}$
be the direct limit of hod pairs in
![]() $\mathcal {F}^+$
. Because
$\mathcal {F}^+$
. Because
![]() $\mathcal {F}$
covers
$\mathcal {F}$
covers
![]() $\mathcal {F}^+$
, we also have that
$\mathcal {F}^+$
, we also have that
![]() $\mathcal {H}^-$
is the direct limit of hod pairs in
$\mathcal {H}^-$
is the direct limit of hod pairs in
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Fix
![]() $({\mathcal {M}}, \Sigma )\in \mathcal {F}^+$
such that
$({\mathcal {M}}, \Sigma )\in \mathcal {F}^+$
such that
![]() ${\mathcal {M}}_{\infty }({\mathcal {M}}, \Sigma )=_{def}{\mathcal {Q}}\unlhd _{hod} \mathcal {H}^-$
. We let
${\mathcal {M}}_{\infty }({\mathcal {M}}, \Sigma )=_{def}{\mathcal {Q}}\unlhd _{hod} \mathcal {H}^-$
. We let
![]() $\Psi _{\mathcal {Q}}=\Sigma ^+_{{\mathcal {Q}}}$
.
$\Psi _{\mathcal {Q}}=\Sigma ^+_{{\mathcal {Q}}}$
.
![]() $\Psi _{\mathcal {Q}}$
only depends on
$\Psi _{\mathcal {Q}}$
only depends on
![]() ${\mathcal {Q}}$
and does not depend on any particular choice of
${\mathcal {Q}}$
and does not depend on any particular choice of
![]() $({\mathcal {M}},\Sigma )\in \mathcal {F}^+$
. Let
$({\mathcal {M}},\Sigma )\in \mathcal {F}^+$
. Let
![]() $({\mathcal { H}}^-(\alpha ): \alpha < \lambda )$
be the layers of
$({\mathcal { H}}^-(\alpha ): \alpha < \lambda )$
be the layers of
![]() ${\mathcal { H}}^-$
(in the sense of [Reference Sargsyan and Trang38] and [Reference Sargsyan34]) and let
${\mathcal { H}}^-$
(in the sense of [Reference Sargsyan and Trang38] and [Reference Sargsyan34]) and let
![]() $\Psi _{\alpha }$
be the strategy of
$\Psi _{\alpha }$
be the strategy of
![]() ${\mathcal { H}}^-(\alpha )$
for each
${\mathcal { H}}^-(\alpha )$
for each
![]() $\alpha <\lambda $
.
$\alpha <\lambda $
.
![]() $\Psi _{\alpha }$
is the tail strategy
$\Psi _{\alpha }$
is the tail strategy
![]() $\Sigma _{\mathcal {Q}}$
for
$\Sigma _{\mathcal {Q}}$
for
![]() ${\mathcal {Q}} = {\mathcal {M}}_{\infty }({\mathcal {M}},\Sigma )$
for any
${\mathcal {Q}} = {\mathcal {M}}_{\infty }({\mathcal {M}},\Sigma )$
for any
![]() $({\mathcal {M}},\Sigma )\in {\mathcal {F}}^+$
such that
$({\mathcal {M}},\Sigma )\in {\mathcal {F}}^+$
such that
![]() ${\mathcal {M}}_{\infty }({\mathcal {M}},\Sigma )={\mathcal { H}}^-(\alpha )$
. We now set
${\mathcal {M}}_{\infty }({\mathcal {M}},\Sigma )={\mathcal { H}}^-(\alpha )$
. We now set
Definition 4.2. Suppose x is a set in
![]() $V({\mathbb {R}}_g)$
and
$V({\mathbb {R}}_g)$
and
![]() $\Phi $
is an iteration strategy with hull condensation. Working in
$\Phi $
is an iteration strategy with hull condensation. Working in
![]() $V({\mathbb {R}}^*)$
, let
$V({\mathbb {R}}^*)$
, let
![]() $Lp^{cuB, \Phi }(x)$
be the union of all sound
$Lp^{cuB, \Phi }(x)$
be the union of all sound
![]() $\Phi $
-mice
$\Phi $
-mice
![]() ${\mathcal {M}}$
over x that project to x and whenever
${\mathcal {M}}$
over x that project to x and whenever
![]() $\pi : {\mathcal {N}} \rightarrow {\mathcal {M}}$
is elementary,
$\pi : {\mathcal {N}} \rightarrow {\mathcal {M}}$
is elementary,
![]() ${\mathcal {N}}$
is countable and transitive. Then
${\mathcal {N}}$
is countable and transitive. Then
![]() ${\mathcal {N}}$
has a universally Baire iteration strategy.
${\mathcal {N}}$
has a universally Baire iteration strategy.
Continuing, we set
-
1.
 $\mathcal {H} = Lp^{cuB, \Psi }(\mathcal {H}^-)$
(note that
$\mathcal {H} = Lp^{cuB, \Psi }(\mathcal {H}^-)$
(note that
 $\mathcal {H}\in V$
),
$\mathcal {H}\in V$
), -
2.
 $\Theta = o(\mathcal {H}^-)$
,
$\Theta = o(\mathcal {H}^-)$
, -
3.
 $(\theta _{\alpha } : \alpha < \lambda )$
as the
$(\theta _{\alpha } : \alpha < \lambda )$
as the
 $\mathsf {Solovay\ Sequence}$
of
$\mathsf {Solovay\ Sequence}$
of
 $\Gamma ^{\infty }$
. Note that
$\Gamma ^{\infty }$
. Note that
 $\Theta = sup_{\alpha } \theta _{\alpha }$
and
$\Theta = sup_{\alpha } \theta _{\alpha }$
and
 $\theta _{\alpha } = \delta ^{{\mathcal { H}}^-(\alpha )}$
for each
$\theta _{\alpha } = \delta ^{{\mathcal { H}}^-(\alpha )}$
for each
 $\alpha <\lambda $
.
$\alpha <\lambda $
.
We note that all objects defined in this section up to this point depend on
![]() $\mu $
. To stress this, we will use
$\mu $
. To stress this, we will use
![]() $\mu $
as subscript. Thus, we will write, if needed,
$\mu $
as subscript. Thus, we will write, if needed,
![]() $\Psi _{\mu }$
or
$\Psi _{\mu }$
or
![]() ${\mathcal { H}}_{\mu }$
for
${\mathcal { H}}_{\mu }$
for
![]() $\Psi $
and
$\Psi $
and
![]() ${\mathcal { H}}$
, respectively. We will refer to the objects introduced above (e.g.,
${\mathcal { H}}$
, respectively. We will refer to the objects introduced above (e.g.,
![]() ${\mathcal { H}}_{\mu }$
and
${\mathcal { H}}_{\mu }$
and
![]() $\Psi _{\mu }$
) as the CMI objects at
$\Psi _{\mu }$
) as the CMI objects at
![]() $\mu $
.
$\mu $
.
Given a hybrid strategy mouse
![]() ${\mathcal {Q}}$
and an iteration strategy
${\mathcal {Q}}$
and an iteration strategy
![]() $\Lambda $
for
$\Lambda $
for
![]() ${\mathcal {Q}}$
, we say
${\mathcal {Q}}$
, we say
![]() $\Lambda $
is potentially-universally Baire if whenever
$\Lambda $
is potentially-universally Baire if whenever
![]() $g\subseteq Coll(\omega , {\mathcal {Q}})$
is generic, there is a unique
$g\subseteq Coll(\omega , {\mathcal {Q}})$
is generic, there is a unique
![]() $\Phi \in V[g]$
such that
$\Phi \in V[g]$
such that
-
1.
 $\Phi {\restriction } V=\Lambda $
,
$\Phi {\restriction } V=\Lambda $
, -
2. in
 $V[g]$
,
$V[g]$
,
 $\Phi $
is a uB iteration strategy for
$\Phi $
is a uB iteration strategy for
 ${\mathcal {Q}}$
.
${\mathcal {Q}}$
.
Similarly, we can define potentially-
![]() $\eta $
-uB iteration strategies.
$\eta $
-uB iteration strategies.
Definition 4.3. Suppose
![]() $\mu $
is a cardinal and
$\mu $
is a cardinal and
![]() $({\mathcal {Q}}, \Lambda )$
is such that
$({\mathcal {Q}}, \Lambda )$
is such that
![]() ${\mathcal {Q}}\in H_{\mu ^+}$
,
${\mathcal {Q}}\in H_{\mu ^+}$
,
![]() ${\mathcal {Q}}$
is a hybrid strategy mouse and
${\mathcal {Q}}$
is a hybrid strategy mouse and
![]() $\Lambda $
is a potentially-uB strategy for
$\Lambda $
is a potentially-uB strategy for
![]() ${\mathcal {Q}}$
. Suppose
${\mathcal {Q}}$
. Suppose
![]() $X\in H_{\mu ^+}$
. We then let
$X\in H_{\mu ^+}$
. We then let
![]() $Lp^{puB, \Lambda }(X)$
be the union of all sound
$Lp^{puB, \Lambda }(X)$
be the union of all sound
![]() $\Lambda $
-mice over X that project to X and have a potentially-uB iteration strategy.
$\Lambda $
-mice over X that project to X and have a potentially-uB iteration strategy.
Clearly,
![]() $Lp^{puB, \Lambda }(X){\trianglelefteq } Lp^{cuB, \Lambda }(X)$
. In many core model induction applications, it is important to show that, in fact,
$Lp^{puB, \Lambda }(X){\trianglelefteq } Lp^{cuB, \Lambda }(X)$
. In many core model induction applications, it is important to show that, in fact,
![]() $Lp^{puB, \Lambda }(X)= Lp^{cuB, \Lambda }(X)$
. The reason this fact is important is that the first is the stack that we can prove is computed by the maximal model of determinacy containing X after we collapse X to be countable while if
$Lp^{puB, \Lambda }(X)= Lp^{cuB, \Lambda }(X)$
. The reason this fact is important is that the first is the stack that we can prove is computed by the maximal model of determinacy containing X after we collapse X to be countable while if
![]() ${\mathcal {Q}}, X$
are already countable, the
${\mathcal {Q}}, X$
are already countable, the
![]() $OD(\Lambda , {\mathcal {Q}}, X)$
information inside the maximal model is captured by
$OD(\Lambda , {\mathcal {Q}}, X)$
information inside the maximal model is captured by
![]() $Lp^{cuB, \Lambda }(X)$
. This is because for countable
$Lp^{cuB, \Lambda }(X)$
. This is because for countable
![]() ${\mathcal {Q}}, X$
,
${\mathcal {Q}}, X$
,
![]() $Lp^{cuB, \Lambda }(X)=Lp^{uB, \Lambda }(X)$
where the mice appearing in the latter stack have universally Baire strategies. The equality
$Lp^{cuB, \Lambda }(X)=Lp^{uB, \Lambda }(X)$
where the mice appearing in the latter stack have universally Baire strategies. The equality
![]() $Lp^{puB, \Lambda }(X)= Lp^{cuB, \Lambda }(X)$
is important for covering type arguments that appear in the proof of Proposition 5.9.
$Lp^{puB, \Lambda }(X)= Lp^{cuB, \Lambda }(X)$
is important for covering type arguments that appear in the proof of Proposition 5.9.
5.
 $Lp^{cuB}$
and
$Lp^{cuB}$
and
 $Lp^{puB}$
operators
$Lp^{puB}$
operators
The following is the main result of this section, and it is the primary way we will translate strength from our hypothesis over to large cardinals. If
![]() $\mu $
is such that
$\mu $
is such that
![]() $Hom^*_g=\Gamma ^{\infty }_g$
for any
$Hom^*_g=\Gamma ^{\infty }_g$
for any
![]() $g\subseteq Coll(\omega , <\mu )$
, then we say that
$g\subseteq Coll(\omega , <\mu )$
, then we say that
![]() $\mu $
stabilizes uB.
$\mu $
stabilizes uB.
Definition 5.1. For each inaccessible cardinal
![]() $\mu $
, let
$\mu $
, let
![]() $A_{\mu }\subseteq \mu $
be a set that codes
$A_{\mu }\subseteq \mu $
be a set that codes
![]() $V_{\mu }$
. We then say that
$V_{\mu }$
. We then say that
![]() $X\prec H_{\mu ^+}$
captures
$X\prec H_{\mu ^+}$
captures
![]() $Lp^{cuB, \Psi _{\mu }}(A_{\mu })$
if
$Lp^{cuB, \Psi _{\mu }}(A_{\mu })$
if
![]() $Lp^{cuB, \Psi _{\mu }}(A_{\mu })\in X$
and letting
$Lp^{cuB, \Psi _{\mu }}(A_{\mu })\in X$
and letting
![]() $\pi _X: M_X\rightarrow H_{\mu ^+}$
be the uncollapse map and letting
$\pi _X: M_X\rightarrow H_{\mu ^+}$
be the uncollapse map and letting
![]() $\Lambda $
be the
$\Lambda $
be the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Psi _{\mu }$
,
$\Psi _{\mu }$
,
Theorem 5.2. Suppose there is a proper class of Woodin cardinals and a stationary class of measurable cardinals.Footnote 67 Suppose further that
![]() $\Gamma ^{\infty }{\vDash }_{\Omega }\mathsf {AD}_{\mathbb {R}}$
. There is then a stationary class S of measurable cardinals that are limits of Woodin cardinals, a proper class
$\Gamma ^{\infty }{\vDash }_{\Omega }\mathsf {AD}_{\mathbb {R}}$
. There is then a stationary class S of measurable cardinals that are limits of Woodin cardinals, a proper class
![]() $S_0\subseteq S$
, and a regular cardinal
$S_0\subseteq S$
, and a regular cardinal
![]() $\nu \geq \omega _1$
such that the following holds:
$\nu \geq \omega _1$
such that the following holds:
-
1. for any
 $\mu \in S$
,
$\mu \in S$
,
 ${\vert {\mathcal { H}}_{\mu }\vert }<\mu ^+$
,
${\vert {\mathcal { H}}_{\mu }\vert }<\mu ^+$
,
 ${\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu })<\mu $
, and
${\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu })<\mu $
, and
 ${\mathrm cf}(Ord\cap Lp^{cuB,\Psi _{\mu }}(A_{\mu }))<\mu $
;
${\mathrm cf}(Ord\cap Lp^{cuB,\Psi _{\mu }}(A_{\mu }))<\mu $
; -
2. for any
 $\mu \in S_0$
,
$\mu \in S_0$
,
 $\mu $
stabilizes uB,
$\mu $
stabilizes uB,
 ${\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu })<\nu $
, and
${\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu })<\nu $
, and
 ${\mathrm cf}(Ord\cap Lp^{cuB,\Psi _{\mu }}(A_{\mu }))<\nu $
;
${\mathrm cf}(Ord\cap Lp^{cuB,\Psi _{\mu }}(A_{\mu }))<\nu $
; -
3. for any
 $\mu \in S_0$
, there is
$\mu \in S_0$
, there is
 $Y_{\mu }\in {\wp }_{\nu }(H_{\mu ^+})$
such that
$Y_{\mu }\in {\wp }_{\nu }(H_{\mu ^+})$
such that
 $A_{\mu }\in Y_{\mu }$
and whenever
$A_{\mu }\in Y_{\mu }$
and whenever
 $X\prec H_{\mu ^+}$
is of size
$X\prec H_{\mu ^+}$
is of size
 $<\mu $
, is
$<\mu $
, is
 $\nu $
-closed and
$\nu $
-closed and
 $Y_{\mu }\subseteq X$
, X captures
$Y_{\mu }\subseteq X$
, X captures
 $Lp^{cuB, \Psi _{\mu }}(A_{\mu })$
.
$Lp^{cuB, \Psi _{\mu }}(A_{\mu })$
.
We emphasize that the arguments in this section (and in this paper) are carried out entirely in
![]() $\mathsf {ZFC}$
, though it may appear that we are working with proper classes. See Remark 5.10 for a more detailed discussion and summary. First, we prove a useful lemma, pointed out to us by Ralf Schindler. Below, by ‘class’, we of course mean ‘definable class’.
$\mathsf {ZFC}$
, though it may appear that we are working with proper classes. See Remark 5.10 for a more detailed discussion and summary. First, we prove a useful lemma, pointed out to us by Ralf Schindler. Below, by ‘class’, we of course mean ‘definable class’.
Lemma 5.3 (
 $\mathsf {ZFC}$
)
$\mathsf {ZFC}$
)
Suppose S is a stationary class of ordinals. Suppose
![]() $f: S \rightarrow Ord$
is regressive (i.e.,
$f: S \rightarrow Ord$
is regressive (i.e.,
![]() $f(\alpha )<\alpha $
for all
$f(\alpha )<\alpha $
for all
![]() $\alpha \in S$
). There is an ordinal
$\alpha \in S$
). There is an ordinal
![]() $\nu $
and a proper class
$\nu $
and a proper class
![]() $S_0\subseteq S$
such that
$S_0\subseteq S$
such that
![]() $f[S_0] = \{\nu \}$
.
$f[S_0] = \{\nu \}$
.
Proof. Suppose not. For each
![]() $\nu $
, let
$\nu $
, let
![]() $\alpha _{\nu } = sup\{\alpha : f(\alpha ) = \nu \}$
if
$\alpha _{\nu } = sup\{\alpha : f(\alpha ) = \nu \}$
if
![]() $\nu \in rng(f)$
and
$\nu \in rng(f)$
and
![]() $\nu +1$
otherwise.
$\nu +1$
otherwise.
![]() $\alpha _{\nu }$
exists because we are assuming that
$\alpha _{\nu }$
exists because we are assuming that
![]() $f^{-1}(\{\nu \})$
is a set. Let
$f^{-1}(\{\nu \})$
is a set. Let
![]() $g: Ord \rightarrow Ord$
be the function:
$g: Ord \rightarrow Ord$
be the function:
![]() $\nu \mapsto \alpha _{\nu }$
; hence,
$\nu \mapsto \alpha _{\nu }$
; hence,
![]() $g(\nu )>\nu $
for all
$g(\nu )>\nu $
for all
![]() $\nu $
. Let
$\nu $
. Let
![]() $C = \{\mu : g[\mu ] \subseteq \mu \}$
. So C is a club class. Let
$C = \{\mu : g[\mu ] \subseteq \mu \}$
. So C is a club class. Let
![]() $\alpha \in lim(C)\cap S$
. We may assume for unboundedly many
$\alpha \in lim(C)\cap S$
. We may assume for unboundedly many
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $\beta \in rng(f)$
. Then we easily get that
$\beta \in rng(f)$
. Then we easily get that
![]() $f(\alpha )$
is not
$f(\alpha )$
is not
![]() $< \alpha $
. Contradiction.
$< \alpha $
. Contradiction.
Clause 1 of Theorem 5.2 follows easily from the above lemma.
Proposition 5.4. Suppose there is a proper class of Woodin cardinals and S is a stationary class of inaccessible cardinals that are limit of Woodin cardinals. Then there is a proper class
![]() $S^*\subseteq S$
such that whenever
$S^*\subseteq S$
such that whenever
![]() $\mu \in S^*$
and
$\mu \in S^*$
and
![]() $g\subseteq Coll(\omega ,<\mu )$
is V-generic, in
$g\subseteq Coll(\omega ,<\mu )$
is V-generic, in
![]() $V[g]$
,
$V[g]$
,
![]() $Hom^*_g= \Gamma ^{\infty }_g$
.
$Hom^*_g= \Gamma ^{\infty }_g$
.
Proof. Clearly,
![]() $\Gamma ^{\infty }_g\subseteq Hom^*_g$
. Suppose then the claim is false. We then have a club C such that whenever
$\Gamma ^{\infty }_g\subseteq Hom^*_g$
. Suppose then the claim is false. We then have a club C such that whenever
![]() $\mu \in C\cap S$
and
$\mu \in C\cap S$
and
![]() $g\subseteq Coll(\omega , <\mu )$
,
$g\subseteq Coll(\omega , <\mu )$
,
![]() $\Gamma ^{\infty }_g \not =Hom^*_g$
. For each
$\Gamma ^{\infty }_g \not =Hom^*_g$
. For each
![]() $\mu \in C\cap S$
, let
$\mu \in C\cap S$
, let
![]() $\eta _{\mu }<\mu $
be least such that whenever
$\eta _{\mu }<\mu $
be least such that whenever
![]() $g\subseteq Coll(\omega , \eta _{\mu })$
, there are
$g\subseteq Coll(\omega , \eta _{\mu })$
, there are
![]() $\mu $
-complementing trees
$\mu $
-complementing trees
![]() $(T, U)\in V[g]$
with the property that
$(T, U)\in V[g]$
with the property that
![]() $p[T]$
is not uB in
$p[T]$
is not uB in
![]() $V[g][h]$
for any
$V[g][h]$
for any
![]() $V[g]$
-generic
$V[g]$
-generic
![]() $h\subseteq Coll(\omega , <\mu )$
. By Lemma 5.3, we then have a proper class
$h\subseteq Coll(\omega , <\mu )$
. By Lemma 5.3, we then have a proper class
![]() $S_0\subseteq S$
such that for every
$S_0\subseteq S$
such that for every
![]() $\mu _0<\mu _1\in S_0$
,
$\mu _0<\mu _1\in S_0$
,
![]() $\eta _{\mu _0}=\eta _{\mu _1}$
. Let
$\eta _{\mu _0}=\eta _{\mu _1}$
. Let
![]() $\eta $
be this common value of
$\eta $
be this common value of
![]() $\eta _{\mu }$
for
$\eta _{\mu }$
for
![]() $\mu \in S_0$
and
$\mu \in S_0$
and
![]() $g\subseteq Coll(\omega , \eta )$
be V-generic. For each
$g\subseteq Coll(\omega , \eta )$
be V-generic. For each
![]() $\mu \in S_0$
, we have a pair
$\mu \in S_0$
, we have a pair
![]() $(T_{\mu }, U_{\mu })\in V[g]$
that represents a
$(T_{\mu }, U_{\mu })\in V[g]$
that represents a
![]() $\mu $
-uB set that is not uB. A simple counting argument then shows that for a proper class
$\mu $
-uB set that is not uB. A simple counting argument then shows that for a proper class
![]() $S^{*}\subseteq S_0$
, whenever
$S^{*}\subseteq S_0$
, whenever
![]() $\mu _0, \mu _1\in S^{*}$
,
$\mu _0, \mu _1\in S^{*}$
,
![]() $V[g]{\vDash } p[T_{\mu _0}]=p[T_{\mu _1}]$
. Letting
$V[g]{\vDash } p[T_{\mu _0}]=p[T_{\mu _1}]$
. Letting
![]() $A=(p[T_{\mu }])^{V[g]}$
for some
$A=(p[T_{\mu }])^{V[g]}$
for some
![]() $\mu \in S^{*}$
, we get a contradiction as A is uB in
$\mu \in S^{*}$
, we get a contradiction as A is uB in
![]() $V[g]$
.
$V[g]$
.
What follows is a sequence of propositions that collectively imply the remaining clauses of Theorem 5.2. We start by establishing that the two stacks are almost the same.
Proposition 5.5. Suppose
![]() $\mu , ({\mathcal {Q}}, \Lambda ), X$
are as in Definition 4.3 and suppose
$\mu , ({\mathcal {Q}}, \Lambda ), X$
are as in Definition 4.3 and suppose
![]() $\mu $
is in addition a measurable cardinal stabilizing uB. Let
$\mu $
is in addition a measurable cardinal stabilizing uB. Let
![]() $j:V\rightarrow M$
be an embedding witnessing the measurability of
$j:V\rightarrow M$
be an embedding witnessing the measurability of
![]() $\mu $
. Then
$\mu $
. Then
![]() $Lp^{cuB, \Lambda }(X) =(Lp^{puB, \Lambda }(X))^M$
.
$Lp^{cuB, \Lambda }(X) =(Lp^{puB, \Lambda }(X))^M$
.
Proof. Let
![]() $j: V\rightarrow M$
be an embedding witnessing the measurability of
$j: V\rightarrow M$
be an embedding witnessing the measurability of
![]() $\mu $
. Let
$\mu $
. Let
![]() ${\mathcal {M}}{\trianglelefteq } Lp^{cuB, \Lambda }(X) $
be such that
${\mathcal {M}}{\trianglelefteq } Lp^{cuB, \Lambda }(X) $
be such that
![]() $\rho ({\mathcal {M}})=X$
. Let
$\rho ({\mathcal {M}})=X$
. Let
![]() $h\subseteq Coll(\omega , <j(\mu ))$
be generic. Consider
$h\subseteq Coll(\omega , <j(\mu ))$
be generic. Consider
![]() $j({\mathcal {M}})$
. In
$j({\mathcal {M}})$
. In
![]() $M[h]$
,
$M[h]$
,
![]() ${\mathcal {M}}$
, as it embeds into
${\mathcal {M}}$
, as it embeds into
![]() $j({\mathcal {M}})$
, has a uB strategy. It follows that
$j({\mathcal {M}})$
, has a uB strategy. It follows that
![]() ${\mathcal {M}}$
has a potentially-uB strategy in M, and hence,
${\mathcal {M}}$
has a potentially-uB strategy in M, and hence,
![]() ${\mathcal {M}}{\trianglelefteq } (Lp^{puB, \Lambda }(X))^M$
. Conversely, if
${\mathcal {M}}{\trianglelefteq } (Lp^{puB, \Lambda }(X))^M$
. Conversely, if
![]() ${\mathcal {M}}{\trianglelefteq } (Lp^{puB, \Lambda }(X))^M$
is such that
${\mathcal {M}}{\trianglelefteq } (Lp^{puB, \Lambda }(X))^M$
is such that
![]() $\rho ({\mathcal {M}})=X$
, then in M,
$\rho ({\mathcal {M}})=X$
, then in M,
![]() ${\mathcal {M}}$
has a potentially-uB strategy, and hence, in V, any countable
${\mathcal {M}}$
has a potentially-uB strategy, and hence, in V, any countable
![]() $\pi :{\mathcal {M}}^*\rightarrow {\mathcal {M}}$
has a
$\pi :{\mathcal {M}}^*\rightarrow {\mathcal {M}}$
has a
![]() $\mu $
-uB-strategy. As
$\mu $
-uB-strategy. As
![]() $\mu $
-stabilizes uB, we have
$\mu $
-stabilizes uB, we have
![]() ${\mathcal {M}}{\trianglelefteq } Lp^{cuB, \Lambda }(X)$
.
${\mathcal {M}}{\trianglelefteq } Lp^{cuB, \Lambda }(X)$
.
The next two propositions are rather important. Similar propositions hide behind any successful core model induction argument.
Proposition 5.6. Suppose there are unboundedly many Woodin cardinals,
![]() $\mu $
is an inaccessible cardinal and
$\mu $
is an inaccessible cardinal and
![]() $\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. Suppose further that
$\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. Suppose further that
![]() $\Lambda $
is a potentially-uB iteration strategy for some
$\Lambda $
is a potentially-uB iteration strategy for some
![]() ${\mathcal {Q}}\in H_{\mu ^+}$
and
${\mathcal {Q}}\in H_{\mu ^+}$
and
![]() $X\in H_{\mu ^+}$
. Let
$X\in H_{\mu ^+}$
. Let
![]() ${\mathcal {M}}=Lp^{puB, \Lambda }(X)$
. Then
${\mathcal {M}}=Lp^{puB, \Lambda }(X)$
. Then
![]() ${\vert {\mathcal {M}}\vert }<\mu ^+$
.
${\vert {\mathcal {M}}\vert }<\mu ^+$
.
Proof. Suppose
![]() $Ord\cap {\mathcal {M}}=\mu ^+$
. Let
$Ord\cap {\mathcal {M}}=\mu ^+$
. Let
![]() $g\subseteq Coll(\omega , \mu )$
be generic. Then
$g\subseteq Coll(\omega , \mu )$
be generic. Then
Moreover,
![]() $(Lp^{puB, \Lambda }(X))^{V[g]}\in L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
. Hence,
$(Lp^{puB, \Lambda }(X))^{V[g]}\in L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
. Hence,
![]() $L(\Gamma ^{\infty }_g, {\mathbb {R}}_g){\vDash }$
‘there is an
$L(\Gamma ^{\infty }_g, {\mathbb {R}}_g){\vDash }$
‘there is an
![]() $\omega _1$
-sequence of reals’. This contradicts the fact that
$\omega _1$
-sequence of reals’. This contradicts the fact that
![]() $L(\Gamma ^{\infty }_g, {\mathbb {R}}_g){\vDash } \mathsf {AD}^{+}$
.
$L(\Gamma ^{\infty }_g, {\mathbb {R}}_g){\vDash } \mathsf {AD}^{+}$
.
Corollary 5.7. Suppose there are unboundedly many Woodin cardinals,
![]() $\mu $
is a measurable limit of Woodin cardinals that stabilizes uB and
$\mu $
is a measurable limit of Woodin cardinals that stabilizes uB and
![]() $\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. Suppose further that
$\Gamma ^{\infty }{\vDash }_{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. Suppose further that
![]() $\Lambda $
is a potentially-uB iteration strategy for some
$\Lambda $
is a potentially-uB iteration strategy for some
![]() ${\mathcal {Q}}\in H_{\mu ^+}$
and
${\mathcal {Q}}\in H_{\mu ^+}$
and
![]() $X\in H_{\mu ^+}$
. Let
$X\in H_{\mu ^+}$
. Let
![]() ${\mathcal {M}}=Lp^{cuB, \Lambda }(X)$
. Then
${\mathcal {M}}=Lp^{cuB, \Lambda }(X)$
. Then
![]() ${\vert {\mathcal {M}}\vert }<\mu ^+$
and
${\vert {\mathcal {M}}\vert }<\mu ^+$
and
![]() ${\mathrm cf}(Ord\cap {\mathcal {M}})<\mu $
.
${\mathrm cf}(Ord\cap {\mathcal {M}})<\mu $
.
Proof. Fix
![]() $j:V\rightarrow M$
witnessing the measurability of
$j:V\rightarrow M$
witnessing the measurability of
![]() $\mu $
. It follows from Proposition 5.5 that
$\mu $
. It follows from Proposition 5.5 that
![]() ${\mathcal {M}}=(Lp^{puB, \Lambda }(X))^M$
. Applying Proposition 5.6 in M, we get that
${\mathcal {M}}=(Lp^{puB, \Lambda }(X))^M$
. Applying Proposition 5.6 in M, we get that
![]() ${\vert {\mathcal {M}}\vert }<\mu ^+$
.
${\vert {\mathcal {M}}\vert }<\mu ^+$
.
Assume next that
![]() ${\mathrm cf}(Ord\cap {\mathcal {M}})=\mu $
. Let
${\mathrm cf}(Ord\cap {\mathcal {M}})=\mu $
. Let
![]() $\eta =Ord\cap {\mathcal {M}}$
and let
$\eta =Ord\cap {\mathcal {M}}$
and let
![]() $\vec {C}$
be the
$\vec {C}$
be the
![]() $\square (\eta )$
-sequence of
$\square (\eta )$
-sequence of
![]() ${\mathcal {M}}$
. Because
${\mathcal {M}}$
. Because
![]() $\mu $
is measurable, we have that
$\mu $
is measurable, we have that
![]() $\vec {C}$
is threadable. To see there is a thread D, note that
$\vec {C}$
is threadable. To see there is a thread D, note that
![]() $sup \ j[\eta ] =_{def} \gamma < j(\eta )$
. Let
$sup \ j[\eta ] =_{def} \gamma < j(\eta )$
. Let
![]() $E = j(\vec {C})_{\gamma }$
and
$E = j(\vec {C})_{\gamma }$
and
![]() $D = j^{-1}[E]$
. Then D is a thread through
$D = j^{-1}[E]$
. Then D is a thread through
![]() $\vec {C}$
.
$\vec {C}$
.
This implies that there is a
![]() $\Lambda $
-mouse
$\Lambda $
-mouse
![]() ${\mathcal {N}}$
extending
${\mathcal {N}}$
extending
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() $\rho ({\mathcal {N}})=\eta $
and every
$\rho ({\mathcal {N}})=\eta $
and every
![]() $<\mu $
-submodel of
$<\mu $
-submodel of
![]() ${\mathcal {N}}$
embeds into some
${\mathcal {N}}$
embeds into some
![]() ${\mathcal {N}}^*{\trianglelefteq } {\mathcal {M}}$
.Footnote 68 It follows that
${\mathcal {N}}^*{\trianglelefteq } {\mathcal {M}}$
.Footnote 68 It follows that
![]() ${\mathcal {N}}{\trianglelefteq } Lp^{cuB, \Lambda }(X)$
.
${\mathcal {N}}{\trianglelefteq } Lp^{cuB, \Lambda }(X)$
.
Corollary 5.8. Assume there is a class of Woodin cardinals and let
![]() $\mu $
be a measurable limit of Woodin cardinals that stabilizes uB. Assume
$\mu $
be a measurable limit of Woodin cardinals that stabilizes uB. Assume
![]() $\Gamma ^{\infty }{\vDash } _{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. Let
$\Gamma ^{\infty }{\vDash } _{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. Let
![]() $\mathcal {H}^-, \mathcal {H}$
, etc. be defined relative to
$\mathcal {H}^-, \mathcal {H}$
, etc. be defined relative to
![]() $\mu $
as in Section 4. Set
$\mu $
as in Section 4. Set
Then
![]() $\xi < \mu $
.
$\xi < \mu $
.
Proof. We show that
![]() ${\mathrm cf}^V(Ord\cap \mathcal {H})<\mu $
. The second inequality is very similar. Let
${\mathrm cf}^V(Ord\cap \mathcal {H})<\mu $
. The second inequality is very similar. Let
![]() $g\subseteq Coll(\omega , <\mu )$
. Notice that
$g\subseteq Coll(\omega , <\mu )$
. Notice that
![]() ${\vert {\Gamma ^{\infty }_g}\vert }^{V[g]}=\aleph _1=\mu $
. It follows that
${\vert {\Gamma ^{\infty }_g}\vert }^{V[g]}=\aleph _1=\mu $
. It follows that
![]() $\vert {\Theta }\vert <\mu ^+$
(recall that
$\vert {\Theta }\vert <\mu ^+$
(recall that
![]() ${\wp }({\mathbb {R}}_g)\cap L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)=\Gamma ^{\infty }_g$
). The fact that
${\wp }({\mathbb {R}}_g)\cap L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)=\Gamma ^{\infty }_g$
). The fact that
![]() ${\vert {\mathcal {H}\vert }}^V<\mu ^+$
follows from Corollary 5.7. The fact that
${\vert {\mathcal {H}\vert }}^V<\mu ^+$
follows from Corollary 5.7. The fact that
![]() ${\mathrm cf}^V(Ord\cap \mathcal {H})<\mu $
follows from the fact that
${\mathrm cf}^V(Ord\cap \mathcal {H})<\mu $
follows from the fact that
![]() $\square (\mu )$
fails while letting
$\square (\mu )$
fails while letting
![]() $\zeta =Ord\cap \mathcal {H}$
;
$\zeta =Ord\cap \mathcal {H}$
;
![]() ${\mathcal { H}}$
has a
${\mathcal { H}}$
has a
![]() $\square (\zeta )$
-sequence. Let
$\square (\zeta )$
-sequence. Let
![]() $\vec {C}$
be the
$\vec {C}$
be the
![]() $\square (\zeta )$
-sequence constructed via the proof of
$\square (\zeta )$
-sequence constructed via the proof of
![]() $\square $
in
$\square $
in
![]() ${\mathcal { H}}$
.Footnote 69 If
${\mathcal { H}}$
.Footnote 69 If
![]() ${\mathrm cf}(\zeta )=\mu $
, then
${\mathrm cf}(\zeta )=\mu $
, then
![]() $\vec {C}$
has a thread D by measurability of
$\vec {C}$
has a thread D by measurability of
![]() $\mu $
; the existence of D follows by an argument similar to that of Corollary 5.7. Because of the way
$\mu $
; the existence of D follows by an argument similar to that of Corollary 5.7. Because of the way
![]() $\vec {C}$
is defined, D indexes a sequence of models
$\vec {C}$
is defined, D indexes a sequence of models
![]() $({\mathcal {M}}_{\alpha }: {\alpha }\in D)$
such that
$({\mathcal {M}}_{\alpha }: {\alpha }\in D)$
such that
-
1. for every
 ${\alpha }\in D$
,
${\alpha }\in D$
,
 ${\mathcal {M}}_{\alpha }{\trianglelefteq } {\mathcal { H}}$
and
${\mathcal {M}}_{\alpha }{\trianglelefteq } {\mathcal { H}}$
and
 $\rho ({\mathcal {M}}_{\alpha })=\Theta $
, and
$\rho ({\mathcal {M}}_{\alpha })=\Theta $
, and -
2. for
 ${\alpha }<{\beta }, {\alpha }, {\beta }\in D$
, there is an embedding
${\alpha }<{\beta }, {\alpha }, {\beta }\in D$
, there is an embedding
 $\pi _{{\alpha }, {\beta }}:{\mathcal {M}}_{\alpha }\rightarrow {\mathcal {M}}_{\beta }$
.
$\pi _{{\alpha }, {\beta }}:{\mathcal {M}}_{\alpha }\rightarrow {\mathcal {M}}_{\beta }$
.
Let
![]() ${\mathcal {M}}$
be the direct limit along
${\mathcal {M}}$
be the direct limit along
![]() $({\mathcal {M}}_{\alpha }, \pi _{{\alpha }, {\beta }}: {\alpha }\in D)$
. Then every countable submodel of
$({\mathcal {M}}_{\alpha }, \pi _{{\alpha }, {\beta }}: {\alpha }\in D)$
. Then every countable submodel of
![]() ${\mathcal {M}}$
embeds into some
${\mathcal {M}}$
embeds into some
![]() ${\mathcal {M}}_{\alpha }$
, implying that
${\mathcal {M}}_{\alpha }$
, implying that
![]() ${\mathcal {M}}{\trianglelefteq } {\mathcal { H}}$
. However, as D is a thread,
${\mathcal {M}}{\trianglelefteq } {\mathcal { H}}$
. However, as D is a thread,
![]() ${\mathcal { H}}{\trianglelefteq } {\mathcal {M}}$
, contradiction.
${\mathcal { H}}{\trianglelefteq } {\mathcal {M}}$
, contradiction.
The next proposition shows that sufficiently closed Skolem hulls of
![]() $Lp^{cuB}$
-operator condense. The proof of it is very much like the proof of [Reference Sargsyan33, Theorem 10.3] and the proof of [Reference Sargsyan and Trang38, Theorem 9.2.6]. The proof of [Reference Sargsyan and Trang38, Theorem 9.2.6] is done for
$Lp^{cuB}$
-operator condense. The proof of it is very much like the proof of [Reference Sargsyan33, Theorem 10.3] and the proof of [Reference Sargsyan and Trang38, Theorem 9.2.6]. The proof of [Reference Sargsyan and Trang38, Theorem 9.2.6] is done for
![]() ${\mathcal { H}}$
, not
${\mathcal { H}}$
, not
![]() $A_{\mu }$
. The proof of Proposition 5.9 can be obtained from the proof of [Reference Sargsyan and Trang38, Theorem 9.2.6] by simply changing
$A_{\mu }$
. The proof of Proposition 5.9 can be obtained from the proof of [Reference Sargsyan and Trang38, Theorem 9.2.6] by simply changing
![]() ${\mathcal {P}}$
to
${\mathcal {P}}$
to
![]() $A_{\mu }$
everywhere.
$A_{\mu }$
everywhere.
Proposition 5.9. Suppose there is a proper class of Woodin cardinals,
![]() $\mu $
is a measurable limit of Woodin cardinals stabilizing uB and
$\mu $
is a measurable limit of Woodin cardinals stabilizing uB and
![]() $\Gamma ^{\infty }{\vDash } _{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. There is then
$\Gamma ^{\infty }{\vDash } _{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. There is then
![]() $\nu <\mu $
and
$\nu <\mu $
and
![]() $Y_0\in {\wp }_{\nu }( H_{\mu ^+})$
such that
$Y_0\in {\wp }_{\nu }( H_{\mu ^+})$
such that
![]() $A_{\mu }\in Y_0$
and for any
$A_{\mu }\in Y_0$
and for any
![]() $X\prec H_{\mu ^+}$
of size
$X\prec H_{\mu ^+}$
of size
![]() $<\mu $
that is closed under
$<\mu $
that is closed under
![]() $\nu $
-sequences and
$\nu $
-sequences and
![]() $Y_0\subseteq X$
, letting
$Y_0\subseteq X$
, letting
![]() $\pi _X: M_X\rightarrow H_{\mu ^+}$
be the uncollapse map and letting
$\pi _X: M_X\rightarrow H_{\mu ^+}$
be the uncollapse map and letting
![]() $\Lambda $
be the
$\Lambda $
be the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Psi $
,
$\Psi $
,
![]() $\pi _X^{-1}(Lp^{cuB, \Psi }(A_{\mu }))=Lp^{cuB, \Lambda }(\pi _X^{-1}(A_{\mu }))$
.
$\pi _X^{-1}(Lp^{cuB, \Psi }(A_{\mu }))=Lp^{cuB, \Lambda }(\pi _X^{-1}(A_{\mu }))$
.
Proof. Let
![]() $j: V\rightarrow M$
be an embedding witnessing that
$j: V\rightarrow M$
be an embedding witnessing that
![]() $\mu $
is a measurable cardinal. Thus,
$\mu $
is a measurable cardinal. Thus,
![]() $\mathrm {crit }(j)=\mu $
. It follows from Corollary 5.8 that
$\mathrm {crit }(j)=\mu $
. It follows from Corollary 5.8 that
![]() $j[Ord\cap Lp^{cuB, \Psi }(A_{\mu })]$
is cofinal in
$j[Ord\cap Lp^{cuB, \Psi }(A_{\mu })]$
is cofinal in
![]() $Ord\cap j(Lp^{cuB, \Psi }(A_{\mu }))$
.Footnote 70 Below, we use the following information:
$Ord\cap j(Lp^{cuB, \Psi }(A_{\mu }))$
.Footnote 70 Below, we use the following information:
-
○
 ${\mathcal {P}}=Lp^{cuB, \Psi }(A_{\mu })$
,
${\mathcal {P}}=Lp^{cuB, \Psi }(A_{\mu })$
,
 $N=j(H_{\mu ^+})$
,
$N=j(H_{\mu ^+})$
,
 $A=j(A_{\mu })$
,
$A=j(A_{\mu })$
, -
○
 $Y_0^*=j[{\mathcal {P}}]$
and
$Y_0^*=j[{\mathcal {P}}]$
and
 $Y_0=Hull^N(Y_0^*)$
, and
$Y_0=Hull^N(Y_0^*)$
, and -
○ if
 $Y\in {\wp }_{\omega _1}(N)\cap M$
, then we let
$Y\in {\wp }_{\omega _1}(N)\cap M$
, then we let
 $M_Y$
be the transitive collapse of Y,
$M_Y$
be the transitive collapse of Y,
 $\pi _Y:M_Y\rightarrow j(H_{\mu ^+})$
be the inverse of the transitive collapse,
$\pi _Y:M_Y\rightarrow j(H_{\mu ^+})$
be the inverse of the transitive collapse,
 ${\mathcal {P}}_Y=\pi ^{-1}_Y(j({\mathcal {P}}))$
and
${\mathcal {P}}_Y=\pi ^{-1}_Y(j({\mathcal {P}}))$
and
 $\Sigma _Y$
be the
$\Sigma _Y$
be the
 $\pi _Y$
-pullback of
$\pi _Y$
-pullback of
 $\Psi $
,
$\Psi $
, -
○ if
 $Y\subseteq Y'$
, then we let
$Y\subseteq Y'$
, then we let
 $\pi _{Y, Y'}: M_Y\rightarrow M_{Y'}$
be the canonical embedding,
$\pi _{Y, Y'}: M_Y\rightarrow M_{Y'}$
be the canonical embedding, -
○
 ${\mathcal { H}}$
and
${\mathcal { H}}$
and
 ${\mathcal { H}}^-$
are defined relative to
${\mathcal { H}}^-$
are defined relative to
 $\mu $
as in Section 4.
$\mu $
as in Section 4.
We want to show that
(a) if
![]() $Y\in {\wp }_{j(\mu )}(N)\cap M$
is such that
$Y\in {\wp }_{j(\mu )}(N)\cap M$
is such that
![]() $Y_0\subseteq Y$
, then
$Y_0\subseteq Y$
, then
![]() $\pi _Y^{-1}(j({\mathcal {P}}))=Lp^{cuB, \Sigma _Y}(\pi _Y^{-1}(A))$
.
$\pi _Y^{-1}(j({\mathcal {P}}))=Lp^{cuB, \Sigma _Y}(\pi _Y^{-1}(A))$
.
Towards a contradiction, assume that (a) is false. Fix one such Y that is a counterexample to (a) and let
![]() ${\mathcal {M}}{\trianglelefteq } Lp^{cuB, \Sigma _Y}(\pi _Y^{-1}(A))$
be a sound
${\mathcal {M}}{\trianglelefteq } Lp^{cuB, \Sigma _Y}(\pi _Y^{-1}(A))$
be a sound
![]() $\Sigma _Y$
-mouse over
$\Sigma _Y$
-mouse over
![]() $\pi _Y^{-1}(A)$
such that
$\pi _Y^{-1}(A)$
such that
![]() ${\mathcal {M}}\not {\trianglelefteq } \pi _Y^{-1}(j({\mathcal {P}}))$
and
${\mathcal {M}}\not {\trianglelefteq } \pi _Y^{-1}(j({\mathcal {P}}))$
and
![]() $\rho ({\mathcal {M}})=Ord\cap \pi _Y^{-1}(A)$
. We can then find some
$\rho ({\mathcal {M}})=Ord\cap \pi _Y^{-1}(A)$
. We can then find some
![]() $\Sigma _{Y_0}$
-hod pair
$\Sigma _{Y_0}$
-hod pair
![]() $({\mathcal {P}}^+, \Pi )\in M$
Footnote 71 and a hod pair
$({\mathcal {P}}^+, \Pi )\in M$
Footnote 71 and a hod pair
![]() $({\mathcal {S}}, \Phi )\in M$
such that
$({\mathcal {S}}, \Phi )\in M$
such that
-
1.
 ${\mathcal {P}}^+\in H_{j(\mu )}^M$
and
${\mathcal {P}}^+\in H_{j(\mu )}^M$
and
 ${\mathcal {P}}^+$
is a hod premouse over
${\mathcal {P}}^+$
is a hod premouse over
 $A_{\mu }$
extending
$A_{\mu }$
extending
 ${\mathcal {P}}$
,
${\mathcal {P}}$
, -
2.
 $\Pi $
has strong branch condensation,
$\Pi $
has strong branch condensation, -
3.
 ${\mathcal {P}}^+$
is meek and of limit type (see [Reference Sargsyan and Trang38, Definition 2.7.1]),
${\mathcal {P}}^+$
is meek and of limit type (see [Reference Sargsyan and Trang38, Definition 2.7.1]), -
4.
 ${\mathrm cf}^{{\mathcal {P}}^+}({\delta }^{{\mathcal {P}}^+})=\omega $
,
${\mathrm cf}^{{\mathcal {P}}^+}({\delta }^{{\mathcal {P}}^+})=\omega $
, -
5.
 $(Y\cap j({\mathcal { H}}^-))\subseteq {\mathrm rge}(\pi ^{\Phi }_{{\mathcal {S}}, \infty })$
and no proper complete layer of
$(Y\cap j({\mathcal { H}}^-))\subseteq {\mathrm rge}(\pi ^{\Phi }_{{\mathcal {S}}, \infty })$
and no proper complete layer of
 ${\mathcal {S}}$
has this property,Footnote 72
${\mathcal {S}}$
has this property,Footnote 72 -
6.
 $\Pi \in M$
is a
$\Pi \in M$
is a
 $(j(\mu ), j(\mu ))$
-strategy for
$(j(\mu ), j(\mu ))$
-strategy for
 ${\mathcal {P}}^+$
such that if
${\mathcal {P}}^+$
such that if
 $h\subseteq Coll(\omega , <j(\mu ))$
is M-generic, then
$h\subseteq Coll(\omega , <j(\mu ))$
is M-generic, then
 $\Pi $
can be uniquely extended to a strategy
$\Pi $
can be uniquely extended to a strategy
 $\Pi ^{h}\in (\Gamma ^{\infty })^{M[h]}$
, and moreover,
$\Pi ^{h}\in (\Gamma ^{\infty })^{M[h]}$
, and moreover,
 $\Pi $
witnesses that
$\Pi $
witnesses that
 ${\mathcal {P}}^+$
is a
${\mathcal {P}}^+$
is a
 $\Sigma _{Y_0}$
-hod mouse.Footnote 73
$\Sigma _{Y_0}$
-hod mouse.Footnote 73
Let
![]() $\tau : M_{Y_0}\rightarrow M_Y$
be the canonical embedding and let E be the long extender of length
$\tau : M_{Y_0}\rightarrow M_Y$
be the canonical embedding and let E be the long extender of length
![]() $Ord\cap \pi _Y^{-1}(Lp^{cuB, \Psi }(A))$
derived from
$Ord\cap \pi _Y^{-1}(Lp^{cuB, \Psi }(A))$
derived from
![]() $\tau $
. Because
$\tau $
. Because
![]() ${\mathcal {P}}^+$
might have cardinality
${\mathcal {P}}^+$
might have cardinality
![]() $>\mu $
, when we form
$>\mu $
, when we form
![]() ${\mathcal {P}}_Y^+=_{def}Ult({\mathcal {P}}^+, E)$
, we cannot conclude that
${\mathcal {P}}_Y^+=_{def}Ult({\mathcal {P}}^+, E)$
, we cannot conclude that
![]() ${\mathcal {P}}_Y^+$
is iterable in M. This is because we do not know that
${\mathcal {P}}_Y^+$
is iterable in M. This is because we do not know that
![]() $j{\restriction } {\mathcal {P}}^+\in M$
. To resolve this issue, we take a hull of size
$j{\restriction } {\mathcal {P}}^+\in M$
. To resolve this issue, we take a hull of size
![]() $\mu $
. Let
$\mu $
. Let
![]() $\mu _1=(\mu ^+)^V$
.
$\mu _1=(\mu ^+)^V$
.
We work in M. We can now find
![]() $m: W\rightarrow N$
such that
$m: W\rightarrow N$
such that
-
○
 $W\in M$
is transitive and
$W\in M$
is transitive and
 $\mu +1\subseteq W$
,
$\mu +1\subseteq W$
, -
○
 $(j({\mathcal {P}}), Y_0, Y, ({\mathcal {P}}^+, \Pi ), ({\mathcal {S}}, \Phi ))\in {\mathrm rge}(m)$
.
$(j({\mathcal {P}}), Y_0, Y, ({\mathcal {P}}^+, \Pi ), ({\mathcal {S}}, \Phi ))\in {\mathrm rge}(m)$
.
Let
![]() $Z=m^{-1}(Y)$
,
$Z=m^{-1}(Y)$
,
![]() ${\mathcal {N}}=m^{-1}({\mathcal {M}})$
,
${\mathcal {N}}=m^{-1}({\mathcal {M}})$
,
![]() ${\mathcal {R}}=m^{-1}(j({\mathcal {P}}))$
and
${\mathcal {R}}=m^{-1}(j({\mathcal {P}}))$
and
![]() $k: {\mathcal {P}}\rightarrow {\mathcal {R}}$
be
$k: {\mathcal {P}}\rightarrow {\mathcal {R}}$
be
![]() $m^{-1}(j{\restriction } {\mathcal {P}})$
. Working in M, set
$m^{-1}(j{\restriction } {\mathcal {P}})$
. Working in M, set
-
○
 ${\mathcal {Q}}=({\mathcal {P}}_{Z})^W$
,
${\mathcal {Q}}=({\mathcal {P}}_{Z})^W$
, -
○
 $\sigma =(\pi _{m^{-1}(Y_0), Z}{\restriction } {\mathcal {P}})^{W}$
and
$\sigma =(\pi _{m^{-1}(Y_0), Z}{\restriction } {\mathcal {P}})^{W}$
and
 $\tau =(\pi _Z{\restriction } {\mathcal {Q}})^{W}$
,
$\tau =(\pi _Z{\restriction } {\mathcal {Q}})^{W}$
, -
○
 $\overline {{\mathcal {P}}^+}=m^{-1}({\mathcal {P}}^+)$
and
$\overline {{\mathcal {P}}^+}=m^{-1}({\mathcal {P}}^+)$
and
 $\overline {\Pi }=m^{-1}(\Pi )$
,
$\overline {\Pi }=m^{-1}(\Pi )$
, -
○
 $(\overline {{\mathcal {S}}}, \overline {\Phi })=m^{-1}({\mathcal {S}}, \Phi )$
.
$(\overline {{\mathcal {S}}}, \overline {\Phi })=m^{-1}({\mathcal {S}}, \Phi )$
.
Thus, we have that
(A)
![]() $k=\tau \circ \sigma $
,
$k=\tau \circ \sigma $
,
![]() $\sigma :{\mathcal {P}}\rightarrow {\mathcal {Q}}$
and
$\sigma :{\mathcal {P}}\rightarrow {\mathcal {Q}}$
and
![]() $\tau :{\mathcal {Q}}\rightarrow {\mathcal {R}}$
,
$\tau :{\mathcal {Q}}\rightarrow {\mathcal {R}}$
,
(B) in W,
-
1.
 ${\mathcal {N}}$
is a sound
${\mathcal {N}}$
is a sound
 $\Sigma _{Z}$
-mouse over
$\Sigma _{Z}$
-mouse over
 ${\mathcal {Q}}$
that projects to
${\mathcal {Q}}$
that projects to
 $Ord\cap {\mathcal {Q}}$
,
$Ord\cap {\mathcal {Q}}$
, -
2. in any derived model of
 $(\overline {{\mathcal {P}}^+}, \overline {\Pi })$
as computed by an
$(\overline {{\mathcal {P}}^+}, \overline {\Pi })$
as computed by an
 ${\mathbb {R}}$
-genericity iteration,
${\mathbb {R}}$
-genericity iteration,
 ${\mathcal {N}}$
has an
${\mathcal {N}}$
has an
 $\omega _1$
-iteration strategy witnessing that it is a
$\omega _1$
-iteration strategy witnessing that it is a
 $\Sigma _Z$
-mouse,
$\Sigma _Z$
-mouse, -
3.
 ${\mathcal {N}}$
is not an initial segment of
${\mathcal {N}}$
is not an initial segment of
 ${\mathcal {Q}}$
,
${\mathcal {Q}}$
, -
4.
 $\overline {\Phi }$
is in the derived model of
$\overline {\Phi }$
is in the derived model of
 $(\overline {{\mathcal {P}}^+}, \overline {\Pi })$
as computed by any
$(\overline {{\mathcal {P}}^+}, \overline {\Pi })$
as computed by any
 ${\mathbb {R}}$
-genericity iteration,
${\mathbb {R}}$
-genericity iteration, -
5. letting
 $\xi :\sigma ({\mathcal { H}})\rightarrow \overline {{\mathcal {S}}}|{\delta }^{\overline {{\mathcal {S}}}}$
be such that
$\xi :\sigma ({\mathcal { H}})\rightarrow \overline {{\mathcal {S}}}|{\delta }^{\overline {{\mathcal {S}}}}$
be such that
 $\xi =(\pi ^{\overline {\Phi }}_{\overline {{\mathcal {S}}}, \infty })^{-1} \circ \tau $
,
$\xi =(\pi ^{\overline {\Phi }}_{\overline {{\mathcal {S}}}, \infty })^{-1} \circ \tau $
,
 $\Sigma _Z=(\xi $
-pullback of
$\Sigma _Z=(\xi $
-pullback of
 $\overline {\Phi }_{\overline {{\mathcal {S}}}|{\delta }^{\overline {{\mathcal {S}}}}}$
.
$\overline {\Phi }_{\overline {{\mathcal {S}}}|{\delta }^{\overline {{\mathcal {S}}}}}$
.
Let now F be the long extender of length
![]() ${\delta }^{\mathcal {Q}}$
derived from
${\delta }^{\mathcal {Q}}$
derived from
![]() $\sigma $
and set
$\sigma $
and set
![]() ${\mathcal {Q}}^+=Ult(\overline {{\mathcal {P}}^+}, F)$
. Let
${\mathcal {Q}}^+=Ult(\overline {{\mathcal {P}}^+}, F)$
. Let
![]() $\sigma ^+=\pi _F^{{\mathcal {P}}^+}$
. Notice that because
$\sigma ^+=\pi _F^{{\mathcal {P}}^+}$
. Notice that because
![]() $m\circ k=j{\restriction } {\mathcal {P}}$
, we have
$m\circ k=j{\restriction } {\mathcal {P}}$
, we have
![]() $\phi ^+:{\mathcal {Q}}^+\rightarrow j(\overline {{\mathcal {P}}^+})$
such that
$\phi ^+:{\mathcal {Q}}^+\rightarrow j(\overline {{\mathcal {P}}^+})$
such that
(C)
![]() $j{\restriction } \overline {{\mathcal {P}}^+}=\phi ^+\circ \sigma ^+$
.
$j{\restriction } \overline {{\mathcal {P}}^+}=\phi ^+\circ \sigma ^+$
.
Let
![]() $\overline {\Pi }^+$
be the
$\overline {\Pi }^+$
be the
![]() $m{\restriction } \overline {{\mathcal {P}}^+}$
-pullback of
$m{\restriction } \overline {{\mathcal {P}}^+}$
-pullback of
![]() $\Pi $
Footnote 74 and let
$\Pi $
Footnote 74 and let
![]() $\overline {\Phi }^+$
be the m-pullback of
$\overline {\Phi }^+$
be the m-pullback of
![]() $\Phi $
. Notice that
$\Phi $
. Notice that
(D1)
![]() $\overline {\Pi }^+{\restriction } W= \overline {\Pi }$
,Footnote 75
$\overline {\Pi }^+{\restriction } W= \overline {\Pi }$
,Footnote 75
(D2)
![]() $\overline {\Pi }^+$
witnesses that
$\overline {\Pi }^+$
witnesses that
![]() $\overline {{\mathcal {P}}^+}$
is a
$\overline {{\mathcal {P}}^+}$
is a
![]() $\Psi $
-hod mouseFootnote 76 ,
$\Psi $
-hod mouseFootnote 76 ,
(D3)
![]() $\overline {\Phi }^+{\restriction } W= \overline {\Phi }$
.
$\overline {\Phi }^+{\restriction } W= \overline {\Phi }$
.
Notice now that we have
(F) in M,
![]() $j(\overline {\Pi }^+{\restriction } H_{\mu _1}^{M})$
is a
$j(\overline {\Pi }^+{\restriction } H_{\mu _1}^{M})$
is a
![]() $(j(\mu ), j(\mu ))$
-iteration strategy witnessing that
$(j(\mu ), j(\mu ))$
-iteration strategy witnessing that
![]() $j(\overline {{\mathcal {P}}^+})$
is a
$j(\overline {{\mathcal {P}}^+})$
is a
![]() $j(\Psi )$
-hod mouse, and moreover,
$j(\Psi )$
-hod mouse, and moreover,
![]() $j{\restriction } \overline {{\mathcal {P}}^+}\in M$
.Footnote 77
$j{\restriction } \overline {{\mathcal {P}}^+}\in M$
.Footnote 77
We let
![]() $\Gamma =(\Sigma _Z)^{W}$
. Notice that in W,
$\Gamma =(\Sigma _Z)^{W}$
. Notice that in W,
![]() $\Gamma $
is the
$\Gamma $
is the
![]() $\tau $
-pullback of
$\tau $
-pullback of
![]() $m^{-1}(j(\Psi ))$
. Let
$m^{-1}(j(\Psi ))$
. Let
![]() $\Gamma ^+$
be the
$\Gamma ^+$
be the
![]() $\phi ^+{\restriction } {\mathcal {Q}}=m\circ \tau {\restriction } {\mathcal {Q}}$
-pullback of
$\phi ^+{\restriction } {\mathcal {Q}}=m\circ \tau {\restriction } {\mathcal {Q}}$
-pullback of
![]() $j(\Psi )$
. It follows that
$j(\Psi )$
. It follows that
(G)
![]() $\Gamma ^+$
is the
$\Gamma ^+$
is the
![]() $m\circ \xi $
-pullback of
$m\circ \xi $
-pullback of
![]() $\Phi $
, and it is also
$\Phi $
, and it is also
![]() $\xi $
-pullback of
$\xi $
-pullback of
![]() $\overline {\Phi }^+$
.
$\overline {\Phi }^+$
.
We now claim that
(b) in M, in any derived model of
![]() $(\overline {{\mathcal {P}}^+}, \overline {\Pi }^+)$
as computed by an
$(\overline {{\mathcal {P}}^+}, \overline {\Pi }^+)$
as computed by an
![]() ${\mathbb {R}}$
-genericity iteration,
${\mathbb {R}}$
-genericity iteration,
![]() ${\mathcal {N}}$
has an
${\mathcal {N}}$
has an
![]() $\omega _1$
-iteration strategy witnessesing that
$\omega _1$
-iteration strategy witnessesing that
![]() ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
![]() $\Gamma ^+$
-mouse.
$\Gamma ^+$
-mouse.
The proof of (b) is like the proof of Claim 1 of [Reference Sargsyan33, Lemma 10.4], and it is also very similar to the proof of (b) that appears in the proof of [Reference Sargsyan and Trang38, Theorem 9.2.6]. Because of this, we skip the proof of (b).
To finish the proof of Proposition 5.9, it remains to implement the last portion of the proof of [Reference Sargsyan33, Theorem 10.3]. Let
![]() $\Delta _0$
be
$\Delta _0$
be
![]() $\phi ^+$
-pullback of
$\phi ^+$
-pullback of
![]() $j^+(\overline {\Pi }^+{\restriction } N)$
. Notice that it follows from (F) that
$j^+(\overline {\Pi }^+{\restriction } N)$
. Notice that it follows from (F) that
![]() $\Delta _0$
witnesses that
$\Delta _0$
witnesses that
![]() ${\mathcal {Q}}^+$
is a
${\mathcal {Q}}^+$
is a
![]() $\Gamma ^+$
-hod mouse. It then follows from (b) that
$\Gamma ^+$
-hod mouse. It then follows from (b) that
(H) in M, in any derived model of
![]() $({\mathcal {Q}}^+, \Delta _0)$
as computed by an
$({\mathcal {Q}}^+, \Delta _0)$
as computed by an
![]() ${\mathbb {R}}$
-genericity iteration,
${\mathbb {R}}$
-genericity iteration,
![]() ${\mathcal {N}}$
has an
${\mathcal {N}}$
has an
![]() $\omega _1$
-iteration strategy
$\omega _1$
-iteration strategy
![]() $\Delta $
witnessing that
$\Delta $
witnessing that
![]() ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
![]() $\Gamma ^+$
-mouse.
$\Gamma ^+$
-mouse.
(H) gives contradiction, as it implies that
(I)
![]() ${\mathcal {Q}}^+{\vDash } \text {`}Ord\cap {\mathcal {Q}}$
is not a cardinal’,Footnote 78
${\mathcal {Q}}^+{\vDash } \text {`}Ord\cap {\mathcal {Q}}$
is not a cardinal’,Footnote 78
while clearly
![]() $\overline {{\mathcal {P}}^+}{\vDash } \text {`}Ord\cap {\mathcal {P}}$
is a cardinal’, contradicting the elementarity of
$\overline {{\mathcal {P}}^+}{\vDash } \text {`}Ord\cap {\mathcal {P}}$
is a cardinal’, contradicting the elementarity of
![]() $\phi ^+$
.
$\phi ^+$
.
Proof of Theorem 5.2
We now prove Theorem 5.2. First, take S to be the stationary class of measurable cardinals which are limits of Woodin cardinals; for any
![]() $\mu \in S$
,
$\mu \in S$
,
![]() $\mu $
satisfies clause (1) of Theorem 5.2 by Corollary 5.8. To get clauses (2) and (3), we apply Lemma 5.3 to the function f on S that maps each
$\mu $
satisfies clause (1) of Theorem 5.2 by Corollary 5.8. To get clauses (2) and (3), we apply Lemma 5.3 to the function f on S that maps each
![]() $\mu \in S$
to the maximum of the ordinals
$\mu \in S$
to the maximum of the ordinals
![]() $\{\nu , \eta _{\mu }, \xi \}$
, where
$\{\nu , \eta _{\mu }, \xi \}$
, where
![]() $\nu $
appears in Proposition 5.9,
$\nu $
appears in Proposition 5.9,
![]() $\eta _{\nu }$
appears in the proof of Proposition 5.4, and
$\eta _{\nu }$
appears in the proof of Proposition 5.4, and
![]() $\xi $
appears in the statement of Corollary 5.8. Using Lemma 5.3, we obtain proper class
$\xi $
appears in the statement of Corollary 5.8. Using Lemma 5.3, we obtain proper class
![]() $S_0\subseteq S$
such that for each
$S_0\subseteq S$
such that for each
![]() $\mu \in S_0$
,
$\mu \in S_0$
,
![]() $\nu $
witnesses clauses (2) and (3) of Theorem 5.2. This finishes the proof of Theorem 5.2.
$\nu $
witnesses clauses (2) and (3) of Theorem 5.2. This finishes the proof of Theorem 5.2.
![]() $\Box $
$\Box $
Remark 5.10.
-
1. By Lemma 5.3, the existence of
 $S,S_0,\nu $
above can be proved within
$S,S_0,\nu $
above can be proved within
 $\mathsf {ZFC}$
.
$\mathsf {ZFC}$
. -
2. It may appear that we use second-order set theory to ‘pick’ for each measurable limit of Woodin cardinals
 $\mu $
a set
$\mu $
a set
 $A_{\mu }$
that codes
$A_{\mu }$
that codes
 $V_{\mu }$
, but the theory
$V_{\mu }$
, but the theory
 $\mathsf {ZFC} + $
‘there is (global) well-order of V’ is conservative over
$\mathsf {ZFC} + $
‘there is (global) well-order of V’ is conservative over
 $\mathsf {ZFC}$
. Over any
$\mathsf {ZFC}$
. Over any
 $V{\vDash } \mathsf {ZFC}$
, we can find a (class) generic extension
$V{\vDash } \mathsf {ZFC}$
, we can find a (class) generic extension
 $V[g]$
of V such that
$V[g]$
of V such that
 $V[g]{\vDash } \text {`}\mathsf {ZFC} + $
there is a global well order’.
$V[g]{\vDash } \text {`}\mathsf {ZFC} + $
there is a global well order’. -
3. The above two remarks simply say that we may assume as part of the hypothesis that V has a global well-order. This then allows us to get
 $S, S_0, \nu $
and the sequences
$S, S_0, \nu $
and the sequences
 $(Y_{\mu }: \mu \in S_0)$
,
$(Y_{\mu }: \mu \in S_0)$
,
 $(A_{\mu }: \mu \in S)$
in Theorem 5.2.
$(A_{\mu }: \mu \in S)$
in Theorem 5.2.
The rest of the argument does not need the hypothesis that
![]() $\Gamma ^{\infty }{\vDash } _{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. It only needs the conclusion of Theorem 5.2. To stress this point, we make the following definitions.
$\Gamma ^{\infty }{\vDash } _{\Omega } \mathsf {AD}_{{\mathbb {R}}}$
. It only needs the conclusion of Theorem 5.2. To stress this point, we make the following definitions.
Definition 5.11. We let T stand for the following theory.
-
1.
 $T_0$
$T_0$
-
2. There is a stationary class S, a proper class
 $S_0\subseteq S$
, an infinite regular cardinal
$S_0\subseteq S$
, an infinite regular cardinal
 $\nu $
and two sequences
$\nu $
and two sequences
 $\vec {Y}=(Y_{\mu }: \mu \in S_0)$
and
$\vec {Y}=(Y_{\mu }: \mu \in S_0)$
and
 $\vec {A}=(A_{\mu }: \mu \in S)$
such that the following conditions hold for any
$\vec {A}=(A_{\mu }: \mu \in S)$
such that the following conditions hold for any
 $\mu \in S$
:
$\mu \in S$
:-
(a)
 $\mu $
is a measurable limit of Woodin cardinals,
$\mu $
is a measurable limit of Woodin cardinals, -
(b)
 $\mu $
stabilizes uB,
$\mu $
stabilizes uB, -
(c)
 ${\vert {\mathcal {H}}_{\mu }}\vert <\mu ^+$
,
${\vert {\mathcal {H}}_{\mu }}\vert <\mu ^+$
, -
(d)
 $A_{\mu }\subseteq \mu $
codes
$A_{\mu }\subseteq \mu $
codes
 $V_{\mu }$
and
$V_{\mu }$
and
 $\max ({\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu }), {\mathrm cf}(Ord\cap Lp^{cuB, \Psi _{\mu }}(A_{\mu }))<\mu $
;
$\max ({\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu }), {\mathrm cf}(Ord\cap Lp^{cuB, \Psi _{\mu }}(A_{\mu }))<\mu $
;
furthermore, if
 $\mu \in S_0$
, then the following hold:
$\mu \in S_0$
, then the following hold:-
(a)
 $\max ({\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu }), {\mathrm cf}(Ord\cap Lp^{cuB, \Psi _{\mu }}(A_{\mu }))<\nu $
,
$\max ({\mathrm cf}(Ord\cap {\mathcal { H}}_{\mu }), {\mathrm cf}(Ord\cap Lp^{cuB, \Psi _{\mu }}(A_{\mu }))<\nu $
, -
(b)
 $Y_{\mu }\in {\wp }_{\nu }(H_{\mu ^+})$
,
$Y_{\mu }\in {\wp }_{\nu }(H_{\mu ^+})$
, -
(c)
 $A_{\mu }\in Y_{\mu }$
, and
$A_{\mu }\in Y_{\mu }$
, and -
(d) whenever
 $X\prec H_{\mu ^+}$
is of size
$X\prec H_{\mu ^+}$
is of size
 $<\mu $
, is
$<\mu $
, is
 $\nu $
-closed and
$\nu $
-closed and
 $Y_{\mu }\subseteq X$
, X capturesFootnote 79
$Y_{\mu }\subseteq X$
, X capturesFootnote 79
 $Lp^{cuB, \Psi _{\mu }}(A_{\mu })$
.
$Lp^{cuB, \Psi _{\mu }}(A_{\mu })$
.
-
6. Condensing sets
Here, we review some facts about condensing sets that were introduced in [Reference Sargsyan33] and developed further in [Reference Sargsyan and Trang38, Chapter 9.1]. We develop this notion assuming the theory T introduced in Definition 5.11. Let
![]() $(S, S_0, \nu _0,\vec {Y}, \vec {A})$
witness that T is true.
$(S, S_0, \nu _0,\vec {Y}, \vec {A})$
witness that T is true.
Fix
![]() $\mu \in S_0$
and let
$\mu \in S_0$
and let
![]() $g\subseteq Coll(\omega , <\mu )$
be generic. We let
$g\subseteq Coll(\omega , <\mu )$
be generic. We let
![]() $ \mathcal {H}, \Psi $
, etc. stand for the CMI objects associated with
$ \mathcal {H}, \Psi $
, etc. stand for the CMI objects associated with
![]() $\mu $
. We summarize some basic notions and results concerning condensing sets which will play a key role in our
$\mu $
. We summarize some basic notions and results concerning condensing sets which will play a key role in our
![]() $K^c$
-constructions. [Reference Sargsyan and Trang38, Chapter 9] gives more details and proofs of basic facts about these objects.
$K^c$
-constructions. [Reference Sargsyan and Trang38, Chapter 9] gives more details and proofs of basic facts about these objects.
The notion of fullness that we will use is full in
![]() $L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
. Notice that if
$L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
. Notice that if
![]() $\Phi \in L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
is an
$\Phi \in L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
is an
![]() $\omega _1$
-strategy with hull condensation, then in
$\omega _1$
-strategy with hull condensation, then in
![]() $L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
, for any
$L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
, for any
![]() $x\in {\mathbb {R}}_g$
,
$x\in {\mathbb {R}}_g$
,
![]() $OD(\Phi )$
is the stack of
$OD(\Phi )$
is the stack of
![]() $\omega _1$
-iterable
$\omega _1$
-iterable
![]() $\Phi $
-mice over x.Footnote 80 Because any such
$\Phi $
-mice over x.Footnote 80 Because any such
![]() $\Phi $
-mouse has an iteration strategy in
$\Phi $
-mouse has an iteration strategy in
![]() $\Gamma ^{\infty }_g$
, it follows that ‘full in
$\Gamma ^{\infty }_g$
, it follows that ‘full in
![]() $L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
’ is equivalent to ‘full with respect to
$L(\Gamma ^{\infty }_g, {\mathbb {R}}_g)$
’ is equivalent to ‘full with respect to
![]() $Lp^{cuB}$
in
$Lp^{cuB}$
in
![]() $V[g]$
’. Thus, given
$V[g]$
’. Thus, given
![]() ${\mathcal {M}}\in HC^{V[g]}$
, we say
${\mathcal {M}}\in HC^{V[g]}$
, we say
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() $\Phi $
-full if for any
$\Phi $
-full if for any
![]() ${\mathcal {M}}$
-cutpoint
${\mathcal {M}}$
-cutpoint
![]() $\eta $
,
$\eta $
,
![]() $Lp^{cuB, \Phi }({\mathcal {M}}|\eta )\in {\mathcal {M}}$
. If
$Lp^{cuB, \Phi }({\mathcal {M}}|\eta )\in {\mathcal {M}}$
. If
![]() ${\mathcal {M}}$
is a
${\mathcal {M}}$
is a
![]() $\Phi $
-mouse over
$\Phi $
-mouse over
![]() ${\mathcal {M}}|\eta $
, then by ‘
${\mathcal {M}}|\eta $
, then by ‘
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() $\Phi $
-full’, we in fact mean that
$\Phi $
-full’, we in fact mean that
![]() ${\mathcal {M}}|(\eta ^+)^{\mathcal {M}}=Lp^{cuB, \Phi }({\mathcal {M}}|\eta )$
. Here, we note again that ‘
${\mathcal {M}}|(\eta ^+)^{\mathcal {M}}=Lp^{cuB, \Phi }({\mathcal {M}}|\eta )$
. Here, we note again that ‘
![]() $Lp^{cuB,\Phi }$
’ is computed in
$Lp^{cuB,\Phi }$
’ is computed in
![]() $V[g]$
.
$V[g]$
.
We start working in
![]() $V[g]$
. Following [Reference Sargsyan and Trang38, Chapter 9], for each
$V[g]$
. Following [Reference Sargsyan and Trang38, Chapter 9], for each
![]() $Z\subseteq {\mathcal { H}}$
, we let
$Z\subseteq {\mathcal { H}}$
, we let
-
○
 ${\mathcal {Q}}_Z$
be the transitive collapse of
${\mathcal {Q}}_Z$
be the transitive collapse of
 $Hull_1^{\mathcal {H}}(Z)$
,
$Hull_1^{\mathcal {H}}(Z)$
, -
○
 $\tau _Z:{\mathcal {Q}}_Z\rightarrow \mathcal {H}$
be the uncollapse map, and
$\tau _Z:{\mathcal {Q}}_Z\rightarrow \mathcal {H}$
be the uncollapse map, and -
○
 $\delta _Z = \delta ^{{\mathcal {Q}}_Z}$
, where
$\delta _Z = \delta ^{{\mathcal {Q}}_Z}$
, where
 $\tau _Z(\delta _Z) = \Theta = \delta ^{\mathcal {H}}$
.
$\tau _Z(\delta _Z) = \Theta = \delta ^{\mathcal {H}}$
.
For
![]() $X\subseteq Y \in {\wp }_{\omega _1}(\mathcal {H})$
, let
$X\subseteq Y \in {\wp }_{\omega _1}(\mathcal {H})$
, let
Definition 6.1. Let
![]() $Z\in {\wp }_{\omega _1}(\mathcal {H})$
.
$Z\in {\wp }_{\omega _1}(\mathcal {H})$
.
![]() $Y \in {\wp }_{\omega _1}(\mathcal {H}^{-})$
is a simple extension of Z if
$Y \in {\wp }_{\omega _1}(\mathcal {H}^{-})$
is a simple extension of Z if
Let
![]() $Z,Y$
be as in Definition 6.1. Let
$Z,Y$
be as in Definition 6.1. Let
Let
and
we also write
![]() ${\mathcal {Q}}^Z_Y$
for
${\mathcal {Q}}^Z_Y$
for
![]() ${\mathcal {Q}}_{Z\oplus Y}$
and
${\mathcal {Q}}_{Z\oplus Y}$
and
![]() $\delta ^Z_Y$
for
$\delta ^Z_Y$
for
![]() $\delta ^{{\mathcal {Q}}_{Z\oplus Y}}$
. We have that
$\delta ^{{\mathcal {Q}}_{Z\oplus Y}}$
. We have that
Given two simple extensions of Z,
![]() $Y_0 \subseteq Y_1$
, we let
$Y_0 \subseteq Y_1$
, we let
![]() $\pi ^Z_{Y_0,Y_1}:{\mathcal {Q}}^Z_{Y_0} \rightarrow {\mathcal {Q}}^Z_{Y_1}$
be the natural map. We also let
$\pi ^Z_{Y_0,Y_1}:{\mathcal {Q}}^Z_{Y_0} \rightarrow {\mathcal {Q}}^Z_{Y_1}$
be the natural map. We also let
Definition 6.2.
Y is an extension of Z if Y is a simple extension of Z and
![]() $\pi ^Z_Y{\restriction } ( {\mathcal {Q}}_Z|\delta _Z)$
is the iteration embedding according to
$\pi ^Z_Y{\restriction } ( {\mathcal {Q}}_Z|\delta _Z)$
is the iteration embedding according to
![]() $\Psi ^Z_Y$
. Here, we allow Z to be an extension of itself.
$\Psi ^Z_Y$
. Here, we allow Z to be an extension of itself.
Suppose Y is an extension of Z. Let
![]() $\sigma ^Z_{Y}:{\mathcal {Q}}^Z_Y\rightarrow \mathcal {H}$
be given by
$\sigma ^Z_{Y}:{\mathcal {Q}}^Z_Y\rightarrow \mathcal {H}$
be given by
where
![]() $a\in ({\mathcal {Q}}^Z_Y|\delta ^Z_Y)^{<\omega }$
and
$a\in ({\mathcal {Q}}^Z_Y|\delta ^Z_Y)^{<\omega }$
and
![]() $q = \pi ^Z_{Y}(f)(a)$
.
$q = \pi ^Z_{Y}(f)(a)$
.
Definition 6.3. Y is an honest extension of Z if
-
1. Y is an extension of Z,
-
2.
 $\mathrm {dom}(\sigma _Y^Z)={\mathcal {Q}}^Z_Y$
and
$\mathrm {dom}(\sigma _Y^Z)={\mathcal {Q}}^Z_Y$
and
 $\sigma _Y^Z$
is elementary,
$\sigma _Y^Z$
is elementary, -
3.
 $\tau _Z =\sigma _Y^Z \circ \pi _Y^Z$
.Footnote 81
$\tau _Z =\sigma _Y^Z \circ \pi _Y^Z$
.Footnote 81
We say Y is an iteration extension of Z if Y is an honest extension of Z and
![]() $Y=\sigma ^Z_Y[{\mathcal {Q}}^Z_Y|\delta ^Z_Y]$
.
$Y=\sigma ^Z_Y[{\mathcal {Q}}^Z_Y|\delta ^Z_Y]$
.
Definition 6.4. We say Z is a simply condensing set if
-
1. for any extension Y of Z,
 ${\mathcal {Q}}_Y^Z$
is
${\mathcal {Q}}_Y^Z$
is
 $\Psi ^Z_Y$
-full,
$\Psi ^Z_Y$
-full, -
2. all extensions Y of Z are honest.
We say Z is condensing if for every extension Y of Z,
![]() $Z \oplus Y$
is a simply condensing set.
$Z \oplus Y$
is a simply condensing set.
In
![]() $V[g]$
, let
$V[g]$
, let
Results in [Reference Sargsyan and Trang38, Chapter 9] give the following:
Theorem 6.5. In
![]() $V[g]$
,
$V[g]$
,
![]() $Cnd(\mathcal {H})$
is a club in
$Cnd(\mathcal {H})$
is a club in
![]() ${\wp }_{\omega _1}(\mathcal {H})$
(i.e., it is unbounded and is closed under countable unions).
${\wp }_{\omega _1}(\mathcal {H})$
(i.e., it is unbounded and is closed under countable unions).
Furthermore, for any cardinal
![]() $\kappa \geq \nu _0$
and
$\kappa \geq \nu _0$
and
![]() $\kappa <\mu $
,
$\kappa <\mu $
,
![]() $\{X\in V: X \in Cnd(\mathcal {H})\wedge |X|^V \leq \kappa \} $
is a club in
$\{X\in V: X \in Cnd(\mathcal {H})\wedge |X|^V \leq \kappa \} $
is a club in
![]() ${\wp }^V_{\kappa ^+}(\mathcal {H})$
. The same holds if V is replaced by
${\wp }^V_{\kappa ^+}(\mathcal {H})$
. The same holds if V is replaced by
![]() $V[g\cap Coll(\omega , <\kappa )]$
.
$V[g\cap Coll(\omega , <\kappa )]$
.
Furthermore, for each
![]() $Z\in Cnd({\mathcal { H}})$
, if Y is an honest extension of Z, then Y is an iteration extension of Z.
$Z\in Cnd({\mathcal { H}})$
, if Y is an honest extension of Z, then Y is an iteration extension of Z.
Also, the following uniqueness fact is very important for this paper. It follows from Proposition 2.9 and can be proved exactly the same way as [Reference Sargsyan and Trang38, Lemma 9.1.14].
Proposition 6.6. Suppose Z is a condensing set. Suppose Y and W are extensions of Z such that
![]() ${\mathcal {Q}}^Z_Y={\mathcal {Q}}^Z_W$
. Then
${\mathcal {Q}}^Z_Y={\mathcal {Q}}^Z_W$
. Then
![]() $\Psi ^Z_Y=\Psi ^Z_W$
.
$\Psi ^Z_Y=\Psi ^Z_W$
.
The following are easy corollaries of Proposition 6.6.
Corollary 6.7. Suppose Z is a condensing set and
![]() ${\mathcal {Q}}$
is such that for some extension Y of Z,
${\mathcal {Q}}$
is such that for some extension Y of Z,
![]() ${\mathcal {Q}}={\mathcal {Q}}^Z_Y$
. There is then a unique honest extension W of Z such that
${\mathcal {Q}}={\mathcal {Q}}^Z_Y$
. There is then a unique honest extension W of Z such that
![]() ${\mathcal {Q}}={\mathcal {Q}}^Z_W$
.
${\mathcal {Q}}={\mathcal {Q}}^Z_W$
.
Corollary 6.8. Suppose Z is a condensing set. Suppose further that Y and W are two extensions of Z such that there is an embedding
![]() $i:{\mathcal {Q}}^Z_Y\rightarrow _{\Sigma _1} {\mathcal {Q}}^Z_W$
such that
$i:{\mathcal {Q}}^Z_Y\rightarrow _{\Sigma _1} {\mathcal {Q}}^Z_W$
such that
![]() $\tau ^Z_W\circ i[{\mathcal {Q}}^Z_Y]$
is an extension of Z. Then the i-pullback of
$\tau ^Z_W\circ i[{\mathcal {Q}}^Z_Y]$
is an extension of Z. Then the i-pullback of
![]() $\Psi ^Z_W$
is
$\Psi ^Z_W$
is
![]() $\Psi ^Z_Y$
.
$\Psi ^Z_Y$
.
Proof. Let
![]() $Y^*=\tau ^Z_W\circ i[{\mathcal {Q}}^Z_Y]$
. We have that
$Y^*=\tau ^Z_W\circ i[{\mathcal {Q}}^Z_Y]$
. We have that
![]() ${\mathcal {Q}}^Z_{Y}={\mathcal {Q}}^Z_{Y^*}$
. Moreover,
${\mathcal {Q}}^Z_{Y}={\mathcal {Q}}^Z_{Y^*}$
. Moreover,
![]() $\Psi ^Z_Y=\Psi ^Z_{Y^*}$
and
$\Psi ^Z_Y=\Psi ^Z_{Y^*}$
and
![]() $\Psi ^Z_{Y^*}$
is the i-pullback of
$\Psi ^Z_{Y^*}$
is the i-pullback of
![]() $\Psi ^Z_{W}$
.
$\Psi ^Z_{W}$
.
7. Z-realizable iterations
In this section, we fix a condensing set Z.
Definition 7.1. Let Z be a condensing set.
![]() ${\mathcal {Q}}$
nicely extends
${\mathcal {Q}}$
nicely extends
![]() ${\mathcal {Q}}_Z$
if
${\mathcal {Q}}_Z$
if
![]() ${\mathcal {Q}}$
is non-meekFootnote 82 and
${\mathcal {Q}}$
is non-meekFootnote 82 and
![]() ${\mathcal {Q}}^b = {\mathcal {Q}}_Z$
. We also say that
${\mathcal {Q}}^b = {\mathcal {Q}}_Z$
. We also say that
![]() ${\mathcal {Q}}$
is a nice extension of
${\mathcal {Q}}$
is a nice extension of
![]() ${\mathcal {Q}}_Z$
.
${\mathcal {Q}}_Z$
.
Suppose Y is an extension of Z and
![]() ${\mathcal {Q}}$
nicely extends
${\mathcal {Q}}$
nicely extends
![]() ${\mathcal {Q}}^Z_Y$
. We would like to analyze the stacks on
${\mathcal {Q}}^Z_Y$
. We would like to analyze the stacks on
![]() ${\mathcal {Q}}$
, following the terminology and conventions used in [Reference Sargsyan and Trang38]. A stackFootnote 83
${\mathcal {Q}}$
, following the terminology and conventions used in [Reference Sargsyan and Trang38]. A stackFootnote 83
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {Q}}$
has the form
${\mathcal {Q}}$
has the form
where the displayed objects are introduced in [Reference Sargsyan and Trang38, Definition 2.4.1]. The above notation is quite standard. D is the set of drops, R is the set of stages where player I starts a new round of the iteration game,
![]() $(\beta _{\alpha }, m_{\alpha })$
is the place player I drops at the beginning of the
$(\beta _{\alpha }, m_{\alpha })$
is the place player I drops at the beginning of the
![]() ${\alpha }$
th round, and T is the tree order. We adopt an important convention introduced in [Reference Sargsyan and Trang38]. Namely, we assume that all our stacks are proper (see [Reference Sargsyan and Trang38, Remark 2.7.27]). One of the key aspects of being proper is that if
${\alpha }$
th round, and T is the tree order. We adopt an important convention introduced in [Reference Sargsyan and Trang38]. Namely, we assume that all our stacks are proper (see [Reference Sargsyan and Trang38, Remark 2.7.27]). One of the key aspects of being proper is that if
![]() ${\beta }<lh({\vec {\mathcal {T}}})$
is such that
${\beta }<lh({\vec {\mathcal {T}}})$
is such that
![]() ${\vec {\mathcal {T}}}_{\geq {\beta }}$
is a stack on
${\vec {\mathcal {T}}}_{\geq {\beta }}$
is a stack on
![]() ${\mathcal {M}}^{\vec {\mathcal {T}}}_{\beta }$
, then
${\mathcal {M}}^{\vec {\mathcal {T}}}_{\beta }$
, then
![]() ${\beta }\in R$
.Footnote 84 We will also use the notation introduced in [Reference Sargsyan and Trang38, Notation 2.4.4]. In particular, for
${\beta }\in R$
.Footnote 84 We will also use the notation introduced in [Reference Sargsyan and Trang38, Notation 2.4.4]. In particular, for
![]() ${\alpha }\in R^{\vec {\mathcal {T}}}$
,
${\alpha }\in R^{\vec {\mathcal {T}}}$
,
![]() ${\mathsf {next}}^{{\vec {\mathcal {T}}}}({\alpha })=min(R^{{\vec {\mathcal {T}}}}-({\alpha }+1))$
if this minimum exists and otherwise
${\mathsf {next}}^{{\vec {\mathcal {T}}}}({\alpha })=min(R^{{\vec {\mathcal {T}}}}-({\alpha }+1))$
if this minimum exists and otherwise
![]() ${\mathsf {next}}^{{\vec {\mathcal {T}}}}({\alpha })=lh({\vec {\mathcal {T}}})$
. For
${\mathsf {next}}^{{\vec {\mathcal {T}}}}({\alpha })=lh({\vec {\mathcal {T}}})$
. For
![]() ${\alpha }\in R^{\vec {\mathcal {T}}}$
, we also set
${\alpha }\in R^{\vec {\mathcal {T}}}$
, we also set
![]() ${\mathsf {nc}}^{{\vec {\mathcal {T}}}}_{\alpha }={\vec {\mathcal {T}}}_{[{\alpha }, {\alpha }']}$
, where
${\mathsf {nc}}^{{\vec {\mathcal {T}}}}_{\alpha }={\vec {\mathcal {T}}}_{[{\alpha }, {\alpha }']}$
, where
![]() ${\alpha }'={\mathsf {next}}^{{\vec {\mathcal {T}}}}({\alpha })$
.
${\alpha }'={\mathsf {next}}^{{\vec {\mathcal {T}}}}({\alpha })$
.
Definition 7.2. Suppose
![]() $Z\in Cnd({\mathcal { H}})$
and Y is an extension of Z. Suppose further that
$Z\in Cnd({\mathcal { H}})$
and Y is an extension of Z. Suppose further that
![]() ${\mathcal {Q}}$
nicely extends
${\mathcal {Q}}$
nicely extends
![]() ${\mathcal {Q}}^Z_Y$
. Given
${\mathcal {Q}}^Z_Y$
. Given
![]() $E\in \vec {E}^{\mathcal {Q}}$
such that
$E\in \vec {E}^{\mathcal {Q}}$
such that
![]() $\mathrm {crit }(E)={\delta }^{{\mathcal {Q}}^Z_Y}$
, we say E is
$\mathrm {crit }(E)={\delta }^{{\mathcal {Q}}^Z_Y}$
, we say E is
![]() $(Z, Y)$
-realizable if there is W, an extension of
$(Z, Y)$
-realizable if there is W, an extension of
![]() $Z\oplus Y$
such that
$Z\oplus Y$
such that
![]() $E=E^Z_{Y, W}$
, where
$E=E^Z_{Y, W}$
, where
![]() $E^Z_{Y,W}$
is the extender defined by
$E^Z_{Y,W}$
is the extender defined by
for any
![]() $a\in [lh(E)]^{<\omega }$
and
$a\in [lh(E)]^{<\omega }$
and
![]() $A\in {\wp }(\mathrm {crit }(E))^{|a|}\cap {\mathcal {Q}}$
.
$A\in {\wp }(\mathrm {crit }(E))^{|a|}\cap {\mathcal {Q}}$
.
We are continuing with the notation of Definition 7.2. Suppose
![]() ${\vec {\mathcal {T}}}$
is a stack on
${\vec {\mathcal {T}}}$
is a stack on
![]() ${\mathcal {Q}}$
. We say
${\mathcal {Q}}$
. We say
![]() ${\vec {\mathcal {T}}}$
is a
${\vec {\mathcal {T}}}$
is a
![]() $(Z, Y)$
-realizable iteration if there is a sequence
$(Z, Y)$
-realizable iteration if there is a sequence
![]() $(W_{\alpha }: {\alpha } \in R^{{\vec {\mathcal {T}}}})$
such that
$(W_{\alpha }: {\alpha } \in R^{{\vec {\mathcal {T}}}})$
such that
-
1.
 $W_0=Y$
,
$W_0=Y$
, -
2. if
 ${\alpha }, {\beta }\in R^{{\vec {\mathcal {T}}}}$
and
${\alpha }, {\beta }\in R^{{\vec {\mathcal {T}}}}$
and
 ${\alpha }<{\beta }$
, then
${\alpha }<{\beta }$
, then
 $W_{\beta }$
is an extension of
$W_{\beta }$
is an extension of
 $Z\oplus W_{\alpha }$
,
$Z\oplus W_{\alpha }$
, -
3. if
 ${\alpha }, {\beta }\in R^{{\vec {\mathcal {T}}}}$
,
${\alpha }, {\beta }\in R^{{\vec {\mathcal {T}}}}$
,
 ${\alpha }<{\beta }$
and
${\alpha }<{\beta }$
and
 $\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}$
is defined, then
$\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}$
is defined, then
 $\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}=\pi ^Z_{W_{\alpha }, W_{\beta }}$
,Footnote 85 and
$\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}=\pi ^Z_{W_{\alpha }, W_{\beta }}$
,Footnote 85 and -
4. if
 ${\alpha }\in R^{\vec {\mathcal {T}}}$
and
${\alpha }\in R^{\vec {\mathcal {T}}}$
and
 ${\vec {\mathcal {U}}}$
is the largest fragment of
${\vec {\mathcal {U}}}$
is the largest fragment of
 ${\vec {\mathcal {T}}}_{\geq {\alpha }}$
that is based on
${\vec {\mathcal {T}}}_{\geq {\alpha }}$
that is based on
 ${\mathcal {M}}_{\alpha }^b$
, then
${\mathcal {M}}_{\alpha }^b$
, then
 ${\vec {\mathcal {U}}}$
is according to
${\vec {\mathcal {U}}}$
is according to
 $\Psi ^Z_{W_{\alpha }}$
.
$\Psi ^Z_{W_{\alpha }}$
.
We say
![]() ${\vec {\mathcal {T}}}$
is Z
-realizable if Y is an honest extension of Z and
${\vec {\mathcal {T}}}$
is Z
-realizable if Y is an honest extension of Z and
![]() ${\vec {\mathcal {T}}}$
is
${\vec {\mathcal {T}}}$
is
![]() $(Z, Y)$
-realizable.
$(Z, Y)$
-realizable.
The following lemma is a consequence os Proposition 6.6, Corollary 6.7 and Corollary 6.8.
Lemma 7.3. Suppose Y is an extension of Z and
![]() ${\mathcal {Q}}$
nicely extends
${\mathcal {Q}}$
nicely extends
![]() ${\mathcal {Q}}^Z_Y$
. Suppose
${\mathcal {Q}}^Z_Y$
. Suppose
![]() ${\vec {\mathcal {T}}}$
is a
${\vec {\mathcal {T}}}$
is a
![]() $(Z, Y)$
-realizable iteration as witnessed by
$(Z, Y)$
-realizable iteration as witnessed by
![]() $(W^{\prime }_{\alpha }: {\alpha } \in R^{{\vec {\mathcal {T}}}})$
. For
$(W^{\prime }_{\alpha }: {\alpha } \in R^{{\vec {\mathcal {T}}}})$
. For
![]() ${\alpha }\in R^{{\vec {\mathcal {T}}}}$
, let
${\alpha }\in R^{{\vec {\mathcal {T}}}}$
, let
![]() $W_{\alpha }$
be the unique honest extension of Z with the property that
$W_{\alpha }$
be the unique honest extension of Z with the property that
![]() $({\mathcal {M}}_{\alpha }^{{\vec {\mathcal {T}}}})^b={\mathcal {Q}}^Z_{W_{\alpha }}$
. Then
$({\mathcal {M}}_{\alpha }^{{\vec {\mathcal {T}}}})^b={\mathcal {Q}}^Z_{W_{\alpha }}$
. Then
![]() $(W_{\alpha }: {\alpha }\in R^{{\vec {\mathcal {T}}}})$
witnesses that
$(W_{\alpha }: {\alpha }\in R^{{\vec {\mathcal {T}}}})$
witnesses that
![]() ${\mathcal {Q}}$
is Z-realizable.
${\mathcal {Q}}$
is Z-realizable.
Proof. It is enough to show that if
![]() ${\alpha }, {\beta }\in R^{\vec {\mathcal {T}}}$
and
${\alpha }, {\beta }\in R^{\vec {\mathcal {T}}}$
and
![]() ${\beta }=\min (R^{\vec {\mathcal {T}}}-({\alpha }+1))$
, then
${\beta }=\min (R^{\vec {\mathcal {T}}}-({\alpha }+1))$
, then
![]() $\pi ^{\vec {\mathcal {T}}}_{{\alpha }, {\beta }}=\pi ^Z_{W_{\alpha }, W_{\beta }}$
. First, we show that
$\pi ^{\vec {\mathcal {T}}}_{{\alpha }, {\beta }}=\pi ^Z_{W_{\alpha }, W_{\beta }}$
. First, we show that
![]() $W_{\alpha }\subseteq W_{\beta }$
. We have that
$W_{\alpha }\subseteq W_{\beta }$
. We have that
![]() $x\in W_{\alpha }$
if for some
$x\in W_{\alpha }$
if for some
![]() $a\in {\delta }_{Z\oplus W_{\alpha }}$
and some
$a\in {\delta }_{Z\oplus W_{\alpha }}$
and some
![]() $f\in Z$
,
$f\in Z$
,
![]() $x=\tau _Z(f)(\tau ^Z_{W_{\alpha }}(a))$
. Since
$x=\tau _Z(f)(\tau ^Z_{W_{\alpha }}(a))$
. Since
![]() $\tau ^Z_{W_{\alpha }}{\restriction } {\delta }_{Z\oplus W_{\alpha }}$
,
$\tau ^Z_{W_{\alpha }}{\restriction } {\delta }_{Z\oplus W_{\alpha }}$
,
![]() $\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}{\restriction } {\delta }_{Z\oplus W_{\alpha }}$
and
$\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}{\restriction } {\delta }_{Z\oplus W_{\alpha }}$
and
![]() $\tau ^Z_{W_{\beta }}\circ \pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}{\restriction } {\delta }_{Z\oplus W_{\alpha }}$
are all iteration embeddings according to
$\tau ^Z_{W_{\beta }}\circ \pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}{\restriction } {\delta }_{Z\oplus W_{\alpha }}$
are all iteration embeddings according to
![]() $\Psi ^Z_{W_{\alpha }}$
, we have that
$\Psi ^Z_{W_{\alpha }}$
, we have that
![]() $x=\tau _Z(f)(\tau ^Z_{W_{\beta }}(\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}(a))$
. Thus,
$x=\tau _Z(f)(\tau ^Z_{W_{\beta }}(\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}(a))$
. Thus,
![]() $W_{\alpha }\subseteq W_{\beta }$
. A similar argument shows that
$W_{\alpha }\subseteq W_{\beta }$
. A similar argument shows that
![]() $\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}=\tau ^Z_{W_{\alpha }, W_{\beta }}$
.
$\pi ^{{\vec {\mathcal {T}}}, b}_{{\alpha }, {\beta }}=\tau ^Z_{W_{\alpha }, W_{\beta }}$
.
Remark 7.4. It follows from Lemma 7.3 that
![]() $(Z, Y)$
-realizability is equivalent to Z-realizability. Because of this, in this paper, we will mostly use Z-realizability.
$(Z, Y)$
-realizability is equivalent to Z-realizability. Because of this, in this paper, we will mostly use Z-realizability.
Suppose
![]() ${\mathcal {Q}}$
nicely extends
${\mathcal {Q}}$
nicely extends
![]() ${\mathcal {Q}}^Z_Y$
and
${\mathcal {Q}}^Z_Y$
and
![]() ${\vec {\mathcal {T}}}$
is a Z-realizable iteration of
${\vec {\mathcal {T}}}$
is a Z-realizable iteration of
![]() ${\mathcal {Q}}$
. We cannot in general prove that
${\mathcal {Q}}$
. We cannot in general prove that
![]() ${\vec {\mathcal {T}}}$
picks unique branches mainly because we say nothing about
${\vec {\mathcal {T}}}$
picks unique branches mainly because we say nothing about
![]() ${\mathcal {Q}}$
-structures that appear in
${\mathcal {Q}}$
-structures that appear in
![]() ${\vec {\mathcal {T}}}$
when we iterate above
${\vec {\mathcal {T}}}$
when we iterate above
![]() ${\delta }^{{\mathcal {M}}_{\alpha }^b}$
for some
${\delta }^{{\mathcal {M}}_{\alpha }^b}$
for some
![]() ${\alpha }\in R^{\vec {\mathcal {T}}}$
. The next definition introduces a notion of a premouse that resolves this issue.
${\alpha }\in R^{\vec {\mathcal {T}}}$
. The next definition introduces a notion of a premouse that resolves this issue.
Definition 7.5. We say
![]() ${\mathcal {R}}$
is weakly Z
-suitable if
${\mathcal {R}}$
is weakly Z
-suitable if
![]() ${\mathcal {R}}$
is a hod premouse of lsa type such that
${\mathcal {R}}$
is a hod premouse of lsa type such that
![]() ${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^{\#}$
,
${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^{\#}$
,
![]() ${\mathcal {R}}$
has no Woodin cardinals in the interval
${\mathcal {R}}$
has no Woodin cardinals in the interval
![]() $({\delta }^{{\mathcal {R}}^b}, {\delta }^{\mathcal {R}})$
and for some extension Y of Z,
$({\delta }^{{\mathcal {R}}^b}, {\delta }^{\mathcal {R}})$
and for some extension Y of Z,
![]() ${\mathcal {R}}$
nicely extends
${\mathcal {R}}$
nicely extends
![]() ${\mathcal {R}}^b={\mathcal {Q}}^Z_Y$
.
${\mathcal {R}}^b={\mathcal {Q}}^Z_Y$
.
The following lemma says that hulls of Z-realizable iterations are Z-realizable and easily follows from Corollary 6.8.
Proposition 7.6. Suppose
![]() ${\mathcal {R}}$
and
${\mathcal {R}}$
and
![]() ${\mathcal {S}}$
are weakly Z-suitable hod premice. Suppose further that
${\mathcal {S}}$
are weakly Z-suitable hod premice. Suppose further that
![]() ${\vec {\mathcal {T}}}$
is a Z-realizable iteration of
${\vec {\mathcal {T}}}$
is a Z-realizable iteration of
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
![]() ${\vec {\mathcal {U}}}$
is an iteration of
${\vec {\mathcal {U}}}$
is an iteration of
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $({\mathcal {R}}, {\vec {\mathcal {U}}})$
is a hullFootnote 86 of
$({\mathcal {R}}, {\vec {\mathcal {U}}})$
is a hullFootnote 86 of
![]() $({\mathcal {S}}, {\vec {\mathcal {T}}})$
. Then
$({\mathcal {S}}, {\vec {\mathcal {T}}})$
. Then
![]() ${\vec {\mathcal {U}}}$
is Z-realizable.
${\vec {\mathcal {U}}}$
is Z-realizable.
We now define the notion of Z-approved sts premouse of depth n by induction on n. The induction ranges over all weakly Z-suitable hod premice.
Definition 7.7. Suppose
![]() ${\mathcal {R}}$
is weakly Z-suitable hod premouse and for some extension Y of Z,
${\mathcal {R}}$
is weakly Z-suitable hod premouse and for some extension Y of Z,
![]() ${\mathcal {R}}$
nicely extends
${\mathcal {R}}$
nicely extends
![]() ${\mathcal {R}}^b={\mathcal {Q}}^Z_Y$
.
${\mathcal {R}}^b={\mathcal {Q}}^Z_Y$
.
-
1. We say that
 ${\mathcal {M}}$
is a Z
-approved sts premouse over
${\mathcal {M}}$
is a Z
-approved sts premouse over
 ${\mathcal {R}}$
of depth
${\mathcal {R}}$
of depth
 $0$
if
$0$
if
 ${\mathcal {M}}$
is an sts premouse over
${\mathcal {M}}$
is an sts premouse over
 ${\mathcal {R}}$
Footnote 87 such that if
${\mathcal {R}}$
Footnote 87 such that if
 ${\mathcal {T}}\in {\mathcal {M}}$
is according to
${\mathcal {T}}\in {\mathcal {M}}$
is according to
 $S^{\mathcal {M}}$
, then
$S^{\mathcal {M}}$
, then
 ${\mathcal {T}}$
is
${\mathcal {T}}$
is
 $(Z, Y)$
-realizable.
$(Z, Y)$
-realizable. -
2. Suppose
 ${\mathcal {R}}$
is weakly Z-suitable hod premouse. We say that
${\mathcal {R}}$
is weakly Z-suitable hod premouse. We say that
 ${\mathcal {M}}$
is a Z
-approved sts premouse over
${\mathcal {M}}$
is a Z
-approved sts premouse over
 ${\mathcal {R}}$
of depth
${\mathcal {R}}$
of depth
 $n+1$
if
$n+1$
if
 ${\mathcal {M}}$
is a Z-approved sts premouse over
${\mathcal {M}}$
is a Z-approved sts premouse over
 ${\mathcal {R}}$
of depth n such that if
${\mathcal {R}}$
of depth n such that if
 ${\mathcal {T}}\in {\mathcal {M}}$
is
${\mathcal {T}}\in {\mathcal {M}}$
is
 $\mathsf {nuvs}$
and
$\mathsf {nuvs}$
and
 $S^{\mathcal {M}}({\mathcal {T}})$
is defined, then letting
$S^{\mathcal {M}}({\mathcal {T}})$
is defined, then letting
 $b=S^{\mathcal {M}}({\mathcal {T}})$
,
$b=S^{\mathcal {M}}({\mathcal {T}})$
,
 ${\mathcal {Q}}(b, {\mathcal {T}})$
is a Z-approved sts premouse over
${\mathcal {Q}}(b, {\mathcal {T}})$
is a Z-approved sts premouse over
 ${\mathrm m}^+({\mathcal {T}})$
of depth n.
${\mathrm m}^+({\mathcal {T}})$
of depth n.
Definition 7.8. We say
![]() ${\mathcal {M}}$
is a Z
-approved sts premouse over
${\mathcal {M}}$
is a Z
-approved sts premouse over
![]() ${\mathcal {R}}$
if for each
${\mathcal {R}}$
if for each
![]() $n<\omega $
,
$n<\omega $
,
![]() ${\mathcal {M}}$
is a Z-approved sts premouse over
${\mathcal {M}}$
is a Z-approved sts premouse over
![]() ${\mathcal {R}}$
of depth n. We say
${\mathcal {R}}$
of depth n. We say
![]() ${\mathcal {M}}$
as above is a Z
-approved sts mouse (over
${\mathcal {M}}$
as above is a Z
-approved sts mouse (over
![]() ${\mathcal {R}}$
) if
${\mathcal {R}}$
) if
![]() ${\mathcal {M}}$
has a
${\mathcal {M}}$
has a
![]() $\mu $
-strategy
$\mu $
-strategy
![]() $\Sigma $
such that whenever
$\Sigma $
such that whenever
![]() ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {M}}$
,
${\mathcal {M}}$
,
![]() ${\mathcal {N}}$
is a Z-approved sts premouse over
${\mathcal {N}}$
is a Z-approved sts premouse over
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
The following proposition is an immediate consequence of our definitions but perhaps is a bit tedious to prove.
Proposition 7.9. Suppose
![]() ${\mathcal {R}}$
and
${\mathcal {R}}$
and
![]() ${\mathcal {S}}$
are weakly Z-suitable,
${\mathcal {S}}$
are weakly Z-suitable,
![]() ${\mathcal {N}}$
is an sts premouse over
${\mathcal {N}}$
is an sts premouse over
![]() ${\mathcal {R}}$
and
${\mathcal {R}}$
and
![]() ${\mathcal {M}}$
is a Z-approved premouse (mouse) over
${\mathcal {M}}$
is a Z-approved premouse (mouse) over
![]() ${\mathcal {S}}$
. Suppose
${\mathcal {S}}$
. Suppose
![]() $\pi :{\mathcal {N}}\rightarrow _{\Sigma _1} {\mathcal {M}}$
. Then
$\pi :{\mathcal {N}}\rightarrow _{\Sigma _1} {\mathcal {M}}$
. Then
![]() ${\mathcal {N}}$
is also a Z-approved premouse (mouse).
${\mathcal {N}}$
is also a Z-approved premouse (mouse).
Proof. We only show that if
![]() ${\mathcal {T}}^*\in {\mathcal {N}}$
is according to
${\mathcal {T}}^*\in {\mathcal {N}}$
is according to
![]() $S^{\mathcal {N}}$
, then
$S^{\mathcal {N}}$
, then
![]() ${\mathcal {T}}^*$
is Z-realizable. Even less, we show that if
${\mathcal {T}}^*$
is Z-realizable. Even less, we show that if
![]() ${\mathcal {T}}^*={\mathcal {T}}^\frown {\mathcal {U}}$
is such that
${\mathcal {T}}^*={\mathcal {T}}^\frown {\mathcal {U}}$
is such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists and
$\pi ^{{\mathcal {T}}, b}$
exists and
![]() ${\mathcal {U}}$
is based on
${\mathcal {U}}$
is based on
![]() $\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)$
, then there is an extension Y of Z such that
$\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)$
, then there is an extension Y of Z such that
![]() $\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)={\mathcal {Q}}^Z_{Y}$
and
$\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)={\mathcal {Q}}^Z_{Y}$
and
![]() ${\mathcal {U}}$
is according to
${\mathcal {U}}$
is according to
![]() $\Psi ^Z_{Y}$
. The rest of the proof is very similar.
$\Psi ^Z_{Y}$
. The rest of the proof is very similar.
Notice that by elementarity of
![]() $\pi $
,
$\pi $
,
![]() $\pi ({\mathcal {T}}^*)$
is according to
$\pi ({\mathcal {T}}^*)$
is according to
![]() $S^{\mathcal {M}}$
. Therefore, there is some extension W of Z such that
$S^{\mathcal {M}}$
. Therefore, there is some extension W of Z such that
![]() $\pi (\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b))={\mathcal {Q}}^Z_{W}$
and
$\pi (\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b))={\mathcal {Q}}^Z_{W}$
and
![]() $\pi ({\mathcal {U}})$
is according to
$\pi ({\mathcal {U}})$
is according to
![]() $\Psi ^Z_W$
. Set
$\Psi ^Z_W$
. Set
![]() $Y=\tau ^Z_W\circ \pi [\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)]$
. Then
$Y=\tau ^Z_W\circ \pi [\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)]$
. Then
![]() $\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)={\mathcal {Q}}^Z_{Y}$
and
$\pi ^{{\mathcal {T}}, b}({\mathcal {R}}^b)={\mathcal {Q}}^Z_{Y}$
and
![]() ${\mathcal {U}}$
is according to the
${\mathcal {U}}$
is according to the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Psi ^Z_{W}$
. As the
$\Psi ^Z_{W}$
. As the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Psi ^Z_{W}$
is just
$\Psi ^Z_{W}$
is just
![]() $\Psi ^Z_{Y}$
, we are done.
$\Psi ^Z_{Y}$
, we are done.
Definition 7.10. Suppose
![]() ${\mathcal {R}}$
is weakly Z-suitable. We let
${\mathcal {R}}$
is weakly Z-suitable. We let
![]() $Lp^{Za, sts}({\mathcal {R}})$
be the union of all Z-approved sound sts mice
$Lp^{Za, sts}({\mathcal {R}})$
be the union of all Z-approved sound sts mice
![]() ${\mathcal {M}}$
over
${\mathcal {M}}$
over
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $\rho ({\mathcal {M}}) \leq Ord\cap {\mathcal {R}}$
.
$\rho ({\mathcal {M}}) \leq Ord\cap {\mathcal {R}}$
.
Finally, we can define the correctly guided Z-realizable iterations.
Definition 7.11. Suppose
![]() ${\mathcal {R}}$
is a weakly Z-suitable hod premouse and
${\mathcal {R}}$
is a weakly Z-suitable hod premouse and
![]() ${\vec {\mathcal {T}}}$
is a Z-realizable iteration of
${\vec {\mathcal {T}}}$
is a Z-realizable iteration of
![]() ${\mathcal {R}}$
. We say
${\mathcal {R}}$
. We say
![]() ${\vec {\mathcal {T}}}$
is correctly guided if whenever
${\vec {\mathcal {T}}}$
is correctly guided if whenever
![]() ${\alpha }\in R^{\vec {\mathcal {T}}}$
,
${\alpha }\in R^{\vec {\mathcal {T}}}$
,
![]() ${\mathcal {U}}=_{def}{\mathsf {nc}}^{{\vec {\mathcal {T}}}}_{\alpha }$
is above
${\mathcal {U}}=_{def}{\mathsf {nc}}^{{\vec {\mathcal {T}}}}_{\alpha }$
is above
![]() ${\delta }^{{\mathcal {M}}_{\alpha }^b}$
,
${\delta }^{{\mathcal {M}}_{\alpha }^b}$
,
![]() ${\alpha }<lh({\mathcal {U}})$
is a limit ordinal such that
${\alpha }<lh({\mathcal {U}})$
is a limit ordinal such that
![]() ${\mathrm m}^+({\mathcal {U}}{\restriction } {\alpha }){\vDash } \text {`}{\delta }({\mathcal {U}}{\restriction } {\alpha })$
is a Woodin cardinal’. Then, letting
${\mathrm m}^+({\mathcal {U}}{\restriction } {\alpha }){\vDash } \text {`}{\delta }({\mathcal {U}}{\restriction } {\alpha })$
is a Woodin cardinal’. Then, letting
![]() $b=[0, {\alpha }]_{\mathcal {U}}$
,
$b=[0, {\alpha }]_{\mathcal {U}}$
,
![]() ${\mathcal {Q}}(b, {\mathcal {U}}{\restriction }\alpha )$
is a Z-approved sts mouse over
${\mathcal {Q}}(b, {\mathcal {U}}{\restriction }\alpha )$
is a Z-approved sts mouse over
![]() ${\mathrm m}^+({\mathcal {U}}{\restriction } {\alpha })$
.
${\mathrm m}^+({\mathcal {U}}{\restriction } {\alpha })$
.
Combining Proposition 7.6 and Proposition 7.9, we get the following.
Corollary 7.12. Suppose
![]() ${\mathcal {R}}$
and
${\mathcal {R}}$
and
![]() ${\mathcal {S}}$
are weakly Z-suitable hod premice. Suppose further that
${\mathcal {S}}$
are weakly Z-suitable hod premice. Suppose further that
![]() ${\vec {\mathcal {T}}}$
is a correctly guided Z-realizable iteration of
${\vec {\mathcal {T}}}$
is a correctly guided Z-realizable iteration of
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
![]() ${\vec {\mathcal {U}}}$
is an iteration of
${\vec {\mathcal {U}}}$
is an iteration of
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $({\mathcal {R}}, {\vec {\mathcal {U}}})$
is a hull of
$({\mathcal {R}}, {\vec {\mathcal {U}}})$
is a hull of
![]() $({\mathcal {S}}, {\vec {\mathcal {T}}})$
(in the sense of [Reference Sargsyan34, Definition 1.30]). Then
$({\mathcal {S}}, {\vec {\mathcal {T}}})$
(in the sense of [Reference Sargsyan34, Definition 1.30]). Then
![]() ${\vec {\mathcal {U}}}$
is also correctly guided Z-realizable iteration.
${\vec {\mathcal {U}}}$
is also correctly guided Z-realizable iteration.
Our uniqueness theorem applies to
![]() ${\mathcal {R}}$
that are not infinitely descending.
${\mathcal {R}}$
that are not infinitely descending.
Definition 7.13. We say that a weakly Z-suitable hod premouse
![]() ${\mathcal {R}}$
is infinitely descending if there is a sequence
${\mathcal {R}}$
is infinitely descending if there is a sequence
![]() $(p_i, {\mathcal {R}}_i, Y_i: i<\omega )$
such that
$(p_i, {\mathcal {R}}_i, Y_i: i<\omega )$
such that
-
1.
 ${\mathcal {R}}_0={\mathcal {R}}$
,
${\mathcal {R}}_0={\mathcal {R}}$
, -
2. for every
 $i<\omega $
,
$i<\omega $
,
 ${\mathcal {R}}_i$
is weakly Z-suitable,
${\mathcal {R}}_i$
is weakly Z-suitable, -
3. for every
 $i<\omega $
,
$i<\omega $
,
 $p_i$
is a correctly guided Z-realizable iteration of
$p_i$
is a correctly guided Z-realizable iteration of
 ${\mathcal {R}}_i$
,
${\mathcal {R}}_i$
, -
4. for every
 $i<\omega $
,
$i<\omega $
,
 $p_i$
has a last normal component
$p_i$
has a last normal component
 ${\mathcal {T}}_i$
of successor lengthFootnote 88 such that
${\mathcal {T}}_i$
of successor lengthFootnote 88 such that
 ${\alpha }_i=_{def}lh({\mathcal {T}}_i)-1$
is a limit ordinal and
${\alpha }_i=_{def}lh({\mathcal {T}}_i)-1$
is a limit ordinal and
 ${\mathcal {R}}_{i+1}={\mathrm m}^+({\mathcal {T}}_i{\restriction } {\alpha }_i)$
,
${\mathcal {R}}_{i+1}={\mathrm m}^+({\mathcal {T}}_i{\restriction } {\alpha }_i)$
, -
5. for every
 $i<\omega $
, setting
$i<\omega $
, setting
 $b_i=_{def}[0, {\alpha }_i)_{{\mathcal {T}}_i}$
,
$b_i=_{def}[0, {\alpha }_i)_{{\mathcal {T}}_i}$
,
 $b_i$
is a cofinal branch of
$b_i$
is a cofinal branch of
 ${\mathcal {T}}_i$
such that
${\mathcal {T}}_i$
such that
 ${\mathcal {Q}}(b_i, {\mathcal {T}}_i)$
exists and is Z-approved.
${\mathcal {Q}}(b_i, {\mathcal {T}}_i)$
exists and is Z-approved.
Note that in the above definition, for each i,
![]() ${\mathcal {R}}_{i+1}$
is a strict initial segment of
${\mathcal {R}}_{i+1}$
is a strict initial segment of
![]() ${\mathcal {Q}}(b_i, {\mathcal {T}}_i)$
. The following is our uniqueness result.
${\mathcal {Q}}(b_i, {\mathcal {T}}_i)$
. The following is our uniqueness result.
Proposition 7.14. Suppose
![]() ${\mathcal {R}}$
is a weakly Z-suitable hod premouse that is not infinitely descending and
${\mathcal {R}}$
is a weakly Z-suitable hod premouse that is not infinitely descending and
![]() ${\vec {\mathcal {T}}}$
is a correctly guided Z-realizable iteration of limit length on
${\vec {\mathcal {T}}}$
is a correctly guided Z-realizable iteration of limit length on
![]() ${\mathcal {R}}$
. Then there is at most one branch b of
${\mathcal {R}}$
. Then there is at most one branch b of
![]() ${\vec {\mathcal {T}}}$
such that
${\vec {\mathcal {T}}}$
such that
![]() ${\vec {\mathcal {T}}}^\frown \{b\}$
is correctly guided and Z-realizable.
${\vec {\mathcal {T}}}^\frown \{b\}$
is correctly guided and Z-realizable.
Here, we outline the proof. First notice that
(a) if
![]() ${\vec {\mathcal {T}}}$
does not have a last component or
${\vec {\mathcal {T}}}$
does not have a last component or
(b) if there is
![]() ${\alpha }\in R^{\vec {\mathcal {T}}}$
such that
${\alpha }\in R^{\vec {\mathcal {T}}}$
such that
![]() ${\vec {\mathcal {T}}}_{\geq {\alpha }}$
is based on
${\vec {\mathcal {T}}}_{\geq {\alpha }}$
is based on
![]() ${\mathcal {M}}_{\alpha }^b$
,
${\mathcal {M}}_{\alpha }^b$
,
then there is nothing to prove, as letting
![]() $W_{\mathcal {S}}$
be as in Definition 7.2,
$W_{\mathcal {S}}$
be as in Definition 7.2,
![]() $\Psi ^Z_{W_S}$
only depends on
$\Psi ^Z_{W_S}$
only depends on
![]() ${\mathcal {S}}^b$
(e.g., see [Reference Sargsyan and Trang38, Lemma 9.1.9]).Footnote 89 Let now
${\mathcal {S}}^b$
(e.g., see [Reference Sargsyan and Trang38, Lemma 9.1.9]).Footnote 89 Let now
![]() ${\mathcal {T}}={\mathsf {nc}}^{\vec {\mathcal {T}}}_{\alpha }$
be the last normal component of
${\mathcal {T}}={\mathsf {nc}}^{\vec {\mathcal {T}}}_{\alpha }$
be the last normal component of
![]() ${\vec {\mathcal {T}}}$
. If
${\vec {\mathcal {T}}}$
. If
![]() $b, c$
are two different branches of
$b, c$
are two different branches of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() ${\vec {\mathcal {T}}}^\frown \{b\}$
and
${\vec {\mathcal {T}}}^\frown \{b\}$
and
![]() ${\vec {\mathcal {T}}}^\frown \{c\}$
are correctly guided Z-realizable iterations, then
${\vec {\mathcal {T}}}^\frown \{c\}$
are correctly guided Z-realizable iterations, then
![]() ${\mathcal {Q}}(b, {\mathcal {T}})\not ={\mathcal {Q}}(c, {\mathcal {T}})$
and both are Z-approved sts mice over
${\mathcal {Q}}(b, {\mathcal {T}})\not ={\mathcal {Q}}(c, {\mathcal {T}})$
and both are Z-approved sts mice over
![]() ${\mathrm m}^+({\mathcal {T}})$
. It now follows from [Reference Sargsyan and Trang38, Lemma 4.7.2] and the fact that
${\mathrm m}^+({\mathcal {T}})$
. It now follows from [Reference Sargsyan and Trang38, Lemma 4.7.2] and the fact that
![]() ${\mathcal {R}}$
is not infinitely descending that we can reduce the disagreement of
${\mathcal {R}}$
is not infinitely descending that we can reduce the disagreement of
![]() ${\mathcal {Q}}(b, {\mathcal {T}})$
and
${\mathcal {Q}}(b, {\mathcal {T}})$
and
![]() ${\mathcal {Q}}(c, {\mathcal {T}})$
to a disagreement between
${\mathcal {Q}}(c, {\mathcal {T}})$
to a disagreement between
![]() $\Psi ^Z_X$
and
$\Psi ^Z_X$
and
![]() $\Psi ^Z_U$
for some extensions
$\Psi ^Z_U$
for some extensions
![]() $X,U$
of Z with
$X,U$
of Z with
![]() ${\mathcal {Q}}^Z_X={\mathcal {Q}}^Z_U$
. However, this cannot happen by Proposition 6.6 (the proof is given by [Reference Sargsyan and Trang38, Lemma 9.1.9]).
${\mathcal {Q}}^Z_X={\mathcal {Q}}^Z_U$
. However, this cannot happen by Proposition 6.6 (the proof is given by [Reference Sargsyan and Trang38, Lemma 9.1.9]).
8. Z-validated iterations
We continue by assuming T. Let
![]() $(S, S_0, \nu _0,\vec {Y}, \vec {A})$
again witness that T is true and let
$(S, S_0, \nu _0,\vec {Y}, \vec {A})$
again witness that T is true and let
![]() $\mu , g, \mathcal {H}$
, etc. be defined as in Section 4. The goal of this section is to introduce some concepts to be used in the
$\mu , g, \mathcal {H}$
, etc. be defined as in Section 4. The goal of this section is to introduce some concepts to be used in the
![]() $K^c$
construction of the next section. The main new concept here is the concept of Z-validated iterations, which are the kind of iterations that will appear in the
$K^c$
construction of the next section. The main new concept here is the concept of Z-validated iterations, which are the kind of iterations that will appear in the
![]() $K^c$
construction of the next section.
$K^c$
construction of the next section.
The following definition is important for this paper. It introduces the hulls that we will use to Z-validate mice, iterations, etc. It goes back to Steel’s [Reference Steel46].
Definition 8.1. Suppose
![]() ${\lambda }\in S_0-\mu $
and
${\lambda }\in S_0-\mu $
and
![]() $U \prec _1 H_{{\lambda }^+}$
. We say U is
$U \prec _1 H_{{\lambda }^+}$
. We say U is
![]() $(\mu , {\lambda }, Z)$
-good if
$(\mu , {\lambda }, Z)$
-good if
![]() $\mu \in U$
,
$\mu \in U$
,
![]() $(Y_{\mu }\cup Y_{\lambda } \cup Z)\subseteq U$
,
$(Y_{\mu }\cup Y_{\lambda } \cup Z)\subseteq U$
,
![]() $\vert {U}\vert <\mu $
,
$\vert {U}\vert <\mu $
,
![]() $U\cap {\mathcal { H}}^-$
is an honest extension of Z and
$U\cap {\mathcal { H}}^-$
is an honest extension of Z and
![]() $U^{\nu _0}\subseteq U$
. When
$U^{\nu _0}\subseteq U$
. When
![]() $\mu $
and
$\mu $
and
![]() ${\lambda }$
are clear from the context or are not important, we simply say U is a good hull. We say a good hull U is transitive below
${\lambda }$
are clear from the context or are not important, we simply say U is a good hull. We say a good hull U is transitive below
![]() $\mu $
if
$\mu $
if
![]() $U\cap \mu \in \mu $
$U\cap \mu \in \mu $
If U is a good hull, then we let
![]() $\pi _U : M_U = M \rightarrow H_{{\lambda }^+}$
be the inverse of the transitive collapse of U. If, in addition, U is transitive below
$\pi _U : M_U = M \rightarrow H_{{\lambda }^+}$
be the inverse of the transitive collapse of U. If, in addition, U is transitive below
![]() $\mu $
, we let
$\mu $
, we let
![]() $\pi _U^+:M_U[g_{\nu }]\rightarrow H_{\Omega }[g]$
, where
$\pi _U^+:M_U[g_{\nu }]\rightarrow H_{\Omega }[g]$
, where
![]() $\nu =\mathrm {crit }(\pi _U)$
and
$\nu =\mathrm {crit }(\pi _U)$
and
![]() $g_{\nu }=g\cap Coll(\omega , <\nu )$
.
$g_{\nu }=g\cap Coll(\omega , <\nu )$
.
Definition 8.2. Suppose
-
○
 ${\mathcal {R}}_0$
nicely extends
${\mathcal {R}}_0$
nicely extends
 ${\mathcal { H}}$
,
${\mathcal { H}}$
, -
○ p is an iteration of
 ${\mathcal {R}}_0$
,
${\mathcal {R}}_0$
, -
○ if p is
 ${\mathsf {nuvs}}$
, then setting
${\mathsf {nuvs}}$
, then setting
 ${\mathcal {R}}={\mathrm m}^+(p)$
,
${\mathcal {R}}={\mathrm m}^+(p)$
,
 ${\mathcal {M}}$
is an sts mouse over
${\mathcal {M}}$
is an sts mouse over
 ${\mathcal {R}}$
, and
${\mathcal {R}}$
, and -
○
 ${\lambda }\in S$
is the least such that
${\lambda }\in S$
is the least such that
 $({\mathcal {R}}, {\mathcal {M}}, p)\in H_{\lambda }$
.
$({\mathcal {R}}, {\mathcal {M}}, p)\in H_{\lambda }$
.
-
1. We say
 ${\mathcal {R}}$
is not infinitely descending if whenever U is a
${\mathcal {R}}$
is not infinitely descending if whenever U is a
 $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
 ${\mathcal {R}}\in U$
,
${\mathcal {R}}\in U$
,
 $\pi _U^{-1}({\mathcal {R}})$
is not infinitely descending.
$\pi _U^{-1}({\mathcal {R}})$
is not infinitely descending. -
2. We say p is Z -validated if whenever U is a
 $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
 $\{{\mathcal {R}}, p\}\subseteq U$
,
$\{{\mathcal {R}}, p\}\subseteq U$
,
 $\pi _U^{-1}(p)$
is a correctly guidedFootnote 90 Z-realizable iteration of
$\pi _U^{-1}(p)$
is a correctly guidedFootnote 90 Z-realizable iteration of
 $\pi _U^{-1}({\mathcal {R}})$
.
$\pi _U^{-1}({\mathcal {R}})$
. -
3. Suppose
 ${\mathcal {R}}$
is a weakly Z-suitable hod premouse above
${\mathcal {R}}$
is a weakly Z-suitable hod premouse above
 $\mu $
. We say
$\mu $
. We say
 ${\mathcal {M}}$
is a Z
-validated sts premouse over
${\mathcal {M}}$
is a Z
-validated sts premouse over
 ${\mathcal {R}}$
if for every
${\mathcal {R}}$
if for every
 $(\mu , {\lambda }, Z)$
-good hull U such that
$(\mu , {\lambda }, Z)$
-good hull U such that
 $\{{\mathcal {R}}, {\mathcal {M}}\}\subseteq U$
, letting
$\{{\mathcal {R}}, {\mathcal {M}}\}\subseteq U$
, letting
 ${\mathcal {N}}=\pi _U^{-1}({\mathcal {M}})$
,
${\mathcal {N}}=\pi _U^{-1}({\mathcal {M}})$
,
 ${\mathcal {N}}$
is a Z-approvedFootnote 91 sts premouse over
${\mathcal {N}}$
is a Z-approvedFootnote 91 sts premouse over
 $\pi ^{-1}_U({\mathcal {R}})$
.
$\pi ^{-1}_U({\mathcal {R}})$
. -
4. Suppose
 ${\mathcal {M}}$
is a Z-validated sts mouse over
${\mathcal {M}}$
is a Z-validated sts mouse over
 ${\mathcal {R}}$
and
${\mathcal {R}}$
and
 $\xi $
is an ordinal. We say
$\xi $
is an ordinal. We say
 ${\mathcal {M}}$
has a Z-validated
${\mathcal {M}}$
has a Z-validated
 $\xi $
-iteration strategy if there is
$\xi $
-iteration strategy if there is
 $\Sigma $
such that
$\Sigma $
such that
 $\Sigma $
is a
$\Sigma $
is a
 $\xi $
-iteration strategy and whenever
$\xi $
-iteration strategy and whenever
 ${\mathcal {N}}$
is an iterate of
${\mathcal {N}}$
is an iterate of
 ${\mathcal {M}}$
via
${\mathcal {M}}$
via
 $\Sigma $
,
$\Sigma $
,
 ${\mathcal {N}}$
is a Z-validated sts mouse over
${\mathcal {N}}$
is a Z-validated sts mouse over
 ${\mathcal {R}}$
.
${\mathcal {R}}$
. -
5. Suppose q is an iteration of
 ${\mathcal {R}}$
. We say q is Z
-validated if
${\mathcal {R}}$
. We say q is Z
-validated if
 $p^\frown q$
is Z-validated.
$p^\frown q$
is Z-validated.
The following proposition is very useful and is an immediate consequence of Proposition 7.9. When X is a good hull, we will use it as a subscript to denote the
![]() $\pi _X$
-preimages of objects that are in X.
$\pi _X$
-preimages of objects that are in X.
Proposition 8.3. Suppose
![]() $({\mathcal {R}}_0, p, {\mathcal {R}}, {\mathcal {M}}, {\lambda })$
are as in Definition 8.2. Suppose U is a
$({\mathcal {R}}_0, p, {\mathcal {R}}, {\mathcal {M}}, {\lambda })$
are as in Definition 8.2. Suppose U is a
![]() $(Z, \mu , {\lambda })$
-good hull such that
$(Z, \mu , {\lambda })$
-good hull such that
![]() $\{{\mathcal {R}}, {\mathcal {M}}\}\subseteq U$
and
$\{{\mathcal {R}}, {\mathcal {M}}\}\subseteq U$
and
![]() ${\mathcal {M}}_U$
is not Z-approved. Then whenever
${\mathcal {M}}_U$
is not Z-approved. Then whenever
![]() $U^*$
is a
$U^*$
is a
![]() $(Z, \mu , {\lambda })$
-good hull such that
$(Z, \mu , {\lambda })$
-good hull such that
![]() $U\cup \{U\}\subseteq U^*$
,
$U\cup \{U\}\subseteq U^*$
,
![]() ${\mathcal {M}}_{U^*}$
is not Z-approved.Footnote 92
${\mathcal {M}}_{U^*}$
is not Z-approved.Footnote 92
Similarly for iterations.
Proposition 8.4. Suppose
![]() $({\mathcal {R}}_0, p, {\lambda })$
are as in Definition 8.2. Suppose U is a
$({\mathcal {R}}_0, p, {\lambda })$
are as in Definition 8.2. Suppose U is a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() $\{{\mathcal {R}}_0, p\}\subseteq U$
and
$\{{\mathcal {R}}_0, p\}\subseteq U$
and
![]() $p_U$
is not Z-realizable. Then whenever
$p_U$
is not Z-realizable. Then whenever
![]() $U^*$
is a
$U^*$
is a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() $U\cup \{U\}\subseteq U^*$
,
$U\cup \{U\}\subseteq U^*$
,
![]() $p_{U^*}$
is not Z-realizable.Footnote 93
$p_{U^*}$
is not Z-realizable.Footnote 93
Definition 8.5. Suppose
![]() $({\mathcal {R}}_0, p, {\mathcal {R}}, \mu )$
are as in Definition 8.2. We let
$({\mathcal {R}}_0, p, {\mathcal {R}}, \mu )$
are as in Definition 8.2. We let
![]() $Lp^{Zv, sts}({\mathcal {R}})$
be the union of all Z-validated sound sts mice over
$Lp^{Zv, sts}({\mathcal {R}})$
be the union of all Z-validated sound sts mice over
![]() ${\mathcal {R}}$
that project to
${\mathcal {R}}$
that project to
![]() $Ord\cap {\mathcal {R}}$
.
$Ord\cap {\mathcal {R}}$
.
The following proposition is a consequence of Proposition 7.14.
Proposition 8.6. Suppose
![]() $({\mathcal {R}}_0, p, {\mathcal {R}}, \mu )$
are as in Definition 8.2 and
$({\mathcal {R}}_0, p, {\mathcal {R}}, \mu )$
are as in Definition 8.2 and
![]() ${\mathcal {R}}$
is not infinitely descending. Suppose
${\mathcal {R}}$
is not infinitely descending. Suppose
![]() ${\vec {\mathcal {T}}}$
is a Z-validated iteration of
${\vec {\mathcal {T}}}$
is a Z-validated iteration of
![]() ${\mathcal {R}}$
of limit length. Then there is at most one branch b of
${\mathcal {R}}$
of limit length. Then there is at most one branch b of
![]() ${\vec {\mathcal {T}}}$
such that
${\vec {\mathcal {T}}}$
such that
![]() ${\vec {\mathcal {T}}}^\frown \{b\}$
is Z-validated.
${\vec {\mathcal {T}}}^\frown \{b\}$
is Z-validated.
9. Realizability array
We continue with
![]() $(S, S_0, \nu _0,\vec {Y}, \vec {A})$
,
$(S, S_0, \nu _0,\vec {Y}, \vec {A})$
,
![]() $\mu \in S_0$
, etc. We define the notion of an array at
$\mu \in S_0$
, etc. We define the notion of an array at
![]() $\mu $
by induction. We say
$\mu $
by induction. We say
![]() $\vec {{\mathcal {V}}}={\mathcal {V}}_0$
is an array of length
$\vec {{\mathcal {V}}}={\mathcal {V}}_0$
is an array of length
![]() $0$
if
$0$
if
![]() ${\mathcal {V}}_0={\mathcal { H}}$
. Suppose we have already defined the meaning of array of length
${\mathcal {V}}_0={\mathcal { H}}$
. Suppose we have already defined the meaning of array of length
![]() $<\eta $
. We want to define the meaning of array of length
$<\eta $
. We want to define the meaning of array of length
![]() $\eta $
.
$\eta $
.
Definition 9.1. We say
![]() $\vec {{\mathcal {V}}}=({\mathcal {V}}_{\alpha }:{\alpha }\leq \eta )$
is an array of length
$\vec {{\mathcal {V}}}=({\mathcal {V}}_{\alpha }:{\alpha }\leq \eta )$
is an array of length
![]() $\eta $
at
$\eta $
at
![]() $\mu $
if the following conditions hold.
$\mu $
if the following conditions hold.
-
1. For every
 ${\alpha }<\eta $
,
${\alpha }<\eta $
,
 $({\mathcal {V}}_{\beta }:{\beta }\leq {\alpha })$
is an array of length
$({\mathcal {V}}_{\beta }:{\beta }\leq {\alpha })$
is an array of length
 ${\alpha }$
at
${\alpha }$
at
 $\mu $
.
$\mu $
. -
2.
 ${\mathcal {V}}_{\eta }$
nicely extends
${\mathcal {V}}_{\eta }$
nicely extends
 ${\mathcal { H}}$
and is a hod premouse.
${\mathcal { H}}$
and is a hod premouse. -
3. For all
 ${\alpha }<\eta $
, if
${\alpha }<\eta $
, if
 ${\mathcal {V}}_{\alpha }$
is weakly Z-suitable, then there is
${\mathcal {V}}_{\alpha }$
is weakly Z-suitable, then there is
 ${\beta }\leq \eta $
such that
${\beta }\leq \eta $
such that
 ${\mathcal {V}}_{\beta }$
is a Z-validated sts mouse over
${\mathcal {V}}_{\beta }$
is a Z-validated sts mouse over
 ${\mathcal {V}}_{\alpha }$
and
${\mathcal {V}}_{\alpha }$
and
 $rud({\mathcal {V}}_{\beta }){\vDash } $
‘there are no Woodin cardinals
$rud({\mathcal {V}}_{\beta }){\vDash } $
‘there are no Woodin cardinals
 $>{\delta }^{{\mathcal { H}}}$
’.
$>{\delta }^{{\mathcal { H}}}$
’. -
4. For all
 ${\alpha }<\eta $
, if
${\alpha }<\eta $
, if
 $rud({\mathcal {V}}_{\alpha }){\vDash } $
‘there are no Woodin cardinals
$rud({\mathcal {V}}_{\alpha }){\vDash } $
‘there are no Woodin cardinals
 $>{\delta }^{{\mathcal { H}}}$
’, then
$>{\delta }^{{\mathcal { H}}}$
’, then
 ${\mathcal {V}}_{\alpha }$
has a Z-validated iteration strategy.
${\mathcal {V}}_{\alpha }$
has a Z-validated iteration strategy.
We say
![]() $\vec {{\mathcal {V}}}$
is small if
$\vec {{\mathcal {V}}}$
is small if
![]() $rud({\mathcal {V}}_{\eta }){\vDash }$
‘there are no Woodin cardinals
$rud({\mathcal {V}}_{\eta }){\vDash }$
‘there are no Woodin cardinals
![]() $>{\delta }^{\mathcal { H}}$
’. We let
$>{\delta }^{\mathcal { H}}$
’. We let
![]() $\eta =lh(\vec {{\mathcal {V}}})$
and for
$\eta =lh(\vec {{\mathcal {V}}})$
and for
![]() ${\alpha }\leq \eta $
, we let
${\alpha }\leq \eta $
, we let
![]() $\vec {{\mathcal {V}}}{\restriction } {\alpha }=({\mathcal {V}}_{\beta }:{\beta }\leq {\alpha })$
.
$\vec {{\mathcal {V}}}{\restriction } {\alpha }=({\mathcal {V}}_{\beta }:{\beta }\leq {\alpha })$
.
Recall the notions of k-maximal iteration trees in [Reference Steel53, Definition 3.4] and weak k-embeddings [Reference Steel53, Definition 4.1]. For an iteration tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {M}}$
, letting
${\mathcal {M}}$
, letting
![]() ${\mathcal {M}}^{\mathcal {T}}_{\alpha }$
be the
${\mathcal {M}}^{\mathcal {T}}_{\alpha }$
be the
![]() $\alpha $
-th model in the tree; for
$\alpha $
-th model in the tree; for
![]() $\alpha +1<lh({\mathcal {T}})$
, recall the notion of degree
$\alpha +1<lh({\mathcal {T}})$
, recall the notion of degree
![]() $deg^{\mathcal {T}}(\alpha +1)$
[Reference Steel53, Definition 3.7]. Recall the definition of
$deg^{\mathcal {T}}(\alpha +1)$
[Reference Steel53, Definition 3.7]. Recall the definition of
![]() $D^{\mathcal {T}}$
: if
$D^{\mathcal {T}}$
: if
![]() $\alpha +1\in D$
, then the extender
$\alpha +1\in D$
, then the extender
![]() $E^{\mathcal {T}}_{\alpha +1}$
is applied to a strict initial segment of
$E^{\mathcal {T}}_{\alpha +1}$
is applied to a strict initial segment of
![]() ${\mathcal {M}}^{\mathcal {T}}_{\beta }$
, where
${\mathcal {M}}^{\mathcal {T}}_{\beta }$
, where
![]() $\beta = T-pred(\alpha +1)$
. For
$\beta = T-pred(\alpha +1)$
. For
![]() $\lambda $
limit,
$\lambda $
limit,
![]() $deg^{\mathcal {T}}(\lambda )$
is the eventual values of
$deg^{\mathcal {T}}(\lambda )$
is the eventual values of
![]() $deg^{\mathcal {T}}(\alpha +1)$
for
$deg^{\mathcal {T}}(\alpha +1)$
for
![]() $\alpha +1\in [0,\lambda ]_{\mathcal {T}}$
. For a cofinal branch b of
$\alpha +1\in [0,\lambda ]_{\mathcal {T}}$
. For a cofinal branch b of
![]() ${\mathcal {T}}$
,
${\mathcal {T}}$
,
![]() $deg^{\mathcal {T}}(b)$
is defined to be the eventual value of
$deg^{\mathcal {T}}(b)$
is defined to be the eventual value of
![]() $deg^{\mathcal {T}}(\alpha +1)$
for
$deg^{\mathcal {T}}(\alpha +1)$
for
![]() $\alpha +1\in b$
. We write
$\alpha +1\in b$
. We write
![]() $\mathcal {C}_k({\mathcal {M}})$
for the k-th core of
$\mathcal {C}_k({\mathcal {M}})$
for the k-th core of
![]() ${\mathcal {M}}$
. Sometimes, we confuse
${\mathcal {M}}$
. Sometimes, we confuse
![]() $\mathcal {C}_0({\mathcal {M}})$
with
$\mathcal {C}_0({\mathcal {M}})$
with
![]() ${\mathcal {M}}$
itself.
${\mathcal {M}}$
itself.
Definition 9.2. Suppose
![]() $\vec {{\mathcal {V}}}$
is an array at
$\vec {{\mathcal {V}}}$
is an array at
![]() $\mu $
. We say
$\mu $
. We say
![]() $\vec {{\mathcal {V}}}$
has the Z-realizability property if for all
$\vec {{\mathcal {V}}}$
has the Z-realizability property if for all
![]() ${\alpha }<lh({\mathcal {V}})$
,
${\alpha }<lh({\mathcal {V}})$
,
![]() $\vec {{\mathcal {V}}}{\restriction } {\alpha }$
has the Z-realizability property and whenever
$\vec {{\mathcal {V}}}{\restriction } {\alpha }$
has the Z-realizability property and whenever
![]() $g\subseteq Coll(\omega , <\mu )$
is generic, in
$g\subseteq Coll(\omega , <\mu )$
is generic, in
![]() $V[g]$
, whenever
$V[g]$
, whenever
![]() $\pi :{\mathcal {W}}\rightarrow \mathcal {C}_k({\mathcal {V}}_{\eta })$
and
$\pi :{\mathcal {W}}\rightarrow \mathcal {C}_k({\mathcal {V}}_{\eta })$
and
![]() ${\mathcal {T}}$
are such that
${\mathcal {T}}$
are such that
-
1.
 $\pi $
is a weak k-embedding,
$\pi $
is a weak k-embedding, -
2.
 $Z\subseteq rng(\pi )$
,
$Z\subseteq rng(\pi )$
, -
3.
 ${\mathcal {W}}, {\mathcal {T}}\in HC$
,
${\mathcal {W}}, {\mathcal {T}}\in HC$
, -
4.
 ${\mathcal {T}}$
is a correctly guided Z-realizableFootnote 94 k-maximal iteration of
${\mathcal {T}}$
is a correctly guided Z-realizableFootnote 94 k-maximal iteration of
 ${\mathcal {W}}$
that is above
${\mathcal {W}}$
that is above
 ${\delta }^{{\mathcal {W}}^b}$
,
${\delta }^{{\mathcal {W}}^b}$
,
one of the following holds (in
![]() $V[g]$
).
$V[g]$
).
-
1.
 ${\mathcal {T}}$
is of limit length and there is a cofinal well-founded branch c such that c has no drops in model (i.e.,
${\mathcal {T}}$
is of limit length and there is a cofinal well-founded branch c such that c has no drops in model (i.e.,
 $D^{\mathcal {T}}\cap b = \emptyset $
); letting
$D^{\mathcal {T}}\cap b = \emptyset $
); letting
 $l=deg^{\mathcal {T}}(b)$
, there is a weak l-embedding
$l=deg^{\mathcal {T}}(b)$
, there is a weak l-embedding
 $\tau :{\mathcal {M}}^{\mathcal {T}}_c\rightarrow \mathcal {C}_l({\mathcal {V}}_{\eta })$
such that
$\tau :{\mathcal {M}}^{\mathcal {T}}_c\rightarrow \mathcal {C}_l({\mathcal {V}}_{\eta })$
such that
 $\pi {\restriction } {\mathcal {W}}=\tau \circ \pi ^{\mathcal {T}}_c$
.
$\pi {\restriction } {\mathcal {W}}=\tau \circ \pi ^{\mathcal {T}}_c$
. -
2.
 ${\mathcal {T}}$
is of limit length and there is a cofinal well-founded branch c such that c has a drop in model, and there is
${\mathcal {T}}$
is of limit length and there is a cofinal well-founded branch c such that c has a drop in model, and there is
 ${\beta }<\eta $
and a weak l-embedding
${\beta }<\eta $
and a weak l-embedding
 $\tau :{\mathcal {M}}^{\mathcal {T}}_c\rightarrow \mathcal {C}_l({\mathcal {V}}_{\beta })$
such that
$\tau :{\mathcal {M}}^{\mathcal {T}}_c\rightarrow \mathcal {C}_l({\mathcal {V}}_{\beta })$
such that
 $\tau {\restriction } ({\mathcal {M}}^{\mathcal {T}}_c)^b=\pi {\restriction } ({\mathcal {M}}^{\mathcal {T}}_c)^b$
, where
$\tau {\restriction } ({\mathcal {M}}^{\mathcal {T}}_c)^b=\pi {\restriction } ({\mathcal {M}}^{\mathcal {T}}_c)^b$
, where
 $l=deg^{\mathcal {T}}(c)$
.
$l=deg^{\mathcal {T}}(c)$
. -
3.
 ${\mathcal {T}}$
has a last model and letting
${\mathcal {T}}$
has a last model and letting
 ${\gamma }=lh({\mathcal {T}})-1$
,
${\gamma }=lh({\mathcal {T}})-1$
,
 $[0, {\gamma }]_{\mathcal {T}}\cap \mathcal {D}^{\mathcal {T}}=\emptyset $
and there is a weak l-embedding
$[0, {\gamma }]_{\mathcal {T}}\cap \mathcal {D}^{\mathcal {T}}=\emptyset $
and there is a weak l-embedding
 $\tau :{\mathcal {M}}^{\mathcal {T}}_{\gamma }\rightarrow \mathcal {C}_l({\mathcal {V}}_{\eta })$
such that
$\tau :{\mathcal {M}}^{\mathcal {T}}_{\gamma }\rightarrow \mathcal {C}_l({\mathcal {V}}_{\eta })$
such that
 $\pi {\restriction } {\mathcal {W}}=\tau \circ \pi ^{\mathcal {T}}$
, where
$\pi {\restriction } {\mathcal {W}}=\tau \circ \pi ^{\mathcal {T}}$
, where
 $l = deg^{\mathcal {T}}(\gamma )$
.
$l = deg^{\mathcal {T}}(\gamma )$
. -
4.
 ${\mathcal {T}}$
has a last model and letting
${\mathcal {T}}$
has a last model and letting
 ${\gamma }=lh({\mathcal {T}})-1$
,
${\gamma }=lh({\mathcal {T}})-1$
,
 $[0, {\gamma }]_{\mathcal {T}}\cap \mathcal {D}^{\mathcal {T}}\not =\emptyset $
and for some
$[0, {\gamma }]_{\mathcal {T}}\cap \mathcal {D}^{\mathcal {T}}\not =\emptyset $
and for some
 ${\beta }<\eta $
, there is a weak l-embedding
${\beta }<\eta $
, there is a weak l-embedding
 $\tau :{\mathcal {M}}^{\mathcal {T}}_{\gamma }\rightarrow \mathcal {C}_l({\mathcal {V}}_{\beta })$
such that
$\tau :{\mathcal {M}}^{\mathcal {T}}_{\gamma }\rightarrow \mathcal {C}_l({\mathcal {V}}_{\beta })$
such that
 $\tau {\restriction } ({\mathcal {M}}^{\mathcal {T}}_{\gamma })^b=\pi {\restriction } ({\mathcal {M}}^{\mathcal {T}}_{\gamma })^b$
, where
$\tau {\restriction } ({\mathcal {M}}^{\mathcal {T}}_{\gamma })^b=\pi {\restriction } ({\mathcal {M}}^{\mathcal {T}}_{\gamma })^b$
, where
 $l = deg^{\mathcal {T}}(\gamma )$
.
$l = deg^{\mathcal {T}}(\gamma )$
.
When the above 4 clauses hold, we say that
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $(\pi , \vec {{\mathcal {V}}})$
-realizable.
$(\pi , \vec {{\mathcal {V}}})$
-realizable.
In the following, we will follow the convention in [Reference Steel55, Section 1.3]: a (hod, hybrid, or pure extender) premouse has the form
![]() $({\mathcal {M}},k)$
, where
$({\mathcal {M}},k)$
, where
![]() ${\mathcal {M}}$
is a k-sound, acceptable J-structure.
${\mathcal {M}}$
is a k-sound, acceptable J-structure.
![]() $k({\mathcal {M}}) = k$
is the degree of soundness of
$k({\mathcal {M}}) = k$
is the degree of soundness of
![]() ${\mathcal {M}}$
. We write the core
${\mathcal {M}}$
. We write the core
![]() $\mathcal {C}({\mathcal {M}})$
for the (
$\mathcal {C}({\mathcal {M}})$
for the (
![]() $k({\mathcal {M}})+1$
-)core of
$k({\mathcal {M}})+1$
-)core of
![]() ${\mathcal {M}}$
(if this makes sense – that is, when
${\mathcal {M}}$
(if this makes sense – that is, when
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() $k({\mathcal {M}})+1$
-solid). Similarly, we write
$k({\mathcal {M}})+1$
-solid). Similarly, we write
![]() $\rho ({\mathcal {M}})$
for the
$\rho ({\mathcal {M}})$
for the
![]() $k({\mathcal {M}})+1$
-projectum and
$k({\mathcal {M}})+1$
-projectum and
![]() $p({\mathcal {M}})$
for the
$p({\mathcal {M}})$
for the
![]() $k({\mathcal {M}})+1$
-standard parameters of
$k({\mathcal {M}})+1$
-standard parameters of
![]() ${\mathcal {M}}$
. When
${\mathcal {M}}$
. When
![]() $\mathcal {C}({\mathcal {M}})$
exists,
$\mathcal {C}({\mathcal {M}})$
exists,
![]() $k(\mathcal {C}({\mathcal {M}})) = k({\mathcal {M}})+1$
.
$k(\mathcal {C}({\mathcal {M}})) = k({\mathcal {M}})+1$
.
![]() ${\mathcal {M}}$
is sound iff
${\mathcal {M}}$
is sound iff
![]() ${\mathcal {M}} = \mathcal {C}({\mathcal {M}})$
. We allow our iterations (e.g., Z-validated iterations) to consist of stacks of normal trees, where we may drop gratuitously at the start of a tree.
${\mathcal {M}} = \mathcal {C}({\mathcal {M}})$
. We allow our iterations (e.g., Z-validated iterations) to consist of stacks of normal trees, where we may drop gratuitously at the start of a tree.
Proposition 9.3. Suppose
![]() $\vec {{\mathcal {V}}}$
is an array with Z-realizability property. Assume further that p is a Z-validated iteration of
$\vec {{\mathcal {V}}}$
is an array with Z-realizability property. Assume further that p is a Z-validated iteration of
![]() $\mathcal {C}_n({\mathcal {V}}_{\eta })$
(for some n) with last model
$\mathcal {C}_n({\mathcal {V}}_{\eta })$
(for some n) with last model
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $\pi ^p$
exists and all the generators of p are contained in
$\pi ^p$
exists and all the generators of p are contained in
![]() ${\delta }^{{\mathcal {R}}^b}$
. Suppose U is a good hull such that
${\delta }^{{\mathcal {R}}^b}$
. Suppose U is a good hull such that
![]() $(\vec {{\mathcal {V}}}, {\mathcal {R}}, p)\in U$
. Let
$(\vec {{\mathcal {V}}}, {\mathcal {R}}, p)\in U$
. Let
![]() ${\mathcal {R}}_U = \pi _U^{-1}({\mathcal {R}}), p_U = \pi ^{-1}(p), {\mathcal {W}} = \pi ^{-1}(\mathcal {C}({\mathcal {V}}_{\eta }))$
. There is then a weak n-embedding
${\mathcal {R}}_U = \pi _U^{-1}({\mathcal {R}}), p_U = \pi ^{-1}(p), {\mathcal {W}} = \pi ^{-1}(\mathcal {C}({\mathcal {V}}_{\eta }))$
. There is then a weak n-embedding
![]() $k:{\mathcal {R}}_U\rightarrow \mathcal {C}_n({\mathcal {V}}_{\eta })$
such that
$k:{\mathcal {R}}_U\rightarrow \mathcal {C}_n({\mathcal {V}}_{\eta })$
such that
![]() $\pi _U{\restriction } {\mathcal {W}}=k\circ \pi ^{p_U}$
.
$\pi _U{\restriction } {\mathcal {W}}=k\circ \pi ^{p_U}$
.
Proof. As p is Z-realizable, letting
![]() $X=U\cap {\mathcal { H}}^-$
, we can find a Y extending
$X=U\cap {\mathcal { H}}^-$
, we can find a Y extending
![]() $Z\oplus X$
such that
$Z\oplus X$
such that
![]() ${\mathcal {Q}}^Z_Y={\mathcal {R}}^b_U$
and
${\mathcal {Q}}^Z_Y={\mathcal {R}}^b_U$
and
![]() $\tau ^Z_X=\tau ^Z_Y\circ \pi ^{p_U, b}$
. Let E be the
$\tau ^Z_X=\tau ^Z_Y\circ \pi ^{p_U, b}$
. Let E be the
![]() $({\delta }^{{\mathcal {R}}_U^b}, {\delta }^{{\mathcal { H}}})$
-extender derived from
$({\delta }^{{\mathcal {R}}_U^b}, {\delta }^{{\mathcal { H}}})$
-extender derived from
![]() $\tau ^Z_Y$
and
$\tau ^Z_Y$
and
![]() $i:Ult({\mathcal {R}}_U, E)\rightarrow \mathcal {C}_n({\mathcal {V}}_{\eta })$
be the factor map given by
$i:Ult({\mathcal {R}}_U, E)\rightarrow \mathcal {C}_n({\mathcal {V}}_{\eta })$
be the factor map given by
![]() $i(\pi ^p(f)(a))=\pi _U(f)(\tau ^Z_Y(a))$
. It then follows that
$i(\pi ^p(f)(a))=\pi _U(f)(\tau ^Z_Y(a))$
. It then follows that
![]() $i\circ \pi _E$
is as desired.
$i\circ \pi _E$
is as desired.
Next, we introduce a weak notion of realizability.
Definition 9.4. Suppose
![]() $\vec {{\mathcal {V}}}$
is an array of length
$\vec {{\mathcal {V}}}$
is an array of length
![]() $\eta $
that has the Z-realizability property and p is a Z-validated iteration of
$\eta $
that has the Z-realizability property and p is a Z-validated iteration of
![]() $\mathcal {C}_n({\mathcal {V}}_{\eta })$
with last model
$\mathcal {C}_n({\mathcal {V}}_{\eta })$
with last model
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $\pi ^p$
exists and the generators of p are contained in
$\pi ^p$
exists and the generators of p are contained in
![]() ${\delta }^{{\mathcal {R}}^b}$
. Suppose
${\delta }^{{\mathcal {R}}^b}$
. Suppose
![]() ${\mathcal {T}}$
is an
${\mathcal {T}}$
is an
![]() $\mathsf {nuvs}$
iteration of
$\mathsf {nuvs}$
iteration of
![]() ${\mathcal {R}}$
that is above
${\mathcal {R}}$
that is above
![]() ${\delta }^{{\mathcal {R}}^b}$
. We say b is
${\delta }^{{\mathcal {R}}^b}$
. We say b is
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable branch of
$(Z, \vec {{\mathcal {V}}})$
-embeddable branch of
![]() ${\mathcal {T}}$
if whenever
${\mathcal {T}}$
if whenever
![]() ${\lambda }\in S$
is such that
${\lambda }\in S$
is such that
![]() $({\mathcal {R}}, {\mathcal {T}}, \vec {{\mathcal {V}}})\in V_{\lambda }$
and U is a
$({\mathcal {R}}, {\mathcal {T}}, \vec {{\mathcal {V}}})\in V_{\lambda }$
and U is a
![]() $(\mu , {\lambda },Z)$
-good hull with
$(\mu , {\lambda },Z)$
-good hull with
![]() $(\vec {{\mathcal {V}}}, {\mathcal {R}}, {\mathcal {T}}, b)\in U$
, there is
$(\vec {{\mathcal {V}}}, {\mathcal {R}}, {\mathcal {T}}, b)\in U$
, there is
![]() ${\alpha }\leq lh(\vec {{\mathcal {V}}})$
, some l, and a weak l-embedding
${\alpha }\leq lh(\vec {{\mathcal {V}}})$
, some l, and a weak l-embedding
![]() $k:{\mathcal {M}}^{{\mathcal {T}}_U}_{b_U}\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
.
$k:{\mathcal {M}}^{{\mathcal {T}}_U}_{b_U}\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
.
Proposition 9.5. Suppose
![]() $\vec {{\mathcal {V}}}$
is a small array with the Z-realizability property. Set
$\vec {{\mathcal {V}}}$
is a small array with the Z-realizability property. Set
![]() $\eta =lh(\vec {{\mathcal {V}}})$
. Suppose further that p is a Z-validated iteration of
$\eta =lh(\vec {{\mathcal {V}}})$
. Suppose further that p is a Z-validated iteration of
![]() $\mathcal {C}_n({\mathcal {V}}_{\eta })$
with last model
$\mathcal {C}_n({\mathcal {V}}_{\eta })$
with last model
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $\pi ^{p}$
exists and the generators of p are contained in
$\pi ^{p}$
exists and the generators of p are contained in
![]() ${\delta }^{{\mathcal {R}}^b}$
. Additionally, suppose that
${\delta }^{{\mathcal {R}}^b}$
. Additionally, suppose that
![]() ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
![]() ${\mathcal {R}}$
above
${\mathcal {R}}$
above
![]() ${\delta }^{{\mathcal {R}}^b}$
such that
${\delta }^{{\mathcal {R}}^b}$
such that
![]() $p^\frown {\mathcal {T}}$
is Z-validated iteration of
$p^\frown {\mathcal {T}}$
is Z-validated iteration of
![]() ${\mathcal {V}}_{\eta }$
. Then for all limit
${\mathcal {V}}_{\eta }$
. Then for all limit
![]() ${\alpha }<lh({\mathcal {T}})$
, if
${\alpha }<lh({\mathcal {T}})$
, if
![]() ${\mathcal {T}}{\restriction } {\alpha }$
is
${\mathcal {T}}{\restriction } {\alpha }$
is
![]() $\mathsf {nuvs}$
, then
$\mathsf {nuvs}$
, then
![]() $[0, {\alpha }]_{\mathcal {T}}$
is the unique branch c of
$[0, {\alpha }]_{\mathcal {T}}$
is the unique branch c of
![]() ${\mathcal {T}}{\restriction } {\alpha }$
such that
${\mathcal {T}}{\restriction } {\alpha }$
such that
![]() ${\mathcal {Q}}(c, {\mathcal {T}}{\restriction } {\alpha })$
exists and is
${\mathcal {Q}}(c, {\mathcal {T}}{\restriction } {\alpha })$
exists and is
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable.
$(Z, \vec {{\mathcal {V}}})$
-embeddable.
Proof. We first show that
![]() $c=_{def}[0, {\alpha }]_{\mathcal {T}}$
is
$c=_{def}[0, {\alpha }]_{\mathcal {T}}$
is
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable. Towards contradiction, assume not and suppose
$(Z, \vec {{\mathcal {V}}})$
-embeddable. Towards contradiction, assume not and suppose
![]() ${\alpha }$
is least such that
${\alpha }$
is least such that
![]() ${\mathcal {T}}{\restriction } {\alpha }$
is
${\mathcal {T}}{\restriction } {\alpha }$
is
![]() $\mathsf {nuvs}$
but
$\mathsf {nuvs}$
but
![]() $[0, {\alpha }]_{\mathcal {T}}$
is not
$[0, {\alpha }]_{\mathcal {T}}$
is not
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable. Let U be a
$(Z, \vec {{\mathcal {V}}})$
-embeddable. Let U be a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() $({\mathcal {R}}, \vec {{\mathcal {V}}},p, {\mathcal {T}}, {\alpha })\in U$
. Let
$({\mathcal {R}}, \vec {{\mathcal {V}}},p, {\mathcal {T}}, {\alpha })\in U$
. Let
![]() ${\mathcal {V}}'=\pi _U^{-1}(\mathcal {C}_n({\mathcal {V}}_{\eta }))$
and
${\mathcal {V}}'=\pi _U^{-1}(\mathcal {C}_n({\mathcal {V}}_{\eta }))$
and
![]() $k:{\mathcal {R}}_U\rightarrow \mathcal {C}_n({\mathcal {V}}_{\eta })$
be such that
$k:{\mathcal {R}}_U\rightarrow \mathcal {C}_n({\mathcal {V}}_{\eta })$
be such that
![]() $\pi _U{\restriction } {\mathcal {V}}'=k\circ \pi ^{p_U}$
.
$\pi _U{\restriction } {\mathcal {V}}'=k\circ \pi ^{p_U}$
.
We now have a cofinal branch d of
![]() ${\mathcal {T}}_U{\restriction } {\alpha }_U$
such that for some
${\mathcal {T}}_U{\restriction } {\alpha }_U$
such that for some
![]() ${\beta }\leq \eta $
, there is
${\beta }\leq \eta $
, there is
![]() $m:{\mathcal {M}}^{{\mathcal {T}}_U{\restriction } {\alpha }_U}_d\rightarrow {\mathcal {V}}_{\beta }$
and
$m:{\mathcal {M}}^{{\mathcal {T}}_U{\restriction } {\alpha }_U}_d\rightarrow {\mathcal {V}}_{\beta }$
and
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U{\restriction } {\alpha }_U)$
exists.Footnote 95 Let
${\mathcal {Q}}(d, {\mathcal {T}}_U{\restriction } {\alpha }_U)$
exists.Footnote 95 Let
![]() ${\mathcal {M}}={\mathcal {Q}}(d, {\mathcal {T}}_U{\restriction } {\alpha }_U)$
and
${\mathcal {M}}={\mathcal {Q}}(d, {\mathcal {T}}_U{\restriction } {\alpha }_U)$
and
![]() ${\mathcal {N}}={\mathcal {Q}}(c_U, {\mathcal {T}}_U{\restriction } {\alpha }_U)$
. Both
${\mathcal {N}}={\mathcal {Q}}(c_U, {\mathcal {T}}_U{\restriction } {\alpha }_U)$
. Both
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() ${\mathcal {N}}$
are Z-approved. Let
${\mathcal {N}}$
are Z-approved. Let
![]() ${\mathcal {S}}_0={\mathrm m}^+({\mathcal {T}}_U{\restriction } {\alpha }_U)$
. If we could conclude that
${\mathcal {S}}_0={\mathrm m}^+({\mathcal {T}}_U{\restriction } {\alpha }_U)$
. If we could conclude that
![]() ${\mathcal {M}}={\mathcal {N}}$
, then we would get that
${\mathcal {M}}={\mathcal {N}}$
, then we would get that
![]() $c_U=d$
, and that would finish the proof. To conclude that
$c_U=d$
, and that would finish the proof. To conclude that
![]() ${\mathcal {M}}={\mathcal {N}}$
, we need to argue that
${\mathcal {M}}={\mathcal {N}}$
, we need to argue that
![]() ${\mathcal {S}}_0$
is not infinitely descending.Footnote 96 The reader may wish to review Definition 7.13 and the discussion after Proposition 7.14.Footnote 97
${\mathcal {S}}_0$
is not infinitely descending.Footnote 96 The reader may wish to review Definition 7.13 and the discussion after Proposition 7.14.Footnote 97
Claim. Suppose
![]() ${\mathcal {S}}_0$
is infinitely descending. Then there is a sequence
${\mathcal {S}}_0$
is infinitely descending. Then there is a sequence
![]() $(p_i, {\mathcal {S}}_i: i<\omega )$
witnessing that
$(p_i, {\mathcal {S}}_i: i<\omega )$
witnessing that
![]() ${\mathcal {S}}_0$
is infinitely descending such that for some
${\mathcal {S}}_0$
is infinitely descending such that for some
![]() ${\beta }'<\eta $
and for some
${\beta }'<\eta $
and for some
![]() $i_0<\omega $
for every
$i_0<\omega $
for every
![]() $i<j\in (i_0, \omega )$
, there are weak
$i<j\in (i_0, \omega )$
, there are weak
![]() $n_i$
-embeddings
$n_i$
-embeddings
![]() $m_i:{\mathcal {S}}_i\rightarrow \mathcal {C}_{n_i}({\mathcal {V}}_{{\beta }'})$
such that
$m_i:{\mathcal {S}}_i\rightarrow \mathcal {C}_{n_i}({\mathcal {V}}_{{\beta }'})$
such that
![]() $m_i=m_j\circ \pi ^{p_i}$
.
$m_i=m_j\circ \pi ^{p_i}$
.
Proof. Set
![]() $m_0=m$
,
$m_0=m$
,
![]() ${\mathcal {S}}_0={\mathcal {S}}$
and
${\mathcal {S}}_0={\mathcal {S}}$
and
![]() ${\beta }_0=\beta $
. We build the sequence by induction. As the successive steps of the induction are the same as the first step, we only do the first step. Let
${\beta }_0=\beta $
. We build the sequence by induction. As the successive steps of the induction are the same as the first step, we only do the first step. Let
![]() $(p_i', {\mathcal {S}}_i': i<\omega )$
be any sequence witnessing that
$(p_i', {\mathcal {S}}_i': i<\omega )$
be any sequence witnessing that
![]() ${\mathcal {S}}_0$
is infinitely descending. We now have two cases. Suppose first that there is
${\mathcal {S}}_0$
is infinitely descending. We now have two cases. Suppose first that there is
![]() ${\beta }_1\leq {\beta }_0$
and a weak k-embedding
${\beta }_1\leq {\beta }_0$
and a weak k-embedding
![]() $m_1:{\mathcal {S}}_1'\rightarrow \mathcal {C}_k({\mathcal {V}}_{{\beta }_1})$
such that if
$m_1:{\mathcal {S}}_1'\rightarrow \mathcal {C}_k({\mathcal {V}}_{{\beta }_1})$
such that if
![]() ${\beta }_1={\beta }_0$
, then
${\beta }_1={\beta }_0$
, then
![]() $m_0=m_1\circ \pi ^{p_0'}$
. In this case, set
$m_0=m_1\circ \pi ^{p_0'}$
. In this case, set
![]() $p_0=p_0'$
and
$p_0=p_0'$
and
![]() ${\mathcal {S}}_1={\mathcal {S}}_1'$
. Notice that
${\mathcal {S}}_1={\mathcal {S}}_1'$
. Notice that
![]() ${\mathcal {S}}_1$
is infinitely descending. Suppose next that there is no such pair
${\mathcal {S}}_1$
is infinitely descending. Suppose next that there is no such pair
![]() $({\beta }_1, m_1)$
. In this case, we have
$({\beta }_1, m_1)$
. In this case, we have
![]() $d_1, {\beta }_1, m_1, n_1$
such that
$d_1, {\beta }_1, m_1, n_1$
such that
-
1.
 ${\beta }_1\leq {\beta }_0$
,
${\beta }_1\leq {\beta }_0$
, -
2.
 $d_1$
is a maximal branch of
$d_1$
is a maximal branch of
 $p_1'{\restriction } \epsilon $
for some
$p_1'{\restriction } \epsilon $
for some
 $\epsilon <lh(p_1')$
,
$\epsilon <lh(p_1')$
, -
3.
 $m_1:{\mathcal {M}}^{p_1'{\restriction } \epsilon }_{d_1}\rightarrow \mathcal {C}_{n_1}({\mathcal {V}}_{{\beta }_1})$
,
$m_1:{\mathcal {M}}^{p_1'{\restriction } \epsilon }_{d_1}\rightarrow \mathcal {C}_{n_1}({\mathcal {V}}_{{\beta }_1})$
, -
4. if
 ${\beta }_1={\beta }_0$
, then
${\beta }_1={\beta }_0$
, then
 $m_0=m_1\circ \pi ^{p_1'{\restriction } \epsilon }_{d_1}$
.
$m_0=m_1\circ \pi ^{p_1'{\restriction } \epsilon }_{d_1}$
.
In this case, set
![]() $p_1=p_1'{\restriction } \epsilon ^\frown \{d_1\}$
and
$p_1=p_1'{\restriction } \epsilon ^\frown \{d_1\}$
and
![]() ${\mathcal {S}}_1={\mathcal {M}}^{p_1'{\restriction } \epsilon }_{d_1}$
, with
${\mathcal {S}}_1={\mathcal {M}}^{p_1'{\restriction } \epsilon }_{d_1}$
, with
![]() ${\beta }_1$
and
${\beta }_1$
and
![]() $m_1$
as above. We now claim that
$m_1$
as above. We now claim that
![]() ${\mathcal {S}}_1$
is still infinitely descending. To see this, let
${\mathcal {S}}_1$
is still infinitely descending. To see this, let
![]() $c=[0, \epsilon )_{p^{\prime }_1}$
. Notice that we must have that
$c=[0, \epsilon )_{p^{\prime }_1}$
. Notice that we must have that
![]() ${\mathcal {Q}}(c, p^{\prime }_1{\restriction } \epsilon )\not ={\mathcal {Q}}(d_1, p^{\prime }_1{\restriction } \epsilon )$
. As both are Z-approved, we must have that
${\mathcal {Q}}(c, p^{\prime }_1{\restriction } \epsilon )\not ={\mathcal {Q}}(d_1, p^{\prime }_1{\restriction } \epsilon )$
. As both are Z-approved, we must have that
![]() ${\mathcal {S}}_1$
is infinitely descending. Continuing in this manner, we get the sequence we desire.
${\mathcal {S}}_1$
is infinitely descending. Continuing in this manner, we get the sequence we desire.
The existence of a sequence as in the claim above gives us a contradiction, as the sequence must have a well-founded branch. The uniqueness proof is similar to the proof of the claim above, and we leave it to our reader.
Remark 9.6. If the iteration p in Propositions 9.3 and 9.5 drops, we can still embed
![]() ${\mathcal {R}}_U$
by some map
${\mathcal {R}}_U$
by some map
![]() $k: {\mathcal {R}}_U \rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
for some
$k: {\mathcal {R}}_U \rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
for some
![]() $\alpha < \epsilon $
and some
$\alpha < \epsilon $
and some
![]() $l<\omega $
. In this case, there is some model
$l<\omega $
. In this case, there is some model
![]() ${\mathcal {M}}\in p$
such that
${\mathcal {M}}\in p$
such that
![]() $\pi ^{p_U}_{{\mathcal {M}}_U,{\mathcal {R}}_U}$
exists and there is a weak l-embedding
$\pi ^{p_U}_{{\mathcal {M}}_U,{\mathcal {R}}_U}$
exists and there is a weak l-embedding
![]() $\sigma : {\mathcal {M}}_U\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
such that
$\sigma : {\mathcal {M}}_U\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
such that
![]() $\sigma = k\circ \pi ^{p_U}_{{\mathcal {M}}_U,{\mathcal {R}}_U}$
.
$\sigma = k\circ \pi ^{p_U}_{{\mathcal {M}}_U,{\mathcal {R}}_U}$
.
Remark 9.7. The fact that
![]() ${\mathcal {V}}$
is small is key to the proof of Proposition 9.5. See Proposition 10.6, which partially deals with the situation when
${\mathcal {V}}$
is small is key to the proof of Proposition 9.5. See Proposition 10.6, which partially deals with the situation when
![]() ${\mathcal {V}}$
is not small.
${\mathcal {V}}$
is not small.
Motivated by Proposition 9.5, we make the following definitions.
Definition 9.8. We say
![]() ${\mathcal {R}}$
is weakly Z
-suitable above
${\mathcal {R}}$
is weakly Z
-suitable above
![]() $\mu $
if
$\mu $
if
![]() ${\mathcal {R}}$
is a hod premouse of lsa type such that
${\mathcal {R}}$
is a hod premouse of lsa type such that
![]() ${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^{\#}$
and whenever
${\mathcal {R}}=({\mathcal {R}}|{\delta }^{\mathcal {R}})^{\#}$
and whenever
![]() ${\lambda }\in S$
is such that
${\lambda }\in S$
is such that
![]() ${\mathcal {R}}\in V_{\lambda }$
and U is a
${\mathcal {R}}\in V_{\lambda }$
and U is a
![]() $(\mu , {\lambda }, Z)$
-good hull,
$(\mu , {\lambda }, Z)$
-good hull,
![]() ${\mathcal {R}}_U$
is weakly Z-suitable.Footnote 98
${\mathcal {R}}_U$
is weakly Z-suitable.Footnote 98
Definition 9.9. Suppose
![]() ${\mathcal {R}}$
is weakly Z-suitable above
${\mathcal {R}}$
is weakly Z-suitable above
![]() $\mu $
. We say
$\mu $
. We say
![]() ${\mathcal {R}}$
is honest if there is an array
${\mathcal {R}}$
is honest if there is an array
![]() $\vec {{\mathcal {V}}}=({\mathcal {V}}_{\alpha }:{\alpha }\leq \eta )$
at
$\vec {{\mathcal {V}}}=({\mathcal {V}}_{\alpha }:{\alpha }\leq \eta )$
at
![]() $\mu $
with the Z-realizability property such that letting
$\mu $
with the Z-realizability property such that letting
![]() ${\lambda }\in S$
be the least such that
${\lambda }\in S$
be the least such that
![]() ${\mathcal {R}}, \vec {{\mathcal {V}}}\in V_{\lambda }$
, the following conditions hold.
${\mathcal {R}}, \vec {{\mathcal {V}}}\in V_{\lambda }$
, the following conditions hold.
-
1. Either
 ${\mathcal {V}}_{\eta }={\mathcal {R}}$
or there is a Z-validated iteration p of
${\mathcal {V}}_{\eta }={\mathcal {R}}$
or there is a Z-validated iteration p of
 ${\mathcal {V}}_{\eta }$
of limit length such that
${\mathcal {V}}_{\eta }$
of limit length such that
 $\pi ^{p, b}$
exists and
$\pi ^{p, b}$
exists and
 ${\mathcal {R}}={\mathrm m}^+(p)$
.
${\mathcal {R}}={\mathrm m}^+(p)$
. -
2.
 $\vec {{\mathcal {V}}}$
is small if and only if
$\vec {{\mathcal {V}}}$
is small if and only if
 ${\mathcal {V}}_{\eta } \not ={\mathcal {R}}$
.
${\mathcal {V}}_{\eta } \not ={\mathcal {R}}$
.
If
![]() ${\mathcal {R}}$
is honest and
${\mathcal {R}}$
is honest and
![]() $\vec {{\mathcal {V}}}$
is as above, then we say that
$\vec {{\mathcal {V}}}$
is as above, then we say that
![]() $\vec {{\mathcal {V}}}$
is an honesty certificate for
$\vec {{\mathcal {V}}}$
is an honesty certificate for
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
Suppose
![]() ${\mathcal {R}}$
is honest as witnessed by
${\mathcal {R}}$
is honest as witnessed by
![]() $(\vec {{\mathcal {V}}}, p)$
. Then we say
$(\vec {{\mathcal {V}}}, p)$
. Then we say
![]() ${\mathcal {T}}$
is a Z-validated iteration of
${\mathcal {T}}$
is a Z-validated iteration of
![]() ${\mathcal {R}}$
if
${\mathcal {R}}$
if
![]() $p^\frown {\mathcal {T}}$
is a Z-validated iteration of
$p^\frown {\mathcal {T}}$
is a Z-validated iteration of
![]() ${\mathcal {V}}_{\eta }$
where
${\mathcal {V}}_{\eta }$
where
![]() $\eta +1=lh(\vec {{\mathcal {V}}})$
.
$\eta +1=lh(\vec {{\mathcal {V}}})$
.
Proposition 9.10. Suppose
![]() ${\mathcal {R}}$
is weakly Z-suitable above
${\mathcal {R}}$
is weakly Z-suitable above
![]() $\mu $
and
$\mu $
and
![]() $(\vec {{\mathcal {V}}}, p)$
is an honesty witness, and suppose
$(\vec {{\mathcal {V}}}, p)$
is an honesty witness, and suppose
![]() ${\mathcal {T}}$
is a Z-validated
${\mathcal {T}}$
is a Z-validated
![]() $\mathsf {nuvs}$
iteration of
$\mathsf {nuvs}$
iteration of
![]() ${\mathcal {R}}$
with last model
${\mathcal {R}}$
with last model
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() $\pi ^{{\mathcal {T}}}$
exists and the generators of
$\pi ^{{\mathcal {T}}}$
exists and the generators of
![]() ${\mathcal {T}}$
are contained in
${\mathcal {T}}$
are contained in
![]() ${\delta }^{{\mathcal {S}}^b}$
. Suppose U is a good hull such that
${\delta }^{{\mathcal {S}}^b}$
. Suppose U is a good hull such that
![]() $({\mathcal {R}}, \vec {{\mathcal {V}}}, p, {\mathcal {T}}, {\mathcal {S}})\in U$
. There is then
$({\mathcal {R}}, \vec {{\mathcal {V}}}, p, {\mathcal {T}}, {\mathcal {S}})\in U$
. There is then
![]() ${\alpha }\leq lh(\vec {{\mathcal {V}}})$
, a Z-approved sts mouse
${\alpha }\leq lh(\vec {{\mathcal {V}}})$
, a Z-approved sts mouse
![]() ${\mathcal {M}}$
over
${\mathcal {M}}$
over
![]() ${\mathcal {R}}_U$
, an embedding
${\mathcal {R}}_U$
, an embedding
![]() $k:{\mathcal {M}}\rightarrow \mathcal {C}({\mathcal {V}}_{\alpha })$
and an embedding
$k:{\mathcal {M}}\rightarrow \mathcal {C}({\mathcal {V}}_{\alpha })$
and an embedding
![]() $\sigma :{\mathcal {S}}_U\rightarrow \mathcal {C}({\mathcal {V}}_{\alpha })$
such that
$\sigma :{\mathcal {S}}_U\rightarrow \mathcal {C}({\mathcal {V}}_{\alpha })$
such that
-
1.
 ${\mathcal {M}}{\vDash } \text {`}{\delta }^{\mathcal {R}}$
is a Woodin cardinal’,
${\mathcal {M}}{\vDash } \text {`}{\delta }^{\mathcal {R}}$
is a Woodin cardinal’, -
2.
 $k{\restriction } {\mathcal {R}}_U=\sigma \circ \pi ^{{\mathcal {T}}_U}$
,
$k{\restriction } {\mathcal {R}}_U=\sigma \circ \pi ^{{\mathcal {T}}_U}$
, -
3.
 ${\mathcal {M}}\not ={\mathcal {R}}_U$
if and only if
${\mathcal {M}}\not ={\mathcal {R}}_U$
if and only if
 ${\mathcal {R}}\not =\mathcal {C}({\mathcal {V}}_{\eta })$
(so
${\mathcal {R}}\not =\mathcal {C}({\mathcal {V}}_{\eta })$
(so
 $\vec {{\mathcal {V}}}$
is small), and
$\vec {{\mathcal {V}}}$
is small), and -
4. if
 ${\mathcal {M}}\not ={\mathcal {R}}_U$
, then
${\mathcal {M}}\not ={\mathcal {R}}_U$
, then
 $rud({\mathcal {M}}){\vDash } \text {`}{\delta }^{\mathcal {R}}$
is not a Woodin cardinal’.
$rud({\mathcal {M}}){\vDash } \text {`}{\delta }^{\mathcal {R}}$
is not a Woodin cardinal’.
Proof. First, we claim that there is
![]() ${\alpha }\leq lh(\vec {{\mathcal {V}}})$
, an
${\alpha }\leq lh(\vec {{\mathcal {V}}})$
, an
![]() $l<\omega $
, and a weak l-embedding
$l<\omega $
, and a weak l-embedding
![]() $k:{\mathcal {R}}_U\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
such that
$k:{\mathcal {R}}_U\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
such that
![]() $Z\subseteq rng(k)$
. If
$Z\subseteq rng(k)$
. If
![]() ${\mathcal {R}}={\mathcal {V}}_{\eta }$
, then set
${\mathcal {R}}={\mathcal {V}}_{\eta }$
, then set
![]() ${\alpha }=\eta $
and
${\alpha }=\eta $
and
![]() $k=\pi _U{\restriction } {\mathcal {R}}_U$
.
$k=\pi _U{\restriction } {\mathcal {R}}_U$
.
Suppose then
![]() ${\mathcal {R}}\not ={\mathcal {V}}_{\eta }$
. In this case,
${\mathcal {R}}\not ={\mathcal {V}}_{\eta }$
. In this case,
![]() $\vec {{\mathcal {V}}}$
is small. Let
$\vec {{\mathcal {V}}}$
is small. Let
![]() ${\mathcal {W}}$
be the largest node on p such that
${\mathcal {W}}$
be the largest node on p such that
![]() $\pi ^{p_{\leq {\mathcal {W}}}}$
exists and the generators of
$\pi ^{p_{\leq {\mathcal {W}}}}$
exists and the generators of
![]() $p_{\leq {\mathcal {W}}}$
are contained in
$p_{\leq {\mathcal {W}}}$
are contained in
![]() ${\delta }^{{\mathcal {W}}^b}$
. Then
${\delta }^{{\mathcal {W}}^b}$
. Then
![]() $p_{\geq {\mathcal {W}}}$
is above
$p_{\geq {\mathcal {W}}}$
is above
![]() ${\delta }^{{\mathcal {W}}^b}$
. It follows from Proposition 9.5 and the remark after that
${\delta }^{{\mathcal {W}}^b}$
. It follows from Proposition 9.5 and the remark after that
![]() $p_{\geq {\mathcal {W}}}$
is according to
$p_{\geq {\mathcal {W}}}$
is according to
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable branches, and therefore, we must have
$(Z, \vec {{\mathcal {V}}})$
-embeddable branches, and therefore, we must have
![]() ${\alpha }\leq lh(\vec {{\mathcal {V}}})$
and a cofinal branch c of
${\alpha }\leq lh(\vec {{\mathcal {V}}})$
and a cofinal branch c of
![]() $p_U$
such that there is an appropriate weak l-embedding
$p_U$
such that there is an appropriate weak l-embedding
![]() $k:{\mathcal {M}}^{p_U}_c\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
Footnote 99 such that
$k:{\mathcal {M}}^{p_U}_c\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
Footnote 99 such that
![]() $Z\subseteq rng(k)$
. Set then
$Z\subseteq rng(k)$
. Set then
![]() ${\mathcal {M}}={\mathcal {M}}^{p_U}_c$
; note that
${\mathcal {M}}={\mathcal {M}}^{p_U}_c$
; note that
![]() ${\mathcal {R}}_U \lhd {\mathcal {M}}$
and
${\mathcal {R}}_U \lhd {\mathcal {M}}$
and
![]() $rud({\mathcal {M}}) \vDash \text {`}\delta ^{\mathcal {R}}$
is not Woodin’ by smallness of
$rud({\mathcal {M}}) \vDash \text {`}\delta ^{\mathcal {R}}$
is not Woodin’ by smallness of
![]() $\vec {{\mathcal {V}}}$
.
$\vec {{\mathcal {V}}}$
.
We continue with one such pair
![]() $({\alpha }, k)$
. Next, as
$({\alpha }, k)$
. Next, as
![]() ${\mathcal {T}}$
is Z-validated, we must have Y an extension of Z such that
${\mathcal {T}}$
is Z-validated, we must have Y an extension of Z such that
![]() $X=_{def}k[{\mathcal {R}}_U^b]\subseteq Z\oplus Y$
,
$X=_{def}k[{\mathcal {R}}_U^b]\subseteq Z\oplus Y$
,
![]() ${\mathcal {S}}_U^b={\mathcal {Q}}^Z_Y$
and
${\mathcal {S}}_U^b={\mathcal {Q}}^Z_Y$
and
![]() $\tau ^Z_X=\tau ^Z_Y\circ \pi ^{{\mathcal {T}}_U, b}$
. We can then lift
$\tau ^Z_X=\tau ^Z_Y\circ \pi ^{{\mathcal {T}}_U, b}$
. We can then lift
![]() $\tau ^Z_Y$
to
$\tau ^Z_Y$
to
![]() ${\mathcal {S}}$
and obtain some weak l-embedding
${\mathcal {S}}$
and obtain some weak l-embedding
![]() $\sigma :{\mathcal {S}}_U\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
such that
$\sigma :{\mathcal {S}}_U\rightarrow \mathcal {C}_l({\mathcal {V}}_{\alpha })$
such that
![]() $k=\sigma \circ \pi ^{{\mathcal {T}}_U}$
.
$k=\sigma \circ \pi ^{{\mathcal {T}}_U}$
.
![]() $\sigma $
is essentially the ultrapower map by the
$\sigma $
is essentially the ultrapower map by the
![]() $({\delta }^{{\mathcal {S}}_U^b}, {\delta }^{{\mathcal { H}}})$
-extender derived from
$({\delta }^{{\mathcal {S}}_U^b}, {\delta }^{{\mathcal { H}}})$
-extender derived from
![]() $\tau ^Z_Y$
(see the proof of Proposition 9.3).
$\tau ^Z_Y$
(see the proof of Proposition 9.3).
Finally, we discuss iterations that are above
![]() ${\mathcal {S}}^b$
where
${\mathcal {S}}^b$
where
![]() ${\mathcal {S}}$
is as in Proposition 9.10. The proof is just like the proof of Proposition 9.5.
${\mathcal {S}}$
is as in Proposition 9.10. The proof is just like the proof of Proposition 9.5.
Proposition 9.11. Suppose
![]() ${\mathcal {R}}$
is honest weakly Z-suitable above
${\mathcal {R}}$
is honest weakly Z-suitable above
![]() $\mu $
hod premouse and
$\mu $
hod premouse and
![]() $(\vec {{\mathcal {V}}}, p)$
is an honesty witness for
$(\vec {{\mathcal {V}}}, p)$
is an honesty witness for
![]() ${\mathcal {R}}$
. Suppose
${\mathcal {R}}$
. Suppose
![]() ${\mathcal {T}}$
is a normal Z-validated iteration of
${\mathcal {T}}$
is a normal Z-validated iteration of
![]() ${\mathcal {R}}$
. Let
${\mathcal {R}}$
. Let
![]() ${\alpha }'\in R^{\mathcal {T}}$
be the largest such that setting
${\alpha }'\in R^{\mathcal {T}}$
be the largest such that setting
![]() ${\mathcal {S}}={\mathcal {M}}_{\alpha }^{\mathcal {T}}$
,
${\mathcal {S}}={\mathcal {M}}_{\alpha }^{\mathcal {T}}$
,
![]() $\pi ^{{\mathcal {T}}_{\leq {\mathcal {S}}}}$
exists and the generators of
$\pi ^{{\mathcal {T}}_{\leq {\mathcal {S}}}}$
exists and the generators of
![]() ${\mathcal {T}}_{\leq {\mathcal {S}}}$
are contained in
${\mathcal {T}}_{\leq {\mathcal {S}}}$
are contained in
![]() ${\mathcal {S}}^b$
. Suppose
${\mathcal {S}}^b$
. Suppose
![]() ${\mathcal {T}}_{\geq {\mathcal {S}}}$
is above
${\mathcal {T}}_{\geq {\mathcal {S}}}$
is above
![]() $Ord\cap {\mathcal {S}}^b$
. Let U be a good hull such that
$Ord\cap {\mathcal {S}}^b$
. Let U be a good hull such that
![]() $\{{\mathcal {R}},\vec {{\mathcal {V}}}, {\mathcal {T}}\}\in U$
and let
$\{{\mathcal {R}},\vec {{\mathcal {V}}}, {\mathcal {T}}\}\in U$
and let
![]() $({\alpha }, {\mathcal {M}}, k, \sigma )$
be as in Proposition 9.10. Then
$({\alpha }, {\mathcal {M}}, k, \sigma )$
be as in Proposition 9.10. Then
![]() ${\mathcal {T}}_{\geq {\mathcal {S}}}$
is
${\mathcal {T}}_{\geq {\mathcal {S}}}$
is
![]() $(\sigma , \vec {{\mathcal {V}}}{\restriction } {\alpha })$
-realizable. Moreover, for each limit ordinal
$(\sigma , \vec {{\mathcal {V}}}{\restriction } {\alpha })$
-realizable. Moreover, for each limit ordinal
![]() ${\beta }<lh({\mathcal {T}}_{\geq {\mathcal {S}}})$
, if
${\beta }<lh({\mathcal {T}}_{\geq {\mathcal {S}}})$
, if
![]() ${\mathcal {T}}_{\geq {\mathcal {S}}}{\restriction } {\beta }$
is
${\mathcal {T}}_{\geq {\mathcal {S}}}{\restriction } {\beta }$
is
![]() $\mathsf {nuvs}$
, then
$\mathsf {nuvs}$
, then
![]() $d=_{def}[0, {\beta }]_{{\mathcal {T}}_{\geq {\mathcal {S}}}}$
is the unqiue cofinal branch
$d=_{def}[0, {\beta }]_{{\mathcal {T}}_{\geq {\mathcal {S}}}}$
is the unqiue cofinal branch
![]() $d'$
of
$d'$
of
![]() ${\mathcal {T}}_{\geq {\mathcal {S}}}{\restriction } {\beta }$
which is
${\mathcal {T}}_{\geq {\mathcal {S}}}{\restriction } {\beta }$
which is
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable and
$(Z, \vec {{\mathcal {V}}})$
-embeddable and
![]() ${\mathcal {Q}}(d', {\mathcal {T}}_{\geq {\mathcal {S}}}{\restriction } {\beta })$
exists.
${\mathcal {Q}}(d', {\mathcal {T}}_{\geq {\mathcal {S}}}{\restriction } {\beta })$
exists.
Definition 9.12. We say
![]() ${\mathcal {R}}$
is Z
-suitable above
${\mathcal {R}}$
is Z
-suitable above
![]() $\mu $
if it is weakly Z-suitable above
$\mu $
if it is weakly Z-suitable above
![]() $\mu $
and whenever
$\mu $
and whenever
![]() ${\mathcal {M}}$
is a Z-validated sts mouse over
${\mathcal {M}}$
is a Z-validated sts mouse over
![]() ${\mathcal {R}}$
,
${\mathcal {R}}$
,
![]() ${\mathcal {M}}{\vDash } \text {`}{\delta }^{\mathcal {R}}$
is a Woodin cardinal’.
${\mathcal {M}}{\vDash } \text {`}{\delta }^{\mathcal {R}}$
is a Woodin cardinal’.
Our goal is to construct an
![]() ${\mathcal {R}}$
which is Z
-suitable above
${\mathcal {R}}$
which is Z
-suitable above
![]() $\mu $
. We do this in Proposition 10.7.
$\mu $
. We do this in Proposition 10.7.
10. Z-validated sts constructions
We assume that the theory T holds (see Definition 5.11). We then fix
![]() $(S, S_0, \nu _0,\vec {Y}, \vec {A})$
that witness T and let
$(S, S_0, \nu _0,\vec {Y}, \vec {A})$
that witness T and let
![]() $\mu \in S_0$
. We will omit
$\mu \in S_0$
. We will omit
![]() $\mu $
when discussing CMI objects at
$\mu $
when discussing CMI objects at
![]() $\mu $
.
$\mu $
.
The construction that we will perform in the next section will hand us a hod premouse
![]() ${\mathcal {R}}$
that is weakly Z-suitable above
${\mathcal {R}}$
that is weakly Z-suitable above
![]() $\mu $
. The rest of the construction that we will perform will be a fully backgrounded construction over
$\mu $
. The rest of the construction that we will perform will be a fully backgrounded construction over
![]() ${\mathcal {R}}$
whose aim is to either find a Z-validated sts mouse destroying the Woodiness of
${\mathcal {R}}$
whose aim is to either find a Z-validated sts mouse destroying the Woodiness of
![]() ${\delta }^{\mathcal {R}}$
or proving that no such structures exist. In the latter case, we will show that we must produce an excellent hybrid premouse.
${\delta }^{\mathcal {R}}$
or proving that no such structures exist. In the latter case, we will show that we must produce an excellent hybrid premouse.
The construction that we describe in this section is a construction that is searching for the Z-validated sts mouse over
![]() ${\mathcal {R}}$
destroying the Woodiness of
${\mathcal {R}}$
destroying the Woodiness of
![]() ${\delta }^{\mathcal {R}}$
. In this construction, we add two kinds of objects. The first type of objects are extenders, and they are handled exactly the same way that they are handled in all fully backgrounded constructions. The second kind of objects are iterations. Here, the difference with the ordinary is that there is no strategy that we follow as we index branches of iterations that appear in the construction. Instead, when our sts scheme demands that a branch of some iteration p must be indexed, we find an appropriate branch and index it. We will make sure that the iterations that we need to consider in the construction are all Z-validated. It must then be proved that given a Z-validated iteration, there is always a branch that is Z-validated.
${\delta }^{\mathcal {R}}$
. In this construction, we add two kinds of objects. The first type of objects are extenders, and they are handled exactly the same way that they are handled in all fully backgrounded constructions. The second kind of objects are iterations. Here, the difference with the ordinary is that there is no strategy that we follow as we index branches of iterations that appear in the construction. Instead, when our sts scheme demands that a branch of some iteration p must be indexed, we find an appropriate branch and index it. We will make sure that the iterations that we need to consider in the construction are all Z-validated. It must then be proved that given a Z-validated iteration, there is always a branch that is Z-validated.
The solution here has a somewhat magical component to it. As we said above, the fully backgrounded Z-validated sts construction is not a construction relative to a strategy. This is an important point that will be useful to keep in mind. Instead, the construction follows the sts scheme, and the Z-validation method is used to find branches of iterations that come up in the construction. To see that we do not run into trouble, we need to show that any such iteration
![]() ${\mathcal {T}}$
that needs to be indexed according to our sts scheme has a branch b such that
${\mathcal {T}}$
that needs to be indexed according to our sts scheme has a branch b such that
![]() ${\mathcal {T}}^\frown \{b\}$
is Z-validated. Let
${\mathcal {T}}^\frown \{b\}$
is Z-validated. Let
![]() ${\mathcal {M}}$
be the stage of the construction where
${\mathcal {M}}$
be the stage of the construction where
![]() ${\mathcal {T}}$
is produced. Recall now that we have two types of such iterations. If
${\mathcal {T}}$
is produced. Recall now that we have two types of such iterations. If
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\mathsf {uvs}$
, then Z-validation will produce a branch in a more or less straightforward fashion (see Proposition 10.5). If
$\mathsf {uvs}$
, then Z-validation will produce a branch in a more or less straightforward fashion (see Proposition 10.5). If
![]() ${\mathcal {T}}$
is
${\mathcal {T}}$
is
![]() $\mathsf {nuvs}$
, then the fact that we need to index a branch of it suggests that we have also reached an authenticated
$\mathsf {nuvs}$
, then the fact that we need to index a branch of it suggests that we have also reached an authenticated
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() ${\mathcal {T}}$
. We will then show that there must be a branch with this
${\mathcal {T}}$
. We will then show that there must be a branch with this
![]() ${\mathcal {Q}}$
-structure. This is the magical component we speak of above. In general, given an iteration
${\mathcal {Q}}$
-structure. This is the magical component we speak of above. In general, given an iteration
![]() ${\mathcal {T}}$
of a weakly Z-suitable
${\mathcal {T}}$
of a weakly Z-suitable
![]() ${\mathcal {R}}$
that is produced by
${\mathcal {R}}$
that is produced by
![]() $\mathsf {HFBC}(\mu )$
of the next section, there is no reason to believe that there is a
$\mathsf {HFBC}(\mu )$
of the next section, there is no reason to believe that there is a
![]() ${\mathcal {Q}}$
-structure for it of any kind. Even if there is a
${\mathcal {Q}}$
-structure for it of any kind. Even if there is a
![]() ${\mathcal {Q}}$
-structure
${\mathcal {Q}}$
-structure
![]() ${\mathcal {Q}}$
of some kind, there is no reason to believe that sufficiently closed hulls of
${\mathcal {Q}}$
of some kind, there is no reason to believe that sufficiently closed hulls of
![]() ${\mathcal {T}}$
will have branches determined by the pre-image of
${\mathcal {T}}$
will have branches determined by the pre-image of
![]() ${\mathcal {Q}}$
. In our case, what helps is that
${\mathcal {Q}}$
. In our case, what helps is that
![]() ${\mathcal {Q}}\in {\mathcal {M}}$
, and this condition, in the authors’ opinion, is somewhat magical.Footnote 100
${\mathcal {Q}}\in {\mathcal {M}}$
, and this condition, in the authors’ opinion, is somewhat magical.Footnote 100
One particularly unpleasant problem is that we cannot in general prove that the non-weakly Z-suitable levels of the fully backgrounded construction produced in the next sections are iterable. This unpleasantness causes us to work with weakly Z-suitable
![]() ${\mathcal {R}}$
that are iterates of a level of the fully backgrounded construction of the next section. In order to have an abstract exposition of the Z-validated sts construction, we introduce the concept of honest weakly Z-suitable
${\mathcal {R}}$
that are iterates of a level of the fully backgrounded construction of the next section. In order to have an abstract exposition of the Z-validated sts construction, we introduce the concept of honest weakly Z-suitable
![]() ${\mathcal {R}}$
over which we will perform our Z-validated sts constructions. The honest weakly Z-suitable hod premice will have honesty witnesses, and that is the concept we introduce first. The honesty witnesses are essentially models of a
${\mathcal {R}}$
over which we will perform our Z-validated sts constructions. The honest weakly Z-suitable hod premice will have honesty witnesses, and that is the concept we introduce first. The honesty witnesses are essentially models of a
![]() $K^c$
-construction.
$K^c$
-construction.
In this section and subsequent sections, we work with the fine structure in [Reference Steel53].
10.1. The Z-validated sts construction
Suppose
![]() ${\mathcal {R}}$
is honest and
${\mathcal {R}}$
is honest and
![]() $\vec {{\mathcal {V}}}$
is an honesty certificate for
$\vec {{\mathcal {V}}}$
is an honesty certificate for
![]() ${\mathcal {R}}$
. We assume that
${\mathcal {R}}$
. We assume that
![]() ${\mathcal {R}}$
is a
${\mathcal {R}}$
is a
![]() $\#$
-lsa type hod premouse. Let X be any transitive set such that
$\#$
-lsa type hod premouse. Let X be any transitive set such that
![]() ${\mathcal {R}}\in X$
. Let
${\mathcal {R}}\in X$
. Let
![]() ${\lambda } \in S_0$
be such that
${\lambda } \in S_0$
be such that
![]() ${\mathcal {R}}, X\in H_{\lambda }$
. In what follows, we introduce the fully backgrounded
${\mathcal {R}}, X\in H_{\lambda }$
. In what follows, we introduce the fully backgrounded
![]() $(Z, {\lambda })$
-validated sts construction over X.
$(Z, {\lambda })$
-validated sts construction over X.
Definition 10.1. We say
![]() $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq \Omega ^*)$
are the models of the fully backgrounded
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq \Omega ^*)$
are the models of the fully backgrounded
![]() $(Z, {\lambda })$
-validated sts construction over X if the following conditions hold:
$(Z, {\lambda })$
-validated sts construction over X if the following conditions hold:
-
1.
 $\Omega ^*\leq {\lambda }$
, for all
$\Omega ^*\leq {\lambda }$
, for all
 $\xi <{\lambda }$
, if
$\xi <{\lambda }$
, if
 ${\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }$
are defined, then
${\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }$
are defined, then
 ${\mathcal {M}}_{\xi }$
and
${\mathcal {M}}_{\xi }$
and
 ${\mathcal {N}}_{\xi }\in H_{\lambda }$
.
${\mathcal {N}}_{\xi }\in H_{\lambda }$
. -
2. For every
 $\xi \leq \Omega ^*$
,
$\xi \leq \Omega ^*$
,
 ${\mathcal {M}}_{\xi }$
and
${\mathcal {M}}_{\xi }$
and
 ${\mathcal {N}}_{\xi }$
are Z-validated sts hod premice over X.
${\mathcal {N}}_{\xi }$
are Z-validated sts hod premice over X. -
3. Suppose the sequence
 $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
 ${\mathcal {M}}_{\eta }$
have been constructed. Suppose further that there is a total
${\mathcal {M}}_{\eta }$
have been constructed. Suppose further that there is a total
 $({\kappa }, \nu )$
-extender F such that letting
$({\kappa }, \nu )$
-extender F such that letting
 $G={\mathcal {M}}_{\eta }\cap F$
,
$G={\mathcal {M}}_{\eta }\cap F$
,
 $({\mathcal {M}}_{\eta }, G)$
is a Z-validated sts hod premouse over X. Let then
$({\mathcal {M}}_{\eta }, G)$
is a Z-validated sts hod premouse over X. Let then
 ${\mathcal {N}}_{\eta }=({\mathcal {M}}_{\eta }, G)$
and
${\mathcal {N}}_{\eta }=({\mathcal {M}}_{\eta }, G)$
and
 ${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
.Footnote 101
${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
.Footnote 101 -
4. Suppose the sequence
 $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
 ${\mathcal {M}}_{\eta }$
have been constructed and
${\mathcal {M}}_{\eta }$
have been constructed and
 ${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
is the
${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
is the
 $<_{{\mathcal {M}}_{\eta }}$
-least
$<_{{\mathcal {M}}_{\eta }}$
-least
 $\mathsf {uvs}$
treeFootnote 102 without an indexed branch. Suppose further that there is a branch b of
$\mathsf {uvs}$
treeFootnote 102 without an indexed branch. Suppose further that there is a branch b of
 ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
 $({\mathcal {M}}_{\eta }, b)$
is a Z-validated sts hod premouseFootnote 103 over
$({\mathcal {M}}_{\eta }, b)$
is a Z-validated sts hod premouseFootnote 103 over
 ${\mathcal {R}}$
. Let then
${\mathcal {R}}$
. Let then
 ${\mathcal {N}}_{\eta }=({\mathcal {M}}_{\eta }, b)$
and
${\mathcal {N}}_{\eta }=({\mathcal {M}}_{\eta }, b)$
and
 ${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
.
${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
. -
5. Suppose the sequence
 $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
 ${\mathcal {M}}_{\eta }$
has been constructed, and for some
${\mathcal {M}}_{\eta }$
has been constructed, and for some
 $\mathsf {nuvs}$
tree
$\mathsf {nuvs}$
tree
 ${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
there is a branch
${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
there is a branch
 $b\in {\mathcal {M}}_{\eta }$
such that
$b\in {\mathcal {M}}_{\eta }$
such that
 $({\mathcal {M}}_{\eta }, b)$
is a Z-validated sts hod premouse over
$({\mathcal {M}}_{\eta }, b)$
is a Z-validated sts hod premouse over
 ${\mathcal {R}}$
. Let
${\mathcal {R}}$
. Let
 ${\mathcal {T}}$
be the
${\mathcal {T}}$
be the
 $<_{{\mathcal {M}}_{\eta }}$
-least such tree and b be such a branch for
$<_{{\mathcal {M}}_{\eta }}$
-least such tree and b be such a branch for
 ${\mathcal {T}}$
. Then
${\mathcal {T}}$
. Then
 ${\mathcal {N}}_{\eta }=({\mathcal {M}}_{\eta }, b)$
and
${\mathcal {N}}_{\eta }=({\mathcal {M}}_{\eta }, b)$
and
 ${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
.Footnote 104
${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
.Footnote 104 -
6. Suppose the sequence
 $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
and
 ${\mathcal {M}}_{\eta }$
has been constructed and all of the above cases fail. In this case, we let
${\mathcal {M}}_{\eta }$
has been constructed and all of the above cases fail. In this case, we let
 ${\mathcal {N}}_{\eta }=\mathcal {J}_1({\mathcal {M}}_{\eta })$
, provided
${\mathcal {N}}_{\eta }=\mathcal {J}_1({\mathcal {M}}_{\eta })$
, provided
 ${\mathcal {N}}_{\eta }$
is a Z-validated sts hod premouse over
${\mathcal {N}}_{\eta }$
is a Z-validated sts hod premouse over
 ${\mathcal {R}}$
,
${\mathcal {R}}$
,
 ${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
.
${\mathcal {M}}_{\eta +1}=\mathcal {C}({\mathcal {N}}_{\eta })$
. -
7. Suppose the sequence
 $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
has been constructed and
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <\eta )$
has been constructed and
 $\eta $
is a limit ordinal. Then
$\eta $
is a limit ordinal. Then
 ${\mathcal {M}}_{\eta }=liminf_{\xi \rightarrow \eta }{\mathcal {M}}_{\xi }$
.
${\mathcal {M}}_{\eta }=liminf_{\xi \rightarrow \eta }{\mathcal {M}}_{\xi }$
.
If
![]() $\lambda $
is clear from context, then we will omit it from our notation.
$\lambda $
is clear from context, then we will omit it from our notation.
The fully backgrounded (f.b.) Z-validated sts construction can break down for several reasons. Let p be the
![]() ${\mathcal {V}}_{\eta }$
-to-
${\mathcal {V}}_{\eta }$
-to-
![]() ${\mathcal {R}}$
iteration witnessing that
${\mathcal {R}}$
iteration witnessing that
![]() ${\mathcal {R}}$
is honest. Below, we list all of these reasons. We say that f.b. Z-validated sts construction breaks down at
${\mathcal {R}}$
is honest. Below, we list all of these reasons. We say that f.b. Z-validated sts construction breaks down at
![]() $\eta $
if one of the following conditions holds.
$\eta $
if one of the following conditions holds.
Break1.
![]() ${\mathcal {M}}_{\eta }$
is not solid or universal.
${\mathcal {M}}_{\eta }$
is not solid or universal.
Break2.
![]() ${\mathcal {M}}_{\eta }$
is not Z-validated.Footnote 105
${\mathcal {M}}_{\eta }$
is not Z-validated.Footnote 105
Break3. There is an
![]() $\mathsf {uvs}$
tree
$\mathsf {uvs}$
tree
![]() ${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
such that the indexing scheme demands that a branch of
${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
such that the indexing scheme demands that a branch of
![]() ${\mathcal {T}}$
must be indexed, yet
${\mathcal {T}}$
must be indexed, yet
![]() ${\mathcal {T}}$
has no (cofinal well-founded) branch b such that
${\mathcal {T}}$
has no (cofinal well-founded) branch b such that
![]() $({\mathcal {M}}_{\eta }, b)$
is a Z-validated sts premouse over
$({\mathcal {M}}_{\eta }, b)$
is a Z-validated sts premouse over
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
Break4. There is an
![]() $\mathsf {nuvs}$
tree
$\mathsf {nuvs}$
tree
![]() ${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
such that the indexing scheme demands that a branch of
${\mathcal {T}}\in {\mathcal {M}}_{\eta }$
such that the indexing scheme demands that a branch of
![]() ${\mathcal {T}}$
must be indexed, yet letting
${\mathcal {T}}$
must be indexed, yet letting
![]() $b\in {\mathcal {M}}_{\eta }$
be the branch given by the authentication process, b is not
$b\in {\mathcal {M}}_{\eta }$
be the branch given by the authentication process, b is not
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable branch of
$(Z, \vec {{\mathcal {V}}})$
-embeddable branch of
![]() ${\mathcal {T}}^\frown p$
.Footnote 106
${\mathcal {T}}^\frown p$
.Footnote 106
Break5.
![]() $\rho ({\mathcal {M}}_{\eta })\leq {\delta }^{{\mathcal { H}}}$
.
$\rho ({\mathcal {M}}_{\eta })\leq {\delta }^{{\mathcal { H}}}$
.
The argument that the construction does not break down because of Break1 is standard, cf. [Reference Mitchell and Steel28]. It is essentially enough to show that the countable substructures of
![]() ${\mathcal {M}}_{\eta }$
are iterable. We will show that much more complicated forms of iterability hold, and so to save ink and to not repeat ourselves, we will leave this portion to our kind reader. To see that the construction does not break down because of Break2 is not too involved, and we will present that argument below. At this point, we cannot do much about Break5. We will deal with it when X becomes a more meaningful object. The remaining cases will be handled in the next subsections.
${\mathcal {M}}_{\eta }$
are iterable. We will show that much more complicated forms of iterability hold, and so to save ink and to not repeat ourselves, we will leave this portion to our kind reader. To see that the construction does not break down because of Break2 is not too involved, and we will present that argument below. At this point, we cannot do much about Break5. We will deal with it when X becomes a more meaningful object. The remaining cases will be handled in the next subsections.
Proposition 10.2. Suppose
![]() ${\mathcal {R}}$
is an honest weakly Z-suitable hod premouse as witnessed by
${\mathcal {R}}$
is an honest weakly Z-suitable hod premouse as witnessed by
![]() $\vec {{\mathcal {V}}}$
, X is a transitive set such that
$\vec {{\mathcal {V}}}$
, X is a transitive set such that
![]() ${\mathcal {R}}\in X$
and
${\mathcal {R}}\in X$
and
![]() ${\lambda }\in S_0$
is such that
${\lambda }\in S_0$
is such that
![]() $X, \vec {{\mathcal {V}}}\in V_{\lambda }$
. Then the f.b.
$X, \vec {{\mathcal {V}}}\in V_{\lambda }$
. Then the f.b.
![]() $(Z, {\lambda })$
-validated construction over X does not break down because of Break2.
$(Z, {\lambda })$
-validated construction over X does not break down because of Break2.
Proof. Towards contradiction, assume that there is some
![]() ${\alpha }$
such that for all
${\alpha }$
such that for all
![]() ${\beta }<{\alpha }$
, both
${\beta }<{\alpha }$
, both
![]() ${\mathcal {M}}_{\beta }$
and
${\mathcal {M}}_{\beta }$
and
![]() ${\mathcal {N}}_{\beta }$
are Z-validated but
${\mathcal {N}}_{\beta }$
are Z-validated but
![]() ${\mathcal {M}}_{\alpha }$
is not Z-validated. Set
${\mathcal {M}}_{\alpha }$
is not Z-validated. Set
![]() ${\mathcal {W}}={\mathcal {M}}_{\alpha }$
be the least such model.
${\mathcal {W}}={\mathcal {M}}_{\alpha }$
be the least such model.
Suppose first
![]() ${\alpha }$
is a limit ordinal. Let U be a
${\alpha }$
is a limit ordinal. Let U be a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() $ \{{\mathcal {R}}, {\mathcal {W}}\}\subseteq U$
and
$ \{{\mathcal {R}}, {\mathcal {W}}\}\subseteq U$
and
![]() $({\mathcal {M}}_{\beta }:{\beta }\leq {\alpha })\in U$
. Let
$({\mathcal {M}}_{\beta }:{\beta }\leq {\alpha })\in U$
. Let
![]() $({\mathcal { K}}_{\xi }: \xi \leq {\alpha }_U)=\pi ^{-1}_U({\mathcal {M}}_{\beta }:{\beta }\leq {\alpha })$
. Fix
$({\mathcal { K}}_{\xi }: \xi \leq {\alpha }_U)=\pi ^{-1}_U({\mathcal {M}}_{\beta }:{\beta }\leq {\alpha })$
. Fix
![]() ${\mathcal {T}}\in {\mathcal { K}}_{{\alpha }_U}$
according to
${\mathcal {T}}\in {\mathcal { K}}_{{\alpha }_U}$
according to
![]() $S^{{\mathcal { K}}_{{\alpha }_U}}$
. We need to see that
$S^{{\mathcal { K}}_{{\alpha }_U}}$
. We need to see that
![]() ${\mathcal {T}}$
is Z-approved. Fix
${\mathcal {T}}$
is Z-approved. Fix
![]() $\xi <{\alpha }_U$
such that
$\xi <{\alpha }_U$
such that
![]() ${\mathcal {T}}\in {\mathcal { K}}_{\xi }$
and is according to
${\mathcal {T}}\in {\mathcal { K}}_{\xi }$
and is according to
![]() $S^{{\mathcal { K}}_{\xi }}$
. Then
$S^{{\mathcal { K}}_{\xi }}$
. Then
![]() $\pi _U({\mathcal {T}})\in {\mathcal {M}}_{\pi _U(\xi )}$
and is according to
$\pi _U({\mathcal {T}})\in {\mathcal {M}}_{\pi _U(\xi )}$
and is according to
![]() $S^{{\mathcal {M}}_{\pi _U(\xi )}}$
. Therefore,
$S^{{\mathcal {M}}_{\pi _U(\xi )}}$
. Therefore,
![]() ${\mathcal {T}}$
is Z-approved.
${\mathcal {T}}$
is Z-approved.
Suppose next that
![]() ${\alpha }={\beta }+1$
. Because we are assuming the least model that is not Z-validated is
${\alpha }={\beta }+1$
. Because we are assuming the least model that is not Z-validated is
![]() ${\mathcal {M}}_{\alpha }$
, we must have that
${\mathcal {M}}_{\alpha }$
, we must have that
![]() ${\mathcal {N}}_{\beta }$
is Z-validated. Let now U be a
${\mathcal {N}}_{\beta }$
is Z-validated. Let now U be a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() $\{{\mathcal {R}}, {\mathcal {W}}\}\subseteq U$
. But then
$\{{\mathcal {R}}, {\mathcal {W}}\}\subseteq U$
. But then
![]() $\pi _U^{-1}({\mathcal {M}}_{\alpha })=\mathcal {C}(\pi ^{-1}_U({\mathcal {N}}_{\beta }))$
. It then follows that
$\pi _U^{-1}({\mathcal {M}}_{\alpha })=\mathcal {C}(\pi ^{-1}_U({\mathcal {N}}_{\beta }))$
. It then follows that
![]() $\pi _U^{-1}({\mathcal {M}}_{\alpha })$
is Z-approved (see Proposition 7.9).
$\pi _U^{-1}({\mathcal {M}}_{\alpha })$
is Z-approved (see Proposition 7.9).
10.2. Break3 never happens
In this subsection,
![]() ${\mathcal {R}}$
is an honest weakly Z-suitable, X is a transitive set containing
${\mathcal {R}}$
is an honest weakly Z-suitable, X is a transitive set containing
![]() ${\mathcal {R}}$
and
${\mathcal {R}}$
and
![]() ${\lambda }\in S_0$
is such that
${\lambda }\in S_0$
is such that
![]() $({\mathcal {R}}, X)\in V_{\lambda }$
. Our main goal here is to prove that the
$({\mathcal {R}}, X)\in V_{\lambda }$
. Our main goal here is to prove that the
![]() $(Z, {\lambda })$
-validated sts construction over X does not break down because of Break3. First, we prove the following general lemma.
$(Z, {\lambda })$
-validated sts construction over X does not break down because of Break3. First, we prove the following general lemma.
Lemma 10.3. Suppose
![]() ${\mathcal {M}}$
is a hod premouse for which
${\mathcal {M}}$
is a hod premouse for which
![]() ${\mathcal {M}}^b$
is defined and p is an iteration of
${\mathcal {M}}^b$
is defined and p is an iteration of
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() $\pi ^{p, b}$
exists. Let
$\pi ^{p, b}$
exists. Let
![]() ${\delta }$
be a Woodin cardinal of
${\delta }$
be a Woodin cardinal of
![]() $\pi ^{p, b}({\mathcal {M}}^b)$
and let
$\pi ^{p, b}({\mathcal {M}}^b)$
and let
![]() $\xi $
be least such that
$\xi $
be least such that
![]() $\pi ^{p, b}(\xi )\geq {\delta }$
. Then
$\pi ^{p, b}(\xi )\geq {\delta }$
. Then
![]() ${\mathrm cf}({\delta })={\mathrm cf}((\xi ^+)^{\mathcal {M}})$
.
${\mathrm cf}({\delta })={\mathrm cf}((\xi ^+)^{\mathcal {M}})$
.
Proof. Let
![]() ${\mathcal {Q}}$
be the least model of p such that
${\mathcal {Q}}$
be the least model of p such that
![]() ${\mathcal {Q}}^b=\pi ^{p, b}({\mathcal {M}}^b)$
and set
${\mathcal {Q}}^b=\pi ^{p, b}({\mathcal {M}}^b)$
and set
![]() $q=p_{\leq {\mathcal {Q}}}$
. Let
$q=p_{\leq {\mathcal {Q}}}$
. Let
![]() ${\mathcal {N}}$
be the least model on q such that
${\mathcal {N}}$
be the least model on q such that
![]() ${\delta }\in rng(\pi ^q_{{\mathcal {N}}, {\mathcal {Q}}})$
. Without losing generality, we can assume
${\delta }\in rng(\pi ^q_{{\mathcal {N}}, {\mathcal {Q}}})$
. Without losing generality, we can assume
![]() ${\mathcal {Q}}={\mathcal {N}}$
as
${\mathcal {Q}}={\mathcal {N}}$
as
![]() $rng(\pi ^q_{{\mathcal {N}}, {\mathcal {Q}}})\cap {\delta }$
is cofinal in
$rng(\pi ^q_{{\mathcal {N}}, {\mathcal {Q}}})\cap {\delta }$
is cofinal in
![]() ${\delta }$
. As the iteration embeddings are cofinal at Woodin cardinals, if
${\delta }$
. As the iteration embeddings are cofinal at Woodin cardinals, if
![]() $\pi ^q(\xi )={\delta }$
, then again there is nothing to prove. Assume then
$\pi ^q(\xi )={\delta }$
, then again there is nothing to prove. Assume then
![]() $\pi ^q(\xi )>{\delta }$
. Without loss of generality, we can assume that
$\pi ^q(\xi )>{\delta }$
. Without loss of generality, we can assume that
![]() $\xi ={\delta }^{{\mathcal {M}}^b}$
. If
$\xi ={\delta }^{{\mathcal {M}}^b}$
. If
![]() $\xi <{\delta }^{{\mathcal {M}}^b}$
, then we need to redefine
$\xi <{\delta }^{{\mathcal {M}}^b}$
, then we need to redefine
![]() ${\mathcal {M}}$
as
${\mathcal {M}}$
as
![]() ${\mathcal {M}}|\zeta $
, where
${\mathcal {M}}|\zeta $
, where
![]() $\zeta $
is the
$\zeta $
is the
![]() ${\mathcal {M}}$
-successor of
${\mathcal {M}}$
-successor of
![]() $o^{\mathcal {M}}(\xi )$
.
$o^{\mathcal {M}}(\xi )$
.
Because
![]() ${\mathcal {N}}$
is the least model that has
${\mathcal {N}}$
is the least model that has
![]() ${\delta }$
in it, it must be case that
${\delta }$
in it, it must be case that
![]() ${\mathcal {N}}=Ult({\mathcal {W}}, E)$
, where
${\mathcal {N}}=Ult({\mathcal {W}}, E)$
, where
![]() ${\mathcal {W}}$
is a node in q and E is an extender used in q to obtain
${\mathcal {W}}$
is a node in q and E is an extender used in q to obtain
![]() ${\mathcal {N}}$
. Moreover,
${\mathcal {N}}$
. Moreover,
![]() $\mathrm {crit }(E)={\delta }^{{\mathcal {W}}^b}$
. Below,
$\mathrm {crit }(E)={\delta }^{{\mathcal {W}}^b}$
. Below,
![]() $\pi _E$
is used for
$\pi _E$
is used for
![]() $\pi _E^{\mathcal {W}}$
.
$\pi _E^{\mathcal {W}}$
.
Suppose
![]() $\pi _E(f)(a)=\delta $
and
$\pi _E(f)(a)=\delta $
and
![]() $\pi _E(g)(a)= \nu _E$
, where
$\pi _E(g)(a)= \nu _E$
, where
-
1.
 $\nu _E$
is the supremum of the generators of E,
$\nu _E$
is the supremum of the generators of E, -
2.
 $f,g: {\delta }^{{\mathcal {W}}^b} \rightarrow {\delta }^{{\mathcal {W}}^b}$
are functions in
$f,g: {\delta }^{{\mathcal {W}}^b} \rightarrow {\delta }^{{\mathcal {W}}^b}$
are functions in
 ${\mathcal {W}}$
,
${\mathcal {W}}$
, -
3.
 $a \in [\nu _E+1]^{<\omega }$
.
$a \in [\nu _E+1]^{<\omega }$
.
Note that
![]() $\nu _E < \delta $
.
$\nu _E < \delta $
.
We first show that
(1)
![]() $\sup (\{ \pi _E(k)(a): k:{\delta }^{{\mathcal {W}}^b}\rightarrow {\delta }^{{\mathcal {W}}^b}, k\in {\mathcal {W}}\}\cap {\delta })={\delta }$
.
$\sup (\{ \pi _E(k)(a): k:{\delta }^{{\mathcal {W}}^b}\rightarrow {\delta }^{{\mathcal {W}}^b}, k\in {\mathcal {W}}\}\cap {\delta })={\delta }$
.
To see (1), fix
![]() $h:{\delta }^{{\mathcal {W}}^b} \rightarrow {\delta }^{{\mathcal {W}}^b}$
in
$h:{\delta }^{{\mathcal {W}}^b} \rightarrow {\delta }^{{\mathcal {W}}^b}$
in
![]() ${\mathcal {W}}$
and let s in
${\mathcal {W}}$
and let s in
![]() $[\nu _E+1]^{<\omega }$
be such that
$[\nu _E+1]^{<\omega }$
be such that
![]() $\pi _E(h)(s) < \delta $
. We want to find k such that
$\pi _E(h)(s) < \delta $
. We want to find k such that
![]() $\pi _E(k)(a)$
is in
$\pi _E(k)(a)$
is in
![]() $[\pi _E(h)(s), \delta ]$
. Set
$[\pi _E(h)(s), \delta ]$
. Set
![]() $k(u)=$
the supremum of points of the form
$k(u)=$
the supremum of points of the form
![]() $h(t)$
such that
$h(t)$
such that
![]() $h(t)< f(u)$
and t is a finite sequence from
$h(t)< f(u)$
and t is a finite sequence from
![]() $g(u)$
.
$g(u)$
.
![]() $f(u)$
is a Woodin cardinal (in
$f(u)$
is a Woodin cardinal (in
![]() ${\mathcal {R}}$
), so
${\mathcal {R}}$
), so
![]() $k(u)< f(u)$
for
$k(u)< f(u)$
for
![]() $E_a$
-almost all u, so
$E_a$
-almost all u, so
Also,
by the definition of k.
Let
![]() ${\lambda }=Ord\cap {\mathcal {W}}^b$
. We have that
${\lambda }=Ord\cap {\mathcal {W}}^b$
. We have that
![]() ${\mathrm cf}({\lambda })={\mathrm cf}(Ord\cap {\mathcal {M}}^b)$
. Thus, it is enough to show that
${\mathrm cf}({\lambda })={\mathrm cf}(Ord\cap {\mathcal {M}}^b)$
. Thus, it is enough to show that
![]() ${\mathrm cf}({\delta })={\mathrm cf}({\lambda })$
. Let
${\mathrm cf}({\delta })={\mathrm cf}({\lambda })$
. Let
![]() $\eta ={\mathrm cf}({\delta })$
and let
$\eta ={\mathrm cf}({\delta })$
and let
![]() $(k_{\alpha }: {\alpha }<\eta )\subseteq {\mathcal {W}}$
be such that
$(k_{\alpha }: {\alpha }<\eta )\subseteq {\mathcal {W}}$
be such that
-
1. for
 ${\alpha }<\eta $
,
${\alpha }<\eta $
,
 $k_{\alpha }:{\delta }^{{\mathcal {W}}^b} \rightarrow {\delta }^{{\mathcal {W}}^b}$
,
$k_{\alpha }:{\delta }^{{\mathcal {W}}^b} \rightarrow {\delta }^{{\mathcal {W}}^b}$
, -
2. for
 ${\alpha }<\eta $
,
${\alpha }<\eta $
,
 $k_{\alpha }\in {\mathcal {W}}$
,
$k_{\alpha }\in {\mathcal {W}}$
, -
3. for
 ${\alpha }<{\beta }<\eta $
,
${\alpha }<{\beta }<\eta $
,
 $\pi _E(k_{\alpha })(a)<\pi _E(k_{\beta })(a)<{\delta }$
.
$\pi _E(k_{\alpha })(a)<\pi _E(k_{\beta })(a)<{\delta }$
.
Let
![]() $\vec {{\gamma }}=({\gamma }_{\alpha }:{\alpha }<\eta )$
be increasing and such that
$\vec {{\gamma }}=({\gamma }_{\alpha }:{\alpha }<\eta )$
be increasing and such that
-
1.
 $k_{\alpha }\in {\mathcal {W}}|{\gamma }_{\alpha }$
,
$k_{\alpha }\in {\mathcal {W}}|{\gamma }_{\alpha }$
, -
2.
 $\rho ({\mathcal {W}}|{\gamma }_{\alpha })={\delta }^{{\mathcal {W}}^b}$
.
$\rho ({\mathcal {W}}|{\gamma }_{\alpha })={\delta }^{{\mathcal {W}}^b}$
.
We claim that
![]() $\vec {{\gamma }}$
is cofinal in
$\vec {{\gamma }}$
is cofinal in
![]() ${\lambda }$
. Suppose it is not. In that case, we can fix
${\lambda }$
. Suppose it is not. In that case, we can fix
![]() $\zeta>\sup \vec {{\gamma }}$
such that
$\zeta>\sup \vec {{\gamma }}$
such that
![]() $\rho _1({\mathcal {W}}|\zeta )={\delta }^{{\mathcal {W}}^b}$
. Let p be the first standard parameter of
$\rho _1({\mathcal {W}}|\zeta )={\delta }^{{\mathcal {W}}^b}$
. Let p be the first standard parameter of
![]() ${\mathcal {W}}|\zeta $
. For each
${\mathcal {W}}|\zeta $
. For each
![]() ${\alpha }<\eta $
, let
${\alpha }<\eta $
, let
![]() $a_{\alpha }\in [{\delta }^{{\mathcal {W}}^b}]^{<\omega }$
be such that
$a_{\alpha }\in [{\delta }^{{\mathcal {W}}^b}]^{<\omega }$
be such that
![]() $k_{\alpha }$
is definable from p and
$k_{\alpha }$
is definable from p and
![]() $a_{\alpha }$
in
$a_{\alpha }$
in
![]() ${\mathcal {W}}|\zeta $
. It then follows that
${\mathcal {W}}|\zeta $
. It then follows that
as witnessed by
![]() $(a_{\alpha }: {\alpha }<\eta )$
. As
$(a_{\alpha }: {\alpha }<\eta )$
. As
![]() $Hull_1^{\pi _E({\mathcal {W}}|\zeta )}(\pi _E(p), {\delta }^{{\mathcal {W}}^b})\in Ult({\mathcal {W}}, E)={\mathcal {N}}$
, the above equality implies that
$Hull_1^{\pi _E({\mathcal {W}}|\zeta )}(\pi _E(p), {\delta }^{{\mathcal {W}}^b})\in Ult({\mathcal {W}}, E)={\mathcal {N}}$
, the above equality implies that
![]() ${\delta }$
is singular in
${\delta }$
is singular in
![]() ${\mathcal {N}}$
; a contradiction. Thus,
${\mathcal {N}}$
; a contradiction. Thus,
![]() $\vec {{\gamma }}$
must be cofinal in
$\vec {{\gamma }}$
must be cofinal in
![]() ${\lambda }$
. Therefore,
${\lambda }$
. Therefore,
![]() ${\mathrm cf}({\lambda })=\eta $
.
${\mathrm cf}({\lambda })=\eta $
.
Recall that we are working under theory T; see Definition 5.11.
Corollary 10.4. Suppose
![]() ${\mathcal {T}}$
is a normal tree on
${\mathcal {T}}$
is a normal tree on
![]() ${\mathcal {R}}$
such that
${\mathcal {R}}$
such that
![]() $\pi ^{{\mathcal {T}}, b}$
exists and
$\pi ^{{\mathcal {T}}, b}$
exists and
![]() $\delta $
is a Woodin cardinal of
$\delta $
is a Woodin cardinal of
![]() $\pi ^{{\mathcal {T}}, b}({\mathcal { H}})$
. Then
$\pi ^{{\mathcal {T}}, b}({\mathcal { H}})$
. Then
![]() ${\mathrm cf}(\delta ) < \mu $
and if
${\mathrm cf}(\delta ) < \mu $
and if
![]() ${\delta }>\sup (\pi ^{{\mathcal {T}}, b}[{\delta }^{{\mathcal { H}}}])$
, then
${\delta }>\sup (\pi ^{{\mathcal {T}}, b}[{\delta }^{{\mathcal { H}}}])$
, then
![]() ${\mathrm cf}({\delta })<\nu _0$
.
${\mathrm cf}({\delta })<\nu _0$
.
Proof. First note that if
![]() $\delta $
is a Woodin cardinal of
$\delta $
is a Woodin cardinal of
![]() $\mathcal {H}$
, then
$\mathcal {H}$
, then
![]() ${\mathrm cf}(\delta ) < \mu $
. This is because there is a hod pair
${\mathrm cf}(\delta ) < \mu $
. This is because there is a hod pair
![]() $({\mathcal {P}},\Sigma )\in \mathcal {F}$
, a
$({\mathcal {P}},\Sigma )\in \mathcal {F}$
, a
![]() $\delta ^*$
such that
$\delta ^*$
such that
![]() ${\mathcal {P}}{\vDash } \delta ^*$
is Woodin and
${\mathcal {P}}{\vDash } \delta ^*$
is Woodin and
![]() $\delta = \pi _{{\mathcal {P}},\infty }(\delta ^*)$
. Now, if
$\delta = \pi _{{\mathcal {P}},\infty }(\delta ^*)$
. Now, if
![]() ${\delta }>\sup (\pi ^{{\mathcal {T}}, b}[{\delta }^{{\mathcal { H}}}])$
, then by Lemma 10.3,
${\delta }>\sup (\pi ^{{\mathcal {T}}, b}[{\delta }^{{\mathcal { H}}}])$
, then by Lemma 10.3,
![]() ${\mathrm cf}({\delta })={\mathrm cf}(Ord\cap {\mathcal { H}})<\nu _0$
.
${\mathrm cf}({\delta })={\mathrm cf}(Ord\cap {\mathcal { H}})<\nu _0$
.
We now state and prove our main proposition of this subsection.
Proposition 10.5. The
![]() $(Z, {\lambda })$
-validated sts construction over X does not break down because of Break3.
$(Z, {\lambda })$
-validated sts construction over X does not break down because of Break3.
Proof. [Reference Sargsyan and Trang38, Section 12] handles a similar situation, and the proof here is very much like the proofs in [Reference Sargsyan and Trang38, Section 12]. Because of this, we give an outline of the proof.
Suppose
![]() ${\mathcal {M}}$
is a model appearing in the
${\mathcal {M}}$
is a model appearing in the
![]() $(Z, {\lambda })$
-validated sts construction over X and
$(Z, {\lambda })$
-validated sts construction over X and
![]() ${\mathcal {T}}^*\in {\mathcal {M}}$
is an
${\mathcal {T}}^*\in {\mathcal {M}}$
is an
![]() $\mathsf {uvs}$
iteration of
$\mathsf {uvs}$
iteration of
![]() ${\mathcal {R}}$
such that the indexing scheme requires that we index a branch of
${\mathcal {R}}$
such that the indexing scheme requires that we index a branch of
![]() ${\mathcal {T}}^*$
at
${\mathcal {T}}^*$
at
![]() $Ord\cap {\mathcal {M}}$
. We need to show that there is a branch b of
$Ord\cap {\mathcal {M}}$
. We need to show that there is a branch b of
![]() ${\mathcal {T}}^*$
such that
${\mathcal {T}}^*$
such that
![]() $({\mathcal {M}}, b)$
is Z-validated. Because of Proposition 8.6 and Proposition 9.11, there can be at most one such branch.
$({\mathcal {M}}, b)$
is Z-validated. Because of Proposition 8.6 and Proposition 9.11, there can be at most one such branch.
Because
![]() ${\mathcal {T}}^*$
is
${\mathcal {T}}^*$
is
![]() $\mathsf {uvs}$
, we have a normal iteration
$\mathsf {uvs}$
, we have a normal iteration
![]() ${\mathcal {T}}\in {\mathcal {M}}$
with last model
${\mathcal {T}}\in {\mathcal {M}}$
with last model
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() $\pi ^{{\mathcal {T}}}$
is defined and a normal iteration
$\pi ^{{\mathcal {T}}}$
is defined and a normal iteration
![]() ${\mathcal {U}}$
based on
${\mathcal {U}}$
based on
![]() ${\mathcal {S}}^b$
such that
${\mathcal {S}}^b$
such that
![]() ${\mathcal {T}}^\frown {\mathcal {U}}={\mathcal {T}}^*$
. Because the construction does not break because of Break2 (see Proposition 10.2), we have that
${\mathcal {T}}^\frown {\mathcal {U}}={\mathcal {T}}^*$
. Because the construction does not break because of Break2 (see Proposition 10.2), we have that
![]() ${\mathcal {M}}$
is Z-validated, and therefore,
${\mathcal {M}}$
is Z-validated, and therefore,
![]() ${\mathcal {T}}$
is Z-validated. Also, we can assume that
${\mathcal {T}}$
is Z-validated. Also, we can assume that
![]() ${\mathcal {U}}$
is not based on
${\mathcal {U}}$
is not based on
![]() ${\mathcal {S}}|\xi $
where
${\mathcal {S}}|\xi $
where
![]() $\xi =\sup (\pi ^{\mathcal {T}}[{\delta }^{\mathcal { H}}])$
, as otherwise the desired branch of
$\xi =\sup (\pi ^{\mathcal {T}}[{\delta }^{\mathcal { H}}])$
, as otherwise the desired branch of
![]() ${\mathcal {U}}$
is given by
${\mathcal {U}}$
is given by
![]() $\Psi $
.
$\Psi $
.
We now show that
![]() ${\mathcal {U}}$
has a branch b such that
${\mathcal {U}}$
has a branch b such that
![]() $({\mathcal {M}}, b)$
is Z-validated. Let
$({\mathcal {M}}, b)$
is Z-validated. Let
![]() ${\lambda }\in S$
be least such that
${\lambda }\in S$
be least such that
![]() ${\mathcal {R}}, {\mathcal {M}}\in H_{\lambda }$
. Given a
${\mathcal {R}}, {\mathcal {M}}\in H_{\lambda }$
. Given a
![]() $(\mu , {\lambda }, Z)$
-good hull U such that
$(\mu , {\lambda }, Z)$
-good hull U such that
![]() $\{{\mathcal {M}}, {\mathcal {T}}, {\mathcal {S}}, {\mathcal {U}}\}\subseteq U$
, let
$\{{\mathcal {M}}, {\mathcal {T}}, {\mathcal {S}}, {\mathcal {U}}\}\subseteq U$
, let
![]() $b_U=\Psi ^Z_W(\pi ^{-1}_U({\mathcal {U}}))$
, where W is any extension of Z such that
$b_U=\Psi ^Z_W(\pi ^{-1}_U({\mathcal {U}}))$
, where W is any extension of Z such that
![]() $\pi ^{-1}_U({\mathcal {S}}^b)={\mathcal {Q}}^Z_W$
. First, we claim that for all U as above,
$\pi ^{-1}_U({\mathcal {S}}^b)={\mathcal {Q}}^Z_W$
. First, we claim that for all U as above,
Claim 1.
![]() $b_U\in M_U$
.
$b_U\in M_U$
.
Proof. Given a U as above, we will use it as a subscript to denote the
![]() $\pi _U$
-preimages of the relevant objects. Fix then a U as above. Suppose first that
$\pi _U$
-preimages of the relevant objects. Fix then a U as above. Suppose first that
![]() ${\mathcal {Q}}(b_U, {\mathcal {U}}_U)$
does not exist. As we are assuming
${\mathcal {Q}}(b_U, {\mathcal {U}}_U)$
does not exist. As we are assuming
![]() ${\mathcal {U}}$
is not based on
${\mathcal {U}}$
is not based on
![]() ${\mathcal {S}}|\xi $
, Corollary 10.4 implies that
${\mathcal {S}}|\xi $
, Corollary 10.4 implies that
![]() ${\mathrm cf}({\delta }({\mathcal {U}}))\leq \nu _0$
. Because
${\mathrm cf}({\delta }({\mathcal {U}}))\leq \nu _0$
. Because
![]() $M_U$
is
$M_U$
is
![]() $\nu _0$
-closed, it follows that
$\nu _0$
-closed, it follows that
![]() $b_U\in M_U$
.
$b_U\in M_U$
.
Suppose next that
![]() ${\mathcal {Q}}(b_U, {\mathcal {U}}_U)$
exists. Let
${\mathcal {Q}}(b_U, {\mathcal {U}}_U)$
exists. Let
![]() $A_U$
be the preimage of
$A_U$
be the preimage of
![]() $A_{\lambda }$
. Notice now that letting
$A_{\lambda }$
. Notice now that letting
![]() $\Phi $
be the
$\Phi $
be the
![]() $\pi _U$
-pullback of
$\pi _U$
-pullback of
![]() $\Psi _{\lambda }$
, we have that
$\Psi _{\lambda }$
, we have that
![]() $Lp^{cuB, \Phi }(A_U)\in M_U$
.
$Lp^{cuB, \Phi }(A_U)\in M_U$
.
Let
![]() $Y=U\cap {\mathcal { H}}$
. Clearly, Y is an extension of Z and because
$Y=U\cap {\mathcal { H}}$
. Clearly, Y is an extension of Z and because
![]() ${\mathcal {M}}$
is Z-validated, we must have
${\mathcal {M}}$
is Z-validated, we must have
![]() $W^*$
an extension of
$W^*$
an extension of
![]() $Z\cup Y$
such that
$Z\cup Y$
such that
![]() ${\mathcal {S}}_U^b={\mathcal {Q}}^Z_{W^*}$
. Notice that because
${\mathcal {S}}_U^b={\mathcal {Q}}^Z_{W^*}$
. Notice that because
![]() $\Psi ^Z_{W^*}$
is computable from
$\Psi ^Z_{W^*}$
is computable from
![]() $\Phi $
and because
$\Phi $
and because
![]() $Lp^{cuB, \Phi }(A_U)\in M_U$
, we must have that
$Lp^{cuB, \Phi }(A_U)\in M_U$
, we must have that
![]() ${\mathcal {Q}}(b_U, {\mathcal {U}}_U)\in M_U$
. Hence,
${\mathcal {Q}}(b_U, {\mathcal {U}}_U)\in M_U$
. Hence,
![]() $b_U\in M_U$
.
$b_U\in M_U$
.
Suppose first that
![]() ${\mathrm cf}(lh({\mathcal {U}}))>\omega $
. In this case, let
${\mathrm cf}(lh({\mathcal {U}}))>\omega $
. In this case, let
![]() ${\mathcal {U}}$
be as above and set
${\mathcal {U}}$
be as above and set
![]() $c=\pi _U(b_U)$
. Then c is the unique well-founded branch of
$c=\pi _U(b_U)$
. Then c is the unique well-founded branch of
![]() ${\mathcal {U}}$
, and hence, for any
${\mathcal {U}}$
, and hence, for any
![]() $(\mu , {\lambda }, Z)$
-good hull
$(\mu , {\lambda }, Z)$
-good hull
![]() $X'$
such that
$X'$
such that
![]() $U\cup \{({\mathcal {M}}, c), U\}\in X'$
,
$U\cup \{({\mathcal {M}}, c), U\}\in X'$
,
![]() $c_{X'}=b_{X'}$
. Hence,
$c_{X'}=b_{X'}$
. Hence,
![]() $({\mathcal {M}}, c)$
is Z-validated (see Proposition 8.3).
$({\mathcal {M}}, c)$
is Z-validated (see Proposition 8.3).
Suppose then
![]() $lh({\mathcal {U}})=\omega $
. We now claim that
$lh({\mathcal {U}})=\omega $
. We now claim that
Claim. there is a
![]() $(\mu , {\lambda }, Z)$
-good hullFootnote 107
$(\mu , {\lambda }, Z)$
-good hullFootnote 107
![]() $X_0$
such that for all
$X_0$
such that for all
![]() $(\mu , {\lambda }, Z)$
-good hulls Y such that
$(\mu , {\lambda }, Z)$
-good hulls Y such that
![]() $X_0\cup \{{\mathcal {M}}, X_0\}\in Y$
,
$X_0\cup \{{\mathcal {M}}, X_0\}\in Y$
,
![]() $\pi _{X_0, Y}(b_{X'})=b_Y$
.
$\pi _{X_0, Y}(b_{X'})=b_Y$
.
Proof. Assuming not, we get a continuous chain
![]() $(X_{\alpha }: {\alpha }<\mu )$
such that
$(X_{\alpha }: {\alpha }<\mu )$
such that
-
1.
 ${\mathcal {M}}, {\mathcal {U}}\in X_0$
,
${\mathcal {M}}, {\mathcal {U}}\in X_0$
, -
2. for all
 ${\alpha }<\mu $
,
${\alpha }<\mu $
,
 $X_{{\alpha }+1}$
is a
$X_{{\alpha }+1}$
is a
 $(\mu , {\lambda }, Z)$
-good hull,
$(\mu , {\lambda }, Z)$
-good hull, -
3. for all
 ${\alpha }<\mu $
,
${\alpha }<\mu $
,
 $X_{{\alpha }}\cup \{X_{{\alpha }}\}\in X_{{\alpha }+1}$
,
$X_{{\alpha }}\cup \{X_{{\alpha }}\}\in X_{{\alpha }+1}$
, -
4. for all
 ${\alpha }<\mu $
,
${\alpha }<\mu $
,
 $\pi _{X_{{\alpha }+1}, X_{{\alpha }+2}}(b_{X_{{\alpha }+1}})\not =b_{X_{{\alpha }+1}}$
.
$\pi _{X_{{\alpha }+1}, X_{{\alpha }+2}}(b_{X_{{\alpha }+1}})\not =b_{X_{{\alpha }+1}}$
.
Let
![]() $\nu \in (\nu _0, \mu )$
be an inaccessible cardinal such that
$\nu \in (\nu _0, \mu )$
be an inaccessible cardinal such that
![]() $X_{\nu }\cap \mu =\nu $
. Fix now
$X_{\nu }\cap \mu =\nu $
. Fix now
![]() ${\alpha }<\nu $
such that
${\alpha }<\nu $
such that
As
![]() ${\mathrm cf}(lh({\mathcal {U}}_{X_{\nu }}))=\omega $
, this is easy to achieve. For
${\mathrm cf}(lh({\mathcal {U}}_{X_{\nu }}))=\omega $
, this is easy to achieve. For
![]() ${\beta }\in [{\alpha }, \nu )$
, let
${\beta }\in [{\alpha }, \nu )$
, let
![]() $c_{\beta }$
be the
$c_{\beta }$
be the
![]() $\pi _{X_{\alpha }, X_{\nu }}$
-pullback of
$\pi _{X_{\alpha }, X_{\nu }}$
-pullback of
![]() $b_{X_{\nu }}$
. Let for
$b_{X_{\nu }}$
. Let for
![]() ${\beta }\in [{\alpha }, \nu ]$
,
${\beta }\in [{\alpha }, \nu ]$
,
![]() $W_{\beta }$
be such that
$W_{\beta }$
be such that
![]() ${\mathcal {S}}^b_{X_{\beta }}={\mathcal {Q}}^Z_{W_{\beta }}$
. It follows that
${\mathcal {S}}^b_{X_{\beta }}={\mathcal {Q}}^Z_{W_{\beta }}$
. It follows that
![]() $c_{\beta }$
is according to the
$c_{\beta }$
is according to the
![]() $\pi _{X_{\beta }, X_{\nu }}$
-pullback of
$\pi _{X_{\beta }, X_{\nu }}$
-pullback of
![]() $\Psi ^Z_{W_{\nu }}$
. Because
$\Psi ^Z_{W_{\nu }}$
. Because
![]() $\Psi ^Z_{W_{\beta }}$
depends only on
$\Psi ^Z_{W_{\beta }}$
depends only on
![]() ${\mathcal {S}}^b_{X_{\beta }}$
, we have that
${\mathcal {S}}^b_{X_{\beta }}$
, we have that
![]() $c_{\beta }=b_{X_{\beta }}$
(this is because the
$c_{\beta }=b_{X_{\beta }}$
(this is because the
![]() $\pi _{X_{\beta }, X_{\nu }}$
-pullback of
$\pi _{X_{\beta }, X_{\nu }}$
-pullback of
![]() $\Psi ^Z_{W_{\nu }}$
is a strategy of the form
$\Psi ^Z_{W_{\nu }}$
is a strategy of the form
![]() $\Psi ^Z_Y$
, where
$\Psi ^Z_Y$
, where
![]() ${\mathcal {Q}}^Z_Y={\mathcal {S}}^b_{X_{\beta }}$
). It follows that for all
${\mathcal {Q}}^Z_Y={\mathcal {S}}^b_{X_{\beta }}$
). It follows that for all
![]() ${\beta }<{\gamma }\in [{\alpha }, \nu )$
,
${\beta }<{\gamma }\in [{\alpha }, \nu )$
,
![]() $\pi _{X_{\beta }, X_{\gamma }}(b_{X_{\beta }})=b_{X_{\gamma }}$
.
$\pi _{X_{\beta }, X_{\gamma }}(b_{X_{\beta }})=b_{X_{\gamma }}$
.
Fix now an
![]() $X_0$
as in the Claim. Set
$X_0$
as in the Claim. Set
![]() $c=\pi _{X_0}(b_{X_0})$
. The above property of
$c=\pi _{X_0}(b_{X_0})$
. The above property of
![]() $X_0$
guarantees that
$X_0$
guarantees that
![]() $({\mathcal {M}}, c)$
is Z-validated. Indeed, fix a
$({\mathcal {M}}, c)$
is Z-validated. Indeed, fix a
![]() $(\mu , {\lambda }, Z)$
-good hull U such that
$(\mu , {\lambda }, Z)$
-good hull U such that
![]() ${\mathcal {M}}, c\in U$
. Let Y be a
${\mathcal {M}}, c\in U$
. Let Y be a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() $X_0\cup U \cup \{X_0, U\}\in Y$
. Then
$X_0\cup U \cup \{X_0, U\}\in Y$
. Then
![]() $\pi _{U, Y}(c_U)=\pi _{X_0, Y}(b_{X_0})=b_Y$
. It follows that
$\pi _{U, Y}(c_U)=\pi _{X_0, Y}(b_{X_0})=b_Y$
. It follows that
![]() $c_U$
is the
$c_U$
is the
![]() $\pi _{U, Y}$
-pullback of
$\pi _{U, Y}$
-pullback of
![]() $\Psi ^Z_W$
, where W is such that
$\Psi ^Z_W$
, where W is such that
![]() ${\mathcal {S}}^b_Y={\mathcal {Q}}^Z_W$
. Hence,
${\mathcal {S}}^b_Y={\mathcal {Q}}^Z_W$
. Hence,
![]() $c_U=b_U$
.
$c_U=b_U$
.
10.3. Break4 never happens
The following is the main proposition of this subsection. We continue with
![]() $({\mathcal {R}}, X, \vec {{\mathcal {V}}}, {\lambda })$
of the previous section.
$({\mathcal {R}}, X, \vec {{\mathcal {V}}}, {\lambda })$
of the previous section.
Proposition 10.6. Suppose the
![]() $(Z, {\lambda })$
-validated sts construction over X breaks because of Break4 and that X is a transitive set such that
$(Z, {\lambda })$
-validated sts construction over X breaks because of Break4 and that X is a transitive set such that
![]() $H_{{\delta }^{\mathcal {R}}}^X$
is the universe of
$H_{{\delta }^{\mathcal {R}}}^X$
is the universe of
![]() ${\mathcal {R}}|{\delta }^{\mathcal {R}}$
and
${\mathcal {R}}|{\delta }^{\mathcal {R}}$
and
![]() ${\delta }^{\mathcal {R}}$
is a Woodin cardinal in X. Then
${\delta }^{\mathcal {R}}$
is a Woodin cardinal in X. Then
-
1.
 $\vec {{\mathcal {V}}}$
is not small (implying
$\vec {{\mathcal {V}}}$
is not small (implying
 ${\mathcal {V}}_{\eta }={\mathcal {R}}$
) and
${\mathcal {V}}_{\eta }={\mathcal {R}}$
) and -
2. letting
 $\eta '$
be such that Break4 occurs at
$\eta '$
be such that Break4 occurs at
 $\eta '$
and letting
$\eta '$
and letting
 $({\mathcal {T}}, b)\in {\mathcal {M}}_{\eta '}$
witness Break4 at
$({\mathcal {T}}, b)\in {\mathcal {M}}_{\eta '}$
witness Break4 at
 $\eta '$
, either
$\eta '$
, either
 ${\delta }^{\mathcal {R}}$
is not a Woodin cardinal of
${\delta }^{\mathcal {R}}$
is not a Woodin cardinal of
 ${\mathcal {M}}_{\eta '}$
or
${\mathcal {M}}_{\eta '}$
or
 $H_{{\delta }^{\mathcal {R}}}^{{\mathcal {M}}_{\eta '}}$
is not the universe of
$H_{{\delta }^{\mathcal {R}}}^{{\mathcal {M}}_{\eta '}}$
is not the universe of
 ${\mathcal {R}}|{\delta }^{\mathcal {R}}$
.
${\mathcal {R}}|{\delta }^{\mathcal {R}}$
.
Proof. Let p be the
![]() ${\mathcal {V}}_{\eta '}$
-to-
${\mathcal {V}}_{\eta '}$
-to-
![]() ${\mathcal {R}}$
iteration. Setting
${\mathcal {R}}$
iteration. Setting
![]() ${\mathcal {W}}={\mathcal {M}}_{\eta '}$
, we have that
${\mathcal {W}}={\mathcal {M}}_{\eta '}$
, we have that
-
1.
 ${\mathcal {W}}$
is Z-validated and
${\mathcal {W}}$
is Z-validated and -
2. b is not
 $(Z, \vec {{\mathcal {V}}})$
-embeddable (see Definition 9.4).
$(Z, \vec {{\mathcal {V}}})$
-embeddable (see Definition 9.4).
Let
![]() ${\beta }$
be such that
${\beta }$
be such that
![]() ${\mathcal {W}}|{\beta }$
authenticates b. Thus,
${\mathcal {W}}|{\beta }$
authenticates b. Thus,
![]() ${\mathcal {W}}|{\beta }$
is a model of
${\mathcal {W}}|{\beta }$
is a model of
![]() $\mathsf {ZFC}$
in which there is a limit of Woodin cardinals
$\mathsf {ZFC}$
in which there is a limit of Woodin cardinals
![]() $\nu $
and the derived model of
$\nu $
and the derived model of
![]() ${\mathcal {W}}|{\beta }$
at
${\mathcal {W}}|{\beta }$
at
![]() $\nu $
has a strategy for
$\nu $
has a strategy for
![]() ${\mathcal {Q}}(b, {\mathcal {T}})$
that is
${\mathcal {Q}}(b, {\mathcal {T}})$
that is
![]() ${\mathcal {W}}|{\beta }$
-authenticated.
${\mathcal {W}}|{\beta }$
-authenticated.
Claim 1.
![]() $p^\frown {\mathcal {T}}^\frown \{b\}$
is a Z-validated iteration (see Definition 8.2).
$p^\frown {\mathcal {T}}^\frown \{b\}$
is a Z-validated iteration (see Definition 8.2).
Proof. Towards a contradiction, suppose
![]() $p^\frown {\mathcal {T}}^\frown \{b\}$
is not Z-validated. Fix now a
$p^\frown {\mathcal {T}}^\frown \{b\}$
is not Z-validated. Fix now a
![]() $(\mu , {\lambda }, Z)$
-good hull U such that
$(\mu , {\lambda }, Z)$
-good hull U such that
![]() $({\mathcal {R}}, {\mathcal {W}}, p, {\mathcal {T}}, b) \in U$
and
$({\mathcal {R}}, {\mathcal {W}}, p, {\mathcal {T}}, b) \in U$
and
![]() $p_U^\frown {\mathcal {T}}_U^\frown \{b_U\}$
is not a correctly guided Z-realizable iteration of
$p_U^\frown {\mathcal {T}}_U^\frown \{b_U\}$
is not a correctly guided Z-realizable iteration of
![]() ${\mathcal {R}}_U$
. Because
${\mathcal {R}}_U$
. Because
![]() ${\mathcal {W}}$
is Z-validated, we can assume that
${\mathcal {W}}$
is Z-validated, we can assume that
![]() $p_U^\frown {\mathcal {T}}_U$
is a correctly guided Z-realizable iteration. It must then be that
$p_U^\frown {\mathcal {T}}_U$
is a correctly guided Z-realizable iteration. It must then be that
![]() ${\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
is not Z-approved.
${\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
is not Z-approved.
To save ink, let us prove that, in fact,
![]() ${\mathcal {N}}=_{def}{\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
is Z-approved of depth 1. As the proof of depth n is the same, we will leave the rest to the reader. To start with, notice that since
${\mathcal {N}}=_{def}{\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
is Z-approved of depth 1. As the proof of depth n is the same, we will leave the rest to the reader. To start with, notice that since
![]() ${\mathcal {T}}_U$
itself is correctly guided Z-realizable, we have that
${\mathcal {T}}_U$
itself is correctly guided Z-realizable, we have that
![]() ${\mathcal {S}}={\mathrm m}^+({\mathcal {T}}_U)$
is weakly Z-suitable. To prove that
${\mathcal {S}}={\mathrm m}^+({\mathcal {T}}_U)$
is weakly Z-suitable. To prove that
![]() ${\mathcal {N}}$
is Z-approved of depth 1, we need to show that if
${\mathcal {N}}$
is Z-approved of depth 1, we need to show that if
![]() ${\mathcal {U}}\in {\mathcal {N}}$
is according to
${\mathcal {U}}\in {\mathcal {N}}$
is according to
![]() $S^{{\mathcal {N}}}$
, then
$S^{{\mathcal {N}}}$
, then
![]() ${\mathcal {U}}$
is Z-realizable.
${\mathcal {U}}$
is Z-realizable.
Fix then
![]() ${\alpha }\in R^{\mathcal {U}}$
and set
${\alpha }\in R^{\mathcal {U}}$
and set
![]() ${\mathcal {X}}={\mathcal {M}}_{\alpha }^{\mathcal {U}}$
. First, let us show that there is
${\mathcal {X}}={\mathcal {M}}_{\alpha }^{\mathcal {U}}$
. First, let us show that there is
![]() $Z'$
an extension of Z such that
$Z'$
an extension of Z such that
![]() ${\mathcal {Q}}^Z_{Z'}={\mathcal {X}}^b$
. Because
${\mathcal {Q}}^Z_{Z'}={\mathcal {X}}^b$
. Because
![]() ${\mathcal {T}}_U^\frown \{b_U\}$
is authenticated inside
${\mathcal {T}}_U^\frown \{b_U\}$
is authenticated inside
![]() ${\mathcal {W}}_U|{\beta }_U$
, we must have an iteration
${\mathcal {W}}_U|{\beta }_U$
, we must have an iteration
![]() ${\mathcal {Y}}$
of
${\mathcal {Y}}$
of
![]() ${\mathcal {R}}_U$
according to
${\mathcal {R}}_U$
according to
![]() $S^{{\mathcal {W}}_U}$
with last model
$S^{{\mathcal {W}}_U}$
with last model
![]() ${\mathcal {R}}_1$
such that there is an embedding
${\mathcal {R}}_1$
such that there is an embedding
![]() $k:{\mathcal {X}}^b\rightarrow {\mathcal {R}}_1^b$
with the property that
$k:{\mathcal {X}}^b\rightarrow {\mathcal {R}}_1^b$
with the property that
![]() $\pi ^{{\mathcal {Y}}, b}=k\circ \pi ^{{\mathcal {U}}_{\leq {\mathcal {X}}}, b}$
. Because
$\pi ^{{\mathcal {Y}}, b}=k\circ \pi ^{{\mathcal {U}}_{\leq {\mathcal {X}}}, b}$
. Because
![]() ${\mathcal {Y}}$
is Z-realizable, we must have Y an extension of Z such that
${\mathcal {Y}}$
is Z-realizable, we must have Y an extension of Z such that
![]() ${\mathcal {R}}_1^b={\mathcal {Q}}^Z_Y$
. Composing k with
${\mathcal {R}}_1^b={\mathcal {Q}}^Z_Y$
. Composing k with
![]() $\tau ^Z_Y$
, we have that
$\tau ^Z_Y$
, we have that
![]() ${\mathcal {X}}^b={\mathcal {Q}}^Z_{Z'}$
for some
${\mathcal {X}}^b={\mathcal {Q}}^Z_{Z'}$
for some
![]() $Z'$
.
$Z'$
.
The rest is similar. If
![]() ${\mathcal {U}}^*$
is the longest initial segment of
${\mathcal {U}}^*$
is the longest initial segment of
![]() ${\mathcal {U}}_{\geq {\mathcal {X}}}$
that is based on
${\mathcal {U}}_{\geq {\mathcal {X}}}$
that is based on
![]() ${\mathcal {X}}^b$
, then there are
${\mathcal {X}}^b$
, then there are
![]() ${\mathcal {Y}}$
and k as above such that
${\mathcal {Y}}$
and k as above such that
![]() ${\mathcal {U}}^*$
is according to the k-pullback of
${\mathcal {U}}^*$
is according to the k-pullback of
![]() $S^{{\mathcal {M}}_U}_{{\mathcal {R}}_1^b}$
. But because
$S^{{\mathcal {M}}_U}_{{\mathcal {R}}_1^b}$
. But because
![]() ${\mathcal {W}}_U$
is Z-approved,
${\mathcal {W}}_U$
is Z-approved,
![]() $S^{{\mathcal {W}}_U}_{{\mathcal {R}}_1^b}$
is a fragment of
$S^{{\mathcal {W}}_U}_{{\mathcal {R}}_1^b}$
is a fragment of
![]() $\Psi ^Z_Y$
, where Y is as above. Hence,
$\Psi ^Z_Y$
, where Y is as above. Hence,
![]() ${\mathcal {U}}^*$
is according to
${\mathcal {U}}^*$
is according to
![]() $\Psi ^Z_X$
for some X (see Corollary 6.8).
$\Psi ^Z_X$
for some X (see Corollary 6.8).
Let now U be a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() $({\mathcal {R}}, {\mathcal {W}}, {\mathcal {T}}, b,{\mathcal {Q}})\in U$
. Because
$({\mathcal {R}}, {\mathcal {W}}, {\mathcal {T}}, b,{\mathcal {Q}})\in U$
. Because
![]() ${\mathcal {T}}$
is Z-validated, we have that the
${\mathcal {T}}$
is Z-validated, we have that the
![]() $\pi _U$
-realizable branch d of
$\pi _U$
-realizable branch d of
![]() ${\mathcal {T}}_U$
is cofinal. Suppose then
${\mathcal {T}}_U$
is cofinal. Suppose then
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists. Then because it is Z-approved, we must have that
${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists. Then because it is Z-approved, we must have that
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)={\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
(for example, see Proposition 9.5). It follows that
${\mathcal {Q}}(d, {\mathcal {T}}_U)={\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
(for example, see Proposition 9.5). It follows that
![]() $d=b_U$
, and so b is
$d=b_U$
, and so b is
![]() $(Z, \vec {{\mathcal {V}}})$
-embeddable.
$(Z, \vec {{\mathcal {V}}})$
-embeddable.
Assume now that clause 1 fails. Because
![]() ${\mathcal {V}}$
is not small, we must have that
${\mathcal {V}}$
is not small, we must have that
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists (as d is the realizable branch of
${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists (as d is the realizable branch of
![]() $p^\frown {\mathcal {T}}_U$
). Assume now that
$p^\frown {\mathcal {T}}_U$
). Assume now that
![]() ${\mathcal {V}}$
is not small. This means that
${\mathcal {V}}$
is not small. This means that
![]() ${\mathcal {R}}={\mathcal {V}}_{\eta }$
. Assume now that clause 2 fails. Since
${\mathcal {R}}={\mathcal {V}}_{\eta }$
. Assume now that clause 2 fails. Since
![]() ${\delta }^{\mathcal {R}}$
is a regular cardinal of
${\delta }^{\mathcal {R}}$
is a regular cardinal of
![]() ${\mathcal {W}}$
,
${\mathcal {W}}$
,
![]() $H_{{\delta }^{\mathcal {R}}}^{{\mathcal {W}}}$
is the universe of
$H_{{\delta }^{\mathcal {R}}}^{{\mathcal {W}}}$
is the universe of
![]() ${\mathcal {R}}|{\delta }^{\mathcal {R}}$
and
${\mathcal {R}}|{\delta }^{\mathcal {R}}$
and
![]() ${\mathcal {R}}={\mathcal {V}}_{\eta }$
. If
${\mathcal {R}}={\mathcal {V}}_{\eta }$
. If
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_{\mathcal {U}})$
does not exist, then the d realizes back into
${\mathcal {Q}}(d, {\mathcal {T}}_{\mathcal {U}})$
does not exist, then the d realizes back into
![]() ${\mathcal {W}}$
. We now argue that
${\mathcal {W}}$
. We now argue that
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists.
${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists.
Claim 2.
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists.
${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists.
Proof. Towards a contradiction, assume
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)$
does not exist. Thus,
${\mathcal {Q}}(d, {\mathcal {T}}_U)$
does not exist. Thus,
![]() $d\cap D^{{\mathcal {T}}_U}=\emptyset $
and
$d\cap D^{{\mathcal {T}}_U}=\emptyset $
and
![]() $\pi ^{{\mathcal {T}}_U}({\delta }^{{\mathcal {R}}_U})={\delta }({\mathcal {T}}_U)$
. Set
$\pi ^{{\mathcal {T}}_U}({\delta }^{{\mathcal {R}}_U})={\delta }({\mathcal {T}}_U)$
. Set
![]() ${\mathcal {N}}={\mathcal {M}}^{{\mathcal {T}}_U}_d$
and
${\mathcal {N}}={\mathcal {M}}^{{\mathcal {T}}_U}_d$
and
![]() $j=\pi ^{{\mathcal {T}}_U}_d$
Footnote 108. Because
$j=\pi ^{{\mathcal {T}}_U}_d$
Footnote 108. Because
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)$
does not exist, we have that
${\mathcal {Q}}(d, {\mathcal {T}}_U)$
does not exist, we have that
![]() ${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}}_U)$
is a Woodin cardinal’.
${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}}_U)$
is a Woodin cardinal’.
We have that
![]() $j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))\in {\mathcal {N}}$
and is authenticated in
$j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))\in {\mathcal {N}}$
and is authenticated in
![]() ${\mathcal {N}}$
. Let
${\mathcal {N}}$
. Let
![]() ${\gamma }=j({\beta }_U)$
. Then
${\gamma }=j({\beta }_U)$
. Then
![]() ${\mathcal {N}}|{\gamma }$
has Woodin cardinals that are bigger than
${\mathcal {N}}|{\gamma }$
has Woodin cardinals that are bigger than
![]() ${\delta }(j({\mathcal {T}}_U))$
. Let
${\delta }(j({\mathcal {T}}_U))$
. Let
![]() ${\delta }$
be the least one that is bigger than
${\delta }$
be the least one that is bigger than
![]() $Ord\cap j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))$
. We can now iterate
$Ord\cap j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))$
. We can now iterate
![]() ${\mathcal {N}}$
below
${\mathcal {N}}$
below
![]() ${\delta }$
but above
${\delta }$
but above
![]() $Ord\cap j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))$
to make
$Ord\cap j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))$
to make
![]() ${\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
generic for the extender algebra at the image of
${\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
generic for the extender algebra at the image of
![]() ${\delta }$
. This iteration produces
${\delta }$
. This iteration produces
![]() $i:{\mathcal {N}}\rightarrow {\mathcal {N}}_1$
such that
$i:{\mathcal {N}}\rightarrow {\mathcal {N}}_1$
such that
![]() $\mathrm {crit }(i)>{\delta }(j({\mathcal {T}}_U))$
. Letting
$\mathrm {crit }(i)>{\delta }(j({\mathcal {T}}_U))$
. Letting
![]() $h\subseteq Coll(\omega , i({\delta }))$
be
$h\subseteq Coll(\omega , i({\delta }))$
be
![]() ${\mathcal {N}}_1$
-generic such that
${\mathcal {N}}_1$
-generic such that
![]() ${\mathcal {Q}}(b_U, {\mathcal {T}}_U)\in {\mathcal {N}}_1[h]$
, we can find
${\mathcal {Q}}(b_U, {\mathcal {T}}_U)\in {\mathcal {N}}_1[h]$
, we can find
such that
-
○
 $l\in {\mathcal {N}}_1[h]$
,
$l\in {\mathcal {N}}_1[h]$
, -
○
 $l{\restriction } ({\mathrm m}^+({\mathcal {T}}_U))^b=\pi ^{j({\mathcal {T}}_U), b}$
.
$l{\restriction } ({\mathrm m}^+({\mathcal {T}}_U))^b=\pi ^{j({\mathcal {T}}_U), b}$
.
As
![]() ${\mathcal {N}}_1[h]{\vDash } \text {`}j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))$
is authenticated and has an authenticated strategy’,
${\mathcal {N}}_1[h]{\vDash } \text {`}j({\mathcal {Q}}(b_U, {\mathcal {T}}_U))$
is authenticated and has an authenticated strategy’,
![]() ${\mathcal {N}}_1[h]{\vDash } \text {`}{\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
has an authenticated iteration strategy’, and hence,
${\mathcal {N}}_1[h]{\vDash } \text {`}{\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
has an authenticated iteration strategy’, and hence,
![]() ${\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
is definable in
${\mathcal {Q}}(b_U, {\mathcal {T}}_U)$
is definable in
![]() ${\mathcal {N}}_1[h]$
from objects in
${\mathcal {N}}_1[h]$
from objects in
![]() ${\mathcal {N}}_1$
. It follows that
${\mathcal {N}}_1$
. It follows that
![]() ${\mathcal {Q}}(b_U, {\mathcal {T}}_U)\in {\mathcal {N}}_1$
, implying that
${\mathcal {Q}}(b_U, {\mathcal {T}}_U)\in {\mathcal {N}}_1$
, implying that
![]() ${\mathcal {N}}_1{\vDash } \text {`}{\delta }({\mathcal {T}}_U)$
is not a Woodin cardinal’. Hence,
${\mathcal {N}}_1{\vDash } \text {`}{\delta }({\mathcal {T}}_U)$
is not a Woodin cardinal’. Hence,
![]() ${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}}_U)$
is not a Woodin cardinal’. Therefore,
${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}}_U)$
is not a Woodin cardinal’. Therefore,
![]() ${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists.
${\mathcal {Q}}(d, {\mathcal {T}}_U)$
exists.
10.4. A conclusion
Proposition 10.7. Suppose
![]() $\vec {{\mathcal {V}}}$
is a small array with the Z-realizability property. Then either
$\vec {{\mathcal {V}}}$
is a small array with the Z-realizability property. Then either
-
1.
 ${\mathcal {V}}_{\eta }$
has a Z-validated iteration strategy
${\mathcal {V}}_{\eta }$
has a Z-validated iteration strategyor
-
2. there is a Z-validated
 $\mathsf {nuvs}$
iteration p of
$\mathsf {nuvs}$
iteration p of
 ${\mathcal {V}}_{\eta }$
such that
${\mathcal {V}}_{\eta }$
such that
 ${\mathrm m}^+(p)$
is Z-suitable.Footnote 110
${\mathrm m}^+(p)$
is Z-suitable.Footnote 110
Proof. The proof has already been given in the previous subsections. Suppose that
![]() ${\mathcal {V}}_{\eta }$
does not have a Z-validated iteration strategy. The proof of Proposition 10.5 shows that if p is a Z-validated
${\mathcal {V}}_{\eta }$
does not have a Z-validated iteration strategy. The proof of Proposition 10.5 shows that if p is a Z-validated
![]() $\mathsf {uvs}$
iteration of
$\mathsf {uvs}$
iteration of
![]() ${\mathcal {V}}_{\eta }$
of limit length, then there is a unique branch b of p such that
${\mathcal {V}}_{\eta }$
of limit length, then there is a unique branch b of p such that
![]() $p^\frown \{b\}$
is Z-validated. Therefore, since picking Z-validated branches is not defining an iteration strategy for
$p^\frown \{b\}$
is Z-validated. Therefore, since picking Z-validated branches is not defining an iteration strategy for
![]() ${\mathcal {V}}_{\eta }$
, we must have a
${\mathcal {V}}_{\eta }$
, we must have a
![]() $\mathsf {nuvs}$
Z-validated iteration p of
$\mathsf {nuvs}$
Z-validated iteration p of
![]() ${\mathcal {V}}_{\eta }$
which does not have a Z-validated branch.Footnote 111
${\mathcal {V}}_{\eta }$
which does not have a Z-validated branch.Footnote 111
We now claim that
![]() ${\mathrm m}^+(p)$
is a Z-suitable hod premouse. Indeed, suppose there is some Z-validated sts premouse
${\mathrm m}^+(p)$
is a Z-suitable hod premouse. Indeed, suppose there is some Z-validated sts premouse
![]() ${\mathcal {Q}}$
extending
${\mathcal {Q}}$
extending
![]() ${\mathcal {R}}=_{def}{\mathrm m}^+(p)$
such that
${\mathcal {R}}=_{def}{\mathrm m}^+(p)$
such that
![]() ${\mathcal {Q}}$
is a
${\mathcal {Q}}$
is a
![]() ${\mathcal {Q}}$
-structure for p. Let then U be a good hull such that
${\mathcal {Q}}$
-structure for p. Let then U be a good hull such that
![]() $\{\vec {{\mathcal {V}}}, p, {\mathcal {Q}}\}\in U$
. Appealing to Proposition 9.10, we now have
$\{\vec {{\mathcal {V}}}, p, {\mathcal {Q}}\}\in U$
. Appealing to Proposition 9.10, we now have
![]() ${\beta }\leq lh(\vec {{\mathcal {V}}})$
, a branch b of
${\beta }\leq lh(\vec {{\mathcal {V}}})$
, a branch b of
![]() $p_U$
such that
$p_U$
such that
![]() ${\mathcal {Q}}(b, p_U)$
exists and a weak l-embedding
${\mathcal {Q}}(b, p_U)$
exists and a weak l-embedding
![]() $k:{\mathcal {M}}_b^{p_U}\rightarrow \mathcal {C}_l({\mathcal {V}}_{\beta })$
for an appropriate l. It follows that
$k:{\mathcal {M}}_b^{p_U}\rightarrow \mathcal {C}_l({\mathcal {V}}_{\beta })$
for an appropriate l. It follows that
![]() ${\mathcal {Q}}(b, p_U)$
is Z-approved, and hence,
${\mathcal {Q}}(b, p_U)$
is Z-approved, and hence,
![]() ${\mathcal {Q}}(b, p_U)={\mathcal {Q}}_U$
. Because
${\mathcal {Q}}(b, p_U)={\mathcal {Q}}_U$
. Because
![]() ${\mathcal {Q}}_U\in M_U$
, we have that
${\mathcal {Q}}_U\in M_U$
, we have that
![]() $b\in M_U$
. Then
$b\in M_U$
. Then
![]() $c=_{def}\pi _U(b)$
is a (cofinal) branch of p such that
$c=_{def}\pi _U(b)$
is a (cofinal) branch of p such that
![]() $p^\frown \{c\}$
is Z-validated.
$p^\frown \{c\}$
is Z-validated.
11. Hybrid fully backgrounded constructions
The goal of this section is to adopt the
![]() $K^c$
-construction used in [Reference Sargsyan and Trang38] to our current situation. As we have the large cardinals in V, it is easier to perform fully backgrounded constructions than using partial background certificates. For instance, proofs of iterability will be easier.
$K^c$
-construction used in [Reference Sargsyan and Trang38] to our current situation. As we have the large cardinals in V, it is easier to perform fully backgrounded constructions than using partial background certificates. For instance, proofs of iterability will be easier.
The construction that we intend to perform will produce an almost excellent (see Definition 2.7) hod premouse
![]() ${\mathcal {P}}$
extending
${\mathcal {P}}$
extending
![]() ${\mathcal { H}}$
. The construction will be done in V.
${\mathcal { H}}$
. The construction will be done in V.
The fully backgrounded construction that we have in mind has two different backgrounding conditions for extenders. The extenders with critical point
![]() $>\Theta =_{def} \delta ^{\mathcal {H}}$
will have total extenders as their background certificates. The extenders with critical point
$>\Theta =_{def} \delta ^{\mathcal {H}}$
will have total extenders as their background certificates. The extenders with critical point
![]() $\Theta $
will be authenticated by good hulls. We call this construction the the hybrid fully backgrounded construction over
$\Theta $
will be authenticated by good hulls. We call this construction the the hybrid fully backgrounded construction over
![]() ${\mathcal { H}}$
and denote it by
${\mathcal { H}}$
and denote it by
![]() $\mathsf {HFBC}(\mu )$
.
$\mathsf {HFBC}(\mu )$
.
We fix a condensing set
![]() $Z\in Cnd({\mathcal { H}})\cap V$
. While Z will appear in our authentication definitions, it can be shown that
$Z\in Cnd({\mathcal { H}})\cap V$
. While Z will appear in our authentication definitions, it can be shown that
![]() $\mathsf {HFBC}(\mu )$
does not depend on Z.
$\mathsf {HFBC}(\mu )$
does not depend on Z.
![]() $\mathsf {HFBC}(\mu )$
proceeds more or less according to the usual procedure for building hod pairs until we reach a weakly Z-suitable stage
$\mathsf {HFBC}(\mu )$
proceeds more or less according to the usual procedure for building hod pairs until we reach a weakly Z-suitable stage
![]() ${\mathcal {R}}$
. At this stage, we must continue with a fully backgrounded Z-validated sts construction over
${\mathcal {R}}$
. At this stage, we must continue with a fully backgrounded Z-validated sts construction over
![]() ${\mathcal {R}}$
. If this construction produces a
${\mathcal {R}}$
. If this construction produces a
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() ${\mathcal {R}}$
, then we attempt to construct a Z-validated strategy for it. Failing to do so will produce our honest Z-suitable
${\mathcal {R}}$
, then we attempt to construct a Z-validated strategy for it. Failing to do so will produce our honest Z-suitable
![]() ${\mathcal {R}}$
as in Proposition 10.7.
${\mathcal {R}}$
as in Proposition 10.7.
![]() $\mathsf {HFBC}$
can fail in the usual ways by producing a level whose countable substructures are not iterable.Footnote 112 However, our constructions are aimed at producing models with strictly weaker large cardinal structure than those for which we know how to prove iterability. In particular, the main theorem of [Reference Neeman31] implies that
$\mathsf {HFBC}$
can fail in the usual ways by producing a level whose countable substructures are not iterable.Footnote 112 However, our constructions are aimed at producing models with strictly weaker large cardinal structure than those for which we know how to prove iterability. In particular, the main theorem of [Reference Neeman31] implies that
![]() $\mathsf {HFBC}$
does not fail because of issues having to do with iterability.
$\mathsf {HFBC}$
does not fail because of issues having to do with iterability.
We should say that the construction that follows is an adaptation of a similar construction introduced in [Reference Sargsyan and Trang38, Section 10.2.9 and 12.2]. Because of this we will not dwell too much on how extenders with critical point
![]() ${\delta }^{\mathcal {H}}$
are chosen. The reader may consult [Reference Sargsyan and Trang38, Lemma 12.3.15]. The first of these constructions used fully backgrounded certificates like we will do in the next subsection. It was used to prove the Mouse Set Conjecture in the minimal model of
${\delta }^{\mathcal {H}}$
are chosen. The reader may consult [Reference Sargsyan and Trang38, Lemma 12.3.15]. The first of these constructions used fully backgrounded certificates like we will do in the next subsection. It was used to prove the Mouse Set Conjecture in the minimal model of
![]() $\mathsf {LSA}$
. The second was used to construct a model of
$\mathsf {LSA}$
. The second was used to construct a model of
![]() $\mathsf {LSA}$
from
$\mathsf {LSA}$
from
![]() $\mathsf {PFA}$
.
$\mathsf {PFA}$
.
11.1. The levels of
 $\mathsf {HFBC}(\mu )$
$\mathsf {HFBC}(\mu )$
We assume that T holds and let
![]() $(S, S_0, \nu _0,\vec {Y}, \vec {A})$
witness it. Let
$(S, S_0, \nu _0,\vec {Y}, \vec {A})$
witness it. Let
![]() $\mu \in S_0$
. When discussing the CMI objects at
$\mu \in S_0$
. When discussing the CMI objects at
![]() $\mu $
, we will omit
$\mu $
, we will omit
![]() $\mu $
from our notation.
$\mu $
from our notation.
Below, we will define the sequence
![]() $({\mathcal {M}}_{\xi },\Sigma _{\xi }: \xi \leq \Omega ')$
, where
$({\mathcal {M}}_{\xi },\Sigma _{\xi }: \xi \leq \Omega ')$
, where
![]() $\Omega ' \leq Ord$
, of levels of the hybrid fully backgrounded construction at
$\Omega ' \leq Ord$
, of levels of the hybrid fully backgrounded construction at
![]() $\mu $
. Here, we develop the terminology that we will use to describe the passage from
$\mu $
. Here, we develop the terminology that we will use to describe the passage from
![]() ${\mathcal {M}}_{\xi }$
to
${\mathcal {M}}_{\xi }$
to
![]() ${\mathcal {M}}_{\xi +1}$
.
${\mathcal {M}}_{\xi +1}$
.
![]() $\mathsf {HFBC}$
resembles the
$\mathsf {HFBC}$
resembles the
![]() $K^c$
-construction of [Reference Sargsyan and Trang38, Section 12.2] except that we require that the extenders with critical point
$K^c$
-construction of [Reference Sargsyan and Trang38, Section 12.2] except that we require that the extenders with critical point
![]() $>\delta ^{\mathcal { H}}$
used in the construction have total certificates in the sense of [Reference Mitchell and Steel28, Chapter 12]. Because our construction does not reach a Woodin cardinal that is a limit of Woodin cardinals, the results of [Reference Neeman31] apply. For instance, [Reference Neeman31, Theorem 1.1] will be used to conclude that the countable submodels of each
$>\delta ^{\mathcal { H}}$
used in the construction have total certificates in the sense of [Reference Mitchell and Steel28, Chapter 12]. Because our construction does not reach a Woodin cardinal that is a limit of Woodin cardinals, the results of [Reference Neeman31] apply. For instance, [Reference Neeman31, Theorem 1.1] will be used to conclude that the countable submodels of each
![]() ${\mathcal {M}}_{\xi }$
are
${\mathcal {M}}_{\xi }$
are
![]() $\omega _1+1$
-iterable. Other theorems that we will use from [Reference Neeman31] are [Reference Neeman31, Theorem 2.1, 2.10, 3.11 and Corollary 3.14].
$\omega _1+1$
-iterable. Other theorems that we will use from [Reference Neeman31] are [Reference Neeman31, Theorem 2.1, 2.10, 3.11 and Corollary 3.14].
Say that
![]() ${\mathcal {M}}$
nicely extends
${\mathcal {M}}$
nicely extends
![]() ${\mathcal { H}}$
if there is a
${\mathcal { H}}$
if there is a
![]() $(\mu , \mu , Z)$
-good hull U such that
$(\mu , \mu , Z)$
-good hull U such that
![]() ${\mathcal {M}}_U$
nicely extends
${\mathcal {M}}_U$
nicely extends
![]() ${\mathcal {Q}}^Z_{U\cap {\mathcal { H}}}$
. Suppose now that
${\mathcal {Q}}^Z_{U\cap {\mathcal { H}}}$
. Suppose now that
![]() ${\mathcal {M}}$
is a Z-validated hod premouse nicely extending
${\mathcal {M}}$
is a Z-validated hod premouse nicely extending
![]() ${\mathcal { H}}$
. Set
${\mathcal { H}}$
. Set
![]() $mo({\mathcal {M}})=o^{\mathcal {M}}({\delta }^{{\mathcal { H}}})$
.Footnote 113
$mo({\mathcal {M}})=o^{\mathcal {M}}({\delta }^{{\mathcal { H}}})$
.Footnote 113
Definition 11.1. Given a Z-validated hod premouse nicely extending
![]() ${\mathcal { H}}$
, we say
${\mathcal { H}}$
, we say
![]() ${\mathcal {M}}$
is appropriate if
${\mathcal {M}}$
is appropriate if
![]() $Ord\cap {\mathcal {M}}=mo({\mathcal {M}})$
and
$Ord\cap {\mathcal {M}}=mo({\mathcal {M}})$
and
![]() ${\mathcal {M}}{\vDash }$
‘there are no Woodin cardinals in the interval
${\mathcal {M}}{\vDash }$
‘there are no Woodin cardinals in the interval
![]() $[{\delta }^{{\mathcal { H}}}, mo({\mathcal {M}}))'$
.
$[{\delta }^{{\mathcal { H}}}, mo({\mathcal {M}}))'$
.
Given an appropriate
![]() ${\mathcal {M}}$
, we would like to describe the next appropriate Z-validated hod premouse. We do this by preparing
${\mathcal {M}}$
, we would like to describe the next appropriate Z-validated hod premouse. We do this by preparing
![]() ${\mathcal {M}}$
, which involves building over
${\mathcal {M}}$
, which involves building over
![]() ${\mathcal {M}}$
some mild structures in order to reach the next stage that is either a stage where we can add an extender or is a weakly Z-suitable stage. In the latter case, we will put
${\mathcal {M}}$
some mild structures in order to reach the next stage that is either a stage where we can add an extender or is a weakly Z-suitable stage. In the latter case, we will put
![]() $\mathsf {HFBC}(\mu )$
on hold and continue with the Z-validated sts construction. The preparation of
$\mathsf {HFBC}(\mu )$
on hold and continue with the Z-validated sts construction. The preparation of
![]() ${\mathcal {M}}$
has two stages. We first add a sharp to
${\mathcal {M}}$
has two stages. We first add a sharp to
![]() ${\mathcal {M}}$
and then close the resulting hod premouse under its strategy. Each of these constructions can change
${\mathcal {M}}$
and then close the resulting hod premouse under its strategy. Each of these constructions can change
![]() ${\mathcal {M}}$
as they can reach levels that project across
${\mathcal {M}}$
as they can reach levels that project across
![]() ${\mathcal {M}}$
. The functions that we referred to above are
${\mathcal {M}}$
. The functions that we referred to above are
![]() $next_{\#}$
,
$next_{\#}$
,
![]() $next_s$
,
$next_s$
,
![]() $next_{bex}$
and
$next_{bex}$
and
![]() $next_{\Theta -ex}$
.
$next_{\Theta -ex}$
.
![]() $next_{bex}({\mathcal {M}})$
$next_{bex}({\mathcal {M}})$
This function simply adds a backgrounded extender to
![]() ${\mathcal {M}}$
. Suppose that
${\mathcal {M}}$
. Suppose that
![]() ${\mathcal {M}}$
is appropriate. We say
${\mathcal {M}}$
is appropriate. We say
![]() $next_{bex}({\mathcal {M}})$
is almost successful if there is a triple
$next_{bex}({\mathcal {M}})$
is almost successful if there is a triple
![]() $({\kappa }, {\lambda }, F)$
such that
$({\kappa }, {\lambda }, F)$
such that
-
1.
 ${\kappa }<{\lambda }$
are inaccessible cardinals
${\kappa }<{\lambda }$
are inaccessible cardinals
 $>{\delta }^{\mathcal { H}}$
,
$>{\delta }^{\mathcal { H}}$
, -
2. F is a
 $({\kappa }, {\lambda })$
-extender such that
$({\kappa }, {\lambda })$
-extender such that
 $V_{\lambda }\subseteq Ult(V, F)$
,
$V_{\lambda }\subseteq Ult(V, F)$
, -
3. letting
 $G=F\cap {\mathcal {M}}$
,
$G=F\cap {\mathcal {M}}$
,
 $({\mathcal {M}}, G)$
is hod premouse.
$({\mathcal {M}}, G)$
is hod premouse.
We say
![]() $next_{bex}({\mathcal {M}})$
is successful if it is almost successful and there is a unique triple
$next_{bex}({\mathcal {M}})$
is successful if it is almost successful and there is a unique triple
![]() $({\kappa }, {\lambda }, F)$
as above such that if
$({\kappa }, {\lambda }, F)$
as above such that if
![]() $G=F\cap {\mathcal {M}}$
,
$G=F\cap {\mathcal {M}}$
,
![]() $({\mathcal {M}}, G)$
is a solid and universal Z-validated hod premouse with a Z-validated strategy and such that
$({\mathcal {M}}, G)$
is a solid and universal Z-validated hod premouse with a Z-validated strategy and such that
![]() $\rho ({\mathcal {M}}, G)>{\delta }^{{\mathcal { H}}}$
.
$\rho ({\mathcal {M}}, G)>{\delta }^{{\mathcal { H}}}$
.
Suppose now that
![]() ${\mathcal {M}}$
is appropriate. We say
${\mathcal {M}}$
is appropriate. We say
![]() ${\mathcal {M}}$
has badness type 0 if
${\mathcal {M}}$
has badness type 0 if
![]() $next_{bex}({\mathcal {M}})$
is almost successful but is not successful. We write
$next_{bex}({\mathcal {M}})$
is almost successful but is not successful. We write
![]() $bad({\mathcal {M}})=0$
. If
$bad({\mathcal {M}})=0$
. If
![]() $next_{bex}({\mathcal {M}})$
is successful or not almost successful, then
$next_{bex}({\mathcal {M}})$
is successful or not almost successful, then
-
1. if
 $next_{bex}({\mathcal {M}})$
is successful, then letting
$next_{bex}({\mathcal {M}})$
is successful, then letting
 $({\kappa }, {\lambda }, F)$
be the unique triple witnessing the success of
$({\kappa }, {\lambda }, F)$
be the unique triple witnessing the success of
 $next_{bex}({\mathcal {M}})$
, we let
$next_{bex}({\mathcal {M}})$
, we let
 $next_{bex}({\mathcal {M}})=({\mathcal {M}}, G)$
, where
$next_{bex}({\mathcal {M}})=({\mathcal {M}}, G)$
, where
 $G=F\cap {\mathcal {M}}$
.
$G=F\cap {\mathcal {M}}$
. -
2. If
 $next_{bex}({\mathcal {M}})$
is not almost successful, then we let
$next_{bex}({\mathcal {M}})$
is not almost successful, then we let
 $next_{bex}({\mathcal {M}})={\mathcal {M}}$
.
$next_{bex}({\mathcal {M}})={\mathcal {M}}$
.
![]() $next_{\#}({\mathcal {M}})$
$next_{\#}({\mathcal {M}})$
Suppose
![]() ${\mathcal {M}}$
is appropriate and
${\mathcal {M}}$
is appropriate and
![]() $bad({\mathcal {M}})\not =0$
. We let
$bad({\mathcal {M}})\not =0$
. We let
![]() $next_{\#}({\mathcal {M}})$
be built as follows. Let
$next_{\#}({\mathcal {M}})$
be built as follows. Let
![]() $({\mathcal {M}}_i: i\leq k)$
be a sequence of Z-validated hod premice defined as follows:
$({\mathcal {M}}_i: i\leq k)$
be a sequence of Z-validated hod premice defined as follows:
-
1.
 ${\mathcal {M}}_0=next_{bex}({\mathcal {M}})$
.
${\mathcal {M}}_0=next_{bex}({\mathcal {M}})$
. -
2. If
 $i+1\leq k$
, then there is
$i+1\leq k$
, then there is
 ${\mathcal {M}}^*$
that is an initial segment of
${\mathcal {M}}^*$
that is an initial segment of
 $J[{\mathcal {M}}_i]$
such that
$J[{\mathcal {M}}_i]$
such that
 $\rho ({\mathcal {M}}^*)<mo({\mathcal {M}}_i)$
, and letting
$\rho ({\mathcal {M}}^*)<mo({\mathcal {M}}_i)$
, and letting
 ${\mathcal {M}}^*$
be the least such initial segment of
${\mathcal {M}}^*$
be the least such initial segment of
 $J[{\mathcal {M}}_i]$
,
$J[{\mathcal {M}}_i]$
,
 ${\mathcal {M}}^*$
is solid and universal,
${\mathcal {M}}^*$
is solid and universal,
 $\rho ({\mathcal {M}}^*)>{\delta }^{{\mathcal { H}}}$
and
$\rho ({\mathcal {M}}^*)>{\delta }^{{\mathcal { H}}}$
and
 ${\mathcal {M}}_{i+1}=\mathcal {C}({\mathcal {M}}^*)$
.
${\mathcal {M}}_{i+1}=\mathcal {C}({\mathcal {M}}^*)$
. -
3. k is least such that either (i) no level of
 $J[{\mathcal {M}}_k]$
projects across
$J[{\mathcal {M}}_k]$
projects across
 $mo({\mathcal {M}}_k)$
or (ii) some level of
$mo({\mathcal {M}}_k)$
or (ii) some level of
 $J[{\mathcal {M}}_k]$
projects to or below
$J[{\mathcal {M}}_k]$
projects to or below
 ${\delta }^{{\mathcal { H}}}$
.
${\delta }^{{\mathcal { H}}}$
.
We say
![]() $next_{\#}({\mathcal {M}})$
is successful if
$next_{\#}({\mathcal {M}})$
is successful if
-
(a) clause 3(ii) does not happen,
-
(b)
 ${\mathcal {M}}_k^{\#}$
is solid and universal,
${\mathcal {M}}_k^{\#}$
is solid and universal, -
(c)
 $\rho ({\mathcal {M}}_k^{\#})>{\delta }^{{\mathcal { H}}}$
.
$\rho ({\mathcal {M}}_k^{\#})>{\delta }^{{\mathcal { H}}}$
.
If
![]() $next_{\#}({\mathcal {M}})$
is successful, then let
$next_{\#}({\mathcal {M}})$
is successful, then let
![]() $next_{\#}({\mathcal {M}})=\mathcal {C}({\mathcal {M}}_k^\#)$
.
$next_{\#}({\mathcal {M}})=\mathcal {C}({\mathcal {M}}_k^\#)$
.
Suppose now that
![]() ${\mathcal {M}}$
is appropriate. We say
${\mathcal {M}}$
is appropriate. We say
![]() ${\mathcal {M}}$
has badness type is 1 if
${\mathcal {M}}$
has badness type is 1 if
![]() $next_{\#}({\mathcal {M}})$
is not successful. We write
$next_{\#}({\mathcal {M}})$
is not successful. We write
![]() $bad({\mathcal {M}})=1$
.
$bad({\mathcal {M}})=1$
.
Suppose now that
![]() ${\mathcal {M}}$
is appropriate and
${\mathcal {M}}$
is appropriate and
![]() $bad({\mathcal {M}})\not =0, 1$
. We say
$bad({\mathcal {M}})\not =0, 1$
. We say
![]() ${\mathcal {M}}$
has badness type 2 if
${\mathcal {M}}$
has badness type 2 if
![]() $next_{\#}({\mathcal {M}})$
is not weakly Z-suitable and does not have a Z-validated strategy. We write
$next_{\#}({\mathcal {M}})$
is not weakly Z-suitable and does not have a Z-validated strategy. We write
![]() $bad({\mathcal {M}})=2$
.
$bad({\mathcal {M}})=2$
.
![]() $next_s({\mathcal {M}})$
$next_s({\mathcal {M}})$
Suppose now that
![]() ${\mathcal {M}}$
is appropriate,
${\mathcal {M}}$
is appropriate,
![]() $bad({\mathcal {M}})\not =0,1, 2$
and
$bad({\mathcal {M}})\not =0,1, 2$
and
![]() $next_{\#}({\mathcal {M}})$
is not weakly Z-suitable. Let
$next_{\#}({\mathcal {M}})$
is not weakly Z-suitable. Let
![]() $\Sigma $
be the unique Z-validated strategy of
$\Sigma $
be the unique Z-validated strategy of
![]() $next_{\#}({\mathcal {M}})$
. We now define
$next_{\#}({\mathcal {M}})$
. We now define
![]() $next_s({\mathcal {M}})$
, which, in a sense, adds
$next_s({\mathcal {M}})$
, which, in a sense, adds
![]() $Lp^{\Sigma }(next_s({\mathcal {M}}))$
to
$Lp^{\Sigma }(next_s({\mathcal {M}}))$
to
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
We let
![]() $next_s({\mathcal {M}})$
be build as follows. Let
$next_s({\mathcal {M}})$
be build as follows. Let
![]() $({\mathcal {M}}_i, \Sigma _i: i\leq k)$
be a sequence of Z-validated hod premice along with their Z-validated strategies defined as follows:
$({\mathcal {M}}_i, \Sigma _i: i\leq k)$
be a sequence of Z-validated hod premice along with their Z-validated strategies defined as follows:
-
1.
 ${\mathcal {M}}_0={\mathcal {N}}$
and
${\mathcal {M}}_0={\mathcal {N}}$
and
 $\Sigma _0=\Sigma $
.
$\Sigma _0=\Sigma $
. -
2. If
 $i+1\leq k$
, then there is
$i+1\leq k$
, then there is
 ${\mathcal {M}}^*$
that is an initial segment of
${\mathcal {M}}^*$
that is an initial segment of
 $J[\vec {E}, \Sigma _i]({\mathcal {M}}_i)$
Footnote 114 such that
$J[\vec {E}, \Sigma _i]({\mathcal {M}}_i)$
Footnote 114 such that
 $\rho ({\mathcal {M}}^*)<mo({\mathcal {M}}_i)$
, and letting
$\rho ({\mathcal {M}}^*)<mo({\mathcal {M}}_i)$
, and letting
 ${\mathcal {M}}^*$
be the least such initial segment of
${\mathcal {M}}^*$
be the least such initial segment of
 $J[\vec {E}, \Sigma _i]({\mathcal {M}}_i)$
,
$J[\vec {E}, \Sigma _i]({\mathcal {M}}_i)$
,
 ${\mathcal {M}}^*$
is solid and universal,
${\mathcal {M}}^*$
is solid and universal,
 $\rho ({\mathcal {M}}^*)>{\delta }^{\mathcal { H}}$
,
$\rho ({\mathcal {M}}^*)>{\delta }^{\mathcal { H}}$
,
 ${\mathcal {M}}_{i+1}=\mathcal {C}({\mathcal {M}}^*)$
and
${\mathcal {M}}_{i+1}=\mathcal {C}({\mathcal {M}}^*)$
and
 $\Sigma _{i+1}$
is the unique Z-validated strategy of
$\Sigma _{i+1}$
is the unique Z-validated strategy of
 ${\mathcal {M}}_{i+1}$
.
${\mathcal {M}}_{i+1}$
. -
3. k is least such that either (i) no level of
 $J[\vec {E}, \Sigma _k]({\mathcal {M}}_k)$
projects across
$J[\vec {E}, \Sigma _k]({\mathcal {M}}_k)$
projects across
 $mo({\mathcal {M}}_k)$
or (ii)
$mo({\mathcal {M}}_k)$
or (ii)
 ${\mathcal {M}}_k$
does not have a Z-validated strategy, or (iii) some level of
${\mathcal {M}}_k$
does not have a Z-validated strategy, or (iii) some level of
 $J[\vec {E}, \Sigma _k]({\mathcal {M}}_k)$
projects to or below
$J[\vec {E}, \Sigma _k]({\mathcal {M}}_k)$
projects to or below
 ${\delta }^{{\mathcal { H}}}$
.
${\delta }^{{\mathcal { H}}}$
.
We say
![]() $next_s({\mathcal {M}})$
is successful if clause 3(ii)–(iii) do not happen. If
$next_s({\mathcal {M}})$
is successful if clause 3(ii)–(iii) do not happen. If
![]() $next_s({\mathcal {M}})$
is successful, then let
$next_s({\mathcal {M}})$
is successful, then let
![]() $next_{s}({\mathcal {M}})=J[\vec {E}, \Sigma _k]({\mathcal {M}}_k)|{\alpha }$
, where
$next_{s}({\mathcal {M}})=J[\vec {E}, \Sigma _k]({\mathcal {M}}_k)|{\alpha }$
, where
Suppose now that
![]() ${\mathcal {M}}$
is appropriate. We say
${\mathcal {M}}$
is appropriate. We say
![]() ${\mathcal {M}}$
has badness type 3 if
${\mathcal {M}}$
has badness type 3 if
![]() $bad({\mathcal {M}})\not =0,1, 2$
and
$bad({\mathcal {M}})\not =0,1, 2$
and
![]() $next_{s}({\mathcal {M}})$
is not successful. We write
$next_{s}({\mathcal {M}})$
is not successful. We write
![]() $bad({\mathcal {M}})=3$
. We say
$bad({\mathcal {M}})=3$
. We say
![]() ${\mathcal {M}}$
has badness type is 4 if
${\mathcal {M}}$
has badness type is 4 if
![]() $bad({\mathcal {M}})\not =0,1,2, 3$
and
$bad({\mathcal {M}})\not =0,1,2, 3$
and
![]() $next_s({\mathcal {M}})$
does not have a Z-validated strategy.
$next_s({\mathcal {M}})$
does not have a Z-validated strategy.
![]() $next_{\Theta -ex}$
$next_{\Theta -ex}$
Suppose now that
![]() ${\mathcal {M}}$
is appropriate and
${\mathcal {M}}$
is appropriate and
![]() $bad({\mathcal {M}})\not \in 5$
. Let
$bad({\mathcal {M}})\not \in 5$
. Let
![]() $\Sigma $
be the unique Z-validated strategy of
$\Sigma $
be the unique Z-validated strategy of
![]() $next_s({\mathcal {M}})$
. We say that
$next_s({\mathcal {M}})$
. We say that
![]() $next_{\Theta -ex}({\mathcal {M}})$
is successful if there is a unique
$next_{\Theta -ex}({\mathcal {M}})$
is successful if there is a unique
![]() ${\mathcal {M}}$
-extender F such that
${\mathcal {M}}$
-extender F such that
-
1.
 $\mathrm {crit }(F)={\delta }^{{\mathcal { H}}}$
,
$\mathrm {crit }(F)={\delta }^{{\mathcal { H}}}$
, -
2.
 $({\mathcal {M}}, F)$
is a Z-validated hod mouse,
$({\mathcal {M}}, F)$
is a Z-validated hod mouse, -
3.
 $\rho (({\mathcal {M}}, F))>{\delta }^{{\mathcal { H}}}$
.
$\rho (({\mathcal {M}}, F))>{\delta }^{{\mathcal { H}}}$
.
If
![]() $next_{\Theta -ex}({\mathcal {M}})$
is successful, then we let
$next_{\Theta -ex}({\mathcal {M}})$
is successful, then we let
![]() $next_{\Theta -ex}({\mathcal {M}})=\mathcal {C}(({\mathcal {M}}, F))$
, where F is as above. We say
$next_{\Theta -ex}({\mathcal {M}})=\mathcal {C}(({\mathcal {M}}, F))$
, where F is as above. We say
![]() ${\mathcal {M}}$
has badness type 5 if
${\mathcal {M}}$
has badness type 5 if
![]() $next_{\Theta -ex}({\mathcal {M}})$
is not successful. In this case, we write
$next_{\Theta -ex}({\mathcal {M}})$
is not successful. In this case, we write
![]() $bad({\mathcal {M}})=5$
.
$bad({\mathcal {M}})=5$
.
Definition 11.2. Suppose
![]() ${\mathcal {M}}$
is appropriate. We say
${\mathcal {M}}$
is appropriate. We say
![]() ${\mathcal {M}}$
is bad if
${\mathcal {M}}$
is bad if
![]() $bad({\mathcal {M}})$
is defined.
$bad({\mathcal {M}})$
is defined.
Definition 11.3. Suppose
![]() ${\mathcal {M}}$
is appropriate. If
${\mathcal {M}}$
is appropriate. If
![]() ${\mathcal {M}}$
is not bad, then we let
${\mathcal {M}}$
is not bad, then we let
![]() $next({\mathcal {M}})=next_{\Theta -ex}({\mathcal {M}})$
.
$next({\mathcal {M}})=next_{\Theta -ex}({\mathcal {M}})$
.
Remark 11.4. In order for
![]() ${\mathcal {M}}\in dom(next)$
, it is necessary that
${\mathcal {M}}\in dom(next)$
, it is necessary that
![]() $next_{\#}({\mathcal {M}})$
is not a weakly Z-suitable level.
$next_{\#}({\mathcal {M}})$
is not a weakly Z-suitable level.
The
![]() $next$
function defined above gives us the next model in
$next$
function defined above gives us the next model in
![]() $\mathsf {HFBC}(\mu )$
, but it does not tell us how to start the construction. We will start
$\mathsf {HFBC}(\mu )$
, but it does not tell us how to start the construction. We will start
![]() $\mathsf {HFBC}(\mu )$
with
$\mathsf {HFBC}(\mu )$
with
![]() ${\mathcal { H}}$
, which is an appropriate hod premouse. However, if we encounter
${\mathcal { H}}$
, which is an appropriate hod premouse. However, if we encounter
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() $next_{\#}({\mathcal {M}})$
is weakly Z-suitable, then we have to continue with the Z-validated sts construction. We get back to
$next_{\#}({\mathcal {M}})$
is weakly Z-suitable, then we have to continue with the Z-validated sts construction. We get back to
![]() $\mathsf {HFBC}(\mu )$
once we produce the canonical witness to non-Woodiness of
$\mathsf {HFBC}(\mu )$
once we produce the canonical witness to non-Woodiness of
![]() ${\delta }^{next_{\#}({\mathcal {M}})}$
. What we do next is we define the
${\delta }^{next_{\#}({\mathcal {M}})}$
. What we do next is we define the
![]() $start$
function whose domain will consist of objects that the Z-validated sts construction produces on top of
$start$
function whose domain will consist of objects that the Z-validated sts construction produces on top of
![]() $next_{\#}({\mathcal {M}})$
.
$next_{\#}({\mathcal {M}})$
.
![]() $start({\mathcal {R}})$
$start({\mathcal {R}})$
Suppose
![]() ${\mathcal {R}}$
is a Z-validated hod mouse such that
${\mathcal {R}}$
is a Z-validated hod mouse such that
-
1.
 $mo({\mathcal {R}})$
is a Woodin cardinal of
$mo({\mathcal {R}})$
is a Woodin cardinal of
 ${\mathcal {R}}$
,
${\mathcal {R}}$
, -
2.
 $({\mathcal {R}}|mo({\mathcal {R}}))^\#{\trianglelefteq } {\mathcal {R}}$
,
$({\mathcal {R}}|mo({\mathcal {R}}))^\#{\trianglelefteq } {\mathcal {R}}$
, -
3.
 ${\mathcal {R}}$
is sound,
${\mathcal {R}}$
is sound, -
4.
 ${\mathcal {R}}$
is an sts premouse over
${\mathcal {R}}$
is an sts premouse over
 $({\mathcal {R}}|mo({\mathcal {R}}))^\#$
such that
$({\mathcal {R}}|mo({\mathcal {R}}))^\#$
such that
 $rud({\mathcal {R}}){\vDash } \text {`}mo({\mathcal {R}})$
is not a Woodin cardinal’.
$rud({\mathcal {R}}){\vDash } \text {`}mo({\mathcal {R}})$
is not a Woodin cardinal’.
If
![]() ${\mathcal {R}}$
is as above, then we write
${\mathcal {R}}$
is as above, then we write
![]() ${\mathcal {R}}\in dom(stop)$
. Let
${\mathcal {R}}\in dom(stop)$
. Let
![]() $\Sigma $
be the Z-validated strategy of
$\Sigma $
be the Z-validated strategy of
![]() ${\mathcal {R}}$
if it exists; in the case it does not exist, we declare
${\mathcal {R}}$
if it exists; in the case it does not exist, we declare
![]() $start_0({\mathcal {R}})$
is unsuccessful, and letting p on
$start_0({\mathcal {R}})$
is unsuccessful, and letting p on
![]() ${\mathcal {R}}$
as in Proposition 10.7, we then switch to the f.b.
${\mathcal {R}}$
as in Proposition 10.7, we then switch to the f.b.
![]() $(Z, \lambda )$
-validated sts construction over
$(Z, \lambda )$
-validated sts construction over
![]() ${\mathrm m}^+(p)$
. In the case
${\mathrm m}^+(p)$
. In the case
![]() $\Sigma $
exists, we define
$\Sigma $
exists, we define
![]() $start_0({\mathcal {R}})$
just like we defined
$start_0({\mathcal {R}})$
just like we defined
![]() $next_{s}({\mathcal {M}})$
above. If
$next_{s}({\mathcal {M}})$
above. If
![]() $start_0({\mathcal {R}})$
is successful, then it will output a Z-validated hod mouse
$start_0({\mathcal {R}})$
is successful, then it will output a Z-validated hod mouse
![]() ${\mathcal {W}}$
that nicely extends
${\mathcal {W}}$
that nicely extends
![]() ${\mathcal { H}}$
and has a Z-validated strategy
${\mathcal { H}}$
and has a Z-validated strategy
![]() $\Lambda $
. Moreover, for some
$\Lambda $
. Moreover, for some
![]() ${\delta }\in {\mathcal {W}}$
,
${\delta }\in {\mathcal {W}}$
,
-
1.
 $({\mathcal {W}}|{\delta })^\#{\trianglelefteq } {\mathcal {W}}$
is of lsa type,
$({\mathcal {W}}|{\delta })^\#{\trianglelefteq } {\mathcal {W}}$
is of lsa type, -
2.
 ${\mathcal {W}}{\vDash } \text {`}{\delta }$
is not a Woodin cardinal’,
${\mathcal {W}}{\vDash } \text {`}{\delta }$
is not a Woodin cardinal’, -
3. letting
 ${\mathcal {W}}^*{\trianglelefteq }{\mathcal {W}}$
be largest such that
${\mathcal {W}}^*{\trianglelefteq }{\mathcal {W}}$
be largest such that
 ${\mathcal {W}}^*{\vDash } yy{\delta }$
is a Woodin cardinal’,
${\mathcal {W}}^*{\vDash } yy{\delta }$
is a Woodin cardinal’,
 ${\mathcal {W}}^*$
is a
${\mathcal {W}}^*$
is a
 $\Lambda ^{stc}_{({\mathcal {W}}|{\delta })^\#}$
-sts mouse over
$\Lambda ^{stc}_{({\mathcal {W}}|{\delta })^\#}$
-sts mouse over
 $({\mathcal {W}}|{\delta })^\#$
and
$({\mathcal {W}}|{\delta })^\#$
and
 ${\mathcal {W}}=J[\vec {E}, \Lambda _{{\mathcal {W}}^*}]|({\delta }^+)^{J[\vec {E}, \Lambda _{{\mathcal {W}}^*}]}$
.
${\mathcal {W}}=J[\vec {E}, \Lambda _{{\mathcal {W}}^*}]|({\delta }^+)^{J[\vec {E}, \Lambda _{{\mathcal {W}}^*}]}$
.
Next, let
![]() $start_1({\mathcal {R}})$
be defined just like
$start_1({\mathcal {R}})$
be defined just like
![]() $next_{\Theta -ex}({\mathcal {M}})$
starting with
$next_{\Theta -ex}({\mathcal {M}})$
starting with
![]() $start_0({\mathcal {R}})$
. For
$start_0({\mathcal {R}})$
. For
![]() ${\mathcal {R}}\in dom(start)$
, we say
${\mathcal {R}}\in dom(start)$
, we say
![]() $start({\mathcal {R}})$
is successful if both
$start({\mathcal {R}})$
is successful if both
![]() $start_0({\mathcal {R}})$
and
$start_0({\mathcal {R}})$
and
![]() $start_1({\mathcal {R}})$
are successful, and we let
$start_1({\mathcal {R}})$
are successful, and we let
![]() $start({\mathcal {R}})$
be the model that
$start({\mathcal {R}})$
be the model that
![]() $start_1({\mathcal {R}})$
outputs.
$start_1({\mathcal {R}})$
outputs.
Definition 11.5. Suppose
![]() ${\mathcal {R}}\in dom(start)$
. We say
${\mathcal {R}}\in dom(start)$
. We say
![]() ${\mathcal {R}}$
is ready for
${\mathcal {R}}$
is ready for
![]() $\mathsf {HFBC}(\mu )$
if
$\mathsf {HFBC}(\mu )$
if
![]() $start({\mathcal {R}})$
is successful.
$start({\mathcal {R}})$
is successful.
Notice that if
![]() $start({\mathcal {R}})$
is successful, then
$start({\mathcal {R}})$
is successful, then
![]() $mo(start({\mathcal {R}}))=Ord\cap start({\mathcal {R}})$
. We end this subsection with the definition of
$mo(start({\mathcal {R}}))=Ord\cap start({\mathcal {R}})$
. We end this subsection with the definition of
![]() $\mathsf {HFBC}(\mu )$
.
$\mathsf {HFBC}(\mu )$
.
Levels of
![]() $\mathsf {HFBC}$
$\mathsf {HFBC}$
Suppose
![]() ${\mathcal {M}}={\mathcal { H}}$
or
${\mathcal {M}}={\mathcal { H}}$
or
![]() ${\mathcal {M}}=start({\mathcal {R}})$
for some
${\mathcal {M}}=start({\mathcal {R}})$
for some
![]() ${\mathcal {R}}\in dom(start)$
such that
${\mathcal {R}}\in dom(start)$
such that
![]() $start({\mathcal {R}})$
is successful. Let
$start({\mathcal {R}})$
is successful. Let
![]() $\Sigma $
be the unique Z-validated strategy of
$\Sigma $
be the unique Z-validated strategy of
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
Definition 11.6. We say
![]() $({\mathcal {M}}_{\xi },\Sigma _{\xi }, : \xi < \Omega ')$
, where
$({\mathcal {M}}_{\xi },\Sigma _{\xi }, : \xi < \Omega ')$
, where
![]() $\Omega ' \leq Ord$
, are the levels of the hybrid fully backgrounded construction at
$\Omega ' \leq Ord$
, are the levels of the hybrid fully backgrounded construction at
![]() $\mu $
(
$\mu $
(
![]() $\mathsf {HFBC}(\mu )$
) done with respect to
$\mathsf {HFBC}(\mu )$
) done with respect to
![]() $({\mathcal {M}}, \Sigma )$
if the following conditions hold.
$({\mathcal {M}}, \Sigma )$
if the following conditions hold.
-
1.
 ${\mathcal {M}}_0={\mathcal {M}}$
and
${\mathcal {M}}_0={\mathcal {M}}$
and
 $\Sigma _0=\Sigma $
.
$\Sigma _0=\Sigma $
. -
2. For each
 $\xi <\Omega '$
,
$\xi <\Omega '$
,
 ${\mathcal {M}}_{\xi }$
is appropriate and
${\mathcal {M}}_{\xi }$
is appropriate and
 $\Sigma _{\xi }$
is the unique Z-validated strategy of
$\Sigma _{\xi }$
is the unique Z-validated strategy of
 ${\mathcal {M}}_{\xi }$
.
${\mathcal {M}}_{\xi }$
. -
3. For all
 $\xi <\Omega '$
, if
$\xi <\Omega '$
, if
 $\xi +1<\Omega '$
, then
$\xi +1<\Omega '$
, then
 ${\mathcal {M}}_{\xi }$
is not bad and
${\mathcal {M}}_{\xi }$
is not bad and
 ${\mathcal {M}}_{\xi +1}=next({\mathcal {M}}_{\xi })$
.
${\mathcal {M}}_{\xi +1}=next({\mathcal {M}}_{\xi })$
. -
4. For all
 $\xi < \Omega '$
, if
$\xi < \Omega '$
, if
 $\xi $
is a limit ordinal, then letting
$\xi $
is a limit ordinal, then letting
 ${\mathcal {M}}^*_{\xi }=_{def}liminf_{{\alpha }\rightarrow \xi }{\mathcal {M}}_{\alpha }$
,
${\mathcal {M}}^*_{\xi }=_{def}liminf_{{\alpha }\rightarrow \xi }{\mathcal {M}}_{\alpha }$
,
 ${\mathcal {M}}^*_{\xi }$
is appropriate and not bad and
${\mathcal {M}}^*_{\xi }$
is appropriate and not bad and
 ${\mathcal {M}}_{\xi }=next({\mathcal {M}}_{\xi }^*)$
.
${\mathcal {M}}_{\xi }=next({\mathcal {M}}_{\xi }^*)$
. -
5.
 $\Omega '$
is the least ordinal
$\Omega '$
is the least ordinal
 ${\alpha }$
such that one of the following conditions hold:
${\alpha }$
such that one of the following conditions hold:-
(a)
 ${\alpha }$
is a limit ordinal and
${\alpha }$
is a limit ordinal and
 ${\mathcal {M}}^*_{\alpha }$
is bad.
${\mathcal {M}}^*_{\alpha }$
is bad. -
(b)
 ${\alpha }$
is a limit ordinal and
${\alpha }$
is a limit ordinal and
 $next_{\#}({\mathcal {M}}^*_{\alpha })$
is weakly Z-suitable.
$next_{\#}({\mathcal {M}}^*_{\alpha })$
is weakly Z-suitable. -
(c)
 ${\alpha }={\beta }+1$
and
${\alpha }={\beta }+1$
and
 ${\mathcal {M}}_{\beta }$
is bad.
${\mathcal {M}}_{\beta }$
is bad.
-
We say
![]() $\mathsf {HFBC}(\mu )$
converges if
$\mathsf {HFBC}(\mu )$
converges if
![]() $\Omega '$
is as in clause 5(b) (i.e.,
$\Omega '$
is as in clause 5(b) (i.e.,
![]() $next_{\#}({\mathcal {M}}^*_{\Omega '})$
is weakly Z-suitable). The following proposition is essentially [Reference Mitchell and Steel28, Theorem 11.3].
$next_{\#}({\mathcal {M}}^*_{\Omega '})$
is weakly Z-suitable). The following proposition is essentially [Reference Mitchell and Steel28, Theorem 11.3].
Proposition 11.7. Suppose
![]() ${\delta }>\mu $
is a Woodin cardinal. Then if for all
${\delta }>\mu $
is a Woodin cardinal. Then if for all
![]() $\xi <{\delta }$
,
$\xi <{\delta }$
,
![]() ${\mathcal {M}}_{\xi }$
is defined, then
${\mathcal {M}}_{\xi }$
is defined, then
![]() $\Omega '={\delta }$
and
$\Omega '={\delta }$
and
![]() $\mathsf {HFBC}$
converges. Moreover, letting
$\mathsf {HFBC}$
converges. Moreover, letting
![]() ${\mathcal {P}}^-=liminf_{\xi \rightarrow {\delta }}{\mathcal {M}}_{\xi }$
and
${\mathcal {P}}^-=liminf_{\xi \rightarrow {\delta }}{\mathcal {M}}_{\xi }$
and
![]() ${\mathcal {P}}=({\mathcal {P}}^-)^\#$
, then
${\mathcal {P}}=({\mathcal {P}}^-)^\#$
, then
![]() ${\mathcal {P}}$
is weakly Z-suitable.
${\mathcal {P}}$
is weakly Z-suitable.
Letting
![]() ${\delta }>\mu $
be the least Woodin cardinal
${\delta }>\mu $
be the least Woodin cardinal
![]() $>\mu $
, we need to show that
$>\mu $
, we need to show that
![]() $\mathsf {HFBC}(\mu )$
either lasts
$\mathsf {HFBC}(\mu )$
either lasts
![]() ${\delta }$
steps or encounters a weakly Z-suitable stage. Recall that we defined
${\delta }$
steps or encounters a weakly Z-suitable stage. Recall that we defined
![]() $\mathsf {HFBC}(\mu )$
over some
$\mathsf {HFBC}(\mu )$
over some
![]() $({\mathcal {M}}, \Sigma )$
.
$({\mathcal {M}}, \Sigma )$
.
12. Putting it all together
We are assuming theory T and let
![]() $(S, S_0, \nu _0, \vec {Y}, \vec {A})$
witness it; let
$(S, S_0, \nu _0, \vec {Y}, \vec {A})$
witness it; let
![]() $\mu \in S_0$
. Combining
$\mu \in S_0$
. Combining
![]() $\mathsf {HFBC}(\mu )$
with the fully backgrounded Z-validated sts construction, as shown by Proposition 10.7, we see that we reach an honest Z-suitable
$\mathsf {HFBC}(\mu )$
with the fully backgrounded Z-validated sts construction, as shown by Proposition 10.7, we see that we reach an honest Z-suitable
![]() ${\mathcal {R}}$
. In this section, we would like to continue the Z-validated sts construction over
${\mathcal {R}}$
. In this section, we would like to continue the Z-validated sts construction over
![]() ${\mathcal {R}}$
and show that it must reach an excellent
${\mathcal {R}}$
and show that it must reach an excellent
![]() ${\mathcal {P}}$
. To do this, we will stack fully backgrounded Z-validated sts constructions one on the top of another to reach an almost excellent hybrid premouse which we will show has external iterability. We will then need some arguments that translate iterable almost excellent hybrid premice into an excellent ones.
${\mathcal {P}}$
. To do this, we will stack fully backgrounded Z-validated sts constructions one on the top of another to reach an almost excellent hybrid premouse which we will show has external iterability. We will then need some arguments that translate iterable almost excellent hybrid premice into an excellent ones.
This stacking idea might be a little bit unnatural but it seems the most straightforward way of dealing with the two main issues at hand. What we would really like to do is to perform the fully backgrounded Z-validated sts construction over
![]() ${\mathcal {R}}$
and hope that it will reach an excellent hybrid premouse. There are two key issues that arise. The final model of our construction has to inherit a stationary class of measurable cardinals. Perhaps the most straightforward way of dealing with this issue is to attempt to show that every measurable cardinal
${\mathcal {R}}$
and hope that it will reach an excellent hybrid premouse. There are two key issues that arise. The final model of our construction has to inherit a stationary class of measurable cardinals. Perhaps the most straightforward way of dealing with this issue is to attempt to show that every measurable cardinal
![]() ${\kappa }$
such that no cardinal is
${\kappa }$
such that no cardinal is
![]() ${\kappa }$
-strong remains measurable in the output of the backgrounded construction. We do not know how to show this without working with more complex forms of backgrounded constructions. Our solution involves just adding the measure by ‘brute force’. Once the construction reaches one such
${\kappa }$
-strong remains measurable in the output of the backgrounded construction. We do not know how to show this without working with more complex forms of backgrounded constructions. Our solution involves just adding the measure by ‘brute force’. Once the construction reaches one such
![]() ${\kappa }$
, we will continue by adding the measure coarsely, much like one does in the construction of
${\kappa }$
, we will continue by adding the measure coarsely, much like one does in the construction of
![]() $L[\mu ]$
.
$L[\mu ]$
.
The next issue is to guarantee window-based iterability. The most natural way of accomplishing this is by showing that the models of our backgrounded construction are iterable. However, this may not work, and if it fails, it fails as follows. Suppose
![]() ${\mathcal {N}}$
is a model appearing in the fully backgrounded Z-validated sts construction over
${\mathcal {N}}$
is a model appearing in the fully backgrounded Z-validated sts construction over
![]() ${\mathcal {R}}$
and
${\mathcal {R}}$
and
![]() ${\kappa }$
is a cutpoint cardinal of
${\kappa }$
is a cutpoint cardinal of
![]() ${\mathcal {N}}$
. Suppose
${\mathcal {N}}$
. Suppose
![]() ${\mathcal {N}}$
has no Woodin cardinals above
${\mathcal {N}}$
has no Woodin cardinals above
![]() ${\kappa }$
. We now seek a Z-validated strategy for
${\kappa }$
. We now seek a Z-validated strategy for
![]() ${\mathcal {N}}$
that acts on iterations above
${\mathcal {N}}$
that acts on iterations above
![]() ${\kappa }$
. If such a strategy does not exist, then we must have a tree
${\kappa }$
. If such a strategy does not exist, then we must have a tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {N}}$
above
${\mathcal {N}}$
above
![]() $\kappa $
which does not have a Z-validated
$\kappa $
which does not have a Z-validated
![]() ${\mathcal {Q}}$
-structure. Let then
${\mathcal {Q}}$
-structure. Let then
![]() ${\mathcal {N}}_1^-={\mathrm m}({\mathcal {T}})$
. It follows that if we perform a fully backgrounded Z-validated sts construction over
${\mathcal {N}}_1^-={\mathrm m}({\mathcal {T}})$
. It follows that if we perform a fully backgrounded Z-validated sts construction over
![]() ${\mathcal {N}}_1^-$
, we will not reach a
${\mathcal {N}}_1^-$
, we will not reach a
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() ${\mathcal {T}}$
. Let then
${\mathcal {T}}$
. Let then
![]() ${\mathcal {N}}_1$
be the one cardinal extension of
${\mathcal {N}}_1$
be the one cardinal extension of
![]() ${\mathcal {N}}_1^-$
built by the fully backgrounded Z-validated sts construction over
${\mathcal {N}}_1^-$
built by the fully backgrounded Z-validated sts construction over
![]() ${\mathcal {N}}_1^-$
. We thus have that
${\mathcal {N}}_1^-$
. We thus have that
![]() ${\mathcal {N}}_1{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’.
${\mathcal {N}}_1{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’.
We now want to see that
![]() ${\mathcal {N}}_1$
has a window-based iterability. Let then
${\mathcal {N}}_1$
has a window-based iterability. Let then
![]() $\eta _1\in ({\kappa }, {\delta }({\mathcal {T}}))$
be a regular cardinal of
$\eta _1\in ({\kappa }, {\delta }({\mathcal {T}}))$
be a regular cardinal of
![]() ${\mathcal {N}}_1$
, and we want to argue that
${\mathcal {N}}_1$
, and we want to argue that
![]() ${\mathcal {N}}_1|\eta _1$
is iterable. The strategy we seek is again a Z-validated strategy. If it does not exist, then we get a tree
${\mathcal {N}}_1|\eta _1$
is iterable. The strategy we seek is again a Z-validated strategy. If it does not exist, then we get a tree
![]() ${\mathcal {T}}_1$
on
${\mathcal {T}}_1$
on
![]() ${\mathcal {N}}_1|\eta _1$
such that
${\mathcal {N}}_1|\eta _1$
such that
![]() ${\mathcal {T}}_1$
does not have a Z-validated
${\mathcal {T}}_1$
does not have a Z-validated
![]() ${\mathcal {Q}}$
-structure. The construction above produced
${\mathcal {Q}}$
-structure. The construction above produced
![]() ${\mathcal {N}}_2$
extending
${\mathcal {N}}_2$
extending
![]() ${\mathrm m}({\mathcal {T}}_1)$
. The goal now is to show that
${\mathrm m}({\mathcal {T}}_1)$
. The goal now is to show that
![]() ${\mathcal {N}}_2$
has window-based iterability. Failure of such a strategy produced
${\mathcal {N}}_2$
has window-based iterability. Failure of such a strategy produced
![]() $\eta _2\in ({\kappa }, {\delta }({\mathcal {T}}_1))$
,
$\eta _2\in ({\kappa }, {\delta }({\mathcal {T}}_1))$
,
![]() ${\mathcal {T}}_2$
based on
${\mathcal {T}}_2$
based on
![]() ${\mathcal {N}}_2$
that is above
${\mathcal {N}}_2$
that is above
![]() ${\kappa }$
and a model
${\kappa }$
and a model
![]() ${\mathcal {N}}_3$
extending
${\mathcal {N}}_3$
extending
![]() ${\mathrm m}({\mathcal {T}}_2)$
. The process outlined above cannot last
${\mathrm m}({\mathcal {T}}_2)$
. The process outlined above cannot last
![]() $\omega $
many steps, for if it did, we will have a sequence
$\omega $
many steps, for if it did, we will have a sequence
![]() $({\mathcal {N}}_i, {\mathcal {T}}_i: i<\omega )$
and a reflected version of this sequence cannot have a well-founded direct limit along the realizable branches.
$({\mathcal {N}}_i, {\mathcal {T}}_i: i<\omega )$
and a reflected version of this sequence cannot have a well-founded direct limit along the realizable branches.
There is yet another issue that we need to deal with which is not connected with the stacking construction but has to do with other aspects of the construction. We will need arguments that will show window-based iterability in V can somehow be reflected inside the sts premice alluded above. To show this, we will need to break into cases and examine exactly how we ended up with the model we seek. For this reason, we isolate the following hypothesis.
![]() $\mathsf {Hypo}:$
For some X containing
$\mathsf {Hypo}:$
For some X containing
![]() ${\mathcal {R}}$
, there is a sound Z-validated almost excellent mouse
${\mathcal {R}}$
, there is a sound Z-validated almost excellent mouse
![]() ${\mathcal {M}}$
over X that is based on
${\mathcal {M}}$
over X that is based on
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
The following essentially follows from the main results of [Reference Neeman31].
Proposition 12.1. Assume
![]() $\neg \mathsf {Hypo}$
. Then for any X containing
$\neg \mathsf {Hypo}$
. Then for any X containing
![]() ${\mathcal {R}}$
, letting
${\mathcal {R}}$
, letting
![]() ${\delta }$
be the least Woodin cardinal such that
${\delta }$
be the least Woodin cardinal such that
![]() $X\in V_{\delta }$
, no model of the Z-validated sts construction of
$X\in V_{\delta }$
, no model of the Z-validated sts construction of
![]() $V_{\delta }$
that is based on
$V_{\delta }$
that is based on
![]() ${\mathcal {R}}$
and is done over X reaches an almost excellent hybrid premouse.
${\mathcal {R}}$
and is done over X reaches an almost excellent hybrid premouse.
12.1. The prototypical branch existence argument
Here, we present an argument due to John Steel that we will use over and over again. The argument is general and can be used in many settings. We will refer to this argument as the prototypical branch existence argument. In the sequel, when we need to prove something via the same argument, we will just say that ‘the prototypical branch existence argument shows…’.
The prototypical branch existence argument
Suppose
![]() ${\delta }$
is a Woodin cardinal,
${\delta }$
is a Woodin cardinal,
![]() $X\in V_{\delta }$
is a set such that
$X\in V_{\delta }$
is a set such that
![]() ${\mathcal {R}}\in X$
and
${\mathcal {R}}\in X$
and
![]() $({\mathcal {M}}_{\alpha }, {\mathcal {N}}_{\alpha }: {\alpha }\leq {\delta })$
are the models of the fully backgrounded Z-validated sts construction done over X. Fix
$({\mathcal {M}}_{\alpha }, {\mathcal {N}}_{\alpha }: {\alpha }\leq {\delta })$
are the models of the fully backgrounded Z-validated sts construction done over X. Fix
![]() ${\alpha }\leq {\delta }$
and suppose that
${\alpha }\leq {\delta }$
and suppose that
![]() ${\mathcal {N}}_{\alpha }$
has no Woodin cardinals (as an sts premouse over X). Let
${\mathcal {N}}_{\alpha }$
has no Woodin cardinals (as an sts premouse over X). Let
![]() ${\mathcal {T}}$
be a normal Z-validated iteration of
${\mathcal {T}}$
be a normal Z-validated iteration of
![]() ${\mathcal {N}}_{\alpha }$
such that for every limit
${\mathcal {N}}_{\alpha }$
such that for every limit
![]() ${\beta }<lh({\mathcal {T}})$
, if
${\beta }<lh({\mathcal {T}})$
, if
![]() $c_{\beta }=[0, {\beta }]_T$
, then
$c_{\beta }=[0, {\beta }]_T$
, then
![]() ${\mathcal {Q}}(c_{\beta }, {\mathcal {T}}{\restriction } {\beta })$
exists and is Z-validated. Suppose that
${\mathcal {Q}}(c_{\beta }, {\mathcal {T}}{\restriction } {\beta })$
exists and is Z-validated. Suppose that
![]() ${\mathcal {T}}$
has limit length and there is a Z-validated sts mouse
${\mathcal {T}}$
has limit length and there is a Z-validated sts mouse
![]() ${\mathcal {Q}}$
such that
${\mathcal {Q}}$
such that
![]() ${\mathrm m}({\mathcal {T}}){\trianglelefteq } {\mathcal {Q}}$
and
${\mathrm m}({\mathcal {T}}){\trianglelefteq } {\mathcal {Q}}$
and
![]() $rud({\mathcal {Q}}){\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. Then there is a branch b of
$rud({\mathcal {Q}}){\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. Then there is a branch b of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() ${\mathcal {Q}}(b, {\mathcal {T}})$
exists and is equal to
${\mathcal {Q}}(b, {\mathcal {T}})$
exists and is equal to
![]() ${\mathcal {Q}}$
.
${\mathcal {Q}}$
.
The argument proceeds as follows. Fix some
![]() $\lambda \in S_0-{\delta }$
and let
$\lambda \in S_0-{\delta }$
and let
![]() $\pi _U: M_U\rightarrow H_{\zeta }$
be a
$\pi _U: M_U\rightarrow H_{\zeta }$
be a
![]() $(\mu , {\lambda }, Z)$
-good hull such that
$(\mu , {\lambda }, Z)$
-good hull such that
![]() ${\mathcal {T}}, {\mathcal {Q}}\in rng(\pi )$
. Let
${\mathcal {T}}, {\mathcal {Q}}\in rng(\pi )$
. Let
![]() $\nu =\vert {M_U}\vert $
and let
$\nu =\vert {M_U}\vert $
and let
![]() $g\subseteq Coll(\omega , \nu )$
be generic. Then there is a maximal branch c of
$g\subseteq Coll(\omega , \nu )$
be generic. Then there is a maximal branch c of
![]() ${\mathcal {T}}_U$
,
${\mathcal {T}}_U$
,
![]() ${\beta }\leq {\alpha }$
and a (weak) embedding
${\beta }\leq {\alpha }$
and a (weak) embedding
![]() $\sigma :{\mathcal {M}}^{{\mathcal {T}}_U}_c\rightarrow {\mathcal {N}}_{\beta }$
such that if c is nondropping, then
$\sigma :{\mathcal {M}}^{{\mathcal {T}}_U}_c\rightarrow {\mathcal {N}}_{\beta }$
such that if c is nondropping, then
![]() ${\beta }={\alpha }$
and
${\beta }={\alpha }$
and
![]() $\pi _U=\sigma \circ \pi ^{{\mathcal {T}}_U}$
. Arguing as in Proposition 9.5, we get that c must be a cofinal branch and that
$\pi _U=\sigma \circ \pi ^{{\mathcal {T}}_U}$
. Arguing as in Proposition 9.5, we get that c must be a cofinal branch and that
![]() ${\mathcal {Q}}(c, {\mathcal {T}}_U)$
must exist and be equal to
${\mathcal {Q}}(c, {\mathcal {T}}_U)$
must exist and be equal to
![]() ${\mathcal {Q}}_U$
. It follows then that
${\mathcal {Q}}_U$
. It follows then that
![]() $c\in M_U$
. Hence,
$c\in M_U$
. Hence,
![]() $\pi _U(c)$
is as desired.
$\pi _U(c)$
is as desired.
Remark 12.2. It is important to keep in mind that the argument does not work when
![]() ${\mathcal {N}}_{\alpha }$
has Woodin cardinals, as then
${\mathcal {N}}_{\alpha }$
has Woodin cardinals, as then
![]() ${\mathcal {Q}}(c, {\mathcal {T}}_U)$
may not exist. Thus, this argument cannot in general be used to show that levels of
${\mathcal {Q}}(c, {\mathcal {T}}_U)$
may not exist. Thus, this argument cannot in general be used to show that levels of
![]() $K^c$
are short-tree iterable.
$K^c$
are short-tree iterable.
12.2. One step construction
Suppose X is a set such that
![]() ${\mathcal {R}}\in X$
. The main goal of this section is to produce a short-tree-iterable Z-suitable sts hod premouse over X. Here, short-tree iterability is in the sense of the
${\mathcal {R}}\in X$
. The main goal of this section is to produce a short-tree-iterable Z-suitable sts hod premouse over X. Here, short-tree iterability is in the sense of the
![]() ${\mathrm {HOD}}$
analysis (cf. [Reference Steel, Woodin, Kechris, Löwe and Steel14]).
${\mathrm {HOD}}$
analysis (cf. [Reference Steel, Woodin, Kechris, Löwe and Steel14]).
Definition 12.3. Suppose
![]() ${\mathcal {P}}$
is a Z-validated sts premouse over X based on
${\mathcal {P}}$
is a Z-validated sts premouse over X based on
![]() ${\mathcal {R}}$
. We say
${\mathcal {R}}$
. We say
![]() ${\mathcal {P}}$
is almost Z
-good if
${\mathcal {P}}$
is almost Z
-good if
![]() ${\mathcal {P}}$
, as an sts premouse over X, has a unique Woodin cardinal
${\mathcal {P}}$
, as an sts premouse over X, has a unique Woodin cardinal
![]() ${\delta }^{\mathcal {P}}$
such that
${\delta }^{\mathcal {P}}$
such that
-
1.
 ${\mathcal {P}}=({\mathcal {P}}|{\delta }^{\mathcal {P}})^\#$
,
${\mathcal {P}}=({\mathcal {P}}|{\delta }^{\mathcal {P}})^\#$
, -
2. if
 ${\mathcal {M}}$
is a sound Z-validated sts mouse over
${\mathcal {M}}$
is a sound Z-validated sts mouse over
 ${\mathcal {P}}$
, then
${\mathcal {P}}$
, then
 ${\mathcal {M}}{\vDash } \text {`}{\delta }^{\mathcal {P}}$
is a Woodin cardinal’.
${\mathcal {M}}{\vDash } \text {`}{\delta }^{\mathcal {P}}$
is a Woodin cardinal’.
We say
![]() ${\mathcal {P}}$
is Z
-good if
${\mathcal {P}}$
is Z
-good if
![]() ${\mathcal {P}}$
has a unique Woodin cardinal
${\mathcal {P}}$
has a unique Woodin cardinal
![]() ${\delta }^{\mathcal {P}}$
such that
${\delta }^{\mathcal {P}}$
such that
-
1.
 $({\mathcal {P}}|{\delta }^{\mathcal {P}})^\#$
is almost Z-good,
$({\mathcal {P}}|{\delta }^{\mathcal {P}})^\#$
is almost Z-good, -
2.
 ${\mathcal {P}}=Lp^{Zv, sts}({\mathcal {P}}|{\delta }^{\mathcal {P}})$
,
${\mathcal {P}}=Lp^{Zv, sts}({\mathcal {P}}|{\delta }^{\mathcal {P}})$
, -
3. for every regular cardinal
 $\eta <{\delta }^{\mathcal {P}}$
,
$\eta <{\delta }^{\mathcal {P}}$
,
 ${\mathcal {P}}|\eta $
has a Z-validated strategy.
${\mathcal {P}}|\eta $
has a Z-validated strategy.
We say that the Z-good
![]() ${\mathcal {P}}$
is fully backgrounded if for some maximal window w and for some
${\mathcal {P}}$
is fully backgrounded if for some maximal window w and for some
![]() $\xi \in w$
,
$\xi \in w$
,
![]() ${\mathcal {P}}|{\delta }^{\mathcal {P}}$
is a model appearing in the fully backgrounded Z-validated sts construction of
${\mathcal {P}}|{\delta }^{\mathcal {P}}$
is a model appearing in the fully backgrounded Z-validated sts construction of
![]() $V_{\eta }$
which uses extenders with critical point
$V_{\eta }$
which uses extenders with critical point
![]() $>\xi $
.
$>\xi $
.
Proposition 12.4. Assume
![]() $\neg \mathsf {Hypo}$
. There is a Z-good fully backgrounded sts premouse over X based on
$\neg \mathsf {Hypo}$
. There is a Z-good fully backgrounded sts premouse over X based on
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
We spend this entire subsection proving Proposition 12.4. We will do it in two steps. In the first step, we will produce a fully backgrounded almost Z-good
![]() ${\mathcal {N}}$
. Then we will obtain a fully backgrounded Z-good
${\mathcal {N}}$
. Then we will obtain a fully backgrounded Z-good
![]() ${\mathcal {P}}$
. We start with the first step.
${\mathcal {P}}$
. We start with the first step.
Lemma 12.5. Assume
![]() $\neg \mathsf {Hypo}$
. There is an almost Z-good fully backgrounded sts premouse over X based on
$\neg \mathsf {Hypo}$
. There is an almost Z-good fully backgrounded sts premouse over X based on
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
Proof. Let
![]() ${\delta }$
be the least Woodin cardinal of V such that
${\delta }$
be the least Woodin cardinal of V such that
![]() $X\in V_{\delta }$
. Let
$X\in V_{\delta }$
. Let
![]() $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq \Omega ^*)$
be the models of the fully backgrounded Z-validated sts construction of
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq \Omega ^*)$
be the models of the fully backgrounded Z-validated sts construction of
![]() $V_{\delta }$
done over X (based on
$V_{\delta }$
done over X (based on
![]() ${\mathcal {R}}$
). Because we are assuming
${\mathcal {R}}$
). Because we are assuming
![]() $\neg \mathsf {Hypo}$
,
$\neg \mathsf {Hypo}$
,
![]() $\Omega ^*={\delta }$
. We claim the following.
$\Omega ^*={\delta }$
. We claim the following.
Claim. There is
![]() $\xi \leq {\delta }$
such that
$\xi \leq {\delta }$
such that
![]() ${\mathcal {N}}_{\xi }$
is an almost Z-good sts premouse.
${\mathcal {N}}_{\xi }$
is an almost Z-good sts premouse.
Proof. Suppose for every
![]() $\xi <{\delta }$
,
$\xi <{\delta }$
,
![]() ${\mathcal {N}}_{\xi }$
is not almost Z-good. We show that
${\mathcal {N}}_{\xi }$
is not almost Z-good. We show that
![]() ${\mathcal {N}}=({\mathcal {N}}_{\delta })^\#$
is an almost Z-good sts premouse. A standard reflection argument shows that
${\mathcal {N}}=({\mathcal {N}}_{\delta })^\#$
is an almost Z-good sts premouse. A standard reflection argument shows that
![]() $\rho _{\omega }({\mathcal {N}})<{\delta }$
. Suppose then
$\rho _{\omega }({\mathcal {N}})<{\delta }$
. Suppose then
![]() ${\mathcal {N}}$
is not almost Z-good and fix
${\mathcal {N}}$
is not almost Z-good and fix
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
-
1.
 ${\mathcal {N}}{\trianglelefteq } {\mathcal {M}}$
,
${\mathcal {N}}{\trianglelefteq } {\mathcal {M}}$
, -
2.
 ${\mathcal {M}}$
is sound above
${\mathcal {M}}$
is sound above
 ${\delta }$
,
${\delta }$
, -
3.
 $\rho _{\omega }({\delta })<{\delta }$
,
$\rho _{\omega }({\delta })<{\delta }$
, -
4.
 ${\mathcal {M}}$
is Z-validated and has a Z-validated
${\mathcal {M}}$
is Z-validated and has a Z-validated
 $Ord$
-strategy.
$Ord$
-strategy.
As we are are assuming
![]() $\neg \mathsf {Hypo}$
,
$\neg \mathsf {Hypo}$
,
![]() ${\delta }$
is not a limit of Woodin cardinals in
${\delta }$
is not a limit of Woodin cardinals in
![]() ${\mathcal {N}}$
. Let then
${\mathcal {N}}$
. Let then
![]() $\pi : {\mathcal {M}}^*\rightarrow {\mathcal {M}}$
be such that letting
$\pi : {\mathcal {M}}^*\rightarrow {\mathcal {M}}$
be such that letting
![]() $\mathrm {crit }(\pi )=\nu $
,
$\mathrm {crit }(\pi )=\nu $
,
![]() $\pi (\nu )={\delta }$
and
$\pi (\nu )={\delta }$
and
![]() ${\mathcal {N}}$
has no Woodin cardinals in the interval
${\mathcal {N}}$
has no Woodin cardinals in the interval
![]() $[\nu , {\delta })$
.
$[\nu , {\delta })$
.
Working inside
![]() ${\mathcal {N}}$
, let
${\mathcal {N}}$
, let
![]() ${\mathcal {N}}'$
be the output of the
${\mathcal {N}}'$
be the output of the
![]() $({\mathcal {R}}, {\mathcal {R}}^b, S^{\mathcal {N}})$
-authenticated construction done over
$({\mathcal {R}}, {\mathcal {R}}^b, S^{\mathcal {N}})$
-authenticated construction done over
![]() ${\mathcal {N}}|\nu +1$
using extenders with critical points
${\mathcal {N}}|\nu +1$
using extenders with critical points
![]() $>\nu $
. Let
$>\nu $
. Let
![]() ${\mathcal {M}}'$
be the result of translating
${\mathcal {M}}'$
be the result of translating
![]() ${\mathcal {M}}$
over to
${\mathcal {M}}$
over to
![]() ${\mathcal {N}}'$
via the S-construction (see [Reference Sargsyan and Trang38, Chapter 6.4]). Similarly, for each
${\mathcal {N}}'$
via the S-construction (see [Reference Sargsyan and Trang38, Chapter 6.4]). Similarly, for each
![]() ${\mathcal {N}}$
-cardinal
${\mathcal {N}}$
-cardinal
![]() $\xi>\nu $
such that
$\xi>\nu $
such that
![]() $({\mathcal {N}}|\xi )^\#{\vDash } \text {`}\xi $
is a Woodin cardinal’, let
$({\mathcal {N}}|\xi )^\#{\vDash } \text {`}\xi $
is a Woodin cardinal’, let
![]() ${\mathcal {M}}_{\xi }$
witness that our proposition fails for
${\mathcal {M}}_{\xi }$
witness that our proposition fails for
![]() $({\mathcal {N}}|\xi )^\#$
. For each such
$({\mathcal {N}}|\xi )^\#$
. For each such
![]() $\xi $
, let
$\xi $
, let
![]() ${\mathcal {M}}^{\prime }_{\xi }$
be the result of translating
${\mathcal {M}}^{\prime }_{\xi }$
be the result of translating
![]() ${\mathcal {M}}_{\xi }$
over to
${\mathcal {M}}_{\xi }$
over to
![]() ${\mathcal {N}}'|\xi $
.
${\mathcal {N}}'|\xi $
.
We now compare
![]() ${\mathcal {M}}^*$
with the construction producing
${\mathcal {M}}^*$
with the construction producing
![]() ${\mathcal {N}}'$
. In this comparison, only
${\mathcal {N}}'$
. In this comparison, only
![]() ${\mathcal {M}}^*$
is moving. We claim that this comparison lasts
${\mathcal {M}}^*$
is moving. We claim that this comparison lasts
![]() ${\delta }+1$
-steps producing a tree
${\delta }+1$
-steps producing a tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {M}}^*$
with last model
${\mathcal {M}}^*$
with last model
![]() ${\mathcal {M}}'$
. Indeed, given
${\mathcal {M}}'$
. Indeed, given
![]() ${\mathcal {T}}{\restriction } {\alpha }$
, where
${\mathcal {T}}{\restriction } {\alpha }$
, where
![]() ${\alpha }\leq {\delta }$
is a limit ordinal, if
${\alpha }\leq {\delta }$
is a limit ordinal, if
![]() ${\mathrm m}^+({\mathcal {T}}{\restriction } {\alpha }){\vDash } \text {`}{\delta }({\mathcal {T}}{\restriction } {\alpha })$
is a Woodin cardinal’, then
${\mathrm m}^+({\mathcal {T}}{\restriction } {\alpha }){\vDash } \text {`}{\delta }({\mathcal {T}}{\restriction } {\alpha })$
is a Woodin cardinal’, then
![]() ${\mathcal {M}}_{\alpha }'$
is defined. Because
${\mathcal {M}}_{\alpha }'$
is defined. Because
![]() ${\mathcal {M}}$
is a Z-validated sts mouse, we must have a unique cofinal well-founded branch
${\mathcal {M}}$
is a Z-validated sts mouse, we must have a unique cofinal well-founded branch
![]() $b_{\alpha }$
of
$b_{\alpha }$
of
![]() ${\mathcal {T}}{\restriction } {\alpha }$
such that
${\mathcal {T}}{\restriction } {\alpha }$
such that
![]() ${\mathcal {Q}}(b, {\mathcal {T}}{\restriction } {\alpha })$
is defined and is equal to
${\mathcal {Q}}(b, {\mathcal {T}}{\restriction } {\alpha })$
is defined and is equal to
![]() ${\mathcal {M}}_{\alpha }'$
. We then pick this branch
${\mathcal {M}}_{\alpha }'$
. We then pick this branch
![]() $b_{\alpha }$
at stage
$b_{\alpha }$
at stage
![]() ${\alpha }$
.
${\alpha }$
.
It must now be clear that the existence of
![]() ${\mathcal {T}}$
violates universality; this implies by standard results that there must be a superstrong cardinal in
${\mathcal {T}}$
violates universality; this implies by standard results that there must be a superstrong cardinal in
![]() ${\mathcal {N}}$
. The reader may consult [Reference Sargsyan34, Lemma 5.4].
${\mathcal {N}}$
. The reader may consult [Reference Sargsyan34, Lemma 5.4].
The claim finishes the proof.
We now start the proof of Proposition 12.4. Towards a contradiction, we assume that there is no fully backgrounded Z-good sts premouse over X based on
![]() ${\mathcal {R}}$
. Let
${\mathcal {R}}$
. Let
![]() ${\mathcal {N}}_0$
be a fully backgrounded almost Z-good sts premouse over X based on
${\mathcal {N}}_0$
be a fully backgrounded almost Z-good sts premouse over X based on
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
Below, given
![]() ${\mathcal {S}}$
,
${\mathcal {S}}$
,
![]() ${\delta }^{\mathcal {S}}$
will always denote the largest Woodin of
${\delta }^{\mathcal {S}}$
will always denote the largest Woodin of
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
![]() $w^{\mathcal {S}}$
will denote the maximal window w of
$w^{\mathcal {S}}$
will denote the maximal window w of
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() ${\delta }^w={\delta }^{\mathcal {S}}$
.
${\delta }^w={\delta }^{\mathcal {S}}$
.
We now by induction produce an infinite sequence
![]() $({\mathcal {N}}_i, \nu _i, {\mathcal {T}}_i: i<\omega )$
such that
$({\mathcal {N}}_i, \nu _i, {\mathcal {T}}_i: i<\omega )$
such that
-
1. for every
 $i<\omega $
,
$i<\omega $
,
 ${\mathcal {N}}_i$
is a fully backgrounded almost Z-good sts premouse over X based on
${\mathcal {N}}_i$
is a fully backgrounded almost Z-good sts premouse over X based on
 ${\mathcal {R}}$
,
${\mathcal {R}}$
, -
2. for every
 $i<\omega $
,
$i<\omega $
,
 $\nu _i$
is a successor cardinal of
$\nu _i$
is a successor cardinal of
 ${\mathcal {N}}_i$
,
${\mathcal {N}}_i$
, -
3. for every
 $i<\omega $
,
$i<\omega $
,
 ${\mathcal {T}}_i$
is a normal Z-validated iteration of
${\mathcal {T}}_i$
is a normal Z-validated iteration of
 ${\mathcal {N}}_i|\nu _i$
such that
${\mathcal {N}}_i|\nu _i$
such that
 ${\mathcal {T}}_i$
has no cofinal well-founded branch b such that
${\mathcal {T}}_i$
has no cofinal well-founded branch b such that
 ${\mathcal {Q}}(b, {\mathcal {T}}_i)$
exists and is a Z-validated mouse,
${\mathcal {Q}}(b, {\mathcal {T}}_i)$
exists and is a Z-validated mouse, -
4. for every
 $i<\omega $
,
$i<\omega $
,
 ${\mathcal {N}}_{i+1}={\mathrm m}^+({\mathcal {T}}_i)$
.
${\mathcal {N}}_{i+1}={\mathrm m}^+({\mathcal {T}}_i)$
.
A simple reflection argument shows that such a sequence cannot exist. The fact that for
![]() $i>0$
,
$i>0$
,
![]() ${\mathcal {N}}_i$
is fully backgrounded is irrelevant for the reflected argument alluded in the previous sentence. It is enough that
${\mathcal {N}}_i$
is fully backgrounded is irrelevant for the reflected argument alluded in the previous sentence. It is enough that
![]() ${\mathcal {N}}_0$
is fully backgrounded.
${\mathcal {N}}_0$
is fully backgrounded.
Assume then we have built
![]() ${\mathcal {N}}_i$
, and we now describe the procedure for getting
${\mathcal {N}}_i$
, and we now describe the procedure for getting
![]() $(\nu _i, {\mathcal {T}}_i, {\mathcal {N}}_{i+1})$
. Because
$(\nu _i, {\mathcal {T}}_i, {\mathcal {N}}_{i+1})$
. Because
![]() ${\mathcal {N}}_i$
is not Z-good, there is a
${\mathcal {N}}_i$
is not Z-good, there is a
![]() $\nu _i\in w^{{\mathcal {N}}_i}$
which is a successor cardinal of
$\nu _i\in w^{{\mathcal {N}}_i}$
which is a successor cardinal of
![]() ${\mathcal {N}}_i$
and
${\mathcal {N}}_i$
and
![]() ${\mathcal {N}}_i|\nu _i$
does not have a Z-validated strategy.
${\mathcal {N}}_i|\nu _i$
does not have a Z-validated strategy.
Let
![]() $\eta $
be some Woodin cardinal such that
$\eta $
be some Woodin cardinal such that
![]() ${\mathcal {N}}_i\in V_{\eta }$
and let
${\mathcal {N}}_i\in V_{\eta }$
and let
![]() $\xi _{\eta }<\eta $
be such that
$\xi _{\eta }<\eta $
be such that
![]() ${\mathcal {N}}_i\in H_{\xi _{\eta }}$
and there are no Woodin cardinals in the interval
${\mathcal {N}}_i\in H_{\xi _{\eta }}$
and there are no Woodin cardinals in the interval
![]() $(\xi _{\eta }, \eta )$
. Let
$(\xi _{\eta }, \eta )$
. Let
![]() $({\mathcal {M}}^\eta _{\alpha }, {\mathcal {S}}^\eta _{\alpha }: {\alpha }\leq \eta )$
be the models of the fully backgrounded Z-validated sts construction of
$({\mathcal {M}}^\eta _{\alpha }, {\mathcal {S}}^\eta _{\alpha }: {\alpha }\leq \eta )$
be the models of the fully backgrounded Z-validated sts construction of
![]() $V_{\eta }$
done over X using extenders with critical points
$V_{\eta }$
done over X using extenders with critical points
![]() $>\xi _{\eta }$
.
$>\xi _{\eta }$
.
As
![]() ${\mathcal {N}}_i\in H_{\xi }$
, in the comparison of
${\mathcal {N}}_i\in H_{\xi }$
, in the comparison of
![]() ${\mathcal {W}}=_{def}{\mathcal {N}}_i|\nu _i$
with the construction
${\mathcal {W}}=_{def}{\mathcal {N}}_i|\nu _i$
with the construction
![]() $({\mathcal {M}}_{\alpha }^\eta , {\mathcal {S}}^\eta _{\alpha }: {\alpha }\leq \eta )$
, only
$({\mathcal {M}}_{\alpha }^\eta , {\mathcal {S}}^\eta _{\alpha }: {\alpha }\leq \eta )$
, only
![]() ${\mathcal {W}}$
moves. We now analyze the tree on
${\mathcal {W}}$
moves. We now analyze the tree on
![]() ${\mathcal {W}}$
. Suppose
${\mathcal {W}}$
. Suppose
![]() ${\mathcal {T}}^\eta $
is the tree on
${\mathcal {T}}^\eta $
is the tree on
![]() ${\mathcal {W}}$
built via the above comparison and suppose
${\mathcal {W}}$
built via the above comparison and suppose
![]() ${\mathcal {T}}^\eta $
has a limit length. We now have two cases.
${\mathcal {T}}^\eta $
has a limit length. We now have two cases.
Case1. Suppose there is
![]() ${\alpha }$
such that
${\alpha }$
such that
![]() ${\mathcal {S}}^\eta _{\alpha }{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. It follows from the prototypical argument that there must be a cofinal branch b of
${\mathcal {S}}^\eta _{\alpha }{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. It follows from the prototypical argument that there must be a cofinal branch b of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() ${\mathcal {Q}}(b, {\mathcal {T}})$
exists and is a Z-validated mouse. We then extend
${\mathcal {Q}}(b, {\mathcal {T}})$
exists and is a Z-validated mouse. We then extend
![]() ${\mathcal {T}}^\eta $
by adding b.
${\mathcal {T}}^\eta $
by adding b.
Case2. Suppose there is no
![]() ${\alpha }\leq \eta $
such that
${\alpha }\leq \eta $
such that
![]() ${\mathcal {S}}^\eta _{\alpha }{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. In this case, we stop the construction and set
${\mathcal {S}}^\eta _{\alpha }{\vDash } \text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. In this case, we stop the construction and set
![]() ${\mathcal {N}}_{i+1}={\mathrm m}^+({\mathcal {T}})$
and
${\mathcal {N}}_{i+1}={\mathrm m}^+({\mathcal {T}})$
and
![]() ${\mathcal {T}}_i={\mathcal {T}}$
.
${\mathcal {T}}_i={\mathcal {T}}$
.
We stop the construction if either Case2 holds or for some
![]() ${\alpha }$
,
${\alpha }$
,
![]() ${\mathcal {M}}^\eta _{\alpha }$
is the last model of
${\mathcal {M}}^\eta _{\alpha }$
is the last model of
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() $\pi ^{\mathcal {T}}$
exists.
$\pi ^{\mathcal {T}}$
exists.
We now claim that for some
![]() $\eta $
, the construction of
$\eta $
, the construction of
![]() ${\mathcal {T}}^\eta $
stops because of Case2. Assume otherwise. Then for each Woodin cardinal
${\mathcal {T}}^\eta $
stops because of Case2. Assume otherwise. Then for each Woodin cardinal
![]() $\eta $
, we have
$\eta $
, we have
![]() ${\alpha }_{\eta }$
and an embedding
${\alpha }_{\eta }$
and an embedding
![]() $\pi :{\mathcal {W}}\rightarrow {\mathcal {M}}^\eta _{{\alpha }_{\eta }}$
. As
$\pi :{\mathcal {W}}\rightarrow {\mathcal {M}}^\eta _{{\alpha }_{\eta }}$
. As
![]() ${\mathcal {W}}$
has no Woodin cardinals, it follows that for every
${\mathcal {W}}$
has no Woodin cardinals, it follows that for every
![]() $\eta $
,
$\eta $
,
![]() ${\mathcal {W}}$
is
${\mathcal {W}}$
is
![]() $\xi _{\eta }$
-iterable via a Z-validated strategy. As
$\xi _{\eta }$
-iterable via a Z-validated strategy. As
![]() $Ord=\bigcup _{\eta } \xi _{\eta }$
, we have that
$Ord=\bigcup _{\eta } \xi _{\eta }$
, we have that
![]() ${\mathcal {W}}$
is
${\mathcal {W}}$
is
![]() $Ord$
-iterable via a Z-validated strategy. Hence, for some
$Ord$
-iterable via a Z-validated strategy. Hence, for some
![]() $\eta $
, Case2 must be the cause for stopping the construction of
$\eta $
, Case2 must be the cause for stopping the construction of
![]() ${\mathcal {T}}^\eta $
. Below, we drop
${\mathcal {T}}^\eta $
. Below, we drop
![]() $\eta $
from subscripts.
$\eta $
from subscripts.
To finish the proof of Proposition 12.4, we need to show that
![]() ${\mathcal {N}}_{i+1}$
is almost Z-good. This easily follows from universality. Because
${\mathcal {N}}_{i+1}$
is almost Z-good. This easily follows from universality. Because
![]() ${\delta }({\mathcal {T}} )$
is Woodin in
${\delta }({\mathcal {T}} )$
is Woodin in
![]() ${\mathcal {S}}_{\eta }$
, we must have that
${\mathcal {S}}_{\eta }$
, we must have that
![]() ${\mathcal {N}}_{i+1}{\trianglelefteq } {\mathcal {S}}_{\eta }$
. If now
${\mathcal {N}}_{i+1}{\trianglelefteq } {\mathcal {S}}_{\eta }$
. If now
![]() ${\mathcal {M}}$
is a
${\mathcal {M}}$
is a
![]() ${\delta }({\mathcal {T}})$
-sound Z-validated sts mouse, then because
${\delta }({\mathcal {T}})$
-sound Z-validated sts mouse, then because
![]() ${\mathcal {T}}$
has no
${\mathcal {T}}$
has no
![]() ${\mathcal {Q}}$
-structure, we must have that
${\mathcal {Q}}$
-structure, we must have that
![]() $\rho ({\mathcal {M}})\geq {\delta }({\mathcal {T}})$
and
$\rho ({\mathcal {M}})\geq {\delta }({\mathcal {T}})$
and
![]() ${\mathcal {M}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ (as otherwise the prototypical argument would yield a branch of
${\mathcal {M}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ (as otherwise the prototypical argument would yield a branch of
![]() ${\mathcal {T}}$
).
${\mathcal {T}}$
).
12.3. Stacking suitable sts mice
In this section, assuming
![]() $\neg \mathsf {Hypo}$
, we build an almost excellent hybrid premouse. We achieve this by stacking fully backgrounded Z-good sts premice. As we said in the introduction to this section, we will make sure that a stationary set of measurable cardinals will remain measurable in the model produced by our construction. This will be achieved by adding each such measures by brute force.
$\neg \mathsf {Hypo}$
, we build an almost excellent hybrid premouse. We achieve this by stacking fully backgrounded Z-good sts premice. As we said in the introduction to this section, we will make sure that a stationary set of measurable cardinals will remain measurable in the model produced by our construction. This will be achieved by adding each such measures by brute force.
By induction, we define a sequence
![]() $\vec {{\mathcal { K}}}=({\mathcal { K}}_{\alpha }: {\alpha }\in \Omega )$
, called a Z-good stack,Footnote 115 such that
$\vec {{\mathcal { K}}}=({\mathcal { K}}_{\alpha }: {\alpha }\in \Omega )$
, called a Z-good stack,Footnote 115 such that
-
1.
 ${\mathcal { K}}_0$
is a fully backgrounded Z-good sts premouse over
${\mathcal { K}}_0$
is a fully backgrounded Z-good sts premouse over
 ${\mathcal {R}}$
,
${\mathcal {R}}$
, -
2. for every
 ${\alpha }$
,
${\alpha }$
,
 ${\mathcal { K}}_{{\alpha }+1}$
is a fully backgrounded Z-good sts hod premouse over
${\mathcal { K}}_{{\alpha }+1}$
is a fully backgrounded Z-good sts hod premouse over
 ${\mathcal { K}}_{\alpha }$
,
${\mathcal { K}}_{\alpha }$
, -
3. if
 ${\alpha }$
is a limit ordinal and
${\alpha }$
is a limit ordinal and
 $Ord\cap \bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta }\not \in S$
, then
$Ord\cap \bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta }\not \in S$
, then
 ${\mathcal { K}}_{\alpha }=Lp^{Zv, sts}(\bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta })$
,
${\mathcal { K}}_{\alpha }=Lp^{Zv, sts}(\bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta })$
, -
4. if
 ${\alpha }$
is a limit ordinal and
${\alpha }$
is a limit ordinal and
 ${\lambda }=_{def}Ord\cap \bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta } \in S$
, then letting U be a normal measure on
${\lambda }=_{def}Ord\cap \bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta } \in S$
, then letting U be a normal measure on
 ${\lambda }$
and setting
${\lambda }$
and setting
 ${\mathcal { K}}^{\prime }_{\alpha }=\bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta }$
and
${\mathcal { K}}^{\prime }_{\alpha }=\bigcup _{{\beta }<{\alpha }}{\mathcal { K}}_{\beta }$
and
 ${\mathcal { K}}^{\prime \prime }_{\alpha }=\pi _U({\mathcal { K}}^{\prime }_{\alpha })|({\lambda }^{++})^{\pi _U({\mathcal { K}}^{\prime }_{\alpha })}$
,
${\mathcal { K}}^{\prime \prime }_{\alpha }=\pi _U({\mathcal { K}}^{\prime }_{\alpha })|({\lambda }^{++})^{\pi _U({\mathcal { K}}^{\prime }_{\alpha })}$
,
 ${\mathcal { K}}^{\prime \prime \prime }_{\alpha }=({\mathcal { K}}^{\prime \prime }_{\alpha }, E)$
where E is the
${\mathcal { K}}^{\prime \prime \prime }_{\alpha }=({\mathcal { K}}^{\prime \prime }_{\alpha }, E)$
where E is the
 $({\lambda }, ({\lambda }^{+})^{\pi _U({\mathcal { K}}^{\prime }_{\alpha })})$
-extender derived from
$({\lambda }, ({\lambda }^{+})^{\pi _U({\mathcal { K}}^{\prime }_{\alpha })})$
-extender derived from
 $\pi _U$
and
$\pi _U$
and
 ${\mathcal { K}}_{\alpha }$
is the core of
${\mathcal { K}}_{\alpha }$
is the core of
 ${\mathcal { K}}^{\prime \prime \prime }_{\alpha }$
.
${\mathcal { K}}^{\prime \prime \prime }_{\alpha }$
.
We call
![]() $\vec {{\mathcal { K}}}$
the
$\vec {{\mathcal { K}}}$
the
![]() $(f.b. Z)$
-validated stack. The construction of
$(f.b. Z)$
-validated stack. The construction of
![]() $\vec {{\mathcal { K}}}$
is straightforward. However, we need to verify the following three statements.
$\vec {{\mathcal { K}}}$
is straightforward. However, we need to verify the following three statements.
(S1) For
![]() ${\alpha }<{\beta }$
, if
${\alpha }<{\beta }$
, if
![]() ${\delta }$
is a Woodin cardinal of
${\delta }$
is a Woodin cardinal of
![]() ${\mathcal { K}}_{\alpha }$
, then no level of
${\mathcal { K}}_{\alpha }$
, then no level of
![]() ${\mathcal { K}}_{\beta }$
projects across
${\mathcal { K}}_{\beta }$
projects across
![]() ${\delta }$
and
${\delta }$
and
![]() ${\mathcal { K}}_{\beta }{\vDash } \text {`}{\delta }$
is a Woodin cardinal’.
${\mathcal { K}}_{\beta }{\vDash } \text {`}{\delta }$
is a Woodin cardinal’.
(S2) If
![]() $Ord\cap \bigcup _{{\beta }<{\lambda }}{\mathcal { K}}_{\beta } \in S$
, then
$Ord\cap \bigcup _{{\beta }<{\lambda }}{\mathcal { K}}_{\beta } \in S$
, then
![]() ${\lambda }$
is a measurable cardinal in
${\lambda }$
is a measurable cardinal in
![]() ${\mathcal { K}}_{{\lambda }+1}$
.
${\mathcal { K}}_{{\lambda }+1}$
.
(S3) The class of
![]() ${\lambda }$
such that
${\lambda }$
such that
![]() $Ord\cap \bigcup _{{\beta }<{\lambda }}{\mathcal { K}}_{\beta } \in S$
is stationary.
$Ord\cap \bigcup _{{\beta }<{\lambda }}{\mathcal { K}}_{\beta } \in S$
is stationary.
We now prove the above three clauses by proving a sequence of lemmas.
Lemma 12.6. For every
![]() ${\alpha }$
,
${\alpha }$
,
![]() ${\mathcal { K}}_{\alpha }$
is a Z-validated mouse. If
${\mathcal { K}}_{\alpha }$
is a Z-validated mouse. If
![]() ${\alpha }\in S$
is such that
${\alpha }\in S$
is such that
![]() $Ord\cap \bigcup _{{\beta }<{\lambda }}{\mathcal { K}}_{\beta } \in S$
, then
$Ord\cap \bigcup _{{\beta }<{\lambda }}{\mathcal { K}}_{\beta } \in S$
, then
![]() ${\mathcal { K}}^{\prime }_{\alpha }$
,
${\mathcal { K}}^{\prime }_{\alpha }$
,
![]() ${\mathcal { K}}^{\prime \prime }_{\alpha }$
,
${\mathcal { K}}^{\prime \prime }_{\alpha }$
,
![]() ${\mathcal { K}}^{\prime \prime \prime }_{\alpha }$
are also Z-validated mice.
${\mathcal { K}}^{\prime \prime \prime }_{\alpha }$
are also Z-validated mice.
Lemma 12.6 is a consequence of [Reference Neeman31, Corollary 3.16]. This corollary shows that if U is a good hull, then the pre-images of the relevant objects have iteration strategies that pick realizable branches, which implies that they have Z-approved strategies.
Lemma 12.7. (S1) holds.
Proof. Fix
![]() ${\alpha }<{\beta }$
and
${\alpha }<{\beta }$
and
![]() ${\delta }$
as in the statement of (S1). Suppose
${\delta }$
as in the statement of (S1). Suppose
![]() ${\mathcal {M}}{\trianglelefteq } {\mathcal { K}}_{{\beta }}$
is such that
${\mathcal {M}}{\trianglelefteq } {\mathcal { K}}_{{\beta }}$
is such that
![]() $\rho ({\mathcal {M}})< {\delta }$
. It follows from our construction that for some
$\rho ({\mathcal {M}})< {\delta }$
. It follows from our construction that for some
![]() ${\gamma }+1\leq {\alpha }$
,
${\gamma }+1\leq {\alpha }$
,
![]() ${\delta }={\delta }^{{\mathcal { K}}_{{\gamma }+1}}$
. Let
${\delta }={\delta }^{{\mathcal { K}}_{{\gamma }+1}}$
. Let
![]() $p=p_{n+1}({\mathcal {M}})$
be the standard parameter of
$p=p_{n+1}({\mathcal {M}})$
be the standard parameter of
![]() ${\mathcal {M}}$
and n be least such that
${\mathcal {M}}$
and n be least such that
![]() $\rho _{n+1}({\mathcal {M}})=\rho ({\mathcal {M}})<{\delta }$
. Let
$\rho _{n+1}({\mathcal {M}})=\rho ({\mathcal {M}})<{\delta }$
. Let
![]() ${\mathcal {W}}$
be the canonical decoding structure of
${\mathcal {W}}$
be the canonical decoding structure of
![]() $Hull_1^{{\mathcal {M}}^n}({\delta }\cup \{p\})$
, where
$Hull_1^{{\mathcal {M}}^n}({\delta }\cup \{p\})$
, where
![]() ${\mathcal {M}}^n$
is the n-th reduct of
${\mathcal {M}}^n$
is the n-th reduct of
![]() ${\mathcal {M}}$
. As
${\mathcal {M}}$
. As
![]() ${\mathcal {M}}$
is a Z-validated sts premouse and
${\mathcal {M}}$
is a Z-validated sts premouse and
![]() ${\mathcal { K}}_{{\gamma }+1}$
is Z-suitable, we must have that
${\mathcal { K}}_{{\gamma }+1}$
is Z-suitable, we must have that
![]() $rud({\mathcal {W}}){\vDash } \text {`}{\delta }$
is a Woodin cardinal’. Hence,
$rud({\mathcal {W}}){\vDash } \text {`}{\delta }$
is a Woodin cardinal’. Hence,
![]() $\rho ({\mathcal {W}})={\delta }$
, a contradiction. A similar argument shows that
$\rho ({\mathcal {W}})={\delta }$
, a contradiction. A similar argument shows that
![]() ${\mathcal { K}}_{\beta }{\vDash } \text {`}{\delta }$
is a Woodin cardinal’.
${\mathcal { K}}_{\beta }{\vDash } \text {`}{\delta }$
is a Woodin cardinal’.
Lemma 12.8. (S2) holds.
Proof. First, we claim that
![]() $\rho ({\mathcal { K}}_{\lambda })>{\lambda }$
. Lemma 12.7 shows that
$\rho ({\mathcal { K}}_{\lambda })>{\lambda }$
. Lemma 12.7 shows that
![]() $\rho ({\mathcal { K}}_{\lambda })\geq {\lambda }$
. Assume then that
$\rho ({\mathcal { K}}_{\lambda })\geq {\lambda }$
. Assume then that
![]() $\rho ({\mathcal { K}}_{\lambda })={\lambda }$
. Let
$\rho ({\mathcal { K}}_{\lambda })={\lambda }$
. Let
![]() ${\mathcal {W}}=Core({\mathcal { K}}_{\lambda })$
and U be the normal measure on
${\mathcal {W}}=Core({\mathcal { K}}_{\lambda })$
and U be the normal measure on
![]() ${\lambda }$
. Because of our definition of
${\lambda }$
. Because of our definition of
![]() $\vec {{\mathcal { K}}}$
, we have that
$\vec {{\mathcal { K}}}$
, we have that
Let now F be the last extender of
![]() ${\mathcal {W}}$
. As
${\mathcal {W}}$
. As
![]() ${\vert {\mathcal {W}}\vert }={\lambda }$
, we have
${\vert {\mathcal {W}}\vert }={\lambda }$
, we have
![]() $\sigma : Ult({\mathcal {W}}, F)\rightarrow \pi _U({\mathcal {W}})$
such that
$\sigma : Ult({\mathcal {W}}, F)\rightarrow \pi _U({\mathcal {W}})$
such that
![]() $\sigma \in Ult(V, U)$
. It follows that
$\sigma \in Ult(V, U)$
. It follows that
Hence,
![]() $Ult({\mathcal {W}}, F){\trianglelefteq } {\mathcal { K}}^{\prime \prime }_{\lambda }$
implying that
$Ult({\mathcal {W}}, F){\trianglelefteq } {\mathcal { K}}^{\prime \prime }_{\lambda }$
implying that
![]() ${\mathcal {W}}\in {\mathcal { K}}^{\prime \prime }_{\lambda }$
. Thus,
${\mathcal {W}}\in {\mathcal { K}}^{\prime \prime }_{\lambda }$
. Thus,
![]() $\rho ({\mathcal { K}}_{\lambda })>{\lambda }$
.
$\rho ({\mathcal { K}}_{\lambda })>{\lambda }$
.
The same argument shows that if
![]() ${\mathcal {M}}{\trianglelefteq } {\mathcal { K}}_{{\lambda }+1}$
, then
${\mathcal {M}}{\trianglelefteq } {\mathcal { K}}_{{\lambda }+1}$
, then
![]() $\rho ({\mathcal {M}})>{\lambda }$
. Thus,
$\rho ({\mathcal {M}})>{\lambda }$
. Thus,
![]() ${\lambda }$
must be a measurable cardinal in
${\lambda }$
must be a measurable cardinal in
![]() ${\mathcal { K}}_{{\lambda }+1}$
.
${\mathcal { K}}_{{\lambda }+1}$
.
(S3) is trivial. It then follows that
![]() $\bigcup _{{\alpha }\in Ord}{\mathcal { K}}_{\alpha }$
is an almost excellent hybrid premouse.
$\bigcup _{{\alpha }\in Ord}{\mathcal { K}}_{\alpha }$
is an almost excellent hybrid premouse.
12.4. The conclusion assuming
 $\neg \mathsf {Hypo}$
$\neg \mathsf {Hypo}$
We remind our reader that we have gotten to this point by assuming that
![]() $\neg \mathsf {Hypo}$
holds. The following summarizes the results of the previous subsection.
$\neg \mathsf {Hypo}$
holds. The following summarizes the results of the previous subsection.
Corollary 12.9. Assume
![]() $\neg \mathsf {Hypo}$
. Then there is an honest Z-suitable
$\neg \mathsf {Hypo}$
. Then there is an honest Z-suitable
![]() ${\mathcal {R}}$
and a Z-validated almost excellent class size premouse
${\mathcal {R}}$
and a Z-validated almost excellent class size premouse
![]() ${\mathcal { K}}$
based on
${\mathcal { K}}$
based on
![]() ${\mathcal {R}}$
satisfying the following conditions.
${\mathcal {R}}$
satisfying the following conditions.
-
1. For each maximal window w of
 ${\mathcal { K}}$
and for each
${\mathcal { K}}$
and for each
 $\eta \in (\nu ^w, {\delta }^w)$
that is a regular cardinal in
$\eta \in (\nu ^w, {\delta }^w)$
that is a regular cardinal in
 ${\mathcal { K}}$
,
${\mathcal { K}}$
,
 ${\mathcal { K}}$
has a Z-validated iteration strategy
${\mathcal { K}}$
has a Z-validated iteration strategy
 $\Sigma $
that acts on normal iterations that are based on
$\Sigma $
that acts on normal iterations that are based on
 ${\mathcal { K}}|\eta $
and are above
${\mathcal { K}}|\eta $
and are above
 $\nu ^w$
.
$\nu ^w$
. -
2. For each maximal window w of
 ${\mathcal { K}}$
,
${\mathcal { K}}$
,
 ${\mathcal { K}}|{\delta }^w$
is a fully backgrounded Z-good sts premouse over
${\mathcal { K}}|{\delta }^w$
is a fully backgrounded Z-good sts premouse over
 ${\mathcal { K}}|\nu ^w$
.
${\mathcal { K}}|\nu ^w$
. -
3. For each Woodin cardinal
 ${\delta }$
of
${\delta }$
of
 ${\mathcal { K}}$
and for each Z-validated sound sts mouse
${\mathcal { K}}$
and for each Z-validated sound sts mouse
 ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
 ${\mathcal { K}}|{\delta }{\trianglelefteq } {\mathcal {M}}$
,
${\mathcal { K}}|{\delta }{\trianglelefteq } {\mathcal {M}}$
,
 ${\mathcal {M}}{\vDash } \text {`}{\delta }$
is a Woodin cardinal’.
${\mathcal {M}}{\vDash } \text {`}{\delta }$
is a Woodin cardinal’.
The next proposition completes the proof Theorem 1.4 and Theorem 1.7 assuming
![]() $\neg \mathsf {Hypo}$
.
$\neg \mathsf {Hypo}$
.
Proposition 12.10. Assume
![]() $\neg \mathsf {Hypo}$
. Then there is a class size excellent hybrid premouse.
$\neg \mathsf {Hypo}$
. Then there is a class size excellent hybrid premouse.
We spend the rest of this subsection proving Proposition 12.10. Let
![]() ${\mathcal {R}}$
and
${\mathcal {R}}$
and
![]() ${\mathcal { K}}$
be as in Corollary 12.9. We claim that, in fact,
${\mathcal { K}}$
be as in Corollary 12.9. We claim that, in fact,
![]() ${\mathcal { K}}$
is excellent. To see this, let w be a maximal window of
${\mathcal { K}}$
is excellent. To see this, let w be a maximal window of
![]() ${\mathcal { K}}$
and let
${\mathcal { K}}$
and let
![]() $\eta \in (\nu ^w, {\delta }^w)$
be a regular cardinal of
$\eta \in (\nu ^w, {\delta }^w)$
be a regular cardinal of
![]() ${\mathcal { K}}$
. We want to see that in
${\mathcal { K}}$
. We want to see that in
![]() ${\mathcal { K}}$
,
${\mathcal { K}}$
,
![]() ${\mathcal { K}}|\eta $
has an iteration strategy that acts on normal iterations that are above
${\mathcal { K}}|\eta $
has an iteration strategy that acts on normal iterations that are above
![]() $\nu ^w$
. Let
$\nu ^w$
. Let
![]() $\Sigma $
be the Z-validated strategy of
$\Sigma $
be the Z-validated strategy of
![]() ${\mathcal { K}}|\eta $
that acts on normal iterations that are above
${\mathcal { K}}|\eta $
that acts on normal iterations that are above
![]() $\nu ^w$
. It is enough to show that
$\nu ^w$
. It is enough to show that
![]() $\Sigma {\restriction } {\mathcal { K}}$
is definable over
$\Sigma {\restriction } {\mathcal { K}}$
is definable over
![]() ${\mathcal { K}}$
.
${\mathcal { K}}$
.
We work inside
![]() ${\mathcal { K}}$
. Given a normal iteration
${\mathcal { K}}$
. Given a normal iteration
![]() ${\mathcal {T}}$
of
${\mathcal {T}}$
of
![]() ${\mathcal { K}}|\eta $
that is above
${\mathcal { K}}|\eta $
that is above
![]() $\nu ^w$
, we will say
$\nu ^w$
, we will say
![]() ${\mathcal {T}}$
has a correct
${\mathcal {T}}$
has a correct
![]() ${\mathcal {Q}}$
-structure if letting
${\mathcal {Q}}$
-structure if letting
![]() $(u, \zeta , ({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq {\delta }^u))$
be such that
$(u, \zeta , ({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq {\delta }^u))$
be such that
-
1. u is the least maximal window of
 ${\mathcal { K}}$
with the property that
${\mathcal { K}}$
with the property that
 ${\mathcal {T}}\in {\mathcal { K}}|{\delta }^u$
,
${\mathcal {T}}\in {\mathcal { K}}|{\delta }^u$
, -
2.
 $\zeta \in (\nu ^u, {\delta }^u)$
is such that
$\zeta \in (\nu ^u, {\delta }^u)$
is such that
 ${\mathcal {T}}\in {\mathcal { K}}|\zeta $
,
${\mathcal {T}}\in {\mathcal { K}}|\zeta $
, -
3.
 $({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <{\delta }^u)$
are the models of the fully backgrounded
$({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi <{\delta }^u)$
are the models of the fully backgrounded
 $({\mathcal {R}}, {\mathcal {R}}^b, S^{\mathcal { K}})$
-authenticated sts construction of
$({\mathcal {R}}, {\mathcal {R}}^b, S^{\mathcal { K}})$
-authenticated sts construction of
 ${\mathcal { K}}|{\delta }^u$
done over
${\mathcal { K}}|{\delta }^u$
done over
 ${\mathrm m}({\mathcal {T}})$
using extenders with critical points
${\mathrm m}({\mathcal {T}})$
using extenders with critical points
 $>\zeta $
,
$>\zeta $
,
for some
![]() $\xi <{\delta }^u$
,
$\xi <{\delta }^u$
,
![]() ${\mathcal {M}}_{\xi }{\vDash }\text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. We then say that
${\mathcal {M}}_{\xi }{\vDash }\text {`}{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. We then say that
![]() ${\mathcal {M}}_{\xi }$
is the correct
${\mathcal {M}}_{\xi }$
is the correct
![]() ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
![]() ${\mathcal {T}}$
. We have that
${\mathcal {T}}$
. We have that
![]() ${\mathcal {M}}_{\xi }$
has a Z-validated iteration strategy, and hence, if it exists, it is unique (i.e., does not depend on
${\mathcal {M}}_{\xi }$
has a Z-validated iteration strategy, and hence, if it exists, it is unique (i.e., does not depend on
![]() $\zeta $
).
$\zeta $
).
Continuing our work in
![]() ${\mathcal { K}}$
, given
${\mathcal { K}}$
, given
![]() ${\mathcal {T}}$
as above, we say
${\mathcal {T}}$
as above, we say
![]() ${\mathcal {T}}$
is correctly guided if for every limit
${\mathcal {T}}$
is correctly guided if for every limit
![]() ${\alpha }<lh({\mathcal {T}})$
, letting
${\alpha }<lh({\mathcal {T}})$
, letting
![]() $b=[0, {\alpha }]_{\mathcal {T}}$
,
$b=[0, {\alpha }]_{\mathcal {T}}$
,
![]() ${\mathcal {Q}}(b, {\mathcal {T}}{\restriction } {\alpha })$
exists and is the correct
${\mathcal {Q}}(b, {\mathcal {T}}{\restriction } {\alpha })$
exists and is the correct
![]() ${\mathcal {Q}}$
-structure of
${\mathcal {Q}}$
-structure of
![]() ${\mathcal {T}}$
. The following lemma finishes the proof of Proposition 12.10.
${\mathcal {T}}$
. The following lemma finishes the proof of Proposition 12.10.
Lemma 12.11. Suppose
![]() ${\mathcal {T}}\in {\mathcal { K}}$
is a normal iteration of
${\mathcal {T}}\in {\mathcal { K}}$
is a normal iteration of
![]() ${\mathcal { K}}|\eta $
of limit length that is according to
${\mathcal { K}}|\eta $
of limit length that is according to
![]() $\Sigma $
. Then
$\Sigma $
. Then
![]() ${\mathcal {T}}$
is correctly guided, and if
${\mathcal {T}}$
is correctly guided, and if
![]() ${\mathcal {T}}$
is of limit length, then
${\mathcal {T}}$
is of limit length, then
![]() ${\mathcal {T}}$
has a correct
${\mathcal {T}}$
has a correct
![]() ${\mathcal {Q}}$
-structure.
${\mathcal {Q}}$
-structure.
Proof. The second part of the conclusion of the lemma implies the first as we can apply it to the initial segments of
![]() ${\mathcal {T}}$
. Thus, assume that
${\mathcal {T}}$
. Thus, assume that
![]() ${\mathcal {T}}$
is correctly guided and is of limit length. Let
${\mathcal {T}}$
is correctly guided and is of limit length. Let
![]() $b=\Sigma ({\mathcal {T}})$
. Then
$b=\Sigma ({\mathcal {T}})$
. Then
![]() ${\mathcal {Q}}(b, {\mathcal {T}})$
exists and is Z-validated. Set
${\mathcal {Q}}(b, {\mathcal {T}})$
exists and is Z-validated. Set
![]() ${\mathcal {Q}}={\mathcal {Q}}(b, {\mathcal {T}})$
.
${\mathcal {Q}}={\mathcal {Q}}(b, {\mathcal {T}})$
.
Let
![]() $(u, \zeta , ({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq {\delta }^u))$
be as in the definition of the correct
$(u, \zeta , ({\mathcal {M}}_{\xi }, {\mathcal {N}}_{\xi }: \xi \leq {\delta }^u))$
be as in the definition of the correct
![]() ${\mathcal {Q}}$
-structure. Towards a contradiction, assume that letting
${\mathcal {Q}}$
-structure. Towards a contradiction, assume that letting
![]() ${\mathcal {N}}=_{def}{\mathcal {M}}_{{\delta }^u}$
,
${\mathcal {N}}=_{def}{\mathcal {M}}_{{\delta }^u}$
,
![]() ${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Notice that
${\mathcal {N}}{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Notice that
![]() ${\mathcal { K}}|{\delta }^u$
is generic over
${\mathcal { K}}|{\delta }^u$
is generic over
![]() ${\mathcal {N}}$
, implying that we can translate
${\mathcal {N}}$
, implying that we can translate
![]() ${\mathcal { K}}$
via S-constructions into an sts premouse over
${\mathcal { K}}$
via S-constructions into an sts premouse over
![]() ${\mathcal {N}}$
; call it
${\mathcal {N}}$
; call it
![]() ${\mathcal { K}}'$
. We have that
${\mathcal { K}}'$
. We have that
![]() ${\mathcal { K}}'{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ and
${\mathcal { K}}'{\vDash } \text {`}{\delta }({\mathcal {T}})$
is a Woodin cardinal’ and
![]() ${\mathcal { K}}'$
is almost excellent.
${\mathcal { K}}'$
is almost excellent.
Next, we compare
![]() ${\mathcal {Q}}$
with
${\mathcal {Q}}$
with
![]() ${\mathcal { K}}'$
. All of the extenders on the extender sequence of
${\mathcal { K}}'$
. All of the extenders on the extender sequence of
![]() ${\mathcal { K}}'$
have fully backgrounded certificates, which implies that in the aforementioned comparison, only the
${\mathcal { K}}'$
have fully backgrounded certificates, which implies that in the aforementioned comparison, only the
![]() ${\mathcal {Q}}$
-side moves. Let
${\mathcal {Q}}$
-side moves. Let
![]() $\Lambda $
be the unique Z-validated strategy of
$\Lambda $
be the unique Z-validated strategy of
![]() ${\mathcal {Q}}$
and let
${\mathcal {Q}}$
and let
![]() ${\mathcal {U}}$
be the tree on
${\mathcal {U}}$
be the tree on
![]() ${\mathcal {Q}}$
of limit length such that
${\mathcal {Q}}$
of limit length such that
![]() ${\mathrm m}({\mathcal {U}})={\mathcal { K}}'|{\delta }^u$
. Set
${\mathrm m}({\mathcal {U}})={\mathcal { K}}'|{\delta }^u$
. Set
![]() $c=\Lambda ({\mathcal {U}})$
and
$c=\Lambda ({\mathcal {U}})$
and
![]() ${\mathcal {M}}={\mathcal {Q}}(c, {\mathcal {U}})$
.Footnote 116
${\mathcal {M}}={\mathcal {Q}}(c, {\mathcal {U}})$
.Footnote 116
Notice now that
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() ${\delta }^u$
-sound,
${\delta }^u$
-sound,
![]() ${\delta }^u$
is a cutpoint in
${\delta }^u$
is a cutpoint in
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() ${\mathcal {M}}$
has no extenders with critical point
${\mathcal {M}}$
has no extenders with critical point
![]() ${\delta }^u$
. Moreover,
${\delta }^u$
. Moreover,
![]() ${\mathcal {M}}$
is a Z-validated sts mouse over
${\mathcal {M}}$
is a Z-validated sts mouse over
![]() ${\mathcal { K}}'|{\delta }^u$
, and therefore, it can be translated into a Z-validated sts mouse
${\mathcal { K}}'|{\delta }^u$
, and therefore, it can be translated into a Z-validated sts mouse
![]() ${\mathcal {X}}$
over
${\mathcal {X}}$
over
![]() ${\mathcal { K}}|{\delta }^u$
. We must then have that
${\mathcal { K}}|{\delta }^u$
. We must then have that
![]() $rud({\mathcal {X}}){\vDash } \text {`}{\delta }^u$
is a Woodin cardinal’. But then
$rud({\mathcal {X}}){\vDash } \text {`}{\delta }^u$
is a Woodin cardinal’. But then
![]() $rud({\mathcal {M}}){\vDash } \text {`}{\delta }^u$
is a Woodin cardinal’, a contradiction.
$rud({\mathcal {M}}){\vDash } \text {`}{\delta }^u$
is a Woodin cardinal’, a contradiction.
Notice now that for
![]() ${\mathcal {T}}\in {\mathcal { K}}$
, we have the following equivalences.
${\mathcal {T}}\in {\mathcal { K}}$
, we have the following equivalences.
-
1.
 ${\mathcal {T}}\in dom(\Sigma )$
if and only if
${\mathcal {T}}\in dom(\Sigma )$
if and only if
 ${\mathcal { K}}{\vDash } \text {`}{\mathcal {T}}$
is correctly guided’,
${\mathcal { K}}{\vDash } \text {`}{\mathcal {T}}$
is correctly guided’, -
2.
 $\Sigma ({\mathcal {T}})=b$
if and only if
$\Sigma ({\mathcal {T}})=b$
if and only if
 ${\mathcal {Q}}(b, {\mathcal {T}})$
exists and
${\mathcal {Q}}(b, {\mathcal {T}})$
exists and
 ${\mathcal { K}}{\vDash } \text {`}{\mathcal {Q}}(b, {\mathcal {T}})$
is the correct
${\mathcal { K}}{\vDash } \text {`}{\mathcal {Q}}(b, {\mathcal {T}})$
is the correct
 ${\mathcal {Q}}$
-structure for
${\mathcal {Q}}$
-structure for
 ${\mathcal {T}}$
’.
${\mathcal {T}}$
’.
12.5. Excellent hybrid premouse from
 $\mathsf {Hypo}$
$\mathsf {Hypo}$
Finally, we show how to get an excellent hybrid premouse from
![]() $\mathsf {Hypo}$
. This will complete the proof of Theorem 1.4 and Theorem 1.7. Suppose then
$\mathsf {Hypo}$
. This will complete the proof of Theorem 1.4 and Theorem 1.7. Suppose then
![]() ${\mathcal {R}}$
is an honest Z-suitable hod premouse, X is a set such that
${\mathcal {R}}$
is an honest Z-suitable hod premouse, X is a set such that
![]() ${\mathcal {R}}\in X$
and
${\mathcal {R}}\in X$
and
![]() ${\mathcal {M}}$
is an almost excellent Z-validated sts premouse over X. In particular,
${\mathcal {M}}$
is an almost excellent Z-validated sts premouse over X. In particular,
![]() ${\mathcal {M}}$
is a model of
${\mathcal {M}}$
is a model of
![]() $\mathsf {ZFC}$
. It must be clear from our construction that we can assume that X has a well-ordering in
$\mathsf {ZFC}$
. It must be clear from our construction that we can assume that X has a well-ordering in
![]() $L[X]$
. Let then
$L[X]$
. Let then
![]() ${\kappa }=({\vert {X}\vert }^+)^{\mathcal {M}}$
. Let
${\kappa }=({\vert {X}\vert }^+)^{\mathcal {M}}$
. Let
![]() ${\delta }$
be the least Woodin cardinal of
${\delta }$
be the least Woodin cardinal of
![]() ${\mathcal {M}}$
that is
${\mathcal {M}}$
that is
![]() $>{\kappa }$
and let
$>{\kappa }$
and let
![]() ${\mathcal {N}}$
be the output of the fully backgrounded
${\mathcal {N}}$
be the output of the fully backgrounded
![]() $({\mathcal {R}}, {\mathcal {R}}^b, S^{\mathcal {M}})$
-authenticated sts construction of
$({\mathcal {R}}, {\mathcal {R}}^b, S^{\mathcal {M}})$
-authenticated sts construction of
![]() ${\mathcal {M}}|{\delta }$
done over
${\mathcal {M}}|{\delta }$
done over
![]() ${\mathcal {R}}$
. Once again, using S-constructions, we can translate
${\mathcal {R}}$
. Once again, using S-constructions, we can translate
![]() ${\mathcal {M}}$
over to an sts mouse
${\mathcal {M}}$
over to an sts mouse
![]() ${\mathcal {P}}$
over
${\mathcal {P}}$
over
![]() ${\mathcal {N}}$
such that
${\mathcal {N}}$
such that
![]() ${\mathcal {P}}[{\mathcal {M}}|{\delta }]={\mathcal {M}}$
. Moreover,
${\mathcal {P}}[{\mathcal {M}}|{\delta }]={\mathcal {M}}$
. Moreover,
![]() ${\mathcal {P}}$
is almost excellent and is a Z-validated sts mouse over
${\mathcal {P}}$
is almost excellent and is a Z-validated sts mouse over
![]() ${\mathcal {R}}$
. Because good hulls of
${\mathcal {R}}$
. Because good hulls of
![]() ${\mathcal {P}}$
are iterable via a Z-approved strategy, we can assume, by minimizing if necessary, that
${\mathcal {P}}$
are iterable via a Z-approved strategy, we can assume, by minimizing if necessary, that
![]() ${\mathcal {P}}$
is minimal in the sense that for each
${\mathcal {P}}$
is minimal in the sense that for each
![]() $\eta \in ({\delta }^{\mathcal {R}}, Ord\cap {\mathcal {P}})$
,
$\eta \in ({\delta }^{\mathcal {R}}, Ord\cap {\mathcal {P}})$
,
![]() ${\mathcal {P}}|\eta $
is not an almost excellent sts premouse over
${\mathcal {P}}|\eta $
is not an almost excellent sts premouse over
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
The rest of the proof follows the same argument as the one given in the previous subsection. We show that
![]() ${\mathcal {P}}$
is, in fact, excellent. As before, this amounts to showing that for a window w of
${\mathcal {P}}$
is, in fact, excellent. As before, this amounts to showing that for a window w of
![]() ${\mathcal {P}}$
such that
${\mathcal {P}}$
such that
![]() ${\delta }^w>{\delta }^{\mathcal {R}}$
, and for any
${\delta }^w>{\delta }^{\mathcal {R}}$
, and for any
![]() $\eta \in (\nu ^w, {\delta }^w)$
, if
$\eta \in (\nu ^w, {\delta }^w)$
, if
![]() $\eta $
is a regular cardinal of
$\eta $
is a regular cardinal of
![]() ${\mathcal {P}}$
, then
${\mathcal {P}}$
, then
![]() ${\mathcal {P}}{\vDash } \text {`}{\mathcal {P}}|\eta $
has
${\mathcal {P}}{\vDash } \text {`}{\mathcal {P}}|\eta $
has
![]() $Ord$
-iteration strategy’. Towards a contradiction, assume not.
$Ord$
-iteration strategy’. Towards a contradiction, assume not.
Let U be a good hull such that
![]() ${\mathcal {P}}\in U$
. Set
${\mathcal {P}}\in U$
. Set
![]() ${\mathcal {S}}={\mathcal {P}}_U$
,
${\mathcal {S}}={\mathcal {P}}_U$
,
![]() ${\mathcal {W}}={\mathcal {R}}_U$
and
${\mathcal {W}}={\mathcal {R}}_U$
and
![]() ${\lambda }=\eta _U$
. Let
${\lambda }=\eta _U$
. Let
![]() $\Lambda $
be the Z-approved strategy of
$\Lambda $
be the Z-approved strategy of
![]() ${\mathcal {S}}$
and let
${\mathcal {S}}$
and let
![]() $\Sigma $
be the fragment of
$\Sigma $
be the fragment of
![]() $\Lambda $
that acts on normal iterations of
$\Lambda $
that acts on normal iterations of
![]() ${\mathcal {S}}|{\lambda }$
that are above
${\mathcal {S}}|{\lambda }$
that are above
![]() $\nu ^{w_U}$
. The following lemma can be proved via a proof almost identical to the proof of Lemma 12.11. We define correct
$\nu ^{w_U}$
. The following lemma can be proved via a proof almost identical to the proof of Lemma 12.11. We define correct
![]() ${\mathcal {Q}}$
-structure and correctly guided exactly the same way as we defined them in the previous subsection, except the definition now takes place in
${\mathcal {Q}}$
-structure and correctly guided exactly the same way as we defined them in the previous subsection, except the definition now takes place in
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
Lemma 12.12. Suppose
![]() ${\mathcal {T}}\in {\mathcal {S}}$
is a normal iteration of
${\mathcal {T}}\in {\mathcal {S}}$
is a normal iteration of
![]() ${\mathcal {S}}|\eta $
of limit length that is according to
${\mathcal {S}}|\eta $
of limit length that is according to
![]() $\Sigma $
. Then
$\Sigma $
. Then
![]() ${\mathcal {T}}$
is correctly guided and if
${\mathcal {T}}$
is correctly guided and if
![]() ${\mathcal {T}}$
is of limit length, then
${\mathcal {T}}$
is of limit length, then
![]() ${\mathcal {T}}$
has a correct
${\mathcal {T}}$
has a correct
![]() ${\mathcal {Q}}$
-structure.
${\mathcal {Q}}$
-structure.
There is only one difference between the proofs of Lemma 12.11 and Lemma 12.12. In the proof of Lemma 12.11, we concluded that
![]() $rud({\mathcal {X}}){\vDash } \text {`}{\delta }^u$
is a Woodin cardinal’ using the fact that
$rud({\mathcal {X}}){\vDash } \text {`}{\delta }^u$
is a Woodin cardinal’ using the fact that
![]() $({\mathcal { K}}|{\delta }^u)^\#$
is Z-suitable sts premouse. Here, we no longer have such a fact, but here we can use minimality of
$({\mathcal { K}}|{\delta }^u)^\#$
is Z-suitable sts premouse. Here, we no longer have such a fact, but here we can use minimality of
![]() ${\mathcal {P}}$
to derive the same conclusion.
${\mathcal {P}}$
to derive the same conclusion.
As in the previous subsection, Lemma 12.12 easily implies that
![]() $\Sigma {\restriction } {\mathcal {P}}$
is definable over
$\Sigma {\restriction } {\mathcal {P}}$
is definable over
![]() ${\mathcal {P}}$
. This completes the proof of Theorem 1.4 and Theorem 1.7.
${\mathcal {P}}$
. This completes the proof of Theorem 1.4 and Theorem 1.7.
13. Open problems and questions
The rather mild assumption that the class of measurable cardinals is stationary is used in various ‘pressing down’ arguments in the proof of Theorem 1.4 and Theorem 1.7, and also in stabilization arguments like those of Theorem 5.2. This assumption is probably not needed, though proving some sort of stabilization lemma like the aforementioned one is probably necessary.
Question 13.1. Are the following theories equiconsistent?
-
1.
 $\mathsf {Sealing} $
+ ‘There is a proper class of Woodin cardinals’.
$\mathsf {Sealing} $
+ ‘There is a proper class of Woodin cardinals’. -
2.
 $\mathsf {LSA-over-uB} $
+ ‘There is a proper class of Woodin cardinals’.
$\mathsf {LSA-over-uB} $
+ ‘There is a proper class of Woodin cardinals’. -
3.
 $\mathsf {Tower\ \ Sealing} $
+ ‘There is a proper class of Woodin cardinals’.
$\mathsf {Tower\ \ Sealing} $
+ ‘There is a proper class of Woodin cardinals’.
As mentioned above, CMI becomes very difficult past
![]() $\mathsf {Sealing}$
. A good test question for CMI practitioners is the following.
$\mathsf {Sealing}$
. A good test question for CMI practitioners is the following.
Open Problem 13.2. Prove that Con
![]() $(\mathsf {PFA})$
implies Con(
$(\mathsf {PFA})$
implies Con(
![]() $\mathsf {WLW}$
).
$\mathsf {WLW}$
).
We know from the results above that
![]() $\mathsf {WLW}$
is stronger than
$\mathsf {WLW}$
is stronger than
![]() $\mathsf {Sealing}$
and is roughly the strongest natural theory at the limit of traditional methods for proving iterability. We believe it is plausible to develop CMI methods for obtaining canonical models of
$\mathsf {Sealing}$
and is roughly the strongest natural theory at the limit of traditional methods for proving iterability. We believe it is plausible to develop CMI methods for obtaining canonical models of
![]() $\mathsf {WLW}$
from just
$\mathsf {WLW}$
from just
![]() $\mathsf {PFA}$
.Footnote 117
$\mathsf {PFA}$
.Footnote 117
Remark 13.3.
-
1. By the above discussion, we also get in
 $V={\mathcal {P}}[g]$
that for every generic h,
$V={\mathcal {P}}[g]$
that for every generic h,
 $(\Gamma ^{\infty }_h)^\#$
exists and by Lemma 3.2,
$(\Gamma ^{\infty }_h)^\#$
exists and by Lemma 3.2,
 $L(\Gamma ^{\infty }_h) \vDash \mathsf {AD}_{\mathbb {R}} + \Theta $
is regular. So we have the following strengthening of
$L(\Gamma ^{\infty }_h) \vDash \mathsf {AD}_{\mathbb {R}} + \Theta $
is regular. So we have the following strengthening of
 $\mathsf {Sealing}$
:
$\mathsf {Sealing}$
:
 $\mathsf {Sealing}^+ $
for all V-generic g, in
$\mathsf {Sealing}^+ $
for all V-generic g, in
 $V[g]$
,
$V[g]$
,
 $L(\Gamma ^{\infty },\mathbb {R}) \vDash \mathsf {AD}_{\mathbb {R}} + \Theta $
is regular. We call this theory
$L(\Gamma ^{\infty },\mathbb {R}) \vDash \mathsf {AD}_{\mathbb {R}} + \Theta $
is regular. We call this theory
 $\mathsf {Sealing}^+$
.
$\mathsf {Sealing}^+$
. -
2. The conclusion of
 $\mathsf {LSA-over-uB}$
can be weakened to the following: For all V-generic g, there is
$\mathsf {LSA-over-uB}$
can be weakened to the following: For all V-generic g, there is
 $A\subseteq {\mathbb {R}}^{V[g]}$
such that
$A\subseteq {\mathbb {R}}^{V[g]}$
such that
 $L(A, {\mathbb {R}}^{V[g]}){\vDash } \mathsf {LSA}$
and
$L(A, {\mathbb {R}}^{V[g]}){\vDash } \mathsf {LSA}$
and
 $\Gamma ^{\infty }_g$
is contained in
$\Gamma ^{\infty }_g$
is contained in
 $L(A, {\mathbb {R}}^{V[g]})$
. We call this theory
$L(A, {\mathbb {R}}^{V[g]})$
. We call this theory
 $\mathsf {LSA-over-uB}^-$
.
$\mathsf {LSA-over-uB}^-$
. -
3. The results of this paper show the following. Let
 $T=$
‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’. Then the following theories are equiconsistent:
$T=$
‘there exists a proper class of Woodin cardinals and the class of measurable cardinals is stationary’. Then the following theories are equiconsistent:-
(a)
 $\mathsf {Sealing}+T$
.
$\mathsf {Sealing}+T$
. -
(b)
 $\mathsf {Sealing}^++T$
.
$\mathsf {Sealing}^++T$
. -
(c)
 $\mathsf {Tower\ \ Sealing} + T$
.
$\mathsf {Tower\ \ Sealing} + T$
. -
(d)
 $\mathsf {LSA-over-uB}+T$
.
$\mathsf {LSA-over-uB}+T$
. -
(e)
 $\mathsf {LSA-over-uB}^-+T$
.
$\mathsf {LSA-over-uB}^-+T$
. -
(f)
 $\mathsf {Weak\ \ Sealing} + T$
.
$\mathsf {Weak\ \ Sealing} + T$
. -
(g)
 $\mathsf {Sealing}^{-} + T$
$\mathsf {Sealing}^{-} + T$
-
We end the paper with the following conjecture; if true, it would be an ultimate analog of the main result of [Reference Steel50].
Conjecture 13.4. Suppose there are unboundedly many Woodin cardinals and the class of measurable cardinals is stationary. Then the following are equivalent.
-
1.
 $\mathsf {Sealing}$
.
$\mathsf {Sealing}$
. -
2.
 $\mathsf {Sealing}^{+}$
.
$\mathsf {Sealing}^{+}$
. -
3.
 $\mathsf {Weak\ Sealing}$
.
$\mathsf {Weak\ Sealing}$
. -
4.
 $\mathsf {Sealing}^{-}$
.
$\mathsf {Sealing}^{-}$
. -
5.
 $\mathsf {Tower\ Sealing}$
.
$\mathsf {Tower\ Sealing}$
.
Acknowledgement
We would like to thank Hugh Woodin for many comments made about the earlier drafts of this paper, and especially for pointing out an easier argument demonstrating that
![]() $\mathsf {LSA-over-uB}$
is not equivalent to
$\mathsf {LSA-over-uB}$
is not equivalent to
![]() $\mathsf {Sealing}$
and for bringing the
$\mathsf {Sealing}$
and for bringing the
![]() $\mathsf {Tower\ Sealing}$
to our attention. We also thank Ralf Schindler for useful suggestion regarding our use of second-order set theory. The authors are grateful for the referees’ enormous efforts to make the manuscript better. The authors would like to thank the NSF for its generous support. The first author was supported by NSF Career Award DMS-1352034 and by NCN Grant WEAVE-UNISONO, Id: 567137. The second author is supported by NSF Grant No DMS-1565808 and DMS-1849295.
$\mathsf {Tower\ Sealing}$
to our attention. We also thank Ralf Schindler for useful suggestion regarding our use of second-order set theory. The authors are grateful for the referees’ enormous efforts to make the manuscript better. The authors would like to thank the NSF for its generous support. The first author was supported by NSF Career Award DMS-1352034 and by NCN Grant WEAVE-UNISONO, Id: 567137. The second author is supported by NSF Grant No DMS-1565808 and DMS-1849295.
Competing interest
None.