Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-12T21:19:16.303Z Has data issue: false hasContentIssue false
  • English
  • Français

DIVERGENT MODELS WITH THE FAILURE OF THE CONTINUUM HYPOTHESIS

Part of: Set theory

Published online by Cambridge University Press:  06 December 2023

NAM TRANG
NAM TRANG*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NORTH TEXAS DENTON, TX 76205, USA
*
E-mail: Nam.Trang@unt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct divergent models of $\mathsf {AD}^+$ along with the failure of the Continuum Hypothesis ($\mathsf {CH}$) under various assumptions. Divergent models of $\mathsf {AD}^+$ play an important role in descriptive inner model theory; all known analyses of HOD in $\mathsf {AD}^+$ models (without extra iterability assumptions) are carried out in the region below the existence of divergent models of $\mathsf {AD}^+$. Our results are the first step toward resolving various open questions concerning the length of definable prewellorderings of the reals and principles implying 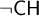$\neg \mathsf {CH}$, like 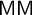$\mathsf {MM}$, that divergent models shed light on, see Question 5.1.

Keywords

divergent modelsinner model theorydescriptive set theory

MSC classification

Primary: 03E15: Descriptive set theory 03E45: Inner models, including constructibility, ordinal definability, and core models 03E60: Determinacy principles
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Farah, I., The extender algebra and ${\varSigma}_1^2$ -absoluteness, preprint, 2016, arXiv:1005.4193.Google Scholar
Neeman, I., Inner models in the region of a Woodin limit of Woodin cardinals . Annals of Pure and Applied Logic, vol. 116 (2002), nos. 1–3, pp. 67–155.CrossRefGoogle Scholar
Sargsyan, G., Hod Mice and the Mouse Set Conjecture, Memoirs of the American Mathematical Society, vol. 236(1111), American Mathematical Society, Providence, 2014.Google Scholar
Sargsyan, G. and Trang, N., The exact consistency strength of the generic absoluteness for the universally Baire sets. Forum of Mathematics, Sigma , 2019, to appear.Google Scholar
Sargsyan, G. and Trang, N., The Largest Suslin Axiom, Lecture Notes in Logic, vol. 56, Cambridge University Press, Cambridge, 2023, to appear.Google Scholar
Steel, J. R., The derived model theorem , Logic Colloquium 2006, Lecture Notes in Logic, vol. 32, Association for Symbolic Logic, Chicago, 2009, pp. 280–327 CrossRefGoogle Scholar
Steel, J. R., An outline of inner model theory , Handbook of Set Theory, Springer, Dordrecht, 2010, pp. 1595–1684.CrossRefGoogle Scholar
Steel, J. R., A Comparison Process for Mouse Pairs, Lecture Notes in Logic, vol. 51, Cambridge University Press, Cambridge, 2022.CrossRefGoogle Scholar
Woodin, W. H., The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, revised ed., De Gruyter Series in Logic and Its Applications, vol. 1, Walter de Gruyter, Berlin, 2010.CrossRefGoogle Scholar