Introduction
Measurements of temperature below the penetration depth of the annual cycle of surface temperature (the “10 m temperature”) have traditionally been used to determine mean annual temperature on the surface of polar ice sheets (see discussions by Reference Hooke, Gould and BrzozowskiHooke and others, 1983; Reference Echelmeyer, Harrison, Clarke and BensonEchelmeyer and others, 1992). Similar measurements and interpretations have been made in permafrost terrains (e.g. Reference LachenbruchLachenbruch, 1994; Reference Osterkamp and RomanovskyOsterkamp and Romanovsky, 1996). Repeat application of the method provides an efficient way to monitor changes of the mean annual surface temperature over interannual and decadal time-scales, but only if the mean annual surface temperature is below freezing and heat transport is limited to thermal diffusion. On polar glaciers the first requirement is satisfied by definition. The second requirement implies no vertical transport and refreezing of liquid water; this is satisfied in the dry-snow zone (if present) and also approximately in the ablation area. In the ablation area of a polar glacier, meltwater may be produced during the short summer but it does not penetrate the cold surface ice. In the absence of horizontal advection, steady-state heat transport can be idealized within vertical columns of ice. In such an ice column the vertical gradient of the mean annual ice temperature depends on the Péclet numberl, as well as the thickness and the temperature difference across the sub-freezing portion of the ice column (see Appendix A). In the accumulation area, vertical temperature gradients near the ice surface are generally small; in the ablation area this is true if ice thickness is large and ablation (i.e. vertical advection) is relatively small. As a consequence, over much of the surface of the polar ice sheets the ice temperature at 10–14 m is a direct measure of mean annual surface temperature. In contrast, the ablation areas of polar valley glaciers typically have large temperature gradients, mainly because they are much thinner than the ice sheets. If, superimposed on these large temperature gradients, there is significant surface lowering, such as that accompanying periods of negative mass balance, then changes in the 10 m temperature will not provide a direct measurement of the change in mean annual surface temperature. This complication makes the interpretation of 10 m ice-temperature changes in terms of climate change difficult. However, for polythermal McCall Glacier in arctic Alaska, we demonstrate that a relatively small number of ice-temperature measurements can be interpreted for a climatological signal with success, provided that both near-surface (10 m) temperatures and temperature gradients can be derived from the observations.
For the Pacific region of North America, Reference Ebbesmeyer, Cayan, McLain, Nichols, Peterson, Redmond, Betancourt and TharpEbbesmeyer and others (1991) demonstrate a statistically significant change in the mid-1970s in a set of variables ranging from sea-ice extent in the Bering Strait to the number of goose nests along the Columbia River. At the same time (around 1977) the mean annual air temperature of several Alaskan weather stations showed an increase of 1–1.5 K. However, interpretation of this change may be biased, as some stations have experienced heat-island effects (Reference Bowling, Weller, Wilson and SeverinBowling, 1991). Independent assessments of climate change in pristine parts of the Arctic are therefore of interest.
The reasonably long background of studies on McCall Glacier provides observations of this type. These include the observation that the annual rate of surface lowering at a transverse profile located in the ablation area of McCall Glacier increased from 0.3 m a−l to 1 m a−l between 1975 and 1987 (Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995), and that the long-term mass balance of McCall Glacier over the period 1972–93 was more negative by a factor two or more than that measured over the period 1958–71. Reference Rabus and EchelmeyerRabus and Echelmeyer (1998) explain these observations in terms of a synoptic-scale climate change. They find that the seasonal and long-term trends of temperature and precipitation on McCall Glacier are well correlated with meteorological observations at Inuvik, Canada, located 400 km northeast of the glacier. Modeling the mass balance of McCall Glacier using these observations showed that the observed mass-balance changes were mainly due to climate warming, aided by lower snowfall. The positive degree-day sum (a measure of summer temperature) increased by about 10% from the earlier to the later mass-balance period, while the winter precipitation decreased by a similar amount. The annual temperature measured above Inuvik at the elevation of the glacier showed an increase of about 0.5 K. However, we note that while the temporal patterns of temperature change appear to be correlated between McCall Glacier and Inuvik, the amplitude of the temperature change need not be the same at both locations. Thus we seek an independent and more robust measure of the mean annual surface temperature change in this region of the Arctic. In the present paper, we use changes in the 10 m ice temperatures, corrected for the known glacier thinning through measured temperature gradients, to determine the change in the mean annual temperature between 1972 and 1995 on McCall Glacier.
Temperature Measurements, 1972 and 1995
McCall Glacier is a small, polythermal valley glacier located in the Brooks Range of northern Alaska, U.S.A. The glacier has been thinning and retreating since the 1950s, with strongly negative mass balances throughout much of the 1990s (Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995; Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998; K. A. Echelmeyer and L. Cox, unpublished data).
Temperature measurements were made in 1972 at a number of locations in both the ablation and accumulation area of McCall Glacier using thermocouples that were installed at initial depths of 5, 10 and l5 m (Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others, 1975). At one location in the ablation area (about 3 km up-glacier from the 1972 terminus) ice temperatures were measured with thermistors down to 75 m depth. In 1995 we reoccupied five of the original thermocouple sites in the ablation area and two near the equilibrium line (Fig. 1).We chose sites that presumably had reliable readings above and below the 10 m depth (D. C. Trabant, unpublished information). Due to the mass wastage of the glacier, the surface elevations at the same horizontal positions were 5–30 m lower in 1995 than in 1972. We installed two thermocouples at each site in mid-June 1995. The installation depths of the thermocouples in each hole were such that, by late summer 1995, ablation had placed them to within a few centimeters of the corresponding 1972 depths at each location. In late June, mid-July, and late August 1995, and again in late April 1996, measurements were carried out using a 0°C bath. The reso1ution of the calibrated voltmeter was 10 μV, corresponding to 0.06°C, and the typical accuracy of our measurements was about 0.1°C.

Fig. 1. McCall Glacier location map.The shift of the elevation contours from 1993 to 1958 above 1900 m is negligible for this study.
Figure 2 shows the 1995/96 data (symbols with error bars); to compress the time axis, the April 1996 reading was shifted by 1 year to April 1995. Separate symbols are used for upper and lower thermocouples. In a similar representation, Figure 3 shows individual measurements from the 1970s for one location, TC2.5 (D. C. Trabant, unpublished information), which was also the site of the 75 m thermistor cable. Three thermocouples were installed at that time. The original 1970s data records exist for only TC2.5 and the thermistor cable; for all other sites, we rely on Trabant and others’ (1975) interpretation of the data in terms of the 1972 mean annual temperatures. We note that the annual cycle has an amplitude of about 5% at 10 m depth for reasons discussed by Reference Hooke, Gould and BrzozowskiHooke and others (1983) and Reference Echelmeyer, Harrison, Clarke and BensonEchelmeyer and others (1992).

Fig. 2. Analysis of shallow ice-temperature measurements from the 1990s. The April 1996 readings have been shifted backwards by 1 year to bring out more clearly the portion of the annual cycle where data are available. “Shallow” (z s ) and “deep” (z d ) denote depth below the glacier surface in August 1995 of the upper (<10 m) and lower (>10 m) thermocouple, respectively.

Fig. 3. Analysis of shallow ice-temperature measurements from the 1970s. “Shallow” (z s ), “medium” (z m ) and “deep”(z d ) denote depth below the glacier surface in August 1971 of the upper, middle and lower thermocouple, respectively.
From our measurements we wish to infer the mean annual surface temperature ![]() at each of the sites in Figure 1. This quantity is related to the mean annual temperature at 10 m depth
at each of the sites in Figure 1. This quantity is related to the mean annual temperature at 10 m depth ![]() and the mean annual vertical temperature gradient (dT
10/dz, where z is the depth below the surface) by
and the mean annual vertical temperature gradient (dT
10/dz, where z is the depth below the surface) by
![]() and dT
10/dz are interpolated from the mean annual temperatures,
and dT
10/dz are interpolated from the mean annual temperatures, ![]() and
and ![]() , at the two thermocouples, one at z
1 < 10 m and the other at z
2 > 10 m according to
, at the two thermocouples, one at z
1 < 10 m and the other at z
2 > 10 m according to

The annual cycle of temperature at a depth z is determined by the diffusion–advection Equation (A.1) given in Appendix A. We assume a constant thermal diffusivity κ and restrict advection to the vertical (z) direction, following the magnitude analysis of Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others (1975) for McCall Glacier. Prescribing a sinusoidal surface temperature cycle with an annual period τ = 365 days at z = 0 gives

with

and
Here, t s is the time in the spring/summer when the surface temperature equals the annual mean surface temperature (the “zero-pass time”) given as
and t 0(z), ΔT, z 0, and τ = 1 year are lag time at depth z, surface amplitude, penetration depth, and period of the annual temperature cycle, respectively. Equation (4) includes the effects of surface ablation a to first order, following Reference Echelmeyer, Harrison, Clarke and BensonEchelmeyer and others (1992). We take κ ≈ κ(−5°C) = 36.3 m2 a−1. The thickness of the seasonal snow layer was typically < 0.4 m for all thermocouple sites, so its influence on κ is neglected.
One might worry that the sinusoid in Equation (4) might not represent the annual course of the ice surface temperature properly, as it neglects the clipping of the ice surface temperature at 0°C during summer melt. However, this effect turns out to be negligible for the severe climate of McCall Glacier. In the 1970s, mean annual air temperature was measured to be −14°C at 1700 m. This suggests negative maximum temperatures of the sinusoidal cycle for the entire glacier because the absolute value of the mean annual temperature is larger than the value found for ΔT (9.6 K; see next paragraph). In the 1990s, mean annual air temperatures were somewhat warmer, with −12.5°C measured at 2100 m, but maximum temperatures of the sinusoid are still expected negative for most of the ablation area. Even for the lowermost thermocouple at 1500 m it is justified to neglect the clipping at 0°C, as the corresponding maximum temperature of the sinusoid should be <1°C there (assuming a lapse rate of 0.6 K per 100 m elevation). Melt does of course occur on McCall Glacier. However, the brief summers on McCall Glacier really consist of a fluctuation of brief warm spells (air temperatures up to +10°C) in between cold spells (air temperatures down to −10°C) through which the sinusoid interpolates an overall summer temperature < 0°C.
We initially attempted to directly solve for the mean annual temperature at the two thermocouples, ![]() ,
, ![]() , the amplitude ΔT and the “zero-pass time”, t
s. We did this by setting up four equations for the temperature at two times at the two depths, with the observed temperatures in August 1995 (t
i) and April 1996 (t
2) as input. However, at several sites this method produced inconsistent results for ΔT and t
s, which in turn lead to unreasonable values for the temperature gradient in Equation (2). The reason for this is that there are relatively large errors in some of the measurements. In an improved approach, ΔT and t
s are obtained independently by fitting a sinusoidal temperature function to a multi-year temperature record measured on the moraine at an elevation of 2135 m (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998). Using that record we found that ΔT = 9.6 K and t
s = 104 d, where d is days since 1 January.
, the amplitude ΔT and the “zero-pass time”, t
s. We did this by setting up four equations for the temperature at two times at the two depths, with the observed temperatures in August 1995 (t
i) and April 1996 (t
2) as input. However, at several sites this method produced inconsistent results for ΔT and t
s, which in turn lead to unreasonable values for the temperature gradient in Equation (2). The reason for this is that there are relatively large errors in some of the measurements. In an improved approach, ΔT and t
s are obtained independently by fitting a sinusoidal temperature function to a multi-year temperature record measured on the moraine at an elevation of 2135 m (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998). Using that record we found that ΔT = 9.6 K and t
s = 104 d, where d is days since 1 January. ![]() and
and ![]() were then found by a least-squares fit of Equation (4) to the data. These results are shown as continuous curves in Figures 2 and 3. Before final least-squares fits were carried out, identifiable outliers were eliminated from the data, as is explained in the following.
were then found by a least-squares fit of Equation (4) to the data. These results are shown as continuous curves in Figures 2 and 3. Before final least-squares fits were carried out, identifiable outliers were eliminated from the data, as is explained in the following.
Figures 2 and 3 reveal that about 20% of the individual measurements have a systematic error of up to 0.5 K. The source of this error remains obscure; perhaps they were due to uncompensated contact potentials. However, there is only one case (deep thermocouple at TC11 in Fig. 2) with less than three data points aligned along the predicted curve within the expected error bounds. Furthermore, the sign of the observed erroneous deviations from the curve appears to be random. We thus argue that the likelihood of three or more erroneous readings lying accidentally on a predicted curve is small and, consequently, the large errors appear to be of “on/off” type. Either a reading is correct to within expected error bounds or it is a clear outlier. This assumption makes it possible to identify and discard the affected measurements for cases in which there is only one outlier. The only ambiguous case with two outliers (deep sensor at TC11) is discarded from all subsequent analysis.
Propagating random measurement errors gives estimated errors, ε, in the mean annual temperature at 10 m and the gradient at that depth:

Here m = 3 or 4 is the number of individual temperature readings (after discarding outliers), and the only free-fit parameter in Equation (4) is ![]() . The error in the temperature measurements is ε(T) = 0.1 K. In the error estimate for
. The error in the temperature measurements is ε(T) = 0.1 K. In the error estimate for ![]() we have neglected the small uncertainty in the depths. For m = 3 (one discarded outlier for each of the two thermocouples) and z
2 − z
1 = 5 m, we obtain
we have neglected the small uncertainty in the depths. For m = 3 (one discarded outlier for each of the two thermocouples) and z
2 − z
1 = 5 m, we obtain ![]() and
and ![]() . The error in the mean annual surface temperature is given by
. The error in the mean annual surface temperature is given by
This error analysis does not consider systematic errors that may arise because of our assumption of a uniform ΔT and t
s at each site. The uniform value of t
s is likely a robust assumption at the few-days level. On the other hand, some differences in surface temperature amplitude between the sites is likely. Additionally, the occurrence of positive temperatures in the weather-station record during June-August will introduce a small positive bias into ΔT, because these are not present in the ice. An empirical estimate of the sensitivity may be obtained by using ΔT ± 1.0 K in Equation (4). The corresponding maximum variations in ![]() and
and ![]() are less than 0.12 K and 0.007 K m−1, respectively. This would increase the overall error to
are less than 0.12 K and 0.007 K m−1, respectively. This would increase the overall error to ![]() , which we judge to be a conservative upper bound.
, which we judge to be a conservative upper bound.
Changes in Ice Temperature and the Temperature Gradientat 10m Depth
Figure 4a and b show ![]() and
and ![]() as calculated using Equations (1–4) for the 1990s data, after outlier elimination (triangles), and the corresponding values for the 1970s data (squares). Solid and open symbols denote sites located in the ablation and accumulation areas, respectively. With the exception of TC2.5, the values of
as calculated using Equations (1–4) for the 1990s data, after outlier elimination (triangles), and the corresponding values for the 1970s data (squares). Solid and open symbols denote sites located in the ablation and accumulation areas, respectively. With the exception of TC2.5, the values of ![]() for the 1970s are taken from Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others (1975). Because the actual 1972 field observations were available to us for TC2.5, we used the same data-reduction method as we did for the 1990s data, with the medium and deep thermocouples in Figure 3. This also led to the only gradient calculation available from the 1970s thermocouple data.
for the 1970s are taken from Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others (1975). Because the actual 1972 field observations were available to us for TC2.5, we used the same data-reduction method as we did for the 1990s data, with the medium and deep thermocouples in Figure 3. This also led to the only gradient calculation available from the 1970s thermocouple data.

Fig. 4. Mean annual values of ice temperature and ice-temperature gradient at 10 m depth plotted against ice surface elevation, (a) Measured ice temperature T10 in 1972 and 1995. Temperature trends shown by dotted lines, (b) Ice-temperature gradient dT10/dz, measured (symbols) and steady-state values calculated from advection and ice depth (lines). Labels near the data points in (a) are site locations shown in Figure 1. Data points for the 1972 measurements (squares) lie directly below the corresponding 1995 data points (triangles) at a given site in the ablation area. Model curves in (b) come from Equation (7).
Mean annual temperature at 10 m depth shows a pronounced warming trend of > 1 K for the lower sites in the ablation area (Fig. 4a). In contrast, there is no clear trend near and above the equilibrium line (about 2000–2200 m elevation), where temperature changes are generally much smaller and of arbitrary sign. As discussed in Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others (1975), percolation in the accumulation area, as well as horizontal advection, cause anomalous ice temperatures close to the equilibrium line. The interannual variability of these effects, together with a general up-glacier migration of the ablation area (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998), explain the scattered nature of the observed temperature changes at these higher elevations. Site TC11.5 was in the accumulation area in the 1970s and in the ablation area in the 1990s; this leads to the deviation of the apparent temperature change at this site from the nearly constant offset.
The measured gradients of mean annual temperature at 10 m depth in the 1990s and the one value in the 1970s are shown in Figure 4b. These are to be compared with the temperature gradients calculated using the measured emergence velocities and ice depths (data from Rabus and Reference Rabus and EchelmeyerEchelmeyer, 1997, figs 9 and 10). These calculated gradients are evaluated from the expression (see derivation in Appendix A)

where the Péclet number is defined as
This is valid for steady-state vertical heat transport in an ice column with the melting isotherm occurring within or at the bottom of the column. Here, θ s is the mean annual surface temperature measured in °C, H is the thickness of the sub-freezing portion of the ice column and v is the vertical advection rate (assumed constant through the sub-freezing portion of the ice column). For the calculation we take v equal to the average value of the emergence velocity over the period 1993–95 as measured by repetitive surveying of surface markers at each site (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1997). θ s is taken to be the approximate value of −10°C, which is reasonable, at least for the ablation area. The correct choice for H at each site is the actual ice depth minus the thickness of a layer of temperate ice at the bed. Such a temperate basal layer is likely present under much of the ablation area; at site TC2.5 its thickness is about 30 m (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1997). At the other sites the thickness of the temperate layer is not known, and to bracket the effect of possible spatial variations in its thickness, we solved Equation (5) for the two limiting cases of: (1) a uniform layer thickness of 30 m (solid line), and (2) no temperate basal layer (H = 0, dashed line). In the latter case, only the glacier sole is at the melting point.
Random errors in ![]() estimated using Equation (7) are <0.02 K m−1. Given our assumptions, the fits between measured and predicted gradients of mean annual ice temperature are satisfactory. In the uppermost and lowermost ablation areas, the Péclet number is small because of the small emergence velocity and shallow ice depth, respectively. In these regions the dashed line (calculated assuming no temperate layer) shows a poor fit to the observations, while that calculated assuming a 30 m thick layer shows a better fit. This gives further support to the idea that there is a finite layer of temperate ice beneath the ablation area of McCall Glacier, as originally proposed by Reference Rabus and EchelmeyerRabus and Echelmeyer (1997) based on ice dynamics.
estimated using Equation (7) are <0.02 K m−1. Given our assumptions, the fits between measured and predicted gradients of mean annual ice temperature are satisfactory. In the uppermost and lowermost ablation areas, the Péclet number is small because of the small emergence velocity and shallow ice depth, respectively. In these regions the dashed line (calculated assuming no temperate layer) shows a poor fit to the observations, while that calculated assuming a 30 m thick layer shows a better fit. This gives further support to the idea that there is a finite layer of temperate ice beneath the ablation area of McCall Glacier, as originally proposed by Reference Rabus and EchelmeyerRabus and Echelmeyer (1997) based on ice dynamics.
Interpretation of the Observed ice-Temperature Changes: Climate Warming or Glacier Thinning?
In this section we investigate the warming at 10 m depth using a simple heat-diffusion model to calculate changes of ![]() and
and ![]() at site TC2.5. We allow the surface of the glacier to lower as a consequence of the observed negative mass balances. The measured 75 m temperature profile at this site is imposed as an initial condition in 1972, and the model is run forward in time until 1995. In a first model, we show that by imposing the observed surface lowering of 20 m (Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995) and using extreme values of vertical advection we can produce the observed 10 m temperature increase of 1.2 K at site TC2.5 (Fig. 4a). No temperature change at the glacier surface is required to achieve this. However, the modeled values of the temperature gradient are unrealistic, being significantly outside the error bound of the observed gradient. In order to reproduce the observed values of both the mean annual 10 m temperature and the gradient there within their respective error bounds, we must impose a significant climate warming.
at site TC2.5. We allow the surface of the glacier to lower as a consequence of the observed negative mass balances. The measured 75 m temperature profile at this site is imposed as an initial condition in 1972, and the model is run forward in time until 1995. In a first model, we show that by imposing the observed surface lowering of 20 m (Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995) and using extreme values of vertical advection we can produce the observed 10 m temperature increase of 1.2 K at site TC2.5 (Fig. 4a). No temperature change at the glacier surface is required to achieve this. However, the modeled values of the temperature gradient are unrealistic, being significantly outside the error bound of the observed gradient. In order to reproduce the observed values of both the mean annual 10 m temperature and the gradient there within their respective error bounds, we must impose a significant climate warming.
We calculate the mean annual ice temperature ![]() for year t and depth z by solving the time-dependent heat-diffusion equation (e.g. Reference Carslaw and JaegerCarslaw and Jaeger, 1959) with constant vertical advection v and constant thermal diffusivity κ,
for year t and depth z by solving the time-dependent heat-diffusion equation (e.g. Reference Carslaw and JaegerCarslaw and Jaeger, 1959) with constant vertical advection v and constant thermal diffusivity κ,
We apply a finite-difference scheme using Δz = 1 m steps in depth and choosing the time-step Δt ≤ Δz)2/(2κ) ≈ 5 days to insure numerical stability. A specified surface lowering v sl over the modeled time period is accommodated by shifting the surface downwards at each time-step at a constant rate. In detail, this is accommodated by removing a surface layer from the temperature profile rather than compressing the profile. In terms of physical processes causing the surface lowering, our implementation therefore favors surface ablation over horizontal stretching and basal melting. Corresponding biases of the model results are, however, expected to be negligible due to the smallness of the chosen time-step. The time-dependent surface boundary condition at z = 0 is approximated as a step change ΔT S in ice surface temperature occurring at the onset of the simulation in 1972,

The initial condition is a vertical profile of annual temperature, ![]() , as compiled from the available 1972 temperature data
, as compiled from the available 1972 temperature data
Thermistors were spaced every 5 m along this profile, with the uppermost being located 7 m below the surface (Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others, 1975), and the near-surface annual temperatures were obtained from our re-analysis of the data from the three thermocouples at the same site, following Figure 3.
The simplicity of our heat-diffusion model is justified by the relatively large uncertainties in some of the model inputs, such as an approximate 30% uncertainty in vertical advection (Table 1a). Sophistication of the model, such as a temperature-dependent thermal diffusivity, an uneven distribution of the surface lowering rate over the year, a linear reduction of the advection rate with depth, and/or detailed modeling of the annual temperature cycle, led to negligible changes in the model fit to the observations, and thus to our main conclusions.
Table 1. Input parameters and results for temperature model at TC2.5, 1972–95

Table 1 presents inputs and results of our model experiments, with each row representing one set of input parameters. The surface lowering v sl is well known over the periods 1972–93 and 1958–72 (Reference Dorrer and WendlerDorrer and Wendler, 1976; Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998). We varied either v or ΔT S until the model reproduced the observed change in T 10.
In the first set of experiments (Table 1a) we investigated scenarios with no change in surface temperature (ΔT
S = 0). The first two rows of Table 1a show that the 1972 deep temperature profile was in equilibrium prior to 1972, as indicated by both ![]() and
and ![]() remaining constant. This holds for the scenario of a reasonable advection rate of 0.8 m a−1 and no surface lowering, as well as for a scenario in which the measured surface lowering rate for the period 1958–72 and a reduced advection rate of 0.6 m a−1 are imposed. This later advection rate is close to that obtained by repeat surveying in the 1990s (as emergence velocity) at this site (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1997). These findings suggest that the deep temperature profile was in equilibrium for some decades before 1972, as suggested by Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others (1975).
remaining constant. This holds for the scenario of a reasonable advection rate of 0.8 m a−1 and no surface lowering, as well as for a scenario in which the measured surface lowering rate for the period 1958–72 and a reduced advection rate of 0.6 m a−1 are imposed. This later advection rate is close to that obtained by repeat surveying in the 1990s (as emergence velocity) at this site (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1997). These findings suggest that the deep temperature profile was in equilibrium for some decades before 1972, as suggested by Reference Trabant, Harrison, Benson, Weller and BowlingTrabant and others (1975).
If, however, we impose the observed surface lowering rate for the 1972–93 period, then an unreasonably large advection rate of v = 1.1 m a−1 is required to match the observed change in 10 m temperature. More important, for this set of input parameters the resulting temperature gradient is much larger than that observed. Thus, the last row in Table 1a leads to the conclusion that the observed warming at 10 m depth cannot be explained without a corresponding warming at the ice surface.
The numerical experiments presented in Table 1b assume a surface temperature increase (ΔT S > 0). The observed surface lowering rate for 1972–93 is used in all cases. For the measured value of v, as well as its lower and upper error bound, ΔT S is varied to match the observed warming at 10 m depth. The imposed surface warming ranges from 0.8 to 1.3 K, which is close to the observed 1.2 K warming at 10 m depth. The best fit to both the observed 10 m temperature change and the observed temperature gradient (0.18 K m−1) is achieved for our lower bound of the vertical advection rate (first row in Table 1b). Using the measured value of v (second row in Table 1b) we obtain the measured temperature change and a gradient that is still within the error margin of the observed value, while for larger advection rates the gradient is unreasonably large.
The results of these numerical experiments thus indicate that: (1) the deep temperature profile was in equilibrium until about 1972, (2) the observed temperature change and gradient at 10 m depth are not consistent with any model with zero surface temperature change, and (3) there is clear evidence of a surface warming of about 1.1 ±0.3 K in the lower ablation area of McCall Glacier. This surface warming is apparent at all sites in the ablation area (Fig. 4), and modeling at these sites leads to similar but less robust conclusions, due to the lack of deep temperature data at these other locations.
A warming of the glacier surface is not automatically equivalent to a climate warming. Two additional factors that need to be considered are: (1) lower surface elevation at the measurement sites, and (2) increased thickness of the seasonal snow cover. The first effect can be estimated by assuming a constant surface lowering rate and an adiabatic lapse rate of 0.6 K per 100 m. This leads to an associated temperature increase for site TC2.5 of about 0.06 K, while for TC2.2 the associated increase would be 0.09 K. Consequently, the effect of lower surface elevation on the surface temperature is negligible compared to the inferred surface warming of 1.1 ±0.03 K.
A change in the annual mean thickness of the seasonal snow cover can be discarded on grounds of the characteristics of seasonal snow accumulation observed on McCall Glacier (Reference RabusRabus, 1997). During the period 1993–97 the surface of the lower ablation area was usually bare ice; in some cases there was a discontinuous snow cover <0.1 m thick. During 1996, continuous automatic measurements of the snow surface height were carried out with a sonic ranger in the upper ablation area close to TC11. Results show the seasonal maximum of snow thickness was reached in early June. Maximum snow thicknesses at TC11 were about 0.5 m, with a mean annual snow thickness of about 0.2 m. From Equation (B.3) in Appendix B we can quantify the ice surface temperature increase Δθ s expected from a change in mean snow thickness Δd snow as

where the thermal conductivities K
ice (= 2.2 W m−1K−1) for ice at −10°C and K
snow for snow of density 400 kg m−3 (= 0. 33 W m−1 K−1) are taken from Reference PatersonPaterson (1994). For ![]() we find that an increase in the mean annual seasonal snow thickness of 0.1 m would lead to an ice surface warming of about 0.13 K. Realistic snow-thickness changes therefore cannot explain the observed warming of the ice surface. In addition, our mass-balance modeling suggests that snowfall has decreased on McCall Glacier rather than increased (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998). Consequently, the calculated increase of ice surface temperature on McCall Glacier might be an underestimate of the corresponding increase of air temperature.
we find that an increase in the mean annual seasonal snow thickness of 0.1 m would lead to an ice surface warming of about 0.13 K. Realistic snow-thickness changes therefore cannot explain the observed warming of the ice surface. In addition, our mass-balance modeling suggests that snowfall has decreased on McCall Glacier rather than increased (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998). Consequently, the calculated increase of ice surface temperature on McCall Glacier might be an underestimate of the corresponding increase of air temperature.
Conclusions
Shallow ice temperatures have been widely used on ice sheets as a measure of mean annual air temperature, and changes of shallow ice temperature consequently are believed to reflect changes of climate. In contrast, such a direct interpretation of shallow ice-temperature changes is not allowed for a polythermal valley glacier with a non-steady-state surface and significant near-surface vertical gradients of mean annual ice temperature. To generalize the method for this case, we need to (1) measure and model both the near-surface mean annual ice temperature and its vertical gradient in the ablation zone, (2) estimate vertical advection, and (3) provide a history of surface elevation changes. This generalized method requires more measurements in the near-surface environment, well distributed over the year. Temperature measurements should be made to an accuracy of better than 0.1 K.
In our model of the observed 1972–95 changes in 10 m ice temperatures on McCall Glacier, we have used both the observed surface lowering and the measured vertical advection rate at the surface. We are able to match the observed changes in temperature and temperature gradients only by imposing a significant increase (1.1 ±0.3 K) of surface air temperature during the period 1972–95. This is in agreement with previous mass-balance modeling results on McCall Glacier (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998).
Our present result suggests spatial variations in the synoptic-scale climatic warming trend that has affected arctic Alaska since the 1970s.We find an increase in the mean annual temperature on McCall Glacier of + 1.1 K, while our previous analysis of meteorological data from Inuvik, Canada, some 400 km to the northwest of the glacier, suggested an increase of at least +0.5 K (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998).
Acknowledgements
This study was supported by U.S. National Science Foundation grant NSF-OPP-9214954. We wish to thank G. Aðalgeirsdóttir, U. Adolphs, J. DeMallie, S. Campbell, J. Sapiano, K. Swanson, D. C. Trabant and C. Trabant for help with the fieldwork. Special thanks are given to D. C. Trabant for access to his data, and to W. D. Harrison for stimulating discussions in the early stages of this work, as well as providing further important comments on the final manuscript. Thanks also go to K. Cuffey for being the scientific editor, and to T. Pfeffer and C. Hulbe for their careful reviews that helped to improve the manuscript. We are also grateful to the refuge manager and other personnel of the Arctic National Wildlife Refuge for providing valuable support.
Appendix A: Relation Between Mean Annual Nearsurface Temperature and its Vertical Gradient for Avertical Ice Column
The diffusion equation for ice temperature T, no horizontal advection and constant thermal diffusivity κ is given by:

Here, v is the (depth-independent) vertical advection rate (v > 0 in the ablation area, v < 0 in the accumulation area) and z is the vertical coordinate measured upward. For steady-state conditions, this becomes

Two cases are considered: (a) there is a layer of temperate ice at the bottom, with thickness H, and (b) no temperate ice layer, but the bed may be at the melting point. The origin z = 0 denotes either the bottom of the sub-freezing part of the ice column in case (a) or the bottom of the ice column itself in case (b). The ice surface is defined by z = H. By rearranging Equation (A.2) and integrating from 0 to z we obtain

The upper boundary condition is T| z = H = T s, while the lower boundary condition is T| z = 0 = T m in case (a) or dT/dz| z = 0 = Γgeo in case (b). Here, T s, T m and Γgeo are mean annual surface temperature, the melting point and geothermal gradient, respectively. For case (b)

showing that the temperature gradient is unrelated to the surface temperature, but it does depend exponentially on the advection rate. In case (a) we integrate Equation (A.3) from 0 to H, and apply the boundary conditions, giving

Defining θ s = T s − T m, which is essentially the surface temperature measured in °C, and rearranging, we obtain

for the relation between surface temperature gradient and surface temperature. For the ablation area Pe > 0. For small Péclet number, which corresponds to small advection rate and/or ice depth, Equation (A.6) can be approximated as

For the other extreme, Pe ≫ 1, which represents strong vertical advection, Equation (A.6) is approximated by

i.e. the near-surface temperature gradient depends linearly on both the surface temperature and the advection rate.
Appendix B: Relation Between Mean Annual Surface Temperature and Mean Annual Air Temperature Under the Presence of a Seasonal Snow Layer
The heat fluxes Q ice from the ice surface and Q snow through the snow layer are given by

and

Here, d snow is the thickness of the snow layer averaged over the year, Ki ce, K snow are the thermal conductivities of snow and ice, and θ a, θ s are mean annual air and ice surface temperatures, respectively. Continuity of the heat flux across the ice–snow interface requires Q ice = Q snow, which gives

as an expression for the mean annual air temperature.


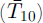 have systematically increased by > 1 K for the ablation area (1400–1900 m), while closer to the firn area, where meltwater percolation and refreezing play a role, they remained approximately unchanged. Interpreting these findings in terms of climate change requires careful consideration of the observed thinning of the glacier, which causes lowering of the surface through an existing vertical temperature gradient. Such temperature gradients can be particularly large in the ablation areas of polythermal glaciers; on McCall Glacier they are on the order of 0.2 K m
have systematically increased by > 1 K for the ablation area (1400–1900 m), while closer to the firn area, where meltwater percolation and refreezing play a role, they remained approximately unchanged. Interpreting these findings in terms of climate change requires careful consideration of the observed thinning of the glacier, which causes lowering of the surface through an existing vertical temperature gradient. Such temperature gradients can be particularly large in the ablation areas of polythermal glaciers; on McCall Glacier they are on the order of 0.2 K m




