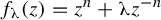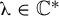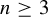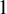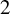1 Introduction
1.1 Background and main result
In 1988, McMullen [Reference McMullen, Drasin, Kra, Earle, Marden and GehringMcM88] introduced a rational map
![]() $f_{\unicode{x3bb} }(z)=z^{2}+\unicode{x3bb} z^{-3}$
as a singular perturbation of
$f_{\unicode{x3bb} }(z)=z^{2}+\unicode{x3bb} z^{-3}$
as a singular perturbation of
![]() $z \mapsto z^{2}$
. In his article, McMullen showed that for
$z \mapsto z^{2}$
. In his article, McMullen showed that for
![]() $\unicode{x3bb} $
sufficiently small, the Julia set
$\unicode{x3bb} $
sufficiently small, the Julia set
![]() $J(f_{\unicode{x3bb} })$
of
$J(f_{\unicode{x3bb} })$
of
![]() $f_{\unicode{x3bb} }$
is a Cantor circle (homeomorphic to a product of a Cantor set and a circle).
$f_{\unicode{x3bb} }$
is a Cantor circle (homeomorphic to a product of a Cantor set and a circle).
In 2005, Devaney and his group [Reference Blanchard, Devaney, Look, Seal and ShapiroBDL+05, Reference Devaney and LookDL05, Reference Devaney, Look and UminskyDLU05] generalized the work of McMullen and studied a more general family of McMullen maps:
with
![]() $\unicode{x3bb} \in \mathbb {C}^{*}=\mathbb {C}\setminus \{0\}$
and
$\unicode{x3bb} \in \mathbb {C}^{*}=\mathbb {C}\setminus \{0\}$
and
![]() $n \geq 2 $
,
$n \geq 2 $
,
![]() $m \geq 1$
. They showed that this family exhibits a very rich dynamical behavior while it has such a simple form. In [Reference Devaney, Look and UminskyDLU05], the authors showed that if the free critical orbits escape to
$m \geq 1$
. They showed that this family exhibits a very rich dynamical behavior while it has such a simple form. In [Reference Devaney, Look and UminskyDLU05], the authors showed that if the free critical orbits escape to
![]() $\infty $
, then its Julia set is either a Cantor set, a Cantor circle, or a Sierpiński carpet. Later on, Devaney and his group published a variety of papers on this McMullen family, see [Reference DevaneyDev04, Reference DevaneyDev05, Reference DevaneyDev06, Reference DevaneyDev07, Reference Devaney, Lyubich and YampolskyDev08, Reference DevaneyDev13, Reference Devaney and LookDL05, Reference Devaney, Look and UminskyDLU05, Reference Devaney and MarottaDM07, Reference Devaney and PilgrimDP09]. Among these articles, lots of them devoted to the particular case of
$\infty $
, then its Julia set is either a Cantor set, a Cantor circle, or a Sierpiński carpet. Later on, Devaney and his group published a variety of papers on this McMullen family, see [Reference DevaneyDev04, Reference DevaneyDev05, Reference DevaneyDev06, Reference DevaneyDev07, Reference Devaney, Lyubich and YampolskyDev08, Reference DevaneyDev13, Reference Devaney and LookDL05, Reference Devaney, Look and UminskyDLU05, Reference Devaney and MarottaDM07, Reference Devaney and PilgrimDP09]. Among these articles, lots of them devoted to the particular case of
![]() $n=m$
in equation (1.1), that is,
$n=m$
in equation (1.1), that is,
with
![]() $\unicode{x3bb} \in \mathbb {C}^{*}$
and
$\unicode{x3bb} \in \mathbb {C}^{*}$
and
![]() $n \geq 3 $
. In the following, we only study this family.
$n \geq 3 $
. In the following, we only study this family.
In the parameter plane, we study the escape locus of this family which consists of those maps such that all critical orbits are attracted by the super-attracting fixed point
![]() $\infty $
. Every connected component of the escape locus is a hyperbolic component, called an escape component. It was proved in [Reference Qiu, Roesch, Wang and YinQRWY15] that every escape component is bounded by a Jordan curve. It can also be shown that each hyperbolic component outside the escape locus belongs to a homeomorphic copy of the Mandelbrot set.
$\infty $
. Every connected component of the escape locus is a hyperbolic component, called an escape component. It was proved in [Reference Qiu, Roesch, Wang and YinQRWY15] that every escape component is bounded by a Jordan curve. It can also be shown that each hyperbolic component outside the escape locus belongs to a homeomorphic copy of the Mandelbrot set.
In this article, we explore the geometric regularity of the boundaries of escape components. There is a unique unbounded escape component which is called the Cantor locus. Like in the case of polynomials, a map in the Cantor locus has all of its critical values in the Fatou component of
![]() $\infty $
. Hence, its Julia set is a Cantor set. In [Reference Qiu, Roesch, Wang and YinQRWY15], the authors proved that cusps are dense on the boundary of the Cantor locus. In the bounded escape components, the McMullen maps behave more like non-polynomial rational maps. A map in a bounded escape component has one of its finite critical values belonging to a strict pre-image of the Fatou component of
$\infty $
. Hence, its Julia set is a Cantor set. In [Reference Qiu, Roesch, Wang and YinQRWY15], the authors proved that cusps are dense on the boundary of the Cantor locus. In the bounded escape components, the McMullen maps behave more like non-polynomial rational maps. A map in a bounded escape component has one of its finite critical values belonging to a strict pre-image of the Fatou component of
![]() $\infty $
. There is a unique escape component centered at the origin which is called the McMullen domain such that a map in it has its Julia set as a Cantor circle. All the other escape components are called Sierpiński holes since maps in them have Julia sets as Sierpiński carpets. The main purpose of this article is to characterize the geometric property of all bounded escape components. We obtain the following result.
$\infty $
. There is a unique escape component centered at the origin which is called the McMullen domain such that a map in it has its Julia set as a Cantor circle. All the other escape components are called Sierpiński holes since maps in them have Julia sets as Sierpiński carpets. The main purpose of this article is to characterize the geometric property of all bounded escape components. We obtain the following result.
Theorem 1.1. The boundary of each bounded escape component is a quasi-circle with Hausdorff dimension strictly between
![]() $1$
and
$1$
and
![]() $2$
.
$2$
.
We show that these geometric properties can be deduced from the following more precise topological characterization about the closures of escape components.
Theorem 1.2. The closures of escape components are pairwise disjoint.
1.2 Idea of proof
The proof of Theorem 1.2 proceeds by seeking contradiction. The key step is to show that the boundary of each bounded escape component does not intersect with the boundary of the Cantor locus. To prove this, we first construct a local para-puzzle system in the parameter space which is the counterpart of a dynamical puzzle system introduced in [Reference Qiu, Wang and YinQWY12, Reference Qiu, Roesch, Wang and YinQRWY15]. With the aid of this para-puzzle system, we can characterize the dynamical behavior of the hypothetical intersection points. We exclude all possibilities except the intersections at parabolic parameters. Then we use the parabolic implosion theory introduced in [Reference Lei and LeiLei00, Reference Shishikura and LeiShi00] to exclude the parabolic case. Indeed, on one hand, the intersection point could be accessed by a parameter ray which consists of maps with critical values in a strict pre-image of the Fatou component of
![]() $\infty $
. On the other hand, according to the parabolic implosion theory, the Fatou coordinate remains stable under a perturbation within a particular sector. After showing that the parameter ray is contained in the sector, we conclude that the maps on this parameter ray should have critical points in the Fatou component of
$\infty $
. On the other hand, according to the parabolic implosion theory, the Fatou coordinate remains stable under a perturbation within a particular sector. After showing that the parameter ray is contained in the sector, we conclude that the maps on this parameter ray should have critical points in the Fatou component of
![]() $\infty $
(not in a strict pre-image of the Fatou component of
$\infty $
(not in a strict pre-image of the Fatou component of
![]() $\infty $
). This is a contradiction. Finally, we show that the closures of bounded escape components are pairwise disjoint. One hidden difficulty is to exclude the intersection of two bounded escape components with potentially the same dynamical property. We solve this by establishing a rigidity result of bounded escape components.
$\infty $
). This is a contradiction. Finally, we show that the closures of bounded escape components are pairwise disjoint. One hidden difficulty is to exclude the intersection of two bounded escape components with potentially the same dynamical property. We solve this by establishing a rigidity result of bounded escape components.
To prove Theorem 1.1, we first observe the boundary of the Fatou component of
![]() $\infty $
is a quasi-circle with Hausdorff dimension strictly between
$\infty $
is a quasi-circle with Hausdorff dimension strictly between
![]() $1$
and
$1$
and
![]() $2$
for the map which does not belong to the closure of the Cantor locus. Then, Theorem 1.2 allows us to transfer this property to the boundaries of bounded escape components in the parameter space via a holomorphic motion.
$2$
for the map which does not belong to the closure of the Cantor locus. Then, Theorem 1.2 allows us to transfer this property to the boundaries of bounded escape components in the parameter space via a holomorphic motion.
1.3 Outline of the article
The content is arranged as follows. Section 2 includes some basic terminology and results for the McMullen family, and the construction of the dynamical puzzle system with some relevant results. In §3, we construct a local para-puzzle system which reveals the relation between the position of the parameter and the structure of its corresponding dynamical puzzle system. Section 4 presents a rigidity result of post-critically finite McMullen maps in the escape locus. In §5, we use the local para-puzzle system to study the properties of the maps which belong to the boundaries of escape components. In §6, we use the parabolic implosion theory to exclude the possibility that any bounded escape component and the Cantor locus have no common boundary point. In §7, we finish the proofs of Theorems 1.1 and 1.2.
2 Preliminary
2.1 Overview of McMullen family
The McMullen family in equation (1.2) admits a symmetric conjugacy
for all
![]() $\unicode{x3bb} \in \mathbb {C}^{*}$
. Hence, it suffices to study maps whose parameters belong to the sector
$\unicode{x3bb} \in \mathbb {C}^{*}$
. Hence, it suffices to study maps whose parameters belong to the sector
 $$ \begin{align} \mathscr{F}_{0}:=\bigg \{\unicode{x3bb} \in \mathbb{C}^{*}: 0 \leq \arg \unicode{x3bb} \leq \frac{2\pi}{n-1} \bigg \}. \end{align} $$
$$ \begin{align} \mathscr{F}_{0}:=\bigg \{\unicode{x3bb} \in \mathbb{C}^{*}: 0 \leq \arg \unicode{x3bb} \leq \frac{2\pi}{n-1} \bigg \}. \end{align} $$
We denote the interior of
![]() $\mathscr {F}_{0}$
as
$\mathscr {F}_{0}$
as
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
The critical set of
![]() $f_{\unicode{x3bb} }$
is
$f_{\unicode{x3bb} }$
is
![]() $\{ 0, \infty \} \cup C_{\unicode{x3bb} }$
, where
$\{ 0, \infty \} \cup C_{\unicode{x3bb} }$
, where
![]() $C_{\unicode{x3bb} }=\{ c \in \mathbb {C}: c^{2n}=\unicode{x3bb} \}$
. Here,
$C_{\unicode{x3bb} }=\{ c \in \mathbb {C}: c^{2n}=\unicode{x3bb} \}$
. Here,
![]() $\infty $
is a super-attracting fixed point of
$\infty $
is a super-attracting fixed point of
![]() $f_{\unicode{x3bb} }$
which has only two pre-images
$f_{\unicode{x3bb} }$
which has only two pre-images
![]() $0$
and
$0$
and
![]() $\infty $
. There are only two critical values
$\infty $
. There are only two critical values
![]() $v^{\pm }_{\unicode{x3bb} }=\pm 2 \sqrt {\unicode{x3bb} }$
other than
$v^{\pm }_{\unicode{x3bb} }=\pm 2 \sqrt {\unicode{x3bb} }$
other than
![]() $\infty $
(here,
$\infty $
(here,
![]() $v^{\pm }_{\unicode{x3bb} }$
is well defined for
$v^{\pm }_{\unicode{x3bb} }$
is well defined for
![]() $\unicode{x3bb} \in \mathscr {F}_{0}$
,
$\unicode{x3bb} \in \mathscr {F}_{0}$
,
![]() $v^{+}_{\unicode{x3bb} }$
is defined to be the one belonging to
$v^{+}_{\unicode{x3bb} }$
is defined to be the one belonging to
![]() $\{z \in \mathbb {C}: 0 \leq \arg z<\pi \}$
). Let
$\{z \in \mathbb {C}: 0 \leq \arg z<\pi \}$
). Let
 $$ \begin{align} Z_{k}(\unicode{x3bb}):= \begin{cases} \{\infty\}, &{k=0,}\\ \{ z \in \mathbb{C}: f^{k-2}_{\unicode{x3bb}}(z)=0 \}, & {k \geq 2.}\\ \end{cases} \end{align} $$
$$ \begin{align} Z_{k}(\unicode{x3bb}):= \begin{cases} \{\infty\}, &{k=0,}\\ \{ z \in \mathbb{C}: f^{k-2}_{\unicode{x3bb}}(z)=0 \}, & {k \geq 2.}\\ \end{cases} \end{align} $$
For
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $Z_k(\unicode{x3bb} )$
is the set of all
$Z_k(\unicode{x3bb} )$
is the set of all
![]() $(k-1)$
th iterated pre-images of
$(k-1)$
th iterated pre-images of
![]() $\infty $
under
$\infty $
under
![]() $f_{\unicode{x3bb} }$
with
$f_{\unicode{x3bb} }$
with
![]() $\infty $
itself excluded.
$\infty $
itself excluded.
Lemma 2.1. (Böttcher coordinate)
For each
![]() $z_{k}(\unicode{x3bb} ) \in Z_{k}(\unicode{x3bb} )$
, the Böttcher coordinate
$z_{k}(\unicode{x3bb} ) \in Z_{k}(\unicode{x3bb} )$
, the Böttcher coordinate
![]() $\phi _{z_{k}(\unicode{x3bb} )}$
near
$\phi _{z_{k}(\unicode{x3bb} )}$
near
![]() $z_{k}(\unicode{x3bb} )$
is defined in the following.
$z_{k}(\unicode{x3bb} )$
is defined in the following.
-
(1) For
 $k=0$
,
$k=0$
,
 $z_{0}(\unicode{x3bb} )=\infty $
,
$z_{0}(\unicode{x3bb} )=\infty $
,
 $\phi _{\infty (\unicode{x3bb} )}$
is defined to be (2.4)with
$\phi _{\infty (\unicode{x3bb} )}$
is defined to be (2.4)with $$ \begin{align} \phi_{\infty(\unicode{x3bb})}(z)=\lim_{k \rightarrow \infty}\sqrt[n^{k}]{f^{k}_{\unicode{x3bb}}(z)} \end{align} $$
$$ \begin{align} \phi_{\infty(\unicode{x3bb})}(z)=\lim_{k \rightarrow \infty}\sqrt[n^{k}]{f^{k}_{\unicode{x3bb}}(z)} \end{align} $$
 $\phi _{\infty (\unicode{x3bb} )}'(\infty )=1$
. It satisfies the equation
$\phi _{\infty (\unicode{x3bb} )}'(\infty )=1$
. It satisfies the equation
 $\phi _{\infty (\unicode{x3bb} )}(f_{\unicode{x3bb} }(z))=(\phi _{\infty (\unicode{x3bb} )}(z))^{n}$
and
$\phi _{\infty (\unicode{x3bb} )}(f_{\unicode{x3bb} }(z))=(\phi _{\infty (\unicode{x3bb} )}(z))^{n}$
and
 $\phi _{\infty (\unicode{x3bb} )}(e^{\pi i/n}z)=e^{\pi i/n} \phi _{\infty (\unicode{x3bb} )}(z)$
.
$\phi _{\infty (\unicode{x3bb} )}(e^{\pi i/n}z)=e^{\pi i/n} \phi _{\infty (\unicode{x3bb} )}(z)$
.
-
(2) For
 $k=2$
,
$k=2$
,
 $z_{2}(\unicode{x3bb} )=0$
,
$z_{2}(\unicode{x3bb} )=0$
,
 $\phi _{0(\unicode{x3bb} )}$
is defined to be
$\phi _{0(\unicode{x3bb} )}$
is defined to be
 $\phi _{0(\unicode{x3bb} )}:=\sqrt [n]{{\phi _{\infty (\unicode{x3bb} )}} \circ f_{\unicode{x3bb} }}$
which satisfies that
$\phi _{0(\unicode{x3bb} )}:=\sqrt [n]{{\phi _{\infty (\unicode{x3bb} )}} \circ f_{\unicode{x3bb} }}$
which satisfies that
 $\phi _{0(\unicode{x3bb} )}'(0)=\sqrt [n]{{\unicode{x3bb} }}$
.
$\phi _{0(\unicode{x3bb} )}'(0)=\sqrt [n]{{\unicode{x3bb} }}$
. -
(3) For
 $k \geq 3$
and
$k \geq 3$
and
 $z_{k}(\unicode{x3bb} ) \in Z_{k}(\unicode{x3bb} ) \setminus \bigcup _{l \geq 0}f^{-l}_{\unicode{x3bb} }(C_{\unicode{x3bb} })$
,
$z_{k}(\unicode{x3bb} ) \in Z_{k}(\unicode{x3bb} ) \setminus \bigcup _{l \geq 0}f^{-l}_{\unicode{x3bb} }(C_{\unicode{x3bb} })$
,
 $\phi _{z_{k}(\unicode{x3bb} )}$
is defined to be
$\phi _{z_{k}(\unicode{x3bb} )}$
is defined to be
 $\phi _{z_{k}(\unicode{x3bb} )}:=\phi _{0(\unicode{x3bb} )} \circ f^{k-2}_{\unicode{x3bb} }.$
$\phi _{z_{k}(\unicode{x3bb} )}:=\phi _{0(\unicode{x3bb} )} \circ f^{k-2}_{\unicode{x3bb} }.$
Remark 2.1. Let
![]() $\mathbb D(a,r)$
denote the disk with the center at a and radius r, and let
$\mathbb D(a,r)$
denote the disk with the center at a and radius r, and let
![]() $\mathbb D_r=\mathbb D(0,r)$
. By §9 in [Reference Milnor and MilnorMil11],
$\mathbb D_r=\mathbb D(0,r)$
. By §9 in [Reference Milnor and MilnorMil11],
![]() $\phi _{z_{k}(\unicode{x3bb} )}^{-1}$
can be extended on a maximal disk
$\phi _{z_{k}(\unicode{x3bb} )}^{-1}$
can be extended on a maximal disk
![]() $\overline {\mathbb {C}} \setminus \overline {\mathbb {D}_{s_{z_k}(\unicode{x3bb} )}}$
with
$\overline {\mathbb {C}} \setminus \overline {\mathbb {D}_{s_{z_k}(\unicode{x3bb} )}}$
with
![]() $s_{z_k}(\unicode{x3bb} )=1$
or with
$s_{z_k}(\unicode{x3bb} )=1$
or with
![]() $s_{z_k}(\unicode{x3bb} )>1$
such that
$s_{z_k}(\unicode{x3bb} )>1$
such that
![]() $\partial \phi _{z_{k}(\unicode{x3bb} )}^{-1}(\mathbb {D}_{s_{z_k}(\unicode{x3bb} )}) \cap \bigcup _{l \geq 0}f_{\unicode{x3bb} }^{-l}(C_{\unicode{x3bb} }) \neq \emptyset $
.
$\partial \phi _{z_{k}(\unicode{x3bb} )}^{-1}(\mathbb {D}_{s_{z_k}(\unicode{x3bb} )}) \cap \bigcup _{l \geq 0}f_{\unicode{x3bb} }^{-l}(C_{\unicode{x3bb} }) \neq \emptyset $
.
Each Böttcher coordinate
![]() $\phi _{z_{k}(\unicode{x3bb} )}$
introduces a system of dynamical rays and equipotential curves near
$\phi _{z_{k}(\unicode{x3bb} )}$
introduces a system of dynamical rays and equipotential curves near
![]() $z_{k}(\unicode{x3bb} )$
. The dynamical ray
$z_{k}(\unicode{x3bb} )$
. The dynamical ray
![]() $R_{z_{k}(\unicode{x3bb} )}^{t}$
with angle
$R_{z_{k}(\unicode{x3bb} )}^{t}$
with angle
![]() $t \in \mathbb {R}/\mathbb {Z}$
is defined to be
$t \in \mathbb {R}/\mathbb {Z}$
is defined to be
![]() $R_{z_{k}(\unicode{x3bb} )}^{t}:=\phi _{z_{k}(\unicode{x3bb} )}^{-1}((s_{z_k}(\unicode{x3bb} ), \infty ]e^{2\pi it})$
. The equipotential curve
$R_{z_{k}(\unicode{x3bb} )}^{t}:=\phi _{z_{k}(\unicode{x3bb} )}^{-1}((s_{z_k}(\unicode{x3bb} ), \infty ]e^{2\pi it})$
. The equipotential curve
![]() $E_{z_{k}(\unicode{x3bb} )}^{s}$
with
$E_{z_{k}(\unicode{x3bb} )}^{s}$
with
![]() $s \geq s_{z_k}$
is defined to be
$s \geq s_{z_k}$
is defined to be
![]() $E_{z_{k}(\unicode{x3bb} )}^{s}:=\phi _{z_{k}(\unicode{x3bb} )}^{-1}(se^{2\pi i \mathbb {R}/\mathbb {Z}})$
.
$E_{z_{k}(\unicode{x3bb} )}^{s}:=\phi _{z_{k}(\unicode{x3bb} )}^{-1}(se^{2\pi i \mathbb {R}/\mathbb {Z}})$
.
Consider the subset of the parameter plane, called the escape locus, which consists of parameters of maps all of whose critical orbits escape to infinity. That is,
The escape locus
![]() $\mathscr {H}$
is an open subset of the parameter plane. Maps inside
$\mathscr {H}$
is an open subset of the parameter plane. Maps inside
![]() $\mathscr {H}$
are called escape maps. Connected components of
$\mathscr {H}$
are called escape maps. Connected components of
![]() $\mathscr {H}$
are called escape components. It is worth mentioning that all escape components are hyperbolic components. According to the discussion in [Reference Qiu, Roesch, Wang and YinQRWY15], hyperbolic components not in
$\mathscr {H}$
are called escape components. It is worth mentioning that all escape components are hyperbolic components. According to the discussion in [Reference Qiu, Roesch, Wang and YinQRWY15], hyperbolic components not in
![]() $\mathscr {H}$
have ‘renormalizable’ type. It could be proved that all hyperbolic components of this type belong to small copies of the Mandelbrot set, see Figures 1 and 2.
$\mathscr {H}$
have ‘renormalizable’ type. It could be proved that all hyperbolic components of this type belong to small copies of the Mandelbrot set, see Figures 1 and 2.

Figure 1 Parameter plane for
![]() $n=3$
.
$n=3$
.

Figure 2 Parameter plane for
![]() $n=4$
.
$n=4$
.
Let
![]() $B_{\unicode{x3bb} }$
denote the Fatou component containing
$B_{\unicode{x3bb} }$
denote the Fatou component containing
![]() $\infty $
. Let
$\infty $
. Let
![]() $T_{\unicode{x3bb} }$
denote the Fatou component containing
$T_{\unicode{x3bb} }$
denote the Fatou component containing
![]() $0$
, which is the unique component of
$0$
, which is the unique component of
![]() $f_{\unicode{x3bb} }^{-1}(B_{\unicode{x3bb} })$
different from
$f_{\unicode{x3bb} }^{-1}(B_{\unicode{x3bb} })$
different from
![]() $B_{\unicode{x3bb} }$
itself. We can further distinguish those escape components by counting the number of iterations needed for
$B_{\unicode{x3bb} }$
itself. We can further distinguish those escape components by counting the number of iterations needed for
![]() $C_{\unicode{x3bb} }$
to be mapped into
$C_{\unicode{x3bb} }$
to be mapped into
![]() $B_{\unicode{x3bb} }$
. For
$B_{\unicode{x3bb} }$
. For
![]() $\unicode{x3bb} \in \mathscr {H}$
, we define its order
$\unicode{x3bb} \in \mathscr {H}$
, we define its order
![]() $N(\unicode{x3bb} )$
to be
$N(\unicode{x3bb} )$
to be
It is obvious that the order
![]() $N(\unicode{x3bb} )$
takes a constant value on each component of
$N(\unicode{x3bb} )$
takes a constant value on each component of
![]() $\mathscr {H}$
. Hence, we can decompose the escape locus such that
$\mathscr {H}$
. Hence, we can decompose the escape locus such that
![]() $\mathscr {H} =\bigcup _{k\geq 0}\mathscr {H}_{k}$
, where
$\mathscr {H} =\bigcup _{k\geq 0}\mathscr {H}_{k}$
, where
![]() $\mathscr {H}_{k}=\{ \unicode{x3bb} \in \mathscr {H}: N(\unicode{x3bb} )=k \}$
consists of all escape maps with order k.
$\mathscr {H}_{k}=\{ \unicode{x3bb} \in \mathscr {H}: N(\unicode{x3bb} )=k \}$
consists of all escape maps with order k.
Remark 2.2. It is known that
![]() $\unicode{x3bb} \in \mathscr H_0$
if and only if
$\unicode{x3bb} \in \mathscr H_0$
if and only if
![]() $v_{\unicode{x3bb} }^{\pm }\in B_{\unicode{x3bb} }$
,
$v_{\unicode{x3bb} }^{\pm }\in B_{\unicode{x3bb} }$
,
![]() $\mathscr H_1=\emptyset $
, and
$\mathscr H_1=\emptyset $
, and
![]() $\unicode{x3bb} \in \mathscr H_k$
for
$\unicode{x3bb} \in \mathscr H_k$
for
![]() $k\geq 2$
if and only if
$k\geq 2$
if and only if
![]() $f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{\pm })\in T_{\unicode{x3bb} }$
.
$f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{\pm })\in T_{\unicode{x3bb} }$
.
According to [Reference Devaney, Look and UminskyDLU05, Reference Roesch, Lude Peterson and HjorthRoe06, Reference SteinmetzSte06], we have the following escape trichotomy and parameterization for escape components.
Theorem 2.2. (Escape trichotomy and parameterization)
We have the following trichotomy and the parameterization.
-
(1) The Cantor locus
 $\mathscr {H}_{0}$
is the unique unbounded hyperbolic component. The parameterization map
$\mathscr {H}_{0}$
is the unique unbounded hyperbolic component. The parameterization map
 $\Phi _{\mathscr {H}_{0}} : \mathscr {H}_{0} \rightarrow \mathbb {C} \setminus \overline {\mathbb {D}}$
defined by
$\Phi _{\mathscr {H}_{0}} : \mathscr {H}_{0} \rightarrow \mathbb {C} \setminus \overline {\mathbb {D}}$
defined by
 $\Phi _{\mathscr {H}_{0}}(\unicode{x3bb} ):=\phi _{\infty (\unicode{x3bb} )}(v^{+}_{\unicode{x3bb} })^{2}$
is a holomorphic homeomorphism. For
$\Phi _{\mathscr {H}_{0}}(\unicode{x3bb} ):=\phi _{\infty (\unicode{x3bb} )}(v^{+}_{\unicode{x3bb} })^{2}$
is a holomorphic homeomorphism. For
 $\unicode{x3bb} \in \mathscr {H}_{0}$
, its Julia set
$\unicode{x3bb} \in \mathscr {H}_{0}$
, its Julia set
 $J(f_{\unicode{x3bb} })$
is a Cantor set, see Figure 3.
$J(f_{\unicode{x3bb} })$
is a Cantor set, see Figure 3. -
(2) The McMullen domain
 $\mathscr {H}_{2}$
is the unique hyperbolic component containing
$\mathscr {H}_{2}$
is the unique hyperbolic component containing
 $0$
. The parameterization map
$0$
. The parameterization map
 $\Phi _{\mathscr {H}_{2}} : \mathscr {H}_{2} \rightarrow \mathbb {C} \setminus \overline {\mathbb {D}}$
defined by
$\Phi _{\mathscr {H}_{2}} : \mathscr {H}_{2} \rightarrow \mathbb {C} \setminus \overline {\mathbb {D}}$
defined by
 $\Phi _{\mathscr {H}_{2}}(\unicode{x3bb} )^{n-2}:=(\phi _{\infty (\unicode{x3bb} )}\circ f_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }))^{2}$
is a holomorphic homeomorphism with
$\Phi _{\mathscr {H}_{2}}(\unicode{x3bb} )^{n-2}:=(\phi _{\infty (\unicode{x3bb} )}\circ f_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }))^{2}$
is a holomorphic homeomorphism with
 $\lim \nolimits _{\unicode{x3bb} \to 0}\unicode{x3bb} \Phi _{\mathscr {H}_{2}}(\unicode{x3bb} )=2^{{2n}/({n-2})}$
. For
$\lim \nolimits _{\unicode{x3bb} \to 0}\unicode{x3bb} \Phi _{\mathscr {H}_{2}}(\unicode{x3bb} )=2^{{2n}/({n-2})}$
. For
 $\unicode{x3bb} \in \mathscr {H}_{2}$
, its Julia set
$\unicode{x3bb} \in \mathscr {H}_{2}$
, its Julia set
 $J(f_{\unicode{x3bb} })$
is a Cantor circle, see Figure 4.
$J(f_{\unicode{x3bb} })$
is a Cantor circle, see Figure 4. -
(3) Sierpiński holes are connected components of
 $\mathscr {H}_{k}$
with order
$\mathscr {H}_{k}$
with order
 $k \geq 3$
. For each Sierpiński hole
$k \geq 3$
. For each Sierpiński hole
 $\mathscr {U}$
, the parameterization map
$\mathscr {U}$
, the parameterization map
 $\Phi _{\mathscr {U}} : \mathscr {U} \rightarrow \overline {\mathbb {C}} \setminus \overline {\mathbb {D}}$
defined by
$\Phi _{\mathscr {U}} : \mathscr {U} \rightarrow \overline {\mathbb {C}} \setminus \overline {\mathbb {D}}$
defined by
 $\Phi _{\mathscr {U}}(\unicode{x3bb} ) :=\phi _{0(\unicode{x3bb} )}\circ f_{\unicode{x3bb} }^{k-2}(v^{+}_{\unicode{x3bb} })$
is a holomorphic homeomorphism. For
$\Phi _{\mathscr {U}}(\unicode{x3bb} ) :=\phi _{0(\unicode{x3bb} )}\circ f_{\unicode{x3bb} }^{k-2}(v^{+}_{\unicode{x3bb} })$
is a holomorphic homeomorphism. For
 $\unicode{x3bb} \in \mathscr {U}$
, its Julia set
$\unicode{x3bb} \in \mathscr {U}$
, its Julia set
 $J(f_{\unicode{x3bb} })$
is a Sierpiński carpet, see Figure 5.
$J(f_{\unicode{x3bb} })$
is a Sierpiński carpet, see Figure 5.
Remark 2.3. Hyperbolic components not in
![]() $\mathscr {H}$
are called non-escape components. All non-escape hyperbolic components are contained in small copies of the Mandelbrot set. A map belonging to a non-escape hyperbolic component has its critical orbit
$\mathscr {H}$
are called non-escape components. All non-escape hyperbolic components are contained in small copies of the Mandelbrot set. A map belonging to a non-escape hyperbolic component has its critical orbit
![]() $\bigcup _{k \geq 0}f^{k}_{\unicode{x3bb} }(C_{\unicode{x3bb} })$
attracted by attracting periodic orbits different from
$\bigcup _{k \geq 0}f^{k}_{\unicode{x3bb} }(C_{\unicode{x3bb} })$
attracted by attracting periodic orbits different from
![]() $\infty $
, see Figure 6.
$\infty $
, see Figure 6.

Figure 3 For
![]() $\unicode{x3bb} \in \mathscr {H}_{0}$
in Cantor locus,
$\unicode{x3bb} \in \mathscr {H}_{0}$
in Cantor locus,
![]() $J(f_{\unicode{x3bb} })$
is a Cantor set.
$J(f_{\unicode{x3bb} })$
is a Cantor set.

Figure 4 For
![]() $\unicode{x3bb} \in \mathscr {H}_{2}$
in the McMullen domain,
$\unicode{x3bb} \in \mathscr {H}_{2}$
in the McMullen domain,
![]() $J(f_{\unicode{x3bb} })$
is a Cantor circle.
$J(f_{\unicode{x3bb} })$
is a Cantor circle.

Figure 5 For
![]() $\unicode{x3bb} $
in a Sierpiński hole,
$\unicode{x3bb} $
in a Sierpiński hole,
![]() $J(f_{\unicode{x3bb} })$
is a Sierpiński carpet.
$J(f_{\unicode{x3bb} })$
is a Sierpiński carpet.

Figure 6 For
![]() $f_\unicode{x3bb} $
is a non-escape hyperbolic map,
$f_\unicode{x3bb} $
is a non-escape hyperbolic map,
![]() $J(f_{\unicode{x3bb} })$
is connected.
$J(f_{\unicode{x3bb} })$
is connected.
It is easy to verify that for
![]() $\unicode{x3bb} \in \mathscr {H}_{0}$
,
$\unicode{x3bb} \in \mathscr {H}_{0}$
,
and
Let
![]() $\mathscr {U} \subset \mathscr {H}$
be an escape component. The parameter ray
$\mathscr {U} \subset \mathscr {H}$
be an escape component. The parameter ray
![]() $\mathscr {R}_{\mathscr {U}}^{t}$
in
$\mathscr {R}_{\mathscr {U}}^{t}$
in
![]() $\mathscr {U}$
with angle
$\mathscr {U}$
with angle
![]() $t \in \mathbb {R}/\mathbb {Z}$
is defined to be
$t \in \mathbb {R}/\mathbb {Z}$
is defined to be
![]() $\mathscr {R}_{\mathscr {U}}^{t}:=\Phi _{\mathscr {U}}^{-1} ((1,\infty ) e^{2\pi i t} )$
. The equipotential curve
$\mathscr {R}_{\mathscr {U}}^{t}:=\Phi _{\mathscr {U}}^{-1} ((1,\infty ) e^{2\pi i t} )$
. The equipotential curve
![]() $\mathscr {E}^{s}_{\mathscr {U}}$
in
$\mathscr {E}^{s}_{\mathscr {U}}$
in
![]() $\mathscr {U}$
with level s is defined to be
$\mathscr {U}$
with level s is defined to be
![]() $\mathscr {E}^{s}_{\mathscr {U}}:=\Phi _{\mathscr {U}}^{-1}(se^{2\pi i \mathbb {R}/\mathbb {Z}} )$
.
$\mathscr {E}^{s}_{\mathscr {U}}:=\Phi _{\mathscr {U}}^{-1}(se^{2\pi i \mathbb {R}/\mathbb {Z}} )$
.
2.2 Dynamical puzzles
Let
![]() $\Lambda \subset \mathbb {C}$
be a hyperbolic region and X be a subset of
$\Lambda \subset \mathbb {C}$
be a hyperbolic region and X be a subset of
![]() $\overline {\mathbb {C}}$
. Let
$\overline {\mathbb {C}}$
. Let
![]() $\pi _{1}: \Lambda \times X \to \Lambda $
and
$\pi _{1}: \Lambda \times X \to \Lambda $
and
![]() $\pi _{2}: \Lambda \times X \to X$
be two projections defined by
$\pi _{2}: \Lambda \times X \to X$
be two projections defined by
![]() $\pi _{1}(\unicode{x3bb} ,z)=\unicode{x3bb} $
and
$\pi _{1}(\unicode{x3bb} ,z)=\unicode{x3bb} $
and
![]() $\pi _{2}(\unicode{x3bb} ,z)=z$
respectively. A holomorphic motion of X, parameterized by
$\pi _{2}(\unicode{x3bb} ,z)=z$
respectively. A holomorphic motion of X, parameterized by
![]() $\Lambda $
, with the base point at
$\Lambda $
, with the base point at
![]() $\unicode{x3bb} _{0} \in \Lambda $
, is a map
$\unicode{x3bb} _{0} \in \Lambda $
, is a map
![]() $h: \Lambda \times X \to \Lambda \times \overline {\mathbb {C}}$
such that:
$h: \Lambda \times X \to \Lambda \times \overline {\mathbb {C}}$
such that:
-
(1) for each
 $x \in X$
, the map
$x \in X$
, the map
 $\unicode{x3bb} \mapsto \pi _{1} \circ h(\unicode{x3bb} ,x)$
is the identity map;
$\unicode{x3bb} \mapsto \pi _{1} \circ h(\unicode{x3bb} ,x)$
is the identity map; -
(2) for each
 $x \in X$
, the map
$x \in X$
, the map
 $\unicode{x3bb} \mapsto \pi _{2} \circ h(\unicode{x3bb} ,x)$
is holomorphic;
$\unicode{x3bb} \mapsto \pi _{2} \circ h(\unicode{x3bb} ,x)$
is holomorphic; -
(3) for each
 $\unicode{x3bb} \in \Lambda $
, the map
$\unicode{x3bb} \in \Lambda $
, the map
 $x \mapsto \pi _{2} \circ h(\unicode{x3bb} ,x)$
is injective;
$x \mapsto \pi _{2} \circ h(\unicode{x3bb} ,x)$
is injective; -
(4) the map
 $x \mapsto \pi _{2} \circ h(\unicode{x3bb} _{0},x)$
is the identity map.
$x \mapsto \pi _{2} \circ h(\unicode{x3bb} _{0},x)$
is the identity map.
Let us denote
![]() $h_{\unicode{x3bb} }: X \to \overline {\mathbb {C}}$
for the map
$h_{\unicode{x3bb} }: X \to \overline {\mathbb {C}}$
for the map
![]() $x \mapsto \pi _{2} \circ h(\unicode{x3bb} ,x)$
.
$x \mapsto \pi _{2} \circ h(\unicode{x3bb} ,x)$
.
Theorem 2.3. (Slodkowski [Reference DouadyDou95, Reference SlodkowskiSlo95])
Suppose
![]() $h: \Lambda \times X \to \Lambda \times \overline {\mathbb {C}}$
is a holomorphic motion, then h can be extended to a holomorphic motion
$h: \Lambda \times X \to \Lambda \times \overline {\mathbb {C}}$
is a holomorphic motion, then h can be extended to a holomorphic motion
![]() ${h}: \Lambda \times \overline {\mathbb {C}} \to \Lambda \times \overline {\mathbb {C}}$
. For the extended holomorphic motion h, for each
${h}: \Lambda \times \overline {\mathbb {C}} \to \Lambda \times \overline {\mathbb {C}}$
. For the extended holomorphic motion h, for each
![]() $\unicode{x3bb} \in \Lambda $
, the map
$\unicode{x3bb} \in \Lambda $
, the map
![]() $h_{\unicode{x3bb} }: \overline {\mathbb {C}} \to \overline {\mathbb {C}}$
is a quasi-conformal homeomorphism. Furthermore, the Beltrami coefficient
$h_{\unicode{x3bb} }: \overline {\mathbb {C}} \to \overline {\mathbb {C}}$
is a quasi-conformal homeomorphism. Furthermore, the Beltrami coefficient
![]() $\mu _{\unicode{x3bb} }=\overline {\partial } h_{\unicode{x3bb} }/{\partial } h_{\unicode{x3bb} }$
of
$\mu _{\unicode{x3bb} }=\overline {\partial } h_{\unicode{x3bb} }/{\partial } h_{\unicode{x3bb} }$
of
![]() $h_{\unicode{x3bb} }$
satisfies
$h_{\unicode{x3bb} }$
satisfies
 $$ \begin{align} \Vert \mu_{\unicode{x3bb}} \Vert_{\infty}=\mathop{\mathrm{ess\,sup}}_{x \in X}\vert \mu_{\unicode{x3bb}}(x) \vert \leq \frac{e^{\rho(\unicode{x3bb},\unicode{x3bb}_{0})}-1}{e^{\rho(\unicode{x3bb},\unicode{x3bb}_{0})}+1}, \end{align} $$
$$ \begin{align} \Vert \mu_{\unicode{x3bb}} \Vert_{\infty}=\mathop{\mathrm{ess\,sup}}_{x \in X}\vert \mu_{\unicode{x3bb}}(x) \vert \leq \frac{e^{\rho(\unicode{x3bb},\unicode{x3bb}_{0})}-1}{e^{\rho(\unicode{x3bb},\unicode{x3bb}_{0})}+1}, \end{align} $$
where
![]() $\rho (\unicode{x3bb} ,\unicode{x3bb} _{0})$
is the hyperbolic distance between
$\rho (\unicode{x3bb} ,\unicode{x3bb} _{0})$
is the hyperbolic distance between
![]() $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
![]() $\unicode{x3bb} _{0}$
in
$\unicode{x3bb} _{0}$
in
![]() $\Lambda $
.
$\Lambda $
.
Let
![]() $\tau : \mathbb {R}/\mathbb {Z} \rightarrow \mathbb {R}/\mathbb {Z}$
be defined by
$\tau : \mathbb {R}/\mathbb {Z} \rightarrow \mathbb {R}/\mathbb {Z}$
be defined by
![]() $\tau (\theta )=n \theta \mod \mathbb {Z}$
. Let
$\tau (\theta )=n \theta \mod \mathbb {Z}$
. Let
![]() $\Theta _{k}=({k}/{2n}, ({k+1})/{2n}]$
for
$\Theta _{k}=({k}/{2n}, ({k+1})/{2n}]$
for
![]() $0 \leq k \leq n$
and
$0 \leq k \leq n$
and
![]() $\Theta _{-k}=({k}/{2n}+\tfrac 12, ({k+1})/{2n}+\tfrac {1}{2}]$
for
$\Theta _{-k}=({k}/{2n}+\tfrac 12, ({k+1})/{2n}+\tfrac {1}{2}]$
for
![]() $1 \leq k \leq n-1$
. Obviously,
$1 \leq k \leq n-1$
. Obviously,
![]() $(0,1]=\bigcup _{-n<j\leq n}\Theta _{j}$
. Let
$(0,1]=\bigcup _{-n<j\leq n}\Theta _{j}$
. Let
![]() $\Theta $
be the set of all angles
$\Theta $
be the set of all angles
![]() $\theta \in (0,1]$
whose orbits remain in
$\theta \in (0,1]$
whose orbits remain in
![]() $\bigcup _{k=1}^{n-1}(\Theta _{k}\cup \Theta _{-k})$
under iterations of
$\bigcup _{k=1}^{n-1}(\Theta _{k}\cup \Theta _{-k})$
under iterations of
![]() $\tau $
. Let
$\tau $
. Let
 $$ \begin{align*} \Theta_{per}=\bigg(\bigcup_{p \geq 1}\{\theta \in \Theta:\tau^{p} \theta=\theta \}\bigg) \setminus \bigg \{ 1, \frac{1}{2} \bigg \}. \end{align*} $$
$$ \begin{align*} \Theta_{per}=\bigg(\bigcup_{p \geq 1}\{\theta \in \Theta:\tau^{p} \theta=\theta \}\bigg) \setminus \bigg \{ 1, \frac{1}{2} \bigg \}. \end{align*} $$
Then,
![]() $\Theta $
is a Cantor set and
$\Theta $
is a Cantor set and
![]() $\Theta _{per}$
is a dense subset of
$\Theta _{per}$
is a dense subset of
![]() $\Theta $
. Following [Reference DevaneyDev04, Reference Qiu, Roesch, Wang and YinQRWY15], for each
$\Theta $
. Following [Reference DevaneyDev04, Reference Qiu, Roesch, Wang and YinQRWY15], for each
![]() $\theta \in \Theta $
, there is a cut ray
$\theta \in \Theta $
, there is a cut ray
![]() $\Omega ^{\theta }_{\unicode{x3bb} }$
which cuts the Julia set into two parts. Instead of giving the precise definition of cut rays, we summarize the essential properties of cut rays in the following Theorem 2.4. It is the combination of Theorem 3.2, Lemma 3.3, Theorem 3.4 in [Reference Qiu, Roesch, Wang and YinQRWY15].
$\Omega ^{\theta }_{\unicode{x3bb} }$
which cuts the Julia set into two parts. Instead of giving the precise definition of cut rays, we summarize the essential properties of cut rays in the following Theorem 2.4. It is the combination of Theorem 3.2, Lemma 3.3, Theorem 3.4 in [Reference Qiu, Roesch, Wang and YinQRWY15].
Theorem 2.4. (Properties of cut rays)
For any
![]() $\theta \in \Theta _{per}$
and
$\theta \in \Theta _{per}$
and
![]() $\unicode{x3bb} \in \mathscr F_0$
, the cut ray
$\unicode{x3bb} \in \mathscr F_0$
, the cut ray
![]() $\Omega _{\unicode{x3bb} }^{\theta }$
with angle
$\Omega _{\unicode{x3bb} }^{\theta }$
with angle
![]() $\theta $
is a Jordan curve containing
$\theta $
is a Jordan curve containing
![]() $0$
and
$0$
and
![]() $\infty $
and symmetric with respect to
$\infty $
and symmetric with respect to
![]() $0$
satisfies the following properties:
$0$
satisfies the following properties:
-
(1)
 $f_{\unicode{x3bb} }^p(\Omega _{\unicode{x3bb} }^{\theta })\subset \Omega _{\unicode{x3bb} }^{\theta }$
, where p is the period of
$f_{\unicode{x3bb} }^p(\Omega _{\unicode{x3bb} }^{\theta })\subset \Omega _{\unicode{x3bb} }^{\theta }$
, where p is the period of
 $\theta $
;
$\theta $
; -
(2)
 $\Omega ^{\theta }_{\unicode{x3bb} } \cap J(f_{\unicode{x3bb} })$
is a Cantor set, and
$\Omega ^{\theta }_{\unicode{x3bb} } \cap J(f_{\unicode{x3bb} })$
is a Cantor set, and
 $\Omega _{\unicode{x3bb} }^{\theta }\cap B_{\unicode{x3bb} }= R_{\infty (\unicode{x3bb} )}^{\theta }\cup R_{\infty (\unicode{x3bb} )}^{\theta +1/2}$
;
$\Omega _{\unicode{x3bb} }^{\theta }\cap B_{\unicode{x3bb} }= R_{\infty (\unicode{x3bb} )}^{\theta }\cup R_{\infty (\unicode{x3bb} )}^{\theta +1/2}$
; -
(3) fix any
 $\unicode{x3bb} _{0} \in \mathscr {F}$
, there is a holomorphic motion
$\unicode{x3bb} _{0} \in \mathscr {F}$
, there is a holomorphic motion
 $h: \mathscr {F} \times \Omega ^{\theta }_{\unicode{x3bb} _{0}} \to \mathscr {F} \times \overline {\mathbb {C}}$
based at
$h: \mathscr {F} \times \Omega ^{\theta }_{\unicode{x3bb} _{0}} \to \mathscr {F} \times \overline {\mathbb {C}}$
based at
 $\unicode{x3bb} _{0}$
such that
$\unicode{x3bb} _{0}$
such that
 $h_{\unicode{x3bb} }(\Omega ^{\theta }_{\unicode{x3bb} _{0}})=\Omega ^{\theta }_{\unicode{x3bb} }$
;
$h_{\unicode{x3bb} }(\Omega ^{\theta }_{\unicode{x3bb} _{0}})=\Omega ^{\theta }_{\unicode{x3bb} }$
; -
(4) fix any
 $\unicode{x3bb} _{0} \in \mathbb {R}_{+}$
, there exists a neighborhood
$\unicode{x3bb} _{0} \in \mathbb {R}_{+}$
, there exists a neighborhood
 $\mathscr {W}_{\theta }$
containing
$\mathscr {W}_{\theta }$
containing
 $\mathbb {R}_{+}$
and a holomorphic motion
$\mathbb {R}_{+}$
and a holomorphic motion
 $h: \mathscr {W}_{\theta } \times \Omega ^{\theta }_{\unicode{x3bb} _{0}} \to \mathscr {W}_{\theta } \times \overline {\mathbb {C}}$
based at
$h: \mathscr {W}_{\theta } \times \Omega ^{\theta }_{\unicode{x3bb} _{0}} \to \mathscr {W}_{\theta } \times \overline {\mathbb {C}}$
based at
 $\unicode{x3bb} _{0}$
such that
$\unicode{x3bb} _{0}$
such that
 $h_{\unicode{x3bb} }(\Omega ^{\theta }_{\unicode{x3bb} _{0}})=\Omega ^{\theta }_{\unicode{x3bb} }$
.
$h_{\unicode{x3bb} }(\Omega ^{\theta }_{\unicode{x3bb} _{0}})=\Omega ^{\theta }_{\unicode{x3bb} }$
.
If for some
![]() $N \geq 1$
,
$N \geq 1$
,
![]() $(\Omega ^{\theta }_{\unicode{x3bb} }\setminus \{0,\infty \}) \cap (\bigcup _{1 \leq k \leq N }f^{k}_{\unicode{x3bb} }(C_{\unicode{x3bb} }))= \emptyset $
, then for any
$(\Omega ^{\theta }_{\unicode{x3bb} }\setminus \{0,\infty \}) \cap (\bigcup _{1 \leq k \leq N }f^{k}_{\unicode{x3bb} }(C_{\unicode{x3bb} }))= \emptyset $
, then for any
![]() $\alpha \in \bigcup _{0 \leq k \leq N}\tau ^{-k}(\theta )$
, there is a unique Jordan curve
$\alpha \in \bigcup _{0 \leq k \leq N}\tau ^{-k}(\theta )$
, there is a unique Jordan curve
![]() $\Omega ^{\alpha }_{\unicode{x3bb} }$
containing
$\Omega ^{\alpha }_{\unicode{x3bb} }$
containing
![]() $0$
and
$0$
and
![]() $\infty $
such that
$\infty $
such that
![]() $f_{\unicode{x3bb} }(\Omega ^{\alpha }_{\unicode{x3bb} })=\Omega ^{\tau (\alpha )}_{\unicode{x3bb} }$
and
$f_{\unicode{x3bb} }(\Omega ^{\alpha }_{\unicode{x3bb} })=\Omega ^{\tau (\alpha )}_{\unicode{x3bb} }$
and
![]() $R_{\infty (\unicode{x3bb} )}^{\alpha } \cup R_{\infty (\unicode{x3bb} )}^{\alpha +1/2} = \Omega ^{\alpha }_{\unicode{x3bb} }\cap B_{\unicode{x3bb} }$
. Under this circumstance, the Jordan curve
$R_{\infty (\unicode{x3bb} )}^{\alpha } \cup R_{\infty (\unicode{x3bb} )}^{\alpha +1/2} = \Omega ^{\alpha }_{\unicode{x3bb} }\cap B_{\unicode{x3bb} }$
. Under this circumstance, the Jordan curve
![]() $\Omega _{\unicode{x3bb} }^{\alpha }$
is also called a cut ray (see Figure 7).
$\Omega _{\unicode{x3bb} }^{\alpha }$
is also called a cut ray (see Figure 7).

Figure 7 Cut ray
![]() $\Omega _{\unicode{x3bb} }^{\theta }$
with angle
$\Omega _{\unicode{x3bb} }^{\theta }$
with angle
![]() $\theta =\tfrac 14,\tfrac 13,\tfrac 12$
, (
$\theta =\tfrac 14,\tfrac 13,\tfrac 12$
, (
![]() $n=3$
).
$n=3$
).
Lemma 2.5. [Reference Qiu, Roesch, Wang and YinQRWY15, Lemma 3.7]
Let
![]() $\unicode{x3bb} \in \mathscr {F}_{0}$
, and
$\unicode{x3bb} \in \mathscr {F}_{0}$
, and
![]() $R_{\infty (\unicode{x3bb} )}^{t_{0}}$
and
$R_{\infty (\unicode{x3bb} )}^{t_{0}}$
and
![]() $R_{\infty (\unicode{x3bb} )}^{t_{1}}$
be two dynamical rays with distinct angles
$R_{\infty (\unicode{x3bb} )}^{t_{1}}$
be two dynamical rays with distinct angles
![]() $t_0$
and
$t_0$
and
![]() $t_1$
. If
$t_1$
. If
 $$ \begin{align} (\Omega^{\theta}_{\unicode{x3bb}}\setminus \{0,\infty \} ) \cap \bigg(\bigcup_{k \geq 1}f^{k}_{\unicode{x3bb}}(C_{\unicode{x3bb}}) \bigg)=\emptyset \end{align} $$
$$ \begin{align} (\Omega^{\theta}_{\unicode{x3bb}}\setminus \{0,\infty \} ) \cap \bigg(\bigcup_{k \geq 1}f^{k}_{\unicode{x3bb}}(C_{\unicode{x3bb}}) \bigg)=\emptyset \end{align} $$
for
![]() $\theta \in \Theta _{per}$
, then there is a cut ray
$\theta \in \Theta _{per}$
, then there is a cut ray
![]() $\Omega _{\unicode{x3bb} }^{\alpha }$
with angle
$\Omega _{\unicode{x3bb} }^{\alpha }$
with angle
![]() $\alpha \in \bigcup _{k\geq 0}\tau ^{-k}(\theta )$
separating
$\alpha \in \bigcup _{k\geq 0}\tau ^{-k}(\theta )$
separating
![]() $R_{\infty (\unicode{x3bb} )}^{t_{0}}$
from
$R_{\infty (\unicode{x3bb} )}^{t_{0}}$
from
![]() $R_{\infty (\unicode{x3bb} )}^{t_{1}}$
.
$R_{\infty (\unicode{x3bb} )}^{t_{1}}$
.
In [Reference Qiu, Wang and YinQWY12], the authors used cut rays to construct a puzzle system for the McMullen family and studied the local connectivity of Julia sets. Puzzles are a regular tool in studying holomorphic dynamics, see [Reference Branner and HubbardBH92, Reference Hubbard, Goldberg and PhillipsHub93, Reference Kahn and LyubichKL09, Reference Kozlovski, Shen and van StrienKSvS07, Reference Levin and van StrienLvS98, Reference PetersenPet96, Reference Qiu and YinQY09, Reference RoeschRoe07, Reference RoeschRoe08, Reference Schleicher, Lapidus and FrankenhuijsenSch04].
For any
![]() $L>1$
, denote
$L>1$
, denote
![]() $X^{L}_{\unicode{x3bb} }:=\{ z \in B_{\unicode{x3bb} }: |\phi _{\infty (\unicode{x3bb} )}(z)|>L \}$
. Given a parameter
$X^{L}_{\unicode{x3bb} }:=\{ z \in B_{\unicode{x3bb} }: |\phi _{\infty (\unicode{x3bb} )}(z)|>L \}$
. Given a parameter
![]() $\unicode{x3bb} \in \mathscr {F}_{0}$
, we can find
$\unicode{x3bb} \in \mathscr {F}_{0}$
, we can find
![]() $\Theta _{\unicode{x3bb} }=\{\theta _{1}, \theta _{2}, \ldots , \theta _{N}\} \subset \Theta _{per}$
and
$\Theta _{\unicode{x3bb} }=\{\theta _{1}, \theta _{2}, \ldots , \theta _{N}\} \subset \Theta _{per}$
and
![]() $L> 1$
such that each cut ray
$L> 1$
such that each cut ray
![]() $\Omega ^{\theta }_{\unicode{x3bb} }$
with
$\Omega ^{\theta }_{\unicode{x3bb} }$
with
![]() $\theta \in \Theta _{\unicode{x3bb} }$
is well defined and
$\theta \in \Theta _{\unicode{x3bb} }$
is well defined and
![]() $C_{\unicode{x3bb} } \cap X^{L}_{\unicode{x3bb} }=\emptyset $
. In the dynamical plane of
$C_{\unicode{x3bb} } \cap X^{L}_{\unicode{x3bb} }=\emptyset $
. In the dynamical plane of
![]() $f_{\unicode{x3bb} }$
, the graph of depth
$f_{\unicode{x3bb} }$
, the graph of depth
![]() $0$
associated with
$0$
associated with
![]() $\Theta _{\unicode{x3bb} }$
is defined to be
$\Theta _{\unicode{x3bb} }$
is defined to be
 $$ \begin{align*}I^{0}_{\unicode{x3bb}}(\Theta_{\unicode{x3bb}})=\partial{X^{L}_{\unicode{x3bb}}} \cup ( (\mathbb{C} \setminus X^{L}_{\unicode{x3bb}}) \cap \bigcup_{m \geq 0} (\Omega^{\tau^{m}(\theta_{1})}_{\unicode{x3bb}} \cup \Omega^{\tau^{m}(\theta_{2})}_{\unicode{x3bb}} \cup \cdots \cup \Omega^{\tau^{m}(\theta_{N})}_{\unicode{x3bb}}) ).\end{align*} $$
$$ \begin{align*}I^{0}_{\unicode{x3bb}}(\Theta_{\unicode{x3bb}})=\partial{X^{L}_{\unicode{x3bb}}} \cup ( (\mathbb{C} \setminus X^{L}_{\unicode{x3bb}}) \cap \bigcup_{m \geq 0} (\Omega^{\tau^{m}(\theta_{1})}_{\unicode{x3bb}} \cup \Omega^{\tau^{m}(\theta_{2})}_{\unicode{x3bb}} \cup \cdots \cup \Omega^{\tau^{m}(\theta_{N})}_{\unicode{x3bb}}) ).\end{align*} $$
The graph of depth k is defined to be
![]() $I^{k}_{\unicode{x3bb} }=f^{-k}_{\unicode{x3bb} }(I^{0}_{\unicode{x3bb} }(\Theta _{\unicode{x3bb} }))$
. A puzzle piece
$I^{k}_{\unicode{x3bb} }=f^{-k}_{\unicode{x3bb} }(I^{0}_{\unicode{x3bb} }(\Theta _{\unicode{x3bb} }))$
. A puzzle piece
![]() $P^{k}_{\unicode{x3bb} }$
of depth k is a connected component of
$P^{k}_{\unicode{x3bb} }$
of depth k is a connected component of
![]() $f^{-k}_{\unicode{x3bb} }(({\mathbb {C}} \setminus X^{L}_{\unicode{x3bb} }) \setminus I^{0}_{\unicode{x3bb} })$
. The puzzle piece of depth k containing
$f^{-k}_{\unicode{x3bb} }(({\mathbb {C}} \setminus X^{L}_{\unicode{x3bb} }) \setminus I^{0}_{\unicode{x3bb} })$
. The puzzle piece of depth k containing
![]() $z\in J(f_{\unicode{x3bb} })$
is denoted by
$z\in J(f_{\unicode{x3bb} })$
is denoted by
![]() $P^{k}_{\unicode{x3bb} }(z)$
. In [Reference Qiu, Roesch, Wang and YinQRWY15, Reference Qiu, Wang and YinQWY12], the authors used the puzzle system
$P^{k}_{\unicode{x3bb} }(z)$
. In [Reference Qiu, Roesch, Wang and YinQRWY15, Reference Qiu, Wang and YinQWY12], the authors used the puzzle system
![]() $(f_{\unicode{x3bb} }, I^{k}_{\unicode{x3bb} }, P^{k}_{\unicode{x3bb} })$
to study the dynamics of McMullen maps and obtained the following results (Theorems 1.1, 1.2, 1.4 in [Reference Qiu, Wang and YinQWY12] and Theorem 1.1 in [Reference Qiu, Roesch, Wang and YinQRWY15]).
$(f_{\unicode{x3bb} }, I^{k}_{\unicode{x3bb} }, P^{k}_{\unicode{x3bb} })$
to study the dynamics of McMullen maps and obtained the following results (Theorems 1.1, 1.2, 1.4 in [Reference Qiu, Wang and YinQWY12] and Theorem 1.1 in [Reference Qiu, Roesch, Wang and YinQRWY15]).
Theorem 2.6. For the McMullen family,
![]() $f_{\unicode{x3bb} }(z)=z^{n}+{\unicode{x3bb} }/{z^{n}}$
with
$f_{\unicode{x3bb} }(z)=z^{n}+{\unicode{x3bb} }/{z^{n}}$
with
![]() $n \geq 3$
and
$n \geq 3$
and
![]() $\unicode{x3bb} \in \mathbb {C}^{*}$
.
$\unicode{x3bb} \in \mathbb {C}^{*}$
.
-
(1) If
 $\unicode{x3bb} \notin \mathscr {H}_{0}$
, then
$\unicode{x3bb} \notin \mathscr {H}_{0}$
, then
 $\partial {B_{\unicode{x3bb} }}$
is a Jordan curve. Furthermore, if
$\partial {B_{\unicode{x3bb} }}$
is a Jordan curve. Furthermore, if
 $\partial B_{\unicode{x3bb} }$
contains neither a parabolic point nor a recurrent critical point, then
$\partial B_{\unicode{x3bb} }$
contains neither a parabolic point nor a recurrent critical point, then
 $\partial B_{\unicode{x3bb} }$
is a quasi-circle.
$\partial B_{\unicode{x3bb} }$
is a quasi-circle. -
(2) Suppose
 $\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
$\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
 $k \geq 2$
and
$k \geq 2$
and
 $\unicode{x3bb} \in \partial {\mathscr {U}} \setminus \partial \mathscr {H}_{0}$
, then for each
$\unicode{x3bb} \in \partial {\mathscr {U}} \setminus \partial \mathscr {H}_{0}$
, then for each
 $z \in J(f_{\unicode{x3bb} })$
,
$z \in J(f_{\unicode{x3bb} })$
,
 $\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }(z)=\{z\}$
and
$\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }(z)=\{z\}$
and
 $J(f_{\unicode{x3bb} })$
is locally connected.
$J(f_{\unicode{x3bb} })$
is locally connected. -
(3) Suppose
 $\mathscr {U} \subset \mathscr {H}$
is an escape component, then
$\mathscr {U} \subset \mathscr {H}$
is an escape component, then
 $\partial {\mathscr {U}}$
is a Jordan curve.
$\partial {\mathscr {U}}$
is a Jordan curve.
By part (1) of Theorem 2.6, for
![]() $\unicode{x3bb} \notin \mathscr {H}_{0}$
, the Böttcher coordinate
$\unicode{x3bb} \notin \mathscr {H}_{0}$
, the Böttcher coordinate
![]() $\phi _{\infty (\unicode{x3bb} )}$
can be extended to a homeomorphism
$\phi _{\infty (\unicode{x3bb} )}$
can be extended to a homeomorphism
![]() $\phi _{\infty (\unicode{x3bb} )} : \overline {B_{\unicode{x3bb} }} \to \overline {\mathbb {C}} \setminus {\mathbb {D}}$
. By part (3) of Theorem 2.6, for each escape component
$\phi _{\infty (\unicode{x3bb} )} : \overline {B_{\unicode{x3bb} }} \to \overline {\mathbb {C}} \setminus {\mathbb {D}}$
. By part (3) of Theorem 2.6, for each escape component
![]() $\mathscr {U} \subset \mathscr {H}$
, the parameterization map
$\mathscr {U} \subset \mathscr {H}$
, the parameterization map
![]() $\Phi _{\mathscr {U}}$
defined in Theorem 2.2 can be extended to a homeomorphism on its closure.
$\Phi _{\mathscr {U}}$
defined in Theorem 2.2 can be extended to a homeomorphism on its closure.
3 Local para-puzzles
In this section, we construct a local-puzzle system at
![]() $\unicode{x3bb} _{0} \in \mathscr {F} \setminus \mathscr {H}$
to study the bifurcation of the puzzle systems
$\unicode{x3bb} _{0} \in \mathscr {F} \setminus \mathscr {H}$
to study the bifurcation of the puzzle systems
![]() $(f_{\unicode{x3bb} }, I^{k}_{\unicode{x3bb} }, P^{k}_{\unicode{x3bb} })$
when the parameter
$(f_{\unicode{x3bb} }, I^{k}_{\unicode{x3bb} }, P^{k}_{\unicode{x3bb} })$
when the parameter
![]() $\unicode{x3bb} $
varies near
$\unicode{x3bb} $
varies near
![]() $\unicode{x3bb} _{0}$
(see Figures 8 and 9). This is a local version of the para-puzzle constructed for polynomials, see [Reference Avila, Lyubich and ShenALS10, Reference FaughtFau93, Reference Hubbard, Goldberg and PhillipsHub93, Reference LyubichLyu00, Reference Roesch and LeiRoe00, Reference RoeschRoe07].
$\unicode{x3bb} _{0}$
(see Figures 8 and 9). This is a local version of the para-puzzle constructed for polynomials, see [Reference Avila, Lyubich and ShenALS10, Reference FaughtFau93, Reference Hubbard, Goldberg and PhillipsHub93, Reference LyubichLyu00, Reference Roesch and LeiRoe00, Reference RoeschRoe07].
Proposition 3.1. (Existence of para-puzzles)
For each
![]() $\unicode{x3bb} _{0} \in \mathscr {F}_{0} \setminus \mathscr {H}$
, there exists a sequence of simply connected open neighborhoods
$\unicode{x3bb} _{0} \in \mathscr {F}_{0} \setminus \mathscr {H}$
, there exists a sequence of simply connected open neighborhoods
![]() $\{ \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \}_{k \geq 0}$
of
$\{ \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \}_{k \geq 0}$
of
![]() $\unicode{x3bb} _{0}$
, which are called para-puzzle pieces, such that the following hold.
$\unicode{x3bb} _{0}$
, which are called para-puzzle pieces, such that the following hold.
-
(1)
 $ \mathscr {P}^{0}_{\unicode{x3bb} _{0}} \supset \mathscr {P}^{1}_{\unicode{x3bb} _{0}} \supset \cdots \supset \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \supset \cdots \supset \{\unicode{x3bb} _{0}\}.$
$ \mathscr {P}^{0}_{\unicode{x3bb} _{0}} \supset \mathscr {P}^{1}_{\unicode{x3bb} _{0}} \supset \cdots \supset \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \supset \cdots \supset \{\unicode{x3bb} _{0}\}.$
-
(2) For each
 $k \geq 0$
, there exists a holomorphic motion
$k \geq 0$
, there exists a holomorphic motion
 $H_{k}: \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times I^{k}_{\unicode{x3bb} _{0}} \rightarrow \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
such that for each
$H_{k}: \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times I^{k}_{\unicode{x3bb} _{0}} \rightarrow \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
such that for each
 $\unicode{x3bb} \in \mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
,
$\unicode{x3bb} \in \mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
,
 $H_{k}(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} })$
.
$H_{k}(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} })$
.
Proof. Proposition 3.1 will be proved by induction. By parts (3) and (4) of Theorem 2.4, there exists a simply connected region
![]() $\mathscr {W}$
containing
$\mathscr {W}$
containing
![]() $\unicode{x3bb} _0$
such that
$\unicode{x3bb} _0$
such that
![]() $h: \mathscr {W} \times \bigcup _{\theta \in \Theta _{\unicode{x3bb} _0}} \Omega _{\unicode{x3bb} _0}^{\theta } \to \mathscr {W} \times \overline {\mathbb {C}}$
is a holomorphic motion. Here,
$h: \mathscr {W} \times \bigcup _{\theta \in \Theta _{\unicode{x3bb} _0}} \Omega _{\unicode{x3bb} _0}^{\theta } \to \mathscr {W} \times \overline {\mathbb {C}}$
is a holomorphic motion. Here,
![]() $\Theta _{\unicode{x3bb} _0}$
is a set of angles
$\Theta _{\unicode{x3bb} _0}$
is a set of angles
![]() $\theta $
of cut rays
$\theta $
of cut rays
![]() $\Omega _{\unicode{x3bb} }^{\theta }$
we picked to construct the graph
$\Omega _{\unicode{x3bb} }^{\theta }$
we picked to construct the graph
![]() $I_{\unicode{x3bb} _0}^{0}(\Theta _{\unicode{x3bb} _0})$
. It is not hard to find a simply connected region
$I_{\unicode{x3bb} _0}^{0}(\Theta _{\unicode{x3bb} _0})$
. It is not hard to find a simply connected region
![]() $\mathscr {P}^{0}_{\unicode{x3bb} _{0}} \subset \mathscr {W}$
containing
$\mathscr {P}^{0}_{\unicode{x3bb} _{0}} \subset \mathscr {W}$
containing
![]() $\unicode{x3bb} _{0}$
such that the map
$\unicode{x3bb} _{0}$
such that the map
![]() $H_{0} : \mathscr {P}^{0}_{\unicode{x3bb} _{0}} \times I^{0}_{\unicode{x3bb} _0} \rightarrow \mathscr {P}^{0}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
defined by
$H_{0} : \mathscr {P}^{0}_{\unicode{x3bb} _{0}} \times I^{0}_{\unicode{x3bb} _0} \rightarrow \mathscr {P}^{0}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
defined by
 $$ \begin{align} H_{0}(\unicode{x3bb},z):= \begin{cases} h(\unicode{x3bb}, z), & {(\unicode{x3bb},z) \in \mathscr{P}_{\unicode{x3bb}_0}^0\times\bigcup_{\theta \in \Theta_{\unicode{x3bb}_0}} \Omega_{\unicode{x3bb}_0}^{\theta},}\\[2pt] (\unicode{x3bb},\phi_{\infty(\unicode{x3bb})}^{-1} \circ \phi_{\infty(\unicode{x3bb}_{0})}(z)), & {(\unicode{x3bb},z) \in \mathscr{P}_{\unicode{x3bb}_0}^0\times \partial X^{L}_{\unicode{x3bb}_{0}}} \end{cases} \end{align} $$
$$ \begin{align} H_{0}(\unicode{x3bb},z):= \begin{cases} h(\unicode{x3bb}, z), & {(\unicode{x3bb},z) \in \mathscr{P}_{\unicode{x3bb}_0}^0\times\bigcup_{\theta \in \Theta_{\unicode{x3bb}_0}} \Omega_{\unicode{x3bb}_0}^{\theta},}\\[2pt] (\unicode{x3bb},\phi_{\infty(\unicode{x3bb})}^{-1} \circ \phi_{\infty(\unicode{x3bb}_{0})}(z)), & {(\unicode{x3bb},z) \in \mathscr{P}_{\unicode{x3bb}_0}^0\times \partial X^{L}_{\unicode{x3bb}_{0}}} \end{cases} \end{align} $$
is a well-defined holomorphic motion which satisfies
![]() $H_{0}(\unicode{x3bb} ,I^{0}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,I^{0}_{\unicode{x3bb} })$
.
$H_{0}(\unicode{x3bb} ,I^{0}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,I^{0}_{\unicode{x3bb} })$
.

Figure 8 The graph
![]() $I_{\unicode{x3bb} }^{0}(\{ \tfrac 12 \})$
for
$I_{\unicode{x3bb} }^{0}(\{ \tfrac 12 \})$
for
![]() $n=3$
.
$n=3$
.

Figure 9 The graph
![]() $I_{\unicode{x3bb} }^{1}(\{ \tfrac 12 \})$
for
$I_{\unicode{x3bb} }^{1}(\{ \tfrac 12 \})$
for
![]() $n=3$
.
$n=3$
.
Assume the para-puzzle pieces
![]() $\mathscr {P}^{m}_{\unicode{x3bb} _0}$
and the holomorphic motion
$\mathscr {P}^{m}_{\unicode{x3bb} _0}$
and the holomorphic motion
![]() $H_{m}: \mathscr {P}^{m}_{\unicode{x3bb} _{0}} \times I^{m}_{\unicode{x3bb} _{0}} \rightarrow \mathscr {P}^{m}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
are already constructed for
$H_{m}: \mathscr {P}^{m}_{\unicode{x3bb} _{0}} \times I^{m}_{\unicode{x3bb} _{0}} \rightarrow \mathscr {P}^{m}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
are already constructed for
![]() $0 \leq m \leq k-1$
. The local parameter graph of depth
$0 \leq m \leq k-1$
. The local parameter graph of depth
![]() $k-1$
in the para-puzzle piece
$k-1$
in the para-puzzle piece
![]() $\mathscr {P}_{\unicode{x3bb} _0}^{k-1}$
is defined to be
$\mathscr {P}_{\unicode{x3bb} _0}^{k-1}$
is defined to be
By the construction of puzzle system
![]() $(f_{\unicode{x3bb} _{0}}, I^{k}_{\unicode{x3bb} _{0}}, P^{k}_{\unicode{x3bb} _{0}})$
,
$(f_{\unicode{x3bb} _{0}}, I^{k}_{\unicode{x3bb} _{0}}, P^{k}_{\unicode{x3bb} _{0}})$
,
![]() $v^{+}_{\unicode{x3bb} _{0}} \notin I^{k-1}_{\unicode{x3bb} _{0}}$
. Hence,
$v^{+}_{\unicode{x3bb} _{0}} \notin I^{k-1}_{\unicode{x3bb} _{0}}$
. Hence,
![]() $\unicode{x3bb} _{0} \notin \mathscr {I}^{k-1}$
. Let
$\unicode{x3bb} _{0} \notin \mathscr {I}^{k-1}$
. Let
![]() $\unicode{x3bb} _{j} \to \unicode{x3bb} \in \mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
as
$\unicode{x3bb} _{j} \to \unicode{x3bb} \in \mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
as
![]() $j \to \infty $
with
$j \to \infty $
with
![]() $\{\unicode{x3bb} _{j}: j \geq 1\} \subset \mathscr {I}^{k-1}$
. Since
$\{\unicode{x3bb} _{j}: j \geq 1\} \subset \mathscr {I}^{k-1}$
. Since
![]() $H_{k-1}$
is a holomorphic motion,
$H_{k-1}$
is a holomorphic motion,
![]() $v^{+}_{\unicode{x3bb} _{j}} \in I^{k-1}_{\unicode{x3bb} _{j}}$
for each
$v^{+}_{\unicode{x3bb} _{j}} \in I^{k-1}_{\unicode{x3bb} _{j}}$
for each
![]() $j \geq 1$
implies that
$j \geq 1$
implies that
![]() $v^{+}_{\unicode{x3bb} } \in I^{k-1}_{\unicode{x3bb} }$
. Hence,
$v^{+}_{\unicode{x3bb} } \in I^{k-1}_{\unicode{x3bb} }$
. Hence,
![]() $\mathscr {I}^{k-1}$
is relatively closed in
$\mathscr {I}^{k-1}$
is relatively closed in
![]() $\mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
. Define
$\mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
. Define
![]() $\mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
to be a simply connected open subset of
$\mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
to be a simply connected open subset of
![]() $\mathscr {P}^{k-1}_{\unicode{x3bb} _{0}} \setminus \mathscr {I}^{k-1}$
containing
$\mathscr {P}^{k-1}_{\unicode{x3bb} _{0}} \setminus \mathscr {I}^{k-1}$
containing
![]() $\unicode{x3bb} _{0}$
(
$\unicode{x3bb} _{0}$
(
![]() $\mathscr {P}^{k}_{\unicode{x3bb} _{0}} = \mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
if
$\mathscr {P}^{k}_{\unicode{x3bb} _{0}} = \mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
if
![]() $\mathscr {I}^{k-1}=\emptyset $
). Since
$\mathscr {I}^{k-1}=\emptyset $
). Since
![]() $v^{+}_{\unicode{x3bb} } \notin I^{k-1}_{\unicode{x3bb} }$
for
$v^{+}_{\unicode{x3bb} } \notin I^{k-1}_{\unicode{x3bb} }$
for
![]() $\unicode{x3bb} \in \mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
, there exists a holomorphic motion
$\unicode{x3bb} \in \mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
, there exists a holomorphic motion
![]() $H_{k}$
such that the following diagram commutes:
$H_{k}$
such that the following diagram commutes:

where
![]() $i. : \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \rightarrow \mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
denotes the inclusion map. By diagram (3.2),
$i. : \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \rightarrow \mathscr {P}^{k-1}_{\unicode{x3bb} _{0}}$
denotes the inclusion map. By diagram (3.2),
![]() $H_{k}(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} })$
. Hence, Proposition 3.1 holds for
$H_{k}(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,I^{k}_{\unicode{x3bb} })$
. Hence, Proposition 3.1 holds for
![]() $m=k$
.
$m=k$
.
Corollary 3.2. There exists a holomorphic motion
![]() $h_{k} : \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times (I^{k-1}_{\unicode{x3bb} _{0}}\cup \{v^{+}_{\unicode{x3bb} _{0}} \} )\to \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
such that
$h_{k} : \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times (I^{k-1}_{\unicode{x3bb} _{0}}\cup \{v^{+}_{\unicode{x3bb} _{0}} \} )\to \mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times \overline {\mathbb {C}}$
such that
![]() $h_{k}|_{\mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times I^{k-1}_{\unicode{x3bb} _{0}}}=H_{k-1}$
and
$h_{k}|_{\mathscr {P}^{k}_{\unicode{x3bb} _{0}} \times I^{k-1}_{\unicode{x3bb} _{0}}}=H_{k-1}$
and
![]() $h_{k}(\unicode{x3bb} , v^{+}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,v^{+}_{\unicode{x3bb} })$
.
$h_{k}(\unicode{x3bb} , v^{+}_{\unicode{x3bb} _{0}})=(\unicode{x3bb} ,v^{+}_{\unicode{x3bb} })$
.
Proof. This follows immediately from
![]() $v^{+}_{\unicode{x3bb} } \notin I^{k-1}_{\unicode{x3bb} }$
for
$v^{+}_{\unicode{x3bb} } \notin I^{k-1}_{\unicode{x3bb} }$
for
![]() $\unicode{x3bb} \in \mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
.
$\unicode{x3bb} \in \mathscr {P}^{k}_{\unicode{x3bb} _{0}}$
.
4 Centers of
 $\mathscr {H}$
$\mathscr {H}$
In this section, we discuss the relation between the centers of hyperbolic components of
![]() $\mathscr {H}$
and the iterated pre-images of
$\mathscr {H}$
and the iterated pre-images of
![]() $\infty $
in the dynamical plane.
$\infty $
in the dynamical plane.
Suppose that
![]() $\mathscr {U}_{k}$
is a connected component of
$\mathscr {U}_{k}$
is a connected component of
![]() $\mathscr {H}_{k}$
,
$\mathscr {H}_{k}$
,
![]() $k\geq 2$
. Recall the parameterization map
$k\geq 2$
. Recall the parameterization map
![]() $\Phi _{\mathscr {U}_{k}}$
defined in Theorem 2.2. The center of
$\Phi _{\mathscr {U}_{k}}$
defined in Theorem 2.2. The center of
![]() $\mathscr {U}_{k}$
is defined to be
$\mathscr {U}_{k}$
is defined to be
![]() $\unicode{x3bb} _{\mathscr {U}_{k}}:=\Phi _{\mathscr {U}_{k}}^{-1}(\infty )$
(for the McMullen domain
$\unicode{x3bb} _{\mathscr {U}_{k}}:=\Phi _{\mathscr {U}_{k}}^{-1}(\infty )$
(for the McMullen domain
![]() $\mathscr {H}_{2}$
, define
$\mathscr {H}_{2}$
, define
![]() $\unicode{x3bb} _{\mathscr {H}_{2}}:=0$
), which satisfies the equation
$\unicode{x3bb} _{\mathscr {H}_{2}}:=0$
), which satisfies the equation
![]() $f_{\unicode{x3bb} }^{k-2}(v_{\unicode{x3bb} }^{+})=0$
. Let
$f_{\unicode{x3bb} }^{k-2}(v_{\unicode{x3bb} }^{+})=0$
. Let
![]() $\Lambda _{k}:= \{ \unicode{x3bb} \in {\mathbb {C}^{*}}: f_{\unicode{x3bb} }^{k-2}(v_{\unicode{x3bb} }^{+})=0 \}$
. Then
$\Lambda _{k}:= \{ \unicode{x3bb} \in {\mathbb {C}^{*}}: f_{\unicode{x3bb} }^{k-2}(v_{\unicode{x3bb} }^{+})=0 \}$
. Then
![]() $\Lambda _{k}$
is a finite set since
$\Lambda _{k}$
is a finite set since
![]() $f_{\unicode{x3bb} }^{k-2}(v_{\unicode{x3bb} }^{+})=0$
is an algebraic equation. It follows that
$f_{\unicode{x3bb} }^{k-2}(v_{\unicode{x3bb} }^{+})=0$
is an algebraic equation. It follows that
![]() $\mathscr {H}_{k}$
has finitely many connected components since the number of connected components of
$\mathscr {H}_{k}$
has finitely many connected components since the number of connected components of
![]() $\mathscr {H}_{k}$
is equal to
$\mathscr {H}_{k}$
is equal to
![]() $\# \Lambda _{k}$
.
$\# \Lambda _{k}$
.
Lemma 4.1. Let
![]() $\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
be a simply connected region, then there exist
$\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
be a simply connected region, then there exist
![]() $(2n)^{k-2}$
distinct holomorphic functions
$(2n)^{k-2}$
distinct holomorphic functions
![]() $z^{i}_{k}(\unicode{x3bb} )$
defined on
$z^{i}_{k}(\unicode{x3bb} )$
defined on
![]() $\mathscr {V}$
such that
$\mathscr {V}$
such that
![]() $f_{\unicode{x3bb} }^{k-2}(z^{i}_{k}(\unicode{x3bb} ))=0$
,
$f_{\unicode{x3bb} }^{k-2}(z^{i}_{k}(\unicode{x3bb} ))=0$
,
![]() $i=1,2,\ldots ,(2n)^{k-2}$
.
$i=1,2,\ldots ,(2n)^{k-2}$
.
Proof. Consider the algebraic equation
For
![]() $k=2$
, Lemma 4.1 is trivial. For
$k=2$
, Lemma 4.1 is trivial. For
![]() $k \geq 3$
, since
$k \geq 3$
, since
![]() $\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
, for each
$\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
, for each
![]() $\unicode{x3bb} \in \mathscr {V}$
, the solution z of equation (4.1) cannot be a critical point of
$\unicode{x3bb} \in \mathscr {V}$
, the solution z of equation (4.1) cannot be a critical point of
![]() $f_{\unicode{x3bb} }^{k-1}$
. For otherwise, by
$f_{\unicode{x3bb} }^{k-1}$
. For otherwise, by
there is an
![]() $0 \leq i \leq k-3$
such that
$0 \leq i \leq k-3$
such that
![]() $f_{\unicode{x3bb} }^{i}(z) \in C_{\unicode{x3bb} }$
which implies
$f_{\unicode{x3bb} }^{i}(z) \in C_{\unicode{x3bb} }$
which implies
![]() $f_{\unicode{x3bb} }^{i+1}(z)=v_{\unicode{x3bb} }^{\pm }$
. Hence,
$f_{\unicode{x3bb} }^{i+1}(z)=v_{\unicode{x3bb} }^{\pm }$
. Hence,
![]() $f_{\unicode{x3bb} }^{k-3-i}(v_{\unicode{x3bb} }^{+})=0$
, which implies that
$f_{\unicode{x3bb} }^{k-3-i}(v_{\unicode{x3bb} }^{+})=0$
, which implies that
![]() $\unicode{x3bb} \in \Lambda _{k-i-1}$
. This is a contradiction. It follows that equation (4.1) has
$\unicode{x3bb} \in \Lambda _{k-i-1}$
. This is a contradiction. It follows that equation (4.1) has
![]() $(2n)^{k-2}$
distinct roots
$(2n)^{k-2}$
distinct roots
![]() $z_{i}$
for
$z_{i}$
for
![]() $1\leq i\leq (2n)^{k-2}$
. By the implicit function theorem, there exist
$1\leq i\leq (2n)^{k-2}$
. By the implicit function theorem, there exist
![]() $(2n)^{k-2}$
distinct holomorphic functions
$(2n)^{k-2}$
distinct holomorphic functions
![]() $z^{i}_{k}(\unicode{x3bb} )$
defined near
$z^{i}_{k}(\unicode{x3bb} )$
defined near
![]() $\unicode{x3bb} _{0}$
such that
$\unicode{x3bb} _{0}$
such that
![]() $f_{\unicode{x3bb} }^{k-2}(z^{i}_{k}(\unicode{x3bb} ))=0$
and
$f_{\unicode{x3bb} }^{k-2}(z^{i}_{k}(\unicode{x3bb} ))=0$
and
![]() $z^{i}_{k}(\unicode{x3bb} _{0})=z_{i}$
for
$z^{i}_{k}(\unicode{x3bb} _{0})=z_{i}$
for
![]() $1 \leq i \leq (2n)^{k-2}$
. Since
$1 \leq i \leq (2n)^{k-2}$
. Since
![]() $\mathscr {V}$
is simply connected, the
$\mathscr {V}$
is simply connected, the
![]() $(2n)^{k-2}$
holomorphic functions
$(2n)^{k-2}$
holomorphic functions
![]() $z^{i}_{k}(\unicode{x3bb} )$
can be extended to the whole region
$z^{i}_{k}(\unicode{x3bb} )$
can be extended to the whole region
![]() $\mathscr {V}$
.
$\mathscr {V}$
.
Define
![]() $z_{0}: \mathbb {C}^{*} \to \mathbb {C}$
to be the constant map
$z_{0}: \mathbb {C}^{*} \to \mathbb {C}$
to be the constant map
![]() $z_{0}(\unicode{x3bb} )=\infty $
. The functions
$z_{0}(\unicode{x3bb} )=\infty $
. The functions
![]() $z_{0}$
and each
$z_{0}$
and each
![]() $z^{i}_{k}$
for
$z^{i}_{k}$
for
![]() $1 \leq i \leq (2n)^{k-2}$
defined in Lemma 4.1 are called root functions.
$1 \leq i \leq (2n)^{k-2}$
defined in Lemma 4.1 are called root functions.
Recall the definition of Thurston’s combinatorial equivalence and Thurston’s rigidity theorem, see [Reference Douady and HubbardDH93, Reference HubbardHub06].
Definition 4.2. (Thurston’s combinatorial equivalence)
Let
![]() $f,g : S^{2} \rightarrow S^{2}$
be post- critically finite branched coverings with post-critical sets
$f,g : S^{2} \rightarrow S^{2}$
be post- critically finite branched coverings with post-critical sets
![]() $P(f)$
and
$P(f)$
and
![]() $P(g)$
, respectively. Suppose that there exist two orientation-preserving homeomorphisms
$P(g)$
, respectively. Suppose that there exist two orientation-preserving homeomorphisms
![]() $\phi , \psi $
from
$\phi , \psi $
from
![]() $S^{2}$
to itself such that the following diagram commutes.
$S^{2}$
to itself such that the following diagram commutes.

Furthermore,
![]() $\phi $
and
$\phi $
and
![]() $\psi $
satisfy that
$\psi $
satisfy that
![]() $\phi |_{P(f)}=\psi |_{P(f)}$
, and
$\phi |_{P(f)}=\psi |_{P(f)}$
, and
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are isotopic to each other relatively to the post-critical set
$\psi $
are isotopic to each other relatively to the post-critical set
![]() $ P(f)$
. Then we say the maps f and g are Thurston combinatorially equivalent.
$ P(f)$
. Then we say the maps f and g are Thurston combinatorially equivalent.
Remark 4.1. If
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are both quasi-conformal homeomorphisms, then the condition of isotopy in Definition 4.2 can be replaced by homotopy, see [Reference HubbardHub06].
$\psi $
are both quasi-conformal homeomorphisms, then the condition of isotopy in Definition 4.2 can be replaced by homotopy, see [Reference HubbardHub06].
Theorem 4.3. (Thurston’s rigidity)
If two post-critically finite rational maps
![]() $f,g$
are Thurston combinatorially equivalent, then
$f,g$
are Thurston combinatorially equivalent, then
![]() $f,g$
are conformally conjugated.
$f,g$
are conformally conjugated.
Proposition 4.4. Let
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
be a simply connected region. For
$\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
be a simply connected region. For
![]() $ \unicode{x3bb} _{1}, \unicode{x3bb} _{2} \in \mathscr {V}\cap \mathscr {F}_{0}$
, if there exists a root function
$ \unicode{x3bb} _{1}, \unicode{x3bb} _{2} \in \mathscr {V}\cap \mathscr {F}_{0}$
, if there exists a root function
![]() $z^{i}_{k}$
such that
$z^{i}_{k}$
such that
![]() $z^{i}_{k}(\unicode{x3bb} _{1})=v^{+}_{\unicode{x3bb} _{1}}$
and
$z^{i}_{k}(\unicode{x3bb} _{1})=v^{+}_{\unicode{x3bb} _{1}}$
and
![]() $z^{i}_{k}(\unicode{x3bb} _{2})=v^{+}_{\unicode{x3bb} _{2}}$
, then
$z^{i}_{k}(\unicode{x3bb} _{2})=v^{+}_{\unicode{x3bb} _{2}}$
, then
![]() $\unicode{x3bb} _{1}=\unicode{x3bb} _{2}$
.
$\unicode{x3bb} _{1}=\unicode{x3bb} _{2}$
.
Proof. Let
![]() $\mathscr {W}:= \{ \unicode{x3bb} \in \mathbb {C}^{*}: f^{l}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }), 0\leq l \leq k-3, \text {are } $
k-2
$\mathscr {W}:= \{ \unicode{x3bb} \in \mathbb {C}^{*}: f^{l}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }), 0\leq l \leq k-3, \text {are } $
k-2
![]() $ \text { distinct points} \}$
. It is obvious that
$ \text { distinct points} \}$
. It is obvious that
![]() $\mathbb {C}^{*}\setminus \mathscr {W}$
is a finite set, so we may assume that
$\mathbb {C}^{*}\setminus \mathscr {W}$
is a finite set, so we may assume that
![]() $\mathscr {V} \subset \mathscr {W}$
. Define
$\mathscr {V} \subset \mathscr {W}$
. Define
![]() $\Phi : \mathscr {V} \times P(f_{\unicode{x3bb} _{1}}) \rightarrow \mathscr {V} \times \overline {\mathbb {C}}$
by
$\Phi : \mathscr {V} \times P(f_{\unicode{x3bb} _{1}}) \rightarrow \mathscr {V} \times \overline {\mathbb {C}}$
by
 $$ \begin{align} \Phi(\unicode{x3bb},f^{l}_{\unicode{x3bb}_{1}}(v^{\pm}_{\unicode{x3bb}_{1}})):= \begin{cases} (\unicode{x3bb}, f^{l}_{\unicode{x3bb}}(v^{\pm}_{\unicode{x3bb}})), & {0 \leq l \leq k-3,}\\[2pt] (\unicode{x3bb}, \mathrm{id}), & {l \geq k-2.} \end{cases} \end{align} $$
$$ \begin{align} \Phi(\unicode{x3bb},f^{l}_{\unicode{x3bb}_{1}}(v^{\pm}_{\unicode{x3bb}_{1}})):= \begin{cases} (\unicode{x3bb}, f^{l}_{\unicode{x3bb}}(v^{\pm}_{\unicode{x3bb}})), & {0 \leq l \leq k-3,}\\[2pt] (\unicode{x3bb}, \mathrm{id}), & {l \geq k-2.} \end{cases} \end{align} $$
It is easy to check that
![]() $ \{f^{l}_{\unicode{x3bb} }(v^{\pm }_{\unicode{x3bb} }) : 0\leq l \leq k-3 \} \cup \{0,\infty \}$
contains exactly
$ \{f^{l}_{\unicode{x3bb} }(v^{\pm }_{\unicode{x3bb} }) : 0\leq l \leq k-3 \} \cup \{0,\infty \}$
contains exactly
![]() $2k-2$
(or
$2k-2$
(or
![]() $k+1$
) distinct points for
$k+1$
) distinct points for
![]() $\unicode{x3bb} \in \mathscr {W} \setminus \bigcup _{j \leq k-1}\Lambda _{j}$
if n is odd (or even). Each of them is holomorphically dependent on the parameter
$\unicode{x3bb} \in \mathscr {W} \setminus \bigcup _{j \leq k-1}\Lambda _{j}$
if n is odd (or even). Each of them is holomorphically dependent on the parameter
![]() $\unicode{x3bb} $
. This implies that
$\unicode{x3bb} $
. This implies that
![]() $\Phi $
is a holomorphic motion based at
$\Phi $
is a holomorphic motion based at
![]() $\unicode{x3bb} _{1}$
. By Theorem 2.3,
$\unicode{x3bb} _{1}$
. By Theorem 2.3,
![]() $\Phi $
can be extended to a holomorphic motion
$\Phi $
can be extended to a holomorphic motion
![]() $\Phi : \mathscr {V} \times \overline {\mathbb {C}} \to \mathscr {V} \times \overline {\mathbb {C}}$
. Let
$\Phi : \mathscr {V} \times \overline {\mathbb {C}} \to \mathscr {V} \times \overline {\mathbb {C}}$
. Let
![]() $F(\unicode{x3bb} ,z):=(\unicode{x3bb} ,f_{\unicode{x3bb} }(z))$
for
$F(\unicode{x3bb} ,z):=(\unicode{x3bb} ,f_{\unicode{x3bb} }(z))$
for
![]() $(\unicode{x3bb} ,z) \in \mathscr {V} \times \overline {\mathbb {C}}$
.
$(\unicode{x3bb} ,z) \in \mathscr {V} \times \overline {\mathbb {C}}$
.
Claim 1. There exists a lifting mapping
![]() $\Psi :\mathscr {V} \times \overline {\mathbb {C}} \rightarrow \mathscr {V} \times \overline {\mathbb {C}}$
of
$\Psi :\mathscr {V} \times \overline {\mathbb {C}} \rightarrow \mathscr {V} \times \overline {\mathbb {C}}$
of
![]() $\Phi $
which is also a holomorphic motion such that the following diagram commutes.
$\Phi $
which is also a holomorphic motion such that the following diagram commutes.

Furthermore,
![]() $\Psi $
satisfies the following property on the post-critical set
$\Psi $
satisfies the following property on the post-critical set
![]() $P( f_{\unicode{x3bb} _{1}} )$
of
$P( f_{\unicode{x3bb} _{1}} )$
of
![]() $f_{\unicode{x3bb} _1}$
:
$f_{\unicode{x3bb} _1}$
:
 $$ \begin{align} \Psi(\unicode{x3bb},f^{l}_{\unicode{x3bb}_{1}}(v^{\pm}_{\unicode{x3bb}_{1}}))=\begin{cases} (\unicode{x3bb}, f^{l}_{\unicode{x3bb}}(v^{\pm}_{\unicode{x3bb}})), & {0 \leq l \leq k-4,}\\[3pt] \unicode{x3bb}, f^{l}_{\unicode{x3bb}}(\pm z^{i}_{k}(\unicode{x3bb}))), & {l=k-3,}\\[3pt] (\unicode{x3bb}, \mathrm{id}), & {l \geq k-2.} \end{cases}\end{align} $$
$$ \begin{align} \Psi(\unicode{x3bb},f^{l}_{\unicode{x3bb}_{1}}(v^{\pm}_{\unicode{x3bb}_{1}}))=\begin{cases} (\unicode{x3bb}, f^{l}_{\unicode{x3bb}}(v^{\pm}_{\unicode{x3bb}})), & {0 \leq l \leq k-4,}\\[3pt] \unicode{x3bb}, f^{l}_{\unicode{x3bb}}(\pm z^{i}_{k}(\unicode{x3bb}))), & {l=k-3,}\\[3pt] (\unicode{x3bb}, \mathrm{id}), & {l \geq k-2.} \end{cases}\end{align} $$
Proof. Since the map
![]() $\Phi (\unicode{x3bb} , v^{\pm }_{\unicode{x3bb} _{1}})=(\unicode{x3bb} , v^{\pm }_{\unicode{x3bb} })$
and
$\Phi (\unicode{x3bb} , v^{\pm }_{\unicode{x3bb} _{1}})=(\unicode{x3bb} , v^{\pm }_{\unicode{x3bb} })$
and
![]() $\Phi (\unicode{x3bb} , \infty )=(\unicode{x3bb} ,\infty )$
, there exists a unique lifting map
$\Phi (\unicode{x3bb} , \infty )=(\unicode{x3bb} ,\infty )$
, there exists a unique lifting map
![]() $\Psi :\mathscr {V} \times \overline {\mathbb {C}} \rightarrow \mathscr {V} \times \overline {\mathbb {C}}$
such that it is a holomorphic motion and satisfies the diagram (4.4).
$\Psi :\mathscr {V} \times \overline {\mathbb {C}} \rightarrow \mathscr {V} \times \overline {\mathbb {C}}$
such that it is a holomorphic motion and satisfies the diagram (4.4).
For
![]() $l=k-3$
, denote
$l=k-3$
, denote
![]() $h^{\pm }(\unicode{x3bb} )=\Psi _{\unicode{x3bb} }\circ f^{k-3}_{\unicode{x3bb} _{1}} (v^{\pm }_{\unicode{x3bb} _{1}})$
. By equation (4.3) and diagram (4.4),
$h^{\pm }(\unicode{x3bb} )=\Psi _{\unicode{x3bb} }\circ f^{k-3}_{\unicode{x3bb} _{1}} (v^{\pm }_{\unicode{x3bb} _{1}})$
. By equation (4.3) and diagram (4.4),
![]() $f_{\unicode{x3bb} }(h^{\pm }(\unicode{x3bb} )) =f_{\unicode{x3bb} _1}^{k-2}(v_{\unicode{x3bb} _1}^{\pm })=0$
. Since
$f_{\unicode{x3bb} }(h^{\pm }(\unicode{x3bb} )) =f_{\unicode{x3bb} _1}^{k-2}(v_{\unicode{x3bb} _1}^{\pm })=0$
. Since
![]() $z^{i}_{k}(\unicode{x3bb} _{1})=v^{+}_{\unicode{x3bb} _{1}}$
, then
$z^{i}_{k}(\unicode{x3bb} _{1})=v^{+}_{\unicode{x3bb} _{1}}$
, then
![]() $h^{\pm }(\unicode{x3bb} _{1})=f^{k-3}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=f^{k-3}_{\unicode{x3bb} _{1}} (\pm z^{i}_{k}(\unicode{x3bb} _{1}))$
. By Lemma 4.1, there are
$h^{\pm }(\unicode{x3bb} _{1})=f^{k-3}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=f^{k-3}_{\unicode{x3bb} _{1}} (\pm z^{i}_{k}(\unicode{x3bb} _{1}))$
. By Lemma 4.1, there are
![]() $2n$
distinct pre-images of
$2n$
distinct pre-images of
![]() $0$
which are holomorphic with respect to
$0$
which are holomorphic with respect to
![]() $\unicode{x3bb} \in \mathscr {V}$
. Hence,
$\unicode{x3bb} \in \mathscr {V}$
. Hence,
![]() $h^{\pm }(\unicode{x3bb} )=f^{k-3}_{\unicode{x3bb} }(\pm z^{i}_{k}(\unicode{x3bb} ))$
for
$h^{\pm }(\unicode{x3bb} )=f^{k-3}_{\unicode{x3bb} }(\pm z^{i}_{k}(\unicode{x3bb} ))$
for
![]() $\unicode{x3bb} $
near
$\unicode{x3bb} $
near
![]() $\unicode{x3bb} _{1}$
. Since
$\unicode{x3bb} _{1}$
. Since
![]() $\mathscr {V}$
is connected, then
$\mathscr {V}$
is connected, then
![]() $h^{\pm }(\unicode{x3bb} )=f^{k-3}_{\unicode{x3bb} }(\pm z^{i}_{k}(\unicode{x3bb} ))$
for all
$h^{\pm }(\unicode{x3bb} )=f^{k-3}_{\unicode{x3bb} }(\pm z^{i}_{k}(\unicode{x3bb} ))$
for all
![]() $\unicode{x3bb} \in \mathscr {V}$
. The proofs for
$\unicode{x3bb} \in \mathscr {V}$
. The proofs for
![]() $l \leq k-4$
and
$l \leq k-4$
and
![]() $l \geq k-2$
are very similar and will be omitted here.
$l \geq k-2$
are very similar and will be omitted here.
The proof of Proposition 4.4 continues. By Claim 1 and the condition
![]() $z^{i}_{k}(\unicode{x3bb} _{2})=v^{+}_{\unicode{x3bb} _{2}}$
, we have
$z^{i}_{k}(\unicode{x3bb} _{2})=v^{+}_{\unicode{x3bb} _{2}}$
, we have
![]() $\Psi _{\unicode{x3bb} _{2}}\circ f^{k-3}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=f^{k-3}_{\unicode{x3bb} _{2}}(\pm z^{i}_{k}(\unicode{x3bb} _{2}))=f^{k-3}_{\unicode{x3bb} _{2}}(v^{\pm }_{\unicode{x3bb} _{2}})$
. Hence,
$\Psi _{\unicode{x3bb} _{2}}\circ f^{k-3}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=f^{k-3}_{\unicode{x3bb} _{2}}(\pm z^{i}_{k}(\unicode{x3bb} _{2}))=f^{k-3}_{\unicode{x3bb} _{2}}(v^{\pm }_{\unicode{x3bb} _{2}})$
. Hence,
![]() $\Phi _{\unicode{x3bb} _{2}}\circ f^{l}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=\Psi _{\unicode{x3bb} _{2}}\circ f^{l}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=f^{l}_{\unicode{x3bb} _{2}}(v^{\pm }_{\unicode{x3bb} _{2}})$
for all
$\Phi _{\unicode{x3bb} _{2}}\circ f^{l}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=\Psi _{\unicode{x3bb} _{2}}\circ f^{l}_{\unicode{x3bb} _{1}}(v^{\pm }_{\unicode{x3bb} _{1}})=f^{l}_{\unicode{x3bb} _{2}}(v^{\pm }_{\unicode{x3bb} _{2}})$
for all
![]() $l \geq 0$
. By diagram (4.4), we have
$l \geq 0$
. By diagram (4.4), we have

Let
![]() $H: [0,1] \times \overline {\mathbb {C}} \rightarrow \overline {\mathbb {C}}$
be defined by
$H: [0,1] \times \overline {\mathbb {C}} \rightarrow \overline {\mathbb {C}}$
be defined by
It is easy to check that
![]() $H_{1}=\Psi _{\unicode{x3bb} _{2}}$
,
$H_{1}=\Psi _{\unicode{x3bb} _{2}}$
,
![]() $H_{0}=\Phi _{\unicode{x3bb} _{2}}$
, and
$H_{0}=\Phi _{\unicode{x3bb} _{2}}$
, and
![]() $H_{t} |_{P(f_{\unicode{x3bb} _{1}})}=\Psi _{\unicode{x3bb} _{2}}$
. Hence,
$H_{t} |_{P(f_{\unicode{x3bb} _{1}})}=\Psi _{\unicode{x3bb} _{2}}$
. Hence,
![]() $\Psi _{\unicode{x3bb} _{2}}$
and
$\Psi _{\unicode{x3bb} _{2}}$
and
![]() $\Phi _{\unicode{x3bb} _{2}}$
are homotopic relative to
$\Phi _{\unicode{x3bb} _{2}}$
are homotopic relative to
![]() $P(f_{\unicode{x3bb} _{1}})$
. Since
$P(f_{\unicode{x3bb} _{1}})$
. Since
![]() $\Phi _{\unicode{x3bb} _{2}}$
and
$\Phi _{\unicode{x3bb} _{2}}$
and
![]() $\Psi _{\unicode{x3bb} _{2}}$
are both quasi-conformal homeomorphisms, by Remark 4.1 and Theorem 4.3,
$\Psi _{\unicode{x3bb} _{2}}$
are both quasi-conformal homeomorphisms, by Remark 4.1 and Theorem 4.3,
![]() $f_{\unicode{x3bb} _{1}}$
and
$f_{\unicode{x3bb} _{1}}$
and
![]() $f_{\unicode{x3bb} _{2}}$
are conformally conjugated. Since
$f_{\unicode{x3bb} _{2}}$
are conformally conjugated. Since
![]() $\unicode{x3bb} _{1}, \unicode{x3bb} _{2} \in \mathscr {F}_{0}$
, it is easy to check that
$\unicode{x3bb} _{1}, \unicode{x3bb} _{2} \in \mathscr {F}_{0}$
, it is easy to check that
![]() $\unicode{x3bb} _{1}=\unicode{x3bb} _{2}$
.
$\unicode{x3bb} _{1}=\unicode{x3bb} _{2}$
.
Corollary 4.5. Let
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component and
$\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component and
![]() $\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(re^{2\pi i t}) \cap \mathscr {F}_{0}$
. Let
$\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(re^{2\pi i t}) \cap \mathscr {F}_{0}$
. Let
![]() $\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
be a simply connected region containing
$\mathscr {V} \subset {\mathbb {C}^{*}} \setminus \bigcup _{2 \leq j \leq k-1}\Lambda _{j}$
be a simply connected region containing
![]() $\overline {\mathscr {U}}$
, then there exists a unique root function
$\overline {\mathscr {U}}$
, then there exists a unique root function
![]() $z^{i}_{k}(\unicode{x3bb} )$
defined on
$z^{i}_{k}(\unicode{x3bb} )$
defined on
![]() $\mathscr {V}$
such that
$\mathscr {V}$
such that
![]() $v^{+}_{\unicode{x3bb} }=\phi _{z_{k}(\unicode{x3bb} )}^{-1}(\rho _{k}(r)e^{2\pi i \theta _{k}(t)})$
, where
$v^{+}_{\unicode{x3bb} }=\phi _{z_{k}(\unicode{x3bb} )}^{-1}(\rho _{k}(r)e^{2\pi i \theta _{k}(t)})$
, where
 $$ \begin{align} \theta_{k}(t):=\begin{cases} \dfrac{t}{2}, & {k=0,}\\[4pt] \dfrac{2nt}{n-2}, & {k=2,}\\ t, & {k \geq 3}, \end{cases} \end{align} $$
$$ \begin{align} \theta_{k}(t):=\begin{cases} \dfrac{t}{2}, & {k=0,}\\[4pt] \dfrac{2nt}{n-2}, & {k=2,}\\ t, & {k \geq 3}, \end{cases} \end{align} $$
and
 $$ \begin{align}\rho_{k}(r):=\begin{cases} \sqrt{r}, & {k=0,}\\[2pt] \sqrt[n-2]{r^{2n}}, & {k=2},\\ r, & {k \geq 3.} \end{cases} \end{align} $$
$$ \begin{align}\rho_{k}(r):=\begin{cases} \sqrt{r}, & {k=0,}\\[2pt] \sqrt[n-2]{r^{2n}}, & {k=2},\\ r, & {k \geq 3.} \end{cases} \end{align} $$
Proof. First, let us show the existence and uniqueness of the root function. Since
![]() $f_{\unicode{x3bb} }^{k-2}(v^{+}_{\unicode{x3bb} _{\mathscr U}})=0$
, by Lemma 4.1 and Proposition 4.4, there exists a unique root function
$f_{\unicode{x3bb} }^{k-2}(v^{+}_{\unicode{x3bb} _{\mathscr U}})=0$
, by Lemma 4.1 and Proposition 4.4, there exists a unique root function
![]() $z^{i}_{k}(\unicode{x3bb} )$
defined on
$z^{i}_{k}(\unicode{x3bb} )$
defined on
![]() $\mathscr {V}$
such that
$\mathscr {V}$
such that
![]() $z^{i}_{k}(\unicode{x3bb} _{\mathscr U})=v^{+}_{\unicode{x3bb} _{\mathscr U}}$
(the uniqueness is trivial for
$z^{i}_{k}(\unicode{x3bb} _{\mathscr U})=v^{+}_{\unicode{x3bb} _{\mathscr U}}$
(the uniqueness is trivial for
![]() $k\leq 2$
and insured by Proposition 4.4 for
$k\leq 2$
and insured by Proposition 4.4 for
![]() $k \geq 3$
).
$k \geq 3$
).
It follows easily that if
![]() $\unicode{x3bb} \in \mathscr {U}$
,
$\unicode{x3bb} \in \mathscr {U}$
,
![]() $v_{\unicode{x3bb} }^{+}$
is contained in the Fatou component containing
$v_{\unicode{x3bb} }^{+}$
is contained in the Fatou component containing
![]() $z^{i}_{k}(\unicode{x3bb} )$
. By Remark 2.1, the Böttcher coordinates
$z^{i}_{k}(\unicode{x3bb} )$
. By Remark 2.1, the Böttcher coordinates
![]() $\phi _{z^{i}_{k}(\unicode{x3bb} )}$
defined in Lemma 2.1 can be extended to
$\phi _{z^{i}_{k}(\unicode{x3bb} )}$
defined in Lemma 2.1 can be extended to
![]() $v_{\unicode{x3bb} }^{+}$
. The rest of the proof follows easily from the asymptotic behavior of the parameterization maps defined in Theorem 2.2 and dynamical Böttcher coordinates defined in Lemma 2.1.
$v_{\unicode{x3bb} }^{+}$
. The rest of the proof follows easily from the asymptotic behavior of the parameterization maps defined in Theorem 2.2 and dynamical Böttcher coordinates defined in Lemma 2.1.
5 Dynamics of maps on
 $\partial {\mathscr {H}}$
$\partial {\mathscr {H}}$
Let
![]() $\mathscr {U} \subset \mathscr {H}$
be an escape component. In this section, we describe the dynamics of
$\mathscr {U} \subset \mathscr {H}$
be an escape component. In this section, we describe the dynamics of
![]() $f_{\unicode{x3bb} }$
for
$f_{\unicode{x3bb} }$
for
![]() $\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t}) \in \partial \mathscr {U} \cap \mathscr {F}_{0}$
, where
$\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t}) \in \partial \mathscr {U} \cap \mathscr {F}_{0}$
, where
![]() $t \in \mathbb {R}/\mathbb {Z}$
via the puzzle system
$t \in \mathbb {R}/\mathbb {Z}$
via the puzzle system
![]() $(f_{\unicode{x3bb} }, I^{k}_{\unicode{x3bb} }, P^{k}_{\unicode{x3bb} })$
.
$(f_{\unicode{x3bb} }, I^{k}_{\unicode{x3bb} }, P^{k}_{\unicode{x3bb} })$
.
Lemma 5.1. If
![]() $\unicode{x3bb} \in \mathscr {F}_{0} \setminus \mathscr {H}_0$
, then for any sequence of puzzle pieces
$\unicode{x3bb} \in \mathscr {F}_{0} \setminus \mathscr {H}_0$
, then for any sequence of puzzle pieces
![]() $\{P_{\unicode{x3bb} }^k\}_{k\geq 0}$
,
$\{P_{\unicode{x3bb} }^k\}_{k\geq 0}$
,
![]() $(\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
is either empty or a singleton.
$(\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
is either empty or a singleton.
Proof. Suppose
![]() $(\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} } \neq \emptyset $
. Then,
$(\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} } \neq \emptyset $
. Then,
![]() $\{P_{\unicode{x3bb} }^k\}$
is a nested sequence of puzzle pieces. By part (1) in Theorem 2.6, every point in
$\{P_{\unicode{x3bb} }^k\}$
is a nested sequence of puzzle pieces. By part (1) in Theorem 2.6, every point in
![]() $(\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
is a landing point of a dynamical ray. Suppose that
$(\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
is a landing point of a dynamical ray. Suppose that
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi i t_{0}}) \in (\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
. It suffices to show for
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi i t_{0}}) \in (\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
. It suffices to show for
![]() $t \neq t_{0}$
,
$t \neq t_{0}$
,
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi i t}) \notin (\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
. Since each
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi i t}) \notin (\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
. Since each
![]() $\theta \in \Theta _{\unicode{x3bb} }$
satisfies equation (2.8) in Lemma 2.5, by the construction of graphs, there is an angle
$\theta \in \Theta _{\unicode{x3bb} }$
satisfies equation (2.8) in Lemma 2.5, by the construction of graphs, there is an angle
![]() $\alpha \in \bigcup _{k \geq 0} \tau ^{-k}(\theta )$
such that the cut ray
$\alpha \in \bigcup _{k \geq 0} \tau ^{-k}(\theta )$
such that the cut ray
![]() $\Omega ^{\alpha }_{\unicode{x3bb} }$
separates
$\Omega ^{\alpha }_{\unicode{x3bb} }$
separates
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it})$
from
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it})$
from
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it_{0}})$
. Note that there must be a k such that
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it_{0}})$
. Note that there must be a k such that
![]() $\alpha \in \tau ^{-k}(\theta )$
which implies that
$\alpha \in \tau ^{-k}(\theta )$
which implies that
![]() $\Omega _{\unicode{x3bb} }^{\alpha }\subset I_{\unicode{x3bb} }^k$
. We get that
$\Omega _{\unicode{x3bb} }^{\alpha }\subset I_{\unicode{x3bb} }^k$
. We get that
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it})$
and
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it})$
and
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it_{0}})$
are separated by the graph
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it_{0}})$
are separated by the graph
![]() $I_{\unicode{x3bb} }^k$
of depth k. This follows that
$I_{\unicode{x3bb} }^k$
of depth k. This follows that
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it}) \notin P^{k}_{\unicode{x3bb} }(\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it_{0}}) )=P^{k}_{\unicode{x3bb} }$
, and hence
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it}) \notin P^{k}_{\unicode{x3bb} }(\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it_{0}}) )=P^{k}_{\unicode{x3bb} }$
, and hence
![]() $\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it}) \notin (\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
.
$\phi _{\infty (\unicode{x3bb} )}^{-1}(e^{2\pi it}) \notin (\bigcap _{k \geq 0}P^{k}_{\unicode{x3bb} }) \cap \partial {B}_{\unicode{x3bb} }$
.
Let us denote
![]() $K^{\pm }_{\unicode{x3bb} }:=\bigcap _{k \geq 0}P_{\unicode{x3bb} }^{k}(v^{\pm }_{\unicode{x3bb} })$
.
$K^{\pm }_{\unicode{x3bb} }:=\bigcap _{k \geq 0}P_{\unicode{x3bb} }^{k}(v^{\pm }_{\unicode{x3bb} })$
.
Proposition 5.2. Let
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component with
$\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component with
![]() $k \geq 0$
. If
$k \geq 0$
. If
![]() $\unicode{x3bb} _{0}=\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t}) \in \mathscr {F}_{0}$
, then there exists
$\unicode{x3bb} _{0}=\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t}) \in \mathscr {F}_{0}$
, then there exists
![]() $z^{i}_{k}(\unicode{x3bb} _0) \in Z_{k}(\unicode{x3bb} _0)$
such that
$z^{i}_{k}(\unicode{x3bb} _0) \in Z_{k}(\unicode{x3bb} _0)$
such that
where
![]() $\theta _k(t)$
is defined in equation (4.7).
$\theta _k(t)$
is defined in equation (4.7).
Proof. For
![]() $k=0$
,
$k=0$
,
![]() $z^{i}_{k}(\unicode{x3bb} _0)=\infty $
. For
$z^{i}_{k}(\unicode{x3bb} _0)=\infty $
. For
![]() $k \geq 2$
, there is a simply connected region
$k \geq 2$
, there is a simply connected region
![]() $\mathscr {U}^{*} \supset \overline {\mathscr {U}}$
such that
$\mathscr {U}^{*} \supset \overline {\mathscr {U}}$
such that
![]() $\mathscr {U}^{*} \cap (\bigcup _{2 \leq l\leq k-1} \Lambda _{l})=\emptyset $
. Let
$\mathscr {U}^{*} \cap (\bigcup _{2 \leq l\leq k-1} \Lambda _{l})=\emptyset $
. Let
![]() $z^{i}_{k}(\unicode{x3bb} )$
denote the root function obtained in Corollary 4.5. In the following, we prove that for any
$z^{i}_{k}(\unicode{x3bb} )$
denote the root function obtained in Corollary 4.5. In the following, we prove that for any
![]() $m \geq k+2$
,
$m \geq k+2$
,
Here, L is the number we choose for
![]() $X_{\unicode{x3bb} _0}^{L}$
to construct puzzles in §2.2. For each
$X_{\unicode{x3bb} _0}^{L}$
to construct puzzles in §2.2. For each
![]() $m \geq k+2$
, choose
$m \geq k+2$
, choose
![]() $r_{m}$
such that
$r_{m}$
such that
![]() $1< \rho _{k}(r_{m}) \leq \sqrt [n^{m-k+2}]{L}$
and
$1< \rho _{k}(r_{m}) \leq \sqrt [n^{m-k+2}]{L}$
and
![]() $\unicode{x3bb} _{m}=\Phi _{\mathscr {U}}^{-1}( r_{m} e^{2\pi it} ) \in \mathscr {P}^{m+2}_{\unicode{x3bb} _{0}}\cap \mathscr {R}^{t}_{\mathscr {U}}$
. Here,
$\unicode{x3bb} _{m}=\Phi _{\mathscr {U}}^{-1}( r_{m} e^{2\pi it} ) \in \mathscr {P}^{m+2}_{\unicode{x3bb} _{0}}\cap \mathscr {R}^{t}_{\mathscr {U}}$
. Here,
![]() $\rho _{k}$
is the function we defined in equation (4.8). By Corollary 4.5,
$\rho _{k}$
is the function we defined in equation (4.8). By Corollary 4.5,
![]() $v^{+}_{\unicode{x3bb} _{m}}=\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} _{m})}( \rho _{k}(r_{m}) e^{2\pi i\theta _{k}(t)} )$
. By Corollary 3.2, there is no critical value in
$v^{+}_{\unicode{x3bb} _{m}}=\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} _{m})}( \rho _{k}(r_{m}) e^{2\pi i\theta _{k}(t)} )$
. By Corollary 3.2, there is no critical value in
![]() $f^{-m-1}_{\unicode{x3bb} }(X^{L}_{\unicode{x3bb} })\setminus \{\infty \}$
for
$f^{-m-1}_{\unicode{x3bb} }(X^{L}_{\unicode{x3bb} })\setminus \{\infty \}$
for
![]() $\unicode{x3bb} \in \mathscr {P}^{m+1}_{\unicode{x3bb} _{0}}$
since there are no critical values of
$\unicode{x3bb} \in \mathscr {P}^{m+1}_{\unicode{x3bb} _{0}}$
since there are no critical values of
![]() $f_{\unicode{x3bb} _0}$
in
$f_{\unicode{x3bb} _0}$
in
![]() $f^{-m-1}_{\unicode{x3bb} _0}(X^{L}_{\unicode{x3bb} _0})\setminus \{\infty \}$
. Hence,
$f^{-m-1}_{\unicode{x3bb} _0}(X^{L}_{\unicode{x3bb} _0})\setminus \{\infty \}$
. Hence,
![]() $\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} )}(\!\sqrt [n^{m-k+2}]{L}e^{2\pi i\theta _{k}(t)}) \in I^{m+2}_{\unicode{x3bb} }$
is well defined for
$\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} )}(\!\sqrt [n^{m-k+2}]{L}e^{2\pi i\theta _{k}(t)}) \in I^{m+2}_{\unicode{x3bb} }$
is well defined for
![]() $\unicode{x3bb} \in \mathscr {P}^{m+2}_{\unicode{x3bb} _{0}}$
. Since both
$\unicode{x3bb} \in \mathscr {P}^{m+2}_{\unicode{x3bb} _{0}}$
. Since both
![]() $v^{+}_{\unicode{x3bb} _{m}}=\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} _{m})}( \rho _{k}(r_{m}) e^{2\pi i\theta _{k}(t)} )$
and
$v^{+}_{\unicode{x3bb} _{m}}=\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} _{m})}( \rho _{k}(r_{m}) e^{2\pi i\theta _{k}(t)} )$
and
![]() $\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} _{m})}(\!\sqrt [n^{m-k+2}]{L}e^{2\pi i\theta _{k}(t)})$
belong to the dynamical ray
$\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} _{m})}(\!\sqrt [n^{m-k+2}]{L}e^{2\pi i\theta _{k}(t)})$
belong to the dynamical ray
![]() $R_{z^{i}_{k}(\unicode{x3bb} _{m})}^{\theta _{k}(t)}$
, and
$R_{z^{i}_{k}(\unicode{x3bb} _{m})}^{\theta _{k}(t)}$
, and
![]() $I_{\unicode{x3bb} }^{m-1}$
does not contain the equipotential curve
$I_{\unicode{x3bb} }^{m-1}$
does not contain the equipotential curve
![]() $E_{z^{i}_{k}(\unicode{x3bb} _{m})}^{s}$
with
$E_{z^{i}_{k}(\unicode{x3bb} _{m})}^{s}$
with
![]() $1<s< \sqrt [n^{m-k+2}]{L}$
, we have
$1<s< \sqrt [n^{m-k+2}]{L}$
, we have
By Corollary 3.2,
is a holomorphic motion. Hence, equation (5.2) implies that
for all
![]() $\unicode{x3bb} \in \mathscr {P}^{m}_{\unicode{x3bb} _{0}}$
. Then equation (5.1) follows by setting
$\unicode{x3bb} \in \mathscr {P}^{m}_{\unicode{x3bb} _{0}}$
. Then equation (5.1) follows by setting
![]() $\unicode{x3bb} =\unicode{x3bb} _0$
.
$\unicode{x3bb} =\unicode{x3bb} _0$
.
Certainly, for
![]() $1<s< \sqrt [n^{m-k+2}]{L}$
, we also have
$1<s< \sqrt [n^{m-k+2}]{L}$
, we also have
Let
![]() $s \to 1$
. Then,
$s \to 1$
. Then,
![]() $w^{t}_{k}(\unicode{x3bb} _0):=\lim \nolimits _{s \to 1}\phi _{z^{i}_{k}(\unicode{x3bb} _0)}^{-1}(se^{2\pi i \theta _{k}(t)}) \in {P^{m-1}_{\unicode{x3bb} _{0}}(v^{+}_{\unicode{x3bb} _{0}})}$
for all
$w^{t}_{k}(\unicode{x3bb} _0):=\lim \nolimits _{s \to 1}\phi _{z^{i}_{k}(\unicode{x3bb} _0)}^{-1}(se^{2\pi i \theta _{k}(t)}) \in {P^{m-1}_{\unicode{x3bb} _{0}}(v^{+}_{\unicode{x3bb} _{0}})}$
for all
![]() $m \geq k+2$
. This follows that
$m \geq k+2$
. This follows that
![]() $w^{t}_{k}(\unicode{x3bb} _0) \in \bigcap _{m \geq k+2} {P^{m-1}_{\unicode{x3bb} _{0}}(v^{+}_{\unicode{x3bb} _{0}})}=K_{\unicode{x3bb} _{0}}^{+}$
.
$w^{t}_{k}(\unicode{x3bb} _0) \in \bigcap _{m \geq k+2} {P^{m-1}_{\unicode{x3bb} _{0}}(v^{+}_{\unicode{x3bb} _{0}})}=K_{\unicode{x3bb} _{0}}^{+}$
.
For
![]() $\mathscr {H}_{0}$
,
$\mathscr {H}_{0}$
,
![]() $\unicode{x3bb} =\Phi _{\mathscr {H}_{0}}^{-1}(e^{2\pi i t})\in \mathscr {F}_{0}$
if and only if
$\unicode{x3bb} =\Phi _{\mathscr {H}_{0}}^{-1}(e^{2\pi i t})\in \mathscr {F}_{0}$
if and only if
![]() $t \in (0,{1}/({n-1}) )$
and
$t \in (0,{1}/({n-1}) )$
and
![]() $\Phi _{\mathscr {H}_{0}}^{-1}(1)\in \partial \mathscr {F}_0$
.
$\Phi _{\mathscr {H}_{0}}^{-1}(1)\in \partial \mathscr {F}_0$
.
Corollary 5.3. Suppose
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component. Then for
$\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component. Then for
![]() $\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t})\cap \mathscr {F}_{0}$
,
$\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t})\cap \mathscr {F}_{0}$
,
Proof. By Proposition 5.2,
![]() $f^{k-1}_{\unicode{x3bb} } (w^{t}_{k}(\unicode{x3bb} )) \in f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })$
. Note that
$f^{k-1}_{\unicode{x3bb} } (w^{t}_{k}(\unicode{x3bb} )) \in f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })$
. Note that
yields
![]() $f^{k-1}_{\unicode{x3bb} } (w^{t}_{k}(\unicode{x3bb} )) \in f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })\cap \partial {B_{\unicode{x3bb} }}$
. Conversely, by Lemma 5.1,
$f^{k-1}_{\unicode{x3bb} } (w^{t}_{k}(\unicode{x3bb} )) \in f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })\cap \partial {B_{\unicode{x3bb} }}$
. Conversely, by Lemma 5.1,
![]() $f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })\cap \partial {B_{\unicode{x3bb} }}=(\bigcap _{n \geq 0}P^{n}_{\unicode{x3bb} }(f^{k-1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }) ))\cap \partial B_{\unicode{x3bb} }$
contains at most one point. This implies that
$f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })\cap \partial {B_{\unicode{x3bb} }}=(\bigcap _{n \geq 0}P^{n}_{\unicode{x3bb} }(f^{k-1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }) ))\cap \partial B_{\unicode{x3bb} }$
contains at most one point. This implies that
![]() $f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })\cap \partial {B_{\unicode{x3bb} }}= \{ f_{\unicode{x3bb} }^{k-1}(w^{t}_{k}(\unicode{x3bb} ) ) \}$
.
$f_{\unicode{x3bb} }^{k-1}(K^{+}_{\unicode{x3bb} })\cap \partial {B_{\unicode{x3bb} }}= \{ f_{\unicode{x3bb} }^{k-1}(w^{t}_{k}(\unicode{x3bb} ) ) \}$
.
6 No bounded escape components attached on
 $\partial {\mathscr {H}_{0}}$
$\partial {\mathscr {H}_{0}}$
The purpose of this section is to prove that the boundary of the Cantor locus is disjoint with the boundary of any bounded escape component. This result is also the key step of proving Theorem 1.2.
6.1 Assumptions
Let
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
be an escape hyperbolic component with order
$\mathscr {U} \subset \mathscr {H}_{k}$
be an escape hyperbolic component with order
![]() $k \geq 2$
. To prove that
$k \geq 2$
. To prove that
![]() $\partial \mathscr {U} \cap \partial \mathcal {H}_{0}=\emptyset $
, it suffices to show that
$\partial \mathscr {U} \cap \partial \mathcal {H}_{0}=\emptyset $
, it suffices to show that
![]() $\overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0}= \emptyset $
for any
$\overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0}= \emptyset $
for any
![]() $t_{0},t_{1}\in \mathbb {R}/\mathbb {Z}$
. Here,
$t_{0},t_{1}\in \mathbb {R}/\mathbb {Z}$
. Here,
![]() $\mathscr {R}_{\mathscr {H}_0}^{f_0}$
and
$\mathscr {R}_{\mathscr {H}_0}^{f_0}$
and
![]() $\mathscr {R}_{\mathcal {U}}^{t_1}$
are parameter rays in
$\mathscr {R}_{\mathcal {U}}^{t_1}$
are parameter rays in
![]() $\mathscr {H}_0$
and
$\mathscr {H}_0$
and
![]() $\mathscr {U}$
, respectively. We prove this by seeking a contradiction under the assumption
$\mathscr {U}$
, respectively. We prove this by seeking a contradiction under the assumption
![]() $\overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0} \neq \emptyset $
. Let us use the notation in the proof of Proposition 5.2. The function
$\overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0} \neq \emptyset $
. Let us use the notation in the proof of Proposition 5.2. The function
![]() $z^{i}_{k}$
is the root function defined on
$z^{i}_{k}$
is the root function defined on
![]() $\mathscr {U}^{*} \supset \overline {\mathscr {U}}$
, such that
$\mathscr {U}^{*} \supset \overline {\mathscr {U}}$
, such that
![]() $v^{+}_{\unicode{x3bb} _{\mathscr {U}}}=z^{i}_{k}(\unicode{x3bb} _{\mathscr {U}} )$
.
$v^{+}_{\unicode{x3bb} _{\mathscr {U}}}=z^{i}_{k}(\unicode{x3bb} _{\mathscr {U}} )$
.
Proposition 6.1. Let
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
be an escape hyperbolic component with order
$\mathscr {U} \subset \mathscr {H}_{k}$
be an escape hyperbolic component with order
![]() $k \geq 2$
. If
$k \geq 2$
. If
![]() $\overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0} \neq \emptyset $
, then
$\overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0} \neq \emptyset $
, then
![]() $\tau ^{k-1}(t_{0})=t_{0}$
.
$\tau ^{k-1}(t_{0})=t_{0}$
.
Proof. Suppose
![]() $\unicode{x3bb} _{0} \in \overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0}$
. By Proposition 5.2,
$\unicode{x3bb} _{0} \in \overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0}$
. By Proposition 5.2,
![]() $ \{w^{t_0}_{0}(\unicode{x3bb} _{0}), w^{t_{1}}_{k}(\unicode{x3bb} _{0}) \}\subset K^{+}_{\unicode{x3bb} _{0}}$
. Then,
$ \{w^{t_0}_{0}(\unicode{x3bb} _{0}), w^{t_{1}}_{k}(\unicode{x3bb} _{0}) \}\subset K^{+}_{\unicode{x3bb} _{0}}$
. Then,
and
By Corollary 5.3, we get
If
![]() $f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))\neq f^{k-2}_{\unicode{x3bb} _{0}}( w^{t_{1}}_{k}(\unicode{x3bb} _{0}))$
, then by equations (6.1), (6.2), and the fact
$f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))\neq f^{k-2}_{\unicode{x3bb} _{0}}( w^{t_{1}}_{k}(\unicode{x3bb} _{0}))$
, then by equations (6.1), (6.2), and the fact
for all integers
![]() $m\geq 0$
, we have that
$m\geq 0$
, we have that
is a ramified covering of degree at least two. Since the puzzle pieces are all simply connected,
![]() $P_{\unicode{x3bb} _0}^m (f_{\unicode{x3bb} _0}^{k-1}(w_0^{t_0}(\unicode{x3bb} _0)))$
must contain a critical value for all
$P_{\unicode{x3bb} _0}^m (f_{\unicode{x3bb} _0}^{k-1}(w_0^{t_0}(\unicode{x3bb} _0)))$
must contain a critical value for all
![]() $m\geq 0$
. It follows that
$m\geq 0$
. It follows that
![]() $f^{k-1}_{\unicode{x3bb} _{0}}(K^{+}_{\unicode{x3bb} _{0}})$
contains a critical value
$f^{k-1}_{\unicode{x3bb} _{0}}(K^{+}_{\unicode{x3bb} _{0}})$
contains a critical value
![]() $v^{+}_{\unicode{x3bb} _{0}}$
or
$v^{+}_{\unicode{x3bb} _{0}}$
or
![]() $v^{-}_{\unicode{x3bb} _{0}}$
, that is,
$v^{-}_{\unicode{x3bb} _{0}}$
, that is,
![]() $f^{k-1}_{\unicode{x3bb} _{0}}(K^{+}_{\unicode{x3bb} _{0}}) = K^{+}_{\unicode{x3bb} _{0}}$
or
$f^{k-1}_{\unicode{x3bb} _{0}}(K^{+}_{\unicode{x3bb} _{0}}) = K^{+}_{\unicode{x3bb} _{0}}$
or
![]() $=K^{-}_{\unicode{x3bb} _{0}}$
. This implies that
$=K^{-}_{\unicode{x3bb} _{0}}$
. This implies that
![]() $\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}$
or
$\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}$
or
![]() $\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
. Both lead to the consequence that
$\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
. Both lead to the consequence that
![]() $\tau ^{k-1}(t_{0})=t_{0}$
.
$\tau ^{k-1}(t_{0})=t_{0}$
.
If
![]() $f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0})) = f^{k-2}_{\unicode{x3bb} _{0}}( w^{t_{1}}_{k}(\unicode{x3bb} _{0}))$
, then both dynamical rays
$f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0})) = f^{k-2}_{\unicode{x3bb} _{0}}( w^{t_{1}}_{k}(\unicode{x3bb} _{0}))$
, then both dynamical rays
![]() $f_{\unicode{x3bb} _0}^{k-2}(R_{z_k^i(\unicode{x3bb} _0)}^{\theta _k(t_1)}) \subset T_{\unicode{x3bb} _0}$
and
$f_{\unicode{x3bb} _0}^{k-2}(R_{z_k^i(\unicode{x3bb} _0)}^{\theta _k(t_1)}) \subset T_{\unicode{x3bb} _0}$
and
![]() $f_{\unicode{x3bb} _0}^{k-2}(R_{\infty (\unicode{x3bb} _0)}^{\theta _0(t_0)}) \subset B_{\unicode{x3bb} _0}$
land on the common point
$f_{\unicode{x3bb} _0}^{k-2}(R_{\infty (\unicode{x3bb} _0)}^{\theta _0(t_0)}) \subset B_{\unicode{x3bb} _0}$
land on the common point
![]() $f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))$
. Note that
$f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))$
. Note that
![]() $f_{\unicode{x3bb} _0}^{k-1} (R_{z_k^i(\unicode{x3bb} _0)}^{\theta _k(t_1)}) = f_{\unicode{x3bb} _0}^{k-1} (R_{\infty (\unicode{x3bb} _0)}^{\theta _0(t_0)}) \subset B_{\unicode{x3bb} _0}$
is the external ray landing on
$f_{\unicode{x3bb} _0}^{k-1} (R_{z_k^i(\unicode{x3bb} _0)}^{\theta _k(t_1)}) = f_{\unicode{x3bb} _0}^{k-1} (R_{\infty (\unicode{x3bb} _0)}^{\theta _0(t_0)}) \subset B_{\unicode{x3bb} _0}$
is the external ray landing on
![]() $f^{k-1}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))$
. It follows that
$f^{k-1}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))$
. It follows that
![]() $f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))$
is a critical point and
$f^{k-2}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0}))$
is a critical point and
![]() $f^{k-1}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0})) \in f_{\unicode{x3bb} _0}^{k-1}(K_{\unicode{x3bb} _0}^+)$
is a critical value
$f^{k-1}_{\unicode{x3bb} _{0}}(w^{t_0}_{0}(\unicode{x3bb} _{0})) \in f_{\unicode{x3bb} _0}^{k-1}(K_{\unicode{x3bb} _0}^+)$
is a critical value
![]() $v^{+}_{\unicode{x3bb} _{0}}$
or
$v^{+}_{\unicode{x3bb} _{0}}$
or
![]() $v^{-}_{\unicode{x3bb} _{0}}$
. We again obtain that
$v^{-}_{\unicode{x3bb} _{0}}$
. We again obtain that
![]() $\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}$
or
$\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}$
or
![]() $\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
, and then
$\tau ^{k-1}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
, and then
![]() $\tau ^{k-1}(t_{0})=t_{0}$
.
$\tau ^{k-1}(t_{0})=t_{0}$
.
Suppose that
![]() $t_0 \in [0,{1}/({n-1}) )$
satisfies
$t_0 \in [0,{1}/({n-1}) )$
satisfies
![]() $\tau ^{p}t_0=t_0$
for an integer
$\tau ^{p}t_0=t_0$
for an integer
![]() $p\geq 1$
. Let
$p\geq 1$
. Let
![]() $\unicode{x3bb} _0=\Phi _{\mathscr {H}_{0}}^{-1}(e^{2\pi i t_0} )$
. It follows from [Reference Qiu, Roesch, Wang and YinQRWY15] (Lemmas 4.6, 4.8, Theorem 6.2, and Remark 6.3) that there is a quadratic-like map
$\unicode{x3bb} _0=\Phi _{\mathscr {H}_{0}}^{-1}(e^{2\pi i t_0} )$
. It follows from [Reference Qiu, Roesch, Wang and YinQRWY15] (Lemmas 4.6, 4.8, Theorem 6.2, and Remark 6.3) that there is a quadratic-like map
![]() $g_{\unicode{x3bb} _0}: U\to V$
with a parabolic fixed point
$g_{\unicode{x3bb} _0}: U\to V$
with a parabolic fixed point
![]() $\beta _{\unicode{x3bb} _0}\in U$
satisfying
$\beta _{\unicode{x3bb} _0}\in U$
satisfying
which is defined according to the following three cases.
-
(1) If
 $\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}$
, then
$\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}$
, then
 $g_{\unicode{x3bb} _0}=f_{\unicode{x3bb} _0}^{p}$
,
$g_{\unicode{x3bb} _0}=f_{\unicode{x3bb} _0}^{p}$
,
 $U= P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{+} )$
, and
$U= P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{+} )$
, and
 $V= P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+} )$
for an N large,
$V= P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+} )$
for an N large,
 $\beta _{\unicode{x3bb} _0}=w^{t_{0}}_{0}(\unicode{x3bb} _0)$
, and
$\beta _{\unicode{x3bb} _0}=w^{t_{0}}_{0}(\unicode{x3bb} _0)$
, and
 $v_{\unicode{x3bb} _0}^{+}$
is the unique critical value.
$v_{\unicode{x3bb} _0}^{+}$
is the unique critical value. -
(2) If
 $\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
and
$\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
and
 $\tau ^{p}({t_{0}}/{2}+\tfrac 12) ={t_{0}}/{2}+\tfrac 12$
, then
$\tau ^{p}({t_{0}}/{2}+\tfrac 12) ={t_{0}}/{2}+\tfrac 12$
, then
 $g_{\unicode{x3bb} _0}=f_{\unicode{x3bb} _0}^{p}$
,
$g_{\unicode{x3bb} _0}=f_{\unicode{x3bb} _0}^{p}$
,
 $U= P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{-} )$
, and
$U= P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{-} )$
, and
 $V= P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{-} )$
for an N large,
$V= P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{-} )$
for an N large,
 $\beta _{\unicode{x3bb} _0}=-w^{t_{0}}_{0}(\unicode{x3bb} _0)$
, and
$\beta _{\unicode{x3bb} _0}=-w^{t_{0}}_{0}(\unicode{x3bb} _0)$
, and
 $v_{\unicode{x3bb} _0}^{-}$
is the unique critical value.
$v_{\unicode{x3bb} _0}^{-}$
is the unique critical value. -
(3) If
 $\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
and
$\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}+\tfrac 12$
and
 $\tau ^{p}({t_{0}}/{2}+\tfrac 12)={t_{0}}/{2}$
, then
$\tau ^{p}({t_{0}}/{2}+\tfrac 12)={t_{0}}/{2}$
, then
 $g_{\unicode{x3bb} _0}=-f_{\unicode{x3bb} _0}^{p}$
,
$g_{\unicode{x3bb} _0}=-f_{\unicode{x3bb} _0}^{p}$
,
 $U= P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{+} )$
, and
$U= P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{+} )$
, and
 $V= P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+} )$
for an N large,
$V= P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+} )$
for an N large,
 $\beta _{\unicode{x3bb} _0}=w^{t_{0}}_{0}(\unicode{x3bb} _0)$
, and
$\beta _{\unicode{x3bb} _0}=w^{t_{0}}_{0}(\unicode{x3bb} _0)$
, and
 $v_{\unicode{x3bb} _0}^{+}$
is the unique critical value.
$v_{\unicode{x3bb} _0}^{+}$
is the unique critical value.
Remark 6.1. In the above, we have assumed that
![]() $\unicode{x3bb} _0\notin \mathbb R^{+}$
. When
$\unicode{x3bb} _0\notin \mathbb R^{+}$
. When
![]() $\unicode{x3bb} _0\in \mathbb R^{+}$
, the regions
$\unicode{x3bb} _0\in \mathbb R^{+}$
, the regions
![]() $U, V$
will be taken as those constructed in the proof of Lemma 7.2 in [Reference Qiu, Wang and YinQWY12].
$U, V$
will be taken as those constructed in the proof of Lemma 7.2 in [Reference Qiu, Wang and YinQWY12].
In the following discussion, without loss of generality, we may assume that we are in case (1). Hence, we have the following Assumption 6.2.
Assumption 6.2. Suppose that
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
$\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\unicode{x3bb} _{0} \in \overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0}$
, and
$\unicode{x3bb} _{0} \in \overline {\mathscr {R}^{t_{0}}_{\mathscr {H}_{0}}} \cap \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}}} \cap \mathscr {F}_{0}$
, and
![]() $p|(k-1)$
is a positive integer such that
$p|(k-1)$
is a positive integer such that
![]() $\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}$
. Then:
$\tau ^{p}({t_{0}}/{2})={t_{0}}/{2}$
. Then:
-
(1) there exists N such that
 $g_{\unicode{x3bb} _0}=f_{\unicode{x3bb} _0}^p: P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{+} ) \to P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+} )$
is a quadratic-like map with unique critical value
$g_{\unicode{x3bb} _0}=f_{\unicode{x3bb} _0}^p: P_{\unicode{x3bb} _0}^{N}(v_{\unicode{x3bb} _0}^{+} ) \to P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+} )$
is a quadratic-like map with unique critical value
 $v_{\unicode{x3bb} _0}^{+}$
;
$v_{\unicode{x3bb} _0}^{+}$
; -
(2)
 $g_{\unicode{x3bb} _{0}}(w^{t_{0}}_{0}(\unicode{x3bb} _{0})) =w^{t_{0}}_{0}(\unicode{x3bb} _0)$
,
$g_{\unicode{x3bb} _{0}}(w^{t_{0}}_{0}(\unicode{x3bb} _{0})) =w^{t_{0}}_{0}(\unicode{x3bb} _0)$
,
 $g_{\unicode{x3bb} _{0}}'(w^{t_{0}}_{0}(\unicode{x3bb} _{0}))=1$
, and
$g_{\unicode{x3bb} _{0}}'(w^{t_{0}}_{0}(\unicode{x3bb} _{0}))=1$
, and
 $g_{\unicode{x3bb} _{0}}"(w^{t_{0}}_{0}(\unicode{x3bb} _{0})) \neq 0$
;
$g_{\unicode{x3bb} _{0}}"(w^{t_{0}}_{0}(\unicode{x3bb} _{0})) \neq 0$
; -
(3)
 $g_{\unicode{x3bb} _{0}}^{(k-1)/{p}}(w^{t_{1}}_{k}(\unicode{x3bb} _{0}) )=w^{t_{0}}_{0}(\unicode{x3bb} _{0})$
, where
$g_{\unicode{x3bb} _{0}}^{(k-1)/{p}}(w^{t_{1}}_{k}(\unicode{x3bb} _{0}) )=w^{t_{0}}_{0}(\unicode{x3bb} _{0})$
, where
 $w^{t_{0}}_{0}(\unicode{x3bb} _{0})$
is the landing point of ray
$w^{t_{0}}_{0}(\unicode{x3bb} _{0})$
is the landing point of ray
 $R_{\infty (\unicode{x3bb} _{0})}^{\theta _{0}(t_{0})}$
and
$R_{\infty (\unicode{x3bb} _{0})}^{\theta _{0}(t_{0})}$
and
 $w^{t_{1}}_{k}(\unicode{x3bb} _{0})$
is the landing point of ray
$w^{t_{1}}_{k}(\unicode{x3bb} _{0})$
is the landing point of ray
 $R^{\theta _{k}(t_{1})}_{z^{i}_{k}(\unicode{x3bb} _0)}$
.
$R^{\theta _{k}(t_{1})}_{z^{i}_{k}(\unicode{x3bb} _0)}$
.
6.2 Rational family with parabolic implosion
The original parabolic implosion theory is established by Douady and Lavaurs [Reference LavaursLav89], see [Reference Douady and HubbardDH84]. This theory is further developed by Shishikura, see [Reference ShishikuraShi98, Reference Shishikura and LeiShi00]. Here, we use the terminology and results given in [Reference Lei and LeiLei00, Reference Shishikura and LeiShi00].
Let
![]() $\Delta _{\rho ,\theta }$
be a bounded connected open set with
$\Delta _{\rho ,\theta }$
be a bounded connected open set with
![]() $0$
on its boundary, and
$0$
on its boundary, and
![]() $F: \overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb {C}} \rightarrow \overline {\mathbb {C}}$
,
$F: \overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb {C}} \rightarrow \overline {\mathbb {C}}$
,
![]() $(u,z)\mapsto F_u(z)$
be a map satisfying the following conditions.
$(u,z)\mapsto F_u(z)$
be a map satisfying the following conditions.
-
(1)
 $F: (u,z) \mapsto F_{u}(z)$
is continuous on
$F: (u,z) \mapsto F_{u}(z)$
is continuous on
 $\overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb C}$
, holomorphic on
$\overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb C}$
, holomorphic on
 $\Delta _{\rho ,\theta }\times \overline {\mathbb {C}}$
, and
$\Delta _{\rho ,\theta }\times \overline {\mathbb {C}}$
, and
 $F_u(z)$
is a rational map for each
$F_u(z)$
is a rational map for each
 $u\in \overline {\Delta _{\rho ,\theta }}$
.
$u\in \overline {\Delta _{\rho ,\theta }}$
. -
(2)
 $F_{u}(z)=m(u)z+O(z^{2})$
as
$F_{u}(z)=m(u)z+O(z^{2})$
as
 $z\to 0$
with
$z\to 0$
with
 $m(0)=1$
,
$m(0)=1$
,
 $F_{0}"(0) \neq 0$
, and
$F_{0}"(0) \neq 0$
, and
 $F_{0}$
has a unique simple critical value
$F_{0}$
has a unique simple critical value
 $v_{0}$
contained in the parabolic basin of
$v_{0}$
contained in the parabolic basin of
 $0$
.
$0$
. -
(3)
 $\sigma (u):=({m(u)-1})/{2\pi i}$
maps
$\sigma (u):=({m(u)-1})/{2\pi i}$
maps
 $\Delta _{\rho ,\theta }$
univalently onto
$\Delta _{\rho ,\theta }$
univalently onto
 $ \{ z \in \mathbb {C} : |z|<\rho , |\arg z|< \theta \}$
with
$ \{ z \in \mathbb {C} : |z|<\rho , |\arg z|< \theta \}$
with
 $\rho>0$
small and
$\rho>0$
small and
 $\theta \in (0, \pi )$
.
$\theta \in (0, \pi )$
.
By equation (2),
![]() $F_{u}$
has two fixed points
$F_{u}$
has two fixed points
![]() $0$
and
$0$
and
![]() $q(u)$
when
$q(u)$
when
![]() $u\in \overline {\Delta _{\rho ,\theta }}\setminus \!\{0\}$
. The parabolic implosion phenomenon for such a family
$u\in \overline {\Delta _{\rho ,\theta }}\setminus \!\{0\}$
. The parabolic implosion phenomenon for such a family
![]() $F_u$
was given as the Douday–Lavaurs–Shishikura theorem (see Theorem 2.1 in [Reference Lei and LeiLei00]). Since we need only to use the attracting part of Theorem 2.1 in [Reference Lei and LeiLei00], we translate it to the following Theorem 6.3. Set
$F_u$
was given as the Douday–Lavaurs–Shishikura theorem (see Theorem 2.1 in [Reference Lei and LeiLei00]). Since we need only to use the attracting part of Theorem 2.1 in [Reference Lei and LeiLei00], we translate it to the following Theorem 6.3. Set
![]() $S_M =\{z\in \mathbb {C}: 0<\Re (z)<M+1\}$
for any
$S_M =\{z\in \mathbb {C}: 0<\Re (z)<M+1\}$
for any
![]() $M\in \mathbb N$
.
$M\in \mathbb N$
.
Theorem 6.3. (Douady–Lavaurs–Shishikura)
Let
![]() $F: \overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb C} \rightarrow \overline {\mathbb {C}}$
,
$F: \overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb C} \rightarrow \overline {\mathbb {C}}$
,
![]() $(u,z)\mapsto F_u(z)$
satisfy the conditions given above. For any given
$(u,z)\mapsto F_u(z)$
satisfy the conditions given above. For any given
![]() $M\in \mathbb N$
large, when
$M\in \mathbb N$
large, when
![]() $\rho $
is small enough, there exists a continuous map
$\rho $
is small enough, there exists a continuous map
![]() $\Psi : \overline {\Delta _{\rho , \theta }} \times {S}_{M} \rightarrow \mathbb {C}$
,
$\Psi : \overline {\Delta _{\rho , \theta }} \times {S}_{M} \rightarrow \mathbb {C}$
,
![]() $(u,z)\mapsto \Psi _u(z)$
satisfying the following properties (see Figure 10).
$(u,z)\mapsto \Psi _u(z)$
satisfying the following properties (see Figure 10).
-
(1) For
 $u=0$
,
$u=0$
,
 $\Psi _{0}:{S}_{M}\to \Psi _0({S}_M)\subset \Omega _0$
is a univalent map where
$\Psi _{0}:{S}_{M}\to \Psi _0({S}_M)\subset \Omega _0$
is a univalent map where
 $\Omega _0$
is the attracting petal of
$\Omega _0$
is the attracting petal of
 $F_0$
with the parabolic fixed point
$F_0$
with the parabolic fixed point
 $0$
on its boundary, and
$0$
on its boundary, and
 $\Psi _{0}^{-1}$
is the restriction of the usual Fatou coordinate
$\Psi _{0}^{-1}$
is the restriction of the usual Fatou coordinate
 $\varphi _0:\Omega _0\to \{z:\Re (z)>0\}$
.
$\varphi _0:\Omega _0\to \{z:\Re (z)>0\}$
. -
(2) For
 $u \in \overline {\Delta _{\rho , \theta }} \setminus \! \{0\}$
,
$u \in \overline {\Delta _{\rho , \theta }} \setminus \! \{0\}$
,
 $\Psi _u: {S}_M\to \mathbb C$
is a univalent map such that
$\Psi _u: {S}_M\to \mathbb C$
is a univalent map such that
 $\Psi _{u}({S}_{M})$
is a Jordan region containing two fixed points
$\Psi _{u}({S}_{M})$
is a Jordan region containing two fixed points
 $0$
and
$0$
and
 $q(u)$
of
$q(u)$
of
 $F_{u}$
on its boundary.
$F_{u}$
on its boundary. -
(3) Whenever
 $z, z+1\in {S}_M$
, Furthermore,
$z, z+1\in {S}_M$
, Furthermore, $$ \begin{align*} \Psi_{u}(z+1)=F_{u}(\Psi_{u}(z)). \end{align*} $$
$$ \begin{align*} \Psi_{u}(z+1)=F_{u}(\Psi_{u}(z)). \end{align*} $$
 $\Psi _{u}(S_{0})$
contains the critical value
$\Psi _{u}(S_{0})$
contains the critical value
 $v(u)$
of
$v(u)$
of
 $F_u$
with
$F_u$
with
 $v(0)=v_{0}$
.
$v(0)=v_{0}$
.

Figure 10 Illustration of Theorem 6.3.
By this theorem, we call the map F or the family
![]() $F_{u}$
the rational family with parabolic implosion (RFPI).
$F_{u}$
the rational family with parabolic implosion (RFPI).
Remark 6.2. From equation (3),
![]() $\Psi _u(S_0)$
is a fundamental region of
$\Psi _u(S_0)$
is a fundamental region of
![]() $F_u$
, and
$F_u$
, and
![]() $F_u^m$
is well defined and univalent on
$F_u^m$
is well defined and univalent on
![]() $\Psi _u(S_0)$
for any
$\Psi _u(S_0)$
for any
![]() $1\leq m\leq M$
.
$1\leq m\leq M$
.
6.3 Application to McMullen family
Set
![]() $g_{\unicode{x3bb} }:=f_{\unicode{x3bb} }^p$
, where p is given in Assumption 6.2. Consider the equation
$g_{\unicode{x3bb} }:=f_{\unicode{x3bb} }^p$
, where p is given in Assumption 6.2. Consider the equation
![]() $g_{\unicode{x3bb} }(z)-z=0$
. By part (2) of Assumption 6.2, the fixed points of
$g_{\unicode{x3bb} }(z)-z=0$
. By part (2) of Assumption 6.2, the fixed points of
![]() $g_{\unicode{x3bb} }(z)$
for
$g_{\unicode{x3bb} }(z)$
for
![]() $(\unicode{x3bb} ,z)$
near
$(\unicode{x3bb} ,z)$
near
![]() $(\unicode{x3bb} _0, w_0^{t_0}(\unicode{x3bb} _0))$
can be uniformized by setting
$(\unicode{x3bb} _0, w_0^{t_0}(\unicode{x3bb} _0))$
can be uniformized by setting
![]() $\unicode{x3bb} =\unicode{x3bb} _0+u^2$
. That is, there exists
$\unicode{x3bb} =\unicode{x3bb} _0+u^2$
. That is, there exists
![]() $r>0$
small enough such that
$r>0$
small enough such that
![]() $\mathbb D(\unicode{x3bb} _0,r)\subset \mathscr {U}^{*}$
(
$\mathbb D(\unicode{x3bb} _0,r)\subset \mathscr {U}^{*}$
(
![]() $\mathscr {U}^{*}$
is defined in Proposition 5.2), a local change of coordinates
$\mathscr {U}^{*}$
is defined in Proposition 5.2), a local change of coordinates
![]() $\unicode{x3bb} : \mathbb {D}(0,\sqrt {r}) \to \mathbb {D}(\unicode{x3bb} _0,r)$
given by
$\unicode{x3bb} : \mathbb {D}(0,\sqrt {r}) \to \mathbb {D}(\unicode{x3bb} _0,r)$
given by
![]() $u \mapsto \unicode{x3bb} _{0}+u^{2}$
, and a holomorphic function
$u \mapsto \unicode{x3bb} _{0}+u^{2}$
, and a holomorphic function
![]() $p: \mathbb {D}(0,\sqrt {r}) \to \mathbb {C}$
such that
$p: \mathbb {D}(0,\sqrt {r}) \to \mathbb {C}$
such that
![]() $p(u)$
and
$p(u)$
and
![]() $p(-u)$
are the two local fixed points of
$p(-u)$
are the two local fixed points of
![]() $g_{\unicode{x3bb} _{0}+u^{2}}$
satisfying
$g_{\unicode{x3bb} _{0}+u^{2}}$
satisfying
![]() $p(u)=w^{t_{0}}_{0}(\unicode{x3bb} _{0}+u^{2})$
for
$p(u)=w^{t_{0}}_{0}(\unicode{x3bb} _{0}+u^{2})$
for
![]() $\unicode{x3bb} _{0}+u^{2} \in \mathbb {D}(0,\sqrt {r}) \setminus \mathscr {H}_{0}$
. Let
$\unicode{x3bb} _{0}+u^{2} \in \mathbb {D}(0,\sqrt {r}) \setminus \mathscr {H}_{0}$
. Let
![]() $m: \mathbb {D}(0,\sqrt {r}) \to \mathbb {C}, u \mapsto g_{\unicode{x3bb} _{0}+u^{2}}'(p(u))$
be the multiplier of the fixed point
$m: \mathbb {D}(0,\sqrt {r}) \to \mathbb {C}, u \mapsto g_{\unicode{x3bb} _{0}+u^{2}}'(p(u))$
be the multiplier of the fixed point
![]() $p(u)$
. Then,
$p(u)$
. Then,
![]() $m(u)$
is holomorphic on
$m(u)$
is holomorphic on
![]() $\mathbb {D}(0,\sqrt {r})$
and
$\mathbb {D}(0,\sqrt {r})$
and
![]() $m(0)=1$
. It is evident that
$m(0)=1$
. It is evident that
Let
![]() $T_{u}(z):=z-p(u)$
and
$T_{u}(z):=z-p(u)$
and
![]() $F_{u}(\omega ):=T_{u} \circ g_{\unicode{x3bb} _{0}+u^{2}} \circ T_{u}^{-1}(\omega )$
. Then, equation (6.3) becomes
$F_{u}(\omega ):=T_{u} \circ g_{\unicode{x3bb} _{0}+u^{2}} \circ T_{u}^{-1}(\omega )$
. Then, equation (6.3) becomes
Remark 6.3. It is obvious that another fixed point
![]() $p(-u)$
of
$p(-u)$
of
![]() $g_{\unicode{x3bb} _{0}+u^{2}}$
has the multiplier
$g_{\unicode{x3bb} _{0}+u^{2}}$
has the multiplier
![]() $m(-u)$
. So, except the fixed point
$m(-u)$
. So, except the fixed point
![]() $0$
, the other fixed point of
$0$
, the other fixed point of
![]() $F_u$
is
$F_u$
is
![]() $q(u)=p(-u)-p(u)$
with the multiplier
$q(u)=p(-u)-p(u)$
with the multiplier
![]() $m(-u)$
when
$m(-u)$
when
![]() $u\neq 0$
.
$u\neq 0$
.
Let
![]() $v(u):=T_{u}(v^{+}_{\unicode{x3bb} _{0}+u^{2}})$
be the critical value of
$v(u):=T_{u}(v^{+}_{\unicode{x3bb} _{0}+u^{2}})$
be the critical value of
![]() $F_u(\omega )$
. Let
$F_u(\omega )$
. Let
![]() $U_{0}=T_{0}(P_{\unicode{x3bb} _0}^N(v_{\unicode{x3bb} _0}^{+}))$
and
$U_{0}=T_{0}(P_{\unicode{x3bb} _0}^N(v_{\unicode{x3bb} _0}^{+}))$
and
![]() $V_{0}:=T_{0}(P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+}))$
. Then by equation (1) of Assumption 6.2,
$V_{0}:=T_{0}(P_{\unicode{x3bb} _0}^{N-p}(v_{\unicode{x3bb} _0}^{+}))$
. Then by equation (1) of Assumption 6.2,
![]() $F_0: U_{0}\to V_{0}$
is a quadratic-like map with the unique critical value
$F_0: U_{0}\to V_{0}$
is a quadratic-like map with the unique critical value
![]() $v(0)\in U_{0}$
, which is obviously contained in the parabolic basin of
$v(0)\in U_{0}$
, which is obviously contained in the parabolic basin of
![]() $0$
. When
$0$
. When
![]() $r>0$
is small enough, then by the continuity of
$r>0$
is small enough, then by the continuity of
![]() $F_u$
with respect to
$F_u$
with respect to
![]() $u\in \mathbb D(0,\sqrt {r})$
, it is easy to find a simply connected region
$u\in \mathbb D(0,\sqrt {r})$
, it is easy to find a simply connected region
![]() $U_{u}\subset U_{0}$
such that
$U_{u}\subset U_{0}$
such that
![]() $F_u: U_{u}\to V_u:=F_u(U_{u})$
is also a quadratic-like map with the unique critical value
$F_u: U_{u}\to V_u:=F_u(U_{u})$
is also a quadratic-like map with the unique critical value
![]() $v(u)\in U_u$
. Furthermore
$v(u)\in U_u$
. Furthermore
![]() $U_{u} \to U_{0}$
as
$U_{u} \to U_{0}$
as
![]() $u \to 0$
in Hausdorff topology.
$u \to 0$
in Hausdorff topology.
Let
![]() $\Gamma _{\pm }:=\unicode{x3bb} ^{-1}( \mathscr {R}^{t_{1}}_{\mathscr {U}} )$
denote the two pre-images of
$\Gamma _{\pm }:=\unicode{x3bb} ^{-1}( \mathscr {R}^{t_{1}}_{\mathscr {U}} )$
denote the two pre-images of
![]() $\mathscr {R}^{t_{1}}_{\mathscr {U}}$
in the u-plane which can be parameterized by
$\mathscr {R}^{t_{1}}_{\mathscr {U}}$
in the u-plane which can be parameterized by
![]() $\Gamma _{\pm }(s):=\unicode{x3bb} ^{-1}( \Phi _{\mathscr {U}}(se^{2\pi i t_{1}}) )$
. Obviously,
$\Gamma _{\pm }(s):=\unicode{x3bb} ^{-1}( \Phi _{\mathscr {U}}(se^{2\pi i t_{1}}) )$
. Obviously,
![]() $\Gamma _{\pm }(s)\to 0$
as
$\Gamma _{\pm }(s)\to 0$
as
![]() $s\to 1$
.
$s\to 1$
.
Proposition 6.4. For any
![]() $\theta \in (0,\pi /2)$
, there exist
$\theta \in (0,\pi /2)$
, there exist
![]() $\rho>0$
and
$\rho>0$
and
![]() $\Delta _{\rho ,\theta } \subset \mathbb {D}(0,\sqrt {r})$
which is mapped univalently onto
$\Delta _{\rho ,\theta } \subset \mathbb {D}(0,\sqrt {r})$
which is mapped univalently onto
![]() $ \{ z \in \mathbb {C} : |z|<\rho , |\arg z|< \theta \}$
by
$ \{ z \in \mathbb {C} : |z|<\rho , |\arg z|< \theta \}$
by
![]() $\sigma =(m-1)/(2\pi i)$
such that
$\sigma =(m-1)/(2\pi i)$
such that
![]() $\Gamma _{+}(s) \in \Delta _{\rho ,\theta }$
or
$\Gamma _{+}(s) \in \Delta _{\rho ,\theta }$
or
![]() $\Gamma _{-}(s) \in \Delta _{\rho ,\theta }$
for s sufficiently close to
$\Gamma _{-}(s) \in \Delta _{\rho ,\theta }$
for s sufficiently close to
![]() $1$
.
$1$
.
The proof of Proposition 6.4 will be given in the next subsection. By Proposition 6.4 and the discussion above,
![]() $F: \overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb {C}} \to \overline {\mathbb {C}}$
defined by
$F: \overline {\Delta _{\rho ,\theta }} \times \overline {\mathbb {C}} \to \overline {\mathbb {C}}$
defined by
![]() $F(u,z):=F_{u}(z)$
is an RFPI.
$F(u,z):=F_{u}(z)$
is an RFPI.
Proposition 6.5. For any escape component
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
with
$\mathscr {U} \subset \mathscr {H}_{k}$
with
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\overline {\mathscr {U}}\cap \overline {\mathscr {H}_{0}}=\emptyset $
.
$\overline {\mathscr {U}}\cap \overline {\mathscr {H}_{0}}=\emptyset $
.
Proof. If the proposition is not true, we may assume Assumption 6.2 holds. By Proposition 6.4, without loss of generality, let us assume
![]() $\Gamma _{+}(s) \in \Delta _{\rho ,\theta }$
for
$\Gamma _{+}(s) \in \Delta _{\rho ,\theta }$
for
![]() $s(>1)$
close to
$s(>1)$
close to
![]() $1$
.
$1$
.
Let
![]() $R_{u}:=T_{u}(R_{\infty (\unicode{x3bb} _{0})}^{\theta _{0}(t_{0})} )$
be parameterized by
$R_{u}:=T_{u}(R_{\infty (\unicode{x3bb} _{0})}^{\theta _{0}(t_{0})} )$
be parameterized by
![]() $R_{u}(s):=T_{u}( \phi _{\infty (\unicode{x3bb} )}^{-1}(se^{2\pi i \theta _{0}(t_{0})}) )$
and
$R_{u}(s):=T_{u}( \phi _{\infty (\unicode{x3bb} )}^{-1}(se^{2\pi i \theta _{0}(t_{0})}) )$
and
![]() $\tilde {R}_{u}:=T_{u} ( R^{\theta _{k}(t_{1})}_{z^{i}_{k}(\unicode{x3bb} _0+u^2)} )$
be parameterized by
$\tilde {R}_{u}:=T_{u} ( R^{\theta _{k}(t_{1})}_{z^{i}_{k}(\unicode{x3bb} _0+u^2)} )$
be parameterized by
![]() $\tilde {R}_{u}(s):=T_{u}( \phi _{z^{i}_{k}(\unicode{x3bb} _0+u^2)}^{-1}(se^{2\pi i \theta _{k}(t_{1})}) )$
. Then we have
$\tilde {R}_{u}(s):=T_{u}( \phi _{z^{i}_{k}(\unicode{x3bb} _0+u^2)}^{-1}(se^{2\pi i \theta _{k}(t_{1})}) )$
. Then we have
![]() $F_u(R_u)=R_u$
and
$F_u(R_u)=R_u$
and
![]() $F_{u}^{(k-1)/{p}}(\tilde {R}_{u})=R_{u}$
by equation (3) of Assumption 6.2. Note that by Corollary 4.5, the critical value
$F_{u}^{(k-1)/{p}}(\tilde {R}_{u})=R_{u}$
by equation (3) of Assumption 6.2. Note that by Corollary 4.5, the critical value
![]() $v(u)= \tilde {R}_{u}(\rho _{k}(s))$
for
$v(u)= \tilde {R}_{u}(\rho _{k}(s))$
for
![]() $u=\Gamma _{+}(s) \in \Delta _{\rho ,\theta }$
is close to
$u=\Gamma _{+}(s) \in \Delta _{\rho ,\theta }$
is close to
![]() $0$
. Hence,
$0$
. Hence,
![]() $F^{(k-1)/{p}}_{u}(v(u)) = R_{u}( s_{0} )\in R_u$
for some
$F^{(k-1)/{p}}_{u}(v(u)) = R_{u}( s_{0} )\in R_u$
for some
![]() $s_0>1$
. Take
$s_0>1$
. Take
![]() $M=(k-1)/p$
and
$M=(k-1)/p$
and
![]() $\Psi : \overline {\Delta _{\rho ,\theta }}\times S_M\to \mathbb C$
, as given in Theorem 6.3. Then by part (3) of Theorem 6.3 (see Remark 6.2),
$\Psi : \overline {\Delta _{\rho ,\theta }}\times S_M\to \mathbb C$
, as given in Theorem 6.3. Then by part (3) of Theorem 6.3 (see Remark 6.2),
![]() $v(u) \in \Psi _{u}(S_{0})$
and
$v(u) \in \Psi _{u}(S_{0})$
and
![]() $R_u(s_0)=F^{M}_{u}(v(u)) \in \Psi _{u}(S_{M} )$
.
$R_u(s_0)=F^{M}_{u}(v(u)) \in \Psi _{u}(S_{M} )$
.
However, in Remark 2.1, it is pointed out that
![]() $R_{u}$
can be extended continuously to
$R_{u}$
can be extended continuously to
![]() $R_{u}(\!\sqrt [n^{M}]{s_{0}} )$
such that
$R_{u}(\!\sqrt [n^{M}]{s_{0}} )$
such that
![]() $F^{M}_{u}( R_{u}(\!\sqrt [n^{M}]{s_{0}} ) )=R_{u}( s_{0} )$
. The invariance and continuity of
$F^{M}_{u}( R_{u}(\!\sqrt [n^{M}]{s_{0}} ) )=R_{u}( s_{0} )$
. The invariance and continuity of
![]() $R_u$
ensure that
$R_u$
ensure that
![]() $R_{u}(\!\sqrt [n^{M}]{s_{0}} )\in \Psi _{u}(S_{0})$
. By Remark 6.2,
$R_{u}(\!\sqrt [n^{M}]{s_{0}} )\in \Psi _{u}(S_{0})$
. By Remark 6.2,
![]() $F^{M}_{u}$
is univalent on
$F^{M}_{u}$
is univalent on
![]() $\Psi _{u}(S_{0})$
. Hence,
$\Psi _{u}(S_{0})$
. Hence,
![]() $F_u^M(v(u))=F_u^M(R_u(\!\sqrt [n^M]{s_0}))=R_u(s_0)$
implies that
$F_u^M(v(u))=F_u^M(R_u(\!\sqrt [n^M]{s_0}))=R_u(s_0)$
implies that
![]() $v(u)=R_{u}(\!\sqrt [n^{M}]{s_{0}} )\in R_u$
. This contradicts with
$v(u)=R_{u}(\!\sqrt [n^{M}]{s_{0}} )\in R_u$
. This contradicts with
![]() $v(u)=\tilde {R}_{u}(\rho _{k}(s)) \in \tilde {R}_{u}$
, where
$v(u)=\tilde {R}_{u}(\rho _{k}(s)) \in \tilde {R}_{u}$
, where
![]() $\rho _k$
is defined in equation (4.8) (see Figure 11).
$\rho _k$
is defined in equation (4.8) (see Figure 11).

Figure 11 Illustration for the proof of Proposition 6.5.
6.4 Proof of Proposition 6.4
Let
![]() $X_{\rho ,\theta }:= \{|z-1|<2\pi \rho : \vert \arg (z-1)\vert \leq {\pi }/{2}-\theta \} $
and
$X_{\rho ,\theta }:= \{|z-1|<2\pi \rho : \vert \arg (z-1)\vert \leq {\pi }/{2}-\theta \} $
and
![]() $Y^{\pm }_{\rho ,\theta }:=\{z \in \mathbb {H}_{\pm }: |z-1|<2\pi \rho \} \setminus (-X_{\rho ,\theta } \cup X_{\rho ,\theta } )$
. By part (3) of the definition of RFPI, it suffices to show that either
$Y^{\pm }_{\rho ,\theta }:=\{z \in \mathbb {H}_{\pm }: |z-1|<2\pi \rho \} \setminus (-X_{\rho ,\theta } \cup X_{\rho ,\theta } )$
. By part (3) of the definition of RFPI, it suffices to show that either
![]() $m(\Gamma _{+}(s)) \in Y^{+}_{\rho ,\theta }$
or
$m(\Gamma _{+}(s)) \in Y^{+}_{\rho ,\theta }$
or
![]() $m(\Gamma _{-}(s)) \in Y^{+}_{\rho ,\theta }$
for s large. Recall that by the conjugacy under affine transformation
$m(\Gamma _{-}(s)) \in Y^{+}_{\rho ,\theta }$
for s large. Recall that by the conjugacy under affine transformation
![]() $T_{u}(z)=z-p(u)$
,
$T_{u}(z)=z-p(u)$
,
![]() $g_{\unicode{x3bb} _{0}+u^{2}}$
is conjugated to
$g_{\unicode{x3bb} _{0}+u^{2}}$
is conjugated to
Since the multiplier
![]() $m(u)$
is a non-constant holomorphic function in
$m(u)$
is a non-constant holomorphic function in
![]() $\mathbb D(0,\sqrt {r})$
and
$\mathbb D(0,\sqrt {r})$
and
![]() $m(0)=1$
,
$m(0)=1$
,
![]() $m(u)$
has the following expansion:
$m(u)$
has the following expansion:
where
![]() $\ell $
is a positive integer and
$\ell $
is a positive integer and
![]() $a\neq 0$
.
$a\neq 0$
.
Lemma 6.6.
![]() $\ell $
is an odd number.
$\ell $
is an odd number.
Proof. It is known that for
![]() $u\in \mathbb D(0,\sqrt {r})$
with
$u\in \mathbb D(0,\sqrt {r})$
with
![]() $r>0$
small,
$r>0$
small,
![]() $F_u: U_{0}\to V_u:=F_u(U_{0})$
is a quadratic-like map with the unique critical value
$F_u: U_{0}\to V_u:=F_u(U_{0})$
is a quadratic-like map with the unique critical value
![]() $v(u)\in U_0$
. From Remark 6.3,
$v(u)\in U_0$
. From Remark 6.3,
![]() $F_u$
has two fixed points
$F_u$
has two fixed points
![]() $0$
and
$0$
and
![]() $q(u)=p(-u)-p(u)$
contained in
$q(u)=p(-u)-p(u)$
contained in
![]() $U_0$
with the multipliers
$U_0$
with the multipliers
![]() $m(u)$
and
$m(u)$
and
![]() $m(-u)$
, respectively. Suppose
$m(-u)$
, respectively. Suppose
![]() $\ell $
is even, then from equation (6.5), we have
$\ell $
is even, then from equation (6.5), we have
![]() $m(u)-m(-u)=o(u^{\ell })$
, which implies that
$m(u)-m(-u)=o(u^{\ell })$
, which implies that
![]() $|m(u)-m(-u)|<|m(u)-1|$
for u small since
$|m(u)-m(-u)|<|m(u)-1|$
for u small since
![]() $m(u)-1\sim au^{\ell }$
. It follows that
$m(u)-1\sim au^{\ell }$
. It follows that
 $$ \begin{align} \begin{aligned} |m(-u)|&\leq|m(u)-m(-u)|+|m(u)| \\[4pt] &<|1-m(u)|+|m(u)| \\[4pt] &=1-|m(u)|+|m(u)|=1. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |m(-u)|&\leq|m(u)-m(-u)|+|m(u)| \\[4pt] &<|1-m(u)|+|m(u)| \\[4pt] &=1-|m(u)|+|m(u)|=1. \end{aligned} \end{align} $$
Hence,
![]() $q(u)=p(-u)-p(u)$
is an attracting fixed point of
$q(u)=p(-u)-p(u)$
is an attracting fixed point of
![]() $F_{u}$
.
$F_{u}$
.
However, by the open mapping theorem, we can find u close to
![]() $0$
and
$0$
and
![]() $q(u) \in U_{u}$
such that
$q(u) \in U_{u}$
such that
![]() $|m(u)|<1$
. So
$|m(u)|<1$
. So
![]() $0$
is also an attracting fixed point of
$0$
is also an attracting fixed point of
![]() $F_u$
for such u. This is impossible since
$F_u$
for such u. This is impossible since
![]() $F_{u}$
is a quadratic-like map on
$F_{u}$
is a quadratic-like map on
![]() $U_{u}$
.
$U_{u}$
.
Lemma 6.7. For any
![]() $\theta \in (0,{\pi }/{2} )$
, if u is small and
$\theta \in (0,{\pi }/{2} )$
, if u is small and
![]() $|\arg (m(u)-1)|<{\pi }/{2}-\theta $
, then
$|\arg (m(u)-1)|<{\pi }/{2}-\theta $
, then
![]() $m(-u) \in \mathbb {D}$
.
$m(-u) \in \mathbb {D}$
.
Proof. By equation (6.5) and Lemma 6.6 (see Figure 12),
![]() $m(u)+m(-u)-2=o(u^{\ell })$
, and then
$m(u)+m(-u)-2=o(u^{\ell })$
, and then
for u small. Let
![]() $r(u):=|m(u)-2|$
and
$r(u):=|m(u)-2|$
and
![]() $\theta (u):=\arg (m(u)-1)$
. It follows that for u small,
$\theta (u):=\arg (m(u)-1)$
. It follows that for u small,
 $$ \begin{align*} |m(u)-1|&=\cos(\theta(u))-\sqrt{(r(u))^{2}-\sin^{2}(\theta(u))} \\ &=\cos(\theta(u))-\sqrt{(r(u)-1)^{2}+2(r(u)-1)+\cos^{2}(\theta(u))} \\ &=\cos(\theta(u))-\cos(\theta(u))\sqrt{1+\frac{2r(u)-2+(r(u)-1)^{2}}{\cos^{2}(\theta(u))} }\\ &=\cos(\theta(u))-\cos(\theta(u))\bigg(1+\frac{r(u)-1}{\cos^{2}(\theta(u))}+o(r(u)-1)\bigg) \\ &=\frac{1-r(u)}{\cos(\theta(u))}+o(r(u)-1). \end{align*} $$
$$ \begin{align*} |m(u)-1|&=\cos(\theta(u))-\sqrt{(r(u))^{2}-\sin^{2}(\theta(u))} \\ &=\cos(\theta(u))-\sqrt{(r(u)-1)^{2}+2(r(u)-1)+\cos^{2}(\theta(u))} \\ &=\cos(\theta(u))-\cos(\theta(u))\sqrt{1+\frac{2r(u)-2+(r(u)-1)^{2}}{\cos^{2}(\theta(u))} }\\ &=\cos(\theta(u))-\cos(\theta(u))\bigg(1+\frac{r(u)-1}{\cos^{2}(\theta(u))}+o(r(u)-1)\bigg) \\ &=\frac{1-r(u)}{\cos(\theta(u))}+o(r(u)-1). \end{align*} $$
Hence, for u small and
![]() $|\theta (u)| \leq {\pi }/{2}-\theta <{\pi }/{2}$
, we have
$|\theta (u)| \leq {\pi }/{2}-\theta <{\pi }/{2}$
, we have
Coupling it with equation (6.7) gives that
![]() $|m(u)+m(-u)-2|<1-|2-m(u)|$
for u small. Hence,
$|m(u)+m(-u)-2|<1-|2-m(u)|$
for u small. Hence,
 $$ \begin{align} \begin{aligned} |m(-u)|&\leq|m(u)+m(-u)-2|+|m(u)-2| \\ &<1-|2-m(u)|+|m(u)-2|=1.\\[-2.1pc] \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |m(-u)|&\leq|m(u)+m(-u)-2|+|m(u)-2| \\ &<1-|2-m(u)|+|m(u)-2|=1.\\[-2.1pc] \end{aligned} \end{align} $$

Figure 12 Illustration for the proof of Lemma 6.7.
Proposition 6.8. For any
![]() $\theta \in (0,{\pi }/{2} )$
and
$\theta \in (0,{\pi }/{2} )$
and
![]() $\rho>0$
, one of the following is true:
$\rho>0$
, one of the following is true:
-
•
 $m(\Gamma _{+}(s)) \in Y^{+}_{\rho ,\theta }$
for all
$m(\Gamma _{+}(s)) \in Y^{+}_{\rho ,\theta }$
for all
 $s>1$
sufficiently close to
$s>1$
sufficiently close to
 $1$
;
$1$
; -
•
 $m(\Gamma _{-}(s)) \in Y^{+}_{\rho ,\theta }$
for all
$m(\Gamma _{-}(s)) \in Y^{+}_{\rho ,\theta }$
for all
 $s>1$
sufficiently close to
$s>1$
sufficiently close to
 $1$
.
$1$
.
Proof. Fix any
![]() $\theta \in (0,{\pi }/{2})$
and
$\theta \in (0,{\pi }/{2})$
and
![]() $\rho>0$
. Since
$\rho>0$
. Since
![]() $\Gamma _{\pm }(s)\to 0$
and
$\Gamma _{\pm }(s)\to 0$
and
![]() $m(\Gamma _{\pm }(s)) \to 1$
as
$m(\Gamma _{\pm }(s)) \to 1$
as
![]() $s\to 1$
, we have
$s\to 1$
, we have
![]() $|m(\Gamma _{\pm }(s))-1|<\rho $
for
$|m(\Gamma _{\pm }(s))-1|<\rho $
for
![]() $s>1$
sufficiently close to
$s>1$
sufficiently close to
![]() $1$
. Since
$1$
. Since
![]() $f_{\unicode{x3bb} _{0}+u^{2}}$
is an escape map for
$f_{\unicode{x3bb} _{0}+u^{2}}$
is an escape map for
![]() $u=\Gamma _{\pm }(s)$
,
$u=\Gamma _{\pm }(s)$
,
![]() $F_{u}$
has no attracting fixed points in
$F_{u}$
has no attracting fixed points in
![]() $\mathbb C$
. Hence, it follows from Lemma 6.7,
$\mathbb C$
. Hence, it follows from Lemma 6.7,
![]() $m(\Gamma _{\pm }(s)) \in (Y^{+}_{\rho ,\theta } \cup Y^{-}_{\rho ,\theta } )$
for all s close to
$m(\Gamma _{\pm }(s)) \in (Y^{+}_{\rho ,\theta } \cup Y^{-}_{\rho ,\theta } )$
for all s close to
![]() $1$
.
$1$
.
Assume that
![]() $m(\Gamma _{-}(s)) \in Y^{-}_{\rho ,\theta }$
for an
$m(\Gamma _{-}(s)) \in Y^{-}_{\rho ,\theta }$
for an
![]() $s>1$
, then by continuity,
$s>1$
, then by continuity,
![]() $m(\Gamma _{-}(s))\in Y^{-}_{\rho ,\theta }$
for all
$m(\Gamma _{-}(s))\in Y^{-}_{\rho ,\theta }$
for all
![]() $s>1$
close to
$s>1$
close to
![]() $1$
. It follows that
$1$
. It follows that
Since
![]() $\Gamma _{+}(s)=-\Gamma _{-}(s)$
, we have from equations (6.7) and (6.10) that
$\Gamma _{+}(s)=-\Gamma _{-}(s)$
, we have from equations (6.7) and (6.10) that
It follows that
 $$ \begin{align} \begin{aligned} \Im(m(\Gamma_{+}(s)))&=\Im(2-m(\Gamma_{-}(s)))-\Im(2-m(\Gamma_{-}(s))-m(\Gamma_{+}(s)))\\ &=\Im(1-m(\Gamma_{-}(s)))-\Im(2-m(\Gamma_{-}(t))-m(\Gamma_{+}(s)))\\ &>\Im(1-m(\Gamma_{-}(s)))-|2-m(\Gamma_{-}(s))-m(\Gamma_{+}(s))|\\ &>\Im(1-m(\Gamma_{-}(s)))-\Im(1-m(\Gamma_{-}(s)))=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Im(m(\Gamma_{+}(s)))&=\Im(2-m(\Gamma_{-}(s)))-\Im(2-m(\Gamma_{-}(s))-m(\Gamma_{+}(s)))\\ &=\Im(1-m(\Gamma_{-}(s)))-\Im(2-m(\Gamma_{-}(t))-m(\Gamma_{+}(s)))\\ &>\Im(1-m(\Gamma_{-}(s)))-|2-m(\Gamma_{-}(s))-m(\Gamma_{+}(s))|\\ &>\Im(1-m(\Gamma_{-}(s)))-\Im(1-m(\Gamma_{-}(s)))=0. \end{aligned} \end{align} $$
Hence,
![]() $m(\Gamma _{+}(s)) \in Y^{+}_{\rho ,\theta }$
for all
$m(\Gamma _{+}(s)) \in Y^{+}_{\rho ,\theta }$
for all
![]() $s>1$
close to
$s>1$
close to
![]() $1$
.
$1$
.
Proof of Proposition 6.4
Take
![]() $\rho $
small enough. By Proposition 6.8, we can choose an inverse branch
$\rho $
small enough. By Proposition 6.8, we can choose an inverse branch
![]() $m^{-1}$
of m such that
$m^{-1}$
of m such that
![]() $m^{-1}(Y^{+}_{\rho ,\theta })$
contains
$m^{-1}(Y^{+}_{\rho ,\theta })$
contains
![]() $\Gamma _{+}(s)$
or
$\Gamma _{+}(s)$
or
![]() $\Gamma _{-}$
for s close to
$\Gamma _{-}$
for s close to
![]() $1$
. Let
$1$
. Let
![]() $\Delta _{\rho ,\theta }:=m^{-1}(Y^{+}_{\rho ,\theta }) \subset \mathbb {D}(0,\sqrt {r})$
. Then
$\Delta _{\rho ,\theta }:=m^{-1}(Y^{+}_{\rho ,\theta }) \subset \mathbb {D}(0,\sqrt {r})$
. Then
![]() $m: \Delta _{\rho ,\theta }\to Y_{\rho ,\theta }^{+}$
is a univalent map. According to the relation of
$m: \Delta _{\rho ,\theta }\to Y_{\rho ,\theta }^{+}$
is a univalent map. According to the relation of
![]() $\sigma $
and m, the result follows directly.
$\sigma $
and m, the result follows directly.
7 Proofs of Theorems 1.1 and 1.2
In this section, we will present the proofs of Theorems 1.2 and 1.1.
7.1 Closures of escape components are pairwise disjoint
In this subsection, we finish the proof of Theorem 1.2. By Proposition 6.5, it remains to show that the closures of escape components with order at least 2 are pairwise disjoint.
Lemma 7.1. There is no parameter
![]() $\unicode{x3bb} \in \partial {\mathscr {H}}$
such that
$\unicode{x3bb} \in \partial {\mathscr {H}}$
such that
![]() $f^{m}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }) \in C_{\unicode{x3bb} }$
with
$f^{m}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }) \in C_{\unicode{x3bb} }$
with
![]() $m \geq 0$
.
$m \geq 0$
.
Proof. Suppose that
![]() $\unicode{x3bb} $
satisfies
$\unicode{x3bb} $
satisfies
![]() $f^{m}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }) \in C_{\unicode{x3bb} }$
with
$f^{m}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} }) \in C_{\unicode{x3bb} }$
with
![]() $m \geq 0$
. Then, either
$m \geq 0$
. Then, either
![]() $f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{+}_{\unicode{x3bb} }$
or
$f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{+}_{\unicode{x3bb} }$
or
![]() $f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{-}_{\unicode{x3bb} }$
. In the first case, we get
$f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{-}_{\unicode{x3bb} }$
. In the first case, we get
![]() $f^{m}_{\unicode{x3bb} }(v_{\unicode{x3bb} }^{+} )$
is a periodic critical point, which is clearly impossible.
$f^{m}_{\unicode{x3bb} }(v_{\unicode{x3bb} }^{+} )$
is a periodic critical point, which is clearly impossible.
In the second case, recall the McMullen map satisfies
![]() $f^{m+1}_{\unicode{x3bb} }(-z)=-f^{m+1}_{\unicode{x3bb} }(z)$
or
$f^{m+1}_{\unicode{x3bb} }(-z)=-f^{m+1}_{\unicode{x3bb} }(z)$
or
![]() $f^{m+1}_{\unicode{x3bb} }(-z)=f^{m+1}_{\unicode{x3bb} }(z)$
depending on whether n is odd or even. So if n is odd, then
$f^{m+1}_{\unicode{x3bb} }(-z)=f^{m+1}_{\unicode{x3bb} }(z)$
depending on whether n is odd or even. So if n is odd, then
![]() $f^{m+1}_{\unicode{x3bb} }(v^{-}_{\unicode{x3bb} })=-f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{+}_{\unicode{x3bb} }$
. This means
$f^{m+1}_{\unicode{x3bb} }(v^{-}_{\unicode{x3bb} })=-f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{+}_{\unicode{x3bb} }$
. This means
![]() $f^{2m+2}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{+}_{\unicode{x3bb} }$
, which deduces to the first case. If n is even, then
$f^{2m+2}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{+}_{\unicode{x3bb} }$
, which deduces to the first case. If n is even, then
![]() $f^{m+1}_{\unicode{x3bb} }(v^{-}_{\unicode{x3bb} })=f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{-}_{\unicode{x3bb} }$
. So
$f^{m+1}_{\unicode{x3bb} }(v^{-}_{\unicode{x3bb} })=f^{m+1}_{\unicode{x3bb} }(v^{+}_{\unicode{x3bb} })=v^{-}_{\unicode{x3bb} }$
. So
![]() $f^{m}_{\unicode{x3bb} }(v^{-}_{\unicode{x3bb} })$
is a periodic critical point with period
$f^{m}_{\unicode{x3bb} }(v^{-}_{\unicode{x3bb} })$
is a periodic critical point with period
![]() $m+1$
, which is also clearly impossible.
$m+1$
, which is also clearly impossible.
Proposition 7.2. Suppose
![]() $\mathscr {U}_{1} \subset \mathscr {H}_{k_{1}}$
and
$\mathscr {U}_{1} \subset \mathscr {H}_{k_{1}}$
and
![]() $\mathscr {U}_{2} \subset \mathscr {H}_{k_{2}}$
are two distinct escape components with order
$\mathscr {U}_{2} \subset \mathscr {H}_{k_{2}}$
are two distinct escape components with order
![]() $k_{1}, k_{2} \geq 2$
, then
$k_{1}, k_{2} \geq 2$
, then
![]() $\partial {\mathscr {U}_{1}}\cap \partial {\mathscr {U}_{2}}=\emptyset $
.
$\partial {\mathscr {U}_{1}}\cap \partial {\mathscr {U}_{2}}=\emptyset $
.
Proof. Suppose
![]() $\unicode{x3bb} _{0}=\overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cap \overline {\mathscr {R}^{t_{2}}_{\mathscr {U}_{2}}}\in \partial {\mathscr {U}_{1}}\cap \partial {\mathscr {U}_{2}}$
. Without loss of generality, we may assume that
$\unicode{x3bb} _{0}=\overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cap \overline {\mathscr {R}^{t_{2}}_{\mathscr {U}_{2}}}\in \partial {\mathscr {U}_{1}}\cap \partial {\mathscr {U}_{2}}$
. Without loss of generality, we may assume that
![]() $\unicode{x3bb} _{0} \in \mathscr {F}_{0}$
. Let
$\unicode{x3bb} _{0} \in \mathscr {F}_{0}$
. Let
![]() $\mathscr {V}_j$
be a simply connected open subset of
$\mathscr {V}_j$
be a simply connected open subset of
![]() $\mathbb {C}^{*}\setminus \bigcup _{2\leq \ell \leq k_{j}-1}\Lambda _{\ell }$
containing
$\mathbb {C}^{*}\setminus \bigcup _{2\leq \ell \leq k_{j}-1}\Lambda _{\ell }$
containing
![]() $\unicode{x3bb} _{0}$
and
$\unicode{x3bb} _{0}$
and
![]() $\unicode{x3bb} _{\mathscr {U}_{j}}$
for
$\unicode{x3bb} _{\mathscr {U}_{j}}$
for
![]() $j=1,2$
. Here,
$j=1,2$
. Here,
![]() $\Lambda _{l}$
for
$\Lambda _{l}$
for
![]() $l \geq 2$
is defined in §4. By Lemma 4.1, there exist two root functions
$l \geq 2$
is defined in §4. By Lemma 4.1, there exist two root functions
![]() $z^{i_{j}}_{k_{j}}(\unicode{x3bb} )$
defined on
$z^{i_{j}}_{k_{j}}(\unicode{x3bb} )$
defined on
![]() $\mathscr V_j$
for
$\mathscr V_j$
for
![]() $j=1,2$
such that
$j=1,2$
such that
![]() $v^{+}_{\unicode{x3bb} _{\mathscr {U}_{j}}} =z^{i_{j}}_{k_{j}}(\unicode{x3bb} _{\mathscr {U}_{j}})$
. Then both
$v^{+}_{\unicode{x3bb} _{\mathscr {U}_{j}}} =z^{i_{j}}_{k_{j}}(\unicode{x3bb} _{\mathscr {U}_{j}})$
. Then both
![]() $z_{k_1}^{i_1}(\unicode{x3bb} _0)$
and
$z_{k_1}^{i_1}(\unicode{x3bb} _0)$
and
![]() $z_{k_2}^{i_2}(\unicode{x3bb} _0)$
are well defined.
$z_{k_2}^{i_2}(\unicode{x3bb} _0)$
are well defined.
Let
![]() $U^{i_{j}}_{k_{j}}(\unicode{x3bb} _0)$
denote the Fatou component containing
$U^{i_{j}}_{k_{j}}(\unicode{x3bb} _0)$
denote the Fatou component containing
![]() $z^{i_{j}}_{k_{j}}(\unicode{x3bb} _0)$
and let
$z^{i_{j}}_{k_{j}}(\unicode{x3bb} _0)$
and let
 $$ \begin{align*} w^{t_{j}}_{k_j}(\unicode{x3bb}_{0}):=\lim_{s \rightarrow 1} \phi^{-1}_{z^{i_{j}}_{k_{j}}(\unicode{x3bb}_{0})}(se^{2\pi i\, \theta_{k_{j}}(t_{j})}) \end{align*} $$
$$ \begin{align*} w^{t_{j}}_{k_j}(\unicode{x3bb}_{0}):=\lim_{s \rightarrow 1} \phi^{-1}_{z^{i_{j}}_{k_{j}}(\unicode{x3bb}_{0})}(se^{2\pi i\, \theta_{k_{j}}(t_{j})}) \end{align*} $$
for
![]() $j=1,2$
. That is,
$j=1,2$
. That is,
![]() $w^{t_{j}}_{k_j}(\unicode{x3bb} _{0})$
is the landing point of dynamical ray
$w^{t_{j}}_{k_j}(\unicode{x3bb} _{0})$
is the landing point of dynamical ray
 $R_{j}:=R_{z_{k_j}^{i_j}(\unicode{x3bb} _0)}^{t_j}$
in
$R_{j}:=R_{z_{k_j}^{i_j}(\unicode{x3bb} _0)}^{t_j}$
in
![]() $U_{k_j}^{i_j}(\unicode{x3bb} _0)$
. By Proposition 5.2,
$U_{k_j}^{i_j}(\unicode{x3bb} _0)$
. By Proposition 5.2,
![]() $ \{ w^{t_{1}}_{k_1}(\unicode{x3bb} _{0}), w^{t_{2}}_{k_2}(\unicode{x3bb} _{0}) \} \subset K^{+}_{\unicode{x3bb} _{0}}$
. By part (2) of Theorem 2.6,
$ \{ w^{t_{1}}_{k_1}(\unicode{x3bb} _{0}), w^{t_{2}}_{k_2}(\unicode{x3bb} _{0}) \} \subset K^{+}_{\unicode{x3bb} _{0}}$
. By part (2) of Theorem 2.6,
![]() $K^{+}_{\unicode{x3bb} _{0}}= \{v^{+}_{\unicode{x3bb} _{0}} \}$
. It follows that
$K^{+}_{\unicode{x3bb} _{0}}= \{v^{+}_{\unicode{x3bb} _{0}} \}$
. It follows that
![]() $w^{t_{1}}_{k_1}(\unicode{x3bb} _{0})=w^{t_{2}}_{k_2}(\unicode{x3bb} _{0}) =v^{+}_{\unicode{x3bb} _{0}}$
, which implies the dynamical rays
$w^{t_{1}}_{k_1}(\unicode{x3bb} _{0})=w^{t_{2}}_{k_2}(\unicode{x3bb} _{0}) =v^{+}_{\unicode{x3bb} _{0}}$
, which implies the dynamical rays
![]() $R_1$
and
$R_1$
and
![]() $R_2$
land together at the common point
$R_2$
land together at the common point
![]() $v_{\unicode{x3bb} _0}^+\in \partial U_{k_1}^{i_1}(\unicode{x3bb} _0)\cap \partial U_{k_2}^{i_2}(\unicode{x3bb} _0)$
.
$v_{\unicode{x3bb} _0}^+\in \partial U_{k_1}^{i_1}(\unicode{x3bb} _0)\cap \partial U_{k_2}^{i_2}(\unicode{x3bb} _0)$
.
Suppose
![]() $z^{i_{1}}_{k_{1}}(\unicode{x3bb} _{0}) \neq z^{i_{2}}_{k_{2}}(\unicode{x3bb} _{0})$
. Notice that both
$z^{i_{1}}_{k_{1}}(\unicode{x3bb} _{0}) \neq z^{i_{2}}_{k_{2}}(\unicode{x3bb} _{0})$
. Notice that both
![]() $U_{k_1}^{i_1}(\unicode{x3bb} _0)$
and
$U_{k_1}^{i_1}(\unicode{x3bb} _0)$
and
![]() $U_{k_2}^{i_2}(\unicode{x3bb} _0)$
will be mapped eventually to the Fatou component
$U_{k_2}^{i_2}(\unicode{x3bb} _0)$
will be mapped eventually to the Fatou component
![]() $B_{\unicode{x3bb} _0}$
, and
$B_{\unicode{x3bb} _0}$
, and
![]() $B_{\unicode{x3bb} _0}$
is invariant. We get that there exists
$B_{\unicode{x3bb} _0}$
is invariant. We get that there exists
![]() $m>0$
such that
$m>0$
such that
![]() $f_{\unicode{x3bb} _0}^m(U_{k_1}^{i_1}(\unicode{x3bb} _0))\neq f_{\unicode{x3bb} _0}^m(U_{k_2}^{i_2}(\unicode{x3bb} _0))$
, but
$f_{\unicode{x3bb} _0}^m(U_{k_1}^{i_1}(\unicode{x3bb} _0))\neq f_{\unicode{x3bb} _0}^m(U_{k_2}^{i_2}(\unicode{x3bb} _0))$
, but
![]() $f_{\unicode{x3bb} _0}^{m+1}(U_{k_1}^{i_1}(\unicode{x3bb} _0)) = f_{\unicode{x3bb} _0}^{m+1}(U_{k_2}^{i_2}(\unicode{x3bb} _0))$
. (In fact, if
$f_{\unicode{x3bb} _0}^{m+1}(U_{k_1}^{i_1}(\unicode{x3bb} _0)) = f_{\unicode{x3bb} _0}^{m+1}(U_{k_2}^{i_2}(\unicode{x3bb} _0))$
. (In fact, if
![]() $k_1\neq k_2$
, then
$k_1\neq k_2$
, then
![]() $m=\max \{k_1,k_2\}-2$
; if
$m=\max \{k_1,k_2\}-2$
; if
![]() $k_1=k_2$
, then
$k_1=k_2$
, then
![]() $m < k_1-2$
.) Thus,
$m < k_1-2$
.) Thus,
![]() $f_{\unicode{x3bb} _0}^m(R_1)$
and
$f_{\unicode{x3bb} _0}^m(R_1)$
and
![]() $f_{\unicode{x3bb} _0}^m(R_2)$
are two different dynamical rays which land together at
$f_{\unicode{x3bb} _0}^m(R_2)$
are two different dynamical rays which land together at
![]() $f_{\unicode{x3bb} _0}^m(v_{\unicode{x3bb} _0}^+)$
, but
$f_{\unicode{x3bb} _0}^m(v_{\unicode{x3bb} _0}^+)$
, but
![]() $f_{\unicode{x3bb} _0}^{m+1}(R_1)=f_{\unicode{x3bb} _0}^{m+1}(R_2)$
is a dynamical ray landing on
$f_{\unicode{x3bb} _0}^{m+1}(R_1)=f_{\unicode{x3bb} _0}^{m+1}(R_2)$
is a dynamical ray landing on
![]() $f_{\unicode{x3bb} _0}^{m+1}(v_{\unicode{x3bb} _0}^+)$
since the Fatou component
$f_{\unicode{x3bb} _0}^{m+1}(v_{\unicode{x3bb} _0}^+)$
since the Fatou component
![]() $f_{\unicode{x3bb} _0}^{m+1}(U_{k_1}^{i_1}) = f_{\unicode{x3bb} _0}^{m+1}(U_{k_2}^{i_2})$
is a Jordan domain (see part (1) of Theorem 2.6) and there is only one dynamical ray landing on
$f_{\unicode{x3bb} _0}^{m+1}(U_{k_1}^{i_1}) = f_{\unicode{x3bb} _0}^{m+1}(U_{k_2}^{i_2})$
is a Jordan domain (see part (1) of Theorem 2.6) and there is only one dynamical ray landing on
![]() $f_{\unicode{x3bb} _0}^{m+1}(v_{\unicode{x3bb} _0}^+)$
. This implies
$f_{\unicode{x3bb} _0}^{m+1}(v_{\unicode{x3bb} _0}^+)$
. This implies
![]() $f_{\unicode{x3bb} _0}^{m}(v_{\unicode{x3bb} _0}^{+})\in C_{\unicode{x3bb} _0}$
, which contradicts with Lemma 7.1.
$f_{\unicode{x3bb} _0}^{m}(v_{\unicode{x3bb} _0}^{+})\in C_{\unicode{x3bb} _0}$
, which contradicts with Lemma 7.1.
Suppose
![]() $z^{i_{1}}_{k_{1}}(\unicode{x3bb} _{0})=z^{i_{2}}_{k_{2}}(\unicode{x3bb} _{0})$
. In this case,
$z^{i_{1}}_{k_{1}}(\unicode{x3bb} _{0})=z^{i_{2}}_{k_{2}}(\unicode{x3bb} _{0})$
. In this case,
![]() $k_{1}=k_{2} \geq 3$
and
$k_{1}=k_{2} \geq 3$
and
![]() $U_{k_1}^{i_1}(\unicode{x3bb} _0)= U_{k_2}^{i_2}(\unicode{x3bb} _0)$
. Since
$U_{k_1}^{i_1}(\unicode{x3bb} _0)= U_{k_2}^{i_2}(\unicode{x3bb} _0)$
. Since
![]() $\partial U_{k_1}^{i_1}(\unicode{x3bb} _0)$
is a Jordan curve and
$\partial U_{k_1}^{i_1}(\unicode{x3bb} _0)$
is a Jordan curve and
![]() $w^{t_{1}}_{k_1}(\unicode{x3bb} _{0})=w^{t_{2}}_{k_2}(\unicode{x3bb} _{0})$
, we have
$w^{t_{1}}_{k_1}(\unicode{x3bb} _{0})=w^{t_{2}}_{k_2}(\unicode{x3bb} _{0})$
, we have
![]() $t_{1}=t_{2}$
. By the discreteness of pre-images of
$t_{1}=t_{2}$
. By the discreteness of pre-images of
![]() $0$
, it is not hard to see that
$0$
, it is not hard to see that
![]() $z^{i_{1}}_{k_{1}}(\unicode{x3bb} )=z^{i_{2}}_{k_{2}}(\unicode{x3bb} )$
for
$z^{i_{1}}_{k_{1}}(\unicode{x3bb} )=z^{i_{2}}_{k_{2}}(\unicode{x3bb} )$
for
![]() $\unicode{x3bb} $
near
$\unicode{x3bb} $
near
![]() $\unicode{x3bb} _{0}$
. Hence, we can find a simply connected region
$\unicode{x3bb} _{0}$
. Hence, we can find a simply connected region
![]() $\mathcal {V}\subset \mathscr {V}_{1} \cup \mathscr {V}_{2}$
containing
$\mathcal {V}\subset \mathscr {V}_{1} \cup \mathscr {V}_{2}$
containing
![]() $\unicode{x3bb} _{\mathscr {U}_{1}}$
,
$\unicode{x3bb} _{\mathscr {U}_{1}}$
,
![]() $\unicode{x3bb} _{\mathscr {U}_{2}}$
, and
$\unicode{x3bb} _{\mathscr {U}_{2}}$
, and
![]() $\unicode{x3bb} _{0}$
such that
$\unicode{x3bb} _{0}$
such that
![]() $z^{i_{1}}_{k_{1}}(\unicode{x3bb} )=z^{i_{2}}_{k_{2}}(\unicode{x3bb} )$
for
$z^{i_{1}}_{k_{1}}(\unicode{x3bb} )=z^{i_{2}}_{k_{2}}(\unicode{x3bb} )$
for
![]() $\unicode{x3bb} \in \mathcal {V}$
. By Proposition 4.4, we have
$\unicode{x3bb} \in \mathcal {V}$
. By Proposition 4.4, we have
![]() $\unicode{x3bb} _{\mathscr {U}_{2}}=e^{{2m\pi i}/({n-1})}\unicode{x3bb} _{\mathscr {U}_{1}}$
for some
$\unicode{x3bb} _{\mathscr {U}_{2}}=e^{{2m\pi i}/({n-1})}\unicode{x3bb} _{\mathscr {U}_{1}}$
for some
![]() $m \in \mathbb {N}$
. It follows that
$m \in \mathbb {N}$
. It follows that
![]() $\overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cup \overline {\mathscr {R}^{t_{2}}_{\mathscr {U}_{2}}} \cap \mathbb {R}^{+} \neq \emptyset $
. Without loss of generality, we may suppose
$\overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cup \overline {\mathscr {R}^{t_{2}}_{\mathscr {U}_{2}}} \cap \mathbb {R}^{+} \neq \emptyset $
. Without loss of generality, we may suppose
![]() $\overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cap \mathbb {R}^{+} \neq \emptyset $
and
$\overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cap \mathbb {R}^{+} \neq \emptyset $
and
![]() $\unicode{x3bb} ' \in \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cap \mathbb {R}^{+}$
. It is not hard to check that for
$\unicode{x3bb} ' \in \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}} \cap \mathbb {R}^{+}$
. It is not hard to check that for
![]() $\unicode{x3bb} \in \mathbb {R}^{+}$
, both
$\unicode{x3bb} \in \mathbb {R}^{+}$
, both
![]() $B_{\unicode{x3bb} } \cap \mathbb {R}^{+}$
and
$B_{\unicode{x3bb} } \cap \mathbb {R}^{+}$
and
![]() $T_{\unicode{x3bb} } \cap \mathbb {R}^{+}$
are connected. Hence, we may suppose
$T_{\unicode{x3bb} } \cap \mathbb {R}^{+}$
are connected. Hence, we may suppose
![]() $B_{\unicode{x3bb} '} \cap \mathbb {R}^{+}=(z_{0},\infty )$
,
$B_{\unicode{x3bb} '} \cap \mathbb {R}^{+}=(z_{0},\infty )$
,
![]() $T_{\unicode{x3bb} '} \cap \mathbb {R}^{+}=(0,z_{1})$
. Since
$T_{\unicode{x3bb} '} \cap \mathbb {R}^{+}=(0,z_{1})$
. Since
![]() $\unicode{x3bb} ' \in \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}}$
, then
$\unicode{x3bb} ' \in \overline {\mathscr {R}^{t_{1}}_{\mathscr {U}_{1}}}$
, then
![]() $v_{\unicode{x3bb} '}^{+} \in [z_{1},z_{0}]$
and
$v_{\unicode{x3bb} '}^{+} \in [z_{1},z_{0}]$
and
![]() $f_{\unicode{x3bb} '}^{k_{1}}( v_{\unicode{x3bb} '}^{+} ) \in [0,z_{1}]$
. Notice that
$f_{\unicode{x3bb} '}^{k_{1}}( v_{\unicode{x3bb} '}^{+} ) \in [0,z_{1}]$
. Notice that
![]() $v^{+}_{\unicode{x3bb} '}=\min _{z \in \mathbb {R}^{+}}f_{\unicode{x3bb} '}(z)$
. It follows that
$v^{+}_{\unicode{x3bb} '}=\min _{z \in \mathbb {R}^{+}}f_{\unicode{x3bb} '}(z)$
. It follows that
![]() $\unicode{x3bb} '=\unicode{x3bb} _{0}$
$\unicode{x3bb} '=\unicode{x3bb} _{0}$
![]() $v^{+}_{\unicode{x3bb} '}=z_{1} \in \partial T_{\unicode{x3bb} '} \cap \partial U^{i_{1}}_{k_{1}}(\unicode{x3bb} ')$
which can be deduced to the previous case.
$v^{+}_{\unicode{x3bb} '}=z_{1} \in \partial T_{\unicode{x3bb} '} \cap \partial U^{i_{1}}_{k_{1}}(\unicode{x3bb} ')$
which can be deduced to the previous case.
A combination of Propositions 6.5 and 7.2 completes the proof of Theorem 1.2. The proof of Proposition 7.2 also implies the following.
Corollary 7.3. Suppose
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
$\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
![]() $k \geq 2$
. If
$k \geq 2$
. If
![]() $\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t} ) \in \partial \mathscr {U}$
, then
$\unicode{x3bb} =\Phi _{\mathscr {U}}^{-1}(e^{2\pi i t} ) \in \partial \mathscr {U}$
, then
![]() $v^{+}_{\unicode{x3bb} }=\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} )} (e^{2\pi i \theta _{k}(t)} )\in \partial U_{k}^{i}(\unicode{x3bb} )$
, where
$v^{+}_{\unicode{x3bb} }=\phi ^{-1}_{z^{i}_{k}(\unicode{x3bb} )} (e^{2\pi i \theta _{k}(t)} )\in \partial U_{k}^{i}(\unicode{x3bb} )$
, where
![]() $z^{i}_{k}$
is the root function defined on a neighborhood of
$z^{i}_{k}$
is the root function defined on a neighborhood of
![]() $\overline {\mathscr {U}}$
satisfying that
$\overline {\mathscr {U}}$
satisfying that
![]() $v^{+}_{\unicode{x3bb} _{\mathscr {U}}}=z^{i}_{k}(\unicode{x3bb} _{\mathscr {U}})$
and
$v^{+}_{\unicode{x3bb} _{\mathscr {U}}}=z^{i}_{k}(\unicode{x3bb} _{\mathscr {U}})$
and
![]() $U_{k}^{i}(\unicode{x3bb} )$
is the Fatou component containing
$U_{k}^{i}(\unicode{x3bb} )$
is the Fatou component containing
![]() $z_k^i(\unicode{x3bb} )$
. In particular,
$z_k^i(\unicode{x3bb} )$
. In particular,
![]() $v^{\pm }_{\unicode{x3bb} } \notin \partial B_{\unicode{x3bb} }$
.
$v^{\pm }_{\unicode{x3bb} } \notin \partial B_{\unicode{x3bb} }$
.
7.2 McMullen domain and Sierpiński holes are quasi-disks
In this section, we prove that the McMullen domain and all Sierpiński holes are all bounded by quasi-circles. Recall that
![]() $\mathscr U$
is a McMullen domain or a Sierpiński hole if and only if
$\mathscr U$
is a McMullen domain or a Sierpiński hole if and only if
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
$\mathscr {U} \subset \mathscr {H}_{k}$
is an escape component with
![]() $k \geq 2$
.
$k \geq 2$
.
Lemma 7.4. Let
![]() $\mathscr {W}= \mathbb {C} \setminus \overline {\mathscr {H}_{0}}$
. Then for any
$\mathscr {W}= \mathbb {C} \setminus \overline {\mathscr {H}_{0}}$
. Then for any
![]() $\unicode{x3bb} _{0} \in \mathscr {W}$
, there is a holomorphic motion based at
$\unicode{x3bb} _{0} \in \mathscr {W}$
, there is a holomorphic motion based at
![]() $\unicode{x3bb} _{0}$
:
$\unicode{x3bb} _{0}$
:
Proof. When
![]() $\unicode{x3bb} \in \mathscr {W}\setminus \{0\}$
,
$\unicode{x3bb} \in \mathscr {W}\setminus \{0\}$
,
![]() $C_{\unicode{x3bb} } \cap B_{\unicode{x3bb} }=\emptyset $
and
$C_{\unicode{x3bb} } \cap B_{\unicode{x3bb} }=\emptyset $
and
![]() $B_{\unicode{x3bb} }$
is a Jordan region. The Böttcher coordinate
$B_{\unicode{x3bb} }$
is a Jordan region. The Böttcher coordinate
![]() $\phi _{\infty (\unicode{x3bb} )}$
is a holomorphic homeomorphism from
$\phi _{\infty (\unicode{x3bb} )}$
is a holomorphic homeomorphism from
![]() $B_{\unicode{x3bb} }$
to
$B_{\unicode{x3bb} }$
to
![]() $\overline {\mathbb {C}} \setminus \overline {\mathbb {D}}$
. When
$\overline {\mathbb {C}} \setminus \overline {\mathbb {D}}$
. When
![]() $\unicode{x3bb} =0$
, set
$\unicode{x3bb} =0$
, set
![]() $B_{0}=\overline {\mathbb C}\setminus \overline {\mathbb D}$
and
$B_{0}=\overline {\mathbb C}\setminus \overline {\mathbb D}$
and
![]() $\phi _{\infty (0)}=\mathrm {id}$
. By the usual construction of the Böttcher coordinates, it is easy to check
$\phi _{\infty (0)}=\mathrm {id}$
. By the usual construction of the Böttcher coordinates, it is easy to check
![]() $\phi _{\infty (\unicode{x3bb} )}$
is holomorphic with respect to
$\phi _{\infty (\unicode{x3bb} )}$
is holomorphic with respect to
![]() $\unicode{x3bb} \in \mathscr W$
, even at
$\unicode{x3bb} \in \mathscr W$
, even at
![]() $\unicode{x3bb} =0$
. Hence,
$\unicode{x3bb} =0$
. Hence,
is well defined for
![]() $\unicode{x3bb} \in \mathscr W$
. Then it is direct to verify that
$\unicode{x3bb} \in \mathscr W$
. Then it is direct to verify that
![]() $H:\mathscr W\times B_{\unicode{x3bb} _0}\to \mathscr W\times \overline {\mathbb C}$
,
$H:\mathscr W\times B_{\unicode{x3bb} _0}\to \mathscr W\times \overline {\mathbb C}$
,
![]() $(\unicode{x3bb} , z)\mapsto (\unicode{x3bb} ,H_{\unicode{x3bb} }(z))$
is a holomorphic motion.
$(\unicode{x3bb} , z)\mapsto (\unicode{x3bb} ,H_{\unicode{x3bb} }(z))$
is a holomorphic motion.
By Theorem 2.3, the holomorphic motion defined in Lemma 7.4 can be extended to a holomorphic motion
![]() $H: \mathscr {W} \times \overline {\mathbb {C}} \to \mathscr {W} \times \overline {\mathbb {C}}$
. It follows that the following map:
$H: \mathscr {W} \times \overline {\mathbb {C}} \to \mathscr {W} \times \overline {\mathbb {C}}$
. It follows that the following map:
 $$ \begin{align} \Phi_k(\unicode{x3bb}):= \begin{cases} H_{\unicode{x3bb}}^{-1}(f_{\unicode{x3bb}}^{k-1}(v_{\unicode{x3bb}}^{+})),& \unicode{x3bb} \in \mathscr W\setminus\{0\},\\[2pt] \infty,& \unicode{x3bb}=0 \end{cases} \end{align} $$
$$ \begin{align} \Phi_k(\unicode{x3bb}):= \begin{cases} H_{\unicode{x3bb}}^{-1}(f_{\unicode{x3bb}}^{k-1}(v_{\unicode{x3bb}}^{+})),& \unicode{x3bb} \in \mathscr W\setminus\{0\},\\[2pt] \infty,& \unicode{x3bb}=0 \end{cases} \end{align} $$
is well defined on
![]() $\mathscr {W}$
for all
$\mathscr {W}$
for all
![]() $k\geq 2$
. Noting that when
$k\geq 2$
. Noting that when
![]() $\unicode{x3bb} \to 0$
,
$\unicode{x3bb} \to 0$
,
![]() $H_{\unicode{x3bb} }^{-1}(f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+}))\to \infty $
,
$H_{\unicode{x3bb} }^{-1}(f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+}))\to \infty $
,
![]() $\Phi _k(\unicode{x3bb} )$
is continuous even at
$\Phi _k(\unicode{x3bb} )$
is continuous even at
![]() $\unicode{x3bb} =0$
.
$\unicode{x3bb} =0$
.
In the following, we always assume that
![]() $\unicode{x3bb} _0\in \mathscr W$
is given.
$\unicode{x3bb} _0\in \mathscr W$
is given.
Lemma 7.5. The map
![]() $\Phi _k :\mathscr {W} \rightarrow \overline {\mathbb {C}}$
defined by equation (7.2) is quasi-regular on any region
$\Phi _k :\mathscr {W} \rightarrow \overline {\mathbb {C}}$
defined by equation (7.2) is quasi-regular on any region
![]() $\mathscr W^*\Subset ~\mathscr W$
.
$\mathscr W^*\Subset ~\mathscr W$
.
Proof. Consider the derivative of equation
![]() $H_{\unicode{x3bb} } \circ \Phi _k(\unicode{x3bb} )=f_{\unicode{x3bb} }^{k-1}(v^{+}_{\unicode{x3bb} })$
. Since
$H_{\unicode{x3bb} } \circ \Phi _k(\unicode{x3bb} )=f_{\unicode{x3bb} }^{k-1}(v^{+}_{\unicode{x3bb} })$
. Since
![]() $H_{\unicode{x3bb} }$
and
$H_{\unicode{x3bb} }$
and
![]() $f_{\unicode{x3bb} }^{k-1}(v^{+}_{\unicode{x3bb} })$
are all holomorphic in
$f_{\unicode{x3bb} }^{k-1}(v^{+}_{\unicode{x3bb} })$
are all holomorphic in
![]() $\unicode{x3bb} $
, therefore,
$\unicode{x3bb} $
, therefore,
![]() $\partial H_{\unicode{x3bb} }/\partial {\overline{\unicode{x3bb}}} =\partial f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+})/\partial {\overline{\unicode{x3bb}}} =0$
, and we have
$\partial H_{\unicode{x3bb} }/\partial {\overline{\unicode{x3bb}}} =\partial f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+})/\partial {\overline{\unicode{x3bb}}} =0$
, and we have
 $$ \begin{align} \frac{\partial H_{\unicode{x3bb}}}{\partial z}\bigg|_{\Phi_k(\unicode{x3bb})} \frac{\partial \Phi_k}{\partial {\overline{\unicode{x3bb}}}}\bigg|_{\unicode{x3bb}} +\frac{\partial H_{\unicode{x3bb}}}{\partial\overline z}\bigg|_{\Phi_k(\unicode{x3bb})}\frac{\partial\overline \Phi_k}{\partial{\overline{\unicode{x3bb}}}} \bigg|_{\unicode{x3bb}}=0, \end{align} $$
$$ \begin{align} \frac{\partial H_{\unicode{x3bb}}}{\partial z}\bigg|_{\Phi_k(\unicode{x3bb})} \frac{\partial \Phi_k}{\partial {\overline{\unicode{x3bb}}}}\bigg|_{\unicode{x3bb}} +\frac{\partial H_{\unicode{x3bb}}}{\partial\overline z}\bigg|_{\Phi_k(\unicode{x3bb})}\frac{\partial\overline \Phi_k}{\partial{\overline{\unicode{x3bb}}}} \bigg|_{\unicode{x3bb}}=0, \end{align} $$
where
![]() $\partial H_{\unicode{x3bb} }/\partial z$
and
$\partial H_{\unicode{x3bb} }/\partial z$
and
![]() $\partial H_{\unicode{x3bb} }/\partial \overline {z}$
exist almost everywhere since
$\partial H_{\unicode{x3bb} }/\partial \overline {z}$
exist almost everywhere since
![]() $H_{\unicode{x3bb} }$
is quasi-conformal. Thus,
$H_{\unicode{x3bb} }$
is quasi-conformal. Thus,
 $$ \begin{align} \bigg|\frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial \Phi_k/\partial \unicode{x3bb}}\bigg|_{\unicode{x3bb}}\bigg| =\bigg|\frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial\overline \Phi_k/\partial{\overline{\unicode{x3bb}}}}\bigg|_{\unicode{x3bb}}\bigg| =\bigg|\frac{\partial H_{\unicode{x3bb}}/\partial \overline z}{\partial H_{\unicode{x3bb}}/\partial z}\bigg|_{\Phi_k(\unicode{x3bb})}\bigg| =|\mu_\unicode{x3bb}(\Phi_k(\unicode{x3bb}))|, \end{align} $$
$$ \begin{align} \bigg|\frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial \Phi_k/\partial \unicode{x3bb}}\bigg|_{\unicode{x3bb}}\bigg| =\bigg|\frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial\overline \Phi_k/\partial{\overline{\unicode{x3bb}}}}\bigg|_{\unicode{x3bb}}\bigg| =\bigg|\frac{\partial H_{\unicode{x3bb}}/\partial \overline z}{\partial H_{\unicode{x3bb}}/\partial z}\bigg|_{\Phi_k(\unicode{x3bb})}\bigg| =|\mu_\unicode{x3bb}(\Phi_k(\unicode{x3bb}))|, \end{align} $$
where
![]() $\mu _{\unicode{x3bb} }$
is the Beltrami coefficient of
$\mu _{\unicode{x3bb} }$
is the Beltrami coefficient of
![]() $H_{\unicode{x3bb} }$
.
$H_{\unicode{x3bb} }$
.
Let
![]() $\rho (\cdot ,\cdot )$
denote the hyperbolic distance of
$\rho (\cdot ,\cdot )$
denote the hyperbolic distance of
![]() $\mathscr W$
. Then,
$\mathscr W$
. Then,
By Theorem 2.3, for any
![]() $\unicode{x3bb} \in \mathscr W^*$
,
$\unicode{x3bb} \in \mathscr W^*$
,
 $$ \begin{align} \mathop{\mathrm{ess\,sup}}_{z \in \overline{\mathbb{C}}}| \mu_{\unicode{x3bb}}(z)| \leq \frac{e^{\rho(\unicode{x3bb},\unicode{x3bb}_0)}-1}{e^{\rho(\unicode{x3bb},\unicode{x3bb}_0)}+1}\leq k:=\frac{e^{\rho^*}-1}{e^{\rho^*}+1} <1. \end{align} $$
$$ \begin{align} \mathop{\mathrm{ess\,sup}}_{z \in \overline{\mathbb{C}}}| \mu_{\unicode{x3bb}}(z)| \leq \frac{e^{\rho(\unicode{x3bb},\unicode{x3bb}_0)}-1}{e^{\rho(\unicode{x3bb},\unicode{x3bb}_0)}+1}\leq k:=\frac{e^{\rho^*}-1}{e^{\rho^*}+1} <1. \end{align} $$
Therefore,
 $$ \begin{align} \bigg \Vert \frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial \Phi_k/\partial \unicode{x3bb}} \bigg \Vert_{\infty}=\mathop{\mathrm{ess\,sup}}\limits_{\unicode{x3bb} \in \mathscr{W}^*} \bigg| \frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial \Phi_k/\partial \unicode{x3bb}} \bigg|=\mathop{\mathrm{ess\,sup}}_{\unicode{x3bb} \in \mathscr{W}^*}|\mu_\unicode{x3bb}(\Phi_k(\unicode{x3bb}))| \leq k<1. \end{align} $$
$$ \begin{align} \bigg \Vert \frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial \Phi_k/\partial \unicode{x3bb}} \bigg \Vert_{\infty}=\mathop{\mathrm{ess\,sup}}\limits_{\unicode{x3bb} \in \mathscr{W}^*} \bigg| \frac{\partial \Phi_k/\partial{\overline{\unicode{x3bb}}}}{\partial \Phi_k/\partial \unicode{x3bb}} \bigg|=\mathop{\mathrm{ess\,sup}}_{\unicode{x3bb} \in \mathscr{W}^*}|\mu_\unicode{x3bb}(\Phi_k(\unicode{x3bb}))| \leq k<1. \end{align} $$
It means that
![]() $\Phi _k$
is a quasi-regular map on the region
$\Phi _k$
is a quasi-regular map on the region
![]() $\mathscr W^*$
.
$\mathscr W^*$
.
From the proof of Lemma 7.5, we have the following corollary.
Corollary 7.6. Let
![]() $\mu _{\Phi _k}(\unicode{x3bb} )=(\partial \Phi _k/\partial \overline {\unicode{x3bb} }) /(\partial \Phi _k/\partial \unicode{x3bb} )$
be the Beltrami coefficient of
$\mu _{\Phi _k}(\unicode{x3bb} )=(\partial \Phi _k/\partial \overline {\unicode{x3bb} }) /(\partial \Phi _k/\partial \unicode{x3bb} )$
be the Beltrami coefficient of
![]() $\Phi _k(\unicode{x3bb} )$
. Let
$\Phi _k(\unicode{x3bb} )$
. Let
![]() $\mathscr D_m=\mathbb D(\unicode{x3bb} _0, 1/m)$
for
$\mathscr D_m=\mathbb D(\unicode{x3bb} _0, 1/m)$
for
![]() $m>0$
large such that
$m>0$
large such that
![]() $\mathscr D_m\subset \mathscr W$
. Then,
$\mathscr D_m\subset \mathscr W$
. Then,
Proof. It follows immediately from equations (7.5), (7.6), and the fact that
![]() $\sup _{\unicode{x3bb} \in \mathscr D_m} \rho (\unicode{x3bb} ,\unicode{x3bb} _0)\to 0$
as
$\sup _{\unicode{x3bb} \in \mathscr D_m} \rho (\unicode{x3bb} ,\unicode{x3bb} _0)\to 0$
as
![]() $m\to \infty $
.
$m\to \infty $
.
Proposition 7.7. Let
![]() $\mathscr U$
be an escape component of
$\mathscr U$
be an escape component of
![]() $\mathscr H_k$
with
$\mathscr H_k$
with
![]() $k\geq 2$
. Then there is a neighborhood
$k\geq 2$
. Then there is a neighborhood
![]() $\mathscr {V}$
of
$\mathscr {V}$
of
![]() $\overline {\mathscr {U}}$
and a quasi-conformal homeomorphism
$\overline {\mathscr {U}}$
and a quasi-conformal homeomorphism
![]() $\Psi _k: \mathscr V\to \overline {\mathbb C}$
such that
$\Psi _k: \mathscr V\to \overline {\mathbb C}$
such that
![]() $\Psi _k(\overline {\mathscr {U}})=\overline {B_{\unicode{x3bb} _{0}}}$
.
$\Psi _k(\overline {\mathscr {U}})=\overline {B_{\unicode{x3bb} _{0}}}$
.
Proof. Set
![]() $\Psi _k :\mathscr W\to \overline {\mathbb C}$
be defined by
$\Psi _k :\mathscr W\to \overline {\mathbb C}$
be defined by
 $$ \begin{align} \Psi_k:= \begin{cases} \phi_{\infty(\unicode{x3bb}_{0})}^{-1} \circ (\phi_{\infty(\unicode{x3bb}_{0})} \circ \Phi_k)^{2/(n-2)}, & {k=2},\\[5pt] \phi_{\infty(\unicode{x3bb}_{0})}^{-1} \circ (\phi_{\infty(\unicode{x3bb}_{0})} \circ \Phi_k)^{1/n}, & {k \geq 3}, \end{cases} \end{align} $$
$$ \begin{align} \Psi_k:= \begin{cases} \phi_{\infty(\unicode{x3bb}_{0})}^{-1} \circ (\phi_{\infty(\unicode{x3bb}_{0})} \circ \Phi_k)^{2/(n-2)}, & {k=2},\\[5pt] \phi_{\infty(\unicode{x3bb}_{0})}^{-1} \circ (\phi_{\infty(\unicode{x3bb}_{0})} \circ \Phi_k)^{1/n}, & {k \geq 3}, \end{cases} \end{align} $$
or more clearly, using equation (7.2),
![]() $\Psi _k(0)=\infty $
and for
$\Psi _k(0)=\infty $
and for
![]() $\unicode{x3bb} \neq 0$
,
$\unicode{x3bb} \neq 0$
,
 $$ \begin{align} \Psi_k(\unicode{x3bb})= \begin{cases} \phi_{\infty(\unicode{x3bb}_0)}^{-1}\circ (\phi_{\infty(\unicode{x3bb}_0)}\circ H_{\unicode{x3bb}}^{-1}(f_{\unicode{x3bb}}(v_{\unicode{x3bb}}^{+})))^{{2}/(n-2)}, & k=2,\\[2pt] \phi_{\infty(\unicode{x3bb}_0)}^{-1}\circ (\phi_{\infty(\unicode{x3bb}_0)}\circ H_{\unicode{x3bb}}^{-1}(f_{\unicode{x3bb}}^{k-1}(v_{\unicode{x3bb}}^{+})))^{1/n}, & k\geq 3. \end{cases} \end{align} $$
$$ \begin{align} \Psi_k(\unicode{x3bb})= \begin{cases} \phi_{\infty(\unicode{x3bb}_0)}^{-1}\circ (\phi_{\infty(\unicode{x3bb}_0)}\circ H_{\unicode{x3bb}}^{-1}(f_{\unicode{x3bb}}(v_{\unicode{x3bb}}^{+})))^{{2}/(n-2)}, & k=2,\\[2pt] \phi_{\infty(\unicode{x3bb}_0)}^{-1}\circ (\phi_{\infty(\unicode{x3bb}_0)}\circ H_{\unicode{x3bb}}^{-1}(f_{\unicode{x3bb}}^{k-1}(v_{\unicode{x3bb}}^{+})))^{1/n}, & k\geq 3. \end{cases} \end{align} $$
When
![]() $\unicode{x3bb} \in \mathscr U$
, it is easy to check that
$\unicode{x3bb} \in \mathscr U$
, it is easy to check that
where
![]() $\Phi _{\mathscr {U}}(\unicode{x3bb} )$
is defined in Theorem 2.2 which is a holomorphic homeomorphism from
$\Phi _{\mathscr {U}}(\unicode{x3bb} )$
is defined in Theorem 2.2 which is a holomorphic homeomorphism from
![]() $\mathscr U$
to
$\mathscr U$
to
![]() $\overline {\mathbb C}\setminus \overline {\mathbb D}$
(here for
$\overline {\mathbb C}\setminus \overline {\mathbb D}$
(here for
![]() $k=2$
, we need to extend the definition of
$k=2$
, we need to extend the definition of
![]() $\Phi _{\mathscr {U}}$
such that
$\Phi _{\mathscr {U}}$
such that
![]() $\Phi _{\mathscr {U}}(0)=\infty $
). It follows that
$\Phi _{\mathscr {U}}(0)=\infty $
). It follows that
![]() $\Psi _k: {\mathscr {U}} \to {B_{\unicode{x3bb} _{0}}}$
is a holomorphic homeomorphism. By parts (1), (3) of Theorem 2.6, both
$\Psi _k: {\mathscr {U}} \to {B_{\unicode{x3bb} _{0}}}$
is a holomorphic homeomorphism. By parts (1), (3) of Theorem 2.6, both
![]() $\partial {\mathscr {U}}$
and
$\partial {\mathscr {U}}$
and
![]() $\partial {B_{\unicode{x3bb} _{0}}}$
are Jordan curves. Hence,
$\partial {B_{\unicode{x3bb} _{0}}}$
are Jordan curves. Hence,
![]() $\Psi _k: \overline {\mathscr {U}} \to \overline {B_{\unicode{x3bb} _{0}}}$
is a homeomorphism with
$\Psi _k: \overline {\mathscr {U}} \to \overline {B_{\unicode{x3bb} _{0}}}$
is a homeomorphism with
![]() $\Psi _k(\partial {\mathscr {U}}) =\partial {B_{\unicode{x3bb} _{0}}}$
.
$\Psi _k(\partial {\mathscr {U}}) =\partial {B_{\unicode{x3bb} _{0}}}$
.
By Propositions 6.5 and 7.2, we have
![]() $\overline {\mathscr U}\cap \overline {\mathscr U'}=\emptyset $
for any escape component
$\overline {\mathscr U}\cap \overline {\mathscr U'}=\emptyset $
for any escape component
![]() $\mathscr U'$
different from
$\mathscr U'$
different from
![]() $\mathscr U$
. Since for fixed
$\mathscr U$
. Since for fixed
![]() $\ell \leq k$
,
$\ell \leq k$
,
![]() $\mathscr H_{\ell }$
has only finitely many components, there exists a simply connected region
$\mathscr H_{\ell }$
has only finitely many components, there exists a simply connected region
![]() $\mathscr W^*$
such that
$\mathscr W^*$
such that
![]() $\mathscr U\Subset \mathscr W^*\Subset \mathscr W$
and
$\mathscr U\Subset \mathscr W^*\Subset \mathscr W$
and
![]() $\overline {\mathscr W^*}\cap \overline {\mathscr U'}=\emptyset $
for all components
$\overline {\mathscr W^*}\cap \overline {\mathscr U'}=\emptyset $
for all components
![]() $\mathscr U'$
of
$\mathscr U'$
of
![]() $\mathscr H_{\ell }$
with
$\mathscr H_{\ell }$
with
![]() $0\leq \ell \leq k$
which are different from
$0\leq \ell \leq k$
which are different from
![]() $\mathscr U$
.
$\mathscr U$
.
Now, we restrict
![]() $\Psi _k$
on
$\Psi _k$
on
![]() $\mathscr W^*$
and then show that
$\mathscr W^*$
and then show that
![]() $\Psi _k^{-1}(\overline {B_{\unicode{x3bb} _{0}}} )=\overline {\mathscr {U}}$
. That is, if
$\Psi _k^{-1}(\overline {B_{\unicode{x3bb} _{0}}} )=\overline {\mathscr {U}}$
. That is, if
![]() $\unicode{x3bb} \in \mathscr W^*$
such that
$\unicode{x3bb} \in \mathscr W^*$
such that
![]() $\Psi _k(\unicode{x3bb} )\in \overline {B_{\unicode{x3bb} _0}}$
, then
$\Psi _k(\unicode{x3bb} )\in \overline {B_{\unicode{x3bb} _0}}$
, then
![]() $\unicode{x3bb} \in \overline {\mathscr U}$
.
$\unicode{x3bb} \in \overline {\mathscr U}$
.
We first prove that
![]() $\Psi _k(\unicode{x3bb} )\in B_{\unicode{x3bb} _0}$
implies
$\Psi _k(\unicode{x3bb} )\in B_{\unicode{x3bb} _0}$
implies
![]() $\unicode{x3bb} \in \mathscr U$
. From equation (7.9) and the definition of
$\unicode{x3bb} \in \mathscr U$
. From equation (7.9) and the definition of
![]() $\phi _{\infty (\unicode{x3bb} )}$
, we have that
$\phi _{\infty (\unicode{x3bb} )}$
, we have that
![]() $\Psi _k(\unicode{x3bb} )\in B_{\unicode{x3bb} _0}$
implies
$\Psi _k(\unicode{x3bb} )\in B_{\unicode{x3bb} _0}$
implies
![]() $H_{\unicode{x3bb} }^{-1}(f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+})) \in B_{\unicode{x3bb} _0}$
. Since
$H_{\unicode{x3bb} }^{-1}(f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+})) \in B_{\unicode{x3bb} _0}$
. Since
![]() $H_{\unicode{x3bb} }:\mathbb C\to \mathbb C$
is a quasi-conformal homeomorphism and
$H_{\unicode{x3bb} }:\mathbb C\to \mathbb C$
is a quasi-conformal homeomorphism and
![]() $H_{\unicode{x3bb} }(B_{\unicode{x3bb} _0})=B_{\unicode{x3bb} }$
, we get that
$H_{\unicode{x3bb} }(B_{\unicode{x3bb} _0})=B_{\unicode{x3bb} }$
, we get that
![]() $f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+})\in B_{\unicode{x3bb} }$
. This shows that
$f_{\unicode{x3bb} }^{k-1}(v_{\unicode{x3bb} }^{+})\in B_{\unicode{x3bb} }$
. This shows that
![]() $\unicode{x3bb} \in \mathscr H_{\ell }$
for some
$\unicode{x3bb} \in \mathscr H_{\ell }$
for some
![]() $\ell \leq k$
. However, by the definition of
$\ell \leq k$
. However, by the definition of
![]() $\mathscr W^*$
,
$\mathscr W^*$
,
![]() $\mathscr W^*\cap \bigcup _{\ell \leq k}\mathscr H_{\ell }=\mathscr U$
. We get that
$\mathscr W^*\cap \bigcup _{\ell \leq k}\mathscr H_{\ell }=\mathscr U$
. We get that
![]() $\unicode{x3bb} \in \mathscr U$
.
$\unicode{x3bb} \in \mathscr U$
.
Suppose that
![]() $\Psi _k(\unicode{x3bb} ) \in \partial B_{\unicode{x3bb} _{0}}$
. Since
$\Psi _k(\unicode{x3bb} ) \in \partial B_{\unicode{x3bb} _{0}}$
. Since
![]() $\Phi _k$
is quasi-regular by Lemma 7.5,
$\Phi _k$
is quasi-regular by Lemma 7.5,
![]() $\Psi _k$
is also quasi-regular and obviously non-constant. Thus,
$\Psi _k$
is also quasi-regular and obviously non-constant. Thus,
![]() $\Psi _k$
is an open map. It follows that for any neighborhood
$\Psi _k$
is an open map. It follows that for any neighborhood
![]() $\mathscr {N}$
of
$\mathscr {N}$
of
![]() $\unicode{x3bb} $
,
$\unicode{x3bb} $
,
![]() $\Psi _k(\mathscr {N}) \cap B_{\unicode{x3bb} _{0}} \neq \emptyset $
. Hence,
$\Psi _k(\mathscr {N}) \cap B_{\unicode{x3bb} _{0}} \neq \emptyset $
. Hence,
![]() $\mathscr {N} \cap \mathscr {U} \neq \emptyset $
, which implies that
$\mathscr {N} \cap \mathscr {U} \neq \emptyset $
, which implies that
![]() $\unicode{x3bb} \in \partial \mathscr {U}$
.
$\unicode{x3bb} \in \partial \mathscr {U}$
.
Finally, we take a Jordan region
![]() $\mathscr V'$
satisfying
$\mathscr V'$
satisfying
![]() $\mathscr U\Subset \mathscr V\Subset \mathscr W^*$
. Let
$\mathscr U\Subset \mathscr V\Subset \mathscr W^*$
. Let
![]() $\gamma =\partial \mathscr V$
and
$\gamma =\partial \mathscr V$
and
![]() $\Gamma =\Psi _k(\partial \mathscr V)$
. Then, by the discussion above,
$\Gamma =\Psi _k(\partial \mathscr V)$
. Then, by the discussion above,
![]() $\Gamma \cap \overline {B_{\unicode{x3bb} _0}}=\emptyset $
. Let
$\Gamma \cap \overline {B_{\unicode{x3bb} _0}}=\emptyset $
. Let
![]() $B'$
be the component of
$B'$
be the component of
![]() $\mathbb C\setminus \Gamma $
which contains
$\mathbb C\setminus \Gamma $
which contains
![]() $B_{\unicode{x3bb} _0}$
. Noting that a quasi-regular map is the composition of a holomorphic map and a quasi-conformal homeomorphism, the argument principle can be applied. Since the point
$B_{\unicode{x3bb} _0}$
. Noting that a quasi-regular map is the composition of a holomorphic map and a quasi-conformal homeomorphism, the argument principle can be applied. Since the point
![]() $z\in B_{\unicode{x3bb} _0}\subset B'$
has only one pre-image of
$z\in B_{\unicode{x3bb} _0}\subset B'$
has only one pre-image of
![]() $\Psi _k$
in
$\Psi _k$
in
![]() $\mathscr U\subset \mathscr V'$
, we get that every
$\mathscr U\subset \mathscr V'$
, we get that every
![]() $z\in B'$
has only one pre-image in
$z\in B'$
has only one pre-image in
![]() $\mathscr V'$
. Take
$\mathscr V'$
. Take
![]() $\mathscr V=\Psi _k(U')\subset \mathscr V'$
. Then,
$\mathscr V=\Psi _k(U')\subset \mathscr V'$
. Then,
![]() $\mathscr V$
is a neighborhood of
$\mathscr V$
is a neighborhood of
![]() $\mathscr U$
and
$\mathscr U$
and
![]() $\Psi _k: \mathscr V\to \Psi _k(\mathscr V)=B'$
is a quasi-conformal homeomorphism.
$\Psi _k: \mathscr V\to \Psi _k(\mathscr V)=B'$
is a quasi-conformal homeomorphism.
Corollary 7.8.
![]() $\partial \mathscr {U}$
is a quasi-circle.
$\partial \mathscr {U}$
is a quasi-circle.
Proof. Take
![]() $\unicode{x3bb} _0=\unicode{x3bb} _{\mathscr U}$
as the center of
$\unicode{x3bb} _0=\unicode{x3bb} _{\mathscr U}$
as the center of
![]() $\mathscr U$
. Then,
$\mathscr U$
. Then,
![]() $f_{\unicode{x3bb} _0}$
is hyperbolic and hence
$f_{\unicode{x3bb} _0}$
is hyperbolic and hence
![]() $\unicode{x3bb} _0$
satisfies the condition of part (1) of Theorem 2.6. Hence,
$\unicode{x3bb} _0$
satisfies the condition of part (1) of Theorem 2.6. Hence,
![]() $\partial {B_{\unicode{x3bb} _0}}$
is a quasi-circle. By Proposition 7.7,
$\partial {B_{\unicode{x3bb} _0}}$
is a quasi-circle. By Proposition 7.7,
![]() $\partial \mathscr U$
is also a quasi-circle.
$\partial \mathscr U$
is also a quasi-circle.
7.3 Hausdorff dimension of the boundary of escape component
Let
![]() $\dim _H X$
denote the Hausdorff dimension of a Borel subset X of
$\dim _H X$
denote the Hausdorff dimension of a Borel subset X of
![]() $\mathbb C$
. The following results are well known, see [Reference FalconerFal04].
$\mathbb C$
. The following results are well known, see [Reference FalconerFal04].
Lemma 7.9. Let
![]() $X \subset \mathbb {C}$
be a Borel subset. If
$X \subset \mathbb {C}$
be a Borel subset. If
![]() $f : X \rightarrow \mathbb {C}$
satisfies the Hölder condition
$f : X \rightarrow \mathbb {C}$
satisfies the Hölder condition
then
Lemma 7.10. If f is a non-constant holomorphic map defined on a neighborhood of
![]() $X\subset ~{\mathbb {C}}$
, then
$X\subset ~{\mathbb {C}}$
, then
Recall that for a K-quasi-conformal homeomorphism, we have the following Mori’s theorem, see [Reference AhlforsAhl06].
Theorem 7.11. (Mori)
Suppose
![]() $f: \mathbb {D} \rightarrow \mathbb {D}$
is a K-quasi-conformal homeomorphism. Then for each
$f: \mathbb {D} \rightarrow \mathbb {D}$
is a K-quasi-conformal homeomorphism. Then for each
![]() $z_{1}, z_{2} \in \mathbb {D}$
,
$z_{1}, z_{2} \in \mathbb {D}$
,
We also need the following theorem due to Przytycki [Reference PrzytyckiPrz06] as we know.
Theorem 7.12. (Przytycki)
Let
![]() $f : \overline {\mathbb {C}} \rightarrow \overline {\mathbb {C}}$
be a rational map of degree
$f : \overline {\mathbb {C}} \rightarrow \overline {\mathbb {C}}$
be a rational map of degree
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\Omega $
be a simply connected immediate basin of attraction to a periodic attracting point. Then, provided f is not a Blaschke product in some holomorphic coordinates or a quotient of a Blaschke product by a rational function of degree
$\Omega $
be a simply connected immediate basin of attraction to a periodic attracting point. Then, provided f is not a Blaschke product in some holomorphic coordinates or a quotient of a Blaschke product by a rational function of degree
![]() $2$
, the Hausdorff dimension of
$2$
, the Hausdorff dimension of
![]() $\partial {\Omega }$
is greater than 1.
$\partial {\Omega }$
is greater than 1.
Corollary 7.13. Let
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component with order
$\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component with order
![]() $k \geq 2$
. If
$k \geq 2$
. If
![]() $\unicode{x3bb} _{0} \in \partial {\mathscr {U}}$
and
$\unicode{x3bb} _{0} \in \partial {\mathscr {U}}$
and
![]() $z_{0} \in \partial B_{\unicode{x3bb} _{0}}$
, then for any neighborhood U of
$z_{0} \in \partial B_{\unicode{x3bb} _{0}}$
, then for any neighborhood U of
![]() $z_0$
,
$z_0$
,
Proof. From Theorem 7.12, we have that
![]() $\dim _H \partial B_{\unicode{x3bb} _{0}}>1$
as long as
$\dim _H \partial B_{\unicode{x3bb} _{0}}>1$
as long as
![]() $\unicode{x3bb} _0\in \mathscr W\setminus \{0\}$
. So
$\unicode{x3bb} _0\in \mathscr W\setminus \{0\}$
. So
![]() $\dim _H \partial B_{\unicode{x3bb} _{0}}>1$
if
$\dim _H \partial B_{\unicode{x3bb} _{0}}>1$
if
![]() $\unicode{x3bb} _0\in \partial \mathscr U$
. For any neighborhood U of
$\unicode{x3bb} _0\in \partial \mathscr U$
. For any neighborhood U of
![]() $z_0\in \partial B_{\unicode{x3bb} _0}$
,
$z_0\in \partial B_{\unicode{x3bb} _0}$
,
as m is sufficiently large. By Lemma 7.10,
Proposition 7.14. Let
![]() $\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component with order
$\mathscr {U} \subset \mathscr {H}_{k}$
be an escape component with order
![]() $k \geq 2$
. Then the Hausdorff dimension of
$k \geq 2$
. Then the Hausdorff dimension of
![]() $\partial \mathscr {U}$
satisfies
$\partial \mathscr {U}$
satisfies
Proof. Astala [Reference AstalaAst94] proved that the image of a set of Hausdorff dimension 1 under a K-quasi-conformal homeomorphism has the Hausdorff dimension at most
![]() $1+k$
, where
$1+k$
, where
![]() $k=(K-1)/(K+1)<1$
. It follows that any quasi-circle has the Hausdorff dimension less than
$k=(K-1)/(K+1)<1$
. It follows that any quasi-circle has the Hausdorff dimension less than
![]() $2$
. So,
$2$
. So,
![]() $\dim _{H} \partial {\mathscr {U}}<2$
since
$\dim _{H} \partial {\mathscr {U}}<2$
since
![]() $\partial \mathscr U$
is a quasi-circle by Corollary 7.8. It remains to show that
$\partial \mathscr U$
is a quasi-circle by Corollary 7.8. It remains to show that
![]() $\dim _{H}\partial {\mathscr {U}}>1$
.
$\dim _{H}\partial {\mathscr {U}}>1$
.
Choose a
![]() $\unicode{x3bb} _{0} \in \partial {\mathscr {U}}$
and let
$\unicode{x3bb} _{0} \in \partial {\mathscr {U}}$
and let
![]() $\mathscr {D}_{m}=\mathbb D(\unicode{x3bb} _0,1/m)$
for
$\mathscr {D}_{m}=\mathbb D(\unicode{x3bb} _0,1/m)$
for
![]() $m>0$
large such that
$m>0$
large such that
![]() $\mathscr D_m\subset \mathscr V$
, where
$\mathscr D_m\subset \mathscr V$
, where
![]() $\mathscr V$
is given in Proposition 7.7. By Corollary 7.6, equation (7.7) holds, that is,
$\mathscr V$
is given in Proposition 7.7. By Corollary 7.6, equation (7.7) holds, that is,
Then,
![]() $\Phi _k$
, as a quasi-regular map restricted on
$\Phi _k$
, as a quasi-regular map restricted on
![]() $\mathscr D_m$
, has its maximal dilatation
$\mathscr D_m$
, has its maximal dilatation
 $$ \begin{align} K_{m,k}:=\frac{1+\|\mu\|_{k,m}}{1-\|\mu\|_{k,m}}\to 1\quad \mbox{as } m\to\infty. \end{align} $$
$$ \begin{align} K_{m,k}:=\frac{1+\|\mu\|_{k,m}}{1-\|\mu\|_{k,m}}\to 1\quad \mbox{as } m\to\infty. \end{align} $$
Let
![]() $\Psi _k$
be the quasi-conformal homeomorphism defined in equation (7.8), let
$\Psi _k$
be the quasi-conformal homeomorphism defined in equation (7.8), let
![]() $\eta _{m,k}$
be the Riemann map from
$\eta _{m,k}$
be the Riemann map from
![]() $\Psi _k(\mathscr {D}_{m})$
onto
$\Psi _k(\mathscr {D}_{m})$
onto
![]() $\mathbb {D}$
, and let
$\mathbb {D}$
, and let
![]() $\xi _{m}(\unicode{x3bb} ):\mathscr D_m \to \mathbb D$
be the affine map defined by
$\xi _{m}(\unicode{x3bb} ):\mathscr D_m \to \mathbb D$
be the affine map defined by
![]() $\xi _m(\unicode{x3bb} )=m(\unicode{x3bb} - \unicode{x3bb} _{0})$
. Then,
$\xi _m(\unicode{x3bb} )=m(\unicode{x3bb} - \unicode{x3bb} _{0})$
. Then,
![]() $\widetilde {\Psi }_{m,k}: \mathbb {D} \to \mathbb {D}$
defined by
$\widetilde {\Psi }_{m,k}: \mathbb {D} \to \mathbb {D}$
defined by
![]() $\widetilde {\Psi }_{m,k}:= \eta _{m,k} \circ \Psi _k \circ \xi _{m}^{-1}$
is a quasi-conformal homeomorphism. It has the same maximal dilatation as
$\widetilde {\Psi }_{m,k}:= \eta _{m,k} \circ \Psi _k \circ \xi _{m}^{-1}$
is a quasi-conformal homeomorphism. It has the same maximal dilatation as
![]() $\Phi _k$
since
$\Phi _k$
since
![]() $\phi _{\infty (\unicode{x3bb} _0)}$
,
$\phi _{\infty (\unicode{x3bb} _0)}$
,
![]() $\eta _{m,k}$
, and
$\eta _{m,k}$
, and
![]() $\xi _m$
are all conformal. By Theorem 7.11 and Lemmas 7.9, 7.10,
$\xi _m$
are all conformal. By Theorem 7.11 and Lemmas 7.9, 7.10,
By Corollary 7.13, there exists a constant
![]() $c>1$
such that
$c>1$
such that
where
![]() $U_{m,k}=\Psi _k(\mathscr D_m)$
is a neighborhood of
$U_{m,k}=\Psi _k(\mathscr D_m)$
is a neighborhood of
![]() $z_0:=\Psi _k(\unicode{x3bb} _0)\in \partial B_{\unicode{x3bb} _0}$
. Since
$z_0:=\Psi _k(\unicode{x3bb} _0)\in \partial B_{\unicode{x3bb} _0}$
. Since
![]() $K_{m} \to 1$
as
$K_{m} \to 1$
as
![]() $m \to ~\infty $
, then
$m \to ~\infty $
, then
![]() $\dim _{H} (\partial {\mathscr {U}}\cap \mathscr {D}_{m})>1$
for m large enough. Hence,
$\dim _{H} (\partial {\mathscr {U}}\cap \mathscr {D}_{m})>1$
for m large enough. Hence,
Acknowledgement
This work was supported by NNSF grant nos. 11731003 and 12071118 for the second author.