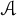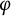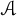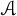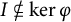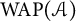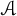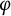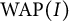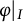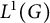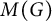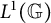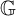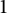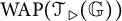1 Introduction
Let
![]() ${\mathcal A}$
be a Banach algebra. Then
${\mathcal A}$
be a Banach algebra. Then
![]() ${\mathcal A}^*$
is canonically a Banach
${\mathcal A}^*$
is canonically a Banach
![]() ${\mathcal A}$
-bimodule with the actions
${\mathcal A}$
-bimodule with the actions
for all
![]() $a,b\in {\mathcal A}$
and
$a,b\in {\mathcal A}$
and
![]() $x\in {\mathcal A}^*$
. There are two naturally defined products, which we denote by
$x\in {\mathcal A}^*$
. There are two naturally defined products, which we denote by
![]() $\square $
and
$\square $
and
![]() $\Diamond $
on the second dual
$\Diamond $
on the second dual
![]() $\mathcal {A}^{* *}$
of
$\mathcal {A}^{* *}$
of
![]() $\mathcal {A},$
each extending the product on
$\mathcal {A},$
each extending the product on
![]() $\mathcal {A}$
. For
$\mathcal {A}$
. For
![]() $m, n \in \mathcal {A}^{* *}$
and
$m, n \in \mathcal {A}^{* *}$
and
![]() $x \in \mathcal {A}^{*},$
the first Arens product
$x \in \mathcal {A}^{*},$
the first Arens product
![]() $\square $
in
$\square $
in
![]() $\mathcal {A}^{* *}$
is given as follows:
$\mathcal {A}^{* *}$
is given as follows:
where
![]() $n \cdot x \in \mathcal {A}^{*}$
is defined by
$n \cdot x \in \mathcal {A}^{*}$
is defined by
![]() $\langle n \cdot x, a\rangle =\langle n, x \cdot a\rangle $
for all
$\langle n \cdot x, a\rangle =\langle n, x \cdot a\rangle $
for all
![]() $a \in \mathcal {A}$
. Similarly, the second Arens product
$a \in \mathcal {A}$
. Similarly, the second Arens product
![]() $\Diamond $
in
$\Diamond $
in
![]() $\mathcal {A}^{* *}$
satisfies
$\mathcal {A}^{* *}$
satisfies
where
![]() $x \cdot m \in \mathcal {A}^{*}$
is given by
$x \cdot m \in \mathcal {A}^{*}$
is given by
![]() $\langle x \cdot m, a\rangle =\langle m, a \cdot x\rangle $
for all
$\langle x \cdot m, a\rangle =\langle m, a \cdot x\rangle $
for all
![]() $a \in \mathcal {A} .$
The Banach algebra
$a \in \mathcal {A} .$
The Banach algebra
![]() $\mathcal {A}$
is called Arens regular if
$\mathcal {A}$
is called Arens regular if
![]() $\square $
and
$\square $
and
![]() $\Diamond $
coincide on
$\Diamond $
coincide on
![]() $\mathcal {A}^{* *}$
.
$\mathcal {A}^{* *}$
.
We denote the spectrum of
![]() $\mathcal {A}$
by
$\mathcal {A}$
by
![]() $\operatorname {sp}(\mathcal {A})$
. Let
$\operatorname {sp}(\mathcal {A})$
. Let
![]() $\varphi \in \operatorname {sp}(\mathcal {A}),$
and let X be a Banach right
$\varphi \in \operatorname {sp}(\mathcal {A}),$
and let X be a Banach right
![]() $\mathcal {A}$
-submodule of
$\mathcal {A}$
-submodule of
![]() ${\mathcal A}^*$
with
${\mathcal A}^*$
with
![]() $\varphi \in X$
. Then a left invariant
$\varphi \in X$
. Then a left invariant
![]() $\varphi $
-mean on X is a functional
$\varphi $
-mean on X is a functional
![]() $m\in X^*$
satisfying
$m\in X^*$
satisfying
Right and (two-sided) invariant
![]() $\varphi $
-means are defined similarly. The Banach algebra
$\varphi $
-means are defined similarly. The Banach algebra
![]() $\mathcal {A}$
is called left
$\mathcal {A}$
is called left
![]() $\varphi $
-amenable if there exists a left invariant
$\varphi $
-amenable if there exists a left invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() ${\mathcal A}^*$
(see [Reference Kaniuth, Lau and Pym7]). This notion generalizes the concept of left amenability for Lau algebras, a class of Banach algebras including all convolution quantum group algebras, which was first introduced and studied in [Reference Lau10].
${\mathcal A}^*$
(see [Reference Kaniuth, Lau and Pym7]). This notion generalizes the concept of left amenability for Lau algebras, a class of Banach algebras including all convolution quantum group algebras, which was first introduced and studied in [Reference Lau10].
A Banach right (resp. left)
![]() $\mathcal {A}$
-submodule X of
$\mathcal {A}$
-submodule X of
![]() $\mathcal {A}^{*}$
is called left (resp. right) introverted if
$\mathcal {A}^{*}$
is called left (resp. right) introverted if
![]() $X^{*} \cdot X \subseteq X$
(resp.
$X^{*} \cdot X \subseteq X$
(resp.
![]() $X \cdot X^* \subseteq X$
). In this case,
$X \cdot X^* \subseteq X$
). In this case,
![]() $X^{*}$
is a Banach algebra with the multiplication induced by the first (resp. second) Arens product
$X^{*}$
is a Banach algebra with the multiplication induced by the first (resp. second) Arens product
![]() $\square $
(resp.
$\square $
(resp.
![]() $\Diamond $
) inherited from
$\Diamond $
) inherited from
![]() $\mathcal {A}^{* *}$
. A Banach
$\mathcal {A}^{* *}$
. A Banach
![]() $\mathcal {A}$
-subbimodule X of
$\mathcal {A}$
-subbimodule X of
![]() $\mathcal {A}^{*}$
is called introverted if it is both left and right introverted (see [Reference Dales and Lau2, Chapter 5] for details).
$\mathcal {A}^{*}$
is called introverted if it is both left and right introverted (see [Reference Dales and Lau2, Chapter 5] for details).
An element x of
![]() $\mathcal {A}^{*}$
is weakly almost periodic if the map
$\mathcal {A}^{*}$
is weakly almost periodic if the map
![]() $\lambda _x: a \mapsto a\cdot x $
from
$\lambda _x: a \mapsto a\cdot x $
from
![]() $\mathcal {A}$
into
$\mathcal {A}$
into
![]() $\mathcal {A}^{*}$
is a weakly compact operator. Let
$\mathcal {A}^{*}$
is a weakly compact operator. Let
![]() $\operatorname {WAP}(\mathcal {A})$
denote the closed subspace of
$\operatorname {WAP}(\mathcal {A})$
denote the closed subspace of
![]() ${\mathcal A}^*$
consisting of the weakly almost periodic functionals on
${\mathcal A}^*$
consisting of the weakly almost periodic functionals on
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
![]() $\operatorname {WAP}(\mathcal {A})$
is an introverted subspace of
$\operatorname {WAP}(\mathcal {A})$
is an introverted subspace of
![]() $\mathcal {A}^{*}$
containing
$\mathcal {A}^{*}$
containing
![]() $\operatorname {sp}(\mathcal {A})$
. We would like to recall from [Reference Dales and Lau2, Proposition 3.11] that
$\operatorname {sp}(\mathcal {A})$
. We would like to recall from [Reference Dales and Lau2, Proposition 3.11] that
![]() $m\square n= m\Diamond n $
for all
$m\square n= m\Diamond n $
for all
![]() $m,n\in \operatorname {WAP}(\mathcal {A})^*$
. Now suppose that I is a closed ideal in
$m,n\in \operatorname {WAP}(\mathcal {A})^*$
. Now suppose that I is a closed ideal in
![]() ${\mathcal A}$
with a bounded approximate identity. Then, by [Reference Dales and Lau2, Proposition 3.12]
${\mathcal A}$
with a bounded approximate identity. Then, by [Reference Dales and Lau2, Proposition 3.12]
![]() $\operatorname {WAP}(I)$
is a neo-unital Banach I-bimodule; that is,
$\operatorname {WAP}(I)$
is a neo-unital Banach I-bimodule; that is,
![]() $\operatorname {WAP}(I) = I\cdot \operatorname {WAP}(I) = \operatorname {WAP}(I)\cdot I$
. Moreover,
$\operatorname {WAP}(I) = I\cdot \operatorname {WAP}(I) = \operatorname {WAP}(I)\cdot I$
. Moreover,
![]() $\operatorname {WAP}(I)$
becomes a Banach
$\operatorname {WAP}(I)$
becomes a Banach
![]() ${\mathcal A}$
-bimodule (see [Reference Runde14, Proposition 2.1.6]).
${\mathcal A}$
-bimodule (see [Reference Runde14, Proposition 2.1.6]).
In the case that A is the group algebra
![]() $L^1(G)$
of a locally compact group G, it is known that
$L^1(G)$
of a locally compact group G, it is known that
![]() $\operatorname {WAP}(L^1(G))$
admits an invariant mean, which is unique, that is, a norm one functional
$\operatorname {WAP}(L^1(G))$
admits an invariant mean, which is unique, that is, a norm one functional
![]() $m\in L^1(G)^{**}$
with
$m\in L^1(G)^{**}$
with
![]() $\langle m, 1\rangle = 1$
and
$\langle m, 1\rangle = 1$
and
for all
![]() $x\in \operatorname {WAP}(L^1(G))$
and
$x\in \operatorname {WAP}(L^1(G))$
and
![]() $f\in L^1(G)$
(see [Reference Wong17]).
$f\in L^1(G)$
(see [Reference Wong17]).
Furthermore, it is known from [Reference Dales, Lau and Strauss3, Proposition 5.16] that if G is discrete or amenable, then
![]() $\operatorname {WAP}(M(G))$
admits an invariant mean, which is unique, where
$\operatorname {WAP}(M(G))$
admits an invariant mean, which is unique, where
![]() $M(G)$
denotes the measure algebra of G. Recently, Neufang in [Reference Neufang12] generalized this latter result to arbitrary locally compact groups, thereby answering a question posed in [Reference Dales, Lau and Strauss3].
$M(G)$
denotes the measure algebra of G. Recently, Neufang in [Reference Neufang12] generalized this latter result to arbitrary locally compact groups, thereby answering a question posed in [Reference Dales, Lau and Strauss3].
In this article, we generalize the main result of [Reference Neufang12] to an arbitrary Banach algebra
![]() ${\mathcal A}$
. More precisely, for
${\mathcal A}$
. More precisely, for
![]() $\varphi \in \operatorname {sp}({\mathcal A})$
, we show that if I is a closed ideal of
$\varphi \in \operatorname {sp}({\mathcal A})$
, we show that if I is a closed ideal of
![]() ${\mathcal A}$
with a bounded approximate identity such that
${\mathcal A}$
with a bounded approximate identity such that
![]() $I\not \subseteq \ker \varphi $
, then
$I\not \subseteq \ker \varphi $
, then
![]() $\operatorname {WAP}(\mathcal {A})$
admits a right (left) invariant
$\operatorname {WAP}(\mathcal {A})$
admits a right (left) invariant
![]() $\varphi $
-mean if and only if
$\varphi $
-mean if and only if
![]() $\operatorname {WAP}(I)$
admits a right (left) invariant
$\operatorname {WAP}(I)$
admits a right (left) invariant
![]() $\varphi |_I$
-mean. Applying our results to algebras over locally compact (quantum) groups, we show that, if I is a closed ideal of
$\varphi |_I$
-mean. Applying our results to algebras over locally compact (quantum) groups, we show that, if I is a closed ideal of
![]() $L^1(G)$
with a bounded approximate identity such that
$L^1(G)$
with a bounded approximate identity such that
![]() $I\not \subseteq \ker 1$
, then I is Arens regular if and only if it is reflexive.
$I\not \subseteq \ker 1$
, then I is Arens regular if and only if it is reflexive.
Finally, for a locally compact quantum group
![]() ${\mathbb G}$
, we characterize the existence of left and right invariant
${\mathbb G}$
, we characterize the existence of left and right invariant
![]() $1$
-means on
$1$
-means on
![]() $ \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, where
$ \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, where
![]() $\mathcal {T}_{\triangleright }({\mathbb G})$
denotes the trace class operators on
$\mathcal {T}_{\triangleright }({\mathbb G})$
denotes the trace class operators on
![]() $L^2({\mathbb G})$
, but equipped with a product different from composition (see [Reference Hu, Neufang and Ruan6].
$L^2({\mathbb G})$
, but equipped with a product different from composition (see [Reference Hu, Neufang and Ruan6].
2 Preliminaries
The class of locally compact quantum groups was first introduced and studied by Kustermans and Vaes [Reference Kustermans and Vaes8, Reference Kustermans and Vaes9]. Recall that a (von Neumann algebraic) locally compact quantum group is a quadruple
![]() ${\mathbb G}=(L^{\infty }({\mathbb G}), \Delta , \phi , \psi )$
, where
${\mathbb G}=(L^{\infty }({\mathbb G}), \Delta , \phi , \psi )$
, where
![]() $L^{\infty }({\mathbb G})$
is a von Neumann algebra with identity element
$L^{\infty }({\mathbb G})$
is a von Neumann algebra with identity element
![]() $1$
and a co-multiplication
$1$
and a co-multiplication
![]() $ \Delta : L^{\infty }({\mathbb G})\rightarrow L^{\infty }({\mathbb G})\bar {\otimes }L^{\infty }({\mathbb G}). $
Moreover,
$ \Delta : L^{\infty }({\mathbb G})\rightarrow L^{\infty }({\mathbb G})\bar {\otimes }L^{\infty }({\mathbb G}). $
Moreover,
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are normal faithful semifinite left and right Haar weights on
$\psi $
are normal faithful semifinite left and right Haar weights on
![]() $L^{\infty }({\mathbb G})$
, respectively. Here,
$L^{\infty }({\mathbb G})$
, respectively. Here,
![]() $\bar {\otimes }$
denotes the von Neumann algebra tensor product.
$\bar {\otimes }$
denotes the von Neumann algebra tensor product.
The predual of
![]() $L^{\infty }({\mathbb G})$
is denoted by
$L^{\infty }({\mathbb G})$
is denoted by
![]() $L^1({\mathbb G})$
which is called quantum group algebra of
$L^1({\mathbb G})$
which is called quantum group algebra of
![]() $\mathbb {G}$
. Then the pre-adjoint of the co-multiplication
$\mathbb {G}$
. Then the pre-adjoint of the co-multiplication
![]() $\Delta $
induces on
$\Delta $
induces on
![]() $L^1({\mathbb G})$
an associative completely contractive multiplication
$L^1({\mathbb G})$
an associative completely contractive multiplication
![]() $\Delta _*:L^1({\mathbb G})\widehat {\otimes }L^1({\mathbb G})\rightarrow L^1({\mathbb G})$
, where
$\Delta _*:L^1({\mathbb G})\widehat {\otimes }L^1({\mathbb G})\rightarrow L^1({\mathbb G})$
, where
![]() $\widehat {\otimes }$
is the operator space projective tensor product. Therefore,
$\widehat {\otimes }$
is the operator space projective tensor product. Therefore,
![]() $L^1({\mathbb G})$
is a Banach algebra under the product
$L^1({\mathbb G})$
is a Banach algebra under the product
![]() $*$
given by
$*$
given by
![]() $f*g:=\Delta _*(f\otimes g)\in L^1({\mathbb G})$
for all
$f*g:=\Delta _*(f\otimes g)\in L^1({\mathbb G})$
for all
![]() $f,g\in L^1({\mathbb G})$
. Moreover, the module actions of
$f,g\in L^1({\mathbb G})$
. Moreover, the module actions of
![]() $L^1({\mathbb G})$
on
$L^1({\mathbb G})$
on
![]() $L^{\infty }({\mathbb G})$
are given by
$L^{\infty }({\mathbb G})$
are given by
for all
![]() $f\in L^1({\mathbb G})$
and
$f\in L^1({\mathbb G})$
and
![]() $x\in L^{\infty }({\mathbb G})$
.
$x\in L^{\infty }({\mathbb G})$
.
For every locally compact quantum group
![]() $\mathbb {G}$
, there is a left fundamental unitary operator
$\mathbb {G}$
, there is a left fundamental unitary operator
![]() $W\in L^{\infty }(\mathbb {G})\bar {\otimes } L^{\infty }(\widehat {\mathbb {G}})$
and a right fundamental unitary operator
$W\in L^{\infty }(\mathbb {G})\bar {\otimes } L^{\infty }(\widehat {\mathbb {G}})$
and a right fundamental unitary operator
![]() $V\in L^{\infty }(\widehat {\mathbb {G}})'\bar {\otimes } L^{\infty }(\mathbb {G}) $
which the co-multiplication
$V\in L^{\infty }(\widehat {\mathbb {G}})'\bar {\otimes } L^{\infty }(\mathbb {G}) $
which the co-multiplication
![]() $\Delta $
can be given in terms of W and V by the formula
$\Delta $
can be given in terms of W and V by the formula
where
![]() $ L^{\infty }(\widehat {\mathbb G}):={\{(f\otimes \mathrm {id})(W)\;:\; f\in L^1(\mathbb G)\}}^{"} $
. The Gelfand–Naimark–Segal (GNS) representation space for the left Haar weight will be denoted by
$ L^{\infty }(\widehat {\mathbb G}):={\{(f\otimes \mathrm {id})(W)\;:\; f\in L^1(\mathbb G)\}}^{"} $
. The Gelfand–Naimark–Segal (GNS) representation space for the left Haar weight will be denoted by
![]() $L^2({\mathbb G})$
. Put
$L^2({\mathbb G})$
. Put
![]() $\widehat {W}=\sigma W^*\sigma $
, where
$\widehat {W}=\sigma W^*\sigma $
, where
![]() $\sigma $
denotes the flip operator on
$\sigma $
denotes the flip operator on
![]() $B(L^2({\mathbb G})\otimes L^2({\mathbb G}))$
, and define
$B(L^2({\mathbb G})\otimes L^2({\mathbb G}))$
, and define
which is a co-multiplication. One can also define a left Haar weight
![]() $\hat {\varphi }$
and a right Haar weight
$\hat {\varphi }$
and a right Haar weight
![]() $\hat {\psi }$
on
$\hat {\psi }$
on
![]() $L^{\infty }(\widehat {\mathbb G})$
that
$L^{\infty }(\widehat {\mathbb G})$
that
![]() $\widehat {\mathbb G}=(L^{\infty }(\widehat {\mathbb G}),\widehat {\Gamma }, \hat {\varphi }, \hat {\psi }),$
the dual quantum group of
$\widehat {\mathbb G}=(L^{\infty }(\widehat {\mathbb G}),\widehat {\Gamma }, \hat {\varphi }, \hat {\psi }),$
the dual quantum group of
![]() ${\mathbb G}$
, turn it into a locally compact quantum group. Moreover, a Pontryagin duality theorem holds, that is,
${\mathbb G}$
, turn it into a locally compact quantum group. Moreover, a Pontryagin duality theorem holds, that is,
![]() $\widehat {\widehat {\mathbb G}}={\mathbb G}$
(for more details, see [Reference Kustermans and Vaes8, Reference Kustermans and Vaes9]). The reduced quantum group
$\widehat {\widehat {\mathbb G}}={\mathbb G}$
(for more details, see [Reference Kustermans and Vaes8, Reference Kustermans and Vaes9]). The reduced quantum group
![]() $C^*$
-algebra of
$C^*$
-algebra of
![]() $L^{\infty }({\mathbb G})$
is defined as
$L^{\infty }({\mathbb G})$
is defined as
We say that
![]() ${\mathbb G}$
is compact if
${\mathbb G}$
is compact if
![]() $C_0({\mathbb G})$
is a unital
$C_0({\mathbb G})$
is a unital
![]() $C^*$
-algebra. The co-multiplication
$C^*$
-algebra. The co-multiplication
![]() $\Delta $
maps
$\Delta $
maps
![]() $C_0({\mathbb G})$
into the multiplier algebra
$C_0({\mathbb G})$
into the multiplier algebra
![]() $M(C_0({\mathbb G})\otimes C_0({\mathbb G}))$
of the minimal
$M(C_0({\mathbb G})\otimes C_0({\mathbb G}))$
of the minimal
![]() $C^*$
-algebra tensor product
$C^*$
-algebra tensor product
![]() $C_0({\mathbb G})\otimes C_0({\mathbb G})$
. Thus, we can define the completely contractive product
$C_0({\mathbb G})\otimes C_0({\mathbb G})$
. Thus, we can define the completely contractive product
![]() $*$
on
$*$
on
![]() $C_0({\mathbb G})^*=M({\mathbb G})$
by
$C_0({\mathbb G})^*=M({\mathbb G})$
by
whence
![]() $(M({\mathbb G}), *)$
is a completely contractive Banach algebra and contains
$(M({\mathbb G}), *)$
is a completely contractive Banach algebra and contains
![]() $L^1({\mathbb G})$
as a norm closed two-sided ideal. If X is a Banach right
$L^1({\mathbb G})$
as a norm closed two-sided ideal. If X is a Banach right
![]() $L^1({\mathbb G})$
-submodule of
$L^1({\mathbb G})$
-submodule of
![]() $L^{\infty }({\mathbb G})$
with
$L^{\infty }({\mathbb G})$
with
![]() $1\in X$
, then a left invariant mean on X, is a functional
$1\in X$
, then a left invariant mean on X, is a functional
![]() $m\in X^*$
satisfying
$m\in X^*$
satisfying
Right and (two-sided) invariant means are defined similarly. A locally compact quantum group
![]() ${\mathbb G}$
is said to be amenable if there exists a left (equivalently, right, or two-sided) invariant mean on
${\mathbb G}$
is said to be amenable if there exists a left (equivalently, right, or two-sided) invariant mean on
![]() $L^{\infty }({\mathbb G})$
(see [Reference Desmedt, Quaegebeur and Vaes4, Proposition 3]). A standard argument, used in the proof of [Reference Lau10, Theorem 4.1] on Lau algebras shows that
$L^{\infty }({\mathbb G})$
(see [Reference Desmedt, Quaegebeur and Vaes4, Proposition 3]). A standard argument, used in the proof of [Reference Lau10, Theorem 4.1] on Lau algebras shows that
![]() ${\mathbb G}$
is amenable if and only if
${\mathbb G}$
is amenable if and only if
![]() $L^1({\mathbb G})$
is left
$L^1({\mathbb G})$
is left
![]() $1$
-amenable. We also recall that,
$1$
-amenable. We also recall that,
![]() $\mathbb {G}$
is called co-amenable if
$\mathbb {G}$
is called co-amenable if
![]() $L^1({\mathbb G})$
has a bounded approximate identity.
$L^1({\mathbb G})$
has a bounded approximate identity.
The right fundamental unitary V of
![]() $\mathbb {G}$
induces a co-associative co-multiplication
$\mathbb {G}$
induces a co-associative co-multiplication
and the restriction of
![]() $\Delta ^{r}$
to
$\Delta ^{r}$
to
![]() $L^{\infty }(\mathbb {G})$
yields the original co-multiplication
$L^{\infty }(\mathbb {G})$
yields the original co-multiplication
![]() $\Delta $
on
$\Delta $
on
![]() $L^{\infty }(\mathbb {G})$
. The pre-adjoint of
$L^{\infty }(\mathbb {G})$
. The pre-adjoint of
![]() $\Delta ^{r}$
induces an associative completely contractive multiplication on space
$\Delta ^{r}$
induces an associative completely contractive multiplication on space
![]() $\mathcal {T}\left (L^{2}(\mathbb {G})\right )$
of trace class operators on
$\mathcal {T}\left (L^{2}(\mathbb {G})\right )$
of trace class operators on
![]() $L^{2}(\mathbb {G})$
, defined by
$L^{2}(\mathbb {G})$
, defined by
where
![]() $\widehat {\otimes }$
denotes the operator space projective tensor product.
$\widehat {\otimes }$
denotes the operator space projective tensor product.
It was shown in [Reference Hu, Neufang and Ruan6, Lemma 5.2], that the pre-annihilator
![]() $L^{\infty }(\mathbb {G})_{\perp }$
of
$L^{\infty }(\mathbb {G})_{\perp }$
of
![]() $L^{\infty }(\mathbb {G})$
in
$L^{\infty }(\mathbb {G})$
in
![]() $\mathcal {T}\left (L^{2}(\mathbb {G})\right )$
is a norm closed two-sided ideal in
$\mathcal {T}\left (L^{2}(\mathbb {G})\right )$
is a norm closed two-sided ideal in
![]() $\left (\mathcal {T}\left (L^{2}(\mathbb {G})\right ), \triangleright \right )$
and the complete quotient map
$\left (\mathcal {T}\left (L^{2}(\mathbb {G})\right ), \triangleright \right )$
and the complete quotient map
is a completely contractive algebra homomorphism from
![]() $\mathcal {T}_{\triangleright }({\mathbb G}):=\left (\mathcal {T}\left (L^{2}(\mathbb {G})\right ), \triangleright \right )$
onto
$\mathcal {T}_{\triangleright }({\mathbb G}):=\left (\mathcal {T}\left (L^{2}(\mathbb {G})\right ), \triangleright \right )$
onto
![]() $L^{1}(\mathbb {G})$
. The multiplication
$L^{1}(\mathbb {G})$
. The multiplication
![]() $\triangleright $
defines a canonical
$\triangleright $
defines a canonical
![]() $\mathcal {T}_{\triangleright }({\mathbb G})$
-bimodule structure on
$\mathcal {T}_{\triangleright }({\mathbb G})$
-bimodule structure on
![]() $\mathcal {B}\left (L^{2}(\mathbb {G})\right )$
. Note that since
$\mathcal {B}\left (L^{2}(\mathbb {G})\right )$
. Note that since
![]() $V \in L^{\infty }(\widehat {\mathbb {G}}^{\prime }) \bar {\otimes } L^{\infty }(\mathbb {G})$
, the bimodule action on
$V \in L^{\infty }(\widehat {\mathbb {G}}^{\prime }) \bar {\otimes } L^{\infty }(\mathbb {G})$
, the bimodule action on
![]() $L^{\infty }(\widehat {\mathbb {G}})$
becomes rather trivial. Indeed, for
$L^{\infty }(\widehat {\mathbb {G}})$
becomes rather trivial. Indeed, for
![]() $\hat {x} \in L^{\infty }(\widehat {\mathbb {G}})$
and
$\hat {x} \in L^{\infty }(\widehat {\mathbb {G}})$
and
![]() $\omega \in \mathcal {T}_{\triangleright }({\mathbb G}),$
we have
$\omega \in \mathcal {T}_{\triangleright }({\mathbb G}),$
we have
This implies that
![]() $L^{\infty }(\widehat {\mathbb {G}})\subseteq \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. It is also known from [Reference Hu, Neufang and Ruan6, Proposition 5.3] that
$L^{\infty }(\widehat {\mathbb {G}})\subseteq \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. It is also known from [Reference Hu, Neufang and Ruan6, Proposition 5.3] that
![]() $B(L^2({\mathbb G}))\triangleright \mathcal {T}_{\triangleright }({\mathbb G})\subseteq L^{\infty }({\mathbb G}).$
In particular, the actions of
$B(L^2({\mathbb G}))\triangleright \mathcal {T}_{\triangleright }({\mathbb G})\subseteq L^{\infty }({\mathbb G}).$
In particular, the actions of
![]() $\mathcal {T}_{\triangleright }({\mathbb G})$
on
$\mathcal {T}_{\triangleright }({\mathbb G})$
on
![]() $L^{\infty }(\mathbb {G})$
satisfies
$L^{\infty }(\mathbb {G})$
satisfies
for all
![]() $\omega \in \mathcal {T}_{\triangleright }({\mathbb G})$
and
$\omega \in \mathcal {T}_{\triangleright }({\mathbb G})$
and
![]() $ x\in L^{\infty }(\mathbb {G})$
.
$ x\in L^{\infty }(\mathbb {G})$
.
3 Invariant means on weakly almost periodic functionals
Let I be a closed ideal of the Banach algebra
![]() $\mathcal {A}$
. Then for every
$\mathcal {A}$
. Then for every
![]() $b \in I$
and
$b \in I$
and
![]() $x \in I^{*}$
, define
$x \in I^{*}$
, define
![]() $x \bullet b, b \bullet x \in \mathcal {A}^*$
as follows:
$x \bullet b, b \bullet x \in \mathcal {A}^*$
as follows:
We note that, given
![]() $a\in {\mathcal A}, b_1, b_2\in I$
, and
$a\in {\mathcal A}, b_1, b_2\in I$
, and
![]() $x\in I^*$
, for
$x\in I^*$
, for
![]() $a'\in {\mathcal A}$
, we have
$a'\in {\mathcal A}$
, we have
 $$ \begin{align*} \langle a\cdot((b_1\cdot x)\bullet b_2), a'\rangle &=\langle (b_1\cdot x)\bullet b_2, a'a\rangle =\langle b_1\cdot x, b_2a'a\rangle =\langle x, b_2a'ab_1\rangle\\ &= \langle ab_1\cdot x, b_2a'\rangle =\langle (ab_1\cdot x)\bullet b_2, a'\rangle, \end{align*} $$
$$ \begin{align*} \langle a\cdot((b_1\cdot x)\bullet b_2), a'\rangle &=\langle (b_1\cdot x)\bullet b_2, a'a\rangle =\langle b_1\cdot x, b_2a'a\rangle =\langle x, b_2a'ab_1\rangle\\ &= \langle ab_1\cdot x, b_2a'\rangle =\langle (ab_1\cdot x)\bullet b_2, a'\rangle, \end{align*} $$
so that,
![]() $ a\cdot ((b_1\cdot x)\bullet b_2)=(ab_1\cdot x)\bullet b_2$
.
$ a\cdot ((b_1\cdot x)\bullet b_2)=(ab_1\cdot x)\bullet b_2$
.
Lemma 3.1 Let
![]() ${\mathcal A}$
be a Banach algebra, and let I be a closed ideal of
${\mathcal A}$
be a Banach algebra, and let I be a closed ideal of
![]() ${\mathcal A}$
with a bounded approximate identity. Then
${\mathcal A}$
with a bounded approximate identity. Then
Proof Let
![]() $x\in \mathrm {WAP}(I)$
and
$x\in \mathrm {WAP}(I)$
and
![]() $b_1, b_2\in I$
. Suppose that
$b_1, b_2\in I$
. Suppose that
![]() $(a_n)$
is a bounded sequence in
$(a_n)$
is a bounded sequence in
![]() ${\mathcal A}$
. Then
${\mathcal A}$
. Then
![]() $(a_nb_1)$
is a bounded sequence in I and so by weak compactness of the map
$(a_nb_1)$
is a bounded sequence in I and so by weak compactness of the map
![]() $\lambda _x: I\rightarrow I^*$
, there is a subsequence
$\lambda _x: I\rightarrow I^*$
, there is a subsequence
![]() $(a_{n_j}b_1)$
of
$(a_{n_j}b_1)$
of
![]() $(a_nb_1)$
such that
$(a_nb_1)$
such that
![]() $(a_{n_j}b_1\cdot x)$
converges weakly in
$(a_{n_j}b_1\cdot x)$
converges weakly in
![]() $I^*$
to some
$I^*$
to some
![]() $y\in I^*$
. Now, for each
$y\in I^*$
. Now, for each
![]() $m\in {\mathcal A}^{**}$
, define the functional
$m\in {\mathcal A}^{**}$
, define the functional
![]() $b_2\bullet m\in I^{**}$
as follows:
$b_2\bullet m\in I^{**}$
as follows:
It follows that
 $$ \begin{align*} \langle m,a_{n_j}\cdot((b_1\cdot x)\bullet b_2)\rangle &= \langle m,(a_{n_j}b_1\cdot x)\bullet b_2\rangle \\ &= \langle b_2\bullet m, a_{n_j}b_1\cdot x\rangle \rightarrow \langle b_2\bullet m, y\rangle\\ &= \langle m, y\bullet b_2\rangle \end{align*} $$
$$ \begin{align*} \langle m,a_{n_j}\cdot((b_1\cdot x)\bullet b_2)\rangle &= \langle m,(a_{n_j}b_1\cdot x)\bullet b_2\rangle \\ &= \langle b_2\bullet m, a_{n_j}b_1\cdot x\rangle \rightarrow \langle b_2\bullet m, y\rangle\\ &= \langle m, y\bullet b_2\rangle \end{align*} $$
for all
![]() $m\in {\mathcal A}^{**}$
. That is,
$m\in {\mathcal A}^{**}$
. That is,
![]() $(b_1\cdot x)\bullet b_2\in \mathrm {WAP}(\mathcal {A})$
. Since I has a bounded right approximate identity, it follows from [Reference Dales and Lau2, Proposition 3.12] that
$(b_1\cdot x)\bullet b_2\in \mathrm {WAP}(\mathcal {A})$
. Since I has a bounded right approximate identity, it follows from [Reference Dales and Lau2, Proposition 3.12] that
![]() $I\cdot \mathrm {WAP}(I)=\mathrm {WAP}(I)$
. This shows that
$I\cdot \mathrm {WAP}(I)=\mathrm {WAP}(I)$
. This shows that
![]() $\mathrm {WAP}(I)\bullet I\subseteq \mathrm {WAP}(\mathcal {A})$
. The inclusion
$\mathrm {WAP}(I)\bullet I\subseteq \mathrm {WAP}(\mathcal {A})$
. The inclusion
![]() $I\bullet \mathrm {WAP}(I)\subseteq \mathrm {WAP}(\mathcal {A})$
can be proved similarly.
$I\bullet \mathrm {WAP}(I)\subseteq \mathrm {WAP}(\mathcal {A})$
can be proved similarly.
Theorem 3.2 Let
![]() ${\mathcal A}$
be a Banach algebra with
${\mathcal A}$
be a Banach algebra with
![]() $\varphi \in \operatorname {sp}(\mathcal {A})$
, and let I be a closed ideal of
$\varphi \in \operatorname {sp}(\mathcal {A})$
, and let I be a closed ideal of
![]() ${\mathcal A}$
with a bounded approximate identity such that
${\mathcal A}$
with a bounded approximate identity such that
![]() $I\not \subseteq \ker \varphi $
. Then the following statements are equivalent:
$I\not \subseteq \ker \varphi $
. Then the following statements are equivalent:
-
(i)
 $\mathrm {WAP}(I)$
has a right (left) invariant
$\mathrm {WAP}(I)$
has a right (left) invariant
 $\varphi |_I$
-mean.
$\varphi |_I$
-mean. -
(ii)
 $\mathrm {WAP}(A)$
has a right (left) invariant
$\mathrm {WAP}(A)$
has a right (left) invariant
 $\varphi $
-mean.
$\varphi $
-mean.
Proof We only prove the right version of the theorem. Similar arguments will establish the left side version.
(i)
![]() $\Rightarrow $
(ii). Let m be a right invariant
$\Rightarrow $
(ii). Let m be a right invariant
![]() $\varphi |_I$
-mean on
$\varphi |_I$
-mean on
![]() $\mathrm {WAP}(I)$
. This means that for every
$\mathrm {WAP}(I)$
. This means that for every
![]() $x\in \mathrm {WAP}(I)$
and
$x\in \mathrm {WAP}(I)$
and
![]() $b\in I,$
we have
$b\in I,$
we have
We denote by
![]() $\imath :I\rightarrow {\mathcal A}$
the canonical embedding map. By [Reference Young18, Corollary to Lemma 1], the map
$\imath :I\rightarrow {\mathcal A}$
the canonical embedding map. By [Reference Young18, Corollary to Lemma 1], the map
![]() $R:=\imath ^*: {\mathcal A}^*\rightarrow I^*$
maps
$R:=\imath ^*: {\mathcal A}^*\rightarrow I^*$
maps
![]() $\operatorname {WAP}({\mathcal A})$
to
$\operatorname {WAP}({\mathcal A})$
to
![]() $\mathrm {WAP}(I)$
. Define
$\mathrm {WAP}(I)$
. Define
![]() ${\widetilde m}:=m\circ R\in {\mathcal A}^{**}$
. It is easy to see that
${\widetilde m}:=m\circ R\in {\mathcal A}^{**}$
. It is easy to see that
![]() $ \langle {\widetilde m}, \varphi \rangle =1. $
Let
$ \langle {\widetilde m}, \varphi \rangle =1. $
Let
![]() $(e_{\alpha })$
be a bounded approximate identity for I. By [Reference Dales and Lau2, Proposition 3.12], we have
$(e_{\alpha })$
be a bounded approximate identity for I. By [Reference Dales and Lau2, Proposition 3.12], we have
![]() $I\cdot \operatorname {WAP}(I)=\operatorname {WAP}(I)\cdot I=\operatorname {WAP}(I)$
. Thus,
$I\cdot \operatorname {WAP}(I)=\operatorname {WAP}(I)\cdot I=\operatorname {WAP}(I)$
. Thus,
![]() $\lim _{\alpha } e_{\alpha }\cdot R(y)=R(y)$
for all
$\lim _{\alpha } e_{\alpha }\cdot R(y)=R(y)$
for all
![]() $y\in \operatorname {WAP}({\mathcal A})$
. Moreover, by [Reference Runde14, Proposition 2.1.6],
$y\in \operatorname {WAP}({\mathcal A})$
. Moreover, by [Reference Runde14, Proposition 2.1.6],
![]() $\mathrm {WAP}(I)$
becomes a Banach
$\mathrm {WAP}(I)$
becomes a Banach
![]() ${\mathcal A}$
-bimodule and since I is an ideal in
${\mathcal A}$
-bimodule and since I is an ideal in
![]() ${\mathcal A}$
, it is not hard check that
${\mathcal A}$
, it is not hard check that
![]() $R(a\cdot y)=a\cdot R(y)$
for all
$R(a\cdot y)=a\cdot R(y)$
for all
![]() $a\in {\mathcal A}$
and
$a\in {\mathcal A}$
and
![]() $y\in \operatorname {WAP}({\mathcal A})$
. Therefore, for every
$y\in \operatorname {WAP}({\mathcal A})$
. Therefore, for every
![]() $a\in {\mathcal A}$
and
$a\in {\mathcal A}$
and
![]() $y\in \operatorname {WAP}({\mathcal A})$
, we have
$y\in \operatorname {WAP}({\mathcal A})$
, we have
 $$ \begin{align*} \langle {\widetilde m}, a\cdot y\rangle&=\langle m,R(a\cdot y)\rangle =\langle m,a\cdot R(y)\rangle\\ &=\lim_{\alpha}\langle m,a\cdot (e_{\alpha}\cdot R(y))\rangle =\lim_{\alpha}\langle m, ae_{\alpha}\cdot R(y)\rangle\\ &=\lim_{\alpha}\varphi(ae_{\alpha})\langle m, R(y)\rangle =\varphi(a)\varphi(e_{\alpha})\langle {\widetilde m}, y\rangle=\varphi(a)\langle {\widetilde m}, y\rangle. \end{align*} $$
$$ \begin{align*} \langle {\widetilde m}, a\cdot y\rangle&=\langle m,R(a\cdot y)\rangle =\langle m,a\cdot R(y)\rangle\\ &=\lim_{\alpha}\langle m,a\cdot (e_{\alpha}\cdot R(y))\rangle =\lim_{\alpha}\langle m, ae_{\alpha}\cdot R(y)\rangle\\ &=\lim_{\alpha}\varphi(ae_{\alpha})\langle m, R(y)\rangle =\varphi(a)\varphi(e_{\alpha})\langle {\widetilde m}, y\rangle=\varphi(a)\langle {\widetilde m}, y\rangle. \end{align*} $$
Thus,
![]() ${\widetilde m}$
is a right invariant
${\widetilde m}$
is a right invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() $\operatorname {WAP}({\mathcal A})$
.
$\operatorname {WAP}({\mathcal A})$
.
(ii)
![]() $\Rightarrow $
(i). Let
$\Rightarrow $
(i). Let
![]() $m \in {\mathcal A}^{**}$
be a right invariant
$m \in {\mathcal A}^{**}$
be a right invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() $\operatorname {WAP}({\mathcal A})$
. Fix
$\operatorname {WAP}({\mathcal A})$
. Fix
![]() $b_{0} \in I$
with
$b_{0} \in I$
with
![]() $\varphi (b_0)=1$
. Since
$\varphi (b_0)=1$
. Since
![]() $\operatorname {WAP}(I)\bullet b_0\subseteq \operatorname {WAP}({\mathcal A})$
, by Lemma 3.1, we can define
$\operatorname {WAP}(I)\bullet b_0\subseteq \operatorname {WAP}({\mathcal A})$
, by Lemma 3.1, we can define
![]() $\tilde {m} \in \operatorname {WAP}(I)^{*}$
as follows:
$\tilde {m} \in \operatorname {WAP}(I)^{*}$
as follows:
It is easily verified that
Moreover, for every
![]() $b\in I$
and
$b\in I$
and
![]() $x \in \operatorname {WAP}(I)$
, we have
$x \in \operatorname {WAP}(I)$
, we have
 $$ \begin{align*} \begin{aligned} \langle\tilde{m}, b \cdot x\rangle =\left\langle m, (b\cdot x)\bullet b_{0}\right\rangle &= \left\langle m, b\cdot(x\bullet b_0) \right\rangle \\ &=\left.\varphi\right|{}_{I}\left(b\right)\left\langle m, x \bullet b_0\right\rangle \\ &=\left.\varphi\right|{}_{I}\left(b\right)\langle\tilde{m}, x\rangle. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \langle\tilde{m}, b \cdot x\rangle =\left\langle m, (b\cdot x)\bullet b_{0}\right\rangle &= \left\langle m, b\cdot(x\bullet b_0) \right\rangle \\ &=\left.\varphi\right|{}_{I}\left(b\right)\left\langle m, x \bullet b_0\right\rangle \\ &=\left.\varphi\right|{}_{I}\left(b\right)\langle\tilde{m}, x\rangle. \end{aligned} \end{align*} $$
Therefore,
![]() $\tilde {m}$
is a right
$\tilde {m}$
is a right
![]() $\left .\varphi \right |{}_{I}$
-mean on
$\left .\varphi \right |{}_{I}$
-mean on
![]() $\operatorname {WAP}(I)$
.
$\operatorname {WAP}(I)$
.
Remark 3.3 We would like to point out the following fact related to right and left invariant
![]() $\varphi $
-means on
$\varphi $
-means on
![]() $\mathrm {WAP}({\mathcal A})$
. Suppose that m is a left invariant
$\mathrm {WAP}({\mathcal A})$
. Suppose that m is a left invariant
![]() $\varphi $
-mean and n is a right invariant
$\varphi $
-mean and n is a right invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() $\mathrm {WAP}({\mathcal A})$
. Using weak
$\mathrm {WAP}({\mathcal A})$
. Using weak
![]() $^*$
-continuity of the maps
$^*$
-continuity of the maps
![]() $p\mapsto p\square m$
and
$p\mapsto p\square m$
and
![]() $p\mapsto n\Diamond p$
on
$p\mapsto n\Diamond p$
on
![]() $\mathrm {WAP}({\mathcal A})^*$
, we obtain that
$\mathrm {WAP}({\mathcal A})^*$
, we obtain that
![]() $m=n(\varphi )m=n\square m=n\Diamond m=m(\varphi )n=n$
. In particular, if there is an invariant
$m=n(\varphi )m=n\square m=n\Diamond m=m(\varphi )n=n$
. In particular, if there is an invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() $\mathrm {WAP}({\mathcal A})$
, then it is unique.
$\mathrm {WAP}({\mathcal A})$
, then it is unique.
We now consider some special cases. Suppose that
![]() ${\mathbb G}$
is a locally compact quantum group. Then
${\mathbb G}$
is a locally compact quantum group. Then
![]() ${\Bbb G}$
has a canonical co-involution
${\Bbb G}$
has a canonical co-involution
![]() ${\mathcal R}$
, called the unitary antipode of
${\mathcal R}$
, called the unitary antipode of
![]() ${\Bbb G}$
. That is,
${\Bbb G}$
. That is,
![]() ${\mathcal R}: L^{\infty }({\Bbb G})\longrightarrow L^{\infty }({\Bbb G})$
is a
${\mathcal R}: L^{\infty }({\Bbb G})\longrightarrow L^{\infty }({\Bbb G})$
is a
![]() $^*$
-anti-homomorphism satisfying
$^*$
-anti-homomorphism satisfying
![]() ${\mathcal R}^2=\mathrm {id}$
and
${\mathcal R}^2=\mathrm {id}$
and
![]() $ \Delta \circ {\mathcal R}=\sigma ({\mathcal R}\otimes {\mathcal R})\circ \Delta , $
where
$ \Delta \circ {\mathcal R}=\sigma ({\mathcal R}\otimes {\mathcal R})\circ \Delta , $
where
![]() $\sigma $
is the flip map on
$\sigma $
is the flip map on
![]() $L^2({\Bbb G})\otimes L^2({\Bbb G})$
. Then
$L^2({\Bbb G})\otimes L^2({\Bbb G})$
. Then
![]() ${\mathcal R}$
induces a completely isometric involution on
${\mathcal R}$
induces a completely isometric involution on
![]() $L^1({\Bbb G})$
defined by
$L^1({\Bbb G})$
defined by
Hence,
![]() $L^1({\Bbb G})$
becomes an involutive Banach algebra.
$L^1({\Bbb G})$
becomes an involutive Banach algebra.
Now, assume that m is a left (resp. right) invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(L^1({\mathbb G}))$
, and let
$\operatorname {WAP}(L^1({\mathbb G}))$
, and let
![]() $\widetilde {m}\in L^{\infty }({\mathbb G})^*$
be a Hahn–Banach extension of m. It is not hard to see that
$\widetilde {m}\in L^{\infty }({\mathbb G})^*$
be a Hahn–Banach extension of m. It is not hard to see that
![]() $n:=\widetilde {m}^{\circ }|_{\operatorname {WAP}(L^1({\mathbb G})}$
is a right (resp. left) invariant
$n:=\widetilde {m}^{\circ }|_{\operatorname {WAP}(L^1({\mathbb G})}$
is a right (resp. left) invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(L^1({\mathbb G}))$
, where
$\operatorname {WAP}(L^1({\mathbb G}))$
, where
![]() $\circ : L^{\infty }({\mathbb G})^*\rightarrow L^{\infty }({\mathbb G})^*, m\mapsto m^{\circ }$
is the unique weak
$\circ : L^{\infty }({\mathbb G})^*\rightarrow L^{\infty }({\mathbb G})^*, m\mapsto m^{\circ }$
is the unique weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
continuous extension of the involution on
$^*$
continuous extension of the involution on
![]() $L^1({\mathbb G})$
which is called the linear involution (see [Reference Dales and Lau2, Chapter 2, p. 18]. Thus, by Remark 3.3, we obtain that any left (resp. right) invariant
$L^1({\mathbb G})$
which is called the linear involution (see [Reference Dales and Lau2, Chapter 2, p. 18]. Thus, by Remark 3.3, we obtain that any left (resp. right) invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(L^1({\mathbb G}))$
is unique and (two-sided) invariant.
$\operatorname {WAP}(L^1({\mathbb G}))$
is unique and (two-sided) invariant.
Our next result yields a generalization of [Reference Neufang12, Theorem 2.3] which is concerned with the group algebra
![]() $L^1(G)$
as an ideal in the measure algebra
$L^1(G)$
as an ideal in the measure algebra
![]() $M(G)$
, for a locally compact group G.
$M(G)$
, for a locally compact group G.
Corollary 3.4 Let
![]() ${\mathbb G}$
be a co-amenable locally compact quantum group. Then
${\mathbb G}$
be a co-amenable locally compact quantum group. Then
![]() $\operatorname {WAP}(L^1({\mathbb G}))$
has a right invariant
$\operatorname {WAP}(L^1({\mathbb G}))$
has a right invariant
![]() $1$
-mean or equivalently has an invariant
$1$
-mean or equivalently has an invariant
![]() $1$
-mean if and only if
$1$
-mean if and only if
![]() $\operatorname {WAP}(M({\mathbb G}))$
has an invariant
$\operatorname {WAP}(M({\mathbb G}))$
has an invariant
![]() $1$
-mean.
$1$
-mean.
Proposition 3.5 Let
![]() ${\mathcal A}$
is a Banach algebra, and let I is a closed ideal in
${\mathcal A}$
is a Banach algebra, and let I is a closed ideal in
![]() ${\mathcal A}$
. Let
${\mathcal A}$
. Let
![]() $\varphi \in \operatorname {sp}(\mathcal {A})$
be such that
$\varphi \in \operatorname {sp}(\mathcal {A})$
be such that
![]() $I\not \subseteq \ker \varphi $
. Then
$I\not \subseteq \ker \varphi $
. Then
![]() ${\mathcal A}^*$
admits a right invariant
${\mathcal A}^*$
admits a right invariant
![]() $\varphi $
-mean if and only if
$\varphi $
-mean if and only if
![]() $I^*$
admits a right invariant
$I^*$
admits a right invariant
![]() $\varphi |_I$
-mean.
$\varphi |_I$
-mean.
Proof To see this, first note that, since we can identify
![]() $I^{**}$
with
$I^{**}$
with
![]() $I^{\perp \perp }$
, it follows that
$I^{\perp \perp }$
, it follows that
![]() $I^{**}$
is a closed ideal in
$I^{**}$
is a closed ideal in
![]() ${\mathcal A}^{**}$
(see [Reference Dales and Lau2, p. 17]). Fix
${\mathcal A}^{**}$
(see [Reference Dales and Lau2, p. 17]). Fix
![]() $b_0\in I$
with
$b_0\in I$
with
![]() $\varphi (b_0)=1$
. Now, suppose that
$\varphi (b_0)=1$
. Now, suppose that
![]() $m\in {\mathcal A}^{**}$
is a right invariant
$m\in {\mathcal A}^{**}$
is a right invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() ${\mathcal A}^*$
. Since
${\mathcal A}^*$
. Since
![]() $I^{**}$
is an ideal in
$I^{**}$
is an ideal in
![]() ${\mathcal A}^{**}$
, we obtain that
${\mathcal A}^{**}$
, we obtain that
![]() $b_0\square m\in I^{**}$
. Furthermore,
$b_0\square m\in I^{**}$
. Furthermore,
![]() $\langle b_0\square m, \varphi \rangle =1$
and
$\langle b_0\square m, \varphi \rangle =1$
and
for all
![]() $b\in I$
. Thus,
$b\in I$
. Thus,
![]() $b_0\square m$
is a right invariant
$b_0\square m$
is a right invariant
![]() $\varphi |_I$
-mean on
$\varphi |_I$
-mean on
![]() ${I}^*$
. For the converse, suppose that
${I}^*$
. For the converse, suppose that
![]() $m\in {I}^{**}$
is a right invariant
$m\in {I}^{**}$
is a right invariant
![]() $\varphi |_I$
-mean on
$\varphi |_I$
-mean on
![]() $I^*$
. Then
$I^*$
. Then
for all
![]() $a\in {\mathcal A}$
. This shows that m is a right invariant
$a\in {\mathcal A}$
. This shows that m is a right invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() ${\mathcal A}^*$
.
${\mathcal A}^*$
.
Before giving the next result, we recall that a Banach algebra
![]() ${\mathcal A}$
is weakly sequentially complete if every weakly Cauchy sequence in
${\mathcal A}$
is weakly sequentially complete if every weakly Cauchy sequence in
![]() ${\mathcal A}$
is weakly convergent in
${\mathcal A}$
is weakly convergent in
![]() ${\mathcal A}$
. For example, preduals of von Neumann algebras are weakly sequentially complete (see [Reference Takesaki15]).
${\mathcal A}$
. For example, preduals of von Neumann algebras are weakly sequentially complete (see [Reference Takesaki15]).
Proposition 3.6 Let
![]() ${\mathbb G}$
be a locally compact quantum group such that
${\mathbb G}$
be a locally compact quantum group such that
![]() $\operatorname {WAP}(L^1({\mathbb G}))$
has an invariant
$\operatorname {WAP}(L^1({\mathbb G}))$
has an invariant
![]() $1$
-mean, and let I be a closed ideal of
$1$
-mean, and let I be a closed ideal of
![]() $L^1({\mathbb G})$
with a bounded approximate identity such that
$L^1({\mathbb G})$
with a bounded approximate identity such that
![]() $I\not \subseteq \ker 1$
. If I is Arens regular, then
$I\not \subseteq \ker 1$
. If I is Arens regular, then
![]() ${\mathbb G}$
is compact.
${\mathbb G}$
is compact.
Proof By assumption and Theorem 3.2, we conclude that
![]() $\operatorname {WAP}(I)$
has a right invariant
$\operatorname {WAP}(I)$
has a right invariant
![]() $1$
-mean. Since I is Arens regular, we have that
$1$
-mean. Since I is Arens regular, we have that
![]() $\operatorname {WAP}(I)=I^*$
. This implies that I is right
$\operatorname {WAP}(I)=I^*$
. This implies that I is right
![]() $1$
-amenable. Now, by Proposition 3.5, we obtain that
$1$
-amenable. Now, by Proposition 3.5, we obtain that
![]() $L^1({\mathbb G})$
is right
$L^1({\mathbb G})$
is right
![]() $1$
-amenable or equivalently,
$1$
-amenable or equivalently,
![]() ${\mathbb G}$
is amenable. Thus, there is an invariant
${\mathbb G}$
is amenable. Thus, there is an invariant
![]() $1$
-mean on
$1$
-mean on
![]() $L^{\infty }({\mathbb G})$
. Again by two-sided version of Proposition 3.5, we conclude that there is an invariant
$L^{\infty }({\mathbb G})$
. Again by two-sided version of Proposition 3.5, we conclude that there is an invariant
![]() $1$
-mean m on
$1$
-mean m on
![]() $I^*$
. Since I is Arens regular and weakly sequentially complete, it follows from [Reference Kaniuth, Lau and Pym7, Theorem 3.9] that
$I^*$
. Since I is Arens regular and weakly sequentially complete, it follows from [Reference Kaniuth, Lau and Pym7, Theorem 3.9] that
![]() $m\in I$
. Therefore, for every
$m\in I$
. Therefore, for every
![]() $f\in L^1({\mathbb G})$
, we have
$f\in L^1({\mathbb G})$
, we have
Thus, m is a left invariant
![]() $1$
-mean belonging to
$1$
-mean belonging to
![]() $L^1({\mathbb G})$
, and equivalently
$L^1({\mathbb G})$
, and equivalently
![]() ${\mathbb G}$
is compact (see [Reference Bédos and Tuset1, Proposition 3.1]).
${\mathbb G}$
is compact (see [Reference Bédos and Tuset1, Proposition 3.1]).
Theorem 3.7 Let
![]() ${\mathbb G}$
be a locally compact quantum group such that
${\mathbb G}$
be a locally compact quantum group such that
![]() $\operatorname {WAP}(L^1({\mathbb G}))$
has an invariant
$\operatorname {WAP}(L^1({\mathbb G}))$
has an invariant
![]() $1$
-mean, and let I be a closed ideal of
$1$
-mean, and let I be a closed ideal of
![]() $L^1({\mathbb G})$
with a bounded approximate identity such that
$L^1({\mathbb G})$
with a bounded approximate identity such that
![]() $I\not \subseteq \ker 1$
. Then I is Arens regular if and only if it is reflexive.
$I\not \subseteq \ker 1$
. Then I is Arens regular if and only if it is reflexive.
Proof If I is reflexive, then I is clearly Arens regular. Conversely, suppose that I is Arens regular. Then
![]() ${\mathbb G}$
is compact by Proposition 3.6 and so by [Reference Runde13, Theorem 3.8],
${\mathbb G}$
is compact by Proposition 3.6 and so by [Reference Runde13, Theorem 3.8],
![]() $L^1({\mathbb G})$
is an ideal in its bidual. Since I has a bounded approximate identity, Cohen’s Factorization theorem implies that
$L^1({\mathbb G})$
is an ideal in its bidual. Since I has a bounded approximate identity, Cohen’s Factorization theorem implies that
![]() $I*I=\{a*b: a, b\in I\}=I$
. Hence, we drive that
$I*I=\{a*b: a, b\in I\}=I$
. Hence, we drive that
This shows that I is a right ideal in its bidual. Thus, by [Reference Ulger16, Corollar ies 3.7 and 3.9], we obtain that I is reflexive.
Dually to [Reference Forrest5, Proposition 3.14], we obtain the result below for the group algebra
![]() $L^1(G)$
of a locally compact group G. We would like to recall that
$L^1(G)$
of a locally compact group G. We would like to recall that
![]() $\operatorname {WAP}(L^1(G))$
admits an invariant mean.
$\operatorname {WAP}(L^1(G))$
admits an invariant mean.
Corollary 3.8 Let G be a locally compact group, and let I be a closed ideal of
![]() $L^1(G)$
with a bounded approximate identity such that
$L^1(G)$
with a bounded approximate identity such that
![]() $I\not \subseteq \ker 1$
. Then I is Arens regular if and only if it is reflexive.
$I\not \subseteq \ker 1$
. Then I is Arens regular if and only if it is reflexive.
4 Convolution trace class operators
We recall from [Reference Lau10] that a Lau algebra
![]() ${\mathcal A}$
is a Banach algebra such that
${\mathcal A}$
is a Banach algebra such that
![]() ${\mathcal A}^*$
is a von Neumann algebra whose unit
${\mathcal A}^*$
is a von Neumann algebra whose unit
![]() $1$
lies in the spectrum of
$1$
lies in the spectrum of
![]() ${\mathcal A}$
. Let
${\mathcal A}$
. Let
![]() ${\mathbb G}$
be a locally compact quantum group. Then it is easy to see that
${\mathbb G}$
be a locally compact quantum group. Then it is easy to see that
![]() $1=1\circ \pi \in \operatorname {sp}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Now, since
$1=1\circ \pi \in \operatorname {sp}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Now, since
![]() $B(L^{2}(\mathbb {G}))$
is a von Neumann algebra, it follows that
$B(L^{2}(\mathbb {G}))$
is a von Neumann algebra, it follows that
![]() $\mathcal {T}_{\triangleright }({\mathbb G})$
is a Lau algebra. In this section, we are interested to study the relation between the existence of left or right invariant
$\mathcal {T}_{\triangleright }({\mathbb G})$
is a Lau algebra. In this section, we are interested to study the relation between the existence of left or right invariant
![]() $1$
-means on
$1$
-means on
![]() $ \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
and on
$ \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
and on
![]() $\operatorname {WAP}(L^1(\mathbb {G}))$
.
$\operatorname {WAP}(L^1(\mathbb {G}))$
.
Lemma 4.1 Let
![]() ${\mathbb G}$
be a locally compact quantum group. Then
${\mathbb G}$
be a locally compact quantum group. Then
Proof Suppose that
![]() $x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
and
$x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
and
![]() $w\in \mathcal {T}_{\triangleright }({\mathbb G})$
. Let
$w\in \mathcal {T}_{\triangleright }({\mathbb G})$
. Let
![]() $(f_k)_k$
be a bounded sequence in
$(f_k)_k$
be a bounded sequence in
![]() $L^1(\mathbb {G})$
. For each k, let
$L^1(\mathbb {G})$
. For each k, let
![]() $w_k\in \mathcal {T}_{\triangleright }({\mathbb G})$
be a normal extension of
$w_k\in \mathcal {T}_{\triangleright }({\mathbb G})$
be a normal extension of
![]() $f_k$
. By weak compactness of the map
$f_k$
. By weak compactness of the map
![]() $\lambda _x: \mathcal {T}_{\triangleright }({\mathbb G})\rightarrow B(L^{2}(\mathbb {G}))$
, there is a subsequence
$\lambda _x: \mathcal {T}_{\triangleright }({\mathbb G})\rightarrow B(L^{2}(\mathbb {G}))$
, there is a subsequence
![]() $(w_{k_j})$
of
$(w_{k_j})$
of
![]() $(w_k)$
such that
$(w_k)$
such that
![]() $(w_{k_j}\triangleright x)$
converges weakly in
$(w_{k_j}\triangleright x)$
converges weakly in
![]() $B(L^{2}(\mathbb {G}))$
to some
$B(L^{2}(\mathbb {G}))$
to some
![]() $y\in B(L^{2}(\mathbb {G}))$
. It is easy to check that
$y\in B(L^{2}(\mathbb {G}))$
. It is easy to check that
![]() $(w_{k_j}\triangleright x \triangleright w)$
converges weakly in
$(w_{k_j}\triangleright x \triangleright w)$
converges weakly in
![]() $B(L^{2}(\mathbb {G}))$
to
$B(L^{2}(\mathbb {G}))$
to
![]() $y \triangleright w$
. Now, let
$y \triangleright w$
. Now, let
![]() $m\in L^{\infty }(\mathbb {G})^*$
, and let
$m\in L^{\infty }(\mathbb {G})^*$
, and let
![]() $\widetilde {m}\in B(L^{2}(\mathbb {G}))^*$
be a Hahn–Banach extension of m. Since
$\widetilde {m}\in B(L^{2}(\mathbb {G}))^*$
be a Hahn–Banach extension of m. Since
![]() $B(L^{2}(\mathbb {G}))\triangleright \mathcal {T}_{\triangleright }({\mathbb G})\subseteq L^{\infty }(\mathbb {G})$
, we have
$B(L^{2}(\mathbb {G}))\triangleright \mathcal {T}_{\triangleright }({\mathbb G})\subseteq L^{\infty }(\mathbb {G})$
, we have
This shows that
![]() $x\triangleright w\in \operatorname {WAP}(L^{1}(\mathbb {G}))$
.
$x\triangleright w\in \operatorname {WAP}(L^{1}(\mathbb {G}))$
.
Theorem 4.2 Let
![]() ${\mathbb G}$
be a locally compact quantum group. Then
${\mathbb G}$
be a locally compact quantum group. Then
![]() $\operatorname {WAP}(L^{1}(\mathbb {G}))$
has a right invariant
$\operatorname {WAP}(L^{1}(\mathbb {G}))$
has a right invariant
![]() $1$
-mean if and only if
$1$
-mean if and only if
![]() $\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
has a right invariant
$\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
has a right invariant
![]() $1$
-mean.
$1$
-mean.
Proof Let m be a right invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(L^{1}(\mathbb {G}))$
. Define
$\operatorname {WAP}(L^{1}(\mathbb {G}))$
. Define
![]() $\widetilde {m}\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))^*$
by
$\widetilde {m}\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))^*$
by
![]() $\langle \widetilde {m}, x\rangle =\langle m, x\triangleright w_0\rangle $
for all
$\langle \widetilde {m}, x\rangle =\langle m, x\triangleright w_0\rangle $
for all
![]() $x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, where
$x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, where
![]() $w_0\in \mathcal {T}_{\triangleright }({\mathbb G})$
with
$w_0\in \mathcal {T}_{\triangleright }({\mathbb G})$
with
![]() $\|w_0\|=\langle w_0 ,1\rangle =1$
. Then it is easy to check that
$\|w_0\|=\langle w_0 ,1\rangle =1$
. Then it is easy to check that
![]() $\langle \widetilde {m}, 1\rangle =1$
. Moreover, we have
$\langle \widetilde {m}, 1\rangle =1$
. Moreover, we have
 $$ \begin{align*} \langle\widetilde{m}, w\triangleright x\rangle&=\langle m, w\triangleright (x\triangleright w_0)\rangle\\ &=\langle m, \pi(w)\cdot(x\triangleright w_0)\rangle\\ &= \langle w, 1\rangle\langle m, x\triangleright w_0\rangle\\ &=\langle w, 1\rangle\langle\widetilde{m}, x\rangle \end{align*} $$
$$ \begin{align*} \langle\widetilde{m}, w\triangleright x\rangle&=\langle m, w\triangleright (x\triangleright w_0)\rangle\\ &=\langle m, \pi(w)\cdot(x\triangleright w_0)\rangle\\ &= \langle w, 1\rangle\langle m, x\triangleright w_0\rangle\\ &=\langle w, 1\rangle\langle\widetilde{m}, x\rangle \end{align*} $$
for all
![]() $w\in \mathcal {T}_{\triangleright }({\mathbb G})$
and
$w\in \mathcal {T}_{\triangleright }({\mathbb G})$
and
![]() $x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, proving that
$x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, proving that
![]() $\widetilde {m}$
is a right invariant
$\widetilde {m}$
is a right invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
.
$\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
.
Conversely, suppose that n is a right invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Since
$\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Since
![]() $\pi : \mathcal {T}_{\triangleright }({\mathbb G})\rightarrow L^{1}(\mathbb {G})$
is a continuous algebra homomorphism, it follows from [Reference Young18, Corollary to Lemma 1] that the map
$\pi : \mathcal {T}_{\triangleright }({\mathbb G})\rightarrow L^{1}(\mathbb {G})$
is a continuous algebra homomorphism, it follows from [Reference Young18, Corollary to Lemma 1] that the map
![]() $\pi ^*$
maps
$\pi ^*$
maps
![]() $\operatorname {WAP}(L^{1}(\mathbb {G}))$
to
$\operatorname {WAP}(L^{1}(\mathbb {G}))$
to
![]() $\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Thus, we can define
$\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Thus, we can define
![]() $\widetilde {n}\in \operatorname {WAP}(L^{1}(\mathbb {G}))^*$
by
$\widetilde {n}\in \operatorname {WAP}(L^{1}(\mathbb {G}))^*$
by
![]() $\widetilde {n}:=n\circ \pi ^*$
. It is easily verified that
$\widetilde {n}:=n\circ \pi ^*$
. It is easily verified that
![]() $\langle \widetilde {n}, 1\rangle =1$
. For every
$\langle \widetilde {n}, 1\rangle =1$
. For every
![]() $f\in L^1(\mathbb {G})$
and
$f\in L^1(\mathbb {G})$
and
![]() $x\in \operatorname {WAP}(L^{1}(\mathbb {G}))$
, let
$x\in \operatorname {WAP}(L^{1}(\mathbb {G}))$
, let
![]() $w\in \mathcal {T}_{\triangleright }({\mathbb G})$
be a normal extension of f. Then we have
$w\in \mathcal {T}_{\triangleright }({\mathbb G})$
be a normal extension of f. Then we have
 $$ \begin{align*} \langle\pi^*(f\cdot x),w'\rangle=\langle f\cdot x,\pi(w')\rangle &=\langle x, \pi(w')*\pi(w)\rangle\\ &=\langle\pi^*(x),w'\triangleright w\rangle\\ &=\langle w\triangleright \pi^*(x),w'\rangle, \end{align*} $$
$$ \begin{align*} \langle\pi^*(f\cdot x),w'\rangle=\langle f\cdot x,\pi(w')\rangle &=\langle x, \pi(w')*\pi(w)\rangle\\ &=\langle\pi^*(x),w'\triangleright w\rangle\\ &=\langle w\triangleright \pi^*(x),w'\rangle, \end{align*} $$
for all
![]() $w'\in \mathcal {T}_{\triangleright }({\mathbb G})$
. Therefore,
$w'\in \mathcal {T}_{\triangleright }({\mathbb G})$
. Therefore,
 $$ \begin{align*} \langle\widetilde{n}, f\cdot x\rangle&=\langle n, \pi^*(f\cdot x)\rangle\\ &=\langle n, w\triangleright \pi^*(x)\rangle\\ &=\langle w, 1\rangle\langle n, \pi^*(x)\rangle\\ &=\langle f, 1\rangle\langle\widetilde{n}, x\rangle. \end{align*} $$
$$ \begin{align*} \langle\widetilde{n}, f\cdot x\rangle&=\langle n, \pi^*(f\cdot x)\rangle\\ &=\langle n, w\triangleright \pi^*(x)\rangle\\ &=\langle w, 1\rangle\langle n, \pi^*(x)\rangle\\ &=\langle f, 1\rangle\langle\widetilde{n}, x\rangle. \end{align*} $$
That is,
![]() $\widetilde {n}$
is a right invariant
$\widetilde {n}$
is a right invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(L^{1}(\mathbb {G}))$
.
$\operatorname {WAP}(L^{1}(\mathbb {G}))$
.
Before giving the next result, recall that if
![]() ${\mathbb G}= L^{\infty }(G)$
for a locally compact group G, then
${\mathbb G}= L^{\infty }(G)$
for a locally compact group G, then
![]() $\mathcal {T}_{\triangleright }(\mathbb {G})$
is the convolution algebra introduced by Neufang in [Reference Neufang11].
$\mathcal {T}_{\triangleright }(\mathbb {G})$
is the convolution algebra introduced by Neufang in [Reference Neufang11].
Corollary 4.3 Let G be a locally compact group, and let
![]() ${\mathbb G}= L^{\infty }(G)$
. Then
${\mathbb G}= L^{\infty }(G)$
. Then
![]() $\operatorname {WAP}(\mathcal {T}_{\triangleright }(\mathbb {G}))$
admits a right invariant
$\operatorname {WAP}(\mathcal {T}_{\triangleright }(\mathbb {G}))$
admits a right invariant
![]() $1$
-mean.
$1$
-mean.
Theorem 4.4 Let
![]() $\mathbb {G}$
be a locally compact quantum group. Then
$\mathbb {G}$
be a locally compact quantum group. Then
![]() $\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
has a left invariant
$\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
has a left invariant
![]() $1$
-mean if and only if
$1$
-mean if and only if
![]() $\mathbb {G}$
is trivial.
$\mathbb {G}$
is trivial.
Proof Let m be a left invariant
![]() $1$
-mean on
$1$
-mean on
![]() $\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Then for every
$\operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Then for every
![]() $x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, we have
$x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
, we have
![]() $m\cdot x=\langle m, x\rangle 1$
, by left invariance. Now, consider the map
$m\cdot x=\langle m, x\rangle 1$
, by left invariance. Now, consider the map
defined by
![]() $E(x)=m\cdot x=\langle m, x\rangle 1$
for all
$E(x)=m\cdot x=\langle m, x\rangle 1$
for all
![]() $x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Then for every
$x\in \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$
. Then for every
![]() $\hat {x}\in L^{\infty }(\hat {\mathbb {G}})$
, we have
$\hat {x}\in L^{\infty }(\hat {\mathbb {G}})$
, we have
These prove that
![]() $L^{\infty }(\widehat {\mathbb {G}})=E(L^{\infty }(\widehat {\mathbb {G}}))\subseteq \mathbb {C}1$
. Therefore,
$L^{\infty }(\widehat {\mathbb {G}})=E(L^{\infty }(\widehat {\mathbb {G}}))\subseteq \mathbb {C}1$
. Therefore,
![]() $L^{\infty }(\widehat {\mathbb {G}})=\mathbb {C}1$
and so
$L^{\infty }(\widehat {\mathbb {G}})=\mathbb {C}1$
and so
![]() ${\mathbb G}$
is trivial.
${\mathbb G}$
is trivial.
Acknowledgment
The authors are grateful to the referee for his/her careful reading of the paper and valuable suggestions.