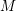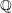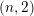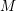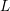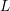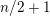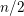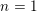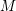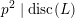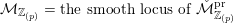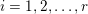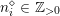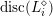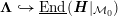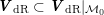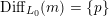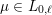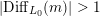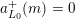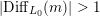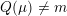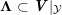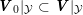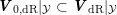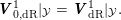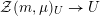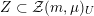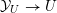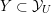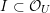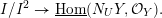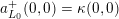1 Introduction
In this paper we prove a generalization, conjectured by Bruinier and Yang [Reference Bruinier and YangBY09], of the Gross–Zagier theorem on heights of Heegner points on modular curves.
Instead of a modular curve we work on the Shimura variety defined by a reductive group over
![]() $\mathbb{Q}$
of type
$\mathbb{Q}$
of type
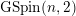 $\text{GSpin}(n,2)$
. The Heegner points are replaced by
$\text{GSpin}(n,2)$
. The Heegner points are replaced by
![]() $0$
-cycles arising from embeddings of rank-two tori into
$0$
-cycles arising from embeddings of rank-two tori into
 $\text{GSpin}(n,2)$
, and by divisors arising from embeddings of
$\text{GSpin}(n,2)$
, and by divisors arising from embeddings of
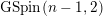 $\text{GSpin}(n-1,2)$
into
$\text{GSpin}(n-1,2)$
into
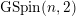 $\text{GSpin}(n,2)$
. We prove that the arithmetic intersections of these special cycles are related to the central derivatives of certain Rankin–Selberg convolution
$\text{GSpin}(n,2)$
. We prove that the arithmetic intersections of these special cycles are related to the central derivatives of certain Rankin–Selberg convolution
![]() $L$
-functions.
$L$
-functions.
1.1 The Shimura variety
Fix an integer
![]() $n\geqslant 1$
and a quadratic space
$n\geqslant 1$
and a quadratic space
![]() $(V,Q)$
over
$(V,Q)$
over
![]() $\mathbb{Q}$
of signature
$\mathbb{Q}$
of signature
![]() $(n,2)$
. From
$(n,2)$
. From
![]() $V$
one can construct a Shimura datum
$V$
one can construct a Shimura datum
![]() $(G,{\mathcal{D}})$
, in which
$(G,{\mathcal{D}})$
, in which
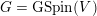 $G=\text{GSpin}(V)$
is a reductive group over
$G=\text{GSpin}(V)$
is a reductive group over
![]() $\mathbb{Q}$
sitting in an exact sequence
$\mathbb{Q}$
sitting in an exact sequence
 $$\begin{eqnarray}1\rightarrow \mathbb{G}_{m}\rightarrow \text{GSpin}(V)\rightarrow \text{SO}(V)\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \mathbb{G}_{m}\rightarrow \text{GSpin}(V)\rightarrow \text{SO}(V)\rightarrow 1,\end{eqnarray}$$
and the hermitian domain
![]() ${\mathcal{D}}$
is an open subset of the space of isotropic lines in
${\mathcal{D}}$
is an open subset of the space of isotropic lines in
![]() $\mathbb{P}^{1}(V_{\mathbb{C}})$
.
$\mathbb{P}^{1}(V_{\mathbb{C}})$
.
Any choice of lattice
![]() $L\subset V$
on which
$L\subset V$
on which
![]() $Q$
is
$Q$
is
![]() $\mathbb{Z}$
-valued determines a compact open subgroup
$\mathbb{Z}$
-valued determines a compact open subgroup
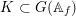 $K\subset G(\mathbb{A}_{f})$
. We fix such a lattice, and assume that
$K\subset G(\mathbb{A}_{f})$
. We fix such a lattice, and assume that
![]() $L$
is maximal, in the sense that it admits no superlattice on which
$L$
is maximal, in the sense that it admits no superlattice on which
![]() $Q$
is
$Q$
is
![]() $\mathbb{Z}$
-valued. The data
$\mathbb{Z}$
-valued. The data
![]() $L\subset V$
now determines a complex orbifold
$L\subset V$
now determines a complex orbifold
 $$\begin{eqnarray}M(\mathbb{C})=G(\mathbb{Q})\backslash {\mathcal{D}}\times G(\mathbb{A}_{f})/K\end{eqnarray}$$
$$\begin{eqnarray}M(\mathbb{C})=G(\mathbb{Q})\backslash {\mathcal{D}}\times G(\mathbb{A}_{f})/K\end{eqnarray}$$
which, by the theory of canonical models of Shimura varieties, is the space of complex points of an algebraic stack
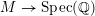 $M\rightarrow \text{Spec}(\mathbb{Q})$
. (Throughout this article stack means Deligne–Mumford stack.)
$M\rightarrow \text{Spec}(\mathbb{Q})$
. (Throughout this article stack means Deligne–Mumford stack.)
Except for small values of
![]() $n$
, the Shimura variety
$n$
, the Shimura variety
![]() $M$
is not of PEL (polarization, endomorphism, and level) type; that is, it is not naturally a moduli space of abelian varieties with PEL structures. It is, however, of Hodge type, and so the recent work of Kisin [Reference KisinKis10] (and its extension in [Reference Madapusi PeraMad16, Reference Kim and Madapusi PeraKM16]) provides us with a regular and flat integral model
$M$
is not of PEL (polarization, endomorphism, and level) type; that is, it is not naturally a moduli space of abelian varieties with PEL structures. It is, however, of Hodge type, and so the recent work of Kisin [Reference KisinKis10] (and its extension in [Reference Madapusi PeraMad16, Reference Kim and Madapusi PeraKM16]) provides us with a regular and flat integral model
 $$\begin{eqnarray}{\mathcal{M}}\rightarrow \text{Spec}(\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}\rightarrow \text{Spec}(\mathbb{Z}).\end{eqnarray}$$
1.2 Special divisors
The integral model carries over it a canonical family of abelian varieties: the Kuga–Satake abelian scheme
 $$\begin{eqnarray}{\mathcal{A}}\rightarrow {\mathcal{M}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}\rightarrow {\mathcal{M}}.\end{eqnarray}$$
The Kuga–Satake abelian scheme is endowed with an action of the Clifford algebra
![]() $C(L)$
, and with a
$C(L)$
, and with a
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading
$\mathbb{Z}/2\mathbb{Z}$
-grading
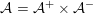 ${\mathcal{A}}={\mathcal{A}}^{+}\times {\mathcal{A}}^{-}$
.
${\mathcal{A}}={\mathcal{A}}^{+}\times {\mathcal{A}}^{-}$
.
For any scheme
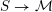 $S\rightarrow {\mathcal{M}}$
, the pullback
$S\rightarrow {\mathcal{M}}$
, the pullback
![]() ${\mathcal{A}}_{S}$
comes with a distinguished
${\mathcal{A}}_{S}$
comes with a distinguished
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
 $$\begin{eqnarray}V({\mathcal{A}}_{S})\subset \text{End}({\mathcal{A}}_{S})\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{A}}_{S})\subset \text{End}({\mathcal{A}}_{S})\end{eqnarray}$$
of special endomorphisms, and there is a positive definite quadratic form
 $$\begin{eqnarray}Q:V({\mathcal{A}}_{S})\rightarrow \mathbb{Z}\end{eqnarray}$$
$$\begin{eqnarray}Q:V({\mathcal{A}}_{S})\rightarrow \mathbb{Z}\end{eqnarray}$$
characterized by
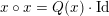 $x\circ x=Q(x)\cdot \text{Id}$
. Slightly more generally, there is a distinguished subset
$x\circ x=Q(x)\cdot \text{Id}$
. Slightly more generally, there is a distinguished subset
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})\subset V({\mathcal{A}}_{S})\otimes _{\mathbb{Z}}\mathbb{Q}\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})\subset V({\mathcal{A}}_{S})\otimes _{\mathbb{Z}}\mathbb{Q}\end{eqnarray}$$
for each coset
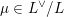 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
, where
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
, where
![]() $L^{\vee }$
is the dual lattice of
$L^{\vee }$
is the dual lattice of
![]() $L$
. Taking
$L$
. Taking
![]() $\unicode[STIX]{x1D707}=0$
recovers
$\unicode[STIX]{x1D707}=0$
recovers
![]() $V({\mathcal{A}}_{S})$
.
$V({\mathcal{A}}_{S})$
.
The special endomorphisms allow us to define a family of special divisors on
![]() ${\mathcal{M}}$
. For
${\mathcal{M}}$
. For
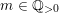 $m\in \mathbb{Q}_{{>}0}$
and
$m\in \mathbb{Q}_{{>}0}$
and
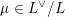 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
, let
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
, let
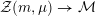 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
be the moduli stack that assigns to any
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
be the moduli stack that assigns to any
![]() ${\mathcal{M}}$
-scheme
${\mathcal{M}}$
-scheme
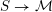 $S\rightarrow {\mathcal{M}}$
the set
$S\rightarrow {\mathcal{M}}$
the set
 $$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})(S)=\{x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S}):Q(x)=m\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})(S)=\{x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S}):Q(x)=m\}.\end{eqnarray}$$
The morphism
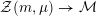 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
is relatively representable, finite, and unramified, and allows us to view
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
is relatively representable, finite, and unramified, and allows us to view
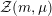 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
as a Cartier divisor on
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
as a Cartier divisor on
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
In the generic fiber of
![]() ${\mathcal{M}}$
the special divisors agree with the divisors appearing in [Reference BorcherdsBor98, Reference BruinierBru02, Reference Bruinier and YangBY09, Reference KudlaKud04]. In special cases where
${\mathcal{M}}$
the special divisors agree with the divisors appearing in [Reference BorcherdsBor98, Reference BruinierBru02, Reference Bruinier and YangBY09, Reference KudlaKud04]. In special cases where
![]() $V$
has signature
$V$
has signature
![]() $(1,2)$
,
$(1,2)$
,
![]() $(2,2)$
, or
$(2,2)$
, or
![]() $(3,2)$
, the Shimura variety
$(3,2)$
, the Shimura variety
![]() ${\mathcal{M}}$
is (a quaternionic version of) a modular curve, Hilbert modular surface, or Siegel threefold, respectively. In these cases the special divisors are traditionally known as complex multiplication points, Hirzebruch–Zagier divisors, and Humbert surfaces. See, for example, [Reference van der GeervdG88, Reference Kudla and RapoportKR99, Reference Kudla and RapoportKR00, Reference Kudla, Rapoport and YangKRY06].
${\mathcal{M}}$
is (a quaternionic version of) a modular curve, Hilbert modular surface, or Siegel threefold, respectively. In these cases the special divisors are traditionally known as complex multiplication points, Hirzebruch–Zagier divisors, and Humbert surfaces. See, for example, [Reference van der GeervdG88, Reference Kudla and RapoportKR99, Reference Kudla and RapoportKR00, Reference Kudla, Rapoport and YangKRY06].
1.3 Complex multiplication points
Let
![]() $V_{0}\subset V$
be a negative definite plane in
$V_{0}\subset V$
be a negative definite plane in
![]() $V$
, and set
$V$
, and set
 $L_{0}=V_{0}\cap L$
. The Clifford algebra
$L_{0}=V_{0}\cap L$
. The Clifford algebra
![]() $C(L_{0})$
is an order in a quaternion algebra over
$C(L_{0})$
is an order in a quaternion algebra over
![]() $\mathbb{Q}$
, and its even part
$\mathbb{Q}$
, and its even part
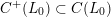 $C^{+}(L_{0})\subset C(L_{0})$
is an order in a quadratic imaginary field
$C^{+}(L_{0})\subset C(L_{0})$
is an order in a quadratic imaginary field
![]() $\boldsymbol{k}$
. Fix an embedding
$\boldsymbol{k}$
. Fix an embedding
![]() $\boldsymbol{k}\rightarrow \mathbb{C}$
, and assume from now on that
$\boldsymbol{k}\rightarrow \mathbb{C}$
, and assume from now on that
 $C^{+}(L_{0})={\mathcal{O}}_{\boldsymbol{k}}$
is the maximal order in
$C^{+}(L_{0})={\mathcal{O}}_{\boldsymbol{k}}$
is the maximal order in
![]() $\boldsymbol{k}$
.
$\boldsymbol{k}$
.
The group
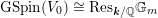 $\text{GSpin}(V_{0})\cong \text{Res}_{\boldsymbol{k}/\mathbb{Q}}\mathbb{G}_{m}$
is a rank-two torus, and has associated to it a zero-dimensional Shimura variety
$\text{GSpin}(V_{0})\cong \text{Res}_{\boldsymbol{k}/\mathbb{Q}}\mathbb{G}_{m}$
is a rank-two torus, and has associated to it a zero-dimensional Shimura variety
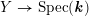 $Y\rightarrow \text{Spec}(\boldsymbol{k})$
, which can be reinterpreted as the moduli stack of elliptic curves with complex multiplication (CM) by
$Y\rightarrow \text{Spec}(\boldsymbol{k})$
, which can be reinterpreted as the moduli stack of elliptic curves with complex multiplication (CM) by
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. This allows us to construct a smooth integral model
${\mathcal{O}}_{\boldsymbol{k}}$
. This allows us to construct a smooth integral model
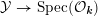 ${\mathcal{Y}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
. If
${\mathcal{Y}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
. If
![]() $\boldsymbol{k}$
has odd discriminant the inclusion
$\boldsymbol{k}$
has odd discriminant the inclusion
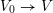 $V_{0}\rightarrow V$
induces an embedding
$V_{0}\rightarrow V$
induces an embedding
 $\text{GSpin}(V_{0})\rightarrow G$
and a relatively representable, finite, and unramified morphism
$\text{GSpin}(V_{0})\rightarrow G$
and a relatively representable, finite, and unramified morphism
 $$\begin{eqnarray}i:{\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}.\end{eqnarray}$$
$$\begin{eqnarray}i:{\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}.\end{eqnarray}$$
The stack
![]() ${\mathcal{Y}}$
has its own Kuga–Satake abelian scheme
${\mathcal{Y}}$
has its own Kuga–Satake abelian scheme
 ${\mathcal{A}}_{0}\rightarrow {\mathcal{Y}}$
, endowed with a
${\mathcal{A}}_{0}\rightarrow {\mathcal{Y}}$
, endowed with a
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading
$\mathbb{Z}/2\mathbb{Z}$
-grading
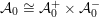 ${\mathcal{A}}_{0}\cong {\mathcal{A}}_{0}^{+}\times {\mathcal{A}}_{0}^{-}$
, and an action of
${\mathcal{A}}_{0}\cong {\mathcal{A}}_{0}^{+}\times {\mathcal{A}}_{0}^{-}$
, and an action of
![]() $C(L_{0})$
. Here
$C(L_{0})$
. Here
![]() ${\mathcal{A}}_{0}^{+}$
is the universal elliptic curve with CM by
${\mathcal{A}}_{0}^{+}$
is the universal elliptic curve with CM by
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
and
${\mathcal{O}}_{\boldsymbol{k}}$
and
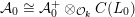 ${\mathcal{A}}_{0}\cong {\mathcal{A}}_{0}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L_{0})$
. It is related to the Kuga–Satake abelian scheme
${\mathcal{A}}_{0}\cong {\mathcal{A}}_{0}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L_{0})$
. It is related to the Kuga–Satake abelian scheme
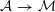 ${\mathcal{A}}\rightarrow {\mathcal{M}}$
by a
${\mathcal{A}}\rightarrow {\mathcal{M}}$
by a
![]() $C(L)$
-linear isomorphism
$C(L)$
-linear isomorphism
 $$\begin{eqnarray}{\mathcal{A}}|_{{\mathcal{Y}}}\cong {\mathcal{A}}_{0}|_{{\mathcal{Y}}}\otimes _{C(L_{0})}C(L).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}|_{{\mathcal{Y}}}\cong {\mathcal{A}}_{0}|_{{\mathcal{Y}}}\otimes _{C(L_{0})}C(L).\end{eqnarray}$$
Let
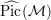 $\widehat{\text{Pic}}({\mathcal{M}})$
denote the group of metrized line bundles on
$\widehat{\text{Pic}}({\mathcal{M}})$
denote the group of metrized line bundles on
![]() ${\mathcal{M}}$
, and similarly with
${\mathcal{M}}$
, and similarly with
![]() ${\mathcal{M}}$
replaced by
${\mathcal{M}}$
replaced by
![]() ${\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
or
${\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
or
![]() ${\mathcal{Y}}$
. The composition
${\mathcal{Y}}$
. The composition
 $$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\rightarrow \widehat{\text{Pic}}({\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\widehat{\deg }}\mathbb{R}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\rightarrow \widehat{\text{Pic}}({\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\widehat{\deg }}\mathbb{R}\end{eqnarray}$$
is denoted
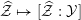 $\widehat{{\mathcal{Z}}}\mapsto [\widehat{{\mathcal{Z}}}:{\mathcal{Y}}]$
. We call it arithmetic degree along
$\widehat{{\mathcal{Z}}}\mapsto [\widehat{{\mathcal{Z}}}:{\mathcal{Y}}]$
. We call it arithmetic degree along
![]() ${\mathcal{Y}}$
.
${\mathcal{Y}}$
.
1.4 Harmonic modular forms
Denote by
![]() $\widetilde{\text{SL}}_{2}(\mathbb{Z})$
the metaplectic double cover of
$\widetilde{\text{SL}}_{2}(\mathbb{Z})$
the metaplectic double cover of
![]() $\text{SL}_{2}(\mathbb{Z})$
, and by
$\text{SL}_{2}(\mathbb{Z})$
, and by
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{L}:\widetilde{\text{SL}}_{2}(\mathbb{Z})\rightarrow \text{Aut}_{\mathbb{C}}(\mathfrak{S}_{L})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{L}:\widetilde{\text{SL}}_{2}(\mathbb{Z})\rightarrow \text{Aut}_{\mathbb{C}}(\mathfrak{S}_{L})\end{eqnarray}$$
the Weil representation on the space
![]() $\mathfrak{S}_{L}$
of
$\mathfrak{S}_{L}$
of
![]() $\mathbb{C}$
-valued functions on
$\mathbb{C}$
-valued functions on
![]() $L^{\vee }/L$
. There is a complex conjugate representation
$L^{\vee }/L$
. There is a complex conjugate representation
![]() $\overline{\unicode[STIX]{x1D714}}_{L}$
on the same space, and a contragredient action
$\overline{\unicode[STIX]{x1D714}}_{L}$
on the same space, and a contragredient action
![]() $\unicode[STIX]{x1D714}_{L}^{\vee }$
on the dual space
$\unicode[STIX]{x1D714}_{L}^{\vee }$
on the dual space
![]() $\mathfrak{S}_{L}^{\vee }$
.
$\mathfrak{S}_{L}^{\vee }$
.
Bruinier and Funke [Reference Bruinier and FunkeBF04] have defined a surjective conjugate-linear differential operator
 $$\begin{eqnarray}\unicode[STIX]{x1D709}:H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}:H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L}).\end{eqnarray}$$
Here
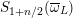 $S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L})$
is the space of weight
$S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L})$
is the space of weight
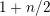 $1+n/2$
cusp forms valued in
$1+n/2$
cusp forms valued in
![]() $\mathfrak{S}_{L}$
, and transforming according to the representation
$\mathfrak{S}_{L}$
, and transforming according to the representation
![]() $\overline{\unicode[STIX]{x1D714}}_{L}$
. The space
$\overline{\unicode[STIX]{x1D714}}_{L}$
. The space
 $H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
is defined similarly, but the forms are harmonic weak Mass forms in the sense of [Reference Bruinier and YangBY09, § 3.1].
$H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
is defined similarly, but the forms are harmonic weak Mass forms in the sense of [Reference Bruinier and YangBY09, § 3.1].
To any
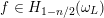 $f\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
there is associated a formal
$f\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
there is associated a formal
![]() $q$
-expansion
$q$
-expansion
 $$\begin{eqnarray}f^{+}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\substack{ m\in \mathbb{Q} \\ m\gg -\infty }}c_{f}^{+}(m)q^{m}\in \mathfrak{S}_{L}[[q]],\end{eqnarray}$$
$$\begin{eqnarray}f^{+}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\substack{ m\in \mathbb{Q} \\ m\gg -\infty }}c_{f}^{+}(m)q^{m}\in \mathfrak{S}_{L}[[q]],\end{eqnarray}$$
and each coefficient is uniquely a linear combination
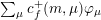 $\sum _{\unicode[STIX]{x1D707}}c_{f}^{+}(m,\unicode[STIX]{x1D707})\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$
of the characteristic functions
$\sum _{\unicode[STIX]{x1D707}}c_{f}^{+}(m,\unicode[STIX]{x1D707})\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$
of the characteristic functions
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$
of cosets
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$
of cosets
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
. Assuming that
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
. Assuming that
![]() $f^{+}$
has integral principal part, in the sense that
$f^{+}$
has integral principal part, in the sense that
 $c_{f}^{+}(m,\unicode[STIX]{x1D707})\in \mathbb{Z}$
whenever
$c_{f}^{+}(m,\unicode[STIX]{x1D707})\in \mathbb{Z}$
whenever
![]() $m<0$
, we may form the Cartier divisor
$m<0$
, we may form the Cartier divisor
 $$\begin{eqnarray}{\mathcal{Z}}(f)=\mathop{\sum }_{m>0}\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\vee }/L}c_{f}^{+}(-m,\unicode[STIX]{x1D707})\cdot {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(f)=\mathop{\sum }_{m>0}\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\vee }/L}c_{f}^{+}(-m,\unicode[STIX]{x1D707})\cdot {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\end{eqnarray}$$
(the sum is finite) on the integral model
![]() ${\mathcal{M}}$
, following the work of Borcherds [Reference BorcherdsBor98], Bruinier [Reference BruinierBru02], and Bruinier and Yang [Reference Bruinier and YangBY09].
${\mathcal{M}}$
, following the work of Borcherds [Reference BorcherdsBor98], Bruinier [Reference BruinierBru02], and Bruinier and Yang [Reference Bruinier and YangBY09].
Using the formalism of regularized theta lifts developed in [Reference BorcherdsBor98], Bruinier [Reference BruinierBru02] defined a Green function
![]() $\unicode[STIX]{x1D6F7}(f)$
for
$\unicode[STIX]{x1D6F7}(f)$
for
![]() ${\mathcal{Z}}(f)$
. This Green function determines a metric on the corresponding line bundle, yielding a metrized line bundle
${\mathcal{Z}}(f)$
. This Green function determines a metric on the corresponding line bundle, yielding a metrized line bundle
 $$\begin{eqnarray}\widehat{{\mathcal{Z}}}(f)\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{Z}}}(f)\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
1.5 The main result
The central problem is to compute the arithmetic degree
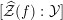 $[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]$
. Assuming that the divisor
$[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]$
. Assuming that the divisor
![]() ${\mathcal{Z}}(f)_{{\mathcal{O}}_{\boldsymbol{k}}}$
intersects the cycle
${\mathcal{Z}}(f)_{{\mathcal{O}}_{\boldsymbol{k}}}$
intersects the cycle
![]() ${\mathcal{Y}}$
properly, the arithmetic degree decomposes as a sum of local contributions. The calculation of the archimedean contribution, which is essentially the sum of the values of
${\mathcal{Y}}$
properly, the arithmetic degree decomposes as a sum of local contributions. The calculation of the archimedean contribution, which is essentially the sum of the values of
![]() $\unicode[STIX]{x1D6F7}(f)$
at all
$\unicode[STIX]{x1D6F7}(f)$
at all
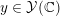 $y\in {\mathcal{Y}}(\mathbb{C})$
, is the main result of [Reference Bruinier and YangBY09].
$y\in {\mathcal{Y}}(\mathbb{C})$
, is the main result of [Reference Bruinier and YangBY09].
Based on their calculation of the archimedean contribution, Bruinier and Yang formulated a conjecture [Reference Bruinier and YangBY09, Conjecture 1.1] relating
 $[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]$
to the derivative of an
$[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]$
to the derivative of an
![]() $L$
-function. Our main result is a proof of this conjecture.
$L$
-function. Our main result is a proof of this conjecture.
The statement of the result requires two more ingredients. The first is the metrized cotautological bundle
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
By definition, the hermitian domain
![]() ${\mathcal{D}}$
is an open subset of the space of isotropic lines in
${\mathcal{D}}$
is an open subset of the space of isotropic lines in
![]() $\mathbb{P}^{1}(V_{\mathbb{C}})$
. Restricting the tautological bundle on
$\mathbb{P}^{1}(V_{\mathbb{C}})$
. Restricting the tautological bundle on
![]() $\mathbb{P}^{1}(V_{\mathbb{C}})$
yields a line bundle
$\mathbb{P}^{1}(V_{\mathbb{C}})$
yields a line bundle
![]() $\unicode[STIX]{x1D714}_{{\mathcal{D}}}$
on
$\unicode[STIX]{x1D714}_{{\mathcal{D}}}$
on
![]() ${\mathcal{D}}$
, which descends first to the orbifold
${\mathcal{D}}$
, which descends first to the orbifold
![]() $M(\mathbb{C})$
, and then to the canonical model
$M(\mathbb{C})$
, and then to the canonical model
![]() $M$
. The resulting line bundle,
$M$
. The resulting line bundle,
![]() $\unicode[STIX]{x1D714}$
, is the tautological bundle on
$\unicode[STIX]{x1D714}$
, is the tautological bundle on
![]() $M$
, also called the line bundle of weight 1 modular forms. There is a natural metric (5.8) on
$M$
, also called the line bundle of weight 1 modular forms. There is a natural metric (5.8) on
![]() $\unicode[STIX]{x1D714}$
, and our
$\unicode[STIX]{x1D714}$
, and our
![]() $\widehat{\boldsymbol{T}}$
is an integral model of
$\widehat{\boldsymbol{T}}$
is an integral model of
![]() $\widehat{\unicode[STIX]{x1D714}}^{-1}$
.
$\widehat{\unicode[STIX]{x1D714}}^{-1}$
.
The second ingredient is a classical vector valued theta series. From the
![]() $\mathbb{Z}$
-quadratic space
$\mathbb{Z}$
-quadratic space
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}=\{x\in L:x\bot L_{0}\}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}=\{x\in L:x\bot L_{0}\}\end{eqnarray}$$
of signature
![]() $(n,0)$
, one can construct a half-integral weight theta series
$(n,0)$
, one can construct a half-integral weight theta series
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})\in M_{n/2}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})\in M_{n/2}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee }).\end{eqnarray}$$
Here
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}$
is the Weil representation of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}$
is the Weil representation of
![]() $\widetilde{\text{SL}}_{2}(\mathbb{Z})$
on the space
$\widetilde{\text{SL}}_{2}(\mathbb{Z})$
on the space
![]() $\mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
of functions on
$\mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
of functions on
![]() $\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
, and
$\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
, and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee }$
is its contragredient. See § 3.3 for the precise definition.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee }$
is its contragredient. See § 3.3 for the precise definition.
The following appears in the text as Theorem 5.7.3.
Theorem A. Assume that the discriminant of
![]() $\boldsymbol{k}$
is odd, and let
$\boldsymbol{k}$
is odd, and let
![]() $h_{\boldsymbol{k}}$
and
$h_{\boldsymbol{k}}$
and
![]() $w_{\boldsymbol{k}}$
be the class number and number of roots of unity in
$w_{\boldsymbol{k}}$
be the class number and number of roots of unity in
![]() $\boldsymbol{k}$
, respectively. Every weak harmonic Maass form
$\boldsymbol{k}$
, respectively. Every weak harmonic Maass form
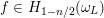 $f\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
with integral principal part satisfies
$f\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
with integral principal part satisfies
 $$\begin{eqnarray}[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]+c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0),\end{eqnarray}$$
$$\begin{eqnarray}[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]+c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0),\end{eqnarray}$$
where
 $c_{f}^{+}(0,0)$
is the value of
$c_{f}^{+}(0,0)$
is the value of
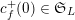 $c_{f}^{+}(0)\in \mathfrak{S}_{L}$
at the trivial coset in
$c_{f}^{+}(0)\in \mathfrak{S}_{L}$
at the trivial coset in
![]() $L^{\vee }/L$
, and
$L^{\vee }/L$
, and
 $L(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)$
is the Rankin–Selberg convolution
$L(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)$
is the Rankin–Selberg convolution
![]() $L$
-function of § 3.3.
$L$
-function of § 3.3.
Remark 1.5.1. The analogous theorem for Shimura varieties associated with unitary similitude groups was proved in [Reference Bruinier, Howard and YangBHY15].
Remark 1.5.2. The convolution
![]() $L$
-function appearing in the theorem can be realized by integrating
$L$
-function appearing in the theorem can be realized by integrating
![]() $\unicode[STIX]{x1D709}(f)$
and
$\unicode[STIX]{x1D709}(f)$
and
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}$
against a certain Eisenstein series
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}$
against a certain Eisenstein series
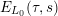 $E_{L_{0}}(\unicode[STIX]{x1D70F},s)$
. This Eisenstein series vanishes at
$E_{L_{0}}(\unicode[STIX]{x1D70F},s)$
. This Eisenstein series vanishes at
![]() $s=0$
, and hence the same is true of
$s=0$
, and hence the same is true of
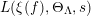 $L(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)$
.
$L(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)$
.
Remark 1.5.3. As noted earlier, our cycles
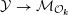 ${\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
arise from embeddings of rank-two tori into
${\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
arise from embeddings of rank-two tori into
 $\text{GSpin}(n,2)$
. One could instead look at the cycles defined by embeddings of maximal tori; these are the big CM cycles of [Reference Bruinier, Kudla and YangBKY12]. In [Reference Andreatta, Goren, Howard and Madapusi PeraAGHM15] we prove a result analogous to Theorem A in this setting. We show that it implies an averaged form of Colmez’s conjecture on the Faltings heights of CM abelian varieties (via the method of Yang [Reference YangYan10]). This has provided a key ingredient in Tsimerman’s recent proof of the André–Oort conjecture [Reference TsimermanTsi15], which characterizes Shimura subvarieties of Shimura varieties of Hodge type by means of special points.
$\text{GSpin}(n,2)$
. One could instead look at the cycles defined by embeddings of maximal tori; these are the big CM cycles of [Reference Bruinier, Kudla and YangBKY12]. In [Reference Andreatta, Goren, Howard and Madapusi PeraAGHM15] we prove a result analogous to Theorem A in this setting. We show that it implies an averaged form of Colmez’s conjecture on the Faltings heights of CM abelian varieties (via the method of Yang [Reference YangYan10]). This has provided a key ingredient in Tsimerman’s recent proof of the André–Oort conjecture [Reference TsimermanTsi15], which characterizes Shimura subvarieties of Shimura varieties of Hodge type by means of special points.
Remark 1.5.4. If one is willing to have the equality of Theorem A only up to rational multiples of
![]() $\log (2)$
, in principle it should be possible to drop the assumption that
$\log (2)$
, in principle it should be possible to drop the assumption that
![]() $d_{\boldsymbol{k}}$
is odd or that
$d_{\boldsymbol{k}}$
is odd or that
 $C^{+}(L_{0})$
is maximal and replace it by the weaker assumption that
$C^{+}(L_{0})$
is maximal and replace it by the weaker assumption that
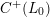 $C^{+}(L_{0})$
is maximal away from
$C^{+}(L_{0})$
is maximal away from
![]() $2$
. Such improvements come at a cost: under these weaker hypotheses one does not know anything like the explicit formulas appearing in Proposition 3.3.1 and Theorem 4.5.1.
$2$
. Such improvements come at a cost: under these weaker hypotheses one does not know anything like the explicit formulas appearing in Proposition 3.3.1 and Theorem 4.5.1.
Instead, one should be able (we have not checked the details) to prove the main result by using the Siegel–Weil arguments of [Reference Bruinier, Kudla and YangBKY12, Reference Kudla and YangKY13]. In essence, the Siegel–Weil formula allows one to compare the point counting part of Theorem 4.5.1 with the values of certain Whittaker functions appearing in the Eisenstein series coefficients of Proposition 3.3.1, without deriving explicit formulas for either one.
A rough outline of the contents is as follows.
In § 2 we establish the basic properties of the Shimura variety
![]() ${\mathcal{M}}$
on which we will be performing intersection theory, and of the special cycles
${\mathcal{M}}$
on which we will be performing intersection theory, and of the special cycles
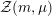 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
. We prove that the
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
. We prove that the
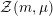 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
define Cartier divisors on
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
define Cartier divisors on
![]() ${\mathcal{M}}$
, and explore the functoriality of the formation of
${\mathcal{M}}$
, and explore the functoriality of the formation of
![]() ${\mathcal{M}}$
and its divisors with respect to the quadratic space
${\mathcal{M}}$
and its divisors with respect to the quadratic space
![]() $L$
. More precisely, given an isometric embedding
$L$
. More precisely, given an isometric embedding
 $L_{0}{\hookrightarrow}L$
of maximal
$L_{0}{\hookrightarrow}L$
of maximal
![]() $\mathbb{Z}$
-quadratic spaces of signatures
$\mathbb{Z}$
-quadratic spaces of signatures
![]() $(n_{0},2)$
and
$(n_{0},2)$
and
![]() $(n,2)$
, with
$(n,2)$
, with
 $1\leqslant n_{0}\leqslant n$
, we prove the existence of a canonical morphism
$1\leqslant n_{0}\leqslant n$
, we prove the existence of a canonical morphism
 ${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
between the associated integral models, and show that the pullback of a special divisor on
${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
between the associated integral models, and show that the pullback of a special divisor on
![]() ${\mathcal{M}}$
is a prescribed linear combination of special divisors on
${\mathcal{M}}$
is a prescribed linear combination of special divisors on
![]() ${\mathcal{M}}_{0}$
.
${\mathcal{M}}_{0}$
.
In § 3 we remind the reader of some of the analytic theory used in [Reference Bruinier and YangBY09]. In particular, we recall the essential properties of harmonic weak Maass forms, the divisors
![]() $Z(f)$
on
$Z(f)$
on
![]() $M$
associated to such forms, and the Green functions
$M$
associated to such forms, and the Green functions
![]() $\unicode[STIX]{x1D6F7}(f)$
for these divisors, which are defined as regularized theta lifts. We also recall the theta series and convolution
$\unicode[STIX]{x1D6F7}(f)$
for these divisors, which are defined as regularized theta lifts. We also recall the theta series and convolution
![]() $L$
-functions that appear in the main theorem, and Schofer’s [Reference SchoferSch09] calculation of the Fourier coefficients of the Eisenstein series of Remark 1.5.2. The only thing new here is that, thanks to the constructions of § 2, we are able to define an extension of the divisor
$L$
-functions that appear in the main theorem, and Schofer’s [Reference SchoferSch09] calculation of the Fourier coefficients of the Eisenstein series of Remark 1.5.2. The only thing new here is that, thanks to the constructions of § 2, we are able to define an extension of the divisor
![]() $Z(f)$
on
$Z(f)$
on
![]() $M$
to a divisor
$M$
to a divisor
![]() ${\mathcal{Z}}(f)$
on the integral model
${\mathcal{Z}}(f)$
on the integral model
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
In § 4 we fix a quadratic space
![]() $L_{0}$
over
$L_{0}$
over
![]() $\mathbb{Z}$
of signature
$\mathbb{Z}$
of signature
![]() $(0,2)$
, whose even Clifford algebra is isomorphic to the maximal order in a quadratic imaginary field
$(0,2)$
, whose even Clifford algebra is isomorphic to the maximal order in a quadratic imaginary field
![]() $\boldsymbol{k}$
. The Clifford algebra of
$\boldsymbol{k}$
. The Clifford algebra of
![]() $L_{0}$
then has the form
$L_{0}$
then has the form
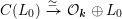 $C(L_{0})\xrightarrow[{}]{\simeq }{\mathcal{O}}_{\boldsymbol{k}}\oplus L_{0}$
. The Shimura variety associated to the rank-two torus
$C(L_{0})\xrightarrow[{}]{\simeq }{\mathcal{O}}_{\boldsymbol{k}}\oplus L_{0}$
. The Shimura variety associated to the rank-two torus
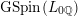 $\text{GSpin}(L_{0\mathbb{Q}})$
has dimension
$\text{GSpin}(L_{0\mathbb{Q}})$
has dimension
![]() $0$
, and can be realized as the moduli stack of elliptic curves with complex multiplication by
$0$
, and can be realized as the moduli stack of elliptic curves with complex multiplication by
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. Using this interpretation we define an integral model
${\mathcal{O}}_{\boldsymbol{k}}$
. Using this interpretation we define an integral model
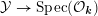 ${\mathcal{Y}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
, and define the Kuga–Satake abelian scheme as
${\mathcal{Y}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
, and define the Kuga–Satake abelian scheme as
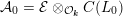 ${\mathcal{A}}_{0}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L_{0})$
, where
${\mathcal{A}}_{0}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L_{0})$
, where
![]() ${\mathcal{E}}\rightarrow {\mathcal{Y}}$
is the universal CM elliptic curve. All of the results of § 2 are then extended to this new setting.
${\mathcal{E}}\rightarrow {\mathcal{Y}}$
is the universal CM elliptic curve. All of the results of § 2 are then extended to this new setting.
In particular, we define a family of divisors
 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
on the arithmetic curve
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
on the arithmetic curve
![]() ${\mathcal{Y}}$
, each of which can be characterized as the locus of points where
${\mathcal{Y}}$
, each of which can be characterized as the locus of points where
![]() ${\mathcal{A}}_{0}$
has an extra quasi-endomorphism with prescribed properties. This can also be expressed in terms of endomorphisms of the universal CM elliptic curve: along each special divisor the action of
${\mathcal{A}}_{0}$
has an extra quasi-endomorphism with prescribed properties. This can also be expressed in terms of endomorphisms of the universal CM elliptic curve: along each special divisor the action of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
on
${\mathcal{O}}_{\boldsymbol{k}}$
on
![]() ${\mathcal{E}}$
extends to an action of an order in a definite quaternion algebra. Theorem 4.5.1 gives explicit formulas for the degrees of the divisors
${\mathcal{E}}$
extends to an action of an order in a definite quaternion algebra. Theorem 4.5.1 gives explicit formulas for the degrees of the divisors
 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
, and these degrees match up with Schofer’s formulas for the coefficients of Eisenstein series. Many cases of Theorem 4.5.1 already appear in work of Kudla et al. [Reference Kudla, Rapoport and YangKRY99] and Kudla and Yang [Reference Kudla and YangKY13], and our proof, like theirs, makes essential use of Gross’s calculation [Reference GrossGro86] of the endomorphism rings of canonical lifts of CM elliptic curves.
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
, and these degrees match up with Schofer’s formulas for the coefficients of Eisenstein series. Many cases of Theorem 4.5.1 already appear in work of Kudla et al. [Reference Kudla, Rapoport and YangKRY99] and Kudla and Yang [Reference Kudla and YangKY13], and our proof, like theirs, makes essential use of Gross’s calculation [Reference GrossGro86] of the endomorphism rings of canonical lifts of CM elliptic curves.
In § 5 we prove Theorem A. The greatest difficulty comes from the fact that the
![]() $1$
-cycle
$1$
-cycle
![]() ${\mathcal{Y}}$
on
${\mathcal{Y}}$
on
![]() ${\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
may have irreducible components contained entirely within
${\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
may have irreducible components contained entirely within
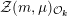 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{{\mathcal{O}}_{\boldsymbol{k}}}$
. Thus we must compute improper intersections. Our techniques for doing this are a blend of the methods used in [Reference Bruinier, Howard and YangBHY15] on unitary Shimura varieties, and the methods of Hu’s thesis [Reference HuHu99], which reconstructs the arithmetic intersection theory of Gillet and Soulé [Reference Gillet and SouléGS90] using Fulton’s method of deformation to the normal cone.
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{{\mathcal{O}}_{\boldsymbol{k}}}$
. Thus we must compute improper intersections. Our techniques for doing this are a blend of the methods used in [Reference Bruinier, Howard and YangBHY15] on unitary Shimura varieties, and the methods of Hu’s thesis [Reference HuHu99], which reconstructs the arithmetic intersection theory of Gillet and Soulé [Reference Gillet and SouléGS90] using Fulton’s method of deformation to the normal cone.
The cycle
![]() ${\mathcal{Y}}$
has a normal bundle
${\mathcal{Y}}$
has a normal bundle
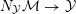 $N_{{\mathcal{Y}}}{\mathcal{M}}\rightarrow {\mathcal{Y}}$
, and the arithmetic divisor
$N_{{\mathcal{Y}}}{\mathcal{M}}\rightarrow {\mathcal{Y}}$
, and the arithmetic divisor
![]() $\widehat{{\mathcal{Z}}}(f)$
on
$\widehat{{\mathcal{Z}}}(f)$
on
![]() ${\mathcal{M}}$
has a specialization to the normal bundle
${\mathcal{M}}$
has a specialization to the normal bundle
 $\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(f))$
, which is an arithmetic divisor on
$\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(f))$
, which is an arithmetic divisor on
![]() $N_{{\mathcal{Y}}}{\mathcal{M}}$
. The specialization is defined in such a way that the arithmetic degree of
$N_{{\mathcal{Y}}}{\mathcal{M}}$
. The specialization is defined in such a way that the arithmetic degree of
![]() $\widehat{{\mathcal{Z}}}(f)$
along
$\widehat{{\mathcal{Z}}}(f)$
along
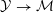 ${\mathcal{Y}}\rightarrow {\mathcal{M}}$
is equal to the arithmetic degree of
${\mathcal{Y}}\rightarrow {\mathcal{M}}$
is equal to the arithmetic degree of
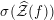 $\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(f))$
along the zero section
$\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(f))$
along the zero section
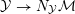 ${\mathcal{Y}}\rightarrow N_{{\mathcal{Y}}}{\mathcal{M}}$
. What we are able to show, essentially, is that every component of the arithmetic divisor
${\mathcal{Y}}\rightarrow N_{{\mathcal{Y}}}{\mathcal{M}}$
. What we are able to show, essentially, is that every component of the arithmetic divisor
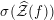 $\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(f))$
that meets the zero section improperly has
$\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(f))$
that meets the zero section improperly has
![]() $\unicode[STIX]{x1D70E}(\widehat{\boldsymbol{T}})$
, the specialization of the cotautological bundle, as its associated line bundle. This implies that every component of
$\unicode[STIX]{x1D70E}(\widehat{\boldsymbol{T}})$
, the specialization of the cotautological bundle, as its associated line bundle. This implies that every component of
![]() $\widehat{{\mathcal{Z}}}(f)$
that meets
$\widehat{{\mathcal{Z}}}(f)$
that meets
![]() ${\mathcal{Y}}$
improperly contributes the same quantity,
${\mathcal{Y}}$
improperly contributes the same quantity,
![]() $[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]$
, to the degree
$[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]$
, to the degree
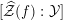 $[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]$
. The contribution to the intersection of the remaining components can be read off from the degrees of the divisors
$[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]$
. The contribution to the intersection of the remaining components can be read off from the degrees of the divisors
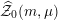 $\widehat{{\mathcal{Z}}}_{0}(m,\unicode[STIX]{x1D707})$
computed in § 4, and the calculation of
$\widehat{{\mathcal{Z}}}_{0}(m,\unicode[STIX]{x1D707})$
computed in § 4, and the calculation of
![]() $[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]$
quickly reduces to the Chowla–Selberg formula.
$[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]$
quickly reduces to the Chowla–Selberg formula.
Finally, we remark that the proof of Theorem A makes essential use of the Bruinier–Yang calculation (following Schofer [Reference SchoferSch09]) of the values of
![]() $\unicode[STIX]{x1D6F7}(f)$
at the points of
$\unicode[STIX]{x1D6F7}(f)$
at the points of
![]() ${\mathcal{Y}}(\mathbb{C})$
. Because of the particular way in which the divergent integral defining
${\mathcal{Y}}(\mathbb{C})$
. Because of the particular way in which the divergent integral defining
![]() $\unicode[STIX]{x1D6F7}(f)$
is regularized, the Green function
$\unicode[STIX]{x1D6F7}(f)$
is regularized, the Green function
![]() $\unicode[STIX]{x1D6F7}(f)$
has a well-defined value even at points of divisor
$\unicode[STIX]{x1D6F7}(f)$
has a well-defined value even at points of divisor
![]() ${\mathcal{Z}}(f)$
along which
${\mathcal{Z}}(f)$
along which
![]() $\unicode[STIX]{x1D6F7}(f)$
has a logarithmic singularity. In other words, the Green function comes, by construction, with a discontinuous extension to all points of
$\unicode[STIX]{x1D6F7}(f)$
has a logarithmic singularity. In other words, the Green function comes, by construction, with a discontinuous extension to all points of
![]() ${\mathcal{M}}(\mathbb{C})$
. Hu’s thesis sheds some light on this phenomenon, and the over-regularized values of
${\mathcal{M}}(\mathbb{C})$
. Hu’s thesis sheds some light on this phenomenon, and the over-regularized values of
![]() $\unicode[STIX]{x1D6F7}(f)$
at the points of
$\unicode[STIX]{x1D6F7}(f)$
at the points of
![]() ${\mathcal{Z}}(f)$
will play an essential role in our calculation of improper intersections.
${\mathcal{Z}}(f)$
will play an essential role in our calculation of improper intersections.
2 The GSpin Shimura variety and its special divisors
2.1 Preliminaries
Let
![]() $R$
be a commutative ring. A quadratic space over
$R$
be a commutative ring. A quadratic space over
![]() $R$
is a projective
$R$
is a projective
![]() $R$
-module
$R$
-module
![]() $V$
of finite rank, equipped with a homogenous function
$V$
of finite rank, equipped with a homogenous function
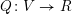 $Q:V\rightarrow R$
of degree
$Q:V\rightarrow R$
of degree
![]() $2$
for which the symmetric pairing
$2$
for which the symmetric pairing
 $$\begin{eqnarray}[x,y]=Q(x+y)-Q(x)-Q(y)\end{eqnarray}$$
$$\begin{eqnarray}[x,y]=Q(x+y)-Q(x)-Q(y)\end{eqnarray}$$
is
![]() $R$
-bilinear. We say that
$R$
-bilinear. We say that
![]() $V$
is self-dual if this pairing induces an isomorphism
$V$
is self-dual if this pairing induces an isomorphism
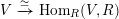 $V\xrightarrow[{}]{\simeq }\text{Hom}_{R}(V,R)$
.
$V\xrightarrow[{}]{\simeq }\text{Hom}_{R}(V,R)$
.
The Clifford algebra
![]() $C(V)$
is the quotient of the tensor algebra
$C(V)$
is the quotient of the tensor algebra
![]() $\bigotimes V$
by the ideal generated by elements of the form
$\bigotimes V$
by the ideal generated by elements of the form
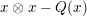 $x\otimes x-Q(x)$
. The
$x\otimes x-Q(x)$
. The
![]() $R$
-algebra
$R$
-algebra
![]() $C(V)$
is generated by the image of the natural injection
$C(V)$
is generated by the image of the natural injection
 $V\rightarrow C(V)$
, and the grading on
$V\rightarrow C(V)$
, and the grading on
![]() $\bigotimes V$
induces a
$\bigotimes V$
induces a
![]() $\mathbb{Z}/2\mathbb{Z}$
grading
$\mathbb{Z}/2\mathbb{Z}$
grading
 $$\begin{eqnarray}C(V)=C^{+}(V)\oplus C^{-}(V).\end{eqnarray}$$
$$\begin{eqnarray}C(V)=C^{+}(V)\oplus C^{-}(V).\end{eqnarray}$$
The Clifford algebra
![]() $C(V)$
has the following universal property: given an associative algebra
$C(V)$
has the following universal property: given an associative algebra
![]() $B$
over
$B$
over
![]() $R$
and a map of
$R$
and a map of
![]() $R$
-modules
$R$
-modules
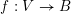 $f:V\rightarrow B$
satisfying
$f:V\rightarrow B$
satisfying
 $f(x)^{2}=Q(x)$
for all
$f(x)^{2}=Q(x)$
for all
![]() $x\in V$
, there is a unique map of
$x\in V$
, there is a unique map of
![]() $R$
-algebras
$R$
-algebras
 $\tilde{f}:C(V)\rightarrow B$
satisfying
$\tilde{f}:C(V)\rightarrow B$
satisfying
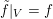 $\tilde{f}|_{V}=f$
. In particular, applying this property with
$\tilde{f}|_{V}=f$
. In particular, applying this property with
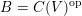 $B=C(V)^{\text{op}}$
and
$B=C(V)^{\text{op}}$
and
![]() $f$
the natural inclusion of
$f$
the natural inclusion of
![]() $V$
in
$V$
in
![]() $C(V)^{\text{op}}$
, we obtain a canonical anti-involution
$C(V)^{\text{op}}$
, we obtain a canonical anti-involution
![]() $\ast$
on
$\ast$
on
![]() $C(V)$
satisfying
$C(V)$
satisfying
 $$\begin{eqnarray}(x_{1}x_{2}\cdots x_{r-1}x_{r})^{\ast }=x_{r}x_{r-1}\cdots x_{2}x_{1}\end{eqnarray}$$
$$\begin{eqnarray}(x_{1}x_{2}\cdots x_{r-1}x_{r})^{\ast }=x_{r}x_{r-1}\cdots x_{2}x_{1}\end{eqnarray}$$
for any
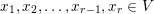 $x_{1},x_{2},\ldots ,x_{r-1},x_{r}\in V$
.
$x_{1},x_{2},\ldots ,x_{r-1},x_{r}\in V$
.
To a self-dual quadratic space
![]() $V$
, we can attach the reductive group scheme
$V$
, we can attach the reductive group scheme
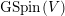 $\text{GSpin}(V)$
over
$\text{GSpin}(V)$
over
![]() $R$
with functor of points
$R$
with functor of points
 $$\begin{eqnarray}\text{GSpin}(V)(S)=\{g\in C^{+}(V)_{S}^{\times }:gV_{S}g^{-1}=V_{S}\}\end{eqnarray}$$
$$\begin{eqnarray}\text{GSpin}(V)(S)=\{g\in C^{+}(V)_{S}^{\times }:gV_{S}g^{-1}=V_{S}\}\end{eqnarray}$$
for any
![]() $R$
-algebra
$R$
-algebra
![]() $S$
. Denote by
$S$
. Denote by
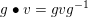 $g\bullet v=gvg^{-1}$
the natural action of
$g\bullet v=gvg^{-1}$
the natural action of
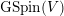 $\text{GSpin}(V)$
on
$\text{GSpin}(V)$
on
![]() $V$
. For any
$V$
. For any
![]() $R$
-algebra
$R$
-algebra
![]() $S$
, the map
$S$
, the map
 $g\mapsto g^{\ast }g$
on
$g\mapsto g^{\ast }g$
on
 $\text{GSpin}(V)(S)$
takes values in
$\text{GSpin}(V)(S)$
takes values in
![]() $S^{\times }$
[Reference BassBas74, 3.2.1], and so defines a canonical homomorphism of
$S^{\times }$
[Reference BassBas74, 3.2.1], and so defines a canonical homomorphism of
![]() $R$
-group schemes
$R$
-group schemes
 $$\begin{eqnarray}\unicode[STIX]{x1D708}:\text{GSpin}(V)\rightarrow \mathbb{G}_{m,R},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}:\text{GSpin}(V)\rightarrow \mathbb{G}_{m,R},\end{eqnarray}$$
which we call the spinor norm.
Choose an element
 $\unicode[STIX]{x1D6FF}\in C^{+}(V)^{\times }$
satisfying
$\unicode[STIX]{x1D6FF}\in C^{+}(V)^{\times }$
satisfying
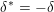 $\unicode[STIX]{x1D6FF}^{\ast }=-\unicode[STIX]{x1D6FF}$
. We can use this element to define a symplectic pairing on
$\unicode[STIX]{x1D6FF}^{\ast }=-\unicode[STIX]{x1D6FF}$
. We can use this element to define a symplectic pairing on
![]() $C(V)$
as follows (see [Reference Madapusi PeraMad16, (1.6)]). The self-duality hypothesis on
$C(V)$
as follows (see [Reference Madapusi PeraMad16, (1.6)]). The self-duality hypothesis on
![]() $V$
implies that
$V$
implies that
![]() $C(V)$
is a graded Azumaya algebra over
$C(V)$
is a graded Azumaya algebra over
![]() $R$
in the sense of [Reference BassBas74, § 2.3, Theorem]. In particular, there is a canonical reduced trace form
$R$
in the sense of [Reference BassBas74, § 2.3, Theorem]. In particular, there is a canonical reduced trace form
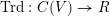 $\text{Trd}:C(V)\rightarrow R$
, and the pairing
$\text{Trd}:C(V)\rightarrow R$
, and the pairing
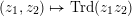 $(z_{1},z_{2})\mapsto \text{Trd}(z_{1}z_{2})$
is a perfect symmetric bilinear form on
$(z_{1},z_{2})\mapsto \text{Trd}(z_{1}z_{2})$
is a perfect symmetric bilinear form on
![]() $C(V)$
. The desired symplectic pairing on
$C(V)$
. The desired symplectic pairing on
![]() $C(V)$
is
$C(V)$
is
 $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(z_{1},z_{2})=\text{Trd}(z_{1}\unicode[STIX]{x1D6FF}z_{2}^{\ast })$
.
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(z_{1},z_{2})=\text{Trd}(z_{1}\unicode[STIX]{x1D6FF}z_{2}^{\ast })$
.
It is easily checked that
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(gz_{1},gz_{2})=\unicode[STIX]{x1D708}(g)\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(z_{1},z_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(gz_{1},gz_{2})=\unicode[STIX]{x1D708}(g)\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(z_{1},z_{2})\end{eqnarray}$$
for any
![]() $R$
-algebra
$R$
-algebra
![]() $S$
,
$S$
,
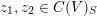 $z_{1},z_{2}\in C(V)_{S}$
, and
$z_{1},z_{2}\in C(V)_{S}$
, and
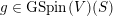 $g\in \text{GSpin}(V)(S)$
. In other words, the action of
$g\in \text{GSpin}(V)(S)$
. In other words, the action of
 $\text{GSpin}(V)$
on
$\text{GSpin}(V)$
on
![]() $C(V)$
by left multiplication realizes
$C(V)$
by left multiplication realizes
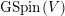 $\text{GSpin}(V)$
as a subgroup of the
$\text{GSpin}(V)$
as a subgroup of the
![]() $R$
-group scheme
$R$
-group scheme
![]() $\text{GSp}_{\unicode[STIX]{x1D6FF}}$
of symplectic similitudes of
$\text{GSp}_{\unicode[STIX]{x1D6FF}}$
of symplectic similitudes of
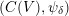 $(C(V),\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}})$
, and the symplectic similitude character restricts to the spinor norm on
$(C(V),\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}})$
, and the symplectic similitude character restricts to the spinor norm on
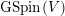 $\text{GSpin}(V)$
.
$\text{GSpin}(V)$
.
2.2 The complex Shimura variety
Let
![]() $n\geqslant 1$
be an integer. Fix a quadratic space
$n\geqslant 1$
be an integer. Fix a quadratic space
![]() $(L,Q)$
over
$(L,Q)$
over
![]() $\mathbb{Z}$
of signature
$\mathbb{Z}$
of signature
![]() $(n,2)$
, and set
$(n,2)$
, and set
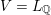 $V=L_{\mathbb{Q}}$
. We assume throughout that
$V=L_{\mathbb{Q}}$
. We assume throughout that
![]() $L$
is maximal in the sense that there is no lattice
$L$
is maximal in the sense that there is no lattice
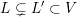 $L\subsetneq L^{\prime }\subset V$
satisfying
$L\subsetneq L^{\prime }\subset V$
satisfying
 $Q(L^{\prime })\subset \mathbb{Z}$
. Set
$Q(L^{\prime })\subset \mathbb{Z}$
. Set
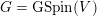 $G=\text{GSpin}(V)$
; this is a reductive group over
$G=\text{GSpin}(V)$
; this is a reductive group over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Let
![]() ${\mathcal{D}}$
be the space of oriented negative
${\mathcal{D}}$
be the space of oriented negative
![]() $2$
-planes
$2$
-planes
![]() $\boldsymbol{h}\subset V_{\mathbb{R}}$
. If we extend the
$\boldsymbol{h}\subset V_{\mathbb{R}}$
. If we extend the
![]() $\mathbb{Q}$
-bilinear form on
$\mathbb{Q}$
-bilinear form on
![]() $V$
to a
$V$
to a
![]() $\mathbb{C}$
-bilinear form on
$\mathbb{C}$
-bilinear form on
![]() $V_{\mathbb{C}}$
, the real manifold
$V_{\mathbb{C}}$
, the real manifold
![]() ${\mathcal{D}}$
is isomorphic to the Grassmannian
${\mathcal{D}}$
is isomorphic to the Grassmannian
 $$\begin{eqnarray}\displaystyle {\mathcal{D}}\xrightarrow[{}]{\simeq }\{z\in V_{\mathbb{C}}\smallsetminus \{0\}:[z,z]=0\text{ and }[z,\overline{z}]<0\}/\mathbb{C}^{\times }, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}\xrightarrow[{}]{\simeq }\{z\in V_{\mathbb{C}}\smallsetminus \{0\}:[z,z]=0\text{ and }[z,\overline{z}]<0\}/\mathbb{C}^{\times }, & & \displaystyle\end{eqnarray}$$
and in particular is naturally a complex manifold. The isomorphism is as follows: for each
![]() $\boldsymbol{h}$
pick an oriented basis
$\boldsymbol{h}$
pick an oriented basis
![]() $\{x,y\}$
so that
$\{x,y\}$
so that
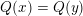 $Q(x)=Q(y)$
and
$Q(x)=Q(y)$
and
 $[x,y]=0$
, and let
$[x,y]=0$
, and let
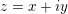 $z=x+iy$
. The inverse construction is obvious.
$z=x+iy$
. The inverse construction is obvious.
There are canonical inclusions of
![]() $\mathbb{R}$
-algebras
$\mathbb{R}$
-algebras
 $\mathbb{C}{\hookrightarrow}C(\boldsymbol{h}){\hookrightarrow}C(V_{\mathbb{R}})$
, where the first is determined by
$\mathbb{C}{\hookrightarrow}C(\boldsymbol{h}){\hookrightarrow}C(V_{\mathbb{R}})$
, where the first is determined by
 $$\begin{eqnarray}i\mapsto \frac{xy}{\sqrt{Q(x)Q(y)}}.\end{eqnarray}$$
$$\begin{eqnarray}i\mapsto \frac{xy}{\sqrt{Q(x)Q(y)}}.\end{eqnarray}$$
The induced map
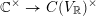 $\mathbb{C}^{\times }\rightarrow C(V_{\mathbb{R}})^{\times }$
takes values in
$\mathbb{C}^{\times }\rightarrow C(V_{\mathbb{R}})^{\times }$
takes values in
![]() $G(\mathbb{R})$
, and arises from a morphism of real algebraic groups
$G(\mathbb{R})$
, and arises from a morphism of real algebraic groups
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{\boldsymbol{h}}:\text{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m}\rightarrow G_{\mathbb{R}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{\boldsymbol{h}}:\text{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m}\rightarrow G_{\mathbb{R}}. & & \displaystyle\end{eqnarray}$$
In this way we identify
![]() ${\mathcal{D}}$
with a
${\mathcal{D}}$
with a
![]() $G(\mathbb{R})$
-conjugacy class in
$G(\mathbb{R})$
-conjugacy class in
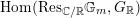 $\text{Hom}(\text{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m},G_{\mathbb{R}})$
.
$\text{Hom}(\text{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m},G_{\mathbb{R}})$
.
Set
![]() $\widehat{L}=L_{\widehat{\mathbb{Z}}}$
, and define a compact open subgroup
$\widehat{L}=L_{\widehat{\mathbb{Z}}}$
, and define a compact open subgroup
 $$\begin{eqnarray}K=G(\mathbb{A}_{f})\cap C(\widehat{L})^{\times }\end{eqnarray}$$
$$\begin{eqnarray}K=G(\mathbb{A}_{f})\cap C(\widehat{L})^{\times }\end{eqnarray}$$
of
![]() $G(\mathbb{A}_{f})$
. Note that
$G(\mathbb{A}_{f})$
. Note that
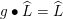 $g\bullet \widehat{L}=\widehat{L}$
for all
$g\bullet \widehat{L}=\widehat{L}$
for all
![]() $g\in K$
. Denote by
$g\in K$
. Denote by
 $$\begin{eqnarray}L^{\vee }=\{x\in V:[x,L]\subset \mathbb{Z}\}\end{eqnarray}$$
$$\begin{eqnarray}L^{\vee }=\{x\in V:[x,L]\subset \mathbb{Z}\}\end{eqnarray}$$
the dual lattice of
![]() $L$
. As in the proof of [Reference Madapusi PeraMad16, (2.6)], the action of
$L$
. As in the proof of [Reference Madapusi PeraMad16, (2.6)], the action of
![]() $K$
on
$K$
on
![]() $\widehat{L}$
defines a homomorphism
$\widehat{L}$
defines a homomorphism
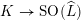 $K\rightarrow \text{SO}(\widehat{L})$
whose image is precisely the subgroup of elements acting trivially on the discriminant group
$K\rightarrow \text{SO}(\widehat{L})$
whose image is precisely the subgroup of elements acting trivially on the discriminant group
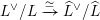 $L^{\vee }/L\xrightarrow[{}]{\simeq }\widehat{L}^{\vee }/\widehat{L}$
.
$L^{\vee }/L\xrightarrow[{}]{\simeq }\widehat{L}^{\vee }/\widehat{L}$
.
The pair
![]() $(G,{\mathcal{D}})$
is a Shimura datum, and
$(G,{\mathcal{D}})$
is a Shimura datum, and
 $$\begin{eqnarray}\displaystyle M(\mathbb{C})=G(\mathbb{Q})\backslash {\mathcal{D}}\times G(\mathbb{A}_{f})/K\mathop{\xrightarrow[{}]{\simeq }\bigsqcup }\nolimits_{g\in G(\mathbb{Q})\backslash G(\mathbb{A}_{f})/K}\unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M(\mathbb{C})=G(\mathbb{Q})\backslash {\mathcal{D}}\times G(\mathbb{A}_{f})/K\mathop{\xrightarrow[{}]{\simeq }\bigsqcup }\nolimits_{g\in G(\mathbb{Q})\backslash G(\mathbb{A}_{f})/K}\unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}, & & \displaystyle\end{eqnarray}$$
is the complex orbifold of
![]() $\mathbb{C}$
-points of the Shimura variety attached to this datum and level subgroup
$\mathbb{C}$
-points of the Shimura variety attached to this datum and level subgroup
![]() $K$
. Here we have set
$K$
. Here we have set
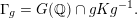 $\unicode[STIX]{x1D6E4}_{g}=G(\mathbb{Q})\cap gKg^{-1}.$
We will refer to
$\unicode[STIX]{x1D6E4}_{g}=G(\mathbb{Q})\cap gKg^{-1}.$
We will refer to
![]() $M(\mathbb{C})$
as the GSpin Shimura variety associated with
$M(\mathbb{C})$
as the GSpin Shimura variety associated with
![]() $L$
.
$L$
.
Given an algebraic representation
 $G\rightarrow \text{}\underline{\text{Aut}}(N)$
on a finite-dimensional
$G\rightarrow \text{}\underline{\text{Aut}}(N)$
on a finite-dimensional
![]() $\mathbb{Q}$
-vector space, and a
$\mathbb{Q}$
-vector space, and a
![]() $K$
-stable lattice
$K$
-stable lattice
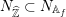 $N_{\widehat{\mathbb{Z}}}\subset N_{\mathbb{A}_{f}}$
, we obtain a
$N_{\widehat{\mathbb{Z}}}\subset N_{\mathbb{A}_{f}}$
, we obtain a
![]() $\mathbb{Z}$
-local system
$\mathbb{Z}$
-local system
![]() $\boldsymbol{N}_{\text{Be}}$
on
$\boldsymbol{N}_{\text{Be}}$
on
![]() $M(\mathbb{C})$
whose fiber at a point
$M(\mathbb{C})$
whose fiber at a point
 $[(\boldsymbol{h},g)]\in M(\mathbb{C})$
is identified with
$[(\boldsymbol{h},g)]\in M(\mathbb{C})$
is identified with
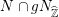 $N\cap gN_{\widehat{\mathbb{Z}}}$
. The corresponding vector bundle
$N\cap gN_{\widehat{\mathbb{Z}}}$
. The corresponding vector bundle
 $$\begin{eqnarray}\boldsymbol{N}_{\text{dR},M(\mathbb{C})}={\mathcal{O}}_{M(\mathbb{C})}\otimes \boldsymbol{N}_{\text{Be}}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{N}_{\text{dR},M(\mathbb{C})}={\mathcal{O}}_{M(\mathbb{C})}\otimes \boldsymbol{N}_{\text{Be}}\end{eqnarray}$$
is equipped with a filtration
 $\text{Fil}^{\bullet }\boldsymbol{N}_{\text{dR},M(\mathbb{C})}$
, which at any point
$\text{Fil}^{\bullet }\boldsymbol{N}_{\text{dR},M(\mathbb{C})}$
, which at any point
![]() $[(\boldsymbol{h},g)]$
equips the fiber of
$[(\boldsymbol{h},g)]$
equips the fiber of
![]() $\boldsymbol{N}_{\text{Be}}$
with the Hodge structure determined by (2.2). This gives us a functorial assignment from pairs
$\boldsymbol{N}_{\text{Be}}$
with the Hodge structure determined by (2.2). This gives us a functorial assignment from pairs
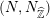 $(N,N_{\widehat{\mathbb{Z}}})$
as above to variations of
$(N,N_{\widehat{\mathbb{Z}}})$
as above to variations of
![]() $\mathbb{Z}$
-Hodge structures over
$\mathbb{Z}$
-Hodge structures over
![]() $M(\mathbb{C})$
.
$M(\mathbb{C})$
.
Applying this to
![]() $V$
and the lattice
$V$
and the lattice
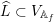 $\widehat{L}\subset V_{\mathbb{A}_{f}}$
, we obtain a canonical variation of polarized
$\widehat{L}\subset V_{\mathbb{A}_{f}}$
, we obtain a canonical variation of polarized
![]() $\mathbb{Z}$
-Hodge structures
$\mathbb{Z}$
-Hodge structures
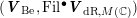 $(\boldsymbol{V}_{\text{Be}},\text{Fil}^{\bullet }\boldsymbol{V}_{\text{dR},M(\mathbb{C})})$
. For each point
$(\boldsymbol{V}_{\text{Be}},\text{Fil}^{\bullet }\boldsymbol{V}_{\text{dR},M(\mathbb{C})})$
. For each point
![]() $z$
of (2.1) the induced Hodge decomposition of
$z$
of (2.1) the induced Hodge decomposition of
![]() $V_{\mathbb{C}}$
has
$V_{\mathbb{C}}$
has
 $$\begin{eqnarray}V_{\mathbb{C}}^{(1,-1)}=\mathbb{C}z,\quad V_{\mathbb{ C}}^{(-1,1)}=\mathbb{C}\overline{z},\quad V_{\mathbb{ C}}^{(0,0)}=(\mathbb{C}z+\mathbb{C}\overline{z})^{\bot }.\end{eqnarray}$$
$$\begin{eqnarray}V_{\mathbb{C}}^{(1,-1)}=\mathbb{C}z,\quad V_{\mathbb{ C}}^{(-1,1)}=\mathbb{C}\overline{z},\quad V_{\mathbb{ C}}^{(0,0)}=(\mathbb{C}z+\mathbb{C}\overline{z})^{\bot }.\end{eqnarray}$$
It follows that
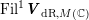 $\text{Fil}^{1}\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
is an isotropic line and
$\text{Fil}^{1}\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
is an isotropic line and
 $\text{Fil}^{0}\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
is its annihilator with respect to the pairing on
$\text{Fil}^{0}\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
is its annihilator with respect to the pairing on
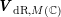 $\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
induced from that on
$\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
induced from that on
![]() $L$
.
$L$
.
Similarly, viewing
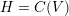 $H=C(V)$
as a representation of
$H=C(V)$
as a representation of
![]() $G$
by left multiplication, with its lattice
$G$
by left multiplication, with its lattice
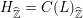 $H_{\widehat{\mathbb{Z}}}=C(L)_{\widehat{\mathbb{Z}}}$
, we obtain a variation of
$H_{\widehat{\mathbb{Z}}}=C(L)_{\widehat{\mathbb{Z}}}$
, we obtain a variation of
![]() $\mathbb{Z}$
-Hodge structures
$\mathbb{Z}$
-Hodge structures
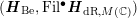 $(\boldsymbol{H}_{\text{Be}},\text{Fil}^{\bullet }\boldsymbol{H}_{\text{dR},M(\mathbb{C})})$
. This variation has type
$(\boldsymbol{H}_{\text{Be}},\text{Fil}^{\bullet }\boldsymbol{H}_{\text{dR},M(\mathbb{C})})$
. This variation has type
 $(-1,0),(0,-1)$
and is therefore the homology of a family of complex tori over
$(-1,0),(0,-1)$
and is therefore the homology of a family of complex tori over
![]() $M(\mathbb{C})$
.
$M(\mathbb{C})$
.
This variation of
![]() $\mathbb{Z}$
-Hodge structures is polarizable, and so the family of complex tori in fact arises from an abelian scheme over
$\mathbb{Z}$
-Hodge structures is polarizable, and so the family of complex tori in fact arises from an abelian scheme over
![]() $M(\mathbb{C})$
. To see this, first consider the representation of
$M(\mathbb{C})$
. To see this, first consider the representation of
![]() $G$
on
$G$
on
![]() $\mathbb{Q}$
afforded by the spinor norm
$\mathbb{Q}$
afforded by the spinor norm
![]() $\unicode[STIX]{x1D708}$
, along with the obvious
$\unicode[STIX]{x1D708}$
, along with the obvious
![]() $K$
-stable lattice
$K$
-stable lattice
![]() $\widehat{\mathbb{Z}}\subset \mathbb{A}_{f}$
. For any
$\widehat{\mathbb{Z}}\subset \mathbb{A}_{f}$
. For any
![]() $\boldsymbol{h}\in {\mathcal{D}}$
, the composition
$\boldsymbol{h}\in {\mathcal{D}}$
, the composition
![]() $\unicode[STIX]{x1D708}\circ \unicode[STIX]{x1D6FC}_{\boldsymbol{h}}$
is the homomorphism
$\unicode[STIX]{x1D708}\circ \unicode[STIX]{x1D6FC}_{\boldsymbol{h}}$
is the homomorphism
 $$\begin{eqnarray}\text{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m}\xrightarrow[{}]{z\mapsto z\overline{z}}\mathbb{G}_{m,\mathbb{R}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m}\xrightarrow[{}]{z\mapsto z\overline{z}}\mathbb{G}_{m,\mathbb{R}}.\end{eqnarray}$$
From this, we see that the associated variation of
![]() $\mathbb{Z}$
-Hodge structures is the Tate twist
$\mathbb{Z}$
-Hodge structures is the Tate twist
![]() $\text{}\underline{\mathbb{Z}}(1)$
, whose underlying
$\text{}\underline{\mathbb{Z}}(1)$
, whose underlying
![]() $\mathbb{Z}$
-local system is just the constant sheaf
$\mathbb{Z}$
-local system is just the constant sheaf
![]() $\text{}\underline{\mathbb{Z}}$
, but whose (constant) Hodge filtration is concentrated in degree
$\text{}\underline{\mathbb{Z}}$
, but whose (constant) Hodge filtration is concentrated in degree
![]() $-1$
.
$-1$
.
Now, choose
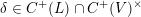 $\unicode[STIX]{x1D6FF}\in C^{+}(L)\cap C^{+}(V)^{\times }$
satisfying
$\unicode[STIX]{x1D6FF}\in C^{+}(L)\cap C^{+}(V)^{\times }$
satisfying
 $\unicode[STIX]{x1D6FF}^{\ast }=-\unicode[STIX]{x1D6FF}$
. As explained in § 2.1, this defines a
$\unicode[STIX]{x1D6FF}^{\ast }=-\unicode[STIX]{x1D6FF}$
. As explained in § 2.1, this defines a
![]() $G$
-equivariant symplectic pairing
$G$
-equivariant symplectic pairing
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}:C(V)\times C(V)\rightarrow \mathbb{Q}(\unicode[STIX]{x1D708})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}:C(V)\times C(V)\rightarrow \mathbb{Q}(\unicode[STIX]{x1D708})\end{eqnarray}$$
by
 $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(x,y)=\text{Trd}(x\unicode[STIX]{x1D6FF}y^{\ast })$
. Since
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(x,y)=\text{Trd}(x\unicode[STIX]{x1D6FF}y^{\ast })$
. Since
![]() $\unicode[STIX]{x1D6FF}$
lies in
$\unicode[STIX]{x1D6FF}$
lies in
![]() $C^{+}(L)$
, the restriction of this form to
$C^{+}(L)$
, the restriction of this form to
![]() $C(L)$
is
$C(L)$
is
![]() $\mathbb{Z}$
-valued, and in particular induces a
$\mathbb{Z}$
-valued, and in particular induces a
![]() $K$
-invariant alternating form on
$K$
-invariant alternating form on
![]() $C(L)_{\widehat{\mathbb{Z}}}$
with values in
$C(L)_{\widehat{\mathbb{Z}}}$
with values in
![]() $\widehat{\mathbb{Z}}(\unicode[STIX]{x1D708})$
.
$\widehat{\mathbb{Z}}(\unicode[STIX]{x1D708})$
.
We can arrange our choice of
![]() $\unicode[STIX]{x1D6FF}$
to have the following positivity property: for every
$\unicode[STIX]{x1D6FF}$
to have the following positivity property: for every
![]() $\boldsymbol{h}\in {\mathcal{D}}$
, the Hermitian form
$\boldsymbol{h}\in {\mathcal{D}}$
, the Hermitian form
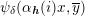 $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D6FC}_{\boldsymbol{h}}(i)x,\overline{y})$
on
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D6FC}_{\boldsymbol{h}}(i)x,\overline{y})$
on
![]() $C(V)_{\mathbb{C}}$
is (positive or negative) definite. To produce a concrete such choice, choose a negative definite plane
$C(V)_{\mathbb{C}}$
is (positive or negative) definite. To produce a concrete such choice, choose a negative definite plane
![]() $\boldsymbol{h}_{0}\subset V$
defined over
$\boldsymbol{h}_{0}\subset V$
defined over
![]() $\mathbb{Q}$
, and an oriented basis
$\mathbb{Q}$
, and an oriented basis
 $x,y\in \boldsymbol{h}_{0}\cap L$
for
$x,y\in \boldsymbol{h}_{0}\cap L$
for
![]() $\boldsymbol{h}_{0}$
satisfying
$\boldsymbol{h}_{0}$
satisfying
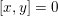 $[x,y]=0$
. Then it can be checked that
$[x,y]=0$
. Then it can be checked that
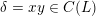 $\unicode[STIX]{x1D6FF}=xy\in C(L)$
has the desired positivity property. Any such choice of
$\unicode[STIX]{x1D6FF}=xy\in C(L)$
has the desired positivity property. Any such choice of
![]() $\unicode[STIX]{x1D6FF}$
produces an alternating morphism
$\unicode[STIX]{x1D6FF}$
produces an alternating morphism
 $$\begin{eqnarray}\displaystyle \boldsymbol{H}_{\text{Be}}\otimes \boldsymbol{H}_{\text{Be}}\rightarrow \text{}\underline{\mathbb{Z}}(1) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{H}_{\text{Be}}\otimes \boldsymbol{H}_{\text{Be}}\rightarrow \text{}\underline{\mathbb{Z}}(1) & & \displaystyle \nonumber\end{eqnarray}$$
of variations of Hodge structures, and the positivity property implies that this is a polarization.
Remark 2.2.1. By our construction, any choice of
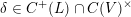 $\unicode[STIX]{x1D6FF}\in C^{+}(L)\cap C(V)^{\times }$
with the required positivity property produces a polarization on
$\unicode[STIX]{x1D6FF}\in C^{+}(L)\cap C(V)^{\times }$
with the required positivity property produces a polarization on
![]() ${\mathcal{A}}_{M(\mathbb{C})}$
. While the polarization on
${\mathcal{A}}_{M(\mathbb{C})}$
. While the polarization on
![]() ${\mathcal{A}}_{M(\mathbb{C})}$
depends on the choice of
${\mathcal{A}}_{M(\mathbb{C})}$
depends on the choice of
![]() $\unicode[STIX]{x1D6FF}$
, the abelian scheme itself does not.
$\unicode[STIX]{x1D6FF}$
, the abelian scheme itself does not.
In sum, we have produced an abelian scheme
 ${\mathcal{A}}_{M(\mathbb{C})}\rightarrow M(\mathbb{C})$
, whose homology is canonically identified with the polarizable variation of Hodge structures
${\mathcal{A}}_{M(\mathbb{C})}\rightarrow M(\mathbb{C})$
, whose homology is canonically identified with the polarizable variation of Hodge structures
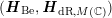 $(\boldsymbol{H}_{\text{Be}},\boldsymbol{H}_{\text{dR},M(\mathbb{C})})$
. We call this the Kuga–Satake abelian scheme. It has relative dimension
$(\boldsymbol{H}_{\text{Be}},\boldsymbol{H}_{\text{dR},M(\mathbb{C})})$
. We call this the Kuga–Satake abelian scheme. It has relative dimension
![]() $2^{n+1}$
.
$2^{n+1}$
.
The action of
![]() $G$
on
$G$
on
![]() $H$
commutes with the right multiplication action of
$H$
commutes with the right multiplication action of
![]() $C(V)$
, and also respects the
$C(V)$
, and also respects the
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading
$\mathbb{Z}/2\mathbb{Z}$
-grading
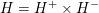 $H=H^{+}\times H^{-}$
defined by
$H=H^{+}\times H^{-}$
defined by
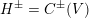 $H^{\pm }=C^{\pm }(V)$
. Thus the Kuga–Satake abelian scheme inherits a right action of
$H^{\pm }=C^{\pm }(V)$
. Thus the Kuga–Satake abelian scheme inherits a right action of
![]() $C(L)$
, and a
$C(L)$
, and a
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading
$\mathbb{Z}/2\mathbb{Z}$
-grading
 $$\begin{eqnarray}{\mathcal{A}}_{M(\mathbb{C})}={\mathcal{A}}_{M(\mathbb{C})}^{+}\times {\mathcal{A}}_{M(\mathbb{C})}^{-}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{M(\mathbb{C})}={\mathcal{A}}_{M(\mathbb{C})}^{+}\times {\mathcal{A}}_{M(\mathbb{C})}^{-}.\end{eqnarray}$$
Elements of
![]() $C^{+}(L)$
and
$C^{+}(L)$
and
![]() $C^{-}(L)$
act as homogeneous endomorphisms of graded degrees zero and one, respectively. The left multiplication action of
$C^{-}(L)$
act as homogeneous endomorphisms of graded degrees zero and one, respectively. The left multiplication action of
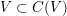 $V\subset C(V)$
on
$V\subset C(V)$
on
![]() $H$
induces an embedding
$H$
induces an embedding
 $$\begin{eqnarray}(\boldsymbol{V}_{\text{Be}},\text{Fil}^{\bullet }\boldsymbol{V}_{\text{dR},M(\mathbb{C})})\subset (\text{}\underline{\text{End}}(\boldsymbol{H}_{\text{Be}}),\text{Fil}^{\bullet }\text{}\underline{\text{End}}(\boldsymbol{H}_{\text{dR},M(\mathbb{C})}))\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{V}_{\text{Be}},\text{Fil}^{\bullet }\boldsymbol{V}_{\text{dR},M(\mathbb{C})})\subset (\text{}\underline{\text{End}}(\boldsymbol{H}_{\text{Be}}),\text{Fil}^{\bullet }\text{}\underline{\text{End}}(\boldsymbol{H}_{\text{dR},M(\mathbb{C})}))\end{eqnarray}$$
of variations of Hodge structures.
For
![]() $x\in V$
of positive length, define a divisor on
$x\in V$
of positive length, define a divisor on
![]() ${\mathcal{D}}$
by
${\mathcal{D}}$
by
 $$\begin{eqnarray}{\mathcal{D}}(x)=\{z\in {\mathcal{D}}:z\bot x\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}(x)=\{z\in {\mathcal{D}}:z\bot x\}.\end{eqnarray}$$
As in the work of Borcherds [Reference BorcherdsBor98], Bruinier [Reference BruinierBru02], and Kudla [Reference KudlaKud04], for every
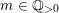 $m\in \mathbb{Q}_{{>}0}$
and
$m\in \mathbb{Q}_{{>}0}$
and
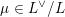 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
we define a complex orbifold
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
we define a complex orbifold
 $$\begin{eqnarray}\displaystyle Z(m,\unicode[STIX]{x1D707})(\mathbb{C})=\bigsqcup _{g\in G(\mathbb{Q})\backslash G(\mathbb{A}_{f})/K}\unicode[STIX]{x1D6E4}_{g}\bigg\backslash\biggl(\bigsqcup _{\substack{ x\in \unicode[STIX]{x1D707}_{g}+L_{g} \\ Q(x)=m}}{\mathcal{D}}(x)\biggr). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z(m,\unicode[STIX]{x1D707})(\mathbb{C})=\bigsqcup _{g\in G(\mathbb{Q})\backslash G(\mathbb{A}_{f})/K}\unicode[STIX]{x1D6E4}_{g}\bigg\backslash\biggl(\bigsqcup _{\substack{ x\in \unicode[STIX]{x1D707}_{g}+L_{g} \\ Q(x)=m}}{\mathcal{D}}(x)\biggr). & & \displaystyle\end{eqnarray}$$
Here
![]() $L_{g}\subset V$
is the
$L_{g}\subset V$
is the
![]() $\mathbb{Z}$
-lattice determined by
$\mathbb{Z}$
-lattice determined by
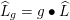 $\widehat{L}_{g}=g\bullet \widehat{L}$
, and
$\widehat{L}_{g}=g\bullet \widehat{L}$
, and
 $\unicode[STIX]{x1D707}_{g}=g\bullet \unicode[STIX]{x1D707}\in L_{g}^{\vee }/L_{g}.$
Comparing with (2.3), the natural finite and unramified morphism
$\unicode[STIX]{x1D707}_{g}=g\bullet \unicode[STIX]{x1D707}\in L_{g}^{\vee }/L_{g}.$
Comparing with (2.3), the natural finite and unramified morphism
 $$\begin{eqnarray}Z(m,\unicode[STIX]{x1D707})(\mathbb{C})\rightarrow M(\mathbb{C})\end{eqnarray}$$
$$\begin{eqnarray}Z(m,\unicode[STIX]{x1D707})(\mathbb{C})\rightarrow M(\mathbb{C})\end{eqnarray}$$
allows us to view (2.4) as an effective Cartier divisor on
![]() $M(\mathbb{C})$
. We will see below that (2.4) admits a moduli interpretation in terms of the Kuga–Satake abelian scheme.
$M(\mathbb{C})$
. We will see below that (2.4) admits a moduli interpretation in terms of the Kuga–Satake abelian scheme.
2.3 Canonical models over
 $\mathbb{Q}$
$\mathbb{Q}$
The reflex field of the Shimura datum
![]() $(G,{\mathcal{D}})$
is
$(G,{\mathcal{D}})$
is
![]() $\mathbb{Q}$
, and hence
$\mathbb{Q}$
, and hence
![]() $M(\mathbb{C})$
is the complex fiber of an algebraic stack
$M(\mathbb{C})$
is the complex fiber of an algebraic stack
![]() $M$
over
$M$
over
![]() $\mathbb{Q}$
. By [Reference Madapusi PeraMad16, § 3] the Kuga–Satake abelian scheme, along with all its additional structures, has a canonical descent
$\mathbb{Q}$
. By [Reference Madapusi PeraMad16, § 3] the Kuga–Satake abelian scheme, along with all its additional structures, has a canonical descent
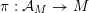 $\unicode[STIX]{x1D70B}:{\mathcal{A}}_{M}\rightarrow M$
.
$\unicode[STIX]{x1D70B}:{\mathcal{A}}_{M}\rightarrow M$
.
We denote byFootnote 1
 $$\begin{eqnarray}\boldsymbol{H}_{\text{dR},M}=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\text{Zar},\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}_{M}/M}^{\bullet },{\mathcal{O}}_{M})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{H}_{\text{dR},M}=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\text{Zar},\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}_{M}/M}^{\bullet },{\mathcal{O}}_{M})\end{eqnarray}$$
the first de Rham homology of
![]() ${\mathcal{A}}_{M}$
relative to
${\mathcal{A}}_{M}$
relative to
![]() $M$
: that is, the dual of the first relative hypercohomology of the de Rham complex. It is a locally free
$M$
: that is, the dual of the first relative hypercohomology of the de Rham complex. It is a locally free
![]() ${\mathcal{O}}_{M}$
-module of rank
${\mathcal{O}}_{M}$
-module of rank
![]() $2^{n+2}$
, equipped with its Hodge filtration
$2^{n+2}$
, equipped with its Hodge filtration
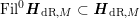 $\text{Fil}^{0}\boldsymbol{H}_{\text{dR},M}\subset \boldsymbol{H}_{\text{dR},M}$
and Gauss–Manin connection. It also has a
$\text{Fil}^{0}\boldsymbol{H}_{\text{dR},M}\subset \boldsymbol{H}_{\text{dR},M}$
and Gauss–Manin connection. It also has a
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading
$\mathbb{Z}/2\mathbb{Z}$
-grading
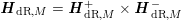 $\boldsymbol{H}_{\text{dR},M}=\boldsymbol{H}_{\text{dR},M}^{+}\times \boldsymbol{H}_{\text{dR},M}^{-}$
arising from the grading
$\boldsymbol{H}_{\text{dR},M}=\boldsymbol{H}_{\text{dR},M}^{+}\times \boldsymbol{H}_{\text{dR},M}^{-}$
arising from the grading
 ${\mathcal{A}}_{M}={\mathcal{A}}_{M}^{+}\times {\mathcal{A}}_{M}^{-}$
on the Kuga–Satake abelian scheme, and similarly a right action of
${\mathcal{A}}_{M}={\mathcal{A}}_{M}^{+}\times {\mathcal{A}}_{M}^{-}$
on the Kuga–Satake abelian scheme, and similarly a right action of
![]() $C(L)$
induced from that on
$C(L)$
induced from that on
![]() ${\mathcal{A}}_{M}$
. Over
${\mathcal{A}}_{M}$
. Over
![]() $M(\mathbb{C})$
, it is canonically identified with
$M(\mathbb{C})$
, it is canonically identified with
 $\boldsymbol{H}_{\text{dR},M(\mathbb{C})}$
with its filtration and integrable connection.
$\boldsymbol{H}_{\text{dR},M(\mathbb{C})}$
with its filtration and integrable connection.
From [Reference Madapusi PeraMad16, (3.12)], we find that there is a canonical descent
![]() $\boldsymbol{V}_{\text{dR},M}$
of
$\boldsymbol{V}_{\text{dR},M}$
of
 $\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
, along with its filtration and integrable connection, so that we have an embedding
$\boldsymbol{V}_{\text{dR},M(\mathbb{C})}$
, along with its filtration and integrable connection, so that we have an embedding
 $$\begin{eqnarray}\boldsymbol{V}_{\text{dR},M}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},M})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\text{dR},M}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},M})\end{eqnarray}$$
of filtered vector bundles over
![]() $M$
with integrable connection. This embedding is a descent of the one already available over
$M$
with integrable connection. This embedding is a descent of the one already available over
![]() $M(\mathbb{C})$
. There is a canonical quadratic form
$M(\mathbb{C})$
. There is a canonical quadratic form
 $\boldsymbol{Q}:\boldsymbol{V}_{\text{dR},M}\rightarrow {\mathcal{O}}_{M}$
given on sections by
$\boldsymbol{Q}:\boldsymbol{V}_{\text{dR},M}\rightarrow {\mathcal{O}}_{M}$
given on sections by
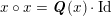 $x\circ x=\boldsymbol{Q}(x)\cdot \text{Id}$
, where the composition takes place in
$x\circ x=\boldsymbol{Q}(x)\cdot \text{Id}$
, where the composition takes place in
 $\text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},M})$
.
$\text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},M})$
.
In the same way we define
 $$\begin{eqnarray}\boldsymbol{H}_{\ell ,\acute{\text{e}}\text{t}}=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\acute{\text{e}}\text{t},\ast }\text{}\underline{\mathbb{Z}}_{\ell },\text{}\underline{\mathbb{Z}}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{H}_{\ell ,\acute{\text{e}}\text{t}}=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\acute{\text{e}}\text{t},\ast }\text{}\underline{\mathbb{Z}}_{\ell },\text{}\underline{\mathbb{Z}}_{\ell })\end{eqnarray}$$
to be the first
![]() $\ell$
-adic étale homology of
$\ell$
-adic étale homology of
![]() ${\mathcal{A}}_{M}$
relative to
${\mathcal{A}}_{M}$
relative to
![]() $M$
. Over
$M$
. Over
![]() $M(\mathbb{C})$
, it is canonically identified with
$M(\mathbb{C})$
, it is canonically identified with
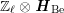 $\mathbb{Z}_{\ell }\otimes \boldsymbol{H}_{\text{Be}}$
. The local system
$\mathbb{Z}_{\ell }\otimes \boldsymbol{H}_{\text{Be}}$
. The local system
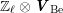 $\mathbb{Z}_{\ell }\otimes \boldsymbol{V}_{\text{Be}}$
descends to an
$\mathbb{Z}_{\ell }\otimes \boldsymbol{V}_{\text{Be}}$
descends to an
![]() $\ell$
-adic sheaf
$\ell$
-adic sheaf
![]() $\boldsymbol{V}_{\ell ,\acute{\text{e}}\text{t}}$
over
$\boldsymbol{V}_{\ell ,\acute{\text{e}}\text{t}}$
over
![]() $M$
, and there is a canonical embedding as a local direct summand
$M$
, and there is a canonical embedding as a local direct summand
 $$\begin{eqnarray}\boldsymbol{V}_{\ell ,\acute{\text{e}}\text{t}}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\ell ,\acute{\text{e}}\text{t}}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\ell ,\acute{\text{e}}\text{t}}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\ell ,\acute{\text{e}}\text{t}}).\end{eqnarray}$$
Again, composition on the right-hand side induces a quadratic form on
![]() $\boldsymbol{V}_{\ell ,\acute{\text{e}}\text{t}}$
with values in the constant sheaf
$\boldsymbol{V}_{\ell ,\acute{\text{e}}\text{t}}$
with values in the constant sheaf
![]() $\text{}\underline{\mathbb{Z}}_{\ell }$
.
$\text{}\underline{\mathbb{Z}}_{\ell }$
.
2.4 Integral models
The stack
![]() $M$
admits a regular integral model
$M$
admits a regular integral model
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
![]() $\mathbb{Z}$
, which we construct in this section following [Reference Madapusi PeraMad16, § 7]. In [Reference Madapusi PeraMad16] such a model is constructed over
$\mathbb{Z}$
, which we construct in this section following [Reference Madapusi PeraMad16, § 7]. In [Reference Madapusi PeraMad16] such a model is constructed over
![]() $\mathbb{Z}[1/2]$
as one uses the main result of [Reference KisinKis10], where
$\mathbb{Z}[1/2]$
as one uses the main result of [Reference KisinKis10], where
![]() $2$
is assumed to be invertible. As we shall see, most of the results extend also to the case of the prime
$2$
is assumed to be invertible. As we shall see, most of the results extend also to the case of the prime
![]() $p=2$
replacing [Reference KisinKis10] with [Reference Kim and Madapusi PeraKM16]. The construction is involved, and the final definition of
$p=2$
replacing [Reference KisinKis10] with [Reference Kim and Madapusi PeraKM16]. The construction is involved, and the final definition of
![]() ${\mathcal{M}}$
is given in Proposition 2.4.6.
${\mathcal{M}}$
is given in Proposition 2.4.6.
It follows from [Reference Madapusi PeraMad16, (6.8)] that we may fix an isometric embedding
![]() $L\subset L^{\diamond }$
, where
$L\subset L^{\diamond }$
, where
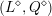 $(L^{\diamond },Q^{\diamond })$
is a maximal quadratic space over
$(L^{\diamond },Q^{\diamond })$
is a maximal quadratic space over
![]() $\mathbb{Z}$
, self-dual at
$\mathbb{Z}$
, self-dual at
![]() $p$
and of signature
$p$
and of signature
![]() $(n^{\diamond },2)$
. Set
$(n^{\diamond },2)$
. Set
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}=L^{\bot }=\{x\in L^{\diamond }:x\bot L\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}=L^{\bot }=\{x\in L^{\diamond }:x\bot L\}.\end{eqnarray}$$
The construction of the integral model over
![]() $\mathbb{Z}_{(p)}$
of
$\mathbb{Z}_{(p)}$
of
![]() $M$
will proceed by first constructing a smooth integral model for the larger Shimura variety
$M$
will proceed by first constructing a smooth integral model for the larger Shimura variety
![]() $M^{\diamond }$
associated with
$M^{\diamond }$
associated with
![]() $L^{\diamond }$
. There is a finite and unramified morphism
$L^{\diamond }$
. There is a finite and unramified morphism
 $M\rightarrow M^{\diamond }$
over
$M\rightarrow M^{\diamond }$
over
![]() $\mathbb{Q}$
which we will extend to integral models, and the integral model for
$\mathbb{Q}$
which we will extend to integral models, and the integral model for
![]() $M$
will inherit extra structure (for example, the vector bundles of Proposition 2.4.5 below) realized by pulling back structures from the larger integral model.
$M$
will inherit extra structure (for example, the vector bundles of Proposition 2.4.5 below) realized by pulling back structures from the larger integral model.
Over
![]() $M^{\diamond }$
we have the vector bundle
$M^{\diamond }$
we have the vector bundle
![]() $\boldsymbol{V}_{\text{dR},M^{\diamond }}^{\diamond }$
associated with
$\boldsymbol{V}_{\text{dR},M^{\diamond }}^{\diamond }$
associated with
![]() $L^{\diamond }$
. Let
$L^{\diamond }$
. Let
![]() $\boldsymbol{V}_{\text{dR},M}^{\diamond }$
be its restriction to
$\boldsymbol{V}_{\text{dR},M}^{\diamond }$
be its restriction to
![]() $M$
. By construction, we have an isometric embedding
$M$
. By construction, we have an isometric embedding
 $$\begin{eqnarray}\boldsymbol{V}_{\text{dR},M}{\hookrightarrow}\boldsymbol{V}_{\text{dR},M}^{\diamond }\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\text{dR},M}{\hookrightarrow}\boldsymbol{V}_{\text{dR},M}^{\diamond }\end{eqnarray}$$
of filtered vector bundles with integrable connections over
![]() $M$
. Setting
$M$
. Setting
 $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},M}=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}{\mathcal{O}}_{M}$
, we obtain an injection of vector bundles
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},M}=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}{\mathcal{O}}_{M}$
, we obtain an injection of vector bundles
 $$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},M}{\hookrightarrow}\boldsymbol{V}_{\text{dR},M}^{\diamond } & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},M}{\hookrightarrow}\boldsymbol{V}_{\text{dR},M}^{\diamond } & & \displaystyle\end{eqnarray}$$
identifying
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},M}$
with a local direct summand of
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},M}$
with a local direct summand of
![]() $\boldsymbol{V}_{\text{dR},M}^{\diamond }$
.
$\boldsymbol{V}_{\text{dR},M}^{\diamond }$
.
The Shimura variety
![]() $M^{\diamond }$
admits a smooth canonical model
$M^{\diamond }$
admits a smooth canonical model
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
over
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
over
![]() $\mathbb{Z}_{(p)}$
. This is the main theorem of [Reference KisinKis10] for
$\mathbb{Z}_{(p)}$
. This is the main theorem of [Reference KisinKis10] for
![]() $p\neq 2$
and it is proven in general in [Reference Kim and Madapusi PeraKM16]. We now recall the construction. Choose
$p\neq 2$
and it is proven in general in [Reference Kim and Madapusi PeraKM16]. We now recall the construction. Choose
 $\unicode[STIX]{x1D6FF}\in C^{+}(L^{\diamond })\cap C(V^{\diamond })^{\times }$
as in § 2.2, so that the associated symplectic pairing
$\unicode[STIX]{x1D6FF}\in C^{+}(L^{\diamond })\cap C(V^{\diamond })^{\times }$
as in § 2.2, so that the associated symplectic pairing
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}$
on
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}$
on
![]() $C(L^{\diamond })$
produces a polarization on the Kuga–Satake abelian scheme
$C(L^{\diamond })$
produces a polarization on the Kuga–Satake abelian scheme
 $$\begin{eqnarray}A_{M^{\diamond }(\mathbb{C})}^{\diamond }\rightarrow M^{\diamond }(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}A_{M^{\diamond }(\mathbb{C})}^{\diamond }\rightarrow M^{\diamond }(\mathbb{C}).\end{eqnarray}$$
This polarization has degree
![]() $d^{\diamond }$
, where
$d^{\diamond }$
, where
![]() $d^{\diamond }$
is the discriminant of the restriction of
$d^{\diamond }$
is the discriminant of the restriction of
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}$
to
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}$
to
![]() $C(L^{\diamond })$
. The polarized Kuga–Satake abelian scheme defines a morphism of complex algebraic stacks
$C(L^{\diamond })$
. The polarized Kuga–Satake abelian scheme defines a morphism of complex algebraic stacks
 $$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF}}:M_{\mathbb{C}}^{\diamond }\rightarrow {\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{C}}^{\text{Siegel}},\end{eqnarray}$$
$$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF}}:M_{\mathbb{C}}^{\diamond }\rightarrow {\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{C}}^{\text{Siegel}},\end{eqnarray}$$
where
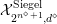 ${\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond }}^{\text{Siegel}}$
is the Siegel moduli stack over
${\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond }}^{\text{Siegel}}$
is the Siegel moduli stack over
![]() $\mathbb{Z}$
parameterizing polarized abelian schemes of dimension
$\mathbb{Z}$
parameterizing polarized abelian schemes of dimension
![]() $2^{n^{\diamond }+1}$
of degree
$2^{n^{\diamond }+1}$
of degree
![]() $d^{\diamond }$
. It can be checked using complex uniformization that this map is finite and unramified. The theory of canonical models of Shimura varieties implies that
$d^{\diamond }$
. It can be checked using complex uniformization that this map is finite and unramified. The theory of canonical models of Shimura varieties implies that
![]() $i_{\unicode[STIX]{x1D6FF}}$
descends to a finite and unramified map of
$i_{\unicode[STIX]{x1D6FF}}$
descends to a finite and unramified map of
![]() $\mathbb{Q}$
-stacks
$\mathbb{Q}$
-stacks
 $$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF}}:M^{\diamond }\rightarrow {\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{Q}}^{\text{Siegel}}.\end{eqnarray}$$
$$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF}}:M^{\diamond }\rightarrow {\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{Q}}^{\text{Siegel}}.\end{eqnarray}$$
The integral model
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is defined as the normalization of
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is defined as the normalization of
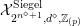 ${\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{Z}_{(p)}}^{\text{Siegel}}$
in
${\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{Z}_{(p)}}^{\text{Siegel}}$
in
![]() $M^{\diamond }$
, in the following sense.
$M^{\diamond }$
, in the following sense.
Definition 2.4.1. Given an algebraic stack
![]() ${\mathcal{X}}$
over
${\mathcal{X}}$
over
![]() $\mathbb{Z}_{(p)}$
, and a normal algebraic stack
$\mathbb{Z}_{(p)}$
, and a normal algebraic stack
![]() $Y$
over
$Y$
over
![]() $\mathbb{Q}$
equipped with a finite map
$\mathbb{Q}$
equipped with a finite map
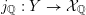 $j_{\mathbb{Q}}:Y\rightarrow {\mathcal{X}}_{\mathbb{Q}}$
, the normalization of
$j_{\mathbb{Q}}:Y\rightarrow {\mathcal{X}}_{\mathbb{Q}}$
, the normalization of
![]() ${\mathcal{X}}$
in
${\mathcal{X}}$
in
![]() $Y$
is the finite
$Y$
is the finite
![]() ${\mathcal{X}}$
-stack
${\mathcal{X}}$
-stack
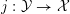 $j:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
, characterized by the property that
$j:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
, characterized by the property that
![]() $j_{\ast }{\mathcal{O}}_{{\mathcal{Y}}}$
is the integral closure of
$j_{\ast }{\mathcal{O}}_{{\mathcal{Y}}}$
is the integral closure of
![]() ${\mathcal{O}}_{{\mathcal{X}}}$
in
${\mathcal{O}}_{{\mathcal{X}}}$
in
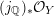 $(j_{\mathbb{Q}})_{\ast }{\mathcal{O}}_{Y}$
.
$(j_{\mathbb{Q}})_{\ast }{\mathcal{O}}_{Y}$
.
The normalization is uniquely determined by the following universal property: given a finite morphism
 ${\mathcal{Z}}\rightarrow {\mathcal{X}}$
with
${\mathcal{Z}}\rightarrow {\mathcal{X}}$
with
![]() ${\mathcal{Z}}$
a normal algebraic stack, flat over
${\mathcal{Z}}$
a normal algebraic stack, flat over
![]() $\mathbb{Z}_{(p)}$
, any map of
$\mathbb{Z}_{(p)}$
, any map of
![]() ${\mathcal{X}}_{\mathbb{Q}}$
-stacks
${\mathcal{X}}_{\mathbb{Q}}$
-stacks
 ${\mathcal{Z}}_{\mathbb{Q}}\rightarrow Y$
extends uniquely to a map of
${\mathcal{Z}}_{\mathbb{Q}}\rightarrow Y$
extends uniquely to a map of
![]() ${\mathcal{X}}$
-stacks
${\mathcal{X}}$
-stacks
![]() ${\mathcal{Z}}\rightarrow {\mathcal{Y}}$
.
${\mathcal{Z}}\rightarrow {\mathcal{Y}}$
.
Proposition 2.4.2. The stack
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is smooth over
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is smooth over
![]() $\mathbb{Z}_{(p)}$
. It does not depend on the choice of
$\mathbb{Z}_{(p)}$
. It does not depend on the choice of
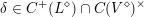 $\unicode[STIX]{x1D6FF}\in C^{+}(L^{\diamond })\cap C(V^{\diamond })^{\times }$
.
$\unicode[STIX]{x1D6FF}\in C^{+}(L^{\diamond })\cap C(V^{\diamond })^{\times }$
.
Proof. This essentially follows from [Reference KisinKis10, (2.3.8)] if
![]() $p\neq 2$
and from [Reference Kim and Madapusi PeraKM16, Theorem 3.10] in general. We provide some of the details.
$p\neq 2$
and from [Reference Kim and Madapusi PeraKM16, Theorem 3.10] in general. We provide some of the details.
Abbreviate
 $$\begin{eqnarray}{\mathcal{X}}^{\text{Siegel}}={\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{Z}_{(p)}}^{\text{Siegel}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}^{\text{Siegel}}={\mathcal{X}}_{2^{n^{\diamond }+1},d^{\diamond },\mathbb{Z}_{(p)}}^{\text{Siegel}},\end{eqnarray}$$
and let
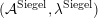 $({\mathcal{A}}^{\text{Siegel}},\unicode[STIX]{x1D706}^{\text{Siegel}})$
be the universal polarized abelian scheme over
$({\mathcal{A}}^{\text{Siegel}},\unicode[STIX]{x1D706}^{\text{Siegel}})$
be the universal polarized abelian scheme over
![]() ${\mathcal{X}}^{\text{Siegel}}$
. For any
${\mathcal{X}}^{\text{Siegel}}$
. For any
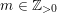 $m\in \mathbb{Z}_{{>}0}$
coprime to
$m\in \mathbb{Z}_{{>}0}$
coprime to
![]() $pd^{\diamond }$
, let
$pd^{\diamond }$
, let
 ${\mathcal{X}}_{m}^{\text{Siegel}}\rightarrow {\mathcal{X}}^{\text{Siegel}}$
be the finite étale cover parameterizing full level-
${\mathcal{X}}_{m}^{\text{Siegel}}\rightarrow {\mathcal{X}}^{\text{Siegel}}$
be the finite étale cover parameterizing full level-
![]() $m$
structures on
$m$
structures on
![]() ${\mathcal{A}}^{\text{Siegel}}$
: that is, parametrizing isomorphisms of group schemes
${\mathcal{A}}^{\text{Siegel}}$
: that is, parametrizing isomorphisms of group schemes
 $$\begin{eqnarray}C(L^{\diamond })\otimes \text{}\underline{\mathbb{Z}/m\mathbb{Z}}\xrightarrow[{}]{\simeq }{\mathcal{A}}^{\text{Siegel}}[m]\end{eqnarray}$$
$$\begin{eqnarray}C(L^{\diamond })\otimes \text{}\underline{\mathbb{Z}/m\mathbb{Z}}\xrightarrow[{}]{\simeq }{\mathcal{A}}^{\text{Siegel}}[m]\end{eqnarray}$$
that carry the symplectic form
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}\otimes 1$
on the left-hand side to a
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}}\otimes 1$
on the left-hand side to a
 $(\mathbb{Z}/m\mathbb{Z})^{\times }$
-multiple of the Weil pairing on
$(\mathbb{Z}/m\mathbb{Z})^{\times }$
-multiple of the Weil pairing on
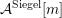 ${\mathcal{A}}^{\text{Siegel}}[m]$
induced by
${\mathcal{A}}^{\text{Siegel}}[m]$
induced by
![]() $\unicode[STIX]{x1D706}^{\text{Siegel}}$
. For
$\unicode[STIX]{x1D706}^{\text{Siegel}}$
. For
![]() $m\geqslant 3$
the stack
$m\geqslant 3$
the stack
![]() ${\mathcal{X}}_{m}^{\text{Siegel}}$
is a scheme over
${\mathcal{X}}_{m}^{\text{Siegel}}$
is a scheme over
![]() $\mathbb{Z}_{(p)}$
.
$\mathbb{Z}_{(p)}$
.
Write
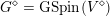 $G^{\diamond }=\text{GSpin}(V^{\diamond })$
, and set
$G^{\diamond }=\text{GSpin}(V^{\diamond })$
, and set
 $$\begin{eqnarray}K^{\diamond }=G^{\diamond }(\mathbb{A}_{f})\cap C(L^{\diamond })_{\widehat{\mathbb{ Z}}}^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}K^{\diamond }=G^{\diamond }(\mathbb{A}_{f})\cap C(L^{\diamond })_{\widehat{\mathbb{ Z}}}^{\times }.\end{eqnarray}$$
Let
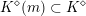 $K^{\diamond }(m)\subset K^{\diamond }$
be the largest subgroup acting trivially on
$K^{\diamond }(m)\subset K^{\diamond }$
be the largest subgroup acting trivially on
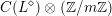 $C(L^{\diamond })\otimes (\mathbb{Z}/m\mathbb{Z})$
. We obtain a finite étale cover
$C(L^{\diamond })\otimes (\mathbb{Z}/m\mathbb{Z})$
. We obtain a finite étale cover
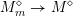 $M_{m}^{\diamond }\rightarrow M^{\diamond }$
of Shimura varieties with Galois group
$M_{m}^{\diamond }\rightarrow M^{\diamond }$
of Shimura varieties with Galois group
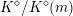 $K^{\diamond }/K^{\diamond }(m)$
, where
$K^{\diamond }/K^{\diamond }(m)$
, where
 $$\begin{eqnarray}M_{m}^{\diamond }(\mathbb{C})=G^{\diamond }(\mathbb{Q})\backslash {\mathcal{D}}^{\diamond }\times G^{\diamond }(\mathbb{A}_{f})/K^{\diamond }(m)\end{eqnarray}$$
$$\begin{eqnarray}M_{m}^{\diamond }(\mathbb{C})=G^{\diamond }(\mathbb{Q})\backslash {\mathcal{D}}^{\diamond }\times G^{\diamond }(\mathbb{A}_{f})/K^{\diamond }(m)\end{eqnarray}$$
and
![]() ${\mathcal{D}}^{\diamond }$
is the space of oriented negative definite planes in
${\mathcal{D}}^{\diamond }$
is the space of oriented negative definite planes in
![]() $V_{\mathbb{R}}^{\diamond }$
.
$V_{\mathbb{R}}^{\diamond }$
.
The map
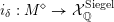 $i_{\unicode[STIX]{x1D6FF}}:M^{\diamond }\rightarrow {\mathcal{X}}_{\mathbb{Q}}^{\text{Siegel}}$
lifts to a map
$i_{\unicode[STIX]{x1D6FF}}:M^{\diamond }\rightarrow {\mathcal{X}}_{\mathbb{Q}}^{\text{Siegel}}$
lifts to a map
 $$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF},m}:M_{m}^{\diamond }\rightarrow {\mathcal{X}}_{m,\mathbb{Q}}^{\text{Siegel}}.\end{eqnarray}$$
$$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF},m}:M_{m}^{\diamond }\rightarrow {\mathcal{X}}_{m,\mathbb{Q}}^{\text{Siegel}}.\end{eqnarray}$$
From [Reference KisinKis10, (2.1.2)] we find that
![]() $i_{\unicode[STIX]{x1D6FF},m}$
is a closed immersion of
$i_{\unicode[STIX]{x1D6FF},m}$
is a closed immersion of
![]() $\mathbb{Q}$
-schemes for sufficiently large
$\mathbb{Q}$
-schemes for sufficiently large
![]() $m$
. Fix such an
$m$
. Fix such an
![]() $m$
, and let
$m$
, and let
 ${\mathcal{M}}_{m,\mathbb{Z}_{(p)}}^{\diamond }$
be the normalization of
${\mathcal{M}}_{m,\mathbb{Z}_{(p)}}^{\diamond }$
be the normalization of
![]() ${\mathcal{X}}_{m}^{\text{Siegel}}$
in
${\mathcal{X}}_{m}^{\text{Siegel}}$
in
![]() $M_{m}^{\diamond }$
. Since
$M_{m}^{\diamond }$
. Since
![]() $i_{\unicode[STIX]{x1D6FF},m}$
is a closed immersion, this is simply the normalization of the Zariski closure of
$i_{\unicode[STIX]{x1D6FF},m}$
is a closed immersion, this is simply the normalization of the Zariski closure of
![]() $M_{m}^{\diamond }$
in
$M_{m}^{\diamond }$
in
![]() ${\mathcal{X}}_{m}^{\text{Siegel}}$
. It now follows from [Reference KisinKis10, (2.3.8)] and [Reference Kim and Madapusi PeraKM16, Theorem 3.10] that
${\mathcal{X}}_{m}^{\text{Siegel}}$
. It now follows from [Reference KisinKis10, (2.3.8)] and [Reference Kim and Madapusi PeraKM16, Theorem 3.10] that
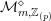 ${\mathcal{M}}_{m,\mathbb{Z}_{(p)}}^{\diamond }$
is smooth over
${\mathcal{M}}_{m,\mathbb{Z}_{(p)}}^{\diamond }$
is smooth over
![]() $\mathbb{Z}_{(p)}$
, and, moreover, that it is, up to unique isomorphism, independent of the choice of
$\mathbb{Z}_{(p)}$
, and, moreover, that it is, up to unique isomorphism, independent of the choice of
![]() $\unicode[STIX]{x1D6FF}$
.
$\unicode[STIX]{x1D6FF}$
.
The stack
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is the étale quotient of
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is the étale quotient of
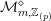 ${\mathcal{M}}_{m,\mathbb{Z}_{(p)}}^{\diamond }$
by the action of
${\mathcal{M}}_{m,\mathbb{Z}_{(p)}}^{\diamond }$
by the action of
 $K^{\diamond }/K^{\diamond }(m)$
, and so the proposition follows.◻
$K^{\diamond }/K^{\diamond }(m)$
, and so the proposition follows.◻
By the construction of the integral model
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
, the Kuga–Satake abelian scheme
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
, the Kuga–Satake abelian scheme
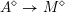 $A^{\diamond }\rightarrow M^{\diamond }$
extends to
$A^{\diamond }\rightarrow M^{\diamond }$
extends to
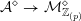 ${\mathcal{A}}^{\diamond }\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
. A non-trivial consequence of the construction is that the vector bundle
${\mathcal{A}}^{\diamond }\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
. A non-trivial consequence of the construction is that the vector bundle
![]() $\boldsymbol{V}_{\text{dR},M^{\diamond }}^{\diamond }$
, with its integrable connection and filtration, extends to a filtered vector bundle with integrable connection
$\boldsymbol{V}_{\text{dR},M^{\diamond }}^{\diamond }$
, with its integrable connection and filtration, extends to a filtered vector bundle with integrable connection
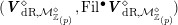 $(\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond },\text{Fil}^{\bullet }\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }}^{\diamond }\!)$
over
$(\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond },\text{Fil}^{\bullet }\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }}^{\diamond }\!)$
over
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
(see [Reference Madapusi PeraMad16, § 4] for details).
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
(see [Reference Madapusi PeraMad16, § 4] for details).
Let
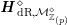 $\boldsymbol{H}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }$
be the first de Rham homology of
$\boldsymbol{H}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }$
be the first de Rham homology of
![]() ${\mathcal{A}}^{\diamond }$
, so that we have an embedding of filtered vector bundles
${\mathcal{A}}^{\diamond }$
, so that we have an embedding of filtered vector bundles
 $$\begin{eqnarray}\displaystyle \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }}^{\diamond }\!) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }}^{\diamond }\!) & & \displaystyle\end{eqnarray}$$
extending that in the generic fiber and exhibiting its source as a local direct summand of the target. Composition in the endomorphism ring gives a non-degenerate quadratic form on
 $$\begin{eqnarray}\boldsymbol{Q}^{\diamond }:\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }}^{\diamond }\rightarrow {\mathcal{O}}_{{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Q}^{\diamond }:\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }}^{\diamond }\rightarrow {\mathcal{O}}_{{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}\end{eqnarray}$$
again extending that on its generic fiber.
Similarly, let
 $$\begin{eqnarray}\boldsymbol{H}_{\text{crys}}^{\diamond }=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\text{crys},\ast }{\mathcal{O}}_{{\mathcal{A}}_{\mathbb{F}_{p}}^{\diamond }/\mathbb{Z}_{p}}^{\text{crys}},{\mathcal{O}}_{{\mathcal{M}}_{\mathbb{ F}_{p}}^{\diamond }/\mathbb{Z}_{p}}^{\text{crys}})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{H}_{\text{crys}}^{\diamond }=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\text{crys},\ast }{\mathcal{O}}_{{\mathcal{A}}_{\mathbb{F}_{p}}^{\diamond }/\mathbb{Z}_{p}}^{\text{crys}},{\mathcal{O}}_{{\mathcal{M}}_{\mathbb{ F}_{p}}^{\diamond }/\mathbb{Z}_{p}}^{\text{crys}})\end{eqnarray}$$
be the first crystalline homology of
![]() ${\mathcal{A}}_{\mathbb{F}_{p}}^{\diamond }$
relative to
${\mathcal{A}}_{\mathbb{F}_{p}}^{\diamond }$
relative to
![]() ${\mathcal{M}}_{\mathbb{F}_{p}}^{\diamond }$
. As
${\mathcal{M}}_{\mathbb{F}_{p}}^{\diamond }$
. As
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is smooth over
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
is smooth over
![]() $\mathbb{Z}_{(p)}$
, the vector bundle with integrable connection (2.6) determines a crystal
$\mathbb{Z}_{(p)}$
, the vector bundle with integrable connection (2.6) determines a crystal
![]() $\boldsymbol{V}_{\text{crys}}^{\diamond }$
over
$\boldsymbol{V}_{\text{crys}}^{\diamond }$
over
![]() ${\mathcal{M}}_{\mathbb{F}_{p}}^{\diamond }$
equipped with an embedding
${\mathcal{M}}_{\mathbb{F}_{p}}^{\diamond }$
equipped with an embedding
 $$\begin{eqnarray}\boldsymbol{V}_{\text{crys}}^{\diamond }\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{crys}}^{\diamond })\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\text{crys}}^{\diamond }\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{crys}}^{\diamond })\end{eqnarray}$$
as a local direct summand; see [Reference Madapusi PeraMad16, (4.14)] for details.
We are now ready to give the construction of the desired integral model
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
for
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
for
![]() $M$
. The isometric embedding
$M$
. The isometric embedding
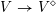 $V\rightarrow V^{\diamond }$
induces a homomorphism of Clifford algebras, which restricts to a closed immersion
$V\rightarrow V^{\diamond }$
induces a homomorphism of Clifford algebras, which restricts to a closed immersion
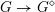 $G\rightarrow G^{\diamond }$
. This induces a morphism of Shimura varieties
$G\rightarrow G^{\diamond }$
. This induces a morphism of Shimura varieties
 $M\rightarrow M^{\diamond }$
. The direct summands
$M\rightarrow M^{\diamond }$
. The direct summands
 $\unicode[STIX]{x1D6EC}_{\mathbb{Q}}\subset V^{\diamond }$
and
$\unicode[STIX]{x1D6EC}_{\mathbb{Q}}\subset V^{\diamond }$
and
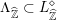 $\unicode[STIX]{x1D6EC}_{\widehat{\mathbb{Z}}}\subset L_{\widehat{\mathbb{Z}}}^{\diamond }$
are pointwise stabilized by
$\unicode[STIX]{x1D6EC}_{\widehat{\mathbb{Z}}}\subset L_{\widehat{\mathbb{Z}}}^{\diamond }$
are pointwise stabilized by
![]() $G(\mathbb{Q})$
and
$G(\mathbb{Q})$
and
![]() $K$
, respectively. From this, arguing as in [Reference Madapusi PeraMad16, (6.5)], we find that there is a canonical embedding
$K$
, respectively. From this, arguing as in [Reference Madapusi PeraMad16, (6.5)], we find that there is a canonical embedding
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}\subset \text{End}_{C(L^{\diamond })}({\mathcal{A}}^{\diamond }|_{M}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}\subset \text{End}_{C(L^{\diamond })}({\mathcal{A}}^{\diamond }|_{M}) & & \displaystyle\end{eqnarray}$$
whose de Rham realization is (2.5). Let
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
be the normalization of
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
be the normalization of
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
in
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
in
![]() $M$
. Then, by [Reference Faltings and ChaiFC90, Proposition 2.7], the embedding (2.7) extends to
$M$
. Then, by [Reference Faltings and ChaiFC90, Proposition 2.7], the embedding (2.7) extends to
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}\subset \text{End}_{C(L^{\diamond })}({\mathcal{A}}^{\diamond }|_{\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}}\!). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}\subset \text{End}_{C(L^{\diamond })}({\mathcal{A}}^{\diamond }|_{\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}}\!). & & \displaystyle\end{eqnarray}$$
Since
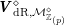 $\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }$
is a direct summand of
$\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }$
is a direct summand of
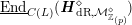 $\text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }\!)$
, the de Rham realization of (2.8) provides us with an extension
$\text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}^{\diamond }\!)$
, the de Rham realization of (2.8) provides us with an extension
 $$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}\rightarrow \boldsymbol{V}_{\text{dR},\check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}}^{\diamond } & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}\rightarrow \boldsymbol{V}_{\text{dR},\check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}}^{\diamond } & & \displaystyle\end{eqnarray}$$
of (2.5), where
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}{\mathcal{O}}_{\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}}\!.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}{\mathcal{O}}_{\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}}\!.\end{eqnarray}$$
Let
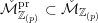 $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}\subset \check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}$
be the open locus where the cokernel of (2.9) is a vector bundle of rank
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}\subset \check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}$
be the open locus where the cokernel of (2.9) is a vector bundle of rank
![]() $n$
(see [Reference Madapusi PeraMad16, 6.16(i)]). This is also the locus over which the image of (2.9) is a local direct summand. In particular, it contains the generic fiber
$n$
(see [Reference Madapusi PeraMad16, 6.16(i)]). This is also the locus over which the image of (2.9) is a local direct summand. In particular, it contains the generic fiber
![]() $M$
of
$M$
of
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
.
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
.
Let
 $\text{M}^{\text{loc}}(L)$
be the projective scheme over
$\text{M}^{\text{loc}}(L)$
be the projective scheme over
![]() $\mathbb{Z}$
parameterizing isotropic lines
$\mathbb{Z}$
parameterizing isotropic lines
![]() $L^{1}\subset L$
. The following can be deduced from [Reference Madapusi PeraMad16, (6.16), (6.20), (2.16)].
$L^{1}\subset L$
. The following can be deduced from [Reference Madapusi PeraMad16, (6.16), (6.20), (2.16)].
Proposition 2.4.3. (i) Around any point of
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
, we can find an étale neighborhood
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
, we can find an étale neighborhood
![]() $T$
such that there exists an isometry
$T$
such that there exists an isometry
 $$\begin{eqnarray}\unicode[STIX]{x1D709}:{\mathcal{O}}_{T}\otimes L^{\diamond }\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR},T}^{\diamond }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}:{\mathcal{O}}_{T}\otimes L^{\diamond }\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR},T}^{\diamond }\end{eqnarray}$$
satisfying
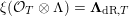 $\unicode[STIX]{x1D709}({\mathcal{O}}_{T}\otimes \unicode[STIX]{x1D6EC})=\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},T}$
, and such that the morphism
$\unicode[STIX]{x1D709}({\mathcal{O}}_{T}\otimes \unicode[STIX]{x1D6EC})=\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR},T}$
, and such that the morphism
 $T\rightarrow \text{M}^{\text{loc}}(L)$
determined by the isotropic line
$T\rightarrow \text{M}^{\text{loc}}(L)$
determined by the isotropic line
 $$\begin{eqnarray}\unicode[STIX]{x1D709}^{-1}(\text{Fil}^{1}\boldsymbol{V}_{\text{dR},T}^{\diamond })\subset {\mathcal{O}}_{T}\otimes L^{\diamond }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{-1}(\text{Fil}^{1}\boldsymbol{V}_{\text{dR},T}^{\diamond })\subset {\mathcal{O}}_{T}\otimes L^{\diamond }\end{eqnarray}$$
is étale.
(ii) If
![]() $L_{(p)}$
is self-dual, or if
$L_{(p)}$
is self-dual, or if
![]() $p>2$
and
$p>2$
and
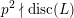 $p^{2}\nmid \text{disc}(L)$
, then
$p^{2}\nmid \text{disc}(L)$
, then
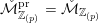 $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}=\check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}\!$
.
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}=\check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}\!$
.
(iii) If
![]() $p>2$
and
$p>2$
and
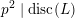 $p^{2}\mid \text{disc}(L)$
, then
$p^{2}\mid \text{disc}(L)$
, then
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
is regular outside of a zero-dimensional closed substack.
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
is regular outside of a zero-dimensional closed substack.
We now define:
-
–
 ${\mathcal{M}}_{\mathbb{Z}_{(p)}}=\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
if
${\mathcal{M}}_{\mathbb{Z}_{(p)}}=\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
if
 $L_{(p)}$
is self-dual, or if
$L_{(p)}$
is self-dual, or if
 $p>2$
and
$p>2$
and
 $p^{2}\nmid \text{disc}(L)$
;
$p^{2}\nmid \text{disc}(L)$
; -
–
 ${\mathcal{M}}_{\mathbb{Z}_{(p)}}=\text{the regular locus of }\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
if
${\mathcal{M}}_{\mathbb{Z}_{(p)}}=\text{the regular locus of }\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
if
 $p>2$
and
$p>2$
and
 $p^{2}\mid \text{disc}(L)$
;
$p^{2}\mid \text{disc}(L)$
; -
–
 ${\mathcal{M}}_{\mathbb{Z}_{(p)}}=\text{the smooth locus of }\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
if
${\mathcal{M}}_{\mathbb{Z}_{(p)}}=\text{the smooth locus of }\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
if
 $p=2$
.
$p=2$
.
Then
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
is the desired regular integral model for
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
is the desired regular integral model for
![]() $M$
over
$M$
over
![]() $\mathbb{Z}_{(p)}$
.
$\mathbb{Z}_{(p)}$
.
Remark 2.4.4. If
![]() $p=2$
and
$p=2$
and
![]() $L_{(2)}$
is not self-dual, or if
$L_{(2)}$
is not self-dual, or if
![]() $p>2$
and
$p>2$
and
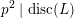 $p^{2}\mid \text{disc}(L)$
, this is certainly not the optimal definition of the regular model
$p^{2}\mid \text{disc}(L)$
, this is certainly not the optimal definition of the regular model
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
. For a discussion and examples of this when
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
. For a discussion and examples of this when
![]() $p$
is odd, see [Reference Madapusi PeraMad16, (6.27), (6.28)].
$p$
is odd, see [Reference Madapusi PeraMad16, (6.27), (6.28)].
Equip
 $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}{\mathcal{O}}_{{\mathcal{M}}_{\mathbb{Z}_{(p)}}}$
with the integrable connection
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}{\mathcal{O}}_{{\mathcal{M}}_{\mathbb{Z}_{(p)}}}$
with the integrable connection
![]() $1\otimes \text{d}$
, and the trivial filtration concentrated in degree
$1\otimes \text{d}$
, and the trivial filtration concentrated in degree
![]() $0$
. By construction, over
$0$
. By construction, over
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
we have a canonical isometric embedding
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
we have a canonical isometric embedding
 $$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}\subset \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond } & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}\subset \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond } & & \displaystyle \nonumber\end{eqnarray}$$
of filtered vector bundles with integrable connections. Therefore, since the quadratic form on
 $\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }$
is self-dual, the orthogonal complement
$\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }$
is self-dual, the orthogonal complement
 $$\begin{eqnarray}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}=\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}^{\bot }\subset \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond }\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}=\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}^{\bot }\subset \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond }\end{eqnarray}$$
is again a vector sub-bundle with integrable connection. Indeed, it is precisely the kernel of the surjection of vector bundles
 $$\begin{eqnarray}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond ,\vee }\rightarrow \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond ,\vee }/\text{ann}(\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond ,\vee }\rightarrow \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond ,\vee }/\text{ann}(\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}).\end{eqnarray}$$
Moreover, the isotropic line
 $\text{Fil}^{1}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }$
is actually contained in
$\text{Fil}^{1}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }$
is actually contained in
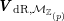 $\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}$
. For convenience, we abbreviate
$\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}$
. For convenience, we abbreviate
 $$\begin{eqnarray}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{1}=\text{Fil}^{1}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond }\!.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{1}=\text{Fil}^{1}\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond }\!.\end{eqnarray}$$
Proposition 2.4.5. The integral models
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
and
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
and
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
are, up to unique isomorphism, independent of the auxiliary choice of
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
are, up to unique isomorphism, independent of the auxiliary choice of
![]() $L^{\diamond }$
. Furthermore, the vector bundle
$L^{\diamond }$
. Furthermore, the vector bundle
 $\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}$
and the isotropic line
$\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}$
and the isotropic line
 $\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{1}\subset \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}$
are also independent of this auxiliary choice.
$\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{1}\subset \boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}$
are also independent of this auxiliary choice.
Proof. Suppose that we have a different embedding
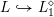 $L{\hookrightarrow}L_{1}^{\diamond }$
with
$L{\hookrightarrow}L_{1}^{\diamond }$
with
![]() $L_{1}^{\diamond }$
maximal, self-dual at
$L_{1}^{\diamond }$
maximal, self-dual at
![]() $p$
, and of signature
$p$
, and of signature
![]() $(n_{1}^{\diamond },2)$
.
$(n_{1}^{\diamond },2)$
.
First, assume that the embedding
 $L{\hookrightarrow}L_{1}^{\diamond }$
factors as
$L{\hookrightarrow}L_{1}^{\diamond }$
factors as
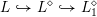 $L{\hookrightarrow}L^{\diamond }{\hookrightarrow}L_{1}^{\diamond }$
. The construction of Kisin in [Reference KisinKis10] and its generalization in [Reference Kim and Madapusi PeraKM16] show that the map of integral models
$L{\hookrightarrow}L^{\diamond }{\hookrightarrow}L_{1}^{\diamond }$
. The construction of Kisin in [Reference KisinKis10] and its generalization in [Reference Kim and Madapusi PeraKM16] show that the map of integral models
 ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }\rightarrow {\mathcal{M}}_{1,\mathbb{Z}_{(p)}}^{\diamond }$
associated with
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }\rightarrow {\mathcal{M}}_{1,\mathbb{Z}_{(p)}}^{\diamond }$
associated with
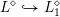 $L^{\diamond }{\hookrightarrow}L_{1}^{\diamond }$
is finite and unramified. Moreover, Proposition 2.4.3 shows that, if
$L^{\diamond }{\hookrightarrow}L_{1}^{\diamond }$
is finite and unramified. Moreover, Proposition 2.4.3 shows that, if
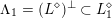 $\unicode[STIX]{x1D6EC}_{1}=(L^{\diamond })^{\bot }\subset L_{1}^{\diamond }$
, then the corresponding map
$\unicode[STIX]{x1D6EC}_{1}=(L^{\diamond })^{\bot }\subset L_{1}^{\diamond }$
, then the corresponding map
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EC}}_{1,\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}\rightarrow \boldsymbol{V}_{1,\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond }\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EC}}_{1,\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}^{\diamond }}\rightarrow \boldsymbol{V}_{1,\text{dR},{\mathcal{M}}_{\mathbb{Z}_{(p)}}}^{\diamond }\end{eqnarray}$$
is an embedding of vector bundles, and that its orthogonal complement is exactly
 $\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }\!$
. From this, we easily deduce that the constructions of both
$\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}^{\diamond }\!$
. From this, we easily deduce that the constructions of both
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
and
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
and
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
do not depend on the choice of isometric embedding. The proof also shows that the vector bundle
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}^{\text{pr}}$
do not depend on the choice of isometric embedding. The proof also shows that the vector bundle
 $\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}\!$
, along with its isotropic line, is also independent of this choice.
$\boldsymbol{V}_{\text{dR},{\mathcal{M}}_{\mathbb{ Z}_{(p)}}}\!$
, along with its isotropic line, is also independent of this choice.
For the general case, consider the embedding
 $\unicode[STIX]{x1D6E5}:L{\hookrightarrow}L^{\diamond }\oplus L_{1}^{\diamond }$
defined by
$\unicode[STIX]{x1D6E5}:L{\hookrightarrow}L^{\diamond }\oplus L_{1}^{\diamond }$
defined by
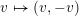 $v\mapsto (v,-v)$
. The quadratic form on
$v\mapsto (v,-v)$
. The quadratic form on
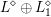 $L^{\diamond }\oplus L_{1}^{\diamond }$
given by the orthogonal sum of those on its individual summands induces a quadratic form on the quotient
$L^{\diamond }\oplus L_{1}^{\diamond }$
given by the orthogonal sum of those on its individual summands induces a quadratic form on the quotient
 $$\begin{eqnarray}L_{2}^{\diamond }=(L^{\diamond }\oplus L_{1}^{\diamond })/\unicode[STIX]{x1D6E5}(L)\end{eqnarray}$$
$$\begin{eqnarray}L_{2}^{\diamond }=(L^{\diamond }\oplus L_{1}^{\diamond })/\unicode[STIX]{x1D6E5}(L)\end{eqnarray}$$
of signature
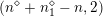 $(n^{\diamond }+n_{1}^{\diamond }-n,2)$
. Moreover, the natural maps
$(n^{\diamond }+n_{1}^{\diamond }-n,2)$
. Moreover, the natural maps
 $L^{\diamond }\rightarrow L_{2}^{\diamond }$
and
$L^{\diamond }\rightarrow L_{2}^{\diamond }$
and
 $L_{1}^{\diamond }\rightarrow L_{2}^{\diamond }$
are isometric inclusions of direct summands, whose restrictions to
$L_{1}^{\diamond }\rightarrow L_{2}^{\diamond }$
are isometric inclusions of direct summands, whose restrictions to
![]() $L$
coincide.
$L$
coincide.
Now,
![]() $L_{2}^{\diamond }$
need not be self-dual at
$L_{2}^{\diamond }$
need not be self-dual at
![]() $p$
, but, via the argument in [Reference Madapusi PeraMad16, (6.8)], we can embed it isometrically as a direct summand in a maximal quadratic space
$p$
, but, via the argument in [Reference Madapusi PeraMad16, (6.8)], we can embed it isometrically as a direct summand in a maximal quadratic space
![]() $L_{3}^{\diamond }$
of signature
$L_{3}^{\diamond }$
of signature
![]() $(n_{3}^{\diamond },2)$
, which is self-dual at
$(n_{3}^{\diamond },2)$
, which is self-dual at
![]() $p$
. In particular, replacing
$p$
. In particular, replacing
![]() $L_{1}^{\diamond }$
with
$L_{1}^{\diamond }$
with
![]() $L_{3}^{\diamond }$
, we are reduced to the already considered case where
$L_{3}^{\diamond }$
, we are reduced to the already considered case where
![]() $L^{\diamond }$
is an isometric direct summand of
$L^{\diamond }$
is an isometric direct summand of
![]() $L_{1}^{\diamond }$
.◻
$L_{1}^{\diamond }$
.◻
We can now give the construction of the stack
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
![]() $\mathbb{Z}$
. It is simply obtained by patching together the spaces
$\mathbb{Z}$
. It is simply obtained by patching together the spaces
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
. To do this rigorously, we choose a finite collection of maximal quadratic spaces
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
. To do this rigorously, we choose a finite collection of maximal quadratic spaces
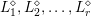 $L_{1}^{\diamond },L_{2}^{\diamond },\ldots ,L_{r}^{\diamond }$
with the following properties.
$L_{1}^{\diamond },L_{2}^{\diamond },\ldots ,L_{r}^{\diamond }$
with the following properties.
-
– For each
 $i=1,2,\ldots ,r$
,
$i=1,2,\ldots ,r$
,
 $L_{i}^{\diamond }$
has signature
$L_{i}^{\diamond }$
has signature
 $(n_{i}^{\diamond },2)$
, for
$(n_{i}^{\diamond },2)$
, for
 $n_{i}^{\diamond }\in \mathbb{Z}_{{>}0}$
.
$n_{i}^{\diamond }\in \mathbb{Z}_{{>}0}$
. -
– For each
 $i$
, there is an isometric embedding
$i$
, there is an isometric embedding
 $L{\hookrightarrow}L_{i}^{\diamond }$
.
$L{\hookrightarrow}L_{i}^{\diamond }$
. -
– If, for each
 $i$
, we denote by
$i$
, we denote by
 $S_{i}$
the set of primes dividing
$S_{i}$
the set of primes dividing
 $\text{disc}(L_{i}^{\diamond })$
, then
$\text{disc}(L_{i}^{\diamond })$
, then
 $\bigcap _{i=1}^{r}S_{i}=\emptyset$
.
$\bigcap _{i=1}^{r}S_{i}=\emptyset$
.
It is always possible to find such a collection. For instance, first choose any maximal quadratic lattice of signature
![]() $(n_{1}^{\diamond },2)$
, admitting
$(n_{1}^{\diamond },2)$
, admitting
![]() $L$
as an isometric direct summand. Let
$L$
as an isometric direct summand. Let
 $\{p_{2},\ldots ,p_{r}\}$
be the set of primes dividing the discriminant of
$\{p_{2},\ldots ,p_{r}\}$
be the set of primes dividing the discriminant of
![]() $L_{1}^{\diamond }$
. Now, for each
$L_{1}^{\diamond }$
. Now, for each
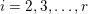 $i=2,3,\ldots ,r$
, let
$i=2,3,\ldots ,r$
, let
![]() $L_{i}^{\diamond }$
be a maximal quadratic lattice, self-dual at
$L_{i}^{\diamond }$
be a maximal quadratic lattice, self-dual at
![]() $p_{i}$
, of signature
$p_{i}$
, of signature
![]() $(n_{i}^{\diamond },2)$
, admitting
$(n_{i}^{\diamond },2)$
, admitting
![]() $L$
as an isometric direct summand. Then the collection
$L$
as an isometric direct summand. Then the collection
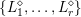 $\{L_{1}^{\diamond },\ldots ,L_{r}^{\diamond }\}$
does the job.
$\{L_{1}^{\diamond },\ldots ,L_{r}^{\diamond }\}$
does the job.
For
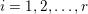 $i=1,2,\ldots ,r$
, let
$i=1,2,\ldots ,r$
, let
![]() $M_{i}^{\diamond }$
be the GSpin Shimura variety over
$M_{i}^{\diamond }$
be the GSpin Shimura variety over
![]() $\mathbb{Q}$
attached to
$\mathbb{Q}$
attached to
![]() $L_{i}^{\diamond }$
. Given an appropriate choice of
$L_{i}^{\diamond }$
. Given an appropriate choice of
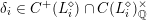 $\unicode[STIX]{x1D6FF}_{i}\in C^{+}(L_{i}^{\diamond })\cap C(L_{i}^{\diamond })_{\mathbb{Q}}^{\times }$
, with associated alternating form
$\unicode[STIX]{x1D6FF}_{i}\in C^{+}(L_{i}^{\diamond })\cap C(L_{i}^{\diamond })_{\mathbb{Q}}^{\times }$
, with associated alternating form
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}_{i}}$
on
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}_{i}}$
on
![]() $C(L_{i}^{\diamond })$
, we obtain a sequence of finite and unramified map of
$C(L_{i}^{\diamond })$
, we obtain a sequence of finite and unramified map of
![]() $\mathbb{Q}$
-stacks
$\mathbb{Q}$
-stacks
 $$\begin{eqnarray}M\rightarrow M_{i}^{\diamond }\xrightarrow[{}]{i_{\unicode[STIX]{x1D6FF}_{i}}}{\mathcal{X}}_{2^{n_{i}^{\diamond }+1},d_{i}^{\diamond },\mathbb{Q}}^{\text{Siegel}}\!.\end{eqnarray}$$
$$\begin{eqnarray}M\rightarrow M_{i}^{\diamond }\xrightarrow[{}]{i_{\unicode[STIX]{x1D6FF}_{i}}}{\mathcal{X}}_{2^{n_{i}^{\diamond }+1},d_{i}^{\diamond },\mathbb{Q}}^{\text{Siegel}}\!.\end{eqnarray}$$
Here,
![]() $d_{i}^{\diamond }$
is the discriminant of
$d_{i}^{\diamond }$
is the discriminant of
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}_{i}}$
.
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FF}_{i}}$
.
Let
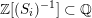 $\mathbb{Z}[(S_{i})^{-1}]\subset \mathbb{Q}$
be the localization of
$\mathbb{Z}[(S_{i})^{-1}]\subset \mathbb{Q}$
be the localization of
![]() $\mathbb{Z}$
obtained by inverting the primes in
$\mathbb{Z}$
obtained by inverting the primes in
![]() $S_{i}$
. Let
$S_{i}$
. Let
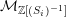 ${\mathcal{M}}_{\mathbb{Z}[(S_{i})^{-1}]}$
be the stack over
${\mathcal{M}}_{\mathbb{Z}[(S_{i})^{-1}]}$
be the stack over
 $\mathbb{Z}[(S_{i})^{-1}]$
obtained by normalizing
$\mathbb{Z}[(S_{i})^{-1}]$
obtained by normalizing
 ${\mathcal{X}}_{2^{n_{i}^{\diamond }+1},d_{i}^{\diamond },\mathbb{Z}[(S_{i})^{-1}]}^{\text{Siegel}}$
in
${\mathcal{X}}_{2^{n_{i}^{\diamond }+1},d_{i}^{\diamond },\mathbb{Z}[(S_{i})^{-1}]}^{\text{Siegel}}$
in
![]() $M$
.
$M$
.
Proposition 2.4.6. There is a regular, flat, algebraic
![]() $\mathbb{Z}$
-stack
$\mathbb{Z}$
-stack
![]() ${\mathcal{M}}$
such that for each
${\mathcal{M}}$
such that for each
![]() $i$
the restriction of
$i$
the restriction of
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
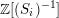 $\mathbb{Z}[(S_{i})^{-1}]$
is isomorphic to
$\mathbb{Z}[(S_{i})^{-1}]$
is isomorphic to
 ${\mathcal{M}}_{\mathbb{Z}[(S_{i})^{-1}]}$
. Moreover, the vector bundle
${\mathcal{M}}_{\mathbb{Z}[(S_{i})^{-1}]}$
. Moreover, the vector bundle
![]() $\boldsymbol{V}_{\text{dR},M}$
on
$\boldsymbol{V}_{\text{dR},M}$
on
![]() $M$
, along with its integrable connection and the isotropic line
$M$
, along with its integrable connection and the isotropic line
![]() $\boldsymbol{V}_{\text{dR},M}^{1}$
, has a canonical extension
$\boldsymbol{V}_{\text{dR},M}^{1}$
, has a canonical extension
 $(\boldsymbol{V}_{\text{dR}},\boldsymbol{V}_{\text{dR}}^{1})$
over
$(\boldsymbol{V}_{\text{dR}},\boldsymbol{V}_{\text{dR}}^{1})$
over
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Proof. This is immediate from Proposition 2.4.5. ◻
Definition 2.4.7. The line bundle
 $\boldsymbol{V}_{\text{dR}}^{1}\subset \boldsymbol{V}_{\text{dR}}$
is the tautological bundle on
$\boldsymbol{V}_{\text{dR}}^{1}\subset \boldsymbol{V}_{\text{dR}}$
is the tautological bundle on
![]() ${\mathcal{M}}$
. Its dual is the cotautological bundle.
${\mathcal{M}}$
. Its dual is the cotautological bundle.
Remark 2.4.8. Under the uniformization
 ${\mathcal{D}}\rightarrow \unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}\subset {\mathcal{M}}(\mathbb{C}),$
of (2.3), and using the notation of (2.1), the tautological bundle and cotautological bundle pull back to the line bundles
${\mathcal{D}}\rightarrow \unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}\subset {\mathcal{M}}(\mathbb{C}),$
of (2.3), and using the notation of (2.1), the tautological bundle and cotautological bundle pull back to the line bundles
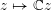 $z\mapsto \mathbb{C}z$
and
$z\mapsto \mathbb{C}z$
and
 $z\mapsto V_{\mathbb{C}}/(\mathbb{C}z)^{\bot }$
, respectively.
$z\mapsto V_{\mathbb{C}}/(\mathbb{C}z)^{\bot }$
, respectively.
By [Reference Madapusi PeraMad16, (7.12)], the Kuga–Satake abelian scheme over
![]() $M$
extends (necessarily uniquely) to an abelian scheme
$M$
extends (necessarily uniquely) to an abelian scheme
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{A}}\rightarrow {\mathcal{M}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{A}}\rightarrow {\mathcal{M}}\end{eqnarray}$$
endowed with a right
![]() $C(L)$
-action and
$C(L)$
-action and
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading. The de Rham realization of
$\mathbb{Z}/2\mathbb{Z}$
-grading. The de Rham realization of
![]() ${\mathcal{A}}$
provides us with an extension
${\mathcal{A}}$
provides us with an extension
![]() $\boldsymbol{H}_{\text{dR}}$
over
$\boldsymbol{H}_{\text{dR}}$
over
![]() ${\mathcal{M}}$
of the filtered vector bundle with connection
${\mathcal{M}}$
of the filtered vector bundle with connection
![]() $\boldsymbol{H}_{\text{dR},M}$
, equipped with its
$\boldsymbol{H}_{\text{dR},M}$
, equipped with its
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading and right
$\mathbb{Z}/2\mathbb{Z}$
-grading and right
![]() $C(L)$
-action. Let
$C(L)$
-action. Let
 $$\begin{eqnarray}\boldsymbol{H}_{\text{crys}}=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\text{crys},\ast }{\mathcal{O}}_{{\mathcal{A}}_{\mathbb{F}_{p}}/\mathbb{Z}_{p}}^{\text{crys}},{\mathcal{O}}_{{\mathcal{M}}_{\mathbb{ F}_{p}}/\mathbb{Z}_{p}}^{\text{crys}})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{H}_{\text{crys}}=\text{}\underline{\text{Hom}}(R^{1}\unicode[STIX]{x1D70B}_{\text{crys},\ast }{\mathcal{O}}_{{\mathcal{A}}_{\mathbb{F}_{p}}/\mathbb{Z}_{p}}^{\text{crys}},{\mathcal{O}}_{{\mathcal{M}}_{\mathbb{ F}_{p}}/\mathbb{Z}_{p}}^{\text{crys}})\end{eqnarray}$$
be the first crystalline homology of
![]() ${\mathcal{A}}_{\mathbb{F}_{p}}$
relative to
${\mathcal{A}}_{\mathbb{F}_{p}}$
relative to
![]() ${\mathcal{M}}_{\mathbb{F}_{p}}$
.
${\mathcal{M}}_{\mathbb{F}_{p}}$
.
Denote by
![]() $\mathbf{1}$
the structure sheaf
$\mathbf{1}$
the structure sheaf
![]() ${\mathcal{O}}_{{\mathcal{M}}}$
with its standard connection and trivial filtration in the de Rham case; the constant sheaf
${\mathcal{O}}_{{\mathcal{M}}}$
with its standard connection and trivial filtration in the de Rham case; the constant sheaf
![]() $\text{}\underline{\mathbb{Z}}_{p}$
on
$\text{}\underline{\mathbb{Z}}_{p}$
on
![]() ${\mathcal{M}}[1/p]$
in the étale case; the crystal
${\mathcal{M}}[1/p]$
in the étale case; the crystal
 ${\mathcal{O}}_{{\mathcal{M}}_{\mathbb{F}_{p}},\text{crys}}$
in the crystalline case; and the trivial variation of
${\mathcal{O}}_{{\mathcal{M}}_{\mathbb{F}_{p}},\text{crys}}$
in the crystalline case; and the trivial variation of
![]() $\mathbb{Z}$
-Hodge structures over
$\mathbb{Z}$
-Hodge structures over
![]() $M_{\mathbb{C}}^{\text{an}}$
in the Betti case. If
$M_{\mathbb{C}}^{\text{an}}$
in the Betti case. If
![]() $\boldsymbol{H}$
is any one of
$\boldsymbol{H}$
is any one of
![]() $\boldsymbol{H}_{\text{dR}}$
,
$\boldsymbol{H}_{\text{dR}}$
,
![]() $\boldsymbol{H}_{\ell ,\acute{\text{e}}\text{t}}$
,
$\boldsymbol{H}_{\ell ,\acute{\text{e}}\text{t}}$
,
![]() $\boldsymbol{H}_{\text{crys}}$
, or
$\boldsymbol{H}_{\text{crys}}$
, or
![]() $\boldsymbol{H}_{\text{Be}}$
, then
$\boldsymbol{H}_{\text{Be}}$
, then
![]() $\boldsymbol{H}$
is a
$\boldsymbol{H}$
is a
![]() $\mathbf{1}$
-module in the appropriate category.
$\mathbf{1}$
-module in the appropriate category.
It follows from [Reference Madapusi PeraMad16, (3.12), (7.13)] that there is a canonical local direct summand
 $$\begin{eqnarray}\displaystyle \boldsymbol{V}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{V}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}) & & \displaystyle\end{eqnarray}$$
of grade-shifting endomorphisms. In fact, as we will see below in Proposition 2.5.1, the homological realizations of the canonical isometric embedding
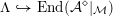 $\unicode[STIX]{x1D6EC}{\hookrightarrow}\text{End}({\mathcal{A}}^{\diamond }|_{{\mathcal{M}}})$
exhibit
$\unicode[STIX]{x1D6EC}{\hookrightarrow}\text{End}({\mathcal{A}}^{\diamond }|_{{\mathcal{M}}})$
exhibit
![]() $\unicode[STIX]{x1D6EC}\otimes \mathbf{1}$
as an isometric local direct summand of
$\unicode[STIX]{x1D6EC}\otimes \mathbf{1}$
as an isometric local direct summand of
![]() $\boldsymbol{V}^{\diamond }|_{{\mathcal{M}}}$
, and
$\boldsymbol{V}^{\diamond }|_{{\mathcal{M}}}$
, and
 $$\begin{eqnarray}\boldsymbol{V}=(\unicode[STIX]{x1D6EC}\otimes \mathbf{1})^{\bot }\subset \boldsymbol{V}^{\diamond }|_{{\mathcal{M}}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}=(\unicode[STIX]{x1D6EC}\otimes \mathbf{1})^{\bot }\subset \boldsymbol{V}^{\diamond }|_{{\mathcal{M}}}.\end{eqnarray}$$
In the de Rham or Betti case,
![]() $\boldsymbol{V}$
is identified with the realizations already constructed above. Moreover, for any prime
$\boldsymbol{V}$
is identified with the realizations already constructed above. Moreover, for any prime
![]() $p$
, the étale realization
$p$
, the étale realization
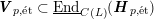 $\boldsymbol{V}_{p,\acute{\text{e}}\text{t}}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{p,\acute{\text{e}}\text{t}})$
is the unique extension of that over
$\boldsymbol{V}_{p,\acute{\text{e}}\text{t}}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}_{p,\acute{\text{e}}\text{t}})$
is the unique extension of that over
![]() ${\mathcal{M}}[1/p]$
. Here, we are using the following fact: given a normal flat Noetherian algebraic
${\mathcal{M}}[1/p]$
. Here, we are using the following fact: given a normal flat Noetherian algebraic
![]() $\mathbb{Z}[1/p]$
-stack
$\mathbb{Z}[1/p]$
-stack
![]() $S$
, and a lisse
$S$
, and a lisse
![]() $p$
-adic sheaf
$p$
-adic sheaf
![]() $F$
over
$F$
over
![]() $S$
, any lisse subsheaf of
$S$
, any lisse subsheaf of
![]() $F|_{S_{\mathbb{Q}}}$
extends uniquely to a lisse subsheaf of
$F|_{S_{\mathbb{Q}}}$
extends uniquely to a lisse subsheaf of
![]() $F$
. To see this, we can reduce to the case where
$F$
. To see this, we can reduce to the case where
![]() $S$
is a normal, connected, flat Noetherian
$S$
is a normal, connected, flat Noetherian
![]() $\mathbb{Z}[1/p]$
-scheme, where the assertion amounts to saying that the map of étale fundamental groups
$\mathbb{Z}[1/p]$
-scheme, where the assertion amounts to saying that the map of étale fundamental groups
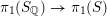 $\unicode[STIX]{x1D70B}_{1}(S_{\mathbb{Q}})\rightarrow \unicode[STIX]{x1D70B}_{1}(S)$
is surjective. This is shown in [Reference GrothendieckSGA1, Example V, Proposition 8.2].
$\unicode[STIX]{x1D70B}_{1}(S_{\mathbb{Q}})\rightarrow \unicode[STIX]{x1D70B}_{1}(S)$
is surjective. This is shown in [Reference GrothendieckSGA1, Example V, Proposition 8.2].
For any section
![]() $x$
of
$x$
of
![]() $\boldsymbol{V}$
, the element
$\boldsymbol{V}$
, the element
![]() $x\circ x$
is a scalar endomorphism of
$x\circ x$
is a scalar endomorphism of
![]() $\boldsymbol{H}$
. Define a quadratic form
$\boldsymbol{H}$
. Define a quadratic form
 $$\begin{eqnarray}\boldsymbol{Q}:\boldsymbol{V}\rightarrow \mathbf{1}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Q}:\boldsymbol{V}\rightarrow \mathbf{1}\end{eqnarray}$$
by
 $x\circ x=\boldsymbol{Q}(x)\cdot \text{Id}$
.
$x\circ x=\boldsymbol{Q}(x)\cdot \text{Id}$
.
Remark 2.4.9. Although we will not require this in what follows, we note that there is a certain compatibility between the crystalline realization
![]() $\boldsymbol{V}_{\text{crys}}$
over
$\boldsymbol{V}_{\text{crys}}$
over
![]() ${\mathcal{M}}_{\mathbb{F}_{p}}$
and the
${\mathcal{M}}_{\mathbb{F}_{p}}$
and the
![]() $p$
-adic realization
$p$
-adic realization
![]() $\boldsymbol{V}_{p,\acute{\text{e}}\text{t}}$
over
$\boldsymbol{V}_{p,\acute{\text{e}}\text{t}}$
over
![]() ${\mathcal{M}}[1/p]$
. Suppose that we are given a finite extension
${\mathcal{M}}[1/p]$
. Suppose that we are given a finite extension
![]() $F/\mathbb{Q}_{p}$
, contained in an algebraic closure
$F/\mathbb{Q}_{p}$
, contained in an algebraic closure
![]() $\overline{\mathbb{Q}}_{p}$
of
$\overline{\mathbb{Q}}_{p}$
of
![]() $\mathbb{Q}_{p}$
, with residue field
$\mathbb{Q}_{p}$
, with residue field
![]() $k$
. Write
$k$
. Write
![]() $F_{0}\subset F$
for the maximal unramified subextension of
$F_{0}\subset F$
for the maximal unramified subextension of
![]() $F$
. Suppose that we are given a point
$F$
. Suppose that we are given a point
 $s\in {\mathcal{M}}(F)$
specializing to a point
$s\in {\mathcal{M}}(F)$
specializing to a point
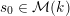 $s_{0}\in {\mathcal{M}}(k)$
. Write
$s_{0}\in {\mathcal{M}}(k)$
. Write
![]() $\overline{s}$
for the corresponding
$\overline{s}$
for the corresponding
![]() $\overline{\mathbb{Q}}_{p}$
-point of
$\overline{\mathbb{Q}}_{p}$
-point of
![]() ${\mathcal{M}}$
. Then the comparison isomorphism between the crystalline cohomology of
${\mathcal{M}}$
. Then the comparison isomorphism between the crystalline cohomology of
![]() ${\mathcal{A}}_{s_{0}}$
with respect to
${\mathcal{A}}_{s_{0}}$
with respect to
 $W(k)={\mathcal{O}}_{F_{0}}$
and the
$W(k)={\mathcal{O}}_{F_{0}}$
and the
![]() $p$
-adic étale cohomology of
$p$
-adic étale cohomology of
![]() ${\mathcal{A}}_{\overline{s}}$
induces, by [Reference Madapusi PeraMad16, (7.11)], an isometry
${\mathcal{A}}_{\overline{s}}$
induces, by [Reference Madapusi PeraMad16, (7.11)], an isometry
 $$\begin{eqnarray}\boldsymbol{V}_{\text{crys},s_{0}}\otimes _{F_{0}}B_{\text{crys}}\xrightarrow[{}]{\simeq }\boldsymbol{V}_{p,\acute{\text{e}}\text{t},\overline{s}}\otimes _{\mathbb{Q}_{p}}B_{\text{crys}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{\text{crys},s_{0}}\otimes _{F_{0}}B_{\text{crys}}\xrightarrow[{}]{\simeq }\boldsymbol{V}_{p,\acute{\text{e}}\text{t},\overline{s}}\otimes _{\mathbb{Q}_{p}}B_{\text{crys}}.\end{eqnarray}$$
2.5 Functoriality of integral models
We consider the question of functoriality of the previous constructions with respect to the maximal quadratic space
![]() $L$
. Let
$L$
. Let
![]() $L_{0}\subset L$
be an isometric embedding of maximal quadratic spaces over
$L_{0}\subset L$
be an isometric embedding of maximal quadratic spaces over
![]() $\mathbb{Z}$
, of signatures
$\mathbb{Z}$
, of signatures
![]() $(n_{0},2)$
and
$(n_{0},2)$
and
![]() $(n,2)$
, respectively. This implies that
$(n,2)$
, respectively. This implies that
![]() $L_{0}$
is a
$L_{0}$
is a
![]() $\mathbb{Z}$
-module direct summand of
$\mathbb{Z}$
-module direct summand of
![]() $L$
. We will maintain our assumption that
$L$
. We will maintain our assumption that
![]() $n_{0}\geqslant 1$
.
$n_{0}\geqslant 1$
.
The quadratic spaces
![]() $L_{0}$
and
$L_{0}$
and
![]() $L$
have associated Shimura varieties
$L$
have associated Shimura varieties
![]() $M_{0}$
and
$M_{0}$
and
![]() $M$
, with level structure defined by the compact open subgroups
$M$
, with level structure defined by the compact open subgroups
 $$\begin{eqnarray}\displaystyle K_{0} & = & \displaystyle \text{GSpin}(L_{0}\otimes \mathbb{A}_{f})\cap C(\widehat{L}_{0})^{\times },\nonumber\\ \displaystyle K & = & \displaystyle \text{GSpin}(L\otimes \mathbb{A}_{f})\cap C(\widehat{L})^{\times }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{0} & = & \displaystyle \text{GSpin}(L_{0}\otimes \mathbb{A}_{f})\cap C(\widehat{L}_{0})^{\times },\nonumber\\ \displaystyle K & = & \displaystyle \text{GSpin}(L\otimes \mathbb{A}_{f})\cap C(\widehat{L})^{\times }.\nonumber\end{eqnarray}$$
The inclusion
 $L_{0}{\hookrightarrow}L$
induces a homomorphism of Clifford algebras, which then restricts to an inclusion of algebraic groups
$L_{0}{\hookrightarrow}L$
induces a homomorphism of Clifford algebras, which then restricts to an inclusion of algebraic groups
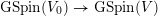 $\text{GSpin}(V_{0})\rightarrow \text{GSpin}(V)$
satisfying
$\text{GSpin}(V_{0})\rightarrow \text{GSpin}(V)$
satisfying
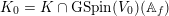 $K_{0}=K\cap \text{GSpin}(V_{0})(\mathbb{A}_{f})$
. By the theory of canonical models of Shimura varieties, there is an induced finite and unramified morphism of
$K_{0}=K\cap \text{GSpin}(V_{0})(\mathbb{A}_{f})$
. By the theory of canonical models of Shimura varieties, there is an induced finite and unramified morphism of
![]() $\mathbb{Q}$
-stacks
$\mathbb{Q}$
-stacks
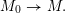 $M_{0}\rightarrow M.$
$M_{0}\rightarrow M.$
Let
![]() ${\mathcal{M}}_{0}$
and
${\mathcal{M}}_{0}$
and
![]() ${\mathcal{M}}$
be the integral models over
${\mathcal{M}}$
be the integral models over
![]() $\mathbb{Z}$
, and let
$\mathbb{Z}$
, and let
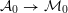 ${\mathcal{A}}_{0}\rightarrow {\mathcal{M}}_{0}$
and
${\mathcal{A}}_{0}\rightarrow {\mathcal{M}}_{0}$
and
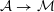 ${\mathcal{A}}\rightarrow {\mathcal{M}}$
be their Kuga–Satake abelian schemes. They are equipped with actions of
${\mathcal{A}}\rightarrow {\mathcal{M}}$
be their Kuga–Satake abelian schemes. They are equipped with actions of
![]() $C(L_{0})$
and
$C(L_{0})$
and
![]() $C(L)$
, respectively. Let
$C(L)$
, respectively. Let
![]() $\boldsymbol{H}_{0}$
and
$\boldsymbol{H}_{0}$
and
![]() $\boldsymbol{H}$
stand for the various homological realizations of
$\boldsymbol{H}$
stand for the various homological realizations of
![]() ${\mathcal{A}}_{0}$
and
${\mathcal{A}}_{0}$
and
![]() ${\mathcal{A}}$
, respectively. We have the canonical sub-objects
${\mathcal{A}}$
, respectively. We have the canonical sub-objects
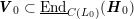 $\boldsymbol{V}_{0}\subset \text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0})$
and
$\boldsymbol{V}_{0}\subset \text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0})$
and
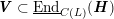 $\boldsymbol{V}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H})$
introduced in § 2.4.
$\boldsymbol{V}\subset \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H})$
introduced in § 2.4.
The Kuga–Satake abelian schemes over
![]() $M_{0}$
and
$M_{0}$
and
![]() $M$
are determined by the lattices
$M$
are determined by the lattices
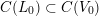 $C(L_{0})\subset C(V_{0})$
and
$C(L_{0})\subset C(V_{0})$
and
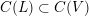 $C(L)\subset C(V)$
(in the sense of [Reference DeligneDel72, § 4.12]), and the argument in [Reference Madapusi PeraMad16, (6.4)] shows that there is a
$C(L)\subset C(V)$
(in the sense of [Reference DeligneDel72, § 4.12]), and the argument in [Reference Madapusi PeraMad16, (6.4)] shows that there is a
![]() $C(L)$
-linear isomorphism of abelian schemes
$C(L)$
-linear isomorphism of abelian schemes
 $$\begin{eqnarray}\displaystyle ({\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L))|_{M_{0}}\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{M_{0}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L))|_{M_{0}}\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{M_{0}} & & \displaystyle\end{eqnarray}$$
over the generic fiber
![]() $M_{0}$
of
$M_{0}$
of
![]() ${\mathcal{M}}_{0}$
. As
${\mathcal{M}}_{0}$
. As
![]() $L_{0}$
is a direct summand of
$L_{0}$
is a direct summand of
![]() $L$
, one easily checks that
$L$
, one easily checks that
![]() $C(L)$
is a free
$C(L)$
is a free
![]() $C(L_{0})$
-module, and so the tensor construction
$C(L_{0})$
-module, and so the tensor construction
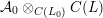 ${\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L)$
in (2.11) is defined.
${\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L)$
in (2.11) is defined.
Proposition 2.5.1. The morphism
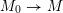 $M_{0}\rightarrow M$
extends uniquely to an unramified morphism
$M_{0}\rightarrow M$
extends uniquely to an unramified morphism
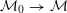 ${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
, and (2.11) extends to a
${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
, and (2.11) extends to a
![]() $C(L)$
-linear isomorphism of abelian schemes
$C(L)$
-linear isomorphism of abelian schemes
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{{\mathcal{M}}_{0}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{{\mathcal{M}}_{0}} & & \displaystyle\end{eqnarray}$$
over
![]() ${\mathcal{M}}_{0}$
. In particular,
${\mathcal{M}}_{0}$
. In particular,
 $$\begin{eqnarray}\displaystyle \boldsymbol{H}_{0}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }\boldsymbol{H}|_{{\mathcal{M}}_{0}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{H}_{0}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }\boldsymbol{H}|_{{\mathcal{M}}_{0}}. & & \displaystyle\end{eqnarray}$$
Furthermore, if we set
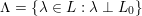 $\unicode[STIX]{x1D6EC}=\{\unicode[STIX]{x1D706}\in L:\unicode[STIX]{x1D706}\bot L_{0}\}$
and define a sheaf
$\unicode[STIX]{x1D6EC}=\{\unicode[STIX]{x1D706}\in L:\unicode[STIX]{x1D706}\bot L_{0}\}$
and define a sheaf
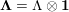 $\boldsymbol{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}\otimes \mathbf{1}$
on
$\boldsymbol{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}\otimes \mathbf{1}$
on
![]() ${\mathcal{M}}_{0}$
, then there is a canonical embedding
${\mathcal{M}}_{0}$
, then there is a canonical embedding
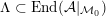 $\unicode[STIX]{x1D6EC}\subset \text{End}({\mathcal{A}}|_{{\mathcal{M}}_{0}})$
with the following properties.
$\unicode[STIX]{x1D6EC}\subset \text{End}({\mathcal{A}}|_{{\mathcal{M}}_{0}})$
with the following properties.
-
(i) Its homological realization
 $\boldsymbol{\unicode[STIX]{x1D6EC}}{\hookrightarrow}\text{}\underline{\text{End}}(\boldsymbol{H}|_{{\mathcal{M}}_{0}})$
arises from an isometric map
$\boldsymbol{\unicode[STIX]{x1D6EC}}{\hookrightarrow}\text{}\underline{\text{End}}(\boldsymbol{H}|_{{\mathcal{M}}_{0}})$
arises from an isometric map
 $\boldsymbol{\unicode[STIX]{x1D6EC}}{\hookrightarrow}\boldsymbol{V}|_{{\mathcal{M}}_{0}}$
, and exhibits
$\boldsymbol{\unicode[STIX]{x1D6EC}}{\hookrightarrow}\boldsymbol{V}|_{{\mathcal{M}}_{0}}$
, and exhibits
 $\boldsymbol{\unicode[STIX]{x1D6EC}}$
as a local direct summand of
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
as a local direct summand of
 $\boldsymbol{V}|_{{\mathcal{M}}_{0}}$
.
$\boldsymbol{V}|_{{\mathcal{M}}_{0}}$
. -
(ii) The injection
induced by (2.13) identifies $$\begin{eqnarray}\text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0})\rightarrow \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}|_{{\mathcal{M}}_{0}})\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0})\rightarrow \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}|_{{\mathcal{M}}_{0}})\end{eqnarray}$$
 $\boldsymbol{V}_{0}$
with the submodule of all elements of
$\boldsymbol{V}_{0}$
with the submodule of all elements of
 $\boldsymbol{V}|_{{\mathcal{M}}_{0}}$
anticommuting with all elements of
$\boldsymbol{V}|_{{\mathcal{M}}_{0}}$
anticommuting with all elements of
 $\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Furthermore,
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Furthermore,
 $\boldsymbol{V}_{0}\subset \boldsymbol{V}|_{{\mathcal{M}}_{0}}$
is locally a direct summand.
$\boldsymbol{V}_{0}\subset \boldsymbol{V}|_{{\mathcal{M}}_{0}}$
is locally a direct summand.
-
(iii) In the de Rham case, the inclusion
 $\boldsymbol{V}_{\text{dR}}\subset \boldsymbol{V}_{\text{dR}}|_{{\mathcal{M}}_{0}}$
identifies
$\boldsymbol{V}_{\text{dR}}\subset \boldsymbol{V}_{\text{dR}}|_{{\mathcal{M}}_{0}}$
identifies  $$\begin{eqnarray}\boldsymbol{V}_{0,\text{dR}}^{1}\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR}}^{1}|_{{\mathcal{M}}_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{0,\text{dR}}^{1}\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR}}^{1}|_{{\mathcal{M}}_{0}}.\end{eqnarray}$$
Proof. It suffices to construct the morphism
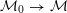 ${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
after localizing at a prime
${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
after localizing at a prime
![]() $p$
. Hence we can assume that we have a sequence of isometric embeddings
$p$
. Hence we can assume that we have a sequence of isometric embeddings
 $L_{0}{\hookrightarrow}L{\hookrightarrow}L^{\diamond }$
, where
$L_{0}{\hookrightarrow}L{\hookrightarrow}L^{\diamond }$
, where
![]() $L^{\diamond }$
is maximal and self-dual at
$L^{\diamond }$
is maximal and self-dual at
![]() $p$
.
$p$
.
By taking the normalizations of
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
in
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
in
![]() $M_{0}$
and
$M_{0}$
and
![]() $M$
, respectively, we see that the finite morphism
$M$
, respectively, we see that the finite morphism
 $M_{0}\rightarrow M$
extends to a map
$M_{0}\rightarrow M$
extends to a map
 $$\begin{eqnarray}\displaystyle \check{{\mathcal{M}}}_{0,\mathbb{Z}_{(p)}}\rightarrow \check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}\!. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \check{{\mathcal{M}}}_{0,\mathbb{Z}_{(p)}}\rightarrow \check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}\!. & & \displaystyle\end{eqnarray}$$
Set
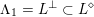 $\unicode[STIX]{x1D6EC}_{1}=L^{\bot }\subset L^{\diamond }$
and
$\unicode[STIX]{x1D6EC}_{1}=L^{\bot }\subset L^{\diamond }$
and
 $\widetilde{\unicode[STIX]{x1D6EC}}=L_{0}^{\bot }\subset L^{\diamond }$
, so that
$\widetilde{\unicode[STIX]{x1D6EC}}=L_{0}^{\bot }\subset L^{\diamond }$
, so that
![]() $\unicode[STIX]{x1D6EC}_{1}$
is a direct summand in
$\unicode[STIX]{x1D6EC}_{1}$
is a direct summand in
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
with orthogonal complement
$\widetilde{\unicode[STIX]{x1D6EC}}$
with orthogonal complement
![]() $\unicode[STIX]{x1D6EC}$
. From this, it is clear that (2.14) restricts to a map
$\unicode[STIX]{x1D6EC}$
. From this, it is clear that (2.14) restricts to a map
 $\check{{\mathcal{M}}}_{0,\mathbb{Z}_{(p)}}^{\text{pr}}\rightarrow \check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}^{\text{pr}}$
. We can deduce from Proposition 2.4.3 that, étale locally on the source, this map is isomorphic to an étale neighborhood of the map of quadrics
$\check{{\mathcal{M}}}_{0,\mathbb{Z}_{(p)}}^{\text{pr}}\rightarrow \check{{\mathcal{M}}}_{\mathbb{ Z}_{(p)}}^{\text{pr}}$
. We can deduce from Proposition 2.4.3 that, étale locally on the source, this map is isomorphic to an étale neighborhood of the map of quadrics
 $\text{M}^{\text{loc}}(L_{0})\rightarrow \text{M}^{\text{loc}}(L)$
. In particular, it is unramified.
$\text{M}^{\text{loc}}(L_{0})\rightarrow \text{M}^{\text{loc}}(L)$
. In particular, it is unramified.
To check that this carries
![]() ${\mathcal{M}}_{0,\mathbb{Z}_{(p)}}$
to
${\mathcal{M}}_{0,\mathbb{Z}_{(p)}}$
to
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
it suffices now to show that the map
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
it suffices now to show that the map
 $$\begin{eqnarray}\text{M}^{\text{loc}}(L_{0})_{\mathbb{Z}_{(p)}}\rightarrow \text{M}^{\text{loc}}(L)_{\mathbb{Z}_{(p)}}\end{eqnarray}$$
$$\begin{eqnarray}\text{M}^{\text{loc}}(L_{0})_{\mathbb{Z}_{(p)}}\rightarrow \text{M}^{\text{loc}}(L)_{\mathbb{Z}_{(p)}}\end{eqnarray}$$
of quadrics over
![]() $\mathbb{Z}_{(p)}$
carries the smooth locus to the smooth locus and, if
$\mathbb{Z}_{(p)}$
carries the smooth locus to the smooth locus and, if
![]() $p\neq 2$
, the regular locus of the source into that of the target.
$p\neq 2$
, the regular locus of the source into that of the target.
For the first assertion, observe that an
![]() $\overline{\mathbb{F}}_{p}$
-valued point of the space is in the smooth locus if and only if it corresponds to an isotropic line that is not contained in the radical of
$\overline{\mathbb{F}}_{p}$
-valued point of the space is in the smooth locus if and only if it corresponds to an isotropic line that is not contained in the radical of
![]() $L_{0,\overline{\mathbb{F}}_{p}}$
. But then it is a fortiori not in the radical of
$L_{0,\overline{\mathbb{F}}_{p}}$
. But then it is a fortiori not in the radical of
![]() $L_{\overline{\mathbb{F}}_{p}}$
, and hence corresponds to a smooth point of
$L_{\overline{\mathbb{F}}_{p}}$
, and hence corresponds to a smooth point of
 $\text{M}^{\text{loc}}(L)$
as well.
$\text{M}^{\text{loc}}(L)$
as well.
We are left to prove the second claim, so that we can assume that
![]() $p$
is odd.
$p$
is odd.
If the discriminant of
![]() $L_{\mathbb{Z}_{(p)}}$
is not divisible by
$L_{\mathbb{Z}_{(p)}}$
is not divisible by
![]() $p^{2}$
, the entire target is regular (see [Reference Madapusi PeraMad16, (2.16)]), and there is nothing to check. Otherwise, the locus where
$p^{2}$
, the entire target is regular (see [Reference Madapusi PeraMad16, (2.16)]), and there is nothing to check. Otherwise, the locus where
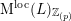 $\text{M}^{\text{loc}}(L)_{\mathbb{Z}_{(p)}}$
is not regular consists exactly of the two
$\text{M}^{\text{loc}}(L)_{\mathbb{Z}_{(p)}}$
is not regular consists exactly of the two
![]() $\mathbb{F}_{p^{2}}$
-valued points where the corresponding isotropic line
$\mathbb{F}_{p^{2}}$
-valued points where the corresponding isotropic line
 $L^{1}\subset L_{\mathbb{F}_{p^{2}}}$
lies in the radical
$L^{1}\subset L_{\mathbb{F}_{p^{2}}}$
lies in the radical
 $\text{rad}(L_{\mathbb{F}_{p^{2}}})$
and is also isotropic for the non-degenerate quadratic form on this radical (see [Reference Madapusi PeraMad16]).
$\text{rad}(L_{\mathbb{F}_{p^{2}}})$
and is also isotropic for the non-degenerate quadratic form on this radical (see [Reference Madapusi PeraMad16]).
Suppose therefore that we have an isotropic line
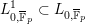 $L_{0,\overline{\mathbb{F}}_{p}}^{1}\subset L_{0,\overline{\mathbb{F}}_{p}}$
. We need to show: if, as an isotropic line in
$L_{0,\overline{\mathbb{F}}_{p}}^{1}\subset L_{0,\overline{\mathbb{F}}_{p}}$
. We need to show: if, as an isotropic line in
![]() $L_{\overline{\mathbb{F}}_{p}}$
, it corresponds to one of the two singular points above, then the discriminant of
$L_{\overline{\mathbb{F}}_{p}}$
, it corresponds to one of the two singular points above, then the discriminant of
![]() $L_{0}$
is also divisible by
$L_{0}$
is also divisible by
![]() $p^{2}$
, and
$p^{2}$
, and
![]() $L_{0,\overline{\mathbb{F}}_{p}}^{1}$
corresponds to a singular point of
$L_{0,\overline{\mathbb{F}}_{p}}^{1}$
corresponds to a singular point of
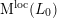 $\text{M}^{\text{loc}}(L_{0})$
.
$\text{M}^{\text{loc}}(L_{0})$
.
As any smooth point of
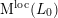 $\text{M}^{\text{loc}}(L_{0})$
(that is, a point at which the space is smooth over
$\text{M}^{\text{loc}}(L_{0})$
(that is, a point at which the space is smooth over
![]() $\mathbb{Z}$
) maps to a smooth point of
$\mathbb{Z}$
) maps to a smooth point of
 $\text{M}^{\text{loc}}(L)$
, the only remaining possibility is that the discriminant of
$\text{M}^{\text{loc}}(L)$
, the only remaining possibility is that the discriminant of
![]() $L_{0}$
is divisible exactly by
$L_{0}$
is divisible exactly by
![]() $p$
, and that
$p$
, and that
![]() $L_{0,\overline{\mathbb{F}}_{p}}^{1}$
is just the radical of
$L_{0,\overline{\mathbb{F}}_{p}}^{1}$
is just the radical of
![]() $L_{0,\overline{\mathbb{F}}_{p}}$
, corresponding to the unique non-smooth point of
$L_{0,\overline{\mathbb{F}}_{p}}$
, corresponding to the unique non-smooth point of
 $\text{M}^{\text{loc}}(L_{0})_{\mathbb{Z}_{(p)}}$
. However, this point is defined over
$\text{M}^{\text{loc}}(L_{0})_{\mathbb{Z}_{(p)}}$
. However, this point is defined over
![]() $\mathbb{F}_{p}$
, whereas both the singular points of
$\mathbb{F}_{p}$
, whereas both the singular points of
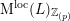 $\text{M}^{\text{loc}}(L)_{\mathbb{Z}_{(p)}}$
are only defined over
$\text{M}^{\text{loc}}(L)_{\mathbb{Z}_{(p)}}$
are only defined over
![]() $\mathbb{F}_{p^{2}}$
. Hence this possibility can also be excluded.
$\mathbb{F}_{p^{2}}$
. Hence this possibility can also be excluded.
Now, the fact that the isomorphism of abelian schemes also extends over
![]() ${\mathcal{M}}_{0}$
is a consequence of [Reference Faltings and ChaiFC90, Proposition I.2.7].
${\mathcal{M}}_{0}$
is a consequence of [Reference Faltings and ChaiFC90, Proposition I.2.7].
The canonical embedding
 $\unicode[STIX]{x1D6EC}\subset \text{End}({\mathcal{A}}|_{{\mathcal{M}}_{0,\mathbb{Z}_{(p)}}}\!)$
is constructed as follows. First, we will define an action of
$\unicode[STIX]{x1D6EC}\subset \text{End}({\mathcal{A}}|_{{\mathcal{M}}_{0,\mathbb{Z}_{(p)}}}\!)$
is constructed as follows. First, we will define an action of
![]() $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
 $$\begin{eqnarray}{\mathcal{A}}_{0}\otimes _{\mathbb{Z}}C(L)=({\mathcal{A}}_{0}^{+}\otimes _{\mathbb{ Z}}C(L))\times ({\mathcal{A}}_{0}^{-}\otimes _{\mathbb{ Z}}C(L)).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{0}\otimes _{\mathbb{Z}}C(L)=({\mathcal{A}}_{0}^{+}\otimes _{\mathbb{ Z}}C(L))\times ({\mathcal{A}}_{0}^{-}\otimes _{\mathbb{ Z}}C(L)).\end{eqnarray}$$
Given a section of the form
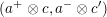 $(a^{+}\otimes c,a^{-}\otimes c^{\prime })$
of this product and an element
$(a^{+}\otimes c,a^{-}\otimes c^{\prime })$
of this product and an element
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, we set
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, we set
 $$\begin{eqnarray}\unicode[STIX]{x1D706}\cdot (a^{+}\otimes c,a^{-}\otimes c^{\prime })=(a^{+}\otimes \unicode[STIX]{x1D706}c,-a^{-}\otimes \unicode[STIX]{x1D706}c^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}\cdot (a^{+}\otimes c,a^{-}\otimes c^{\prime })=(a^{+}\otimes \unicode[STIX]{x1D706}c,-a^{-}\otimes \unicode[STIX]{x1D706}c^{\prime }).\end{eqnarray}$$
As
![]() $L_{0}$
anti-commutes with
$L_{0}$
anti-commutes with
![]() $\unicode[STIX]{x1D6EC}$
within
$\unicode[STIX]{x1D6EC}$
within
![]() $C(L)$
, it is easy to check that this action of
$C(L)$
, it is easy to check that this action of
![]() $\unicode[STIX]{x1D6EC}$
descends to one on
$\unicode[STIX]{x1D6EC}$
descends to one on
 $$\begin{eqnarray}{\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L)\xrightarrow[{\simeq }]{(2.12)}{\mathcal{A}}|_{{\mathcal{M}}_{0,\mathbb{Z}_{(p)}}}\!.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L)\xrightarrow[{\simeq }]{(2.12)}{\mathcal{A}}|_{{\mathcal{M}}_{0,\mathbb{Z}_{(p)}}}\!.\end{eqnarray}$$
Claims (i)–(iii) are now shown in [Reference Madapusi PeraMad16, (7.13)] for the crystalline realizations over
![]() ${\mathcal{M}}_{0,\mathbb{F}_{p}}$
, but in the case where
${\mathcal{M}}_{0,\mathbb{F}_{p}}$
, but in the case where
![]() $L$
is self-dual at
$L$
is self-dual at
![]() $p$
. From this, we can easily deduce the general case, just as above, by embedding everything in a quadratic space that is self-dual at
$p$
. From this, we can easily deduce the general case, just as above, by embedding everything in a quadratic space that is self-dual at
![]() $p$
.◻
$p$
.◻
2.6 Special endomorphisms
For any scheme
 $S\rightarrow {\mathcal{M}}$
the pullback
$S\rightarrow {\mathcal{M}}$
the pullback
![]() ${\mathcal{A}}_{S}$
of the Kuga–Satake abelian scheme has a distinguished submodule
${\mathcal{A}}_{S}$
of the Kuga–Satake abelian scheme has a distinguished submodule
 $$\begin{eqnarray}V({\mathcal{A}}_{S})\subset \text{End}_{C(L)}({\mathcal{A}}_{S})\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{A}}_{S})\subset \text{End}_{C(L)}({\mathcal{A}}_{S})\end{eqnarray}$$
of special endomorphisms, defined in [Reference Madapusi PeraMad16, (5.4)]. If
![]() $S$
is connected and
$S$
is connected and
![]() $s\rightarrow S$
is any geometric point, there is a cartesian diagram
$s\rightarrow S$
is any geometric point, there is a cartesian diagram

In other words, if
![]() $S$
is connected, an endomorphism is special if and only if it is special at one (equivalently, all) geometric points of
$S$
is connected, an endomorphism is special if and only if it is special at one (equivalently, all) geometric points of
![]() $S$
.
$S$
.
At a geometric point
![]() $s$
, the property of being special can be characterized homologically, using the subspace
$s$
, the property of being special can be characterized homologically, using the subspace
 $$\begin{eqnarray}\displaystyle \boldsymbol{V}_{s}\subset \text{End}_{C(L)}(\boldsymbol{H}_{s}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{V}_{s}\subset \text{End}_{C(L)}(\boldsymbol{H}_{s}). & & \displaystyle\end{eqnarray}$$
If
 $s=\text{Spec}(\mathbb{C})$
then
$s=\text{Spec}(\mathbb{C})$
then
 $x\in \text{End}_{C(L)}({\mathcal{A}}_{s})$
is special if and only if its Betti realization lies in the subspace (2.15). This is equivalent to the
$x\in \text{End}_{C(L)}({\mathcal{A}}_{s})$
is special if and only if its Betti realization lies in the subspace (2.15). This is equivalent to the
![]() $\ell$
-adic étale realization of
$\ell$
-adic étale realization of
![]() $x$
lying in (2.15) for one (equivalently, all) primes
$x$
lying in (2.15) for one (equivalently, all) primes
![]() $\ell$
. It is also equivalent to requiring that the de Rham realization
$\ell$
. It is also equivalent to requiring that the de Rham realization
 $t_{\text{dR}}(x)\in \text{End}_{C(L)}(\boldsymbol{H}_{\text{dR},s})$
lie in the subspace
$t_{\text{dR}}(x)\in \text{End}_{C(L)}(\boldsymbol{H}_{\text{dR},s})$
lie in the subspace
![]() $\boldsymbol{V}_{\text{dR},s}$
.
$\boldsymbol{V}_{\text{dR},s}$
.
If
![]() $s$
is a geometric point of characteristic
$s$
is a geometric point of characteristic
![]() $p$
, then
$p$
, then
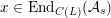 $x\in \text{End}_{C(L)}({\mathcal{A}}_{s})$
is special if and only if its crystalline realization lies in (2.15). This implies that the
$x\in \text{End}_{C(L)}({\mathcal{A}}_{s})$
is special if and only if its crystalline realization lies in (2.15). This implies that the
![]() $\ell$
-adic étale realization lies in (2.15) for all
$\ell$
-adic étale realization lies in (2.15) for all
![]() $\ell$
different from the characteristic of
$\ell$
different from the characteristic of
![]() $s$
; cf. [Reference Madapusi PeraMad16, (5.22)].
$s$
; cf. [Reference Madapusi PeraMad16, (5.22)].
Fix an element
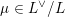 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
and a prime
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
and a prime
![]() $p>0$
, and suppose that we are given an embedding
$p>0$
, and suppose that we are given an embedding
 $L{\hookrightarrow}L^{\diamond }$
of maximal quadratic lattices with
$L{\hookrightarrow}L^{\diamond }$
of maximal quadratic lattices with
![]() $L^{\diamond }$
self-dual at
$L^{\diamond }$
self-dual at
![]() $p$
. Let
$p$
. Let
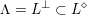 $\unicode[STIX]{x1D6EC}=L^{\bot }\subset L^{\diamond }$
be the subspace of elements orthogonal to
$\unicode[STIX]{x1D6EC}=L^{\bot }\subset L^{\diamond }$
be the subspace of elements orthogonal to
![]() $L$
.
$L$
.
There are canonical isomorphisms
 $$\begin{eqnarray}\displaystyle \mathbb{Z}_{p}\otimes (L^{\vee }/L)\xleftarrow[{}]{\simeq }\mathbb{Z}_{p}\otimes (L^{\diamond }/(L\oplus \unicode[STIX]{x1D6EC}))\xrightarrow[{}]{\simeq }\mathbb{Z}_{p}\otimes (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{Z}_{p}\otimes (L^{\vee }/L)\xleftarrow[{}]{\simeq }\mathbb{Z}_{p}\otimes (L^{\diamond }/(L\oplus \unicode[STIX]{x1D6EC}))\xrightarrow[{}]{\simeq }\mathbb{Z}_{p}\otimes (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}), & & \displaystyle\end{eqnarray}$$
which allow us to view
![]() $\unicode[STIX]{x1D707}_{p}$
as an element of
$\unicode[STIX]{x1D707}_{p}$
as an element of
 $\mathbb{Z}_{p}\otimes (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC})$
. Fix a lift
$\mathbb{Z}_{p}\otimes (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC})$
. Fix a lift
 $\tilde{\unicode[STIX]{x1D707}}_{p}\in \unicode[STIX]{x1D6EC}^{\vee }$
of
$\tilde{\unicode[STIX]{x1D707}}_{p}\in \unicode[STIX]{x1D6EC}^{\vee }$
of
![]() $\unicode[STIX]{x1D707}_{p}$
.
$\unicode[STIX]{x1D707}_{p}$
.
By construction, the map
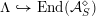 $\unicode[STIX]{x1D6EC}{\hookrightarrow}\text{End}({\mathcal{A}}_{S}^{\diamond })$
from Proposition 2.5.1 factors through an isometric embedding
$\unicode[STIX]{x1D6EC}{\hookrightarrow}\text{End}({\mathcal{A}}_{S}^{\diamond })$
from Proposition 2.5.1 factors through an isometric embedding
 $\unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S}^{\diamond })$
. Via this embedding, we can view
$\unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S}^{\diamond })$
. Via this embedding, we can view
![]() $\tilde{\unicode[STIX]{x1D707}}_{p}$
as an element of
$\tilde{\unicode[STIX]{x1D707}}_{p}$
as an element of
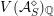 $V({\mathcal{A}}_{S}^{\diamond })_{\mathbb{Q}}$
.
$V({\mathcal{A}}_{S}^{\diamond })_{\mathbb{Q}}$
.
Lemma 2.6.1. The subset
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})_{(p)}=\{x\in V({\mathcal{A}}_{S})_{\mathbb{Q}}:x+\tilde{\unicode[STIX]{x1D707}}_{p}\in V({\mathcal{A}}_{S}^{\diamond })\otimes \mathbb{Z}_{(p)}\}\subset V({\mathcal{A}}_{S})_{\mathbb{Q}}\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})_{(p)}=\{x\in V({\mathcal{A}}_{S})_{\mathbb{Q}}:x+\tilde{\unicode[STIX]{x1D707}}_{p}\in V({\mathcal{A}}_{S}^{\diamond })\otimes \mathbb{Z}_{(p)}\}\subset V({\mathcal{A}}_{S})_{\mathbb{Q}}\end{eqnarray}$$
is functorial in
![]() $S$
, and is independent of the choice of embedding
$S$
, and is independent of the choice of embedding
 $L{\hookrightarrow}L^{\diamond }$
of maximal lattices with
$L{\hookrightarrow}L^{\diamond }$
of maximal lattices with
![]() $L^{\diamond }$
self-dual at
$L^{\diamond }$
self-dual at
![]() $p$
.
$p$
.
Proof. Note that the definition is clearly independent of the choice of lift
![]() $\tilde{\unicode[STIX]{x1D707}}_{p}$
.
$\tilde{\unicode[STIX]{x1D707}}_{p}$
.
The functoriality of the subset is clear, so it only remains to prove the independence from the choice of embedding into a self-dual at
![]() $p$
maximal lattice. For this, as in the proof of Proposition 2.4.5 we can reduce to the case where both
$p$
maximal lattice. For this, as in the proof of Proposition 2.4.5 we can reduce to the case where both
![]() $L$
and
$L$
and
![]() $L^{\diamond }$
are self-dual at
$L^{\diamond }$
are self-dual at
![]() $p$
, where we have to show that the definition using the identity
$p$
, where we have to show that the definition using the identity
![]() $L\rightarrow L$
is equivalent to the one given using the embedding
$L\rightarrow L$
is equivalent to the one given using the embedding
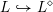 $L{\hookrightarrow}L^{\diamond }$
.
$L{\hookrightarrow}L^{\diamond }$
.
In this case,
![]() $\tilde{\unicode[STIX]{x1D707}}_{p}$
can be chosen to be
$\tilde{\unicode[STIX]{x1D707}}_{p}$
can be chosen to be
![]() $0$
, and we are reduced to checking that an element
$0$
, and we are reduced to checking that an element
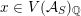 $x\in V({\mathcal{A}}_{S})_{\mathbb{Q}}$
maps into
$x\in V({\mathcal{A}}_{S})_{\mathbb{Q}}$
maps into
 $V({\mathcal{A}}_{S})\otimes \mathbb{Z}_{(p)}$
if and only if it maps into
$V({\mathcal{A}}_{S})\otimes \mathbb{Z}_{(p)}$
if and only if it maps into
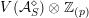 $V({\mathcal{A}}_{S}^{\diamond })\otimes \mathbb{Z}_{(p)}$
. For this, it is enough to verify that the inclusion of abelian groups
$V({\mathcal{A}}_{S}^{\diamond })\otimes \mathbb{Z}_{(p)}$
. For this, it is enough to verify that the inclusion of abelian groups
 $$\begin{eqnarray}V({\mathcal{A}}_{S})\subset V({\mathcal{A}}_{S}^{\diamond })\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{A}}_{S})\subset V({\mathcal{A}}_{S}^{\diamond })\end{eqnarray}$$
maps onto a
![]() $\mathbb{Z}$
-direct summand. However, this follows from the fact that
$\mathbb{Z}$
-direct summand. However, this follows from the fact that
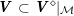 $\boldsymbol{V}\subset \boldsymbol{V}^{\diamond }|_{{\mathcal{M}}}$
is a local direct summand; see Proposition 2.5.1(ii).◻
$\boldsymbol{V}\subset \boldsymbol{V}^{\diamond }|_{{\mathcal{M}}}$
is a local direct summand; see Proposition 2.5.1(ii).◻
Remark 2.6.2. When
![]() $S$
is a scheme over
$S$
is a scheme over
![]() ${\mathcal{M}}[p^{-1}]$
, there is a more intrinsic description of the subset above. Note that the natural action of the compact open subgroup
${\mathcal{M}}[p^{-1}]$
, there is a more intrinsic description of the subset above. Note that the natural action of the compact open subgroup
 $K\subset G(\mathbb{A}_{f})$
on
$K\subset G(\mathbb{A}_{f})$
on
![]() $\widehat{L}^{\diamond }$
preserves
$\widehat{L}^{\diamond }$
preserves
![]() $\widehat{L}$
, and induces the trivial action on all the quotients involved in (2.16). Therefore, over
$\widehat{L}$
, and induces the trivial action on all the quotients involved in (2.16). Therefore, over
![]() ${\mathcal{M}}[p^{-1}]$
, we have a canonical isometry
${\mathcal{M}}[p^{-1}]$
, we have a canonical isometry
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}:\text{}\underline{\mathbb{Z}}_{p}\otimes (L^{\vee }/L)\xrightarrow[{}]{\simeq }\boldsymbol{V}_{p}^{\vee }/\boldsymbol{V}_{p}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}:\text{}\underline{\mathbb{Z}}_{p}\otimes (L^{\vee }/L)\xrightarrow[{}]{\simeq }\boldsymbol{V}_{p}^{\vee }/\boldsymbol{V}_{p}\end{eqnarray}$$
of
![]() $p$
-torsion étale sheaves. In particular, by taking the pre-image of
$p$
-torsion étale sheaves. In particular, by taking the pre-image of
 $\unicode[STIX]{x1D6FC}_{p}(1\otimes \unicode[STIX]{x1D707}_{p})$
in
$\unicode[STIX]{x1D6FC}_{p}(1\otimes \unicode[STIX]{x1D707}_{p})$
in
![]() $\boldsymbol{V}_{p}^{\vee }$
, we obtain a subsheaf of sets
$\boldsymbol{V}_{p}^{\vee }$
, we obtain a subsheaf of sets
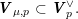 $\boldsymbol{V}_{\unicode[STIX]{x1D707},p}\subset \boldsymbol{V}_{p}^{\vee }.$
The subset
$\boldsymbol{V}_{\unicode[STIX]{x1D707},p}\subset \boldsymbol{V}_{p}^{\vee }.$
The subset
 $V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})_{(p)}$
consists precisely of those elements of
$V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})_{(p)}$
consists precisely of those elements of
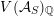 $V({\mathcal{A}}_{S})_{\mathbb{Q}}$
, whose
$V({\mathcal{A}}_{S})_{\mathbb{Q}}$
, whose
![]() $p$
-adic realizations land in
$p$
-adic realizations land in
![]() $\boldsymbol{V}_{\unicode[STIX]{x1D707},p}$
.
$\boldsymbol{V}_{\unicode[STIX]{x1D707},p}$
.
For a scheme
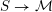 $S\rightarrow {\mathcal{M}}$
, we now define a natural subset
$S\rightarrow {\mathcal{M}}$
, we now define a natural subset
 $V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})\subset V({\mathcal{A}}_{S})_{\mathbb{Q}}$
by setting
$V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})\subset V({\mathcal{A}}_{S})_{\mathbb{Q}}$
by setting
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})=\mathop{\bigcap }_{p}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})_{(p)}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})=\mathop{\bigcap }_{p}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})_{(p)}.\end{eqnarray}$$
We record some properties of these spaces.
Proposition 2.6.3. (i) If
![]() $\unicode[STIX]{x1D707}=0$
, then
$\unicode[STIX]{x1D707}=0$
, then
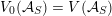 $V_{0}({\mathcal{A}}_{S})=V({\mathcal{A}}_{S})$
.
$V_{0}({\mathcal{A}}_{S})=V({\mathcal{A}}_{S})$
.
(ii) Each
 $x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})$
, viewed as an element of
$x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})$
, viewed as an element of
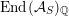 $\text{End}({\mathcal{A}}_{S})_{\mathbb{Q}}$
, shifts the grading on
$\text{End}({\mathcal{A}}_{S})_{\mathbb{Q}}$
, shifts the grading on
![]() ${\mathcal{A}}_{S}$
and commutes with the right action of
${\mathcal{A}}_{S}$
and commutes with the right action of
![]() $C(L)$
.
$C(L)$
.
(iii) Moreover,
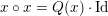 $x\circ x=Q(x)\cdot \text{Id}$
for some non-negative
$x\circ x=Q(x)\cdot \text{Id}$
for some non-negative
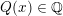 $Q(x)\in \mathbb{Q}$
satisfying
$Q(x)\in \mathbb{Q}$
satisfying
 $$\begin{eqnarray}\displaystyle Q(x)\equiv Q(\unicode[STIX]{x1D707})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q(x)\equiv Q(\unicode[STIX]{x1D707})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}), & & \displaystyle\end{eqnarray}$$
and
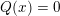 $Q(x)=0$
if and only if
$Q(x)=0$
if and only if
![]() $x=0$
.
$x=0$
.
Proof. The first statement was shown in the course of the proof of Lemma 2.6.1, where we found that
![]() $V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})$
is a subset of
$V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})$
is a subset of
 $V({\mathcal{A}}_{S})\otimes \mathbb{Z}_{(p)}$
whenever
$V({\mathcal{A}}_{S})\otimes \mathbb{Z}_{(p)}$
whenever
![]() $\unicode[STIX]{x1D707}_{p}=0$
.
$\unicode[STIX]{x1D707}_{p}=0$
.
The second follows from the construction of the space
![]() $V({\mathcal{A}}_{S})$
, and the fact that the endomorphisms
$V({\mathcal{A}}_{S})$
, and the fact that the endomorphisms
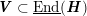 $\boldsymbol{V}\subset \text{}\underline{\text{End}}(\boldsymbol{H})$
of (2.15) are grade shifting and commute with
$\boldsymbol{V}\subset \text{}\underline{\text{End}}(\boldsymbol{H})$
of (2.15) are grade shifting and commute with
![]() $C(L)$
.
$C(L)$
.
For the third, we first check that the quadratic form
![]() $Q(x)$
is positive definite. But this follows from the existence of a polarization on
$Q(x)$
is positive definite. But this follows from the existence of a polarization on
![]() ${\mathcal{A}}_{S}$
such that every element of
${\mathcal{A}}_{S}$
such that every element of
 $V({\mathcal{A}}_{S})\otimes \mathbb{Q}$
is fixed under the corresponding Rosati involution; see the proof of [Reference Madapusi PeraMad16, (5.12)]. We also have to show that, for each prime
$V({\mathcal{A}}_{S})\otimes \mathbb{Q}$
is fixed under the corresponding Rosati involution; see the proof of [Reference Madapusi PeraMad16, (5.12)]. We also have to show that, for each prime
![]() $p$
, we have
$p$
, we have
 $$\begin{eqnarray}Q(x)\equiv Q(\unicode[STIX]{x1D707})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}).\end{eqnarray}$$
$$\begin{eqnarray}Q(x)\equiv Q(\unicode[STIX]{x1D707})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}).\end{eqnarray}$$
We can assume that we have chosen an embedding
 $L{\hookrightarrow}L^{\diamond }$
with
$L{\hookrightarrow}L^{\diamond }$
with
![]() $L^{\diamond }$
self-dual at
$L^{\diamond }$
self-dual at
![]() $p$
. In this case, with
$p$
. In this case, with
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $\tilde{\unicode[STIX]{x1D707}}_{p}$
as in Lemma 2.6.1, we find that, in terms of the quadratic form
$\tilde{\unicode[STIX]{x1D707}}_{p}$
as in Lemma 2.6.1, we find that, in terms of the quadratic form
![]() $Q^{\diamond }$
on
$Q^{\diamond }$
on
![]() $V({\mathcal{A}}_{S}^{\diamond })$
, we have
$V({\mathcal{A}}_{S}^{\diamond })$
, we have
 $$\begin{eqnarray}Q^{\diamond }(x+\tilde{\unicode[STIX]{x1D707}}_{p})\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}).\end{eqnarray}$$
$$\begin{eqnarray}Q^{\diamond }(x+\tilde{\unicode[STIX]{x1D707}}_{p})\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}).\end{eqnarray}$$
It can be checked using Proposition 2.5.1(ii) that
![]() $V({\mathcal{A}}_{S})$
is orthogonal to
$V({\mathcal{A}}_{S})$
is orthogonal to
![]() $\tilde{\unicode[STIX]{x1D707}}_{p}$
as a subspace of
$\tilde{\unicode[STIX]{x1D707}}_{p}$
as a subspace of
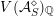 $V({\mathcal{A}}_{S}^{\diamond })_{\mathbb{Q}}$
. Therefore, we have
$V({\mathcal{A}}_{S}^{\diamond })_{\mathbb{Q}}$
. Therefore, we have
 $$\begin{eqnarray}\displaystyle Q(x)=Q^{\diamond }(x)\equiv -Q^{\diamond }(\tilde{\unicode[STIX]{x1D707}}_{p})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q(x)=Q^{\diamond }(x)\equiv -Q^{\diamond }(\tilde{\unicode[STIX]{x1D707}}_{p})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}). & & \displaystyle\end{eqnarray}$$
On the other hand, recall that
 $\tilde{\unicode[STIX]{x1D707}}_{p}\subset \unicode[STIX]{x1D6EC}^{\vee }$
was defined to be a lift of the image of
$\tilde{\unicode[STIX]{x1D707}}_{p}\subset \unicode[STIX]{x1D6EC}^{\vee }$
was defined to be a lift of the image of
![]() $\unicode[STIX]{x1D707}_{p}$
under the canonical isomorphism
$\unicode[STIX]{x1D707}_{p}$
under the canonical isomorphism
 $$\begin{eqnarray}(L^{\vee }/L)\otimes \mathbb{Z}_{(p)}\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}\otimes \mathbb{Z}_{(p)}\end{eqnarray}$$
$$\begin{eqnarray}(L^{\vee }/L)\otimes \mathbb{Z}_{(p)}\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}\otimes \mathbb{Z}_{(p)}\end{eqnarray}$$
associated with the embedding
 $L{\hookrightarrow}L^{\diamond }$
. In other words, if
$L{\hookrightarrow}L^{\diamond }$
. In other words, if
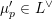 $\unicode[STIX]{x1D707}_{p}^{\prime }\in L^{\vee }$
is any lift of
$\unicode[STIX]{x1D707}_{p}^{\prime }\in L^{\vee }$
is any lift of
![]() $\unicode[STIX]{x1D707}_{p}$
, we have
$\unicode[STIX]{x1D707}_{p}$
, we have
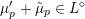 $\unicode[STIX]{x1D707}_{p}^{\prime }+\tilde{\unicode[STIX]{x1D707}}_{p}\in L^{\diamond }$
. Hence, arguing just as in the previous paragraph, we find
$\unicode[STIX]{x1D707}_{p}^{\prime }+\tilde{\unicode[STIX]{x1D707}}_{p}\in L^{\diamond }$
. Hence, arguing just as in the previous paragraph, we find
 $$\begin{eqnarray}\displaystyle Q(\unicode[STIX]{x1D707}_{p}^{\prime })\equiv -Q^{\diamond }(\tilde{\unicode[STIX]{x1D707}}_{p})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q(\unicode[STIX]{x1D707}_{p}^{\prime })\equiv -Q^{\diamond }(\tilde{\unicode[STIX]{x1D707}}_{p})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}_{(p)}). & & \displaystyle\end{eqnarray}$$
As before, suppose that we are given an embedding of maximal quadratic spaces
 $L_{0}{\hookrightarrow}L$
with
$L_{0}{\hookrightarrow}L$
with
 $\unicode[STIX]{x1D6EC}=L_{0}^{\bot }\subset L$
. In particular the inclusion
$\unicode[STIX]{x1D6EC}=L_{0}^{\bot }\subset L$
. In particular the inclusion
 $L^{\vee }{\hookrightarrow}L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
induces an injection
$L^{\vee }{\hookrightarrow}L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
induces an injection
 $$\begin{eqnarray}L^{\vee }/(L_{0}\oplus \unicode[STIX]{x1D6EC}){\hookrightarrow}(L_{0}^{\vee }/L_{0})\oplus (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
$$\begin{eqnarray}L^{\vee }/(L_{0}\oplus \unicode[STIX]{x1D6EC}){\hookrightarrow}(L_{0}^{\vee }/L_{0})\oplus (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
Fix an
![]() ${\mathcal{M}}_{0}$
-scheme
${\mathcal{M}}_{0}$
-scheme
 $S\rightarrow {\mathcal{M}}_{0}$
. Then, by construction, the map
$S\rightarrow {\mathcal{M}}_{0}$
. Then, by construction, the map
 $\unicode[STIX]{x1D6EC}{\hookrightarrow}\text{End}({\mathcal{A}}_{S})$
from Proposition 2.5.1 factors through an isometric embedding
$\unicode[STIX]{x1D6EC}{\hookrightarrow}\text{End}({\mathcal{A}}_{S})$
from Proposition 2.5.1 factors through an isometric embedding
 $\unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S})$
.
$\unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S})$
.
Proposition 2.6.4. Fix an
![]() ${\mathcal{M}}_{0}$
-scheme
${\mathcal{M}}_{0}$
-scheme
 $S\rightarrow {\mathcal{M}}_{0}$
.
$S\rightarrow {\mathcal{M}}_{0}$
.
-
(i) There is a canonical isometry
(2.20)where here $$\begin{eqnarray}\displaystyle V({\mathcal{A}}_{0,S})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\bot }\subset V({\mathcal{A}}_{S}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V({\mathcal{A}}_{0,S})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\bot }\subset V({\mathcal{A}}_{S}), & & \displaystyle\end{eqnarray}$$
 $\unicode[STIX]{x1D6EC}^{\bot }$
is calculated inside
$\unicode[STIX]{x1D6EC}^{\bot }$
is calculated inside
 $V({\mathcal{A}}_{S})$
.
$V({\mathcal{A}}_{S})$
.
-
(ii) For every
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
and every
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
and every
 $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
the map (2.20), tensored with
$(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
the map (2.20), tensored with
 $\mathbb{Q}$
, restricts to an injection
$\mathbb{Q}$
, restricts to an injection  $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{A}}_{0,S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}){\hookrightarrow}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S}).\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{A}}_{0,S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}){\hookrightarrow}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S}).\end{eqnarray}$$
-
(iii) The above injections determine a decomposition
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})=\bigsqcup _{(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{A}}_{0,S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})=\bigsqcup _{(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{A}}_{0,S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
Proof. Claim (i) follows from the definitions and Proposition 2.5.1; see also [Reference Madapusi PeraMad16, (7.15)]. In particular, any element
 $x\in V({\mathcal{A}}_{S})\otimes \mathbb{Q}$
admits a decomposition
$x\in V({\mathcal{A}}_{S})\otimes \mathbb{Q}$
admits a decomposition
 $$\begin{eqnarray}x=(x_{0},\unicode[STIX]{x1D708})\in (V({\mathcal{A}}_{0,S})\otimes \mathbb{Q})\times (\unicode[STIX]{x1D6EC}\otimes \mathbb{Q}).\end{eqnarray}$$
$$\begin{eqnarray}x=(x_{0},\unicode[STIX]{x1D708})\in (V({\mathcal{A}}_{0,S})\otimes \mathbb{Q})\times (\unicode[STIX]{x1D6EC}\otimes \mathbb{Q}).\end{eqnarray}$$
Using this decomposition, it is an easy exercise to deduce claims (ii) and (iii) from the definitions. The main input is Lemma 2.6.1, which permits us to study all spaces in question by embedding
![]() $L$
into a maximal quadratic lattice that is self-dual at any given prime
$L$
into a maximal quadratic lattice that is self-dual at any given prime
![]() $p$
.◻
$p$
.◻
2.7 Special divisors
For
 $m\in \mathbb{Q}_{{>}0}$
and
$m\in \mathbb{Q}_{{>}0}$
and
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
, define the special cycle
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
, define the special cycle
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
as the stack over
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
as the stack over
![]() ${\mathcal{M}}$
with functor of points
${\mathcal{M}}$
with functor of points
 $$\begin{eqnarray}\displaystyle {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(S)=\{x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S}):Q(x)=m\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(S)=\{x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S}):Q(x)=m\} & & \displaystyle\end{eqnarray}$$
for any scheme
 $S\rightarrow {\mathcal{M}}$
. Note that, by (2.17), the stack (2.21) is empty unless the image of
$S\rightarrow {\mathcal{M}}$
. Note that, by (2.17), the stack (2.21) is empty unless the image of
![]() $m$
in
$m$
in
![]() $\mathbb{Q}/\mathbb{Z}$
agrees with
$\mathbb{Q}/\mathbb{Z}$
agrees with
![]() $Q(\unicode[STIX]{x1D707})$
.
$Q(\unicode[STIX]{x1D707})$
.
For later purposes we also define the stacks
![]() ${\mathcal{Z}}(0,\unicode[STIX]{x1D707})$
in exactly the same way. As the only special endomorphism
${\mathcal{Z}}(0,\unicode[STIX]{x1D707})$
in exactly the same way. As the only special endomorphism
![]() $x$
with
$x$
with
 $Q(x)=0$
is the zero map, we have
$Q(x)=0$
is the zero map, we have
 $$\begin{eqnarray}{\mathcal{Z}}(0,\unicode[STIX]{x1D707})=\left\{\begin{array}{@{}ll@{}}\emptyset \quad & \text{if }\unicode[STIX]{x1D707}\neq 0,\\ {\mathcal{M}}\quad & \text{if }\unicode[STIX]{x1D707}=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(0,\unicode[STIX]{x1D707})=\left\{\begin{array}{@{}ll@{}}\emptyset \quad & \text{if }\unicode[STIX]{x1D707}\neq 0,\\ {\mathcal{M}}\quad & \text{if }\unicode[STIX]{x1D707}=0.\end{array}\right.\end{eqnarray}$$
The special cycles behave nicely under pullback by the morphism of Proposition 2.5.1. Indeed, the following is an immediate consequence of Proposition 2.6.4.
Proposition 2.7.1. Suppose that we are given an embedding of maximal quadratic spaces
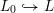 $L_{0}{\hookrightarrow}L$
, and let
$L_{0}{\hookrightarrow}L$
, and let
![]() $\unicode[STIX]{x1D6EC}\subset L$
be the submodule of vectors orthogonal to
$\unicode[STIX]{x1D6EC}\subset L$
be the submodule of vectors orthogonal to
![]() $L_{0}$
. Let
$L_{0}$
. Let
 ${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
be the corresponding morphism of Shimura varieties, as in Proposition 2.5.1. Thus, for any
${\mathcal{M}}_{0}\rightarrow {\mathcal{M}}$
be the corresponding morphism of Shimura varieties, as in Proposition 2.5.1. Thus, for any
 $m\in \mathbb{Q}_{{\geqslant}0}$
and
$m\in \mathbb{Q}_{{\geqslant}0}$
and
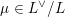 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
there is a special cycle
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
there is a special cycle
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
, and for any
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
, and for any
 $m_{1}\in \mathbb{Q}_{{\geqslant}0}$
and
$m_{1}\in \mathbb{Q}_{{\geqslant}0}$
and
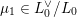 $\unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0}$
there is a special cycle
$\unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0}$
there is a special cycle
 ${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\rightarrow {\mathcal{M}}_{0}$
.
${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\rightarrow {\mathcal{M}}_{0}$
.
Then, there is an isomorphism of
![]() ${\mathcal{M}}_{0}$
-stacks
${\mathcal{M}}_{0}$
-stacks
 $$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{M}}_{0}\simeq \bigsqcup _{\substack{ m_{1}+m_{2}=m \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{M}}_{0}\simeq \bigsqcup _{\substack{ m_{1}+m_{2}=m \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}=\{x\in \unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}:Q(x)=m_{2}\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}=\{x\in \unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}:Q(x)=m_{2}\},\end{eqnarray}$$
and
 ${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
denotes the disjoint union of
${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
denotes the disjoint union of
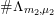 $\#\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
copies of
$\#\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
copies of
 ${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})$
.
${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})$
.
Proposition 2.7.2. For every
 $m\in \mathbb{Q}_{{\geqslant}0}$
and
$m\in \mathbb{Q}_{{\geqslant}0}$
and
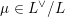 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
, the morphism
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
, the morphism
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
is relatively representable, finite, and unramified.
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
is relatively representable, finite, and unramified.
Proof. Suppose that we have an embedding
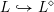 $L{\hookrightarrow}L^{\diamond }$
of maximal quadratic spaces with
$L{\hookrightarrow}L^{\diamond }$
of maximal quadratic spaces with
![]() $\unicode[STIX]{x1D6EC}\subset L^{\diamond }$
the submodule of vectors orthogonal to
$\unicode[STIX]{x1D6EC}\subset L^{\diamond }$
the submodule of vectors orthogonal to
![]() $L$
. Suppose also that
$L$
. Suppose also that
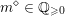 $m^{\diamond }\in \mathbb{Q}_{{\geqslant}0}$
,
$m^{\diamond }\in \mathbb{Q}_{{\geqslant}0}$
,
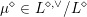 $\unicode[STIX]{x1D707}^{\diamond }\in L^{\diamond ,\vee }/L^{\diamond }$
, and
$\unicode[STIX]{x1D707}^{\diamond }\in L^{\diamond ,\vee }/L^{\diamond }$
, and
 $\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
are such that
$\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
are such that
 $$\begin{eqnarray}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime })\in (\unicode[STIX]{x1D707}^{\diamond }+L^{\diamond })/(L\oplus \unicode[STIX]{x1D6EC}),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime })\in (\unicode[STIX]{x1D707}^{\diamond }+L^{\diamond })/(L\oplus \unicode[STIX]{x1D6EC}),\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle Q(\unicode[STIX]{x1D707}^{\diamond }) & \equiv & \displaystyle m^{\diamond }\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}),\nonumber\\ \displaystyle Q(\unicode[STIX]{x1D707}^{\prime }) & \equiv & \displaystyle m^{\diamond }-m\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q(\unicode[STIX]{x1D707}^{\diamond }) & \equiv & \displaystyle m^{\diamond }\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}),\nonumber\\ \displaystyle Q(\unicode[STIX]{x1D707}^{\prime }) & \equiv & \displaystyle m^{\diamond }-m\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z}).\nonumber\end{eqnarray}$$
Let
 ${\mathcal{Z}}(m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })\rightarrow {\mathcal{M}}^{\diamond }$
be the morphism of stacks associated with the triple
${\mathcal{Z}}(m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })\rightarrow {\mathcal{M}}^{\diamond }$
be the morphism of stacks associated with the triple
 $(L^{\diamond },m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })$
. Suppose that we know that
$(L^{\diamond },m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })$
. Suppose that we know that
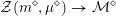 ${\mathcal{Z}}(m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })\rightarrow {\mathcal{M}}^{\diamond }$
is relatively representable, finite, and unramified. Then Proposition 2.7.1 implies that
${\mathcal{Z}}(m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })\rightarrow {\mathcal{M}}^{\diamond }$
is relatively representable, finite, and unramified. Then Proposition 2.7.1 implies that
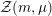 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
can be viewed as a closed and open substack of
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
can be viewed as a closed and open substack of
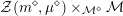 ${\mathcal{Z}}(m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })\times _{{\mathcal{M}}^{\diamond }}{\mathcal{M}}$
, and is thus finite and unramified over
${\mathcal{Z}}(m^{\diamond },\unicode[STIX]{x1D707}^{\diamond })\times _{{\mathcal{M}}^{\diamond }}{\mathcal{M}}$
, and is thus finite and unramified over
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Therefore, by replacing
![]() $L$
with an appropriate choice of
$L$
with an appropriate choice of
![]() $L^{\diamond }$
, one reduces the problem to studying the morphism
$L^{\diamond }$
, one reduces the problem to studying the morphism
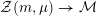 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
under the additional assumption that
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
under the additional assumption that
![]() $L$
is self-dual. Of course this implies that
$L$
is self-dual. Of course this implies that
![]() $\unicode[STIX]{x1D707}=0$
.
$\unicode[STIX]{x1D707}=0$
.
Suppose we have a Noetherian scheme
![]() $S$
and a morphism
$S$
and a morphism
 $S\rightarrow {\mathcal{M}}$
. Recall that the étale sheaf
$S\rightarrow {\mathcal{M}}$
. Recall that the étale sheaf
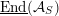 $\text{}\underline{\text{End}}({\mathcal{A}}_{S})$
on
$\text{}\underline{\text{End}}({\mathcal{A}}_{S})$
on
![]() $S$
is represented by a formally unramified scheme over
$S$
is represented by a formally unramified scheme over
![]() $S$
, whose connected components are projective. Formal unramifiedness follows from the rigidity of morphisms of abelian schemes [Reference Mumford, Fogarty and KirwanMFK94, Corollary 6.2]. Representability and projectiveness of the components follows from the theory of Hilbert schemes and the valuative criterion of properness, as in [Reference HidaHida04, §§ 6.1.5 and 6.1.6].
$S$
, whose connected components are projective. Formal unramifiedness follows from the rigidity of morphisms of abelian schemes [Reference Mumford, Fogarty and KirwanMFK94, Corollary 6.2]. Representability and projectiveness of the components follows from the theory of Hilbert schemes and the valuative criterion of properness, as in [Reference HidaHida04, §§ 6.1.5 and 6.1.6].
As in [Reference Madapusi PeraMad16, Proposition 6.13],
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is represented by a formally unramified
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is represented by a formally unramified
![]() $S$
-scheme whose connected components are projective. More precisely, it is isomorphic to a union of connected components of
$S$
-scheme whose connected components are projective. More precisely, it is isomorphic to a union of connected components of
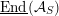 $\text{}\underline{\text{End}}({\mathcal{A}}_{S})$
. This is a consequence of the fact that, for any
$\text{}\underline{\text{End}}({\mathcal{A}}_{S})$
. This is a consequence of the fact that, for any
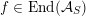 $f\in \text{End}({\mathcal{A}}_{S})$
, the property of being special can be checked at any geometric point of a connected component of
$f\in \text{End}({\mathcal{A}}_{S})$
, the property of being special can be checked at any geometric point of a connected component of
![]() $S$
, and similarly for the property
$S$
, and similarly for the property
 $f\circ f=m$
.
$f\circ f=m$
.
The only thing left to prove is that
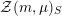 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is of finite type over
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is of finite type over
![]() $S$
. For this, one first notes that, for any projective scheme
$S$
. For this, one first notes that, for any projective scheme
![]() $X$
over
$X$
over
![]() $S$
, the Hilbert scheme parameterizing closed subschemes of
$S$
, the Hilbert scheme parameterizing closed subschemes of
![]() $X$
with fixed Hilbert polynomial is projective, and hence of finite type, over
$X$
with fixed Hilbert polynomial is projective, and hence of finite type, over
![]() $S$
. See [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and VistoliFGIKNV05, § 5.6]. We will realize
$S$
. See [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and VistoliFGIKNV05, § 5.6]. We will realize
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
as a closed subscheme of such a Hilbert scheme with
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
as a closed subscheme of such a Hilbert scheme with
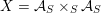 $X={\mathcal{A}}_{S}\times _{S}{\mathcal{A}}_{S}$
.
$X={\mathcal{A}}_{S}\times _{S}{\mathcal{A}}_{S}$
.
Of course, the Hilbert polynomial depends on the choice of an ample line bundle on
![]() $X$
. We will choose our line bundle as follows: Let
$X$
. We will choose our line bundle as follows: Let
![]() ${\mathcal{A}}_{S}^{\vee }$
be the dual abelian scheme, and let
${\mathcal{A}}_{S}^{\vee }$
be the dual abelian scheme, and let
![]() ${\mathcal{P}}$
be the Poincaré line bundle on
${\mathcal{P}}$
be the Poincaré line bundle on
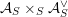 ${\mathcal{A}}_{S}\times _{S}{\mathcal{A}}_{S}^{\vee }$
. As in Proposition 2.6.3, one can choose a polarization
${\mathcal{A}}_{S}\times _{S}{\mathcal{A}}_{S}^{\vee }$
. As in Proposition 2.6.3, one can choose a polarization
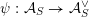 $\unicode[STIX]{x1D713}:{\mathcal{A}}_{S}\rightarrow {\mathcal{A}}_{S}^{\vee }$
such that the associated Rosati involution fixes all special endomorphisms of
$\unicode[STIX]{x1D713}:{\mathcal{A}}_{S}\rightarrow {\mathcal{A}}_{S}^{\vee }$
such that the associated Rosati involution fixes all special endomorphisms of
![]() ${\mathcal{A}}_{S}$
. Define an ample line bundle on
${\mathcal{A}}_{S}$
. Define an ample line bundle on
![]() ${\mathcal{A}}_{S}$
by
${\mathcal{A}}_{S}$
by
 $$\begin{eqnarray}{\mathcal{O}}(1)=(1\times \unicode[STIX]{x1D713})^{\ast }{\mathcal{P}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}(1)=(1\times \unicode[STIX]{x1D713})^{\ast }{\mathcal{P}}.\end{eqnarray}$$
As usual, for any
![]() $n\in \mathbb{Z}$
, set
$n\in \mathbb{Z}$
, set
 ${\mathcal{O}}(n)={\mathcal{O}}(1)^{\otimes n}$
. Define an ample line bundle on
${\mathcal{O}}(n)={\mathcal{O}}(1)^{\otimes n}$
. Define an ample line bundle on
![]() $X$
by
$X$
by
 $p_{1}^{\ast }{\mathcal{O}}(1)\otimes p_{2}^{\ast }{\mathcal{O}}(1)$
, where
$p_{1}^{\ast }{\mathcal{O}}(1)\otimes p_{2}^{\ast }{\mathcal{O}}(1)$
, where
 $p_{i}:X\rightarrow {\mathcal{A}}_{S}$
are the two projections.
$p_{i}:X\rightarrow {\mathcal{A}}_{S}$
are the two projections.
Suppose that
 $s\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is a geometric point. It determines a geometric point
$s\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is a geometric point. It determines a geometric point
![]() $s\rightarrow S$
, along with a special endomorphism
$s\rightarrow S$
, along with a special endomorphism
 $x\in V({\mathcal{A}}_{s})$
with
$x\in V({\mathcal{A}}_{s})$
with
 $Q(x)=m$
. The Hilbert polynomial of the graph
$Q(x)=m$
. The Hilbert polynomial of the graph
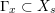 $\unicode[STIX]{x1D6E4}_{x}\subset X_{s}$
is associated with the function
$\unicode[STIX]{x1D6E4}_{x}\subset X_{s}$
is associated with the function
 $$\begin{eqnarray}n\mapsto h^{0}({\mathcal{A}}_{s},{\mathcal{O}}(n)\otimes x^{\ast }{\mathcal{O}}(n)).\end{eqnarray}$$
$$\begin{eqnarray}n\mapsto h^{0}({\mathcal{A}}_{s},{\mathcal{O}}(n)\otimes x^{\ast }{\mathcal{O}}(n)).\end{eqnarray}$$
Since
![]() $x$
is fixed by the Rosati involution, one easily checks that
$x$
is fixed by the Rosati involution, one easily checks that
 $x^{\ast }{\mathcal{O}}(n)={\mathcal{O}}(mn)$
. Therefore the Hilbert polynomial in question is the one attached to
$x^{\ast }{\mathcal{O}}(n)={\mathcal{O}}(mn)$
. Therefore the Hilbert polynomial in question is the one attached to
 $$\begin{eqnarray}n\mapsto h^{0}({\mathcal{A}}_{s},{\mathcal{O}}((m+1)n)),\end{eqnarray}$$
$$\begin{eqnarray}n\mapsto h^{0}({\mathcal{A}}_{s},{\mathcal{O}}((m+1)n)),\end{eqnarray}$$
which clearly depends only on
![]() $m$
.
$m$
.
Sending a point of
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
to the graph of the corresponding special endomorphism defines a closed immersion of
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
to the graph of the corresponding special endomorphism defines a closed immersion of
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
into the Hilbert scheme of closed subschemes of
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
into the Hilbert scheme of closed subschemes of
![]() $X$
with fixed Hilbert polynomial. This proves that
$X$
with fixed Hilbert polynomial. This proves that
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is of finite type over
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{S}$
is of finite type over
![]() $S$
, and completes the proof.◻
$S$
, and completes the proof.◻
Lemma 2.7.3. For any positive
![]() $m$
and any
$m$
and any
![]() $\unicode[STIX]{x1D707}$
, the complex orbifold
$\unicode[STIX]{x1D707}$
, the complex orbifold
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C})$
just defined agrees with (2.4).
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C})$
just defined agrees with (2.4).
Proof. Consider the uniformization
 $M(\mathbb{C})=G(\mathbb{Q})\backslash {\mathcal{D}}\times G(\mathbb{A}_{f})/K$
. By construction, for every
$M(\mathbb{C})=G(\mathbb{Q})\backslash {\mathcal{D}}\times G(\mathbb{A}_{f})/K$
. By construction, for every
 $$\begin{eqnarray}z=(\boldsymbol{h},g)\in {\mathcal{D}}\times G(\mathbb{A}_{f}),\end{eqnarray}$$
$$\begin{eqnarray}z=(\boldsymbol{h},g)\in {\mathcal{D}}\times G(\mathbb{A}_{f}),\end{eqnarray}$$
the fiber of
![]() $\boldsymbol{V}_{\text{Be},\mathbb{Q}}$
at
$\boldsymbol{V}_{\text{Be},\mathbb{Q}}$
at
![]() $z$
is the
$z$
is the
![]() $\mathbb{Q}$
-vector space
$\mathbb{Q}$
-vector space
![]() $V$
with Hodge structure determined by the negative plane
$V$
with Hodge structure determined by the negative plane
![]() $\boldsymbol{h}\subset V_{\mathbb{R}}$
. The
$\boldsymbol{h}\subset V_{\mathbb{R}}$
. The
![]() $(0,0)$
part of
$(0,0)$
part of
![]() $\boldsymbol{V}_{\text{Be},\mathbb{Q},z}$
is
$\boldsymbol{V}_{\text{Be},\mathbb{Q},z}$
is
![]() $V\cap \boldsymbol{h}^{\bot }$
. The fibers of the subsheaves
$V\cap \boldsymbol{h}^{\bot }$
. The fibers of the subsheaves
![]() $\boldsymbol{V}_{\text{Be}}$
and
$\boldsymbol{V}_{\text{Be}}$
and
![]() $\boldsymbol{V}_{\text{Be}}^{\vee }$
of
$\boldsymbol{V}_{\text{Be}}^{\vee }$
of
![]() $\boldsymbol{V}_{\text{Be},\mathbb{Q}}$
at
$\boldsymbol{V}_{\text{Be},\mathbb{Q}}$
at
![]() $z$
are
$z$
are
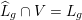 $\widehat{L}_{g}\cap V=L_{g}$
and
$\widehat{L}_{g}\cap V=L_{g}$
and
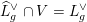 $\widehat{L}_{g}^{\vee }\cap V=L_{g}^{\vee }$
, respectively. Here, using the notation of § 2.2,
$\widehat{L}_{g}^{\vee }\cap V=L_{g}^{\vee }$
, respectively. Here, using the notation of § 2.2,
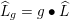 $\widehat{L}_{g}=g\bullet \widehat{L}$
and
$\widehat{L}_{g}=g\bullet \widehat{L}$
and
 $\widehat{L}_{g}^{\vee }=g\bullet \widehat{L}^{\vee }$
.
$\widehat{L}_{g}^{\vee }=g\bullet \widehat{L}^{\vee }$
.
By definition, we now have
 $$\begin{eqnarray}V({\mathcal{A}}_{z})=\text{End}({\mathcal{A}}_{z})\cap \boldsymbol{V}_{\text{Be},z}=(\boldsymbol{V}_{\text{Be},z})^{(0,0)}=L_{g}\cap \boldsymbol{h}^{\bot }.\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{A}}_{z})=\text{End}({\mathcal{A}}_{z})\cap \boldsymbol{V}_{\text{Be},z}=(\boldsymbol{V}_{\text{Be},z})^{(0,0)}=L_{g}\cap \boldsymbol{h}^{\bot }.\end{eqnarray}$$
This proves the lemma for the trivial class
![]() $\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D707}$
.
Now, since
![]() $K$
acts trivially on
$K$
acts trivially on
![]() $L^{\vee }/L$
, there is a canonical isometry
$L^{\vee }/L$
, there is a canonical isometry
 $\boldsymbol{V}_{\text{Be}}^{\vee }/\boldsymbol{V}_{\text{Be}}\simeq L^{\vee }/L\otimes \mathbf{1}$
of torsion sheaves on
$\boldsymbol{V}_{\text{Be}}^{\vee }/\boldsymbol{V}_{\text{Be}}\simeq L^{\vee }/L\otimes \mathbf{1}$
of torsion sheaves on
![]() $M(\mathbb{C})$
. This determines, for every
$M(\mathbb{C})$
. This determines, for every
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
, a locally constant intermediate sheaf of sets
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
, a locally constant intermediate sheaf of sets
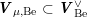 $\boldsymbol{V}_{\unicode[STIX]{x1D707},\text{Be}}\subset \boldsymbol{V}_{\text{Be}}^{\vee }$
whose fiber
$\boldsymbol{V}_{\unicode[STIX]{x1D707},\text{Be}}\subset \boldsymbol{V}_{\text{Be}}^{\vee }$
whose fiber
![]() $\boldsymbol{V}_{\unicode[STIX]{x1D707},\text{Be},z}$
is
$\boldsymbol{V}_{\unicode[STIX]{x1D707},\text{Be},z}$
is
 $\unicode[STIX]{x1D707}_{g}+L_{g}$
. It is not hard to deduce from Remark 2.6.2 that
$\unicode[STIX]{x1D707}_{g}+L_{g}$
. It is not hard to deduce from Remark 2.6.2 that
![]() $V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})$
consists precisely of those elements of
$V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})$
consists precisely of those elements of
 $V({\mathcal{A}}_{z})_{\mathbb{Q}}$
whose Betti realization lands in
$V({\mathcal{A}}_{z})_{\mathbb{Q}}$
whose Betti realization lands in
![]() $\boldsymbol{V}_{\unicode[STIX]{x1D707},\text{Be}}$
. It follows that
$\boldsymbol{V}_{\unicode[STIX]{x1D707},\text{Be}}$
. It follows that
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})=(\unicode[STIX]{x1D707}_{g}+L_{g})\cap \boldsymbol{h}^{\bot },\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})=(\unicode[STIX]{x1D707}_{g}+L_{g})\cap \boldsymbol{h}^{\bot },\end{eqnarray}$$
which proves the lemma for non-trivial
![]() $\unicode[STIX]{x1D707}$
.◻
$\unicode[STIX]{x1D707}$
.◻
We now show that the stacks
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
with
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
with
![]() $m>0$
define (étale local) Cartier divisors on
$m>0$
define (étale local) Cartier divisors on
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Proposition 2.7.4. Suppose
![]() $m>0$
. Then étale locally on the source,
$m>0$
. Then étale locally on the source,
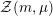 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
defines a Cartier divisor on
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
defines a Cartier divisor on
![]() ${\mathcal{M}}$
. More precisely: around every geometric point of
${\mathcal{M}}$
. More precisely: around every geometric point of
![]() ${\mathcal{M}}$
there is an étale neighborhood
${\mathcal{M}}$
there is an étale neighborhood
![]() $U$
such that for every connected component
$U$
such that for every connected component
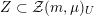 $Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
, the map
$Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
, the map
![]() $Z\rightarrow U$
is a closed immersion defined by a single non-zero equation.
$Z\rightarrow U$
is a closed immersion defined by a single non-zero equation.
Proof. Suppose that we are given a geometric point
![]() $z$
of
$z$
of
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
, corresponding to an element
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
, corresponding to an element
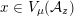 $x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})$
. Let
$x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})$
. Let
 $R={\mathcal{O}}_{{\mathcal{M}},z}$
be the étale local ring of
$R={\mathcal{O}}_{{\mathcal{M}},z}$
be the étale local ring of
![]() ${\mathcal{M}}$
at
${\mathcal{M}}$
at
![]() $z$
. Since
$z$
. Since
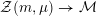 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
is unramified, it follows that
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
is unramified, it follows that
 $$\begin{eqnarray}{\mathcal{O}}_{{\mathcal{Z}}(m,\unicode[STIX]{x1D707}),z}\xrightarrow[{}]{\simeq }R/J_{x}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{{\mathcal{Z}}(m,\unicode[STIX]{x1D707}),z}\xrightarrow[{}]{\simeq }R/J_{x}\end{eqnarray}$$
for some ideal
![]() $J_{x}\subset R$
. Set
$J_{x}\subset R$
. Set
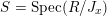 $S=\text{Spec}(R/J_{x})$
, so that
$S=\text{Spec}(R/J_{x})$
, so that
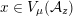 $x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})$
has a universal deformation to
$x\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{z})$
has a universal deformation to
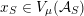 $x_{S}\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})$
.
$x_{S}\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})$
.
Fix an embedding
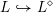 $L{\hookrightarrow}L^{\diamond }$
so that
$L{\hookrightarrow}L^{\diamond }$
so that
![]() $L^{\diamond }$
is maximal and self-dual at
$L^{\diamond }$
is maximal and self-dual at
![]() $p$
of signature
$p$
of signature
![]() $(n^{\diamond },2)$
, and let
$(n^{\diamond },2)$
, and let
![]() $\unicode[STIX]{x1D6EC}\subset L^{\diamond }$
be the subset of vectors orthogonal to
$\unicode[STIX]{x1D6EC}\subset L^{\diamond }$
be the subset of vectors orthogonal to
![]() $L$
. Let
$L$
. Let
 ${\mathcal{A}}^{\diamond }\rightarrow {\mathcal{M}}^{\diamond }$
be the Kuga–Satake abelian scheme over the integral model of the Shimura variety determined by
${\mathcal{A}}^{\diamond }\rightarrow {\mathcal{M}}^{\diamond }$
be the Kuga–Satake abelian scheme over the integral model of the Shimura variety determined by
![]() $L^{\diamond }$
. Proposition 2.6.4 (with
$L^{\diamond }$
. Proposition 2.6.4 (with
![]() ${\mathcal{A}}_{0}$
and
${\mathcal{A}}_{0}$
and
![]() ${\mathcal{A}}$
replaced by
${\mathcal{A}}$
replaced by
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{A}}^{\diamond }$
) gives an inclusion
${\mathcal{A}}^{\diamond }$
) gives an inclusion
 $$\begin{eqnarray}V({\mathcal{A}}_{S})\oplus \unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S}^{\diamond }),\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{A}}_{S})\oplus \unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S}^{\diamond }),\end{eqnarray}$$
which becomes an isomorphism after tensoring with
![]() $\mathbb{Q}$
. There is a
$\mathbb{Q}$
. There is a
![]() $\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}^{\vee }$
such that the vector
$\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}^{\vee }$
such that the vector
 $$\begin{eqnarray}x_{S}^{\diamond }:=x_{S}+\unicode[STIX]{x1D708}\in (V({\mathcal{A}}_{S})\otimes \mathbb{Q})\oplus (\unicode[STIX]{x1D6EC}\otimes \mathbb{Q})\end{eqnarray}$$
$$\begin{eqnarray}x_{S}^{\diamond }:=x_{S}+\unicode[STIX]{x1D708}\in (V({\mathcal{A}}_{S})\otimes \mathbb{Q})\oplus (\unicode[STIX]{x1D6EC}\otimes \mathbb{Q})\end{eqnarray}$$
lies in the
![]() $\mathbb{Z}$
-lattice
$\mathbb{Z}$
-lattice
![]() $V({\mathcal{A}}_{S}^{\diamond })$
. The crystalline realization
$V({\mathcal{A}}_{S}^{\diamond })$
. The crystalline realization
 $t_{\text{crys}}(x^{\diamond })$
allows us to canonically lift the de Rham realization
$t_{\text{crys}}(x^{\diamond })$
allows us to canonically lift the de Rham realization
 $$\begin{eqnarray}t_{\text{dR}}(x_{S}^{\diamond })\in \boldsymbol{V}_{\text{dR},R/J_{x}}^{\diamond }\end{eqnarray}$$
$$\begin{eqnarray}t_{\text{dR}}(x_{S}^{\diamond })\in \boldsymbol{V}_{\text{dR},R/J_{x}}^{\diamond }\end{eqnarray}$$
to an element
 $$\begin{eqnarray}t_{\text{crys}}(x_{S}^{\diamond })\in \boldsymbol{V}_{\text{ dR},R/J_{x}^{2}}^{\diamond },\end{eqnarray}$$
$$\begin{eqnarray}t_{\text{crys}}(x_{S}^{\diamond })\in \boldsymbol{V}_{\text{ dR},R/J_{x}^{2}}^{\diamond },\end{eqnarray}$$
through the divided power thickening
 $S{\hookrightarrow}\text{Spec}(R/J_{x}^{2})$
.
$S{\hookrightarrow}\text{Spec}(R/J_{x}^{2})$
.
It follows from [Reference Madapusi PeraMad16, (5.15)] that
![]() $t_{\text{dR}}(x_{S}^{\diamond })$
is orthogonal to
$t_{\text{dR}}(x_{S}^{\diamond })$
is orthogonal to
![]() $\boldsymbol{V}_{\text{dR},S}^{\diamond ,1}$
. Thus, if
$\boldsymbol{V}_{\text{dR},S}^{\diamond ,1}$
. Thus, if
 $$\begin{eqnarray}\unicode[STIX]{x1D714}\in \boldsymbol{V}_{\text{dR},R/J_{x}^{2}}^{1}\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR},R/J_{x}^{2}}^{\diamond ,1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}\in \boldsymbol{V}_{\text{dR},R/J_{x}^{2}}^{1}\xrightarrow[{}]{\simeq }\boldsymbol{V}_{\text{dR},R/J_{x}^{2}}^{\diamond ,1}\end{eqnarray}$$
is an
![]() $R$
-module generator, we obtain an element
$R$
-module generator, we obtain an element
 $\big[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S}^{\diamond })\big]\in J_{x}/J_{x}^{2}$
using the pairing on
$\big[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S}^{\diamond })\big]\in J_{x}/J_{x}^{2}$
using the pairing on
![]() $\boldsymbol{V}_{\text{dR}}^{\diamond }$
. In fact, Grothendieck–Messing theory [Reference Madapusi PeraMad16, (5.17)] shows that
$\boldsymbol{V}_{\text{dR}}^{\diamond }$
. In fact, Grothendieck–Messing theory [Reference Madapusi PeraMad16, (5.17)] shows that
 $[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S}^{\diamond })]$
generates
$[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S}^{\diamond })]$
generates
![]() $J_{x}/J_{x}^{2}$
. The element
$J_{x}/J_{x}^{2}$
. The element
 $$\begin{eqnarray}t_{\text{crys}}(x_{S}):=t_{\text{crys}}(x_{S}^{\diamond })-\unicode[STIX]{x1D708}\end{eqnarray}$$
$$\begin{eqnarray}t_{\text{crys}}(x_{S}):=t_{\text{crys}}(x_{S}^{\diamond })-\unicode[STIX]{x1D708}\end{eqnarray}$$
lies in
 $\boldsymbol{V}_{\text{dR},R/J_{x}^{2}}^{\vee }$
, and the orthogonality relation
$\boldsymbol{V}_{\text{dR},R/J_{x}^{2}}^{\vee }$
, and the orthogonality relation
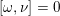 $[\unicode[STIX]{x1D714},\unicode[STIX]{x1D708}]=0$
implies
$[\unicode[STIX]{x1D714},\unicode[STIX]{x1D708}]=0$
implies
 $$\begin{eqnarray}[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S})]=[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S}^{\diamond })].\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S})]=[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S}^{\diamond })].\end{eqnarray}$$
Lemma 2.7.5. The element
 $[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S})]$
generates
$[\unicode[STIX]{x1D714},t_{\text{crys}}(x_{S})]$
generates
![]() $J_{x}/J_{x}^{2}$
as an
$J_{x}/J_{x}^{2}$
as an
![]() $R$
-module. In particular,
$R$
-module. In particular,
![]() $J_{x}\subset R$
is a principal ideal.
$J_{x}\subset R$
is a principal ideal.
Proof. The discussion above proves the first assertion. The second follows by Nakayama’s lemma. ◻
Proposition 2.7.4 follows immediately from the lemma. ◻
Remark 2.7.6. It follows from Proposition 2.7.4 that
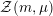 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
is of pure dimension
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
is of pure dimension
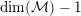 $\dim ({\mathcal{M}})-1$
. The morphism to
$\dim ({\mathcal{M}})-1$
. The morphism to
![]() ${\mathcal{M}}$
is not itself a closed immersion, but nevertheless
${\mathcal{M}}$
is not itself a closed immersion, but nevertheless
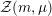 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
defines a Cartier divisor on
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
defines a Cartier divisor on
![]() ${\mathcal{M}}$
, as in [Reference Bruinier, Howard and YangBHY15, § 3.1].
${\mathcal{M}}$
, as in [Reference Bruinier, Howard and YangBHY15, § 3.1].
3 Harmonic modular forms and special divisors
Fix a maximal quadratic space
![]() $L$
over
$L$
over
![]() $\mathbb{Z}$
of signature
$\mathbb{Z}$
of signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n\geqslant 1$
, set
$n\geqslant 1$
, set
 $V=L_{\mathbb{Q}}$
, and let
$V=L_{\mathbb{Q}}$
, and let
 ${\mathcal{M}}\rightarrow \text{Spec}(\mathbb{Z})$
be the corresponding integral model of the Shimura variety (2.3) defined in § 2.
${\mathcal{M}}\rightarrow \text{Spec}(\mathbb{Z})$
be the corresponding integral model of the Shimura variety (2.3) defined in § 2.
This section is a rapid review of some results and constructions of Bruinier [Reference BruinierBru02], Bruinier and Funke [Reference Bruinier and FunkeBF04], and Bruinier and Yang [Reference Bruinier and YangBY09]. In particular, we recall the construction of a divisor
![]() ${\mathcal{Z}}(f)$
and a Green function
${\mathcal{Z}}(f)$
and a Green function
![]() $\unicode[STIX]{x1D6F7}(f)$
on
$\unicode[STIX]{x1D6F7}(f)$
on
![]() ${\mathcal{M}}$
from a harmonic weak Maass form
${\mathcal{M}}$
from a harmonic weak Maass form
![]() $f$
.
$f$
.
3.1 Vector valued modular forms
Let
![]() $\mathfrak{S}_{L}$
be the (finite-dimensional) space of
$\mathfrak{S}_{L}$
be the (finite-dimensional) space of
![]() $\mathbb{C}$
-valued functions on
$\mathbb{C}$
-valued functions on
![]() $L^{\vee }/L$
. As in [Reference Bruinier and YangBY09] there is a Weil representation
$L^{\vee }/L$
. As in [Reference Bruinier and YangBY09] there is a Weil representation
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{L}:\widetilde{\text{SL}}_{2}(\mathbb{Z})\rightarrow \text{Aut}_{\mathbb{C}}(\mathfrak{S}_{L}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{L}:\widetilde{\text{SL}}_{2}(\mathbb{Z})\rightarrow \text{Aut}_{\mathbb{C}}(\mathfrak{S}_{L}),\end{eqnarray}$$
where
![]() $\widetilde{\text{SL}}_{2}(\mathbb{Z})$
is the metaplectic double cover of
$\widetilde{\text{SL}}_{2}(\mathbb{Z})$
is the metaplectic double cover of
![]() $\text{SL}_{2}(\mathbb{Z})$
. Define the conjugate action
$\text{SL}_{2}(\mathbb{Z})$
. Define the conjugate action
![]() $\overline{\unicode[STIX]{x1D714}}_{L}$
by
$\overline{\unicode[STIX]{x1D714}}_{L}$
by
 $\overline{\unicode[STIX]{x1D714}}_{L}(\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D711}=\overline{\unicode[STIX]{x1D714}_{L}(\unicode[STIX]{x1D6FE})\overline{\unicode[STIX]{x1D711}}}.$
We denote by
$\overline{\unicode[STIX]{x1D714}}_{L}(\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D711}=\overline{\unicode[STIX]{x1D714}_{L}(\unicode[STIX]{x1D6FE})\overline{\unicode[STIX]{x1D711}}}.$
We denote by
![]() $\unicode[STIX]{x1D714}_{L}^{\vee }$
the contragredient action of
$\unicode[STIX]{x1D714}_{L}^{\vee }$
the contragredient action of
![]() $\widetilde{\text{SL}}_{2}(\mathbb{Z})$
on the complex linear dual
$\widetilde{\text{SL}}_{2}(\mathbb{Z})$
on the complex linear dual
![]() $\mathfrak{S}_{L}^{\vee }$
.
$\mathfrak{S}_{L}^{\vee }$
.
Remark 3.1.1. Our
![]() $\overline{\unicode[STIX]{x1D714}}_{L}$
is the representation denoted
$\overline{\unicode[STIX]{x1D714}}_{L}$
is the representation denoted
![]() $\unicode[STIX]{x1D70C}_{L}$
in [Reference BorcherdsBor98, Reference BruinierBru02, Reference Bruinier and FunkeBF04, Reference Bruinier and YangBY09]. If we denote by
$\unicode[STIX]{x1D70C}_{L}$
in [Reference BorcherdsBor98, Reference BruinierBru02, Reference Bruinier and FunkeBF04, Reference Bruinier and YangBY09]. If we denote by
![]() $-L$
the quadratic space over
$-L$
the quadratic space over
![]() $\mathbb{Z}$
whose underlying
$\mathbb{Z}$
whose underlying
![]() $\mathbb{Z}$
-module is
$\mathbb{Z}$
-module is
![]() $L$
, but endowed with the quadratic form
$L$
, but endowed with the quadratic form
![]() $-Q$
, then
$-Q$
, then
 $\mathfrak{S}_{L}=\mathfrak{S}_{-L}$
as vector spaces, but
$\mathfrak{S}_{L}=\mathfrak{S}_{-L}$
as vector spaces, but
 $\unicode[STIX]{x1D714}_{L}=\unicode[STIX]{x1D70C}_{-L}$
.
$\unicode[STIX]{x1D714}_{L}=\unicode[STIX]{x1D70C}_{-L}$
.
For a half-integer
![]() $k$
, denote by
$k$
, denote by
![]() $H_{k}(\unicode[STIX]{x1D714}_{L})$
the
$H_{k}(\unicode[STIX]{x1D714}_{L})$
the
![]() $\mathbb{C}$
-vector space of
$\mathbb{C}$
-vector space of
![]() $\mathfrak{S}_{L}$
-valued harmonic weak Maass forms of weight
$\mathfrak{S}_{L}$
-valued harmonic weak Maass forms of weight
![]() $k$
and representation
$k$
and representation
![]() $\unicode[STIX]{x1D714}_{L}$
, in the senseFootnote
2
of [Reference Bruinier and YangBY09, § 3.1]. As in [Reference Bruinier and YangBY09, § 3] there are subspaces
$\unicode[STIX]{x1D714}_{L}$
, in the senseFootnote
2
of [Reference Bruinier and YangBY09, § 3.1]. As in [Reference Bruinier and YangBY09, § 3] there are subspaces
 $$\begin{eqnarray}S_{k}(\unicode[STIX]{x1D714}_{L})\subset M_{k}^{!}(\unicode[STIX]{x1D714}_{L})\subset H_{k}(\unicode[STIX]{x1D714}_{L})\end{eqnarray}$$
$$\begin{eqnarray}S_{k}(\unicode[STIX]{x1D714}_{L})\subset M_{k}^{!}(\unicode[STIX]{x1D714}_{L})\subset H_{k}(\unicode[STIX]{x1D714}_{L})\end{eqnarray}$$
of cusp forms and weakly modular forms. Define similar spaces of modular forms for the representation
![]() $\overline{\unicode[STIX]{x1D714}}_{L}$
. Bruinier and Funke [Reference Bruinier and FunkeBF04] have defined a differential operator
$\overline{\unicode[STIX]{x1D714}}_{L}$
. Bruinier and Funke [Reference Bruinier and FunkeBF04] have defined a differential operator
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}:H_{k}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{2-k}(\overline{\unicode[STIX]{x1D714}}_{L}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}:H_{k}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{2-k}(\overline{\unicode[STIX]{x1D714}}_{L}) & & \displaystyle\end{eqnarray}$$
by
 $\unicode[STIX]{x1D709}(f)=2iv^{k}\overline{(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70F}})}$
, where
$\unicode[STIX]{x1D709}(f)=2iv^{k}\overline{(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70F}})}$
, where
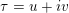 $\unicode[STIX]{x1D70F}=u+iv$
is the variable on the upper half-plane, and have proved the exactness of the sequence
$\unicode[STIX]{x1D70F}=u+iv$
is the variable on the upper half-plane, and have proved the exactness of the sequence
 $$\begin{eqnarray}0\rightarrow M_{k}^{!}(\unicode[STIX]{x1D714}_{L})\rightarrow H_{k}(\unicode[STIX]{x1D714}_{L})\xrightarrow[{}]{\unicode[STIX]{x1D709}}S_{2-k}(\overline{\unicode[STIX]{x1D714}}_{L})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M_{k}^{!}(\unicode[STIX]{x1D714}_{L})\rightarrow H_{k}(\unicode[STIX]{x1D714}_{L})\xrightarrow[{}]{\unicode[STIX]{x1D709}}S_{2-k}(\overline{\unicode[STIX]{x1D714}}_{L})\rightarrow 0.\end{eqnarray}$$
Every
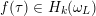 $f(\unicode[STIX]{x1D70F})\in H_{k}(\unicode[STIX]{x1D714}_{L})$
has an associated formal
$f(\unicode[STIX]{x1D70F})\in H_{k}(\unicode[STIX]{x1D714}_{L})$
has an associated formal
![]() $q$
-expansion
$q$
-expansion
 $$\begin{eqnarray}f^{+}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\substack{ m\in \mathbb{Q} \\ -\infty \ll m}}c_{f}^{+}(m)\cdot q^{m},\end{eqnarray}$$
$$\begin{eqnarray}f^{+}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\substack{ m\in \mathbb{Q} \\ -\infty \ll m}}c_{f}^{+}(m)\cdot q^{m},\end{eqnarray}$$
called the holomorphic part of
![]() $f$
, with
$f$
, with
 $c_{f}^{+}(m)\in \mathfrak{S}_{L}$
. The delta functions
$c_{f}^{+}(m)\in \mathfrak{S}_{L}$
. The delta functions
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$
at elements
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}$
at elements
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
form a basis for
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
form a basis for
![]() $\mathfrak{S}_{L}$
, and so each coefficient
$\mathfrak{S}_{L}$
, and so each coefficient
![]() $c_{f}^{+}(m)$
can be decomposed as a sum
$c_{f}^{+}(m)$
can be decomposed as a sum
 $$\begin{eqnarray}c_{f}^{+}(m)=\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\vee }/L}c_{f}^{+}(m,\unicode[STIX]{x1D707})\cdot \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}\end{eqnarray}$$
$$\begin{eqnarray}c_{f}^{+}(m)=\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\vee }/L}c_{f}^{+}(m,\unicode[STIX]{x1D707})\cdot \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}\end{eqnarray}$$
with
 $c_{f}^{+}(m,\unicode[STIX]{x1D707})\in \mathbb{C}$
. The transformation laws satisfied by
$c_{f}^{+}(m,\unicode[STIX]{x1D707})\in \mathbb{C}$
. The transformation laws satisfied by
![]() $f$
imply that
$f$
imply that
 $$\begin{eqnarray}c_{f}^{+}(m,\unicode[STIX]{x1D707})=c_{f}^{+}(m,-\unicode[STIX]{x1D707}),\end{eqnarray}$$
$$\begin{eqnarray}c_{f}^{+}(m,\unicode[STIX]{x1D707})=c_{f}^{+}(m,-\unicode[STIX]{x1D707}),\end{eqnarray}$$
and also that
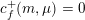 $c_{f}^{+}(m,\unicode[STIX]{x1D707})=0$
, unless the image of
$c_{f}^{+}(m,\unicode[STIX]{x1D707})=0$
, unless the image of
![]() $m$
in
$m$
in
![]() $\mathbb{Q}/\mathbb{Z}$
is equal to
$\mathbb{Q}/\mathbb{Z}$
is equal to
![]() $-Q(\unicode[STIX]{x1D707})$
.
$-Q(\unicode[STIX]{x1D707})$
.
3.2 Divisors and Green functions
Suppose we are given a harmonic weak Maass form
 $$\begin{eqnarray}f(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\end{eqnarray}$$
$$\begin{eqnarray}f(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\end{eqnarray}$$
having integral principal part, in the sense that
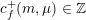 $c_{f}^{+}(m,\unicode[STIX]{x1D707})\in \mathbb{Z}$
for all
$c_{f}^{+}(m,\unicode[STIX]{x1D707})\in \mathbb{Z}$
for all
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
and all
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
and all
![]() $m<0$
. Define a divisor on
$m<0$
. Define a divisor on
![]() ${\mathcal{M}}$
by
${\mathcal{M}}$
by
 $$\begin{eqnarray}\displaystyle {\mathcal{Z}}(f)=\mathop{\sum }_{m\in \mathbb{Q}_{{>}0}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\vee }/L}c_{f}^{+}(-m,\unicode[STIX]{x1D707}){\mathcal{Z}}(m,\unicode[STIX]{x1D707}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{Z}}(f)=\mathop{\sum }_{m\in \mathbb{Q}_{{>}0}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\vee }/L}c_{f}^{+}(-m,\unicode[STIX]{x1D707}){\mathcal{Z}}(m,\unicode[STIX]{x1D707}). & & \displaystyle \nonumber\end{eqnarray}$$
Bruinier [Reference BruinierBru02], following ideas of Borcherds [Reference BorcherdsBor98] and Harvey–Moore, constructed a Green function
![]() $\unicode[STIX]{x1D6F7}(f)$
for
$\unicode[STIX]{x1D6F7}(f)$
for
![]() ${\mathcal{Z}}(f)$
as follows (see also [Reference Bruinier and YangBY09, § 4]). Let
${\mathcal{Z}}(f)$
as follows (see also [Reference Bruinier and YangBY09, § 4]). Let
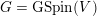 $G=\text{GSpin}(V)$
as in § 2. For each coset
$G=\text{GSpin}(V)$
as in § 2. For each coset
 $g\in G(\mathbb{A}_{f})/K$
there is a Siegel theta function
$g\in G(\mathbb{A}_{f})/K$
there is a Siegel theta function
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z,g):{\mathcal{H}}\times {\mathcal{D}}\rightarrow \mathfrak{S}_{L}^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z,g):{\mathcal{H}}\times {\mathcal{D}}\rightarrow \mathfrak{S}_{L}^{\vee }\end{eqnarray}$$
as in [Reference Bruinier and YangBY09, (2.4)], which is
![]() $\unicode[STIX]{x1D6E4}_{g}$
-invariant in the variable
$\unicode[STIX]{x1D6E4}_{g}$
-invariant in the variable
![]() $z\in {\mathcal{D}}$
, and transforms in the variable
$z\in {\mathcal{D}}$
, and transforms in the variable
 $\unicode[STIX]{x1D70F}=u+iv\in {\mathcal{H}}$
like a modular form of representation
$\unicode[STIX]{x1D70F}=u+iv\in {\mathcal{H}}$
like a modular form of representation
![]() $\unicode[STIX]{x1D714}_{L}^{\vee }$
.
$\unicode[STIX]{x1D714}_{L}^{\vee }$
.
The regularized theta integral
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(f,z,g)=\int _{{\mathcal{F}}}^{\text{reg}}\{f(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z,g)\}\frac{du\,dv}{v^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(f,z,g)=\int _{{\mathcal{F}}}^{\text{reg}}\{f(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z,g)\}\frac{du\,dv}{v^{2}}\end{eqnarray}$$
of [Reference Bruinier and YangBY09, (4.7)] defines a
![]() $\unicode[STIX]{x1D6E4}_{g}$
-invariant function on
$\unicode[STIX]{x1D6E4}_{g}$
-invariant function on
![]() ${\mathcal{D}}$
, where
${\mathcal{D}}$
, where
 $$\begin{eqnarray}\{\cdot ,\cdot \}:\mathfrak{S}_{L}\times \mathfrak{S}_{L}^{\vee }\rightarrow \mathbb{C}\end{eqnarray}$$
$$\begin{eqnarray}\{\cdot ,\cdot \}:\mathfrak{S}_{L}\times \mathfrak{S}_{L}^{\vee }\rightarrow \mathbb{C}\end{eqnarray}$$
is the tautological pairing. Letting
![]() $g$
vary and using the uniformization (2.3) yields a function
$g$
vary and using the uniformization (2.3) yields a function
![]() $\unicode[STIX]{x1D6F7}(f)$
on the orbifold
$\unicode[STIX]{x1D6F7}(f)$
on the orbifold
![]() ${\mathcal{M}}(\mathbb{C})$
. This function is smooth on the complement of
${\mathcal{M}}(\mathbb{C})$
. This function is smooth on the complement of
![]() ${\mathcal{Z}}(f)$
, and has a logarithmic singularity along
${\mathcal{Z}}(f)$
, and has a logarithmic singularity along
![]() ${\mathcal{Z}}(f)$
in the sense that for any local equation
${\mathcal{Z}}(f)$
in the sense that for any local equation
 $\unicode[STIX]{x1D6F9}(z)=0$
defining
$\unicode[STIX]{x1D6F9}(z)=0$
defining
 ${\mathcal{Z}}(f)(\mathbb{C})$
, the function
${\mathcal{Z}}(f)(\mathbb{C})$
, the function
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(f,z)+\text{log}|\unicode[STIX]{x1D6F9}(z)|^{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(f,z)+\text{log}|\unicode[STIX]{x1D6F9}(z)|^{2}\end{eqnarray}$$
on
 ${\mathcal{M}}(\mathbb{C})\smallsetminus {\mathcal{Z}}(f)(\mathbb{C})$
has a smooth extension across
${\mathcal{M}}(\mathbb{C})\smallsetminus {\mathcal{Z}}(f)(\mathbb{C})$
has a smooth extension across
 ${\mathcal{Z}}(f)(\mathbb{C})$
.
${\mathcal{Z}}(f)(\mathbb{C})$
.
Remark 3.2.1. Amazingly, the regularized integral defining
 $\unicode[STIX]{x1D6F7}(f,z,g)$
converges at every point of
$\unicode[STIX]{x1D6F7}(f,z,g)$
converges at every point of
![]() ${\mathcal{D}}$
, and so the function
${\mathcal{D}}$
, and so the function
![]() $\unicode[STIX]{x1D6F7}(f)$
has a well-defined value even at points of the divisor
$\unicode[STIX]{x1D6F7}(f)$
has a well-defined value even at points of the divisor
 ${\mathcal{Z}}(f)(\mathbb{C})$
. The value of the discontinuous function
${\mathcal{Z}}(f)(\mathbb{C})$
. The value of the discontinuous function
![]() $\unicode[STIX]{x1D6F7}(f)$
at the points of
$\unicode[STIX]{x1D6F7}(f)$
at the points of
 ${\mathcal{Z}}(f)(\mathbb{C})$
will play a key role in our later calculations of improper intersection.
${\mathcal{Z}}(f)(\mathbb{C})$
will play a key role in our later calculations of improper intersection.
Among the harmonic weak Maass forms of weight
 $1-n/2$
are the Hejhal–Poincarè series
$1-n/2$
are the Hejhal–Poincarè series
 $$\begin{eqnarray}F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L}),\end{eqnarray}$$
$$\begin{eqnarray}F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L}),\end{eqnarray}$$
defined for all
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
and positive
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
and positive
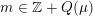 $m\in \mathbb{Z}+Q(\unicode[STIX]{x1D707})$
, which may be rescaled to have holomorphic parts
$m\in \mathbb{Z}+Q(\unicode[STIX]{x1D707})$
, which may be rescaled to have holomorphic parts
 $$\begin{eqnarray}F_{m,\unicode[STIX]{x1D707}}^{+}(\unicode[STIX]{x1D70F})={\textstyle \frac{1}{2}}(q^{-m}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}+q^{-m}\unicode[STIX]{x1D711}_{-\unicode[STIX]{x1D707}})+O(1).\end{eqnarray}$$
$$\begin{eqnarray}F_{m,\unicode[STIX]{x1D707}}^{+}(\unicode[STIX]{x1D70F})={\textstyle \frac{1}{2}}(q^{-m}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}+q^{-m}\unicode[STIX]{x1D711}_{-\unicode[STIX]{x1D707}})+O(1).\end{eqnarray}$$
In particular
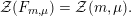 ${\mathcal{Z}}(F_{m,\unicode[STIX]{x1D707}})={\mathcal{Z}}(m,\unicode[STIX]{x1D707}).$
See [Reference BruinierBru02, Definition 1.8 and Proposition 1.10] and [Reference Bruinier and FunkeBF04, Remark 3.10] for details.
${\mathcal{Z}}(F_{m,\unicode[STIX]{x1D707}})={\mathcal{Z}}(m,\unicode[STIX]{x1D707}).$
See [Reference BruinierBru02, Definition 1.8 and Proposition 1.10] and [Reference Bruinier and FunkeBF04, Remark 3.10] for details.
3.3 Eisenstein series and the Rankin–Selberg integral
Fix a rational negative
![]() $2$
-plane
$2$
-plane
![]() $V_{0}\subset V$
, and let
$V_{0}\subset V$
, and let
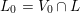 $L_{0}=V_{0}\cap L$
. We assume that
$L_{0}=V_{0}\cap L$
. We assume that
 $C^{+}(L_{0})$
is the maximal order in the quadratic imaginary field
$C^{+}(L_{0})$
is the maximal order in the quadratic imaginary field
![]() $C^{+}(V_{0})$
. This implies, in particular, that
$C^{+}(V_{0})$
. This implies, in particular, that
![]() $L_{0}$
is a maximal quadratic space. Let
$L_{0}$
is a maximal quadratic space. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}=\{x\in L:x\bot L_{0}\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}=\{x\in L:x\bot L_{0}\},\end{eqnarray}$$
so that
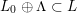 $L_{0}\oplus \unicode[STIX]{x1D6EC}\subset L$
with finite index, and
$L_{0}\oplus \unicode[STIX]{x1D6EC}\subset L$
with finite index, and
![]() $\unicode[STIX]{x1D6EC}$
is also a maximal quadratic space.
$\unicode[STIX]{x1D6EC}$
is also a maximal quadratic space.
Let
![]() $\mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
be the space of complex-valued functions on
$\mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
be the space of complex-valued functions on
![]() $\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
, and let
$\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
, and let
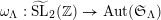 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}:\widetilde{\text{SL}}_{2}(\mathbb{Z})\rightarrow \text{Aut}(\mathfrak{S}_{\unicode[STIX]{x1D6EC}})$
be the Weil representation. Let
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}:\widetilde{\text{SL}}_{2}(\mathbb{Z})\rightarrow \text{Aut}(\mathfrak{S}_{\unicode[STIX]{x1D6EC}})$
be the Weil representation. Let
![]() $\mathfrak{S}_{\unicode[STIX]{x1D6EC}}^{\vee }$
be the complex linear dual of
$\mathfrak{S}_{\unicode[STIX]{x1D6EC}}^{\vee }$
be the complex linear dual of
![]() $\mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
, and for each
$\mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
, and for each
![]() $m\in \mathbb{Q}$
define the representation number
$m\in \mathbb{Q}$
define the representation number
 $R_{\unicode[STIX]{x1D6EC}}(m)\in \mathfrak{S}_{\unicode[STIX]{x1D6EC}}^{\vee }$
by
$R_{\unicode[STIX]{x1D6EC}}(m)\in \mathfrak{S}_{\unicode[STIX]{x1D6EC}}^{\vee }$
by
 $$\begin{eqnarray}R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D711})=\mathop{\sum }_{\substack{ x\in \unicode[STIX]{x1D6EC}^{\vee } \\ Q(x)=m}}\unicode[STIX]{x1D711}(x)\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D711})=\mathop{\sum }_{\substack{ x\in \unicode[STIX]{x1D6EC}^{\vee } \\ Q(x)=m}}\unicode[STIX]{x1D711}(x)\end{eqnarray}$$
for any
![]() $\unicode[STIX]{x1D711}\in \mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
. As in [Reference Bruinier and YangBY09, § 2], these representation numbers are the Fourier coefficients of a vector-valued modular form
$\unicode[STIX]{x1D711}\in \mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
. As in [Reference Bruinier and YangBY09, § 2], these representation numbers are the Fourier coefficients of a vector-valued modular form
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Q}}R_{\unicode[STIX]{x1D6EC}}(m)q^{m}\in M_{n/2}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Q}}R_{\unicode[STIX]{x1D6EC}}(m)q^{m}\in M_{n/2}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee }).\end{eqnarray}$$
Abbreviate
 $R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})=R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}),$
where
$R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})=R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}),$
where
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}\in \mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
is the characteristic function of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}\in \mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
is the characteristic function of
 $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
, so that
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
, so that
 $$\begin{eqnarray}R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})=\#\{x\in \unicode[STIX]{x1D707}+\unicode[STIX]{x1D6EC}:Q(x)=m\}.\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})=\#\{x\in \unicode[STIX]{x1D707}+\unicode[STIX]{x1D6EC}:Q(x)=m\}.\end{eqnarray}$$
Let
![]() $F(\unicode[STIX]{x1D70F})$
be a cuspidal modular form
$F(\unicode[STIX]{x1D70F})$
be a cuspidal modular form
 $$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Q}_{{>}0}}b_{F}(m)q^{m}\in S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L}).\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Q}_{{>}0}}b_{F}(m)q^{m}\in S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L}).\end{eqnarray}$$
Using the natural inclusion
 $L^{\vee }\subset L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
, every function on
$L^{\vee }\subset L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
, every function on
![]() $L^{\vee }$
extends to a function on
$L^{\vee }$
extends to a function on
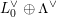 $L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
identically zero off of
$L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
identically zero off of
![]() $L^{\vee }$
. Thus, there is a natural ‘extension by zero’ map
$L^{\vee }$
. Thus, there is a natural ‘extension by zero’ map
 $$\begin{eqnarray}\displaystyle \mathfrak{S}_{L}\rightarrow \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{L}\rightarrow \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}, & & \displaystyle\end{eqnarray}$$
which allows us to view
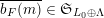 $\overline{b_{F}(m)}\in \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}$
. The inclusion
$\overline{b_{F}(m)}\in \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}$
. The inclusion
 $\unicode[STIX]{x1D6EC}^{\vee }\rightarrow L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
defines a restriction of functions homomorphism
$\unicode[STIX]{x1D6EC}^{\vee }\rightarrow L_{0}^{\vee }\oplus \unicode[STIX]{x1D6EC}^{\vee }$
defines a restriction of functions homomorphism
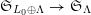 $\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}\rightarrow \mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
. Using this, we can view
$\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}\rightarrow \mathfrak{S}_{\unicode[STIX]{x1D6EC}}$
. Using this, we can view
 $R_{\unicode[STIX]{x1D6EC}}(m)\in \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }$
. This allows us to define the Rankin–Selberg convolution
$R_{\unicode[STIX]{x1D6EC}}(m)\in \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }$
. This allows us to define the Rankin–Selberg convolution
![]() $L$
-function
$L$
-function
 $$\begin{eqnarray}L(F,\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)=\unicode[STIX]{x1D6E4}\biggl(\frac{s+n}{2}\biggr)\mathop{\sum }_{m\in \mathbb{Q}^{+}}\frac{\{\overline{b_{F}(m)},R_{\unicode[STIX]{x1D6EC}}(m)\}}{(4\unicode[STIX]{x1D70B}m)^{(s+n)/2}},\end{eqnarray}$$
$$\begin{eqnarray}L(F,\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)=\unicode[STIX]{x1D6E4}\biggl(\frac{s+n}{2}\biggr)\mathop{\sum }_{m\in \mathbb{Q}^{+}}\frac{\{\overline{b_{F}(m)},R_{\unicode[STIX]{x1D6EC}}(m)\}}{(4\unicode[STIX]{x1D70B}m)^{(s+n)/2}},\end{eqnarray}$$
in which the pairing on the right is the tautological pairing
 $$\begin{eqnarray}\displaystyle \{\cdot ,\cdot \}:\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}\times \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }\rightarrow \mathbb{C}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{\cdot ,\cdot \}:\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}\times \mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }\rightarrow \mathbb{C}. & & \displaystyle\end{eqnarray}$$
Define an
![]() $\mathfrak{S}_{L_{0}}^{\vee }$
-valued Eisenstein series
$\mathfrak{S}_{L_{0}}^{\vee }$
-valued Eisenstein series
 $E_{L_{0}}(\unicode[STIX]{x1D70F},s)$
by
$E_{L_{0}}(\unicode[STIX]{x1D70F},s)$
by
 $$\begin{eqnarray}E_{L_{0}}(\unicode[STIX]{x1D70F},s,\unicode[STIX]{x1D711})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in B\backslash \text{SL}_{2}(\mathbb{Z})}(\unicode[STIX]{x1D714}_{L_{0}}(\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D711})(0)\cdot \frac{\text{Im}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{s/2}}{c\unicode[STIX]{x1D70F}+d}\end{eqnarray}$$
$$\begin{eqnarray}E_{L_{0}}(\unicode[STIX]{x1D70F},s,\unicode[STIX]{x1D711})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in B\backslash \text{SL}_{2}(\mathbb{Z})}(\unicode[STIX]{x1D714}_{L_{0}}(\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D711})(0)\cdot \frac{\text{Im}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{s/2}}{c\unicode[STIX]{x1D70F}+d}\end{eqnarray}$$
for all
 $\unicode[STIX]{x1D711}\in \mathfrak{S}_{L_{0}}$
, where
$\unicode[STIX]{x1D711}\in \mathfrak{S}_{L_{0}}$
, where
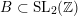 $B\subset \text{SL}_{2}(\mathbb{Z})$
is the subset of upper triangular matrices, and
$B\subset \text{SL}_{2}(\mathbb{Z})$
is the subset of upper triangular matrices, and
![]() $\unicode[STIX]{x1D714}_{L_{0}}$
is the Weil representation of
$\unicode[STIX]{x1D714}_{L_{0}}$
is the Weil representation of
![]() $\text{SL}_{2}(\mathbb{Z})$
on
$\text{SL}_{2}(\mathbb{Z})$
on
![]() $\mathfrak{S}_{L_{0}}$
. The Eisenstein series
$\mathfrak{S}_{L_{0}}$
. The Eisenstein series
 $E_{L_{0}}(\unicode[STIX]{x1D70F},s)$
, which is precisely the incoherent Eisenstein series denoted
$E_{L_{0}}(\unicode[STIX]{x1D70F},s)$
, which is precisely the incoherent Eisenstein series denoted
 $E_{L_{0}}(\unicode[STIX]{x1D70F},s;1)$
in [Reference Bruinier and YangBY09, § 2.2], transforms in the variable
$E_{L_{0}}(\unicode[STIX]{x1D70F},s;1)$
in [Reference Bruinier and YangBY09, § 2.2], transforms in the variable
![]() $\unicode[STIX]{x1D70F}$
like a weight
$\unicode[STIX]{x1D70F}$
like a weight
![]() $1$
modular form of representation
$1$
modular form of representation
![]() $\unicode[STIX]{x1D714}_{L_{0}}^{\vee }$
. It is initially defined for
$\unicode[STIX]{x1D714}_{L_{0}}^{\vee }$
. It is initially defined for
 $\text{Re}(s)\gg 0$
, but has meromorphic continuation to all
$\text{Re}(s)\gg 0$
, but has meromorphic continuation to all
![]() $s$
, and vanishes at
$s$
, and vanishes at
![]() $s=0$
. The usual Rankin–Selberg unfolding method shows that
$s=0$
. The usual Rankin–Selberg unfolding method shows that
 $$\begin{eqnarray}L(F,\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)=\int _{\text{SL}_{2}(\mathbb{Z})\backslash {\mathcal{H}}}\{\overline{F},E_{L_{0}}(s)\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}\frac{du\,dv}{v^{1-n/2}},\end{eqnarray}$$
$$\begin{eqnarray}L(F,\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)=\int _{\text{SL}_{2}(\mathbb{Z})\backslash {\mathcal{H}}}\{\overline{F},E_{L_{0}}(s)\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}\frac{du\,dv}{v^{1-n/2}},\end{eqnarray}$$
where the pairing on the right is (3.3), and we are using the isomorphism
 $$\begin{eqnarray}\mathfrak{S}_{L_{0}}^{\vee }\otimes \mathfrak{S}_{\unicode[STIX]{x1D6EC}}^{\vee }\xrightarrow[{}]{\simeq }\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{L_{0}}^{\vee }\otimes \mathfrak{S}_{\unicode[STIX]{x1D6EC}}^{\vee }\xrightarrow[{}]{\simeq }\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }\end{eqnarray}$$
to view
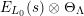 $E_{L_{0}}(s)\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}$
as a smooth modular form valued in
$E_{L_{0}}(s)\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}$
as a smooth modular form valued in
![]() $\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }$
.
$\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}^{\vee }$
.
The central derivative
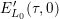 $E_{L_{0}}^{\prime }(\unicode[STIX]{x1D70F},0)$
is a harmonic
$E_{L_{0}}^{\prime }(\unicode[STIX]{x1D70F},0)$
is a harmonic
![]() $\mathfrak{S}_{L_{0}}^{\vee }$
-valued function transforming like a weight
$\mathfrak{S}_{L_{0}}^{\vee }$
-valued function transforming like a weight
![]() $1$
modular form of representation
$1$
modular form of representation
![]() $\unicode[STIX]{x1D714}_{L_{0}}^{\vee }$
. Denote the holomorphic part of the central derivative by
$\unicode[STIX]{x1D714}_{L_{0}}^{\vee }$
. Denote the holomorphic part of the central derivative by
 $$\begin{eqnarray}{\mathcal{E}}_{L_{0}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Q}}a_{L_{0}}^{+}(m)\cdot q^{m}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{L_{0}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Q}}a_{L_{0}}^{+}(m)\cdot q^{m}.\end{eqnarray}$$
We will sometimes abbreviate
 $a_{L_{0}}^{+}(m,\unicode[STIX]{x1D707})=a_{L_{0}}^{+}(m,\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}),$
where
$a_{L_{0}}^{+}(m,\unicode[STIX]{x1D707})=a_{L_{0}}^{+}(m,\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}),$
where
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}\in \mathfrak{S}_{L_{0}}$
is the characteristic function of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D707}}\in \mathfrak{S}_{L_{0}}$
is the characteristic function of
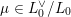 $\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
. Note that our
$\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
. Note that our
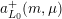 $a_{L_{0}}^{+}(m,\unicode[STIX]{x1D707})$
is exactly the
$a_{L_{0}}^{+}(m,\unicode[STIX]{x1D707})$
is exactly the
![]() $\unicode[STIX]{x1D705}(m,\unicode[STIX]{x1D707})$
of [Reference Bruinier and YangBY09, (2.25)].
$\unicode[STIX]{x1D705}(m,\unicode[STIX]{x1D707})$
of [Reference Bruinier and YangBY09, (2.25)].
Abbreviate
 $\boldsymbol{k}=C^{+}(V_{0})$
, and recall that
$\boldsymbol{k}=C^{+}(V_{0})$
, and recall that
![]() $\boldsymbol{k}$
is a quadratic imaginary field. For any positive rational number
$\boldsymbol{k}$
is a quadratic imaginary field. For any positive rational number
![]() $m$
, define a finite set of primes
$m$
, define a finite set of primes
 $$\begin{eqnarray}\displaystyle \text{Diff}_{L_{0}}(m)=\{\text{primes }p<\infty :L_{0}\otimes _{\mathbb{Z}}\mathbb{Q}_{p}\text{ does not represent }m\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Diff}_{L_{0}}(m)=\{\text{primes }p<\infty :L_{0}\otimes _{\mathbb{Z}}\mathbb{Q}_{p}\text{ does not represent }m\}. & & \displaystyle\end{eqnarray}$$
Note that all primes in this set are non-split in
![]() $\boldsymbol{k}$
. Because
$\boldsymbol{k}$
. Because
![]() $L_{0}$
is negative definite, the set
$L_{0}$
is negative definite, the set
 $\text{Diff}_{L_{0}}(m)$
has odd cardinality; in particular,
$\text{Diff}_{L_{0}}(m)$
has odd cardinality; in particular,
 $\text{Diff}_{L_{0}}(m)\not =\emptyset$
. For
$\text{Diff}_{L_{0}}(m)\not =\emptyset$
. For
 $m\in \mathbb{Z}_{{>}0}$
, set
$m\in \mathbb{Z}_{{>}0}$
, set
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}(m)=\#\{\text{nonzero ideals }\mathfrak{m}\subset {\mathcal{O}}_{\boldsymbol{k}}:\text{N}(\mathfrak{m})=m\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}(m)=\#\{\text{nonzero ideals }\mathfrak{m}\subset {\mathcal{O}}_{\boldsymbol{k}}:\text{N}(\mathfrak{m})=m\}.\end{eqnarray}$$
We will extend
![]() $\unicode[STIX]{x1D70C}$
to a function on all rational numbers by setting
$\unicode[STIX]{x1D70C}$
to a function on all rational numbers by setting
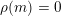 $\unicode[STIX]{x1D70C}(m)=0$
for all
$\unicode[STIX]{x1D70C}(m)=0$
for all
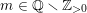 $m\in \mathbb{Q}\smallsetminus \mathbb{Z}_{{>}0}$
.
$m\in \mathbb{Q}\smallsetminus \mathbb{Z}_{{>}0}$
.
The coefficients
![]() $a_{L_{0}}^{+}(m)$
were computed by Schofer [Reference SchoferSch09], but those formulas contain a minor misstatement. This misstatement was corrected when Schofer’s formulas were reproduced in [Reference Bruinier and YangBY09, Theorem 2.6], but the formula for the constant term
$a_{L_{0}}^{+}(m)$
were computed by Schofer [Reference SchoferSch09], but those formulas contain a minor misstatement. This misstatement was corrected when Schofer’s formulas were reproduced in [Reference Bruinier and YangBY09, Theorem 2.6], but the formula for the constant term
![]() $a_{L_{0}}^{+}(0)$
in [Reference Bruinier and YangBY09] is misstated.Footnote
3
We record now the corrected formulas.
$a_{L_{0}}^{+}(0)$
in [Reference Bruinier and YangBY09] is misstated.Footnote
3
We record now the corrected formulas.
Proposition 3.3.1 (Schofer).
Let
![]() $d_{\boldsymbol{k}}$
,
$d_{\boldsymbol{k}}$
,
![]() $h_{\boldsymbol{k}}$
, and
$h_{\boldsymbol{k}}$
, and
![]() $w_{\boldsymbol{k}}$
be the discriminant of
$w_{\boldsymbol{k}}$
be the discriminant of
![]() $\boldsymbol{k}$
, the class number of
$\boldsymbol{k}$
, the class number of
![]() $\boldsymbol{k}$
, and number of roots of unity in
$\boldsymbol{k}$
, and number of roots of unity in
![]() $\boldsymbol{k}$
, respectively, and assume that
$\boldsymbol{k}$
, respectively, and assume that
![]() $d_{\boldsymbol{k}}$
is odd. The coefficients
$d_{\boldsymbol{k}}$
is odd. The coefficients
![]() $a_{L_{0}}^{+}(m)$
are as follows.
$a_{L_{0}}^{+}(m)$
are as follows.
-
(i) The constant term is
Here $$\begin{eqnarray}a_{L_{0}}^{+}(0,\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}(0)\cdot \biggl(\unicode[STIX]{x1D6FE}+\text{log}\biggl|\frac{4\unicode[STIX]{x1D70B}}{d_{\boldsymbol{k}}}\biggr|-2\frac{L^{\prime }(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}{L(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}a_{L_{0}}^{+}(0,\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}(0)\cdot \biggl(\unicode[STIX]{x1D6FE}+\text{log}\biggl|\frac{4\unicode[STIX]{x1D70B}}{d_{\boldsymbol{k}}}\biggr|-2\frac{L^{\prime }(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}{L(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}\biggr).\end{eqnarray}$$
 $\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6E4}^{\prime }(1)$
is the Euler–Mascheroni constant, and
$\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6E4}^{\prime }(1)$
is the Euler–Mascheroni constant, and
 $\unicode[STIX]{x1D712}_{\boldsymbol{k}}$
is the quadratic Dirichlet character associated with
$\unicode[STIX]{x1D712}_{\boldsymbol{k}}$
is the quadratic Dirichlet character associated with
 $\boldsymbol{k}/\mathbb{Q}$
.
$\boldsymbol{k}/\mathbb{Q}$
.
-
(ii) If
 $m>0$
and
$m>0$
and
 $\text{Diff}_{L_{0}}(m)=\{p\}$
for a single prime
$\text{Diff}_{L_{0}}(m)=\{p\}$
for a single prime
 $p$
, then On the right-hand side,
$p$
, then On the right-hand side, $$\begin{eqnarray}a_{L_{0}}^{+}(m,\unicode[STIX]{x1D711})=-\frac{w_{\boldsymbol{k}}}{2h_{\boldsymbol{k}}}\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr)\cdot \text{ord}_{p}(pm)\cdot \log (p)\mathop{\sum }_{\substack{ \unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0} \\ Q(\unicode[STIX]{x1D707})=m}}2^{s(\unicode[STIX]{x1D707})}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
$$\begin{eqnarray}a_{L_{0}}^{+}(m,\unicode[STIX]{x1D711})=-\frac{w_{\boldsymbol{k}}}{2h_{\boldsymbol{k}}}\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr)\cdot \text{ord}_{p}(pm)\cdot \log (p)\mathop{\sum }_{\substack{ \unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0} \\ Q(\unicode[STIX]{x1D707})=m}}2^{s(\unicode[STIX]{x1D707})}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
 $s(\unicode[STIX]{x1D707})$
is the number of primes
$s(\unicode[STIX]{x1D707})$
is the number of primes
 $\ell \mid \text{disc}(L_{0})$
such that
$\ell \mid \text{disc}(L_{0})$
such that
 $\unicode[STIX]{x1D707}\in L_{0,\ell }$
, and
$\unicode[STIX]{x1D707}\in L_{0,\ell }$
, and $$\begin{eqnarray}\unicode[STIX]{x1D716}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }p\text{ is inert in }\boldsymbol{k},\\ 0\quad & \text{if }p\text{is ramified in }\boldsymbol{ k},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }p\text{ is inert in }\boldsymbol{k},\\ 0\quad & \text{if }p\text{is ramified in }\boldsymbol{ k},\end{array}\right.\end{eqnarray}$$
 $Q(\unicode[STIX]{x1D707})=m$
is understood as an equality in
$Q(\unicode[STIX]{x1D707})=m$
is understood as an equality in
 $\mathbb{Q}/\mathbb{Z}$
.
$\mathbb{Q}/\mathbb{Z}$
.
-
(iii) If
 $m>0$
and
$m>0$
and
 $|\text{Diff}_{L_{0}}(m)|>1$
, or if
$|\text{Diff}_{L_{0}}(m)|>1$
, or if
 $m<0$
, then
$m<0$
, then
 $a_{L_{0}}^{+}(m)=0$
.
$a_{L_{0}}^{+}(m)=0$
.
4 Complex multiplication cycles
Keep
 $L_{0}\oplus \unicode[STIX]{x1D6EC}\subset L$
as in § 3.3, so that
$L_{0}\oplus \unicode[STIX]{x1D6EC}\subset L$
as in § 3.3, so that
![]() $L$
is a maximal lattice of signature
$L$
is a maximal lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $L_{0}$
is a sublattice of signature
$L_{0}$
is a sublattice of signature
![]() $(0,2)$
, and
$(0,2)$
, and
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}=L_{0}^{\bot }=\{x\in L:x\bot L_{0}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}=L_{0}^{\bot }=\{x\in L:x\bot L_{0}\}.\end{eqnarray}$$
Abbreviate
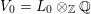 $V_{0}=L_{0}\otimes _{\mathbb{Z}}\mathbb{Q}$
and
$V_{0}=L_{0}\otimes _{\mathbb{Z}}\mathbb{Q}$
and
 $V=L\otimes _{\mathbb{Z}}\mathbb{Q}$
. The even part
$V=L\otimes _{\mathbb{Z}}\mathbb{Q}$
. The even part
![]() $C^{+}(V_{0})$
of the Clifford algebra is isomorphic to a quadratic imaginary field
$C^{+}(V_{0})$
of the Clifford algebra is isomorphic to a quadratic imaginary field
![]() $\boldsymbol{k}$
, and we continue to assume that
$\boldsymbol{k}$
, and we continue to assume that
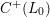 $C^{+}(L_{0})$
is its maximal order.
$C^{+}(L_{0})$
is its maximal order.
In this section we construct an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-stack
${\mathcal{O}}_{\boldsymbol{k}}$
-stack
![]() ${\mathcal{Y}}$
from the quadratic space
${\mathcal{Y}}$
from the quadratic space
![]() $L_{0}$
. Assuming that the discriminant of
$L_{0}$
. Assuming that the discriminant of
![]() $\boldsymbol{k}$
is odd, the inclusion
$\boldsymbol{k}$
is odd, the inclusion
![]() $L_{0}\subset L$
induces a morphism
$L_{0}\subset L$
induces a morphism
 ${\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}},$
where
${\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}},$
where
![]() ${\mathcal{M}}$
is the stack over
${\mathcal{M}}$
is the stack over
![]() $\mathbb{Z}$
determined by the quadratic space
$\mathbb{Z}$
determined by the quadratic space
![]() $L$
. We define special divisors on
$L$
. We define special divisors on
![]() ${\mathcal{Y}}$
, compute their degrees explicitly, and compare them with the special divisors on
${\mathcal{Y}}$
, compute their degrees explicitly, and compare them with the special divisors on
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
4.1 Preliminaries
Fix once and for all an isomorphism of
 $C^{+}(L_{0})$
with the maximal order
$C^{+}(L_{0})$
with the maximal order
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
in a quadratic imaginary subfield
${\mathcal{O}}_{\boldsymbol{k}}$
in a quadratic imaginary subfield
![]() $\boldsymbol{k}\subset \mathbb{C}$
. Let
$\boldsymbol{k}\subset \mathbb{C}$
. Let
![]() $d_{\boldsymbol{k}}$
,
$d_{\boldsymbol{k}}$
,
![]() $h_{\boldsymbol{k}}$
, and
$h_{\boldsymbol{k}}$
, and
![]() $w_{\boldsymbol{k}}$
be as in Proposition 3.3.1. The
$w_{\boldsymbol{k}}$
be as in Proposition 3.3.1. The
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading on
$\mathbb{Z}/2\mathbb{Z}$
-grading on
![]() $C(L_{0})$
takes the form
$C(L_{0})$
takes the form
 $$\begin{eqnarray}\displaystyle C(L_{0})={\mathcal{O}}_{\boldsymbol{k}}\oplus L_{0}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C(L_{0})={\mathcal{O}}_{\boldsymbol{k}}\oplus L_{0}, & & \displaystyle\end{eqnarray}$$
and
![]() $L_{0}$
is both a left and right
$L_{0}$
is both a left and right
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-module; the two actions are related by
${\mathcal{O}}_{\boldsymbol{k}}$
-module; the two actions are related by
 $x\unicode[STIX]{x1D6FC}=\overline{\unicode[STIX]{x1D6FC}}x$
for every
$x\unicode[STIX]{x1D6FC}=\overline{\unicode[STIX]{x1D6FC}}x$
for every
![]() $x\in L_{0}$
and
$x\in L_{0}$
and
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
.
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
.
There is a fractional
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-ideal
${\mathcal{O}}_{\boldsymbol{k}}$
-ideal
![]() $\mathfrak{a}$
and an isomorphism
$\mathfrak{a}$
and an isomorphism
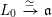 $L_{0}\xrightarrow[{}]{\simeq }\mathfrak{a}$
of left
$L_{0}\xrightarrow[{}]{\simeq }\mathfrak{a}$
of left
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-modules identifying the quadratic form on
${\mathcal{O}}_{\boldsymbol{k}}$
-modules identifying the quadratic form on
![]() $L_{0}$
with the form
$L_{0}$
with the form
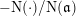 $-\text{N}(\cdot )/\text{N}(\mathfrak{a})$
on
$-\text{N}(\cdot )/\text{N}(\mathfrak{a})$
on
![]() $\mathfrak{a}$
, and an easy exercise shows that
$\mathfrak{a}$
, and an easy exercise shows that
 $$\begin{eqnarray}\displaystyle L_{0}^{\vee }=\mathfrak{d}_{\boldsymbol{k}}^{-1}L_{0}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{0}^{\vee }=\mathfrak{d}_{\boldsymbol{k}}^{-1}L_{0}, & & \displaystyle\end{eqnarray}$$
where
![]() $\mathfrak{d}_{\boldsymbol{k}}$
is the different of
$\mathfrak{d}_{\boldsymbol{k}}$
is the different of
![]() $\boldsymbol{k}/\mathbb{Q}$
.
$\boldsymbol{k}/\mathbb{Q}$
.
4.2 The zero-dimensional Shimura variety
Let
![]() $T$
be the group scheme over
$T$
be the group scheme over
![]() $\mathbb{Z}$
with functor of points
$\mathbb{Z}$
with functor of points
 $$\begin{eqnarray}T(R)=(C^{+}(L_{0})\otimes _{\mathbb{Z}}R)^{\times }\end{eqnarray}$$
$$\begin{eqnarray}T(R)=(C^{+}(L_{0})\otimes _{\mathbb{Z}}R)^{\times }\end{eqnarray}$$
for any
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $R$
. Thus
$R$
. Thus
 $T_{\mathbb{Q}}=\text{GSpin}(V_{0})$
is a torus of rank two and can be identified with the maximal subgroup of
$T_{\mathbb{Q}}=\text{GSpin}(V_{0})$
is a torus of rank two and can be identified with the maximal subgroup of
![]() $G$
that acts trivially on the subspace
$G$
that acts trivially on the subspace
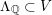 $\unicode[STIX]{x1D6EC}_{\mathbb{Q}}\subset V$
. Set
$\unicode[STIX]{x1D6EC}_{\mathbb{Q}}\subset V$
. Set
 $K_{0}=T(\widehat{\mathbb{Z}})$
.
$K_{0}=T(\widehat{\mathbb{Z}})$
.
Using our fixed embedding
 ${\mathcal{O}}_{\boldsymbol{k}}\subset \mathbb{C}$
, left multiplication makes
${\mathcal{O}}_{\boldsymbol{k}}\subset \mathbb{C}$
, left multiplication makes
![]() $V_{0,\mathbb{R}}$
into a complex vector space. This determines an orientation on
$V_{0,\mathbb{R}}$
into a complex vector space. This determines an orientation on
![]() $V_{0,\mathbb{R}}$
, and the oriented negative plane
$V_{0,\mathbb{R}}$
, and the oriented negative plane
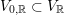 $V_{0,\mathbb{R}}\subset V_{\mathbb{R}}$
determines a point
$V_{0,\mathbb{R}}\subset V_{\mathbb{R}}$
determines a point
![]() $\boldsymbol{h}_{0}\in {\mathcal{D}}$
. The isomorphism of (2.1) then associates to
$\boldsymbol{h}_{0}\in {\mathcal{D}}$
. The isomorphism of (2.1) then associates to
![]() $\boldsymbol{h}_{0}$
an isotropic line in
$\boldsymbol{h}_{0}$
an isotropic line in
![]() $V_{0,\mathbb{C}}$
; explicitly, this is the line on which the right action of
$V_{0,\mathbb{C}}$
; explicitly, this is the line on which the right action of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
agrees with the inclusion
${\mathcal{O}}_{\boldsymbol{k}}$
agrees with the inclusion
 ${\mathcal{O}}_{\boldsymbol{k}}\subset \mathbb{C}=\text{End}_{\mathbb{C}}(V_{0,\mathbb{C}})$
.
${\mathcal{O}}_{\boldsymbol{k}}\subset \mathbb{C}=\text{End}_{\mathbb{C}}(V_{0,\mathbb{C}})$
.
The pair
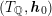 $(T_{\mathbb{Q}},\boldsymbol{h}_{0})$
is a Shimura datum with reflex field
$(T_{\mathbb{Q}},\boldsymbol{h}_{0})$
is a Shimura datum with reflex field
![]() $\boldsymbol{k}\subset \mathbb{C}$
, and the zero-dimensional complex orbifold
$\boldsymbol{k}\subset \mathbb{C}$
, and the zero-dimensional complex orbifold
 $$\begin{eqnarray}Y(\mathbb{C})=T(\mathbb{Q})\backslash \{\boldsymbol{h}_{0}\}\times T(\mathbb{A}_{f})/K_{0}\end{eqnarray}$$
$$\begin{eqnarray}Y(\mathbb{C})=T(\mathbb{Q})\backslash \{\boldsymbol{h}_{0}\}\times T(\mathbb{A}_{f})/K_{0}\end{eqnarray}$$
is the complex fiber of a
![]() $\boldsymbol{k}$
-stack
$\boldsymbol{k}$
-stack
![]() $Y$
. As in § 2.2, the representation of
$Y$
. As in § 2.2, the representation of
![]() $T_{\mathbb{Q}}$
on
$T_{\mathbb{Q}}$
on
![]() $V_{0}$
and the lattice
$V_{0}$
and the lattice
 $$\begin{eqnarray}L_{0}\otimes \widehat{\mathbb{Z}}\subset V_{0}\otimes \mathbb{A}_{f}\end{eqnarray}$$
$$\begin{eqnarray}L_{0}\otimes \widehat{\mathbb{Z}}\subset V_{0}\otimes \mathbb{A}_{f}\end{eqnarray}$$
determine a variation of polarized
![]() $\mathbb{Z}$
-Hodge structures
$\mathbb{Z}$
-Hodge structures
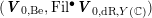 $(\boldsymbol{V}_{0,\text{Be}},\text{Fil}^{\bullet }\boldsymbol{V}_{0,\text{dR},Y(\mathbb{C})})$
of type
$(\boldsymbol{V}_{0,\text{Be}},\text{Fil}^{\bullet }\boldsymbol{V}_{0,\text{dR},Y(\mathbb{C})})$
of type
![]() $(-1,1)$
,
$(-1,1)$
,
![]() $(1,-1)$
over
$(1,-1)$
over
![]() $Y(\mathbb{C})$
.
$Y(\mathbb{C})$
.
Similarly, the representation of
![]() $T_{\mathbb{Q}}$
on
$T_{\mathbb{Q}}$
on
![]() $C(V_{0})$
by left multiplication, together with the lattice
$C(V_{0})$
by left multiplication, together with the lattice
 $$\begin{eqnarray}C(L_{0})_{\widehat{\mathbb{Z}}}\subset C(V_{0})_{\mathbb{A}_{f}},\end{eqnarray}$$
$$\begin{eqnarray}C(L_{0})_{\widehat{\mathbb{Z}}}\subset C(V_{0})_{\mathbb{A}_{f}},\end{eqnarray}$$
determine a variation of
![]() $\mathbb{Z}$
-Hodge structures
$\mathbb{Z}$
-Hodge structures
 $(\boldsymbol{H}_{0,\text{Be}},\text{Fil}^{\bullet }\boldsymbol{H}_{0,\text{dR},{\mathcal{Y}}(\mathbb{C})})$
of type
$(\boldsymbol{H}_{0,\text{Be}},\text{Fil}^{\bullet }\boldsymbol{H}_{0,\text{dR},{\mathcal{Y}}(\mathbb{C})})$
of type
![]() $(-1,0)$
,
$(-1,0)$
,
![]() $(0,-1)$
. As in § 2.3, this is the homology of an abelian scheme
$(0,-1)$
. As in § 2.3, this is the homology of an abelian scheme
 $$\begin{eqnarray}{\mathcal{A}}_{0,Y}\rightarrow Y\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{0,Y}\rightarrow Y\end{eqnarray}$$
of relative dimension
![]() $2$
, equipped with a right
$2$
, equipped with a right
![]() $C(L_{0})$
-action and a compatible
$C(L_{0})$
-action and a compatible
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading
$\mathbb{Z}/2\mathbb{Z}$
-grading
 $$\begin{eqnarray}{\mathcal{A}}_{0,Y}={\mathcal{A}}_{0,Y}^{+}\times {\mathcal{A}}_{0,Y}^{-}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{0,Y}={\mathcal{A}}_{0,Y}^{+}\times {\mathcal{A}}_{0,Y}^{-}.\end{eqnarray}$$
As before, we will refer to this abelian scheme as the Kuga–Satake abelian scheme over
![]() $Y$
.
$Y$
.
4.3 The integral model
We now define integral models of
![]() $Y$
and
$Y$
and
![]() ${\mathcal{A}}_{0,Y}$
over
${\mathcal{A}}_{0,Y}$
over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
.
${\mathcal{O}}_{\boldsymbol{k}}$
.
Definition 4.3.1. If
![]() $S$
is an
$S$
is an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-scheme, an
${\mathcal{O}}_{\boldsymbol{k}}$
-scheme, an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve over
${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve over
![]() $S$
is an elliptic curve
$S$
is an elliptic curve
![]() ${\mathcal{E}}\rightarrow S$
endowed with an action of
${\mathcal{E}}\rightarrow S$
endowed with an action of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
in such a way that the induced action on the
${\mathcal{O}}_{\boldsymbol{k}}$
in such a way that the induced action on the
![]() ${\mathcal{O}}_{S}$
-module
${\mathcal{O}}_{S}$
-module
![]() $\text{Lie}({\mathcal{E}})$
is through the structure morphism
$\text{Lie}({\mathcal{E}})$
is through the structure morphism
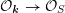 ${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{S}$
.
${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{S}$
.
Remark 4.3.2. Our convention is that the
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-action on any
${\mathcal{O}}_{\boldsymbol{k}}$
-action on any
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve is written on the right.
${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve is written on the right.
Denote by
![]() ${\mathcal{Y}}$
the
${\mathcal{Y}}$
the
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-stack classifying
${\mathcal{O}}_{\boldsymbol{k}}$
-stack classifying
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curves over
${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curves over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-schemes. Every point
${\mathcal{O}}_{\boldsymbol{k}}$
-schemes. Every point
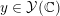 $y\in {\mathcal{Y}}(\mathbb{C})$
has automorphism group
$y\in {\mathcal{Y}}(\mathbb{C})$
has automorphism group
![]() ${\mathcal{O}}_{\boldsymbol{k}}^{\times }$
, and
${\mathcal{O}}_{\boldsymbol{k}}^{\times }$
, and
 $$\begin{eqnarray}\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{1}{\#\text{Aut}(y)}=\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{1}{\#\text{Aut}(y)}=\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}.\end{eqnarray}$$
As in [Reference Kudla, Rapoport and YangKRY99, Proposition 5.1], the stack
![]() ${\mathcal{Y}}$
is finite étale over
${\mathcal{Y}}$
is finite étale over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. In particular
${\mathcal{O}}_{\boldsymbol{k}}$
. In particular
![]() ${\mathcal{Y}}$
is regular of dimension
${\mathcal{Y}}$
is regular of dimension
![]() $1$
, and is flat over
$1$
, and is flat over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
.
${\mathcal{O}}_{\boldsymbol{k}}$
.
The positive graded part
![]() ${\mathcal{A}}_{0,Y}^{+}$
of the Kuga–Satake abelian scheme, with its right action of
${\mathcal{A}}_{0,Y}^{+}$
of the Kuga–Satake abelian scheme, with its right action of
 $C^{+}(L_{0})={\mathcal{O}}_{\boldsymbol{k}}$
, is an
$C^{+}(L_{0})={\mathcal{O}}_{\boldsymbol{k}}$
, is an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve over
${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve over
![]() $Y$
(for the obvious extension of this notion over algebraic stacks). Therefore, it defines a morphism
$Y$
(for the obvious extension of this notion over algebraic stacks). Therefore, it defines a morphism
![]() $Y\rightarrow {\mathcal{Y}}$
. By checking on complex points, we see that this map defines an isomorphism
$Y\rightarrow {\mathcal{Y}}$
. By checking on complex points, we see that this map defines an isomorphism
 $Y\xrightarrow[{}]{\simeq }{\mathcal{Y}}_{\boldsymbol{k}}.$
Again by checking on complex points, one can show that the natural map
$Y\xrightarrow[{}]{\simeq }{\mathcal{Y}}_{\boldsymbol{k}}.$
Again by checking on complex points, one can show that the natural map
 $$\begin{eqnarray}{\mathcal{A}}_{0,Y}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}C(L_{0})\rightarrow {\mathcal{A}}_{0,Y}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{0,Y}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}C(L_{0})\rightarrow {\mathcal{A}}_{0,Y}\end{eqnarray}$$
is an isomorphism, from which it follows that
 $$\begin{eqnarray}{\mathcal{A}}_{0,Y}^{-}\xrightarrow[{}]{\simeq }{\mathcal{A}}_{0,Y}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}L_{0}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{0,Y}^{-}\xrightarrow[{}]{\simeq }{\mathcal{A}}_{0,Y}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}L_{0}.\end{eqnarray}$$
From these observations, we can use the universal
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve
${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve
![]() ${\mathcal{E}}\rightarrow {\mathcal{Y}}$
to extend the Kuga–Satake abelian scheme
${\mathcal{E}}\rightarrow {\mathcal{Y}}$
to extend the Kuga–Satake abelian scheme
 ${\mathcal{A}}_{0,Y}\rightarrow Y$
to an abelian scheme
${\mathcal{A}}_{0,Y}\rightarrow Y$
to an abelian scheme
 $$\begin{eqnarray}{\mathcal{A}}_{0}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L_{0})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{0}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L_{0})\end{eqnarray}$$
over
![]() ${\mathcal{Y}}$
of relative dimension
${\mathcal{Y}}$
of relative dimension
![]() $2$
. By construction,
$2$
. By construction,
![]() ${\mathcal{A}}_{0}$
carries a right action of
${\mathcal{A}}_{0}$
carries a right action of
![]() $C(L_{0})$
and a
$C(L_{0})$
and a
![]() $\mathbb{Z}/2\mathbb{Z}$
-grading
$\mathbb{Z}/2\mathbb{Z}$
-grading
 ${\mathcal{A}}_{0}={\mathcal{A}}_{0}^{+}\times {\mathcal{A}}_{0}^{-}$
induced by (4.1), where
${\mathcal{A}}_{0}={\mathcal{A}}_{0}^{+}\times {\mathcal{A}}_{0}^{-}$
induced by (4.1), where
 ${\mathcal{A}}_{0}^{+}={\mathcal{E}}$
and
${\mathcal{A}}_{0}^{+}={\mathcal{E}}$
and
 ${\mathcal{A}}_{0}^{-}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
.
${\mathcal{A}}_{0}^{-}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
.
Remark 4.3.3. Note that the tensor product
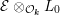 ${\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
is with respect to the left action of
${\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
is with respect to the left action of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
on
${\mathcal{O}}_{\boldsymbol{k}}$
on
![]() $L_{0}$
, and
$L_{0}$
, and
 ${\mathcal{O}}_{\boldsymbol{k}}\subset C(L_{0})$
acts on
${\mathcal{O}}_{\boldsymbol{k}}\subset C(L_{0})$
acts on
 ${\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
through right multiplication on
${\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
through right multiplication on
![]() $L_{0}$
. From the relation
$L_{0}$
. From the relation
 $x\unicode[STIX]{x1D6FC}=\overline{\unicode[STIX]{x1D6FC}}x$
for
$x\unicode[STIX]{x1D6FC}=\overline{\unicode[STIX]{x1D6FC}}x$
for
![]() $x\in L_{0}$
and
$x\in L_{0}$
and
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
, it follows that
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
, it follows that
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
acts on
${\mathcal{O}}_{\boldsymbol{k}}$
acts on
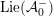 $\text{Lie}({\mathcal{A}}_{0}^{-})$
through the conjugate of the structure morphism
$\text{Lie}({\mathcal{A}}_{0}^{-})$
through the conjugate of the structure morphism
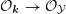 ${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}$
.
${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}$
.
There are obvious analogues on
![]() ${\mathcal{Y}}$
of the sheaves
${\mathcal{Y}}$
of the sheaves
![]() $\boldsymbol{H}$
defined in § 2.4. Denote by
$\boldsymbol{H}$
defined in § 2.4. Denote by
![]() $\boldsymbol{H}_{0,\text{dR}}$
the first de Rham homology of
$\boldsymbol{H}_{0,\text{dR}}$
the first de Rham homology of
![]() ${\mathcal{A}}_{0}$
relative to
${\mathcal{A}}_{0}$
relative to
![]() ${\mathcal{Y}}$
. Similarly, denote by
${\mathcal{Y}}$
. Similarly, denote by
![]() $\boldsymbol{H}_{0,p,\acute{\text{e}}\text{t}}$
the first
$\boldsymbol{H}_{0,p,\acute{\text{e}}\text{t}}$
the first
![]() $p$
-adic étale homology of
$p$
-adic étale homology of
![]() ${\mathcal{A}}_{0}$
relative to
${\mathcal{A}}_{0}$
relative to
![]() ${\mathcal{Y}}[1/p]$
, and by
${\mathcal{Y}}[1/p]$
, and by
![]() $\boldsymbol{H}_{0,\text{crys}}$
the first crystalline homology of the special fiber of
$\boldsymbol{H}_{0,\text{crys}}$
the first crystalline homology of the special fiber of
![]() ${\mathcal{A}}_{0}$
at a prime
${\mathcal{A}}_{0}$
at a prime
![]() $p$
relative to
$p$
relative to
![]() ${\mathcal{Y}}_{\mathbb{F}_{p}}$
. These sheaves come with right actions of
${\mathcal{Y}}_{\mathbb{F}_{p}}$
. These sheaves come with right actions of
![]() $C(L_{0})$
, and
$C(L_{0})$
, and
![]() $\mathbb{Z}/2\mathbb{Z}$
-gradings
$\mathbb{Z}/2\mathbb{Z}$
-gradings
 $\boldsymbol{H}_{0}=\boldsymbol{H}_{0}^{+}\times \boldsymbol{H}_{0}^{-}$
in such a way that
$\boldsymbol{H}_{0}=\boldsymbol{H}_{0}^{+}\times \boldsymbol{H}_{0}^{-}$
in such a way that
 $\boldsymbol{H}_{0}^{-}=\boldsymbol{H}_{0}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
. As in the higher-dimensional case, over
$\boldsymbol{H}_{0}^{-}=\boldsymbol{H}_{0}^{+}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
. As in the higher-dimensional case, over
![]() ${\mathcal{Y}}(\mathbb{C})$
the de Rham and étale sheaves arise from the Betti realization
${\mathcal{Y}}(\mathbb{C})$
the de Rham and étale sheaves arise from the Betti realization
![]() $\boldsymbol{H}_{0,\text{Be}}$
.
$\boldsymbol{H}_{0,\text{Be}}$
.
Define
 $$\begin{eqnarray}\boldsymbol{V}_{0}\subset \text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{0}\subset \text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0})\end{eqnarray}$$
as the submodule of grade-shifting endomorphisms. As can be checked from the complex uniformization, over
![]() ${\mathcal{Y}}(\mathbb{C})$
this definition recovers the local system
${\mathcal{Y}}(\mathbb{C})$
this definition recovers the local system
![]() $\boldsymbol{V}_{0,\text{Be}}$
(for the Betti realization) and the vector bundle
$\boldsymbol{V}_{0,\text{Be}}$
(for the Betti realization) and the vector bundle
 $\boldsymbol{V}_{0,\text{dR},Y(\mathbb{C})}$
(for the de Rham realization). Indeed, this amounts to the fact that the embedding of
$\boldsymbol{V}_{0,\text{dR},Y(\mathbb{C})}$
(for the de Rham realization). Indeed, this amounts to the fact that the embedding of
![]() $L_{0}$
into
$L_{0}$
into
 $\text{End}(C(L_{0}))$
via left multiplication identifies it with the space of grade-shifting endomorphisms of
$\text{End}(C(L_{0}))$
via left multiplication identifies it with the space of grade-shifting endomorphisms of
![]() $C(L_{0})$
that commute with right multiplication by
$C(L_{0})$
that commute with right multiplication by
![]() $C(L_{0})$
.
$C(L_{0})$
.
Restriction to
![]() $\boldsymbol{H}_{0}^{+}$
defines an isomorphism
$\boldsymbol{H}_{0}^{+}$
defines an isomorphism
 $$\begin{eqnarray}\displaystyle \boldsymbol{V}_{0}\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0}^{+},\boldsymbol{H}_{0}^{-}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{V}_{0}\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0}^{+},\boldsymbol{H}_{0}^{-}). & & \displaystyle\end{eqnarray}$$
As
![]() $\boldsymbol{H}_{0}^{\pm }$
is a locally free
$\boldsymbol{H}_{0}^{\pm }$
is a locally free
![]() ${\mathcal{O}}_{\boldsymbol{k}}\otimes \mathbf{1}$
-module of rank one, the same is true of
${\mathcal{O}}_{\boldsymbol{k}}\otimes \mathbf{1}$
-module of rank one, the same is true of
![]() $\boldsymbol{V}_{0}$
. In particular,
$\boldsymbol{V}_{0}$
. In particular,
![]() $\boldsymbol{V}_{0}$
is a locally free
$\boldsymbol{V}_{0}$
is a locally free
![]() $\mathbf{1}$
-module of rank two. In the de Rham case, the Hodge filtration on
$\mathbf{1}$
-module of rank two. In the de Rham case, the Hodge filtration on
![]() $\boldsymbol{H}_{0,\text{dR}}$
determines a submodule
$\boldsymbol{H}_{0,\text{dR}}$
determines a submodule
 $\boldsymbol{V}_{0,\text{dR}}^{1}\subset \boldsymbol{V}_{0,\text{dR}}$
by
$\boldsymbol{V}_{0,\text{dR}}^{1}\subset \boldsymbol{V}_{0,\text{dR}}$
by
 $$\begin{eqnarray}\boldsymbol{V}_{0,\text{dR}}^{1}=\boldsymbol{V}_{0,\text{dR}}\cap \text{Fil}^{1}\text{}\underline{\text{End}}(\boldsymbol{H}_{0,\text{dR}}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{0,\text{dR}}^{1}=\boldsymbol{V}_{0,\text{dR}}\cap \text{Fil}^{1}\text{}\underline{\text{End}}(\boldsymbol{H}_{0,\text{dR}}).\end{eqnarray}$$
Definition 4.3.4. As in Definition 2.4.7, the line bundle
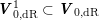 $\boldsymbol{V}_{0,\text{dR}}^{1}\subset \boldsymbol{V}_{0,\text{dR}}$
is the tautological bundle on
$\boldsymbol{V}_{0,\text{dR}}^{1}\subset \boldsymbol{V}_{0,\text{dR}}$
is the tautological bundle on
![]() ${\mathcal{Y}}$
, and its dual is the cotautological bundle.
${\mathcal{Y}}$
, and its dual is the cotautological bundle.
The following proposition makes the cotautological bundle more explicit.
Proposition 4.3.5. There are canonical isomorphisms of
![]() ${\mathcal{O}}_{{\mathcal{Y}}}$
-modules
${\mathcal{O}}_{{\mathcal{Y}}}$
-modules
 $$\begin{eqnarray}\displaystyle (\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{A}}_{0}^{+})\otimes \text{Lie}({\mathcal{A}}_{0}^{-})\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{E}})^{\otimes 2}\otimes \boldsymbol{L}_{0}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{A}}_{0}^{+})\otimes \text{Lie}({\mathcal{A}}_{0}^{-})\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{E}})^{\otimes 2}\otimes \boldsymbol{L}_{0}, & & \displaystyle\end{eqnarray}$$
where
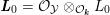 $\boldsymbol{L}_{0}={\mathcal{O}}_{{\mathcal{Y}}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
.
$\boldsymbol{L}_{0}={\mathcal{O}}_{{\mathcal{Y}}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
.
Proof. We have canonical isomorphisms of line bundles over
![]() ${\mathcal{Y}}$
${\mathcal{Y}}$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{H}_{0,\text{dR}}^{+}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{+}\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{A}}_{0}^{+}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \boldsymbol{H}_{0,\text{dR}}^{-}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-}\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{A}}_{0}^{-}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{H}_{0,\text{dR}}^{+}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{+}\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{A}}_{0}^{+}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \boldsymbol{H}_{0,\text{dR}}^{-}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-}\xrightarrow[{}]{\simeq }\text{Lie}({\mathcal{A}}_{0}^{-}), & \displaystyle \nonumber\end{eqnarray}$$
and the (de Rham realization of the) unique principal polarization on
![]() ${\mathcal{A}}_{0}^{-}$
induces an isomorphism of
${\mathcal{A}}_{0}^{-}$
induces an isomorphism of
![]() ${\mathcal{O}}_{{\mathcal{Y}}}$
-modules
${\mathcal{O}}_{{\mathcal{Y}}}$
-modules
 $$\begin{eqnarray}\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-}\xrightarrow[{}]{\simeq }(\boldsymbol{H}_{0,\text{dR}}^{-}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-})^{\vee }=\text{Lie}({\mathcal{A}}_{0}^{-})^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-}\xrightarrow[{}]{\simeq }(\boldsymbol{H}_{0,\text{dR}}^{-}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-})^{\vee }=\text{Lie}({\mathcal{A}}_{0}^{-})^{\vee }.\end{eqnarray}$$
The isomorphism (4.3) restricts to
 $$\begin{eqnarray}\displaystyle \boldsymbol{V}_{0,\text{dR}}^{1} & \xrightarrow[{}]{\simeq } & \displaystyle \text{Fil}^{1}\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0,\text{dR}}^{+},\boldsymbol{H}_{0,\text{dR}}^{-})\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0,\text{dR}}^{+}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{+},\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-})\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \text{}\underline{\text{Hom}}(\text{Lie}({\mathcal{A}}_{0}^{+}),\text{Lie}({\mathcal{A}}_{0}^{-})^{\vee }),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{V}_{0,\text{dR}}^{1} & \xrightarrow[{}]{\simeq } & \displaystyle \text{Fil}^{1}\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0,\text{dR}}^{+},\boldsymbol{H}_{0,\text{dR}}^{-})\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0,\text{dR}}^{+}/\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{+},\text{Fil}^{0}\boldsymbol{H}_{0,\text{dR}}^{-})\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \text{}\underline{\text{Hom}}(\text{Lie}({\mathcal{A}}_{0}^{+}),\text{Lie}({\mathcal{A}}_{0}^{-})^{\vee }),\end{eqnarray}$$
and dualizing yields the first isomorphism in (4.4). The second isomorphism is clear from the definition of
![]() ${\mathcal{A}}_{0}^{\pm }$
and the relation
${\mathcal{A}}_{0}^{\pm }$
and the relation
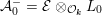 ${\mathcal{A}}_{0}^{-}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
.◻
${\mathcal{A}}_{0}^{-}={\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
.◻
Remark 4.3.6. It is clear from (4.5) that the isotropic line
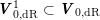 $\boldsymbol{V}_{0,\text{dR}}^{1}\subset \boldsymbol{V}_{0,\text{dR}}$
is stable under the action of
$\boldsymbol{V}_{0,\text{dR}}^{1}\subset \boldsymbol{V}_{0,\text{dR}}$
is stable under the action of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
induced by (4.3), and that
${\mathcal{O}}_{\boldsymbol{k}}$
induced by (4.3), and that
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
acts on this line through the structure morphism
${\mathcal{O}}_{\boldsymbol{k}}$
acts on this line through the structure morphism
 ${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}$
.
${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}$
.
4.4 Special endomorphisms
If
![]() ${\mathcal{E}}_{1}$
and
${\mathcal{E}}_{1}$
and
![]() ${\mathcal{E}}_{2}$
are any elliptic curves with right actions of
${\mathcal{E}}_{2}$
are any elliptic curves with right actions of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
, we make
${\mathcal{O}}_{\boldsymbol{k}}$
, we make
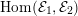 $\text{Hom}({\mathcal{E}}_{1},{\mathcal{E}}_{2})$
into a right
$\text{Hom}({\mathcal{E}}_{1},{\mathcal{E}}_{2})$
into a right
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-module via
${\mathcal{O}}_{\boldsymbol{k}}$
-module via
 $$\begin{eqnarray}(f\cdot \unicode[STIX]{x1D6FC})(-)=f(-)\cdot \unicode[STIX]{x1D6FC}\end{eqnarray}$$
$$\begin{eqnarray}(f\cdot \unicode[STIX]{x1D6FC})(-)=f(-)\cdot \unicode[STIX]{x1D6FC}\end{eqnarray}$$
for all
 $f\in \text{Hom}({\mathcal{E}}_{1},{\mathcal{E}}_{2})$
and
$f\in \text{Hom}({\mathcal{E}}_{1},{\mathcal{E}}_{2})$
and
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
. With this convention, for any
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
. With this convention, for any
![]() ${\mathcal{Y}}$
-scheme
${\mathcal{Y}}$
-scheme
![]() $S$
there is an isomorphism of right
$S$
there is an isomorphism of right
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-modules
${\mathcal{O}}_{\boldsymbol{k}}$
-modules
 $$\begin{eqnarray}\text{Hom}({\mathcal{E}}_{S},{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0})\xrightarrow[{}]{\simeq }\text{End}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}({\mathcal{E}}_{S},{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0})\xrightarrow[{}]{\simeq }\text{End}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}.\end{eqnarray}$$
This restricts to an isomorphism
 $$\begin{eqnarray}\text{Hom}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{E}}_{S},{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0})\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0},\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{E}}_{S},{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0})\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0},\end{eqnarray}$$
which we rewrite as
 $$\begin{eqnarray}\displaystyle \text{Hom}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{A}}_{0,S}^{+},{\mathcal{A}}_{0,S}^{-})\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{A}}_{0,S}^{+},{\mathcal{A}}_{0,S}^{-})\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}. & & \displaystyle\end{eqnarray}$$
Here the subscripts
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
and
${\mathcal{O}}_{\boldsymbol{k}}$
and
![]() $\overline{{\mathcal{O}}}_{\boldsymbol{k}}$
indicate
$\overline{{\mathcal{O}}}_{\boldsymbol{k}}$
indicate
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-linear and
${\mathcal{O}}_{\boldsymbol{k}}$
-linear and
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-conjugate-linear maps, respectively. The quadratic form
${\mathcal{O}}_{\boldsymbol{k}}$
-conjugate-linear maps, respectively. The quadratic form
![]() $\deg$
on the left-hand side of (4.6) corresponds to the quadratic form
$\deg$
on the left-hand side of (4.6) corresponds to the quadratic form
 $$\begin{eqnarray}\displaystyle x\otimes v\mapsto -\text{deg}(x)\cdot Q(v) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x\otimes v\mapsto -\text{deg}(x)\cdot Q(v) & & \displaystyle\end{eqnarray}$$
on the right-hand side (which is positive definite, as
![]() $\deg$
and
$\deg$
and
![]() $-Q$
are positive definite).
$-Q$
are positive definite).
Elements of
 $\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}$
are special quasi-endomorphisms of
$\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}$
are special quasi-endomorphisms of
![]() ${\mathcal{E}}_{S}$
. For every
${\mathcal{E}}_{S}$
. For every
![]() $\unicode[STIX]{x1D707}\in L_{0}^{\vee }$
define a collection of special quasi-endomorphisms by
$\unicode[STIX]{x1D707}\in L_{0}^{\vee }$
define a collection of special quasi-endomorphisms by
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{E}}_{S})=\{x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}^{\vee }:x-\text{id}\otimes \unicode[STIX]{x1D707}\in \text{End}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{E}}_{S})=\{x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}^{\vee }:x-\text{id}\otimes \unicode[STIX]{x1D707}\in \text{End}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\}.\end{eqnarray}$$
This collection depends only on the coset
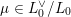 $\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
. We will sometimes abbreviate
$\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
. We will sometimes abbreviate
 $$\begin{eqnarray}V({\mathcal{E}}_{S})=\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{E}}_{S})=\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\end{eqnarray}$$
for the space defined by the coset
![]() $\unicode[STIX]{x1D707}=0$
.
$\unicode[STIX]{x1D707}=0$
.
Remark 4.4.1. For any
![]() $S\rightarrow {\mathcal{Y}}$
as above, let
$S\rightarrow {\mathcal{Y}}$
as above, let
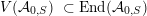 $V({\mathcal{A}}_{0,S})~\subset \text{End}({\mathcal{A}}_{0,S})$
be the submodule of
$V({\mathcal{A}}_{0,S})~\subset \text{End}({\mathcal{A}}_{0,S})$
be the submodule of
![]() $C(L_{0})$
-linear grade-shifting endomorphisms of
$C(L_{0})$
-linear grade-shifting endomorphisms of
![]() ${\mathcal{A}}_{0,S}$
. Equivalently,
${\mathcal{A}}_{0,S}$
. Equivalently,
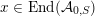 $x\in \text{End}({\mathcal{A}}_{0,S})$
lies in
$x\in \text{End}({\mathcal{A}}_{0,S})$
lies in
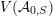 $V({\mathcal{A}}_{0,S})$
if and only if all of its homological realizations lie in the subsheaf
$V({\mathcal{A}}_{0,S})$
if and only if all of its homological realizations lie in the subsheaf
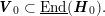 $\boldsymbol{V}_{0}\subset \text{}\underline{\text{End}}(\boldsymbol{H}_{0}).$
Restriction to the positive graded part identifies
$\boldsymbol{V}_{0}\subset \text{}\underline{\text{End}}(\boldsymbol{H}_{0}).$
Restriction to the positive graded part identifies
 $$\begin{eqnarray}\displaystyle V({\mathcal{A}}_{0,S})\xrightarrow[{}]{\simeq }\text{Hom}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{A}}_{0,S}^{+},{\mathcal{A}}_{0,S}^{-})\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\xrightarrow[{}]{\simeq }V({\mathcal{E}}_{S}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V({\mathcal{A}}_{0,S})\xrightarrow[{}]{\simeq }\text{Hom}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{A}}_{0,S}^{+},{\mathcal{A}}_{0,S}^{-})\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\xrightarrow[{}]{\simeq }V({\mathcal{E}}_{S}), & & \displaystyle\end{eqnarray}$$
where the middle isomorphism is (4.6).
4.5 Degrees of special divisors
In this subsection we define the special divisors
 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{Y}}$
and compute their degrees.
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{Y}}$
and compute their degrees.
For a non-negative rational number
![]() $m$
and a class
$m$
and a class
 $\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
, define
$\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
, define
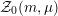 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
to be the
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
to be the
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-stack that assigns to an
${\mathcal{O}}_{\boldsymbol{k}}$
-stack that assigns to an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-scheme
${\mathcal{O}}_{\boldsymbol{k}}$
-scheme
![]() $S$
the groupoid of pairs
$S$
the groupoid of pairs
![]() $({\mathcal{E}}_{S},x)$
in which
$({\mathcal{E}}_{S},x)$
in which
![]() ${\mathcal{E}}_{S}$
is an
${\mathcal{E}}_{S}$
is an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve over
${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve over
![]() $S$
, and
$S$
, and
 $x\in V_{\unicode[STIX]{x1D707}}({\mathcal{E}}_{S})$
satisfies
$x\in V_{\unicode[STIX]{x1D707}}({\mathcal{E}}_{S})$
satisfies
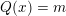 $Q(x)=m$
. Note that for
$Q(x)=m$
. Note that for
![]() $m=0$
we have
$m=0$
we have
 $$\begin{eqnarray}{\mathcal{Z}}_{0}(0,\unicode[STIX]{x1D707})=\left\{\begin{array}{@{}ll@{}}\emptyset \quad & \text{if }\unicode[STIX]{x1D707}\neq 0,\\ {\mathcal{Y}}\quad & \text{if }\unicode[STIX]{x1D707}=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{0}(0,\unicode[STIX]{x1D707})=\left\{\begin{array}{@{}ll@{}}\emptyset \quad & \text{if }\unicode[STIX]{x1D707}\neq 0,\\ {\mathcal{Y}}\quad & \text{if }\unicode[STIX]{x1D707}=0.\end{array}\right.\end{eqnarray}$$
The following theorem is due to Kudla et al. [Reference Kudla, Rapoport and YangKRY99] in the special case where
![]() $\boldsymbol{k}$
has prime discriminant and
$\boldsymbol{k}$
has prime discriminant and
![]() $\unicode[STIX]{x1D707}=0$
. Subsequent generalizations and variants can be found in [Reference Kudla and YangKY13, Reference Bruinier, Howard and YangBHY15, Reference HowardHow12].
$\unicode[STIX]{x1D707}=0$
. Subsequent generalizations and variants can be found in [Reference Kudla and YangKY13, Reference Bruinier, Howard and YangBHY15, Reference HowardHow12].
Theorem 4.5.1. Assume that
![]() $d_{\boldsymbol{k}}$
is odd, and recall the finite set of primes
$d_{\boldsymbol{k}}$
is odd, and recall the finite set of primes
 $\text{Diff}_{L_{0}}(m)$
of (3.4). For
$\text{Diff}_{L_{0}}(m)$
of (3.4). For
![]() $m>0$
the stack
$m>0$
the stack
 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
has the following properties.
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
has the following properties.
-
(i) If
 $|\text{Diff}_{L_{0}}(m)|>1$
, or if
$|\text{Diff}_{L_{0}}(m)|>1$
, or if
 $Q(\unicode[STIX]{x1D707})\not =m$
in
$Q(\unicode[STIX]{x1D707})\not =m$
in
 $\mathbb{Q}/\mathbb{Z}$
, then
$\mathbb{Q}/\mathbb{Z}$
, then
 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})=\emptyset$
.
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})=\emptyset$
. -
(ii) If
 $\text{Diff}_{L_{0}}(m)=\{p\}$
and
$\text{Diff}_{L_{0}}(m)=\{p\}$
and
 $Q(\unicode[STIX]{x1D707})=m$
in
$Q(\unicode[STIX]{x1D707})=m$
in
 $\mathbb{Q}/\mathbb{Z}$
, then
$\mathbb{Q}/\mathbb{Z}$
, then
 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
has dimension
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})$
has dimension
 $0$
and is supported in characteristic
$0$
and is supported in characteristic
 $p$
. Furthermore, where
$p$
. Furthermore, where $$\begin{eqnarray}\frac{\log (\text{N}(\mathfrak{p}))}{\log (p)}\mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{\text{length}({\mathcal{O}}_{{\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707}),z})}{\#\text{Aut}(z)}=2^{s(\unicode[STIX]{x1D707})-1}\cdot \text{ord}_{p}(pm)\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\log (\text{N}(\mathfrak{p}))}{\log (p)}\mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{\text{length}({\mathcal{O}}_{{\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707}),z})}{\#\text{Aut}(z)}=2^{s(\unicode[STIX]{x1D707})-1}\cdot \text{ord}_{p}(pm)\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr),\end{eqnarray}$$
 $\mathfrak{p}$
is the unique prime of
$\mathfrak{p}$
is the unique prime of
 $\boldsymbol{k}$
above
$\boldsymbol{k}$
above
 $p$
, and
$p$
, and
 $\unicode[STIX]{x1D716}$
,
$\unicode[STIX]{x1D716}$
,
 $\unicode[STIX]{x1D70C}$
, and
$\unicode[STIX]{x1D70C}$
, and
 $s(\unicode[STIX]{x1D707})$
are as in Proposition 3.3.1.
$s(\unicode[STIX]{x1D707})$
are as in Proposition 3.3.1.
In either case
 $$\begin{eqnarray}\mathop{\sum }_{\mathfrak{p}\subset {\mathcal{O}}_{\boldsymbol{k}}}\log (\text{N}(\mathfrak{p}))\mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{\text{length}({\mathcal{O}}_{{\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707}),z})}{\#\text{Aut}(z)}=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot a_{L_{0}}(m,\unicode[STIX]{x1D707}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\mathfrak{p}\subset {\mathcal{O}}_{\boldsymbol{k}}}\log (\text{N}(\mathfrak{p}))\mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{\text{length}({\mathcal{O}}_{{\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707}),z})}{\#\text{Aut}(z)}=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot a_{L_{0}}(m,\unicode[STIX]{x1D707}).\end{eqnarray}$$
Proof. Let
![]() $\mathfrak{p}$
be a prime of
$\mathfrak{p}$
be a prime of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
, and let
${\mathcal{O}}_{\boldsymbol{k}}$
, and let
![]() $p$
be the rational prime below it. Suppose we have a point
$p$
be the rational prime below it. Suppose we have a point
 $$\begin{eqnarray}\displaystyle z=({\mathcal{E}},x)\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z=({\mathcal{E}},x)\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}}). & & \displaystyle\end{eqnarray}$$
The existence of
 $x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
already implies that
$x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
already implies that
![]() ${\mathcal{E}}$
is supersingular,
${\mathcal{E}}$
is supersingular,
![]() $p$
is non-split in
$p$
is non-split in
![]() $\boldsymbol{k}$
, and
$\boldsymbol{k}$
, and
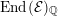 $\text{End}({\mathcal{E}})_{\mathbb{Q}}$
is the quaternion division algebra ramified at
$\text{End}({\mathcal{E}})_{\mathbb{Q}}$
is the quaternion division algebra ramified at
![]() $\infty$
and
$\infty$
and
![]() $p$
.
$p$
.
As
 ${\mathcal{O}}_{\boldsymbol{k}}{\hookrightarrow}\text{End}(E)$
we can extend this to an inclusion
${\mathcal{O}}_{\boldsymbol{k}}{\hookrightarrow}\text{End}(E)$
we can extend this to an inclusion
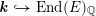 $\boldsymbol{k}{\hookrightarrow}\text{End}(E)_{\mathbb{Q}}$
. Since
$\boldsymbol{k}{\hookrightarrow}\text{End}(E)_{\mathbb{Q}}$
. Since
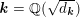 $\boldsymbol{k}=\mathbb{Q}(\sqrt{d_{\boldsymbol{k}}})$
there is an
$\boldsymbol{k}=\mathbb{Q}(\sqrt{d_{\boldsymbol{k}}})$
there is an
![]() $\unicode[STIX]{x1D702}\in \mathbb{Q}^{\times }$
such that
$\unicode[STIX]{x1D702}\in \mathbb{Q}^{\times }$
such that
 $$\begin{eqnarray}\text{End}(E)_{\mathbb{Q}}=\biggl(\frac{d_{\boldsymbol{k}},\unicode[STIX]{x1D702}}{\mathbb{Q}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\text{End}(E)_{\mathbb{Q}}=\biggl(\frac{d_{\boldsymbol{k}},\unicode[STIX]{x1D702}}{\mathbb{Q}}\biggr).\end{eqnarray}$$
Consequently
 $\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E)_{\mathbb{Q}}=\boldsymbol{k}\cdot j$
, where
$\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E)_{\mathbb{Q}}=\boldsymbol{k}\cdot j$
, where
![]() $j^{2}=\unicode[STIX]{x1D702}$
and
$j^{2}=\unicode[STIX]{x1D702}$
and
 $j\unicode[STIX]{x1D6FC}=\bar{\unicode[STIX]{x1D6FC}}j,\forall \unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
. Further,
$j\unicode[STIX]{x1D6FC}=\bar{\unicode[STIX]{x1D6FC}}j,\forall \unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{\boldsymbol{k}}$
. Further,
 $\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E)_{\mathbb{Q}}=\boldsymbol{k}\cdot j$
is a one-dimensional
$\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E)_{\mathbb{Q}}=\boldsymbol{k}\cdot j$
is a one-dimensional
![]() $\boldsymbol{k}$
-vector space equipped with the quadratic form
$\boldsymbol{k}$
-vector space equipped with the quadratic form
![]() $\deg$
, which is just the reduced norm of the quaternion algebra. As
$\deg$
, which is just the reduced norm of the quaternion algebra. As
![]() $j$
has reduced norm
$j$
has reduced norm
![]() $-\unicode[STIX]{x1D702}$
, we deduce that there is an isomorphism of quadratic spaces
$-\unicode[STIX]{x1D702}$
, we deduce that there is an isomorphism of quadratic spaces
 $$\begin{eqnarray}\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E)_{\mathbb{Q}}\cong W_{-\unicode[STIX]{x1D702}},\end{eqnarray}$$
$$\begin{eqnarray}\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E)_{\mathbb{Q}}\cong W_{-\unicode[STIX]{x1D702}},\end{eqnarray}$$
where for every
![]() $\unicode[STIX]{x1D6FE}\in \mathbb{Q}^{\times }$
we let
$\unicode[STIX]{x1D6FE}\in \mathbb{Q}^{\times }$
we let
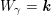 $W_{\unicode[STIX]{x1D6FE}}=\boldsymbol{k}$
equipped with the quadratic form
$W_{\unicode[STIX]{x1D6FE}}=\boldsymbol{k}$
equipped with the quadratic form
 $Q(w)=\unicode[STIX]{x1D6FE}w\overline{w}.$
$Q(w)=\unicode[STIX]{x1D6FE}w\overline{w}.$
As
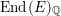 $\text{End}(E)_{\mathbb{Q}}$
is a quaternion algebra ramified precisely at
$\text{End}(E)_{\mathbb{Q}}$
is a quaternion algebra ramified precisely at
![]() $p$
and
$p$
and
![]() $\infty$
, it follows that
$\infty$
, it follows that
![]() $\unicode[STIX]{x1D702}$
is a local norm from
$\unicode[STIX]{x1D702}$
is a local norm from
![]() $\boldsymbol{k}$
everywhere but at
$\boldsymbol{k}$
everywhere but at
![]() $p$
and
$p$
and
![]() $\infty$
.
$\infty$
.
Recalling that
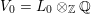 $V_{0}=L_{0}\otimes _{\mathbb{Z}}\mathbb{Q}$
, any choice of left
$V_{0}=L_{0}\otimes _{\mathbb{Z}}\mathbb{Q}$
, any choice of left
![]() $\boldsymbol{k}$
-module generator
$\boldsymbol{k}$
-module generator
![]() $v\in V_{0}$
identifies
$v\in V_{0}$
identifies
 $V_{0}\xrightarrow[{}]{\simeq }W_{\unicode[STIX]{x1D6FE}}$
, where
$V_{0}\xrightarrow[{}]{\simeq }W_{\unicode[STIX]{x1D6FE}}$
, where
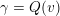 $\unicode[STIX]{x1D6FE}=Q(v)$
. Recalling (4.7), we deduce that there an isomorphism of quadratic spaces
$\unicode[STIX]{x1D6FE}=Q(v)$
. Recalling (4.7), we deduce that there an isomorphism of quadratic spaces
 $$\begin{eqnarray}\displaystyle \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\xrightarrow[{}]{\simeq }W_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\xrightarrow[{}]{\simeq }W_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}}. & & \displaystyle\end{eqnarray}$$
The existence of
![]() $x$
shows that the quadratic space on the left represents
$x$
shows that the quadratic space on the left represents
![]() $m$
globally, and hence
$m$
globally, and hence
![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}/m$
is a norm from
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FE}/m$
is a norm from
![]() $\boldsymbol{k}$
. This implies that
$\boldsymbol{k}$
. This implies that
![]() $\unicode[STIX]{x1D6FE}/m$
, hence
$\unicode[STIX]{x1D6FE}/m$
, hence
![]() $\unicode[STIX]{x1D6FE}m$
, is a norm from
$\unicode[STIX]{x1D6FE}m$
, is a norm from
![]() $\boldsymbol{k}$
everywhere locally except at
$\boldsymbol{k}$
everywhere locally except at
![]() $\infty$
and
$\infty$
and
![]() $p$
, from which we deduce
$p$
, from which we deduce
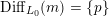 $\text{Diff}_{L_{0}}(m)=\{p\}$
. The equality
$\text{Diff}_{L_{0}}(m)=\{p\}$
. The equality
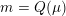 $m=Q(\unicode[STIX]{x1D707})$
in
$m=Q(\unicode[STIX]{x1D707})$
in
![]() $\mathbb{Q}/\mathbb{Z}$
can be checked directly, but it also follows from (2.17) and Proposition 4.6.3.
$\mathbb{Q}/\mathbb{Z}$
can be checked directly, but it also follows from (2.17) and Proposition 4.6.3.
We have now proved that
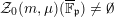 ${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})\not =\emptyset$
only when
${\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})\not =\emptyset$
only when
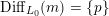 $\text{Diff}_{L_{0}}(m)=\{p\}$
and
$\text{Diff}_{L_{0}}(m)=\{p\}$
and
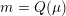 $m=Q(\unicode[STIX]{x1D707})$
in
$m=Q(\unicode[STIX]{x1D707})$
in
![]() $\mathbb{Q}/\mathbb{Z}$
, and hence have proved property (i). The proof of property (ii) requires a lemma.
$\mathbb{Q}/\mathbb{Z}$
, and hence have proved property (i). The proof of property (ii) requires a lemma.
Lemma 4.5.2. The existence of a point (4.9) implies
 $\unicode[STIX]{x1D707}\in L_{0,p}$
.
$\unicode[STIX]{x1D707}\in L_{0,p}$
.
Proof. By (4.2) we may assume that
![]() $p$
is ramified in
$p$
is ramified in
![]() $\boldsymbol{k}$
. Fix a generator
$\boldsymbol{k}$
. Fix a generator
![]() $\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}\in \mathfrak{d}_{\boldsymbol{k}}$
, so that
$\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}\in \mathfrak{d}_{\boldsymbol{k}}$
, so that
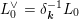 $L_{0}^{\vee }=\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}^{-1}L_{0}$
. Let
$L_{0}^{\vee }=\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}^{-1}L_{0}$
. Let
![]() $E_{p}$
be the
$E_{p}$
be the
![]() $p$
-divisible group of
$p$
-divisible group of
![]() ${\mathcal{E}}$
with its induced
${\mathcal{E}}$
with its induced
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-action.
${\mathcal{O}}_{\boldsymbol{k}}$
-action.
If
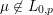 $\unicode[STIX]{x1D707}\not \in L_{0,p}$
then
$\unicode[STIX]{x1D707}\not \in L_{0,p}$
then
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}$
generates
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}$
generates
![]() $L_{0,p}$
as an
$L_{0,p}$
as an
![]() ${\mathcal{O}}_{\boldsymbol{k},p}$
-module. If we use this generator to identify
${\mathcal{O}}_{\boldsymbol{k},p}$
-module. If we use this generator to identify
 $$\begin{eqnarray}\text{End}(E_{p})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\xrightarrow[{}]{\simeq }\text{End}(E_{p})\end{eqnarray}$$
$$\begin{eqnarray}\text{End}(E_{p})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\xrightarrow[{}]{\simeq }\text{End}(E_{p})\end{eqnarray}$$
and multiply both sides of the relation
 $x-\text{id}\otimes \unicode[STIX]{x1D707}\in \text{End}(E_{p})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
on the right by
$x-\text{id}\otimes \unicode[STIX]{x1D707}\in \text{End}(E_{p})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
on the right by
![]() $\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}$
, we obtain
$\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}$
, we obtain
 $$\begin{eqnarray}\displaystyle y-\text{id}\in \text{End}(E_{p})\cdot \unicode[STIX]{x1D6FF}_{\boldsymbol{k}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y-\text{id}\in \text{End}(E_{p})\cdot \unicode[STIX]{x1D6FF}_{\boldsymbol{k}}, & & \displaystyle\end{eqnarray}$$
where we have set
 $y=x\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{p})$
.
$y=x\unicode[STIX]{x1D6FF}_{\boldsymbol{k}}\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{p})$
.
The ring
 $\text{End}(E_{p})$
is the maximal order in the division quaternion algebra over
$\text{End}(E_{p})$
is the maximal order in the division quaternion algebra over
![]() $\mathbb{Q}_{p}$
, and this maximal order is a (noncommutative) discrete valuation ring with
$\mathbb{Q}_{p}$
, and this maximal order is a (noncommutative) discrete valuation ring with
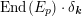 $\text{End}(E_{p})\cdot \unicode[STIX]{x1D6FF}_{\boldsymbol{k}}$
as its unique maximal ideal. Using
$\text{End}(E_{p})\cdot \unicode[STIX]{x1D6FF}_{\boldsymbol{k}}$
as its unique maximal ideal. Using
 $yv=\overline{v}y$
for all
$yv=\overline{v}y$
for all
 $v\in {\mathcal{O}}_{\boldsymbol{k},p}$
, an exercise with quaternion algebras shows that
$v\in {\mathcal{O}}_{\boldsymbol{k},p}$
, an exercise with quaternion algebras shows that
![]() $y$
has reduced trace
$y$
has reduced trace
![]() $0$
. Taking the reduced trace of (4.11) now implies that
$0$
. Taking the reduced trace of (4.11) now implies that
![]() $-2\cdot \text{id}$
lies in the maximal ideal of
$-2\cdot \text{id}$
lies in the maximal ideal of
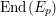 $\text{End}(E_{p})$
, which is absurd, as our assumption that
$\text{End}(E_{p})$
, which is absurd, as our assumption that
![]() $d_{\boldsymbol{k}}$
is odd implies
$d_{\boldsymbol{k}}$
is odd implies
![]() $p>2$
.◻
$p>2$
.◻
It follows from Lemma 4.5.2 and the Serre–Tate theorem that we may completely ignore
![]() $\unicode[STIX]{x1D707}$
in the deformation problem that computes the length of the étale local ring at
$\unicode[STIX]{x1D707}$
in the deformation problem that computes the length of the étale local ring at
![]() $z$
. Gross’s results on canonical liftings [Reference GrossGro86] therefore imply
$z$
. Gross’s results on canonical liftings [Reference GrossGro86] therefore imply
 $$\begin{eqnarray}\frac{\log (\text{N}(\mathfrak{p}))}{\log (p)}\cdot \text{length}({\mathcal{O}}_{{\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707}),z})=\text{ord}_{p}(pm)\end{eqnarray}$$
$$\begin{eqnarray}\frac{\log (\text{N}(\mathfrak{p}))}{\log (p)}\cdot \text{length}({\mathcal{O}}_{{\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707}),z})=\text{ord}_{p}(pm)\end{eqnarray}$$
for every point (4.9).
If
 $\text{ord}_{p}(m)<0$
then the relation
$\text{ord}_{p}(m)<0$
then the relation
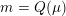 $m=Q(\unicode[STIX]{x1D707})$
in
$m=Q(\unicode[STIX]{x1D707})$
in
![]() $\mathbb{Q}/\mathbb{Z}$
implies
$\mathbb{Q}/\mathbb{Z}$
implies
 $\unicode[STIX]{x1D707}\not \in L_{0,p}$
, and hence, using Lemma 4.5.2, both sides of the desired equality in property (ii) of Theorem 4.5.1 are equal to
$\unicode[STIX]{x1D707}\not \in L_{0,p}$
, and hence, using Lemma 4.5.2, both sides of the desired equality in property (ii) of Theorem 4.5.1 are equal to
![]() $0$
. Thus it only remains to prove
$0$
. Thus it only remains to prove
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{1}{\#\text{Aut}(z)}=2^{s(\unicode[STIX]{x1D707})-1}\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{1}{\#\text{Aut}(z)}=2^{s(\unicode[STIX]{x1D707})-1}\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr) & & \displaystyle\end{eqnarray}$$
under the assumption
 $\text{ord}_{p}(m)\geqslant 0$
. The argument is very similar to that of [Reference Kudla and YangKY13, Proposition 3.1], [Reference Howard and YangHY12, Proposition 2.18], [Reference Bruinier, Howard and YangBHY15, Theorem 5.5], and [Reference HowardHow12, Theorem 3.5.3], and hence we omit some details.
$\text{ord}_{p}(m)\geqslant 0$
. The argument is very similar to that of [Reference Kudla and YangKY13, Proposition 3.1], [Reference Howard and YangHY12, Proposition 2.18], [Reference Bruinier, Howard and YangBHY15, Theorem 5.5], and [Reference HowardHow12, Theorem 3.5.3], and hence we omit some details.
Fix one elliptic curve
![]() ${\mathcal{E}}$
over
${\mathcal{E}}$
over
![]() $\overline{\mathbb{F}}_{\mathfrak{p}}$
with complex multiplication by
$\overline{\mathbb{F}}_{\mathfrak{p}}$
with complex multiplication by
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. As the ideal class group of
${\mathcal{O}}_{\boldsymbol{k}}$
. As the ideal class group of
![]() $\boldsymbol{k}$
acts simply transitively on the elliptic curves with complex multiplication by
$\boldsymbol{k}$
acts simply transitively on the elliptic curves with complex multiplication by
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
, we find
${\mathcal{O}}_{\boldsymbol{k}}$
, we find
 $$\begin{eqnarray}\mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{1}{\#\text{Aut}(z)}=\mathop{\sum }_{\mathfrak{a}\in \text{Pic}({\mathcal{O}}_{\boldsymbol{ k}})}\mathop{\sum }_{\substack{ x\in V_{\unicode[STIX]{x1D707}}({\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}\mathfrak{a}) \\ \deg (x)=m}}\frac{1}{w_{\boldsymbol{k}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{1}{\#\text{Aut}(z)}=\mathop{\sum }_{\mathfrak{a}\in \text{Pic}({\mathcal{O}}_{\boldsymbol{ k}})}\mathop{\sum }_{\substack{ x\in V_{\unicode[STIX]{x1D707}}({\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}\mathfrak{a}) \\ \deg (x)=m}}\frac{1}{w_{\boldsymbol{k}}}.\end{eqnarray}$$
As in the argument surrounding (4.10), the assumption
 $\text{Diff}_{L_{0}}(m)=\{p\}$
implies that there is some vector
$\text{Diff}_{L_{0}}(m)=\{p\}$
implies that there is some vector
 $$\begin{eqnarray}x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\end{eqnarray}$$
$$\begin{eqnarray}x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\end{eqnarray}$$
with
 $Q(x)=m$
, and the group
$Q(x)=m$
, and the group
 $\boldsymbol{k}^{1}=\{s\in \boldsymbol{k}^{\times }:s\overline{s}=1\}$
acts transitively (by right multiplication on
$\boldsymbol{k}^{1}=\{s\in \boldsymbol{k}^{\times }:s\overline{s}=1\}$
acts transitively (by right multiplication on
![]() $V_{0}$
) on the set of all such
$V_{0}$
) on the set of all such
![]() $x$
. Using
$x$
. Using
 $t\mapsto t/\overline{t}$
to identify
$t\mapsto t/\overline{t}$
to identify
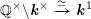 $\mathbb{Q}^{\times }\backslash \boldsymbol{k}^{\times }\xrightarrow[{}]{\simeq }\boldsymbol{k}^{1}$
and arguing as in the proof of [Reference Howard and YangHY12, Proposition 2.18], we obtain a factorization into orbital integrals
$\mathbb{Q}^{\times }\backslash \boldsymbol{k}^{\times }\xrightarrow[{}]{\simeq }\boldsymbol{k}^{1}$
and arguing as in the proof of [Reference Howard and YangHY12, Proposition 2.18], we obtain a factorization into orbital integrals
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{1}{\#\text{Aut}(z)} & = & \displaystyle \frac{1}{w_{\boldsymbol{k}}}\mathop{\sum }_{\mathfrak{a}\in \text{Pic}({\mathcal{O}}_{\boldsymbol{ k}})}\mathop{\sum }_{t\in \mathbb{Q}^{\times }\backslash \boldsymbol{k}^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}({\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}\mathfrak{a})}(xt\overline{t}^{-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\mathop{\prod }_{\ell }\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{z\in {\mathcal{Z}}_{0}(m,\unicode[STIX]{x1D707})(\overline{\mathbb{F}}_{\mathfrak{p}})}\frac{1}{\#\text{Aut}(z)} & = & \displaystyle \frac{1}{w_{\boldsymbol{k}}}\mathop{\sum }_{\mathfrak{a}\in \text{Pic}({\mathcal{O}}_{\boldsymbol{ k}})}\mathop{\sum }_{t\in \mathbb{Q}^{\times }\backslash \boldsymbol{k}^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}({\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{ k}}}\mathfrak{a})}(xt\overline{t}^{-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\mathop{\prod }_{\ell }\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1}).\end{eqnarray}$$
Here
![]() $\mathbf{1}$
indicates characteristic function,
$\mathbf{1}$
indicates characteristic function,
![]() $E_{\ell }$
is the
$E_{\ell }$
is the
![]() $\ell$
-divisible group of
$\ell$
-divisible group of
![]() ${\mathcal{E}}$
, and
${\mathcal{E}}$
, and
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}(E_{\ell })=\{y\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}^{\vee }:y-\text{id}\otimes \unicode[STIX]{x1D707}\in \text{End}(E_{\ell })\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}(E_{\ell })=\{y\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}^{\vee }:y-\text{id}\otimes \unicode[STIX]{x1D707}\in \text{End}(E_{\ell })\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}\}.\end{eqnarray}$$
On the right-hand side of the first equality of (4.13) we are viewing
 $$\begin{eqnarray}xt\overline{t}^{-1}\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{ k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}\mathfrak{a})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\end{eqnarray}$$
$$\begin{eqnarray}xt\overline{t}^{-1}\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{ k}}}({\mathcal{E}})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\xrightarrow[{}]{\simeq }\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}\mathfrak{a})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}V_{0}\end{eqnarray}$$
using the quasi-isogeny from
![]() ${\mathcal{E}}$
to
${\mathcal{E}}$
to
 ${\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}\mathfrak{a}$
defined by
${\mathcal{E}}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}\mathfrak{a}$
defined by
 $P\mapsto P\otimes 1$
.
$P\mapsto P\otimes 1$
.
A choice of left
![]() ${\mathcal{O}}_{\boldsymbol{k},\ell }$
-module isomorphism
${\mathcal{O}}_{\boldsymbol{k},\ell }$
-module isomorphism
 $L_{0,\ell }\xrightarrow[{}]{\simeq }{\mathcal{O}}_{\boldsymbol{k},\ell }$
identifies
$L_{0,\ell }\xrightarrow[{}]{\simeq }{\mathcal{O}}_{\boldsymbol{k},\ell }$
identifies
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}(E_{\ell })=\{y\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\cdot \mathfrak{d}_{\boldsymbol{k}}^{-1}:y-\unicode[STIX]{x1D707}\in \text{End}(E_{\ell })\},\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}(E_{\ell })=\{y\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\cdot \mathfrak{d}_{\boldsymbol{k}}^{-1}:y-\unicode[STIX]{x1D707}\in \text{End}(E_{\ell })\},\end{eqnarray}$$
where
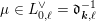 $\unicode[STIX]{x1D707}\in L_{0,\ell }^{\vee }=\mathfrak{d}_{\boldsymbol{k},\ell }^{-1}$
is viewed as a quasi-endomorphism of
$\unicode[STIX]{x1D707}\in L_{0,\ell }^{\vee }=\mathfrak{d}_{\boldsymbol{k},\ell }^{-1}$
is viewed as a quasi-endomorphism of
![]() $E_{\ell }$
using the complex multiplication. From now on we use this identification to view
$E_{\ell }$
using the complex multiplication. From now on we use this identification to view
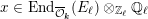 $x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\otimes _{\mathbb{Z}_{\ell }}\mathbb{Q}_{\ell }$
and
$x\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\otimes _{\mathbb{Z}_{\ell }}\mathbb{Q}_{\ell }$
and
![]() $\unicode[STIX]{x1D707}\in \boldsymbol{k}_{\ell }$
. Using (4.7), the condition
$\unicode[STIX]{x1D707}\in \boldsymbol{k}_{\ell }$
. Using (4.7), the condition
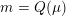 $m=Q(\unicode[STIX]{x1D707})$
in
$m=Q(\unicode[STIX]{x1D707})$
in
![]() $\mathbb{Q}/\mathbb{Z}$
translates to
$\mathbb{Q}/\mathbb{Z}$
translates to
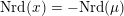 $\text{Nrd}(x)=-\text{Nrd}(\unicode[STIX]{x1D707})$
in
$\text{Nrd}(x)=-\text{Nrd}(\unicode[STIX]{x1D707})$
in
![]() $\mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }$
, where
$\mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }$
, where
![]() $\text{Nrd}$
is the reduced norm on the quaternion algebra
$\text{Nrd}$
is the reduced norm on the quaternion algebra
 $$\begin{eqnarray}\text{End}(E_{\ell })\otimes _{\mathbb{Z}_{\ell }}\mathbb{Q}_{\ell }=\boldsymbol{k}_{\ell }\oplus (\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\otimes _{\mathbb{Z}_{\ell }}\mathbb{Q}_{\ell }).\end{eqnarray}$$
$$\begin{eqnarray}\text{End}(E_{\ell })\otimes _{\mathbb{Z}_{\ell }}\mathbb{Q}_{\ell }=\boldsymbol{k}_{\ell }\oplus (\text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}(E_{\ell })\otimes _{\mathbb{Z}_{\ell }}\mathbb{Q}_{\ell }).\end{eqnarray}$$
An explicit description (in terms of this decomposition) of the maximal order
 $\text{End}(E_{\ell })$
can be found in [Reference Kudla and YangKY13, Lemma 3.3].
$\text{End}(E_{\ell })$
can be found in [Reference Kudla and YangKY13, Lemma 3.3].
Using the explicit description of
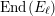 $\text{End}(E_{\ell })$
, the local factors on the right-hand side of (4.13) can be computed directly. We demonstrate the method for a prime
$\text{End}(E_{\ell })$
, the local factors on the right-hand side of (4.13) can be computed directly. We demonstrate the method for a prime
![]() $\ell$
ramified in
$\ell$
ramified in
![]() $\boldsymbol{k}$
. For such an
$\boldsymbol{k}$
. For such an
![]() $\ell$
we have
$\ell$
we have
 $$\begin{eqnarray}\mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{ k},\ell }^{\times }=\{1,t\}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{ k},\ell }^{\times }=\{1,t\}\end{eqnarray}$$
where
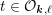 $t\in {\mathcal{O}}_{\boldsymbol{k},\ell }$
is any uniformizer. As
$t\in {\mathcal{O}}_{\boldsymbol{k},\ell }$
is any uniformizer. As
![]() $\ell >2$
, we may choose
$\ell >2$
, we may choose
![]() $t$
so that
$t$
so that
![]() $\overline{t}=-t$
, and so
$\overline{t}=-t$
, and so
 $$\begin{eqnarray}\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(x)+\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(-x).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(x)+\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(-x).\end{eqnarray}$$
We now consider the two sub-cases
![]() $\ell =p$
and
$\ell =p$
and
![]() $\ell \not =p$
.
$\ell \not =p$
.
If
![]() $\ell =p$
, our assumption
$\ell =p$
, our assumption
 $\text{ord}_{p}(m)\geqslant 0$
and the relation
$\text{ord}_{p}(m)\geqslant 0$
and the relation
 $m=Q(\unicode[STIX]{x1D707})$
in
$m=Q(\unicode[STIX]{x1D707})$
in
![]() $\mathbb{Q}/\mathbb{Z}$
imply that
$\mathbb{Q}/\mathbb{Z}$
imply that
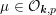 $\unicode[STIX]{x1D707}\in {\mathcal{O}}_{\boldsymbol{k},p}$
, and that
$\unicode[STIX]{x1D707}\in {\mathcal{O}}_{\boldsymbol{k},p}$
, and that
 $\text{Nrd}(x)\in \mathbb{Z}_{p}$
. As
$\text{Nrd}(x)\in \mathbb{Z}_{p}$
. As
 $\text{End}(E_{p})$
is the maximal order in the ramified quaternion algebra over
$\text{End}(E_{p})$
is the maximal order in the ramified quaternion algebra over
![]() $\mathbb{Q}_{p}$
, this implies that
$\mathbb{Q}_{p}$
, this implies that
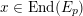 $x\in \text{End}(E_{p})$
. From this it follows that both
$x\in \text{End}(E_{p})$
. From this it follows that both
![]() $x$
and
$x$
and
![]() $-x$
lie in
$-x$
lie in
![]() $V_{\unicode[STIX]{x1D707}}(E_{p})$
, and so
$V_{\unicode[STIX]{x1D707}}(E_{p})$
, and so
 $$\begin{eqnarray}\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=2.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=2.\end{eqnarray}$$
Now suppose
![]() $\ell \not =p$
. If
$\ell \not =p$
. If
 $\unicode[STIX]{x1D707}\in {\mathcal{O}}_{\boldsymbol{k},\ell }$
then
$\unicode[STIX]{x1D707}\in {\mathcal{O}}_{\boldsymbol{k},\ell }$
then
 $\text{Nrd}(\unicode[STIX]{x1D707})\in \mathbb{Z}_{\ell }$
, and hence
$\text{Nrd}(\unicode[STIX]{x1D707})\in \mathbb{Z}_{\ell }$
, and hence
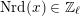 $\text{Nrd}(x)\in \mathbb{Z}_{\ell }$
. The description of
$\text{Nrd}(x)\in \mathbb{Z}_{\ell }$
. The description of
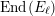 $\text{End}(E_{\ell })$
in [Reference Kudla and YangKY13, Lemma 3.3] now implies that
$\text{End}(E_{\ell })$
in [Reference Kudla and YangKY13, Lemma 3.3] now implies that
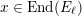 $x\in \text{End}(E_{\ell })$
, and again both
$x\in \text{End}(E_{\ell })$
, and again both
![]() $x$
and
$x$
and
![]() $-x$
lie in
$-x$
lie in
![]() $V_{\unicode[STIX]{x1D707}}(E_{p})$
. If
$V_{\unicode[STIX]{x1D707}}(E_{p})$
. If
 $\unicode[STIX]{x1D707}\not \in {\mathcal{O}}_{\boldsymbol{k},\ell }$
then
$\unicode[STIX]{x1D707}\not \in {\mathcal{O}}_{\boldsymbol{k},\ell }$
then
 $\ell \cdot \text{Nrd}(\unicode[STIX]{x1D707})\in \mathbb{Z}_{\ell }^{\times }$
, and hence the relation
$\ell \cdot \text{Nrd}(\unicode[STIX]{x1D707})\in \mathbb{Z}_{\ell }^{\times }$
, and hence the relation
 $\text{Nrd}(x)+\text{Nrd}(\unicode[STIX]{x1D707})\in \mathbb{Z}_{\ell }$
noted above implies
$\text{Nrd}(x)+\text{Nrd}(\unicode[STIX]{x1D707})\in \mathbb{Z}_{\ell }$
noted above implies
 $\ell \cdot \text{Nrd}(x)\in \mathbb{Z}_{\ell }^{\times }$
. Using the same relation, and the description of
$\ell \cdot \text{Nrd}(x)\in \mathbb{Z}_{\ell }^{\times }$
. Using the same relation, and the description of
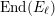 $\text{End}(E_{\ell })$
in [Reference Kudla and YangKY13, Lemma 3.3], one can show that exactly one of
$\text{End}(E_{\ell })$
in [Reference Kudla and YangKY13, Lemma 3.3], one can show that exactly one of
![]() $x\pm \unicode[STIX]{x1D707}$
lies in
$x\pm \unicode[STIX]{x1D707}$
lies in
 $\text{End}(E_{\ell })$
. Thus exactly one of
$\text{End}(E_{\ell })$
. Thus exactly one of
![]() $x$
and
$x$
and
![]() $-x$
lies in
$-x$
lies in
![]() $V_{\unicode[STIX]{x1D707}}(E_{\ell })$
, and we have proved
$V_{\unicode[STIX]{x1D707}}(E_{\ell })$
, and we have proved
 $$\begin{eqnarray}\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\unicode[STIX]{x1D707}\not \in L_{0,\ell },\\ 2\quad & \text{if }\unicode[STIX]{x1D707}\in L_{0,\ell }.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\unicode[STIX]{x1D707}\not \in L_{0,\ell },\\ 2\quad & \text{if }\unicode[STIX]{x1D707}\in L_{0,\ell }.\end{array}\right.\end{eqnarray}$$
From similar calculations at the unramified primes, one can deduce the relation
 $$\begin{eqnarray}\mathop{\prod }_{\ell }\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=2^{s(\unicode[STIX]{x1D707})}\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\ell }\mathop{\sum }_{t\in \mathbb{Q}_{\ell }^{\times }\backslash \boldsymbol{k}_{\ell }^{\times }/{\mathcal{O}}_{\boldsymbol{k},\ell }^{\times }}\mathbf{1}_{V_{\unicode[STIX]{x1D707}}(E_{\ell })}(xt\overline{t}^{-1})=2^{s(\unicode[STIX]{x1D707})}\cdot \unicode[STIX]{x1D70C}\biggl(\frac{m|d_{\boldsymbol{k}}|}{p^{\unicode[STIX]{x1D716}}}\biggr)\end{eqnarray}$$
(the right-hand side has an obvious product factorization, and one verifies equality prime-by-prime). The equality (4.12) follows immediately.
The final claim of the theorem follows by comparing the above formulas with Proposition 3.3.1. ◻
4.6 Mapping to the orthogonal Shimura variety
Recall from § 2.3 the
![]() $\text{GSpin}$
Shimura variety
$\text{GSpin}$
Shimura variety
![]() $M$
over
$M$
over
![]() $\mathbb{Q}$
defined by the quadratic space
$\mathbb{Q}$
defined by the quadratic space
![]() $L$
. In § 2.4 we defined the integral model
$L$
. In § 2.4 we defined the integral model
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
![]() $\mathbb{Z}$
, and the Kuga–Satake abelian scheme
$\mathbb{Z}$
, and the Kuga–Satake abelian scheme
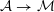 ${\mathcal{A}}\rightarrow {\mathcal{M}}$
. The integral model
${\mathcal{A}}\rightarrow {\mathcal{M}}$
. The integral model
![]() ${\mathcal{M}}$
carries over it the collection of sheaves
${\mathcal{M}}$
carries over it the collection of sheaves
 $\boldsymbol{V}\subset \text{}\underline{\text{End}}(\boldsymbol{H})$
of (2.10).
$\boldsymbol{V}\subset \text{}\underline{\text{End}}(\boldsymbol{H})$
of (2.10).
The inclusion
 $L_{0}\rightarrow L$
extends to a homomorphism
$L_{0}\rightarrow L$
extends to a homomorphism
 $C(V_{0})\rightarrow C(V)$
of Clifford algebras, which then induces a morphism
$C(V_{0})\rightarrow C(V)$
of Clifford algebras, which then induces a morphism
 $\text{GSpin}(V_{0})\rightarrow \text{GSpin}(V)$
. The theory of canonical models shows that the induced map of complex orbifolds
$\text{GSpin}(V_{0})\rightarrow \text{GSpin}(V)$
. The theory of canonical models shows that the induced map of complex orbifolds
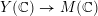 $Y(\mathbb{C})\rightarrow M(\mathbb{C})$
descends to a finite and unramified morphism of
$Y(\mathbb{C})\rightarrow M(\mathbb{C})$
descends to a finite and unramified morphism of
![]() $\boldsymbol{k}$
-stacks
$\boldsymbol{k}$
-stacks
 $$\begin{eqnarray}\displaystyle Y\rightarrow M_{\boldsymbol{k}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y\rightarrow M_{\boldsymbol{k}}. & & \displaystyle\end{eqnarray}$$
In this section we assume that the discriminant of
![]() $\boldsymbol{k}$
is odd. We will extend this morphism to a morphism
$\boldsymbol{k}$
is odd. We will extend this morphism to a morphism
 ${\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
of integral models, and explain the how the various structures (special cycles, sheaves, and Kuga–Satake abelian schemes) on the source and target are related.
${\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}$
of integral models, and explain the how the various structures (special cycles, sheaves, and Kuga–Satake abelian schemes) on the source and target are related.
As noted earlier,
![]() ${\mathcal{Y}}$
is finite étale over
${\mathcal{Y}}$
is finite étale over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. The proof of Proposition 4.6.1 below will require a slightly different perspective on this, couched in the language of local models.
${\mathcal{O}}_{\boldsymbol{k}}$
. The proof of Proposition 4.6.1 below will require a slightly different perspective on this, couched in the language of local models.
Let
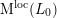 $\text{M}^{\text{loc}}(L_{0})$
be the quadric over
$\text{M}^{\text{loc}}(L_{0})$
be the quadric over
![]() $\mathbb{Z}$
that parameterizes isotropic lines in
$\mathbb{Z}$
that parameterizes isotropic lines in
![]() $L_{0}$
. There is an isomorphism of
$L_{0}$
. There is an isomorphism of
![]() $\mathbb{Z}$
-schemes
$\mathbb{Z}$
-schemes
 $$\begin{eqnarray}\displaystyle \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})\xrightarrow[{}]{\simeq }\text{M}^{\text{loc}}(L_{0}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})\xrightarrow[{}]{\simeq }\text{M}^{\text{loc}}(L_{0}) & & \displaystyle\end{eqnarray}$$
determined as follows. Consider the map
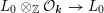 $L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{\boldsymbol{k}}\rightarrow L_{0}$
defined by
$L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{\boldsymbol{k}}\rightarrow L_{0}$
defined by
 $v\otimes \unicode[STIX]{x1D6FC}\mapsto v\overline{\unicode[STIX]{x1D6FC}}.$
The kernel of this map is an isotropic rank-one
$v\otimes \unicode[STIX]{x1D6FC}\mapsto v\overline{\unicode[STIX]{x1D6FC}}.$
The kernel of this map is an isotropic rank-one
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-module corresponding to a map
${\mathcal{O}}_{\boldsymbol{k}}$
-module corresponding to a map
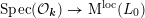 $\text{Spec}({\mathcal{O}}_{\boldsymbol{k}})\rightarrow \text{M}^{\text{loc}}(L_{0})$
, which is the desired isomorphism (4.15).
$\text{Spec}({\mathcal{O}}_{\boldsymbol{k}})\rightarrow \text{M}^{\text{loc}}(L_{0})$
, which is the desired isomorphism (4.15).
Now, consider the functor
![]() ${\mathcal{P}}_{0}$
on
${\mathcal{P}}_{0}$
on
![]() ${\mathcal{Y}}$
-schemes parameterizing
${\mathcal{Y}}$
-schemes parameterizing
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-equivariant isomorphisms of rank-two vector bundles
${\mathcal{O}}_{\boldsymbol{k}}$
-equivariant isomorphisms of rank-two vector bundles
 $$\begin{eqnarray}{\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{{\mathcal{Y}}}\xrightarrow[{}]{\simeq }\boldsymbol{H}_{0,\text{dR}}^{+}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{{\mathcal{Y}}}\xrightarrow[{}]{\simeq }\boldsymbol{H}_{0,\text{dR}}^{+}.\end{eqnarray}$$
This is represented over
![]() ${\mathcal{Y}}$
by a
${\mathcal{Y}}$
by a
![]() $T$
-torsor
$T$
-torsor
 ${\mathcal{P}}_{0}\rightarrow {\mathcal{Y}}$
. Indeed, we only need to observe that, étale locally on
${\mathcal{P}}_{0}\rightarrow {\mathcal{Y}}$
. Indeed, we only need to observe that, étale locally on
![]() ${\mathcal{Y}}$
,
${\mathcal{Y}}$
,
![]() $\boldsymbol{H}_{0,\text{dR}}^{+}$
is a free
$\boldsymbol{H}_{0,\text{dR}}^{+}$
is a free
 ${\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{{\mathcal{Y}}}$
-module of rank one.
${\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{{\mathcal{Y}}}$
-module of rank one.
Suppose that we are given a scheme
![]() $U\rightarrow {\mathcal{Y}}$
over
$U\rightarrow {\mathcal{Y}}$
over
![]() ${\mathcal{Y}}$
and a section
${\mathcal{Y}}$
and a section
 $U\rightarrow {\mathcal{P}}_{0}$
, corresponding to an
$U\rightarrow {\mathcal{P}}_{0}$
, corresponding to an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-equivariant isomorphism
${\mathcal{O}}_{\boldsymbol{k}}$
-equivariant isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D709}_{0}:{\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\boldsymbol{H}_{0,\text{dR}}^{+}|_{U}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{0}:{\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\boldsymbol{H}_{0,\text{dR}}^{+}|_{U}.\end{eqnarray}$$
This determines an isomorphism
 $$\begin{eqnarray}L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\boldsymbol{H}_{0,\text{dR}}^{+}|_{U}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}=\boldsymbol{H}_{0,\text{dR}}^{-}|_{U}.\end{eqnarray}$$
$$\begin{eqnarray}L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\boldsymbol{H}_{0,\text{dR}}^{+}|_{U}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}=\boldsymbol{H}_{0,\text{dR}}^{-}|_{U}.\end{eqnarray}$$
Combining the above isomorphisms with the canonical isomorphism
 $$\begin{eqnarray}L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U},L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U})\end{eqnarray}$$
$$\begin{eqnarray}L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}({\mathcal{O}}_{\boldsymbol{k}}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U},L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U})\end{eqnarray}$$
yields an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-linear isometry
${\mathcal{O}}_{\boldsymbol{k}}$
-linear isometry
 $$\begin{eqnarray}\unicode[STIX]{x1D709}_{0}:L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0,\text{dR}}^{+}|_{U},\boldsymbol{H}_{0,\text{dR}}^{-}|_{U})=\boldsymbol{V}_{0,\text{dR}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{0}:L_{0}\otimes _{\mathbb{Z}}{\mathcal{O}}_{U}\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}_{{\mathcal{O}}_{\boldsymbol{k}}}(\boldsymbol{H}_{0,\text{dR}}^{+}|_{U},\boldsymbol{H}_{0,\text{dR}}^{-}|_{U})=\boldsymbol{V}_{0,\text{dR}}.\end{eqnarray}$$
The preimage
 $\unicode[STIX]{x1D709}_{0}^{-1}(\boldsymbol{V}_{0,\text{dR}}^{1})\subset L_{0}\otimes {\mathcal{O}}_{U}$
is an isotropic line, and so corresponds to a point in
$\unicode[STIX]{x1D709}_{0}^{-1}(\boldsymbol{V}_{0,\text{dR}}^{1})\subset L_{0}\otimes {\mathcal{O}}_{U}$
is an isotropic line, and so corresponds to a point in
 $\text{M}^{\text{loc}}(L_{0})(U)$
. We therefore obtain a map
$\text{M}^{\text{loc}}(L_{0})(U)$
. We therefore obtain a map
 $U\rightarrow \text{M}^{\text{loc}}(L_{0})$
. It is not hard to see that the composition of this map with the isomorphism (4.15) is just the structure map
$U\rightarrow \text{M}^{\text{loc}}(L_{0})$
. It is not hard to see that the composition of this map with the isomorphism (4.15) is just the structure map
 $U\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
. The main point is that, as in Remark 4.3.6,
$U\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
. The main point is that, as in Remark 4.3.6,
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
acts on
${\mathcal{O}}_{\boldsymbol{k}}$
acts on
![]() $\boldsymbol{V}_{0,\text{dR}}^{1}$
through the structure map
$\boldsymbol{V}_{0,\text{dR}}^{1}$
through the structure map
 ${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}$
, and on the quotient
${\mathcal{O}}_{\boldsymbol{k}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}$
, and on the quotient
 $\boldsymbol{V}_{0,\text{dR}}/\boldsymbol{V}_{0,\text{dR}}^{1}$
through the conjugate of the structure map. Hence the quotient
$\boldsymbol{V}_{0,\text{dR}}/\boldsymbol{V}_{0,\text{dR}}^{1}$
through the conjugate of the structure map. Hence the quotient
 $\boldsymbol{V}_{0,\text{dR}}/\boldsymbol{V}_{0,\text{dR}}^{1}$
is obtained from
$\boldsymbol{V}_{0,\text{dR}}/\boldsymbol{V}_{0,\text{dR}}^{1}$
is obtained from
![]() $\boldsymbol{V}_{0,\text{dR}}$
via base-change along the augmentation map
$\boldsymbol{V}_{0,\text{dR}}$
via base-change along the augmentation map
 $$\begin{eqnarray}{\mathcal{O}}_{\boldsymbol{k}}\otimes {\mathcal{O}}_{{\mathcal{Y}}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\boldsymbol{k}}\otimes {\mathcal{O}}_{{\mathcal{Y}}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\end{eqnarray}$$
defined by
 $\unicode[STIX]{x1D6FC}\otimes f\mapsto \overline{\unicode[STIX]{x1D6FC}}f.$
$\unicode[STIX]{x1D6FC}\otimes f\mapsto \overline{\unicode[STIX]{x1D6FC}}f.$
In particular, since
![]() ${\mathcal{Y}}$
is étale over
${\mathcal{Y}}$
is étale over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
, if
${\mathcal{O}}_{\boldsymbol{k}}$
, if
![]() $U$
is étale over
$U$
is étale over
![]() ${\mathcal{Y}}$
, then the map
${\mathcal{Y}}$
, then the map
 $U\rightarrow \text{M}^{\text{loc}}(L_{0})$
will also be étale. This can also be shown directly using Grothendieck–Messing theory.
$U\rightarrow \text{M}^{\text{loc}}(L_{0})$
will also be étale. This can also be shown directly using Grothendieck–Messing theory.
The following result is analogous to Proposition 2.5.1.
Proposition 4.6.1. The morphism (4.14) extends uniquely to a finite and unramified morphism
 $$\begin{eqnarray}\displaystyle {\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{Y}}\rightarrow {\mathcal{M}}_{{\mathcal{O}}_{\boldsymbol{k}}}, & & \displaystyle\end{eqnarray}$$
and there is a canonical
![]() $C(L)$
-equivariant isomorphism
$C(L)$
-equivariant isomorphism
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{0}|_{{\mathcal{Y}}}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{{\mathcal{Y}}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{0}|_{{\mathcal{Y}}}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{{\mathcal{Y}}} & & \displaystyle\end{eqnarray}$$
of
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded abelian schemes over
$\mathbb{Z}/2\mathbb{Z}$
-graded abelian schemes over
![]() ${\mathcal{Y}}$
. In particular,
${\mathcal{Y}}$
. In particular,
 $$\begin{eqnarray}\displaystyle \boldsymbol{H}_{0}|_{{\mathcal{Y}}}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }\boldsymbol{H}|_{{\mathcal{Y}}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{H}_{0}|_{{\mathcal{Y}}}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }\boldsymbol{H}|_{{\mathcal{Y}}}. & & \displaystyle\end{eqnarray}$$
Furthermore, set
 $\boldsymbol{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}\otimes \mathbf{1}$
, and recall the space of special endomorphisms
$\boldsymbol{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}\otimes \mathbf{1}$
, and recall the space of special endomorphisms
 $$\begin{eqnarray}V({\mathcal{A}}|_{{\mathcal{Y}}})\subset \text{End}_{C(L)}({\mathcal{A}}|_{{\mathcal{Y}}})\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{A}}|_{{\mathcal{Y}}})\subset \text{End}_{C(L)}({\mathcal{A}}|_{{\mathcal{Y}}})\end{eqnarray}$$
of § 2.6. There is a canonical embedding
 $\unicode[STIX]{x1D6EC}\subset V({\mathcal{A}}|_{{\mathcal{Y}}})$
with the following properties.
$\unicode[STIX]{x1D6EC}\subset V({\mathcal{A}}|_{{\mathcal{Y}}})$
with the following properties.
-
(i) Its homological realization exhibits
 $\boldsymbol{\unicode[STIX]{x1D6EC}}\subset \boldsymbol{V}|_{{\mathcal{Y}}}$
as a local direct summand.
$\boldsymbol{\unicode[STIX]{x1D6EC}}\subset \boldsymbol{V}|_{{\mathcal{Y}}}$
as a local direct summand. -
(ii) The injection
induced by (4.18) identifies $$\begin{eqnarray}\text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0}|_{{\mathcal{Y}}})\rightarrow \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}|_{{\mathcal{Y}}})\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\text{End}}_{C(L_{0})}(\boldsymbol{H}_{0}|_{{\mathcal{Y}}})\rightarrow \text{}\underline{\text{End}}_{C(L)}(\boldsymbol{H}|_{{\mathcal{Y}}})\end{eqnarray}$$
 $\boldsymbol{V}_{0}|_{{\mathcal{Y}}}$
with the submodule of all elements of
$\boldsymbol{V}_{0}|_{{\mathcal{Y}}}$
with the submodule of all elements of
 $\boldsymbol{V}|_{{\mathcal{Y}}}$
anticommuting with all elements of
$\boldsymbol{V}|_{{\mathcal{Y}}}$
anticommuting with all elements of
 $\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Furthermore
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Furthermore
 $\boldsymbol{V}_{0}|_{{\mathcal{Y}}}\subset \boldsymbol{V}|_{{\mathcal{Y}}}$
is locally a direct summand.
$\boldsymbol{V}_{0}|_{{\mathcal{Y}}}\subset \boldsymbol{V}|_{{\mathcal{Y}}}$
is locally a direct summand.
-
(iii) In the de Rham case, the inclusion
 $\boldsymbol{V}_{0,\text{dR}}|_{{\mathcal{Y}}}\subset \boldsymbol{V}_{\text{dR}}|_{{\mathcal{Y}}}$
identifies
$\boldsymbol{V}_{0,\text{dR}}|_{{\mathcal{Y}}}\subset \boldsymbol{V}_{\text{dR}}|_{{\mathcal{Y}}}$
identifies
 $\boldsymbol{V}_{0,\text{dR}}^{1}|_{{\mathcal{Y}}}=\boldsymbol{V}_{\text{dR}}^{1}|_{{\mathcal{Y}}}.$
$\boldsymbol{V}_{0,\text{dR}}^{1}|_{{\mathcal{Y}}}=\boldsymbol{V}_{\text{dR}}^{1}|_{{\mathcal{Y}}}.$
Proof. Just as in (2.11), there is a
![]() $C(L)$
-equivariant isomorphism
$C(L)$
-equivariant isomorphism
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{0}|_{Y}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{Y} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{0}|_{Y}\otimes _{C(L_{0})}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{Y} & & \displaystyle\end{eqnarray}$$
of
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded abelian schemes over
$\mathbb{Z}/2\mathbb{Z}$
-graded abelian schemes over
![]() $Y$
.
$Y$
.
Extending the map of (4.14) of
![]() $\boldsymbol{k}$
-stacks to a map (4.16) of
$\boldsymbol{k}$
-stacks to a map (4.16) of
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-stacks is equivalent to extending the map of
${\mathcal{O}}_{\boldsymbol{k}}$
-stacks is equivalent to extending the map of
![]() $\mathbb{Q}$
-stacks
$\mathbb{Q}$
-stacks
 $Y\rightarrow M$
to a map of
$Y\rightarrow M$
to a map of
![]() $\mathbb{Z}$
-stacks
$\mathbb{Z}$
-stacks
 ${\mathcal{Y}}_{\mathbb{Z}}\rightarrow {\mathcal{M}}$
. Here we write
${\mathcal{Y}}_{\mathbb{Z}}\rightarrow {\mathcal{M}}$
. Here we write
![]() ${\mathcal{Y}}_{\mathbb{Z}}$
for the stack
${\mathcal{Y}}_{\mathbb{Z}}$
for the stack
![]() ${\mathcal{Y}}$
viewed over
${\mathcal{Y}}$
viewed over
 $\text{Spec}(\mathbb{Z})$
.
$\text{Spec}(\mathbb{Z})$
.
To do this, fix a prime
![]() $p>0$
, and assume first that
$p>0$
, and assume first that
![]() $L_{\mathbb{Z}_{(p)}}$
is self-dual. As observed in § 2.4, an appropriate choice of
$L_{\mathbb{Z}_{(p)}}$
is self-dual. As observed in § 2.4, an appropriate choice of
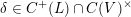 $\unicode[STIX]{x1D6FF}\in C^{+}(L)\cap C(V)^{\times }$
determines a degree
$\unicode[STIX]{x1D6FF}\in C^{+}(L)\cap C(V)^{\times }$
determines a degree
![]() $d$
polarization of the Kuga–Satake abelian scheme
$d$
polarization of the Kuga–Satake abelian scheme
 ${\mathcal{A}}_{M}\rightarrow M$
, inducing a finite unramified map
${\mathcal{A}}_{M}\rightarrow M$
, inducing a finite unramified map
 $$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF}}:M\rightarrow {\mathcal{X}}_{2^{n+1},d,\mathbb{Q}}^{\text{Siegel}}\end{eqnarray}$$
$$\begin{eqnarray}i_{\unicode[STIX]{x1D6FF}}:M\rightarrow {\mathcal{X}}_{2^{n+1},d,\mathbb{Q}}^{\text{Siegel}}\end{eqnarray}$$
to a moduli stack of polarized abelian varieties. The integral model
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
is then simply the normalization of
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
is then simply the normalization of
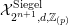 ${\mathcal{X}}_{2^{n+1},d,\mathbb{Z}_{(p)}}^{\text{Siegel}}$
in
${\mathcal{X}}_{2^{n+1},d,\mathbb{Z}_{(p)}}^{\text{Siegel}}$
in
![]() $M$
.
$M$
.
The composition
 $$\begin{eqnarray}Y\rightarrow M\rightarrow {\mathcal{X}}_{2^{n+1},d,\mathbb{Q}}^{\text{Siegel}}\end{eqnarray}$$
$$\begin{eqnarray}Y\rightarrow M\rightarrow {\mathcal{X}}_{2^{n+1},d,\mathbb{Q}}^{\text{Siegel}}\end{eqnarray}$$
determines a polarized abelian scheme over
![]() $Y$
, which is precisely (4.19). The polarized abelian scheme
$Y$
, which is precisely (4.19). The polarized abelian scheme
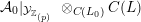 ${\mathcal{A}}_{0}|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}~\otimes _{C(L_{0})}C(L)$
defines an extension of (4.19) to
${\mathcal{A}}_{0}|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}~\otimes _{C(L_{0})}C(L)$
defines an extension of (4.19) to
![]() ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
, which shows that the above composition extends to a morphism
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
, which shows that the above composition extends to a morphism
 $$\begin{eqnarray}{\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{X}}_{2^{n+1},d,\mathbb{Z}_{(p)}}^{\text{Siegel}}\!.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{X}}_{2^{n+1},d,\mathbb{Z}_{(p)}}^{\text{Siegel}}\!.\end{eqnarray}$$
Since
![]() ${\mathcal{Y}}$
is regular, and hence normal, this extension must lift to a map
${\mathcal{Y}}$
is regular, and hence normal, this extension must lift to a map
 ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}},$
and by construction (4.19) extends to an isomorphism
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}},$
and by construction (4.19) extends to an isomorphism
 $$\begin{eqnarray}({\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L))|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}\!.\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{A}}_{0}\otimes _{C(L_{0})}C(L))|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}\xrightarrow[{}]{\simeq }{\mathcal{A}}|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}\!.\end{eqnarray}$$
The construction of the embedding
 $\unicode[STIX]{x1D6EC}{\hookrightarrow}({\mathcal{A}}|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}),$
as well as the proofs of assertions (i), (ii) and (iii) over
$\unicode[STIX]{x1D6EC}{\hookrightarrow}({\mathcal{A}}|_{{\mathcal{Y}}_{\mathbb{Z}_{(p)}}}),$
as well as the proofs of assertions (i), (ii) and (iii) over
![]() ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
, now proceed exactly as in Proposition 2.5.1.
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
, now proceed exactly as in Proposition 2.5.1.
It remains to show (under our self-duality assumption on
![]() $L_{\mathbb{Z}_{(p)}}$
) that the map
$L_{\mathbb{Z}_{(p)}}$
) that the map
 ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}}$
is finite and unramified. For this, using Proposition 2.4.3 and the above discussion of local models, we see that the map is étale locally on the source isomorphic to an étale neighborhood of the closed immersion
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}}$
is finite and unramified. For this, using Proposition 2.4.3 and the above discussion of local models, we see that the map is étale locally on the source isomorphic to an étale neighborhood of the closed immersion
 $\text{M}^{\text{loc}}(L_{0})\rightarrow \text{M}^{\text{loc}}(L)$
. This shows that
$\text{M}^{\text{loc}}(L_{0})\rightarrow \text{M}^{\text{loc}}(L)$
. This shows that
![]() ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
is unramified over
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
is unramified over
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}\!$
. That it is also finite is immediate from the fact that
${\mathcal{M}}_{\mathbb{Z}_{(p)}}\!$
. That it is also finite is immediate from the fact that
![]() ${\mathcal{Y}}$
is finite over
${\mathcal{Y}}$
is finite over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
.
${\mathcal{O}}_{\boldsymbol{k}}$
.
It remains to deal with the primes
![]() $p$
where
$p$
where
![]() $L_{\mathbb{Z}_{(p)}}$
is not self-dual. For this, embed
$L_{\mathbb{Z}_{(p)}}$
is not self-dual. For this, embed
![]() $L$
as an isometric direct summand of a maximal lattice
$L$
as an isometric direct summand of a maximal lattice
![]() $L^{\diamond }$
of signature
$L^{\diamond }$
of signature
![]() $(n^{\diamond },2)$
for which
$(n^{\diamond },2)$
for which
![]() $L_{\mathbb{Z}_{(p)}}^{\diamond }$
is self-dual. Let
$L_{\mathbb{Z}_{(p)}}^{\diamond }$
is self-dual. Let
![]() ${\mathcal{M}}^{\diamond }$
be the regular integral model over
${\mathcal{M}}^{\diamond }$
be the regular integral model over
![]() $\mathbb{Z}$
for the Shimura variety
$\mathbb{Z}$
for the Shimura variety
![]() $M^{\diamond }$
associated with
$M^{\diamond }$
associated with
![]() $L^{\diamond }$
. As in (2.4), let
$L^{\diamond }$
. As in (2.4), let
![]() $\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
be the normalization of
$\check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
be the normalization of
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
in
${\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond }$
in
![]() $M$
.
$M$
.
From what we have shown above, the composition
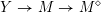 $Y\rightarrow M\rightarrow M^{\diamond }$
extends to a map
$Y\rightarrow M\rightarrow M^{\diamond }$
extends to a map
 ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond },$
which, since
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow {\mathcal{M}}_{\mathbb{Z}_{(p)}}^{\diamond },$
which, since
![]() ${\mathcal{Y}}$
is a normal stack over
${\mathcal{Y}}$
is a normal stack over
![]() $\mathbb{Z}$
, must lift to a finite map
$\mathbb{Z}$
, must lift to a finite map
 ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow \check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
. As in the proof of Proposition 2.5.1, we find that this lift must map
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}\rightarrow \check{{\mathcal{M}}}_{\mathbb{Z}_{(p)}}$
. As in the proof of Proposition 2.5.1, we find that this lift must map
![]() ${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
to
${\mathcal{Y}}_{\mathbb{Z}_{(p)}}$
to
![]() ${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
and must also be unramified, being, étale locally on the source, isomorphic to an étale neighborhood of
${\mathcal{M}}_{\mathbb{Z}_{(p)}}$
and must also be unramified, being, étale locally on the source, isomorphic to an étale neighborhood of
 $$\begin{eqnarray}\displaystyle \text{M}^{\text{loc}}(L_{0})_{\mathbb{Z}}\rightarrow \text{M}^{\text{loc}}(L). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{M}^{\text{loc}}(L_{0})_{\mathbb{Z}}\rightarrow \text{M}^{\text{loc}}(L). & & \displaystyle\end{eqnarray}$$
If
![]() $p=2$
the assumption that
$p=2$
the assumption that
 $C^{+}(L_{0})$
is a maximal order of odd discriminant implies that
$C^{+}(L_{0})$
is a maximal order of odd discriminant implies that
![]() $L_{0,\mathbb{F}_{2}}$
is self-dual so that (4.20) must map into the smooth locus of the target.
$L_{0,\mathbb{F}_{2}}$
is self-dual so that (4.20) must map into the smooth locus of the target.
For
![]() $p>2$
the key point is that the radical of
$p>2$
the key point is that the radical of
![]() $L_{0,\mathbb{F}_{p}}$
, if non-zero, defines an
$L_{0,\mathbb{F}_{p}}$
, if non-zero, defines an
![]() $\mathbb{F}_{p}$
-valued point of the quadric
$\mathbb{F}_{p}$
-valued point of the quadric
 $\text{M}^{\text{loc}}(L_{0})$
associated with
$\text{M}^{\text{loc}}(L_{0})$
associated with
![]() $L_{0}$
. Therefore (4.20) must map into the regular locus (see the proof of Proposition 2.5.1).
$L_{0}$
. Therefore (4.20) must map into the regular locus (see the proof of Proposition 2.5.1).
Finally, the extension (4.17) of the isomorphism (4.19) once again follows from the property of Néron models, and the remaining assertions follow from Proposition 2.5.1 and from what we have already shown in the self-dual case.◻
Remark 4.6.2. The proof of Proposition 4.6.1 actually proves the stronger claim that the morphism
 ${\mathcal{Y}}\rightarrow {\mathcal{M}}$
is finite and unramified.
${\mathcal{Y}}\rightarrow {\mathcal{M}}$
is finite and unramified.
Now suppose that
![]() $S$
is a scheme over
$S$
is a scheme over
![]() ${\mathcal{Y}}$
. Then Proposition 4.6.1 gives us an isometric embedding
${\mathcal{Y}}$
. Then Proposition 4.6.1 gives us an isometric embedding
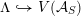 $\unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S})$
. We obtain the following analogue of Proposition 2.6.4.
$\unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S})$
. We obtain the following analogue of Proposition 2.6.4.
Proposition 4.6.3. (i) There is a canonical isometry
 $$\begin{eqnarray}V({\mathcal{E}}_{S})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\bot }\subset V({\mathcal{A}}_{S}).\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{E}}_{S})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\bot }\subset V({\mathcal{A}}_{S}).\end{eqnarray}$$
(ii) The induced map
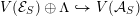 $V({\mathcal{E}}_{S})\oplus \unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S})$
, tensored with
$V({\mathcal{E}}_{S})\oplus \unicode[STIX]{x1D6EC}{\hookrightarrow}V({\mathcal{A}}_{S})$
, tensored with
![]() $\mathbb{Q}$
, restricts to an injection
$\mathbb{Q}$
, restricts to an injection
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}){\hookrightarrow}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}){\hookrightarrow}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})\end{eqnarray}$$
for every
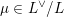 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
and every
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
and every
 $$\begin{eqnarray}(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})\subset (L_{0}^{\vee }/L_{0})\oplus (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})\subset (L_{0}^{\vee }/L_{0})\oplus (\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
(iii) The above injections determine a decomposition
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})=\bigsqcup _{(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{S})=\bigsqcup _{(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}).\end{eqnarray}$$
Proof. Exactly as in the proof Proposition 2.6.4, Proposition 4.6.1 implies that there is a canonical isometry
 $$\begin{eqnarray}V({\mathcal{A}}_{0,S})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\bot }\subset V({\mathcal{A}}_{S}).\end{eqnarray}$$
$$\begin{eqnarray}V({\mathcal{A}}_{0,S})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\bot }\subset V({\mathcal{A}}_{S}).\end{eqnarray}$$
Thus assertion (i) is clear from (4.8).
In particular, there is a canonical inclusion
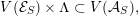 $V({\mathcal{E}}_{S})\times \unicode[STIX]{x1D6EC}\subset V({\mathcal{A}}_{S}),$
which we can make explicit using the
$V({\mathcal{E}}_{S})\times \unicode[STIX]{x1D6EC}\subset V({\mathcal{A}}_{S}),$
which we can make explicit using the
![]() $C(L)$
-equivariant isomorphism
$C(L)$
-equivariant isomorphism
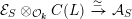 ${\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}$
of (4.17). Indeed, each
${\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}$
of (4.17). Indeed, each
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
induces a special endomorphism
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
induces a special endomorphism
 $$\begin{eqnarray}{\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto e\otimes \unicode[STIX]{x1D706}c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto e\otimes \unicode[STIX]{x1D706}c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S},\end{eqnarray}$$
while each
 $\unicode[STIX]{x1D719}\otimes \ell \in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}=V({\mathcal{E}}_{S})$
induces a special endomorphism
$\unicode[STIX]{x1D719}\otimes \ell \in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}=V({\mathcal{E}}_{S})$
induces a special endomorphism
 $$\begin{eqnarray}{\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto \unicode[STIX]{x1D719}(e)\otimes \ell c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto \unicode[STIX]{x1D719}(e)\otimes \ell c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}.\end{eqnarray}$$
With this in mind, assertions (ii) and (iii) amount to unwinding the definitions. By embedding
![]() $L$
into a unimodular lattice and using Proposition 2.6.4, we may reduce to the case where
$L$
into a unimodular lattice and using Proposition 2.6.4, we may reduce to the case where
![]() $L$
is itself unimodular. In this case, we have canonical isometries
$L$
is itself unimodular. In this case, we have canonical isometries
 $$\begin{eqnarray}L_{0}^{\vee }/L_{0}\xleftarrow[{}]{\simeq }L/(L_{0}\oplus \unicode[STIX]{x1D6EC})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC},\end{eqnarray}$$
$$\begin{eqnarray}L_{0}^{\vee }/L_{0}\xleftarrow[{}]{\simeq }L/(L_{0}\oplus \unicode[STIX]{x1D6EC})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC},\end{eqnarray}$$
and
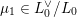 $\unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0}$
corresponds to
$\unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0}$
corresponds to
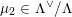 $\unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
if and only if
$\unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
if and only if
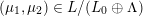 $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in L/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
.
$(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in L/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
.
If
 $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in L/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
and
$(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in L/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
and
 $$\begin{eqnarray}(x,\unicode[STIX]{x1D706})\in V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC})\end{eqnarray}$$
$$\begin{eqnarray}(x,\unicode[STIX]{x1D706})\in V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})\times (\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC})\end{eqnarray}$$
then we may write
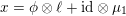 $x=\unicode[STIX]{x1D719}\otimes \ell +\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
for some
$x=\unicode[STIX]{x1D719}\otimes \ell +\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
for some
 $\unicode[STIX]{x1D719}\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})$
and
$\unicode[STIX]{x1D719}\in \text{End}_{\overline{{\mathcal{O}}}_{\boldsymbol{k}}}({\mathcal{E}}_{S})$
and
![]() $\ell \in L_{0}$
. As
$\ell \in L_{0}$
. As
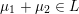 $\unicode[STIX]{x1D707}_{1}+\unicode[STIX]{x1D707}_{2}\in L$
, the quasi-endomorphism
$\unicode[STIX]{x1D707}_{1}+\unicode[STIX]{x1D707}_{2}\in L$
, the quasi-endomorphism
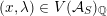 $(x,\unicode[STIX]{x1D706})\in V({\mathcal{A}}_{S})_{\mathbb{Q}}$
is equal to
$(x,\unicode[STIX]{x1D706})\in V({\mathcal{A}}_{S})_{\mathbb{Q}}$
is equal to
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto \unicode[STIX]{x1D719}(e)\otimes \ell c+e\otimes (\unicode[STIX]{x1D707}_{1}+\unicode[STIX]{x1D707}_{2})c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto \unicode[STIX]{x1D719}(e)\otimes \ell c+e\otimes (\unicode[STIX]{x1D707}_{1}+\unicode[STIX]{x1D707}_{2})c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}, & & \displaystyle\end{eqnarray}$$
and so lies in
![]() $V({\mathcal{A}}_{S})$
.
$V({\mathcal{A}}_{S})$
.
Conversely, any element of
![]() $V({\mathcal{A}}_{S})$
is given by a pair
$V({\mathcal{A}}_{S})$
is given by a pair
 $$\begin{eqnarray}(x,\unicode[STIX]{x1D706})\in V({\mathcal{E}}_{S})_{\mathbb{Q}}\times \unicode[STIX]{x1D6EC}_{\mathbb{Q}},\end{eqnarray}$$
$$\begin{eqnarray}(x,\unicode[STIX]{x1D706})\in V({\mathcal{E}}_{S})_{\mathbb{Q}}\times \unicode[STIX]{x1D6EC}_{\mathbb{Q}},\end{eqnarray}$$
and it is easy to see that we must have
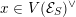 $x\in V({\mathcal{E}}_{S})^{\vee }$
and
$x\in V({\mathcal{E}}_{S})^{\vee }$
and
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}^{\vee }$
. Let
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}^{\vee }$
. Let
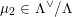 $\unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
be the coset of
$\unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
be the coset of
![]() $\unicode[STIX]{x1D706}$
, and let
$\unicode[STIX]{x1D706}$
, and let
 $\unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0}$
be the unique element for which
$\unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0}$
be the unique element for which
 $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in L/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
. If we write
$(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in L/(L_{0}\oplus \unicode[STIX]{x1D6EC})$
. If we write
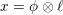 $x=\unicode[STIX]{x1D719}\otimes \ell$
with
$x=\unicode[STIX]{x1D719}\otimes \ell$
with
![]() $\ell \in V_{0}$
then, by assumption, the quasi-endomorphism of
$\ell \in V_{0}$
then, by assumption, the quasi-endomorphism of
![]() ${\mathcal{A}}_{S}$
determined by
${\mathcal{A}}_{S}$
determined by
![]() $(x,\unicode[STIX]{x1D706})$
is the (integral) endomorphism (4.21), while
$(x,\unicode[STIX]{x1D706})$
is the (integral) endomorphism (4.21), while
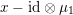 $x-\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
is the quasi-endomorphism
$x-\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
is the quasi-endomorphism
 $$\begin{eqnarray}{\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto \unicode[STIX]{x1D719}(e)\otimes \ell c-e\otimes \unicode[STIX]{x1D707}_{1}c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{S}\xrightarrow[{}]{\simeq }{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{e\otimes c\mapsto \unicode[STIX]{x1D719}(e)\otimes \ell c-e\otimes \unicode[STIX]{x1D707}_{1}c}{\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)\xrightarrow[{}]{\simeq }{\mathcal{A}}_{S}.\end{eqnarray}$$
These differ by the endomorphism
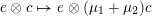 $e\otimes c\mapsto e\otimes (\unicode[STIX]{x1D707}_{1}+\unicode[STIX]{x1D707}_{2})c$
, and so
$e\otimes c\mapsto e\otimes (\unicode[STIX]{x1D707}_{1}+\unicode[STIX]{x1D707}_{2})c$
, and so
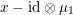 $x-\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
is an (integral) endomorphism of
$x-\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
is an (integral) endomorphism of
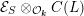 ${\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)$
. As
${\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}C(L)$
. As
 $L_{0}\subset C(L)$
as an
$L_{0}\subset C(L)$
as an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-module direct summand, it follows that
${\mathcal{O}}_{\boldsymbol{k}}$
-module direct summand, it follows that
 $x-\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
restricts to a homomorphism
$x-\text{id}\otimes \unicode[STIX]{x1D707}_{1}$
restricts to a homomorphism
 ${\mathcal{E}}_{S}\rightarrow {\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
. This proves that
${\mathcal{E}}_{S}\rightarrow {\mathcal{E}}_{S}\otimes _{{\mathcal{O}}_{\boldsymbol{k}}}L_{0}$
. This proves that
 $x\in V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})$
, and all parts of the claim follow.◻
$x\in V_{\unicode[STIX]{x1D707}_{1}}({\mathcal{E}}_{S})$
, and all parts of the claim follow.◻
We immediately obtain from Proposition 4.6.3 the following analogue of Proposition 2.7.1.
Proposition 4.6.4. There is an isomorphism of
![]() ${\mathcal{Y}}$
-stacks
${\mathcal{Y}}$
-stacks
 $$\begin{eqnarray}\displaystyle {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{Y}}~\xrightarrow[{}]{\simeq }~\bigsqcup _{\substack{ m_{1}+m_{2}=m \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{Y}}~\xrightarrow[{}]{\simeq }~\bigsqcup _{\substack{ m_{1}+m_{2}=m \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}, & & \displaystyle\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}=\{x\in \unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}:Q(x)=m_{2}\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}=\{x\in \unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D6EC}:Q(x)=m_{2}\},\end{eqnarray}$$
and
 ${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
denotes the disjoint union of
${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
denotes the disjoint union of
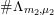 $\#\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
copies of
$\#\unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}$
copies of
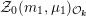 ${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}$
.
${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}$
.
Remark 4.6.5. The terms
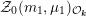 ${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}$
in the decomposition (4.22) define
${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})_{{\mathcal{O}}_{\boldsymbol{k}}}$
in the decomposition (4.22) define
![]() $0$
-cycles on
$0$
-cycles on
![]() ${\mathcal{Y}}$
when
${\mathcal{Y}}$
when
![]() $m_{1}\neq 0$
. The remaining terms
$m_{1}\neq 0$
. The remaining terms
 $$\begin{eqnarray}\bigsqcup _{(0,\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}{\mathcal{Z}}_{0}(0,0)_{{\mathcal{O}}_{\boldsymbol{k}}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}_{2}}=\bigsqcup _{(0,\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}{\mathcal{Y}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}_{2}}\end{eqnarray}$$
$$\begin{eqnarray}\bigsqcup _{(0,\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}{\mathcal{Z}}_{0}(0,0)_{{\mathcal{O}}_{\boldsymbol{k}}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}_{2}}=\bigsqcup _{(0,\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}{\mathcal{Y}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}_{2}}\end{eqnarray}$$
are those with
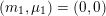 $(m_{1},\unicode[STIX]{x1D707}_{1})=(0,0)$
, and account for the improper intersection between the cycles
$(m_{1},\unicode[STIX]{x1D707}_{1})=(0,0)$
, and account for the improper intersection between the cycles
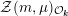 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{{\mathcal{O}}_{\boldsymbol{k}}}$
and
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{{\mathcal{O}}_{\boldsymbol{k}}}$
and
![]() ${\mathcal{Y}}$
.
${\mathcal{Y}}$
.
5 Degrees of metrized line bundles
As in previous sections, fix a maximal quadratic space
![]() $L$
over
$L$
over
![]() $\mathbb{Z}$
of signature
$\mathbb{Z}$
of signature
![]() $(n,2)$
, and a
$(n,2)$
, and a
![]() $\mathbb{Z}$
-module direct summand
$\mathbb{Z}$
-module direct summand
![]() $L_{0}\subset L$
of signature
$L_{0}\subset L$
of signature
![]() $(0,2)$
. Assume the even Clifford algebra
$(0,2)$
. Assume the even Clifford algebra
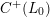 $C^{+}(L_{0})$
is isomorphic to the maximal order in a quadratic imaginary field
$C^{+}(L_{0})$
is isomorphic to the maximal order in a quadratic imaginary field
![]() $\boldsymbol{k}\subset \mathbb{C}$
of odd discriminant. Set
$\boldsymbol{k}\subset \mathbb{C}$
of odd discriminant. Set
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}=\{x\in L:x\bot L_{0}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}=\{x\in L:x\bot L_{0}\}.\end{eqnarray}$$
Recall from § 2.4 that we have associated with
![]() $L$
an algebraic stack
$L$
an algebraic stack
 $$\begin{eqnarray}\displaystyle {\mathcal{M}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{M}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}}). & & \displaystyle\end{eqnarray}$$
Similarly, in § 4.3 we constructed from
![]() $L_{0}$
an algebraic stack
$L_{0}$
an algebraic stack
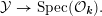 ${\mathcal{Y}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}}).$
The functoriality results of Proposition 4.6.1 provide us with a finite and unramified morphism
${\mathcal{Y}}\rightarrow \text{Spec}({\mathcal{O}}_{\boldsymbol{k}}).$
The functoriality results of Proposition 4.6.1 provide us with a finite and unramified morphism
 $$\begin{eqnarray}i:{\mathcal{Y}}\rightarrow {\mathcal{M}}.\end{eqnarray}$$
$$\begin{eqnarray}i:{\mathcal{Y}}\rightarrow {\mathcal{M}}.\end{eqnarray}$$
Of course the stack
![]() ${\mathcal{M}}$
was originally constructed over
${\mathcal{M}}$
was originally constructed over
![]() $\mathbb{Z}$
. Its restriction to
$\mathbb{Z}$
. Its restriction to
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
is all that we will use in this section.
${\mathcal{O}}_{\boldsymbol{k}}$
is all that we will use in this section.
5.1 Metrized line bundles
We will need some basic notions of arithmetic intersection theory on the stack
![]() ${\mathcal{M}}$
. For more details see [Reference Gillet and SouléGS90, Reference Kudla, Rapoport and YangKRY04, Reference Kudla, Rapoport and YangKRY06], or [Reference VistoliVis89].
${\mathcal{M}}$
. For more details see [Reference Gillet and SouléGS90, Reference Kudla, Rapoport and YangKRY04, Reference Kudla, Rapoport and YangKRY06], or [Reference VistoliVis89].
Although the integral model over
![]() $\mathbb{Z}$
described in § 2.4 is regular, its base change (5.1) to
$\mathbb{Z}$
described in § 2.4 is regular, its base change (5.1) to
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
need not be. This is not a serious problem: the first part of the following proposition implies that
${\mathcal{O}}_{\boldsymbol{k}}$
need not be. This is not a serious problem: the first part of the following proposition implies that
![]() ${\mathcal{M}}$
has a perfectly good theory of Cartier divisors. Whenever we speak of ‘divisors’ on
${\mathcal{M}}$
has a perfectly good theory of Cartier divisors. Whenever we speak of ‘divisors’ on
![]() ${\mathcal{M}}$
we always mean ‘Cartier divisors.’
${\mathcal{M}}$
we always mean ‘Cartier divisors.’
Proposition 5.1.1. The stack
![]() ${\mathcal{M}}$
is locally integral. If
${\mathcal{M}}$
is locally integral. If
![]() $D$
denotes the greatest common divisor of
$D$
denotes the greatest common divisor of
 $\text{disc}(L_{0})$
and
$\text{disc}(L_{0})$
and
![]() $\text{disc}(L)$
, then the restriction of
$\text{disc}(L)$
, then the restriction of
![]() ${\mathcal{M}}$
to
${\mathcal{M}}$
to
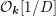 ${\mathcal{O}}_{\boldsymbol{k}}[1/D]$
is regular.
${\mathcal{O}}_{\boldsymbol{k}}[1/D]$
is regular.
Proof. Using Proposition 2.4.3 and the definition of
![]() ${\mathcal{M}}$
, to show that
${\mathcal{M}}$
, to show that
![]() ${\mathcal{M}}$
is locally integral, it suffices to show that the regular locus of the quadric
${\mathcal{M}}$
is locally integral, it suffices to show that the regular locus of the quadric
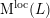 $\text{M}^{\text{loc}}(L)$
associated with the quadratic space
$\text{M}^{\text{loc}}(L)$
associated with the quadratic space
![]() $L$
is integral after base change to
$L$
is integral after base change to
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. In explicit terms, the complete local rings of this locus at its
${\mathcal{O}}_{\boldsymbol{k}}$
. In explicit terms, the complete local rings of this locus at its
![]() $\overline{\mathbb{F}}_{p}$
-points are either formally smooth over
$\overline{\mathbb{F}}_{p}$
-points are either formally smooth over
![]() $\mathbb{Z}_{p}$
, or are isomorphic to one of the two following
$\mathbb{Z}_{p}$
, or are isomorphic to one of the two following
![]() $W(\overline{\mathbb{F}}_{p})$
-algebras [Reference Madapusi PeraMad16, (2.16)]:
$W(\overline{\mathbb{F}}_{p})$
-algebras [Reference Madapusi PeraMad16, (2.16)]:
 $$\begin{eqnarray}W(\overline{\mathbb{F}}_{p})\frac{[[u_{1},\ldots ,u_{n+1}]]}{(\mathop{\sum }_{i}u_{i}^{2}+p)}\quad \text{or}\quad W(\overline{\mathbb{F}}_{p})\frac{[[u_{1},\ldots ,u_{n},w]]}{(\mathop{\sum }_{i}u_{i}^{2}+p(w+1))}.\end{eqnarray}$$
$$\begin{eqnarray}W(\overline{\mathbb{F}}_{p})\frac{[[u_{1},\ldots ,u_{n+1}]]}{(\mathop{\sum }_{i}u_{i}^{2}+p)}\quad \text{or}\quad W(\overline{\mathbb{F}}_{p})\frac{[[u_{1},\ldots ,u_{n},w]]}{(\mathop{\sum }_{i}u_{i}^{2}+p(w+1))}.\end{eqnarray}$$
Since
![]() $n\geqslant 1$
, it is easily checked that, in all three cases, tensoring with
$n\geqslant 1$
, it is easily checked that, in all three cases, tensoring with
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
over
${\mathcal{O}}_{\boldsymbol{k}}$
over
![]() $\mathbb{Z}$
gives us something locally integral.
$\mathbb{Z}$
gives us something locally integral.
The claim about regularity over
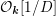 ${\mathcal{O}}_{\boldsymbol{k}}[1/D]$
follows from the smoothness of the integral model of § 2.4 over
${\mathcal{O}}_{\boldsymbol{k}}[1/D]$
follows from the smoothness of the integral model of § 2.4 over
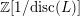 $\mathbb{Z}[1/\text{disc}(L)]$
and of
$\mathbb{Z}[1/\text{disc}(L)]$
and of
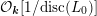 ${\mathcal{O}}_{\boldsymbol{k}}[1/\text{disc}(L_{0})]$
over
${\mathcal{O}}_{\boldsymbol{k}}[1/\text{disc}(L_{0})]$
over
![]() $\mathbb{Z}$
.◻
$\mathbb{Z}$
.◻
An arithmetic divisor on
![]() ${\mathcal{M}}$
is a pair
${\mathcal{M}}$
is a pair
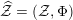 $\widehat{{\mathcal{Z}}}=({\mathcal{Z}},\unicode[STIX]{x1D6F7})$
consisting of a Cartier divisor
$\widehat{{\mathcal{Z}}}=({\mathcal{Z}},\unicode[STIX]{x1D6F7})$
consisting of a Cartier divisor
![]() ${\mathcal{Z}}$
on
${\mathcal{Z}}$
on
![]() ${\mathcal{M}}$
and a Green function
${\mathcal{M}}$
and a Green function
![]() $\unicode[STIX]{x1D6F7}$
for
$\unicode[STIX]{x1D6F7}$
for
![]() ${\mathcal{Z}}(\mathbb{C})$
on
${\mathcal{Z}}(\mathbb{C})$
on
![]() ${\mathcal{M}}(\mathbb{C})$
. Thus if
${\mathcal{M}}(\mathbb{C})$
. Thus if
![]() $\unicode[STIX]{x1D6F9}=0$
is a local equation for
$\unicode[STIX]{x1D6F9}=0$
is a local equation for
![]() ${\mathcal{Z}}(\mathbb{C})$
, the function
${\mathcal{Z}}(\mathbb{C})$
, the function
 $\unicode[STIX]{x1D6F7}+\text{log}|\unicode[STIX]{x1D6F9}|^{2}$
, initially defined on the complement of
$\unicode[STIX]{x1D6F7}+\text{log}|\unicode[STIX]{x1D6F9}|^{2}$
, initially defined on the complement of
![]() ${\mathcal{Z}}(\mathbb{C})$
, is required to extend smoothly across the singularity
${\mathcal{Z}}(\mathbb{C})$
, is required to extend smoothly across the singularity
![]() ${\mathcal{Z}}(\mathbb{C})$
. A principal arithmetic divisor is an arithmetic divisor of the form
${\mathcal{Z}}(\mathbb{C})$
. A principal arithmetic divisor is an arithmetic divisor of the form
 $$\begin{eqnarray}\widehat{\text{div}}(\unicode[STIX]{x1D6F9})=(\text{div}(\unicode[STIX]{x1D6F9}),-\text{log}|\unicode[STIX]{x1D6F9}|^{2})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{div}}(\unicode[STIX]{x1D6F9})=(\text{div}(\unicode[STIX]{x1D6F9}),-\text{log}|\unicode[STIX]{x1D6F9}|^{2})\end{eqnarray}$$
for a rational function
![]() $\unicode[STIX]{x1D6F9}$
on
$\unicode[STIX]{x1D6F9}$
on
![]() ${\mathcal{M}}$
. The group of all arithmetic divisors is denoted
${\mathcal{M}}$
. The group of all arithmetic divisors is denoted
 $\widehat{\text{Div}}({\mathcal{M}})$
, and its quotient by the subgroup of principal arithmetic divisors is the arithmetic Chow group
$\widehat{\text{Div}}({\mathcal{M}})$
, and its quotient by the subgroup of principal arithmetic divisors is the arithmetic Chow group
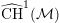 $\widehat{\text{CH}}^{1}({\mathcal{M}})$
of Gillet and Soulé.
$\widehat{\text{CH}}^{1}({\mathcal{M}})$
of Gillet and Soulé.
A metrized line bundle on
![]() ${\mathcal{M}}$
is a line bundle endowed with a smoothly varying Hermitian metric on its complex points. The isomorphism classes of metrized line bundles form a group
${\mathcal{M}}$
is a line bundle endowed with a smoothly varying Hermitian metric on its complex points. The isomorphism classes of metrized line bundles form a group
 $\widehat{\text{Pic}}({\mathcal{M}})$
under tensor product.
$\widehat{\text{Pic}}({\mathcal{M}})$
under tensor product.
There is an isomorphism
 $$\begin{eqnarray}\widehat{\text{CH}}^{1}({\mathcal{M}})\xrightarrow[{}]{\simeq }\widehat{\text{Pic}}({\mathcal{M}})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{CH}}^{1}({\mathcal{M}})\xrightarrow[{}]{\simeq }\widehat{\text{Pic}}({\mathcal{M}})\end{eqnarray}$$
defined as follows. Given an arithmetic divisor
![]() $({\mathcal{Z}},\unicode[STIX]{x1D6F7})$
, the line bundle
$({\mathcal{Z}},\unicode[STIX]{x1D6F7})$
, the line bundle
 ${\mathcal{L}}={\mathcal{O}}({\mathcal{Z}})$
is endowed with a canonical rational section
${\mathcal{L}}={\mathcal{O}}({\mathcal{Z}})$
is endowed with a canonical rational section
![]() $s$
with divisor
$s$
with divisor
![]() ${\mathcal{Z}}$
. This section is nothing more than the constant function
${\mathcal{Z}}$
. This section is nothing more than the constant function
![]() $1$
on
$1$
on
![]() ${\mathcal{M}}$
, viewed as a section of
${\mathcal{M}}$
, viewed as a section of
![]() ${\mathcal{L}}$
. We endow
${\mathcal{L}}$
. We endow
![]() ${\mathcal{L}}$
with the metric defined by
${\mathcal{L}}$
with the metric defined by
 $-\text{log}\Vert s\Vert ^{2}=\unicode[STIX]{x1D6F7}.$
For the inverse construction, start with a metrized line bundle
$-\text{log}\Vert s\Vert ^{2}=\unicode[STIX]{x1D6F7}.$
For the inverse construction, start with a metrized line bundle
![]() $\widehat{{\mathcal{L}}}$
on
$\widehat{{\mathcal{L}}}$
on
![]() ${\mathcal{M}}$
and let
${\mathcal{M}}$
and let
![]() $s$
be any non-zero rational section. The associated arithmetic divisor, well-defined modulo principal arithmetic divisors, is
$s$
be any non-zero rational section. The associated arithmetic divisor, well-defined modulo principal arithmetic divisors, is
 $$\begin{eqnarray}\widehat{\text{div}}(s)=(\text{div}(s),-\text{log}\Vert s\Vert ^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{div}}(s)=(\text{div}(s),-\text{log}\Vert s\Vert ^{2}).\end{eqnarray}$$
Of course there is a similar discussion with
![]() ${\mathcal{M}}$
replaced by
${\mathcal{M}}$
replaced by
![]() ${\mathcal{Y}}$
. As
${\mathcal{Y}}$
. As
![]() ${\mathcal{Y}}$
is smooth of relative dimension
${\mathcal{Y}}$
is smooth of relative dimension
![]() $0$
over
$0$
over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
, all divisors on
${\mathcal{O}}_{\boldsymbol{k}}$
, all divisors on
![]() ${\mathcal{Y}}$
are supported in non-zero characteristics; thus, a Green function for a divisor on
${\mathcal{Y}}$
are supported in non-zero characteristics; thus, a Green function for a divisor on
![]() ${\mathcal{Y}}$
is any complex-valued function on the zero-dimensional orbifold
${\mathcal{Y}}$
is any complex-valued function on the zero-dimensional orbifold
![]() ${\mathcal{Y}}(\mathbb{C})$
. In particular any arithmetic divisor
${\mathcal{Y}}(\mathbb{C})$
. In particular any arithmetic divisor
![]() $({\mathcal{Z}},\unicode[STIX]{x1D6F7})$
decomposes as
$({\mathcal{Z}},\unicode[STIX]{x1D6F7})$
decomposes as
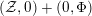 $({\mathcal{Z}},0)+(0,\unicode[STIX]{x1D6F7})$
, and
$({\mathcal{Z}},0)+(0,\unicode[STIX]{x1D6F7})$
, and
![]() ${\mathcal{Z}}$
can be further decomposed as the difference of two effective Cartier divisors.
${\mathcal{Z}}$
can be further decomposed as the difference of two effective Cartier divisors.
To define the arithmetic degree (as in [Reference Kudla, Rapoport and YangKRY04] or [Reference Kudla, Rapoport and YangKRY06]) of an arithmetic divisor
![]() $\widehat{{\mathcal{Z}}}$
on
$\widehat{{\mathcal{Z}}}$
on
![]() ${\mathcal{Y}}$
we first assume that
${\mathcal{Y}}$
we first assume that
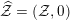 $\widehat{{\mathcal{Z}}}=({\mathcal{Z}},0)$
with
$\widehat{{\mathcal{Z}}}=({\mathcal{Z}},0)$
with
![]() ${\mathcal{Z}}$
effective. Then
${\mathcal{Z}}$
effective. Then
 $$\begin{eqnarray}\widehat{\deg }(\widehat{{\mathcal{Z}}})=\mathop{\sum }_{\mathfrak{p}\subset {\mathcal{O}}_{\boldsymbol{k}}}\log \text{N}(\mathfrak{p})\mathop{\sum }_{z\in {\mathcal{Z}}(\overline{\mathbb{F}}_{\mathfrak{ p}})}\frac{\text{length}({\mathcal{O}}_{{\mathcal{Z}},z})}{\#\text{Aut}(z)}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\deg }(\widehat{{\mathcal{Z}}})=\mathop{\sum }_{\mathfrak{p}\subset {\mathcal{O}}_{\boldsymbol{k}}}\log \text{N}(\mathfrak{p})\mathop{\sum }_{z\in {\mathcal{Z}}(\overline{\mathbb{F}}_{\mathfrak{ p}})}\frac{\text{length}({\mathcal{O}}_{{\mathcal{Z}},z})}{\#\text{Aut}(z)}\end{eqnarray}$$
where
![]() ${\mathcal{O}}_{{\mathcal{Z}},z}$
is the étale local ring of
${\mathcal{O}}_{{\mathcal{Z}},z}$
is the étale local ring of
![]() ${\mathcal{Z}}$
at
${\mathcal{Z}}$
at
![]() $z$
. If
$z$
. If
 $\widehat{{\mathcal{Z}}}=(0,\unicode[STIX]{x1D6F7})$
is purely archimedean, then
$\widehat{{\mathcal{Z}}}=(0,\unicode[STIX]{x1D6F7})$
is purely archimedean, then
 $$\begin{eqnarray}\widehat{\deg }(\widehat{{\mathcal{Z}}})=\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}(y)}{\#\text{Aut}(y)}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\deg }(\widehat{{\mathcal{Z}}})=\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}(y)}{\#\text{Aut}(y)}.\end{eqnarray}$$
The arithmetic degree extends linearly to all arithmetic divisors, and defines a homomorphism
 $$\begin{eqnarray}\widehat{\deg }:\widehat{\text{Pic}}({\mathcal{Y}})\rightarrow \mathbb{R}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\deg }:\widehat{\text{Pic}}({\mathcal{Y}})\rightarrow \mathbb{R}.\end{eqnarray}$$
We now define a homomorphism
 $$\begin{eqnarray}[\cdot :{\mathcal{Y}}]:\widehat{\text{Pic}}({\mathcal{M}})\rightarrow \mathbb{R},\end{eqnarray}$$
$$\begin{eqnarray}[\cdot :{\mathcal{Y}}]:\widehat{\text{Pic}}({\mathcal{M}})\rightarrow \mathbb{R},\end{eqnarray}$$
the arithmetic degree along
![]() ${\mathcal{Y}}$
, as the composition
${\mathcal{Y}}$
, as the composition
 $$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\widehat{\deg }}\mathbb{R}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\widehat{\deg }}\mathbb{R}.\end{eqnarray}$$
5.2 Specialization to the normal bundle
Fix a positive
![]() $m\in \mathbb{Q}$
and a
$m\in \mathbb{Q}$
and a
 $\unicode[STIX]{x1D707}\in L^{\vee }/L$
, and denote by
$\unicode[STIX]{x1D707}\in L^{\vee }/L$
, and denote by
 $$\begin{eqnarray}\displaystyle {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}} & & \displaystyle\end{eqnarray}$$
the stack obtained from (2.21) by base change from
![]() $\mathbb{Z}$
to
$\mathbb{Z}$
to
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. The fact that (5.2) and
${\mathcal{O}}_{\boldsymbol{k}}$
. The fact that (5.2) and
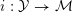 $i:{\mathcal{Y}}\rightarrow {\mathcal{M}}$
are not closed immersions is a minor nuisance. The following definition is introduced to address technical difficulties arising from this defect.
$i:{\mathcal{Y}}\rightarrow {\mathcal{M}}$
are not closed immersions is a minor nuisance. The following definition is introduced to address technical difficulties arising from this defect.
Definition 5.2.1. A sufficiently small étale open chart of
![]() ${\mathcal{M}}$
is a scheme
${\mathcal{M}}$
is a scheme
![]() $U$
together with an étale morphism
$U$
together with an étale morphism
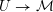 $U\rightarrow {\mathcal{M}}$
such that the following hold.
$U\rightarrow {\mathcal{M}}$
such that the following hold.
-
(i) The natural map
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}\rightarrow U$
restricts to a closed immersion on every connected component
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}\rightarrow U$
restricts to a closed immersion on every connected component
 $Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
.
$Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
. -
(ii) The natural map
 ${\mathcal{Y}}_{U}\rightarrow U$
restricts to a closed immersion on every connected component
${\mathcal{Y}}_{U}\rightarrow U$
restricts to a closed immersion on every connected component
 $Y\subset {\mathcal{Y}}_{U}$
.
$Y\subset {\mathcal{Y}}_{U}$
.
Remark 5.2.2. The stack
![]() ${\mathcal{M}}$
admits a covering by sufficiently small étale open charts. This is a consequence of [Reference VistoliVis89, Lemma 1.19] and the fact that
${\mathcal{M}}$
admits a covering by sufficiently small étale open charts. This is a consequence of [Reference VistoliVis89, Lemma 1.19] and the fact that
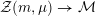 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
and
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})\rightarrow {\mathcal{M}}$
and
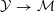 ${\mathcal{Y}}\rightarrow {\mathcal{M}}$
are finite and unramified. Note that these two morphisms are relatively representable, and so for any
${\mathcal{Y}}\rightarrow {\mathcal{M}}$
are finite and unramified. Note that these two morphisms are relatively representable, and so for any
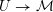 $U\rightarrow {\mathcal{M}}$
as above the pullbacks
$U\rightarrow {\mathcal{M}}$
as above the pullbacks
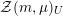 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
and
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
and
![]() ${\mathcal{Y}}_{U}$
are actually schemes.
${\mathcal{Y}}_{U}$
are actually schemes.
Remark 5.2.3. When we think of
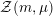 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
as a Cartier divisor on
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
as a Cartier divisor on
![]() ${\mathcal{M}}$
, its pullback to
${\mathcal{M}}$
, its pullback to
![]() $U$
is simply the sum of the connected components of
$U$
is simply the sum of the connected components of
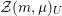 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
, each viewed as closed subscheme of
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
, each viewed as closed subscheme of
![]() $U$
.
$U$
.
Remark 5.2.4. In § 4 the notation
![]() $Y$
was used for the generic fiber of
$Y$
was used for the generic fiber of
![]() ${\mathcal{Y}}$
. Throughout § 5 the notation
${\mathcal{Y}}$
. Throughout § 5 the notation
![]() $Y$
is only used for a connected component of
$Y$
is only used for a connected component of
![]() ${\mathcal{Y}}_{U}$
, and so no confusion should arise.
${\mathcal{Y}}_{U}$
, and so no confusion should arise.
Fix a sufficiently small
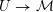 $U\rightarrow {\mathcal{M}}$
and a connected component
$U\rightarrow {\mathcal{M}}$
and a connected component
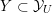 $Y\subset {\mathcal{Y}}_{U}$
. The smoothness of
$Y\subset {\mathcal{Y}}_{U}$
. The smoothness of
![]() ${\mathcal{Y}}$
over
${\mathcal{Y}}$
over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
implies that
${\mathcal{O}}_{\boldsymbol{k}}$
implies that
![]() $Y$
is a regular integral scheme of dimension
$Y$
is a regular integral scheme of dimension
![]() $1$
. Let
$1$
. Let
![]() $I\subset {\mathcal{O}}_{U}$
be the ideal sheaf defining the closed immersion
$I\subset {\mathcal{O}}_{U}$
be the ideal sheaf defining the closed immersion
 $Y\rightarrow U$
, and recall that the normal bundle of
$Y\rightarrow U$
, and recall that the normal bundle of
![]() $Y\subset U$
is the
$Y\subset U$
is the
![]() ${\mathcal{O}}_{Y}$
-module
${\mathcal{O}}_{Y}$
-module
 $$\begin{eqnarray}N_{Y}U=\text{}\underline{\text{Hom}}(I/I^{2},{\mathcal{O}}_{Y}).\end{eqnarray}$$
$$\begin{eqnarray}N_{Y}U=\text{}\underline{\text{Hom}}(I/I^{2},{\mathcal{O}}_{Y}).\end{eqnarray}$$
As
![]() $Y\rightarrow U$
may not be a regular immersion, the
$Y\rightarrow U$
may not be a regular immersion, the
![]() ${\mathcal{O}}_{Y}$
-module
${\mathcal{O}}_{Y}$
-module
![]() $I/I^{2}$
may not be locally free. However, we will see below in Proposition 5.4.1 that
$I/I^{2}$
may not be locally free. However, we will see below in Proposition 5.4.1 that
![]() $N_{Y}U$
is locally free of rank
$N_{Y}U$
is locally free of rank
![]() $n$
, and so defines a vector bundle
$n$
, and so defines a vector bundle
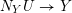 $N_{Y}U\rightarrow Y$
. By taking the disjoint union over all connected components
$N_{Y}U\rightarrow Y$
. By taking the disjoint union over all connected components
 $Y\subset {\mathcal{Y}}_{U}$
we obtain a vector bundle on
$Y\subset {\mathcal{Y}}_{U}$
we obtain a vector bundle on
![]() ${\mathcal{Y}}_{U}$
. Letting
${\mathcal{Y}}_{U}$
. Letting
![]() $U$
vary over a cover of
$U$
vary over a cover of
![]() ${\mathcal{M}}$
by sufficiently small étale open charts and glueing defines the normal bundle
${\mathcal{M}}$
by sufficiently small étale open charts and glueing defines the normal bundle
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:N_{{\mathcal{Y}}}{\mathcal{M}}\rightarrow {\mathcal{Y}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:N_{{\mathcal{Y}}}{\mathcal{M}}\rightarrow {\mathcal{Y}}. & & \displaystyle\end{eqnarray}$$
Recall the Hejhal–Poincaré series
 $$\begin{eqnarray}F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\end{eqnarray}$$
$$\begin{eqnarray}F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\end{eqnarray}$$
of § 3.2. The discussion of § 3.2 endows the divisor
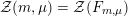 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})={\mathcal{Z}}(F_{m,\unicode[STIX]{x1D707}})$
with a Green function
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})={\mathcal{Z}}(F_{m,\unicode[STIX]{x1D707}})$
with a Green function
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6F7}(F_{m,\unicode[STIX]{x1D707}},\cdot ),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6F7}(F_{m,\unicode[STIX]{x1D707}},\cdot ),\end{eqnarray}$$
which is defined at every point of
![]() ${\mathcal{M}}(\mathbb{C})$
, but is discontinuous at points of the divisor
${\mathcal{M}}(\mathbb{C})$
, but is discontinuous at points of the divisor
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
. The corresponding arithmetic divisor is denoted
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
. The corresponding arithmetic divisor is denoted
 $$\begin{eqnarray}\displaystyle \widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})=({\mathcal{Z}}(m,\unicode[STIX]{x1D707}),\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})\in \widehat{\text{Div}}({\mathcal{M}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})=({\mathcal{Z}}(m,\unicode[STIX]{x1D707}),\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})\in \widehat{\text{Div}}({\mathcal{M}}). & & \displaystyle\end{eqnarray}$$
From the arithmetic divisor (5.4) we will construct a new arithmetic divisor
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))\in \widehat{\text{Div}}(N_{{\mathcal{Y}}}{\mathcal{M}}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))\in \widehat{\text{Div}}(N_{{\mathcal{Y}}}{\mathcal{M}}) & & \displaystyle\end{eqnarray}$$
called the specialization to the normal bundle. Fix a cover of
![]() ${\mathcal{M}}$
by sufficiently small étale open charts. Given a chart
${\mathcal{M}}$
by sufficiently small étale open charts. Given a chart
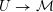 $U\rightarrow {\mathcal{M}}$
in the cover, fix a connected component
$U\rightarrow {\mathcal{M}}$
in the cover, fix a connected component
 $Y\subset {\mathcal{Y}}_{U}$
and decompose
$Y\subset {\mathcal{Y}}_{U}$
and decompose
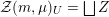 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}=\bigsqcup Z$
as the union of its connected components. By refining our cover, we may assume that each closed subscheme
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}=\bigsqcup Z$
as the union of its connected components. By refining our cover, we may assume that each closed subscheme
![]() $Z\rightarrow U$
is defined by a single equation
$Z\rightarrow U$
is defined by a single equation
![]() $f_{Z}=0$
.
$f_{Z}=0$
.
Lemma 5.2.5. For every connected component
 $Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
the intersection
$Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
the intersection
 $$\begin{eqnarray}Y\cap Z:=Y\times _{U}Z\end{eqnarray}$$
$$\begin{eqnarray}Y\cap Z:=Y\times _{U}Z\end{eqnarray}$$
satisfies one of the following (mutually exclusive) properties.
-
(i) The intersection
 $Y\cap Z$
has dimension
$Y\cap Z$
has dimension
 $0$
, and
$0$
, and
 $f_{Z}$
restricts to a non-zero section of
$f_{Z}$
restricts to a non-zero section of
 ${\mathcal{O}}_{U}/I$
.
${\mathcal{O}}_{U}/I$
. -
(ii) The intersection
 $Y\cap Z$
equals
$Y\cap Z$
equals
 $Y$
, and
$Y$
, and
 $f_{Z}$
defines a section of
$f_{Z}$
defines a section of
 $I\subset {\mathcal{O}}_{U}$
with non-zero image under the natural map
$I\subset {\mathcal{O}}_{U}$
with non-zero image under the natural map
 $I/I^{2}\rightarrow \text{}\underline{\text{Hom}}(N_{U}Y,{\mathcal{O}}_{Y}).$
$I/I^{2}\rightarrow \text{}\underline{\text{Hom}}(N_{U}Y,{\mathcal{O}}_{Y}).$
Proof. As
![]() $Y$
is an integral scheme of dimension
$Y$
is an integral scheme of dimension
![]() $1$
, its closed subscheme
$1$
, its closed subscheme
![]() $Y\cap Z$
is either all of
$Y\cap Z$
is either all of
![]() $Y$
or of dimension
$Y$
or of dimension
![]() $0$
. Given this, the only non-trivial thing to check is that when
$0$
. Given this, the only non-trivial thing to check is that when
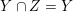 $Y\cap Z=Y$
, the image of
$Y\cap Z=Y$
, the image of
![]() $f_{Z}$
under
$f_{Z}$
under
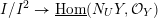 $I/I^{2}\rightarrow \text{}\underline{\text{Hom}}(N_{U}Y,{\mathcal{O}}_{Y})$
is non-zero. This can be checked after restricting to the complex fiber, where it follows from the smoothness of the divisor
$I/I^{2}\rightarrow \text{}\underline{\text{Hom}}(N_{U}Y,{\mathcal{O}}_{Y})$
is non-zero. This can be checked after restricting to the complex fiber, where it follows from the smoothness of the divisor
![]() $Z(\mathbb{C})$
on
$Z(\mathbb{C})$
on
![]() $U(\mathbb{C})$
. This smoothness can be checked using the complex uniformization (2.4).◻
$U(\mathbb{C})$
. This smoothness can be checked using the complex uniformization (2.4).◻
If
![]() $Y\cap Z$
has dimension
$Y\cap Z$
has dimension
![]() $0$
, then restricting
$0$
, then restricting
![]() $f_{Z}$
to
$f_{Z}$
to
![]() $Y$
and pulling back via
$Y$
and pulling back via
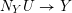 $N_{Y}U\rightarrow Y$
results in a function
$N_{Y}U\rightarrow Y$
results in a function
![]() $\unicode[STIX]{x1D70E}(f_{Z})$
on
$\unicode[STIX]{x1D70E}(f_{Z})$
on
![]() $N_{Y}U$
, which is homogeneous of degree
$N_{Y}U$
, which is homogeneous of degree
![]() $0$
. On the other hand, if
$0$
. On the other hand, if
 $Y\cap Z=Y$
then the image of
$Y\cap Z=Y$
then the image of
![]() $f_{Z}$
in
$f_{Z}$
in
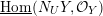 $\text{}\underline{\text{Hom}}(N_{U}Y,{\mathcal{O}}_{Y})$
defines a function
$\text{}\underline{\text{Hom}}(N_{U}Y,{\mathcal{O}}_{Y})$
defines a function
![]() $\unicode[STIX]{x1D70E}(f_{Z})$
on
$\unicode[STIX]{x1D70E}(f_{Z})$
on
![]() $N_{U}Y$
, which is homogeneous of degree
$N_{U}Y$
, which is homogeneous of degree
![]() $1$
. In either case, define an effective Cartier divisor on
$1$
. In either case, define an effective Cartier divisor on
![]() $N_{Y}U$
by
$N_{Y}U$
by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}({\mathcal{Z}}(m,\unicode[STIX]{x1D707}))=\mathop{\sum }_{Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}}\text{div}(\unicode[STIX]{x1D70E}(f_{Z})). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}({\mathcal{Z}}(m,\unicode[STIX]{x1D707}))=\mathop{\sum }_{Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}}\text{div}(\unicode[STIX]{x1D70E}(f_{Z})). & & \displaystyle\end{eqnarray}$$
The function
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}}\text{log}|f_{Z}|^{2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}}\text{log}|f_{Z}|^{2},\end{eqnarray}$$
initially defined on the complex fiber of
 $U\smallsetminus {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
, extends smoothly to all of
$U\smallsetminus {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
, extends smoothly to all of
![]() $U(\mathbb{C})$
. By restricting to
$U(\mathbb{C})$
. By restricting to
![]() ${\mathcal{Y}}(\mathbb{C})$
and then pulling back via (5.3) we obtain a smooth function
${\mathcal{Y}}(\mathbb{C})$
and then pulling back via (5.3) we obtain a smooth function
 $\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}$
on
 $(N_{Y}U)(\mathbb{C})$
. Define
$(N_{Y}U)(\mathbb{C})$
. Define
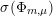 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})$
by the relation
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})$
by the relation
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})+\mathop{\sum }_{Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}}\text{log}|\unicode[STIX]{x1D70E}(f_{Z})|^{2}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})+\mathop{\sum }_{Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}}\text{log}|\unicode[STIX]{x1D70E}(f_{Z})|^{2}. & & \displaystyle\end{eqnarray}$$
The resulting arithmetic divisor
 $$\begin{eqnarray}(\unicode[STIX]{x1D70E}({\mathcal{Z}}(m,\unicode[STIX]{x1D707})),\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}))\in \widehat{\text{Div}}(N_{Y}U)\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70E}({\mathcal{Z}}(m,\unicode[STIX]{x1D707})),\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}))\in \widehat{\text{Div}}(N_{Y}U)\end{eqnarray}$$
does not depend on the choice of
![]() $f_{Z}$
used in its construction. Using étale descent these arithmetic divisors glue together to form the desired arithmetic divisor (5.5).
$f_{Z}$
used in its construction. Using étale descent these arithmetic divisors glue together to form the desired arithmetic divisor (5.5).
Proposition 5.2.6. The composition
 $$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}\widehat{\text{Pic}}(N_{{\mathcal{Y}}}{\mathcal{M}})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}\widehat{\text{Pic}}(N_{{\mathcal{Y}}}{\mathcal{M}})\end{eqnarray}$$
sends the metrized line bundle defined by
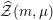 $\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})$
to the metrized line bundle defined by
$\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})$
to the metrized line bundle defined by
 $\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))$
.
$\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))$
.
Proof. Let
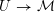 $U\rightarrow {\mathcal{M}}$
be a sufficiently small étale open chart, and write
$U\rightarrow {\mathcal{M}}$
be a sufficiently small étale open chart, and write
 $$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}=\bigsqcup Z\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}=\bigsqcup Z\end{eqnarray}$$
as the union of its connected components. Each connected component determines a line bundle
 ${\mathcal{O}}(Z)=f_{Z}^{-1}{\mathcal{O}}_{U}$
, and
${\mathcal{O}}(Z)=f_{Z}^{-1}{\mathcal{O}}_{U}$
, and
 $$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}\xrightarrow[{}]{\simeq }\bigotimes {\mathcal{O}}(Z)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}\xrightarrow[{}]{\simeq }\bigotimes {\mathcal{O}}(Z)\end{eqnarray}$$
as line bundles on
![]() $U$
.
$U$
.
Let
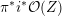 $\unicode[STIX]{x1D70B}^{\ast }i^{\ast }{\mathcal{O}}(Z)$
be the pullback of
$\unicode[STIX]{x1D70B}^{\ast }i^{\ast }{\mathcal{O}}(Z)$
be the pullback of
![]() ${\mathcal{O}}(Z)$
via
${\mathcal{O}}(Z)$
via
 $N_{Y}U\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Y\xrightarrow[{}]{i}U.$
If we denote by
$N_{Y}U\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Y\xrightarrow[{}]{i}U.$
If we denote by
![]() $s_{Z}$
the constant function
$s_{Z}$
the constant function
![]() $1$
on
$1$
on
![]() $U$
viewed as a section of
$U$
viewed as a section of
![]() ${\mathcal{O}}(Z)$
, then
${\mathcal{O}}(Z)$
, then
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(s_{Z})=\unicode[STIX]{x1D70E}(f_{Z})\unicode[STIX]{x1D70B}^{\ast }i^{\ast }(f_{Z}^{-1}s_{Z})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(s_{Z})=\unicode[STIX]{x1D70E}(f_{Z})\unicode[STIX]{x1D70B}^{\ast }i^{\ast }(f_{Z}^{-1}s_{Z})\end{eqnarray}$$
is a non-zero section of
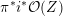 $\unicode[STIX]{x1D70B}^{\ast }i^{\ast }{\mathcal{O}}(Z)$
, and does not depend on the choice of
$\unicode[STIX]{x1D70B}^{\ast }i^{\ast }{\mathcal{O}}(Z)$
, and does not depend on the choice of
![]() $f_{Z}$
. The tensor product
$f_{Z}$
. The tensor product
 $\unicode[STIX]{x1D70E}(s)=\otimes \unicode[STIX]{x1D70E}(s_{Z})$
over all
$\unicode[STIX]{x1D70E}(s)=\otimes \unicode[STIX]{x1D70E}(s_{Z})$
over all
![]() $Z$
is a global section of the metrized line bundle
$Z$
is a global section of the metrized line bundle
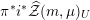 $\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})_{U}$
, and these section glue together over an étale cover of
$\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})_{U}$
, and these section glue together over an étale cover of
![]() ${\mathcal{M}}$
to define a global section
${\mathcal{M}}$
to define a global section
![]() $\unicode[STIX]{x1D70E}(s)$
of
$\unicode[STIX]{x1D70E}(s)$
of
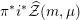 $\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})$
.
$\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})$
.
Tracing through the definitions shows that
 $\widehat{\text{div}}(\unicode[STIX]{x1D70E}(s))=\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})),$
as arithmetic divisors, and so
$\widehat{\text{div}}(\unicode[STIX]{x1D70E}(s))=\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})),$
as arithmetic divisors, and so
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))\end{eqnarray}$$
as metrized line bundles. ◻
Remark 5.2.7. The construction (5.5) and Proposition 5.2.6 will be our main tools for computing improper intersections. The technique is based on the thesis of Hu [Reference HuHu99], which reconstructs the arithmetic intersection theory of Gillet and Soulé [Reference Gillet and SouléGS90] using Fulton’s method of deformation to the normal cone.
Letting
![]() $C_{{\mathcal{Y}}}{\mathcal{M}}$
denote the normal cone of
$C_{{\mathcal{Y}}}{\mathcal{M}}$
denote the normal cone of
![]() ${\mathcal{Y}}$
in
${\mathcal{Y}}$
in
![]() ${\mathcal{M}}$
, HuFootnote
4
constructs a specialization to the normal cone map
${\mathcal{M}}$
, HuFootnote
4
constructs a specialization to the normal cone map
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}:\widehat{\text{Div}}({\mathcal{M}})\rightarrow \widehat{\text{Div}}(C_{{\mathcal{Y}}}{\mathcal{M}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}:\widehat{\text{Div}}({\mathcal{M}})\rightarrow \widehat{\text{Div}}(C_{{\mathcal{Y}}}{\mathcal{M}}),\end{eqnarray}$$
and shows that
 $$\begin{eqnarray}[\widehat{{\mathcal{Z}}}:{\mathcal{Y}}]=[\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}):{\mathcal{Y}}]\end{eqnarray}$$
$$\begin{eqnarray}[\widehat{{\mathcal{Z}}}:{\mathcal{Y}}]=[\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}):{\mathcal{Y}}]\end{eqnarray}$$
for any arithmetic divisor
![]() $\widehat{{\mathcal{Z}}}$
. Here the intersection pairing on the right is defined using the canonical closed immersion
$\widehat{{\mathcal{Z}}}$
. Here the intersection pairing on the right is defined using the canonical closed immersion
 ${\mathcal{Y}}\rightarrow C_{{\mathcal{Y}}}{\mathcal{M}}$
.
${\mathcal{Y}}\rightarrow C_{{\mathcal{Y}}}{\mathcal{M}}$
.
The normal bundle
![]() $N_{{\mathcal{Y}}}{\mathcal{M}}$
is essentially a first order approximation to
$N_{{\mathcal{Y}}}{\mathcal{M}}$
is essentially a first order approximation to
![]() $C_{{\mathcal{Y}}}{\mathcal{M}}$
, and our construction (5.5) and Proposition 5.2.6 amount to truncating Hu’s theory to first order. In order to use this to compute arithmetic intersections, it is essential to know that our divisors satisfy Lemma 5.2.5, which says, loosely speaking, that the functions
$C_{{\mathcal{Y}}}{\mathcal{M}}$
, and our construction (5.5) and Proposition 5.2.6 amount to truncating Hu’s theory to first order. In order to use this to compute arithmetic intersections, it is essential to know that our divisors satisfy Lemma 5.2.5, which says, loosely speaking, that the functions
![]() $f_{Z}$
vanish along
$f_{Z}$
vanish along
![]() $Y$
to at most order
$Y$
to at most order
![]() $1$
. This guarantees that the specialization (5.5) to the normal bundle does not lose too much information about the divisor
$1$
. This guarantees that the specialization (5.5) to the normal bundle does not lose too much information about the divisor
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
.
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
.
To be clear: we are exploiting here a special property of the divisors
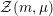 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
and their relative positions with respect to
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
and their relative positions with respect to
![]() ${\mathcal{Y}}$
. It would not be very useful to define the specialization (5.5) for an arbitrary divisor on
${\mathcal{Y}}$
. It would not be very useful to define the specialization (5.5) for an arbitrary divisor on
![]() ${\mathcal{M}}$
, as truncating Hu’s specialization map to first order would lose essential higher order information.
${\mathcal{M}}$
, as truncating Hu’s specialization map to first order would lose essential higher order information.
5.3 The cotautological bundle
Recall from (2.10) the vector bundle
![]() $\boldsymbol{V}_{\text{dR}}$
on
$\boldsymbol{V}_{\text{dR}}$
on
![]() ${\mathcal{M}}$
with its isotropic line
${\mathcal{M}}$
with its isotropic line
![]() $\boldsymbol{V}_{\text{dR}}^{1}$
, and from (4.3) the line bundle
$\boldsymbol{V}_{\text{dR}}^{1}$
, and from (4.3) the line bundle
![]() $\boldsymbol{V}_{0,\text{dR}}$
on
$\boldsymbol{V}_{0,\text{dR}}$
on
![]() ${\mathcal{Y}}$
. Proposition 4.6.1 implies that
${\mathcal{Y}}$
. Proposition 4.6.1 implies that
 $\boldsymbol{V}_{0,\text{dR}}\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
in such a way that
$\boldsymbol{V}_{0,\text{dR}}\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
in such a way that
 $\boldsymbol{V}_{0,\text{dR}}^{1}=i^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
.
$\boldsymbol{V}_{0,\text{dR}}^{1}=i^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
.
Denote by
 $\boldsymbol{T}=(\boldsymbol{V}_{\text{dR}}^{1})^{\vee }$
and
$\boldsymbol{T}=(\boldsymbol{V}_{\text{dR}}^{1})^{\vee }$
and
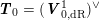 $\boldsymbol{T}_{0}=(\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }$
the cotautological bundles on
$\boldsymbol{T}_{0}=(\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }$
the cotautological bundles on
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
![]() ${\mathcal{Y}}$
, respectively, so that
${\mathcal{Y}}$
, respectively, so that
 $\boldsymbol{T}_{0}=i^{\ast }\boldsymbol{T}$
. Under the complex uniformization
$\boldsymbol{T}_{0}=i^{\ast }\boldsymbol{T}$
. Under the complex uniformization
 $\unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}\rightarrow {\mathcal{M}}(\mathbb{C})$
of (2.3) the fiber of
$\unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}\rightarrow {\mathcal{M}}(\mathbb{C})$
of (2.3) the fiber of
![]() $\boldsymbol{V}_{\text{dR}}^{1}$
at
$\boldsymbol{V}_{\text{dR}}^{1}$
at
![]() $z\in {\mathcal{D}}$
is identified with the tautological line
$z\in {\mathcal{D}}$
is identified with the tautological line
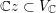 $\mathbb{C}z\subset V_{\mathbb{C}}$
, which we endow with the metric
$\mathbb{C}z\subset V_{\mathbb{C}}$
, which we endow with the metric
 $$\begin{eqnarray}\displaystyle \Vert z\Vert ^{2}=\frac{-1}{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}}[z,\overline{z}]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert z\Vert ^{2}=\frac{-1}{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}}[z,\overline{z}]. & & \displaystyle\end{eqnarray}$$
Here, as before,
 $\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6E4}^{\prime }(1)$
is the Euler–Mascheroni constant. Dualizing, we obtain a metric on the cotautological bundle, and the resulting metrized line bundle is denoted
$\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6E4}^{\prime }(1)$
is the Euler–Mascheroni constant. Dualizing, we obtain a metric on the cotautological bundle, and the resulting metrized line bundle is denoted
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
We endow
![]() $\boldsymbol{T}_{0}$
with the unique metric for which
$\boldsymbol{T}_{0}$
with the unique metric for which
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{0}\xrightarrow[{}]{\simeq }i^{\ast }\widehat{\boldsymbol{T}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{0}\xrightarrow[{}]{\simeq }i^{\ast }\widehat{\boldsymbol{T}}.\end{eqnarray}$$
Proposition 5.3.1. The metrized cotautological bundle satisfies
 $$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=2\frac{L^{\prime }(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}{L(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}+\text{log}\biggl|\frac{d_{\boldsymbol{k}}}{4\unicode[STIX]{x1D70B}}\biggr|-\unicode[STIX]{x1D6FE}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=2\frac{L^{\prime }(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}{L(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}+\text{log}\biggl|\frac{d_{\boldsymbol{k}}}{4\unicode[STIX]{x1D70B}}\biggr|-\unicode[STIX]{x1D6FE}.\end{eqnarray}$$
Proof. This is virtually identical to the proof of [Reference Bruinier, Howard and YangBHY15, Theorem 6.4], and so we only give an outline. Let
![]() ${\mathcal{E}}\rightarrow {\mathcal{Y}}$
be the universal
${\mathcal{E}}\rightarrow {\mathcal{Y}}$
be the universal
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve. If we endow the
${\mathcal{O}}_{\boldsymbol{k}}$
-elliptic curve. If we endow the
![]() ${\mathcal{O}}_{{\mathcal{Y}}}$
-module
${\mathcal{O}}_{{\mathcal{Y}}}$
-module
![]() $\text{Lie}({\mathcal{E}})$
with the Faltings metric, the Chowla–Selberg formula implies
$\text{Lie}({\mathcal{E}})$
with the Faltings metric, the Chowla–Selberg formula implies
 $$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot \widehat{\deg }~\widehat{\text{Lie}}({\mathcal{E}})=\frac{L^{\prime }(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}{L(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}+\log (2\unicode[STIX]{x1D70B})+\frac{1}{2}\text{log}|d_{\boldsymbol{k}}|.\end{eqnarray}$$
$$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot \widehat{\deg }~\widehat{\text{Lie}}({\mathcal{E}})=\frac{L^{\prime }(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}{L(\unicode[STIX]{x1D712}_{\boldsymbol{k}},0)}+\log (2\unicode[STIX]{x1D70B})+\frac{1}{2}\text{log}|d_{\boldsymbol{k}}|.\end{eqnarray}$$
Now view
![]() $L_{0}$
as an
$L_{0}$
as an
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-module through left multiplication, and endow the corresponding line bundle
${\mathcal{O}}_{\boldsymbol{k}}$
-module through left multiplication, and endow the corresponding line bundle
![]() $\boldsymbol{L}_{0}$
on
$\boldsymbol{L}_{0}$
on
 $\text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
with the metric
$\text{Spec}({\mathcal{O}}_{\boldsymbol{k}})$
with the metric
 $$\begin{eqnarray}\Vert x\Vert ^{2}=-16\unicode[STIX]{x1D70B}^{3}e^{\unicode[STIX]{x1D6FE}}\cdot Q(x).\end{eqnarray}$$
$$\begin{eqnarray}\Vert x\Vert ^{2}=-16\unicode[STIX]{x1D70B}^{3}e^{\unicode[STIX]{x1D6FE}}\cdot Q(x).\end{eqnarray}$$
Pulling back
![]() $\boldsymbol{L}_{0}$
to
$\boldsymbol{L}_{0}$
to
![]() ${\mathcal{Y}}$
via the structure morphism yields a metrized line bundle
${\mathcal{Y}}$
via the structure morphism yields a metrized line bundle
![]() $\widehat{\boldsymbol{L}}_{0}$
on
$\widehat{\boldsymbol{L}}_{0}$
on
![]() ${\mathcal{Y}}$
satisfying
${\mathcal{Y}}$
satisfying
 $$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot \widehat{\deg }~\widehat{\boldsymbol{L}}_{0}=-\text{log}(16\unicode[STIX]{x1D70B}^{3}e^{\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot \widehat{\deg }~\widehat{\boldsymbol{L}}_{0}=-\text{log}(16\unicode[STIX]{x1D70B}^{3}e^{\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
By keeping track of the metrics, the isomorphism (4.4) defines an isomorphism of metrized line bundles
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{0}\xrightarrow[{}]{\simeq }\widehat{\text{Lie}}({\mathcal{E}})^{\otimes 2}\otimes \widehat{\boldsymbol{L}}_{0}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{0}\xrightarrow[{}]{\simeq }\widehat{\text{Lie}}({\mathcal{E}})^{\otimes 2}\otimes \widehat{\boldsymbol{L}}_{0}\end{eqnarray}$$
on
![]() ${\mathcal{Y}}$
, and the claim follows.◻
${\mathcal{Y}}$
, and the claim follows.◻
Comparing with Proposition 3.3.1 proves the following.
Corollary 5.3.2. The coefficient
 $a_{L_{0}}^{+}(0)\in \mathfrak{S}_{L_{0}}^{\vee }$
satisfies
$a_{L_{0}}^{+}(0)\in \mathfrak{S}_{L_{0}}^{\vee }$
satisfies
 $$\begin{eqnarray}a_{L_{0}}^{+}(0,\unicode[STIX]{x1D707})=-\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot \left\{\begin{array}{@{}ll@{}}[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]\quad & \text{if }\unicode[STIX]{x1D707}=0,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}a_{L_{0}}^{+}(0,\unicode[STIX]{x1D707})=-\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\cdot \left\{\begin{array}{@{}ll@{}}[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]\quad & \text{if }\unicode[STIX]{x1D707}=0,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
for every
 $\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
.
$\unicode[STIX]{x1D707}\in L_{0}^{\vee }/L_{0}$
.
5.4 The normal bundle at CM points
Consider the orthogonal complement
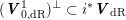 $(\boldsymbol{V}_{0,\text{dR}}^{1})^{\bot }\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
. Since
$(\boldsymbol{V}_{0,\text{dR}}^{1})^{\bot }\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
. Since
![]() ${\mathcal{Y}}$
is regular of dimension
${\mathcal{Y}}$
is regular of dimension
![]() $1$
, this complement is torsion-free and is therefore a vector sub-bundle of
$1$
, this complement is torsion-free and is therefore a vector sub-bundle of
![]() $i^{\ast }\boldsymbol{V}_{\text{dR}}$
of co-rank one. (Note that the corresponding assertion over
$i^{\ast }\boldsymbol{V}_{\text{dR}}$
of co-rank one. (Note that the corresponding assertion over
![]() ${\mathcal{M}}$
may not be true; the orthogonal complement of
${\mathcal{M}}$
may not be true; the orthogonal complement of
![]() $\boldsymbol{V}_{\text{dR}}^{1}$
in
$\boldsymbol{V}_{\text{dR}}^{1}$
in
![]() $\boldsymbol{V}_{\text{dR}}$
will in general not be a vector bundle unless
$\boldsymbol{V}_{\text{dR}}$
will in general not be a vector bundle unless
![]() $L$
is unimodular.)
$L$
is unimodular.)
Set
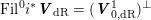 $\text{Fil}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}=(\boldsymbol{V}_{0,\text{dR}}^{1})^{\bot }$
and
$\text{Fil}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}=(\boldsymbol{V}_{0,\text{dR}}^{1})^{\bot }$
and
 $\text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}=\text{Fil}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}^{1}$
.
$\text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}=\text{Fil}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}^{1}$
.
Proposition 5.4.1. There is a canonical isomorphism of
![]() ${\mathcal{O}}_{{\mathcal{Y}}}$
-modules
${\mathcal{O}}_{{\mathcal{Y}}}$
-modules
 $$\begin{eqnarray}N_{{\mathcal{Y}}}{\mathcal{M}}\xrightarrow[{}]{\simeq }\boldsymbol{T}_{0}\otimes \text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}.\end{eqnarray}$$
$$\begin{eqnarray}N_{{\mathcal{Y}}}{\mathcal{M}}\xrightarrow[{}]{\simeq }\boldsymbol{T}_{0}\otimes \text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}.\end{eqnarray}$$
In particular, the normal bundle is locally free of rank
![]() $n$
, and is therefore relatively representable over
$n$
, and is therefore relatively representable over
![]() ${\mathcal{Y}}$
.
${\mathcal{Y}}$
.
Proof. Fix a sufficiently small étale open chart
 $U\rightarrow {\mathcal{M}}$
, and let
$U\rightarrow {\mathcal{M}}$
, and let
 $Y\subset {\mathcal{Y}}_{U}$
be a connected component. Let
$Y\subset {\mathcal{Y}}_{U}$
be a connected component. Let
 $Y[\unicode[STIX]{x1D700}]=Y\times _{\mathbb{Z}}\text{Spec}(\mathbb{Z}[\unicode[STIX]{x1D700}])$
be the scheme of dual numbers relative to
$Y[\unicode[STIX]{x1D700}]=Y\times _{\mathbb{Z}}\text{Spec}(\mathbb{Z}[\unicode[STIX]{x1D700}])$
be the scheme of dual numbers relative to
![]() $Y$
, and let
$Y$
, and let
![]() $\text{Def}_{i}$
be the Zariski sheaf of infinitesimal deformations of
$\text{Def}_{i}$
be the Zariski sheaf of infinitesimal deformations of
 $i:Y\rightarrow U$
. By this we mean the sheaf associating to an open subscheme
$i:Y\rightarrow U$
. By this we mean the sheaf associating to an open subscheme
![]() $S\subset Y$
the set
$S\subset Y$
the set
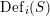 $\text{Def}_{i}(S)$
of morphisms
$\text{Def}_{i}(S)$
of morphisms
 $j_{S}:S[\unicode[STIX]{x1D700}]\rightarrow U$
such that
$j_{S}:S[\unicode[STIX]{x1D700}]\rightarrow U$
such that
 $j_{S}|_{S}=i_{S}$
. Here we are writing
$j_{S}|_{S}=i_{S}$
. Here we are writing
![]() $i_{S}$
for the inclusion
$i_{S}$
for the inclusion
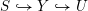 $S{\hookrightarrow}Y{\hookrightarrow}U$
.
$S{\hookrightarrow}Y{\hookrightarrow}U$
.
Lemma 5.4.2. There is a canonical isomorphism of functors
 $$\begin{eqnarray}\displaystyle \text{Def}_{i}\xrightarrow[{}]{\simeq }N_{Y}U. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Def}_{i}\xrightarrow[{}]{\simeq }N_{Y}U. & & \displaystyle\end{eqnarray}$$
Proof. The morphism (5.9) is defined in the usual way: every
 $j_{S}\in \text{Def}_{i}(S)$
defines a map
$j_{S}\in \text{Def}_{i}(S)$
defines a map
 ${\mathcal{O}}_{U}/I^{2}\rightarrow {\mathcal{O}}_{S}[\unicode[STIX]{x1D700}]$
, whose restriction
${\mathcal{O}}_{U}/I^{2}\rightarrow {\mathcal{O}}_{S}[\unicode[STIX]{x1D700}]$
, whose restriction
 $$\begin{eqnarray}I/I^{2}\rightarrow {\mathcal{O}}_{S}\cdot \unicode[STIX]{x1D700}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{S}\end{eqnarray}$$
$$\begin{eqnarray}I/I^{2}\rightarrow {\mathcal{O}}_{S}\cdot \unicode[STIX]{x1D700}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{S}\end{eqnarray}$$
defines an element of
 $(N_{Y}U)(S)$
.
$(N_{Y}U)(S)$
.
To construct an inverse to (5.9), first recall that
![]() ${\mathcal{Y}}$
is formally étale over
${\mathcal{Y}}$
is formally étale over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
. This implies that the surjection
${\mathcal{O}}_{\boldsymbol{k}}$
. This implies that the surjection
 ${\mathcal{O}}_{U}/I^{2}\rightarrow {\mathcal{O}}_{Y}$
admits a canonical section, and so
${\mathcal{O}}_{U}/I^{2}\rightarrow {\mathcal{O}}_{Y}$
admits a canonical section, and so
 $$\begin{eqnarray}{\mathcal{O}}_{U}/I^{2}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{Y}\oplus I/I^{2}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{U}/I^{2}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{Y}\oplus I/I^{2}\end{eqnarray}$$
as sheaves of rings on
![]() ${\mathcal{O}}_{Y}$
. Any
${\mathcal{O}}_{Y}$
. Any
![]() $S$
-point
$S$
-point
 $s\in (N_{Y}U)(S)$
therefore defines a homomorphism
$s\in (N_{Y}U)(S)$
therefore defines a homomorphism
 $$\begin{eqnarray}{\mathcal{O}}_{U}/I^{2}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{Y}\oplus I/I^{2}\xrightarrow[{}]{1\oplus s\cdot \unicode[STIX]{x1D716}}{\mathcal{O}}_{S}[\unicode[STIX]{x1D716}],\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{U}/I^{2}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{Y}\oplus I/I^{2}\xrightarrow[{}]{1\oplus s\cdot \unicode[STIX]{x1D716}}{\mathcal{O}}_{S}[\unicode[STIX]{x1D716}],\end{eqnarray}$$
which in turn determines a deformation
 $j_{S}:S[\unicode[STIX]{x1D716}]\rightarrow U$
of
$j_{S}:S[\unicode[STIX]{x1D716}]\rightarrow U$
of
![]() $i_{S}$
.◻
$i_{S}$
.◻
Lemma 5.4.3. There is a canonical isomorphism
 $$\begin{eqnarray}\text{Def}_{i}\xrightarrow[{}]{\simeq }(\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }\otimes _{{\mathcal{O}}_{Y}}\text{gr}_{\text{Fil}}^{0}(i^{\ast }\boldsymbol{V}_{\text{dR}})\end{eqnarray}$$
$$\begin{eqnarray}\text{Def}_{i}\xrightarrow[{}]{\simeq }(\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }\otimes _{{\mathcal{O}}_{Y}}\text{gr}_{\text{Fil}}^{0}(i^{\ast }\boldsymbol{V}_{\text{dR}})\end{eqnarray}$$
of sheaves of sets on
![]() $Y$
.
$Y$
.
Proof. Let
![]() $S\subset Y$
be an open subscheme, and let
$S\subset Y$
be an open subscheme, and let
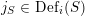 $j_{S}\in \text{Def}_{i}(S)$
. The pullback
$j_{S}\in \text{Def}_{i}(S)$
. The pullback
![]() $j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}$
is a locally free sheaf of
$j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}$
is a locally free sheaf of
![]() ${\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
-modules of rank
${\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
-modules of rank
![]() $n+2$
, endowed with an
$n+2$
, endowed with an
![]() ${\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
-submodule
${\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
-submodule
![]() $j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
of rank one, locally a direct summand. As
$j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
of rank one, locally a direct summand. As
![]() $\boldsymbol{V}_{\text{dR}}$
is a vector bundle with integrable connection, the retraction
$\boldsymbol{V}_{\text{dR}}$
is a vector bundle with integrable connection, the retraction
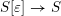 $S[\unicode[STIX]{x1D700}]\rightarrow S$
induces a canonical isomorphism
$S[\unicode[STIX]{x1D700}]\rightarrow S$
induces a canonical isomorphism
 $$\begin{eqnarray}j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\xrightarrow[{}]{\simeq }i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}.\end{eqnarray}$$
$$\begin{eqnarray}j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\xrightarrow[{}]{\simeq }i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}.\end{eqnarray}$$
We claim that, under this isomorphism,
![]() $j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
maps into
$j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
maps into
 $\text{Fil}^{0}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
; in other words, the image of
$\text{Fil}^{0}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
; in other words, the image of
![]() $j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
is orthogonal to
$j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
is orthogonal to
 $i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
. This is easily deduced from the fact that both this image and
$i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
. This is easily deduced from the fact that both this image and
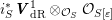 $i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
are isotropic lines lifting
$i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}$
are isotropic lines lifting
![]() $i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
.
$i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}$
.
Consider the composition
 $$\begin{eqnarray}j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}{\hookrightarrow}\text{Fil}^{0}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}\rightarrow \text{gr}_{\text{Fil}}^{0}(i_{S}^{\ast }\boldsymbol{V}_{\text{dR}})\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}.\end{eqnarray}$$
$$\begin{eqnarray}j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}{\hookrightarrow}\text{Fil}^{0}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}\rightarrow \text{gr}_{\text{Fil}}^{0}(i_{S}^{\ast }\boldsymbol{V}_{\text{dR}})\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}.\end{eqnarray}$$
The reduction of this map modulo
![]() $(\unicode[STIX]{x1D700})$
is
$(\unicode[STIX]{x1D700})$
is
![]() $0$
, and therefore it must factor through a map
$0$
, and therefore it must factor through a map
 $$\begin{eqnarray}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\rightarrow \unicode[STIX]{x1D700}\cdot (\text{gr}_{\text{Fil}}^{0}(i_{S}^{\ast }\boldsymbol{V}_{\text{dR}})\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]})\xrightarrow[{}]{\simeq }\text{gr}_{\text{Fil}}^{0}(i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}).\end{eqnarray}$$
$$\begin{eqnarray}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\rightarrow \unicode[STIX]{x1D700}\cdot (\text{gr}_{\text{Fil}}^{0}(i_{S}^{\ast }\boldsymbol{V}_{\text{dR}})\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]})\xrightarrow[{}]{\simeq }\text{gr}_{\text{Fil}}^{0}(i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}).\end{eqnarray}$$
Thus, we have produced a canonical morphism
 $$\begin{eqnarray}\text{Def}_{i}\rightarrow (\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }\otimes _{{\mathcal{O}}_{Y}}\text{gr}_{\text{Fil}}^{0}(i^{\ast }\boldsymbol{V}_{\text{dR}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Def}_{i}\rightarrow (\boldsymbol{V}_{0,\text{dR}}^{1})^{\vee }\otimes _{{\mathcal{O}}_{Y}}\text{gr}_{\text{Fil}}^{0}(i^{\ast }\boldsymbol{V}_{\text{dR}}).\end{eqnarray}$$
To show that this is an isomorphism, we can, by Proposition 2.4.3 and the above discussion of local models, assume that the immersion
![]() $Y\subset U$
is isomorphic to an étale neighborhood of the closed immersion
$Y\subset U$
is isomorphic to an étale neighborhood of the closed immersion
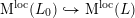 $\text{M}^{\text{loc}}(L_{0}){\hookrightarrow}\text{M}^{\text{loc}}(L)$
. Moreover, we can choose this isomorphism in such a way that it identifies
$\text{M}^{\text{loc}}(L_{0}){\hookrightarrow}\text{M}^{\text{loc}}(L)$
. Moreover, we can choose this isomorphism in such a way that it identifies
![]() $\boldsymbol{V}_{0,\text{dR}}$
and
$\boldsymbol{V}_{0,\text{dR}}$
and
![]() $\boldsymbol{V}_{\text{dR}}$
with the trivial vector bundles
$\boldsymbol{V}_{\text{dR}}$
with the trivial vector bundles
![]() $\mathbf{1}\otimes L_{0}$
and
$\mathbf{1}\otimes L_{0}$
and
![]() $\mathbf{1}\otimes L$
, respectively, and such that
$\mathbf{1}\otimes L$
, respectively, and such that
![]() $\boldsymbol{V}_{0,\text{dR}}^{1}$
and
$\boldsymbol{V}_{0,\text{dR}}^{1}$
and
![]() $\boldsymbol{V}_{\text{dR}}^{1}$
get identified with the tautological isotropic lines in
$\boldsymbol{V}_{\text{dR}}^{1}$
get identified with the tautological isotropic lines in
![]() $\mathbf{1}\otimes L_{0}$
and
$\mathbf{1}\otimes L_{0}$
and
![]() $\mathbf{1}\otimes L$
, respectively.
$\mathbf{1}\otimes L$
, respectively.
So, if
 $\boldsymbol{L}_{0}^{1}\subset \mathbf{1}\otimes L_{0}$
is the tautological isotropic line over
$\boldsymbol{L}_{0}^{1}\subset \mathbf{1}\otimes L_{0}$
is the tautological isotropic line over
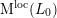 $\text{M}^{\text{loc}}(L_{0})$
, and
$\text{M}^{\text{loc}}(L_{0})$
, and
 $\boldsymbol{L}^{0}\subset \mathbf{1}\otimes L$
is its orthogonal complement, we are reduced to showing the elementary fact that there is a canonical isomorphism
$\boldsymbol{L}^{0}\subset \mathbf{1}\otimes L$
is its orthogonal complement, we are reduced to showing the elementary fact that there is a canonical isomorphism
 $$\begin{eqnarray}N_{\text{M}^{\text{loc}}(L_{0})}(\text{M}^{\text{loc}}(L))\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}(\boldsymbol{L}_{0}^{1},\boldsymbol{L}^{0}/\boldsymbol{L}_{0}^{1})\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{M}^{\text{loc}}(L_{0})}(\text{M}^{\text{loc}}(L))\xrightarrow[{}]{\simeq }\text{}\underline{\text{Hom}}(\boldsymbol{L}_{0}^{1},\boldsymbol{L}^{0}/\boldsymbol{L}_{0}^{1})\end{eqnarray}$$
of Zariski sheaves over
 $\text{M}^{\text{loc}}(L_{0})$
. We leave this as an exercise to the reader.◻
$\text{M}^{\text{loc}}(L_{0})$
. We leave this as an exercise to the reader.◻
The proof of Proposition 5.4.1 now follows by combining Lemmas (5.4.2) and (5.4.3) and glueing over an étale cover of
![]() ${\mathcal{M}}$
.◻
${\mathcal{M}}$
.◻
We will have use for the following composition:
 $$\begin{eqnarray}\displaystyle N_{{\mathcal{Y}}}{\mathcal{M}}\xrightarrow[{(5.4.1)}]{\simeq }\boldsymbol{T}_{0}\otimes \text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow \boldsymbol{T}_{0}\otimes (i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{{\mathcal{Y}}}{\mathcal{M}}\xrightarrow[{(5.4.1)}]{\simeq }\boldsymbol{T}_{0}\otimes \text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow \boldsymbol{T}_{0}\otimes (i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}). & & \displaystyle\end{eqnarray}$$
Here, the map on the right is induced by the natural map
 $$\begin{eqnarray}\text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{\text{dR}}^{0}.\end{eqnarray}$$
$$\begin{eqnarray}\text{gr}_{\text{Fil}}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{\text{dR}}^{0}.\end{eqnarray}$$
Note that this last map is an isomorphism over the generic fiber of
![]() ${\mathcal{Y}}$
. Indeed, it amounts to knowing that the inclusion
${\mathcal{Y}}$
. Indeed, it amounts to knowing that the inclusion
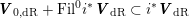 $\boldsymbol{V}_{0,\text{dR}}+\text{Fil}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
is an isomorphism over the generic fiber. This follows from the self-duality of the quadratic form on
$\boldsymbol{V}_{0,\text{dR}}+\text{Fil}^{0}i^{\ast }\boldsymbol{V}_{\text{dR}}\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
is an isomorphism over the generic fiber. This follows from the self-duality of the quadratic form on
![]() $\boldsymbol{V}_{\text{dR},M}$
.
$\boldsymbol{V}_{\text{dR},M}$
.
On the other hand, over the generic fiber, the map
 $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}\rightarrow i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{\text{dR}}^{0}$
is also an isomorphism. Therefore, for any point
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\text{dR}}\rightarrow i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{\text{dR}}^{0}$
is also an isomorphism. Therefore, for any point
 $y\in {\mathcal{Y}}(\mathbb{C})$
, (5.10) induces a canonical isomorphism
$y\in {\mathcal{Y}}(\mathbb{C})$
, (5.10) induces a canonical isomorphism
 $$\begin{eqnarray}\displaystyle (N_{{\mathcal{Y}}}{\mathcal{M}})_{y}\xrightarrow[{}]{\simeq }\boldsymbol{T}_{0,y}\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (N_{{\mathcal{Y}}}{\mathcal{M}})_{y}\xrightarrow[{}]{\simeq }\boldsymbol{T}_{0,y}\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}. & & \displaystyle\end{eqnarray}$$
We will now give an explicit description of this isomorphism. To begin,
![]() $y$
determines an isotropic line
$y$
determines an isotropic line
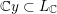 $\mathbb{C}y\subset L_{\mathbb{C}}$
, whose dual can be naturally identified with the fiber
$\mathbb{C}y\subset L_{\mathbb{C}}$
, whose dual can be naturally identified with the fiber
![]() $\boldsymbol{T}_{0,y}$
of
$\boldsymbol{T}_{0,y}$
of
![]() $\boldsymbol{T}_{0}$
at
$\boldsymbol{T}_{0}$
at
![]() $y$
. The construction of the isomorphism (5.11) proceeded by choosing an appropriate local trivialization of
$y$
. The construction of the isomorphism (5.11) proceeded by choosing an appropriate local trivialization of
![]() $\boldsymbol{V}_{\text{dR}}$
. In an analytic neighborhood of
$\boldsymbol{V}_{\text{dR}}$
. In an analytic neighborhood of
![]() $y$
, this simply means that we choose a local section
$y$
, this simply means that we choose a local section
![]() $U\rightarrow {\mathcal{D}}$
of the complex analytic uniformization carrying
$U\rightarrow {\mathcal{D}}$
of the complex analytic uniformization carrying
![]() $y$
to
$y$
to
![]() $\mathbb{C}y$
.
$\mathbb{C}y$
.
Note that
![]() ${\mathcal{D}}$
is contained in the complex quadric
${\mathcal{D}}$
is contained in the complex quadric
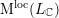 $\text{M}^{\text{loc}}(L_{\mathbb{C}})$
. We therefore see that it is enough to describe the induced isomorphism:
$\text{M}^{\text{loc}}(L_{\mathbb{C}})$
. We therefore see that it is enough to describe the induced isomorphism:
 $$\begin{eqnarray}\displaystyle T_{\mathbb{C}y}{\mathcal{D}}=T_{\mathbb{C}y}\text{M}^{\text{loc}}(L_{\mathbb{C}})\xrightarrow[{}]{\simeq }(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{\mathbb{C}y}{\mathcal{D}}=T_{\mathbb{C}y}\text{M}^{\text{loc}}(L_{\mathbb{C}})\xrightarrow[{}]{\simeq }(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}. & & \displaystyle\end{eqnarray}$$
Here,
![]() $T_{\mathbb{C}y}{\mathcal{D}}$
is the tangent space of
$T_{\mathbb{C}y}{\mathcal{D}}$
is the tangent space of
![]() ${\mathcal{D}}$
at
${\mathcal{D}}$
at
![]() $\mathbb{C}y$
.
$\mathbb{C}y$
.
We consider the local immersion
 $$\begin{eqnarray}\displaystyle \text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}})=(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}\rightarrow \text{M}^{\text{loc}}(L_{\mathbb{C}}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}})=(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}\rightarrow \text{M}^{\text{loc}}(L_{\mathbb{C}}), & & \displaystyle \nonumber\end{eqnarray}$$
which carries a section
![]() $\unicode[STIX]{x1D709}$
to the isotropic line spanned by
$\unicode[STIX]{x1D709}$
to the isotropic line spanned by
 $$\begin{eqnarray}y+\unicode[STIX]{x1D709}(y)-\frac{Q(\unicode[STIX]{x1D709}(y))}{[y,\overline{y}]}\overline{y}.\end{eqnarray}$$
$$\begin{eqnarray}y+\unicode[STIX]{x1D709}(y)-\frac{Q(\unicode[STIX]{x1D709}(y))}{[y,\overline{y}]}\overline{y}.\end{eqnarray}$$
This carries
![]() $0$
to
$0$
to
![]() $\mathbb{C}y$
, and the derivative at
$\mathbb{C}y$
, and the derivative at
![]() $0$
is exactly the inverse to (5.12).
$0$
is exactly the inverse to (5.12).
5.5 Specialization of the Green function
Suppose we have a complex point
 $y\in {\mathcal{Y}}(\mathbb{C})$
. Under the uniformization
$y\in {\mathcal{Y}}(\mathbb{C})$
. Under the uniformization
 $$\begin{eqnarray}{\mathcal{Y}}(\mathbb{C})\xrightarrow[{}]{\simeq }T(\mathbb{Q})\backslash \{\boldsymbol{h}_{0}\}\times T(\mathbb{A}_{f})/\widehat{{\mathcal{O}}}_{\boldsymbol{k}}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Y}}(\mathbb{C})\xrightarrow[{}]{\simeq }T(\mathbb{Q})\backslash \{\boldsymbol{h}_{0}\}\times T(\mathbb{A}_{f})/\widehat{{\mathcal{O}}}_{\boldsymbol{k}}^{\times }\end{eqnarray}$$
of § 4.2, the point
![]() $y$
is represented by a pair
$y$
is represented by a pair
![]() $(\boldsymbol{h}_{0},g)$
with
$(\boldsymbol{h}_{0},g)$
with
 $$\begin{eqnarray}g\in T(\mathbb{A}_{f})\subset G(\mathbb{A}_{f}),\end{eqnarray}$$
$$\begin{eqnarray}g\in T(\mathbb{A}_{f})\subset G(\mathbb{A}_{f}),\end{eqnarray}$$
and so its image in
![]() ${\mathcal{M}}(\mathbb{C})$
lies on the component
${\mathcal{M}}(\mathbb{C})$
lies on the component
![]() $\unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}$
of (2.3). Here
$\unicode[STIX]{x1D6E4}_{g}\backslash {\mathcal{D}}$
of (2.3). Here
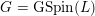 $G=\text{GSpin}(L)$
. By mild abuse of notation we also let
$G=\text{GSpin}(L)$
. By mild abuse of notation we also let
![]() $\mathbb{C}y\in {\mathcal{D}}$
denote the isotropic line corresponding to the oriented negative plane
$\mathbb{C}y\in {\mathcal{D}}$
denote the isotropic line corresponding to the oriented negative plane
 $\boldsymbol{h}_{0}=L_{0\mathbb{R}}$
, so that
$\boldsymbol{h}_{0}=L_{0\mathbb{R}}$
, so that
![]() $\mathbb{C}y$
is a lift of
$\mathbb{C}y$
is a lift of
![]() $y$
under
$y$
under
 ${\mathcal{D}}\rightarrow {\mathcal{M}}(\mathbb{C}),$
and
${\mathcal{D}}\rightarrow {\mathcal{M}}(\mathbb{C}),$
and
 $L_{\mathbb{C}}=\mathbb{C}y\oplus \mathbb{C}\overline{y}\oplus \unicode[STIX]{x1D6EC}_{\mathbb{C}}$
.
$L_{\mathbb{C}}=\mathbb{C}y\oplus \mathbb{C}\overline{y}\oplus \unicode[STIX]{x1D6EC}_{\mathbb{C}}$
.
From (2.4), we find that a neighborhood of
![]() $y$
admits a complex analytic uniformization
$y$
admits a complex analytic uniformization
 $$\begin{eqnarray}\bigsqcup _{\substack{ x\in \unicode[STIX]{x1D707}_{g}+L_{g} \\ Q(x)=m}}{\mathcal{D}}(x)\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}\bigsqcup _{\substack{ x\in \unicode[STIX]{x1D707}_{g}+L_{g} \\ Q(x)=m}}{\mathcal{D}}(x)\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C}).\end{eqnarray}$$
The components
![]() ${\mathcal{D}}(x)$
passing through
${\mathcal{D}}(x)$
passing through
![]() $\mathbb{C}y$
are precisely those for which
$\mathbb{C}y$
are precisely those for which
![]() $x$
is orthogonal to
$x$
is orthogonal to
![]() $y$
. But, since
$y$
. But, since
![]() $x$
is rational, this is equivalent to requiring that
$x$
is rational, this is equivalent to requiring that
![]() $x$
be orthogonal to both
$x$
be orthogonal to both
![]() $y$
and
$y$
and
![]() $\overline{y}$
; or, in other words, that
$\overline{y}$
; or, in other words, that
![]() $x$
lies in
$x$
lies in
![]() $\unicode[STIX]{x1D6EC}^{\vee }$
.
$\unicode[STIX]{x1D6EC}^{\vee }$
.
As the orthogonal transformation
 $g\in \text{SO}(L\otimes \mathbb{A}_{f})$
acts trivially on the direct summand
$g\in \text{SO}(L\otimes \mathbb{A}_{f})$
acts trivially on the direct summand
![]() $\unicode[STIX]{x1D6EC}\otimes \mathbb{A}_{f}$
, we see that such
$\unicode[STIX]{x1D6EC}\otimes \mathbb{A}_{f}$
, we see that such
![]() $x$
in fact lie in
$x$
in fact lie in
![]() $\unicode[STIX]{x1D707}+L$
. This shows that in a small enough analytic neighborhood
$\unicode[STIX]{x1D707}+L$
. This shows that in a small enough analytic neighborhood
![]() $U$
of
$U$
of
![]() $\mathbb{C}y$
there is an isomorphism of divisors
$\mathbb{C}y$
there is an isomorphism of divisors
 $$\begin{eqnarray}\displaystyle U\cap \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}{\mathcal{D}}(\unicode[STIX]{x1D706})\xrightarrow[{}]{\simeq }U\cap {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U\cap \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}{\mathcal{D}}(\unicode[STIX]{x1D706})\xrightarrow[{}]{\simeq }U\cap {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C}), & & \displaystyle\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}=\left\{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}^{\vee }:\begin{array}{@{}c@{}}Q(\unicode[STIX]{x1D706})=m\\ \unicode[STIX]{x1D706}\in \unicode[STIX]{x1D707}+L\end{array}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}=\left\{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}^{\vee }:\begin{array}{@{}c@{}}Q(\unicode[STIX]{x1D706})=m\\ \unicode[STIX]{x1D706}\in \unicode[STIX]{x1D707}+L\end{array}\right\}.\end{eqnarray}$$
Recall that each isotropic line
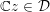 $\mathbb{C}z\in {\mathcal{D}}$
corresponds to a negative plane
$\mathbb{C}z\in {\mathcal{D}}$
corresponds to a negative plane
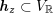 $\boldsymbol{h}_{z}\subset V_{\mathbb{R}}$
. For each
$\boldsymbol{h}_{z}\subset V_{\mathbb{R}}$
. For each
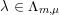 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
let
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
let
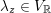 $\unicode[STIX]{x1D706}_{z}\in V_{\mathbb{R}}$
be the orthogonal projection of
$\unicode[STIX]{x1D706}_{z}\in V_{\mathbb{R}}$
be the orthogonal projection of
![]() $\unicode[STIX]{x1D706}$
to
$\unicode[STIX]{x1D706}$
to
![]() $\boldsymbol{h}_{z}$
. Simple linear algebra gives
$\boldsymbol{h}_{z}$
. Simple linear algebra gives
 $$\begin{eqnarray}Q(\unicode[STIX]{x1D706}_{z})=\frac{[\unicode[STIX]{x1D706},\bar{z}]\cdot [\unicode[STIX]{x1D706},z]}{[z,\bar{z}]}.\end{eqnarray}$$
$$\begin{eqnarray}Q(\unicode[STIX]{x1D706}_{z})=\frac{[\unicode[STIX]{x1D706},\bar{z}]\cdot [\unicode[STIX]{x1D706},z]}{[z,\bar{z}]}.\end{eqnarray}$$
Define a function on
 $U\smallsetminus {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C})$
by
$U\smallsetminus {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C})$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{log}|4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}\cdot Q(\unicode[STIX]{x1D706}_{z})|.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{log}|4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}\cdot Q(\unicode[STIX]{x1D706}_{z})|.\end{eqnarray}$$
Recall that the function
 $\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(z)$
is defined, but discontinuous, at
$\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(z)$
is defined, but discontinuous, at
![]() $z=y$
. The following proposition gives us a method of computing the value of this function at the discontinuity
$z=y$
. The following proposition gives us a method of computing the value of this function at the discontinuity
![]() $z=y$
.
$z=y$
.
Proposition 5.5.1. The function
![]() $\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}$
extends smoothly to all of
$\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}$
extends smoothly to all of
![]() $U$
, and this extension satisfies
$U$
, and this extension satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}(y)=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}(y)=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y).\end{eqnarray}$$
Proof. Let
 $\unicode[STIX]{x1D70F}=u+iv\in {\mathcal{H}}$
be the variable on the upper half-plane. The function
$\unicode[STIX]{x1D70F}=u+iv\in {\mathcal{H}}$
be the variable on the upper half-plane. The function
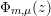 $\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(z)$
is defined, as in [Reference Bruinier and YangBY09, (4.8)], as the constant term of the Laurent expansion at
$\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(z)$
is defined, as in [Reference Bruinier and YangBY09, (4.8)], as the constant term of the Laurent expansion at
![]() $s=0$
of
$s=0$
of
 $$\begin{eqnarray}\displaystyle \lim _{T\rightarrow \infty }\int _{{\mathcal{F}}_{T}}\{F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z)\}\frac{du\,dv}{v^{s+2}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{T\rightarrow \infty }\int _{{\mathcal{F}}_{T}}\{F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z)\}\frac{du\,dv}{v^{s+2}}, & & \displaystyle\end{eqnarray}$$
where
 $$\begin{eqnarray}{\mathcal{F}}_{T}=\{\unicode[STIX]{x1D70F}=u+iv\in {\mathcal{H}}:|u|\leqslant 1/2,|\unicode[STIX]{x1D70F}|\geqslant 1,v\leqslant T\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{T}=\{\unicode[STIX]{x1D70F}=u+iv\in {\mathcal{H}}:|u|\leqslant 1/2,|\unicode[STIX]{x1D70F}|\geqslant 1,v\leqslant T\}.\end{eqnarray}$$
Now substitute the definition [Reference Bruinier and YangBY09, (2.4)] of
![]() $\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z)$
and the Fourier expansion of
$\unicode[STIX]{x1D703}_{L}(\unicode[STIX]{x1D70F},z)$
and the Fourier expansion of
![]() $F_{m,\unicode[STIX]{x1D707}}$
into (5.14), and argue as in [Reference BorcherdsBor98, Theorem 6.2]. Using the decomposition
$F_{m,\unicode[STIX]{x1D707}}$
into (5.14), and argue as in [Reference BorcherdsBor98, Theorem 6.2]. Using the decomposition
 $F_{m,\unicode[STIX]{x1D707}}=F_{m,\unicode[STIX]{x1D707}}^{+}+F_{m,\unicode[STIX]{x1D707}}^{-}$
of [Reference Bruinier and YangBY09, (3.4a) and (3.4b)] and the rapid decay as
$F_{m,\unicode[STIX]{x1D707}}=F_{m,\unicode[STIX]{x1D707}}^{+}+F_{m,\unicode[STIX]{x1D707}}^{-}$
of [Reference Bruinier and YangBY09, (3.4a) and (3.4b)] and the rapid decay as
![]() $v\rightarrow \infty$
of the Fourier coefficients of
$v\rightarrow \infty$
of the Fourier coefficients of
![]() $F_{m,\unicode[STIX]{x1D707}}^{-}$
, we find
$F_{m,\unicode[STIX]{x1D707}}^{-}$
, we find
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(z)=\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}(z)+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{CT}_{s=0}\biggl[\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v^{s+1}}\biggr] & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(z)=\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}(z)+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{CT}_{s=0}\biggl[\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v^{s+1}}\biggr] & & \displaystyle\end{eqnarray}$$
for some smooth function
![]() $\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}$
on
![]() $U$
, where
$U$
, where
![]() $\text{CT}_{s=0}$
means take the constant term at
$\text{CT}_{s=0}$
means take the constant term at
![]() $s=0$
.
$s=0$
.
Each
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
is orthogonal to
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
is orthogonal to
![]() $y$
, and so
$y$
, and so
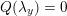 $Q(\unicode[STIX]{x1D706}_{y})=0$
. Thus setting
$Q(\unicode[STIX]{x1D706}_{y})=0$
. Thus setting
![]() $z=y$
in (5.15) and computing the constant term at
$z=y$
in (5.15) and computing the constant term at
![]() $s=0$
shows that
$s=0$
shows that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)=\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}(y).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)=\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}(y).\end{eqnarray}$$
On the other hand, for any
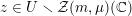 $z\in U\smallsetminus {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C})$
we have
$z\in U\smallsetminus {\mathcal{Z}}(m,\unicode[STIX]{x1D707})(\mathbb{C})$
we have
 $Q(\unicode[STIX]{x1D706}_{z})<0$
for every
$Q(\unicode[STIX]{x1D706}_{z})<0$
for every
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
, and so
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
, and so
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{CT}_{s=0}\biggl[\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v^{s+1}}\biggr] & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D6E4}(0,-4\unicode[STIX]{x1D70B}Q(\unicode[STIX]{x1D706}_{z})),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{CT}_{s=0}\biggl[\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v^{s+1}}\biggr] & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D6E4}(0,-4\unicode[STIX]{x1D70B}Q(\unicode[STIX]{x1D706}_{z})),\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(0,x)=\int _{x}^{\infty }e^{-t}\,\frac{dt}{t}=-\unicode[STIX]{x1D6FE}-\text{log}(x)-\mathop{\sum }_{k=1}^{\infty }\frac{(-x)^{k}}{k\cdot k!}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(0,x)=\int _{x}^{\infty }e^{-t}\,\frac{dt}{t}=-\unicode[STIX]{x1D6FE}-\text{log}(x)-\mathop{\sum }_{k=1}^{\infty }\frac{(-x)^{k}}{k\cdot k!}. & & \displaystyle\end{eqnarray}$$
Comparing (5.16) with (5.17) shows that
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{log}|4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}\cdot Q(\unicode[STIX]{x1D706}_{z})|=-\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{CT}_{s=0}\biggl[\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v^{s+1}}\biggr]\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{log}|4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}\cdot Q(\unicode[STIX]{x1D706}_{z})|=-\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{CT}_{s=0}\biggl[\int _{1}^{\infty }e^{4\unicode[STIX]{x1D70B}vQ(\unicode[STIX]{x1D706}_{z})}\,\frac{dv}{v^{s+1}}\biggr]\end{eqnarray}$$
up to a smooth function on
![]() $U$
, vanishing at
$U$
, vanishing at
![]() $z=y$
. Adding this equality to (5.15) proves that
$z=y$
. Adding this equality to (5.15) proves that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}(z)=\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}(z)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}(z)=\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D707}}(z)\end{eqnarray}$$
up to a smooth function vanishing at
![]() $z=y$
, and completes the proof.◻
$z=y$
, and completes the proof.◻
For any
 $y\in {\mathcal{Y}}(\mathbb{C})$
, we have a canonical isomorphism (see (5.11))
$y\in {\mathcal{Y}}(\mathbb{C})$
, we have a canonical isomorphism (see (5.11))
 $$\begin{eqnarray}\displaystyle (N_{{\mathcal{Y}}}{\mathcal{M}})_{y}\xrightarrow[{}]{\simeq }(\mathbb{C}y)^{\vee }\otimes _{\mathbb{C}}\unicode[STIX]{x1D6EC}_{\mathbb{C}}=\text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (N_{{\mathcal{Y}}}{\mathcal{M}})_{y}\xrightarrow[{}]{\simeq }(\mathbb{C}y)^{\vee }\otimes _{\mathbb{C}}\unicode[STIX]{x1D6EC}_{\mathbb{C}}=\text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}}). & & \displaystyle\end{eqnarray}$$
For each
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
, define a function
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
, define a function
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
on
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
on
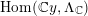 $\text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}})$
by
$\text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}})$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})=-\text{log}\biggl|\frac{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(y)]^{2}}{[y,\bar{y}]}\biggr|.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})=-\text{log}\biggl|\frac{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(y)]^{2}}{[y,\bar{y}]}\biggr|.\end{eqnarray}$$
This function has a logarithmic singularity along the hyperplane
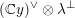 $(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D706}^{\bot }$
. Letting
$(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D706}^{\bot }$
. Letting
![]() $y$
vary over
$y$
vary over
![]() ${\mathcal{Y}}(\mathbb{C})$
yields a function
${\mathcal{Y}}(\mathbb{C})$
yields a function
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
on the vector bundle
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
on the vector bundle
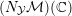 $(N_{{\mathcal{Y}}}{\mathcal{M}})(\mathbb{C})$
having a logarithmic singularity along a sub-bundle of hyperplanes.
$(N_{{\mathcal{Y}}}{\mathcal{M}})(\mathbb{C})$
having a logarithmic singularity along a sub-bundle of hyperplanes.
Proposition 5.5.2. The Green function
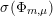 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})$
defined by (5.7) satisfies
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})$
defined by (5.7) satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})=\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})=\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}},\end{eqnarray}$$
where
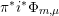 $\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}$
denotes the pullback of
$\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}$
denotes the pullback of
![]() $\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}$
via
$\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}$
via
 $$\begin{eqnarray}(N_{{\mathcal{Y}}}{\mathcal{M}})(\mathbb{C})\xrightarrow[{}]{\unicode[STIX]{x1D70B}}{\mathcal{Y}}(\mathbb{C})\xrightarrow[{}]{i}{\mathcal{M}}(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}(N_{{\mathcal{Y}}}{\mathcal{M}})(\mathbb{C})\xrightarrow[{}]{\unicode[STIX]{x1D70B}}{\mathcal{Y}}(\mathbb{C})\xrightarrow[{}]{i}{\mathcal{M}}(\mathbb{C}).\end{eqnarray}$$
Proof. As above, fix a point
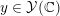 $y\in {\mathcal{Y}}(\mathbb{C})$
and let
$y\in {\mathcal{Y}}(\mathbb{C})$
and let
![]() $U\subset {\mathcal{D}}$
be a neighborhood of the isotropic line
$U\subset {\mathcal{D}}$
be a neighborhood of the isotropic line
 $\mathbb{C}y\subset L_{\mathbb{C}}$
. As in § 5.4, we can define a holomorphic local immersion
$\mathbb{C}y\subset L_{\mathbb{C}}$
. As in § 5.4, we can define a holomorphic local immersion
 $$\begin{eqnarray}\text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}})=(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{ C}}\rightarrow \text{M}^{\text{loc}}(L_{\mathbb{ C}})\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}(\mathbb{C}y,\unicode[STIX]{x1D6EC}_{\mathbb{C}})=(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{ C}}\rightarrow \text{M}^{\text{loc}}(L_{\mathbb{ C}})\end{eqnarray}$$
by sending
![]() $\unicode[STIX]{x1D709}$
to the
$\unicode[STIX]{x1D709}$
to the
![]() $\mathbb{C}$
-span of
$\mathbb{C}$
-span of
 $$\begin{eqnarray}y+\unicode[STIX]{x1D709}(y)-\frac{Q(\unicode[STIX]{x1D709}(y))\overline{y}}{[y,\overline{y}]}.\end{eqnarray}$$
$$\begin{eqnarray}y+\unicode[STIX]{x1D709}(y)-\frac{Q(\unicode[STIX]{x1D709}(y))\overline{y}}{[y,\overline{y}]}.\end{eqnarray}$$
As we saw at the end of § 5.4, the induced isomorphism on tangent spaces
 $$\begin{eqnarray}(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{ C}}\rightarrow T_{y}{\mathcal{D}}\xrightarrow[{}]{\simeq }(N_{{\mathcal{Y}}}{\mathcal{M}})_{y}\end{eqnarray}$$
$$\begin{eqnarray}(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{ C}}\rightarrow T_{y}{\mathcal{D}}\xrightarrow[{}]{\simeq }(N_{{\mathcal{Y}}}{\mathcal{M}})_{y}\end{eqnarray}$$
agrees with the isomorphism of (5.18).
From now on we use the above map to identify
![]() $U$
with an open neighborhood of the origin of
$U$
with an open neighborhood of the origin of
 $(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}$
. Each divisor
$(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}$
. Each divisor
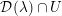 ${\mathcal{D}}(\unicode[STIX]{x1D706})\cap U$
appearing in (5.13) is identified with the zero locus of
${\mathcal{D}}(\unicode[STIX]{x1D706})\cap U$
appearing in (5.13) is identified with the zero locus of
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})=[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(y)]\cdot \biggl|\frac{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}}{[y,\overline{y}]}\biggr|^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})=[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(y)]\cdot \biggl|\frac{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}}{[y,\overline{y}]}\biggr|^{1/2}.\end{eqnarray}$$
This function is already linear, and so when we apply the construction
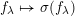 $f_{\unicode[STIX]{x1D706}}\mapsto \unicode[STIX]{x1D70E}(f_{\unicode[STIX]{x1D706}})$
of the discussion preceding (5.7) and identify
$f_{\unicode[STIX]{x1D706}}\mapsto \unicode[STIX]{x1D70E}(f_{\unicode[STIX]{x1D706}})$
of the discussion preceding (5.7) and identify
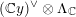 $(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}$
with its own tangent space at the origin, we obtain
$(\mathbb{C}y)^{\vee }\otimes \unicode[STIX]{x1D6EC}_{\mathbb{C}}$
with its own tangent space at the origin, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(f_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D709})=[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(\boldsymbol{v})]\cdot \biggl|\frac{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}}{[\boldsymbol{v},\overline{\boldsymbol{v}}]}\biggr|^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(f_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D709})=[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(\boldsymbol{v})]\cdot \biggl|\frac{4\unicode[STIX]{x1D70B}e^{\unicode[STIX]{x1D6FE}}}{[\boldsymbol{v},\overline{\boldsymbol{v}}]}\biggr|^{1/2}.\end{eqnarray}$$
Thus
 $-\text{log}|\unicode[STIX]{x1D70E}(f_{\unicode[STIX]{x1D706}})|^{2}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}.$
$-\text{log}|\unicode[STIX]{x1D70E}(f_{\unicode[STIX]{x1D706}})|^{2}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}.$
If we define a smooth function on
![]() $U$
by
$U$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{log}|f_{\unicode[STIX]{x1D706}}|^{2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\text{log}|f_{\unicode[STIX]{x1D706}}|^{2},\end{eqnarray}$$
then directly from the definition (5.7) and the paragraph above we see that
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})=\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})=\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
Now use
 $\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}(y)=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}(y)=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)$
to complete the proof.◻
$\unicode[STIX]{x1D719}_{m,\unicode[STIX]{x1D707}}(y)=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}^{\text{reg}}(y)=\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)$
to complete the proof.◻
5.6 The calculation of the pullback
Recall that the Kuga–Satake abelian scheme
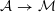 ${\mathcal{A}}\rightarrow {\mathcal{M}}$
restricts to the abelian scheme
${\mathcal{A}}\rightarrow {\mathcal{M}}$
restricts to the abelian scheme
 $$\begin{eqnarray}{\mathcal{A}}_{{\mathcal{Y}}}={\mathcal{E}}\otimes _{C^{+}(L_{0})}C(L)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{{\mathcal{Y}}}={\mathcal{E}}\otimes _{C^{+}(L_{0})}C(L)\end{eqnarray}$$
over
![]() ${\mathcal{Y}}$
, where
${\mathcal{Y}}$
, where
![]() ${\mathcal{E}}\rightarrow {\mathcal{Y}}$
is the universal elliptic curve.
${\mathcal{E}}\rightarrow {\mathcal{Y}}$
is the universal elliptic curve.
By Proposition 4.6.3, every
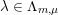 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
determines a canonical special endomorphism
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
determines a canonical special endomorphism
 $\boldsymbol{\ell }_{\unicode[STIX]{x1D706}}\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{{\mathcal{Y}}})$
, and the pair
$\boldsymbol{\ell }_{\unicode[STIX]{x1D706}}\in V_{\unicode[STIX]{x1D707}}({\mathcal{A}}_{{\mathcal{Y}}})$
, and the pair
 $({\mathcal{A}}_{{\mathcal{Y}}},\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})$
is a
$({\mathcal{A}}_{{\mathcal{Y}}},\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})$
is a
![]() ${\mathcal{Y}}$
-valued point of
${\mathcal{Y}}$
-valued point of
 ${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
. The corresponding map
${\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
. The corresponding map
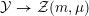 ${\mathcal{Y}}\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
is finite and unramified, and so we may define an
${\mathcal{Y}}\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
is finite and unramified, and so we may define an
![]() ${\mathcal{O}}_{{\mathcal{Y}}}$
-submodule
${\mathcal{O}}_{{\mathcal{Y}}}$
-submodule
 $$\begin{eqnarray}\displaystyle {\mathcal{Z}}_{\unicode[STIX]{x1D706}}=N_{{\mathcal{Y}}}{\mathcal{Z}}(m,\unicode[STIX]{x1D707}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{Z}}_{\unicode[STIX]{x1D706}}=N_{{\mathcal{Y}}}{\mathcal{Z}}(m,\unicode[STIX]{x1D707}) & & \displaystyle\end{eqnarray}$$
of
![]() $N_{{\mathcal{Y}}}{\mathcal{M}}$
in exactly the same way that
$N_{{\mathcal{Y}}}{\mathcal{M}}$
in exactly the same way that
![]() $N_{{\mathcal{Y}}}{\mathcal{M}}$
was defined.
$N_{{\mathcal{Y}}}{\mathcal{M}}$
was defined.
Proposition 4.6.1 provides us with a canonical morphism
 $\unicode[STIX]{x1D6EC}\rightarrow i^{\ast }\boldsymbol{V}_{\text{dR}}$
such that
$\unicode[STIX]{x1D6EC}\rightarrow i^{\ast }\boldsymbol{V}_{\text{dR}}$
such that
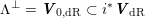 $\unicode[STIX]{x1D6EC}^{\bot }=\boldsymbol{V}_{0,\text{dR}}\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
. Thus, the bilinear pairing on
$\unicode[STIX]{x1D6EC}^{\bot }=\boldsymbol{V}_{0,\text{dR}}\subset i^{\ast }\boldsymbol{V}_{\text{dR}}$
. Thus, the bilinear pairing on
![]() $i^{\ast }\boldsymbol{V}_{\text{dR}}$
gives us a map
$i^{\ast }\boldsymbol{V}_{\text{dR}}$
gives us a map
 $$\begin{eqnarray}i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\otimes \unicode[STIX]{x1D6EC}^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\otimes \unicode[STIX]{x1D6EC}^{\vee }\end{eqnarray}$$
of vector bundles over
![]() ${\mathcal{Y}}$
. This map is injective, and using local trivializations, one sees that its image is identified precisely with the inclusion
${\mathcal{Y}}$
. This map is injective, and using local trivializations, one sees that its image is identified precisely with the inclusion
 $$\begin{eqnarray}{\mathcal{O}}_{{\mathcal{Y}}}\otimes (L/L_{0}){\hookrightarrow}{\mathcal{O}}_{{\mathcal{Y}}}\otimes \unicode[STIX]{x1D6EC}^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{{\mathcal{Y}}}\otimes (L/L_{0}){\hookrightarrow}{\mathcal{O}}_{{\mathcal{Y}}}\otimes \unicode[STIX]{x1D6EC}^{\vee }.\end{eqnarray}$$
This latter inclusion is the natural one induced by the bilinear pairing on
![]() $L$
.
$L$
.
Now, by definition,
![]() $\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
is contained in
$\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
is contained in
 $(L/L_{0})^{\vee }\subset L^{\vee }$
. Therefore, we obtain a morphism,
$(L/L_{0})^{\vee }\subset L^{\vee }$
. Therefore, we obtain a morphism,
 $$\begin{eqnarray}[\,\cdot \,,\unicode[STIX]{x1D706}]:i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\otimes (L/L_{0})\xrightarrow[{}]{1\otimes \unicode[STIX]{x1D706}}{\mathcal{O}}_{{\mathcal{Y}}},\end{eqnarray}$$
$$\begin{eqnarray}[\,\cdot \,,\unicode[STIX]{x1D706}]:i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\rightarrow {\mathcal{O}}_{{\mathcal{Y}}}\otimes (L/L_{0})\xrightarrow[{}]{1\otimes \unicode[STIX]{x1D706}}{\mathcal{O}}_{{\mathcal{Y}}},\end{eqnarray}$$
of
![]() ${\mathcal{O}}_{{\mathcal{Y}}}$
-modules.
${\mathcal{O}}_{{\mathcal{Y}}}$
-modules.
Here is another way to describe this morphism. Recall from § 4.6 that we have a canonical
![]() $T$
-torsor over
$T$
-torsor over
![]() ${\mathcal{Y}}$
parameterizing
${\mathcal{Y}}$
parameterizing
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
-equivariant trivializations of
${\mathcal{O}}_{\boldsymbol{k}}$
-equivariant trivializations of
![]() $\boldsymbol{H}_{0,\text{dR}}^{+}$
. Using this torsor of local trivializations, we get a canonical functor from representations of
$\boldsymbol{H}_{0,\text{dR}}^{+}$
. Using this torsor of local trivializations, we get a canonical functor from representations of
![]() $T$
to vector bundles over
$T$
to vector bundles over
![]() ${\mathcal{Y}}$
with integrable connection.
${\mathcal{Y}}$
with integrable connection.
The map
![]() $[\,\cdot \,,\unicode[STIX]{x1D706}]$
is now simply obtained by applying this functor to the
$[\,\cdot \,,\unicode[STIX]{x1D706}]$
is now simply obtained by applying this functor to the
![]() $T$
-invariant functional
$T$
-invariant functional
 $L/L_{0}\rightarrow \mathbb{Z}$
given by pairing with
$L/L_{0}\rightarrow \mathbb{Z}$
given by pairing with
![]() $\unicode[STIX]{x1D706}$
. In particular, if
$\unicode[STIX]{x1D706}$
. In particular, if
![]() $t_{\text{dR}}(\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})$
is the de Rham realization of
$t_{\text{dR}}(\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})$
is the de Rham realization of
![]() $\boldsymbol{\ell }_{\unicode[STIX]{x1D706}}$
(it is a section of
$\boldsymbol{\ell }_{\unicode[STIX]{x1D706}}$
(it is a section of
![]() $i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{\vee }$
), we find that functionals
$i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{\vee }$
), we find that functionals
 $$\begin{eqnarray}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\xrightarrow[{}]{[\cdot ,\unicode[STIX]{x1D706}]}{\mathcal{O}}_{S}\end{eqnarray}$$
$$\begin{eqnarray}i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\xrightarrow[{}]{[\cdot ,\unicode[STIX]{x1D706}]}{\mathcal{O}}_{S}\end{eqnarray}$$
and
 $$\begin{eqnarray}[\,\cdot \,,t_{\text{dR}}(\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})]:i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow {\mathcal{O}}_{S}\end{eqnarray}$$
$$\begin{eqnarray}[\,\cdot \,,t_{\text{dR}}(\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})]:i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}\rightarrow {\mathcal{O}}_{S}\end{eqnarray}$$
are identical.
Proposition 5.6.1. Fix any
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
.
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
.
-
(i) The divisor
 ${\mathcal{Z}}_{\unicode[STIX]{x1D706}}$
is canonically identified with the kernel of
${\mathcal{Z}}_{\unicode[STIX]{x1D706}}$
is canonically identified with the kernel of  $$\begin{eqnarray}N_{{\mathcal{Y}}}{\mathcal{M}}\xrightarrow[{}]{(5.10)}\boldsymbol{T}_{0}\otimes (i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}})\xrightarrow[{}]{[\cdot ,\unicode[STIX]{x1D706}]}\boldsymbol{T}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}N_{{\mathcal{Y}}}{\mathcal{M}}\xrightarrow[{}]{(5.10)}\boldsymbol{T}_{0}\otimes (i^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}})\xrightarrow[{}]{[\cdot ,\unicode[STIX]{x1D706}]}\boldsymbol{T}_{0}.\end{eqnarray}$$
-
(ii) The metrized line bundle
 $\unicode[STIX]{x1D70B}^{\ast }\widehat{\boldsymbol{T}}_{0}$
is represented by the arithmetic divisor
$\unicode[STIX]{x1D70B}^{\ast }\widehat{\boldsymbol{T}}_{0}$
is represented by the arithmetic divisor  $$\begin{eqnarray}({\mathcal{Z}}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})\in \widehat{\text{Div}}(N_{{\mathcal{Y}}}{\mathcal{M}}).\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{Z}}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})\in \widehat{\text{Div}}(N_{{\mathcal{Y}}}{\mathcal{M}}).\end{eqnarray}$$
Proof. We work over a sufficiently small étale neighborhood
![]() $Y\subset U$
of
$Y\subset U$
of
 ${\mathcal{Y}}\rightarrow {\mathcal{M}}$
. Suppose that we are given an open subspace
${\mathcal{Y}}\rightarrow {\mathcal{M}}$
. Suppose that we are given an open subspace
![]() $S\subset Y$
and
$S\subset Y$
and
 $j_{S}\in \text{Def}_{i}(S)$
. By the construction of the map (5.10), to prove the first claim, we have to show that
$j_{S}\in \text{Def}_{i}(S)$
. By the construction of the map (5.10), to prove the first claim, we have to show that
![]() $\boldsymbol{\ell }_{\unicode[STIX]{x1D706}}$
lifts to an element in
$\boldsymbol{\ell }_{\unicode[STIX]{x1D706}}$
lifts to an element in
 $V_{\unicode[STIX]{x1D707}}(j_{S}^{\ast }{\mathcal{A}})$
if and only if the composition
$V_{\unicode[STIX]{x1D707}}(j_{S}^{\ast }{\mathcal{A}})$
if and only if the composition
 $$\begin{eqnarray}j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\rightarrow i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}\xrightarrow[{}]{[\,\cdot \,,\unicode[STIX]{x1D706}]}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}\end{eqnarray}$$
$$\begin{eqnarray}j_{S}^{\ast }\boldsymbol{V}_{\text{dR}}^{1}\rightarrow i_{S}^{\ast }\boldsymbol{V}_{\text{dR}}/\boldsymbol{V}_{0,\text{dR}}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}\xrightarrow[{}]{[\,\cdot \,,\unicode[STIX]{x1D706}]}{\mathcal{O}}_{S[\unicode[STIX]{x1D700}]}\end{eqnarray}$$
is identically
![]() $0$
. This follows from Lemma 2.7.5 and the identification we made above of
$0$
. This follows from Lemma 2.7.5 and the identification we made above of
![]() $[\,\cdot \,,\unicode[STIX]{x1D706}]$
with pairing against
$[\,\cdot \,,\unicode[STIX]{x1D706}]$
with pairing against
![]() $t_{\text{dR}}(\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})$
.
$t_{\text{dR}}(\boldsymbol{\ell }_{\unicode[STIX]{x1D706}})$
.
The second claim follows from the first, as the map
 $[\,\cdot \,,\unicode[STIX]{x1D706}]:N_{{\mathcal{Y}}}{\mathcal{M}}\rightarrow \boldsymbol{T}_{0}$
defines a section
$[\,\cdot \,,\unicode[STIX]{x1D706}]:N_{{\mathcal{Y}}}{\mathcal{M}}\rightarrow \boldsymbol{T}_{0}$
defines a section
![]() $s_{\unicode[STIX]{x1D706}}$
of
$s_{\unicode[STIX]{x1D706}}$
of
![]() $\unicode[STIX]{x1D70B}^{\ast }\boldsymbol{T}_{0}$
with
$\unicode[STIX]{x1D70B}^{\ast }\boldsymbol{T}_{0}$
with
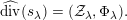 $\widehat{\text{div}}(s_{\unicode[STIX]{x1D706}})=({\mathcal{Z}}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}).$
Indeed, using the notation of (5.18), the norm of this section at a complex point
$\widehat{\text{div}}(s_{\unicode[STIX]{x1D706}})=({\mathcal{Z}}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}).$
Indeed, using the notation of (5.18), the norm of this section at a complex point
 $\unicode[STIX]{x1D709}\in (N_{{\mathcal{Y}}}{\mathcal{M}})_{y}$
in the fiber over
$\unicode[STIX]{x1D709}\in (N_{{\mathcal{Y}}}{\mathcal{M}})_{y}$
in the fiber over
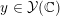 $y\in {\mathcal{Y}}(\mathbb{C})$
is
$y\in {\mathcal{Y}}(\mathbb{C})$
is
 $$\begin{eqnarray}-\text{log}\Vert s_{\unicode[STIX]{x1D706}}\Vert ^{2}=-\text{log}\biggl|\frac{[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(y)]}{\Vert y\Vert }\biggr|^{2}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709}),\end{eqnarray}$$
$$\begin{eqnarray}-\text{log}\Vert s_{\unicode[STIX]{x1D706}}\Vert ^{2}=-\text{log}\biggl|\frac{[\unicode[STIX]{x1D706},\unicode[STIX]{x1D709}(y)]}{\Vert y\Vert }\biggr|^{2}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709}),\end{eqnarray}$$
where the second equality is by definition (5.8) of the metric on
![]() $\widehat{\boldsymbol{T}}_{0}$
.◻
$\widehat{\boldsymbol{T}}_{0}$
.◻
As in [Reference Bruinier, Howard and YangBHY15, § 7.3], we define a new metrized line bundle
 $$\begin{eqnarray}\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})\otimes \widehat{\boldsymbol{T}}^{\otimes -\#\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707})\otimes \widehat{\boldsymbol{T}}^{\otimes -\#\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}\in \widehat{\text{Pic}}({\mathcal{M}}).\end{eqnarray}$$
Proposition 5.6.2. The image of
 $\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})$
under the pullback
$\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})$
under the pullback
 $$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\end{eqnarray}$$
is represented by the arithmetic divisor
 $$\begin{eqnarray}\biggl(\mathop{\sum }_{\substack{ m_{1}>0 \\ m_{2}\geqslant 0 \\ m_{1}+m_{2}=m}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0} \\ \unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC} \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\cdot {\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1}),i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}\biggr)\in \widehat{\text{Div}}({\mathcal{Y}}).\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\mathop{\sum }_{\substack{ m_{1}>0 \\ m_{2}\geqslant 0 \\ m_{1}+m_{2}=m}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0} \\ \unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC} \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\cdot {\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1}),i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}\biggr)\in \widehat{\text{Div}}({\mathcal{Y}}).\end{eqnarray}$$
Proof. By Proposition 4.6.4 there is a decomposition of
![]() ${\mathcal{Y}}$
-stacks
${\mathcal{Y}}$
-stacks
 $$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{Y}}=\bigsqcup _{\substack{ m_{1},m_{2}\in \mathbb{Q}_{{\geqslant}0} \\ m_{1}+m_{2}=m}}\bigsqcup _{\substack{ \unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0} \\ \unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC} \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{Y}}=\bigsqcup _{\substack{ m_{1},m_{2}\in \mathbb{Q}_{{\geqslant}0} \\ m_{1}+m_{2}=m}}\bigsqcup _{\substack{ \unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0} \\ \unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC} \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}.\end{eqnarray}$$
Using Remark 4.6.5 we may therefore decompose
 $$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{Y}}={\mathcal{Z}}_{0}^{\text{prop}}\,\sqcup ({\mathcal{Y}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})\times _{{\mathcal{M}}}{\mathcal{Y}}={\mathcal{Z}}_{0}^{\text{prop}}\,\sqcup ({\mathcal{Y}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}),\end{eqnarray}$$
where
 $$\begin{eqnarray}{\mathcal{Z}}_{0}^{\text{prop}}=\bigsqcup _{\substack{ m_{1}>0 \\ m_{2}\geqslant 0 \\ m_{1}+m_{2}=m}}\bigsqcup _{\substack{ \unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0} \\ \unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC} \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{0}^{\text{prop}}=\bigsqcup _{\substack{ m_{1}>0 \\ m_{2}\geqslant 0 \\ m_{1}+m_{2}=m}}\bigsqcup _{\substack{ \unicode[STIX]{x1D707}_{1}\in L_{0}^{\vee }/L_{0} \\ \unicode[STIX]{x1D707}_{2}\in \unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC} \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\times \unicode[STIX]{x1D6EC}_{m_{2},\unicode[STIX]{x1D707}_{2}}\end{eqnarray}$$
is a
![]() ${\mathcal{Y}}$
-stack of dimension
${\mathcal{Y}}$
-stack of dimension
![]() $0$
. Moreover, the induced map
$0$
. Moreover, the induced map
 $$\begin{eqnarray}{\mathcal{Y}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Y}}\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})\end{eqnarray}$$
determines, for each
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
, a map
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
, a map
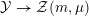 ${\mathcal{Y}}\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
, which is none other than the map used in the definition (5.19) of
${\mathcal{Y}}\rightarrow {\mathcal{Z}}(m,\unicode[STIX]{x1D707})$
, which is none other than the map used in the definition (5.19) of
![]() ${\mathcal{Z}}_{\unicode[STIX]{x1D706}}$
.
${\mathcal{Z}}_{\unicode[STIX]{x1D706}}$
.
Over a sufficiently small étale open chart
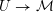 $U\rightarrow {\mathcal{M}}$
we may fix a connected component
$U\rightarrow {\mathcal{M}}$
we may fix a connected component
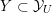 $Y\subset {\mathcal{Y}}_{U}$
, and decompose
$Y\subset {\mathcal{Y}}_{U}$
, and decompose
 $$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}=Z^{\text{prop}}\,\sqcup (Y\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}=Z^{\text{prop}}\,\sqcup (Y\times \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}})\end{eqnarray}$$
where
![]() $Z^{\text{prop}}$
is the union of all connected components
$Z^{\text{prop}}$
is the union of all connected components
 $Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
for which
$Z\subset {\mathcal{Z}}(m,\unicode[STIX]{x1D707})_{U}$
for which
![]() $Z\cap Y$
has dimension
$Z\cap Y$
has dimension
![]() $0$
. If we apply the specialization to the normal bundle construction of (5.6) separately to
$0$
. If we apply the specialization to the normal bundle construction of (5.6) separately to
![]() $Z^{\text{prop}}$
and to each of the
$Z^{\text{prop}}$
and to each of the
![]() $\#\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
copies of
$\#\unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}$
copies of
![]() $Y$
, and then glue over an étale cover, we find the equality
$Y$
, and then glue over an étale cover, we find the equality
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}({\mathcal{Z}}(m,\unicode[STIX]{x1D707}))=\unicode[STIX]{x1D70B}^{\ast }{\mathcal{Z}}_{0}^{\text{prop}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}{\mathcal{Z}}_{\unicode[STIX]{x1D706}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}({\mathcal{Z}}(m,\unicode[STIX]{x1D707}))=\unicode[STIX]{x1D70B}^{\ast }{\mathcal{Z}}_{0}^{\text{prop}}+\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}{\mathcal{Z}}_{\unicode[STIX]{x1D706}} & & \displaystyle\end{eqnarray}$$
of divisors on
![]() $N_{{\mathcal{Y}}}{\mathcal{M}}$
.
$N_{{\mathcal{Y}}}{\mathcal{M}}$
.
By Propositions 5.2.6 and 5.6.1 the image of
 $\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})$
under
$\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})$
under
 $$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}\widehat{\text{Pic}}(N_{{\mathcal{Y}}}{\mathcal{M}})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\text{Pic}}({\mathcal{M}})\xrightarrow[{}]{i^{\ast }}\widehat{\text{Pic}}({\mathcal{Y}})\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}\widehat{\text{Pic}}(N_{{\mathcal{Y}}}{\mathcal{M}})\end{eqnarray}$$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))-\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}({\mathcal{Z}}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=\unicode[STIX]{x1D70E}(\widehat{{\mathcal{Z}}}(m,\unicode[STIX]{x1D707}))-\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{m,\unicode[STIX]{x1D707}}}({\mathcal{Z}}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\end{eqnarray}$$
and Proposition 5.5.2 and (5.20) allow us to rewrite this as an equality of metrized line bundles
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=\unicode[STIX]{x1D70B}^{\ast }({\mathcal{Z}}_{0}^{\text{prop}},i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }i^{\ast }\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=\unicode[STIX]{x1D70B}^{\ast }({\mathcal{Z}}_{0}^{\text{prop}},i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})\end{eqnarray}$$
on
![]() $N_{{\mathcal{Y}}}{\mathcal{M}}$
. Pulling back by the zero section
$N_{{\mathcal{Y}}}{\mathcal{M}}$
. Pulling back by the zero section
 ${\mathcal{Y}}\rightarrow N_{{\mathcal{Y}}}{\mathcal{M}}$
yields an isomorphism
${\mathcal{Y}}\rightarrow N_{{\mathcal{Y}}}{\mathcal{M}}$
yields an isomorphism
 $$\begin{eqnarray}i^{\ast }\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=({\mathcal{Z}}_{0}^{\text{prop}},i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})\end{eqnarray}$$
$$\begin{eqnarray}i^{\ast }\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})=({\mathcal{Z}}_{0}^{\text{prop}},i^{\ast }\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}})\end{eqnarray}$$
of metrized line bundles on
![]() ${\mathcal{Y}}$
.◻
${\mathcal{Y}}$
.◻
5.7 The main result
We are now ready to prove our main result. For the reader’s convenience, we review the dramatis personae.
The lattices
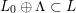 $L_{0}\oplus \unicode[STIX]{x1D6EC}\subset L$
determine a finite and unramified morphism of stacks
$L_{0}\oplus \unicode[STIX]{x1D6EC}\subset L$
determine a finite and unramified morphism of stacks
 ${\mathcal{Y}}\rightarrow {\mathcal{M}}$
over
${\mathcal{Y}}\rightarrow {\mathcal{M}}$
over
![]() ${\mathcal{O}}_{\boldsymbol{k}}$
, and hence a linear functional
${\mathcal{O}}_{\boldsymbol{k}}$
, and hence a linear functional
 $$\begin{eqnarray}[\cdot :{\mathcal{Y}}]:\widehat{\text{CH}}^{1}({\mathcal{M}})\rightarrow \mathbb{R}\end{eqnarray}$$
$$\begin{eqnarray}[\cdot :{\mathcal{Y}}]:\widehat{\text{CH}}^{1}({\mathcal{M}})\rightarrow \mathbb{R}\end{eqnarray}$$
defined in § 5.1.
Fix a weak harmonic Maass form
 $f(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
. The holomorphic part
$f(\unicode[STIX]{x1D70F})\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
. The holomorphic part
 $$\begin{eqnarray}f^{+}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\gg -\infty }c_{f}^{+}(m)\cdot q^{m}\end{eqnarray}$$
$$\begin{eqnarray}f^{+}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\gg -\infty }c_{f}^{+}(m)\cdot q^{m}\end{eqnarray}$$
is a formal
![]() $q$
-expansion valued in the finite-dimensional vector space
$q$
-expansion valued in the finite-dimensional vector space
![]() $\mathfrak{S}_{L}$
of complex functions on
$\mathfrak{S}_{L}$
of complex functions on
![]() $L^{\vee }/L$
. We assume that
$L^{\vee }/L$
. We assume that
![]() $f^{+}$
has integral principal part, so that the constructions of § 3.2 provide us with an arithmetic divisor
$f^{+}$
has integral principal part, so that the constructions of § 3.2 provide us with an arithmetic divisor
 $$\begin{eqnarray}\widehat{{\mathcal{Z}}}(f)=({\mathcal{Z}}(f),\unicode[STIX]{x1D6F7}(f))\in \widehat{\text{CH}}^{1}({\mathcal{M}}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{Z}}}(f)=({\mathcal{Z}}(f),\unicode[STIX]{x1D6F7}(f))\in \widehat{\text{CH}}^{1}({\mathcal{M}}).\end{eqnarray}$$
We also have, from § 5.3, the metrized cotautological bundle
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}\in \widehat{\text{CH}}^{1}({\mathcal{M}}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}\in \widehat{\text{CH}}^{1}({\mathcal{M}}).\end{eqnarray}$$
Recalling the Bruinier–Funke differential operator
 $$\begin{eqnarray}\unicode[STIX]{x1D709}:H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}:H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L})\end{eqnarray}$$
from (3.1), we may form the convolution
![]() $L$
-function
$L$
-function
 $L(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)$
of
$L(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},s)$
of
![]() $\unicode[STIX]{x1D709}(f)$
with the theta series
$\unicode[STIX]{x1D709}(f)$
with the theta series
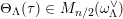 $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})\in M_{n/2}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee })$
of § 3.3. The convolution
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})\in M_{n/2}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{\vee })$
of § 3.3. The convolution
![]() $L$
-function vanishes at
$L$
-function vanishes at
![]() $s=0$
, the center of the functional equation.
$s=0$
, the center of the functional equation.
Recall the
![]() $\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}$
-valued formal
$\mathfrak{S}_{L_{0}\oplus \unicode[STIX]{x1D6EC}}$
-valued formal
![]() $q$
-expansion
$q$
-expansion
 ${\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}$
of § 3.3. Using (3.2) and (3.3), we obtain a scalar-valued
${\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}$
of § 3.3. Using (3.2) and (3.3), we obtain a scalar-valued
![]() $q$
-expansion
$q$
-expansion
 $$\begin{eqnarray}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}=\mathop{\sum }_{m_{1},m_{2},m_{3}\in \mathbb{Q}}\{c_{f}^{+}(m_{1}),a_{L_{0}}^{+}(m_{2})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{3})\}\cdot q^{m_{1}+m_{2}+m_{3}}\end{eqnarray}$$
$$\begin{eqnarray}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}=\mathop{\sum }_{m_{1},m_{2},m_{3}\in \mathbb{Q}}\{c_{f}^{+}(m_{1}),a_{L_{0}}^{+}(m_{2})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{3})\}\cdot q^{m_{1}+m_{2}+m_{3}}\end{eqnarray}$$
with constant term
 $$\begin{eqnarray}\displaystyle \text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}=\mathop{\sum }_{m_{1}+m_{2}+m_{3}=0}\{c_{f}^{+}(m_{1}),a_{L_{0}}^{+}(m_{2})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{3})\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}=\mathop{\sum }_{m_{1}+m_{2}+m_{3}=0}\{c_{f}^{+}(m_{1}),a_{L_{0}}^{+}(m_{2})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{3})\}. & & \displaystyle\end{eqnarray}$$
The following CM value formula was proved by Schofer [Reference SchoferSch09] for weakly holomorphic modular forms, and then generalized to harmonic weak Maass forms by Bruinier and Yang [Reference Bruinier and YangBY09]. We repeat here the statement of [Reference Bruinier and YangBY09, Theorem 4.7], with a sign error corrected. See also [Reference Bruinier, Howard and YangBHY15, Theorem 5.3.6].
Theorem 5.7.1 (Schofer, Bruinier and Yang).
The Green function
![]() $\unicode[STIX]{x1D6F7}(f)$
satisfies
$\unicode[STIX]{x1D6F7}(f)$
satisfies
 $$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}(f,y)}{\#\text{Aut}(y)}=-L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\},\end{eqnarray}$$
$$\begin{eqnarray}\frac{w_{\boldsymbol{k}}}{h_{\boldsymbol{k}}}\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}(f,y)}{\#\text{Aut}(y)}=-L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D709}:H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}:H_{1-n/2}(\unicode[STIX]{x1D714}_{L})\rightarrow S_{1+n/2}(\overline{\unicode[STIX]{x1D714}}_{L})\end{eqnarray}$$
is the Bruinier–Funke differential operator of (3.1).
Remark 5.7.2. Recalling Remark 3.2.1, Theorem 5.7.1 holds even when some points of
![]() ${\mathcal{Y}}(\mathbb{C})$
lie on
${\mathcal{Y}}(\mathbb{C})$
lie on
 ${\mathcal{Z}}(f)(\mathbb{C})$
, the divisor along which
${\mathcal{Z}}(f)(\mathbb{C})$
, the divisor along which
![]() $\unicode[STIX]{x1D6F7}(f)$
has its logarithmic singularities.
$\unicode[STIX]{x1D6F7}(f)$
has its logarithmic singularities.
Inspired by Theorem 5.7.1, the following formula was conjectured by Bruinier and Yang [Reference Bruinier and YangBY09].
Theorem 5.7.3. Assume
![]() $d_{\boldsymbol{k}}$
is odd. Every weak harmonic Maass form
$d_{\boldsymbol{k}}$
is odd. Every weak harmonic Maass form
 $f\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
with integral principal part satisfies
$f\in H_{1-n/2}(\unicode[STIX]{x1D714}_{L})$
with integral principal part satisfies
 $$\begin{eqnarray}[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]+c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0),\end{eqnarray}$$
$$\begin{eqnarray}[\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}]+c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0),\end{eqnarray}$$
where
 $c_{f}^{+}(0,0)$
is the value of
$c_{f}^{+}(0,0)$
is the value of
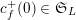 $c_{f}^{+}(0)\in \mathfrak{S}_{L}$
at the trivial coset in
$c_{f}^{+}(0)\in \mathfrak{S}_{L}$
at the trivial coset in
![]() $L^{\vee }/L$
.
$L^{\vee }/L$
.
Proof. First assume
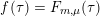 $f(\unicode[STIX]{x1D70F})=F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})$
is the Hejhal–Poincaré series of § 3.2, so that
$f(\unicode[STIX]{x1D70F})=F_{m,\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})$
is the Hejhal–Poincaré series of § 3.2, so that
 $$\begin{eqnarray}\widehat{{\mathcal{Z}}}(f)=\big({\mathcal{Z}}(m,\unicode[STIX]{x1D707}),\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}\big)=\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})\otimes \widehat{\boldsymbol{T}}^{\otimes R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{Z}}}(f)=\big({\mathcal{Z}}(m,\unicode[STIX]{x1D707}),\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}\big)=\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707})\otimes \widehat{\boldsymbol{T}}^{\otimes R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})}.\end{eqnarray}$$
By Proposition 5.6.2 there is a decomposition
 $$\begin{eqnarray}\displaystyle [\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707}):{\mathcal{Y}}] & = & \displaystyle \mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0 \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\cdot \widehat{\deg }\,{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)}{\#\text{Aut}(y)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707}):{\mathcal{Y}}] & = & \displaystyle \mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0 \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\cdot \widehat{\deg }\,{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)}{\#\text{Aut}(y)},\nonumber\end{eqnarray}$$
where we view
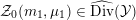 ${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\in \widehat{\text{Div}}({\mathcal{Y}})$
as an arithmetic divisor with trivial Green function. Theorem 4.5.1 shows that the first term is
${\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\in \widehat{\text{Div}}({\mathcal{Y}})$
as an arithmetic divisor with trivial Green function. Theorem 4.5.1 shows that the first term is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0 \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\cdot \widehat{\deg }\,{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\nonumber\\ \displaystyle & & \displaystyle \qquad =-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0 \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}a_{L_{0}}^{+}(m_{1},\unicode[STIX]{x1D707}_{1})R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad =-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0}}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(m_{1})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{2})\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0 \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\cdot \widehat{\deg }\,{\mathcal{Z}}_{0}(m_{1},\unicode[STIX]{x1D707}_{1})\nonumber\\ \displaystyle & & \displaystyle \qquad =-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0 \\ (\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2})\in (\unicode[STIX]{x1D707}+L)/(L_{0}\oplus \unicode[STIX]{x1D6EC})}}a_{L_{0}}^{+}(m_{1},\unicode[STIX]{x1D707}_{1})R_{\unicode[STIX]{x1D6EC}}(m_{2},\unicode[STIX]{x1D707}_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad =-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\mathop{\sum }_{\substack{ m_{1}+m_{2}=m \\ m_{1}>0}}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(m_{1})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{2})\}.\nonumber\end{eqnarray}$$
For our special choice of
![]() $f(\unicode[STIX]{x1D70F})$
the constant term (5.21) simplifies to
$f(\unicode[STIX]{x1D70F})$
the constant term (5.21) simplifies to
 $$\begin{eqnarray}\displaystyle \text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\} & = & \displaystyle \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m_{1}+m_{2}=m}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(m_{1})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{2})\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\} & = & \displaystyle \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{m_{1}+m_{2}=m}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(m_{1})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{2})\}\nonumber\end{eqnarray}$$
and so Theorem 5.7.1 becomes
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)}{\#\text{Aut}(y)} & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\mathop{\sum }_{m_{1}+m_{2}=m}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(m_{1})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{2})\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}_{m,\unicode[STIX]{x1D707}}(y)}{\#\text{Aut}(y)} & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\mathop{\sum }_{m_{1}+m_{2}=m}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(m_{1})\otimes R_{\unicode[STIX]{x1D6EC}}(m_{2})\}.\nonumber\end{eqnarray}$$
We have now proved
 $$\begin{eqnarray}\displaystyle [\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707}):{\mathcal{Y}}] & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(m)\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707}):{\mathcal{Y}}] & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\{c_{f}^{+}(-m),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(m)\}.\nonumber\end{eqnarray}$$
Corollary 5.3.2 implies both
 $$\begin{eqnarray}c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\end{eqnarray}$$
$$\begin{eqnarray}c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}\end{eqnarray}$$
and
 $$\begin{eqnarray}R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(-m),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(m)\},\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(-m),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(m)\},\end{eqnarray}$$
leaving
 $$\begin{eqnarray}[\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707}):{\mathcal{Y}}]+[\widehat{\boldsymbol{T}}^{\otimes R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})}:{\mathcal{Y}}]+c_{f}^{+}(0,0)[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0),\end{eqnarray}$$
$$\begin{eqnarray}[\widehat{{\mathcal{Z}}}^{\heartsuit }(m,\unicode[STIX]{x1D707}):{\mathcal{Y}}]+[\widehat{\boldsymbol{T}}^{\otimes R_{\unicode[STIX]{x1D6EC}}(m,\unicode[STIX]{x1D707})}:{\mathcal{Y}}]+c_{f}^{+}(0,0)[\widehat{\boldsymbol{T}}:{\mathcal{Y}}]=-\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0),\end{eqnarray}$$
and proving the desired formula in the special case of
 $f=F_{m,\unicode[STIX]{x1D707}}$
.
$f=F_{m,\unicode[STIX]{x1D707}}$
.
Now assume that
![]() $f$
satisfies
$f$
satisfies
 $f^{+}(\unicode[STIX]{x1D70F})=O(1)$
. In particular,
$f^{+}(\unicode[STIX]{x1D70F})=O(1)$
. In particular,
 ${\mathcal{Z}}(f)=\emptyset$
and the Green function
${\mathcal{Z}}(f)=\emptyset$
and the Green function
![]() $\unicode[STIX]{x1D6F7}(f)$
is a smooth function on
$\unicode[STIX]{x1D6F7}(f)$
is a smooth function on
![]() ${\mathcal{M}}(\mathbb{C})$
. The arithmetic intersection is purely archimedean, and Theorem 5.7.1 shows that
${\mathcal{M}}(\mathbb{C})$
. The arithmetic intersection is purely archimedean, and Theorem 5.7.1 shows that
 $$\begin{eqnarray}\displaystyle [\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}] & = & \displaystyle \mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}(f,y)}{\#\text{Aut}(y)}\nonumber\\ \displaystyle & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}\nonumber\\ \displaystyle & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\widehat{{\mathcal{Z}}}(f):{\mathcal{Y}}] & = & \displaystyle \mathop{\sum }_{y\in {\mathcal{Y}}(\mathbb{C})}\frac{\unicode[STIX]{x1D6F7}(f,y)}{\#\text{Aut}(y)}\nonumber\\ \displaystyle & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \text{CT}\{f^{+},{\mathcal{E}}_{L_{0}}\otimes \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}}\}\nonumber\\ \displaystyle & = & \displaystyle -\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot L^{\prime }(\unicode[STIX]{x1D709}(f),\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6EC}},0)+\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}.\nonumber\end{eqnarray}$$
Corollary 5.3.2 implies that
 $$\begin{eqnarray}\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}=\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot c_{f}^{+}(0,0)\cdot a_{L_{0}}^{+}(0,0)=-c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}],\end{eqnarray}$$
$$\begin{eqnarray}\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot \{c_{f}^{+}(0),a_{L_{0}}^{+}(0)\otimes R_{\unicode[STIX]{x1D6EC}}(0)\}=\frac{h_{\boldsymbol{k}}}{w_{\boldsymbol{k}}}\cdot c_{f}^{+}(0,0)\cdot a_{L_{0}}^{+}(0,0)=-c_{f}^{+}(0,0)\cdot [\widehat{\boldsymbol{T}}:{\mathcal{Y}}],\end{eqnarray}$$
completing the proof in this case.
Finally, every weak harmonic Maass form can be written as a linear combination of the Hejhal–Poincaré series, and a form with holomorphic part
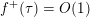 $f^{+}(\unicode[STIX]{x1D70F})=O(1)$
. Thus the claim follows from the linearity in
$f^{+}(\unicode[STIX]{x1D70F})=O(1)$
. Thus the claim follows from the linearity in
![]() $f$
of both sides of the desired equality.◻
$f$
of both sides of the desired equality.◻
Acknowledgements
The authors thank Jan Bruinier, José Burgos Gil, Steve Kudla, and Tonghai Yang for helpful conversations and insights. They also thank the referees for useful comments.