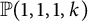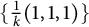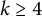A note on the smooth blowups of $\mathbb {P}(1,1,1,k)$ in torus-invariant subvarieties

Abstract

This papers classifies toric Fano threefolds with singular locus $\{ \frac {1}{k}(1,1,1) \}$ for $k \in \mathbb {Z}_{\geq 1}$ building on the work of Batyrev (1981, Nauk SSSR Ser. Mat. 45, 704–717) and Watanabe–Watanabe (1982, Tokyo J. Math. 5, 37–48). This is achieved by completing an equivalent problem in the language of Fano polytopes. Furthermore, we identify birational relationships between entries of the classification. For a fixed value $k \geq 4$, there are exactly two such toric Fano threefolds linked by a blowup in a torus-invariant line.

1 Introduction

A projective algebraic variety over $\mathbb {C}$ is Fano if the anticanonical divisor $-K_{X}$ is ample. Classifications of Fano varieties is an area of substantial interest in algebraic geometry. Most famously, del Pezzo classified the smooth Fano varieties in dimension $2$ , known as the 10 smooth del Pezzo surfaces. Mori–Mukai completed the classification of smooth Fano threefolds finding 105 varieties [11].

Restricting the class of varieties in dimension d to toric varieties, that is, varieties with a suitable embedding of the algebraic torus $(\mathbb {C}^{*})^{d}$ , allows for a combinatorial reinterpretation of the problem. The classification of toric d-dimensional Fano varieties is equivalent to the classification of specific d-dimensional lattice polytopes, known as Fano polytopes, up to a change of basis on the lattice.

A number of classifications of toric Fano varieties exist in the literature. Most notably Batyrev [1] and Watanabe–Watanabe [14] simultaneously classified smooth toric Fano threefolds. Batyrev further classified smooth toric Fano fourfolds [2]. Moving into the non-singular situation Kruezer–Skarke [7–9] classify Gorenstein toric Fano varieties in dimensions $2, 3$ , and $4$ . Kasprzyk classifies toric Fano threefolds with at worst terminal/canonical singularities in [5, 6].

Definition 1.1 Let $N \cong \mathbb {Z}^{n}$ be a lattice. A Fano polytope $P \subset N_{\mathbb {R}}=N \otimes \mathbb {R}$ is a full-dimensional convex polytope such that $\mathbf {0} \in \text {int}(P)$ and all vertices $v \in \mathcal {V}(P)$ have primitive coordinates.

The spanning fan $\Sigma _{P}$ of a Fano polytope P gives rise to a toric variety $X_{P}$ , leading to the previously mentioned equivalence for Fano variety classifications. Geometric properties of the toric variety can be seen at the level of the combinatorics of P. In particular, one can observe the singularities of $X_{P}$ ; each maximal cone of $\Sigma _{P}$ describes a toric singularity on $X_{P}$ .

Definition 1.2 Consider the action of $\mu _{r}$ , the cyclic group of order r, on $\mathbb {C}^{3}$ by

$$\begin{align*}\epsilon \cdot (x,y,z) = (\epsilon^{a}x,\epsilon^{b}y, \epsilon^{c}z), \end{align*}$$

where $\epsilon $ is an rth root of unity. The germ of the origin of $\text {Spec}(\mathbb {C}[x,y,z]^{\mu _{r}})$ is known as a quotient singularity $\frac {1}{r}(a,b,c)$ . A cyclic quotient singularity is a quotient singularity $\frac {1}{r}(a,b,c)$ such that $\gcd (r,a)=\gcd (r,b)= \gcd (r,c)=1$ .

Cyclic quotient singularities are toric, and the corresponding cone is simplicial. Of particular interest for this paper are: (i) the simplicial cone whose generating rays form a basis of the lattice N, which describes a smooth patch $\mathbb {C}^{n} \subset X_{P}$ , and is subsequently known as a smooth cone, and (ii) the cone over $\text {conv} \left \{ (1,0,0), (0,1,0), (-1,-1,-k) \right \}$ , considered up to a change of basis, which describes a $\frac {1}{k}(1,1,1)$ singularity and is subsequently denoted $C_{\frac {1}{k}(1,1,1)}$ .

As mentioned, Batyrev [1] and Watanabe–Watanabe [14] classify smooth toric Fano threefolds, and further identify any birational relations, that is, blowups or blowdowns, within this classification. The resulting 18 varieties are outlined in Table 1 and fall into a cascade structure, terminology coined by Reid–Suzuki [12], rooted at $\mathbb {P}^{3}$ shown in Figure 1. Here, and indeed throughout the paper, a blue line indicates a blowup in a smooth point and a red line indicates a blowup in a smooth torus-invariant line.

Table 1 Smooth toric Fano threefolds V.

Figure 1 Cascade of varieties rooted at $\mathbb {P}^{3}$ .

Motivated by the above, one may ask how this cascade generalizes if we were to replace $\mathbb {P}^{3}$ by $\mathbb {P}(1,1,1,k)$ for $k \geq 2$ . To answer this question, we classify the toric Fano threefolds V with singular locus $\text {Sing}(V)= \left \{ \frac {1}{k}(1,1,1) \right \}$ using the combinatorial language introduced.

The cases $k=2$ and $k=3$ are terminal and canonical, respectively, and so the classifications are readily available via a quick search of the Graded Ring Database [13] which includes the results obtained by Kasprzyk [5, 6]. The results are given in the following propositions.

Theorem 1.1 Let V be a toric Fano threefold, $\text {Sing}(V) = \left \{ \frac {1}{2}(1,1,1) \right \}$ . Then V is isomorphic to one of the 18 varieties in Table 2. Furthermore, these varieties admit the birational relationships illustrated in Figure 2.

Table 2 Toric Fano threefolds V, $\text {Sing}(V)= \left \{ \frac {1}{2}(1,1,1) \right \}$ .

Figure 2 Cascade of varieties rooted at $\mathbb {P}(1,1,1,2)$ .

Theorem 1.2 Let V be a toric Fano threefold, $\text {Sing}(V) = \left \{ \frac {1}{3}(1,1,1) \right \}$ . Then V is isomorphic to one of the two varieties in Table 3. Furthermore, these two varieties are related birationally, as illustrated in Figure 3.

Table 3 Toric Fano threefolds V, $\text {Sing}(V)= \left \{ \frac {1}{3}(1,1,1) \right \}$ .

Figure 3 Cascade of varieties rooted at $\mathbb {P}(1,1,1,3)$ .

The original material of this paper is then to deal with the case $k>3$ , that is, when the varieties are no longer canonical.

Theorem 1.3 For $k \geq 4$ , let V be a toric Fano threefold, $\text {Sing}(V) = \left \{ \frac {1}{k}(1,1,1) \right \}$ . Then V is isomorphic to one of the two varieties in Table 4. Furthermore, these two varieties are related birationally, as illustrated in Figure 4.

Table 4 Toric Fano threefolds V, $\text {Sing}(V)= \left \{ \frac {1}{k}(1,1,1) \right \}$ .

Figure 4 Cascade of varieties rooted at $\mathbb {P}(1,1,1,k)$ .

In dimension 2, it is shown in [3] that the $\mathbb {P}^{2}$ cascade generalizes in some sense to the cascade of $\mathbb {P}(1,1,k)$ for $k>1$ . This does not seem to be the case in the threefold setting. The majority of the birational relationships between threefolds in the $\mathbb {P}^{3}$ cascade above, or indeed the $\mathbb {P}(1,1,1,2)$ cascade, do not generalize to a birational relationship on the $\mathbb {P}(1,1,1,k)$ cascade. One could hypothesize that the majority of threefolds birationally related to $\mathbb {P}^{3}$ and $\mathbb {P}(1,1,1,2)$ are suitably interesting Fano threefolds in a fashion analogous to the rich geometry of the low-degree del Pezzo surfaces. Further it is worth remarking that variety 2.18 is the unique toric Fano threefold with singular locus $\left \{ \frac {1}{k}(1,1,1) \right \}$ which is not a smooth blow up of $\mathbb {P}(1,1,1,k)$ for any value of k, and is of particular intrigue.

The method outlined in this paper could be replicated if one wished to classify toric Fano threefolds whose singular locus consists of any one fixed cyclic quotient singularity that is of particular interest to the reader.

2 Proof of Theorem 1.5

Lemma 2.1 Let $k>3$ . Let P be a Fano polytope. Assume that P has a $C_{\frac {1}{k}(1,1,1)}$ cone over $\text {conv} \{ (1,0,0),(0,1,0),(-1,-1,-k) \}$ , and that all other cones of P are smooth. Then there exists a finite set $U^{(k)}$ such that

$$\begin{align*}\mathcal{V}(P) \backslash \big\{ (1,0,0),(0,1,0),(-1,-1,-k) \big\} \quad \subset \quad U^{(k)}. \end{align*}$$

Proof We aim to find all lattice points that could be added to the vertex set of P that would not violate the assumptions on P. Convexity dictates that the plane through $(1,0,0), (0,1,0)$ , and $(-1,-1,-k)$ defines a closed half-space $kx+ky-3z \geq k$ of $N_{\mathbb {R}}$ in which no new vertex can belong.

To sort through the remaining lattice points, we define an algorithm. The algorithm is based on the fact that P cannot contain interior points or non-vertex boundary points other than those in $C_{\frac {1}{k}(1,1,1)}$ . For a lattice point $p \notin C_{\frac {1}{k}(1,1,1)}$ , define $C_p$ to be the cone based at p, generated by rays laying on the three lines $L_{1}, L_{2}, L_{3}$ , where $L_{1}, L_{2}, L_{3}$ are the lines through p and $(1,0,0), (0,1,0), (-1,-1,-k)$ , respectively, and where the rays point away from $(1,0,0)$ , $(0,1,0)$ , $(-1,-1,-k)$ , respectively. It follows by convexity that p will be a non-vertex lattice point in P if $\mathcal {V}(P)$ contains a lattice point belonging to the polyhedral cone $C_{p}$ . So to determine all possible vertices, we perform the following steps:

1. (i) Define a set A of the lattice points in the open half-space $kx+ky-3z<k$ .

2. (ii) Pick a lattice point $p \in A$ , and construct the cone $C_{p}$ described above.

3. (iii) Remove from A all lattice points in $C_{p}$ .

4. (iv) Return to step (ii) and pick a point $p \in A$ that has not been chosen before.

5. (v) Continue repeating until all points of A have been chosen as p.

It remains to check that the algorithm does indeed terminate. It is enough to show that we can assume A starts off as a finite set. To do this, we use a bound, given by Hensley [4] and later improved by Lagarias–Ziegler [10], on the volume of a dimension d polytope with $n>0$ interior points:

$$\begin{align*}\text{Vol}(P) \leq d! \cdot (8d)! \cdot 15^{d \cdot 2^{2d+1} \cdot n}. \end{align*}$$

Since P is a threedimensional polytope with at least one interior point, namely, the origin, it follows that the volume is bounded by some $R \in \mathbb {Z}_{>0}$ .

Consider $(x,y,z) \in A$ . Define three lattice polytopes:

$$ \begin{align*} T_{1} :=& \text{conv} \left\{ (0,0,0), (1,0,0), (0,1,0), (x,y,z) \right\}. \\ T_{2} :=& \text{conv} \left\{ (0,0,0), (1,0,0), (-1,-1,-k), (x,y,z) \right\}. \\ T_{3} :=& \text{conv} \left\{ (0,0,0), (0,1,0), (-1,-1,-k), (x,y,z) \right\}. \end{align*} $$

If there exists P with $(x,y,z) \in \mathcal {V}(P)$ , then $T_{i} \subset P$ , $\forall i$ . It follows that the volume of $T_{i}$ is bounded by R. Calculate that

$$ \begin{align*} \text{Vol}(T_{1}) &= \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ x & y & z \end{vmatrix} = \lvert z \rvert, \\ \text{Vol}(T_{2}) &= \begin{vmatrix} 1 & 0 & 0 \\ -1 & -1 & -k \\ x & y & z \end{vmatrix} = \lvert ky-z \rvert, \\[2pt] \text{Vol}(T_{3}) &= \begin{vmatrix} 0 & 1 & 0 \\ -1 & -1 & -k \\ x & y & z \end{vmatrix} = \lvert kx-z \rvert. \end{align*} $$

It follows that $x,y,z$ are all bounded and so A is finite. It is worth noting that the authors of [4, 10] do not claim R to be a sharp bound on the volume. Even if it was sharp, we do not believe R would subsequently provide a sharp bound on the values that $x,y,z$ can take. However, it is enough to assume that A can be taken as finite in the algorithm and proves that the algorithm will indeed terminate. The set $U^{(K)}$ that is left after running the algorithm is finite.

Indeed, further to Lemma 2.1, running the algorithm determines the set $U^{(K)}$ as

$$\begin{align*}U^{(k)} := U_{1}^{(k)} \cup U_{2}^{(k)} \cup \cdots \cup U_{10}^{(k)},\end{align*}$$

where:

where:

$$\begin{align*}a := \begin{cases} \frac{4}{3}k-1, & \text{if } k \equiv 0 \quad \text{(mod 3),} \\ \frac{4}{3}(k-1)+1, & \text{if } k \equiv 1 \quad \text{(mod 3),} \\ \frac{4}{3}(k-2)+1, & \text{if } k \equiv 2 \quad \text{(mod 3),} \end{cases} \end{align*}$$

$$\begin{align*}b := \begin{cases} \frac{2}{3}k-1, & \text{if } k \equiv 0 \quad \text{(mod 3),} \\ \frac{2}{3}(k-1), & \text{if } k \equiv 1 \quad \text{(mod 3),} \\ \frac{2}{3}(k-2)+1, & \text{if } k \equiv 2 \quad \text{(mod 3),} \end{cases} \end{align*}$$

$$\begin{align*}c := \begin{cases} \frac{1}{3}k+1, & \text{if } k \equiv 0 \quad \text{(mod 6),} \\ \frac{1}{3}(k-1), & \text{if } k \equiv 1 \quad \text{(mod 6),} \\ \frac{1}{3}(k-2)+1, & \text{if } k \equiv 2 \quad \text{(mod 6),} \\ \frac{1}{3}(k-3), & \text{if } k \equiv 3 \quad \text{(mod 6),} \\ \frac{1}{3}(k-4)-1, & \text{if } k \equiv 4 \quad \text{(mod 6),} \\ \frac{1}{3}(k-5), & \text{if } k \equiv 5 \quad \text{(mod 6),} \end{cases} \end{align*}$$

$$\begin{align*}d := \begin{cases} \frac{1}{3}k+1, & \text{if } k \equiv 0 \quad \text{(mod 3),} \\ \frac{1}{3}(k-1)+1, & \text{if } k \equiv 1 \quad \text{(mod 3),} \\ \frac{1}{3}(k-2)+1, & \text{if } k \equiv 2 \quad \text{(mod 3),} \end{cases} \end{align*}$$

$$\begin{align*}e := \begin{cases} \frac{2}{3}k+1, & \text{if } k \equiv 0 \quad \text{(mod 3),} \\ \frac{2}{3}(k-1)+1, & \text{if } k \equiv 1 \quad \text{(mod 3),} \\ \frac{2}{3}(k-2)+3, & \text{if } k \equiv 2 \quad \text{(mod 3).} \end{cases} \end{align*}$$

We are now ready to prove Theorem 1.3.

Proof “Theorem 1.5” Consider the Fano polytope P of a toric Fano threefold V, $\text {Sing}(V) = \left \{ \frac {1}{k}(1,1,1) \right \}$ . Without loss of generality, assume that the face of P corresponding to the unique singularity is given by $\text {conv} \left \{ (1,0,0), (0,1,0), (-1,-1,-k) \right \}$ . Since all other faces of P must define a smooth cone, it follows from Lemma 2.1 that $\mathcal {V}(P) \subset U^{(k)}$ .

In particular, there exists a vertex $v_{1} \in \mathcal {V}(P), v_{1} \neq (-1,-1,-k)$ , such that $\text {conv} \{ (1,0,0), (0,1,0), v_{1} \}$ defines a face of P. This face will define a smooth cone and it must not determine that $\mathbf {0} \notin P$ by convexity. With this in mind define:

$$\begin{align*}L_{1}^{(k)} := \left\{ (x,y,z) \in U^{(k)} : \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ x & y & z \end{vmatrix} = 1 \quad \text{and} \quad \begin{array}{c} \text{sign} ( n \cdot (-1,-1,-k) ) \neq \text{sign} (n \cdot v), \\ \text{where } n \text{ is the inward pointing normal} \\ \text{of conv}\{ (1,0,0), (0,1,0), (x,y,z) \} \end{array} \!\right\}. \end{align*}$$

Define $v_{2} \neq (0,1,0)$ to be the vertex creating a face with $(1,0,0)$ and $(-1,-1,-k)$ , and $v_{3} \neq (1,0,0)$ to be the vertex creating a face with $(0,1,0)$ and $(-1,-1,-k)$ . Therefore, consider two further similarly motivated sets of lattice points:

$$\begin{align*}L_{2}^{(k)} := \left\{ (x,y,z) \in U^{(k)} : \begin{vmatrix} 1 & 0 & 0 \\ -1 & -1 & -k \\ x & y & z \end{vmatrix} = 1 \quad \text{and} \quad \begin{array}{c} \text{sign} ( n \cdot (0,1,0) ) \neq \text{sign} (n \cdot v), \\ \text{where } n \text{ is the inward pointing normal} \\ \text{of conv}\{ (1,0,0), (-1,-1,-k), (x,y,z) \} \end{array} \!\!\right\}\kern-1pt, \end{align*}$$

$$\begin{align*}L_{3}^{(k)} := \left\{ (x,y,z) \in U^{(k)} : \begin{vmatrix} 0 & 1 & 0 \\ -1 & -1 & -k \\ x & y & z \end{vmatrix} = 1 \quad \text{and} \quad \begin{array}{c} \text{sign} ( n \cdot (1,0,0) ) \neq \text{sign} (n \cdot v), \\ \text{where } n \text{ is the inward pointing normal} \\ \text{of conv}\{ (0,1,0), (-1,-1,-k), (x,y,z) \} \end{array} \!\!\right\}\kern-1pt. \end{align*}$$

Using the list in the statement of Lemma 2.1, we can calculate $L_{1}, L_{2}, L_{3}$ explicitly:

$$\begin{align*}L_{1}^{(k)} = \left\{ \begin{array}{c} (-2,-1,1), (-1,-2,1), (-1,0,1), (-1,1,1), (-1,2,1), (0,-1,1) \\ (0,0,1), (0,1,1), (1,-1,1), (1,0,1), (2,-1,1) \end{array} \!\!\right\}\kern-1pt, \end{align*}$$

$$\begin{align*}L_{2}^{(k)} = \left\{ \begin{array}{c} (-3,-2,-2k+1), (-2,-1,-k+1), (-1,-1,-k+1), (-1,0,1), (-1,1,k+1), \\ (0,0,1), (1,0,1), (1,1,k+1), (1,2,2k+1), (2,1,k+1), (3,1,k+1) \!\!\end{array} \right\}\kern-1pt, \end{align*}$$

$$\begin{align*}L_{3}^{(k)} = \left\{ \begin{array}{c} (-2,-3,-2k+1), (-1,-2,-k+1), (-1,-1,-k+1), (0,-1,1), (0,0,1), (0,1,1) \\ (1,-1,k+1), (1,1,k+1), (1,2,k+1), (1,3,k+1), (2,1,2k+1) \!\!\end{array} \right\}\kern-1pt. \end{align*}$$

It is worth noting that, while choices for each of the $v_{i}$ must be made, it is not necessarily true that $v_{i} \neq v_{j}$ for $i \neq j$ .

From here, we construct sets $\mathcal {V}(P)$ defining the vertices of a suitable Fano polytope:

1. (i) Iterate through the possibilities for $v_{1}$ .

2. (ii) Each choice for $v_{1}$ narrows down the possibilities for $v_{2}$ and $v_{3}$ from $L_{2}^{(k)}$ and $L_{3}^{(k)}$ , respectively, by convexity.

3. (iii) Iterating through choices for $v_{2}$ narrows down the possibilities for $v_{3}$ from $L_{3}^{(k)}$ .

4. (iv) Lattice points in $U^{(k)}$ which satisfy the three new convexity conditions can be added to $\mathcal {V}(P)$ .

In attempting to do this a number of things can go wrong. For example, if there is a non-vertex lattice point in $\text {conv} \left \{ (1,0,0), (0,1,0), (-1,-1,-k), v_{1}, v_{2} \right \}$ , other than those in $C_{\frac {1}{k}(1,1,1)}$ , then P would contain this lattice point and would therefore contain a second singular cone. This could also happen after adding $v_{3}$ or a vertex from $U^{(k)}$ . Alternatively, convexity requirements from adding $v_{1}$ and $v_{2}$ could leave us with no options for $v_{3}$ , meaning a suitable P cannot exist. Similarly, it could happen that there a no possibilities in $U^{(k)}$ due to convexity from adding $v_{1}, v_{2}, v_{3}$ and the convex hull of the current set of vertices has a second singular cone meaning, we cannot complete to the construction of a suitable polytope P. We demonstrate a sample computation for a particular choice of $v_{1}$ .

Choose $v_{1}=(-2,-1,1) \in L_{1}^{(k)}$ . It is worth noting that $(-2,-1,1) \notin L_{2}^{(k)}, L_{3}^{(k)}$ and so is not a suitable choice for $v_{2}$ or $v_{3}$ . The new face $\text {conv} \left \{ (1,0,0), (0,1,0), (-2,-1,-1) \right \}$ bounds P by the plane $x+y+4z < 1$ . There are only three points in $L_{2}^{(k)}$ satisfying this bound and so are suitable choices of $v_{2}$ , namely, $(-3,-2,-2k+1), (-2,-1,-k+1)$ , and $(-1,-1,-k+1)$ . For $(-3,-2,-2k+1)$ , note that $\text {conv} \big \{ (0,1,0), (-2,-1,1), (-3,-2,-2k+1) \big \}$ contains an interior point and so this is not a suitable choice for $v_{2}$ . Similarly, $\text {conv} \left \{ (-2,-1,-k+1), (-2,-1,1) \right \}$ contains interior points ruling out $v_{2} = (-2,-1,1)$ . Therefore, $v_{2}=(-1,-1,-k+1)$ . Note that $v_{2} = (-1,-1,k+1) \in L_{3}^{(k)}$ . Suppose initially that $v_{3} \neq (-1,-1,-k+1)$ . Adding $v_{2}$ gave P an additional bounding plane, $x-2y<1$ , along with the preexisting bound $x+y+4z<1$ . No points in $L_{3}^{(k)}$ satisfy both these equations and so there would no possible choice for $v_{3}$ . The only remaining choice for $v_{3}$ is $(-1,-1,-k+1)$ . The polytope $\text {conv} \left \{ (1,0,0), (0,1,0), (-1,-1,-k), (-2,-1,1), (-1,-1,-k+1) \right \}$ has a singular cone over the face $\text {conv} \left \{ (1,0,0), (0,1,0), (-1,-1,-k+1) \right \}$ , and it is necessary to add vertices from $U^{(k)}$ to change this. However, we now have three bounding planes coming from adding $v_{1},v_{2}$ , and $v_{3}$ , namely, $x+y+4z<1, x-2y<1$ , and $y-2x<1$ , respectively, and one can check that no points of $U^{(k)}$ satisfy all three of these bounds. Therefore, there are no possible polytope constructions here.

The only suitable Fano polytopes that are constructed through this method are the two that are listed in the statement of the theorem. It is routine to observe the blow up relation between the two varieties.