Transpiration through hydrogels

Abstract

We present experiments and theory relating to transpiration through unrestrained hydrogel beads in contact with a water reservoir below and air above. Experimentally, we find that saturated hydrogel beads shrink until a steady state is reached in which water flows continuously through the beads. The size of the bead in steady state is sensitive to the evaporation rate, which depends on the relative humidity and speed of the surrounding air, and to the pressure head imposed by the fluid reservoir. Specifically, the bead size decreases with increasing pressure head or evaporation rate. Our one-dimensional model proposes that transport in the hydrogel is driven by gradients in osmotic pressure, caused by gradients in polymer concentration in the hydrogel that correspond to gradients in swelling. If the evaporation rate or the pressure head changes, the adjustment of this gradient requires the bead to change shape and size. Smaller beads have larger gradients of osmotic pressure, which drive higher transpiration rates and can draw water against larger pressure heads.

1. Introduction

Hydrogels consist of cross-linked polymer molecules that form three-dimensional networks (Laftah, Hashim & Ibrahim 2011) of macroscopic extent (Vervoort 2006), which can absorb large quantities of water. Depending on the chemical composition of the polymer and the chain architecture, the water content can exceed 99 %. The short-time behaviour of a hydrogel is that of an elastic, incompressible solid (Yoon et al. 2010), while at long times hydrogels can respond to changing external conditions (stress, temperature, humidity) by swelling, shrinking or deformation. Hydrogels represent an intermediate state between liquid and solid (Tanaka 1981) and are of enormous technical importance for biomedical applications (Hoare & Kohane 2008; Van Vlierberghe, Dubruel & Schacht 2011), oil recovery (Pu et al. 2017), agriculture (Guilherme et al. 2015) and many more.

Transpiration is the process of transporting water driven by evaporation from a suitable surface and has intrigued scientists for more than a century (see references in Thut 1928) due to its crucial role in plant metabolism (Zimmermann et al. 2004). Transpiration surfaces are either microporous solids or polymeric gels, even though some authors treat both as porous solids. The physical chemistry of such systems is fascinating: for microporous substrates the Laplace equation indicates that minisci in small pores can support enormous pressure gradients. In gel systems, water transport is attributed to gradients in chemical potential, which, between a liquid water reservoir and air of 40 % relative humidity, corresponds to a pressure difference of more than 1000 bar ($10^7\ {\rm kPa}$) (Wheeler & Stroock 2008). This theoretical pressure drop within a hydrogel under transpiration has been used to study water under tension. Some of these studies consider the stability of water droplets enclosed in hydrogel (Wheeler & Stroock 2008, 2009) which are progressively dehydrated by evaporation (Wheeler & Stroock 2008, 2009; Vincent et al. 2012; Bruning et al. 2019). One of the earliest hydrogel evaporation experiments was reported by Thut (1928), who used gel-coated cylinders made of porous porcelain to lift water. They report pressure heads between 1.5 and 2 atmospheres (100–200 kPa). Wheeler & Stroock (2008) designed a microfluidic synthetic tree with a high internal flow resistance. They infer internal pressure drops in these systems from the flow rate via Poiseuille's law and report values between $7\times 10^4$ and $4\times 10^5\ {\rm Pa}$ and argue that the water entering the evaporation hydrogel is therefore under tension for cases with higher pressure drops. Experiments with a similar set-up studying cavitation dynamics were also reported by Roper, Euliss & Nguyen (2012) who give no pressure drops.

Since transpiration requires neither moving parts nor a complex external power source, transpiration from hydrogels has been used in technical applications such as cooling (Qian et al. 2019) and for lab-on-a-chip applications. Choi, Lee & Chung (2010) integrated agarose and polyacrylamide gels into a microfluidic network and demonstrated the ability of this network to pump water and blood. Li et al. (2011) integrated an agarose sheet into a microfluidic network, covered by a porous screen plate to imitate the stomata of plants. Refined manufacturing processes generate large pores within the hydrogels via freeze drying to increase the flow rate (Lee, Kim & Ahn 2015) and the addition of titanium nanoparticles to further increase the wettability of the system (Lee, Lim & Lee 2017). Other design improvements are the introduction of flow control elements (Jingmin et al. 2012) such as stomata-like layers made of thermo-responsive materials (Kim & Lee 2015; Kim, Kim & Lee 2017). Wu, Patil & Chen (2018) used a hydrogel as polyelectrolyte in a fuel cell, where transpiration of water from the air cathode ensures the continuous supply of fuel. Hydrogels are also used in some solar evaporators which seem to be operated close to saturated conditions (e.g. Zhou et al. 2018).

Transpiration through hydrogels has also been identified to cause corneal desiccation in users of soft contact lenses (SCL), which has led to a small number of studies of the transpiration rate through hydrogel membranes and contact lenses with increasingly sophisticated evaporation cells. Martin (1995) integrated different SCL into an apparatus similar to ours and measured the evaporation rate. The contact lenses were treated as a rigid porous medium and the flow resistance was treated as Darcy permeability; the analysis focused on steady states. Similarly, Hoch, Chauhan & Radke (2003) and Fornasiero et al. (2005a,b) measured the transpiration rate through hydrogel membrane and SLC with the aim to obtain transport coefficients. Their innovative set-up used an impinging airflow; thus, measurements at different air velocities and subsequent extrapolation to infinite flow rates led to data independent of external mass transfer resistance. They used these data to calculate Fickian diffusion coefficients of water within the hydrogel and a Stefan–Maxwell diffusion coefficient using a model which we will discuss below. These experiments were refined further to reduce external mass-transfer resistance by evaporation into a pure water atmosphere without air (Fornasiero et al. 2008) and by the development of a fan-driven evaporation cell (Boushehri et al. 2010). Most notably, this last paper focused on the computation of the Fickian diffusion coefficient and did not consider the Stefan–Maxwell diffusion coefficient. Some of the literature above indicates that lens dehydration may affect fitting and corrective strength of hydrogel SCL, but this is not elaborated further.

None of the studies above nor others we are aware of considered the mechanical meaning of the chemical potential, which is that of a pressure (see § 3), and its consequences for the behaviour of the gel supporting a transpiration flux. This can be illustrated by considering an elementary hydrogel micropump, a piece of hydrogel mounted at the end of an upright tube. The pressure at the surface in contact with water is set by the water pressure, which we assume to be either atmospheric or below to avoid flow driven by an external pressure gradient. Pressure at the evaporation surfaces is necessarily ambient pressure. Evaporation generates a gradient in chemical potential, which acts as a pressure gradient within the hydrogel and may enable flow against the external pressure gradient if the pressure in the water reservoir is below ambient pressure.

Basic mechanical equilibrium at the hydrogel surfaces requires that the internal pressure within the gel is balanced by an external force. Therefore, a clamped hydrogel under transpiration is expected to exert a force on the clamps. If the remaining surfaces are exposed to atmospheric pressure, the stress must be supported by the hydrogel itself. Stiff hydrogels with high polymer content such as those used by Wheeler & Stroock (2008) (with 28 % to 32 % water) may do so, while in soft hydrogels, particularly those with high water content, one expects potentially large changes in size and volume.

However, the literature reviewed above reports no direct observations of shape changes of hydrogels, even though photos shown by Lee et al. (2017) indicate some shrinkage and deformation of their agarose gel cylinder which is not discussed further. This lack of observation is in most cases probably due to the choice of experimental set-ups which restrict the ability of the sample to change size and/or the use of relatively stiff gels. The only exceptions are those who use the Stefan–Maxwell model presented first by Hoch et al. (2003). The model attributes transport to gradients in chemical potential, which are obtained via Flory–Rehner theory and, therefore, depend on the polymer volume fraction. Thus their model contains a change of membrane thickness as a fitting parameter, but this is not analysed further.

To the best of our knowledge, we are the first to demonstrate the connection between shape and transpiration for a polymeric gel experimentally by placing a high-swelling hydrogel bead in contact with a water reservoir at sub-atmospheric pressure without mechanical constraints. Therefore, in contrast to the experiments reviewed above, free swelling and shrinking is possible. Our experiments show that, during transpiration of a hydrogel, shrinkage of its free surface towards its rigid, porous boundary is associated with flow away from the rigid boundary. This is in striking contrast to the flow through a soft porous medium driven by external pressure gradients, in which the free surface of the medium is compressed in the direction of flow towards its constraining rigid, porous boundary (e.g. Hewitt et al. 2016; MacMinn, Dufresne & Wettlaufer 2016). We present a semi-quantitative phenomenological model, which explains how transport in the hydrogel is caused by gradients in osmotic pressure, which, in turn are caused by gradients in polymer volume fraction and, therefore, differential shrinkage of the bead. We discuss briefly how this implies that the direction and rates of steady-state transport in unrestrained hydrogels determine the shape and size of the deformed gel under transpiration. We propose potential applications for this phenomenon such as flow control and evaporation-rate sensing.

2. Experiments

2.1. Apparatus

Our experimental apparatus is shown in figure 1(a). It consisted of a 9.5 mm (inner diameter) Perspex tube of 10 cm length, connected by a polyvinyl chloride tube to a 50 ml reservoir. The inner diameter at the upper end of the Perspex tube was increased to 12.5 mm to accept a bead holder machined from polyoxymethylene (trade name Delrin), which is shown black in the figure. It consisted of a 3.86 mm deep approximately half-spherical indentation with a 2 mm diameter hole at its lowest point. During the experiment, the hole connected the hydrogel bead via a continuous water column to the reservoir. Therefore, the distance between the hydrogel bead and the reservoir determines the sub-atmospheric pressure $P=P_a - \rho g H$ under the bead, where $P_a$ is atmospheric pressure, $\rho$ is the density of water, $g$ is the acceleration due to gravity and $H$ is the hydraulic pressure head. The remainder of the bead surface was exposed to the surrounding atmosphere, allowing evaporation.

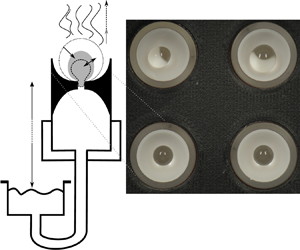
Figure 1. Schematic of the apparatus used for the experiment. (a) Detailed view of an individual bead holder with reservoir assembly. We approximate the bead as a sphere of diameter $d$, while the actual form (for the upright state) is shown with a dotted outline. (b) Evaporation chamber assembly – four (only two visible) of the bead holders shown in (a) were inserted into a cylindrical evaporation chamber. Note the humidity sensors at inflow and outflow. Conditioned air is delivered by the bubbler assembly shown in (c). The photograph (d) shows the hydrogel beads as seen by the camera. The deformation associated with the experiment makes larger beads unstable, which causes them to fall over (on-side state). Larger pressure heads cause smaller beads to remain in the upright state.

We controlled the atmospheric conditions around the beads by inserting four of these tubes into an evaporation chamber of approximately 6 cm diameter and 5 cm height as shown in figure 1(b) (only two tubes are visible). The four tubes were arranged in a square with a centre-to-centre distance of approximately 2.5 cm as shown in figure 1(d). The top of the chamber was sealed with a circular glass plate, 50 cm above which was an SLR camera used to monitor the changes in diameter $d$ of the hydrogel beads. A typical image is shown in figure 1(d). The four reservoirs were mounted on vertical rails so that the pressure heads could be changed easily.

The atmospheric conditions in the evaporation chamber were controlled by continuously purging it with air of relative humidity $\mathcal {RH}_i$ and flow rate $\mathcal {Q}$. The air entered through two ports in opposite side walls and left through a single port. The figure shows only two inlets and two outlets. The relative humidity $\mathcal {RH}_o$ of the outflow was measured to determine the evaporation rate, as described below.

Air of defined relative humidity was generated by bubbling air through saturated salt solutions (Greenspan 1977; Wedler 2004) using the apparatus illustrated in figure 1(c). The first flask contained pure water to saturate the air, while the second and third flask contained the salt solutions required to set the desired relative humidity. A full list of salt solutions is provided in the supplementary material available at https://doi.org/10.1017/jfm.2021.608. A second air pump (see figure 1b) was used for the dataset shown in figure 3 to increase the air velocity in the evaporation chamber without changing the relative humidity.

The procedure for calibration of the sensors and correction of other minor differences between the set-ups used in different experimental runs is described in the supplementary material.

2.2. Procedure

In these experiments, it is important that no air bubbles interfere with the flow of water from the reservoir to the bead. For each bead holder, the reservoir was initially placed such that the bead holder held a small pool of water. A saturated ionic hydrogel bead (poly[acrylamide-co-(potassium acrylate)] more details in the supplementary material) was then placed in the pool to cover the hole and the reservoir was lowered to the desired height. There was sufficient contact between the bead and the rim of the hole to prevent air being drawn into the system by the negative pressure head below the bead. Excess water was carefully removed with a tissue, and the remaining water around the bead evaporated after a few hours. The beads then shrank until a steady state was reached. Our standard procedure was initially to flush the chamber with air at $\mathcal {RH}_i \approx 0.43$ and ${\mathcal {Q}}=0.65 - 1.0\ {\rm l}\ {\rm min}^{-1}$, which led to the first steady state after four to five days.

After the first steady state was reached, we explored the response of the beads to variations in $\mathcal {RH}_i$, $\mathcal {Q}$, the air velocity in the humidity chamber and the pressure head $H$. The datasets used in this paper are summarised in table 1. The full datasets are provided with further explanations in the supplementary material.

Table 1. Overview of the datasets included. The size $d_0$ of the saturated bead was determined after the experiment. The time-resolved data of D, E and F are provided in the supplementary material.

2.3. General observations

More than half of the beads did not reach a steady state but dried out within a few days. We attribute this to a compromised seal between the hydrogel and the bead holder, which allowed an air bubble to form beneath the bead, drastically decreasing the availability of water. Even if the beads reached the first steady state, beads often dried out at later stages for no apparent reason. This unresolved problem with the experiments is a consequence of the fact that the hydrogel is not constrained but free to change its size and shape. For some experiments, we attempted to reset these beads by lifting the reservoir so that the air was pushed out from below the bead holder; this is indicated in the appropriate table.

A typical image of beads in steady state is shown in figure 1(d). Although whole beads or parts thereof appear dark, they actually remain transparent. The dark regions are due to the projection of the hole in the bead holder onto the bead surface. Changes in this projection could sometimes be used to determine whether air had accumulated under the bead. We also observed that larger beads tended to appear moist (shiny), while smaller beads in steady state appeared dry (dull).

Figure 1(d) is representative of the two distinct configurations found for the hydrogel beads in steady state. The top row shows an on-side configuration. The beads are slightly elongated and seem to have fallen over. The bottom row in the figure shows beads in an upright state. These beads are also slightly elongated but sit upright in the bead holder. We observed that larger pressure heads $H$ (i.e. lower pressure under the bead) tended to give rise to the upright state. We were unable to investigate this systematically but discuss it further in the context of § 2.4.3 below.

When experiments were terminated with beads still in steady state (i.e. had not dried out), a small dimple was found where the beads were in contact with water through the hole in the bead holder. The dimple disappeared within approximately ten minutes of removing the bead from the holder and appeared to be more pronounced for beads in the upright state. We therefore believe that the larger pressure heads pulled the bead into the bead holder, stabilising the upright state.

We note that the saturated bead sizes after the experiment reported in table 1 are larger than the average bead sizes reported in the supplementary material, probably because the hydrogel beads for the experiments were chosen with a bias towards the largest swollen beads available. Slower relaxation processes could occur which alter the swelling properties when the beads remain swollen for a long time. An indication of this is that the beads received from the manufacturer are clear, while swollen and subsequently dried beads become turbid and are of yellowish colour.

2.4. Results

2.4.1. Changes of humidity

In the first set of experiments we describe, the volume flux of conditioned air through the evaporation chamber was held constant at ${\mathcal {Q}}=0.65\ {\rm l}\ {\rm min}^{-1}$ and the pressure head was maintained at $H=10.7$ cm while the input relative humidity $\mathcal {RH}_i$ was cycled through the values {0.43, 0.73, 0.43, 0.73, 0.43, 0.53, 0.43, 0.23} and held fixed for periods of 3–5 days, as shown by the solid curves in figure 2(b). We have omitted the initial transient during the first 4 days when the beads shrank from their fully saturated size to an approximately steady size of approximately half their original diameter. In these experiments, all of the beads adopted the on-side state during the initial transient and remained so for the rest of the experiment.

Figure 2. Experimentally observed response of hydrogel beads to changes in relative humidity. (a) Normalised bead size $d/d_0$ as a function of time. Black curves represent individual beads, red dotted curves are fits of (2.1) to determine steady-state behaviour and the time scale of change, which is shown for each transition together with the standard deviation to indicate variation between different beads. (b) Relative humidity of air entering ($\mathcal {RH}_i$) and leaving ($\mathcal {RH}_o$) the evaporation chamber, while the purge flow rate was kept constant at 0.65 l min$^{-1}$. (c) Computed total evaporation rate $Q$ (black) and per unit area of bead surface $q$ (red). Horizontal numbered arrows relate the transition periods to the parameters given for each period in the supplementary material.

Owing to evaporation from the surface of the beads, the relative humidity of the outflow from the chamber $\mathcal {RH}_o$ was higher than $\mathcal {RH}_i$, as shown by the dotted curves in figure 2(b). Note the transient response of the outflow humidity after each change of inflow humidity, which is caused by the transient change in evaporation rate of the beads.

The response of the beads to these changes in relative humidity is shown in figure 2(a), where we show with black curves the diameter $d$ of each of the four beads normalised by its diameter $d_0$ when fully saturated. The beads had not reached a completely steady state even after five days and so we extrapolated the response of each bead by fitting an exponential curve

(2.1)\begin{equation} d(t) = d_\infty+(d_i - d_\infty) \exp[-(t-t_i)/\tau_e], \end{equation}

to determine a final steady size $d_{\infty }$ and a characteristic experimental relaxation time $\tau _e$, where $d_i = d(t_i)$ and $t_i$ are the experimental values when the change in relative humidity was made, as shown by the red dotted curves in figure 2(a). Typical values for $\tau _e$ in this experiment were between 1.1 and 1.6 d. Detailed steady-state data for this and other datasets are included as a table in the supplementary material.

In these experiments, there is a clear correlation between the steady-state size of each bead and the relative humidity of the inflow into the chamber (compare figures 2a and 2b). However, in other experiments, we varied the inflow rate and also introduced an additional wind with a secondary circulation (see figure 1b), both of which affected the evaporation rate and size of the beads. It is therefore better to correlate bead size with the evaporation rate per unit area (evaporation flux)

(2.2)\begin{equation} q = \frac{Q} {\sum_{\mathit{beads}}{\rm \pi} d^2}, \end{equation}

which we compute from the total evaporation flux $Q$ as

(2.3)\begin{equation} Q = \frac{1}{\rho_w}C_s(T)(\mathcal{RH}_o - \mathcal{RH}_i){\mathcal{Q}}, \end{equation}

where $C_s(T)$ is the vapour content (mass of water per volume of air) of saturated air at temperature $T$, which was kept at $22 \pm 1.5\,^\circ \textrm {C}$, and $\rho _w$ is the density of liquid water. We note that $C_s(T)$ varies approximately 10 % for temperature changes of ${\pm } 1.5\,^\circ \textrm {C}$, which has to be taken as the error measure for experimentally determined $q$.

Figure 2(c) shows $Q$ and $q$ from the beads determined by (2.2). A change in relative humidity causes a spike of typically half-hour duration, which is probably related to the transient flushing of the humidity chamber. Indeed, during the calibration of the humidity sensors spikes of similar duration were observed. Following an increase in inflow humidity, $q$ is fairly constant after the initial spike. However, following a decrease in inflow humidity, the evaporation rate experiences a transient with a duration of more than one day. This phenomenon, which is not visible in all our datasets, cannot be explained by transients due to the humidity change alone (see also the data in the supplementary material). Instead, it indicates an asymmetry between shrinking and swelling, which we will revisit in the discussion in § 5.

2.4.2. Changes of air flow

In order to confirm the hypothesis that the evaporation flux $q$ is indeed the critical parameter, we also varied the flow rate $\mathcal {Q}$ of the purging air and the air velocity within the humidity chamber using the circulation pump shown in figure 1(b). The resulting data are shown in figure 3.

Figure 3. Experimentally observed response of hydrogel beads to changes in evaporation conditions. Evaporation conditions were varied by changing the purge air flow rate, the relative humidity (only once, after 18 d) and the air velocity in the evaporation chamber by using a mixing pump (only once, after 15 d). (a) Normalised size $d/d_0$ of three hydrogel breads as a function of time. Black curves describe individual beads, the red dotted curve indicates fits of (2.1) to determine steady-state behaviour and characteristic time scales for each transition with the associated standard deviation. (b) Relative humidity of air entering ($\mathcal {RH}_i$) and leaving ($\mathcal {RH}_o$) the evaporation chamber and purge air flow rate $\mathcal {Q}$ (red curve). (c) Computed total evaporation rate $Q$ (black) and per unit area of bead surface $q$ (red). Horizontal numbered arrows relate the transition periods to the parameters given for each period in the supplementary material.

The inflow humidity is shown by the solid black curve in figure 3(b). It was kept constant at $\mathcal {RH}_i \approx 0.43$ for the first 18 days (the period labelled A) and then changed to $\mathcal {RH}_i \approx 0.73$ for the remainder of the experiment (the period labelled C). The small daily oscillations in relative humidity around these mean values is a consequence of the varying temperature in the laboratory. The secondary pump with a flow rate of approximately 3.5 l min$^{-1}$ was switched on after 16 days, so that the airflow over the beads just resulted from the initial inflow during period A but was greatly enhanced in periods B and C. Within these general environments, the inflow rate $\mathcal {Q}$ was varied as indicated by the solid red curve in figure 3(b). These different environmental forcings resulted in different evaporation rates, leading to different values of the outflow humidity, indicated by the dotted curve in figure 3(b). The evaporation flux calculated using (2.2) is shown in figure 3(c). We note that Martin (1995) reports a similar transient response of hydrogel contact lenses under transpiration when the flow rates were changed.

We noticed that the response of the beads was a little more rapid in response to changes in inflow rates than was typical of the previous experiments in which the inflow humidity was changed. Consequently, we often changed conditions after just 2 or 3 days. The normalised bead sizes are shown in figure 3(a). Notice the significant decrease in bead size at letter B (16 days) when the secondary flow was introduced, which provided some forced convection and an increase in the evaporation rate, as seen in figure 3(c). As before, exponential fits according to (2.1) were made to each section corresponding to constant external forcing (inflow rate, inflow humidity, secondary flow) in order to determine the characteristic relaxation time and extrapolate the steady-state bead size. A few of these fits are shown with red dotted curves in figure 3(a) for illustration.

2.4.3. Changes in pressure head

We also investigated the response to changes in the pressure head supported by the bead. Although these experiments were difficult to reproduce quantitatively, we are confident to report qualitative trends and orders of magnitude.

In figure 4, an experiment with a single bead (the other three beads dried out) is shown with an initial pressure head of 0.2 cm. Figure 4(a) shows how the bead size initially adjusts until the first steady state is reached after approximately 3 days. At this stage, the bead was in the on-side state. On the sixth day the pressure head was increased by 10 cm, causing the bead to shrink and change into the upright state. Note that there appears to be a slight delay between the increase in pressure head and beginning of shrinking. Increasing the head by an additional 10 cm on the eighth day caused the bead to shrink further, but less than after the initial head change. While figure 4(b) indicates that the outlet relative humidity $\mathcal {RH}_o$ is only mildly affected by the size changes of the bead, we find that $q$ increases considerably as the bead shrinks. Despite the data being too noisy to make quantitative deductions, this dataset also indicates that the evaporation rate depends inversely on the bead size as one might expect for evaporation into a stationary atmosphere (Morse 1910; Langmuir 1918; Houghton 1933). We explore the consequences of this coupling in § 5.

Figure 4. Experimentally observed response of a single hydrogel bead to changes in pressure head. After the bead reached steady state ($t>3$ d), the bead was in the on-side state until the head was increased (see label, $t\approx 6$ d), which caused the bead to shrink and change into the upright state. A subsequent increase in head caused the bead to shrink again. (a) Normalised size $d/d_0$ of the hydrogel bead. (b) Relative humidity of air entering ($\mathcal {RH}_i$) and leaving ($\mathcal {RH}_o$) the evaporation chamber and pure air flow rate $\mathcal {Q}$ (red curve). (c) Computed total evaporation rate ${Q}$ (black) and per unit area of bead surface ${q}$ (red). Horizontal numbered arrows relate the transition periods to the parameters given for each period in the supplementary material.

In general, decreasing the pressure head did not cause the beads to swell, regardless of whether the initial steady state was reached for a large pressure head or had been decreased during the experiment. Most experiments which involved changes of the reservoir head dried out after a head change. Our analysis, presented in § 3.6.2, finds that increases in pressure head cause shrinking of the hydrogel to propagate from the bottom of the bead upwards. It is likely that this weakens the seal around the bead when $H$ is increased. This may also allow the bead to be pulled deeper into the holder, stabilising its position so that the upright state becomes stable. In contrast, decreasing $H$ causes the bottom of the bead to expand first, probably jamming the bead in the bead holder.

Owing to these difficulties, we decided to investigate the dependence between bead size and pressure head by repeating the experiments introduced in § 2.4.1 using different fixed pressure heads. The time-dependent data are provided in the supplementary material but the principal results are briefly summarised in the next section and discussed in light of the model in § 4.

2.4.4. Steady states and relaxation times

As a result of the problems in conducting successful experiments which involve changes of the pressure head, we decided to keep the pressure head constant during an experiment and vary the evaporation rate by changing $\mathcal {RH}_i$ or $\mathcal {Q}$. As described above, we used (2.1) to determine the steady-state bead sizes $d_\infty$ and the experimental relaxation times $\tau _e$ as functions of the steady-state evaporation flux $q_\infty$.

In figure 5 (cf. § 4), the datasets obtained under consistent experimental conditions for constant $H$ by changing $\mathcal {RH}_i$ or $\mathcal {Q}$ are shown. Each symbol represents the average over all beads within the experiment; error bars indicate the standard deviation over these. These data confirm the dependence of the bead size on $q_\infty$ within each dataset, where, as already discussed above, larger beads correspond to smaller evaporation rates. For all datasets shown, the sensitivity of the bead size to changes in $q_\infty$ seems to decrease with increasing $q_\infty$. We also find that the typical bead size decreases with increasing $H$. However, the two datasets with smaller $H$ (circles, lozenges) can be barely distinguished from each other.

Figure 5. Overview of the steady-state data from datasets obtained under consistent experimental conditions for constant $H$. Blue circle – dataset B ($H=2.6$ cm), orange diamond – dataset D ($H=5.2$ cm), green triangle – dataset E ($H=10$ cm), red fatplus – dataset F ($H=20$ cm), see table 1 for further details.

The time scales determined by the fit of (2.1) covered a range between 0.27 and 1.2 d for the datasets included in the figure; detailed values are provided in a table in the supplementary material. Within a given dataset, smaller size changes appear to be faster. Further analysis is deferred to § 4 in the context of a simple phenomenological model.

3. One-dimensional phenomenological model

In this section, we present a simple one-dimensional model to explain the fundamental principles of transpiration through the hydrogel bead. Our analysis is based on ideas previously developed in the literature to understand swelling and/or drying of unconstrained hydrogels (e.g. Tanaka & Fillmore 1979; Tanaka et al. 1980; Tomari & Doi 1995; Yoon et al. 2010; Engelsberg & Barros 2013; Bertrand et al. 2016), the influence of various constraints on swelling such as on thin films chemically bonded to rigid substrates (Yoon et al. 2010), and the relaxation of gels under mechanical stress (Hecht & Geissler 1980; Li et al. 2012).

After early work by Fatt & Goldstick (1965) and Tanaka & Fillmore (1979), more recent hydrogel models are poroelastic models. Within a continuum thermodynamics framework, they are constructed by formulating the free energy of swelling, which, analogous to Flory–Rehner (e.g. Flory 1953; Treloar 1975), consists of a contribution due to the deformation of the polymer chains, a contribution from the mixing between water and polymer, and a contribution due to the chemical potential of the mixed water. Linear poroelasticity assumes that the two former contributions can be described by a quadratic strain energy density (Yoon et al. 2010) and are restricted to infinitesimal strains, which leads to expressions analogous to Biot's poroelasticity (Biot 1941). However, as Doi (2009) notes, the volume modulus describes the resistance of the material against changes in water content rather than changes in total volume as a bulk modulus would do. Nonlinear poroelasticity allows for finite deformations by using nonlinear measures of deformation. In the theories proposed by Hong et al. (2008), Doi (2009) and Chester & Anand (2010) the mixing contribution to the free energy is obtained from Flory–Huggins theory, which combines a lattice model for the entropy of mixing with an enthalpic term describing the pairwise interactions. The contribution due to the deformation of the polymer is modelled as a strain energy density function for a hyperelastic material. The most common choice appears to be a Gaussian chain model (Flory 1953), which as Chester & Anand (2010) note is only valid for moderate extensions, and more refined models exist (Boyce & Arruda 2000). These models are closed by assuming mechanical equilibrium and conservation of volume. Fluid flow within the gel is either treated as Darcy flow (Tomari & Doi 1995; Doi 2009; Chester & Anand 2010; Bertrand et al. 2016) or as diffusion (Hong et al. 2008). The linear poroelastic models can be recovered from these models in the limit of small deformations (Doi 2009; Bouklas & Huang 2012).

However, as MacMinn, Dufresne & Wettlaufer (2015) observe, the computational machinery required to solve nonlinear poromechanical problems in more than one dimension often obstructs the key physics driving the process; a comment which applies equally to linearised models in more than one dimension. A rigorous model of our experiment would require at least a two-dimensional model with rotational symmetry and therefore would rely on such a machinery. At this stage, we present a conceptual one-dimensional model, which is illustrated in figure 6, with a simplified one-dimensional constitutive equation. We observe that numerous authors, for example Chester & Anand (2010) and MacMinn et al. (2016) present mathematically one-dimensional nonlinear models for pressure-driven fluid flow through quasi-one-dimensional media. However, the constitutive equations in these models remain fully three-dimensional; a uniform extension is enforced via a stress boundary condition (a restraint) which would make adoption of these models to our experiment misleading. A one-dimensional model necessarily restricts our analysis to isotropic elastic stresses. Therefore, certain hysteresis phenomena (Tomari & Doi 1995) or the squeezing of swollen regions by less-swollen regions (Bertrand et al. 2016) cannot be modelled. The aim of our modelling section is to demonstrate how certain key physics can semi-quantitatively reproduce the observed behaviour without going into the full complexity of a nonlinear theory.

Figure 6. Overview of the one-dimensional transport model and its boundary conditions.

Note that the applied pressure head means that the water below the bead is at lower than atmospheric pressure, so fluid motion upwards through the bead is not driven mechanically by external pressures. Rather, it is driven by gradients in pore water pressure (a formal definition will follow) that are generated by gradients in polymer concentration within the hydrogel bead. Water transport in this system is an osmotic process, which is usually described in terms of chemical potential gradients in the case of solutions. On the other hand, the cross-linking in hydrogels creates a structure that is more familiarly described in fluid-mechanical terms as a porous medium, more specifically as a poroelastic medium, in which flow is driven by pressure gradients. The relationship between these two descriptions can be elucidated by considering a thought experiment described by Peppin, Elliott & Worster (2005) to define what they call ‘pervadic pressure’. The pervadic pressure $p$ is the pressure measured in a chamber filled with pure liquid water connected to the medium (here the hydrogel) via a semi-permeable (water-permeable) membrane. In equilibrium, the chemical potentials of the water in the medium and the chamber are equal and so the chemical potential of the water $\mu _w$ is related to the pervadic pressure, at constant temperature, by

(3.1)\begin{equation} \mu_w - \mu_{wa} = v_w (p-P_a), \end{equation}

where $P$ is the total pressure, the subscript $a$ indicates ambient conditions, $v_w$ denotes the molar volume of liquid water and we have assumed the water to be incompressible. Therefore, the role of the chemical potential in the porous medium is that of the water pressure inside the pores.

3.1. Constitutive equation for transport

Relative motion between the constituents of an aqueous binary system can be described by Darcy's law

(3.2)\begin{equation} \eta \boldsymbol{u} ={-}K\nabla p, \end{equation}

where $\boldsymbol u$ is the volume flux of water relative to the polymer skeleton (see below), $\eta$ is the dynamic viscosity of water and $K(\phi )$ is the permeability of the medium, which is a function of the porosity $(1-\phi )$  where $\phi$ is the volume fraction of polymer in the gel. This is equivalent to equation (17) of Bertrand et al. (2016). Our formulation, which follows Peppin et al. (2005), leads us to associate the pervadic pressure with the pore pressure that drives flow through the medium.

3.2. Constitutive relation for osmotic pressure

The polymer that forms the skeleton of a hydrogel is soluble in water but is prevented from dispersing completely by cross-links between polymer chains. The strands of polymer between cross-links act as (entropic) springs. Our one-dimensional model considers only isotropic stresses (pressures). Thus, at any point $z$, we express the total pressure as

(3.3)\begin{equation} P = {\rm \pi}+ p_e +p, \end{equation}

where ${\rm \pi} (\phi )$ is the osmotic pressure of solution (due to mixing of polymer and water) and $p_e(\phi )$ is a contribution to the total pressure from internal elasticity. This arrangement highlights the fact that the total mechanical pressure $P$ on the gel is given by the sum of the pervadic pore pressure $p$, the elastic pressure $p_e$, sometimes called the effective pressure of a porous medium especially in the context of soil science, and the osmotic pressure of solution ${\rm \pi}$. Note that in a three-dimensional description a constitutive equation for the Cauchy stress tensor is required, where $p_e+{\rm \pi}$ is the isotropic part of Terzhagi's effective stress tensor and $P$ the isotropic part of the Cauchy stress tensor.

The constitutive equation (3.3) is expected to have the general property that ${\rm \pi} (\phi )$ is an increasing function of $\phi$ (the swelling pressure is large when the polymer fraction is high) and that $p_e(\phi )$ is negative with magnitude decreasing with increasing $\phi$ (the stretched polymer strands are in tension). It is common to obtain ${\rm \pi}$ from Flory–Huggins theory and to use an expression obtained from a polymer chain model for $p_e$ (Tomari & Doi 1995; Hong et al. 2008; Doi 2009; Chester & Anand 2010; Engelsberg & Barros 2013; Bertrand et al. 2016).

Given the simplifications we have already made, we avoid the complexity introduced by the aforementioned references and use simplified expressions which represent the key properties mentioned above. We therefore take Flory–Huggins theory in the limit of small polymer volume fraction for ${\rm \pi}$ (also known as van't Hoff's law), which yields ${\rm \pi} = {\mathcal {A}}\phi$. In our model, $\mathcal {A}$ sets the magnitude of the osmotic pressure. For a hydrogel with charged groups, as we use in our experiments, the magnitude of $\mathcal {A}$ is likely to be determined by ionic effects and may be larger than for an uncharged polymer (see e.g. Tanaka et al. 1980, for the osmotic pressure of an ionic gel). To avoid issues in the limit of large swelling (as pointed out by Chester & Anand 2010), we chose a simple expression for $p_e$, which we only require to diverge for large swelling, consistent with our physical expectation. Our choice is $p_e=-k/\phi ^{2/3}$, but the precise detail of this is, eventually, immaterial owing to the steps that follow.

We use as a reference state the equilibrium in which the hydrogel is immersed in water at atmospheric pressure, so that $P=p = P_a$ and the equilibrium polymer volume fraction is $\phi _0$, in which case

(3.4)\begin{equation} \phi = \phi_0 \equiv \left(\frac{k}{\mathcal{A}}\right)^{3/5}. \end{equation}

For small departures from such an equilibrium, we use the leading-order Taylor expansion

(3.5)\begin{equation} P-p \approx A(\phi - \phi_0)={\rm \pi}_0\frac{\phi-\phi_0}{\phi_0}, \end{equation}

where $A = 5{\mathcal {A}}/3$ and ${\rm \pi} _0=A\phi _0$ corresponds to the osmotic modulus (Doi 2009). In general, ${\rm \pi} _0 = \phi ({\partial }/{\partial \phi })({\rm \pi} + p_e)|_{\phi =\phi _0}$ with $\phi _0$ being the root of ${\rm \pi} (\phi ) + p_e(\phi ) = 0$. Note that ${\rm \pi} _0$ describes the combined effect of mixing and stretching of the polymer chains around the fully swollen state.

3.3. Transpiration flow

We consider one-dimensional flow of water through hydrogel of height $a(t)$ placed on a fixed water-permeable membrane at $z=0$, evaporating at the surface $z=a(t)$ with prescribed flux $q(t)$, as shown in figure 6(a). The region $z<0$ is filled with liquid water, which enters the hydrogel via the membrane with derived flux $u_0(t)$. The bulk pressure $P$ is equal to atmospheric pressure $P_a$ at the surface $z=a$ and to the reduced pressure $P_a - \rho g H$ below the membrane at $z=0-$. We present a fluid-mechanical model to determine the concentration of polymer $\phi (z, t)$ and the height of the gel $a(t)$.

3.3.1. Governing equations

The evolution of this system is very slow and so we neglect inertia. For simplicity, we also assume (reasonably) that the polymer and water have equal densities $\rho$ in pure and mixed state. Therefore, mechanical equilibrium gives

(3.6)\begin{equation} \frac{\partial P}{\partial z} ={-}\rho g \ \Rightarrow \ P = P_a + \rho g (a-z). \end{equation}

Note that $P(z=0+)=P_a +\rho g a$, which is greater than the pressure $P_a-\rho g H$ in the liquid beneath the semi-permeable membrane at $z=0-$. The resultant force is balanced by the rigidity of the membrane in our model and the bead holder in our experiment.

We assume ideal mixing so that both mass and volume of polymer and water are conserved locally. The continuity equations for polymer and water are therefore

(3.7a,b)\begin{equation} \frac{\partial \phi_w}{\partial t} + \frac{\partial (\phi_w u_w)}{\partial z} = 0 \quad\mathrm{and}\quad \frac{\partial \phi}{\partial t}+\frac{\partial (\phi u_p)}{\partial z}=0 , \end{equation}

where $\phi _w=1-\phi$ is the volume fraction of water, $u_w$ and $u_p$ are the water and polymer velocities and $t$ denotes time. Summing these equations, noting that $\phi _w + \phi = 1$ is independent of time, and then integrating with respect to $z$, we find that

(3.8)\begin{equation} (1-\phi) u_w + \phi u_p = q_0, \end{equation}

given that at $z=0$ the polymer velocity $u_p$ is zero and the water flux $(1-\phi ) u_w$ is equal to the flux of water entering from below the membrane $q_0(t)$. This expression can be rearranged to show that the polymer velocity is

(3.9)\begin{equation} u_p = q_0 - u, \end{equation}

where the Darcy flux $u \equiv (1-\phi )(u_w - u_p)$ is the volume flux of water relative to the polymer skeleton of the hydrogel. Hence, (3.7a,b) can be written as

(3.10)\begin{equation} \frac{\partial \phi}{\partial t} = \frac{\partial }{\partial z}[\phi (u-q_0)]. \end{equation}

This hyperbolic nonlinear equation is a conservation equation for polymer, which is coupled to Darcy's equation (3.2) for the relative water flux, which can be written as

(3.11)\begin{equation} u = \frac{K(\phi)}{\eta}\left(\frac{{\rm \pi}_0}{\phi_0}\frac{\partial \phi}{\partial z} + \rho g\right), \end{equation}

using (3.5) and (3.6). Equations (3.10) and (3.11) can be combined to give a nonlinear advection–diffusion equation for the polymer concentration

(3.12)\begin{equation} \frac{\partial \phi}{\partial t} + q_0\frac{\partial \phi}{\partial z} = \frac{\partial}{\partial z}\left[\frac{\phi K(\phi)}{\eta}\left(\frac{{\rm \pi}_0}{\phi_0}\frac{\partial \phi}{\partial z} + \rho g\right)\right] \end{equation}

but the physics is perhaps more clearly represented by the separate (3.10) and (3.11).

Note that there is a static equilibrium, which can be achieved by maintaining the atmosphere above the hydrogel bead fully saturated, in which ${\partial \phi /\partial z} = -\rho g /A$ is negative: the polymer concentration decreases slightly upwards to provide a generalised osmotic pressure gradient that balances the force of gravity.

The equations are completed with a specification of the permeability $K(\phi )$. It is common to use expressions similar to the Kozeny–Carman equation, such as $K(\phi ) \propto (1-\phi )^3/\phi ^\beta$, with various values of $\beta$ suggested in different contexts. In Appendix A.1, we argue that the appropriate value for hydrogels, given conservation of polymer, is $\beta = 2/3$. For now we choose a general expression but make use of the fact that $\phi \ll 1$ to approximate

(3.13)\begin{equation} K(\phi) = K_0\left(\frac{\phi_0}{\phi}\right)^{\beta}, \end{equation}

where $K_0$ is the permeability of the swollen gel.

3.3.2. Boundary conditions

By definition, the pervadic pressure $p$ is continuous across the semi-permeable membrane at $z=0$, and it is equal to the bulk pressure $P=P_a - \rho g H$ in the liquid just below the membrane $z=0-$. Therefore, using (3.5) and (3.6) we determine that the polymer concentration satisfies the Dirichlet boundary condition

(3.14)\begin{equation} \phi = \phi_0\left[1 + \frac{\rho g}{{\rm \pi}_0}(H+a)\right] \quad (z=0). \end{equation}

At the upper surface of the bead, the relative flux of water through the gel is equal to the evaporation flux, $u=q$, so the polymer concentration satisfies the Neumann boundary condition

(3.15)\begin{equation} u=\frac{K(\phi)}{\eta} \left(\frac{{\rm \pi}_0}{\phi_0}\frac{\partial \phi}{\partial z} + \rho g\right) = q \quad (z=a (t)). \end{equation}

An additional constraint is needed to determine the unknown boundary position of the hydrogel surface, $z=a(t)$. This is obtained from an expression for the conservation of polymer in the hydrogel bead. Here, we make the approximation of isotropic expansion of the hydrogel to give

(3.16)\begin{equation} a^2\int_0^a\phi\,\mathrm{d}z = \phi_0a_0^3 \end{equation}

to use our one-dimensional model to reflect more closely the three-dimensional swelling and de-swelling observed experimentally. This is an important dimensional consideration in order to obtain appropriate orders of magnitude for the polymer volume fraction, and hence the pore size relevant to the permeability, used in Darcy's equation for the flow.

Equation (3.12) also requires an initial condition. An example would be to start with a bead taken from an equilibrium state immersed in water (in which it is neutrally buoyant by assumption that the densities of water and polymer are equal), in which case $\phi \equiv \phi _0$ and $a = a_0$.

3.4. Non-dimensionalisation

We introduce non-dimensional variables,

(3.17a–d)\begin{equation} \tilde{\phi}=\frac{\phi}{\phi_0},\quad \tilde{u} = \frac{u\tau}{ a_0},\quad \tilde{z}=\frac{z}{a_0}, \quad \tilde{t}=\frac{t}{\tau}, \end{equation}

where the poroelastic time scale is

(3.18)\begin{equation} \tau = \frac{a_0^2\eta}{K_0 {\rm \pi}_0}. \end{equation}

The complete problem in non-dimensional quantities is then

(3.19a)$$\begin{gather} \frac{\partial \tilde{\phi}}{\partial \tilde{t}} + \tilde{q_0} \frac{\partial \tilde{\phi}}{\partial \tilde{z}} = \frac{\partial }{\partial \tilde{z}}(\tilde{\phi}\tilde{u}), \end{gather}$$

(3.19b)$$\begin{gather}\tilde{u} = \tilde{\phi}^{- \beta}\left(\frac{\partial \tilde{\phi}}{\partial \tilde{z}} + \epsilon\right), \end{gather}$$

with boundary conditions

(3.20a)$$\begin{gather} \tilde{\phi} = 1+\tilde{H} + \tilde{\epsilon} \quad (\tilde{z} = 0), \end{gather}$$

(3.20b)$$\begin{gather}\tilde{u} = \tilde{q} \quad (\tilde{z} = \tilde{a}), \end{gather}$$

(3.20c)$$\begin{gather}\tilde{a}^2\int_0^{\tilde{a}(t)}\tilde{\phi} \,\textrm{d}\tilde{z} = 1 \end{gather}$$

and initial condition

(3.21)\begin{equation} \tilde{\phi} = 1 \quad (\tilde{t} = 0). \end{equation}

The dimensionless parameters in this system are the dimensionless evaporative flux

(3.22)\begin{equation} \tilde{q} = \frac{a_0 \eta}{K_0 {\rm \pi}_0}q, \end{equation}

the dimensionless pressure head

(3.23)\begin{equation} \tilde{H} =\frac{\rho g}{{\rm \pi}_0}H, \end{equation}

and the dimensionless head associated with the bead

(3.24)\begin{equation} \tilde{\epsilon} =\frac{\rho g a_0}{{\rm \pi}_0}. \end{equation}

In our experiments, we have seen changes in $\tilde {a}$ of several tenths (order unity) related to evaporation rates $q\approx 10^{-7}\ {\rm ms}^{-1}$ or pressure heads $H\approx 10$ cm. We therefore require that $\tilde {q}$ and $\tilde {H}$ are of order unity but, given that $a_0\approx 1$ cm, we assume $\epsilon \ll 1$ and neglect it in the subsequent analysis.

These observations also allow us to estimate some of the physical parameters of our experimental system. If $\tilde {H}\approx 1$ when $H\approx 10$ cm then (3.23) gives ${\rm \pi} _0 \approx 10^3\ {\rm Pa}$, given $\rho \approx 10^3\ {\rm kg}\ {\rm m}^{-3}$ and $g\approx 10\ {\rm m}\ {\rm s}^{-2}$. If $\tilde {q}\approx 1$ when $q\approx 10^{-7}\ {\rm ms}^{-1}$ then (3.22) gives $K_0\approx 10^{-15}\ {\rm m}^2$, given $a_0\approx 1$ cm and $\eta \approx 10^{-3}\ {\rm Pa}\ {\rm s}$. This permeability corresponds to a pore size of approximately 300 nm. This is based on the estimate that for many natural porous media the length scale $l$ is related to the permeability $K$ by $l^2\approx 10^2 K$. For example, Cubaud & Ho (2004) find $l^2=28.43K$ for square channels. This estimate of permeability and corresponding pore size appears reasonable, as Gombert et al. (2020) report hierarchical structures in polyacrylamide hydrogels with features up to 100 nm size.

Finally, (3.18) gives an estimated time scale of $\tau \approx 10^{5}$ s, which is approximately 1 day, consistent with our experimental observations. These estimates will be refined below using comparisons between our theoretical predictions and experimental results.

3.5. Steady states

Steady-state solutions to (3.19) with $\beta =2/3$ can be found by integration between 0 and $a$, which leads to an expression for the polymer concentration,

(3.25)\begin{equation} \tilde{\phi} = \left(\frac{1}{3}\tilde{q}\tilde{z}+(1+\tilde{H})^{1/3}\right)^{3}, \end{equation}

with $0<\tilde {z}<\tilde {a}$, where $\tilde {a}$ remains undetermined. We see that $\tilde {\phi }$ increases from $1+\tilde {H}$ at the bottom of the bead $\tilde {z}=0$ to $((1+\tilde {H})^{1/3}+(1/3)\tilde {q}\tilde {a})^{3}$ at the top of the bead $\tilde {z}=\tilde {a}$. It is this gradient in concentration of the hydrophilic polymer that causes transpiration through the bead. Increasing $\tilde {H}$ increases the polymer volume fraction everywhere in the domain, which means that the domain has to shrink due to conservation of volume. Similarly, increasing $\tilde {q}$ increases the polymer volume fraction everywhere but at $z=0$, again causing the domain to shrink.

The domain size $a$ is then obtained by integration and application of (3.20c). The results are shown in figure 7 and confirm the observations made above. Note in particular that order-one values of $\tilde {q}$ at $\tilde {H}=0$ and order-one values of $\tilde {H}$ at $\tilde {q}=0$ cause order-one changes to the dimensionless size $\tilde {a}$, as assumed in the scaling analysis above. Note also that in the limit of no evaporation $\tilde {q}\to 0$ the bead has size $\tilde {a} = 1/(1+\tilde {H})$. It is important to realise that this reduction in size is not a purely mechanical response to external loading of the bead but an equilibrium in which the gravitational loading from $H$ and the compressive force from the extended polymer matrix is balanced by the osmotic forces in the gel.

Figure 7. Steady-state domain sizes $\tilde {a}$ plotted as a function of $\tilde {q}$. In-line labels mark the value of $\tilde {H}$ for each line.

3.6. Transient solutions

We use a finite-volume method (described in Appendix A.3) to solve the full, time-dependent problem (3.19) with $\beta = 2/3$ and boundary conditions (3.20) and explore the response of the hydrogel to changes in $\tilde {H}$ and $\tilde {q}$.

3.6.1. Response to changes in evaporation rate

In figure 8 we plot $\tilde {a}$ as a function of time. The hydrogel is saturated at $\tilde {t}=0$ and we set $\tilde {q}=10$, $\tilde {H} = 0$. The bead shrinks from its saturated size ($\tilde {a}=1$) until a steady state with $\tilde {a}\approx 0.5$ is reached. Similar to our experiments, we then change the evaporation rate to $\tilde {q}=4.74$, which is the expected change in evaporation rate for a change in relative humidity from 0.43 to 0.73. This leads to a transition to a new steady state with $\tilde {a}\approx 0.65$. A subsequent step change to $\tilde {q}=10$ causes the hydrogel to return to the previous value at $\tilde {a}\approx 0.5$. This cycle is repeated (approximately $0.8<\tilde {t}<1.3$), followed by a cycle with a smaller step in $\tilde {q}$, $10 \rightarrow 8.25 \rightarrow 10$ for approximately $1.3<\tilde {t}<1.75$. We note that the model results are in qualitative agreement with the experimental data shown in figure 2.

Figure 8. Model solutions resembling the experiment shown in figure 2. At $\tilde {t}=0$, the hydrogel is saturated with water, $\tilde {q}=10$ and $\tilde{H}=0$. The hydrogel reaches steady state for $\tilde {t}>0.25$ and is subject to a series of changes in evaporation rate ($\Delta \tilde {q}=\{-5.26,5.26,-5.26,5.26,-1.76,1.76\}$) similar to those in figure 2, causing the domain to swell and to shrink. Red curves represent fits of (2.1) to extract the dimensionless time scales $\tau _m$ predicted by a model for a transition between representative steady states.

For both growth and shrinking, the response to step changes in $\tilde {q}$ is rapid at first and slows down as the new steady state is approached. Since we only have a numerical solution, we extract characteristic dimensionless relaxation times $\tilde {\tau }_m$ by fitting an exponential (2.1), as was done for the experimental data. This is shown as red dashed lines in figure 8. A near perfect fit is obtained for growth processes, while fits for shrinking are less good, indicating a slightly different functional form. The fits indicate that $\tilde {\tau }_m$ takes values of $\tilde {\tau }_m \approx 0.04$ for the larger and $\tilde {\tau }_m \approx 0.03$ for the smaller swelling shown in the figure. Shrinking is consistently slightly faster, with $\tilde {\tau }_m\approx 0.03$ for the larger and $\tilde {\tau }_m\approx 0.02$ for the smaller changes. The reason for $\tau _m$ to be smaller than one is that $\tau$ is the diffusion time scale through a hydrogel domain of $\tilde {a}=1$, while we analyse changes for $\tilde {a}$ between 0.5 and 0.8. The largest change in $\phi$, and therefore the greatest contraction/expansion of the hydrogel, occurs close the evaporation surface, reducing the effective diffusion length scale and therefore the observed time scale for the problem even further.

In figure 9, we show the distributions of $\tilde {\phi }$ for swelling (a) and shrinking (b) for the first cycle ($0.25<\tilde {t}<0.8$) in figure 8. The inset shows the domain size as a function of time for both processes and crosses indicate the time points when distributions were plotted. Arrows in the main figures indicate the evolution of time.

Figure 9. Change of $\tilde {\phi }$ in response to changes in evaporation rate $\tilde {q}$ during swelling (a) and shrinking (b); corresponding to the first swelling–shrinking cycle in figure 8. Steady states are shown by the outer red lines, the inner black lines represent transients at times shown as crosses in the insets.

Swelling and shrinking is due to the instantaneous change of $\tilde {q}$, which by (3.20) corresponds to an adjustment of the gradient of $\tilde {\phi }$. As can be seen in panel (a) for swelling, a decrease in $\tilde {q}$ reduces the gradient of $\tilde {\phi }$ close to the surface. The remainder of the hydrogel maintains the steeper gradient, which corresponds by (3.19b) to a larger Darcy flux. Thus, the bottom of the hydrogel continues to pump water into the upper part, causing it to swell. The mechanism of shrinking is similar. Here, an increase of $\tilde {q}$ increases the gradient of $\tilde {\phi }$, therefore increasing the Darcy flux beyond its value in the yet unaffected regions of the hydrogel, thereby causing shrinking.

The different time scales of the process are due to the different permeabilities of the regions during which water has to be transported. As can be seen in panel (a), swelling requires transport of water through the dense regions with high $\tilde {\phi }$ at the bottom of the hydrogel, which has a lower permeability. In contrast, during shrinking in response to a change in $\tilde {q}$, the water is removed directly through the evaporation surface, which initially has a lower $\tilde {\phi }$ and therefore higher permeability. Additionally, in our experiment, similar to Bertrand et al. (2016), the drying of the outer shell of the hydrogel may impose a stress on the swollen inner parts of the hydrogel beads accelerating drying which cannot be captured by our model.

3.6.2. Response to changes in $\tilde {H}$

In figure 10 we explore the response of the hydrogel to a step change of $\tilde {H}$ while $\tilde {q}$ is kept constant. In panel (a) we see that, during swelling, a decrease in $\tilde {H}$ leads, due to boundary condition (3.20a), to an immediate increase of $\tilde {\phi }$ at $z=0$, which propagates upwards over time, since less osmotic pressure is required to balance the hydrostatic head.

Figure 10. Changes of $\tilde {\phi }$ in response to changes of $\tilde {H}$ with constant $\tilde {q}$ during (a) swelling ($\tilde {H}:\: 2\rightarrow 0$) and (b) shrinking ($\tilde {H}:\: 0\rightarrow 2$). Steady states are shown by the outer red lines, the inner black lines represent transients at times shown as crosses in the insets.

Similarly, we show in panel (b) the response to an increase in $\tilde {H}$ leads to an immediate adjustment of $\tilde {\phi }$ at $\tilde {z}=0$. This adjustment of $\tilde {\phi }$ leads to a negative gradient in $\tilde {\phi }$ close to $\tilde {z}=0$, which corresponds to water leaving the hydrogel not only through the evaporation surface but also through its bottom surface.

This means, in particular, that a decrease of $\tilde {H}$ triggers swelling of the lower part of the hydrogel first. In our experimental geometry this could have been hindered by the funnel-shaped bead holder and, therefore, be responsible for the irreversibility we observed.

4. Comparison between experiment and model

The model proposed in § 3 is qualitatively in good agreement with our experiments, in particular figures 2 and 8 agree well. In this section we explore whether the model can reproduce the experimental data with physically reasonable parameters. Two dimensional parameters, ${\rm \pi} _0$ and $K_0$, are unknown from the dimensional parameters grouped in the dimensionless pressure head (3.23) and the dimensionless evaporation flux (3.22). These are material properties of the hydrogel and must be determined by fitting. We chose to simultaneously fit the steady-state solution of the model (§ 3.5) to all the steady-state datasets included in figure 5 (see Appendix A.4 for details).

In figure 11(a) the coloured symbols (filled circles, diamonds, triangles and pluses) represent the data shown in figure 5. Dashed lines represent the model predictions for the set of the same colour; the parameters used are marked by a red cross in figure 11(b) and are ${\rm \pi} _0=117\ {\rm Pa}$ and $K_0 = 3.8\times 10^{-16}\ {\rm m}^2$. The surrounding contours mark the parameter range in which the sum of residuals is within 1 % and 5 % (dashes) of the minimum value.

Figure 11. (a) Steady-state data with fits of steady-state solutions for datasets obtained with consistent experimental conditions. (b) Fit parameters ${\rm \pi} _0$ and $K_0$ and contours corresponding to an increase of the sum of residuals by 1 % and 5 % (dashed) from its minimum value. Blue circle – dataset B ($H=2.6$ cm), orange diamond – dataset D ($H=5.2$ cm), green triangle – dataset E ($H=10$ cm), red fatplus – dataset F ($H=20$ cm), coloured dotted lines represent the steady states predicted by the model for the dataset of the same colour with the parameters given by the red cross in (b).

Given the simplifications inherent of the model, in particular the restriction to one-dimensional transport, we do not expect an accurate fit of the data. Instead, we look merely for an indication of the parameter variation and order-of-magnitude estimation of the dimensionless parameters.

It appears from figure 11(a) that the model is capable of capturing the relative position of the datasets and the general trends of the functional forms correctly. We discuss in § 5 how the aforementioned simplifications may affect the functional forms of the steady-state curves predicted by the model.

The parameter values of the best fit are broadly consistent with the scaling analysis made in § 3, the primary difference is that we initially assumed an order-one change in $\tilde {q}$ to cause an order-one change in $a$; while we find in § 3.5 that due to (3.16) such a change requires $\tilde {q}$ to change by 10. The permeability values correspond, using the approximation introduced before, to a pore size of approximately 200 nm. This is of the same order of magnitude as the size of larger features of a hydrogel structure proposed by Gombert et al. (2020) ($\approx$100 nm). The fit parameters correspond to a poroelastic time scale (3.18) of $\approx$4 d. Thus, with the dimensionless times predicted by the model for typical transitions (see figure 8), $\tilde {\tau }_m\approx 0.02 - 0.04$, the model predicts transition times between 0.08 and 0.16 d. While this is somewhat smaller that the experimentally observed transition times (0.26–1.2 d) for these datasets, the prediction is of the correct order of magnitude.

The presented fit demonstrates that our model can reproduce the general trend found experimentally for steady-state bead sizes with a single set of fitted material parameters. With these parameters, derived from steady-state information, our model can just about predict the order of magnitude of the independently measured transition times between steady states. We take this ability of the model to deduce dynamic information from steady-state information and its general agreement with the steady-state distribution as evidence that it captures the key physics, despite the drastic simplifications made.

5. Discussion

The experimental work presented in this paper was extraordinarily challenging owing to the slow processes involved. This precluded further iterative experimental development and hindered a more detailed investigation of numerous phenomena at this stage. Nevertheless, a consistent picture has emerged from the experiments.

Each dataset obtained by varying the relative humidity is self-consistent, demonstrating the link between bead size and evaporation flux. Steady-state datasets obtained for different parameters follow a consistent, monotonic trend (increasing $H$ or $q$ leads to smaller beads).

Our conceptual model explains flow in the hydrogel as driven by gradients in pervadic pressure, caused by gradients in polymer concentration and therefore gradients in differential swelling. The parameters necessary to fit the model to the experimental data appear to have physically reasonable orders of magnitude. The predictions for the typical time scale obtained from the model are broadly consistent with the values obtained independently from the experiment. This indicates that we capture the key physics of the system despite the simplifications made.

In § 2.4.1 (figure 2) we reported that a step increase of $\mathcal {RH}$ leads to a step decrease of $q$, while a step decrease of $\mathcal {RH}$ does not immediately change $q$ to a new constant value. We attempt to explain these observations by linking the evaporative flux to the relative humidity via a simple mass-transfer model for evaporation into still air (Morse 1910; Langmuir 1918; Houghton 1933) with

(5.1a)$$\begin{gather} \tilde{q} = \frac{\mathrm{G}{\rm R}}{\tilde{a}}(\mathcal{RH}_s-\mathcal{RH}_\infty), \end{gather}$$

(5.1b)$$\begin{gather}\mathcal{RH}_s=\exp(-\mathrm{P}{\rm A} (\tilde{\phi}-1)) \end{gather}$$

and $\mathrm {G}{\rm R}=D_vC_s\tau /(\rho _wa_0^2)$, where $C_s$ is the saturated water content of air, $D_v$ is the water vapour diffusion coefficient in air and the non-dimensional parameter $\mathrm {P} {\rm A}={\rm \pi} _0 v_w/(RT)$ determines the sensitivity of $\mathcal {RH}_s$ to changes in $\tilde {\phi }$. Equation (5.1a) is consistent with experimental observations shown in figure 4 which indicate that the evaporation rate increases with decreasing bead size. Note that the vapour concentration difference driving diffusion is given as ($\mathcal {RH}_s-\mathcal {RH}_\infty )$. For a pure water surface, the equilibrium relative humidity at the surface would be $\mathcal {RH}_s=1$. However, for water bound in a hydrogel it should depend on the pervadic pressure of the water in the hydrogel; the argument leading to the exponential expression in (5.1b) is presented in Appendix A.2.

In figure 12(a) the model result for evaporation into still air with $\mathrm {P}{\rm A}=0$ (no dependence of $\mathcal {RH}_s$ on $\phi (\tilde {a})$) is shown. Since $\tilde {q}\propto \tilde {a}^{-1}$, the evaporation rate varies strongly with the bead size, which slows down the processes relative to an ideal step change (figure 8a) of the evaporation rate. Step changes in relative humidity lead to a step change in evaporation rate followed by a slow, monotonic adjustment towards the final value as shown in the insets. This is similar to the experimental observation in figure 2(c), particularly for an increase in $\mathcal {RH}$.

Figure 12. Plots illustrating the response of our model to changes in background relative humidity $\mathcal {RH}_\infty$ for evaporation into still air with $\mathrm {G} {\rm R}=2.2$. (a) Solutions of the hydrogel model coupled with evaporation model (5.1a) and $\mathcal {RH}_S\equiv 1$ (equivalent to $\mathrm {P}{\rm A} \equiv 0$). Note the adjustment of $\tilde {q}$ after the step change in $\mathcal {RH}_\infty$ which is due to the change in $\tilde {a}$. (b) Similar to (a) but with $\mathrm {P}{\rm A} \equiv 10^{-2}$. The asymmetry in $\tilde {q}$ for increasing $\mathcal {RH}_\infty$ (nearly ideal step) and decreasing $\mathcal {RH}_\infty$ (step followed by slow adjustment) is similar to the experimental data shown in figure 2.

In figure 12(b) we set $\mathrm {P}{\rm A}=0.01$, so that $\mathcal {RH}_s$ depends on the surface polymer volume fraction. We now find an asymmetric response to step changes in relative humidity. For increases in relative humidity, the evaporation rate undergoes a near perfect step change towards the new value with only minor adjustments (see inset). However, a decrease in relative humidity leads to a step change followed by near linear adjustment to a final value. Qualitatively this is very similar to the experimental data shown in figure 2(c).

The functional form of $\tilde {q}$ in figure 12(b, insets) is due to two opposing physical effects. The immediate consequence of a step change is a change in $\tilde {\phi }$ at the bead surface, which, due to the exponential term in (5.1a) changes the driving force $\mathcal {RH}_s-\mathcal {RH}_\infty$. The change in $\phi$ also causes an opposing change in $1/a$. The adjustment in $\mathcal {RH}_s$ is only at the surface and therefore quick compared with the change in $a$, which requires the propagation of change through the hydrogel domain.

This indicates that the transport process in the hydrogel is indeed coupled to the transport process in the gas phase and the choice of a Neumann boundary condition on the hydrogel surface is justified for our case. This is consistent with recent work by Bertrand et al. (2016), who also found that the rate of drying of beads is limited by the evaporation rate.

The solutions shown here were computed with $\mathrm {G} {\rm R}=2.2$, chosen such that $\tilde {a}\approx 0.5$ for $\mathcal {RH}_\infty =0.43$. Using our values obtained from fitting the steady states (§ 4), we find that $\mathrm {G} {\rm R}\approx 10.5$. Since we continuously purge the chamber, a still-air model may underestimate the mass transfer compared with our experiment and an advective diffusive boundary layer model with a weaker size dependence of $\tilde {q}$ (e.g. the Lévêque approximation would lead to $q \propto a^{-1/3}$) may represent the experiment more accurately. Nevertheless, the value of $\mathrm {P}{\rm A}=0.01$ corresponds to ${\rm \pi} _0 \approx 14\times 10^5\ {\rm Pa}$, which is four orders of magnitude larger than the estimates obtained from the steady state experiments.

Our one-dimensional simplification means that we do not consider the effect of the three-dimensional stress distribution within the material. Nonlinear theories in the literature propose that, in the three-dimensional case, the pervadic pressure (chemical potential) does not depend on the polymer volume fraction and thermodynamic pressure alone but on the generally anisotropic stress state (e.g. Hong et al. 2008; Doi 2009; Li et al. 2012; Engelsberg & Barros 2013; Bertrand et al. 2016). It is known that in swelling/drying and volume phase transitions the squeezing effect of hoop stresses (Tomari & Doi 1995; Bertrand et al. 2016) may lead to hysteresis and a different dynamics during swelling and drying. In our experiment, these are likely to be caused by a relatively wet bead centre surrounded by a dry evaporation surface. This may be of particular relevance during transitioning between steady states and therefore explain the inconsistently high value of $\mathrm {P}{\rm A}$ discussed in the previous paragraph. Three-dimensional effects could reduce the shrinking of the outer layers with increasing evaporation rate as its shrinking would create a stress normal to the direction of transport which might balance the pervadic pressures. Furthermore, the one-dimensional model does not consider changes in cross-section which affect the order of magnitude of $u$, and therefore of the gradient in swelling, in the hydrogel. Therefore, the sensitivity of the bead size to small changes of the evaporation rate could be increased compared with a one-dimensional model. Consequently, the aforementioned mechanisms are expected to affect the functional form of the steady-state solutions and could therefore explain the differences between model and experiment.

The absence of any experimentally observed swelling when $H$ was decreased could also be attributed to effects of the three-dimensional deformation of the hydrogel. As already discussed in § 2.3, the beads form a small dimple at their contact point with water. This dimple could be pulled into the bead holder. When $H$ is decreased, swelling commences at the bottom of the bead (see § 3.6.2), which might cause the bead to be trapped within the bead holder.

Therefore, while our model captures most of the experimental observations semi-quantitatively, there is likely additional insight about the dynamics of our particular system to be gained from a three-dimensional analysis (see, among others, Hong et al. 2008; Doi 2009; Bertrand et al. 2016). We plan to investigate these fascinating aspects in a separate study.

We observe that (3.12) is formally identical with those found for an elastic macroscopically porous medium with large deformation (Hewitt et al. 2016; MacMinn et al. 2016). However, the physical origins of the phenomenon are different. In their case compression of the porous medium is resisted by elasticity of the matrix, whereas in a hydrogel deformation is resisted by the combination of osmotic pressure of solution (resists compression) and the elasticity of the polymer (aids compression). Therefore, the apparent permeability of a gel depends on the pressure difference applied, as noted previously by other authors such as Scherer (1989) for similar systems.

This pressure dependence is of potential consequence for the pressure-bomb method employed in tree hydrodynamics, the initial motivation of this work. The pressure-bomb method seeks to measure the transpiration pressure by inserting a twig with leaves into a pressure chamber such that only the cut surface is outside the chamber. The pressure in this chamber is increased until reverse flow is visible on the cut surface extending from the chamber (Scholander et al. 1965; Venturas, Sperry & Hacke 2017). If hydrogel-like materials are present in the mesophyll (leaf tissue) and xylem, they may resist the pressure-driven flow imposed by the pressure chamber, possibly leading to erroneously high mechanical pressure measurements that may not be representative of the transpiration process.

Lastly, we briefly note two potential applications of our findings. Since the shape of the hydrogel in transpiration depends on the evaporation rate rather the external relative humidity, hydrogels under transpiration could act as compact sensors for the evaporation rate. Furthermore, since an increase in evaporation rate decreases the surface available for evaporation, the size changes of the hydrogel could be used as a flow control measure in evaporation pumps to stabilise the flow rate in such systems.

6. Conclusion

We have shown that transpiration through the surface of an unrestrained hydrogel bead causes the gel to change size and shape. Our experiments link this phenomenon to the evaporation flux and the pressure head that the gel has to overcome to maintain flow. In our model, we show that flow is possible since the gradient in pervadic pressure (chemical potential) that drives flow is of opposite sign to the difference in mechanical pressure between bottom and evaporation surface of the gel. In an unrestrained gel this gradient corresponds to gradients in polymer volume fraction and therefore to gradients in local swelling, which cause a macroscopic adjustment in size and shape. As discussed in § 5, our experiments raise many open questions, against which we offered some speculative suggestions. The fluid-mechanical study of flow through hydrogels is ripe for extensive future exploration.