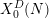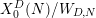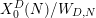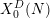1 Introduction
For an indefinite quaternion algebra
![]() $B$
of discriminant
$B$
of discriminant
![]() $D$
over
$D$
over
![]() $\mathbb{Q}$
and a positive integer
$\mathbb{Q}$
and a positive integer
![]() $N$
with
$N$
with
 $(D,N)=1$
, we let
$(D,N)=1$
, we let
 $X_{0}^{D}(N)$
be the Shimura curve associated to an Eichler order
$X_{0}^{D}(N)$
be the Shimura curve associated to an Eichler order
![]() ${\mathcal{O}}$
of level
${\mathcal{O}}$
of level
![]() $N$
in
$N$
in
![]() $B$
. When
$B$
. When
![]() $D=1$
, the Shimura curve
$D=1$
, the Shimura curve
![]() $X_{0}^{D}(N)$
is simply the classical modular curve
$X_{0}^{D}(N)$
is simply the classical modular curve
![]() $X_{0}(N)$
, which is the coarse moduli space of elliptic curves together with a cyclic subgroup of order
$X_{0}(N)$
, which is the coarse moduli space of elliptic curves together with a cyclic subgroup of order
![]() $N$
and has been studied extensively in the literature. When
$N$
and has been studied extensively in the literature. When
![]() $D>1$
, the curve
$D>1$
, the curve
![]() $X_{0}^{D}(N)$
is the coarse moduli space of principally polarized abelian surfaces with multiplication by
$X_{0}^{D}(N)$
is the coarse moduli space of principally polarized abelian surfaces with multiplication by
![]() ${\mathcal{O}}$
. The arithmetic of such a Shimura curve is similar to those of classical modular curves, but the lack of cusps makes the Diophantine geometry and explicit calculation of such a Shimura curve more interesting and challenging than those of classical modular curves. The primary purpose of the present paper is to address the problem of determining equations of Shimura curves.
${\mathcal{O}}$
. The arithmetic of such a Shimura curve is similar to those of classical modular curves, but the lack of cusps makes the Diophantine geometry and explicit calculation of such a Shimura curve more interesting and challenging than those of classical modular curves. The primary purpose of the present paper is to address the problem of determining equations of Shimura curves.
In the classical modular case, which has been studied extensively and is well known for admitting Fourier expansions around the cusps, there are many constructions of modular forms and modular functions, such as Eisenstein series, the Dedekind function, theta series, etc., and there are formulas for their Fourier expansions. Thus, it is often easy to determine equations of modular curves. We refer the reader to Galbraith [Reference GalbraithGal96], Yang [Reference YangYan06], and the references contained therein for more information about equations of modular curves.
On the other hand, when
![]() $D\neq 1$
, the absence of cusps has been an obstacle for explicit approaches to Shimura curves since modular forms or modular functions on Shimura curves do not have Fourier expansions and, as a result, most of the methods for classical modular curves cannot possibly be extended to the case of general Shimura curves. Up to now, only a few equations of Shimura curves are known. Ihara [Reference IharaIha79] was perhaps the first to give defining equations of Shimura curves. For example, he found an equation for the curve
$D\neq 1$
, the absence of cusps has been an obstacle for explicit approaches to Shimura curves since modular forms or modular functions on Shimura curves do not have Fourier expansions and, as a result, most of the methods for classical modular curves cannot possibly be extended to the case of general Shimura curves. Up to now, only a few equations of Shimura curves are known. Ihara [Reference IharaIha79] was perhaps the first to give defining equations of Shimura curves. For example, he found an equation for the curve
![]() $X_{0}^{6}(1)$
of genus zero. Kurihara [Reference KuriharaKur79] extended Ihara’s method and determined equations of
$X_{0}^{6}(1)$
of genus zero. Kurihara [Reference KuriharaKur79] extended Ihara’s method and determined equations of
![]() $X_{0}^{10}(1)$
and
$X_{0}^{10}(1)$
and
![]() $X_{0}^{22}(1)$
of genus zero and
$X_{0}^{22}(1)$
of genus zero and
![]() $X_{0}^{14}(1)$
,
$X_{0}^{14}(1)$
,
![]() $X_{0}^{21}(1)$
, and
$X_{0}^{21}(1)$
, and
![]() $X_{0}^{46}(1)$
of genus one. Jordan [Reference JordanJor81] computed equations of two Shimura curves
$X_{0}^{46}(1)$
of genus one. Jordan [Reference JordanJor81] computed equations of two Shimura curves
![]() $X_{0}^{15}(1)$
and
$X_{0}^{15}(1)$
and
![]() $X_{0}^{33}(1)$
of genus one. Later on, González and Rotger [Reference González and RotgerGR04, Reference González and RotgerGR06] completed the list of equations of Shimura curves
$X_{0}^{33}(1)$
of genus one. Later on, González and Rotger [Reference González and RotgerGR04, Reference González and RotgerGR06] completed the list of equations of Shimura curves
 $X_{0}^{D}(N)$
of genus one and two. For Shimura curves
$X_{0}^{D}(N)$
of genus one and two. For Shimura curves
![]() $X_{0}^{D}(N)$
of higher genus, Elkies [Reference ElkiesElk08] found equations of Shimura curves
$X_{0}^{D}(N)$
of higher genus, Elkies [Reference ElkiesElk08] found equations of Shimura curves
![]() $X_{0}^{57}(1)$
and
$X_{0}^{57}(1)$
and
 $X_{0}^{206}(1)$
using the fact that some families of
$X_{0}^{206}(1)$
using the fact that some families of
![]() $K3$
surfaces are parameterized by Shimura curves. More recently, Molina [Reference MolinaMol12] found equations of
$K3$
surfaces are parameterized by Shimura curves. More recently, Molina [Reference MolinaMol12] found equations of
![]() $X_{0}^{39}(1)$
and
$X_{0}^{39}(1)$
and
![]() $X_{0}^{55}(1)$
and Atkin–Lehner quotients of some Shimura curves. Also, González and Molina [Reference González and MolinaGM16] determine equations of all Shimura curves
$X_{0}^{55}(1)$
and Atkin–Lehner quotients of some Shimura curves. Also, González and Molina [Reference González and MolinaGM16] determine equations of all Shimura curves
![]() $X_{0}^{D}(1)$
of genus three. (Note that it happens that all of these curves are hyperelliptic.) We remark that all of the methods in the above-mentioned works other than those in [Reference ElkiesElk08] are strongly based on the Cerednik–Drinfeld theory of
$X_{0}^{D}(1)$
of genus three. (Note that it happens that all of these curves are hyperelliptic.) We remark that all of the methods in the above-mentioned works other than those in [Reference ElkiesElk08] are strongly based on the Cerednik–Drinfeld theory of
![]() $p$
-adic uniformization of Shimura curves [Reference Boutot and CarayolBC92],
$p$
-adic uniformization of Shimura curves [Reference Boutot and CarayolBC92],
![]() $p|D$
, and arithmetic properties of CM points. In addition, other than [Reference ElkiesElk08], their methods do not allow us to locate general CM points on the curves.
$p|D$
, and arithmetic properties of CM points. In addition, other than [Reference ElkiesElk08], their methods do not allow us to locate general CM points on the curves.
In this paper, we will adopt a very different approach, using the theory of Borcherds forms and explicit formulas for values of Borcherds forms at CM points to obtain equations of Shimura curves. (See § 2 for a quick introduction to Borcherds forms.) The main result of this paper is a complete list of equations of all hyperelliptic Shimura curves
 $X_{0}^{D}(N)$
.
$X_{0}^{D}(N)$
.
Theorem 1. The tables in Appendix A give a complete list of equations of hyperelliptic Shimura curves
![]() $X_{0}^{D}(N)$
,
$X_{0}^{D}(N)$
,
![]() $D>1$
.
$D>1$
.
The idea of realizing modular forms on Shimura curves as Borcherds forms is not new. For example, as a corollary to his formula for average values of Borcherds forms at CM points, Schofer [Reference SchoferSch09] proved a weak analogue of Gross and Zagier’s result [Reference Gross and ZagierGZ85] on the prime factorization of the norm of the difference of two singular moduli on the classical modular curve
![]() $X_{0}(1)$
for the case of Shimura curves. Later on, Errthum [Reference ErrthumErr11] applied Schofers formula to compute singular moduli on
$X_{0}(1)$
for the case of Shimura curves. Later on, Errthum [Reference ErrthumErr11] applied Schofers formula to compute singular moduli on
 $X_{0}^{6}(1)/W_{6,1}$
and
$X_{0}^{6}(1)/W_{6,1}$
and
 $X_{0}^{10}(1)/W_{10,1}$
, verifying Elkies numerical computation [Reference ElkiesElk98], where
$X_{0}^{10}(1)/W_{10,1}$
, verifying Elkies numerical computation [Reference ElkiesElk98], where
![]() $W_{D,N}$
denotes the full Atkin–Lehner group on
$W_{D,N}$
denotes the full Atkin–Lehner group on
![]() $X_{0}^{D}(N)$
. However, applications of Borcherds forms to the theory of Shimura curves were not explored any further in the literature. One possible reason is that in order to successfully use Borcherds forms to perform computation on Shimura curves, one needs a systematic method to construct them in the first place, but such a method has not yet been developed in the literature. Thus, our first task here is to develop a systematic method to construct Borcherds forms. We will see that the problem of constructing Borcherds forms reduces to that of solving certain integer programming problems, which we solve by using the AMPL modeling language (http://www.ampl.com) and the Gurobi solver (http://www.gurobi.com).
$X_{0}^{D}(N)$
. However, applications of Borcherds forms to the theory of Shimura curves were not explored any further in the literature. One possible reason is that in order to successfully use Borcherds forms to perform computation on Shimura curves, one needs a systematic method to construct them in the first place, but such a method has not yet been developed in the literature. Thus, our first task here is to develop a systematic method to construct Borcherds forms. We will see that the problem of constructing Borcherds forms reduces to that of solving certain integer programming problems, which we solve by using the AMPL modeling language (http://www.ampl.com) and the Gurobi solver (http://www.gurobi.com).
Note that our method works for any Shimura curve
 $X_{0}^{D}(N)$
such that
$X_{0}^{D}(N)$
such that
 $X_{0}^{D}(N)/W_{D,N}$
has genus zero, but because there are too many of them, here we consider only the hyperelliptic cases. (There are more than
$X_{0}^{D}(N)/W_{D,N}$
has genus zero, but because there are too many of them, here we consider only the hyperelliptic cases. (There are more than
![]() $110$
non-hyperelliptic Shimura curves
$110$
non-hyperelliptic Shimura curves
![]() $X_{0}^{D}(N)$
whose Atkin–Lehner quotient
$X_{0}^{D}(N)$
whose Atkin–Lehner quotient
 $X_{0}^{D}(N)/W_{D,N}$
has genus zero.) In addition, under a certain technical assumption (Assumption 40), it is also possible to determine equations of
$X_{0}^{D}(N)/W_{D,N}$
has genus zero.) In addition, under a certain technical assumption (Assumption 40), it is also possible to determine equations of
 $X_{0}^{D}(N)/W_{D,N}$
even if it is not of genus zero. In § 4.3, we give two such examples. However, the method becomes less systematic and it is not clear whether it will always work in general.
$X_{0}^{D}(N)/W_{D,N}$
even if it is not of genus zero. In § 4.3, we give two such examples. However, the method becomes less systematic and it is not clear whether it will always work in general.
In principle, our list of equations should also be obtainable using Elkies’ approach [Reference ElkiesElk08], but our approach via Borcherds forms have potential applications to other problems about Shimura curves beyond the scope of the present paper. To illustrate our point, in the arXiv version of the present paper (http://arxiv.org/pdf/1510.06193), we also discuss how our construction of Borcherds forms leads to a method to compute heights of CM points on Shimura curves, again under Assumption 40. Note that both Elkies’ and our approaches have an advantage over other methods in that we can determine the coordinates of CM points on Shimura curves, although Elkies’ approach sometimes involves exhaustive search and it is not clear whether the method is always guaranteed to work. In the arXiv version of the present paper, we also list the coordinates of the CM points used in determining our equations of Shimura curves.
The rest of the paper is organized as follows. In § 2, we give a quick overview of the theory of Borcherds forms and explain the idea of realizing modular forms on Shimura curves in terms of Borcherds forms. The exposition of this section follows [Reference YangYan15]. In § 3, we discuss how to construct Borcherds forms by solving certain integer programming problems. For our purpose, the case of odd
![]() $D$
needs special attention. As a byproduct, we find that for
$D$
needs special attention. As a byproduct, we find that for
![]() $(D,N)$
in Theorem 1 with even
$(D,N)$
in Theorem 1 with even
![]() $D$
, all meromorphic modular forms with divisors supported on CM divisors (Definition 21) can be realized as Borcherds forms. (We believe that this is also true for odd
$D$
, all meromorphic modular forms with divisors supported on CM divisors (Definition 21) can be realized as Borcherds forms. (We believe that this is also true for odd
![]() $D$
, but since it is not the main problem we are concerned with, we will not prove this assertion here.) In § 4, we will give several examples illustrating how to obtain equations of Shimura curves using Borcherds forms we constructed in § 3 and Schofer’s formula for values of Borcherds forms at CM points. In § 4.3, we give additional examples where the genus of
$D$
, but since it is not the main problem we are concerned with, we will not prove this assertion here.) In § 4, we will give several examples illustrating how to obtain equations of Shimura curves using Borcherds forms we constructed in § 3 and Schofer’s formula for values of Borcherds forms at CM points. In § 4.3, we give additional examples where the genus of
 $X_{0}^{D}(N)/W_{D,N}$
is not zero. Specifically, we determine equations of
$X_{0}^{D}(N)/W_{D,N}$
is not zero. Specifically, we determine equations of
 $X_{0}^{142}(1)/W_{142,1}$
and
$X_{0}^{142}(1)/W_{142,1}$
and
 $X_{0}^{302}(1)/W_{302,1}$
, under Assumption 40.
$X_{0}^{302}(1)/W_{302,1}$
, under Assumption 40.
2 Borcherds forms
2.1 Basic theory
We give a quick introduction to Borcherds forms. For details, see [Reference BorcherdsBor98, Reference BorcherdsBor00, Reference BruinierBru02] for the classical setting and [Reference ErrthumErr11, Reference KudlaKud03, Reference SchoferSch09] for the adelic setting.
Let
![]() $L$
be an even lattice with symmetric bilinear form
$L$
be an even lattice with symmetric bilinear form
![]() $\langle \cdot \,,\cdot \rangle$
of signature
$\langle \cdot \,,\cdot \rangle$
of signature
![]() $(n,2)$
and let
$(n,2)$
and let
![]() $L^{\vee }$
be the dual lattice of
$L^{\vee }$
be the dual lattice of
![]() $L$
. We assume that
$L$
. We assume that
![]() $L$
is nondegenerate and denote by
$L$
is nondegenerate and denote by
 $$\begin{eqnarray}\{e_{\unicode[STIX]{x1D702}}:\unicode[STIX]{x1D702}\in L^{\vee }/L\}\end{eqnarray}$$
$$\begin{eqnarray}\{e_{\unicode[STIX]{x1D702}}:\unicode[STIX]{x1D702}\in L^{\vee }/L\}\end{eqnarray}$$
the standard basis for the group algebra
 $\mathbb{C}[L^{\vee }/L]$
. Associated to the lattice
$\mathbb{C}[L^{\vee }/L]$
. Associated to the lattice
![]() $L$
, we have a unitary Weil representation
$L$
, we have a unitary Weil representation
![]() $\unicode[STIX]{x1D70C}_{L}$
of the metaplectic group
$\unicode[STIX]{x1D70C}_{L}$
of the metaplectic group
 $$\begin{eqnarray}\widetilde{\operatorname{SL}}(2,\mathbb{Z})=\left\{\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\sqrt{c\unicode[STIX]{x1D70F}+d}\right):\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \operatorname{SL}(2,\mathbb{Z})\right\}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\operatorname{SL}}(2,\mathbb{Z})=\left\{\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\sqrt{c\unicode[STIX]{x1D70F}+d}\right):\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \operatorname{SL}(2,\mathbb{Z})\right\}\end{eqnarray}$$
on the group algebra
 $\mathbb{C}[L^{\vee }/L]$
defined by
$\mathbb{C}[L^{\vee }/L]$
defined by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{L}(T)e_{\unicode[STIX]{x1D702}} & = & \displaystyle e^{-2\unicode[STIX]{x1D70B}i\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D702}\rangle /2}e_{\unicode[STIX]{x1D702}},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{L}(S)e_{\unicode[STIX]{x1D702}} & = & \displaystyle \frac{e^{2\unicode[STIX]{x1D70B}i(n-2)/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in L^{\vee }/L}e^{2\unicode[STIX]{x1D70B}i\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D6FF}\rangle }e_{\unicode[STIX]{x1D6FF}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{L}(T)e_{\unicode[STIX]{x1D702}} & = & \displaystyle e^{-2\unicode[STIX]{x1D70B}i\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D702}\rangle /2}e_{\unicode[STIX]{x1D702}},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{L}(S)e_{\unicode[STIX]{x1D702}} & = & \displaystyle \frac{e^{2\unicode[STIX]{x1D70B}i(n-2)/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in L^{\vee }/L}e^{2\unicode[STIX]{x1D70B}i\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D6FF}\rangle }e_{\unicode[STIX]{x1D6FF}},\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}S=\left(\left(\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right),\sqrt{\unicode[STIX]{x1D70F}}\right)\quad \text{and}\quad T=\left(\left(\begin{array}{@{}cc@{}}1 & 1\\ 0 & 1\end{array}\right),1\right),\end{eqnarray}$$
$$\begin{eqnarray}S=\left(\left(\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right),\sqrt{\unicode[STIX]{x1D70F}}\right)\quad \text{and}\quad T=\left(\left(\begin{array}{@{}cc@{}}1 & 1\\ 0 & 1\end{array}\right),1\right),\end{eqnarray}$$
which generate
 $\widetilde{\operatorname{SL}}(2,\mathbb{Z})$
.
$\widetilde{\operatorname{SL}}(2,\mathbb{Z})$
.
Definition 1. A holomorphic function
 $F:\mathfrak{H}\rightarrow \mathbb{C}[L^{\vee }/L]$
is called a weakly holomorphic vector-valued modular form of weight
$F:\mathfrak{H}\rightarrow \mathbb{C}[L^{\vee }/L]$
is called a weakly holomorphic vector-valued modular form of weight
![]() $k\in \frac{1}{2}\mathbb{Z}$
and type
$k\in \frac{1}{2}\mathbb{Z}$
and type
![]() $\unicode[STIX]{x1D70C}_{L}$
on
$\unicode[STIX]{x1D70C}_{L}$
on
 $\widetilde{\operatorname{SL}}(2,\mathbb{Z})$
if it satisfies
$\widetilde{\operatorname{SL}}(2,\mathbb{Z})$
if it satisfies
 $$\begin{eqnarray}F\biggl(\frac{a\unicode[STIX]{x1D70F}+b}{c\unicode[STIX]{x1D70F}+d}\biggr)=(c\unicode[STIX]{x1D70F}+d)^{k}\unicode[STIX]{x1D70C}\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\sqrt{c\unicode[STIX]{x1D70F}+d}\right)F(\unicode[STIX]{x1D70F})\end{eqnarray}$$
$$\begin{eqnarray}F\biggl(\frac{a\unicode[STIX]{x1D70F}+b}{c\unicode[STIX]{x1D70F}+d}\biggr)=(c\unicode[STIX]{x1D70F}+d)^{k}\unicode[STIX]{x1D70C}\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\sqrt{c\unicode[STIX]{x1D70F}+d}\right)F(\unicode[STIX]{x1D70F})\end{eqnarray}$$
for all
![]() $\unicode[STIX]{x1D70F}\in \mathfrak{H}$
and all
$\unicode[STIX]{x1D70F}\in \mathfrak{H}$
and all
 $(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \operatorname{SL}(2,\mathbb{Z})$
and
$(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \operatorname{SL}(2,\mathbb{Z})$
and
![]() $F$
is meromorphic at the cusp
$F$
is meromorphic at the cusp
![]() $\infty$
. The last condition means that the Fourier expansion of
$\infty$
. The last condition means that the Fourier expansion of
![]() $F$
is of the form
$F$
is of the form
 $$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}~\mathop{\sum }_{m\in \mathbb{Z}-\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D702}\rangle /2,~m>-m_{0}}c_{\unicode[STIX]{x1D702}}(m)q^{m}e_{\unicode[STIX]{x1D702}},\quad q=e^{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}},\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}~\mathop{\sum }_{m\in \mathbb{Z}-\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D702}\rangle /2,~m>-m_{0}}c_{\unicode[STIX]{x1D702}}(m)q^{m}e_{\unicode[STIX]{x1D702}},\quad q=e^{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}},\end{eqnarray}$$
for some rational number
![]() $m_{0}$
.
$m_{0}$
.
For
![]() $k=\mathbb{Q}$
,
$k=\mathbb{Q}$
,
![]() $\mathbb{R}$
or
$\mathbb{R}$
or
![]() $\mathbb{C}$
, let
$\mathbb{C}$
, let
 $V(k)=L\otimes k$
and extend the definition of
$V(k)=L\otimes k$
and extend the definition of
![]() $\langle \cdot \,,\cdot \rangle$
to
$\langle \cdot \,,\cdot \rangle$
to
![]() $V(k)$
by linearity. Define
$V(k)$
by linearity. Define
![]() $O_{V}(\mathbb{R})$
to be the orthogonal group of the bilinear form
$O_{V}(\mathbb{R})$
to be the orthogonal group of the bilinear form
![]() $\langle \cdot \,,\cdot \rangle$
and its subgroup
$\langle \cdot \,,\cdot \rangle$
and its subgroup
 $$\begin{eqnarray}O_{V}^{+}(\mathbb{R}):=\{\unicode[STIX]{x1D70E}\in O_{V}(\mathbb{R}):\operatorname{spin}\unicode[STIX]{x1D70E}=\operatorname{sgn}\det \unicode[STIX]{x1D70E}\},\end{eqnarray}$$
$$\begin{eqnarray}O_{V}^{+}(\mathbb{R}):=\{\unicode[STIX]{x1D70E}\in O_{V}(\mathbb{R}):\operatorname{spin}\unicode[STIX]{x1D70E}=\operatorname{sgn}\det \unicode[STIX]{x1D70E}\},\end{eqnarray}$$
where if
![]() $\unicode[STIX]{x1D70E}$
is equal to the product of
$\unicode[STIX]{x1D70E}$
is equal to the product of
![]() $n$
reflections with respect to the vectors
$n$
reflections with respect to the vectors
 $v_{1},\ldots ,v_{n}$
, then its spinor norm is defined by
$v_{1},\ldots ,v_{n}$
, then its spinor norm is defined by
 $\operatorname{spin}\unicode[STIX]{x1D70E}=(-1)^{n}\prod _{i=1}^{n}\operatorname{sgn}\langle v_{i},v_{i}\rangle$
. We also define
$\operatorname{spin}\unicode[STIX]{x1D70E}=(-1)^{n}\prod _{i=1}^{n}\operatorname{sgn}\langle v_{i},v_{i}\rangle$
. We also define
 $$\begin{eqnarray}O_{L}^{+}:=\{\unicode[STIX]{x1D70E}\in O_{V}^{+}(\mathbb{R}):\unicode[STIX]{x1D70E}(L)=L\}\end{eqnarray}$$
$$\begin{eqnarray}O_{L}^{+}:=\{\unicode[STIX]{x1D70E}\in O_{V}^{+}(\mathbb{R}):\unicode[STIX]{x1D70E}(L)=L\}\end{eqnarray}$$
to be the orthogonal group of the lattice
![]() $L$
. As the orthogonal group
$L$
. As the orthogonal group
![]() $O_{L}^{+}$
acts on the dual lattice
$O_{L}^{+}$
acts on the dual lattice
![]() $L^{\vee }$
, there is an induced operation on
$L^{\vee }$
, there is an induced operation on
 $\mathbb{C}[L^{\vee }/L]$
given by
$\mathbb{C}[L^{\vee }/L]$
given by
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}c_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D702}}\longmapsto \mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}c_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D702}},\quad \unicode[STIX]{x1D70E}\in O_{L}^{+}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}c_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D702}}\longmapsto \mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}c_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D702}},\quad \unicode[STIX]{x1D70E}\in O_{L}^{+}.\end{eqnarray}$$
Definition 2. Suppose that
 $F=\sum _{\unicode[STIX]{x1D702}\in L^{\vee }/L}F_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D702}}$
is a vector-valued modular form. We define the automorphism group
$F=\sum _{\unicode[STIX]{x1D702}\in L^{\vee }/L}F_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D702}}$
is a vector-valued modular form. We define the automorphism group
![]() $O_{L,F}^{+}$
of
$O_{L,F}^{+}$
of
![]() $F$
by
$F$
by
 $$\begin{eqnarray}O_{L,F}^{+}=\{\unicode[STIX]{x1D70E}\in O_{L}^{+}:F_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D702}}=F_{\unicode[STIX]{x1D702}}~\text{for all }\unicode[STIX]{x1D702}\text{ in }L^{\vee }/L\}.\end{eqnarray}$$
$$\begin{eqnarray}O_{L,F}^{+}=\{\unicode[STIX]{x1D70E}\in O_{L}^{+}:F_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D702}}=F_{\unicode[STIX]{x1D702}}~\text{for all }\unicode[STIX]{x1D702}\text{ in }L^{\vee }/L\}.\end{eqnarray}$$
Consider the subset
 $$\begin{eqnarray}K=\{[z]\in \mathbb{P}(V(\mathbb{C})):\langle z,z\rangle =0,\langle z,\bar{z}\rangle <0\}\end{eqnarray}$$
$$\begin{eqnarray}K=\{[z]\in \mathbb{P}(V(\mathbb{C})):\langle z,z\rangle =0,\langle z,\bar{z}\rangle <0\}\end{eqnarray}$$
of the projective space
 $\mathbb{P}(V(\mathbb{C}))$
. This set
$\mathbb{P}(V(\mathbb{C}))$
. This set
![]() $K$
consists of two connected components and the orthogonal group
$K$
consists of two connected components and the orthogonal group
![]() $O_{V}^{+}(\mathbb{R})$
preserves the components. Pick one of them to be
$O_{V}^{+}(\mathbb{R})$
preserves the components. Pick one of them to be
![]() $K^{+}$
. Then it can be checked that
$K^{+}$
. Then it can be checked that
![]() $O_{V}^{+}(\mathbb{R})$
acts transitively on
$O_{V}^{+}(\mathbb{R})$
acts transitively on
![]() $K^{+}$
.
$K^{+}$
.
Definition 3. Let
 $\widetilde{K}^{+}=\{z\in V(\mathbb{C}):[z]\in K^{+}\}$
. For each subgroup of
$\widetilde{K}^{+}=\{z\in V(\mathbb{C}):[z]\in K^{+}\}$
. For each subgroup of
![]() $\unicode[STIX]{x1D6E4}$
of finite index of
$\unicode[STIX]{x1D6E4}$
of finite index of
![]() $O_{L}^{+}$
, we call a meromorphic function
$O_{L}^{+}$
, we call a meromorphic function
 $\unicode[STIX]{x1D6F9}:\widetilde{K}^{+}\rightarrow \mathbb{P}(\mathbb{C})$
a modular form of weight
$\unicode[STIX]{x1D6F9}:\widetilde{K}^{+}\rightarrow \mathbb{P}(\mathbb{C})$
a modular form of weight
![]() $k$
and character
$k$
and character
![]() $\unicode[STIX]{x1D712}$
on
$\unicode[STIX]{x1D712}$
on
![]() $\unicode[STIX]{x1D6E4}$
if
$\unicode[STIX]{x1D6E4}$
if
![]() $\unicode[STIX]{x1D6F9}$
satisfies:
$\unicode[STIX]{x1D6F9}$
satisfies:
-
(i)
 $\unicode[STIX]{x1D6F9}(cz)=c^{-k}\widetilde{\unicode[STIX]{x1D6F9}}(z)$
for all
$\unicode[STIX]{x1D6F9}(cz)=c^{-k}\widetilde{\unicode[STIX]{x1D6F9}}(z)$
for all
 $c\in \mathbb{C}^{\ast }$
and
$c\in \mathbb{C}^{\ast }$
and
 $z\in \widetilde{K}$
;
$z\in \widetilde{K}$
; -
(ii)
 $\unicode[STIX]{x1D6F9}(hz)=\unicode[STIX]{x1D712}(h)\widetilde{\unicode[STIX]{x1D6F9}}(z)$
for all
$\unicode[STIX]{x1D6F9}(hz)=\unicode[STIX]{x1D712}(h)\widetilde{\unicode[STIX]{x1D6F9}}(z)$
for all
 $h\in \unicode[STIX]{x1D6E4}$
and
$h\in \unicode[STIX]{x1D6E4}$
and
 $z\in \widetilde{K}$
.
$z\in \widetilde{K}$
.
Theorem A [Reference BorcherdsBor98, Theorem 13.3].
Let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
and
$(n,2)$
and
![]() $F(\unicode[STIX]{x1D70F})$
be a weakly holomorphic vector-valued modular forms of weigh
$F(\unicode[STIX]{x1D70F})$
be a weakly holomorphic vector-valued modular forms of weigh
 $1-n/2$
and type
$1-n/2$
and type
![]() $\unicode[STIX]{x1D70C}_{L}$
with Fourier expansion
$\unicode[STIX]{x1D70C}_{L}$
with Fourier expansion
 $F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{n}c_{\unicode[STIX]{x1D702}}(n)q^{n})e_{\unicode[STIX]{x1D702}}$
. Suppose that
$F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{n}c_{\unicode[STIX]{x1D702}}(n)q^{n})e_{\unicode[STIX]{x1D702}}$
. Suppose that
 $c_{\unicode[STIX]{x1D702}}(n)\in \mathbb{Z}$
for any
$c_{\unicode[STIX]{x1D702}}(n)\in \mathbb{Z}$
for any
 $\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
$\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
![]() $n\leqslant 0$
. Then there corresponds a meromorphic function
$n\leqslant 0$
. Then there corresponds a meromorphic function
 $\unicode[STIX]{x1D6F9}_{F}(z),~z\in \widetilde{K}^{+}$
with the following properties.
$\unicode[STIX]{x1D6F9}_{F}(z),~z\in \widetilde{K}^{+}$
with the following properties.
-
(i) Here
 $\unicode[STIX]{x1D6F9}_{F}(z)$
is a meromorphic modular forms of weight
$\unicode[STIX]{x1D6F9}_{F}(z)$
is a meromorphic modular forms of weight
 $c_{0}(0)/2$
for the group
$c_{0}(0)/2$
for the group
 $O_{L,F}^{+}$
with respect to some unitary character
$O_{L,F}^{+}$
with respect to some unitary character
 $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
 $O_{L,F}^{+}$
.
$O_{L,F}^{+}$
. -
(ii) The only zeros or poles of
 $\unicode[STIX]{x1D6F9}_{F}(z)$
lie on the rational quadratic divisor for
$\unicode[STIX]{x1D6F9}_{F}(z)$
lie on the rational quadratic divisor for $$\begin{eqnarray}\unicode[STIX]{x1D706}^{\bot }=\{z\in \widetilde{K}^{+}:\langle z,\unicode[STIX]{x1D706}\rangle =0\}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}^{\bot }=\{z\in \widetilde{K}^{+}:\langle z,\unicode[STIX]{x1D706}\rangle =0\}\end{eqnarray}$$
 $\unicode[STIX]{x1D706}$
in
$\unicode[STIX]{x1D706}$
in
 $L$
,
$L$
,
 $\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D706}\rangle >0$
, and are of order
$\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D706}\rangle >0$
, and are of order  $$\begin{eqnarray}\mathop{\sum }_{0<r\in \mathbb{Q},r\unicode[STIX]{x1D706}\in L^{\vee }}c_{r\unicode[STIX]{x1D706}}(-r^{2}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D706}\rangle /2).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{0<r\in \mathbb{Q},r\unicode[STIX]{x1D706}\in L^{\vee }}c_{r\unicode[STIX]{x1D706}}(-r^{2}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D706}\rangle /2).\end{eqnarray}$$
Definition 4. We call the function
![]() $\unicode[STIX]{x1D6F9}_{F}(z)$
the Borcherds form associated to
$\unicode[STIX]{x1D6F9}_{F}(z)$
the Borcherds form associated to
![]() $F$
.
$F$
.
2.2 Borcherds forms on Shimura curves
We now explain how to realize modular forms on Shimura curves as Borcherds forms. We follow the exposition in [Reference YangYan15]. See also [Reference ErrthumErr11].
Let
![]() $B$
be an indefinite quaternion algebra of discriminant
$B$
be an indefinite quaternion algebra of discriminant
![]() $D$
over
$D$
over
![]() $\mathbb{Q}$
. Consider the vector space
$\mathbb{Q}$
. Consider the vector space
 $$\begin{eqnarray}V=V(\mathbb{Q})=\{x\in B:\operatorname{tr}(x)=0\}\end{eqnarray}$$
$$\begin{eqnarray}V=V(\mathbb{Q})=\{x\in B:\operatorname{tr}(x)=0\}\end{eqnarray}$$
over
![]() $\mathbb{Q}$
with the natural bilinear form
$\mathbb{Q}$
with the natural bilinear form
 $\langle x,y\rangle =\operatorname{tr}(x\overline{y})=-\text{tr}(xy)$
. Then
$\langle x,y\rangle =\operatorname{tr}(x\overline{y})=-\text{tr}(xy)$
. Then
![]() $V$
has signature
$V$
has signature
![]() $(1,2)$
and the associated quadratic form is
$(1,2)$
and the associated quadratic form is
 $\operatorname{nrd}(x)=-x^{2}$
, where
$\operatorname{nrd}(x)=-x^{2}$
, where
![]() $\operatorname{nrd}(x)$
denotes the reduced norm of
$\operatorname{nrd}(x)$
denotes the reduced norm of
![]() $x\in B$
. Given an Eichler order
$x\in B$
. Given an Eichler order
![]() ${\mathcal{O}}$
of level
${\mathcal{O}}$
of level
![]() $N$
in
$N$
in
![]() $B$
, we let
$B$
, we let
![]() $L$
be the lattice
$L$
be the lattice
 $$\begin{eqnarray}L={\mathcal{O}}\cap V=\{x\in {\mathcal{O}}:\operatorname{tr}(x)=0\}.\end{eqnarray}$$
$$\begin{eqnarray}L={\mathcal{O}}\cap V=\{x\in {\mathcal{O}}:\operatorname{tr}(x)=0\}.\end{eqnarray}$$
For an invertible element
![]() $\unicode[STIX]{x1D6FD}$
in
$\unicode[STIX]{x1D6FD}$
in
![]() $B\otimes \mathbb{R}$
, define
$B\otimes \mathbb{R}$
, define
 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:V(\mathbb{R})\rightarrow V(\mathbb{R})$
by
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:V(\mathbb{R})\rightarrow V(\mathbb{R})$
by
 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{-1}$
. Then, we can show that
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{-1}$
. Then, we can show that
 $$\begin{eqnarray}O_{V}^{+}(\mathbb{R})=\{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:\unicode[STIX]{x1D6FD}\in (B\otimes \mathbb{R})^{\ast }/\mathbb{R}^{\ast },\operatorname{nrd}(\unicode[STIX]{x1D6FD})>0\}\times \{\pm 1\}\end{eqnarray}$$
$$\begin{eqnarray}O_{V}^{+}(\mathbb{R})=\{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:\unicode[STIX]{x1D6FD}\in (B\otimes \mathbb{R})^{\ast }/\mathbb{R}^{\ast },\operatorname{nrd}(\unicode[STIX]{x1D6FD})>0\}\times \{\pm 1\}\end{eqnarray}$$
and
 $$\begin{eqnarray}O_{L}^{+}=\{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:\unicode[STIX]{x1D6FD}\in N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }\}\times \{\pm 1\}.\end{eqnarray}$$
$$\begin{eqnarray}O_{L}^{+}=\{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:\unicode[STIX]{x1D6FD}\in N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }\}\times \{\pm 1\}.\end{eqnarray}$$
If we assume that the quaternion algebra is represented by
 $B=(\frac{a,b}{\mathbb{Q}})$
with
$B=(\frac{a,b}{\mathbb{Q}})$
with
![]() $a>0$
and
$a>0$
and
![]() $b>0$
, that is,
$b>0$
, that is,
 $B=\mathbb{Q}+\mathbb{Q}i+\mathbb{Q}j+\mathbb{Q}ij$
with
$B=\mathbb{Q}+\mathbb{Q}i+\mathbb{Q}j+\mathbb{Q}ij$
with
 $i^{2}=a,j^{2}=b$
, and
$i^{2}=a,j^{2}=b$
, and
 $ij=-ji$
, and fix an embedding
$ij=-ji$
, and fix an embedding
 $\unicode[STIX]{x1D704}:B{\hookrightarrow}M(2,\mathbb{R})$
by
$\unicode[STIX]{x1D704}:B{\hookrightarrow}M(2,\mathbb{R})$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D704}:i\longmapsto \left(\begin{array}{@{}cc@{}}0 & \sqrt{a}\\ \sqrt{a} & 0\end{array}\right),\quad j\mapsto \left(\begin{array}{@{}cc@{}}\sqrt{b} & 0\\ 0 & -\sqrt{b}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}:i\longmapsto \left(\begin{array}{@{}cc@{}}0 & \sqrt{a}\\ \sqrt{a} & 0\end{array}\right),\quad j\mapsto \left(\begin{array}{@{}cc@{}}\sqrt{b} & 0\\ 0 & -\sqrt{b}\end{array}\right),\end{eqnarray}$$
then each class in
 $K=\{z\in \mathbb{P}(V(\mathbb{C})):\langle z,z\rangle =0,\langle z,\bar{z}\rangle <0\}$
contains a unique representative of the form
$K=\{z\in \mathbb{P}(V(\mathbb{C})):\langle z,z\rangle =0,\langle z,\bar{z}\rangle <0\}$
contains a unique representative of the form
 $$\begin{eqnarray}z(\unicode[STIX]{x1D70F})=\frac{1-\unicode[STIX]{x1D70F}^{2}}{2\sqrt{a}}i+\frac{\unicode[STIX]{x1D70F}}{\sqrt{b}}j+\frac{1+\unicode[STIX]{x1D70F}^{2}}{2\sqrt{ab}}ij\end{eqnarray}$$
$$\begin{eqnarray}z(\unicode[STIX]{x1D70F})=\frac{1-\unicode[STIX]{x1D70F}^{2}}{2\sqrt{a}}i+\frac{\unicode[STIX]{x1D70F}}{\sqrt{b}}j+\frac{1+\unicode[STIX]{x1D70F}^{2}}{2\sqrt{ab}}ij\end{eqnarray}$$
for some
![]() $\unicode[STIX]{x1D70F}\in \mathfrak{H}^{\pm }$
, the union of upper and lower half-plane. The mapping
$\unicode[STIX]{x1D70F}\in \mathfrak{H}^{\pm }$
, the union of upper and lower half-plane. The mapping
 $\unicode[STIX]{x1D70F}\mapsto z(\unicode[STIX]{x1D70F})~\text{mod}~\mathbb{C}^{\ast }$
is a bijection of between
$\unicode[STIX]{x1D70F}\mapsto z(\unicode[STIX]{x1D70F})~\text{mod}~\mathbb{C}^{\ast }$
is a bijection of between
![]() $\mathfrak{H}^{\pm }$
and
$\mathfrak{H}^{\pm }$
and
![]() $K$
.
$K$
.
Let
![]() $K^{+}$
be the image of
$K^{+}$
be the image of
 $\mathfrak{H}^{+}=\mathfrak{H}$
under the mapping. Then we obtain compatible actions of
$\mathfrak{H}^{+}=\mathfrak{H}$
under the mapping. Then we obtain compatible actions of
 $N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }$
on
$N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }$
on
![]() $K^{\ast }$
and
$K^{\ast }$
and
![]() $\mathfrak{H}$
with the action on
$\mathfrak{H}$
with the action on
![]() $K^{+}$
by conjugation and the action on
$K^{+}$
by conjugation and the action on
![]() $\mathfrak{H}$
by linear fraction transformation. More precisely, this means that for
$\mathfrak{H}$
by linear fraction transformation. More precisely, this means that for
 $\unicode[STIX]{x1D6FC}\in N_{B}^{+}({\mathcal{O}})$
, if we write
$\unicode[STIX]{x1D6FC}\in N_{B}^{+}({\mathcal{O}})$
, if we write
 $\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=(\!\begin{smallmatrix}c_{1} & c_{2}\\ c_{3} & c_{4}\end{smallmatrix}\!)$
, then
$\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=(\!\begin{smallmatrix}c_{1} & c_{2}\\ c_{3} & c_{4}\end{smallmatrix}\!)$
, then
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}z(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6FC}^{-1}=\frac{(c_{3}\unicode[STIX]{x1D70F}+c_{4})^{2}}{\operatorname{nrd}(\unicode[STIX]{x1D6FC})}z\biggl(\frac{c_{1}\unicode[STIX]{x1D70F}+c_{2}}{c_{3}\unicode[STIX]{x1D70F}+c_{4}}\biggr)\equiv z(\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70F})\quad \text{mod}~\mathbb{C}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}z(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6FC}^{-1}=\frac{(c_{3}\unicode[STIX]{x1D70F}+c_{4})^{2}}{\operatorname{nrd}(\unicode[STIX]{x1D6FC})}z\biggl(\frac{c_{1}\unicode[STIX]{x1D70F}+c_{2}}{c_{3}\unicode[STIX]{x1D70F}+c_{4}}\biggr)\equiv z(\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70F})\quad \text{mod}~\mathbb{C}^{\ast }.\end{eqnarray}$$
Lemma 5 [Reference YangYan15, Lemma 6].
Let
 $F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{n}c_{\unicode[STIX]{x1D702}}(n)q^{n})e_{\unicode[STIX]{x1D702}}$
be a weakly holomorphic vector-valued modular form of weight
$F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{n}c_{\unicode[STIX]{x1D702}}(n)q^{n})e_{\unicode[STIX]{x1D702}}$
be a weakly holomorphic vector-valued modular form of weight
![]() $1/2$
and type
$1/2$
and type
![]() $\unicode[STIX]{x1D70C}_{L}$
such that
$\unicode[STIX]{x1D70C}_{L}$
such that
 $O_{L,F}^{+}=O_{L}^{+}$
and
$O_{L,F}^{+}=O_{L}^{+}$
and
 $c_{\unicode[STIX]{x1D702}}(n)\in \mathbb{Z}$
whenever
$c_{\unicode[STIX]{x1D702}}(n)\in \mathbb{Z}$
whenever
 $\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
$\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
![]() $n\leqslant 0$
. Then the function
$n\leqslant 0$
. Then the function
![]() $\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
defined by
$\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
defined by
 $\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6F9}_{F}(z(\unicode[STIX]{x1D70F}))$
is a meromorphic modular forms of weight
$\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6F9}_{F}(z(\unicode[STIX]{x1D70F}))$
is a meromorphic modular forms of weight
![]() $c_{0}(0)$
with certain unitary character
$c_{0}(0)$
with certain unitary character
![]() $\unicode[STIX]{x1D712}$
on the Shimura curve
$\unicode[STIX]{x1D712}$
on the Shimura curve
 $X_{0}^{D}(N)/W_{D,N}$
.
$X_{0}^{D}(N)/W_{D,N}$
.
Definition 6. With assumptions given as in the lemma, the function
![]() $\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
defined by
$\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6F9}_{F}(z(\unicode[STIX]{x1D70F}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6F9}_{F}(z(\unicode[STIX]{x1D70F}))\end{eqnarray}$$
is called the Borcherds forms on the Shimura curve
 $X_{0}^{D}(N)/W_{D,N}$
associated to
$X_{0}^{D}(N)/W_{D,N}$
associated to
![]() $F$
.
$F$
.
The next lemma gives us the criterion when the character of a Borcherds form
![]() $\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
is trivial, under the assumption that the genus of
$\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
is trivial, under the assumption that the genus of
 $N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
is zero.
$N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
is zero.
Lemma 7 [Reference YangYan15, Lemma 8].
Assume that the genus of
 $X=N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
is zero. Let
$X=N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
is zero. Let
 $\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{r}$
be the elliptic points of
$\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{r}$
be the elliptic points of
![]() $X$
and assume that their orders are
$X$
and assume that their orders are
 $b_{1},\ldots ,b_{r}$
, respectively. Assume further that, as
$b_{1},\ldots ,b_{r}$
, respectively. Assume further that, as
![]() $\text{CM}$
points, the discriminant of
$\text{CM}$
points, the discriminant of
 $\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{r}$
are
$\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{r}$
are
 $d_{1},\ldots ,d_{r}$
, respectively. Let
$d_{1},\ldots ,d_{r}$
, respectively. Let
 $F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{m}c_{\unicode[STIX]{x1D702}}(n)q^{m})e_{\unicode[STIX]{x1D702}}$
be a weakly holomorphic vector-valued modular form of weight
$F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{m}c_{\unicode[STIX]{x1D702}}(n)q^{m})e_{\unicode[STIX]{x1D702}}$
be a weakly holomorphic vector-valued modular form of weight
![]() $1/2$
and type
$1/2$
and type
![]() $\unicode[STIX]{x1D70C}_{L}$
such that
$\unicode[STIX]{x1D70C}_{L}$
such that
 $O_{L,F}^{+}=O_{L}^{+}$
and
$O_{L,F}^{+}=O_{L}^{+}$
and
 $c_{\unicode[STIX]{x1D702}}(m)\in \mathbb{Z}$
whenever
$c_{\unicode[STIX]{x1D702}}(m)\in \mathbb{Z}$
whenever
 $\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
$\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
![]() $m\leqslant 0$
. Assume that
$m\leqslant 0$
. Assume that
![]() $c_{0}(0)$
is even. Then the Borcherds form
$c_{0}(0)$
is even. Then the Borcherds form
![]() $\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
is a modular form with trivial character on
$\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})$
is a modular form with trivial character on
![]() $X$
if and only if for
$X$
if and only if for
![]() $j$
such that
$j$
such that
![]() $b_{j}\neq 3$
, the order of
$b_{j}\neq 3$
, the order of
![]() $\unicode[STIX]{x1D6F9}_{F}(z)$
at
$\unicode[STIX]{x1D6F9}_{F}(z)$
at
![]() $z(\unicode[STIX]{x1D70F}_{j})$
has the same parity as
$z(\unicode[STIX]{x1D70F}_{j})$
has the same parity as
![]() $c_{0}(0)/2$
.
$c_{0}(0)/2$
.
We now state Schofer’s formula [Reference SchoferSch09, Corollaries 1.2 and 3.5] in the setting of Shimura curves as follows.
Theorem B [Reference SchoferSch09, Corollaries 1.2 and 3.5].
Let
 $F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{m}c_{\unicode[STIX]{x1D702}}(n)q^{m})e_{\unicode[STIX]{x1D702}}$
be a weakly holomorphic vector-valued modular form of weight
$F(\unicode[STIX]{x1D70F})=\sum _{\unicode[STIX]{x1D702}}(\sum _{m}c_{\unicode[STIX]{x1D702}}(n)q^{m})e_{\unicode[STIX]{x1D702}}$
be a weakly holomorphic vector-valued modular form of weight
![]() $1/2$
and type
$1/2$
and type
![]() $\unicode[STIX]{x1D70C}_{L}$
for
$\unicode[STIX]{x1D70C}_{L}$
for
 $\widetilde{\operatorname{SL}}(2,\mathbb{Z})$
such that
$\widetilde{\operatorname{SL}}(2,\mathbb{Z})$
such that
 $O_{L,F}^{+}=O_{L}^{+}$
,
$O_{L,F}^{+}=O_{L}^{+}$
,
 $c_{0}(0)=0$
and
$c_{0}(0)=0$
and
 $c_{\unicode[STIX]{x1D702}}(m)\in \mathbb{Z}$
whenever
$c_{\unicode[STIX]{x1D702}}(m)\in \mathbb{Z}$
whenever
 $\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
$\unicode[STIX]{x1D702}\in L^{\vee }/L$
and
![]() $n\leqslant 0$
. Let
$n\leqslant 0$
. Let
![]() $d<0$
be a fundamental discriminant such that the set
$d<0$
be a fundamental discriminant such that the set
![]() $\text{CM}(d)$
of CM points of discriminant
$\text{CM}(d)$
of CM points of discriminant
![]() $d$
on
$d$
on
 $N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
is not empty and that the support of
$N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
is not empty and that the support of
 $\operatorname{div}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70F})$
does not intersect
$\operatorname{div}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70F})$
does not intersect
![]() $\text{CM}(d)$
. Then we have
$\text{CM}(d)$
. Then we have
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \text{CM}(d)}\text{log}|\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})|=-\frac{|\text{CM}(d)|}{4}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in L^{\vee }/L}\mathop{\sum }_{m\geqslant 0}c_{\unicode[STIX]{x1D6FE}}(-m)\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FE}}(m),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \text{CM}(d)}\text{log}|\unicode[STIX]{x1D713}_{F}(\unicode[STIX]{x1D70F})|=-\frac{|\text{CM}(d)|}{4}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in L^{\vee }/L}\mathop{\sum }_{m\geqslant 0}c_{\unicode[STIX]{x1D6FE}}(-m)\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FE}}(m),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FE}}(m)$
are certain sums involving derivatives of Fourier coefficients of some incoherent Eisenstein series.
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FE}}(m)$
are certain sums involving derivatives of Fourier coefficients of some incoherent Eisenstein series.
We refer the reader to [Reference ErrthumErr11, Reference YangYan15] for strategies to compute
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FE}}(m)$
explicitly.
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FE}}(m)$
explicitly.
3 Construction of Borcherds forms
3.1 Errthum’s method
In this section, we will review Errthum’s method [Reference ErrthumErr11] for constructing vector-valued modular forms out of scalar-valued modular forms. Here the notation
![]() $D$
,
$D$
,
![]() $N$
,
$N$
,
![]() ${\mathcal{O}}$
,
${\mathcal{O}}$
,
![]() $L$
, etc. has the same meaning as in § 2.2. The level
$L$
, etc. has the same meaning as in § 2.2. The level
![]() $N$
is always assumed to be squarefree.
$N$
is always assumed to be squarefree.
Let us first describe the structure of the lattice
![]() $L$
.
$L$
.
Lemma 8. Assume that
![]() $N$
is squarefree. Let
$N$
is squarefree. Let
![]() $q$
be a prime number such that
$q$
be a prime number such that
 $q\equiv 1~\text{mod}~4$
and
$q\equiv 1~\text{mod}~4$
and
 $$\begin{eqnarray}\biggl(\frac{q}{p}\biggr)=\left\{\begin{array}{@{}ll@{}}-1\quad & \text{if }p|D,\\ 1\quad & \text{if }p|N.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{q}{p}\biggr)=\left\{\begin{array}{@{}ll@{}}-1\quad & \text{if }p|D,\\ 1\quad & \text{if }p|N.\end{array}\right.\end{eqnarray}$$
Then
 $B=(\frac{DN,q}{\mathbb{Q}})$
is a quaternion algebra of discriminant
$B=(\frac{DN,q}{\mathbb{Q}})$
is a quaternion algebra of discriminant
![]() $D$
over
$D$
over
![]() $\mathbb{Q}$
. Moreover, let
$\mathbb{Q}$
. Moreover, let
![]() $a$
be an integer such that
$a$
be an integer such that
 $a^{2}DN\equiv 1~\text{mod}~q$
. Then the
$a^{2}DN\equiv 1~\text{mod}~q$
. Then the
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() ${\mathcal{O}}$
generated by
${\mathcal{O}}$
generated by
 $$\begin{eqnarray}e_{1}=1,\quad e_{2}=\frac{1+j}{2},\quad e_{3}=\frac{i+ij}{2},\quad e_{4}=\frac{aDNj+ij}{q}\end{eqnarray}$$
$$\begin{eqnarray}e_{1}=1,\quad e_{2}=\frac{1+j}{2},\quad e_{3}=\frac{i+ij}{2},\quad e_{4}=\frac{aDNj+ij}{q}\end{eqnarray}$$
is an Eichler order of level
![]() $N$
in
$N$
in
![]() $B$
. Also, let
$B$
. Also, let
![]() $L$
be the set of elements of trace zero in
$L$
be the set of elements of trace zero in
![]() ${\mathcal{O}}$
and let
${\mathcal{O}}$
and let
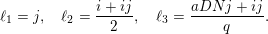 $$\begin{eqnarray}\ell _{1}=j,\quad \ell _{2}=\frac{i+ij}{2},\quad \ell _{3}=\frac{aDNj+ij}{q}.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{1}=j,\quad \ell _{2}=\frac{i+ij}{2},\quad \ell _{3}=\frac{aDNj+ij}{q}.\end{eqnarray}$$
Then
 $$\begin{eqnarray}L=\mathbb{Z}\ell _{1}+\mathbb{Z}\ell _{2}+\mathbb{Z}\ell _{3},\quad L^{\vee }=\mathbb{Z}\frac{\ell _{1}}{2}+\mathbb{Z}\frac{\ell _{2}}{DN}+\mathbb{Z}\frac{\ell _{3}}{DN}.\end{eqnarray}$$
$$\begin{eqnarray}L=\mathbb{Z}\ell _{1}+\mathbb{Z}\ell _{2}+\mathbb{Z}\ell _{3},\quad L^{\vee }=\mathbb{Z}\frac{\ell _{1}}{2}+\mathbb{Z}\frac{\ell _{2}}{DN}+\mathbb{Z}\frac{\ell _{3}}{DN}.\end{eqnarray}$$
Proof. The conditions in (2) imply that
![]() $B$
is ramified at prime divisors of
$B$
is ramified at prime divisors of
![]() $D$
and unramified at prime divisors of
$D$
and unramified at prime divisors of
![]() $N$
. Also, by the quadratic reciprocity law, we have
$N$
. Also, by the quadratic reciprocity law, we have
 $(\frac{DN}{q})=1$
. Thus, the discriminant of
$(\frac{DN}{q})=1$
. Thus, the discriminant of
![]() $B$
is
$B$
is
![]() $D$
.
$D$
.
We check that
 $$\begin{eqnarray}\displaystyle e_{2}^{2} & = & \displaystyle \frac{q-1}{4}e_{1}+e_{2},\nonumber\\ \displaystyle e_{2}e_{3} & = & \displaystyle \frac{aDN(q-1)}{4}e_{1}+\frac{aDN(1-q)}{2}e_{2}+\frac{1-q}{2}e_{3}+\frac{q(q-1)}{4}e_{4},\nonumber\\ \displaystyle e_{2}e_{4} & = & \displaystyle aDNe_{1}-aDNe_{2}-e_{3}+\frac{q+1}{2}e_{4},\nonumber\\ \displaystyle e_{3}^{2} & = & \displaystyle \frac{DN(1-q)}{4}e_{1},\nonumber\\ \displaystyle e_{3}e_{4} & = & \displaystyle -\frac{DN(a^{2}DN(q-1)+q+1)}{2q}e_{1}+\frac{DN(a^{2}DN(q-1)+1)}{q}e_{2}\nonumber\\ \displaystyle & & \displaystyle +\,aDNe_{3}+\frac{aDN(1-q)}{2}e_{4},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{2}^{2} & = & \displaystyle \frac{q-1}{4}e_{1}+e_{2},\nonumber\\ \displaystyle e_{2}e_{3} & = & \displaystyle \frac{aDN(q-1)}{4}e_{1}+\frac{aDN(1-q)}{2}e_{2}+\frac{1-q}{2}e_{3}+\frac{q(q-1)}{4}e_{4},\nonumber\\ \displaystyle e_{2}e_{4} & = & \displaystyle aDNe_{1}-aDNe_{2}-e_{3}+\frac{q+1}{2}e_{4},\nonumber\\ \displaystyle e_{3}^{2} & = & \displaystyle \frac{DN(1-q)}{4}e_{1},\nonumber\\ \displaystyle e_{3}e_{4} & = & \displaystyle -\frac{DN(a^{2}DN(q-1)+q+1)}{2q}e_{1}+\frac{DN(a^{2}DN(q-1)+1)}{q}e_{2}\nonumber\\ \displaystyle & & \displaystyle +\,aDNe_{3}+\frac{aDN(1-q)}{2}e_{4},\nonumber\end{eqnarray}$$
so that
 $\mathbb{Z}e_{1}+\mathbb{Z}e_{2}+\mathbb{Z}e_{3}+\mathbb{Z}e_{4}$
is an order in
$\mathbb{Z}e_{1}+\mathbb{Z}e_{2}+\mathbb{Z}e_{3}+\mathbb{Z}e_{4}$
is an order in
![]() $B$
. Also, the Gram matrix
$B$
. Also, the Gram matrix
 $$\begin{eqnarray}(\operatorname{tr}(e_{i}\overline{e}_{j}))=\left(\begin{array}{@{}cccc@{}}2 & 1 & 0 & 0\\ 1 & (q-1)/2 & 0 & -aDN\\ 0 & 0 & DN(q-1)/2 & DN\\ 0 & -aDN & DN & 2DN(1-a^{2}DN)/q\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{tr}(e_{i}\overline{e}_{j}))=\left(\begin{array}{@{}cccc@{}}2 & 1 & 0 & 0\\ 1 & (q-1)/2 & 0 & -aDN\\ 0 & 0 & DN(q-1)/2 & DN\\ 0 & -aDN & DN & 2DN(1-a^{2}DN)/q\end{array}\right)\end{eqnarray}$$
has determinant
![]() $(DN)^{2}$
. Thus, it is an Eichler order of level
$(DN)^{2}$
. Thus, it is an Eichler order of level
![]() $N$
.
$N$
.
Moreover, it is clear that
![]() $\ell _{1}$
,
$\ell _{1}$
,
![]() $\ell _{2}$
and
$\ell _{2}$
and
![]() $\ell _{3}$
span
$\ell _{3}$
span
![]() $L$
. Also, the Gram matrix of
$L$
. Also, the Gram matrix of
![]() $L$
with respect to this basis is
$L$
with respect to this basis is
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}-2q & 0 & -2aDN\\ 0 & DN(q-1)/2 & DN\\ -2aDN & DN & 2DN(1-a^{2}DN)/q\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}-2q & 0 & -2aDN\\ 0 & DN(q-1)/2 & DN\\ -2aDN & DN & 2DN(1-a^{2}DN)/q\end{array}\right),\end{eqnarray}$$
and its determinant is
![]() $2D^{2}N^{2}$
. From the Gram matrix of
$2D^{2}N^{2}$
. From the Gram matrix of
![]() $L$
, it is easy to check that
$L$
, it is easy to check that
![]() $L^{\vee }$
is spanned by
$L^{\vee }$
is spanned by
![]() $\ell _{1}/2$
,
$\ell _{1}/2$
,
![]() $\ell _{2}/DN$
and
$\ell _{2}/DN$
and
![]() $\ell _{3}/DN$
. This proves the lemma.◻
$\ell _{3}/DN$
. This proves the lemma.◻
Corollary 9. Assume that
![]() $N$
is squarefree. The discriminant of the lattice
$N$
is squarefree. The discriminant of the lattice
![]() $L$
is
$L$
is
 $$\begin{eqnarray}|L^{\vee }/L|=2(DN)^{2}\end{eqnarray}$$
$$\begin{eqnarray}|L^{\vee }/L|=2(DN)^{2}\end{eqnarray}$$
and the level of
![]() $L$
is
$L$
is
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}4DN\quad & \text{ if }DN\text{ is odd},\\ 2DN\quad & \text{if }DN\text{ is even}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}4DN\quad & \text{ if }DN\text{ is odd},\\ 2DN\quad & \text{if }DN\text{ is even}.\end{array}\right.\end{eqnarray}$$
Proof. The result follows directly from the proof of the previous lemma since the determinant of the Gram matrix in (5) is
 $2(DN)^{2}$
and
$2(DN)^{2}$
and
 $L^{\vee }/L\simeq (\mathbb{Z}/2)\times (\mathbb{Z}/DN)^{2}$
.◻
$L^{\vee }/L\simeq (\mathbb{Z}/2)\times (\mathbb{Z}/DN)^{2}$
.◻
We now recall Errthum’s method [Reference ErrthumErr11] for constructing weakly holomorphic vector-valued modular forms. Let
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}$
denote the character associated to the Jacobi theta function
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}$
denote the character associated to the Jacobi theta function
 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})=\sum _{n\in \mathbb{Z}}q^{n^{2}}$
. That is,
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})=\sum _{n\in \mathbb{Z}}q^{n^{2}}$
. That is,
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}$
is defined by
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}$
is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FE})(c\unicode[STIX]{x1D70F}+d)^{1/2}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FE})(c\unicode[STIX]{x1D70F}+d)^{1/2}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})\end{eqnarray}$$
for all
 $\unicode[STIX]{x1D6FE}=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \unicode[STIX]{x1D6E4}_{0}(4)$
and all
$\unicode[STIX]{x1D6FE}=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \unicode[STIX]{x1D6E4}_{0}(4)$
and all
![]() $\unicode[STIX]{x1D70F}\in \mathfrak{H}$
.
$\unicode[STIX]{x1D70F}\in \mathfrak{H}$
.
Lemma 10 [Reference BarnardBar03, Theorem 4.2.9].
Let
![]() $M$
be the level of the lattice
$M$
be the level of the lattice
![]() $L$
. Suppose that
$L$
. Suppose that
![]() $f(\unicode[STIX]{x1D70F})$
is a weakly holomorphic scalar-valued modular form of weight
$f(\unicode[STIX]{x1D70F})$
is a weakly holomorphic scalar-valued modular form of weight
![]() $1/2$
such that
$1/2$
such that
 $$\begin{eqnarray}f(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FE})(c\unicode[STIX]{x1D70F}+d)^{1/2}f(\unicode[STIX]{x1D70F})\end{eqnarray}$$
$$\begin{eqnarray}f(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FE})(c\unicode[STIX]{x1D70F}+d)^{1/2}f(\unicode[STIX]{x1D70F})\end{eqnarray}$$
for all
 $\unicode[STIX]{x1D6FE}=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \unicode[STIX]{x1D6E4}_{0}(M)$
. Then the function
$\unicode[STIX]{x1D6FE}=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \unicode[STIX]{x1D6E4}_{0}(M)$
. Then the function
![]() $F_{f}(\unicode[STIX]{x1D70F})$
defined by
$F_{f}(\unicode[STIX]{x1D70F})$
defined by
 $$\begin{eqnarray}F_{f}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \widetilde{\unicode[STIX]{x1D6E4}}_{0}(M)\backslash \widetilde{\operatorname{SL}}(2,\mathbb{Z})}f|_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70C}_{L}(\unicode[STIX]{x1D6FE}^{-1})e_{0}\end{eqnarray}$$
$$\begin{eqnarray}F_{f}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \widetilde{\unicode[STIX]{x1D6E4}}_{0}(M)\backslash \widetilde{\operatorname{SL}}(2,\mathbb{Z})}f|_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70C}_{L}(\unicode[STIX]{x1D6FE}^{-1})e_{0}\end{eqnarray}$$
is a weakly holomorphic vector-valued modular form of weight
![]() $1/2$
and type
$1/2$
and type
![]() $\unicode[STIX]{x1D70C}_{L}$
.
$\unicode[STIX]{x1D70C}_{L}$
.
Lemma 11 [Reference ErrthumErr11, Theorem 5.8].
Let
![]() $f(\unicode[STIX]{x1D70F})$
and
$f(\unicode[STIX]{x1D70F})$
and
![]() $F_{f}(\unicode[STIX]{x1D70F})$
be given as in the previous lemma. Then for
$F_{f}(\unicode[STIX]{x1D70F})$
be given as in the previous lemma. Then for
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
 $\unicode[STIX]{x1D702}^{\prime }\in L^{\vee }/L$
with
$\unicode[STIX]{x1D702}^{\prime }\in L^{\vee }/L$
with
 $\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D702}\rangle =\langle \unicode[STIX]{x1D702}^{\prime },\unicode[STIX]{x1D702}^{\prime }\rangle$
, the
$\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D702}\rangle =\langle \unicode[STIX]{x1D702}^{\prime },\unicode[STIX]{x1D702}^{\prime }\rangle$
, the
![]() $e_{\unicode[STIX]{x1D702}}$
component and
$e_{\unicode[STIX]{x1D702}}$
component and
![]() $e_{\unicode[STIX]{x1D702}^{\prime }}$
component of
$e_{\unicode[STIX]{x1D702}^{\prime }}$
component of
![]() $F_{f}(\unicode[STIX]{x1D70F})$
are equal. Consequently, we have
$F_{f}(\unicode[STIX]{x1D70F})$
are equal. Consequently, we have
 $O_{L,F_{f}}^{+}=O_{L}^{+}$
.
$O_{L,F_{f}}^{+}=O_{L}^{+}$
.
Lemma 12 [Reference BorcherdsBor00, Theorem 6.2].
Let
![]() $M$
be the level of the lattice
$M$
be the level of the lattice
![]() $L$
. Suppose that
$L$
. Suppose that
![]() $r_{d}$
,
$r_{d}$
,
![]() $d|M$
, are integers satisfying the conditions:
$d|M$
, are integers satisfying the conditions:
-
(i)
 $\sum _{d|M}r_{d}=1$
;
$\sum _{d|M}r_{d}=1$
; -
(ii)
 $|L^{\vee }/L|\prod _{d|M}d^{r_{d}}$
is a square in
$|L^{\vee }/L|\prod _{d|M}d^{r_{d}}$
is a square in
 $\mathbb{Q}^{\ast }$
;
$\mathbb{Q}^{\ast }$
; -
(iii)
 $\sum _{d|M}dr_{d}\equiv 0~\text{mod}~24$
; and
$\sum _{d|M}dr_{d}\equiv 0~\text{mod}~24$
; and -
(iv)
 $\sum _{d|M}(M/d)r_{d}\equiv 0~\text{mod}~24$
.
$\sum _{d|M}(M/d)r_{d}\equiv 0~\text{mod}~24$
.
Then
 $\prod _{d|M}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
is a weakly holomorphic scalar-valued modular form satisfying the condition for
$\prod _{d|M}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
is a weakly holomorphic scalar-valued modular form satisfying the condition for
![]() $f(\unicode[STIX]{x1D70F})$
in Lemma 10.
$f(\unicode[STIX]{x1D70F})$
in Lemma 10.
Definition 13. If an eta product satisfies the conditions in Lemma 12, then we say it is admissible.
To have a better control over the divisors of Borcherds forms constructed, we will use certain special admissible eta products.
Definition 14. Let
![]() $M$
be the level of the lattice
$M$
be the level of the lattice
![]() $L$
and let
$L$
and let
![]() $S$
be a subset of the cusps of
$S$
be a subset of the cusps of
![]() $\unicode[STIX]{x1D6E4}_{0}(M)$
. If
$\unicode[STIX]{x1D6E4}_{0}(M)$
. If
![]() $f$
is a weakly holomorphic modular form of weight
$f$
is a weakly holomorphic modular form of weight
![]() $1/2$
on
$1/2$
on
![]() $\unicode[STIX]{x1D6E4}_{0}(M)$
whose only poles are at the cusps in
$\unicode[STIX]{x1D6E4}_{0}(M)$
whose only poles are at the cusps in
![]() $S$
, then we say
$S$
, then we say
![]() $f$
is a
$f$
is a
![]() $S$
-weakly holomorphic scalar-valued modular form of weight
$S$
-weakly holomorphic scalar-valued modular form of weight
![]() $1/2$
on
$1/2$
on
![]() $\unicode[STIX]{x1D6E4}_{0}(M)$
.
$\unicode[STIX]{x1D6E4}_{0}(M)$
.
Later on, we will use
![]() $\{\infty \}$
-weakly holomorphic modular forms to construct Borcherds forms for the case of even
$\{\infty \}$
-weakly holomorphic modular forms to construct Borcherds forms for the case of even
![]() $D$
and
$D$
and
![]() $\{\infty ,0\}$
-weakly holomorphic modular forms for the case of odd
$\{\infty ,0\}$
-weakly holomorphic modular forms for the case of odd
![]() $D$
. Therefore, let us introduce the following definitions.
$D$
. Therefore, let us introduce the following definitions.
Definition 15. Let
![]() $D_{0}$
be the odd part of
$D_{0}$
be the odd part of
![]() $DN$
. We let
$DN$
. We let
 $M^{!}(4D_{0})$
denote the space of all
$M^{!}(4D_{0})$
denote the space of all
![]() $\{\infty \}$
-weakly holomorphic modular forms of weight
$\{\infty \}$
-weakly holomorphic modular forms of weight
![]() $1/2$
on
$1/2$
on
 $\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
. Also, for a nonnegative integer
$\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
. Also, for a nonnegative integer
![]() $n$
, let
$n$
, let
 $M_{n}^{!}(4D_{0})$
be the subspace of
$M_{n}^{!}(4D_{0})$
be the subspace of
 $M^{!}(4D_{0})$
consisting of modular forms with a pole of order at most
$M^{!}(4D_{0})$
consisting of modular forms with a pole of order at most
![]() $n$
at
$n$
at
![]() $\infty$
. If
$\infty$
. If
![]() $j$
is a positive integer such that there does not exist a modular form in
$j$
is a positive integer such that there does not exist a modular form in
 $M^{!}(4D_{0})$
with a pole of order
$M^{!}(4D_{0})$
with a pole of order
![]() $j$
at
$j$
at
![]() $\infty$
, then we say
$\infty$
, then we say
![]() $j$
is a gap of
$j$
is a gap of
 $M^{!}(4D_{0})$
.
$M^{!}(4D_{0})$
.
Similarly, we let
 $M^{!,!}(4D_{0})$
be the space of all
$M^{!,!}(4D_{0})$
be the space of all
![]() $\{\infty ,0\}$
-weakly holomorphic modular forms of weight
$\{\infty ,0\}$
-weakly holomorphic modular forms of weight
![]() $1/2$
on
$1/2$
on
 $\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
. For nonnegative integers
$\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
. For nonnegative integers
![]() $m$
and
$m$
and
![]() $n$
, let
$n$
, let
 $M_{m,n}^{!,!}(4D_{0})$
be the subspace of
$M_{m,n}^{!,!}(4D_{0})$
be the subspace of
 $M^{!,!}(4D_{0})$
consisting of modular forms with a pole of order at most
$M^{!,!}(4D_{0})$
consisting of modular forms with a pole of order at most
![]() $m$
at
$m$
at
![]() $\infty$
and a pole of order at most
$\infty$
and a pole of order at most
![]() $n$
at zero.
$n$
at zero.
Remark 16. Note that the space
 $M_{0}^{!}(4D_{0})$
is simply the space of holomorphic modular forms of weight
$M_{0}^{!}(4D_{0})$
is simply the space of holomorphic modular forms of weight
![]() $1/2$
on
$1/2$
on
 $\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
. Since
$\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
. Since
![]() $D_{0}$
is assumed to be squarefree, by [Reference Serre and StarkSS77, Theorem A], the space
$D_{0}$
is assumed to be squarefree, by [Reference Serre and StarkSS77, Theorem A], the space
 $M_{0}^{!}(4D_{0})$
is one-dimensional and spanned by
$M_{0}^{!}(4D_{0})$
is one-dimensional and spanned by
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})$
.
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})$
.
3.2 Case of even
 $D$
$D$
In this section, we assume that
![]() $D$
is even and
$D$
is even and
![]() $N$
is squarefree. In Proposition 18, we will see how the problem of constructing Borcherds forms becomes the problem of solving certain integer programming problem. Ultimately, in Proposition 23, we will show that for
$N$
is squarefree. In Proposition 18, we will see how the problem of constructing Borcherds forms becomes the problem of solving certain integer programming problem. Ultimately, in Proposition 23, we will show that for
![]() $(D,N)$
in Theorem 1 with
$(D,N)$
in Theorem 1 with
![]() $2|D$
, every meromorphic modular form of even weight on
$2|D$
, every meromorphic modular form of even weight on
 $X_{0}^{D}(N)/W_{D,N}$
with divisor supported on CM divisors (see Definition 21) can be realized as a Borcherds form. Note that Bruinier [Reference BruinierBru14] and Heim and Murase [Reference Heim and MuraseHM15] studied when a modular form on an orthogonal group
$X_{0}^{D}(N)/W_{D,N}$
with divisor supported on CM divisors (see Definition 21) can be realized as a Borcherds form. Note that Bruinier [Reference BruinierBru14] and Heim and Murase [Reference Heim and MuraseHM15] studied when a modular form on an orthogonal group
![]() $O(n,2)$
can be realized as a Borcherds form, but as the integer
$O(n,2)$
can be realized as a Borcherds form, but as the integer
![]() $n$
is assumed to be at least two, their results do not apply to the case of Shimura curves. In fact, it is pointed out in [Reference BruinierBru14, §1] that counterexamples exist in the case
$n$
is assumed to be at least two, their results do not apply to the case of Shimura curves. In fact, it is pointed out in [Reference BruinierBru14, §1] that counterexamples exist in the case
![]() $n=1$
(see also [Reference Bruinier and OnoBO10, §8.3]). It will be a very interesting problem to characterize those modular forms on Shimura curves
$n=1$
(see also [Reference Bruinier and OnoBO10, §8.3]). It will be a very interesting problem to characterize those modular forms on Shimura curves
 $X_{0}^{D}(N)/W_{D,N}$
that can be realized as Borcherds forms.
$X_{0}^{D}(N)/W_{D,N}$
that can be realized as Borcherds forms.
Let
![]() $D_{0}$
be the odd part of
$D_{0}$
be the odd part of
![]() $DN$
. Then according to Corollary 9, the level of the lattice under consideration is
$DN$
. Then according to Corollary 9, the level of the lattice under consideration is
![]() $4D_{0}$
. Let us first determine the dimensions of
$4D_{0}$
. Let us first determine the dimensions of
 $M_{n}^{!}(4D_{0})$
.
$M_{n}^{!}(4D_{0})$
.
Lemma 17. Let
![]() $D_{0}$
be the odd part of
$D_{0}$
be the odd part of
![]() $DN$
and
$DN$
and
![]() $g$
be the genus of the modular curve
$g$
be the genus of the modular curve
 $X_{0}(4D_{0})$
. Then for a nonnegative integer
$X_{0}(4D_{0})$
. Then for a nonnegative integer
![]() $n$
with
$n$
with
 $$\begin{eqnarray}n\geqslant 2g-2-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor ,\end{eqnarray}$$
$$\begin{eqnarray}n\geqslant 2g-2-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor ,\end{eqnarray}$$
we have
 $$\begin{eqnarray}\dim _{\mathbb{C}}M_{n}^{!}(4D_{0})=n+\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor +1-g.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbb{C}}M_{n}^{!}(4D_{0})=n+\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor +1-g.\end{eqnarray}$$
Moreover, the number of gaps of
 $M^{!}(4D_{0})$
is
$M^{!}(4D_{0})$
is
 $g-\sum _{d|D_{0}}\lfloor d/4\rfloor$
.
$g-\sum _{d|D_{0}}\lfloor d/4\rfloor$
.
Proof. Let
 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})=\sum _{n}q^{n^{2}}$
be the Jacobi theta function. For a divisor
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F})=\sum _{n}q^{n^{2}}$
be the Jacobi theta function. For a divisor
![]() $d$
of
$d$
of
![]() $4D_{0}$
, let
$4D_{0}$
, let
![]() $C_{d}$
represent the cusp
$C_{d}$
represent the cusp
![]() $1/d$
. As a modular form on
$1/d$
. As a modular form on
 $\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
, we have
$\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
, we have
 $$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D703}=\mathop{\sum }_{d|D_{0}}\frac{d}{4}(C_{2d}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D703}=\mathop{\sum }_{d|D_{0}}\frac{d}{4}(C_{2d}).\end{eqnarray}$$
A modular form
![]() $f$
is contained in
$f$
is contained in
 $M_{n}^{!}(4D_{0})$
if and only if the modular function
$M_{n}^{!}(4D_{0})$
if and only if the modular function
 $g=f/\unicode[STIX]{x1D703}$
on
$g=f/\unicode[STIX]{x1D703}$
on
 $\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
satisfies
$\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
satisfies
 $$\begin{eqnarray}\operatorname{div}g\geqslant -n(\infty )-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor (C_{2d}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{div}g\geqslant -n(\infty )-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor (C_{2d}).\end{eqnarray}$$
Then by the Riemann–Roch theorem, when
![]() $n$
is a nonnegative integer such that
$n$
is a nonnegative integer such that
 $n\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
, the dimension of the space
$n\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
, the dimension of the space
 $M_{n}^{!}(4D_{0})$
is
$M_{n}^{!}(4D_{0})$
is
 $$\begin{eqnarray}n+\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor +1-g.\end{eqnarray}$$
$$\begin{eqnarray}n+\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor +1-g.\end{eqnarray}$$
Now since
![]() $D_{0}$
is squarefree, by [Reference Serre and StarkSS77, Theorem A], the space
$D_{0}$
is squarefree, by [Reference Serre and StarkSS77, Theorem A], the space
 $M_{0}^{!}(4D_{0})$
is one-dimensional and spanned by
$M_{0}^{!}(4D_{0})$
is one-dimensional and spanned by
![]() $\unicode[STIX]{x1D703}$
, which implies that there is no modular form in
$\unicode[STIX]{x1D703}$
, which implies that there is no modular form in
 $M^{!}(4D_{0})$
having a zero at
$M^{!}(4D_{0})$
having a zero at
![]() $\infty$
. Therefore, from the dimension formula for
$\infty$
. Therefore, from the dimension formula for
 $M_{n}^{!}(4D_{0})$
, we see that the number of gaps is
$M_{n}^{!}(4D_{0})$
, we see that the number of gaps is
 $n+1-\dim M_{n}^{!}(4D_{0})=g-\sum _{d|D_{0}}\lfloor d/4\rfloor$
.◻
$n+1-\dim M_{n}^{!}(4D_{0})=g-\sum _{d|D_{0}}\lfloor d/4\rfloor$
.◻
Proposition 18. For
![]() $(D,N)$
in Theorem 1 with even
$(D,N)$
in Theorem 1 with even
![]() $D$
, the space
$D$
, the space
 $M^{!}(4D_{0})$
is spanned by admissible eta products. Moreover, there exists a positive integer
$M^{!}(4D_{0})$
is spanned by admissible eta products. Moreover, there exists a positive integer
![]() $m$
such that, for each positive integer
$m$
such that, for each positive integer
![]() $j\geqslant m$
, there exists a modular form
$j\geqslant m$
, there exists a modular form
![]() $f_{j}$
in
$f_{j}$
in
 $M^{!}(4D_{0})\cap \mathbb{Z}((q))$
whose order of pole at
$M^{!}(4D_{0})\cap \mathbb{Z}((q))$
whose order of pole at
![]() $\infty$
is
$\infty$
is
![]() $j$
and whose leading coefficient is one.
$j$
and whose leading coefficient is one.
Proof. Let
![]() $g$
be the genus of the modular curve
$g$
be the genus of the modular curve
 $X_{0}(4D_{0})$
and set
$X_{0}(4D_{0})$
and set
 $$\begin{eqnarray}n_{0}=\max \biggl(2g-2-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor ,0\biggr).\end{eqnarray}$$
$$\begin{eqnarray}n_{0}=\max \biggl(2g-2-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor ,0\biggr).\end{eqnarray}$$
According to Lemma 17, if
![]() $n$
is an integer such that
$n$
is an integer such that
![]() $n\geqslant n_{0}$
, then there exists a modular form in
$n\geqslant n_{0}$
, then there exists a modular form in
 $M^{!}(4D_{0})$
with a pole of order
$M^{!}(4D_{0})$
with a pole of order
![]() $n$
at
$n$
at
![]() $\infty$
. Now suppose that we can find an eta product
$\infty$
. Now suppose that we can find an eta product
![]() $t(\unicode[STIX]{x1D70F})$
such that
$t(\unicode[STIX]{x1D70F})$
such that
![]() $t$
is a modular function on
$t$
is a modular function on
 $\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
with a unique pole at
$\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
with a unique pole at
![]() $\infty$
. Let
$\infty$
. Let
![]() $k$
be the order of the pole of
$k$
be the order of the pole of
![]() $t$
at
$t$
at
![]() $\infty$
. Now Lemma 17 implies that for each integer
$\infty$
. Now Lemma 17 implies that for each integer
![]() $j\geqslant n_{0}$
, there is a modular form in
$j\geqslant n_{0}$
, there is a modular form in
 $M^{!}(4D_{0})$
with a pole of order
$M^{!}(4D_{0})$
with a pole of order
![]() $j$
at
$j$
at
![]() $\infty$
. Thus, for all
$\infty$
. Thus, for all
![]() $n\geqslant n_{0}$
, we have
$n\geqslant n_{0}$
, we have
 $$\begin{eqnarray}M_{n+k}^{!}(4D_{0})=M_{n}^{!}(4D_{0})+tM_{n}^{!}(4D_{0}).\end{eqnarray}$$
$$\begin{eqnarray}M_{n+k}^{!}(4D_{0})=M_{n}^{!}(4D_{0})+tM_{n}^{!}(4D_{0}).\end{eqnarray}$$
Therefore, to prove the assertion about
 $M^{!}(4D_{0})$
, it suffices to find such a modular function
$M^{!}(4D_{0})$
, it suffices to find such a modular function
![]() $t$
and show that the space
$t$
and show that the space
 $M_{n_{0}+k}^{!}(4D_{0})$
can be spanned by eta products and that there exists a positive integer
$M_{n_{0}+k}^{!}(4D_{0})$
can be spanned by eta products and that there exists a positive integer
![]() $m\geqslant n_{0}$
such that for each integer
$m\geqslant n_{0}$
such that for each integer
![]() $j$
with
$j$
with
 $m\leqslant j\leqslant m+k-1$
, there exists a modular form in
$m\leqslant j\leqslant m+k-1$
, there exists a modular form in
 $M_{j}^{!}(4D_{0})\cap \mathbb{Z}((q))$
whose order of pole at
$M_{j}^{!}(4D_{0})\cap \mathbb{Z}((q))$
whose order of pole at
![]() $\infty$
is
$\infty$
is
![]() $j$
and whose leading coefficient is one.
$j$
and whose leading coefficient is one.
Consider the case of a maximal order first. Assume that
 $D=2p$
for some odd prime
$D=2p$
for some odd prime
![]() $p$
. By Lemma 12, for an eta product
$p$
. By Lemma 12, for an eta product
 $\prod _{d|4p}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
to be admissible, the integers
$\prod _{d|4p}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
to be admissible, the integers
![]() $r_{d}$
must satisfy
$r_{d}$
must satisfy
 $$\begin{eqnarray}\begin{array}{@{}rcrcrcrcrcrcl@{}}r_{1} & + & r_{2} & + & r_{4} & + & r_{p} & + & r_{2p} & + & r_{4p} & = & 1\\ & & r_{2} & & & & & + & r_{2p} & & & = & 1+2\unicode[STIX]{x1D6FF}_{2}\\ & & & & & & r_{p} & + & r_{2p} & + & r_{4p} & = & 2\unicode[STIX]{x1D6FF}_{p}\\ r_{1} & + & 2r_{2} & + & 4r_{4} & + & pr_{p} & + & 2pr_{2p} & + & 4pr_{4p} & = & 24\unicode[STIX]{x1D716}_{1}\\ 4pr_{1} & + & 2pr_{2} & + & pr_{4} & + & 4r_{p} & + & 2r_{2p} & + & r_{4p} & = & 24\unicode[STIX]{x1D716}_{2}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcrcrcrcrcrcl@{}}r_{1} & + & r_{2} & + & r_{4} & + & r_{p} & + & r_{2p} & + & r_{4p} & = & 1\\ & & r_{2} & & & & & + & r_{2p} & & & = & 1+2\unicode[STIX]{x1D6FF}_{2}\\ & & & & & & r_{p} & + & r_{2p} & + & r_{4p} & = & 2\unicode[STIX]{x1D6FF}_{p}\\ r_{1} & + & 2r_{2} & + & 4r_{4} & + & pr_{p} & + & 2pr_{2p} & + & 4pr_{4p} & = & 24\unicode[STIX]{x1D716}_{1}\\ 4pr_{1} & + & 2pr_{2} & + & pr_{4} & + & 4r_{p} & + & 2r_{2p} & + & r_{4p} & = & 24\unicode[STIX]{x1D716}_{2}\end{array}\end{eqnarray}$$
for some integers
![]() $\unicode[STIX]{x1D6FF}_{2}$
,
$\unicode[STIX]{x1D6FF}_{2}$
,
![]() $\unicode[STIX]{x1D6FF}_{p}$
,
$\unicode[STIX]{x1D6FF}_{p}$
,
![]() $\unicode[STIX]{x1D716}_{1}$
and
$\unicode[STIX]{x1D716}_{1}$
and
![]() $\unicode[STIX]{x1D716}_{2}$
. Moreover, the congruence subgroup
$\unicode[STIX]{x1D716}_{2}$
. Moreover, the congruence subgroup
![]() $\unicode[STIX]{x1D6E4}_{0}(4p)$
has six cusps, represented by
$\unicode[STIX]{x1D6E4}_{0}(4p)$
has six cusps, represented by
![]() $1/c$
with
$1/c$
with
![]() $c|4p$
. The orders of the eta function
$c|4p$
. The orders of the eta function
![]() $\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})$
at these cusps, multiplied by
$\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})$
at these cusps, multiplied by
![]() $24$
, are given by the following.
$24$
, are given by the following.

Thus, in order for an eta product to be in
 $M_{n}^{!}(4p)$
, the exponents
$M_{n}^{!}(4p)$
, the exponents
![]() $r_{d}$
should satisfy
$r_{d}$
should satisfy
 $$\begin{eqnarray}\begin{array}{@{}rcrcrcrcrcrcl@{}}r_{1} & + & 2r_{2} & + & 4r_{4} & + & pr_{p} & + & 2pr_{2p} & + & 4pr_{4p} & {\geqslant} & -24n\\ r_{1} & + & 2r_{2} & + & r_{4} & + & pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ 4r_{1} & + & 2r_{2} & + & r_{4} & + & 4pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & 4pr_{4} & + & r_{p} & + & 2r_{2p} & + & 4r_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & pr_{4} & + & r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & 0\\ 4pr_{1} & + & 2pr_{2} & + & pr_{4} & + & 4r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & 0\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcrcrcrcrcrcl@{}}r_{1} & + & 2r_{2} & + & 4r_{4} & + & pr_{p} & + & 2pr_{2p} & + & 4pr_{4p} & {\geqslant} & -24n\\ r_{1} & + & 2r_{2} & + & r_{4} & + & pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ 4r_{1} & + & 2r_{2} & + & r_{4} & + & 4pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & 4pr_{4} & + & r_{p} & + & 2r_{2p} & + & 4r_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & pr_{4} & + & r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & 0\\ 4pr_{1} & + & 2pr_{2} & + & pr_{4} & + & 4r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & 0\end{array}\end{eqnarray}$$
In literature, problems of solving a set of equalities and inequalities in integers are called integer programming problems. Solving (7) and (8) using the AMPL modeling language (http://www.ampl.com) and the gurobi solver (http://www.gurobi.com), we can produce many admissible eta products.
To find
![]() $t$
, we replace the first two equations in (7) by
$t$
, we replace the first two equations in (7) by
 $r_{1}+r_{2}+r_{4}+r_{p}+r_{2p}+r_{4p}=0$
and
$r_{1}+r_{2}+r_{4}+r_{p}+r_{2p}+r_{4p}=0$
and
 $r_{2}+r_{2p}=2\unicode[STIX]{x1D6FF}_{2}$
and solve the integer programming problem. We find that we can choose
$r_{2}+r_{2p}=2\unicode[STIX]{x1D6FF}_{2}$
and solve the integer programming problem. We find that we can choose
 $$\begin{eqnarray}t(\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(2p\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(4p\unicode[STIX]{x1D70F})^{4}}\end{eqnarray}$$
$$\begin{eqnarray}t(\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(2p\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(4p\unicode[STIX]{x1D70F})^{4}}\end{eqnarray}$$
with
 $k=(p-1)/2$
.
$k=(p-1)/2$
.
In the other cases when
![]() $N>1$
,
$N>1$
,
![]() $N$
is always a prime. The modular curve
$N$
is always a prime. The modular curve
 $X_{0}(4D_{0})$
has
$X_{0}(4D_{0})$
has
![]() $12$
cusps and there are more inequalities and equalities in the integer programming problem. Nevertheless, we can easily find
$12$
cusps and there are more inequalities and equalities in the integer programming problem. Nevertheless, we can easily find
![]() $t$
and many admissible eta products by solving the integer programming problem.
$t$
and many admissible eta products by solving the integer programming problem.
Having found
![]() $t(\unicode[STIX]{x1D70F})$
and many admissible eta products, we check case by case that eta products do span
$t(\unicode[STIX]{x1D70F})$
and many admissible eta products, we check case by case that eta products do span
 $M_{n_{0}+k}^{!}(4p)$
and that there exists positive integer
$M_{n_{0}+k}^{!}(4p)$
and that there exists positive integer
![]() $m\geqslant n_{0}$
such that for each integer
$m\geqslant n_{0}$
such that for each integer
![]() $j$
with
$j$
with
 $m\leqslant j\leqslant m+k-1$
, there exists a modular form
$m\leqslant j\leqslant m+k-1$
, there exists a modular form
 $f_{j}\in M_{n_{0}+k}^{!}(4D_{0})\cap \mathbb{Z}((q))$
whose order of pole at
$f_{j}\in M_{n_{0}+k}^{!}(4D_{0})\cap \mathbb{Z}((q))$
whose order of pole at
![]() $\infty$
is
$\infty$
is
![]() $j$
and whose leading coefficient is one. (Sometimes,
$j$
and whose leading coefficient is one. (Sometimes,
![]() $f_{j}$
will be a linear combination of eta products with rational coefficients. To show that all Fourier coefficients are integers, we use Sturm’s theorem.) Here we omit the details, providing only one example as below.◻
$f_{j}$
will be a linear combination of eta products with rational coefficients. To show that all Fourier coefficients are integers, we use Sturm’s theorem.) Here we omit the details, providing only one example as below.◻
Example 19. Consider the case
![]() $D=26$
and
$D=26$
and
![]() $N=1$
. The modular curve
$N=1$
. The modular curve
![]() $X_{0}(52)$
has genus five. Thus, by Lemma 17, the number of gaps of
$X_{0}(52)$
has genus five. Thus, by Lemma 17, the number of gaps of
![]() $M^{!}(52)$
is
$M^{!}(52)$
is
 $5-\sum _{d|13}\lfloor d/4\rfloor =2$
. The modular function
$5-\sum _{d|13}\lfloor d/4\rfloor =2$
. The modular function
 $$\begin{eqnarray}t(\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(26\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(52\unicode[STIX]{x1D70F})^{4}}\end{eqnarray}$$
$$\begin{eqnarray}t(\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(26\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(52\unicode[STIX]{x1D70F})^{4}}\end{eqnarray}$$
has a unique pole of order six at
![]() $\infty$
. According to the proof of Proposition 18, we need to show that the space
$\infty$
. According to the proof of Proposition 18, we need to show that the space
 $M_{11}^{!}(52)$
can be spanned by eta products. Using the gurobi solver, we find the following solutions
$M_{11}^{!}(52)$
can be spanned by eta products. Using the gurobi solver, we find the following solutions
 $(r_{1},r_{2},r_{4},r_{13},r_{26},r_{52})$
to the integer programming problem in (7) and (8) with
$(r_{1},r_{2},r_{4},r_{13},r_{26},r_{52})$
to the integer programming problem in (7) and (8) with
![]() $n=11$
$n=11$
 $$\begin{eqnarray}\displaystyle & \displaystyle (-3,6,0,-3,11,-10),~(-1,3,1,3,2,-7),~(3,-3,3,-1,8,-9),~(1,1,1,1,4,-7), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (-1,1,1,3,4,-7),~(0,-3,6,-2,8,-8),~(3,-1,1,-1,6,-7),~(-5,12,-4,-1,5,-6), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (-1,2,0,-5,15,-10),~(1,-1,1,1,6,-7),~(1,3,-1,1,2,-5),~(-1,3,-1,3,2,-5), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (3,1,-1,-1,4,-5),~(-2,3,2,0,2,-4),~(0,-1,2,-2,6,-4),~(-2,5,-2,0,0,0). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (-3,6,0,-3,11,-10),~(-1,3,1,3,2,-7),~(3,-3,3,-1,8,-9),~(1,1,1,1,4,-7), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (-1,1,1,3,4,-7),~(0,-3,6,-2,8,-8),~(3,-1,1,-1,6,-7),~(-5,12,-4,-1,5,-6), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (-1,2,0,-5,15,-10),~(1,-1,1,1,6,-7),~(1,3,-1,1,2,-5),~(-1,3,-1,3,2,-5), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (3,1,-1,-1,4,-5),~(-2,3,2,0,2,-4),~(0,-1,2,-2,6,-4),~(-2,5,-2,0,0,0). & \displaystyle \nonumber\end{eqnarray}$$
Suitable linear combinations of these eta products
 $\prod _{d|52}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
yield a basis consisting of
$\prod _{d|52}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
yield a basis consisting of
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}f_{0}\ & =\ & 1+2q+2q^{4}+2q^{9}+\cdots \,,\quad & f_{3}\ & =\ & q^{-3}+q^{-1}+q^{3}+q^{9}+\cdots \,,\\ f_{4}\ & =\ & q^{-4}-q^{-1}-q+q^{3}+\cdots \,,\quad & f_{5}\ & =\ & q^{-5}+q^{-2}-2q+q^{2}+\cdots \,,\\ f_{6}\ & =\ & q^{-6}+q^{-2}-2q+2q^{2}+\cdots \,,\quad & f_{7}\ & =\ & q^{-7}-q^{-2}+2q-q^{2}+\cdots \,,\\ f_{8}\ & =\ & q^{-8}+q^{-2}+q^{2}+2q^{5}+\cdots \,,\quad & f_{9}\ & =\ & q^{-9}+2q^{-1}+3q+2q^{3}+\cdots \,,\\ f_{10}\ & =\ & q^{-10}+3q^{-1}+q-q^{3}+\cdots \,,\quad & f_{11}\ & =\ & q^{-11}+2q^{2}+q^{5}+4q^{7}+\cdots \,,\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}f_{0}\ & =\ & 1+2q+2q^{4}+2q^{9}+\cdots \,,\quad & f_{3}\ & =\ & q^{-3}+q^{-1}+q^{3}+q^{9}+\cdots \,,\\ f_{4}\ & =\ & q^{-4}-q^{-1}-q+q^{3}+\cdots \,,\quad & f_{5}\ & =\ & q^{-5}+q^{-2}-2q+q^{2}+\cdots \,,\\ f_{6}\ & =\ & q^{-6}+q^{-2}-2q+2q^{2}+\cdots \,,\quad & f_{7}\ & =\ & q^{-7}-q^{-2}+2q-q^{2}+\cdots \,,\\ f_{8}\ & =\ & q^{-8}+q^{-2}+q^{2}+2q^{5}+\cdots \,,\quad & f_{9}\ & =\ & q^{-9}+2q^{-1}+3q+2q^{3}+\cdots \,,\\ f_{10}\ & =\ & q^{-10}+3q^{-1}+q-q^{3}+\cdots \,,\quad & f_{11}\ & =\ & q^{-11}+2q^{2}+q^{5}+4q^{7}+\cdots \,,\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
for the space
 $M_{11}^{!}(52)$
. In fact, since all of these modular forms have integral coefficients, multiplying these
$M_{11}^{!}(52)$
. In fact, since all of these modular forms have integral coefficients, multiplying these
![]() $f_{j}$
by powers of
$f_{j}$
by powers of
![]() $t$
, we find that for each non-gap positive integer
$t$
, we find that for each non-gap positive integer
![]() $j$
, there exists a modular form
$j$
, there exists a modular form
![]() $f_{j}$
in
$f_{j}$
in
 $M^{!}(52)\cap \mathbb{Z}((q))$
with a pole of order
$M^{!}(52)\cap \mathbb{Z}((q))$
with a pole of order
![]() $j$
at
$j$
at
![]() $\infty$
and a leading coefficient of one.
$\infty$
and a leading coefficient of one.
Remark 20. Quite curiously, our computation shows that whenever
![]() $N=1$
, i.e. whenever
$N=1$
, i.e. whenever
![]() $D_{0}=p$
is an odd prime, the space
$D_{0}=p$
is an odd prime, the space
 $M^{!}(4D_{0})$
has the property that for each non-gap positive integer
$M^{!}(4D_{0})$
has the property that for each non-gap positive integer
![]() $j$
, there exists a modular form
$j$
, there exists a modular form
![]() $f$
in
$f$
in
 $M^{!}(4D_{0})\cap \mathbb{Z}((q))$
such that
$M^{!}(4D_{0})\cap \mathbb{Z}((q))$
such that
![]() $f$
has a pole of order
$f$
has a pole of order
![]() $j$
at
$j$
at
![]() $\infty$
with leading coefficient one.
$\infty$
with leading coefficient one.
The smallest
![]() $D_{0}$
such that
$D_{0}$
such that
 $M^{!}(4D_{0})$
does not have this property is
$M^{!}(4D_{0})$
does not have this property is
 $D_{0}=51$
. We can show that the gaps of
$D_{0}=51$
. We can show that the gaps of
 $M^{!}(204)$
are
$M^{!}(204)$
are
 $1,\ldots ,14$
, and
$1,\ldots ,14$
, and
![]() $20$
and there exists a modular form
$20$
and there exists a modular form
![]() $f$
in
$f$
in
 $M^{!}(204)\cap \mathbb{Z}((q))$
with a Fourier expansion
$M^{!}(204)\cap \mathbb{Z}((q))$
with a Fourier expansion
 $2q^{-22}-q^{-20}-2q^{-14}+2q^{-12}+\cdots \,.$
As
$2q^{-22}-q^{-20}-2q^{-14}+2q^{-12}+\cdots \,.$
As
![]() $20$
is a gap, there cannot exist
$20$
is a gap, there cannot exist
 $g\in M^{!}(204)\cap \mathbb{Z}((q))$
with a Fourier expansion
$g\in M^{!}(204)\cap \mathbb{Z}((q))$
with a Fourier expansion
 $q^{-22}+\cdots \,.$
$q^{-22}+\cdots \,.$
We now show that for
![]() $(D,N)$
in Theorem 1 with even
$(D,N)$
in Theorem 1 with even
![]() $D$
, all meromorphic modular forms of even weights on
$D$
, all meromorphic modular forms of even weights on
 $X_{0}^{D}(N)/W_{D,N}$
with divisors supported on CM divisors, which we define below, can be realized as Borcherds forms.
$X_{0}^{D}(N)/W_{D,N}$
with divisors supported on CM divisors, which we define below, can be realized as Borcherds forms.
Definition 21. For a negative discriminant
![]() $d$
, we let
$d$
, we let
![]() $\operatorname{CM}(d)$
denote the set of CM points of discriminant
$\operatorname{CM}(d)$
denote the set of CM points of discriminant
![]() $d$
on
$d$
on
 $X_{0}^{D}(N)/W_{D,N}$
,
$X_{0}^{D}(N)/W_{D,N}$
,
 $h_{d}=|\!\operatorname{CM}(d)|$
, and
$h_{d}=|\!\operatorname{CM}(d)|$
, and
![]() $P_{d}$
be the divisor
$P_{d}$
be the divisor
 $$\begin{eqnarray}P_{d}=\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \operatorname{CM}(d)}\unicode[STIX]{x1D70F}.\end{eqnarray}$$
$$\begin{eqnarray}P_{d}=\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \operatorname{CM}(d)}\unicode[STIX]{x1D70F}.\end{eqnarray}$$
(If
![]() $h_{d}=0$
, then
$h_{d}=0$
, then
![]() $P_{d}$
simply means zero.) We call
$P_{d}$
simply means zero.) We call
![]() $P_{d}$
the
$P_{d}$
the
![]() $\operatorname{CM}$
divisor of discriminant
$\operatorname{CM}$
divisor of discriminant
![]() $d$
. Note that sometimes we wish to keep track the degree of the divisor
$d$
. Note that sometimes we wish to keep track the degree of the divisor
![]() $P_{d}$
. In such as a case, we will write
$P_{d}$
. In such as a case, we will write
![]() $P_{d}^{\times h_{d}}$
instead of
$P_{d}^{\times h_{d}}$
instead of
![]() $P_{d}$
.
$P_{d}$
.
Lemma 22. Let
![]() $f$
be an element in
$f$
be an element in
 $M^{!}(4D_{0})\cap \mathbb{Z}((q))$
,
$M^{!}(4D_{0})\cap \mathbb{Z}((q))$
,
![]() $F_{f}$
be the vector-valued modular form constructed using
$F_{f}$
be the vector-valued modular form constructed using
![]() $f$
as given by (6), and
$f$
as given by (6), and
![]() $\unicode[STIX]{x1D713}_{F_{f}}(\unicode[STIX]{x1D70F})$
be the Borcherds form on
$\unicode[STIX]{x1D713}_{F_{f}}(\unicode[STIX]{x1D70F})$
be the Borcherds form on
 $X_{0}^{D}(N)/W_{D,N}$
corresponding to
$X_{0}^{D}(N)/W_{D,N}$
corresponding to
![]() $F_{f}$
as defined in Definition 6. Suppose that the Fourier expansion of
$F_{f}$
as defined in Definition 6. Suppose that the Fourier expansion of
![]() $f$
is
$f$
is
 $\sum _{m}c_{m}q^{m}$
. Then
$\sum _{m}c_{m}q^{m}$
. Then
 $$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=\mathop{\sum }_{m<0}c_{m}\mathop{\sum }_{r\in \mathbb{Z}^{+},4m/r^{2}~\text{is a discriminant}}\frac{1}{e_{4m/r^{2}}}P_{4m/r^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=\mathop{\sum }_{m<0}c_{m}\mathop{\sum }_{r\in \mathbb{Z}^{+},4m/r^{2}~\text{is a discriminant}}\frac{1}{e_{4m/r^{2}}}P_{4m/r^{2}},\end{eqnarray}$$
where
![]() $e_{d}$
is the cardinality of the stabilizer subgroup of
$e_{d}$
is the cardinality of the stabilizer subgroup of
 $\unicode[STIX]{x1D70F}\in \operatorname{CM}(d)$
in
$\unicode[STIX]{x1D70F}\in \operatorname{CM}(d)$
in
 $N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }$
.
$N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }$
.
Proof. This follows from [Reference ErrthumErr11, Proposition 5.4] and [Reference YangYan15, Lemma 7].◻
Proposition 23. For
![]() $(D,N)$
in Theorem 1 with
$(D,N)$
in Theorem 1 with
![]() $2|D$
, all meromorphic modular forms of even weights on
$2|D$
, all meromorphic modular forms of even weights on
 $X_{0}^{D}(N)/W_{D,N}$
with a divisor supported on CM divisors can be realized as Borcherds forms.
$X_{0}^{D}(N)/W_{D,N}$
with a divisor supported on CM divisors can be realized as Borcherds forms.
Proof. We will prove only the case
 $(D,N)=(26,1)$
. The proof of the other cases is similar.
$(D,N)=(26,1)$
. The proof of the other cases is similar.
We claim that:
-
(i) there is a Borcherds form
 $\unicode[STIX]{x1D713}$
of weight two with a trivial character; and
$\unicode[STIX]{x1D713}$
of weight two with a trivial character; and -
(ii) every modular function on
 $X_{0}^{26}(1)/W_{26,1}$
with divisor supported on CM divisors can be realized as a Borcherds form.
$X_{0}^{26}(1)/W_{26,1}$
with divisor supported on CM divisors can be realized as a Borcherds form.
Then observe that if
![]() $\unicode[STIX]{x1D719}$
is a modular form of even weight
$\unicode[STIX]{x1D719}$
is a modular form of even weight
![]() $k$
, then
$k$
, then
![]() $\unicode[STIX]{x1D719}/\unicode[STIX]{x1D713}^{k/2}$
has weight zero. The two claims imply that
$\unicode[STIX]{x1D719}/\unicode[STIX]{x1D713}^{k/2}$
has weight zero. The two claims imply that
![]() $\unicode[STIX]{x1D719}$
can be realized as a Borcherds form.
$\unicode[STIX]{x1D719}$
can be realized as a Borcherds form.
The Shimura curve
 $X_{0}^{26}(1)/W_{26,1}$
has genus zero and precisely five elliptic points of order two. Among the five elliptic points, one is a CM point of discriminant
$X_{0}^{26}(1)/W_{26,1}$
has genus zero and precisely five elliptic points of order two. Among the five elliptic points, one is a CM point of discriminant
![]() $-8$
, one is a CM point of discriminant
$-8$
, one is a CM point of discriminant
![]() $-52$
and the remaining three are CM points of discriminant
$-52$
and the remaining three are CM points of discriminant
![]() $-104$
. Also, if
$-104$
. Also, if
![]() $\unicode[STIX]{x1D713}$
is a meromorphic modular form of even weight
$\unicode[STIX]{x1D713}$
is a meromorphic modular form of even weight
![]() $k$
on
$k$
on
 $X_{0}^{26}(1)/W_{26,1}$
, then the degree of
$X_{0}^{26}(1)/W_{26,1}$
, then the degree of
![]() $\operatorname{div}\unicode[STIX]{x1D713}$
is
$\operatorname{div}\unicode[STIX]{x1D713}$
is
![]() $k/4$
. Thus, by Lemmas 7 and 22, for
$k/4$
. Thus, by Lemmas 7 and 22, for
 $f=\sum _{m}c_{m}q^{m}\in M^{!}(52)\cap \mathbb{Z}((q))$
, the Borcherds form
$f=\sum _{m}c_{m}q^{m}\in M^{!}(52)\cap \mathbb{Z}((q))$
, the Borcherds form
![]() $\unicode[STIX]{x1D713}_{F_{f}}$
has even weight
$\unicode[STIX]{x1D713}_{F_{f}}$
has even weight
![]() $k$
and a trivial character if and only if
$k$
and a trivial character if and only if
 $$\begin{eqnarray}\mathop{\sum }_{m<0}c_{m}\mathop{\sum }_{r\in \mathbb{Z}^{+},4m/r^{2}~\text{is a discriminant}}\frac{1}{e_{4m/r^{2}}}|\!\operatorname{CM}(4m/r^{2})|=k/4\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m<0}c_{m}\mathop{\sum }_{r\in \mathbb{Z}^{+},4m/r^{2}~\text{is a discriminant}}\frac{1}{e_{4m/r^{2}}}|\!\operatorname{CM}(4m/r^{2})|=k/4\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathop{\sum }_{m=-2n^{2}}c_{m}\equiv \mathop{\sum }_{m=-13n^{2}}c_{m}\equiv \mathop{\sum }_{m=-26n^{2}}c_{m}\equiv k/2\quad \text{mod}~2.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=-2n^{2}}c_{m}\equiv \mathop{\sum }_{m=-13n^{2}}c_{m}\equiv \mathop{\sum }_{m=-26n^{2}}c_{m}\equiv k/2\quad \text{mod}~2.\end{eqnarray}$$
Now from Example 19, we know that for each
![]() $j\geqslant 3$
, there exists a unique element
$j\geqslant 3$
, there exists a unique element
![]() $f_{j}$
in
$f_{j}$
in
 $M^{!}(52)\cap \mathbb{Z}((q))$
such that its Fourier expansion is of the form
$M^{!}(52)\cap \mathbb{Z}((q))$
such that its Fourier expansion is of the form
 $f_{j}=q^{-j}+c_{-2}q^{-2}+c_{-1}q^{-1}+\cdots \,.$
In particular, we find
$f_{j}=q^{-j}+c_{-2}q^{-2}+c_{-1}q^{-1}+\cdots \,.$
In particular, we find
 $$\begin{eqnarray}\displaystyle f_{7} & = & \displaystyle q^{-7}-q^{-2}+2q+\cdots \,,\nonumber\\ \displaystyle f_{13} & = & \displaystyle q^{-13}-q^{-2}-2q^{-1}+q+\cdots \,,\nonumber\\ \displaystyle f_{26} & = & \displaystyle q^{-26}+q^{-1}-q+\cdots \,.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{7} & = & \displaystyle q^{-7}-q^{-2}+2q+\cdots \,,\nonumber\\ \displaystyle f_{13} & = & \displaystyle q^{-13}-q^{-2}-2q^{-1}+q+\cdots \,,\nonumber\\ \displaystyle f_{26} & = & \displaystyle q^{-26}+q^{-1}-q+\cdots \,.\nonumber\end{eqnarray}$$
The modular form
 $$\begin{eqnarray}f=f_{26}-f_{13}+2f_{7}=q^{-26}-q^{-13}+2q^{-7}-q^{-2}+3q^{-1}+2q+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}f=f_{26}-f_{13}+2f_{7}=q^{-26}-q^{-13}+2q^{-7}-q^{-2}+3q^{-1}+2q+\cdots \,,\end{eqnarray}$$
satisfies the conditions in (9) and (10) with
![]() $k=2$
. (Note that no CM points of discriminants
$k=2$
. (Note that no CM points of discriminants
![]() $-4$
and
$-4$
and
![]() $-7$
exist on the Shimura curve
$-7$
exist on the Shimura curve
![]() $X_{0}^{26}(1)$
, so the presence of the terms
$X_{0}^{26}(1)$
, so the presence of the terms
![]() $q^{-7}$
and
$q^{-7}$
and
![]() $q^{-1}$
will not contribute anything to the divisor of the Borcherds form.) This proves claim (i).
$q^{-1}$
will not contribute anything to the divisor of the Borcherds form.) This proves claim (i).
To prove claim (ii), it suffices to show that for each discriminant
![]() $d<0$
, there exists a modular form
$d<0$
, there exists a modular form
![]() $f$
in
$f$
in
 $M^{!}(52)\cap \mathbb{Z}((q))$
satisfying (9) and (10) with
$M^{!}(52)\cap \mathbb{Z}((q))$
satisfying (9) and (10) with
![]() $k=0$
such that
$k=0$
such that
 $\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=P_{d}^{\times h_{d}}-h_{d}P_{-8}$
. For the special cases
$\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=P_{d}^{\times h_{d}}-h_{d}P_{-8}$
. For the special cases
 $d=-52$
and
$d=-52$
and
 $d=-104$
, we may choose
$d=-104$
, we may choose
![]() $f$
to be
$f$
to be
![]() $2f_{13}$
and
$2f_{13}$
and
 $2f_{26}+6f_{7}$
, respectively. If
$2f_{26}+6f_{7}$
, respectively. If
 $d\neq -52,-104$
and
$d\neq -52,-104$
and
![]() $d$
is a fundamental discriminant, we choose
$d$
is a fundamental discriminant, we choose
![]() $f$
to be
$f$
to be
 $f_{|d|}+af_{7}$
with a proper integer
$f_{|d|}+af_{7}$
with a proper integer
![]() $a$
such that the coefficient of
$a$
such that the coefficient of
![]() $q^{-2}$
is
$q^{-2}$
is
![]() $-2h_{d}$
. (If
$-2h_{d}$
. (If
![]() $4|d$
, we may choose
$4|d$
, we may choose
 $f_{|d|/4}+bf_{7}$
instead.) Now assume that
$f_{|d|/4}+bf_{7}$
instead.) Now assume that
![]() $d$
is not a fundamental discriminant, say,
$d$
is not a fundamental discriminant, say,
 $d=d_{0}n^{2}$
for some fundamental discriminant
$d=d_{0}n^{2}$
for some fundamental discriminant
![]() $d_{0}$
. We let
$d_{0}$
. We let
![]() $a$
be the integer such that the coefficient of
$a$
be the integer such that the coefficient of
![]() $q^{-2}$
in
$q^{-2}$
in
 $f=\sum _{r|n}\unicode[STIX]{x1D707}(r)f_{|d|/r^{2}}+af_{7}$
is
$f=\sum _{r|n}\unicode[STIX]{x1D707}(r)f_{|d|/r^{2}}+af_{7}$
is
![]() $-2h_{d}$
, where
$-2h_{d}$
, where
![]() $\unicode[STIX]{x1D707}(r)$
is the Möbius function. Then
$\unicode[STIX]{x1D707}(r)$
is the Möbius function. Then
 $\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=P_{d}^{\times h_{d}}-h_{d}P_{-8}$
. (The case
$\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=P_{d}^{\times h_{d}}-h_{d}P_{-8}$
. (The case
 $d_{0}=-8$
needs a special treatment, but it is completely analogous.) This proves claim (ii) and, hence, the proposition for the case
$d_{0}=-8$
needs a special treatment, but it is completely analogous.) This proves claim (ii) and, hence, the proposition for the case
 $(D,N)=(26,1)$
.◻
$(D,N)=(26,1)$
.◻
3.3 Case of odd
 $D$
$D$
The construction of Borcherds forms in the case of odd
![]() $D$
is a little more complicated than the case of even
$D$
is a little more complicated than the case of even
![]() $D$
. The idea of using
$D$
. The idea of using
![]() $\{\infty \}$
-weakly holomorphic modular forms to construct Borcherds forms is no longer sufficient for our purpose. The reason is that if the divisor of a Borcherds form arising from a
$\{\infty \}$
-weakly holomorphic modular forms to construct Borcherds forms is no longer sufficient for our purpose. The reason is that if the divisor of a Borcherds form arising from a
![]() $\{\infty \}$
-weakly holomorphic modular form is supported at a CM point of discriminant
$\{\infty \}$
-weakly holomorphic modular form is supported at a CM point of discriminant
![]() $d$
,
$d$
,
 $d\equiv 1~\text{mod}~4$
, then it also is supported at CM points of discriminant
$d\equiv 1~\text{mod}~4$
, then it also is supported at CM points of discriminant
![]() $4d$
. However, in practice, we are often required to construct Borcherds forms whose divisors are supported at CM points of discriminant
$4d$
. However, in practice, we are often required to construct Borcherds forms whose divisors are supported at CM points of discriminant
![]() $d$
, but not at CM points of discriminant
$d$
, but not at CM points of discriminant
![]() $4d$
. Thus, in the case of odd
$4d$
. Thus, in the case of odd
![]() $D$
, we will need to use
$D$
, we will need to use
![]() $\{\infty ,0\}$
-weakly holomorphic modular forms to construct desired Borcherds forms.
$\{\infty ,0\}$
-weakly holomorphic modular forms to construct desired Borcherds forms.
Assume that
![]() $D$
is odd and
$D$
is odd and
![]() $N$
is squarefree. As usual, we let
$N$
is squarefree. As usual, we let
![]() ${\mathcal{O}}$
be an Eichler order of level
${\mathcal{O}}$
be an Eichler order of level
![]() $N$
in the quaternion algebra
$N$
in the quaternion algebra
![]() $B$
of discriminant
$B$
of discriminant
![]() $D$
, and
$D$
, and
![]() $L$
be the lattice formed by elements of trace
$L$
be the lattice formed by elements of trace
![]() $0$
in
$0$
in
![]() ${\mathcal{O}}$
. For convenience, for a modular form
${\mathcal{O}}$
. For convenience, for a modular form
![]() $f$
, we let
$f$
, we let
![]() $P(f)$
denote the principal part of
$P(f)$
denote the principal part of
![]() $f$
at
$f$
at
![]() $\infty$
, i.e. the sums of the terms with negative exponents in the Fourier expansion of
$\infty$
, i.e. the sums of the terms with negative exponents in the Fourier expansion of
![]() $f$
. Similarly, for a vector-valued modular form
$f$
. Similarly, for a vector-valued modular form
 $F=\sum _{\unicode[STIX]{x1D702}\in L^{\vee }/L}F_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D702}}$
, we let
$F=\sum _{\unicode[STIX]{x1D702}\in L^{\vee }/L}F_{\unicode[STIX]{x1D702}}e_{\unicode[STIX]{x1D702}}$
, we let
 $$\begin{eqnarray}P(F)=\mathop{\sum }_{\unicode[STIX]{x1D702}}P(F_{\unicode[STIX]{x1D702}})e_{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
$$\begin{eqnarray}P(F)=\mathop{\sum }_{\unicode[STIX]{x1D702}}P(F_{\unicode[STIX]{x1D702}})e_{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
Lemma 24. Let
![]() $M$
be the level of
$M$
be the level of
![]() $L$
. Suppose that
$L$
. Suppose that
![]() $f$
is a
$f$
is a
![]() $\{\infty ,0\}$
-weakly holomorphic scalar-valued modular of weight
$\{\infty ,0\}$
-weakly holomorphic scalar-valued modular of weight
![]() $1/2$
on
$1/2$
on
![]() $\unicode[STIX]{x1D6E4}_{0}(M)$
and
$\unicode[STIX]{x1D6E4}_{0}(M)$
and
![]() $F_{f}$
was given in Lemma 10. Assume that
$F_{f}$
was given in Lemma 10. Assume that
 $P(f|_{1/2}S)=\sum _{n>0}b_{n}q^{-n/M}$
. Then
$P(f|_{1/2}S)=\sum _{n>0}b_{n}q^{-n/M}$
. Then
 $$\begin{eqnarray}P(F_{f})=P(f)e_{0}+\frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{n>0}b_{n}q^{-n/M}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L,\operatorname{nrd}(\unicode[STIX]{x1D702})\in n/M+\mathbb{Z}}e_{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
$$\begin{eqnarray}P(F_{f})=P(f)e_{0}+\frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{n>0}b_{n}q^{-n/M}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L,\operatorname{nrd}(\unicode[STIX]{x1D702})\in n/M+\mathbb{Z}}e_{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
Proof. Since
![]() $f$
is of
$f$
is of
![]() $\{\infty ,0\}$
-weakly holomorphic, if
$\{\infty ,0\}$
-weakly holomorphic, if
![]() $\unicode[STIX]{x1D6FE}$
is an element of
$\unicode[STIX]{x1D6FE}$
is an element of
 $\operatorname{SL}(2,\mathbb{Z})$
such that
$\operatorname{SL}(2,\mathbb{Z})$
such that
![]() $\unicode[STIX]{x1D6FE}\infty$
is not equivalent to the cusp
$\unicode[STIX]{x1D6FE}\infty$
is not equivalent to the cusp
![]() $\infty$
or zero, then we have
$\infty$
or zero, then we have
 $P(f|_{1/2}\unicode[STIX]{x1D6FE})=0$
. Now
$P(f|_{1/2}\unicode[STIX]{x1D6FE})=0$
. Now
![]() $\unicode[STIX]{x1D6FE}=I$
is the only right coset representative of
$\unicode[STIX]{x1D6FE}=I$
is the only right coset representative of
![]() $\unicode[STIX]{x1D6E4}_{0}(M)$
in
$\unicode[STIX]{x1D6E4}_{0}(M)$
in
 $\operatorname{SL}(2,\mathbb{Z})$
with
$\operatorname{SL}(2,\mathbb{Z})$
with
 $\unicode[STIX]{x1D6FE}\infty \sim \infty$
and
$\unicode[STIX]{x1D6FE}\infty \sim \infty$
and
 $\unicode[STIX]{x1D6FE}=ST^{j}$
,
$\unicode[STIX]{x1D6FE}=ST^{j}$
,
 $j=0,\ldots ,M-1$
, are the only right coset representatives with
$j=0,\ldots ,M-1$
, are the only right coset representatives with
 $\unicode[STIX]{x1D6FE}\infty \sim 0$
. Thus,
$\unicode[STIX]{x1D6FE}\infty \sim 0$
. Thus,
 $$\begin{eqnarray}P(F_{f})=P(f)e_{0}+\mathop{\sum }_{j=0}^{M-1}P(f|_{1/2}ST^{j})\unicode[STIX]{x1D70C}_{L}(T^{-j}S^{-1})e_{0}.\end{eqnarray}$$
$$\begin{eqnarray}P(F_{f})=P(f)e_{0}+\mathop{\sum }_{j=0}^{M-1}P(f|_{1/2}ST^{j})\unicode[STIX]{x1D70C}_{L}(T^{-j}S^{-1})e_{0}.\end{eqnarray}$$
Since
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{L}(S^{-1})e_{\unicode[STIX]{x1D6FF}}=\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}e^{-\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D6FF}\rangle }e_{\unicode[STIX]{x1D702}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{L}(S^{-1})e_{\unicode[STIX]{x1D6FF}}=\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}e^{-\langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D6FF}\rangle }e_{\unicode[STIX]{x1D702}},\end{eqnarray}$$
we find
 $$\begin{eqnarray}\displaystyle P(F_{f}) & = & \displaystyle P(f)e_{0}+\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{j=0}^{M-1}P(f|_{1/2}ST^{j})\unicode[STIX]{x1D70C}_{L}(T^{-j})\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}e_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle P(f)e_{0}+\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{n>0}b_{n}q^{-n/M}\mathop{\sum }_{j=0}^{M-1}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}e^{2\unicode[STIX]{x1D70B}ij(-n/M+\operatorname{nrd}(\unicode[STIX]{x1D702}))}e_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle P(f)e_{0}+\frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{n>0}b_{n}q^{-n/M}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L,\operatorname{nrd}(\unicode[STIX]{x1D702})\in n/M+\mathbb{Z}}e_{\unicode[STIX]{x1D702}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(F_{f}) & = & \displaystyle P(f)e_{0}+\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{j=0}^{M-1}P(f|_{1/2}ST^{j})\unicode[STIX]{x1D70C}_{L}(T^{-j})\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}e_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle P(f)e_{0}+\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{n>0}b_{n}q^{-n/M}\mathop{\sum }_{j=0}^{M-1}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L}e^{2\unicode[STIX]{x1D70B}ij(-n/M+\operatorname{nrd}(\unicode[STIX]{x1D702}))}e_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & = & \displaystyle P(f)e_{0}+\frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}\mathop{\sum }_{n>0}b_{n}q^{-n/M}\mathop{\sum }_{\unicode[STIX]{x1D702}\in L^{\vee }/L,\operatorname{nrd}(\unicode[STIX]{x1D702})\in n/M+\mathbb{Z}}e_{\unicode[STIX]{x1D702}}.\nonumber\end{eqnarray}$$
This proves the lemma.◻
In general, the principal part
 $e^{2\unicode[STIX]{x1D70B}i/8}|L^{\vee }/L|^{-1/2}P(f|_{1/2}S)$
in the lemma lie in
$e^{2\unicode[STIX]{x1D70B}i/8}|L^{\vee }/L|^{-1/2}P(f|_{1/2}S)$
in the lemma lie in
 $\mathbb{C}[q^{-1/M}]$
. For our purpose, we will only consider those
$\mathbb{C}[q^{-1/M}]$
. For our purpose, we will only consider those
![]() $f$
such that
$f$
such that
 $$\begin{eqnarray}P(f)\in \mathbb{Z}[q^{-1}],\quad \frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}P(f|_{1/2}S)\in \mathbb{Z}[q^{-1/4}].\end{eqnarray}$$
$$\begin{eqnarray}P(f)\in \mathbb{Z}[q^{-1}],\quad \frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}P(f|_{1/2}S)\in \mathbb{Z}[q^{-1/4}].\end{eqnarray}$$
Lemma 25. Let
![]() $f$
be as in the lemma above. Suppose that
$f$
be as in the lemma above. Suppose that
![]() $P(f)$
and
$P(f)$
and
 $P(f|_{1/2}S)$
are of the form
$P(f|_{1/2}S)$
are of the form
 $$\begin{eqnarray}P(f)=\mathop{\sum }_{n>0,n\in \mathbb{Z}}a_{n}q^{-n},\quad \frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}P(f|_{1/2}S)=\mathop{\sum }_{n>0,n\in \mathbb{Z}}b_{n}q^{-n/4}\end{eqnarray}$$
$$\begin{eqnarray}P(f)=\mathop{\sum }_{n>0,n\in \mathbb{Z}}a_{n}q^{-n},\quad \frac{Me^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}P(f|_{1/2}S)=\mathop{\sum }_{n>0,n\in \mathbb{Z}}b_{n}q^{-n/4}\end{eqnarray}$$
for some integers
![]() $a_{n}$
and
$a_{n}$
and
![]() $b_{n}$
. Then
$b_{n}$
. Then
 $$\begin{eqnarray}\displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{F_{f}} & = & \displaystyle \mathop{\sum }_{n}a_{n}\mathop{\sum }_{r\in \mathbb{Z}^{+},-4n/r^{2}\text{ is a discriminant}}\frac{1}{e_{-4n/r^{2}}}P_{-4n/r^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n}b_{n}\mathop{\sum }_{r\in \mathbb{Z}^{+},-N^{2}n/r^{2}\text{ is a discriminant}}\frac{1}{e_{-N^{2}n/r^{2}}}P_{-N^{2}n/r^{2}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{F_{f}} & = & \displaystyle \mathop{\sum }_{n}a_{n}\mathop{\sum }_{r\in \mathbb{Z}^{+},-4n/r^{2}\text{ is a discriminant}}\frac{1}{e_{-4n/r^{2}}}P_{-4n/r^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n}b_{n}\mathop{\sum }_{r\in \mathbb{Z}^{+},-N^{2}n/r^{2}\text{ is a discriminant}}\frac{1}{e_{-N^{2}n/r^{2}}}P_{-N^{2}n/r^{2}},\nonumber\end{eqnarray}$$
where
![]() $e_{d}$
is the cardinality of the stabilizer subgroup of a CM point of discriminant
$e_{d}$
is the cardinality of the stabilizer subgroup of a CM point of discriminant
![]() $d$
in
$d$
in
 $N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }$
.
$N_{B}^{+}({\mathcal{O}})/\mathbb{Q}^{\ast }$
.
Proof. Let
![]() $q$
be a prime satisfying the condition in Lemma 8 so that
$q$
be a prime satisfying the condition in Lemma 8 so that
 $B=(\frac{DN,q}{\mathbb{Q}})$
is a quaternion algebra of discriminant
$B=(\frac{DN,q}{\mathbb{Q}})$
is a quaternion algebra of discriminant
![]() $D$
. Let
$D$
. Let
![]() ${\mathcal{O}}$
be the Eichler order of level
${\mathcal{O}}$
be the Eichler order of level
![]() $N$
spanned by
$N$
spanned by
 $e_{1},\ldots ,e_{4}$
given in (3) and
$e_{1},\ldots ,e_{4}$
given in (3) and
 $\{\ell _{1},\ell _{2},\ell _{3}\}$
be given as in (4). The contribution from
$\{\ell _{1},\ell _{2},\ell _{3}\}$
be given as in (4). The contribution from
![]() $P(f)e_{0}$
to the divisor of
$P(f)e_{0}$
to the divisor of
![]() $\unicode[STIX]{x1D713}_{F_{f}}$
is described in Lemma 22. Here we are mainly concerned with the contribution from
$\unicode[STIX]{x1D713}_{F_{f}}$
is described in Lemma 22. Here we are mainly concerned with the contribution from
![]() $P(f|S)$
.
$P(f|S)$
.
Consider the case of odd
![]() $N$
first. Let
$N$
first. Let
![]() $\unicode[STIX]{x1D706}$
be an element in
$\unicode[STIX]{x1D706}$
be an element in
 $L^{\vee }=\mathbb{Z}\ell _{1}/2+\mathbb{Z}\ell _{2}/DN+\mathbb{Z}\ell _{3}/DN$
satisfying
$L^{\vee }=\mathbb{Z}\ell _{1}/2+\mathbb{Z}\ell _{2}/DN+\mathbb{Z}\ell _{3}/DN$
satisfying
 $\operatorname{nrd}(\unicode[STIX]{x1D706})=n/4$
for some positive integer
$\operatorname{nrd}(\unicode[STIX]{x1D706})=n/4$
for some positive integer
![]() $n$
. We need to determine the discriminant of the optimal embedding
$n$
. We need to determine the discriminant of the optimal embedding
 $\unicode[STIX]{x1D719}:\mathbb{Q}(\sqrt{-n}){\hookrightarrow}B$
that maps
$\unicode[STIX]{x1D719}:\mathbb{Q}(\sqrt{-n}){\hookrightarrow}B$
that maps
![]() $\sqrt{-n}$
to
$\sqrt{-n}$
to
![]() $2\unicode[STIX]{x1D706}$
.
$2\unicode[STIX]{x1D706}$
.
Observe that
 $2DN\unicode[STIX]{x1D706}\in {\mathcal{O}}$
and
$2DN\unicode[STIX]{x1D706}\in {\mathcal{O}}$
and
 $\operatorname{nrd}(2DN\unicode[STIX]{x1D706})=-D^{2}N^{2}n$
. By [Reference Alsina and BayerAB04, Proposition 1.53], we must have
$\operatorname{nrd}(2DN\unicode[STIX]{x1D706})=-D^{2}N^{2}n$
. By [Reference Alsina and BayerAB04, Proposition 1.53], we must have
 $2N\unicode[STIX]{x1D706}\in {\mathcal{O}}$
, i.e.
$2N\unicode[STIX]{x1D706}\in {\mathcal{O}}$
, i.e.
 $\unicode[STIX]{x1D706}=c_{1}\ell _{1}/2+c_{2}\ell _{2}/N+c_{3}\ell _{3}/N$
for some integers
$\unicode[STIX]{x1D706}=c_{1}\ell _{1}/2+c_{2}\ell _{2}/N+c_{3}\ell _{3}/N$
for some integers
![]() $c_{1}$
,
$c_{1}$
,
![]() $c_{2}$
and
$c_{2}$
and
![]() $c_{3}$
, and the discriminant of the optimal embedding
$c_{3}$
, and the discriminant of the optimal embedding
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
 $-4N^{2}n/r^{2}$
for some integer
$-4N^{2}n/r^{2}$
for some integer
![]() $r$
.
$r$
.
From the Gram matrix in (5), we have
 $$\begin{eqnarray}\operatorname{nrd}(N\unicode[STIX]{x1D706})=-\frac{qN^{2}c_{1}^{2}}{4}+\frac{q-1}{4}DNc_{2}^{2}+\frac{1-a^{2}DN}{q}DNc_{3}^{2}-aDN^{2}c_{1}c_{3}+DNc_{2}c_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{nrd}(N\unicode[STIX]{x1D706})=-\frac{qN^{2}c_{1}^{2}}{4}+\frac{q-1}{4}DNc_{2}^{2}+\frac{1-a^{2}DN}{q}DNc_{3}^{2}-aDN^{2}c_{1}c_{3}+DNc_{2}c_{3}.\end{eqnarray}$$
As
![]() $q$
is congruent to
$q$
is congruent to
![]() $1$
modulo
$1$
modulo
![]() $4$
, this shows that
$4$
, this shows that
 $\operatorname{nrd}(2N\unicode[STIX]{x1D706})\equiv 0,3~\text{mod}~4$
. Therefore, if
$\operatorname{nrd}(2N\unicode[STIX]{x1D706})\equiv 0,3~\text{mod}~4$
. Therefore, if
 $n\equiv 1,2~\text{mod}~4$
, then there does not exist
$n\equiv 1,2~\text{mod}~4$
, then there does not exist
![]() $\unicode[STIX]{x1D706}\in L^{\vee }$
such that
$\unicode[STIX]{x1D706}\in L^{\vee }$
such that
 $\operatorname{nrd}(\unicode[STIX]{x1D706})=n/4$
. Also, if
$\operatorname{nrd}(\unicode[STIX]{x1D706})=n/4$
. Also, if
 $n\equiv 3~\text{mod}~4$
, then
$n\equiv 3~\text{mod}~4$
, then
![]() $c_{1}$
must be odd and
$c_{1}$
must be odd and
 $$\begin{eqnarray}\frac{1+N\unicode[STIX]{x1D706}}{2}=\frac{1-Nc_{1}}{2}e_{1}+Nc_{1}e_{2}+c_{2}e_{3}+c_{3}e_{4}\in {\mathcal{O}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1+N\unicode[STIX]{x1D706}}{2}=\frac{1-Nc_{1}}{2}e_{1}+Nc_{1}e_{2}+c_{2}e_{3}+c_{3}e_{4}\in {\mathcal{O}}.\end{eqnarray}$$
In this case, the discriminant of the optimal embedding is
 $-N^{2}n/r^{2}$
for some
$-N^{2}n/r^{2}$
for some
![]() $r$
. If
$r$
. If
 $n\equiv 0~\text{mod}~4$
, then
$n\equiv 0~\text{mod}~4$
, then
![]() $c_{1}$
is even. It follows that
$c_{1}$
is even. It follows that
 $N\unicode[STIX]{x1D706}\in {\mathcal{O}}$
and the optimal embedding has discriminant
$N\unicode[STIX]{x1D706}\in {\mathcal{O}}$
and the optimal embedding has discriminant
 $-N^{2}n/r^{2}$
for some
$-N^{2}n/r^{2}$
for some
![]() $r$
.
$r$
.
Conversely, given a CM point
![]() $\unicode[STIX]{x1D70F}$
of discriminant
$\unicode[STIX]{x1D70F}$
of discriminant
 $-N^{2}n/r^{2}$
, there exists an element
$-N^{2}n/r^{2}$
, there exists an element
 $\unicode[STIX]{x1D706}=d_{1}\ell _{1}+d_{2}\ell _{2}+d_{3}\ell _{3}\in L$
fixing
$\unicode[STIX]{x1D706}=d_{1}\ell _{1}+d_{2}\ell _{2}+d_{3}\ell _{3}\in L$
fixing
![]() $\unicode[STIX]{x1D70F}$
and having norm
$\unicode[STIX]{x1D70F}$
and having norm
 $$\begin{eqnarray}\operatorname{nrd}(\unicode[STIX]{x1D706})=\left\{\begin{array}{@{}ll@{}}-N^{2}n/4\quad & \text{if }n\equiv 0~\text{mod}~4,\\ -N^{2}n\quad & \text{if }n\equiv 3~\text{mod}~4.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{nrd}(\unicode[STIX]{x1D706})=\left\{\begin{array}{@{}ll@{}}-N^{2}n/4\quad & \text{if }n\equiv 0~\text{mod}~4,\\ -N^{2}n\quad & \text{if }n\equiv 3~\text{mod}~4.\end{array}\right.\end{eqnarray}$$
Note that if
![]() $n$
is odd, then we must have
$n$
is odd, then we must have
 $(1+\unicode[STIX]{x1D706})/2\in {\mathcal{O}}$
. In other words,
$(1+\unicode[STIX]{x1D706})/2\in {\mathcal{O}}$
. In other words,
![]() $d_{2}$
and
$d_{2}$
and
![]() $d_{3}$
are even and
$d_{3}$
are even and
![]() $d_{1}$
is odd. On the other hand,
$d_{1}$
is odd. On the other hand,
 $$\begin{eqnarray}\operatorname{nrd}(\unicode[STIX]{x1D706})=-qd_{1}^{2}+\frac{q-1}{4}DNd_{2}^{2}+\frac{1-a^{2}DN}{q}DNd_{3}^{2}-2aDNd_{1}d_{3}+DNd_{2}d_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{nrd}(\unicode[STIX]{x1D706})=-qd_{1}^{2}+\frac{q-1}{4}DNd_{2}^{2}+\frac{1-a^{2}DN}{q}DNd_{3}^{2}-2aDNd_{1}d_{3}+DNd_{2}d_{3}.\end{eqnarray}$$
Since
![]() $N$
is squarefree, this implies that
$N$
is squarefree, this implies that
![]() $N|d_{1}$
. Setting
$N|d_{1}$
. Setting
 $$\begin{eqnarray}\unicode[STIX]{x1D706}^{\prime }=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D706}/N\quad & \text{if }n\equiv 0~\text{mod}~4,\\ \unicode[STIX]{x1D706}/(2N)\quad & \text{if }n\equiv 3~\text{mod}~4,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}^{\prime }=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D706}/N\quad & \text{if }n\equiv 0~\text{mod}~4,\\ \unicode[STIX]{x1D706}/(2N)\quad & \text{if }n\equiv 3~\text{mod}~4,\end{array}\right.\end{eqnarray}$$
we find
 $\unicode[STIX]{x1D706}^{\prime }\in L^{\vee }$
with
$\unicode[STIX]{x1D706}^{\prime }\in L^{\vee }$
with
 $\operatorname{nrd}(\unicode[STIX]{x1D706}^{\prime })=n/4$
. This proves the lemma for the case of odd
$\operatorname{nrd}(\unicode[STIX]{x1D706}^{\prime })=n/4$
. This proves the lemma for the case of odd
![]() $N$
. The proof of the case of even
$N$
. The proof of the case of even
![]() $N$
is similar and is omitted.◻
$N$
is similar and is omitted.◻
Lemma 26. Let
![]() $M$
be the level of the lattice
$M$
be the level of the lattice
![]() $L$
and let
$L$
and let
 $f(\unicode[STIX]{x1D70F})=\prod _{d|M}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
be an admissible eta product. (See Definition 13.) Then we have
$f(\unicode[STIX]{x1D70F})=\prod _{d|M}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
be an admissible eta product. (See Definition 13.) Then we have
 $$\begin{eqnarray}\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}(f|_{1/2}S)(\unicode[STIX]{x1D70F})=\frac{1}{\sqrt{|L^{\vee }/L|}}\mathop{\prod }_{d|M}\frac{1}{d^{r_{d}/2}}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F}/d)^{r_{d}}\in \mathbb{Q}((q^{1/M})).\end{eqnarray}$$
$$\begin{eqnarray}\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}(f|_{1/2}S)(\unicode[STIX]{x1D70F})=\frac{1}{\sqrt{|L^{\vee }/L|}}\mathop{\prod }_{d|M}\frac{1}{d^{r_{d}/2}}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F}/d)^{r_{d}}\in \mathbb{Q}((q^{1/M})).\end{eqnarray}$$
Proof. The lemma follows immediately from the formula
 $\unicode[STIX]{x1D702}(-1/\unicode[STIX]{x1D70F})=e^{-2\unicode[STIX]{x1D70B}i/8}\sqrt{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})$
and the assumptions that
$\unicode[STIX]{x1D702}(-1/\unicode[STIX]{x1D70F})=e^{-2\unicode[STIX]{x1D70B}i/8}\sqrt{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})$
and the assumptions that
 $\sum r_{d}=1$
and that
$\sum r_{d}=1$
and that
 $|L^{\vee }/L|\prod _{d|M}d^{r_{d}}$
is a square in
$|L^{\vee }/L|\prod _{d|M}d^{r_{d}}$
is a square in
![]() $\mathbb{Q}^{\ast }$
.◻
$\mathbb{Q}^{\ast }$
.◻
Lemma 27. Let
![]() $D_{0}$
be the odd part of
$D_{0}$
be the odd part of
![]() $DN$
and
$DN$
and
![]() $g$
be the genus of the modular curve
$g$
be the genus of the modular curve
 $X_{0}(4D_{0})$
.
$X_{0}(4D_{0})$
.
-
(1) For nonnegative integers
 $m$
and
$m$
and
 $n$
with we have
$n$
with we have $$\begin{eqnarray}m+n\geqslant 2g-2-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor ,\end{eqnarray}$$
$$\begin{eqnarray}m+n\geqslant 2g-2-\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor ,\end{eqnarray}$$
 $$\begin{eqnarray}\dim _{\mathbb{C}}M_{m,n}^{!,!}(4D_{0})=m+n+\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor +1-g.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbb{C}}M_{m,n}^{!,!}(4D_{0})=m+n+\mathop{\sum }_{d|D_{0}}\lfloor d/4\rfloor +1-g.\end{eqnarray}$$
-
(2) Let
 $m$
be a nonnegative integers such that
$m$
be a nonnegative integers such that
 $m\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
. Then for each positive integer
$m\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
. Then for each positive integer
 $n$
, there exists a modular form
$n$
, there exists a modular form
 $f_{n}$
in
$f_{n}$
in
 $M_{m,n}^{!,!}(4D_{0})$
with a pole of order
$M_{m,n}^{!,!}(4D_{0})$
with a pole of order
 $n$
at
$n$
at
 $0$
. Furthermore, the space
$0$
. Furthermore, the space
 $M^{!,!}(4D_{0})$
is spanned by
$M^{!,!}(4D_{0})$
is spanned by
 $M^{!}(4D_{0})$
and
$M^{!}(4D_{0})$
and
 $f_{1},f_{2},\ldots .$
$f_{1},f_{2},\ldots .$
Proof. The proof of part (1) is similar to that of Lemma 17 and is omitted. To prove part (2), we note that part (1) implies that when
 $m\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
, the space
$m\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
, the space
 $M_{m,0}^{!,!}(4D_{0})$
has co-dimension
$M_{m,0}^{!,!}(4D_{0})$
has co-dimension
![]() $n$
in
$n$
in
 $M_{m,n}^{!,!}(4D_{0})$
. It follows that for each integer
$M_{m,n}^{!,!}(4D_{0})$
. It follows that for each integer
![]() $k$
with
$k$
with
 $1\leqslant k\leqslant n$
, there exists a modular form
$1\leqslant k\leqslant n$
, there exists a modular form
![]() $f_{k}$
in
$f_{k}$
in
 $M_{m,n}^{!,!}(4D_{0})$
with a pole of order
$M_{m,n}^{!,!}(4D_{0})$
with a pole of order
![]() $k$
at zero. Now if
$k$
at zero. Now if
![]() $f$
is a modular form in
$f$
is a modular form in
 $M^{!,!}(4D_{0})$
, then for some linear combination
$M^{!,!}(4D_{0})$
, then for some linear combination
![]() $\sum c_{n}f_{n}$
, we have
$\sum c_{n}f_{n}$
, we have
 $f-\sum c_{n}f_{n}\in M^{!}(4D_{0})$
. This proves part (2).◻
$f-\sum c_{n}f_{n}\in M^{!}(4D_{0})$
. This proves part (2).◻
Proposition 28. For
![]() $(D,N)$
in Theorem 1 with odd
$(D,N)$
in Theorem 1 with odd
![]() $D$
and squarefree
$D$
and squarefree
![]() $N$
, the space
$N$
, the space
 $M^{!,!}(4D_{0})$
is spanned by admissible eta products. Moreover, if
$M^{!,!}(4D_{0})$
is spanned by admissible eta products. Moreover, if
 $f(\unicode[STIX]{x1D70F})\in M^{!,!}(4D_{0})\cap \mathbb{Q}((q))$
, then
$f(\unicode[STIX]{x1D70F})\in M^{!,!}(4D_{0})\cap \mathbb{Q}((q))$
, then
 $$\begin{eqnarray}\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}(f|_{1/2}S)(\unicode[STIX]{x1D70F})\in \mathbb{Q}((q^{1/(4D_{0})})).\end{eqnarray}$$
$$\begin{eqnarray}\frac{e^{2\unicode[STIX]{x1D70B}i/8}}{\sqrt{|L^{\vee }/L|}}(f|_{1/2}S)(\unicode[STIX]{x1D70F})\in \mathbb{Q}((q^{1/(4D_{0})})).\end{eqnarray}$$
Proof. Suppose that we can find an eta product
![]() $t(\unicode[STIX]{x1D70F})$
such that
$t(\unicode[STIX]{x1D70F})$
such that
![]() $t(\unicode[STIX]{x1D70F})$
is a modular function on
$t(\unicode[STIX]{x1D70F})$
is a modular function on
 $X_{0}(4D_{0})$
with a unique pole at
$X_{0}(4D_{0})$
with a unique pole at
![]() $\infty$
. Let
$\infty$
. Let
![]() $k$
be the order of pole of
$k$
be the order of pole of
![]() $t(\unicode[STIX]{x1D70F})$
at
$t(\unicode[STIX]{x1D70F})$
at
![]() $\infty$
. Then
$\infty$
. Then
 $t(-1/(4D_{0}\unicode[STIX]{x1D70F}))$
is a modular function on
$t(-1/(4D_{0}\unicode[STIX]{x1D70F}))$
is a modular function on
 $X_{0}(4D_{0})$
with a unique pole of order
$X_{0}(4D_{0})$
with a unique pole of order
![]() $k$
at zero. Let
$k$
at zero. Let
![]() $g$
be the genus of
$g$
be the genus of
 $X_{0}(4D_{0})$
and
$X_{0}(4D_{0})$
and
![]() $m$
be an integer with
$m$
be an integer with
 $m\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
. By Lemma 27, for each positive integer
$m\geqslant 2g-2-\sum _{d|D_{0}}\lfloor d/4\rfloor$
. By Lemma 27, for each positive integer
![]() $j$
, there exist a modular form in
$j$
, there exist a modular form in
 $M_{m,j}^{!,!}(4D_{0})$
with a pole of order
$M_{m,j}^{!,!}(4D_{0})$
with a pole of order
![]() $j$
at zero. It follows that
$j$
at zero. It follows that
 $$\begin{eqnarray}M_{m,n+k}^{!,!}(4D_{0})=M_{m,n}^{!,!}(4D_{0})+t(-1/4D_{0}\unicode[STIX]{x1D70F})M_{m,n}^{!,!}(4D_{0}).\end{eqnarray}$$
$$\begin{eqnarray}M_{m,n+k}^{!,!}(4D_{0})=M_{m,n}^{!,!}(4D_{0})+t(-1/4D_{0}\unicode[STIX]{x1D70F})M_{m,n}^{!,!}(4D_{0}).\end{eqnarray}$$
Thus, to prove the proposition, it suffices to show that:
-
(i) there exists an eta product
 $t(\unicode[STIX]{x1D70F})$
such that
$t(\unicode[STIX]{x1D70F})$
such that
 $t(\unicode[STIX]{x1D70F})$
is a modular function on
$t(\unicode[STIX]{x1D70F})$
is a modular function on
 $\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
with a unique pole of at
$\unicode[STIX]{x1D6E4}_{0}(4D_{0})$
with a unique pole of at
 $\infty$
;
$\infty$
; -
(ii) admissible eta products span
 $M^{!}(4D_{0})$
; and
$M^{!}(4D_{0})$
; and -
(iii) admissible eta products span
 $M_{m,k}^{!,!}(4D_{0})$
, where
$M_{m,k}^{!,!}(4D_{0})$
, where
 $k$
is the order of pole of
$k$
is the order of pole of
 $t(\unicode[STIX]{x1D70F})$
at
$t(\unicode[STIX]{x1D70F})$
at
 $\infty$
.
$\infty$
.
For conditions (i) and (ii), the integer programming problem involved in the construction of
![]() $t(\unicode[STIX]{x1D70F})$
and admissible eta products is the same as that in Proposition 18. For condition (iii), the integer programming problem is slightly different. For the case
$t(\unicode[STIX]{x1D70F})$
and admissible eta products is the same as that in Proposition 18. For condition (iii), the integer programming problem is slightly different. For the case
![]() $D_{0}=p$
is a prime, instead of (8), we have
$D_{0}=p$
is a prime, instead of (8), we have
 $$\begin{eqnarray}\begin{array}{@{}rcrcrcrcrcrcl@{}}r_{1} & + & 2r_{2} & + & 4r_{4} & + & pr_{p} & + & 2pr_{2p} & + & 4pr_{4p} & {\geqslant} & -24m\\ r_{1} & + & 2r_{2} & + & r_{4} & + & pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ 4r_{1} & + & 2r_{2} & + & r_{4} & + & 4pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & 4pr_{4} & + & r_{p} & + & 2r_{2p} & + & 4r_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & pr_{4} & + & r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & 0\\ 4pr_{1} & + & 2pr_{2} & + & pr_{4} & + & 4r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & -24k\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcrcrcrcrcrcl@{}}r_{1} & + & 2r_{2} & + & 4r_{4} & + & pr_{p} & + & 2pr_{2p} & + & 4pr_{4p} & {\geqslant} & -24m\\ r_{1} & + & 2r_{2} & + & r_{4} & + & pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ 4r_{1} & + & 2r_{2} & + & r_{4} & + & 4pr_{p} & + & 2pr_{2p} & + & pr_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & 4pr_{4} & + & r_{p} & + & 2r_{2p} & + & 4r_{4p} & {\geqslant} & 0\\ pr_{1} & + & 2pr_{2} & + & pr_{4} & + & r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & 0\\ 4pr_{1} & + & 2pr_{2} & + & pr_{4} & + & 4r_{p} & + & 2r_{2p} & + & r_{4p} & {\geqslant} & -24k\end{array}\end{eqnarray}$$
where the last inequality corresponds to the condition that the order of the pole at zero is at most
![]() $k$
. After setting up the integer programming problems, we check case by case that admissible eta products do expand
$k$
. After setting up the integer programming problems, we check case by case that admissible eta products do expand
 $M^{!,!}(4D_{0})$
.
$M^{!,!}(4D_{0})$
.
Since every modular form
![]() $f(\unicode[STIX]{x1D70F})$
in
$f(\unicode[STIX]{x1D70F})$
in
 $M^{!,!}(4D_{0})\cap \mathbb{Q}((q))$
is a
$M^{!,!}(4D_{0})\cap \mathbb{Q}((q))$
is a
![]() $\mathbb{Q}$
-linear combination of admissible eta products, the assertion about rationality of Fourier coefficients of
$\mathbb{Q}$
-linear combination of admissible eta products, the assertion about rationality of Fourier coefficients of
![]() $f|_{1/2}S$
follows from Lemma 26.◻
$f|_{1/2}S$
follows from Lemma 26.◻
Example 29. Consider the Shimura curve
 $X_{0}^{15}(1)/W_{15,1}$
. We have
$X_{0}^{15}(1)/W_{15,1}$
. We have
 $|L^{\vee }/L|=450$
and the level of the lattice
$|L^{\vee }/L|=450$
and the level of the lattice
![]() $L$
is
$L$
is
![]() $60$
. By solving the relevant integer programming problem, we find that
$60$
. By solving the relevant integer programming problem, we find that
 $$\begin{eqnarray}t(\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(20\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})^{3}}{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})^{6}}=q^{-8}-q^{-6}+q^{-4}+q^{-2}+q^{4}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}t(\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(20\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})^{3}}{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})^{6}}=q^{-8}-q^{-6}+q^{-4}+q^{-2}+q^{4}+\cdots \,.\end{eqnarray}$$
is a modular function on
![]() $\unicode[STIX]{x1D6E4}_{0}(60)$
with a unique pole of order eight at
$\unicode[STIX]{x1D6E4}_{0}(60)$
with a unique pole of order eight at
![]() $\infty$
. Also, the genus of
$\infty$
. Also, the genus of
![]() $X_{0}(60)$
is seven. By Lemma 17, the number of gaps of
$X_{0}(60)$
is seven. By Lemma 17, the number of gaps of
![]() $M^{!}(60)$
is three, and for
$M^{!}(60)$
is three, and for
![]() $n\geqslant 8$
, we have
$n\geqslant 8$
, we have
 $\dim M_{n}^{!}(60)=n-2$
. According to the proof of Proposition 18, we should find an integer
$\dim M_{n}^{!}(60)=n-2$
. According to the proof of Proposition 18, we should find an integer
![]() $n_{0}$
such that
$n_{0}$
such that
 $M_{n_{0}+8}^{!}(60)$
is spanned by eta products and for each integer
$M_{n_{0}+8}^{!}(60)$
is spanned by eta products and for each integer
![]() $j$
with
$j$
with
 $n_{0}<j\leqslant n_{0}+8$
, there exists a modular form in
$n_{0}<j\leqslant n_{0}+8$
, there exists a modular form in
 $M_{n_{0}+8}^{!}(60)$
with a pole of order
$M_{n_{0}+8}^{!}(60)$
with a pole of order
![]() $j$
at
$j$
at
![]() $\infty$
. It turns out that we can choose
$\infty$
. It turns out that we can choose
![]() $n_{0}=3$
. (In other words, we will see that the gaps are
$n_{0}=3$
. (In other words, we will see that the gaps are
![]() $1,2,3$
.)
$1,2,3$
.)
For convenience, we let
 $(r_{1},r_{2},r_{3},r_{4},r_{5},r_{6},r_{10},r_{12},r_{15},r_{20},r_{30},r_{60})$
represents the eta product
$(r_{1},r_{2},r_{3},r_{4},r_{5},r_{6},r_{10},r_{12},r_{15},r_{20},r_{30},r_{60})$
represents the eta product
 $\prod _{d|60}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
. By solving the integer programming program, we find that there are at least
$\prod _{d|60}\unicode[STIX]{x1D702}(d\unicode[STIX]{x1D70F})^{r_{d}}$
. By solving the integer programming program, we find that there are at least
![]() $96$
eta products in
$96$
eta products in
 $M_{11}^{!}(60)$
. Among them, we choose
$M_{11}^{!}(60)$
. Among them, we choose
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}f_{11}\ & =\ & (0,1,0,-1,-1,-1,0,2,5,2,1,-7),\quad & f_{10}\ & =\ & (0,0,-1,0,2,1,0,1,1,1,2,-6),\\ f_{9}\ & =\ & (0,0,-1,0,-1,2,-1,0,2,3,4,-7),\quad & f_{8}\ & =\ & (0,0,-1,1,-2,0,1,1,5,1,0,-5),\\ f_{7}\ & =\ & (0,1,1,-1,2,-1,-2,1,-1,3,3,-5),\quad & f_{6}\ & =\ & (0,1,0,-1,0,-1,0,2,2,1,1,-4),\\ f_{5}\ & =\ & (0,0,-1,0,-1,1,2,1,2,0,0,-3),\quad & f_{4}\ & =\ & (0,0,-1,0,0,2,-1,0,-1,2,4,-4),\\ f_{0}\ & =\ & (-2,5,0,-2,0,0,0,0,0,0,0,0).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}f_{11}\ & =\ & (0,1,0,-1,-1,-1,0,2,5,2,1,-7),\quad & f_{10}\ & =\ & (0,0,-1,0,2,1,0,1,1,1,2,-6),\\ f_{9}\ & =\ & (0,0,-1,0,-1,2,-1,0,2,3,4,-7),\quad & f_{8}\ & =\ & (0,0,-1,1,-2,0,1,1,5,1,0,-5),\\ f_{7}\ & =\ & (0,1,1,-1,2,-1,-2,1,-1,3,3,-5),\quad & f_{6}\ & =\ & (0,1,0,-1,0,-1,0,2,2,1,1,-4),\\ f_{5}\ & =\ & (0,0,-1,0,-1,1,2,1,2,0,0,-3),\quad & f_{4}\ & =\ & (0,0,-1,0,0,2,-1,0,-1,2,4,-4),\\ f_{0}\ & =\ & (-2,5,0,-2,0,0,0,0,0,0,0,0).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
They form a basis for
 $M_{11}^{!}(60)$
. (The subscripts are the orders of poles at
$M_{11}^{!}(60)$
. (The subscripts are the orders of poles at
![]() $\infty$
.) Then multiplying those modular forms by suitable powers of
$\infty$
.) Then multiplying those modular forms by suitable powers of
![]() $t(\unicode[STIX]{x1D70F})$
, we get, for each a non-gap integer
$t(\unicode[STIX]{x1D70F})$
, we get, for each a non-gap integer
![]() $j>0$
, a modular form in
$j>0$
, a modular form in
 $M^{!}(60)\cap \mathbb{Z}((q))$
with a unique pole of order
$M^{!}(60)\cap \mathbb{Z}((q))$
with a unique pole of order
![]() $j$
at
$j$
at
![]() $\infty$
and a leading coefficient of one.
$\infty$
and a leading coefficient of one.
Furthermore, we find that there are at least
![]() $102$
eta products in
$102$
eta products in
 $M_{3,8}^{!,!}(60)$
. Among them, we choose
$M_{3,8}^{!,!}(60)$
. Among them, we choose
 $$\begin{eqnarray}\displaystyle g_{1}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})^{2}}=q^{-3}+2q^{-2}+4q^{-1}+\cdots \,,\nonumber\\ \displaystyle g_{2}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(20\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+3q^{-1}+5+8q+\cdots \,,\nonumber\\ \displaystyle g_{3}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(20\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+2q^{-1}+5+10q+18q^{2}+\cdots \,,\nonumber\\ \displaystyle g_{4}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-1}+4+11q+24q^{2}+\cdots \,,\nonumber\\ \displaystyle g_{5}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+5q^{-1}+15+39q+90q^{2}+\cdots \,,\nonumber\\ \displaystyle g_{6}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+5q^{-1}+17+48q+\cdots \,,\nonumber\\ \displaystyle g_{7}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})}=1+5q+18q^{2}+54q^{3}+\cdots \,,\nonumber\\ \displaystyle g_{8}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-1}+6+23q+72q^{2}+\cdots \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{1}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})^{2}}=q^{-3}+2q^{-2}+4q^{-1}+\cdots \,,\nonumber\\ \displaystyle g_{2}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(20\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+3q^{-1}+5+8q+\cdots \,,\nonumber\\ \displaystyle g_{3}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(20\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+2q^{-1}+5+10q+18q^{2}+\cdots \,,\nonumber\\ \displaystyle g_{4}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-1}+4+11q+24q^{2}+\cdots \,,\nonumber\\ \displaystyle g_{5}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+5q^{-1}+15+39q+90q^{2}+\cdots \,,\nonumber\\ \displaystyle g_{6}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{2}}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-2}+5q^{-1}+17+48q+\cdots \,,\nonumber\\ \displaystyle g_{7}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{5}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})}=1+5q+18q^{2}+54q^{3}+\cdots \,,\nonumber\\ \displaystyle g_{8}(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{4}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(12\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(4\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(60\unicode[STIX]{x1D70F})}=q^{-1}+6+23q+72q^{2}+\cdots \nonumber\end{eqnarray}$$
of weight
![]() $1/2$
on
$1/2$
on
![]() $\unicode[STIX]{x1D6E4}_{0}(60)$
. By Lemma 26,
$\unicode[STIX]{x1D6E4}_{0}(60)$
. By Lemma 26,
 $$\begin{eqnarray}\displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{1}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{2}{3}(q^{-2/60}+2q^{-1/60}+4+8q^{1/60}+14q^{2/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{2}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle q^{-2/60}+q^{-1/60}+2+4q^{1/60}+6q^{2/60}+8q^{3/60}+\cdots \,,\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{3}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle 2(q^{-3/60}+q^{-2/60}+2q^{-1/60}+4+6q^{1/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{4}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle 2(q^{-4/60}+q^{-3/60}+q^{-2/60}+2q^{-1/60}+3+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{5}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle q^{-5/60}+q^{-4/60}+2q^{-3/60}+3q^{-2/60}+5q^{-1/60}+\cdots \,,\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{6}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{2}{3}(q^{-6/60}+q^{-5/60}+2q^{-4/60}+3q^{-3/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{7}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{1}{5}(q^{-7/60}+q^{-3/60}+q^{-2/60}+2q^{1/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{8}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{2}{15}(q^{-8/60}+q^{-7/60}+2q^{-6/60}+3q^{-5/60}+\cdots \,).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{1}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{2}{3}(q^{-2/60}+2q^{-1/60}+4+8q^{1/60}+14q^{2/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{2}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle q^{-2/60}+q^{-1/60}+2+4q^{1/60}+6q^{2/60}+8q^{3/60}+\cdots \,,\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{3}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle 2(q^{-3/60}+q^{-2/60}+2q^{-1/60}+4+6q^{1/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{4}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle 2(q^{-4/60}+q^{-3/60}+q^{-2/60}+2q^{-1/60}+3+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{5}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle q^{-5/60}+q^{-4/60}+2q^{-3/60}+3q^{-2/60}+5q^{-1/60}+\cdots \,,\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{6}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{2}{3}(q^{-6/60}+q^{-5/60}+2q^{-4/60}+3q^{-3/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{7}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{1}{5}(q^{-7/60}+q^{-3/60}+q^{-2/60}+2q^{1/60}+\cdots \,),\nonumber\\ \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(g_{8}|S)(\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{2}{15}(q^{-8/60}+q^{-7/60}+2q^{-6/60}+3q^{-5/60}+\cdots \,).\nonumber\end{eqnarray}$$
Thus, letting
 $$\begin{eqnarray}h_{1}=3g_{1}/2-g_{2},\quad h_{2}=g_{2},\quad h_{3}=g_{3}/2,\quad h_{4}=g_{4}/2,\end{eqnarray}$$
$$\begin{eqnarray}h_{1}=3g_{1}/2-g_{2},\quad h_{2}=g_{2},\quad h_{3}=g_{3}/2,\quad h_{4}=g_{4}/2,\end{eqnarray}$$
and
 $$\begin{eqnarray}h_{5}=g_{5},\quad h_{6}=3g_{6}/2,\quad h_{7}=5g_{7},\quad h_{8}=15g_{8}/2,\end{eqnarray}$$
$$\begin{eqnarray}h_{5}=g_{5},\quad h_{6}=3g_{6}/2,\quad h_{7}=5g_{7},\quad h_{8}=15g_{8}/2,\end{eqnarray}$$
we get a sequence
![]() $h_{j}$
,
$h_{j}$
,
 $j=1,\ldots ,8$
, of modular forms such that
$j=1,\ldots ,8$
, of modular forms such that
 $$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h_{j}|S)(\unicode[STIX]{x1D70F})=q^{-j/60}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h_{j}|S)(\unicode[STIX]{x1D70F})=q^{-j/60}+\cdots \,.\end{eqnarray}$$
Now we have
 $$\begin{eqnarray}t(-1/60\unicode[STIX]{x1D70F})=5\frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})^{2}}=5+30q+120q^{2}+390q^{3}+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}t(-1/60\unicode[STIX]{x1D70F})=5\frac{\unicode[STIX]{x1D702}(2\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{2}\unicode[STIX]{x1D702}(5\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(30\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(6\unicode[STIX]{x1D70F})\unicode[STIX]{x1D702}(10\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(15\unicode[STIX]{x1D70F})^{2}}=5+30q+120q^{2}+390q^{3}+\cdots \,,\end{eqnarray}$$
which is a modular function on
![]() $\unicode[STIX]{x1D6E4}_{0}(60)$
having a unique pole of order eight at the cusp zero. Thus, by multiplying
$\unicode[STIX]{x1D6E4}_{0}(60)$
having a unique pole of order eight at the cusp zero. Thus, by multiplying
![]() $h_{j}$
with suitable powers of
$h_{j}$
with suitable powers of
 $t(-1/60\unicode[STIX]{x1D70F})$
, we get, for each positive integer
$t(-1/60\unicode[STIX]{x1D70F})$
, we get, for each positive integer
![]() $m$
, an
$m$
, an
![]() $\{\infty ,0\}$
-weakly holomorphic modular form
$\{\infty ,0\}$
-weakly holomorphic modular form
![]() $h_{m}$
whose order of pole at
$h_{m}$
whose order of pole at
![]() $\infty$
is bounded by three, while
$\infty$
is bounded by three, while
 $$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h_{m}|S)(\unicode[STIX]{x1D70F})=q^{-m/60}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h_{m}|S)(\unicode[STIX]{x1D70F})=q^{-m/60}+\cdots \,.\end{eqnarray}$$
Remark 30. We expect that, as in the case of even
![]() $D$
, for
$D$
, for
![]() $(D,N)$
in Theorem 1 with odd
$(D,N)$
in Theorem 1 with odd
![]() $D$
and squarefree
$D$
and squarefree
![]() $N$
, all meromorphic modular forms of even weights on
$N$
, all meromorphic modular forms of even weights on
 $X_{0}^{D}(N)/W_{D,N}$
with a divisor supported on CM divisors can be realized as a Borcherds form. However, a proof along the line of that of Proposition 23 will be a little complicated because the Fourier expansions at zero of a modular form in
$X_{0}^{D}(N)/W_{D,N}$
with a divisor supported on CM divisors can be realized as a Borcherds form. However, a proof along the line of that of Proposition 23 will be a little complicated because the Fourier expansions at zero of a modular form in
 $M^{!,!}(4D_{0})\cap \mathbb{Z}((q))$
may not be integral.
$M^{!,!}(4D_{0})\cap \mathbb{Z}((q))$
may not be integral.
Example 31. Here we give an example showing how to construct a Borcherds form with a desired divisor on
 $X_{0}^{15}(1)/W_{15,1}$
using modular forms in
$X_{0}^{15}(1)/W_{15,1}$
using modular forms in
 $M^{!,!}(60)$
.
$M^{!,!}(60)$
.
Suppose that we wish to construct a Borcherds form with a divisor
 $P_{-12}-P_{-3}$
. For a positive integer
$P_{-12}-P_{-3}$
. For a positive integer
![]() $j$
, we let
$j$
, we let
![]() $h_{j}$
be the modular form in
$h_{j}$
be the modular form in
 $M^{!,!}(60)$
constructed in Example 29 with the properties that its order of pole at
$M^{!,!}(60)$
constructed in Example 29 with the properties that its order of pole at
![]() $\infty$
is bounded by three and
$\infty$
is bounded by three and
 $$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h_{j}|S)(\unicode[STIX]{x1D70F})=q^{-j/60}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h_{j}|S)(\unicode[STIX]{x1D70F})=q^{-j/60}+\cdots \,.\end{eqnarray}$$
A suitable linear combination of these
![]() $h_{m}$
will yield a function
$h_{m}$
will yield a function
![]() $h$
with
$h$
with
 $$\begin{eqnarray}h(\unicode[STIX]{x1D70F})=q^{-2}+11+\cdots \,,\quad \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h|S)(\unicode[STIX]{x1D70F})=2q^{-3/4}+4q^{1/60}+4q^{2/60}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}h(\unicode[STIX]{x1D70F})=q^{-2}+11+\cdots \,,\quad \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(h|S)(\unicode[STIX]{x1D70F})=2q^{-3/4}+4q^{1/60}+4q^{2/60}+\cdots \,.\end{eqnarray}$$
By Lemma 25,
 $$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{F_{h}}={\textstyle \frac{1}{3}}P_{-3}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{F_{h}}={\textstyle \frac{1}{3}}P_{-3}.\end{eqnarray}$$
Let
 $$\begin{eqnarray}f=f_{8}-f_{5}+f_{4}=q^{-8}+2q^{-3}+q^{-2}+2q^{2}+\cdots\end{eqnarray}$$
$$\begin{eqnarray}f=f_{8}-f_{5}+f_{4}=q^{-8}+2q^{-3}+q^{-2}+2q^{2}+\cdots\end{eqnarray}$$
where
![]() $f_{j}$
are as given in Example 29. By Lemma 25,
$f_{j}$
are as given in Example 29. By Lemma 25,
 $$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=P_{-12}+{\textstyle \frac{1}{3}}P_{-3}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{F_{f}}=P_{-12}+{\textstyle \frac{1}{3}}P_{-3}.\end{eqnarray}$$
Therefore, we find that
![]() $\unicode[STIX]{x1D713}_{F_{f-4h}}$
is a Borcherds form with a divisor
$\unicode[STIX]{x1D713}_{F_{f-4h}}$
is a Borcherds form with a divisor
 $P_{-12}-P_{-3}$
.
$P_{-12}-P_{-3}$
.
4 Equations of hyperelliptic Shimura curves
Recall that a compact Riemann surface
![]() $X$
of genus at least two is hyperelliptic if and only if there exists a double covering
$X$
of genus at least two is hyperelliptic if and only if there exists a double covering
 $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}(\mathbb{C})$
or, equivalently, if there exists an involution
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}(\mathbb{C})$
or, equivalently, if there exists an involution
 $w:X\rightarrow X$
such that
$w:X\rightarrow X$
such that
![]() $X/w$
has genus zero. The involution
$X/w$
has genus zero. The involution
![]() $w$
is unique and is called the hyperelliptic involution.
$w$
is unique and is called the hyperelliptic involution.
Theorem C [Reference OggOgg83, Theorems 7 and 8].
Let
 $g(D,N)$
denote the genus of
$g(D,N)$
denote the genus of
 $X_{0}^{D}(N)$
. Table 1 gives the full list of hyperelliptic Shimura curves,
$X_{0}^{D}(N)$
. Table 1 gives the full list of hyperelliptic Shimura curves,
![]() $D>1$
, and their hyperelliptic involutions.
$D>1$
, and their hyperelliptic involutions.
Table 1. List of hyperelliptic Shimura curves and their hyperelliptic involutions.

4.1 Method
Let us briefly explain our method to compute equations of these hyperelliptic Shimura curves. Before doing that, we remark that in addition to Borcherds forms and Schofer’s formula, arithmetic properties of CM points are also crucial in our computation. We refer the reader to [Reference González and RotgerGR06, §5] for an explicit description of the Shimura reciprocity law.
Let
 $X_{0}^{D}(N)$
be one of the curves in Ogg’s list. Since the hyperelliptic involution of
$X_{0}^{D}(N)$
be one of the curves in Ogg’s list. Since the hyperelliptic involution of
![]() $X_{0}^{D}(N)$
is an Atkin–Lehner involution, the genus of
$X_{0}^{D}(N)$
is an Atkin–Lehner involution, the genus of
 $X_{0}^{D}(N)/W_{D,N}$
is necessarily zero. Moreover, it turns out that any of these
$X_{0}^{D}(N)/W_{D,N}$
is necessarily zero. Moreover, it turns out that any of these
 $X_{0}^{D}(N)/W_{D,N}$
has at least three rational CM points
$X_{0}^{D}(N)/W_{D,N}$
has at least three rational CM points
![]() $\unicode[STIX]{x1D70F}_{1}$
,
$\unicode[STIX]{x1D70F}_{1}$
,
![]() $\unicode[STIX]{x1D70F}_{2}$
and
$\unicode[STIX]{x1D70F}_{2}$
and
![]() $\unicode[STIX]{x1D70F}_{3}$
of discriminants
$\unicode[STIX]{x1D70F}_{3}$
of discriminants
![]() $d_{1}$
,
$d_{1}$
,
![]() $d_{2}$
and
$d_{2}$
and
![]() $d_{3}$
, respectively. Thus, there is a Hauptmodul
$d_{3}$
, respectively. Thus, there is a Hauptmodul
![]() $s(\unicode[STIX]{x1D70F})$
on
$s(\unicode[STIX]{x1D70F})$
on
 $X_{0}^{D}(N)/W_{D,N}$
with
$X_{0}^{D}(N)/W_{D,N}$
with
 $s(\unicode[STIX]{x1D70F}_{1})=\infty$
,
$s(\unicode[STIX]{x1D70F}_{1})=\infty$
,
 $s(\unicode[STIX]{x1D70F}_{2})=0$
and
$s(\unicode[STIX]{x1D70F}_{2})=0$
and
 $s(\unicode[STIX]{x1D70F}_{3})\in \mathbb{Q}$
.
$s(\unicode[STIX]{x1D70F}_{3})\in \mathbb{Q}$
.
Let
![]() $W$
be a subgroup of index two of
$W$
be a subgroup of index two of
![]() $W_{D,N}$
. Suppose that
$W_{D,N}$
. Suppose that
![]() $w_{m}$
is an element of
$w_{m}$
is an element of
![]() $W_{D,N}$
not in
$W_{D,N}$
not in
![]() $W$
. Then
$W$
. Then
 $X_{0}^{D}(N)/W\rightarrow X_{0}^{D}(N)/W_{D,N}$
is a double cover ramified at certain CM points that are fixed points of the Atkin–Lehner involutions
$X_{0}^{D}(N)/W\rightarrow X_{0}^{D}(N)/W_{D,N}$
is a double cover ramified at certain CM points that are fixed points of the Atkin–Lehner involutions
 $w_{mn/\text{gcd}(m,n)^{2}}$
,
$w_{mn/\text{gcd}(m,n)^{2}}$
,
 $w_{n}\in W$
. Thus, an equation of
$w_{n}\in W$
. Thus, an equation of
 $X_{0}^{D}(N)/W$
is
$X_{0}^{D}(N)/W$
is
 $$\begin{eqnarray}y^{2}=a\mathop{\prod }_{\unicode[STIX]{x1D70F}\,\text{ramified},s(\unicode[STIX]{x1D70F})\neq \infty }(s-s(\unicode[STIX]{x1D70F})),\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=a\mathop{\prod }_{\unicode[STIX]{x1D70F}\,\text{ramified},s(\unicode[STIX]{x1D70F})\neq \infty }(s-s(\unicode[STIX]{x1D70F})),\end{eqnarray}$$
where
![]() $a$
is a rational number depending on the arithmetic of
$a$
is a rational number depending on the arithmetic of
 $X_{0}^{D}(N)/W$
. Specifically,
$X_{0}^{D}(N)/W$
. Specifically,
![]() $a$
must be a rational number such that
$a$
must be a rational number such that
 $(a\prod _{\unicode[STIX]{x1D70F}\text{ramified}}(-s(\unicode[STIX]{x1D70F})))^{1/2}$
is in the field of definition of a CM point of discriminant
$(a\prod _{\unicode[STIX]{x1D70F}\text{ramified}}(-s(\unicode[STIX]{x1D70F})))^{1/2}$
is in the field of definition of a CM point of discriminant
![]() $d_{2}$
on
$d_{2}$
on
 $X_{0}^{D}(N)/W$
. As an additional check, note that when
$X_{0}^{D}(N)/W$
. As an additional check, note that when
![]() $\unicode[STIX]{x1D70F}_{1}$
is not a ramified point, the right-hand side of (12) is a polynomial of even degree and
$\unicode[STIX]{x1D70F}_{1}$
is not a ramified point, the right-hand side of (12) is a polynomial of even degree and
![]() $a$
must be a rational number such that
$a$
must be a rational number such that
![]() $\sqrt{a}$
is in the field of definition of a CM point of discriminant
$\sqrt{a}$
is in the field of definition of a CM point of discriminant
![]() $d_{1}$
on
$d_{1}$
on
 $X_{0}^{D}(N)/W$
.
$X_{0}^{D}(N)/W$
.
To determine the coefficients of the polynomial on the right-hand side of (12), we simply have to know the values of
![]() $s$
and
$s$
and
![]() $y^{2}$
at sufficiently many points. For this purpose, we observe that
$y^{2}$
at sufficiently many points. For this purpose, we observe that
![]() $s$
and
$s$
and
![]() $y^{2}$
are both modular functions on
$y^{2}$
are both modular functions on
 $X_{0}^{D}(N)/W_{D,N}$
with divisors supported on CM divisors. Thus, they are both realizable as Borcherds forms. (This is proved in Proposition 23 for the case of even
$X_{0}^{D}(N)/W_{D,N}$
with divisors supported on CM divisors. Thus, they are both realizable as Borcherds forms. (This is proved in Proposition 23 for the case of even
![]() $D$
. We do not try to give a proof for the case of odd
$D$
. We do not try to give a proof for the case of odd
![]() $D$
, but, in practice, we are always able to realize modular forms encountered as Borcherds forms.) Then Schofer’s formula gives us the absolute values of norms of values of
$D$
, but, in practice, we are always able to realize modular forms encountered as Borcherds forms.) Then Schofer’s formula gives us the absolute values of norms of values of
![]() $s$
and
$s$
and
![]() $y^{2}$
at CM points.
$y^{2}$
at CM points.
In order to obtain the actual values of
![]() $s$
, not just the absolute values, we let
$s$
, not just the absolute values, we let
![]() $\widetilde{s}$
be another Hauptmodul with
$\widetilde{s}$
be another Hauptmodul with
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{1})=\infty$
,
$\widetilde{s}(\unicode[STIX]{x1D70F}_{1})=\infty$
,
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{3})=0$
and
$\widetilde{s}(\unicode[STIX]{x1D70F}_{3})=0$
and
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{2})\in \mathbb{Q}$
. We may also realize
$\widetilde{s}(\unicode[STIX]{x1D70F}_{2})\in \mathbb{Q}$
. We may also realize
![]() $\widetilde{s}$
as a Borcherds form. Then the absolute values of
$\widetilde{s}$
as a Borcherds form. Then the absolute values of
![]() $s(\unicode[STIX]{x1D70F}_{3})$
and
$s(\unicode[STIX]{x1D70F}_{3})$
and
![]() $\widetilde{s}(\unicode[STIX]{x1D70F}_{2})$
obtained using Schofer’s formula determine the relation
$\widetilde{s}(\unicode[STIX]{x1D70F}_{2})$
obtained using Schofer’s formula determine the relation
 $\widetilde{s}=bs+c$
between
$\widetilde{s}=bs+c$
between
![]() $s$
and
$s$
and
![]() $\widetilde{s}$
. If
$\widetilde{s}$
. If
![]() $d$
is a discriminant such that there is only one CM point
$d$
is a discriminant such that there is only one CM point
![]() $\unicode[STIX]{x1D70F}_{d}$
of discriminant
$\unicode[STIX]{x1D70F}_{d}$
of discriminant
![]() $d$
, then knowing the values of
$d$
, then knowing the values of
![]() $|s(\unicode[STIX]{x1D70F}_{d})|$
and
$|s(\unicode[STIX]{x1D70F}_{d})|$
and
 $|\widetilde{s}(\unicode[STIX]{x1D70F}_{d})|=|bs(\unicode[STIX]{x1D70F}_{d})+c|$
from Schofer’s formula is enough to determine the value of
$|\widetilde{s}(\unicode[STIX]{x1D70F}_{d})|=|bs(\unicode[STIX]{x1D70F}_{d})+c|$
from Schofer’s formula is enough to determine the value of
![]() $s(\unicode[STIX]{x1D70F}_{d})$
. If there are two CM points
$s(\unicode[STIX]{x1D70F}_{d})$
. If there are two CM points
![]() $\unicode[STIX]{x1D70F}_{d}$
and
$\unicode[STIX]{x1D70F}_{d}$
and
![]() $\unicode[STIX]{x1D70F}_{d}^{\prime }$
of discriminant
$\unicode[STIX]{x1D70F}_{d}^{\prime }$
of discriminant
![]() $d$
, then from the values of
$d$
, then from the values of
 $|s(\unicode[STIX]{x1D70F}_{d})s(\unicode[STIX]{x1D70F}_{d}^{\prime })|$
and
$|s(\unicode[STIX]{x1D70F}_{d})s(\unicode[STIX]{x1D70F}_{d}^{\prime })|$
and
 $|(bs(\unicode[STIX]{x1D70F}_{d})+c)(bs(\unicode[STIX]{x1D70F}_{d}^{\prime })+c)|$
we get four possible candidates for the minimal polynomial of
$|(bs(\unicode[STIX]{x1D70F}_{d})+c)(bs(\unicode[STIX]{x1D70F}_{d}^{\prime })+c)|$
we get four possible candidates for the minimal polynomial of
![]() $s(\unicode[STIX]{x1D70F}_{d})$
. In almost all cases we consider, there is precisely one of the four candidates that have roots in the correct field. This gives us the values of
$s(\unicode[STIX]{x1D70F}_{d})$
. In almost all cases we consider, there is precisely one of the four candidates that have roots in the correct field. This gives us the values of
![]() $s(\unicode[STIX]{x1D70F}_{d})$
and
$s(\unicode[STIX]{x1D70F}_{d})$
and
![]() $s(\unicode[STIX]{x1D70F}_{d}^{\prime })$
. In practice, we do not need information from discriminants with more than two CM points.
$s(\unicode[STIX]{x1D70F}_{d}^{\prime })$
. In practice, we do not need information from discriminants with more than two CM points.
The determination of values of
![]() $y^{2}$
from absolute values is easier. For example, when
$y^{2}$
from absolute values is easier. For example, when
![]() $d$
is a discriminant such that there is only one CM point of discriminant
$d$
is a discriminant such that there is only one CM point of discriminant
![]() $d$
on
$d$
on
 $X_{0}^{D}(N)/W_{D,N}$
,
$X_{0}^{D}(N)/W_{D,N}$
,
![]() $y(\unicode[STIX]{x1D70F}_{d})$
is either
$y(\unicode[STIX]{x1D70F}_{d})$
is either
 $\sqrt{|y(\unicode[STIX]{x1D70F}_{d})^{2}|}$
or
$\sqrt{|y(\unicode[STIX]{x1D70F}_{d})^{2}|}$
or
 $\sqrt{-|y(\unicode[STIX]{x1D70F}_{d})^{2}|}$
, but only one of them is in the correct field.
$\sqrt{-|y(\unicode[STIX]{x1D70F}_{d})^{2}|}$
, but only one of them is in the correct field.
Having determined values of
![]() $s$
and
$s$
and
![]() $y^{2}$
at sufficiently many CM points, it is straightforward to determine the equation of
$y^{2}$
at sufficiently many CM points, it is straightforward to determine the equation of
 $X_{0}^{D}(N)/W$
. Then we will either work out equations of
$X_{0}^{D}(N)/W$
. Then we will either work out equations of
 $X_{0}^{D}(N)/W^{\prime }$
for various other subgroups
$X_{0}^{D}(N)/W^{\prime }$
for various other subgroups
![]() $W^{\prime }$
of
$W^{\prime }$
of
![]() $W_{D,N}$
of index two or use arithmetic properties of
$W_{D,N}$
of index two or use arithmetic properties of
 $X_{0}^{D}(N)$
to determine equations of
$X_{0}^{D}(N)$
to determine equations of
![]() $X_{0}^{D}(N)$
. We will give several examples in the next section.
$X_{0}^{D}(N)$
. We will give several examples in the next section.
4.2 Examples
Example 32. Consider
![]() $X_{0}^{15}(1)$
. In [Reference JordanJor81, Proposition 3.2.1], it is shown that an equation of
$X_{0}^{15}(1)$
. In [Reference JordanJor81, Proposition 3.2.1], it is shown that an equation of
![]() $X_{0}^{15}(1)$
is
$X_{0}^{15}(1)$
is
 $$\begin{eqnarray}3y^{2}+(x^{2}+3)(x^{2}+243)=0.\end{eqnarray}$$
$$\begin{eqnarray}3y^{2}+(x^{2}+3)(x^{2}+243)=0.\end{eqnarray}$$
In this example, we will use Borcherds forms and Schofer’s formula to obtain this result.
The curve
 $X=X_{0}^{15}(1)$
and its various Atkin–Lehner quotients have the following geometric information.
$X=X_{0}^{15}(1)$
and its various Atkin–Lehner quotients have the following geometric information.

According to the method described in the previous section, we should first determine the equation of
![]() $X/W$
for some subgroup
$X/W$
for some subgroup
![]() $W$
of
$W$
of
![]() $W_{15,1}$
of index two. Here we choose
$W_{15,1}$
of index two. Here we choose
 $W=\langle w_{3}\rangle$
. The double cover
$W=\langle w_{3}\rangle$
. The double cover
 $X/w_{3}\rightarrow X/W_{15,1}$
is ramified at the CM points
$X/w_{3}\rightarrow X/W_{15,1}$
is ramified at the CM points
![]() $\unicode[STIX]{x1D70F}_{-15}$
and
$\unicode[STIX]{x1D70F}_{-15}$
and
![]() $\unicode[STIX]{x1D70F}_{-60}$
of discriminants
$\unicode[STIX]{x1D70F}_{-60}$
of discriminants
![]() $-15$
and
$-15$
and
![]() $-60$
. Let
$-60$
. Let
![]() $s(\unicode[STIX]{x1D70F})$
be a Hauptmodul on
$s(\unicode[STIX]{x1D70F})$
be a Hauptmodul on
 $X/W_{15,1}$
taking values zero and
$X/W_{15,1}$
taking values zero and
![]() $\infty$
at CM points
$\infty$
at CM points
![]() $\unicode[STIX]{x1D70F}_{-12}$
and
$\unicode[STIX]{x1D70F}_{-12}$
and
![]() $\unicode[STIX]{x1D70F}_{-3}$
of discriminants
$\unicode[STIX]{x1D70F}_{-3}$
of discriminants
![]() $-12$
and
$-12$
and
![]() $-3$
, respectively, and satisfying
$-3$
, respectively, and satisfying
 $s(\unicode[STIX]{x1D70F}_{-40})\in \mathbb{Q}$
, where
$s(\unicode[STIX]{x1D70F}_{-40})\in \mathbb{Q}$
, where
![]() $\unicode[STIX]{x1D70F}_{-40}$
is the unique CM point of discriminant
$\unicode[STIX]{x1D70F}_{-40}$
is the unique CM point of discriminant
![]() $-40$
on
$-40$
on
 $X/W_{15,1}$
. Then an equation of
$X/W_{15,1}$
. Then an equation of
![]() $X/w_{3}$
is
$X/w_{3}$
is
 $$\begin{eqnarray}y^{2}=a(s-s(\unicode[STIX]{x1D70F}_{-15}))(s-s(\unicode[STIX]{x1D70F}_{-60})),\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=a(s-s(\unicode[STIX]{x1D70F}_{-15}))(s-s(\unicode[STIX]{x1D70F}_{-60})),\end{eqnarray}$$
where
 $a=-3r^{2}$
for some
$a=-3r^{2}$
for some
![]() $r\in \mathbb{Q}$
since a CM point of discriminant
$r\in \mathbb{Q}$
since a CM point of discriminant
![]() $-3$
on
$-3$
on
![]() $X/w_{3}$
is defined over
$X/w_{3}$
is defined over
 $\mathbb{Q}(\sqrt{-3})$
. The divisor of
$\mathbb{Q}(\sqrt{-3})$
. The divisor of
![]() $y^{2}$
, as a function on
$y^{2}$
, as a function on
 $X/W_{15,1}$
, is
$X/W_{15,1}$
, is
 $P_{-15}+P_{-60}-2P_{-3}$
. Let also
$P_{-15}+P_{-60}-2P_{-3}$
. Let also
![]() $\widetilde{s}$
be a Hauptmodul with
$\widetilde{s}$
be a Hauptmodul with
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=\infty$
,
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=\infty$
,
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{40})=0$
, and
$\widetilde{s}(\unicode[STIX]{x1D70F}_{40})=0$
, and
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-60})\in \mathbb{Q}$
. According to our method, we should construct Borcherds forms with divisors
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-60})\in \mathbb{Q}$
. According to our method, we should construct Borcherds forms with divisors
 $P_{-12}-P_{-3}$
,
$P_{-12}-P_{-3}$
,
 $P_{-40}-P_{-3}$
and
$P_{-40}-P_{-3}$
and
 $P_{-15}+P_{-60}-2P_{-3}$
. A Borcherds form
$P_{-15}+P_{-60}-2P_{-3}$
. A Borcherds form
 $P_{-12}-P_{-3}$
is constructed in Example 31. Denote this Borcherds form by
$P_{-12}-P_{-3}$
is constructed in Example 31. Denote this Borcherds form by
![]() $\unicode[STIX]{x1D713}_{1}$
. Here let us construct the other two Borcherds forms.
$\unicode[STIX]{x1D713}_{1}$
. Here let us construct the other two Borcherds forms.
Using the notation in Example 29 and letting
![]() $h$
be the modular form in (11), we find that
$h$
be the modular form in (11), we find that
 $$\begin{eqnarray}f_{10}-f_{7}+f_{5}-2f_{4}-3h=q^{-10}-3q^{-2}+q^{-1}-35+\cdots\end{eqnarray}$$
$$\begin{eqnarray}f_{10}-f_{7}+f_{5}-2f_{4}-3h=q^{-10}-3q^{-2}+q^{-1}-35+\cdots\end{eqnarray}$$
and
 $$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(f_{10}-f_{7}+f_{5}-2f_{4}-3h)|S=6q^{-3/4}+c_{0}+c_{1}q^{1/60}+\cdots\end{eqnarray}$$
$$\begin{eqnarray}\frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(f_{10}-f_{7}+f_{5}-2f_{4}-3h)|S=6q^{-3/4}+c_{0}+c_{1}q^{1/60}+\cdots\end{eqnarray}$$
for some
![]() $c_{j}$
. Thus, by Lemma 25, the Borcherds form
$c_{j}$
. Thus, by Lemma 25, the Borcherds form
![]() $\unicode[STIX]{x1D713}_{2}$
associated to this modular form has a divisor
$\unicode[STIX]{x1D713}_{2}$
associated to this modular form has a divisor
 $P_{-40}-P_{-3}$
. Also, we have
$P_{-40}-P_{-3}$
. Also, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle 2f_{15}+4f_{13}+2f_{12}-2f_{10}-4f_{9}-7f_{8}-10f_{7}+10f_{6}+3f_{5}-23f_{4}-6h\nonumber\\ \displaystyle & & \displaystyle \quad =2q^{-15}-q^{-8}-5q^{-2}-2q^{-1}-78+\cdots \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2f_{15}+4f_{13}+2f_{12}-2f_{10}-4f_{9}-7f_{8}-10f_{7}+10f_{6}+3f_{5}-23f_{4}-6h\nonumber\\ \displaystyle & & \displaystyle \quad =2q^{-15}-q^{-8}-5q^{-2}-2q^{-1}-78+\cdots \nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(2f_{15}+4f_{13}+2f_{12}-2f_{10}-4f_{9}-7f_{8}-10f_{7}+10f_{6}+3f_{5}-23f_{4}-6h)|S\nonumber\\ \displaystyle & & \displaystyle \quad =12q^{-3/4}+c_{0}^{\prime }+c_{1}^{\prime }q^{1/60}+\cdots \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{60e^{2\unicode[STIX]{x1D70B}i/8}}{15\sqrt{2}}(2f_{15}+4f_{13}+2f_{12}-2f_{10}-4f_{9}-7f_{8}-10f_{7}+10f_{6}+3f_{5}-23f_{4}-6h)|S\nonumber\\ \displaystyle & & \displaystyle \quad =12q^{-3/4}+c_{0}^{\prime }+c_{1}^{\prime }q^{1/60}+\cdots \nonumber\end{eqnarray}$$
for some
![]() $c_{j}^{\prime }$
. Therefore, the Borcherds form
$c_{j}^{\prime }$
. Therefore, the Borcherds form
![]() $\unicode[STIX]{x1D713}_{3}$
associated to this modular form has a divisor
$\unicode[STIX]{x1D713}_{3}$
associated to this modular form has a divisor
 $P_{-15}+P_{-60}-2P_{-3}$
. An application of Schofer’s formula yields the following values of Borcherds forms at CM points.
$P_{-15}+P_{-60}-2P_{-3}$
. An application of Schofer’s formula yields the following values of Borcherds forms at CM points.

Observe that multiplying
![]() $\unicode[STIX]{x1D713}_{j}$
by a scalar of absolute value
$\unicode[STIX]{x1D713}_{j}$
by a scalar of absolute value
![]() $1$
does not change the absolute value of its value at a CM point. Thus, we may as well assume that
$1$
does not change the absolute value of its value at a CM point. Thus, we may as well assume that
 $\unicode[STIX]{x1D713}_{1}(\unicode[STIX]{x1D70F}_{-15})=-3$
,
$\unicode[STIX]{x1D713}_{1}(\unicode[STIX]{x1D70F}_{-15})=-3$
,
 $5^{-3/2}\unicode[STIX]{x1D713}_{2}(\unicode[STIX]{x1D70F}_{-15})=5/27$
and
$5^{-3/2}\unicode[STIX]{x1D713}_{2}(\unicode[STIX]{x1D70F}_{-15})=5/27$
and
 $\unicode[STIX]{x1D713}_{3}(\unicode[STIX]{x1D70F}_{-7})=-35/3^{6}$
. Also, we choose
$\unicode[STIX]{x1D713}_{3}(\unicode[STIX]{x1D70F}_{-7})=-35/3^{6}$
. Also, we choose
![]() $s$
,
$s$
,
![]() $\widetilde{s}$
and
$\widetilde{s}$
and
![]() $y$
such that
$y$
such that
 $s(\unicode[STIX]{x1D70F}_{-15})=-243$
,
$s(\unicode[STIX]{x1D70F}_{-15})=-243$
,
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=5$
and
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=5$
and
 $y(\unicode[STIX]{x1D70F}_{-7})^{2}=-2^{4}3^{4}7$
. Therefore, we have
$y(\unicode[STIX]{x1D70F}_{-7})^{2}=-2^{4}3^{4}7$
. Therefore, we have
 $$\begin{eqnarray}s=81\unicode[STIX]{x1D713}_{1},\quad \widetilde{s}=27\cdot 5^{-3/2}\unicode[STIX]{x1D713}_{2},\quad y^{2}=\frac{2^{4}3^{10}}{5}\unicode[STIX]{x1D713}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}s=81\unicode[STIX]{x1D713}_{1},\quad \widetilde{s}=27\cdot 5^{-3/2}\unicode[STIX]{x1D713}_{2},\quad y^{2}=\frac{2^{4}3^{10}}{5}\unicode[STIX]{x1D713}_{3}.\end{eqnarray}$$
Then from the table above, we obtain
 $$\begin{eqnarray}|s(\unicode[STIX]{x1D70F}_{-12})|=0,\quad |\widetilde{s}(\unicode[STIX]{x1D70F}_{-12})|=1,\quad |s(\unicode[STIX]{x1D70F}_{-40})|=81/2,\quad |\widetilde{s}(\unicode[STIX]{x1D70F}_{-40})|=0,\end{eqnarray}$$
$$\begin{eqnarray}|s(\unicode[STIX]{x1D70F}_{-12})|=0,\quad |\widetilde{s}(\unicode[STIX]{x1D70F}_{-12})|=1,\quad |s(\unicode[STIX]{x1D70F}_{-40})|=81/2,\quad |\widetilde{s}(\unicode[STIX]{x1D70F}_{-40})|=0,\end{eqnarray}$$
which implies that
![]() $\widetilde{s}$
is equal to one of
$\widetilde{s}$
is equal to one of
 $\pm 2s/81\pm 1$
. As
$\pm 2s/81\pm 1$
. As
 $s(\unicode[STIX]{x1D70F}_{-15})=-243$
and
$s(\unicode[STIX]{x1D70F}_{-15})=-243$
and
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=5$
, we find that
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=5$
, we find that
 $\widetilde{s}=-2s/81-1$
. Then the table above and the requirement that
$\widetilde{s}=-2s/81-1$
. Then the table above and the requirement that
![]() $y(\unicode[STIX]{x1D70F}_{d})$
must lie in the correct field yield the following.
$y(\unicode[STIX]{x1D70F}_{d})$
must lie in the correct field yield the following.

It follows that an equation of
![]() $X/w_{3}$
is
$X/w_{3}$
is
 $3y^{2}+(s+243)(s+3)=0$
.
$3y^{2}+(s+243)(s+3)=0$
.
Furthermore, the double cover
 $X/w_{15}\rightarrow X/W_{15,1}$
is ramified at CM points of discriminants
$X/w_{15}\rightarrow X/W_{15,1}$
is ramified at CM points of discriminants
![]() $-3$
and
$-3$
and
![]() $-12$
. Thus, an equation of
$-12$
. Thus, an equation of
![]() $X/w_{15}$
is
$X/w_{15}$
is
![]() $x^{2}=bs$
for some
$x^{2}=bs$
for some
![]() $b$
. As CM points of discriminant
$b$
. As CM points of discriminant
![]() $-7$
are rational points on
$-7$
are rational points on
![]() $X/w_{15}$
, we find that
$X/w_{15}$
, we find that
![]() $b$
must be a square, which we may assume to be one. That is, we have
$b$
must be a square, which we may assume to be one. That is, we have
![]() $s=x^{2}$
. Therefore, we have
$s=x^{2}$
. Therefore, we have
 $3y^{2}+(x^{2}+243)(x^{2}+3)=0$
, which can be taken to be an equation of
$3y^{2}+(x^{2}+243)(x^{2}+3)=0$
, which can be taken to be an equation of
![]() $X$
, agreeing with Jordan’s result.
$X$
, agreeing with Jordan’s result.
We remark that Elkies [Reference ElkiesElk98] has used Schwarzian differential equations to compute numerically the values of
![]() $s$
at many CM points. (His modular function differs from our
$s$
at many CM points. (His modular function differs from our
![]() $s$
by a factor of
$s$
by a factor of
![]() $-3$
.) Using Borcherds forms, we verify that all of the entries in [Reference ElkiesElk98, Table 6] are correct.
$-3$
.) Using Borcherds forms, we verify that all of the entries in [Reference ElkiesElk98, Table 6] are correct.
Example 33. Consider the Shimura curve
 $X=X_{0}^{26}(1)$
. In [Reference González and RotgerGR04], González and Rotger proved that an equation of
$X=X_{0}^{26}(1)$
. In [Reference González and RotgerGR04], González and Rotger proved that an equation of
![]() $X$
is
$X$
is
 $$\begin{eqnarray}y^{2}=-2x^{6}+19x^{4}-24x^{2}-169.\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-2x^{6}+19x^{4}-24x^{2}-169.\end{eqnarray}$$
In this example, we will obtain this result using Borcherds forms.
We have the following information about
![]() $X$
and its Atkin–Lehner quotients.
$X$
and its Atkin–Lehner quotients.

The double cover
 $X/w_{13}\rightarrow X/W_{26,1}$
is ramified at the CM point of discriminant
$X/w_{13}\rightarrow X/W_{26,1}$
is ramified at the CM point of discriminant
![]() $-8$
and the three CM points of discriminant
$-8$
and the three CM points of discriminant
![]() $-104$
. Let
$-104$
. Let
![]() $s$
be a Hauptmodul on
$s$
be a Hauptmodul on
 $X/W_{26,1}$
with
$X/W_{26,1}$
with
 $s(\unicode[STIX]{x1D70F}_{-8})=\infty$
,
$s(\unicode[STIX]{x1D70F}_{-8})=\infty$
,
 $s(\unicode[STIX]{x1D70F}_{-52})=0$
, and
$s(\unicode[STIX]{x1D70F}_{-52})=0$
, and
 $s(\unicode[STIX]{x1D70F}_{-11})\in \mathbb{Q}$
. Then an equation of
$s(\unicode[STIX]{x1D70F}_{-11})\in \mathbb{Q}$
. Then an equation of
![]() $X/w_{13}$
is
$X/w_{13}$
is
 $$\begin{eqnarray}y^{2}=a\mathop{\prod }_{\unicode[STIX]{x1D70F}:\operatorname{CM}\text{points of discriminant}-104}(s-s(\unicode[STIX]{x1D70F}))\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=a\mathop{\prod }_{\unicode[STIX]{x1D70F}:\operatorname{CM}\text{points of discriminant}-104}(s-s(\unicode[STIX]{x1D70F}))\end{eqnarray}$$
for some nonzero rational number
![]() $a$
. As a modular function on
$a$
. As a modular function on
 $X/W_{26,1}$
, we have
$X/W_{26,1}$
, we have
 $\operatorname{div}y^{2}=P_{-104}-3P_{-8}$
. Let
$\operatorname{div}y^{2}=P_{-104}-3P_{-8}$
. Let
![]() $\widetilde{s}$
be another Hauptmodul on
$\widetilde{s}$
be another Hauptmodul on
 $X/W_{26,1}$
with
$X/W_{26,1}$
with
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-8})=\infty$
,
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-8})=\infty$
,
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-11})=0$
, and
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-11})=0$
, and
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-52})\in \mathbb{Q}$
. We now realize
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-52})\in \mathbb{Q}$
. We now realize
![]() $s$
,
$s$
,
![]() $\widetilde{s}$
, and
$\widetilde{s}$
, and
![]() $y^{2}$
as Borcherds forms.
$y^{2}$
as Borcherds forms.
Let
![]() $f_{j}$
be modular forms in
$f_{j}$
be modular forms in
 $M^{!}(52)\cap \mathbb{Z}((q))$
with a pole of order
$M^{!}(52)\cap \mathbb{Z}((q))$
with a pole of order
![]() $j$
at
$j$
at
![]() $\infty$
and a leading coefficient of one constructed in Example 19. Using these
$\infty$
and a leading coefficient of one constructed in Example 19. Using these
![]() $f_{j}$
, we find three modular forms
$f_{j}$
, we find three modular forms
 $$\begin{eqnarray}\displaystyle g_{1} & = & \displaystyle 2q^{-13}-2q^{-2}-4q^{-1}+2q-2q^{2}-2q^{3}+\cdots \,,\nonumber\\ \displaystyle g_{2} & = & \displaystyle q^{-11}+2q^{-7}-2q^{-2}+4q+4q^{4}+\cdots \,,\nonumber\\ \displaystyle g_{3} & = & \displaystyle 2q^{-26}+6q^{-7}-6q^{-2}+2q^{-1}+10q-8q^{2}+\cdots \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{1} & = & \displaystyle 2q^{-13}-2q^{-2}-4q^{-1}+2q-2q^{2}-2q^{3}+\cdots \,,\nonumber\\ \displaystyle g_{2} & = & \displaystyle q^{-11}+2q^{-7}-2q^{-2}+4q+4q^{4}+\cdots \,,\nonumber\\ \displaystyle g_{3} & = & \displaystyle 2q^{-26}+6q^{-7}-6q^{-2}+2q^{-1}+10q-8q^{2}+\cdots \nonumber\end{eqnarray}$$
in
![]() $M^{!}(52)$
. Let
$M^{!}(52)$
. Let
![]() $\unicode[STIX]{x1D713}_{j}$
,
$\unicode[STIX]{x1D713}_{j}$
,
 $j=1,2,3$
, be the Borcherds forms associated to
$j=1,2,3$
, be the Borcherds forms associated to
![]() $g_{j}$
. By Lemma 22,
$g_{j}$
. By Lemma 22,
 $$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{1}=P_{-52}-P_{-8},\quad \operatorname{div}\unicode[STIX]{x1D713}_{2}=P_{-11}-P_{-8},\quad \operatorname{div}\unicode[STIX]{x1D713}_{3}=P_{-104}-3P_{-8}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{div}\unicode[STIX]{x1D713}_{1}=P_{-52}-P_{-8},\quad \operatorname{div}\unicode[STIX]{x1D713}_{2}=P_{-11}-P_{-8},\quad \operatorname{div}\unicode[STIX]{x1D713}_{3}=P_{-104}-3P_{-8}.\end{eqnarray}$$
Thus,
![]() $\unicode[STIX]{x1D713}_{j}$
are scalar multiples of
$\unicode[STIX]{x1D713}_{j}$
are scalar multiples of
![]() $s$
,
$s$
,
![]() $\widetilde{s}$
and
$\widetilde{s}$
and
![]() $y^{2}$
, respectively. Applying Schofer’s formula, we obtain the following result.
$y^{2}$
, respectively. Applying Schofer’s formula, we obtain the following result.

Since multiplying
![]() $\unicode[STIX]{x1D713}_{j}$
by a suitable factor of absolute value one does not change the absolute value of its value at a CM point, we may as well assume that
$\unicode[STIX]{x1D713}_{j}$
by a suitable factor of absolute value one does not change the absolute value of its value at a CM point, we may as well assume that
 $\unicode[STIX]{x1D713}_{1}(\unicode[STIX]{x1D70F}_{-11})=1$
,
$\unicode[STIX]{x1D713}_{1}(\unicode[STIX]{x1D70F}_{-11})=1$
,
 $\unicode[STIX]{x1D713}_{2}(\unicode[STIX]{x1D70F}_{-52})=8$
and
$\unicode[STIX]{x1D713}_{2}(\unicode[STIX]{x1D70F}_{-52})=8$
and
 $\unicode[STIX]{x1D713}_{3}(\unicode[STIX]{x1D70F}_{-11})=-2^{10}11^{1}13^{3}$
. Also, we choose
$\unicode[STIX]{x1D713}_{3}(\unicode[STIX]{x1D70F}_{-11})=-2^{10}11^{1}13^{3}$
. Also, we choose
![]() $s$
,
$s$
,
![]() $\widetilde{s}$
and
$\widetilde{s}$
and
![]() $y$
in a way such that
$y$
in a way such that
 $s(\unicode[STIX]{x1D70F}_{-11})=1$
,
$s(\unicode[STIX]{x1D70F}_{-11})=1$
,
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-52})=1$
and
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-52})=1$
and
 $y(\unicode[STIX]{x1D70F}_{-11})^{2}=-2^{4}11$
, i.e.
$y(\unicode[STIX]{x1D70F}_{-11})^{2}=-2^{4}11$
, i.e.
![]() $s=\unicode[STIX]{x1D713}_{1}$
,
$s=\unicode[STIX]{x1D713}_{1}$
,
 $\widetilde{s}=\unicode[STIX]{x1D713}_{2}/8$
and
$\widetilde{s}=\unicode[STIX]{x1D713}_{2}/8$
and
 $y^{2}=\unicode[STIX]{x1D713}_{3}/2^{6}13^{3}$
. Then we have
$y^{2}=\unicode[STIX]{x1D713}_{3}/2^{6}13^{3}$
. Then we have
 $\widetilde{s}=1-s$
and from the table above we obtain the following result.
$\widetilde{s}=1-s$
and from the table above we obtain the following result.

(The signs of
![]() $y(\unicode[STIX]{x1D70F}_{d})^{2}$
are determined by the Shimura reciprocity law.) From the data, we easily deduce that the relation between
$y(\unicode[STIX]{x1D70F}_{d})^{2}$
are determined by the Shimura reciprocity law.) From the data, we easily deduce that the relation between
![]() $y$
and
$y$
and
![]() $s$
is
$s$
is
 $$\begin{eqnarray}y^{2}=-2s^{3}+19s^{2}-24s-169,\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-2s^{3}+19s^{2}-24s-169,\end{eqnarray}$$
which is an equation for
 $X_{0}^{26}(1)/w_{13}$
.
$X_{0}^{26}(1)/w_{13}$
.
On the other hand, the cover
 $X_{0}^{26}(1)/w_{26}\rightarrow X_{0}^{26}(1)/W_{26,1}$
is ramified at the CM points of discriminants
$X_{0}^{26}(1)/w_{26}\rightarrow X_{0}^{26}(1)/W_{26,1}$
is ramified at the CM points of discriminants
![]() $-8$
and
$-8$
and
![]() $-52$
. Thus, there is a modular function
$-52$
. Thus, there is a modular function
![]() $x$
on
$x$
on
 $X_{0}^{26}(1)/w_{26}$
with
$X_{0}^{26}(1)/w_{26}$
with
![]() $x^{2}=cs$
for some rational number
$x^{2}=cs$
for some rational number
![]() $c$
. Since CM points of discriminant
$c$
. Since CM points of discriminant
![]() $-11$
are rational points on
$-11$
are rational points on
 $X_{0}^{26}(1)/w_{26}$
, we conclude that
$X_{0}^{26}(1)/w_{26}$
, we conclude that
![]() $c$
can be chosen to be
$c$
can be chosen to be
![]() $1$
. Hence,
$1$
. Hence,
 $y^{2}=-2x^{6}+19x^{4}-24x^{2}-169$
is an equation for
$y^{2}=-2x^{6}+19x^{4}-24x^{2}-169$
is an equation for
![]() $X_{0}^{26}(1)$
and the Atkin–Lehner involutions are given by
$X_{0}^{26}(1)$
and the Atkin–Lehner involutions are given by
 $$\begin{eqnarray}w_{2}:(x,y)\mapsto (-x,-y),\quad w_{26}:(x,y)\mapsto (x,-y).\end{eqnarray}$$
$$\begin{eqnarray}w_{2}:(x,y)\mapsto (-x,-y),\quad w_{26}:(x,y)\mapsto (x,-y).\end{eqnarray}$$
Example 34. Consider
 $X=X_{0}^{111}(1)$
. We have the following information.
$X=X_{0}^{111}(1)$
. We have the following information.

Let
![]() $s$
and
$s$
and
![]() $\widetilde{s}$
be modular functions on
$\widetilde{s}$
be modular functions on
 $X/W_{111,1}$
such that
$X/W_{111,1}$
such that
 $s(\unicode[STIX]{x1D70F}_{-15})=\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=\infty$
,
$s(\unicode[STIX]{x1D70F}_{-15})=\widetilde{s}(\unicode[STIX]{x1D70F}_{-15})=\infty$
,
 $s(\unicode[STIX]{x1D70F}_{-60})=0$
,
$s(\unicode[STIX]{x1D70F}_{-60})=0$
,
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-24})=0$
,
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-24})=0$
,
 $s(\unicode[STIX]{x1D70F}_{-24})=1$
and
$s(\unicode[STIX]{x1D70F}_{-24})=1$
and
 $\widetilde{s}(\unicode[STIX]{x1D70F}_{-60})=1$
, so that
$\widetilde{s}(\unicode[STIX]{x1D70F}_{-60})=1$
, so that
 $\widetilde{s}=1-s$
. Then an equation for
$\widetilde{s}=1-s$
. Then an equation for
![]() $X/w_{37}$
is
$X/w_{37}$
is
 $$\begin{eqnarray}y^{2}=a\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \operatorname{CM}(-111),\operatorname{CM}(-444)}(s-s(\unicode[STIX]{x1D70F})).\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=a\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \operatorname{CM}(-111),\operatorname{CM}(-444)}(s-s(\unicode[STIX]{x1D70F})).\end{eqnarray}$$
As CM points of discriminant
![]() $-60$
on
$-60$
on
![]() $X/w_{37}$
lie in
$X/w_{37}$
lie in
 $\mathbb{Q}(\sqrt{-3})$
, we choose
$\mathbb{Q}(\sqrt{-3})$
, we choose
![]() $y$
such that
$y$
such that
 $y(\unicode[STIX]{x1D70F}_{-60})^{2}=-27$
. Then realizing
$y(\unicode[STIX]{x1D70F}_{-60})^{2}=-27$
. Then realizing
![]() $s$
,
$s$
,
![]() $\widetilde{s}$
and
$\widetilde{s}$
and
![]() $y^{2}$
as Borcherds forms and using Schofer’s formula, we deduce the following values of these modular functions at rational CM points.
$y^{2}$
as Borcherds forms and using Schofer’s formula, we deduce the following values of these modular functions at rational CM points.

As the right-hand side of (13) is a polynomial of degree eight, these CM values are not sufficient to determine the equation and we will need values of
![]() $s$
and
$s$
and
![]() $y^{2}$
at some degree-two CM points.
$y^{2}$
at some degree-two CM points.
Let
![]() $\unicode[STIX]{x1D70F}_{-39}$
and
$\unicode[STIX]{x1D70F}_{-39}$
and
![]() $\unicode[STIX]{x1D70F}_{-39}^{\prime }$
be the two CM points of discriminant
$\unicode[STIX]{x1D70F}_{-39}^{\prime }$
be the two CM points of discriminant
![]() $-39$
on
$-39$
on
 $X/W_{111,1}$
. Schofer’s formula yields
$X/W_{111,1}$
. Schofer’s formula yields
 $$\begin{eqnarray}|s(\unicode[STIX]{x1D70F}_{-39})s(\unicode[STIX]{x1D70F}_{-39}^{\prime })|=3,\quad |(1-s(\unicode[STIX]{x1D70F}_{-39}))(1-s(\unicode[STIX]{x1D70F}_{-39}^{\prime }))|=4.\end{eqnarray}$$
$$\begin{eqnarray}|s(\unicode[STIX]{x1D70F}_{-39})s(\unicode[STIX]{x1D70F}_{-39}^{\prime })|=3,\quad |(1-s(\unicode[STIX]{x1D70F}_{-39}))(1-s(\unicode[STIX]{x1D70F}_{-39}^{\prime }))|=4.\end{eqnarray}$$
From the Shimura reciprocity law, we know that
 $s(\unicode[STIX]{x1D70F}_{-39})\in \mathbb{Q}(\sqrt{-3})$
. Thus,
$s(\unicode[STIX]{x1D70F}_{-39})\in \mathbb{Q}(\sqrt{-3})$
. Thus,
 $$\begin{eqnarray}s(\unicode[STIX]{x1D70F}_{-39})s(\unicode[STIX]{x1D70F}_{-39}^{\prime })=3,\quad (1-s(\unicode[STIX]{x1D70F}_{-39}))(1-s(\unicode[STIX]{x1D70F}_{-39}^{\prime }))=4.\end{eqnarray}$$
$$\begin{eqnarray}s(\unicode[STIX]{x1D70F}_{-39})s(\unicode[STIX]{x1D70F}_{-39}^{\prime })=3,\quad (1-s(\unicode[STIX]{x1D70F}_{-39}))(1-s(\unicode[STIX]{x1D70F}_{-39}^{\prime }))=4.\end{eqnarray}$$
From these, we deduce that
 $s(\unicode[STIX]{x1D70F}_{-39})=\pm \sqrt{-3}$
. Likewise, we find that the values of
$s(\unicode[STIX]{x1D70F}_{-39})=\pm \sqrt{-3}$
. Likewise, we find that the values of
![]() $s$
at the two CM points
$s$
at the two CM points
 $\unicode[STIX]{x1D70F}_{-52},\unicode[STIX]{x1D70F}_{-52}^{\prime }$
of discriminants
$\unicode[STIX]{x1D70F}_{-52},\unicode[STIX]{x1D70F}_{-52}^{\prime }$
of discriminants
![]() $-52$
are
$-52$
are
 $1\pm 2\sqrt{-1}$
. Also, we have
$1\pm 2\sqrt{-1}$
. Also, we have
 $$\begin{eqnarray}y(\unicode[STIX]{x1D70F}_{-39})^{2}y(\unicode[STIX]{x1D70F}_{-39}^{\prime })^{2}=2^{16}3^{2}13,\quad y(\unicode[STIX]{x1D70F}_{-52})^{2}y(\unicode[STIX]{x1D70F}_{-52}^{\prime })^{2}=2^{16}13^{2}.\end{eqnarray}$$
$$\begin{eqnarray}y(\unicode[STIX]{x1D70F}_{-39})^{2}y(\unicode[STIX]{x1D70F}_{-39}^{\prime })^{2}=2^{16}3^{2}13,\quad y(\unicode[STIX]{x1D70F}_{-52})^{2}y(\unicode[STIX]{x1D70F}_{-52}^{\prime })^{2}=2^{16}13^{2}.\end{eqnarray}$$
These data are enough to determine the equation of
![]() $X/w_{37}$
. We find that it is
$X/w_{37}$
. We find that it is
 $$\begin{eqnarray}y^{2}=-(3s^{4}-6s^{3}+28s^{2}-10s+1)(s^{4}-2s^{3}+4s^{2}+18s+27).\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-(3s^{4}-6s^{3}+28s^{2}-10s+1)(s^{4}-2s^{3}+4s^{2}+18s+27).\end{eqnarray}$$
Similarly, we can compute an equation for
![]() $X/w_{111}$
by observing that
$X/w_{111}$
by observing that
 $X/w_{111}\rightarrow X/W_{111,1}$
is ramified at the two CM points of discriminant
$X/w_{111}\rightarrow X/W_{111,1}$
is ramified at the two CM points of discriminant
![]() $-148$
, constructing a Borcherds form with divisor
$-148$
, constructing a Borcherds form with divisor
 $P_{-148}-2P_{-15}$
, and evaluating at various CM points and obtain
$P_{-148}-2P_{-15}$
, and evaluating at various CM points and obtain
 $$\begin{eqnarray}t^{2}=5s^{2}-18s+45.\end{eqnarray}$$
$$\begin{eqnarray}t^{2}=5s^{2}-18s+45.\end{eqnarray}$$
The conic has rational points
 $(s,t)=(3,\pm 6)$
corresponding the two CM points of discriminant
$(s,t)=(3,\pm 6)$
corresponding the two CM points of discriminant
![]() $-19$
on
$-19$
on
![]() $X/w_{111}$
, so it admits a rational parameterization. Specifically, let
$X/w_{111}$
, so it admits a rational parameterization. Specifically, let
![]() $x$
be a Hauptmodul on
$x$
be a Hauptmodul on
![]() $X/w_{111}$
that has a pole and a zero at the two CM points of discriminant
$X/w_{111}$
that has a pole and a zero at the two CM points of discriminant
![]() $-19$
, respectively, and takes rational values at CM points of discriminant
$-19$
, respectively, and takes rational values at CM points of discriminant
![]() $-43$
. (In terms of
$-43$
. (In terms of
![]() $(s,t)$
, the coordinates are
$(s,t)$
, the coordinates are
 $(-3,\pm 12)$
.) Then
$(-3,\pm 12)$
.) Then
 $$\begin{eqnarray}x=\frac{c(s-3)}{s-t+3}\end{eqnarray}$$
$$\begin{eqnarray}x=\frac{c(s-3)}{s-t+3}\end{eqnarray}$$
for some rational number
![]() $c$
. Choose
$c$
. Choose
![]() $c=2$
so that it takes values
$c=2$
so that it takes values
![]() $\pm 1$
at the CM points of discriminant
$\pm 1$
at the CM points of discriminant
![]() $-43$
. We have
$-43$
. We have
 $$\begin{eqnarray}(s,t)=\biggl(\frac{3x^{2}-3x-3}{x^{2}+x-1},\frac{6x^{2}+6}{x^{2}+x-1}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}(s,t)=\biggl(\frac{3x^{2}-3x-3}{x^{2}+x-1},\frac{6x^{2}+6}{x^{2}+x-1}\biggr).\end{eqnarray}$$
Plugging in
 $s=(3x^{2}-3x-3)/(x^{2}+x-1)$
in (14) and making a slight change of variables, we find that an equation of
$s=(3x^{2}-3x-3)/(x^{2}+x-1)$
in (14) and making a slight change of variables, we find that an equation of
 $X_{0}^{111}(1)$
is
$X_{0}^{111}(1)$
is
 $$\begin{eqnarray}\displaystyle z^{2} & = & \displaystyle -(x^{8}-3x^{5}-x^{4}+3x^{3}+1)\nonumber\\ \displaystyle & & \displaystyle \times \,(19x^{8}-44x^{7}-16x^{6}+55x^{5}+37x^{4}-55x^{3}-16x^{2}+44x+19)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z^{2} & = & \displaystyle -(x^{8}-3x^{5}-x^{4}+3x^{3}+1)\nonumber\\ \displaystyle & & \displaystyle \times \,(19x^{8}-44x^{7}-16x^{6}+55x^{5}+37x^{4}-55x^{3}-16x^{2}+44x+19)\nonumber\end{eqnarray}$$
with the actions of the Atkin–Lehner involutions given by
 $$\begin{eqnarray}w_{37}:(x,z)\mapsto \biggl(-\frac{1}{x},\frac{z}{x^{8}}\biggr),\quad w_{111}:(x,z)\mapsto (x,-z).\end{eqnarray}$$
$$\begin{eqnarray}w_{37}:(x,z)\mapsto \biggl(-\frac{1}{x},\frac{z}{x^{8}}\biggr),\quad w_{111}:(x,z)\mapsto (x,-z).\end{eqnarray}$$
Example 35. Consider
 $X=X_{0}^{146}(1)$
. Let
$X=X_{0}^{146}(1)$
. Let
![]() $s$
be the Hauptmodul of
$s$
be the Hauptmodul of
 $X/W_{146,1}$
such that
$X/W_{146,1}$
such that
 $s(\unicode[STIX]{x1D70F}_{-43})=0$
,
$s(\unicode[STIX]{x1D70F}_{-43})=0$
,
 $s(\unicode[STIX]{x1D70F}_{-11})=\infty$
and
$s(\unicode[STIX]{x1D70F}_{-11})=\infty$
and
 $s(\unicode[STIX]{x1D70F}_{-20})=1$
. Let
$s(\unicode[STIX]{x1D70F}_{-20})=1$
. Let
![]() $y$
be a modular function on
$y$
be a modular function on
![]() $X/w_{73}$
such that
$X/w_{73}$
such that
![]() $y^{2}$
is a modular function on
$y^{2}$
is a modular function on
 $X/W_{146,1}$
with
$X/W_{146,1}$
with
 $\operatorname{div}y^{2}=P_{-584}-8P_{-11}$
. Realizing
$\operatorname{div}y^{2}=P_{-584}-8P_{-11}$
. Realizing
![]() $s$
and
$s$
and
![]() $y^{2}$
as Borcherds forms and suitably scaling
$y^{2}$
as Borcherds forms and suitably scaling
![]() $y^{2}$
, we find that an equation for
$y^{2}$
, we find that an equation for
![]() $X/w_{73}$
is
$X/w_{73}$
is
 $$\begin{eqnarray}y^{2}=-11s^{8}+82s^{7}-309s^{6}+788s^{5}-1413s^{4}+1858s^{3}-1803s^{2}+1240s-688.\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-11s^{8}+82s^{7}-309s^{6}+788s^{5}-1413s^{4}+1858s^{3}-1803s^{2}+1240s-688.\end{eqnarray}$$
Similarly, we find that an equation for
![]() $X/w_{146}$
is
$X/w_{146}$
is
 $t^{2}=s^{2}+4$
, where the roots of
$t^{2}=s^{2}+4$
, where the roots of
![]() $s^{2}+4$
correspond the to CM points of discriminant
$s^{2}+4$
correspond the to CM points of discriminant
![]() $-292$
. We choose a rational parameterization of the conic to be
$-292$
. We choose a rational parameterization of the conic to be
 $$\begin{eqnarray}(s,t)=\biggl(\frac{x^{2}-1}{x},\frac{x^{2}+1}{x}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}(s,t)=\biggl(\frac{x^{2}-1}{x},\frac{x^{2}+1}{x}\biggr),\end{eqnarray}$$
where
![]() $x$
is actually a modular function on
$x$
is actually a modular function on
 $X/w_{146}$
that has a pole and a zero at the two CM points of discriminant
$X/w_{146}$
that has a pole and a zero at the two CM points of discriminant
![]() $-11$
and is equal to
$-11$
and is equal to
![]() $\pm 1$
at the two CM points of discriminant
$\pm 1$
at the two CM points of discriminant
![]() $-43$
on
$-43$
on
 $X/w_{146}$
. Substituting
$X/w_{146}$
. Substituting
 $s=(x^{2}-1)/x$
in (15) and making a change of variables, we find that an equation for
$s=(x^{2}-1)/x$
in (15) and making a change of variables, we find that an equation for
![]() $X$
is
$X$
is
 $$\begin{eqnarray}\displaystyle z^{2} & = & \displaystyle -11x^{16}+82x^{15}-221x^{14}+214x^{13}+133x^{12}-360x^{11}-170x^{10}+676x^{9}\nonumber\\ \displaystyle & & \displaystyle -\,150x^{8}-676x^{7}-170x^{6}+360x^{5}+133x^{4}-214x^{3}-221x^{2}-82x-11,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z^{2} & = & \displaystyle -11x^{16}+82x^{15}-221x^{14}+214x^{13}+133x^{12}-360x^{11}-170x^{10}+676x^{9}\nonumber\\ \displaystyle & & \displaystyle -\,150x^{8}-676x^{7}-170x^{6}+360x^{5}+133x^{4}-214x^{3}-221x^{2}-82x-11,\nonumber\end{eqnarray}$$
where the Atkin–Lehner involutions are given by
 $$\begin{eqnarray}w_{73}:(x,y)\mapsto \biggl(-\frac{1}{x},\frac{y}{x^{8}}\biggr),\quad w_{146}:(x,y)\mapsto (x,-y).\end{eqnarray}$$
$$\begin{eqnarray}w_{73}:(x,y)\mapsto \biggl(-\frac{1}{x},\frac{y}{x^{8}}\biggr),\quad w_{146}:(x,y)\mapsto (x,-y).\end{eqnarray}$$
Example 36. Let
 $X=X_{0}^{14}(5)$
. Let
$X=X_{0}^{14}(5)$
. Let
![]() $s$
be the Hauptmodul of
$s$
be the Hauptmodul of
 $X/W_{14,5}$
such that
$X/W_{14,5}$
such that
 $s(\unicode[STIX]{x1D70F}_{-4})=\infty$
,
$s(\unicode[STIX]{x1D70F}_{-4})=\infty$
,
 $s(\unicode[STIX]{x1D70F}_{-11})=1$
and
$s(\unicode[STIX]{x1D70F}_{-11})=1$
and
 $s(\unicode[STIX]{x1D70F}_{-35})=0$
. We find that an equation for
$s(\unicode[STIX]{x1D70F}_{-35})=0$
. We find that an equation for
 $X/\langle w_{5},w_{7}\rangle$
is
$X/\langle w_{5},w_{7}\rangle$
is
 $$\begin{eqnarray}y^{2}=-16s^{3}-347s^{2}+222s-35,\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-16s^{3}-347s^{2}+222s-35,\end{eqnarray}$$
which is isomorphic to the elliptic curve
![]() $E_{\text{14A5}}$
in Cremona’s table [Reference CremonaCre97]. (In fact, we can use the Cerednik–Drinfeld theory of
$E_{\text{14A5}}$
in Cremona’s table [Reference CremonaCre97]. (In fact, we can use the Cerednik–Drinfeld theory of
![]() $p$
-adic uniformization of Shimura curves [Reference Boutot and CarayolBC92] to determine the singular fibers of
$p$
-adic uniformization of Shimura curves [Reference Boutot and CarayolBC92] to determine the singular fibers of
 $X/\langle w_{5},w_{7}\rangle$
and conclude that it is isomorphic to
$X/\langle w_{5},w_{7}\rangle$
and conclude that it is isomorphic to
![]() $E_{\text{14A5}}$
.) The double cover
$E_{\text{14A5}}$
.) The double cover
 $X/\langle w_{5},w_{14}\rangle \rightarrow X/W_{14,5}$
is ramified at the CM point of discriminant
$X/\langle w_{5},w_{14}\rangle \rightarrow X/W_{14,5}$
is ramified at the CM point of discriminant
![]() $-4$
and the CM point of discriminant
$-4$
and the CM point of discriminant
![]() $-35$
, so that there is a Hauptmodul
$-35$
, so that there is a Hauptmodul
![]() $t$
of
$t$
of
 $X/\langle w_{5},w_{14}\rangle$
such that
$X/\langle w_{5},w_{14}\rangle$
such that
![]() $t^{2}=cs$
for some rational number
$t^{2}=cs$
for some rational number
![]() $c$
. In addition, the CM points of discriminant
$c$
. In addition, the CM points of discriminant
![]() $-11$
on
$-11$
on
 $X/\langle w_{5},w_{14}\rangle$
are rational points. Thus, we may choose
$X/\langle w_{5},w_{14}\rangle$
are rational points. Thus, we may choose
![]() $c=1$
and find that an equation for
$c=1$
and find that an equation for
![]() $X/w_{5}$
is
$X/w_{5}$
is
 $$\begin{eqnarray}y^{2}=-16t^{6}-347t^{4}+222t^{2}-35.\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-16t^{6}-347t^{4}+222t^{2}-35.\end{eqnarray}$$
We next determine an equation of
![]() $X/w_{14}$
. The double cover
$X/w_{14}$
. The double cover
 $X/w_{14}\rightarrow X/\langle w_{5},w_{14}\rangle$
is ramified at the two CM points of discriminant
$X/w_{14}\rightarrow X/\langle w_{5},w_{14}\rangle$
is ramified at the two CM points of discriminant
![]() $-280$
. Using Schofer’s formula, we find
$-280$
. Using Schofer’s formula, we find
 $s(\unicode[STIX]{x1D70F}_{-280})=5/16$
and, thus, an equation for
$s(\unicode[STIX]{x1D70F}_{-280})=5/16$
and, thus, an equation for
![]() $X/w_{14}$
is
$X/w_{14}$
is
 $u^{2}=d(16t^{2}-5)$
for some rational number. The point such that
$u^{2}=d(16t^{2}-5)$
for some rational number. The point such that
![]() $t=0$
is the CM point of discriminant
$t=0$
is the CM point of discriminant
![]() $-35$
. Therefore, we may choose
$-35$
. Therefore, we may choose
![]() $d=-1$
and find that an equation for
$d=-1$
and find that an equation for
![]() $X/w_{14}$
is
$X/w_{14}$
is
 $$\begin{eqnarray}u^{2}+16t^{2}=5.\end{eqnarray}$$
$$\begin{eqnarray}u^{2}+16t^{2}=5.\end{eqnarray}$$
This is a conic with rational points and a rational parameterization is
 $$\begin{eqnarray}(t,u)=\biggl(\frac{x^{2}-x-1}{2x^{2}+2},\frac{x^{2}+4x-1}{x^{2}+1}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}(t,u)=\biggl(\frac{x^{2}-x-1}{2x^{2}+2},\frac{x^{2}+4x-1}{x^{2}+1}\biggr).\end{eqnarray}$$
Substituting
 $t=(x^{2}-x-1)/(2x^{2}+2)$
into (16) and making a change of variables, we conclude that an equation for
$t=(x^{2}-x-1)/(2x^{2}+2)$
into (16) and making a change of variables, we conclude that an equation for
![]() $X_{0}^{14}(5)$
is
$X_{0}^{14}(5)$
is
 $$\begin{eqnarray}z^{2}=-23x^{8}-180x^{7}-358x^{6}-168x^{5}-677x^{4}+168x^{3}-358x^{2}+180x-23,\end{eqnarray}$$
$$\begin{eqnarray}z^{2}=-23x^{8}-180x^{7}-358x^{6}-168x^{5}-677x^{4}+168x^{3}-358x^{2}+180x-23,\end{eqnarray}$$
on which the actions of the Atkin–Lehner operators are given by
 $$\begin{eqnarray}w_{2}:(x,z)\mapsto \biggl(-\frac{1}{x},\frac{z}{x^{4}}\biggr),\quad w_{14}:(x,z)\mapsto (x,-z),\end{eqnarray}$$
$$\begin{eqnarray}w_{2}:(x,z)\mapsto \biggl(-\frac{1}{x},\frac{z}{x^{4}}\biggr),\quad w_{14}:(x,z)\mapsto (x,-z),\end{eqnarray}$$
and
 $$\begin{eqnarray}w_{35}:(x,z)\mapsto \biggl(\frac{x+2}{2x-1},\frac{25z}{(2x-1)^{4}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}w_{35}:(x,z)\mapsto \biggl(\frac{x+2}{2x-1},\frac{25z}{(2x-1)^{4}}\biggr).\end{eqnarray}$$
Note that
 $X_{0}^{14}(5)/w_{14}$
is an example of Shimura curves of genus zero that is isomorphic to
$X_{0}^{14}(5)/w_{14}$
is an example of Shimura curves of genus zero that is isomorphic to
![]() $\mathbb{P}^{1}$
over
$\mathbb{P}^{1}$
over
![]() $\mathbb{Q}$
but none of the rational points is a CM point.
$\mathbb{Q}$
but none of the rational points is a CM point.
Example 37. Let
 $X=X_{0}^{10}(19)$
. Let
$X=X_{0}^{10}(19)$
. Let
![]() $s$
be the Hauptmodul of
$s$
be the Hauptmodul of
 $X/W_{10,19}$
such that
$X/W_{10,19}$
such that
 $s(\unicode[STIX]{x1D70F}_{-8})=0$
,
$s(\unicode[STIX]{x1D70F}_{-8})=0$
,
 $s(\unicode[STIX]{x1D70F}_{-40})=\infty$
, and
$s(\unicode[STIX]{x1D70F}_{-40})=\infty$
, and
 $s(\unicode[STIX]{x1D70F}_{-3})=1$
. We find that an equation for
$s(\unicode[STIX]{x1D70F}_{-3})=1$
. We find that an equation for
 $X/\langle w_{2},w_{95}\rangle$
is
$X/\langle w_{2},w_{95}\rangle$
is
 $$\begin{eqnarray}y^{2}=-8s^{3}+57s^{2}-40s+16,\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-8s^{3}+57s^{2}-40s+16,\end{eqnarray}$$
which is isomorphic to the elliptic curve
![]() $E_{\text{190A1}}$
in Cremona’s table [Reference CremonaCre97]. Also, the double cover
$E_{\text{190A1}}$
in Cremona’s table [Reference CremonaCre97]. Also, the double cover
 $X/\langle w_{5},w_{38}\rangle \rightarrow X/W_{10,19}$
is ramified at the CM point of discriminant
$X/\langle w_{5},w_{38}\rangle \rightarrow X/W_{10,19}$
is ramified at the CM point of discriminant
![]() $-8$
and the CM point of discriminant
$-8$
and the CM point of discriminant
![]() $-40$
. The CM points of discriminant
$-40$
. The CM points of discriminant
![]() $-3$
are rational points on
$-3$
are rational points on
 $X/\langle w_{5},w_{38}\rangle$
. Thus, arguing as before, we deduce that an equation for
$X/\langle w_{5},w_{38}\rangle$
. Thus, arguing as before, we deduce that an equation for
![]() $X/w_{190}$
is
$X/w_{190}$
is
 $y^{2}=-8x^{6}+57x^{4}-40x^{2}+16$
. Moreover, the double cover
$y^{2}=-8x^{6}+57x^{4}-40x^{2}+16$
. Moreover, the double cover
 $X/w_{38}\rightarrow X/\langle w_{5},w_{38}\rangle$
is ramified at the two CM points of discriminant
$X/w_{38}\rightarrow X/\langle w_{5},w_{38}\rangle$
is ramified at the two CM points of discriminant
![]() $-760$
. Since
$-760$
. Since
 $s(\unicode[STIX]{x1D70F}_{760})=32/5$
and the point with
$s(\unicode[STIX]{x1D70F}_{760})=32/5$
and the point with
![]() $s=0$
is a CM point of discriminant
$s=0$
is a CM point of discriminant
![]() $-8$
, we see that an equation for
$-8$
, we see that an equation for
![]() $X/w_{38}$
is
$X/w_{38}$
is
 $z^{2}=5x^{2}-32$
. We conclude that an equation for
$z^{2}=5x^{2}-32$
. We conclude that an equation for
![]() $X$
is
$X$
is
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}y^{2}=-8x^{6}+57x^{4}-40x^{2}+16,\quad \\ z^{2}=5x^{2}-32,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}y^{2}=-8x^{6}+57x^{4}-40x^{2}+16,\quad \\ z^{2}=5x^{2}-32,\quad \end{array}\right.\end{eqnarray}$$
with the actions of the Atkin–Lehner involutions given by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}w_{2}:(x,y,z)\ & \mapsto \ & (-x,y,z),\\ w_{5}:(x,y,z)\ & \mapsto \ & (x,-y,-z),\\ w_{19}:(x,y,z)\ & \mapsto \ & (-x,-y,z).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}w_{2}:(x,y,z)\ & \mapsto \ & (-x,y,z),\\ w_{5}:(x,y,z)\ & \mapsto \ & (x,-y,-z),\\ w_{19}:(x,y,z)\ & \mapsto \ & (-x,-y,z).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Note that as the conic
 $z^{2}=5x^{2}-32$
has only real points, but no rational points, the Shimura curve
$z^{2}=5x^{2}-32$
has only real points, but no rational points, the Shimura curve
![]() $X$
is hyperelliptic over
$X$
is hyperelliptic over
![]() $\mathbb{R}$
, but not over
$\mathbb{R}$
, but not over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Remark 38. In [Reference OggOgg83], Ogg mentioned that
 $X_{0}^{10}(19)$
and
$X_{0}^{10}(19)$
and
![]() $X_{0}^{14}(5)$
are the only two hyperelliptic curves that he could not determine whether they are hyperelliptic over
$X_{0}^{14}(5)$
are the only two hyperelliptic curves that he could not determine whether they are hyperelliptic over
![]() $\mathbb{Q}$
. Our computation shows that
$\mathbb{Q}$
. Our computation shows that
![]() $X_{0}^{14}(5)$
is hyperelliptic over
$X_{0}^{14}(5)$
is hyperelliptic over
![]() $\mathbb{Q}$
because the curve
$\mathbb{Q}$
because the curve
 $X_{0}^{14}(5)/w_{14}$
has rational points, but
$X_{0}^{14}(5)/w_{14}$
has rational points, but
 $X_{0}^{10}(19)$
is not hyperelliptic over
$X_{0}^{10}(19)$
is not hyperelliptic over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Remark 39. Note that there is a curve, namely,
 $X=X_{0}^{15}(4)$
, whose equation is not obtained using our method. This is because the normalizer of the Eichler order in this case is larger than the Atkin–Lehner group. For this special curve, we use the result of Tu [Reference TuTu14]. In [Reference TuTu14, Lemma 13], it is shown that there is a Hauptmodul
$X=X_{0}^{15}(4)$
, whose equation is not obtained using our method. This is because the normalizer of the Eichler order in this case is larger than the Atkin–Lehner group. For this special curve, we use the result of Tu [Reference TuTu14]. In [Reference TuTu14, Lemma 13], it is shown that there is a Hauptmodul
![]() $t_{4}$
on
$t_{4}$
on
 $X/\langle w_{3},w_{5}\rangle$
that takes values
$X/\langle w_{3},w_{5}\rangle$
that takes values
 $\pm 1/\sqrt{-3}$
,
$\pm 1/\sqrt{-3}$
,
 $\pm \sqrt{-15}/5$
and
$\pm \sqrt{-15}/5$
and
 $(\pm 1\pm \sqrt{-15})/8$
at CM points of discriminants
$(\pm 1\pm \sqrt{-15})/8$
at CM points of discriminants
![]() $-12$
,
$-12$
,
![]() $-15$
and
$-15$
and
![]() $-60$
, respectively. Since the double cover
$-60$
, respectively. Since the double cover
 $X/w_{3}\rightarrow X/\langle w_{3},w_{5}\rangle$
ramifies at CM points of discriminants
$X/w_{3}\rightarrow X/\langle w_{3},w_{5}\rangle$
ramifies at CM points of discriminants
![]() $-15$
and
$-15$
and
![]() $-60$
, while the cover
$-60$
, while the cover
 $X/w_{15}\rightarrow X/\langle w_{3},w_{5}\rangle$
ramifies at CM points of discriminant
$X/w_{15}\rightarrow X/\langle w_{3},w_{5}\rangle$
ramifies at CM points of discriminant
![]() $-12$
, we find that there are rational numbers
$-12$
, we find that there are rational numbers
![]() $a$
and
$a$
and
![]() $b$
such that the equations of
$b$
such that the equations of
![]() $X/w_{3}$
and
$X/w_{3}$
and
![]() $X/w_{15}$
are
$X/w_{15}$
are
 $$\begin{eqnarray}y^{2}=a(4t_{4}^{2}-t_{4}+1)(4t_{4}^{2}+t_{4}+1)(5t_{4}^{2}+3),\quad z^{2}=b(3t_{4}^{2}+1),\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=a(4t_{4}^{2}-t_{4}+1)(4t_{4}^{2}+t_{4}+1)(5t_{4}^{2}+3),\quad z^{2}=b(3t_{4}^{2}+1),\end{eqnarray}$$
respectively. To determine the constants
![]() $a$
and
$a$
and
![]() $b$
, we further recall that [Reference TuTu14, Lemma 13] shows that there is a Hauptmodul
$b$
, we further recall that [Reference TuTu14, Lemma 13] shows that there is a Hauptmodul
![]() $t_{2}$
on
$t_{2}$
on
 $X_{0}^{15}(2)/\langle w_{3},w_{5}\rangle$
with
$X_{0}^{15}(2)/\langle w_{3},w_{5}\rangle$
with
 $$\begin{eqnarray}t_{2}=\frac{5t_{4}^{2}+2t_{4}+1}{7t_{4}^{2}-2t_{4}+3}.\end{eqnarray}$$
$$\begin{eqnarray}t_{2}=\frac{5t_{4}^{2}+2t_{4}+1}{7t_{4}^{2}-2t_{4}+3}.\end{eqnarray}$$
From this, the CM values of
![]() $t_{2}$
obtained using Schofer’s formula, and arithmetic properties of CM points, we see that we can choose
$t_{2}$
obtained using Schofer’s formula, and arithmetic properties of CM points, we see that we can choose
 $a=b=-1$
. Note that
$a=b=-1$
. Note that
![]() $X_{0}^{15}(4)$
is one of the hyperelliptic Shimura curves that are not hyperelliptic over
$X_{0}^{15}(4)$
is one of the hyperelliptic Shimura curves that are not hyperelliptic over
![]() $\mathbb{R}$
(see [Reference OggOgg83]).
$\mathbb{R}$
(see [Reference OggOgg83]).
4.3 Additional examples
In the previous section, we determine the equations of hyperelliptic Shimura curves
![]() $X_{0}^{D}(N)$
whose Atkin–Lehner involutions act as hyperelliptic involutions. In particular, the curves
$X_{0}^{D}(N)$
whose Atkin–Lehner involutions act as hyperelliptic involutions. In particular, the curves
 $X_{0}^{D}(N)/W_{D,N}$
are of genus zero, so that Lemma 7 applies and we have a simple criterion for a Borcherds form to have a trivial character. Throughout this section, we make the following assumption.
$X_{0}^{D}(N)/W_{D,N}$
are of genus zero, so that Lemma 7 applies and we have a simple criterion for a Borcherds form to have a trivial character. Throughout this section, we make the following assumption.
Assumption 40. The criterion for a Borcherds form to have a trivial character is also valid for the case when
 $N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
has a positive genus.
$N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
has a positive genus.
Remark 41. Recall that a Fuchsian group of the first kind is generated by some elements
 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{g},\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n}$
with defining relations
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{g},\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n}$
with defining relations
 $$\begin{eqnarray}[\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1}]\ldots [\unicode[STIX]{x1D6FC}_{g},\unicode[STIX]{x1D6FD}_{g}]\unicode[STIX]{x1D6FE}_{1}\ldots \unicode[STIX]{x1D6FE}_{n}=1,\quad \unicode[STIX]{x1D6FE}_{i}^{k_{i}}=1,~i=1,\ldots ,n,\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1}]\ldots [\unicode[STIX]{x1D6FC}_{g},\unicode[STIX]{x1D6FD}_{g}]\unicode[STIX]{x1D6FE}_{1}\ldots \unicode[STIX]{x1D6FE}_{n}=1,\quad \unicode[STIX]{x1D6FE}_{i}^{k_{i}}=1,~i=1,\ldots ,n,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}$
are hyperbolic elements,
$\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}$
are hyperbolic elements,
![]() $[\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}]$
denotes the commutator,
$[\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}]$
denotes the commutator,
![]() $g$
is the genus and
$g$
is the genus and
![]() $k_{i}$
is an integer at least two or
$k_{i}$
is an integer at least two or
![]() $\infty$
. (See, for instance, [Reference KatokKat92].) Let
$\infty$
. (See, for instance, [Reference KatokKat92].) Let
![]() $\unicode[STIX]{x1D712}$
be the character of a Borcherds form on
$\unicode[STIX]{x1D712}$
be the character of a Borcherds form on
 $N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
. The proof of Lemma 7 given in [Reference YangYan15] shows that
$N_{B}^{+}({\mathcal{O}})\backslash \mathfrak{H}$
. The proof of Lemma 7 given in [Reference YangYan15] shows that
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE}_{i})=1$
for all
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE}_{i})=1$
for all
![]() $i$
if and only if the condition in Lemma 7 holds. Thus, what we really assume in Assumption 40 is that for all hyperbolic elements
$i$
if and only if the condition in Lemma 7 holds. Thus, what we really assume in Assumption 40 is that for all hyperbolic elements
![]() $\unicode[STIX]{x1D6FC}$
, we have
$\unicode[STIX]{x1D6FC}$
, we have
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})=1$
.
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})=1$
.
It turns out that sometimes our methods can also be used to determine equations of
 $X_{0}^{D}(N)/W_{D,N}$
even when they have positive genera, under Assumption 40. However, the method becomes less systematic and it is not clear whether our methods will always work in general, so we will only give two examples in this section.
$X_{0}^{D}(N)/W_{D,N}$
even when they have positive genera, under Assumption 40. However, the method becomes less systematic and it is not clear whether our methods will always work in general, so we will only give two examples in this section.
Example 42. Let
 $X=X_{0}^{142}(1)/W_{142,1}$
. It is of genus one and has rational points (for instance, the CM point of discriminant
$X=X_{0}^{142}(1)/W_{142,1}$
. It is of genus one and has rational points (for instance, the CM point of discriminant
![]() $-3$
). Thus,
$-3$
). Thus,
![]() $X$
is a rational elliptic curve. From the Jacquet–Langlands correspondence, we know that it must lie in the isogeny class 142A in Cremona’s table [Reference CremonaCre97], whose corresponding cusp form on
$X$
is a rational elliptic curve. From the Jacquet–Langlands correspondence, we know that it must lie in the isogeny class 142A in Cremona’s table [Reference CremonaCre97], whose corresponding cusp form on
 $\unicode[STIX]{x1D6E4}_{0}(142)$
has eigenvalues
$\unicode[STIX]{x1D6E4}_{0}(142)$
has eigenvalues
![]() $-1$
for the Atkin–Lehner involutions
$-1$
for the Atkin–Lehner involutions
![]() $w_{2}$
and
$w_{2}$
and
![]() $w_{71}$
. Since the isogeny class contains only one curve, we immediately conclude that the equation for
$w_{71}$
. Since the isogeny class contains only one curve, we immediately conclude that the equation for
![]() $X$
is
$X$
is
 $E_{\text{142A1}}:y^{2}+xy+y=x^{3}-x^{2}-12x+15$
. Here we will use our method to obtain the same conclusion. An advantage of our method is that we can determine the coordinates of all CM points on the curve. In the arXiv version of this paper, we discuss the heights of these CM points and verify Zhang’s formula [Reference ZhangZha01] for heights of CM points in this particular case.
$E_{\text{142A1}}:y^{2}+xy+y=x^{3}-x^{2}-12x+15$
. Here we will use our method to obtain the same conclusion. An advantage of our method is that we can determine the coordinates of all CM points on the curve. In the arXiv version of this paper, we discuss the heights of these CM points and verify Zhang’s formula [Reference ZhangZha01] for heights of CM points in this particular case.
By finding many suitable eta products, we construct four modular forms
 $f_{1},f_{2},f_{3},f_{4}$
in
$f_{1},f_{2},f_{3},f_{4}$
in
 $M^{!}(284)$
with Fourier expansions
$M^{!}(284)$
with Fourier expansions
 $$\begin{eqnarray}\displaystyle f_{1} & = & \displaystyle -2q^{-87}-2q^{-71}-2q^{-48}-2q^{-36}+2q^{-16}-2q^{-15}-2q^{-12}+2q^{-9}\nonumber\\ \displaystyle & & \displaystyle -\,2q^{-7}-2q^{-3}+2q^{-2}+2q^{-1}-4q\cdots \,,\nonumber\\ \displaystyle f_{2} & = & \displaystyle 2q^{-116}-q^{-87}-q^{-79}+2q^{-71}+2q^{-60}-2q^{-48}+q^{-43}-2q^{-29}\nonumber\\ \displaystyle & & \displaystyle +\,q^{-19}-4q^{-15}-2q^{-12}+2q^{-7}-2q^{-3}-4q+\cdots \,,\nonumber\\ \displaystyle f_{3} & = & \displaystyle q^{-87}-2q^{-79}+q^{-76}-2q^{-71}+2q^{-48}-q^{-40}+3q^{-32}-2q^{-20}\nonumber\\ \displaystyle & & \displaystyle -\,q^{-19}-2q^{-12}+2q^{-10}+q^{-8}-2q^{-7}-2q^{-2}+4q+\cdots \,,\nonumber\\ \displaystyle f_{4} & = & \displaystyle -q^{-79}+q^{-76}+q^{-48}-q^{-40}+q^{-32}-q^{-20}-q^{-12}+q^{-10}+q^{-6}\nonumber\\ \displaystyle & & \displaystyle -\,q^{-5}-q^{-2}-q^{7}+\cdots \,.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{1} & = & \displaystyle -2q^{-87}-2q^{-71}-2q^{-48}-2q^{-36}+2q^{-16}-2q^{-15}-2q^{-12}+2q^{-9}\nonumber\\ \displaystyle & & \displaystyle -\,2q^{-7}-2q^{-3}+2q^{-2}+2q^{-1}-4q\cdots \,,\nonumber\\ \displaystyle f_{2} & = & \displaystyle 2q^{-116}-q^{-87}-q^{-79}+2q^{-71}+2q^{-60}-2q^{-48}+q^{-43}-2q^{-29}\nonumber\\ \displaystyle & & \displaystyle +\,q^{-19}-4q^{-15}-2q^{-12}+2q^{-7}-2q^{-3}-4q+\cdots \,,\nonumber\\ \displaystyle f_{3} & = & \displaystyle q^{-87}-2q^{-79}+q^{-76}-2q^{-71}+2q^{-48}-q^{-40}+3q^{-32}-2q^{-20}\nonumber\\ \displaystyle & & \displaystyle -\,q^{-19}-2q^{-12}+2q^{-10}+q^{-8}-2q^{-7}-2q^{-2}+4q+\cdots \,,\nonumber\\ \displaystyle f_{4} & = & \displaystyle -q^{-79}+q^{-76}+q^{-48}-q^{-40}+q^{-32}-q^{-20}-q^{-12}+q^{-10}+q^{-6}\nonumber\\ \displaystyle & & \displaystyle -\,q^{-5}-q^{-2}-q^{7}+\cdots \,.\nonumber\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D713}_{j}$
,
$\unicode[STIX]{x1D713}_{j}$
,
 $j=1,\ldots ,4$
, be the Borcherds form associated to
$j=1,\ldots ,4$
, be the Borcherds form associated to
![]() $f_{j}$
. Under Assumption 40, these Borcherds forms have trivial characters. We have
$f_{j}$
. Under Assumption 40, these Borcherds forms have trivial characters. We have
 $$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{1}=P_{-4}+P_{-8}-2P_{-3},\quad \operatorname{div}\unicode[STIX]{x1D713}_{2}=P_{-19}+P_{-43}-2P_{-3}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{3}=P_{-8}+P_{-40}-2P_{-20},\quad \operatorname{div}\unicode[STIX]{x1D713}_{4}=P_{-19}+P_{-24}-2P_{-20}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{1}=P_{-4}+P_{-8}-2P_{-3},\quad \operatorname{div}\unicode[STIX]{x1D713}_{2}=P_{-19}+P_{-43}-2P_{-3}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{3}=P_{-8}+P_{-40}-2P_{-20},\quad \operatorname{div}\unicode[STIX]{x1D713}_{4}=P_{-19}+P_{-24}-2P_{-20}. & \displaystyle \nonumber\end{eqnarray}$$
It is easy to show that
![]() $\unicode[STIX]{x1D713}_{2}$
is a polynomial of degree one in
$\unicode[STIX]{x1D713}_{2}$
is a polynomial of degree one in
![]() $\unicode[STIX]{x1D713}_{1}$
and
$\unicode[STIX]{x1D713}_{1}$
and
![]() $\unicode[STIX]{x1D713}_{4}$
is a polynomial of degree one in
$\unicode[STIX]{x1D713}_{4}$
is a polynomial of degree one in
![]() $\unicode[STIX]{x1D713}_{3}$
. Thus, there are modular functions
$\unicode[STIX]{x1D713}_{3}$
. Thus, there are modular functions
![]() $x$
and
$x$
and
![]() $y$
on
$y$
on
![]() $X$
such that
$X$
such that
![]() $x$
has a double pole at
$x$
has a double pole at
![]() $\unicode[STIX]{x1D70F}_{-3}$
with
$\unicode[STIX]{x1D70F}_{-3}$
with
 $x(\unicode[STIX]{x1D70F}_{-4})=x(\unicode[STIX]{x1D70F}_{-8})=0$
and
$x(\unicode[STIX]{x1D70F}_{-4})=x(\unicode[STIX]{x1D70F}_{-8})=0$
and
 $x(\unicode[STIX]{x1D70F}_{-19})=x(\unicode[STIX]{x1D70F}_{-43})=1$
and
$x(\unicode[STIX]{x1D70F}_{-19})=x(\unicode[STIX]{x1D70F}_{-43})=1$
and
![]() $y$
has a double pole at
$y$
has a double pole at
![]() $\unicode[STIX]{x1D70F}_{-20}$
with
$\unicode[STIX]{x1D70F}_{-20}$
with
 $y(\unicode[STIX]{x1D70F}_{-8})=y(\unicode[STIX]{x1D70F}_{-20})=0$
and
$y(\unicode[STIX]{x1D70F}_{-8})=y(\unicode[STIX]{x1D70F}_{-20})=0$
and
 $y(\unicode[STIX]{x1D70F}_{-19})=y(\unicode[STIX]{x1D70F}_{-24})=1$
. Computing singular moduli using Schofer’s formula and choosing proper scalars of modulus one for
$y(\unicode[STIX]{x1D70F}_{-19})=y(\unicode[STIX]{x1D70F}_{-24})=1$
. Computing singular moduli using Schofer’s formula and choosing proper scalars of modulus one for
![]() $\unicode[STIX]{x1D713}_{j}$
, we find
$\unicode[STIX]{x1D713}_{j}$
, we find
 $$\begin{eqnarray}x=2^{-10}\unicode[STIX]{x1D713}_{1},\quad 1-x=\unicode[STIX]{x1D713}_{2},\quad y=\unicode[STIX]{x1D713}_{3}/2,\quad 1-y=\unicode[STIX]{x1D713}_{4}/2,\end{eqnarray}$$
$$\begin{eqnarray}x=2^{-10}\unicode[STIX]{x1D713}_{1},\quad 1-x=\unicode[STIX]{x1D713}_{2},\quad y=\unicode[STIX]{x1D713}_{3}/2,\quad 1-y=\unicode[STIX]{x1D713}_{4}/2,\end{eqnarray}$$
and the values of
![]() $x$
and
$x$
and
![]() $y$
at various CM points are given in the following table.
$y$
at various CM points are given in the following table.

Since
 $y(\unicode[STIX]{x1D70F}_{-4})\neq y(\unicode[STIX]{x1D70F}_{-8})$
,
$y(\unicode[STIX]{x1D70F}_{-4})\neq y(\unicode[STIX]{x1D70F}_{-8})$
,
![]() $y$
cannot lie in
$y$
cannot lie in
![]() $\mathbb{C}(x)$
. Therefore,
$\mathbb{C}(x)$
. Therefore,
![]() $x$
and
$x$
and
![]() $y$
generate the field of modular functions on
$y$
generate the field of modular functions on
![]() $X$
. From the table above, we determine that the relation between
$X$
. From the table above, we determine that the relation between
![]() $x$
and
$x$
and
![]() $y$
is
$y$
is
 $$\begin{eqnarray}2(x+1)^{2}y^{2}-(8x^{2}+11x+1)y+4x(2x+1)=0.\end{eqnarray}$$
$$\begin{eqnarray}2(x+1)^{2}y^{2}-(8x^{2}+11x+1)y+4x(2x+1)=0.\end{eqnarray}$$
Set
 $$\begin{eqnarray}\displaystyle x_{1} & = & \displaystyle -\frac{2(x+1)^{2}y-5x^{2}-3x-1}{x^{2}},\nonumber\\ \displaystyle y_{1} & = & \displaystyle -\frac{(4x^{3}+6x^{2}-2)y-5x^{3}-6x^{2}+x+1}{x^{3}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{1} & = & \displaystyle -\frac{2(x+1)^{2}y-5x^{2}-3x-1}{x^{2}},\nonumber\\ \displaystyle y_{1} & = & \displaystyle -\frac{(4x^{3}+6x^{2}-2)y-5x^{3}-6x^{2}+x+1}{x^{3}}.\nonumber\end{eqnarray}$$
We find
 $y_{1}^{2}+x_{1}y_{1}+y_{1}=x_{1}^{3}-x_{1}^{2}-12x_{1}+15$
, which is indeed the elliptic curve
$y_{1}^{2}+x_{1}y_{1}+y_{1}=x_{1}^{3}-x_{1}^{2}-12x_{1}+15$
, which is indeed the elliptic curve
![]() $E_{\text{142A1}}$
. The coordinates of the CM points above on this model are given in the following table.
$E_{\text{142A1}}$
. The coordinates of the CM points above on this model are given in the following table.

Here
 $Q=(1,1)$
generates the group of rational points on
$Q=(1,1)$
generates the group of rational points on
![]() $E_{\text{142A1}}$
.
$E_{\text{142A1}}$
.
Example 43. We next consider
 $X=X_{0}^{302}(1)/W_{302,1}$
, which has genus two. We can construct four modular forms
$X=X_{0}^{302}(1)/W_{302,1}$
, which has genus two. We can construct four modular forms
 $f_{1},\ldots ,f_{4}$
in
$f_{1},\ldots ,f_{4}$
in
 $M^{!}(604)$
whose associated Borcherds forms
$M^{!}(604)$
whose associated Borcherds forms
 $\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{4}$
have divisors
$\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{4}$
have divisors
 $$\begin{eqnarray}\displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{1} & = & \displaystyle P_{-43}+P_{-72}-P_{-19}-P_{-88},\nonumber\\ \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{2} & = & \displaystyle P_{-20}+P_{-36}-P_{-19}-P_{-88},\nonumber\\ \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{3} & = & \displaystyle P_{-8}+2P_{-40}-P_{-4}-2P_{-88},\nonumber\\ \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{4} & = & \displaystyle P_{-11}+P_{-19}+P_{-43}-P_{-4}-2P_{-88},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{1} & = & \displaystyle P_{-43}+P_{-72}-P_{-19}-P_{-88},\nonumber\\ \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{2} & = & \displaystyle P_{-20}+P_{-36}-P_{-19}-P_{-88},\nonumber\\ \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{3} & = & \displaystyle P_{-8}+2P_{-40}-P_{-4}-2P_{-88},\nonumber\\ \displaystyle \operatorname{div}\unicode[STIX]{x1D713}_{4} & = & \displaystyle P_{-11}+P_{-19}+P_{-43}-P_{-4}-2P_{-88},\nonumber\end{eqnarray}$$
respectively. In addition, under Assumption 40, they have trivial characters. Thus,
![]() $\unicode[STIX]{x1D713}_{1}$
generates the unique genus-zero subfield of degree two of the hyperelliptic function field, and
$\unicode[STIX]{x1D713}_{1}$
generates the unique genus-zero subfield of degree two of the hyperelliptic function field, and
![]() $\unicode[STIX]{x1D713}_{2}$
is a polynomial of degree one in
$\unicode[STIX]{x1D713}_{2}$
is a polynomial of degree one in
![]() $\unicode[STIX]{x1D713}_{1}$
. Also,
$\unicode[STIX]{x1D713}_{1}$
. Also,
![]() $\unicode[STIX]{x1D713}_{4}$
must be a polynomial of degree one in
$\unicode[STIX]{x1D713}_{4}$
must be a polynomial of degree one in
![]() $\unicode[STIX]{x1D713}_{3}$
. To see this, we observe that there exists a suitable linear combination
$\unicode[STIX]{x1D713}_{3}$
. To see this, we observe that there exists a suitable linear combination
 $a\unicode[STIX]{x1D713}_{3}+b\unicode[STIX]{x1D713}_{4}$
such that it is a function of degree at most two on
$a\unicode[STIX]{x1D713}_{3}+b\unicode[STIX]{x1D713}_{4}$
such that it is a function of degree at most two on
![]() $X$
and, hence, is contained in
$X$
and, hence, is contained in
![]() $\mathbb{C}(\unicode[STIX]{x1D713}_{1})$
. If this linear combination is not a constant function, then it must have a pole at
$\mathbb{C}(\unicode[STIX]{x1D713}_{1})$
. If this linear combination is not a constant function, then it must have a pole at
![]() $\unicode[STIX]{x1D70F}_{-88}$
; otherwise it will have only a pole of order one at
$\unicode[STIX]{x1D70F}_{-88}$
; otherwise it will have only a pole of order one at
![]() $\unicode[STIX]{x1D70F}_{-4}$
, which is impossible. It follows that
$\unicode[STIX]{x1D70F}_{-4}$
, which is impossible. It follows that
![]() $\unicode[STIX]{x1D70F}_{-19}$
is also a pole of this linear combination. However,
$\unicode[STIX]{x1D70F}_{-19}$
is also a pole of this linear combination. However,
![]() $\unicode[STIX]{x1D70F}_{-19}$
can never be a pole of this function. Therefore, we conclude that this linear combination is a constant function.
$\unicode[STIX]{x1D70F}_{-19}$
can never be a pole of this function. Therefore, we conclude that this linear combination is a constant function.
Let
![]() $x$
be the unique function on
$x$
be the unique function on
![]() $X$
with
$X$
with
 $\operatorname{div}x=\operatorname{div}\unicode[STIX]{x1D713}_{1}$
and
$\operatorname{div}x=\operatorname{div}\unicode[STIX]{x1D713}_{1}$
and
 $x(\unicode[STIX]{x1D70F}_{-20})=2$
and
$x(\unicode[STIX]{x1D70F}_{-20})=2$
and
![]() $y$
be the unique function with
$y$
be the unique function with
 $\operatorname{div}y=\operatorname{div}\unicode[STIX]{x1D713}_{3}$
and
$\operatorname{div}y=\operatorname{div}\unicode[STIX]{x1D713}_{3}$
and
 $y(\unicode[STIX]{x1D70F}_{-11})=1$
. Computing using Schofer’s formula, we find the following result.
$y(\unicode[STIX]{x1D70F}_{-11})=1$
. Computing using Schofer’s formula, we find the following result.

From the coordinates at
![]() $\unicode[STIX]{x1D70F}_{-4}$
,
$\unicode[STIX]{x1D70F}_{-4}$
,
![]() $\unicode[STIX]{x1D70F}_{-8}$
,
$\unicode[STIX]{x1D70F}_{-8}$
,
![]() $\unicode[STIX]{x1D70F}_{-19}$
,
$\unicode[STIX]{x1D70F}_{-19}$
,
![]() $\unicode[STIX]{x1D70F}_{-40}$
and
$\unicode[STIX]{x1D70F}_{-40}$
and
![]() $\unicode[STIX]{x1D70F}_{-88}$
, we see that the relation between
$\unicode[STIX]{x1D70F}_{-88}$
, we see that the relation between
![]() $x$
and
$x$
and
![]() $y$
is
$y$
is
 $$\begin{eqnarray}a(x+1)y^{2}+(-2x^{3}+bx^{2}+cx+d)y+(2x-3)(x-1)^{2}=0\end{eqnarray}$$
$$\begin{eqnarray}a(x+1)y^{2}+(-2x^{3}+bx^{2}+cx+d)y+(2x-3)(x-1)^{2}=0\end{eqnarray}$$
for some rational numbers
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
, and
$c$
, and
![]() $d$
. Then the information at the other CM points yields
$d$
. Then the information at the other CM points yields
 $$\begin{eqnarray}a=1,\quad b=11,\quad c=-13,\quad d=2.\end{eqnarray}$$
$$\begin{eqnarray}a=1,\quad b=11,\quad c=-13,\quad d=2.\end{eqnarray}$$
Setting
 $$\begin{eqnarray}x_{0}=\frac{3-x}{1-x},\quad y_{0}=\frac{4(2x^{3}-11x^{2}+13x-2-2xy-2y)}{(1-x)^{3}},\end{eqnarray}$$
$$\begin{eqnarray}x_{0}=\frac{3-x}{1-x},\quad y_{0}=\frac{4(2x^{3}-11x^{2}+13x-2-2xy-2y)}{(1-x)^{3}},\end{eqnarray}$$
we obtain a Weierstrass model
 $$\begin{eqnarray}y_{0}^{2}=x_{0}^{6}-18x_{0}^{4}+113x_{0}^{2}-32\end{eqnarray}$$
$$\begin{eqnarray}y_{0}^{2}=x_{0}^{6}-18x_{0}^{4}+113x_{0}^{2}-32\end{eqnarray}$$
for
![]() $X$
. Then letting
$X$
. Then letting
 $$\begin{eqnarray}x_{1}=x_{0}^{2},\quad y_{1}=y_{0},\quad x_{2}=-32/x_{0}^{2},\quad y_{2}=32y_{0}/x_{0}^{3},\end{eqnarray}$$
$$\begin{eqnarray}x_{1}=x_{0}^{2},\quad y_{1}=y_{0},\quad x_{2}=-32/x_{0}^{2},\quad y_{2}=32y_{0}/x_{0}^{3},\end{eqnarray}$$
we obtain modular parameterization of two elliptic curves
 $$\begin{eqnarray}y_{1}^{2}=x_{1}^{3}-18x_{1}^{2}+113x_{1}-32,\quad y_{2}^{2}=x_{2}^{3}+113x_{2}^{2}+576x_{2}+1024.\end{eqnarray}$$
$$\begin{eqnarray}y_{1}^{2}=x_{1}^{3}-18x_{1}^{2}+113x_{1}-32,\quad y_{2}^{2}=x_{2}^{3}+113x_{2}^{2}+576x_{2}+1024.\end{eqnarray}$$
The minimal models of these two elliptic curves are
 $E_{\text{302C1}}:Y^{2}+XY+Y=X^{3}-X^{2}+3$
and
$E_{\text{302C1}}:Y^{2}+XY+Y=X^{3}-X^{2}+3$
and
 $E_{\text{302A1}}:Y^{2}+XY+Y=X^{3}+X^{2}-230X+1251$
, respectively, in Cremona’s table. The coordinates of the CM points on the two curves are as follows.
$E_{\text{302A1}}:Y^{2}+XY+Y=X^{3}+X^{2}-230X+1251$
, respectively, in Cremona’s table. The coordinates of the CM points on the two curves are as follows.

Here
 $P=(-32,256)$
generates the torsion subgroup of order five and
$P=(-32,256)$
generates the torsion subgroup of order five and
 $Q=(-96,320)$
generates the free part of
$Q=(-96,320)$
generates the free part of
 $E_{\text{302A1}}(\mathbb{Q})$
, and
$E_{\text{302A1}}(\mathbb{Q})$
, and
 $R=(9,16)$
generates the group of rational points on
$R=(9,16)$
generates the group of rational points on
![]() $E_{\text{302C1}}$
. In the arXiv version of the present paper, we also address the issue of heights of CM points on the Jacobians of these elliptic curves.
$E_{\text{302C1}}$
. In the arXiv version of the present paper, we also address the issue of heights of CM points on the Jacobians of these elliptic curves.
Acknowledgements
The authors would like to thank Dr Yi-Hsuan Lin for his masterfully written code. It would have been impossible to construct required Borcherds forms without the code. The authors would also like to thank the referee for carefully reading the manuscript and providing valuable comments.
Appendix A Tables for equations of hyperelliptic Shimura curves
We list defining equations of hyperelliptic Shimura curves in Tables A.1 and A.2.
Table A.1. Equations of level one.

Table A.2. Equations of level greater than one.