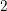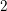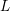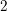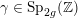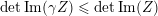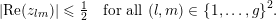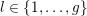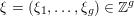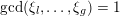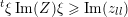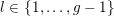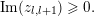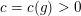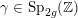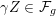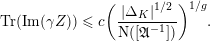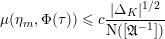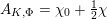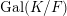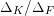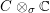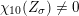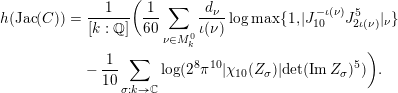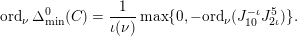1 Introduction
By a curve we mean a smooth, geometrically connected, projective curve
![]() $C$
defined over a field
$C$
defined over a field
![]() $k$
. Its jacobian variety
$k$
. Its jacobian variety
![]() $\operatorname{Jac}(C)$
is a principally polarised abelian variety defined over
$\operatorname{Jac}(C)$
is a principally polarised abelian variety defined over
![]() $k$
. For any abelian variety
$k$
. For any abelian variety
![]() $A$
defined over
$A$
defined over
![]() $k$
, we write
$k$
, we write
![]() $\operatorname{End}(A)$
for the ring of geometric endomorphisms of
$\operatorname{End}(A)$
for the ring of geometric endomorphisms of
![]() $A$
, i.e., the ring of endomorphisms of the base change of
$A$
, i.e., the ring of endomorphisms of the base change of
![]() $A$
to a given algebraic closure of
$A$
to a given algebraic closure of
![]() $k$
. For brevity we say that
$k$
. For brevity we say that
![]() $A$
has CM if its base change to an algebraic closure of
$A$
has CM if its base change to an algebraic closure of
![]() $k$
has complex multiplication and if
$k$
has complex multiplication and if
![]() $k$
has characteristic
$k$
has characteristic
![]() $0$
. We also say that
$0$
. We also say that
![]() $C$
has CM if
$C$
has CM if
![]() $\operatorname{Jac}(C)$
does. A curve defined over
$\operatorname{Jac}(C)$
does. A curve defined over
![]() $\overline{\mathbb{Q}}$
is said to have good reduction everywhere if it has potentially good reduction at all finite places of a number field over which it is defined.
$\overline{\mathbb{Q}}$
is said to have good reduction everywhere if it has potentially good reduction at all finite places of a number field over which it is defined.
By the work of Serre and Tate [Reference Serre and TateST68], an abelian variety defined over a number field with CM has potentially good reduction at all finite places. If a curve of positive genus which is defined over a number field has good reduction at a given finite place, then so does its jacobian variety. However, the converse statement is false in the genus
![]() $2$
case; cf. entry [
$2$
case; cf. entry [
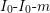 $I_{0}\text{-}I_{0}\text{-}m$
] in Namikawa and Ueno’s classification table [Reference Namikawa and UenoNU73] in equicharacteristic
$I_{0}\text{-}I_{0}\text{-}m$
] in Namikawa and Ueno’s classification table [Reference Namikawa and UenoNU73] in equicharacteristic
![]() $0$
. The main result of our paper, which we discuss in greater detail below, states that this phenomenon prevails for certain families of CM curves of genus
$0$
. The main result of our paper, which we discuss in greater detail below, states that this phenomenon prevails for certain families of CM curves of genus
![]() $2$
.
$2$
.
Theorem 1.1. Let
![]() $F$
be a real quadratic number field. Up to isomorphism there are only finitely many curves
$F$
be a real quadratic number field. Up to isomorphism there are only finitely many curves
![]() $C$
of genus
$C$
of genus
![]() $2$
defined over
$2$
defined over
![]() $\overline{\mathbb{Q}}$
with good reduction everywhere and such that
$\overline{\mathbb{Q}}$
with good reduction everywhere and such that
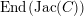 $\operatorname{End}(\operatorname{Jac}(C))$
is the maximal order of a quartic, cyclic, totally imaginary number field containing
$\operatorname{End}(\operatorname{Jac}(C))$
is the maximal order of a quartic, cyclic, totally imaginary number field containing
![]() $F$
.
$F$
.
This finiteness result is of a familiar type for objects in arithmetic geometry. A number field has only finitely many unramified extensions of given degree due to the theorem of Hermite–Minkowski. The Shafarevich conjecture, proved by Faltings [Reference FaltingsFal83], ensures that again there are only finitely many curves defined over a fixed number field, of fixed positive genus, with good reduction outside a fixed finite set of places. Fontaine [Reference FontaineFon85, p. 517] proved that there is no non-zero abelian variety of any dimension with good reduction at all finite places if one fixes the field of definition to be
![]() $\mathbb{Q}$
,
$\mathbb{Q}$
,
![]() $\mathbb{Q}(i)$
,
$\mathbb{Q}(i)$
,
![]() $\mathbb{Q}(i\sqrt{3})$
, or
$\mathbb{Q}(i\sqrt{3})$
, or
![]() $\mathbb{Q}(\sqrt{5})$
. In particular, there exists no curve over
$\mathbb{Q}(\sqrt{5})$
. In particular, there exists no curve over
![]() $\mathbb{Q}$
of positive genus that has good reduction at all primes. Schoof obtained finiteness results along these lines for certain additional cyclotomic fields [Reference SchoofSch03].
$\mathbb{Q}$
of positive genus that has good reduction at all primes. Schoof obtained finiteness results along these lines for certain additional cyclotomic fields [Reference SchoofSch03].
Let us stress here that there are infinitely many curves of genus
![]() $2$
defined over
$2$
defined over
![]() $\overline{\mathbb{Q}}$
with good reduction everywhere. One can deduce this fact from Moret-Bailly [Reference Moret-BaillyMB01, Exemple 0.9].
$\overline{\mathbb{Q}}$
with good reduction everywhere. One can deduce this fact from Moret-Bailly [Reference Moret-BaillyMB01, Exemple 0.9].
Our result does not seem to be a direct consequence of the theorems mentioned above. Instead of working over a fixed number field our finiteness result concerns curves over the algebraically closed field
![]() $\overline{\mathbb{Q}}$
. Indeed, it is not possible to uniformly bound the degree over
$\overline{\mathbb{Q}}$
. Indeed, it is not possible to uniformly bound the degree over
![]() $\mathbb{Q}$
of a curve of genus
$\mathbb{Q}$
of a curve of genus
![]() $2$
whose jacobian variety has complex multiplication.
$2$
whose jacobian variety has complex multiplication.
Example 1.2. Let us exhibit an infinite family of genus
![]() $2$
curves with CM such that the endomorphism ring is the ring of algebraic integers in a cyclic extension of
$2$
curves with CM such that the endomorphism ring is the ring of algebraic integers in a cyclic extension of
![]() $\mathbb{Q}$
that contains
$\mathbb{Q}$
that contains
![]() $\mathbb{Q}(\sqrt{5})$
.
$\mathbb{Q}(\sqrt{5})$
.
Suppose that
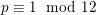 $p\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}12$
is a prime; then
$p\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}12$
is a prime; then
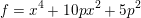 $$\begin{eqnarray}f=x^{4}+10px^{2}+5p^{2}\end{eqnarray}$$
$$\begin{eqnarray}f=x^{4}+10px^{2}+5p^{2}\end{eqnarray}$$
has roots
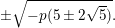 $$\begin{eqnarray}\pm \sqrt{-p(5\pm 2\sqrt{5})}.\end{eqnarray}$$
$$\begin{eqnarray}\pm \sqrt{-p(5\pm 2\sqrt{5})}.\end{eqnarray}$$
So, the splitting field
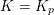 $K=K_{p}$
of
$K=K_{p}$
of
![]() $f$
over
$f$
over
![]() $\mathbb{Q}$
is a CM field with maximal totally real subfield
$\mathbb{Q}$
is a CM field with maximal totally real subfield
![]() $\mathbb{Q}(\sqrt{5})$
. The product of two roots lies in
$\mathbb{Q}(\sqrt{5})$
. The product of two roots lies in
![]() $\mathbb{Q}(\sqrt{5})$
, so
$\mathbb{Q}(\sqrt{5})$
, so
![]() $K/\mathbb{Q}$
is a Galois extension. But such a product does not lie in
$K/\mathbb{Q}$
is a Galois extension. But such a product does not lie in
![]() $\mathbb{Q}$
, so the Galois group of
$\mathbb{Q}$
, so the Galois group of
![]() $K/\mathbb{Q}$
is not isomorphic to
$K/\mathbb{Q}$
is not isomorphic to
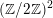 $(\mathbb{Z}/2\mathbb{Z})^{2}$
. This means that
$(\mathbb{Z}/2\mathbb{Z})^{2}$
. This means that
![]() $K/\mathbb{Q}$
is a cyclic extension.
$K/\mathbb{Q}$
is a cyclic extension.
By (1.1),
![]() $K$
is ramified above
$K$
is ramified above
![]() $p$
, so we obtain infinitely many fields
$p$
, so we obtain infinitely many fields
![]() $K$
as infinitely many primes
$K$
as infinitely many primes
![]() $p$
satisfy
$p$
satisfy
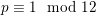 $p\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}12$
.
$p\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}12$
.
There exists a principally polarised abelian surface whose endomorphism ring is the ring of algebraic integers in
![]() $K$
; see for example the paragraph after the proof of Theorem 4 of van Wamelen [Reference van WamelenvWa99a].
$K$
; see for example the paragraph after the proof of Theorem 4 of van Wamelen [Reference van WamelenvWa99a].
In our situation this abelian surface is necessarily simple; cf. Lemma 3.10 below.
A principally polarised abelian surface that is not a product of elliptic curves with the product polarisation is the jacobian of a curve of genus
![]() $2$
by [Reference Birkenhake and LangeBL04, Corollary 11.8.2]. Therefore, there is a curve
$2$
by [Reference Birkenhake and LangeBL04, Corollary 11.8.2]. Therefore, there is a curve
![]() $C=C_{p}$
defined over a number field such that
$C=C_{p}$
defined over a number field such that
![]() $\operatorname{Jac}(C)$
has complex multiplication by the ring of algebraic integers in
$\operatorname{Jac}(C)$
has complex multiplication by the ring of algebraic integers in
![]() $K$
. According to Theorem 1.1, the curve
$K$
. According to Theorem 1.1, the curve
![]() $C$
has potentially good reduction everywhere for at most finitely many
$C$
has potentially good reduction everywhere for at most finitely many
![]() $p$
.
$p$
.
We set
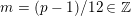 $m=(p-1)/12\in \mathbb{Z}$
and observe that
$m=(p-1)/12\in \mathbb{Z}$
and observe that
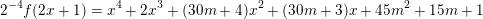 $$\begin{eqnarray}2^{-4}f(2x+1)=x^{4}+2x^{3}+(30m+4)x^{2}+(30m+3)x+45m^{2}+15m+1\end{eqnarray}$$
$$\begin{eqnarray}2^{-4}f(2x+1)=x^{4}+2x^{3}+(30m+4)x^{2}+(30m+3)x+45m^{2}+15m+1\end{eqnarray}$$
is irreducible modulo
![]() $2$
and modulo
$2$
and modulo
![]() $3$
. This implies that
$3$
. This implies that
![]() $K/\mathbb{Q}$
is unramified above these primes and even that they are inert in
$K/\mathbb{Q}$
is unramified above these primes and even that they are inert in
![]() $K$
. We may apply Goren [Reference GorenGor97, Theorem 1] to see that the semi-stable reduction of
$K$
. We may apply Goren [Reference GorenGor97, Theorem 1] to see that the semi-stable reduction of
![]() $\operatorname{Jac}(C)$
at all places above
$\operatorname{Jac}(C)$
at all places above
![]() $2$
and
$2$
and
![]() $3$
is isogenous but not isomorphic to a product of supersingular elliptic curves. By the paragraph before Proposition 2 of Liu [Reference LiuLiu93], the curve
$3$
is isogenous but not isomorphic to a product of supersingular elliptic curves. By the paragraph before Proposition 2 of Liu [Reference LiuLiu93], the curve
![]() $C$
has potentially good reduction at places above
$C$
has potentially good reduction at places above
![]() $2$
and
$2$
and
![]() $3$
. So, bad reduction is not a consequence of the obstruction described by Ibukiyama et al. [Reference Ibukiyama, Katsura and OortIKO86, Theorem 3.3(III)]; cf. Goren and Lauter’s comment of [Reference Goren and LauterGL07, p. 477].
$3$
. So, bad reduction is not a consequence of the obstruction described by Ibukiyama et al. [Reference Ibukiyama, Katsura and OortIKO86, Theorem 3.3(III)]; cf. Goren and Lauter’s comment of [Reference Goren and LauterGL07, p. 477].
The proof of Theorem 1.1 relies heavily on various aspects of the stable Faltings height
![]() $h(A)$
of an abelian variety
$h(A)$
of an abelian variety
![]() $A$
defined over a number field. Indeed, it follows by computing the said height of
$A$
defined over a number field. Indeed, it follows by computing the said height of
![]() $\operatorname{Jac}(C)$
in two different ways if
$\operatorname{Jac}(C)$
in two different ways if
![]() $C$
is a genus
$C$
is a genus
![]() $2$
curve defined over
$2$
curve defined over
![]() $\overline{\mathbb{Q}}$
. We will be able to bound one of these expressions from below and the other one from above. The resulting inequality will yield Theorem 1.4 below, a more precise version of our result above.
$\overline{\mathbb{Q}}$
. We will be able to bound one of these expressions from below and the other one from above. The resulting inequality will yield Theorem 1.4 below, a more precise version of our result above.
The first expression of the Faltings height of
![]() $\operatorname{Jac}(C)$
uses the additional hypothesis that
$\operatorname{Jac}(C)$
uses the additional hypothesis that
![]() $C$
has CM as in Theorem 1.1. We will use Colmez’s conjecture, a theorem in our case due to Colmez [Reference ColmezCol93] and Obus [Reference ObusObu13], as the CM field
$C$
has CM as in Theorem 1.1. We will use Colmez’s conjecture, a theorem in our case due to Colmez [Reference ColmezCol93] and Obus [Reference ObusObu13], as the CM field
![]() $K$
is an abelian extension of
$K$
is an abelian extension of
![]() $\mathbb{Q}$
. Yang [Reference YangYan10] was the first to prove the Colmez conjecture in some non-abelian quartic cases. Colmez’s conjecture enables us to express
$\mathbb{Q}$
. Yang [Reference YangYan10] was the first to prove the Colmez conjecture in some non-abelian quartic cases. Colmez’s conjecture enables us to express
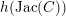 $h(\operatorname{Jac}(C))$
in terms of the logarithmic derivative of an
$h(\operatorname{Jac}(C))$
in terms of the logarithmic derivative of an
![]() $L$
-function. Using this presentation, Colmez [Reference ColmezCol98] found a lower bound for the Faltings height of an elliptic curve with CM when the endomorphism ring is a maximal order. The bound grows logarithmically in the discriminant of the CM field. We recall that the discriminant
$L$
-function. Using this presentation, Colmez [Reference ColmezCol98] found a lower bound for the Faltings height of an elliptic curve with CM when the endomorphism ring is a maximal order. The bound grows logarithmically in the discriminant of the CM field. We recall that the discriminant
![]() $\unicode[STIX]{x1D6E5}_{K}$
of
$\unicode[STIX]{x1D6E5}_{K}$
of
![]() $K$
is a positive integer as
$K$
is a positive integer as
![]() $K$
is a quartic CM field. In our case we obtain a lower bound which is linear in
$K$
is a quartic CM field. In our case we obtain a lower bound which is linear in
![]() $\log \unicode[STIX]{x1D6E5}_{K}$
. Let
$\log \unicode[STIX]{x1D6E5}_{K}$
. Let
![]() $B$
be a real number. So, by the theorem of Hermite–Minkowski, there are only finitely many possibilities for
$B$
be a real number. So, by the theorem of Hermite–Minkowski, there are only finitely many possibilities for
![]() $K$
up to isomorphism if
$K$
up to isomorphism if
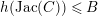 $h(\operatorname{Jac}(C))\leqslant B$
. In the situation of Theorem 1.1, the endomorphism ring of
$h(\operatorname{Jac}(C))\leqslant B$
. In the situation of Theorem 1.1, the endomorphism ring of
![]() $\operatorname{Jac}(C)$
is the maximal order of
$\operatorname{Jac}(C)$
is the maximal order of
![]() $K$
. So, there are only finitely many possibilities for
$K$
. So, there are only finitely many possibilities for
![]() $\operatorname{Jac}(C)$
up to isomorphism for fixed
$\operatorname{Jac}(C)$
up to isomorphism for fixed
![]() $B$
. Torelli’s theorem will imply that there are at most finitely many possibilities for
$B$
. Torelli’s theorem will imply that there are at most finitely many possibilities for
![]() $C$
up to isomorphism.
$C$
up to isomorphism.
Our theorem would follow if we could establish a uniform height upper bound
![]() $B$
as before. We were not able to do this directly. Instead, we will show that for any
$B$
as before. We were not able to do this directly. Instead, we will show that for any
![]() $\unicode[STIX]{x1D716}>0$
there is a constant
$\unicode[STIX]{x1D716}>0$
there is a constant
![]() $c(\unicode[STIX]{x1D716},F)$
with
$c(\unicode[STIX]{x1D716},F)$
with
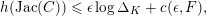 $$\begin{eqnarray}h(\operatorname{Jac}(C))\leqslant \unicode[STIX]{x1D716}\log \unicode[STIX]{x1D6E5}_{K}+c(\unicode[STIX]{x1D716},F),\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))\leqslant \unicode[STIX]{x1D716}\log \unicode[STIX]{x1D6E5}_{K}+c(\unicode[STIX]{x1D716},F),\end{eqnarray}$$
with
![]() $F$
the maximal totally real subfield of
$F$
the maximal totally real subfield of
![]() $K$
. For small
$K$
. For small
![]() $\unicode[STIX]{x1D716}$
this upper bound is strong enough to compete with the logarithmic lower bound coming from Colmez’s conjecture because
$\unicode[STIX]{x1D716}$
this upper bound is strong enough to compete with the logarithmic lower bound coming from Colmez’s conjecture because
![]() $F$
is fixed in our Theorem 1.1. It would be interesting to know if this inequality could be made uniform in
$F$
is fixed in our Theorem 1.1. It would be interesting to know if this inequality could be made uniform in
![]() $F$
.
$F$
.
The upper bound requires the second expression for the Faltings height of
![]() $\operatorname{Jac}(C)$
alluded to above. We still work with a curve
$\operatorname{Jac}(C)$
alluded to above. We still work with a curve
![]() $C$
of genus
$C$
of genus
![]() $2$
defined over
$2$
defined over
![]() $\overline{\mathbb{Q}}$
, but now do not require that
$\overline{\mathbb{Q}}$
, but now do not require that
![]() $\operatorname{Jac}(C)$
has CM. Suppose that
$\operatorname{Jac}(C)$
has CM. Suppose that
![]() $C$
is the base change to
$C$
is the base change to
![]() $\overline{\mathbb{Q}}$
of a curve
$\overline{\mathbb{Q}}$
of a curve
![]() $C_{k}$
defined over a number field
$C_{k}$
defined over a number field
![]() $k\subseteq \overline{\mathbb{Q}}$
. If
$k\subseteq \overline{\mathbb{Q}}$
. If
![]() $C_{k}$
has good reduction at all places above
$C_{k}$
has good reduction at all places above
![]() $2$
, then Ueno [Reference UenoUen88] decomposed
$2$
, then Ueno [Reference UenoUen88] decomposed
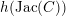 $h(\operatorname{Jac}(C))$
into a sum over all places of
$h(\operatorname{Jac}(C))$
into a sum over all places of
![]() $k$
.Footnote
1
We present another expression for the Faltings height in Theorem 4.5 by decomposing it into local terms. In contrast to Ueno’s formula and with our application in mind, we require that
$k$
.Footnote
1
We present another expression for the Faltings height in Theorem 4.5 by decomposing it into local terms. In contrast to Ueno’s formula and with our application in mind, we require that
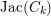 $\operatorname{Jac}(C_{k})$
has good reduction at all finite places but in turn allow
$\operatorname{Jac}(C_{k})$
has good reduction at all finite places but in turn allow
![]() $C_{k}$
to have bad reduction above
$C_{k}$
to have bad reduction above
![]() $2$
. Our proof of Theorem 4.5 makes use of the reduction theory of genus
$2$
. Our proof of Theorem 4.5 makes use of the reduction theory of genus
![]() $2$
curves as developed by Igusa [Reference IgusaIgu60] and later by Liu [Reference LiuLiu93, Reference LiuLiu94] as well as Saito’s generalisation [Reference SaitoSai88] of Ogg’s formula for the conductor of an elliptic curve. In our decomposition of
$2$
curves as developed by Igusa [Reference IgusaIgu60] and later by Liu [Reference LiuLiu93, Reference LiuLiu94] as well as Saito’s generalisation [Reference SaitoSai88] of Ogg’s formula for the conductor of an elliptic curve. In our decomposition of
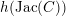 $h(\operatorname{Jac}(C))$
into local terms a non-zero contribution at a finite place indicates that the curve
$h(\operatorname{Jac}(C))$
into local terms a non-zero contribution at a finite place indicates that the curve
![]() $C_{k}$
has bad stable reduction at the said place. In other words, if
$C_{k}$
has bad stable reduction at the said place. In other words, if
![]() $C$
has good reduction everywhere, as in Theorem 1.1, then the finite places do not contribute to
$C$
has good reduction everywhere, as in Theorem 1.1, then the finite places do not contribute to
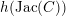 $h(\operatorname{Jac}(C))$
. We will also express the local contribution in
$h(\operatorname{Jac}(C))$
. We will also express the local contribution in
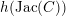 $h(\operatorname{Jac}(C))$
at the finite places in terms of the classical Igusa invariants attached to
$h(\operatorname{Jac}(C))$
at the finite places in terms of the classical Igusa invariants attached to
![]() $C$
.
$C$
.
The terms at the archimedean places in Theorem 4.5 are expressed using a Siegel modular cusp form of degree
![]() $2$
and weight
$2$
and weight
![]() $10$
. We must bound these infinite places from above in order to arrive at (1.2). One issue is that the archimedean local term has a logarithmic singularity along the divisor where the cusp form vanishes. This vanishing locus corresponds to the principally polarised abelian surfaces that are isomorphic to a product of elliptic curves with the product polarisation. The jacobian variety of a genus
$10$
. We must bound these infinite places from above in order to arrive at (1.2). One issue is that the archimedean local term has a logarithmic singularity along the divisor where the cusp form vanishes. This vanishing locus corresponds to the principally polarised abelian surfaces that are isomorphic to a product of elliptic curves with the product polarisation. The jacobian variety of a genus
![]() $2$
curve defined over
$2$
curve defined over
![]() $\mathbb{C}$
is never such a product. So, in our application, we are never on the logarithmic singularity.
$\mathbb{C}$
is never such a product. So, in our application, we are never on the logarithmic singularity.
To obtain the upper bound for
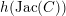 $h(\operatorname{Jac}(C))$
we must ensure first that not too many period matrices coming from the conjugates of
$h(\operatorname{Jac}(C))$
we must ensure first that not too many period matrices coming from the conjugates of
![]() $\operatorname{Jac}(C)$
are close to the logarithmic singularity. Second, we must show that no period matrix is excessively close to the said singularity.
$\operatorname{Jac}(C)$
are close to the logarithmic singularity. Second, we must show that no period matrix is excessively close to the said singularity.
To achieve the first goal we require Zhang’s equidistribution theorem [Reference ZhangZha05] for Galois orbits of CM points on Hilbert modular surfaces. Zhang’s result relies on the powerful subconvexity estimate due to Michel and Venkatesh [Reference Michel and VenkateshMV10]; Cohen [Reference CohenCoh05] and Clozel and Ullmo [Reference Clozel and UllmoCU05] have related equidistribution results. Roughly speaking, equidistribution guarantees that only a small proportion of period matrices coming from the Galois orbit of
![]() $\operatorname{Jac}(C)$
lie close to the problematic divisor.
$\operatorname{Jac}(C)$
lie close to the problematic divisor.
However, equidistribution does not rule out the possibility that some period matrix is excessively close to the singular locus. To handle this contingency we use the following simple but crucial observation. Inside Siegel’s fundamental domain, the divisor consists of diagonal period matrices
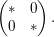 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\ast & 0\\ 0 & \ast \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\ast & 0\\ 0 & \ast \end{array}\right).\end{eqnarray}$$
A period matrix lying close to this divisor has small off-diagonal entries. It is a classical fact that the period matrix of a CM abelian variety is algebraic. Moreover, the degree over
![]() $\mathbb{Q}$
of each entry is bounded from above in terms of the dimension of the abelian variety. We will use Liouville’s inequality to bound the modulus of the off-diagonal entries from below. This enables us to handle the contribution coming from the vanishing locus of the cusp form.
$\mathbb{Q}$
of each entry is bounded from above in terms of the dimension of the abelian variety. We will use Liouville’s inequality to bound the modulus of the off-diagonal entries from below. This enables us to handle the contribution coming from the vanishing locus of the cusp form.
The archimedean contribution to the Faltings height of
![]() $\operatorname{Jac}(C)$
is also unbounded near the cusp in the Siegel upper half-space. We will again use the subconvexity estimates to control this contribution on average.
$\operatorname{Jac}(C)$
is also unbounded near the cusp in the Siegel upper half-space. We will again use the subconvexity estimates to control this contribution on average.
Our efforts at the archimedean places can be reduced to obtaining an upper bound for the archimedean contribution to the Faltings height of
![]() $\operatorname{Jac}(C)$
. We state this bound separately.
$\operatorname{Jac}(C)$
. We state this bound separately.
Theorem 1.3. For any
![]() $\unicode[STIX]{x1D716}>0$
and any real quadratic field
$\unicode[STIX]{x1D716}>0$
and any real quadratic field
![]() $F$
, there exists a constant
$F$
, there exists a constant
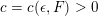 $c=c(\unicode[STIX]{x1D716},F)>0$
with the following property. Let
$c=c(\unicode[STIX]{x1D716},F)>0$
with the following property. Let
![]() $C$
be a curve of genus
$C$
be a curve of genus
![]() $2$
defined over a number field
$2$
defined over a number field
![]() $k$
such that its jacobian
$k$
such that its jacobian
![]() $\operatorname{Jac}(C)$
has complex multiplication by the ring of integers of a CM field
$\operatorname{Jac}(C)$
has complex multiplication by the ring of integers of a CM field
![]() $K$
containing
$K$
containing
![]() $F$
that is quartic and cyclic over
$F$
that is quartic and cyclic over
![]() $\mathbb{Q}$
. For an embedding
$\mathbb{Q}$
. For an embedding
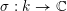 $\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
, let
$\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
, let
![]() $Z_{\unicode[STIX]{x1D70E}}$
denote a period matrix of
$Z_{\unicode[STIX]{x1D70E}}$
denote a period matrix of
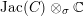 $\operatorname{Jac}(C)\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
. Then
$\operatorname{Jac}(C)\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
. Then
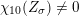 $\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})\not =0$
and
$\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})\not =0$
and
 $$\begin{eqnarray}-\frac{1}{[k:\mathbb{Q}]}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}\,\operatorname{Im}(Z_{\unicode[STIX]{x1D70E}})^{5})\leqslant \unicode[STIX]{x1D716}(\log \unicode[STIX]{x1D6E5}_{K})+c,\end{eqnarray}$$
$$\begin{eqnarray}-\frac{1}{[k:\mathbb{Q}]}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}\,\operatorname{Im}(Z_{\unicode[STIX]{x1D70E}})^{5})\leqslant \unicode[STIX]{x1D716}(\log \unicode[STIX]{x1D6E5}_{K})+c,\end{eqnarray}$$
where
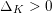 $\unicode[STIX]{x1D6E5}_{K}>0$
is the discriminant of
$\unicode[STIX]{x1D6E5}_{K}>0$
is the discriminant of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D712}_{10}$
is the Siegel cusp mentioned above. (The value of
$\unicode[STIX]{x1D712}_{10}$
is the Siegel cusp mentioned above. (The value of
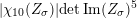 $|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}\operatorname{Im}(Z_{\unicode[STIX]{x1D70E}})^{5}$
does not depend on the choice of period matrix.)
$|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}\operatorname{Im}(Z_{\unicode[STIX]{x1D70E}})^{5}$
does not depend on the choice of period matrix.)
These various estimates combine to give (1.2). The quantitative nature of our approach allows for the following quantitative estimate, which implies Theorem 1.1, as we will see. We will measure the amount of bad stable reduction of a curve
![]() $C_{k}$
of genus
$C_{k}$
of genus
![]() $2$
defined over a number field
$2$
defined over a number field
![]() $k$
using the minimal discriminant
$k$
using the minimal discriminant
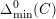 $\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
in the sense of Definition 4.4. It is a non-zero ideal in the ring of integers of
$\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
in the sense of Definition 4.4. It is a non-zero ideal in the ring of integers of
![]() $k$
and
$k$
and
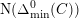 $\text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))$
denotes its norm below.
$\text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))$
denotes its norm below.
Theorem 1.4. Let
![]() $F$
be a real quadratic number field. There exists a constant
$F$
be a real quadratic number field. There exists a constant
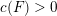 $c(F)>0$
with the following property. Let
$c(F)>0$
with the following property. Let
![]() $C$
be a curve of genus
$C$
be a curve of genus
![]() $2$
defined over
$2$
defined over
![]() $\overline{\mathbb{Q}}$
such that
$\overline{\mathbb{Q}}$
such that
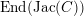 $\operatorname{End}(\operatorname{Jac}(C))$
is the maximal order of an imaginary quadratic extension
$\operatorname{End}(\operatorname{Jac}(C))$
is the maximal order of an imaginary quadratic extension
![]() $K$
of
$K$
of
![]() $F$
with
$F$
with
![]() $K/\mathbb{Q}$
cyclic. Then
$K/\mathbb{Q}$
cyclic. Then
![]() $C$
is the base change to
$C$
is the base change to
![]() $\overline{\mathbb{Q}}$
of a curve
$\overline{\mathbb{Q}}$
of a curve
![]() $C_{k}$
defined over a number field
$C_{k}$
defined over a number field
![]() $k\subseteq \overline{\mathbb{Q}}$
with
$k\subseteq \overline{\mathbb{Q}}$
with
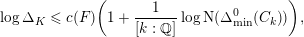 $$\begin{eqnarray}\log \unicode[STIX]{x1D6E5}_{K}\leqslant c(F)\biggl(1+\frac{1}{[k:\mathbb{Q}]}\log \text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C_{k}))\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\log \unicode[STIX]{x1D6E5}_{K}\leqslant c(F)\biggl(1+\frac{1}{[k:\mathbb{Q}]}\log \text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C_{k}))\biggr),\end{eqnarray}$$
where the normalised norm on the right is invariant under finite field extensions of
![]() $k$
.
$k$
.
The choice of
![]() $k$
will be made during the proof.
$k$
will be made during the proof.
In Theorem 4.5(ii), we will be able to express the normalised norm in terms of the Igusa invariants of the curve
![]() $C$
.
$C$
.
Theorem 1.4 implies finiteness results for more general families than curves with potentially good reduction everywhere. Indeed, an analog of Theorem 1.1 is obtained for any collection where the normalised norm of
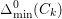 $\unicode[STIX]{x1D6E5}_{\min }^{0}(C_{k})$
is uniformly bounded from above.
$\unicode[STIX]{x1D6E5}_{\min }^{0}(C_{k})$
is uniformly bounded from above.
Let
![]() $K$
be a quartic CM field that is not bi-quadratic. Goren and Lauter [Reference Goren and LauterGL06] called a rational prime
$K$
be a quartic CM field that is not bi-quadratic. Goren and Lauter [Reference Goren and LauterGL06] called a rational prime
![]() $p$
evil for
$p$
evil for
![]() $K$
if there is a principally polarised abelian variety with CM by the maximal order of
$K$
if there is a principally polarised abelian variety with CM by the maximal order of
![]() $K$
whose reduction over a place above
$K$
whose reduction over a place above
![]() $p$
is a product of two supersingular elliptic curves with the product polarisation. This corresponds to a genus
$p$
is a product of two supersingular elliptic curves with the product polarisation. This corresponds to a genus
![]() $2$
curve whose semi-stable reduction is bad at a place above
$2$
curve whose semi-stable reduction is bad at a place above
![]() $p$
and whose jacobian variety has CM by the maximal order of
$p$
and whose jacobian variety has CM by the maximal order of
![]() $K$
. Goren and Lauter proved that evilness prevails by showing that a given prime is evil for infinitely many
$K$
. Goren and Lauter proved that evilness prevails by showing that a given prime is evil for infinitely many
![]() $K$
containing a fixed real quadratic field with trivial narrow-class group. In our Theorem 1.1, the prime
$K$
containing a fixed real quadratic field with trivial narrow-class group. In our Theorem 1.1, the prime
![]() $p$
varies; using Goren and Lauter’s terminology we can restate our result as follows. For all but finitely many quartic and cyclic CM number fields containing a given real quadratic field, there is an evil prime.
$p$
varies; using Goren and Lauter’s terminology we can restate our result as follows. For all but finitely many quartic and cyclic CM number fields containing a given real quadratic field, there is an evil prime.
Let us now recall the fundamental result of Deligne and Mumford of [Reference Deligne and MumfordDM69, Theorem 2.4, p. 89].
Theorem 1.5 (Deligne–Mumford).
Let
![]() $k$
be a field with a discrete valuation and with algebraically closed residue field. Let
$k$
be a field with a discrete valuation and with algebraically closed residue field. Let
![]() $C$
be a curve over
$C$
be a curve over
![]() $k$
of genus at least
$k$
of genus at least
![]() $2$
. Then the jacobian variety
$2$
. Then the jacobian variety
![]() $\operatorname{Jac}(C)$
has semi-stable reduction if and only if
$\operatorname{Jac}(C)$
has semi-stable reduction if and only if
![]() $C$
has semi-stable reduction.
$C$
has semi-stable reduction.
The reader should keep in mind that even though a curve and its jacobian variety have semi-stable reduction simultaneously, it does not mean that the type of reduction (good or bad) is the same.
We conclude this introduction by posing some questions related to our results and to
![]() ${\mathcal{A}}_{g}$
, the coarse moduli space of principally polarised abelian varieties of dimension
${\mathcal{A}}_{g}$
, the coarse moduli space of principally polarised abelian varieties of dimension
![]() $g\geqslant 1$
.
$g\geqslant 1$
.
The authors conjecture that there are only finitely many curves
![]() $C$
of genus
$C$
of genus
![]() $2$
defined over
$2$
defined over
![]() $\overline{\mathbb{Q}}$
which have good reduction everywhere and for which
$\overline{\mathbb{Q}}$
which have good reduction everywhere and for which
![]() $\operatorname{Jac}(C)$
has complex multiplication by an order containing the ring of integers of
$\operatorname{Jac}(C)$
has complex multiplication by an order containing the ring of integers of
![]() $F$
.
$F$
.
Our restriction in Theorem 1.1 that
![]() $K/\mathbb{Q}$
is abelian reflects the current status of Colmez’s conjecture. This conjecture is open for general quartic extensions of
$K/\mathbb{Q}$
is abelian reflects the current status of Colmez’s conjecture. This conjecture is open for general quartic extensions of
![]() $\mathbb{Q}$
. However, Yang [Reference YangYan10] has proved some non-abelian cases for quartic CM fields. Recently, Andreatta–Goren–Howard–Madapusi Pera and independently Yuan–Zhang announced a version of Colmez’s conjecture when averaging over all CM types of a CM field. An averaged version is not strong enough for our purposes. It is, however, if all members in the average have the same Faltings height (which is the case in our paper). We hope that this will allow us to extend our theorems above to quartic CM fields that are not normal over
$\mathbb{Q}$
. However, Yang [Reference YangYan10] has proved some non-abelian cases for quartic CM fields. Recently, Andreatta–Goren–Howard–Madapusi Pera and independently Yuan–Zhang announced a version of Colmez’s conjecture when averaging over all CM types of a CM field. An averaged version is not strong enough for our purposes. It is, however, if all members in the average have the same Faltings height (which is the case in our paper). We hope that this will allow us to extend our theorems above to quartic CM fields that are not normal over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Nakkajima and Taguchi [Reference Nakkajima and TaguchiNT91] computed the Faltings height of an elliptic curve with complex multiplication by a general order. They reduced the computation to the case of a maximal order which is covered by the Chowla–Selberg formula. Very recently, Mocz has announced a variant of Nakkajima–Taguchi’s result for abelian varieties in higher dimension.
Our approach relies heavily on equidistribution of Galois orbits on Hilbert modular surfaces. For this reason we must fix the maximal total real subfield in our theorem. However, it is natural to ask if the finiteness statement in Theorem 1.1 holds without fixing
![]() $F$
. For example, is the set of points in
$F$
. For example, is the set of points in
![]() ${\mathcal{A}}_{2}$
consisting of jacobians of curves defined over
${\mathcal{A}}_{2}$
consisting of jacobians of curves defined over
![]() $\overline{\mathbb{Q}}$
with CM and with good reduction everywhere Zariski non-dense in
$\overline{\mathbb{Q}}$
with CM and with good reduction everywhere Zariski non-dense in
![]() ${\mathcal{A}}_{2}$
? One could even speculate whether this set is finite.
${\mathcal{A}}_{2}$
? One could even speculate whether this set is finite.
In genus
![]() $g=3$
the image of the Torelli morphism again dominates
$g=3$
the image of the Torelli morphism again dominates
![]() ${\mathcal{A}}_{3}$
. Here too this image contains infinitely many jacobian varieties with CM. So, we ask whether the set of CM points that come from genus
${\mathcal{A}}_{3}$
. Here too this image contains infinitely many jacobian varieties with CM. So, we ask whether the set of CM points that come from genus
![]() $3$
curves with good reduction everywhere is Zariski non-dense in
$3$
curves with good reduction everywhere is Zariski non-dense in
![]() ${\mathcal{A}}_{3}$
or perhaps even finite. A simplified variant of this question would ask for non-denseness or finiteness under the restriction that the CM field contains a fixed totally real cubic subfield. Hyperelliptic curves of genus
${\mathcal{A}}_{3}$
or perhaps even finite. A simplified variant of this question would ask for non-denseness or finiteness under the restriction that the CM field contains a fixed totally real cubic subfield. Hyperelliptic curves of genus
![]() $3$
do not lie Zariski dense in the moduli space of genus
$3$
do not lie Zariski dense in the moduli space of genus
![]() $3$
curves. Thus, a statement like Theorem 4.5 for non-hyperelliptic curves would be necessary. This would be interesting in its own right.
$3$
curves. Thus, a statement like Theorem 4.5 for non-hyperelliptic curves would be necessary. This would be interesting in its own right.
Starting from genus
![]() $g=4$
it is no longer true that the Torelli morphism dominates
$g=4$
it is no longer true that the Torelli morphism dominates
![]() ${\mathcal{A}}_{4}$
. The André–Oort conjecture, which is known unconditionally in this case by work of Pila and Tsimerman [Reference Pila and TsimermanPT14], yields an additional obstruction for a curve of genus
${\mathcal{A}}_{4}$
. The André–Oort conjecture, which is known unconditionally in this case by work of Pila and Tsimerman [Reference Pila and TsimermanPT14], yields an additional obstruction for a curve of genus
![]() $4$
to have CM. Coleman conjectured that there are only finitely many curves of fixed genus
$4$
to have CM. Coleman conjectured that there are only finitely many curves of fixed genus
![]() $g\geqslant 4$
with CM. However, this conjecture is known to be false for
$g\geqslant 4$
with CM. However, this conjecture is known to be false for
![]() $g=4$
and
$g=4$
and
![]() $g=6$
by work of de Jong and Noot [Reference de Jong and NootdJN91]. In any case, a version of Theorem 1.1 for higher genus curves is entangled with other problems in arithmetic geometry.
$g=6$
by work of de Jong and Noot [Reference de Jong and NootdJN91]. In any case, a version of Theorem 1.1 for higher genus curves is entangled with other problems in arithmetic geometry.
In genus
![]() $g=1$
no finiteness result such as Theorem 1.1 can hold true, as an elliptic curve with complex multiplication has potentially good reduction at all finite places. However, the first-named author proved [Reference HabeggerHab15] the following finiteness result, which is reminiscent of the current work. Up to
$g=1$
no finiteness result such as Theorem 1.1 can hold true, as an elliptic curve with complex multiplication has potentially good reduction at all finite places. However, the first-named author proved [Reference HabeggerHab15] the following finiteness result, which is reminiscent of the current work. Up to
![]() $\overline{\mathbb{Q}}$
-isomorphism there are only finitely many elliptic curves with complex multiplication whose
$\overline{\mathbb{Q}}$
-isomorphism there are only finitely many elliptic curves with complex multiplication whose
![]() $j$
-invariants are algebraic units. This connection reinforces the heuristics that CM points behave similarly to integral points on a curve in the context of Siegel’s theorem. Indeed, the jacobian variety of a curve of genus
$j$
-invariants are algebraic units. This connection reinforces the heuristics that CM points behave similarly to integral points on a curve in the context of Siegel’s theorem. Indeed, the jacobian variety of a curve of genus
![]() $2$
defined over
$2$
defined over
![]() $\overline{\mathbb{Q}}$
and with good reduction everywhere corresponds to an algebraic point on
$\overline{\mathbb{Q}}$
and with good reduction everywhere corresponds to an algebraic point on
![]() ${\mathcal{A}}_{2}$
that is integral with respect to the divisor given by products of elliptic curves with their product polarisation. Theorem 1.1 is a finiteness result on the set of certain CM points of
${\mathcal{A}}_{2}$
that is integral with respect to the divisor given by products of elliptic curves with their product polarisation. Theorem 1.1 is a finiteness result on the set of certain CM points of
![]() ${\mathcal{A}}_{2}$
that are integral with respect to the said divisor. It would be interesting to know if, e.g., Vojta’s Theorem 0.4 on integral points on semi-abelian varieties [Reference VojtaVoj99] has an analog for
${\mathcal{A}}_{2}$
that are integral with respect to the said divisor. It would be interesting to know if, e.g., Vojta’s Theorem 0.4 on integral points on semi-abelian varieties [Reference VojtaVoj99] has an analog for
![]() ${\mathcal{A}}_{g}$
and other Shimura varieties.
${\mathcal{A}}_{g}$
and other Shimura varieties.
Finally, one can ask if the questions posed above remain valid in an
![]() $S$
-integer setting. In other words, are there only finitely many curves
$S$
-integer setting. In other words, are there only finitely many curves
![]() $C$
of genus
$C$
of genus
![]() $2$
or
$2$
or
![]() $3$
which have good reduction above the complement of a finite set of primes, where
$3$
which have good reduction above the complement of a finite set of primes, where
![]() $\operatorname{Jac}(C)$
has CM, and where possibly further conditions are met?
$\operatorname{Jac}(C)$
has CM, and where possibly further conditions are met?
The paper is structured as follows. In the next section we introduce some basic notation. In § 3 we cover some properties of abelian varieties with complex multiplication, and recall Shimura’s theorem on the Galois orbit for the cases we are interested in. In § 4 we recall first the Faltings height of an abelian variety. Then in § 4.2 we use a case of Colmez’s conjecture to express the Faltings height of certain abelian varieties with CM. Section 4.4 contains the local decomposition of the Faltings height of a jacobian surface with good reduction at all finite places. The archimedean places in this decomposition are bounded from above in § 5. Finally, the proof of both our theorems is completed in § 6. In the appendix we both express, using Colmez’s conjecture, and approximate numerically, using the result in § 4.4, the Faltings height of three jacobian varieties of genus
![]() $2$
curves. Each pair of heights are equal up to the prescribed precision. The computations and statements made in the appendix are not necessary for the proof of our theorems.
$2$
curves. Each pair of heights are equal up to the prescribed precision. The computations and statements made in the appendix are not necessary for the proof of our theorems.
2 Notation
In this paper it will be convenient to take
![]() $\overline{\mathbb{Q}}$
as the algebraic closure of
$\overline{\mathbb{Q}}$
as the algebraic closure of
![]() $\mathbb{Q}$
in
$\mathbb{Q}$
in
![]() $\mathbb{C}$
and all number fields to be subfields of
$\mathbb{C}$
and all number fields to be subfields of
![]() $\overline{\mathbb{Q}}$
.
$\overline{\mathbb{Q}}$
.
The letter
![]() $i$
stands for an element of
$i$
stands for an element of
![]() $\overline{\mathbb{Q}}$
such that
$\overline{\mathbb{Q}}$
such that
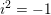 $i^{2}=-1$
.
$i^{2}=-1$
.
We let
![]() $K^{\times }$
denote the multiplicative group of any field
$K^{\times }$
denote the multiplicative group of any field
![]() $K$
. If
$K$
. If
![]() $K$
is a number field, then
$K$
is a number field, then
![]() $\unicode[STIX]{x1D6E5}_{K}$
is its discriminant and
$\unicode[STIX]{x1D6E5}_{K}$
is its discriminant and
![]() $\operatorname{Cl}_{K}$
is the class group of
$\operatorname{Cl}_{K}$
is the class group of
![]() $K$
. We use the symbol
$K$
. We use the symbol
![]() ${\mathcal{O}}_{K}$
for the ring of integers of
${\mathcal{O}}_{K}$
for the ring of integers of
![]() $K$
and
$K$
and
![]() ${{\mathcal{O}}_{K}}^{\times }$
is the group of units of
${{\mathcal{O}}_{K}}^{\times }$
is the group of units of
![]() ${\mathcal{O}}_{K}$
. If
${\mathcal{O}}_{K}$
. If
![]() $\mathfrak{A}$
is a fractional ideal of
$\mathfrak{A}$
is a fractional ideal of
![]() $K$
, then
$K$
, then
![]() $[\mathfrak{A}]$
denotes its class in
$[\mathfrak{A}]$
denotes its class in
![]() $\operatorname{Cl}_{K}$
. If
$\operatorname{Cl}_{K}$
. If
![]() $K/F$
is an extension of number fields, then
$K/F$
is an extension of number fields, then
![]() $\mathscr{D}_{K/F}$
is its different and
$\mathscr{D}_{K/F}$
is its different and
![]() $\mathfrak{d}_{K/F}$
is its relative discriminant. The norm of
$\mathfrak{d}_{K/F}$
is its relative discriminant. The norm of
![]() $\mathfrak{A}$
is
$\mathfrak{A}$
is
![]() $\text{N}(\mathfrak{A})$
, so
$\text{N}(\mathfrak{A})$
, so
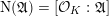 $\text{N}(\mathfrak{A})=[{\mathcal{O}}_{K}:\mathfrak{A}]$
if
$\text{N}(\mathfrak{A})=[{\mathcal{O}}_{K}:\mathfrak{A}]$
if
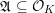 $\mathfrak{A}\subseteq {\mathcal{O}}_{K}$
. For the norm of
$\mathfrak{A}\subseteq {\mathcal{O}}_{K}$
. For the norm of
![]() $\mathfrak{A}$
relative to
$\mathfrak{A}$
relative to
![]() $K/F$
, a fractional ideal of
$K/F$
, a fractional ideal of
![]() $F$
, we use the symbol
$F$
, we use the symbol
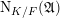 $\text{N}_{K/F}(\mathfrak{A})$
. If
$\text{N}_{K/F}(\mathfrak{A})$
. If
![]() $\unicode[STIX]{x1D6FC}\in K$
, then
$\unicode[STIX]{x1D6FC}\in K$
, then
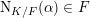 $\text{N}_{K/F}(\unicode[STIX]{x1D6FC})\in F$
and
$\text{N}_{K/F}(\unicode[STIX]{x1D6FC})\in F$
and
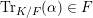 $\operatorname{Tr}_{K/F}(\unicode[STIX]{x1D6FC})\in F$
are norm and trace, respectively, of
$\operatorname{Tr}_{K/F}(\unicode[STIX]{x1D6FC})\in F$
are norm and trace, respectively, of
![]() $\unicode[STIX]{x1D6FC}$
relative to
$\unicode[STIX]{x1D6FC}$
relative to
![]() $K/F$
.
$K/F$
.
A place
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $K$
is an absolute value on
$K$
is an absolute value on
![]() $K$
whose restriction to
$K$
whose restriction to
![]() $\mathbb{Q}$
is the standard absolute value on
$\mathbb{Q}$
is the standard absolute value on
![]() $\mathbb{Q}$
or a
$\mathbb{Q}$
or a
![]() $p$
-adic absolute value for some prime number
$p$
-adic absolute value for some prime number
![]() $p$
. The former places are called infinite or archimedean and we write
$p$
. The former places are called infinite or archimedean and we write
![]() $\unicode[STIX]{x1D708}\mid \infty$
whereas the latter are called finite or non-archimedean and we write
$\unicode[STIX]{x1D708}\mid \infty$
whereas the latter are called finite or non-archimedean and we write
![]() $\unicode[STIX]{x1D708}\nmid \infty$
or
$\unicode[STIX]{x1D708}\nmid \infty$
or
![]() $\unicode[STIX]{x1D708}\mid p$
. The set of finite places is
$\unicode[STIX]{x1D708}\mid p$
. The set of finite places is
![]() $M_{K}^{0}$
. Any
$M_{K}^{0}$
. Any
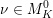 $\unicode[STIX]{x1D708}\in M_{K}^{0}$
corresponds to a maximal ideal of
$\unicode[STIX]{x1D708}\in M_{K}^{0}$
corresponds to a maximal ideal of
![]() ${\mathcal{O}}_{K}$
and we write
${\mathcal{O}}_{K}$
and we write
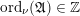 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(\mathfrak{A})\in \mathbb{Z}$
for the power with which this ideal appears in the factorisation of
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(\mathfrak{A})\in \mathbb{Z}$
for the power with which this ideal appears in the factorisation of
![]() $\mathfrak{A}$
. If
$\mathfrak{A}$
. If
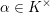 $\unicode[STIX]{x1D6FC}\in K^{\times }$
, then
$\unicode[STIX]{x1D6FC}\in K^{\times }$
, then
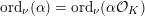 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FC})=\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{K})$
. We write
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FC})=\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{K})$
. We write
![]() $K_{\unicode[STIX]{x1D708}}$
for the completion of
$K_{\unicode[STIX]{x1D708}}$
for the completion of
![]() $K$
with respect to
$K$
with respect to
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
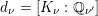 $d_{\unicode[STIX]{x1D708}}=[K_{\unicode[STIX]{x1D708}}:\mathbb{Q}_{\unicode[STIX]{x1D708}^{\prime }}]$
, where
$d_{\unicode[STIX]{x1D708}}=[K_{\unicode[STIX]{x1D708}}:\mathbb{Q}_{\unicode[STIX]{x1D708}^{\prime }}]$
, where
![]() $\unicode[STIX]{x1D708}^{\prime }$
is the restriction of
$\unicode[STIX]{x1D708}^{\prime }$
is the restriction of
![]() $\unicode[STIX]{x1D708}$
to
$\unicode[STIX]{x1D708}$
to
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
We will often use
![]() $K$
to denote a CM field and
$K$
to denote a CM field and
![]() $F$
its totally real subfield. Complex conjugation on
$F$
its totally real subfield. Complex conjugation on
![]() $K$
will be denoted by
$K$
will be denoted by
![]() $\unicode[STIX]{x1D6FC}\mapsto \overline{\unicode[STIX]{x1D6FC}}$
. If a CM type
$\unicode[STIX]{x1D6FC}\mapsto \overline{\unicode[STIX]{x1D6FC}}$
. If a CM type
![]() $\unicode[STIX]{x1D6F7}$
of
$\unicode[STIX]{x1D6F7}$
of
![]() $K$
is given, then we write
$K$
is given, then we write
![]() $K^{\ast }$
for the associated reflex field.
$K^{\ast }$
for the associated reflex field.
For the field of definition of an algebraic variety we use lower case letters,
![]() $k$
for instance.
$k$
for instance.
Let
![]() $g\geqslant 1$
be an integer and
$g\geqslant 1$
be an integer and
![]() $\mathbb{H}_{g}$
the Siegel upper half-space, i.e.,
$\mathbb{H}_{g}$
the Siegel upper half-space, i.e.,
![]() $g\times g$
symmetric matrices with entries in
$g\times g$
symmetric matrices with entries in
![]() $\mathbb{C}$
and positive-definite imaginary parts. For brevity,
$\mathbb{C}$
and positive-definite imaginary parts. For brevity,
![]() $\mathbb{H}=\mathbb{H}_{1}$
denotes the upper half-plane. The symplectic group
$\mathbb{H}=\mathbb{H}_{1}$
denotes the upper half-plane. The symplectic group
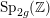 $\operatorname{Sp}_{2g}(\mathbb{Z})$
acts on
$\operatorname{Sp}_{2g}(\mathbb{Z})$
acts on
![]() $\mathbb{H}_{g}$
by
$\mathbb{H}_{g}$
by
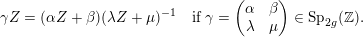 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}Z=(\unicode[STIX]{x1D6FC}Z+\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D706}Z+\unicode[STIX]{x1D707})^{-1}\quad \text{if}~\unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FD}\\ \unicode[STIX]{x1D706} & \unicode[STIX]{x1D707}\end{array}\right)\in \operatorname{Sp}_{2g}(\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}Z=(\unicode[STIX]{x1D6FC}Z+\unicode[STIX]{x1D6FD})(\unicode[STIX]{x1D706}Z+\unicode[STIX]{x1D707})^{-1}\quad \text{if}~\unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FD}\\ \unicode[STIX]{x1D706} & \unicode[STIX]{x1D707}\end{array}\right)\in \operatorname{Sp}_{2g}(\mathbb{Z}).\end{eqnarray}$$
We recall that
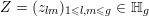 $Z=(z_{lm})_{1\leqslant l,m\leqslant g}\in \mathbb{H}_{g}$
is called Siegel reduced and lies in Siegel’s fundamental domain
$Z=(z_{lm})_{1\leqslant l,m\leqslant g}\in \mathbb{H}_{g}$
is called Siegel reduced and lies in Siegel’s fundamental domain
![]() ${\mathcal{F}}_{g}$
if and only if the following properties are met; cf. [Reference KlingenKli90, §§ 2 and 3].
${\mathcal{F}}_{g}$
if and only if the following properties are met; cf. [Reference KlingenKli90, §§ 2 and 3].
- (i)
-
For every
 $\unicode[STIX]{x1D6FE}\in \operatorname{Sp}_{2g}(\mathbb{Z})$
, one has
$\unicode[STIX]{x1D6FE}\in \operatorname{Sp}_{2g}(\mathbb{Z})$
, one has
 $\det \operatorname{Im}(\unicode[STIX]{x1D6FE}Z)\leqslant \det \operatorname{Im}(Z)$
, where
$\det \operatorname{Im}(\unicode[STIX]{x1D6FE}Z)\leqslant \det \operatorname{Im}(Z)$
, where
 $\operatorname{Im}(\cdot )$
denotes the imaginary part.
$\operatorname{Im}(\cdot )$
denotes the imaginary part. - (ii)
-
The real part is bounded by
 $$\begin{eqnarray}|\text{Re}(z_{lm})|\leqslant {\textstyle \frac{1}{2}}\quad \text{for all}~(l,m)\in \{1,\ldots ,g\}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}|\text{Re}(z_{lm})|\leqslant {\textstyle \frac{1}{2}}\quad \text{for all}~(l,m)\in \{1,\ldots ,g\}^{2}.\end{eqnarray}$$
- (iii)
 $_{a}$
$_{a}$
-
For all
 $l\in \{1,\ldots ,g\}$
and all
$l\in \{1,\ldots ,g\}$
and all
 $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{g})\in \mathbb{Z}^{g}$
with
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{g})\in \mathbb{Z}^{g}$
with
 $\text{gcd}(\unicode[STIX]{x1D709}_{l},\ldots ,\unicode[STIX]{x1D709}_{g})=1$
, we have
$\text{gcd}(\unicode[STIX]{x1D709}_{l},\ldots ,\unicode[STIX]{x1D709}_{g})=1$
, we have
 $\text{}^{t}\unicode[STIX]{x1D709}\operatorname{Im}(Z)\unicode[STIX]{x1D709}\geqslant \operatorname{Im}(z_{ll})$
.
$\text{}^{t}\unicode[STIX]{x1D709}\operatorname{Im}(Z)\unicode[STIX]{x1D709}\geqslant \operatorname{Im}(z_{ll})$
. - (iii)
 $_{b}$
$_{b}$
-
For all
 $l\in \{1,\ldots ,g-1\}$
, we have
$l\in \{1,\ldots ,g-1\}$
, we have
 $\operatorname{Im}(z_{l,l+1})\geqslant 0.$
$\operatorname{Im}(z_{l,l+1})\geqslant 0.$
The properties (iii)
![]() $_{a}$
and (iii)
$_{a}$
and (iii)
![]() $_{b}$
state that
$_{b}$
state that
![]() $\operatorname{Im}(Z)$
is Minkowski reduced.
$\operatorname{Im}(Z)$
is Minkowski reduced.
We write
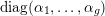 $\operatorname{diag}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g})$
for the diagonal matrix with diagonal elements
$\operatorname{diag}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g})$
for the diagonal matrix with diagonal elements
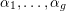 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g}$
which are contained in some field.
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g}$
which are contained in some field.
3 Abelian varieties
In the next sections we collect some statements on Hilbert modular varieties and abelian varieties that we require later on.
3.1 Hilbert modular varieties
Theorem 1.1 concerns jacobian varieties whose endomorphism algebras contain a fixed real quadratic number field. So, Hilbert modular surfaces arise naturally. In this section we discuss some properties of a fundamental set of the action of Hilbert modular groups on
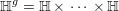 $\mathbb{H}^{g}=\mathbb{H}\,\times \,\cdots \,\times \,\mathbb{H}$
, the
$\mathbb{H}^{g}=\mathbb{H}\,\times \,\cdots \,\times \,\mathbb{H}$
, the
![]() $g$
-fold product of the complex upper half-plane
$g$
-fold product of the complex upper half-plane
![]() $\mathbb{H}\subseteq \mathbb{C}$
. Our main reference for this section is Chapter I of van der Geer’s book [Reference van der GeervdG88]. However, we will work in a slightly modified setting and therefore provide some additional details.
$\mathbb{H}\subseteq \mathbb{C}$
. Our main reference for this section is Chapter I of van der Geer’s book [Reference van der GeervdG88]. However, we will work in a slightly modified setting and therefore provide some additional details.
Let
![]() $F$
be a totally real number field of degree
$F$
be a totally real number field of degree
![]() $g$
with distinct real embeddings
$g$
with distinct real embeddings
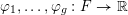 $\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}:F\rightarrow \mathbb{R}$
. Throughout this section
$\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}:F\rightarrow \mathbb{R}$
. Throughout this section
![]() $\mathfrak{a}$
is a fractional ideal of
$\mathfrak{a}$
is a fractional ideal of
![]() ${\mathcal{O}}_{F}$
. Later on we will be mainly interested in the case
${\mathcal{O}}_{F}$
. Later on we will be mainly interested in the case
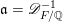 $\mathfrak{a}=\mathscr{D}_{F/\mathbb{Q}}^{-1}$
, the inverse of the different of
$\mathfrak{a}=\mathscr{D}_{F/\mathbb{Q}}^{-1}$
, the inverse of the different of
![]() $F/\mathbb{Q}$
.
$F/\mathbb{Q}$
.
Let
![]() ${\mathcal{O}}_{F}^{\times ,+}$
be the group of totally positive units in
${\mathcal{O}}_{F}^{\times ,+}$
be the group of totally positive units in
![]() ${\mathcal{O}}_{F}$
and
${\mathcal{O}}_{F}$
and
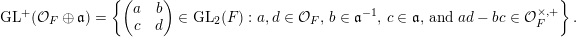 $$\begin{eqnarray}\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \operatorname{GL}_{2}(F):a,d\in {\mathcal{O}}_{F},\,b\in \mathfrak{a}^{-1},\,c\in \mathfrak{a},\,\text{and }ad-bc\in {\mathcal{O}}_{F}^{\times ,+}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \operatorname{GL}_{2}(F):a,d\in {\mathcal{O}}_{F},\,b\in \mathfrak{a}^{-1},\,c\in \mathfrak{a},\,\text{and }ad-bc\in {\mathcal{O}}_{F}^{\times ,+}\right\}.\end{eqnarray}$$
The group
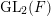 $\operatorname{GL}_{2}(F)$
acts on
$\operatorname{GL}_{2}(F)$
acts on
![]() $\mathbb{P}^{1}(F)$
. Its subgroup
$\mathbb{P}^{1}(F)$
. Its subgroup
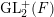 $\operatorname{GL}_{2}^{+}(F)$
of matrices with totally positive determinant acts on
$\operatorname{GL}_{2}^{+}(F)$
of matrices with totally positive determinant acts on
![]() $\mathbb{H}^{g}$
by fractional linear transformations through the
$\mathbb{H}^{g}$
by fractional linear transformations through the
![]() $g$
embeddings
$g$
embeddings
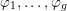 $\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}$
.
$\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}$
.
We are interested in the restriction of this action to the subgroup
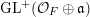 $\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})$
. As this group’s center acts trivially on
$\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})$
. As this group’s center acts trivially on
![]() $\mathbb{H}^{g}$
, let us consider also
$\mathbb{H}^{g}$
, let us consider also
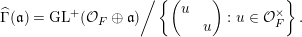 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})=\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})\bigg/\left\{\left(\begin{array}{@{}cc@{}}u & \\ & u\end{array}\right):u\in {\mathcal{O}}_{F}^{\times }\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})=\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})\bigg/\left\{\left(\begin{array}{@{}cc@{}}u & \\ & u\end{array}\right):u\in {\mathcal{O}}_{F}^{\times }\right\}.\end{eqnarray}$$
The group
![]() $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
also acts on
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
also acts on
![]() $\mathbb{P}^{1}(F)$
.
$\mathbb{P}^{1}(F)$
.
The
![]() $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
-action on
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
-action on
![]() $\mathbb{P}^{1}(F)$
consists of
$\mathbb{P}^{1}(F)$
consists of
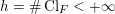 $h=\#\operatorname{Cl}_{F}<+\infty$
orbits which represent the cusps of
$h=\#\operatorname{Cl}_{F}<+\infty$
orbits which represent the cusps of
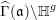 $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})\backslash \mathbb{H}^{g}$
. For
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})\backslash \mathbb{H}^{g}$
. For
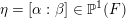 $\unicode[STIX]{x1D702}=[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]\in \mathbb{P}^{1}(F)$
with
$\unicode[STIX]{x1D702}=[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]\in \mathbb{P}^{1}(F)$
with
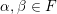 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in F$
and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in F$
and
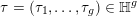 $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{g})\in \mathbb{H}^{g}$
, we define
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{g})\in \mathbb{H}^{g}$
, we define
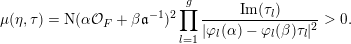 $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})=\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1})^{2}\mathop{\prod }_{l=1}^{g}\frac{\operatorname{Im}(\unicode[STIX]{x1D70F}_{l})}{|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D70F}_{l}|^{2}}>0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})=\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1})^{2}\mathop{\prod }_{l=1}^{g}\frac{\operatorname{Im}(\unicode[STIX]{x1D70F}_{l})}{|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D70F}_{l}|^{2}}>0.\end{eqnarray}$$
The quantity
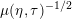 $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{-1/2}$
measures the distance of the point in
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{-1/2}$
measures the distance of the point in
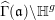 $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})\backslash \mathbb{H}^{g}$
represented by
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})\backslash \mathbb{H}^{g}$
represented by
![]() $\unicode[STIX]{x1D70F}$
to the cusp represented by
$\unicode[STIX]{x1D70F}$
to the cusp represented by
![]() $\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}$
.
If
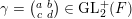 $\unicode[STIX]{x1D6FE}=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \operatorname{GL}_{2}^{+}(F)$
, then
$\unicode[STIX]{x1D6FE}=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \operatorname{GL}_{2}^{+}(F)$
, then
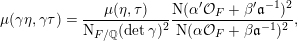 $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})}{\text{N}_{F/\mathbb{Q}}(\det \unicode[STIX]{x1D6FE})^{2}}\frac{\text{N}(\unicode[STIX]{x1D6FC}^{\prime }{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}^{\prime }\mathfrak{a}^{-1})^{2}}{\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1})^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})}{\text{N}_{F/\mathbb{Q}}(\det \unicode[STIX]{x1D6FE})^{2}}\frac{\text{N}(\unicode[STIX]{x1D6FC}^{\prime }{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}^{\prime }\mathfrak{a}^{-1})^{2}}{\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1})^{2}},\end{eqnarray}$$
where
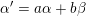 $\unicode[STIX]{x1D6FC}^{\prime }=a\unicode[STIX]{x1D6FC}+b\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FC}^{\prime }=a\unicode[STIX]{x1D6FC}+b\unicode[STIX]{x1D6FD}$
and
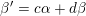 $\unicode[STIX]{x1D6FD}^{\prime }=c\unicode[STIX]{x1D6FC}+d\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}^{\prime }=c\unicode[STIX]{x1D6FC}+d\unicode[STIX]{x1D6FD}$
.
Let us study two important special cases. First, if
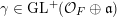 $\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})$
, then
$\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})$
, then
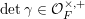 $\det \unicode[STIX]{x1D6FE}\in {\mathcal{O}}_{F}^{\times ,+}$
and the ideals appearing on the right of (3.3) coincide. So, the equality simplifies to
$\det \unicode[STIX]{x1D6FE}\in {\mathcal{O}}_{F}^{\times ,+}$
and the ideals appearing on the right of (3.3) coincide. So, the equality simplifies to
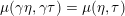 $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})$
. Second, let us suppose that
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})$
. Second, let us suppose that
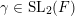 $\unicode[STIX]{x1D6FE}\in \operatorname{SL}_{2}(F)$
and fix a positive integer
$\unicode[STIX]{x1D6FE}\in \operatorname{SL}_{2}(F)$
and fix a positive integer
![]() $\unicode[STIX]{x1D706}$
with
$\unicode[STIX]{x1D706}$
with
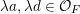 $\unicode[STIX]{x1D706}a,\unicode[STIX]{x1D706}d\in {\mathcal{O}}_{F}$
,
$\unicode[STIX]{x1D706}a,\unicode[STIX]{x1D706}d\in {\mathcal{O}}_{F}$
,
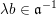 $\unicode[STIX]{x1D706}b\in \mathfrak{a}^{-1}$
, and
$\unicode[STIX]{x1D706}b\in \mathfrak{a}^{-1}$
, and
![]() $\unicode[STIX]{x1D706}c\in \mathfrak{a}$
. Then
$\unicode[STIX]{x1D706}c\in \mathfrak{a}$
. Then
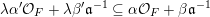 $\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}^{\prime }{\mathcal{O}}_{F}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}^{\prime }\mathfrak{a}^{-1}\subseteq \unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1}$
and so the norm of the ideal on the left is at least the norm of the ideal on the right. Equality (3.3) implies that
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}^{\prime }{\mathcal{O}}_{F}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}^{\prime }\mathfrak{a}^{-1}\subseteq \unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1}$
and so the norm of the ideal on the left is at least the norm of the ideal on the right. Equality (3.3) implies that
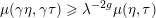 $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})\geqslant \unicode[STIX]{x1D706}^{-2g}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})$
.
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})\geqslant \unicode[STIX]{x1D706}^{-2g}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})$
.
On applying the same argument to
![]() $\unicode[STIX]{x1D6FE}^{-1}$
, we find
$\unicode[STIX]{x1D6FE}^{-1}$
, we find
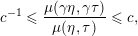 $$\begin{eqnarray}c^{-1}\leqslant \frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})}\leqslant c,\end{eqnarray}$$
$$\begin{eqnarray}c^{-1}\leqslant \frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})}\leqslant c,\end{eqnarray}$$
where
![]() $c>0$
depends only on
$c>0$
depends only on
![]() $\unicode[STIX]{x1D6FE}$
and not on
$\unicode[STIX]{x1D6FE}$
and not on
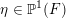 $\unicode[STIX]{x1D702}\in \mathbb{P}^{1}(F)$
or on
$\unicode[STIX]{x1D702}\in \mathbb{P}^{1}(F)$
or on
![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}^{g}$
.
$\unicode[STIX]{x1D70F}\in \mathbb{H}^{g}$
.
A fundamental set for the action of
![]() $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
on
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
on
![]() $\mathbb{H}^{g}$
is a subset of
$\mathbb{H}^{g}$
is a subset of
![]() $\mathbb{H}^{g}$
that meets all
$\mathbb{H}^{g}$
that meets all
![]() $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
-orbits. We do not require a fundamental set to be connected and we do not exclude that two distinct points are in the same orbit. In the following we will describe a fundamental set much as van der Geer’s construction of a fundamental domain for the action of
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
-orbits. We do not require a fundamental set to be connected and we do not exclude that two distinct points are in the same orbit. In the following we will describe a fundamental set much as van der Geer’s construction of a fundamental domain for the action of
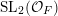 $\operatorname{SL}_{2}({\mathcal{O}}_{F})$
on
$\operatorname{SL}_{2}({\mathcal{O}}_{F})$
on
![]() $\mathbb{H}^{g}$
in [Reference van der GeervdG88, ch. I.3].
$\mathbb{H}^{g}$
in [Reference van der GeervdG88, ch. I.3].
First, let us fix a set of representatives
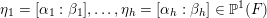 $\unicode[STIX]{x1D702}_{1}=[\unicode[STIX]{x1D6FC}_{1}:\unicode[STIX]{x1D6FD}_{1}],\ldots ,\unicode[STIX]{x1D702}_{h}=[\unicode[STIX]{x1D6FC}_{h}:\unicode[STIX]{x1D6FD}_{h}]\in \mathbb{P}^{1}(F)$
of the cusps. We may assume that
$\unicode[STIX]{x1D702}_{1}=[\unicode[STIX]{x1D6FC}_{1}:\unicode[STIX]{x1D6FD}_{1}],\ldots ,\unicode[STIX]{x1D702}_{h}=[\unicode[STIX]{x1D6FC}_{h}:\unicode[STIX]{x1D6FD}_{h}]\in \mathbb{P}^{1}(F)$
of the cusps. We may assume that
![]() $\unicode[STIX]{x1D6FC}_{1}=1$
and
$\unicode[STIX]{x1D6FC}_{1}=1$
and
![]() $\unicode[STIX]{x1D6FD}_{1}=0$
, i.e.,
$\unicode[STIX]{x1D6FD}_{1}=0$
, i.e.,
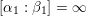 $[\unicode[STIX]{x1D6FC}_{1}:\unicode[STIX]{x1D6FD}_{1}]=\infty$
. Only a slight variation in the argument of [Reference van der GeervdG88, Lemma I.2.2] is required to obtain
$[\unicode[STIX]{x1D6FC}_{1}:\unicode[STIX]{x1D6FD}_{1}]=\infty$
. Only a slight variation in the argument of [Reference van der GeervdG88, Lemma I.2.2] is required to obtain
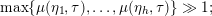 $$\begin{eqnarray}\max \{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{h},\unicode[STIX]{x1D70F})\}\gg 1;\end{eqnarray}$$
$$\begin{eqnarray}\max \{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{h},\unicode[STIX]{x1D70F})\}\gg 1;\end{eqnarray}$$
the constants implicit in
![]() $\ll$
and
$\ll$
and
![]() $\gg$
here and below depend only on
$\gg$
here and below depend only on
![]() $\mathfrak{a}$
and the
$\mathfrak{a}$
and the
![]() $\unicode[STIX]{x1D6FC}_{m},\unicode[STIX]{x1D6FD}_{m}$
.
$\unicode[STIX]{x1D6FC}_{m},\unicode[STIX]{x1D6FD}_{m}$
.
Proposition 3.1. There is a closed fundamental set
![]() ${\mathcal{F}}(\mathfrak{a})$
for the action of
${\mathcal{F}}(\mathfrak{a})$
for the action of
![]() $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
on
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
on
![]() $\mathbb{H}^{g}$
with the following property. If
$\mathbb{H}^{g}$
with the following property. If
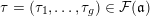 $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{g})\in {\mathcal{F}}(\mathfrak{a})$
, then
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{g})\in {\mathcal{F}}(\mathfrak{a})$
, then
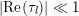 $|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
and
$|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
and
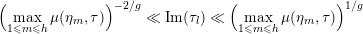 $$\begin{eqnarray}\Bigl(\max _{1\leqslant m\leqslant h}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D70F})\Bigr)^{-2/g}\ll \operatorname{Im}(\unicode[STIX]{x1D70F}_{l})\ll \Bigl(\max _{1\leqslant m\leqslant h}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D70F})\Bigr)^{1/g}\end{eqnarray}$$
$$\begin{eqnarray}\Bigl(\max _{1\leqslant m\leqslant h}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D70F})\Bigr)^{-2/g}\ll \operatorname{Im}(\unicode[STIX]{x1D70F}_{l})\ll \Bigl(\max _{1\leqslant m\leqslant h}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D70F})\Bigr)^{1/g}\end{eqnarray}$$
for all
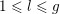 $1\leqslant l\leqslant g$
.
$1\leqslant l\leqslant g$
.
Proof. A given
![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}^{g}$
is in
$\unicode[STIX]{x1D70F}\in \mathbb{H}^{g}$
is in
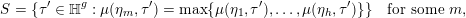 $$\begin{eqnarray}S=\{\unicode[STIX]{x1D70F}^{\prime }\in \mathbb{H}^{g}:\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D70F}^{\prime })=\max \{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D70F}^{\prime }),\ldots ,\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{h},\unicode[STIX]{x1D70F}^{\prime })\}\}\quad \text{for some}~m,\end{eqnarray}$$
$$\begin{eqnarray}S=\{\unicode[STIX]{x1D70F}^{\prime }\in \mathbb{H}^{g}:\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D70F}^{\prime })=\max \{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D70F}^{\prime }),\ldots ,\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{h},\unicode[STIX]{x1D70F}^{\prime })\}\}\quad \text{for some}~m,\end{eqnarray}$$
the sphere of influence of the cusp
![]() $\unicode[STIX]{x1D702}_{m}$
. We abbreviate
$\unicode[STIX]{x1D702}_{m}$
. We abbreviate
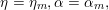 $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{m},$
and
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{m},$
and
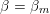 $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{m}$
. Thus,
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{m}$
. Thus,
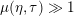 $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})\gg 1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})\gg 1\end{eqnarray}$$
by (3.5). Let us define the fractional ideal
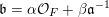 $\mathfrak{b}=\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1}$
of
$\mathfrak{b}=\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathfrak{a}^{-1}$
of
![]() ${\mathcal{O}}_{F}$
. Next we choose
${\mathcal{O}}_{F}$
. Next we choose
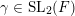 $\unicode[STIX]{x1D6FE}\in \operatorname{SL}_{2}(F)$
with
$\unicode[STIX]{x1D6FE}\in \operatorname{SL}_{2}(F)$
with
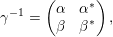 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}^{-1}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FC}^{\ast }\\ \unicode[STIX]{x1D6FD} & \unicode[STIX]{x1D6FD}^{\ast }\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}^{-1}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FC}^{\ast }\\ \unicode[STIX]{x1D6FD} & \unicode[STIX]{x1D6FD}^{\ast }\end{array}\right),\end{eqnarray}$$
where
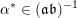 $\unicode[STIX]{x1D6FC}^{\ast }\in (\mathfrak{a}\mathfrak{b})^{-1}$
and
$\unicode[STIX]{x1D6FC}^{\ast }\in (\mathfrak{a}\mathfrak{b})^{-1}$
and
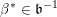 $\unicode[STIX]{x1D6FD}^{\ast }\in \mathfrak{b}^{-1}$
. So,
$\unicode[STIX]{x1D6FD}^{\ast }\in \mathfrak{b}^{-1}$
. So,
 $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702}=\infty$
and we observe that an application of (3.4) and (3.7) yields
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702}=\infty$
and we observe that an application of (3.4) and (3.7) yields
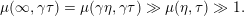 $$\begin{eqnarray}\unicode[STIX]{x1D707}(\infty ,\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})\gg \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})\gg 1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\infty ,\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})\gg \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})\gg 1.\end{eqnarray}$$
The left-hand side is
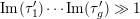 $\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime })\gg 1$
, where
$\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime })\gg 1$
, where
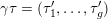 $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D70F}_{g}^{\prime })$
.
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D70F}_{g}^{\prime })$
.
We observe that
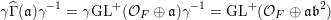 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})\unicode[STIX]{x1D6FE}^{-1}=\unicode[STIX]{x1D6FE}\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})\unicode[STIX]{x1D6FE}^{-1}=\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a}\mathfrak{b}^{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})\unicode[STIX]{x1D6FE}^{-1}=\unicode[STIX]{x1D6FE}\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a})\unicode[STIX]{x1D6FE}^{-1}=\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a}\mathfrak{b}^{2})\end{eqnarray}$$
and use
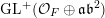 $\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a}\mathfrak{b}^{2})$
to act on
$\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a}\mathfrak{b}^{2})$
to act on
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
. In fact, we will use only elements in the stabiliser of
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
. In fact, we will use only elements in the stabiliser of
![]() $\infty$
, i.e., the subgroup of upper triangular matrices in
$\infty$
, i.e., the subgroup of upper triangular matrices in
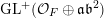 $\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a}\mathfrak{b}^{2})$
. As in [Reference van der GeervdG88, ch. I.3], we find
$\operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathfrak{a}\mathfrak{b}^{2})$
. As in [Reference van der GeervdG88, ch. I.3], we find
![]() $\unicode[STIX]{x1D6FE}^{\prime }$
in the said group such that if
$\unicode[STIX]{x1D6FE}^{\prime }$
in the said group such that if
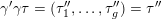 $\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1}^{\prime \prime },\ldots ,\unicode[STIX]{x1D70F}_{g}^{\prime \prime })=\unicode[STIX]{x1D70F}^{\prime \prime }$
, then
$\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}_{1}^{\prime \prime },\ldots ,\unicode[STIX]{x1D70F}_{g}^{\prime \prime })=\unicode[STIX]{x1D70F}^{\prime \prime }$
, then
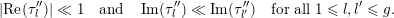 $$\begin{eqnarray}|\text{Re}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })|\ll 1\quad \text{and}\quad \operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \operatorname{Im}(\unicode[STIX]{x1D70F}_{l^{\prime }}^{\prime })\quad \text{for all}~1\leqslant l,l^{\prime }\leqslant g.\end{eqnarray}$$
$$\begin{eqnarray}|\text{Re}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })|\ll 1\quad \text{and}\quad \operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \operatorname{Im}(\unicode[STIX]{x1D70F}_{l^{\prime }}^{\prime })\quad \text{for all}~1\leqslant l,l^{\prime }\leqslant g.\end{eqnarray}$$
We note that
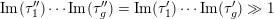 $\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime \prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime \prime })=\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime })\gg 1$
and thus
$\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime \prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime \prime })=\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime })\gg 1$
and thus
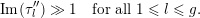 $$\begin{eqnarray}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\gg 1\quad \text{for all}~1\leqslant l\leqslant g.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\gg 1\quad \text{for all}~1\leqslant l\leqslant g.\end{eqnarray}$$
The point
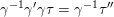 $\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime }$
lies in the
$\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime }$
lies in the
![]() $\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
-orbit of
$\widehat{\unicode[STIX]{x1D6E4}}(\mathfrak{a})$
-orbit of
![]() $\unicode[STIX]{x1D70F}$
by (3.8). We define
$\unicode[STIX]{x1D70F}$
by (3.8). We define
![]() $D$
as the set of
$D$
as the set of
![]() $\unicode[STIX]{x1D70F}^{\prime \prime }$
that satisfy (3.9) and (3.10). We take
$\unicode[STIX]{x1D70F}^{\prime \prime }$
that satisfy (3.9) and (3.10). We take
![]() $\unicode[STIX]{x1D6FE}^{-1}D$
as a part of the fundamental set whose entirety
$\unicode[STIX]{x1D6FE}^{-1}D$
as a part of the fundamental set whose entirety
![]() ${\mathcal{F}}(\mathfrak{a})$
is obtained by taking the union of the sets coming from all
${\mathcal{F}}(\mathfrak{a})$
is obtained by taking the union of the sets coming from all
![]() $h$
cusps. Observe that
$h$
cusps. Observe that
![]() $\unicode[STIX]{x1D6FE}^{-1}D$
is closed in
$\unicode[STIX]{x1D6FE}^{-1}D$
is closed in
![]() $\mathbb{H}^{g}$
and so
$\mathbb{H}^{g}$
and so
![]() ${\mathcal{F}}(\mathfrak{a})$
is closed too.
${\mathcal{F}}(\mathfrak{a})$
is closed too.
It remains to prove that the various bounds in the assertion hold for
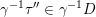 $\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime }\in \unicode[STIX]{x1D6FE}^{-1}D$
. To simplify notation we write
$\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime }\in \unicode[STIX]{x1D6FE}^{-1}D$
. To simplify notation we write
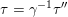 $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime }$
and recall that
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime }$
and recall that
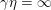 $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702}=\infty$
still holds. We use the second set of inequalities in (3.9) to bound
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702}=\infty$
still holds. We use the second set of inequalities in (3.9) to bound
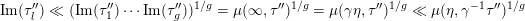 $\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll (\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime \prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime \prime }))^{1/g}=\unicode[STIX]{x1D707}(\infty ,\unicode[STIX]{x1D70F}^{\prime \prime })^{1/g}=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F}^{\prime \prime })^{1/g}\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime })^{1/g}$
. So,
$\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll (\operatorname{Im}(\unicode[STIX]{x1D70F}_{1}^{\prime \prime })\cdots \operatorname{Im}(\unicode[STIX]{x1D70F}_{g}^{\prime \prime }))^{1/g}=\unicode[STIX]{x1D707}(\infty ,\unicode[STIX]{x1D70F}^{\prime \prime })^{1/g}=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F}^{\prime \prime })^{1/g}\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}^{\prime \prime })^{1/g}$
. So,
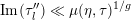 $\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
and in particular
$\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
and in particular
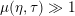 $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})\gg 1$
by (3.10). We find that
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})\gg 1$
by (3.10). We find that
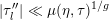 $|\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
as the real part of
$|\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
as the real part of
![]() $\unicode[STIX]{x1D70F}_{l}^{\prime \prime }$
is bounded by (3.9). Now
$\unicode[STIX]{x1D70F}_{l}^{\prime \prime }$
is bounded by (3.9). Now
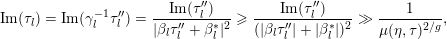 $$\begin{eqnarray}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l})=\operatorname{Im}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })=\frac{\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })}{|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }+\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}}\geqslant \frac{\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })}{(|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|+|\unicode[STIX]{x1D6FD}_{l}^{\ast }|)^{2}}\gg \frac{1}{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{2/g}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l})=\operatorname{Im}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })=\frac{\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })}{|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }+\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}}\geqslant \frac{\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })}{(|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|+|\unicode[STIX]{x1D6FD}_{l}^{\ast }|)^{2}}\gg \frac{1}{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{2/g}},\end{eqnarray}$$
where the subscript
![]() $l$
in
$l$
in
![]() $\unicode[STIX]{x1D6FD}_{l},\unicode[STIX]{x1D6FD}_{l}^{\ast },$
and
$\unicode[STIX]{x1D6FD}_{l},\unicode[STIX]{x1D6FD}_{l}^{\ast },$
and
![]() $\unicode[STIX]{x1D6FE}_{l}$
indicates that
$\unicode[STIX]{x1D6FE}_{l}$
indicates that
![]() $\unicode[STIX]{x1D711}_{l}$
was applied. This yields the lower bound in (3.6).
$\unicode[STIX]{x1D711}_{l}$
was applied. This yields the lower bound in (3.6).
To deduce the upper bound, we split up into two cases. If
![]() $\unicode[STIX]{x1D6FD}_{l}\not =0$
, then
$\unicode[STIX]{x1D6FD}_{l}\not =0$
, then
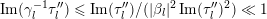 $\operatorname{Im}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\leqslant \operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })/(|\unicode[STIX]{x1D6FD}_{l}|^{2}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })^{2})\ll 1$
and in particular
$\operatorname{Im}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\leqslant \operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })/(|\unicode[STIX]{x1D6FD}_{l}|^{2}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })^{2})\ll 1$
and in particular
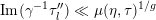 $\operatorname{Im}(\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
. So, the upper bound holds in this case. What if
$\operatorname{Im}(\unicode[STIX]{x1D6FE}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
. So, the upper bound holds in this case. What if
![]() $\unicode[STIX]{x1D6FD}_{l}=0$
? Then
$\unicode[STIX]{x1D6FD}_{l}=0$
? Then
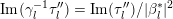 $\operatorname{Im}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })=\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })/|\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}$
. Further up we have seen that
$\operatorname{Im}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })=\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })/|\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}$
. Further up we have seen that
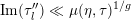 $\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
and the upper bound follows from this.
$\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })\ll \unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D70F})^{1/g}$
and the upper bound follows from this.
To bound the real part, we use
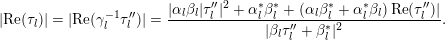 $$\begin{eqnarray}|\text{Re}(\unicode[STIX]{x1D70F}_{l})|=|\text{Re}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })|=\frac{|\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D6FD}_{l}|\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|^{2}+\unicode[STIX]{x1D6FC}_{l}^{\ast }\unicode[STIX]{x1D6FD}_{l}^{\ast }+(\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D6FD}_{l}^{\ast }+\unicode[STIX]{x1D6FC}_{l}^{\ast }\unicode[STIX]{x1D6FD}_{l})\operatorname{Re}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })|}{|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }+\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}|\text{Re}(\unicode[STIX]{x1D70F}_{l})|=|\text{Re}(\unicode[STIX]{x1D6FE}_{l}^{-1}\unicode[STIX]{x1D70F}_{l}^{\prime \prime })|=\frac{|\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D6FD}_{l}|\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|^{2}+\unicode[STIX]{x1D6FC}_{l}^{\ast }\unicode[STIX]{x1D6FD}_{l}^{\ast }+(\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D6FD}_{l}^{\ast }+\unicode[STIX]{x1D6FC}_{l}^{\ast }\unicode[STIX]{x1D6FD}_{l})\operatorname{Re}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })|}{|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }+\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}}.\end{eqnarray}$$
The denominator is at least
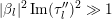 $|\unicode[STIX]{x1D6FD}_{l}|^{2}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })^{2}\gg 1$
if
$|\unicode[STIX]{x1D6FD}_{l}|^{2}\operatorname{Im}(\unicode[STIX]{x1D70F}_{l}^{\prime \prime })^{2}\gg 1$
if
![]() $\unicode[STIX]{x1D6FD}_{l}\not =0$
and it equals
$\unicode[STIX]{x1D6FD}_{l}\not =0$
and it equals
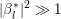 $|\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}\gg 1$
if
$|\unicode[STIX]{x1D6FD}_{l}^{\ast }|^{2}\gg 1$
if
![]() $\unicode[STIX]{x1D6FD}_{l}=0$
. Using elementary estimates we conclude that
$\unicode[STIX]{x1D6FD}_{l}=0$
. Using elementary estimates we conclude that
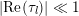 $|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
by treating separately the cases
$|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
by treating separately the cases
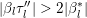 $|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|>2|\unicode[STIX]{x1D6FD}_{l}^{\ast }|$
and
$|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|>2|\unicode[STIX]{x1D6FD}_{l}^{\ast }|$
and
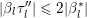 $|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|\leqslant 2|\unicode[STIX]{x1D6FD}_{l}^{\ast }|$
.◻
$|\unicode[STIX]{x1D6FD}_{l}\unicode[STIX]{x1D70F}_{l}^{\prime \prime }|\leqslant 2|\unicode[STIX]{x1D6FD}_{l}^{\ast }|$
.◻
3.2 Abelian varieties with complex multiplication
In this section we recall some basic facts on a certain class of abelian varieties with CM. Furthermore, we prove several estimates that will play important roles in sections to come.
Let
![]() $K$
be a CM field with
$K$
be a CM field with
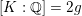 $[K:\mathbb{Q}]=2g$
and
$[K:\mathbb{Q}]=2g$
and
![]() $F$
the maximal, totally real subfield of
$F$
the maximal, totally real subfield of
![]() $K$
.
$K$
.
We suppose that
![]() $A$
is an abelian variety of dimension
$A$
is an abelian variety of dimension
![]() $g$
defined over
$g$
defined over
![]() $\mathbb{C}$
such that there is a ring homomorphism from an order
$\mathbb{C}$
such that there is a ring homomorphism from an order
![]() ${\mathcal{O}}$
of
${\mathcal{O}}$
of
![]() $K$
into
$K$
into
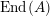 $\operatorname{End}(A)$
which maps
$\operatorname{End}(A)$
which maps
![]() $1$
to the identity map on
$1$
to the identity map on
![]() $A$
. In addition, we suppose that
$A$
. In addition, we suppose that
![]() $A$
is principally polarised.
$A$
is principally polarised.
As
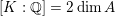 $[K:\mathbb{Q}]=2\dim A$
, the natural action of
$[K:\mathbb{Q}]=2\dim A$
, the natural action of
![]() $K$
on the tangent space of
$K$
on the tangent space of
![]() $A$
at
$A$
at
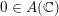 $0\in A(\mathbb{C})$
is equivalent to a direct sum of embeddings
$0\in A(\mathbb{C})$
is equivalent to a direct sum of embeddings
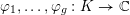 $\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}:K\rightarrow \mathbb{C}$
, which are distinct modulo complex conjugation. In this way,
$\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}:K\rightarrow \mathbb{C}$
, which are distinct modulo complex conjugation. In this way,
![]() $A$
gives rise to a CM type
$A$
gives rise to a CM type
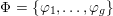 $\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}\}$
of
$\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}\}$
of
![]() $K$
. To keep notation elementary we fix a basis of the said tangent space and identify it with
$K$
. To keep notation elementary we fix a basis of the said tangent space and identify it with
![]() $\mathbb{C}^{g}$
such that the action of
$\mathbb{C}^{g}$
such that the action of
![]() $K$
is given by
$K$
is given by
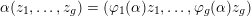 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(z_{1},\ldots ,z_{g})=(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D6FC})z_{1},\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D6FC})z_{g})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(z_{1},\ldots ,z_{g})=(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D6FC})z_{1},\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D6FC})z_{g})\end{eqnarray}$$
for
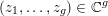 $(z_{1},\ldots ,z_{g})\in \mathbb{C}^{g}$
.
$(z_{1},\ldots ,z_{g})\in \mathbb{C}^{g}$
.
By abuse of notation, we write
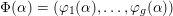 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})=(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D6FC}),\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D6FC}))$
if
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})=(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D6FC}),\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D6FC}))$
if
![]() $\unicode[STIX]{x1D6FC}\in K$
.
$\unicode[STIX]{x1D6FC}\in K$
.
The period lattice of
![]() $A$
is a discrete subgroup
$A$
is a discrete subgroup
![]() $\unicode[STIX]{x1D6F1}\subseteq \mathbb{C}^{g}$
of rank
$\unicode[STIX]{x1D6F1}\subseteq \mathbb{C}^{g}$
of rank
![]() $2g$
. After scaling coordinates we may suppose that
$2g$
. After scaling coordinates we may suppose that
 $(1,\ldots ,1)\in \unicode[STIX]{x1D6F1}$
.
$(1,\ldots ,1)\in \unicode[STIX]{x1D6F1}$
.
The set
 $$\begin{eqnarray}\mathfrak{M}=\{\unicode[STIX]{x1D6FC}\in K:\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})\in \unicode[STIX]{x1D6F1}\}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{M}=\{\unicode[STIX]{x1D6FC}\in K:\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})\in \unicode[STIX]{x1D6F1}\}\end{eqnarray}$$
is an
![]() ${\mathcal{O}}_{F}$
-module since
${\mathcal{O}}_{F}$
-module since
![]() ${\mathcal{O}}_{F}$
acts on the period lattice via
${\mathcal{O}}_{F}$
acts on the period lattice via
![]() $\unicode[STIX]{x1D6F7}$
. It is finitely generated as such and it contains an order of
$\unicode[STIX]{x1D6F7}$
. It is finitely generated as such and it contains an order of
![]() $K$
. Moreover,
$K$
. Moreover,
![]() $\mathfrak{M}$
is torsion-free and
$\mathfrak{M}$
is torsion-free and
![]() ${\mathcal{O}}_{F}$
is a Dedekind ring; thus,
${\mathcal{O}}_{F}$
is a Dedekind ring; thus,
![]() $\mathfrak{M}$
is a projective
$\mathfrak{M}$
is a projective
![]() ${\mathcal{O}}_{F}$
-module. It is of rank
${\mathcal{O}}_{F}$
-module. It is of rank
![]() $2$
making it isomorphic to
$2$
making it isomorphic to
![]() ${\mathcal{O}}_{F}\oplus \mathfrak{a}$
, where
${\mathcal{O}}_{F}\oplus \mathfrak{a}$
, where
![]() $\mathfrak{a}$
is a fractional ideal of
$\mathfrak{a}$
is a fractional ideal of
![]() ${\mathcal{O}}_{F}$
. Now
${\mathcal{O}}_{F}$
. Now
![]() $\mathfrak{a}$
is uniquely determined by its ideal class and later on we will show that
$\mathfrak{a}$
is uniquely determined by its ideal class and later on we will show that
![]() $\mathfrak{a}$
lies in the class of
$\mathfrak{a}$
lies in the class of
![]() $\mathscr{D}_{F/\mathbb{Q}}^{-1}$
. Let us fix
$\mathscr{D}_{F/\mathbb{Q}}^{-1}$
. Let us fix
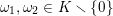 $\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}\in K\smallsetminus \{0\}$
with
$\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}\in K\smallsetminus \{0\}$
with
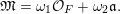 $$\begin{eqnarray}\mathfrak{M}=\unicode[STIX]{x1D714}_{1}{\mathcal{O}}_{F}+\unicode[STIX]{x1D714}_{2}\mathfrak{a}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{M}=\unicode[STIX]{x1D714}_{1}{\mathcal{O}}_{F}+\unicode[STIX]{x1D714}_{2}\mathfrak{a}.\end{eqnarray}$$
We note that
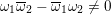 $\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}-\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}\not =0$
, where as usual
$\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}-\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}\not =0$
, where as usual
![]() $\overline{\cdot }$
denotes complex conjugation on
$\overline{\cdot }$
denotes complex conjugation on
![]() $K$
, and define
$K$
, and define
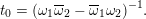 $$\begin{eqnarray}t_{0}=(\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}-\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2})^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}t_{0}=(\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}-\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2})^{-1}.\end{eqnarray}$$
Observe that if the order
![]() ${\mathcal{O}}$
equals
${\mathcal{O}}$
equals
![]() ${\mathcal{O}}_{K}$
, then
${\mathcal{O}}_{K}$
, then
![]() $\mathfrak{M}$
is a fractional ideal of
$\mathfrak{M}$
is a fractional ideal of
![]() ${\mathcal{O}}_{K}$
. In this case we will use the symbol
${\mathcal{O}}_{K}$
. In this case we will use the symbol
![]() $\mathfrak{A}$
to denote
$\mathfrak{A}$
to denote
![]() $\mathfrak{M}$
.
$\mathfrak{M}$
.
As
![]() $A$
is principally polarised, it comes with an
$A$
is principally polarised, it comes with an
![]() $\mathbb{R}$
-bilinear form
$\mathbb{R}$
-bilinear form
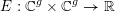 $E:\mathbb{C}^{g}\times \mathbb{C}^{g}\rightarrow \mathbb{R}$
which restricts to an integral symplectic form of determinant
$E:\mathbb{C}^{g}\times \mathbb{C}^{g}\rightarrow \mathbb{R}$
which restricts to an integral symplectic form of determinant
![]() $1$
on
$1$
on
![]() $\unicode[STIX]{x1D6F1}\times \unicode[STIX]{x1D6F1}$
. We note that
$\unicode[STIX]{x1D6F1}\times \unicode[STIX]{x1D6F1}$
. We note that
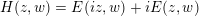 $$\begin{eqnarray}H(z,w)=E(iz,w)+iE(z,w)\end{eqnarray}$$
$$\begin{eqnarray}H(z,w)=E(iz,w)+iE(z,w)\end{eqnarray}$$
is a positive-definite hermitian form whose imaginary part is integral on
![]() $\unicode[STIX]{x1D6F1}\times \unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}\times \unicode[STIX]{x1D6F1}$
.
Our form
![]() $E$
satisfies the condition of Theorem 4, ch. II in Shimura’s book [Reference ShimuraShi97]. So, there is
$E$
satisfies the condition of Theorem 4, ch. II in Shimura’s book [Reference ShimuraShi97]. So, there is
![]() $t\in K$
with
$t\in K$
with
![]() $\overline{t}=-t$
and
$\overline{t}=-t$
and
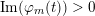 $\operatorname{Im}(\unicode[STIX]{x1D711}_{m}(t))>0$
for all
$\operatorname{Im}(\unicode[STIX]{x1D711}_{m}(t))>0$
for all
![]() $m$
such that
$m$
such that
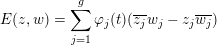 $$\begin{eqnarray}E(z,w)=\mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(t)(\overline{z_{j}}w_{j}-z_{j}\overline{w_{j}})\end{eqnarray}$$
$$\begin{eqnarray}E(z,w)=\mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(t)(\overline{z_{j}}w_{j}-z_{j}\overline{w_{j}})\end{eqnarray}$$
for all
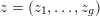 $z=(z_{1},\ldots ,z_{g})$
and
$z=(z_{1},\ldots ,z_{g})$
and
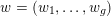 $w=(w_{1},\ldots ,w_{g})$
in
$w=(w_{1},\ldots ,w_{g})$
in
![]() $\mathbb{C}^{g}$
. Then
$\mathbb{C}^{g}$
. Then
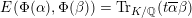 $$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FD}))=\operatorname{Tr}_{K/\mathbb{Q}}(t\overline{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD})\end{eqnarray}$$
$$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FD}))=\operatorname{Tr}_{K/\mathbb{Q}}(t\overline{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD})\end{eqnarray}$$
for all
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in K$
.
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in K$
.
Lemma 3.2. Let us keep the notation from above and also set
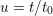 $u=t/t_{0}$
.
$u=t/t_{0}$
.
-
(i) We have
 $u\in F$
and for all
$u\in F$
and for all $$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))=\operatorname{Tr}_{F/\mathbb{Q}}(u(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }))\end{eqnarray}$$
$$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))=\operatorname{Tr}_{F/\mathbb{Q}}(u(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }))\end{eqnarray}$$
 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D707},\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in F$
.
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D707},\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in F$
.
-
(ii) We have
 $u\mathfrak{a}=\mathscr{D}_{F/\mathbb{Q}}^{-1}$
.
$u\mathfrak{a}=\mathscr{D}_{F/\mathbb{Q}}^{-1}$
.
Proof. As
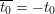 $\overline{t_{0}}=-t_{0}$
, we find that
$\overline{t_{0}}=-t_{0}$
, we find that
![]() $\overline{u}=u$
and thus
$\overline{u}=u$
and thus
![]() $u\in F$
. We find that
$u\in F$
. We find that
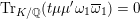 $\operatorname{Tr}_{K/\mathbb{Q}}(t\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{1})=0$
as
$\operatorname{Tr}_{K/\mathbb{Q}}(t\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{1})=0$
as
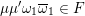 $\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{1}\in F$
and similarly
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{1}\in F$
and similarly
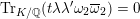 $\operatorname{Tr}_{K/\mathbb{Q}}(t\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}\overline{\unicode[STIX]{x1D714}}_{2})=0$
. Therefore, by (3.14),
$\operatorname{Tr}_{K/\mathbb{Q}}(t\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}\overline{\unicode[STIX]{x1D714}}_{2})=0$
. Therefore, by (3.14),
 $$\begin{eqnarray}\displaystyle E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2})) & = & \displaystyle \operatorname{Tr}_{K/\mathbb{Q}}(t(\unicode[STIX]{x1D707}\overline{\unicode[STIX]{x1D714}}_{1}+\unicode[STIX]{x1D706}\overline{\unicode[STIX]{x1D714}}_{2})(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Tr}_{K/\mathbb{Q}}(t(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(t(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Tr}_{F/\mathbb{Q}}(u(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime })),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2})) & = & \displaystyle \operatorname{Tr}_{K/\mathbb{Q}}(t(\unicode[STIX]{x1D707}\overline{\unicode[STIX]{x1D714}}_{1}+\unicode[STIX]{x1D706}\overline{\unicode[STIX]{x1D714}}_{2})(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Tr}_{K/\mathbb{Q}}(t(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(t(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }\overline{\unicode[STIX]{x1D714}}_{1}\unicode[STIX]{x1D714}_{2}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}}_{2}))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Tr}_{F/\mathbb{Q}}(u(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime })),\nonumber\end{eqnarray}$$
where the final equality used
![]() $t=ut_{0}$
and (3.12). Part (i) follows.
$t=ut_{0}$
and (3.12). Part (i) follows.
The symplectic form
![]() $E$
has determinant
$E$
has determinant
![]() $1$
as it corresponds to a principal polarisation of
$1$
as it corresponds to a principal polarisation of
![]() $A$
. So, there exist a
$A$
. So, there exist a
![]() $\mathbb{Z}$
-basis
$\mathbb{Z}$
-basis
 $(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{g})$
of
$(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{g})$
of
![]() ${\mathcal{O}}_{F}$
and a
${\mathcal{O}}_{F}$
and a
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
 $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{g})$
of
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{g})$
of
![]() $\mathfrak{a}$
such that
$\mathfrak{a}$
such that
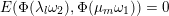 $E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{m}\unicode[STIX]{x1D714}_{1}))=0$
except if
$E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{m}\unicode[STIX]{x1D714}_{1}))=0$
except if
![]() $l=m$
when the value is
$l=m$
when the value is
![]() $1$
. Part (i) yields
$1$
. Part (i) yields
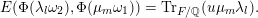 $$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{m}\unicode[STIX]{x1D714}_{1}))=\operatorname{Tr}_{F/\mathbb{Q}}(u\unicode[STIX]{x1D707}_{m}\unicode[STIX]{x1D706}_{l}).\end{eqnarray}$$
$$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{m}\unicode[STIX]{x1D714}_{1}))=\operatorname{Tr}_{F/\mathbb{Q}}(u\unicode[STIX]{x1D707}_{m}\unicode[STIX]{x1D706}_{l}).\end{eqnarray}$$
So, if we arrange the
![]() $g$
column vectors
$g$
column vectors
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{m})$
to a square matrix
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{m})$
to a square matrix
![]() $U$
and do the same with
$U$
and do the same with
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{l})$
to obtain
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{l})$
to obtain
![]() $\unicode[STIX]{x1D6EC}$
, then
$\unicode[STIX]{x1D6EC}$
, then
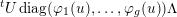 $\text{}^{t}U\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(u),\ldots ,\unicode[STIX]{x1D711}_{g}(u))\unicode[STIX]{x1D6EC}$
is the
$\text{}^{t}U\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(u),\ldots ,\unicode[STIX]{x1D711}_{g}(u))\unicode[STIX]{x1D6EC}$
is the
![]() $g\,\times \,g$
unit matrix. Thus,
$g\,\times \,g$
unit matrix. Thus,
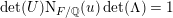 $\det (U)\text{N}_{F/\mathbb{Q}}(u)\det (\unicode[STIX]{x1D6EC})=1$
. Now
$\det (U)\text{N}_{F/\mathbb{Q}}(u)\det (\unicode[STIX]{x1D6EC})=1$
. Now
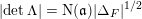 $|\text{det}\,\unicode[STIX]{x1D6EC}|=\text{N}(\mathfrak{a})|\unicode[STIX]{x1D6E5}_{F}|^{1/2}$
and
$|\text{det}\,\unicode[STIX]{x1D6EC}|=\text{N}(\mathfrak{a})|\unicode[STIX]{x1D6E5}_{F}|^{1/2}$
and
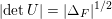 $|\text{det}\,U|=|\unicode[STIX]{x1D6E5}_{F}|^{1/2}$
and thus
$|\text{det}\,U|=|\unicode[STIX]{x1D6E5}_{F}|^{1/2}$
and thus
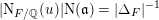 $|\text{N}_{F/\mathbb{Q}}(u)|\text{N}(\mathfrak{a})=|\unicode[STIX]{x1D6E5}_{F}|^{-1}$
. We conclude that
$|\text{N}_{F/\mathbb{Q}}(u)|\text{N}(\mathfrak{a})=|\unicode[STIX]{x1D6E5}_{F}|^{-1}$
. We conclude that
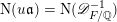 $\text{N}(u\mathfrak{a})=\text{N}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
.
$\text{N}(u\mathfrak{a})=\text{N}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
.
If
![]() $\unicode[STIX]{x1D706}\in \mathfrak{a}$
is arbitrary, then
$\unicode[STIX]{x1D706}\in \mathfrak{a}$
is arbitrary, then
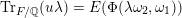 $\operatorname{Tr}_{F/\mathbb{Q}}(u\unicode[STIX]{x1D706})=E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{1}))$
by part (i). This is an integer and so
$\operatorname{Tr}_{F/\mathbb{Q}}(u\unicode[STIX]{x1D706})=E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{1}))$
by part (i). This is an integer and so
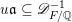 $u\mathfrak{a}\subseteq \mathscr{D}_{F/\mathbb{Q}}^{-1}$
. But we proved above that these two fractional ideals have equal norm; thus, part (ii) follows.◻
$u\mathfrak{a}\subseteq \mathscr{D}_{F/\mathbb{Q}}^{-1}$
. But we proved above that these two fractional ideals have equal norm; thus, part (ii) follows.◻
Part (ii) of the lemma above establishes our claim that
![]() $\mathfrak{a}$
and
$\mathfrak{a}$
and
![]() $\mathscr{D}_{F/\mathbb{Q}}^{-1}$
are in the same ideal class. So, we can take
$\mathscr{D}_{F/\mathbb{Q}}^{-1}$
are in the same ideal class. So, we can take
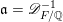 $\mathfrak{a}=\mathscr{D}_{F/\mathbb{Q}}^{-1}$
to start out with. Part (ii) of the previous lemma implies that
$\mathfrak{a}=\mathscr{D}_{F/\mathbb{Q}}^{-1}$
to start out with. Part (ii) of the previous lemma implies that
![]() $u\in {\mathcal{O}}_{F}^{\times }$
. We now replace
$u\in {\mathcal{O}}_{F}^{\times }$
. We now replace
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $\unicode[STIX]{x1D714}_{2}$
with
$\unicode[STIX]{x1D714}_{2}$
with
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $u^{-1}\unicode[STIX]{x1D714}_{2}$
, respectively. With these new periods,
$u^{-1}\unicode[STIX]{x1D714}_{2}$
, respectively. With these new periods,
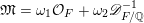 $$\begin{eqnarray}\mathfrak{M}=\unicode[STIX]{x1D714}_{1}{\mathcal{O}}_{F}+\unicode[STIX]{x1D714}_{2}\mathscr{D}_{F/\mathbb{Q}}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{M}=\unicode[STIX]{x1D714}_{1}{\mathcal{O}}_{F}+\unicode[STIX]{x1D714}_{2}\mathscr{D}_{F/\mathbb{Q}}^{-1}\end{eqnarray}$$
remains true but now
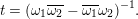 $$\begin{eqnarray}t=(\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}_{2}}-\overline{\unicode[STIX]{x1D714}_{1}}\unicode[STIX]{x1D714}_{2})^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}t=(\unicode[STIX]{x1D714}_{1}\overline{\unicode[STIX]{x1D714}_{2}}-\overline{\unicode[STIX]{x1D714}_{1}}\unicode[STIX]{x1D714}_{2})^{-1}.\end{eqnarray}$$
Moreover, the formula in Lemma 3.2(i) simplifies to
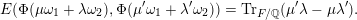 $$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))=\operatorname{Tr}_{F/\mathbb{Q}}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))=\operatorname{Tr}_{F/\mathbb{Q}}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }).\end{eqnarray}$$
Next let us consider
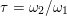 $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
. We compute
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
. We compute
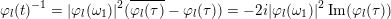 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{l}(t)^{-1}=|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{1})|^{2}(\overline{\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F})}-\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))=-2i|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{1})|^{2}\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{l}(t)^{-1}=|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{1})|^{2}(\overline{\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F})}-\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))=-2i|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{1})|^{2}\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))\end{eqnarray}$$
for all
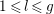 $1\,\leqslant \,l\,\leqslant \,g$
. Our
$1\,\leqslant \,l\,\leqslant \,g$
. Our
![]() $t$
satisfies
$t$
satisfies
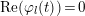 $\operatorname{Re}(\unicode[STIX]{x1D711}_{l}(t))\,=\,0$
and
$\operatorname{Re}(\unicode[STIX]{x1D711}_{l}(t))\,=\,0$
and
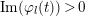 $\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(t))\,>\,0$
. We conclude that
$\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(t))\,>\,0$
. We conclude that
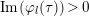 $\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))\,>\,0$
for all
$\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))\,>\,0$
for all
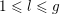 $1\leqslant l\leqslant g$
. In particular,
$1\leqslant l\leqslant g$
. In particular,
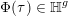 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})\in \mathbb{H}^{g}$
.
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})\in \mathbb{H}^{g}$
.
Recall that the group
 $\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
, defined in (3.2), acts on
$\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
, defined in (3.2), acts on
![]() $\mathbb{H}^{g}$
and that we described a fundamental set for this action in Proposition 3.1. In the proposition below we use this group to transform
$\mathbb{H}^{g}$
and that we described a fundamental set for this action in Proposition 3.1. In the proposition below we use this group to transform
![]() $\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
to the said fundamental set.
$\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
to the said fundamental set.
Let
 $V\subseteq {\mathcal{O}}_{F}^{\times ,+}$
be a set of representatives of
$V\subseteq {\mathcal{O}}_{F}^{\times ,+}$
be a set of representatives of
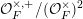 ${\mathcal{O}}_{F}^{\times ,+}/({\mathcal{O}}_{F}^{\times })^{2}$
. Note that
${\mathcal{O}}_{F}^{\times ,+}/({\mathcal{O}}_{F}^{\times })^{2}$
. Note that
![]() $V$
is finite.
$V$
is finite.
Proposition 3.3. There exist
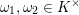 $\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}\in K^{\times }$
as in (3.15),
$\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}\in K^{\times }$
as in (3.15),
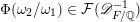 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1})\in {\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
, and such that there is
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1})\in {\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
, and such that there is
![]() $v\in V$
with
$v\in V$
with
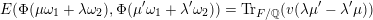 $$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))=\operatorname{Tr}_{F/\mathbb{Q}}(v(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }-\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D707}))\end{eqnarray}$$
$$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}))=\operatorname{Tr}_{F/\mathbb{Q}}(v(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }-\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D707}))\end{eqnarray}$$
for all
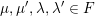 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime },\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in F$
.
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime },\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in F$
.
Proof. According to Proposition 3.1, there is
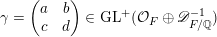 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathscr{D}_{F/\mathbb{Q}}^{-1})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \operatorname{GL}_{}^{+}({\mathcal{O}}_{F}\oplus \mathscr{D}_{F/\mathbb{Q}}^{-1})\end{eqnarray}$$
with
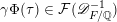 $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})\in {\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
. Multiplying
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})\in {\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
. Multiplying
![]() $\unicode[STIX]{x1D6FE}$
by a scalar matrix with diagonal entry
$\unicode[STIX]{x1D6FE}$
by a scalar matrix with diagonal entry
![]() $u\in {\mathcal{O}}_{F}^{\times }$
does not affect
$u\in {\mathcal{O}}_{F}^{\times }$
does not affect
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})$
and replaces
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})$
and replaces
![]() $\det \unicode[STIX]{x1D6FE}$
by
$\det \unicode[STIX]{x1D6FE}$
by
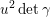 $u^{2}\det \unicode[STIX]{x1D6FE}$
. So, we may assume that
$u^{2}\det \unicode[STIX]{x1D6FE}$
. So, we may assume that
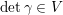 $\det \unicode[STIX]{x1D6FE}\in V$
. We set
$\det \unicode[STIX]{x1D6FE}\in V$
. We set
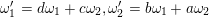 $\unicode[STIX]{x1D714}_{1}^{\prime }=d\unicode[STIX]{x1D714}_{1}+c\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{2}^{\prime }=b\unicode[STIX]{x1D714}_{1}+a\unicode[STIX]{x1D714}_{2}$
and find, using the definition (3.1), that (3.15) again remains true. Using (3.17), we obtain
$\unicode[STIX]{x1D714}_{1}^{\prime }=d\unicode[STIX]{x1D714}_{1}+c\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{2}^{\prime }=b\unicode[STIX]{x1D714}_{1}+a\unicode[STIX]{x1D714}_{2}$
and find, using the definition (3.1), that (3.15) again remains true. Using (3.17), we obtain
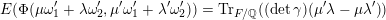 $$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}^{\prime }+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}^{\prime },\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}^{\prime }+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}^{\prime }))=\operatorname{Tr}_{F/\mathbb{Q}}((\det \unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }))\end{eqnarray}$$
$$\begin{eqnarray}E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}\unicode[STIX]{x1D714}_{1}^{\prime }+\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{2}^{\prime },\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D714}_{1}^{\prime }+\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D714}_{2}^{\prime }))=\operatorname{Tr}_{F/\mathbb{Q}}((\det \unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{\prime }))\end{eqnarray}$$
for all
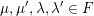 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime },\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in F$
. The proposition follows on replacing
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime },\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in F$
. The proposition follows on replacing
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $\unicode[STIX]{x1D714}_{2}$
by
$\unicode[STIX]{x1D714}_{2}$
by
![]() $\unicode[STIX]{x1D714}_{1}^{\prime }$
and
$\unicode[STIX]{x1D714}_{1}^{\prime }$
and
![]() $\unicode[STIX]{x1D714}_{2}^{\prime }$
, respectively. ◻
$\unicode[STIX]{x1D714}_{2}^{\prime }$
, respectively. ◻
Let
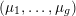 $(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{g})$
be any
$(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{g})$
be any
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
![]() ${\mathcal{O}}_{F}$
. We may find a
${\mathcal{O}}_{F}$
. We may find a
![]() $\mathbb{Z}$
-basis
$\mathbb{Z}$
-basis
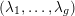 $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{g})$
of
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{g})$
of
![]() $\mathscr{D}_{F/\mathbb{Q}}^{-1}$
such that
$\mathscr{D}_{F/\mathbb{Q}}^{-1}$
such that
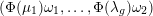 $(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{1})\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{g})\unicode[STIX]{x1D714}_{2})$
is a symplectic basis for
$(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{1})\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{g})\unicode[STIX]{x1D714}_{2})$
is a symplectic basis for
![]() $E$
. We note that the
$E$
. We note that the
![]() $\unicode[STIX]{x1D706}_{l}$
may depend on the symplectic form
$\unicode[STIX]{x1D706}_{l}$
may depend on the symplectic form
![]() $E$
and thus on
$E$
and thus on
![]() $\mathfrak{M}$
, whereas the
$\mathfrak{M}$
, whereas the
![]() $\unicode[STIX]{x1D707}_{m}$
depend only on
$\unicode[STIX]{x1D707}_{m}$
depend only on
![]() $F$
. Let us see how to retrieve the
$F$
. Let us see how to retrieve the
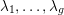 $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{g}$
from the other data. We define
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{g}$
from the other data. We define
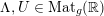 $\unicode[STIX]{x1D6EC},U\in \text{Mat}_{g}(\mathbb{R})$
as the square matrices with columns
$\unicode[STIX]{x1D6EC},U\in \text{Mat}_{g}(\mathbb{R})$
as the square matrices with columns
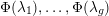 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{1}),\ldots ,\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{g})$
and
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{1}),\ldots ,\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D706}_{g})$
and
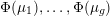 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{1}),\ldots ,\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{g})$
, respectively. Relation (3.18) yields
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{1}),\ldots ,\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}_{g})$
, respectively. Relation (3.18) yields
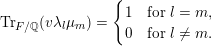 $$\begin{eqnarray}\operatorname{Tr}_{F/\mathbb{Q}}(v\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D707}_{m})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{for}~l=m,\\ 0\quad & \text{for}~l\not =m.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tr}_{F/\mathbb{Q}}(v\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D707}_{m})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{for}~l=m,\\ 0\quad & \text{for}~l\not =m.\end{array}\right.\end{eqnarray}$$
So,
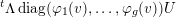 $\text{}^{t}\unicode[STIX]{x1D6EC}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(v),\ldots ,\unicode[STIX]{x1D711}_{g}(v))U$
is the
$\text{}^{t}\unicode[STIX]{x1D6EC}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(v),\ldots ,\unicode[STIX]{x1D711}_{g}(v))U$
is the
![]() $g\times g$
unit matrix. The period matrix with respect to the symplectic basis is
$g\times g$
unit matrix. The period matrix with respect to the symplectic basis is
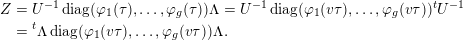 $$\begin{eqnarray}\displaystyle Z & = & \displaystyle U^{-1}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D70F}))\unicode[STIX]{x1D6EC}=U^{-1}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(v\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D711}_{g}(v\unicode[STIX]{x1D70F}))\text{}^{t}U^{-1}\nonumber\\ \displaystyle & = & \displaystyle \text{}^{t}\unicode[STIX]{x1D6EC}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(v\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D711}_{g}(v\unicode[STIX]{x1D70F}))\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z & = & \displaystyle U^{-1}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D70F}))\unicode[STIX]{x1D6EC}=U^{-1}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(v\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D711}_{g}(v\unicode[STIX]{x1D70F}))\text{}^{t}U^{-1}\nonumber\\ \displaystyle & = & \displaystyle \text{}^{t}\unicode[STIX]{x1D6EC}\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(v\unicode[STIX]{x1D70F}),\ldots ,\unicode[STIX]{x1D711}_{g}(v\unicode[STIX]{x1D70F}))\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
It is well known that
![]() $Z$
lies in the Siegel upper half-space
$Z$
lies in the Siegel upper half-space
![]() $\mathbb{H}_{g}$
.
$\mathbb{H}_{g}$
.
Remark 3.4. Let us assume that
![]() $g=2$
and
$g=2$
and
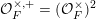 ${\mathcal{O}}_{F}^{\times ,+}=({\mathcal{O}}_{F}^{\times })^{2}$
. So,
${\mathcal{O}}_{F}^{\times ,+}=({\mathcal{O}}_{F}^{\times })^{2}$
. So,
![]() $F$
is a real quadratic field of discriminant
$F$
is a real quadratic field of discriminant
![]() $\unicode[STIX]{x1D6E5}>0$
, say, and we may take
$\unicode[STIX]{x1D6E5}>0$
, say, and we may take
![]() $V$
as above Proposition 3.3 to contain only
$V$
as above Proposition 3.3 to contain only
![]() $1$
. Thus,
$1$
. Thus,
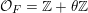 ${\mathcal{O}}_{F}=\mathbb{Z}+\unicode[STIX]{x1D703}\mathbb{Z}$
with
${\mathcal{O}}_{F}=\mathbb{Z}+\unicode[STIX]{x1D703}\mathbb{Z}$
with
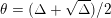 $\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D6E5}+\sqrt{\unicode[STIX]{x1D6E5}})/2$
. The conjugate of
$\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D6E5}+\sqrt{\unicode[STIX]{x1D6E5}})/2$
. The conjugate of
![]() $\unicode[STIX]{x1D703}$
over
$\unicode[STIX]{x1D703}$
over
![]() $\mathbb{Q}$
is
$\mathbb{Q}$
is
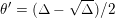 $\unicode[STIX]{x1D703}^{\prime }=(\unicode[STIX]{x1D6E5}-\sqrt{\unicode[STIX]{x1D6E5}})/2$
and we consider
$\unicode[STIX]{x1D703}^{\prime }=(\unicode[STIX]{x1D6E5}-\sqrt{\unicode[STIX]{x1D6E5}})/2$
and we consider
![]() $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }$
as real numbers. So,
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }$
as real numbers. So,
becomes an admissible choice for
![]() $U$
as above. Say
$U$
as above. Say
![]() $\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}$
are as in Proposition 3.3 with
$\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}$
are as in Proposition 3.3 with
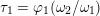 $\unicode[STIX]{x1D70F}_{1}=\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1})$
and
$\unicode[STIX]{x1D70F}_{1}=\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1})$
and
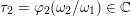 $\unicode[STIX]{x1D70F}_{2}=\unicode[STIX]{x1D711}_{2}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1})\in \mathbb{C}$
. A brief calculation using
$\unicode[STIX]{x1D70F}_{2}=\unicode[STIX]{x1D711}_{2}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1})\in \mathbb{C}$
. A brief calculation using
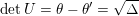 $\det U=\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}^{\prime }=\sqrt{\unicode[STIX]{x1D6E5}}$
yields the period matrix
$\det U=\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}^{\prime }=\sqrt{\unicode[STIX]{x1D6E5}}$
yields the period matrix
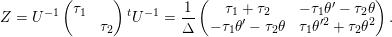 $$\begin{eqnarray}Z=U^{-1}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D70F}_{1} & \\ & \unicode[STIX]{x1D70F}_{2}\end{array}\right)\text{}^{t}U^{-1}=\frac{1}{\unicode[STIX]{x1D6E5}}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D70F}_{1}+\unicode[STIX]{x1D70F}_{2} & -\unicode[STIX]{x1D70F}_{1}\unicode[STIX]{x1D703}^{\prime }-\unicode[STIX]{x1D70F}_{2}\unicode[STIX]{x1D703}\\ -\unicode[STIX]{x1D70F}_{1}\unicode[STIX]{x1D703}^{\prime }-\unicode[STIX]{x1D70F}_{2}\unicode[STIX]{x1D703} & \unicode[STIX]{x1D70F}_{1}{\unicode[STIX]{x1D703}^{\prime }}^{2}+\unicode[STIX]{x1D70F}_{2}\unicode[STIX]{x1D703}^{2}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}Z=U^{-1}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D70F}_{1} & \\ & \unicode[STIX]{x1D70F}_{2}\end{array}\right)\text{}^{t}U^{-1}=\frac{1}{\unicode[STIX]{x1D6E5}}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D70F}_{1}+\unicode[STIX]{x1D70F}_{2} & -\unicode[STIX]{x1D70F}_{1}\unicode[STIX]{x1D703}^{\prime }-\unicode[STIX]{x1D70F}_{2}\unicode[STIX]{x1D703}\\ -\unicode[STIX]{x1D70F}_{1}\unicode[STIX]{x1D703}^{\prime }-\unicode[STIX]{x1D70F}_{2}\unicode[STIX]{x1D703} & \unicode[STIX]{x1D70F}_{1}{\unicode[STIX]{x1D703}^{\prime }}^{2}+\unicode[STIX]{x1D70F}_{2}\unicode[STIX]{x1D703}^{2}\end{array}\right).\end{eqnarray}$$
For the remainder of this section we suppose that
 ${\mathcal{O}}={\mathcal{O}}_{K}$
and thus that
${\mathcal{O}}={\mathcal{O}}_{K}$
and thus that
![]() $\mathfrak{M}=\mathfrak{A}$
is a fractional ideal of
$\mathfrak{M}=\mathfrak{A}$
is a fractional ideal of
![]() ${\mathcal{O}}_{K}$
.
${\mathcal{O}}_{K}$
.
Next we will bound how close the point represented by
![]() $Z$
lies to the boundary of the coarse moduli space of principally polarised abelian varieties of dimension
$Z$
lies to the boundary of the coarse moduli space of principally polarised abelian varieties of dimension
![]() $g$
. We will do the same for the point in
$g$
. We will do the same for the point in
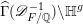 $\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})\backslash \mathbb{H}^{g}$
represented by
$\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})\backslash \mathbb{H}^{g}$
represented by
![]() $\unicode[STIX]{x1D70F}$
from Proposition 3.3.
$\unicode[STIX]{x1D70F}$
from Proposition 3.3.
We define the norm of any ideal class
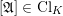 $[\mathfrak{A}]\in \operatorname{Cl}_{K}$
as the least norm of an ideal representing the said class, i.e.,
$[\mathfrak{A}]\in \operatorname{Cl}_{K}$
as the least norm of an ideal representing the said class, i.e.,
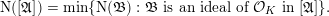 $$\begin{eqnarray}\text{N}([\mathfrak{A}])=\min \{\text{N}(\mathfrak{B}):\mathfrak{B}\text{ is an ideal of}~{\mathcal{O}}_{K}~\text{in }[\mathfrak{A}]\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{N}([\mathfrak{A}])=\min \{\text{N}(\mathfrak{B}):\mathfrak{B}\text{ is an ideal of}~{\mathcal{O}}_{K}~\text{in }[\mathfrak{A}]\}.\end{eqnarray}$$
Recall that
![]() ${\mathcal{F}}_{g}$
denotes Siegel’s fundamental domain; see § 2.
${\mathcal{F}}_{g}$
denotes Siegel’s fundamental domain; see § 2.
Lemma 3.5. Let
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $\unicode[STIX]{x1D714}_{2}$
be as in Proposition 3.3. Then
$\unicode[STIX]{x1D714}_{2}$
be as in Proposition 3.3. Then
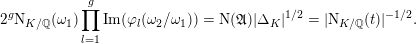 $$\begin{eqnarray}2^{g}\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714}_{1})\mathop{\prod }_{l=1}^{g}\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}))=\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}=|\text{N}_{K/\mathbb{Q}}(t)|^{-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}2^{g}\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714}_{1})\mathop{\prod }_{l=1}^{g}\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}))=\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}=|\text{N}_{K/\mathbb{Q}}(t)|^{-1/2}.\end{eqnarray}$$
Proof. We let
 $U,\unicode[STIX]{x1D6EC}\in \text{Mat}_{g}(\mathbb{R})$
denote matrices as in (3.20). Let
$U,\unicode[STIX]{x1D6EC}\in \text{Mat}_{g}(\mathbb{R})$
denote matrices as in (3.20). Let
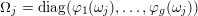 $\unicode[STIX]{x1D6FA}_{j}=\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D714}_{j}),\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D714}_{j}))$
for
$\unicode[STIX]{x1D6FA}_{j}=\operatorname{diag}(\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D714}_{j}),\ldots ,\unicode[STIX]{x1D711}_{g}(\unicode[STIX]{x1D714}_{j}))$
for
 $1\leqslant j\leqslant 2$
. Then the columns of
$1\leqslant j\leqslant 2$
. Then the columns of
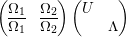 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FA}_{1} & \unicode[STIX]{x1D6FA}_{2}\\ \overline{\unicode[STIX]{x1D6FA}_{1}} & \overline{\unicode[STIX]{x1D6FA}_{2}}\end{array}\right)\left(\begin{array}{@{}cc@{}}U & \\ & \unicode[STIX]{x1D6EC}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FA}_{1} & \unicode[STIX]{x1D6FA}_{2}\\ \overline{\unicode[STIX]{x1D6FA}_{1}} & \overline{\unicode[STIX]{x1D6FA}_{2}}\end{array}\right)\left(\begin{array}{@{}cc@{}}U & \\ & \unicode[STIX]{x1D6EC}\end{array}\right)\end{eqnarray}$$
constitute a
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
 $\unicode[STIX]{x1D6F7}\times \overline{\unicode[STIX]{x1D6F7}}(\mathfrak{A})\subseteq \mathbb{C}^{2g}$
. The determinant of this product has modulus
$\unicode[STIX]{x1D6F7}\times \overline{\unicode[STIX]{x1D6F7}}(\mathfrak{A})\subseteq \mathbb{C}^{2g}$
. The determinant of this product has modulus
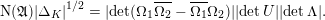 $$\begin{eqnarray}\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}=|\text{det}(\unicode[STIX]{x1D6FA}_{1}\overline{\unicode[STIX]{x1D6FA}_{2}}-\overline{\unicode[STIX]{x1D6FA}_{1}}\unicode[STIX]{x1D6FA}_{2})||\text{det}\,U||\text{det}\,\unicode[STIX]{x1D6EC}|.\end{eqnarray}$$
$$\begin{eqnarray}\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}=|\text{det}(\unicode[STIX]{x1D6FA}_{1}\overline{\unicode[STIX]{x1D6FA}_{2}}-\overline{\unicode[STIX]{x1D6FA}_{1}}\unicode[STIX]{x1D6FA}_{2})||\text{det}\,U||\text{det}\,\unicode[STIX]{x1D6EC}|.\end{eqnarray}$$
The first equality follows since
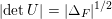 $|\text{det}\,U|=|\unicode[STIX]{x1D6E5}_{F}|^{1/2}$
and
$|\text{det}\,U|=|\unicode[STIX]{x1D6E5}_{F}|^{1/2}$
and
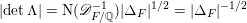 $|\text{det}\,\unicode[STIX]{x1D6EC}|=\text{N}(\mathscr{D}_{F/\mathbb{Q}}^{-1})|\unicode[STIX]{x1D6E5}_{F}|^{1/2}=|\unicode[STIX]{x1D6E5}_{F}|^{-1/2}$
.
$|\text{det}\,\unicode[STIX]{x1D6EC}|=\text{N}(\mathscr{D}_{F/\mathbb{Q}}^{-1})|\unicode[STIX]{x1D6E5}_{F}|^{1/2}=|\unicode[STIX]{x1D6E5}_{F}|^{-1/2}$
.
To prove the second equality, let
 $(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{2g})$
be a
$(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{2g})$
be a
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
![]() $\mathfrak{A}$
. The entries of the matrix
$\mathfrak{A}$
. The entries of the matrix
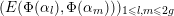 $(E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{l}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{m})))_{1\leqslant l,m\leqslant 2g}$
can be expressed using the trace by (3.14). We find that
$(E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{l}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{m})))_{1\leqslant l,m\leqslant 2g}$
can be expressed using the trace by (3.14). We find that
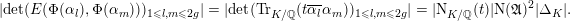 $$\begin{eqnarray}|\text{det}(E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{l}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{m})))_{1\leqslant l,m\leqslant 2g}|=|\text{det}(\operatorname{Tr}_{K/\mathbb{Q}}(t\overline{\unicode[STIX]{x1D6FC}_{l}}\unicode[STIX]{x1D6FC}_{m}))_{1\leqslant l,m\leqslant 2g}|=|\text{N}_{K/\mathbb{Q}}(t)|\text{N}(\mathfrak{A})^{2}|\unicode[STIX]{x1D6E5}_{K}|.\end{eqnarray}$$
$$\begin{eqnarray}|\text{det}(E(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{l}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC}_{m})))_{1\leqslant l,m\leqslant 2g}|=|\text{det}(\operatorname{Tr}_{K/\mathbb{Q}}(t\overline{\unicode[STIX]{x1D6FC}_{l}}\unicode[STIX]{x1D6FC}_{m}))_{1\leqslant l,m\leqslant 2g}|=|\text{N}_{K/\mathbb{Q}}(t)|\text{N}(\mathfrak{A})^{2}|\unicode[STIX]{x1D6E5}_{K}|.\end{eqnarray}$$
The absolute value on the left is
![]() $1$
as the polarisation on
$1$
as the polarisation on
![]() $A$
is principal. Our claim follows after taking the square root and rearranging terms.◻
$A$
is principal. Our claim follows after taking the square root and rearranging terms.◻
For the next lemma we fix representatives
 $\unicode[STIX]{x1D702}_{m}\in \mathbb{P}^{1}(F)$
of the
$\unicode[STIX]{x1D702}_{m}\in \mathbb{P}^{1}(F)$
of the
![]() $\#\operatorname{Cl}_{F}$
cusps of
$\#\operatorname{Cl}_{F}$
cusps of
 $\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})\backslash \mathbb{H}^{g}$
as in § 3.1.
$\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})\backslash \mathbb{H}^{g}$
as in § 3.1.
Lemma 3.6. Let
![]() $Z$
be the period matrix (3.20), let
$Z$
be the period matrix (3.20), let
![]() $\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}$
be as in Proposition 3.3, and set
$\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}$
be as in Proposition 3.3, and set
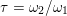 $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
.
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
.
-
(i) There exists a constant
 $c=c(g)>0$
which depends only on
$c=c(g)>0$
which depends only on
 $g$
with the following property. If
$g$
with the following property. If
 $\unicode[STIX]{x1D6FE}\in \operatorname{Sp}_{2g}(\mathbb{Z})$
with
$\unicode[STIX]{x1D6FE}\in \operatorname{Sp}_{2g}(\mathbb{Z})$
with
 $\unicode[STIX]{x1D6FE}Z\in {\mathcal{F}}_{g}$
, then
$\unicode[STIX]{x1D6FE}Z\in {\mathcal{F}}_{g}$
, then  $$\begin{eqnarray}\operatorname{Tr}_{}(\operatorname{Im}(\unicode[STIX]{x1D6FE}Z))\leqslant c\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/g}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tr}_{}(\operatorname{Im}(\unicode[STIX]{x1D6FE}Z))\leqslant c\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/g}.\end{eqnarray}$$
-
(ii) There exists a constant
 $c>0$
which depends only on
$c>0$
which depends only on
 $F$
and the
$F$
and the
 $\unicode[STIX]{x1D702}_{m}$
such that for all
$\unicode[STIX]{x1D702}_{m}$
such that for all $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\leqslant c\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\leqslant c\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\end{eqnarray}$$
 $m$
.
$m$
.
Proof. Let
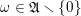 $\unicode[STIX]{x1D714}\in \mathfrak{A}\smallsetminus \{0\}$
witness the injectivity diameter
$\unicode[STIX]{x1D714}\in \mathfrak{A}\smallsetminus \{0\}$
witness the injectivity diameter
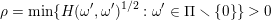 $$\begin{eqnarray}\unicode[STIX]{x1D70C}=\min \{H(\unicode[STIX]{x1D714}^{\prime },\unicode[STIX]{x1D714}^{\prime })^{1/2}:\unicode[STIX]{x1D714}^{\prime }\in \unicode[STIX]{x1D6F1}\smallsetminus \{0\}\}>0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}=\min \{H(\unicode[STIX]{x1D714}^{\prime },\unicode[STIX]{x1D714}^{\prime })^{1/2}:\unicode[STIX]{x1D714}^{\prime }\in \unicode[STIX]{x1D6F1}\smallsetminus \{0\}\}>0\end{eqnarray}$$
of
![]() $A$
with its polarisation, i.e.,
$A$
with its polarisation, i.e.,
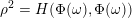 $\unicode[STIX]{x1D70C}^{2}=H(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}))$
. Then
$\unicode[STIX]{x1D70C}^{2}=H(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}))$
. Then
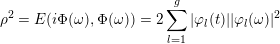 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}=E(i\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}))=2\mathop{\sum }_{l=1}^{g}|\unicode[STIX]{x1D711}_{l}(t)||\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714})|^{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}=E(i\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}))=2\mathop{\sum }_{l=1}^{g}|\unicode[STIX]{x1D711}_{l}(t)||\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714})|^{2}\end{eqnarray}$$
by (3.13). The inequality between the arithmetic mean and the geometric mean implies that
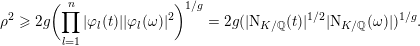 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}\geqslant 2g\biggl(\mathop{\prod }_{l=1}^{n}|\unicode[STIX]{x1D711}_{l}(t)||\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714})|^{2}\biggr)^{1/g}=2g(|\text{N}_{K/\mathbb{Q}}(t)|^{1/2}|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714})|)^{1/g}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}\geqslant 2g\biggl(\mathop{\prod }_{l=1}^{n}|\unicode[STIX]{x1D711}_{l}(t)||\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714})|^{2}\biggr)^{1/g}=2g(|\text{N}_{K/\mathbb{Q}}(t)|^{1/2}|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714})|)^{1/g}.\end{eqnarray}$$
By the second equality in Lemma 3.5, we deduce that
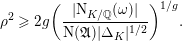 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}\geqslant 2g\biggl(\frac{|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714})|}{\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}\biggr)^{1/g}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}\geqslant 2g\biggl(\frac{|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714})|}{\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}\biggr)^{1/g}.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D714}\in \mathfrak{A}$
is non-zero, there is an ideal
$\unicode[STIX]{x1D714}\in \mathfrak{A}$
is non-zero, there is an ideal
![]() $\mathfrak{B}$
of
$\mathfrak{B}$
of
![]() ${\mathcal{O}}_{K}$
with
${\mathcal{O}}_{K}$
with
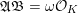 $\mathfrak{A}\mathfrak{B}=\unicode[STIX]{x1D714}{\mathcal{O}}_{K}$
. Thus,
$\mathfrak{A}\mathfrak{B}=\unicode[STIX]{x1D714}{\mathcal{O}}_{K}$
. Thus,
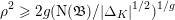 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}\geqslant 2g(\text{N}(\mathfrak{B})/|\unicode[STIX]{x1D6E5}_{K}|^{1/2})^{1/g}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{2}\geqslant 2g(\text{N}(\mathfrak{B})/|\unicode[STIX]{x1D6E5}_{K}|^{1/2})^{1/g}\end{eqnarray}$$
since
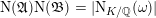 $\text{N}(\mathfrak{A})\text{N}(\mathfrak{B})=|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714})|$
. So,
$\text{N}(\mathfrak{A})\text{N}(\mathfrak{B})=|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714})|$
. So,
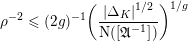 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{-2}\leqslant (2g)^{-1}\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/g}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{-2}\leqslant (2g)^{-1}\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/g}\end{eqnarray}$$
since
![]() $\mathfrak{B}$
is in the class
$\mathfrak{B}$
is in the class
![]() $[\mathfrak{A}^{-1}]$
.
$[\mathfrak{A}^{-1}]$
.
Next we write
 $Z_{\text{red}}=\unicode[STIX]{x1D6FE}Z$
with
$Z_{\text{red}}=\unicode[STIX]{x1D6FE}Z$
with
![]() $\unicode[STIX]{x1D6FE}$
as in (i). As
$\unicode[STIX]{x1D6FE}$
as in (i). As
![]() $Z_{\text{red}}$
lies in Siegel’s fundamental domain, its imaginary part is Minkowski reduced. The matrix
$Z_{\text{red}}$
lies in Siegel’s fundamental domain, its imaginary part is Minkowski reduced. The matrix
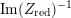 $\operatorname{Im}(Z_{\text{red}})^{-1}$
represents the hermitian form
$\operatorname{Im}(Z_{\text{red}})^{-1}$
represents the hermitian form
![]() $H$
with respect to the standard basis on
$H$
with respect to the standard basis on
![]() $\mathbb{C}^{g}$
. If
$\mathbb{C}^{g}$
. If
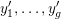 $y_{1}^{\prime },\ldots ,y_{g}^{\prime }$
are the diagonal elements of
$y_{1}^{\prime },\ldots ,y_{g}^{\prime }$
are the diagonal elements of
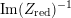 $\operatorname{Im}(Z_{\text{red}})^{-1}$
, then we find that
$\operatorname{Im}(Z_{\text{red}})^{-1}$
, then we find that
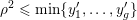 $\unicode[STIX]{x1D70C}^{2}\leqslant \min \{y_{1}^{\prime },\ldots ,y_{g}^{\prime }\}$
on testing with standard basis vectors. The diagonal entries
$\unicode[STIX]{x1D70C}^{2}\leqslant \min \{y_{1}^{\prime },\ldots ,y_{g}^{\prime }\}$
on testing with standard basis vectors. The diagonal entries
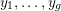 $y_{1},\ldots ,y_{g}$
of
$y_{1},\ldots ,y_{g}$
of
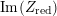 $\operatorname{Im}(Z_{\text{red}})$
are positive and satisfy
$\operatorname{Im}(Z_{\text{red}})$
are positive and satisfy
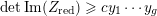 $\det \operatorname{Im}(Z_{\text{red}})\geqslant cy_{1}\cdots y_{g}$
by [Reference KlingenKli90, Proposition 1(iii), § 2], where
$\det \operatorname{Im}(Z_{\text{red}})\geqslant cy_{1}\cdots y_{g}$
by [Reference KlingenKli90, Proposition 1(iii), § 2], where
![]() $c>0$
depends only on
$c>0$
depends only on
![]() $g$
. Part (ii) of the same proposition provides a bound for the off-diagonal entries of
$g$
. Part (ii) of the same proposition provides a bound for the off-diagonal entries of
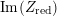 $\operatorname{Im}(Z_{\text{red}})$
in terms of the
$\operatorname{Im}(Z_{\text{red}})$
in terms of the
![]() $y_{l}$
. This allows us to bound the cofactors of
$y_{l}$
. This allows us to bound the cofactors of
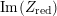 $\operatorname{Im}(Z_{\text{red}})$
using the triangle inequality. The lower bound for
$\operatorname{Im}(Z_{\text{red}})$
using the triangle inequality. The lower bound for
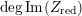 $\deg \operatorname{Im}(Z_{\text{red}})$
then leads to
$\deg \operatorname{Im}(Z_{\text{red}})$
then leads to
 $y_{l}^{\prime }\leqslant c/y_{l}$
after possibly increasing
$y_{l}^{\prime }\leqslant c/y_{l}$
after possibly increasing
![]() $c$
.
$c$
.
So,
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{-2}\geqslant \max \{y_{1},\ldots ,y_{g}\}/c\geqslant \operatorname{Tr}_{}(\operatorname{Im}(Y))/(cg).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{-2}\geqslant \max \{y_{1},\ldots ,y_{g}\}/c\geqslant \operatorname{Tr}_{}(\operatorname{Im}(Y))/(cg).\end{eqnarray}$$
We combine this inequality with (3.21) to deduce part (i).
For the proof of (ii), we abbreviate
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{m}$
and fix
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{m}$
and fix
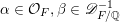 $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{F},\unicode[STIX]{x1D6FD}\in \mathscr{D}_{F/\mathbb{Q}}^{-1}$
with
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{F},\unicode[STIX]{x1D6FD}\in \mathscr{D}_{F/\mathbb{Q}}^{-1}$
with
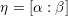 $\unicode[STIX]{x1D702}=[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]$
. Then
$\unicode[STIX]{x1D702}=[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]$
. Then
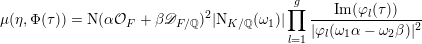 $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))=\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathscr{D}_{F/\mathbb{Q}})^{2}|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714}_{1})|\mathop{\prod }_{l=1}^{g}\frac{\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))}{|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD})|^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))=\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathscr{D}_{F/\mathbb{Q}})^{2}|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714}_{1})|\mathop{\prod }_{l=1}^{g}\frac{\operatorname{Im}(\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D70F}))}{|\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD})|^{2}}\end{eqnarray}$$
and so
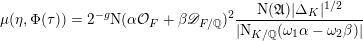 $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))=2^{-g}\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathscr{D}_{F/\mathbb{Q}})^{2}\frac{\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD})|}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))=2^{-g}\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathscr{D}_{F/\mathbb{Q}})^{2}\frac{\text{N}(\mathfrak{A})|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{|\text{N}_{K/\mathbb{Q}}(\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD})|}\end{eqnarray}$$
by the first equality of Lemma 3.5. We observe that
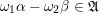 $\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD}\in \mathfrak{A}$
is non-zero. As above,
$\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD}\in \mathfrak{A}$
is non-zero. As above,
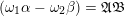 $(\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD})=\mathfrak{A}\mathfrak{B}$
for some ideal
$(\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D6FD})=\mathfrak{A}\mathfrak{B}$
for some ideal
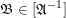 $\mathfrak{B}\in [\mathfrak{A}^{-1}]$
. We conclude that
$\mathfrak{B}\in [\mathfrak{A}^{-1}]$
. We conclude that
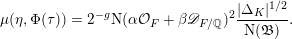 $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))=2^{-g}\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathscr{D}_{F/\mathbb{Q}})^{2}\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}(\mathfrak{B})}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))=2^{-g}\text{N}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{F}+\unicode[STIX]{x1D6FD}\mathscr{D}_{F/\mathbb{Q}})^{2}\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}(\mathfrak{B})}.\end{eqnarray}$$
With this, part (ii) follows since
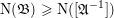 $\text{N}(\mathfrak{B})\geqslant \text{N}([\mathfrak{A}^{-1}])$
and because
$\text{N}(\mathfrak{B})\geqslant \text{N}([\mathfrak{A}^{-1}])$
and because
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
depend only on
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
depend only on
![]() $F$
and the
$F$
and the
![]() $\unicode[STIX]{x1D702}_{m}$
.◻
$\unicode[STIX]{x1D702}_{m}$
.◻
The fact that the exponent
![]() $1/g$
in (i) is strictly less than one for the jacobian of a genus
$1/g$
in (i) is strictly less than one for the jacobian of a genus
![]() $g=2$
curve will prove crucial later on.
$g=2$
curve will prove crucial later on.
The period matrix
![]() $Z$
we constructed above may not lie in Siegel’s fundamental domain
$Z$
we constructed above may not lie in Siegel’s fundamental domain
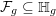 ${\mathcal{F}}_{g}\subseteq \mathbb{H}_{g}$
defined in § 2. We rectify this in the next lemma by using Minkowski and Siegel’s reduction theory.
${\mathcal{F}}_{g}\subseteq \mathbb{H}_{g}$
defined in § 2. We rectify this in the next lemma by using Minkowski and Siegel’s reduction theory.
Lemma 3.7. Let
![]() $\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}$
be as in Proposition 3.3 and set
$\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2}$
be as in Proposition 3.3 and set
 $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
. For given
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{1}$
. For given
![]() $M>0$
, there is a finite set
$M>0$
, there is a finite set
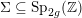 $\unicode[STIX]{x1D6F4}\subseteq \operatorname{Sp}_{2g}(\mathbb{Z})$
such that if
$\unicode[STIX]{x1D6F4}\subseteq \operatorname{Sp}_{2g}(\mathbb{Z})$
such that if
 $\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\leqslant M$
, then there exists
$\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\leqslant M$
, then there exists
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}$
with
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}$
with
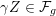 $\unicode[STIX]{x1D6FE}Z\in {\mathcal{F}}_{g}$
.
$\unicode[STIX]{x1D6FE}Z\in {\mathcal{F}}_{g}$
.
Proof. In this proof, all constants implicit in
![]() $\ll$
and
$\ll$
and
![]() $\gg$
depend on
$\gg$
depend on
![]() $F,$
the set
$F,$
the set
![]() $V$
, the matrix
$V$
, the matrix
![]() $U$
, the choice of cusp representatives
$U$
, the choice of cusp representatives
![]() $\unicode[STIX]{x1D702}_{m}$
, and
$\unicode[STIX]{x1D702}_{m}$
, and
![]() $M$
. So,
$M$
. So,
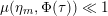 $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\ll 1$
for all cusp representatives
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\ll 1$
for all cusp representatives
![]() $\unicode[STIX]{x1D702}_{m}$
. Recall that
$\unicode[STIX]{x1D702}_{m}$
. Recall that
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})$
lies in the fundamental set
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})$
lies in the fundamental set
 ${\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
coming from Proposition 3.1. If
${\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
coming from Proposition 3.1. If
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})$
is equal to
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F})$
is equal to
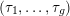 $(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{g})$
, then
$(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{g})$
, then
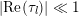 $|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
and
$|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
and
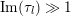 $\operatorname{Im}(\unicode[STIX]{x1D70F}_{l})\gg 1$
for all
$\operatorname{Im}(\unicode[STIX]{x1D70F}_{l})\gg 1$
for all
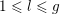 $1\leqslant l\leqslant g$
.
$1\leqslant l\leqslant g$
.
There are at most finitely many possible
![]() $\unicode[STIX]{x1D6EC}$
as in (3.20). Let us write
$\unicode[STIX]{x1D6EC}$
as in (3.20). Let us write
![]() $z_{lm}$
for the entries of
$z_{lm}$
for the entries of
![]() $Z$
. The entries of
$Z$
. The entries of
![]() $\unicode[STIX]{x1D6EC}$
are
$\unicode[STIX]{x1D6EC}$
are
![]() $\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D706}_{m})$
. So,
$\unicode[STIX]{x1D711}_{l}(\unicode[STIX]{x1D706}_{m})$
. So,
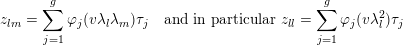 $$\begin{eqnarray}z_{lm}=\mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D706}_{m})\unicode[STIX]{x1D70F}_{j}\quad \text{and in particular}~z_{ll}=\mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}^{2})\unicode[STIX]{x1D70F}_{j}\end{eqnarray}$$
$$\begin{eqnarray}z_{lm}=\mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D706}_{m})\unicode[STIX]{x1D70F}_{j}\quad \text{and in particular}~z_{ll}=\mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}^{2})\unicode[STIX]{x1D70F}_{j}\end{eqnarray}$$
for some
![]() $v\in V$
. We observe that
$v\in V$
. We observe that
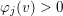 $\unicode[STIX]{x1D711}_{j}(v)>0$
as
$\unicode[STIX]{x1D711}_{j}(v)>0$
as
 $V\subseteq {\mathcal{O}}_{F}^{\times ,+}$
and
$V\subseteq {\mathcal{O}}_{F}^{\times ,+}$
and
 $\unicode[STIX]{x1D711}_{j}(\unicode[STIX]{x1D706}_{l})\in \mathbb{R}\smallsetminus \{0\}$
. So,
$\unicode[STIX]{x1D711}_{j}(\unicode[STIX]{x1D706}_{l})\in \mathbb{R}\smallsetminus \{0\}$
. So,
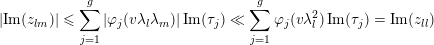 $$\begin{eqnarray}|\text{Im}(z_{lm})|\leqslant \mathop{\sum }_{j=1}^{g}|\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D706}_{m})|\operatorname{Im}(\unicode[STIX]{x1D70F}_{j})\ll \mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}^{2})\operatorname{Im}(\unicode[STIX]{x1D70F}_{j})=\operatorname{Im}(z_{ll})\end{eqnarray}$$
$$\begin{eqnarray}|\text{Im}(z_{lm})|\leqslant \mathop{\sum }_{j=1}^{g}|\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}\unicode[STIX]{x1D706}_{m})|\operatorname{Im}(\unicode[STIX]{x1D70F}_{j})\ll \mathop{\sum }_{j=1}^{g}\unicode[STIX]{x1D711}_{j}(v\unicode[STIX]{x1D706}_{l}^{2})\operatorname{Im}(\unicode[STIX]{x1D70F}_{j})=\operatorname{Im}(z_{ll})\end{eqnarray}$$
for all
 $1\leqslant l,m\leqslant g$
. Taking the determinant of the imaginary part of (3.20) yields
$1\leqslant l,m\leqslant g$
. Taking the determinant of the imaginary part of (3.20) yields
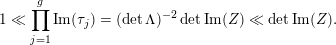 $$\begin{eqnarray}1\ll \mathop{\prod }_{j=1}^{g}\operatorname{Im}(\unicode[STIX]{x1D70F}_{j})=(\det \unicode[STIX]{x1D6EC})^{-2}\det \operatorname{Im}(Z)\ll \det \operatorname{Im}(Z).\end{eqnarray}$$
$$\begin{eqnarray}1\ll \mathop{\prod }_{j=1}^{g}\operatorname{Im}(\unicode[STIX]{x1D70F}_{j})=(\det \unicode[STIX]{x1D6EC})^{-2}\det \operatorname{Im}(Z)\ll \det \operatorname{Im}(Z).\end{eqnarray}$$
So,
![]() $\operatorname{Im}(Z)$
lies in the set
$\operatorname{Im}(Z)$
lies in the set
![]() $Q_{g}(t)$
from [Reference KlingenKli90, Definition 2, § 2] for all sufficiently large
$Q_{g}(t)$
from [Reference KlingenKli90, Definition 2, § 2] for all sufficiently large
![]() $t$
.
$t$
.
On considering the real part, we obtain
 $|\text{Re}(z_{lm})|\ll 1$
from (3.20) and
$|\text{Re}(z_{lm})|\ll 1$
from (3.20) and
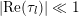 $|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
. Moreover,
$|\text{Re}(\unicode[STIX]{x1D70F}_{l})|\ll 1$
. Moreover,
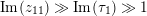 $\operatorname{Im}(z_{11})\gg \operatorname{Im}(\unicode[STIX]{x1D70F}_{1})\gg 1$
.
$\operatorname{Im}(z_{11})\gg \operatorname{Im}(\unicode[STIX]{x1D70F}_{1})\gg 1$
.
Hence,
![]() $Z$
lies in
$Z$
lies in
![]() $L_{g}(t)$
as in [Reference KlingenKli90, Definition 2, § 3] for all large
$L_{g}(t)$
as in [Reference KlingenKli90, Definition 2, § 3] for all large
![]() $t$
. The existence of the finite set
$t$
. The existence of the finite set
![]() $\unicode[STIX]{x1D6F4}$
now follows from [Reference KlingenKli90, Theorem 1].◻
$\unicode[STIX]{x1D6F4}$
now follows from [Reference KlingenKli90, Theorem 1].◻
By our relation (3.20), the entries of
![]() $Z$
are contained in the normal closure of
$Z$
are contained in the normal closure of
![]() $K/\mathbb{Q}$
. In particular, the entries of
$K/\mathbb{Q}$
. In particular, the entries of
![]() $Z$
are contained in a number field whose degree over
$Z$
are contained in a number field whose degree over
![]() $\mathbb{Q}$
is bounded by a constant depending only on
$\mathbb{Q}$
is bounded by a constant depending only on
![]() $g$
.
$g$
.
We use a recent result of Pila and Tsimerman to bound the height of a reduced period matrix.
Lemma 3.8. Let us suppose that
![]() $A$
is simple. If
$A$
is simple. If
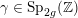 $\unicode[STIX]{x1D6FE}\in \operatorname{Sp}_{2g}(\mathbb{Z})$
with
$\unicode[STIX]{x1D6FE}\in \operatorname{Sp}_{2g}(\mathbb{Z})$
with
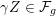 $\unicode[STIX]{x1D6FE}Z\in {\mathcal{F}}_{g}$
, then
$\unicode[STIX]{x1D6FE}Z\in {\mathcal{F}}_{g}$
, then
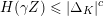 $H(\unicode[STIX]{x1D6FE}Z)\leqslant |\unicode[STIX]{x1D6E5}_{K}|^{c}$
for a constant
$H(\unicode[STIX]{x1D6FE}Z)\leqslant |\unicode[STIX]{x1D6E5}_{K}|^{c}$
for a constant
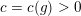 $c=c(g)>0$
that depends only on
$c=c(g)>0$
that depends only on
![]() $g$
.
$g$
.
Proof. This follows from Pila and Tsimerman [Reference Pila and TsimermanPT13, Theorem 3.1] as the endomorphism ring of
![]() $A$
equals
$A$
equals
![]() ${\mathcal{O}}_{K}$
under the simplicity assumption on
${\mathcal{O}}_{K}$
under the simplicity assumption on
![]() $A$
.◻
$A$
.◻
3.3 The Galois orbit
We keep the notation of the previous two sections.
Any field automorphism
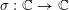 $\unicode[STIX]{x1D70E}:\mathbb{C}\rightarrow \mathbb{C}$
determines a new abelian variety
$\unicode[STIX]{x1D70E}:\mathbb{C}\rightarrow \mathbb{C}$
determines a new abelian variety
![]() $A^{\unicode[STIX]{x1D70E}}$
with complex multiplication. Let
$A^{\unicode[STIX]{x1D70E}}$
with complex multiplication. Let
 $\operatorname{Aut}(\mathbb{C}/K^{\ast })$
denote the group of automorphisms that restrict to the identity on
$\operatorname{Aut}(\mathbb{C}/K^{\ast })$
denote the group of automorphisms that restrict to the identity on
![]() $K^{\ast }$
, the reflex field of
$K^{\ast }$
, the reflex field of
![]() $(K,\unicode[STIX]{x1D6F7})$
. Shimura [Reference ShimuraShi97, Theorem 18.6] described how to recover a period lattice of
$(K,\unicode[STIX]{x1D6F7})$
. Shimura [Reference ShimuraShi97, Theorem 18.6] described how to recover a period lattice of
![]() $A^{\unicode[STIX]{x1D70E}}$
if
$A^{\unicode[STIX]{x1D70E}}$
if
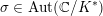 $\unicode[STIX]{x1D70E}\in \operatorname{Aut}(\mathbb{C}/K^{\ast })$
. We only state a special case of Shimura’s theorem and avoid the language of idèles. Indeed, by the assumptions of this section
$\unicode[STIX]{x1D70E}\in \operatorname{Aut}(\mathbb{C}/K^{\ast })$
. We only state a special case of Shimura’s theorem and avoid the language of idèles. Indeed, by the assumptions of this section
![]() $\mathfrak{A}$
is a fractional ideal in
$\mathfrak{A}$
is a fractional ideal in
![]() $K$
and the ideal-theoretic formulation suffices.
$K$
and the ideal-theoretic formulation suffices.
To this extent let
![]() $H^{\ast }$
denote the Hilbert class field of
$H^{\ast }$
denote the Hilbert class field of
![]() $K^{\ast }$
and
$K^{\ast }$
and
 $$\begin{eqnarray}\operatorname{art}:\operatorname{Cl}_{K^{\ast }}\rightarrow \operatorname{Gal}(H^{\ast }/K^{\ast })\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{art}:\operatorname{Cl}_{K^{\ast }}\rightarrow \operatorname{Gal}(H^{\ast }/K^{\ast })\end{eqnarray}$$
the group isomorphism coming from class field theory.
Let
![]() $\unicode[STIX]{x1D6F7}^{\ast }$
denote the CM type attached to the reflex of
$\unicode[STIX]{x1D6F7}^{\ast }$
denote the CM type attached to the reflex of
![]() $(K,\unicode[STIX]{x1D6F7})$
. The reflex norm
$(K,\unicode[STIX]{x1D6F7})$
. The reflex norm
 $\text{N}_{\unicode[STIX]{x1D6F7}}:(K^{\ast })^{\times }\rightarrow K^{\times }$
attached to
$\text{N}_{\unicode[STIX]{x1D6F7}}:(K^{\ast })^{\times }\rightarrow K^{\times }$
attached to
![]() $(K,\unicode[STIX]{x1D6F7})$
is
$(K,\unicode[STIX]{x1D6F7})$
is
 $$\begin{eqnarray}\text{N}_{\unicode[STIX]{x1D6F7}}(a)=\mathop{\prod }_{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}^{\ast }}\unicode[STIX]{x1D711}(a);\end{eqnarray}$$
$$\begin{eqnarray}\text{N}_{\unicode[STIX]{x1D6F7}}(a)=\mathop{\prod }_{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}^{\ast }}\unicode[STIX]{x1D711}(a);\end{eqnarray}$$
cf. [Reference ShimuraShi97, § 8.3] for standard properties including the fact that the target is indeed
![]() $K^{\times }$
. If
$K^{\times }$
. If
![]() $\mathfrak{B}^{\ast }$
is a fractional ideal of
$\mathfrak{B}^{\ast }$
is a fractional ideal of
![]() $K^{\ast }$
, then
$K^{\ast }$
, then
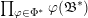 $\prod _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}^{\ast }}\unicode[STIX]{x1D711}(\mathfrak{B}^{\ast })$
is a fractional ideal of
$\prod _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}^{\ast }}\unicode[STIX]{x1D711}(\mathfrak{B}^{\ast })$
is a fractional ideal of
![]() $K$
, which we denote with
$K$
, which we denote with
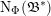 $\text{N}_{\unicode[STIX]{x1D6F7}}(\mathfrak{B}^{\ast })$
. Observe that
$\text{N}_{\unicode[STIX]{x1D6F7}}(\mathfrak{B}^{\ast })$
. Observe that
![]() $\text{N}_{\unicode[STIX]{x1D6F7}}$
also induces a homomorphism of class groups
$\text{N}_{\unicode[STIX]{x1D6F7}}$
also induces a homomorphism of class groups
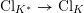 $\operatorname{Cl}_{K^{\ast }}\rightarrow \operatorname{Cl}_{K}$
, which we also denote by
$\operatorname{Cl}_{K^{\ast }}\rightarrow \operatorname{Cl}_{K}$
, which we also denote by
![]() $\text{N}_{\unicode[STIX]{x1D6F7}}$
.
$\text{N}_{\unicode[STIX]{x1D6F7}}$
.
Theorem 3.9 (Shimura).
Let
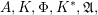 $A,K,\unicode[STIX]{x1D6F7},K^{\ast },\mathfrak{A},$
and
$A,K,\unicode[STIX]{x1D6F7},K^{\ast },\mathfrak{A},$
and
![]() $t$
be as above and as in the last section.
$t$
be as above and as in the last section.
Suppose that
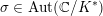 $\unicode[STIX]{x1D70E}\in \operatorname{Aut}(\mathbb{C}/K^{\ast })$
; we consider
$\unicode[STIX]{x1D70E}\in \operatorname{Aut}(\mathbb{C}/K^{\ast })$
; we consider
![]() $A^{\unicode[STIX]{x1D70E}}$
as an abelian variety over
$A^{\unicode[STIX]{x1D70E}}$
as an abelian variety over
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $\mathfrak{B}^{\ast }$
be a fractional ideal of
$\mathfrak{B}^{\ast }$
be a fractional ideal of
![]() $K^{\ast }$
with
$K^{\ast }$
with
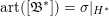 $\operatorname{art}([\mathfrak{B}^{\ast }])=\unicode[STIX]{x1D70E}|_{H^{\ast }}$
. Then
$\operatorname{art}([\mathfrak{B}^{\ast }])=\unicode[STIX]{x1D70E}|_{H^{\ast }}$
. Then
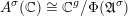 $A^{\unicode[STIX]{x1D70E}}(\mathbb{C})\cong \mathbb{C}^{g}/\unicode[STIX]{x1D6F7}(\mathfrak{A}^{\unicode[STIX]{x1D70E}})$
, where
$A^{\unicode[STIX]{x1D70E}}(\mathbb{C})\cong \mathbb{C}^{g}/\unicode[STIX]{x1D6F7}(\mathfrak{A}^{\unicode[STIX]{x1D70E}})$
, where
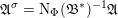 $\mathfrak{A}^{\unicode[STIX]{x1D70E}}=\text{N}_{\unicode[STIX]{x1D6F7}}(\mathfrak{B}^{\ast })^{-1}\mathfrak{A}$
and
$\mathfrak{A}^{\unicode[STIX]{x1D70E}}=\text{N}_{\unicode[STIX]{x1D6F7}}(\mathfrak{B}^{\ast })^{-1}\mathfrak{A}$
and
![]() $t$
transforms to
$t$
transforms to
![]() $\text{N}(\mathfrak{B}^{\ast })t$
.
$\text{N}(\mathfrak{B}^{\ast })t$
.
In particular, the set of period lattices in the
 $\operatorname{Aut}(\mathbb{C}/K^{\ast })$
-orbit are represented by
$\operatorname{Aut}(\mathbb{C}/K^{\ast })$
-orbit are represented by
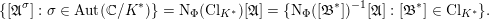 $$\begin{eqnarray}\{[\mathfrak{A}^{\unicode[STIX]{x1D70E}}]:\unicode[STIX]{x1D70E}\in \operatorname{Aut}(\mathbb{C}/K^{\ast })\}=\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})[\mathfrak{A}]=\{\text{N}_{\unicode[STIX]{x1D6F7}}([\mathfrak{B}^{\ast }])^{-1}[\mathfrak{A}]:[\mathfrak{B}^{\ast }]\in \operatorname{Cl}_{K^{\ast }}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{[\mathfrak{A}^{\unicode[STIX]{x1D70E}}]:\unicode[STIX]{x1D70E}\in \operatorname{Aut}(\mathbb{C}/K^{\ast })\}=\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})[\mathfrak{A}]=\{\text{N}_{\unicode[STIX]{x1D6F7}}([\mathfrak{B}^{\ast }])^{-1}[\mathfrak{A}]:[\mathfrak{B}^{\ast }]\in \operatorname{Cl}_{K^{\ast }}\}.\end{eqnarray}$$
Proof. The first statement follows from [Reference ShimuraShi97, Theorem 18.6 part (1)]. Observe that
![]() $\mathfrak{A}$
is a fractional ideal, so the action by the finite idèles factors through the maximal compact subgroup. The second statement is a consequence of the fact that the Artin homomorphism is bijective.◻
$\mathfrak{A}$
is a fractional ideal, so the action by the finite idèles factors through the maximal compact subgroup. The second statement is a consequence of the fact that the Artin homomorphism is bijective.◻
If
![]() $G$
is an abelian group, then
$G$
is an abelian group, then
![]() $G[2]$
denotes its subgroup of elements that have order dividing
$G[2]$
denotes its subgroup of elements that have order dividing
![]() $2$
.
$2$
.
We now specialise to the case we are interested in. The following lemma is well known.
Lemma 3.10. Suppose that
![]() $K/\mathbb{Q}$
is cyclic of degree
$K/\mathbb{Q}$
is cyclic of degree
![]() $4$
. Then
$4$
. Then
![]() $(K,\unicode[STIX]{x1D6F7})$
is primitive,
$(K,\unicode[STIX]{x1D6F7})$
is primitive,
![]() $A$
is a simple abelian variety,
$A$
is a simple abelian variety,
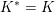 $K^{\ast }=K$
, and
$K^{\ast }=K$
, and
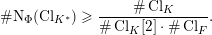 $$\begin{eqnarray}\#\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})\geqslant \frac{\#\operatorname{Cl}_{K}}{\#\operatorname{Cl}_{K}[2]\cdot \#\operatorname{Cl}_{F}}.\end{eqnarray}$$
$$\begin{eqnarray}\#\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})\geqslant \frac{\#\operatorname{Cl}_{K}}{\#\operatorname{Cl}_{K}[2]\cdot \#\operatorname{Cl}_{F}}.\end{eqnarray}$$
Proof. In this lemma we identify the embeddings in the CM type
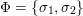 $\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}\}$
with automorphisms of
$\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}\}$
with automorphisms of
![]() $K$
. By hypothesis,
$K$
. By hypothesis,
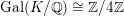 $\operatorname{Gal}(K/\mathbb{Q})\cong \mathbb{Z}/4\mathbb{Z}$
. As
$\operatorname{Gal}(K/\mathbb{Q})\cong \mathbb{Z}/4\mathbb{Z}$
. As
![]() $\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{1}^{-1}$
is neither the identity nor complex conjugation, it must generate the Galois group. So,
$\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{1}^{-1}$
is neither the identity nor complex conjugation, it must generate the Galois group. So,
![]() $(K,\unicode[STIX]{x1D6F7})$
is primitive by [Reference ShimuraShi97, Proposition 26, ch. II]. Therefore,
$(K,\unicode[STIX]{x1D6F7})$
is primitive by [Reference ShimuraShi97, Proposition 26, ch. II]. Therefore,
![]() $A$
is simple.
$A$
is simple.
Further down in [Reference ShimuraShi97, Example 8.4], Shimura remarks that
 $K^{\ast }=K$
and
$K^{\ast }=K$
and
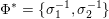 $\unicode[STIX]{x1D6F7}^{\ast }=\{\unicode[STIX]{x1D70E}_{1}^{-1},\unicode[STIX]{x1D70E}_{2}^{-1}\}$
under the assumption that
$\unicode[STIX]{x1D6F7}^{\ast }=\{\unicode[STIX]{x1D70E}_{1}^{-1},\unicode[STIX]{x1D70E}_{2}^{-1}\}$
under the assumption that
![]() $(K,\unicode[STIX]{x1D6F7})$
is primitive and
$(K,\unicode[STIX]{x1D6F7})$
is primitive and
![]() $K/\mathbb{Q}$
is abelian.
$K/\mathbb{Q}$
is abelian.
Observe that
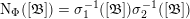 $\text{N}_{\unicode[STIX]{x1D6F7}}([\mathfrak{B}])=\unicode[STIX]{x1D70E}_{1}^{-1}([\mathfrak{B}])\unicode[STIX]{x1D70E}_{2}^{-1}([\mathfrak{B}])$
if
$\text{N}_{\unicode[STIX]{x1D6F7}}([\mathfrak{B}])=\unicode[STIX]{x1D70E}_{1}^{-1}([\mathfrak{B}])\unicode[STIX]{x1D70E}_{2}^{-1}([\mathfrak{B}])$
if
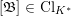 $[\mathfrak{B}]\in \operatorname{Cl}_{K^{\ast }}$
and recall that
$[\mathfrak{B}]\in \operatorname{Cl}_{K^{\ast }}$
and recall that
![]() $\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{1}^{-1}$
generates
$\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{1}^{-1}$
generates
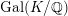 $\operatorname{Gal}(K/\mathbb{Q})$
. To prove the final claim, it suffices to consider the case where
$\operatorname{Gal}(K/\mathbb{Q})$
. To prove the final claim, it suffices to consider the case where
![]() $\unicode[STIX]{x1D70E}_{1}$
is the identity and
$\unicode[STIX]{x1D70E}_{1}$
is the identity and
![]() $\unicode[STIX]{x1D70E}_{2}$
generates the Galois group. We abbreviate
$\unicode[STIX]{x1D70E}_{2}$
generates the Galois group. We abbreviate
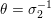 $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70E}_{2}^{-1}$
. Let
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70E}_{2}^{-1}$
. Let
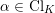 $\unicode[STIX]{x1D6FC}\in \operatorname{Cl}_{K}$
be arbitrary. As
$\unicode[STIX]{x1D6FC}\in \operatorname{Cl}_{K}$
be arbitrary. As
![]() $K$
is a CM field with totally real subfield
$K$
is a CM field with totally real subfield
![]() $F$
, the class
$F$
, the class
![]() $\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}$
is represented by an ideal generated by an ideal of
$\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}$
is represented by an ideal generated by an ideal of
![]() ${\mathcal{O}}_{F}$
. Thus, there are at most
${\mathcal{O}}_{F}$
. Thus, there are at most
![]() $\#\operatorname{Cl}_{F}$
different possibilities for the class
$\#\operatorname{Cl}_{F}$
different possibilities for the class
![]() $\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}$
. On the other hand,
$\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}$
. On the other hand,
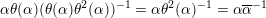 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D703}^{2}(\unicode[STIX]{x1D6FC}))^{-1}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{2}(\unicode[STIX]{x1D6FC})^{-1}=\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}^{-1}$
lies in
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D703}^{2}(\unicode[STIX]{x1D6FC}))^{-1}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D703}^{2}(\unicode[STIX]{x1D6FC})^{-1}=\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}^{-1}$
lies in
 $\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})$
. So,
$\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})$
. So,
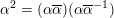 $\unicode[STIX]{x1D6FC}^{2}=(\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}})(\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}^{-1})$
lies in at most
$\unicode[STIX]{x1D6FC}^{2}=(\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}})(\unicode[STIX]{x1D6FC}\overline{\unicode[STIX]{x1D6FC}}^{-1})$
lies in at most
![]() $\#\operatorname{Cl}_{F}$
translates of
$\#\operatorname{Cl}_{F}$
translates of
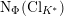 $\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})$
. The bound (3.22) follows because
$\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})$
. The bound (3.22) follows because
![]() $\operatorname{Cl}_{K}$
contains precisely
$\operatorname{Cl}_{K}$
contains precisely
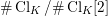 $\#\operatorname{Cl}_{K}/\#\operatorname{Cl}_{K}[2]$
squares.◻
$\#\operatorname{Cl}_{K}/\#\operatorname{Cl}_{K}[2]$
squares.◻
Lemma 3.11. Let
![]() $\unicode[STIX]{x1D716}>0$
. There exists a constant
$\unicode[STIX]{x1D716}>0$
. There exists a constant
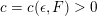 $c=c(\unicode[STIX]{x1D716},F)>0$
depending only on
$c=c(\unicode[STIX]{x1D716},F)>0$
depending only on
![]() $\unicode[STIX]{x1D716}$
and the totally real field
$\unicode[STIX]{x1D716}$
and the totally real field
![]() $F$
with the following property. Suppose that
$F$
with the following property. Suppose that
![]() $K/\mathbb{Q}$
is cyclic of degree
$K/\mathbb{Q}$
is cyclic of degree
![]() $4$
; then
$4$
; then
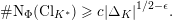 $$\begin{eqnarray}\#\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})\geqslant c|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D716}}.\end{eqnarray}$$
$$\begin{eqnarray}\#\text{N}_{\unicode[STIX]{x1D6F7}}(\operatorname{Cl}_{K^{\ast }})\geqslant c|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D716}}.\end{eqnarray}$$
Proof. Zhang’s proposition [Reference ZhangZha05, Proposition 6.3(2)] implies that
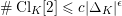 $\#\operatorname{Cl}_{K}[2]\leqslant c|\unicode[STIX]{x1D6E5}_{K}|^{\unicode[STIX]{x1D716}}$
, where
$\#\operatorname{Cl}_{K}[2]\leqslant c|\unicode[STIX]{x1D6E5}_{K}|^{\unicode[STIX]{x1D716}}$
, where
![]() $c$
depends only on
$c$
depends only on
![]() $\unicode[STIX]{x1D716}>0$
.
$\unicode[STIX]{x1D716}>0$
.
Next we bound the class number of
![]() $K$
from below using the Brauer–Siegel theorem. For any imaginary quadratic extension
$K$
from below using the Brauer–Siegel theorem. For any imaginary quadratic extension
![]() $K$
of
$K$
of
![]() $F$
that is Galois over
$F$
that is Galois over
![]() $\mathbb{Q}$
, we have
$\mathbb{Q}$
, we have
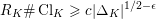 $R_{K}\#\operatorname{Cl}_{K}\geqslant c|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D716}}$
with a possibly smaller constant
$R_{K}\#\operatorname{Cl}_{K}\geqslant c|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D716}}$
with a possibly smaller constant
![]() $c>0$
; here
$c>0$
; here
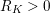 $R_{K}>0$
denotes the regulator of
$R_{K}>0$
denotes the regulator of
![]() $K$
. By [Reference WashingtonWas82, Proposition 4.16],
$K$
. By [Reference WashingtonWas82, Proposition 4.16],
![]() $R_{K}$
is at most twice the regulator of
$R_{K}$
is at most twice the regulator of
![]() $F$
. As we allow
$F$
. As we allow
![]() $c$
to depend on
$c$
to depend on
![]() $F$
, our lemma follows from Lemma 3.10 on decreasing this constant
$F$
, our lemma follows from Lemma 3.10 on decreasing this constant
![]() $c$
if necessary.◻
$c$
if necessary.◻
4 Faltings height
We begin by recalling the definition of the Faltings height of an abelian variety. Then we apply a known case of Colmez’s conjecture to compute the Faltings height of certain CM abelian varieties in terms of the
![]() $L$
-functions. Finally, we will give an alternative formula for the Faltings height for an abelian variety that has good reduction everywhere and that is the jacobian of a hyperelliptic curve in genus
$L$
-functions. Finally, we will give an alternative formula for the Faltings height for an abelian variety that has good reduction everywhere and that is the jacobian of a hyperelliptic curve in genus
![]() $2$
.
$2$
.
4.1 General abelian varieties
Let
![]() $A$
be an abelian variety of dimension
$A$
be an abelian variety of dimension
![]() $g\geqslant 1$
defined over a number field
$g\geqslant 1$
defined over a number field
![]() $k$
. After extending
$k$
. After extending
![]() $k$
, we may suppose that
$k$
, we may suppose that
![]() $A$
has semi-stable reduction at all finite places of
$A$
has semi-stable reduction at all finite places of
![]() $k$
.
$k$
.
Put
 $S=\operatorname{Spec}{\mathcal{O}}_{k}$
, where
$S=\operatorname{Spec}{\mathcal{O}}_{k}$
, where
![]() ${\mathcal{O}}_{k}$
is the ring of integers of
${\mathcal{O}}_{k}$
is the ring of integers of
![]() $k$
. Let
$k$
. Let
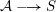 ${\mathcal{A}}\longrightarrow S$
be the Néron model of
${\mathcal{A}}\longrightarrow S$
be the Néron model of
![]() $A$
. We shall denote by
$A$
. We shall denote by
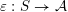 $\unicode[STIX]{x1D700}:S\rightarrow {\mathcal{A}}$
the zero section.
$\unicode[STIX]{x1D700}:S\rightarrow {\mathcal{A}}$
the zero section.
We write
![]() $\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}$
for the
$\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}$
for the
![]() $g$
th exterior power of the sheaf of relative differentials of the smooth morphism
$g$
th exterior power of the sheaf of relative differentials of the smooth morphism
![]() ${\mathcal{A}}\rightarrow S$
. This is an invertible sheaf on
${\mathcal{A}}\rightarrow S$
. This is an invertible sheaf on
![]() ${\mathcal{A}}$
and its pull-back
${\mathcal{A}}$
and its pull-back
![]() $\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}$
is an invertible sheaf on
$\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}$
is an invertible sheaf on
 $\operatorname{Spec}{\mathcal{O}}_{k}$
.
$\operatorname{Spec}{\mathcal{O}}_{k}$
.
For any embedding
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $k$
in
$k$
in
![]() $\mathbb{C}$
, the base change
$\mathbb{C}$
, the base change
 ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}={\mathcal{A}}\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
is an abelian variety over
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}={\mathcal{A}}\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
is an abelian variety over
![]() $\operatorname{Spec}\mathbb{C}$
. There is a canonical isomorphism
$\operatorname{Spec}\mathbb{C}$
. There is a canonical isomorphism
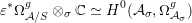 $$\begin{eqnarray}\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}\simeq H^{0}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D6FA}_{{\mathcal{A}}_{\unicode[STIX]{x1D70E}}}^{g})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}\simeq H^{0}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D6FA}_{{\mathcal{A}}_{\unicode[STIX]{x1D70E}}}^{g})\end{eqnarray}$$
as vector spaces over
![]() $\mathbb{C}$
. So, we can equip the first vector space with the
$\mathbb{C}$
. So, we can equip the first vector space with the
![]() $L^{2}$
-metric
$L^{2}$
-metric
![]() $\Vert \cdot \Vert _{\unicode[STIX]{x1D70E}}$
defined by
$\Vert \cdot \Vert _{\unicode[STIX]{x1D70E}}$
defined by
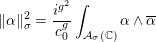 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FC}\Vert _{\unicode[STIX]{x1D70E}}^{2}=\frac{i^{g^{2}}}{c_{0}^{g}}\int _{{\mathcal{A}}_{\unicode[STIX]{x1D70E}}(\mathbb{C})}\unicode[STIX]{x1D6FC}\wedge \overline{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FC}\Vert _{\unicode[STIX]{x1D70E}}^{2}=\frac{i^{g^{2}}}{c_{0}^{g}}\int _{{\mathcal{A}}_{\unicode[STIX]{x1D70E}}(\mathbb{C})}\unicode[STIX]{x1D6FC}\wedge \overline{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
for a normalising universal constant
![]() $c_{0}>0$
.
$c_{0}>0$
.
The rank-one
![]() ${\mathcal{O}}_{k}$
-module
${\mathcal{O}}_{k}$
-module
![]() $\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}$
, together with the hermitian norms
$\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}$
, together with the hermitian norms
![]() $\Vert \cdot \Vert _{\unicode[STIX]{x1D70E}}$
at infinity, defines a hermitian line bundle over
$\Vert \cdot \Vert _{\unicode[STIX]{x1D70E}}$
at infinity, defines a hermitian line bundle over
![]() $S$
.
$S$
.
Recall that for any hermitian line bundle
![]() $\overline{\unicode[STIX]{x1D714}}$
over
$\overline{\unicode[STIX]{x1D714}}$
over
![]() $S$
, the Arakelov degree of
$S$
, the Arakelov degree of
![]() $\overline{\unicode[STIX]{x1D714}}$
is defined as
$\overline{\unicode[STIX]{x1D714}}$
is defined as
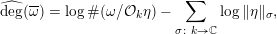 $$\begin{eqnarray}\widehat{\operatorname{deg}}(\overline{\unicode[STIX]{x1D714}})=\log \#(\unicode[STIX]{x1D714}/{\mathcal{O}}_{k}\unicode[STIX]{x1D702})-\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log \Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\operatorname{deg}}(\overline{\unicode[STIX]{x1D714}})=\log \#(\unicode[STIX]{x1D714}/{\mathcal{O}}_{k}\unicode[STIX]{x1D702})-\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log \Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D702}$
is any non-zero section of
$\unicode[STIX]{x1D702}$
is any non-zero section of
![]() $\overline{\unicode[STIX]{x1D714}}$
. The Arakelov degree is independent of the choice of
$\overline{\unicode[STIX]{x1D714}}$
. The Arakelov degree is independent of the choice of
![]() $\unicode[STIX]{x1D702}$
by the product formula.
$\unicode[STIX]{x1D702}$
by the product formula.
We now give the definition of the Faltings height, see [Reference FaltingsFal83, p. 354], which is sometimes also called the differential height.
Definition 4.1. The stable Faltings height of
![]() $A$
is
$A$
is
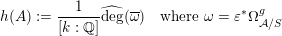 $$\begin{eqnarray}h(A):=\frac{1}{[k:\mathbb{Q}]}\widehat{\operatorname{deg}}(\overline{\unicode[STIX]{x1D714}})\quad \text{where}~\unicode[STIX]{x1D714}=\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}\end{eqnarray}$$
$$\begin{eqnarray}h(A):=\frac{1}{[k:\mathbb{Q}]}\widehat{\operatorname{deg}}(\overline{\unicode[STIX]{x1D714}})\quad \text{where}~\unicode[STIX]{x1D714}=\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{g}\end{eqnarray}$$
becomes a hermitian line bundle
![]() $\overline{\unicode[STIX]{x1D714}}$
when equipped with the metrics mentioned above and
$\overline{\unicode[STIX]{x1D714}}$
when equipped with the metrics mentioned above and
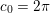 $c_{0}=2\unicode[STIX]{x1D70B}$
.
$c_{0}=2\unicode[STIX]{x1D70B}$
.
To see that it satisfies a Northcott theorem, see for instance Faltings’s Satz 1 [Reference FaltingsFal83, pp. 356 and 357] or the theorem of Bost–David made available in [Reference PazukiPaz12a].
For a discussion on some interesting values for
![]() $c_{0}$
, see [Reference PazukiPaz12b]. Faltings uses
$c_{0}$
, see [Reference PazukiPaz12b]. Faltings uses
![]() $c_{0}=2$
. In this paper, the choice will be
$c_{0}=2$
. In this paper, the choice will be
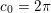 $c_{0}=2\unicode[STIX]{x1D70B}$
, following Deligne and Bost. This choice removes the
$c_{0}=2\unicode[STIX]{x1D70B}$
, following Deligne and Bost. This choice removes the
![]() $\unicode[STIX]{x1D70B}$
in the expression derived from the Chowla–Selberg formula in the CM case. The choice
$\unicode[STIX]{x1D70B}$
in the expression derived from the Chowla–Selberg formula in the CM case. The choice
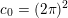 $c_{0}=(2\unicode[STIX]{x1D70B})^{2}$
leads to a non-negative height
$c_{0}=(2\unicode[STIX]{x1D70B})^{2}$
leads to a non-negative height
![]() $h_{F^{+}}(A)$
due to a result of Bost. In any case, one has the easy relations
$h_{F^{+}}(A)$
due to a result of Bost. In any case, one has the easy relations
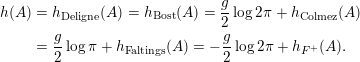 $$\begin{eqnarray}\displaystyle h(A) & = & \displaystyle h_{\text{Deligne}}(A)=h_{\text{Bost}}(A)=\frac{g}{2}\log 2\unicode[STIX]{x1D70B}+h_{\text{Colmez}}(A)\nonumber\\ \displaystyle & = & \displaystyle \frac{g}{2}\log \unicode[STIX]{x1D70B}+h_{\text{Faltings}}(A)=-\frac{g}{2}\log 2\unicode[STIX]{x1D70B}+h_{F^{+}}(A).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(A) & = & \displaystyle h_{\text{Deligne}}(A)=h_{\text{Bost}}(A)=\frac{g}{2}\log 2\unicode[STIX]{x1D70B}+h_{\text{Colmez}}(A)\nonumber\\ \displaystyle & = & \displaystyle \frac{g}{2}\log \unicode[STIX]{x1D70B}+h_{\text{Faltings}}(A)=-\frac{g}{2}\log 2\unicode[STIX]{x1D70B}+h_{F^{+}}(A).\nonumber\end{eqnarray}$$
4.2 Colmez’s conjecture
Colmez’s conjecture [Reference ColmezCol93] relates the Faltings height of an abelian variety with complex multiplication and the logarithmic derivative of certain Artin
![]() $L$
-functions at
$L$
-functions at
![]() $s=0$
. In the same paper Colmez proved his conjecture for CM fields that are abelian extensions of
$s=0$
. In the same paper Colmez proved his conjecture for CM fields that are abelian extensions of
![]() $\mathbb{Q}$
and satisfy a ramification condition above
$\mathbb{Q}$
and satisfy a ramification condition above
![]() $2$
. Obus [Reference ObusObu13] then generalised the result by dropping the ramification restriction. Yang [Reference YangYan10] verified the conjecture for certain abelian surfaces where the CM field is not Galois over
$2$
. Obus [Reference ObusObu13] then generalised the result by dropping the ramification restriction. Yang [Reference YangYan10] verified the conjecture for certain abelian surfaces where the CM field is not Galois over
![]() $\mathbb{Q}$
. Our work will rely only on the case when the CM field is a cyclic, quartic extension of the rationals.
$\mathbb{Q}$
. Our work will rely only on the case when the CM field is a cyclic, quartic extension of the rationals.
Let us briefly recall Colmez’s conjecture when the CM field
![]() $K$
is an abelian extension of
$K$
is an abelian extension of
![]() $\mathbb{Q}$
of degree
$\mathbb{Q}$
of degree
![]() $2g$
.
$2g$
.
Let
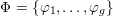 $\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}\}$
be a CM type of
$\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{g}\}$
be a CM type of
![]() $K$
. If
$K$
. If
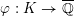 $\unicode[STIX]{x1D711}:K\rightarrow \overline{\mathbb{Q}}$
is an embedding, Colmez sets
$\unicode[STIX]{x1D711}:K\rightarrow \overline{\mathbb{Q}}$
is an embedding, Colmez sets
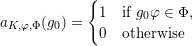 $$\begin{eqnarray}a_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(g_{0})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }g_{0}\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7},\\ 0\quad & \text{otherwise}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}a_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(g_{0})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }g_{0}\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7},\\ 0\quad & \text{otherwise}\end{array}\right.\end{eqnarray}$$
for all
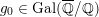 $g_{0}\in \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
and
$g_{0}\in \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
and
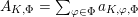 $A_{K,\unicode[STIX]{x1D6F7}}=\sum _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}}a_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}$
. Then
$A_{K,\unicode[STIX]{x1D6F7}}=\sum _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}}a_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}$
. Then
![]() $A_{K,\unicode[STIX]{x1D6F7}}$
factors through
$A_{K,\unicode[STIX]{x1D6F7}}$
factors through
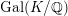 $\operatorname{Gal}(K/\mathbb{Q})$
and by abuse of notation we sometimes consider
$\operatorname{Gal}(K/\mathbb{Q})$
and by abuse of notation we sometimes consider
![]() $A_{K,\unicode[STIX]{x1D6F7}}$
as a function on this Galois group. It is a
$A_{K,\unicode[STIX]{x1D6F7}}$
as a function on this Galois group. It is a
![]() $\mathbb{C}$
-linear combination of the irreducible characters of
$\mathbb{C}$
-linear combination of the irreducible characters of
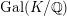 $\operatorname{Gal}(K/\mathbb{Q})$
. Moreover, the Artin
$\operatorname{Gal}(K/\mathbb{Q})$
. Moreover, the Artin
![]() $L$
-series attached to any character that contributes to this sum is holomorphic and non-zero at
$L$
-series attached to any character that contributes to this sum is holomorphic and non-zero at
![]() $s=0$
. If
$s=0$
. If
![]() $\unicode[STIX]{x1D712}$
is any character of
$\unicode[STIX]{x1D712}$
is any character of
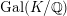 $\operatorname{Gal}(K/\mathbb{Q})$
, then
$\operatorname{Gal}(K/\mathbb{Q})$
, then
![]() $f_{\unicode[STIX]{x1D712}}$
denotes the conductor of
$f_{\unicode[STIX]{x1D712}}$
denotes the conductor of
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
In the following result we use the normalisation of the Faltings height used in § 4.1.
Theorem 4.2 (Colmez, Obus).
Let
![]() $A$
be an abelian variety defined over a number field that is a subfield of
$A$
be an abelian variety defined over a number field that is a subfield of
![]() $\mathbb{C}$
. We suppose that
$\mathbb{C}$
. We suppose that
![]() $A$
has complex multiplication by the ring of integers of a CM field
$A$
has complex multiplication by the ring of integers of a CM field
![]() $K$
of degree
$K$
of degree
![]() $2\dim A$
over
$2\dim A$
over
![]() $\mathbb{Q}$
. This data provides a CM type
$\mathbb{Q}$
. This data provides a CM type
![]() $\unicode[STIX]{x1D6F7}$
of
$\unicode[STIX]{x1D6F7}$
of
![]() $K$
. Suppose in addition that
$K$
. Suppose in addition that
![]() $K/\mathbb{Q}$
is an abelian extension. We decompose
$K/\mathbb{Q}$
is an abelian extension. We decompose
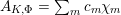 $A_{K,\unicode[STIX]{x1D6F7}}=\sum _{m}c_{m}\unicode[STIX]{x1D712}_{m}$
, where the
$A_{K,\unicode[STIX]{x1D6F7}}=\sum _{m}c_{m}\unicode[STIX]{x1D712}_{m}$
, where the
![]() $\unicode[STIX]{x1D712}_{m}$
denote the irreducible characters of
$\unicode[STIX]{x1D712}_{m}$
denote the irreducible characters of
 $\operatorname{Gal}(K/\mathbb{Q})$
. Then
$\operatorname{Gal}(K/\mathbb{Q})$
. Then
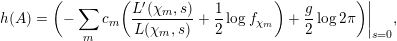 $$\begin{eqnarray}h(A)=\biggl(-\mathop{\sum }_{m}c_{m}\biggl(\frac{L^{\prime }(\unicode[STIX]{x1D712}_{m},s)}{L(\unicode[STIX]{x1D712}_{m},s)}+\frac{1}{2}\log f_{\unicode[STIX]{x1D712}_{m}}\biggr)+\frac{g}{2}\log 2\unicode[STIX]{x1D70B}\biggr)\biggr|_{s=0},\end{eqnarray}$$
$$\begin{eqnarray}h(A)=\biggl(-\mathop{\sum }_{m}c_{m}\biggl(\frac{L^{\prime }(\unicode[STIX]{x1D712}_{m},s)}{L(\unicode[STIX]{x1D712}_{m},s)}+\frac{1}{2}\log f_{\unicode[STIX]{x1D712}_{m}}\biggr)+\frac{g}{2}\log 2\unicode[STIX]{x1D70B}\biggr)\biggr|_{s=0},\end{eqnarray}$$
where the right-hand side is evaluated at
![]() $s=0$
.
$s=0$
.
Proof. We refer to Colmez [Reference ColmezCol93, Théorèmes 0.3(ii) and III.2.9], from which the result follows modulo a rational multiple of
![]() $\log 2$
. Subsequent work of Obus [Reference ObusObu13] removed this ambiguity.◻
$\log 2$
. Subsequent work of Obus [Reference ObusObu13] removed this ambiguity.◻
Let us consider what happens for an abelian surface when
![]() $K/\mathbb{Q}$
is cyclic.
$K/\mathbb{Q}$
is cyclic.
Proposition 4.3. Suppose that
![]() $K$
is a CM field with
$K$
is a CM field with
![]() $K/\mathbb{Q}$
cyclic of degree
$K/\mathbb{Q}$
cyclic of degree
![]() $4$
and let
$4$
and let
![]() $F$
be the real quadratic subfield of
$F$
be the real quadratic subfield of
![]() $K$
.
$K$
.
-
(i) Let
 $\unicode[STIX]{x1D6F7}$
be any CM type of
$\unicode[STIX]{x1D6F7}$
be any CM type of
 $K$
. If
$K$
. If
 $g_{0}\in \operatorname{Gal}(K/\mathbb{Q})$
, then
$g_{0}\in \operatorname{Gal}(K/\mathbb{Q})$
, then  $$\begin{eqnarray}A_{K,\unicode[STIX]{x1D6F7}}(g_{0})=\left\{\begin{array}{@{}ll@{}}2\quad & \text{if}~g_{0}=1,\\ 0\quad & \text{if}~g_{0}~\text{has order}~2,\\ 1\quad & \text{if}~g_{0}~\text{has order}~4.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A_{K,\unicode[STIX]{x1D6F7}}(g_{0})=\left\{\begin{array}{@{}ll@{}}2\quad & \text{if}~g_{0}=1,\\ 0\quad & \text{if}~g_{0}~\text{has order}~2,\\ 1\quad & \text{if}~g_{0}~\text{has order}~4.\end{array}\right.\end{eqnarray}$$
-
(ii) As a function on
 $\operatorname{Gal}(K/\mathbb{Q})$
, we can decompose
$\operatorname{Gal}(K/\mathbb{Q})$
, we can decompose
 $A_{K,\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D712}_{0}+\frac{1}{2}\unicode[STIX]{x1D712}$
, where
$A_{K,\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D712}_{0}+\frac{1}{2}\unicode[STIX]{x1D712}$
, where
 $\unicode[STIX]{x1D712}_{0}$
is the trivial character and
$\unicode[STIX]{x1D712}_{0}$
is the trivial character and
 $\unicode[STIX]{x1D712}$
is induced by the non-trivial character of
$\unicode[STIX]{x1D712}$
is induced by the non-trivial character of
 $\operatorname{Gal}(K/F)$
. Moreover, the conductor
$\operatorname{Gal}(K/F)$
. Moreover, the conductor
 $f_{\unicode[STIX]{x1D712}}$
of
$f_{\unicode[STIX]{x1D712}}$
of
 $\unicode[STIX]{x1D712}$
is
$\unicode[STIX]{x1D712}$
is
 $\unicode[STIX]{x1D6E5}_{K}/\unicode[STIX]{x1D6E5}_{F}$
.
$\unicode[STIX]{x1D6E5}_{K}/\unicode[STIX]{x1D6E5}_{F}$
. -
(iii) Let
 $A$
be a simple abelian surface with endomorphism ring
$A$
be a simple abelian surface with endomorphism ring
 ${\mathcal{O}}_{K}$
. Then where
${\mathcal{O}}_{K}$
. Then where $$\begin{eqnarray}h(A)=-\frac{1}{2}\frac{L^{\prime }(0)}{L(0)}-\frac{1}{4}\log \frac{\unicode[STIX]{x1D6E5}_{K}}{\unicode[STIX]{x1D6E5}_{F}}=\frac{1}{2}\frac{L^{\prime }(1)}{L(1)}+\frac{1}{4}\log \frac{\unicode[STIX]{x1D6E5}_{K}}{\unicode[STIX]{x1D6E5}_{F}}-\log (2\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D6FE}_{\mathbb{Q}},\end{eqnarray}$$
$$\begin{eqnarray}h(A)=-\frac{1}{2}\frac{L^{\prime }(0)}{L(0)}-\frac{1}{4}\log \frac{\unicode[STIX]{x1D6E5}_{K}}{\unicode[STIX]{x1D6E5}_{F}}=\frac{1}{2}\frac{L^{\prime }(1)}{L(1)}+\frac{1}{4}\log \frac{\unicode[STIX]{x1D6E5}_{K}}{\unicode[STIX]{x1D6E5}_{F}}-\log (2\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D6FE}_{\mathbb{Q}},\end{eqnarray}$$
 $L(s)=\unicode[STIX]{x1D701}_{K}(s)/\unicode[STIX]{x1D701}_{F}(s)$
is a quotient of the Dedekind
$L(s)=\unicode[STIX]{x1D701}_{K}(s)/\unicode[STIX]{x1D701}_{F}(s)$
is a quotient of the Dedekind
 $\unicode[STIX]{x1D701}$
-functions of
$\unicode[STIX]{x1D701}$
-functions of
 $K$
and
$K$
and
 $F$
, respectively, and
$F$
, respectively, and
 $\unicode[STIX]{x1D6FE}_{\mathbb{Q}}=0.577215\ldots$
denotes Euler’s constant.
$\unicode[STIX]{x1D6FE}_{\mathbb{Q}}=0.577215\ldots$
denotes Euler’s constant.
-
(iv) Let
 $A$
be as in (iii). Then where
$A$
be as in (iii). Then where $$\begin{eqnarray}h(A)\geqslant -c+\frac{\sqrt{5}}{20}\log \unicode[STIX]{x1D6E5}_{K},\end{eqnarray}$$
$$\begin{eqnarray}h(A)\geqslant -c+\frac{\sqrt{5}}{20}\log \unicode[STIX]{x1D6E5}_{K},\end{eqnarray}$$
 $c$
is a constant that depends only on
$c$
is a constant that depends only on
 $F$
.
$F$
.
Proof. Let us write
 $\operatorname{Gal}(K/\mathbb{Q})=\{1,h,h^{2},h^{3}\}$
. Then
$\operatorname{Gal}(K/\mathbb{Q})=\{1,h,h^{2},h^{3}\}$
. Then
![]() $h$
has order
$h$
has order
![]() $4$
and
$4$
and
![]() $h^{2}$
is complex conjugation on
$h^{2}$
is complex conjugation on
![]() $K$
. By definition, we have
$K$
. By definition, we have
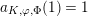 $a_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(1)=1$
for all
$a_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(1)=1$
for all
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}$
. So,
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}$
. So,
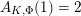 $A_{K,\unicode[STIX]{x1D6F7}}(1)=2$
. On the other hand, no two elements of
$A_{K,\unicode[STIX]{x1D6F7}}(1)=2$
. On the other hand, no two elements of
![]() $\unicode[STIX]{x1D6F7}$
are equal modulo complex conjugation. So,
$\unicode[STIX]{x1D6F7}$
are equal modulo complex conjugation. So,
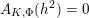 $A_{K,\unicode[STIX]{x1D6F7}}(h^{2})=0$
. Finally,
$A_{K,\unicode[STIX]{x1D6F7}}(h^{2})=0$
. Finally,
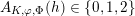 $A_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(h)\in \{0,1,2\}$
. If
$A_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(h)\in \{0,1,2\}$
. If
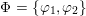 $\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2}\}$
, then simultaneous equalities
$\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2}\}$
, then simultaneous equalities
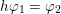 $h\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{2}$
and
$h\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{2}$
and
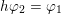 $h\unicode[STIX]{x1D711}_{2}=\unicode[STIX]{x1D711}_{1}$
are impossible. This rules out
$h\unicode[STIX]{x1D711}_{2}=\unicode[STIX]{x1D711}_{1}$
are impossible. This rules out
![]() $2$
. We can also rule out
$2$
. We can also rule out
![]() $0$
since
$0$
since
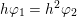 $h\unicode[STIX]{x1D711}_{1}=h^{2}\unicode[STIX]{x1D711}_{2}$
and
$h\unicode[STIX]{x1D711}_{1}=h^{2}\unicode[STIX]{x1D711}_{2}$
and
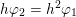 $h\unicode[STIX]{x1D711}_{2}=h^{2}\unicode[STIX]{x1D711}_{1}$
are impossible too. Thus,
$h\unicode[STIX]{x1D711}_{2}=h^{2}\unicode[STIX]{x1D711}_{1}$
are impossible too. Thus,
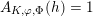 $A_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(h)=1$
and by symmetry we also find that
$A_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(h)=1$
and by symmetry we also find that
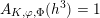 $A_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(h^{3})=1$
. This completes the proof of part (i).
$A_{K,\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}}(h^{3})=1$
. This completes the proof of part (i).
If
![]() $\unicode[STIX]{x1D712}$
is the character of
$\unicode[STIX]{x1D712}$
is the character of
 $\operatorname{Gal}(K/\mathbb{Q})$
induced by the non-trivial irreducible representation of
$\operatorname{Gal}(K/\mathbb{Q})$
induced by the non-trivial irreducible representation of
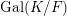 $\operatorname{Gal}(K/F)$
, then
$\operatorname{Gal}(K/F)$
, then
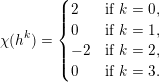 $$\begin{eqnarray}\unicode[STIX]{x1D712}(h^{k})=\left\{\begin{array}{@{}ll@{}}2\quad & \text{if}~k=0,\\ 0\quad & \text{if}~k=1,\\ -2\quad & \text{if}~k=2,\\ 0\quad & \text{if}~k=3.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(h^{k})=\left\{\begin{array}{@{}ll@{}}2\quad & \text{if}~k=0,\\ 0\quad & \text{if}~k=1,\\ -2\quad & \text{if}~k=2,\\ 0\quad & \text{if}~k=3.\end{array}\right.\end{eqnarray}$$
We observe that
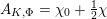 $A_{K,\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D712}_{0}+\frac{1}{2}\unicode[STIX]{x1D712}$
and this yields the first part of (ii).
$A_{K,\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D712}_{0}+\frac{1}{2}\unicode[STIX]{x1D712}$
and this yields the first part of (ii).
The conductor
![]() $f_{\unicode[STIX]{x1D712}}$
equals
$f_{\unicode[STIX]{x1D712}}$
equals
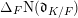 $\unicode[STIX]{x1D6E5}_{F}\text{N}(\mathfrak{d}_{K/F})$
by [Reference NeukirchNeu99, Proposition VII.11.7(iii)], where
$\unicode[STIX]{x1D6E5}_{F}\text{N}(\mathfrak{d}_{K/F})$
by [Reference NeukirchNeu99, Proposition VII.11.7(iii)], where
![]() $\mathfrak{d}_{K/F}$
is the relative discriminant of
$\mathfrak{d}_{K/F}$
is the relative discriminant of
![]() $K/F$
. The final statement of part (ii) follows as
$K/F$
. The final statement of part (ii) follows as
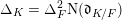 $\unicode[STIX]{x1D6E5}_{K}=\unicode[STIX]{x1D6E5}_{F}^{2}\text{N}(\mathfrak{d}_{K/F})$
.
$\unicode[STIX]{x1D6E5}_{K}=\unicode[STIX]{x1D6E5}_{F}^{2}\text{N}(\mathfrak{d}_{K/F})$
.
To prove (iii), we first remark that
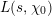 $L(s,\unicode[STIX]{x1D712}_{0})$
is the Riemann
$L(s,\unicode[STIX]{x1D712}_{0})$
is the Riemann
![]() $\unicode[STIX]{x1D701}$
-function and that
$\unicode[STIX]{x1D701}$
-function and that
![]() $\unicode[STIX]{x1D701}_{K}(s)$
factors as
$\unicode[STIX]{x1D701}_{K}(s)$
factors as
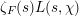 $\unicode[STIX]{x1D701}_{F}(s)L(s,\unicode[STIX]{x1D712})$
with
$\unicode[STIX]{x1D701}_{F}(s)L(s,\unicode[STIX]{x1D712})$
with
![]() $L(\cdot ,\unicode[STIX]{x1D712})$
the Artin
$L(\cdot ,\unicode[STIX]{x1D712})$
the Artin
![]() $L$
-function attached to the character
$L$
-function attached to the character
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
The first equality in (iii) now follows from Theorem 4.2 applied to (ii) and since
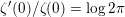 $\unicode[STIX]{x1D701}^{\prime }(0)/\unicode[STIX]{x1D701}(0)=\log 2\unicode[STIX]{x1D70B}$
. The second equality follows from the functional equation of the Dedekind
$\unicode[STIX]{x1D701}^{\prime }(0)/\unicode[STIX]{x1D701}(0)=\log 2\unicode[STIX]{x1D70B}$
. The second equality follows from the functional equation of the Dedekind
![]() $\unicode[STIX]{x1D701}$
-function.
$\unicode[STIX]{x1D701}$
-function.
If
![]() $M$
is any number field, then
$M$
is any number field, then
![]() $\unicode[STIX]{x1D6FE}_{M}$
denotes the constant term in the Taylor expansion around
$\unicode[STIX]{x1D6FE}_{M}$
denotes the constant term in the Taylor expansion around
![]() $s=1$
of the logarithmic derivative of the Dedekind
$s=1$
of the logarithmic derivative of the Dedekind
![]() $\unicode[STIX]{x1D701}$
-function of
$\unicode[STIX]{x1D701}$
-function of
![]() $M$
. Then
$M$
. Then
![]() $\unicode[STIX]{x1D6FE}_{M}$
is called the Euler–Kronecker constant of
$\unicode[STIX]{x1D6FE}_{M}$
is called the Euler–Kronecker constant of
![]() $M$
and generalises Euler’s constant
$M$
and generalises Euler’s constant
![]() $\unicode[STIX]{x1D6FE}_{\mathbb{Q}}$
to number fields. Badzyan’s theorem [Reference BadzyanBad10, Theorem 1] yields the lower bound
$\unicode[STIX]{x1D6FE}_{\mathbb{Q}}$
to number fields. Badzyan’s theorem [Reference BadzyanBad10, Theorem 1] yields the lower bound
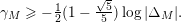 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{M}\geqslant -{\textstyle \frac{1}{2}}(1-{\textstyle \frac{\sqrt{5}}{5}})\log |\unicode[STIX]{x1D6E5}_{M}|.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{M}\geqslant -{\textstyle \frac{1}{2}}(1-{\textstyle \frac{\sqrt{5}}{5}})\log |\unicode[STIX]{x1D6E5}_{M}|.\end{eqnarray}$$
We have
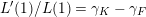 $L^{\prime }(1)/L(1)=\unicode[STIX]{x1D6FE}_{K}-\unicode[STIX]{x1D6FE}_{F}$
and so part (iv) follows from Badzyan’s bound together with part (iii).◻
$L^{\prime }(1)/L(1)=\unicode[STIX]{x1D6FE}_{K}-\unicode[STIX]{x1D6FE}_{F}$
and so part (iv) follows from Badzyan’s bound together with part (iii).◻
Colmez [Reference ColmezCol98] also obtained a lower bound for the Faltings height related to (iv) above.
Part (i) together with Theorem 4.2 implies that the Faltings height does not depend on the CM type of
![]() $K$
. This was originally observed by Yang [Reference YangYan10] and is specific to degree
$K$
. This was originally observed by Yang [Reference YangYan10] and is specific to degree
![]() $4$
.
$4$
.
4.3 Models of curves of genus
 $2$
$2$
This section explains the choice of models used in the next section to give an explicit formula for the Faltings height of abelian surfaces. We will use Weierstrass models of degree 5 and of degree 6 for our curves of genus 2. To be able to choose models of degree 5 for a curve
![]() $C$
, one needs to have at least one rational Weierstrass point on
$C$
, one needs to have at least one rational Weierstrass point on
![]() $C$
, which can be obtained by passing to a finite field extension if needed. As plane models they are singular at infinity; one will recover the curve
$C$
, which can be obtained by passing to a finite field extension if needed. As plane models they are singular at infinity; one will recover the curve
![]() $C$
through desingularisation.
$C$
through desingularisation.
We work with hyperelliptic equations for a curve
![]() $C$
of genus
$C$
of genus
![]() $2$
defined over a field
$2$
defined over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
.
$0$
.
Suppose that
![]() $C(k)$
contains a Weierstrass point of
$C(k)$
contains a Weierstrass point of
![]() $C$
. By Lockhart [Reference LockhartLoc94, Proposition 1.2], there is a monic polynomial
$C$
. By Lockhart [Reference LockhartLoc94, Proposition 1.2], there is a monic polynomial
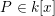 $P\in k[x]$
of degree
$P\in k[x]$
of degree
![]() $5$
such that an open, affine subset of
$5$
such that an open, affine subset of
![]() $C$
is isomorphic to the affine curve determined by the equation
$C$
is isomorphic to the affine curve determined by the equation
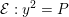 ${\mathcal{E}}:y^{2}=P$
. We call
${\mathcal{E}}:y^{2}=P$
. We call
![]() ${\mathcal{E}}$
a restricted Weierstrass equation for
${\mathcal{E}}$
a restricted Weierstrass equation for
![]() $C$
. Lockhart defined the discriminant of
$C$
. Lockhart defined the discriminant of
![]() ${\mathcal{E}}$
as
${\mathcal{E}}$
as
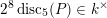 $2^{8}\operatorname{disc}_{5}(P)\in k^{\times }$
.
$2^{8}\operatorname{disc}_{5}(P)\in k^{\times }$
.
Say
![]() $k$
is a subfield of
$k$
is a subfield of
![]() $\mathbb{C}$
. As on [Reference LockhartLoc94, p. 740], we fix an ordering on the roots of
$\mathbb{C}$
. As on [Reference LockhartLoc94, p. 740], we fix an ordering on the roots of
![]() $P$
and attach a rank-
$P$
and attach a rank-
![]() $4$
discrete subgroup
$4$
discrete subgroup
![]() $\unicode[STIX]{x1D6EC}$
of
$\unicode[STIX]{x1D6EC}$
of
![]() $\mathbb{C}^{2}$
and a period matrix
$\mathbb{C}^{2}$
and a period matrix
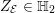 $Z_{{\mathcal{E}}}\in \mathbb{H}_{2}$
to
$Z_{{\mathcal{E}}}\in \mathbb{H}_{2}$
to
![]() ${\mathcal{E}}$
. We write
${\mathcal{E}}$
. We write
![]() $V_{{\mathcal{E}}}>0$
for the covolume of
$V_{{\mathcal{E}}}>0$
for the covolume of
![]() $\unicode[STIX]{x1D6EC}$
in
$\unicode[STIX]{x1D6EC}$
in
![]() $\mathbb{C}^{2}$
.
$\mathbb{C}^{2}$
.
Now we define a larger class of Weierstrass equations.
Definition 4.4. A Weierstrass equation
![]() ${\mathcal{E}}$
for
${\mathcal{E}}$
for
![]() $C/k$
is an equation
$C/k$
is an equation
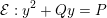 $$\begin{eqnarray}{\mathcal{E}}:y^{2}+Qy=P\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}:y^{2}+Qy=P\end{eqnarray}$$
that describes an open, affine subset of
![]() $C$
, where
$C$
, where
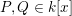 $P,Q\in k[x]$
with
$P,Q\in k[x]$
with
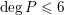 $\deg P\leqslant 6$
and
$\deg P\leqslant 6$
and
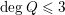 $\deg Q\leqslant 3$
. The discriminant of
$\deg Q\leqslant 3$
. The discriminant of
![]() ${\mathcal{E}}$
is defined as
${\mathcal{E}}$
is defined as
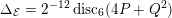 $\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}=2^{-12}\operatorname{disc}_{6}(4P+Q^{2})$
; it is a non-zero element of
$\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}=2^{-12}\operatorname{disc}_{6}(4P+Q^{2})$
; it is a non-zero element of
![]() $k$
.
$k$
.
Suppose that
![]() $k$
is the field of fractions of a discrete valuation ring. We call
$k$
is the field of fractions of a discrete valuation ring. We call
![]() ${\mathcal{E}}$
integral if
${\mathcal{E}}$
integral if
![]() $P$
and
$P$
and
![]() $Q$
have integral coefficients. The minimal discriminant
$Q$
have integral coefficients. The minimal discriminant
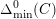 $\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
of
$\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
of
![]() $C$
is the ideal of the ring of integers generated by a discriminant with minimal valuation among the discriminants of the integral equations of
$C$
is the ideal of the ring of integers generated by a discriminant with minimal valuation among the discriminants of the integral equations of
![]() $C$
. In Liu’s terminology [Reference LiuLiu94],
$C$
. In Liu’s terminology [Reference LiuLiu94],
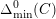 $\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
is called the naive minimal discriminant. If
$\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
is called the naive minimal discriminant. If
![]() $k$
is a number field, then by abuse of notation we let
$k$
is a number field, then by abuse of notation we let
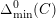 $\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
denote the ideal of
$\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
denote the ideal of
![]() ${\mathcal{O}}_{k}$
that is minimal at each finite place of
${\mathcal{O}}_{k}$
that is minimal at each finite place of
![]() $k$
.
$k$
.
If
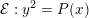 ${\mathcal{E}}:y^{2}=P(x)$
is a restricted Weierstrass equation as in Lockhart’s work, then his notation of discriminant coincides with the one used above, i.e.,
${\mathcal{E}}:y^{2}=P(x)$
is a restricted Weierstrass equation as in Lockhart’s work, then his notation of discriminant coincides with the one used above, i.e.,
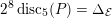 $2^{8}\operatorname{disc}_{5}(P)=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}$
follows from basic properties of the discriminant.
$2^{8}\operatorname{disc}_{5}(P)=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}$
follows from basic properties of the discriminant.
Weierstrass equations are unique up to the following change of variables, see [Reference LiuLiu02, Corollary 4.33],
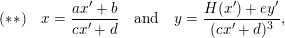 $$\begin{eqnarray}(\ast \ast )\quad x=\frac{ax^{\prime }+b}{cx^{\prime }+d}\quad \text{and}\quad y=\frac{H(x^{\prime })+ey^{\prime }}{(cx^{\prime }+d)^{3}},\end{eqnarray}$$
$$\begin{eqnarray}(\ast \ast )\quad x=\frac{ax^{\prime }+b}{cx^{\prime }+d}\quad \text{and}\quad y=\frac{H(x^{\prime })+ey^{\prime }}{(cx^{\prime }+d)^{3}},\end{eqnarray}$$
where
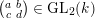 $(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \text{GL}_{2}(k)$
,
$(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \text{GL}_{2}(k)$
,
![]() $e\in k^{\ast }$
,
$e\in k^{\ast }$
,
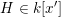 $H\in k[x^{\prime }]$
with
$H\in k[x^{\prime }]$
with
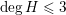 $\deg H\leqslant 3$
.
$\deg H\leqslant 3$
.
4.4 Hyperelliptic jacobians in genus
 $2$
$2$
In this section we state a formula for the Faltings height of the jacobian of a genus
![]() $2$
curve if the said jacobian has potentially good reduction at all finite places. Ueno [Reference UenoUen88] had a related expression for the Faltings height, but with a restriction on reduction type which is incommensurable with ours. The second-named author proved [Reference PazukiPaz12b] another formula for the Faltings height of the jacobian of a hyperelliptic curve of arbitrary genus.
$2$
curve if the said jacobian has potentially good reduction at all finite places. Ueno [Reference UenoUen88] had a related expression for the Faltings height, but with a restriction on reduction type which is incommensurable with ours. The second-named author proved [Reference PazukiPaz12b] another formula for the Faltings height of the jacobian of a hyperelliptic curve of arbitrary genus.
In order to formulate our result, we recall the definition of relevant theta functions and the
![]() $10$
non-trivial theta constants in dimension
$10$
non-trivial theta constants in dimension
![]() $2$
. The latter correspond precisely to the even characteristics
$2$
. The latter correspond precisely to the even characteristics
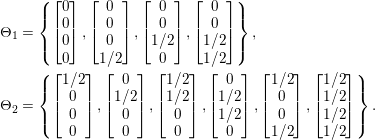 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{1} & = & \displaystyle \left\{\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 1/2\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 0\\ 1/2\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 0\\ 1/2\\ 1/2\end{array}\right]\right\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6E9}_{2} & = & \displaystyle \left\{\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}1/2\\ 1/2\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 1/2\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 0\\ 1/2\end{array}\right],\left[\begin{array}{@{}c@{}}1/2\\ 1/2\\ 1/2\\ 1/2\end{array}\right]\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{1} & = & \displaystyle \left\{\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 1/2\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 0\\ 1/2\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 0\\ 1/2\\ 1/2\end{array}\right]\right\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6E9}_{2} & = & \displaystyle \left\{\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}1/2\\ 1/2\\ 0\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 1/2\\ 0\end{array}\right],\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 0\\ 1/2\end{array}\right],\left[\begin{array}{@{}c@{}}1/2\\ 1/2\\ 1/2\\ 1/2\end{array}\right]\right\}.\nonumber\end{eqnarray}$$
We abbreviate
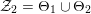 ${\mathcal{Z}}_{2}=\unicode[STIX]{x1D6E9}_{1}\cup \unicode[STIX]{x1D6E9}_{2}$
, the union being disjoint. Say
${\mathcal{Z}}_{2}=\unicode[STIX]{x1D6E9}_{1}\cup \unicode[STIX]{x1D6E9}_{2}$
, the union being disjoint. Say
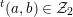 $\text{}^{t}(a,b)\in {\mathcal{Z}}_{2}$
with
$\text{}^{t}(a,b)\in {\mathcal{Z}}_{2}$
with
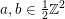 $a,b\in \frac{1}{2}\mathbb{Z}^{2}$
. We denote
$a,b\in \frac{1}{2}\mathbb{Z}^{2}$
. We denote
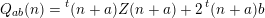 $$\begin{eqnarray}Q_{ab}(n)=\text{}^{t}(n+a)Z(n+a)+2\,\text{}^{t}(n+a)b\end{eqnarray}$$
$$\begin{eqnarray}Q_{ab}(n)=\text{}^{t}(n+a)Z(n+a)+2\,\text{}^{t}(n+a)b\end{eqnarray}$$
for
![]() $n\in \mathbb{Z}^{2}$
and thus get a theta function
$n\in \mathbb{Z}^{2}$
and thus get a theta function
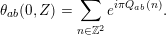 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{ab}(0,Z)=\mathop{\sum }_{n\in \mathbb{Z}^{2}}e^{i\unicode[STIX]{x1D70B}Q_{ab}(n)}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{ab}(0,Z)=\mathop{\sum }_{n\in \mathbb{Z}^{2}}e^{i\unicode[STIX]{x1D70B}Q_{ab}(n)}.\end{eqnarray}$$
We will use the classical Siegel cusp form
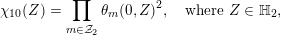 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{10}(Z)=\mathop{\prod }_{m\in {\mathcal{Z}}_{2}}\unicode[STIX]{x1D703}_{m}(0,Z)^{2},\quad \text{where}~Z\in \mathbb{H}_{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{10}(Z)=\mathop{\prod }_{m\in {\mathcal{Z}}_{2}}\unicode[STIX]{x1D703}_{m}(0,Z)^{2},\quad \text{where}~Z\in \mathbb{H}_{2},\end{eqnarray}$$
of weight
![]() $10$
; cf. the second Remark after Proposition 2, [Reference KlingenKli90, §9]. So,
$10$
; cf. the second Remark after Proposition 2, [Reference KlingenKli90, §9]. So,
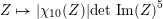 $$\begin{eqnarray}Z\mapsto |\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\,\operatorname{Im}(Z)^{5}\end{eqnarray}$$
$$\begin{eqnarray}Z\mapsto |\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\,\operatorname{Im}(Z)^{5}\end{eqnarray}$$
is an
![]() $\operatorname{Sp}_{4}(\mathbb{Z})$
-invariant, real analytic map
$\operatorname{Sp}_{4}(\mathbb{Z})$
-invariant, real analytic map
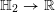 $\mathbb{H}_{2}\rightarrow \mathbb{R}$
.
$\mathbb{H}_{2}\rightarrow \mathbb{R}$
.
For a finite place
![]() $\unicode[STIX]{x1D708}$
of a number field, we write
$\unicode[STIX]{x1D708}$
of a number field, we write
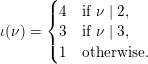 $$\begin{eqnarray}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})=\left\{\begin{array}{@{}ll@{}}4\quad & \text{if }\unicode[STIX]{x1D708}\mid 2,\\ 3\quad & \text{if }\unicode[STIX]{x1D708}\mid 3,\\ 1\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})=\left\{\begin{array}{@{}ll@{}}4\quad & \text{if }\unicode[STIX]{x1D708}\mid 2,\\ 3\quad & \text{if }\unicode[STIX]{x1D708}\mid 3,\\ 1\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
We recall that
![]() $d_{\unicode[STIX]{x1D708}}$
denotes a local degree and is defined in § 2.
$d_{\unicode[STIX]{x1D708}}$
denotes a local degree and is defined in § 2.
Theorem 4.5. Let
![]() $C$
be a curve of genus
$C$
be a curve of genus
![]() $2$
defined over a number field
$2$
defined over a number field
![]() $k$
such that
$k$
such that
![]() $C(k)$
contains a Weierstrass point of
$C(k)$
contains a Weierstrass point of
![]() $C$
and such that
$C$
and such that
![]() $\operatorname{Jac}(C)$
has good reduction at all finite places of
$\operatorname{Jac}(C)$
has good reduction at all finite places of
![]() $k$
. Let
$k$
. Let
 $J_{2},J_{6},J_{8},J_{10}\in k$
be Igusa’s invariants attached to
$J_{2},J_{6},J_{8},J_{10}\in k$
be Igusa’s invariants attached to
![]() $C$
. The following properties hold true.
$C$
. The following properties hold true.
-
(i) For any embedding
 $\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
, let
$\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
, let
 $Z_{\unicode[STIX]{x1D70E}}$
be a period matrix coming from a restricted Weierstrass model of
$Z_{\unicode[STIX]{x1D70E}}$
be a period matrix coming from a restricted Weierstrass model of
 $C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
as in § 4.3; then
$C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
as in § 4.3; then
 $\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})\not =0$
. Moreover, we have
$\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})\not =0$
. Moreover, we have  $$\begin{eqnarray}\displaystyle h(\operatorname{Jac}(C)) & = & \displaystyle \frac{1}{[k:\mathbb{Q}]}\biggl(\frac{1}{60}\mathop{\sum }_{\unicode[STIX]{x1D708}\in M_{k}^{0}}\frac{d_{\unicode[STIX]{x1D708}}}{\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}\log \max \{1,|J_{10}^{-\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}J_{2\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}^{5}|_{\unicode[STIX]{x1D708}}\}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{10}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log (2^{8}\unicode[STIX]{x1D70B}^{10}|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}(\operatorname{Im}Z_{\unicode[STIX]{x1D70E}})^{5})\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(\operatorname{Jac}(C)) & = & \displaystyle \frac{1}{[k:\mathbb{Q}]}\biggl(\frac{1}{60}\mathop{\sum }_{\unicode[STIX]{x1D708}\in M_{k}^{0}}\frac{d_{\unicode[STIX]{x1D708}}}{\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}\log \max \{1,|J_{10}^{-\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}J_{2\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}^{5}|_{\unicode[STIX]{x1D708}}\}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{10}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log (2^{8}\unicode[STIX]{x1D70B}^{10}|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}(\operatorname{Im}Z_{\unicode[STIX]{x1D70E}})^{5})\biggr).\nonumber\end{eqnarray}$$
-
(ii) Let
 $\unicode[STIX]{x1D708}$
be a finite place of
$\unicode[STIX]{x1D708}$
be a finite place of
 $k$
; then
$k$
; then  $$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6E5}_{\min }^{0}(C)=\frac{1}{\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}\max \{0,-\text{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{-\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{5})\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6E5}_{\min }^{0}(C)=\frac{1}{\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})}\max \{0,-\text{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{-\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{5})\}.\end{eqnarray}$$
We will prove this theorem after some preliminary work. But first we state an immediate corollary.
Corollary 4.6. Let
![]() $C,k,$
and the
$C,k,$
and the
![]() $Z_{\unicode[STIX]{x1D70E}}$
be as in Theorem 4.5; then
$Z_{\unicode[STIX]{x1D70E}}$
be as in Theorem 4.5; then
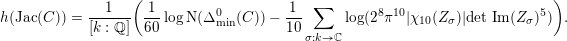 $$\begin{eqnarray}h(\operatorname{Jac}(C))=\frac{1}{[k:\mathbb{Q}]}\biggl(\frac{1}{60}\log \text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))-\frac{1}{10}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log (2^{8}\unicode[STIX]{x1D70B}^{10}|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}\,\operatorname{Im}(Z_{\unicode[STIX]{x1D70E}})^{5})\biggr).\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))=\frac{1}{[k:\mathbb{Q}]}\biggl(\frac{1}{60}\log \text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))-\frac{1}{10}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\log (2^{8}\unicode[STIX]{x1D70B}^{10}|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}\,\operatorname{Im}(Z_{\unicode[STIX]{x1D70E}})^{5})\biggr).\end{eqnarray}$$
Suppose that
![]() $C$
is a curve of genus
$C$
is a curve of genus
![]() $2$
defined over a number field
$2$
defined over a number field
![]() $k$
and presented by a Weierstrass equation as in Definition 4.4. There exists a classical basis for
$k$
and presented by a Weierstrass equation as in Definition 4.4. There exists a classical basis for
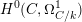 $H^{0}(C,\unicode[STIX]{x1D6FA}_{C/k}^{1})$
given by
$H^{0}(C,\unicode[STIX]{x1D6FA}_{C/k}^{1})$
given by
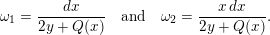 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{dx}{2y+Q(x)}\quad \text{and}\quad \unicode[STIX]{x1D714}_{2}=\frac{x\,dx}{2y+Q(x)}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{dx}{2y+Q(x)}\quad \text{and}\quad \unicode[STIX]{x1D714}_{2}=\frac{x\,dx}{2y+Q(x)}.\end{eqnarray}$$
Consider the section
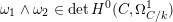 $\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}\in \det H^{0}(C,\unicode[STIX]{x1D6FA}_{C/k}^{1})$
. A change of variables in the Weierstrass models of
$\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}\in \det H^{0}(C,\unicode[STIX]{x1D6FA}_{C/k}^{1})$
. A change of variables in the Weierstrass models of
![]() $C$
leaves
$C$
leaves
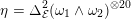 $$\begin{eqnarray}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}^{2}(\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2})^{\otimes 20}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}^{2}(\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2})^{\otimes 20}\end{eqnarray}$$
invariant; cf. [Reference LiuLiu94, § 1.3].
We now show how to use
![]() $\unicode[STIX]{x1D702}$
, a differential form on the curve
$\unicode[STIX]{x1D702}$
, a differential form on the curve
![]() $C$
, to compute the Faltings height of the jacobian
$C$
, to compute the Faltings height of the jacobian
![]() $\operatorname{Jac}(C)$
.
$\operatorname{Jac}(C)$
.
Suppose that
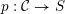 $p:{\mathcal{C}}\rightarrow S$
is a regular semi-stable model of
$p:{\mathcal{C}}\rightarrow S$
is a regular semi-stable model of
![]() $C$
over
$C$
over
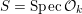 $S=\operatorname{Spec}{\mathcal{O}}_{k}$
. We now prove that
$S=\operatorname{Spec}{\mathcal{O}}_{k}$
. We now prove that
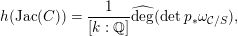 $$\begin{eqnarray}h(\operatorname{Jac}(C))=\frac{1}{[k:\mathbb{Q}]}\widehat{\deg }(\det p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}),\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))=\frac{1}{[k:\mathbb{Q}]}\widehat{\deg }(\det p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}$
denotes the relative canonical bundle and where the hermitian metrics on
$\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}$
denotes the relative canonical bundle and where the hermitian metrics on
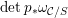 $\det p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}$
are determined by
$\det p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}$
are determined by
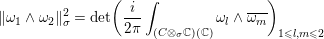 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}\Vert _{\unicode[STIX]{x1D70E}}^{2}=\det \biggl(\frac{i}{2\unicode[STIX]{x1D70B}}\int _{(C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C})(\mathbb{C})}\unicode[STIX]{x1D714}_{l}\wedge \overline{\unicode[STIX]{x1D714}_{m}}\biggr)_{1\leqslant l,m\leqslant 2}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}\Vert _{\unicode[STIX]{x1D70E}}^{2}=\det \biggl(\frac{i}{2\unicode[STIX]{x1D70B}}\int _{(C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C})(\mathbb{C})}\unicode[STIX]{x1D714}_{l}\wedge \overline{\unicode[STIX]{x1D714}_{m}}\biggr)_{1\leqslant l,m\leqslant 2}\end{eqnarray}$$
with
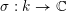 $\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
an embedding. Indeed, suppose that
$\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
an embedding. Indeed, suppose that
![]() $\unicode[STIX]{x1D700}$
is a section of
$\unicode[STIX]{x1D700}$
is a section of
![]() ${\mathcal{C}}\rightarrow S$
and let
${\mathcal{C}}\rightarrow S$
and let
![]() $\operatorname{Pic}_{{\mathcal{C}}/S}^{0}$
be the relative Picard scheme of degree
$\operatorname{Pic}_{{\mathcal{C}}/S}^{0}$
be the relative Picard scheme of degree
![]() $0$
. Then
$0$
. Then
![]() $\operatorname{Pic}_{{\mathcal{C}}/S}^{0}$
is the identity component of the Néron model
$\operatorname{Pic}_{{\mathcal{C}}/S}^{0}$
is the identity component of the Néron model
![]() ${\mathcal{A}}$
of the jacobian of
${\mathcal{A}}$
of the jacobian of
![]() $C$
by [Reference Bosch, Lütkebohmert and RaynaudBLR90, Theorem 4, ch. 9.5]. This is an open subscheme of
$C$
by [Reference Bosch, Lütkebohmert and RaynaudBLR90, Theorem 4, ch. 9.5]. This is an open subscheme of
![]() ${\mathcal{A}}$
which contains the image of
${\mathcal{A}}$
which contains the image of
![]() $\unicode[STIX]{x1D700}$
. Therefore,
$\unicode[STIX]{x1D700}$
. Therefore,
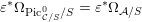 $\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{\text{Pic}_{{\mathcal{C}}/S}^{0}/S}=\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}$
, which allows us to replace
$\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{\text{Pic}_{{\mathcal{C}}/S}^{0}/S}=\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}$
, which allows us to replace
![]() ${\mathcal{A}}$
by
${\mathcal{A}}$
by
![]() $\operatorname{Pic}_{{\mathcal{C}}/S}^{0}$
in the computations below. Then
$\operatorname{Pic}_{{\mathcal{C}}/S}^{0}$
in the computations below. Then
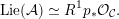 $$\begin{eqnarray}\operatorname{Lie}({\mathcal{A}})\simeq R^{1}p_{\ast }{\mathcal{O}}_{{\mathcal{C}}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Lie}({\mathcal{A}})\simeq R^{1}p_{\ast }{\mathcal{O}}_{{\mathcal{C}}}.\end{eqnarray}$$
Moreover, by Grothendieck duality (see [Reference LiuLiu02, 6.4.3, p. 243]), we have
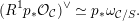 $$\begin{eqnarray}(R^{1}p_{\ast }{\mathcal{O}}_{{\mathcal{C}}})^{\vee }\simeq p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}.\end{eqnarray}$$
$$\begin{eqnarray}(R^{1}p_{\ast }{\mathcal{O}}_{{\mathcal{C}}})^{\vee }\simeq p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}.\end{eqnarray}$$
Then
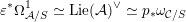 $$\begin{eqnarray}\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{1}\simeq \operatorname{Lie}({\mathcal{A}})^{\vee }\simeq p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{1}\simeq \operatorname{Lie}({\mathcal{A}})^{\vee }\simeq p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S}\end{eqnarray}$$
and hence
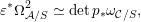 $$\begin{eqnarray}\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{2}\simeq \det p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}^{\ast }\unicode[STIX]{x1D6FA}_{{\mathcal{A}}/S}^{2}\simeq \det p_{\ast }\unicode[STIX]{x1D714}_{{\mathcal{C}}/S},\end{eqnarray}$$
which turns out to be an isometry by 4.15 of the second lecture of [Reference SzpiroSzp85]. We conclude (4.5) by taking the Arakelov degree.
4.4.1 Archimedean places
We use Lockhart [Reference LockhartLoc94] and Mumford [Reference MumfordMum84] as references for these places. If
![]() $T$
is a subset of
$T$
is a subset of
 $\{1,2,3,4,5\}$
, one then defines
$\{1,2,3,4,5\}$
, one then defines
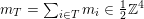 $m_{T}=\sum _{i\in T}m_{i}\in \frac{1}{2}\mathbb{Z}^{4}$
with
$m_{T}=\sum _{i\in T}m_{i}\in \frac{1}{2}\mathbb{Z}^{4}$
with
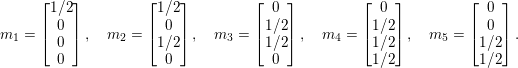 $$\begin{eqnarray}m_{1}=\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 0\\ 0\end{array}\right],\quad m_{2}=\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 1/2\\ 0\end{array}\right],\quad m_{3}=\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 1/2\\ 0\end{array}\right],\quad m_{4}=\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 1/2\\ 1/2\end{array}\right],\quad m_{5}=\left[\begin{array}{@{}c@{}}0\\ 0\\ 1/2\\ 1/2\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}m_{1}=\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 0\\ 0\end{array}\right],\quad m_{2}=\left[\begin{array}{@{}c@{}}1/2\\ 0\\ 1/2\\ 0\end{array}\right],\quad m_{3}=\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 1/2\\ 0\end{array}\right],\quad m_{4}=\left[\begin{array}{@{}c@{}}0\\ 1/2\\ 1/2\\ 1/2\end{array}\right],\quad m_{5}=\left[\begin{array}{@{}c@{}}0\\ 0\\ 1/2\\ 1/2\end{array}\right].\end{eqnarray}$$
In the notation of Lockhart’s definition [Reference LockhartLoc94, Definition 3.1],
![]() $\unicode[STIX]{x1D711}(Z)$
is the fourth power of
$\unicode[STIX]{x1D711}(Z)$
is the fourth power of
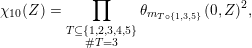 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{10}(Z)=\mathop{\prod }_{\substack{ T\subseteq \{1,2,3,4,5\} \\ \#T=3}}\unicode[STIX]{x1D703}_{m_{T\circ \{1,3,5\}}}(0,Z)^{2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{10}(Z)=\mathop{\prod }_{\substack{ T\subseteq \{1,2,3,4,5\} \\ \#T=3}}\unicode[STIX]{x1D703}_{m_{T\circ \{1,3,5\}}}(0,Z)^{2},\end{eqnarray}$$
where
![]() $\circ$
denotes the symmetric difference of sets and
$\circ$
denotes the symmetric difference of sets and
![]() $\unicode[STIX]{x1D703}_{m}$
are theta functions from § 4.4.
$\unicode[STIX]{x1D703}_{m}$
are theta functions from § 4.4.
The following result is from Lockhart [Reference LockhartLoc94, Proposition 3.3]. In his notation, we have
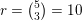 $r=\binom{5}{3}=10$
and
$r=\binom{5}{3}=10$
and
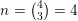 $n=\binom{4}{3}=4$
.
$n=\binom{4}{3}=4$
.
Proposition 4.7. Let
![]() $C$
be a curve of genus
$C$
be a curve of genus
![]() $2$
defined over
$2$
defined over
![]() $\mathbb{C}$
and suppose that
$\mathbb{C}$
and suppose that
![]() ${\mathcal{E}}$
is a restricted Weierstrass equation for
${\mathcal{E}}$
is a restricted Weierstrass equation for
![]() $C$
. One has the uniformisation
$C$
. One has the uniformisation
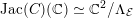 $\operatorname{Jac}(C)(\mathbb{C})\simeq \mathbb{C}^{2}/\unicode[STIX]{x1D6EC}_{{\mathcal{E}}}$
with the lattice
$\operatorname{Jac}(C)(\mathbb{C})\simeq \mathbb{C}^{2}/\unicode[STIX]{x1D6EC}_{{\mathcal{E}}}$
with the lattice
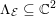 $\unicode[STIX]{x1D6EC}_{{\mathcal{E}}}\subseteq \mathbb{C}^{2}$
, its period matrix
$\unicode[STIX]{x1D6EC}_{{\mathcal{E}}}\subseteq \mathbb{C}^{2}$
, its period matrix
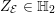 $Z_{{\mathcal{E}}}\in \mathbb{H}_{2}$
and covolume
$Z_{{\mathcal{E}}}\in \mathbb{H}_{2}$
and covolume
![]() $V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})$
, both as near the beginning of § 4.3. Then
$V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})$
, both as near the beginning of § 4.3. Then
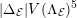 $|\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})^{5}$
is independent of the equation
$|\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})^{5}$
is independent of the equation
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
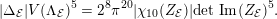 $$\begin{eqnarray}|\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})^{5}=2^{8}\unicode[STIX]{x1D70B}^{20}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|\text{det}\,\operatorname{Im}(Z_{{\mathcal{E}}})^{5}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})^{5}=2^{8}\unicode[STIX]{x1D70B}^{20}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|\text{det}\,\operatorname{Im}(Z_{{\mathcal{E}}})^{5}.\end{eqnarray}$$
Next comes the archimedean contribution of the section
![]() $\unicode[STIX]{x1D702}$
from (4.4).
$\unicode[STIX]{x1D702}$
from (4.4).
Proposition 4.8. Let
![]() $C$
be a curve of genus
$C$
be a curve of genus
![]() $2$
defined over a number field
$2$
defined over a number field
![]() $k$
. Let
$k$
. Let
 $\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
be an embedding and suppose that
$\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}$
be an embedding and suppose that
![]() ${\mathcal{E}}$
is a restricted Weierstrass equation for
${\mathcal{E}}$
is a restricted Weierstrass equation for
 $C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
. We write
$C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C}$
. We write
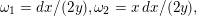 $\unicode[STIX]{x1D714}_{1}=dx/(2y),\unicode[STIX]{x1D714}_{2}=x\,dx/(2y),$
and
$\unicode[STIX]{x1D714}_{1}=dx/(2y),\unicode[STIX]{x1D714}_{2}=x\,dx/(2y),$
and
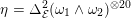 $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}^{2}(\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2})^{\otimes 20}$
. Then
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}^{2}(\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2})^{\otimes 20}$
. Then
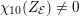 $\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})\not =0$
and
$\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})\not =0$
and
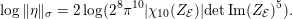 $$\begin{eqnarray}\log \Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}}=2\log (2^{8}\unicode[STIX]{x1D70B}^{10}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|\text{det}\operatorname{Im}(Z_{{\mathcal{E}}})^{5}).\end{eqnarray}$$
$$\begin{eqnarray}\log \Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}}=2\log (2^{8}\unicode[STIX]{x1D70B}^{10}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|\text{det}\operatorname{Im}(Z_{{\mathcal{E}}})^{5}).\end{eqnarray}$$
Proof. We use Proposition 4.7 to compute
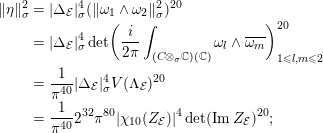 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}}^{2} & = & \displaystyle |\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|_{\unicode[STIX]{x1D70E}}^{4}(\Vert \unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}\Vert _{\unicode[STIX]{x1D70E}}^{2})^{20}\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|_{\unicode[STIX]{x1D70E}}^{4}\det \biggl(\frac{i}{2\unicode[STIX]{x1D70B}}\int _{(C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C})(\mathbb{C})}\unicode[STIX]{x1D714}_{l}\wedge \overline{\unicode[STIX]{x1D714}_{m}}\biggr)_{1\leqslant l,m\leqslant 2}^{20}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}^{40}}|\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|_{\unicode[STIX]{x1D70E}}^{4}V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})^{20}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}^{40}}2^{32}\unicode[STIX]{x1D70B}^{80}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|^{4}\det (\operatorname{Im}Z_{{\mathcal{E}}})^{20};\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}}^{2} & = & \displaystyle |\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|_{\unicode[STIX]{x1D70E}}^{4}(\Vert \unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}\Vert _{\unicode[STIX]{x1D70E}}^{2})^{20}\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|_{\unicode[STIX]{x1D70E}}^{4}\det \biggl(\frac{i}{2\unicode[STIX]{x1D70B}}\int _{(C\otimes _{\unicode[STIX]{x1D70E}}\mathbb{C})(\mathbb{C})}\unicode[STIX]{x1D714}_{l}\wedge \overline{\unicode[STIX]{x1D714}_{m}}\biggr)_{1\leqslant l,m\leqslant 2}^{20}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}^{40}}|\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}|_{\unicode[STIX]{x1D70E}}^{4}V(\unicode[STIX]{x1D6EC}_{{\mathcal{E}}})^{20}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70B}^{40}}2^{32}\unicode[STIX]{x1D70B}^{80}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|^{4}\det (\operatorname{Im}Z_{{\mathcal{E}}})^{20};\nonumber\end{eqnarray}$$
here the second equality requires the definition (4.6), the next one is classical, cf. [Reference Griffiths and HarrisGH78, ch. 2.2], and the fourth one is Proposition 4.7.
Hence,
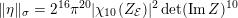 $\Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}}=2^{16}\unicode[STIX]{x1D70B}^{20}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|^{2}\det (\operatorname{Im}Z)^{10}$
and it follows in particular that
$\Vert \unicode[STIX]{x1D702}\Vert _{\unicode[STIX]{x1D70E}}=2^{16}\unicode[STIX]{x1D70B}^{20}|\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})|^{2}\det (\operatorname{Im}Z)^{10}$
and it follows in particular that
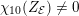 $\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})\not =0$
.◻
$\unicode[STIX]{x1D712}_{10}(Z_{{\mathcal{E}}})\not =0$
.◻
4.4.2 Non-archimedean places
Proposition 4.9. Let
![]() $C$
be a curve of genus
$C$
be a curve of genus
![]() $2$
defined over a number field
$2$
defined over a number field
![]() $k$
. Let
$k$
. Let
![]() $\unicode[STIX]{x1D708}$
be a finite place of
$\unicode[STIX]{x1D708}$
be a finite place of
![]() $k$
at which
$k$
at which
![]() $\operatorname{Jac}(C)$
has good reduction. If
$\operatorname{Jac}(C)$
has good reduction. If
![]() $\unicode[STIX]{x1D702}$
is as in (4.4), then
$\unicode[STIX]{x1D702}$
is as in (4.4), then
 $$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D702})=\frac{1}{3\unicode[STIX]{x1D704}}\max \{0,\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\}=\frac{1}{3}\operatorname{ord}_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6E5}_{\min }^{0}(C),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D702})=\frac{1}{3\unicode[STIX]{x1D704}}\max \{0,\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\}=\frac{1}{3}\operatorname{ord}_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6E5}_{\min }^{0}(C),\end{eqnarray}$$
where
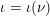 $\unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})$
is as in (4.3) and where the
$\unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D708})$
is as in (4.3) and where the
 $J_{2},J_{6},J_{8},J_{10}$
are as in Theorem 4.5.
$J_{2},J_{6},J_{8},J_{10}$
are as in Theorem 4.5.
Proof. Let
![]() $k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
be the maximal unramified extension of
$k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
be the maximal unramified extension of
![]() $k_{\unicode[STIX]{x1D708}}$
inside a fixed algebraic closure of
$k_{\unicode[STIX]{x1D708}}$
inside a fixed algebraic closure of
![]() $k_{\unicode[STIX]{x1D708}}$
. This is a strictly henselian field equipped with a discrete valuation whose ring of integers
$k_{\unicode[STIX]{x1D708}}$
. This is a strictly henselian field equipped with a discrete valuation whose ring of integers
![]() ${\mathcal{O}}$
has an algebraically closed residue field. Thus,
${\mathcal{O}}$
has an algebraically closed residue field. Thus,
![]() ${\mathcal{O}}$
satisfies the hypothesis needed for the references below.
${\mathcal{O}}$
satisfies the hypothesis needed for the references below.
Recall that
 $\operatorname{Jac}(C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}})$
has good reduction by hypothesis; it has in particular semi-stable reduction. So, the curve
$\operatorname{Jac}(C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}})$
has good reduction by hypothesis; it has in particular semi-stable reduction. So, the curve
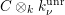 $C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
has semi-stable reduction by Deligne and Mumford’s theorem cited in the introduction. The minimal regular model
$C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
has semi-stable reduction by Deligne and Mumford’s theorem cited in the introduction. The minimal regular model
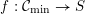 $f:{\mathcal{C}}_{\min }\rightarrow S$
of
$f:{\mathcal{C}}_{\min }\rightarrow S$
of
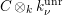 $C\,\otimes _{k}\,k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
over
$C\,\otimes _{k}\,k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
over
 $S=\operatorname{Spec}{\mathcal{O}}$
is semi-stable by [Reference LiuLiu02, Theorem 10.3.34(a)]. The canonical model
$S=\operatorname{Spec}{\mathcal{O}}$
is semi-stable by [Reference LiuLiu02, Theorem 10.3.34(a)]. The canonical model
![]() ${\mathcal{C}}_{\text{st}}$
, obtained via a contraction
${\mathcal{C}}_{\text{st}}$
, obtained via a contraction
 ${\mathcal{C}}_{\min }\rightarrow {\mathcal{C}}_{\text{st}}$
, is stable by part (b) of the same theorem [Reference LiuLiu02]. It is well known that exactly seven geometric configurations can arise for the geometric special fibre of the stable model. They are pictured in [Reference LiuLiu02, Example 10.3.6].
${\mathcal{C}}_{\min }\rightarrow {\mathcal{C}}_{\text{st}}$
, is stable by part (b) of the same theorem [Reference LiuLiu02]. It is well known that exactly seven geometric configurations can arise for the geometric special fibre of the stable model. They are pictured in [Reference LiuLiu02, Example 10.3.6].
We infer from a theorem of Raynaud that the special fibre of
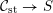 ${\mathcal{C}}_{\text{st}}\rightarrow S$
is either smooth or a union of two elliptic curves meeting at a point; see the paragraph before [Reference LiuLiu93, Proposition 2].
${\mathcal{C}}_{\text{st}}\rightarrow S$
is either smooth or a union of two elliptic curves meeting at a point; see the paragraph before [Reference LiuLiu93, Proposition 2].
Later on, we will consider these two cases separately. But first let us fix a Weierstrass equation
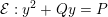 ${\mathcal{E}}:y^{2}+Qy=P$
for
${\mathcal{E}}:y^{2}+Qy=P$
for
 $C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
such that
$C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}}$
such that
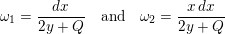 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{dx}{2y+Q}\quad \text{and}\quad \unicode[STIX]{x1D714}_{2}=\frac{x\,dx}{2y+Q}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}=\frac{dx}{2y+Q}\quad \text{and}\quad \unicode[STIX]{x1D714}_{2}=\frac{x\,dx}{2y+Q}\end{eqnarray}$$
constitute an
![]() ${\mathcal{O}}$
-basis of
${\mathcal{O}}$
-basis of
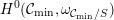 $H^{0}({\mathcal{C}}_{\min },\unicode[STIX]{x1D714}_{{\mathcal{C}}_{\min }/S})$
; its existence is guaranteed by [Reference LiuLiu94, Proposition 2(a)].
$H^{0}({\mathcal{C}}_{\min },\unicode[STIX]{x1D714}_{{\mathcal{C}}_{\min }/S})$
; its existence is guaranteed by [Reference LiuLiu94, Proposition 2(a)].
Then
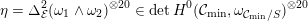 $$\begin{eqnarray}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}^{2}(\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2})^{\otimes 20}\in \det H^{0}({\mathcal{C}}_{ min},\unicode[STIX]{x1D714}_{{\mathcal{C}}_{\min }/S})^{\otimes 20}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6E5}_{{\mathcal{E}}}^{2}(\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2})^{\otimes 20}\in \det H^{0}({\mathcal{C}}_{ min},\unicode[STIX]{x1D714}_{{\mathcal{C}}_{\min }/S})^{\otimes 20}\end{eqnarray}$$
by the invariance under coordinate change mentioned after Theorem 4.5. The equation
![]() ${\mathcal{E}}$
is minimal in Ueno’s sense [Reference LiuLiu94, Definition 1], and we use
${\mathcal{E}}$
is minimal in Ueno’s sense [Reference LiuLiu94, Definition 1], and we use
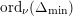 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })$
to denote the order of Ueno’s minimal discriminant; cf. the same definition. Observe that this order is non-negative, but may be less than the order of the minimal discriminant
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })$
to denote the order of Ueno’s minimal discriminant; cf. the same definition. Observe that this order is non-negative, but may be less than the order of the minimal discriminant
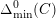 $\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
. By Proposition 3 and its corollary, both in [Reference LiuLiu94], we find that
$\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
. By Proposition 3 and its corollary, both in [Reference LiuLiu94], we find that
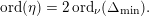 $$\begin{eqnarray}\text{ord}(\unicode[STIX]{x1D702})=2\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }).\end{eqnarray}$$
$$\begin{eqnarray}\text{ord}(\unicode[STIX]{x1D702})=2\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }).\end{eqnarray}$$
First, let us suppose that the special fibre of the stable model is not smooth. Then we are in [Reference LiuLiu93, case (V) of Théorème 1] and by [Reference LiuLiu93, Proposition 2]
![]() ${\mathcal{C}}_{\min }$
is of type [
${\mathcal{C}}_{\min }$
is of type [
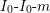 $I_{0}\text{-}I_{0}\text{-}m$
] in Namikawa and Ueno’s classification [Reference Namikawa and UenoNU73]. The value
$I_{0}\text{-}I_{0}\text{-}m$
] in Namikawa and Ueno’s classification [Reference Namikawa and UenoNU73]. The value
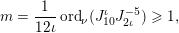 $$\begin{eqnarray}m=\frac{1}{12\unicode[STIX]{x1D704}}\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\geqslant 1,\end{eqnarray}$$
$$\begin{eqnarray}m=\frac{1}{12\unicode[STIX]{x1D704}}\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\geqslant 1,\end{eqnarray}$$
computed in part (v) of the proposition, is the thickness of the singular point in the special fibre of
![]() ${\mathcal{C}}_{\text{st}}$
, see [Reference LiuLiu02, Definition 3.23]; here we used that
${\mathcal{C}}_{\text{st}}$
, see [Reference LiuLiu02, Definition 3.23]; here we used that
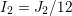 $I_{2}=J_{2}/12$
,
$I_{2}=J_{2}/12$
,
![]() $I_{6}=J_{6}$
, and
$I_{6}=J_{6}$
, and
![]() $I_{8}=J_{8}$
as in Liu’s paper [Reference LiuLiu93].
$I_{8}=J_{8}$
as in Liu’s paper [Reference LiuLiu93].
The fibre of
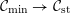 ${\mathcal{C}}_{\min }\rightarrow {\mathcal{C}}_{\text{st}}$
above the unique singular point is a chain of
${\mathcal{C}}_{\min }\rightarrow {\mathcal{C}}_{\text{st}}$
above the unique singular point is a chain of
![]() $m-1$
copies of the projective line. We shall use the Artin conductor of
$m-1$
copies of the projective line. We shall use the Artin conductor of
![]() ${\mathcal{C}}_{\min }/S$
; see the introduction [Reference LiuLiu94] for a definition. By [Reference LiuLiu94, Proposition 1],
${\mathcal{C}}_{\min }/S$
; see the introduction [Reference LiuLiu94] for a definition. By [Reference LiuLiu94, Proposition 1],
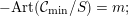 $$\begin{eqnarray}-\text{Art}({\mathcal{C}}_{\min }/S)=m;\end{eqnarray}$$
$$\begin{eqnarray}-\text{Art}({\mathcal{C}}_{\min }/S)=m;\end{eqnarray}$$
indeed, the conductor mentioned in the reference has exponent
![]() $0$
because
$0$
because
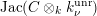 $\operatorname{Jac}(C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}})$
has good reduction at
$\operatorname{Jac}(C\otimes _{k}k_{\unicode[STIX]{x1D708}}^{\text{unr}})$
has good reduction at
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
Saito proved in [Reference SaitoSai88, Theorem 1] that
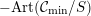 $-\text{Art}({\mathcal{C}}_{\min }/S)$
equals the order of yet a further discriminant attached to
$-\text{Art}({\mathcal{C}}_{\min }/S)$
equals the order of yet a further discriminant attached to
![]() ${\mathcal{C}}_{\min }/S$
; its definition is given in [Reference SaitoSai88] and relies on unpublished work of Deligne. Saito attributed this equality to Deligne in the semi-stable case, which covers our application.
${\mathcal{C}}_{\min }/S$
; its definition is given in [Reference SaitoSai88] and relies on unpublished work of Deligne. Saito attributed this equality to Deligne in the semi-stable case, which covers our application.
Proposition [Reference SaitoSai89] yields
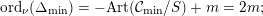 $$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })=-\text{Art}({\mathcal{C}}_{\min }/S)+m=2m;\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })=-\text{Art}({\mathcal{C}}_{\min }/S)+m=2m;\end{eqnarray}$$
cf. also [Reference LiuLiu94, § 2.1]. Using this we can relate the section
![]() $\unicode[STIX]{x1D702}$
to the Igusa invariants as follows:
$\unicode[STIX]{x1D702}$
to the Igusa invariants as follows:
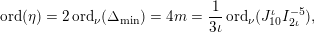 $$\begin{eqnarray}\operatorname{ord}(\unicode[STIX]{x1D702})=2\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })=4m=\frac{1}{3\unicode[STIX]{x1D704}}\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}I_{2\unicode[STIX]{x1D704}}^{-5}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ord}(\unicode[STIX]{x1D702})=2\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })=4m=\frac{1}{3\unicode[STIX]{x1D704}}\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}I_{2\unicode[STIX]{x1D704}}^{-5}),\end{eqnarray}$$
where the first equality used (4.8) and the last equality used (4.9). We obtain
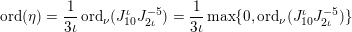 $$\begin{eqnarray}\operatorname{ord}(\unicode[STIX]{x1D702})=\frac{1}{3\unicode[STIX]{x1D704}}\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})=\frac{1}{3\unicode[STIX]{x1D704}}\max \{0,\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ord}(\unicode[STIX]{x1D702})=\frac{1}{3\unicode[STIX]{x1D704}}\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})=\frac{1}{3\unicode[STIX]{x1D704}}\max \{0,\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\}\end{eqnarray}$$
and hence the first equality of this proposition in the current case.
Next we apply a result of Liu to relate
![]() $\operatorname{ord}(\unicode[STIX]{x1D702})$
to the order of the minimal discriminant
$\operatorname{ord}(\unicode[STIX]{x1D702})$
to the order of the minimal discriminant
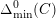 $\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
. In Liu’s notation [Reference LiuLiu94], we have
$\unicode[STIX]{x1D6E5}_{\min }^{0}(C)$
. In Liu’s notation [Reference LiuLiu94], we have
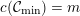 $c({\mathcal{C}}_{\text{min}})=m$
. Théorème 2 of [Reference LiuLiu94] implies that
$c({\mathcal{C}}_{\text{min}})=m$
. Théorème 2 of [Reference LiuLiu94] implies that
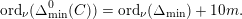 $$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))=\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{ min})+10m.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))=\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{ min})+10m.\end{eqnarray}$$
So,
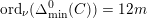 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))=12m$
by (4.11). The second equality in the assertion follows from (4.12).
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))=12m$
by (4.11). The second equality in the assertion follows from (4.12).
Second, suppose that the special fibre of
![]() ${\mathcal{C}}_{\text{st}}$
is smooth. Using [Reference LiuLiu94], we find that the Artin conductor of
${\mathcal{C}}_{\text{st}}$
is smooth. Using [Reference LiuLiu94], we find that the Artin conductor of
![]() ${\mathcal{C}}/S$
vanishes. Just as near (4.11), we find that
${\mathcal{C}}/S$
vanishes. Just as near (4.11), we find that
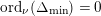 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })=0$
and thus
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })=0$
and thus
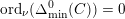 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))=0$
as
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))=0$
as
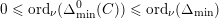 $0\leqslant \operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))\leqslant \operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })$
holds in general by [Reference LiuLiu94, Proposition 2(d)]. Using (4.8), we conclude that
$0\leqslant \operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))\leqslant \operatorname{ord}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D6E5}_{\min })$
holds in general by [Reference LiuLiu94, Proposition 2(d)]. Using (4.8), we conclude that
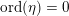 $\operatorname{ord}(\unicode[STIX]{x1D702})=0$
. Théorème 1 of [Reference LiuLiu93], attributed to Igusa, states that
$\operatorname{ord}(\unicode[STIX]{x1D702})=0$
. Théorème 1 of [Reference LiuLiu93], attributed to Igusa, states that
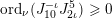 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{-\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{5})\geqslant 0$
for all
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{-\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{5})\geqslant 0$
for all
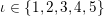 $\unicode[STIX]{x1D704}\in \{1,2,3,4,5\}$
. In particular,
$\unicode[STIX]{x1D704}\in \{1,2,3,4,5\}$
. In particular,
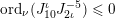 $\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\leqslant 0$
and so the proposition holds true in this case too.◻
$\operatorname{ord}_{\unicode[STIX]{x1D708}}(J_{10}^{\unicode[STIX]{x1D704}}J_{2\unicode[STIX]{x1D704}}^{-5})\leqslant 0$
and so the proposition holds true in this case too.◻
4.4.3 Proof of Theorem 4.5
Since there is a
![]() $k$
-rational Weierstrass point by hypothesis, there is a restricted Weierstrass equation as in Proposition 4.8, with coefficients in
$k$
-rational Weierstrass point by hypothesis, there is a restricted Weierstrass equation as in Proposition 4.8, with coefficients in
![]() $k$
. Part (i) of the theorem follows by studying the local contributions to the Faltings height. The infinite places are handled by Proposition 4.8 and the finite places are dealt with by Proposition 4.9. Observe that the Arakelov degree of
$k$
. Part (i) of the theorem follows by studying the local contributions to the Faltings height. The infinite places are handled by Proposition 4.8 and the finite places are dealt with by Proposition 4.9. Observe that the Arakelov degree of
![]() $\unicode[STIX]{x1D702}$
is
$\unicode[STIX]{x1D702}$
is
![]() $20$
times the desired Faltings height of
$20$
times the desired Faltings height of
![]() $\operatorname{Jac}(C)$
.
$\operatorname{Jac}(C)$
.
Part (ii) is the second equality in Proposition 4.9.
5 Archimedean estimates
5.1 Lower bounds for the Siegel modular form of weight
 $10$
in degree
$10$
in degree
 $2$
$2$
The contribution of the infinite places to the Faltings height in Theorem 4.5 involves the Siegel modular form
![]() $\unicode[STIX]{x1D712}_{10}$
of weight
$\unicode[STIX]{x1D712}_{10}$
of weight
![]() $10$
and degree
$10$
and degree
![]() $2$
defined in (4.2). A lower bound for the modulus of
$2$
defined in (4.2). A lower bound for the modulus of
![]() $\unicode[STIX]{x1D712}_{10}$
can be used to bound the height from below.
$\unicode[STIX]{x1D712}_{10}$
can be used to bound the height from below.
In this section the period matrix
![]() $Z$
lies in Siegel’s fundamental domain
$Z$
lies in Siegel’s fundamental domain
![]() ${\mathcal{F}}_{2}$
described in § 2.
${\mathcal{F}}_{2}$
described in § 2.
The modular form
![]() $\unicode[STIX]{x1D712}_{10}$
vanishes at those elements
$\unicode[STIX]{x1D712}_{10}$
vanishes at those elements
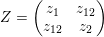 $$\begin{eqnarray}Z=\left(\begin{array}{@{}cc@{}}z_{1} & z_{12}\\ z_{12} & z_{2}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}Z=\left(\begin{array}{@{}cc@{}}z_{1} & z_{12}\\ z_{12} & z_{2}\end{array}\right)\end{eqnarray}$$
of
![]() ${\mathcal{F}}_{2}$
for which
${\mathcal{F}}_{2}$
for which
![]() $z_{12}$
vanishes and only at those; cf. [Reference KlingenKli90, the proof of Proposition 2, § 9]. They correspond to abelian surfaces that are products of elliptic curves; thus, they are not jacobians of genus
$z_{12}$
vanishes and only at those; cf. [Reference KlingenKli90, the proof of Proposition 2, § 9]. They correspond to abelian surfaces that are products of elliptic curves; thus, they are not jacobians of genus
![]() $2$
curves.
$2$
curves.
In the following lemmas we implicitly use techniques from the second-named author’s work [Reference PazukiPaz13] and obtain some minor numerical improvements. We will use
![]() $a$
and
$a$
and
![]() $b$
to denote components of the even characteristic
$b$
to denote components of the even characteristic
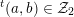 $\text{}^{t}(a,b)\in {\mathcal{Z}}_{2}$
from § 4.4 and abbreviate
$\text{}^{t}(a,b)\in {\mathcal{Z}}_{2}$
from § 4.4 and abbreviate
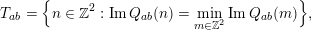 $$\begin{eqnarray}T_{ab}=\Bigl\{\displaystyle n\in \mathbb{Z}^{2}:\operatorname{Im}Q_{ab}(n)=\min _{m\in \mathbb{Z}^{2}}\operatorname{Im}Q_{ab}(m)\Bigr\},\end{eqnarray}$$
$$\begin{eqnarray}T_{ab}=\Bigl\{\displaystyle n\in \mathbb{Z}^{2}:\operatorname{Im}Q_{ab}(n)=\min _{m\in \mathbb{Z}^{2}}\operatorname{Im}Q_{ab}(m)\Bigr\},\end{eqnarray}$$
where
![]() $Q_{ab}$
was defined in (4.1).
$Q_{ab}$
was defined in (4.1).
Lemma 5.1. For all
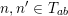 $n,n^{\prime }\in T_{ab}$
, we have
$n,n^{\prime }\in T_{ab}$
, we have
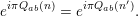 $$\begin{eqnarray}e^{i\unicode[STIX]{x1D70B}Q_{ab}(n)}=e^{i\unicode[STIX]{x1D70B}Q_{ab}(n^{\prime })}.\end{eqnarray}$$
$$\begin{eqnarray}e^{i\unicode[STIX]{x1D70B}Q_{ab}(n)}=e^{i\unicode[STIX]{x1D70B}Q_{ab}(n^{\prime })}.\end{eqnarray}$$
Moreover,
![]() $T_{ab}$
is finite and
$T_{ab}$
is finite and
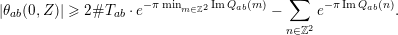 $$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 2\#T_{ab}\cdot e^{-\unicode[STIX]{x1D70B}\min _{m\in \mathbb{Z}^{2}}\operatorname{Im}Q_{ab}(m)}-\mathop{\sum }_{n\in \mathbb{Z}^{2}}e^{-\unicode[STIX]{x1D70B}\operatorname{Im}Q_{ab}(n)}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 2\#T_{ab}\cdot e^{-\unicode[STIX]{x1D70B}\min _{m\in \mathbb{Z}^{2}}\operatorname{Im}Q_{ab}(m)}-\mathop{\sum }_{n\in \mathbb{Z}^{2}}e^{-\unicode[STIX]{x1D70B}\operatorname{Im}Q_{ab}(n)}.\end{eqnarray}$$
Proof. This is [Reference PazukiPaz13, Lemma 4.18]. ◻
Lemma 5.2. If
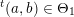 $\text{}^{t}(a,b)\in \unicode[STIX]{x1D6E9}_{1}$
, i.e.,
$\text{}^{t}(a,b)\in \unicode[STIX]{x1D6E9}_{1}$
, i.e.,
![]() $a=0$
, one has
$a=0$
, one has
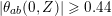 $$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 0.44\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 0.44\end{eqnarray}$$
for all
![]() $Z\in {\mathcal{F}}_{2}$
.
$Z\in {\mathcal{F}}_{2}$
.
Proof. This follows from [Reference PazukiPaz13, Proposition 4.19]. ◻
Lemma 5.3. If
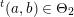 $\text{}^{t}(a,b)\in \unicode[STIX]{x1D6E9}_{2}$
with
$\text{}^{t}(a,b)\in \unicode[STIX]{x1D6E9}_{2}$
with
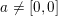 $a\not =[0,0]$
and
$a\not =[0,0]$
and
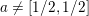 $a\not =[1/2,1/2]$
, one has
$a\not =[1/2,1/2]$
, one has
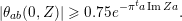 $$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 0.75e^{-\unicode[STIX]{x1D70B}\text{}^{t}a\operatorname{Im}Za}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 0.75e^{-\unicode[STIX]{x1D70B}\text{}^{t}a\operatorname{Im}Za}.\end{eqnarray}$$
Proof. This follows from [Reference PazukiPaz13, Proposition 4.20]. ◻
The crucial case is
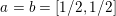 $a=b=[1/2,1/2]$
as the corresponding theta constant vanishes on diagonal matrices in Siegel’s fundamental domain.
$a=b=[1/2,1/2]$
as the corresponding theta constant vanishes on diagonal matrices in Siegel’s fundamental domain.
Lemma 5.4. If
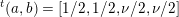 $\text{}^{t}(a,b)=[1/2,1/2,\unicode[STIX]{x1D708}/2,\unicode[STIX]{x1D708}/2]$
with
$\text{}^{t}(a,b)=[1/2,1/2,\unicode[STIX]{x1D708}/2,\unicode[STIX]{x1D708}/2]$
with
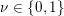 $\unicode[STIX]{x1D708}\in \{0,1\}$
, one has
$\unicode[STIX]{x1D708}\in \{0,1\}$
, one has
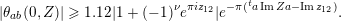 $$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 1.12|1+(-1)^{\unicode[STIX]{x1D708}}e^{\unicode[STIX]{x1D70B}iz_{12}}|e^{-\unicode[STIX]{x1D70B}(\text{}^{t}a\operatorname{Im}Za-\operatorname{Im}z_{12})}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D703}_{ab}(0,Z)|\geqslant 1.12|1+(-1)^{\unicode[STIX]{x1D708}}e^{\unicode[STIX]{x1D70B}iz_{12}}|e^{-\unicode[STIX]{x1D70B}(\text{}^{t}a\operatorname{Im}Za-\operatorname{Im}z_{12})}.\end{eqnarray}$$
Proof. This follows from [Reference PazukiPaz13, Proposition 4.22] and from
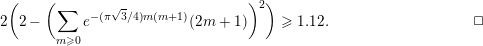 $$\begin{eqnarray}2\biggl(2-\biggl(\mathop{\sum }_{m\geqslant 0}e^{-(\unicode[STIX]{x1D70B}\sqrt{3}/4)m(m+1)}(2m+1)\biggr)^{2}\biggr)\geqslant 1.12.\square\end{eqnarray}$$
$$\begin{eqnarray}2\biggl(2-\biggl(\mathop{\sum }_{m\geqslant 0}e^{-(\unicode[STIX]{x1D70B}\sqrt{3}/4)m(m+1)}(2m+1)\biggr)^{2}\biggr)\geqslant 1.12.\square\end{eqnarray}$$
Lemma 5.5. Let
![]() $z$
be a complex number with
$z$
be a complex number with
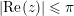 $|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
. Then
$|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
. Then
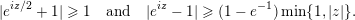 $$\begin{eqnarray}\displaystyle |e^{iz/2}+1|\geqslant 1\quad \text{and}\quad \displaystyle |e^{iz}-1|\geqslant (1-e^{-1})\min \{1,|z|\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |e^{iz/2}+1|\geqslant 1\quad \text{and}\quad \displaystyle |e^{iz}-1|\geqslant (1-e^{-1})\min \{1,|z|\}.\end{eqnarray}$$
Proof. The first inequality follows from
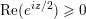 $\operatorname{Re}(e^{iz/2})\geqslant 0$
. For the second inequality, we note that
$\operatorname{Re}(e^{iz/2})\geqslant 0$
. For the second inequality, we note that
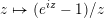 $z\mapsto (e^{iz}-1)/z$
is entire and does not vanish if
$z\mapsto (e^{iz}-1)/z$
is entire and does not vanish if
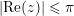 $|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
and
$|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
and
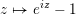 $z\mapsto e^{iz}-1$
does not vanish if
$z\mapsto e^{iz}-1$
does not vanish if
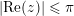 $|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
and
$|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
and
![]() $|z|\geqslant 1$
. By the maximum modulus principle applied to the reciprocals, we deduce that the minimum of
$|z|\geqslant 1$
. By the maximum modulus principle applied to the reciprocals, we deduce that the minimum of
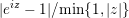 $|e^{iz}-1|/\text{min}\{1,|z|\}$
subject to
$|e^{iz}-1|/\text{min}\{1,|z|\}$
subject to
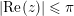 $|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
is attained on
$|\text{Re}(z)|\leqslant \unicode[STIX]{x1D70B}$
is attained on
![]() $|z|=1$
or
$|z|=1$
or
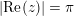 $|\text{Re}(z)|=\unicode[STIX]{x1D70B}$
. In the latter case the quotient is
$|\text{Re}(z)|=\unicode[STIX]{x1D70B}$
. In the latter case the quotient is
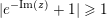 $|e^{-\text{Im}(z)}+1|\geqslant 1$
, which is better than the claim. Let us now suppose that
$|e^{-\text{Im}(z)}+1|\geqslant 1$
, which is better than the claim. Let us now suppose that
![]() $|z|=1$
. We assume that
$|z|=1$
. We assume that
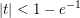 $|t|<1-e^{-1}$
with
$|t|<1-e^{-1}$
with
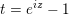 $t=e^{iz}-1$
; this will lead to a contradiction and will thus complete this proof. The logarithm
$t=e^{iz}-1$
; this will lead to a contradiction and will thus complete this proof. The logarithm
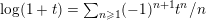 $\log (1+t)=\sum _{n\geqslant 1}(-1)^{n+1}t^{n}/n$
converges and satisfies
$\log (1+t)=\sum _{n\geqslant 1}(-1)^{n+1}t^{n}/n$
converges and satisfies
 $e^{\log (1+t)}=1+t=e^{iz}$
. So,
$e^{\log (1+t)}=1+t=e^{iz}$
. So,
 $\log (1+t)=iz+2\unicode[STIX]{x1D70B}ik$
for an integer
$\log (1+t)=iz+2\unicode[STIX]{x1D70B}ik$
for an integer
![]() $k$
. We bound the modulus of
$k$
. We bound the modulus of
 $\log (1+t)$
from above using the triangle inequality and obtain
$\log (1+t)$
from above using the triangle inequality and obtain
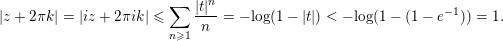 $$\begin{eqnarray}|z+2\unicode[STIX]{x1D70B}k|=|iz+2\unicode[STIX]{x1D70B}ik|\leqslant \mathop{\sum }_{n\geqslant 1}\frac{|t|^{n}}{n}=-\text{log}(1-|t|)<-\text{log}(1-(1-e^{-1}))=1.\end{eqnarray}$$
$$\begin{eqnarray}|z+2\unicode[STIX]{x1D70B}k|=|iz+2\unicode[STIX]{x1D70B}ik|\leqslant \mathop{\sum }_{n\geqslant 1}\frac{|t|^{n}}{n}=-\text{log}(1-|t|)<-\text{log}(1-(1-e^{-1}))=1.\end{eqnarray}$$
This is impossible since
![]() $|z|=1$
.◻
$|z|=1$
.◻
The next proposition combines the previous lemmas.
Proposition 5.6. For any
![]() $Z\in {\mathcal{F}}_{2}$
as in (5.1), one has
$Z\in {\mathcal{F}}_{2}$
as in (5.1), one has
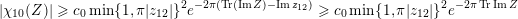 $$\begin{eqnarray}|\unicode[STIX]{x1D712}_{10}(Z)|\geqslant c_{0}\min \{1,\unicode[STIX]{x1D70B}|z_{12}|\}^{2}e^{-2\unicode[STIX]{x1D70B}(\operatorname{Tr}(\operatorname{Im}Z)-\operatorname{Im}z_{12})}\geqslant c_{0}\min \{1,\unicode[STIX]{x1D70B}|z_{12}|\}^{2}e^{-2\unicode[STIX]{x1D70B}\operatorname{Tr}\operatorname{Im}Z}\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D712}_{10}(Z)|\geqslant c_{0}\min \{1,\unicode[STIX]{x1D70B}|z_{12}|\}^{2}e^{-2\unicode[STIX]{x1D70B}(\operatorname{Tr}(\operatorname{Im}Z)-\operatorname{Im}z_{12})}\geqslant c_{0}\min \{1,\unicode[STIX]{x1D70B}|z_{12}|\}^{2}e^{-2\unicode[STIX]{x1D70B}\operatorname{Tr}\operatorname{Im}Z}\end{eqnarray}$$
with
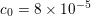 $c_{0}=8\times 10^{-5}$
.
$c_{0}=8\times 10^{-5}$
.
Proof. We use Lemmas 5.2–5.4 in connection with the definition (4.2) to obtain
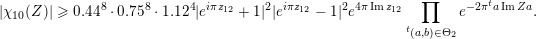 $$\begin{eqnarray}|\unicode[STIX]{x1D712}_{10}(Z)|\geqslant 0.44^{8}\cdot 0.75^{8}\cdot 1.12^{4}|e^{i\unicode[STIX]{x1D70B}z_{12}}+1|^{2}|e^{i\unicode[STIX]{x1D70B}z_{12}}-1|^{2}e^{4\unicode[STIX]{x1D70B}\operatorname{Im}z_{12}}\mathop{\prod }_{\text{}^{t}(a,b)\in \unicode[STIX]{x1D6E9}_{2}}e^{-2\unicode[STIX]{x1D70B}\text{}^{t}a\operatorname{Im}Za}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D712}_{10}(Z)|\geqslant 0.44^{8}\cdot 0.75^{8}\cdot 1.12^{4}|e^{i\unicode[STIX]{x1D70B}z_{12}}+1|^{2}|e^{i\unicode[STIX]{x1D70B}z_{12}}-1|^{2}e^{4\unicode[STIX]{x1D70B}\operatorname{Im}z_{12}}\mathop{\prod }_{\text{}^{t}(a,b)\in \unicode[STIX]{x1D6E9}_{2}}e^{-2\unicode[STIX]{x1D70B}\text{}^{t}a\operatorname{Im}Za}.\end{eqnarray}$$
Observe that
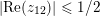 $|\text{Re}(z_{12})|\leqslant 1/2$
. The first inequality in the assertion follows from this, Lemma 5.5 applied to
$|\text{Re}(z_{12})|\leqslant 1/2$
. The first inequality in the assertion follows from this, Lemma 5.5 applied to
![]() $2\unicode[STIX]{x1D70B}z_{12}$
and
$2\unicode[STIX]{x1D70B}z_{12}$
and
![]() $\unicode[STIX]{x1D70B}z_{12}$
, and since the product over
$\unicode[STIX]{x1D70B}z_{12}$
, and since the product over
![]() $\unicode[STIX]{x1D6E9}_{2}$
equals
$\unicode[STIX]{x1D6E9}_{2}$
equals
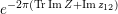 $e^{-2\unicode[STIX]{x1D70B}(\operatorname{Tr}\operatorname{Im}Z+\operatorname{Im}z_{12})}$
. The second inequality follows as
$e^{-2\unicode[STIX]{x1D70B}(\operatorname{Tr}\operatorname{Im}Z+\operatorname{Im}z_{12})}$
. The second inequality follows as
![]() $Z\in {\mathcal{F}}_{2}$
entails
$Z\in {\mathcal{F}}_{2}$
entails
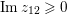 $\operatorname{Im}z_{12}\geqslant 0$
.◻
$\operatorname{Im}z_{12}\geqslant 0$
.◻
5.2 Subconvexity
Let
![]() $K$
be a number field. Say
$K$
be a number field. Say
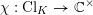 $\unicode[STIX]{x1D712}:\operatorname{Cl}_{K}\rightarrow \mathbb{C}^{\times }$
is a character of the class group. We may also think of
$\unicode[STIX]{x1D712}:\operatorname{Cl}_{K}\rightarrow \mathbb{C}^{\times }$
is a character of the class group. We may also think of
![]() $\unicode[STIX]{x1D712}$
as a Hecke character of conductor
$\unicode[STIX]{x1D712}$
as a Hecke character of conductor
![]() ${\mathcal{O}}_{K}$
. The
${\mathcal{O}}_{K}$
. The
![]() $L$
-series attached to the character
$L$
-series attached to the character
![]() $\unicode[STIX]{x1D712}$
is
$\unicode[STIX]{x1D712}$
is
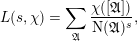 $$\begin{eqnarray}L(s,\unicode[STIX]{x1D712})=\mathop{\sum }_{\mathfrak{A}}\frac{\unicode[STIX]{x1D712}([\mathfrak{A}])}{\text{N}(\mathfrak{A})^{s}},\end{eqnarray}$$
$$\begin{eqnarray}L(s,\unicode[STIX]{x1D712})=\mathop{\sum }_{\mathfrak{A}}\frac{\unicode[STIX]{x1D712}([\mathfrak{A}])}{\text{N}(\mathfrak{A})^{s}},\end{eqnarray}$$
where here and below we sum over non-zero ideals
![]() $\mathfrak{A}$
of
$\mathfrak{A}$
of
![]() ${\mathcal{O}}_{K}$
.
${\mathcal{O}}_{K}$
.
It is well known that this Dirichlet series determines a meromorphic function on
![]() $\mathbb{C}$
with at most a simple pole at
$\mathbb{C}$
with at most a simple pole at
![]() $s=1$
if
$s=1$
if
![]() $\unicode[STIX]{x1D712}$
is the trivial character.
$\unicode[STIX]{x1D712}$
is the trivial character.
The following subconvexity estimate follows from Michel and Venkatesh’s deep Theorem 1.1 [Reference Michel and VenkateshMV10].
Theorem 5.7. Let
![]() $F$
be a totally real number field. There exist constants
$F$
be a totally real number field. There exist constants
 $c_{1}>0,N>0$
, and
$c_{1}>0,N>0$
, and
 $\unicode[STIX]{x1D6FF}\in (0,1/4)$
depending on
$\unicode[STIX]{x1D6FF}\in (0,1/4)$
depending on
![]() $F$
with the following property. If
$F$
with the following property. If
![]() $K/F$
is an imaginary quadratic extension and
$K/F$
is an imaginary quadratic extension and
 $\unicode[STIX]{x1D712}:\operatorname{Cl}_{K}\rightarrow \mathbb{C}^{\times }$
is a character, then
$\unicode[STIX]{x1D712}:\operatorname{Cl}_{K}\rightarrow \mathbb{C}^{\times }$
is a character, then
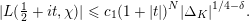 $$\begin{eqnarray}|L({\textstyle \frac{1}{2}}+it,\unicode[STIX]{x1D712})|\leqslant c_{1}(1+|t|)^{N}|\unicode[STIX]{x1D6E5}_{K}|^{1/4-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}|L({\textstyle \frac{1}{2}}+it,\unicode[STIX]{x1D712})|\leqslant c_{1}(1+|t|)^{N}|\unicode[STIX]{x1D6E5}_{K}|^{1/4-\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
The following lemma involves a well-known trick in analytic number theory; cf. work of Duke et al. [Reference Iwaniec, Duke and FriedlanderID02, p. 574]. We shift a contour integral into the critical strip and apply the subconvexity result cited above.
Lemma 5.8. Let
![]() $F$
be a totally real number field and let
$F$
be a totally real number field and let
![]() $\unicode[STIX]{x1D6FF}$
be from Theorem 5.7. There is a constant
$\unicode[STIX]{x1D6FF}$
be from Theorem 5.7. There is a constant
![]() $c_{2}>0$
depending only on
$c_{2}>0$
depending only on
![]() $F$
with the following property. Say
$F$
with the following property. Say
![]() $K$
is a totally imaginary quadratic extension of
$K$
is a totally imaginary quadratic extension of
![]() $F$
and let
$F$
and let
![]() $H$
be a coset of a subgroup of
$H$
be a coset of a subgroup of
![]() $\operatorname{Cl}_{K}$
. If
$\operatorname{Cl}_{K}$
. If
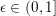 $\unicode[STIX]{x1D716}\in (0,1]$
and
$\unicode[STIX]{x1D716}\in (0,1]$
and
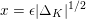 $x=\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
, then
$x=\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
, then
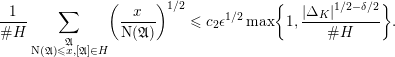 $$\begin{eqnarray}\frac{1}{\#H}\mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{1/2}\leqslant c_{2}\unicode[STIX]{x1D716}^{1/2}\max \biggl\{1,\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\#H}\mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{1/2}\leqslant c_{2}\unicode[STIX]{x1D716}^{1/2}\max \biggl\{1,\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}.\end{eqnarray}$$
Proof. We fix a smooth test function
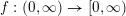 $f:(0,\infty )\rightarrow [0,\infty )$
that satisfies
$f:(0,\infty )\rightarrow [0,\infty )$
that satisfies
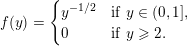 $$\begin{eqnarray}f(y)=\left\{\begin{array}{@{}ll@{}}y^{-1/2}\quad & \text{if}\;y\in (0,1],\\ 0\quad & \text{if}\;y\geqslant 2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f(y)=\left\{\begin{array}{@{}ll@{}}y^{-1/2}\quad & \text{if}\;y\in (0,1],\\ 0\quad & \text{if}\;y\geqslant 2.\end{array}\right.\end{eqnarray}$$
Its Mellin transform
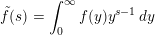 $$\begin{eqnarray}\tilde{f}(s)=\int _{0}^{\infty }f(y)y^{s-1}\,dy\end{eqnarray}$$
$$\begin{eqnarray}\tilde{f}(s)=\int _{0}^{\infty }f(y)y^{s-1}\,dy\end{eqnarray}$$
exists if
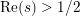 $\operatorname{Re}(s)>1/2$
and the Mellin inversion formula holds; cf. [Reference CohenCoh07, Proposition 9.7.7]. Using in addition [Reference CohenCoh07, Theorem 9.7.5(4)], we see that
$\operatorname{Re}(s)>1/2$
and the Mellin inversion formula holds; cf. [Reference CohenCoh07, Proposition 9.7.7]. Using in addition [Reference CohenCoh07, Theorem 9.7.5(4)], we see that
![]() $\tilde{f}$
decays rapidly; here this means that if
$\tilde{f}$
decays rapidly; here this means that if
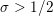 $\unicode[STIX]{x1D70E}>1/2$
is fixed and
$\unicode[STIX]{x1D70E}>1/2$
is fixed and
![]() $N\geqslant 1$
, then
$N\geqslant 1$
, then
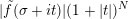 $|\tilde{f}(\unicode[STIX]{x1D70E}+it)|(1+|t|)^{N}$
is a bounded function in
$|\tilde{f}(\unicode[STIX]{x1D70E}+it)|(1+|t|)^{N}$
is a bounded function in
![]() $t\in \mathbb{R}$
.
$t\in \mathbb{R}$
.
For a real number
![]() $x>0$
and a character
$x>0$
and a character
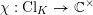 $\unicode[STIX]{x1D712}:\operatorname{Cl}_{K}\rightarrow \mathbb{C}^{\times }$
, we define
$\unicode[STIX]{x1D712}:\operatorname{Cl}_{K}\rightarrow \mathbb{C}^{\times }$
, we define
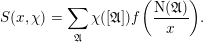 $$\begin{eqnarray}S(x,\unicode[STIX]{x1D712})=\mathop{\sum }_{\mathfrak{A}}\unicode[STIX]{x1D712}([\mathfrak{A}])f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}S(x,\unicode[STIX]{x1D712})=\mathop{\sum }_{\mathfrak{A}}\unicode[STIX]{x1D712}([\mathfrak{A}])f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr).\end{eqnarray}$$
The sum is finite since
![]() $f$
vanishes at large arguments. If
$f$
vanishes at large arguments. If
![]() $\unicode[STIX]{x1D70E}\in \mathbb{R}$
, then
$\unicode[STIX]{x1D70E}\in \mathbb{R}$
, then
![]() $\int _{(\unicode[STIX]{x1D70E})}$
signifies the integral along the vertical line
$\int _{(\unicode[STIX]{x1D70E})}$
signifies the integral along the vertical line
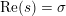 $\operatorname{Re}(s)=\unicode[STIX]{x1D70E}$
. The Mellin inversion formula leads to
$\operatorname{Re}(s)=\unicode[STIX]{x1D70E}$
. The Mellin inversion formula leads to
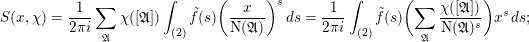 $$\begin{eqnarray}\displaystyle S(x,\unicode[STIX]{x1D712})=\frac{1}{2\unicode[STIX]{x1D70B}i}\mathop{\sum }_{\mathfrak{A}}\unicode[STIX]{x1D712}([\mathfrak{A}])\int _{(2)}\tilde{f}(s)\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{s}\,ds=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(2)}\tilde{f}(s)\biggl(\mathop{\sum }_{\mathfrak{A}}\frac{\unicode[STIX]{x1D712}([\mathfrak{A}])}{\text{N}(\mathfrak{A})^{s}}\biggr)x^{s}\,ds; & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(x,\unicode[STIX]{x1D712})=\frac{1}{2\unicode[STIX]{x1D70B}i}\mathop{\sum }_{\mathfrak{A}}\unicode[STIX]{x1D712}([\mathfrak{A}])\int _{(2)}\tilde{f}(s)\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{s}\,ds=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(2)}\tilde{f}(s)\biggl(\mathop{\sum }_{\mathfrak{A}}\frac{\unicode[STIX]{x1D712}([\mathfrak{A}])}{\text{N}(\mathfrak{A})^{s}}\biggr)x^{s}\,ds; & & \displaystyle \nonumber\end{eqnarray}$$
the sum and the integral commute by the dominant convergence theorem. The inner sum is the
![]() $L$
-function
$L$
-function
![]() $L(s,\unicode[STIX]{x1D712})$
and hence
$L(s,\unicode[STIX]{x1D712})$
and hence
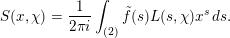 $$\begin{eqnarray}S(x,\unicode[STIX]{x1D712})=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(2)}\tilde{f}(s)L(s,\unicode[STIX]{x1D712})x^{s}\,ds.\end{eqnarray}$$
$$\begin{eqnarray}S(x,\unicode[STIX]{x1D712})=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(2)}\tilde{f}(s)L(s,\unicode[STIX]{x1D712})x^{s}\,ds.\end{eqnarray}$$
Let
![]() $H_{0}$
denote the translate of
$H_{0}$
denote the translate of
![]() $H$
containing the unit element; it is a subgroup of
$H$
containing the unit element; it is a subgroup of
![]() $\operatorname{Cl}_{K}$
. Suppose that
$\operatorname{Cl}_{K}$
. Suppose that
![]() $\unicode[STIX]{x1D712}$
is any character with
$\unicode[STIX]{x1D712}$
is any character with
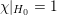 $\unicode[STIX]{x1D712}|_{H_{0}}=1$
. The function
$\unicode[STIX]{x1D712}|_{H_{0}}=1$
. The function
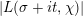 $|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712})|$
has at most polynomial growth in the imaginary part
$|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712})|$
has at most polynomial growth in the imaginary part
![]() $t$
if
$t$
if
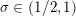 $\unicode[STIX]{x1D70E}\in (1/2,1)$
is fixed. By a contour shift and by the decay property of
$\unicode[STIX]{x1D70E}\in (1/2,1)$
is fixed. By a contour shift and by the decay property of
![]() $\tilde{f}$
, we arrive at
$\tilde{f}$
, we arrive at
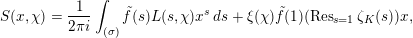 $$\begin{eqnarray}S(x,\unicode[STIX]{x1D712})=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(\unicode[STIX]{x1D70E})}\tilde{f}(s)L(s,\unicode[STIX]{x1D712})x^{s}\,ds+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})\tilde{f}(1)(\operatorname{Res}_{s=1}\unicode[STIX]{x1D701}_{K}(s))x,\end{eqnarray}$$
$$\begin{eqnarray}S(x,\unicode[STIX]{x1D712})=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(\unicode[STIX]{x1D70E})}\tilde{f}(s)L(s,\unicode[STIX]{x1D712})x^{s}\,ds+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})\tilde{f}(1)(\operatorname{Res}_{s=1}\unicode[STIX]{x1D701}_{K}(s))x,\end{eqnarray}$$
where
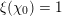 $\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712}_{0})=1$
for
$\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712}_{0})=1$
for
![]() $\unicode[STIX]{x1D712}_{0}$
the trivial character and
$\unicode[STIX]{x1D712}_{0}$
the trivial character and
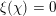 $\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})=0$
if
$\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})=0$
if
![]() $\unicode[STIX]{x1D712}\not =\unicode[STIX]{x1D712}_{0}$
.
$\unicode[STIX]{x1D712}\not =\unicode[STIX]{x1D712}_{0}$
.
Here and below
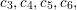 $c_{3},c_{4},c_{5},c_{6},$
and
$c_{3},c_{4},c_{5},c_{6},$
and
![]() $c_{7}$
denote positive constants that depend only on
$c_{7}$
denote positive constants that depend only on
![]() $F,f,\unicode[STIX]{x1D6FF}$
, and
$F,f,\unicode[STIX]{x1D6FF}$
, and
![]() $\unicode[STIX]{x1D70E}$
but not on
$\unicode[STIX]{x1D70E}$
but not on
![]() $K,\unicode[STIX]{x1D712},\unicode[STIX]{x1D716},$
or
$K,\unicode[STIX]{x1D712},\unicode[STIX]{x1D716},$
or
![]() $H$
.
$H$
.
Let
![]() $h_{K}$
denote the class number of
$h_{K}$
denote the class number of
![]() $K$
,
$K$
,
![]() $R_{K}$
the regulator of
$R_{K}$
the regulator of
![]() $K$
, and
$K$
, and
![]() $\unicode[STIX]{x1D714}_{K}$
the number of roots of unity in
$\unicode[STIX]{x1D714}_{K}$
the number of roots of unity in
![]() $K$
. The residue of
$K$
. The residue of
![]() $\unicode[STIX]{x1D701}_{K}$
at
$\unicode[STIX]{x1D701}_{K}$
at
![]() $s=1$
is positive and at most
$s=1$
is positive and at most
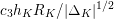 $c_{3}h_{K}R_{K}/|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
by the analytic class number formula. The unit groups of
$c_{3}h_{K}R_{K}/|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
by the analytic class number formula. The unit groups of
![]() $K$
and
$K$
and
![]() $F$
have equal rank. As in the proof of Lemma 3.11, we have
$F$
have equal rank. As in the proof of Lemma 3.11, we have
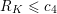 $R_{K}\leqslant c_{4}$
, where
$R_{K}\leqslant c_{4}$
, where
![]() $c_{4}$
may depend on
$c_{4}$
may depend on
![]() $F$
. Hence,
$F$
. Hence,
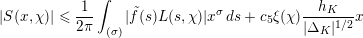 $$\begin{eqnarray}|S(x,\unicode[STIX]{x1D712})|\leqslant \frac{1}{2\unicode[STIX]{x1D70B}}\int _{(\unicode[STIX]{x1D70E})}|\tilde{f}(s)L(s,\unicode[STIX]{x1D712})|x^{\unicode[STIX]{x1D70E}}\,ds+c_{5}\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})\frac{h_{K}}{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}x\end{eqnarray}$$
$$\begin{eqnarray}|S(x,\unicode[STIX]{x1D712})|\leqslant \frac{1}{2\unicode[STIX]{x1D70B}}\int _{(\unicode[STIX]{x1D70E})}|\tilde{f}(s)L(s,\unicode[STIX]{x1D712})|x^{\unicode[STIX]{x1D70E}}\,ds+c_{5}\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})\frac{h_{K}}{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}x\end{eqnarray}$$
with
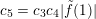 $c_{5}=c_{3}c_{4}|\tilde{f}(1)|$
.
$c_{5}=c_{3}c_{4}|\tilde{f}(1)|$
.
Soon we will apply the Phragmén–Lindelöf principle, cf. [Reference Iwaniec and KowalskiIK04, Theorem 5.53], to bound
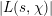 $|L(s,\unicode[STIX]{x1D712})|$
from above in terms of
$|L(s,\unicode[STIX]{x1D712})|$
from above in terms of
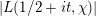 $|L(1/2+it,\unicode[STIX]{x1D712})|$
and
$|L(1/2+it,\unicode[STIX]{x1D712})|$
and
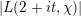 $|L(2+it,\unicode[STIX]{x1D712})|$
; here
$|L(2+it,\unicode[STIX]{x1D712})|$
; here
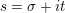 $s=\unicode[STIX]{x1D70E}+it$
. Indeed, the bound
$s=\unicode[STIX]{x1D70E}+it$
. Indeed, the bound
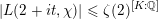 $|L(2+it,\unicode[STIX]{x1D712})|\leqslant \unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}]}$
is elementary but to bound
$|L(2+it,\unicode[STIX]{x1D712})|\leqslant \unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}]}$
is elementary but to bound
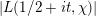 $|L(1/2+it,\unicode[STIX]{x1D712})|$
we need Theorem 5.7. We abbreviate
$|L(1/2+it,\unicode[STIX]{x1D712})|$
we need Theorem 5.7. We abbreviate
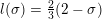 $$\begin{eqnarray}l(\unicode[STIX]{x1D70E})={\textstyle \frac{2}{3}}(2-\unicode[STIX]{x1D70E})\end{eqnarray}$$
$$\begin{eqnarray}l(\unicode[STIX]{x1D70E})={\textstyle \frac{2}{3}}(2-\unicode[STIX]{x1D70E})\end{eqnarray}$$
whose graph linearly interpolates
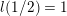 $l(1/2)=1$
and
$l(1/2)=1$
and
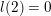 $l(2)=0$
.
$l(2)=0$
.
We suppose first that
![]() $\unicode[STIX]{x1D712}\not =\unicode[STIX]{x1D712}_{0}$
. Then
$\unicode[STIX]{x1D712}\not =\unicode[STIX]{x1D712}_{0}$
. Then
![]() $L(\cdot ,\unicode[STIX]{x1D712})$
is an entire function and we may apply the Phragmén–Lindelöf principle directly. So,
$L(\cdot ,\unicode[STIX]{x1D712})$
is an entire function and we may apply the Phragmén–Lindelöf principle directly. So,
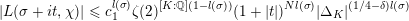 $$\begin{eqnarray}|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712})|\leqslant c_{1}^{l(\unicode[STIX]{x1D70E})}\unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}](1-l(\unicode[STIX]{x1D70E}))}(1+|t|)^{Nl(\unicode[STIX]{x1D70E})}|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})}\end{eqnarray}$$
$$\begin{eqnarray}|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712})|\leqslant c_{1}^{l(\unicode[STIX]{x1D70E})}\unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}](1-l(\unicode[STIX]{x1D70E}))}(1+|t|)^{Nl(\unicode[STIX]{x1D70E})}|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})}\end{eqnarray}$$
for all
![]() $t\in \mathbb{R}$
, where we may assume that
$t\in \mathbb{R}$
, where we may assume that
![]() $c_{1}\geqslant 1$
. To treat the trivial character, we work with the entire function
$c_{1}\geqslant 1$
. To treat the trivial character, we work with the entire function
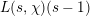 $L(s,\unicode[STIX]{x1D712})(s-1)$
. As
$L(s,\unicode[STIX]{x1D712})(s-1)$
. As
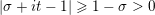 $|\unicode[STIX]{x1D70E}+it-1|\geqslant 1-\unicode[STIX]{x1D70E}>0$
, we obtain
$|\unicode[STIX]{x1D70E}+it-1|\geqslant 1-\unicode[STIX]{x1D70E}>0$
, we obtain
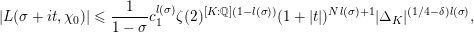 $$\begin{eqnarray}|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712}_{0})|\leqslant \frac{1}{1-\unicode[STIX]{x1D70E}}c_{1}^{l(\unicode[STIX]{x1D70E})}\unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}](1-l(\unicode[STIX]{x1D70E}))}(1+|t|)^{Nl(\unicode[STIX]{x1D70E})+1}|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})},\end{eqnarray}$$
$$\begin{eqnarray}|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712}_{0})|\leqslant \frac{1}{1-\unicode[STIX]{x1D70E}}c_{1}^{l(\unicode[STIX]{x1D70E})}\unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}](1-l(\unicode[STIX]{x1D70E}))}(1+|t|)^{Nl(\unicode[STIX]{x1D70E})+1}|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})},\end{eqnarray}$$
where the additional
![]() $1+|t|$
appears since
$1+|t|$
appears since
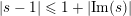 $|s-1|\leqslant 1+|\text{Im}(s)|$
if
$|s-1|\leqslant 1+|\text{Im}(s)|$
if
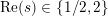 $\operatorname{Re}(s)\in \{1/2,2\}$
.
$\operatorname{Re}(s)\in \{1/2,2\}$
.
In any case, we have
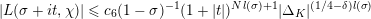 $|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712})|\leqslant c_{6}(1-\unicode[STIX]{x1D70E})^{-1}(1+|t|)^{Nl(\unicode[STIX]{x1D70E})+1}|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})}$
with
$|L(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D712})|\leqslant c_{6}(1-\unicode[STIX]{x1D70E})^{-1}(1+|t|)^{Nl(\unicode[STIX]{x1D70E})+1}|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})}$
with
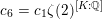 $c_{6}=c_{1}\unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}]}$
. Together with (5.5) and the decay property of
$c_{6}=c_{1}\unicode[STIX]{x1D701}(2)^{[K:\mathbb{Q}]}$
. Together with (5.5) and the decay property of
![]() $\tilde{f}$
, we obtain
$\tilde{f}$
, we obtain
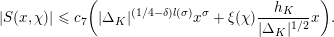 $$\begin{eqnarray}|S(x,\unicode[STIX]{x1D712})|\leqslant c_{7}\biggl(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})}x^{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})\frac{h_{K}}{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}x\biggr).\end{eqnarray}$$
$$\begin{eqnarray}|S(x,\unicode[STIX]{x1D712})|\leqslant c_{7}\biggl(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})}x^{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})\frac{h_{K}}{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}x\biggr).\end{eqnarray}$$
We substitute
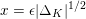 $x=\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
to find
$x=\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
to find
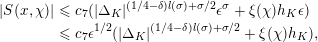 $$\begin{eqnarray}\displaystyle |S(x,\unicode[STIX]{x1D712})| & {\leqslant} & \displaystyle c_{7}(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})h_{K}\unicode[STIX]{x1D716})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c_{7}\unicode[STIX]{x1D716}^{1/2}(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})h_{K}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |S(x,\unicode[STIX]{x1D712})| & {\leqslant} & \displaystyle c_{7}(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})h_{K}\unicode[STIX]{x1D716})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c_{7}\unicode[STIX]{x1D716}^{1/2}(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}+\unicode[STIX]{x1D709}(\unicode[STIX]{x1D712})h_{K}),\end{eqnarray}$$
where we used
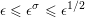 $\unicode[STIX]{x1D716}\leqslant \unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70E}}\leqslant \unicode[STIX]{x1D716}^{1/2}$
as
$\unicode[STIX]{x1D716}\leqslant \unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70E}}\leqslant \unicode[STIX]{x1D716}^{1/2}$
as
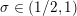 $\unicode[STIX]{x1D70E}\in (1/2,1)$
and
$\unicode[STIX]{x1D70E}\in (1/2,1)$
and
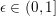 $\unicode[STIX]{x1D716}\in (0,1]$
.
$\unicode[STIX]{x1D716}\in (0,1]$
.
We consider the mean
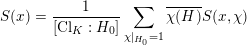 $$\begin{eqnarray}S(x)=\frac{1}{[\operatorname{Cl}_{K}:H_{0}]}\mathop{\sum }_{\unicode[STIX]{x1D712}|_{H_{0}}=1}\overline{\unicode[STIX]{x1D712}(H)}S(x,\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}S(x)=\frac{1}{[\operatorname{Cl}_{K}:H_{0}]}\mathop{\sum }_{\unicode[STIX]{x1D712}|_{H_{0}}=1}\overline{\unicode[STIX]{x1D712}(H)}S(x,\unicode[STIX]{x1D712})\end{eqnarray}$$
over all characters
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\operatorname{Cl}_{K}$
that are constant on
$\operatorname{Cl}_{K}$
that are constant on
![]() $H$
. Since
$H$
. Since
![]() $\unicode[STIX]{x1D712}$
takes values on the unit circle, we may bound
$\unicode[STIX]{x1D712}$
takes values on the unit circle, we may bound
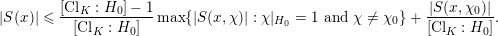 $$\begin{eqnarray}|S(x)|\leqslant \frac{[\operatorname{Cl}_{K}:H_{0}]-1}{[\operatorname{Cl}_{K}:H_{0}]}\max \{|S(x,\unicode[STIX]{x1D712})|:\unicode[STIX]{x1D712}|_{H_{0}}=1\text{ and }\unicode[STIX]{x1D712}\not =\unicode[STIX]{x1D712}_{0}\}+\frac{|S(x,\unicode[STIX]{x1D712}_{0})|}{[\operatorname{Cl}_{K}:H_{0}]}.\end{eqnarray}$$
$$\begin{eqnarray}|S(x)|\leqslant \frac{[\operatorname{Cl}_{K}:H_{0}]-1}{[\operatorname{Cl}_{K}:H_{0}]}\max \{|S(x,\unicode[STIX]{x1D712})|:\unicode[STIX]{x1D712}|_{H_{0}}=1\text{ and }\unicode[STIX]{x1D712}\not =\unicode[STIX]{x1D712}_{0}\}+\frac{|S(x,\unicode[STIX]{x1D712}_{0})|}{[\operatorname{Cl}_{K}:H_{0}]}.\end{eqnarray}$$
We observe that
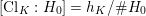 $[\operatorname{Cl}_{K}:H_{0}]=h_{K}/\#H_{0}$
. The bound (5.7) yields
$[\operatorname{Cl}_{K}:H_{0}]=h_{K}/\#H_{0}$
. The bound (5.7) yields
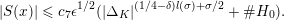 $$\begin{eqnarray}|S(x)|\leqslant c_{7}\unicode[STIX]{x1D716}^{1/2}(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}+\#H_{0}).\end{eqnarray}$$
$$\begin{eqnarray}|S(x)|\leqslant c_{7}\unicode[STIX]{x1D716}^{1/2}(|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}+\#H_{0}).\end{eqnarray}$$
We insert the finite sum (5.4) into (5.8) and rearrange the order of summation to obtain
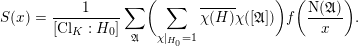 $$\begin{eqnarray}S(x)=\frac{1}{[\operatorname{Cl}_{K}:H_{0}]}\mathop{\sum }_{\mathfrak{A}}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D712}|_{H_{0}}=1}\overline{\unicode[STIX]{x1D712}(H)}\unicode[STIX]{x1D712}([\mathfrak{A}])\biggr)f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}S(x)=\frac{1}{[\operatorname{Cl}_{K}:H_{0}]}\mathop{\sum }_{\mathfrak{A}}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D712}|_{H_{0}}=1}\overline{\unicode[STIX]{x1D712}(H)}\unicode[STIX]{x1D712}([\mathfrak{A}])\biggr)f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr).\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D712}$
from the inner sum, we have
$\unicode[STIX]{x1D712}$
from the inner sum, we have
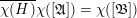 $\overline{\unicode[STIX]{x1D712}(H)}\unicode[STIX]{x1D712}([\mathfrak{A}])=\unicode[STIX]{x1D712}([\mathfrak{B}])$
for a fractional ideal
$\overline{\unicode[STIX]{x1D712}(H)}\unicode[STIX]{x1D712}([\mathfrak{A}])=\unicode[STIX]{x1D712}([\mathfrak{B}])$
for a fractional ideal
![]() $\mathfrak{B}$
with
$\mathfrak{B}$
with
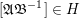 $[\mathfrak{A}\mathfrak{B}^{-1}]\in H$
. But
$[\mathfrak{A}\mathfrak{B}^{-1}]\in H$
. But
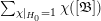 $\sum _{\unicode[STIX]{x1D712}|_{H_{0}}=1}\unicode[STIX]{x1D712}([\mathfrak{B}])$
equals
$\sum _{\unicode[STIX]{x1D712}|_{H_{0}}=1}\unicode[STIX]{x1D712}([\mathfrak{B}])$
equals
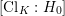 $[\operatorname{Cl}_{K}:H_{0}]$
if
$[\operatorname{Cl}_{K}:H_{0}]$
if
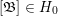 $[\mathfrak{B}]\in H_{0}$
and
$[\mathfrak{B}]\in H_{0}$
and
![]() $0$
otherwise. Hence,
$0$
otherwise. Hence,
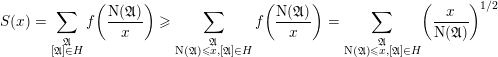 $$\begin{eqnarray}S(x)=\mathop{\sum }_{\substack{ \mathfrak{A} \\ [\mathfrak{A}]\in H}}f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr)\geqslant \mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr)=\mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{1/2}\end{eqnarray}$$
$$\begin{eqnarray}S(x)=\mathop{\sum }_{\substack{ \mathfrak{A} \\ [\mathfrak{A}]\in H}}f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr)\geqslant \mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}f\biggl(\frac{\text{N}(\mathfrak{A})}{x}\biggr)=\mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{1/2}\end{eqnarray}$$
as
![]() $f$
is non-negative and by (5.3). We divide by
$f$
is non-negative and by (5.3). We divide by
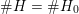 $\#H=\#H_{0}$
and use (5.9) to obtain
$\#H=\#H_{0}$
and use (5.9) to obtain
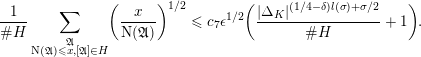 $$\begin{eqnarray}\frac{1}{\#H}\mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{1/2}\leqslant c_{7}\unicode[STIX]{x1D716}^{1/2}\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}}{\#H}+1\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\#H}\mathop{\sum }_{\substack{ \mathfrak{A} \\ \text{N}(\mathfrak{A})\leqslant x,[\mathfrak{A}]\in H}}\biggl(\frac{x}{\text{N}(\mathfrak{A})}\biggr)^{1/2}\leqslant c_{7}\unicode[STIX]{x1D716}^{1/2}\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2}}{\#H}+1\biggr).\end{eqnarray}$$
The lemma follows as we may fix
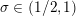 $\unicode[STIX]{x1D70E}\in (1/2,1)$
with
$\unicode[STIX]{x1D70E}\in (1/2,1)$
with
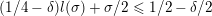 $(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2\leqslant 1/2-\unicode[STIX]{x1D6FF}/2$
.◻
$(1/4-\unicode[STIX]{x1D6FF})l(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D70E}/2\leqslant 1/2-\unicode[STIX]{x1D6FF}/2$
.◻
Next we state two simple consequences of the previous proposition that we need for our main result. Recall that the norm
![]() $\text{N}([\mathfrak{A}])$
of an ideal class in
$\text{N}([\mathfrak{A}])$
of an ideal class in
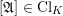 $[\mathfrak{A}]\in \operatorname{Cl}_{K}$
is the smallest norm of a representative.
$[\mathfrak{A}]\in \operatorname{Cl}_{K}$
is the smallest norm of a representative.
Proposition 5.9. Let
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D6FF}$
be as in Lemma 5.8. There is a constant
$\unicode[STIX]{x1D6FF}$
be as in Lemma 5.8. There is a constant
![]() $c_{8}>0$
depending only on
$c_{8}>0$
depending only on
![]() $F$
with the following property. Say
$F$
with the following property. Say
![]() $K$
is a totally imaginary quadratic extension of
$K$
is a totally imaginary quadratic extension of
![]() $F$
and let
$F$
and let
![]() $H$
be a coset of a subgroup of
$H$
be a coset of a subgroup of
![]() $\operatorname{Cl}_{K}$
; then the following two properties hold.
$\operatorname{Cl}_{K}$
; then the following two properties hold.
-
(i) We have
 $$\begin{eqnarray}\frac{1}{\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/2}\leqslant c_{8}\max \biggl\{1,\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\biggl(\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/2}\leqslant c_{8}\max \biggl\{1,\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}.\end{eqnarray}$$
-
(ii) Let
 $\unicode[STIX]{x1D716}\in (0,1]$
; then
$\unicode[STIX]{x1D716}\in (0,1]$
; then  $$\begin{eqnarray}\frac{1}{\#H}\#\{[\mathfrak{A}]\in H:\text{N}([\mathfrak{A}^{-1}])\leqslant \unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}\}\leqslant c_{2}\unicode[STIX]{x1D716}^{1/2}\max \biggl\{1,\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\#H}\#\{[\mathfrak{A}]\in H:\text{N}([\mathfrak{A}^{-1}])\leqslant \unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}\}\leqslant c_{2}\unicode[STIX]{x1D716}^{1/2}\max \biggl\{1,\frac{|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}.\end{eqnarray}$$
Proof. Let
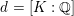 $d=[K:\mathbb{Q}]$
. By a theorem of Minkowski, any ideal class of
$d=[K:\mathbb{Q}]$
. By a theorem of Minkowski, any ideal class of
![]() $K$
is represented by an ideal whose norm is at most
$K$
is represented by an ideal whose norm is at most
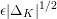 $\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
, where
$\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
, where
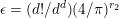 $\unicode[STIX]{x1D716}=(d!/d^{d})(4/\unicode[STIX]{x1D70B})^{r_{2}}$
and
$\unicode[STIX]{x1D716}=(d!/d^{d})(4/\unicode[STIX]{x1D70B})^{r_{2}}$
and
![]() $2r_{2}$
is the number of non-real embeddings
$2r_{2}$
is the number of non-real embeddings
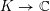 $K\rightarrow \mathbb{C}$
. It is well known that
$K\rightarrow \mathbb{C}$
. It is well known that
![]() $\unicode[STIX]{x1D716}\leqslant 1$
. Part (i) follows from Lemma 5.8 applied to
$\unicode[STIX]{x1D716}\leqslant 1$
. Part (i) follows from Lemma 5.8 applied to
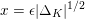 $x=\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
and to the coset
$x=\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
and to the coset
![]() $H^{-1}$
since
$H^{-1}$
since
![]() $\unicode[STIX]{x1D716}$
depends only on
$\unicode[STIX]{x1D716}$
depends only on
![]() $F$
.
$F$
.
Part (ii) follows from Lemma 5.8 applied to
![]() $H^{-1}$
since the terms in the sum on the left of (5.2) are at least
$H^{-1}$
since the terms in the sum on the left of (5.2) are at least
![]() $1$
.◻
$1$
.◻
In our application, the coset
![]() $H$
will generally have more than
$H$
will generally have more than
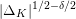 $|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}$
elements. In this case, the upper bound in part (i) simplifies to
$|\unicode[STIX]{x1D6E5}_{K}|^{1/2-\unicode[STIX]{x1D6FF}/2}$
elements. In this case, the upper bound in part (i) simplifies to
![]() $c_{8}$
, which depends only on
$c_{8}$
, which depends only on
![]() $F$
. Also, if
$F$
. Also, if
![]() $\unicode[STIX]{x1D716}$
is sufficiently small in part (ii), then we find that only a small proportion of elements of
$\unicode[STIX]{x1D716}$
is sufficiently small in part (ii), then we find that only a small proportion of elements of
![]() $H^{-1}$
will have norm less than
$H^{-1}$
will have norm less than
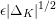 $\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
. Geometrically speaking, these ideal classes correspond to Galois conjugates of a CM abelian variety that lie close to the cusp in the moduli space. So, only a small proportion of said conjugates are near the cusp.
$\unicode[STIX]{x1D716}|\unicode[STIX]{x1D6E5}_{K}|^{1/2}$
. Geometrically speaking, these ideal classes correspond to Galois conjugates of a CM abelian variety that lie close to the cusp in the moduli space. So, only a small proportion of said conjugates are near the cusp.
6 Proof of the theorems
We begin this section by proving Theorems 1.3 and 1.4.
Let
![]() $F$
be a real quadratic field. We fix representatives
$F$
be a real quadratic field. We fix representatives
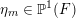 $\unicode[STIX]{x1D702}_{m}\in \mathbb{P}^{1}(F)$
of cusps of
$\unicode[STIX]{x1D702}_{m}\in \mathbb{P}^{1}(F)$
of cusps of
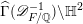 $\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})\backslash \mathbb{H}^{2}$
as in § 3.1. In particular,
$\widehat{\unicode[STIX]{x1D6E4}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})\backslash \mathbb{H}^{2}$
as in § 3.1. In particular,
![]() $\unicode[STIX]{x1D702}_{1}=\infty$
. We will work with a parameter
$\unicode[STIX]{x1D702}_{1}=\infty$
. We will work with a parameter
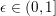 $\unicode[STIX]{x1D716}\in (0,1]$
that depends only on
$\unicode[STIX]{x1D716}\in (0,1]$
that depends only on
![]() $F$
and a second parameter
$F$
and a second parameter
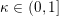 $\unicode[STIX]{x1D705}\in (0,1]$
that depends only on
$\unicode[STIX]{x1D705}\in (0,1]$
that depends only on
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D716}$
. We regard
$\unicode[STIX]{x1D716}$
. We regard
![]() $\unicode[STIX]{x1D705}$
as small with respect to
$\unicode[STIX]{x1D705}$
as small with respect to
![]() $\unicode[STIX]{x1D716}$
. We will see how to fix these parameters in due course.
$\unicode[STIX]{x1D716}$
. We will see how to fix these parameters in due course.
Let
![]() $C$
be as in Theorem 1.4 and suppose that
$C$
be as in Theorem 1.4 and suppose that
![]() $k\subseteq \mathbb{C}$
is a number field over which
$k\subseteq \mathbb{C}$
is a number field over which
![]() $C$
is defined which we will increase at will. Let
$C$
is defined which we will increase at will. Let
![]() $K$
be the CM field of
$K$
be the CM field of
![]() $\operatorname{Jac}(C)$
. We may suppose that
$\operatorname{Jac}(C)$
. We may suppose that
![]() $k\supseteq K$
.
$k\supseteq K$
.
As discussed in greater detail in the introduction, the basic strategy is to let the lower bound coming from Proposition 4.3 compete with an upper bound of the Faltings height. To estimate the Faltings height from above we need its expression in Corollary 4.6. Observe that this corollary is applicable as, after possibly increasing
![]() $k$
, the classical theorem of Serre and Tate [Reference Serre and TateST68] states that the CM abelian variety
$k$
, the classical theorem of Serre and Tate [Reference Serre and TateST68] states that the CM abelian variety
![]() $\operatorname{Jac}(C)$
has good reduction everywhere. We will show that the archimedean contribution to the Faltings height is negligible when compared to the non-archimedean contribution. We use notation introduced in Theorem 4.5 and Corollary 4.6. Observe that
$\operatorname{Jac}(C)$
has good reduction everywhere. We will show that the archimedean contribution to the Faltings height is negligible when compared to the non-archimedean contribution. We use notation introduced in Theorem 4.5 and Corollary 4.6. Observe that
![]() $k$
satisfies the hypothesis of the theorem after passing to a finite field extension. By part (ii) of the theorem, the normalised norm in (1.4) does not change after passing to a further finite extension of
$k$
satisfies the hypothesis of the theorem after passing to a finite field extension. By part (ii) of the theorem, the normalised norm in (1.4) does not change after passing to a further finite extension of
![]() $k$
. This settles the last statement of Theorem 1.4.
$k$
. This settles the last statement of Theorem 1.4.
We thus decompose
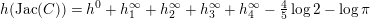 $h(\operatorname{Jac}(C))=h^{0}+h_{1}^{\infty }+h_{2}^{\infty }+h_{3}^{\infty }+h_{4}^{\infty }-\frac{4}{5}\log 2-\log \unicode[STIX]{x1D70B}$
, where
$h(\operatorname{Jac}(C))=h^{0}+h_{1}^{\infty }+h_{2}^{\infty }+h_{3}^{\infty }+h_{4}^{\infty }-\frac{4}{5}\log 2-\log \unicode[STIX]{x1D70B}$
, where
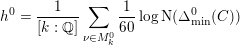 $$\begin{eqnarray}h^{0}=\frac{1}{[k:\mathbb{Q}]}\mathop{\sum }_{\unicode[STIX]{x1D708}\in M_{k}^{0}}\frac{1}{60}\log \text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))\end{eqnarray}$$
$$\begin{eqnarray}h^{0}=\frac{1}{[k:\mathbb{Q}]}\mathop{\sum }_{\unicode[STIX]{x1D708}\in M_{k}^{0}}\frac{1}{60}\log \text{N}(\unicode[STIX]{x1D6E5}_{\min }^{0}(C))\end{eqnarray}$$
is the finite part and
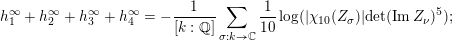 $$\begin{eqnarray}h_{1}^{\infty }+h_{2}^{\infty }+h_{3}^{\infty }+h_{4}^{\infty }=-\frac{1}{[k:\mathbb{Q}]}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\frac{1}{10}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}(\operatorname{Im}Z_{\unicode[STIX]{x1D708}})^{5});\end{eqnarray}$$
$$\begin{eqnarray}h_{1}^{\infty }+h_{2}^{\infty }+h_{3}^{\infty }+h_{4}^{\infty }=-\frac{1}{[k:\mathbb{Q}]}\mathop{\sum }_{\unicode[STIX]{x1D70E}:k\rightarrow \mathbb{C}}\frac{1}{10}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D70E}})|\text{det}(\operatorname{Im}Z_{\unicode[STIX]{x1D708}})^{5});\end{eqnarray}$$
here the single
![]() $h_{m}^{\infty }$
for
$h_{m}^{\infty }$
for
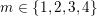 $m\in \{1,2,3,4\}$
are determined as follows.
$m\in \{1,2,3,4\}$
are determined as follows.
Shimura’s theorem 3.9 describes the period matrices coming from a Galois orbit that fixes the reflex field
![]() $K^{\ast }$
. Observe that
$K^{\ast }$
. Observe that
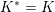 $K^{\ast }=K$
by Lemma 3.10 because
$K^{\ast }=K$
by Lemma 3.10 because
![]() $K/\mathbb{Q}$
is cyclic. So, (6.1) holds, where each
$K/\mathbb{Q}$
is cyclic. So, (6.1) holds, where each
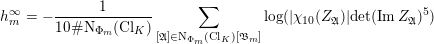 $$\begin{eqnarray}h_{m}^{\infty }=-\frac{1}{10\#\text{N}_{\unicode[STIX]{x1D6F7}_{m}}(\operatorname{Cl}_{K})}\mathop{\sum }_{[\mathfrak{A}]\in \text{N}_{\unicode[STIX]{x1D6F7}_{m}}(\operatorname{Cl}_{K})[\mathfrak{B}_{m}]}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\mathfrak{A}})|\text{det}(\operatorname{Im}Z_{\mathfrak{A}})^{5})\end{eqnarray}$$
$$\begin{eqnarray}h_{m}^{\infty }=-\frac{1}{10\#\text{N}_{\unicode[STIX]{x1D6F7}_{m}}(\operatorname{Cl}_{K})}\mathop{\sum }_{[\mathfrak{A}]\in \text{N}_{\unicode[STIX]{x1D6F7}_{m}}(\operatorname{Cl}_{K})[\mathfrak{B}_{m}]}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\mathfrak{A}})|\text{det}(\operatorname{Im}Z_{\mathfrak{A}})^{5})\end{eqnarray}$$
corresponds to one of the four cosets of
 $\operatorname{Aut}(\mathbb{C}/K)$
in
$\operatorname{Aut}(\mathbb{C}/K)$
in
 $\operatorname{Aut}(\mathbb{C}/\mathbb{Q})$
; here
$\operatorname{Aut}(\mathbb{C}/\mathbb{Q})$
; here
![]() $\unicode[STIX]{x1D6F7}_{m}$
is a CM type of
$\unicode[STIX]{x1D6F7}_{m}$
is a CM type of
![]() $K$
and
$K$
and
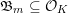 $\mathfrak{B}_{m}\subseteq {\mathcal{O}}_{K}$
is a fractional ideal. Observe that the terms on the right of (6.2) do not depend on the choice of a representative
$\mathfrak{B}_{m}\subseteq {\mathcal{O}}_{K}$
is a fractional ideal. Observe that the terms on the right of (6.2) do not depend on the choice of a representative
![]() $\mathfrak{A}\in [\mathfrak{A}]$
. Indeed, we already observed that
$\mathfrak{A}\in [\mathfrak{A}]$
. Indeed, we already observed that
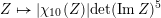 $Z\mapsto |\unicode[STIX]{x1D712}_{10}(Z)|\text{det}(\operatorname{Im}Z)^{5}$
is
$Z\mapsto |\unicode[STIX]{x1D712}_{10}(Z)|\text{det}(\operatorname{Im}Z)^{5}$
is
![]() $\operatorname{Sp}_{4}(\mathbb{Z})$
-invariant in § 4.4.
$\operatorname{Sp}_{4}(\mathbb{Z})$
-invariant in § 4.4.
For any
![]() $\mathfrak{A}$
as in the sum (6.2), Proposition 3.3 provides
$\mathfrak{A}$
as in the sum (6.2), Proposition 3.3 provides
![]() $\unicode[STIX]{x1D70F}_{\mathfrak{A}}$
with
$\unicode[STIX]{x1D70F}_{\mathfrak{A}}$
with
![]() $\unicode[STIX]{x1D6F7}_{m}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
in the fundamental set
$\unicode[STIX]{x1D6F7}_{m}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
in the fundamental set
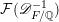 ${\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
from § 3.1. The period matrices
${\mathcal{F}}(\mathscr{D}_{F/\mathbb{Q}}^{-1})$
from § 3.1. The period matrices
![]() $Z_{\mathfrak{A}}$
are as described in (3.20).
$Z_{\mathfrak{A}}$
are as described in (3.20).
Later on we will show that there exists
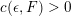 $c(\unicode[STIX]{x1D716},F)>0$
depending only on
$c(\unicode[STIX]{x1D716},F)>0$
depending only on
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $F$
such that
$F$
such that
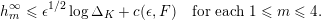 $$\begin{eqnarray}h_{m}^{\infty }\leqslant \unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}+c(\unicode[STIX]{x1D716},F)\quad \text{for each}~1\leqslant m\leqslant 4.\end{eqnarray}$$
$$\begin{eqnarray}h_{m}^{\infty }\leqslant \unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}+c(\unicode[STIX]{x1D716},F)\quad \text{for each}~1\leqslant m\leqslant 4.\end{eqnarray}$$
Our Theorem 1.4 follows from this inequality and from Proposition 4.3.
But also Theorem 1.3 follows from (6.3) after adjusting
![]() $\unicode[STIX]{x1D716}$
. Indeed, the archimedean contribution to the Faltings height of
$\unicode[STIX]{x1D716}$
. Indeed, the archimedean contribution to the Faltings height of
![]() $\operatorname{Jac}(C)$
is invariant under replacing the field of definition by a finite extension; so the extensions of
$\operatorname{Jac}(C)$
is invariant under replacing the field of definition by a finite extension; so the extensions of
![]() $k$
made before are harmless.
$k$
made before are harmless.
Of course, all
![]() $m$
can be treated in a similar manner. So, we simplify notation by abbreviating
$m$
can be treated in a similar manner. So, we simplify notation by abbreviating
 $h^{\infty }=h_{m}^{\infty },$
writing
$h^{\infty }=h_{m}^{\infty },$
writing
![]() $H$
for
$H$
for
 $\text{N}_{\unicode[STIX]{x1D6F7}_{m}}(\operatorname{Cl}_{K})[\mathfrak{B}_{m}]$
and
$\text{N}_{\unicode[STIX]{x1D6F7}_{m}}(\operatorname{Cl}_{K})[\mathfrak{B}_{m}]$
and
![]() $\unicode[STIX]{x1D6F7}$
for the CM type
$\unicode[STIX]{x1D6F7}$
for the CM type
![]() $\unicode[STIX]{x1D6F7}_{m}$
. Observe that
$\unicode[STIX]{x1D6F7}_{m}$
. Observe that
![]() $H$
is a coset in the class group
$H$
is a coset in the class group
![]() $\operatorname{Cl}_{K}$
.
$\operatorname{Cl}_{K}$
.
In this new notation, we have
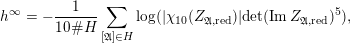 $$\begin{eqnarray}h^{\infty }=-\frac{1}{10\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\mathfrak{A},\text{red}})|\text{det}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})^{5}),\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }=-\frac{1}{10\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\log (|\unicode[STIX]{x1D712}_{10}(Z_{\mathfrak{A},\text{red}})|\text{det}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})^{5}),\end{eqnarray}$$
where
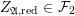 $Z_{\mathfrak{A},\text{red}}\in {\mathcal{F}}_{2}$
is in the
$Z_{\mathfrak{A},\text{red}}\in {\mathcal{F}}_{2}$
is in the
![]() $\operatorname{Sp}_{4}(\mathbb{Z})$
-orbit of
$\operatorname{Sp}_{4}(\mathbb{Z})$
-orbit of
![]() $Z_{\mathfrak{A}}$
.
$Z_{\mathfrak{A}}$
.
Below,
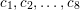 $c_{1},c_{2},\ldots ,c_{8}$
denote positive constants that depend only on the real quadratic field
$c_{1},c_{2},\ldots ,c_{8}$
denote positive constants that depend only on the real quadratic field
![]() $F$
.
$F$
.
Taking the sign in
![]() $h^{\infty }$
into account, we would like to bound each logarithm in
$h^{\infty }$
into account, we would like to bound each logarithm in
![]() $h^{\infty }$
from below using Proposition 5.6. If
$h^{\infty }$
from below using Proposition 5.6. If
![]() $z_{\mathfrak{A},12}$
is the off-diagonal entry of the Siegel reduced matrix
$z_{\mathfrak{A},12}$
is the off-diagonal entry of the Siegel reduced matrix
![]() $Z_{\mathfrak{A},\text{red}}$
, then
$Z_{\mathfrak{A},\text{red}}$
, then
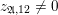 $z_{\mathfrak{A},12}\not =0$
. Indeed, otherwise
$z_{\mathfrak{A},12}\not =0$
. Indeed, otherwise
![]() $Z_{\mathfrak{A},\text{red}}$
is diagonal. But this is impossible because
$Z_{\mathfrak{A},\text{red}}$
is diagonal. But this is impossible because
![]() $\operatorname{Jac}(C)$
is not a product of elliptic curves due to the fact that
$\operatorname{Jac}(C)$
is not a product of elliptic curves due to the fact that
![]() $K/\mathbb{Q}$
is cyclic; see [Reference Birkenhake and LangeBL04, Corollary 11.8.2] and Lemma 3.10. Another way to see that
$K/\mathbb{Q}$
is cyclic; see [Reference Birkenhake and LangeBL04, Corollary 11.8.2] and Lemma 3.10. Another way to see that
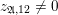 $z_{\mathfrak{A},12}\not =0$
is by noting that
$z_{\mathfrak{A},12}\not =0$
is by noting that
![]() $\unicode[STIX]{x1D712}_{10}$
restricted to
$\unicode[STIX]{x1D712}_{10}$
restricted to
![]() ${\mathcal{F}}_{2}$
vanishes only on diagonal matrices and by using the proof of Proposition 4.8. By Proposition 5.6, we obtain
${\mathcal{F}}_{2}$
vanishes only on diagonal matrices and by using the proof of Proposition 4.8. By Proposition 5.6, we obtain
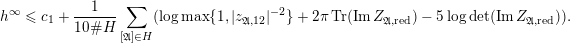 $$\begin{eqnarray}h^{\infty }\leqslant c_{1}+\frac{1}{10\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}(\log \max \{1,|z_{\mathfrak{A},12}|^{-2}\}+2\unicode[STIX]{x1D70B}\operatorname{Tr}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})-5\log \det (\operatorname{Im}Z_{\mathfrak{A},\text{red}})).\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{1}+\frac{1}{10\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}(\log \max \{1,|z_{\mathfrak{A},12}|^{-2}\}+2\unicode[STIX]{x1D70B}\operatorname{Tr}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})-5\log \det (\operatorname{Im}Z_{\mathfrak{A},\text{red}})).\end{eqnarray}$$
Since
![]() $Z_{\mathfrak{A},\text{red}}$
is Siegel reduced, we have
$Z_{\mathfrak{A},\text{red}}$
is Siegel reduced, we have
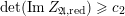 $\det (\operatorname{Im}Z_{\mathfrak{A},\text{red}})\geqslant c_{2}$
. So, the average value of the quantity
$\det (\operatorname{Im}Z_{\mathfrak{A},\text{red}})\geqslant c_{2}$
. So, the average value of the quantity
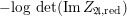 $-\text{log}\,\det (\operatorname{Im}Z_{\mathfrak{A},\text{red}})$
is bounded from above uniformly. After possibly increasing
$-\text{log}\,\det (\operatorname{Im}Z_{\mathfrak{A},\text{red}})$
is bounded from above uniformly. After possibly increasing
![]() $c_{1}$
, we find
$c_{1}$
, we find
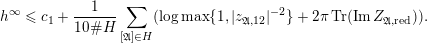 $$\begin{eqnarray}h^{\infty }\leqslant c_{1}+\frac{1}{10\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}(\log \max \{1,|z_{\mathfrak{A},12}|^{-2}\}+2\unicode[STIX]{x1D70B}\operatorname{Tr}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})).\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{1}+\frac{1}{10\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}(\log \max \{1,|z_{\mathfrak{A},12}|^{-2}\}+2\unicode[STIX]{x1D70B}\operatorname{Tr}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})).\end{eqnarray}$$
Next we use Lemma 3.6(i) to bound each
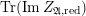 $\operatorname{Tr}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})$
from above to get
$\operatorname{Tr}(\operatorname{Im}Z_{\mathfrak{A},\text{red}})$
from above to get
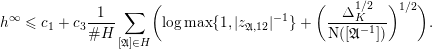 $$\begin{eqnarray}h^{\infty }\leqslant c_{1}+c_{3}\frac{1}{\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\biggl(\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}+\biggl(\frac{\unicode[STIX]{x1D6E5}_{K}^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/2}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{1}+c_{3}\frac{1}{\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\biggl(\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}+\biggl(\frac{\unicode[STIX]{x1D6E5}_{K}^{1/2}}{\text{N}([\mathfrak{A}^{-1}])}\biggr)^{1/2}\biggr).\end{eqnarray}$$
We continue by tackling the terms
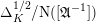 $\unicode[STIX]{x1D6E5}_{K}^{1/2}/\text{N}([\mathfrak{A}^{-1}])$
. The trivial bound that follows from
$\unicode[STIX]{x1D6E5}_{K}^{1/2}/\text{N}([\mathfrak{A}^{-1}])$
. The trivial bound that follows from
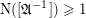 $\text{N}([\mathfrak{A}^{-1}])\geqslant 1$
is of little use here as it leads to an upper bound for
$\text{N}([\mathfrak{A}^{-1}])\geqslant 1$
is of little use here as it leads to an upper bound for
![]() $h^{\infty }$
of the magnitude
$h^{\infty }$
of the magnitude
![]() $\unicode[STIX]{x1D6E5}_{K}^{1/4}$
. When compared with the logarithmic lower bound coming from Proposition 4.3, this is not good enough to conclude (6.3). We need the subconvexity bound. Proposition 5.9(i) combined with the lower bound for
$\unicode[STIX]{x1D6E5}_{K}^{1/4}$
. When compared with the logarithmic lower bound coming from Proposition 4.3, this is not good enough to conclude (6.3). We need the subconvexity bound. Proposition 5.9(i) combined with the lower bound for
![]() $\#H$
from Lemma 3.11 implies that the average contribution of
$\#H$
from Lemma 3.11 implies that the average contribution of
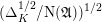 $(\unicode[STIX]{x1D6E5}_{K}^{1/2}/\text{N}(\mathfrak{A}))^{1/2}$
is bounded from above. Thus,
$(\unicode[STIX]{x1D6E5}_{K}^{1/2}/\text{N}(\mathfrak{A}))^{1/2}$
is bounded from above. Thus,
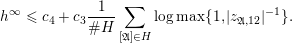 $$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{3}\frac{1}{\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}.\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{3}\frac{1}{\#H}\mathop{\sum }_{[\mathfrak{A}]\in H}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}.\end{eqnarray}$$
Recall that
![]() $z_{\mathfrak{A},12}$
is a non-zero algebraic number of absolute logarithmic Weil height at most
$z_{\mathfrak{A},12}$
is a non-zero algebraic number of absolute logarithmic Weil height at most
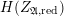 $H(Z_{\mathfrak{A},\text{red}})$
. As
$H(Z_{\mathfrak{A},\text{red}})$
. As
![]() $K/\mathbb{Q}$
is Galois, we conclude that
$K/\mathbb{Q}$
is Galois, we conclude that
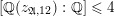 $[\mathbb{Q}(z_{\mathfrak{A},12}):\mathbb{Q}]\leqslant 4$
using the expression (3.20). The fundamental inequality of Liouville found in [Reference Bombieri and GublerBG06, 1.5.19] thus implies that
$[\mathbb{Q}(z_{\mathfrak{A},12}):\mathbb{Q}]\leqslant 4$
using the expression (3.20). The fundamental inequality of Liouville found in [Reference Bombieri and GublerBG06, 1.5.19] thus implies that
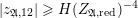 $|z_{\mathfrak{A},12}|\geqslant H(Z_{\mathfrak{A},\text{red}})^{-4}$
. The height of this reduced period matrix is bounded from above polynomially in
$|z_{\mathfrak{A},12}|\geqslant H(Z_{\mathfrak{A},\text{red}})^{-4}$
. The height of this reduced period matrix is bounded from above polynomially in
![]() $\unicode[STIX]{x1D6E5}_{K}$
by Lemma 3.8. Therefore, taking the logarithm yields
$\unicode[STIX]{x1D6E5}_{K}$
by Lemma 3.8. Therefore, taking the logarithm yields
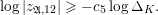 $$\begin{eqnarray}\log |z_{\mathfrak{A},12}|\geqslant -c_{5}\log \unicode[STIX]{x1D6E5}_{K}.\end{eqnarray}$$
$$\begin{eqnarray}\log |z_{\mathfrak{A},12}|\geqslant -c_{5}\log \unicode[STIX]{x1D6E5}_{K}.\end{eqnarray}$$
We use this inequality to bound from above the terms in (6.4) for which
![]() $\unicode[STIX]{x1D70F}_{\mathfrak{A}}$
is close to one of the cusps, i.e.,
$\unicode[STIX]{x1D70F}_{\mathfrak{A}}$
is close to one of the cusps, i.e.,
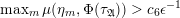 $\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}}))>c_{6}\unicode[STIX]{x1D716}^{-1}$
with
$\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}}))>c_{6}\unicode[STIX]{x1D716}^{-1}$
with
![]() $c_{6}=c$
the constant from Lemma 3.6(ii). We have
$c_{6}=c$
the constant from Lemma 3.6(ii). We have
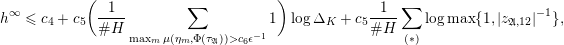 $$\begin{eqnarray}\displaystyle h^{\infty }\leqslant c_{4}+c_{5}\biggl(\frac{1}{\#H}\mathop{\sum }_{\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}}))>c_{6}\unicode[STIX]{x1D716}^{-1}}1\biggr)\log \unicode[STIX]{x1D6E5}_{K}+c_{5}\frac{1}{\#H}\mathop{\sum }_{(\ast )}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{\infty }\leqslant c_{4}+c_{5}\biggl(\frac{1}{\#H}\mathop{\sum }_{\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}}))>c_{6}\unicode[STIX]{x1D716}^{-1}}1\biggr)\log \unicode[STIX]{x1D6E5}_{K}+c_{5}\frac{1}{\#H}\mathop{\sum }_{(\ast )}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}, & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $(\ast )$
abbreviates the condition
$(\ast )$
abbreviates the condition
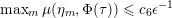 $\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\leqslant c_{6}\unicode[STIX]{x1D716}^{-1}$
here and in the sums below. Observe that being close to a cusp entails
$\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}))\leqslant c_{6}\unicode[STIX]{x1D716}^{-1}$
here and in the sums below. Observe that being close to a cusp entails
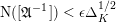 $\text{N}([\mathfrak{A}^{-1}])<\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{K}^{1/2}$
by Lemma 3.6(ii). Part (ii) of Proposition 5.9 tells us that not too many
$\text{N}([\mathfrak{A}^{-1}])<\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{K}^{1/2}$
by Lemma 3.6(ii). Part (ii) of Proposition 5.9 tells us that not too many
![]() $\unicode[STIX]{x1D70F}_{\mathfrak{A}}$
are close to a cusp. We obtain
$\unicode[STIX]{x1D70F}_{\mathfrak{A}}$
are close to a cusp. We obtain
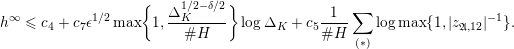 $$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{7}\unicode[STIX]{x1D716}^{1/2}\max \biggl\{1,\frac{\unicode[STIX]{x1D6E5}_{K}^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}\log \unicode[STIX]{x1D6E5}_{K}+c_{5}\frac{1}{\#H}\mathop{\sum }_{(\ast )}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}.\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{7}\unicode[STIX]{x1D716}^{1/2}\max \biggl\{1,\frac{\unicode[STIX]{x1D6E5}_{K}^{1/2-\unicode[STIX]{x1D6FF}/2}}{\#H}\biggr\}\log \unicode[STIX]{x1D6E5}_{K}+c_{5}\frac{1}{\#H}\mathop{\sum }_{(\ast )}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}.\end{eqnarray}$$
We apply Lemma 3.11 again to bound
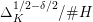 $\unicode[STIX]{x1D6E5}_{K}^{1/2-\unicode[STIX]{x1D6FF}/2}/\#H$
from above. Thus,
$\unicode[STIX]{x1D6E5}_{K}^{1/2-\unicode[STIX]{x1D6FF}/2}/\#H$
from above. Thus,
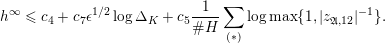 $$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{7}\unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}+c_{5}\frac{1}{\#H}\mathop{\sum }_{(\ast )}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}.\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{7}\unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}+c_{5}\frac{1}{\#H}\mathop{\sum }_{(\ast )}\log \max \{1,|z_{\mathfrak{A},12}|^{-1}\}.\end{eqnarray}$$
It remains to bound the sum on the right. If some
![]() $|z_{\mathfrak{A},12}|$
is small, then the corresponding conjugate of
$|z_{\mathfrak{A},12}|$
is small, then the corresponding conjugate of
![]() $\operatorname{Jac}(C)$
is close to a product of elliptic curves in the appropriate coarse moduli space. To measure this proximity we require the second parameter
$\operatorname{Jac}(C)$
is close to a product of elliptic curves in the appropriate coarse moduli space. To measure this proximity we require the second parameter
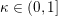 $\unicode[STIX]{x1D705}\in (0,1]$
. We split the upper bound for
$\unicode[STIX]{x1D705}\in (0,1]$
. We split the upper bound for
![]() $h^{\infty }$
up into a subsum where
$h^{\infty }$
up into a subsum where
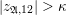 $|z_{\mathfrak{A},12}|>\unicode[STIX]{x1D705}$
holds and one where it does not. The first subsum is at most
$|z_{\mathfrak{A},12}|>\unicode[STIX]{x1D705}$
holds and one where it does not. The first subsum is at most
![]() $|\text{log}\,\unicode[STIX]{x1D705}|$
and so
$|\text{log}\,\unicode[STIX]{x1D705}|$
and so
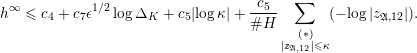 $$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{7}\unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}+c_{5}|\text{log}\,\unicode[STIX]{x1D705}|+\frac{c_{5}}{\#H}\mathop{\sum }_{\substack{ (\ast ) \\ |z_{\mathfrak{A},12}|\leqslant \unicode[STIX]{x1D705}}}(-\text{log}\,|z_{\mathfrak{A},12}|).\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{4}+c_{7}\unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}+c_{5}|\text{log}\,\unicode[STIX]{x1D705}|+\frac{c_{5}}{\#H}\mathop{\sum }_{\substack{ (\ast ) \\ |z_{\mathfrak{A},12}|\leqslant \unicode[STIX]{x1D705}}}(-\text{log}\,|z_{\mathfrak{A},12}|).\end{eqnarray}$$
We use (6.5) again to obtain
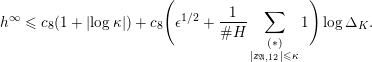 $$\begin{eqnarray}h^{\infty }\leqslant c_{8}(1+|\text{log}\,\unicode[STIX]{x1D705}|)+c_{8}\left(\unicode[STIX]{x1D716}^{1/2}+\frac{1}{\#H}\mathop{\sum }_{\substack{ (\ast ) \\ |z_{\mathfrak{A},12}|\leqslant \unicode[STIX]{x1D705}}}1\right)\log \unicode[STIX]{x1D6E5}_{K}.\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{8}(1+|\text{log}\,\unicode[STIX]{x1D705}|)+c_{8}\left(\unicode[STIX]{x1D716}^{1/2}+\frac{1}{\#H}\mathop{\sum }_{\substack{ (\ast ) \\ |z_{\mathfrak{A},12}|\leqslant \unicode[STIX]{x1D705}}}1\right)\log \unicode[STIX]{x1D6E5}_{K}.\end{eqnarray}$$
To conclude, we must bound the remaining sum in (6.6). So, say
![]() $[\mathfrak{A}]$
corresponds to one of its terms. The property
$[\mathfrak{A}]$
corresponds to one of its terms. The property
![]() $(\ast )$
implies that
$(\ast )$
implies that
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
is bounded away from all cusps. So,
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
is bounded away from all cusps. So,
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
lies in a compact subset
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
lies in a compact subset
![]() ${\mathcal{K}}$
of
${\mathcal{K}}$
of
![]() $\mathbb{H}^{2}$
, cf. Proposition 3.1, which depends only on
$\mathbb{H}^{2}$
, cf. Proposition 3.1, which depends only on
![]() $\unicode[STIX]{x1D716}$
. Being bounded away from the cusps entails that reducing
$\unicode[STIX]{x1D716}$
. Being bounded away from the cusps entails that reducing
![]() $Z_{\mathfrak{A}}$
to
$Z_{\mathfrak{A}}$
to
![]() $Z_{\mathfrak{A},\text{red}}$
requires only a finite subset of
$Z_{\mathfrak{A},\text{red}}$
requires only a finite subset of
![]() $\operatorname{Sp}_{4}(\mathbb{Z})$
. Indeed, we apply Lemma 3.7 to
$\operatorname{Sp}_{4}(\mathbb{Z})$
. Indeed, we apply Lemma 3.7 to
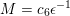 $M=c_{6}\unicode[STIX]{x1D716}^{-1}$
to obtain a finite set
$M=c_{6}\unicode[STIX]{x1D716}^{-1}$
to obtain a finite set
 $\unicode[STIX]{x1D6F4}\subseteq \operatorname{Sp}_{4}(\mathbb{Z})$
, which depends only on
$\unicode[STIX]{x1D6F4}\subseteq \operatorname{Sp}_{4}(\mathbb{Z})$
, which depends only on
![]() $c_{6}$
and
$c_{6}$
and
![]() $\unicode[STIX]{x1D716}$
, such that
$\unicode[STIX]{x1D716}$
, such that
 $Z_{\mathfrak{A},\text{red}}=\unicode[STIX]{x1D6FE}Z_{\mathfrak{A}}$
for some
$Z_{\mathfrak{A},\text{red}}=\unicode[STIX]{x1D6FE}Z_{\mathfrak{A}}$
for some
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}$
. Therefore,
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}$
. Therefore,
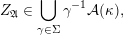 $$\begin{eqnarray}Z_{\mathfrak{A}}\in \mathop{\bigcup }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FE}^{-1}{\mathcal{A}}(\unicode[STIX]{x1D705}),\end{eqnarray}$$
$$\begin{eqnarray}Z_{\mathfrak{A}}\in \mathop{\bigcup }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FE}^{-1}{\mathcal{A}}(\unicode[STIX]{x1D705}),\end{eqnarray}$$
where
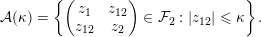 $$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D705})=\left\{\left(\begin{array}{@{}cc@{}}z_{1} & z_{12}\\ z_{12} & z_{2}\end{array}\right)\in {\mathcal{F}}_{2}:|z_{12}|\leqslant \unicode[STIX]{x1D705}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D705})=\left\{\left(\begin{array}{@{}cc@{}}z_{1} & z_{12}\\ z_{12} & z_{2}\end{array}\right)\in {\mathcal{F}}_{2}:|z_{12}|\leqslant \unicode[STIX]{x1D705}\right\}.\end{eqnarray}$$
Each
![]() ${\mathcal{A}}(\unicode[STIX]{x1D705})$
is closed in
${\mathcal{A}}(\unicode[STIX]{x1D705})$
is closed in
 $\text{Mat}_{2}(\mathbb{C})$
and
$\text{Mat}_{2}(\mathbb{C})$
and
 $\bigcap _{\unicode[STIX]{x1D705}>0}{\mathcal{A}}(\unicode[STIX]{x1D705})$
contains only diagonal elements.
$\bigcap _{\unicode[STIX]{x1D705}>0}{\mathcal{A}}(\unicode[STIX]{x1D705})$
contains only diagonal elements.
We can reconstruct
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
from
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
from
![]() $Z_{\mathfrak{A}}$
as follows. The expression (3.20) determines
$Z_{\mathfrak{A}}$
as follows. The expression (3.20) determines
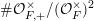 $\#{\mathcal{O}}_{F,+}^{\times }/({\mathcal{O}}_{F}^{\times })^{2}$
holomorphic mappings
$\#{\mathcal{O}}_{F,+}^{\times }/({\mathcal{O}}_{F}^{\times })^{2}$
holomorphic mappings
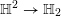 $\mathbb{H}^{2}\rightarrow \mathbb{H}_{2}$
. So,
$\mathbb{H}^{2}\rightarrow \mathbb{H}_{2}$
. So,
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
lies in the pre-image of
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
lies in the pre-image of
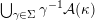 $\bigcup _{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FE}^{-1}{\mathcal{A}}(\unicode[STIX]{x1D705})$
under one of them. Recall that
$\bigcup _{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FE}^{-1}{\mathcal{A}}(\unicode[STIX]{x1D705})$
under one of them. Recall that
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
lies in the compact set
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}})$
lies in the compact set
![]() ${\mathcal{K}}$
. As
${\mathcal{K}}$
. As
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
, the hyperbolic measure of the intersection of the said pre-image and
$\unicode[STIX]{x1D705}\rightarrow 0$
, the hyperbolic measure of the intersection of the said pre-image and
![]() ${\mathcal{K}}$
tends to
${\mathcal{K}}$
tends to
![]() $0$
.
$0$
.
Galois orbits are equidistributed by Zhang’s Corollary 3.3 [Reference ZhangZha05] and [Reference Michel and VenkateshMV10, Theorem 1.2] by Michel and Venkatesh. In particular,
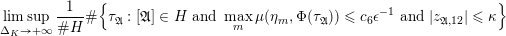 $$\begin{eqnarray}\limsup _{\unicode[STIX]{x1D6E5}_{K}\rightarrow +\infty }\frac{1}{\#H}\#\Bigl\{\unicode[STIX]{x1D70F}_{\mathfrak{A}}:[\mathfrak{A}]\in H\text{ and }\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}}))\leqslant c_{6}\unicode[STIX]{x1D716}^{-1}\text{ and }|z_{\mathfrak{ A},12}|\leqslant \unicode[STIX]{x1D705}\Bigr\}\end{eqnarray}$$
$$\begin{eqnarray}\limsup _{\unicode[STIX]{x1D6E5}_{K}\rightarrow +\infty }\frac{1}{\#H}\#\Bigl\{\unicode[STIX]{x1D70F}_{\mathfrak{A}}:[\mathfrak{A}]\in H\text{ and }\max _{m}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D702}_{m},\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F}_{\mathfrak{A}}))\leqslant c_{6}\unicode[STIX]{x1D716}^{-1}\text{ and }|z_{\mathfrak{ A},12}|\leqslant \unicode[STIX]{x1D705}\Bigr\}\end{eqnarray}$$
is bounded above by an expression that tends to
![]() $0$
as
$0$
as
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
. We fix
$\unicode[STIX]{x1D705}\rightarrow 0$
. We fix
![]() $\unicode[STIX]{x1D705}$
sufficiently small in terms of
$\unicode[STIX]{x1D705}$
sufficiently small in terms of
![]() $\unicode[STIX]{x1D716}$
such that this limit superior is at most
$\unicode[STIX]{x1D716}$
such that this limit superior is at most
![]() $\unicode[STIX]{x1D716}^{1/2}$
.
$\unicode[STIX]{x1D716}^{1/2}$
.
We can now continue bounding (6.6) from above. If
![]() $\unicode[STIX]{x1D6E5}_{K}$
is sufficiently large with respect to
$\unicode[STIX]{x1D6E5}_{K}$
is sufficiently large with respect to
![]() $\unicode[STIX]{x1D716}$
, then the number of terms in the sum is at most
$\unicode[STIX]{x1D716}$
, then the number of terms in the sum is at most
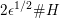 $2\unicode[STIX]{x1D716}^{1/2}\#H$
by the last paragraph. Therefore,
$2\unicode[STIX]{x1D716}^{1/2}\#H$
by the last paragraph. Therefore,
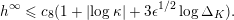 $$\begin{eqnarray}h^{\infty }\leqslant c_{8}(1+|\text{log}\,\unicode[STIX]{x1D705}|+3\unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}).\end{eqnarray}$$
$$\begin{eqnarray}h^{\infty }\leqslant c_{8}(1+|\text{log}\,\unicode[STIX]{x1D705}|+3\unicode[STIX]{x1D716}^{1/2}\log \unicode[STIX]{x1D6E5}_{K}).\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D6E5}_{K}$
is not large enough, we have a similar bound with a possibly larger
$\unicode[STIX]{x1D6E5}_{K}$
is not large enough, we have a similar bound with a possibly larger
![]() $c_{8}$
. We have thus verified the inequality (6.3) and therefore Theorem 1.4.◻
$c_{8}$
. We have thus verified the inequality (6.3) and therefore Theorem 1.4.◻
Proof of Theorem 1.1.
We have seen essentially the same argument in the introduction; let us repeat it here again. Let
![]() $F$
and
$F$
and
![]() $C$
be as in the theorem. Then we take
$C$
be as in the theorem. Then we take
![]() $C$
as defined over a sufficiently large number field
$C$
as defined over a sufficiently large number field
![]() $k$
with
$k$
with
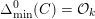 $\unicode[STIX]{x1D6E5}_{\text{min}}^{0}(C)={\mathcal{O}}_{k}$
. If
$\unicode[STIX]{x1D6E5}_{\text{min}}^{0}(C)={\mathcal{O}}_{k}$
. If
![]() $K$
is the CM field of
$K$
is the CM field of
![]() $\operatorname{Jac}(C)$
, then its discriminant
$\operatorname{Jac}(C)$
, then its discriminant
![]() $\unicode[STIX]{x1D6E5}_{K}$
is bounded from above by a constant depending only on
$\unicode[STIX]{x1D6E5}_{K}$
is bounded from above by a constant depending only on
![]() $F$
by Theorem 1.4. By the theorem of Hermite–Minkowski, there are only finitely many possibilities for
$F$
by Theorem 1.4. By the theorem of Hermite–Minkowski, there are only finitely many possibilities for
![]() $K$
. As there are only finitely many abelian surfaces over
$K$
. As there are only finitely many abelian surfaces over
![]() $\overline{\mathbb{Q}}$
with CM by the maximal order of
$\overline{\mathbb{Q}}$
with CM by the maximal order of
![]() $K$
, this leaves at most finitely many possibilities for
$K$
, this leaves at most finitely many possibilities for
![]() $\operatorname{Jac}(C)$
as an abelian variety. But each abelian variety, such as
$\operatorname{Jac}(C)$
as an abelian variety. But each abelian variety, such as
![]() $\operatorname{Jac}(C)$
, carries only finitely many principal polarisations up to equivalence; this follows from the general Narasimhan–Nori theorem, or from more elementary considerations as
$\operatorname{Jac}(C)$
, carries only finitely many principal polarisations up to equivalence; this follows from the general Narasimhan–Nori theorem, or from more elementary considerations as
![]() $\operatorname{Jac}(C)$
is simple, or in a direct way using the arguments in § 3.2. Thus, up to
$\operatorname{Jac}(C)$
is simple, or in a direct way using the arguments in § 3.2. Thus, up to
![]() $\overline{\mathbb{Q}}$
-isomorphism, there are only finitely many possibilities for
$\overline{\mathbb{Q}}$
-isomorphism, there are only finitely many possibilities for
![]() $\operatorname{Jac}(C)$
as a principally polarised abelian variety. By Torelli’s theorem this leaves only finitely many
$\operatorname{Jac}(C)$
as a principally polarised abelian variety. By Torelli’s theorem this leaves only finitely many
![]() $\overline{\mathbb{Q}}$
-isomorphism classes for the curve
$\overline{\mathbb{Q}}$
-isomorphism classes for the curve
![]() $C$
.◻
$C$
.◻
Acknowledgements
The authors thank Qing Liu and Shou-Wu Zhang for helpful conversations. They also thank Javier Fresan and Marco Streng for their remarks on Colmez on average as well as the referees for helpful suggestions that improved the manuscript. The second-named author is supported by ANR-10-BLAN-0115 Hamot, ANR-10-JCJC-0107 Arivaf, and a DNRF Niels Bohr Professorship. Both authors thank the Université de Bordeaux, the Technical University of Darmstadt, and the University of Frankfurt. They also thank the DFG for supporting this collaboration through the project ‘Heights and unlikely intersections’ HA 6828/1-1.
Appendix A Numerical examples
In this section we provide some numerical examples for our expression of the Faltings height in Theorem 4.5. We will approximate
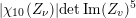 $|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D708}})|\text{det}\operatorname{Im}(Z_{v})^{5}$
numerically and compare the resulting sum with the conclusion of Colmez’s conjecture, Proposition 4.3(iii).
$|\unicode[STIX]{x1D712}_{10}(Z_{\unicode[STIX]{x1D708}})|\text{det}\operatorname{Im}(Z_{v})^{5}$
numerically and compare the resulting sum with the conclusion of Colmez’s conjecture, Proposition 4.3(iii).
Let
![]() $K$
be a CM field that is a quartic, cyclic extension of
$K$
be a CM field that is a quartic, cyclic extension of
![]() $\mathbb{Q}$
and has maximal totally real subfield
$\mathbb{Q}$
and has maximal totally real subfield
![]() $F$
. Let
$F$
. Let
![]() $A$
be an abelian surface defined over a number field whose endomorphism ring is
$A$
be an abelian surface defined over a number field whose endomorphism ring is
![]() ${\mathcal{O}}_{K}$
.
${\mathcal{O}}_{K}$
.
First we describe how to compute
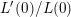 $L^{\prime }(0)/L(0)$
, where
$L^{\prime }(0)/L(0)$
, where
![]() $L$
is as in Proposition 4.3. For this, let
$L$
is as in Proposition 4.3. For this, let
![]() $f_{K}\geqslant 1$
be the finite part of the conductor of
$f_{K}\geqslant 1$
be the finite part of the conductor of
![]() $K/\mathbb{Q}$
. In other words,
$K/\mathbb{Q}$
. In other words,
![]() $f_{K}$
is the least positive integer such that
$f_{K}$
is the least positive integer such that
![]() $K$
is a subfield of the cyclotomic field generated by a root of unity of order
$K$
is a subfield of the cyclotomic field generated by a root of unity of order
![]() $f_{K}$
. Recall that
$f_{K}$
. Recall that
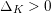 $\unicode[STIX]{x1D6E5}_{K}>0$
, as
$\unicode[STIX]{x1D6E5}_{K}>0$
, as
![]() $K/\mathbb{Q}$
is a CM field of degree
$K/\mathbb{Q}$
is a CM field of degree
![]() $4$
, and
$4$
, and
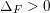 $\unicode[STIX]{x1D6E5}_{F}>0$
, since
$\unicode[STIX]{x1D6E5}_{F}>0$
, since
![]() $F/\mathbb{Q}$
is real quadratic. By [Reference NeukirchNeu99, Propositions 11.9 and 11.10, ch. VII], we have
$F/\mathbb{Q}$
is real quadratic. By [Reference NeukirchNeu99, Propositions 11.9 and 11.10, ch. VII], we have
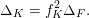 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{K}=f_{K}^{2}\unicode[STIX]{x1D6E5}_{F}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{K}=f_{K}^{2}\unicode[STIX]{x1D6E5}_{F}.\end{eqnarray}$$
The
![]() $L$
-function
$L$
-function
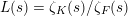 $L(s)=\unicode[STIX]{x1D701}_{K}(s)/\unicode[STIX]{x1D701}_{F}(s)$
is a product
$L(s)=\unicode[STIX]{x1D701}_{K}(s)/\unicode[STIX]{x1D701}_{F}(s)$
is a product
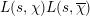 $L(s,\unicode[STIX]{x1D712})L(s,\overline{\unicode[STIX]{x1D712}})$
of Dirichlet
$L(s,\unicode[STIX]{x1D712})L(s,\overline{\unicode[STIX]{x1D712}})$
of Dirichlet
![]() $L$
-functions for some character
$L$
-functions for some character
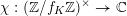 $\unicode[STIX]{x1D712}:(\mathbb{Z}/f_{K}\mathbb{Z})^{\times }\rightarrow \mathbb{C}$
of order
$\unicode[STIX]{x1D712}:(\mathbb{Z}/f_{K}\mathbb{Z})^{\times }\rightarrow \mathbb{C}$
of order
![]() $4$
. If
$4$
. If
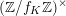 $(\mathbb{Z}/f_{K}\mathbb{Z})^{\times }$
is cyclic, e.g., if
$(\mathbb{Z}/f_{K}\mathbb{Z})^{\times }$
is cyclic, e.g., if
![]() $f_{K}$
is a prime, then
$f_{K}$
is a prime, then
![]() $\unicode[STIX]{x1D712}$
is uniquely determined up to complex conjugation.
$\unicode[STIX]{x1D712}$
is uniquely determined up to complex conjugation.
We use (A 1) and Proposition 4.3(iii) to compute
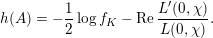 $$\begin{eqnarray}h(A)=-\frac{1}{2}\log f_{K}-\operatorname{Re}\frac{L^{\prime }(0,\unicode[STIX]{x1D712})}{L(0,\unicode[STIX]{x1D712})}.\end{eqnarray}$$
$$\begin{eqnarray}h(A)=-\frac{1}{2}\log f_{K}-\operatorname{Re}\frac{L^{\prime }(0,\unicode[STIX]{x1D712})}{L(0,\unicode[STIX]{x1D712})}.\end{eqnarray}$$
Observe that
![]() $\unicode[STIX]{x1D712}$
is an odd character. Corollary 10.3.2 and Proposition 10.3.5(1) of Cohen [Reference CohenCoh07] allow us to compute
$\unicode[STIX]{x1D712}$
is an odd character. Corollary 10.3.2 and Proposition 10.3.5(1) of Cohen [Reference CohenCoh07] allow us to compute
![]() $L(0,\unicode[STIX]{x1D712})$
and
$L(0,\unicode[STIX]{x1D712})$
and
![]() $L^{\prime }(0,\unicode[STIX]{x1D712})$
, respectively. We find
$L^{\prime }(0,\unicode[STIX]{x1D712})$
, respectively. We find
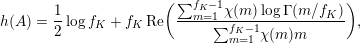 $$\begin{eqnarray}h(A)=\frac{1}{2}\log f_{K}+f_{K}\operatorname{Re}\biggl(\frac{\mathop{\sum }_{m=1}^{f_{K}-1}\unicode[STIX]{x1D712}(m)\log \unicode[STIX]{x1D6E4}(m/f_{K})}{\mathop{\sum }_{m=1}^{f_{K}-1}\unicode[STIX]{x1D712}(m)m}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}h(A)=\frac{1}{2}\log f_{K}+f_{K}\operatorname{Re}\biggl(\frac{\mathop{\sum }_{m=1}^{f_{K}-1}\unicode[STIX]{x1D712}(m)\log \unicode[STIX]{x1D6E4}(m/f_{K})}{\mathop{\sum }_{m=1}^{f_{K}-1}\unicode[STIX]{x1D712}(m)m}\biggr),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}(\cdot )$
is the gamma function.
$\unicode[STIX]{x1D6E4}(\cdot )$
is the gamma function.
To compute the Igusa invariants
 $J_{2},J_{4},J_{6},J_{8},J_{10}$
of a hyperelliptic equation, we use the pari/gp package of Rodriguez–Villegas, based on work of Mestre and Liu. We used the same software to determine the places of potentially good reduction for the curves listed below.
$J_{2},J_{4},J_{6},J_{8},J_{10}$
of a hyperelliptic equation, we use the pari/gp package of Rodriguez–Villegas, based on work of Mestre and Liu. We used the same software to determine the places of potentially good reduction for the curves listed below.
We consider three curves of genus
![]() $2$
defined over the rationals. The first quite obviously has a jacobian variety with CM. Van Wamelen [Reference van WamelenvWa99a, Reference van WamelenvWa99b] verified this in the remaining two cases. The source of the CM fields
$2$
defined over the rationals. The first quite obviously has a jacobian variety with CM. Van Wamelen [Reference van WamelenvWa99a, Reference van WamelenvWa99b] verified this in the remaining two cases. The source of the CM fields
![]() $K$
in the second and third examples is van Wamelen’s table [Reference van WamelenvWa99a]. For examples 2 and 3, van Wamelen does not prove that the endomorphism ring is the full ring of integers of
$K$
in the second and third examples is van Wamelen’s table [Reference van WamelenvWa99a]. For examples 2 and 3, van Wamelen does not prove that the endomorphism ring is the full ring of integers of
![]() $K$
. But equality is compatible with our computations below. We use the symbol
$K$
. But equality is compatible with our computations below. We use the symbol
![]() $\dot{=}$
to denote conditional equality, subject to the hypothesis that the endomorphism ring of the jacobian under consideration is indeed the full ring of integers of the CM field. In all three cases,
$\dot{=}$
to denote conditional equality, subject to the hypothesis that the endomorphism ring of the jacobian under consideration is indeed the full ring of integers of the CM field. In all three cases,
![]() $K$
has trivial class group.
$K$
has trivial class group.
Example A.1. We consider the curve
![]() $C$
defined by
$C$
defined by
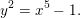 $$\begin{eqnarray}y^{2}=x^{5}-1.\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=x^{5}-1.\end{eqnarray}$$
Let
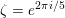 $\unicode[STIX]{x1D701}=e^{2\unicode[STIX]{x1D70B}i/5}$
be a primitive
$\unicode[STIX]{x1D701}=e^{2\unicode[STIX]{x1D70B}i/5}$
be a primitive
![]() $5$
th root of unity. Then
$5$
th root of unity. Then
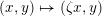 $(x,y)\mapsto (\unicode[STIX]{x1D701}x,y)$
is a automorphism of
$(x,y)\mapsto (\unicode[STIX]{x1D701}x,y)$
is a automorphism of
![]() $C$
of order
$C$
of order
![]() $5$
defined over the cyclotomic field
$5$
defined over the cyclotomic field
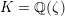 $K=\mathbb{Q}(\unicode[STIX]{x1D701})$
. So, the endomorphism ring of
$K=\mathbb{Q}(\unicode[STIX]{x1D701})$
. So, the endomorphism ring of
![]() $\operatorname{Jac}(C)$
over the algebraic closure contains
$\operatorname{Jac}(C)$
over the algebraic closure contains
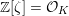 $\mathbb{Z}[\unicode[STIX]{x1D701}]={\mathcal{O}}_{K}$
. The two must be equal. Observe that
$\mathbb{Z}[\unicode[STIX]{x1D701}]={\mathcal{O}}_{K}$
. The two must be equal. Observe that
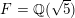 $F=\mathbb{Q}(\sqrt{5})$
is the maximal totally real subfield of
$F=\mathbb{Q}(\sqrt{5})$
is the maximal totally real subfield of
![]() $K$
and
$K$
and
![]() $f_{K}=5$
. As a character
$f_{K}=5$
. As a character
![]() $\unicode[STIX]{x1D712}$
near (A 2), we take for example
$\unicode[STIX]{x1D712}$
near (A 2), we take for example
 $\unicode[STIX]{x1D712}(1)=1,\unicode[STIX]{x1D712}(2)=i,\unicode[STIX]{x1D712}(3)=-i,\unicode[STIX]{x1D712}(4)=-1$
. So,
$\unicode[STIX]{x1D712}(1)=1,\unicode[STIX]{x1D712}(2)=i,\unicode[STIX]{x1D712}(3)=-i,\unicode[STIX]{x1D712}(4)=-1$
. So,
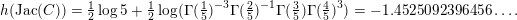 $$\begin{eqnarray}h(\operatorname{Jac}(C))={\textstyle \frac{1}{2}}\log 5+{\textstyle \frac{1}{2}}\log (\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{5}})^{-3}\unicode[STIX]{x1D6E4}({\textstyle \frac{2}{5}})^{-1}\unicode[STIX]{x1D6E4}({\textstyle \frac{3}{5}})\unicode[STIX]{x1D6E4}({\textstyle \frac{4}{5}})^{3})=-1.4525092396456\ldots .\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))={\textstyle \frac{1}{2}}\log 5+{\textstyle \frac{1}{2}}\log (\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{5}})^{-3}\unicode[STIX]{x1D6E4}({\textstyle \frac{2}{5}})^{-1}\unicode[STIX]{x1D6E4}({\textstyle \frac{3}{5}})\unicode[STIX]{x1D6E4}({\textstyle \frac{4}{5}})^{3})=-1.4525092396456\ldots .\end{eqnarray}$$
Bost et al. [Reference Bost, Mestre and Moret-BaillyBMM90] computed this Faltings height using a different approach to be
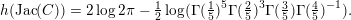 $$\begin{eqnarray}h(\operatorname{Jac}(C))=2\log 2\unicode[STIX]{x1D70B}-{\textstyle \frac{1}{2}}\log (\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{5}})^{5}\unicode[STIX]{x1D6E4}({\textstyle \frac{2}{5}})^{3}\unicode[STIX]{x1D6E4}({\textstyle \frac{3}{5}})\unicode[STIX]{x1D6E4}({\textstyle \frac{4}{5}})^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))=2\log 2\unicode[STIX]{x1D70B}-{\textstyle \frac{1}{2}}\log (\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{5}})^{5}\unicode[STIX]{x1D6E4}({\textstyle \frac{2}{5}})^{3}\unicode[STIX]{x1D6E4}({\textstyle \frac{3}{5}})\unicode[STIX]{x1D6E4}({\textstyle \frac{4}{5}})^{-1}).\end{eqnarray}$$
This expression equals (A 3) by classical properties of the gamma function.
The Igusa invariants of
![]() $C$
are
$C$
are
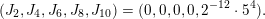 $$\begin{eqnarray}(J_{2},J_{4},J_{6},J_{8},J_{10})=(0,0,0,0,2^{-12}\cdot 5^{4}).\end{eqnarray}$$
$$\begin{eqnarray}(J_{2},J_{4},J_{6},J_{8},J_{10})=(0,0,0,0,2^{-12}\cdot 5^{4}).\end{eqnarray}$$
So, there is no contribution to the finite places in Theorem 4.5. In fact,
![]() $C$
has potentially good reduction everywhere. This was already observed by Bost et al.
$C$
has potentially good reduction everywhere. This was already observed by Bost et al.
The different ideal
![]() $\mathscr{D}_{F/\mathbb{Q}}$
equals
$\mathscr{D}_{F/\mathbb{Q}}$
equals
![]() $\sqrt{5}{\mathcal{O}}_{F}$
. If
$\sqrt{5}{\mathcal{O}}_{F}$
. If
![]() $\unicode[STIX]{x1D714}_{1}=1$
and
$\unicode[STIX]{x1D714}_{1}=1$
and
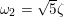 $\unicode[STIX]{x1D714}_{2}=\sqrt{5}\unicode[STIX]{x1D701}$
, then
$\unicode[STIX]{x1D714}_{2}=\sqrt{5}\unicode[STIX]{x1D701}$
, then
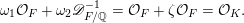 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}{\mathcal{O}}_{F}+\unicode[STIX]{x1D714}_{2}\mathscr{D}_{F/\mathbb{Q}}^{-1}={\mathcal{O}}_{F}+\unicode[STIX]{x1D701}{\mathcal{O}}_{F}={\mathcal{O}}_{K}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{1}{\mathcal{O}}_{F}+\unicode[STIX]{x1D714}_{2}\mathscr{D}_{F/\mathbb{Q}}^{-1}={\mathcal{O}}_{F}+\unicode[STIX]{x1D701}{\mathcal{O}}_{F}={\mathcal{O}}_{K}.\end{eqnarray}$$
The period matrix of
![]() ${\mathcal{O}}_{K}$
can be computed using Remark 3.4 with
${\mathcal{O}}_{K}$
can be computed using Remark 3.4 with
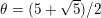 $\unicode[STIX]{x1D703}=(5+\sqrt{5})/2$
,
$\unicode[STIX]{x1D703}=(5+\sqrt{5})/2$
,
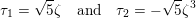 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{1}=\sqrt{5}\unicode[STIX]{x1D701}\quad \text{and}\quad \unicode[STIX]{x1D70F}_{2}=-\sqrt{5}\unicode[STIX]{x1D701}^{3}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{1}=\sqrt{5}\unicode[STIX]{x1D701}\quad \text{and}\quad \unicode[STIX]{x1D70F}_{2}=-\sqrt{5}\unicode[STIX]{x1D701}^{3}\end{eqnarray}$$
as
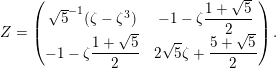 $$\begin{eqnarray}Z=\left(\begin{array}{@{}cc@{}}\sqrt{5}^{-1}(\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}^{3}) & \displaystyle -1-\unicode[STIX]{x1D701}\frac{1+\sqrt{5}}{2}\\ \displaystyle -1-\unicode[STIX]{x1D701}\frac{1+\sqrt{5}}{2} & \displaystyle 2\sqrt{5}\unicode[STIX]{x1D701}+\frac{5+\sqrt{5}}{2}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}Z=\left(\begin{array}{@{}cc@{}}\sqrt{5}^{-1}(\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}^{3}) & \displaystyle -1-\unicode[STIX]{x1D701}\frac{1+\sqrt{5}}{2}\\ \displaystyle -1-\unicode[STIX]{x1D701}\frac{1+\sqrt{5}}{2} & \displaystyle 2\sqrt{5}\unicode[STIX]{x1D701}+\frac{5+\sqrt{5}}{2}\end{array}\right).\end{eqnarray}$$
We observe that
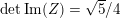 $\det \operatorname{Im}(Z)=\sqrt{5}/4$
and use a computer to approximate
$\det \operatorname{Im}(Z)=\sqrt{5}/4$
and use a computer to approximate
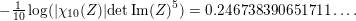 $$\begin{eqnarray}-{\textstyle \frac{1}{10}}\log (|\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\operatorname{Im}(Z)^{5})=0.246738390651711\ldots .\end{eqnarray}$$
$$\begin{eqnarray}-{\textstyle \frac{1}{10}}\log (|\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\operatorname{Im}(Z)^{5})=0.246738390651711\ldots .\end{eqnarray}$$
We add
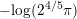 $-\text{log}(2^{4/5}\unicode[STIX]{x1D70B})$
in accordance with Theorem 4.5 and find that the sum approximates (A 3) up to the displayed digits.
$-\text{log}(2^{4/5}\unicode[STIX]{x1D70B})$
in accordance with Theorem 4.5 and find that the sum approximates (A 3) up to the displayed digits.
Example A.2. The second example concerns the new curve
![]() $C$
$C$
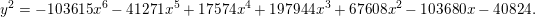 $$\begin{eqnarray}y^{2}=-103615x^{6}-41271x^{5}+17574x^{4}+197944x^{3}+67608x^{2}-103680x-40824.\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-103615x^{6}-41271x^{5}+17574x^{4}+197944x^{3}+67608x^{2}-103680x-40824.\end{eqnarray}$$
The endomorphism ring of the jacobian
![]() $\operatorname{Jac}(C)$
has complex multiplication by the ring of algebraic integers in
$\operatorname{Jac}(C)$
has complex multiplication by the ring of algebraic integers in
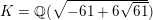 $K=\mathbb{Q}(\sqrt{-61+6\sqrt{61}})$
. The real quadratic subfield of
$K=\mathbb{Q}(\sqrt{-61+6\sqrt{61}})$
. The real quadratic subfield of
![]() $K$
is
$K$
is
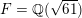 $F=\mathbb{Q}(\sqrt{61})$
. We have
$F=\mathbb{Q}(\sqrt{61})$
. We have
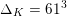 $\unicode[STIX]{x1D6E5}_{K}=61^{3}$
and
$\unicode[STIX]{x1D6E5}_{K}=61^{3}$
and
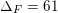 $\unicode[STIX]{x1D6E5}_{F}=61$
, so the conductor of
$\unicode[STIX]{x1D6E5}_{F}=61$
, so the conductor of
![]() $K$
is
$K$
is
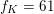 $f_{K}=61$
. Now
$f_{K}=61$
. Now
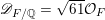 $\mathscr{D}_{F/\mathbb{Q}}=\sqrt{61}{\mathcal{O}}_{F}$
. Let
$\mathscr{D}_{F/\mathbb{Q}}=\sqrt{61}{\mathcal{O}}_{F}$
. Let
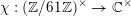 $\unicode[STIX]{x1D712}:(\mathbb{Z}/61\mathbb{Z})^{\times }\rightarrow \mathbb{C}^{\times }$
be the character of order
$\unicode[STIX]{x1D712}:(\mathbb{Z}/61\mathbb{Z})^{\times }\rightarrow \mathbb{C}^{\times }$
be the character of order
![]() $4$
with
$4$
with
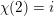 $\unicode[STIX]{x1D712}(2)=i$
; observe that
$\unicode[STIX]{x1D712}(2)=i$
; observe that
![]() $2$
generates
$2$
generates
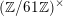 $(\mathbb{Z}/61\mathbb{Z})^{\times }$
. Then
$(\mathbb{Z}/61\mathbb{Z})^{\times }$
. Then
 $$\begin{eqnarray}\mathop{\sum }_{m=1}^{60}\unicode[STIX]{x1D712}(m)m=-61(1-i)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=1}^{60}\unicode[STIX]{x1D712}(m)m=-61(1-i)\end{eqnarray}$$
and so
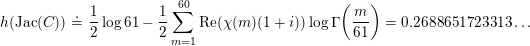 $$\begin{eqnarray}h(\operatorname{Jac}(C))~\dot{=}~\frac{1}{2}\log 61-\frac{1}{2}\mathop{\sum }_{m=1}^{60}\operatorname{Re}(\unicode[STIX]{x1D712}(m)(1+i))\log \unicode[STIX]{x1D6E4}\biggl(\frac{m}{61}\biggr)=0.2688651723313\ldots\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))~\dot{=}~\frac{1}{2}\log 61-\frac{1}{2}\mathop{\sum }_{m=1}^{60}\operatorname{Re}(\unicode[STIX]{x1D712}(m)(1+i))\log \unicode[STIX]{x1D6E4}\biggl(\frac{m}{61}\biggr)=0.2688651723313\ldots\end{eqnarray}$$
by (A 2).
The Igusa invariants satisfy
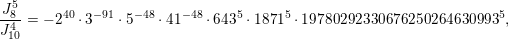 $$\begin{eqnarray}\frac{J_{8}^{5}}{J_{10}^{4}}=-2^{40}\cdot 3^{-91}\cdot 5^{-48}\cdot 41^{-48}\cdot 643^{5}\cdot 1871^{5}\cdot 19780292330676250264630993^{5},\end{eqnarray}$$
$$\begin{eqnarray}\frac{J_{8}^{5}}{J_{10}^{4}}=-2^{40}\cdot 3^{-91}\cdot 5^{-48}\cdot 41^{-48}\cdot 643^{5}\cdot 1871^{5}\cdot 19780292330676250264630993^{5},\end{eqnarray}$$
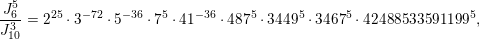 $$\begin{eqnarray}\frac{J_{6}^{5}}{J_{10}^{3}}=2^{25}\cdot 3^{-72}\cdot 5^{-36}\cdot 7^{5}\cdot 41^{-36}\cdot 487^{5}\cdot 3449^{5}\cdot 3467^{5}\cdot 42488533591199^{5},\end{eqnarray}$$
$$\begin{eqnarray}\frac{J_{6}^{5}}{J_{10}^{3}}=2^{25}\cdot 3^{-72}\cdot 5^{-36}\cdot 7^{5}\cdot 41^{-36}\cdot 487^{5}\cdot 3449^{5}\cdot 3467^{5}\cdot 42488533591199^{5},\end{eqnarray}$$
and
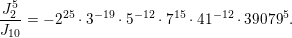 $$\begin{eqnarray}\frac{J_{2}^{5}}{J_{10}}=-2^{25}\cdot 3^{-19}\cdot 5^{-12}\cdot 7^{15}\cdot 41^{-12}\cdot 39079^{5}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{J_{2}^{5}}{J_{10}}=-2^{25}\cdot 3^{-19}\cdot 5^{-12}\cdot 7^{15}\cdot 41^{-12}\cdot 39079^{5}.\end{eqnarray}$$
The quotient (A 5) yields the contribution of
![]() $3$
to the Faltings height and (A 6) the contributions of
$3$
to the Faltings height and (A 6) the contributions of
![]() $5$
and
$5$
and
![]() $41$
. Explicitly, the finite contribution to
$41$
. Explicitly, the finite contribution to
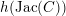 $h(\operatorname{Jac}(C))$
as in Theorem 4.5 is
$h(\operatorname{Jac}(C))$
as in Theorem 4.5 is
 $$\begin{eqnarray}{\textstyle \frac{2}{5}}\log 3+{\textstyle \frac{1}{5}}\log 5+{\textstyle \frac{1}{5}}\log 41.\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{2}{5}}\log 3+{\textstyle \frac{1}{5}}\log 5+{\textstyle \frac{1}{5}}\log 41.\end{eqnarray}$$
Our curve has potentially good reduction away from
![]() $3,5,$
and
$3,5,$
and
![]() $41$
.
$41$
.
We fix roots
 $\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}\in \mathbb{H}$
of
$\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}\in \mathbb{H}$
of
 $x^{4}-61x^{3}+6039x^{2}-137677x+889319$
. They are suitable diagonal elements as in Remark 3.4 and can be used to construct a period matrix
$x^{4}-61x^{3}+6039x^{2}-137677x+889319$
. They are suitable diagonal elements as in Remark 3.4 and can be used to construct a period matrix
![]() $Z$
with
$Z$
with
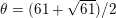 $\unicode[STIX]{x1D703}=(61+\sqrt{61})/2$
. We approximate
$\unicode[STIX]{x1D703}=(61+\sqrt{61})/2$
. We approximate
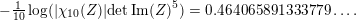 $$\begin{eqnarray}-{\textstyle \frac{1}{10}}\log (|\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\operatorname{Im}(Z)^{5})=0.464065891333779\ldots .\end{eqnarray}$$
$$\begin{eqnarray}-{\textstyle \frac{1}{10}}\log (|\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\operatorname{Im}(Z)^{5})=0.464065891333779\ldots .\end{eqnarray}$$
We add (A 7) and
 $-\text{log}(2^{4/5}\unicode[STIX]{x1D70B})$
from Theorem 4.5 to this value and see that the resulting value approximates (A 4) well.
$-\text{log}(2^{4/5}\unicode[STIX]{x1D70B})$
from Theorem 4.5 to this value and see that the resulting value approximates (A 4) well.
Example A.3. Our final example has bad reduction above
![]() $2$
. Let
$2$
. Let
![]() $C$
be given by
$C$
be given by
 $$\begin{eqnarray}y^{2}=-x^{5}+3x^{4}+2x^{3}-6x^{2}-3x+1.\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=-x^{5}+3x^{4}+2x^{3}-6x^{2}-3x+1.\end{eqnarray}$$
The endomorphism ring of
![]() $\operatorname{Jac}(C)$
is the ring of integers in
$\operatorname{Jac}(C)$
is the ring of integers in
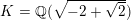 $K=\mathbb{Q}(\sqrt{-2+\sqrt{2}})$
which contains
$K=\mathbb{Q}(\sqrt{-2+\sqrt{2}})$
which contains
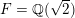 $F=\mathbb{Q}(\sqrt{2})$
. We have
$F=\mathbb{Q}(\sqrt{2})$
. We have
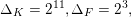 $\unicode[STIX]{x1D6E5}_{K}=2^{11},\unicode[STIX]{x1D6E5}_{F}=2^{3},$
and
$\unicode[STIX]{x1D6E5}_{K}=2^{11},\unicode[STIX]{x1D6E5}_{F}=2^{3},$
and
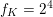 $f_{K}=2^{4}$
. We must take slightly more care when finding
$f_{K}=2^{4}$
. We must take slightly more care when finding
![]() $\unicode[STIX]{x1D712}$
as
$\unicode[STIX]{x1D712}$
as
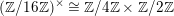 $(\mathbb{Z}/16\mathbb{Z})^{\times }\cong \mathbb{Z}/4\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
is not cyclic and admits four characters of order
$(\mathbb{Z}/16\mathbb{Z})^{\times }\cong \mathbb{Z}/4\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
is not cyclic and admits four characters of order
![]() $4$
. The kernel of
$4$
. The kernel of
![]() $\unicode[STIX]{x1D712}$
we are interested in corresponds to the fixed field of
$\unicode[STIX]{x1D712}$
we are interested in corresponds to the fixed field of
![]() $K$
in the number field generated by a root of unity of order
$K$
in the number field generated by a root of unity of order
![]() $16$
. The non-trivial element in
$16$
. The non-trivial element in
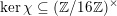 $\ker \unicode[STIX]{x1D712}\subseteq (\mathbb{Z}/16\mathbb{Z})^{\times }$
is represented by
$\ker \unicode[STIX]{x1D712}\subseteq (\mathbb{Z}/16\mathbb{Z})^{\times }$
is represented by
![]() $7,9,$
or
$7,9,$
or
![]() $-1$
. However,
$-1$
. However,
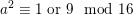 $a^{2}\equiv 1\text{ or }9\hspace{0.6em}{\rm mod}\hspace{0.2em}16$
if
$a^{2}\equiv 1\text{ or }9\hspace{0.6em}{\rm mod}\hspace{0.2em}16$
if
![]() $a$
is odd. This rules our
$a$
is odd. This rules our
![]() $9$
as a representative because
$9$
as a representative because
![]() $K/\mathbb{Q}$
is cyclic of order
$K/\mathbb{Q}$
is cyclic of order
![]() $4$
. Moreover,
$4$
. Moreover,
![]() $-1$
is also impossible because it represents complex conjugation in the Galois group. This leaves
$-1$
is also impossible because it represents complex conjugation in the Galois group. This leaves
![]() $7$
, i.e.,
$7$
, i.e.,
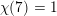 $\unicode[STIX]{x1D712}(7)=1$
. We must have
$\unicode[STIX]{x1D712}(7)=1$
. We must have
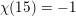 $\unicode[STIX]{x1D712}(15)=-1$
and
$\unicode[STIX]{x1D712}(15)=-1$
and
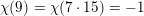 $\unicode[STIX]{x1D712}(9)=\unicode[STIX]{x1D712}(7\cdot 15)=-1$
. Again up to complex conjugation there are at most two choices for
$\unicode[STIX]{x1D712}(9)=\unicode[STIX]{x1D712}(7\cdot 15)=-1$
. Again up to complex conjugation there are at most two choices for
![]() $\unicode[STIX]{x1D712}$
. As
$\unicode[STIX]{x1D712}$
. As
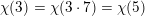 $\unicode[STIX]{x1D712}(3)=\unicode[STIX]{x1D712}(3\cdot 7)=\unicode[STIX]{x1D712}(5)$
, one choice is
$\unicode[STIX]{x1D712}(3)=\unicode[STIX]{x1D712}(3\cdot 7)=\unicode[STIX]{x1D712}(5)$
, one choice is
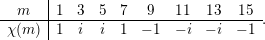
Thus,
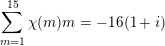 $$\begin{eqnarray}\mathop{\sum }_{m=1}^{15}\unicode[STIX]{x1D712}(m)m=-16(1+i)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m=1}^{15}\unicode[STIX]{x1D712}(m)m=-16(1+i)\end{eqnarray}$$
and so
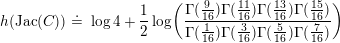 $$\begin{eqnarray}h(\operatorname{Jac}(C))~\dot{=}~\log 4+\frac{1}{2}\log \biggl(\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{9}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{11}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{13}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{15}{16}})}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{3}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{5}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{7}{16}})}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))~\dot{=}~\log 4+\frac{1}{2}\log \biggl(\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{9}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{11}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{13}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{15}{16}})}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{3}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{5}{16}})\unicode[STIX]{x1D6E4}({\textstyle \frac{7}{16}})}\biggr)\end{eqnarray}$$
by (A 2). Numerically, we find
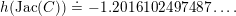 $$\begin{eqnarray}h(\operatorname{Jac}(C))~\dot{=}~-1.2016102497487\ldots .\end{eqnarray}$$
$$\begin{eqnarray}h(\operatorname{Jac}(C))~\dot{=}~-1.2016102497487\ldots .\end{eqnarray}$$
The Igusa invariants satisfy
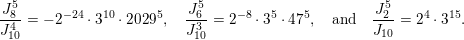 $$\begin{eqnarray}\frac{J_{8}^{5}}{J_{10}^{4}}=-2^{-24}\cdot 3^{10}\cdot 2029^{5},\quad \frac{J_{6}^{5}}{J_{10}^{3}}=2^{-8}\cdot 3^{5}\cdot 47^{5},\quad \text{and}\quad \frac{J_{2}^{5}}{J_{10}}=2^{4}\cdot 3^{15}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{J_{8}^{5}}{J_{10}^{4}}=-2^{-24}\cdot 3^{10}\cdot 2029^{5},\quad \frac{J_{6}^{5}}{J_{10}^{3}}=2^{-8}\cdot 3^{5}\cdot 47^{5},\quad \text{and}\quad \frac{J_{2}^{5}}{J_{10}}=2^{4}\cdot 3^{15}.\end{eqnarray}$$
So, only
![]() $2$
contributes to the finite part of the height in Theorem 4.5. In fact,
$2$
contributes to the finite part of the height in Theorem 4.5. In fact,
![]() $C$
has potentially good reduction outside of
$C$
has potentially good reduction outside of
![]() $2$
. The contribution to the finite part is
$2$
. The contribution to the finite part is
We can take
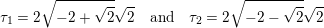 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{1}=2\sqrt{-2+\sqrt{2}}\sqrt{2}\quad \text{and}\quad \unicode[STIX]{x1D70F}_{2}=2\sqrt{-2-\sqrt{2}}\sqrt{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{1}=2\sqrt{-2+\sqrt{2}}\sqrt{2}\quad \text{and}\quad \unicode[STIX]{x1D70F}_{2}=2\sqrt{-2-\sqrt{2}}\sqrt{2}\end{eqnarray}$$
to construct
![]() $Z$
, now with
$Z$
, now with
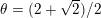 $\unicode[STIX]{x1D703}=(2+\sqrt{2})/2$
, and find
$\unicode[STIX]{x1D703}=(2+\sqrt{2})/2$
, and find
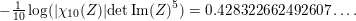 $$\begin{eqnarray}-{\textstyle \frac{1}{10}}\log (|\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\operatorname{Im}(Z)^{5})=0.428322662492607\ldots .\end{eqnarray}$$
$$\begin{eqnarray}-{\textstyle \frac{1}{10}}\log (|\unicode[STIX]{x1D712}_{10}(Z)|\text{det}\operatorname{Im}(Z)^{5})=0.428322662492607\ldots .\end{eqnarray}$$
We must add
 $(\log 2)/10$
to this value to compensate for bad reduction and
$(\log 2)/10$
to this value to compensate for bad reduction and
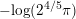 $-\text{log}(2^{4/5}\unicode[STIX]{x1D70B})$
due to the normalisation of the archimedean places. We end up with a good match with (A 8).
$-\text{log}(2^{4/5}\unicode[STIX]{x1D70B})$
due to the normalisation of the archimedean places. We end up with a good match with (A 8).