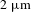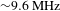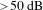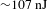Generation of 100 nJ pulse, 1 W average power at $2~\unicode[STIX]{x03BC}\text{m}$ from an intermode beating mode-locked all-fiber laser

Abstract

We report on the investigation of intermode beating mode-locked (IBML) pulse generation in a simple all-fiber Tm$^{3+}$-doped double clad fiber laser (TDFL). This IBML TDFL is implemented by matching longitudinal-mode frequency between 793 nm laser and TDFL without extra mode locker. The central wavelength of ${\sim}1983~\text{nm}$, the fundamental pulse frequency of ${\sim}9.6~\text{MHz}$ and the signal-to-noise ratio (SNR) of ${>}50~\text{dB}$ are achieved in this IBML TDFL. With laser cavity optimization, the IBML TDFL can finally generate an average output power of 1.03 W with corresponding pulse energy of ${\sim}107~\text{nJ}$. These results can provide an easily accessible way to develop compact large-energy, high-power TDFLs.

1 Introduction

Eye-safe $2~\unicode[STIX]{x03BC}\text{m}$ pulsed fiber lasers have boomed in recent years due to their extensive use in medicine, material processing and national defense. Some characteristics crucial for practical applications of $2~\unicode[STIX]{x03BC}\text{m}$ pulsed fiber lasers are large pulse energy, high output power and high laser stability. The pulsed operation of fiber lasers is typically implemented with $Q$ -switching and mode-locking techniques. $Q$ -switched pulse trains are capable of large pulse energy and high average output power, but unstable pulse repetition rate caused by variable pump power. In contrast, mode-locked pulse trains are more expected to meet all the above conditions.

The well-established ways to generate $2~\unicode[STIX]{x03BC}\text{m}$ mode-locked pulse trains are employing active mode lockers or passive mode lockers to modulate fiber lasers. The common $2~\unicode[STIX]{x03BC}\text{m}$ active mode lockers are acousto-optic modulator (AOM) and electro-optic modulator (EOM)^[1–3]. For instance, Kneis et al. have demonstrated a 66 MHz actively mode-locked Tm $^{3+}$ -doped double clad fiber laser (TDFL) with pulse energy of $0.8~\unicode[STIX]{x03BC}\text{J}$ by using a free space AOM^[1]. Nevertheless, the $2~\unicode[STIX]{x03BC}\text{m}$ AOM and EOM are often with tremendous cost and nonintegrated structure, which should be driven by an additional digital frequency synthesizer and pulse generator. Differently, passive mode lockers can spontaneously modulate lasers by means of their nonlinear optical properties. Low-dimension materials and semiconductor saturable absorption mirrors (SESAMs) are the best known types of passive mode lockers. Their presence can always be seen in mode-locked TDFLs^[4–10], but none is perfect. For example, thermal accumulation under strong light illumination for low-dimension materials is severe. The improvement of cost and fabrication process of SESAMs has a long way to go.

Besides these real saturable absorbers (SAs), some other artificial SAs-based passive mode lockers have gradually come into researchers’ sight and attracted great attention, e.g., nonlinear polarization rotation (NPR)^[11–17], nonlinear amplifying loop mirror (NALM)^[18–21], and self-phase modulation (SPM)^[22]. Among them, NPR is the most studied and applied mode locking method. For instance, 330 fs, 248 MHz ultra-short pulse train has been generated in an NPR mode-locked 1950 nm TDFL^[12]. 1.446 GHz NPR mode-locked pulse is achieved in a $1.85~\unicode[STIX]{x03BC}\text{m}$ TDFL^[13]. However, environmental stability of NPR is challengeable. The pulse energy of NPR pulse still needs to be perfected. For NALM-based TDFLs, the mode-locking type is often dissipative soliton resonance (DSR). For example, 19.51 nJ, 6.19 ns NALM mode-locked pulse has been obtained from a $1.9~\unicode[STIX]{x03BC}\text{m}$ DSR TDFL^[18]. 353 nJ, 13.7 ns DSR pulse has been output from a 2005.9 nm NALM mode-locked TDFL^[19]. Nevertheless, the NALM mode-locked TDFLs are always restricted to rectangular pulse shapes and $\unicode[STIX]{x03C3}$ -shaped laser structures. More recently, Luo et al. have successfully demonstrated a 352 pJ pulse energy, 12.2 mW average output power mode-locked TDFL through cavity length matching method^[23], which is known as intermode beating mode-locking^[23–27]. Neither additional mode lockers nor special cavity structures are required in intermode beating mode-locked (IBML) fiber lasers. Therefore, IBML fiber lasers can be cost-effective, fairly compact, and with a high damage threshold, which are expected to become high performance $2~\unicode[STIX]{x03BC}\text{m}$ pulsed fiber laser sources. In this letter, we propose a simple all-fiber IBML TDFL through cavity length matching. With further optimization, the IBML TDFL can generate stable short pulses with large pulse energy and high average output power.

2 Principle of intermode beating mode locking

The mechanism of IBML fiber laser can be briefly described as follows. Pump source possesses multi-longitudinal modes with mode frequencies $(f_{m})$ of

(1) $$\begin{eqnarray}f_{m}=m\frac{c}{2nL},\end{eqnarray}$$

where $m$ is a positive integer, $c$ is the speed of light, $n$ is the refractive index and $L$ is the cavity length. The intermode beating among these longitudinal modes can lead to a periodic weak jitter $(T)$ of pump source’s output power.

(2) $$\begin{eqnarray}T=\frac{1}{f_{m}}.\end{eqnarray}$$

This phenomenon can be observed in a frequency spectrum analyzer, showing weak frequency lines. But it shows no periodic pulse trains on the oscilloscope. The periodic weak jitter of laser intensity can transfer from pump source to gain fiber, modulating the intensity of the intracavity laser, just like an active modulator.

(3) $$\begin{eqnarray}I_{p}(f_{m},t)\xrightarrow[{}]{\hspace{5.0pt}g(f_{m},t)\hspace{5.0pt}}I_{L}(f_{m},t).\end{eqnarray}$$

If a certain longitudinal-mode frequency $(f_{n})$ of fiber laser matches with a pump source one, the laser intensity modulation will be rapidly enhanced.

(4) $$\begin{eqnarray}f_{m}=f_{n}.\end{eqnarray}$$

Then, mode-locked pulses with a repetition rate of $f_{m}$ will be generated in the fiber laser. Otherwise, the fiber laser will oscillate in a consuetudinary continuous wave (CW) state. In short, the key step of IBML process is to match the longitudinal-mode frequency between pump source and fiber laser, i.e., cavity length of lasers. Compared to a synchronously pumped mode-locking one, the IBML technique is more competitive since it goes without a pulsed pump source.

3 Experimental setup

Figure 1(a) presents the schematic diagram of an IBML TDFL. It is a compact all-fiber laser with linear cavity structure. The pump source is a $793~\text{nm}/8~\text{W}$ composite-cavity semiconductor laser diode (SLD). The external cavity is derived from the Fresnel reflection of coupled fiber. A $793/1980~\text{nm}$ multi-mode pump and signal fiber combiner is applied to couple the pump light into gain fiber. The coupling efficiency of pump laser is ${\sim}90\%$ . The gain fiber is a 4 m Tm $^{3+}$ -doped double clad fiber (Nufern, SM-TDF-10P/130-M) with cladding absorption coefficient of $4.5~\text{dB}/\text{m}$ at 793 nm. A 50:50 1980 nm optical fiber coupler (OC) is made into a fiber loop mirror (FLM), acting as a reflective mirror with high reflectivity of ${\sim}100\%$ ^[28]. The other reflector mirror is a fiber Bragg grating (FBG). Its optical reflection spectrum is shown in Figure 1(b). The central wavelength is at ${\sim}1983~\text{nm}$ with a 3 dB bandwidth of ${\sim}2~\text{nm}$ . This FBG can reduce the laser’s quantum noise, making the laser’s central wavelength stable and the timing jitter weak^{[29, 30]}. Then, the other 1980 nm OC is used to output the intracavity laser. During our experimental process, the output ratios of 10%, 50% and 90% are investigated, respectively. To achieve intermode beating mode locking in this TDFL, the cavity length of TDFL is purposely controlled by inserting a matching fiber (SMF28e+). Firstly, the radio frequency (RF) spectrum of a 793 nm laser is measured by an RF spectrum analyzer (Keysight, 9 kHz, 7.5 GHz) together with a 12.5 GHz photodetector (Newport, 818-BB-51F). Figure 1(c) shows its longitudinal-mode frequency line of 9.68 MHz, 19.4 MHz and 29.1 MHz, which has a low signal-to-noise ratio (SNR) of ${\sim}11.5~\text{dB}$ , ${\sim}5~\text{dB}$ and ${\sim}4~\text{dB}$ . Then, an oscilloscope trace of 793 nm laser is also measured (Yokogawa, $2.5~\text{GS}/\text{s}$ , 500 MHz) and given in Figure 1(d). There is no regular pulse on the oscilloscope, confirming the CW operation state of 793 nm laser. At last, the length of matching fiber is precisely optimized until some longitudinal-mode frequencies between TDFL and 793 nm laser mutual matching. The total effective cavity length is modulated to be ${\sim}20.8~\text{m}$ , corresponding to a longitudinal-mode frequency of ${\sim}9.6~\text{MHz}$ . As the dispersion parameter $\unicode[STIX]{x1D6FD}_{2}$ of the single-mode fiber and the $\text{Tm}^{3+}$ -doped fiber is about $-71~\text{ps}^{2}/\text{km}$ and $-78.53~\text{ps}^{2}/\text{km}$ at 1950 nm, the net dispersion of this IBML laser is calculated to be about $-1.51~\text{ps}^{2}$ .

Figure 1. (a) Experimental setup of IBML TDFL with a simple linear cavity, (b) optical reflection spectrum of the 1983 nm FBG, (c) RF spectrum of 793 nm laser and (d) oscilloscope trace of 793 nm laser.

Figure 2. The average output power of TDFLs versus pump power with laser output ratios of 10%, 50% and 90%, respectively.

4 Results and discussion

When 10% intracavity laser is output, this TDFL emits CW laser at a pump power of 2 W. Further increase in the pump power to 2.5 W initiates the IBML operation. The stable mode-locked pulse can keep running with the pump power ranging from 2.5 to 3.4 W. The maximum average output power of this IBML TDFL is ${\sim}76.4~\text{mW}$ . In consideration of the large laser gain provided by the 4 m TDF and 8 W 793 nm laser in this TDFL, 50% laser output ratio is then used. The thresholds of CW and IBML operations are 2.5 W and 2.8 W, respectively. The stable mode-locked operation range is from 2.8 to 4.9 W. Under the pump power of 4.9 W, the average output power is measured to be ${\sim}496.6~\text{mW}$ . It is nearly 6.5 times of the 10% one. In order to further enhance the output power, 90% laser output ratio is also demonstrated. The thresholds of CW and IBML operations in this condition are 3.3 W and 3.4 W, respectively. With the pump power changing from 3.4 to 5.4 W, the IBML operation can stably work. The maximum average output power of this IBML TDFL with 90% output ratio is 1.03 W, which is much higher than in the other two cases. Figure 2 presents the average output power of the three TDFLs as a function of pump power. From Figure 2, all the laser output powers linearly increase with pump powers without a saturation phenomenon. The laser conversion efficiencies are measured to be 4.4%, 16.7% and 32.5%, respectively. If the laser output ratio continues to enlarge (e.g., 99%), there stands a good chance of further increasing the IBML TDFL’s average output power.

Figure 3. Optical spectrum of the IBML TDFL with 90% output ratio.

Figure 4. The output pulse trains of IBML TDFL with 90% output ratio: (a)  $200~\text{ns}/\text{div}$ , (b)  $10~\text{ns}/\text{div}$ and (c)  $2~\unicode[STIX]{x03BC}\text{s}/\text{div}$ .

Take the IBML TDFL with 90% output ratio as an example; the detailed laser outputs are exhibited. Figure 3 is the laser’s optical spectrum under the pump power of 5.4 W (Yokogawa, AQ6375, 1200–2400 nm). The central wavelength locates at 1983.7 nm. The full width at half maximum (FWHM) of this laser is ${\sim}0.05~\text{nm}$ . Then, the pulse trains of this IBML TDFL at the pump power of 5.4 W are shown in Figure 4. From Figure 4(a), the time interval of adjacent pulses is 104 ns, which corresponds well to the laser cavity round trip time. Figure 4(b) presents a single pulse. The FWHM of this pulse is measured to be 45 ns. With pump power varying from 3.4 to 5.4 W, the pulse width exhibits random variation from 45 to 47.5 ns. This pulse width is much wider than that of the traditional mode-locked pulse (e.g., ps and fs). To compress the pulse width, a piece of 8.5 m ultra-high numerical aperture 4 (UHNA4) fiber with positive dispersion at 1983 nm is connected to the laser output. However, the pulse width does not change after passing through the UHNA4 fiber, just like an actively mode-locked pulse. With reference to the actively mode-locked pulse, the pulse width $(\unicode[STIX]{x0394}t)$ of IBML TDFL can be determined by

(5) $$\begin{eqnarray}\unicode[STIX]{x0394}t=0.445\left(\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x0394}m}\right)^{\frac{1}{4}}\left(\frac{1}{f_{m}\unicode[STIX]{x0394}f_{g}}\right)^{\frac{1}{2}},\end{eqnarray}$$

where $\unicode[STIX]{x1D6FE}$ is the total TDFL’s gain coefficient, $2\unicode[STIX]{x0394}m$ is the 793 nm laser’s peak-to-peak value of modulation amplitude and $\unicode[STIX]{x0394}f_{g}$ is the gain bandwidth of TDF. Compared to the other IBML laser^[23], our IBML TDFL possesses a larger total gain coefficient and a smaller longitudinal-mode frequency, and hence a wider pulse width. From the above, the pulse width of this IBML TDFL can be further improved by decreasing the laser gain and increasing the longitudinal-mode frequency (e.g., intermode beating mode locking at larger longitudinal-mode frequency). Then, Figure 4(c) shows a wideband IBML pulse train. The pulse repetition rate is measured to be 9.615 MHz. The amplitude fluctuation of this pulse train is very weak, indicating the high amplitude stability of this IBML pulse. To further verify the stability of our IBML pulse, RF spectrum is recorded and shown in Figure 5. The fundamental pulse frequency in Figure 5(a) is measured to be 9.644 MHz with SNR of 57 dB, which is comparable to traditional mode-locked pulse. One will notice that there exist two sidebands in the RF spectrum which is introduced by the low pulse phase jitter. However, it can be further improved by reducing the pump-induced gain fluctuations, the quantum noise in the amplification process and the laser cavity length fluctuations. The broadband RF spectrum without spectral modulation is also given in Figure 5(b), further indicating the relative stability of our IBML pulse.

According to the pulse repetition rate measured by the frequency spectrum analyzer, the single pulse energy of the IBML TDFL with laser output ratio of 90% is calculated and presented in Figure 6. The single pulse energy almost linearly increases as the pump power. When the pump power is 5.4 W, the maximum single pulse energy of this IBML TDFL is 106.8 nJ. This pulse energy is ${\sim}300$ times of the previous 0.352 nJ one^[23]. Therefore, we have successfully constructed a simple all-fiber high performance mode-locked TDFL.

At last, the typical output characteristic parameters of the IBML TDFLs with different laser output ratios are summarized in Table 1. Their central wavelength and pulse repetition rate all locate at ${\sim}1983~\text{nm}$ and ${\sim}9.6~\text{MHz}$ . Their pulse trains are relatively stable with an SNR of ${>}50~\text{dB}$ . Moreover, their IBML operation ranges are wide, e.g., 2 W tunable pump power range in IBML TDFL with 90% output ratio. With laser output ratio optimization, the laser average output power and single pulse energy have been greatly improved.

Figure 5. (a) RF spectrum of IBML TDFL with 90% output ratio and (b) broadband RF spectrum.

Figure 6. The single pulse energy of IBML TDFL with laser output ratio of 90% versus pump power.

5 Conclusion

To conclude, we have successfully demonstrated the IBML operation in a simple linear cavity 1983 nm TDFL by matching longitudinal-mode frequency between 793 nm laser and TDFL for the first time, to the best of our knowledge. The generated IBML pulse has the repetition rate of ${\sim}9.6~\text{MHz}$ and the SNR of ${>}50~\text{dB}$ . To improve the laser output performance, laser output ratio of this IBML TDFL has been optimized. With enlarging the laser output ratio from 10% to 90%, the average output power and single pulse energy have been raised from 76.4 mW and 7.9 nJ to 1.03 W and 106.8 nJ, respectively. This IBML pulse energy can be further improved by continuing to increase the laser output ratio.

Table 1. Comparison of the IBML TDFLs with different laser output ratios.