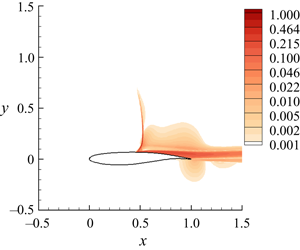
The original paper Crouch, Garbaruk & Strelets (Reference Crouch, Garbaruk and Strelets2019) identified three global modes of instability associated with swept-wing buffet: long-wavelength modes, intermediate-wavelength modes, and short-wavelength modes.
Following that earlier investigation, an independent study using an alternative formulation for the stability equations (Paladini et al. Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019) was not able to reproduce the growth characteristics for the short-wavelength modes. Meanwhile, we also applied a new formulation based on a fully three-dimensional eigenfunction to independently assess the initial results. In the course of this work, an error was identified in the numerical results by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) associated with a term in the eddy-viscosity equation. The error (here corrected) had minimal impact on the frequencies but a larger impact on the growth rates, with the error increasing with the spanwise wave number. While the long-wavelength and intermediate-wavelength growth rates are weakly altered, the short-wavelength growth rates are significantly modified.
Figures 3, 4, 6, and 7, and figures 10 through 14 are replotted here based on the original formulation by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) with corrected numerics. The discussion and overall findings by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) remain unchanged, with the exception that the peak growth rate for the short-wavelength modes occurs at ![]() $\beta \approx 25$ as opposed to
$\beta \approx 25$ as opposed to ![]() $\beta \approx 45$, and the short-wavelength onset of instability is now consistently supercritical to the long-wavelength oscillatory modes. The overall agreement between the stability analysis and the URANS is slightly improved. The new figures provide a quantitative correction to the growth rates and stability boundaries, but are qualitatively the same.
$\beta \approx 45$, and the short-wavelength onset of instability is now consistently supercritical to the long-wavelength oscillatory modes. The overall agreement between the stability analysis and the URANS is slightly improved. The new figures provide a quantitative correction to the growth rates and stability boundaries, but are qualitatively the same.

Figure 3. Instability growth rates at ![]() $M=0.73$,
$M=0.73$, ![]() $Re=3 \times 10^{6}$ as a function of
$Re=3 \times 10^{6}$ as a function of ![]() $\beta$ for (a) oscillatory modes and (b) stationary modes (OAT15A).
$\beta$ for (a) oscillatory modes and (b) stationary modes (OAT15A).

Figure 4. Magnitude of ![]() $u$ component of instability for
$u$ component of instability for ![]() $M=0.73$,
$M=0.73$, ![]() $\alpha =3.6^{\circ }$, and
$\alpha =3.6^{\circ }$, and ![]() $Re=3 \times 10^{6}$ with different values of
$Re=3 \times 10^{6}$ with different values of ![]() $\beta$: (a)
$\beta$: (a) ![]() $\beta =0$ oscillatory, (b)
$\beta =0$ oscillatory, (b) ![]() $\beta =6$ stationary, (c)
$\beta =6$ stationary, (c) ![]() $\beta =12$ stationary, (d)
$\beta =12$ stationary, (d) ![]() $\beta =45$ stationary (OAT15A).
$\beta =45$ stationary (OAT15A).
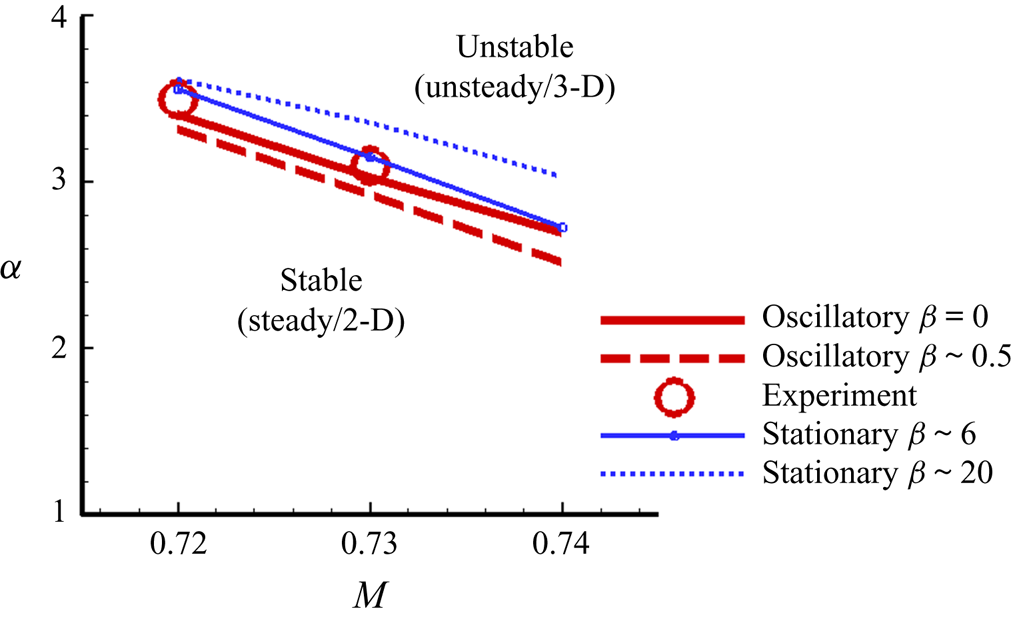
Figure 6. Stability boundaries for different ![]() $\beta$ values corresponding to local maxima of the growth rate at
$\beta$ values corresponding to local maxima of the growth rate at ![]() $Re=3 \times 10^{6}$ (OAT15A).
$Re=3 \times 10^{6}$ (OAT15A).

Figure 7. Variation with angle of attack for (a) growth rates of the stationary and oscillatory modes, and (b) oscillatory-mode frequencies for the dominant range of ![]() $\beta$. Results at
$\beta$. Results at ![]() $M=0.73$ and
$M=0.73$ and ![]() $Re=3 \times 10^{6}$ (RA16SC1).
$Re=3 \times 10^{6}$ (RA16SC1).

Figure 10. Neutral stability curves for (a) oscillatory modes, and (b) stationary modes, with S and U showing stable and unstable regions, respectively. Solid symbols are results from URANS, and open symbols are extrapolated URANS results at instability onset. Results at ![]() $M=0.72$,
$M=0.72$, ![]() $0.73$,
$0.73$, ![]() $0.74$ and
$0.74$ and ![]() $Re=3 \times 10^{6}$ (OAT15A).
$Re=3 \times 10^{6}$ (OAT15A).

Figure 13. Oscillatory mode (a) growth rates and (b) frequencies for different sweep angles ![]() $\varLambda =0^{\circ }$,
$\varLambda =0^{\circ }$, ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$,
$20^{\circ }$, ![]() $30^{\circ }$ at
$30^{\circ }$ at ![]() $M_n=0.73$,
$M_n=0.73$, ![]() $\alpha _n =3.2^{\circ }$ and
$\alpha _n =3.2^{\circ }$ and ![]() $Re_n=3 \times 10^{6}$ (OAT15A).
$Re_n=3 \times 10^{6}$ (OAT15A).

Figure 12. Travelling mode growth rate and frequency as a function of ![]() $\beta$ for infinite swept wing with: (a,b)
$\beta$ for infinite swept wing with: (a,b) ![]() $\varLambda =10^{\circ }$, (c,d)
$\varLambda =10^{\circ }$, (c,d) ![]() $\varLambda =20^{\circ }$, (e,f)
$\varLambda =20^{\circ }$, (e,f) ![]() $\varLambda =30^{\circ }$, at
$\varLambda =30^{\circ }$, at ![]() $M_n=0.73$ and
$M_n=0.73$ and ![]() $Re_n=3 \times 10^{6}$ (OAT15A).
$Re_n=3 \times 10^{6}$ (OAT15A).

Figure 11. Travelling mode (a) growth rate and (b) frequency as a function of ![]() $\beta$ for
$\beta$ for ![]() $\varLambda =30^{\circ }$. Results for different values of
$\varLambda =30^{\circ }$. Results for different values of ![]() $\alpha _n$ with
$\alpha _n$ with ![]() $M_n=0.73$,
$M_n=0.73$, ![]() $Re_n=3 \times 10^{6}$ (OAT15A).
$Re_n=3 \times 10^{6}$ (OAT15A).

Figure 14. Stability boundaries as a function of sweep for different ![]() $\beta$ values corresponding to local maxima of the growth rate. Results in terms of (a)
$\beta$ values corresponding to local maxima of the growth rate. Results in terms of (a) ![]() $\alpha _n$ and (b)
$\alpha _n$ and (b) ![]() $\alpha$ for
$\alpha$ for ![]() $M_n=0.73$ and
$M_n=0.73$ and ![]() $Re_n=3 \times 10^{6}$ (OAT15A).
$Re_n=3 \times 10^{6}$ (OAT15A).
Declaration of interests
The authors report no conflict of interest.