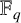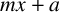1. Introduction
Let p be an odd prime and q a power of p. We use
![]() ${\mathbb F}_{q}$
to denote the finite field of order q. Throughout,
${\mathbb F}_{q}$
to denote the finite field of order q. Throughout,
![]() $\zeta $
denotes a primitive element of
$\zeta $
denotes a primitive element of
![]() ${\mathbb F}_{q}$
, so that
${\mathbb F}_{q}$
, so that
![]() $\langle \zeta \rangle ={\mathbb F}_{q}^\star $
, the set of nonzero elements of
$\langle \zeta \rangle ={\mathbb F}_{q}^\star $
, the set of nonzero elements of
![]() ${\mathbb F}_{q}$
. We also use
${\mathbb F}_{q}$
. We also use
![]() $\square _q$
and
$\square _q$
and ![]() to denote the squares and nonsquares, respectively, of
to denote the squares and nonsquares, respectively, of
![]() ${\mathbb F}_{q}$
. The quadratic character
${\mathbb F}_{q}$
. The quadratic character
![]() $\eta $
over
$\eta $
over
![]() ${\mathbb F}_{q}$
is the finite field extension of the Legendre symbol:
${\mathbb F}_{q}$
is the finite field extension of the Legendre symbol:

The problem of considering when an element and a linear translate of that element are both quadratic residues dates back at least to Gauss. Davenport comments in [Reference Davenport2, page 63] that Gauss determined the number of pairs
![]() $x,x+1 \in {\mathbb F}_{p}^\star $
for which x and
$x,x+1 \in {\mathbb F}_{p}^\star $
for which x and
![]() $x+1$
had prescribed characters. Of course, these results have since been extended to arbitrary fields: for example, Dickson gives the generalisation for square x in [Reference Dickson3, Theorem 67]. Davenport ascribes the full enumeration over arbitrary fields to Dickson also. More modern treatments of this count were given by Raber [Reference Raber8] and Ralston [Reference Ralston9] in the 1970s. In 2002, Sun [Reference Sun10] gave an explicit description of those x in
$x+1$
had prescribed characters. Of course, these results have since been extended to arbitrary fields: for example, Dickson gives the generalisation for square x in [Reference Dickson3, Theorem 67]. Davenport ascribes the full enumeration over arbitrary fields to Dickson also. More modern treatments of this count were given by Raber [Reference Raber8] and Ralston [Reference Ralston9] in the 1970s. In 2002, Sun [Reference Sun10] gave an explicit description of those x in
![]() ${\mathbb F}_{p}$
for which x and
${\mathbb F}_{p}$
for which x and
![]() $x+1$
were both squares or both nonsquares, thereby extending the original results of Gauss. In this note, we extend Sun’s results to all finite fields and all possible prescribed character values, and for any linear translate.
$x+1$
were both squares or both nonsquares, thereby extending the original results of Gauss. In this note, we extend Sun’s results to all finite fields and all possible prescribed character values, and for any linear translate.
To be more precise, let us fix
![]() $m,a\in {\mathbb F}_{q}^\star $
. We define four subsets of
$m,a\in {\mathbb F}_{q}^\star $
. We define four subsets of
![]() ${\mathbb F}_{q}^\star $
:
${\mathbb F}_{q}^\star $
:
 $$ \begin{align*} K_1(a,m) &= \{x : \eta(x) = \eta(mx+a) = 1 \},\\ K_2(a,m) &= \{x : \eta(x) = \eta(mx+a) = -1 \},\\ K_3(a,m) &= \{x : \eta(x) = -1,\ \eta(mx+a) = 1\},\\ K_4(a,m) &= \{x : \eta(x) = 1,\ \eta(mx+a) = -1\}. \end{align*} $$
$$ \begin{align*} K_1(a,m) &= \{x : \eta(x) = \eta(mx+a) = 1 \},\\ K_2(a,m) &= \{x : \eta(x) = \eta(mx+a) = -1 \},\\ K_3(a,m) &= \{x : \eta(x) = -1,\ \eta(mx+a) = 1\},\\ K_4(a,m) &= \{x : \eta(x) = 1,\ \eta(mx+a) = -1\}. \end{align*} $$
The historical results described above all relate to the sets
![]() $K_i(1,1)$
. As mentioned, Sun gave explicit descriptions of the sets
$K_i(1,1)$
. As mentioned, Sun gave explicit descriptions of the sets
![]() $K_1(1,1)$
and
$K_1(1,1)$
and
![]() $K_2(1,1)$
over prime fields in [Reference Sun10]. Here, we provide an explicit description of each of the sets
$K_2(1,1)$
over prime fields in [Reference Sun10]. Here, we provide an explicit description of each of the sets
![]() $K_i(a,m)$
for any nonzero
$K_i(a,m)$
for any nonzero
![]() $a,m$
in any finite field. To do so, we first show how to relate each of these sets to an explicit description of
$a,m$
in any finite field. To do so, we first show how to relate each of these sets to an explicit description of
![]() $K_i(1,1)$
and then give a complete description of the sets
$K_i(1,1)$
and then give a complete description of the sets
![]() $K_i(a,m)$
. The reduction to
$K_i(a,m)$
. The reduction to
![]() $K_i(1,1)$
is shown in the next section. The explicit descriptions of the sets
$K_i(1,1)$
is shown in the next section. The explicit descriptions of the sets
![]() $K_i(a,m)$
over an arbitrary finite field of odd order are given in Section 3. As shall be seen, the main tool used to obtain these descriptions is the ‘S-set’ representation of a finite field (see Lemma 3.1), which allows for a uniform treatment of all the sets
$K_i(a,m)$
over an arbitrary finite field of odd order are given in Section 3. As shall be seen, the main tool used to obtain these descriptions is the ‘S-set’ representation of a finite field (see Lemma 3.1), which allows for a uniform treatment of all the sets
![]() $K_i(a,m)$
.
$K_i(a,m)$
.
2. Reduction process
Our first step is to reduce our problem to dealing with the sets
![]() $K_i(1,1)$
. The reduction step is completely reversible so that having complete descriptions of the sets
$K_i(1,1)$
. The reduction step is completely reversible so that having complete descriptions of the sets
![]() $K_i(1,1)$
suffices for our purposes.
$K_i(1,1)$
suffices for our purposes.
The first and simplest reductions are those reductions involving m. As might be expected, these reductions split based on the value of
![]() $\eta (m)$
.
$\eta (m)$
.
Lemma 2.1. Let
![]() ${\mathbb F}_{q}$
be a finite field and
${\mathbb F}_{q}$
be a finite field and
![]() $a,m\in {\mathbb F}_{q}^\star $
.
$a,m\in {\mathbb F}_{q}^\star $
.
-
(i) If
 $\eta (m) = 1$
, then
$\eta (m) = 1$
, then  $$ \begin{align*}K_i(a,m) = m^{-1}K_i(a,1).\end{align*} $$
$$ \begin{align*}K_i(a,m) = m^{-1}K_i(a,1).\end{align*} $$
-
(ii) If
 $\eta (m) = -1$
, then
$\eta (m) = -1$
, then  $$ \begin{align*} K_1(a,m) &= m^{-1}K_3(a,1),\\ K_2(a,m) &= m^{-1}K_4(a,1),\\ K_3(a,m) &= m^{-1}K_1(a,1),\\ K_4(a,m) &= m^{-1}K_2(a,1). \end{align*} $$
$$ \begin{align*} K_1(a,m) &= m^{-1}K_3(a,1),\\ K_2(a,m) &= m^{-1}K_4(a,1),\\ K_3(a,m) &= m^{-1}K_1(a,1),\\ K_4(a,m) &= m^{-1}K_2(a,1). \end{align*} $$
Proof. Suppose
![]() $\eta (m) = 1$
. Then,
$\eta (m) = 1$
. Then,
![]() $\eta (x) = \eta (mx)$
for all
$\eta (x) = \eta (mx)$
for all
![]() $x\in {\mathbb F}_{q}$
. So, if
$x\in {\mathbb F}_{q}$
. So, if
![]() $x\in K_i(a,m)$
, then
$x\in K_i(a,m)$
, then
![]() $mx\in K_i(a,1)$
and vice versa. Thus,
$mx\in K_i(a,1)$
and vice versa. Thus,
![]() $K_i(a,m) = m^{-1}K_i(a,1)$
for
$K_i(a,m) = m^{-1}K_i(a,1)$
for
![]() $i = 1,2,3,4.$
$i = 1,2,3,4.$
For the remainder, assume
![]() $\eta (m)=-1$
. If
$\eta (m)=-1$
. If
![]() $x\in K_1(a,m)$
, then
$x\in K_1(a,m)$
, then
![]() $\eta (x) = 1 = \eta (mx+a)$
. Since
$\eta (x) = 1 = \eta (mx+a)$
. Since
![]() $\eta (m)=-1$
,
$\eta (m)=-1$
,
![]() $\eta (mx) = -1$
. Hence,
$\eta (mx) = -1$
. Hence,
![]() $mx\in K_3(a,1)$
. Thus,
$mx\in K_3(a,1)$
. Thus,
![]() $K_1(a,m) = m^{-1}K_3(a,1)$
. The other three cases follow similarly.
$K_1(a,m) = m^{-1}K_3(a,1)$
. The other three cases follow similarly.
We now deal with the reduction of the a. In light of the previous lemma, we may restrict ourselves to reducing the sets
![]() $K_i(a,1)$
. For ease of notation, we denote
$K_i(a,1)$
. For ease of notation, we denote
![]() $K_i(a,1)$
by
$K_i(a,1)$
by
![]() $K_i(a)$
for
$K_i(a)$
for
![]() $i = 1,\ldots ,4$
.
$i = 1,\ldots ,4$
.
Lemma 2.2. Let
![]() $a\in {\mathbb F}_{q}^\star $
. The following statements hold.
$a\in {\mathbb F}_{q}^\star $
. The following statements hold.
-
(i) If
 $\eta (a) = 1$
, then
$\eta (a) = 1$
, then  $$ \begin{align*}K_i(a) = aK_i(1).\end{align*} $$
$$ \begin{align*}K_i(a) = aK_i(1).\end{align*} $$
-
(ii) If
 $\eta (a) = -1$
, then
$\eta (a) = -1$
, then  $$ \begin{align*} K_1(a) &= aK_2(1),\\ K_2(a) &= aK_1(1),\\ K_3(a) &= aK_4(1),\\ K_4(a) &= aK_3(1). \end{align*} $$
$$ \begin{align*} K_1(a) &= aK_2(1),\\ K_2(a) &= aK_1(1),\\ K_3(a) &= aK_4(1),\\ K_4(a) &= aK_3(1). \end{align*} $$
Proof. First, notice that
![]() $\eta (x) = \eta (a)\eta (a^{-1}x)$
and
$\eta (x) = \eta (a)\eta (a^{-1}x)$
and
![]() $\eta (x+a) = \eta (a)\eta (a^{-1}x + 1)$
.
$\eta (x+a) = \eta (a)\eta (a^{-1}x + 1)$
.
If
![]() $\eta (a) = 1$
, then
$\eta (a) = 1$
, then
![]() $x\in K_i(a)$
implies
$x\in K_i(a)$
implies
![]() $a^{-1}x\in K_i(1)$
as
$a^{-1}x\in K_i(1)$
as
![]() $\eta (x) = \eta (a^{-1}x)$
and
$\eta (x) = \eta (a^{-1}x)$
and
![]() $\eta (x+a) = \eta (a^{-1}x+1)$
.
$\eta (x+a) = \eta (a^{-1}x+1)$
.
Now suppose
![]() $\eta (a) = -1$
. As with the previous lemma, we prove one equality, with the others following nearly identically. Let
$\eta (a) = -1$
. As with the previous lemma, we prove one equality, with the others following nearly identically. Let
![]() $x\in K_3(a)$
. Then,
$x\in K_3(a)$
. Then,
![]() $\eta (x) = -1$
and
$\eta (x) = -1$
and
![]() ${\eta (x+a) = 1}$
. So
${\eta (x+a) = 1}$
. So
![]() $\eta (a^{-1}x) = 1$
and
$\eta (a^{-1}x) = 1$
and
![]() $\eta (a^{-1}x+1) = -1$
and hence,
$\eta (a^{-1}x+1) = -1$
and hence,
![]() $a^{-1}x\in K_4(1)$
.
$a^{-1}x\in K_4(1)$
.
3. Explicit representations
We now move to providing the explicit representations of the sets
![]() $K_i(1)$
. Our results make use of the following useful partition of a finite field. We provide a proof for completeness.
$K_i(1)$
. Our results make use of the following useful partition of a finite field. We provide a proof for completeness.
Lemma 3.1. Let q be an odd prime power and
![]() $a\in {\mathbb F}_{q}^\star $
.
$a\in {\mathbb F}_{q}^\star $
.
-
(1) If
 $a\in \square _q^\ast $
, then
$a\in \square _q^\ast $
, then
 ${\mathbb F}_{q}=S_0(a)\cup S_1(a)\cup S_2(a)$
, where
${\mathbb F}_{q}=S_0(a)\cup S_1(a)\cup S_2(a)$
, where  $$ \begin{align*} S_0(a) &=\{ \pm 2\sqrt{a} \},\\ S_1(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q-1} = 1 \text{ and } u\ne\pm\sqrt{a}\},\\ S_2(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q+1} = a \text{ and } u\ne\pm\sqrt{a}\}. \end{align*} $$
$$ \begin{align*} S_0(a) &=\{ \pm 2\sqrt{a} \},\\ S_1(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q-1} = 1 \text{ and } u\ne\pm\sqrt{a}\},\\ S_2(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q+1} = a \text{ and } u\ne\pm\sqrt{a}\}. \end{align*} $$
-
(2) If
 , then
, then
 ${\mathbb F}_{q}=S_1(a)\cup S_2(a)$
, where
${\mathbb F}_{q}=S_1(a)\cup S_2(a)$
, where  $$ \begin{align*} S_1(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q-1} = 1\}\\ S_2(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q+1} = a\}. \end{align*} $$
$$ \begin{align*} S_1(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q-1} = 1\}\\ S_2(a) &= \{ u+au^{-1} : u\in{\mathbb F}_{q^2} \text{ and } u^{q+1} = a\}. \end{align*} $$
Proof. We first show that for fixed
![]() $a\in {\mathbb F}_{q}^\star $
, any
$a\in {\mathbb F}_{q}^\star $
, any
![]() $x\in {\mathbb F}_{q}$
can be written as
$x\in {\mathbb F}_{q}$
can be written as
![]() $x=u+au^{-1}$
for some
$x=u+au^{-1}$
for some
![]() $u\in {\mathbb F}_{q^2}^\star $
with
$u\in {\mathbb F}_{q^2}^\star $
with
![]() $u^{q-1}=1$
or
$u^{q-1}=1$
or
![]() $u^{q+1}=a$
. To see this, consider the quadratic polynomial
$u^{q+1}=a$
. To see this, consider the quadratic polynomial
![]() $Y^2-xY-a$
over
$Y^2-xY-a$
over
![]() ${\mathbb F}_{q}$
. This factorises completely in
${\mathbb F}_{q}$
. This factorises completely in
![]() ${\mathbb F}_{q^2}$
. Let
${\mathbb F}_{q^2}$
. Let
![]() $u\in {\mathbb F}_{q^2}$
be a root of
$u\in {\mathbb F}_{q^2}$
be a root of
![]() $Y^2-xY-a$
, that is to say,
$Y^2-xY-a$
, that is to say,
![]() $u^2-xu+a=0$
and note that
$u^2-xu+a=0$
and note that
![]() $u\neq 0$
as
$u\neq 0$
as
![]() $a\neq 0$
. Isolating x, we have
$a\neq 0$
. Isolating x, we have
![]() $x=u+au^{-1}$
, where
$x=u+au^{-1}$
, where
![]() $u\in {\mathbb F}_{q^2}$
. As
$u\in {\mathbb F}_{q^2}$
. As
![]() $x\in {\mathbb F}_{q}$
, we have
$x\in {\mathbb F}_{q}$
, we have
![]() $x^q=x$
, from which we obtain
$x^q=x$
, from which we obtain
![]() $u^q+au^{-q}=u+au^{-1}$
, and rearranging yields
$u^q+au^{-q}=u+au^{-1}$
, and rearranging yields
Thus,
![]() $u^{q-1}=1$
or
$u^{q-1}=1$
or
![]() $u^{q+1}=a$
.
$u^{q+1}=a$
.
Now suppose
![]() $a\in \square _q$
. We have
$a\in \square _q$
. We have
![]() $x=u+au^{-1}$
for
$x=u+au^{-1}$
for
![]() $u\in {\mathbb F}_{q^2}^\star $
. If
$u\in {\mathbb F}_{q^2}^\star $
. If
![]() $x\in S_0$
, then
$x\in S_0$
, then
![]() ${x=\pm 2\sqrt {a}}$
. Therefore,
${x=\pm 2\sqrt {a}}$
. Therefore,
![]() $\pm 2\sqrt {a}=u+au^{-1}$
, or multiplying through by u and rearranging,
$\pm 2\sqrt {a}=u+au^{-1}$
, or multiplying through by u and rearranging,
![]() ${u^2- \pm 2\sqrt {a}u+a=0}$
. Factoring gives
${u^2- \pm 2\sqrt {a}u+a=0}$
. Factoring gives
![]() $(u-\pm \sqrt {a})^2=0$
, or in other words,
$(u-\pm \sqrt {a})^2=0$
, or in other words,
![]() $u=\pm \sqrt {a}$
. It follows that
$u=\pm \sqrt {a}$
. It follows that
![]() $S_0$
is disjoint from both
$S_0$
is disjoint from both
![]() $S_1$
and
$S_1$
and
![]() $S_2$
.
$S_2$
.
It remains to show
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are disjoint. Suppose
$S_2$
are disjoint. Suppose
![]() $x\in S_1\cap S_2$
. Then,
$x\in S_1\cap S_2$
. Then,
![]() ${x=u+au^{-1}}$
for some
${x=u+au^{-1}}$
for some
![]() $u\in {\mathbb F}_{q^2}^\star $
with
$u\in {\mathbb F}_{q^2}^\star $
with
![]() $u^{q-1}=1$
and where
$u^{q-1}=1$
and where
![]() $u\neq \pm \sqrt {a}$
. Also,
$u\neq \pm \sqrt {a}$
. Also,
![]() $x=v+av^{-1}$
for some
$x=v+av^{-1}$
for some
![]() ${v\in {\mathbb F}_{q^2}^\star }$
with
${v\in {\mathbb F}_{q^2}^\star }$
with
![]() $v^{q+1}=a$
and where
$v^{q+1}=a$
and where
![]() $v\neq \pm \sqrt {a}$
. So we have
$v\neq \pm \sqrt {a}$
. So we have
![]() $u+au^{-1}=v+av^{-1}$
, or multiplying through by
$u+au^{-1}=v+av^{-1}$
, or multiplying through by
![]() $uv$
and rearranging,
$uv$
and rearranging,
![]() $uv(u-v)=a(u-v)$
. So
$uv(u-v)=a(u-v)$
. So
![]() $u=v$
or
$u=v$
or
![]() $uv=a$
. If
$uv=a$
. If
![]() $u=v$
, then
$u=v$
, then
![]() $1=u^{q-1}=v^{q-1}$
. Therefore,
$1=u^{q-1}=v^{q-1}$
. Therefore,
![]() $v^{q+1}=v^2=a$
, which implies
$v^{q+1}=v^2=a$
, which implies
![]() $v=\pm \sqrt {a}$
, so that
$v=\pm \sqrt {a}$
, so that
![]() $x\in S_0$
, which is a contradiction. If
$x\in S_0$
, which is a contradiction. If
![]() $uv=a$
, then we again find
$uv=a$
, then we again find
![]() $v^{q-1}=1$
, which we know produces a contradiction. So,
$v^{q-1}=1$
, which we know produces a contradiction. So,
![]() $S_1\cap S_2=\varnothing $
and
$S_1\cap S_2=\varnothing $
and
![]() ${\mathbb F}_{q}=S_0\cup S_1\cup S_2$
where the S-sets are pairwise disjoint. The case where
${\mathbb F}_{q}=S_0\cup S_1\cup S_2$
where the S-sets are pairwise disjoint. The case where ![]() is almost the same, except that we no longer have the set
is almost the same, except that we no longer have the set
![]() $S_0$
to contend with.
$S_0$
to contend with.
The S-set representation of a finite field is certainly not new and has been used in a number of places over time. While it may appear so, it is not necessary to work in the quadratic extension, as you can compute
![]() $S_0$
(when required) and
$S_0$
(when required) and
![]() $S_1$
from within
$S_1$
from within
![]() ${\mathbb F}_{q}$
as
${\mathbb F}_{q}$
as
![]() $u\in {\mathbb F}_{q}^\star $
for
$u\in {\mathbb F}_{q}^\star $
for
![]() $S_1$
. One can then obtain
$S_1$
. One can then obtain
![]() $S_2$
as the complement. A specific and important instance of their application has been in the study of the Dickson polynomials of the first and second kind. The functional behaviour of both polynomial classes is intimately tied to the S-sets. Indeed, practically all of the permutation polynomial results for either class have relied specifically on the S-sets. (See Nöbauer [Reference Nöbauer7] for a full classification of permutation polynomials among the Dickson polynomials of the first kind, and Henderson [Reference Henderson4], Henderson and Matthews [Reference Henderson and Matthews5, Reference Henderson and Matthews6] and Coulter and Matthews [Reference Coulter and Matthews1] for establishing classes of permutation polynomials among the Dickson polynomials of the second kind.) We note, in passing, that Henderson and Matthews made a conjecture in [Reference Henderson and Matthews6] concerning permutation polynomials among the Dickson polynomials of the second kind that remains unresolved.
$S_2$
as the complement. A specific and important instance of their application has been in the study of the Dickson polynomials of the first and second kind. The functional behaviour of both polynomial classes is intimately tied to the S-sets. Indeed, practically all of the permutation polynomial results for either class have relied specifically on the S-sets. (See Nöbauer [Reference Nöbauer7] for a full classification of permutation polynomials among the Dickson polynomials of the first kind, and Henderson [Reference Henderson4], Henderson and Matthews [Reference Henderson and Matthews5, Reference Henderson and Matthews6] and Coulter and Matthews [Reference Coulter and Matthews1] for establishing classes of permutation polynomials among the Dickson polynomials of the second kind.) We note, in passing, that Henderson and Matthews made a conjecture in [Reference Henderson and Matthews6] concerning permutation polynomials among the Dickson polynomials of the second kind that remains unresolved.
Our main results will make use of the partition of
![]() ${\mathbb F}_{q}$
given in Lemma 3.1 as it allows us to obtain a consistent form for all four sets. Below, when we write
${\mathbb F}_{q}$
given in Lemma 3.1 as it allows us to obtain a consistent form for all four sets. Below, when we write
![]() $S_i^\star $
, we mean the nonzero elements of
$S_i^\star $
, we mean the nonzero elements of
![]() $S_i$
, though it is not necessarily the case that 0 will lie in the set
$S_i$
, though it is not necessarily the case that 0 will lie in the set
![]() $S_i$
. We start with the explicit descriptions of the sets
$S_i$
. We start with the explicit descriptions of the sets
![]() $K_i(1)$
, which are given in the following two theorems.
$K_i(1)$
, which are given in the following two theorems.
Theorem 3.2. For arbitrary odd q,
Proof. For ease, define
Lemma 3.1 shows that the sets A and B contain all nonzero squares except for
![]() $-1$
when
$-1$
when
![]() $-1$
is a square. So we have
$-1$
is a square. So we have
![]() $K_1(1) \cup K_4(1) = A\cup B$
. Now if
$K_1(1) \cup K_4(1) = A\cup B$
. Now if
![]() $a\in A$
, then
$a\in A$
, then
![]() $a = \tfrac {1}{4}(u - u^{-1})^2$
for some u such that
$a = \tfrac {1}{4}(u - u^{-1})^2$
for some u such that
![]() $u\in {\mathbb F}_{q}$
. So we can rewrite
$u\in {\mathbb F}_{q}$
. So we can rewrite
for some primitive element
![]() $\zeta $
of
$\zeta $
of
![]() ${\mathbb F}_{q}$
and integer k. From here, we can see that
${\mathbb F}_{q}$
and integer k. From here, we can see that
![]() $a + 1 = \tfrac {1}{4}(\zeta ^{k}+ \zeta ^{-k})^2$
which is a square in
$a + 1 = \tfrac {1}{4}(\zeta ^{k}+ \zeta ^{-k})^2$
which is a square in
![]() ${\mathbb F}_{q}$
, so that
${\mathbb F}_{q}$
, so that
![]() $A \subseteq K_1(1)$
. It now suffices to show that
$A \subseteq K_1(1)$
. It now suffices to show that
![]() $\#K_1(1) = \#A$
. Towards this end, consider
$\#K_1(1) = \#A$
. Towards this end, consider
![]() $S_1^\star (-1)$
. If
$S_1^\star (-1)$
. If
![]() $q \equiv 1 \pmod {4}$
, then
$q \equiv 1 \pmod {4}$
, then
![]() $-1$
is a square in
$-1$
is a square in
![]() ${\mathbb F}_{q}$
so
${\mathbb F}_{q}$
so
![]() $\#S_1^\star (-1) = \tfrac {1}{2}{(q-3)}-1$
. Similarly, if
$\#S_1^\star (-1) = \tfrac {1}{2}{(q-3)}-1$
. Similarly, if
![]() $q\equiv -1\pmod {4}$
, then
$q\equiv -1\pmod {4}$
, then
![]() $\#S_1^\star (-1) = \tfrac 12{(q-1)}-1$
. Since
$\#S_1^\star (-1) = \tfrac 12{(q-1)}-1$
. Since
![]() $S_1^\star (-1)$
is closed under negation, we have
$S_1^\star (-1)$
is closed under negation, we have
![]() $\#A = \tfrac {1}{2}{\#S_1^\star (-1)}$
and thus
$\#A = \tfrac {1}{2}{\#S_1^\star (-1)}$
and thus
![]() $A = K_1(1)$
in each case by [Reference Ralston9]. This then gives
$A = K_1(1)$
in each case by [Reference Ralston9]. This then gives
![]() $B = K_4(1)$
since A and B are disjoint.
$B = K_4(1)$
since A and B are disjoint.
Theorem 3.3. Let
![]() $\zeta $
be a primitive element of
$\zeta $
be a primitive element of
![]() ${\mathbb F}_{q}$
. Then,
${\mathbb F}_{q}$
. Then,
 $$ \begin{align*} K_2(1) = \Bigg\{ \frac{1}{4\zeta}\alpha^2 : \alpha \in S_1^\star(-\zeta)\Bigg\} \quad\text{and}\quad K_3(1) = \Bigg\{\frac{1}{4\zeta}\alpha^2 : \alpha \in S_2^\star(-\zeta)\Bigg\}. \end{align*} $$
$$ \begin{align*} K_2(1) = \Bigg\{ \frac{1}{4\zeta}\alpha^2 : \alpha \in S_1^\star(-\zeta)\Bigg\} \quad\text{and}\quad K_3(1) = \Bigg\{\frac{1}{4\zeta}\alpha^2 : \alpha \in S_2^\star(-\zeta)\Bigg\}. \end{align*} $$
Proof. Let
 $$ \begin{align*} A = \Bigg\{ \frac{1}{4\zeta}\alpha^2 : \alpha \in S_1^\star(-\zeta)\Bigg\} \quad\text{and}\quad B = \Bigg\{\frac{1}{4\zeta}\alpha^2 : \alpha \in S_2^\star(-\zeta)\Bigg\}. \end{align*} $$
$$ \begin{align*} A = \Bigg\{ \frac{1}{4\zeta}\alpha^2 : \alpha \in S_1^\star(-\zeta)\Bigg\} \quad\text{and}\quad B = \Bigg\{\frac{1}{4\zeta}\alpha^2 : \alpha \in S_2^\star(-\zeta)\Bigg\}. \end{align*} $$
Similar to Theorem 3.2, we can see that
![]() $A\cup B = K_2(1) \cup K_3(1)$
and that
$A\cup B = K_2(1) \cup K_3(1)$
and that
![]() $A\cap B = \emptyset $
. Let
$A\cap B = \emptyset $
. Let
![]() $a \in A$
. Then,
$a \in A$
. Then,
![]() $a = \tfrac {1}{4\zeta }(\zeta ^k-\zeta ^{1-k})^2$
for some integer k, and thus,
$a = \tfrac {1}{4\zeta }(\zeta ^k-\zeta ^{1-k})^2$
for some integer k, and thus,
 $$ \begin{align*}a+1 = \frac{1}{4\zeta}(\zeta^k+\zeta^{1-k})^2.\end{align*} $$
$$ \begin{align*}a+1 = \frac{1}{4\zeta}(\zeta^k+\zeta^{1-k})^2.\end{align*} $$
So we have
![]() $A\subseteq K_2(1)$
. To finish the proof, we need only show that
$A\subseteq K_2(1)$
. To finish the proof, we need only show that
![]() $\#A = \#K_1(1)$
.
$\#A = \#K_1(1)$
.
Again, consider
![]() $S_1^\star (-\zeta )$
. If
$S_1^\star (-\zeta )$
. If
![]() $q \equiv 1 \pmod {4}$
, then
$q \equiv 1 \pmod {4}$
, then
![]() $-\zeta $
is a nonsquare, so
$-\zeta $
is a nonsquare, so
![]() $\#S_1^\star (-\zeta ) = \tfrac {1}{2}{(q-1)}$
since
$\#S_1^\star (-\zeta ) = \tfrac {1}{2}{(q-1)}$
since
![]() $S_1^\star (-\zeta ) = S_1$
. So
$S_1^\star (-\zeta ) = S_1$
. So
![]() $\#A = \tfrac {1}{4}{(q-1)}$
and
$\#A = \tfrac {1}{4}{(q-1)}$
and
![]() $\#B = \tfrac {1}{4}{(q-1)}$
. If
$\#B = \tfrac {1}{4}{(q-1)}$
. If
![]() $q \equiv 3 \pmod {4}$
, then
$q \equiv 3 \pmod {4}$
, then
![]() $-\zeta $
is a square and so
$-\zeta $
is a square and so
![]() $\#S_1^\star (-\zeta ) = \tfrac {1}{2}{(q-3)}$
, and so
$\#S_1^\star (-\zeta ) = \tfrac {1}{2}{(q-3)}$
, and so
![]() $\#A = \tfrac {1}{4}{(q-3)}$
and
$\#A = \tfrac {1}{4}{(q-3)}$
and
![]() $\#B = \tfrac {1}{4}{(q-3)}$
giving
$\#B = \tfrac {1}{4}{(q-3)}$
giving
![]() $A = K_2(1)$
and
$A = K_2(1)$
and
![]() $B= K_3(1)$
.
$B= K_3(1)$
.
A nearly identical proof to the two above yields the following corollary, though you could also use Lemma 2.2.
Theorem 3.4. Let
![]() ${\mathbb F}_{q}$
be a finite field,
${\mathbb F}_{q}$
be a finite field,
![]() $\zeta $
a primitive element of
$\zeta $
a primitive element of
![]() ${\mathbb F}_{q}$
, and
${\mathbb F}_{q}$
, and
![]() $a\in {\mathbb F}_{q}^\star $
. Then,
$a\in {\mathbb F}_{q}^\star $
. Then,
 $$ \begin{align*} K_1(a) &= \{ \tfrac{1}{4}\alpha^2 : \alpha \in S_1^\star(-a)\},\\ K_2(a) &=\Bigg\{ \frac{1}{4\zeta}\alpha^2 : \alpha \in S_1^\star(-a\zeta)\Bigg\},\\ K_3(a) &= \Bigg\{\frac{1}{4\zeta}\alpha^2 : \alpha \in S_2^\star(-a\zeta)\Bigg\},\\ K_4(a) &= \{\tfrac{1}{4}\alpha^2 : \alpha \in S_2^\star(-a)\}. \end{align*} $$
$$ \begin{align*} K_1(a) &= \{ \tfrac{1}{4}\alpha^2 : \alpha \in S_1^\star(-a)\},\\ K_2(a) &=\Bigg\{ \frac{1}{4\zeta}\alpha^2 : \alpha \in S_1^\star(-a\zeta)\Bigg\},\\ K_3(a) &= \Bigg\{\frac{1}{4\zeta}\alpha^2 : \alpha \in S_2^\star(-a\zeta)\Bigg\},\\ K_4(a) &= \{\tfrac{1}{4}\alpha^2 : \alpha \in S_2^\star(-a)\}. \end{align*} $$
We now use Lemma 2.1 to get the representations of
![]() $K_i(a,m)$
.
$K_i(a,m)$
.
Theorem 3.5. Let
![]() ${\mathbb F}_{q}$
be a finite field,
${\mathbb F}_{q}$
be a finite field,
![]() $\zeta $
a primitive element of
$\zeta $
a primitive element of
![]() ${\mathbb F}_{q}$
, and
${\mathbb F}_{q}$
, and
![]() $a,m\in {\mathbb F}_{q}^\star $
.
$a,m\in {\mathbb F}_{q}^\star $
.
-
(i) If
 $\eta (m) = 1$
, then
$\eta (m) = 1$
, then  $$ \begin{align*} K_1(a,m) &= \bigg\{ \frac{1}{4m}\alpha^2 : \alpha \in S_1^\star(-a)\bigg\},\\[4pt] K_2(a,m) &= \bigg\{ \frac{1}{4m\zeta}\alpha^2 : \alpha \in S_1^\star(-a\zeta)\bigg\},\\[4pt] K_3(a,m) &= \bigg\{\frac{1}{4m\zeta}\alpha^2 : \alpha \in S_2^\star(-a\zeta)\bigg\},\\[4pt] K_4(a,m) &= \bigg\{\frac{1}{4m}\alpha^2 : \alpha \in S_2^\star(-a)\bigg\}. \end{align*} $$
$$ \begin{align*} K_1(a,m) &= \bigg\{ \frac{1}{4m}\alpha^2 : \alpha \in S_1^\star(-a)\bigg\},\\[4pt] K_2(a,m) &= \bigg\{ \frac{1}{4m\zeta}\alpha^2 : \alpha \in S_1^\star(-a\zeta)\bigg\},\\[4pt] K_3(a,m) &= \bigg\{\frac{1}{4m\zeta}\alpha^2 : \alpha \in S_2^\star(-a\zeta)\bigg\},\\[4pt] K_4(a,m) &= \bigg\{\frac{1}{4m}\alpha^2 : \alpha \in S_2^\star(-a)\bigg\}. \end{align*} $$
-
(ii) If
 $\eta (m) = -1$
, then
$\eta (m) = -1$
, then  $$ \begin{align*} K_1(a,m) &= \bigg\{\frac{1}{4m}\alpha^2 : \alpha \in S_2^\star(-a\zeta)\bigg\},\\[4pt] K_2(a,m) &= \bigg\{\frac{1}{4m\zeta}\alpha^2 : \alpha \in S_2^\star(-a)\bigg\},\\[4pt] K_3(a,m) &= \bigg\{ \frac{1}{4m\zeta}\alpha^2 : \alpha \in S_1^\star(-a)\bigg\},\\[4pt] K_4(a,m) &= \bigg\{ \frac{1}{4m}\alpha^2 : \alpha \in S_1^\star(-a\zeta)\bigg\}. \end{align*} $$
$$ \begin{align*} K_1(a,m) &= \bigg\{\frac{1}{4m}\alpha^2 : \alpha \in S_2^\star(-a\zeta)\bigg\},\\[4pt] K_2(a,m) &= \bigg\{\frac{1}{4m\zeta}\alpha^2 : \alpha \in S_2^\star(-a)\bigg\},\\[4pt] K_3(a,m) &= \bigg\{ \frac{1}{4m\zeta}\alpha^2 : \alpha \in S_1^\star(-a)\bigg\},\\[4pt] K_4(a,m) &= \bigg\{ \frac{1}{4m}\alpha^2 : \alpha \in S_1^\star(-a\zeta)\bigg\}. \end{align*} $$
Finally, Sun determined in [Reference Sun10] forms for
![]() $K_1(1)$
and
$K_1(1)$
and
![]() $K_2(1)$
over prime fields. However, Sun’s results do not have the same format as our general results above for
$K_2(1)$
over prime fields. However, Sun’s results do not have the same format as our general results above for
![]() $K_1(1)$
and
$K_1(1)$
and
![]() $K_2(1)$
, even when we restrict to the prime case. For completeness, we give the representations of
$K_2(1)$
, even when we restrict to the prime case. For completeness, we give the representations of
![]() $K_i(1)$
in terms similar to Sun’s.
$K_i(1)$
in terms similar to Sun’s.
Corollary 3.6. Let
![]() $\zeta $
be a primitive element of
$\zeta $
be a primitive element of
![]() ${\mathbb F}_{q}$
. Then,
${\mathbb F}_{q}$
. Then,
 $$ \begin{align*} K_1(1) &= \bigg\{ b_k : b_k = \frac{(\zeta^{2k}-1)^2}{4\zeta^{2k}} \text{ and } k = 1,\ldots, \bigg\lfloor \frac{q-3}{4}\bigg\rfloor \bigg\},\\[4pt] K_2(1) &= \bigg\{ b_k : b_k = \frac{(\zeta^{2k-1}-1)^2}{4\zeta^{2k-1}} \text{ and } k = 1,\ldots, \bigg\lfloor \frac{q-1}{4}\bigg\rfloor \bigg\},\\[4pt] K_3(1) &= \bigg\{ b_k : b_k = \frac{4\zeta^{2k-1}}{(\zeta^{2k-1}-1)^2} \text{ and } k = 1,\ldots, \bigg\lfloor\frac{q-1}{4}\bigg\rfloor\bigg\}. \end{align*} $$
$$ \begin{align*} K_1(1) &= \bigg\{ b_k : b_k = \frac{(\zeta^{2k}-1)^2}{4\zeta^{2k}} \text{ and } k = 1,\ldots, \bigg\lfloor \frac{q-3}{4}\bigg\rfloor \bigg\},\\[4pt] K_2(1) &= \bigg\{ b_k : b_k = \frac{(\zeta^{2k-1}-1)^2}{4\zeta^{2k-1}} \text{ and } k = 1,\ldots, \bigg\lfloor \frac{q-1}{4}\bigg\rfloor \bigg\},\\[4pt] K_3(1) &= \bigg\{ b_k : b_k = \frac{4\zeta^{2k-1}}{(\zeta^{2k-1}-1)^2} \text{ and } k = 1,\ldots, \bigg\lfloor\frac{q-1}{4}\bigg\rfloor\bigg\}. \end{align*} $$
Additionally, if
![]() $q\equiv 1\bmod 4$
, then
$q\equiv 1\bmod 4$
, then
 $$ \begin{align*} K_4(1) = \bigg\{ b_k : b_k = \frac{-(\zeta^{2k-1}-1)^2}{(\zeta^{2k-1}+1)^2} \text{ and } k = 1,\ldots, \frac{q-1}{4}\bigg\}.\end{align*} $$
$$ \begin{align*} K_4(1) = \bigg\{ b_k : b_k = \frac{-(\zeta^{2k-1}-1)^2}{(\zeta^{2k-1}+1)^2} \text{ and } k = 1,\ldots, \frac{q-1}{4}\bigg\}.\end{align*} $$
Proof. Here,
![]() $K_1(1)$
follows from the fact that
$K_1(1)$
follows from the fact that
 $$ \begin{align*} \frac{(\zeta^{2k}-1)^2}{4\zeta^{2k}} = \frac{1}{4\zeta}(\zeta^{k}-\zeta^{-k})^2\end{align*} $$
$$ \begin{align*} \frac{(\zeta^{2k}-1)^2}{4\zeta^{2k}} = \frac{1}{4\zeta}(\zeta^{k}-\zeta^{-k})^2\end{align*} $$
and we have seen that this is exactly the form of
![]() $K_1(1)$
from Theorem 3.2. Similarly,
$K_1(1)$
from Theorem 3.2. Similarly,
![]() $K_2(1)$
follows from the fact that
$K_2(1)$
follows from the fact that
 $$ \begin{align*}\frac{(\zeta^{2k-1}-1)^2}{4\zeta^{2k-1}} = \frac{1}{4\zeta}(\zeta^k - \zeta^{1-k})^2\end{align*} $$
$$ \begin{align*}\frac{(\zeta^{2k-1}-1)^2}{4\zeta^{2k-1}} = \frac{1}{4\zeta}(\zeta^k - \zeta^{1-k})^2\end{align*} $$
as seen in Theorem 3.3, and
![]() $K_3(1)$
follows from the fact that
$K_3(1)$
follows from the fact that
and so if
![]() $x\in K_2(1)$
, then
$x\in K_2(1)$
, then
![]() $x^{-1} \in K_3(1)$
and vice versa.
$x^{-1} \in K_3(1)$
and vice versa.
To finish, for
![]() $K_4(1)$
,
$K_4(1)$
,
![]() $-1$
is a square when
$-1$
is a square when
![]() $q\equiv 1\bmod 4$
and we can write
$q\equiv 1\bmod 4$
and we can write
Now, we see
![]() $x\in K_4(1)$
if and only if
$x\in K_4(1)$
if and only if
![]() $-1-x^{-1}\in K_3(1)$
and some simple arithmetic produces the claimed description.
$-1-x^{-1}\in K_3(1)$
and some simple arithmetic produces the claimed description.
We note that this second ‘explicit’ format, as given in Corollary 3.6, is missing the
![]() $q\equiv 3\bmod 4$
case for
$q\equiv 3\bmod 4$
case for
![]() $K_4(1)$
. The tricks we have used here do not work for this last case where
$K_4(1)$
. The tricks we have used here do not work for this last case where ![]() , as they end up producing another element in
, as they end up producing another element in
![]() $K_4$
. In particular, we find that when
$K_4$
. In particular, we find that when
![]() $q\equiv 3\bmod 4$
,
$q\equiv 3\bmod 4$
,
![]() $x\in K_4(1)$
if and only if
$x\in K_4(1)$
if and only if
![]() $-1-x^{-1}\in K_4(1)$
. While this gives us some structural information about
$-1-x^{-1}\in K_4(1)$
. While this gives us some structural information about
![]() $K_4(1)$
, it does not appear to lead to an explicit description of its elements in the format of Corollary 3.6.
$K_4(1)$
, it does not appear to lead to an explicit description of its elements in the format of Corollary 3.6.
Acknowledgement
The authors gratefully acknowledge the contribution of an anonymous referee, whose suggestions both improved the exposition and provided a cleaner explanation of how the representation of
![]() $K_4(1)$
just given follows from the results in this paper.
$K_4(1)$
just given follows from the results in this paper.