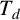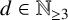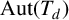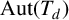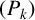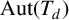1 Introduction
In the structure theory of locally compact (l.c.) groups, totally disconnected (t.d.) ones are in focus because any locally compact group G is an extension of its connected component
![]() $G_{0}$
by the totally disconnected quotient
$G_{0}$
by the totally disconnected quotient
![]() $G/G_{0}$
,
$G/G_{0}$
,
and connected l.c. groups have been identified as inverse limits of Lie groups in seminal work by Gleason [Reference Gleason13], Montgomery and Zippin [Reference Montgomery and Zippin20] and Yamabe [Reference Yamabe35].
Every t.d.l.c. group can be viewed as a directed union of compactly generated open subgroups. Among the latter, groups acting on regular graphs and trees stand out due to the Cayley–Abels graph construction: every compactly generated t.d.l.c. group G acts vertex-transitively on a connected regular graph
![]() $\Gamma $
of finite degree d with compact kernel K. In particular, the universal cover of
$\Gamma $
of finite degree d with compact kernel K. In particular, the universal cover of
![]() $\Gamma $
is the d-regular tree
$\Gamma $
is the d-regular tree
![]() $T_{d}$
and we obtain a cocompact subgroup
$T_{d}$
and we obtain a cocompact subgroup
![]() $\smash {\widetilde {G}}$
of its automorphism group
$\smash {\widetilde {G}}$
of its automorphism group
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
,
$\operatorname {\mathrm {Aut}}(T_{d})$
,
as an extension of
![]() $\pi _{1}(\Gamma )$
by
$\pi _{1}(\Gamma )$
by
![]() $G/K$
; see [Reference Monod19, Section 11.3] and [Reference Krön and Möller15] for details.
$G/K$
; see [Reference Monod19, Section 11.3] and [Reference Krön and Möller15] for details.
In studying the automorphism group
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
of a locally finite, connected graph
$\operatorname {\mathrm {Aut}}(\Gamma )$
of a locally finite, connected graph
![]() $\Gamma =(V,E)$
, we follow the notation of Serre [Reference Serre25]. The group
$\Gamma =(V,E)$
, we follow the notation of Serre [Reference Serre25]. The group
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
is t.d.l.c. when equipped with the permutation topology for its action on
$\operatorname {\mathrm {Aut}}(\Gamma )$
is t.d.l.c. when equipped with the permutation topology for its action on
![]() $V\cup E$
; see Section 2.1. Given a subgroup
$V\cup E$
; see Section 2.1. Given a subgroup
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
and a vertex
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
and a vertex
![]() $x\in V$
, the stabilizer
$x\in V$
, the stabilizer
![]() $H_{x}$
of x in H induces a permutation group on the set
$H_{x}$
of x in H induces a permutation group on the set
![]() $E(x):=\{e\in E\mid o(e)=x\}$
of edges issuing from x. We say that H is locally ‘X’ if for every
$E(x):=\{e\in E\mid o(e)=x\}$
of edges issuing from x. We say that H is locally ‘X’ if for every
![]() $x\in V$
the said permutation group satisfies property ‘X’ (for example, being transitive, semiprimitive or quasiprimitive).
$x\in V$
the said permutation group satisfies property ‘X’ (for example, being transitive, semiprimitive or quasiprimitive).
In [Reference Burger and Mozes2], Burger and Mozes develop a remarkable structure theory of closed, nondiscrete, locally quasiprimitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
, which resembles the theory of semisimple Lie groups; see Theorem 2.2. In Section 3 (specifically Theorem 3.14) we show that this theory readily carries over to the semiprimitive case.
$\operatorname {\mathrm {Aut}}(\Gamma )$
, which resembles the theory of semisimple Lie groups; see Theorem 2.2. In Section 3 (specifically Theorem 3.14) we show that this theory readily carries over to the semiprimitive case.
Let
![]() $\Omega $
be a set of cardinality
$\Omega $
be a set of cardinality
![]() $d\!\in \!\operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and let
$d\!\in \!\operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and let
![]() $T_{d}\!=\!(V,E)$
be the d-regular tree. Burger and Mozes complement their structure theory with a particularly accessible class of subgroups of
$T_{d}\!=\!(V,E)$
be the d-regular tree. Burger and Mozes complement their structure theory with a particularly accessible class of subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
with prescribed local action. Given
$\operatorname {\mathrm {Aut}}(T_{d})$
with prescribed local action. Given
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
, their universal group
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
, their universal group
![]() $\mathrm {U}(F)$
is closed in
$\mathrm {U}(F)$
is closed in
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
, vertex-transitive, compactly generated and locally permutation isomorphic to F. It is discrete if and only if F is semiregular. When F is transitive,
$\operatorname {\mathrm {Aut}}(T_{d})$
, vertex-transitive, compactly generated and locally permutation isomorphic to F. It is discrete if and only if F is semiregular. When F is transitive,
![]() $\mathrm {U}(F)$
is maximal up to conjugation among vertex-transitive subgroups of
$\mathrm {U}(F)$
is maximal up to conjugation among vertex-transitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
that are locally permutation isomorphic to F, hence universal.
$\operatorname {\mathrm {Aut}}(T_{d})$
that are locally permutation isomorphic to F, hence universal.
We generalize the universal groups by prescribing the local action on balls of a given radius
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
, the Burger–Mozes construction corresponding to the case
$k\in \operatorname {\mathrm {\mathbb {N}}}$
, the Burger–Mozes construction corresponding to the case
![]() $k\!=\!1$
. Equip
$k\!=\!1$
. Equip
![]() $T_{d}$
with a labelling, that is, a map
$T_{d}$
with a labelling, that is, a map
![]() $l:E\to \Omega $
such that for every
$l:E\to \Omega $
such that for every
![]() $x\in V$
the map
$x\in V$
the map
![]() $l_{x}\!:\! E(x)\!\to \!\Omega,\, e\!\mapsto \! l(e)$
is a bijection, and
$l_{x}\!:\! E(x)\!\to \!\Omega,\, e\!\mapsto \! l(e)$
is a bijection, and
![]() $l(e)\!=\!l(\overline {e})$
for all
$l(e)\!=\!l(\overline {e})$
for all
![]() $e\!\in \! E$
. Also, fix a tree
$e\!\in \! E$
. Also, fix a tree
![]() $B_{d,k}$
that is isomorphic to a ball of radius k around a vertex in the labelled tree
$B_{d,k}$
that is isomorphic to a ball of radius k around a vertex in the labelled tree
![]() $T_{d}$
and let
$T_{d}$
and let
![]() $l_{x}^{k}:B(x,k)\to B_{d,k}$
(
$l_{x}^{k}:B(x,k)\to B_{d,k}$
(
![]() $x\in V$
) be the unique label-respecting isomorphism. Then
$x\in V$
) be the unique label-respecting isomorphism. Then
captures the k-local action of g at the vertex
![]() $x\in V$
.
$x\in V$
.
Definition 1.1. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Define
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Define
While
![]() $\mathrm {U}_{k}(F)$
is always closed, vertex-transitive and compactly generated, other properties of
$\mathrm {U}_{k}(F)$
is always closed, vertex-transitive and compactly generated, other properties of
![]() $\mathrm {U}(F)$
need not carry over. In particular, the group
$\mathrm {U}(F)$
need not carry over. In particular, the group
![]() $\mathrm {U}_{k}(F)$
need not be locally action isomorphic to F; we say that
$\mathrm {U}_{k}(F)$
need not be locally action isomorphic to F; we say that
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfies condition (C) if it is. This can be viewed as an interchangeability condition on neighbouring local actions; see Section 4.4. There also is a discreteness condition (D) on
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfies condition (C) if it is. This can be viewed as an interchangeability condition on neighbouring local actions; see Section 4.4. There also is a discreteness condition (D) on
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
in terms of certain stabilizers in F under which
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
in terms of certain stabilizers in F under which
![]() $\mathrm {U}_{k}(F)$
is discrete; see Section 4.2.2. Finally, the groups
$\mathrm {U}_{k}(F)$
is discrete; see Section 4.2.2. Finally, the groups
![]() $\mathrm {U}_{k}(\! F)$
are universal in a sense akin to the above by Theorem 4.34.
$\mathrm {U}_{k}(\! F)$
are universal in a sense akin to the above by Theorem 4.34.
For
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
, let
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
, let
![]() $\smash {F:=\pi \widetilde {F}\le \operatorname {\mathrm {Sym}}(\Omega )}$
denote its projection to
$\smash {F:=\pi \widetilde {F}\le \operatorname {\mathrm {Sym}}(\Omega )}$
denote its projection to
![]() $\operatorname {\mathrm {Aut}}(B_{d,1})$
, which is naturally permutation isomorphic to
$\operatorname {\mathrm {Aut}}(B_{d,1})$
, which is naturally permutation isomorphic to
![]() $\operatorname {\mathrm {Sym}}(\Omega )$
via the labelling of
$\operatorname {\mathrm {Sym}}(\Omega )$
via the labelling of
![]() $B_{d,1}$
. The following rigidity theorem is inspired by [Reference Burger and Mozes2, Proposition 3.3.1].
$B_{d,1}$
. The following rigidity theorem is inspired by [Reference Burger and Mozes2, Proposition 3.3.1].
Theorem 1.2. Let
![]() $F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be
$F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be
![]() $2$
-transitive and
$2$
-transitive and
![]() $F_{\omega }\ (\omega \!\in \!\Omega )$
simple nonabelian. Further, let
$F_{\omega }\ (\omega \!\in \!\Omega )$
simple nonabelian. Further, let
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
with
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
with
![]() $\smash {\pi \widetilde {F}=F}$
satisfy (C). Then
$\smash {\pi \widetilde {F}=F}$
satisfy (C). Then
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})}$
equals either
$\smash {\mathrm {U}_{k}(\widetilde {F})}$
equals either
Here, the groups
![]() $\Gamma (F),\Delta (F)\!\le \!\operatorname {\mathrm {Aut}}(B_{d,2})$
of Section 4.4 satisfy both (C) and (D) and therefore yield discrete universal groups. Illustrating the necessity of the assumptions in Theorem 4.32, we construct further universal groups in the case where either point-stabilizers in F are not simple, F is not primitive, or F is not perfect; see, for example,
$\Gamma (F),\Delta (F)\!\le \!\operatorname {\mathrm {Aut}}(B_{d,2})$
of Section 4.4 satisfy both (C) and (D) and therefore yield discrete universal groups. Illustrating the necessity of the assumptions in Theorem 4.32, we construct further universal groups in the case where either point-stabilizers in F are not simple, F is not primitive, or F is not perfect; see, for example,
![]() $\Phi (F,N), \Phi (F,\operatorname {\mathrm {\mathcal {P}}}),\Pi (F,\rho ,X)\le \operatorname {\mathrm {Aut}}(B_{d,2})$
in Section 4.4.
$\Phi (F,N), \Phi (F,\operatorname {\mathrm {\mathcal {P}}}),\Pi (F,\rho ,X)\le \operatorname {\mathrm {Aut}}(B_{d,2})$
in Section 4.4.
In Section 5 we present three applications of the framework of universal groups. First, we study the quasicentre of subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
. The quasicentre
$\operatorname {\mathrm {Aut}}(T_{d})$
. The quasicentre
![]() $\mathrm {QZ}(G)$
of a topological group G consists of those elements whose centralizer in G is open. It plays a major role in the Burger–Mozes structure theorem (Theorem 2.2): a nondiscrete, locally quasiprimitive subgroup of
$\mathrm {QZ}(G)$
of a topological group G consists of those elements whose centralizer in G is open. It plays a major role in the Burger–Mozes structure theorem (Theorem 2.2): a nondiscrete, locally quasiprimitive subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
does not feature any nontrivial quasicentral elliptic elements. We extend this fact to the following local-to-global-type characterization of the automorphism types that the quasicentre of a nondiscrete subgroup of
$\operatorname {\mathrm {Aut}}(T_{d})$
does not feature any nontrivial quasicentral elliptic elements. We extend this fact to the following local-to-global-type characterization of the automorphism types that the quasicentre of a nondiscrete subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
may feature in terms of the group’s local action.
$\operatorname {\mathrm {Aut}}(T_{d})$
may feature in terms of the group’s local action.
Theorem 1.3. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete. If H is locally:
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete. If H is locally:
-
(i) Transitive, then
 $\mathrm {QZ}(H)$
contains no inversion.
$\mathrm {QZ}(H)$
contains no inversion. -
(ii) Semiprimitive, then
 $\mathrm {QZ}(H)$
contains no nontrivial edge-fixating element.
$\mathrm {QZ}(H)$
contains no nontrivial edge-fixating element. -
(iii) Quasiprimitive, then
 $\mathrm {QZ}(H)$
contains no nontrivial elliptic element.
$\mathrm {QZ}(H)$
contains no nontrivial elliptic element. -
(iv) k-transitive,
 $(k\in \operatorname {\mathrm {\mathbb {N}}})$
then
$(k\in \operatorname {\mathrm {\mathbb {N}}})$
then
 $\mathrm {QZ}(H)$
contains no hyperbolic element of length k.
$\mathrm {QZ}(H)$
contains no hyperbolic element of length k.
More importantly, the proof of the above theorem suggests using groups of the form
![]() $\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
for appropriate local actions
$\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
for appropriate local actions
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
in order to explicitly construct nondiscrete subgroups of
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
in order to explicitly construct nondiscrete subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
whose quasicentres contain certain types of automorphisms. This leads to the following sharpness result.
$\operatorname {\mathrm {Aut}}(T_{d})$
whose quasicentres contain certain types of automorphisms. This leads to the following sharpness result.
Theorem 1.4. There exist a
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated subgroup of
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
that is locally:
$\operatorname {\mathrm {Aut}}(T_{d})$
that is locally:
-
(i) Intransitive and contains a quasicentral inversion.
-
(ii) Transitive and contains a nontrivial quasicentral edge-fixating element.
-
(iii) Semiprimitive and contains a nontrivial quasicentral elliptic element.
-
(iv)
-
(a) Intransitive and contains a quasicentral hyperbolic element of length
 $1$
.
$1$
. -
(b) Quasiprimitive and contains a quasicentral hyperbolic element of length
 $2$
.
$2$
.
-
Part (ii) of this theorem can be strengthened to the following result which shows that the Burger–Mozes theory does not extend further to locally transitive groups.
Theorem 1.5. There exist
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated, locally transitive subgroup of
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated, locally transitive subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
with open, hence nondiscrete, quasicentre.
$\operatorname {\mathrm {Aut}}(T_{d})$
with open, hence nondiscrete, quasicentre.
We also give an algebraic characterization of the
![]() $(P_{k})$
-closures of locally transitive subgroups of
$(P_{k})$
-closures of locally transitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
which contain an involutive inversion. Thereby, we partially answer two questions by Banks et al. [Reference Banks, Elder and Willis1, page 259] who introduced the term
$\operatorname {\mathrm {Aut}}(T_{d})$
which contain an involutive inversion. Thereby, we partially answer two questions by Banks et al. [Reference Banks, Elder and Willis1, page 259] who introduced the term
![]() $(P_{k})$
-closure in [Reference Banks, Elder and Willis1] and called it k-closure; however the term k-closure has an established meaning for permutation groups due to Wielandt, so we use
$(P_{k})$
-closure in [Reference Banks, Elder and Willis1] and called it k-closure; however the term k-closure has an established meaning for permutation groups due to Wielandt, so we use
![]() $(P_{k})$
-closure here. Recall (Section 2.2.2) that the
$(P_{k})$
-closure here. Recall (Section 2.2.2) that the
![]() $(P_{k})$
-closure
$(P_{k})$
-closure
![]() $(k\in \operatorname {\mathrm {\mathbb {N}}})$
of a subgroup
$(k\in \operatorname {\mathrm {\mathbb {N}}})$
of a subgroup
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
is given by
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
is given by
Theorem 1.6. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and contain an involutive inversion. Then
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and contain an involutive inversion. Then
![]() $\smash {H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})}$
for some labelling l of
$\smash {H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})}$
for some labelling l of
![]() $T_{d}$
and
$T_{d}$
and
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
.
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
.
Combined with the independence properties
![]() $(\!P_{k}\!)$
,
$(\!P_{k}\!)$
,
![]() $k\!\in \!\operatorname {\mathrm {\mathbb {N}}}$
(Section 2.2.2), introduced by Banks et al. [Reference Banks, Elder and Willis1] as generalizations of Tits’ independence property, Theorem 5.31 entails the following characterization of universal groups.
$k\!\in \!\operatorname {\mathrm {\mathbb {N}}}$
(Section 2.2.2), introduced by Banks et al. [Reference Banks, Elder and Willis1] as generalizations of Tits’ independence property, Theorem 5.31 entails the following characterization of universal groups.
Corollary 1.7. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed, locally transitive and contain an involutive inversion. Then
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed, locally transitive and contain an involutive inversion. Then
![]() $H=\mathrm {U}_{k}(F^{(k)})$
if and only if H satisfies property
$H=\mathrm {U}_{k}(F^{(k)})$
if and only if H satisfies property
![]() $(P_{k})$
.
$(P_{k})$
.
Banks, Elder and Willis use subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
with pairwise distinct
$\operatorname {\mathrm {Aut}}(T_{d})$
with pairwise distinct
![]() $(P_{k})$
-closures to construct infinitely many, pairwise nonconjugate, nondiscrete simple subgroups of
$(P_{k})$
-closures to construct infinitely many, pairwise nonconjugate, nondiscrete simple subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
via Theorem 2.1 and ask whether they are also pairwise nonisomorphic as topological groups. We partially answer this question in the following theorem.
$\operatorname {\mathrm {Aut}}(T_{d})$
via Theorem 2.1 and ask whether they are also pairwise nonisomorphic as topological groups. We partially answer this question in the following theorem.
Theorem 1.8. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete, locally permutation isomorphic to
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete, locally permutation isomorphic to
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
and contain an involutive inversion. Suppose that F is transitive and that every nontrivial subnormal subgroup of
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
and contain an involutive inversion. Suppose that F is transitive and that every nontrivial subnormal subgroup of
![]() $F_{\omega }\ (\omega \!\in \!\Omega )$
is transitive on
$F_{\omega }\ (\omega \!\in \!\Omega )$
is transitive on
![]() $\Omega \backslash \{\omega \}$
. If
$\Omega \backslash \{\omega \}$
. If
![]() $H^{(P_{k})}\neq H^{(P_{l})}$
for some
$H^{(P_{k})}\neq H^{(P_{l})}$
for some
![]() $k,l\in \operatorname {\mathrm {\mathbb {N}}}$
then
$k,l\in \operatorname {\mathrm {\mathbb {N}}}$
then
![]() $(H^{(P_{k})})^{+_{k}}$
and
$(H^{(P_{k})})^{+_{k}}$
and
![]() $(H^{(P_{l})})^{+_{l}}$
are nonisomorphic.
$(H^{(P_{l})})^{+_{l}}$
are nonisomorphic.
Infinitely many families of pairwise nonisomorphic simple groups of this type, each sharing a certain transitive local action, are constructed in Example 5.37.
Finally, Section 5.3 offers a new view on the Weiss conjecture [Reference Weiss33] which states that there are only finitely many conjugacy classes of discrete, locally primitive and vertex-transitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
for a given
$\operatorname {\mathrm {Aut}}(T_{d})$
for a given
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
. This conjecture was extended by Potočnik et al. in [Reference Potočnik, Spiga and Verret21] to semiprimitive local actions, and impressive partial results have been obtained by the same authors as well as by Giudici and Morgan [Reference Giudici and Morgan11]. We show that under the additional assumption that each group contains an involutive inversion, it suffices to show that for every semiprimitive
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
. This conjecture was extended by Potočnik et al. in [Reference Potočnik, Spiga and Verret21] to semiprimitive local actions, and impressive partial results have been obtained by the same authors as well as by Giudici and Morgan [Reference Giudici and Morgan11]. We show that under the additional assumption that each group contains an involutive inversion, it suffices to show that for every semiprimitive
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
there are only finitely many
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
there are only finitely many
![]() ${\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}\ (k\in \operatorname {\mathrm {\mathbb {N}}})}$
with
${\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}\ (k\in \operatorname {\mathrm {\mathbb {N}}})}$
with
![]() $\smash {\pi \widetilde {F}=F}$
that satisfy conditions (C) and (D) in a minimal fashion; see Definition 5.42.
$\smash {\pi \widetilde {F}=F}$
that satisfy conditions (C) and (D) in a minimal fashion; see Definition 5.42.
2 Preliminaries
This section gathers together preliminaries on permutation groups, graph theory and Burger–Mozes theory. References are given in each subsection.
2.1 Permutation groups
Let
![]() $\Omega $
be a set. In this section we give definitions and results concerning the group
$\Omega $
be a set. In this section we give definitions and results concerning the group
![]() $\operatorname {\mathrm {Sym}}(\Omega )$
of bijections of
$\operatorname {\mathrm {Sym}}(\Omega )$
of bijections of
![]() $\Omega $
. Refer to [Reference Dixon and Mortimer6, Reference Giudici and Morgan12, Reference Praeger22] and [Reference Krön and Möller15, Section 1.2] for further details.
$\Omega $
. Refer to [Reference Dixon and Mortimer6, Reference Giudici and Morgan12, Reference Praeger22] and [Reference Krön and Möller15, Section 1.2] for further details.
Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
. The degree of F is
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
. The degree of F is
![]() $|\Omega |$
. For
$|\Omega |$
. For
![]() $\omega \in \Omega $
, the stabilizer of
$\omega \in \Omega $
, the stabilizer of
![]() $\omega $
in F is
$\omega $
in F is
![]() $F_{\omega }:=\{\sigma \in F\mid \sigma \omega =\omega \}$
. The subgroup of F generated by its point-stabilizers is denoted by
$F_{\omega }:=\{\sigma \in F\mid \sigma \omega =\omega \}$
. The subgroup of F generated by its point-stabilizers is denoted by
![]() $F^{+}:=\langle \{F_{\omega }\mid \omega \in \Omega \}\rangle $
. The permutation group F is semiregular, or free, if
$F^{+}:=\langle \{F_{\omega }\mid \omega \in \Omega \}\rangle $
. The permutation group F is semiregular, or free, if
![]() $F_{\omega }=\{\operatorname {\mathrm {id}}\}$
for all
$F_{\omega }=\{\operatorname {\mathrm {id}}\}$
for all
![]() $\omega \in \Omega $
; equivalently, if
$\omega \in \Omega $
; equivalently, if
![]() $F^{+}$
is trivial. It is transitive if its action on
$F^{+}$
is trivial. It is transitive if its action on
![]() $\Omega $
is transitive, and regular if it is both semiregular and transitive.
$\Omega $
is transitive, and regular if it is both semiregular and transitive.
Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. The rank of F is the number
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. The rank of F is the number
![]() $\operatorname {\mathrm {rank}}(F):=|F\backslash \Omega ^{2}|$
of orbits of the diagonal action
$\operatorname {\mathrm {rank}}(F):=|F\backslash \Omega ^{2}|$
of orbits of the diagonal action
![]() $\sigma \cdot (\omega ,\omega '):=(\sigma \omega ,\sigma \omega ')$
of F on
$\sigma \cdot (\omega ,\omega '):=(\sigma \omega ,\sigma \omega ')$
of F on
![]() $\Omega ^{2}$
. Equivalently,
$\Omega ^{2}$
. Equivalently,
![]() $\operatorname {\mathrm {rank}}(F)=|F_{\omega }\backslash \Omega |$
for all
$\operatorname {\mathrm {rank}}(F)=|F_{\omega }\backslash \Omega |$
for all
![]() $\omega \in \Omega $
. Note that the diagonal
$\omega \in \Omega $
. Note that the diagonal
![]() $\Delta (\Omega ):=\{(\omega ,\omega )\mid \omega \in \Omega \}$
is always an orbit of the diagonal action
$\Delta (\Omega ):=\{(\omega ,\omega )\mid \omega \in \Omega \}$
is always an orbit of the diagonal action
![]() $F\curvearrowright \Omega ^{2}$
. The permutation group F is
$F\curvearrowright \Omega ^{2}$
. The permutation group F is
![]() $2$
-transitive if it acts transitively on
$2$
-transitive if it acts transitively on
![]() $\Omega ^{2}\backslash \Delta (\Omega )$
. In other words,
$\Omega ^{2}\backslash \Delta (\Omega )$
. In other words,
![]() $\operatorname {\mathrm {rank}}(F)=2$
.
$\operatorname {\mathrm {rank}}(F)=2$
.
We now define several classes of permutation groups lying in between the classes of transitive and
![]() $2$
-transitive permutation groups. Let
$2$
-transitive permutation groups. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
. A partition
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
. A partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
is preserved by F, or F-invariant, if for all
$\Omega $
is preserved by F, or F-invariant, if for all
![]() $\sigma \in F$
we have that
$\sigma \in F$
we have that
![]() ${\{\sigma \Omega _{i}\mid i\in ~I\}=\{\Omega _{i}\mid i\in I\}}$
. The partitions
${\{\sigma \Omega _{i}\mid i\in ~I\}=\{\Omega _{i}\mid i\in I\}}$
. The partitions
![]() $\Omega =\Omega $
and
$\Omega =\Omega $
and
![]() $\Omega =\bigsqcup _{\omega \in \Omega }\{\omega \}$
are trivial. A map
$\Omega =\bigsqcup _{\omega \in \Omega }\{\omega \}$
are trivial. A map
![]() $a:\Omega \to F$
is constant with respect to (w.r.t.)
$a:\Omega \to F$
is constant with respect to (w.r.t.)
![]() $\operatorname {\mathrm {\mathcal {P}}}$
if
$\operatorname {\mathrm {\mathcal {P}}}$
if
![]() $a(\omega )=a(\omega ')$
whenever
$a(\omega )=a(\omega ')$
whenever
![]() $\omega ,\omega '\in \Omega _{i}$
for some
$\omega ,\omega '\in \Omega _{i}$
for some
![]() $i\in I$
. The permutation group F is primitive if it is transitive and preserves no nontrivial partition of
$i\in I$
. The permutation group F is primitive if it is transitive and preserves no nontrivial partition of
![]() $\Omega $
. Equivalently, F is transitive and its point-stabilizers are maximal subgroups. Given a normal subgroup N of F, the partition of
$\Omega $
. Equivalently, F is transitive and its point-stabilizers are maximal subgroups. Given a normal subgroup N of F, the partition of
![]() $\Omega $
into N-orbits is F-invariant. Consequently, every nontrivial normal subgroup of a primitive group is transitive. The permutation group F is quasiprimitive if it is transitive and all its nontrivial normal subgroups are transitive. Finally, F is semiprimitive if it is transitive and all its normal subgroups are either transitive or semiregular. The following implications among the above properties follow from the definitions; we list examples illustrating that each implication is strict:
$\Omega $
into N-orbits is F-invariant. Consequently, every nontrivial normal subgroup of a primitive group is transitive. The permutation group F is quasiprimitive if it is transitive and all its nontrivial normal subgroups are transitive. Finally, F is semiprimitive if it is transitive and all its normal subgroups are either transitive or semiregular. The following implications among the above properties follow from the definitions; we list examples illustrating that each implication is strict:
Note that
![]() $A_{5}$
is simple and that
$A_{5}$
is simple and that
![]() $C_{5}\lneq D_{5}\lneq A_{5}$
is a nonmaximal subgroup of
$C_{5}\lneq D_{5}\lneq A_{5}$
is a nonmaximal subgroup of
![]() $A_{5}$
.
$A_{5}$
.
2.1.1 Permutation topology
Let X be a set and
![]() $H\le \operatorname {\mathrm {Sym}}(X)$
. The basic open sets of the permutation topology on H are
$H\le \operatorname {\mathrm {Sym}}(X)$
. The basic open sets of the permutation topology on H are
![]() $U_{x,y}:=\{h\in H\mid \text { for all } i\in \{1,\ldots ,n\}:h(x_{i})=y_{i}\}$
, where
$U_{x,y}:=\{h\in H\mid \text { for all } i\in \{1,\ldots ,n\}:h(x_{i})=y_{i}\}$
, where
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
and
$n\in \operatorname {\mathrm {\mathbb {N}}}$
and
![]() $x=(x_{1},\ldots ,x_{n}), y=(y_{1},\ldots ,y_{n})\in X^{n}$
. This turns H into a Hausdorff, t.d. group and makes the action map
$x=(x_{1},\ldots ,x_{n}), y=(y_{1},\ldots ,y_{n})\in X^{n}$
. This turns H into a Hausdorff, t.d. group and makes the action map
![]() $H\times X\to X$
continuous for the discrete topology on X. The group H is discrete if and only if the stabilizer in H of a finite subset of X is trivial. It is compact if and only if it is closed and all its orbits are finite. Finally,
$H\times X\to X$
continuous for the discrete topology on X. The group H is discrete if and only if the stabilizer in H of a finite subset of X is trivial. It is compact if and only if it is closed and all its orbits are finite. Finally,
![]() $\operatorname {\mathrm {Sym}}(X)$
is second-countable if and only if X is countable.
$\operatorname {\mathrm {Sym}}(X)$
is second-countable if and only if X is countable.
2.2 Graph theory
We first recall Serre’s [Reference Serre25] notation and definitions in the context of graphs and trees, and then give generalities about automorphisms of trees. We conclude with an important simplicity criterion.
2.2.1 Definitions and notation
A graph
![]() $\Gamma $
is a tuple
$\Gamma $
is a tuple
![]() $(V,E)$
consisting of a vertex set V and an edge set E, together with a fixed-point-free involution of E, denoted by
$(V,E)$
consisting of a vertex set V and an edge set E, together with a fixed-point-free involution of E, denoted by
![]() $e\mapsto \overline {e}$
, and maps
$e\mapsto \overline {e}$
, and maps
![]() $o,t:E\to V$
, providing the origin and terminus of an edge, such that
$o,t:E\to V$
, providing the origin and terminus of an edge, such that
![]() $o(\overline {e})=t(e)$
and
$o(\overline {e})=t(e)$
and
![]() $t(\overline {e})=o(e)$
for all
$t(\overline {e})=o(e)$
for all
![]() $e\in E$
. Given
$e\in E$
. Given
![]() $e\in E$
, the pair
$e\in E$
, the pair
![]() $\{e,\overline {e}\}$
is a geometric edge. For
$\{e,\overline {e}\}$
is a geometric edge. For
![]() $x\in V$
, we let
$x\in V$
, we let
![]() $E(x):=o^{-1}(x)=\{e\in E\mid o(e)=x\}$
be the set of edges issuing from x. The valency of
$E(x):=o^{-1}(x)=\{e\in E\mid o(e)=x\}$
be the set of edges issuing from x. The valency of
![]() $x\in V$
is
$x\in V$
is
![]() $|E(x)|$
. A vertex of valency
$|E(x)|$
. A vertex of valency
![]() $1$
is a leaf. A morphism between graphs
$1$
is a leaf. A morphism between graphs
![]() $\Gamma _{1}=(V_{1},E_{1})$
and
$\Gamma _{1}=(V_{1},E_{1})$
and
![]() $\Gamma _{2}=(V_{2},E_{2})$
is a pair
$\Gamma _{2}=(V_{2},E_{2})$
is a pair
![]() $(\alpha _{V},\alpha _{E})$
of maps
$(\alpha _{V},\alpha _{E})$
of maps
![]() $\alpha _{V}:V_{1}\to V_{2}$
and
$\alpha _{V}:V_{1}\to V_{2}$
and
![]() $\alpha _{E}:E_{1}\to E_{2}$
preserving the graph structure, that is,
$\alpha _{E}:E_{1}\to E_{2}$
preserving the graph structure, that is,
![]() $\alpha _{V}(o(e))=o(\alpha _{E}(e))$
and
$\alpha _{V}(o(e))=o(\alpha _{E}(e))$
and
![]() $\alpha _{V}(t(e))=t(\alpha _{E}(e))$
for all
$\alpha _{V}(t(e))=t(\alpha _{E}(e))$
for all
![]() $e\in E$
.
$e\in E$
.
For
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
, let
$n\in \operatorname {\mathrm {\mathbb {N}}}$
, let
![]() $\mathrm {Path}_{n}$
denote the graph with vertex set
$\mathrm {Path}_{n}$
denote the graph with vertex set
![]() $\{0,\ldots ,n\}$
and edge set
$\{0,\ldots ,n\}$
and edge set
![]() $\smash {\{(k,k+1),\overline {(k,k+1)}\mid k\in \{0,\ldots ,n-1\}\}}$
. A path of length n in a graph
$\smash {\{(k,k+1),\overline {(k,k+1)}\mid k\in \{0,\ldots ,n-1\}\}}$
. A path of length n in a graph
![]() $\Gamma $
is a morphism
$\Gamma $
is a morphism
![]() $\gamma $
from
$\gamma $
from
![]() $\mathrm {Path}_{n}$
to
$\mathrm {Path}_{n}$
to
![]() $\Gamma $
. It can be identified with
$\Gamma $
. It can be identified with
![]() $\smash {(e_{1},\ldots ,e_{n})\in E(\Gamma )^{n}}$
, where
$\smash {(e_{1},\ldots ,e_{n})\in E(\Gamma )^{n}}$
, where
![]() $e_{k}=\gamma ((k-1,k))$
for
$e_{k}=\gamma ((k-1,k))$
for
![]() $k\in \{1,\ldots ,n\}$
. In this case,
$k\in \{1,\ldots ,n\}$
. In this case,
![]() $\gamma $
is a path from
$\gamma $
is a path from
![]() $o(e_{1})$
to
$o(e_{1})$
to
![]() $t(e_{n})$
.
$t(e_{n})$
.
Similarly, let
![]() $\mathrm {Path}_{\operatorname {\mathrm {\mathbb {N}}}_{0}}$
and
$\mathrm {Path}_{\operatorname {\mathrm {\mathbb {N}}}_{0}}$
and
![]() $\mathrm {Path}_{\operatorname {\mathrm {\mathbb {Z}}}}$
be the graphs with vertex sets
$\mathrm {Path}_{\operatorname {\mathrm {\mathbb {Z}}}}$
be the graphs with vertex sets
![]() $\operatorname {\mathrm {\mathbb {N}}}_{0}$
and
$\operatorname {\mathrm {\mathbb {N}}}_{0}$
and
![]() $\operatorname {\mathrm {\mathbb {Z}}}$
, and edge sets
$\operatorname {\mathrm {\mathbb {Z}}}$
, and edge sets
![]() $\smash {\{(k,k+1),\overline {(k,k+1)}\mid k\in \operatorname {\mathrm {\mathbb {N}}}_{0}\}}$
and
$\smash {\{(k,k+1),\overline {(k,k+1)}\mid k\in \operatorname {\mathrm {\mathbb {N}}}_{0}\}}$
and
![]() $\smash {\{(k,k+1),\overline {(k,k+1)}\mid k\in \operatorname {\mathrm {\mathbb {Z}}}\}}$
, respectively. A half-infinite path, or ray, in a graph
$\smash {\{(k,k+1),\overline {(k,k+1)}\mid k\in \operatorname {\mathrm {\mathbb {Z}}}\}}$
, respectively. A half-infinite path, or ray, in a graph
![]() $\Gamma $
is a morphism
$\Gamma $
is a morphism
![]() $\gamma $
from
$\gamma $
from
![]() $\mathrm {Path}_{\operatorname {\mathrm {\mathbb {N}}}_{0}}$
to
$\mathrm {Path}_{\operatorname {\mathrm {\mathbb {N}}}_{0}}$
to
![]() $\Gamma $
. It can be identified with
$\Gamma $
. It can be identified with
![]() $(e_{k})_{k\in \operatorname {\mathrm {\mathbb {N}}}}\in E(\Gamma )^{\operatorname {\mathrm {\mathbb {N}}}}$
where
$(e_{k})_{k\in \operatorname {\mathrm {\mathbb {N}}}}\in E(\Gamma )^{\operatorname {\mathrm {\mathbb {N}}}}$
where
![]() $e_{k}=\gamma ((k-1,k))$
for
$e_{k}=\gamma ((k-1,k))$
for
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
. In this case,
$k\in \operatorname {\mathrm {\mathbb {N}}}$
. In this case,
![]() $\gamma $
originates at, or issues from,
$\gamma $
originates at, or issues from,
![]() $o(e_{1})$
. An infinite path, or line, in a graph
$o(e_{1})$
. An infinite path, or line, in a graph
![]() $\Gamma $
is a morphism from
$\Gamma $
is a morphism from
![]() $\mathrm {Path}_{\operatorname {\mathrm {\mathbb {Z}}}}$
to
$\mathrm {Path}_{\operatorname {\mathrm {\mathbb {Z}}}}$
to
![]() $\Gamma $
. A pair
$\Gamma $
. A pair
![]() $\smash {(e_{k},e_{k+1})=(e_{k},\overline {e_{k}})}$
of edges in a path is a backtracking. A graph is connected if any two of its vertices can be joined by a path. The maximal connected subgraphs of a graph are its connected components.
$\smash {(e_{k},e_{k+1})=(e_{k},\overline {e_{k}})}$
of edges in a path is a backtracking. A graph is connected if any two of its vertices can be joined by a path. The maximal connected subgraphs of a graph are its connected components.
A forest is a graph in which there are no nonbacktracking paths
![]() $(e_{1},\ldots ,e_{n})$
with
$(e_{1},\ldots ,e_{n})$
with
![]() $o(e_{1})=t(e_{n})$
,
$o(e_{1})=t(e_{n})$
,
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
. Consequently, a morphism of forests is determined by the underlying vertex map. In particular, a path of length
$n\in \operatorname {\mathrm {\mathbb {N}}}$
. Consequently, a morphism of forests is determined by the underlying vertex map. In particular, a path of length
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
in a forest is determined by the images of the vertices of
$n\in \operatorname {\mathrm {\mathbb {N}}}$
in a forest is determined by the images of the vertices of
![]() $\mathrm {Path}_{n}$
.
$\mathrm {Path}_{n}$
.
A tree is a connected forest. As a consequence of the above, the vertex set V of a tree T admits a natural metric. Given
![]() $x,y\in V$
, define
$x,y\in V$
, define
![]() $d(x,y)$
as the minimal length of a path from x to y. A tree in which every vertex has valency
$d(x,y)$
as the minimal length of a path from x to y. A tree in which every vertex has valency
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}$
is d-regular. It is unique up to isomorphism and denoted by
$d\in \operatorname {\mathrm {\mathbb {N}}}$
is d-regular. It is unique up to isomorphism and denoted by
![]() $T_{d}$
.
$T_{d}$
.
Let
![]() $T=(V,E)$
be a tree. For
$T=(V,E)$
be a tree. For
![]() $S\subseteq V\cup E$
, the subtree spanned by S is the unique minimal subtree of T containing S. For
$S\subseteq V\cup E$
, the subtree spanned by S is the unique minimal subtree of T containing S. For
![]() $x\in V$
and
$x\in V$
and
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}_{0}$
, the subtree spanned by
$n\in \operatorname {\mathrm {\mathbb {N}}}_{0}$
, the subtree spanned by
![]() $\{y\in V\mid d(y,x)\le n\}$
is the ball of radius n around x, denoted by
$\{y\in V\mid d(y,x)\le n\}$
is the ball of radius n around x, denoted by
![]() $B(x,n)$
. Similarly,
$B(x,n)$
. Similarly,
![]() $S(x,n)=\{y\in V\mid d(y,x)\!=\! n\}$
is the sphere of radius n around x, and the set of edges within distance n of x is
$S(x,n)=\{y\in V\mid d(y,x)\!=\! n\}$
is the sphere of radius n around x, and the set of edges within distance n of x is
![]() $E(x,n):=\{e\in E\mid d(o(e),x),d(t(e),x)\le n\}$
. For a subtree
$E(x,n):=\{e\in E\mid d(o(e),x),d(t(e),x)\le n\}$
. For a subtree
![]() ${T'\subseteq T}$
, let
${T'\subseteq T}$
, let
![]() $\pi :V\to V(T')$
denote the closest point projection, that is,
$\pi :V\to V(T')$
denote the closest point projection, that is,
![]() $\pi (x)=y$
whenever
$\pi (x)=y$
whenever
![]() ${d(x,y)=\min _{z\in V(T')}\{d(x,z)\}}$
. In the case of an edge
${d(x,y)=\min _{z\in V(T')}\{d(x,z)\}}$
. In the case of an edge
![]() $e=(x,y)\in E$
, the half-trees
$e=(x,y)\in E$
, the half-trees
![]() $T_{x}$
and
$T_{x}$
and
![]() $T_{y}$
are the subtrees spanned by
$T_{y}$
are the subtrees spanned by
![]() $\pi ^{-1}(x)$
and
$\pi ^{-1}(x)$
and
![]() $\pi ^{-1}(y)$
, respectively.
$\pi ^{-1}(y)$
, respectively.
Two nonbacktracking rays
![]() $\gamma _{1},\gamma _{2}:\mathrm {Path}_{\operatorname {\mathrm {\mathbb {N}}}}\to T$
in T are equivalent,
$\gamma _{1},\gamma _{2}:\mathrm {Path}_{\operatorname {\mathrm {\mathbb {N}}}}\to T$
in T are equivalent,
![]() $\gamma _{1}\sim \gamma _{2}$
, if there exist
$\gamma _{1}\sim \gamma _{2}$
, if there exist
![]() $N,d\in \operatorname {\mathrm {\mathbb {N}}}$
such that
$N,d\in \operatorname {\mathrm {\mathbb {N}}}$
such that
![]() $\gamma _{1}(n)=\gamma _{2}(n+d)$
for all
$\gamma _{1}(n)=\gamma _{2}(n+d)$
for all
![]() $n\ge N$
. The boundary, or set of ends, of T is the set
$n\ge N$
. The boundary, or set of ends, of T is the set
![]() $\partial T$
of equivalence classes of nonbacktracking rays in T.
$\partial T$
of equivalence classes of nonbacktracking rays in T.
2.2.2 Automorphism groups of graphs
Let
![]() $\Gamma =(V,E)$
be a graph. We equip the group
$\Gamma =(V,E)$
be a graph. We equip the group
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
of automorphisms of
$\operatorname {\mathrm {Aut}}(\Gamma )$
of automorphisms of
![]() $\Gamma $
with the permutation topology for its action on
$\Gamma $
with the permutation topology for its action on
![]() $V\cup E$
.
$V\cup E$
.
Notation. Let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
. Given a subgraph
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
. Given a subgraph
![]() $\Gamma '\subseteq \Gamma $
, the pointwise stabilizer of
$\Gamma '\subseteq \Gamma $
, the pointwise stabilizer of
![]() $\Gamma '$
in H is denoted by
$\Gamma '$
in H is denoted by
![]() $H_{\Gamma '}$
. Similarly, the setwise stabilizer of
$H_{\Gamma '}$
. Similarly, the setwise stabilizer of
![]() $\Gamma '$
in H is denoted by
$\Gamma '$
in H is denoted by
![]() $H_{\{\Gamma '\}}$
. In the case where
$H_{\{\Gamma '\}}$
. In the case where
![]() $\Gamma '$
is a single vertex x, the permutation group that
$\Gamma '$
is a single vertex x, the permutation group that
![]() $H_{x}$
induces on
$H_{x}$
induces on
![]() $E(x)$
is denoted by
$E(x)$
is denoted by
![]() $\smash {H_{x}^{(1)}\le \operatorname {\mathrm {Sym}}(E(x))}$
. Given a property ‘X’ of permutation groups, the group H is locally ‘X’ if for every
$\smash {H_{x}^{(1)}\le \operatorname {\mathrm {Sym}}(E(x))}$
. Given a property ‘X’ of permutation groups, the group H is locally ‘X’ if for every
![]() $x\in V$
the permutation group
$x\in V$
the permutation group
![]() $\smash {H_{x}^{(1)}}$
has ‘X’; with the exception that H is locally k-transitive
$\smash {H_{x}^{(1)}}$
has ‘X’; with the exception that H is locally k-transitive
![]() $(k\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3})$
if
$(k\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3})$
if
![]() $H_{x}$
acts transitively on the set of nonbacktracking paths of length k issuing from x. It is locally
$H_{x}$
acts transitively on the set of nonbacktracking paths of length k issuing from x. It is locally
![]() $\infty $
-transitive if it is locally k-transitive for all
$\infty $
-transitive if it is locally k-transitive for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
.
$k\in \operatorname {\mathrm {\mathbb {N}}}$
.
Let
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and
![]() $T_{d}=(V,E)$
the d-regular tree. Then
$T_{d}=(V,E)$
the d-regular tree. Then
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
acts on
$\operatorname {\mathrm {Aut}}(T_{d})$
acts on
![]() $\partial T_{d}$
by
$\partial T_{d}$
by
![]() $g\cdot [\gamma ]\kern-1pt :=\kern-1pt [g\circ \gamma ]$
. Given
$g\cdot [\gamma ]\kern-1pt :=\kern-1pt [g\circ \gamma ]$
. Given
![]() $[\gamma ]\in \partial T_{d}$
, the stabilizer of
$[\gamma ]\in \partial T_{d}$
, the stabilizer of
![]() $[\gamma ]$
in H is
$[\gamma ]$
in H is
![]() $H_{[\gamma ]}\kern-1pt =\kern-1pt \{h\!\in \! H\mid h\circ \gamma \sim \gamma \}$
.
$H_{[\gamma ]}\kern-1pt =\kern-1pt \{h\!\in \! H\mid h\circ \gamma \sim \gamma \}$
.
We let
denote the subgroup of H generated by vertex-stabilizers and
![]() $H^{+}\!=\!\langle \{H_{e}\!\mid \! e\in E\}\rangle $
the subgroup generated by edge-stabilizers. For a subtree
$H^{+}\!=\!\langle \{H_{e}\!\mid \! e\in E\}\rangle $
the subgroup generated by edge-stabilizers. For a subtree
![]() $T\subseteq T_{d}$
and
$T\subseteq T_{d}$
and
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
, let
$k\in \operatorname {\mathrm {\mathbb {N}}}$
, let
![]() $T^{k}$
denote the subtree of
$T^{k}$
denote the subtree of
![]() $T_{d}$
spanned by
$T_{d}$
spanned by
![]() $\{x\in V\mid d(x,T)\le k\}$
. We set
$\{x\in V\mid d(x,T)\le k\}$
. We set
![]() $H^{+_{k}}=\langle \{H_{e^{k-1}}\!\mid \! e\in E\}\rangle $
. Then
$H^{+_{k}}=\langle \{H_{e^{k-1}}\!\mid \! e\in E\}\rangle $
. Then
![]() $H^{+_{1}}=H^{+}$
and
$H^{+_{1}}=H^{+}$
and
Classification of automorphisms. Automorphisms of
![]() $T_{d}$
can be divided into three distinct types. Refer to [Reference Garrido, Glasner, Tornier, Caprace and Monod10, Section 6.2.2] for details.
$T_{d}$
can be divided into three distinct types. Refer to [Reference Garrido, Glasner, Tornier, Caprace and Monod10, Section 6.2.2] for details.
For
![]() $g\!\in \!\operatorname {\mathrm {Aut}}(T_{d})$
, set
$g\!\in \!\operatorname {\mathrm {Aut}}(T_{d})$
, set
![]() $l(g)\!:=\!\min _{x\in V}d(x,gx)$
and
$l(g)\!:=\!\min _{x\in V}d(x,gx)$
and
![]() $V(g)\!:=\!\{x\in V\!\mid \! d(x,gx)=l(g)\}$
. If
$V(g)\!:=\!\{x\in V\!\mid \! d(x,gx)=l(g)\}$
. If
![]() $l(g)=0$
then g fixes a vertex. An automorphism of this kind is elliptic. Suppose now that
$l(g)=0$
then g fixes a vertex. An automorphism of this kind is elliptic. Suppose now that
![]() $l(g)>0$
. If
$l(g)>0$
. If
![]() $V(g)$
is infinite then g is hyperbolic. Geometrically, it is a translation of length
$V(g)$
is infinite then g is hyperbolic. Geometrically, it is a translation of length
![]() $l(g)$
along the line in
$l(g)$
along the line in
![]() $T_{d}$
defined by
$T_{d}$
defined by
![]() $V(g)$
. If
$V(g)$
. If
![]() $V(g)$
is finite then
$V(g)$
is finite then
![]() $l(g)=1$
and g maps some edge
$l(g)=1$
and g maps some edge
![]() $e\in E$
to
$e\in E$
to
![]() $\overline {e}$
and is termed an inversion.
$\overline {e}$
and is termed an inversion.
Independence and simplicity. The base case of the simplicity criterion presented below is due to Tits [Reference Tits29] and applies to sufficiently rich subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
. The generalized version is due to Banks et al. [Reference Banks, Elder and Willis1]; see also [Reference Garrido, Glasner, Tornier, Caprace and Monod10].
$\operatorname {\mathrm {Aut}}(T_{d})$
. The generalized version is due to Banks et al. [Reference Banks, Elder and Willis1]; see also [Reference Garrido, Glasner, Tornier, Caprace and Monod10].
Let C denote a path in
![]() $T_{d}$
(finite, half-infinite or infinite). For every
$T_{d}$
(finite, half-infinite or infinite). For every
![]() $x\in V(C)$
and
$x\in V(C)$
and
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}_{0}$
, the pointwise stabilizer
$k\in \operatorname {\mathrm {\mathbb {N}}}_{0}$
, the pointwise stabilizer
![]() $H_{C^{k}}$
of
$H_{C^{k}}$
of
![]() $C^{k}$
induces an action
$C^{k}$
induces an action
![]() $\smash {H_{C^{k}}^{(x)}\le \operatorname {\mathrm {Aut}}(\pi ^{-1}(x))}$
on
$\smash {H_{C^{k}}^{(x)}\le \operatorname {\mathrm {Aut}}(\pi ^{-1}(x))}$
on
![]() $\pi ^{-1}(x)$
, the subtree spanned by those vertices of T whose closest vertex in C is x. We therefore obtain an injective homomorphism
$\pi ^{-1}(x)$
, the subtree spanned by those vertices of T whose closest vertex in C is x. We therefore obtain an injective homomorphism
 $$ \begin{align*} \varphi_{C}^{(k)}:H_{C^{k}}\to\prod\limits_{x\in V(C)}H_{C^{k}}^{(x)}. \end{align*} $$
$$ \begin{align*} \varphi_{C}^{(k)}:H_{C^{k}}\to\prod\limits_{x\in V(C)}H_{C^{k}}^{(x)}. \end{align*} $$
A subgroup
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
satisfies property
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
satisfies property
![]() $(P_{k}) \ (k\in \operatorname {\mathrm {\mathbb {N}}})$
if
$(P_{k}) \ (k\in \operatorname {\mathrm {\mathbb {N}}})$
if
![]() $\varphi _{C}^{(k-1)}$
is an isomorphism for every path C in
$\varphi _{C}^{(k-1)}$
is an isomorphism for every path C in
![]() $T_{d}$
. If
$T_{d}$
. If
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
is closed, it suffices to check the above properties in the case where C is a single edge. For example, given a closed subgroup
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
is closed, it suffices to check the above properties in the case where C is a single edge. For example, given a closed subgroup
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
, property
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
, property
![]() $(P_{k})$
is satisfied by its
$(P_{k})$
is satisfied by its
![]() $(P_{k})$
-closure:
$(P_{k})$
-closure:
Theorem 2.1 [Reference Banks, Elder and Willis1, Theorem 7.3].
Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
. Suppose H neither fixes an end nor stabilizes a proper subtree of
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
. Suppose H neither fixes an end nor stabilizes a proper subtree of
![]() $T_{d}$
setwise, and that H satisfies property
$T_{d}$
setwise, and that H satisfies property
![]() $(P_{k})$
. Then the group
$(P_{k})$
. Then the group
![]() $H^{+_{k}}$
is either trivial or simple.
$H^{+_{k}}$
is either trivial or simple.
2.3 Burger–Mozes theory
In [Reference Burger and Mozes2], Burger and Mozes develop a structure theory of certain locally quasiprimitive automorphism groups of graphs which resembles the theory of semisimple Lie groups. Their fundamental definitions are meaningful in the setting of t.d.l.c. groups. Let H be a t.d.l.c. group. Define
alternatively the intersection of all open finite-index subgroups of H, and
the quasicentre of H. Both
![]() $H^{(\infty )}$
and
$H^{(\infty )}$
and
![]() $\mathrm {QZ}(H)$
are topologically characteristic subgroups of H, that is, they are preserved by continuous automorphisms of H. Whereas
$\mathrm {QZ}(H)$
are topologically characteristic subgroups of H, that is, they are preserved by continuous automorphisms of H. Whereas
![]() $H^{(\infty )}\le H$
is closed, the quasicentre need not be so.
$H^{(\infty )}\le H$
is closed, the quasicentre need not be so.
Whereas for a general t.d.l.c. group H nothing much can be said about the size of
![]() $H^{(\infty )}$
and
$H^{(\infty )}$
and
![]() $\mathrm {QZ}(H)$
, Burger and Mozes show that good control can be obtained in the case of certain locally quasiprimitive automorphism groups of graphs. The following result summarizes their structure theory. It is a combination of Proposition 1.2.1, Corollary 1.5.1, Theorem 1.7.1 and Corollary 1.7.2 in [Reference Burger and Mozes2].
$\mathrm {QZ}(H)$
, Burger and Mozes show that good control can be obtained in the case of certain locally quasiprimitive automorphism groups of graphs. The following result summarizes their structure theory. It is a combination of Proposition 1.2.1, Corollary 1.5.1, Theorem 1.7.1 and Corollary 1.7.2 in [Reference Burger and Mozes2].
Theorem 2.2. Let
![]() $\Gamma $
be a locally finite, connected graph. Further, let
$\Gamma $
be a locally finite, connected graph. Further, let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally quasiprimitive. Then
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally quasiprimitive. Then
-
(i)
 $H^{(\infty )}$
is minimal closed normal cocompact in H;
$H^{(\infty )}$
is minimal closed normal cocompact in H; -
(ii)
 $\mathrm {QZ}(H)$
is maximal discrete normal, and noncocompact in H; and
$\mathrm {QZ}(H)$
is maximal discrete normal, and noncocompact in H; and -
(iii)
 $H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})\!=\! H^{(\infty )}\!/(\mathrm {QZ}(H)\cap H^{(\infty )})$
admits minimal, nontrivial closed normal subgroups finite in number, H-conjugate and topologically simple.
$H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})\!=\! H^{(\infty )}\!/(\mathrm {QZ}(H)\cap H^{(\infty )})$
admits minimal, nontrivial closed normal subgroups finite in number, H-conjugate and topologically simple.
If
![]() $\Gamma $
is a tree and moreover H is locally primitive then
$\Gamma $
is a tree and moreover H is locally primitive then
-
(iv)
 $H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
is a direct product of topologically simple groups.
$H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
is a direct product of topologically simple groups.
2.3.1 Burger–Mozes universal groups
The first introduction of Burger–Mozes universal groups in [Reference Burger and Mozes2, Section 3.2] was expanded in the introductory article [Reference Garrido, Glasner, Tornier, Caprace and Monod10], which we follow closely. Most results are generalized in Section 4.
Let
![]() $\Omega $
be a set of cardinality
$\Omega $
be a set of cardinality
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and let
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and let
![]() $T_{d}=(V,E)$
denote the d-regular tree. A labelling l of
$T_{d}=(V,E)$
denote the d-regular tree. A labelling l of
![]() $T_{d}$
is a map
$T_{d}$
is a map
![]() $l:E\to \Omega $
such that for every
$l:E\to \Omega $
such that for every
![]() $x\in V$
the map
$x\in V$
the map
![]() $l_{x}:E(x)\to \Omega ,\ e\mapsto l(e)$
is a bijection, and
$l_{x}:E(x)\to \Omega ,\ e\mapsto l(e)$
is a bijection, and
![]() $l(e)\!=\!l(\overline {e})$
for all
$l(e)\!=\!l(\overline {e})$
for all
![]() $e\in E$
. The local action
$e\in E$
. The local action
![]() $\sigma (g,x)\in \operatorname {\mathrm {Sym}}(\Omega )$
of an automorphism
$\sigma (g,x)\in \operatorname {\mathrm {Sym}}(\Omega )$
of an automorphism
![]() $g\in \operatorname {\mathrm {Aut}}(T_{d})$
at a vertex
$g\in \operatorname {\mathrm {Aut}}(T_{d})$
at a vertex
![]() $x\in V$
is defined via
$x\in V$
is defined via
Definition 2.3. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
and l a labelling of
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
and l a labelling of
![]() $T_{d}$
. Define
$T_{d}$
. Define
The map
![]() $\sigma $
satisfies a cocycle identity: for all
$\sigma $
satisfies a cocycle identity: for all
![]() $g,h\in \operatorname {\mathrm {Aut}}(T_{d})$
and
$g,h\in \operatorname {\mathrm {Aut}}(T_{d})$
and
![]() $x\in V$
we have
$x\in V$
we have
![]() $\sigma (gh,x)=\sigma (g,hx)\sigma (h,x)$
. As a consequence,
$\sigma (gh,x)=\sigma (g,hx)\sigma (h,x)$
. As a consequence,
![]() $\mathrm {U}^{(l)}(F)$
is a subgroup of
$\mathrm {U}^{(l)}(F)$
is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
.
$\operatorname {\mathrm {Aut}}(T_{d})$
.
Passing to a different labelling amounts to passing to a conjugate of
![]() $\mathrm {U}^{(l)}(F)$
inside
$\mathrm {U}^{(l)}(F)$
inside
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
. We therefore omit reference to an explicit labelling from here onwards.
$\operatorname {\mathrm {Aut}}(T_{d})$
. We therefore omit reference to an explicit labelling from here onwards.
The following proposition collects several basic properties of Burger–Mozes groups. We refer the reader to [Reference Garrido, Glasner, Tornier, Caprace and Monod10, Section 6.4] for proofs.
Proposition 2.4. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
. The group
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
. The group
![]() $\mathrm {U}(F)$
is
$\mathrm {U}(F)$
is
-
(i) closed in
 $\mathrm {Aut}(T_{d})$
,
$\mathrm {Aut}(T_{d})$
, -
(ii) vertex-transitive,
-
(iii) compactly generated,
-
(iv) locally permutation isomorphic to F,
-
(v) edge-transitive if and only if F is transitive, and
-
(vi) discrete if and only if F is semiregular.
Part (iii) of Proposition 2.4 relies on the following result which we include for future reference. Given
![]() $x\in V$
and
$x\in V$
and
![]() $\omega \in \Omega $
, let
$\omega \in \Omega $
, let
![]() $\smash {\iota _{\omega }^{(x)}\in \mathrm {U}(\{\operatorname {\mathrm {id}}\})}$
denote the unique label-respecting inversion of the edge
$\smash {\iota _{\omega }^{(x)}\in \mathrm {U}(\{\operatorname {\mathrm {id}}\})}$
denote the unique label-respecting inversion of the edge
![]() $e_{\omega }\in E$
with
$e_{\omega }\in E$
with
![]() $o(e_{\omega })=x$
and
$o(e_{\omega })=x$
and
![]() $l(e_{\omega })=\omega $
.
$l(e_{\omega })=\omega $
.
Lemma 2.5. Let
![]() $x\in V$
. Then
$x\in V$
. Then
![]() .
.
Proof. Every element of
![]() $\mathrm {U}(\{\operatorname {\mathrm {id}}\})$
is determined by its image on x. Hence, it suffices to show that
$\mathrm {U}(\{\operatorname {\mathrm {id}}\})$
is determined by its image on x. Hence, it suffices to show that
![]() $\smash {\langle \{\iota _{\omega }^{(x)}\mid \omega \in \Omega \}\rangle }$
is vertex-transitive and has the asserted structure. Indeed, let
$\smash {\langle \{\iota _{\omega }^{(x)}\mid \omega \in \Omega \}\rangle }$
is vertex-transitive and has the asserted structure. Indeed, let
![]() $y\in V\backslash \{x\}$
, and let
$y\in V\backslash \{x\}$
, and let
![]() $\omega _{1},\ldots ,\omega _{n}\in \Omega $
be the labels of the shortest path from x to y. Then
$\omega _{1},\ldots ,\omega _{n}\in \Omega $
be the labels of the shortest path from x to y. Then
![]() $\smash {\iota _{\omega _{1}}^{(x)}\circ \cdots \circ \iota _{\omega _{n}}^{(x)}}$
maps x to y as every
$\smash {\iota _{\omega _{1}}^{(x)}\circ \cdots \circ \iota _{\omega _{n}}^{(x)}}$
maps x to y as every
![]() $\smash {\iota _{\omega }^{(x)}}\ (\omega \in \Omega )$
is label-respecting. Setting
$\smash {\iota _{\omega }^{(x)}}\ (\omega \in \Omega )$
is label-respecting. Setting
![]() $X_{\omega }:=T_{t(e_{\omega })}$
, we have
$X_{\omega }:=T_{t(e_{\omega })}$
, we have
![]() $\iota _{\omega }(X_{\omega '})\subseteq X_{\omega }$
for all distinct
$\iota _{\omega }(X_{\omega '})\subseteq X_{\omega }$
for all distinct
![]() $\omega ,\omega '\in \Omega $
. Hence, the assertion follows from the ping-pong lemma.
$\omega ,\omega '\in \Omega $
. Hence, the assertion follows from the ping-pong lemma.
The name universal group is due to the following maximality statement. Its proof (see [Reference Burger and Mozes2, Proposition 3.2.2]) should be compared with the proof of Theorem 4.34.
Proposition 2.6. 5 Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and vertex-transitive. Then there is a labelling l of
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and vertex-transitive. Then there is a labelling l of
![]() $T_{d}$
such that
$T_{d}$
such that
![]() $H\le \mathrm {U}^{(l)}(F)$
where
$H\le \mathrm {U}^{(l)}(F)$
where
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
is action isomorphic to the local action of H.
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
is action isomorphic to the local action of H.
3 Structure theory of locally semiprimitive groups
We generalize the Burger–Mozes theory of locally quasiprimitive automorphism groups of graphs to the semiprimitive case. While this adjustment of Sections 1.1–1.5 in [Reference Burger and Mozes2] is straightforward and was initiated in [Reference Tornier30, Section II.7] and [Reference Caprace and Le Boudec3, Section 6.2], we provide a full account for the reader’s convenience.
3.1 General facts
Let
![]() $\Gamma =(V,E)$
be a connected graph. We first present a few general facts about several classes of subgroups of
$\Gamma =(V,E)$
be a connected graph. We first present a few general facts about several classes of subgroups of
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
for future reference.
$\operatorname {\mathrm {Aut}}(\Gamma )$
for future reference.
Lemma 3.1. Let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be locally transitive. Then
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be locally transitive. Then
![]() is geometric edge transitive and of index at most
is geometric edge transitive and of index at most
![]() $2$
in H.
$2$
in H.
Proof. Since H is locally transitive, so is
![]() , given that
, given that
![]() for all
for all
![]() $x\in V$
. Hence, it is geometric edge transitive. In particular, it has at most two vertex orbits, which implies the second assertion.
$x\in V$
. Hence, it is geometric edge transitive. In particular, it has at most two vertex orbits, which implies the second assertion.
Lemma 3.2. Let
![]() $H\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
and let
$H\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
and let
![]() $\Gamma '=(V',E')$
be a connected subgraph of
$\Gamma '=(V',E')$
be a connected subgraph of
![]() $\Gamma $
. Suppose
$\Gamma $
. Suppose
![]() $R\subseteq H$
is such that for every
$R\subseteq H$
is such that for every
![]() $x'\in V'$
and
$x'\in V'$
and
![]() $e\in E(x')$
there is
$e\in E(x')$
there is
![]() $r\in R$
such that
$r\in R$
such that
![]() $re\in E'$
. Then
$re\in E'$
. Then
![]() $\Lambda :=\langle R\rangle $
satisfies
$\Lambda :=\langle R\rangle $
satisfies
![]() $\bigcup _{\lambda \in \Lambda }\lambda \Gamma '=\Gamma $
.
$\bigcup _{\lambda \in \Lambda }\lambda \Gamma '=\Gamma $
.
Proof. By assumption,
![]() $B(\Gamma ',1)\subseteq \bigcup _{\lambda \in \Lambda }\lambda \Gamma '$
. Now suppose
$B(\Gamma ',1)\subseteq \bigcup _{\lambda \in \Lambda }\lambda \Gamma '$
. Now suppose
![]() $B(\Gamma ',n)\subseteq \bigcup _{\lambda \in \Lambda }\lambda \Gamma '$
for some
$B(\Gamma ',n)\subseteq \bigcup _{\lambda \in \Lambda }\lambda \Gamma '$
for some
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
. Let
$n\in \operatorname {\mathrm {\mathbb {N}}}$
. Let
![]() $x'\in V(B(\Gamma ',n))$
. Pick
$x'\in V(B(\Gamma ',n))$
. Pick
![]() $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
![]() $\lambda (x')\!\in \! V'$
. Since
$\lambda (x')\!\in \! V'$
. Since
![]() $\lambda $
induces a bijection between
$\lambda $
induces a bijection between
![]() $E(x')$
and
$E(x')$
and
![]() $E(\lambda (x'))$
we conclude that
$E(\lambda (x'))$
we conclude that
![]() $B(\Gamma ',n+1)\subseteq \bigcup _{\lambda \in \Lambda }\lambda \Gamma '$
.
$B(\Gamma ',n+1)\subseteq \bigcup _{\lambda \in \Lambda }\lambda \Gamma '$
.
Assume from now on that
![]() $\Gamma $
is a locally finite, connected graph.
$\Gamma $
is a locally finite, connected graph.
Lemma 3.3. Let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
. If
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
. If
![]() $H\backslash \Gamma $
is finite then there is a finitely generated subgroup
$H\backslash \Gamma $
is finite then there is a finitely generated subgroup
![]() $\Lambda \le H$
such that
$\Lambda \le H$
such that
![]() $\Lambda \backslash \Gamma $
is finite.
$\Lambda \backslash \Gamma $
is finite.
Proof. Let
![]() $\Gamma '=(V',E')\subseteq \Gamma $
be a connected subgraph that projects onto
$\Gamma '=(V',E')\subseteq \Gamma $
be a connected subgraph that projects onto
![]() $H\backslash \Gamma $
. For every
$H\backslash \Gamma $
. For every
![]() $x'\in V'$
and
$x'\in V'$
and
![]() $e\in E(x')$
, pick
$e\in E(x')$
, pick
![]() $\lambda _{x',e}\in H$
such that
$\lambda _{x',e}\in H$
such that
![]() $\lambda _{x',e}(e)\in E'$
. Then the group
$\lambda _{x',e}(e)\in E'$
. Then the group
![]() ${\Lambda :=\langle \{\lambda _{x',e}\mid x'\in X,\ e\in E(x')\}\rangle }$
satisfies the conclusion by Lemma 3.2.
${\Lambda :=\langle \{\lambda _{x',e}\mid x'\in X,\ e\in E(x')\}\rangle }$
satisfies the conclusion by Lemma 3.2.
Lemma 3.4. Let
![]() $\Lambda \le \operatorname {\mathrm {Aut}}(\Gamma )$
. If
$\Lambda \le \operatorname {\mathrm {Aut}}(\Gamma )$
. If
![]() $\Lambda \backslash \Gamma $
is finite then
$\Lambda \backslash \Gamma $
is finite then
![]() $Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
is discrete.
$Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
is discrete.
Proof. Let
![]() $F\subseteq E$
be finite such that
$F\subseteq E$
be finite such that
![]() $\bigcup _{\lambda \in \Lambda }\lambda F=E$
and
$\bigcup _{\lambda \in \Lambda }\lambda F=E$
and
![]() $U:=\Lambda _{F}\cap Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
, which is open in
$U:=\Lambda _{F}\cap Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
, which is open in
![]() $Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
. Given that U and
$Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
. Given that U and
![]() $\Lambda $
commute, U acts trivially on
$\Lambda $
commute, U acts trivially on
![]() $E=\bigcup _{\lambda \in \Lambda }\lambda F$
. Hence,
$E=\bigcup _{\lambda \in \Lambda }\lambda F$
. Hence,
![]() $U=\{\operatorname {\mathrm {id}}\}$
and
$U=\{\operatorname {\mathrm {id}}\}$
and
![]() $Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
is discrete.
$Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
is discrete.
Lemma 3.5. Let
![]() $\Lambda _{1},\Lambda _{2}\le \operatorname {\mathrm {Aut}}(\Gamma )$
. If
$\Lambda _{1},\Lambda _{2}\le \operatorname {\mathrm {Aut}}(\Gamma )$
. If
![]() $\Lambda _{1}\backslash \Gamma $
is finite and
$\Lambda _{1}\backslash \Gamma $
is finite and
![]() $[\Lambda _{1},\Lambda _{2}]\le \operatorname {\mathrm {Aut}}(\Gamma )$
is discrete then
$[\Lambda _{1},\Lambda _{2}]\le \operatorname {\mathrm {Aut}}(\Gamma )$
is discrete then
![]() $\Lambda _{2}\le \operatorname {\mathrm {Aut}}(\Gamma )$
is discrete.
$\Lambda _{2}\le \operatorname {\mathrm {Aut}}(\Gamma )$
is discrete.
Proof. Using Lemma 3.3 pick
![]() $R\subseteq \Lambda _{1}$
such that
$R\subseteq \Lambda _{1}$
such that
![]() $\langle R\rangle \backslash \Gamma $
is finite. As
$\langle R\rangle \backslash \Gamma $
is finite. As
![]() $[\Lambda _{1},\Lambda _{2}]\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
is discrete, there is an open subgroup
$[\Lambda _{1},\Lambda _{2}]\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
is discrete, there is an open subgroup
![]() $U\le \Lambda _{2}$
such that
$U\le \Lambda _{2}$
such that
![]() $[r,U]=\{e\}$
for all
$[r,U]=\{e\}$
for all
![]() $r\in R$
. That is,
$r\in R$
. That is,
![]() $U\le Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\langle R\rangle )$
. Hence, U is discrete by Lemma 3.4, and so is
$U\le Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\langle R\rangle )$
. Hence, U is discrete by Lemma 3.4, and so is
![]() $\Lambda _{2}$
.
$\Lambda _{2}$
.
Lemma 3.6. Let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be nondiscrete. Then
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be nondiscrete. Then
![]() $\mathrm {QZ}(H)\backslash \Gamma $
is infinite.
$\mathrm {QZ}(H)\backslash \Gamma $
is infinite.
Proof. If
![]() $\mathrm {QZ}(H)\backslash \Gamma $
is finite, there is a finitely generated subgroup
$\mathrm {QZ}(H)\backslash \Gamma $
is finite, there is a finitely generated subgroup
![]() $\Lambda \le \mathrm {QZ}(H)$
such that
$\Lambda \le \mathrm {QZ}(H)$
such that
![]() $\Lambda \backslash \Gamma $
is finite as well by Lemma 3.3. Hence, there is an open subgroup
$\Lambda \backslash \Gamma $
is finite as well by Lemma 3.3. Hence, there is an open subgroup
![]() $U\le H$
with
$U\le H$
with
![]() $U\le Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
. Hence, U and therefore H are discrete by Lemma 3.4.
$U\le Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
. Hence, U and therefore H are discrete by Lemma 3.4.
Lemma 3.7. Let
![]() $\Lambda \!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
be discrete. If
$\Lambda \!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
be discrete. If
![]() $\Lambda \backslash \Gamma $
is finite then
$\Lambda \backslash \Gamma $
is finite then
![]() $N_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
is discrete.
$N_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
is discrete.
Proof. Apply Lemma 3.5 to
![]() $\Lambda _{1}:=\Lambda $
and
$\Lambda _{1}:=\Lambda $
and
![]() $\Lambda _{2}:=N_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
.
$\Lambda _{2}:=N_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Lambda )$
.
3.2 Normal subgroups
Let
![]() $\Gamma =(V,E)$
denote a locally finite, connected graph. For closed subgroups
$\Gamma =(V,E)$
denote a locally finite, connected graph. For closed subgroups
![]() $\Lambda \unlhd H$
of
$\Lambda \unlhd H$
of
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
we define
$\operatorname {\mathrm {Aut}}(\Gamma )$
we define
the set of closed normal subgroups of H that contain
![]() $\Lambda $
and do not act freely on E. The set
$\Lambda $
and do not act freely on E. The set
![]() $\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
is partially ordered by inclusion. We let
$\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
is partially ordered by inclusion. We let
![]() $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\Lambda )\subseteq \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
denote the set of minimal elements in
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\Lambda )\subseteq \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
denote the set of minimal elements in
![]() $\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
.
$\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
.
Lemma 3.8. Let
![]() $\Gamma \!=\!(V,E)$
be a locally finite, connected graph and
$\Gamma \!=\!(V,E)$
be a locally finite, connected graph and
![]() $\Lambda \unlhd H\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
. If
$\Lambda \unlhd H\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
. If
![]() $H\backslash \Gamma $
is finite and H does not act freely on E then
$H\backslash \Gamma $
is finite and H does not act freely on E then
![]() $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\Lambda )\neq \emptyset $
.
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\Lambda )\neq \emptyset $
.
Proof. We argue using Zorn’s lemma. First note that
![]() $\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
is nonempty as it contains H. Let
$\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
is nonempty as it contains H. Let
![]() $C\subseteq \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
be a chain. Pick a finite set
$C\subseteq \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\Lambda )$
be a chain. Pick a finite set
![]() $F\subseteq E$
of representatives of
$F\subseteq E$
of representatives of
![]() $H\backslash E$
. For every
$H\backslash E$
. For every
![]() $N\in C$
, the set
$N\in C$
, the set
![]() $F_{N}:=\{e\in F\mid N|_{e^{1}}\le \operatorname {\mathrm {Aut}}(e^{1}) \text { is nontrivial}\}$
is nonempty. Since F is finite and C is a chain it follows that
$F_{N}:=\{e\in F\mid N|_{e^{1}}\le \operatorname {\mathrm {Aut}}(e^{1}) \text { is nontrivial}\}$
is nonempty. Since F is finite and C is a chain it follows that
![]() $\bigcap _{N\in C}F_{N}$
is nonempty, that is, there exists
$\bigcap _{N\in C}F_{N}$
is nonempty, that is, there exists
![]() $e\in F$
such that
$e\in F$
such that
![]() $N|_{e^{1}}$
is nontrivial for every
$N|_{e^{1}}$
is nontrivial for every
![]() $N\in C$
. As before, we conclude that
$N\in C$
. As before, we conclude that
![]() $M:=\bigcap _{N\in C}N|_{e^{1}}$
is nontrivial. For
$M:=\bigcap _{N\in C}N|_{e^{1}}$
is nontrivial. For
![]() $\alpha \in M\backslash \{\operatorname {\mathrm {id}}\}$
,
$\alpha \in M\backslash \{\operatorname {\mathrm {id}}\}$
,
![]() $N^{\alpha }:=\{g\in N_{e}\mid g|_{e^{1}}=\alpha \}$
is a nonempty compact subset of
$N^{\alpha }:=\{g\in N_{e}\mid g|_{e^{1}}=\alpha \}$
is a nonempty compact subset of
![]() $H_{e}$
, and since C is a chain every finite subset of
$H_{e}$
, and since C is a chain every finite subset of
![]() $\{N^{\alpha }\mid N\in C\}$
has nonempty intersection. Hence,
$\{N^{\alpha }\mid N\in C\}$
has nonempty intersection. Hence,
![]() $\bigcap _{N\in C}N^{\alpha }$
is nonempty and therefore
$\bigcap _{N\in C}N^{\alpha }$
is nonempty and therefore
![]() $N_{C}:=\bigcap _{N\in C}N$
is a closed normal subgroup of H containing
$N_{C}:=\bigcap _{N\in C}N$
is a closed normal subgroup of H containing
![]() $\Lambda $
that does not act freely on E. Overall,
$\Lambda $
that does not act freely on E. Overall,
![]() $N_{C}\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\Lambda )$
.
$N_{C}\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\Lambda )$
.
The following lemma is contained in the author’s PhD thesis [Reference Tornier30, Section II.7] and, independently, in Caprace and Le Boudec [Reference Caprace and Le Boudec3, Section 6.2].
Lemma 3.9. Let
![]() $\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
$\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be locally semiprimitive and
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be locally semiprimitive and
![]() $N\unlhd H$
. Define
$N\unlhd H$
. Define
-
 $V_{1}:=\{x\in V\mid N_{x}\curvearrowright S(x,1) \text { is transitive and not semiregular}\}$
,
$V_{1}:=\{x\in V\mid N_{x}\curvearrowright S(x,1) \text { is transitive and not semiregular}\}$
, -
 $V_{2}:=\{x\in V\mid N_{x}\curvearrowright S(x,1) \text { is semiregular}\}$
.
$V_{2}:=\{x\in V\mid N_{x}\curvearrowright S(x,1) \text { is semiregular}\}$
.
Then one of the following assertions holds.
-
(i)
 $V=V_{2}$
and N acts freely on E.
$V=V_{2}$
and N acts freely on E. -
(ii)
 $V=V_{1}$
and N is geometric edge transitive.
$V=V_{1}$
and N is geometric edge transitive. -
(iii)
 $V=V_{1}\sqcup V_{2}$
is an H-invariant partition of V and
$V=V_{1}\sqcup V_{2}$
is an H-invariant partition of V and
 $B(x,1)$
is a fundamental domain for the action of N on
$B(x,1)$
is a fundamental domain for the action of N on
 $\Gamma $
for any
$\Gamma $
for any
 $x\in V_{2}$
.
$x\in V_{2}$
.
Proof. Since H is locally semiprimitive and N is normal in H, we have
![]() $V=V_{1}\sqcup V_{2}$
. If N does not act freely on E then there exist an edge
$V=V_{1}\sqcup V_{2}$
. If N does not act freely on E then there exist an edge
![]() $e\in E$
with
$e\in E$
with
![]() $N_{e}\neq \{\operatorname {\mathrm {id}}\}$
and an
$N_{e}\neq \{\operatorname {\mathrm {id}}\}$
and an
![]() $N_{e}$
-fixed vertex
$N_{e}$
-fixed vertex
![]() $x\in V$
for which
$x\in V$
for which
![]() $N_{x}\curvearrowright S(x,1)$
is not semiregular, hence transitive. That is,
$N_{x}\curvearrowright S(x,1)$
is not semiregular, hence transitive. That is,
![]() $V_{1}\neq \emptyset $
. Now, either
$V_{1}\neq \emptyset $
. Now, either
![]() $V_{2}(N)=\emptyset $
in which case N is locally transitive and we are in case (ii), or
$V_{2}(N)=\emptyset $
in which case N is locally transitive and we are in case (ii), or
![]() $V_{2}(N)\neq \emptyset $
. Being locally transitive, H acts transitively on the set of geometric edges and therefore has at most two vertex orbits. Given that both
$V_{2}(N)\neq \emptyset $
. Being locally transitive, H acts transitively on the set of geometric edges and therefore has at most two vertex orbits. Given that both
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are nonempty and H-invariant, they constitute exactly the said orbits. Since any pair of adjacent vertices
$V_{2}$
are nonempty and H-invariant, they constitute exactly the said orbits. Since any pair of adjacent vertices
![]() $(x,y)$
is a fundamental domain for the H-action on V, we conclude that if
$(x,y)$
is a fundamental domain for the H-action on V, we conclude that if
![]() $y\in V_{2}$
then
$y\in V_{2}$
then
![]() $x\in V_{1}$
. Thus every leaf of
$x\in V_{1}$
. Thus every leaf of
![]() $B(y,1)$
is in
$B(y,1)$
is in
![]() $V_{1}$
and we are in case (iii) by Lemma 3.2.
$V_{1}$
and we are in case (iii) by Lemma 3.2.
3.3 The subquotient
 $H^{\textbf{(}\infty \textbf{)}}/{QZ}\textbf{(}H^{\textbf{(}\infty \textbf{)}}$
$H^{\textbf{(}\infty \textbf{)}}/{QZ}\textbf{(}H^{\textbf{(}\infty \textbf{)}}$
In this section, we achieve control over
![]() $H^{(\infty )}$
and
$H^{(\infty )}$
and
![]() $\mathrm {QZ}(H)$
as well as the normal subgroups of H in the semiprimitive case. We then describe the structure of the subquotient
$\mathrm {QZ}(H)$
as well as the normal subgroups of H in the semiprimitive case. We then describe the structure of the subquotient
![]() $H^{(\infty )}/\mathrm {QZ}(H^{(\infty )})$
. First, recall the following lemma from topological group theory.
$H^{(\infty )}/\mathrm {QZ}(H^{(\infty )})$
. First, recall the following lemma from topological group theory.
Lemma 3.10. Let G be a topological group. If
![]() $H\unlhd G$
is discrete then
$H\unlhd G$
is discrete then
![]() $H\subseteq \mathrm {QZ}(G)$
.
$H\subseteq \mathrm {QZ}(G)$
.
Proof. For
![]() $h\in H$
, the map
$h\in H$
, the map
![]() $\varphi _{h}:G\to H$
,
$\varphi _{h}:G\to H$
,
![]() $g\mapsto ghg^{-1}$
is well defined because
$g\mapsto ghg^{-1}$
is well defined because
![]() $H\unlhd G$
, and continuous. Hence, there is an open set
$H\unlhd G$
, and continuous. Hence, there is an open set
![]() $U\subseteq G$
containing
$U\subseteq G$
containing
![]() $1\in G$
and such that
$1\in G$
and such that
![]() $\varphi _{h}(U)\subseteq \{h\}$
, that is,
$\varphi _{h}(U)\subseteq \{h\}$
, that is,
![]() $U\subseteq Z_{G}(h)$
.
$U\subseteq Z_{G}(h)$
.
Proposition 3.11. Let
![]() $\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
$\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Then the following assertions hold.
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Then the following assertions hold.
-
(i)
 $H/H^{(\infty )}$
is compact.
$H/H^{(\infty )}$
is compact. -
(ii)
 $\mathrm {QZ}(H)$
acts freely on E, and is discrete noncocompact in H.
$\mathrm {QZ}(H)$
acts freely on E, and is discrete noncocompact in H. -
(iii) For any closed normal subgroup
 $N\unlhd H$
, either N is nondiscrete cocompact and
$N\unlhd H$
, either N is nondiscrete cocompact and
 $N\unrhd H^{(\infty )}$
, or N is discrete and
$N\unrhd H^{(\infty )}$
, or N is discrete and
 $N\unlhd \mathrm {QZ}(H)$
.
$N\unlhd \mathrm {QZ}(H)$
. -
(iv)
 $\mathrm {QZ}(H^{(\infty )})=\mathrm {QZ}(H)\cap H^{(\infty )}$
acts freely on E without inversions.
$\mathrm {QZ}(H^{(\infty )})=\mathrm {QZ}(H)\cap H^{(\infty )}$
acts freely on E without inversions. -
(v) For any open normal subgroup
 $N\unlhd H^{(\infty )}$
we have
$N\unlhd H^{(\infty )}$
we have
 $N=H^{(\infty )}$
.
$N=H^{(\infty )}$
. -
(vi)
 $H^{(\infty )}$
is topologically perfect, that is,
$H^{(\infty )}$
is topologically perfect, that is,
 $H^{(\infty )}=[H^{(\infty )},H^{(\infty )}]$
.
$H^{(\infty )}=[H^{(\infty )},H^{(\infty )}]$
.
Proof. For (i), let
![]() $N\unlhd H$
be closed and cocompact. Since H is nondiscrete, so is N in view of Lemma 3.7. Hence,
$N\unlhd H$
be closed and cocompact. Since H is nondiscrete, so is N in view of Lemma 3.7. Hence,
![]() $N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. Conversely, if
$N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. Conversely, if
![]() $N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
then N is cocompact in H by Lemma 3.9. We conclude that
$N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
then N is cocompact in H by Lemma 3.9. We conclude that
![]() $H^{(\infty )}=\bigcap \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. This intersection is in fact given by a single minimal element of
$H^{(\infty )}=\bigcap \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. This intersection is in fact given by a single minimal element of
![]() $\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. Using Lemma 3.8, pick
$\operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. Using Lemma 3.8, pick
![]() $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
, and let
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
, and let
![]() $N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. Suppose
$N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})$
. Suppose
![]() $N\not \supseteq M$
. Because M is minimal,
$N\not \supseteq M$
. Because M is minimal,
![]() $N\cap M$
acts freely on E. In particular,
$N\cap M$
acts freely on E. In particular,
![]() $N\cap M$
is discrete. Since both N and M are normal in H, we also have
$N\cap M$
is discrete. Since both N and M are normal in H, we also have
![]() $N\cap M\supseteq [N,M]$
and hence N and M are discrete by Lemma 3.5. Then so is
$N\cap M\supseteq [N,M]$
and hence N and M are discrete by Lemma 3.5. Then so is
![]() $H\subseteq N_{\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {\mathfrak {g}}})}(H)$
by Lemma 3.7. Overall,
$H\subseteq N_{\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {\mathfrak {g}}})}(H)$
by Lemma 3.7. Overall,
![]() $\smash {H^{(\infty )}\!=\!M\!\in \!\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})}$
and the assertion now follows from Lemma 3.9.
$\smash {H^{(\infty )}\!=\!M\!\in \!\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H,\{\operatorname {\mathrm {id}}\})}$
and the assertion now follows from Lemma 3.9.
As to (ii), the group
![]() $\mathrm {QZ}(H)$
is noncocompact by Lemma 3.6 and therefore acts freely on E by Lemma 3.9. In particular, it is discrete.
$\mathrm {QZ}(H)$
is noncocompact by Lemma 3.6 and therefore acts freely on E by Lemma 3.9. In particular, it is discrete.
For (iii), let
![]() $N\unlhd H$
be a closed normal subgroup. If N acts freely on E, then N is discrete and hence contained in
$N\unlhd H$
be a closed normal subgroup. If N acts freely on E, then N is discrete and hence contained in
![]() $\mathrm {QZ}(H)$
by Lemma 3.10. If N does not act freely on E then N is cocompact in H by Lemma 3.9 and therefore contains
$\mathrm {QZ}(H)$
by Lemma 3.10. If N does not act freely on E then N is cocompact in H by Lemma 3.9 and therefore contains
![]() $H^{(\infty )}$
.
$H^{(\infty )}$
.
Concerning (iv), the inclusion
![]() $\mathrm {QZ}(H)\cap H^{(\infty )}\subseteq \mathrm {QZ}(H^{(\infty )})$
is automatic. Further,
$\mathrm {QZ}(H)\cap H^{(\infty )}\subseteq \mathrm {QZ}(H^{(\infty )})$
is automatic. Further,
![]() $\mathrm {QZ}(H^{(\infty )})$
is normal in H because it is topologically characteristic in
$\mathrm {QZ}(H^{(\infty )})$
is normal in H because it is topologically characteristic in
![]() $H^{(\infty )}\unlhd H$
. Therefore, if
$H^{(\infty )}\unlhd H$
. Therefore, if
![]() $\mathrm {QZ}(H^{(\infty )})\not \subseteq \mathrm {QZ}(H)$
, then
$\mathrm {QZ}(H^{(\infty )})\not \subseteq \mathrm {QZ}(H)$
, then
![]() $\mathrm {QZ}(H^{(\infty )})$
is nondiscrete by part (iii) and does not act freely on E. Then
$\mathrm {QZ}(H^{(\infty )})$
is nondiscrete by part (iii) and does not act freely on E. Then
![]() $\mathrm {QZ}(H^{(\infty )})\backslash \Gamma $
is finite by Lemma 3.9, contradicting Lemma 3.6 applied to
$\mathrm {QZ}(H^{(\infty )})\backslash \Gamma $
is finite by Lemma 3.9, contradicting Lemma 3.6 applied to
![]() $H^{(\infty )}$
which is nondiscrete because
$H^{(\infty )}$
which is nondiscrete because
![]() $\mathrm {QZ}(H^{(\infty )})\le H^{(\infty )}$
is. Consequently,
$\mathrm {QZ}(H^{(\infty )})\le H^{(\infty )}$
is. Consequently,
![]() $\mathrm {QZ}(H^{(\infty )})\le \mathrm {QZ}(H)$
, which proves the assertion.
$\mathrm {QZ}(H^{(\infty )})\le \mathrm {QZ}(H)$
, which proves the assertion.
For part (v), note that
![]() $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\{\operatorname {\mathrm {id}}\})$
is nonempty by Lemma 3.8 as
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\{\operatorname {\mathrm {id}}\})$
is nonempty by Lemma 3.8 as
![]() $H^{(\infty )}$
is cocompact in
$H^{(\infty )}$
is cocompact in
![]() $\operatorname {\mathrm {Aut}}(\Gamma )$
by part (i) and nondiscrete by part (iii). Further, since
$\operatorname {\mathrm {Aut}}(\Gamma )$
by part (i) and nondiscrete by part (iii). Further, since
![]() $\mathrm {QZ}(H^{(\infty )})$
acts freely on E, every
$\mathrm {QZ}(H^{(\infty )})$
acts freely on E, every
![]() $N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H^{(\infty )},\{\operatorname {\mathrm {id}}\})$
is nondiscrete by part (iii) as well. Given an open subgroup
$N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H^{(\infty )},\{\operatorname {\mathrm {id}}\})$
is nondiscrete by part (iii) as well. Given an open subgroup
![]() $U\unlhd H^{(\infty )}$
and
$U\unlhd H^{(\infty )}$
and
![]() $N\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{\infty },\{\operatorname {\mathrm {id}}\})$
, the group
$N\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{\infty },\{\operatorname {\mathrm {id}}\})$
, the group
![]() $U\cap N$
is normal in
$U\cap N$
is normal in
![]() $H^{(\infty )}$
and nondiscrete. In particular,
$H^{(\infty )}$
and nondiscrete. In particular,
![]() $U\cap N$
does not act freely on E and hence
$U\cap N$
does not act freely on E and hence
![]() $U\cap N=N$
. Thus U contains the subgroup of
$U\cap N=N$
. Thus U contains the subgroup of
![]() $H^{(\infty )}$
generated by the elements of
$H^{(\infty )}$
generated by the elements of
![]() $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\{\operatorname {\mathrm {id}}\})$
, which is closed, normal and nondiscrete. Hence,
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\{\operatorname {\mathrm {id}}\})$
, which is closed, normal and nondiscrete. Hence,
![]() $U= H^{(\infty )}$
.
$U= H^{(\infty )}$
.
As to (vi), the group
![]() $[H^{(\infty )},H^{(\infty )}]$
is nondiscrete by part (i) and Lemma 3.5. Hence, so is
$[H^{(\infty )},H^{(\infty )}]$
is nondiscrete by part (i) and Lemma 3.5. Hence, so is
![]() $\smash {\overline {[H^{(\infty )},H^{(\infty )}]}\unlhd H^{(\infty )}}$
. Now apply part (iii).
$\smash {\overline {[H^{(\infty )},H^{(\infty )}]}\unlhd H^{(\infty )}}$
. Now apply part (iii).
Proposition 3.12. Let
![]() $\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
$\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Finally, let
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Finally, let
![]() $\Lambda \unlhd H$
such that
$\Lambda \unlhd H$
such that
![]() $\Lambda \le \mathrm {QZ}(H^{(\infty )})$
. Then the following assertions hold.
$\Lambda \le \mathrm {QZ}(H^{(\infty )})$
. Then the following assertions hold.
-
(i)
-
(a) The group H acts transitively on
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
.
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. -
(b) The set
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is finite and nonempty.
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is finite and nonempty.
-
-
(ii) Let
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
.
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
.-
(a) The group
 $M/\Lambda $
is topologically perfect.
$M/\Lambda $
is topologically perfect. -
(b) The group
 $\mathrm {QZ}(M)$
acts freely on E and
$\mathrm {QZ}(M)$
acts freely on E and
 $\mathrm {QZ}(M)=\mathrm {QZ}(H^{(\infty )})\cap M$
.
$\mathrm {QZ}(M)=\mathrm {QZ}(H^{(\infty )})\cap M$
. -
(c) The group
 $M/\mathrm {QZ}(M)$
is topologically simple.
$M/\mathrm {QZ}(M)$
is topologically simple.
-
-
(iii) For every
 $N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
there is
$N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
there is
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
 $N\supseteq M$
.
$N\supseteq M$
.
Proof. Since every discrete normal subgroup of
![]() $H^{(\infty )}$
is contained in
$H^{(\infty )}$
is contained in
![]() $\mathrm {QZ}(H^{(\infty )})$
by Lemma 3.10 (iii), and the latter acts freely on E by Proposition 3.11(iii), every element of
$\mathrm {QZ}(H^{(\infty )})$
by Lemma 3.10 (iii), and the latter acts freely on E by Proposition 3.11(iii), every element of
![]() $\mathcal {N}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is nondiscrete. We proceed with a number of claims.
$\mathcal {N}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is nondiscrete. We proceed with a number of claims.
-
(1) For every
 $N\in \mathcal {N}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
we have
$N\in \mathcal {N}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
we have
 $[H^{(\infty )},N]\not \subseteq \mathrm {QZ}(H^{(\infty )})$
.
$[H^{(\infty )},N]\not \subseteq \mathrm {QZ}(H^{(\infty )})$
.This follows from the above combined with Proposition 3.11(i) and Lemma 3.5.
In the following, given
![]() $S\subseteq \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
, we let
$S\subseteq \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
, we let
![]() $M_{S}:=\langle M\mid M\in S\rangle \le H^{(\infty )}$
denote the subgroup of
$M_{S}:=\langle M\mid M\in S\rangle \le H^{(\infty )}$
denote the subgroup of
![]() $H^{(\infty )}$
generated by
$H^{(\infty )}$
generated by
![]() $\bigcup _{M\in S}M$
.
$\bigcup _{M\in S}M$
.
-
(2) The group H acts transitively on
 $\mathcal {M}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
.
$\mathcal {M}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
.Let
 $ S$
be an orbit for the action of H on
$ S$
be an orbit for the action of H on
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
, and suppose there is an element
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
, and suppose there is an element
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )\backslash S$
. For every
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )\backslash S$
. For every
 $N\in S$
, the subgroup
$N\in S$
, the subgroup
 $N\cap M$
is normal in
$N\cap M$
is normal in
 $H^{(\infty )}$
and acts freely on E by minimality of M, hence is discrete. The same therefore holds for
$H^{(\infty )}$
and acts freely on E by minimality of M, hence is discrete. The same therefore holds for
 $[N,M]\subseteq N\cap M$
. Thus
$[N,M]\subseteq N\cap M$
. Thus
 $[N,M]\subseteq \mathrm {QZ}(H^{(\infty )})$
. As
$[N,M]\subseteq \mathrm {QZ}(H^{(\infty )})$
. As
 $\mathrm {QZ}(H^{(\infty )})$
is discrete by Proposition 3.11 and therefore closed in
$\mathrm {QZ}(H^{(\infty )})$
is discrete by Proposition 3.11 and therefore closed in
 $H^{(\infty )}$
we conclude
$H^{(\infty )}$
we conclude
 $[\overline {M_{ S}},M]\subseteq \mathrm {QZ}(H^{(\infty )})$
. On the other hand,
$[\overline {M_{ S}},M]\subseteq \mathrm {QZ}(H^{(\infty )})$
. On the other hand,
 $\overline {M_{S}}$
is normal in H since S is an H-orbit. It is also closed in H, and nondiscrete by the above. Thus
$\overline {M_{S}}$
is normal in H since S is an H-orbit. It is also closed in H, and nondiscrete by the above. Thus
 $\overline {M_{S}}=H^{(\infty )}$
by Proposition 3.11(iii), and
$\overline {M_{S}}=H^{(\infty )}$
by Proposition 3.11(iii), and
 $[H^{(\infty )},M]\subseteq \mathrm {QZ}(H^{(\infty )})$
, which contradicts part (1).
$[H^{(\infty )},M]\subseteq \mathrm {QZ}(H^{(\infty )})$
, which contradicts part (1). -
(3) For every
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
we have
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
we have
 $\smash {\overline {[M,M]\cdot \Lambda }=M}$
.
$\smash {\overline {[M,M]\cdot \Lambda }=M}$
.Note that
 $\overline {[M,M]\cdot \Lambda }$
is a group because
$\overline {[M,M]\cdot \Lambda }$
is a group because
 $\Lambda $
is normal in M. Suppose there is an element
$\Lambda $
is normal in M. Suppose there is an element
 $M_{0}\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
$M_{0}\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
 $\overline {[M_{0},M_{0}]\cdot \Lambda }\lneq M_{0}$
. Then
$\overline {[M_{0},M_{0}]\cdot \Lambda }\lneq M_{0}$
. Then
 $\overline {[M_{0},M_{0}]\cdot \Lambda }$
acts freely on E by minimality of
$\overline {[M_{0},M_{0}]\cdot \Lambda }$
acts freely on E by minimality of
 $M_{0}$
and is discrete. Since
$M_{0}$
and is discrete. Since
 $[M_{0},M_{0}]$
is also normal in
$[M_{0},M_{0}]$
is also normal in
 $H^{(\infty)}$
, we obtain
$H^{(\infty)}$
, we obtain
 $[M_{0},M_{0}]\subseteq\mathrm{QZ}(H^{(\infty)})$
.Part (2) now implies that
$[M_{0},M_{0}]\subseteq\mathrm{QZ}(H^{(\infty)})$
.Part (2) now implies that
 $[M,M]\subseteq \mathrm {QZ}(H^{(\infty )})$
for all
$[M,M]\subseteq \mathrm {QZ}(H^{(\infty )})$
for all
 $M\in \mathcal {M}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Given that
$M\in \mathcal {M}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Given that
 $[M,M']\subseteq \mathrm {QZ}(H^{(\infty )})$
for all distinct
$[M,M']\subseteq \mathrm {QZ}(H^{(\infty )})$
for all distinct
 $M,M'$
in
$M,M'$
in
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
as well, we conclude that
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
as well, we conclude that
 $[H^{(\infty )},H^{(\infty )}]\subseteq \mathrm {QZ}(H^{(\infty )})$
, which contradicts part (1).
$[H^{(\infty )},H^{(\infty )}]\subseteq \mathrm {QZ}(H^{(\infty )})$
, which contradicts part (1). -
(4) For every
 $N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
there is
$N\in \operatorname {\mathrm {\mathcal {N}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
there is
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
 $N\supseteq M$
.
$N\supseteq M$
.Let
 $ S\!:=\!\{M\!\in \!\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )\!\mid \! N\not \supseteq M\}$
. Then
$ S\!:=\!\{M\!\in \!\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )\!\mid \! N\not \supseteq M\}$
. Then
 $[\overline {M_{S}},N]\!\subseteq \!\mathrm {QZ}(H^{(\infty )})$
as above. On the other hand, for
$[\overline {M_{S}},N]\!\subseteq \!\mathrm {QZ}(H^{(\infty )})$
as above. On the other hand, for
 $T:=\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
, the group
$T:=\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
, the group
 $\overline {M_{T}}\subseteq H^{(\infty )}$
is closed, nondiscrete and normal in H, thus
$\overline {M_{T}}\subseteq H^{(\infty )}$
is closed, nondiscrete and normal in H, thus
 $\overline {M_{T}}=H^{(\infty )}$
. Using (1), we conclude that
$\overline {M_{T}}=H^{(\infty )}$
. Using (1), we conclude that
 $ S\neq T$
, which proves the assertion.
$ S\neq T$
, which proves the assertion. -
(5) Let
 $S, S'$
be disjoint subsets of
$S, S'$
be disjoint subsets of
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Then
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Then
 $\overline {M_{S}}\cap \overline {M_{S'}}\subseteq \mathrm {QZ}(H^{(\infty )})$
.
$\overline {M_{S}}\cap \overline {M_{S'}}\subseteq \mathrm {QZ}(H^{(\infty )})$
.If not, we have
 $\smash {\overline {M_{ S}}\cap \overline {M_{ S'}}\!\in \!\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )}$
and there is, by part (4), an element
$\smash {\overline {M_{ S}}\cap \overline {M_{ S'}}\!\in \!\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )}$
and there is, by part (4), an element
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
 $\smash {M\subseteq \overline {M_{S}}\cap \overline {M_{ S'}}}$
. However, this implies that
$\smash {M\subseteq \overline {M_{S}}\cap \overline {M_{ S'}}}$
. However, this implies that
 $[M,M]\subseteq [\overline {M_{S}},\overline {M_{S'}}]\subseteq \mathrm {QZ}(H^{(\infty )})$
, which contradicts part (3).
$[M,M]\subseteq [\overline {M_{S}},\overline {M_{S'}}]\subseteq \mathrm {QZ}(H^{(\infty )})$
, which contradicts part (3). -
(6) The set
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is finite and nonempty.
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is finite and nonempty.The set
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is nonempty by Lemma 3.8. Let
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is nonempty by Lemma 3.8. Let
 $G=\bigcup \overline {M_{S}}$
, where the union is taken over all finite subsets S of the set
$G=\bigcup \overline {M_{S}}$
, where the union is taken over all finite subsets S of the set
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Then G is nondiscrete and normal in H. Hence,
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Then G is nondiscrete and normal in H. Hence,
 $\overline {G}=H^{(\infty )}$
by Proposition 3.11(iii). Since H is second-countable and locally compact, it is metrizable. Hence,
$\overline {G}=H^{(\infty )}$
by Proposition 3.11(iii). Since H is second-countable and locally compact, it is metrizable. Hence,
 $H^{(\infty )}$
is a separable metric space and the same holds for G. Let
$H^{(\infty )}$
is a separable metric space and the same holds for G. Let
 $L\subseteq G$
be a countable dense subgroup, and fix an exhaustion
$L\subseteq G$
be a countable dense subgroup, and fix an exhaustion
 $F_{1}\subseteq F_{2}\subseteq \cdots \subseteq F$
of F by finite sets. Let
$F_{1}\subseteq F_{2}\subseteq \cdots \subseteq F$
of F by finite sets. Let
 $( S_{n})_{n\in \operatorname {\mathrm {\mathbb {N}}}}$
be an increasing sequence of finite subsets of
$( S_{n})_{n\in \operatorname {\mathrm {\mathbb {N}}}}$
be an increasing sequence of finite subsets of
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
such that
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
such that
 $F_{n}\subseteq \overline {M_{S_{n}}}$
. In particular, which by (5) and (1) implies
$F_{n}\subseteq \overline {M_{S_{n}}}$
. In particular, which by (5) and (1) implies $$ \begin{align*} L\subseteq\overline{M_{\bigcup_{n\in\operatorname{\mathrm{\mathbb{N}}}} S_{n}}} \quad\text{and thus}\quad \overline{M_{\bigcup_{n\in\operatorname{\mathrm{\mathbb{N}}}} S_{n}}}=H^{(\infty)}, \end{align*} $$
$$ \begin{align*} L\subseteq\overline{M_{\bigcup_{n\in\operatorname{\mathrm{\mathbb{N}}}} S_{n}}} \quad\text{and thus}\quad \overline{M_{\bigcup_{n\in\operatorname{\mathrm{\mathbb{N}}}} S_{n}}}=H^{(\infty)}, \end{align*} $$
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )=\bigcup _{n\in \operatorname {\mathrm {\mathbb {N}}}} S_{n}$
. Thus
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )=\bigcup _{n\in \operatorname {\mathrm {\mathbb {N}}}} S_{n}$
. Thus
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is countable. Next, fix
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is countable. Next, fix
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Then
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
. Then
 $N_{H}(M)$
is closed and of countable index in H, and thus has nonempty interior as H is a Baire space. Hence,
$N_{H}(M)$
is closed and of countable index in H, and thus has nonempty interior as H is a Baire space. Hence,
 $N_{H}(M)$
is open in H. Given that
$N_{H}(M)$
is open in H. Given that
 $N_{H}(M)$
contains
$N_{H}(M)$
contains
 $H^{(\infty )}$
, we conclude that
$H^{(\infty )}$
, we conclude that
 $N_{H}(M)$
is of finite index in H using Proposition 3.11(i). Since H acts transitively on
$N_{H}(M)$
is of finite index in H using Proposition 3.11(i). Since H acts transitively on
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
by (2) we conclude that
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
by (2) we conclude that
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is finite by the orbit–stabilizer theorem.
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is finite by the orbit–stabilizer theorem.
The above claims yield parts (i)(a), (i)(b), (ii)(a) and (iii) of Proposition 3.12. We now turn to parts (ii)(b) and (ii)(c).
-
(ii)(b) Using part (6), let
 $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )=\{M_{1},\ldots ,M_{r}\}$
and define Note that since
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )=\{M_{1},\ldots ,M_{r}\}$
and define Note that since $$ \begin{align*} \Omega:=\mathrm{QZ}(M_{1})\cdot\cdots\cdot\mathrm{QZ}(M_{r}). \end{align*} $$
$$ \begin{align*} \Omega:=\mathrm{QZ}(M_{1})\cdot\cdots\cdot\mathrm{QZ}(M_{r}). \end{align*} $$
 $\mathrm {QZ}(M_{i})$
is characteristic in
$\mathrm {QZ}(M_{i})$
is characteristic in
 $M_{i}$
, which is normal in
$M_{i}$
, which is normal in
 $H^{(\infty )}$
, the quasicentres in the above definition normalize each other, so
$H^{(\infty )}$
, the quasicentres in the above definition normalize each other, so
 $\Omega $
is a group. It is then normal in H. If
$\Omega $
is a group. It is then normal in H. If
 $\Omega $
does not act freely on E then
$\Omega $
does not act freely on E then
 $\Omega \backslash \Gamma $
is finite by Lemma 3.9 and there exist
$\Omega \backslash \Gamma $
is finite by Lemma 3.9 and there exist
 $\lambda _{1},\ldots ,\lambda _{k}\in \Omega $
by Lemma 3.3 such that for
$\lambda _{1},\ldots ,\lambda _{k}\in \Omega $
by Lemma 3.3 such that for
 $\Omega ':=\langle \lambda _{1},\ldots ,\lambda _{k}\rangle $
the quotient
$\Omega ':=\langle \lambda _{1},\ldots ,\lambda _{k}\rangle $
the quotient
 $\Omega '\backslash \Gamma $
is finite. For every
$\Omega '\backslash \Gamma $
is finite. For every
 $i\in \{1,\ldots ,k\}$
, write
$i\in \{1,\ldots ,k\}$
, write
 $\lambda _{i}=a_{i}b_{i}$
where
$\lambda _{i}=a_{i}b_{i}$
where
 $a_{i}\in \mathrm {QZ}(M_{1})$
and
$a_{i}\in \mathrm {QZ}(M_{1})$
and
 $b_{i}\in \mathrm {QZ}(M_{2})\cdot \cdots \cdot \mathrm {QZ}(M_{r})$
. Let
$b_{i}\in \mathrm {QZ}(M_{2})\cdot \cdots \cdot \mathrm {QZ}(M_{r})$
. Let
 $U_{1}\le M_{1}$
be an open subgroup such that
$U_{1}\le M_{1}$
be an open subgroup such that
 $[a_{i},U_{1}]=\{e\}$
for all
$[a_{i},U_{1}]=\{e\}$
for all
 $i\in \{1,\ldots ,k\}$
. Since
$i\in \{1,\ldots ,k\}$
. Since
 $[M_{2}\cdots M_{r},M_{1}]\subseteq \mathrm {QZ}(H^{(\infty )})$
, there is an open subgroup
$[M_{2}\cdots M_{r},M_{1}]\subseteq \mathrm {QZ}(H^{(\infty )})$
, there is an open subgroup
 $U_{2}\le M_{1}$
such that
$U_{2}\le M_{1}$
such that
 $[b_{i},U_{2}]=\{e\}$
for all
$[b_{i},U_{2}]=\{e\}$
for all
 $i\in \{1,\ldots ,k\}$
. Hence,
$i\in \{1,\ldots ,k\}$
. Hence,
 $U:=U_{1}\cap U_{2}\le M_{1}$
is contained in
$U:=U_{1}\cap U_{2}\le M_{1}$
is contained in
 $Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Omega ')$
, which by Lemma 3.4 implies that U and hence
$Z_{\operatorname {\mathrm {Aut}}(\Gamma )}(\Omega ')$
, which by Lemma 3.4 implies that U and hence
 $M_{1}$
is discrete, a contradiction. Thus
$M_{1}$
is discrete, a contradiction. Thus
 $\Omega $
acts freely on E, is discrete and therefore
$\Omega $
acts freely on E, is discrete and therefore
 $\Omega \subseteq \mathrm {QZ}(H^{(\infty )})$
. That is,
$\Omega \subseteq \mathrm {QZ}(H^{(\infty )})$
. That is,
 $\mathrm {QZ}(M_{i})\subseteq \mathrm {QZ}(H^{(\infty )})\cap M_{i}$
. The opposite inclusion follows from the definitions.
$\mathrm {QZ}(M_{i})\subseteq \mathrm {QZ}(H^{(\infty )})\cap M_{i}$
. The opposite inclusion follows from the definitions.
-
(ii)(c) Let
 $M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
and let
$M\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
and let
 $N\unlhd M$
be a closed subgroup containing
$N\unlhd M$
be a closed subgroup containing
 $\mathrm {QZ}(M)$
. For every
$\mathrm {QZ}(M)$
. For every
 $M'\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
$M'\in \operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
with
 $M\neq M'$
we have This implies
$M\neq M'$
we have This implies $$ \begin{align*} [M',M]\subseteq M'\subseteq M\subseteq\mathrm{QZ}(H^{(\infty)}). \end{align*} $$
$$ \begin{align*} [M',M]\subseteq M'\subseteq M\subseteq\mathrm{QZ}(H^{(\infty)}). \end{align*} $$
 $[M',N]\subseteq \mathrm {QZ}(H^{(\infty )})\cap M=\mathrm {QZ}(M)\subseteq N$
; that is,
$[M',N]\subseteq \mathrm {QZ}(H^{(\infty )})\cap M=\mathrm {QZ}(M)\subseteq N$
; that is,
 $M'$
normalizes N. Since
$M'$
normalizes N. Since
 $N\unlhd M$
, this implies
$N\unlhd M$
, this implies
 $N\unlhd H^{(\infty )}$
; and hence, by minimality of M, we have either that
$N\unlhd H^{(\infty )}$
; and hence, by minimality of M, we have either that
 $N=M$
or else that N acts freely on E and
$N=M$
or else that N acts freely on E and
 ${N\subseteq \mathrm {QZ}(H^{(\infty )})\cap M=\mathrm {QZ}(M)}$
.
${N\subseteq \mathrm {QZ}(H^{(\infty )})\cap M=\mathrm {QZ}(M)}$
.
Corollary 3.13. Let
![]() $\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
$\Gamma =(V,E)$
be a locally finite, connected graph. Further, let
![]() $H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Minimal, nontrivial closed normal subgroups of
$H\le \operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Minimal, nontrivial closed normal subgroups of
![]() $H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
exist. They are all H-conjugate, finite in number and topologically simple.
$H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
exist. They are all H-conjugate, finite in number and topologically simple.
Proof. Apply Proposition 3.12 to
![]() $\Lambda =\mathrm {QZ}(H^{(\infty )})$
.
$\Lambda =\mathrm {QZ}(H^{(\infty )})$
.
We summarize the previous results in the following theorem, which is a verbatim copy of Burger and Mozes’ Theorem 2.2, except that the local action need only be semiprimitive, not quasiprimitive.
Theorem 3.14. Let
![]() $\Gamma $
be a locally finite, connected graph. Further, let
$\Gamma $
be a locally finite, connected graph. Further, let
![]() $H\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Then the following assertions hold.
$H\!\le \!\operatorname {\mathrm {Aut}}(\Gamma )$
be closed, nondiscrete and locally semiprimitive. Then the following assertions hold.
-
(i)
 $H^{(\infty )}$
is minimal closed normal cocompact in H.
$H^{(\infty )}$
is minimal closed normal cocompact in H. -
(ii)
 $\mathrm {QZ}(H)$
is maximal discrete normal, and noncocompact in H.
$\mathrm {QZ}(H)$
is maximal discrete normal, and noncocompact in H. -
(iii)
 $H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})\!=\! H^{(\infty )}\!/(\mathrm {QZ}(H)\cap H^{(\infty )})$
admits minimal, nontrivial closed normal subgroups finite in number, H-conjugate and topologically simple.
$H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})\!=\! H^{(\infty )}\!/(\mathrm {QZ}(H)\cap H^{(\infty )})$
admits minimal, nontrivial closed normal subgroups finite in number, H-conjugate and topologically simple.
If
![]() $\Gamma $
is a tree, and, in addition, H is locally primitive then
$\Gamma $
is a tree, and, in addition, H is locally primitive then
-
(iv)
 $H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
is a direct product of topologically simple groups.
$H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
is a direct product of topologically simple groups.
Proof. Parts (i) and (ii) stem from parts (i), (ii) and (iii) of Proposition 3.11 in combination with Section 2.3. For part (iii), use part (iv) of Proposition 3.11 and Corollary 3.13. Finally, part (iv) is Corollary 1.7.2 in [Reference Burger and Mozes2]. It follows from Theorem 1.7.1 in [Reference Burger and Mozes2] as the commutator of any two distinct elements in
![]() $\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is contained in
$\operatorname {\mathrm {\mathcal {M}}}_{\mathrm {nf}}(H^{(\infty )},\Lambda )$
is contained in
![]() $\mathrm {QZ}(H^{(\infty )})$
.
$\mathrm {QZ}(H^{(\infty )})$
.
4 Universal groups
In this section, we develop a generalization of Burger–Mozes universal groups that arises through prescribing the local action on balls of a given radius
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
around vertices. The Burger–Mozes construction corresponds to the case
$k\in \operatorname {\mathrm {\mathbb {N}}}$
around vertices. The Burger–Mozes construction corresponds to the case
![]() $k=1$
.
$k=1$
.
Whereas many properties of the original construction carry over to the new set-up, others require adjustments. Notably, there are compatibility and discreteness conditions on the local action F under which the associated universal group is locally action isomorphic to F and discrete, respectively.
We then exhibit examples and (non)rigidity phenomena of our construction. Finally, a universality statement holds under an additional assumption.
4.1 Definition and basic properties
4.1.1 Definition
Let
![]() $\Omega $
be a set of cardinality
$\Omega $
be a set of cardinality
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and let
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and let
![]() $T_{d}=(V,E)$
denote the d-regular tree. A labelling l of
$T_{d}=(V,E)$
denote the d-regular tree. A labelling l of
![]() $T_{d}$
is a map
$T_{d}$
is a map
![]() $l:E\to \Omega $
such that for every
$l:E\to \Omega $
such that for every
![]() $x\in V$
the map
$x\in V$
the map
![]() $l_{x}\!:E(x)\to \Omega ,\ e\mapsto l(e)$
is a bijection, and
$l_{x}\!:E(x)\to \Omega ,\ e\mapsto l(e)$
is a bijection, and
![]() $l(e)=l(\overline {e})$
for all
$l(e)=l(\overline {e})$
for all
![]() $e\in E$
.
$e\in E$
.
For every
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
, fix a tree
$k\in \operatorname {\mathrm {\mathbb {N}}}$
, fix a tree
![]() $B_{d,k}$
that is isomorphic to a ball of radius k around a vertex in
$B_{d,k}$
that is isomorphic to a ball of radius k around a vertex in
![]() $T_{d}$
. Let b denote its centre and carry over the labelling of
$T_{d}$
. Let b denote its centre and carry over the labelling of
![]() $T_{d}$
to
$T_{d}$
to
![]() $B_{d,k}$
via the chosen isomorphism. Then for every
$B_{d,k}$
via the chosen isomorphism. Then for every
![]() $x\in V$
there is a unique, label-respecting isomorphism
$x\in V$
there is a unique, label-respecting isomorphism
![]() $l_{x}^{k}:B(x,k)\to B_{d,k}$
. We define the k-local action
$l_{x}^{k}:B(x,k)\to B_{d,k}$
. We define the k-local action
![]() $\sigma _{k}(g,x)\!\in \!\operatorname {\mathrm {Aut}}(B_{d,k})$
of an automorphism
$\sigma _{k}(g,x)\!\in \!\operatorname {\mathrm {Aut}}(B_{d,k})$
of an automorphism
![]() $g\!\in \!\operatorname {\mathrm {Aut}}(T_{d})$
at a vertex
$g\!\in \!\operatorname {\mathrm {Aut}}(T_{d})$
at a vertex
![]() $x\in V$
via
$x\in V$
via
Definition 4.1. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
and l be a labelling of
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
and l be a labelling of
![]() $T_{d}$
. Define
$T_{d}$
. Define
The following lemma states that the maps
![]() $\sigma _{k}$
satisfy a cocycle identity which implies that
$\sigma _{k}$
satisfy a cocycle identity which implies that
![]() $\smash {\mathrm {U}_{k}^{(l)}(F)}$
is a subgroup of
$\smash {\mathrm {U}_{k}^{(l)}(F)}$
is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
for every
$\operatorname {\mathrm {Aut}}(T_{d})$
for every
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
.
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
.
Lemma 4.2. Let
![]() $x\in V$
and
$x\in V$
and
![]() $g,h\in \operatorname {\mathrm {Aut}}(T_{d})$
. Then
$g,h\in \operatorname {\mathrm {Aut}}(T_{d})$
. Then
![]() $\sigma _{k}(gh,x)=\sigma _{k}(g,hx)\sigma _{k}(h,x)$
.
$\sigma _{k}(gh,x)=\sigma _{k}(g,hx)\sigma _{k}(h,x)$
.
Proof. We compute
 $$ \begin{align*} \sigma_{k}(gh,x)&=l_{(gh)x}^{k}\circ gh\circ (l_{x}^{k})^{-1}=l_{(gh)x}^{k}\circ g\circ h\circ(l_{x}^{k})^{-1} \\ &=l_{(gh)x}^{k}\circ g\circ (l_{hx}^{k})^{-1}\circ l_{hx}^{k}\circ h\circ(l_{x}^{k})^{-1}=\sigma_{k}(g,hx)\sigma_{k}(h,x).\\[-2.9pc] \end{align*} $$
$$ \begin{align*} \sigma_{k}(gh,x)&=l_{(gh)x}^{k}\circ gh\circ (l_{x}^{k})^{-1}=l_{(gh)x}^{k}\circ g\circ h\circ(l_{x}^{k})^{-1} \\ &=l_{(gh)x}^{k}\circ g\circ (l_{hx}^{k})^{-1}\circ l_{hx}^{k}\circ h\circ(l_{x}^{k})^{-1}=\sigma_{k}(g,hx)\sigma_{k}(h,x).\\[-2.9pc] \end{align*} $$
4.1.2 Basic properties
Note that the group
![]() $\smash {\mathrm {U}_{1}^{(l)}(F)}$
of Definition 4.1 coincides with the Burger–Mozes universal group
$\smash {\mathrm {U}_{1}^{(l)}(F)}$
of Definition 4.1 coincides with the Burger–Mozes universal group
![]() $\smash {\mathrm {U}_{(l)}(F)}$
introduced in [Reference Burger and Mozes2, Section 3.2] under the natural isomorphism
$\smash {\mathrm {U}_{(l)}(F)}$
introduced in [Reference Burger and Mozes2, Section 3.2] under the natural isomorphism
![]() $\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
. Several basic properties of the latter group carry over to the generalized set-up. First of all, passing between different labellings of
$\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
. Several basic properties of the latter group carry over to the generalized set-up. First of all, passing between different labellings of
![]() $T_{d}$
amounts to conjugating in
$T_{d}$
amounts to conjugating in
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
. Subsequently, we therefore omit the reference to an explicit labelling.
$\operatorname {\mathrm {Aut}}(T_{d})$
. Subsequently, we therefore omit the reference to an explicit labelling.
Lemma 4.3. For every quadruple
![]() $(l,l',x,x')$
of labellings
$(l,l',x,x')$
of labellings
![]() $l,l'$
of
$l,l'$
of
![]() $T_{d}$
and vertices
$T_{d}$
and vertices
![]() $x,x'\in V$
, there is a unique automorphism
$x,x'\in V$
, there is a unique automorphism
![]() $g\in \operatorname {\mathrm {Aut}}(T_{d})$
with
$g\in \operatorname {\mathrm {Aut}}(T_{d})$
with
![]() $gx=x'$
and
$gx=x'$
and
![]() $l'=l\circ g$
.
$l'=l\circ g$
.
Proof. Set
![]() $gx:=x'$
. Now assume inductively that g is uniquely determined on
$gx:=x'$
. Now assume inductively that g is uniquely determined on
![]() $B(x,n)$
,
$B(x,n)$
,
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}_{0}$
, and let
$n\in \operatorname {\mathrm {\mathbb {N}}}_{0}$
, and let
![]() $v\in S(x,n)$
. Then g is also uniquely determined on
$v\in S(x,n)$
. Then g is also uniquely determined on
![]() $E(v)$
by the requirement
$E(v)$
by the requirement
![]() $l'=l\circ g$
, namely
$l'=l\circ g$
, namely
![]() $g|_{E(v)}:=l|_{E(gv)}^{-1}\circ l'|_{E(v)}$
.
$g|_{E(v)}:=l|_{E(gv)}^{-1}\circ l'|_{E(v)}$
.
Proposition 4.4. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Further, let l and
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Further, let l and
![]() $l'$
be labellings of
$l'$
be labellings of
![]() $T_{d}$
. Then the groups
$T_{d}$
. Then the groups
![]() $\smash {\mathrm {U}_{k}^{(l)}(F)}$
and
$\smash {\mathrm {U}_{k}^{(l)}(F)}$
and
![]() $\smash {\mathrm {U}_{k}^{(l')}(F)}$
are conjugate in
$\smash {\mathrm {U}_{k}^{(l')}(F)}$
are conjugate in
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
.
$\operatorname {\mathrm {Aut}}(T_{d})$
.
Proof. Choose
![]() $x\in V$
. Let
$x\in V$
. Let
![]() $\tau \in \operatorname {\mathrm {Aut}}(T_{d})$
denote the automorphism of
$\tau \in \operatorname {\mathrm {Aut}}(T_{d})$
denote the automorphism of
![]() $T_{d}$
associated to
$T_{d}$
associated to
![]() $(l,l',x,x)$
by Lemma 4.3. Then
$(l,l',x,x)$
by Lemma 4.3. Then
![]() $\smash {\mathrm {U}_{k}^{(l)}(F)=\tau \mathrm {U}_{k}^{(l')}(F)\tau ^{-1}}$
.
$\smash {\mathrm {U}_{k}^{(l)}(F)=\tau \mathrm {U}_{k}^{(l')}(F)\tau ^{-1}}$
.
The following basic properties of
![]() $\mathrm {U}_{k}(F)$
are as in Proposition 2.4.
$\mathrm {U}_{k}(F)$
are as in Proposition 2.4.
Proposition 4.5. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. The group
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. The group
![]() $\mathrm {U}_{k}(F)$
is
$\mathrm {U}_{k}(F)$
is
-
(i) closed in
 $\operatorname {\mathrm {Aut}}(T_{d})$
,
$\operatorname {\mathrm {Aut}}(T_{d})$
, -
(ii) vertex-transitive, and
-
(iii) compactly generated.
Proof. For (i), note that if
![]() $g\notin \mathrm {U}_{k}(F)$
then
$g\notin \mathrm {U}_{k}(F)$
then
![]() $\sigma _{k}(g,x)\notin F$
for some
$\sigma _{k}(g,x)\notin F$
for some
![]() $x\in V$
. In this case, the open neighbourhood
$x\in V$
. In this case, the open neighbourhood
![]() $\{h\in \operatorname {\mathrm {Aut}}(T_{d})\mid h|_{B(x,k)}=g|_{B(x,k)}\}$
of g in
$\{h\in \operatorname {\mathrm {Aut}}(T_{d})\mid h|_{B(x,k)}=g|_{B(x,k)}\}$
of g in
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
is also contained in the complement of
$\operatorname {\mathrm {Aut}}(T_{d})$
is also contained in the complement of
![]() $\mathrm {U}_{k}(F)$
.
$\mathrm {U}_{k}(F)$
.
For (ii), let
![]() $x,x'\in V$
and let
$x,x'\in V$
and let
![]() $g\in \operatorname {\mathrm {Aut}}(T_{d})$
be the automorphism of
$g\in \operatorname {\mathrm {Aut}}(T_{d})$
be the automorphism of
![]() $T_{d}$
associated to
$T_{d}$
associated to
![]() $(l,l,x,x')$
by Lemma 4.3. Then
$(l,l,x,x')$
by Lemma 4.3. Then
![]() $g\in \mathrm {U}_{k}(F)$
as
$g\in \mathrm {U}_{k}(F)$
as
![]() $\sigma _{k}(g,v)=\operatorname {\mathrm {id}}\in F$
for all
$\sigma _{k}(g,v)=\operatorname {\mathrm {id}}\in F$
for all
![]() $v\in V$
.
$v\in V$
.
To prove (iii), fix
![]() $x\in V$
. We show that
$x\in V$
. We show that
![]() $\mathrm {U}_{k}(F)$
is generated by the join of the compact set
$\mathrm {U}_{k}(F)$
is generated by the join of the compact set
![]() $\mathrm {U}_{k}(F)_{x}$
and the finite generating set of
$\mathrm {U}_{k}(F)_{x}$
and the finite generating set of
![]() $\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})=\mathrm {U}_{k}(\{\operatorname {\mathrm {id}}\})\le \mathrm {U}_{k}(F)$
guaranteed by Lemma 2.5. Indeed, for
$\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})=\mathrm {U}_{k}(\{\operatorname {\mathrm {id}}\})\le \mathrm {U}_{k}(F)$
guaranteed by Lemma 2.5. Indeed, for
![]() $g\in \mathrm {U}_{k}(F)$
pick
$g\in \mathrm {U}_{k}(F)$
pick
![]() $g'$
in the finitely generated, vertex-transitive subgroup
$g'$
in the finitely generated, vertex-transitive subgroup
![]() $\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})$
of
$\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})$
of
![]() $\mathrm {U}_{k}(F)$
such that
$\mathrm {U}_{k}(F)$
such that
![]() $g'gx=x$
. We then have
$g'gx=x$
. We then have
![]() $g'g\in \mathrm {U}_{k}(F)_{x}$
and the assertion follows.
$g'g\in \mathrm {U}_{k}(F)_{x}$
and the assertion follows.
For completeness, we explicitly state the following proposition.
Proposition 4.6. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
![]() $\mathrm {U}_{k}(F)$
is a compactly generated, totally disconnected, locally compact, second countable group.
$\mathrm {U}_{k}(F)$
is a compactly generated, totally disconnected, locally compact, second countable group.
Proof. The group
![]() $\mathrm {U}_{k}(F)$
is totally disconnected, locally compact, second countable as a closed subgroup of
$\mathrm {U}_{k}(F)$
is totally disconnected, locally compact, second countable as a closed subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
, and compactly generated by Proposition 4.5.
$\operatorname {\mathrm {Aut}}(T_{d})$
, and compactly generated by Proposition 4.5.
Finally, we record that the groups
![]() $\mathrm {U}_{k}(F)$
are
$\mathrm {U}_{k}(F)$
are
![]() $(P_{k})$
-closed.
$(P_{k})$
-closed.
Proposition 4.7. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
![]() $\mathrm {U}_{k}(F)$
satisfies property
$\mathrm {U}_{k}(F)$
satisfies property
![]() $(P_{k})$
.
$(P_{k})$
.
Proof. Let
![]() $e=(x,y)\in E$
. Clearly,
$e=(x,y)\in E$
. Clearly,
![]() $\mathrm {U}_{k}(F)_{e^{k}}\supseteq \mathrm {U}_{k}(F)_{e^{k},T_{y}}\cdot \mathrm {U}_{k}(F)_{e^{k},T_{x}}$
. Conversely, consider
$\mathrm {U}_{k}(F)_{e^{k}}\supseteq \mathrm {U}_{k}(F)_{e^{k},T_{y}}\cdot \mathrm {U}_{k}(F)_{e^{k},T_{x}}$
. Conversely, consider
![]() $g\in \mathrm {U}_{k}(F)_{e^{k}}$
and define
$g\in \mathrm {U}_{k}(F)_{e^{k}}$
and define
![]() $g_{y}\in \operatorname {\mathrm {Aut}}(T_{d})$
and
$g_{y}\in \operatorname {\mathrm {Aut}}(T_{d})$
and
![]() $g_{x}\in \operatorname {\mathrm {Aut}}(T_{d})$
by
$g_{x}\in \operatorname {\mathrm {Aut}}(T_{d})$
by
 $$ \begin{align*} \sigma_{k}(g_{y},v)=\begin{cases}\sigma_{k}(g,v) & v\in V(T_{x}) \\ \operatorname{\mathrm{id}} & v\in V(T_{y})\end{cases} \quad\text{and}\quad \sigma_{k}(g_{x},v)=\begin{cases}\operatorname{\mathrm{id}} & v\in V(T_{x}) \\ \sigma_{k}(g,v) & v\in V(T_{y}),\end{cases} \end{align*} $$
$$ \begin{align*} \sigma_{k}(g_{y},v)=\begin{cases}\sigma_{k}(g,v) & v\in V(T_{x}) \\ \operatorname{\mathrm{id}} & v\in V(T_{y})\end{cases} \quad\text{and}\quad \sigma_{k}(g_{x},v)=\begin{cases}\operatorname{\mathrm{id}} & v\in V(T_{x}) \\ \sigma_{k}(g,v) & v\in V(T_{y}),\end{cases} \end{align*} $$
respectively. Then
![]() $g_{y}\in \mathrm {U}_{k}(F)_{e^{k},T_{y}}$
,
$g_{y}\in \mathrm {U}_{k}(F)_{e^{k},T_{y}}$
,
![]() $g_{x}\in \mathrm {U}_{k}(F)_{e^{k},T_{x}}$
and
$g_{x}\in \mathrm {U}_{k}(F)_{e^{k},T_{x}}$
and
![]() $g=g_{y}\circ g_{x}$
.
$g=g_{y}\circ g_{x}$
.
4.2 Compatibility and discreteness
We now generalize parts (iv) and (vi) of Burger and Mozes’ Proposition 2.4. There are compatibility and discreteness conditions (C) and (D) on subgroups
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
that hold if and only if the associated universal group is locally action isomorphic to F and discrete, respectively.
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
that hold if and only if the associated universal group is locally action isomorphic to F and discrete, respectively.
We introduce the following notation for vertices in the labelled tree
![]() $(T_{d},l)$
. Given
$(T_{d},l)$
. Given
![]() $x\in V$
and
$x\in V$
and
![]() $\xi =(\omega _{1},\ldots ,\omega _{n})\in \Omega ^{n} (n\in \operatorname {\mathrm {\mathbb {N}}}_{0})$
, set
$\xi =(\omega _{1},\ldots ,\omega _{n})\in \Omega ^{n} (n\in \operatorname {\mathrm {\mathbb {N}}}_{0})$
, set
![]() $x_{\xi }:=\gamma _{x,\xi }(n)$
where
$x_{\xi }:=\gamma _{x,\xi }(n)$
where

is the unique label-respecting morphism sending
![]() $0$
to
$0$
to
![]() $x\in V$
. If
$x\in V$
. If
![]() $\xi $
is the empty word, set
$\xi $
is the empty word, set
![]() $x_{\xi }:=x$
. Whenever admissible, we also adopt this notation in the case of
$x_{\xi }:=x$
. Whenever admissible, we also adopt this notation in the case of
![]() $B_{d,k}$
and its labelling. In particular,
$B_{d,k}$
and its labelling. In particular,
![]() $S(x,n)$
is in natural bijection with the set
$S(x,n)$
is in natural bijection with the set
![]() $\Omega ^{(n)}:=\{(\omega _{1},\ldots ,\omega _{n})\in \Omega ^{n}\mid \text { for all } k\in \{1,\ldots ,n-1\}:\omega _{k+1}\neq \omega _{k}\}$
.
$\Omega ^{(n)}:=\{(\omega _{1},\ldots ,\omega _{n})\in \Omega ^{n}\mid \text { for all } k\in \{1,\ldots ,n-1\}:\omega _{k+1}\neq \omega _{k}\}$
.
4.2.1 Compatibility
First, we ask whether
![]() $\mathrm {U}_{k}(F)$
locally acts like F, that is, whether the actions
$\mathrm {U}_{k}(F)$
locally acts like F, that is, whether the actions
![]() $\mathrm {U}_{k}(F)_{x}\curvearrowright B(x,k)$
and
$\mathrm {U}_{k}(F)_{x}\curvearrowright B(x,k)$
and
![]() $F\curvearrowright B_{d,k}$
are isomorphic for every
$F\curvearrowright B_{d,k}$
are isomorphic for every
![]() $x\in V$
. Whereas this always holds for
$x\in V$
. Whereas this always holds for
![]() $k=1$
by Proposition 2.4(iv), it need not be true for
$k=1$
by Proposition 2.4(iv), it need not be true for
![]() $k\ge 2$
, the issue being (non)compatibility among elements of F. See Example 4.9. The condition developed in this section allows for computations. A more practical version from a theoretical viewpoint follows in Section 4.4.
$k\ge 2$
, the issue being (non)compatibility among elements of F. See Example 4.9. The condition developed in this section allows for computations. A more practical version from a theoretical viewpoint follows in Section 4.4.
Now, let
![]() $x\in V$
and suppose that
$x\in V$
and suppose that
![]() $\alpha \in \mathrm {U}_{k}(F)_{x}$
realizes
$\alpha \in \mathrm {U}_{k}(F)_{x}$
realizes
![]() $a\in F$
at x, that is,
$a\in F$
at x, that is,
Then given the condition that
![]() $\sigma _{k}(\alpha ,x_{\omega })$
is in F for all
$\sigma _{k}(\alpha ,x_{\omega })$
is in F for all
![]() $\omega \in \Omega $
, we obtain the following necessary compatibility condition on F for
$\omega \in \Omega $
, we obtain the following necessary compatibility condition on F for
![]() $\mathrm {U}_{k}(F)$
to act like F at
$\mathrm {U}_{k}(F)$
to act like F at
![]() $x\in V$
:
$x\in V$
:
 $$ \begin{align*} &\text{ for all } a\in F,\text{ for all } \omega\in\Omega:\text{there exists } a_{\omega}\in F:\\&\quad(l_{x}^{k})^{-1}\circ a\circ l_{x}^{k}|_{S_{\omega}}=(l_{\alpha x_{\omega}}^{k})^{-1}\circ a_{\omega}\circ l_{x_{\omega}}^{k}|_{S_{\omega}} \end{align*} $$
$$ \begin{align*} &\text{ for all } a\in F,\text{ for all } \omega\in\Omega:\text{there exists } a_{\omega}\in F:\\&\quad(l_{x}^{k})^{-1}\circ a\circ l_{x}^{k}|_{S_{\omega}}=(l_{\alpha x_{\omega}}^{k})^{-1}\circ a_{\omega}\circ l_{x_{\omega}}^{k}|_{S_{\omega}} \end{align*} $$
where
![]() $S_{\omega }:=B(x,k)\cap B(x_{\omega },k)\subseteq T_{d}$
. Set
$S_{\omega }:=B(x,k)\cap B(x_{\omega },k)\subseteq T_{d}$
. Set
![]() $T_{\omega }:=l_{x}^{k}(S_{\omega })\subseteq B_{d,k}$
. Then the above condition can be rewritten as
$T_{\omega }:=l_{x}^{k}(S_{\omega })\subseteq B_{d,k}$
. Then the above condition can be rewritten as
 $$ \begin{align*} &\text{ for all } a\in F, \text{ for all } \omega\in\Omega:\text{there exists } a_{\omega}\in F:\\&\quad a_{\omega}|_{T_{\omega}}=l_{\alpha x_{\omega}}^{k}\circ(l_{x}^{k})^{-1}\circ a\circ l_{x}^{k}\circ(l_{x_{\omega}}^{k})^{-1}|_{T_{\omega}}. \end{align*} $$
$$ \begin{align*} &\text{ for all } a\in F, \text{ for all } \omega\in\Omega:\text{there exists } a_{\omega}\in F:\\&\quad a_{\omega}|_{T_{\omega}}=l_{\alpha x_{\omega}}^{k}\circ(l_{x}^{k})^{-1}\circ a\circ l_{x}^{k}\circ(l_{x_{\omega}}^{k})^{-1}|_{T_{\omega}}. \end{align*} $$
Now note the following observations. First,
![]() $\alpha x_{\omega }$
depends only on a. Second, the subtree
$\alpha x_{\omega }$
depends only on a. Second, the subtree
![]() $T_{\omega }$
of
$T_{\omega }$
of
![]() $B_{d,k}$
does not depend on x. Third,
$B_{d,k}$
does not depend on x. Third,
![]() $\iota _{\omega }:=l_{x}^{k}|_{S_{\omega }}^{T_{\omega }}\circ (l_{x_{\omega }}^{k})^{-1}|_{T_{\omega }}^{S_{\omega }}$
is the unique nontrivial, involutive and label-respecting automorphism of
$\iota _{\omega }:=l_{x}^{k}|_{S_{\omega }}^{T_{\omega }}\circ (l_{x_{\omega }}^{k})^{-1}|_{T_{\omega }}^{S_{\omega }}$
is the unique nontrivial, involutive and label-respecting automorphism of
![]() $T_{\omega }$
; it is given by
$T_{\omega }$
; it is given by
for admissible words
![]() $\xi $
. Hence, the above condition may be rewritten as
$\xi $
. Hence, the above condition may be rewritten as
In this situation we say that
![]() $a_{\omega }$
is compatible with a in direction
$a_{\omega }$
is compatible with a in direction
![]() $\omega $
.
$\omega $
.
Proposition 4.8. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
![]() $\mathrm {U}_{k}(F)$
is locally action isomorphic to F if and only if F satisfies (C).
$\mathrm {U}_{k}(F)$
is locally action isomorphic to F if and only if F satisfies (C).
Proof. By the above, condition (C) is necessary. To show that it is also sufficient, let
![]() $x\in V$
and
$x\in V$
and
![]() $a\in F$
. We aim to define an automorphism
$a\in F$
. We aim to define an automorphism
![]() $\alpha \in \mathrm {U}_{k}(F)_{x}$
which realizes a at x. This forces us to define
$\alpha \in \mathrm {U}_{k}(F)_{x}$
which realizes a at x. This forces us to define
Now, assume inductively that
![]() $\alpha $
is defined consistently on
$\alpha $
is defined consistently on
![]() $B(x,n)$
in the sense that
$B(x,n)$
in the sense that
![]() $\sigma _{k}(\alpha ,y)\in F$
for all
$\sigma _{k}(\alpha ,y)\in F$
for all
![]() $y\in B(x,n)$
with
$y\in B(x,n)$
with
![]() $B(y,k)\subseteq B(x,n)$
. In order to extend
$B(y,k)\subseteq B(x,n)$
. In order to extend
![]() $\alpha $
to
$\alpha $
to
![]() $B(x,n+1)$
, let
$B(x,n+1)$
, let
![]() $y\in S(x,n-k+1)$
and let
$y\in S(x,n-k+1)$
and let
![]() $\omega \in \Omega $
be the unique label such that
$\omega \in \Omega $
be the unique label such that
![]() $y_{\omega }\in S(x,n-k)$
. Set
$y_{\omega }\in S(x,n-k)$
. Set
![]() $c:=\sigma _{k}(\alpha ,y_{\omega })$
. Applying condition (C) to the pair
$c:=\sigma _{k}(\alpha ,y_{\omega })$
. Applying condition (C) to the pair
![]() $(c,\omega )$
yields an element
$(c,\omega )$
yields an element
![]() $c_{\omega }\in F$
such that
$c_{\omega }\in F$
such that
where
![]() $S_{\omega }:=B(y,k)\cap B(y_{\omega },k)$
and we have realized
$S_{\omega }:=B(y,k)\cap B(y_{\omega },k)$
and we have realized
Now extend
![]() $\alpha $
consistently to
$\alpha $
consistently to
![]() $B(v,n+1)$
by setting
$B(v,n+1)$
by setting
![]() $\alpha |_{B(x,k)}:=(l_{\alpha x}^{k})^{-1}\circ c_{\omega }\circ l_{x}^{k}$
.
$\alpha |_{B(x,k)}:=(l_{\alpha x}^{k})^{-1}\circ c_{\omega }\circ l_{x}^{k}$
.
Example 4.9. Let
![]() $\Omega :=\{1,2,3\}$
and
$\Omega :=\{1,2,3\}$
and
![]() $a\in \operatorname {\mathrm {Aut}}(B_{3,2})$
be the element that swaps the leaves
$a\in \operatorname {\mathrm {Aut}}(B_{3,2})$
be the element that swaps the leaves
![]() $b_{12}$
and
$b_{12}$
and
![]() $b_{13}$
of
$b_{13}$
of
![]() $B_{3,2}$
. Then
$B_{3,2}$
. Then
![]() $F:=\langle a\rangle =\{\operatorname {\mathrm {id}},a\}$
does not contain an element compatible with a in direction
$F:=\langle a\rangle =\{\operatorname {\mathrm {id}},a\}$
does not contain an element compatible with a in direction
![]() $1\in \Omega $
and hence does not satisfy condition (C).
$1\in \Omega $
and hence does not satisfy condition (C).
We show that it suffices to check condition (C) on the elements of a generating set. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
and
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
and
![]() $a,b\in F$
. Set
$a,b\in F$
. Set
![]() $c:=ab$
. Then
$c:=ab$
. Then
 $$ \begin{align} c_{\omega}|_{T_{\omega}}=\iota_{c\omega}\circ a\circ b\circ\iota_{\omega}&=(\iota_{c\omega}\circ a\circ\iota_{b\omega})\circ(\iota_{b\omega}\circ b\circ\iota_{\omega}) \nonumber \\ &=(\iota_{a(b\omega)}\circ a\circ\iota_{b\omega})\circ(\iota_{b\omega}\circ b\circ\iota_{\omega}). \end{align} $$
$$ \begin{align} c_{\omega}|_{T_{\omega}}=\iota_{c\omega}\circ a\circ b\circ\iota_{\omega}&=(\iota_{c\omega}\circ a\circ\iota_{b\omega})\circ(\iota_{b\omega}\circ b\circ\iota_{\omega}) \nonumber \\ &=(\iota_{a(b\omega)}\circ a\circ\iota_{b\omega})\circ(\iota_{b\omega}\circ b\circ\iota_{\omega}). \end{align} $$
Let
![]() $C_{F}(a,\omega )$
denote the compatibility set of elements in F that are compatible with
$C_{F}(a,\omega )$
denote the compatibility set of elements in F that are compatible with
![]() $a\in F$
in direction
$a\in F$
in direction
![]() $\omega \in \Omega $
. Then (M) shows that
$\omega \in \Omega $
. Then (M) shows that
![]() $C_{F}(ab,\omega )\supseteq C_{F}(a,b\omega )C_{F}(b,\omega )$
. It therefore suffices to check condition (C) on a generating set of F.
$C_{F}(ab,\omega )\supseteq C_{F}(a,b\omega )C_{F}(b,\omega )$
. It therefore suffices to check condition (C) on a generating set of F.
Given
![]() $S\subseteq \Omega $
, we also define
$S\subseteq \Omega $
, we also define
![]() $C_{F}(a,S):=\bigcap _{\omega \in S}C_{F}(a,\omega )$
, the set of elements in F that are compatible with
$C_{F}(a,S):=\bigcap _{\omega \in S}C_{F}(a,\omega )$
, the set of elements in F that are compatible with
![]() $a\in F$
in all directions from S. We omit F in this notation when it is clear from the context.
$a\in F$
in all directions from S. We omit F in this notation when it is clear from the context.
As a consequence, we obtain the following description of the local action of
![]() $\mathrm {U}_{k}(F)$
when F does not satisfy condition (C).
$\mathrm {U}_{k}(F)$
when F does not satisfy condition (C).
Proposition 4.10. Let
![]() $F\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})$
. Then F has a unique maximal subgroup
$F\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})$
. Then F has a unique maximal subgroup
![]() $C(F)$
that satisfies (C). We have
$C(F)$
that satisfies (C). We have
![]() $C(C(F))\!=\!C(F)$
and
$C(C(F))\!=\!C(F)$
and
![]() $\mathrm {U}_{k}(F)\!=\!\mathrm {U}_{k}(C(F))$
.
$\mathrm {U}_{k}(F)\!=\!\mathrm {U}_{k}(C(F))$
.
Proof. By the above,
![]() $C(F)\!:=\!\langle H\le F\mid H \text { satisfies (C)}\rangle \!\le \! F$
satisfies condition (C). It is the unique maximal such subgroup of F by definition, and
$C(F)\!:=\!\langle H\le F\mid H \text { satisfies (C)}\rangle \!\le \! F$
satisfies condition (C). It is the unique maximal such subgroup of F by definition, and
![]() $C(C(F))=C(F)$
.
$C(C(F))=C(F)$
.
Furthermore,
![]() $\mathrm {U}_{k}(C(F))\le \mathrm {U}_{k}(F)$
. Conversely, suppose
$\mathrm {U}_{k}(C(F))\le \mathrm {U}_{k}(F)$
. Conversely, suppose
![]() $g\in \mathrm {U}_{k}(F)\backslash \mathrm {U}_{k}(C(F))$
. Then there is
$g\in \mathrm {U}_{k}(F)\backslash \mathrm {U}_{k}(C(F))$
. Then there is
![]() $x\in V$
such that
$x\in V$
such that
![]() $\sigma _{k}(g,x)\in F\backslash C(F)$
and the group
$\sigma _{k}(g,x)\in F\backslash C(F)$
and the group
satisfies condition (C), too, as can be seen by setting
![]() $\sigma _{k}(g,x)_{\omega }:=\sigma _{k}(g,x_{\omega })$
. This contradicts the maximality of
$\sigma _{k}(g,x)_{\omega }:=\sigma _{k}(g,x_{\omega })$
. This contradicts the maximality of
![]() $C(F)$
.
$C(F)$
.
Remark 4.11. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). The proof of Proposition 4.8 shows that elements of
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). The proof of Proposition 4.8 shows that elements of
![]() $\mathrm {U}_{k}(F)$
are readily constructed. Given
$\mathrm {U}_{k}(F)$
are readily constructed. Given
![]() $x,y\in V(T_{d})$
and
$x,y\in V(T_{d})$
and
![]() $a\in F$
, define
$a\in F$
, define
![]() $g:B(x,k)\to B(y,k)$
by setting
$g:B(x,k)\to B(y,k)$
by setting
![]() $g(x)=y$
and
$g(x)=y$
and
![]() $\sigma _{k}(g,x)=a$
. Then, given elements
$\sigma _{k}(g,x)=a$
. Then, given elements
![]() $a_{\omega }\in F (\omega \in \Omega )$
such that
$a_{\omega }\in F (\omega \in \Omega )$
such that
![]() $a_{\omega }\in C_{F}(a,\omega )$
for all
$a_{\omega }\in C_{F}(a,\omega )$
for all
![]() $\omega \in \Omega $
, there is a unique extension of g to
$\omega \in \Omega $
, there is a unique extension of g to
![]() $B(x,k+1)$
so that
$B(x,k+1)$
so that
![]() $\sigma _{k}(g,x_{\omega })=a_{\omega }$
for all
$\sigma _{k}(g,x_{\omega })=a_{\omega }$
for all
![]() $\omega \in \Omega $
. Proceed iteratively.
$\omega \in \Omega $
. Proceed iteratively.
4.2.2 Discreteness
The group
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
also determines whether or not
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
also determines whether or not
![]() $\mathrm {U}_{k}(F)$
is discrete. In fact, the following proposition generalizes Proposition 2.4(vi).
$\mathrm {U}_{k}(F)$
is discrete. In fact, the following proposition generalizes Proposition 2.4(vi).
Proposition 4.12. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. Then
![]() $\mathrm {U}_{k}(F)$
is discrete if F satisfies
$\mathrm {U}_{k}(F)$
is discrete if F satisfies
Conversely, if
![]() $\mathrm {U}_{k}(F)$
is discrete and F satisfies (C), then F satisfies (D).
$\mathrm {U}_{k}(F)$
is discrete and F satisfies (C), then F satisfies (D).
Alternatively,
![]() $\mathrm {U}_{k}(F)$
is discrete if and only if
$\mathrm {U}_{k}(F)$
is discrete if and only if
![]() $C(F)$
satisfies (D). Example 4.9 shows that condition (C) is necessary for the second part of Proposition 4.12.
$C(F)$
satisfies (D). Example 4.9 shows that condition (C) is necessary for the second part of Proposition 4.12.
Finally, note that F satisfies (D) if and only if
![]() $C_{F}(\operatorname {\mathrm {id}},\omega )=\{\operatorname {\mathrm {id}}\}$
for all
$C_{F}(\operatorname {\mathrm {id}},\omega )=\{\operatorname {\mathrm {id}}\}$
for all
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Proof of Proposition 4.12.
Fix
![]() $x\in V$
. A subgroup
$x\in V$
. A subgroup
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
is nondiscrete if and only if for every
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
is nondiscrete if and only if for every
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
there is
$n\in \operatorname {\mathrm {\mathbb {N}}}$
there is
![]() $h\in H\backslash \{\operatorname {\mathrm {id}}\}$
such that
$h\in H\backslash \{\operatorname {\mathrm {id}}\}$
such that
![]() $h|_{B(x,n)}=\operatorname {\mathrm {id}}$
.
$h|_{B(x,n)}=\operatorname {\mathrm {id}}$
.
Suppose that
![]() $\mathrm {U}_{k}(F)$
is nondiscrete. Then there are
$\mathrm {U}_{k}(F)$
is nondiscrete. Then there are
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}_{\ge k}$
and
$n\in \operatorname {\mathrm {\mathbb {N}}}_{\ge k}$
and
![]() $\alpha \in \text {U}_{k}(F)$
such that
$\alpha \in \text {U}_{k}(F)$
such that
![]() $\alpha |_{B(x,n)}=\operatorname {\mathrm {id}}$
and
$\alpha |_{B(x,n)}=\operatorname {\mathrm {id}}$
and
![]() $\alpha |_{B(x,n+1)}\neq \operatorname {\mathrm {id}}$
. Hence, there is
$\alpha |_{B(x,n+1)}\neq \operatorname {\mathrm {id}}$
. Hence, there is
![]() $y\in S(x,n-k+1)$
with
$y\in S(x,n-k+1)$
with
![]() $a:=\sigma _{k}(\alpha ,y)\neq \operatorname {\mathrm {id}}$
. In particular,
$a:=\sigma _{k}(\alpha ,y)\neq \operatorname {\mathrm {id}}$
. In particular,
![]() $a\in F_{T_{\omega }}\backslash \{\operatorname {\mathrm {id}}\}$
where
$a\in F_{T_{\omega }}\backslash \{\operatorname {\mathrm {id}}\}$
where
![]() $\omega $
is the label of the unique edge
$\omega $
is the label of the unique edge
![]() $e\in E$
with
$e\in E$
with
![]() $o(e)=y$
and
$o(e)=y$
and
![]() $d(x,y)=d(x,t(e))+1$
.
$d(x,y)=d(x,t(e))+1$
.
Conversely, suppose that F satisfies (C) and
![]() $F_{T_{\omega }}\neq \{\operatorname {\mathrm {id}}\}$
for some
$F_{T_{\omega }}\neq \{\operatorname {\mathrm {id}}\}$
for some
![]() $\omega \in \Omega $
. Then for every
$\omega \in \Omega $
. Then for every
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}_{\ge k}$
, we define an automorphism
$n\in \operatorname {\mathrm {\mathbb {N}}}_{\ge k}$
, we define an automorphism
![]() $\alpha \in \text {U}_{k}(F)$
with
$\alpha \in \text {U}_{k}(F)$
with
![]() $\alpha |_{B(x,n)}=\operatorname {\mathrm {id}}$
and
$\alpha |_{B(x,n)}=\operatorname {\mathrm {id}}$
and
![]() $\alpha |_{B(x,n+1)}\neq \operatorname {\mathrm {id}}$
. If
$\alpha |_{B(x,n+1)}\neq \operatorname {\mathrm {id}}$
. If
![]() $\alpha |_{B(x,n)}=\operatorname {\mathrm {id}}$
, then
$\alpha |_{B(x,n)}=\operatorname {\mathrm {id}}$
, then
![]() $\sigma _{k}(\alpha ,y)\in F$
for all
$\sigma _{k}(\alpha ,y)\in F$
for all
![]() $y\in B(x,n-k)$
. Choose
$y\in B(x,n-k)$
. Choose
![]() $e\in E$
with
$e\in E$
with
![]() $y:=o(e)\in S(x,n-k+1)$
and
$y:=o(e)\in S(x,n-k+1)$
and
![]() $t(e)\in S(x,n-k)$
such that
$t(e)\in S(x,n-k)$
such that
![]() $l(e)=\omega $
. We extend
$l(e)=\omega $
. We extend
![]() $\alpha $
to
$\alpha $
to
![]() $B(y,k)$
by setting
$B(y,k)$
by setting
![]() $\alpha |_{B(y,k)}:=l_{y}^{k}\circ s\circ (l_{y}^{k})^{-1}$
where
$\alpha |_{B(y,k)}:=l_{y}^{k}\circ s\circ (l_{y}^{k})^{-1}$
where
![]() $s\in F_{T_{\omega }}\backslash \{\operatorname {\mathrm {id}}\}$
. Finally, we extend
$s\in F_{T_{\omega }}\backslash \{\operatorname {\mathrm {id}}\}$
. Finally, we extend
![]() $\alpha $
to
$\alpha $
to
![]() $T_{d}$
using (C).
$T_{d}$
using (C).
We define the following condition (CD) on
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
as the conjunction of (C) and (D):
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
as the conjunction of (C) and (D):
The following description is immediate from the above. When F satisfies (CD), an element of
![]() $\mathrm {U}_{k}(F)_{x}$
is determined by its action on
$\mathrm {U}_{k}(F)_{x}$
is determined by its action on
![]() $B(x,k)$
. Hence,
$B(x,k)$
. Hence,
![]() $\mathrm {U}_{k}(F)_{x}\cong F$
for every
$\mathrm {U}_{k}(F)_{x}\cong F$
for every
![]() $x\in V$
and
$x\in V$
and
![]() $\mathrm {U}_{k}(F)_{(x,y)}\cong F_{(b,b_{\omega })}$
for every
$\mathrm {U}_{k}(F)_{(x,y)}\cong F_{(b,b_{\omega })}$
for every
![]() $(x,y)\in E$
with
$(x,y)\in E$
with
![]() $l(x,y)=\omega $
. Furthermore, F admits a unique involutive compatibility cocycle, that is, a map
$l(x,y)=\omega $
. Furthermore, F admits a unique involutive compatibility cocycle, that is, a map
![]() $z:F\times \Omega \to F, (a,\omega )\mapsto a_{\omega }$
which for all
$z:F\times \Omega \to F, (a,\omega )\mapsto a_{\omega }$
which for all
![]() $a,b\in F$
and
$a,b\in F$
and
![]() $\omega \in \Omega $
satisfies
$\omega \in \Omega $
satisfies
-
(i) (compatibility)
 $z(a,\omega )\in C_{F}(a,\omega )$
,
$z(a,\omega )\in C_{F}(a,\omega )$
, -
(ii) (cocycle)
 $z(ab,\omega )=z(a,b\omega )z(b,\omega )$
, and
$z(ab,\omega )=z(a,b\omega )z(b,\omega )$
, and -
(iii) (involutive)
 $z(z(a,\omega ),\omega )=a$
.
$z(z(a,\omega ),\omega )=a$
.
Note that z restricts to an automorphism
![]() $z_{\omega }$
of
$z_{\omega }$
of
![]() $F_{(b,b_{\omega })} (\omega \in \Omega )$
of order at most
$F_{(b,b_{\omega })} (\omega \in \Omega )$
of order at most
![]() $2$
.
$2$
.
4.3 Group structure
For
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
, let
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
, let
![]() $\smash {F:=\pi \widetilde {F}\le \operatorname {\mathrm {Sym}}(\Omega )}$
denote the projection of
$\smash {F:=\pi \widetilde {F}\le \operatorname {\mathrm {Sym}}(\Omega )}$
denote the projection of
![]() $\smash {\widetilde {F}}$
onto
$\smash {\widetilde {F}}$
onto
![]() $\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
. As an illustration, we record that the group structure of
$\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
. As an illustration, we record that the group structure of
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})}$
is particularly clear when F is regular.
$\smash {\mathrm {U}_{k}(\widetilde {F})}$
is particularly clear when F is regular.
Proposition 4.13. Let
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C). Suppose
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C). Suppose
![]() $\smash {F:=\pi \widetilde {F}}$
is regular. Then
$\smash {F:=\pi \widetilde {F}}$
is regular. Then
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})=\mathrm {U}_{1}(F)\cong F\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}}$
.
$\smash {\mathrm {U}_{k}(\widetilde {F})=\mathrm {U}_{1}(F)\cong F\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}}$
.
Proof. Fix
![]() $x\in V$
. Since F is transitive, the group
$x\in V$
. Since F is transitive, the group
![]() $\mathrm {U}_{k}(\widetilde {F})$
is generated by
$\mathrm {U}_{k}(\widetilde {F})$
is generated by
![]() $\mathrm {U}_{k}(\widetilde {F})_{x}$
and an involution
$\mathrm {U}_{k}(\widetilde {F})_{x}$
and an involution
![]() $\iota $
inverting an edge with origin x. Given
$\iota $
inverting an edge with origin x. Given
![]() $\smash {\alpha \in \mathrm {U}_{k}(\widetilde {F})_{x}}$
, regularity of F implies that
$\smash {\alpha \in \mathrm {U}_{k}(\widetilde {F})_{x}}$
, regularity of F implies that
![]() $\sigma _{1}(\alpha ,y)=\sigma _{1}(\alpha ,x)\in F$
for all
$\sigma _{1}(\alpha ,y)=\sigma _{1}(\alpha ,x)\in F$
for all
![]() $y\in V$
. Now, the subgroups
$y\in V$
. Now, the subgroups
![]() $H_{1}:=\smash {\mathrm {U}_{k}(\widetilde {F})_{x}\cong F}$
and
$H_{1}:=\smash {\mathrm {U}_{k}(\widetilde {F})_{x}\cong F}$
and
![]() $H_{2}:=\langle \iota \rangle $
of
$H_{2}:=\langle \iota \rangle $
of
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})}$
generate a free product within
$\smash {\mathrm {U}_{k}(\widetilde {F})}$
generate a free product within
![]() $\mathrm {U}_{k}(F)$
by the ping-pong lemma. Put
$\mathrm {U}_{k}(F)$
by the ping-pong lemma. Put
![]() $X_{1}:=V(T_{x})$
and
$X_{1}:=V(T_{x})$
and
![]() $X_{2}:=V(T_{x_{\omega }})$
. Any nontrivial element of
$X_{2}:=V(T_{x_{\omega }})$
. Any nontrivial element of
![]() $H_{1}$
maps
$H_{1}$
maps
![]() $X_{2}$
into
$X_{2}$
into
![]() $X_{1}$
as
$X_{1}$
as
![]() $F_{\omega }=\{\operatorname {\mathrm {id}}\}$
, and
$F_{\omega }=\{\operatorname {\mathrm {id}}\}$
, and
![]() $\iota \in H_{2}$
maps
$\iota \in H_{2}$
maps
![]() $X_{1}$
into
$X_{1}$
into
![]() $X_{2}$
.
$X_{2}$
.
More generally, Bass–Serre theory [Reference Serre25] identifies the universal groups
![]() $\mathrm {U}_{k}(F)$
as amalgamated free products, taking into account that
$\mathrm {U}_{k}(F)$
as amalgamated free products, taking into account that
![]() $\mathrm {U}_{k}(F)$
acts with inversions.
$\mathrm {U}_{k}(F)$
acts with inversions.
Proposition 4.14. Let
![]() $\smash {F\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C) (and (D)). If
$\smash {F\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C) (and (D)). If
![]() $\pi F$
is transitive then
$\pi F$
is transitive then
 $$ \begin{align*} \mathrm{U}_{k}(F)\cong\mathrm{U}_{k}(F)_{x}\!\!\!\!\!\underset{{{{{\scriptstyle\mathrm{U}_{k}(F)_{(x,y)}}}}}}{\ast}\!\!\!\!\!\mathrm{U}_{k}(F)_{\{x,y\}}\bigg(\cong F\!\!\underset{{{{{F_{(b,b_{\omega})}}}}}}{\ast}\!\!(F_{(b,b_{\omega})}\rtimes\operatorname{\mathrm{\mathbb{Z}}}\!/2\operatorname{\mathrm{\mathbb{Z}}})\bigg) \end{align*} $$
$$ \begin{align*} \mathrm{U}_{k}(F)\cong\mathrm{U}_{k}(F)_{x}\!\!\!\!\!\underset{{{{{\scriptstyle\mathrm{U}_{k}(F)_{(x,y)}}}}}}{\ast}\!\!\!\!\!\mathrm{U}_{k}(F)_{\{x,y\}}\bigg(\cong F\!\!\underset{{{{{F_{(b,b_{\omega})}}}}}}{\ast}\!\!(F_{(b,b_{\omega})}\rtimes\operatorname{\mathrm{\mathbb{Z}}}\!/2\operatorname{\mathrm{\mathbb{Z}}})\bigg) \end{align*} $$
for any edge
![]() $(x,y)\in E$
, where
$(x,y)\in E$
, where
![]() $\omega =l(x,y)$
and
$\omega =l(x,y)$
and
![]() $\operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}$
acts on
$\operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}$
acts on
![]() $F_{(b,b_{\omega })}$
as
$F_{(b,b_{\omega })}$
as
![]() $z_{\omega }$
.
$z_{\omega }$
.
Corollary 4.15. Let
![]() $F,F'\!\le \!\operatorname {\mathrm {Aut}}(\! B_{d,k})$
satisfy (CD). If there are
$F,F'\!\le \!\operatorname {\mathrm {Aut}}(\! B_{d,k})$
satisfy (CD). If there are
![]() $\omega ,\omega '\in \Omega $
and an isomorphism
$\omega ,\omega '\in \Omega $
and an isomorphism
![]() $\varphi \!:\!F\!\to \! F'$
such that
$\varphi \!:\!F\!\to \! F'$
such that
![]() $\varphi (F_{(b,b_{\omega })})=F^{\prime }_{(b,b_{\omega '})}$
, then
$\varphi (F_{(b,b_{\omega })})=F^{\prime }_{(b,b_{\omega '})}$
, then
![]() $\mathrm {U}_{k}(F)\cong \mathrm {U}_{k}(F')$
.
$\mathrm {U}_{k}(F)\cong \mathrm {U}_{k}(F')$
.
Note that Corollary 4.15 applies to conjugate subgroups of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
that satisfy (CD). The following example shows that the assumption that both F and
$\operatorname {\mathrm {Aut}}(B_{d,k})$
that satisfy (CD). The following example shows that the assumption that both F and
![]() $F'$
in Corollary 4.15 satisfy (CD) is indeed necessary.
$F'$
in Corollary 4.15 satisfy (CD) is indeed necessary.
Example 4.16. Let
![]() $\Omega :=\{1,2,3\}$
and
$\Omega :=\{1,2,3\}$
and
![]() $t\in \operatorname {\mathrm {Aut}}(B_{3,2})$
be the element that swaps the leaves
$t\in \operatorname {\mathrm {Aut}}(B_{3,2})$
be the element that swaps the leaves
![]() $x_{12}$
and
$x_{12}$
and
![]() $x_{13}$
of
$x_{13}$
of
![]() $B_{3,2}$
. Using the notation of Section 4.4.1 below, consider the group
$B_{3,2}$
. Using the notation of Section 4.4.1 below, consider the group
![]() $\Gamma (A_{3})\!\le \!\operatorname {\mathrm {Aut}}(B_{3,2})$
which satisfies (C). In particular,
$\Gamma (A_{3})\!\le \!\operatorname {\mathrm {Aut}}(B_{3,2})$
which satisfies (C). In particular,
![]() $\mathrm {U}_{2}(\Gamma (A_{3}))\!\cong \! A_{3}\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}$
by Proposition 4.13. On the other hand, set
$\mathrm {U}_{2}(\Gamma (A_{3}))\!\cong \! A_{3}\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}$
by Proposition 4.13. On the other hand, set
![]() $F':=t\Gamma (A_{3})t^{-1}$
. Then
$F':=t\Gamma (A_{3})t^{-1}$
. Then
![]() $\pi F'=A_{3}$
, while for a nontrivial element
$\pi F'=A_{3}$
, while for a nontrivial element
![]() $\alpha $
of
$\alpha $
of
![]() $F'$
we have
$F'$
we have
![]() $\sigma _{1}(\alpha ,b_{\omega })\!\in \! S_{3}\backslash A_{3}$
for some
$\sigma _{1}(\alpha ,b_{\omega })\!\in \! S_{3}\backslash A_{3}$
for some
![]() $\omega \in \Omega $
. Therefore,
$\omega \in \Omega $
. Therefore,
![]() $\mathrm {U}_{2}(F')=\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})$
is isomorphic to
$\mathrm {U}_{2}(F')=\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})$
is isomorphic to
![]() $\operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}$
by Lemma 2.5. In particular,
$\operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}\ast \operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}$
by Lemma 2.5. In particular,
![]() $\mathrm {U}_{2}(\Gamma (A_{3}))$
and
$\mathrm {U}_{2}(\Gamma (A_{3}))$
and
![]() $\mathrm {U}_{2}(t\Gamma (A_{3})t^{-1})$
are not isomorphic.
$\mathrm {U}_{2}(t\Gamma (A_{3})t^{-1})$
are not isomorphic.
Conversely, the following proposition based on [Reference Radu23, Appendix A], which states that in certain cases the tree can be recovered from the topological group structure of a subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
, applies to appropriate universal groups.
$\operatorname {\mathrm {Aut}}(T_{d})$
, applies to appropriate universal groups.
Proposition 4.17. Let
![]() $H,H'\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed and locally transitive with distinct point-stabilizers. Then H and
$H,H'\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed and locally transitive with distinct point-stabilizers. Then H and
![]() $H'$
are isomorphic topological groups if and only if they are conjugate in
$H'$
are isomorphic topological groups if and only if they are conjugate in
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
.
$\operatorname {\mathrm {Aut}}(T_{d})$
.
Proof. By [Reference Figà-Talamanca and Nebbia8], every compact subgroup of H is either contained in a vertex stabilizer
![]() $H_{x} (x\in V)$
or, in case
$H_{x} (x\in V)$
or, in case
![]() $H\not \leq \operatorname {\mathrm {Aut}}(T_{d})^{+}$
, in a geometric edge stabilizer
$H\not \leq \operatorname {\mathrm {Aut}}(T_{d})^{+}$
, in a geometric edge stabilizer
![]() $H_{\{e,\overline {e}\}} (e\in E)$
. Since H is locally transitive, the above are pairwise distinct.
$H_{\{e,\overline {e}\}} (e\in E)$
. Since H is locally transitive, the above are pairwise distinct.
The vertex stabilizers are precisely those maximal compact subgroups
![]() $K\le H$
for which there is no maximal compact subgroup
$K\le H$
for which there is no maximal compact subgroup
![]() $K'$
with
$K'$
with
![]() $[K:K\cap K']=2$
. Indeed, for
$[K:K\cap K']=2$
. Indeed, for
![]() $e\in E$
and
$e\in E$
and
![]() $x\in \{o(e),t(e)\}$
we have
$x\in \{o(e),t(e)\}$
we have
![]() $[H_{\{e,\overline {e}\}}:H_{\{e,\overline {e}\}}\cap H_{x}]=2$
, whereas
$[H_{\{e,\overline {e}\}}:H_{\{e,\overline {e}\}}\cap H_{x}]=2$
, whereas
![]() ${[H_{x}:H_{x}\cap H_{y}]\ge 3}$
and
${[H_{x}:H_{x}\cap H_{y}]\ge 3}$
and
![]() $[H_{x}:H_{x}\cap H_{\{e,\overline{e}\}}]\ge 3$
for all distinct
$[H_{x}:H_{x}\cap H_{\{e,\overline{e}\}}]\ge 3$
for all distinct
![]() $x,y\in V$
and
$x,y\in V$
and
![]() $e\in E$
by the orbit–stabilizer theorem because
$e\in E$
by the orbit–stabilizer theorem because
![]() $d\ge 3$
and H is locally transitive.
$d\ge 3$
and H is locally transitive.
Adjacency can be expressed in terms of indices as well, Let
![]() $x,y\in V$
be distinct. Then
$x,y\in V$
be distinct. Then
![]() $(x,y)\in E$
if and only if
$(x,y)\in E$
if and only if
![]() $[H_{x}:H_{x}\cap H_{y}]\le [H_{x}:H_{x}\cap H_{z}]$
for all
$[H_{x}:H_{x}\cap H_{y}]\le [H_{x}:H_{x}\cap H_{z}]$
for all
![]() $z\in V$
. Indeed, if
$z\in V$
. Indeed, if
![]() $(x,y)\in E$
, then
$(x,y)\in E$
, then
![]() $[H_{x}:H_{x}\cap H_{y}]=d$
by the orbit–stabilizer theorem, given that H is locally transitive. If
$[H_{x}:H_{x}\cap H_{y}]=d$
by the orbit–stabilizer theorem, given that H is locally transitive. If
![]() $z\in V$
is not adjacent to x then
$z\in V$
is not adjacent to x then
![]() $[H_{x}:H_{x}\cap H_{z}]>d$
because point-stabilizers of every local action of H are distinct.
$[H_{x}:H_{x}\cap H_{z}]>d$
because point-stabilizers of every local action of H are distinct.
Now, let
![]() $\Phi :H\to H'$
be an isomorphism of topological groups. Then
$\Phi :H\to H'$
be an isomorphism of topological groups. Then
![]() $\Phi $
induces a bijection between the maximal compact subgroups of H and
$\Phi $
induces a bijection between the maximal compact subgroups of H and
![]() $H'$
, and preserves indices. Hence, there is an automorphism
$H'$
, and preserves indices. Hence, there is an automorphism
![]() $\varphi \in \operatorname {\mathrm {Aut}}(T_{d})$
such that
$\varphi \in \operatorname {\mathrm {Aut}}(T_{d})$
such that
![]() $\Phi (H_{x})=H^{\prime }_{\varphi (x)}$
for all
$\Phi (H_{x})=H^{\prime }_{\varphi (x)}$
for all
![]() $x\in V$
. Furthermore, since vertex stabilizers in
$x\in V$
. Furthermore, since vertex stabilizers in
![]() $H'$
are pairwise distinct and
$H'$
are pairwise distinct and
for all
![]() $x\in V$
, we have
$x\in V$
, we have
![]() $\varphi h\varphi ^{-1}=\Phi (h)$
for all
$\varphi h\varphi ^{-1}=\Phi (h)$
for all
![]() $h\in H$
.
$h\in H$
.
The following corollary uses the notation
![]() $\Phi ^{k}(F')$
from Section 4.4.2.
$\Phi ^{k}(F')$
from Section 4.4.2.
Corollary 4.18. Let
![]() $F\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})$
and
$F\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})$
and
![]() $F'\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k'})$
satisfy (C). Assume
$F'\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k'})$
satisfy (C). Assume
![]() $k\!\ge \! k'$
and
$k\!\ge \! k'$
and
![]() $\pi F,\pi F'\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
are transitive with distinct point-stabilizers. If
$\pi F,\pi F'\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
are transitive with distinct point-stabilizers. If
![]() $\mathrm {U}_{k}(F)$
and
$\mathrm {U}_{k}(F)$
and
![]() $\mathrm {U}_{k'}(F')$
are isomorphic topological groups then
$\mathrm {U}_{k'}(F')$
are isomorphic topological groups then
![]() $F,\Phi ^{k}(F')\!\le \!\operatorname {\mathrm {Aut}}(\!B_{d,k})$
are conjugate.
$F,\Phi ^{k}(F')\!\le \!\operatorname {\mathrm {Aut}}(\!B_{d,k})$
are conjugate.
Proof. By Proposition 4.17, the groups
![]() $\mathrm {U}_{k}(F)$
and
$\mathrm {U}_{k}(F)$
and
![]() $\mathrm {U}_{k}(F')$
are conjugate in
$\mathrm {U}_{k}(F')$
are conjugate in
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
; hence so are
$\operatorname {\mathrm {Aut}}(T_{d})$
; hence so are
![]() $\mathrm {U}_{k}(F)_{x}$
and
$\mathrm {U}_{k}(F)_{x}$
and
![]() $\mathrm {U}_{k'}(F')_{x}$
for every
$\mathrm {U}_{k'}(F')_{x}$
for every
![]() $x\in V$
, and the assertion follows.
$x\in V$
, and the assertion follows.
Example 4.19. Section 4.4.1 introduces the isomorphic, nonconjugate subgroups
![]() $\Pi (S_{3},\mathrm {sgn},\{1\})$
and
$\Pi (S_{3},\mathrm {sgn},\{1\})$
and
![]() $\Pi (S_{3},\mathrm {sgn},\{0,1\})$
of
$\Pi (S_{3},\mathrm {sgn},\{0,1\})$
of
![]() $\operatorname {\mathrm {Aut}}(B_{3,2})$
, both of which project onto
$\operatorname {\mathrm {Aut}}(B_{3,2})$
, both of which project onto
![]() $S_{3}$
and satisfy (C) but not (D). An explicit isomorphism satisfies the assumption of Corollary 4.15. However, by Corollary 4.18 the universal groups
$S_{3}$
and satisfy (C) but not (D). An explicit isomorphism satisfies the assumption of Corollary 4.15. However, by Corollary 4.18 the universal groups
![]() $\mathrm {U}_{2}(\Pi (S_{3},\mathrm {sgn},\{1\}))$
and
$\mathrm {U}_{2}(\Pi (S_{3},\mathrm {sgn},\{1\}))$
and
![]() $\mathrm {U}_{2}(\Pi (S_{3},\mathrm {sgn},\{0,1\}))$
are nonisomorphic. Therefore, Corollary 4.15 does not generalize to the nondiscrete case.
$\mathrm {U}_{2}(\Pi (S_{3},\mathrm {sgn},\{0,1\}))$
are nonisomorphic. Therefore, Corollary 4.15 does not generalize to the nondiscrete case.
Question 4.20. Let
![]() $F,F'\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C) and be conjugate. Are the associated universal groups
$F,F'\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C) and be conjugate. Are the associated universal groups
![]() $\mathrm {U}_{k}(F)$
and
$\mathrm {U}_{k}(F)$
and
![]() $\mathrm {U}_{k}(F')$
necessarily isomorphic?
$\mathrm {U}_{k}(F')$
necessarily isomorphic?
In the following, we determine the Burger–Mozes subquotient
![]() $H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
of Theorem 3.14 for nondiscrete, locally semiprimitive universal groups.
$H^{(\infty )}\!/\mathrm {QZ}(H^{(\infty )})$
of Theorem 3.14 for nondiscrete, locally semiprimitive universal groups.
Proposition 4.21. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). If, in addition, F satisfies (D) then
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). If, in addition, F satisfies (D) then
![]() $\mathrm {QZ}(\mathrm {U}_{k}(F))=\mathrm {U}_{k}(F)$
. Otherwise,
$\mathrm {QZ}(\mathrm {U}_{k}(F))=\mathrm {U}_{k}(F)$
. Otherwise,
![]() $\mathrm {QZ}(\mathrm {U}_{k}(F))=\{\operatorname {\mathrm {id}}\}$
.
$\mathrm {QZ}(\mathrm {U}_{k}(F))=\{\operatorname {\mathrm {id}}\}$
.
Proof. If F satisfies (D) then
![]() $\mathrm {U}_{k}(F)$
is discrete and hence
$\mathrm {U}_{k}(F)$
is discrete and hence
![]() $\mathrm {QZ}(\mathrm {U}_{k}(F))=\mathrm {U}_{k}(F)$
. Conversely, if F satisfies (C) but not (D) then the stabilizer of any half-tree
$\mathrm {QZ}(\mathrm {U}_{k}(F))=\mathrm {U}_{k}(F)$
. Conversely, if F satisfies (C) but not (D) then the stabilizer of any half-tree
![]() $T\subseteq T_{d}$
in
$T\subseteq T_{d}$
in
![]() $\mathrm {U}_{k}(F)$
is nontrivial: we have
$\mathrm {U}_{k}(F)$
is nontrivial: we have
![]() $T\in \{T_{x},T_{y}\}$
for some edge
$T\in \{T_{x},T_{y}\}$
for some edge
![]() $e:=(x,y)\in E$
. Since
$e:=(x,y)\in E$
. Since
![]() $\mathrm {U}_{k}(F)$
is nondiscrete by Proposition 4.12 and has property
$\mathrm {U}_{k}(F)$
is nondiscrete by Proposition 4.12 and has property
![]() $(P_{k})$
by Proposition 4.7, the group
$(P_{k})$
by Proposition 4.7, the group
![]() $\mathrm {U}_{k}(F)_{e^{k}}=\mathrm {U}_{k}(F)_{e^{k},T_{y}}\cdot \mathrm {U}_{k}(F)_{e^{k},T_{x}}$
is nontrivial. In particular, either
$\mathrm {U}_{k}(F)_{e^{k}}=\mathrm {U}_{k}(F)_{e^{k},T_{y}}\cdot \mathrm {U}_{k}(F)_{e^{k},T_{x}}$
is nontrivial. In particular, either
![]() $\mathrm {U}_{k}(F)_{T_{x}}$
or
$\mathrm {U}_{k}(F)_{T_{x}}$
or
![]() $\mathrm {U}_{k}(F)_{T_{y}}$
is nontrivial. In view of the existence of label-respecting inversions, both are nontrivial and hence so is
$\mathrm {U}_{k}(F)_{T_{y}}$
is nontrivial. In view of the existence of label-respecting inversions, both are nontrivial and hence so is
![]() $\mathrm {U}_{k}(F)_{T}$
. Therefore,
$\mathrm {U}_{k}(F)_{T}$
. Therefore,
![]() $\mathrm {U}_{k}(F)$
has Property H of Möller–Vonk [Reference Möller and Vonk18, Definition 2.3] and [Reference Möller and Vonk18, Proposition 2.6] implies that
$\mathrm {U}_{k}(F)$
has Property H of Möller–Vonk [Reference Möller and Vonk18, Definition 2.3] and [Reference Möller and Vonk18, Proposition 2.6] implies that
![]() $\mathrm {U}_{k}(F)$
has trivial quasicentre.
$\mathrm {U}_{k}(F)$
has trivial quasicentre.
Proposition 4.22. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C) but not (D). Suppose that
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C) but not (D). Suppose that
![]() $\pi F$
is semiprimitive. Then
$\pi F$
is semiprimitive. Then
![]() $\mathrm {U}_{k}(F)^{(\infty )}/\mathrm {QZ}(\mathrm {U}_{k}(F)^{(\infty )})=\mathrm {U}_{k}(F)^{(\infty )}=\mathrm {U}_{k}(F)^{+_{k}}$
.
$\mathrm {U}_{k}(F)^{(\infty )}/\mathrm {QZ}(\mathrm {U}_{k}(F)^{(\infty )})=\mathrm {U}_{k}(F)^{(\infty )}=\mathrm {U}_{k}(F)^{+_{k}}$
.
Proof. The subgroup
![]() $\mathrm {U}_{k}(F)^{+_{k}}\le \mathrm {U}_{k}(F)$
is open, hence closed, and normal in
$\mathrm {U}_{k}(F)^{+_{k}}\le \mathrm {U}_{k}(F)$
is open, hence closed, and normal in
![]() $\mathrm {U}_{k}(F)$
by definition. Since
$\mathrm {U}_{k}(F)$
by definition. Since
![]() $\mathrm {U}_{k}(F)$
is nondiscrete by Proposition 4.12, so is
$\mathrm {U}_{k}(F)$
is nondiscrete by Proposition 4.12, so is
![]() $\mathrm {U}_{k}(F)^{+_{k}}$
. Using Proposition 3.11(iii), we conclude that
$\mathrm {U}_{k}(F)^{+_{k}}$
. Using Proposition 3.11(iii), we conclude that
![]() $\mathrm {U}_{k}(F)^{+_{k}}\ge \mathrm {U}_{k}(F)^{(\infty )}$
. Since
$\mathrm {U}_{k}(F)^{+_{k}}\ge \mathrm {U}_{k}(F)^{(\infty )}$
. Since
![]() $\mathrm {U}_{k}(F)$
satisfies property
$\mathrm {U}_{k}(F)$
satisfies property
![]() $(P_{k})$
by Proposition 4.7, the group
$(P_{k})$
by Proposition 4.7, the group
![]() $\mathrm {U}_{k}(F)^{+_{k}}$
is simple due to Theorem 2.1. Thus
$\mathrm {U}_{k}(F)^{+_{k}}$
is simple due to Theorem 2.1. Thus
![]() $\mathrm {U}_{k}(F)^{+_{k}}=\mathrm {U}_{k}(F)^{(\infty )}$
. Given that
$\mathrm {U}_{k}(F)^{+_{k}}=\mathrm {U}_{k}(F)^{(\infty )}$
. Given that
![]() $\mathrm {QZ}(\mathrm {U}_{k}(F)^{(\infty )})=\mathrm {QZ}(\mathrm {U}_{k}(F))\cap \mathrm {U}_{k}(F)^{(\infty )}$
by Proposition 3.11(iv), the assertion follows from Proposition 4.21.
$\mathrm {QZ}(\mathrm {U}_{k}(F)^{(\infty )})=\mathrm {QZ}(\mathrm {U}_{k}(F))\cap \mathrm {U}_{k}(F)^{(\infty )}$
by Proposition 3.11(iv), the assertion follows from Proposition 4.21.
In the context of Proposition 4.22, the group
![]() $\mathrm {U}_{k}(F)^{+_{k}}$
is simple, compactly generated, nondiscrete, totally disconnected, locally compact, second countable. Compact generation follows from [Reference Krön and Möller15, Corollary 2.11], given that
$\mathrm {U}_{k}(F)^{+_{k}}$
is simple, compactly generated, nondiscrete, totally disconnected, locally compact, second countable. Compact generation follows from [Reference Krön and Möller15, Corollary 2.11], given that
![]() $\smash {\mathrm {U}_{k}(F)^{+_{k}}}$
is cocompact in
$\smash {\mathrm {U}_{k}(F)^{+_{k}}}$
is cocompact in
![]() $\mathrm {U}_{k}(F)$
by Proposition 3.11(i).
$\mathrm {U}_{k}(F)$
by Proposition 3.11(i).
4.4 Examples
We now construct various classes of examples of subgroups of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
satisfying (C) or (CD), and prove a rigidity result for certain local actions.
$\operatorname {\mathrm {Aut}}(B_{d,k})$
satisfying (C) or (CD), and prove a rigidity result for certain local actions.
First, we give a suitable realization of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
and conditions (C) and (D). Namely, we view an automorphism
$\operatorname {\mathrm {Aut}}(B_{d,k})$
and conditions (C) and (D). Namely, we view an automorphism
![]() $\alpha $
of
$\alpha $
of
![]() $B_{d,k}$
as the set
$B_{d,k}$
as the set
![]() $\{\sigma _{k-1}(\alpha ,v)\mid v\in B(b,1)\}$
as follows. Let
$\{\sigma _{k-1}(\alpha ,v)\mid v\in B(b,1)\}$
as follows. Let
![]() $\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
be the natural isomorphism. For
$\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
be the natural isomorphism. For
![]() $k\ge 2$
, we iteratively identify
$k\ge 2$
, we iteratively identify
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
with its image under the map
$\operatorname {\mathrm {Aut}}(B_{d,k})$
with its image under the map
where
![]() $\operatorname {\mathrm {Aut}}(B_{d,k-1})$
acts on
$\operatorname {\mathrm {Aut}}(B_{d,k-1})$
acts on
![]() $\smash {\prod _{\omega \in \Omega }\operatorname {\mathrm {Aut}}(B_{d,k-1})}$
by permuting the factors according to its action on
$\smash {\prod _{\omega \in \Omega }\operatorname {\mathrm {Aut}}(B_{d,k-1})}$
by permuting the factors according to its action on
![]() $S(b,1)\cong \Omega $
. That is, multiplication in
$S(b,1)\cong \Omega $
. That is, multiplication in
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
is given by
$\operatorname {\mathrm {Aut}}(B_{d,k})$
is given by
Consider the homomorphism
![]() $\pi _{k-1}:\operatorname {\mathrm {Aut}}(B_{d,k})\to \operatorname {\mathrm {Aut}}(B_{d,k-1}),\ \alpha \mapsto \sigma _{k-1}(\alpha ,b)$
, the projections
$\pi _{k-1}:\operatorname {\mathrm {Aut}}(B_{d,k})\to \operatorname {\mathrm {Aut}}(B_{d,k-1}),\ \alpha \mapsto \sigma _{k-1}(\alpha ,b)$
, the projections
![]() $\operatorname {\mathrm {pr}}_{\omega }:\operatorname {\mathrm {Aut}}(B_{d,k})\to \operatorname {\mathrm {Aut}}(B_{d,k-1}),\ \alpha \mapsto \sigma _{k-1}(\alpha ,b_{\omega }) \ (\omega \in \Omega )$
, and
$\operatorname {\mathrm {pr}}_{\omega }:\operatorname {\mathrm {Aut}}(B_{d,k})\to \operatorname {\mathrm {Aut}}(B_{d,k-1}),\ \alpha \mapsto \sigma _{k-1}(\alpha ,b_{\omega }) \ (\omega \in \Omega )$
, and
whose image we interpret as a relation on
![]() $\operatorname {\mathrm {Aut}}(B_{d,k-1})$
. Conditions (C) and (D) for a subgroup
$\operatorname {\mathrm {Aut}}(B_{d,k-1})$
. Conditions (C) and (D) for a subgroup
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
now read as follows:
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
now read as follows:
4.4.1 The case
 $k=2$
$k=2$
We first consider the case
![]() $k=2$
which is all-encompassing in certain situations; see Theorem 4.32. By the above,
$k=2$
which is all-encompassing in certain situations; see Theorem 4.32. By the above,
![]() $\operatorname {\mathrm {Aut}}(B_{d,2})$
is realized as follows:
$\operatorname {\mathrm {Aut}}(B_{d,2})$
is realized as follows:
![]() $\operatorname {\mathrm {Aut}}(B_{d,2})=\{(a,(a_{\omega })_{\omega \in \Omega })\mid a\in \operatorname {\mathrm {Sym}}(\Omega ), \text { for all }\omega \in \Omega :a_{\omega }\in \operatorname {\mathrm {Sym}}(\Omega ) \text { and } a_{\omega }\omega =a\omega \}$
.
$\operatorname {\mathrm {Aut}}(B_{d,2})=\{(a,(a_{\omega })_{\omega \in \Omega })\mid a\in \operatorname {\mathrm {Sym}}(\Omega ), \text { for all }\omega \in \Omega :a_{\omega }\in \operatorname {\mathrm {Sym}}(\Omega ) \text { and } a_{\omega }\omega =a\omega \}$
.
Consider the map
![]() $\gamma :\operatorname {\mathrm {Sym}}(\Omega )\to \operatorname {\mathrm {Aut}}(B_{d,2})$
,
$\gamma :\operatorname {\mathrm {Sym}}(\Omega )\to \operatorname {\mathrm {Aut}}(B_{d,2})$
,
![]() $a\mapsto (a,(a,\ldots ,a))\in \operatorname {\mathrm {Aut}}(B_{d,2})$
, using the realization of
$a\mapsto (a,(a,\ldots ,a))\in \operatorname {\mathrm {Aut}}(B_{d,2})$
, using the realization of
![]() $\operatorname {\mathrm {Aut}}(B_{d,2})$
from above. For every
$\operatorname {\mathrm {Aut}}(B_{d,2})$
from above. For every
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
, the image
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
, the image
is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(B_{d,2})$
which is isomorphic to F and satisfies both (C) and (D). The involutive compatibility cocycle is given by
$\operatorname {\mathrm {Aut}}(B_{d,2})$
which is isomorphic to F and satisfies both (C) and (D). The involutive compatibility cocycle is given by
![]() $\Gamma (F)\times \Omega \to \Gamma (F),\ (\gamma (a),\omega )\mapsto \gamma (a)$
. Note that
$\Gamma (F)\times \Omega \to \Gamma (F),\ (\gamma (a),\omega )\mapsto \gamma (a)$
. Note that
![]() $\Gamma (F)\!\cong \! F$
implements the diagonal action
$\Gamma (F)\!\cong \! F$
implements the diagonal action
![]() $F\curvearrowright \Omega ^{2}$
on
$F\curvearrowright \Omega ^{2}$
on
![]() $S(b,2)\cong \Omega ^{(2)}\subset \Omega ^{2}$
.
$S(b,2)\cong \Omega ^{(2)}\subset \Omega ^{2}$
.
We obtain
![]() $\mathrm {U}_{2}(\Gamma (F))\kern1.2pt{=}\kern1.2pt\{\alpha \kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {Aut}}(T_{d})\mid \text { there exists } a\in F: \text { for all } x\kern1.2pt{\in}\kern1.2pt V:\sigma _{1}(\alpha ,x)\kern1.2pt{=}\kern1.2pta\}=:\mathrm {D}(F)$
, following the notation of [Reference Banks, Elder and Willis1]. Moreover, there is the following description of all subgroups
$\mathrm {U}_{2}(\Gamma (F))\kern1.2pt{=}\kern1.2pt\{\alpha \kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {Aut}}(T_{d})\mid \text { there exists } a\in F: \text { for all } x\kern1.2pt{\in}\kern1.2pt V:\sigma _{1}(\alpha ,x)\kern1.2pt{=}\kern1.2pta\}=:\mathrm {D}(F)$
, following the notation of [Reference Banks, Elder and Willis1]. Moreover, there is the following description of all subgroups
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,2})}$
with
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,2})}$
with
![]() $\smash {\pi \widetilde {F}=F}$
that satisfy (C) and contain
$\smash {\pi \widetilde {F}=F}$
that satisfy (C) and contain
![]() $\Gamma (F)$
.
$\Gamma (F)$
.
Proposition 4.23. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Given
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Given
![]() $K\le \prod _{\omega \in \Omega }F_{\omega }\cong \ker \pi \le \operatorname {\mathrm {Aut}}(B_{d,2})$
, there is
$K\le \prod _{\omega \in \Omega }F_{\omega }\cong \ker \pi \le \operatorname {\mathrm {Aut}}(B_{d,2})$
, there is
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,2})}$
satisfying (C) and fitting into the split exact sequence
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,2})}$
satisfying (C) and fitting into the split exact sequence
if and only if K is preserved by the action
![]() $F\curvearrowright \prod _{\omega \in \Omega }F_{\omega}, a\cdot (a_{\omega })_{\omega }:=(aa_{a^{-1}\omega }a^{-1})_{\omega }$
.
$F\curvearrowright \prod _{\omega \in \Omega }F_{\omega}, a\cdot (a_{\omega })_{\omega }:=(aa_{a^{-1}\omega }a^{-1})_{\omega }$
.
Proof. If there is a split exact sequence as above then
![]() $K\unlhd \widetilde {F}$
is invariant under conjugation by
$K\unlhd \widetilde {F}$
is invariant under conjugation by
![]() $\smash {\Gamma (F)\le \widetilde {F}}$
, hence the assertion.
$\smash {\Gamma (F)\le \widetilde {F}}$
, hence the assertion.
Conversely, if K is invariant under the given action, then
fits into the sequence. First, note that
![]() $\smash {\widetilde {F}}$
contains both K and
$\smash {\widetilde {F}}$
contains both K and
![]() $\Gamma (F)$
. It is also a subgroup of
$\Gamma (F)$
. It is also a subgroup of
![]() $\operatorname {\mathrm {Aut}}(B_{d,2})$
: for
$\operatorname {\mathrm {Aut}}(B_{d,2})$
: for
![]() $\smash {(a,(aa_{\omega })_{\omega }),\ (b,(bb_{\omega })_{\omega })\in \widetilde {F}}$
we have
$\smash {(a,(aa_{\omega })_{\omega }),\ (b,(bb_{\omega })_{\omega })\in \widetilde {F}}$
we have
by assumption. In particular,
![]() $\widetilde {F}=\langle \Gamma (F),K\rangle $
. It suffices to check condition (C) on these generators of
$\widetilde {F}=\langle \Gamma (F),K\rangle $
. It suffices to check condition (C) on these generators of
![]() $\smash {\widetilde {F}}$
. As before,
$\smash {\widetilde {F}}$
. As before,
![]() $\gamma (a)\in C(\gamma (a),\omega )$
for all
$\gamma (a)\in C(\gamma (a),\omega )$
for all
![]() $a\in F$
and
$a\in F$
and
![]() $\omega \in \Omega $
. Now let
$\omega \in \Omega $
. Now let
![]() $k\in K$
. Then
$k\in K$
. Then
![]() $\gamma (\operatorname {\mathrm {pr}}_{\omega }k)k^{-1}\in C(k,\omega )$
for all
$\gamma (\operatorname {\mathrm {pr}}_{\omega }k)k^{-1}\in C(k,\omega )$
for all
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Example 4.24. We show that for certain dihedral groups there are only four groups of the type given in Proposition 4.23. Set
![]() $F:=D_{p}\le \operatorname {\mathrm {Sym}}(p)$
for some prime
$F:=D_{p}\le \operatorname {\mathrm {Sym}}(p)$
for some prime
![]() $p\ge 3$
. Then
$p\ge 3$
. Then
![]() $F_{\omega }\!\cong \!(\operatorname {\mathrm {\mathbb {F}}}_{2},+)$
. Hence,
$F_{\omega }\!\cong \!(\operatorname {\mathrm {\mathbb {F}}}_{2},+)$
. Hence,
![]() $\smash {U\!:=\!\prod _{\omega \in \Omega }F_{\omega }}$
is a p-dimensional vector space over
$\smash {U\!:=\!\prod _{\omega \in \Omega }F_{\omega }}$
is a p-dimensional vector space over
![]() $\operatorname {\mathrm {\mathbb {F}}}_{2}$
and the F-action on it permutes coordinates. When
$\operatorname {\mathrm {\mathbb {F}}}_{2}$
and the F-action on it permutes coordinates. When
![]() $2\in (\operatorname {\mathrm {\mathbb {Z}}}/p\operatorname {\mathrm {\mathbb {Z}}})^{\ast }$
is primitive, there are only four F-invariant subspaces of U: the trivial subspace; the diagonal subspace
$2\in (\operatorname {\mathrm {\mathbb {Z}}}/p\operatorname {\mathrm {\mathbb {Z}}})^{\ast }$
is primitive, there are only four F-invariant subspaces of U: the trivial subspace; the diagonal subspace
![]() $\langle (1,\ldots ,1)\rangle $
; the whole space; and
$\langle (1,\ldots ,1)\rangle $
; the whole space; and
![]() $\smash {K:=\ker \sigma \cong \operatorname {\mathrm {\mathbb {F}}}_{2}^{(p-1)}}$
where
$\smash {K:=\ker \sigma \cong \operatorname {\mathrm {\mathbb {F}}}_{2}^{(p-1)}}$
where
![]() $\smash {\sigma \!:U\to \operatorname {\mathrm {\mathbb {F}}}_{2}}$
is given by
$\smash {\sigma \!:U\to \operatorname {\mathrm {\mathbb {F}}}_{2}}$
is given by
![]() $\smash {(v_{1},\ldots ,v_{p})\mapsto \sum _{i=1}^{p}v_{i}}$
. Note that K is F-invariant because the homomorphism
$\smash {(v_{1},\ldots ,v_{p})\mapsto \sum _{i=1}^{p}v_{i}}$
. Note that K is F-invariant because the homomorphism
![]() $\sigma $
is. Conjecturally, there are infinitely many primes for which
$\sigma $
is. Conjecturally, there are infinitely many primes for which
![]() $2\in (\operatorname {\mathrm {\mathbb {Z}}}/p\operatorname {\mathrm {\mathbb {Z}}})^{\ast }$
is primitive. The list starts with
$2\in (\operatorname {\mathrm {\mathbb {Z}}}/p\operatorname {\mathrm {\mathbb {Z}}})^{\ast }$
is primitive. The list starts with
![]() $3$
,
$3$
,
![]() $5$
,
$5$
,
![]() $11$
,
$11$
,
![]() $13,\ldots $
; see [Reference Sloane26, A001122].
$13,\ldots $
; see [Reference Sloane26, A001122].
Suppose that
![]() $W\le U$
is F-invariant. It suffices to show that W contains K as soon as
$W\le U$
is F-invariant. It suffices to show that W contains K as soon as
![]() $W\cap \ker \sigma $
contains a nontrivial element w. To see this, we show that the orbit of w under the cyclic group
$W\cap \ker \sigma $
contains a nontrivial element w. To see this, we show that the orbit of w under the cyclic group
![]() $\langle \varrho \rangle =C_{p}\le D_{p}$
generates a
$\langle \varrho \rangle =C_{p}\le D_{p}$
generates a
![]() $(p-1)$
-dimensional subspace of K which hence equals K. Indeed, the rank of the circulant matrix
$(p-1)$
-dimensional subspace of K which hence equals K. Indeed, the rank of the circulant matrix
![]() $C:=(w,\varrho w,\varrho ^{2}w,\ldots ,\varrho ^{(p-1)}w)$
equals
$C:=(w,\varrho w,\varrho ^{2}w,\ldots ,\varrho ^{(p-1)}w)$
equals
![]() $p-\deg (\gcd (x^{p}-1,f(x)))$
where
$p-\deg (\gcd (x^{p}-1,f(x)))$
where
![]() $f(x)\in \operatorname {\mathrm {\mathbb {F}}}_{2}[x]$
is the polynomial
$f(x)\in \operatorname {\mathrm {\mathbb {F}}}_{2}[x]$
is the polynomial
![]() $f(x)=w_{p}x^{p-1}+\cdots +w_{2}x+w_{1}$
; see, for example, [Reference Daykin5, Corollary 1]. The polynomial
$f(x)=w_{p}x^{p-1}+\cdots +w_{2}x+w_{1}$
; see, for example, [Reference Daykin5, Corollary 1]. The polynomial
![]() $x^{p}-1\in \operatorname {\mathrm {\mathbb {F}}}_{2}[x]$
factors into the irreducibles
$x^{p}-1\in \operatorname {\mathrm {\mathbb {F}}}_{2}[x]$
factors into the irreducibles
![]() $(x^{p-1}+x^{p-2}+\cdots +x+1) (x-1)$
by the assumption on p. Since f has an even number of nonzero coefficients, we conclude that
$(x^{p-1}+x^{p-2}+\cdots +x+1) (x-1)$
by the assumption on p. Since f has an even number of nonzero coefficients, we conclude that
![]() $\mathrm {rank}(C)=p-1$
.
$\mathrm {rank}(C)=p-1$
.
The following subgroups of
![]() $\operatorname {\mathrm {Aut}}(B_{d,2})$
are of the type given in Proposition 4.23. Let
$\operatorname {\mathrm {Aut}}(B_{d,2})$
are of the type given in Proposition 4.23. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Fix
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Fix
![]() $\omega _{0}\in \Omega $
, let
$\omega _{0}\in \Omega $
, let
![]() $C\le Z(F_{\omega _{0}})$
and let
$C\le Z(F_{\omega _{0}})$
and let
![]() $N\unlhd F_{\omega _{0}}$
be normal. Furthermore, fix elements
$N\unlhd F_{\omega _{0}}$
be normal. Furthermore, fix elements
![]() $f_{\omega }\in F$
(
$f_{\omega }\in F$
(
![]() $\omega \in \Omega $
) satisfying
$\omega \in \Omega $
) satisfying
![]() $f_{\omega }(\omega _{0})=\omega $
. We define
$f_{\omega }(\omega _{0})=\omega $
. We define
 $$ \begin{align*} \Delta(F,C)&:=\{(a,(a\circ f_{\omega}a_{0}f_{\omega}^{-1})_{\omega})\mid a\in F,\ a_{0}\in C\}\cong F\times C,\\ \Phi(F,N)&:=\{(a,(a\circ f_{\omega}a_{0}^{(\omega)}f_{\omega}^{-1})_{\omega})\mid a\in F,\ \text{for all } \omega\in\Omega:a_{0}^{(\omega)}\in N\}\cong F\ltimes N^{d}. \end{align*} $$
$$ \begin{align*} \Delta(F,C)&:=\{(a,(a\circ f_{\omega}a_{0}f_{\omega}^{-1})_{\omega})\mid a\in F,\ a_{0}\in C\}\cong F\times C,\\ \Phi(F,N)&:=\{(a,(a\circ f_{\omega}a_{0}^{(\omega)}f_{\omega}^{-1})_{\omega})\mid a\in F,\ \text{for all } \omega\in\Omega:a_{0}^{(\omega)}\in N\}\cong F\ltimes N^{d}. \end{align*} $$
In the case of
![]() $\Delta (F,C)$
we have
$\Delta (F,C)$
we have
![]() $K=\{(f_{\omega }a_{0}f_{\omega }^{-1})_{\omega }\mid a_{0}\in C\}$
, whereas in the case of
$K=\{(f_{\omega }a_{0}f_{\omega }^{-1})_{\omega }\mid a_{0}\in C\}$
, whereas in the case of
![]() $\Phi (F,N)$
we have
$\Phi (F,N)$
we have
![]() $\smash {K=\{(f_{\omega }a_{0}^{(\omega )}f_{\omega }^{-1})_{\omega }\mid \text { for all }\omega \in \Omega : a_{0}^{(\omega )}\in N\}}$
. In both cases, invariance under the action of F is readily verified, as is condition (D) for
$\smash {K=\{(f_{\omega }a_{0}^{(\omega )}f_{\omega }^{-1})_{\omega }\mid \text { for all }\omega \in \Omega : a_{0}^{(\omega )}\in N\}}$
. In both cases, invariance under the action of F is readily verified, as is condition (D) for
![]() $\Delta (F,C)$
.
$\Delta (F,C)$
.
The group
![]() $\Delta (F,F_{\omega _{0}})$
can be defined for nonabelian
$\Delta (F,F_{\omega _{0}})$
can be defined for nonabelian
![]() $F_{\omega _{0}}$
as well, namely,
$F_{\omega _{0}}$
as well, namely,
However, it need not contain
![]() $\Gamma (F)$
. Note that
$\Gamma (F)$
. Note that
![]() $\Phi (F,N)$
does not depend on the choice of the elements
$\Phi (F,N)$
does not depend on the choice of the elements
![]() $(f_{\omega })_{\omega \in \Omega }$
as N is normal in
$(f_{\omega })_{\omega \in \Omega }$
as N is normal in
![]() $F_{\omega _{0}}$
, whereas
$F_{\omega _{0}}$
, whereas
![]() $\Delta (F,C)$
and
$\Delta (F,C)$
and
![]() $\Delta (F)$
may. However, any group of the form
$\Delta (F)$
may. However, any group of the form
![]() $\{(a,(z(a,\omega )\alpha _{\omega }(a_{0}))_{\omega })\mid a\in F,\ a_{0}\in F_{\omega _{0}}\}$
, where z is a compatibility cocycle of F and
$\{(a,(z(a,\omega )\alpha _{\omega }(a_{0}))_{\omega })\mid a\in F,\ a_{0}\in F_{\omega _{0}}\}$
, where z is a compatibility cocycle of F and
![]() $\alpha _{\omega }:F_{\omega _{0}}\to F_{\omega } (\omega \in \Omega )$
are isomorphisms, that satisfies (C) and in which
$\alpha _{\omega }:F_{\omega _{0}}\to F_{\omega } (\omega \in \Omega )$
are isomorphisms, that satisfies (C) and in which
![]() $\{(a,(z(a,\omega ))_{\omega })\mid a\in F\}$
and
$\{(a,(z(a,\omega ))_{\omega })\mid a\in F\}$
and
![]() $\{(\operatorname {\mathrm {id}},(\alpha _{\omega }(a_{0}))_{\omega })\mid a_{0}\in F_{\omega _{0}}\}$
commute, will be referred to as
$\{(\operatorname {\mathrm {id}},(\alpha _{\omega }(a_{0}))_{\omega })\mid a_{0}\in F_{\omega _{0}}\}$
commute, will be referred to as
![]() $\Delta (F)$
in view of Corollary 4.15.
$\Delta (F)$
in view of Corollary 4.15.
The group
![]() $\Phi (F,F_{\omega _{0}})$
can be defined without assuming transitivity of F, namely,
$\Phi (F,F_{\omega _{0}})$
can be defined without assuming transitivity of F, namely,
We conclude that
![]() $\mathrm {U}_{2}(\Phi (F))=\mathrm {U}_{1}(F)$
for every
$\mathrm {U}_{2}(\Phi (F))=\mathrm {U}_{1}(F)$
for every
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
.
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
.
When
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
preserves a partition
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
preserves a partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
, we define
$\Omega $
, we define
The group
![]() $\Phi (F,\operatorname {\mathrm {\mathcal {P}}})$
satisfies (C) as well and features prominently in Section 5.1.
$\Phi (F,\operatorname {\mathrm {\mathcal {P}}})$
satisfies (C) as well and features prominently in Section 5.1.
The following kind of
![]() $2$
-local action generalizes the sign construction in [Reference Radu23]. Let
$2$
-local action generalizes the sign construction in [Reference Radu23]. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
and let
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
and let
![]() $\rho :F\twoheadrightarrow A$
be a homomorphism to an abelian group A. Define
$\rho :F\twoheadrightarrow A$
be a homomorphism to an abelian group A. Define
 $$ \begin{align*} \Pi(F,\rho,\{1\})&:=\bigg\{(a,(a_{\omega})_{\omega})\in\Phi(F)\bigg|\ \prod\limits_{\omega\in\Omega}\rho(a_{\omega})=1\bigg\}, \\ \Pi(F,\rho,\{0,1\})&:=\bigg\{(a,(a_{\omega})_{\omega})\in\Phi(F)\bigg|\ \rho(a)\prod\limits_{\omega\in\Omega}\rho(a_{\omega})=1\bigg\}. \end{align*} $$
$$ \begin{align*} \Pi(F,\rho,\{1\})&:=\bigg\{(a,(a_{\omega})_{\omega})\in\Phi(F)\bigg|\ \prod\limits_{\omega\in\Omega}\rho(a_{\omega})=1\bigg\}, \\ \Pi(F,\rho,\{0,1\})&:=\bigg\{(a,(a_{\omega})_{\omega})\in\Phi(F)\bigg|\ \rho(a)\prod\limits_{\omega\in\Omega}\rho(a_{\omega})=1\bigg\}. \end{align*} $$
This construction is generalized to
![]() $k\geq 2$
in Section 4.4.2 where the third entry of
$k\geq 2$
in Section 4.4.2 where the third entry of
![]() $\Pi $
is a set of radii over which the defining product is taken.
$\Pi $
is a set of radii over which the defining product is taken.
Proposition 4.25. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
and let
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
and let
![]() $\rho :F\twoheadrightarrow A$
be a homomorphism to an abelian group A. Let
$\rho :F\twoheadrightarrow A$
be a homomorphism to an abelian group A. Let
![]() $\smash {\widetilde {F}\in \{\Pi (F,\rho ,\{1\}), \Pi (F,\rho ,\{0,1\})\}}$
. If
$\smash {\widetilde {F}\in \{\Pi (F,\rho ,\{1\}), \Pi (F,\rho ,\{0,1\})\}}$
. If
![]() $\rho (F_{\omega })=A$
for all
$\rho (F_{\omega })=A$
for all
![]() $\omega \in \Omega $
then
$\omega \in \Omega $
then
![]() $\smash {\pi \widetilde {F}=F}$
and
$\smash {\pi \widetilde {F}=F}$
and
![]() $\smash {\widetilde {F}}$
satisfies (C).
$\smash {\widetilde {F}}$
satisfies (C).
Proof. As
![]() $C_{F}(a,\omega )\!=\!aF_{\omega }$
, and
$C_{F}(a,\omega )\!=\!aF_{\omega }$
, and
![]() $\rho (F_{\omega })\!=\!A$
for all
$\rho (F_{\omega })\!=\!A$
for all
![]() $\omega \in \Omega $
, an element
$\omega \in \Omega $
, an element
![]() $(a,(a_{\omega })_{\omega })\!\in \!\Phi (F)$
can be turned into an element of
$(a,(a_{\omega })_{\omega })\!\in \!\Phi (F)$
can be turned into an element of
![]() $\smash {\widetilde {F}}$
by changing
$\smash {\widetilde {F}}$
by changing
![]() $a_{\omega }$
for a single, arbitrary
$a_{\omega }$
for a single, arbitrary
![]() $\omega \!\in \!\Omega $
. We conclude that
$\omega \!\in \!\Omega $
. We conclude that
![]() $\smash {\pi \widetilde {F}=F}$
and that
$\smash {\pi \widetilde {F}=F}$
and that
![]() $\smash {\widetilde {F}}$
satisfies (C).
$\smash {\widetilde {F}}$
satisfies (C).
4.4.2 General case
We extend some constructions of Section 4.4.1 to arbitrary k. Given
![]() $\smash {F\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfying (C), define the subgroup
$\smash {F\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfying (C), define the subgroup
Then
![]() $\Phi _{k}(F)$
inherits condition (C) from F and we obtain
$\Phi _{k}(F)$
inherits condition (C) from F and we obtain
![]() $\mathrm {U}_{k+1}(\Phi _{k}(F))=\mathrm {U}_{k}(F)$
. Concerning the construction
$\mathrm {U}_{k+1}(\Phi _{k}(F))=\mathrm {U}_{k}(F)$
. Concerning the construction
![]() $\Gamma $
we have the following proposition.
$\Gamma $
we have the following proposition.
Proposition 4.26. Let
![]() $F\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). Then there exists a group
$F\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). Then there exists a group
![]() satisfying (CD) such that
satisfying (CD) such that
![]() $\pi_{k}|_{\Gamma_{k}(F)}$
is an isomorphism onto F if and only if F admits an involutive compatibility cocycle z.
$\pi_{k}|_{\Gamma_{k}(F)}$
is an isomorphism onto F if and only if F admits an involutive compatibility cocycle z.
Proof. If F admits an involutive compatibility cocycle z, define
Then
![]() $\gamma _{z}:F\to \Gamma _{k}(F),\ \alpha \mapsto (\alpha ,(z(\alpha ,\omega ))_{\omega })$
is an isomorphism and the involutive compatibility cocycle of
$\gamma _{z}:F\to \Gamma _{k}(F),\ \alpha \mapsto (\alpha ,(z(\alpha ,\omega ))_{\omega })$
is an isomorphism and the involutive compatibility cocycle of
![]() $\Gamma _{k}(F)$
is given by
$\Gamma _{k}(F)$
is given by
![]() $\widetilde {z}:(\gamma _{z}(\alpha ),\omega )\mapsto \gamma _{z}(z(\alpha ,\omega ))$
. Conversely, if a group
$\widetilde {z}:(\gamma _{z}(\alpha ),\omega )\mapsto \gamma _{z}(z(\alpha ,\omega ))$
. Conversely, if a group
![]() $\Gamma _{k}(F)$
with the asserted properties exists, set
$\Gamma _{k}(F)$
with the asserted properties exists, set
![]() $\smash {z:(\alpha ,\omega )\mapsto \operatorname {\mathrm {pr}}_{\omega }\pi _{k}^{-1}\alpha }$
.
$\smash {z:(\alpha ,\omega )\mapsto \operatorname {\mathrm {pr}}_{\omega }\pi _{k}^{-1}\alpha }$
.
Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C) and let
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C) and let
![]() $l>k$
. We set
$l>k$
. We set
![]() $\Gamma ^{l}(F):=\Gamma _{l-1}\circ \cdots \circ \Gamma _{k}(F)$
for an implicit sequence of involutive compatibility cocycles. Similarly, we define
$\Gamma ^{l}(F):=\Gamma _{l-1}\circ \cdots \circ \Gamma _{k}(F)$
for an implicit sequence of involutive compatibility cocycles. Similarly, we define
![]() $\Phi ^{l}(F):=\Phi _{l-1}\circ \cdots \circ \Phi _{k}(F)$
. Now, let
$\Phi ^{l}(F):=\Phi _{l-1}\circ \cdots \circ \Phi _{k}(F)$
. Now, let
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
. Assume
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
. Assume
![]() $\smash {F:=\pi \widetilde {F}\le \operatorname {\mathrm {Sym}}(\Omega )}$
preserves a partition
$\smash {F:=\pi \widetilde {F}\le \operatorname {\mathrm {Sym}}(\Omega )}$
preserves a partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
. Define the group
$\Omega $
. Define the group
If
![]() $\smash {C_{\widetilde {F}}(\alpha ,\Omega _{i})}$
is nonempty for all
$\smash {C_{\widetilde {F}}(\alpha ,\Omega _{i})}$
is nonempty for all
![]() $\smash {\alpha \in \widetilde {F}}$
and
$\smash {\alpha \in \widetilde {F}}$
and
![]() $i\in I$
then
$i\in I$
then
![]() $\smash {\Phi _{k}(\widetilde {F},\operatorname {\mathrm {\mathcal {P}}})}$
satisfies (C), and if
$\smash {\Phi _{k}(\widetilde {F},\operatorname {\mathrm {\mathcal {P}}})}$
satisfies (C), and if
![]() $\smash {C_{\widetilde {F}}(\operatorname {\mathrm {id}},\Omega _{i})}$
is nontrivial for all
$\smash {C_{\widetilde {F}}(\operatorname {\mathrm {id}},\Omega _{i})}$
is nontrivial for all
![]() $i\in I$
then
$i\in I$
then
![]() $\smash {\Phi _{k}(\widetilde {F},\operatorname {\mathrm {\mathcal {P}}})}$
does not satisfy (D).
$\smash {\Phi _{k}(\widetilde {F},\operatorname {\mathrm {\mathcal {P}}})}$
does not satisfy (D).
The following statement generalizes Proposition 4.23.
Proposition 4.27. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). Suppose F admits an involutive compatibility cocycle z. Given
$F\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfy (C). Suppose F admits an involutive compatibility cocycle z. Given
![]() $K\le \Phi _{k}(F)\cap \ker (\pi _{k})$
, there is
$K\le \Phi _{k}(F)\cap \ker (\pi _{k})$
, there is
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k+1})}$
satisfying (C) and fitting into the split exact sequence
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k+1})}$
satisfying (C) and fitting into the split exact sequence
if and only if
![]() $\Gamma _{k}(F)$
normalizes K, and for all
$\Gamma _{k}(F)$
normalizes K, and for all
![]() $k\in K$
and
$k\in K$
and
![]() $\omega \in \Omega $
there is
$\omega \in \Omega $
there is
![]() $k_{\omega }\in K$
such that
$k_{\omega }\in K$
such that
![]() $\operatorname {\mathrm {pr}}_{\omega }k_{\omega }=z(\operatorname {\mathrm {pr}}_{\omega }k,\omega )^{-1}$
.
$\operatorname {\mathrm {pr}}_{\omega }k_{\omega }=z(\operatorname {\mathrm {pr}}_{\omega }k,\omega )^{-1}$
.
Proof. If there is a split exact sequence as above then
![]() $K\unlhd \widetilde {F}$
is invariant under conjugation by
$K\unlhd \widetilde {F}$
is invariant under conjugation by
![]() $\Gamma _{k}(F)$
. Moreover, all elements of
$\Gamma _{k}(F)$
. Moreover, all elements of
![]() $\smash {\widetilde {F}}$
have the form
$\smash {\widetilde {F}}$
have the form
![]() $(\alpha ,(z(\alpha ,\omega )\alpha _{\omega })_{\omega })$
for some
$(\alpha ,(z(\alpha ,\omega )\alpha _{\omega })_{\omega })$
for some
![]() $\alpha \!\in \! F$
and
$\alpha \!\in \! F$
and
![]() $(\alpha _{\omega })_{\omega }\in K$
. This implies the second assertion on K.
$(\alpha _{\omega })_{\omega }\in K$
. This implies the second assertion on K.
Conversely, if K satisfies the assumptions, then
fits into the sequence. First, note that
![]() $\widetilde {F}$
contains both K and
$\widetilde {F}$
contains both K and
![]() $\Gamma _{k}(F)$
. It is also a subgroup of
$\Gamma _{k}(F)$
. It is also a subgroup of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k+1})$
: for
$\operatorname {\mathrm {Aut}}(B_{d,k+1})$
: for
![]() $\smash {(\alpha ,(z(\alpha ,\omega )\alpha _{\omega })_{\omega }),\ (\beta ,(z(\beta ,\omega )\beta _{\omega })_{\omega })\in \widetilde {F}}$
we have
$\smash {(\alpha ,(z(\alpha ,\omega )\alpha _{\omega })_{\omega }),\ (\beta ,(z(\beta ,\omega )\beta _{\omega })_{\omega })\in \widetilde {F}}$
we have
 $$ \begin{align*} (\alpha,(z(\alpha,\omega)\alpha_{\omega})_{\omega})&\circ(\beta,(z(\beta,\omega)\beta_{\omega})_{\omega})=(\alpha\beta,(z(\alpha,\beta\omega)\alpha_{\beta\omega}z(\beta,\omega)\beta_{\omega})_{\omega}) \\ &=(\alpha\beta,(z(\alpha,\beta\omega)z(\beta,\omega)\circ z(\beta,\omega)^{-1}\alpha_{\beta\omega}z(\beta,\omega)\circ\beta_{\omega})_{\omega}) \\ &=(\alpha\beta,(z(\alpha\beta,\omega)\alpha_{\omega}'\beta_{\omega})_{\omega})\in\widetilde{F} \end{align*} $$
$$ \begin{align*} (\alpha,(z(\alpha,\omega)\alpha_{\omega})_{\omega})&\circ(\beta,(z(\beta,\omega)\beta_{\omega})_{\omega})=(\alpha\beta,(z(\alpha,\beta\omega)\alpha_{\beta\omega}z(\beta,\omega)\beta_{\omega})_{\omega}) \\ &=(\alpha\beta,(z(\alpha,\beta\omega)z(\beta,\omega)\circ z(\beta,\omega)^{-1}\alpha_{\beta\omega}z(\beta,\omega)\circ\beta_{\omega})_{\omega}) \\ &=(\alpha\beta,(z(\alpha\beta,\omega)\alpha_{\omega}'\beta_{\omega})_{\omega})\in\widetilde{F} \end{align*} $$
for some
![]() $(\alpha _{\omega }')_{\omega }\in K$
because
$(\alpha _{\omega }')_{\omega }\in K$
because
![]() $\Gamma _{k}(F)$
normalizes K. In particular,
$\Gamma _{k}(F)$
normalizes K. In particular,
![]() $\smash {\widetilde {F}=\langle \Gamma _{k}(F),K\rangle }$
. We check condition (C) on these generators. As before,
$\smash {\widetilde {F}=\langle \Gamma _{k}(F),K\rangle }$
. We check condition (C) on these generators. As before,
![]() $\gamma _{z}(z(\alpha ,\omega ))\in C(\gamma _{z}(\alpha ),\omega )$
for all
$\gamma _{z}(z(\alpha ,\omega ))\in C(\gamma _{z}(\alpha ),\omega )$
for all
![]() $\alpha \in F$
and
$\alpha \in F$
and
![]() $\omega \in \Omega $
because z is involutive. Now, let
$\omega \in \Omega $
because z is involutive. Now, let
![]() $k\in K$
. We then have
$k\in K$
. We then have
![]() $\gamma _{z}(\operatorname {\mathrm {pr}}_{\omega }k)k_{\omega }\in C(k,\omega )$
for all
$\gamma _{z}(\operatorname {\mathrm {pr}}_{\omega }k)k_{\omega }\in C(k,\omega )$
for all
![]() $\omega \in \Omega $
by the assumption on
$\omega \in \Omega $
by the assumption on
![]() $k_{\omega }$
.
$k_{\omega }$
.
In the split situation of Proposition 4.27 we also denote
![]() $\smash {\widetilde {F}}$
by
$\smash {\widetilde {F}}$
by
![]() $\Sigma _{k}(F,K)$
. For instance, the group
$\Sigma _{k}(F,K)$
. For instance, the group
![]() $\Pi (S_{3},\mathrm {sgn},\{1\})$
of Proposition 4.25 satisfies (C), admits an involutive compatibility cocycle but does not satisfy (D); see Section 5.3.
$\Pi (S_{3},\mathrm {sgn},\{1\})$
of Proposition 4.25 satisfies (C), admits an involutive compatibility cocycle but does not satisfy (D); see Section 5.3.
Now, let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
and
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
and
![]() $\rho :F\twoheadrightarrow A$
a homomorphism to an abelian group A. Further, let
$\rho :F\twoheadrightarrow A$
a homomorphism to an abelian group A. Further, let
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
and
$k\in \operatorname {\mathrm {\mathbb {N}}}$
and
![]() $X\subseteq \{0,\ldots ,k-1\}$
. Define
$X\subseteq \{0,\ldots ,k-1\}$
. Define
 $$ \begin{align*} \Pi^{k}(F,\rho,X):=\bigg\{\alpha\in\Phi^{k}(F)\bigg|\ \prod\limits_{r\in X}\prod\limits_{x\in S(b,r)}\rho(\sigma_{1}(\alpha,x))=1\bigg\}. \end{align*} $$
$$ \begin{align*} \Pi^{k}(F,\rho,X):=\bigg\{\alpha\in\Phi^{k}(F)\bigg|\ \prod\limits_{r\in X}\prod\limits_{x\in S(b,r)}\rho(\sigma_{1}(\alpha,x))=1\bigg\}. \end{align*} $$
Proposition 4.28. Let
![]() $F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
and let
$F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
and let
![]() $\rho \!:\!F\twoheadrightarrow \! A$
be a homomorphism to an abelian group A. Further, let
$\rho \!:\!F\twoheadrightarrow \! A$
be a homomorphism to an abelian group A. Further, let
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
and
$k\in \operatorname {\mathrm {\mathbb {N}}}$
and
![]() $X\subseteq \{0,\ldots ,k-1\}$
be nonempty and nonzero with
$X\subseteq \{0,\ldots ,k-1\}$
be nonempty and nonzero with
![]() $k\!-\!1\!\in \! X$
. If
$k\!-\!1\!\in \! X$
. If
![]() $\rho (F_{\omega })\!=\!A$
for all
$\rho (F_{\omega })\!=\!A$
for all
![]() $\omega \!\in \!\Omega $
then
$\omega \!\in \!\Omega $
then
![]() $\smash {\pi (\Pi ^{k}(F,\rho ,X))\!=\!F}$
and
$\smash {\pi (\Pi ^{k}(F,\rho ,X))\!=\!F}$
and
![]() $\smash {\Pi ^{k}(F,\rho ,X)}$
has (C).
$\smash {\Pi ^{k}(F,\rho ,X)}$
has (C).
Proof. As
![]() $C_{F}(a,\omega )=aF_{\omega }$
, and
$C_{F}(a,\omega )=aF_{\omega }$
, and
![]() $\rho (F_{\omega })=A$
for all
$\rho (F_{\omega })=A$
for all
![]() $\omega \in \Omega $
, an element
$\omega \in \Omega $
, an element
![]() $\alpha \in \Phi ^{k}(F)$
can be turned into an element of
$\alpha \in \Phi ^{k}(F)$
can be turned into an element of
![]() $\Pi ^{k}(F,\rho ,X)$
by changing
$\Pi ^{k}(F,\rho ,X)$
by changing
![]() $\sigma _{1}(\alpha ,x)$
for a single, arbitrary
$\sigma _{1}(\alpha ,x)$
for a single, arbitrary
![]() $x\in S(b,k-1)$
. When X is nonzero we conclude that
$x\in S(b,k-1)$
. When X is nonzero we conclude that
![]() $\pi (\Pi ^{k}(F,\rho ,X))\!=\!F$
and that
$\pi (\Pi ^{k}(F,\rho ,X))\!=\!F$
and that
![]() $\Pi ^{k}(F,\rho ,X)$
satisfies (C).
$\Pi ^{k}(F,\rho ,X)$
satisfies (C).
4.4.3 A rigid case
For certain
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
the groups
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
the groups
![]() $\Gamma (F)$
,
$\Gamma (F)$
,
![]() $\Delta (F)$
and
$\Delta (F)$
and
![]() $\Phi (F)$
already yield all possible
$\Phi (F)$
already yield all possible
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})}$
with
$\smash {\mathrm {U}_{k}(\widetilde {F})}$
with
![]() $\smash {\pi \widetilde {F}=F}$
. The main argument is based on Sections 3.4 and 3.5 of [Reference Burger and Mozes2]. We first record the following lemma whose proof is due to M. Giudici by personal communication.
$\smash {\pi \widetilde {F}=F}$
. The main argument is based on Sections 3.4 and 3.5 of [Reference Burger and Mozes2]. We first record the following lemma whose proof is due to M. Giudici by personal communication.
Lemma 4.29. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be
![]() $2$
-transitive and
$2$
-transitive and
![]() $F_{\omega }\ (\omega \in \Omega )$
simple nonabelian. Then every extension
$F_{\omega }\ (\omega \in \Omega )$
simple nonabelian. Then every extension
![]() $\smash {\widetilde {F}}$
of
$\smash {\widetilde {F}}$
of
![]() $F_{\omega }$
(
$F_{\omega }$
(
![]() $\omega \in \Omega $
) by F is equivalent to
$\omega \in \Omega $
) by F is equivalent to
![]() $F_{\omega }\times F$
.
$F_{\omega }\times F$
.
Proof. Regarding
![]() $F_{\omega }$
as a normal subgroup of
$F_{\omega }$
as a normal subgroup of
![]() $\smash {\widetilde {F}}$
, consider the conjugation map
$\smash {\widetilde {F}}$
, consider the conjugation map
![]() $\smash {\varphi :\widetilde {F}\to \operatorname {\mathrm {Aut}}(F_{\omega })}$
. We show that
$\smash {\varphi :\widetilde {F}\to \operatorname {\mathrm {Aut}}(F_{\omega })}$
. We show that
![]() $\smash {K:=\ker \varphi =Z_{\widetilde {F}}(F_{\omega })\unlhd \widetilde {F}}$
complements
$\smash {K:=\ker \varphi =Z_{\widetilde {F}}(F_{\omega })\unlhd \widetilde {F}}$
complements
![]() $F_{\omega }$
in
$F_{\omega }$
in
![]() $\widetilde {F}$
. Since
$\widetilde {F}$
. Since
![]() $Z(F_{\omega })=\{\operatorname {\mathrm {id}}\}$
, we have
$Z(F_{\omega })=\{\operatorname {\mathrm {id}}\}$
, we have
![]() $F_{\omega }\cap K=\{\operatorname {\mathrm {id}}\}$
. Hence,
$F_{\omega }\cap K=\{\operatorname {\mathrm {id}}\}$
. Hence,
![]() $\smash {F_{\omega }K\unlhd \widetilde {F}}$
. Next, consider
$\smash {F_{\omega }K\unlhd \widetilde {F}}$
. Next, consider
![]() $\smash {\widetilde {F}/(F_{\omega }K)\lesssim \mathrm {Out}(F_{\omega })}$
. By the solution of Schreier’s conjecture,
$\smash {\widetilde {F}/(F_{\omega }K)\lesssim \mathrm {Out}(F_{\omega })}$
. By the solution of Schreier’s conjecture,
![]() $\mathrm {Out}(F_{\omega })$
is solvable. Since
$\mathrm {Out}(F_{\omega })$
is solvable. Since
![]() $\smash {\widetilde {F}/F_{\omega }\cong F}$
is not solvable we conclude
$\smash {\widetilde {F}/F_{\omega }\cong F}$
is not solvable we conclude
![]() $K\neq \{\operatorname {\mathrm {id}}\}$
. Now, by a theorem of Burnside, every
$K\neq \{\operatorname {\mathrm {id}}\}$
. Now, by a theorem of Burnside, every
![]() $2$
-transitive permutation group F is either almost simple or of affine type; see [Reference Dixon and Mortimer6, Theorem 4.1B and Section 4.8].
$2$
-transitive permutation group F is either almost simple or of affine type; see [Reference Dixon and Mortimer6, Theorem 4.1B and Section 4.8].
In the first case, F is actually simple: Let
![]() $N\unlhd F$
. Then
$N\unlhd F$
. Then
![]() $F_{\omega }\cap N\unlhd F_{\omega }$
. Hence, either
$F_{\omega }\cap N\unlhd F_{\omega }$
. Hence, either
![]() $F_{\omega }\cap N=\{\operatorname {\mathrm {id}}\}$
or
$F_{\omega }\cap N=\{\operatorname {\mathrm {id}}\}$
or
![]() $F_{\omega }\cap N=F_{\omega }$
. Since F is
$F_{\omega }\cap N=F_{\omega }$
. Since F is
![]() $2$
-transitive and therefore primitive, every normal subgroup acts transitively. Hence, in the first case, N is regular, which contradicts F being almost simple. Thus the second case holds and
$2$
-transitive and therefore primitive, every normal subgroup acts transitively. Hence, in the first case, N is regular, which contradicts F being almost simple. Thus the second case holds and
![]() $N=NF_{\omega }=F$
. Now
$N=NF_{\omega }=F$
. Now
![]() $\smash {\widetilde {F}/F_{\omega }K}$
is a proper quotient of F and therefore trivial. We conclude that
$\smash {\widetilde {F}/F_{\omega }K}$
is a proper quotient of F and therefore trivial. We conclude that
![]() $\smash {\widetilde {F}=F_{\omega }K\cong F_{\omega }\times K}$
and
$\smash {\widetilde {F}=F_{\omega }K\cong F_{\omega }\times K}$
and
![]() $\smash {K\cong \widetilde {F}/F_{\omega }\cong F}$
.
$\smash {K\cong \widetilde {F}/F_{\omega }\cong F}$
.
In the second case,
![]() $\smash {F=F_{\omega }\ltimes C_{p}^{d}}$
for some
$\smash {F=F_{\omega }\ltimes C_{p}^{d}}$
for some
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}$
and prime p. Given that K is nontrivial and
$d\in \operatorname {\mathrm {\mathbb {N}}}$
and prime p. Given that K is nontrivial and
![]() , it contains the unique minimal normal subgroup
, it contains the unique minimal normal subgroup
![]() . Since
. Since
![]() $F/C_{p}^{d}\cong F_{\omega }$
is nonabelian simple whereas the proper quotient
$F/C_{p}^{d}\cong F_{\omega }$
is nonabelian simple whereas the proper quotient
![]() $\smash {\widetilde {F}/F_{\omega }K}$
of F is solvable,
$\smash {\widetilde {F}/F_{\omega }K}$
of F is solvable,
![]() $\smash {K\neq C_{p}^{d}}$
. But
$\smash {K\neq C_{p}^{d}}$
. But
![]() $\smash {F/C_{p}^{d}\cong F_{\omega }}$
is simple, so
$\smash {F/C_{p}^{d}\cong F_{\omega }}$
is simple, so
![]() $\smash {\smash {F_{\omega }K=\widetilde {F}}}$
.
$\smash {\smash {F_{\omega }K=\widetilde {F}}}$
.
The following propositions are of independent interest and used in Theorem 4.32 below. We introduce the following notation. Let
![]() $\smash {\widetilde {F}\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})}$
and
$\smash {\widetilde {F}\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})}$
and
![]() $\smash {K\le \widetilde {F}_{b_{\xi }}}$
for some
$\smash {K\le \widetilde {F}_{b_{\xi }}}$
for some
![]() $\xi =(\omega _{1},\ldots ,\omega _{k-1})\in \Omega ^{(k-1)}$
. We set
$\xi =(\omega _{1},\ldots ,\omega _{k-1})\in \Omega ^{(k-1)}$
. We set
![]() $\smash {\pi _{\xi }K:=\sigma _{1}(K,b_{\xi })\le \operatorname {\mathrm {Sym}}(\Omega )_{\omega _{k-1}}}$
.
$\smash {\pi _{\xi }K:=\sigma _{1}(K,b_{\xi })\le \operatorname {\mathrm {Sym}}(\Omega )_{\omega _{k-1}}}$
.
Proposition 4.30. Let
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C). Suppose
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C). Suppose
![]() $\smash {F:=\pi \widetilde {F}}$
is transitive. Further, let
$\smash {F:=\pi \widetilde {F}}$
is transitive. Further, let
![]() $\omega \!\in \!\Omega $
and
$\omega \!\in \!\Omega $
and
![]() $\xi \!=\!(\omega _{1},\ldots ,\omega _{k-1})\!\in \!\Omega ^{(k-1)}$
with
$\xi \!=\!(\omega _{1},\ldots ,\omega _{k-1})\!\in \!\Omega ^{(k-1)}$
with
![]() $\omega _{1}\!\neq \!\omega $
. Then
$\omega _{1}\!\neq \!\omega $
. Then
![]() $\smash {\pi _{\xi }(\widetilde {F}_{b_{\xi }}\!\cap \ker \pi )}$
and
$\smash {\pi _{\xi }(\widetilde {F}_{b_{\xi }}\!\cap \ker \pi )}$
and
![]() $\smash {\pi _{\xi }\widetilde {F}_{T_{\omega }}}$
are subnormal in
$\smash {\pi _{\xi }\widetilde {F}_{T_{\omega }}}$
are subnormal in
![]() $F_{\omega _{k-1}}$
of depth at most
$F_{\omega _{k-1}}$
of depth at most
![]() $k-1$
and k, respectively.
$k-1$
and k, respectively.
Proof. We argue by induction on
![]() $k\!\ge \! 2$
. For
$k\!\ge \! 2$
. For
![]() $k\!=\!2$
, the assertion that
$k\!=\!2$
, the assertion that
![]() $\smash {\pi _{\xi }(\widetilde {F}_{b_{\xi }}\cap \ker \pi )}$
is normal in
$\smash {\pi _{\xi }(\widetilde {F}_{b_{\xi }}\cap \ker \pi )}$
is normal in
![]() $F_{\omega _{1}}$
is a consequence of condition (C). Now, suppose
$F_{\omega _{1}}$
is a consequence of condition (C). Now, suppose
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k+1})}$
satisfies the assumptions, and let
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k+1})}$
satisfies the assumptions, and let
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $\xi =(\omega _{1},\ldots ,\omega _{k})\in \Omega ^{(k)}$
be such that
$\xi =(\omega _{1},\ldots ,\omega _{k})\in \Omega ^{(k)}$
be such that
![]() $\omega _{1}\!\neq \!\omega $
. Since
$\omega _{1}\!\neq \!\omega $
. Since
![]() $\smash {\widetilde {F}}$
satisfies (C), we have
$\smash {\widetilde {F}}$
satisfies (C), we have
![]() $\smash {\operatorname {\mathrm {pr}}_{\omega _{1}}(\widetilde {F}_{b_{\xi }}\cap \ker \pi )\unlhd (\pi _{k}\widetilde {F})_{b_{\xi '}}\cap \ker \pi }$
, where
$\smash {\operatorname {\mathrm {pr}}_{\omega _{1}}(\widetilde {F}_{b_{\xi }}\cap \ker \pi )\unlhd (\pi _{k}\widetilde {F})_{b_{\xi '}}\cap \ker \pi }$
, where
![]() $\xi ':=(\omega _{2},\ldots ,\omega _{k-1})$
and the right-hand-side
$\xi ':=(\omega _{2},\ldots ,\omega _{k-1})$
and the right-hand-side
![]() $\pi $
implicitly has domain
$\pi $
implicitly has domain
![]() $\smash {\pi _{k}\widetilde {F}}$
. Hence,
$\smash {\pi _{k}\widetilde {F}}$
. Hence,
by the induction hypothesis. The second assertion follows as
![]() $\smash {\widetilde {F}_{T_{\omega }}\unlhd \smash {\widetilde {F}_{b_{\xi }}\cap \ker \pi }}$
.
$\smash {\widetilde {F}_{T_{\omega }}\unlhd \smash {\widetilde {F}_{b_{\xi }}\cap \ker \pi }}$
.
Proposition 4.31. Let
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C) but not (D). Suppose
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfy (C) but not (D). Suppose
![]() $\smash {F:=\pi \widetilde {F}}$
is transitive, and every nontrivial subnormal subgroup of
$\smash {F:=\pi \widetilde {F}}$
is transitive, and every nontrivial subnormal subgroup of
![]() $F_{\omega }$
(
$F_{\omega }$
(
![]() $\omega \in \Omega $
) of depth at most
$\omega \in \Omega $
) of depth at most
![]() $k-1$
is transitive on
$k-1$
is transitive on
![]() $\Omega \backslash \{\omega \}$
. Then
$\Omega \backslash \{\omega \}$
. Then
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})}$
is locally k-transitive.
$\smash {\mathrm {U}_{k}(\widetilde {F})}$
is locally k-transitive.
Proof. We argue by induction on k. For
![]() $k=1$
, the assertion follows from transitivity of F. Now, let
$k=1$
, the assertion follows from transitivity of F. Now, let
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k+1})}$
satisfy (C) but not (D). Then the same holds for
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k+1})}$
satisfy (C) but not (D). Then the same holds for
![]() $\smash {F^{(k)}:=\pi _{k}\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
. Given
$\smash {F^{(k)}:=\pi _{k}\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
. Given
![]() $\smash {\widetilde {\xi },\widetilde {\xi }'\in \Omega ^{(k)}}$
, write
$\smash {\widetilde {\xi },\widetilde {\xi }'\in \Omega ^{(k)}}$
, write
![]() $\smash {\widetilde {\xi }=(\xi ,\omega )}$
and
$\smash {\widetilde {\xi }=(\xi ,\omega )}$
and
![]() $\smash {\widetilde {\xi }'=(\xi ',\omega ')}$
where
$\smash {\widetilde {\xi }'=(\xi ',\omega ')}$
where
![]() $\xi ,\xi '\in \Omega ^{(k-1)}$
and
$\xi ,\xi '\in \Omega ^{(k-1)}$
and
![]() $\omega ,\omega '\in \Omega $
. By the induction hypothesis, the group
$\omega ,\omega '\in \Omega $
. By the induction hypothesis, the group
![]() $\smash {F^{(k)}}$
acts transitively on
$\smash {F^{(k)}}$
acts transitively on
![]() $S(b,k)$
. Hence, using (C), there is
$S(b,k)$
. Hence, using (C), there is
![]() $\smash {g\in \widetilde {F}}$
such that
$\smash {g\in \widetilde {F}}$
such that
![]() $gb_{\xi }=b_{\xi '}$
. As
$gb_{\xi }=b_{\xi '}$
. As
![]() $\smash {\widetilde {F}}$
does not satisfy (D) the said transitivity further implies that
$\smash {\widetilde {F}}$
does not satisfy (D) the said transitivity further implies that
![]() $\smash {\pi _{\xi '}(\widetilde {F}_{b_{\xi '}}\cap \ker \pi ))}$
is nontrivial. By Proposition 4.30, it is also subnormal of depth at most
$\smash {\pi _{\xi '}(\widetilde {F}_{b_{\xi '}}\cap \ker \pi ))}$
is nontrivial. By Proposition 4.30, it is also subnormal of depth at most
![]() $k-1$
in
$k-1$
in
![]() $F_{\omega '}$
and thus transitive. Hence, there is
$F_{\omega '}$
and thus transitive. Hence, there is
![]() $\smash {g'\in \widetilde {F}_{b_{\xi '}}}$
with
$\smash {g'\in \widetilde {F}_{b_{\xi '}}}$
with
![]() $g'gb_{\,\widetilde {\xi }}=b_{\,\widetilde {\xi }'}$
.
$g'gb_{\,\widetilde {\xi }}=b_{\,\widetilde {\xi }'}$
.
The following theorem is closely related to [Reference Burger and Mozes2, Proposition 3.3.1].
Theorem 4.32. Let
![]() $F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be
$F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be
![]() $2$
-transitive and
$2$
-transitive and
![]() $F_{\omega }\ (\omega \!\in \!\Omega )$
simple nonabelian. Further, let
$F_{\omega }\ (\omega \!\in \!\Omega )$
simple nonabelian. Further, let
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
with
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
with
![]() $\smash {\pi \widetilde {F}=F}$
satisfy (C). Then
$\smash {\pi \widetilde {F}=F}$
satisfy (C). Then
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})}$
equals
$\smash {\mathrm {U}_{k}(\widetilde {F})}$
equals
Proof. Since
![]() $\mathrm {U}_{1}(F)=\mathrm {U}_{2}(\Phi (F))$
, we may assume
$\mathrm {U}_{1}(F)=\mathrm {U}_{2}(\Phi (F))$
, we may assume
![]() $k\ge 2$
. Given that
$k\ge 2$
. Given that
![]() $\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfies (C), so does the restriction
$\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
satisfies (C), so does the restriction
![]() $\smash {F^{(2)}:=\pi _{2}\widetilde {F}\le \Phi (F)\le \operatorname {\mathrm {Aut}}(B_{d,2})}$
. Consider the projection
$\smash {F^{(2)}:=\pi _{2}\widetilde {F}\le \Phi (F)\le \operatorname {\mathrm {Aut}}(B_{d,2})}$
. Consider the projection
![]() $\smash {\pi :F^{(2)}\twoheadrightarrow F}$
. We have
$\smash {\pi :F^{(2)}\twoheadrightarrow F}$
. We have
![]() $\ker \pi \le \prod _{\omega \in \Omega }F_{\omega }$
and
$\ker \pi \le \prod _{\omega \in \Omega }F_{\omega }$
and
![]() $\operatorname {\mathrm {pr}}_{\omega }\ker \pi \unlhd F_{\omega }$
for all
$\operatorname {\mathrm {pr}}_{\omega }\ker \pi \unlhd F_{\omega }$
for all
![]() $\omega \in \Omega $
by Proposition 4.30. Since
$\omega \in \Omega $
by Proposition 4.30. Since
![]() $F_{\omega }$
is simple,
$F_{\omega }$
is simple,
![]() $\smash {\ker \pi \unlhd F^{(2)}}$
and F is transitive, this implies that either
$\smash {\ker \pi \unlhd F^{(2)}}$
and F is transitive, this implies that either
![]() $\operatorname {\mathrm {pr}}_{\omega }\ker \pi =\{\operatorname {\mathrm {id}}\}$
for all
$\operatorname {\mathrm {pr}}_{\omega }\ker \pi =\{\operatorname {\mathrm {id}}\}$
for all
![]() $\omega \in \Omega $
or
$\omega \in \Omega $
or
![]() $\operatorname {\mathrm {pr}}_{\omega }\ker \pi =F_{\omega }$
for all
$\operatorname {\mathrm {pr}}_{\omega }\ker \pi =F_{\omega }$
for all
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
In the first case,
![]() $\smash {\pi :F^{(2)}\to F}$
is an isomorphism. Hence,
$\smash {\pi :F^{(2)}\to F}$
is an isomorphism. Hence,
![]() $\smash {F^{(2)}}$
satisfies (CD) and
$\smash {F^{(2)}}$
satisfies (CD) and
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})\!=\!\mathrm {U}_{2}(\Gamma _{1}(F))}$
for an involutive compatibility cocycle of F by Proposition 4.26.
$\smash {\mathrm {U}_{k}(\widetilde {F})\!=\!\mathrm {U}_{2}(\Gamma _{1}(F))}$
for an involutive compatibility cocycle of F by Proposition 4.26.
In the second case, fix
![]() $\omega _{0}\in \Omega $
. We have
$\omega _{0}\in \Omega $
. We have
![]() $\ker \pi \le \prod _{\omega \in \Omega }F_{\omega }\cong F_{\omega _{0}}^{d}$
by transitivity of F. Since
$\ker \pi \le \prod _{\omega \in \Omega }F_{\omega }\cong F_{\omega _{0}}^{d}$
by transitivity of F. Since
![]() $F_{\omega _{0}}$
is simple nonabelian, [Reference Radu23, Lemma 2.3] implies that the group
$F_{\omega _{0}}$
is simple nonabelian, [Reference Radu23, Lemma 2.3] implies that the group
![]() $\ker \pi $
is a product of subdiagonals preserved by the primitive action of F on the index set of
$\ker \pi $
is a product of subdiagonals preserved by the primitive action of F on the index set of
![]() $F_{\omega _{0}}^{d}$
. Hence, either there is just one block and
$F_{\omega _{0}}^{d}$
. Hence, either there is just one block and
![]() ${\ker\pi=\{(\text{id},(\alpha_{\omega}(a_{0}))_{\omega})\}}$
for some isomorphisms
${\ker\pi=\{(\text{id},(\alpha_{\omega}(a_{0}))_{\omega})\}}$
for some isomorphisms
![]() $\alpha _{\omega }:F_{\omega _{0}}\to F_{\omega }$
, or all blocks are singletons and
$\alpha _{\omega }:F_{\omega _{0}}\to F_{\omega }$
, or all blocks are singletons and
![]() $\smash {\ker \pi =\prod _{\omega \in \Omega }F_{\omega }\cong F_{\omega _{0}}^{d}}$
. In the first case, there is a compatibility cocycle z of F such that
$\smash {\ker \pi =\prod _{\omega \in \Omega }F_{\omega }\cong F_{\omega _{0}}^{d}}$
. In the first case, there is a compatibility cocycle z of F such that
![]() $F\cong \{(a,(z(a,\omega ))_{\omega })\mid a\in F\}\le F^{(2)}$
commutes with
$F\cong \{(a,(z(a,\omega ))_{\omega })\mid a\in F\}\le F^{(2)}$
commutes with
![]() $\ker \pi \le F^{(2)}$
by Lemma 4.29. Thus
$\ker \pi \le F^{(2)}$
by Lemma 4.29. Thus
![]() $F^{(2)}=\{a,(z(a,\omega )\alpha _{\omega }(a_{0}))_{\omega }\mid a\in F,\ a_{0}\in F_{\omega _{0}}\}$
. In particular,
$F^{(2)}=\{a,(z(a,\omega )\alpha _{\omega }(a_{0}))_{\omega }\mid a\in F,\ a_{0}\in F_{\omega _{0}}\}$
. In particular,
![]() $F^{(2)}$
satisfies (CD). Hence,
$F^{(2)}$
satisfies (CD). Hence,
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})=\mathrm {U}_{2}(\Delta (F))}$
.
$\smash {\mathrm {U}_{k}(\widetilde {F})=\mathrm {U}_{2}(\Delta (F))}$
.
When
![]() $\smash {\ker \pi \cong F_{\omega _{0}}^{d}}$
, we have
$\smash {\ker \pi \cong F_{\omega _{0}}^{d}}$
, we have
![]() $\smash {\mathrm {U}_{k}(\widetilde {F})=\mathrm {U}_{1}(F)}$
by [Reference Burger and Mozes2, Proposition 3.3.1].
$\smash {\mathrm {U}_{k}(\widetilde {F})=\mathrm {U}_{1}(F)}$
by [Reference Burger and Mozes2, Proposition 3.3.1].
If F does not have simple point-stabilizers or preserves a nontrivial partition, more universal groups are given by
![]() $\mathrm {U}_{2}(\Phi (F,N))$
and
$\mathrm {U}_{2}(\Phi (F,N))$
and
![]() $\mathrm {U}_{2}(\Phi (F,\operatorname {\mathrm {\mathcal {P}}}))$
; see Section 4.4.1. When F is
$\mathrm {U}_{2}(\Phi (F,\operatorname {\mathrm {\mathcal {P}}}))$
; see Section 4.4.1. When F is
![]() $2$
-transitive and has abelian point-stabilizers,
$2$
-transitive and has abelian point-stabilizers,
![]() $F\!\cong \!\operatorname {\mathrm {AGL}}(1,q)$
for some prime power q by [Reference Károlyi, Kovács and Pálfy14]. Hence, point-stabilizers in F are isomorphic to
$F\!\cong \!\operatorname {\mathrm {AGL}}(1,q)$
for some prime power q by [Reference Károlyi, Kovács and Pálfy14]. Hence, point-stabilizers in F are isomorphic to
![]() $\operatorname {\mathrm {\mathbb {F}}}_{q}^{\ast }$
and simple if and only if
$\operatorname {\mathrm {\mathbb {F}}}_{q}^{\ast }$
and simple if and only if
![]() $q-1$
is a Mersenne prime. For any value of q, the projection
$q-1$
is a Mersenne prime. For any value of q, the projection
![]() $\rho :\operatorname {\mathrm {AGL}}(1,q)\to \operatorname {\mathrm {\mathbb {F}}}_{q}^{\ast }$
satisfies the assumptions of Proposition 4.28 and so the groups
$\rho :\operatorname {\mathrm {AGL}}(1,q)\to \operatorname {\mathrm {\mathbb {F}}}_{q}^{\ast }$
satisfies the assumptions of Proposition 4.28 and so the groups
![]() $\smash {\mathrm {U}_{k}(\Pi ^{k}(\operatorname {\mathrm {AGL}}(1,q),\rho ,X))}$
provide further examples. The following question remains.
$\smash {\mathrm {U}_{k}(\Pi ^{k}(\operatorname {\mathrm {AGL}}(1,q),\rho ,X))}$
provide further examples. The following question remains.
Question 4.33. Let
![]() $F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be primitive and
$F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be primitive and
![]() $F_{\omega } (\omega \in \Omega )$
simple nonabelian. Is there
$F_{\omega } (\omega \in \Omega )$
simple nonabelian. Is there
![]() $\smash {\widetilde {F}\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})}$
with (C) and
$\smash {\widetilde {F}\!\le \!\operatorname {\mathrm {Aut}}(B_{d,k})}$
with (C) and
![]() $\pi \widetilde {F}\!=\!F$
other than
$\pi \widetilde {F}\!=\!F$
other than
![]() $\Gamma ^{k}(F)$
,
$\Gamma ^{k}(F)$
,
![]() $\Delta (F)$
and
$\Delta (F)$
and
![]() $\Phi ^{k}(F)$
?
$\Phi ^{k}(F)$
?
4.5 Universality
The constructed groups
![]() $\mathrm {U}_{k}(F)$
are universal in the sense of the following maximality statement, which should be compared to Proposition 2.6.
$\mathrm {U}_{k}(F)$
are universal in the sense of the following maximality statement, which should be compared to Proposition 2.6.
Theorem 4.34. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and contain an involutive inversion. Then there is a labelling l of
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and contain an involutive inversion. Then there is a labelling l of
![]() $T_{d}$
such that
$T_{d}$
such that
where
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
is action isomorphic to the k-local action of H.
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
is action isomorphic to the k-local action of H.
Proof. First, we construct a labelling l of
![]() $T_{d}$
such that
$T_{d}$
such that
![]() $H\ge \mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})$
. Fix
$H\ge \mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})$
. Fix
![]() $x\in V$
and choose a bijection
$x\in V$
and choose a bijection
![]() $l_{x}:E(x)\to \Omega $
. By the assumptions, there is an involutive inversion
$l_{x}:E(x)\to \Omega $
. By the assumptions, there is an involutive inversion
![]() $\iota _{\omega }\in H$
of the edge
$\iota _{\omega }\in H$
of the edge
![]() $(x,x_{\omega })\in E$
for every
$(x,x_{\omega })\in E$
for every
![]() $\omega \in \Omega $
. Using these inversions, we define the announced labelling inductively. Set
$\omega \in \Omega $
. Using these inversions, we define the announced labelling inductively. Set
![]() $l|_{E(x)}:=l_{x}$
and assume that l is defined on
$l|_{E(x)}:=l_{x}$
and assume that l is defined on
![]() $E(x,n)$
. For
$E(x,n)$
. For
![]() $e\in E(x,n+1)\backslash E(x,n)$
put
$e\in E(x,n+1)\backslash E(x,n)$
put
![]() $l(e):=l(\iota _{\omega }(e))$
if
$l(e):=l(\iota _{\omega }(e))$
if
![]() $x_{\omega }$
is part of the unique reduced path from x to
$x_{\omega }$
is part of the unique reduced path from x to
![]() $o(e)$
. Since the
$o(e)$
. Since the
![]() $\iota _{\omega }\ (\omega \in \Omega )$
have order
$\iota _{\omega }\ (\omega \in \Omega )$
have order
![]() $2$
, we obtain
$2$
, we obtain
![]() $\sigma _{1}(\iota _{\omega },y)=\operatorname {\mathrm {id}}$
for all
$\sigma _{1}(\iota _{\omega },y)=\operatorname {\mathrm {id}}$
for all
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $y\in V$
. Therefore,
$y\in V$
. Therefore,
![]() $\smash {\langle \{\iota _{\omega }\mid \omega \in \Omega \}\rangle =\mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})\le H}$
, following the proof of Lemma 2.5.
$\smash {\langle \{\iota _{\omega }\mid \omega \in \Omega \}\rangle =\mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})\le H}$
, following the proof of Lemma 2.5.
Now, let
![]() $h\in H$
and
$h\in H$
and
![]() $y\in V$
. Further, let
$y\in V$
. Further, let
![]() $(x,x_{1},\ldots ,x_{n},y)$
and
$(x,x_{1},\ldots ,x_{n},y)$
and
![]() $(x,x_{1}',\ldots ,x_{m}',h(y))$
be the unique reduced paths from x to y and
$(x,x_{1}',\ldots ,x_{m}',h(y))$
be the unique reduced paths from x to y and
![]() $h(y)$
, respectively. Since
$h(y)$
, respectively. Since
![]() $\smash {\mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})}\le H$
, the group H contains the unique label-respecting inversion
$\smash {\mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})}\le H$
, the group H contains the unique label-respecting inversion
![]() $\iota _{e}$
of every edge
$\iota _{e}$
of every edge
![]() $e\in E$
. We therefore have
$e\in E$
. We therefore have
Also, s stabilizes x. The cocycle identity implies for every
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
that
$k\in \operatorname {\mathrm {\mathbb {N}}}$
that
where
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
is defined by
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
is defined by
![]() $l_{x}^{k}\circ H_{x}|_{B(x,k)}\circ (l_{x}^{k})^{-1}$
.
$l_{x}^{k}\circ H_{x}|_{B(x,k)}\circ (l_{x}^{k})^{-1}$
.
Remark 4.35. Retain the notation of Theorem 4.34. By Proposition 2.6, there is a labelling l of
![]() $T_{d}$
such that
$T_{d}$
such that
![]() $\smash {\mathrm {U}_{1}^{(l)}(F^{(1)})\ge H}$
regardless of the minimal order of an inversion in H. This labelling may be distinct from that of Theorem 4.34 which fails without assuming the existence of an involutive inversion. For example, a vertex-stabilizer of the group
$\smash {\mathrm {U}_{1}^{(l)}(F^{(1)})\ge H}$
regardless of the minimal order of an inversion in H. This labelling may be distinct from that of Theorem 4.34 which fails without assuming the existence of an involutive inversion. For example, a vertex-stabilizer of the group
![]() $G_{2}^{1}$
of Example 5.39 below is action isomorphic to
$G_{2}^{1}$
of Example 5.39 below is action isomorphic to
![]() $\Gamma (S_{3})$
but
$\Gamma (S_{3})$
but
![]() $\smash {G_{2}^{1}\not \le \mathrm {U}_{2}^{(l)}(\Gamma (S_{3}))}$
for any labelling l because
$\smash {G_{2}^{1}\not \le \mathrm {U}_{2}^{(l)}(\Gamma (S_{3}))}$
for any labelling l because
![]() $(G_{2}^{1})_{\{b,b_{\omega }\}}\cong \operatorname {\mathrm {\mathbb {Z}}}/4\operatorname {\mathrm {\mathbb {Z}}}$
, whereas
$(G_{2}^{1})_{\{b,b_{\omega }\}}\cong \operatorname {\mathrm {\mathbb {Z}}}/4\operatorname {\mathrm {\mathbb {Z}}}$
, whereas
by Proposition 4.14.
We complement Theorem 4.34 with the following criterion for certain subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
to contain an involutive inversion.
$\operatorname {\mathrm {Aut}}(T_{d})$
to contain an involutive inversion.
Proposition 4.36. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive with odd-order point-stabilizers. If H contains a finite-order inversion then it contains an involutive one.
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive with odd-order point-stabilizers. If H contains a finite-order inversion then it contains an involutive one.
Proof. Let
![]() $\iota \in H$
be a finite-order inversion of an edge
$\iota \in H$
be a finite-order inversion of an edge
![]() $e\in E$
and
$e\in E$
and
![]() $\mathrm {ord}(\iota )=2^{k}\cdot m$
for some odd
$\mathrm {ord}(\iota )=2^{k}\cdot m$
for some odd
![]() $m\in \operatorname {\mathrm {\mathbb {N}}}$
and some
$m\in \operatorname {\mathrm {\mathbb {N}}}$
and some
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
. It suffices to show that
$k\in \operatorname {\mathrm {\mathbb {N}}}$
. It suffices to show that
![]() $k=1$
, in which case
$k=1$
, in which case
![]() $\iota ^{m}$
is an involutive inversion. Suppose
$\iota ^{m}$
is an involutive inversion. Suppose
![]() $k\ge 1$
. Then
$k\ge 1$
. Then
![]() $\smash {\iota ^{2^{k-1}\cdot m}}$
is nontrivial and fixes the edge e. Because point-stabilizers in the local action of H have odd order, it follows that
$\smash {\iota ^{2^{k-1}\cdot m}}$
is nontrivial and fixes the edge e. Because point-stabilizers in the local action of H have odd order, it follows that
![]() $\smash {(\iota ^{2^{k-1}\cdot m})^{2}}$
is nontrivial as well, but
$\smash {(\iota ^{2^{k-1}\cdot m})^{2}}$
is nontrivial as well, but
![]() $\smash {(\iota ^{2^{k-1}\cdot m})^{2}=\iota ^{\mathrm {ord}(\iota )}=\operatorname {\mathrm {id}}}$
.
$\smash {(\iota ^{2^{k-1}\cdot m})^{2}=\iota ^{\mathrm {ord}(\iota )}=\operatorname {\mathrm {id}}}$
.
For example, Proposition 4.36 applies when H is discrete and vertex-transitive: Combined with local transitivity this implies the existence of a finite-order inversion.
We remark that primitive permutation groups with odd-order point-stabilizers were classified in [Reference Liebeck and Saxl17]. For instance, they include
![]() $\mathrm {PSL}(2,q)\curvearrowright \mathrm {P}^{1}(\operatorname {\mathrm {\mathbb {F}}}_{q})$
for any prime power q that satisfies
$\mathrm {PSL}(2,q)\curvearrowright \mathrm {P}^{1}(\operatorname {\mathrm {\mathbb {F}}}_{q})$
for any prime power q that satisfies
![]() $q\equiv 3\ \mathrm {mod}\ 4$
.
$q\equiv 3\ \mathrm {mod}\ 4$
.
4.6 A bipartite version
In this section we introduce a bipartite version of the universal groups developed above which plays a critical role in the proof of Theorem 5.2(iv)(b). As before, let
![]() $T_{d}=(V,E)$
denote the d-regular tree. Fix a regular bipartition
$T_{d}=(V,E)$
denote the d-regular tree. Fix a regular bipartition
![]() $V=V_{1}\sqcup V_{2}$
of
$V=V_{1}\sqcup V_{2}$
of
![]() $T_{d}$
.
$T_{d}$
.
4.6.1 Definition and basic properties
The groups to be defined are subgroups of
![]() $^{+}{\operatorname {\mathrm {Aut}}(T_{d})}{}\le \operatorname {\mathrm {Aut}}(T_{d})$
, the maximal subgroup of
$^{+}{\operatorname {\mathrm {Aut}}(T_{d})}{}\le \operatorname {\mathrm {Aut}}(T_{d})$
, the maximal subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
preserving the bipartition
$\operatorname {\mathrm {Aut}}(T_{d})$
preserving the bipartition
![]() $V=V_{1}\sqcup V_{2}$
. Alternatively, it can be described as the subgroup generated by all point-stabilizers, or all edge-stabilizers.
$V=V_{1}\sqcup V_{2}$
. Alternatively, it can be described as the subgroup generated by all point-stabilizers, or all edge-stabilizers.
Definition 4.37. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
and l be a labelling of
$F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
and l be a labelling of
![]() $T_{d}$
. Define
$T_{d}$
. Define
Note that
![]() $\mathrm {BU}_{2k}^{(l)}(F)$
is a subgroup of
$\mathrm {BU}_{2k}^{(l)}(F)$
is a subgroup of
![]() thanks to Lemma 4.2 and the assumption that it is a subset of
thanks to Lemma 4.2 and the assumption that it is a subset of
![]() . Further, Proposition 4.4 carries over to the groups
. Further, Proposition 4.4 carries over to the groups
![]() $\smash {\mathrm {BU}_{2k}^{(l)}(F)}$
. We therefore omit the reference to an explicit labelling in the following. Also, we recover the following basic properties.
$\smash {\mathrm {BU}_{2k}^{(l)}(F)}$
. We therefore omit the reference to an explicit labelling in the following. Also, we recover the following basic properties.
Proposition 4.38. Let
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
. The group
$F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
. The group
![]() $\mathrm {BU}_{2k}(F)$
is
$\mathrm {BU}_{2k}(F)$
is
-
(i) closed in
 $\operatorname {\mathrm {Aut}}(T_{d})$
$\operatorname {\mathrm {Aut}}(T_{d})$
-
(ii) transitive on both
 $V_{1}$
and
$V_{1}$
and
 $V_{2}$
, and
$V_{2}$
, and -
(iii) compactly generated.
Parts (i) and (ii) are proven as their analogues in Proposition 4.5, whereas part (iii) relies on part (ii) and the subsequent analogue of Lemma 2.5, for which we introduce the following notation: Given
![]() $x\in V$
and
$x\in V$
and
![]() $\smash {\xi \in \Omega ^{(2k)}}$
, let
$\smash {\xi \in \Omega ^{(2k)}}$
, let
![]() $\smash {t_{\xi }^{(x)}\in \mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})}$
denote the unique label-respecting translation with
$\smash {t_{\xi }^{(x)}\in \mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})}$
denote the unique label-respecting translation with
![]() $\smash {t_{\xi }^{(x)}(x)=x_{\xi }}$
. Given an element
$\smash {t_{\xi }^{(x)}(x)=x_{\xi }}$
. Given an element
![]() $\smash {\xi =(\omega _{1},\ldots ,\omega _{2k})\in \Omega ^{(2k)}}$
, we set
$\smash {\xi =(\omega _{1},\ldots ,\omega _{2k})\in \Omega ^{(2k)}}$
, we set
![]() $\smash {\overline {\xi }:=(\omega _{2k},\ldots ,\omega _{1})\in \Omega ^{(2k)}}$
. Then
$\smash {\overline {\xi }:=(\omega _{2k},\ldots ,\omega _{1})\in \Omega ^{(2k)}}$
. Then
![]() $\smash {(t_{\xi }^{(x)})^{-1}=t_{\overline {\xi }}^{(x)}}$
, and if
$\smash {(t_{\xi }^{(x)})^{-1}=t_{\overline {\xi }}^{(x)}}$
, and if
![]() $\smash {\Omega _{+}^{(2k)}\subseteq \Omega ^{(2k)}}$
is such that for every
$\smash {\Omega _{+}^{(2k)}\subseteq \Omega ^{(2k)}}$
is such that for every
![]() $\smash {\xi \in \Omega ^{(2k)}}$
exactly one of
$\smash {\xi \in \Omega ^{(2k)}}$
exactly one of
![]() $\{\xi ,\overline {\xi }\}$
belongs to
$\{\xi ,\overline {\xi }\}$
belongs to
![]() $\smash {\Omega _{+}^{(2k)}}$
, then
$\smash {\Omega _{+}^{(2k)}}$
, then
![]() $\smash {\Omega _{+}^{(2k)}=\Omega _{+}^{(2k)}\sqcup \overline {\Omega }_{+}^{(2k)}}$
where
$\smash {\Omega _{+}^{(2k)}=\Omega _{+}^{(2k)}\sqcup \overline {\Omega }_{+}^{(2k)}}$
where
![]() $\smash {\overline {\Omega }_{+}^{(2k)}:=\{\overline {\xi }\mid \xi \in \Omega _{+}^{(2k)}\}}$
.
$\smash {\overline {\Omega }_{+}^{(2k)}:=\{\overline {\xi }\mid \xi \in \Omega _{+}^{(2k)}\}}$
.
Lemma 4.39. Let
![]() $x\in V_{1}$
. Then
$x\in V_{1}$
. Then
![]() $\smash {\mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})=\langle \{t_{\xi }^{(x)}\mid \xi \in \Omega ^{(2)}\}\rangle \cong F_{\Omega _{+}^{(2)}}}$
, the free group on the set
$\smash {\mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})=\langle \{t_{\xi }^{(x)}\mid \xi \in \Omega ^{(2)}\}\rangle \cong F_{\Omega _{+}^{(2)}}}$
, the free group on the set
![]() $\smash {\Omega _{+}^{(2)}}$
.
$\smash {\Omega _{+}^{(2)}}$
.
Proof. Every element of
![]() $\mathrm {BU}_{2k}(\{\operatorname {\mathrm {id}}\})$
is uniquely determined by its image on x. To see that
$\mathrm {BU}_{2k}(\{\operatorname {\mathrm {id}}\})$
is uniquely determined by its image on x. To see that
![]() $\smash {\mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})=\langle \{t_{\xi }^{(x)}\mid \xi \in \Omega ^{(2)}\}\rangle }$
it thus suffices to show that
$\smash {\mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})=\langle \{t_{\xi }^{(x)}\mid \xi \in \Omega ^{(2)}\}\rangle }$
it thus suffices to show that
![]() $\smash {\{t_{\xi }^{(x)}\!\mid \! \xi \!\in \!\Omega ^{(2)}\}}$
is transitive on
$\smash {\{t_{\xi }^{(x)}\!\mid \! \xi \!\in \!\Omega ^{(2)}\}}$
is transitive on
![]() $V_{1}$
. Indeed, let
$V_{1}$
. Indeed, let
![]() $y\in V_{1}$
. Then
$y\in V_{1}$
. Then
![]() $y=x_{\xi }$
for some
$y=x_{\xi }$
for some
![]() $\xi \in \Omega ^{(2k)}$
where
$\xi \in \Omega ^{(2k)}$
where
![]() $2k=d(x,y)$
. Write
$2k=d(x,y)$
. Write
![]() $\xi =(\xi _{1},\ldots ,\xi _{k})\in (\Omega ^{(2)})^{k}$
. Then
$\xi =(\xi _{1},\ldots ,\xi _{k})\in (\Omega ^{(2)})^{k}$
. Then
![]() $\smash {t_{\xi _{1}}^{(x)}\circ \cdots \circ t_{\xi _{k}}^{(x)}=t_{\xi }^{(x)}}$
as every
$\smash {t_{\xi _{1}}^{(x)}\circ \cdots \circ t_{\xi _{k}}^{(x)}=t_{\xi }^{(x)}}$
as every
![]() $\smash {t_{\xi _{i}}^{(x)}}\ (i\in \{1,\ldots ,k\})$
is label respecting. Hence,
$\smash {t_{\xi _{i}}^{(x)}}\ (i\in \{1,\ldots ,k\})$
is label respecting. Hence,
![]() $\smash {t_{\xi _{1}}^{(x)}\circ \cdots \circ t_{\xi _{k}}^{(x)}(x)=y}$
and
$\smash {t_{\xi _{1}}^{(x)}\circ \cdots \circ t_{\xi _{k}}^{(x)}(x)=y}$
and
 $$ \begin{align*} \langle\{t_{\xi}^{(x)}\!\mid\! \xi\in\Omega^{(2)}\}\rangle\to F_{\Omega_{+}^{(2)}},\quad \begin{cases}t_{\xi}^{(x)}\mapsto \xi & \xi\in\Omega_{+}^{(2)} \\ t_{\xi}^{(x)}\mapsto \overline{\xi}^{-1} & \xi\not\in\Omega_{+}^{(2)}\end{cases} \end{align*} $$
$$ \begin{align*} \langle\{t_{\xi}^{(x)}\!\mid\! \xi\in\Omega^{(2)}\}\rangle\to F_{\Omega_{+}^{(2)}},\quad \begin{cases}t_{\xi}^{(x)}\mapsto \xi & \xi\in\Omega_{+}^{(2)} \\ t_{\xi}^{(x)}\mapsto \overline{\xi}^{-1} & \xi\not\in\Omega_{+}^{(2)}\end{cases} \end{align*} $$
yields a well-defined isomorphism.
4.6.2 Compatibility and discreteness
In order to describe the compatibility and the discreteness condition in the bipartite setting, we first introduce a suitable realization of
![]() $\operatorname {\mathrm {Aut}}(B_{d,2k}) \ (k\in \operatorname {\mathrm {\mathbb {N}}})$
, similar to that at the beginning of Section 4.4. Let
$\operatorname {\mathrm {Aut}}(B_{d,2k}) \ (k\in \operatorname {\mathrm {\mathbb {N}}})$
, similar to that at the beginning of Section 4.4. Let
![]() $\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
and
$\operatorname {\mathrm {Aut}}(B_{d,1})\cong \operatorname {\mathrm {Sym}}(\Omega )$
and
![]() $\operatorname {\mathrm {Aut}}(B_{d,2})$
be as before. For
$\operatorname {\mathrm {Aut}}(B_{d,2})$
be as before. For
![]() $k\ge 2$
, we inductively identify
$k\ge 2$
, we inductively identify
![]() $\operatorname {\mathrm {Aut}}(B_{d,2k})$
with its image under
$\operatorname {\mathrm {Aut}}(B_{d,2k})$
with its image under
 $$ \begin{align*} \operatorname{\mathrm{Aut}}(B_{d,2k})&\to\operatorname{\mathrm{Aut}}(B_{d,2(k-1)})\ltimes\prod_{\xi\in\Omega^{(2)}}\operatorname{\mathrm{Aut}}(B_{d,2(k-1)}) \\ \alpha&\mapsto(\sigma_{2(k-1)}(\alpha,b),(\sigma_{2(k-1)}(\alpha,b_{\xi}))_{\xi}) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Aut}}(B_{d,2k})&\to\operatorname{\mathrm{Aut}}(B_{d,2(k-1)})\ltimes\prod_{\xi\in\Omega^{(2)}}\operatorname{\mathrm{Aut}}(B_{d,2(k-1)}) \\ \alpha&\mapsto(\sigma_{2(k-1)}(\alpha,b),(\sigma_{2(k-1)}(\alpha,b_{\xi}))_{\xi}) \end{align*} $$
where
![]() $\operatorname {\mathrm {Aut}}(B_{d,2(k-1)})$
acts on
$\operatorname {\mathrm {Aut}}(B_{d,2(k-1)})$
acts on
![]() $\Omega ^{(2)}$
by permuting the factors according to its action on
$\Omega ^{(2)}$
by permuting the factors according to its action on
![]() $\smash {S(b,2)\cong \Omega ^{(2)}}$
. In addition, consider the map
$\smash {S(b,2)\cong \Omega ^{(2)}}$
. In addition, consider the map
![]() $\operatorname {\mathrm {pr}}_{\xi }:\operatorname {\mathrm {Aut}}(B_{d,2k})\to \operatorname {\mathrm {Aut}}(B_{d,2(k-1)})$
,
$\operatorname {\mathrm {pr}}_{\xi }:\operatorname {\mathrm {Aut}}(B_{d,2k})\to \operatorname {\mathrm {Aut}}(B_{d,2(k-1)})$
,
![]() $\alpha \mapsto \sigma _{2(k-1)}(\alpha ,b_{\xi })$
for every
$\alpha \mapsto \sigma _{2(k-1)}(\alpha ,b_{\xi })$
for every
![]() $\smash {\xi \in \Omega ^{(2)}}$
, as well as
$\smash {\xi \in \Omega ^{(2)}}$
, as well as
For
![]() $k\ge 2$
, conditions (C) and (D) for
$k\ge 2$
, conditions (C) and (D) for
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
now read as follows:
$F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
now read as follows:
 $$ \begin{align} &\text{for all }\alpha\in F,\ \text{ for all } \xi\in\Omega^{(2)}: \text{there exists } \alpha_{\xi}\in F:\nonumber \\ &\quad\pi_{2(k-1)}(\alpha_{\xi})=\operatorname{\mathrm{pr}}_{\xi}(\alpha),\ \operatorname{\mathrm{pr}}_{\overline{\xi}}(\alpha_{\xi})=\pi_{2(k-1)}(\alpha); \end{align} $$
$$ \begin{align} &\text{for all }\alpha\in F,\ \text{ for all } \xi\in\Omega^{(2)}: \text{there exists } \alpha_{\xi}\in F:\nonumber \\ &\quad\pi_{2(k-1)}(\alpha_{\xi})=\operatorname{\mathrm{pr}}_{\xi}(\alpha),\ \operatorname{\mathrm{pr}}_{\overline{\xi}}(\alpha_{\xi})=\pi_{2(k-1)}(\alpha); \end{align} $$
For
![]() $k=1$
we have, using the maps
$k=1$
we have, using the maps
![]() $\operatorname {\mathrm {pr}}_{\omega }$
(
$\operatorname {\mathrm {pr}}_{\omega }$
(
![]() $\omega \in \Omega $
) as in Section 4.4,
$\omega \in \Omega $
) as in Section 4.4,
Analogues of Proposition 4.12 are proven using the discreteness conditions (D) above. We do not introduce new notation for any of the above as the context always implies which condition is to be considered. The definition of the compatibility sets
![]() $C_{F}(\alpha ,S)$
for
$C_{F}(\alpha ,S)$
for
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
and
$F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
and
![]() $\smash {S\subseteq \Omega ^{(2)}}$
carries over from Section 4.2 in a straightforward fashion.
$\smash {S\subseteq \Omega ^{(2)}}$
carries over from Section 4.2 in a straightforward fashion.
4.6.3 Examples
Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Then the group
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Then the group
![]() $\Gamma (F)\le \operatorname {\mathrm {Aut}}(B_{d,2})$
introduced in Section 4.4.1 satisfies conditions (C) and (D) for the case
$\Gamma (F)\le \operatorname {\mathrm {Aut}}(B_{d,2})$
introduced in Section 4.4.1 satisfies conditions (C) and (D) for the case
![]() $k=1$
above, and we have
$k=1$
above, and we have
![]() .
.
Similarly, the group
![]() $\Phi (F)\le \operatorname {\mathrm {Aut}}(B_{d,2})$
satisfies condition (C) for the case
$\Phi (F)\le \operatorname {\mathrm {Aut}}(B_{d,2})$
satisfies condition (C) for the case
![]() $k=1$
as
$k=1$
as
![]() $\Gamma (F)\le \Phi (F)$
, and we have
$\Gamma (F)\le \Phi (F)$
, and we have
![]() .
.
The following example gives an analogue of the groups
![]() $\Phi (F,N)$
. Notice, however, that in this case the second argument is a subgroup of F rather than
$\Phi (F,N)$
. Notice, however, that in this case the second argument is a subgroup of F rather than
![]() $F_{\omega _{0}}$
and need not be normal, as the
$F_{\omega _{0}}$
and need not be normal, as the
![]() $1$
-local action at vertices in
$1$
-local action at vertices in
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
need not be the same.
$V_{2}$
need not be the same.
Example 4.40. Let
![]() $F'\le F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Then
$F'\le F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Then
satisfies condition (C) for the case
![]() $k=1$
above, given that
$k=1$
above, given that
![]() $\Gamma (F')\le \mathrm {B}\Phi (F,F')$
. If
$\Gamma (F')\le \mathrm {B}\Phi (F,F')$
. If
![]() $F'\backslash \Omega =F\backslash \Omega $
, the
$F'\backslash \Omega =F\backslash \Omega $
, the
![]() $1$
-local action of
$1$
-local action of
![]() $\mathrm {B}\Phi (F,F')$
at vertices in
$\mathrm {B}\Phi (F,F')$
at vertices in
![]() $V_{1}$
is indeed F, whereas it is
$V_{1}$
is indeed F, whereas it is
![]() $F^{\prime +}$
at vertices in
$F^{\prime +}$
at vertices in
![]() $V_{2}$
. This construction is similar to
$V_{2}$
. This construction is similar to
![]() $\operatorname {\mathrm {\mathcal {U}}}_{\operatorname {\mathrm {\mathcal {L}}}}(M,N)$
in [Reference Smith27].
$\operatorname {\mathrm {\mathcal {U}}}_{\operatorname {\mathrm {\mathcal {L}}}}(M,N)$
in [Reference Smith27].
The next example constitutes the base case in Section 5.1.5 below.
Example 4.41. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Suppose F preserves a nontrivial partition
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Suppose F preserves a nontrivial partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
. Then
$\Omega $
. Then
is preserved by the action of
![]() $\Phi (F)$
on
$\Phi (F)$
on
![]() $S(b,2)\cong \Omega ^{(2)}$
. Let
$S(b,2)\cong \Omega ^{(2)}$
. Let
![]() $\alpha \!=\!(a,(a_{\omega })_{\omega })\!\in \!\Phi (F)$
and
$\alpha \!=\!(a,(a_{\omega })_{\omega })\!\in \!\Phi (F)$
and
![]() $\smash {(\omega _{1},\omega _{2})\in \Omega ^{(2)}_{0}}$
. Then
$\smash {(\omega _{1},\omega _{2})\in \Omega ^{(2)}_{0}}$
. Then
![]() $\smash {\alpha (\omega _{1},\omega _{2})=(a\omega _{1},a_{\omega _{1}}\omega _{2})=(a_{\omega _{1}}\omega _{1},a_{\omega _{1}}\omega _{1})\in \Omega ^{(2)}_{0}}$
. Also, note that if
$\smash {\alpha (\omega _{1},\omega _{2})=(a\omega _{1},a_{\omega _{1}}\omega _{2})=(a_{\omega _{1}}\omega _{1},a_{\omega _{1}}\omega _{1})\in \Omega ^{(2)}_{0}}$
. Also, note that if
![]() $\smash {\xi =(\omega _{1},\omega _{2})\in \Omega ^{(2)}_{0}}$
then also
$\smash {\xi =(\omega _{1},\omega _{2})\in \Omega ^{(2)}_{0}}$
then also
![]() $\overline {\xi }=(\omega _{2},\omega _{1})\in \Omega ^{(2)}_{0}$
.
$\overline {\xi }=(\omega _{2},\omega _{1})\in \Omega ^{(2)}_{0}$
.
The subgroup of
![]() $\Phi (F)$
consisting of those elements which are self-compatible in all directions from
$\Phi (F)$
consisting of those elements which are self-compatible in all directions from
![]() $\smash {\Omega ^{(2)}_{0}}$
is precisely given by
$\smash {\Omega ^{(2)}_{0}}$
is precisely given by
in view of condition (C) for the case
![]() $k=1$
above.
$k=1$
above.
Suppose now that
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
satisfies (C). Analogous to the group
$F\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
satisfies (C). Analogous to the group
![]() $\Phi _{k}(F)$
of Section 4.4.2, we define
$\Phi _{k}(F)$
of Section 4.4.2, we define
Then
![]() $\mathrm {B}\Phi _{2k}(F)\le \operatorname {\mathrm {Aut}}(B_{d,2(k+1)})$
satisfies (C) and
$\mathrm {B}\Phi _{2k}(F)\le \operatorname {\mathrm {Aut}}(B_{d,2(k+1)})$
satisfies (C) and
![]() $\mathrm {BU}_{2(k+1)}(\mathrm {B}\Phi _{2k}(F))=\mathrm {BU}_{2k}(F)$
. Given
$\mathrm {BU}_{2(k+1)}(\mathrm {B}\Phi _{2k}(F))=\mathrm {BU}_{2k}(F)$
. Given
![]() $l>k$
, we also set
$l>k$
, we also set
![]() $\mathrm {B}\Phi ^{2l}(F):=\mathrm {B}\Phi _{2(l-1)}\circ \cdots \circ \mathrm {B}\Phi _{2k}(F)$
; cf. Section 4.4.2.
$\mathrm {B}\Phi ^{2l}(F):=\mathrm {B}\Phi _{2(l-1)}\circ \cdots \circ \mathrm {B}\Phi _{2k}(F)$
; cf. Section 4.4.2.
5 Applications
In this section we give three applications of the framework of universal groups. First, we characterize the automorphism types that the quasicentre of a nondiscrete subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
may feature in terms of the group’s local action, and see that the Burger–Mozes theory does not extend to the transitive case. Second, we give an algebraic characterization of the
$\operatorname {\mathrm {Aut}}(T_{d})$
may feature in terms of the group’s local action, and see that the Burger–Mozes theory does not extend to the transitive case. Second, we give an algebraic characterization of the
![]() $(P_{k})$
-closures of locally transitive subgroups of
$(P_{k})$
-closures of locally transitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
containing an involutive inversion, and thereby partially answer two questions by Banks, Elder and Willis. Third, we offer a new view on the Weiss conjecture.
$\operatorname {\mathrm {Aut}}(T_{d})$
containing an involutive inversion, and thereby partially answer two questions by Banks, Elder and Willis. Third, we offer a new view on the Weiss conjecture.
5.1 Groups acting on trees with nontrivial quasicentre
By Proposition 3.11(ii), a nondiscrete, locally semiprimitive subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
does not contain any nontrivial quasicentral edge-fixating elements. We extend this fact to the following local-to-global-type characterization of quasicentral elements.
$\operatorname {\mathrm {Aut}}(T_{d})$
does not contain any nontrivial quasicentral edge-fixating elements. We extend this fact to the following local-to-global-type characterization of quasicentral elements.
Theorem 5.1. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete. If H is locally:
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete. If H is locally:
-
(i) Transitive, then
 $\mathrm {QZ}(H)$
contains no inversion.
$\mathrm {QZ}(H)$
contains no inversion. -
(ii) Semiprimitive, then
 $\mathrm {QZ}(H)$
contains no nontrivial edge-fixating element.
$\mathrm {QZ}(H)$
contains no nontrivial edge-fixating element. -
(iii) Quasiprimitive, then
 $\mathrm {QZ}(H)$
contains no nontrivial elliptic element.
$\mathrm {QZ}(H)$
contains no nontrivial elliptic element. -
(iv) k-transitive,
 $(k\in \operatorname {\mathrm {\mathbb {N}}})$
then
$(k\in \operatorname {\mathrm {\mathbb {N}}})$
then
 $\mathrm {QZ}(H)$
contains no hyperbolic element of length k.
$\mathrm {QZ}(H)$
contains no hyperbolic element of length k.
Theorem 5.2. There is a
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated subgroup of
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
which is locally:
$\operatorname {\mathrm {Aut}}(T_{d})$
which is locally:
-
(i) Intransitive and contains a quasicentral inversion.
-
(ii) Transitive and contains a nontrivial quasicentral edge-fixating element.
-
(iii) Semiprimitive and contains a nontrivial quasicentral elliptic element.
-
(iv)
-
(a) Intransitive and contains a quasicentral hyperbolic element of length
 $1$
.
$1$
. -
(b) Quasiprimitive and contains a quasicentral hyperbolic element of length
 $2$
.
$2$
.
-
Proof of Theorem 5.1.
Fix a labelling of
![]() $T_{d}$
and let
$T_{d}$
and let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete.
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete.
For (i), suppose
![]() $\iota \in \mathrm {QZ}(H)$
inverts
$\iota \in \mathrm {QZ}(H)$
inverts
![]() $(x,x_{\omega })\in E$
. Since H is locally transitive and
$(x,x_{\omega })\in E$
. Since H is locally transitive and
![]() $\mathrm {QZ}(H)\unlhd H$
, there is an inversion
$\mathrm {QZ}(H)\unlhd H$
, there is an inversion
![]() $\iota _{\omega }\in \mathrm {QZ}(H)$
of
$\iota _{\omega }\in \mathrm {QZ}(H)$
of
![]() $(x,x_{\omega })\in E$
for all
$(x,x_{\omega })\in E$
for all
![]() $\omega \in \Omega $
. By definition, the centralizer of
$\omega \in \Omega $
. By definition, the centralizer of
![]() $\iota _{\omega }$
in H is open for all
$\iota _{\omega }$
in H is open for all
![]() $\omega \in \Omega $
. Hence, using the nondiscreteness of H, there is
$\omega \in \Omega $
. Hence, using the nondiscreteness of H, there is
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
such that
$n\in \operatorname {\mathrm {\mathbb {N}}}$
such that
![]() $H_{B(x,n)}$
commutes with
$H_{B(x,n)}$
commutes with
![]() $\iota _{\omega }$
for all
$\iota _{\omega }$
for all
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $H_{B(x,n+1)}\neq \{\operatorname {\mathrm {id}}\}$
. However,
$H_{B(x,n+1)}\neq \{\operatorname {\mathrm {id}}\}$
. However,
![]() $H_{B(x,n)}=\iota _{\omega }H_{B(x,n)}\iota _{\omega }^{-1}=H_{B(x_{\omega },n)}$
for all
$H_{B(x,n)}=\iota _{\omega }H_{B(x,n)}\iota _{\omega }^{-1}=H_{B(x_{\omega },n)}$
for all
![]() $\omega \in \Omega $
; that is,
$\omega \in \Omega $
; that is,
![]() $H_{B(x,n+1)}\subseteq H_{B(x,n)}$
in contradiction to the above.
$H_{B(x,n+1)}\subseteq H_{B(x,n)}$
in contradiction to the above.
Part (ii) is Proposition 3.11(ii) and part (iii) is [Reference Burger and Mozes2, Proposition 1.2.1(ii)]. Here, the closedness assumption is unnecessary.
For part (iv), suppose
![]() $\tau \in \mathrm {QZ}(H)$
is a translation of length k that maps
$\tau \in \mathrm {QZ}(H)$
is a translation of length k that maps
![]() $x\in V$
to
$x\in V$
to
![]() $x_{\xi }\in V$
for some
$x_{\xi }\in V$
for some
![]() $\xi \in \Omega ^{(k)}$
. Since H is locally k-transitive and
$\xi \in \Omega ^{(k)}$
. Since H is locally k-transitive and
![]() $\mathrm {QZ}(H)\unlhd H$
, there is a translation
$\mathrm {QZ}(H)\unlhd H$
, there is a translation
![]() $\tau _{\xi }\in \mathrm {QZ}(H)$
that maps x to
$\tau _{\xi }\in \mathrm {QZ}(H)$
that maps x to
![]() $x_{\xi }$
for all
$x_{\xi }$
for all
![]() $\smash {\xi \in \Omega ^{(k)}}$
. By definition, the centralizer of
$\smash {\xi \in \Omega ^{(k)}}$
. By definition, the centralizer of
![]() $\tau _{\xi }$
in H is open for all
$\tau _{\xi }$
in H is open for all
![]() $\xi \in \Omega ^{(k)}$
. Hence, using the nondiscreteness of H, there is
$\xi \in \Omega ^{(k)}$
. Hence, using the nondiscreteness of H, there is
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
such that
$n\in \operatorname {\mathrm {\mathbb {N}}}$
such that
![]() $H_{B(x,n)}$
commutes with
$H_{B(x,n)}$
commutes with
![]() $\tau _{\xi }$
for all
$\tau _{\xi }$
for all
![]() $\smash {\xi \in \Omega ^{(k)}}$
and
$\smash {\xi \in \Omega ^{(k)}}$
and
![]() $H_{B(x,n+1)}\neq \{\operatorname {\mathrm {id}}\}$
. However,
$H_{B(x,n+1)}\neq \{\operatorname {\mathrm {id}}\}$
. However,
![]() $H_{B(x,n)}=\tau _{\xi }H_{B(x,n)}\tau _{\xi }^{-1}=H_{B(x_{\xi },n)}$
for all
$H_{B(x,n)}=\tau _{\xi }H_{B(x,n)}\tau _{\xi }^{-1}=H_{B(x_{\xi },n)}$
for all
![]() $\smash {\xi \in \Omega ^{(k)}}$
; that is,
$\smash {\xi \in \Omega ^{(k)}}$
; that is,
![]() $H_{B(x,n+k)}\subseteq H_{B(x,n)}$
in contradiction to the above.
$H_{B(x,n+k)}\subseteq H_{B(x,n)}$
in contradiction to the above.
We complement part (ii) of Theorem 5.1 with the following result which is inspired by [Reference Burger and Mozes2, Proposition 3.1.2] and [Reference Rattaggi24, Conjecture 2.63],
Proposition 5.3. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete and locally semiprimitive. If all orbits of
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete and locally semiprimitive. If all orbits of
![]() $H\curvearrowright \partial T_{d}$
are uncountable then
$H\curvearrowright \partial T_{d}$
are uncountable then
![]() $\mathrm {QZ}(H)$
is trivial.
$\mathrm {QZ}(H)$
is trivial.
Proof. By Theorem 5.1, the group
![]() $\mathrm {QZ}(H)$
contains no inversions. Let
$\mathrm {QZ}(H)$
contains no inversions. Let
![]() $S\subseteq \partial T_{d}$
be the set of fixed points of hyperbolic elements in
$S\subseteq \partial T_{d}$
be the set of fixed points of hyperbolic elements in
![]() $\mathrm {QZ}(H)$
. Since
$\mathrm {QZ}(H)$
. Since
![]() $\mathrm {QZ}(H)\unlhd H$
, the set S is H-invariant. Also,
$\mathrm {QZ}(H)\unlhd H$
, the set S is H-invariant. Also,
![]() $\mathrm {QZ}(H)$
is discrete by Theorem 5.1 and hence countable as H is second-countable. Thus S is countable and hence empty. We conclude that
$\mathrm {QZ}(H)$
is discrete by Theorem 5.1 and hence countable as H is second-countable. Thus S is countable and hence empty. We conclude that
![]() $\mathrm {QZ}(H)\unlhd H$
does not contain elliptic elements in view of [Reference Garrido, Glasner, Tornier, Caprace and Monod10, Lemma 6.4].
$\mathrm {QZ}(H)\unlhd H$
does not contain elliptic elements in view of [Reference Garrido, Glasner, Tornier, Caprace and Monod10, Lemma 6.4].
The following strengthening of Theorem 5.2(ii) proved in Section 5.1.2 below shows that the Burger–Mozes theory does not generalize to the locally transitive case.
Theorem 5.4. There exist
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated, locally transitive subgroup of
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
and a closed, nondiscrete, compactly generated, locally transitive subgroup of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
with open, hence nondiscrete, quasicentre.
$\operatorname {\mathrm {Aut}}(T_{d})$
with open, hence nondiscrete, quasicentre.
We prove Theorem 5.2 by construction in the rest of this subsection. Whereas parts (i)–(iv)(a) all use groups of the form
![]() $\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
for appropriate local actions
$\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
for appropriate local actions
![]() $\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
, part (iv)(b) uses a group of the form
$\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
, part (iv)(b) uses a group of the form
![]() $\smash {\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {BU}(F^{(2k)})}$
. The various parts appear similar at first glance but vary in detail.
$\smash {\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {BU}(F^{(2k)})}$
. The various parts appear similar at first glance but vary in detail.
Proof of Theorem 5.2(i).
For certain intransitive
![]() $F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
$F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
![]() $H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
which locally acts like F and contains a quasicentral involutive inversion.
$H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
which locally acts like F and contains a quasicentral involutive inversion.
Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Assume that the partition
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
. Assume that the partition
![]() $F\backslash \Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$F\backslash \Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
into F-orbits has at least three elements and that
$\Omega $
into F-orbits has at least three elements and that
![]() $F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
$F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
![]() $i\in I$
.
$i\in I$
.
Fix an orbit
![]() $\Omega _{0}$
of size at least
$\Omega _{0}$
of size at least
![]() $2$
and
$2$
and
![]() $\omega _{0}\in \Omega _{0}$
. Define groups
$\omega _{0}\in \Omega _{0}$
. Define groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
$k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
![]() $F^{(1)}:=F$
and
$F^{(1)}:=F$
and
Proposition 5.5. The groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
$k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
-
(i) Every
 $\alpha \in F^{(k)}$
is self-compatible in directions from
$\alpha \in F^{(k)}$
is self-compatible in directions from
 $\Omega _{0}$
.
$\Omega _{0}$
. -
(ii) The compatibility set
 $C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
$C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
 $\alpha \in F^{(k)}$
and
$\alpha \in F^{(k)}$
and
 $i\in I$
. In particular, the group
$i\in I$
. In particular, the group
 $F^{(k)}$
satisfies (C).
$F^{(k)}$
satisfies (C). -
(iii) The compatibility set
 $C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
$C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
 $\Omega _{i}\neq \Omega _{0}$
. In particular, the group
$\Omega _{i}\neq \Omega _{0}$
. In particular, the group
 $F^{(k)}$
does not satisfy (D).
$F^{(k)}$
does not satisfy (D).
Proof. We prove all three properties simultaneously by induction. For
![]() $k=1$
, assertions (i) and (ii) are trivial. Assertion (iii) translates to
$k=1$
, assertions (i) and (ii) are trivial. Assertion (iii) translates to
![]() $F_{\Omega _{i}}$
being nontrivial for all
$F_{\Omega _{i}}$
being nontrivial for all
![]() $\Omega _{i}\neq \Omega _{0}$
, which is an assumption. Now, assume that all properties hold for
$\Omega _{i}\neq \Omega _{0}$
, which is an assumption. Now, assume that all properties hold for
![]() $F^{(k)}$
. Then the definition of
$F^{(k)}$
. Then the definition of
![]() $F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
$F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k+1})$
because F preserves each
$\operatorname {\mathrm {Aut}}(B_{d,k+1})$
because F preserves each
![]() $\Omega _{i}\ (i\in I)$
. Assertion (i) is now evident. Assertion (ii) carries over from
$\Omega _{i}\ (i\in I)$
. Assertion (i) is now evident. Assertion (ii) carries over from
![]() $F^{(k)}$
to
$F^{(k)}$
to
![]() $F^{(k+1)}$
. So does (iii) since
$F^{(k+1)}$
. So does (iii) since
![]() $|F\backslash \Omega |\ge 3$
.
$|F\backslash \Omega |\ge 3$
.
Definition 5.6. Retain the above notation. Define
![]() $H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
$H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
Now,
![]() $H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
$H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
![]() $\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
$\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
![]() $H(F)$
is closed as an intersection of closed sets. The
$H(F)$
is closed as an intersection of closed sets. The
![]() $1$
-local action of H is given by
$1$
-local action of H is given by
![]() $F=F^{(1)}$
because
$F=F^{(1)}$
because
![]() $\Gamma ^{k}(F)\le F^{(k)}$
for all
$\Gamma ^{k}(F)\le F^{(k)}$
for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
, and therefore
$k\in \operatorname {\mathrm {\mathbb {N}}}$
, and therefore
![]() $\mathrm {D}(F)\le H(F)$
.
$\mathrm {D}(F)\le H(F)$
.
Lemma 5.7. The group
![]() $H(F)$
is nondiscrete.
$H(F)$
is nondiscrete.
Proof. Let
![]() $x\in V$
and
$x\in V$
and
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
$n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
![]() $h\in H(F)$
which fixes
$h\in H(F)$
which fixes
![]() $B(x,n)$
. Set
$B(x,n)$
. Set
![]() $\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}$
. By parts (i) and (iii) of Proposition 5.5 as well as the definition of
$\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}$
. By parts (i) and (iii) of Proposition 5.5 as well as the definition of
![]() $F^{(n+1)}$
, there is a nontrivial element
$F^{(n+1)}$
, there is a nontrivial element
![]() $\alpha _{n+1}\in F^{(n+1)}$
with
$\alpha _{n+1}\in F^{(n+1)}$
with
![]() $\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying parts (i) and (ii) of Proposition 5.5 repeatedly, we obtain nontrivial elements
$\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying parts (i) and (ii) of Proposition 5.5 repeatedly, we obtain nontrivial elements
![]() $\alpha _{k}\!\in \! F^{(k)}$
for all
$\alpha _{k}\!\in \! F^{(k)}$
for all
![]() $k\ge n+1$
with
$k\ge n+1$
with
![]() $\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
$\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
![]() $\alpha _{k}:=\operatorname {\mathrm {id}}\!\in \! F^{(k)}$
for all
$\alpha _{k}:=\operatorname {\mathrm {id}}\!\in \! F^{(k)}$
for all
![]() $k\!\le \! n$
and define
$k\!\le \! n$
and define
![]() $h\!\in \!\operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
$h\!\in \!\operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
![]() $\sigma _{k}(h,x)\!:=\!\alpha _{k}\in F^{(k)}$
. Since
$\sigma _{k}(h,x)\!:=\!\alpha _{k}\in F^{(k)}$
. Since
![]() $F^{(l)}\!\le \!\Phi ^{l}(F^{(k)})$
for all
$F^{(l)}\!\le \!\Phi ^{l}(F^{(k)})$
for all
![]() $k\!\le \! l$
, we conclude that
$k\!\le \! l$
, we conclude that
![]() $h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
$h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
Proposition 5.8. The quasicentre of
![]() $H(F)$
contains an involutive inversion.
$H(F)$
contains an involutive inversion.
Proof. Let
![]() $x\!\in \! V$
. We show that the group
$x\!\in \! V$
. We show that the group
![]() $\mathrm {QZ}(H(F))$
contains the label-respecting inversion
$\mathrm {QZ}(H(F))$
contains the label-respecting inversion
![]() $\iota _{\omega }$
of
$\iota _{\omega }$
of
![]() $(x,x_{\omega })\!\in \! E$
for all
$(x,x_{\omega })\!\in \! E$
for all
![]() $\omega \!\in \!\Omega _{0}$
. To see this, let
$\omega \!\in \!\Omega _{0}$
. To see this, let
![]() $h\!\in \! H(F)_{B(x,1)}$
and
$h\!\in \! H(F)_{B(x,1)}$
and
![]() $\omega \!\in \!\Omega _{0}$
. Then
$\omega \!\in \!\Omega _{0}$
. Then
![]() $h\iota _{\omega }(x)\!=\!x_{\omega }\!=\!\iota _{\omega }h(x)$
and
$h\iota _{\omega }(x)\!=\!x_{\omega }\!=\!\iota _{\omega }h(x)$
and
![]() $\sigma _{k}(h\iota _{\omega },x)=\sigma _{k}(h,\iota _{\omega }x)\sigma _{k}(\iota _{\omega },x)=\sigma _{k}(h,x_{\omega })=\sigma _{k}(\iota _{\omega },hx) \sigma _{k}(h,x)=\sigma _{k}(\iota _{\omega }h,x)$
for all
$\sigma _{k}(h\iota _{\omega },x)=\sigma _{k}(h,\iota _{\omega }x)\sigma _{k}(\iota _{\omega },x)=\sigma _{k}(h,x_{\omega })=\sigma _{k}(\iota _{\omega },hx) \sigma _{k}(h,x)=\sigma _{k}(\iota _{\omega }h,x)$
for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
since
$k\in \operatorname {\mathrm {\mathbb {N}}}$
since
![]() $h\in \mathrm {U}_{k+1}(F^{(k+1)})$
. That is,
$h\in \mathrm {U}_{k+1}(F^{(k+1)})$
. That is,
![]() $\iota _{\omega }$
commutes with
$\iota _{\omega }$
commutes with
![]() $H(F)_{B(b,1)}$
.
$H(F)_{B(b,1)}$
.
Proof of Theorem 5.2(ii).
For certain transitive
![]() $F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
$F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
![]() $H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and has open quasicentre.
$H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and has open quasicentre.
Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Assume that F preserves a nontrivial partition
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Assume that F preserves a nontrivial partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
and that
$\Omega $
and that
![]() $F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
$F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
![]() $i\in I$
. Further, suppose that
$i\in I$
. Further, suppose that
![]() $F^{+}$
is abelian and preserves
$F^{+}$
is abelian and preserves
![]() $\operatorname {\mathrm {\mathcal {P}}}$
setwise.
$\operatorname {\mathrm {\mathcal {P}}}$
setwise.
Example 5.9. Let
![]() $F'\le \operatorname {\mathrm {Sym}}(\Omega ')$
be regular abelian and
$F'\le \operatorname {\mathrm {Sym}}(\Omega ')$
be regular abelian and
![]() $P\le \operatorname {\mathrm {Sym}}(\Lambda )$
regular. Then
$P\le \operatorname {\mathrm {Sym}}(\Lambda )$
regular. Then
![]() $F:=F'\wr P\le \operatorname {\mathrm {Sym}}(\Omega '\times \Lambda )$
satisfies the above properties as
$F:=F'\wr P\le \operatorname {\mathrm {Sym}}(\Omega '\times \Lambda )$
satisfies the above properties as
![]() $F^{+}=\prod _{\lambda \in \Lambda }F'$
.
$F^{+}=\prod _{\lambda \in \Lambda }F'$
.
Define groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
$k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
![]() $F^{(1)}:=F$
and
$F^{(1)}:=F$
and
Proposition 5.10. The groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
$k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
-
(i) The compatibility set
 $C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
$C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
 $\alpha \in F^{(k)}$
and
$\alpha \in F^{(k)}$
and
 $i\in I$
. In particular, the group
$i\in I$
. In particular, the group
 $F^{(k)}$
satisfies (C).
$F^{(k)}$
satisfies (C). -
(ii) The compatibility set
 $C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
$C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
 $i\in I$
. In particular, the group
$i\in I$
. In particular, the group
 $F^{(k)}$
does not satisfy (D).
$F^{(k)}$
does not satisfy (D). -
(iii) The group
 $F^{(k)}\cap \Phi ^{k}(F^{+})$
is abelian.
$F^{(k)}\cap \Phi ^{k}(F^{+})$
is abelian.
Proof. We prove all three properties simultaneously by induction. For
![]() $k=1$
, assertion (i) is trivial whereas (iii) is an assumption. Assertion (ii) translates to
$k=1$
, assertion (i) is trivial whereas (iii) is an assumption. Assertion (ii) translates to
![]() $F_{\Omega _{i}}$
being nontrivial for all
$F_{\Omega _{i}}$
being nontrivial for all
![]() $i\in I$
, which is an assumption. Now, assume all properties hold for
$i\in I$
, which is an assumption. Now, assume all properties hold for
![]() $F^{(k)}$
. Then the definition of
$F^{(k)}$
. Then the definition of
![]() $F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
$F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
because F preserves
$\operatorname {\mathrm {Aut}}(B_{d,k})$
because F preserves
![]() $\operatorname {\mathrm {\mathcal {P}}}$
. Assertion (ii) carries over from
$\operatorname {\mathrm {\mathcal {P}}}$
. Assertion (ii) carries over from
![]() $F^{(k)}$
to
$F^{(k)}$
to
![]() $F^{(k+1)}$
. Finally, (iii) follows inductively because
$F^{(k+1)}$
. Finally, (iii) follows inductively because
![]() $F^{+}$
preserves
$F^{+}$
preserves
![]() $\operatorname {\mathrm {\mathcal {P}}}$
setwise.
$\operatorname {\mathrm {\mathcal {P}}}$
setwise.
Definition 5.11. Retain the above notation. Define
![]() $H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
$H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
Now,
![]() $H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
$H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
![]() $\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
$\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
![]() $H(F)$
is closed as an intersection of closed sets. The
$H(F)$
is closed as an intersection of closed sets. The
![]() $1$
-local action of H is given by
$1$
-local action of H is given by
![]() $F=F^{(1)}$
because
$F=F^{(1)}$
because
![]() $\Gamma _{k}(F)\le F^{(k)}$
for all
$\Gamma _{k}(F)\le F^{(k)}$
for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
and therefore
$k\in \operatorname {\mathrm {\mathbb {N}}}$
and therefore
![]() $\mathrm {D}(F)\le H(F)$
.
$\mathrm {D}(F)\le H(F)$
.
Lemma 5.12. The group
![]() $H(F)$
is nondiscrete.
$H(F)$
is nondiscrete.
Proof. Let
![]() $x\in V$
and
$x\in V$
and
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
$n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
![]() $h\in H(F)$
that fixes
$h\in H(F)$
that fixes
![]() $B(x,n)$
. Consider
$B(x,n)$
. Consider
![]() $\smash {\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}}$
. By part (ii) of Proposition 5.10 as well as the definition of
$\smash {\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}}$
. By part (ii) of Proposition 5.10 as well as the definition of
![]() $\smash {F^{(n+1)}}$
, there is a nontrivial element
$\smash {F^{(n+1)}}$
, there is a nontrivial element
![]() $\smash {\alpha _{n+1}\in F^{(n+1)}}$
with
$\smash {\alpha _{n+1}\in F^{(n+1)}}$
with
![]() $\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying part (i) of Proposition 5.10 repeatedly, we obtain nontrivial elements
$\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying part (i) of Proposition 5.10 repeatedly, we obtain nontrivial elements
![]() $\smash {\alpha _{k}\in F^{(k)}}$
for all
$\smash {\alpha _{k}\in F^{(k)}}$
for all
![]() $k\ge n+1$
with
$k\ge n+1$
with
![]() $\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
$\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
![]() $\alpha _{k}:=\operatorname {\mathrm {id}}\in F^{(k)}$
for all
$\alpha _{k}:=\operatorname {\mathrm {id}}\in F^{(k)}$
for all
![]() $k\le n$
and define
$k\le n$
and define
![]() $h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
$h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
![]() $\smash {\sigma _{k}(h,x):=\alpha _{k}\in F^{(k)}}$
. Since
$\smash {\sigma _{k}(h,x):=\alpha _{k}\in F^{(k)}}$
. Since
![]() $\smash {F^{(l)}\!\le \!\Phi ^{l}(F^{(k)})}$
for all
$\smash {F^{(l)}\!\le \!\Phi ^{l}(F^{(k)})}$
for all
![]() $k\!\le \! l$
, we conclude that
$k\!\le \! l$
, we conclude that
![]() $h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
$h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
Proposition 5.13. The group
![]() $H(F)$
has open quasicentre.
$H(F)$
has open quasicentre.
Proof. The group
![]() $H(F)_{B(x,1)}$
is a subgroup of the group
$H(F)_{B(x,1)}$
is a subgroup of the group
![]() $H(F^{+})_{x}$
which is abelian by part (iii) of Proposition 5.10. Hence,
$H(F^{+})_{x}$
which is abelian by part (iii) of Proposition 5.10. Hence,
![]() $H(F)_{B(x,1)}\le \mathrm {QZ}(H(F))$
.
$H(F)_{B(x,1)}\le \mathrm {QZ}(H(F))$
.
Remark 5.14. Without assuming local transitivity one can achieve abelian point-stabilizers, following the construction of the previous section. This cannot happen for nondiscrete locally transitive groups
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
that are vertex-transitive as the following argument shows. By Proposition 2.6, the group H is contained in
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
that are vertex-transitive as the following argument shows. By Proposition 2.6, the group H is contained in
![]() $\mathrm {U}(F)$
where
$\mathrm {U}(F)$
where
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
is the local action of H. If
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
is the local action of H. If
![]() $H_{x}$
is abelian, then so is F. Since any transitive abelian permutation group is regular we conclude that
$H_{x}$
is abelian, then so is F. Since any transitive abelian permutation group is regular we conclude that
![]() $\mathrm {U}(F)$
and hence H are discrete. In this sense, the construction of this section is efficient.
$\mathrm {U}(F)$
and hence H are discrete. In this sense, the construction of this section is efficient.
Proof of Theorem 5.2(iii).
For certain semiprimitive
![]() $F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
$F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
![]() $H(F)\!\le \!\operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and contains a nontrivial quasicentral elliptic element.
$H(F)\!\le \!\operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and contains a nontrivial quasicentral elliptic element.
Let
![]() $F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be semiprimitive. Suppose F preserves a nontrivial partition
$F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be semiprimitive. Suppose F preserves a nontrivial partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
and that
$\Omega $
and that
![]() $F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
$F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
![]() $i\in I$
. Further, suppose that F contains a nontrivial central element
$i\in I$
. Further, suppose that F contains a nontrivial central element
![]() $\tau $
which preserves
$\tau $
which preserves
![]() $\operatorname {\mathrm {\mathcal {P}}}$
setwise.
$\operatorname {\mathrm {\mathcal {P}}}$
setwise.
Example 5.15. Consider
![]() $\operatorname {\mathrm {SL}}(2,3)\curvearrowright \operatorname {\mathrm {\mathbb {F}}}_{3}^{2}\backslash \{0\}=\{\pm e_{1},\pm e_{2},\pm (e_{1}+e_{2}),\pm (e_{1}-e_{2})\}$
where
$\operatorname {\mathrm {SL}}(2,3)\curvearrowright \operatorname {\mathrm {\mathbb {F}}}_{3}^{2}\backslash \{0\}=\{\pm e_{1},\pm e_{2},\pm (e_{1}+e_{2}),\pm (e_{1}-e_{2})\}$
where
![]() $e_{1},e_{2}$
are the standard basis vectors. We have
$e_{1},e_{2}$
are the standard basis vectors. We have
![]() $Z(\operatorname {\mathrm {SL}}(2,3))=\{\pm \operatorname {\mathrm {Id}}\}$
. The blocks of size
$Z(\operatorname {\mathrm {SL}}(2,3))=\{\pm \operatorname {\mathrm {Id}}\}$
. The blocks of size
![]() $2$
are as listed above, given that
$2$
are as listed above, given that
![]() $\operatorname {\mathrm {SL}}(2,3)_{e_{1}}\le _{2}\pm \operatorname {\mathrm {SL}}(2,3)_{e_{1}}$
.
$\operatorname {\mathrm {SL}}(2,3)_{e_{1}}\le _{2}\pm \operatorname {\mathrm {SL}}(2,3)_{e_{1}}$
.
Define groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
$k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
![]() $F^{(1)}:=F$
and
$F^{(1)}:=F$
and
Proposition 5.16. The groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
$k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
-
(i) The compatibility set
 $C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
$C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
 $\alpha \in F^{(k)}$
and
$\alpha \in F^{(k)}$
and
 $i\in I$
. In particular, the group
$i\in I$
. In particular, the group
 $F^{(k)}$
satisfies (C).
$F^{(k)}$
satisfies (C). -
(ii) The compatibility set
 $C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
$C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
 $i\in I$
. In particular, the group
$i\in I$
. In particular, the group
 $F^{(k)}$
does not satisfy (D).
$F^{(k)}$
does not satisfy (D). -
(iii) The element
 $\gamma _{k}(\tau )\in \operatorname {\mathrm {Aut}}(B_{d,k})$
is central in
$\gamma _{k}(\tau )\in \operatorname {\mathrm {Aut}}(B_{d,k})$
is central in
 $F^{(k)}$
.
$F^{(k)}$
.
Proof. We prove all three properties simultaneously by induction. For
![]() $k=1$
, assertion (i) is trivial whereas (iii) is an assumption. Assertion (ii) translates to
$k=1$
, assertion (i) is trivial whereas (iii) is an assumption. Assertion (ii) translates to
![]() $F_{\Omega _{i}}$
being nontrivial for all
$F_{\Omega _{i}}$
being nontrivial for all
![]() $i\in I$
, which is an assumption. Now, assume all properties hold for
$i\in I$
, which is an assumption. Now, assume all properties hold for
![]() $F^{(k)}$
. Then the definition of
$F^{(k)}$
. Then the definition of
![]() $F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
$F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k+1})$
because F preserves
$\operatorname {\mathrm {Aut}}(B_{d,k+1})$
because F preserves
![]() $\operatorname {\mathrm {\mathcal {P}}}$
. Assertion (ii) carries over from
$\operatorname {\mathrm {\mathcal {P}}}$
. Assertion (ii) carries over from
![]() $F^{(k)}$
to
$F^{(k)}$
to
![]() $F^{(k+1)}$
. Finally, (iii) follows inductively because
$F^{(k+1)}$
. Finally, (iii) follows inductively because
![]() $\tau $
and hence
$\tau $
and hence
![]() $\tau ^{-1}$
preserves
$\tau ^{-1}$
preserves
![]() $\operatorname {\mathrm {\mathcal {P}}}$
setwise: for
$\operatorname {\mathrm {\mathcal {P}}}$
setwise: for
![]() $\smash {\widetilde {\alpha }=(\alpha ,(\alpha _{\omega })_{\omega })\in F^{(k+1)}}$
we have
$\smash {\widetilde {\alpha }=(\alpha ,(\alpha _{\omega })_{\omega })\in F^{(k+1)}}$
we have
Definition 5.17. Retain the above notation. Define
![]() $H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
$H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
Now,
![]() $H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
$H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
![]() $\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
$\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
![]() $H(F)$
is closed as an intersection of closed sets. The
$H(F)$
is closed as an intersection of closed sets. The
![]() $1$
-local action of H is given by
$1$
-local action of H is given by
![]() $F=F^{(1)}$
because
$F=F^{(1)}$
because
![]() $\Gamma ^{k}(F)\le F^{(k)}$
for all
$\Gamma ^{k}(F)\le F^{(k)}$
for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
and therefore
$k\in \operatorname {\mathrm {\mathbb {N}}}$
and therefore
![]() $\mathrm {D}(F)\le H(F)$
.
$\mathrm {D}(F)\le H(F)$
.
Lemma 5.18. The group
![]() $H(F)$
is nondiscrete.
$H(F)$
is nondiscrete.
Proof. Let
![]() $x\in V$
and
$x\in V$
and
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
$n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
![]() $h\in H(F)$
that fixes
$h\in H(F)$
that fixes
![]() $B(x,n)$
. Consider
$B(x,n)$
. Consider
![]() $\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}$
. By part (ii) of Proposition 5.16 and the definition of
$\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}$
. By part (ii) of Proposition 5.16 and the definition of
![]() $F^{(n+1)}$
, there is a nontrivial
$F^{(n+1)}$
, there is a nontrivial
![]() $\alpha _{n+1}\in F^{(n+1)}$
with
$\alpha _{n+1}\in F^{(n+1)}$
with
![]() $\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying part (i) of Proposition 5.16 repeatedly, we obtain nontrivial elements
$\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying part (i) of Proposition 5.16 repeatedly, we obtain nontrivial elements
![]() $\alpha _{k}\in F^{(k)}$
for all
$\alpha _{k}\in F^{(k)}$
for all
![]() $k\ge n+1$
with
$k\ge n+1$
with
![]() $\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
$\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
![]() $\alpha _{k}:=\operatorname {\mathrm {id}}\in F^{(k)}$
for all
$\alpha _{k}:=\operatorname {\mathrm {id}}\in F^{(k)}$
for all
![]() $k\le n$
and define
$k\le n$
and define
![]() $h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
$h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
![]() $\sigma _{k}(h,x):=\alpha _{k}\in F^{(k)}$
. Since
$\sigma _{k}(h,x):=\alpha _{k}\in F^{(k)}$
. Since
![]() $F^{(l)}\le \Phi ^{l}(F^{(k)})$
for all
$F^{(l)}\le \Phi ^{l}(F^{(k)})$
for all
![]() $k\le l$
, we conclude that
$k\le l$
, we conclude that
![]() $h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
$h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
Proposition 5.19. The quasicentre of
![]() $H(F)$
contains a nontrivial elliptic element.
$H(F)$
contains a nontrivial elliptic element.
Proof. By Proposition 5.16, the element
![]() $d(\tau )$
that fixes x and whose
$d(\tau )$
that fixes x and whose
![]() $1$
-local action is
$1$
-local action is
![]() $\tau $
everywhere commutes with
$\tau $
everywhere commutes with
![]() $H(F)_{x}$
. Hence,
$H(F)_{x}$
. Hence,
![]() $d(\tau )\in \mathrm {QZ}(H(F))$
.
$d(\tau )\in \mathrm {QZ}(H(F))$
.
Remark 5.20. The argument of this section does not work in the quasiprimitive case because a quasiprimitive group
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
with nontrivial centre is abelian and regular. If
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
with nontrivial centre is abelian and regular. If
![]() $Z(F)\unlhd F$
is nontrivial then it is transitive, and it suffices to show that
$Z(F)\unlhd F$
is nontrivial then it is transitive, and it suffices to show that
![]() $F^{+}$
is trivial. Suppose
$F^{+}$
is trivial. Suppose
![]() $a\in F_{\omega }$
moves
$a\in F_{\omega }$
moves
![]() $\omega '\in \Omega $
. Pick
$\omega '\in \Omega $
. Pick
![]() $z\in Z(F)$
with
$z\in Z(F)$
with
![]() $z(\omega )=\omega '$
. Then
$z(\omega )=\omega '$
. Then
![]() $za(\omega )=\omega '\neq az(\omega )$
, contradicting the assumption that
$za(\omega )=\omega '\neq az(\omega )$
, contradicting the assumption that
![]() $z\in Z(F)$
.
$z\in Z(F)$
.
Proof of Theorem 5.2(iv)(a).
For certain intransitive
![]() $F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
$F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated, vertex-transitive group
![]() $H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and contains a quasicentral hyperbolic element of length
$H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and contains a quasicentral hyperbolic element of length
![]() $1$
.
$1$
.
Let
![]() $F\le \mathrm {Sym}(\Omega )$
. Assume that the partition
$F\le \mathrm {Sym}(\Omega )$
. Assume that the partition
![]() $F\backslash \Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$F\backslash \Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
has at least three elements and that
$\Omega $
has at least three elements and that
![]() $Z(F)\neq \{\operatorname {\mathrm {id}}\}$
. Choose a nontrivial element
$Z(F)\neq \{\operatorname {\mathrm {id}}\}$
. Choose a nontrivial element
![]() $\tau \in Z(F)$
and
$\tau \in Z(F)$
and
![]() $\omega _{0}\in \Omega _{0}\in F\backslash \Omega $
with
$\omega _{0}\in \Omega _{0}\in F\backslash \Omega $
with
![]() $\tau (\omega _{0})\neq \omega _{0}$
. Further, suppose that
$\tau (\omega _{0})\neq \omega _{0}$
. Further, suppose that
![]() $F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
$F_{\Omega _{i}}\neq \{\operatorname {\mathrm {id}}\}$
for all
![]() $\Omega _{i}\neq \Omega _{0}$
.
$\Omega _{i}\neq \Omega _{0}$
.
Define groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
for
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
$k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
![]() $F^{(1)}:=F$
and
$F^{(1)}:=F$
and
Proposition 5.21. The groups
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
(
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
$k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
-
(i) Every
 $\alpha \in F^{(k)}$
is self-compatible in directions from
$\alpha \in F^{(k)}$
is self-compatible in directions from
 $\Omega _{0}$
.
$\Omega _{0}$
. -
(ii) The compatibility set
 $C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
$C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
 $\alpha \in F^{(k)}$
and
$\alpha \in F^{(k)}$
and
 $i\in I$
. In particular, the group
$i\in I$
. In particular, the group
 $F^{(k)}$
satisfies (C).
$F^{(k)}$
satisfies (C). -
(iii) The compatibility set
 $C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
$C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
 $i\in I\backslash \{0\}$
. In particular, the group
$i\in I\backslash \{0\}$
. In particular, the group
 $F^{(k)}$
does not satisfy (D).
$F^{(k)}$
does not satisfy (D). -
(iv) The element
 $\gamma _{k}(\tau )\in \operatorname {\mathrm {Aut}}(B_{d,k})$
is central in
$\gamma _{k}(\tau )\in \operatorname {\mathrm {Aut}}(B_{d,k})$
is central in
 $F^{(k)}$
.
$F^{(k)}$
.
Proof. We prove all four properties simultaneously by induction. For
![]() $k=1$
, assertions (i) and (ii) are trivial. Assertion (iii) translates to
$k=1$
, assertions (i) and (ii) are trivial. Assertion (iii) translates to
![]() $F_{\Omega _{i}}$
being nontrivial for all
$F_{\Omega _{i}}$
being nontrivial for all
![]() $i\in I\backslash \{0\}$
, which is an assumption, as is (iv). Now, assume that all properties hold for
$i\in I\backslash \{0\}$
, which is an assumption, as is (iv). Now, assume that all properties hold for
![]() $F^{(k)}$
. Then the definition of
$F^{(k)}$
. Then the definition of
![]() $F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
$F^{(k+1)}$
is meaningful because of (i) and it is a subgroup of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
because F preserves
$\operatorname {\mathrm {Aut}}(B_{d,k})$
because F preserves
![]() $F\backslash \Omega $
. Assertion (i) is now evident. Assertions (ii) and (iii) carry over from
$F\backslash \Omega $
. Assertion (i) is now evident. Assertions (ii) and (iii) carry over from
![]() $F^{(k)}$
to
$F^{(k)}$
to
![]() $F^{(k+1)}$
. Finally, (iv) follows inductively because
$F^{(k+1)}$
. Finally, (iv) follows inductively because
![]() $\tau $
and hence
$\tau $
and hence
![]() $\tau ^{-1}$
preserves
$\tau ^{-1}$
preserves
![]() $F\backslash \Omega $
setwise: for
$F\backslash \Omega $
setwise: for
![]() $\smash {\widetilde {\alpha }=(\alpha ,(\alpha _{\omega })_{\omega })\in F^{(k+1)}}$
we have
$\smash {\widetilde {\alpha }=(\alpha ,(\alpha _{\omega })_{\omega })\in F^{(k+1)}}$
we have
Definition 5.22. Retain the above notation. Define
![]() $H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
$H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
.
Now,
![]() $H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
$H(F)$
is compactly generated, vertex-transitive and contains an involutive inversion because
![]() $\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
$\smash {\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})\le H(F)}$
. Also,
![]() $H(F)$
is closed as the intersection of all its
$H(F)$
is closed as the intersection of all its
![]() $(P_{k})$
-closures. The
$(P_{k})$
-closures. The
![]() $1$
-local action of H is given by
$1$
-local action of H is given by
![]() $F=F^{(1)}$
as
$F=F^{(1)}$
as
![]() $\Gamma ^{k}(F)\le F^{(k)}$
for all
$\Gamma ^{k}(F)\le F^{(k)}$
for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
and therefore
$k\in \operatorname {\mathrm {\mathbb {N}}}$
and therefore
![]() $\mathrm {D}(F)\le H$
.
$\mathrm {D}(F)\le H$
.
Lemma 5.23. The group
![]() $H(F)$
is nondiscrete.
$H(F)$
is nondiscrete.
Proof. Let
![]() $x\in V$
and
$x\in V$
and
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
$n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
![]() $h\in H(F)$
which fixes
$h\in H(F)$
which fixes
![]() $B(x,n)$
. Consider
$B(x,n)$
. Consider
![]() $\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}$
. By parts (i) and (iii) of Proposition 5.21 as well as the definition of
$\alpha _{n}:=\operatorname {\mathrm {id}}\in F^{(n)}$
. By parts (i) and (iii) of Proposition 5.21 as well as the definition of
![]() $F^{(n+1)}$
, there is a nontrivial element
$F^{(n+1)}$
, there is a nontrivial element
![]() $\alpha _{n+1}\in F^{(n+1)}$
with
$\alpha _{n+1}\in F^{(n+1)}$
with
![]() $\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying parts (i) and (ii) of Proposition 5.21 repeatedly, we obtain nontrivial elements
$\pi _{n}\alpha _{n+1}=\alpha _{n}$
. Applying parts (i) and (ii) of Proposition 5.21 repeatedly, we obtain nontrivial elements
![]() $\alpha _{k}\in F^{(k)}$
for all
$\alpha _{k}\in F^{(k)}$
for all
![]() $k\ge n+1$
with
$k\ge n+1$
with
![]() $\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
$\pi _{k}\alpha _{k+1}=\alpha _{k}$
. Set
![]() $\alpha _{k}:=\operatorname {\mathrm {id}}\in F^{(k)}$
for all
$\alpha _{k}:=\operatorname {\mathrm {id}}\in F^{(k)}$
for all
![]() $k\le n$
, and define
$k\le n$
, and define
![]() $h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
$h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
![]() $\sigma _{k}(h,x):=\alpha _{k}\in F^{(k)}$
. Since
$\sigma _{k}(h,x):=\alpha _{k}\in F^{(k)}$
. Since
![]() $F^{(l)}\le \Phi ^{l}(F^{(k)})$
for all
$F^{(l)}\le \Phi ^{l}(F^{(k)})$
for all
![]() $k\le l$
we conclude that
$k\le l$
we conclude that
![]() $h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
$h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})=H(F)$
.
Proposition 5.24. The quasicentre of
![]() $H(F)$
contains a translation of length
$H(F)$
contains a translation of length
![]() $1$
.
$1$
.
Proof. Fix
![]() $x\in V$
and let
$x\in V$
and let
![]() $\tau $
be as above. Consider the line L through x with labels
$\tau $
be as above. Consider the line L through x with labels
Define
![]() $t\in \mathrm {D}(F)$
by
$t\in \mathrm {D}(F)$
by
![]() $t(x)=x_{\omega _{0}}$
and
$t(x)=x_{\omega _{0}}$
and
![]() $\sigma _{1}(t,y)=\tau $
for all
$\sigma _{1}(t,y)=\tau $
for all
![]() $y\in V$
. Then t is a translation of length
$y\in V$
. Then t is a translation of length
![]() $1$
along L. Furthermore, t commutes with
$1$
along L. Furthermore, t commutes with
![]() $H(F)_{B(x,1)}$
. Indeed, let
$H(F)_{B(x,1)}$
. Indeed, let
![]() $g\in H(F)_{B(x,1)}$
. Then
$g\in H(F)_{B(x,1)}$
. Then
![]() $(gt)(x)=t(x)=(tg)(x)$
and
$(gt)(x)=t(x)=(tg)(x)$
and
for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
because
$k\in \operatorname {\mathrm {\mathbb {N}}}$
because
![]() $\sigma _{k}(t,x)=\gamma ^{k}(\tau )\in Z(F^{(k)})$
and
$\sigma _{k}(t,x)=\gamma ^{k}(\tau )\in Z(F^{(k)})$
and
![]() $g\in \mathrm {U}_{k+1}(F^{(k+1)})_{B(x,1)}$
.
$g\in \mathrm {U}_{k+1}(F^{(k+1)})_{B(x,1)}$
.
Proof of Theorem 5.2(iv)(b).
For certain quasiprimitive
![]() $F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated group
$F\le \mathrm {Sym}(\Omega )$
we construct a closed, nondiscrete, compactly generated group
![]() $H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and contains a quasicentral hyperbolic element of length
$H(F)\le \operatorname {\mathrm {Aut}}(T_{d})$
that locally acts like F and contains a quasicentral hyperbolic element of length
![]() $2$
.
$2$
.
Let
![]() $F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be quasiprimitive. Suppose F preserves a nontrivial partition
$F\!\le \!\operatorname {\mathrm {Sym}}(\Omega )$
be quasiprimitive. Suppose F preserves a nontrivial partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
. Further, suppose that
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
. Further, suppose that
![]() $F_{\Omega _{i}}\!\neq \!\{\operatorname {\mathrm {id}}\}$
and that
$F_{\Omega _{i}}\!\neq \!\{\operatorname {\mathrm {id}}\}$
and that
![]() $F_{\omega _{i}}\curvearrowright \Omega _{i}\backslash \{\omega _{i}\}$
is transitive for all
$F_{\omega _{i}}\curvearrowright \Omega _{i}\backslash \{\omega _{i}\}$
is transitive for all
![]() $i\in I$
and
$i\in I$
and
![]() $\omega _{i}\in \Omega _{i}$
.
$\omega _{i}\in \Omega _{i}$
.
Example 5.25. Consider the action
![]() $A_{5}\curvearrowright A_{5}/C_{5}$
. It has blocks of size
$A_{5}\curvearrowright A_{5}/C_{5}$
. It has blocks of size
![]() $[D_{5}:C_{5}]=2$
and nontrivial block stabilizers as
$[D_{5}:C_{5}]=2$
and nontrivial block stabilizers as
![]() $C_{5}\cap \tau C_{5}\tau ^{-1}=C_{5}$
for all
$C_{5}\cap \tau C_{5}\tau ^{-1}=C_{5}$
for all
![]() $\tau \in D_{5}$
given that
$\tau \in D_{5}$
given that
![]() $C_{5}\unlhd D_{5}$
.
$C_{5}\unlhd D_{5}$
.
Retain the notation of Example 4.41. Define groups
![]() $\smash {F^{(2k)}\le \operatorname {\mathrm {Aut}}(B_{d,2k})}$
for
$\smash {F^{(2k)}\le \operatorname {\mathrm {Aut}}(B_{d,2k})}$
for
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
$k\in \operatorname {\mathrm {\mathbb {N}}}$
inductively by
![]() $\smash {F^{(2)}=\{(a,(a_{\omega })_{\omega })\mid a\in F, a_{\omega }\in C_{F}(a,\omega ) \text { constant w.r.t. } \operatorname {\mathrm {\mathcal {P}}}\}}$
and
$\smash {F^{(2)}=\{(a,(a_{\omega })_{\omega })\mid a\in F, a_{\omega }\in C_{F}(a,\omega ) \text { constant w.r.t. } \operatorname {\mathrm {\mathcal {P}}}\}}$
and
Proposition 5.26. The groups
![]() $F^{(2k)}\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
(
$F^{(2k)}\le \operatorname {\mathrm {Aut}}(B_{d,2k})$
(
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
$k\in \operatorname {\mathrm {\mathbb {N}}}$
) defined above satisfy the following assertions.
-
(i) Every
 $\alpha \in F^{(2k)}$
is self-compatible in all directions from
$\alpha \in F^{(2k)}$
is self-compatible in all directions from
 $\Omega ^{(2)}_{0}$
.
$\Omega ^{(2)}_{0}$
. -
(ii) The compatibility set
 $C_{F^{(2k)}}(\alpha ,\xi )$
is nonempty for all
$C_{F^{(2k)}}(\alpha ,\xi )$
is nonempty for all
 $\alpha \!\in \! F^{(2k)}$
and
$\alpha \!\in \! F^{(2k)}$
and
 $\xi \!\in \!\Omega ^{(2)}$
. In particular, the group
$\xi \!\in \!\Omega ^{(2)}$
. In particular, the group
 $F^{(2k)}$
satisfies (C).
$F^{(2k)}$
satisfies (C). -
(iii) The compatibility set
 $C_{F^{(2k)}}(\operatorname {\mathrm {id}},\xi )$
is nontrivial for all
$C_{F^{(2k)}}(\operatorname {\mathrm {id}},\xi )$
is nontrivial for all
 $\xi \in \Omega ^{(2)}$
. In particular, the group
$\xi \in \Omega ^{(2)}$
. In particular, the group
 $F^{(2k)}$
does not satisfy (D).
$F^{(2k)}$
does not satisfy (D).
Proof. We prove all three properties simultaneously by induction. For
![]() $k=1$
, assertion (i) holds by construction of
$k=1$
, assertion (i) holds by construction of
![]() $F^{(2)}$
, as do (ii) and (iii). Now assume that all properties hold for
$F^{(2)}$
, as do (ii) and (iii). Now assume that all properties hold for
![]() $F^{(2k)}$
. Then the definition of
$F^{(2k)}$
. Then the definition of
![]() $F^{(2(k+1))}$
is meaningful because of (i) and it is a subgroup because
$F^{(2(k+1))}$
is meaningful because of (i) and it is a subgroup because
![]() $F^{(2)}$
preserves
$F^{(2)}$
preserves
![]() $\smash {\Omega ^{(2)}_{0}}$
. Also,
$\smash {\Omega ^{(2)}_{0}}$
. Also,
![]() $F^{(2(k+1))}$
satisfies (i) because
$F^{(2(k+1))}$
satisfies (i) because
![]() $\smash {\Omega ^{(2)}_{0}}$
is inversion-closed. Assertions (ii) and (iii) carry over from
$\smash {\Omega ^{(2)}_{0}}$
is inversion-closed. Assertions (ii) and (iii) carry over from
![]() $\smash {F^{(2k)}}$
.
$\smash {F^{(2k)}}$
.
Definition 5.27. Retain the above notation. Define
![]() $H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {BU}_{2k}(F^{(2k)})$
.
$H(F):=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {BU}_{2k}(F^{(2k)})$
.
Now,
![]() $H(F)$
is closed as an intersection of closed sets and compactly generated by
$H(F)$
is closed as an intersection of closed sets and compactly generated by
![]() $H(F)_{x}$
for some
$H(F)_{x}$
for some
![]() $x\in V_{1}$
and a finite generating set of
$x\in V_{1}$
and a finite generating set of
![]() $\mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})^{+}$
; see Lemma 4.39. For vertices in
$\mathrm {BU}_{2}(\{\operatorname {\mathrm {id}}\})^{+}$
; see Lemma 4.39. For vertices in
![]() $V_{1}$
, the
$V_{1}$
, the
![]() $1$
-local action is F because
$1$
-local action is F because
![]() $\Gamma ^{2k}(F)\le F^{(2k)}$
. For vertices in
$\Gamma ^{2k}(F)\le F^{(2k)}$
. For vertices in
![]() $V_{2}$
the
$V_{2}$
the
![]() $1$
-local action is
$1$
-local action is
![]() $F^{+}=F$
as
$F^{+}=F$
as
![]() $\Gamma ^{2}(F)\le F^{(2)}$
.
$\Gamma ^{2}(F)\le F^{(2)}$
.
Lemma 5.28. The group
![]() $H(F)$
is nondiscrete.
$H(F)$
is nondiscrete.
Proof. Let
![]() $x\in V_{1}$
and
$x\in V_{1}$
and
![]() $n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
$n\in \operatorname {\mathrm {\mathbb {N}}}$
. We construct a nontrivial element
![]() $h\in H(F)$
that fixes
$h\in H(F)$
that fixes
![]() $B(x,2n)$
. Consider
$B(x,2n)$
. Consider
![]() $\alpha _{2n}:=\operatorname {\mathrm {id}}\in F^{(2n)}$
: By parts (i) and (iii) of Proposition 5.5 and the definition of
$\alpha _{2n}:=\operatorname {\mathrm {id}}\in F^{(2n)}$
: By parts (i) and (iii) of Proposition 5.5 and the definition of
![]() $F^{(2(n+1))}$
, there is a nontrivial element
$F^{(2(n+1))}$
, there is a nontrivial element
![]() $\smash {\alpha _{2(n+1)}\in F^{(2(n+1))}}$
with
$\smash {\alpha _{2(n+1)}\in F^{(2(n+1))}}$
with
![]() $\pi _{2n}\alpha _{2(n+1)}=\alpha _{2n}$
. Applying parts (i) and (ii) of Proposition 5.26 repeatedly, we obtain nontrivial elements
$\pi _{2n}\alpha _{2(n+1)}=\alpha _{2n}$
. Applying parts (i) and (ii) of Proposition 5.26 repeatedly, we obtain nontrivial elements
![]() $\smash {\alpha _{2k}\in F^{(2k)}}$
for all
$\smash {\alpha _{2k}\in F^{(2k)}}$
for all
![]() $k\ge n+1$
with
$k\ge n+1$
with
![]() $\smash {\pi _{2k}\alpha ^{2(k+1)}=\alpha _{2k}}$
. Set
$\smash {\pi _{2k}\alpha ^{2(k+1)}=\alpha _{2k}}$
. Set
![]() $\smash {\alpha _{2k}:=\operatorname {\mathrm {id}}\in F^{(2k)}}$
for all
$\smash {\alpha _{2k}:=\operatorname {\mathrm {id}}\in F^{(2k)}}$
for all
![]() $k\le n$
and define
$k\le n$
and define
![]() $h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
$h\in \operatorname {\mathrm {Aut}}(T_{d})_{x}$
by fixing x and setting
![]() $\smash {\sigma _{2k}(h,x):=\alpha _{2k}\in F^{(2k)}}$
. Since
$\smash {\sigma _{2k}(h,x):=\alpha _{2k}\in F^{(2k)}}$
. Since
![]() $\smash {F^{(2l)}\!\le \!\mathrm {B}\Phi ^{2l}(F^{(2k)})}$
for all
$\smash {F^{(2l)}\!\le \!\mathrm {B}\Phi ^{2l}(F^{(2k)})}$
for all
![]() $k\!\le \! l$
, we conclude that
$k\!\le \! l$
, we conclude that
![]() $\smash {h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {BU}_{2k}(F^{(2k)})=H(F)}$
.
$\smash {h\in \bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {BU}_{2k}(F^{(2k)})=H(F)}$
.
Proposition 5.29. The quasicentre of
![]() $H(F)$
contains a translation of length
$H(F)$
contains a translation of length
![]() $2$
.
$2$
.
Proof. Fix
![]() $x\!\in \! V_{1}$
and
$x\!\in \! V_{1}$
and
![]() $\xi \!=\!(\omega _{1},\omega _{2})\!\in \!\Omega ^{(2)}_{0}$
. Consider the line L through b with labels
$\xi \!=\!(\omega _{1},\omega _{2})\!\in \!\Omega ^{(2)}_{0}$
. Consider the line L through b with labels
Define
![]() $t\in \mathrm {D}(F)$
by
$t\in \mathrm {D}(F)$
by
![]() $t(x)= x_{\xi }$
and
$t(x)= x_{\xi }$
and
![]() $\sigma _{1}(t,y)=\operatorname {\mathrm {id}}$
for all
$\sigma _{1}(t,y)=\operatorname {\mathrm {id}}$
for all
![]() $y\in V$
. Then t is a translation of length
$y\in V$
. Then t is a translation of length
![]() $2$
along L. Furthermore, t commutes with
$2$
along L. Furthermore, t commutes with
![]() $H(F)_{B(x,2)}$
. Indeed, let
$H(F)_{B(x,2)}$
. Indeed, let
![]() $g\in H(F)_{B(x,2)}$
. Then
$g\in H(F)_{B(x,2)}$
. Then
![]() $gt(x)=t(x)=tg(x)$
and, for all
$gt(x)=t(x)=tg(x)$
and, for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
,
$k\in \operatorname {\mathrm {\mathbb {N}}}$
,
 $$ \begin{align*} \sigma_{2k}(gt,x)=\sigma_{2k}(g,tx)\sigma_{2k}(t,x)&=\sigma_{2k}(g,x_{\xi}) \\ &=\sigma_{2k}(g,x)=\sigma_{2k}(t,gx)\sigma_{2k}(g,x)=\sigma_{2k}(tg,x) \end{align*} $$
$$ \begin{align*} \sigma_{2k}(gt,x)=\sigma_{2k}(g,tx)\sigma_{2k}(t,x)&=\sigma_{2k}(g,x_{\xi}) \\ &=\sigma_{2k}(g,x)=\sigma_{2k}(t,gx)\sigma_{2k}(g,x)=\sigma_{2k}(tg,x) \end{align*} $$
as
![]() $\sigma _{l}(t,y)=\operatorname {\mathrm {id}}$
for all
$\sigma _{l}(t,y)=\operatorname {\mathrm {id}}$
for all
![]() $l\in \operatorname {\mathrm {\mathbb {N}}}$
and
$l\in \operatorname {\mathrm {\mathbb {N}}}$
and
![]() $y\in V(T_{d})$
, and
$y\in V(T_{d})$
, and
![]() $g\in \mathrm {BU}_{2(k+1)}(F^{(2(k+1))})_{B(b,2)}$
.
$g\in \mathrm {BU}_{2(k+1)}(F^{(2(k+1))})_{B(b,2)}$
.
Remark 5.30. We argue that the construction of this section does not carry over to any primitive
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
and
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
and
![]() $\Gamma (F)\le F^{(2)}\le \Phi (F)$
.
$\Gamma (F)\le F^{(2)}\le \Phi (F)$
.
First, note that
![]() $\Phi (F)\backslash \Omega ^{(2)}=\Gamma (F)\backslash \Omega ^{(2)}$
. For
$\Phi (F)\backslash \Omega ^{(2)}=\Gamma (F)\backslash \Omega ^{(2)}$
. For
![]() $\alpha :=(a,(a_{\omega })_{\omega \in \Omega })\in \Phi (F)$
and
$\alpha :=(a,(a_{\omega })_{\omega \in \Omega })\in \Phi (F)$
and
![]() $\smash {(\omega _{1},\omega _{2})\!\in \!\Omega ^{(2)}}$
we have
$\smash {(\omega _{1},\omega _{2})\!\in \!\Omega ^{(2)}}$
we have
![]() $\alpha (\omega _{1},\omega _{2})=(a\omega _{1},a_{\omega _{1}}\omega _{2})\in \{(a\omega _{1},aF_{\omega _{1}}\omega _{2})\}\subseteq \Gamma (F)(\omega _{1},\omega _{2})$
. We now observe the following obstruction to nondiscreteness. Given any orbit
$\alpha (\omega _{1},\omega _{2})=(a\omega _{1},a_{\omega _{1}}\omega _{2})\in \{(a\omega _{1},aF_{\omega _{1}}\omega _{2})\}\subseteq \Gamma (F)(\omega _{1},\omega _{2})$
. We now observe the following obstruction to nondiscreteness. Given any orbit
![]() $\smash {\Omega ^{(2)}_{0}\in \Phi (F)\backslash \Omega ^{(2)}=F^{(2)}\backslash \Omega ^{(2)}}$
, the subgroup of
$\smash {\Omega ^{(2)}_{0}\in \Phi (F)\backslash \Omega ^{(2)}=F^{(2)}\backslash \Omega ^{(2)}}$
, the subgroup of
![]() $\Phi (F)$
consisting of elements that are self-compatible in all directions from
$\Phi (F)$
consisting of elements that are self-compatible in all directions from
![]() $\smash {\Omega ^{(2)}_{0}}$
is precisely
$\smash {\Omega ^{(2)}_{0}}$
is precisely
![]() $\Gamma (F)$
.
$\Gamma (F)$
.
Indeed, every element of
![]() $\Gamma (F)$
is self-compatible in all directions from
$\Gamma (F)$
is self-compatible in all directions from
![]() $\Omega ^{(2)}\!\supseteq \!\Omega _{0}^{2}$
. Conversely, let
$\Omega ^{(2)}\!\supseteq \!\Omega _{0}^{2}$
. Conversely, let
![]() $(a,(a_{\omega })_{\omega })\in \Phi (F)$
be self-compatible in all directions from
$(a,(a_{\omega })_{\omega })\in \Phi (F)$
be self-compatible in all directions from
![]() $\smash {\Omega ^{(2)}_{0}}$
. Consider the equivalence relation on
$\smash {\Omega ^{(2)}_{0}}$
. Consider the equivalence relation on
![]() $\Omega $
defined by
$\Omega $
defined by
![]() $\omega _{1}\sim \omega _{2}$
if and only if
$\omega _{1}\sim \omega _{2}$
if and only if
![]() $a_{\omega _{1}}=a_{\omega _{2}}$
. Since
$a_{\omega _{1}}=a_{\omega _{2}}$
. Since
![]() $a_{\omega _{1}}=a_{\omega _{2}}$
whenever
$a_{\omega _{1}}=a_{\omega _{2}}$
whenever
![]() $\xi :=(\omega _{1},\omega _{2})\in \smash {\Omega ^{(2)}_{0}}$
, this relation is F-invariant. Since
$\xi :=(\omega _{1},\omega _{2})\in \smash {\Omega ^{(2)}_{0}}$
, this relation is F-invariant. Since
![]() $\Gamma (F)\le \Phi (F)$
we have
$\Gamma (F)\le \Phi (F)$
we have
![]() $\smash {\gamma (a)(\omega _{1},\omega _{2})=(a\omega _{1},a\omega _{2})\in \Omega ^{(2)}_{0}}$
for all
$\smash {\gamma (a)(\omega _{1},\omega _{2})=(a\omega _{1},a\omega _{2})\in \Omega ^{(2)}_{0}}$
for all
![]() $a\in F$
whenever
$a\in F$
whenever
![]() $\smash {(\omega _{1},\omega _{2})\in \Omega ^{(2)}_{0}}$
. Since F is primitive, it is the universal relation, so
$\smash {(\omega _{1},\omega _{2})\in \Omega ^{(2)}_{0}}$
. Since F is primitive, it is the universal relation, so
![]() $(a,(a_{\omega })_{\omega })\!\in \!\Gamma (F)$
.
$(a,(a_{\omega })_{\omega })\!\in \!\Gamma (F)$
.
5.2 Banks–Elder–Willis
 $(P_{k})$
-closures
$(P_{k})$
-closures
Theorem 4.34 yields a description of the
![]() $(P_{k})$
-closures of locally transitive subgroups of
$(P_{k})$
-closures of locally transitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
that contain an involutive inversion, and therefore a characterization of the locally transitive universal groups. Recall that the
$\operatorname {\mathrm {Aut}}(T_{d})$
that contain an involutive inversion, and therefore a characterization of the locally transitive universal groups. Recall that the
![]() $(P_{k})$
-closure of a subgroup
$(P_{k})$
-closure of a subgroup
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
is
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
is
Combined with Corollary 4.18 the following partially answers the question for an algebraic description of a group’s
![]() $(P_{k})$
-closure in the last paragraph of [Reference Banks, Elder and Willis1].
$(P_{k})$
-closure in the last paragraph of [Reference Banks, Elder and Willis1].
Theorem 5.31. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and contain an involutive inversion. Then
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be locally transitive and contain an involutive inversion. Then
![]() $\smash {H^{(P_{k})}=\mathrm {U}_{k}^{(l)}(F^{(k)})}$
for some labelling l of
$\smash {H^{(P_{k})}=\mathrm {U}_{k}^{(l)}(F^{(k)})}$
for some labelling l of
![]() $T_{d}$
and
$T_{d}$
and
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
.
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
.
Proof. Let l and
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
be as in Theorem 4.34. Then
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
be as in Theorem 4.34. Then
![]() $\smash {H^{(P_{k})}\!=\!\mathrm {U}_{k}^{(l)}(F^{(k)})}$
.
$\smash {H^{(P_{k})}\!=\!\mathrm {U}_{k}^{(l)}(F^{(k)})}$
.
Let
![]() $\smash {g\in \mathrm {U}_{k}(F^{(k)})}$
and
$\smash {g\in \mathrm {U}_{k}(F^{(k)})}$
and
![]() $x\in V$
. Since
$x\in V$
. Since
![]() $\smash {\mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})\le H}$
there is
$\smash {\mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})\le H}$
there is
![]() $\smash {h'\in \mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})}\le H$
with
$\smash {h'\in \mathrm {U}_{1}^{(l)}(\{\operatorname {\mathrm {id}}\})}\le H$
with
![]() $h'(x)=g(x)$
, and since H is k-locally action isomorphic to
$h'(x)=g(x)$
, and since H is k-locally action isomorphic to
![]() $\smash {F^{(k)}}$
there is
$\smash {F^{(k)}}$
there is
![]() $h"\!\in \! H_{x}$
such that
$h"\!\in \! H_{x}$
such that
![]() $\sigma _{k}(h",x)=\sigma _{k}(g,x)$
. Then
$\sigma _{k}(h",x)=\sigma _{k}(g,x)$
. Then
![]() $h:=h'h"\in H$
satisfies
$h:=h'h"\in H$
satisfies
![]() $g|_{B(x,k)}=h|_{B(x,k)}$
.
$g|_{B(x,k)}=h|_{B(x,k)}$
.
Conversely, let
![]() $\smash {g\in H^{(P_{k})}}$
. Then all k-local actions of g stem from elements of H. Given that
$\smash {g\in H^{(P_{k})}}$
. Then all k-local actions of g stem from elements of H. Given that
![]() $H\le \mathrm {U}_{k}(F^{(k)})$
by Theorem 4.34, we conclude that
$H\le \mathrm {U}_{k}(F^{(k)})$
by Theorem 4.34, we conclude that
![]() $g\in \mathrm {U}_{k}(F^{(k)})$
.
$g\in \mathrm {U}_{k}(F^{(k)})$
.
Corollary 5.32. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed, locally transitive and contain an involutive inversion. Then
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed, locally transitive and contain an involutive inversion. Then
![]() $\smash {H=\mathrm {U}_{k}^{(l)}(F^{(k)})}$
for some labelling l of
$\smash {H=\mathrm {U}_{k}^{(l)}(F^{(k)})}$
for some labelling l of
![]() $T_{d}$
and an action
$T_{d}$
and an action
![]() $\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
if and only if H satisfies property
$\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
if and only if H satisfies property
![]() $(P_{k})$
.
$(P_{k})$
.
Proof. If
![]() $H=\mathrm {U}_{k}^{(l)}(F^{(k)})$
then H satisfies property
$H=\mathrm {U}_{k}^{(l)}(F^{(k)})$
then H satisfies property
![]() $(P_{k})$
by Proposition 4.7. Conversely, if H satisfies Property
$(P_{k})$
by Proposition 4.7. Conversely, if H satisfies Property
![]() $\smash {(P_{k})}$
then
$\smash {(P_{k})}$
then
![]() $\smash {H=\overline {H}\!=\!H^{(P_{k})}}$
by [Reference Banks, Elder and Willis1, Theorem 5.4] and the assertion follows from Theorem 5.31.
$\smash {H=\overline {H}\!=\!H^{(P_{k})}}$
by [Reference Banks, Elder and Willis1, Theorem 5.4] and the assertion follows from Theorem 5.31.
Banks, Elder and Willis use certain subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
with pairwise distinct
$\operatorname {\mathrm {Aut}}(T_{d})$
with pairwise distinct
![]() $(P_{k})$
-closures to construct infinitely many, pairwise nonconjugate, nondiscrete simple subgroups of
$(P_{k})$
-closures to construct infinitely many, pairwise nonconjugate, nondiscrete simple subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
via Theorem 2.1 and [Reference Banks, Elder and Willis1, Theorem 8.2]. For example, the group
$\operatorname {\mathrm {Aut}}(T_{d})$
via Theorem 2.1 and [Reference Banks, Elder and Willis1, Theorem 8.2]. For example, the group
![]() $\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})\!\le \!\operatorname {\mathrm {Aut}}(T_{p+1})$
qualifies by the argument in [Reference Banks, Elder and Willis1, Section 4.1]. Whereas
$\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})\!\le \!\operatorname {\mathrm {Aut}}(T_{p+1})$
qualifies by the argument in [Reference Banks, Elder and Willis1, Section 4.1]. Whereas
![]() $\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})$
has trivial quasicentre given that it is simple, certain groups with nontrivial quasicentre always have infinitely many distinct
$\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})$
has trivial quasicentre given that it is simple, certain groups with nontrivial quasicentre always have infinitely many distinct
![]() $(P_{k})$
-closures.
$(P_{k})$
-closures.
Proposition 5.33. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed, nondiscrete, locally transitive and contain an involutive inversion. If also H has nontrivial quasicentre then H has infinitely many distinct
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be closed, nondiscrete, locally transitive and contain an involutive inversion. If also H has nontrivial quasicentre then H has infinitely many distinct
![]() $(P_{k})$
-closures.
$(P_{k})$
-closures.
Proof. We have
![]() $H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})$
by Theorem 5.31. Therefore,
$H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})$
by Theorem 5.31. Therefore,
![]() $H=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
by [Reference Banks, Elder and Willis1, Proposition 3.4(iii)]. If H had only finitely many distinct
$H=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
by [Reference Banks, Elder and Willis1, Proposition 3.4(iii)]. If H had only finitely many distinct
![]() $(P_{k})$
-closures, the sequence
$(P_{k})$
-closures, the sequence
![]() $(H^{(P_{k})})_{k\in \operatorname {\mathrm {\mathbb {N}}}}$
of subgroups of
$(H^{(P_{k})})_{k\in \operatorname {\mathrm {\mathbb {N}}}}$
of subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
would be eventually constant and equal to, say,
$\operatorname {\mathrm {Aut}}(T_{d})$
would be eventually constant and equal to, say,
![]() $H^{(n)}=\mathrm {U}_{n}(F^{(n)})\ge H$
. However, since H is nondiscrete, so is
$H^{(n)}=\mathrm {U}_{n}(F^{(n)})\ge H$
. However, since H is nondiscrete, so is
![]() $\mathrm {U}_{n}(F^{(n)})$
which thus has trivial quasicentre by Proposition 4.21.
$\mathrm {U}_{n}(F^{(n)})$
which thus has trivial quasicentre by Proposition 4.21.
Banks, Elder and Willis ask whether the infinitely many, pairwise nonconjugate, nondiscrete simple subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
they construct are also pairwise nonisomorphic as topological groups. By Proposition 4.17, this is the case if the said simple groups are locally transitive with distinct point-stabilizers, which can be determined from the original group’s k-local actions thanks to Theorem 5.31.
$\operatorname {\mathrm {Aut}}(T_{d})$
they construct are also pairwise nonisomorphic as topological groups. By Proposition 4.17, this is the case if the said simple groups are locally transitive with distinct point-stabilizers, which can be determined from the original group’s k-local actions thanks to Theorem 5.31.
Theorem 5.34. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete, locally permutation isomorphic to
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be nondiscrete, locally permutation isomorphic to
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
and contain an involutive inversion. Suppose that F is transitive and that every nontrivial subnormal subgroup of
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
and contain an involutive inversion. Suppose that F is transitive and that every nontrivial subnormal subgroup of
![]() $F_{\omega }\ (\omega \!\in \!\Omega )$
is transitive on
$F_{\omega }\ (\omega \!\in \!\Omega )$
is transitive on
![]() $\Omega \backslash \{\omega \}$
. If
$\Omega \backslash \{\omega \}$
. If
![]() $H^{(P_{k})}\neq H^{(P_{l})}$
for some
$H^{(P_{k})}\neq H^{(P_{l})}$
for some
![]() $k,l\in \operatorname {\mathrm {\mathbb {N}}}$
then
$k,l\in \operatorname {\mathrm {\mathbb {N}}}$
then
![]() $(H^{(P_{k})})^{+_{k}}$
and
$(H^{(P_{k})})^{+_{k}}$
and
![]() $(H^{(P_{l})})^{+_{l}}$
are nonisomorphic.
$(H^{(P_{l})})^{+_{l}}$
are nonisomorphic.
Proof. In view of [Reference Banks, Elder and Willis1, Theorem 8.2], the groups
![]() $(H^{(P_{k})})^{+_{k}}$
and
$(H^{(P_{k})})^{+_{k}}$
and
![]() $(H^{(P_{l})})^{+_{l}}$
are nonconjugate. We show that they satisfy the assumptions of Proposition 4.17 which then implies the assertion. It suffices to consider
$(H^{(P_{l})})^{+_{l}}$
are nonconjugate. We show that they satisfy the assumptions of Proposition 4.17 which then implies the assertion. It suffices to consider
![]() $H^{(P_{k})}$
. By Theorem 5.31, we have
$H^{(P_{k})}$
. By Theorem 5.31, we have
![]() $H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})$
for some
$H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})$
for some
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. By virtue of Proposition 4.10, we may assume that
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
. By virtue of Proposition 4.10, we may assume that
![]() $\smash {F^{(k)}}$
satisfies (C). Since H is nondiscrete, so is
$\smash {F^{(k)}}$
satisfies (C). Since H is nondiscrete, so is
![]() $\smash {H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})}$
. Therefore,
$\smash {H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})}$
. Therefore,
![]() $F^{(k)}$
does not satisfy (D); see Proposition 4.12. Hence, in view of the local action of H and Proposition 4.31, the group
$F^{(k)}$
does not satisfy (D); see Proposition 4.12. Hence, in view of the local action of H and Proposition 4.31, the group
![]() $\smash {\pi _{\xi }F^{(k)}_{T_{\omega }}}$
is nontrivial and thus transitive by Proposition 4.30 for all
$\smash {\pi _{\xi }F^{(k)}_{T_{\omega }}}$
is nontrivial and thus transitive by Proposition 4.30 for all
![]() $\smash {\xi =(\omega _{1},\ldots ,\omega _{k-1})\in \Omega ^{(k-1)}}$
and
$\smash {\xi =(\omega _{1},\ldots ,\omega _{k-1})\in \Omega ^{(k-1)}}$
and
![]() $\omega \in \Omega \backslash \{\omega _{1}\}$
. Now, let
$\omega \in \Omega \backslash \{\omega _{1}\}$
. Now, let
![]() $x\in V(T_{d})$
. For every
$x\in V(T_{d})$
. For every
![]() $\omega \in \Omega $
pick
$\omega \in \Omega $
pick
![]() $\xi =(\omega _{1},\ldots ,\omega _{k-2},\omega )\in \Omega ^{(k-1)}$
. Let
$\xi =(\omega _{1},\ldots ,\omega _{k-2},\omega )\in \Omega ^{(k-1)}$
. Let
![]() $y\in V(T_{d})$
be such that
$y\in V(T_{d})$
be such that
![]() $x=y_{\xi }$
. Since
$x=y_{\xi }$
. Since
![]() $\smash {\pi _{\xi }F^{(k)}_{T_{\omega '}}}$
is transitive for every
$\smash {\pi _{\xi }F^{(k)}_{T_{\omega '}}}$
is transitive for every
![]() $\omega '\in \Omega \backslash \{\omega _{1}\}$
we conclude that
$\omega '\in \Omega \backslash \{\omega _{1}\}$
we conclude that
![]() $(H^{(P_{k})})^{+_{k}}$
is locally
$(H^{(P_{k})})^{+_{k}}$
is locally
![]() $2$
-transitive at x. So Proposition 4.17 applies.
$2$
-transitive at x. So Proposition 4.17 applies.
Example 5.35. Theorem 5.34 applies to
![]() $\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})\!\le \!\operatorname {\mathrm {Aut}}(T_{p+1})$
for any prime p by Lemma 5.36 below. In fact, the local action is given by
$\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})\!\le \!\operatorname {\mathrm {Aut}}(T_{p+1})$
for any prime p by Lemma 5.36 below. In fact, the local action is given by
![]() $\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {F}}}_{p})\!\curvearrowright \!\mathrm {P}^{1}(\operatorname {\mathrm {\mathbb {F}}}_{p})$
, point-stabilizers of which act like
$\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {F}}}_{p})\!\curvearrowright \!\mathrm {P}^{1}(\operatorname {\mathrm {\mathbb {F}}}_{p})$
, point-stabilizers of which act like
![]() $\operatorname {\mathrm {AGL}}(1,p)\!=\!\operatorname {\mathrm {\mathbb {F}}}_{p}^{\ast }\ltimes \operatorname {\mathrm {\mathbb {F}}}_{p}\curvearrowright \operatorname {\mathrm {\mathbb {F}}}_{p}$
. Retaining the notation of [Reference Banks, Elder and Willis1, Section 4.1], an involutive inversion in
$\operatorname {\mathrm {AGL}}(1,p)\!=\!\operatorname {\mathrm {\mathbb {F}}}_{p}^{\ast }\ltimes \operatorname {\mathrm {\mathbb {F}}}_{p}\curvearrowright \operatorname {\mathrm {\mathbb {F}}}_{p}$
. Retaining the notation of [Reference Banks, Elder and Willis1, Section 4.1], an involutive inversion in
![]() $\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})$
is given by
$\operatorname {\mathrm {PGL}}(2,\operatorname {\mathrm {\mathbb {Q}}}_{p})$
is given by
 $$ \begin{align*} \sigma:=\begin{bmatrix}0 & 1 \\ p & 0\end{bmatrix} \quad\text{with } \sigma^{2}=\begin{bmatrix}p & 0 \\ 0 & p\end{bmatrix}=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}. \end{align*} $$
$$ \begin{align*} \sigma:=\begin{bmatrix}0 & 1 \\ p & 0\end{bmatrix} \quad\text{with } \sigma^{2}=\begin{bmatrix}p & 0 \\ 0 & p\end{bmatrix}=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}. \end{align*} $$
Indeed,
![]() $\sigma $
swaps the vertices v and
$\sigma $
swaps the vertices v and
![]() $\textbf {L}_{p}$
.
$\textbf {L}_{p}$
.
Lemma 5.36. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be
![]() $2$
-transitive. If
$2$
-transitive. If
![]() $|\Omega |-1$
is prime then every nontrivial subnormal subgroup of
$|\Omega |-1$
is prime then every nontrivial subnormal subgroup of
![]() $F_{\omega }$
(
$F_{\omega }$
(
![]() $\omega \in \Omega $
) acts transitively on
$\omega \in \Omega $
) acts transitively on
![]() $\Omega \backslash \{\omega \}$
.
$\Omega \backslash \{\omega \}$
.
Proof. Since
![]() $F_{\omega }$
acts transitively on
$F_{\omega }$
acts transitively on
![]() $\Omega \backslash \{\omega \}$
, which has prime order,
$\Omega \backslash \{\omega \}$
, which has prime order,
![]() $F_{\omega }$
is primitive. So every nontrivial normal subgroup of
$F_{\omega }$
is primitive. So every nontrivial normal subgroup of
![]() $F_{\omega }$
acts transitively on
$F_{\omega }$
acts transitively on
![]() $\Omega \backslash \{\omega \}$
. Iterate.
$\Omega \backslash \{\omega \}$
. Iterate.
Example 5.37. The proof of Theorem 5.34 shows that the assumptions on F can be replaced with asking that
![]() $(H^{(P_{k})})^{+_{k}}$
be locally transitive with distinct point-stabilizers, which may be feasible to check in a given example.
$(H^{(P_{k})})^{+_{k}}$
be locally transitive with distinct point-stabilizers, which may be feasible to check in a given example.
For instance, let
![]() $F\!\le \!\mathrm {Sym}(\Omega )$
be transitive with distinct point-stabilizers. Assume that F preserves a nontrivial partition
$F\!\le \!\mathrm {Sym}(\Omega )$
be transitive with distinct point-stabilizers. Assume that F preserves a nontrivial partition
![]() $\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
$\operatorname {\mathrm {\mathcal {P}}}:\Omega =\bigsqcup _{i\in I}\Omega _{i}$
of
![]() $\Omega $
and that it is generated by its block stabilizers, that is,
$\Omega $
and that it is generated by its block stabilizers, that is,
![]() $F=\langle \{F_{\Omega _{i}}\mid i\in I\}\rangle $
.
$F=\langle \{F_{\Omega _{i}}\mid i\in I\}\rangle $
.
Let
![]() $p:\Omega \to I$
be such that
$p:\Omega \to I$
be such that
![]() $\omega \in \Omega _{p\omega }$
for all
$\omega \in \Omega _{p\omega }$
for all
![]() $\omega \in \Omega $
. Inductively define groups
$\omega \in \Omega $
. Inductively define groups
![]() $\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
by
$\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
by
![]() $\smash {F^{(1)}:=F}$
and
$\smash {F^{(1)}:=F}$
and
![]() $\smash {F^{(k+1)}\!:=\!\Phi _{k}(F^{(k)},\operatorname {\mathrm {\mathcal {P}}})}$
, and check that
$\smash {F^{(k+1)}\!:=\!\Phi _{k}(F^{(k)},\operatorname {\mathrm {\mathcal {P}}})}$
, and check that
-
(i)
 $C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
$C_{F^{(k)}}(\alpha ,\Omega _{i})$
is nonempty for all
 $\smash {\alpha \in F^{(k)}}$
and
$\smash {\alpha \in F^{(k)}}$
and
 $i\in I$
,
$i\in I$
, -
(ii)
 $C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
$C_{F^{(k)}}(\operatorname {\mathrm {id}},\Omega _{i})$
is nontrivial for all
 $i\in I$
,
$i\in I$
, -
(iii)
 $F^{(k+1)}\lneq \Phi (F^{(k)})$
, and
$F^{(k+1)}\lneq \Phi (F^{(k)})$
, and -
(iv)
 $\smash {\pi _{\xi }F^{(k)}_{T_{\omega }}\!=\!F_{\Omega _{p\omega _{k-1}}}}$
for all
$\smash {\pi _{\xi }F^{(k)}_{T_{\omega }}\!=\!F_{\Omega _{p\omega _{k-1}}}}$
for all
 $\omega \!\in \!\Omega $
and
$\omega \!\in \!\Omega $
and
 $\xi \!=\!(\omega _{1},\ldots ,\omega _{k-1})\!\in \!\Omega ^{(k-1)}$
with
$\xi \!=\!(\omega _{1},\ldots ,\omega _{k-1})\!\in \!\Omega ^{(k-1)}$
with
 $\omega _{1}\!\notin \!\Omega _{p\omega }$
.
$\omega _{1}\!\notin \!\Omega _{p\omega }$
.
In particular,
![]() $F^{(k)}$
satisfies (C) but not (D) for all
$F^{(k)}$
satisfies (C) but not (D) for all
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
. Set
$k\in \operatorname {\mathrm {\mathbb {N}}}$
. Set
![]() $H:=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
. By the above, H is nondiscrete and contains both
$H:=\bigcap _{k\in \operatorname {\mathrm {\mathbb {N}}}}\mathrm {U}_{k}(F^{(k)})$
. By the above, H is nondiscrete and contains both
![]() $D(F)$
and
$D(F)$
and
![]() $\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})$
. Hence, Theorem 5.31 applies and we have
$\mathrm {U}_{1}(\{\operatorname {\mathrm {id}}\})$
. Hence, Theorem 5.31 applies and we have
![]() $H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})$
. From item (iii), we conclude that the
$H^{(P_{k})}=\mathrm {U}_{k}(F^{(k)})$
. From item (iii), we conclude that the
![]() $H^{(P_{k})}$
(
$H^{(P_{k})}$
(
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
) are pairwise distinct. Given that
$k\in \operatorname {\mathrm {\mathbb {N}}}$
) are pairwise distinct. Given that
![]() $(H^{(P_{k})})^{+_{k}}$
locally acts like F due to item (iv), the
$(H^{(P_{k})})^{+_{k}}$
locally acts like F due to item (iv), the
![]() $\smash {(H^{(P_{k})})^{+_{k}}}\ (k\in \operatorname {\mathrm {\mathbb {N}}})$
are hence pairwise nonisomorphic.
$\smash {(H^{(P_{k})})^{+_{k}}}\ (k\in \operatorname {\mathrm {\mathbb {N}}})$
are hence pairwise nonisomorphic.
5.3 A view on the Weiss conjecture
The Weiss conjecture states that there are only finitely many conjugacy classes of discrete, vertex-transitive, locally primitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
for a given
$\operatorname {\mathrm {Aut}}(T_{d})$
for a given
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
. We now study the universal group construction in the discrete case and offer a new view on this conjecture. Under the additional assumption that each group contains an involutive inversion, it suffices to show that for every primitive
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
. We now study the universal group construction in the discrete case and offer a new view on this conjecture. Under the additional assumption that each group contains an involutive inversion, it suffices to show that for every primitive
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
there are only finitely many
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
there are only finitely many
![]() $\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}\ (k\in \operatorname {\mathrm {\mathbb {N}}})$
with
$\smash {\widetilde {F}\le \operatorname {\mathrm {Aut}}(B_{d,k})}\ (k\in \operatorname {\mathrm {\mathbb {N}}})$
with
![]() $\smash {\pi \widetilde {F}=F}$
and that satisfy (CD) in a minimal fashion; see Definition 5.42 and the discussion thereafter.
$\smash {\pi \widetilde {F}=F}$
and that satisfy (CD) in a minimal fashion; see Definition 5.42 and the discussion thereafter.
The following consequence of Theorem 5.31 identifies certain groups relevant to the Weiss conjecture as universal groups for local actions satisfying condition (CD).
Corollary 5.38. Let
![]() $H\le \operatorname {\mathrm {Aut}}(T_{d})$
be discrete, locally transitive and contain an involutive inversion. Then
$H\le \operatorname {\mathrm {Aut}}(T_{d})$
be discrete, locally transitive and contain an involutive inversion. Then
![]() $\smash {H=\mathrm {U}_{k}^{(l)}(F^{(k)})}$
for some
$\smash {H=\mathrm {U}_{k}^{(l)}(F^{(k)})}$
for some
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
, a labelling l of
$k\in \operatorname {\mathrm {\mathbb {N}}}$
, a labelling l of
![]() $T_{d}$
and
$T_{d}$
and
![]() $\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfying (CD) that is isomorphic to the k-local action of H.
$\smash {F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})}$
satisfying (CD) that is isomorphic to the k-local action of H.
Proof. Discreteness of H implies property
![]() $(P_{k})$
for every
$(P_{k})$
for every
![]() $k\in \operatorname {\mathrm {\mathbb {N}}}$
such that stabilizers in H of balls of radius k in
$k\in \operatorname {\mathrm {\mathbb {N}}}$
such that stabilizers in H of balls of radius k in
![]() $T_{d}$
are trivial. Then apply Theorem 5.31.
$T_{d}$
are trivial. Then apply Theorem 5.31.
Therefore, the study of the class of groups given in Corollary 5.38 reduces to the study of subgroups
![]() $F\le \operatorname {\mathrm {Aut}}(B_{d,k}) \ (k\in \operatorname {\mathrm {\mathbb {N}}})$
that satisfy (CD) and for which
$F\le \operatorname {\mathrm {Aut}}(B_{d,k}) \ (k\in \operatorname {\mathrm {\mathbb {N}}})$
that satisfy (CD) and for which
![]() $\pi F$
is transitive. By Corollary 4.15, any two conjugate such groups yield isomorphic universal groups. In this sense, it suffices to examine conjugacy classes of subgroups of
$\pi F$
is transitive. By Corollary 4.15, any two conjugate such groups yield isomorphic universal groups. In this sense, it suffices to examine conjugacy classes of subgroups of
![]() $\operatorname {\mathrm {Aut}}(B_{d,k})$
. This can be done computationally using the description of conditions (C) and (D) developed in Section 4.2, using, for example, [9].
$\operatorname {\mathrm {Aut}}(B_{d,k})$
. This can be done computationally using the description of conditions (C) and (D) developed in Section 4.2, using, for example, [9].
Example 5.39. Consider the case
![]() $d\!=\!3$
. By [Reference Djoković and Miller7, Reference Tutte31, Reference Tutte32], there are, up to conjugacy, seven discrete, vertex-transitive and locally transitive subgroups of
$d\!=\!3$
. By [Reference Djoković and Miller7, Reference Tutte31, Reference Tutte32], there are, up to conjugacy, seven discrete, vertex-transitive and locally transitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{3})$
. We denote them by
$\operatorname {\mathrm {Aut}}(T_{3})$
. We denote them by
![]() $G_{1}$
,
$G_{1}$
,
![]() $G_{2}$
,
$G_{2}$
,
![]() $G_{2}^{1}$
,
$G_{2}^{1}$
,
![]() $G_{3}$
,
$G_{3}$
,
![]() $G_{4}$
,
$G_{4}$
,
![]() $G_{4}^{1}$
and
$G_{4}^{1}$
and
![]() $G_{5}$
. The subscript n determines the isomorphism class of the vertex stabilizer, whose order is
$G_{5}$
. The subscript n determines the isomorphism class of the vertex stabilizer, whose order is
![]() $3\cdot 2^{n-1}$
. A group contains an involutive inversion if and only if it has no superscript. The minimal order of an inversion in
$3\cdot 2^{n-1}$
. A group contains an involutive inversion if and only if it has no superscript. The minimal order of an inversion in
![]() $G_{2}^{1}$
and
$G_{2}^{1}$
and
![]() $G_{4}^{1}$
is
$G_{4}^{1}$
is
![]() $4$
. See also [Reference Conder and Lorimer4]. By Corollary 5.38, the groups
$4$
. See also [Reference Conder and Lorimer4]. By Corollary 5.38, the groups
![]() $G_{n}\ (n\!\in \!\{1,\ldots ,5\})$
are of the form
$G_{n}\ (n\!\in \!\{1,\ldots ,5\})$
are of the form
![]() $\mathrm {U}_{k}(F)$
. We recover their local actions in Table 1. The list is complete for
$\mathrm {U}_{k}(F)$
. We recover their local actions in Table 1. The list is complete for
![]() $k=2$
, and for
$k=2$
, and for
![]() $k=3$
in the case of (CD).
$k=3$
in the case of (CD).
Table. 1 Conjugacy class representatives of subgroups F of
![]() and
and
![]() that satisfy (C) and project onto a transitive subgroup of
that satisfy (C) and project onto a transitive subgroup of
![]() $S_{3}$
.
$S_{3}$
.

The column labelled ‘i.c.c.’ records whether F admits an involutive compatibility cocycle. This can be determined in [9] and is automatic in the case of (CD). The group
![]() $\Pi (S_{3},\mathrm {sgn},\{1\})$
of Proposition 4.25 admits an involutive compatibility cocycle z which we describe as follows. Suppose
$\Pi (S_{3},\mathrm {sgn},\{1\})$
of Proposition 4.25 admits an involutive compatibility cocycle z which we describe as follows. Suppose
![]() $\Omega \!:=\!\{1,2,3\}$
. Let
$\Omega \!:=\!\{1,2,3\}$
. Let
![]() $t_{i}\!\in \!\operatorname {\mathrm {Sym}}(\Omega )$
be the transposition that fixes i, and let
$t_{i}\!\in \!\operatorname {\mathrm {Sym}}(\Omega )$
be the transposition that fixes i, and let
![]() $\tau _{i}\!\in \! \Pi (S_{3},\mathrm {sgn},\{1\})$
be the element whose
$\tau _{i}\!\in \! \Pi (S_{3},\mathrm {sgn},\{1\})$
be the element whose
![]() $1$
-local action is
$1$
-local action is
![]() $t_{i}$
everywhere except at
$t_{i}$
everywhere except at
![]() $b_{i}$
. Then
$b_{i}$
. Then
![]() $\Pi (S_{3},\mathrm {sgn},\{1\})=\langle \tau _{1},\tau _{2},\tau _{3}\rangle $
. Further, let
$\Pi (S_{3},\mathrm {sgn},\{1\})=\langle \tau _{1},\tau _{2},\tau _{3}\rangle $
. Further, let
![]() $\kappa _{i}\in \Pi (S_{3},\mathrm {sgn},\{1\})\cap \ker \pi $
be the nontrivial element with
$\kappa _{i}\in \Pi (S_{3},\mathrm {sgn},\{1\})\cap \ker \pi $
be the nontrivial element with
![]() $\sigma _{1}(\kappa _{i},b_{i})=e$
. We then have
$\sigma _{1}(\kappa _{i},b_{i})=e$
. We then have
![]() $z(\tau _{i},i)=\kappa _{i-1}$
and
$z(\tau _{i},i)=\kappa _{i-1}$
and
![]() $z(\tau _{i},j)=\tau _{i}\kappa _{j}$
for all distinct
$z(\tau _{i},j)=\tau _{i}\kappa _{j}$
for all distinct
![]() $i,j\in \Omega $
, with cyclic notation.
$i,j\in \Omega $
, with cyclic notation.
The kernel
![]() $K_{2}$
is the diagonal subgroup of
$K_{2}$
is the diagonal subgroup of
![]() $\smash {\operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}^{3\cdot (3-1)}\cong \ker \pi _{2}\le \operatorname {\mathrm {Aut}}(B_{3,3})}$
. Using the above, we conclude that
$\smash {\operatorname {\mathrm {\mathbb {Z}}}\!/2\operatorname {\mathrm {\mathbb {Z}}}^{3\cdot (3-1)}\cong \ker \pi _{2}\le \operatorname {\mathrm {Aut}}(B_{3,3})}$
. Using the above, we conclude that
![]() $G_{1}=\mathrm {U}_{1}(A_{3})$
,
$G_{1}=\mathrm {U}_{1}(A_{3})$
,
![]() $G_{2}=\mathrm {U}_{2}(\Gamma (S_{3}))$
,
$G_{2}=\mathrm {U}_{2}(\Gamma (S_{3}))$
,
![]() $G_{3}=\mathrm {U}_{2}(\Delta (S_{3}))$
,
$G_{3}=\mathrm {U}_{2}(\Delta (S_{3}))$
,
![]() $G_{4}=\mathrm {U}_{3}(\Gamma _{2}(\Pi (S_{3},\mathrm {sgn},\{1\})))$
and
$G_{4}=\mathrm {U}_{3}(\Gamma _{2}(\Pi (S_{3},\mathrm {sgn},\{1\})))$
and
![]() $G_{5}=\mathrm {U}_{3}(\Sigma _{2}(\Pi (S_{3},\mathrm {sgn},\{1\}),K_{2}))$
.
$G_{5}=\mathrm {U}_{3}(\Sigma _{2}(\Pi (S_{3},\mathrm {sgn},\{1\}),K_{2}))$
.
Question 5.40. Can the groups
![]() $G_{2}^{1}$
and
$G_{2}^{1}$
and
![]() $G_{4}^{1}$
be described as universal groups with prescribed local actions on edge neighbourhoods that prevent involutive inversions?
$G_{4}^{1}$
be described as universal groups with prescribed local actions on edge neighbourhoods that prevent involutive inversions?
The long-standing Weiss conjecture [Reference Weiss33] states that there are only finitely many conjugacy classes of discrete, vertex-transitive, locally primitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
for a given
$\operatorname {\mathrm {Aut}}(T_{d})$
for a given
![]() $d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
. Potočnic et al. [Reference Potočnik, Spiga and Verret21] show that a permutation group
$d\in \operatorname {\mathrm {\mathbb {N}}}_{\ge 3}$
. Potočnic et al. [Reference Potočnik, Spiga and Verret21] show that a permutation group
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
, for which there are only finitely many conjugacy classes of discrete, vertex-transitive subgroups of
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
, for which there are only finitely many conjugacy classes of discrete, vertex-transitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
that locally act like F, is necessarily semiprimitive, and conjecture the converse. Promising partial results were obtained in the same article as well as by Giudici and Morgan in [Reference Giudici and Morgan11].
$\operatorname {\mathrm {Aut}}(T_{d})$
that locally act like F, is necessarily semiprimitive, and conjecture the converse. Promising partial results were obtained in the same article as well as by Giudici and Morgan in [Reference Giudici and Morgan11].
Corollary 5.38 suggests restricting to discrete, locally semiprimitive subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
containing an involutive inversion.
$\operatorname {\mathrm {Aut}}(T_{d})$
containing an involutive inversion.
Conjecture 5.41. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be semiprimitive. Then there are only finitely many conjugacy classes of discrete subgroups of
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be semiprimitive. Then there are only finitely many conjugacy classes of discrete subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
that locally act like F and contain an involutive inversion.
$\operatorname {\mathrm {Aut}}(T_{d})$
that locally act like F and contain an involutive inversion.
For a transitive permutation group
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
, let
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
, let
![]() $\operatorname {\mathrm {\mathcal {H}}}_{F}$
denote the collection of subgroups of
$\operatorname {\mathrm {\mathcal {H}}}_{F}$
denote the collection of subgroups of
![]() $\operatorname {\mathrm {Aut}}(T_{d})$
that are discrete, locally act like F and contain an involutive inversion. Then the following definition is meaningful by Corollary 5.38.
$\operatorname {\mathrm {Aut}}(T_{d})$
that are discrete, locally act like F and contain an involutive inversion. Then the following definition is meaningful by Corollary 5.38.
Definition 5.42. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Define
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Define
if the maximum exists and
![]() $\dim _{\mathrm {CD}}(F)=\infty $
otherwise.
$\dim _{\mathrm {CD}}(F)=\infty $
otherwise.
Given Definition 5.42, Conjecture 5.41 is equivalent to asserting that
![]() $\dim _{\mathrm {CD}}(F)$
is finite whenever
$\dim _{\mathrm {CD}}(F)$
is finite whenever
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
is semiprimitive. The remainder of this subsection is devoted to determining
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
is semiprimitive. The remainder of this subsection is devoted to determining
![]() $\dim _{\mathrm {CD}}$
for certain classes of transitive permutation groups.
$\dim _{\mathrm {CD}}$
for certain classes of transitive permutation groups.
Proposition 5.43. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Then
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be transitive. Then
![]() $\dim _{\mathrm {CD}}(F)=1$
if and only if F is regular.
$\dim _{\mathrm {CD}}(F)=1$
if and only if F is regular.
Proof. If F is regular, then
![]() $\dim _{\mathrm {CD}}(F)=1$
by Proposition 4.13. Conversely, if
$\dim _{\mathrm {CD}}(F)=1$
by Proposition 4.13. Conversely, if
![]() $\dim _{\mathrm {CD}}(F)=1$
then
$\dim _{\mathrm {CD}}(F)=1$
then
![]() $\mathrm {U}_{2}(\Delta (F))=\mathrm {U}_{1}(F)=\mathrm {U}_{2}(\Gamma (F))$
. Hence,
$\mathrm {U}_{2}(\Delta (F))=\mathrm {U}_{1}(F)=\mathrm {U}_{2}(\Gamma (F))$
. Hence,
![]() $\Gamma (F)\cong \Delta (F)$
, which implies that
$\Gamma (F)\cong \Delta (F)$
, which implies that
![]() $F_{\omega }$
is trivial for all
$F_{\omega }$
is trivial for all
![]() $\omega \in \Omega $
. That is, F is regular.
$\omega \in \Omega $
. That is, F is regular.
The next proposition provides a large class of primitive groups of dimension
![]() $2$
. It relies on the following relations between various characteristic subgroups of a finite group. Recall that the socle of a finite group is the subgroup generated by its minimal normal subgroups, which form a direct product.
$2$
. It relies on the following relations between various characteristic subgroups of a finite group. Recall that the socle of a finite group is the subgroup generated by its minimal normal subgroups, which form a direct product.
Lemma 5.44. Let G be a finite group. Then the following assertions are equivalent.
-
(i) The socle
 $\mathrm {soc}(G)$
has no abelian factor.
$\mathrm {soc}(G)$
has no abelian factor. -
(ii) The solvable radical
 $\operatorname {\mathrm {\mathcal {O}}}_{\infty }(G)$
is trivial.
$\operatorname {\mathrm {\mathcal {O}}}_{\infty }(G)$
is trivial. -
(iii) The nilpotent radical
 $\mathrm {Fit}(G)$
is trivial.
$\mathrm {Fit}(G)$
is trivial.
Proof. If
![]() $\mathrm {soc}(G)$
has no abelian factor then
$\mathrm {soc}(G)$
has no abelian factor then
![]() $\operatorname {\mathrm {\mathcal {O}}}_{\infty }(G)$
is trivial: a nontrivial solvable normal subgroup of G would contain a minimal solvable normal subgroup of G which is necessarily abelian. Next, (ii) implies (iii) as every nilpotent group is solvable. Finally, if
$\operatorname {\mathrm {\mathcal {O}}}_{\infty }(G)$
is trivial: a nontrivial solvable normal subgroup of G would contain a minimal solvable normal subgroup of G which is necessarily abelian. Next, (ii) implies (iii) as every nilpotent group is solvable. Finally, if
![]() $\mathrm {soc}(G)$
has an abelian factor then G contains a (minimal) normal abelian, hence nilpotent subgroup. Thus (iii) implies (i).
$\mathrm {soc}(G)$
has an abelian factor then G contains a (minimal) normal abelian, hence nilpotent subgroup. Thus (iii) implies (i).
Proposition 5.45. Let
![]() $F\le \operatorname {\mathrm {Sym}}(\Omega )$
be primitive, nonregular and assume that
$F\le \operatorname {\mathrm {Sym}}(\Omega )$
be primitive, nonregular and assume that
![]() $F_{\omega }$
has trivial nilpotent radical for all
$F_{\omega }$
has trivial nilpotent radical for all
![]() $\omega \in \Omega $
. Then
$\omega \in \Omega $
. Then
![]() $\dim _{\mathrm {CD}}(F)=2$
.
$\dim _{\mathrm {CD}}(F)=2$
.
Proof. Suppose that
![]() $F^{(2)}\le \operatorname {\mathrm {Aut}}(B_{d,2})$
satisfies (C) and that the sequence
$F^{(2)}\le \operatorname {\mathrm {Aut}}(B_{d,2})$
satisfies (C) and that the sequence
is exact. Fix
![]() $\omega _{0}\in \Omega $
. Then
$\omega _{0}\in \Omega $
. Then
![]() $\ker \pi \le \prod _{\omega \in \Omega }F_{\omega }\cong F_{\omega _{0}}^{d}$
. Since
$\ker \pi \le \prod _{\omega \in \Omega }F_{\omega }\cong F_{\omega _{0}}^{d}$
. Since
![]() $F^{(2)}$
satisfies (C), we have
$F^{(2)}$
satisfies (C), we have
![]() $\operatorname {\mathrm {pr}}_{\omega }(\ker \pi )\unlhd F_{\omega _{0}}$
for all
$\operatorname {\mathrm {pr}}_{\omega }(\ker \pi )\unlhd F_{\omega _{0}}$
for all
![]() $\omega \in \Omega $
, and since F is transitive these projections all coincide with the same
$\omega \in \Omega $
, and since F is transitive these projections all coincide with the same
![]() $N\unlhd F_{\omega _{0}}$
. Now consider
$N\unlhd F_{\omega _{0}}$
. Now consider
![]() $\smash {F^{(2)}_{T_{\omega }}=\ker \operatorname {\mathrm {pr}}_{\omega }|_{\ker \pi }\unlhd \ker \pi }$
for some
$\smash {F^{(2)}_{T_{\omega }}=\ker \operatorname {\mathrm {pr}}_{\omega }|_{\ker \pi }\unlhd \ker \pi }$
for some
![]() $\omega \in \Omega $
. Either
$\omega \in \Omega $
. Either
![]() $\smash {F^{(2)}_{T_{\omega }}}$
is trivial, in which case
$\smash {F^{(2)}_{T_{\omega }}}$
is trivial, in which case
![]() $\smash {F^{(2)}}$
has (CD), or
$\smash {F^{(2)}}$
has (CD), or
![]() $\smash {F^{(2)}_{T_{\omega }}}$
is nontrivial. In the latter case, suppose
$\smash {F^{(2)}_{T_{\omega }}}$
is nontrivial. In the latter case, suppose
![]() $\smash {N_{\omega ,\omega '}:=\operatorname {\mathrm {pr}}_{\omega '}F^{(2)}_{T_{\omega }}}$
is nontrivial for some
$\smash {N_{\omega ,\omega '}:=\operatorname {\mathrm {pr}}_{\omega '}F^{(2)}_{T_{\omega }}}$
is nontrivial for some
![]() $\omega '\in \Omega $
. Then
$\omega '\in \Omega $
. Then
![]() $N_{\omega ,\omega '}$
is subnormal in
$N_{\omega ,\omega '}$
is subnormal in
![]() $F_{\omega _{0}}$
as
$F_{\omega _{0}}$
as
![]() $N_{\omega ,\omega '}\unlhd N\unlhd F_{\omega _{0}}$
and therefore has trivial nilpotent radical. The Thompson–Wielandt theorem [Reference Thompson28, Reference Wielandt34] (cf. [Reference Burger and Mozes2, Theorem 2.1.1]) now implies that there is no
$N_{\omega ,\omega '}\unlhd N\unlhd F_{\omega _{0}}$
and therefore has trivial nilpotent radical. The Thompson–Wielandt theorem [Reference Thompson28, Reference Wielandt34] (cf. [Reference Burger and Mozes2, Theorem 2.1.1]) now implies that there is no
![]() $F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
,
$F^{(k)}\le \operatorname {\mathrm {Aut}}(B_{d,k})$
,
![]() $k\ge 3$
, satisfying
$k\ge 3$
, satisfying
![]() $\pi _{2}F^{(k)}=F^{(2)}$
and (CD). Thus
$\pi _{2}F^{(k)}=F^{(2)}$
and (CD). Thus
![]() $\dim _{\mathrm {CD}}(F)\le 2$
. Equality holds by Proposition 5.43.
$\dim _{\mathrm {CD}}(F)\le 2$
. Equality holds by Proposition 5.43.
Proposition 5.45 applies to
![]() $\operatorname {\mathrm {Alt}}(d)$
and
$\operatorname {\mathrm {Alt}}(d)$
and
![]() $\operatorname {\mathrm {Sym}}(d)$
,
$\operatorname {\mathrm {Sym}}(d)$
,
![]() $d\ge 6$
, whose point-stabilizers have nonabelian simple socle
$d\ge 6$
, whose point-stabilizers have nonabelian simple socle
![]() $\operatorname {\mathrm {Alt}}(d-1)$
. It also applies to primitive groups of O’Nan–Scott type (TW) and (HS), whose point-stabilizers have trivial solvable radical [Reference Dixon and Mortimer6, Theorem 4.7B] and simple nonabelian socle [Reference Liebeck, Praeger and Saxl16], respectively.
$\operatorname {\mathrm {Alt}}(d-1)$
. It also applies to primitive groups of O’Nan–Scott type (TW) and (HS), whose point-stabilizers have trivial solvable radical [Reference Dixon and Mortimer6, Theorem 4.7B] and simple nonabelian socle [Reference Liebeck, Praeger and Saxl16], respectively.
Example 5.46. By Example 5.39, we have
![]() $\dim _{\mathrm {CD}}(S_{3})\ge 3$
. The article [Reference Djoković and Miller7] shows that in fact
$\dim _{\mathrm {CD}}(S_{3})\ge 3$
. The article [Reference Djoković and Miller7] shows that in fact
![]() $\dim _{\mathrm {CD}}(S_{3})=3$
.
$\dim _{\mathrm {CD}}(S_{3})=3$
.
To contrast the primitive case, we show that imprimitive wreath products have dimension at least
![]() $3$
, illustrating the use of involutive compatibility cocycles. Recall that for
$3$
, illustrating the use of involutive compatibility cocycles. Recall that for
![]() $F\le \mathrm {Sym}(\Omega )$
and
$F\le \mathrm {Sym}(\Omega )$
and
![]() $P\le \mathrm {Sym}(\Lambda )$
the wreath product
$P\le \mathrm {Sym}(\Lambda )$
the wreath product
![]() $\smash {F\wr P:=F^{\vert \Lambda \vert }\rtimes P}$
admits a natural imprimitive action on
$\smash {F\wr P:=F^{\vert \Lambda \vert }\rtimes P}$
admits a natural imprimitive action on
![]() $\Omega \times \Lambda $
with the partition
$\Omega \times \Lambda $
with the partition
![]() $\bigsqcup _{\lambda \in \Lambda }\Omega \times \{\lambda \}$
, namely
$\bigsqcup _{\lambda \in \Lambda }\Omega \times \{\lambda \}$
, namely
![]() $((a_{\lambda })_{\lambda },\sigma )\cdot (\omega ,\lambda '):=(a_{\sigma (\lambda ')}\omega ,\sigma \lambda ')$
.
$((a_{\lambda })_{\lambda },\sigma )\cdot (\omega ,\lambda '):=(a_{\sigma (\lambda ')}\omega ,\sigma \lambda ')$
.
Proposition 5.47. Let
![]() $\Omega $
and
$\Omega $
and
![]() $\Lambda $
be finite sets of size at least
$\Lambda $
be finite sets of size at least
![]() $2$
. Furthermore, let
$2$
. Furthermore, let
![]() $F\le \mathrm {Sym}(\Omega )$
and
$F\le \mathrm {Sym}(\Omega )$
and
![]() $P\le \mathrm {Sym}(\Lambda )$
be transitive. Then
$P\le \mathrm {Sym}(\Lambda )$
be transitive. Then
![]() $\dim _{\mathrm {CD}}(F\wr P)\ge 3$
.
$\dim _{\mathrm {CD}}(F\wr P)\ge 3$
.
Proof. We define a subgroup
![]() $W(F,P)\le \operatorname {\mathrm {Aut}}(B_{|\Omega \times \Lambda |,2})$
that projects onto
$W(F,P)\le \operatorname {\mathrm {Aut}}(B_{|\Omega \times \Lambda |,2})$
that projects onto
![]() $F\wr P$
, satisfies (C), does not satisfy (D) but admits an involutive compatibility cocycle. This suffices by Lemma 4.26. For
$F\wr P$
, satisfies (C), does not satisfy (D) but admits an involutive compatibility cocycle. This suffices by Lemma 4.26. For
![]() $\lambda \in \Lambda $
, let
$\lambda \in \Lambda $
, let
![]() $\iota _{\lambda }$
denote the
$\iota _{\lambda }$
denote the
![]() $\lambda $
th embedding of F into
$\lambda $
th embedding of F into
![]() $\smash {F\wr P=(\prod _{\lambda \in \Lambda }F)\rtimes P}$
. Recall the map
$\smash {F\wr P=(\prod _{\lambda \in \Lambda }F)\rtimes P}$
. Recall the map
![]() $\gamma $
from Section 4.4.1 and consider
$\gamma $
from Section 4.4.1 and consider
Furthermore, let
![]() $\iota $
denote the embedding of P into
$\iota $
denote the embedding of P into
![]() $F\wr P$
. We define
$F\wr P$
. We define
By construction,
![]() $W(F,P)$
does not satisfy (D). To see that
$W(F,P)$
does not satisfy (D). To see that
![]() $W(F,P)$
admits an involutive compatibility cocycle, we first determine its group structure. Consider the subgroups
$W(F,P)$
admits an involutive compatibility cocycle, we first determine its group structure. Consider the subgroups
![]() $V:=\langle \gamma _{\lambda }(a)\mid \lambda \in \Lambda ,\ a\in F\rangle $
and
$V:=\langle \gamma _{\lambda }(a)\mid \lambda \in \Lambda ,\ a\in F\rangle $
and
![]() $\smash {\overline {V}:=\langle \gamma _{\lambda }^{(2)}(a)\mid \lambda \in \Lambda ,\ a\in F\rangle }$
. Then
$\smash {\overline {V}:=\langle \gamma _{\lambda }^{(2)}(a)\mid \lambda \in \Lambda ,\ a\in F\rangle }$
. Then
![]() $W(F,P)=\langle V,\overline {V},\Gamma (\iota (P))\rangle $
. Observe that
$W(F,P)=\langle V,\overline {V},\Gamma (\iota (P))\rangle $
. Observe that
![]() $V\cong F^{|\Lambda |}$
and
$V\cong F^{|\Lambda |}$
and
![]() $\overline {V}\cong F^{|\Lambda |}$
commute, intersect trivially, and that
$\overline {V}\cong F^{|\Lambda |}$
commute, intersect trivially, and that
![]() $\Gamma (\iota (P))$
permutes the factors of each product. Hence,
$\Gamma (\iota (P))$
permutes the factors of each product. Hence,
An involutive compatibility cocycle z of
![]() $W(F,P)$
may now be defined by setting
$W(F,P)$
may now be defined by setting
 $$ \begin{align*} z(\gamma_{\lambda}(a),(\omega,\lambda')):=\begin{cases} \gamma_{\lambda}(a) & \lambda=\lambda' \\ \gamma_{\lambda}^{(2)}(a) & \lambda\neq \lambda'\end{cases}, \,z(\gamma_{\lambda}^{(2)}(a),(\omega,\lambda')):=\begin{cases} \gamma_{\lambda}^{(2)}(a) & \lambda=\lambda' \\ \gamma_{\lambda}(a) & \lambda\neq\lambda'\end{cases} \end{align*} $$
$$ \begin{align*} z(\gamma_{\lambda}(a),(\omega,\lambda')):=\begin{cases} \gamma_{\lambda}(a) & \lambda=\lambda' \\ \gamma_{\lambda}^{(2)}(a) & \lambda\neq \lambda'\end{cases}, \,z(\gamma_{\lambda}^{(2)}(a),(\omega,\lambda')):=\begin{cases} \gamma_{\lambda}^{(2)}(a) & \lambda=\lambda' \\ \gamma_{\lambda}(a) & \lambda\neq\lambda'\end{cases} \end{align*} $$
for all
![]() $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
,
![]() $a\in F$
, and
$a\in F$
, and
![]() $z(\gamma (\iota (\varrho )),(\omega ,\lambda )):=\gamma (\iota (\varrho ))$
for all
$z(\gamma (\iota (\varrho )),(\omega ,\lambda )):=\gamma (\iota (\varrho ))$
for all
![]() $\varrho \in P$
. In fact, the map z extends to an involutive compatibility cocycle of
$\varrho \in P$
. In fact, the map z extends to an involutive compatibility cocycle of
![]() $V\times \overline {V}\le W(F,P)$
which in turn extends to an involutive compatibility cocycle of
$V\times \overline {V}\le W(F,P)$
which in turn extends to an involutive compatibility cocycle of
![]() $W(F,P)$
.
$W(F,P)$
.
Acknowledgements
The author is indebted to Marc Burger and George Willis for their support and the suggestion to define generalized universal groups. Thanks are also due to Luke Morgan and Michael Giudici for sharing their insight on permutation groups, and Michael Giudici for providing a proof of Lemma 4.29. Two anonymous referees’ comments were also much appreciated.
A good part of this research was carried out during visits to The University of Newcastle, Australia, for the hospitality of which the author is thankful.