The Extent of Frozen Ground Under the Sea Bottom and Glacier Beds

Abstract

The ground in Spitsbergen is frozen to a depth of about 320 m., as can be seen from observations in the collieries. At a mean surface temperature of −8° C. this corresponds to a geothermal gradient of 1°/40 m. The temperature of the sea water is almost 0° C. Along the coast the land lies very little above the sea level, and here the sea is shallow. One assumes that the land as well as the sea bed is horizontal. Thus the temperature on the land is –8° C., in the sea 0° C. On the coast the temperature must suddenly change. One must also take into account the fact that the temperature rises with depth. A simple calculation leads to the conclusion that the frozen ground below the sea bed must extend about 100 m. from the coast. Investigations near a Swedish colliery have shown this to be the case.

This result also applies to the conditions underneath a glacier. On the same assumptions one can conclude that if the glacier is less than 400 m. wide the frozen ground underneath forms one coherent layer and that this is not the case if the glacier is wider. The same applies to a shallow fjord.

Zusammenfassung

Wie sich aus Beobachtungen in den Kohlenbergenwerken ergibt, ist der Boden in Spitzbergen bis zu einer Tiefe von ca. 320 m. gefroren. Bei einer mittleren Oberflächentemperatur von −8° entspricht dies einer geothermischen Stufe von 1°/140 m. Die Temperatur im Seewasser ist dagegen beinahe 0°. Dem Ufer entlang zieht sich eine nur ganz wenig über dem Seespiegel liegende Strecke, und das Meer ist hier ganz seicht. Man darf annehmen, dass sowohl die Land-Oberfläche als auch der Seeboden auf waagrechter Fläche liegen. Auf dem Lande ist also die Temperatur –8°, im Meere 0°. Gerade am Ufer muss sich die Temperatur sprungweise ändern. Man muss auch die mit der Tiefe steigende Temperatur in Betracht ziehen. Nach einfacher Berechnung kommt man zu dem Schluss, dass sich der gefrorener Boden unter dem Seeboden ungefähr 100 m. vom Ufer aus erstreckt. Dass sich dies so verhält, hat man bei einer schwedischen Kohlenmine festgestellt.

Dieses Ergebnis kann man auf den sich unter einem Gletscher befindenden Zustand anwenden. Unter denselben Annahmen kommt man zu dem Schluss, dass falls der Gletscher weniger als 400 m. breit ist das Eis darunter eine zusammenhängende Schicht bildet, dass dies aber nicht der Fall ist, wenn der Gletscher breiter ist. Dasselbe gilt für einen seichten Fjord.

In countries with a low annual temperature combined with slight snowfall, the subsoil is permanently frozen. In Spitsbergen a great deal of the snow that falls during the winter is blown out of the valleys and deposited on the fjord ice. If the temperature of the subsoil is assumed to rise uniformly with depth by one degree centigrade per 40 metres, the frozen subsoil, earth and rock, should reach the enormous thickness of about 1000 ft. (305 m.), depending upon the mean temperature of the surface.

Near the Swedish colliery in Braganza Bay (Lowe Sound) the melting point of ice was found at a depth of about 320 metres below the surface, and 430 metres from the mouth of the level adit. Assuming the vertical temperature gradient to be q=1/40, the mean annual temperature of the surface should be −8° C.

Along the shore the land is low and flat for a considerable distance from the beach and the sea is very shallow. The temperature of the sea water may be taken to be 0° C.

As an approximation we will assume that both land and sea bottom (and surface) are situated in the same horizontal plane. We then introduce a system of coordinates. The Z-axis coincides with the shore, which is assumed to be straight; the X-axis is horizontal and positive along the surface of the sea; the Y-axis is perpendicular and positive downwards. The soil is assumed to be homogeneous in respect to the conductivity of heat and temperature. Then the following expression holds good:

Dividing the temperature T into two components

we put

to account for the gradual change of temperature between the surface of the land, T ₀, and the temperature of the sea, 0° C. (In the figures we have taken T ₀ = −8° C.) (Fig. 1, p. 199).

Fig. 1

Further T ₂ = qy where y is the depth below the surface and q the temperature gradient below a level surface (Fig. 2).

Fig. 2

These temperature fields can both be represented by simple graphs.

By superposition we obtain

Fig. 3

For the sake of convenience we write

and obtain

For the temperature gradient G we get

where r ²=x ²+y ², r being the distance from the origin.

With increasing distance r, the gradient G approaches the value

and, at the same time, the direction of the gradient becomes more and more vertical. This means that the effect of the disturbance in the temperature field will disappear in the distance.

By putting T=constant, an isothermal curve is obtained. For temperatures between 0° and T ₀, these curves all pass through the origin, which is a singular point in the temperature field. There is another singular point at the intersection of the curve T = 0 and the X-axis, with the coordinates x = h, y = 0. This point marks the edge of the frozen ground at the sea bottom.

By introducing the values T ₀ = −8° and q = 1/40, we obtain h = 100 m. The frozen soil should stretch along the sea bottom to a distance of about 100 metres from the shore, and should there drop off vertically.

From information gathered on the site at this colliery, the ice was found to extend under the sea bottom to a distance of about 100 metres from the shore. This should correspond to a mean temperature T ₀ = −8° C., which may be considered as probable.

Fact and theory seem to be in agreement.

We will suppose now, that a shallow fjord lies between low flat land on both sides. The temperature of the sea water is 0° C., that of the surface of the land, T°. The fjord is assumed to be straight with parallel sides, and with breadth B. We shall consider a plane section, perpendicular to the coasts. As before, we put:

and after calculation we obtain the following results:

The curve T = 0° C. indicates the Iimit of the area of temperatures below zero, that is, the frozen ground. This area is continuous below the fjord from one shore to the other, if B is Iess than 4h (Figs. 4 and 5). In the opposite case, B being greater than 4h, the area of frost is divided into two distinct parts, by an intervening area of temperatures above zero Figs. 6 and 7. The breadth of the ice-free zone is:

But, as 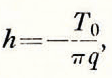then 4h = −50T ₀, approximately

Therefore,

Thus, if the temperature T ₀ = −8° C. for example, then frozen ground will extend continuously from one shore to the other beneath the bed of the sea, provided the width of the fjord does not exceed 400 metres.

Fig. 4

Fig. 5

Fig. 6 Permanently frozen earth continuous from one side of a fjord to the other under the sea bed when the fjord is less than 400 m. across

Fig. 7 Permanently frozen earth near the two shores of a fjord with a zone of unfrozen earth beneath the centre of the fjord bed when the fjord exceeds 400 m. in width

Now, let us consider what happens in glaciers. Below an active glacier the temperature is practically at the melting point of ice; water streams from the snout even during the winter. (There are exceptions.) If now a glacier is broader than the same 4h, where

the frozen soil cannot join below the ice, from one side to the other so that along the central part there will be some unfrozen ground.

Under the central parts of large glaciers, then, the water can sink down into the ground, and pass down through the layer of impervious frozen subsoil. In this way it is possible to account for the origin of the rather numerous springs in the floors of some broad valleys in Spitsbergen.

This theory is only an approximation, but I think that it explains the main facts in substance.