1. Introduction
Particle-laden turbulent flows are widespread in both nature and industry. One of the most important features of turbulence is its ability to effectively transport suspended particles and create highly inhomogeneous particle distributions, which eventually lead to frequent particle collisions or bubble/droplet coalescence (Falkovich, Gawedzki & Vergassola Reference Falkovich, Gawedzki and Vergassola2001; Toschi & Bodenschatz Reference Toschi and Bodenschatz2009; Pumir & Wilkinson Reference Pumir and Wilkinson2016). Typical natural processes can be found as rain formation (Shaw Reference Shaw2003; Grabowski & Wang Reference Grabowski and Wang2013), sandstorms (Zhang & Zhou Reference Zhang and Zhou2020) and the formation of marine snow in the ocean (Arguedas-Leiva et al. Reference Arguedas-Leiva, Słomka, Lalescu, Stocker and Wilczek2022), while in industrial applications turbulence-induced collisions are also shown to be essential in dusty particle removal (Jaworek et al. Reference Jaworek, Marchewicz, Sobczyk, Krupa and Czech2018) and flocculation (Zhao et al. Reference Zhao, Pomes, Vowinckel, Hsu, Bai and Meiburg2021).
It has been widely shown that the spatial distribution of inertial particles is highly non-uniform and intermittent, which is known as preferential concentration (Maxey Reference Maxey1987; Squires & Eaton Reference Squires and Eaton1991). Preferential concentration could significantly enhance the local particle number density and facilitate interparticle collisions (Reade & Collins Reference Reade and Collins2000). At the dissipative range, clustering is driven by Kolmogorov-scale eddies that eject heavy particles out of high-vorticity regions while entrapping light bubbles (Balkovsky, Falkovich & Fouxon Reference Balkovsky, Falkovich and Fouxon2001; Calzavarini et al. Reference Calzavarini, Cencini, Lohse and Toschi2008; Mathai et al. Reference Mathai, Calzavarini, Brons, Sun and Lohse2016). Moreover, later studies show that, in addition to clustering at the dissipative scale, the coexistence of multi-scale vortices in turbulence also affects the dynamics of heavy particles with relaxation times much larger than the Kolmogorov time scale, and drives self-similar clustering at larger scales (Goto & Vassilicos Reference Goto and Vassilicos2006; Bec et al. Reference Bec, Biferale, Cencini, Lanotte, Musacchio and Toschi2007; Yoshimoto & Goto Reference Yoshimoto and Goto2007; Baker et al. Reference Baker, Frankel, Mani and Coletti2017). Besides, the inertial-range clustering of heavy particles can be alternatively explained by the sweep-stick mechanism, where inertial particles are assumed to stick to and move with fluid elements with zero acceleration (Goto & Vassilicos Reference Goto and Vassilicos2008).
Apart from preferential concentration, the sling effect or the formation of caustics becomes more significant with the growth of particle inertia or turbulence intensity (Falkovich, Fouxon & Stepanov Reference Falkovich, Fouxon and Stepanov2002; Wilkinson & Mehlig Reference Wilkinson and Mehlig2005; Wilkinson, Mehlig & Bezuglyy Reference Wilkinson, Mehlig and Bezuglyy2006; Falkovich & Pumir Reference Falkovich and Pumir2007). When sling happens, inertial particles encountering intermittent fluctuations get ejected out of local flow. Then, clouds of particles with different flow histories interpenetrate each other with large relative velocities (Bewley, Saw & Bodenschatz Reference Bewley, Saw and Bodenschatz2013). As a result, the large relative velocity gives rise to an abrupt growth of the collision frequency, and the sling effect becomes the dominant collision mechanism for large-inertia particles (Voßkuhle et al. Reference Voßkuhle, Pumir, Lévêque and Wilkinson2014).
By means of direct numerical simulations (DNSs), the contributions of both preferential concentration and the sling effect (or the turbulence transport effect) to the collision rate could be quantified separately. A framework based on the radial distribution function and the mean relative velocity was proposed to predict the collision kernel function of neutral monodisperse particles with arbitrary inertia (Sundaram & Collins Reference Sundaram and Collins1997; Wang, Wexler & Zhou Reference Wang, Wexler and Zhou2000). Based on this framework, the impacts of turbulence Reynolds number, nonlinear drag, gravity and hydrodynamic interactions were systematically investigated (Ayala, Rosa & Wang Reference Ayala, Rosa and Wang2008a; Ayala et al. Reference Ayala, Rosa, Wang and Grabowski2008b; Ireland, Bragg & Collins Reference Ireland, Bragg and Collins2016a,Reference Ireland, Bragg and Collinsb; Ababaei et al. Reference Ababaei, Rosa, Pozorski and Wang2021; Bragg et al. Reference Bragg, Hammond, Dhariwal and Meng2022). In addition to monodisperse particles, this framework was also extended to bidispersed particle systems. Compared with monodisperse system, the clustering of different-size particles is found to be weaker, while the turbulent transport effect is more pronounced due to the particles’ different responses to turbulent fluctuations (Zhou, Wexler & Wang Reference Zhou, Wexler and Wang2001).
In addition to neutral particles, particles in nature could easily get charged after moving through ionized air (Marshall & Li Reference Marshall and Li2014; van Minderhout et al. Reference van Minderhout, van Huijstee, Rompelberg, Post, Peijnenburg, Blom and Beckers2021) or encountering collisions (Lee et al. Reference Lee, Waitukaitis, Miskin and Jaeger2015). The resulting electrostatic interaction could significantly modulate the fundamental particle dynamics in turbulence, such as clustering, dispersion and agglomeration (Karnik & Shrimpton Reference Karnik and Shrimpton2012; Yao & Capecelatro Reference Yao and Capecelatro2018; Ruan, Chen & Li Reference Ruan, Chen and Li2021; Boutsikakis, Fede & Simonin Reference Boutsikakis, Fede and Simonin2022; Ruan & Li Reference Ruan and Li2022; Zhang, Cui & Zheng Reference Zhang, Cui and Zheng2023). For identically charged particles, it has been shown that the Coulomb repulsion could effectively repel close particle pairs and mitigate particle clustering. By assuming that the drift velocity caused by the Coulomb force can be superposed on the turbulence drift velocity, the radial distribution function of particles with negligible/finite inertia can be derived, which shows good agreement with both experimental and numerical results (Lu et al. Reference Lu, Nordsiek, Saw and Shaw2010a; Lu, Nordsiek & Shaw Reference Lu, Nordsiek and Shaw2010b; Lu & Shaw Reference Lu and Shaw2015).
Different from the like-charged monodisperse system, real charged particle-laden flows may be more complicated because: (i) the size of suspended particles is generally polydispersed (Zhang & Zhou Reference Zhang and Zhou2020), and (ii) the charge polarity varies with the particle size because of charge segregation. That is, after triboelectrification, smaller particles tend to accumulate negative charges while large ones are preferentially positively charged (Forward, Lacks & Sankaran Reference Forward, Lacks and Sankaran2009; Lee et al. Reference Lee, Waitukaitis, Miskin and Jaeger2015). In the previous work by Di Renzo & Urzay (Reference Di Renzo and Urzay2018), DNS of the bidispersed suspensions of oppositely charged particles was performed. It was shown that the aerodynamic response of different-size particles to turbulent fluctuations varies significantly. Although the system is overall neutral, different clustering behaviours lead to a spatial separation of positive and negative charge generating mesoscale electric fields in space.
However, even though the charge segregation is often correlated with the size difference, few studies have been devoted to the dynamics of bidispersed particles with both charge and size differences. In this system, three kinds of electrostatic interactions are introduced simultaneously, i.e. repulsion between small–small/large–large particles and attraction between small–large particles. How these electrostatic forces affect the clustering of bidispersed particles is less understood. Moreover, the collision frequency of charged particles is of great importance to understand the physics of rain initiation (Harrison et al. Reference Harrison, Nicoll, Ambaum, Marlton, Aplin and Lockwood2020) and planet formation (Steinpilz et al. Reference Steinpilz, Joeris, Jungmann, Wolf, Brendel, Teiser, Shinbrot and Wurm2020), and the influence of charge segregation on these processes are still unclear.
To address the above issues, in this study we perform DNSs to investigate the dynamics of bidispersed oppositely charged particles in homogeneous isotropic turbulence. The numerical methods are introduced in § 2. In § 3, the statistics of the radial distribution function and the mean relative velocity are first presented to show the effects of the electrostatic force on the clustering and the relative motion between different kinds of particle pairs. Then, the modulation of collision frequency is quantified using the particle flux, and the mean Coulomb-turbulence parameter is proposed to characterize the relative importance of the electrostatic force compared with particle–turbulence interaction. Finally, the particle flux density in the relative velocity space is discussed, which illustrates in detail how the electrostatic force affects the collision of charged particle pairs with different relative velocities.
2. Methods
2.1. Simulation conditions
The transport of bidispersed solid particles in turbulence is numerically investigated using the Eulerian–Lagrangian framework. The flow field is homogeneous isotropic turbulence with the Taylor Reynolds number ![]() ${Re}_{\lambda }=147.5$. Solid particles are treated as discrete points and their motions are updated based on the Maxey–Riley equation (Maxey & Riley Reference Maxey and Riley1983).
${Re}_{\lambda }=147.5$. Solid particles are treated as discrete points and their motions are updated based on the Maxey–Riley equation (Maxey & Riley Reference Maxey and Riley1983).
Table 1 lists the simulation parameters used in this study. Particle properties are chosen based on typical values of silica particles suspended in gaseous turbulence. Here, the particle density is much larger than that of the air (![]() $\rho _{{p}}/\rho _{{f}} \sim O(10^3)$), and the particle size is smaller than the Kolmogorov length (i.e.
$\rho _{{p}}/\rho _{{f}} \sim O(10^3)$), and the particle size is smaller than the Kolmogorov length (i.e. ![]() $d_{{p,S}}/\eta =0.1, d_{{p,L}}/\eta \approx 0.3$, where
$d_{{p,S}}/\eta =0.1, d_{{p,L}}/\eta \approx 0.3$, where ![]() $d_{p,S}$ and
$d_{p,S}$ and ![]() $d_{p,L}$ are the diameters of small and large particles, respectively, and
$d_{p,L}$ are the diameters of small and large particles, respectively, and ![]() $\eta$ is the Kolmogorov length scale). The particle Stokes number
$\eta$ is the Kolmogorov length scale). The particle Stokes number ![]() $St$, defined as the ratio of the particle relaxation time
$St$, defined as the ratio of the particle relaxation time ![]() $\tau _{{p}}$ to the Kolmogorov time scale
$\tau _{{p}}$ to the Kolmogorov time scale ![]() $\tau _{\eta }$, is given by
$\tau _{\eta }$, is given by
 \begin{equation} St = \frac{\tau_{{p}}}{\tau_{\eta}} = \frac{1}{18} \frac{\rho_{{p}}}{\rho_{{f}}} {\left(\frac{d_{{p}}}{\eta} \right)}^2. \end{equation}
\begin{equation} St = \frac{\tau_{{p}}}{\tau_{\eta}} = \frac{1}{18} \frac{\rho_{{p}}}{\rho_{{f}}} {\left(\frac{d_{{p}}}{\eta} \right)}^2. \end{equation}
In previous field measurements (Zhang & Zhou Reference Zhang and Zhou2020), the Stokes number of sand particles was mainly in the range of ![]() $St = 1\unicode{x2013}10$ in strong sandstorms. We thus choose
$St = 1\unicode{x2013}10$ in strong sandstorms. We thus choose ![]() $St_{{S}}=1$ and
$St_{{S}}=1$ and ![]() $St_{{L}}=10$ as the typical Stokes numbers for small and large particles, respectively. In addition, since the measured particle mass concentration in Zhang & Zhou (Reference Zhang and Zhou2020) is low, the particle volume fraction is set small (
$St_{{L}}=10$ as the typical Stokes numbers for small and large particles, respectively. In addition, since the measured particle mass concentration in Zhang & Zhou (Reference Zhang and Zhou2020) is low, the particle volume fraction is set small (![]() $\phi _{{par}} = 6.87 \times 10^{-6}$) in our simulation, and the force feedback from the dilute particle phase to the fluid phase is omitted (Balachandar & Eaton Reference Balachandar and Eaton2010).
$\phi _{{par}} = 6.87 \times 10^{-6}$) in our simulation, and the force feedback from the dilute particle phase to the fluid phase is omitted (Balachandar & Eaton Reference Balachandar and Eaton2010).
Table 1. Simulation parameters.

When choosing the particle charge, we assume that particles carry a certain amount of charge as a result of triboelectrification. Both small and large particles are assigned the same amount of charge ![]() $q$ but with the opposite polarities. Because of charge segregation, small particles (
$q$ but with the opposite polarities. Because of charge segregation, small particles (![]() $St_{{S}}=1$) are negatively charged while large particles (
$St_{{S}}=1$) are negatively charged while large particles (![]() $St_{{L}}=10$) are positive. In previous measurements of tribocharged particles, the surface charge density could reach
$St_{{L}}=10$) are positive. In previous measurements of tribocharged particles, the surface charge density could reach ![]() $\sigma _{{p}} \approx 10^{-5}\ \mathrm {\mu }\mathrm {C}\ \mathrm {m}^{-2}$ (Waitukaitis et al. Reference Waitukaitis, Lee, Pierson, Forman and Jaeger2014; Lee et al. Reference Lee, Waitukaitis, Miskin and Jaeger2015; Harper et al. Reference Harper, Cimarelli, Cigala, Kueppers and Dufek2021). For a particle size of
$\sigma _{{p}} \approx 10^{-5}\ \mathrm {\mu }\mathrm {C}\ \mathrm {m}^{-2}$ (Waitukaitis et al. Reference Waitukaitis, Lee, Pierson, Forman and Jaeger2014; Lee et al. Reference Lee, Waitukaitis, Miskin and Jaeger2015; Harper et al. Reference Harper, Cimarelli, Cigala, Kueppers and Dufek2021). For a particle size of ![]() $d_{{p}} \sim 10\ \mathrm {\mu }\mathrm {m}$, the order of the particle charge can be estimated as
$d_{{p}} \sim 10\ \mathrm {\mu }\mathrm {m}$, the order of the particle charge can be estimated as ![]() $q = {\rm \pi}d_{{p}}^2 \sigma _{{p}} \sim 10^{-14}\ \mathrm {C}$. Moreover, since the considered particle concentration is low, particle collision is negligible. So the charge transfer is not included and the prescribed charge on each individual particle remains constant.
$q = {\rm \pi}d_{{p}}^2 \sigma _{{p}} \sim 10^{-14}\ \mathrm {C}$. Moreover, since the considered particle concentration is low, particle collision is negligible. So the charge transfer is not included and the prescribed charge on each individual particle remains constant.
2.2. Fluid phase
The DNS of the incompressible homogeneous isotropic turbulence is performed using the pseudo-spectral method. The computation domain is a triply periodic cubic box with the domain size ![]() $L^3={(2 {\rm \pi}\times 10^{-2}\ \mathrm {m})}^3$ and the grid number
$L^3={(2 {\rm \pi}\times 10^{-2}\ \mathrm {m})}^3$ and the grid number ![]() $N_{{grid}}^3=192^3$. The governing equations of the fluid phase are given by
$N_{{grid}}^3=192^3$. The governing equations of the fluid phase are given by
and
Here, ![]() $\boldsymbol {u}(\boldsymbol {x}_i)$ is the fluid velocity at the grid node
$\boldsymbol {u}(\boldsymbol {x}_i)$ is the fluid velocity at the grid node ![]() $\boldsymbol {x}_i$,
$\boldsymbol {x}_i$, ![]() $p$ is the pressure,
$p$ is the pressure, ![]() $\rho _{{f}}$ is the fluid density and
$\rho _{{f}}$ is the fluid density and ![]() $\nu _{{f}}$ is the fluid kinematic viscosity;
$\nu _{{f}}$ is the fluid kinematic viscosity; ![]() $\boldsymbol {f}_{{F}}$ is the forcing term that injects kinetic energy from large scales and keeps the turbulence steady. In the wavenumber space, the forcing term is given by
$\boldsymbol {f}_{{F}}$ is the forcing term that injects kinetic energy from large scales and keeps the turbulence steady. In the wavenumber space, the forcing term is given by
Here, ![]() $C$ is the constant forcing coefficient, the critical wavenumber is
$C$ is the constant forcing coefficient, the critical wavenumber is ![]() $\kappa _{crit} = 5\kappa _{0}$ with
$\kappa _{crit} = 5\kappa _{0}$ with ![]() ${\kappa }_0 = 2 {\rm \pi}/ L$ the smallest wavenumber.
${\kappa }_0 = 2 {\rm \pi}/ L$ the smallest wavenumber.
When evolving the turbulence, the second-order Adam–Bashforth scheme is used for the nonlinear term while the viscous term is integrated exactly (Vincent & Meneguzzi Reference Vincent and Meneguzzi1991). The fluid time step is ![]() $\Delta t_{{F}}=1 \times 10^{-5}\ \mathrm {s}$. Table 1 lists typical parameters of the homogeneous and isotropic turbulence. The fluctuation velocity
$\Delta t_{{F}}=1 \times 10^{-5}\ \mathrm {s}$. Table 1 lists typical parameters of the homogeneous and isotropic turbulence. The fluctuation velocity ![]() $u^\prime$ and the dissipation rate
$u^\prime$ and the dissipation rate ![]() $\epsilon$ can be obtained from the energy spectrum
$\epsilon$ can be obtained from the energy spectrum ![]() $E(\kappa )$ as
$E(\kappa )$ as
The Kolmogorov length and time scales are given by ![]() $\eta = ({\nu _{{f}}}^3 / \epsilon )^{1/4}$ and
$\eta = ({\nu _{{f}}}^3 / \epsilon )^{1/4}$ and ![]() $\tau _{\eta } = (\nu _{{f}} / \epsilon )^{1/2}$, respectively. The integral length scale is
$\tau _{\eta } = (\nu _{{f}} / \epsilon )^{1/2}$, respectively. The integral length scale is ![]() $l= ({{\rm \pi} }/2{u'}^2) \int _{\kappa _{{min}}}^{\kappa _{{max}}} [E(\kappa )/{\kappa }]\, \mathrm {d}{\kappa }$, the eddy turnover time is
$l= ({{\rm \pi} }/2{u'}^2) \int _{\kappa _{{min}}}^{\kappa _{{max}}} [E(\kappa )/{\kappa }]\, \mathrm {d}{\kappa }$, the eddy turnover time is ![]() $\tau _{\mathrm {e}} = l/u^{\prime }$ and the Taylor Reynolds number is
$\tau _{\mathrm {e}} = l/u^{\prime }$ and the Taylor Reynolds number is ![]() ${Re}_{\lambda } = u^{\prime } \lambda / \nu _{{f}}$, with
${Re}_{\lambda } = u^{\prime } \lambda / \nu _{{f}}$, with ![]() $\lambda = u^{\prime } (15 \nu _{{f}} /\epsilon )^{1/2}$ the Taylor microscale.
$\lambda = u^{\prime } (15 \nu _{{f}} /\epsilon )^{1/2}$ the Taylor microscale.
2.3. Particle motion
The movements of charged particles are integrated using the second-order Adam–Bashforth time stepping. The particle time step is ![]() $\Delta t_{{p}} = 2.5 \times 10^{-6}\ \mathrm {s}$. This time step is much smaller than the particle relaxation time to well resolve the particles’ aerodynamic response to the turbulence (
$\Delta t_{{p}} = 2.5 \times 10^{-6}\ \mathrm {s}$. This time step is much smaller than the particle relaxation time to well resolve the particles’ aerodynamic response to the turbulence (![]() $\Delta t_{{p}}/\tau _{{p,S}}=0.23\,\%$). Besides, within each step, particles only move a short distance compared with the Kolmogorov length (
$\Delta t_{{p}}/\tau _{{p,S}}=0.23\,\%$). Besides, within each step, particles only move a short distance compared with the Kolmogorov length (![]() $u^{\prime } \Delta t_{{p}} / \eta = 1.4\,\%$), so that the variation of the electrostatic force is well captured when particles become close. The governing equations of particle motions are
$u^{\prime } \Delta t_{{p}} / \eta = 1.4\,\%$), so that the variation of the electrostatic force is well captured when particles become close. The governing equations of particle motions are
Here, ![]() $\boldsymbol {v}_i$ and
$\boldsymbol {v}_i$ and ![]() $\boldsymbol {x}_i$ are the velocity and the location of particle
$\boldsymbol {x}_i$ are the velocity and the location of particle ![]() $i$, respectively;
$i$, respectively; ![]() $m_i = {\rm \pi}\rho _{{p}} d_{{p},i}^3/6$ is the particle mass, with
$m_i = {\rm \pi}\rho _{{p}} d_{{p},i}^3/6$ is the particle mass, with ![]() $\rho _{{p}}$ the density and
$\rho _{{p}}$ the density and ![]() $d_{{p},i}$ the diameter;
$d_{{p},i}$ the diameter; ![]() $\boldsymbol {F}^{{F}}_i$ and
$\boldsymbol {F}^{{F}}_i$ and ![]() $\boldsymbol {F}^{{E}}_i$ are the fluid force and the electrostatic force acting on particle
$\boldsymbol {F}^{{E}}_i$ are the fluid force and the electrostatic force acting on particle ![]() $i$.
$i$.
Since particles are small (![]() $d_{{p}} < \eta$) and heavy (
$d_{{p}} < \eta$) and heavy (![]() $\rho _{{p}} / \rho _{{f}} \gg 1$), the dominant fluid force comes from the Stokes drag (Maxey & Riley Reference Maxey and Riley1983)
$\rho _{{p}} / \rho _{{f}} \gg 1$), the dominant fluid force comes from the Stokes drag (Maxey & Riley Reference Maxey and Riley1983)
Here, ![]() $\mu _{{f}}$ is the dynamic viscosity of the fluid, and
$\mu _{{f}}$ is the dynamic viscosity of the fluid, and ![]() $\boldsymbol {u}(\boldsymbol {x}_{i})$ is the fluid velocity at the particle position. For two consecutive particle time steps within the same fluid time step, the flow field remains unchanged, and the fluid velocity at the particle location is interpolated at each particle time step using the second-order tri-linear interpolation scheme (Marshall Reference Marshall2009; Qian, Ruan & Li Reference Qian, Ruan and Li2022). The effect of fluid inertia is neglected by assuming that the particle Reynolds number
$\boldsymbol {u}(\boldsymbol {x}_{i})$ is the fluid velocity at the particle position. For two consecutive particle time steps within the same fluid time step, the flow field remains unchanged, and the fluid velocity at the particle location is interpolated at each particle time step using the second-order tri-linear interpolation scheme (Marshall Reference Marshall2009; Qian, Ruan & Li Reference Qian, Ruan and Li2022). The effect of fluid inertia is neglected by assuming that the particle Reynolds number ![]() ${Re}_{{p}}$ is much smaller than unity.
${Re}_{{p}}$ is much smaller than unity.
In this dilute system, the average separation between charged particles is large compared with the particle size (![]() $\bar {l} \gg d_{{p}}$), indicating an insignificant effect of particle polarization (Ruan et al. Reference Ruan, Gorman, Li and Ni2022). Therefore, the electrostatic force acting on each particle
$\bar {l} \gg d_{{p}}$), indicating an insignificant effect of particle polarization (Ruan et al. Reference Ruan, Gorman, Li and Ni2022). Therefore, the electrostatic force acting on each particle ![]() $i$ can be obtained by summing the pairwise Coulomb force from other particles
$i$ can be obtained by summing the pairwise Coulomb force from other particles ![]() $j$, which reads
$j$, which reads
 \begin{equation} \boldsymbol{F}_{i}^{{E}} = \sum_{j {\ne} i} \frac{q_i q_j (\boldsymbol{x}_i - \boldsymbol{x}_j)}{4 {\rm \pi}\varepsilon_0 {|\boldsymbol{x}_i - \boldsymbol{x}_j|}^3}. \end{equation}
\begin{equation} \boldsymbol{F}_{i}^{{E}} = \sum_{j {\ne} i} \frac{q_i q_j (\boldsymbol{x}_i - \boldsymbol{x}_j)}{4 {\rm \pi}\varepsilon_0 {|\boldsymbol{x}_i - \boldsymbol{x}_j|}^3}. \end{equation}
Here, ![]() $\varepsilon _0 = 8.8542 \times 10^{-12}\ \mathrm {F}\,{\rm m}^{-1}$ is the vacuum permittivity,
$\varepsilon _0 = 8.8542 \times 10^{-12}\ \mathrm {F}\,{\rm m}^{-1}$ is the vacuum permittivity, ![]() $q_i$ is the point charge located at the centroid of particle
$q_i$ is the point charge located at the centroid of particle ![]() $i$.
$i$.
To properly apply the periodic boundary condition of the long-range electrostatic force, several layers of image domains are added around the original computation domain (Di Renzo & Urzay Reference Di Renzo and Urzay2018; Boutsikakis, Fede & Simonin Reference Boutsikakis, Fede and Simonin2023). When calculating the electrostatic force acting on the ![]() $i$th particle located at
$i$th particle located at ![]() $\boldsymbol {x}_i$, the contributions from other particles
$\boldsymbol {x}_i$, the contributions from other particles ![]() $j$ at
$j$ at ![]() $\boldsymbol {x}_j$ as well as their images at
$\boldsymbol {x}_j$ as well as their images at ![]() $\boldsymbol {x}_j +(l\boldsymbol {i}+m\boldsymbol {j}+n\boldsymbol {k})L$ are all considered
$\boldsymbol {x}_j +(l\boldsymbol {i}+m\boldsymbol {j}+n\boldsymbol {k})L$ are all considered
 \begin{equation} \boldsymbol{F}_{i}^{{E}} = \sum_{j {\ne} i} \sum_{l,m,n} \frac{q_i q_j \{\boldsymbol{x}_i - [\boldsymbol{x}_j+ (l\boldsymbol{i}+m\boldsymbol{j}+n\boldsymbol{k})L ]\}}{4 {\rm \pi}\varepsilon_0 {|\boldsymbol{x}_i - [\boldsymbol{x}_j+ (l\boldsymbol{i}+m\boldsymbol{j}+n\boldsymbol{k})L]|}^3}, \end{equation}
\begin{equation} \boldsymbol{F}_{i}^{{E}} = \sum_{j {\ne} i} \sum_{l,m,n} \frac{q_i q_j \{\boldsymbol{x}_i - [\boldsymbol{x}_j+ (l\boldsymbol{i}+m\boldsymbol{j}+n\boldsymbol{k})L ]\}}{4 {\rm \pi}\varepsilon_0 {|\boldsymbol{x}_i - [\boldsymbol{x}_j+ (l\boldsymbol{i}+m\boldsymbol{j}+n\boldsymbol{k})L]|}^3}, \end{equation}
where ![]() $l,m,n=-N_{{per}},\ldots, N_{{per}}$. Here,
$l,m,n=-N_{{per}},\ldots, N_{{per}}$. Here, ![]() $\boldsymbol {i}$,
$\boldsymbol {i}$, ![]() $\boldsymbol {j}$ and
$\boldsymbol {j}$ and ![]() $\boldsymbol {k}$ are unit vectors along the
$\boldsymbol {k}$ are unit vectors along the ![]() $x$,
$x$, ![]() $y$ and
$y$ and ![]() $z$ directions.
$z$ directions.
According to (2.9), when computing the electrostatic force acting on the target particle ![]() $i$, the cost is
$i$, the cost is ![]() $O(N_{{s}}) = O((N_{{p}}-1)\times (2N_{{per}}+1)^3)$, where
$O(N_{{s}}) = O((N_{{p}}-1)\times (2N_{{per}}+1)^3)$, where ![]() $O(N_{{s}})$ is the number of source particles to each target particle. The total cost of the electrostatic computation then scales with
$O(N_{{s}})$ is the number of source particles to each target particle. The total cost of the electrostatic computation then scales with ![]() $O(N_{{p}}^2 N_{{per}}^3)$. Considering the large particle number and the addition of image domains, direct summation (2.9) is extremely expensive. Therefore, we employ the fast multipole method (FMM) to accelerate the calculation. In FMM, the field strength generated by neighbouring particles is directly computed using (2.9), while the contribution from clouds of particles far from the target particle is approximated using fast multipole expansion, which reduces the required computation cost to
$O(N_{{p}}^2 N_{{per}}^3)$. Considering the large particle number and the addition of image domains, direct summation (2.9) is extremely expensive. Therefore, we employ the fast multipole method (FMM) to accelerate the calculation. In FMM, the field strength generated by neighbouring particles is directly computed using (2.9), while the contribution from clouds of particles far from the target particle is approximated using fast multipole expansion, which reduces the required computation cost to ![]() $O(N_{{p}}\log (N_{{p}}N_{{per}}^3))$ (Greengard & Rokhlin Reference Greengard and Rokhlin1987, Reference Greengard and Rokhlin1997). In this study, the open-source library FMMLIB3D is employed to conduct the fast electrostatic computation (Gimbutas & Greengard Reference Gimbutas and Greengard2015). The accuracy of FMM with various layers of image domains is compared in Appendix A. Based on the analysis, two layers of image boxes (
$O(N_{{p}}\log (N_{{p}}N_{{per}}^3))$ (Greengard & Rokhlin Reference Greengard and Rokhlin1987, Reference Greengard and Rokhlin1997). In this study, the open-source library FMMLIB3D is employed to conduct the fast electrostatic computation (Gimbutas & Greengard Reference Gimbutas and Greengard2015). The accuracy of FMM with various layers of image domains is compared in Appendix A. Based on the analysis, two layers of image boxes (![]() $N_{{per}}=2$) are added, which is sufficient to ensure the convergence of the electrostatic force acting on all particles in the original domain.
$N_{{per}}=2$) are added, which is sufficient to ensure the convergence of the electrostatic force acting on all particles in the original domain.
Moreover, the Coulomb force is capped if the distance between two particles is smaller than a preset critical distance to avoid a non-physically strong force
 \begin{equation} F_{i \leftarrow j}^{{E}} = \min \left \{ \frac{q_i q_j}{4 {\rm \pi}\varepsilon_0 {|\boldsymbol{x}_i - \boldsymbol{x}_j|}^2}, \frac{q_i q_j}{4 {\rm \pi}\varepsilon_0 {d_{{cap}}}^2} \right \}. \end{equation}
\begin{equation} F_{i \leftarrow j}^{{E}} = \min \left \{ \frac{q_i q_j}{4 {\rm \pi}\varepsilon_0 {|\boldsymbol{x}_i - \boldsymbol{x}_j|}^2}, \frac{q_i q_j}{4 {\rm \pi}\varepsilon_0 {d_{{cap}}}^2} \right \}. \end{equation}
Here, the critical distance is ![]() $d_{{cap}} = d_{{p,SS}}/2$ or
$d_{{cap}} = d_{{p,SS}}/2$ or ![]() $d_{{cap}} = \eta /20$. This value is chosen so that, even for a pair of small particles approaching each other, the Coulomb force between them is still accurate at the collision distance (
$d_{{cap}} = \eta /20$. This value is chosen so that, even for a pair of small particles approaching each other, the Coulomb force between them is still accurate at the collision distance (![]() $|\boldsymbol {x}_i - \boldsymbol {x}_j| = d_{{p,SS}}>d_{{cap}}$). Moreover, since
$|\boldsymbol {x}_i - \boldsymbol {x}_j| = d_{{p,SS}}>d_{{cap}}$). Moreover, since ![]() $d_{{cap}}$ is set small compared with the Kolmogorov length scale
$d_{{cap}}$ is set small compared with the Kolmogorov length scale ![]() $\eta$, capping the electrostatic force does not affect the statistics at larger scales presented below.
$\eta$, capping the electrostatic force does not affect the statistics at larger scales presented below.
In each run, the single-phase turbulence is first evolved until reaching the steady state. Particles are then injected randomly in the domain with their initial velocities equal to the fluid velocity at particle locations. It takes roughly ![]() $3.5 \tau _{{e}}$ for particle dynamics to reach equilibrium, statistics are then taken over another
$3.5 \tau _{{e}}$ for particle dynamics to reach equilibrium, statistics are then taken over another ![]() $5\tau _{{e}}$. Three parallel runs with different initial particle locations are performed for each case, and their results are averaged and presented below.
$5\tau _{{e}}$. Three parallel runs with different initial particle locations are performed for each case, and their results are averaged and presented below.
3. Results and discussions
3.1. Clustering and relative velocity of charged particles
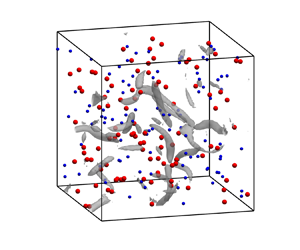
Figure 1 compares the spatial distribution of bidispersed particles within a thin slice ![]() $|z| \leq 20 \eta$. Although oppositely charged bidispersed particles are simulated in each case, we show small and large particles in the left and the right panels separately for better illustration. In the neutral case (figure 1a,b), particle behaviour is solely determined by the particle–turbulence interaction. Small particles (
$|z| \leq 20 \eta$. Although oppositely charged bidispersed particles are simulated in each case, we show small and large particles in the left and the right panels separately for better illustration. In the neutral case (figure 1a,b), particle behaviour is solely determined by the particle–turbulence interaction. Small particles (![]() $St=1$) are responsive to fluctuations at the Kolmogorov length scale. As a result, their spatial distribution is highly non-uniform, and small-scale particle clusters can be observed (figure 1a). Meanwhile, large particles (
$St=1$) are responsive to fluctuations at the Kolmogorov length scale. As a result, their spatial distribution is highly non-uniform, and small-scale particle clusters can be observed (figure 1a). Meanwhile, large particles (![]() $St=10$) are more inertial, so they are more dispersed in the domain (figure 1b).
$St=10$) are more inertial, so they are more dispersed in the domain (figure 1b).

Figure 1. Snapshots of particles in the slice ![]() $|z| \le 20 \eta$ with (a)
$|z| \le 20 \eta$ with (a) ![]() $St=1$ and
$St=1$ and ![]() $q = 0\ \mathrm {C}$, (b)
$q = 0\ \mathrm {C}$, (b) ![]() $St=10$ and
$St=10$ and ![]() $q = 0\ \mathrm {C}$, (c)
$q = 0\ \mathrm {C}$, (c) ![]() $St=1$ and
$St=1$ and ![]() $q = 2 \times 10^{-14}\ \mathrm {C}$, (d)
$q = 2 \times 10^{-14}\ \mathrm {C}$, (d) ![]() $St=10$ and
$St=10$ and ![]() $q = 2 \times 10^{-14}\ \mathrm {C}$. Blue/red dots represent small/large particles. The colour bar indicates the vorticity magnitude normalized by its average over the domain.
$q = 2 \times 10^{-14}\ \mathrm {C}$. Blue/red dots represent small/large particles. The colour bar indicates the vorticity magnitude normalized by its average over the domain.
We employ the radial distribution function (RDF) to quantify how particles from the same (or different) size groups cluster. The RDFs of different kinds of particle pairs, i.e. small–small (SS), large–large (LL) and small–large (SL) pairs, are defined as
In the definition of ![]() $g_{{SS}}(r)$,
$g_{{SS}}(r)$, ![]() $\Delta N_{{SS}}(r)$ is the number of SS pairs with separation distances within the range of
$\Delta N_{{SS}}(r)$ is the number of SS pairs with separation distances within the range of ![]() $r \pm \Delta r/2$, and
$r \pm \Delta r/2$, and ![]() $\Delta V(r) = 4 {\rm \pi}[(r+\Delta r/2)^3-(r-\Delta r/2)^3]/3$ is the shell volume in the separation distance bin;
$\Delta V(r) = 4 {\rm \pi}[(r+\Delta r/2)^3-(r-\Delta r/2)^3]/3$ is the shell volume in the separation distance bin; ![]() $N_{{p,S}}(N_{{p,S}}-1)/2/L^3$ is the average number of SS pairs in the whole domain. Therefore,
$N_{{p,S}}(N_{{p,S}}-1)/2/L^3$ is the average number of SS pairs in the whole domain. Therefore, ![]() $g_{{SS}}(r)>1$ means there is a higher density of SS pairs at a given separation distance of
$g_{{SS}}(r)>1$ means there is a higher density of SS pairs at a given separation distance of ![]() $r$ compared with the average pair density. The definitions of
$r$ compared with the average pair density. The definitions of ![]() $g_{{LL}}(r)$ and
$g_{{LL}}(r)$ and ![]() $g_{{SL}}(r)$ are similar and thus omitted.
$g_{{SL}}(r)$ are similar and thus omitted.
As shown in figure 2(a), ![]() $g_{{SS}}(r)$ for neutral pairs is significantly larger than unity at
$g_{{SS}}(r)$ for neutral pairs is significantly larger than unity at ![]() $r \leq \eta$, indicating strong clustering at the small scale;
$r \leq \eta$, indicating strong clustering at the small scale; ![]() $g_{{SS}}(r)$ also follows a clear power law
$g_{{SS}}(r)$ also follows a clear power law ![]() $g_{{SS}}(r) \sim (r/ \eta )^{-{c}_1}$ with the fitted exponent
$g_{{SS}}(r) \sim (r/ \eta )^{-{c}_1}$ with the fitted exponent ![]() ${c}_1 = 0.69$. The value of
${c}_1 = 0.69$. The value of ![]() ${c}_1$ is close to those reported in previous studies with similar
${c}_1$ is close to those reported in previous studies with similar ![]() ${Re}_{\lambda }$, e.g.
${Re}_{\lambda }$, e.g. ![]() ${c}_1 = 0.67$ for
${c}_1 = 0.67$ for ![]() ${Re}_{\lambda }=143$ (Saw et al. Reference Saw, Salazar, Collins and Shaw2012) and
${Re}_{\lambda }=143$ (Saw et al. Reference Saw, Salazar, Collins and Shaw2012) and ![]() ${c}_1 = 0.68$ for
${c}_1 = 0.68$ for ![]() ${Re}_{\lambda }=140$ (Ireland et al. Reference Ireland, Bragg and Collins2016a). In comparison,
${Re}_{\lambda }=140$ (Ireland et al. Reference Ireland, Bragg and Collins2016a). In comparison, ![]() $g_{{LL}}(r)$ for neutral pairs is only slightly larger than one, which means the clustering of large particles is relatively weak. However,
$g_{{LL}}(r)$ for neutral pairs is only slightly larger than one, which means the clustering of large particles is relatively weak. However, ![]() $g_{{LL}}(r)$ decreases slowly with the increase of
$g_{{LL}}(r)$ decreases slowly with the increase of ![]() $r$ and stays above unity until
$r$ and stays above unity until ![]() $r \approx 100 \eta$, while
$r \approx 100 \eta$, while ![]() $g_{{SS}}(r)$ drops rapidly and approaches unity around
$g_{{SS}}(r)$ drops rapidly and approaches unity around ![]() $20\unicode{x2013}30 \eta$. This is because the clustering of inertial particles with the relaxation time
$20\unicode{x2013}30 \eta$. This is because the clustering of inertial particles with the relaxation time ![]() $\tau _{{p}}$ is driven by vortices whose time scales are comparable to a particle's relaxation time (i.e.
$\tau _{{p}}$ is driven by vortices whose time scales are comparable to a particle's relaxation time (i.e. ![]() $\tau (r) \sim \tau _{{p}}$). In the inertial range, the time scale satisfies
$\tau (r) \sim \tau _{{p}}$). In the inertial range, the time scale satisfies ![]() $\tau (r)\sim \epsilon ^{-1/3} r^{2/3}$, so the relationship can be given as
$\tau (r)\sim \epsilon ^{-1/3} r^{2/3}$, so the relationship can be given as ![]() $r \sim \epsilon ^{1/3} \tau _{{p}}^{3/2}$ (Yoshimoto & Goto Reference Yoshimoto and Goto2007; Bec et al. Reference Bec, Biferale, Cencini, Lanotte and Toschi2011). With the increase of particle inertia, the length and the time scales of vortices that could affect particle behaviours also become larger. As a result, the size of particle clusters also grow larger, leading to the large correlation length in
$r \sim \epsilon ^{1/3} \tau _{{p}}^{3/2}$ (Yoshimoto & Goto Reference Yoshimoto and Goto2007; Bec et al. Reference Bec, Biferale, Cencini, Lanotte and Toschi2011). With the increase of particle inertia, the length and the time scales of vortices that could affect particle behaviours also become larger. As a result, the size of particle clusters also grow larger, leading to the large correlation length in ![]() $g_{{LL}}(r)$ (Yoshimoto & Goto Reference Yoshimoto and Goto2007; Liu et al. Reference Liu, Shen, Zamansky and Coletti2020). Besides, when comparing those particles with a large
$g_{{LL}}(r)$ (Yoshimoto & Goto Reference Yoshimoto and Goto2007; Liu et al. Reference Liu, Shen, Zamansky and Coletti2020). Besides, when comparing those particles with a large ![]() $St$ difference, because their relaxation times differ by a factor of ten, they respond to flows of very different scales. Therefore, there is little spatial correlation between small and large particles, and
$St$ difference, because their relaxation times differ by a factor of ten, they respond to flows of very different scales. Therefore, there is little spatial correlation between small and large particles, and ![]() $g_{{SL}}(r)$ is close to unity at all separation distance
$g_{{SL}}(r)$ is close to unity at all separation distance ![]() $r$ when particles are neutral.
$r$ when particles are neutral.

Figure 2. The RDFs between (a) SS, (b) LL and (c) SL particle pairs with different particle charge ![]() $q$. The inset in (a) shows the full scale of
$q$. The inset in (a) shows the full scale of ![]() $g_{SS}(r)$ in the neutral case. Dashed lines from light to dark correspond to predicted RDFs using (3.12) (or its counterpart for the oppositely charged case) for
$g_{SS}(r)$ in the neutral case. Dashed lines from light to dark correspond to predicted RDFs using (3.12) (or its counterpart for the oppositely charged case) for ![]() $q=5 \times 10^{-15}\ \mathrm {C}$,
$q=5 \times 10^{-15}\ \mathrm {C}$, ![]() $1 \times 10^{-14}\ \mathrm {C}$ and
$1 \times 10^{-14}\ \mathrm {C}$ and ![]() $2 \times 10^{-14}\ \mathrm {C}$, respectively.
$2 \times 10^{-14}\ \mathrm {C}$, respectively.
When particles are charged, since charge segregation correlates with size, the same-size particles will repel each other when they get close. Since the amount of particle charge is the same, the effect of repulsion is more drastic between SS pairs rather than between LL pairs. As a result, the order of ![]() $g_{{SS}}(r)$ at small
$g_{{SS}}(r)$ at small ![]() $r$ drops by several decades as
$r$ drops by several decades as ![]() $q$ increases. The same decreasing trend is observed for
$q$ increases. The same decreasing trend is observed for ![]() $g_{{LL}}(r)$, but the influence is less significant because of the large particle inertia. This can also be shown by comparing the top and the bottom panels in figure 1. In the charged case (
$g_{{LL}}(r)$, but the influence is less significant because of the large particle inertia. This can also be shown by comparing the top and the bottom panels in figure 1. In the charged case (![]() $q=2 \times 10^{-14}\ \mathrm {C}$), the small particles become less concentrated (figure 1c), while no obvious difference is seen in the spatial distribution of large particles (figure 1d). It is worth noting that, since the Coulomb force decays rapidly with
$q=2 \times 10^{-14}\ \mathrm {C}$), the small particles become less concentrated (figure 1c), while no obvious difference is seen in the spatial distribution of large particles (figure 1d). It is worth noting that, since the Coulomb force decays rapidly with ![]() $r$, its effect is only significant within a relatively short range (
$r$, its effect is only significant within a relatively short range (![]() $r \approx 1\unicode{x2013}10 \eta$). Beyond this range, both
$r \approx 1\unicode{x2013}10 \eta$). Beyond this range, both ![]() $g_{{SS}}(r)$ and
$g_{{SS}}(r)$ and ![]() $g_{{LL}}(r)$ in figure 2(a,b) recover to their neutral values again, so clustering could still be observed at large
$g_{{LL}}(r)$ in figure 2(a,b) recover to their neutral values again, so clustering could still be observed at large ![]() $r$. As for
$r$. As for ![]() $g_{{SL}}$, because of the Coulomb attraction, particles of different sizes are more likely to stay close. More specifically, considering the large mass difference between SL pairs (
$g_{{SL}}$, because of the Coulomb attraction, particles of different sizes are more likely to stay close. More specifically, considering the large mass difference between SL pairs (![]() $m_{{L}}/m_{{S}}=(St_{{L}}/St_{{S}})^{1.5}\approx 30$), small particles will always be attracted towards the large ones, giving rise to the rapid growth of
$m_{{L}}/m_{{S}}=(St_{{L}}/St_{{S}})^{1.5}\approx 30$), small particles will always be attracted towards the large ones, giving rise to the rapid growth of ![]() $g_{{SL}}(r)$ at small separation (
$g_{{SL}}(r)$ at small separation (![]() $r \leq \eta$). Again, the opposite-sign attraction decays with increasing
$r \leq \eta$). Again, the opposite-sign attraction decays with increasing ![]() $r$, so
$r$, so ![]() $g_{{SL}}(r)$ approaches one when
$g_{{SL}}(r)$ approaches one when ![]() $r$ is sufficiently large.
$r$ is sufficiently large.
Apart from spatial correlation, it is also of interest to study the relative velocity between particle pairs and focus on the modulation caused by the electrostatic force. For a pair of particles ![]() $i$ and
$i$ and ![]() $j$ with the separation
$j$ with the separation ![]() $r = |\boldsymbol {x}_i-\boldsymbol {x}_j|$, the radial component of the relative velocity is defined as
$r = |\boldsymbol {x}_i-\boldsymbol {x}_j|$, the radial component of the relative velocity is defined as ![]() $w_{{r},ij} = (\boldsymbol {v}_i-\boldsymbol {v}_j) \boldsymbol {\cdot } (\boldsymbol {x}_i-\boldsymbol {x}_j)/|\boldsymbol {x}_i-\boldsymbol {x}_j|$. Taking the ensemble average over SS/LL/SL particle pairs then yields the mean relative velocities between three kinds of particle pairs as
$w_{{r},ij} = (\boldsymbol {v}_i-\boldsymbol {v}_j) \boldsymbol {\cdot } (\boldsymbol {x}_i-\boldsymbol {x}_j)/|\boldsymbol {x}_i-\boldsymbol {x}_j|$. Taking the ensemble average over SS/LL/SL particle pairs then yields the mean relative velocities between three kinds of particle pairs as ![]() $\langle |w_{{r,SS}}| \rangle$,
$\langle |w_{{r,SS}}| \rangle$, ![]() $\langle |w_{r,LL}| \rangle$ and
$\langle |w_{r,LL}| \rangle$ and ![]() $\langle |w_{{r,SL}}| \rangle$, respectively.
$\langle |w_{{r,SL}}| \rangle$, respectively.
Figure 3(a) compares the mean radial relative velocity between SS pairs, ![]() $\langle |w_{{r,SS}}| \rangle$, for various particle charge
$\langle |w_{{r,SS}}| \rangle$, for various particle charge ![]() $q$. For neutral SS pairs, when
$q$. For neutral SS pairs, when ![]() $r$ is in the inertial range (
$r$ is in the inertial range (![]() $\eta \ll r \ll L_{{int}}$),
$\eta \ll r \ll L_{{int}}$), ![]() $\tau _{{p,S}}$ is much smaller than the characteristic time scales of turbulent fluctuations at this length scale. The radial relative velocity between SS pairs,
$\tau _{{p,S}}$ is much smaller than the characteristic time scales of turbulent fluctuations at this length scale. The radial relative velocity between SS pairs, ![]() $\langle |w_{{r,SS}}| \rangle$, thus follows that of fluid tracers
$\langle |w_{{r,SS}}| \rangle$, thus follows that of fluid tracers ![]() $\delta u_{{r}}$. Here, the fluid relative velocity is obtained from the second-order longitudinal structure function as
$\delta u_{{r}}$. Here, the fluid relative velocity is obtained from the second-order longitudinal structure function as ![]() $\delta u_{{r}} = {C_2}^{1/2} \epsilon ^{1/3} r^{1/3}$ and the constant is
$\delta u_{{r}} = {C_2}^{1/2} \epsilon ^{1/3} r^{1/3}$ and the constant is ![]() $C_2=2.13$ (Yeung & Zhou Reference Yeung and Zhou1997) (shown as dash-dotted lines in figure 3). If
$C_2=2.13$ (Yeung & Zhou Reference Yeung and Zhou1997) (shown as dash-dotted lines in figure 3). If ![]() $r$ is within the dissipative range, the time scale of local fluctuations becomes comparable to
$r$ is within the dissipative range, the time scale of local fluctuations becomes comparable to ![]() $\tau _{{p,S}}$. Small neutral particles cannot perfectly follow the background flow at this separation, so
$\tau _{{p,S}}$. Small neutral particles cannot perfectly follow the background flow at this separation, so ![]() $\langle |w_{{r,SS}}| \rangle$ deviates from the fluid relative velocity
$\langle |w_{{r,SS}}| \rangle$ deviates from the fluid relative velocity ![]() $\delta u_{{r}}= (\epsilon /15 \nu )^{1/2} r$ (dashed lines in figure 3).
$\delta u_{{r}}= (\epsilon /15 \nu )^{1/2} r$ (dashed lines in figure 3).

Figure 3. Mean radial relative velocity ![]() $\langle |w_{{r}}| \rangle$ normalized by
$\langle |w_{{r}}| \rangle$ normalized by ![]() $u_{\eta }$ between (a) SS, (b) LL and (c) SL particle pairs with different particle charge
$u_{\eta }$ between (a) SS, (b) LL and (c) SL particle pairs with different particle charge ![]() $q$. The inset in (a) shows the full scale of
$q$. The inset in (a) shows the full scale of![]() $\langle |w_{{r,SS}}| \rangle$ in the neutral case. The red dashed line denotes the velocity scaling
$\langle |w_{{r,SS}}| \rangle$ in the neutral case. The red dashed line denotes the velocity scaling ![]() ${\propto }r$ in the dissipation range, and the red dash-dotted line denotes the velocity scaling
${\propto }r$ in the dissipation range, and the red dash-dotted line denotes the velocity scaling ![]() ${\propto }r^{1/3}$ in the inertial range. Dashed lines from light to dark correspond to predictions using (3.15) (or its counterpart for the oppositely charged case) for
${\propto }r^{1/3}$ in the inertial range. Dashed lines from light to dark correspond to predictions using (3.15) (or its counterpart for the oppositely charged case) for ![]() $q=5 \times 10^{-15}\ \mathrm {C}$,
$q=5 \times 10^{-15}\ \mathrm {C}$, ![]() $1 \times 10^{-14}\ \mathrm {C}$ and
$1 \times 10^{-14}\ \mathrm {C}$ and ![]() $2 \times 10^{-14}\, \mathrm {C}$, respectively.
$2 \times 10^{-14}\, \mathrm {C}$, respectively.
When particles are charged, since the influence of Coulomb force is negligible at large ![]() $r$, curves for different
$r$, curves for different ![]() $q$ collapse. In contrast,
$q$ collapse. In contrast, ![]() $\langle |w_{{r,SS}}| \rangle$ is found to rise significantly as particles get close to each other. When
$\langle |w_{{r,SS}}| \rangle$ is found to rise significantly as particles get close to each other. When ![]() $q$ gets larger, the increase of
$q$ gets larger, the increase of ![]() $\langle |w_{{r,SS}}| \rangle$ becomes more pronounced and the deviation from the neutral result also occurs at a larger
$\langle |w_{{r,SS}}| \rangle$ becomes more pronounced and the deviation from the neutral result also occurs at a larger ![]() $r$. This seems counter-intuitive because the Coulomb repulsion between SS pairs should always slow approaching particles down and reduce the relative velocity. One explanation for this change is as follows. When
$r$. This seems counter-intuitive because the Coulomb repulsion between SS pairs should always slow approaching particles down and reduce the relative velocity. One explanation for this change is as follows. When ![]() $q$ is large, the strong Coulomb repulsion causes biased sampling at small
$q$ is large, the strong Coulomb repulsion causes biased sampling at small ![]() $r$: only those pairs with large inward relative velocity could overcome the energy barrier and get close. Meanwhile, since the electrical potential energy is conserved in the approach-then-depart process, the pairs approaching each other at a high velocity will also be repelled at a high velocity as the electrostatic force pushes them apart. As a result, pairs with a large
$r$: only those pairs with large inward relative velocity could overcome the energy barrier and get close. Meanwhile, since the electrical potential energy is conserved in the approach-then-depart process, the pairs approaching each other at a high velocity will also be repelled at a high velocity as the electrostatic force pushes them apart. As a result, pairs with a large ![]() $|w_{{r,SS}}|$ take a large proportion of the close pairs as
$|w_{{r,SS}}|$ take a large proportion of the close pairs as ![]() $q$ increases, so the mean radial relative velocity between both approaching and departing pairs,
$q$ increases, so the mean radial relative velocity between both approaching and departing pairs, ![]() $\langle w_{{r},ij} \rangle$, shows the increasing trend in figure 3(a). This increasing trend with
$\langle w_{{r},ij} \rangle$, shows the increasing trend in figure 3(a). This increasing trend with ![]() $q$ will be further discussed in § 3.3.
$q$ will be further discussed in § 3.3.
Compared with small particles with ![]() $St=1$, large particles with
$St=1$, large particles with ![]() $St=10$ are very inertial and insensitive to fluctuations even at large separations. The curves of
$St=10$ are very inertial and insensitive to fluctuations even at large separations. The curves of ![]() $\langle |w_{{r,LL}}| \rangle$ are therefore much flatter. Besides, the constant relative velocity between LL pairs at small
$\langle |w_{{r,LL}}| \rangle$ are therefore much flatter. Besides, the constant relative velocity between LL pairs at small ![]() $r$ is also significantly larger, because their relative velocity comes from the energetic large-scale motions. When particles are charged, the same increasing trend with
$r$ is also significantly larger, because their relative velocity comes from the energetic large-scale motions. When particles are charged, the same increasing trend with ![]() $q$ is also observed but is less significant, which can be attributed to the large kinetic energy compared with the electrostatic potential energy.
$q$ is also observed but is less significant, which can be attributed to the large kinetic energy compared with the electrostatic potential energy.
As for SL pairs, ![]() $\langle |w_{{r,SL}}| \rangle$ is larger than both
$\langle |w_{{r,SL}}| \rangle$ is larger than both ![]() $\langle |w_{{r,SS}}| \rangle$ and
$\langle |w_{{r,SS}}| \rangle$ and ![]() $\langle |w_{{r,LL}}| \rangle$ in the neutral cases. This is caused by the different responses of small/large particles to turbulent fluctuations, which is termed the differential inertia effect (Zhou et al. Reference Zhou, Wexler and Wang2001). Interestingly, there is no obvious change when comparing curves between different charges
$\langle |w_{{r,LL}}| \rangle$ in the neutral cases. This is caused by the different responses of small/large particles to turbulent fluctuations, which is termed the differential inertia effect (Zhou et al. Reference Zhou, Wexler and Wang2001). Interestingly, there is no obvious change when comparing curves between different charges ![]() $q$ in figure 3(c). As shown in figure 2(c), the Coulomb force attracts small particles towards large ones and enhances their spatial correlation. Nevertheless, even though charged SL pairs experience a more similar flow history than neutral SL pairs, they will still develop large relative velocities over time because their response to local fluctuations is very different. Therefore, the influence of charge on
$q$ in figure 3(c). As shown in figure 2(c), the Coulomb force attracts small particles towards large ones and enhances their spatial correlation. Nevertheless, even though charged SL pairs experience a more similar flow history than neutral SL pairs, they will still develop large relative velocities over time because their response to local fluctuations is very different. Therefore, the influence of charge on ![]() $\langle |w_{{r,SL}}| \rangle$ is weak.
$\langle |w_{{r,SL}}| \rangle$ is weak.
3.2. Effect of Coulomb force on particle flux
Once the RDF and the radial relative velocity are known, we could further investigate the collision frequency between charged particles. For a steady system, the collision frequency can be measured by the kinematic collision kernel function as (Sundaram & Collins Reference Sundaram and Collins1997; Wang et al. Reference Wang, Wexler and Zhou2000)
Here, ![]() $R_{{C}}=r_{i}+r_{j}$ is the collision radius, which equals the sum of the radii of particles
$R_{{C}}=r_{i}+r_{j}$ is the collision radius, which equals the sum of the radii of particles ![]() $i$ and
$i$ and ![]() $j$;
$j$; ![]() $g_{ij}(R_{{C}})$ is the RDF at
$g_{ij}(R_{{C}})$ is the RDF at ![]() $r=R_{{C}}$, and the mean relative velocity is
$r=R_{{C}}$, and the mean relative velocity is ![]() $\langle |w_{{r},ij}|\rangle = \int _{-\infty }^{\infty } |w_{{r},ij}| p_{ij}(w_{{r},ij})\, \mathrm {d}w_{{r},ij}$, with
$\langle |w_{{r},ij}|\rangle = \int _{-\infty }^{\infty } |w_{{r},ij}| p_{ij}(w_{{r},ij})\, \mathrm {d}w_{{r},ij}$, with ![]() $p_{ij}(w_{{r},ij})$ the probability density function (PDF) of
$p_{ij}(w_{{r},ij})$ the probability density function (PDF) of ![]() $w_{{r},ij}$ at
$w_{{r},ij}$ at ![]() $r=R_{{C}}$.
$r=R_{{C}}$.
Even though other particle parameters (e.g. the Stokes number) are set the same, different choices of ![]() $R_{{C}}$ will affect the final outcome of
$R_{{C}}$ will affect the final outcome of ![]() $\varGamma _{ij}$ by changing the collision geometry. Therefore, instead of directly using
$\varGamma _{ij}$ by changing the collision geometry. Therefore, instead of directly using ![]() $\varGamma _{ij}$, we define the particle flux
$\varGamma _{ij}$, we define the particle flux ![]() $\varPhi _{ij}$ as the ratio of the collision kernel
$\varPhi _{ij}$ as the ratio of the collision kernel ![]() $\varGamma _{ij}(r)$ to the area of the collision sphere
$\varGamma _{ij}(r)$ to the area of the collision sphere ![]() $4 {\rm \pi}r^2$ at
$4 {\rm \pi}r^2$ at ![]() $r$ as
$r$ as
Here, ![]() $\varPhi _{ij}$ can be understood as the number of particles crossing the collision sphere per area per unit time, which is independent of the prescribed
$\varPhi _{ij}$ can be understood as the number of particles crossing the collision sphere per area per unit time, which is independent of the prescribed ![]() $R_{{C}}$.
$R_{{C}}$.
Apart from (3.3) that uses information of both approaching and departing pairs, the particle flux can also be defined using only the approaching or departing pairs. In real situations, it is the approaching pairs that lead to collisions, so a natural way to define particle flux is based on the inward flux as
Here, ![]() $F(w_{{r},ij}<0|r)$ is the fraction of particles moving inwards at
$F(w_{{r},ij}<0|r)$ is the fraction of particles moving inwards at ![]() $r$, and the mean inward relative velocity is
$r$, and the mean inward relative velocity is ![]() $\langle w_{{r},ij}^{-}\rangle = - \int _{-\infty }^{0} w_{{r},ij} p_{ij}(w_{{r},ij})\, \mathrm {d}w_{{r},ij}$. After the system reaches equilibrium, RDFs between particle pairs no longer change, suggesting that the inward flux should balance the outward flux at all
$\langle w_{{r},ij}^{-}\rangle = - \int _{-\infty }^{0} w_{{r},ij} p_{ij}(w_{{r},ij})\, \mathrm {d}w_{{r},ij}$. After the system reaches equilibrium, RDFs between particle pairs no longer change, suggesting that the inward flux should balance the outward flux at all ![]() $r$. Here, the outward particle flux is
$r$. Here, the outward particle flux is
with the mean outward relative velocity given by ![]() $\langle w_{{r},ij}^{+}\rangle = \int _{0}^{\infty } w_{{r},ij} p_{ij}(w_{{r},ij})\, \mathrm {d}w_{{r},ij}$. The definition of
$\langle w_{{r},ij}^{+}\rangle = \int _{0}^{\infty } w_{{r},ij} p_{ij}(w_{{r},ij})\, \mathrm {d}w_{{r},ij}$. The definition of ![]() $\varPhi _{ij}$ is based on a pair of particles
$\varPhi _{ij}$ is based on a pair of particles ![]() $i$ and
$i$ and ![]() $j$ without specifying their sizes. If the average is taken over all SS pairs, the result is the SS particle flux denoted by
$j$ without specifying their sizes. If the average is taken over all SS pairs, the result is the SS particle flux denoted by ![]() $\varPhi _{{SS}}$. The flux between LL pairs (
$\varPhi _{{SS}}$. The flux between LL pairs (![]() $\varPhi _{{LL}}$) and SL pairs (
$\varPhi _{{LL}}$) and SL pairs (![]() $\varPhi _{{SL}}$) can also be obtained by taking the average over corresponding particle pairs.
$\varPhi _{{SL}}$) can also be obtained by taking the average over corresponding particle pairs.
The SS fluxes ![]() $\varPhi _{{SS}}$ defined by (3.3), (3.4) and (3.5) are first compared and show good agreement with each other, indicating that the flux-balance condition is valid. Since (3.3) uses the information of both approaching and departing particle pairs, it is adopted in the following sections for better statistics.
$\varPhi _{{SS}}$ defined by (3.3), (3.4) and (3.5) are first compared and show good agreement with each other, indicating that the flux-balance condition is valid. Since (3.3) uses the information of both approaching and departing particle pairs, it is adopted in the following sections for better statistics.
Figure 4(a) compares the SS fluxes with various ![]() $q$. The flux for neutral pairs remain constant when
$q$. The flux for neutral pairs remain constant when ![]() $r$ is comparable to
$r$ is comparable to ![]() $\eta$. This indicates that, although both
$\eta$. This indicates that, although both ![]() $g_{{SS}}$ (figure 2a) and
$g_{{SS}}$ (figure 2a) and ![]() $\langle |w_{{r,SS}}| \rangle$ (figure 3a) keep changing as
$\langle |w_{{r,SS}}| \rangle$ (figure 3a) keep changing as ![]() $r$ decreases, their product is almost constant for small
$r$ decreases, their product is almost constant for small ![]() $r$. For inertial particle pairs with small
$r$. For inertial particle pairs with small ![]() $r$, it has been shown that
$r$, it has been shown that ![]() $g(r) \propto r^{D_2-3}$, with
$g(r) \propto r^{D_2-3}$, with ![]() $D_2$ the correlation dimension (Bec et al. Reference Bec, Biferale, Cencini, Lanotte, Musacchio and Toschi2007), while the relative velocity follows
$D_2$ the correlation dimension (Bec et al. Reference Bec, Biferale, Cencini, Lanotte, Musacchio and Toschi2007), while the relative velocity follows ![]() $\langle w_{{r,SS}} \rangle \propto r^{3-D_2}$ (Gustavsson & Mehlig Reference Gustavsson and Mehlig2014). Therefore, the dependence of
$\langle w_{{r,SS}} \rangle \propto r^{3-D_2}$ (Gustavsson & Mehlig Reference Gustavsson and Mehlig2014). Therefore, the dependence of ![]() $\varPhi _{{SS}}$ on
$\varPhi _{{SS}}$ on ![]() $r$ is cancelled out. Besides, in practical situations the collision diameter
$r$ is cancelled out. Besides, in practical situations the collision diameter ![]() $R_{{C}}$ between micron particles/droplets is smaller than
$R_{{C}}$ between micron particles/droplets is smaller than ![]() $\eta$, so the constant flux at such separation distance leads to a quadratic dependence of collision kernel on
$\eta$, so the constant flux at such separation distance leads to a quadratic dependence of collision kernel on ![]() $R_{{C}}$ as
$R_{{C}}$ as ![]() $\varGamma _{SS}=4 {\rm \pi}R_{{C,SS}}^2 \varPhi _{{SS}}(R_{{C,SS}})$ (Sundaram & Collins Reference Sundaram and Collins1997).
$\varGamma _{SS}=4 {\rm \pi}R_{{C,SS}}^2 \varPhi _{{SS}}(R_{{C,SS}})$ (Sundaram & Collins Reference Sundaram and Collins1997).

Figure 4. Particle fluxes between (a) SS, (b) LL and (c) SL particle pairs with different particle charge ![]() $q$.
$q$.
When particles are charged, the SS flux is found to decrease rapidly as ![]() $r$ drops. To characterize the effect of Coulomb force on the reduction of
$r$ drops. To characterize the effect of Coulomb force on the reduction of ![]() $\varPhi _{{SS}}$, we need to quantify the competition between the driving force and the resistance of particle collisions. For a pair of same-sign particles
$\varPhi _{{SS}}$, we need to quantify the competition between the driving force and the resistance of particle collisions. For a pair of same-sign particles ![]() $i$ and
$i$ and ![]() $j$ separated by
$j$ separated by ![]() $r$, the driving force can be evaluated by the relative kinetic energy
$r$, the driving force can be evaluated by the relative kinetic energy ![]() $E_{{Kin}}(r)=m_{ij} \langle |w_{{r},ij}| \rangle ^2/2$. Here,
$E_{{Kin}}(r)=m_{ij} \langle |w_{{r},ij}| \rangle ^2/2$. Here, ![]() $m_{ij}=(m_i^{-1}+m_j^{-1})^{-1}$ is the effective mass,
$m_{ij}=(m_i^{-1}+m_j^{-1})^{-1}$ is the effective mass, ![]() $\langle |w_{{r},ij}| \rangle (r)$ is the mean radial relative velocity between neutral pairs with a separation of
$\langle |w_{{r},ij}| \rangle (r)$ is the mean radial relative velocity between neutral pairs with a separation of ![]() $r$. The resistance is the electrical energy barrier
$r$. The resistance is the electrical energy barrier ![]() $E_{{Coul}} = q_i q_j /4 {\rm \pi}\varepsilon _0 r$. The energy ratio is then given as
$E_{{Coul}} = q_i q_j /4 {\rm \pi}\varepsilon _0 r$. The energy ratio is then given as
Note that, in previous studies regarding the clustering of charged particles with weak inertia (Lu et al. Reference Lu, Nordsiek, Saw and Shaw2010a,Reference Lu, Nordsiek and Shawb), the approaching velocity between particle pairs can be directly derived through perturbation expansion in the Stokes number (Chun et al. Reference Chun, Koch, Rani, Ahluwalia and Collins2005). In this work, however, particles are very inertial, so the mean relative velocity ![]() $\langle |w_{{r},ij}| \rangle$ between neutral pairs is used instead. By using the corresponding effective mass (e.g.
$\langle |w_{{r},ij}| \rangle$ between neutral pairs is used instead. By using the corresponding effective mass (e.g. ![]() $m_{{SS}}=m_{{S}}/2$,
$m_{{SS}}=m_{{S}}/2$, ![]() $m_{{LL}}=m_{{L}}/2$, and
$m_{{LL}}=m_{{L}}/2$, and ![]() $m_{{SL}}=m_{{S}}m_{{L}}/(m_{{S}}+m_{{L}})$) and the mean relative velocity (
$m_{{SL}}=m_{{S}}m_{{L}}/(m_{{S}}+m_{{L}})$) and the mean relative velocity (![]() $\langle |w_{{r,SS}}|\rangle$,
$\langle |w_{{r,SS}}|\rangle$, ![]() $\langle |w_{{r,LL}}|\rangle$, and
$\langle |w_{{r,LL}}|\rangle$, and ![]() $\langle |w_{{r,SL}}|\rangle$), (3.6) can quantify the Coulomb-turbulence competition for different kinds of particle pairs. Since
$\langle |w_{{r,SL}}|\rangle$), (3.6) can quantify the Coulomb-turbulence competition for different kinds of particle pairs. Since ![]() ${Ct}_0$ measures the relative importance of the Coulomb force to the mean relative kinetic energy, it is called the mean Coulomb-turbulence parameter hereinafter.
${Ct}_0$ measures the relative importance of the Coulomb force to the mean relative kinetic energy, it is called the mean Coulomb-turbulence parameter hereinafter.
According to the definition in (3.6), the value of ![]() ${Ct}_0$ can be varied as the particle charges or the separation distance changes. Therefore, for each data point in figure 4(a), we plot the ratio of
${Ct}_0$ can be varied as the particle charges or the separation distance changes. Therefore, for each data point in figure 4(a), we plot the ratio of ![]() $\varPhi _{{SS}}(q)$ to its corresponding value in the neutral case
$\varPhi _{{SS}}(q)$ to its corresponding value in the neutral case ![]() $\varPhi _{{SS}}(q=0)$ as a function of
$\varPhi _{{SS}}(q=0)$ as a function of ![]() ${Ct}_0$ in figure 5(a). The flux ratios for different
${Ct}_0$ in figure 5(a). The flux ratios for different ![]() $q$ are found to follow the same trend. The particle flux of charged particles is almost unaffected when
$q$ are found to follow the same trend. The particle flux of charged particles is almost unaffected when ![]() ${Ct}_0$ is small, and a significant decay is observed when
${Ct}_0$ is small, and a significant decay is observed when ![]() ${Ct}_0$ exceeds unity. The LL fluxes
${Ct}_0$ exceeds unity. The LL fluxes ![]() $\varPhi _{{LL}}$ in figure 4(b) are analysed in a similar way, and the results are plotted in figure 5(b). Because of the large kinematic energy between LL pairs, the Coulomb repulsion is relatively weak (
$\varPhi _{{LL}}$ in figure 4(b) are analysed in a similar way, and the results are plotted in figure 5(b). Because of the large kinematic energy between LL pairs, the Coulomb repulsion is relatively weak (![]() ${Ct}_0<1$), so the reduction of
${Ct}_0<1$), so the reduction of ![]() $\varPhi _{{LL}}$ has not yet reached the electrostatic-dominant regime. As for the flux between SL pairs shown in figure 4(c), the opposite trend is seen when plotting the flux ratio as a function of
$\varPhi _{{LL}}$ has not yet reached the electrostatic-dominant regime. As for the flux between SL pairs shown in figure 4(c), the opposite trend is seen when plotting the flux ratio as a function of ![]() ${Ct}_0$ (figure 5c). The increase of
${Ct}_0$ (figure 5c). The increase of ![]() $\varPhi _{{SL}}$ becomes significant when
$\varPhi _{{SL}}$ becomes significant when ![]() ${Ct}_0$ becomes larger than one.
${Ct}_0$ becomes larger than one.

Figure 5. Ratios of charged particle flux ![]() $\varPhi (q)$ to neutral particle flux
$\varPhi (q)$ to neutral particle flux ![]() $\varPhi (q=0)$ as a function of the mean Coulomb-turbulence parameter
$\varPhi (q=0)$ as a function of the mean Coulomb-turbulence parameter ![]() ${Ct}_0$ for (a) SS, (b) LL and (c) SL particle pairs. Blue solid lines are model predictions from (3.16) and (3.17) with fitted
${Ct}_0$ for (a) SS, (b) LL and (c) SL particle pairs. Blue solid lines are model predictions from (3.16) and (3.17) with fitted ![]() $\beta$. Brown dash-dotted lines are predictions with the fixed
$\beta$. Brown dash-dotted lines are predictions with the fixed ![]() $\beta =1$.
$\beta =1$.
We now propose a model to quantify the influence of the electrostatic force on the mean particle flux. For particle pairs with a separation distance ![]() $r$, the mean radial relative velocities between different kinds of particle pairs have been shown in figure 3. We then assume that, for each kind of particle pair, the relative velocity between neutral pairs follows the Gaussian distribution. Taking SS particle pairs as an example, the PDF
$r$, the mean radial relative velocities between different kinds of particle pairs have been shown in figure 3. We then assume that, for each kind of particle pair, the relative velocity between neutral pairs follows the Gaussian distribution. Taking SS particle pairs as an example, the PDF ![]() $p_{{r,SS}}$ of the relative velocity
$p_{{r,SS}}$ of the relative velocity ![]() $w_{{r,SS}}(r)$ is
$w_{{r,SS}}(r)$ is
 \begin{equation} p_{{r,SS}}(w_{{r,SS}}) = \frac{1}{\sqrt{2 {\rm \pi}} \sigma_{{SS}}} \exp{\left(-\frac{w_{{r,SS}}^2}{2 \sigma_{{SS}}^2}\right)}. \end{equation}
\begin{equation} p_{{r,SS}}(w_{{r,SS}}) = \frac{1}{\sqrt{2 {\rm \pi}} \sigma_{{SS}}} \exp{\left(-\frac{w_{{r,SS}}^2}{2 \sigma_{{SS}}^2}\right)}. \end{equation}
The standard deviation is determined by the mean relative velocity at ![]() $r$ as
$r$ as ![]() $\sigma _{{SS}} = \sqrt {{\rm \pi} /2} \cdot \langle |w_{{r,SS}}| \rangle (r)$. It should be noted that the relative velocity distribution is actually non-Gaussian (Sundaram & Collins Reference Sundaram and Collins1997; Wang et al. Reference Wang, Wexler and Zhou2000; Ireland et al. Reference Ireland, Bragg and Collins2016a). However, a Gaussian distribution is sufficient for the first-order assumption, and has already been applied in previous studies (Pan & Padoan Reference Pan and Padoan2010; Lu & Shaw Reference Lu and Shaw2015).
$\sigma _{{SS}} = \sqrt {{\rm \pi} /2} \cdot \langle |w_{{r,SS}}| \rangle (r)$. It should be noted that the relative velocity distribution is actually non-Gaussian (Sundaram & Collins Reference Sundaram and Collins1997; Wang et al. Reference Wang, Wexler and Zhou2000; Ireland et al. Reference Ireland, Bragg and Collins2016a). However, a Gaussian distribution is sufficient for the first-order assumption, and has already been applied in previous studies (Pan & Padoan Reference Pan and Padoan2010; Lu & Shaw Reference Lu and Shaw2015).
We then evaluate the RDF of charged pairs. For neutral SS pairs, all particle pairs with an inward relative velocity (![]() $w_{{r,SS}}<0$) could approach each other. In comparison, when they are identically charged, only those SS pairs whose inward relative velocity exceeds a critical velocity (
$w_{{r,SS}}<0$) could approach each other. In comparison, when they are identically charged, only those SS pairs whose inward relative velocity exceeds a critical velocity (![]() $w_{{r,SS}}<-w_{{C,SS}}$) are able to get close. By balancing the Coulomb energy barrier and the relative kinetic energy, the critical velocity can be given as
$w_{{r,SS}}<-w_{{C,SS}}$) are able to get close. By balancing the Coulomb energy barrier and the relative kinetic energy, the critical velocity can be given as
 \begin{equation} w_{{C,SS}}=\left( \frac{q^2}{2 {\rm \pi}\varepsilon_0 r m_{{SS}}}\right)^{1/2}. \end{equation}
\begin{equation} w_{{C,SS}}=\left( \frac{q^2}{2 {\rm \pi}\varepsilon_0 r m_{{SS}}}\right)^{1/2}. \end{equation}
The critical velocity for LL or SL pairs can be given by replacing ![]() $m_{{SS}}=m_{{S}}/2$ with
$m_{{SS}}=m_{{S}}/2$ with ![]() $m_{{LL}}=m_{{L}}/2$ or
$m_{{LL}}=m_{{L}}/2$ or ![]() $m_{{SL}}=m_{{S}}m_{{L}}/(m_{{S}}+m_{{L}})$. Note that the critical velocity is derived from the interaction between a pair of particles, which could reasonably describe the major effect of the Coulomb force in the current dilution suspension. If the particle concentration becomes higher, the particle number density needs to be included for a more accurate prediction (Boutsikakis et al. Reference Boutsikakis, Fede and Simonin2022, Reference Boutsikakis, Fede and Simonin2023). By assuming a sharp cutoff at
$m_{{SL}}=m_{{S}}m_{{L}}/(m_{{S}}+m_{{L}})$. Note that the critical velocity is derived from the interaction between a pair of particles, which could reasonably describe the major effect of the Coulomb force in the current dilution suspension. If the particle concentration becomes higher, the particle number density needs to be included for a more accurate prediction (Boutsikakis et al. Reference Boutsikakis, Fede and Simonin2022, Reference Boutsikakis, Fede and Simonin2023). By assuming a sharp cutoff at ![]() $w=-w_{{C,SS}}$, Lu & Shaw (Reference Lu and Shaw2015) related the RDF of charged SS pairs
$w=-w_{{C,SS}}$, Lu & Shaw (Reference Lu and Shaw2015) related the RDF of charged SS pairs ![]() $g_{{SS}}(r|q)$ to that of neutral SS pairs
$g_{{SS}}(r|q)$ to that of neutral SS pairs ![]() $g_{{SS}}(r|q=0)$ as
$g_{{SS}}(r|q=0)$ as
 \begin{align} g_{{SS}}(r|q) &= g_{{SS}}(r|q=0) \cdot \frac{\displaystyle\int_{-\infty}^{{-}w_{{C,SS}}} p_{{r,SS}}(w)\,\mathrm{d}w}{\displaystyle \int_{-\infty}^{0} p_{{r,SS}}(w)\,\mathrm{d}w} \nonumber\\ &=g_{{r,SS}}(r|q=0) \cdot \left[1-\mathrm{erf}\left(\frac{w_{{C,SS}}}{\sqrt{2} \sigma_{SS}}\right)\right], \end{align}
\begin{align} g_{{SS}}(r|q) &= g_{{SS}}(r|q=0) \cdot \frac{\displaystyle\int_{-\infty}^{{-}w_{{C,SS}}} p_{{r,SS}}(w)\,\mathrm{d}w}{\displaystyle \int_{-\infty}^{0} p_{{r,SS}}(w)\,\mathrm{d}w} \nonumber\\ &=g_{{r,SS}}(r|q=0) \cdot \left[1-\mathrm{erf}\left(\frac{w_{{C,SS}}}{\sqrt{2} \sigma_{SS}}\right)\right], \end{align}
where ![]() $\mathrm {erf}$ is the error function. However, as the relative velocity magnitude
$\mathrm {erf}$ is the error function. However, as the relative velocity magnitude ![]() $w_{{r}}$ becomes smaller than
$w_{{r}}$ becomes smaller than ![]() $w_{{C,SS}}$, the corresponding flux contribution does not drop sharply to zero. Instead, a smooth transition would be expected, so the ratio of the charged RDF to the neutral RDF should be written as
$w_{{C,SS}}$, the corresponding flux contribution does not drop sharply to zero. Instead, a smooth transition would be expected, so the ratio of the charged RDF to the neutral RDF should be written as
 \begin{equation} \frac{g_{{SS}}(r|q)}{g_{{SS}}(r|q=0)} = \frac{\displaystyle\int_{-\infty}^{0} \varTheta_{{SS}}(w) p_{{r,SS}}(w)\,\mathrm{d}w}{ \displaystyle\int_{-\infty}^{0} p_{{r,SS}}(w)\,\mathrm{d}w}. \end{equation}
\begin{equation} \frac{g_{{SS}}(r|q)}{g_{{SS}}(r|q=0)} = \frac{\displaystyle\int_{-\infty}^{0} \varTheta_{{SS}}(w) p_{{r,SS}}(w)\,\mathrm{d}w}{ \displaystyle\int_{-\infty}^{0} p_{{r,SS}}(w)\,\mathrm{d}w}. \end{equation}
Here, ![]() $\varTheta _{{SS}}(w)$ is the electrical kernel that gradually transitions from one to zero when the magnitude of
$\varTheta _{{SS}}(w)$ is the electrical kernel that gradually transitions from one to zero when the magnitude of ![]() $w_{{r}}$ drops below
$w_{{r}}$ drops below ![]() $w_{{C,SS}}$. The proportion of charged particles that could overcome the Coulomb repulsion is then obtained from the convolution of
$w_{{C,SS}}$. The proportion of charged particles that could overcome the Coulomb repulsion is then obtained from the convolution of ![]() $\varTheta _{{SS}}$ and
$\varTheta _{{SS}}$ and ![]() $p_{{r,SS}}$, which is the numerator of the right-hand term in (3.10). To account for the smooth transition without adding significant complexity, we still adopt the sharp cutoff assumption, but the effective cutoff velocity
$p_{{r,SS}}$, which is the numerator of the right-hand term in (3.10). To account for the smooth transition without adding significant complexity, we still adopt the sharp cutoff assumption, but the effective cutoff velocity ![]() $\beta _{{SS}}w_{{C,SS}}$ is used. Here,
$\beta _{{SS}}w_{{C,SS}}$ is used. Here, ![]() $\beta _{{SS}} \sim O(1)$ is the correction factor that ensures an accurate prediction as
$\beta _{{SS}} \sim O(1)$ is the correction factor that ensures an accurate prediction as
The difference between the effective cutoff and the actual electrical kernel will be further discussed in § 3.3. Consequently, (3.9) becomes
To obtain the mean relative velocity between charged SS pairs, we start by computing the mean relative velocity in the velocity interval ![]() $[-\infty,-\beta _{{SS}} w_{{C,SS}}]$ between neutral SS pairs
$[-\infty,-\beta _{{SS}} w_{{C,SS}}]$ between neutral SS pairs
 \begin{align} \langle |w_{{r,SS}}^{\prime}| \rangle (r|q=0) &= \frac{\displaystyle-\int_{-\infty}^{-\beta_{{SS}} w_{{C,SS}}} w \cdot p_{{r,SS}}(w)\,\mathrm{d}w}{ \displaystyle\int_{-\infty}^{-\beta_{{SS}} w_{{C,SS}}} p_{{r,SS}}(w)\,\mathrm{d}w} \nonumber\\ &= \langle |w_{{r,SS}}| \rangle (r|q=0) \cdot \exp{\left(\frac{-\beta_{{SS}}^2 w_{{C,SS}}^2}{2 \sigma_{SS}^2}\right)\Bigg/ \left[1-\mathrm{erf}\left(\frac{\beta_{{SS}} \cdot w_{{C,SS}}}{\sqrt{2} \sigma_{SS}}\right)\right]}. \end{align}
\begin{align} \langle |w_{{r,SS}}^{\prime}| \rangle (r|q=0) &= \frac{\displaystyle-\int_{-\infty}^{-\beta_{{SS}} w_{{C,SS}}} w \cdot p_{{r,SS}}(w)\,\mathrm{d}w}{ \displaystyle\int_{-\infty}^{-\beta_{{SS}} w_{{C,SS}}} p_{{r,SS}}(w)\,\mathrm{d}w} \nonumber\\ &= \langle |w_{{r,SS}}| \rangle (r|q=0) \cdot \exp{\left(\frac{-\beta_{{SS}}^2 w_{{C,SS}}^2}{2 \sigma_{SS}^2}\right)\Bigg/ \left[1-\mathrm{erf}\left(\frac{\beta_{{SS}} \cdot w_{{C,SS}}}{\sqrt{2} \sigma_{SS}}\right)\right]}. \end{align}
Then, the mean relative velocity of charged SS pairs can be obtained by subtracting the Coulomb potential energy from the mean relative kinetic energy in the velocity interval ![]() $[-\infty,-\beta _{{SS}} w_{{C,SS}}]$
$[-\infty,-\beta _{{SS}} w_{{C,SS}}]$
Here, the correction factor ![]() $\beta _{{SS}}$ is also added to the last term on the right-hand side to account for the smooth transition. Taking (3.13) into (3.14) then yields
$\beta _{{SS}}$ is also added to the last term on the right-hand side to account for the smooth transition. Taking (3.13) into (3.14) then yields
 \begin{align} \langle |w_{{r,SS}}| \rangle (r|q) &= \langle |w_{{r,SS}}| \rangle (r|q=0) \nonumber\\ &\quad \cdot \left[\frac{\displaystyle\exp{\left(-\dfrac{\beta_{{SS}}^2 w_{{C,SS}}^2 }{\sigma_{SS}^2}\right)}}{ \displaystyle\left[1-\mathrm{erf} \left(\dfrac{\beta_{{SS}}w_{{C,SS}}}{\sqrt{2}\sigma_{SS}}\right)\right]^2} - \frac{\beta_{{SS}}^2 q^2}{2 {\rm \pi}\varepsilon_0 m_{{SS}} \cdot \langle |w_{{r,SS}}| \rangle^2 (r|q=0) \cdot r}\right]^{1/2} . \end{align}
\begin{align} \langle |w_{{r,SS}}| \rangle (r|q) &= \langle |w_{{r,SS}}| \rangle (r|q=0) \nonumber\\ &\quad \cdot \left[\frac{\displaystyle\exp{\left(-\dfrac{\beta_{{SS}}^2 w_{{C,SS}}^2 }{\sigma_{SS}^2}\right)}}{ \displaystyle\left[1-\mathrm{erf} \left(\dfrac{\beta_{{SS}}w_{{C,SS}}}{\sqrt{2}\sigma_{SS}}\right)\right]^2} - \frac{\beta_{{SS}}^2 q^2}{2 {\rm \pi}\varepsilon_0 m_{{SS}} \cdot \langle |w_{{r,SS}}| \rangle^2 (r|q=0) \cdot r}\right]^{1/2} . \end{align} Finally, by multiplying (3.9) and (3.15) and taking into account the definition of ![]() ${Ct}_0$ (3.6), the flux ratio can be given as
${Ct}_0$ (3.6), the flux ratio can be given as
 \begin{align} \frac{\varPhi_{{SS}}(q)}{\varPhi_{{SS}}(q=0)} &= \frac{g_{{SS}}(r|q) \cdot \langle |w_{{r,SS}}| \rangle (r|q)}{g_{{SS}}(r|q=0) \cdot \langle |w_{{r,SS}}| \rangle (r|q=0)} \nonumber\\ &= \left\{ \exp{\left(-\frac{2 \beta_{{SS}}^2 {Ct}_0}{\rm \pi}\right)} - \beta_{{SS}}^2 {Ct}_0 [1-\mathrm{erf}(\beta_{{SS}} \sqrt{{Ct}_0 / {\rm \pi}})]^2 \right\}^{1/2}. \end{align}
\begin{align} \frac{\varPhi_{{SS}}(q)}{\varPhi_{{SS}}(q=0)} &= \frac{g_{{SS}}(r|q) \cdot \langle |w_{{r,SS}}| \rangle (r|q)}{g_{{SS}}(r|q=0) \cdot \langle |w_{{r,SS}}| \rangle (r|q=0)} \nonumber\\ &= \left\{ \exp{\left(-\frac{2 \beta_{{SS}}^2 {Ct}_0}{\rm \pi}\right)} - \beta_{{SS}}^2 {Ct}_0 [1-\mathrm{erf}(\beta_{{SS}} \sqrt{{Ct}_0 / {\rm \pi}})]^2 \right\}^{1/2}. \end{align}The flux ratios for LL pairs and SL pairs can be derived in a similar way and are written as
 $$\begin{gather} \frac{\varPhi_{{LL}}(q)}{\varPhi_{{LL}}(q=0)} = \left\{\exp{\left(-\frac{2 \beta_{{LL}}^2 {Ct}_0}{\rm \pi}\right)} - \beta_{{LL}}^2 {Ct}_0 [1-\mathrm{erf}(\beta_{{LL}} \sqrt{{Ct}_0 / {\rm \pi}})]^2\right\}^{1/2}, \end{gather}$$
$$\begin{gather} \frac{\varPhi_{{LL}}(q)}{\varPhi_{{LL}}(q=0)} = \left\{\exp{\left(-\frac{2 \beta_{{LL}}^2 {Ct}_0}{\rm \pi}\right)} - \beta_{{LL}}^2 {Ct}_0 [1-\mathrm{erf}(\beta_{{LL}} \sqrt{{Ct}_0 / {\rm \pi}})]^2\right\}^{1/2}, \end{gather}$$ $$\begin{gather}\frac{\varPhi_{{SL}}(q)}{\varPhi_{{SL}}(q=0)} = \left\{ \exp{\left(-\frac{2 \beta_{{SL}}^2 {Ct}_0}{\rm \pi}\right)} + \beta_{{SL}}^2 {Ct}_0 [1+\mathrm{erf}(\beta_{{SL}} \sqrt{{Ct}_0 / {\rm \pi}})]^2\right\}^{1/2}. \end{gather}$$
$$\begin{gather}\frac{\varPhi_{{SL}}(q)}{\varPhi_{{SL}}(q=0)} = \left\{ \exp{\left(-\frac{2 \beta_{{SL}}^2 {Ct}_0}{\rm \pi}\right)} + \beta_{{SL}}^2 {Ct}_0 [1+\mathrm{erf}(\beta_{{SL}} \sqrt{{Ct}_0 / {\rm \pi}})]^2\right\}^{1/2}. \end{gather}$$ Equations (3.16) and (3.17) are then fitted as blue lines in figure 5, which show good agreement with the simulation results. The fitted correction factors are ![]() $\beta _{{SS}}=0.193$,
$\beta _{{SS}}=0.193$, ![]() $\beta _{{LL}}=0.739$ and
$\beta _{{LL}}=0.739$ and ![]() $\beta _{{SL}}=0.5415$, satisfying the assumption that the correction factors are of the order of unity. The predictions with the fixed
$\beta _{{SL}}=0.5415$, satisfying the assumption that the correction factors are of the order of unity. The predictions with the fixed ![]() $\beta =1$ are also shown as brown dash-dotted lines, which correspond to the original model that assumes the sharp cutoff occurs at the critical velocity
$\beta =1$ are also shown as brown dash-dotted lines, which correspond to the original model that assumes the sharp cutoff occurs at the critical velocity ![]() $w_{{C,SS/LL/SL}}$. Although the trends are similar, models with the fixed
$w_{{C,SS/LL/SL}}$. Although the trends are similar, models with the fixed ![]() $\beta =1$ underestimate the critical
$\beta =1$ underestimate the critical ![]() ${Ct}_0$ at which the transition occurs. Moreover, the proposed model underestimates the SS flux when
${Ct}_0$ at which the transition occurs. Moreover, the proposed model underestimates the SS flux when ![]() ${Ct}_0 \approx 10^2$ in figure 5(a). To find the origin of this discrepancy, the predicted
${Ct}_0 \approx 10^2$ in figure 5(a). To find the origin of this discrepancy, the predicted ![]() $g_{ij}(r)$ using (3.12) and the predicted
$g_{ij}(r)$ using (3.12) and the predicted ![]() $\langle |w_{{r,SS}}| \rangle (r)$ using (3.15) are also plotted as grey dashed lines in figures 2 and 3, respectively. It can be seen that the predicted RDFs are comparable to the simulation results, so the discrepancy of
$\langle |w_{{r,SS}}| \rangle (r)$ using (3.15) are also plotted as grey dashed lines in figures 2 and 3, respectively. It can be seen that the predicted RDFs are comparable to the simulation results, so the discrepancy of ![]() $\varPhi _{{SS}}$ at
$\varPhi _{{SS}}$ at ![]() ${Ct}_0 \approx 10^2$ mainly comes from the underestimation of the mean relative velocity at
${Ct}_0 \approx 10^2$ mainly comes from the underestimation of the mean relative velocity at ![]() $r \sim \eta$ in figure 3(a). Since the PDF of
$r \sim \eta$ in figure 3(a). Since the PDF of ![]() $w_{{r}}$ is assumed Gaussian in our model, the influence of intermittency is not considered. As a result, the proportion of particle pairs with large relative velocity is significantly underestimated.
$w_{{r}}$ is assumed Gaussian in our model, the influence of intermittency is not considered. As a result, the proportion of particle pairs with large relative velocity is significantly underestimated.
3.3. Particle flux density for charged particles
In § 3.2, the mean Coulomb-turbulence parameter ![]() ${Ct}_0$ is defined using the mean relative velocity
${Ct}_0$ is defined using the mean relative velocity ![]() $\langle |w_{{r},ij}| \rangle$, which compares the importance of the Coulomb force with the mean relative motion caused by turbulence. However, it has been known that the relative velocity between particle pairs may vary within a wide range, and the mean Coulomb-turbulence parameter
$\langle |w_{{r},ij}| \rangle$, which compares the importance of the Coulomb force with the mean relative motion caused by turbulence. However, it has been known that the relative velocity between particle pairs may vary within a wide range, and the mean Coulomb-turbulence parameter ![]() ${Ct}_0$ may not be sufficient to fully reveal the physics.
${Ct}_0$ may not be sufficient to fully reveal the physics.
In this section it would be of interest to examine the impacts of the Coulomb force on particle pairs with different relative velocities. For different kinds of particle pairs, the particle flux ![]() $\varPhi _{ij}$ in the relative velocity space is expanded as
$\varPhi _{ij}$ in the relative velocity space is expanded as
Here, ![]() $\phi _{ij}$ is the density of particle flux within each relative velocity interval, which measures the contribution to the total particle flux
$\phi _{ij}$ is the density of particle flux within each relative velocity interval, which measures the contribution to the total particle flux ![]() $\varPhi _{ij}$ by particle pairs whose relative velocity is within the interval
$\varPhi _{ij}$ by particle pairs whose relative velocity is within the interval ![]() $w_{{r}} \pm \Delta w_{{r}}/2$. By comparing (3.18) and (3.3),
$w_{{r}} \pm \Delta w_{{r}}/2$. By comparing (3.18) and (3.3), ![]() $\phi _{ij}$ can be given as
$\phi _{ij}$ can be given as
We start with the effect of the Coulomb force on the PDFs of relative velocity ![]() $p_{ij}(w_{{r},ij})$, because the distribution of
$p_{ij}(w_{{r},ij})$, because the distribution of ![]() $\phi _{ij}$ in (3.19) is strongly dependent on
$\phi _{ij}$ in (3.19) is strongly dependent on ![]() $p_{ij}(w_{{r},ij})$. Figure 6(a) illustrates PDFs of
$p_{ij}(w_{{r},ij})$. Figure 6(a) illustrates PDFs of ![]() $w_{{r,SS}}$ at the separation distance interval
$w_{{r,SS}}$ at the separation distance interval ![]() $r \in [1.15\eta, 2.5\eta )$. The Gaussian distribution defined by (3.7) is also shown as the black dashed line. By comparing the neutral PDFs and the Gaussian curves, it is clear that the Gaussian assumption serves as a reasonable approximation at
$r \in [1.15\eta, 2.5\eta )$. The Gaussian distribution defined by (3.7) is also shown as the black dashed line. By comparing the neutral PDFs and the Gaussian curves, it is clear that the Gaussian assumption serves as a reasonable approximation at ![]() $|w_{{r}}|<3u_\eta$, but significantly underestimates the probability of large
$|w_{{r}}|<3u_\eta$, but significantly underestimates the probability of large ![]() $|w_{{r}}|$. Therefore, the Gaussian assumption is only suitable for modelling low-order effects, not for higher-order statistics. Besides, as will be discussed below, since the Gaussian curve is symmetric, it is not able to capture the asymmetry of the relative velocity between approaching and departing pairs.
$|w_{{r}}|$. Therefore, the Gaussian assumption is only suitable for modelling low-order effects, not for higher-order statistics. Besides, as will be discussed below, since the Gaussian curve is symmetric, it is not able to capture the asymmetry of the relative velocity between approaching and departing pairs.

Figure 6. The PDFs of the relative velocity between (a) SS, (b) LL and (c) SL pairs at ![]() $r \in [ 1.15\eta, 2.5\eta )$. Zoom-in views around
$r \in [ 1.15\eta, 2.5\eta )$. Zoom-in views around ![]() $w_{{r}}=0$ are shown in the insets. Black dashed lines denote the Gaussian distributions defined by (3.7) for different kinds of particle pairs.
$w_{{r}}=0$ are shown in the insets. Black dashed lines denote the Gaussian distributions defined by (3.7) for different kinds of particle pairs.
For SS pairs, compared with the neutral PDF, charged PDFs become wider as ![]() $q$ increases, indicating a lower/higher probability of finding particle pairs with low/high relative velocity within the separation interval. This is consistent with the increase of the mean relative velocity with
$q$ increases, indicating a lower/higher probability of finding particle pairs with low/high relative velocity within the separation interval. This is consistent with the increase of the mean relative velocity with ![]() $q$ in figure 3(a). If we look at the symmetry of
$q$ in figure 3(a). If we look at the symmetry of ![]() $p_{{SS}}$, the neutral PDF is found negatively skewed. This asymmetry is attributed to: (i) the fluid velocity derivative is negatively skewed, and the relative motion between particle pairs with
$p_{{SS}}$, the neutral PDF is found negatively skewed. This asymmetry is attributed to: (i) the fluid velocity derivative is negatively skewed, and the relative motion between particle pairs with ![]() $St=1$ is partially coupled to the local flow and thus exhibits a similar feature (Van Atta & Antonia Reference Van Atta and Antonia1980; Wang et al. Reference Wang, Wexler and Zhou2000); (ii) the asymmetry of particle path history gives rise to a larger relative velocity between approaching pairs than departing pairs (Bragg & Collins Reference Bragg and Collins2014). However, the asymmetry of
$St=1$ is partially coupled to the local flow and thus exhibits a similar feature (Van Atta & Antonia Reference Van Atta and Antonia1980; Wang et al. Reference Wang, Wexler and Zhou2000); (ii) the asymmetry of particle path history gives rise to a larger relative velocity between approaching pairs than departing pairs (Bragg & Collins Reference Bragg and Collins2014). However, the asymmetry of ![]() $p_{{SS}}$ curves are significantly reduced once particles are charged (see table 2), which results from the symmetric nature of the Coulomb force. The magnitude of the Coulomb force relies only on the interparticle distance
$p_{{SS}}$ curves are significantly reduced once particles are charged (see table 2), which results from the symmetric nature of the Coulomb force. The magnitude of the Coulomb force relies only on the interparticle distance ![]() $r$, so the approaching or departing SS pairs experience the same amount of repulsion as long as
$r$, so the approaching or departing SS pairs experience the same amount of repulsion as long as ![]() $r$ is the same, which makes the approaching-then-departing process more symmetric. Therefore, introducing Coulomb force could effectively increase the standard deviation but reduce the skewness of
$r$ is the same, which makes the approaching-then-departing process more symmetric. Therefore, introducing Coulomb force could effectively increase the standard deviation but reduce the skewness of ![]() $w_{{r,SS}}$.
$w_{{r,SS}}$.
Table 2. Normalized skewness of the radial relative velocity ![]() $w_{{r}}$ at
$w_{{r}}$ at ![]() $r \in [ 1.15\eta, 2.5\eta )$.
$r \in [ 1.15\eta, 2.5\eta )$.

For LL pairs, since Coulomb repulsion is only able to repel pairs with small relative velocity, ![]() $p_{{LL}}$ drops slightly as
$p_{{LL}}$ drops slightly as ![]() $w_{{r}}$ approaches zero, but remains almost unchanged at larger
$w_{{r}}$ approaches zero, but remains almost unchanged at larger ![]() $w_{{r}}$. As for
$w_{{r}}$. As for ![]() $p_{{SL}}$, the difference between the neutral and charged case is insignificant, which again demonstrates that the velocity difference between particles of different sizes mainly comes from the differential inertia effect, while the influence of the Coulomb force is limited. Besides, the movement of large particles with
$p_{{SL}}$, the difference between the neutral and charged case is insignificant, which again demonstrates that the velocity difference between particles of different sizes mainly comes from the differential inertia effect, while the influence of the Coulomb force is limited. Besides, the movement of large particles with ![]() $St=10$ has very weak couplings to the local flow fields, so the skewness of
$St=10$ has very weak couplings to the local flow fields, so the skewness of ![]() $p_{{LL}}$ and
$p_{{LL}}$ and ![]() $p_{{SL}}$ in table 2 is negligible.
$p_{{SL}}$ in table 2 is negligible.
We now turn to the distribution of flux density ![]() $\phi _{ij}$ in the velocity space. Figure 7(a,c,e) plots the flux densities between SS, LL and SL pairs, respectively. Different from the unimodal PDFs of the relative velocity shown in figure 6,
$\phi _{ij}$ in the velocity space. Figure 7(a,c,e) plots the flux densities between SS, LL and SL pairs, respectively. Different from the unimodal PDFs of the relative velocity shown in figure 6, ![]() $\phi _{ij}$ are bimodal because the maximum flux density is reached when the product
$\phi _{ij}$ are bimodal because the maximum flux density is reached when the product ![]() $|w_{{r},ij}| \cdot p_{ij}(w_{{r},ij})$ is the largest. Therefore, it is the particle pairs with the intermediate relative velocity that contribute the most to the overall particle flux.
$|w_{{r},ij}| \cdot p_{ij}(w_{{r},ij})$ is the largest. Therefore, it is the particle pairs with the intermediate relative velocity that contribute the most to the overall particle flux.

Figure 7. Particle flux density in the velocity space, ![]() $\phi (w_{{r}})$, between (a) SS, (c) LL and (e) SL pairs at
$\phi (w_{{r}})$, between (a) SS, (c) LL and (e) SL pairs at ![]() $r \in [1.15\eta, 2.5\eta )$. Zoom-in views around
$r \in [1.15\eta, 2.5\eta )$. Zoom-in views around ![]() $w_{{r}}=0$ are shown in the insets. (b,d,f) Dependence of Coulomb kernel
$w_{{r}}=0$ are shown in the insets. (b,d,f) Dependence of Coulomb kernel ![]() $\varTheta _{ij}=\phi _{ij}(q)/\phi _{ij}(q=0)$ on
$\varTheta _{ij}=\phi _{ij}(q)/\phi _{ij}(q=0)$ on ![]() $w_{{r},ij}$ corresponding to (a,c,e), respectively.
$w_{{r},ij}$ corresponding to (a,c,e), respectively.
To better describe the impacts of the Coulomb force, we define the Coulomb kernel ![]() $\varTheta _{ij}$ as the ratios of the charged flux densities to their neutral values, i.e.
$\varTheta _{ij}$ as the ratios of the charged flux densities to their neutral values, i.e. ![]() $\varTheta _{ij}(q) = \phi _{ij}(q)/\phi _{ij}(q=0)$, which are displayed in the right panel (i.e. (b), (d) and (f)) of figure 7. As shown in figure 7(b), the value of
$\varTheta _{ij}(q) = \phi _{ij}(q)/\phi _{ij}(q=0)$, which are displayed in the right panel (i.e. (b), (d) and (f)) of figure 7. As shown in figure 7(b), the value of ![]() $\varTheta _{{SS}}$ varies by more than one order of magnitude, indicating that the influence of the Coulomb force changes significantly as
$\varTheta _{{SS}}$ varies by more than one order of magnitude, indicating that the influence of the Coulomb force changes significantly as ![]() $w_{{r}}$ changes. When
$w_{{r}}$ changes. When ![]() $|w_{{r}}|$ is small,
$|w_{{r}}|$ is small, ![]() $\varTheta _{{SS}}$ decreases drastically as
$\varTheta _{{SS}}$ decreases drastically as ![]() $q$ increases because Coulomb repulsion dominates. In addition,
$q$ increases because Coulomb repulsion dominates. In addition, ![]() $\varTheta _{{SS}}$ is found to be asymmetric. As discussed above, neutral particles with
$\varTheta _{{SS}}$ is found to be asymmetric. As discussed above, neutral particles with ![]() $St=1$ tend to separate at a lower relative velocity compared with the approaching pairs. When they are charged, particle pairs originally separating at low speeds will be accelerated and pushed apart by Coulomb repulsion, which effectively shifts the high flux density from the small positive
$St=1$ tend to separate at a lower relative velocity compared with the approaching pairs. When they are charged, particle pairs originally separating at low speeds will be accelerated and pushed apart by Coulomb repulsion, which effectively shifts the high flux density from the small positive ![]() $w_{{r}}$ to a larger positive
$w_{{r}}$ to a larger positive ![]() $w_{{r}}$ in the velocity space. Consequently,
$w_{{r}}$ in the velocity space. Consequently, ![]() $\varTheta _{{SS}}$ experiences a more significant decrease at
$\varTheta _{{SS}}$ experiences a more significant decrease at ![]() $w_{{r}}$ slightly greater than zero, but quickly exceeds one when
$w_{{r}}$ slightly greater than zero, but quickly exceeds one when ![]() $w_{{r}} \approx 2 u_\eta$. Moreover,
$w_{{r}} \approx 2 u_\eta$. Moreover, ![]() $\varTheta _{{SS}}$ becomes larger than one at large
$\varTheta _{{SS}}$ becomes larger than one at large ![]() $|w_{{r}}|$ for both approaching and departing pairs. The explanation is that, with the increase of
$|w_{{r}}|$ for both approaching and departing pairs. The explanation is that, with the increase of ![]() $q$, small particles are more likely to get attracted towards the large ones and follow their motions. Since the relative velocity between LL pairs is generally much larger, this effect could increase the SS flux density at large
$q$, small particles are more likely to get attracted towards the large ones and follow their motions. Since the relative velocity between LL pairs is generally much larger, this effect could increase the SS flux density at large ![]() $|w_{{r}}|$. However, the contribution of the increased flux at large positive
$|w_{{r}}|$. However, the contribution of the increased flux at large positive ![]() $|w_{{r}}|$ is negligible compared with the decrease at small
$|w_{{r}}|$ is negligible compared with the decrease at small ![]() $|w_{{r}}|$ (see figure 7a), so the major effect of the Coulomb force is to reduce the SS flux through the SS repulsive force.
$|w_{{r}}|$ (see figure 7a), so the major effect of the Coulomb force is to reduce the SS flux through the SS repulsive force.
The kernel ![]() $\varTheta _{{LL}}$ between LL pairs (figure 7d) also drops quickly at small
$\varTheta _{{LL}}$ between LL pairs (figure 7d) also drops quickly at small ![]() $|w_{{r}}|$, but recovers to unity when
$|w_{{r}}|$, but recovers to unity when ![]() $|w_{{r}}| \geq 2u_\eta$. Besides, because of the limited effects of the local fluid velocity gradient mentioned above, the approaching and departing processes are more symmetric for neutral LL pairs, and adding the Coulomb force retains this symmetry. As for
$|w_{{r}}| \geq 2u_\eta$. Besides, because of the limited effects of the local fluid velocity gradient mentioned above, the approaching and departing processes are more symmetric for neutral LL pairs, and adding the Coulomb force retains this symmetry. As for ![]() $\varTheta _{{SL}}$ shown in figure 7(f), the change is still most significant near
$\varTheta _{{SL}}$ shown in figure 7(f), the change is still most significant near ![]() $w_{{r}}=0$. However, different from the kernels of SS/LL pairs where the impact of the same-sign repulsion is only obvious within a narrow interval (i.e.
$w_{{r}}=0$. However, different from the kernels of SS/LL pairs where the impact of the same-sign repulsion is only obvious within a narrow interval (i.e. ![]() $|w_{{r}}|/u_\eta \leq 2$), the opposite-sign attraction seems to increase
$|w_{{r}}|/u_\eta \leq 2$), the opposite-sign attraction seems to increase ![]() $\varTheta _{{SL}}$ in a much wider range of
$\varTheta _{{SL}}$ in a much wider range of ![]() $w_{{r}}$. For instance,
$w_{{r}}$. For instance, ![]() $\varTheta _{{SL}}$ is increased even at
$\varTheta _{{SL}}$ is increased even at ![]() $w_{{r}}/u_\eta =-10$ for
$w_{{r}}/u_\eta =-10$ for ![]() $q=2\times 10^{-14}\ \mathrm {C}$ in figure 7(f). As discussed in § 3.2, the main effect of the opposite-sign attraction is to enhance SL clustering. Then, particles of different sizes, although staying close to each other, will develop a large relative velocity as a result of their different responses to local fluctuations, which leads to the increase of
$q=2\times 10^{-14}\ \mathrm {C}$ in figure 7(f). As discussed in § 3.2, the main effect of the opposite-sign attraction is to enhance SL clustering. Then, particles of different sizes, although staying close to each other, will develop a large relative velocity as a result of their different responses to local fluctuations, which leads to the increase of ![]() $\varTheta _{{SL}}$ in a wide range of
$\varTheta _{{SL}}$ in a wide range of ![]() $w_{{r}}$.
$w_{{r}}$.
The discussion above has shown that the influence of the Coulomb force is different as the particle relative velocity ![]() $w_{{r},ij}$ changes. Therefore, instead of using the mean relative velocity
$w_{{r},ij}$ changes. Therefore, instead of using the mean relative velocity ![]() $\langle |w_{{r},ij}| \rangle$ (3.6), we adopt the median relative velocity
$\langle |w_{{r},ij}| \rangle$ (3.6), we adopt the median relative velocity ![]() $\bar {w}_{{r},ij}$ in each
$\bar {w}_{{r},ij}$ in each ![]() $w_{{r}}$ bin to estimate the relative kinetic energy. For a given separation distance
$w_{{r}}$ bin to estimate the relative kinetic energy. For a given separation distance ![]() $r$ and a certain relative velocity bin with the median
$r$ and a certain relative velocity bin with the median ![]() $\bar {w}_{{r},ij}$, the extended Coulomb-turbulence parameter is given as
$\bar {w}_{{r},ij}$, the extended Coulomb-turbulence parameter is given as
We then examine the dependence of the electrical kernel ![]() $\varTheta _{ij}$ on the extended Coulomb-turbulence parameter
$\varTheta _{ij}$ on the extended Coulomb-turbulence parameter ![]() ${Ct}$. For the data points
${Ct}$. For the data points ![]() $(w_{{r},ij},\varTheta _{ij})$ shown in the right panel (i.e. (b), (d) and (f)) of figure 7, the corresponding values of
$(w_{{r},ij},\varTheta _{ij})$ shown in the right panel (i.e. (b), (d) and (f)) of figure 7, the corresponding values of ![]() ${Ct}$ are calculated using (3.20), and the results are re-plotted as points
${Ct}$ are calculated using (3.20), and the results are re-plotted as points ![]() $({Ct}, \varTheta _{ij})$. Note that to ensure meaningful statistics, only data points satisfying a certain criterion are considered and the reasons are as follows:
$({Ct}, \varTheta _{ij})$. Note that to ensure meaningful statistics, only data points satisfying a certain criterion are considered and the reasons are as follows:
(i) In addition to the separation interval
 $r \in [1.15\eta,2.5\eta )$ shown in figure 7, data from two more separation intervals, i.e.
$r \in [1.15\eta,2.5\eta )$ shown in figure 7, data from two more separation intervals, i.e.  $[0.85\eta,1.15\eta )$ and
$[0.85\eta,1.15\eta )$ and  $[2.5\eta,3.5\eta )$, are also added. At these separation distances, the effect of the electrostatic force is already significant, while the number of samples is large enough for statistics.
$[2.5\eta,3.5\eta )$, are also added. At these separation distances, the effect of the electrostatic force is already significant, while the number of samples is large enough for statistics.(ii) We only consider pairs with their relative velocity in a certain range to avoid using the more scattered data points at large
 $w_{{r}}$. For SS pairs, the relative velocity range is
$w_{{r}}$. For SS pairs, the relative velocity range is  $[-5 u_\eta, 5 u_\eta ]$, while for LL/SL pairs the range considered is
$[-5 u_\eta, 5 u_\eta ]$, while for LL/SL pairs the range considered is  $[-10 u_\eta, 10 u_\eta ]$. The particle flux within the above ranges contributes at least
$[-10 u_\eta, 10 u_\eta ]$. The particle flux within the above ranges contributes at least  $97.1\,\% / 95.6\,\% / 96.3\,\%$ of the total SS/LL/SL particle flux in the neutral case, which reflects the major change of
$97.1\,\% / 95.6\,\% / 96.3\,\%$ of the total SS/LL/SL particle flux in the neutral case, which reflects the major change of  $\varPhi _{ij}$ in each case.
$\varPhi _{ij}$ in each case.(iii) As shown in figure 7(b),
 $\varTheta _{{SS}}$ is not symmetric about
$\varTheta _{{SS}}$ is not symmetric about  $w_{{r}}=0$. When particles are departing, the Coulomb repulsion will redistribute
$w_{{r}}=0$. When particles are departing, the Coulomb repulsion will redistribute  $\phi _{{SS}}$ in the velocity space, which may distort the
$\phi _{{SS}}$ in the velocity space, which may distort the  $\varTheta _{{SS}}-{Ct}$ relationship. We therefore only use the data from approaching pairs (
$\varTheta _{{SS}}-{Ct}$ relationship. We therefore only use the data from approaching pairs ( $w_{{r}}<0$) for later analysis. Since the outward flux is balanced by the inward flux in the steady state, the total flux could still be evaluated as
$w_{{r}}<0$) for later analysis. Since the outward flux is balanced by the inward flux in the steady state, the total flux could still be evaluated as  $\varPhi _{{SS}}(q)=2\int _{-\infty }^{0} \varTheta _{{SS}}({Ct}) \phi _{{SS}}(w_{{r,SS}})\, \mathrm {d} w_{{r,SS}}$.
$\varPhi _{{SS}}(q)=2\int _{-\infty }^{0} \varTheta _{{SS}}({Ct}) \phi _{{SS}}(w_{{r,SS}})\, \mathrm {d} w_{{r,SS}}$.
Figure 8 plots the dependence of ![]() $\varTheta _{ij}$ on
$\varTheta _{ij}$ on ![]() ${Ct}$ for different particle pairs. Despite different particle charge
${Ct}$ for different particle pairs. Despite different particle charge ![]() $q$ and separation
$q$ and separation ![]() $r$, the data points for both SS (figure 8a) and LL (figure 8b) pairs show a similar trend. When
$r$, the data points for both SS (figure 8a) and LL (figure 8b) pairs show a similar trend. When ![]() ${Ct}$ is small, the Coulomb force is weak compared with particle–turbulence interaction, so
${Ct}$ is small, the Coulomb force is weak compared with particle–turbulence interaction, so ![]() $\varTheta _{{SS}}$ and
$\varTheta _{{SS}}$ and ![]() $\varTheta _{{LL}}$ stay close to one. When
$\varTheta _{{LL}}$ stay close to one. When ![]() ${Ct}$ becomes larger than one, the same-sign repulsion starts to significantly reduce the corresponding particle flux density, and a decrease of
${Ct}$ becomes larger than one, the same-sign repulsion starts to significantly reduce the corresponding particle flux density, and a decrease of ![]() $\varTheta$ is observed. In § 3.2, it has been assumed that a sharp cutoff occurs at the effective velocity
$\varTheta$ is observed. In § 3.2, it has been assumed that a sharp cutoff occurs at the effective velocity ![]() $\beta _{{SS}} w_{{C,SS}}$ or
$\beta _{{SS}} w_{{C,SS}}$ or ![]() $\beta _{{LL}} w_{{C,LL}}$ for SS or LL pairs. However, the transitions of
$\beta _{{LL}} w_{{C,LL}}$ for SS or LL pairs. However, the transitions of ![]() $\varTheta _{{SS}}$ and
$\varTheta _{{SS}}$ and ![]() $\varTheta _{{LL}}$ in figure 8(a) turn out to be smooth. Thus, the sharp cutoff can be understood as the first-order approximation of the influence of Coulomb repulsion, which can be written as
$\varTheta _{{LL}}$ in figure 8(a) turn out to be smooth. Thus, the sharp cutoff can be understood as the first-order approximation of the influence of Coulomb repulsion, which can be written as
with ![]() $H(\,\cdot\,)$ being the Heaviside step function. The critical value of
$H(\,\cdot\,)$ being the Heaviside step function. The critical value of ![]() ${Ct}$ describing where
${Ct}$ describing where ![]() $\varTheta _{ij}$ steps down can be related to the fitted correction factors for the effective cutoff velocity as
$\varTheta _{ij}$ steps down can be related to the fitted correction factors for the effective cutoff velocity as
By taking into the fitted results (![]() $\beta _{{SS}}=0.193$ and
$\beta _{{SS}}=0.193$ and ![]() $\beta _{{LL}}=0.739$) from § 3.2, the critical values can be given as
$\beta _{{LL}}=0.739$) from § 3.2, the critical values can be given as ![]() ${Ct}_{{crit,SS}} = 26.85$ and
${Ct}_{{crit,SS}} = 26.85$ and ![]() ${Ct}_{{crit,LL}}=1.83$, respectively.
${Ct}_{{crit,LL}}=1.83$, respectively.

Figure 8. Dependence of the electrical kernel ![]() $\varTheta _{ij}$ on the extended Coulomb-turbulence parameter
$\varTheta _{ij}$ on the extended Coulomb-turbulence parameter ![]() ${Ct}$ for (a) SS, (b) LL and (c) SL particle pairs. Different shapes represent data points from
${Ct}$ for (a) SS, (b) LL and (c) SL particle pairs. Different shapes represent data points from ![]() $r \in [0.85\eta,1.15\eta )$ (circles:
$r \in [0.85\eta,1.15\eta )$ (circles: ![]() $\circ$),
$\circ$), ![]() $r \in [1.15\eta,2.5\eta )$ (diamonds:
$r \in [1.15\eta,2.5\eta )$ (diamonds: ![]() $\diamond$) and
$\diamond$) and ![]() $r \in [2.5\eta,3.5\eta )$ (triangles:
$r \in [2.5\eta,3.5\eta )$ (triangles: ![]() $\triangle$), respectively. Open/filled symbols denote data points for approaching/departing pairs.
$\triangle$), respectively. Open/filled symbols denote data points for approaching/departing pairs.
However, different from ![]() $\varTheta _{{SS}}$ and
$\varTheta _{{SS}}$ and ![]() $\varTheta _{{LL}}$, there is no clear dependence of
$\varTheta _{{LL}}$, there is no clear dependence of ![]() $\varTheta _{{SL}}$ on
$\varTheta _{{SL}}$ on ![]() ${Ct}$ in figure 8(c). The reason is as follows. The opposite-sign Coulomb force will attract SL pairs with a low departing velocity together and promote clustering. However, although these SL pairs have a low relative velocity at first, they will develop a much larger relative velocity over time. As a result, the relative kinetic energy
${Ct}$ in figure 8(c). The reason is as follows. The opposite-sign Coulomb force will attract SL pairs with a low departing velocity together and promote clustering. However, although these SL pairs have a low relative velocity at first, they will develop a much larger relative velocity over time. As a result, the relative kinetic energy ![]() $E_{{Kin}}$ becomes independent of the electrical potential energy
$E_{{Kin}}$ becomes independent of the electrical potential energy ![]() $E_{{Coul}}$, and no clear relationship can be found between
$E_{{Coul}}$, and no clear relationship can be found between ![]() $\varTheta _{{SL}}$ and
$\varTheta _{{SL}}$ and ![]() $\phi _{{SL}}$.
$\phi _{{SL}}$.
4. Conclusions
In this study, we investigate the effects of charge segregation on the dynamics of tribocharged bidispersed particles in homogeneous isotropic turbulence by means of DNS. Using a radial distribution function ![]() $g_{ij}(r)$, we show that Coulomb repulsion/attraction significantly inhibits/promotes particle clustering within a short range, while the clustering at a large separation distance is still determined by particle–turbulence interaction. For same-sign particles, Coulomb repulsion repels an approaching pair with low relative velocity, giving rise to the increase of mean relative velocity
$g_{ij}(r)$, we show that Coulomb repulsion/attraction significantly inhibits/promotes particle clustering within a short range, while the clustering at a large separation distance is still determined by particle–turbulence interaction. For same-sign particles, Coulomb repulsion repels an approaching pair with low relative velocity, giving rise to the increase of mean relative velocity ![]() $\langle |w_{{r},ij}| \rangle$ as the separation distance
$\langle |w_{{r},ij}| \rangle$ as the separation distance ![]() $r$ decreases. In comparison, the relative velocity between different-size particles is almost unchanged for all
$r$ decreases. In comparison, the relative velocity between different-size particles is almost unchanged for all ![]() $q$, which suggests that the differential inertia effect contributes predominantly to
$q$, which suggests that the differential inertia effect contributes predominantly to ![]() $\langle w_{{r,SL}} \rangle$.
$\langle w_{{r,SL}} \rangle$.
By defining the particle flux ![]() $\varPhi _{ij}$ as the number of particles crossing the collision sphere per area per unit time, we are able to quantify the particle collision frequency without a prescribed collision diameter
$\varPhi _{ij}$ as the number of particles crossing the collision sphere per area per unit time, we are able to quantify the particle collision frequency without a prescribed collision diameter ![]() $R_{{C}}$. As expected, the Coulomb repulsion/attraction is found to reduce/increase the total particle flux
$R_{{C}}$. As expected, the Coulomb repulsion/attraction is found to reduce/increase the total particle flux ![]() $\varPhi _{ij}$ when particles are close. When plotted as a function of the mean Coulomb-turbulence parameter
$\varPhi _{ij}$ when particles are close. When plotted as a function of the mean Coulomb-turbulence parameter ![]() ${Ct}_0$ that measures the relative importance of electrostatic potential energy to the mean relative kinetic energy, the particle flux ratio
${Ct}_0$ that measures the relative importance of electrostatic potential energy to the mean relative kinetic energy, the particle flux ratio ![]() $\varPhi _{ij}(q)/\varPhi _{ij}(q=0)$ is shown to follow a similar trend. Specifically, by assuming that the PDF of relative velocity follows a Gaussian distribution, the particle flux can be well modelled by a function of
$\varPhi _{ij}(q)/\varPhi _{ij}(q=0)$ is shown to follow a similar trend. Specifically, by assuming that the PDF of relative velocity follows a Gaussian distribution, the particle flux can be well modelled by a function of ![]() ${Ct}_0$.
${Ct}_0$.
The total particle flux ![]() $\varPhi _{ij}$ is then expanded in the relative velocity space as the flux density
$\varPhi _{ij}$ is then expanded in the relative velocity space as the flux density ![]() $\phi _{ij}$, and the relative change
$\phi _{ij}$, and the relative change ![]() $\varTheta _{ij}=\phi _{ij}(q)/\phi _{ij}(q=0)$ (also termed the Coulomb kernel) in each relative interval exhibits a significant difference. Finally, the extended Coulomb-turbulence parameter
$\varTheta _{ij}=\phi _{ij}(q)/\phi _{ij}(q=0)$ (also termed the Coulomb kernel) in each relative interval exhibits a significant difference. Finally, the extended Coulomb-turbulence parameter ![]() ${Ct}$ is defined using the median
${Ct}$ is defined using the median ![]() $\bar {w}_{{r},ij}$ in each relative velocity bin, which better describes the competition between Coulomb force and the turbulence effect. Then for same-size particle pairs, a clear relationship is found between
$\bar {w}_{{r},ij}$ in each relative velocity bin, which better describes the competition between Coulomb force and the turbulence effect. Then for same-size particle pairs, a clear relationship is found between ![]() $\varTheta _{ij}$ and
$\varTheta _{ij}$ and ![]() ${Ct}$. And the smooth transition of
${Ct}$. And the smooth transition of ![]() $\varTheta _{ij}$ is observed near the critical value
$\varTheta _{ij}$ is observed near the critical value ![]() ${Ct}_{{crit},ij}=1/\beta _{ij}^2$. For SL pairs, however, the relative velocity will grow larger because of the predominant differential inertia effect, so
${Ct}_{{crit},ij}=1/\beta _{ij}^2$. For SL pairs, however, the relative velocity will grow larger because of the predominant differential inertia effect, so ![]() $\varTheta _{{SL}}$ shows no clear dependence on
$\varTheta _{{SL}}$ shows no clear dependence on ![]() $w_{{r,SL}}$ (and therefore on
$w_{{r,SL}}$ (and therefore on ![]() ${Ct}$).
${Ct}$).
Funding
This work was supported by an Early Stage Innovation grant from NASA's Space Technology Research Grants Program under grant no. 80NSSC21K0222. This work was also partially supported by the Office of Naval Research (ONR) under grant no. N00014-21-1-2620.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Validation of the electrostatic calculation
To validate the electrostatic computation introduced in § 2.3, we compute the Coulomb force acting on ![]() $N_{{p}}$ particles in the three-dimensional periodic box using both (i) FMM incorporated with periodic image boxes and (ii) the standard Ewald summation. For the charge-neutral system in this work, the exact Coulomb force acting on particle
$N_{{p}}$ particles in the three-dimensional periodic box using both (i) FMM incorporated with periodic image boxes and (ii) the standard Ewald summation. For the charge-neutral system in this work, the exact Coulomb force acting on particle ![]() $i$ can be computed by Ewald summation (Deserno & Holm Reference Deserno and Holm1998) as
$i$ can be computed by Ewald summation (Deserno & Holm Reference Deserno and Holm1998) as
where the contributions from the real (physical) space ![]() $\boldsymbol {F}^{{(r)}}_i$, the Fourier (wavenumber) space
$\boldsymbol {F}^{{(r)}}_i$, the Fourier (wavenumber) space ![]() $\boldsymbol {F}^{{(k)}}_i$ and the dipole correction
$\boldsymbol {F}^{{(k)}}_i$ and the dipole correction ![]() $\boldsymbol {F}^{{(d)}}_i$ are given as
$\boldsymbol {F}^{{(d)}}_i$ are given as
 $$\begin{gather} \boldsymbol{F}^{{(r)}}_i = \frac{q_i}{4 {\rm \pi}\varepsilon_0} \sum_j q_j \sum_{\boldsymbol{m} \in \mathbb{Z}^3}^{\prime} \left( \frac{2 \alpha}{\sqrt{\rm \pi}} \exp(-\alpha^2 |\boldsymbol{r}_{ij} + \boldsymbol{m}L|^2) + \frac{\mathrm{erfc}(\alpha |\boldsymbol{r}_{ij} +\boldsymbol{m}L|)}{|\boldsymbol{r}_{ij} +\boldsymbol{m}L|} \right) \frac{\boldsymbol{r}_{ij} +\boldsymbol{m}L}{|\boldsymbol{r}_{ij} +\boldsymbol{m}L|^2}, \end{gather}$$
$$\begin{gather} \boldsymbol{F}^{{(r)}}_i = \frac{q_i}{4 {\rm \pi}\varepsilon_0} \sum_j q_j \sum_{\boldsymbol{m} \in \mathbb{Z}^3}^{\prime} \left( \frac{2 \alpha}{\sqrt{\rm \pi}} \exp(-\alpha^2 |\boldsymbol{r}_{ij} + \boldsymbol{m}L|^2) + \frac{\mathrm{erfc}(\alpha |\boldsymbol{r}_{ij} +\boldsymbol{m}L|)}{|\boldsymbol{r}_{ij} +\boldsymbol{m}L|} \right) \frac{\boldsymbol{r}_{ij} +\boldsymbol{m}L}{|\boldsymbol{r}_{ij} +\boldsymbol{m}L|^2}, \end{gather}$$ $$\begin{gather}\boldsymbol{F}^{{(k)}}_i = \frac{q_i}{4 {\rm \pi}\varepsilon_0 L^3} \sum_j q_j \sum_{\boldsymbol{k} {\neq} \boldsymbol{0}} \frac{4 {\rm \pi}\boldsymbol{k}}{k^2} \exp \left( -\frac{k^2}{4\alpha^2}\right) \sin{(\boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{r}_{ij})}, \end{gather}$$
$$\begin{gather}\boldsymbol{F}^{{(k)}}_i = \frac{q_i}{4 {\rm \pi}\varepsilon_0 L^3} \sum_j q_j \sum_{\boldsymbol{k} {\neq} \boldsymbol{0}} \frac{4 {\rm \pi}\boldsymbol{k}}{k^2} \exp \left( -\frac{k^2}{4\alpha^2}\right) \sin{(\boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{r}_{ij})}, \end{gather}$$
Here, ![]() $\alpha$ is the Ewald parameter,
$\alpha$ is the Ewald parameter, ![]() $\mathrm {erfc}$ is the complimentary error function and
$\mathrm {erfc}$ is the complimentary error function and ![]() $\varepsilon ^{\prime }=1$ is the relative dielectric constant of the surrounding medium.
$\varepsilon ^{\prime }=1$ is the relative dielectric constant of the surrounding medium.
Since Ewald summation is computationally expensive, a smaller-scale system with ![]() $N_{{p}}=2000$ oppositely charged particles is used in validation cases. In each case, ten parallel computations with different particle locations are performed to ensure reliable statistics. Table 3 lists parameters used in the Ewald summation. The dimensionless product
$N_{{p}}=2000$ oppositely charged particles is used in validation cases. In each case, ten parallel computations with different particle locations are performed to ensure reliable statistics. Table 3 lists parameters used in the Ewald summation. The dimensionless product ![]() $\alpha r_{{C}}$ equals
$\alpha r_{{C}}$ equals ![]() ${\rm \pi}$ to ensure high accuracy in both real and Fourier spaces. The cutoff radius(
${\rm \pi}$ to ensure high accuracy in both real and Fourier spaces. The cutoff radius(![]() $r_{{C}}$)/wavenumber(
$r_{{C}}$)/wavenumber(![]() $k_{{C}}$) in the real/Fourier space is then determined by
$k_{{C}}$) in the real/Fourier space is then determined by ![]() $r_{{C}}=(\alpha r_{{C}}) L/{\rm \pi} ^{1/2}N_{{p}}^{1/6}$ and
$r_{{C}}=(\alpha r_{{C}}) L/{\rm \pi} ^{1/2}N_{{p}}^{1/6}$ and ![]() $k_{{C}} = 1.8 (\alpha r_{{C}})^2/r_{{C}}$ to balance the computation cost of
$k_{{C}} = 1.8 (\alpha r_{{C}})^2/r_{{C}}$ to balance the computation cost of ![]() $\boldsymbol {F}^{{(r)}}_i$ and
$\boldsymbol {F}^{{(r)}}_i$ and ![]() $\boldsymbol {F}^{{(k)}}_i$ (Fincham Reference Fincham1994).
$\boldsymbol {F}^{{(k)}}_i$ (Fincham Reference Fincham1994).
Table 3. Dimensionless parameters in Ewald summation.

When performing FMM computation, the layer number ![]() $N_{{per}}$ is varied from
$N_{{per}}$ is varied from ![]() $0$ to
$0$ to ![]() $4$ to show the influence of adding image domains. The relative error of FMM compared with Ewald summation is given as
$4$ to show the influence of adding image domains. The relative error of FMM compared with Ewald summation is given as
 \begin{equation} \epsilon^{{FMM}} = \frac{|\boldsymbol{F}^{{E,FMM}}- \boldsymbol{F}^{{E,Ewald}}|}{|\boldsymbol{F}^{{E,Ewald}}|} = \frac{\displaystyle\left[\sum_{i=1}^{N_{p}} (\boldsymbol{F}_i^{{E,FMM}}- \boldsymbol{F}_i^{{E,Ewald}})^2 /N_{{p}}\right]^{1/2}}{\displaystyle\left[\sum_{i=1}^{N_{p}} (\boldsymbol{F}_i^{{E,Ewald}})^2 /N_{{p}}\right]^{1/2}}, \end{equation}
\begin{equation} \epsilon^{{FMM}} = \frac{|\boldsymbol{F}^{{E,FMM}}- \boldsymbol{F}^{{E,Ewald}}|}{|\boldsymbol{F}^{{E,Ewald}}|} = \frac{\displaystyle\left[\sum_{i=1}^{N_{p}} (\boldsymbol{F}_i^{{E,FMM}}- \boldsymbol{F}_i^{{E,Ewald}})^2 /N_{{p}}\right]^{1/2}}{\displaystyle\left[\sum_{i=1}^{N_{p}} (\boldsymbol{F}_i^{{E,Ewald}})^2 /N_{{p}}\right]^{1/2}}, \end{equation}
where the norm of force is defined as the root mean square of the force components following Deserno & Holm (Reference Deserno and Holm1998). The dependence of ![]() $\epsilon ^{{FMM}}$ on
$\epsilon ^{{FMM}}$ on ![]() $N_{{per}}$ is shown in table 4. The relative error is significant (
$N_{{per}}$ is shown in table 4. The relative error is significant (![]() $\epsilon ^{{FMM}} >10\,\%$) if periodicity is not considered. After adding image domains, the relative error drops significantly and almost saturates after
$\epsilon ^{{FMM}} >10\,\%$) if periodicity is not considered. After adding image domains, the relative error drops significantly and almost saturates after ![]() $N_{{per}} \geq 2$. Hence,
$N_{{per}} \geq 2$. Hence, ![]() $N_{{per}} = 2$ is chosen to guarantee sufficient accuracy (
$N_{{per}} = 2$ is chosen to guarantee sufficient accuracy (![]() $\epsilon ^{{FMM}}=0.17\,\%$) while avoiding expensive computation cost.
$\epsilon ^{{FMM}}=0.17\,\%$) while avoiding expensive computation cost.
Table 4. Relative errors of FMM computation compared with Ewald summation.