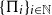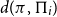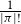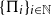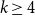Lower bound on the size of a quasirandom forcing set of permutations

Abstract

A set S of permutations is forcing if for any sequence $\{\Pi_i\}_{i \in \mathbb{N}}$ of permutations where the density $d(\pi,\Pi_i)$ converges to $\frac{1}{|\pi|!}$ for every permutation $\pi \in S$ , it holds that $\{\Pi_i\}_{i \in \mathbb{N}}$ is quasirandom. Graham asked whether there exists an integer k such that the set of all permutations of order k is forcing; this has been shown to be true for any $k\ge 4$ . In particular, the set of all 24 permutations of order 4 is forcing. We provide the first non-trivial lower bound on the size of a forcing set of permutations: every forcing set of permutations (with arbitrary orders) contains at least four permutations.

1. Introduction

Random combinatorial structures play an important role in combinatorics and various computer science applications. If a large combinatorial structure shares key properties with a truly random structure, then it is said to be quasirandom. The most studied theory of quasirandomness is that of graphs which originated in the seminal works of Rödl [24], Thomason [25], and Chung, Graham and Wilson [8] in the 1980s. Graph quasirandomness is captured by several seemingly different but in fact equivalent conditions: the density of all subgraphs is close to their expected density in a random graph, all but the largest eigenvalue of the adjacency matrix are small, the density of a graph is uniformly distributed amongst its (linear size) subsets of vertices, all cuts between linear size subsets of vertices have the same density, etc. Besides graphs, there are results on quasirandomness of many different types of combinatorial structures, in particular, tournaments [2, 6, 13, 18], hypergraphs [4, 15, 16, 19, 22], set systems [5], groups [17], subsets of integers [7], and Latin squares [10]. In this paper, we are concerned with quasirandomness of permutations as studied in [3, 11, 23].

One of the equivalent conditions mentioned above says that a large graph is quasirandom if and only if its edge density is $1/2+o(1)$ and the density of cycles of length four is $1/16+o(1)$ . Hence, graph quasirandomness is captured by the density of two specific subgraphs: $K_2$ and $C_4$ . More generally, the Forcing Conjecture posed by Conlon, Fox and Sudakov [9] asserts that $C_4$ can be replaced by any bipartite graph with at least one cycle. Graham (see [11, page 141]) asked whether an analogous result is true for permutations: Does there exists an integer k such that a (large) permutation is quasirandom if and only if the densities of all k-permutation are the same? This question was answered affirmatively by Král’ and Pikhurko [23] by establishing that any $k\ge 4$ has this property; we remark that the answer is negative for $k\in\{1,2,3\}$ [12]. Equivalent results were established in statistics in relation to non-parametric independence tests by Yanagimoto [26], building on an older work by Hoeffding [20]. In this context, we refer the reader to the work by Even-Zohar and Leng [14] on nearly linear time algorithm for counting small permutation occurrences, which can be used for fast implementation of these tests.

We are interested in determining the minimum size of a set of permutations that captures permutation quasirandomness. To state our results precisely, we need to introduce some definitions. A permutation of order n, or briefly an n-permutation, is a bijection from $\{1,\ldots,n\}$ to $\{1,\ldots,n\}$ ; the order of a permutation $\Pi$ is denoted by $|\Pi|$ . If $A=\{a_1,\ldots,a_k\}\subseteq \{1,\ldots,n\}$ , $a_1<\cdots<a_k$ , then the subpermutation of $\Pi$ induced by A is the unique permutation $\pi$ of order $|A|=k$ such that $\pi(i)<\pi(j)$ if and only if $\Pi(a_i)<\Pi(a_j)$ . Subpermutations are often referred to as patterns. The (pattern) density of a k-permutation $\pi$ in an n-permutation $\Pi$ is the probability $d(\pi,\Pi)$ that a randomly chosen k-element subset of $\{1,\ldots,n\}$ induces a subpermutation equal to $\pi$ ; if $k>n$ , we set $d(\pi,\Pi)=0$ . We say that a sequence $\{\Pi_i\}_{i \in \mathbb{N}}$ of permutations satisfying $|\Pi_i|\to \infty$ is quasirandom if for every permutation $\pi$ the limit of its densities in the sequence $\{\Pi_i\}_{i \in \mathbb{N}}$ satisfies

(1) \begin{equation} \lim_{i\to\infty}d(\pi,\Pi_i)=\frac{1}{\lvert\pi\rvert!}.\end{equation}

Finally, we say that a set S of permutations is forcing if any sequence $\{\Pi_i\}_{i\in\mathbb{N}}$ with $|\Pi_i| \to \infty$ satisfying equality (1) for all $\pi \in S$ is quasirandom. In particular, the results of [23, 26] imply that the set of all 4-permutations is forcing.

A natural question is to determine the minimum size of a forcing set of permutations. Inspecting the proof given in [23], Zhang [27] observed that there exists a 16-element forcing set of 4-permutations. Bergsma and Dassios [1] identified an 8-element forcing set of 4-permutations and Chan [3] found three additional 8-element forcing sets of 4-permutations. In fact, these four 8-element forcing sets S of 4-permutations satisfy an even stronger property, which is called $\Sigma$ -forcing, i.e., a sequence of permutations is quasirandom if and only if the limit of the sum of the pattern densities of permutations in S converges to $\lvert S\rvert/24$ . Our main result asserts that there is no forcing set containing less than four permutations.

Theorem 1. Every forcing set of permutations (of arbitrary, possibly different, orders) has at least four elements.

The proof of Theorem 1 is based on analysing perturbations of a truly random large permutation. We present our argument using the language of the theory of combinatorial limits, which we briefly introduce in Section 2. In Section 3, we establish that the change of the density of a pattern after small perturbations can be described by a certain polynomial for each pattern (the values of the polynomial determine the gradient of the density depending on the location of the perturbation) and state a sufficient condition for being non-forcing in terms of these polynomials. In Section 4, we show that every set with fewer than four permutations satisfies this condition with the exception of a few cases. We then analyse these cases separately to conclude the proof of Theorem 1.

2. Preliminaries

In this section, we define notation used in the rest of the paper and present some basic results on permutation limits. The set of all positive integers is denoted by $\mathbb{N}$ , the set of all non-negative integers by $\mathbb{N}_0$ , and for any $n\in \mathbb{N}$ the set $\{1, \ldots, n\}$ is denoted by [n]. We write $f\,:\,[k]\nearrow [n]$ to mean that f is a non-decreasing function from [k] to [n].

The set of all real matrices of order $n \times m$ is denoted by $\mathbb{R} ^ {n \times m}$ . The ith row of a matrix M is denoted by $M_i$ , and its entry in the ith row and jth column is denoted by $M_{i,j}$ . A stochastic matrix is a non-negative square matrix M such that each of its columns sums to one. If the same also holds for all its rows, we say that M is doubly stochastic. We use $\mathbb{J}$ to denote the constant doubly stochastic matrix. The order of $\mathbb{J}$ is always clear from context. For a k-permutation $\pi$ , we define its permutation matrix $A_\pi \in \mathbb{R}^{k \times k}$ by setting

\begin{align*}\left(A_\pi\right)_{i,j} = \begin{cases} 1 & \text{if } \pi(i) = j \text{ and}\\[4pt] 0 & \text{otherwise.}\end{cases}\end{align*}

Note that any permutation matrix is doubly stochastic. By a formal linear combination of permutations, we mean a formal linear combination over real numbers. For a formal linear combination $t_1 \pi_1 + \ldots + t_n \pi_n$ of permutations of equal orders, we define its cover matrix as

\begin{equation*}\textrm{Cvr}({t_1 \pi_1 + \ldots + t_n \pi_n}) = \sum_{i \in [n]} t_i A_{\pi_i}.\end{equation*}

A permuton is a limit object describing convergent sequences of permutations. Formally, a permuton $\mu$ is a Borel probability measure on $[0,1]^2$ that has uniform marginals, i.e., the measure of sets $[0,a]\times [0,1]$ and $[0,1] \times [0,a]$ equals to a for any $a \in [0, 1]$ . The notion of induced subpermutations introduced in Section 1 can be generalized to any set of points $P = \{(x_1, y_1), \ldots, (x_k, y_k)\}$ such that $x_1 < \ldots < x_k$ and all the y-coordinates are pairwise distinct: for such a set P the unique permutation $\pi$ satisfying

\begin{equation*}\pi(i) < \pi(j) \Leftrightarrow y_i < y_j,\end{equation*}

is called the permutation induced by P. Whenever k points are sampled from $\mu$ , they have distinct x and y-coordinates with probability one (since $\mu$ has uniform marginals) and therefore they induce a k-permutation almost surely. Such permutations are referred to as $\mu$ -random permutations. For any k-permutation $\pi$ , the probability that a $\mu$ -random k-permutation is equal to $\pi$ is called the density of $\pi$ in $\mu$ and denoted by $d(\pi, \mu)$ . For example, the uniform Borel measure $\lambda$ on $[0,1]^2$ is a permuton and it holds $d(\pi, \lambda) = \frac{1}{k!}$ for all k-permutations $\pi$ ; in fact, $\lambda$ is the only permuton with this property.

We say that a sequence of permutations $\{\Pi_i\}_{i \in \mathbb{N}}$ with $|\Pi_i| \to \infty$ is convergent if the sequence $\{d(\pi, \Pi_i)\}_{i \in \mathbb{N}}$ converges for any permutation $\pi$ . Additionally, we say it converges to a permuton $\mu$ if the equality

\begin{equation*}\lim_{i \to \infty} d(\pi, \Pi_i) = d(\pi, \mu).\end{equation*}

holds for all permutations $\pi$ . The following lemma asserts that permutons may serve as limits of convergent permutation sequences.

Lemma 2. Given a convergent permutation sequence $\{\Pi_i\}_{i\in\mathbb{N}}$ , there exists a unique permuton $\mu$ such that $\{\Pi_i\}_{i\in\mathbb{N}}$ converges to $\mu$ . Conversely, every permuton $\mu$ is a limit of a convergent permutation sequence, i.e., there is a sequence $\{\Pi_i\}_{i\in\mathbb{N}}$ converging to $\mu$ .

The lemma was first stated as the main result in [21], using a slightly different definition of limit objects; however, both definitions are equivalent. The uniqueness of the limit permuton is then a direct corollary of Theorem 1.7. in [21] (see the discussion after the definition of limit permutations and after Theorem 1.7.). More details can also be found in Section 2 of [23]. Lemma 2 allows us to cast the proof of Theorem 1 in the language of permutons, which we formalize in the following direct corollary of Lemma 2.

Lemma 3. A non-empty finite set of permutations S is forcing if and only if the uniform permuton is the only permuton $\mu$ satisfying $d(\pi, \mu) = \frac{1}{|\pi|!}$ for any $\pi \in S$ .

We associate a doubly stochastic square matrix M of order n with a step permuton $\mu[M]$ as follows: for a Borel set X, the measure of X is

\begin{align*} \mu[M](X) = \sum_{i,j \in [n]}n M_{i,j} \cdot \lambda \left( X \cap \left[\frac{i-1}{n}, \frac{i}{n}\right] \times \left[\frac{j-1}{n}, \frac{j}{n}\right]\right),\end{align*}

where $\lambda$ is the uniform measure. A straightforward computation leads to an explicit formula for the density of a k-permutation $\pi$ in the step permuton $\mu[M]$ .

(2) \begin{align}d(\pi, \mu[M]) = \frac{k!}{n^k} \sum_{f,g\,:\,[k] \nearrow [n]} \frac{1}{\prod_{i \in [n]} |f^{-1}(i)|!|g^{-1}(i)|!} \times \prod_{m \in [k]} M_{f(m), g(\pi(m))},\end{align}

Let us provide a brief explanation of (2). Any set of points $\{(x_1, y_1), \ldots, (x_k, y_k)\} \subseteq [0, 1] ^ 2$ can be uniquely identified with a pair $f,g\,:\,[k] \nearrow [n]$ by setting $f(m) = \lceil x_{i_m} \cdot n \rceil $ and $g(m) = \lceil y_{j_m} \cdot n \rceil$ for any $m \in [k]$ , where $x_{i_1} \leq \ldots \leq x_{i_k}$ and $y_{j_1} \leq \ldots \leq y_{j_k}$ . If we select k random points according to $\mu[M]$ , the probability that they correspond to the same function f is $\frac{k!}{n^k} \cdot \prod_{i\in[n]}\frac{1}{|f^{-1}(i)|!}.$ Subject to this, the conditional probability that these points also correspond to the function g and form the pattern $\pi$ is $\prod_{i\in[n]}\frac{1}{|g^{-1}(i)|!} \prod_{m \in [k]}M_{f(m), g(\pi(m))}$ . Summing over all pairs f,g we obtain formula (2).

3. Perturbing the uniform permuton

In this section, we develop tools for analysing small perturbations of the uniform permuton. First, we describe a method for perturbing a step permuton and formulate a sufficient condition for a set of permutations to be non-forcing. Then, we introduce a so-called gradient polynomial which captures the behaviour of perturbations of step permutons as the order of underlying matrices tends to infinity, and reformulate our sufficient condition in terms of gradient polynomials. Finally, two different presentations of gradient polynomials are given as they are both needed in specific lemmas.

Fix an integer $n > 1$ and let $k, l \in [n-1]$ . We define a matrix $B^{k,l} \in \mathbb{R}^{n \times n}$ by setting

\begin{equation*}B^{k,l}_{i,j} = \begin{cases} 1 & \text{if either } i=k \text{ and } j=l \text{, or } i=k+1 \text{ and } j=l+1 \text{,}\\[4pt] -1 & \text{if either } i=k+1 \text{ and } j=l \text{, or } i=k \text{ and } j=l+1 \text{, and}\\[4pt] 0 & \text{otherwise.}\end{cases}\end{equation*}

See Figure 1(a) for an example. Further, for a matrix $x \in \mathbb{R}^{ (n-1) \times (n - 1)}$ , we define

\begin{equation*}\mathbb{J}^{x} = \mathbb{J} + \sum_{1 \leq i,j < n} x_{i,j}B^{i,j}.\end{equation*}

To simplify the notation, we freely interchange matrices of order ${(n-1) \times (n-1)}$ with vectors of length $(n-1)^2$ obtained by concatenating rows of the matrix. Note that the matrix $B^{k,l}$ is non-zero only on a $2 \times 2$ submatrix, and the sum of all its rows and columns is zero. Thus, for any $x \in [-\frac{1}{4n}, \frac{1}{4n}]^{(n-1) \times (n-1)}$ , the matrix $\mathbb{J}^x$ is doubly stochastic, and therefore it gives rise to a step permuton; see Figure 1(b) for an example. In particular, if x is the zero vector, the permuton $\mu[\mathbb{J}^x]$ is the uniform permuton.

Figure 1. Perturbation of a $3 \times 3$ step permuton.

For a permutation $\pi$ we define the density function $h_{\pi, n} \,:\, \mathbb{R}^{(n-1) \times (n-1)} \rightarrow \mathbb{R}$ where $h_{\pi, n}(x) = d\left(\pi, \mu\left[ \mathbb{J}^x\right]\right)$ . We wish to analyse permutons $\mu[\mathbb{J}^x]$ for x close to the zero vector. In particular, our goal is to find a non-zero x such that the densities of permutations from S in $\mu[\mathbb{J}^x]$ are the same as in $\mu[\mathbb{J}]$ , i.e., in the uniform permuton. In the next lemma, we show that if the gradients of the density functions of the permutations in S satisfy certain conditions, then we are able to find such x using the Implicit Function Theorem. We attach the used version of the theorem for the reader’s convenience.

Theorem 4. (the Implicit Function Theorem) Let $h\,:\, \mathbb{R}^{m+n} \to \mathbb{R}^n$ be a differentiable function, $x_0 \in \mathbb{R}^{m}, y_0 \in \mathbb{R}^{n}$ any points, and $\nabla h(x_0, y_0)$ the Jacobian matrix of h. Let G denote the square matrix consisting of last n columns of $\nabla h(x_0, y_0)$ . If G is regular, then there exists $\varepsilon > 0$ and a continuous function $g\,:\, \mathbb{R}^m \to \mathbb{R}^{m + n}$ such that $g(x_0) = (x_0, y_0)$ and $h(g(x_0 + \Delta x)) = h(x_0, y_0)$ for any $\Delta x \in$ $(-\varepsilon, \varepsilon)^m$ .

Lemma 5. Let S be a non-empty finite set of permutations. If there exists $n \in \mathbb{N}$ such that $(n\,{-}\,1)^2\,{>}\,|S|$ and the gradients $\nabla h_{\pi, n}(0,\ldots,0), \pi \in S$ , are linearly independent, then S is not forcing.

Proof. Note that by the assumption of the lemma, the inequality $(n-1)^2 > |S|$ holds, and so the gradient vectors have at least $|S|+1$ coordinates. Choose indices $i_2, \ldots, i_{|S|+1}$ such that the gradient vectors $\nabla h_{\pi, n}(0,\ldots,0), \pi \in S$ , restricted to these indices are linearly independent. Let $i_{1}$ be any index different from $i_2, \ldots, i_{|S|+1}$ . Define an embedding function $e\,:\,\mathbb{R}^{|S|+1} \rightarrow \mathbb{R}^{(n-1)^2}$ such that $e(x)_{i_k} = x_k$ for $k \in [|S|+1]$ and $e(x)_i=0$ otherwise.

The gradients ${\nabla (h_{\pi, n}\circ e)(0,\ldots, 0)}$ are linearly independent as well; hence we can apply the Implicit Function Theorem for $h_{\pi, n}\circ e$ at the point $(0, \ldots, 0)$ . The theorem yields a continuous function $g\,:\, \mathbb{R} \to \mathbb{R}^{|S|+1}$ defined on $(-\varepsilon, \varepsilon)$ for some $\varepsilon > 0$ , such that $h_{\pi, n}(e(g(t))) = h_{\pi, n}(0, \ldots, 0) = \frac{1}{|\pi|!}$ for all $\pi \in S$ and $t \in (-\varepsilon, \varepsilon)$ . Moreover, by choosing a small enough $\varepsilon$ , we can assume $\textrm{Im}({g}) \subseteq [-\frac{1}{4n}, \frac{1}{4n}]^{|S|+1}$ . Thus, given $t \in (-\varepsilon, \varepsilon)$ , we obtain a permuton $\mu\left[\mathbb{J}^{e(g(t))}\right]$ which satisfies $d(\pi, \mu\left[\mathbb{J}^{e(g(t))}\right]) = h_{\pi, n}(e(g(t))) = \frac{1}{|\pi|!}$ for all $\pi \in S$ . In particular, $\mu\left[\mathbb{J}^{e(g(\varepsilon/2))}\right]$ is a non-uniform permuton that witnesses that S is not forcing.

As the number of parts of a step permuton increases, the probability that two randomly chosen points share the same part tends to zero. This simplifies the analysis of gradients significantly and leads us to defining the gradient polynomial of a permutation $\pi$ —a limit object which captures the behaviour of the gradients $\nabla h_{\pi,n}$ as n tends to infinity. First note that the gradient vector $\nabla h_{\pi, n}(0,\ldots, 0)$ of any permutation $\pi$ can be calculated by a straightforward differentiation of (2). In particular the following holds for any positive integer $n > 1$ and $i, j \in [n]$ :

(3) \begin{align}\frac{\partial}{\partial x_{i,j}} h_{\pi, n}(0, \ldots, 0) = \frac{k!}{n^{2k-1}} \sum_{f,g\,:\,[k]\nearrow [n]} \frac{1}{\prod_{m\in[n]}|f^{-1}(m)|!|g^{-1}(m)|!} \times \sum_{m \in [k]} B^{i,j}_{f(m), g(\pi(m))}.\end{align}

The gradient polynomial $P_\pi(\alpha, \beta)$ is defined as the unique polynomial in two variables which satisfies the equality

\begin{align*}P_\pi(\alpha, \beta) = \lim_{n \rightarrow \infty} n^3 \frac{\partial}{\partial x_{\lfloor \alpha n \rfloor, \lfloor \beta n \rfloor}}h_{\pi, n}(0, \ldots, 0),\end{align*}

for any $\alpha, \beta \in (0, 1)$ . In the following lemmas we show that the limit always exists, indeed yields a polynomial and we provide an explicit formula for its coefficients.

We first show that it is possible to restrict the sum (3) to injective functions when considering the limit.

Lemma 6. For any k-permutation $\pi$ and $\alpha, \beta \in (0,1)$ , the following equality holds if any of the two limits exists:

\begin{equation*}\lim_{n \rightarrow \infty}n^3\frac{\partial}{\partial x_{\lfloor \alpha n \rfloor,\lfloor \beta n \rfloor}} h_{\pi, n}(0, \ldots, 0)= \lim_{n \rightarrow \infty}\frac{k!}{n^{2k-4}} \sum_{ \substack{f,g\,:\,[k]\nearrow [n] \\ f,g \text{ injective}}} \sum_{m \in [k]} B^{\lfloor \alpha n \rfloor,\lfloor \beta n \rfloor}_{f(m), g(\pi(m))}.\end{equation*}

Proof. Let $i_n = \lfloor \alpha n \rfloor$ , $j_n = \lfloor \beta n \rfloor$ . Given $f,g\,:\, [k] \nearrow [n],$ let $S_n(\kern1.4pt f, g)$ denote the summand

\begin{equation*}\frac{1}{\prod_{m\in[n]}|f^{-1}(m)|!|g^{-1}(m)|!} \times \sum_{m \in [k]} B^{i_n,j_n}_{f(m), g(\pi(m))},\end{equation*}

from (3). Note that whenever f and g are injective function, $S_n(\kern1.4pt f, g)$ becomes just $\sum_{m \in [k]} B^{i_n,j_n}_{f(m), g(\pi(m))}$ . By (3), it holds

\begin{equation*} \left|n^3\frac{\partial}{\partial x_{i_n,j_n}} h_{\pi, n}(0, \ldots, 0)- \frac{k!}{n^{2k-4}} \sum_{ \substack{f,g\,:\,[k]\nearrow [n] \\ f,g \text{ injective}}} S_n(\kern1.4pt f, g)\right|= \left|\frac{k!}{n^{2k-4}} \sum_{ \substack{f,g\,:\,[k]\nearrow [n] \\ f \text{ or } g \text{ non-injective}}} S_n(\kern1.4pt f, g) \right|.\end{equation*}

Hence, it is enough to show that the right-hand side converges to zero as n tends to infinity. We denote the right-hand side by $D_n$ .

Whenever f is such that neither $i_n$ nor $i_n + 1$ belongs to $\textrm{Im}(\kern1.4pt f) $ , then $B^{i_n,j_n}_{f(m), g(\pi(m))}$ is simply zero regardless of m or g; hence $S_n(\kern1.4pt f, g)$ is zero as well. In case $\textrm{Im}(\kern1.4pt f)$ contains exactly one of $i_n$ or $i_n + 1$ , let us define a function $\tilde f$ for $m \in [n]$ as

\begin{equation*} \tilde{f}(m) = \begin{cases} i_n & \text{if } m \in f^{-1}(i_n+1)\\[3pt] i_n+1 & \text{if } m \in f^{-1}(i_n)\\[3pt] f(m) & \text{otherwise}. \end{cases}\end{equation*}

Note that the function $\tilde{f}$ is increasing. By definition, it holds that $B^{i_n,j_n}_{i_n, \ell} = - B^{i_n,j_n}_{i_n+1, \ell}$ for any $\ell \in [n]$ ; therefore, $S(\kern1.4pt f, g) + S(\tilde{f}, g) = 0$ regardless of g. Altogether, all the factors $S_n(\kern1.4pt f,g)$ such that $\{i, i+1\} \not \subseteq \textrm{Im}(\kern1.4pt f)$ cancel out from the sum in D. Similarly, all the factors corresponding to g where $\{j, j+1\} \not \subseteq \textrm{Im}(g)$ cancel out.

Note that $\left|S_n(\kern1.4pt f,g)\right|$ is at most k for any f and g. Hence, $D_n$ can be bounded by the product of $\frac{k\cdot k!}{n^{2k-4}}$ and the number of pairs of functions $f,g\,:\, [k] \nearrow [n]$ satisfying $\{i, i+1\} \subseteq \textrm{Im}(\kern1.4pt f)$ , $\{j, j+1\} \subseteq \textrm{Im}(g)$ and f or g is non-injective. Fixing two elements $a, a+1 \in [n]$ , there are at most $\mathcal{O}(n^{k-2})$ non-decreasing functions $[k] \to [n]$ containing both a and $a+1$ in their image. Only $\mathcal{O}(n^{k-3})$ of them are in addition non-injective. Therefore, there are $\mathcal{O} (n^{2k-5}) = 2\mathcal{O} (n^{2k-5}) + \mathcal{O} (n^{2k-6})$ of such pairs (f, g). It follows that $D_n = \mathcal{O}(\frac{1}{n})$ , in particular $D_n$ tends to zero as n goes to infinity.

Using Lemma 6, we find an explicit formula for gradient polynomials. Note that the formula indeed defines a polynomial.

Lemma 7. For any k-permutation $\pi$ , the gradient polynomial is well-defined and is equal to the following formula:

(4) \begin{align}\begin{split} P_\pi(\alpha, \beta) & = k! \sum_{m \in [k]}\left( \frac{k-m}{1 - \alpha} - \frac{m-1}{\alpha} \right)\left( \frac{k-\pi(m)}{1 - \beta} - \frac{\pi(m)-1}{\beta} \right) \\[5pt]& \quad \frac{\alpha^{m-1}(1 - \alpha)^{k-m}\beta^{\pi(m)-1}(1 - \beta)^{k-\pi(m)}}{(m-1)!(k-m)!(\pi(m)-1)!(k-\pi(m))!}.\end{split}\end{align}

Proof. Fix $\alpha, \beta \in (0,1)$ . We introduce $i_n = \lfloor \alpha n \rfloor$ and $j_n = \lfloor \beta n \rfloor$ . We omit the subscript whenever the index is clear from context. By Lemma 6, the following equality holds whenever the right-hand side exists

\begin{align*}P_\pi(\alpha, \beta) = \lim_{n \rightarrow \infty} \frac{k!}{n^{2k-4}} \sum_{ \substack{f,g\,:\,[k]\nearrow [n] \\ f,g \text{ injective}}}\ \ \sum_{m \in [k]} B^{i,j}_{f(m), g(\pi(m))}.\end{align*}

Let $F_n[m \mapsto i]$ denote the number of strictly increasing functions $f\,:\,[k] \nearrow [n]$ satisfying $f(m) = i$ . We can group the summands by m to obtain

\begin{align*}& \frac{k!}{n^{2k-4}} \sum_{m \in [k]}\ \ \sum_{ \substack{f,g\,:\,[k]\nearrow [n] \\ f,g \text{ injective}}} B^{i,j}_{f(m), g(\pi(m))}\\& \quad = \frac{k!}{n^{2k-4}} \sum_{m \in [k]} F[m \mapsto i]F[\pi(m)\mapsto j] + F[m \mapsto i+1]F[\pi(m)\mapsto j+1]\\& \qquad - F[m\mapsto i+1]F[\pi(m)\mapsto j] - F[m\mapsto i]F[\pi(m)\mapsto j+1]\\& \quad = \frac{k!}{n^{2k-4}} \sum_{m \in [k]} \left(F[m \mapsto i]-F[m \mapsto i+1]\right)\left(F[\pi(m)\mapsto j]-F[\pi(m)\mapsto j+1]\right).\end{align*}

Note that for $k \leq i \leq n-k$ the equality $F[m \mapsto i] = {\bigg(\begin{array}{c}i-1\\[-5pt] m-1\end{array}\bigg)}{\bigg(\begin{array}{c}n-i\\[-5pt] k-m\end{array}\bigg)}$ holds. Then we can further simplify the sum using the following:

(5) \begin{align}\begin{split} & F[m \mapsto i]-F[m \mapsto i+1] = {\bigg(\begin{array}{c}i-1\\[-5pt] m-1\end{array}\bigg)}{\bigg(\begin{array}{c}n-i\\[-5pt] k-m\end{array}\bigg)}-{\bigg(\begin{array}{c}i\\[-5pt] m-1\end{array}\bigg)}{\bigg(\begin{array}{c}n-i-1\\[-5pt] k-m\end{array}\bigg)} \\& \quad = \left(\frac{i-m+1}{i}-\frac{n-i-k+m}{n-i}\right){\bigg(\begin{array}{c}i\\[-5pt] m-1\end{array}\bigg)}{\bigg(\begin{array}{c}n-i\\[-5pt] k-m\end{array}\bigg)}\\& \quad = \left(\frac{k-m}{n-i} - \frac{m-1}{i}\right){\bigg(\begin{array}{c}i\\[-5pt] m-1\end{array}\bigg)}{\bigg(\begin{array}{c}n-i\\[-5pt] k-m\end{array}\bigg)}.\end{split}\end{align}

Note that for any $\alpha \in (0,1)$ there exist N such that for any $n \geq N$ it holds $k \leq \lfloor \alpha n \rfloor \leq n-k$ and thus we can always use (5) in the following limit:

\begin{align*}&\lim_{n \rightarrow \infty} \frac{1}{n^{k-2}} \left(F[m \mapsto \lfloor \alpha n \rfloor] - F[m \mapsto \lfloor \alpha n \rfloor + 1] \right)\\[4pt]& \quad = \lim_{n \rightarrow \infty}\frac{1}{n^{k-2}} \left(\frac{k-m}{n-\lfloor \alpha n \rfloor}-\frac{m-1}{\lfloor \alpha n \rfloor}\right){\bigg(\begin{array}{c}\lfloor \alpha n \rfloor\\[-5pt] m-1\end{array}\bigg)}\bigg(\begin{array}{c}{{n}-\lfloor \alpha n \rfloor}\\[-5pt] k-m\end{array}\bigg)\\[4pt]& \quad = \left( \frac{k-m}{1-\alpha} - \frac{m-1}{\alpha} \right)\frac{\alpha^{m-1}(1-\alpha)^{k-m}}{(m-1)!(k-m)!}.\end{align*}

Similarly we compute

\begin{align*}&\lim_{n \rightarrow \infty} \frac{1}{n^{k-2}} \left(F[\pi(m) \mapsto \lfloor \beta n \rfloor] - F[\pi(m) \mapsto \lfloor \beta n \rfloor + 1] \right)\\[4pt]& \quad = \left( \frac{k-\pi(m)}{1-\beta} - \frac{\pi(m)-1}{\beta}\right)\frac{\beta^{\pi(m)-1}(1-\beta)^{k-\pi(m)}}{(\pi(m)-1)!(k-\pi(m))!}.\end{align*}

By multiplying these two limits, we obtain the equality from the statement of the lemma.

We next provide an analog of Lemma 5 for gradient polynomials.

Lemma 8. Let S be a non-empty finite set of permutations. If the gradient polynomials $P_\pi , \pi \in S$ , are linearly independent, then S is not forcing.

Proof. We prove the contrapositive, hence suppose that S is forcing. Denote the elements of S by $\pi_1, \ldots, \pi_m$ , and for any $n>1$ define $g_i^n = \nabla h_{\pi_i, n}(0,\ldots, 0)$ . Lemma 5 yields that the gradients $g_i^n , i \in [m],$ are linearly dependent for any $n > m + 1$ . Therefore, for any such n, there exists a non-zero tuple of reals $t^n = (t_1^n, \ldots, t_m^n)$ such that $\sum_{i \in [m]} t_i^n g_i^n = (0, \ldots, 0)$ . Moreover, without loss of generality, we can assume $\|t^n\|_{\infty} = 1$ . Since $[-1,1]^m$ is a compact set, there exists a convergent subsequence $\{(t_1^{n_j}, \ldots, t_m^{n_j}) \}_{j \in \mathbb{N}}$ converging to a non-zero tuple $(t_1, \ldots, t_m)$ . Hence for any $\alpha, \beta \in (0,1)$ , it holds that

\begin{align*} \sum_{i \in [m]} t_i P_{\pi_i}(\alpha, \beta) = \sum_{i \in [m]} \lim_{j \rightarrow \infty} t_i^{n_j} \lim_{j \rightarrow \infty} {n_j^3} (g_i^{n_j})_{\lfloor \alpha {n_j} \rfloor, \lfloor \beta {n_j} \rfloor} = \lim_{j \rightarrow \infty} \sum_{i \in [m]} t_i^{n_j} {n_j^3} (g_i^{n_j})_{\lfloor \alpha {n_j} \rfloor, \lfloor \beta {n_j} \rfloor} = 0.\end{align*}

Therefore the gradient polynomials are linearly dependent since $\sum_{i \in [m]}t_i P_{\pi_i} = 0$ .

For the analysis of gradient polynomials, we use the following kind of vectors. For an integer $i\in[k]$ we define a vector $\textbf{b}^k_i \in \mathbb{R}^k$ as follows:

\begin{equation*}\left(\textbf{b}^k_i\right)_\ell = \begin{cases}(-1)^{\ell-1} {\bigg(\begin{array}{c}i - 1\\[-5pt] \ell-1\end{array}\bigg)} & \text{for } 1 \leq \ell \leq i\\0 & \text{otherwise}.\\\end{cases}\end{equation*}

For example,

\begin{equation*}\textbf{b}_5^5 = (1, -4, 6, -4, 1)^T \text{ and } \textbf{b}_4^5 = (1, -3, 3, -1, 0)^T.\end{equation*}

We sometimes omit the upper index and write just $\textbf{b}_i$ when the dimension is clear from the context.

Let us denote the linear span of vectors $\textbf{b}^k_2, \ldots, \textbf{b}^k_k$ by $\mathcal{B}$ and let $\textbf{j} = (1,\ldots,1)^T \in \mathbb{R}^k$ . Observe that $\mathcal{B}$ is the orthogonal complement of the vector $\textbf{j}$ . Indeed, by the Binomial Theorem,

\begin{equation*} \langle \textbf{j} , \textbf{b}_i \rangle = \sum_{\ell=1}^i (-1)^{\ell-1}{\bigg(\begin{array}{c}i-1\\[-5pt] \ell-1\end{array}\bigg)} = 0.\end{equation*}

Also observe that for any $i \in [k-1]$ , the vectors $\textbf{b}_2^k, \ldots, \textbf{b}_{i+1}^k$ span an i-dimensional space. In particular, the vectors $\textbf{j}, \textbf{b}_2^k, \ldots, \textbf{b}_k^k$ form a basis of $\mathbb{R}^k$ .

The next lemma provides an explicit formula for the coefficients of the gradient polynomials. Let $P(\alpha, \beta)$ be a polynomial in $\alpha, \beta$ . For any $i,j \in \mathbb{N}_0$ , we use $c_{i,j}(P)$ to denote the coefficient of the monomial $\alpha^i\beta^j$ in P, i.e., it holds that

\begin{equation*}P = \sum_{i,j \in \mathbb{N}_0} c_{i,j}(P)\alpha^i\beta^j.\end{equation*}

Lemma 9. Let $\pi$ be a k-permutation and $i,j \in \mathbb{N}_0$ . Then

\begin{align*}c_{i,j}(P_\pi) = \frac{k!(-1)^{i+j}}{i!j!(k-i-2)!(k-j-2)!} \left( \textbf{b}_{i+2}^T \, A_\pi \, \textbf{b}_{j+2} \right),\end{align*}

if both i and j are at most $k-2$ , and $c_{i,j}(P_\pi)=0$ otherwise.

Proof. For this proof, we set $1/a!= 0$ whenever $a<0$ , and ${\bigg(\begin{array}{c}a\\[-5pt] b\end{array}\bigg)}=0$ whenever $a < b$ . In order to determine the coefficient of $\alpha^i\beta^j$ in $P_\pi$ , we need to compute the coefficient of each summand from (4) and sum them up. For any $m \in [k]$ , the coefficient of $\alpha^i\beta^j$ is the product of the coefficient of $\alpha^i$ in $\left(\frac{k-m}{1 - \alpha} - \frac{m-1}{\alpha} \right)\frac{\alpha^{m-1}(1 - \alpha)^{k-m}}{(m-1)!(k-m)!}$ and the coefficient of $\beta^j$ in $\left(\frac{k-\pi(m)}{1 - \beta} - \frac{\pi(m)-1}{\beta} \right)\frac{\beta^{\pi(m)-1}(1 - \beta)^{k-\pi(m)}}{(\pi(m)-1)!(k-\pi(m))!}.$ We first compute the coefficient of $\alpha^i$ :

\begin{align*} & \left(\frac{k-m}{1 - \alpha} - \frac{m-1}{\alpha} \right)\frac{\alpha^{m-1}(1 - \alpha)^{k-m}}{(m-1)!(k-m)!} \\ &\quad = \frac{\alpha^{m-1}(1 - \alpha)^{k-m-1}}{(m-1)!(k-m-1)!} - \frac{\alpha^{m-2}(1 - \alpha)^{k-m}}{(m-2)!(k-m)!} \\ & \quad = \sum_{\ell=0}^{k-m-1} {\bigg(\begin{array}{c}k-m-1\\[-5pt] \ell\end{array}\bigg)} \frac{\alpha^{m-1+\ell}(-1)^\ell}{(m-1)!(k-m-1)!} - \sum_{\ell'=0}^{k-m} {\bigg(\begin{array}{c}k-m\\[-5pt] \ell'\end{array}\bigg)} \frac{\alpha^{m-2+\ell'}(-1)^{\ell'}}{(m-2)!(k-m)!}.\end{align*}

The last equality is just an expansion of $(1-\alpha)^{k-m-1}$ and $(1-\alpha)^{k-m}$ . The ith power of $\alpha$ appears for $l = i+1-m$ and $l' = i+2-m$ . This yields that the coefficient of $\alpha^i$ is

\begin{align*} &{\bigg(\begin{array}{c}k-m-1\\[-5pt] i+1-m\end{array}\bigg)} \frac{(-1)^{i+1-m}}{(m-1)!(k-m-1)!} - {\bigg(\begin{array}{c}k-m\\[-5pt] i+2-m\end{array}\bigg)} \frac{(-1)^{i-m}}{(m-2)!(k-m)!}\\ &\quad = {\bigg(\begin{array}{c}i\\[-5pt] m-1\end{array}\bigg)} \frac{1}{(k-i-2)!i!}(-1)^{i+1-m} + {\bigg(\begin{array}{c}i\\[-5pt] m-2\end{array}\bigg)} \frac{1}{(k-i-2)!i!}(-1)^{i+1-m}\\ &\quad = {\bigg(\begin{array}{c}i+1\\[-5pt] m-1\end{array}\bigg)} \frac{1}{(k-i-2)!i!}(-1)^{i+1-m}.\end{align*}

Note that if $m > i+2$ , the formula is equal to zero. Similarly, the coefficient of $\beta^j$ in $\left(\frac{k-\pi(m)}{1 - \beta} - \frac{\pi(m)-1}{\beta} \right)\frac{\beta^{\pi(m)-1}(1 - \beta)^{k-\pi(m)}}{(\pi(m)-1)!(k-\pi(m))!}$ is equal to

\begin{equation*}{\bigg(\begin{array}{c}j+1\\[-5pt] \pi(m)-1\end{array}\bigg)} \frac{1}{(k-j-2)!j!}(-1)^{j+1-\pi(m)}.\end{equation*}

Hence, the coefficient of $\alpha^i\beta^j$ is the following:

\begin{align*}c_{i,j}(P_\pi) \,=\, & k!\sum_{m \in [k]}{\bigg(\begin{array}{c}i+1\\[-5pt] m-1\end{array}\bigg)} \frac{(-1)^{i+1-m}}{(k-i-2)!i!}{\bigg(\begin{array}{c}j+1\\[-5pt] \pi(m)-1\end{array}\bigg)} \frac{(-1)^{j+1-\pi(m)}}{(k-j-2)!j!}\\= & \frac{k!(-1)^{i+j}}{i!j!(k-i-2)!(k-j-2)!}\sum_{m \in [k]}(-1)^{m-1}{\bigg(\begin{array}{c}i+1\\[-5pt] m-1\end{array}\bigg)}(-1)^{\pi(m)-1}{\bigg(\begin{array}{c}j+1\\[-5pt] \pi(m)-1\end{array}\bigg)}\\= & \frac{k!(-1)^{i+j}}{i!j!(k-i-2)!(k-j-2)!} \left( {\textbf{b}^T_{i+2}} \, A_\pi \, \textbf{b}_{j+2} \right).\end{align*}

In the following we use

\begin{equation*}K^k_{i,j} = \frac{k!(-1)^{i+j}}{i!j!(k-i-2)!(k-j-2)!},\end{equation*}

and we omit the upper index when it is clear from the context. Thus, it holds that ${c_{i,j}(P_\pi) = K_{i,j} \left( \textbf{b}_{i+2}^T \, A_\pi \, \textbf{b}_{j+2} \right)}$ .

Finally we define the mirror gradient polynomial ${P}^\updownarrow_\pi(\alpha, \beta)$ by setting

\begin{equation*}{P}^\updownarrow_\pi(\alpha, \beta) = P_\pi(1-\alpha, \beta).\end{equation*}

As shown above, the coefficient $c_{i,j}(P_\pi)$ depends on the ‘top’ rows of the matrix $A_\pi$ , i.e., the first $i+2$ rows. For any matrix $M \in \mathbb{R}^{n \times m}$ we define its row mirror image ${M}^\updownarrow$ where ${M}^\updownarrow_{i, j} = M_{n-i+1, j}$ . In the next lemma, we prove that ${P}^\updownarrow_\pi$ behaves in a similar way as $P_\pi$ but its coefficients depend on the ‘top’ $i+2$ rows of the matrix ${{A_\pi}}^\updownarrow$ instead.

Lemma 10. Let $\pi$ be a k-permutation and $i,j \in \mathbb{N}_0$ . Then

\begin{equation*}c_{i,j}({P}^\updownarrow_\pi) = \frac{k!(-1)^{i+j+1}}{i!j!(k-i-2)!(k-j-2)!} \left( \textbf{b}^T_{i+2} \, {A}^\updownarrow_\pi \, \textbf{b}_{j+2} \right) = -K_{i,j} \left( {\textbf{b}^T_{i+2}} \, {A}^\updownarrow_\pi \, \textbf{b}_{j+2} \right),\end{equation*}

if both i and j are at most $k-2$ , and $c_{i,j}({P}^\updownarrow_\pi) = 0$ otherwise.

Proof. We perform similar steps as in the previous proof. By the definition of the mirror polynomial, we can substitute $1-\alpha$ into $(4)$ to obtain

\begin{align*}\begin{split} {P}^\updownarrow_\pi(\alpha, \beta) \,=\, & k! \sum_{m \in [k]}\left( \frac{k-m}{\alpha} - \frac{m-1}{1-\alpha} \right)\left( \frac{k-\pi(m)}{1 - \beta} - \frac{\pi(m)-1}{\beta} \right) \\& \, \frac{(1-\alpha)^{m-1}\alpha^{k-m}\beta^{\pi(m)-1}(1 - \beta)^{k-\pi(m)}}{(m-1)!(k-m)!(\pi(m)-1)!(k-\pi(m))!}.\end{split}\end{align*}

Again, we split each summand into a product of two parts, one depending only on $\alpha$ and the other on $\beta$ . The part involving $\beta$ is the same as in the previous proof. A straightforward computation analogous to the one in the proof of the previous lemma yields that the coefficient of $\alpha ^ i$ in $\left(\frac{k-m}{\alpha} - \frac{m-1}{1 - \alpha} \right)\frac{(1-\alpha)^{m-1}\alpha^{k-m}}{(m-1)!(k-m)!}$ is

\begin{align*}{\bigg(\begin{array}{c}m-1\\[-5pt] i+m-k+1\end{array}\bigg)} \frac{(-1)^{i+m-k+1}}{(m-1)!(k-m-1)!} - {\bigg(\begin{array}{c}m-2\\[-5pt] i+m-k\end{array}\bigg)} \frac{(-1)^{i+m-k}}{(m-2)!(k-m)!}.\end{align*}

This can be further simplified to

\begin{align*}{\bigg(\begin{array}{c}i+1\\[-5pt] k-m\end{array}\bigg)} \frac{1}{(k-i-2)!i!}(-1)^{i-k+m+1}.\end{align*}

Hence, the coefficient $c_{i,j}({P}^\updownarrow_\pi)$ is equal to

\begin{align*} &\frac{k!(-1)^{i+j}}{i!j!(k-i-2)!(k-j-2)!}\sum_{m \in [k]}(-1)^{m-k+1}{\bigg(\begin{array}{c}i+1\\[-5pt] k-m\end{array}\bigg)}(-1)^{\pi(m)+1}{\bigg(\begin{array}{c}j+1\\[-5pt] \pi(m)-1\end{array}\bigg)},\end{align*}

where we can substitute $\ell = k - m + 1$ and reverse the order of the summation to obtain

\begin{align*}&\frac{k!(-1)^{i+j}}{i!j!(k-i-2)!(k-j-2)!}\sum_{\ell \in [k]}(-1)^{-\ell}{\bigg(\begin{array}{c}i+1\\[-5pt] k-(k-\ell+1)\end{array}\bigg)}(-1)^{\pi(k-\ell+1)+1}{\bigg(\begin{array}{c}j+1\\[-5pt] \pi(k-\ell+1)-1\end{array}\bigg)}\\ & \quad = \frac{k!(-1)^{i+j+1}}{i!j!(k-i-2)!(k-j-2)!}\sum_{\ell \in [k]}(-1)^{\ell-1}{\bigg(\begin{array}{c}i+1\\[-5pt] \ell-1\end{array}\bigg)}(-1)^{\pi(k-\ell+1)-1}{\bigg(\begin{array}{c}j+1\\[-5pt] \pi(k-\ell+1)-1\end{array}\bigg)}\\ &\quad = \frac{k!(-1)^{i+j+1}}{i!j!(k-i-2)!(k-j-2)!} \left( {\textbf{b}^k_{ i+2}}^T \, {A}^\updownarrow_\pi \, \textbf{b}^k_{j+2} \right).\end{align*}

4. Sets of linearly dependent polynomials

In this section, we prove our main result. We call the set S of permutations linearly dependent if the gradient polynomials of the permutations in the set S are linearly dependent. In the previous section, we have shown that any forcing set of permutations is linearly dependent. We next establish three lemmas that describe general properties of cover matrices of dependent sets of permutations with respect to orders of their permutations. This renders many triples of permutations to be non-forcing. We then identify all linearly dependent sets of size three and prove none of them is forcing.

Recall that the cover matrix of a formal linear combination of k-permutations $\omega = {\sum_{i \in [m]} t_i \pi_i}$ is the matrix $\textrm{Cvr}({\omega}) = \sum_{i \in [m]} t_i A_{\pi_i}$ . For a dependent set of permutations S, the next lemma states a property of the cover matrix of the permutations with the largest order in S.

Lemma 11. Let $\pi_1, \ldots, \pi_m$ be permutations and $t_1, \ldots, t_m$ be reals such that $\sum_{i \in [m]} t_i P_{\pi_i} = 0$ and set $k = \max\{|\pi_1|, \ldots, |\pi_m|\}$ . Suppose that $\pi_1, \ldots, \pi_n$ are all the permutations from S with order k. Further, let $2 \leq h \leq k$ be any integer such that the order of all the remaining permutations $\pi_{n+1}, \ldots, \pi_m$ is at most $h-1$ . Let $\omega = t_1 \pi_1 + \ldots + t_n \pi_n$ . Then the following holds:

\begin{equation*}\text{Cvr}({\omega}) \, {\textbf{b}}_{h} = (0,\ldots,0)^T\ { \text{and} }\ {\textbf{b}}^T_{h} \, \text{Cvr}({\omega}) = (0,\ldots,0).\end{equation*}

Proof. By Lemma 9, the coefficient $c_{i,j}(P_{\pi_\ell})$ is equal to zero for any $\ell > n$ whenever i or j is at least $h-2$ . Therefore, for any $0 \leq i \leq k-2$ , we have

\begin{align*} 0 = \sum_{\ell \in [m]} t_\ell c_{i, h-2}(P_{\pi_\ell}) = \sum_{\ell \in [n]} t_\ell K_{i,h-2} \left( \textbf{b}_{i+2}^T \, A_{\pi_\ell} \, \textbf{b}_{h} \right) = K_{i,h-2} \left( \textbf{b}_{i+2}^T \, \textrm{Cvr}({\omega}) \, \textbf{b}_{h} \right).\end{align*}

Since $K_{i,h-2}$ is non-zero, it also holds that

(6) \begin{align} 0 = \textbf{b}_{i+2}^T \, \textrm{Cvr}({\omega}) \, \textbf{b}_{h},\end{align}

implying

(7) \begin{align}v^T \, \textrm{Cvr}({\omega}) \, \textbf{b}_{h} = 0.\end{align}

for any $v\in \mathcal{B}$ . Recall that $\mathcal{B}$ is the orthogonal complement of $\,\textbf{j}$ . Since any vector u that has one entry $-1$ , one entry $+1$ , and all the other entries equal to zero belongs to $\mathcal{B}$ , it holds ${u \, \textrm{Cvr}({\omega}) \, \textbf{b}_h = 0}$ , i.e., $\textrm{Cvr}({\omega})_p \, \textbf{b}_{h} - \textrm{Cvr}({\omega})_q \, \textbf{b}_{h} = 0$ for any two rows $\textrm{Cvr}({\omega})_p$ and $\textrm{Cvr}({\omega})_q$ of matrix $\textrm{Cvr}({\omega})$ . This implies $\textrm{Cvr}({\omega})_p \, \textbf{b}_{h} = \textrm{Cvr}({\omega})_q \, \textbf{b}_{h}$ for any $p,q \in [k]$ .

Therefore, for any $p \in [k]$ the equality $\textrm{Cvr}({\omega})_p\, \textbf{b}_{h} = 0$ holds since

\begin{align*} k \, \textrm{Cvr}({\omega})_p\, \textbf{b}_{h} = \sum_{\ell \in [k]} \textrm{Cvr}({\omega})_p\, \textbf{b}_{h} = \sum_{\ell \in [k]} \textrm{Cvr}({\omega})_\ell\, \textbf{b}_{h} = (a, \ldots, a) \, \textbf{b}_{h} = 0,\end{align*}

where $a = \sum_{\ell \in [n]} t_\ell$ is the common sum of all the columns. The first equality of the lemma follows. The other can be proven by a symmetric argument.

If all the permutations in a dependent set have the same order, we can prove the following.

Lemma 12. Let $\omega = t_1\pi_1 + \ldots + t_m \pi_m$ be a formal linear combination of k-permutations. If $\sum_{i \in [m]} t_iP_{\pi_i} = 0$ , then the cover matrix $\mathrm{Cvr}({\omega})$ is constant.

Proof. We first bound the rank of $\textrm{Cvr}({\omega})$ . Recall that the vectors $\textbf{b}^k_{2}, \ldots, \textbf{b}^k_{ k}$ , and $\textbf{j}$ form a basis of $\mathbb{R}^k$ . Call that basis B. The matrix $\textrm{Cvr}({\omega})$ is a matrix of a bilinear functional $\phi\,:\,\mathbb{R}^k \times \mathbb{R}^k \rightarrow \mathbb{R}$ in the canonical basis. Let us express the matrix of the functional $\phi$ in the basis B by computing the values of $\phi$ on the pairs of basis vectors. By Lemma 11, for $2 \leq i, j \leq k$ , it holds $\textbf{b}_{ i}^T \, \textrm{Cvr}({\omega}) \, \textbf{b}_{ j} = 0$ implying $\phi(\textbf{b}_{i}, \textbf{b}_{j}) = 0$ . By the definition of a cover matrix, the sum of any column or row of $\textrm{Cvr}({\omega})$ is equal to a constant $a = \sum_{\ell \in [m]} t_\ell$ . Hence, it holds $\textbf{j} \, \textrm{Cvr}({\omega}) \, \textbf{b}_{ j} = (a,\ldots, a) \, \textbf{b}_{ j} = 0$ for any $2 \leq j \leq k$ and thus $\phi(\textbf{j}, \textbf{b}_{ j}) = 0$ . Similarly, it also holds $\phi(\textbf{b}_{ i}, \textbf{j}) = 0$ for any $2 \leq i \leq k$ .

The rank of the matrix of $\phi$ in the basis B is at most one since the only non-zero entry it could have is the one corresponding to the value $\phi(\textbf{j}, \textbf{j})$ . The change of the basis does not change the rank of the matrix of a functional; therefore, the rank of $\textrm{Cvr}({\omega})$ depends only on the value of $\phi(\textbf{j}, \textbf{j})$ . In particular, it is either zero or one. If it is zero, then the matrix $\textrm{Cvr}({\omega})$ is the constant zero matrix. In the latter case, the columns of $\textrm{Cvr}({\omega})$ are multiple of each other, and since they have constant non-zero sum, they are all equal. Similarly, all the rows of $\textrm{Cvr}({\omega})$ are equal. The fact that $\textrm{Cvr}({\omega})$ is constant follows.

In the next lemma, we prove that if there exists a formal linear combination of gradient polynomials equal to zero but having all coefficients non-zero, then it contains at least two permutations with the maximum order.

Lemma 13. Let $\pi_1, \ldots, \pi_m$ be permutations of order at least two and suppose $|\pi_1| \geq \ldots \geq |\pi_m| $ . If there exist non-zero reals $t_1, \ldots, t_m$ satisfying $\sum_{i \in [m]} t_i P_{\pi_i} = 0$ , then $m \geq 2$ and $|\pi_1|=|\pi_2|$ .

Proof. Suppose for a contradiction that $\pi_1$ is the unique permutation amongst $\pi_1,\ldots, \pi_m$ with the largest order (in particular this holds if $m=1$ ). Then, the cover matrix $\textrm{Cvr}({t_1 \pi_1}) = t_1 A_{\pi_1}$ contains exactly one non-zero element in each row, and therefore the product of any row with the vector $\textbf{b}_k$ is non-zero. This contradicts Lemma 11. Hence, there is at least one permutation with order $|\pi_1|$ other than $\pi_1$ . In particular $m \geq 2$ .

The next lemma combines Lemma 12 and Lemma 13 to exclude most of the sets of two or three permutations of equal orders from being linearly dependent.

Lemma 14. Let S be a linearly dependent set of permutations whose orders are larger than one. Then:

1. (a) S is not a singleton.

2. (b) If $|S|=2$ , then both permutations in S have order two.

3. (c) If $|S|=3$ and all permutations in S have the same order, then their common order is three.

Proof. Let $\pi_1, \ldots, \pi_m, 1 \leq m \leq 3,$ be permutations in S. By Lemma 13, it holds that ${m = |S| \geq 2}$ . Since S is linearly dependent, there exists a non-zero tuple of reals $(t_1, \ldots, t_m)$ such that $\sum_{i \in [m]} t_i P_{\pi_i} = 0$ . Let $\omega$ denote the formal linear combination $\sum_{i \in [m]} t_i \pi_i$ . We first show that regardless whether $m=2$ or $m=3$ , we may assume that all permutation in S have the same order and all the coefficients $t_i, i \in [m],$ are non-zero. Indeed for $m=2$ , both statements follows as a consequence of Lemma 13. For $m=3$ , the equality of orders follows by the assumption of the lemma. Furthermore, observe that if any of the coefficients $t_i$ was equal to zero, we would proceed as in the part (b) and show that two of the permutations in S have order two. By the assumption, the third should have the same order which is impossible since there are only two distinct permutations of order two.

If the order of permutations in S is larger than m, then there exists a zero entry in the matrix $\textrm{Cvr}({\omega})$ . Since m is at most three, there exists $i\in [m]$ and $\pi_j\in S$ such that $\pi_j(i)$ differs from all the other permutations from S evaluated at i, i.e., $\pi_j(i) \neq \pi_{j'}(i)$ for $j' \neq j$ . Otherwise, all permutations would be identical. Hence, the matrix $\textrm{Cvr}({\omega})$ has a non-zero entry, specifically $\textrm{Cvr}({\omega})_{i, \pi_j(i)} = t_j$ . In particular, the matrix $\textrm{Cvr}({\omega})$ is not constant, which contradicts Lemma 12. Therefore, all the permutations in the set S have order m regardless of whether $m=2$ or $m=3$ .

In the next lemma, we exclude all the sets of three permutations containing two ‘large’ permutations from being linearly dependent. More precisely, we show that if a linearly dependent set of three permutations contains a permutation of order greater than three, then it contains a linearly dependent proper subset. By Lemma 14, this subset consist of 2-point permutations 12 and 21.

Lemma 15. There are no three permutations $\pi_1, \pi_2, \pi_3$ and non-zero real coefficients $t_1, t_2, t_3$ such that $\max_{i\in[m]}\{|\pi_i|\} > 3$ and $\sum_{i \in [3]} t_i P_{\pi_i} = 0$ .

Proof. For the contradiction suppose there exist such $\pi_1, \pi_2$ , and $\pi_3$ , and constants $t_1, t_2$ , and $t_3$ . By Lemma 13, at least two of the permutations have the maximum order. At the same time, by Lemma 14, the order of the third permutation is distinct since the order of the largest permutation is greater than three. Hence without loss of generality, we can assume $|\pi_1| = |\pi_2| > |\pi_3|$ and $|t_1| \leq |t_2|$ .

Let k denote the order of the permutations $\pi_1$ and $\pi_2$ , and let $\omega$ denote the formal linear combination $t_1\pi_1 + t_2\pi_2$ . We first show that the absolute values of the coefficients $t_1$ and $t_2$ are, in fact, equal. Lemma 11 asserts that $\textrm{Cvr}({\omega}) \, \textbf{b}_{k} = (0,\ldots,0)^T$ . In particular, the following holds for any $i\in [k]$ :

\begin{equation*} 0 = \textrm{Cvr}({\omega})_i\,\textbf{b}_k= t_1 {\bigg(\begin{array}{c}k-1\\[-5pt] \pi_1(i)-1\end{array}\bigg)} (-1)^{\pi_1(i)-1} + t_2 {\bigg(\begin{array}{c}k-1\\[-5pt] \pi_2(i)-1\end{array}\bigg)} (-1)^{\pi_2(i)-1},\end{equation*}

Choosing i such that $\pi_1(i) = 1$ yields

\begin{equation*} 0 = t_1{\bigg(\begin{array}{c}k-1\\[-5pt] 0\end{array}\bigg)} + t_2{\bigg(\begin{array}{c}k-1\\[-5pt] \pi_2(i)-1\end{array}\bigg)}(-1)^{\pi_2(i)-1},\end{equation*}

which is possible only if $\pi_2(i) \in \{1, k\}$ and $|t_1| = |t_2|$ since we assumed $|t_2|$ to be at least as large as $|t_1|$ .

We next show that $|\pi_3| = k-1$ . Suppose that this is not the case, i.e., $|\pi_3| < k - 1$ . Let i be such that $\pi_1(i)\neq\pi_2(i)$ , i.e., the row $\textrm{Cvr}({\omega})_i$ contains exactly two non-zero entries. By Lemma 11, the following equalities hold:

\begin{align*}\textrm{Cvr}({\omega})_i \, \textbf{b}_{k} & = 0,\\\textrm{Cvr}({\omega})_i \, \textbf{b}_{k-1} & = 0.\end{align*}

The first equality implies that $\pi_1(i) = k + 1 - \pi_2(i)$ since $|t_1|=|t_2|$ , while the second implies that $\pi_1(i) = k - \pi_2(i)$ which is impossible.

We next assume that the order of $\pi_3$ is $k-1$ and find a contradiction. Recall the definition of mirror gradient polynomials ${P}^\updownarrow_\pi(\alpha, \beta) = P_\pi(1 - \alpha, \beta)$ . Note that whenever the equality

(8) \begin{equation} \sum_{i \in [3]}t_i P_{\pi_i} = 0,\end{equation}

holds, it also holds that

(9) \begin{equation} \sum_{i \in [3]}t_i {P}^\updownarrow_{\pi_i} = 0.\end{equation}

Moreover, Lemma 11 yields that the cover matrix $\textrm{Cvr}({\omega})$ is symmetric up to the sign, i.e.,

(10) \begin{equation} {\textrm{Cvr}({\omega})} = (-1)^{k}{\textrm{Cvr}({\omega})}^\updownarrow,\end{equation}

since $\textrm{Cvr}({\omega})$ has at most two non-zero entries in each column and $|t_1| = |t_2|$ . Altogether, given i,j such that $0 \leq i, j \leq k-3$ , we obtain

\begin{align*}&\left|t_3 c_{i,j}({P}^\updownarrow_{\pi_3})\right| &\\= &\left|t_2 c_{i,j}({P}^\updownarrow_{\pi_2}) + t_1 c_{i,j}({P}^\updownarrow_{\pi_1}) \right|& \text{(by equality (9))}\\= &\left|K_{i,j} \left(\textbf{b}_{ i+2}^T \, {\textrm{Cvr}({\omega})}^\updownarrow \, \textbf{b}_{ j+2} \right) \right|& \text{(by Lemma 10)}\\= &\left|K_{i,j} \left(\textbf{b}_{ i+2}^T \, \textrm{Cvr}({\omega}) \, \textbf{b}_{ j+2}\right) \right|& \text{(by equality (10))}\\= &\left|t_2 c_{i,j}(P_{\pi_2}) + t_1 c_{i,j}(P_{\pi_1}) \right|& \text{(by Lemma 9)}\\= &\left|t_3 c_{i, j}(P_{\pi_3}) \right|.& \text{(by equality (8))}\end{align*}

Since $t_3$ is non-zero, it holds that $\Big|c_{i,j}({P}^\updownarrow_{\pi_3})\Big| = \Big|c_{i, j}(P_{\pi_3}) \Big|$ , which, together with the fact that $|\pi_3| \geq 3$ , implies

\begin{align*}\left| \left(\textbf{b}^{|\pi_3|}_{ i+2}\right)^T \, {A}^\updownarrow_{\pi_3} \, \textbf{b}^{|\pi_3|}_{j+2} \right|= \left| \left(\textbf{b}^{|\pi_3|}_{ i+2}\right)^T \, A_{\pi_3} \, \textbf{b}^{|\pi_3|}_{j+2} \right|,\end{align*}

for any $0 \leq i,j \leq k-3$ . We conclude that the equality $\left|u^T \, {A}^\updownarrow_{\pi_3} \, v \right| = \left| u^T \, A_{\pi_3} \, v \right|$ holds for any vectors $u,v \in \mathcal{B}$ . Let $u=(1,-1,0,\ldots) \in \mathcal{B}$ be a vector having two non-zero entries, and let $v\in \mathcal{B}$ be such a vector that $v_{\pi_3(1)} = 1, v_{\pi_3(2)} = -1$ and $v_\ell = 0$ otherwise. The product $u^T \, A_{\pi_3}\, v$ is equal to two but the absolute value of the product $u^T \, {A}^\updownarrow_{\pi_3} \, v$ is at most one since $|\pi_3| = k-1 > 2$ ; which is a contradiction.

The next lemma provides the last ingredient to prove Theorem 1. The lemma can be found, for instance, in [23] but we include a sketch of the proof for completeness.

Lemma 16. There exists a non-uniform permuton $\mu$ such that for any k-permutation $\pi$ with $k < 4$ it holds that $d(\pi, \mu) = \frac{1}{|\pi|!}$ .

For any $\alpha \in [0,1]$ define $M_\alpha$ to be the set of all the points $(x, y) \in [0, 1]^2$ such that $x+y \in \{1-\frac{\alpha}{2}, 1+\frac{\alpha}{2}, \frac{\alpha}{2}, 2-\frac{\alpha}{2}\}$ or $y-x \in \{-\frac{\alpha}{2}, \frac{\alpha}{2}, 1-\frac{\alpha}{2}, \frac{\alpha}{2}-1\}$ . See the illustration in Figure 2. Let $\mu_{\alpha}$ be a permuton that is obtained by uniformly distributing the mass along $M_\alpha$ . Note that $\mu_\alpha$ is invariant under horizontal and vertical reflection, and, therefore, the density of both 12 and 21 in $\mu_\alpha$ is equal to $1/2$ for any $\alpha$ . A simple calculation yields that $d(123, \mu_0) = 1/4$ and $d(123, \mu_1) = 1/8$ . Since $d(123, \mu_{\alpha})$ is a continuous function there exists $\alpha_0 \in (0, 1)$ such that $d(123, \mu_{\alpha_0}) = 1/6$ . The symmetries of the permuton imply that $d(123, \mu_{\alpha_0}) = d(321, \mu_{\alpha_0})$ and $d(132, \mu_{\alpha_0}) = d(312, \mu_{\alpha_0}) = d(213, \mu_{\alpha_0}) = d(231, \mu_{\alpha_0})$ . In addition, the sum of these six densities is one, hence all six densities are equal to $1/6$ .

Figure 2. The sets $M_0$ , $M_{0.5}$ , and $M_1$ .

We are finally ready to prove Theorem 1:

Proof of Theorem 1. Lemmas 14 and 16 yield that there is no forcing set of size one or two. For the contradiction, let $S=\{\pi_1, \pi_2, \pi_3\}$ be a forcing set consisting of three permutations and suppose $|\pi_1| \geq |\pi_2| \geq |\pi_3|$ . Note that we can, without loss of generality, assume that all the permutations have order at least two. Moreover, by Lemma 16, the order of $\pi_1$ is at least four. Further, set S is linearly dependent by Lemma 8; hence there exist reals $t_1, t_2$ , and $t_3$ such that $\sum_{i \in [3]}t_i P_{\pi_i} = 0$ . Lemma 15 together with Lemma 13 then implies that precisely two of the coefficients are non-zero and their corresponding permutations have order two.

It follows that set S contains permutation $\pi_1$ together with permutations 12 and 21. Note that the density of 12 in a permuton is equal to $\frac{1}{2}$ if and only if the density of 21 is since the sum of these two densities is one. Therefore, if the set $\{\pi_1, 12, 21\}$ were forcing, then $\{\pi_1, 12\}$ would also be forcing. However, such a set can not be forcing since we have proven that the size of any forcing set is at least three. We conclude that there does not exist any forcing set consisting of three permutations.