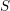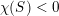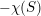1 Introduction
For Riemannian metrics on the closed surface
![]() $S=S_{g}$
of genus
$S=S_{g}$
of genus
![]() $g\geqslant 2$
, the eigenvalue
$g\geqslant 2$
, the eigenvalue
 $\unicode[STIX]{x1D706}_{2g-2}=\unicode[STIX]{x1D706}_{-\unicode[STIX]{x1D712}(S)}$
plays a specific role. Buser gave examples of hyperbolic metrics on
$\unicode[STIX]{x1D706}_{2g-2}=\unicode[STIX]{x1D706}_{-\unicode[STIX]{x1D712}(S)}$
plays a specific role. Buser gave examples of hyperbolic metrics on
![]() $S$
such that the first
$S$
such that the first
![]() $2g-2$
eigenvalues
$2g-2$
eigenvalues
 $$\begin{eqnarray}0=\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D706}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D706}_{2g-3}\end{eqnarray}$$
$$\begin{eqnarray}0=\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D706}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D706}_{2g-3}\end{eqnarray}$$
are arbitrarily small [Reference BuserBus77, Satz 1]. On the other hand, Schoen et al. proved that there is a constant
 $c=c(g)>0$
such that
$c=c(g)>0$
such that
 $\unicode[STIX]{x1D706}_{2g-2}>c$
for any Riemannian metric on
$\unicode[STIX]{x1D706}_{2g-2}>c$
for any Riemannian metric on
![]() $S$
with curvature
$S$
with curvature
 $K\leqslant -1$
[Reference Schoen, Wolpert and YauSWY80]. Buser then showed that, for hyperbolic metrics, the constant
$K\leqslant -1$
[Reference Schoen, Wolpert and YauSWY80]. Buser then showed that, for hyperbolic metrics, the constant
![]() $c$
can be chosen to be independent of the genus [Reference BuserBus10, Theorem 8.1.4]. This development culminated in the work of Otal and Rosas, who showed that
$c$
can be chosen to be independent of the genus [Reference BuserBus10, Theorem 8.1.4]. This development culminated in the work of Otal and Rosas, who showed that
 $\unicode[STIX]{x1D706}_{2g-2}>\unicode[STIX]{x1D706}_{0}(\tilde{S})$
for any analytic Riemannian metric on
$\unicode[STIX]{x1D706}_{2g-2}>\unicode[STIX]{x1D706}_{0}(\tilde{S})$
for any analytic Riemannian metric on
![]() $S$
with curvature
$S$
with curvature
 $K\leqslant -1$
, where
$K\leqslant -1$
, where
![]() $\unicode[STIX]{x1D706}_{0}(\tilde{S})$
denotes the bottom of the spectrum of the universal covering surface
$\unicode[STIX]{x1D706}_{0}(\tilde{S})$
denotes the bottom of the spectrum of the universal covering surface
![]() $\tilde{S}$
of
$\tilde{S}$
of
![]() $S$
, endowed with the lifted Riemannian metric [Reference Otal and RosasOR09, Théorème 1].
$S$
, endowed with the lifted Riemannian metric [Reference Otal and RosasOR09, Théorème 1].
Recall that the bottom of the spectrum of the hyperbolic plane is
![]() $1/4$
and that we have
$1/4$
and that we have
 $\unicode[STIX]{x1D706}_{0}(\tilde{S})\geqslant 1/4$
if
$\unicode[STIX]{x1D706}_{0}(\tilde{S})\geqslant 1/4$
if
 $K\leqslant -1$
; see also (1.1) below.
$K\leqslant -1$
; see also (1.1) below.
Dodziuk et al. extended the work of Schoen et al. to the non-compact surfaces
![]() $S_{g,p}$
of genus
$S_{g,p}$
of genus
![]() $g$
with
$g$
with
![]() $p>0$
punctures (where
$p>0$
punctures (where
 $2g+p>2$
). They showed that there is a constant
$2g+p>2$
). They showed that there is a constant
 $c=c(2g+p)$
such that complete hyperbolic metrics on
$c=c(2g+p)$
such that complete hyperbolic metrics on
![]() $S_{g,p}$
, of finite or infinite area, have at most
$S_{g,p}$
, of finite or infinite area, have at most
 $2g+p-2$
eigenvalues
$2g+p-2$
eigenvalues
![]() $\unicode[STIX]{x1D706}$
, counted with multiplicity, with
$\unicode[STIX]{x1D706}$
, counted with multiplicity, with
![]() $\unicode[STIX]{x1D706}\leqslant c$
[Reference Dodziuk, Pignataro, Randol and SullivanDPRS87, Corollary 1.3]. In [Reference Otal and RosasOR09, Théorème 2], Otal and Rosas improve this for complete hyperbolic metrics of finite area to
$\unicode[STIX]{x1D706}\leqslant c$
[Reference Dodziuk, Pignataro, Randol and SullivanDPRS87, Corollary 1.3]. In [Reference Otal and RosasOR09, Théorème 2], Otal and Rosas improve this for complete hyperbolic metrics of finite area to
 $c=1/4$
.
$c=1/4$
.
At the end of their article, Otal and Rosas discuss the question whether their results also hold for smooth Riemannian metrics. In our previous article [Reference Ballmann, Matthiesen and MondalBMM16a], we showed this for closed surfaces and sharpened their bound
![]() $\unicode[STIX]{x1D706}_{0}(\tilde{S})$
. In the present article, we generalize their results to the case of complete Riemannian metrics on surfaces of finite type with Euler characteristic
$\unicode[STIX]{x1D706}_{0}(\tilde{S})$
. In the present article, we generalize their results to the case of complete Riemannian metrics on surfaces of finite type with Euler characteristic
 $\unicode[STIX]{x1D712}(S)<0$
. We allow the surfaces
$\unicode[STIX]{x1D712}(S)<0$
. We allow the surfaces
![]() $S$
to be compact or non-compact and the metrics to have finite or infinite area. We also allow for non-empty boundary
$S$
to be compact or non-compact and the metrics to have finite or infinite area. We also allow for non-empty boundary
![]() $\unicode[STIX]{x2202}S$
. In that case, our results refer to the Dirichlet spectrum.
$\unicode[STIX]{x2202}S$
. In that case, our results refer to the Dirichlet spectrum.
1.1 Statement of main results
We say that a surface
![]() $S$
with boundary (possibly empty) is of finite type if it is diffeomorphic to a closed surface with
$S$
with boundary (possibly empty) is of finite type if it is diffeomorphic to a closed surface with
![]() $p\geqslant 0$
points and
$p\geqslant 0$
points and
![]() $q\geqslant 0$
open discs removed. Then
$q\geqslant 0$
open discs removed. Then
![]() $S$
has
$S$
has
![]() $p$
ends, represented by the punctures, and
$p$
ends, represented by the punctures, and
![]() $q$
boundary circles, the boundaries of the deleted open discs. Note that we are only concerned with the diffeomorphism type of
$q$
boundary circles, the boundaries of the deleted open discs. Note that we are only concerned with the diffeomorphism type of
![]() $S$
. Thus a puncture has the same effect as the removal of a closed disc.
$S$
. Thus a puncture has the same effect as the removal of a closed disc.
A basis of the neighborhoods of an end of
![]() $S$
consists of punctured discs around the corresponding deleted point. We call these punctured discs funnels and visualize the surface as a steamboat with the funnels pointing upwards and the rest of the surface below them. As already emphasized above, we do not distinguish between different conformal types. For example, in our terminology, a hyperbolic cusp is a funnel.
$S$
consists of punctured discs around the corresponding deleted point. We call these punctured discs funnels and visualize the surface as a steamboat with the funnels pointing upwards and the rest of the surface below them. As already emphasized above, we do not distinguish between different conformal types. For example, in our terminology, a hyperbolic cusp is a funnel.
We assume that
![]() $S$
is endowed with a Riemannian metric which is complete with respect to the associated distance function. The area of the metric may be finite or infinite. We view the Laplacian
$S$
is endowed with a Riemannian metric which is complete with respect to the associated distance function. The area of the metric may be finite or infinite. We view the Laplacian
![]() $\unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6E5}$
of
![]() $S$
as an unbounded operator on the space
$S$
as an unbounded operator on the space
![]() $L^{2}(S)$
of square-integrable functions on
$L^{2}(S)$
of square-integrable functions on
![]() $S$
with domain the space of smooth functions on
$S$
with domain the space of smooth functions on
![]() $S$
with compact support in the interior
$S$
with compact support in the interior
![]() $\mathring{S}$
of
$\mathring{S}$
of
![]() $S$
. Our concern is the spectrum of the Friedrichs extension of
$S$
. Our concern is the spectrum of the Friedrichs extension of
![]() $\unicode[STIX]{x1D6E5}$
, which we call the spectrum of
$\unicode[STIX]{x1D6E5}$
, which we call the spectrum of
![]() $S$
. If the boundary of
$S$
. If the boundary of
![]() $S$
is empty, a case which we include in our discussion, this is the usual spectrum of
$S$
is empty, a case which we include in our discussion, this is the usual spectrum of
![]() $S$
. Otherwise it is the Dirichlet spectrum of
$S$
. Otherwise it is the Dirichlet spectrum of
![]() $S$
.
$S$
.
For any Riemannian manifold
![]() $M$
, with or without boundary, denote by
$M$
, with or without boundary, denote by
![]() $\unicode[STIX]{x1D706}_{0}(M)$
the bottom of the spectrum of the Laplacian
$\unicode[STIX]{x1D706}_{0}(M)$
the bottom of the spectrum of the Laplacian
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $M$
; that is,
$M$
; that is,
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}(M)=\inf R(\unicode[STIX]{x1D711}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}(M)=\inf R(\unicode[STIX]{x1D711}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D711}$
runs over all non-zero smooth functions on
$\unicode[STIX]{x1D711}$
runs over all non-zero smooth functions on
![]() $M$
with compact support in the interior of
$M$
with compact support in the interior of
![]() $M$
and where
$M$
and where
![]() $R(\unicode[STIX]{x1D711})$
denotes the Rayleigh quotient of
$R(\unicode[STIX]{x1D711})$
denotes the Rayleigh quotient of
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
 $$\begin{eqnarray}R(\unicode[STIX]{x1D711})=\frac{\int _{M}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}|^{2}}{\int _{M}\unicode[STIX]{x1D711}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}R(\unicode[STIX]{x1D711})=\frac{\int _{M}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}|^{2}}{\int _{M}\unicode[STIX]{x1D711}^{2}}.\end{eqnarray}$$
As we mentioned above, the bottom of the spectrum of the hyperbolic plane is
![]() $1/4$
. The bottom of the spectrum of the Euclidean plane is 0.
$1/4$
. The bottom of the spectrum of the Euclidean plane is 0.
To state the main result of the present article, we need to introduce one more notion. Let
![]() $S$
be a surface of finite type, with or without boundary, endowed with a complete Riemannian metric. Set
$S$
be a surface of finite type, with or without boundary, endowed with a complete Riemannian metric. Set
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(S)=\inf _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D6FA}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(S)=\inf _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D6FA}),\end{eqnarray}$$
where the infimum is taken over all domains
![]() $\unicode[STIX]{x1D6FA}$
in
$\unicode[STIX]{x1D6FA}$
in
![]() $S$
which are diffeomorphic to an open disc, annulus, or cross cap. The work of Brooks [Reference BrooksBro85, Theorem 1] implies that we always have
$S$
which are diffeomorphic to an open disc, annulus, or cross cap. The work of Brooks [Reference BrooksBro85, Theorem 1] implies that we always have
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})\end{eqnarray}$$
as we will see in Proposition 3.8. The inequality is strict if
![]() $S$
is closed and hyperbolic [Reference MondalMon14]. More generally, it is strict for any Riemannian metric on a compact surface with non-positive Euler characteristic; see [Reference Ballmann, Matthiesen and MondalBMM16b]. However, the strict inequality
$S$
is closed and hyperbolic [Reference MondalMon14]. More generally, it is strict for any Riemannian metric on a compact surface with non-positive Euler characteristic; see [Reference Ballmann, Matthiesen and MondalBMM16b]. However, the strict inequality
 $\unicode[STIX]{x1D6EC}(S)>\unicode[STIX]{x1D706}_{0}(\tilde{S})$
does not hold in general. For example, for a non-compact complete hyperbolic surface
$\unicode[STIX]{x1D6EC}(S)>\unicode[STIX]{x1D706}_{0}(\tilde{S})$
does not hold in general. For example, for a non-compact complete hyperbolic surface
![]() $S$
of finite type without boundary, we have
$S$
of finite type without boundary, we have
 $\unicode[STIX]{x1D6EC}(S)=\unicode[STIX]{x1D706}_{0}(\tilde{S})=1/4$
by the special geometry of the ends of
$\unicode[STIX]{x1D6EC}(S)=\unicode[STIX]{x1D706}_{0}(\tilde{S})=1/4$
by the special geometry of the ends of
![]() $S$
.
$S$
.
We say that an eigenvalue
![]() $\unicode[STIX]{x1D706}$
of a complete Riemannian metric on a surface
$\unicode[STIX]{x1D706}$
of a complete Riemannian metric on a surface
![]() $S$
is small if
$S$
is small if
 $\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6EC}(S)$
. In [Reference Ballmann, Matthiesen and MondalBMM16a] we showed that, on a closed surface
$\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6EC}(S)$
. In [Reference Ballmann, Matthiesen and MondalBMM16a] we showed that, on a closed surface
![]() $S$
with
$S$
with
 $\unicode[STIX]{x1D712}(S)<0$
, a Riemannian metric has at most
$\unicode[STIX]{x1D712}(S)<0$
, a Riemannian metric has at most
![]() $-\unicode[STIX]{x1D712}(S)$
small eigenvalues, counted with multiplicity. The main result of this article is an extension of the latter result to surfaces of finite type.
$-\unicode[STIX]{x1D712}(S)$
small eigenvalues, counted with multiplicity. The main result of this article is an extension of the latter result to surfaces of finite type.
Theorem 1.5. A complete Riemannian metric on a surface
![]() $S$
of finite type with
$S$
of finite type with
 $\unicode[STIX]{x1D712}(S)<0$
has at most
$\unicode[STIX]{x1D712}(S)<0$
has at most
![]() $-\unicode[STIX]{x1D712}(S)$
small eigenvalues, counted with multiplicity.
$-\unicode[STIX]{x1D712}(S)$
small eigenvalues, counted with multiplicity.
With
![]() $p,q$
as further up, the case
$p,q$
as further up, the case
 $p=q=0$
corresponds to closed surfaces, treated in [Reference Ballmann, Matthiesen and MondalBMM16a]. The case
$p=q=0$
corresponds to closed surfaces, treated in [Reference Ballmann, Matthiesen and MondalBMM16a]. The case
![]() $p>0$
,
$p>0$
,
![]() $q=0$
(with orientable
$q=0$
(with orientable
![]() $S$
) extends [Reference Dodziuk, Pignataro, Randol and SullivanDPRS87, Corollary 1.3] of Dodziuk et al. and [Reference Otal and RosasOR09, Théorème 2] of Otal and Rosas to arbitrary complete Riemannian metrics on such surfaces. The case
$S$
) extends [Reference Dodziuk, Pignataro, Randol and SullivanDPRS87, Corollary 1.3] of Dodziuk et al. and [Reference Otal and RosasOR09, Théorème 2] of Otal and Rosas to arbitrary complete Riemannian metrics on such surfaces. The case
![]() $p=0$
,
$p=0$
,
![]() $q>0$
corresponds to the Dirichlet spectrum of compact surfaces with non-empty boundary.
$q>0$
corresponds to the Dirichlet spectrum of compact surfaces with non-empty boundary.
Using the work of Lax and Phillips on so-called embedded eigenvalues [Reference Lax and PhillipsLP82], we will show that Theorem 1.5 has the following consequence.
Theorem 1.6. A complete hyperbolic metric with infinite area on a surface
![]() $S$
of finite type with
$S$
of finite type with
 $\unicode[STIX]{x1D712}(S)<0$
has at most
$\unicode[STIX]{x1D712}(S)<0$
has at most
![]() $-\unicode[STIX]{x1D712}(S)$
eigenvalues, counted with multiplicity, and all of them are contained in
$-\unicode[STIX]{x1D712}(S)$
eigenvalues, counted with multiplicity, and all of them are contained in
![]() $(0,1/4)$
.
$(0,1/4)$
.
In the case where the boundary of
![]() $S$
is empty, Theorem 1.6 is an almost immediate consequence of Theorem 1.5 and the work of Lax and Phillips.
$S$
is empty, Theorem 1.6 is an almost immediate consequence of Theorem 1.5 and the work of Lax and Phillips.
The assertion of Theorem 1.6 also holds if the metric is assumed to be complete with curvature
 $K\leqslant -1$
and to be asymptotically hyperbolic in the sense of Mazzeo [Reference MazzeoMaz91] on at least one of its funnels; see our discussion in § 5.
$K\leqslant -1$
and to be asymptotically hyperbolic in the sense of Mazzeo [Reference MazzeoMaz91] on at least one of its funnels; see our discussion in § 5.
The situation for complete hyperbolic metrics of finite area is much more complicated; see e.g. [Reference SarnakSar03, § 2 and Conjecture 1].
1.2 Remarks and examples
-
(i) The bound
 $-\unicode[STIX]{x1D712}(S)$
in Theorems 1.5 and 1.6 is optimal. Indeed, the construction of Buser in [Reference BuserBus77] applies to surfaces
$-\unicode[STIX]{x1D712}(S)$
in Theorems 1.5 and 1.6 is optimal. Indeed, the construction of Buser in [Reference BuserBus77] applies to surfaces
 $S$
of finite type with
$S$
of finite type with
 $\unicode[STIX]{x1D712}(S)<0$
and shows that, for any
$\unicode[STIX]{x1D712}(S)<0$
and shows that, for any
 $\unicode[STIX]{x1D700}>0$
, there is a complete hyperbolic metric on any such
$\unicode[STIX]{x1D700}>0$
, there is a complete hyperbolic metric on any such
 $S$
(with closed hyperbolic geodesics as boundary circles if the boundary of
$S$
(with closed hyperbolic geodesics as boundary circles if the boundary of
 $S$
is non-empty) such that
$S$
is non-empty) such that
 $S$
has (at least)
$S$
has (at least)
 $-\unicode[STIX]{x1D712}(S)$
eigenvalues
$-\unicode[STIX]{x1D712}(S)$
eigenvalues
 $\unicode[STIX]{x1D706}$
, counted with multiplicity, with
$\unicode[STIX]{x1D706}$
, counted with multiplicity, with
 $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D700}$
. Furthermore, if
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D700}$
. Furthermore, if
 $S$
is non-compact, the metric can be chosen to have finite or infinite area.
$S$
is non-compact, the metric can be chosen to have finite or infinite area. -
(ii) Besides
 $\unicode[STIX]{x1D706}_{0}(\tilde{S})$
and
$\unicode[STIX]{x1D706}_{0}(\tilde{S})$
and
 $\unicode[STIX]{x1D6EC}(S)$
, there is another constant which is of interest in our context. Recall that the spectrum of
$\unicode[STIX]{x1D6EC}(S)$
, there is another constant which is of interest in our context. Recall that the spectrum of
 $S$
is the disjoint union of the discrete and the essential spectrum of
$S$
is the disjoint union of the discrete and the essential spectrum of
 $S$
, where
$S$
, where
 $\unicode[STIX]{x1D706}\in \mathbb{R}$
belongs to the essential spectrum of
$\unicode[STIX]{x1D706}\in \mathbb{R}$
belongs to the essential spectrum of
 $S$
if
$S$
if
 $\unicode[STIX]{x1D6E5}-\unicode[STIX]{x1D706}$
is not a Fredholm operator. The essential spectrum of
$\unicode[STIX]{x1D6E5}-\unicode[STIX]{x1D706}$
is not a Fredholm operator. The essential spectrum of
 $S$
is a closed subset of
$S$
is a closed subset of
 $[0,\infty )$
with bottom denoted by
$[0,\infty )$
with bottom denoted by
 $\unicode[STIX]{x1D706}_{\text{ess}}(S)$
. In Proposition 3.8, we will see that
$\unicode[STIX]{x1D706}_{\text{ess}}(S)$
. In Proposition 3.8, we will see that
 $\unicode[STIX]{x1D706}_{\text{ess}}(S)\geqslant \unicode[STIX]{x1D6EC}(S)$
if
$\unicode[STIX]{x1D706}_{\text{ess}}(S)\geqslant \unicode[STIX]{x1D6EC}(S)$
if
 $S$
is of finite type.
$S$
is of finite type. -
(iii) In [Reference Buser, Colbois and DodziukBCD93, Example 4.1], Buser et al. construct examples of complete hyperbolic surfaces
 $S$
of infinite type with arbitrarily small
$S$
of infinite type with arbitrarily small
 $\unicode[STIX]{x1D706}_{\text{ess}}(S)>0$
which have infinitely many eigenvalues less than
$\unicode[STIX]{x1D706}_{\text{ess}}(S)>0$
which have infinitely many eigenvalues less than
 $\unicode[STIX]{x1D706}_{\text{ess}}(S)$
. Since the eigenvalues are smaller than
$\unicode[STIX]{x1D706}_{\text{ess}}(S)$
. Since the eigenvalues are smaller than
 $\unicode[STIX]{x1D706}_{\text{ess}}(S)$
, they do not belong to the essential spectrum of
$\unicode[STIX]{x1D706}_{\text{ess}}(S)$
, they do not belong to the essential spectrum of
 $S$
, and therefore they are of finite multiplicity. Note that zero is not an eigenvalue of
$S$
, and therefore they are of finite multiplicity. Note that zero is not an eigenvalue of
 $S$
since the area of
$S$
since the area of
 $S$
is infinite so that non-zero constant functions are not square integrable. By Proposition 3.8 and since
$S$
is infinite so that non-zero constant functions are not square integrable. By Proposition 3.8 and since
 $\tilde{S}$
is the hyperbolic plane, we also have that
$\tilde{S}$
is the hyperbolic plane, we also have that
 $\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})=1/4$
.
$\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})=1/4$
. -
(iv) In Examples 3.7(i) and 3.7(ii), we construct complete surfaces of finite type with curvature
 $K\leqslant -1$
, of finite and infinite area, and with empty essential spectrum. Such surfaces have infinitely many eigenvalues, and all of them are of finite multiplicity. In Example 3.7(iii), we construct complete non-compact surfaces
$K\leqslant -1$
, of finite and infinite area, and with empty essential spectrum. Such surfaces have infinitely many eigenvalues, and all of them are of finite multiplicity. In Example 3.7(iii), we construct complete non-compact surfaces
 $S$
of finite type with curvature
$S$
of finite type with curvature
 $K\leqslant 0$
, of finite and infinite area, with
$K\leqslant 0$
, of finite and infinite area, with
 $\unicode[STIX]{x1D6EC}(S)$
arbitrarily small, and
$\unicode[STIX]{x1D6EC}(S)$
arbitrarily small, and
 $\unicode[STIX]{x1D706}_{\text{ess}}(S)=1/4$
.
$\unicode[STIX]{x1D706}_{\text{ess}}(S)=1/4$
. -
(v) Our results refer to the standard spectrum of the surface
 $S$
if
$S$
if
 $\unicode[STIX]{x2202}S=\emptyset$
and to the Dirichlet spectrum of
$\unicode[STIX]{x2202}S=\emptyset$
and to the Dirichlet spectrum of
 $S$
if
$S$
if
 $\unicode[STIX]{x2202}S\neq \emptyset$
. In the latter case, one might also ask for other boundary conditions and, in particular, for the Neumann condition. In fact, our arguments in the proof of Theorem 1.5 still apply. However, for the Neumann condition, the constant
$\unicode[STIX]{x2202}S\neq \emptyset$
. In the latter case, one might also ask for other boundary conditions and, in particular, for the Neumann condition. In fact, our arguments in the proof of Theorem 1.5 still apply. However, for the Neumann condition, the constant
 $\unicode[STIX]{x1D6EC}(S)$
would have to be replaced by a corresponding constant
$\unicode[STIX]{x1D6EC}(S)$
would have to be replaced by a corresponding constant
 $\unicode[STIX]{x1D6EC}_{N}(S)$
, where we would have to consider mixed boundary conditions for the Laplacian on embedded discs, annuli, and cross caps
$\unicode[STIX]{x1D6EC}_{N}(S)$
, where we would have to consider mixed boundary conditions for the Laplacian on embedded discs, annuli, and cross caps
 $\unicode[STIX]{x1D6FA}$
in
$\unicode[STIX]{x1D6FA}$
in
 $S$
with piecewise smooth boundary (Neumann condition on
$S$
with piecewise smooth boundary (Neumann condition on
 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x2202}S$
, Dirichlet condition on
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x2202}S$
, Dirichlet condition on
 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\cap \mathring{S}$
). As of now, we do not see interesting estimates for that constant.
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\cap \mathring{S}$
). As of now, we do not see interesting estimates for that constant.
In the case where the surface is hyperbolic with periodic geodesics as boundary circles, doubling
![]() $S$
along
$S$
along
![]() $\unicode[STIX]{x2202}S$
would lead to the estimate that the number of Dirichlet eigenvalues plus the number of Neumann eigenvalues of
$\unicode[STIX]{x2202}S$
would lead to the estimate that the number of Dirichlet eigenvalues plus the number of Neumann eigenvalues of
![]() $S$
below
$S$
below
![]() $\unicode[STIX]{x1D6EC}(2S)$
is bounded by
$\unicode[STIX]{x1D6EC}(2S)$
is bounded by
![]() $-2\unicode[STIX]{x1D712}(S)$
since the eigenfunctions on the double
$-2\unicode[STIX]{x1D712}(S)$
since the eigenfunctions on the double
![]() $2S$
split into even and odd ones with respect to the isometry of
$2S$
split into even and odd ones with respect to the isometry of
![]() $2S$
which interchanges the two summands of
$2S$
which interchanges the two summands of
![]() $2S$
. Via restriction, the first type corresponds to Neumann eigenfunctions, the second to Dirichlet eigenfunctions on the original
$2S$
. Via restriction, the first type corresponds to Neumann eigenfunctions, the second to Dirichlet eigenfunctions on the original
![]() $S$
. (This observation led to [Reference SchmutzSch91, Conjecture 2].)
$S$
. (This observation led to [Reference SchmutzSch91, Conjecture 2].)
1.3 Structure of the article
In the proof of our main result, Theorem 1.5, our line of arguments is different from the classical one of Buser [Reference BuserBus77], Schoen et al. [Reference Schoen, Wolpert and YauSWY80], and Dodziuk et al. [Reference Dodziuk, Pignataro, Randol and SullivanDPRS87], who rely on decompositions of the surface into appropriate pieces and monotonicity properties of eigenvalues. As in our previous article [Reference Ballmann, Matthiesen and MondalBMM16a], we follow the strategy of Otal and Rosas in [Reference Otal and RosasOR09], which involves a careful examination of topological properties of nodal sets and domains of finite linear combinations of eigenfunctions.
In the cases discussed by Otal and Rosas, the underlying Riemannian metrics are analytic. Then the corresponding eigenfunctions are analytic functions, and hence also finite linear combinations of them. It follows that the nodal set
 $Z_{\unicode[STIX]{x1D711}}=\{\unicode[STIX]{x1D711}=0\}$
of such a linear combination
$Z_{\unicode[STIX]{x1D711}}=\{\unicode[STIX]{x1D711}=0\}$
of such a linear combination
![]() $\unicode[STIX]{x1D711}$
is a locally finite graph with analytic edges. In our situation of smooth Riemannian metrics, nodal sets of eigenfunctions are still locally finite graphs. However, for a finite linear combination
$\unicode[STIX]{x1D711}$
is a locally finite graph with analytic edges. In our situation of smooth Riemannian metrics, nodal sets of eigenfunctions are still locally finite graphs. However, for a finite linear combination
![]() $\unicode[STIX]{x1D711}$
of eigenfunctions, the regularity of the nodal set
$\unicode[STIX]{x1D711}$
of eigenfunctions, the regularity of the nodal set
![]() $Z_{\unicode[STIX]{x1D711}}$
is not clear anymore. Therefore, we investigate approximate nodal sets
$Z_{\unicode[STIX]{x1D711}}$
is not clear anymore. Therefore, we investigate approximate nodal sets
 $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})=\{|\unicode[STIX]{x1D711}|\leqslant \unicode[STIX]{x1D700}\}$
instead and, for that reason, have to face a number of additional problems before we get the main argument of Otal and Rosas to work.
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})=\{|\unicode[STIX]{x1D711}|\leqslant \unicode[STIX]{x1D700}\}$
instead and, for that reason, have to face a number of additional problems before we get the main argument of Otal and Rosas to work.
Our line of proof requires extending the corresponding arguments in [Reference Ballmann, Matthiesen and MondalBMM16a] from closed surfaces to surfaces of finite type. In particular, we do not assume that
![]() $S$
is compact. Hence approximate nodal sets
$S$
is compact. Hence approximate nodal sets
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
and approximate nodal domains, that is, connected components of
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
and approximate nodal domains, that is, connected components of
 $S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, might not be compact, and we have to face the problem of getting a hand on the asymptotic structure of approximate nodal sets and domains at infinity. To that end, we discuss a simultaneous twofold asymptotic behavior, namely the asymptotics of the intersection of approximate nodal sets and domains with compact subsets
$S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, might not be compact, and we have to face the problem of getting a hand on the asymptotic structure of approximate nodal sets and domains at infinity. To that end, we discuss a simultaneous twofold asymptotic behavior, namely the asymptotics of the intersection of approximate nodal sets and domains with compact subsets
![]() $K$
of
$K$
of
![]() $S$
for
$S$
for
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
and
$\unicode[STIX]{x1D700}\rightarrow 0$
and
![]() $K\rightarrow S$
. We actually do not consider approximate nodal sets and domains themselves, but need to study appropriate modifications of them. One of the new technical problems in the non-compact case is that
$K\rightarrow S$
. We actually do not consider approximate nodal sets and domains themselves, but need to study appropriate modifications of them. One of the new technical problems in the non-compact case is that
![]() $\pm \unicode[STIX]{x1D700}$
might be a regular value of
$\pm \unicode[STIX]{x1D700}$
might be a regular value of
![]() $\unicode[STIX]{x1D711}$
, but not for a function
$\unicode[STIX]{x1D711}$
, but not for a function
![]() $\unicode[STIX]{x1D713}$
which is
$\unicode[STIX]{x1D713}$
which is
![]() $C^{2}$
-close to
$C^{2}$
-close to
![]() $\unicode[STIX]{x1D711}$
on a compact subset. Note also that the rather special behavior of nodal lines along hyperbolic cusps, as used by Otal and Rosas, is not at our disposal.
$\unicode[STIX]{x1D711}$
on a compact subset. Note also that the rather special behavior of nodal lines along hyperbolic cusps, as used by Otal and Rosas, is not at our disposal.
In addition to the above, we need the following generalization of Cheng’s structure theorem for nodal lines of eigenfunctions of Schrödinger operators.
Theorem 1.7. Let
![]() $S$
be a surface with smooth boundary (possibly empty), endowed with a Riemannian metric. Let
$S$
be a surface with smooth boundary (possibly empty), endowed with a Riemannian metric. Let
![]() $\unicode[STIX]{x1D711},V$
be smooth functions on
$\unicode[STIX]{x1D711},V$
be smooth functions on
![]() $S$
and suppose that
$S$
and suppose that
![]() $\unicode[STIX]{x1D711}$
vanishes along the boundary of
$\unicode[STIX]{x1D711}$
vanishes along the boundary of
![]() $S$
and solves the Schrödinger equation
$S$
and solves the Schrödinger equation
 $(\unicode[STIX]{x1D6E5}+V)\unicode[STIX]{x1D711}=0$
. Then the
$(\unicode[STIX]{x1D6E5}+V)\unicode[STIX]{x1D711}=0$
. Then the
 $\text{nodal set}$
$\text{nodal set}$
 $Z_{\unicode[STIX]{x1D711}}=\{x\in S\mid \unicode[STIX]{x1D711}(x)=0\}$
of
$Z_{\unicode[STIX]{x1D711}}=\{x\in S\mid \unicode[STIX]{x1D711}(x)=0\}$
of
![]() $\unicode[STIX]{x1D711}$
is a locally finite graph in
$\unicode[STIX]{x1D711}$
is a locally finite graph in
![]() $S$
. Moreover:
$S$
. Moreover:
-
(i)
 $z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
has valence
$z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
has valence
 $2n$
if and only if
$2n$
if and only if
 $\unicode[STIX]{x1D711}$
vanishes to order
$\unicode[STIX]{x1D711}$
vanishes to order
 $n$
at
$n$
at
 $z$
;
$z$
; -
(ii)
 $z\in Z_{\unicode[STIX]{x1D711}}\cap \unicode[STIX]{x2202}S$
has valence
$z\in Z_{\unicode[STIX]{x1D711}}\cap \unicode[STIX]{x2202}S$
has valence
 $n+1$
if and only if
$n+1$
if and only if
 $\unicode[STIX]{x1D711}$
vanishes to order
$\unicode[STIX]{x1D711}$
vanishes to order
 $n$
at
$n$
at
 $z$
.
$z$
.
In both cases, the opening angles between the edges at
![]() $z$
are equal to
$z$
are equal to
![]() $\unicode[STIX]{x1D70B}/n$
.
$\unicode[STIX]{x1D70B}/n$
.
For points
 $z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
, this is [Reference ChengChe76, Theorem 2.5]. The case of boundary points is new. We also note the following consequence of Theorem 1.7.
$z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
, this is [Reference ChengChe76, Theorem 2.5]. The case of boundary points is new. We also note the following consequence of Theorem 1.7.
Corollary 1.8. In the situation of Theorem 1.7,
![]() $Z_{\unicode[STIX]{x1D711}}$
is a locally finite union of immersed circles, line segments with both end points on
$Z_{\unicode[STIX]{x1D711}}$
is a locally finite union of immersed circles, line segments with both end points on
![]() $\unicode[STIX]{x2202}S$
, rays with one end point on
$\unicode[STIX]{x2202}S$
, rays with one end point on
![]() $\unicode[STIX]{x2202}S$
, and lines.
$\unicode[STIX]{x2202}S$
, and lines.
The main part of the proof of Theorem 1.5 is contained in § 4 and is concerned with topological properties of approximate nodal domains and their asymptotic behavior. The analytical part of the proof is concentrated in Lemma 4.10. To prepare the proof of Theorem 1.5, we collect some prerequisites from topology in § 2, with Theorem 2.3 and Lemma 2.5 as our main later tools, and from analysis in § 3. In particular, the latter section contains the proof of Theorem 1.7. The proof of Theorem 1.6 is contained in § 5.
Mutatis mutandis, our arguments in the proof of Theorem 1.5 remain valid for Schrödinger operators
![]() $\unicode[STIX]{x1D6E5}+V$
, where the potential
$\unicode[STIX]{x1D6E5}+V$
, where the potential
![]() $V$
is non-negative or, more or less equivalently, bounded from below. In particular, the analog of Theorem 1.5 holds also for such operators.
$V$
is non-negative or, more or less equivalently, bounded from below. In particular, the analog of Theorem 1.5 holds also for such operators.
2 Prerequisites from topology
In this section, we collect some results about the topology of surfaces. We assume throughout that the concerned surfaces have empty or piecewise smooth boundaries.
Proposition 2.1. The interior of a surface
![]() $S$
is of finite type if and only if the fundamental group of
$S$
is of finite type if and only if the fundamental group of
![]() $S$
is finitely generated.
$S$
is finitely generated.
Among the surfaces with boundary (possibly empty) whose interior is of finite type, we singled out those with compact boundary in the introduction.
For
![]() $n\geqslant 2$
, denote by
$n\geqslant 2$
, denote by
![]() $F_{n}$
the free group in
$F_{n}$
the free group in
![]() $n$
generators and recall that the commutator subgroup of
$n$
generators and recall that the commutator subgroup of
![]() $F_{2}$
is isomorphic to
$F_{2}$
is isomorphic to
![]() $F_{\infty }$
.
$F_{\infty }$
.
Proposition 2.2. For a non-closed surface
![]() $S$
, the following are equivalent.
$S$
, the following are equivalent.
-
(i) The fundamental group of
 $S$
is cyclic.
$S$
is cyclic. -
(ii) The fundamental group of
 $S$
is amenable.
$S$
is amenable. -
(iii) The fundamental group of
 $S$
does not contain
$S$
does not contain
 $F_{2}$
as a subgroup.
$F_{2}$
as a subgroup. -
(iv) The interior of
 $S$
is an open disc, annulus, or cross cap.
$S$
is an open disc, annulus, or cross cap.
We say that a curve in a manifold is a Jordan curve if it is properly embedded. Note that Jordan curves are closed as subsets of the ambient manifold. We will need the following version of the Schoenflies theorem (compare with [Reference BuserBus10, Corollary A.7]).
Theorem 2.3. Any null-homotopic Jordan loop in a surface
![]() $S$
bounds an embedded disc in
$S$
bounds an embedded disc in
![]() $S$
.
$S$
.
Corollary 2.4. Let
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
be Jordan loops in an annulus
$c_{1}$
be Jordan loops in an annulus
![]() $A$
which represent the generator of the fundamental group of
$A$
which represent the generator of the fundamental group of
![]() $A$
(up to orientation) and which do not intersect. Then
$A$
(up to orientation) and which do not intersect. Then
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
are the boundary circles of an embedded annulus
$c_{1}$
are the boundary circles of an embedded annulus
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $A$
.
$A$
.
A subsurface
![]() $C\subseteq S$
is called incompressible in
$C\subseteq S$
is called incompressible in
![]() $S$
if any closed curve in
$S$
if any closed curve in
![]() $C$
, which is homotopic to zero in
$C$
, which is homotopic to zero in
![]() $S$
, is already homotopic to zero in
$S$
, is already homotopic to zero in
![]() $C$
.
$C$
.
Lemma 2.5. Let
![]() $R$
be a compact and connected surface (with piecewise smooth boundary
$R$
be a compact and connected surface (with piecewise smooth boundary
![]() $\unicode[STIX]{x2202}R$
, possibly empty) which is not homeomorphic to the sphere. Let
$\unicode[STIX]{x2202}R$
, possibly empty) which is not homeomorphic to the sphere. Let
![]() $X$
be a non-empty incompressible closed subsurface of
$X$
be a non-empty incompressible closed subsurface of
![]() $R$
with piecewise smooth boundary
$R$
with piecewise smooth boundary
![]() $\unicode[STIX]{x2202}X$
. Assume that
$\unicode[STIX]{x2202}X$
. Assume that
 $\unicode[STIX]{x2202}X\cap \unicode[STIX]{x2202}R$
is a union of piecewise smooth segments and circles (possibly empty) and that
$\unicode[STIX]{x2202}X\cap \unicode[STIX]{x2202}R$
is a union of piecewise smooth segments and circles (possibly empty) and that
![]() $\unicode[STIX]{x2202}X$
and
$\unicode[STIX]{x2202}X$
and
![]() $\unicode[STIX]{x2202}R$
are transversal, where they meet. Then
$\unicode[STIX]{x2202}R$
are transversal, where they meet. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D712}(R)\leqslant \unicode[STIX]{x1D712}(X).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(R)\leqslant \unicode[STIX]{x1D712}(X).\end{eqnarray}$$
In the case of equality, the components of
![]() $R\setminus \mathring{X}$
are annuli, cross caps, and lunes. More precisely, if
$R\setminus \mathring{X}$
are annuli, cross caps, and lunes. More precisely, if
![]() $C$
is a component of
$C$
is a component of
![]() $R\setminus \mathring{X}$
that intersects the boundary of
$R\setminus \mathring{X}$
that intersects the boundary of
![]() $R$
, then
$R$
, then
![]() $C$
is an annulus attached to a boundary circle of
$C$
is an annulus attached to a boundary circle of
![]() $X$
or is a lune attached to a part of a boundary circle of
$X$
or is a lune attached to a part of a boundary circle of
![]() $X$
. Otherwise
$X$
. Otherwise
![]() $C$
is an annulus attached to two boundary circles of
$C$
is an annulus attached to two boundary circles of
![]() $X$
or a cross cap attached to a boundary circle of
$X$
or a cross cap attached to a boundary circle of
![]() $X$
.
$X$
.
Here a lune is a closed disc
![]() $D$
whose boundary is subdivided into two subarcs. Attaching a lune
$D$
whose boundary is subdivided into two subarcs. Attaching a lune
![]() $D$
to
$D$
to
![]() $X$
along
$X$
along
![]() $\unicode[STIX]{x2202}X$
means to glue one of the subarcs of the boundary of
$\unicode[STIX]{x2202}X$
means to glue one of the subarcs of the boundary of
![]() $D$
to an arc in
$D$
to an arc in
![]() $\unicode[STIX]{x2202}X$
. Then
$\unicode[STIX]{x2202}X$
. Then
![]() $X$
is isotopic to
$X$
is isotopic to
![]() $X\cup D$
.
$X\cup D$
.
Proof of Lemma 2.5.
We may assume
![]() $X\subsetneq R$
. Now by the assumptions on the boundaries of
$X\subsetneq R$
. Now by the assumptions on the boundaries of
![]() $R$
and
$R$
and
![]() $X$
, there is a closed collar
$X$
, there is a closed collar
![]() $U$
about
$U$
about
![]() $\unicode[STIX]{x2202}R$
in
$\unicode[STIX]{x2202}R$
in
![]() $R$
such that
$R$
such that
 $Y=X\setminus \mathring{U}$
is a deformation retract of
$Y=X\setminus \mathring{U}$
is a deformation retract of
![]() $X$
in
$X$
in
![]() $R$
. Observe that
$R$
. Observe that
![]() $Y$
does not intersect
$Y$
does not intersect
![]() $\unicode[STIX]{x2202}R$
and that the boundaries of
$\unicode[STIX]{x2202}R$
and that the boundaries of
![]() $R$
and
$R$
and
![]() $Y$
each are disjoint unions of circles.
$Y$
each are disjoint unions of circles.
If a component
![]() $D$
of
$D$
of
![]() $R\setminus \mathring{Y}$
were a closed disc, set
$R\setminus \mathring{Y}$
were a closed disc, set
![]() $c=\unicode[STIX]{x2202}D$
, a circle in
$c=\unicode[STIX]{x2202}D$
, a circle in
![]() $\unicode[STIX]{x2202}Y$
. If
$\unicode[STIX]{x2202}Y$
. If
![]() $c$
were homotopic to zero in
$c$
were homotopic to zero in
![]() $Y$
, then there would be a closed disc
$Y$
, then there would be a closed disc
![]() $D^{\prime }$
in
$D^{\prime }$
in
![]() $Y$
with
$Y$
with
 $\unicode[STIX]{x2202}D^{\prime }=c$
. Thus
$\unicode[STIX]{x2202}D^{\prime }=c$
. Thus
![]() $D\cup D^{\prime }$
would be an embedded sphere in
$D\cup D^{\prime }$
would be an embedded sphere in
![]() $R$
. This is not possible since
$R$
. This is not possible since
![]() $R$
is connected and would have to be equal to that sphere. Thus
$R$
is connected and would have to be equal to that sphere. Thus
![]() $c$
is not homotopic to zero in
$c$
is not homotopic to zero in
![]() $Y$
, hence neither in
$Y$
, hence neither in
![]() $R$
since
$R$
since
![]() $Y$
is incompressible in
$Y$
is incompressible in
![]() $R$
. This is a contradiction, and hence no component of
$R$
. This is a contradiction, and hence no component of
![]() $R\setminus \mathring{Y}$
is a disc. Note also that no component of
$R\setminus \mathring{Y}$
is a disc. Note also that no component of
![]() $R\setminus \mathring{Y}$
is a closed surface since
$R\setminus \mathring{Y}$
is a closed surface since
![]() $R$
is connected and
$R$
is connected and
![]() $Y$
is non-empty.
$Y$
is non-empty.
From the Mayer–Vietoris sequence, we obtain
 $\unicode[STIX]{x1D712}(R)=\unicode[STIX]{x1D712}(Y)+\unicode[STIX]{x1D712}(R\setminus \mathring{Y})$
. Since no component of
$\unicode[STIX]{x1D712}(R)=\unicode[STIX]{x1D712}(Y)+\unicode[STIX]{x1D712}(R\setminus \mathring{Y})$
. Since no component of
![]() $R\setminus \mathring{Y}$
is a disc or a closed surface, we have
$R\setminus \mathring{Y}$
is a disc or a closed surface, we have
 $\unicode[STIX]{x1D712}(R\setminus \mathring{Y})\leqslant 0$
and hence
$\unicode[STIX]{x1D712}(R\setminus \mathring{Y})\leqslant 0$
and hence
 $$\begin{eqnarray}\unicode[STIX]{x1D712}(R)\leqslant \unicode[STIX]{x1D712}(Y)=\unicode[STIX]{x1D712}(X).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(R)\leqslant \unicode[STIX]{x1D712}(Y)=\unicode[STIX]{x1D712}(X).\end{eqnarray}$$
If
 $\unicode[STIX]{x1D712}(R)=\unicode[STIX]{x1D712}(Y)$
, we have
$\unicode[STIX]{x1D712}(R)=\unicode[STIX]{x1D712}(Y)$
, we have
 $\unicode[STIX]{x1D712}(C)=0$
for each component
$\unicode[STIX]{x1D712}(C)=0$
for each component
![]() $C$
of
$C$
of
![]() $R\setminus \mathring{Y}$
. Hence each such
$R\setminus \mathring{Y}$
. Hence each such
![]() $C$
is an annulus or a cross cap. If
$C$
is an annulus or a cross cap. If
![]() $C$
does not intersect
$C$
does not intersect
![]() $U$
, then
$U$
, then
![]() $C$
is also a component of
$C$
is also a component of
![]() $R\setminus X$
.
$R\setminus X$
.
If
![]() $C$
intersects
$C$
intersects
![]() $U$
, it contains the corresponding parts of the boundary of
$U$
, it contains the corresponding parts of the boundary of
![]() $R$
. Since
$R$
. Since
![]() $R$
is connected and
$R$
is connected and
![]() $Y$
is non-empty,
$Y$
is non-empty,
![]() $C$
also contains a part of the boundary of
$C$
also contains a part of the boundary of
![]() $Y$
. Hence the boundary of
$Y$
. Hence the boundary of
![]() $C$
has more than one component, and hence
$C$
has more than one component, and hence
![]() $C$
is an annulus. Therefore
$C$
is an annulus. Therefore
![]() $C$
contains precisely one boundary circle of
$C$
contains precisely one boundary circle of
![]() $R$
and intersects only the corresponding part of
$R$
and intersects only the corresponding part of
![]() $U$
.
$U$
.
Let
![]() $C^{\prime }$
be a component of
$C^{\prime }$
be a component of
![]() $R\setminus \mathring{X}$
that is contained in
$R\setminus \mathring{X}$
that is contained in
![]() $C$
. If
$C$
. If
![]() $C^{\prime }$
contains a component of
$C^{\prime }$
contains a component of
![]() $\unicode[STIX]{x2202}R$
, then
$\unicode[STIX]{x2202}R$
, then
![]() $C=C^{\prime }$
and
$C=C^{\prime }$
and
![]() $C^{\prime }$
is an annulus. If
$C^{\prime }$
is an annulus. If
![]() $C^{\prime }$
intersects a component of
$C^{\prime }$
intersects a component of
![]() $\unicode[STIX]{x2202}R$
but does not contain it, then
$\unicode[STIX]{x2202}R$
but does not contain it, then
![]() $C\setminus C^{\prime }$
is a subdomain of
$C\setminus C^{\prime }$
is a subdomain of
![]() $C$
whose boundary components intersects both boundary circles of
$C$
whose boundary components intersects both boundary circles of
![]() $C$
. This is possible only if
$C$
. This is possible only if
![]() $C\setminus \mathring{X}$
consists of attached lunes. ◻
$C\setminus \mathring{X}$
consists of attached lunes. ◻
3 Prerequisites from analysis
We let
![]() $M$
be a Riemannian manifold, complete or not complete, connected or not connected, with or without (piecewise smooth) boundary. We denote by
$M$
be a Riemannian manifold, complete or not complete, connected or not connected, with or without (piecewise smooth) boundary. We denote by
![]() $C^{k}(M)$
the space of
$C^{k}(M)$
the space of
![]() $C^{k}$
-functions on
$C^{k}$
-functions on
![]() $M$
, by
$M$
, by
 $C_{c}^{k}(M)\subseteq C^{k}(M)$
the space of
$C_{c}^{k}(M)\subseteq C^{k}(M)$
the space of
![]() $C^{k}$
-functions on
$C^{k}$
-functions on
![]() $M$
with compact support, and by
$M$
with compact support, and by
 $C_{cc}^{k}(M)\subseteq C_{c}^{k}(M)$
the space of
$C_{cc}^{k}(M)\subseteq C_{c}^{k}(M)$
the space of
![]() $C^{k}$
-functions on
$C^{k}$
-functions on
![]() $M$
with compact support in the interior
$M$
with compact support in the interior
![]() $\mathring{M}$
of
$\mathring{M}$
of
![]() $M$
, respectively. In the case where the boundary
$M$
, respectively. In the case where the boundary
![]() $\unicode[STIX]{x2202}M$
of
$\unicode[STIX]{x2202}M$
of
![]() $M$
is empty, we have
$M$
is empty, we have
 $C_{cc}^{k}(M)=C_{c}^{k}(M)$
. We use the term smooth to indicate
$C_{cc}^{k}(M)=C_{c}^{k}(M)$
. We use the term smooth to indicate
![]() $C^{\infty }$
.
$C^{\infty }$
.
We let
![]() $L^{2}(M)$
be the space of square-integrable functions on
$L^{2}(M)$
be the space of square-integrable functions on
![]() $M$
and recall that
$M$
and recall that
 $C_{cc}^{\infty }(M)$
is a dense subspace of
$C_{cc}^{\infty }(M)$
is a dense subspace of
![]() $L^{2}(M)$
. We denote by
$L^{2}(M)$
. We denote by
![]() $H^{1}(M)$
the space of functions in
$H^{1}(M)$
the space of functions in
![]() $L^{2}(M)$
which have a square-integrable gradient
$L^{2}(M)$
which have a square-integrable gradient
![]() $\unicode[STIX]{x1D6FB}f$
in the sense of distributions. By the latter we mean that we test
$\unicode[STIX]{x1D6FB}f$
in the sense of distributions. By the latter we mean that we test
![]() $\unicode[STIX]{x1D6FB}f$
against smooth one-forms on
$\unicode[STIX]{x1D6FB}f$
against smooth one-forms on
![]() $M$
with compact support in
$M$
with compact support in
![]() $\mathring{M}$
. Recall that
$\mathring{M}$
. Recall that
![]() $H^{1}(M)$
is a Hilbert space with respect to the
$H^{1}(M)$
is a Hilbert space with respect to the
![]() $H^{1}$
-norm and denote by
$H^{1}$
-norm and denote by
![]() $H_{0}^{1}(M)$
the closure of
$H_{0}^{1}(M)$
the closure of
 $C_{cc}^{\infty }(M)$
in
$C_{cc}^{\infty }(M)$
in
![]() $H^{1}(M)$
.
$H^{1}(M)$
.
Proposition 3.1 (Friedrichs extension).
The Laplacian
![]() $\unicode[STIX]{x1D6E5}$
is self-adjoint as an unbounded operator on
$\unicode[STIX]{x1D6E5}$
is self-adjoint as an unbounded operator on
![]() $L^{2}(M)$
with domain the space of
$L^{2}(M)$
with domain the space of
 $\unicode[STIX]{x1D711}\in H_{0}^{1}(M)$
such that
$\unicode[STIX]{x1D711}\in H_{0}^{1}(M)$
such that
 $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}\in L^{2}(M)$
in the sense of distributions.
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}\in L^{2}(M)$
in the sense of distributions.
Proof. Since
![]() $H_{0}^{1}(M)$
is dense in
$H_{0}^{1}(M)$
is dense in
![]() $L^{2}(M)$
, this follows immediately from the construction of the Friedrichs extension; compare with [Reference TaylorTay96, § A.8].◻
$L^{2}(M)$
, this follows immediately from the construction of the Friedrichs extension; compare with [Reference TaylorTay96, § A.8].◻
We call the spectrum of the Friedrichs extension of
![]() $\unicode[STIX]{x1D6E5}$
as in Proposition 3.1 the spectrum of
$\unicode[STIX]{x1D6E5}$
as in Proposition 3.1 the spectrum of
![]() $M$
. Note that, in the case where
$M$
. Note that, in the case where
![]() $M$
has no boundary, this is the usual spectrum of
$M$
has no boundary, this is the usual spectrum of
![]() $S$
whereas it is the Dirichlet spectrum in the case where the boundary of
$S$
whereas it is the Dirichlet spectrum in the case where the boundary of
![]() $M$
is non-empty and piecewise smooth.
$M$
is non-empty and piecewise smooth.
Set
 $C_{0}^{k}(M)=\{\unicode[STIX]{x1D711}\in C^{k}(M)\mid \unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}M}=0\}$
, and let
$C_{0}^{k}(M)=\{\unicode[STIX]{x1D711}\in C^{k}(M)\mid \unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}M}=0\}$
, and let
 $C_{c,0}^{k}(M)$
be the space of
$C_{c,0}^{k}(M)$
be the space of
![]() $C^{k}$
-functions in
$C^{k}$
-functions in
![]() $C_{0}^{k}(M)$
with compact support. We use a corresponding notation for the space
$C_{0}^{k}(M)$
with compact support. We use a corresponding notation for the space
 $C^{0,1}(M)$
of Lipschitz functions on
$C^{0,1}(M)$
of Lipschitz functions on
![]() $M$
.
$M$
.
Lemma 3.2. If
![]() $M$
is complete as a metric space and the boundary of
$M$
is complete as a metric space and the boundary of
![]() $M$
is piecewise smooth (possibly empty), then
$M$
is piecewise smooth (possibly empty), then
 $$\begin{eqnarray}C_{0}^{0,1}(M)\cap H^{1}(M)\subseteq H_{0}^{1}(M).\end{eqnarray}$$
$$\begin{eqnarray}C_{0}^{0,1}(M)\cap H^{1}(M)\subseteq H_{0}^{1}(M).\end{eqnarray}$$
Proof. Since the boundary of
![]() $M$
is piecewise smooth, there is a sequence of functions
$M$
is piecewise smooth, there is a sequence of functions
![]() $\unicode[STIX]{x1D712}_{n}$
in
$\unicode[STIX]{x1D712}_{n}$
in
![]() $C_{c}^{1}(M)$
such that
$C_{c}^{1}(M)$
such that
 $0\leqslant \unicode[STIX]{x1D712}_{n}\leqslant 1$
and
$0\leqslant \unicode[STIX]{x1D712}_{n}\leqslant 1$
and
 $|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D712}_{n}|\leqslant 1/n$
, such that
$|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D712}_{n}|\leqslant 1/n$
, such that
 $\{\unicode[STIX]{x1D712}_{n}=1\}$
contains the support of
$\{\unicode[STIX]{x1D712}_{n}=1\}$
contains the support of
![]() $\unicode[STIX]{x1D712}_{n-1}$
in its interior, and such that
$\unicode[STIX]{x1D712}_{n-1}$
in its interior, and such that
 $\cup \{\unicode[STIX]{x1D712}_{n}=1\}=M$
. With such a sequence, we can reduce the assertion of Lemma 3.2 to the case of functions in
$\cup \{\unicode[STIX]{x1D712}_{n}=1\}=M$
. With such a sequence, we can reduce the assertion of Lemma 3.2 to the case of functions in
 $C_{c,0}^{0,1}(M)\cap H^{1}(M)$
.
$C_{c,0}^{0,1}(M)\cap H^{1}(M)$
.
Given a compact set
 $K\subseteq M$
, there is a sequence of functions
$K\subseteq M$
, there is a sequence of functions
![]() $\unicode[STIX]{x1D712}_{n}$
in
$\unicode[STIX]{x1D712}_{n}$
in
![]() $C_{c}^{1}(M)$
such that
$C_{c}^{1}(M)$
such that
 $0\leqslant \unicode[STIX]{x1D712}_{n}\leqslant 1$
and
$0\leqslant \unicode[STIX]{x1D712}_{n}\leqslant 1$
and
 $|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D712}_{n}|\leqslant Cn$
for some constant
$|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D712}_{n}|\leqslant Cn$
for some constant
 $C=C(K)$
, such that
$C=C(K)$
, such that
![]() $\unicode[STIX]{x1D712}_{n}=1$
on the set of
$\unicode[STIX]{x1D712}_{n}=1$
on the set of
![]() $x\in K$
with
$x\in K$
with
 $d(x,\unicode[STIX]{x2202}M)\geqslant 2/n$
, and such that
$d(x,\unicode[STIX]{x2202}M)\geqslant 2/n$
, and such that
![]() $\unicode[STIX]{x1D712}_{n}=0$
on the set of
$\unicode[STIX]{x1D712}_{n}=0$
on the set of
![]() $x\in K$
with
$x\in K$
with
 $d(x,\unicode[STIX]{x2202}M)\leqslant 1/n$
.
$d(x,\unicode[STIX]{x2202}M)\leqslant 1/n$
.
Now let
 $\unicode[STIX]{x1D711}\in C_{c,0}^{0,1}(M)\cap H^{1}(M)$
and
$\unicode[STIX]{x1D711}\in C_{c,0}^{0,1}(M)\cap H^{1}(M)$
and
 $K=\operatorname{supp}\unicode[STIX]{x1D711}$
. Choose a sequence of functions
$K=\operatorname{supp}\unicode[STIX]{x1D711}$
. Choose a sequence of functions
![]() $\unicode[STIX]{x1D712}_{n}$
for
$\unicode[STIX]{x1D712}_{n}$
for
![]() $K$
as above. Then
$K$
as above. Then
 $\unicode[STIX]{x1D712}_{n}\unicode[STIX]{x1D711}\rightarrow \unicode[STIX]{x1D711}$
in
$\unicode[STIX]{x1D712}_{n}\unicode[STIX]{x1D711}\rightarrow \unicode[STIX]{x1D711}$
in
![]() $H^{1}(M)$
since the area of the set of
$H^{1}(M)$
since the area of the set of
![]() $x\in K$
with
$x\in K$
with
 $1/n\leqslant d(x,\unicode[STIX]{x2202}M)\leqslant 2/n$
, which contains
$1/n\leqslant d(x,\unicode[STIX]{x2202}M)\leqslant 2/n$
, which contains
 $K\cap \operatorname{supp}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D712}_{n}$
, is bounded by
$K\cap \operatorname{supp}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D712}_{n}$
, is bounded by
![]() $A/n$
for some constant
$A/n$
for some constant
![]() $A$
and since
$A$
and since
 $\unicode[STIX]{x1D711}\leqslant 2B/n$
on this set, where
$\unicode[STIX]{x1D711}\leqslant 2B/n$
on this set, where
![]() $B$
is a Lipschitz constant for
$B$
is a Lipschitz constant for
![]() $\unicode[STIX]{x1D711}$
. This reduces the assertion of Lemma 3.2 to the case where the support of
$\unicode[STIX]{x1D711}$
. This reduces the assertion of Lemma 3.2 to the case where the support of
![]() $\unicode[STIX]{x1D711}$
is contained in
$\unicode[STIX]{x1D711}$
is contained in
![]() $\mathring{M}$
. In this case, the assertion follows from smoothing.◻
$\mathring{M}$
. In this case, the assertion follows from smoothing.◻
As in the introduction, let
 $\unicode[STIX]{x1D706}_{0}(M)=\inf R(\unicode[STIX]{x1D711})$
, where the infimum is taken over all non-zero
$\unicode[STIX]{x1D706}_{0}(M)=\inf R(\unicode[STIX]{x1D711})$
, where the infimum is taken over all non-zero
 $\unicode[STIX]{x1D711}\in C_{cc}^{\infty }(M)$
. Since
$\unicode[STIX]{x1D711}\in C_{cc}^{\infty }(M)$
. Since
![]() $R$
is continuous on
$R$
is continuous on
 $H_{0}^{1}(M)\setminus \{0\}$
and
$H_{0}^{1}(M)\setminus \{0\}$
and
 $C_{cc}^{\infty }(M)$
is dense in
$C_{cc}^{\infty }(M)$
is dense in
![]() $H_{0}^{1}(M)$
, we have
$H_{0}^{1}(M)$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}(M)=\inf \{R(\unicode[STIX]{x1D711})\mid \unicode[STIX]{x1D711}\in H_{0}^{1}(M)\setminus \{0\}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}(M)=\inf \{R(\unicode[STIX]{x1D711})\mid \unicode[STIX]{x1D711}\in H_{0}^{1}(M)\setminus \{0\}\}.\end{eqnarray}$$
Hence
![]() $\unicode[STIX]{x1D706}_{0}(M)$
is the bottom of the spectrum of the Laplacian. By the definition of
$\unicode[STIX]{x1D706}_{0}(M)$
is the bottom of the spectrum of the Laplacian. By the definition of
![]() $\unicode[STIX]{x1D706}_{0}$
, we also have domain monotonicity,
$\unicode[STIX]{x1D706}_{0}$
, we also have domain monotonicity,
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}(M)\geqslant \unicode[STIX]{x1D706}_{0}(M^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}(M)\geqslant \unicode[STIX]{x1D706}_{0}(M^{\prime })\end{eqnarray}$$
for any Riemannian manifold
![]() $M^{\prime }$
containing
$M^{\prime }$
containing
![]() $M$
.
$M$
.
Lemma 3.5. A non-zero
 $\unicode[STIX]{x1D711}\in H_{0}^{1}(M)$
satisfies
$\unicode[STIX]{x1D711}\in H_{0}^{1}(M)$
satisfies
 $R(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D706}_{0}(M)$
if and only if
$R(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D706}_{0}(M)$
if and only if
![]() $\unicode[STIX]{x1D711}$
is an eigenfunction of the Laplacian with eigenvalue
$\unicode[STIX]{x1D711}$
is an eigenfunction of the Laplacian with eigenvalue
![]() $\unicode[STIX]{x1D706}_{0}(M)$
.
$\unicode[STIX]{x1D706}_{0}(M)$
.
Proof. By the spectral theorem, we may represent
![]() $L^{2}(M)$
as the space
$L^{2}(M)$
as the space
![]() $L^{2}(X)$
of square-integrable functions on a measured space
$L^{2}(X)$
of square-integrable functions on a measured space
![]() $X$
such that
$X$
such that
![]() $\unicode[STIX]{x1D6E5}$
corresponds to multiplication by a measurable function
$\unicode[STIX]{x1D6E5}$
corresponds to multiplication by a measurable function
![]() $f$
on
$f$
on
![]() $X$
. By the definition of
$X$
. By the definition of
![]() $\unicode[STIX]{x1D706}_{0}(M)$
, we have
$\unicode[STIX]{x1D706}_{0}(M)$
, we have
 $f\geqslant \unicode[STIX]{x1D706}_{0}(M)\geqslant 0$
almost everywhere on
$f\geqslant \unicode[STIX]{x1D706}_{0}(M)\geqslant 0$
almost everywhere on
![]() $X$
.◻
$X$
.◻
For a self-adjoint operator
![]() $A$
on a Hilbert space
$A$
on a Hilbert space
![]() $H$
, the spectrum
$H$
, the spectrum
![]() $\operatorname{spec}A$
of
$\operatorname{spec}A$
of
![]() $A$
can be decomposed in several ways. By definition, the essential spectrum
$A$
can be decomposed in several ways. By definition, the essential spectrum
 $\operatorname{spec}_{\text{ess}}A\subseteq \operatorname{spec}A$
consists of all
$\operatorname{spec}_{\text{ess}}A\subseteq \operatorname{spec}A$
consists of all
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D706}\in \mathbb{R}$
such that
 $A-\unicode[STIX]{x1D706}\operatorname{id}$
is not a Fredholm operator. The discrete spectrum
$A-\unicode[STIX]{x1D706}\operatorname{id}$
is not a Fredholm operator. The discrete spectrum
![]() $\operatorname{spec}_{d}A$
is the complement,
$\operatorname{spec}_{d}A$
is the complement,
 $$\begin{eqnarray}\operatorname{spec}_{d}A=\operatorname{spec}A\setminus \operatorname{spec}_{\text{ess}}A.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{spec}_{d}A=\operatorname{spec}A\setminus \operatorname{spec}_{\text{ess}}A.\end{eqnarray}$$
The discrete spectrum consists of eigenvalues of finite multiplicity of
![]() $A$
which are isolated points of
$A$
which are isolated points of
![]() $\operatorname{spec}A$
. The essential spectrum is a closed subset of
$\operatorname{spec}A$
. The essential spectrum is a closed subset of
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
The following result shows that the essential spectrum of the Laplacian only depends on the geometry of the underlying manifold at infinity and that the essential spectrum of the Laplacian is empty if
![]() $M$
is compact.
$M$
is compact.
Proposition 3.6. For a complete Riemannian manifold
![]() $M$
with compact boundary (possibly empty),
$M$
with compact boundary (possibly empty),
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}$
belongs to the essential spectrum of
$\unicode[STIX]{x1D706}\in \mathbb{R}$
belongs to the essential spectrum of
![]() $\unicode[STIX]{x1D6E5}$
if and only if there is a
$\unicode[STIX]{x1D6E5}$
if and only if there is a
 $\text{Weyl sequence}$
for
$\text{Weyl sequence}$
for
![]() $\unicode[STIX]{x1D706}$
, that is, a sequence of functions
$\unicode[STIX]{x1D706}$
, that is, a sequence of functions
![]() $\unicode[STIX]{x1D711}_{n}$
in
$\unicode[STIX]{x1D711}_{n}$
in
 $C_{cc}^{\infty }(M)$
such that:
$C_{cc}^{\infty }(M)$
such that:
-
(i) for any compact
 $K\subseteq M$
,
$K\subseteq M$
,
 $\operatorname{supp}\unicode[STIX]{x1D711}_{n}\cap K=\emptyset$
for all sufficiently large
$\operatorname{supp}\unicode[STIX]{x1D711}_{n}\cap K=\emptyset$
for all sufficiently large
 $n$
;
$n$
; -
(ii)
 $\limsup _{n\rightarrow \infty }\Vert \unicode[STIX]{x1D711}_{n}\Vert _{2}>0$
and
$\limsup _{n\rightarrow \infty }\Vert \unicode[STIX]{x1D711}_{n}\Vert _{2}>0$
and
 $\lim _{n\rightarrow \infty }\Vert \unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}_{n}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}_{n}\Vert _{2}=0$
.
$\lim _{n\rightarrow \infty }\Vert \unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}_{n}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}_{n}\Vert _{2}=0$
.
Proof. See the elementary argument in [Reference BärBär00, proof of Proposition 1]. ◻
Examples 3.7.
-
(i) Let
 $F=\{(x,y)\mid x\geqslant 0,y\in \mathbb{R}/L\mathbb{Z}\}$
be a funnel with the expanding hyperbolic metric
$F=\{(x,y)\mid x\geqslant 0,y\in \mathbb{R}/L\mathbb{Z}\}$
be a funnel with the expanding hyperbolic metric
 $dx^{2}+\cosh (x)^{2}\,dy^{2}$
. Let
$dx^{2}+\cosh (x)^{2}\,dy^{2}$
. Let
 $\unicode[STIX]{x1D705}:\mathbb{R}\rightarrow \mathbb{R}$
be a monotonic smooth function with
$\unicode[STIX]{x1D705}:\mathbb{R}\rightarrow \mathbb{R}$
be a monotonic smooth function with
 $\unicode[STIX]{x1D705}(x)=-1$
for
$\unicode[STIX]{x1D705}(x)=-1$
for
 $x\leqslant 1$
and
$x\leqslant 1$
and
 $\unicode[STIX]{x1D705}(x)\rightarrow -\infty$
as
$\unicode[STIX]{x1D705}(x)\rightarrow -\infty$
as
 $x\rightarrow \infty$
. Suppose that
$x\rightarrow \infty$
. Suppose that
 $j:\mathbb{R}\rightarrow \mathbb{R}$
solves
$j:\mathbb{R}\rightarrow \mathbb{R}$
solves
 $j^{\prime \prime }+\unicode[STIX]{x1D705}j=0$
with initial condition
$j^{\prime \prime }+\unicode[STIX]{x1D705}j=0$
with initial condition
 $j(0)=1$
and
$j(0)=1$
and
 $j^{\prime }(0)=0$
. Then
$j^{\prime }(0)=0$
. Then
 $j(x)>\cosh x$
for all
$j(x)>\cosh x$
for all
 $x>1$
. Furthermore, the funnel
$x>1$
. Furthermore, the funnel
 $F$
with Riemannian metric
$F$
with Riemannian metric
 $g=dx^{2}+j(x)^{2}\,dy^{2}$
has curvature
$g=dx^{2}+j(x)^{2}\,dy^{2}$
has curvature
 $K(x,y)=\unicode[STIX]{x1D705}(x)\leqslant -1$
and infinite area. By comparison, the Rayleigh quotient with respect to
$K(x,y)=\unicode[STIX]{x1D705}(x)\leqslant -1$
and infinite area. By comparison, the Rayleigh quotient with respect to
 $g$
of any smooth function
$g$
of any smooth function
 $\unicode[STIX]{x1D711}$
with compact support in the part
$\unicode[STIX]{x1D711}$
with compact support in the part
 $\{x\geqslant x_{0}\}$
of the funnel is at least
$\{x\geqslant x_{0}\}$
of the funnel is at least
 $-\unicode[STIX]{x1D705}(x_{0})/4$
.
$-\unicode[STIX]{x1D705}(x_{0})/4$
.Let
 $S$
be a non-compact surface of finite type. Endow
$S$
be a non-compact surface of finite type. Endow
 $S$
with a hyperbolic metric which is expanding along its funnels as above. Replace the hyperbolic metric on the funnels by the above Riemannian metric
$S$
with a hyperbolic metric which is expanding along its funnels as above. Replace the hyperbolic metric on the funnels by the above Riemannian metric
 $g$
. Then the new Riemannian metric on
$g$
. Then the new Riemannian metric on
 $S$
is complete with curvature
$S$
is complete with curvature
 $K\leqslant -1$
and infinite area. By Proposition 3.6 and by what we said above about the Rayleigh quotients, the essential spectrum of the new Riemannian metric is empty. Hence the eigenspaces of the new metric are finite dimensional and span
$K\leqslant -1$
and infinite area. By Proposition 3.6 and by what we said above about the Rayleigh quotients, the essential spectrum of the new Riemannian metric is empty. Hence the eigenspaces of the new metric are finite dimensional and span
 $L^{2}(S)$
. Therefore
$L^{2}(S)$
. Therefore
 $S$
has infinitely many eigenvalues, and all of them have finite multiplicity.
$S$
has infinitely many eigenvalues, and all of them have finite multiplicity. -
(ii) As a variation of example (i), suppose now that
 $j$
is the unique solution of
$j$
is the unique solution of
 $j^{\prime \prime }+\unicode[STIX]{x1D705}j=0$
which satisfies the boundary condition
$j^{\prime \prime }+\unicode[STIX]{x1D705}j=0$
which satisfies the boundary condition
 $j(0)=1$
and
$j(0)=1$
and
 $j(\infty )=0$
. Then
$j(\infty )=0$
. Then
 $j^{\prime }(0)<-1$
and
$j^{\prime }(0)<-1$
and
 $j(x)<\exp (-x)$
for all
$j(x)<\exp (-x)$
for all
 $x>0$
. The funnel
$x>0$
. The funnel
 $F$
with Riemannian metric
$F$
with Riemannian metric
 $g=dx^{2}+j(x)^{2}\,dy^{2}$
has curvature
$g=dx^{2}+j(x)^{2}\,dy^{2}$
has curvature
 $K(x,y)=\unicode[STIX]{x1D705}(x)$
and finite area. Again by comparison, the Rayleigh quotient with respect to
$K(x,y)=\unicode[STIX]{x1D705}(x)$
and finite area. Again by comparison, the Rayleigh quotient with respect to
 $g$
of any smooth function
$g$
of any smooth function
 $\unicode[STIX]{x1D711}$
with compact support in the part
$\unicode[STIX]{x1D711}$
with compact support in the part
 $\{x\geqslant x_{0}\}$
of the funnel is at least
$\{x\geqslant x_{0}\}$
of the funnel is at least
 $-\unicode[STIX]{x1D705}(x_{0})/4$
.
$-\unicode[STIX]{x1D705}(x_{0})/4$
.Let
 $S$
be a non-compact surface of finite type, and choose
$S$
be a non-compact surface of finite type, and choose
 $r>0$
such that
$r>0$
such that
 $\coth (r)=-j^{\prime }(0)$
. It is not hard to see that
$\coth (r)=-j^{\prime }(0)$
. It is not hard to see that
 $S$
minus the parts
$S$
minus the parts
 $\{x\geqslant r\}$
of its funnels carries hyperbolic metrics which are equal to
$\{x\geqslant r\}$
of its funnels carries hyperbolic metrics which are equal to
 $dx^{2}+j_{0}(x)^{2}\,dy^{2}$
along the parts
$dx^{2}+j_{0}(x)^{2}\,dy^{2}$
along the parts
 $\{x<r\}$
of its funnels, where
$\{x<r\}$
of its funnels, where
 $j_{0}(x)=\sinh (r-x)/\sinh (r)$
. Then
$j_{0}(x)=\sinh (r-x)/\sinh (r)$
. Then
 $j_{0}(x)=j(x)$
for
$j_{0}(x)=j(x)$
for
 $x<\min \{1,r\}$
. Hence any such hyperbolic metric, restricted to
$x<\min \{1,r\}$
. Hence any such hyperbolic metric, restricted to
 $S$
minus the parts
$S$
minus the parts
 $\{x\geqslant \min \{1,r\}\}$
of its funnels, when combined with
$\{x\geqslant \min \{1,r\}\}$
of its funnels, when combined with
 $g$
along the funnels, defines a smooth and complete Riemannian metric on
$g$
along the funnels, defines a smooth and complete Riemannian metric on
 $S$
which has curvature
$S$
which has curvature
 $K\leqslant -1$
and finite area. Again, its essential spectrum is empty, by Proposition 3.6 and by what we said above about the Rayleigh quotients. Again we obtain that
$K\leqslant -1$
and finite area. Again, its essential spectrum is empty, by Proposition 3.6 and by what we said above about the Rayleigh quotients. Again we obtain that
 $S$
has infinitely many eigenvalues, and all of them have finite multiplicity.
$S$
has infinitely many eigenvalues, and all of them have finite multiplicity. -
(iii) Let
 $S$
be a complete non-compact hyperbolic surface without boundary. Replace a simple closed geodesic
$S$
be a complete non-compact hyperbolic surface without boundary. Replace a simple closed geodesic
 $c$
in
$c$
in
 $S$
by a Euclidean cylinder
$S$
by a Euclidean cylinder
 $C=\{(x,y)\mid 0\leqslant x\leqslant h,y\in \mathbb{R}/L\mathbb{Z}\}$
of height
$C=\{(x,y)\mid 0\leqslant x\leqslant h,y\in \mathbb{R}/L\mathbb{Z}\}$
of height
 $h$
and circumference
$h$
and circumference
 $L=L(c)$
and smooth out the resulting Riemannian metric appropriately. Let
$L=L(c)$
and smooth out the resulting Riemannian metric appropriately. Let
 $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(x)$
be a non-vanishing smooth function on
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(x)$
be a non-vanishing smooth function on
 $\mathbb{R}$
with support in
$\mathbb{R}$
with support in
 $[-1,0]$
. Then the support of
$[-1,0]$
. Then the support of
 $\unicode[STIX]{x1D711}_{k,i}=\unicode[STIX]{x1D711}(x/k-i)$
is in
$\unicode[STIX]{x1D711}_{k,i}=\unicode[STIX]{x1D711}(x/k-i)$
is in
 $[(i-1)k,ik]$
and the Rayleigh quotient of
$[(i-1)k,ik]$
and the Rayleigh quotient of
 $\unicode[STIX]{x1D711}_{k,i}$
is
$\unicode[STIX]{x1D711}_{k,i}$
is
 $R(\unicode[STIX]{x1D711})/k^{2}$
. Hence, given
$R(\unicode[STIX]{x1D711})/k^{2}$
. Hence, given
 $\unicode[STIX]{x1D700}>0$
, we have
$\unicode[STIX]{x1D700}>0$
, we have
 $R(\unicode[STIX]{x1D711}_{k,i})<\unicode[STIX]{x1D700}$
if
$R(\unicode[STIX]{x1D711}_{k,i})<\unicode[STIX]{x1D700}$
if
 $k^{2}>R(\unicode[STIX]{x1D711})/\unicode[STIX]{x1D700}$
. We may also view
$k^{2}>R(\unicode[STIX]{x1D711})/\unicode[STIX]{x1D700}$
. We may also view
 $\unicode[STIX]{x1D711}_{k,i}$
as a smooth function on the cylinder
$\unicode[STIX]{x1D711}_{k,i}$
as a smooth function on the cylinder
 $C$
and the surface
$C$
and the surface
 $S$
if
$S$
if
 $h$
is sufficiently large. More specifically, given
$h$
is sufficiently large. More specifically, given
 $n$
, choose
$n$
, choose
 $h>nk$
. Then the functions
$h>nk$
. Then the functions
 $\unicode[STIX]{x1D711}_{k,1},\ldots ,\unicode[STIX]{x1D711}_{k,n}$
have disjoint supports in
$\unicode[STIX]{x1D711}_{k,1},\ldots ,\unicode[STIX]{x1D711}_{k,n}$
have disjoint supports in
 $C$
and Rayleigh quotients less than
$C$
and Rayleigh quotients less than
 $\unicode[STIX]{x1D700}$
. Hence
$\unicode[STIX]{x1D700}$
. Hence
 $S$
has at least
$S$
has at least
 $n$
eigenvalues which are less than
$n$
eigenvalues which are less than
 $\unicode[STIX]{x1D700}$
. Since
$\unicode[STIX]{x1D700}$
. Since
 $C$
is a cylinder, we also have
$C$
is a cylinder, we also have
 $\unicode[STIX]{x1D6EC}(S)<\unicode[STIX]{x1D700}$
. On the other hand, the essential spectrum of
$\unicode[STIX]{x1D6EC}(S)<\unicode[STIX]{x1D700}$
. On the other hand, the essential spectrum of
 $S$
is still contained in
$S$
is still contained in
 $[1/4,\infty )$
, by Proposition 3.6 and the special geometry of the ends of
$[1/4,\infty )$
, by Proposition 3.6 and the special geometry of the ends of
 $S$
.
$S$
.
Proposition 3.8. For a complete Riemannian metric on a surface
![]() $S$
, we have
$S$
, we have
 $\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
. If
$\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
. If
![]() $S$
is of finite type, then
$S$
is of finite type, then
 $\unicode[STIX]{x1D6EC}(S)\leqslant \unicode[STIX]{x1D706}_{\text{ess}}(S)$
.
$\unicode[STIX]{x1D6EC}(S)\leqslant \unicode[STIX]{x1D706}_{\text{ess}}(S)$
.
Proof. Since the ends of surfaces of finite type are funnels and funnels are diffeomorphic to annuli, we have
 $\unicode[STIX]{x1D6EC}(S)\leqslant \unicode[STIX]{x1D706}_{\text{ess}}(S)$
if
$\unicode[STIX]{x1D6EC}(S)\leqslant \unicode[STIX]{x1D706}_{\text{ess}}(S)$
if
![]() $S$
is of finite type.
$S$
is of finite type.
Under a Riemannian covering of complete and connected Riemannian manifolds, the bottom of the spectrum of the covered manifold is at most the bottom of the spectrum of the covering manifold; see e.g. [Reference BrooksBro85, p. 101]. Brooks showed that, under a normal Riemannian covering of complete and connected Riemannian manifolds with an amenable group of covering transformations, the bottom of the spectrum does not change, provided that the covered manifold is of finite topological type [Reference BrooksBro85, Theorem 1]. The relevant arguments of Brooks in [Reference BrooksBro85, proof of Theorem 1] and of Sullivan in [Reference SullivanSul87, proof of Theorem 2.1] remain valid in the more general case of complete Riemannian manifolds of finite topological type with boundary.
Now in our setting, embedded discs in
![]() $S$
lift to embedded discs in
$S$
lift to embedded discs in
![]() $\tilde{S}$
and embedded annuli and cross caps in
$\tilde{S}$
and embedded annuli and cross caps in
![]() $S$
lift to embedded annuli and cross caps in cyclic subcoverings
$S$
lift to embedded annuli and cross caps in cyclic subcoverings
![]() $\bar{S}$
of
$\bar{S}$
of
![]() $\tilde{S}$
. Moreover,
$\tilde{S}$
. Moreover,
![]() $\bar{S}$
is either an annulus or a cross cap, in particular of finite topological type. For any such
$\bar{S}$
is either an annulus or a cross cap, in particular of finite topological type. For any such
![]() $\bar{S}$
, we have
$\bar{S}$
, we have
 $\unicode[STIX]{x1D706}_{0}(\bar{S})=\unicode[STIX]{x1D706}_{0}(\tilde{S})$
since cyclic groups are amenable. Hence
$\unicode[STIX]{x1D706}_{0}(\bar{S})=\unicode[STIX]{x1D706}_{0}(\tilde{S})$
since cyclic groups are amenable. Hence
 $\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
by the definition of
$\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
by the definition of
![]() $\unicode[STIX]{x1D6EC}(S)$
.◻
$\unicode[STIX]{x1D6EC}(S)$
.◻
For a discussion concerning the strictness of the inequality
 $\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
, we refer to [Reference Ballmann, Matthiesen and MondalBMM16b].
$\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
, we refer to [Reference Ballmann, Matthiesen and MondalBMM16b].
We finish this section by discussing the proof of Theorem 1.7.
Proof of Theorem 1.7.
Recall that non-zero eigenfunctions of the Laplacian cannot vanish of infinite order at any point; see e.g. [Reference AronszajnAro57]. Hence by the main result of [Reference BersBer55], at any critical point
 $z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
of
$z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
of
![]() $\unicode[STIX]{x1D711}$
, there are Riemannian normal coordinates
$\unicode[STIX]{x1D711}$
, there are Riemannian normal coordinates
![]() $(x,y)$
about
$(x,y)$
about
![]() $z$
, a spherical harmonic
$z$
, a spherical harmonic
 $p=p(x,y)\neq 0$
of some order
$p=p(x,y)\neq 0$
of some order
![]() $n\geqslant 2$
, and a constant
$n\geqslant 2$
, and a constant
 $\unicode[STIX]{x1D6FC}\in (0,1)$
such that
$\unicode[STIX]{x1D6FC}\in (0,1)$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x,y)=p(x,y)+O(r^{n+\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x,y)=p(x,y)+O(r^{n+\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
where we write
 $(x,y)=(r\cos \unicode[STIX]{x1D703},r\sin \unicode[STIX]{x1D703})$
. By [Reference ChengChe76, Lemma 2.4], there is a local
$(x,y)=(r\cos \unicode[STIX]{x1D703},r\sin \unicode[STIX]{x1D703})$
. By [Reference ChengChe76, Lemma 2.4], there is a local
![]() $C^{1}$
-diffeomorphism
$C^{1}$
-diffeomorphism
![]() $\unicode[STIX]{x1D6F7}$
about
$\unicode[STIX]{x1D6F7}$
about
![]() $0\in \mathbb{R}^{2}$
fixing 0 such that
$0\in \mathbb{R}^{2}$
fixing 0 such that
 $\unicode[STIX]{x1D711}=p\circ \unicode[STIX]{x1D6F7}$
. Note that, up to a rotation of the
$\unicode[STIX]{x1D711}=p\circ \unicode[STIX]{x1D6F7}$
. Note that, up to a rotation of the
![]() $(x,y)$
-plane, we have
$(x,y)$
-plane, we have
 $$\begin{eqnarray}p=p(x,y)=cr^{n}\cos n\unicode[STIX]{x1D703}\end{eqnarray}$$
$$\begin{eqnarray}p=p(x,y)=cr^{n}\cos n\unicode[STIX]{x1D703}\end{eqnarray}$$
for some constant
![]() $c\neq 0$
. It follows that the interior nodal set
$c\neq 0$
. It follows that the interior nodal set
![]() $Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
of
$Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
of
![]() $\unicode[STIX]{x1D711}$
is a locally finite graph with critical points of
$\unicode[STIX]{x1D711}$
is a locally finite graph with critical points of
![]() $\unicode[STIX]{x1D711}$
as vertices and that the valence of points on
$\unicode[STIX]{x1D711}$
as vertices and that the valence of points on
![]() $Z_{\unicode[STIX]{x1D711}}$
is as asserted.
$Z_{\unicode[STIX]{x1D711}}$
is as asserted.
It remains to discuss points
 $z\in Z_{\unicode[STIX]{x1D711}}\cap \unicode[STIX]{x2202}S$
. Since
$z\in Z_{\unicode[STIX]{x1D711}}\cap \unicode[STIX]{x2202}S$
. Since
 $\dim S=2$
, there are isothermal coordinates around
$\dim S=2$
, there are isothermal coordinates around
![]() $z$
, that is, coordinates
$z$
, that is, coordinates
![]() $(x,y)$
about
$(x,y)$
about
![]() $z$
in which the Riemannian metric
$z$
in which the Riemannian metric
![]() $g$
of
$g$
of
![]() $S$
is conformal to the Euclidean metric
$S$
is conformal to the Euclidean metric
![]() $g_{0}$
:
$g_{0}$
:
 $g=fg_{0}$
with
$g=fg_{0}$
with
 $f=f(x,y)>0$
. Then, again since
$f=f(x,y)>0$
. Then, again since
 $\dim S=2$
, the associated Laplacians satisfy
$\dim S=2$
, the associated Laplacians satisfy
 $f\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{0}$
, and hence
$f\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{0}$
, and hence
![]() $\unicode[STIX]{x1D711}$
solves the Schrödinger equation
$\unicode[STIX]{x1D711}$
solves the Schrödinger equation
 $(\unicode[STIX]{x1D6E5}_{0}+fV)\unicode[STIX]{x1D711}=0$
in the domain of the coordinates.
$(\unicode[STIX]{x1D6E5}_{0}+fV)\unicode[STIX]{x1D711}=0$
in the domain of the coordinates.
After an appropriate further conformal change of the coordinates, we can assume that the domain of the coordinates is
 $B_{\unicode[STIX]{x1D700}}(0)\cap \{y\geqslant 0\}$
such that
$B_{\unicode[STIX]{x1D700}}(0)\cap \{y\geqslant 0\}$
such that
![]() $\unicode[STIX]{x2202}S$
corresponds to
$\unicode[STIX]{x2202}S$
corresponds to
 $B_{\unicode[STIX]{x1D700}}(0)\cap \{y=0\}$
. We consider
$B_{\unicode[STIX]{x1D700}}(0)\cap \{y=0\}$
. We consider
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
 $W=fV$
as functions on
$W=fV$
as functions on
 $B^{+}=B_{\unicode[STIX]{x1D700}}(0)\cap \{y\geqslant 0\}$
, where
$B^{+}=B_{\unicode[STIX]{x1D700}}(0)\cap \{y\geqslant 0\}$
, where
 $\unicode[STIX]{x1D711}(x,0)=0$
, and extend them to functions on
$\unicode[STIX]{x1D711}(x,0)=0$
, and extend them to functions on
![]() $B_{\unicode[STIX]{x1D700}}(0)$
by setting
$B_{\unicode[STIX]{x1D700}}(0)$
by setting
 $\unicode[STIX]{x1D711}(x,y)=-\unicode[STIX]{x1D711}(x,-y)$
and
$\unicode[STIX]{x1D711}(x,y)=-\unicode[STIX]{x1D711}(x,-y)$
and
 $W(x,-y)=W(x,y)$
. Then
$W(x,-y)=W(x,y)$
. Then
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $W$
are
$W$
are
![]() $C^{1,1}$
and
$C^{1,1}$
and
![]() $C^{0,1}$
on
$C^{0,1}$
on
![]() $B_{\unicode[STIX]{x1D700}}(0)$
, respectively, and
$B_{\unicode[STIX]{x1D700}}(0)$
, respectively, and
![]() $\unicode[STIX]{x1D711}$
solves
$\unicode[STIX]{x1D711}$
solves
 $(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}=0$
in
$(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}=0$
in
![]() $B^{+}$
. Since the reflection about the
$B^{+}$
. Since the reflection about the
![]() $x$
-axis is an isometry of the Euclidean plane, we also have
$x$
-axis is an isometry of the Euclidean plane, we also have
 $(\unicode[STIX]{x1D6E5}_{0}\unicode[STIX]{x1D711})(x,y)=-(\unicode[STIX]{x1D6E5}_{0}\unicode[STIX]{x1D711})(x,-y)$
. Hence
$(\unicode[STIX]{x1D6E5}_{0}\unicode[STIX]{x1D711})(x,y)=-(\unicode[STIX]{x1D6E5}_{0}\unicode[STIX]{x1D711})(x,-y)$
. Hence
 $$\begin{eqnarray}(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}(x,y)=-(\unicode[STIX]{x1D6E5}_{0}\unicode[STIX]{x1D711})(x,-y)-W(x,y)\unicode[STIX]{x1D711}(x,-y)=0\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}(x,y)=-(\unicode[STIX]{x1D6E5}_{0}\unicode[STIX]{x1D711})(x,-y)-W(x,y)\unicode[STIX]{x1D711}(x,-y)=0\end{eqnarray}$$
in
 $B^{-}=B_{\unicode[STIX]{x1D700}}(0)\cap \{y\leqslant 0\}$
. Since
$B^{-}=B_{\unicode[STIX]{x1D700}}(0)\cap \{y\leqslant 0\}$
. Since
![]() $\unicode[STIX]{x1D711}=0$
along the
$\unicode[STIX]{x1D711}=0$
along the
![]() $x$
-axis, all
$x$
-axis, all
![]() $x$
-derivatives of
$x$
-derivatives of
![]() $\unicode[STIX]{x1D711}$
vanish along the
$\unicode[STIX]{x1D711}$
vanish along the
![]() $x$
-axis. Since
$x$
-axis. Since
![]() $\unicode[STIX]{x1D711}$
solves
$\unicode[STIX]{x1D711}$
solves
 $(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}=0$
, the second derivative of
$(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}=0$
, the second derivative of
![]() $\unicode[STIX]{x1D711}$
in the
$\unicode[STIX]{x1D711}$
in the
![]() $y$
-direction vanishes along the
$y$
-direction vanishes along the
![]() $x$
-axis as well, and hence
$x$
-axis as well, and hence
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() $C^{2,1}$
. We conclude that
$C^{2,1}$
. We conclude that
![]() $\unicode[STIX]{x1D711}$
is a strong solution of
$\unicode[STIX]{x1D711}$
is a strong solution of
 $(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}=0$
on
$(\unicode[STIX]{x1D6E5}_{0}+W)\unicode[STIX]{x1D711}=0$
on
![]() $B_{\unicode[STIX]{x1D700}}(0)$
, and hence the main result of [Reference BersBer55] and [Reference ChengChe76, proof of Lemma 2.4] applies. The remaining assertions follow as in the case of
$B_{\unicode[STIX]{x1D700}}(0)$
, and hence the main result of [Reference BersBer55] and [Reference ChengChe76, proof of Lemma 2.4] applies. The remaining assertions follow as in the case of
 $z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
above.◻
$z\in Z_{\unicode[STIX]{x1D711}}\cap \mathring{S}$
above.◻
We learned from [Reference Helffer, Hoffmann-Ostenhof and TerraciniHHT09, proof of Theorem 2.3] that the reflection about the
![]() $x$
-axis in the Euclidean plane, which we use in the second part of the above proof, might be helpful in the discussion of the boundary regularity of solutions of Schrödinger equations.
$x$
-axis in the Euclidean plane, which we use in the second part of the above proof, might be helpful in the discussion of the boundary regularity of solutions of Schrödinger equations.
4 Estimating the number of small eigenvalues
Throughout this section, let
![]() $\unicode[STIX]{x1D711}$
be a non-vanishing square-integrable smooth function on
$\unicode[STIX]{x1D711}$
be a non-vanishing square-integrable smooth function on
![]() $S$
which is a finite linear combination of eigenfunctions with eigenvalues less than or equal to
$S$
which is a finite linear combination of eigenfunctions with eigenvalues less than or equal to
![]() $\unicode[STIX]{x1D6EC}(S)$
. The set of zeros of
$\unicode[STIX]{x1D6EC}(S)$
. The set of zeros of
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
 $$\begin{eqnarray}Z_{\unicode[STIX]{x1D711}}:=\{x\in S\mid \unicode[STIX]{x1D711}(x)=0\},\end{eqnarray}$$
$$\begin{eqnarray}Z_{\unicode[STIX]{x1D711}}:=\{x\in S\mid \unicode[STIX]{x1D711}(x)=0\},\end{eqnarray}$$
is called the nodal set of
![]() $\unicode[STIX]{x1D711}$
. The connected components of the complement
$\unicode[STIX]{x1D711}$
. The connected components of the complement
![]() $S\setminus Z_{\unicode[STIX]{x1D711}}$
are called nodal domains of
$S\setminus Z_{\unicode[STIX]{x1D711}}$
are called nodal domains of
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
We say that
![]() $\unicode[STIX]{x1D700}>0$
is
$\unicode[STIX]{x1D700}>0$
is
![]() $\unicode[STIX]{x1D711}$
-regular, if
$\unicode[STIX]{x1D711}$
-regular, if
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $-\unicode[STIX]{x1D700}$
are regular values of
$-\unicode[STIX]{x1D700}$
are regular values of
![]() $\unicode[STIX]{x1D711}$
. For any
$\unicode[STIX]{x1D711}$
. For any
![]() $\unicode[STIX]{x1D700}>0$
, we call
$\unicode[STIX]{x1D700}>0$
, we call
 $$\begin{eqnarray}Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}):=\{x\in S\mid |\unicode[STIX]{x1D711}(x)|\leqslant \unicode[STIX]{x1D700}\}\end{eqnarray}$$
$$\begin{eqnarray}Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}):=\{x\in S\mid |\unicode[STIX]{x1D711}(x)|\leqslant \unicode[STIX]{x1D700}\}\end{eqnarray}$$
the
![]() $\unicode[STIX]{x1D700}$
-nodal set of
$\unicode[STIX]{x1D700}$
-nodal set of
![]() $\unicode[STIX]{x1D711}$
. We are only interested in the case where
$\unicode[STIX]{x1D711}$
. We are only interested in the case where
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
![]() $\unicode[STIX]{x1D711}$
-regular. Then
$\unicode[STIX]{x1D711}$
-regular. Then
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is a subsurface of
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is a subsurface of
![]() $S$
with smooth boundary, may consist of more than one component, and the boundary components of
$S$
with smooth boundary, may consist of more than one component, and the boundary components of
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
are embedded smooth circles and lines along which
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
are embedded smooth circles and lines along which
![]() $\unicode[STIX]{x1D711}$
is constant
$\unicode[STIX]{x1D711}$
is constant
![]() $\pm \unicode[STIX]{x1D700}$
.
$\pm \unicode[STIX]{x1D700}$
.
Lemma 4.3. For any
![]() $\unicode[STIX]{x1D711}$
-regular
$\unicode[STIX]{x1D711}$
-regular
![]() $\unicode[STIX]{x1D700}>0$
, consider the function
$\unicode[STIX]{x1D700}>0$
, consider the function
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D711}(x)-\unicode[STIX]{x1D700}\quad & \text{if}~\unicode[STIX]{x1D711}(x)\geqslant \unicode[STIX]{x1D700},\\ \unicode[STIX]{x1D711}(x)+\unicode[STIX]{x1D700}\quad & \text{if}~\unicode[STIX]{x1D711}(x)\leqslant -\unicode[STIX]{x1D700},\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D711}(x)-\unicode[STIX]{x1D700}\quad & \text{if}~\unicode[STIX]{x1D711}(x)\geqslant \unicode[STIX]{x1D700},\\ \unicode[STIX]{x1D711}(x)+\unicode[STIX]{x1D700}\quad & \text{if}~\unicode[STIX]{x1D711}(x)\leqslant -\unicode[STIX]{x1D700},\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}\in H^{1}(M)$
and
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}\in H^{1}(M)$
and
 $\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
in
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
in
![]() $H^{1}(M)$
.
$H^{1}(M)$
.
Proof. For all
![]() $x\in S$
, we have
$x\in S$
, we have
 $|\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)|\leqslant |\unicode[STIX]{x1D711}(x)|$
. Hence
$|\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)|\leqslant |\unicode[STIX]{x1D711}(x)|$
. Hence
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
is in
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
is in
![]() $L^{2}(M)$
. Moreover,
$L^{2}(M)$
. Moreover,
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)\rightarrow \unicode[STIX]{x1D711}(x)$
, and hence
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)\rightarrow \unicode[STIX]{x1D711}(x)$
, and hence
 $\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
in
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
in
![]() $L^{2}(M)$
. Furthermore,
$L^{2}(M)$
. Furthermore,
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
has weak gradient
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
has weak gradient
 $$\begin{eqnarray}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}(x)\quad & \text{if}~|\unicode[STIX]{x1D711}(x)|\geqslant \unicode[STIX]{x1D700},\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}(x)\quad & \text{if}~|\unicode[STIX]{x1D711}(x)|\geqslant \unicode[STIX]{x1D700},\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
It follows that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
is in
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
is in
![]() $H^{1}(M)$
.
$H^{1}(M)$
.
As for the claim about the
![]() $H^{1}$
-convergence
$H^{1}$
-convergence
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}\rightarrow \unicode[STIX]{x1D711}$
, we note that
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}\rightarrow \unicode[STIX]{x1D711}$
, we note that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
on
 $S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
and that the family of sets
$S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
and that the family of sets
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is nested with
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is nested with
 $\bigcap _{\unicode[STIX]{x1D700}>0}Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})=Z_{\unicode[STIX]{x1D711}}$
. Moreover,
$\bigcap _{\unicode[STIX]{x1D700}>0}Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})=Z_{\unicode[STIX]{x1D711}}$
. Moreover,
![]() $\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
vanishes on
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}$
vanishes on
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. On the other hand, with respect to the area element of
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. On the other hand, with respect to the area element of
![]() $S$
, the set of points of density of
$S$
, the set of points of density of
![]() $Z_{\unicode[STIX]{x1D711}}$
has full measure in
$Z_{\unicode[STIX]{x1D711}}$
has full measure in
![]() $Z_{\unicode[STIX]{x1D711}}$
and
$Z_{\unicode[STIX]{x1D711}}$
and
 $\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}(x)=0$
in any such point. It follows that
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}(x)=0$
in any such point. It follows that
 $\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}$
in
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}$
in
![]() $L^{2}(M)$
and hence that
$L^{2}(M)$
and hence that
 $\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
in
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}$
in
![]() $H^{1}(M)$
.◻
$H^{1}(M)$
.◻
In what follows, we assume throughout that
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
![]() $\unicode[STIX]{x1D711}$
-regular. We say that a disc
$\unicode[STIX]{x1D711}$
-regular. We say that a disc
![]() $D$
in
$D$
in
![]() $S$
is an
$S$
is an
![]() $\unicode[STIX]{x1D700}$
-disc if
$\unicode[STIX]{x1D700}$
-disc if
![]() $D$
is closed in
$D$
is closed in
![]() $S$
and
$S$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D711}=+\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})>0\quad \text{or}\quad \unicode[STIX]{x1D711}=-\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})<0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}=+\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})>0\quad \text{or}\quad \unicode[STIX]{x1D711}=-\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})<0\end{eqnarray}$$
along the boundary circle
![]() $\unicode[STIX]{x2202}D$
of
$\unicode[STIX]{x2202}D$
of
![]() $D$
, where
$D$
, where
![]() $\unicode[STIX]{x1D708}$
denotes the outer normal of
$\unicode[STIX]{x1D708}$
denotes the outer normal of
![]() $D$
along
$D$
along
![]() $\unicode[STIX]{x2202}D$
. Note that, for an
$\unicode[STIX]{x2202}D$
. Note that, for an
![]() $\unicode[STIX]{x1D700}$
-disc
$\unicode[STIX]{x1D700}$
-disc
![]() $D$
, a neighborhood of
$D$
, a neighborhood of
![]() $\unicode[STIX]{x2202}D$
inside
$\unicode[STIX]{x2202}D$
inside
![]() $D$
is contained in
$D$
is contained in
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, whereas a neighborhood of
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, whereas a neighborhood of
![]() $\unicode[STIX]{x2202}D$
outside
$\unicode[STIX]{x2202}D$
outside
![]() $D$
belongs to
$D$
belongs to
 $\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
in the first case in (4.5) and
$\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
in the first case in (4.5) and
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
in the second.
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
in the second.
The boundary circles of
![]() $\unicode[STIX]{x1D700}$
-discs are components of
$\unicode[STIX]{x1D700}$
-discs are components of
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
. Since
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
. Since
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
![]() $\unicode[STIX]{x1D711}$
-regular, the normal derivative of
$\unicode[STIX]{x1D711}$
-regular, the normal derivative of
![]() $\unicode[STIX]{x1D711}$
has to be non-zero along
$\unicode[STIX]{x1D711}$
has to be non-zero along
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
. The requirements on the normal derivative in (4.5) fix its sign. As an example where these requirements do not hold, we note that components of
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
. The requirements on the normal derivative in (4.5) fix its sign. As an example where these requirements do not hold, we note that components of
 $\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
or
$\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
or
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
might be discs, but never
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
might be discs, but never
![]() $\unicode[STIX]{x1D700}$
-discs. On the other hand, any component of
$\unicode[STIX]{x1D700}$
-discs. On the other hand, any component of
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, which is a disc, is also an
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, which is a disc, is also an
![]() $\unicode[STIX]{x1D700}$
-disc.
$\unicode[STIX]{x1D700}$
-disc.
By Theorem 2.3, any component
![]() $C$
of
$C$
of
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, which is contained in the interior of a closed disc, is also contained in an
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, which is contained in the interior of a closed disc, is also contained in an
![]() $\unicode[STIX]{x1D700}$
-disc. More precisely, there is an
$\unicode[STIX]{x1D700}$
-disc. More precisely, there is an
![]() $\unicode[STIX]{x1D700}$
-disc
$\unicode[STIX]{x1D700}$
-disc
![]() $D$
such that
$D$
such that
 $\unicode[STIX]{x2202}D\subseteq \unicode[STIX]{x2202}C$
and such that
$\unicode[STIX]{x2202}D\subseteq \unicode[STIX]{x2202}C$
and such that
![]() $C$
is a neighborhood of
$C$
is a neighborhood of
![]() $\unicode[STIX]{x2202}D$
inside
$\unicode[STIX]{x2202}D$
inside
![]() $D$
. We let
$D$
. We let
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
be the union of
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
be the union of
 $S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
with all
$S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
with all
![]() $\unicode[STIX]{x1D700}$
-discs. Note that the union might not be disjoint since
$\unicode[STIX]{x1D700}$
-discs. Note that the union might not be disjoint since
![]() $\unicode[STIX]{x1D700}$
-discs might contain components of
$\unicode[STIX]{x1D700}$
-discs might contain components of
 $\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
and
$\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
and
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
.
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
.
Lemma 4.6.
-
(i) The subsurface
 $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the union of
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the union of
 $S\setminus \mathring{Z}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
with all components of
$S\setminus \mathring{Z}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
with all components of
 $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which are contained in the interior of closed discs in
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which are contained in the interior of closed discs in
 $S$
.
$S$
. -
(ii) The components of
 $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
are incompressible in
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
are incompressible in
 $S$
.
$S$
.
Proof. Part (i) follows immediately from what we said above. As for part (ii), suppose that there is a loop in a component
![]() $C$
of
$C$
of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which is not contractible in
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which is not contractible in
![]() $C$
, but is contractible in
$C$
, but is contractible in
![]() $S$
. Then there is an embedded circle
$S$
. Then there is an embedded circle
![]() $c$
in the interior of
$c$
in the interior of
![]() $C$
with that property. By Theorem 2.3, there is a closed disc
$C$
with that property. By Theorem 2.3, there is a closed disc
![]() $D$
in
$D$
in
![]() $S$
with
$S$
with
 $\unicode[STIX]{x2202}D=c$
. Since
$\unicode[STIX]{x2202}D=c$
. Since
![]() $c$
is not contractible in
$c$
is not contractible in
![]() $C$
, the interior of
$C$
, the interior of
![]() $D$
contains a component of
$D$
contains a component of
 $S\setminus Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. This contradicts part (i).◻
$S\setminus Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. This contradicts part (i).◻
The set of
![]() $\unicode[STIX]{x1D700}$
-discs is ordered by inclusion. It is important that we have maximal elements in this ordered set.
$\unicode[STIX]{x1D700}$
-discs is ordered by inclusion. It is important that we have maximal elements in this ordered set.
Lemma 4.7. If two
![]() $\unicode[STIX]{x1D700}$
-discs intersect, then they are either identical or one is contained in the interior of the other. Moreover, any
$\unicode[STIX]{x1D700}$
-discs intersect, then they are either identical or one is contained in the interior of the other. Moreover, any
![]() $\unicode[STIX]{x1D700}$
-disc is contained in a unique maximal
$\unicode[STIX]{x1D700}$
-disc is contained in a unique maximal
![]() $\unicode[STIX]{x1D700}$
-disc and maximal
$\unicode[STIX]{x1D700}$
-disc and maximal
![]() $\unicode[STIX]{x1D700}$
-discs are either identical or disjoint.
$\unicode[STIX]{x1D700}$
-discs are either identical or disjoint.
Proof. The first statement is clear since
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
![]() $\unicode[STIX]{x1D711}$
-regular.
$\unicode[STIX]{x1D711}$
-regular.
Fix an exhaustion of
![]() $S$
by compact subsurfaces
$S$
by compact subsurfaces
![]() $S_{n}$
such that
$S_{n}$
such that
![]() $S\setminus S_{n}$
consists of cylindrical neighborhoods of the ends of
$S\setminus S_{n}$
consists of cylindrical neighborhoods of the ends of
![]() $S$
and such that
$S$
and such that
![]() $\unicode[STIX]{x2202}S_{n}$
intersects the set
$\unicode[STIX]{x2202}S_{n}$
intersects the set
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
transversally. Then the boundary components of any
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
transversally. Then the boundary components of any
![]() $S_{n}$
are labeled by the ends of
$S_{n}$
are labeled by the ends of
![]() $S$
they belong to, any
$S$
they belong to, any
![]() $S_{n}$
meets only finitely many components of the set
$S_{n}$
meets only finitely many components of the set
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
, and the sets
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
, and the sets
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}\cap \unicode[STIX]{x2202}S_{n}$
are finite.
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}\cap \unicode[STIX]{x2202}S_{n}$
are finite.
Let
 $D_{1}\subseteq D_{2}\subseteq \cdots \,$
be an ascending chain of pairwise distinct
$D_{1}\subseteq D_{2}\subseteq \cdots \,$
be an ascending chain of pairwise distinct
![]() $\unicode[STIX]{x1D700}$
-discs. For
$\unicode[STIX]{x1D700}$
-discs. For
![]() $n$
sufficiently large, we have
$n$
sufficiently large, we have
 $D_{1}\subseteq S_{n}$
. Then
$D_{1}\subseteq S_{n}$
. Then
 $D_{l}\cap S_{n}\neq \emptyset$
and
$D_{l}\cap S_{n}\neq \emptyset$
and
 $\unicode[STIX]{x2202}D_{l}\cap \unicode[STIX]{x2202}S_{n}\subseteq \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}\cap \unicode[STIX]{x2202}S_{n}$
for all
$\unicode[STIX]{x2202}D_{l}\cap \unicode[STIX]{x2202}S_{n}\subseteq \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}\cap \unicode[STIX]{x2202}S_{n}$
for all
![]() $l\geqslant 1$
. Moreover, if
$l\geqslant 1$
. Moreover, if
 $\unicode[STIX]{x2202}D_{l}\cap \unicode[STIX]{x2202}S_{n}=\emptyset$
, then
$\unicode[STIX]{x2202}D_{l}\cap \unicode[STIX]{x2202}S_{n}=\emptyset$
, then
 $D_{l}\subseteq S_{n}$
. Since
$D_{l}\subseteq S_{n}$
. Since
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
![]() $\unicode[STIX]{x1D711}$
-regular, it follows that the chain of discs is finite.
$\unicode[STIX]{x1D711}$
-regular, it follows that the chain of discs is finite.
Let
![]() $D$
and
$D$
and
![]() $D^{\prime }$
be maximal
$D^{\prime }$
be maximal
![]() $\unicode[STIX]{x1D700}$
-discs and suppose that
$\unicode[STIX]{x1D700}$
-discs and suppose that
 $D\cap D^{\prime }\neq \emptyset$
. Note that
$D\cap D^{\prime }\neq \emptyset$
. Note that
![]() $D$
and
$D$
and
![]() $D^{\prime }$
each have only one boundary circle,
$D^{\prime }$
each have only one boundary circle,
![]() $c$
and
$c$
and
![]() $c^{\prime }$
. If
$c^{\prime }$
. If
![]() $c=c^{\prime }$
, then
$c=c^{\prime }$
, then
 $D=D^{\prime }$
by maximality. If
$D=D^{\prime }$
by maximality. If
![]() $c$
is contained in the interior of
$c$
is contained in the interior of
![]() $D^{\prime }$
, then
$D^{\prime }$
, then
![]() $c^{\prime }$
is contained in the interior of
$c^{\prime }$
is contained in the interior of
![]() $D$
, since otherwise
$D$
, since otherwise
![]() $D$
would be contained in the interior of
$D$
would be contained in the interior of
![]() $D^{\prime }$
, contradicting maximality. But then
$D^{\prime }$
, contradicting maximality. But then
![]() $D\cup D^{\prime }$
is a subsurface of
$D\cup D^{\prime }$
is a subsurface of
![]() $S$
without boundary which is closed as a subset, and hence
$S$
without boundary which is closed as a subset, and hence
 $D\cup D^{\prime }=S$
. This is impossible since then
$D\cup D^{\prime }=S$
. This is impossible since then
 $S=D\cup D^{\prime }$
would be a sphere.◻
$S=D\cup D^{\prime }$
would be a sphere.◻
Lemma 4.8. Each component
![]() $C$
of
$C$
of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the union of a component
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the union of a component
![]() $C_{0}$
of
$C_{0}$
of
 $\{\unicode[STIX]{x1D711}\geqslant +\unicode[STIX]{x1D700}\}$
or of
$\{\unicode[STIX]{x1D711}\geqslant +\unicode[STIX]{x1D700}\}$
or of
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
together with maximal
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
together with maximal
![]() $\unicode[STIX]{x1D700}$
-discs attached to them along common boundary circles. In particular,
$\unicode[STIX]{x1D700}$
-discs attached to them along common boundary circles. In particular,
 $\unicode[STIX]{x2202}C\subseteq \unicode[STIX]{x2202}C_{0}$
and
$\unicode[STIX]{x2202}C\subseteq \unicode[STIX]{x2202}C_{0}$
and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}C} & = & \displaystyle +\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})<0\quad \text{if}~C_{0}~\text{is contained in}~\{\unicode[STIX]{x1D711}\geqslant +\unicode[STIX]{x1D700}\},\nonumber\\ \displaystyle \unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}C} & = & \displaystyle -\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})>0\quad \text{if}~C_{0}~\text{is contained in}~\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}C} & = & \displaystyle +\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})<0\quad \text{if}~C_{0}~\text{is contained in}~\{\unicode[STIX]{x1D711}\geqslant +\unicode[STIX]{x1D700}\},\nonumber\\ \displaystyle \unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}C} & = & \displaystyle -\unicode[STIX]{x1D700}\quad \text{and}\quad \unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})>0\quad \text{if}~C_{0}~\text{is contained in}~\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\},\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D708}$
denotes the outer normal field of
$\unicode[STIX]{x1D708}$
denotes the outer normal field of
![]() $C$
.
$C$
.
Proof. By Lemma 4.7,
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the union of
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the union of
 $S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
with all maximal
$S\setminus Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
with all maximal
![]() $\unicode[STIX]{x1D700}$
-discs. By the requirement on the normal derivative in (4.5), the boundary circle
$\unicode[STIX]{x1D700}$
-discs. By the requirement on the normal derivative in (4.5), the boundary circle
![]() $c$
of each maximal
$c$
of each maximal
![]() $\unicode[STIX]{x1D700}$
-disc
$\unicode[STIX]{x1D700}$
-disc
![]() $D$
is attached to a component of
$D$
is attached to a component of
 $\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
if
$\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
if
![]() $\unicode[STIX]{x1D711}|_{c}=\unicode[STIX]{x1D700}$
and a component of
$\unicode[STIX]{x1D711}|_{c}=\unicode[STIX]{x1D700}$
and a component of
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
if
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
if
 $\unicode[STIX]{x1D711}|_{c}=-\unicode[STIX]{x1D700}$
, respectively.◻
$\unicode[STIX]{x1D711}|_{c}=-\unicode[STIX]{x1D700}$
, respectively.◻
By Lemma 4.8, we may write
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
as the disjoint union,
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
as the disjoint union,
 $$\begin{eqnarray}Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})=Y_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})\,\dot{\cup }\,Y_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}),\end{eqnarray}$$
$$\begin{eqnarray}Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})=Y_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})\,\dot{\cup }\,Y_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}),\end{eqnarray}$$
where
![]() $Y_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
and
$Y_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
and
![]() $Y_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})$
consist of the components
$Y_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})$
consist of the components
![]() $C$
of
$C$
of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
such that the corresponding
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
such that the corresponding
![]() $C_{0}$
is contained in
$C_{0}$
is contained in
 $\{\unicode[STIX]{x1D711}\geqslant +\unicode[STIX]{x1D700}\}$
and
$\{\unicode[STIX]{x1D711}\geqslant +\unicode[STIX]{x1D700}\}$
and
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
, respectively.
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}$
, respectively.
For the statement of the following lemma, recall Proposition 2.2.
Lemma 4.10. For any sufficiently small
![]() $\unicode[STIX]{x1D711}$
-regular
$\unicode[STIX]{x1D711}$
-regular
![]() $\unicode[STIX]{x1D700}>0$
, the fundamental group of at least one component of
$\unicode[STIX]{x1D700}>0$
, the fundamental group of at least one component of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
contains the free group
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
contains the free group
![]() $F_{2}$
in two generators. Moreover, if
$F_{2}$
in two generators. Moreover, if
![]() $\unicode[STIX]{x1D711}$
is an eigenfunction, then each nodal domain
$\unicode[STIX]{x1D711}$
is an eigenfunction, then each nodal domain
![]() $C$
of
$C$
of
![]() $\unicode[STIX]{x1D711}$
is incompressible and the fundamental group of
$\unicode[STIX]{x1D711}$
is incompressible and the fundamental group of
![]() $C$
contains
$C$
contains
![]() $F_{2}$
.
$F_{2}$
.
Proof. We may assume that
 $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\neq S$
. We suppose first that the Rayleigh quotient
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\neq S$
. We suppose first that the Rayleigh quotient
 $R(\unicode[STIX]{x1D711})<\unicode[STIX]{x1D6EC}(S)$
and choose
$R(\unicode[STIX]{x1D711})<\unicode[STIX]{x1D6EC}(S)$
and choose
![]() $\unicode[STIX]{x1D6FF}>0$
such that
$\unicode[STIX]{x1D6FF}>0$
such that
 $$\begin{eqnarray}R(\unicode[STIX]{x1D711})\leqslant \unicode[STIX]{x1D6EC}(S)-2\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
$$\begin{eqnarray}R(\unicode[STIX]{x1D711})\leqslant \unicode[STIX]{x1D6EC}(S)-2\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
By Lemma 4.3 and since
 $S\setminus Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, we have, for any sufficiently small
$S\setminus Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
, we have, for any sufficiently small
![]() $\unicode[STIX]{x1D711}$
-regular
$\unicode[STIX]{x1D711}$
-regular
![]() $\unicode[STIX]{x1D700}>0$
,
$\unicode[STIX]{x1D700}>0$
,
 $$\begin{eqnarray}\frac{\mathop{\sum }_{C}\int _{C}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|^{2}}{\mathop{\sum }_{C}\int _{C}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}^{2}}\leqslant \frac{\int _{S}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}|^{2}\,dv}{\int _{S}\unicode[STIX]{x1D711}^{2}\,dv}+\unicode[STIX]{x1D6FF}=R(\unicode[STIX]{x1D711})+\unicode[STIX]{x1D6FF}\leqslant \unicode[STIX]{x1D6EC}(S)-\unicode[STIX]{x1D6FF},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\sum }_{C}\int _{C}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|^{2}}{\mathop{\sum }_{C}\int _{C}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}^{2}}\leqslant \frac{\int _{S}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}|^{2}\,dv}{\int _{S}\unicode[STIX]{x1D711}^{2}\,dv}+\unicode[STIX]{x1D6FF}=R(\unicode[STIX]{x1D711})+\unicode[STIX]{x1D6FF}\leqslant \unicode[STIX]{x1D6EC}(S)-\unicode[STIX]{x1D6FF},\end{eqnarray}$$
where the sums run over the components
![]() $C$
of
$C$
of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. We conclude that there is a component
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. We conclude that there is a component
![]() $C$
of
$C$
of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
such that
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
such that
 $$\begin{eqnarray}R(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|_{C})=\frac{\int _{C}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|^{2}}{\int _{C}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}^{2}}\leqslant \unicode[STIX]{x1D6EC}(S)-\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
$$\begin{eqnarray}R(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|_{C})=\frac{\int _{C}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|^{2}}{\int _{C}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}^{2}}\leqslant \unicode[STIX]{x1D6EC}(S)-\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
Now
![]() $\unicode[STIX]{x1D711}$
is smooth on
$\unicode[STIX]{x1D711}$
is smooth on
![]() $S$
, and hence
$S$
, and hence
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|_{C}$
is smooth on
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|_{C}$
is smooth on
![]() $C$
and vanishes along
$C$
and vanishes along
![]() $\unicode[STIX]{x2202}C$
. Therefore
$\unicode[STIX]{x2202}C$
. Therefore
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|_{C}\in H_{0}^{1}(C)$
, by Lemma 3.2. Now it follows from the definition of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}|_{C}\in H_{0}^{1}(C)$
, by Lemma 3.2. Now it follows from the definition of
![]() $\unicode[STIX]{x1D6EC}(S)$
that the interior of
$\unicode[STIX]{x1D6EC}(S)$
that the interior of
![]() $C$
cannot be diffeomorphic to an open disc, an open annulus, or an open cross cap. Thus the fundamental group of
$C$
cannot be diffeomorphic to an open disc, an open annulus, or an open cross cap. Thus the fundamental group of
![]() $C$
contains
$C$
contains
![]() $F_{2}$
.
$F_{2}$
.
Assume now that
 $R(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D6EC}(S)$
. Recall that
$R(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D6EC}(S)$
. Recall that
![]() $\unicode[STIX]{x1D711}$
is a finite linear combination of eigenfunctions of
$\unicode[STIX]{x1D711}$
is a finite linear combination of eigenfunctions of
![]() $S$
,
$S$
,
 $\unicode[STIX]{x1D711}=\sum c_{i}\unicode[STIX]{x1D711}_{i}$
, where
$\unicode[STIX]{x1D711}=\sum c_{i}\unicode[STIX]{x1D711}_{i}$
, where
![]() $\unicode[STIX]{x1D711}_{i}\in E$
is a
$\unicode[STIX]{x1D711}_{i}\in E$
is a
![]() $\unicode[STIX]{x1D706}_{i}$
-eigenfunction with
$\unicode[STIX]{x1D706}_{i}$
-eigenfunction with
 $\unicode[STIX]{x1D706}_{i}\leqslant \unicode[STIX]{x1D6EC}(S)$
. If there would be an
$\unicode[STIX]{x1D706}_{i}\leqslant \unicode[STIX]{x1D6EC}(S)$
. If there would be an
![]() $i$
with
$i$
with
![]() $c_{i}\neq 0$
and
$c_{i}\neq 0$
and
 $\unicode[STIX]{x1D706}_{i}<\unicode[STIX]{x1D6EC}(S)$
, then we would have
$\unicode[STIX]{x1D706}_{i}<\unicode[STIX]{x1D6EC}(S)$
, then we would have
 $R(\unicode[STIX]{x1D711})<\unicode[STIX]{x1D6EC}(S)$
, a contradiction. It follows that all
$R(\unicode[STIX]{x1D711})<\unicode[STIX]{x1D6EC}(S)$
, a contradiction. It follows that all
![]() $\unicode[STIX]{x1D706}_{i}$
with
$\unicode[STIX]{x1D706}_{i}$
with
![]() $c_{i}\neq 0$
are equal to
$c_{i}\neq 0$
are equal to
![]() $\unicode[STIX]{x1D6EC}(S)$
, and hence that
$\unicode[STIX]{x1D6EC}(S)$
, and hence that
![]() $\unicode[STIX]{x1D711}$
is a
$\unicode[STIX]{x1D711}$
is a
![]() $\unicode[STIX]{x1D6EC}(S)$
-eigenfunction.
$\unicode[STIX]{x1D6EC}(S)$
-eigenfunction.
Suppose now, more generally, that
![]() $\unicode[STIX]{x1D711}$
is an eigenfunction with corresponding eigenvalue
$\unicode[STIX]{x1D711}$
is an eigenfunction with corresponding eigenvalue
 $\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6EC}(S)$
. Then
$\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6EC}(S)$
. Then
![]() $\unicode[STIX]{x1D711}$
is smooth on
$\unicode[STIX]{x1D711}$
is smooth on
![]() $S$
. By Theorem 1.7, the nodal domains of
$S$
. By Theorem 1.7, the nodal domains of
![]() $\unicode[STIX]{x1D711}$
have piecewise smooth boundary. Hence Lemma 3.2 implies that, for any nodal domain
$\unicode[STIX]{x1D711}$
have piecewise smooth boundary. Hence Lemma 3.2 implies that, for any nodal domain
![]() $C$
of
$C$
of
![]() $\unicode[STIX]{x1D711}$
, we have
$\unicode[STIX]{x1D711}$
, we have
 $\unicode[STIX]{x1D711}|_{C}\in H_{0}^{1}(C)$
with
$\unicode[STIX]{x1D711}|_{C}\in H_{0}^{1}(C)$
with
 $R(\unicode[STIX]{x1D711}|_{C})=\unicode[STIX]{x1D706}$
. In particular,
$R(\unicode[STIX]{x1D711}|_{C})=\unicode[STIX]{x1D706}$
. In particular,
 $\unicode[STIX]{x1D706}_{0}(C)\leqslant \unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}_{0}(C)\leqslant \unicode[STIX]{x1D706}$
.
Let
![]() $C^{\prime }$
be a thickening of
$C^{\prime }$
be a thickening of
![]() $C$
, that is,
$C$
, that is,
![]() $C^{\prime }$
is a domain in
$C^{\prime }$
is a domain in
![]() $S$
with piecewise smooth boundary which contains
$S$
with piecewise smooth boundary which contains
![]() $C$
in its interior and such that
$C$
in its interior and such that
![]() $C$
is a deformation retract of
$C$
is a deformation retract of
![]() $C^{\prime }$
. If the fundamental group of
$C^{\prime }$
. If the fundamental group of
![]() $C$
does not contain
$C$
does not contain
![]() $F_{2}$
, then neither does the fundamental group of
$F_{2}$
, then neither does the fundamental group of
![]() $C^{\prime }$
, and then
$C^{\prime }$
, and then
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(S)\leqslant \unicode[STIX]{x1D706}_{0}(C^{\prime })\leqslant \unicode[STIX]{x1D706}_{0}(C).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(S)\leqslant \unicode[STIX]{x1D706}_{0}(C^{\prime })\leqslant \unicode[STIX]{x1D706}_{0}(C).\end{eqnarray}$$
The extension
![]() $\unicode[STIX]{x1D711}^{\prime }$
of
$\unicode[STIX]{x1D711}^{\prime }$
of
![]() $\unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}C}$
to
$\unicode[STIX]{x1D711}|_{\unicode[STIX]{x2202}C}$
to
![]() $C^{\prime }$
, setting
$C^{\prime }$
, setting
 $\unicode[STIX]{x1D711}^{\prime }|_{C^{\prime }\setminus C}=0$
, is in
$\unicode[STIX]{x1D711}^{\prime }|_{C^{\prime }\setminus C}=0$
, is in
![]() $H_{0}^{1}(M)$
and in the domain of the Laplacian of
$H_{0}^{1}(M)$
and in the domain of the Laplacian of
![]() $C^{\prime }$
. Moreover, it has Rayleigh quotient
$C^{\prime }$
. Moreover, it has Rayleigh quotient
 $R(\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D706}$
. Hence Lemma 3.5 applies and shows that
$R(\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D706}$
. Hence Lemma 3.5 applies and shows that
 $\unicode[STIX]{x1D706}_{0}(C^{\prime })=\unicode[STIX]{x1D6EC}(S)$
and
$\unicode[STIX]{x1D706}_{0}(C^{\prime })=\unicode[STIX]{x1D6EC}(S)$
and
 $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}^{\prime }=\unicode[STIX]{x1D6EC}(S)\unicode[STIX]{x1D711}^{\prime }$
. Now
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}^{\prime }=\unicode[STIX]{x1D6EC}(S)\unicode[STIX]{x1D711}^{\prime }$
. Now
![]() $\unicode[STIX]{x1D711}^{\prime }$
does not vanish identically on
$\unicode[STIX]{x1D711}^{\prime }$
does not vanish identically on
![]() $C$
, but vanishes on
$C$
, but vanishes on
![]() $C^{\prime }\setminus C$
. This is in contradiction to the unique continuation property for Laplace operators. Hence the fundamental group of any nodal domain of
$C^{\prime }\setminus C$
. This is in contradiction to the unique continuation property for Laplace operators. Hence the fundamental group of any nodal domain of
![]() $\unicode[STIX]{x1D711}$
contains
$\unicode[STIX]{x1D711}$
contains
![]() $F_{2}$
.
$F_{2}$
.
Let
![]() $C$
be a nodal domain of
$C$
be a nodal domain of
![]() $\unicode[STIX]{x1D711}$
and suppose that
$\unicode[STIX]{x1D711}$
and suppose that
![]() $C$
is not incompressible in
$C$
is not incompressible in
![]() $S$
. Then there is a loop
$S$
. Then there is a loop
![]() $c$
in
$c$
in
![]() $C$
which is not homotopic to zero in
$C$
which is not homotopic to zero in
![]() $C$
, but is homotopic to zero in
$C$
, but is homotopic to zero in
![]() $S$
. Without loss of generality, we may assume that
$S$
. Without loss of generality, we may assume that
![]() $c$
is a Jordan curve in
$c$
is a Jordan curve in
![]() $\mathring{C}$
. Then
$\mathring{C}$
. Then
![]() $c$
bounds a disc in
$c$
bounds a disc in
![]() $S$
, which is not contained in
$S$
, which is not contained in
![]() $C$
, by Theorem 2.3. Again by Theorem 2.3, there would be a nodal domain
$C$
, by Theorem 2.3. Again by Theorem 2.3, there would be a nodal domain
![]() $D$
of
$D$
of
![]() $\unicode[STIX]{x1D711}$
whose closure is a closed disc with piecewise smooth boundary and with
$\unicode[STIX]{x1D711}$
whose closure is a closed disc with piecewise smooth boundary and with
 $\unicode[STIX]{x1D706}_{0}(D)=\unicode[STIX]{x1D6EC}(S)$
. This is impossible, since
$\unicode[STIX]{x1D706}_{0}(D)=\unicode[STIX]{x1D6EC}(S)$
. This is impossible, since
![]() $\unicode[STIX]{x1D6EC}(S)$
is not attained on (embedded) closed discs. Hence all nodal domains of
$\unicode[STIX]{x1D6EC}(S)$
is not attained on (embedded) closed discs. Hence all nodal domains of
![]() $\unicode[STIX]{x1D711}$
are incompressible in
$\unicode[STIX]{x1D711}$
are incompressible in
![]() $S$
.
$S$
.
Let
![]() $C$
be a nodal domain and
$C$
be a nodal domain and
 $c_{1},c_{2}:[0,1]\rightarrow C$
be two loops at a point
$c_{1},c_{2}:[0,1]\rightarrow C$
be two loops at a point
![]() $x\in C$
which generate a free subgroup
$x\in C$
which generate a free subgroup
 $F_{2}\in \unicode[STIX]{x1D70B}_{1}(C,x)$
. By Theorem 1.7, we may assume that the images of
$F_{2}\in \unicode[STIX]{x1D70B}_{1}(C,x)$
. By Theorem 1.7, we may assume that the images of
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are contained in
$c_{2}$
are contained in
![]() $\mathring{C}$
. Without loss of generality, we may also assume that
$\mathring{C}$
. Without loss of generality, we may also assume that
![]() $\unicode[STIX]{x1D711}$
is positive on
$\unicode[STIX]{x1D711}$
is positive on
![]() $\mathring{C}$
. Then
$\mathring{C}$
. Then
 $$\begin{eqnarray}\mathring{C}=\mathop{\bigcup }_{\unicode[STIX]{x1D700}>0}\{y\in C\mid \unicode[STIX]{x1D711}(y)>\unicode[STIX]{x1D700}\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathring{C}=\mathop{\bigcup }_{\unicode[STIX]{x1D700}>0}\{y\in C\mid \unicode[STIX]{x1D711}(y)>\unicode[STIX]{x1D700}\}.\end{eqnarray}$$
Therefore the image of
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
is contained in
$c_{1}$
is contained in
 $\{y\in C\mid \unicode[STIX]{x1D711}(y)>\unicode[STIX]{x1D700}\}$
for all sufficiently small
$\{y\in C\mid \unicode[STIX]{x1D711}(y)>\unicode[STIX]{x1D700}\}$
for all sufficiently small
![]() $\unicode[STIX]{x1D700}>0$
. Hence the fundamental group of the component
$\unicode[STIX]{x1D700}>0$
. Hence the fundamental group of the component
 $C_{0}\subseteq C$
of
$C_{0}\subseteq C$
of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which contains
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which contains
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
also contains
$c_{1}$
also contains
![]() $F_{2}$
. From Lemma 4.8 we conclude that the component of
$F_{2}$
. From Lemma 4.8 we conclude that the component of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
containing
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
containing
![]() $C_{0}$
contains
$C_{0}$
contains
![]() $F_{2}$
.◻
$F_{2}$
.◻
Say that a component
![]() $C$
of
$C$
of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is an
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is an
![]() $F_{2}$
-component if the fundamental group of
$F_{2}$
-component if the fundamental group of
![]() $C$
contains
$C$
contains
![]() $F_{2}$
. By Lemma 4.8, a component
$F_{2}$
. By Lemma 4.8, a component
![]() $C$
of
$C$
of
![]() $Y_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
is an
$Y_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
is an
![]() $F_{2}$
-component if and only if there is a point
$F_{2}$
-component if and only if there is a point
![]() $x$
in the interior of the corresponding component
$x$
in the interior of the corresponding component
![]() $C_{0}$
of
$C_{0}$
of
 $\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
and a pair of loops
$\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
and a pair of loops
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
at
$c_{1}$
at
![]() $x$
which generate an
$x$
which generate an
![]() $F_{2}$
in
$F_{2}$
in
 $\unicode[STIX]{x1D70B}_{1}(C,x)$
such that
$\unicode[STIX]{x1D70B}_{1}(C,x)$
such that
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
are contained in the interior of
$c_{1}$
are contained in the interior of
![]() $C_{0}$
; that is, such that
$C_{0}$
; that is, such that
![]() $\unicode[STIX]{x1D711}>\unicode[STIX]{x1D700}$
along them. The characterization of
$\unicode[STIX]{x1D711}>\unicode[STIX]{x1D700}$
along them. The characterization of
![]() $F_{2}$
-components of
$F_{2}$
-components of
![]() $Y_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})$
is analogous.
$Y_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})$
is analogous.
Lemma 4.14. If
![]() $K$
is a compact subsurface of
$K$
is a compact subsurface of
![]() $S$
such that
$S$
such that
![]() $S\setminus K$
is a cylindrical neighborhood of the ends of
$S\setminus K$
is a cylindrical neighborhood of the ends of
![]() $S$
and
$S$
and
![]() $C$
is a component of
$C$
is a component of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which is contained in
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
which is contained in
![]() $S\setminus K$
, then the interior of
$S\setminus K$
, then the interior of
![]() $C$
is diffeomorphic to an open disc or an open annulus. In particular, we have the following.
$C$
is diffeomorphic to an open disc or an open annulus. In particular, we have the following.
-
(i) Any
 $F_{2}$
-component of
$F_{2}$
-component of
 $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
intersects
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
intersects
 $K$
.
$K$
. -
(ii) The subsurface
 $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
contains only finitely many
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
contains only finitely many
 $F_{2}$
-components.
$F_{2}$
-components.
Components of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
might be non-compact and might have infinitely many boundary components. But since they are incompressible in
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
might be non-compact and might have infinitely many boundary components. But since they are incompressible in
![]() $S$
, their interiors are surfaces of finite type.
$S$
, their interiors are surfaces of finite type.
Proof of Lemma 4.14.
The components of
![]() $S\setminus K$
are diffeomorphic to open annuli, hence their fundamental group is infinite cyclic. Moreover,
$S\setminus K$
are diffeomorphic to open annuli, hence their fundamental group is infinite cyclic. Moreover,
![]() $C$
is incompressible in
$C$
is incompressible in
![]() $S$
, hence also in the component of
$S$
, hence also in the component of
![]() $S\setminus K$
containing it. Therefore the fundamental group of
$S\setminus K$
containing it. Therefore the fundamental group of
![]() $C$
is either trivial or infinite cyclic. Now, as a domain in a cylinder,
$C$
is either trivial or infinite cyclic. Now, as a domain in a cylinder,
![]() $C$
is orientable. Hence the interior of
$C$
is orientable. Hence the interior of
![]() $C$
is diffeomorphic to an open disc or an open annulus.◻
$C$
is diffeomorphic to an open disc or an open annulus.◻
We denote by
![]() $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
the union of the
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
the union of the
![]() $F_{2}$
-components of
$F_{2}$
-components of
![]() $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
and by
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
and by
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
the ones among them which belong to
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
the ones among them which belong to
![]() $Y_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. Then
$Y_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. Then
![]() $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the disjoint union of
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is the disjoint union of
![]() $X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
and
$X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
and
![]() $X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})$
.
$X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})$
.
Lemma 4.15. If
![]() $\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}$
are
$\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}$
are
![]() $\unicode[STIX]{x1D711}$
-regular, then
$\unicode[STIX]{x1D711}$
-regular, then
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime })$
.
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime })$
.
Proof. By definition,
 $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })\subseteq Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. If a component of
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })\subseteq Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
. If a component of
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is contained in the interior of an embedded closed disc, then also all the components of
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})$
is contained in the interior of an embedded closed disc, then also all the components of
![]() $Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
it contains. It follows that
$Z_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
it contains. It follows that
 $Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
. By Lemma 4.6(ii), if
$Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq Y_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
. By Lemma 4.6(ii), if
![]() $C$
is an
$C$
is an
![]() $F_{2}$
-component of
$F_{2}$
-component of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
, then also the component
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
, then also the component
![]() $C^{\prime }$
of
$C^{\prime }$
of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime })$
containing it. Hence
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime })$
containing it. Hence
 $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
.
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
.
Now let
![]() $C$
be a component of
$C$
be a component of
![]() $X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
and suppose that the component
$X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
and suppose that the component
![]() $C^{\prime }$
of
$C^{\prime }$
of
![]() $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
containing
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime })$
containing
![]() $C$
belongs to
$C$
belongs to
![]() $X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime })$
. By Lemma 4.8,
$X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime })$
. By Lemma 4.8,
![]() $C$
is the union of a component
$C$
is the union of a component
![]() $C_{0}$
of
$C_{0}$
of
 $\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
with maximal
$\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}$
with maximal
![]() $\unicode[STIX]{x1D700}$
-discs. Now let
$\unicode[STIX]{x1D700}$
-discs. Now let
![]() $x$
be a point in the interior of
$x$
be a point in the interior of
![]() $C_{0}$
and choose loops
$C_{0}$
and choose loops
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
in the interior of
$c_{1}$
in the interior of
![]() $C_{0}$
generating an
$C_{0}$
generating an
![]() $F_{2}$
in
$F_{2}$
in
 $\unicode[STIX]{x1D70B}_{1}(C,x)$
; compare with our discussion further up. In particular,
$\unicode[STIX]{x1D70B}_{1}(C,x)$
; compare with our discussion further up. In particular,
![]() $\unicode[STIX]{x1D711}>\unicode[STIX]{x1D700}$
along
$\unicode[STIX]{x1D711}>\unicode[STIX]{x1D700}$
along
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
. Under the inclusion
$c_{1}$
. Under the inclusion
 $C\rightarrow C^{\prime }$
,
$C\rightarrow C^{\prime }$
,
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
cannot be contained in the maximal
$c_{1}$
cannot be contained in the maximal
![]() $\unicode[STIX]{x1D700}^{\prime }$
-discs belonging to
$\unicode[STIX]{x1D700}^{\prime }$
-discs belonging to
![]() $C^{\prime }$
because they would be homotopic to zero in
$C^{\prime }$
because they would be homotopic to zero in
![]() $S$
otherwise. But then they must meet
$S$
otherwise. But then they must meet
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}^{\prime }\}$
, a contradiction. We conclude that
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}^{\prime }\}$
, a contradiction. We conclude that
 $X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700}^{\prime })$
; similarly
$X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700}^{\prime })$
; similarly
 $X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime })$
.◻
$X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700})\subseteq X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime })$
.◻
We view the funnels of
![]() $S$
as vertical and pointing upwards. In this picture, a Jordan curve
$S$
as vertical and pointing upwards. In this picture, a Jordan curve
![]() $c$
in a funnel
$c$
in a funnel
![]() $F$
, which is a generator of the fundamental group of
$F$
, which is a generator of the fundamental group of
![]() $F$
, cuts
$F$
, cuts
![]() $S\setminus c$
in two open pieces, the set
$S\setminus c$
in two open pieces, the set
![]() $F_{c}$
of points above
$F_{c}$
of points above
![]() $c$
and the set of remaining points, sometimes called the points below
$c$
and the set of remaining points, sometimes called the points below
![]() $c$
. The set of points above
$c$
. The set of points above
![]() $c$
is contained in
$c$
is contained in
![]() $F$
and is a funnel around the same end as
$F$
and is a funnel around the same end as
![]() $F$
, the set of points below
$F$
, the set of points below
![]() $c$
is not contained in
$c$
is not contained in
![]() $F$
.
$F$
.
We call Jordan curves in
![]() $F$
, which generate the fundamental group of
$F$
, which generate the fundamental group of
![]() $F$
, cross sections of
$F$
, cross sections of
![]() $F$
. We say that a cross section
$F$
. We say that a cross section
![]() $c$
of
$c$
of
![]() $F$
is
$F$
is
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular if it meets the curves
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular if it meets the curves
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
transversally. By transversality theory, any cross section of
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
transversally. By transversality theory, any cross section of
![]() $F$
can be approximated by smooth
$F$
can be approximated by smooth
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross sections of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross sections of
![]() $F$
in any reasonable topology.
$F$
in any reasonable topology.
Our aim is now to describe the structure of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
with respect to
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
with respect to
![]() $F$
. Let
$F$
. Let
![]() $c$
be a
$c$
be a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross section of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross section of
![]() $F$
. Then
$F$
. Then
![]() $c$
intersects
$c$
intersects
 $\{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D700}\}$
transversally. We emphasize the following three cases:
$\{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D700}\}$
transversally. We emphasize the following three cases:
-
(i)
 $F_{c}\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
;
$F_{c}\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
; -
(ii)
 $c\cap X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})=\emptyset$
;
$c\cap X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})=\emptyset$
; -
(iii)
 $c\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\neq \emptyset$
.
$c\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\neq \emptyset$
.
We now want to normalize the position of a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross section
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross section
![]() $c$
of
$c$
of
![]() $F$
in such a way that the part of
$F$
in such a way that the part of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
below
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
below
![]() $c$
is homotopy equivalent to
$c$
is homotopy equivalent to
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. If it is possible to choose
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. If it is possible to choose
![]() $c$
such that case (i) or case (ii) holds, then any such choice will be a normalization. In the remaining case,
$c$
such that case (i) or case (ii) holds, then any such choice will be a normalization. In the remaining case,
 $c\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\neq \emptyset$
for any choice of cross section of
$c\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\neq \emptyset$
for any choice of cross section of
![]() $F$
. Since
$F$
. Since
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
![]() $\unicode[STIX]{x1D711}$
-regular,
$\unicode[STIX]{x1D711}$
-regular,
 $c\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is finite. By Lemma 4.8,
$c\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is finite. By Lemma 4.8,
 $c\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\subseteq c\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
.
$c\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\subseteq c\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
.
Since
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is a properly embedded submanifold (of dimension
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is a properly embedded submanifold (of dimension
![]() $1$
) of
$1$
) of
![]() $S$
, the components of
$S$
, the components of
 $F_{c}\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
above
$F_{c}\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
above
![]() $c$
are of the following two types: either they are Jordan segments with endpoints on
$c$
are of the following two types: either they are Jordan segments with endpoints on
![]() $c$
or they are Jordan rays with one end on
$c$
or they are Jordan rays with one end on
![]() $c$
and escaping to infinity along the other. We call these components recurrent and escaping, respectively. Since
$c$
and escaping to infinity along the other. We call these components recurrent and escaping, respectively. Since
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is properly embedded, escaping components in
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is properly embedded, escaping components in
 $F_{c}\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
extend continuously as Jordan curves to the one point compactification of
$F_{c}\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
extend continuously as Jordan curves to the one point compactification of
![]() $F_{c}$
at infinity.
$F_{c}$
at infinity.
If
![]() $a$
is a recurrent component, then there is a segment
$a$
is a recurrent component, then there is a segment
![]() $b$
in
$b$
in
![]() $c$
such that
$c$
such that
![]() $a\cup b$
is a null homotopic Jordan loop in
$a\cup b$
is a null homotopic Jordan loop in
![]() $F$
. The disc bounded by
$F$
. The disc bounded by
![]() $a\cup b$
will be called the part of
$a\cup b$
will be called the part of
![]() $F_{c}$
below
$F_{c}$
below
![]() $a$
. Since
$a$
. Since
 $c\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is finite, there are only finitely many such discs, and they are ordered by inclusion. The components
$c\cap \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
is finite, there are only finitely many such discs, and they are ordered by inclusion. The components
![]() $a$
above maximal such discs will be called uppermost. We replace the segments
$a$
above maximal such discs will be called uppermost. We replace the segments
![]() $b$
of
$b$
of
![]() $c$
below such maximal discs by the corresponding uppermost components
$c$
below such maximal discs by the corresponding uppermost components
![]() $a$
and obtain a piecewise smooth cross section of
$a$
and obtain a piecewise smooth cross section of
![]() $F$
. Pushing this cross section upwards and smoothing it appropriately, we arrive at the normalized third case:
$F$
. Pushing this cross section upwards and smoothing it appropriately, we arrive at the normalized third case:
![]() $c$
is
$c$
is
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular and the interior of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular and the interior of
 $F_{c}\cap X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
is a finite union of open discs, bounded by segments of
$F_{c}\cap X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
is a finite union of open discs, bounded by segments of
![]() $c$
, escaping components of
$c$
, escaping components of
 $F_{c}\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
, and, possibly, boundary lines of
$F_{c}\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
, and, possibly, boundary lines of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
which start and end at infinity in
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
which start and end at infinity in
![]() $F$
. Note that boundary circles of
$F$
. Note that boundary circles of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
cannot occur, since they would not be null homotopic and we would be in the second case above.
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
cannot occur, since they would not be null homotopic and we would be in the second case above.
Remark 4.16. In all three cases, after normalization, the part of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
below
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
below
![]() $c$
is homotopy equivalent to
$c$
is homotopy equivalent to
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. With a bit of more work, it would be possible to show that the part of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. With a bit of more work, it would be possible to show that the part of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
below
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
below
![]() $c$
is a deformation retract of
$c$
is a deformation retract of
![]() $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. The technical problem consists in handling the components of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
. The technical problem consists in handling the components of
 $F_{c}\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
above
$F_{c}\cap \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700})$
above
![]() $c$
which contain boundary lines which come from and return back to infinity in
$c$
which contain boundary lines which come from and return back to infinity in
![]() $F_{c}$
. These boundary lines cut out infinite peninsulas which are hanging down from infinity in our picture of
$F_{c}$
. These boundary lines cut out infinite peninsulas which are hanging down from infinity in our picture of
![]() $F_{c}$
. Since we do not need more than homotopy equivalence, we leave it with these remarks.
$F_{c}$
. Since we do not need more than homotopy equivalence, we leave it with these remarks.
Consider a pair
![]() $(\unicode[STIX]{x1D700},K)$
, where
$(\unicode[STIX]{x1D700},K)$
, where
![]() $\unicode[STIX]{x1D700}>0$
and
$\unicode[STIX]{x1D700}>0$
and
![]() $K$
is a smooth and compact subdomain of
$K$
is a smooth and compact subdomain of
![]() $S$
such that
$S$
such that
![]() $S\setminus K$
consists of funnels. Say that the pair
$S\setminus K$
consists of funnels. Say that the pair
![]() $(\unicode[STIX]{x1D700},K)$
is
$(\unicode[STIX]{x1D700},K)$
is
![]() $\unicode[STIX]{x1D711}$
-regular if
$\unicode[STIX]{x1D711}$
-regular if
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
![]() $\unicode[STIX]{x1D711}$
-regular and
$\unicode[STIX]{x1D711}$
-regular and
![]() $\unicode[STIX]{x2202}K$
consists of normalized
$\unicode[STIX]{x2202}K$
consists of normalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross sections as above. For any such pair
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D700})$
-regular cross sections as above. For any such pair
![]() $(\unicode[STIX]{x1D700},K)$
, define
$(\unicode[STIX]{x1D700},K)$
, define
 $$\begin{eqnarray}X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)=X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\cap K\quad \text{and}\quad X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)=X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\cap K.\end{eqnarray}$$
$$\begin{eqnarray}X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)=X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700})\cap K\quad \text{and}\quad X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)=X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\cap K.\end{eqnarray}$$
Note that
 $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
is the disjoint union
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
is the disjoint union
 $X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)\,\dot{\cup }\,X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)$
.
$X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)\,\dot{\cup }\,X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)$
.
By what we said above, the inclusions
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)\rightarrow X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
are homotopy equivalences. Since
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)\rightarrow X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})$
are homotopy equivalences. Since
![]() $K$
is a deformation retraction of
$K$
is a deformation retraction of
![]() $S$
, Lemma 2.5 implies
$S$
, Lemma 2.5 implies
 $$\begin{eqnarray}\unicode[STIX]{x1D712}(S)=\unicode[STIX]{x1D712}(K)\leqslant \unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K))+\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))<0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(S)=\unicode[STIX]{x1D712}(K)\leqslant \unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K))+\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))<0.\end{eqnarray}$$
By Lemma 4.6(ii), the components of
 $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
are incompressible in
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
are incompressible in
![]() $S$
. The following result is an immediate consequence of Lemmas 2.5 and 4.15.
$S$
. The following result is an immediate consequence of Lemmas 2.5 and 4.15.
Lemma 4.19. If
![]() $(\unicode[STIX]{x1D700},K)$
and
$(\unicode[STIX]{x1D700},K)$
and
![]() $(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
are
$(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
are
![]() $\unicode[STIX]{x1D711}$
-regular with
$\unicode[STIX]{x1D711}$
-regular with
![]() $\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}$
and
 $K\subseteq K^{\prime }$
, then
$K\subseteq K^{\prime }$
, then
 $$\begin{eqnarray}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })\quad \text{and}\quad \unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))\leqslant \unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)).\end{eqnarray}$$
$$\begin{eqnarray}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })\quad \text{and}\quad \unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))\leqslant \unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)).\end{eqnarray}$$
Moreover, if
 $\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))$
, then
$\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))$
, then
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
arises from
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
arises from
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
by attaching annuli, cross caps, and lunes along boundary curves of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
by attaching annuli, cross caps, and lunes along boundary curves of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
.
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
.
As a direct application of (4.18) and Lemma 4.19, we get the following.
Corollary 4.20. There exists a
![]() $\unicode[STIX]{x1D711}$
-regular pair
$\unicode[STIX]{x1D711}$
-regular pair
 $(\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}},K_{\unicode[STIX]{x1D711}})$
such that
$(\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}},K_{\unicode[STIX]{x1D711}})$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}},K_{\unicode[STIX]{x1D711}}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}},K_{\unicode[STIX]{x1D711}}))\end{eqnarray}$$
for all
![]() $\unicode[STIX]{x1D711}$
-regular pairs
$\unicode[STIX]{x1D711}$
-regular pairs
![]() $(\unicode[STIX]{x1D700},K)$
with
$(\unicode[STIX]{x1D700},K)$
with
![]() $\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}}$
and
$\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}}$
and
 $K_{\unicode[STIX]{x1D711}}\subseteq K$
.
$K_{\unicode[STIX]{x1D711}}\subseteq K$
.
Now we assume throughout that we are in the stable range, that is, we consider
![]() $\unicode[STIX]{x1D711}$
-regular pairs
$\unicode[STIX]{x1D711}$
-regular pairs
![]() $(\unicode[STIX]{x1D700},K)$
with
$(\unicode[STIX]{x1D700},K)$
with
![]() $\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}}$
and
$\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}}$
and
 $K_{\unicode[STIX]{x1D711}}\subseteq K$
. For such a pair
$K_{\unicode[STIX]{x1D711}}\subseteq K$
. For such a pair
![]() $(\unicode[STIX]{x1D700},K)$
, we study the isotopy type of the triples
$(\unicode[STIX]{x1D700},K)$
, we study the isotopy type of the triples
 $(S,X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
. Here and below we mean compactly supported topological isotopy when speaking of isotopy. By the definition of
$(S,X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
. Here and below we mean compactly supported topological isotopy when speaking of isotopy. By the definition of
![]() $\unicode[STIX]{x1D711}$
-regularity and the discussion leading to it, the isotopy type of
$\unicode[STIX]{x1D711}$
-regularity and the discussion leading to it, the isotopy type of
 $(S,X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
does not depend on
$(S,X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
does not depend on
![]() $K$
. Hence to compare it with the isotopy type of another such triple
$K$
. Hence to compare it with the isotopy type of another such triple
 $(S,X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }),X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))$
, we may assume that
$(S,X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }),X_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))$
, we may assume that
![]() $\unicode[STIX]{x1D700}^{\prime }<\unicode[STIX]{x1D700}$
and that
$\unicode[STIX]{x1D700}^{\prime }<\unicode[STIX]{x1D700}$
and that
![]() $K$
is contained in the interior of
$K$
is contained in the interior of
![]() $K^{\prime }$
.
$K^{\prime }$
.
Now
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
has two kinds of boundary circles: the first kind consists of boundary circles in the interior of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
has two kinds of boundary circles: the first kind consists of boundary circles in the interior of
![]() $K$
, the second kind consists of segments of boundary circles of
$K$
, the second kind consists of segments of boundary circles of
![]() $\unicode[STIX]{x2202}K$
concatenated with segments of
$\unicode[STIX]{x2202}K$
concatenated with segments of
 $\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\subseteq \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
that run inside
$\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700})\subseteq \{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
that run inside
![]() $K$
from
$K$
from
![]() $\unicode[STIX]{x2202}K$
to
$\unicode[STIX]{x2202}K$
to
![]() $\unicode[STIX]{x2202}K$
. By the definition of
$\unicode[STIX]{x2202}K$
. By the definition of
![]() $\unicode[STIX]{x1D711}$
-regularity, boundary circles of
$\unicode[STIX]{x1D711}$
-regularity, boundary circles of
![]() $K$
do not occur as boundary circles of
$K$
do not occur as boundary circles of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. The first kind of boundary circles of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. The first kind of boundary circles of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
is smooth, the second kind is piecewise smooth with vertices in the points, where the circle enters or respectively leaves
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
is smooth, the second kind is piecewise smooth with vertices in the points, where the circle enters or respectively leaves
![]() $\unicode[STIX]{x2202}K$
. The boundary of
$\unicode[STIX]{x2202}K$
. The boundary of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
consists of the corresponding two kinds of boundary circles.
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
consists of the corresponding two kinds of boundary circles.
We start with a closer look at the gluings required to obtain
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
from
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
from
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. Since their Euler characteristics coincide, only annuli, cross caps, and lunes are concerned; compare with Lemma 2.5. Now
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. Since their Euler characteristics coincide, only annuli, cross caps, and lunes are concerned; compare with Lemma 2.5. Now
![]() $\unicode[STIX]{x1D700}^{\prime }<\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}^{\prime }<\unicode[STIX]{x1D700}$
and
![]() $K$
is contained in the interior of
$K$
is contained in the interior of
![]() $K^{\prime }$
. Hence the boundaries of
$K^{\prime }$
. Hence the boundaries of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
and
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
and
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
are disjoint, and therefore no lunes occur.
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
are disjoint, and therefore no lunes occur.
Suppose that a boundary circle
![]() $c$
of
$c$
of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bounds a cross cap
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bounds a cross cap
![]() $C$
in the complement (of the interior) of
$C$
in the complement (of the interior) of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
in
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
in
![]() $S$
. Now
$S$
. Now
![]() $C$
decomposes
$C$
decomposes
![]() $S$
into two connected regions, the points inside
$S$
into two connected regions, the points inside
![]() $C$
and the points outside
$C$
and the points outside
![]() $C$
. Since
$C$
. Since
![]() $\unicode[STIX]{x2202}C$
is contained in
$\unicode[STIX]{x2202}C$
is contained in
 $\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, we conclude that a curve from a point inside
$\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, we conclude that a curve from a point inside
![]() $C$
to a point outside of
$C$
to a point outside of
 $C\cup X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
has to pass through
$C\cup X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
has to pass through
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. In particular,
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. In particular,
![]() $C$
cannot contain points on or beyond boundary circles of
$C$
cannot contain points on or beyond boundary circles of
![]() $K$
since otherwise it would also contain the corresponding funnels, a contradiction to the compactness of
$K$
since otherwise it would also contain the corresponding funnels, a contradiction to the compactness of
![]() $C$
. We conclude that in the gluing required to obtain
$C$
. We conclude that in the gluing required to obtain
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
from
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
from
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, the cross caps, including their boundary circles, are contained in the interior of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, the cross caps, including their boundary circles, are contained in the interior of
![]() $K$
. In particular,
$K$
. In particular,
![]() $\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}$
along their boundary circles.
$\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}$
along their boundary circles.
Since an annulus has two boundary circles, there are different ways of attaching them and we need to distinguish two cases. Suppose first that two boundary circles
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
of
$c_{1}$
of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bound a closed annulus
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bound a closed annulus
![]() $A$
in the complement (of the interior) of
$A$
in the complement (of the interior) of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
in
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
in
![]() $S$
. Then any curve from a point inside
$S$
. Then any curve from a point inside
![]() $A$
to a point outside of
$A$
to a point outside of
 $A\cup X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
has to pass through
$A\cup X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
has to pass through
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. As in the case of cross caps, we get that
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. As in the case of cross caps, we get that
![]() $A$
cannot contain points on or beyond boundary circles of
$A$
cannot contain points on or beyond boundary circles of
![]() $K$
since otherwise it would also contain the corresponding funnels, a contradiction to the compactness of
$K$
since otherwise it would also contain the corresponding funnels, a contradiction to the compactness of
![]() $A$
. We conclude that in the gluing required to obtain
$A$
. We conclude that in the gluing required to obtain
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
from
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
from
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, the annuli
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, the annuli
![]() $A$
with
$A$
with
 $\unicode[STIX]{x2202}A\subseteq \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
are contained in the interior of
$\unicode[STIX]{x2202}A\subseteq \unicode[STIX]{x2202}X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
are contained in the interior of
![]() $K$
. In particular,
$K$
. In particular,
![]() $\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}$
along their boundary circles.
$\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}$
along their boundary circles.
Finally, an annulus might be glued to
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
along one boundary circle such that the second boundary circle belongs to the boundary of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
along one boundary circle such that the second boundary circle belongs to the boundary of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
. Such gluings do not change the isotopy type of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
. Such gluings do not change the isotopy type of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
in
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
in
![]() $S$
, but gluings of cross caps and annuli as above do. To remedy this, attach all annuli and cross caps to
$S$
, but gluings of cross caps and annuli as above do. To remedy this, attach all annuli and cross caps to
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
which are contained in the interior of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
which are contained in the interior of
![]() $K$
and have their boundary in
$K$
and have their boundary in
 $X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)$
and call the resulting subsurface
$X_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)$
and call the resulting subsurface
 $S_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
.
$S_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
.
Note that no component of
 $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
is contained in any of the attached cross caps and annuli since the components of
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
is contained in any of the attached cross caps and annuli since the components of
 $X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
are incompressible in
$X_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
are incompressible in
![]() $S$
and their fundamental groups contain an
$S$
and their fundamental groups contain an
![]() $F_{2}$
. Hence
$F_{2}$
. Hence
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)\cap S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)=\emptyset .\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)\cap S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)=\emptyset .\end{eqnarray}$$
Note also that attaching annuli and cross caps does not change the Euler characteristic.
Lemma 4.21. If
 $(\unicode[STIX]{x1D700},K),(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
are
$(\unicode[STIX]{x1D700},K),(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
are
![]() $\unicode[STIX]{x1D711}$
-regular with
$\unicode[STIX]{x1D711}$
-regular with
 $\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}}$
and
$\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{\unicode[STIX]{x1D711}}$
and
 $K_{\unicode[STIX]{x1D711}}\subseteq K\subseteq K^{\prime }$
, then
$K_{\unicode[STIX]{x1D711}}\subseteq K\subseteq K^{\prime }$
, then
 $$\begin{eqnarray}(S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))\quad \text{and}\quad (S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))\end{eqnarray}$$
$$\begin{eqnarray}(S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))\quad \text{and}\quad (S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700}^{\prime },K^{\prime }))\end{eqnarray}$$
are isotopic in
![]() $S$
.
$S$
.
Proof. After the above discussion leading to the definition of
 $S_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, we have the following remaining issues.
$S_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
, we have the following remaining issues.
If a boundary circle
![]() $c$
of
$c$
of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bounds a cross cap
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bounds a cross cap
![]() $C$
in
$C$
in
![]() $S$
, then either already
$S$
, then either already
 $C\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
or else an annulus
$C\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
or else an annulus
![]() $A\subseteq C$
is attached to
$A\subseteq C$
is attached to
![]() $c$
along one of its boundary circles and the other boundary circle
$c$
along one of its boundary circles and the other boundary circle
![]() $c^{\prime }$
belongs to the boundary of
$c^{\prime }$
belongs to the boundary of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
. Then
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
. Then
![]() $c^{\prime }$
bound a cross cap
$c^{\prime }$
bound a cross cap
![]() $C^{\prime }$
in the complement (of the interior) of
$C^{\prime }$
in the complement (of the interior) of
![]() $A$
in
$A$
in
![]() $C$
and
$C$
and
 $C=A\cup C^{\prime }$
.
$C=A\cup C^{\prime }$
.
Conversely, if a boundary circle
![]() $c$
of
$c$
of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
bounds a cross cap
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
bounds a cross cap
![]() $C^{\prime }$
in
$C^{\prime }$
in
![]() $S$
, then
$S$
, then
![]() $c$
is contained in the interior of
$c$
is contained in the interior of
![]() $K^{\prime }$
and thus
$K^{\prime }$
and thus
 $\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}^{\prime }$
along
$\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}^{\prime }$
along
![]() $c$
. We conclude that
$c$
. We conclude that
![]() $c$
is a boundary circle of an annulus
$c$
is a boundary circle of an annulus
![]() $A$
attached to
$A$
attached to
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
along the other boundary circle of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
along the other boundary circle of
![]() $A$
. Thus
$A$
. Thus
 $C=A\cup C^{\prime }$
is a cross cap in
$C=A\cup C^{\prime }$
is a cross cap in
![]() $S$
with
$S$
with
![]() $\unicode[STIX]{x2202}C$
a boundary circle of
$\unicode[STIX]{x2202}C$
a boundary circle of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. By the discussion further up we obtain that
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. By the discussion further up we obtain that
![]() $C$
is in the interior of
$C$
is in the interior of
![]() $K$
.
$K$
.
If boundary circles
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
of
$c_{1}$
of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bound an annulus
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
bound an annulus
![]() $A$
in
$A$
in
![]() $S$
, then either already
$S$
, then either already
 $A\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
or else disjoint annuli
$A\subseteq X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
or else disjoint annuli
 $A_{0},A_{1}\subseteq A$
are attached to
$A_{0},A_{1}\subseteq A$
are attached to
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
, each along one of its boundary circles, and the other boundary circles
$c_{1}$
, each along one of its boundary circles, and the other boundary circles
![]() $c_{0}^{\prime }$
and
$c_{0}^{\prime }$
and
![]() $c_{1}^{\prime }$
bound an annulus
$c_{1}^{\prime }$
bound an annulus
![]() $A^{\prime }\subseteq A$
between
$A^{\prime }\subseteq A$
between
![]() $A_{0}$
and
$A_{0}$
and
![]() $A_{1}$
. Then
$A_{1}$
. Then
 $A=A_{0}\cup A^{\prime }\cup A_{1}$
.
$A=A_{0}\cup A^{\prime }\cup A_{1}$
.
Conversely, if boundary circles
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
of
$c_{1}$
of
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
bound an annulus
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700}^{\prime },K^{\prime })$
bound an annulus
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $S$
, then
$S$
, then
![]() $A^{\prime }$
is contained in the interior of
$A^{\prime }$
is contained in the interior of
![]() $K^{\prime }$
and thus
$K^{\prime }$
and thus
 $\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}^{\prime }$
along
$\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}^{\prime }$
along
![]() $\unicode[STIX]{x2202}A^{\prime }$
. Arguing as in the case of cross caps, we get annuli
$\unicode[STIX]{x2202}A^{\prime }$
. Arguing as in the case of cross caps, we get annuli
![]() $A_{0}$
and
$A_{0}$
and
![]() $A_{1}$
with one boundary circle in
$A_{1}$
with one boundary circle in
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
and the other equal to
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
and the other equal to
![]() $c_{0}$
and
$c_{0}$
and
![]() $c_{1}$
, respectively. Thus
$c_{1}$
, respectively. Thus
 $A=A_{0}\cup A^{\prime }\cup A_{1}$
is an annulus in
$A=A_{0}\cup A^{\prime }\cup A_{1}$
is an annulus in
![]() $S$
such that
$S$
such that
![]() $\unicode[STIX]{x2202}A$
lies in
$\unicode[STIX]{x2202}A$
lies in
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. By the discussion further up we obtain that
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. By the discussion further up we obtain that
![]() $A$
is in the interior of
$A$
is in the interior of
![]() $K$
.◻
$K$
.◻
We call the isotopy type of the triple
 $(S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
the type of
$(S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
the type of
![]() $\unicode[STIX]{x1D711}$
and the Euler characteristic of
$\unicode[STIX]{x1D711}$
and the Euler characteristic of
 $S_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
the characteristic of
$S_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D700},K)$
the characteristic of
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
Lemma 4.22. Let
![]() $L$
be a compact neighborhood of
$L$
be a compact neighborhood of
![]() $K$
which contains all the
$K$
which contains all the
![]() $\unicode[STIX]{x1D700}$
-discs with respect to
$\unicode[STIX]{x1D700}$
-discs with respect to
![]() $\unicode[STIX]{x1D711}$
which intersect
$\unicode[STIX]{x1D711}$
which intersect
![]() $K$
and such that
$K$
and such that
![]() $\unicode[STIX]{x2202}L$
is smooth and transversal to
$\unicode[STIX]{x2202}L$
is smooth and transversal to
 $\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
. Then a non-trivial finite linear combination
$\{\unicode[STIX]{x1D711}=\pm \unicode[STIX]{x1D700}\}$
. Then a non-trivial finite linear combination
![]() $\unicode[STIX]{x1D713}$
of eigenfunctions of
$\unicode[STIX]{x1D713}$
of eigenfunctions of
![]() $S$
with corresponding eigenvalues less than or equal to
$S$
with corresponding eigenvalues less than or equal to
![]() $\unicode[STIX]{x1D6EC}(S)$
, with the same characteristic as
$\unicode[STIX]{x1D6EC}(S)$
, with the same characteristic as
![]() $\unicode[STIX]{x1D711}$
, and sufficiently
$\unicode[STIX]{x1D711}$
, and sufficiently
![]() $C^{2}$
-close to
$C^{2}$
-close to
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $L$
, has the same type as
$L$
, has the same type as
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
Proof. If
![]() $\unicode[STIX]{x1D713}$
is sufficiently
$\unicode[STIX]{x1D713}$
is sufficiently
![]() $C^{2}$
-close to
$C^{2}$
-close to
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $L$
, then
$L$
, then
![]() $\pm \unicode[STIX]{x1D700}$
are regular values of
$\pm \unicode[STIX]{x1D700}$
are regular values of
![]() $\unicode[STIX]{x1D713}|_{L}$
, the curves
$\unicode[STIX]{x1D713}|_{L}$
, the curves
 $\unicode[STIX]{x1D713}|_{L}=\pm \unicode[STIX]{x1D700}$
intersect
$\unicode[STIX]{x1D713}|_{L}=\pm \unicode[STIX]{x1D700}$
intersect
![]() $\unicode[STIX]{x2202}K$
transversally, and there is a small isotopy of
$\unicode[STIX]{x2202}K$
transversally, and there is a small isotopy of
![]() $S$
which leaves
$S$
which leaves
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x2202}K$
invariant which deforms the configuration of curves
$\unicode[STIX]{x2202}K$
invariant which deforms the configuration of curves
 $\{\unicode[STIX]{x1D713}=\unicode[STIX]{x1D700}\}\cap L$
and
$\{\unicode[STIX]{x1D713}=\unicode[STIX]{x1D700}\}\cap L$
and
 $\{\unicode[STIX]{x1D713}=-\unicode[STIX]{x1D700}\}\cap L$
to the configuration of curves
$\{\unicode[STIX]{x1D713}=-\unicode[STIX]{x1D700}\}\cap L$
to the configuration of curves
 $\{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D700}\}\cap L$
respectively
$\{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D700}\}\cap L$
respectively
 $\{\unicode[STIX]{x1D711}=-\unicode[STIX]{x1D700}\}\cap L$
and, therefore, also the subsurfaces
$\{\unicode[STIX]{x1D711}=-\unicode[STIX]{x1D700}\}\cap L$
and, therefore, also the subsurfaces
 $\{\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\}\cap K$
and
$\{\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\}\cap K$
and
 $\{\unicode[STIX]{x1D713}\leqslant -\unicode[STIX]{x1D700}\}\cap K$
to the subsurfaces
$\{\unicode[STIX]{x1D713}\leqslant -\unicode[STIX]{x1D700}\}\cap K$
to the subsurfaces
 $\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}\cap K$
respectively
$\{\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D700}\}\cap K$
respectively
 $\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}\cap K$
.
$\{\unicode[STIX]{x1D711}\leqslant -\unicode[STIX]{x1D700}\}\cap K$
.
Clearly, if a boundary segment of the latter intersects an
![]() $\unicode[STIX]{x1D700}$
-disc
$\unicode[STIX]{x1D700}$
-disc
![]() $D$
of
$D$
of
![]() $\unicode[STIX]{x1D711}$
, then
$\unicode[STIX]{x1D711}$
, then
![]() $D$
is contained in
$D$
is contained in
![]() $L$
and corresponds under the isotopy to an
$L$
and corresponds under the isotopy to an
![]() $\unicode[STIX]{x1D700}$
-disc
$\unicode[STIX]{x1D700}$
-disc
![]() $B$
of
$B$
of
![]() $\unicode[STIX]{x1D713}$
. Attaching the parts
$\unicode[STIX]{x1D713}$
. Attaching the parts
![]() $B\cap K$
of such discs, we get a surface
$B\cap K$
of such discs, we get a surface
![]() $T^{\pm }$
such that the above isotopy deforms
$T^{\pm }$
such that the above isotopy deforms
![]() $T^{\pm }$
to
$T^{\pm }$
to
 $X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. In particular, the fundamental group of
$X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)$
. In particular, the fundamental group of
![]() $T^{\pm }$
contains an
$T^{\pm }$
contains an
![]() $F_{2}$
,
$F_{2}$
,
![]() $T^{\pm }$
is incompressible in
$T^{\pm }$
is incompressible in
![]() $S$
and
$S$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D712}(T^{\pm })=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(T^{\pm })=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K)).\end{eqnarray}$$
By changing
![]() $\unicode[STIX]{x1D700}$
slightly, we can achieve that
$\unicode[STIX]{x1D700}$
slightly, we can achieve that
![]() $\unicode[STIX]{x1D700}$
is also
$\unicode[STIX]{x1D700}$
is also
![]() $\unicode[STIX]{x1D713}$
-regular. Then, by what we said,
$\unicode[STIX]{x1D713}$
-regular. Then, by what we said,
![]() $T^{\pm }$
is a component of
$T^{\pm }$
is a component of
 $X_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K)$
. Moreover, choosing a
$X_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K)$
. Moreover, choosing a
![]() $\unicode[STIX]{x1D713}$
-regular
$\unicode[STIX]{x1D713}$
-regular
![]() $(\unicode[STIX]{x1D700},K^{\prime })$
with
$(\unicode[STIX]{x1D700},K^{\prime })$
with
![]() $K$
in the interior of
$K$
in the interior of
![]() $K^{\prime }$
, we have
$K^{\prime }$
, we have
 $T^{\pm }\subseteq X_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K^{\prime })$
. Hence
$T^{\pm }\subseteq X_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K^{\prime })$
. Hence
 $X_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K^{\prime })$
is obtained from
$X_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K^{\prime })$
is obtained from
![]() $T^{\pm }$
by attaching annuli, cross caps, and lunes. Now annuli where both boundary curves are attached to
$T^{\pm }$
by attaching annuli, cross caps, and lunes. Now annuli where both boundary curves are attached to
![]() $T^{\pm }$
and cross caps attached to
$T^{\pm }$
and cross caps attached to
![]() $T^{\pm }$
are contained in the interior of
$T^{\pm }$
are contained in the interior of
![]() $K$
and belong to
$K$
and belong to
 $S_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K)$
. We (finally) conclude that
$S_{\unicode[STIX]{x1D713}}^{\pm }(\unicode[STIX]{x1D700},K)$
. We (finally) conclude that
 $(S,S_{\unicode[STIX]{x1D713}}^{+}(\unicode[STIX]{x1D700},K^{\prime }),S_{\unicode[STIX]{x1D713}}^{-}(\unicode[STIX]{x1D700},K^{\prime }))$
is isotopic to the triple
$(S,S_{\unicode[STIX]{x1D713}}^{+}(\unicode[STIX]{x1D700},K^{\prime }),S_{\unicode[STIX]{x1D713}}^{-}(\unicode[STIX]{x1D700},K^{\prime }))$
is isotopic to the triple
 $(S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
.◻
$(S,S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K),S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K))$
.◻
End of proof of Theorem 1.5.
Let
![]() $\mathbb{E}$
be a subspace of
$\mathbb{E}$
be a subspace of
![]() $L^{2}(M)$
which is generated by finitely many eigenfunctions with corresponding eigenvalues less than or equal to
$L^{2}(M)$
which is generated by finitely many eigenfunctions with corresponding eigenvalues less than or equal to
![]() $\unicode[STIX]{x1D6EC}(S)$
and denote by
$\unicode[STIX]{x1D6EC}(S)$
and denote by
![]() $\mathbb{S}$
the unit sphere in
$\mathbb{S}$
the unit sphere in
![]() $\mathbb{E}$
and by
$\mathbb{E}$
and by
![]() $\mathbb{P}$
the projective space of
$\mathbb{P}$
the projective space of
![]() $\mathbb{E}$
. Theorem 1.5 follows if any such
$\mathbb{E}$
. Theorem 1.5 follows if any such
![]() $\mathbb{E}$
has dimension at most
$\mathbb{E}$
has dimension at most
![]() $-\unicode[STIX]{x1D712}(S)$
.
$-\unicode[STIX]{x1D712}(S)$
.
Since
 $\unicode[STIX]{x1D712}(S_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K))$
, (4.18) and Lemma 4.21 imply that we obtain a partition of
$\unicode[STIX]{x1D712}(S_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K))=\unicode[STIX]{x1D712}(X_{\unicode[STIX]{x1D711}}^{\pm }(\unicode[STIX]{x1D700},K))$
, (4.18) and Lemma 4.21 imply that we obtain a partition of
![]() $\mathbb{S}$
into the subsets
$\mathbb{S}$
into the subsets
![]() $\mathbb{A}_{i}$
consisting of functions
$\mathbb{A}_{i}$
consisting of functions
![]() $\unicode[STIX]{x1D711}$
with characteristic
$\unicode[STIX]{x1D711}$
with characteristic
 $i\in \{-\unicode[STIX]{x1D712}(S),\ldots ,-1\}$
. By definition,
$i\in \{-\unicode[STIX]{x1D712}(S),\ldots ,-1\}$
. By definition,
![]() $\unicode[STIX]{x1D711}\in \mathbb{A}_{i}$
if and only if
$\unicode[STIX]{x1D711}\in \mathbb{A}_{i}$
if and only if
 $-\unicode[STIX]{x1D711}\in \mathbb{A}_{i}$
. Hence the partition of
$-\unicode[STIX]{x1D711}\in \mathbb{A}_{i}$
. Hence the partition of
![]() $\mathbb{S}$
into the sets
$\mathbb{S}$
into the sets
![]() $\mathbb{A}_{i}$
is the preimage of a partition of
$\mathbb{A}_{i}$
is the preimage of a partition of
![]() $\mathbb{P}$
into subsets
$\mathbb{P}$
into subsets
![]() $\mathbb{B}_{i}$
under the covering projection
$\mathbb{B}_{i}$
under the covering projection
 $\unicode[STIX]{x1D70B}:\mathbb{B}\rightarrow \mathbb{P}$
.
$\unicode[STIX]{x1D70B}:\mathbb{B}\rightarrow \mathbb{P}$
.
Now at least one of the subsurfaces
 $S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)$
or
$S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)$
or
 $S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)$
is non-empty and has negative Euler characteristic. Therefore, it follows from [Reference IvanovIva92, Theorem 1.2] that there is no isotopy of
$S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)$
is non-empty and has negative Euler characteristic. Therefore, it follows from [Reference IvanovIva92, Theorem 1.2] that there is no isotopy of
![]() $S$
which interchanges the disjoint subsurfaces
$S$
which interchanges the disjoint subsurfaces
 $S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)$
and
$S_{\unicode[STIX]{x1D711}}^{+}(\unicode[STIX]{x1D700},K)$
and
 $S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)$
. Hence the type of
$S_{\unicode[STIX]{x1D711}}^{-}(\unicode[STIX]{x1D700},K)$
. Hence the type of
![]() $\unicode[STIX]{x1D711}\in \mathbb{S}$
is different from the type of
$\unicode[STIX]{x1D711}\in \mathbb{S}$
is different from the type of
![]() $-\unicode[STIX]{x1D711}$
. Hence by Lemma 4.22, the covering
$-\unicode[STIX]{x1D711}$
. Hence by Lemma 4.22, the covering
![]() $\unicode[STIX]{x1D70B}$
is trivial over the subsets
$\unicode[STIX]{x1D70B}$
is trivial over the subsets
![]() $\mathbb{A}_{i}$
. Now
$\mathbb{A}_{i}$
. Now
![]() $\mathbb{P}$
cannot be covered by less than
$\mathbb{P}$
cannot be covered by less than
![]() $\dim \mathbb{E}$
subsets over which
$\dim \mathbb{E}$
subsets over which
![]() $\unicode[STIX]{x1D70B}$
is trivial, by [Reference SévennecSév02, Lemma 8]. We conclude that
$\unicode[STIX]{x1D70B}$
is trivial, by [Reference SévennecSév02, Lemma 8]. We conclude that
 $\dim \mathbb{E}\leqslant -\unicode[STIX]{x1D712}(S)$
.◻
$\dim \mathbb{E}\leqslant -\unicode[STIX]{x1D712}(S)$
.◻
5 Applying the absence of large eigenvalues
We say that a subset
![]() $U$
of the hyperbolic plane is an infinite hinge if it is the region in the hyperbolic plane bounded by two geodesic rays which issue from a common point. Besides Theorem 1.5, the other crucial point of our argument in the proof of Theorem 1.6 is the result of Lax and Phillips that an infinite hinge cannot carry a non-trivial square-integrable solution
$U$
of the hyperbolic plane is an infinite hinge if it is the region in the hyperbolic plane bounded by two geodesic rays which issue from a common point. Besides Theorem 1.5, the other crucial point of our argument in the proof of Theorem 1.6 is the result of Lax and Phillips that an infinite hinge cannot carry a non-trivial square-integrable solution
![]() $\unicode[STIX]{x1D711}$
of the equation
$\unicode[STIX]{x1D711}$
of the equation
 $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}$
with
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}$
with
 $\unicode[STIX]{x1D706}\geqslant 1/4$
; see [Reference Lax and PhillipsLP82, Theorem 4.8]. Notice that Theorem 4.8 also applies in dimension two; see the last sentence in [Reference Lax and PhillipsLP82, § 4].
$\unicode[STIX]{x1D706}\geqslant 1/4$
; see [Reference Lax and PhillipsLP82, Theorem 4.8]. Notice that Theorem 4.8 also applies in dimension two; see the last sentence in [Reference Lax and PhillipsLP82, § 4].
Proof of Theorem 1.6.
The proof is straightforward in the case where the boundary of
![]() $S$
is empty. In that case, since the area of
$S$
is empty. In that case, since the area of
![]() $S$
is infinite,
$S$
is infinite,
![]() $S$
has an end
$S$
has an end
 $F=\{(x,y)\mid x\geqslant 0,y\in \mathbb{R}/L\mathbb{Z}\}$
with metric
$F=\{(x,y)\mid x\geqslant 0,y\in \mathbb{R}/L\mathbb{Z}\}$
with metric
 $dx^{2}+\cosh ^{2}(x)\,dy^{2}$
. Clearly, any such metric contains an infinite hinge
$dx^{2}+\cosh ^{2}(x)\,dy^{2}$
. Clearly, any such metric contains an infinite hinge
![]() $U$
as above and hence the restriction of any eigenfunction of
$U$
as above and hence the restriction of any eigenfunction of
![]() $S$
to
$S$
to
![]() $U$
is a square-integrable solution of
$U$
is a square-integrable solution of
 $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}$
on
![]() $U$
. By the unique continuation principle, it is non-trivial if
$U$
. By the unique continuation principle, it is non-trivial if
![]() $\unicode[STIX]{x1D711}$
is no-trivial, and then
$\unicode[STIX]{x1D711}$
is no-trivial, and then
 $\unicode[STIX]{x1D706}<1/4$
by the work of Lax and Phillips. On the other hand, we have
$\unicode[STIX]{x1D706}<1/4$
by the work of Lax and Phillips. On the other hand, we have
 $\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
by (1.4) and
$\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})$
by (1.4) and
 $\unicode[STIX]{x1D706}_{0}(\tilde{S})=1/4$
since
$\unicode[STIX]{x1D706}_{0}(\tilde{S})=1/4$
since
![]() $\tilde{S}$
is the hyperbolic plane. Hence any eigenvalue of
$\tilde{S}$
is the hyperbolic plane. Hence any eigenvalue of
![]() $S$
is small. Therefore Theorem 1.5 applies and shows that
$S$
is small. Therefore Theorem 1.5 applies and shows that
![]() $S$
has at most
$S$
has at most
![]() $-\unicode[STIX]{x1D712}(S)$
eigenvalues.
$-\unicode[STIX]{x1D712}(S)$
eigenvalues.
The case where the boundary of
![]() $S$
is non-empty and the boundary circles of
$S$
is non-empty and the boundary circles of
![]() $S$
are closed geodesics is easy, too. In that case,
$S$
are closed geodesics is easy, too. In that case,
![]() $S$
also has an end
$S$
also has an end
![]() $F$
as above and the same arguments apply. The difficult part of the proof is the case where the boundary of
$F$
as above and the same arguments apply. The difficult part of the proof is the case where the boundary of
![]() $S$
is non-empty, but no restrictions on the geometry of the boundary are assumed. Then
$S$
is non-empty, but no restrictions on the geometry of the boundary are assumed. Then
![]() $S$
contains at least one funnel
$S$
contains at least one funnel
![]() $F$
with infinite area.
$F$
with infinite area.
Let
![]() $c$
be the boundary circle of
$c$
be the boundary circle of
![]() $F$
. Consider a sequence of points
$F$
. Consider a sequence of points
![]() $q_{n}$
in
$q_{n}$
in
![]() $F$
which diverge to infinity and let
$F$
which diverge to infinity and let
![]() $p_{n}$
be a point in
$p_{n}$
be a point in
![]() $c$
with distance
$c$
with distance
 $d(q_{n},p_{n})=d(q_{n},c)$
. Then the minimal geodesic segment
$d(q_{n},p_{n})=d(q_{n},c)$
. Then the minimal geodesic segment
![]() $\unicode[STIX]{x1D6FE}_{n}$
from
$\unicode[STIX]{x1D6FE}_{n}$
from
![]() $p_{n}$
to
$p_{n}$
to
![]() $q_{n}$
is perpendicular to
$q_{n}$
is perpendicular to
![]() $c$
and
$c$
and
 $\unicode[STIX]{x1D6FE}_{n}\cap c=p_{n}$
. Since
$\unicode[STIX]{x1D6FE}_{n}\cap c=p_{n}$
. Since
![]() $c$
separates
$c$
separates
![]() $F$
from
$F$
from
![]() $S\setminus F$
, we conclude that
$S\setminus F$
, we conclude that
![]() $\unicode[STIX]{x1D6FE}_{n}$
is contained in
$\unicode[STIX]{x1D6FE}_{n}$
is contained in
![]() $F$
. Passing to a subsequence if necessary, the sequence
$F$
. Passing to a subsequence if necessary, the sequence
![]() $\unicode[STIX]{x1D6FE}_{n}$
converges to a minimizing geodesic ray
$\unicode[STIX]{x1D6FE}_{n}$
converges to a minimizing geodesic ray
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $F$
, starting from a point
$F$
, starting from a point
![]() $p$
in
$p$
in
![]() $c$
and perpendicular to
$c$
and perpendicular to
![]() $c$
at
$c$
at
![]() $p$
. Parametrizing
$p$
. Parametrizing
![]() $\unicode[STIX]{x1D6FE}$
by unit speed such that
$\unicode[STIX]{x1D6FE}$
by unit speed such that
 $\unicode[STIX]{x1D6FE}(0)=p$
, we get that
$\unicode[STIX]{x1D6FE}(0)=p$
, we get that
 $d(\unicode[STIX]{x1D6FE}(t),c)=t$
for all
$d(\unicode[STIX]{x1D6FE}(t),c)=t$
for all
![]() $t\geqslant 0$
. Now cut
$t\geqslant 0$
. Now cut
![]() $F$
along
$F$
along
![]() $\unicode[STIX]{x1D6FE}$
to obtain an infinite strip
$\unicode[STIX]{x1D6FE}$
to obtain an infinite strip
![]() $P$
, bounded by two copies
$P$
, bounded by two copies
![]() $\unicode[STIX]{x1D6FE}_{0}$
and
$\unicode[STIX]{x1D6FE}_{0}$
and
![]() $\unicode[STIX]{x1D6FE}_{1}$
of
$\unicode[STIX]{x1D6FE}_{1}$
of
![]() $\unicode[STIX]{x1D6FE}$
on the left and right and by
$\unicode[STIX]{x1D6FE}$
on the left and right and by
![]() $c$
at the bottom, now a smooth curve from
$c$
at the bottom, now a smooth curve from
 $p_{0}=\unicode[STIX]{x1D6FE}_{0}(0)$
to
$p_{0}=\unicode[STIX]{x1D6FE}_{0}(0)$
to
![]() $\unicode[STIX]{x1D6FE}_{1}(0)$
.
$\unicode[STIX]{x1D6FE}_{1}(0)$
.
For any
![]() $t\geqslant 1$
, let
$t\geqslant 1$
, let
![]() $\unicode[STIX]{x1D70E}_{t}$
be the unit speed geodesic segment in
$\unicode[STIX]{x1D70E}_{t}$
be the unit speed geodesic segment in
![]() $P$
starting from
$P$
starting from
![]() $\unicode[STIX]{x1D6FE}_{0}(t)$
and perpendicular to
$\unicode[STIX]{x1D6FE}_{0}(t)$
and perpendicular to
![]() $\unicode[STIX]{x1D6FE}_{0}$
, parametrized on the maximal possible interval. Since
$\unicode[STIX]{x1D6FE}_{0}$
, parametrized on the maximal possible interval. Since
![]() $\unicode[STIX]{x1D70E}_{t}$
never hits
$\unicode[STIX]{x1D70E}_{t}$
never hits
![]() $\unicode[STIX]{x1D6FE}_{0}$
again, there are three alternatives.
$\unicode[STIX]{x1D6FE}_{0}$
again, there are three alternatives.
-
(i) If
 $\unicode[STIX]{x1D70E}_{t}$
neither hits
$\unicode[STIX]{x1D70E}_{t}$
neither hits
 $\unicode[STIX]{x1D6FE}_{1}$
nor
$\unicode[STIX]{x1D6FE}_{1}$
nor
 $c$
, then
$c$
, then
 $\unicode[STIX]{x1D6FE}_{0}$
and
$\unicode[STIX]{x1D6FE}_{0}$
and
 $\unicode[STIX]{x1D70E}_{t}$
bound an infinite hinge, isometric to a corresponding hinge in the hyperbolic plane. Then the result of Lax and Phillips and Theorem 1.5 apply to conclude Theorem 1.6.
$\unicode[STIX]{x1D70E}_{t}$
bound an infinite hinge, isometric to a corresponding hinge in the hyperbolic plane. Then the result of Lax and Phillips and Theorem 1.5 apply to conclude Theorem 1.6. -
(ii) Suppose that
 $\unicode[STIX]{x1D70E}_{t}(r)=\unicode[STIX]{x1D6FE}_{1}(s)$
for some
$\unicode[STIX]{x1D70E}_{t}(r)=\unicode[STIX]{x1D6FE}_{1}(s)$
for some
 $r>0$
. Then
$r>0$
. Then
 $\unicode[STIX]{x1D70E}_{t}|_{[0,r]}$
is a Jordan segment in
$\unicode[STIX]{x1D70E}_{t}|_{[0,r]}$
is a Jordan segment in
 $P$
which decomposes
$P$
which decomposes
 $P$
into a bounded part containing
$P$
into a bounded part containing
 $c$
and an unbounded part
$c$
and an unbounded part
 $Q$
. Since the boundary of
$Q$
. Since the boundary of
 $Q$
consists of the three geodesics
$Q$
consists of the three geodesics
 $\unicode[STIX]{x1D6FE}_{1}|_{[t,\infty )}$
,
$\unicode[STIX]{x1D6FE}_{1}|_{[t,\infty )}$
,
 $\unicode[STIX]{x1D70E}_{t}|_{[0,r]}$
, and
$\unicode[STIX]{x1D70E}_{t}|_{[0,r]}$
, and
 $\unicode[STIX]{x1D6FE}_{1}|_{[s,\infty )}$
, we may think of
$\unicode[STIX]{x1D6FE}_{1}|_{[s,\infty )}$
, we may think of
 $Q$
as a part of the hyperbolic plane. Since the area of
$Q$
as a part of the hyperbolic plane. Since the area of
 $Q$
is infinite, the geodesic rays
$Q$
is infinite, the geodesic rays
 $\unicode[STIX]{x1D6FE}_{1}|_{[t,\infty )}$
and
$\unicode[STIX]{x1D6FE}_{1}|_{[t,\infty )}$
and
 $\unicode[STIX]{x1D6FE}_{1}|_{[s,\infty )}$
cannot be asymptotic. Hence
$\unicode[STIX]{x1D6FE}_{1}|_{[s,\infty )}$
cannot be asymptotic. Hence
 $Q$
contains infinite hinges, and then the result of Lax and Phillips and Theorem 1.5 apply again to conclude Theorem 1.6.
$Q$
contains infinite hinges, and then the result of Lax and Phillips and Theorem 1.5 apply again to conclude Theorem 1.6. -
(iii) Let
 $L$
be the length of
$L$
be the length of
 $c$
and parametrize
$c$
and parametrize
 $c$
by unit speed on
$c$
by unit speed on
 $[0,L]$
. Suppose that
$[0,L]$
. Suppose that
 $\unicode[STIX]{x1D70E}_{1}(r_{1})=c(u)$
for some
$\unicode[STIX]{x1D70E}_{1}(r_{1})=c(u)$
for some
 $u\in (0,L)$
. With
$u\in (0,L)$
. With
 $t=L+1$
, we claim that
$t=L+1$
, we claim that
 $\unicode[STIX]{x1D70E}_{t}$
does not hit
$\unicode[STIX]{x1D70E}_{t}$
does not hit
 $c$
. Otherwise we would have
$c$
. Otherwise we would have
 $\unicode[STIX]{x1D70E}_{t}(r_{t})=c(v)$
for some
$\unicode[STIX]{x1D70E}_{t}(r_{t})=c(v)$
for some
 $v\in (u,L)$
. Furthermore, since
$v\in (u,L)$
. Furthermore, since
 $\unicode[STIX]{x1D6FE}_{0}$
is minimizing to
$\unicode[STIX]{x1D6FE}_{0}$
is minimizing to
 $c$
, we have
$c$
, we have
 $r_{t}\geqslant t$
. Now the geodesic segments
$r_{t}\geqslant t$
. Now the geodesic segments
 $\unicode[STIX]{x1D6FE}_{0}|_{[1,t]}$
,
$\unicode[STIX]{x1D6FE}_{0}|_{[1,t]}$
,
 $\unicode[STIX]{x1D70E}_{1}|_{[0,r_{1}]}$
, and
$\unicode[STIX]{x1D70E}_{1}|_{[0,r_{1}]}$
, and
 $\unicode[STIX]{x1D70E}_{t}|_{[0,r_{t}]}$
together with
$\unicode[STIX]{x1D70E}_{t}|_{[0,r_{t}]}$
together with
 $c|_{[u,v]}$
bound a disc which we may view as a part of the hyperbolic plane. Since
$c|_{[u,v]}$
bound a disc which we may view as a part of the hyperbolic plane. Since
 $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
 $\unicode[STIX]{x1D70E}_{t}$
are perpendicular to
$\unicode[STIX]{x1D70E}_{t}$
are perpendicular to
 $\unicode[STIX]{x1D6FE}_{0}$
, we conclude that Since
$\unicode[STIX]{x1D6FE}_{0}$
, we conclude that Since $$\begin{eqnarray}d(\unicode[STIX]{x1D70E}_{1}(r_{1}),\unicode[STIX]{x1D70E}_{t}(r_{t}))>d(\unicode[STIX]{x1D70E}_{1}(0),\unicode[STIX]{x1D70E}_{t}(0))=L.\end{eqnarray}$$
$$\begin{eqnarray}d(\unicode[STIX]{x1D70E}_{1}(r_{1}),\unicode[STIX]{x1D70E}_{t}(r_{t}))>d(\unicode[STIX]{x1D70E}_{1}(0),\unicode[STIX]{x1D70E}_{t}(0))=L.\end{eqnarray}$$
 $c|_{[u,v]}$
connects
$c|_{[u,v]}$
connects
 $\unicode[STIX]{x1D70E}_{1}(r_{1})$
with
$\unicode[STIX]{x1D70E}_{1}(r_{1})$
with
 $\unicode[STIX]{x1D70E}_{t}(r_{t})$
, this contradicts
$\unicode[STIX]{x1D70E}_{t}(r_{t})$
, this contradicts
 $L(c)=L$
. Hence
$L(c)=L$
. Hence
 $\unicode[STIX]{x1D70E}_{t}$
satisfies one of the first two alternatives. ◻
$\unicode[STIX]{x1D70E}_{t}$
satisfies one of the first two alternatives. ◻
In [Reference MazzeoMaz91], Mazzeo introduced the notion of asymptotically hyperbolic Riemannian metrics. In our setting, we now view a funnel
![]() $F$
of
$F$
of
![]() $S$
as a cylinder
$S$
as a cylinder
 $[0,1)\times \mathbb{R}/\mathbb{Z}$
with a boundary circle
$[0,1)\times \mathbb{R}/\mathbb{Z}$
with a boundary circle
 $z=\{1\}\times \mathbb{R}/\mathbb{Z}$
at infinity. We consider Riemannian metrics on
$z=\{1\}\times \mathbb{R}/\mathbb{Z}$
at infinity. We consider Riemannian metrics on
![]() $F$
of the form
$F$
of the form
 $g=\unicode[STIX]{x1D70C}^{-2}h$
, where
$g=\unicode[STIX]{x1D70C}^{-2}h$
, where
![]() $\unicode[STIX]{x1D70C}$
is a smooth function on
$\unicode[STIX]{x1D70C}$
is a smooth function on
 $Z=[0,1]\times \mathbb{R}/\mathbb{Z}$
with
$Z=[0,1]\times \mathbb{R}/\mathbb{Z}$
with
 $\{\unicode[STIX]{x1D70C}=0\}=z$
and
$\{\unicode[STIX]{x1D70C}=0\}=z$
and
![]() $d\unicode[STIX]{x1D70C}\neq 0$
along
$d\unicode[STIX]{x1D70C}\neq 0$
along
![]() $z$
and where
$z$
and where
![]() $h$
is a Riemannian metric on
$h$
is a Riemannian metric on
![]() $Z$
. Note that because of the factor
$Z$
. Note that because of the factor
![]() $\unicode[STIX]{x1D70C}^{-2}$
, such a metric is complete on
$\unicode[STIX]{x1D70C}^{-2}$
, such a metric is complete on
![]() $F$
with the boundary circle
$F$
with the boundary circle
![]() $z$
located at infinity. By the proposition of [Reference MazzeoMaz88, p. 311], the curvature of
$z$
located at infinity. By the proposition of [Reference MazzeoMaz88, p. 311], the curvature of
![]() $g$
tends to
$g$
tends to
 $-(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708})^{2}$
when approaching
$-(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708})^{2}$
when approaching
![]() $z$
, where
$z$
, where
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}$
denotes the
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}$
denotes the
![]() $h$
-normal derivative of
$h$
-normal derivative of
![]() $\unicode[STIX]{x1D70C}$
along
$\unicode[STIX]{x1D70C}$
along
![]() $z$
. Now it follows from [Reference MazzeoMaz91, Theorem 16] (see also the remark on locality in the first paragraph of [Reference MazzeoMaz91, § IV]) that
$z$
. Now it follows from [Reference MazzeoMaz91, Theorem 16] (see also the remark on locality in the first paragraph of [Reference MazzeoMaz91, § IV]) that
![]() $F$
cannot carry a non-trivial
$F$
cannot carry a non-trivial
![]() $L^{2}$
-solution
$L^{2}$
-solution
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
 $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}$
with
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}$
with
 $\unicode[STIX]{x1D706}\geqslant 1/4$
if
$\unicode[STIX]{x1D706}\geqslant 1/4$
if
 $|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|=1$
along
$|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|=1$
along
![]() $z$
(or, more generally, if
$z$
(or, more generally, if
 $|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|\geqslant 1$
along
$|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|\geqslant 1$
along
![]() $z$
such that
$z$
such that
 $\{|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|=1\}$
contains a non-empty open subarc of
$\{|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|=1\}$
contains a non-empty open subarc of
![]() $z$
).
$z$
).
Theorem 5.1. Let
![]() $S$
be a surface of finite type with a complete Riemannian metric with
$S$
be a surface of finite type with a complete Riemannian metric with
 $K\leqslant -1$
and with at least one asymptotically hyperbolic funnel
$K\leqslant -1$
and with at least one asymptotically hyperbolic funnel
![]() $F$
as above such that
$F$
as above such that
 $|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|=1$
along
$|\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D708}|=1$
along
![]() $z$
. Then
$z$
. Then
![]() $S$
has at most
$S$
has at most
![]() $-\unicode[STIX]{x1D712}(S)$
eigenvalues, counted with multiplicity, and all of them are contained in
$-\unicode[STIX]{x1D712}(S)$
eigenvalues, counted with multiplicity, and all of them are contained in
![]() $(0,1/4)$
.
$(0,1/4)$
.
Proof. By what we said above,
![]() $S$
does not have eigenvalues greater than or equal to
$S$
does not have eigenvalues greater than or equal to
![]() $1/4$
. On the other hand, since
$1/4$
. On the other hand, since
 $K\leqslant -1$
, we have
$K\leqslant -1$
, we have
 $\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})\geqslant 1/4$
. Hence all eigenvalues of
$\unicode[STIX]{x1D6EC}(S)\geqslant \unicode[STIX]{x1D706}_{0}(\tilde{S})\geqslant 1/4$
. Hence all eigenvalues of
![]() $S$
are small. By Theorem 1.5, there are at most
$S$
are small. By Theorem 1.5, there are at most
![]() $-\unicode[STIX]{x1D712}(S)$
of them. Since the area of
$-\unicode[STIX]{x1D712}(S)$
of them. Since the area of
![]() $S$
is infinite, 0 is not an eigenvalue, and hence all eigenvalues of
$S$
is infinite, 0 is not an eigenvalue, and hence all eigenvalues of
![]() $S$
are contained in
$S$
are contained in
![]() $(0,1/4)$
.◻
$(0,1/4)$
.◻
Acknowledgements
We thank Eberhard Freitag, Ursula Hamenstädt, Rafe Mazzeo, Werner Müller, and the anony- mous referees for helpful comments and gratefully acknowledge the support and the hospitality of the Max Planck Institute for Mathematics in Bonn, the Hausdorff Center for Mathematics in Bonn, and the Erwin Schrödinger Institute in Vienna.