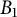Volterra-type operators on the minimal Möbius-invariant space

Abstract

In this note, we mainly study operator-theoretic properties on the Besov space $B_{1}$ on the unit disk. This space is the minimal Möbius-invariant space. First, we consider the boundedness of Volterra-type operators. Second, we prove that Volterra-type operators belong to the Deddens algebra of a composition operator. Third, we obtain estimates for the essential norm of Volterra-type operators. Finally, we give a complete characterization of the spectrum of Volterra-type operators.

1 Introduction and preparation

In this paper, $\mathbb {D}$ denotes the open unit disk and $\mathbb {T}$ be the unit circle. Let $H(\mathbb {D})$ be the space of all analytic functions on $\mathbb {D}$ . For $0<p<\infty $ , the Hardy space $H^p$ consists of analytic functions $f\in \mathbb {D}$ such that

$$ \begin{align*}\|f\|^p_{H^p}=\sup_{0\leq r<1}\frac{1}{2\pi}\int^{2\pi}_{0}|f(re^{i\theta})|^p\,d\theta<\infty. \end{align*} $$

If $p=\infty $ , then $H^{\infty }$ is the space of bounded analytic functions f on $H(\mathbb {D})$ with

$$ \begin{align*}\|f\|_{\infty}=\sup\{|f(z)|:z\in \mathbb{D}\}. \end{align*} $$

For $0<p<\infty $ , the Bergman space $A^p$ consists of all functions f analytic on $\mathbb {D}$ such that

$$ \begin{align*}\|f\|^p_{A^p}=\int_{\mathbb{D}}|f(z)|^p \,dA(z)<\infty, \end{align*} $$

where $dA(z)$ is the normalized Lebesgue area measure on $\mathbb {D}$ . It is clear that $H^p\subset A^p$ . Moreover, $H^p\subset A^{2p}$ and $\|f\|_{A^{2p}}\leq \|f\|_{H^p}$ for $0<p<\infty $ . See [44] for example.

The Dirichlet-type space $\mathcal {D}^p$ is the set of all functions $f\in H(\mathbb {D})$ with

$$ \begin{align*}\|f\|^p_{\mathcal{D}^p}=|f(0)|^p+\int_{\mathbb{D}}|f'(z)|^p \,dA(z)<\infty. \end{align*} $$

The space of all conformal automorphisms of $\mathbb {D}$ forms a group, called the Möbius group, and is denoted by $\mathrm {Aut}\, (\mathbb {D})$ . It is well known that $\varphi $ belongs to $ \mathrm {Aut}\, (\mathbb {D})$ if and only if there exists a real number $\theta $ and a point $a\in \mathbb {D}$ such that

$$ \begin{align*} \varphi(z)=e^{i\theta}\sigma_{a}(z) ~\mbox{ and }~ \sigma_{a}(z)=\frac{a-z}{1-\overline{a}z}, \quad z\in\mathbb{D}. \end{align*} $$

Let X be a Banach space of analytic functions on $\mathbb {D}$ . Then X is said to be Möbius-invariant whenever $f\circ \varphi \in X$ for all $f\in X$ and $\varphi \in \mathrm {Aut}\, (\mathbb {D})$ and $\|f\circ \varphi \|_{X}=\|f\|_{X}$ .

For $1<p<\infty $ , the Besov space $B_p$ consists of analytic functions f on $\mathbb {D}$ such that

$$ \begin{align*}\int_{\mathbb{D}}(1-|z|^2)^{p-2}|f'(z)|^{p}\,dA(z)<\infty. \end{align*} $$

The norm of $B_p$ is defined as

$$ \begin{align*}\|f\|_{B_p}=|f(0)|+\left(\int_{\mathbb{D}}(1-|z|^2)^{p-2}|f'(z)|^{p}\,dA(z)\right)^{\frac{1}{p}}. \end{align*} $$

When $p=\infty $ , $B_{\infty }=: \mathcal {B}$ is called the classical Bloch space. We define a norm on $\mathcal {B}$ as

$$ \begin{align*}\|f\|_{\mathcal{B}}=|f(0)|+\sup_{z\in\mathbb{D}}(1-|z|^2)|f'(z)|<\infty. \end{align*} $$

When $p=2$ , $B_2=:\mathcal {D}$ is the classical Dirichlet space. When $p=1$ , we get the analytic Besov space $B_1$ , which is the minimal Möbius-invariant space consisting of all functions $f\in H(\mathbb {D})$ with

$$ \begin{align*}f(z)=\sum^{\infty}_{k=1}c_k\sigma_{a_k}(z), \end{align*} $$

where the sequences $\{c_k\}_{k\geq 1}\in \ell ^1$ and $\{a_k\}_{k\geq 1}\in \mathbb {D}$ . An equivalent norm of $B_1$ is defined as

$$ \begin{align*}\|f\|_{B_1}=|f(0)|+|f'(0)|+\int_{\mathbb{D}}|f''(z)|\,dA(z). \end{align*} $$

Arazy, Fisher, and Peetre [5] first studied minimal Möbius-invariant space systematically. More results related to minimal Möbius-invariant space may be seen from [6, 7, 9, 32, 33, 45].

Now, we define several operators on $B_1$ . For $g\in H(\mathbb {D})$ , the multiplication operator $M_g$ on $B_1$ is defined as

$$ \begin{align*}(M_{g})f(z)=f(z)g(z),~ f\in B_1,~ z\in\mathbb{D}. \end{align*} $$

The differentiation operator is given by $Df=f'$ for each $f\in H(\mathbb {D})$ . Given $g\in H(\mathbb {D})$ , the Volterra-type operator $T_g$ is defined as

$$ \begin{align*}(T_gf)(z)=\int^{z}_{0}f(w)g'(w)\,dw, ~\mbox{ for all } f\in B_1. \end{align*} $$

When $g(z)=z$ , the operator $T_zf(z)=\int ^{z}_{0}f(w)dw$ becomes the simplest Volterra operator. An integral operator related to $T_g$ , denoted by $I_g$ , is defined as

$$ \begin{align*}(I_gf)(z)=\int^{z}_{0}f'(w)g(w)\,dw, ~\mbox{ for all } f\in B_1. \end{align*} $$

The Volterra-type operator $T_g$ was originally studied by Pommerenke [38]. Later, a series of articles appeared on the study of Volterra-type integration operators on classical spaces of analytic functions, such as Hardy spaces, Bergman spaces, and Dirichlet-type spaces. For more details, please refer to [1, 3, 4, 16, 18]. In [13], Čučković and Paudyal describe the lattice of the closed invariant subspaces of Volterra-type operators. Lin, Liu, and Wu [22] generalized some of the works of [13] to the general case when $1\leq p<\infty $ , and obtained the boundedness of the Volterra-type operators $T_g$ and $I_g$ on the derivative Hardy space $S_p(\mathbb {D})$ . And then, they also considered strict singularity of Volterra-type operators on Hardy spaces in [23]. Meanwhile, Lin [21] characterized the boundedness and compactness of the Volterra-type operators between Bloch-type spaces and weighted Banach spaces. In [31], Miihkinen et al. completely characterize the boundedness of the Volterra-type operators acting from the weighted Bergman spaces to the Hardy spaces of the unit ball.

In this paper, we mainly study the operator-theoretic properties in minimal Möbius-invariant space $B_1$ . The structure of this article is as follows. In Section 2, we discuss the boundedness of the Volterra operator on $B_1$ . In Section 3, it is shown whether the integral operator belongs to Deddens algebras. In Section 4, we will be concerned with the essential norms of integral operators on $B_1$ . Section 5 is devoted to the study of the spectrum of integral operators on $B_1$ .

Throughout this paper, we use the following convention. For two nonnegative functions F and G defined on some function space $X,$ we write $F \lesssim G$ if $F(f) \leq C\cdot G(f)$ for all $f \in X$ and for some positive constant C which is independent of F and $G.$ Denote by $F\approx G$ whenever $F\lesssim G \lesssim F$ .

2 Volterra-type operators on $B_1$

First, we need the following Hardy inequality.

Lemma 1 [15]

If $f\in H^1$ and $f(z)= \sum ^{\infty }_{n=0}a_nz^n$ , then

$$ \begin{align*}\sum^{\infty}_{n=0}\frac{|a_n|}{n+1}\leq\pi\|f\|_{H^1}. \end{align*} $$

The following lemma is a classic exercise in mathematical analysis, but it might be worth to give a brief details of the proof for completeness.

Lemma 2 Suppose that $f(x)$ is a continuously increasing function on $[a,b]$ . Then,

$$ \begin{align*}\int^{b}_{a}xf(x)dx\geq\frac{a+b}{2}\int^{b}_{a}f(x)\,dx. \end{align*} $$

Proof As $f(x)$ is monotonically increasing on $[a,b]$ , the “integral mean value theorem” shows that there exists a $\xi \in [a,b]$ such that

$$ \begin{align*} \int^{b}_{a}\left(x-\frac{a+b}{2}\right)f(x)\,dx=&f(a)\int^{\xi}_{a}\left(x-\frac{a+b}{2}\right)dx+f(b)\int^{b}_{\xi}\left(x-\frac{a+b}{2}\right)dx\\ =&\frac{1}{2}(f(b)-f(a))(a\xi+b\xi-\xi^2-ab)\\ =&\frac{1}{2}(f(b)-f(a))(b-\xi)(\xi-a)\geq0. \end{align*} $$

This completes the proof of the lemma.

Lemma 3 If $f\in \mathcal {D}^1$ , then $\|f\|_{H^1}\leq \|f\|_{\mathcal {D}^1}.$

Proof Let $f\in \mathcal {D}^1.$ Then, we can see that

$$ \begin{align*}|f(e^{i\theta})|-|f(0)|\leq|f(e^{i\theta})-f(0)|\leq\left|\int^1_0f'(re^{i\theta}) \,dr\right|\leq\int^1_0|f'(re^{i\theta})| \,dr. \end{align*} $$

Thus,

$$ \begin{align*} \|f\|_{H_1}=&\frac{1}{2\pi}\int^{2\pi}_{0}|f(e^{i\theta})| \,d\theta\\ \leq&\frac{1}{2\pi}\int^{2\pi}_{0}\left[|f(0)|+\int^{1}_{0}|f'(re^{i\theta})| \,dr\right]d\theta\\ \leq&|f(0)|+\frac{1}{2\pi}\int^{2\pi}_{0}\int^{1}_{0}|f'(re^{i\theta})| \,dr \,d\theta. \end{align*} $$

On the other hand,

$$ \begin{align*} \|f\|_{\mathcal{D}^1}=|f(0)|+\int_{\mathbb{D}}|f'(z)| \,dA(z) =&|f(0)|+\frac{1}{\pi}\int^{2\pi}_{0}\int^{1}_{0}r|f'(re^{i\theta})| \,dr \,d\theta. \end{align*} $$

By Hardy’s convexity theorem (see [28, 46]), we find that

$$ \begin{align*}F(r)=\frac{1}{2\pi}\int^{2\pi}_{0}|f'(re^{i\theta})|\,d\theta,\, ~0<r<1, \end{align*} $$

is a nondecreasing function of r. It follows from Lemma 2 that

$$ \begin{align*}\int^{1}_{0}F(r)dr\leq2\int^{1}_{0}rF(r) \,dr. \end{align*} $$

This shows that $\|f\|_{H^1}\leq \|f\|_{\mathcal {D}^1}$ .

Remark 1 In Lemma 3, set $f(z)=z$ . Then, we see that $1=\|z\|_{H^1}\leq \|z\|_{\mathcal {D}^1}=1$ , showing that the norm estimate is sharp. This improves the previous conclusion, namely, $\|f\|_{H^1}\leq 2\|f\|_{\mathcal {D}^1}$ from the works of Girela and Merchán [17].

Lemma 4 If $f\in B_1$ , then $\|f\|_{\infty }\leq \pi \|f\|_{B_1}$ and $B_1\subset H^{\infty }$ .

Proof Assume that $f\in B_1$ and write $f(z)=\sum ^{\infty }_{k=0}a_kz^k$ . By Lemmas 1 and 3, we have

$$ \begin{align*} |f(z)|=\left|\sum^{\infty}_{k=0}a_kz^k\right|\leq\sum^{\infty}_{k=0}|a_kz^k| \leq&\sum^{\infty}_{k=0}|a_k| \leq \pi\|f'\|_{H^1}+|f(0)| \leq \pi\|f'\|_{\mathcal{D}^1}+|f(0)|\leq\pi\|f\|_{B_1}, \end{align*} $$

for all $z\in \mathbb {D}$ . Hence, we obtain that $\|f\|_{\infty }\leq \pi \|f\|_{B_1}$ .

Remark 2 In [22, Theorem 1], they obtained that $\|f\|_{\infty }\leq \pi \|f\|_{S^1}$ for each $f\in S^1$ , where the space $S^1$ is defined as $S^1=\{f\in H^1:f'\in H^1\}$ . The norm on $S^1$ is given by

$$ \begin{align*}\|f\|_{S^1}=|f(0)|+\|f'\|_{H^1}. \end{align*} $$

Moreover, we obtain the following norm estimate:

$$ \begin{align*} \|f\|_{\infty}\leq\pi\|f\|_{S^1}\leq\pi\|f\|_{B_1},\ \ \mbox{for all} f\in B_1. \end{align*} $$

In the following, we discuss the boundedness of $T_g$ and $I_g$ on minimal Möbius-invariant space.

Theorem 1 The operator $T_g$ is bounded on $B_1$ if and only if $g\in B_1$ . Moreover,

$$ \begin{align*}\|g-g(0)\|\leq \|T_g\|\leq (1+\pi) \|g-g(0)\|_{B_1}. \end{align*} $$

Proof Let $f\in B_{1}$ . By Hölder’s inequality and Lemma 3, we have

$$ \begin{align*} \int_{\mathbb{D}}|f'(z)g'(z)| \,dA(z)&\leq\left(\int_{\mathbb{D}}|f'(z)|^2 \, dA(z)\right)^{\frac{1}{2}}\left(\int_{\mathbb{D}}|g'(z)|^2 \,dA(z)\right)^{\frac{1}{2}} =\|f'\|_{A^2}\|g'\|_{A^2}\\ &\leq\|f'\|_{H^1}\|g'\|_{H^1} \\ &\leq\|f'\|_{\mathcal{D}^1}\|g'\|_{\mathcal{D}^1} \\ &\leq \|f\|_{B_1}\|g-g(0)\|_{B_1}. \end{align*} $$

Hence, we get

$$ \begin{align*} \|T_gf\|_{B_1}&=\|fg'\|_{\mathcal{D}^1(\mathbb{D})} = |f(0)g'(0)|+\!\int_{\mathbb{D}}|f'(z)g'(z)| \,dA(z)+\!\int_{\mathbb{D}}|f(z)g''(z)| \,dA(z)\\ &\leq \|f\|_{B_1}\|g-g(0)\|_{B_1}+\|f\|_{\infty}\|g-g(0)\|_{B_1}\\ &\leq (1+\pi) \|f\|_{B_1}\|g-g(0)\|_{B_1}, \end{align*} $$

showing that $T_g$ is a bounded operator on $B_1$ .

Conversely, assume that $T_g$ is a bounded operator on $B_1$ and let $f=1$ . Then, we obtain

$$ \begin{align*}\|T_g\|\geq\|T_g1\|_{B_1}\geq \|g-g(0)\|_{B_1}, \end{align*} $$

which gives that $g\in B_1$ . Thus,

$$ \begin{align*}\|g-g(0)\|\leq \|T_g\|\leq (1+\pi) \|g-g(0)\|_{B_1}.\\[-2.7pc] \end{align*} $$

For $0<p<\infty $ , $-2<q<\infty $ , and $0\leq s<\infty $ , we define the general family of function spaces $F(p,q,s)$ as the set of all analytic functions f on $\mathbb {D}$ such that

$$ \begin{align*}\|f\|^{p}_{p,q,s}=|f(0)|+\sup_{a\in \mathbb{D}}\int_{\mathbb{D}}|f'(z)|^{p}(1-|z|^2)^{q}g^{s}(z,a) \,dA(z)<\infty, \end{align*} $$

where $g(z,a)=\log \frac {1}{|\sigma _a(z)|}$ . These spaces were introduced by Zhao in [47]. In 2003, Rättyä provided the following nth derivation characterization of functions in spaces $F(p,q,s)$ .

Lemma 5 [39, Theorem 3.2]

Let f be an analytic function on $\mathbb {D}$ , and let $0<p<\infty , -2<q<\infty $ , and $0\leq s<\infty $ . Let $n\in \mathbb {N}$ and $q+s>-1$ ; or $n=0$ and $q+s-p>-1$ . Then, $f\in F(p,q,s)$ if and only if

$$ \begin{align*}\sup_{a\in \mathbb{D}}\int_{\mathbb{D}}|f^{(n)}(z)|^p(1-|z|^2)^{np-p+q}(1-|\varphi_a(z)|^2)^s \,dA(z)<\infty. \end{align*} $$

For $p>0$ , the space $Z_p$ consists of all analytic functions f on $\mathbb {D}$ such that

$$ \begin{align*}\|f\|_{Z_p}=|f(0)|+\sup_{a\in \mathbb{D}}\int_{\mathbb{D}}|(f\circ\sigma_a(z))'|(1-|z|^2)^{p-1} \,dA(z)<\infty. \end{align*} $$

It is clear that $Z_1=F(1,-1,1)$ . For more results about $Z_{p}$ space, see [25, 48].

Theorem 2 The operator $I_g$ is bounded on $B_1$ if and only if $g\in Z_{1}\cap H^{\infty }$ .

Proof Assume that $g \in Z_{1}\cap H^{\infty }$ . Using Lemma $6$ of [25], we obtain that

$$ \begin{align*}\int_{\mathbb{D}}|f'(w)|\cdot|g'(w)| \,dA(w)\lesssim \|g\|_{Z_{1}} \left(|f'(0)|+\int_{\mathbb{D}}|f''(w)| \,dA(w)\right). \end{align*} $$

Thus, we have

$$ \begin{align*} &\|(I_gf)(z)\|_{B_1}=\|f'g\|_{\mathcal{D}^1}\\[3pt] & \quad \leq |f'(0)g(0)|+ \int_{\mathbb{D}}|f''(w)|\cdot|g(w)| \,dA(w)+\int_{\mathbb{D}}|f'(w)|\cdot|g'(w)| \,dA(w)\\[3pt] & \quad \lesssim |f'(0)g(0)|+ \|g\|_{\infty}\int_{\mathbb{D}}|f''(w)| \,dA(w)+\|g\|_{Z_{1}}\left(|f'(0)|+\int_{\mathbb{D}}|f''(w)| \,dA(w)\right)\\[3pt] & \quad \lesssim (\|g\|_{\infty}+\|g\|_{Z_{1}})\|f\|_{B_1} \end{align*} $$

for all $f\in B_1$ . This implies that $I_g$ is a bounded operator on $B_1$ .

Conversely, suppose that $I_g$ is a bounded operator on $B_1$ . For each $a\in \mathbb {D}$ , let $f(z)=\sigma _{a}(z)$ . Then, $\|f\|_{B_1}\lesssim 1$ and

$$ \begin{align*} \|I_g\| &\gtrsim \|I_gf\|_{B_1} =\|g(w)f'(w)\|_{\mathcal{D}^1}\\[3pt] &\geq \|g(w)f'(w)\|_{H^1} =\int^{2\pi}_{0}|g(e^{i\theta})|\cdot|\sigma'_{a}(e^{i\theta})| \,d\theta =\int^{2\pi}_{0}|g(\sigma_{a}(e^{i\theta}))| \,d\theta\\[3pt] &\geq |g(\sigma_{a}(0))|=|g(a)|, \end{align*} $$

which shows that $\|I_g\|\gtrsim \|g\|_{\infty }$ . Hence, $g\in H^{\infty }$ . Moreover,

$$ \begin{align*} \|I_g\| & \gtrsim \|I_g\sigma_a\|_{B_1}\\[3pt] &\geq\int_{\mathbb{D}}|\sigma'_{a}(w)|\cdot|g'(w)| \,dA(w)-\int_{\mathbb{D}}|\sigma"_{a}(w)|\cdot|g(w)| \,dA(w)\\[3pt] &\geq\int_{\mathbb{D}}|\sigma'_{a}(w)|\cdot|g'(w)| \,dA(w)-\|g\|_{\infty}\|\sigma_a\|_{B_1}, \end{align*} $$

from which it follows that

$$ \begin{align*}\|I_g\|+\|g\|_{\infty}\|\sigma_a\|_{B_1} \gtrsim \int_{\mathbb{D}}|\sigma'_{a}(w)|\cdot|g'(w)| \,dA(w). \end{align*} $$

This implies that $g\in Z_1$ . Therefore, $g\in Z_1\cap H^{\infty }$ . This completes the proof of the theorem.

Remark 3 Note that $B_1\subset Z_1\cap H^{\infty }.$ By Lemma 4, we know that $f\in H^{\infty }$ whenever $f\in B_1$ . Using the second derivation characterization of functions on $Z_1$ , we have

$$ \begin{align*} \|f\|_{Z_1}\approx |f(0)|+\sup_{a\in \mathbb{D}}\int_{\mathbb{D}}|f''(z)|(1-|\sigma_a(z)|^2) \,dA(z)\leq |f(0)|+\int_{\mathbb{D}}|f''(z)| \,dA(z)\leq\|f\|_{B_1}. \end{align*} $$

Then $f\in Z_1$ , and thus $B_1\subset Z_1\cap H^{\infty }$ .

Now, we define the space $B^0_1$ as

$$ \begin{align*}B^0_1=\{f\in B_1:f(0)=0\}. \end{align*} $$

The following theorem gives the connection between the Volterra operator $T_z$ on $\mathcal {D}^1$ and the multiplication operator $M_z$ on $B^0_1$ .

Theorem 3 The Volterra-type operator $T_{z}:\mathcal {D}^1\rightarrow B^0_1$ is bounded and invertible with $T^{-1}_z= D .$

Proof First, we show that $T_z(\mathcal {D}^1)=B^0_1.$ For $f\in \mathcal {D}^1$ , we consider

$$ \begin{align*}F(z):=(T_zf)(z)=\int^{z}_{0}f(w)\,dw. \end{align*} $$

Clearly, $F'=f\in \mathcal {D}^1$ so that $F\in B^0_1$ and $T_{z}(\mathcal {D}^1)\subseteq B^0_1.$

Conversely, for each $F\in B^0_1$ , we have $F' \in \mathcal {D}^1$ . Then,

$$ \begin{align*}(T_z(F'(z)))=\int^{z}_{0}F'(w)\,dw=F(z)-F(0)=F(z). \end{align*} $$

Then, $B^0_1 \subseteq T_{z}(\mathcal {D}^1)$ . This implies that $T_{z}(\mathcal {D}^1)=B^0_1$ .

Second, we show that $T_z:\mathcal {D}^1 \rightarrow B^0_1$ is a bounded isomorphism, and its inverse $T^{-1}_{z}= D.$ Recall from the above discussion that $(T_z(F'(z)))=F(z)$ for $F\in B^0_1$ . Then, for each $f\in \mathcal {D}^1$ , we have that $(D(T_zf))(z)=f(z)$ . This implies that $T_z$ is a bijective operator from $\mathcal {D}^1$ onto $B^0_1$ , since $T_z$ is linear and $T_z$ is an isomorphism from $\mathcal {D}^1$ onto $B^0_1$ .

Finally, we need to prove that $T_z$ is a bounded operator on $\mathcal {D}^1$ . For $f\in \mathcal {D}^1$ , we have

$$ \begin{align*}\|T_zf\|_{B_1}\lesssim ( |(T_zf)(0)|+\|f\|_{\mathcal{D}^1})\lesssim \|f\|_{\mathcal{D}^1}. \end{align*} $$

Therefore, $T_z$ is a bounded isomorphism from $\mathcal {D}^1$ onto $B^0_1$ .

Let us introduce an addition operator P defined as

$$ \begin{align*}(Pf)(z)=(M_zf)(z)+(T_zf)(z)\ \mbox{ for } f\in H(\mathbb{D}) \mbox{ and } z\in\mathbb{D}. \end{align*} $$

Theorem 4 Let $T_{z}:\mathcal {D}^1\rightarrow B^0_1$ and $M_z:B^0_1\rightarrow \mathcal {D}^1$ be the Volterra-type operator and the multiplication operator, respectively. Then, P is an operator on $\mathcal {D}^1$ with $P=T^{-1}_{z}M_zT_z.$

Proof Let $f\in \mathcal {D}^1$ and $F=T_zf$ . Then, we get

$$ \begin{align*} (Pf)(z)=&(M_zf)(z)+(T_zf)(z) =zf(z)+F(z) =D(zF(z)) =(T_z^{-1}M_zT_zf)(z), \end{align*} $$

which shows that $P=T^{-1}_{z}M_zT_z$ .

Theorem 5 If $f,g\in B_1$ , then $\|fg\|_{B_1}\leq (2\pi +2)\|f\|_{B_1}\|g\|_{B_1}$ .

Proof For $f,g\in B_1$ , we get

$$ \begin{align*} \|f g\|_{B_1}&=|f(0)g(0)|+|(fg)'(0)|\\& \quad +\int_{\mathbb{D}}|f''(w)g(w)+2f'(w)g'(w)+f(w)g''(w)| \,dA(w)\\& \leq (|f(0)|+|f'(0)|)(|g(0)|+|g'(0)|)+\int_{\mathbb{D}}|f''(w)g(w)| \,dA(w)\\& \quad +2\int_{\mathbb{D}}|f'(w)g'(w)| \,dA(w)+\int_{\mathbb{D}}|f(w)g''(w)| \,dA(w)\\&\leq\|g\|_{B_1}(|f(0)|+|f'(0)|) +\|g\|_{\infty} (\|f\|_{B_1}-|f(0)|-|f'(0)|)\\& \quad +2\|f\|_{B_1}\|g\|_{B_1}+\|f\|_{\infty}\int_{\mathbb{D}}|g''(w)| \,dA(w)\\&\leq\|g\|_{B_1}(|f(0)|+|f'(0)|)+\pi\|g\|_{B_1}(\|f\|_{B_1}-|f(0)|-|f'(0)|)\\& \quad +2\|f\|_{B_1}\|g\|_{B_1}+\pi\|f\|_{B_1}\|g\|_{B_{1}}\\&\leq(2\pi+2)\|f\|_{B_1}\|g\|_{B_1}, \end{align*} $$

and the proof is complete.

Remark 4 In [5, Theorem 10], Arazy et al. obtained $\|fg\|\leq 7\|f\|\|g\|$ for $f,g\in B_1$ , in which they defined the norm of $f\in B_1$ as

$$ \begin{align*}\|f\|=\inf\left\{\sum^{\infty}_{k=1}|c_{k}|:f(z)=\sum^{\infty}_{k=1}c_k\sigma_{a_k}(z)\right\}. \end{align*} $$

Inspired by their work, we derived Theorem 5 and we are not sure whether the constant $2\pi +2$ in Theorem 5 is optimal or not.

3 Deddens algebras

Let $\mathcal {L}(X)$ denote the algebra of all bounded linear operators on a complex Banach space X. A nontrivial invariant subspace of an operator $A\in \mathcal {L}(X)$ is, by definition, a closed subspace M of X such that $M\neq \{0\}$ , $M\neq X$ , and $Ax\in M$ for every $x\in M$ ; or, briefly, $A(M)\subset M$ .

Let $A\in \mathcal {L}(X)$ . The operator T is said to belong to the Deddens algebra $\mathcal {D}_A$ if there exists $M=M(T)>0$ such that

$$ \begin{align*}\|A^nTf\|\leq M\|A^nf\| \end{align*} $$

for each $n\in \mathbb {N}$ and $f\in X$ .

The study of the Deddens algebra was originally introduced by Deddens [14], where he assumed that A is an invertible operator and $\sup _{n\in \mathbb {N}}\|A^nTA^{-n}\|<\infty $ . Later, it received the attention of many scholars (see [14, 19, 20, 34–37, 42, 43]). Recently, Petrovic and Sievewright [37] studied the Deddens algebra associated with compact composition operators $C_{\varphi }$ on Hardy spaces, where A is not necessarily invertible, and they have demonstrated that the operators $M_g$ and $T_z$ belong to the Deddens algebra $\mathcal {D}_{C_{\varphi }}$ . It is worth to point out that compact operators on $H^2$ are not invertible.

Let us begin to present the boundedness of composition operators and multiplication operators on $B_1$ .

Lemma 6 [45]

Let $\varphi $ be an analytic self-map of $\mathbb {D}$ . Then, the composition operator $C_{\varphi }$ is bounded on $B_1$ if and only if

$$ \begin{align*}\sup_{a\in\mathbb{D}}\|C_{\varphi}\sigma_a\|_{B_1}<\infty. \end{align*} $$

In particular, we give another description of sufficiency condition for the boundedness of the composition operator in the following theorem.

Theorem 6 Let $\varphi $ be an analytic self-map of $\mathbb {D}$ such that $\varphi (0)=0$ . Then, the composition operator $C_{\varphi }$ is bounded on $B_1$ whenever $\varphi '\in Z_1\cap H^{\infty }$ .

Proof Suppose that $\varphi '\in Z_1\cap H^{\infty }$ . Then, we get

$$ \begin{align*} \|C_{\varphi}f\|_{B_1}&=\|f(\varphi(z))\|_{B_1}\\&=|f(\varphi(0))|+|f'(\varphi(0))\varphi'(0)|+\int_{\mathbb{D}}|f''(\varphi(w))\cdot(\varphi'(w))^2\\ & \quad + f'(\varphi(w))\cdot\varphi''(w)| \,dA(w)\\&\leq |f(\varphi(0))|+|f'(\varphi(0))\varphi'(0)|+\int_{\mathbb{D}}|f''(\varphi(w))\cdot(\varphi'(w))^2| \,dA(w) \\ & \quad +\int_{\mathbb{D}}|f'(\varphi(w))\cdot\varphi''(w)| \,dA(w)\\ &\lesssim \|f\|_{\infty}+\|\varphi'\|_{\infty} \|f\|_{B_{1}}+\|\varphi'\|^{2}_{\infty} \|f\|_{B_{1}} +\|\varphi\|_{Z_{1}} \|\varphi'\|_{\infty} \|f\|_{B_{1}} \\ &\lesssim (\|\varphi'\|^{2}_{\infty}+\|\varphi\|_{Z_{1}} \|\varphi'\|_{\infty}+ \|\varphi'\|_{\infty} +1)\|f\|_{B_1}, \end{align*} $$

which implies that $C_{\varphi }$ is bounded on $B_1$ if $\varphi '\in Z_1\cap H^{\infty }$ .

Theorem 7 Suppose that $M_g$ is a multiplication operator on $B_1$ . Then, $M_g$ is bounded if and only if $g\in B_1$ .

Proof For any $f\in B_1$ , if $g\in B_1$ , we have $M_g$ is bounded on $B_1,$ by Theorem 5.

Conversely, let $M_g$ be a bounded operator on $B_1.$ Then, with $f=1$ , we get $\|M_g\|\geq \|M_g1\|_{B_1}=\|g\|_{B_1}$ , which implies that $g\in B_1$ .

In the following theorem, we will consider the algebra $\mathcal {D}_{C_{\varphi }}$ , in which the operator $C_{\varphi }$ is a bounded composition operator. For $n\in \mathbb {N}$ , it clear that $C^{n}_{\varphi }f=f\circ \varphi \circ \cdots \circ \varphi $ . For simplicity of the notation, we write $\varphi _{n}$ instead of $\varphi \circ \cdots \circ \varphi $ .

Theorem 8 Let $g\in B_1$ , and let $\varphi $ be an analytic self-map of $\mathbb {D}$ with $\varphi (0)=0$ such that $C_{\varphi }$ is bounded on $B_1$ . Then, the operators $M_g$ , $T_g$ , and $I_g$ belong to the Deddens algebra $\mathcal {D}_{C_{\varphi }}$ .

Proof For each $n\in \mathbb {N}$ , we see that

$$ \begin{align*} C^n_{\varphi}M_gf=&C^{n}_{\varphi}(gf) =(g\circ\varphi_{n})(f\circ\varphi_{n}) =M_{g\circ\varphi_n}C^{n}_{\varphi}f. \end{align*} $$

Since $\varphi _{n}(\mathbb {D})\subset \mathbb {D}$ , it follows that

$$ \begin{align*}\|M_{g\circ\varphi_n}f\|_{B_1}=\|(g\circ\varphi_n)f\|_{B_1}\lesssim\|g\|_{B_1}\|f\|_{B_1}, \end{align*} $$

and therefore

$$ \begin{align*}\|C^n_{\varphi}M_gf\|_{B_1}=\|M_{g\circ\varphi_n}C^{n}_{\varphi}f\|_{B_1}\lesssim\|g\|_{B_1}\|C^{n}_{\varphi}f\|_{B_1}, \end{align*} $$

where $f\in B_{1}(\mathbb {D})$ . This implies that $M_g\in \mathcal {D}_{C_{\varphi }}$ .

Next, we have

$$ \begin{align*}C^n_{\varphi}T_gf(z)=C^n_{\varphi}\left(\int^{z}_{0}f(w)g'(w)dw\right)=\int^{\varphi_{n}(z)}_{0}f(w)g'(w) \,dw. \end{align*} $$

Since $\varphi $ is an analytic self-map of $\mathbb {D}$ satisfying $\varphi (0)=0$ , we have $\varphi _{n}(0)=0$ , and therefore

$$ \begin{align*} T_{g\circ\varphi_n}C^{n}_{\varphi}f(z)&=T_{g\circ\varphi_n}\left(f(\varphi_n(z))\right)\\ &=\int^{z}_{0}f(\varphi_{n}(w))g'(\varphi_{n}(w))\varphi_{n}'(w) \,dw\\ &=\int^{\varphi_{n}(z)}_{0}f(w)g'(w) \,dw, \end{align*} $$

where $f\in B_1$ . It shows that $C^n_{\varphi }T_g=T_{g\circ \varphi _n}C^{n}_{\varphi }$ . By Theorem 1, we have

$$ \begin{align*} \|C^{n}_{\varphi}T_gf(z)\|_{B_1}=&\|T_{g\circ\varphi_n}C^{n}_{\varphi}f(z)\|_{B_1} \lesssim \|g\circ\varphi_n\|_{B_1}\|C^{n}_{\varphi}f(z)\|_{B_1} \lesssim \|g\|_{B_1}\|C^{n}_{\varphi}f(z)\|_{B_1}, \end{align*} $$

which gives $T_g\in \mathcal {D}_{C_{\varphi }}$ .

Finally, we have

$$ \begin{align*}C^n_{\varphi}I_gf(z)=C^{n}_{\varphi}\left(\int^{z}_{0}f'(w)g(w) \,dw\right)=\int^{\varphi_{n}(z)}_{0}f'(w)g(w) \,dw \end{align*} $$

and

$$ \begin{align*} I_{g\circ\varphi_{n}}C^n_{\varphi}f(z)&=I_{g\circ\varphi_{n}}(f(\varphi_{n}(z)))\\ &=\int^{z}_{0}f'(\varphi_{n}(w))g(\varphi_{n}(w))\varphi_{n}'(w) \,dw\\ &=\int^{\varphi_n(z)}_{0}f'(w)g(w) \,dw, \end{align*} $$

where $f\in B_1$ . Therefore, $C^n_{\varphi }I_g=I_{g\circ \varphi _{n}}C^n_{\varphi }$ . By Theorem 2 and Remark 3, we find that

$$ \begin{align*}\|C^n_{\varphi}I_gf(z)\|_{B_1}=\|I_{g\circ\varphi_{n}}C^n_{\varphi}f(z)\|_{B_1} \lesssim\|g\circ\varphi_{n}\|_{B_1}\|C^n_{\varphi}f(z)\|_{B_1}\lesssim\|g\|_{B_1}\|C^n_{\varphi}f(z)\|_{B_1} \end{align*} $$

for all $f\in B_1$ . We thus deduce that $I_g\in \mathcal {D}_{C_{\varphi }}$ .

4 Essential norms of Volterra-type operators on $B_{1}$

Suppose that X is a Banach space and T is a bounded linear operator on X. The essential norm of T is defined to be

$$ \begin{align*}\|T\|_{e}=\inf \{\|T-K\|:K ~\text{is a compact operator on } B_1\}. \end{align*} $$

Obviously, the essential norm of T is 0 if and only if T is compact. For more results, we invite the reader to refer to [26, 41]. In this section, we characterize the essential norm of linear operator on $B_1$ , which generalizes the conclusion of Liu et al. [24]

Theorem 9 Every bounded operator $T_g$ on $B_1$ is compact.

Proof By definition, we know $\|T_{g}\|_{e}\geq 0$ .

Next, we show that $\|T_{g}\|_{e}\leq 0$ . To do this, we define the following operators:

$$ \begin{align*}T_{g_r}f:=\int^z_0rf(w)g_r'(w) \,dw, \end{align*} $$

where $g_r(z)=g(rz)$ and $r\in (0,1)$ . It is easy to see that $T_{g_r}$ is a compact operator on $B_1$ for $g\in B_1$ . In fact, if $T_{g}$ is a bounded operator on $B_1$ , then $g\in B_1$ . Suppose that $\{ f_{n}\}_{n=1}^{\infty } \subset B_1$ with $\|f_{n}\|_{B_1}\leq 1$ , and $f_{n}\rightarrow 0$ uniformly on compact subsets of $\mathbb {D}$ . Then,

$$ \begin{align*} \|T_{g_r}f_n\|_{B_1}&=\|f_{n}(rz)g'(rz)\|_{\mathcal{D}^1}\\ &\lesssim \int_{\mathbb{D}}|f'_{n}(rz)g'(rz)| \,dA(z)+\int_{\mathbb{D}}|f_{n}(rz)g''(rz)| \,dA(z)\\ &=\int_{\mathbb{D}_{\delta_1}}|f'_{n}(rz)g'(rz)| \,dA(z)+\int_{\mathbb{D}\backslash \mathbb{D}_{\delta_1}}|f'_{n}(rz)g'(rz)| \,dA(z)\\ & \quad +\int_{\mathbb{D}_{\delta_1}}|f_{n}(rz)g''(rz)| \,dA(z)+\int_{\mathbb{D}\backslash \mathbb{D}_{\delta_1}}|f_{n}(rz)g''(rz)| \,dA(z), \end{align*} $$

where $\delta _1<1,$ and $\mathbb {D}_{\delta _1}= \{z: |z|<\delta _1\}$ are compact subsets of $\mathbb {D}$ .

Note that

$$ \begin{align*}\int_{\mathbb{D}}|f'_{n}(rz)g'(rz)| \,dA(z)\kern1.4pt{\lesssim}\kern1.4pt \|f_{n}\|_{B_1} \|g\|_{B_1} ~\text{ and }~\! \int_{\mathbb{D}}\kern-1pt|f_{n}(rz)g''(rz)| \,dA(z)\kern1.4pt{\lesssim}\kern1.4pt \|f_{n}\|_{B_1} \|g\|_{B_1}\kern-1pt. \end{align*} $$

Using the theorem of absolute continuity of Lebesgue measure, we conclude that

$$ \begin{align*}\int_{\mathbb{D}\backslash \mathbb{D}_{\delta_1}}|f'_{n}(rz)g'(rz)| \,dA(z) <\epsilon ~\text{ and }~ \int_{\mathbb{D}\backslash \mathbb{D}_{\delta_1}}|f_{n}(rz)g''(rz)| \,dA(z) <\epsilon. \end{align*} $$

On the other hand, using a basic result of complex analysis (see page 151 of [12]), we know that if $f_{n}\rightarrow 0,$ then $f_{n}' \rightarrow 0$ uniformly on compact subsets of $\mathbb {D}$ . Consequently,

$$ \begin{align*}\int_{\mathbb{D}_{\delta_1}}|f'_{n}(rz)g'(rz)| \,dA(z) ~\text{ and }~ \int_{\mathbb{D}_{\delta_1}}|f_{n}(rz)g''(rz)| \,dA(z) \end{align*} $$

converge to $0$ when $n\rightarrow \infty $ . This implies that $T_{g,r}$ is compact.

Meanwhile, we have

$$ \begin{align*}\|T_{g}\|_{e}\leq\|T_{g}-T_{g_r}\|=\|T_{g-g_r}\|\lesssim\|g-g_r\|_{B_1} \end{align*} $$

for $r\in (0,1)$ . Similarly, with the above computation, we have

$$ \begin{align*}\lim_{r\rightarrow 1^{-}}\|g-g_r\|_{B_1}=0, \end{align*} $$

so that $\|T_{g}\|_{e}\leq 0$ . Hence, we deduce that $\|T_{g}\|_{e}=0$ , which completes the proof.

Theorem 10 If $I_{g}$ is bounded operator on $B_1$ , then $\|g\|_{\infty }\leq \|I_{g}\|_{e} \lesssim ( \|g\|_{\infty }+\|g\|_{Z_{1}}).$

Proof From the proof of Theorem 2, we have

$$ \begin{align*}\|I_g\|_{e}=\inf\|I_g-K\|\leq\|I_g\|\leq C(\|g\|_{\infty}+\|g\|_{Z_{1}}), \end{align*} $$

where C is a positive constant.

We next show that $\|I_g\|_{e}\geq \|g\|_{\infty }$ . Choose $a_n\in \mathbb {D}$ such that $|a_n|\rightarrow 1$ as $n\rightarrow \infty $ . Let $f_n(z)=\sigma _{a_n}(z)-a_n$ . It is obvious that $\|f_n\|_{B_1}=1$ . Since $\{f_n\}$ converges to zero uniformly on compact subsets of $\mathbb {D}$ , for every compact operator K on $B_1$ , we obtain $\|Kf_n\|_{B_1}\rightarrow 0$ as $n\rightarrow \infty $ . Therefore,

$$ \begin{align*} \|I_g-K\|&\geq\lim_{n\rightarrow\infty}\sup\|(I_g-K)f_n\|_{B_1}\\ &\geq\lim_{n\rightarrow\infty}\sup(\|I_gf_n\|_{B_1}-\|Kf_n\|_{B_1})\\ &=\lim_{n\rightarrow\infty}\sup\|I_gf_n\|_{B_1}. \end{align*} $$

Similarly to the proof of Theorem 2, we get

$$ \begin{align*} \|I_gf_n\|_{B_1}=\|g(z)f'_n(z)\|_{\mathcal{D}^{1}}\geq|g(\sigma_{a_n}(0))|=|g(a_{n})|. \end{align*} $$

As the choice of the sequence $\{a_n\}\subset \mathbb {D}$ is arbitrary, we have $\|I_g\|_{e}\geq \|g\|_{\infty }$ , which completes the proof.

Theorem 11 Every bounded operator $M_g$ on $B_1$ is compact.

Proof The proof is similar to Theorem 9, so we omit its details.

5 Spectrum of Volterra-type operators on $B_{1}(\mathbb {D})$

The spectrum of integral operators on different spaces has attracted the attention of many scholars. The spectra of integral operators on weighted Bergman spaces are characterized by Aleman and Constantin [2]. Later, Constantin [10] obtained the spectrum of Volterra-type operators on Fock spaces. Mengestie [29] studied the spectrum of Volterra-type operators on Fock–Sobolev spaces. Mengestie [30] also obtained the spectrum of $T_g$ in terms of a closed disk of radius twice the coefficient of the highest degree term in a polynomial expansion of g. For more results, see [8, 27]. Recently, Lin et al. described the spectra of the multiplication operator and the Volterra-type operator $I_g$ in [23], respectively. Inspired by the above results, it is natural to study the spectra of the multiplication operator and the Volterra-type operators on $B_{1}$ .

Theorem 12 Suppose that $M_g$ is bounded on $B_1$ . Then, we have $\sigma (M_g)=\overline {g(\mathbb {D})}.$

Proof Suppose that $\lambda \notin \sigma (M_g)$ . Then, $M_g-\lambda I$ is invertible. As $1 \in B_1,$ there exists an $f\in B_1$ such that $(g(z)-\lambda )f(z)=1$ for all $z\in \mathbb {D}$ , which implies that $\lambda \notin g(\mathbb {D})$ . Thus, $g(\mathbb {D})\subset \sigma (M_g)$ .

For the other way inclusion, we let $\lambda \notin \overline {g(\mathbb {D})}$ . Then, we can choose a $t>0$ such that $|g(z)-\lambda |>t$ for all $z\in \mathbb {D}$ . This shows that $h=(g-\lambda )^{-1}$ is a bounded analytic function on $\mathbb {D}$ . For all $g\in B_1$ , we get

$$ \begin{align*} \|h\|_{B_1}&\leq t(|h(0)|+\|h'\|_{\mathcal{D}^{1}})\\&\leq \left(\frac{1}{|g(0)-\lambda|}+\|\frac{g'}{(g-\lambda)^2}\|_{\mathcal{D}^{1}}\right)\\[-14pt] \\&\leq \left(\frac{1}{|g(0)-\lambda|}+\left|\frac{g'(0)}{(g(0)-\lambda)^2}\right| +\int_{\mathbb{D}}\left|\frac{g''(z)}{(g(z)-\lambda)^2}-\frac{2(g')^2}{(g(z)-\lambda)^{3}}\right| \,dA(z)\right)\\&\lesssim \|g\|_{B_1}+ \|g\|^2_{B_1}. \end{align*} $$

Hence, $h\in B_1$ . Then, $M_h$ is bounded on $B_1,$ by Theorem 7. Since $M_h=M_{(g-\lambda )^{-1}}=M_{g-\lambda }^{-1}$ , we see that $M_{g-\lambda }$ is invertible, and thus $\lambda \notin \sigma (M_g)$ . Therefore, $\sigma (M_g)\subset \overline {g(\mathbb {D})}$ . Since the spectrum set is closed, we conclude that $\sigma (M_g)=\overline {g(\mathbb {D})}$ .

Lemma 7 [40]

Let T be a bounded linear operator on a Banach space X, and let T be compact. If $\dim X=\infty $ , then $\sigma (T)=\{0\} {\cup} $ {eigen values of T}.

Theorem 13 Suppose that $T_g$ is a bounded operator on $B_1$ . Then, $\sigma (T_g)=\{0\}.$

Proof Let $T_g$ be a bounded operator on $B_1.$ Then, $T_g$ is compact, by Theorem 9. By Lemma 7, we obtain $0\in \sigma (T)$ .

Next, we prove that $T_g$ has no nonzero eigenvalue. Assume that $T_g$ has an eigenvalue $\lambda \neq 0$ with eigenvector $f.$ Then,

(1) $$ \begin{align} T_{g}f(z)=\int^{z}_{0}f(w)g'(w) \,dw=\lambda f(z). \end{align} $$

Differentiating equation (1) with respect to z, we get

$$ \begin{align*}f(z)g'(z)=\lambda f'(z). \end{align*} $$

All nonzero solutions of this equation are of the form $f(z)=ce^{\frac {g(z)}{\lambda }}$ for some $c\neq 0$ . Setting $z=0$ in (1) shows that $0=\lambda f(0)$ , which contradicts the last relation about $f.$ Therefore, there is no nonzero eigenvalue for $T_g$ . From this, we deduce that $\sigma (T_g)=\{0\}$ .

Theorem 14 If $I_g$ is a bounded operator on $B_1$ , then

$$ \begin{align*}\sigma(I_g)=\{0\}\cup \overline{g(\mathbb{D})}. \end{align*} $$

Proof For any constant function a, we have

$$ \begin{align*}(I_ga)(z)=\int_{0}^{z}a'(w)g(w)\,dw=0, \end{align*} $$

which gives $0\in \sigma (I_g)$ .

Suppose that $\lambda \in \mathbb {C}\backslash \{0\}$ . Note that the equation

$$ \begin{align*}f-\frac{1}{\lambda}I_gf=h,~\hbox {for} ~h\in B_1, \end{align*} $$

has a unique analytic solution

$$ \begin{align*}f(z)=R_{\lambda,g}h(z)=\int^{z}_{0}\frac{h'(\xi)}{1-\frac{1}{\lambda}g(\xi)} \,d\xi+h(0)=I_{(1-\frac{1}{\lambda}g)^{-1}}h(z)+h(0) \end{align*} $$

(see [11] for more details). Hence, the resolvent set $\rho (I_g)$ of the bounded operator $I_g$ consists precisely of all points $\lambda \in \mathbb {C}$ for which $R_{\lambda ,g}$ is a bounded operator on $B_1$ .

If $\lambda \in \mathbb {C}\backslash (\{0\}\cup \overline {g(D)})$ , then it is clear that $1-\frac {1}{\lambda }g(z)$ is bounded away from $0$ , which implies that $\frac {1}{1-\frac {1}{\lambda }g(z)} \in H^{\infty }$ . If $I_g$ is a bounded operator on $B_1$ , then $g\in H^{\infty }\bigcap Z_{1}$ by Theorem 2. Moreover, it is easy to show that $ \frac {1}{1-\frac {1}{\lambda }g(z)} \in Z_{1}.$ This implies that the operator $R_{\lambda ,g}$ is a bounded operator on $B_1$ . It follows that $\mathbb {C}\backslash (\{0\}\cup \overline {g(\mathbb {D})})\subset \rho (I_g)$ . Thus, $\sigma (I_g)\subset (\{0\}\cup \overline {g(\mathbb {D})})$ .

On the other hand, if $\lambda \in g(\mathbb {D})$ and $\lambda \neq 0$ , then $\frac {1}{1-\frac {1}{\lambda }g(\xi )}$ is not bounded, which shows that the operator $R_{\lambda ,g}$ is not bounded on $B_1$ . Therefore, we obtain that $g(\mathbb {D})\backslash \{0\}\subset \sigma (I_g)$ . This together with the fact that $0\in \sigma (I_g)$ shows that

$$ \begin{align*}g(\mathbb{D})\cup\{0\}\subset\sigma(I_g)\subset \overline{g(\mathbb{D})}\cup\{0\}. \end{align*} $$

Since the spectrum $\sigma (I_g)$ is closed, we deduce that $\sigma (I_g)=\overline {g(\mathbb {D})}\cup \{0\}$ .