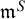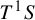1 Introduction
Let S be a closed, orientable, connected surface of genus g endowed with a negatively curved metric and let
![]() $\rho ^S=(\rho _t^S)_{t\in {\mathbb {R}}}$
be the associated geodesic flow on the unit tangent bundle
$\rho ^S=(\rho _t^S)_{t\in {\mathbb {R}}}$
be the associated geodesic flow on the unit tangent bundle
![]() $T^1S$
. We can associate to every primitive periodic
$T^1S$
. We can associate to every primitive periodic
![]() $\rho ^S$
-orbit
$\rho ^S$
-orbit
![]() $\gamma $
, that is, to every non-trivial closed primitive oriented geodesic, a measure
$\gamma $
, that is, to every non-trivial closed primitive oriented geodesic, a measure
![]() $\vec \gamma $
on
$\vec \gamma $
on
![]() $T^1S$
as follow. Choose
$T^1S$
as follow. Choose
![]() $v\in T^1S$
tangent to
$v\in T^1S$
tangent to
![]() $\gamma $
, let
$\gamma $
, let
![]() $\ell _S(\gamma )$
be the length of
$\ell _S(\gamma )$
be the length of
![]() $\gamma $
(that is, the period of the orbit
$\gamma $
(that is, the period of the orbit
![]() $\gamma $
), and set
$\gamma $
), and set
 $$ \begin{align} \int_{T^1S} f\, d\vec\gamma\stackrel{\text{def}}=\int_0^{\ell_S(\gamma)}f(\rho_t(v))\, dt \end{align} $$
$$ \begin{align} \int_{T^1S} f\, d\vec\gamma\stackrel{\text{def}}=\int_0^{\ell_S(\gamma)}f(\rho_t(v))\, dt \end{align} $$
for all
![]() $f\in C^0(T^1S)$
. In [Reference Bowen7] Bowen investigated (for general hyperbolic flows) the distribution of the set
$f\in C^0(T^1S)$
. In [Reference Bowen7] Bowen investigated (for general hyperbolic flows) the distribution of the set
![]() ${\mathcal {P}}_L(S)$
of all primitive periodic
${\mathcal {P}}_L(S)$
of all primitive periodic
![]() $\rho ^S$
-orbits with period at most L. To do so he studied the behaviour, when L tends to
$\rho ^S$
-orbits with period at most L. To do so he studied the behaviour, when L tends to
![]() $\infty $
, of the measures
$\infty $
, of the measures
 $$ \begin{align} b^S_L=\sum_{\gamma\in{\mathcal{P}}_L(S)}\vec\gamma \end{align} $$
$$ \begin{align} b^S_L=\sum_{\gamma\in{\mathcal{P}}_L(S)}\vec\gamma \end{align} $$
and proved that the associated probability measures converge to the measure of maximal entropy of
![]() $\rho ^S$
:
$\rho ^S$
:
 $$ \begin{align*}{\mathfrak{b}}^S=\lim_{L\to\infty}\frac 1{\Vert b^S_L\Vert}b^S_L.\end{align*} $$
$$ \begin{align*}{\mathfrak{b}}^S=\lim_{L\to\infty}\frac 1{\Vert b^S_L\Vert}b^S_L.\end{align*} $$
In this note we study what happens if we condition Bowen’s construction to the set of periodic orbits of a give type. Here we say, à la Mirzakhani, that two closed geodesics are of the same type if their unoriented free homotopy classes differ by a homeomorphism of the surface—for example, any two non-separating simple curves are of the same type. Now, if
![]() $\gamma _0$
is a closed primitive geodesic in S we consider the asymptotic behaviour for
$\gamma _0$
is a closed primitive geodesic in S we consider the asymptotic behaviour for
![]() $L\to \infty $
of the measures
$L\to \infty $
of the measures
 $$ \begin{align} m_L^{S,\gamma_0}=\sum_{\gamma\in{\mathcal{P}}_L(S,\gamma_0)}\vec\gamma \end{align} $$
$$ \begin{align} m_L^{S,\gamma_0}=\sum_{\gamma\in{\mathcal{P}}_L(S,\gamma_0)}\vec\gamma \end{align} $$
where
![]() ${\mathcal {P}}_L(S,\gamma _0)$
is the set of all primitive periodic
${\mathcal {P}}_L(S,\gamma _0)$
is the set of all primitive periodic
![]() $\rho ^S$
-orbits of type
$\rho ^S$
-orbits of type
![]() $\gamma _0$
and with at most length L. We prove the following theorem.
$\gamma _0$
and with at most length L. We prove the following theorem.
Theorem 1.1. Let S be a closed orientable surface of genus g endowed with a negatively curved metric. There is a measure
![]() ${\mathfrak m}^S$
on
${\mathfrak m}^S$
on
![]() $T^1S$
, invariant under both the geodesic flow and the geodesic flip, and with
$T^1S$
, invariant under both the geodesic flow and the geodesic flip, and with
 $$ \begin{align*}\lim_{L\to\infty}\frac 1{\Vert m_L^{S,\gamma_0}\Vert}m_L^{S,\gamma_0}={\mathfrak m}^S\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\frac 1{\Vert m_L^{S,\gamma_0}\Vert}m_L^{S,\gamma_0}={\mathfrak m}^S\end{align*} $$
for every non-trivial closed primitive geodesic
![]() $\gamma _0$
in S.
$\gamma _0$
in S.
The measures
![]() $b_L^S$
and
$b_L^S$
and
![]() $m_L^{S,\gamma _0}$
are very different. For instance, the total measure of the former grows exponentially when
$m_L^{S,\gamma _0}$
are very different. For instance, the total measure of the former grows exponentially when
![]() $L\to \infty $
while, as we will see in Lemma 3.1, the latter has total measure asymptotic to a multiple of
$L\to \infty $
while, as we will see in Lemma 3.1, the latter has total measure asymptotic to a multiple of
![]() $L^{6g-5}$
. Still, since by Bowen’s theorem the set of all geodesics accumulates to the measure of maximal entropy
$L^{6g-5}$
. Still, since by Bowen’s theorem the set of all geodesics accumulates to the measure of maximal entropy
![]() $\mathfrak b^S$
, and since the measure
$\mathfrak b^S$
, and since the measure
![]() ${\mathfrak m}^S$
in Theorem 1.1 is independent of the type of geodesic under consideration, it might sound reasonable to conjecture that
${\mathfrak m}^S$
in Theorem 1.1 is independent of the type of geodesic under consideration, it might sound reasonable to conjecture that
![]() ${\mathfrak m}^S$
is once again the measure of maximal entropy. This is definitely not the case. For example, the measure of maximal entropy of the geodesic flow is ergodic, has positive entropy, and has full support in
${\mathfrak m}^S$
is once again the measure of maximal entropy. This is definitely not the case. For example, the measure of maximal entropy of the geodesic flow is ergodic, has positive entropy, and has full support in
![]() $T^1S$
. None of this is true for the measure
$T^1S$
. None of this is true for the measure
![]() ${\mathfrak m}^S$
.
${\mathfrak m}^S$
.
Theorem 1.2. The measure
![]() ${\mathfrak m}^S$
is not ergodic, has vanishing entropy, and its support has Hausdorff dimension
${\mathfrak m}^S$
is not ergodic, has vanishing entropy, and its support has Hausdorff dimension
![]() $1$
.
$1$
.
Every homeomorphism
![]() $\phi :S\to S'$
between two closed negatively curved surfaces induces an orbit equivalence between the associated geodesic flows. We then get a homeomorphism
$\phi :S\to S'$
between two closed negatively curved surfaces induces an orbit equivalence between the associated geodesic flows. We then get a homeomorphism
![]() $\phi _*$
—see (5.1) below—between the spaces of geodesic flow-invariant measures on
$\phi _*$
—see (5.1) below—between the spaces of geodesic flow-invariant measures on
![]() $T^1S$
and
$T^1S$
and
![]() $T^1S'$
, respectively; moreover
$T^1S'$
, respectively; moreover
![]() $\phi _*$
only depends on the homotopy class of
$\phi _*$
only depends on the homotopy class of
![]() $\phi $
. Anyway,
$\phi $
. Anyway,
![]() $\phi _*$
allows us to compare the measures
$\phi _*$
allows us to compare the measures
![]() $\mathfrak b^S$
and
$\mathfrak b^S$
and
![]() $\mathfrak b^{S'}$
, and it has been conjectured that they are mutually singular unless
$\mathfrak b^{S'}$
, and it has been conjectured that they are mutually singular unless
![]() $\phi _*$
is isotopic to a homothety, an isometry if both surfaces have the same area. In fact, in [Reference Otal19] Otal proved that this conjecture holds if one replaces the measure of maximal entropy by the Liouville measure. We prove that again from this point of view the measure
$\phi _*$
is isotopic to a homothety, an isometry if both surfaces have the same area. In fact, in [Reference Otal19] Otal proved that this conjecture holds if one replaces the measure of maximal entropy by the Liouville measure. We prove that again from this point of view the measure
![]() ${\mathfrak m}^S$
behaves in a very different way than the measure of maximal entropy.
${\mathfrak m}^S$
behaves in a very different way than the measure of maximal entropy.
Theorem 1.3. If
![]() $\phi :S\to S'$
is a homeomorphism between closed negatively curved surfaces then the measures
$\phi :S\to S'$
is a homeomorphism between closed negatively curved surfaces then the measures
![]() $\phi _*({\mathfrak m}^S)$
and
$\phi _*({\mathfrak m}^S)$
and
![]() ${\mathfrak m}^{S'}$
are in the same measure class.
${\mathfrak m}^{S'}$
are in the same measure class.
It may be worth pointing out that in the course of the proof of Theorem 1.3 we will give an explicit formula for the Radon–Nikodym derivative of
![]() $\phi _*({\mathfrak m}^{S})$
with respect to
$\phi _*({\mathfrak m}^{S})$
with respect to
![]() ${\mathfrak m}^{S'}$
.
${\mathfrak m}^{S'}$
.
While, by Theorem 1.3, the measure class of
![]() ${\mathfrak m}^S$
is independent of the particular metric, we prove that the measure
${\mathfrak m}^S$
is independent of the particular metric, we prove that the measure
![]() ${\mathfrak m}^S$
is itself rich enough to distinguish between hyperbolic metrics.
${\mathfrak m}^S$
is itself rich enough to distinguish between hyperbolic metrics.
Theorem 1.4. A homeomorphism
![]() $\phi :S\to S'$
between closed orientable hyperbolic surfaces is isotopic to an isometry if and only if
$\phi :S\to S'$
between closed orientable hyperbolic surfaces is isotopic to an isometry if and only if
![]() $\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
.
$\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
.
One should keep in mind that Theorem 1.4 fails for variable curvature metrics. Indeed, as we will see in §6, there are S and
![]() $S'$
negatively curved, with the same area, and non-isometric to each other, but such that there is a homeomorphism
$S'$
negatively curved, with the same area, and non-isometric to each other, but such that there is a homeomorphism
![]() $\phi :S\to S'$
with
$\phi :S\to S'$
with
![]() $\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. Moreover, here the surface S can be chosen to be hyperbolic.
$\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. Moreover, here the surface S can be chosen to be hyperbolic.
Having presented the results of this paper, let us give a brief indication of the tools used in the proofs. We rely heavily on the work of Mirzakhani [Reference Mirzakhani16, Reference Mirzakhani17] on counting geodesics of a given type
![]() $\gamma _0$
and with at most length L. More concretely, she proved that
$\gamma _0$
and with at most length L. More concretely, she proved that
where
![]() $C=C(\gamma _0,S)$
is a constant and where
$C=C(\gamma _0,S)$
is a constant and where
![]() $\approx $
indicates that the ratio between both sides tends to 1 as L grows. In [Reference Erlandsson and Souto11] we recovered this result, proving that the limit
$\approx $
indicates that the ratio between both sides tends to 1 as L grows. In [Reference Erlandsson and Souto11] we recovered this result, proving that the limit
 $$ \begin{align} \lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\gamma} \end{align} $$
$$ \begin{align} \lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\gamma} \end{align} $$
exists on the space of measures on the space
![]() ${\mathcal {C}}(S)$
of currents on S—here
${\mathcal {C}}(S)$
of currents on S—here
![]() $\delta _x$
is the Dirac measure centred at x and
$\delta _x$
is the Dirac measure centred at x and
![]() $\gamma \sim \gamma _0$
means that they are both of the same type. The relation between the existence of this limit and the results mentioned earlier is via the fact that the space of currents on S is naturally homeomorphic to the space of measures on
$\gamma \sim \gamma _0$
means that they are both of the same type. The relation between the existence of this limit and the results mentioned earlier is via the fact that the space of currents on S is naturally homeomorphic to the space of measures on
![]() $T^1S$
which are invariant under the geodesic flow and the geodesic flip
$T^1S$
which are invariant under the geodesic flow and the geodesic flip
![]() $v\mapsto -v$
.
$v\mapsto -v$
.
In §1.1.3 we recall the definition of currents, as well as the homeomorphism between the spaces of currents and of flip- and flow-invariant measures. In §2 we recall the Thurston measure on the space of measured laminations, discussing briefly how to write it in polar coordinates and stating (1.5) precisely. In §3, the bulk of the paper, we prove Theorem 1.1. In §§4–6 we prove the other three theorems mentioned above. Finally, in §7 we discuss briefly what happens if the surface has punctures.
1.1 Comments
Before moving on, let us comment briefly on the assumptions on the surface S and on a subtlety in what we do here.
1.1.1 Punctures
The reader might be wondering how important it ist hat we are dealing with a closed surface. Not at all. All theorems hold as stated and we only consider the case of closed surfaces to improve the readability of the paper. Indeed, while it is not hard to work with currents on surfaces which are not closed, it definitely needs more attention to detail and one needs to keep making sure to point out that everything happens on compact sets. As stated above, we will discuss in §7 the changes needed to extend the results to the case with punctures.
1.1.2 Orientability
As we used to do ourselves, the reader might well embrace the belief that non-orientable surfaces are an urban myth, or rather that everything that is true for orientable surfaces is, after minimal thought, also true for non-orientable surfaces. Well, in this area things are definitely different. For example, it is due to Gendulphe [Reference Gendulphe13] that there is no integer with which one can replace
![]() $6g-6$
so that (1.5) still holds if the surface is not orientable. This means that our proof really uses the fact that S is orientable, and that we do not know what to do in the non-orientable setting.
$6g-6$
so that (1.5) still holds if the surface is not orientable. This means that our proof really uses the fact that S is orientable, and that we do not know what to do in the non-orientable setting.
1.1.3 Time reversal
Since the geodesic flow commutes with the geodesic flip we get that the measures
![]() $b^S_L$
in (1.2) are not only flow invariant but also flip invariant. We then defined the measures
$b^S_L$
in (1.2) are not only flow invariant but also flip invariant. We then defined the measures
![]() $m_L^{S,\gamma _0}$
so that they are also flip invariant, referring to the type of a geodesic instead of its oriented type. So far, all seems identical. However, there is a difference. Bowen’s result applies to Axiom A flows, and in particular to any perturbation of the geodesic flow, flip invariant or not. In this case the flip invariance of the measures (1.2) is lost, but Bowen’s theorem holds. Flip invariance is, however, key for us. The reason is that currents, as least in the setting needed to establish (1.5), are inherently flip invariant. This means we do not know what to do if instead of working with type we work with oriented type.
$m_L^{S,\gamma _0}$
so that they are also flip invariant, referring to the type of a geodesic instead of its oriented type. So far, all seems identical. However, there is a difference. Bowen’s result applies to Axiom A flows, and in particular to any perturbation of the geodesic flow, flip invariant or not. In this case the flip invariance of the measures (1.2) is lost, but Bowen’s theorem holds. Flip invariance is, however, key for us. The reason is that currents, as least in the setting needed to establish (1.5), are inherently flip invariant. This means we do not know what to do if instead of working with type we work with oriented type.
1.2 Currents
In this section we recall a few definitions and facts about currents. We refer to [Reference Aramayona and Leininger1, Reference Bonahon4–Reference Bonahon and Alperin6, Reference Erlandsson and Souto11] for background and details.
Denoting by S a closed surface of negative curvature, let
![]() ${\tilde {S}}$
be its universal cover and
${\tilde {S}}$
be its universal cover and
![]() ${\mathcal {G}}({\tilde {S}})$
the set of unoriented geodesics therein. Since geodesics in
${\mathcal {G}}({\tilde {S}})$
the set of unoriented geodesics therein. Since geodesics in
![]() ${\tilde {S}}$
are determined by their end points, we have an identification
${\tilde {S}}$
are determined by their end points, we have an identification
where
![]() $\partial _{\infty }{\tilde {S}}$
is the boundary at infinity and where
$\partial _{\infty }{\tilde {S}}$
is the boundary at infinity and where
![]() $\Delta $
is the diagonal. The fundamental group
$\Delta $
is the diagonal. The fundamental group
![]() $\pi _1(S)$
acts by deck transformation on
$\pi _1(S)$
acts by deck transformation on
![]() ${\tilde {S}}$
and hence on
${\tilde {S}}$
and hence on
![]() ${\mathcal {G}}({\tilde {S}})$
. A (geodesic) current on S is a
${\mathcal {G}}({\tilde {S}})$
. A (geodesic) current on S is a
![]() $\pi _1(S)$
-invariant Radon measure on
$\pi _1(S)$
-invariant Radon measure on
![]() ${\mathcal {G}}({\tilde {S}})$
. There are plenty of currents. For example, if
${\mathcal {G}}({\tilde {S}})$
. There are plenty of currents. For example, if
![]() $\gamma $
is a closed unoriented geodesic in S then
$\gamma $
is a closed unoriented geodesic in S then
defines a current, the so-called counting current associated to
![]() $\gamma $
. The set
$\gamma $
. The set
![]() ${\mathcal {C}}(S)$
of all currents in S is, when endowed with the weak-* topology, a cone in a linear space and multiples of counting currents are dense therein [Reference Bonahon4, Reference Erlandsson and Souto11].
${\mathcal {C}}(S)$
of all currents in S is, when endowed with the weak-* topology, a cone in a linear space and multiples of counting currents are dense therein [Reference Bonahon4, Reference Erlandsson and Souto11].
It will be important for us that homeomorphisms
![]() $\phi :S\to S'$
between closed negatively curved surfaces induce homeomorphisms between the associated spaces of currents. Indeed, it follows for instance from the Milnor–Svarc lemma that their lifts
$\phi :S\to S'$
between closed negatively curved surfaces induce homeomorphisms between the associated spaces of currents. Indeed, it follows for instance from the Milnor–Svarc lemma that their lifts
![]() $\tilde \phi :{\tilde {S}}\to {\tilde {S}}'$
to the universal cover are quasi-isometries. This implies, in particular, that they have extensions
$\tilde \phi :{\tilde {S}}\to {\tilde {S}}'$
to the universal cover are quasi-isometries. This implies, in particular, that they have extensions
to the boundary at infinity—extensions which are equivariant under the same homomorphism
![]() $\phi _*:\pi _1(S)\to \pi _1(S')$
with respect to which the chosen lift
$\phi _*:\pi _1(S)\to \pi _1(S')$
with respect to which the chosen lift
![]() $\tilde \phi $
was equivariant.
$\tilde \phi $
was equivariant.
The boundary map
![]() $\partial _{\infty }\tilde \phi $
induces an again equivariant map between the sets of unoriented geodesics
$\partial _{\infty }\tilde \phi $
induces an again equivariant map between the sets of unoriented geodesics
and hence a map, actually a homeomorphism,
between the corresponding spaces of currents. Note that this homeomorphism just depends on the free homotopy class of the map
![]() $\phi $
and that it satisfies
$\phi $
and that it satisfies
for every curve
![]() $\gamma $
. In words,
$\gamma $
. In words,
![]() $\phi _*$
maps the counting current associated to the geodesic
$\phi _*$
maps the counting current associated to the geodesic
![]() $\gamma $
to the counting current associated to the geodesic freely homotopic to
$\gamma $
to the counting current associated to the geodesic freely homotopic to
![]() $\phi (\gamma )$
.
$\phi (\gamma )$
.
The space
![]() ${\mathcal {C}}(S)$
of currents on S is closely related to the space
${\mathcal {C}}(S)$
of currents on S is closely related to the space
![]() ${\mathcal {M}}_{\text {flip-flow}}(S)$
of Radon measures on
${\mathcal {M}}_{\text {flip-flow}}(S)$
of Radon measures on
![]() $T^1S$
which are invariant both under the geodesic flow and the geodesic flip. Indeed, every current
$T^1S$
which are invariant both under the geodesic flow and the geodesic flip. Indeed, every current
![]() $\widehat {\mu }\in {\mathcal {C}}(S)$
induces a flip- and flow-invariant measure
$\widehat {\mu }\in {\mathcal {C}}(S)$
induces a flip- and flow-invariant measure
![]() $\overline \mu =dt\otimes \widehat {\mu }$
on
$\overline \mu =dt\otimes \widehat {\mu }$
on
![]() $T^1S$
as follows: If
$T^1S$
as follows: If
![]() $Z\subset T^1{\tilde {S}}$
is a transversal to the geodesic flow on the universal cover meeting each geodesic at most once then the
$Z\subset T^1{\tilde {S}}$
is a transversal to the geodesic flow on the universal cover meeting each geodesic at most once then the
![]() $\overline \mu $
-measure of the flow box
$\overline \mu $
-measure of the flow box
 $$ \begin{align*} [0,t_0]\times Z=\bigcup_{t\in[0,t_0]}\rho_t^{{\tilde{S}}}(Z)\subset T^1{\tilde{S}} \end{align*} $$
$$ \begin{align*} [0,t_0]\times Z=\bigcup_{t\in[0,t_0]}\rho_t^{{\tilde{S}}}(Z)\subset T^1{\tilde{S}} \end{align*} $$
is given by
where
![]() $\widehat {\mu }(Z)$
is the
$\widehat {\mu }(Z)$
is the
![]() $\widehat {\mu }$
-measure of the subset of
$\widehat {\mu }$
-measure of the subset of
![]() ${\mathcal {G}}({\tilde {S}})$
represented by the orbits
${\mathcal {G}}({\tilde {S}})$
represented by the orbits
![]() $t\mapsto \rho _t^{{\tilde {S}}}(v)$
with
$t\mapsto \rho _t^{{\tilde {S}}}(v)$
with
![]() $v\in Z$
. The measure
$v\in Z$
. The measure
![]() $\overline \mu =dt\otimes \widehat {\mu }$
is
$\overline \mu =dt\otimes \widehat {\mu }$
is
![]() $\pi _1(S)$
-invariant and hence descends to a measure which we still denote by
$\pi _1(S)$
-invariant and hence descends to a measure which we still denote by
![]() $\overline \mu =dt\otimes \widehat {\mu }$
on
$\overline \mu =dt\otimes \widehat {\mu }$
on
![]() $T^1S$
. This is, by construction, flip and flow invariant. In other words, we have given a map
$T^1S$
. This is, by construction, flip and flow invariant. In other words, we have given a map
It is well known that this map is a homeomorphism [Reference Aramayona and Leininger1, Reference Erlandsson and Souto11].
Notation. As we have been doing so far, we will decorate currents with ‘hats’ and flip- and flow-invariant measures by ‘bars’. If we write
![]() and
and
![]() then the former is a current, the latter is a flip- and flow-invariant measure, and one is the image of the other under the homeomorphisms (1.8).
then the former is a current, the latter is a flip- and flow-invariant measure, and one is the image of the other under the homeomorphisms (1.8).
We now explain the pesky
![]() $\tfrac 12$
in (1.7). The flip- and flow-invariant measure
$\tfrac 12$
in (1.7). The flip- and flow-invariant measure
![]() $\bar {\gamma }$
associated to the counting current
$\bar {\gamma }$
associated to the counting current
![]() $\widehat {\gamma }$
is given by
$\widehat {\gamma }$
is given by
where we have chosen an orientation of
![]() $\gamma $
, where
$\gamma $
, where
![]() $\vec \gamma $
is as in (1.1), and where
$\vec \gamma $
is as in (1.1), and where
![]() $\gamma _{\text {flip}}$
stands for the oppositely oriented orbit. The factor
$\gamma _{\text {flip}}$
stands for the oppositely oriented orbit. The factor
![]() $\tfrac 12$
is thus there to guarantee that the measure
$\tfrac 12$
is thus there to guarantee that the measure
![]() $\overline {\gamma }$
has total measure
$\overline {\gamma }$
has total measure
![]() $\ell _S(\gamma )$
for every curve
$\ell _S(\gamma )$
for every curve
![]() $\gamma $
:
$\gamma $
:
Note also that these
![]() $\tfrac 12$
factors disappear when we normalize measures to be probability measures. For example, if we set
$\tfrac 12$
factors disappear when we normalize measures to be probability measures. For example, if we set
then the map
![]() ${\mathcal {P}}_L(S,\gamma _0)\to \mathcal S_L(S,\gamma _0)$
is two-to-one: both
${\mathcal {P}}_L(S,\gamma _0)\to \mathcal S_L(S,\gamma _0)$
is two-to-one: both
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma _{\text {flip}}$
, and only those, get mapped to the same unoriented geodesic. This means that the measure
$\gamma _{\text {flip}}$
, and only those, get mapped to the same unoriented geodesic. This means that the measure
 $$ \begin{align} \overline m^{S,\gamma_0}_L=\sum_{\gamma\in\mathcal S_L(S,\gamma_0)}\overline{\gamma} \end{align} $$
$$ \begin{align} \overline m^{S,\gamma_0}_L=\sum_{\gamma\in\mathcal S_L(S,\gamma_0)}\overline{\gamma} \end{align} $$
is exactly half of the measure
![]() $m^{S,\gamma _0}_L$
defined in (1.3):
$m^{S,\gamma _0}_L$
defined in (1.3):
We thus get the following fact that we record here for later use.
Lemma 1.5. For any
![]() $\gamma _0$
and any L large enough we have
$\gamma _0$
and any L large enough we have
 $$ \begin{align} \frac 1{\Vert\overline m^{S,\gamma_0}_L\Vert}\overline m^{S,\gamma_0}_L=\frac 1{\Vert m^{S,\gamma_0}_L\Vert} m^{S,\gamma_0}_L \end{align} $$
$$ \begin{align} \frac 1{\Vert\overline m^{S,\gamma_0}_L\Vert}\overline m^{S,\gamma_0}_L=\frac 1{\Vert m^{S,\gamma_0}_L\Vert} m^{S,\gamma_0}_L \end{align} $$
where
![]() $m^{S,\gamma _0}_L$
is as in (1.3) and
$m^{S,\gamma _0}_L$
is as in (1.3) and
![]() $\overline m^{S,\gamma _0}_L$
is as in (1.10).
$\overline m^{S,\gamma _0}_L$
is as in (1.10).
Anyway, the reader might well be thinking that those
![]() $\tfrac 12$
factors are perhaps not that painful, and might indeed agree that they are necessary because one is working with unoriented geodesics.
$\tfrac 12$
factors are perhaps not that painful, and might indeed agree that they are necessary because one is working with unoriented geodesics.
![]() $\ldots $
But why is one working with unoriented geodesics in the first place? The main reason is that, other than the counting currents
$\ldots $
But why is one working with unoriented geodesics in the first place? The main reason is that, other than the counting currents
![]() $\widehat {\gamma }$
associated to closed geodesics, the main currents for us are measured laminations, and measured laminations are by their own nature unoriented.
$\widehat {\gamma }$
associated to closed geodesics, the main currents for us are measured laminations, and measured laminations are by their own nature unoriented.
2 Thurston measure
Let
![]() ${\mathcal {M}}\mathcal L(S)$
be the set of measured laminations on S. We can consider measured laminations as currents. Indeed,
${\mathcal {M}}\mathcal L(S)$
be the set of measured laminations on S. We can consider measured laminations as currents. Indeed,
![]() ${\mathcal {M}}\mathcal L(S)$
is nothing other than the set of currents whose support projects to a lamination of S, that is, a compact set foliated by disjoint simple geodesics. As for curves, we will denote by
${\mathcal {M}}\mathcal L(S)$
is nothing other than the set of currents whose support projects to a lamination of S, that is, a compact set foliated by disjoint simple geodesics. As for curves, we will denote by
![]() the current associated to the measured lamination
the current associated to the measured lamination
![]() . We refer to [Reference Aramayona and Leininger1, Reference Bonahon5, Reference Erlandsson and Souto11] for basic facts about measured laminations and their relation to currents.
. We refer to [Reference Aramayona and Leininger1, Reference Bonahon5, Reference Erlandsson and Souto11] for basic facts about measured laminations and their relation to currents.
What will be very important for us is that the set
![]() ${\mathcal {M}}\mathcal L(S)$
of all measured laminations on S is naturally endowed with a measure, the Thurston measure
${\mathcal {M}}\mathcal L(S)$
of all measured laminations on S is naturally endowed with a measure, the Thurston measure
![]() ${\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
. There are different ways of obtaining the Thurston measure. For example, one can get it via the standard symplectic structure on the space of measured laminations, but the more natural way here is as a scaling limit
${\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
. There are different ways of obtaining the Thurston measure. For example, one can get it via the standard symplectic structure on the space of measured laminations, but the more natural way here is as a scaling limit
 $$ \begin{align} {\mathfrak{m}}_{\operatorname{\mathrm{Thu}}}=\lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\in{{\mathcal{M}}}{\mathcal L}_{\mathbb{Z}}(S)}\delta_{(1/L)\widehat{\gamma}} \end{align} $$
$$ \begin{align} {\mathfrak{m}}_{\operatorname{\mathrm{Thu}}}=\lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\in{{\mathcal{M}}}{\mathcal L}_{\mathbb{Z}}(S)}\delta_{(1/L)\widehat{\gamma}} \end{align} $$
where g is the genus of S, where
![]() ${{\mathcal {M}}}{\mathcal L}_{\mathbb {Z}}(S)$
is the set of integrally weighted simple multicurves on S, where we denote by
${{\mathcal {M}}}{\mathcal L}_{\mathbb {Z}}(S)$
is the set of integrally weighted simple multicurves on S, where we denote by
![]() $\widehat {\gamma }$
the counting current associated to the multicurve
$\widehat {\gamma }$
the counting current associated to the multicurve
![]() $\gamma $
, and where the limit is taken with respect to the weak-* topology on the space of currents. See, for example, [Reference Erlandsson and Souto11, Reference Mirzakhani16] for the construction of the Thurston measures and [Reference Monin and Telpukhovskiy18] for the relations between the two possible constructions just mentioned. Anyway, the reason why we care about the Thurston measure is that we have the following theorem.
$\gamma $
, and where the limit is taken with respect to the weak-* topology on the space of currents. See, for example, [Reference Erlandsson and Souto11, Reference Mirzakhani16] for the construction of the Thurston measures and [Reference Monin and Telpukhovskiy18] for the relations between the two possible constructions just mentioned. Anyway, the reason why we care about the Thurston measure is that we have the following theorem.
Theorem 2.1. For every closed geodesic
![]() $\gamma _0$
in S there is a positive constant
$\gamma _0$
in S there is a positive constant
![]() $C(\gamma _0)$
such that
$C(\gamma _0)$
such that
 $$ \begin{align*}\lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}=C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}=C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
Here
![]() $\delta _x$
stands for the Dirac measure centred at x, the sum is taken over all
$\delta _x$
stands for the Dirac measure centred at x, the sum is taken over all
![]() $\gamma $
of type
$\gamma $
of type
![]() $\gamma _0$
, and the convergence takes place with respect to the weak-* topology on the space
$\gamma _0$
, and the convergence takes place with respect to the weak-* topology on the space
![]() ${\mathcal {C}}(S)$
.
${\mathcal {C}}(S)$
.
Theorem 2.1 is due to Mirzakhani [Reference Mirzakhani16] when
![]() $\gamma _0$
is a simple multicurve, and a complete proof for arbitrary curves appears in [Reference Erlandsson and Souto11, Ch. 8]. Theorem 2.1 also appears as Theorem 5.1 in [Reference Erlandsson, Parlier and Souto8], where it is explained how to deduce it from Mirzakhani’s (1.4) together with [Reference Erlandsson and Souto9, Proposition 4.1]. Now, as the referee reminded us, Mirzakhani never came to completely ironing out [Reference Mirzakhani17] and not everyone agrees whether her proof of (1.4) is complete or not when
$\gamma _0$
is a simple multicurve, and a complete proof for arbitrary curves appears in [Reference Erlandsson and Souto11, Ch. 8]. Theorem 2.1 also appears as Theorem 5.1 in [Reference Erlandsson, Parlier and Souto8], where it is explained how to deduce it from Mirzakhani’s (1.4) together with [Reference Erlandsson and Souto9, Proposition 4.1]. Now, as the referee reminded us, Mirzakhani never came to completely ironing out [Reference Mirzakhani17] and not everyone agrees whether her proof of (1.4) is complete or not when
![]() $\gamma _0$
is not filling. This is not a worry because in [Reference Erlandsson and Souto10] we used results from [Reference Erlandsson and Souto9] and from Mirzakhani’s original paper [Reference Mirzakhani16] (the one about simple curves) to give a very short proof of (1.4) in full generality. We should also point out that in the present paper we could bypass (1.4) altogether. Indeed, since the measures in Theorem 1.1 are normalized to be probability measures, we could make do with a version of Theorem 2.1 which holds only up to taking subsequences—this is Proposition 4.1 in [Reference Erlandsson and Souto9] (see [Reference Erlandsson and Souto11, Ch. 6] for a nicer exposition of this result).
$\gamma _0$
is not filling. This is not a worry because in [Reference Erlandsson and Souto10] we used results from [Reference Erlandsson and Souto9] and from Mirzakhani’s original paper [Reference Mirzakhani16] (the one about simple curves) to give a very short proof of (1.4) in full generality. We should also point out that in the present paper we could bypass (1.4) altogether. Indeed, since the measures in Theorem 1.1 are normalized to be probability measures, we could make do with a version of Theorem 2.1 which holds only up to taking subsequences—this is Proposition 4.1 in [Reference Erlandsson and Souto9] (see [Reference Erlandsson and Souto11, Ch. 6] for a nicer exposition of this result).
The Thurston measure
![]() ${\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
has many similarities with Lebesgue measure on
${\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
has many similarities with Lebesgue measure on
![]() ${\mathbb {R}}^{6g-6}$
. For example, it is homogeneous of degree
${\mathbb {R}}^{6g-6}$
. For example, it is homogeneous of degree
![]() $6g-6$
, meaning that for all
$6g-6$
, meaning that for all
![]() $U\subset {\mathcal {C}}(S)$
measurable we have
$U\subset {\mathcal {C}}(S)$
measurable we have
for all
![]() $t\geqslant 0$
. It follows that if
$t\geqslant 0$
. It follows that if
![]() $X\subset {\mathcal {C}}(S)$
is a compact set such that for every
$X\subset {\mathcal {C}}(S)$
is a compact set such that for every
![]() $\alpha \in {\mathcal {C}}(S)\setminus \{0\}$
there is a unique
$\alpha \in {\mathcal {C}}(S)\setminus \{0\}$
there is a unique
![]() $t\in {\mathbb {R}}_{>0}$
with
$t\in {\mathbb {R}}_{>0}$
with
![]() $t\cdot \alpha \in X$
, then there is a unique measure
$t\cdot \alpha \in X$
, then there is a unique measure
![]() $\mathfrak n$
on X such that the map
$\mathfrak n$
on X such that the map
is a measure-preserving homeomorphism. The measure
![]() $\mathfrak n(U)$
of
$\mathfrak n(U)$
of
![]() $U\subset X$
is given by
$U\subset X$
is given by
Combining all of this together we have the following lemma.
Lemma 2.2. Let
![]() $X\subset {\mathcal {C}}(S)$
be a compact set so that for every
$X\subset {\mathcal {C}}(S)$
be a compact set so that for every
![]() $\alpha \in {\mathcal {C}}(S)\setminus \{0\}$
there is a unique
$\alpha \in {\mathcal {C}}(S)\setminus \{0\}$
there is a unique
![]() $t\in {\mathbb {R}}_{>0}$
with
$t\in {\mathbb {R}}_{>0}$
with
![]() $t\cdot \alpha \in X$
. There is a measure
$t\cdot \alpha \in X$
. There is a measure
![]() $\mathfrak n$
on the set X such that the map
$\mathfrak n$
on the set X such that the map
is a measure-preserving homeomorphism.
Continuous homogeneous positive functions
![]() $F:{\mathcal {C}}(S)\to {\mathbb {R}}_{\geqslant 0}$
on the space of currents are a particular source of such sets X, where positive means that
$F:{\mathcal {C}}(S)\to {\mathbb {R}}_{\geqslant 0}$
on the space of currents are a particular source of such sets X, where positive means that
![]() $F(\alpha )>0$
for all
$F(\alpha )>0$
for all
![]() $\alpha \neq 0$
and homogeneous means that
$\alpha \neq 0$
and homogeneous means that
![]() $F(t\cdot \alpha )=t\cdot F(\alpha )$
. Indeed, if we are given any such function F then the set
$F(t\cdot \alpha )=t\cdot F(\alpha )$
. Indeed, if we are given any such function F then the set
![]() $X_F=F^{-1}(1)$
satisfies the condition in Lemma 2.2. Let
$X_F=F^{-1}(1)$
satisfies the condition in Lemma 2.2. Let
![]() $\mathfrak n_F$
be the measure on
$\mathfrak n_F$
be the measure on
![]() $X_F$
provided by the said lemma. This measure comes in particularly handy when integrating functions on
$X_F$
provided by the said lemma. This measure comes in particularly handy when integrating functions on
![]() ${\mathcal {C}}(S)$
whose value at
${\mathcal {C}}(S)$
whose value at
![]() $\widehat {\alpha }$
solely depends on
$\widehat {\alpha }$
solely depends on
![]() $F(\widehat {\alpha })$
. For example, with notation as in Lemma 2.2, we have
$F(\widehat {\alpha })$
. For example, with notation as in Lemma 2.2, we have
 $$ \begin{align} \int_{\{F(\cdot)\leqslant 1\}}F(\widehat{\unicode{x3bb}})^n\ d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\widehat{\unicode{x3bb}})=\frac 1{6g-6+n}\mathfrak n_F(X_F) \end{align} $$
$$ \begin{align} \int_{\{F(\cdot)\leqslant 1\}}F(\widehat{\unicode{x3bb}})^n\ d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\widehat{\unicode{x3bb}})=\frac 1{6g-6+n}\mathfrak n_F(X_F) \end{align} $$
for every
![]() $n\geqslant 0$
. Taking
$n\geqslant 0$
. Taking
![]() $n=0$
, we get in particular that
$n=0$
, we get in particular that
The reason why we care about continuous, homogeneous and positive functions on
![]() ${\mathcal {C}}(S)$
is that there is such a function
${\mathcal {C}}(S)$
is that there is such a function
satisfying
![]() $\ell _S(\widehat {\gamma })=\ell _S(\gamma )$
for every closed geodesic
$\ell _S(\widehat {\gamma })=\ell _S(\gamma )$
for every closed geodesic
![]() $\gamma $
, where the first
$\gamma $
, where the first
![]() $\ell _S(\cdot )$
is the function we are talking about and where the second one is just the length of the geodesic
$\ell _S(\cdot )$
is the function we are talking about and where the second one is just the length of the geodesic
![]() $\gamma $
. The reader can see [Reference Erlandsson, Parlier and Souto8, Reference Martínez-Granado and Thurston14] for other examples of continuous homogeneous functions on the space of currents—in fact we will encounter yet other such functions below.
$\gamma $
. The reader can see [Reference Erlandsson, Parlier and Souto8, Reference Martínez-Granado and Thurston14] for other examples of continuous homogeneous functions on the space of currents—in fact we will encounter yet other such functions below.
3 Proof of Theorem 1.1
We are now ready to prove Theorem 1.1. The first step is to compute the total measure of the measures
![]() $m_L^{S,\gamma _0}$
introduced above.
$m_L^{S,\gamma _0}$
introduced above.
Lemma 3.1. Let S be a closed orientable surface of genus g endowed with a negatively curved metric and denote by
![]() $\ell _S(\cdot )$
the associated length function. For every closed geodesic
$\ell _S(\cdot )$
the associated length function. For every closed geodesic
![]() $\gamma _0$
, we have
$\gamma _0$
, we have
 $$ \begin{align*}\lim_{L\to\infty}\frac 1{L^{6g-5}}\Vert\overline m_L^{S,\gamma_0}\Vert=\frac{6g-6}{6g-5}\cdot C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\frac 1{L^{6g-5}}\Vert\overline m_L^{S,\gamma_0}\Vert=\frac{6g-6}{6g-5}\cdot C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})\end{align*} $$
where
![]() $\overline m_L^{S,\gamma _0}$
is as in (1.10) and where
$\overline m_L^{S,\gamma _0}$
is as in (1.10) and where
![]() $C(\gamma _0)$
is as in Theorem 2.1.
$C(\gamma _0)$
is as in Theorem 2.1.
Note that the exponents of L in Theorem 2.1 and Lemma 3.1 differ,
![]() $6g-6$
versus
$6g-6$
versus
![]() $6g-5$
.
$6g-5$
.
Proof. Still writing
![]() $\gamma \sim \gamma _0$
to indicate that two closed unoriented geodesics are of the same type, we have
$\gamma \sim \gamma _0$
to indicate that two closed unoriented geodesics are of the same type, we have
 $$ \begin{align*} \frac 1{L^{6g-5}}\Vert\overline m_L^{S,\gamma_0}\Vert &=\frac 1{L^{6g-5}}\sum_{\gamma\in\mathcal S_L(S,\gamma_0)}\Vert\overline{\gamma}\Vert=\frac 1{L^{6g-5}}\sum_{\tiny\begin{array}{c}\gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\ell_S(\gamma)\\ &=\frac 1{L^{6g-5}}\int_{\{\ell_S(\cdot)\leqslant L\}}\ell_S(\cdot)\, d\bigg(\sum_{\gamma\sim\gamma_0}\delta_{\widehat{\gamma}}\bigg)\\ &=\int_{\{\ell_S(\cdot)\leqslant L\}}\frac{\ell_S(\cdot)}L\, d\bigg(\frac 1{L^{6g-6}} \sum_{\gamma\sim\gamma_0}\delta_{\widehat{\gamma}}\bigg)\\ &=\int_{\{\ell_S(\cdot)\leqslant 1\}}\ell_S(\cdot)\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg). \end{align*} $$
$$ \begin{align*} \frac 1{L^{6g-5}}\Vert\overline m_L^{S,\gamma_0}\Vert &=\frac 1{L^{6g-5}}\sum_{\gamma\in\mathcal S_L(S,\gamma_0)}\Vert\overline{\gamma}\Vert=\frac 1{L^{6g-5}}\sum_{\tiny\begin{array}{c}\gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\ell_S(\gamma)\\ &=\frac 1{L^{6g-5}}\int_{\{\ell_S(\cdot)\leqslant L\}}\ell_S(\cdot)\, d\bigg(\sum_{\gamma\sim\gamma_0}\delta_{\widehat{\gamma}}\bigg)\\ &=\int_{\{\ell_S(\cdot)\leqslant L\}}\frac{\ell_S(\cdot)}L\, d\bigg(\frac 1{L^{6g-6}} \sum_{\gamma\sim\gamma_0}\delta_{\widehat{\gamma}}\bigg)\\ &=\int_{\{\ell_S(\cdot)\leqslant 1\}}\ell_S(\cdot)\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg). \end{align*} $$
Now, Theorem 2.1 asserts that the measures on the last line converge:
 $$ \begin{align*}\lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}=C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}=C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
It follows that
 $$ \begin{align*} \lim_{L\to\infty}\frac 1{L^{6g-5}}\Vert\overline m_L^{S,\gamma_0}\Vert &=C(\gamma_0)\cdot\int_{\{\ell_S(\cdot)\leqslant 1\}}\ell_S(\cdot)\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}\\ &=\frac{6g-6}{6g-5}\cdot C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\}) \end{align*} $$
$$ \begin{align*} \lim_{L\to\infty}\frac 1{L^{6g-5}}\Vert\overline m_L^{S,\gamma_0}\Vert &=C(\gamma_0)\cdot\int_{\{\ell_S(\cdot)\leqslant 1\}}\ell_S(\cdot)\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}\\ &=\frac{6g-6}{6g-5}\cdot C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\}) \end{align*} $$
where we have used (2.2) and (2.3) to get the last equality.
Recall at this point the identification (1.8) between the spaces
![]() ${\mathcal {M}}_{\text {flip-flow}}(S)$
of flip- and flow-invariant measures and
${\mathcal {M}}_{\text {flip-flow}}(S)$
of flip- and flow-invariant measures and
![]() ${\mathcal {C}}(S)$
of currents, and suppose that we are given a continuous function
${\mathcal {C}}(S)$
of currents, and suppose that we are given a continuous function
![]() $f\in C^0(T^1S)$
. Then we get a continuous function
$f\in C^0(T^1S)$
. Then we get a continuous function
on the space of currents. It is continuous and homogeneous.
Lemma 3.2. We have
 $$ \begin{align*} &\lim_{L\to\infty}\int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)\\[4pt] &\quad=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})} \cdot\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}\end{align*} $$
$$ \begin{align*} &\lim_{L\to\infty}\int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)\\[4pt] &\quad=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})} \cdot\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}\end{align*} $$
for every
![]() $f\in C^0(T^1S)$
.
$f\in C^0(T^1S)$
.
Proof. We compute as in Lemma 3.1:
 $$ \begin{align*} \int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg) &=\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\sum_{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\int_{T^1S}f\, d\overline{\gamma}\\ &=\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\sum_{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\widehat f(\widehat{\gamma})\\ &=\frac L{\Vert\overline m_L^{S,\gamma_0}\Vert}\sum_{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\widehat f\,\bigg((1/L)\widehat{\gamma}\bigg)\\ &=\frac L{\Vert\overline m_L^{S,\gamma_0}\Vert}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg) \end{align*} $$
$$ \begin{align*} \int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg) &=\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\sum_{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\int_{T^1S}f\, d\overline{\gamma}\\ &=\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\sum_{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\widehat f(\widehat{\gamma})\\ &=\frac L{\Vert\overline m_L^{S,\gamma_0}\Vert}\sum_{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}\widehat f\,\bigg((1/L)\widehat{\gamma}\bigg)\\ &=\frac L{\Vert\overline m_L^{S,\gamma_0}\Vert}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg) \end{align*} $$
In light of Lemma 3.1 we get that
 $$ \begin{align} \int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg) &\approx \frac K{C(\gamma_0)\cdot L^{6g-6}}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg)\nonumber\\[4pt] &= \frac K{C(\gamma_0)}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg) \end{align} $$
$$ \begin{align} \int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg) &\approx \frac K{C(\gamma_0)\cdot L^{6g-6}}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg)\nonumber\\[4pt] &= \frac K{C(\gamma_0)}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg) \end{align} $$
where
![]() $\approx $
means that the ratio between both sides tends to
$\approx $
means that the ratio between both sides tends to
![]() $1$
when L tends to
$1$
when L tends to
![]() $\infty $
, and where
$\infty $
, and where
 $$ \begin{align*}K=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}.\end{align*} $$
$$ \begin{align*}K=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}.\end{align*} $$
Now, again invoking Theorem 2.1, we get that the measure at the very end of (3.1) converges to
![]() $C(\gamma _0)\cdot {\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
, meaning that
$C(\gamma _0)\cdot {\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
, meaning that
 $$ \begin{align*}\lim_{L\to\infty}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg)=C(\gamma_0)\int_{\{l_S(\cdot)\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}\bigg)=C(\gamma_0)\int_{\{l_S(\cdot)\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
Putting all of this together, we get that
 $$ \begin{align*}\lim_{L\to\infty}\int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)= K\cdot\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)= K\cdot\int_{\{\ell_S(\cdot)\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}\end{align*} $$
as claimed.
We are basically home and dry.
Proof of Theorem 1.1
nf your party affiliation, from the very definition of measure) that there is a unique measure
![]() ${\mathfrak m}$
on
${\mathfrak m}$
on
![]() $T^1S$
with
$T^1S$
with
 $$ \begin{align*}\int_{T^1S}f\, d{\mathfrak m}=\int_{\{\ell_S(\cdot)\leqslant 1\}}\bigg(\int_{T^1S} f\, d\overline{\unicode{x3bb}}\bigg)\,d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}({\unicode{x3bb}})\end{align*} $$
$$ \begin{align*}\int_{T^1S}f\, d{\mathfrak m}=\int_{\{\ell_S(\cdot)\leqslant 1\}}\bigg(\int_{T^1S} f\, d\overline{\unicode{x3bb}}\bigg)\,d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}({\unicode{x3bb}})\end{align*} $$
where, as usual, we denote by
![]() the flip- and flow-invariant measure associated to the measured lamination
the flip- and flow-invariant measure associated to the measured lamination
![]() .
.
In those terms, Lemma 3.2 says that
 $$ \begin{align*}\lim_{L\to\infty}\int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}\cdot\int_{T^1S}f\, d{\mathfrak m}.\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\int_{T^1S}f\, d\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}\cdot\int_{T^1S}f\, d{\mathfrak m}.\end{align*} $$
This just means that the measures
![]() $ (1/{\Vert \overline m_L^{S,\gamma _0}\Vert })\overline m_L^{S,\gamma _0}$
converge, when L tends to
$ (1/{\Vert \overline m_L^{S,\gamma _0}\Vert })\overline m_L^{S,\gamma _0}$
converge, when L tends to
![]() $\infty $
, to the measure
$\infty $
, to the measure
 $$ \begin{align*}{\mathfrak m}^S=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}\cdot{\mathfrak m}.\end{align*} $$
$$ \begin{align*}{\mathfrak m}^S=\frac{6g-5}{(6g-6)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}\cdot{\mathfrak m}.\end{align*} $$
Since, by (1.11), we have
 $$ \begin{align*}\frac 1{\Vert m_L^{S,\gamma_0}\Vert}m_L^{S,\gamma_0}=\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0},\end{align*} $$
$$ \begin{align*}\frac 1{\Vert m_L^{S,\gamma_0}\Vert}m_L^{S,\gamma_0}=\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0},\end{align*} $$
we are done.
4 Proof of Theorem 1.2
We are now ready to prove Theorem 1.2. We recall the statement for the convenience of the reader.
Theorem 1.2. The measure
![]() ${\mathfrak m}^S$
is not ergodic, has vanishing entropy, and its support has Hausdorff dimension
${\mathfrak m}^S$
is not ergodic, has vanishing entropy, and its support has Hausdorff dimension
![]() $1$
.
$1$
.
Proof. We start by proving that the measure
![]() ${\mathfrak m}^S$
is not ergodic. To begin with, recall that the set
${\mathfrak m}^S$
is not ergodic. To begin with, recall that the set
of uniquely ergodic measured laminations has full Thurston measure by a result of Masur [Reference Masur15]. Decompose the associated projective space
into two disjoint measurable sets
such that the associated subsets of
![]() ${\mathcal {M}}\mathcal L(S)$
have positive Thurston measure
${\mathcal {M}}\mathcal L(S)$
have positive Thurston measure
The sets
![]() $\mathcal A_1,\mathcal A_2\subset T^1S$
given by
$\mathcal A_1,\mathcal A_2\subset T^1S$
given by
are then disjoint and invariant under the geodesic flow. In turn, (4.1) implies that both have positive
![]() ${\mathfrak m}^S$
-measure:
${\mathfrak m}^S$
-measure:
This proves that
![]() ${\mathfrak m}^S$
is not ergodic.
${\mathfrak m}^S$
is not ergodic.
Note that the support of
![]() ${\mathfrak m}^S$
is the set
${\mathfrak m}^S$
is the set
![]() ${\mathcal {K}}$
of vectors tangent to a leaf in the support of some measured lamination. The projection of
${\mathcal {K}}$
of vectors tangent to a leaf in the support of some measured lamination. The projection of
![]() ${\mathcal {K}}$
to the surface S has Hausdorff dimension
${\mathcal {K}}$
to the surface S has Hausdorff dimension
![]() $1$
by the well-known Birman–Series theorem [Reference Birman and Series3]. That
$1$
by the well-known Birman–Series theorem [Reference Birman and Series3]. That
![]() ${\mathcal {K}}$
itself has Hausdorff dimension
${\mathcal {K}}$
itself has Hausdorff dimension
![]() $1$
was proved by Fathi [Reference Fathi12, Theorem 3.1], who also obtained in Corollary 3.4 of the same paper that the topological entropy of the restriction of the geodesic flow to
$1$
was proved by Fathi [Reference Fathi12, Theorem 3.1], who also obtained in Corollary 3.4 of the same paper that the topological entropy of the restriction of the geodesic flow to
![]() ${\mathcal {K}}$
vanishes—this implies that every measure supported by
${\mathcal {K}}$
vanishes—this implies that every measure supported by
![]() ${\mathcal {K}}$
, and in particular
${\mathcal {K}}$
, and in particular
![]() ${\mathfrak m}^S$
, has vanishing entropy.
${\mathfrak m}^S$
, has vanishing entropy.
5 Proof of Theorem 1.3
We will now prove Theorem 1.3. First recall that, as in (1.6), every homeomorphism
between negatively curved surfaces induces a homeomorphism
between the spaces of currents on the domain and target. Since we also have the homeomorphism (1.8) between the space of currents and the space of flip- and flow-invariant measures on the unit tangent bundle, we get an induced homeomorphism
Our first goal is to figure out the image of
![]() ${\mathfrak m}^S$
under this map.
${\mathfrak m}^S$
under this map.
Lemma 5.1. For every
![]() $f\in C^0(T^1S')$
we have
$f\in C^0(T^1S')$
we have
 $$ \begin{align*}\int_{T^1S'}f\, d\phi_*({\mathfrak m}^{S})=\frac{6g-5}{6g-6}\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})\cdot\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}},\end{align*} $$
$$ \begin{align*}\int_{T^1S'}f\, d\phi_*({\mathfrak m}^{S})=\frac{6g-5}{6g-6}\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})\cdot\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}},\end{align*} $$
where the second integral is taken over the set
of those measured laminations in
![]() ${\mathcal {M}}\mathcal L(S')$
which have length at most
${\mathcal {M}}\mathcal L(S')$
which have length at most
![]() $1$
in the surface S.
$1$
in the surface S.
Proof. We start by tracking what the map
![]() $\phi _*$
does to the flip- and flow-invariant measure
$\phi _*$
does to the flip- and flow-invariant measure
![]() $\overline {\gamma }$
on
$\overline {\gamma }$
on
![]() $T^1S$
associated to a free homotopy class
$T^1S$
associated to a free homotopy class
![]() $\gamma $
:
$\gamma $
:
 $$ \begin{align*}\matrix{ {\mathcal{M}}_{\text{flip-flow}}(S) \rightarrow & {\mathcal{C}}(S) \rightarrow & {\mathcal{C}}(S') \rightarrow & {\mathcal{M}}_{\text{flip-flow}}(S')\\ \overline{\gamma}\rightarrow & \widehat{\gamma} \rightarrow & \widehat{\phi(\gamma)} \rightarrow & \overline{\phi(\gamma)}}\end{align*} $$
$$ \begin{align*}\matrix{ {\mathcal{M}}_{\text{flip-flow}}(S) \rightarrow & {\mathcal{C}}(S) \rightarrow & {\mathcal{C}}(S') \rightarrow & {\mathcal{M}}_{\text{flip-flow}}(S')\\ \overline{\gamma}\rightarrow & \widehat{\gamma} \rightarrow & \widehat{\phi(\gamma)} \rightarrow & \overline{\phi(\gamma)}}\end{align*} $$
Now, linearity of (5.1) implies that
 $$ \begin{align*}\phi_*(m^{S,\gamma_0}_L)=\sum_{{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}}\overline{\phi(\gamma)}\end{align*} $$
$$ \begin{align*}\phi_*(m^{S,\gamma_0}_L)=\sum_{{\tiny\begin{array}{c} \gamma\sim\gamma_0\\ \ell_S(\gamma)\leqslant L\end{array}}}\overline{\phi(\gamma)}\end{align*} $$
where
![]() $\gamma _0$
is some arbitrary but otherwise fixed closed geodesic in S.
$\gamma _0$
is some arbitrary but otherwise fixed closed geodesic in S.
Then, exactly the same computation as we used in the first part of the proof of Lemma 3.2 shows that for any continuous function
![]() $f\in C^0(T^1S')$
we have
$f\in C^0(T^1S')$
we have
 $$ \begin{align*}\int_{T^1S'}f\, d\phi_*\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)=\frac L{\Vert\overline m_L^{S,\gamma_0}\Vert}\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d\bigg(\sum_{\gamma\sim\phi(\gamma_0)}\delta_{(1/L)\widehat{\gamma}}\bigg)\end{align*} $$
$$ \begin{align*}\int_{T^1S'}f\, d\phi_*\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)=\frac L{\Vert\overline m_L^{S,\gamma_0}\Vert}\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d\bigg(\sum_{\gamma\sim\phi(\gamma_0)}\delta_{(1/L)\widehat{\gamma}}\bigg)\end{align*} $$
where the integral is taken over the set (5.2). Still as in the proof of Lemma 3.2, we get that
 $$ \begin{align*}\int_{T^1S'}f\, d\phi_*\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)\approx\frac{K(S)}{C(\gamma_0)}\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\phi(\gamma_0)}\delta_{(1/L)\widehat{\gamma}}\bigg)\end{align*} $$
$$ \begin{align*}\int_{T^1S'}f\, d\phi_*\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)\approx\frac{K(S)}{C(\gamma_0)}\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d\bigg(\frac 1{L^{6g-6}}\sum_{\gamma\sim\phi(\gamma_0)}\delta_{(1/L)\widehat{\gamma}}\bigg)\end{align*} $$
where
 $$ \begin{align*}K(S)=\frac{6g-5}{6g-6}\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\}).\end{align*} $$
$$ \begin{align*}K(S)=\frac{6g-5}{6g-6}\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\}).\end{align*} $$
At this point, still as in Lemma 3.2, we get that
 $$ \begin{align*}\lim_{L\to\infty}\int_{T^1S'}f\, d\phi_*\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)=K(S)\cdot\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\int_{T^1S'}f\, d\phi_*\bigg(\frac 1{\Vert\overline m_L^{S,\gamma_0}\Vert}\overline m_L^{S,\gamma_0}\bigg)=K(S)\cdot\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}.\end{align*} $$
Since
![]() ${\mathfrak m}^{S}$
arises by Theorem 1.1 as the limit of the measures
${\mathfrak m}^{S}$
arises by Theorem 1.1 as the limit of the measures
![]() $( 1/{\Vert \overline m_L^{S,\gamma _0}\Vert })\overline m_L^{S,\gamma _0}$
and since
$( 1/{\Vert \overline m_L^{S,\gamma _0}\Vert })\overline m_L^{S,\gamma _0}$
and since
![]() $\phi _*$
is continuous, we get
$\phi _*$
is continuous, we get
 $$ \begin{align*}\int_{T^1S'}f\, d\phi_*({\mathfrak m}^{S})=K(S)\cdot\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}},\end{align*} $$
$$ \begin{align*}\int_{T^1S'}f\, d\phi_*({\mathfrak m}^{S})=K(S)\cdot\int_{\{\ell_S(\phi^{-1}(\cdot))\leqslant 1\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}},\end{align*} $$
as claimed.
We will now rewrite the integral on the right in Lemma 5.1 using polar coordinates in
![]() ${\mathcal {M}}\mathcal L(S')$
. To that end we choose a compact set
${\mathcal {M}}\mathcal L(S')$
. To that end we choose a compact set
![]() $X\subset {\mathcal {C}}(S')$
such that for every
$X\subset {\mathcal {C}}(S')$
such that for every
![]() $\alpha \in {\mathcal {C}}(S')\setminus \{0\}$
there is a uniquely determined
$\alpha \in {\mathcal {C}}(S')\setminus \{0\}$
there is a uniquely determined
![]() $t>0$
with
$t>0$
with
![]() $t\cdot \alpha \in X$
. Let
$t\cdot \alpha \in X$
. Let
![]() $\mathfrak n$
be the measure on X such that the map
$\mathfrak n$
be the measure on X such that the map
is a measure-preserving homeomorphism. Note that this induces a homeomorphism between
We then have for every
![]() $f\in C^0(T^1S')$
that
$f\in C^0(T^1S')$
that
 $$ \begin{align*} \int_{\{\ell_S(\phi^{-1}(\cdot))\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}} &=\int_{\{\ell_S(\phi^{-1}(\cdot))\}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}({\unicode{x3bb}})\\ &=\int_X\int_0^{ 1/{\ell_S(\phi^{-1}({\unicode{x3bb}}))}}\bigg(\int_{T^1S'}f\, d(\overline{t\cdot{\unicode{x3bb}}})\bigg) t^{6g-7}\cdot dt\cdot d\mathfrak n({\unicode{x3bb}})\\ &=\int_X\int_0^{1/{\ell_S(\phi^{-1}({\unicode{x3bb}}))}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg) t^{6g-6}\cdot dt\cdot d\mathfrak n({\unicode{x3bb}})\\ &=\int_X \frac 1{(6g-5)\cdot\ell_S(\phi^{-1}({\unicode{x3bb}}))^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}). \end{align*} $$
$$ \begin{align*} \int_{\{\ell_S(\phi^{-1}(\cdot))\}}\widehat f\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}} &=\int_{\{\ell_S(\phi^{-1}(\cdot))\}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d{\mathfrak m}_{\operatorname{\mathrm{Thu}}}({\unicode{x3bb}})\\ &=\int_X\int_0^{ 1/{\ell_S(\phi^{-1}({\unicode{x3bb}}))}}\bigg(\int_{T^1S'}f\, d(\overline{t\cdot{\unicode{x3bb}}})\bigg) t^{6g-7}\cdot dt\cdot d\mathfrak n({\unicode{x3bb}})\\ &=\int_X\int_0^{1/{\ell_S(\phi^{-1}({\unicode{x3bb}}))}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg) t^{6g-6}\cdot dt\cdot d\mathfrak n({\unicode{x3bb}})\\ &=\int_X \frac 1{(6g-5)\cdot\ell_S(\phi^{-1}({\unicode{x3bb}}))^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}). \end{align*} $$
In light of Lemma 5.1, we get
 $$ \begin{align*}\int_{T^1S'}f\, d\phi_*({\mathfrak m}^S)=\frac{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}{6g-6}\int_X \frac 1{\ell_S(\phi^{-1}({\unicode{x3bb}}))^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}).\end{align*} $$
$$ \begin{align*}\int_{T^1S'}f\, d\phi_*({\mathfrak m}^S)=\frac{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_S(\cdot)\leqslant 1\})}{6g-6}\int_X \frac 1{\ell_S(\phi^{-1}({\unicode{x3bb}}))^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}).\end{align*} $$
Applying this computation to
![]() $S=S'$
and
$S=S'$
and
![]() $\phi =\operatorname {\mathrm {Id}}$
, we also get
$\phi =\operatorname {\mathrm {Id}}$
, we also get
 $$ \begin{align*}\int_{T^1S'}f\, d{\mathfrak m}^{S'}=\frac{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_{S'}(\cdot)\leqslant 1\})}{6g-6}\int_X \frac 1{\ell_{S'}({\unicode{x3bb}})^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}).\end{align*} $$
$$ \begin{align*}\int_{T^1S'}f\, d{\mathfrak m}^{S'}=\frac{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_{S'}(\cdot)\leqslant 1\})}{6g-6}\int_X \frac 1{\ell_{S'}({\unicode{x3bb}})^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}).\end{align*} $$
Let us now denote by
![]() $\mathcal U\mathcal E\subset {\mathcal {M}}\mathcal L(S')$
the set of uniquely ergodic laminations and consider the function
$\mathcal U\mathcal E\subset {\mathcal {M}}\mathcal L(S')$
the set of uniquely ergodic laminations and consider the function
given by
 $$ \begin{align*}\xi^{\phi,S}_{S'}(v)=\left\{\begin{array}{ll} \bigg(\frac{\ell_{S'}({\unicode{x3bb}})}{\ell_S(\phi^{-1}({\unicode{x3bb}}))}\bigg)^{6g-5} & \text{ if }v\text{ is tangent to }{\unicode{x3bb}}\in\mathcal U\mathcal E,\\ 0 & \text{ otherwise}. \end{array}\right.\end{align*} $$
$$ \begin{align*}\xi^{\phi,S}_{S'}(v)=\left\{\begin{array}{ll} \bigg(\frac{\ell_{S'}({\unicode{x3bb}})}{\ell_S(\phi^{-1}({\unicode{x3bb}}))}\bigg)^{6g-5} & \text{ if }v\text{ is tangent to }{\unicode{x3bb}}\in\mathcal U\mathcal E,\\ 0 & \text{ otherwise}. \end{array}\right.\end{align*} $$
Since the set of uniquely ergodic measured laminations has full Thurston measure
![]() ${\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
[Reference Masur15] we get that
${\mathfrak m}_{\operatorname {\mathrm {Thu}}}$
[Reference Masur15] we get that
 $$ \begin{align*}\int_X \frac 1{\ell_S(\phi^{-1}({\unicode{x3bb}}))^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}})=\int_X \frac 1{\ell_{S'}({\unicode{x3bb}})^{6g-5}}\bigg(\int_{T^1S'}f\xi^{\phi,S}_{S'}\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}).\end{align*} $$
$$ \begin{align*}\int_X \frac 1{\ell_S(\phi^{-1}({\unicode{x3bb}}))^{6g-5}}\bigg(\int_{T^1S'}f\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}})=\int_X \frac 1{\ell_{S'}({\unicode{x3bb}})^{6g-5}}\bigg(\int_{T^1S'}f\xi^{\phi,S}_{S'}\, d\overline{\unicode{x3bb}}\bigg)\, d\mathfrak n({\unicode{x3bb}}).\end{align*} $$
Taking all of this together, we get
Since this holds true for all continuous functions
![]() $f\in C^0(T^1S')$
, we get that indeed
$f\in C^0(T^1S')$
, we get that indeed
![]() $\phi _*({\mathfrak m}^S)$
is absolutely continuous with respect to
$\phi _*({\mathfrak m}^S)$
is absolutely continuous with respect to
![]() ${\mathfrak m}^{S'}$
with Radon–Nikodym derivative
${\mathfrak m}^{S'}$
with Radon–Nikodym derivative
 $$ \begin{align} \frac{d\phi_*({\mathfrak m}^S)}{d{\mathfrak m}^{S'}}=\frac{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_{S}(\cdot)\leqslant 1\})}{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_{S'}(\cdot)\leqslant 1\})}\cdot\xi^{\phi,S}_{S'}. \end{align} $$
$$ \begin{align} \frac{d\phi_*({\mathfrak m}^S)}{d{\mathfrak m}^{S'}}=\frac{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_{S}(\cdot)\leqslant 1\})}{{\mathfrak m}_{\operatorname{\mathrm{Thu}}}(\{\ell_{S'}(\cdot)\leqslant 1\})}\cdot\xi^{\phi,S}_{S'}. \end{align} $$
Since the Radon–Nikodym derivative is essentially positive on the support of
![]() ${\mathfrak m}^{S'}$
, we get that indeed both measures are in the same measure class. We have proved Theorem 1.3, which we restate for the convenience of the reader.
${\mathfrak m}^{S'}$
, we get that indeed both measures are in the same measure class. We have proved Theorem 1.3, which we restate for the convenience of the reader.
Theorem 1.3. If
![]() $\phi :S\to S'$
is a homeomorphism between closed negatively curved surfaces then the measures
$\phi :S\to S'$
is a homeomorphism between closed negatively curved surfaces then the measures
![]() $\phi _*({\mathfrak m}^S)$
and
$\phi _*({\mathfrak m}^S)$
and
![]() ${\mathfrak m}^{S'}$
are in the same measure class.
${\mathfrak m}^{S'}$
are in the same measure class.
All that is left to do is to prove Theorem 1.4, which we do in the next section.
6 Proof of Theorem 1.4
Let us remind the reader what we need to prove.
Theorem 1.4. A homeomorphism
![]() $\phi :S\to S'$
between closed orientable hyperbolic surfaces is isotopic to an isometry if and only if
$\phi :S\to S'$
between closed orientable hyperbolic surfaces is isotopic to an isometry if and only if
![]() $\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
.
$\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
.
Proof. One direction is clear: if
![]() $\phi $
is an isometry, then
$\phi $
is an isometry, then
![]() $\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. Suppose conversely that S and
$\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. Suppose conversely that S and
![]() $S'$
are hyperbolic surfaces and that
$S'$
are hyperbolic surfaces and that
![]() $\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. This means that the Radon–Nikodym derivative (5.3) is identically
$\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. This means that the Radon–Nikodym derivative (5.3) is identically
![]() $1$
. This means that we have
$1$
. This means that we have
for almost every uniquely ergodic
![]() . The density of the set of uniquely ergodic laminations and continuity of the length function imply that (6.1) holds for all
. The density of the set of uniquely ergodic laminations and continuity of the length function imply that (6.1) holds for all
![]() . The following claim implies that this cannot happen unless
. The following claim implies that this cannot happen unless
![]() $\phi $
is homotopic, and hence isotopic, to an isometry.
$\phi $
is homotopic, and hence isotopic, to an isometry.
Claim. If
![]() $\phi :S\to S'$
is not homotopic to an isometry then there are
$\phi :S\to S'$
is not homotopic to an isometry then there are
![]() $\alpha ,\beta \in {\mathcal {M}}{\mathcal {L}}(S)$
with
$\alpha ,\beta \in {\mathcal {M}}{\mathcal {L}}(S)$
with
![]() $\ell _S(\alpha )<\ell _{S'}(\phi (\alpha ))$
and
$\ell _S(\alpha )<\ell _{S'}(\phi (\alpha ))$
and
![]() $\ell _S(\beta )>\ell _{S'}(\phi (\beta ))$
.
$\ell _S(\beta )>\ell _{S'}(\phi (\beta ))$
.
Proof. Let
![]() $\operatorname {\mathrm {Lip}}(\phi )$
denote the infimum of the Lipschitz constants over all maps homotopic to
$\operatorname {\mathrm {Lip}}(\phi )$
denote the infimum of the Lipschitz constants over all maps homotopic to
![]() $\phi $
. It is due to Thurston [Reference Thurston20] that
$\phi $
. It is due to Thurston [Reference Thurston20] that
![]() $\operatorname {\mathrm {Lip}}(\phi )>1$
unless
$\operatorname {\mathrm {Lip}}(\phi )>1$
unless
![]() $\phi $
is homotopic to an isometry and that
$\phi $
is homotopic to an isometry and that
The existence of
![]() $\alpha $
follows. The existence of
$\alpha $
follows. The existence of
![]() $\beta $
follows as well once we repeat the argument replacing
$\beta $
follows as well once we repeat the argument replacing
![]() $\phi $
by
$\phi $
by
![]() $\phi ^{-1}$
.
$\phi ^{-1}$
.
Having proved the claim, we have proved that if S and
![]() $S'$
are hyperbolic and if
$S'$
are hyperbolic and if
![]() $\phi ({\mathfrak m}^S)={\mathfrak m}^{S'}$
then
$\phi ({\mathfrak m}^S)={\mathfrak m}^{S'}$
then
![]() $\phi $
is homotopic to an isometry.
$\phi $
is homotopic to an isometry.
Let us now construct an example showing that Theorem 1.4 fails if, say,
![]() $S'$
is allowed to have variable curvature, even after we normalize the area to be equal to that of S. Let us start by choosing S hyperbolic and recall that, by Theorem 1.2, the support
$S'$
is allowed to have variable curvature, even after we normalize the area to be equal to that of S. Let us start by choosing S hyperbolic and recall that, by Theorem 1.2, the support
![]() ${\mathcal {K}}\subset T^1S$
of
${\mathcal {K}}\subset T^1S$
of
![]() ${\mathfrak m}^S$
has Hausdorff dimension
${\mathfrak m}^S$
has Hausdorff dimension
![]() $1$
. Its projection
$1$
. Its projection
![]() ${\mathcal {K}}'\subset S$
to the surface is closed and also has Hausdorff dimension
${\mathcal {K}}'\subset S$
to the surface is closed and also has Hausdorff dimension
![]() $1$
. Denoting by
$1$
. Denoting by
![]() $\sigma _0$
the hyperbolic metric on S, let
$\sigma _0$
the hyperbolic metric on S, let
![]() $\sigma $
be another metric (with same area) obtained by very slightly perturbing
$\sigma $
be another metric (with same area) obtained by very slightly perturbing
![]() $\sigma _0$
on some open set whose closure does not meet
$\sigma _0$
on some open set whose closure does not meet
![]() ${\mathcal {K}}'$
. Let
${\mathcal {K}}'$
. Let
![]() $S'=(S,\sigma )$
and
$S'=(S,\sigma )$
and
![]() $\phi =\operatorname {\mathrm {Id}}$
. Then the map
$\phi =\operatorname {\mathrm {Id}}$
. Then the map
is an isometry on the set
![]() ${\mathcal {K}}'$
and hence satisfies that
${\mathcal {K}}'$
and hence satisfies that
![]() for all
for all
![]() . It follows that the Radon–Nikodym derivative (5.3) of
. It follows that the Radon–Nikodym derivative (5.3) of
![]() $\phi _*({\mathfrak m}^S)$
with respect to
$\phi _*({\mathfrak m}^S)$
with respect to
![]() ${\mathfrak m}^{S'}$
is identically
${\mathfrak m}^{S'}$
is identically
![]() $1$
, meaning that
$1$
, meaning that
![]() $\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. On the other hand, there is no isometry from a hyperbolic surface to one with non-constant curvature.
$\phi _*({\mathfrak m}^S)={\mathfrak m}^{S'}$
. On the other hand, there is no isometry from a hyperbolic surface to one with non-constant curvature.
7 Surfaces with cusps
So far we have been considering closed surfaces. We explain briefly how to modify the proofs of the theorems in the introduction so that they apply to surfaces with cusps. Actually, we will just focus on Theorem 1.1, leaving to the reader the pleasure of modifying the other proofs.
Let us suppose that S is a complete hyperbolic surface of finite area and let
![]() $\gamma _0$
be a closed primitive geodesic in S. We also suppose that S is not a thrice punctured sphere—all results are trivial in that case.
$\gamma _0$
be a closed primitive geodesic in S. We also suppose that S is not a thrice punctured sphere—all results are trivial in that case.
The first basic fact (see, for example, [Reference Erlandsson, Parlier and Souto8, Lemma 5.2], [Reference Erlandsson and Souto11, Lemma 2.8], or [Reference Bell2, Lemma 4]) is that there is a compact subsurface
![]() $S_0\subset S$
which contains every closed geodesic of the same type as
$S_0\subset S$
which contains every closed geodesic of the same type as
![]() $\gamma _0$
, or indeed any closed geodesic
$\gamma _0$
, or indeed any closed geodesic
![]() $\gamma $
with
$\gamma $
with
![]() $\iota (\gamma ,\gamma )\leqslant \iota (\gamma _0,\gamma _0)$
. It follows that the measures
$\iota (\gamma ,\gamma )\leqslant \iota (\gamma _0,\gamma _0)$
. It follows that the measures
![]() $m_L^{S,\gamma _0}$
and
$m_L^{S,\gamma _0}$
and
![]() $\overline m_L^{S,\gamma _0}$
are supported by
$\overline m_L^{S,\gamma _0}$
are supported by
![]() $S_0$
for all L.
$S_0$
for all L.
This means that in the proofs one does not need to worry about the measure wandering off to infinity. But this is only one of the issues one faces when the surface is non-compact. The point is that for technical reasons, when working with currents (and wanting to have a continuous and homogeneous extension of
![]() $\iota (\cdot ,\cdot )$
to the space of currents) one is forced by nature to work on compact surfaces. However, while the surfaces have to be compact, they can have a boundary.
$\iota (\cdot ,\cdot )$
to the space of currents) one is forced by nature to work on compact surfaces. However, while the surfaces have to be compact, they can have a boundary.
Let
![]() $S'\subset S$
be a compact subsurface such that
$S'\subset S$
be a compact subsurface such that
-
•
 $S_0\subset S'\setminus \partial S'$
, and
$S_0\subset S'\setminus \partial S'$
, and -
•
 $S\setminus S'$
is a union of annular components, one for each cusps of S.
$S\setminus S'$
is a union of annular components, one for each cusps of S.
Endow
![]() $S'$
with a negatively curved metric with totally geodesic boundary and which agrees with the metric of S near
$S'$
with a negatively curved metric with totally geodesic boundary and which agrees with the metric of S near
![]() $S_0$
.
$S_0$
.
By definition, a current on
![]() $S'$
is a
$S'$
is a
![]() $\pi _1(S')$
-invariant Radon measure on the space
$\pi _1(S')$
-invariant Radon measure on the space
![]() ${\mathcal {G}}({\tilde {S}}')$
of complete geodesics on the universal cover of
${\mathcal {G}}({\tilde {S}}')$
of complete geodesics on the universal cover of
![]() $S'$
. Denote by
$S'$
. Denote by
![]() ${\mathcal {C}}_{S_0}(S')$
be the set of currents on
${\mathcal {C}}_{S_0}(S')$
be the set of currents on
![]() $S'$
supported by geodesics which project into
$S'$
supported by geodesics which project into
![]() $S_0$
. For example, the current
$S_0$
. For example, the current
![]() $\widehat {\gamma }$
belongs to
$\widehat {\gamma }$
belongs to
![]() ${\mathcal {C}}_{S_0}(S')$
for every
${\mathcal {C}}_{S_0}(S')$
for every
![]() $\gamma $
of the same type as
$\gamma $
of the same type as
![]() $\gamma _0$
.
$\gamma _0$
.
Note also that
![]() $S'$
-geodesics contained in
$S'$
-geodesics contained in
![]() $S_0$
are, by the choice of the metric on S, also S-geodesics. It follows that we can consider currents
$S_0$
are, by the choice of the metric on S, also S-geodesics. It follows that we can consider currents
![]() $\widehat {\mu }\in {\mathcal {C}}_{S_0}(S')$
as
$\widehat {\mu }\in {\mathcal {C}}_{S_0}(S')$
as
![]() $\pi _1(S)$
-invariant measures on the set of geodesics on S. We thus get a continuous map
$\pi _1(S)$
-invariant measures on the set of geodesics on S. We thus get a continuous map
where the measure
![]() $\overline \mu $
is still given by (1.7). This maps is also proper.
$\overline \mu $
is still given by (1.7). This maps is also proper.
Now, Theorem 2.1 is proved in [Reference Erlandsson and Souto11] not only for closed but also for general compact connected orientable surfaces of negative Euler characteristic (other than the pair of pants). Applying it to
![]() $\gamma _0$
when seen as a curve in
$\gamma _0$
when seen as a curve in
![]() $S'$
, we get that
$S'$
, we get that
 $$ \begin{align} \lim_{L\to\infty}\frac 1{L^{6g-6+2r}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}=C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}. \end{align} $$
$$ \begin{align} \lim_{L\to\infty}\frac 1{L^{6g-6+2r}}\sum_{\gamma\sim\gamma_0}\delta_{(1/L)\widehat{\gamma}}=C(\gamma_0)\cdot{\mathfrak m}_{\operatorname{\mathrm{Thu}}}. \end{align} $$
Here g and r are the genus and number of cusps of S and the convergence takes place with respect to the weak-* topology on the space of Radon measures on
![]() ${\mathcal {C}}_{S_0}(S')$
.
${\mathcal {C}}_{S_0}(S')$
.
Armed with (7.1) and (7.2), we can repeat word by word the proof of Lemmas 3.1 and 3.2. Theorem 1.1 follows.
The reader might be wondering if this is actually true. Earlier we were making a big deal of the fact that the space of currents is homeomorphic to that of flip- and flow-invariant measures, and the map (7.1) is obviously not a homeomorphism. If the reader is worried about this, then they can really go back to the proof of Lemmas 3.1 and 3.2 and check that we are only using the continuity and properness of (1.8).
Acknowledgements
We are grateful to Scott Wolpert and especially to Steven Zelditch not only for asking the question leading to this paper, but also for the ensuing discussions. All of this happened after a talk by the first author at the conference Analysis and Geometry—A Symposium to Honor the 70th birthday of Scott Wolpert, and she thanks the organizers for the invitation. The first author gratefully acknowledges support from EPSRC grant EP/T015926/1.