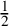1 Introduction
The last two decades have seen an explosion of physics research on the behavior of isolated quantum systems in which both disorder and interactions are present. The appearance of these two features has been linked to the existence of materials that fail to thermalize and consequently cannot be described using equilibrium statistical mechanics. These materials are presumed to remain insulators at nonzero temperature, a phenomenon called many-body localization (MBL). We refer the reader to the physics reviews [Reference Abanin, Altman, Bloch and Serbyn1,Reference Alet and Laflorencie9,Reference Nandkishore and Huse38] for the general description of this phenomenon. MBL-type behavior has been observed in cold atoms experiments [Reference Lukin, Rispoli, Schittko, Tai, Kaufman, Choi, Khemani, Léonard and Greiner31, Reference Schreiber, Hodgman, Bordia, Lüschen, Fischer, Vosk, Altman, Schneider and Bloch41]. The stability of the MBL phase for infinite systems and all times remains a topic of intense debate [Reference Kiefer-Emmanouilidis, Unanyan, Fleischhauer and Sirker25, Reference Morningstar, Colmenarez, Khemani, Luitz and Huse35, Reference Sels and Polkovnikov43, Reference Sierant, Delande and Zakrzewski44, Reference Sierant and Zakrzewski45].
In this paper, we consider the random spin-
![]() $\tfrac 12$
Heisenberg XXZ chain in the Ising phase, a one-dimensional random quantum spin system. This is the most studied model in the context of MBL both in the physics and mathematics literature (going back to [Reference Pal and Huse39, Reference Žnidarič, Prosen and Prelovšek47]). It can be mapped by the Jordan-Wigner transformation into an interacting spinless fermionic model closely related to the disordered Fermi-Hubbard Hamiltonian, a paradigmatic model in condensed matter physics that provides crucial insights into the electronic and magnetic properties of materials. One interesting feature of the random one-dimensional XXZ quantum spin system is the emergence of a many-body localization-delocalization transition. (In contrast, prototypical non-interacting one-dimensional random Schrödinger operators do not exhibit a phase transition and are completely localized.) Numerical evidence for this transition in the disordered XXZ model has been provided in a number of simulations (e.g., [Reference Agarwal, Gopalakrishnan, Knap, Müller and Demler3, Reference Bardarson, Pollmann and Moore10, Reference Baygan, Lim and Sheng11, Reference Luitz, Laflorencie and Alet30, Reference Pal and Huse39]), but remains contested on theoretical grounds (e.g., [Reference De Roeck, Huveneers, Müller and Schiulaz14]).
$\tfrac 12$
Heisenberg XXZ chain in the Ising phase, a one-dimensional random quantum spin system. This is the most studied model in the context of MBL both in the physics and mathematics literature (going back to [Reference Pal and Huse39, Reference Žnidarič, Prosen and Prelovšek47]). It can be mapped by the Jordan-Wigner transformation into an interacting spinless fermionic model closely related to the disordered Fermi-Hubbard Hamiltonian, a paradigmatic model in condensed matter physics that provides crucial insights into the electronic and magnetic properties of materials. One interesting feature of the random one-dimensional XXZ quantum spin system is the emergence of a many-body localization-delocalization transition. (In contrast, prototypical non-interacting one-dimensional random Schrödinger operators do not exhibit a phase transition and are completely localized.) Numerical evidence for this transition in the disordered XXZ model has been provided in a number of simulations (e.g., [Reference Agarwal, Gopalakrishnan, Knap, Müller and Demler3, Reference Bardarson, Pollmann and Moore10, Reference Baygan, Lim and Sheng11, Reference Luitz, Laflorencie and Alet30, Reference Pal and Huse39]), but remains contested on theoretical grounds (e.g., [Reference De Roeck, Huveneers, Müller and Schiulaz14]).
Until quite recently, mathematical results related to the proposed MBL characteristics, including zero-velocity Lieb-Robinson bounds, exponential clustering, quasi-locality, slow spreading of information and area laws, have been confined to quasi-free systems. The latter are models whose study can effectively be reduced to one of a (disordered) one-particle Hamiltonian. Examples of such systems include the XY spin chain in a random transversal field (going back to [Reference Klein and Perez29]; see [Reference Abdul-Rahman, Nachtergaele, Sims and Stolz2] for a review on this topic), the disordered Tonks-Girardeau gas [Reference Seiringer and Warzel42] and systems of quantum harmonic oscillators [Reference Nachtergaele, Sims and Stolz36]. Another direction of research considers the effect of many-body interaction on a single-particle localization (rather than MBL) within the framework of the effective field theories. This allows to consider a realistic Hilbert space for a single particle, such as
![]() $\ell ^2(\mathbb Z^d)$
, rather than finite dimensional ones that are typically used in the MBL context. In particular, the persistence of the dynamical localization in the Hartree-Fock approximation for the disordered Hubbard model has been established in [Reference Ducatez16, Reference Matos and Schenker34].
$\ell ^2(\mathbb Z^d)$
, rather than finite dimensional ones that are typically used in the MBL context. In particular, the persistence of the dynamical localization in the Hartree-Fock approximation for the disordered Hubbard model has been established in [Reference Ducatez16, Reference Matos and Schenker34].
In the last few years, there has been some (modest) progress in understanding genuine many-body systems, all of which is concerned with the XXZ model, either in the quasi-periodic setting (where the exponential clustering property for the ground state of the André-Aubry model has been established [Reference Mastropietro32, Reference Mastropietro33]) or in the droplet spectrum regime in the random case [Reference Beaud and Warzel12, Reference Elgart, Klein and Stolz19]. In the latter case, several MBL manifestations have been established, including some that have never been previously discussed in the physics literature [Reference Elgart, Klein and Stolz18].
While not exactly solvable, the XXZ spin chain does have a symmetry; namely, it preserves the particle number. This enables a reduction to an infinite system of discrete N-body Schrödinger operators on the fermionic subspaces of
![]() $\mathbb Z^N$
[Reference Fischbacher and Stolz21, Reference Nachtergaele and Starr37]. For the XXZ spin chain in the Ising phase, in the absence of a magnetic field, the low energy eigenstates above the ground state are characterized by a droplet regime. In this regime, spins form a droplet (i.e., a single cluster of down spins (particles) in a sea of up spins). This reduction has been effectively exploited inside the droplet spectrum (the interval
$\mathbb Z^N$
[Reference Fischbacher and Stolz21, Reference Nachtergaele and Starr37]. For the XXZ spin chain in the Ising phase, in the absence of a magnetic field, the low energy eigenstates above the ground state are characterized by a droplet regime. In this regime, spins form a droplet (i.e., a single cluster of down spins (particles) in a sea of up spins). This reduction has been effectively exploited inside the droplet spectrum (the interval
![]() $ I_1$
in (2.14) below) using methods that resemble the fractional moment method for random Schrödinger operators, yielding the small number of rigorous results [Reference Beaud and Warzel12, Reference Elgart, Klein and Stolz19]. However, these methods seem to be inadequate above this energy interval (i.e, inside the multi-cluster spectrum), and a new set of ideas that do not rely on a reduction to Schrödinger operators are required to tackle this case.
$ I_1$
in (2.14) below) using methods that resemble the fractional moment method for random Schrödinger operators, yielding the small number of rigorous results [Reference Beaud and Warzel12, Reference Elgart, Klein and Stolz19]. However, these methods seem to be inadequate above this energy interval (i.e, inside the multi-cluster spectrum), and a new set of ideas that do not rely on a reduction to Schrödinger operators are required to tackle this case.
In this paper, we extend the energy interval for which MBL holds well beyond the droplet spectrum, deep inside the multi-cluster spectrum. We develop a suitable method, formulated and proved in terms of spin systems concepts. In particular, our method does not rely on the reduction of the XXZ Hamiltonian to a direct sum of Schrodinger operators (and the subsequent analysis that uses single-particle tools).
Localization phenomenon in condensed matter physics is usually associated with non-spreading of wave packets in a disordered medium. Experimentally, it is observed in semiconductors whose properties are predominantly caused by crystal defects or impurities, as well as in the variety of other systems. This phenomenon is by now well understood for quantum single particle models. A prototypical system studied in this context is the Anderson Hamiltonian
![]() $H_A$
, which is a self-adjoint operator acting on the Hilbert space
$H_A$
, which is a self-adjoint operator acting on the Hilbert space
![]() $\mathcal H=\ell ^2(\mathbb Z^d)$
of the form
$\mathcal H=\ell ^2(\mathbb Z^d)$
of the form
![]() $H_A=-\Delta +\lambda V_\omega $
. Here,
$H_A=-\Delta +\lambda V_\omega $
. Here,
![]() $\Delta $
is the (discrete) Laplacian describing the kinetic hopping,
$\Delta $
is the (discrete) Laplacian describing the kinetic hopping,
![]() $V_\omega $
is a randomly generated multiplication operator (
$V_\omega $
is a randomly generated multiplication operator (
![]() $\omega $
is the random parameter) describing the electric potential, and
$\omega $
is the random parameter) describing the electric potential, and
![]() $\lambda $
is a parameter measuring the strength of the disorder.
$\lambda $
is a parameter measuring the strength of the disorder.
Let us denote by
![]() $\delta _x\in \mathcal H$
the indicator of
$\delta _x\in \mathcal H$
the indicator of
![]() $x\in \mathbb Z^d$
, and fix the random parameter
$x\in \mathbb Z^d$
, and fix the random parameter
![]() $\omega $
. An important feature of
$\omega $
. An important feature of
![]() $H_A$
as a map on
$H_A$
as a map on
![]() $\ell ^2(\mathbb Z^d)$
is its locality, meaning
$\ell ^2(\mathbb Z^d)$
is its locality, meaning
![]() $\langle \delta _x,H_A\delta _y\rangle =0$
if
$\langle \delta _x,H_A\delta _y\rangle =0$
if
![]() $\left \lvert x-y \right \rvert>1$
. As a consequence, the resolvent
$\left \lvert x-y \right \rvert>1$
. As a consequence, the resolvent
![]() $(H_A-z)^{-1} $
retain a measure of locality, which we will call quasi-locality, given by the Combes-Thomas estimate
$(H_A-z)^{-1} $
retain a measure of locality, which we will call quasi-locality, given by the Combes-Thomas estimate
where
![]() $C_z$
and
$C_z$
and
![]() $m_z$
are constants independent of
$m_z$
are constants independent of
![]() $\omega $
such that
$\omega $
such that
![]() $C_z <\infty $
and
$C_z <\infty $
and
![]() $m_z>0$
if
$m_z>0$
if
![]() $z\in \mathbb C$
is outside the spectrum of
$z\in \mathbb C$
is outside the spectrum of
![]() $H_A$
. Maps given by smooth functions of
$H_A$
. Maps given by smooth functions of
![]() $H_A$
also express a measure of quasi-locality – namely,
$H_A$
also express a measure of quasi-locality – namely,
where
![]() $C_{f,n} <\infty $
for all
$C_{f,n} <\infty $
for all
![]() $n\in \mathbb N$
and infinitely differentiable functions f. Moreover, these quasi-locality estimate hold with the same constants for the restriction
$n\in \mathbb N$
and infinitely differentiable functions f. Moreover, these quasi-locality estimate hold with the same constants for the restriction
![]() $H_A^\Lambda $
of
$H_A^\Lambda $
of
![]() $H_A$
to a finite volume
$H_A$
to a finite volume
![]() $\Lambda \subset \mathbb Z^d$
. (See, for example, [Reference Kirsch26, Reference Germinet and Klein24, Reference Remling40].)
$\Lambda \subset \mathbb Z^d$
. (See, for example, [Reference Kirsch26, Reference Germinet and Klein24, Reference Remling40].)
The two mainstream approaches for proving localization in the single particle setting, the multi-scale analysis (MSA) and the fractional moment method (FMM), going back to [Reference von Dreifus and Klein15, Reference Fröhlich and Spencer23, Reference Fröhlich, Martinelli, Scoppola and Spencer22] and [Reference Aizenman4, Reference Aizenman and Molchanov6], respectively – establish localization for the (random) Anderson model
![]() $H_A$
by proving quasi-locality estimates for the finite volume resolvent inside the spectrum of
$H_A$
by proving quasi-locality estimates for the finite volume resolvent inside the spectrum of
![]() $H_A$
. In particular, the fractional moment method shows that, fixing
$H_A$
. In particular, the fractional moment method shows that, fixing
![]() $s\in (0,1)$
, for large disorder
$s\in (0,1)$
, for large disorder
![]() $\lambda $
, we have
$\lambda $
, we have
for all finite
![]() $\Lambda \subset \mathbb Z^d$
,
$\Lambda \subset \mathbb Z^d$
,
![]() $ x,y\in \Lambda $
, and energies
$ x,y\in \Lambda $
, and energies
![]() $E\in \mathbb R$
, where the constants
$E\in \mathbb R$
, where the constants
![]() $C<\infty $
and
$C<\infty $
and
![]() $m>0$
are in dependent of
$m>0$
are in dependent of
![]() $\Lambda $
. Moreover, one also gets a quasi-locality estimate for Borel functions of
$\Lambda $
. Moreover, one also gets a quasi-locality estimate for Borel functions of
![]() $H^A$
(dynamical localization),
$H^A$
(dynamical localization),
 $$ \begin{align}\begin{aligned} \mathbb E\left\{ \sup_{f} \left\lvert \left\langle {\delta_x,f(H^\Lambda_A)\delta_y } \right\rangle \right\rvert \right\}\le C\mathrm{e}^{-m \left\lvert x-y \right\rvert}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E\left\{ \sup_{f} \left\lvert \left\langle {\delta_x,f(H^\Lambda_A)\delta_y } \right\rangle \right\rvert \right\}\le C\mathrm{e}^{-m \left\lvert x-y \right\rvert}, \end{aligned}\end{align} $$
where the supremum is taken over all Borel functions on
![]() $\mathbb R$
bounded by one. Various manifestations of one-particle localization, such as non-spreading of wave packets, vanishing of conductivity in response to electric field, and statistics of the spacing between nearby energy levels, can be derived from these quasi-locality estimates. (See, for example, [Reference Aizenman and Warzel8].) On the mathematical level, the quasi-locality estimates provides an effective description of single particle localization.
$\mathbb R$
bounded by one. Various manifestations of one-particle localization, such as non-spreading of wave packets, vanishing of conductivity in response to electric field, and statistics of the spacing between nearby energy levels, can be derived from these quasi-locality estimates. (See, for example, [Reference Aizenman and Warzel8].) On the mathematical level, the quasi-locality estimates provides an effective description of single particle localization.
The MSA and the FMM prove localization for random Schrödinger operators, both in the discrete and continuum settings. We refer the reader to the lecture notes [Reference Kirsch26, Reference Klein27] and the monograph [Reference Aizenman and Warzel8] for an introduction to the multi-scale analysis and the fractional moment method, respectively.
Both methods have been extended to quantum system consisting of an arbitrary, but fixed, number of interacting particles, showing that many characteristics of single-particle localization remain valid in this case (e.g., [Reference Aizenman and Warzel7, Reference Chulaevsky and Suhov13, Reference Klein and Nguyen28]). But truly many-body systems (where the number of particles is proportional to the system’s size) present new challenges. A major difficulty lies in the fact that the concepts of MBL proposed in the physics literature are not easily tractable on the mathematical level, and it is not clear what could be chosen as the fundamental description of the theory from which other properties can be derived, as in a single particle case. For example, the available concept of quasi-locality in the many-body systems looks very different from the one for single particle quantum systems.
To introduce a simple many-body system Hamiltonian, we consider a finite graph
![]() $\mathbf {\Gamma }=\left ( \mathcal V,\mathcal E \right )$
(where
$\mathbf {\Gamma }=\left ( \mathcal V,\mathcal E \right )$
(where
![]() $\mathcal V$
is the set of vertices and
$\mathcal V$
is the set of vertices and
![]() $\mathcal E$
is the set of edges) and a family
$\mathcal E$
is the set of edges) and a family
![]() $\left \{ \mathcal H_i \right \}_{i\in \mathcal V}$
of Hilbert spaces. The Hilbert space of the subsystem associated with a set
$\left \{ \mathcal H_i \right \}_{i\in \mathcal V}$
of Hilbert spaces. The Hilbert space of the subsystem associated with a set
![]() $X\subset \mathcal V$
is given by
$X\subset \mathcal V$
is given by
![]() $\mathcal H_X=\bigotimes _{i\in X}\mathcal H_i$
, and the full Hilbert space (we ignore particles’ statistics) is
$\mathcal H_X=\bigotimes _{i\in X}\mathcal H_i$
, and the full Hilbert space (we ignore particles’ statistics) is
![]() $\mathcal H_{\mathcal V}$
. For each
$\mathcal H_{\mathcal V}$
. For each
![]() $X\subset \mathcal V$
, one introduces the algebra of observables
$X\subset \mathcal V$
, one introduces the algebra of observables
![]() $\mathcal A_X$
measurable in this subsystem, which is the collection
$\mathcal A_X$
measurable in this subsystem, which is the collection
![]() $\mathcal B(\mathcal H_X)$
of bounded linear operators on the Hilbert space
$\mathcal B(\mathcal H_X)$
of bounded linear operators on the Hilbert space
![]() $\mathcal {H}_X$
. An observable
$\mathcal {H}_X$
. An observable
![]() $\mathcal O\in \mathcal A_{\mathcal V}$
is said to be supported by
$\mathcal O\in \mathcal A_{\mathcal V}$
is said to be supported by
![]() $X\subset \mathcal V$
if
$X\subset \mathcal V$
if ![]() , where
, where
![]() $\mathcal O_{X}\in \mathcal A_{X}$
(i.e., if
$\mathcal O_{X}\in \mathcal A_{X}$
(i.e., if
![]() $\mathcal O$
acts trivially on
$\mathcal O$
acts trivially on
![]() $\mathcal H_{\mathcal V\setminus X}$
). Slightly abusing the notation, we will usually identify
$\mathcal H_{\mathcal V\setminus X}$
). Slightly abusing the notation, we will usually identify
![]() $\mathcal O$
with
$\mathcal O$
with
![]() $\mathcal O_{X}$
and call X a support for
$\mathcal O_{X}$
and call X a support for
![]() $\mathcal O$
. Since we are primarily interested here in understanding the way particles interact, the structure of a single particle Hilbert space
$\mathcal O$
. Since we are primarily interested here in understanding the way particles interact, the structure of a single particle Hilbert space
![]() $\mathcal H_i$
will be only of marginal importance for us. So we will be considering the simplest possible realization of such system, where each
$\mathcal H_i$
will be only of marginal importance for us. So we will be considering the simplest possible realization of such system, where each
![]() $\mathcal H_i$
is the two dimensional vector space
$\mathcal H_i$
is the two dimensional vector space
![]() $\mathbb C^2$
describing a spin-
$\mathbb C^2$
describing a spin-
![]() $\frac 12$
particle.
$\frac 12$
particle.
We next describe the interactions between our spins. We again are going to consider the simplest possible arrangement, where only nearest neighboring spins are allowed to interact. Explicitly, for each pair of vertices
![]() $(i,j)\in \mathcal V$
that share an edge (i.e.,
$(i,j)\in \mathcal V$
that share an edge (i.e.,
![]() $\left \{ i,j \right \} \in \mathcal {E}$
), we pick an observable (called an interaction)
$\left \{ i,j \right \} \in \mathcal {E}$
), we pick an observable (called an interaction)
![]() $h_{i,j}\in \mathcal A_{\left \{ i,j \right \}}$
such that
$h_{i,j}\in \mathcal A_{\left \{ i,j \right \}}$
such that
![]() $h_{i,j}=h^*_{i,j}$
, an observable (called a local transverse field)
$h_{i,j}=h^*_{i,j}$
, an observable (called a local transverse field)
![]() $v_i=v_i^*\in \mathcal {A}_{\left \{ i \right \}}$
, and associate a Hamiltonian
$v_i=v_i^*\in \mathcal {A}_{\left \{ i \right \}}$
, and associate a Hamiltonian
![]() $H^{\mathcal V}=\sum _{\left \{ i,j \right \} \in \mathcal E}h_{i,j}+\sum _{i\in {\mathcal V}} v_i$
with our spin system. In particular,
$H^{\mathcal V}=\sum _{\left \{ i,j \right \} \in \mathcal E}h_{i,j}+\sum _{i\in {\mathcal V}} v_i$
with our spin system. In particular,
![]() $H^{\mathcal V}$
is the sum of local observables and is consequently referred to as a local Hamiltonian. Locality is manifested by
$H^{\mathcal V}$
is the sum of local observables and is consequently referred to as a local Hamiltonian. Locality is manifested by
![]() $[[H^{\mathcal V},\mathcal O],\mathcal O^\prime ]=0$
for any pair of observables
$[[H^{\mathcal V},\mathcal O],\mathcal O^\prime ]=0$
for any pair of observables
![]() $\mathcal O\in \mathcal A_X$
,
$\mathcal O\in \mathcal A_X$
,
![]() $\mathcal O^\prime \in \mathcal A_Y$
, with
$\mathcal O^\prime \in \mathcal A_Y$
, with
![]() $\operatorname {\mathrm {dist}}(X,Y)>1$
. (To compare it with the concept of (single particle) locality for the map
$\operatorname {\mathrm {dist}}(X,Y)>1$
. (To compare it with the concept of (single particle) locality for the map
![]() $H_A$
, we need to define a local observable for the space
$H_A$
, we need to define a local observable for the space
![]() $\ell ^2(\mathbb Z^d)$
. We will say that an observable
$\ell ^2(\mathbb Z^d)$
. We will say that an observable
![]() $\mathcal O\in \mathcal L(\ell ^2(\mathbb Z^d))$
has support
$\mathcal O\in \mathcal L(\ell ^2(\mathbb Z^d))$
has support
![]() $X\subset \mathbb Z^d$
if
$X\subset \mathbb Z^d$
if
![]() $\mathcal O=\mathcal O_{X} \oplus 0_{\ell ^2(\mathbb Z^d\setminus X)}$
with
$\mathcal O=\mathcal O_{X} \oplus 0_{\ell ^2(\mathbb Z^d\setminus X)}$
with
![]() $\mathcal O_{X}\in \mathcal L(\ell ^2(X))$
. With this definition, locality of the map
$\mathcal O_{X}\in \mathcal L(\ell ^2(X))$
. With this definition, locality of the map
![]() $H_A$
(i.e., the property
$H_A$
(i.e., the property
![]() $\langle \delta _x,H_A\delta _y\rangle =0$
whenever
$\langle \delta _x,H_A\delta _y\rangle =0$
whenever
![]() $\left \lvert x-y \right \rvert>1$
) is equivalent to the statement that
$\left \lvert x-y \right \rvert>1$
) is equivalent to the statement that
![]() $[[H_{A},\mathcal O],\mathcal O']=0$
for any pair of observables
$[[H_{A},\mathcal O],\mathcal O']=0$
for any pair of observables
![]() $\mathcal O,\mathcal O'$
with
$\mathcal O,\mathcal O'$
with
![]() $\operatorname {\mathrm {dist}}(\operatorname {\mathrm {supp}}(\mathcal O),\operatorname {\mathrm {supp}}(\mathcal O'))>1$
.)
$\operatorname {\mathrm {dist}}(\operatorname {\mathrm {supp}}(\mathcal O),\operatorname {\mathrm {supp}}(\mathcal O'))>1$
.)
The XXZ spin chain is defined as above on finite subgraphs
![]() $\Lambda $
of the graph
$\Lambda $
of the graph
![]() $\mathbb Z$
(see Section 2.1). Consider
$\mathbb Z$
(see Section 2.1). Consider
![]() $\Lambda \subset \mathbb Z$
connected, and let
$\Lambda \subset \mathbb Z$
connected, and let
![]() $\left \lvert \Lambda \right \rvert $
be its cardinality. We say we have a particle at the site
$\left \lvert \Lambda \right \rvert $
be its cardinality. We say we have a particle at the site
![]() $i\in \Lambda $
if we have spin down in the copy
$i\in \Lambda $
if we have spin down in the copy
![]() $\mathcal {H}_i$
of
$\mathcal {H}_i$
of
![]() $\mathbb C^2$
. Let
$\mathbb C^2$
. Let
![]() $\mathcal {N}_i$
be the orthogonal projection onto configurations with a particle at the site i, and set
$\mathcal {N}_i$
be the orthogonal projection onto configurations with a particle at the site i, and set
![]() $[i]^\Lambda _p= \left \{ j\in \Lambda , \left \lvert j-i \right \rvert \le p \right \}$
for
$[i]^\Lambda _p= \left \{ j\in \Lambda , \left \lvert j-i \right \rvert \le p \right \}$
for
![]() $p=0,1,\ldots $
. Given
$p=0,1,\ldots $
. Given
![]() $B\subset \Lambda $
, let
$B\subset \Lambda $
, let
![]() $P_+^B$
be the orthogonal projection onto configurations with no particles in B. In the Ising phase,
$P_+^B$
be the orthogonal projection onto configurations with no particles in B. In the Ising phase,
![]() $H^\Lambda $
is a
$H^\Lambda $
is a
![]() $2$
-local, gapped, frustration-free system, and
$2$
-local, gapped, frustration-free system, and
![]() $P_+^\Lambda $
describes the projection onto the ground state of
$P_+^\Lambda $
describes the projection onto the ground state of
![]() $H^\Lambda $
(see Remark 2.3).
$H^\Lambda $
(see Remark 2.3).
We can now informally state our main results. We first prove that the resolvent
![]() $R^\Lambda _z=(H^\Lambda -z)^{-1}$
exhibits quasi-locality in the form (see Lemma 3.1 and Remark 3.2)
$R^\Lambda _z=(H^\Lambda -z)^{-1}$
exhibits quasi-locality in the form (see Lemma 3.1 and Remark 3.2)
 $$ \begin{align}\begin{aligned} \left\lVert \mathcal{N}_i R_z^ \Lambda P_+^{[i]^\Lambda_p} \right\rVert\le C_z \mathrm{e}^{-m_z p}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert \mathcal{N}_i R_z^ \Lambda P_+^{[i]^\Lambda_p} \right\rVert\le C_z \mathrm{e}^{-m_z p}, \end{aligned}\end{align} $$
where
![]() $C_z$
and
$C_z$
and
![]() $m_z$
are constants, independent of
$m_z$
are constants, independent of
![]() $\Lambda $
and of the transverse field, such that
$\Lambda $
and of the transverse field, such that
![]() $C_z <\infty $
and
$C_z <\infty $
and
![]() $m_z>0$
if
$m_z>0$
if
![]() $z\in \mathbb C$
is outside the spectrum of
$z\in \mathbb C$
is outside the spectrum of
![]() $H^\Lambda $
. We also establish the many-body analogue of (1.2):
$H^\Lambda $
. We also establish the many-body analogue of (1.2):
 $$ \begin{align}\begin{aligned} \left\lVert \mathcal{N}_i f(H^ \Lambda) P_+^{[i]^\Lambda_p} \right\rVert\le C_{f,n} \left( 1 +p \right)^{-n}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert \mathcal{N}_i f(H^ \Lambda) P_+^{[i]^\Lambda_p} \right\rVert\le C_{f,n} \left( 1 +p \right)^{-n}, \end{aligned}\end{align} $$
where
![]() $C_{f,n} <\infty $
for all
$C_{f,n} <\infty $
for all
![]() $n\in \mathbb N$
and infinitely differentiable functions f on
$n\in \mathbb N$
and infinitely differentiable functions f on
![]() $\mathbb R$
with compact support. (See Appendix B.)
$\mathbb R$
with compact support. (See Appendix B.)
We next consider the random XXZ spin chain (see Definition 2.2). The relations (1.5)–(1.6) suggest, by analogy with random Schrödinger operators, that localization should be manifested as quasi-locality inside the spectrum of
![]() $H^\Lambda $
. This is indeed what we prove in Theorem 2.4. We introduce increasing energy intervals
$H^\Lambda $
. This is indeed what we prove in Theorem 2.4. We introduce increasing energy intervals
![]() $I_{\le k} $
,
$I_{\le k} $
,
![]() $k=0,1,2,\ldots $
, in (2.14) and prove that quasi-locality of the form given in (1.5) holds for the resolvent for energies in
$k=0,1,2,\ldots $
, in (2.14) and prove that quasi-locality of the form given in (1.5) holds for the resolvent for energies in
![]() $I_{\le k} $
for any fixed
$I_{\le k} $
for any fixed
![]() $ k$
. In particular, given
$ k$
. In particular, given
![]() $s\in (0,\frac 1 3)$
, we prove, in the appropriate (k dependent) parameter region, that
$s\in (0,\frac 1 3)$
, we prove, in the appropriate (k dependent) parameter region, that
 $$ \begin{align}\begin{aligned} \mathbb E\left\{ \left\lVert \mathcal{N}_i R_E^ \Lambda P_+^{[i]^\Lambda_p} \right\rVert^s \right\}\le C_k\left\lvert \Lambda \right\rvert^{\xi_k} \mathrm{e}^{-m_k p} \quad\text{for all}\quad E\in I_{\le k} , \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E\left\{ \left\lVert \mathcal{N}_i R_E^ \Lambda P_+^{[i]^\Lambda_p} \right\rVert^s \right\}\le C_k\left\lvert \Lambda \right\rvert^{\xi_k} \mathrm{e}^{-m_k p} \quad\text{for all}\quad E\in I_{\le k} , \end{aligned}\end{align} $$
where the constants
![]() $C_k<\infty $
,
$C_k<\infty $
,
![]() $ \xi _k>0$
,
$ \xi _k>0$
,
![]() $m_k>0$
do not depend on
$m_k>0$
do not depend on
![]() $\Lambda $
. As a consequence, we derive a quasi-locality estimate for Borel functions of
$\Lambda $
. As a consequence, we derive a quasi-locality estimate for Borel functions of
![]() $H^\Lambda $
(Corollary 2.6):
$H^\Lambda $
(Corollary 2.6):
 $$ \begin{align}\begin{aligned} \mathbb E\left( \sup_f {\left\lVert \mathcal{N}_i f(H^\Lambda)P_+^{[i]^\Lambda_p} \right\rVert} \right)\le C_k\left\lvert \Lambda \right\rvert^{\xi_k} \mathrm{e}^{-m_k p}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E\left( \sup_f {\left\lVert \mathcal{N}_i f(H^\Lambda)P_+^{[i]^\Lambda_p} \right\rVert} \right)\le C_k\left\lvert \Lambda \right\rvert^{\xi_k} \mathrm{e}^{-m_k p}, \end{aligned}\end{align} $$
where the supremum is taken over all Borel functions on
![]() $\mathbb R$
that are equal to zero outside the interval
$\mathbb R$
that are equal to zero outside the interval
![]() $I_{\le k}$
and bounded by one.
$I_{\le k}$
and bounded by one.
While the estimates (1.7) and (1.8) are very natural from the mathematical perspective, it is far from obvious whether they yield any of the MBL-type features proposed by physicists. Nevertheless, in a sequel to this paper [Reference Elgart and Klein17], we derive slow propagation of information, a putative MBL manifestation, from Theorem 2.4 and Corollary 2.6, for any
![]() $k\in \mathbb N$
.
$k\in \mathbb N$
.
In the droplet spectrum, [Reference Elgart, Klein and Stolz19, Theorem 2.1] imply Corollary 2.6 (with
![]() $k=1$
), and a converse can established using [Reference Elgart and Klein17, Remark 3.3]. While [Reference Elgart, Klein and Stolz19] and the follow-up paper [Reference Elgart, Klein and Stolz18] contain several MBL-type properties such as the (dynamical) exponential clustering property, (properly defined) zero-velocity Lieb-Robinson bounds, and slow propagation (non-spreading) of information, they are all derived using [Reference Elgart, Klein and Stolz19, Theorem 2.1] as the starting point. We stress that [Reference Elgart, Klein and Stolz19, Theorem 2.1], by its very nature, can only hold in the droplet regime, so while it provides us with very strong consequences in the
$k=1$
), and a converse can established using [Reference Elgart and Klein17, Remark 3.3]. While [Reference Elgart, Klein and Stolz19] and the follow-up paper [Reference Elgart, Klein and Stolz18] contain several MBL-type properties such as the (dynamical) exponential clustering property, (properly defined) zero-velocity Lieb-Robinson bounds, and slow propagation (non-spreading) of information, they are all derived using [Reference Elgart, Klein and Stolz19, Theorem 2.1] as the starting point. We stress that [Reference Elgart, Klein and Stolz19, Theorem 2.1], by its very nature, can only hold in the droplet regime, so while it provides us with very strong consequences in the
![]() $k=1$
case, we do not expect the methods of [Reference Elgart, Klein and Stolz19, Reference Elgart, Klein and Stolz18] to be of any use in the multi-cluster case – that is, for
$k=1$
case, we do not expect the methods of [Reference Elgart, Klein and Stolz19, Reference Elgart, Klein and Stolz18] to be of any use in the multi-cluster case – that is, for
![]() $k\ge 2$
.
$k\ge 2$
.
Although the methods derived in this work are not universal (which is typical for many-body results), they are sufficiently powerful for investigation of MBL phenomena in this context, as shown in [Reference Elgart and Klein17]. We have to admit, however, that in the physics literature, MBL is usually associated with energies that are not fixed (as we assumed in this work) but are comparable with the system size
![]() $\left \lvert \Lambda \right \rvert $
. We do not expect that our techniques will be sufficient to probe such energies. To be able to do so would require non-perturbative techniques similar to the ones used in the investigations of one dimensional random Schrödinger operators.
$\left \lvert \Lambda \right \rvert $
. We do not expect that our techniques will be sufficient to probe such energies. To be able to do so would require non-perturbative techniques similar to the ones used in the investigations of one dimensional random Schrödinger operators.
The model description and main results (Theorem 2.4 and Corollary 2.6) are presented in Section 2. In Section 3, we outline the main ideas used in the proof of Theorem 2.4, which is completed in Section 4. Corollary 2.6 is proven in Section 5. Appendix A contains some useful identities. Appendix B contains the proof of of the many-body quasi-locality estimate (1.6).
Throughout the paper, we will use generic constants
![]() $C, c,m$
, etc., whose values will be allowed to change from line to line, even in a displayed equation. These constants will not depend on subsets of
$C, c,m$
, etc., whose values will be allowed to change from line to line, even in a displayed equation. These constants will not depend on subsets of
![]() $\mathbb Z$
, but they will, in general, depend on the parameters of the model introduced in Section 2.1 (such as
$\mathbb Z$
, but they will, in general, depend on the parameters of the model introduced in Section 2.1 (such as
![]() $\mu $
, k,
$\mu $
, k,
![]() $\Delta _0$
,
$\Delta _0$
,
![]() $ \lambda _0$
and s). When necessary, we will indicate the dependence of a constant on k explicitly by writing it as
$ \lambda _0$
and s). When necessary, we will indicate the dependence of a constant on k explicitly by writing it as
![]() $C_k, m_k$
, etc. These constants can always be estimated from the arguments, but we will not track the changes to avoid complicating the arguments.
$C_k, m_k$
, etc. These constants can always be estimated from the arguments, but we will not track the changes to avoid complicating the arguments.
2 Model description and main results
2.1 Model description
The random XXZ quantum spin-
![]() $\frac 12$
chain on an finite subset
$\frac 12$
chain on an finite subset
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathbb Z$
is given by a self-adjoint Hamiltonian
$\mathbb Z$
is given by a self-adjoint Hamiltonian
![]() $H^\Lambda $
acting on the finite dimensional Hilbert space
$H^\Lambda $
acting on the finite dimensional Hilbert space
![]() $\mathcal H_\Lambda =\otimes _{i\in \Lambda } \mathcal {H}_i$
, where
$\mathcal H_\Lambda =\otimes _{i\in \Lambda } \mathcal {H}_i$
, where
![]() $\mathcal {H}_i=\mathbb C^2$
for each
$\mathcal {H}_i=\mathbb C^2$
for each
![]() $i\in \Lambda $
. For a vector
$i\in \Lambda $
. For a vector
![]() $\phi \in \mathbb C^2$
, we let
$\phi \in \mathbb C^2$
, we let
![]() $\phi _i$
denote the vector as an element of
$\phi _i$
denote the vector as an element of
![]() $\mathcal {H}_i$
; for an operator (
$\mathcal {H}_i$
; for an operator (
![]() $2\times 2$
matrix) A on
$2\times 2$
matrix) A on
![]() $\mathbb C^2$
, we let
$\mathbb C^2$
, we let
![]() $A_i$
denote the operator acting on
$A_i$
denote the operator acting on
![]() $\mathcal {H}_i$
.
$\mathcal {H}_i$
.
We consider only finite subsets of
![]() $\mathbb Z$
, so by a subset of
$\mathbb Z$
, so by a subset of
![]() $\mathbb Z$
we will always mean a finite subset. If
$\mathbb Z$
we will always mean a finite subset. If
![]() $S\subset T\subset \mathbb Z$
, and
$S\subset T\subset \mathbb Z$
, and
![]() $A_S$
is an operator on
$A_S$
is an operator on
![]() $\mathcal {H}_S$
, we consider
$\mathcal {H}_S$
, we consider
![]() $A_S$
as operator on
$A_S$
as operator on
![]() $\mathcal {H}_T$
by identifying it with
$\mathcal {H}_T$
by identifying it with ![]() , where
, where ![]() denotes the identity operator on
denotes the identity operator on
![]() $\mathcal {H}_R$
. We thus identify
$\mathcal {H}_R$
. We thus identify
![]() $\mathcal {A}_S$
with a subset of
$\mathcal {A}_S$
with a subset of
![]() $\mathcal {A}_T$
, where
$\mathcal {A}_T$
, where
![]() $\mathcal {A}_R$
denotes the algebra of bounded operators on
$\mathcal {A}_R$
denotes the algebra of bounded operators on
![]() $\mathcal {H}_R$
.
$\mathcal {H}_R$
.
We now fix
![]() $\Lambda \subset \mathbb Z$
, and consider
$\Lambda \subset \mathbb Z$
, and consider
![]() $\Lambda $
as a subgraph of
$\Lambda $
as a subgraph of
![]() $\mathbb Z$
. We denote by
$\mathbb Z$
. We denote by
![]() $\operatorname {\mathrm {dist}}_\Lambda $
the graph distance in
$\operatorname {\mathrm {dist}}_\Lambda $
the graph distance in
![]() $\Lambda $
, which can be infinite if
$\Lambda $
, which can be infinite if
![]() $\Lambda $
is not a connected subset of
$\Lambda $
is not a connected subset of
![]() $\mathbb Z$
. We write
$\mathbb Z$
. We write
![]() $K^c=\Lambda \setminus K$
for
$K^c=\Lambda \setminus K$
for
![]() $K\subset \Lambda $
. To define
$K\subset \Lambda $
. To define
![]() $H^\Lambda $
, we introduce some notation and definitons.
$H^\Lambda $
, we introduce some notation and definitons.
-
1. By
 $\sigma ^{x,y,z}$
and
$\sigma ^{x,y,z}$
and
 $\sigma ^\pm =\frac 12( \sigma ^x \pm i \sigma ^y)$
we will denote the standard Pauli matrices and ladder operators, respectively.
$\sigma ^\pm =\frac 12( \sigma ^x \pm i \sigma ^y)$
we will denote the standard Pauli matrices and ladder operators, respectively. -
2. By
 $\uparrow \rangle : = \begin {pmatrix} 1 \\ 0 \end {pmatrix} $
and
$\uparrow \rangle : = \begin {pmatrix} 1 \\ 0 \end {pmatrix} $
and
 $\downarrow \rangle = \begin {pmatrix} 0 \\ 1 \end {pmatrix} $
we will denote the elements of the canonical basis of
$\downarrow \rangle = \begin {pmatrix} 0 \\ 1 \end {pmatrix} $
we will denote the elements of the canonical basis of
 $\mathbb C^2$
, called spin-up and spin-down, respectively. Letting
$\mathbb C^2$
, called spin-up and spin-down, respectively. Letting  , we note that
, we note that
 $\mathcal {N} \uparrow \rangle =0$
and
$\mathcal {N} \uparrow \rangle =0$
and
 $\mathcal {N} \downarrow \rangle =\downarrow \rangle $
, and interpret
$\mathcal {N} \downarrow \rangle =\downarrow \rangle $
, and interpret
 $\downarrow \rangle $
as a particle.
$\downarrow \rangle $
as a particle. -
3.
 $\mathcal {N}_i$
, the matrix
$\mathcal {N}_i$
, the matrix
 $ \mathcal {N}$
acting on
$ \mathcal {N}$
acting on
 $\mathcal {H}_i$
, is the projection onto the spin-down state (also called the local number operator) at site i. Given
$\mathcal {H}_i$
, is the projection onto the spin-down state (also called the local number operator) at site i. Given
 $S\subset \Lambda $
,
$S\subset \Lambda $
,
 $\mathcal {N}_{S} = \sum _{i\in S} \mathcal {N}_i$
is the total (spin-down) number operator in S.
$\mathcal {N}_{S} = \sum _{i\in S} \mathcal {N}_i$
is the total (spin-down) number operator in S. -
4. The total number operator
 $\mathcal {N}_\Lambda $
has eigenvalues
$\mathcal {N}_\Lambda $
has eigenvalues
 $0,1,2,\ldots , \left \lvert \Lambda \right \rvert $
. (
$0,1,2,\ldots , \left \lvert \Lambda \right \rvert $
. (
 $\left \lvert S \right \rvert $
denotes the cardinality of
$\left \lvert S \right \rvert $
denotes the cardinality of
 $S\subset \mathbb Z$
.) We set
$S\subset \mathbb Z$
.) We set
 $\mathcal {H}_\Lambda ^{\left (N\right )}=\operatorname {\mathrm {Ran}}\left ( \chi _N(\mathcal N_\Lambda ) \right )$
, obtaining the Hilbert space decomposition
$\mathcal {H}_\Lambda ^{\left (N\right )}=\operatorname {\mathrm {Ran}}\left ( \chi _N(\mathcal N_\Lambda ) \right )$
, obtaining the Hilbert space decomposition
 $ \mathcal {H}_\Lambda = \bigoplus _{N=0}^{\left \lvert \Lambda \right \rvert } \mathcal {H}_\Lambda ^{\left (N\right )}$
. We will use the notation
$ \mathcal {H}_\Lambda = \bigoplus _{N=0}^{\left \lvert \Lambda \right \rvert } \mathcal {H}_\Lambda ^{\left (N\right )}$
. We will use the notation
 $\chi ^\Lambda _{N}=\chi _{\left \{ N \right \}}(\mathcal N_\Lambda )$
.
$\chi ^\Lambda _{N}=\chi _{\left \{ N \right \}}(\mathcal N_\Lambda )$
. -
5. The canonical (orthonormal) basis
 $\Phi _\Lambda $
for
$\Phi _\Lambda $
for
 $\mathcal {H}_\Lambda $
is constructed as follows: Let
$\mathcal {H}_\Lambda $
is constructed as follows: Let
 $\Omega _\Lambda =\phi _\emptyset =\otimes _{i \in \Lambda }\uparrow \rangle _i$
be the vacuum state. Then (2.1)where
$\Omega _\Lambda =\phi _\emptyset =\otimes _{i \in \Lambda }\uparrow \rangle _i$
be the vacuum state. Then (2.1)where $$ \begin{align}\begin{aligned} & \Phi_\Lambda =\left\{ \phi_A=\left( \prod_{i\in A}\sigma_i^- \right)\Omega_\Lambda:\ A\subset \Lambda \right\} =\bigcup_{N=0}^{\left\lvert \Lambda \right\rvert} \Phi_\Lambda^{\left(N\right)}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} & \Phi_\Lambda =\left\{ \phi_A=\left( \prod_{i\in A}\sigma_i^- \right)\Omega_\Lambda:\ A\subset \Lambda \right\} =\bigcup_{N=0}^{\left\lvert \Lambda \right\rvert} \Phi_\Lambda^{\left(N\right)}, \end{aligned}\end{align} $$
 $\Phi _\Lambda ^{\left (N\right )}= \left \{ \phi _A: A\subset \Lambda , \ \left \lvert A \right \rvert =N \right \}$
. Note that
$\Phi _\Lambda ^{\left (N\right )}= \left \{ \phi _A: A\subset \Lambda , \ \left \lvert A \right \rvert =N \right \}$
. Note that
 $ \Phi _\Lambda ^{\left (0\right )}=\left \{ \Omega _\Lambda \right \}$
.
$ \Phi _\Lambda ^{\left (0\right )}=\left \{ \Omega _\Lambda \right \}$
.
We now define the free XXZ quantum spin-
![]() $\frac 12$
Hamiltonian on
$\frac 12$
Hamiltonian on
![]() $\Lambda \subset \mathbb Z$
by
$\Lambda \subset \mathbb Z$
by
where
and
![]() $\Delta>1$
is the anisotropy parameter, specifying the Ising phase (
$\Delta>1$
is the anisotropy parameter, specifying the Ising phase (
![]() $\Delta =1$
selects the Heisenberg chain and
$\Delta =1$
selects the Heisenberg chain and
![]() $\Delta =\infty $
corresponds to the the Ising chain).
$\Delta =\infty $
corresponds to the the Ising chain).
We will consider the XXZ model in the presence of a transversal field
![]() $\lambda V^\Lambda _\omega $
, given by
$\lambda V^\Lambda _\omega $
, given by
![]() $V^\Lambda _\omega =\sum _{i\in \Lambda } \omega _i \mathcal {N}_i$
, where
$V^\Lambda _\omega =\sum _{i\in \Lambda } \omega _i \mathcal {N}_i$
, where
![]() $\omega _i\ge 0$
, and the parameter
$\omega _i\ge 0$
, and the parameter
![]() $\lambda>0$
is used to modulate the strength of the field. The full Hamiltonian is then
$\lambda>0$
is used to modulate the strength of the field. The full Hamiltonian is then
Remark 2.1.
-
1. The operator
 $\boldsymbol {\Delta }^\Lambda $
can be viewed as the analog of the Laplacian operator on
$\boldsymbol {\Delta }^\Lambda $
can be viewed as the analog of the Laplacian operator on
 $\mathcal {H}_\Lambda $
.
$\mathcal {H}_\Lambda $
. -
2.
 $\mathcal {N}_i$
is diagonalized by the canonical basis for all
$\mathcal {N}_i$
is diagonalized by the canonical basis for all
 $i\in \Lambda $
:
$i\in \Lambda $
:
 $\mathcal {N}_i \phi _A= \phi _A$
if
$\mathcal {N}_i \phi _A= \phi _A$
if
 $i\in A$
and
$i\in A$
and
 $0$
otherwise. It follows that the total number operator
$0$
otherwise. It follows that the total number operator
 $\mathcal {N}_\Lambda $
is also diagonalized by the canonical basis:
$\mathcal {N}_\Lambda $
is also diagonalized by the canonical basis:
 $\mathcal {N}_\Lambda \phi _A= \left \lvert A \right \rvert \phi _A$
.
$\mathcal {N}_\Lambda \phi _A= \left \lvert A \right \rvert \phi _A$
. -
3.
 $\mathcal {W}^\Lambda $
, the number of clusters operator, is diagonalized by the canonical basis:
$\mathcal {W}^\Lambda $
, the number of clusters operator, is diagonalized by the canonical basis:
 $\mathcal {W}^\Lambda \phi _A= W^\Lambda _A \phi _A$
, where
$\mathcal {W}^\Lambda \phi _A= W^\Lambda _A \phi _A$
, where
 $W^\Lambda _A\in [0,\left \lvert A \right \rvert ]\cap \mathbb Z$
is the number of clusters of A in
$W^\Lambda _A\in [0,\left \lvert A \right \rvert ]\cap \mathbb Z$
is the number of clusters of A in
 $\Lambda $
(i.e., the number of connected components of A in
$\Lambda $
(i.e., the number of connected components of A in
 $\Lambda $
(considered as a subgraph of
$\Lambda $
(considered as a subgraph of
 $\mathbb Z$
)).
$\mathbb Z$
)). -
4.
 $V^\Lambda _\omega $
is diagonalized by the canonical basis:
$V^\Lambda _\omega $
is diagonalized by the canonical basis:
 $V^\Lambda _\omega \phi _A= \omega ^{\left (A\right )} \phi _A$
, where
$V^\Lambda _\omega \phi _A= \omega ^{\left (A\right )} \phi _A$
, where
 $\omega ^{\left (A\right )}=\sum _{i\in A} \omega _i$
.
$\omega ^{\left (A\right )}=\sum _{i\in A} \omega _i$
. -
5. The operators
 $\mathcal {N}_\Lambda $
,
$\mathcal {N}_\Lambda $
,
 $\mathcal {W}^\Lambda $
, and
$\mathcal {W}^\Lambda $
, and
 $V^\Lambda _\omega $
commute.
$V^\Lambda _\omega $
commute. -
6. The XXZ Hamiltonian
 $H^\Lambda $
preserves the total particle number, (2.6)
$H^\Lambda $
preserves the total particle number, (2.6) $$ \begin{align} [H^\Lambda,\mathcal{N}_\Lambda]= -\tfrac{1}{2\Delta}[ \boldsymbol{\Delta}^\Lambda,\mathcal{N}_\Lambda] =0. \end{align} $$
$$ \begin{align} [H^\Lambda,\mathcal{N}_\Lambda]= -\tfrac{1}{2\Delta}[ \boldsymbol{\Delta}^\Lambda,\mathcal{N}_\Lambda] =0. \end{align} $$
We will consider the XXZ model in the presence of a random transversal field; that is,
![]() $\omega = \left \{ \omega _i \right \}_{i\in \mathbb Z}$
is a family of random variables. More precisely, we make the following definition.
$\omega = \left \{ \omega _i \right \}_{i\in \mathbb Z}$
is a family of random variables. More precisely, we make the following definition.
Definition 2.2. The random XXZ spin Hamiltonian on
![]() $\Lambda \subset \mathbb Z$
is the operator
$\Lambda \subset \mathbb Z$
is the operator
![]() $H^\Lambda =H^\Lambda _\omega (\Delta ,\lambda )$
given in (2.5), where
$H^\Lambda =H^\Lambda _\omega (\Delta ,\lambda )$
given in (2.5), where
![]() $\Delta>1$
,
$\Delta>1$
,
![]() $\lambda>0$
, and
$\lambda>0$
, and
![]() $\omega = \left \{ \omega _i \right \}_{i\in \mathbb Z}$
is a family of independent identically distributed random variables, whose common probability distribution
$\omega = \left \{ \omega _i \right \}_{i\in \mathbb Z}$
is a family of independent identically distributed random variables, whose common probability distribution
![]() $\mu $
satisfies
$\mu $
satisfies
and is assumed to be absolutely continuous with a bounded density.
From now on,
![]() $H^\Lambda $
always denotes the random XXZ spin Hamiltonian on
$H^\Lambda $
always denotes the random XXZ spin Hamiltonian on
![]() $\Lambda $
. The corresponding resolvent is given by
$\Lambda $
. The corresponding resolvent is given by
![]() $R_E^\Lambda =\left ( H^\Lambda -E \right )^{-1}$
, which is well-defined for almost every energy
$R_E^\Lambda =\left ( H^\Lambda -E \right )^{-1}$
, which is well-defined for almost every energy
![]() $E\in \mathbb R$
. We set
$E\in \mathbb R$
. We set
![]() $\omega _S = \left \{ \omega _i \right \}_{i\in S}$
for
$\omega _S = \left \{ \omega _i \right \}_{i\in S}$
for
![]() $S\subset \mathbb Z$
and denote the corresponding expectation and probability by
$S\subset \mathbb Z$
and denote the corresponding expectation and probability by
![]() $\mathbb E_S$
and
$\mathbb E_S$
and
![]() $\mathbb P_S$
.
$\mathbb P_S$
.
It is convenient to introduce the local interaction terms
which allows us to rewrite
It can be verified that on
![]() $\mathcal {H}_{\left \{ i,i+1 \right \}}=\mathcal {H}_i^2\otimes \mathcal {H}_{i+1}^2$
, we have
$\mathcal {H}_{\left \{ i,i+1 \right \}}=\mathcal {H}_i^2\otimes \mathcal {H}_{i+1}^2$
, we have
which implies that
![]() $\mathcal {W}_\Lambda \pm \tfrac 1 2\boldsymbol {\Delta }_\Lambda \ge 0$
; that is,
$\mathcal {W}_\Lambda \pm \tfrac 1 2\boldsymbol {\Delta }_\Lambda \ge 0$
; that is,
It follows that
We conclude that the spectrum of
![]() $H^\Lambda $
is of the form
$H^\Lambda $
is of the form
The lower bound in (2.12) suggests the introduction of the energy thresholds
![]() $k\left ( 1- \tfrac {1}{\Delta } \right )$
,
$k\left ( 1- \tfrac {1}{\Delta } \right )$
,
![]() $ k=0, 1,2\ldots $
. We define the energy intervals
$ k=0, 1,2\ldots $
. We define the energy intervals
 $$ \begin{align}\begin{aligned} \widehat I_{\le k}&=\left(-\infty, (k+1)\left( 1- \tfrac{1}{\Delta} \right)\right), \quad \widehat I_{ k}= \left[1- \tfrac{1}{\Delta}, (k+1)\left( 1- \tfrac{1}{\Delta} \right)\right),\\ I_{\le k}&= \left(-\infty, (k+\tfrac 3 4)\left( 1- \tfrac{1}{\Delta} \right)\right) ,\quad I_k= \left[1- \tfrac{1}{\Delta}, (k+\tfrac 3 4)\left( 1- \tfrac{1}{\Delta} \right)\right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \widehat I_{\le k}&=\left(-\infty, (k+1)\left( 1- \tfrac{1}{\Delta} \right)\right), \quad \widehat I_{ k}= \left[1- \tfrac{1}{\Delta}, (k+1)\left( 1- \tfrac{1}{\Delta} \right)\right),\\ I_{\le k}&= \left(-\infty, (k+\tfrac 3 4)\left( 1- \tfrac{1}{\Delta} \right)\right) ,\quad I_k= \left[1- \tfrac{1}{\Delta}, (k+\tfrac 3 4)\left( 1- \tfrac{1}{\Delta} \right)\right). \end{aligned}\end{align} $$
We call
![]() $\widehat I_{ k}$
the k-cluster spectrum.
$\widehat I_{ k}$
the k-cluster spectrum.
Given
![]() $\emptyset \ne S\subset \Lambda$
, we define the orthogonal projections
$\emptyset \ne S\subset \Lambda$
, we define the orthogonal projections
![]() $P_\pm ^{S}$
on
$P_\pm ^{S}$
on
![]() $\mathcal {H}_\Lambda $
by
$\mathcal {H}_\Lambda $
by
![]() $P_+^{S}$
is the orthogonal projection onto states with no particles in the set S;
$P_+^{S}$
is the orthogonal projection onto states with no particles in the set S;
![]() $P_-^{S}$
is the orthogonal projection onto states with at least one particle in S. We also set
$P_-^{S}$
is the orthogonal projection onto states with at least one particle in S. We also set
Remark 2.3. In the Ising phase (i.e.,
![]() $\Delta>1$
), we have (2.12) and (2.13) for all
$\Delta>1$
), we have (2.12) and (2.13) for all
![]() $\Lambda \subset \mathbb Z$
. It follows that the XXZ chain Hamiltonian
$\Lambda \subset \mathbb Z$
. It follows that the XXZ chain Hamiltonian
![]() $H^\Lambda $
has ground state
$H^\Lambda $
has ground state
![]() $\Omega _\Lambda $
and the ground state energy is
$\Omega _\Lambda $
and the ground state energy is
![]() $0$
(
$0$
(
![]() $H_\Lambda \Omega _\Lambda $
=0), and, moreover, the ground state energy is gapped. This makes
$H_\Lambda \Omega _\Lambda $
=0), and, moreover, the ground state energy is gapped. This makes
![]() $H^\Lambda $
a
$H^\Lambda $
a
![]() $2$
-local, gapped, frustration-free system. These features, plus the preservation of the total particle number, make the XXZ model especially amenable to analysis. In particular, the number of eigenstates of
$2$
-local, gapped, frustration-free system. These features, plus the preservation of the total particle number, make the XXZ model especially amenable to analysis. In particular, the number of eigenstates of
![]() $H^\Lambda $
in the intervals
$H^\Lambda $
in the intervals
![]() $I_{\le k}$
grows only polynomially in the volume of
$I_{\le k}$
grows only polynomially in the volume of
![]() $\Lambda $
(not exponentially as the dimension of
$\Lambda $
(not exponentially as the dimension of
![]() $\mathcal {H}_\Lambda $
) as shown in Lemma 3.5 below.
$\mathcal {H}_\Lambda $
) as shown in Lemma 3.5 below.
2.2 Main results
Our main result establishes quasi-locality for the resolvent of the random XXZ chain inside the spectrum of
![]() $H^\Lambda $
.
$H^\Lambda $
.
Theorem 2.4 (Quasi-locality for resolvents)
Fix
![]() $\Delta _0>1$
,
$\Delta _0>1$
,
![]() $ \lambda _0>0$
, and let
$ \lambda _0>0$
, and let
![]() $s\in (0,\frac 1 3)$
. Then for all
$s\in (0,\frac 1 3)$
. Then for all
![]() $k\in {\mathbb {N}}^0$
, there exist constants
$k\in {\mathbb {N}}^0$
, there exist constants
![]() $D_k,F_k,\xi _k, \theta _k>0$
(depending on k,
$D_k,F_k,\xi _k, \theta _k>0$
(depending on k,
![]() $\Delta _0$
,
$\Delta _0$
,
![]() $ \lambda _0$
and s) such that, for all
$ \lambda _0$
and s) such that, for all
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
with
$\lambda \ge \lambda _0$
with
![]() $\lambda \Delta ^2\ge D_k$
,
$\lambda \Delta ^2\ge D_k$
,
![]() $\Lambda \subset \mathbb Z$
finite, and energy
$\Lambda \subset \mathbb Z$
finite, and energy
![]() $E\in I_{\le k}$
, we have
$E\in I_{\le k}$
, we have
for
![]() $A\subset B\subset \Lambda $
with A connected in
$A\subset B\subset \Lambda $
with A connected in
![]() $\Lambda $
.
$\Lambda $
.
The theorem is proven in Section 4.
Remark 2.5. If A is not connected in
![]() $\Lambda $
, the theorem still holds with (2.17) replaced by
$\Lambda $
, the theorem still holds with (2.17) replaced by
where
![]() ${\Upsilon }^\Lambda _A$
denotes the number of connected components of A in
${\Upsilon }^\Lambda _A$
denotes the number of connected components of A in
![]() $\Lambda $
. This follows from (2.17) and
$\Lambda $
. This follows from (2.17) and
 $$ \begin{align} P_-^{A}=\sum_{j=1}^{{\Upsilon}^\Lambda_A} P_+^{\bigcup_{i=i}^{j-1} A_i}P_-^{A_j}, \end{align} $$
$$ \begin{align} P_-^{A}=\sum_{j=1}^{{\Upsilon}^\Lambda_A} P_+^{\bigcup_{i=i}^{j-1} A_i}P_-^{A_j}, \end{align} $$
where
![]() $A_j$
,
$A_j$
,
![]() $j=1,2,\ldots , {\Upsilon }^\Lambda _A$
, are the connected components of A in
$j=1,2,\ldots , {\Upsilon }^\Lambda _A$
, are the connected components of A in
![]() $\Lambda $
.
$\Lambda $
.
As a consequence of Theorem 2.4, we prove the following quasi-locality estimate for Borel functions of
![]() $H^\Lambda $
. By
$H^\Lambda $
. By
![]() $B(I_{\le k})$
we denote the collection of Borel functions on
$B(I_{\le k})$
we denote the collection of Borel functions on
![]() $\mathbb R$
that are equal to zero outside the interval
$\mathbb R$
that are equal to zero outside the interval
![]() $I_{\le k}$
.
$I_{\le k}$
.
Corollary 2.6 (Quasi-locality for Borel functions)
Assume the hypotheses and conclusions of Theorem 2.4, Then for all
![]() $k\in {\mathbb {N}}^0$
, there exist constants
$k\in {\mathbb {N}}^0$
, there exist constants
![]() $\widetilde F_k,\widetilde \xi _k, \widetilde \theta _k>0$
(depending on k,
$\widetilde F_k,\widetilde \xi _k, \widetilde \theta _k>0$
(depending on k,
![]() $\Delta _0$
,
$\Delta _0$
,
![]() $ \lambda _0$
and s) such that, for all
$ \lambda _0$
and s) such that, for all
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
with
$\lambda \ge \lambda _0$
with
![]() $\lambda \Delta ^2\ge D_k$
, and
$\lambda \Delta ^2\ge D_k$
, and
![]() $\Lambda \subset \mathbb Z$
finite, we have
$\Lambda \subset \mathbb Z$
finite, we have
 $$ \begin{align}\begin{aligned} \mathbb E_{\Lambda}\left( \sup_{\substack{f\in B(I_{\le k}):\\\|f\|_\infty\le1}}\left\lVert P_-^{A}f(H^\Lambda) P_+^{B} \right\rVert \right)\le \widetilde F_k\left\lvert \Lambda \right\rvert^{\widetilde \xi_k} \mathrm{e}^{-\widetilde \theta_k\operatorname{\mathrm{dist}}_\Lambda(A,B^c)} , \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E_{\Lambda}\left( \sup_{\substack{f\in B(I_{\le k}):\\\|f\|_\infty\le1}}\left\lVert P_-^{A}f(H^\Lambda) P_+^{B} \right\rVert \right)\le \widetilde F_k\left\lvert \Lambda \right\rvert^{\widetilde \xi_k} \mathrm{e}^{-\widetilde \theta_k\operatorname{\mathrm{dist}}_\Lambda(A,B^c)} , \end{aligned}\end{align} $$
for all
![]() $A\subset B\subset \Lambda $
, A connected in
$A\subset B\subset \Lambda $
, A connected in
![]() $\Lambda $
.
$\Lambda $
.
The proof of the Corollary is given in Section 5.
3 Key ingredients for the proofs
In this section, we collect a number of definitions, statements and lemmas that will facilitate the proof of Theorem 2.4.
![]() $\Lambda $
will always denote a finite subset of
$\Lambda $
will always denote a finite subset of
![]() $\mathbb Z$
, and
$\mathbb Z$
, and
![]() $A\subset \Lambda $
will always denote a nonempty subset connected in
$A\subset \Lambda $
will always denote a nonempty subset connected in
![]() $\Lambda $
. (
$\Lambda $
. (
![]() $B\subset \Lambda $
,
$B\subset \Lambda $
,
![]() $S\subset \Lambda $
, etc., may not be connected in
$S\subset \Lambda $
, etc., may not be connected in
![]() $\Lambda $
.)
$\Lambda $
.)
3.1 Some definitions
-
○ Given
 $ M\subset \Lambda $
and
$ M\subset \Lambda $
and
 $q\in \mathbb Z$
, we define enlarged (for
$q\in \mathbb Z$
, we define enlarged (for
 $q\ge 0$
) and trimmed (for
$q\ge 0$
) and trimmed (for
 $q<0$
) set
$q<0$
) set
 $[M]^\Lambda _q $
by (3.1)Note that
$[M]^\Lambda _q $
by (3.1)Note that $$ \begin{align}\begin{aligned} {[M]^\Lambda_q } &:=\begin{cases}\left\{ x\in\Lambda: \operatorname{\mathrm{dist}}_\Lambda\left( x,M \right)\le q \right\} &\;\text{if}\; q\in {\mathbb{N}}^0=\left\{ 0 \right\} \cup \mathbb N \\ \left\{ x\in\Lambda:\operatorname{\mathrm{dist}}_\Lambda\left( x, M^c \right)\ge 1-q \right\}= M\setminus [M^c]^\Lambda_{-q}&\;\text{if}\; q\in-\mathbb N\\ \left\{ x\in \Lambda: \operatorname{\mathrm{dist}}_\Lambda\left( x,M \right)<\infty \right\}= \bigcup_{p\in {\mathbb{N}}^0} [M]^\Lambda_p & \;\text{if}\;q=\infty \end{cases}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {[M]^\Lambda_q } &:=\begin{cases}\left\{ x\in\Lambda: \operatorname{\mathrm{dist}}_\Lambda\left( x,M \right)\le q \right\} &\;\text{if}\; q\in {\mathbb{N}}^0=\left\{ 0 \right\} \cup \mathbb N \\ \left\{ x\in\Lambda:\operatorname{\mathrm{dist}}_\Lambda\left( x, M^c \right)\ge 1-q \right\}= M\setminus [M^c]^\Lambda_{-q}&\;\text{if}\; q\in-\mathbb N\\ \left\{ x\in \Lambda: \operatorname{\mathrm{dist}}_\Lambda\left( x,M \right)<\infty \right\}= \bigcup_{p\in {\mathbb{N}}^0} [M]^\Lambda_p & \;\text{if}\;q=\infty \end{cases}. \end{aligned}\end{align} $$
 $ [M]^\Lambda _{-\left \lvert M \right \rvert }=\emptyset $
. Moreover,
$ [M]^\Lambda _{-\left \lvert M \right \rvert }=\emptyset $
. Moreover,
 $[M]^\Lambda _\infty = [M]^\Lambda _{\left \lvert \Lambda \right \rvert -1} $
is the connected component of
$[M]^\Lambda _\infty = [M]^\Lambda _{\left \lvert \Lambda \right \rvert -1} $
is the connected component of
 $\Lambda $
containing M, and we have (3.2)We define
$\Lambda $
containing M, and we have (3.2)We define $$ \begin{align}[H^\Lambda, P_\pm^{[M]^\Lambda_\infty}]=0.\end{align} $$
$$ \begin{align}[H^\Lambda, P_\pm^{[M]^\Lambda_\infty}]=0.\end{align} $$
 $\partial _{ex}^\Lambda M$
(the external boundary of M in
$\partial _{ex}^\Lambda M$
(the external boundary of M in
 $\Lambda $
),
$\Lambda $
),
 $\partial _{in}^\Lambda M$
(the inner boundary of M in
$\partial _{in}^\Lambda M$
(the inner boundary of M in
 $\Lambda $
), and
$\Lambda $
), and
 $ \partial ^\Lambda M$
(the boundary of
$ \partial ^\Lambda M$
(the boundary of
 $M $
in
$M $
in
 $\Lambda $
), by (3.3)It follows that
$\Lambda $
), by (3.3)It follows that $$ \begin{align}\begin{aligned} \partial_{ex}^\Lambda M&:=\left\{ x\in\Lambda:\ \operatorname{\mathrm{dist}}_\Lambda\left( x,M \right)=1 \right\}= [M]^\Lambda_1\setminus M,\\ \partial_{in}^\Lambda M&:=\left\{ x\in\Lambda:\ \operatorname{\mathrm{dist}}_\Lambda \left( x, M^c \right)=1 \right\}=M\setminus [M]^\Lambda_{-1},\\ \partial^\Lambda M &:= \partial_{in}^\Lambda M \cup \partial_{ex}^\Lambda M. \end{aligned}\end{align} $$
(3.4)and we have
$$ \begin{align}\begin{aligned} \partial_{ex}^\Lambda M&:=\left\{ x\in\Lambda:\ \operatorname{\mathrm{dist}}_\Lambda\left( x,M \right)=1 \right\}= [M]^\Lambda_1\setminus M,\\ \partial_{in}^\Lambda M&:=\left\{ x\in\Lambda:\ \operatorname{\mathrm{dist}}_\Lambda \left( x, M^c \right)=1 \right\}=M\setminus [M]^\Lambda_{-1},\\ \partial^\Lambda M &:= \partial_{in}^\Lambda M \cup \partial_{ex}^\Lambda M. \end{aligned}\end{align} $$
(3.4)and we have $$ \begin{align}\begin{aligned} ]M[^\Lambda_q:= [M]^\Lambda_{q+1}\setminus [M]^\Lambda_{q}&=\begin{cases} {\partial^\Lambda_{ex}{[M]^\Lambda_{q}}}, & q\in {\mathbb{N}}^0\\ {\partial^\Lambda_{in }{[M]^\Lambda_{q+1}}} & q\in-\mathbb N \end{cases}, \end{aligned}\end{align} $$
(3.5)If
$$ \begin{align}\begin{aligned} ]M[^\Lambda_q:= [M]^\Lambda_{q+1}\setminus [M]^\Lambda_{q}&=\begin{cases} {\partial^\Lambda_{ex}{[M]^\Lambda_{q}}}, & q\in {\mathbb{N}}^0\\ {\partial^\Lambda_{in }{[M]^\Lambda_{q+1}}} & q\in-\mathbb N \end{cases}, \end{aligned}\end{align} $$
(3.5)If $$ \begin{align}\begin{aligned} ]M[^\Lambda_p= ] M^c[^\Lambda_{-p-1} \quad\text{for}\quad p\in\mathbb Z. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} ]M[^\Lambda_p= ] M^c[^\Lambda_{-p-1} \quad\text{for}\quad p\in\mathbb Z. \end{aligned}\end{align} $$
 $M=\left \{ j \right \}$
, we write
$M=\left \{ j \right \}$
, we write
 ${[j]^\Lambda _q }={[\left \{ j \right \}]^\Lambda _q }$
.
${[j]^\Lambda _q }={[\left \{ j \right \}]^\Lambda _q }$
.
-
○ Given
 $A\subset B \subset \Lambda $
, we let
$A\subset B \subset \Lambda $
, we let
 $\rho ^\Lambda (A,B)$
be the largest
$\rho ^\Lambda (A,B)$
be the largest
 $q\in {\mathbb {N}}^0 \cup \left \{ \infty \right \}$
such that
$q\in {\mathbb {N}}^0 \cup \left \{ \infty \right \}$
such that
 $ [A]^\Lambda _q \subset B$
; that is, (3.6)It will be more convenient to use
$ [A]^\Lambda _q \subset B$
; that is, (3.6)It will be more convenient to use $$ \begin{align}\begin{aligned} \rho^\Lambda (A,B)= \sup \left\{ q\in {\mathbb{N}}^0: [A]^\Lambda_q \subset B \right\} =\operatorname{\mathrm{dist}}_\Lambda (A, B^c)-1. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \rho^\Lambda (A,B)= \sup \left\{ q\in {\mathbb{N}}^0: [A]^\Lambda_q \subset B \right\} =\operatorname{\mathrm{dist}}_\Lambda (A, B^c)-1. \end{aligned}\end{align} $$
 $ \rho ^\Lambda (A,B)$
instead of
$ \rho ^\Lambda (A,B)$
instead of
 $\operatorname {\mathrm {dist}}_\Lambda (A, B^c)$
in the proofs.Note that (3.7)
$\operatorname {\mathrm {dist}}_\Lambda (A, B^c)$
in the proofs.Note that (3.7) $$ \begin{align}\begin{aligned} \rho^\Lambda (A,B)=\infty \iff \operatorname{\mathrm{dist}}_\Lambda (A, B^c)=\infty \iff [A]^\Lambda_\infty \subset B. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \rho^\Lambda (A,B)=\infty \iff \operatorname{\mathrm{dist}}_\Lambda (A, B^c)=\infty \iff [A]^\Lambda_\infty \subset B. \end{aligned}\end{align} $$
-
○ It follows from (3.2) and (3.7) that
(3.8)so it suffices to prove Theorem 2.4 for $$ \begin{align}\begin{aligned} P_-^A R_{E}^{\Lambda} P_+^{B}=0 \quad\text{if}\quad A\subset B\subset \Lambda \quad\text{and}\quad\rho^\Lambda(A,B)=\infty, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_-^A R_{E}^{\Lambda} P_+^{B}=0 \quad\text{if}\quad A\subset B\subset \Lambda \quad\text{and}\quad\rho^\Lambda(A,B)=\infty, \end{aligned}\end{align} $$
 $\rho ^\Lambda (A,B)<\infty $
. Moreover, since
$\rho ^\Lambda (A,B)<\infty $
. Moreover, since
 $A \subset B$
, we have
$A \subset B$
, we have
 $[A]^\Lambda _{\rho ^\Lambda (A,B)}\subset B$
, and hence, (3.9)so without loss of generality, it suffices to prove (2.17) for
$[A]^\Lambda _{\rho ^\Lambda (A,B)}\subset B$
, and hence, (3.9)so without loss of generality, it suffices to prove (2.17) for $$ \begin{align}\begin{aligned} \left\lVert P_-^{A}R_E^\Lambda P_+^{B} \right\rVert\le \left\lVert P_-^{A}R_E^\Lambda P_+^{[A]^\Lambda_{\rho^\Lambda(A,B)}} \right\rVert, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert P_-^{A}R_E^\Lambda P_+^{B} \right\rVert\le \left\lVert P_-^{A}R_E^\Lambda P_+^{[A]^\Lambda_{\rho^\Lambda(A,B)}} \right\rVert, \end{aligned}\end{align} $$
 $B=[A]^\Lambda _{\rho }$
with
$B=[A]^\Lambda _{\rho }$
with
 $\rho \in {\mathbb {N}}^0$
.
$\rho \in {\mathbb {N}}^0$
.
-
○ Given
 $K\subset \Lambda $
, we consider the operator
$K\subset \Lambda $
, we consider the operator  acting on
acting on
 $\mathcal {H}_\Lambda $
. We also consider the operators on
$\mathcal {H}_\Lambda $
. We also consider the operators on
 $\mathcal {H}_\Lambda $
given by (3.10)
$\mathcal {H}_\Lambda $
given by (3.10) $$ \begin{align}\begin{aligned} H^{K,K^c}= H^{K}+H^{K^c}, \quad R^{K,K^c}_E=\left( H^{K,K^c}-E \right)^{-1}, \quad \Gamma^K=H^\Lambda-H^{K,K^c}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} H^{K,K^c}= H^{K}+H^{K^c}, \quad R^{K,K^c}_E=\left( H^{K,K^c}-E \right)^{-1}, \quad \Gamma^K=H^\Lambda-H^{K,K^c}. \end{aligned}\end{align} $$
3.2 Quasi-locality for resolvents
The following lemma and remark yields (deterministic) quasi-locality for the resolvent of the XXZ chain outside the spectrum of
![]() $H^\Lambda $
.
$H^\Lambda $
.
Lemma 3.1. Let
![]() ${\Theta }\subset {\Lambda }$
, and consider the Hilbert space
${\Theta }\subset {\Lambda }$
, and consider the Hilbert space
![]() $\mathcal {H}_{\Lambda }$
. Let the operator
$\mathcal {H}_{\Lambda }$
. Let the operator
![]() $T\in \mathcal A_{\Lambda }$
be of the form
$T\in \mathcal A_{\Lambda }$
be of the form
and let
![]() $\mathcal {X}\in \mathcal {A}_{\Lambda }$
be a projection such that
$\mathcal {X}\in \mathcal {A}_{\Lambda }$
be a projection such that
![]() $[ \mathcal {X},T]=0$
and
$[ \mathcal {X},T]=0$
and
![]() $[\mathcal {X}, P_\pm ^K]=0 $
for all
$[\mathcal {X}, P_\pm ^K]=0 $
for all
![]() $K\subset {\Theta }$
.
$K\subset {\Theta }$
.
Suppose
-
1. For all
 $K \subset {\Theta } $
, we have
$K \subset {\Theta } $
, we have
 $[P_-^{K},T]P_+^{[K]_1^{\Theta }}=0$
.
$[P_-^{K},T]P_+^{[K]_1^{\Theta }}=0$
. -
2. For all
 $K \subset {\Theta } $
, with K connected in
$K \subset {\Theta } $
, with K connected in
 $\Theta $
, we have
$\Theta $
, we have
 $\left \lVert [P_-^{K},T] \right \rVert \le \gamma $
.
$\left \lVert [P_-^{K},T] \right \rVert \le \gamma $
. -
3.
 $T_{\mathcal {X}}$
, the restriction of the operator T to
$T_{\mathcal {X}}$
, the restriction of the operator T to
 $\operatorname {\mathrm {Ran}} \mathcal {X}$
, is invertible with
$\operatorname {\mathrm {Ran}} \mathcal {X}$
, is invertible with
 $ \left \lVert T_{\mathcal {X}}^{-1} \right \rVert _{\operatorname {\mathrm {Ran}} \mathcal {X}} \le \eta ^{-1}$
, where
$ \left \lVert T_{\mathcal {X}}^{-1} \right \rVert _{\operatorname {\mathrm {Ran}} \mathcal {X}} \le \eta ^{-1}$
, where
 $\eta>0$
.
$\eta>0$
.
Then for all
![]() $A\subset B\subset {\Theta }$
, with A connected in
$A\subset B\subset {\Theta }$
, with A connected in
![]() ${\Theta }$
, we have
${\Theta }$
, we have
Proof. We consider first the case ![]() . Let
. Let
![]() $A\subset B\subset {\Theta }$
, with A connected in
$A\subset B\subset {\Theta }$
, with A connected in
![]() ${\Theta }$
. Let
${\Theta }$
. Let
![]() $1\le t \le \rho ^{\Theta } (A,B)$
, so
$1\le t \le \rho ^{\Theta } (A,B)$
, so
![]() $[A]_{t}^\Theta \subset B$
. We have
$[A]_{t}^\Theta \subset B$
. We have
using condition (i) of the Lemma. Proceeding recursively, we get
 $$ \begin{align}\begin{aligned} P_-^{ A}\,T^{-1}\,P_+^{B}= \left( \prod_{p=0}^{t-1}{T^{-1}[T,P_-^{ [A]_p^\Theta}]} \right) P_-^{ [A]^\Theta_{t}}T^{-1}\,P_+^{B}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_-^{ A}\,T^{-1}\,P_+^{B}= \left( \prod_{p=0}^{t-1}{T^{-1}[T,P_-^{ [A]_p^\Theta}]} \right) P_-^{ [A]^\Theta_{t}}T^{-1}\,P_+^{B}. \end{aligned}\end{align} $$
Since A is connected in
![]() $\Theta $
,
$\Theta $
,
![]() $[ A]_{r}^{\Theta }$
,
$[ A]_{r}^{\Theta }$
,
![]() $r=1,2,\ldots ,t$
, are also connected in
$r=1,2,\ldots ,t$
, are also connected in
![]() $\Theta $
. Using assumptions (ii) and (iii), we get
$\Theta $
. Using assumptions (ii) and (iii), we get
Since (3.15) holds for all
![]() $1\le t \le \rho ^{\Theta } (A,B)$
, we get
$1\le t \le \rho ^{\Theta } (A,B)$
, we get
If condition (iii) holds with a projection
![]() $\mathcal {X}\in \mathcal {A}_{\Lambda }$
such that
$\mathcal {X}\in \mathcal {A}_{\Lambda }$
such that
![]() $[ \mathcal {X},T]=0$
and
$[ \mathcal {X},T]=0$
and
![]() $[\mathcal {X}, P_\pm ^K]=0 $
for all
$[\mathcal {X}, P_\pm ^K]=0 $
for all
![]() $K\subset {\Theta }$
, then
$K\subset {\Theta }$
, then
![]() $\widetilde T= T\mathcal {X} + \eta (1-\mathcal {X})$
satisfies conditions (i), (ii), and condition (iii) with
$\widetilde T= T\mathcal {X} + \eta (1-\mathcal {X})$
satisfies conditions (i), (ii), and condition (iii) with ![]() , and the estimate (3.16) for
, and the estimate (3.16) for
![]() $\widetilde T$
implies (3.12).
$\widetilde T$
implies (3.12).
Remark 3.2. Lemma 3.1 yields quasi-locality for the resolvent of the operator
![]() $H^\Lambda $
. The operator
$H^\Lambda $
. The operator
![]() $H^\Lambda -z$
satisfies the hypotheses of Lemma 3.1 for
$H^\Lambda -z$
satisfies the hypotheses of Lemma 3.1 for
![]() $z\notin \sigma (H^\Lambda )$
, with
$z\notin \sigma (H^\Lambda )$
, with
![]() $\Theta =\Lambda $
,
$\Theta =\Lambda $
,
![]() $\gamma = \frac 1 {\Delta }$
(use (A.6)),
$\gamma = \frac 1 {\Delta }$
(use (A.6)), ![]() , and
, and
![]() $\eta = \operatorname {\mathrm {dist}} (z,\sigma (H^\Lambda ))$
. It follows that, with
$\eta = \operatorname {\mathrm {dist}} (z,\sigma (H^\Lambda ))$
. It follows that, with
![]() $R_z^\Lambda = (H^\Lambda -z)^{-1}$
, for all
$R_z^\Lambda = (H^\Lambda -z)^{-1}$
, for all
![]() $A\subset B\subset \Lambda $
, we have
$A\subset B\subset \Lambda $
, we have
From now on, we fix
![]() $\Delta _0>5$
,
$\Delta _0>5$
,
![]() $ \lambda _0>0$
, and assume
$ \lambda _0>0$
, and assume
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
. The constants will depend on
$\lambda \ge \lambda _0$
. The constants will depend on
![]() $\Delta _0$
and
$\Delta _0$
and
![]() $\lambda _0$
.
$\lambda _0$
.
Given
![]() $m \in {\mathbb {N}}^0$
, we set
$m \in {\mathbb {N}}^0$
, we set
![]() $Q_m^\Lambda =\chi _{\left \{ m \right \}}\left ( \mathcal {W}^\Lambda \right )$
, the orthogonal projection onto configurations with exactly m clusters, and let
$Q_m^\Lambda =\chi _{\left \{ m \right \}}\left ( \mathcal {W}^\Lambda \right )$
, the orthogonal projection onto configurations with exactly m clusters, and let
![]() $Q_B^\Lambda =\chi _{B}\left ( \mathcal {W}^\Lambda \right )=\sum _{m\in B} Q_m^\Lambda $
for
$Q_B^\Lambda =\chi _{B}\left ( \mathcal {W}^\Lambda \right )=\sum _{m\in B} Q_m^\Lambda $
for
![]() $ B\subset {\mathbb {N}}^0$
. Note that
$ B\subset {\mathbb {N}}^0$
. Note that
![]() $Q_0^\Lambda = P_+^\Lambda $
and
$Q_0^\Lambda = P_+^\Lambda $
and
![]() $Q_{\mathbb {N}}^\Lambda = \chi _{\mathbb N}({\mathcal {N}}^\Lambda )$
. For
$Q_{\mathbb {N}}^\Lambda = \chi _{\mathbb N}({\mathcal {N}}^\Lambda )$
. For
![]() $k\in \mathbb N$
, we set
$k\in \mathbb N$
, we set
 $$ \begin{align}\begin{aligned} Q_{\le k}^\Lambda =Q_{\left\{ 1,2,\ldots,k \right\}}^\Lambda =\sum_{ m=1}^k Q_m^\Lambda \quad\text{and}\quad \widehat Q_{\le k}^\Lambda =Q_{\le k}^\Lambda + \tfrac {k+1} k Q_0^\Lambda. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} Q_{\le k}^\Lambda =Q_{\left\{ 1,2,\ldots,k \right\}}^\Lambda =\sum_{ m=1}^k Q_m^\Lambda \quad\text{and}\quad \widehat Q_{\le k}^\Lambda =Q_{\le k}^\Lambda + \tfrac {k+1} k Q_0^\Lambda. \end{aligned}\end{align} $$
We also set
 $$ \begin{align}\begin{aligned} \widehat H_0^{ \Lambda}&=H^{\Lambda}+\left( 1- \tfrac{1}{\Delta} \right) Q_0^\Lambda,\\ \widehat H_k^{ \Lambda}&=H^{\Lambda}+{k}\left( 1- \tfrac{1}{\Delta} \right) \widehat Q_{\le k}^{\Lambda} \quad\text{for}\quad k\in \mathbb N. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \widehat H_0^{ \Lambda}&=H^{\Lambda}+\left( 1- \tfrac{1}{\Delta} \right) Q_0^\Lambda,\\ \widehat H_k^{ \Lambda}&=H^{\Lambda}+{k}\left( 1- \tfrac{1}{\Delta} \right) \widehat Q_{\le k}^{\Lambda} \quad\text{for}\quad k\in \mathbb N. \end{aligned}\end{align} $$
We use the notation
It follows from (2.12) and (2.14) that for
![]() $k\in {\mathbb {N}}^0$
, we have
$k\in {\mathbb {N}}^0$
, we have
For
![]() $k\in {\mathbb {N}}^0$
and
$k\in {\mathbb {N}}^0$
and
![]() $E\in I_{\le k}$
, the operator
$E\in I_{\le k}$
, the operator
![]() $T= \widehat H_k^{ \Lambda }-E$
satisfies the assumptions of Lemma 3.1 with
$T= \widehat H_k^{ \Lambda }-E$
satisfies the assumptions of Lemma 3.1 with
![]() $\Theta =\Lambda $
,
$\Theta =\Lambda $
,
![]() $\gamma = \frac 1 {\Delta }$
,
$\gamma = \frac 1 {\Delta }$
, ![]() and
and
![]() $\eta = \frac 1{4}\left ( 1- \frac {1}{\Delta } \right ) $
(see (3.21)). In this case,
$\eta = \frac 1{4}\left ( 1- \frac {1}{\Delta } \right ) $
(see (3.21)). In this case,
![]() $ m =\ln \frac {\Delta -1}{4}$
, and hence, for
$ m =\ln \frac {\Delta -1}{4}$
, and hence, for
![]() $A\subset B\subset {\Lambda }$
, (3.12) yields
$A\subset B\subset {\Lambda }$
, (3.12) yields
To have decay in (3.22), we need
![]() $ \frac {\Delta -1} {4}>1$
; that is,
$ \frac {\Delta -1} {4}>1$
; that is,
![]() $\Delta>5 $
. In the proof of Theorem 2.4, we will fix
$\Delta>5 $
. In the proof of Theorem 2.4, we will fix
![]() $\Delta _0> 5 $
and
$\Delta _0> 5 $
and
![]() $\lambda _0>0$
and require
$\lambda _0>0$
and require
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
. In this case, we have
$\lambda \ge \lambda _0$
. In this case, we have
![]() $\tfrac 4 {1- \frac {1}{\Delta }} \le \tfrac 4 {1-\frac 1 {\Delta _0}} $
and
$\tfrac 4 {1- \frac {1}{\Delta }} \le \tfrac 4 {1-\frac 1 {\Delta _0}} $
and
![]() $ \ln \tfrac {\Delta -1} 4\ge \ln \tfrac {\Delta _0-1} 4$
, so we have
$ \ln \tfrac {\Delta -1} 4\ge \ln \tfrac {\Delta _0-1} 4$
, so we have
It follows from (3.2), which also holds for the operator
![]() $\widehat H_k^{ \Lambda }$
, that
$\widehat H_k^{ \Lambda }$
, that
Remark 3.3. We will prove Theorem 2.4 with
![]() $\Delta _0> 5$
to simplify our analysis. The proof can be extended to arbitrary
$\Delta _0> 5$
to simplify our analysis. The proof can be extended to arbitrary
![]() $\Delta _0> 1$
with minor modifications. Specifically, for
$\Delta _0> 1$
with minor modifications. Specifically, for
![]() $1<\Delta _0 \le 5$
, we need to improve the decay rate in (3.22), which is derived from the lower bound in (3.21). To do so, we would replace
$1<\Delta _0 \le 5$
, we need to improve the decay rate in (3.22), which is derived from the lower bound in (3.21). To do so, we would replace
![]() $\widehat H_k^{ \Lambda }$
in the proof by
$\widehat H_k^{ \Lambda }$
in the proof by
![]() $\widehat H_{k+r}^{ \Lambda }$
, where
$\widehat H_{k+r}^{ \Lambda }$
, where
![]() $r\in \mathbb N$
, so (3.21) yields
$r\in \mathbb N$
, so (3.21) yields
![]() $\widehat H_{k+r}^{ \Lambda }-E \ge (r+ \frac 1 4)\left ( 1- \tfrac {1}{\Delta } \right )$
for
$\widehat H_{k+r}^{ \Lambda }-E \ge (r+ \frac 1 4)\left ( 1- \tfrac {1}{\Delta } \right )$
for
![]() $E\in I_{\le k}$
, leading to
$E\in I_{\le k}$
, leading to
![]() $m_0= \ln \left ( (r + \frac 1 4) \left ( \Delta _0-1 \right ) \right )>0 $
for an appropriate choice of r.
$m_0= \ln \left ( (r + \frac 1 4) \left ( \Delta _0-1 \right ) \right )>0 $
for an appropriate choice of r.
3.3 An a priori estimate
The first step toward the proof of Theorem 2.4 is to understand why the expression on the left-hand side of (2.17) is actually finite. A useful technical device for this purpose is the following bound, where
![]() $\left \lVert T \right \rVert _{HS}$
denotes the Hilbert-Schmidt norm of the operator T.
$\left \lVert T \right \rVert _{HS}$
denotes the Hilbert-Schmidt norm of the operator T.
Lemma 3.4 (A priori estimate)
Let
![]() $i,j\in \Lambda $
(
$i,j\in \Lambda $
(
![]() $i=j$
is allowed), and let
$i=j$
is allowed), and let
![]() $T_{1},T_2$
be a pair of Hilbert-Schmidt operators on
$T_{1},T_2$
be a pair of Hilbert-Schmidt operators on
![]() $\mathcal {H}_\Lambda $
that are
$\mathcal {H}_\Lambda $
that are
![]() $\omega _{\left \{ i,j \right \}}$
-independent. Then we have
$\omega _{\left \{ i,j \right \}}$
-independent. Then we have
The lemma follows from [Reference Aizenman, Elgart, Naboko, Schenker and Stolz5, Proposition 3.2], used with
![]() $U_1=\mathcal {N}_j$
,
$U_1=\mathcal {N}_j$
,
![]() $U_2=\mathcal {N}_k$
there, and the layer-cake representation for a non-negative random variable
$U_2=\mathcal {N}_k$
there, and the layer-cake representation for a non-negative random variable
![]() $X_\omega $
:
$X_\omega $
:
![]() $\mathbb E(X_\omega ^s)=\int _0^\infty \mathbb P(X_\omega>t^{1/s})\, dt$
for
$\mathbb E(X_\omega ^s)=\int _0^\infty \mathbb P(X_\omega>t^{1/s})\, dt$
for
![]() $s\in (0,1)$
.
$s\in (0,1)$
.
The Hilbert-Schmidt operators for Lemma 3.4 are provided by the following result.
Lemma 3.5. Let
![]() $k\in \mathbb N$
. Then
$k\in \mathbb N$
. Then
Proof. For
![]() $m\ge 1$
and
$m\ge 1$
and
![]() $N \ge 1$
, we have the rough estimate
$N \ge 1$
, we have the rough estimate
Thus,
 $$ \begin{align} \operatorname{\mathrm{tr}} \chi^\Lambda_N Q_{\le k}^{\Lambda}\le \sum_{m=1}^k \left\lvert \Lambda \right\rvert^m N^{m-1}= \tfrac 1 N \tfrac {(\left\lvert \Lambda \right\rvert N)^{k+1}-(\left\lvert \Lambda \right\rvert N)}{(\left\lvert \Lambda \right\rvert N)-1}\le k \left\lvert \Lambda \right\rvert^k N^{k-1}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{tr}} \chi^\Lambda_N Q_{\le k}^{\Lambda}\le \sum_{m=1}^k \left\lvert \Lambda \right\rvert^m N^{m-1}= \tfrac 1 N \tfrac {(\left\lvert \Lambda \right\rvert N)^{k+1}-(\left\lvert \Lambda \right\rvert N)}{(\left\lvert \Lambda \right\rvert N)-1}\le k \left\lvert \Lambda \right\rvert^k N^{k-1}. \end{align} $$
It follows that
 $$ \begin{align} \operatorname{\mathrm{tr}} Q_{\le k}^{\Lambda}\le k \left\lvert \Lambda \right\rvert^k \sum_{N=1}^{\left\lvert \Lambda \right\rvert} N^{k-1}\le k\left\lvert \Lambda \right\rvert^{2k}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{tr}} Q_{\le k}^{\Lambda}\le k \left\lvert \Lambda \right\rvert^k \sum_{N=1}^{\left\lvert \Lambda \right\rvert} N^{k-1}\le k\left\lvert \Lambda \right\rvert^{2k}. \end{align} $$
To prove (3.27), let
![]() $\widehat {H}^\Lambda _k$
be as in (3.19), and note that (3.21) implies
$\widehat {H}^\Lambda _k$
be as in (3.19), and note that (3.21) implies
![]() $\operatorname {\mathrm {tr}} \chi _{\widehat I_{\le k}}(\widehat {H}^\Lambda _k)=0$
. Since the spectral shift is bounded by the rank of the perturbation, it follows from (3.19) that
$\operatorname {\mathrm {tr}} \chi _{\widehat I_{\le k}}(\widehat {H}^\Lambda _k)=0$
. Since the spectral shift is bounded by the rank of the perturbation, it follows from (3.19) that
Lemmas 3.4 and 3.5 yield the a priori estimate
More generally, we have
Those a priori estimates are only useful if we can ‘dress’ the resolvent with factors of
![]() $Q^\Lambda _{\le k}$
on both sides. To be able to do so, we will decorate
$Q^\Lambda _{\le k}$
on both sides. To be able to do so, we will decorate
![]() $R^{\Lambda }_{E}$
with resolvents of positive operators that satisfy the quasi-locality property.
$R^{\Lambda }_{E}$
with resolvents of positive operators that satisfy the quasi-locality property.
3.4 Dressing resolvents with Hilbert-Schmidt operators
For
![]() $k=1,2,\ldots $
, and
$k=1,2,\ldots $
, and
![]() $E\in I_{\le k}$
, we use the resolvent identity
$E\in I_{\le k}$
, we use the resolvent identity
Using it twice, we get
We use the notation
![]() $(p)_+=\max \left ( p,0 \right )$
for
$(p)_+=\max \left ( p,0 \right )$
for
![]() $p\in \mathbb R$
.
$p\in \mathbb R$
.
Lemma 3.6. Let
![]() $\mathcal {X}$
denote a spectral projection of
$\mathcal {X}$
denote a spectral projection of
![]() $\mathcal {N}_\Lambda $
(say,
$\mathcal {N}_\Lambda $
(say, ![]() or
or
![]() $\mathcal {X}= \chi _N^\Lambda $
). Let
$\mathcal {X}= \chi _N^\Lambda $
). Let
![]() $A\subset B\subset \Lambda $
, and
$A\subset B\subset \Lambda $
, and
![]() $1\le t=\rho ^\Lambda \left ( A, B \right )<\infty $
. Let
$1\le t=\rho ^\Lambda \left ( A, B \right )<\infty $
. Let
![]() $E\in I_{\le k}$
, and let
$E\in I_{\le k}$
, and let
![]() $m_0$
be as in (3.23).
$m_0$
be as in (3.23).
-
1. We have the following estimate on operator norms:
(3.36) $$ \begin{align}\begin{aligned} &{\left\lVert \mathcal{X} P_-^AR_E^\Lambda P_+^B \right\rVert}\le C_k\Big(\left\lvert \Lambda \right\rvert\mathrm{e}^{- m_0 t} + \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(p)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\left\lVert \mathcal{X} F^\Lambda_{p,q}(E,A) \right\rVert\Big),\\ &\text{where}\quad F^\Lambda_{p,q}(E,A)=Q^\Lambda_{\le k}P_+^{[A]^\Lambda_{p}}P_-^{]A[^\Lambda_{p}} R^{\Lambda}_{E} P_+^{[A]^\Lambda_q}P_-^{]A[^\Lambda_{q}}Q^\Lambda_{\le k} \quad\text{for}\quad p,q\in \mathbb Z. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &{\left\lVert \mathcal{X} P_-^AR_E^\Lambda P_+^B \right\rVert}\le C_k\Big(\left\lvert \Lambda \right\rvert\mathrm{e}^{- m_0 t} + \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(p)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\left\lVert \mathcal{X} F^\Lambda_{p,q}(E,A) \right\rVert\Big),\\ &\text{where}\quad F^\Lambda_{p,q}(E,A)=Q^\Lambda_{\le k}P_+^{[A]^\Lambda_{p}}P_-^{]A[^\Lambda_{p}} R^{\Lambda}_{E} P_+^{[A]^\Lambda_q}P_-^{]A[^\Lambda_{q}}Q^\Lambda_{\le k} \quad\text{for}\quad p,q\in \mathbb Z. \end{aligned}\end{align} $$
-
2. We have the following estimates on Hilbert-Schmidt norms:
(3.37)Moreover, for $$ \begin{align}\begin{aligned} \left\lVert \mathcal{X} P_-^AR_E^\Lambda P_+^B Q^\Lambda_{\le k} \right\rVert_{HS} \le C_k\Big(\left\lvert \Lambda \right\rvert^{k}\mathrm{e}^{-m_0 t}+ \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \mathrm{e}^{-m_0\left( q \right)_+} {\left\lVert \mathcal{X} Q^\Lambda_{\le k}P_-^{]A[_{q}}R^{\Lambda}_{E}P_+^BQ^\Lambda_{\le k} \right\rVert}_{HS}\Big). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert \mathcal{X} P_-^AR_E^\Lambda P_+^B Q^\Lambda_{\le k} \right\rVert_{HS} \le C_k\Big(\left\lvert \Lambda \right\rvert^{k}\mathrm{e}^{-m_0 t}+ \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \mathrm{e}^{-m_0\left( q \right)_+} {\left\lVert \mathcal{X} Q^\Lambda_{\le k}P_-^{]A[_{q}}R^{\Lambda}_{E}P_+^BQ^\Lambda_{\le k} \right\rVert}_{HS}\Big). \end{aligned}\end{align} $$
 $s\in (0,1)$
, we have (3.38)
$s\in (0,1)$
, we have (3.38) $$ \begin{align}\begin{aligned} \mathbb E\left( \left\lVert \mathcal{X} P_-^AR_E^\Lambda P_+^B Q^\Lambda_{\le k} \right\rVert_{HS} ^s \right) \le C_{k,s} \left\lvert \Lambda \right\rvert^{2sk+3}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E\left( \left\lVert \mathcal{X} P_-^AR_E^\Lambda P_+^B Q^\Lambda_{\le k} \right\rVert_{HS} ^s \right) \le C_{k,s} \left\lvert \Lambda \right\rvert^{2sk+3}. \end{aligned}\end{align} $$
Proof. Let
![]() $A\subset B\subset \Lambda $
, A connected in
$A\subset B\subset \Lambda $
, A connected in
![]() $\Lambda $
. Since
$\Lambda $
. Since
![]() $\mathcal {X}$
commutes with all the relevants operators, we will just do the proof for
$\mathcal {X}$
commutes with all the relevants operators, we will just do the proof for
![]() $\mathcal {X}=I$
.
$\mathcal {X}=I$
.
Using (3.35), (3.18) and (3.23), we get
Using (3.24), (A.7) and the fact that
![]() $Q^\Lambda _{\le k}$
commutes with
$Q^\Lambda _{\le k}$
commutes with
![]() $P_\pm $
operators, we get
$P_\pm $
operators, we get
 $$ \begin{align}\begin{aligned} &{\left\lVert P_-^A\widehat R^{\Lambda}_{k,E} Q^\Lambda_{\le k+1}\widehat R^{\Lambda}_{k,E} P_+^B \right\rVert}\le \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} {\left\lVert D_q \right\rVert}{\left\lVert E_q \right\rVert}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &{\left\lVert P_-^A\widehat R^{\Lambda}_{k,E} Q^\Lambda_{\le k+1}\widehat R^{\Lambda}_{k,E} P_+^B \right\rVert}\le \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} {\left\lVert D_q \right\rVert}{\left\lVert E_q \right\rVert}, \end{aligned}\end{align} $$
where
Using (3.21), (3.23) and
![]() $ ]A[_{q} \subset B$
for
$ ]A[_{q} \subset B$
for
![]() $q+1\le t$
, we get
$q+1\le t$
, we get
It follows that
 $$ \begin{align}\begin{aligned} {\left\lVert P_-^A\widehat R^{\Lambda}_{k,E}Q^\Lambda_{\le k+1}\widehat R^{\Lambda}_{k,E} P_+^B \right\rVert}\le C_0^2 \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(q)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\le C_0^\prime \left\lvert \Lambda \right\rvert\mathrm{e}^{- m_0 t}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\left\lVert P_-^A\widehat R^{\Lambda}_{k,E}Q^\Lambda_{\le k+1}\widehat R^{\Lambda}_{k,E} P_+^B \right\rVert}\le C_0^2 \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(q)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\le C_0^\prime \left\lvert \Lambda \right\rvert\mathrm{e}^{- m_0 t}. \end{aligned}\end{align} $$
This leaves us with the estimation of the last term in (3.39). To this end, we use (3.24), (A.7) and (3.42) to obtain
 $$ \begin{align}\begin{aligned} &{\left\lVert P_-^A\widehat R^{\Lambda}_{k,E}Q^\Lambda_{\le k+1} R^{\Lambda}_{E}Q^\Lambda_{\le k+1}\widehat R^{\Lambda}_{k,E} P_+^B \right\rVert}\le \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} {\left\lVert D_p \right\rVert}\left\lVert F_{p,q} \right\rVert{\left\lVert E_q \right\rVert}\\ & \qquad \qquad\le C _0^2 \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(p)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\left\lVert F_{p,q} \right\rVert, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &{\left\lVert P_-^A\widehat R^{\Lambda}_{k,E}Q^\Lambda_{\le k+1} R^{\Lambda}_{E}Q^\Lambda_{\le k+1}\widehat R^{\Lambda}_{k,E} P_+^B \right\rVert}\le \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} {\left\lVert D_p \right\rVert}\left\lVert F_{p,q} \right\rVert{\left\lVert E_q \right\rVert}\\ & \qquad \qquad\le C _0^2 \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(p)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\left\lVert F_{p,q} \right\rVert, \end{aligned}\end{align} $$
where
![]() $F_{p,q}=F_{p,q}^\Lambda (E,A)$
is as in (3.36) for
$F_{p,q}=F_{p,q}^\Lambda (E,A)$
is as in (3.36) for
![]() $p,q \in \mathbb Z$
.
$p,q \in \mathbb Z$
.
Combining (3.39), (3.43) and (3.44), we get (3.36).
To prove (3.37), we proceed as in (3.39) using (3.34), exploit
![]() $\left \lVert T_1T_2 \right \rVert _{HS}\le \left \lVert T_1 \right \rVert \left \lVert T_2 \right \rVert _{HS}$
, and use (3.26), obtaining
$\left \lVert T_1T_2 \right \rVert _{HS}\le \left \lVert T_1 \right \rVert \left \lVert T_2 \right \rVert _{HS}$
, and use (3.26), obtaining
We then use (3.24), (A.7) and (3.42) to get
 $$ \begin{align}\begin{aligned} {\left\lVert P_-^A\widehat R^{\Lambda}_{k,E}Q^\Lambda_{\le k} R^{\Lambda}_{E} P_+^B Q^\Lambda_{\le k} \right\rVert}_{HS} &\le \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} {\left\lVert D_q \right\rVert} {\left\lVert Q^\Lambda_{\le k}P_-^{]A[_{q}}R^{\Lambda}_{E}P_+^BQ^\Lambda_{\le k} \right\rVert}_{HS} \\ &\le \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} C_0 \mathrm{e}^{-m_0\left( q \right)_+} {\left\lVert Q^\Lambda_{\le k}P_-^{]A[_{q}}R^{\Lambda}_{E}P_+^BQ^\Lambda_{\le k} \right\rVert}_{HS}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\left\lVert P_-^A\widehat R^{\Lambda}_{k,E}Q^\Lambda_{\le k} R^{\Lambda}_{E} P_+^B Q^\Lambda_{\le k} \right\rVert}_{HS} &\le \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} {\left\lVert D_q \right\rVert} {\left\lVert Q^\Lambda_{\le k}P_-^{]A[_{q}}R^{\Lambda}_{E}P_+^BQ^\Lambda_{\le k} \right\rVert}_{HS} \\ &\le \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} C_0 \mathrm{e}^{-m_0\left( q \right)_+} {\left\lVert Q^\Lambda_{\le k}P_-^{]A[_{q}}R^{\Lambda}_{E}P_+^BQ^\Lambda_{\le k} \right\rVert}_{HS}. \end{aligned}\end{align} $$
Given
![]() $s\in (0,1)$
, it follows from (3.37) and (3.33) that
$s\in (0,1)$
, it follows from (3.37) and (3.33) that
3.5 Large deviation estimate
Using a large deviation argument, we get the following refinement of (3.33). Recall we may assume
![]() $\rho ^\Lambda (A,B)<\infty $
in view of (3.8).
$\rho ^\Lambda (A,B)<\infty $
in view of (3.8).
Lemma 3.7. Let
![]() $k\in \mathbb N$
. Let
$k\in \mathbb N$
. Let
![]() $A\subset B\subset \Lambda $
, with
$A\subset B\subset \Lambda $
, with
![]() $\rho ^\Lambda (A,B)<\infty $
. Given
$\rho ^\Lambda (A,B)<\infty $
. Given
![]() $s\in (0,\frac 12)$
, there exist constants
$s\in (0,\frac 12)$
, there exist constants
![]() $C_{k,s} ,c_\mu>0$
such that for all
$C_{k,s} ,c_\mu>0$
such that for all
![]() $E \in I_{\le k}$
, we have
$E \in I_{\le k}$
, we have
In particular,
where
![]() $m_ {0,\mu }>0$
.
$m_ {0,\mu }>0$
.
Proof. Recall
![]() $\mathcal {H}_\Lambda ^{\left (N\right )}= \operatorname {\mathrm {Ran}} \chi ^\Lambda _N$
, and let
$\mathcal {H}_\Lambda ^{\left (N\right )}= \operatorname {\mathrm {Ran}} \chi ^\Lambda _N$
, and let
![]() $\mathcal {H}_\Lambda ^{\left (N,k\right )}= \operatorname {\mathrm {Ran}} \chi ^\Lambda _N Q^\Lambda _{\le k}$
. Recall also that the restriction of
$\mathcal {H}_\Lambda ^{\left (N,k\right )}= \operatorname {\mathrm {Ran}} \chi ^\Lambda _N Q^\Lambda _{\le k}$
. Recall also that the restriction of
![]() $V_\omega ^\Lambda $
to
$V_\omega ^\Lambda $
to
![]() $\mathcal {H}_\Lambda ^{\left (N\right )}$
is diagonalized by the canonical basis
$\mathcal {H}_\Lambda ^{\left (N\right )}$
is diagonalized by the canonical basis
![]() $ \Phi _\Lambda ^{\left (N\right )}$
as in Remark 2.1(iii).
$ \Phi _\Lambda ^{\left (N\right )}$
as in Remark 2.1(iii).
Let us first assume that N is such that
![]() $N \lambda \bar {\mu }\ge 2k\left ( 1- \tfrac {1}{\Delta } \right )$
, where
$N \lambda \bar {\mu }\ge 2k\left ( 1- \tfrac {1}{\Delta } \right )$
, where
![]() $ \bar {\mu }$
denotes the mean of the probability distribution
$ \bar {\mu }$
denotes the mean of the probability distribution
![]() $\mu $
(see Definition 2.2). The standard large deviation estimate (Cramer’s Theorem) gives
$\mu $
(see Definition 2.2). The standard large deviation estimate (Cramer’s Theorem) gives
where
![]() $c_\mu $
is a constant depending only on the probability distribution
$c_\mu $
is a constant depending only on the probability distribution
![]() $\mu $
. This implies that there exists
$\mu $
. This implies that there exists
![]() $C_k>0$
such that
$C_k>0$
such that
It follows that for the event
we have
where we also used Lemma 3.5. On the complementary event
![]() $\left ( \mathcal B_k^N \right )^c$
, we have
$\left ( \mathcal B_k^N \right )^c$
, we have
If (3.54) holds, we conclude that
 $$ \begin{align}\begin{aligned} H^{\Lambda,N}&\ge \left( 1- \tfrac{1}{\Delta} \right) \mathcal{W}^\Lambda + \lambda V_\omega= \left( Q_{\le k}^{\Lambda,N} + Q_{\ge k+1 }^{\Lambda,N} \right)\left( \left( 1- \tfrac{1}{\Delta} \right) \mathcal{W}^\Lambda + \lambda V_\omega \right)\\ & \ge \left( 1- \tfrac{1}{\Delta} \right) Q_{\ge k+1 }^{\Lambda,N} \mathcal{W}^\Lambda +Q_{\le k}^{\Lambda,N} \left( \left( 1- \tfrac{1}{\Delta} \right) \mathcal{W}^\Lambda + \lambda V_\omega \right)\ge (k+1) \left( 1- \tfrac{1}{\Delta} \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} H^{\Lambda,N}&\ge \left( 1- \tfrac{1}{\Delta} \right) \mathcal{W}^\Lambda + \lambda V_\omega= \left( Q_{\le k}^{\Lambda,N} + Q_{\ge k+1 }^{\Lambda,N} \right)\left( \left( 1- \tfrac{1}{\Delta} \right) \mathcal{W}^\Lambda + \lambda V_\omega \right)\\ & \ge \left( 1- \tfrac{1}{\Delta} \right) Q_{\ge k+1 }^{\Lambda,N} \mathcal{W}^\Lambda +Q_{\le k}^{\Lambda,N} \left( \left( 1- \tfrac{1}{\Delta} \right) \mathcal{W}^\Lambda + \lambda V_\omega \right)\ge (k+1) \left( 1- \tfrac{1}{\Delta} \right). \end{aligned}\end{align} $$
We deduce that for
![]() $\omega \in \left ( \mathcal B_k^N \right )^c$
and
$\omega \in \left ( \mathcal B_k^N \right )^c$
and
![]() $E \in I_{\le k}$
, we have
$E \in I_{\le k}$
, we have
Proceeding as in the derivation of (3.23), it follows from Lemma 3.1 and Remark 3.2 that for
![]() $\omega \in \left ( \mathcal B_k^N \right )^c$
, we have, for
$\omega \in \left ( \mathcal B_k^N \right )^c$
, we have, for
![]() $A\subset B\subset {\Lambda }$
with A connected in
$A\subset B\subset {\Lambda }$
with A connected in
![]() ${\Lambda }$
, that
${\Lambda }$
, that
Given
![]() $E \in I_{\le k}$
, and letting
$E \in I_{\le k}$
, and letting
![]() $T =\chi _N Q_{\le k}^\Lambda P_-^{A} R_E^\Lambda P_+^{B}Q_{\le k}^\Lambda $
, we obtain
$T =\chi _N Q_{\le k}^\Lambda P_-^{A} R_E^\Lambda P_+^{B}Q_{\le k}^\Lambda $
, we obtain
 $$ \begin{align}\begin{aligned} \mathbb E\left( \left\lVert T \right\rVert_{HS}^s \right) & \le \mathbb E\left( \chi_{\mathcal B_k^N}\left\lVert T \right\rVert_{HS}^s \right)+\mathbb E\left( \chi_{\left( \mathcal B_k^N \right)^c}\left\lVert T \right\rVert_{HS}^s \right)\\ &\le \left( \mathbb P \left( \mathcal B_k^N \right) \right)^{\frac 1 2} \left( \mathbb E\left( \left\lVert T \right\rVert_{HS}^{2s} \right) \right)^{\frac 12}+ C_0 \mathrm{e}^{-m_0 \rho^\Lambda(A,B)}\left\lVert \chi_N Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \\ &\le C_{k,s} \left\lvert \Lambda \right\rvert^{2(sk+1)} \left( \mathrm{e}^{- {\frac 1 2} c_\mu N}+ \mathrm{e}^{-m_0 \rho^\Lambda (A,B)} \right), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E\left( \left\lVert T \right\rVert_{HS}^s \right) & \le \mathbb E\left( \chi_{\mathcal B_k^N}\left\lVert T \right\rVert_{HS}^s \right)+\mathbb E\left( \chi_{\left( \mathcal B_k^N \right)^c}\left\lVert T \right\rVert_{HS}^s \right)\\ &\le \left( \mathbb P \left( \mathcal B_k^N \right) \right)^{\frac 1 2} \left( \mathbb E\left( \left\lVert T \right\rVert_{HS}^{2s} \right) \right)^{\frac 12}+ C_0 \mathrm{e}^{-m_0 \rho^\Lambda(A,B)}\left\lVert \chi_N Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \\ &\le C_{k,s} \left\lvert \Lambda \right\rvert^{2(sk+1)} \left( \mathrm{e}^{- {\frac 1 2} c_\mu N}+ \mathrm{e}^{-m_0 \rho^\Lambda (A,B)} \right), \end{aligned}\end{align} $$
where we used (3.53), Lemma 3.5 and (3.33) with
![]() $2s$
instead of s. This estimate is (3.48), up to a redefinition of the constant
$2s$
instead of s. This estimate is (3.48), up to a redefinition of the constant
![]() $c_\mu $
.
$c_\mu $
.
3.6 Decoupling of resolvents
We now illustrate the basic idea that allows us to obtain the exponential decay of the left-hand side in (2.17), analogous to the decoupling argument in the single particle localization literature. For this purpose, we will consider a more convenient object than the one in (2.17). To do so, let
![]() $A\subset M\subset B\subset \Lambda $
, and consider
$A\subset M\subset B\subset \Lambda $
, and consider
![]() $P_+^{M^c} P_-^AR_E^\Lambda P_+^{B}.$
Let
$P_+^{M^c} P_-^AR_E^\Lambda P_+^{B}.$
Let
![]() $K\subset \mathbb Z$
be such that
$K\subset \mathbb Z$
be such that
![]() $M\subset [K]_{-1}\subset K\subset [K]_1\subset B$
. The resolvent identity yields (recall (3.10))
$M\subset [K]_{-1}\subset K\subset [K]_1\subset B$
. The resolvent identity yields (recall (3.10))
 $$ \begin{align}\begin{aligned} P_+^{M^c} P_-^{A}R_E^\Lambda P_+^{B}& = - P_+^{M^c} P_-^{A}R^{K,K^c}_E \Gamma^K R_E^\Lambda P_+^{B} =- P_+^{M^c} P_-^{A}R^{K,K^c}_EP_+^{K^c} \Gamma^K R_E^\Lambda P_+^{B}\\ & =- P_+^{M^c} P_-^{A}R_E^{K}P_+^{K^c}\Gamma^K R^\Lambda_E P_+^{B}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_+^{M^c} P_-^{A}R_E^\Lambda P_+^{B}& = - P_+^{M^c} P_-^{A}R^{K,K^c}_E \Gamma^K R_E^\Lambda P_+^{B} =- P_+^{M^c} P_-^{A}R^{K,K^c}_EP_+^{K^c} \Gamma^K R_E^\Lambda P_+^{B}\\ & =- P_+^{M^c} P_-^{A}R_E^{K}P_+^{K^c}\Gamma^K R^\Lambda_E P_+^{B}, \end{aligned}\end{align} $$
where we used that
![]() $P_-^{A} R^{K,K^c}_E P_+^{K}=0$
by (3.2) since
$P_-^{A} R^{K,K^c}_E P_+^{K}=0$
by (3.2) since
![]() $[A]_\infty ^K \subset K$
,
$[A]_\infty ^K \subset K$
,
![]() $P_+^{M^c}R^{K,K^c}_E=P_+^{M^c} R^{K,K^c}_EP_+^{K^c}$
by (3.2) since
$P_+^{M^c}R^{K,K^c}_E=P_+^{M^c} R^{K,K^c}_EP_+^{K^c}$
by (3.2) since
![]() $K^c\subset M^c$
, and
$K^c\subset M^c$
, and
![]() $R^{K,K^c}_EP_+^{K^c}=R^{K}_EP_+^{K^c}$
. Using the specific structure of the XXZ Hamiltonian – that is, (A.3)–(A.5) – we have
$R^{K,K^c}_EP_+^{K^c}=R^{K}_EP_+^{K^c}$
. Using the specific structure of the XXZ Hamiltonian – that is, (A.3)–(A.5) – we have
![]() $P_+^{K^c}\Gamma ^K= P_+^{K^c}P_-^{ \partial ^\Lambda K} \Gamma ^K P_-^{ \partial ^\Lambda K}= P_+^{K^c}P_-^{\partial _{in}^\Lambda K}\Gamma ^K P_-^{\partial _{ex}^\Lambda K} $
, so it follows from (3.59) that
$P_+^{K^c}\Gamma ^K= P_+^{K^c}P_-^{ \partial ^\Lambda K} \Gamma ^K P_-^{ \partial ^\Lambda K}= P_+^{K^c}P_-^{\partial _{in}^\Lambda K}\Gamma ^K P_-^{\partial _{ex}^\Lambda K} $
, so it follows from (3.59) that
We now use the resolvent identity for the operator
![]() $H^{ [K]_1^\Lambda ,([K]^\Lambda _1)^c}$
and (A.3), obtaining
$H^{ [K]_1^\Lambda ,([K]^\Lambda _1)^c}$
and (A.3), obtaining
Combining (3.60)–(3.61), we obtain
 $$ \begin{align}\begin{aligned} &P_+^{M^c} P_-^{A}R_E^\Lambda P_+^{B}= \\& (P_-^{A}{P_+^{M^c\cap K}R_E^{K}P_-^{\partial_{in}^\Lambda K}})P_+^{K^c}\Gamma^K \left( P_-^{\partial_{ex}^\Lambda K}R_E^\Lambda P_-^{\partial_{ex}^\Lambda K} \right) \Gamma^{[K]_1} P_+^{[K]_1}{\left( P_-^{\partial_{ex}^\Lambda [K]_1} R_E^{[K]_1^c} P_+^{B\cap [K]_1^c} \right)}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &P_+^{M^c} P_-^{A}R_E^\Lambda P_+^{B}= \\& (P_-^{A}{P_+^{M^c\cap K}R_E^{K}P_-^{\partial_{in}^\Lambda K}})P_+^{K^c}\Gamma^K \left( P_-^{\partial_{ex}^\Lambda K}R_E^\Lambda P_-^{\partial_{ex}^\Lambda K} \right) \Gamma^{[K]_1} P_+^{[K]_1}{\left( P_-^{\partial_{ex}^\Lambda [K]_1} R_E^{[K]_1^c} P_+^{B\cap [K]_1^c} \right)}. \end{aligned}\end{align} $$
This is the basic decoupling formula, in a sense that the expressions in the first and last parentheses on the last line are statistically independent and of the same form as the left-hand side of (2.17). So, if we can perform the averaging over the random variables at sites
![]() $r\in \partial _{ex}^\Lambda K$
to get rid of the middle resolvent, we will effectively decouple the system into pieces supported by the disjoint subsets K and
$r\in \partial _{ex}^\Lambda K$
to get rid of the middle resolvent, we will effectively decouple the system into pieces supported by the disjoint subsets K and
![]() $[K]_1^c$
. (Note that these pieces do not depend on the random variables at sites
$[K]_1^c$
. (Note that these pieces do not depend on the random variables at sites
![]() $r\in \partial _{ex}^\Lambda K$
.) This decoupling will be performed using the a priori estimate (3.33), after we dress the corresponding resolvents with Hilbert-Schmidt operators on both sides as in Lemma 3.6. In broad strokes, we then will extract the (initial) exponential decay from the expression in the first parenthesis in (3.62) using reduction to lower energies and obtain the full exponential decay using a sub-harmonicity argument. We flesh out details of this process as we proceed with the proof.
$r\in \partial _{ex}^\Lambda K$
.) This decoupling will be performed using the a priori estimate (3.33), after we dress the corresponding resolvents with Hilbert-Schmidt operators on both sides as in Lemma 3.6. In broad strokes, we then will extract the (initial) exponential decay from the expression in the first parenthesis in (3.62) using reduction to lower energies and obtain the full exponential decay using a sub-harmonicity argument. We flesh out details of this process as we proceed with the proof.
3.7 Clusters classification
In preparation to initiate the FMM, we first inspect the structure of states in
![]() $\operatorname {\mathrm {Ran}} Q^\Lambda _{\le k}$
. Since
$\operatorname {\mathrm {Ran}} Q^\Lambda _{\le k}$
. Since
![]() $Q^\Lambda _{\le k}$
is a multiplication operator in the canonical basis
$Q^\Lambda _{\le k}$
is a multiplication operator in the canonical basis
![]() $\left \{ \Phi _\Lambda ^{\left (N\right )} \right \}_{N=0}^{\left \lvert \Lambda \right \rvert }$
introduced in (2.1), we just need to consider the elements
$\left \{ \Phi _\Lambda ^{\left (N\right )} \right \}_{N=0}^{\left \lvert \Lambda \right \rvert }$
introduced in (2.1), we just need to consider the elements
![]() $\varphi _M$
of this basis with M that belong to a set
$\varphi _M$
of this basis with M that belong to a set
![]() $\mathcal S_{N,k}^\Lambda :=\left \{ M\subset \Lambda :\ \left \lvert M \right \rvert =N,\ 1\le W^\Lambda _M\le k \right \}$
,
$\mathcal S_{N,k}^\Lambda :=\left \{ M\subset \Lambda :\ \left \lvert M \right \rvert =N,\ 1\le W^\Lambda _M\le k \right \}$
,
![]() $N\ge 1$
. (Recall that
$N\ge 1$
. (Recall that
![]() $W^\Lambda _M$
is the number of clusters of the configuration M – that is, the number of connected components of M in the graph
$W^\Lambda _M$
is the number of clusters of the configuration M – that is, the number of connected components of M in the graph
![]() $\Lambda $
.) Denoting by
$\Lambda $
.) Denoting by
![]() $ \pi _{\varphi }$
the orthogonal projection onto
$ \pi _{\varphi }$
the orthogonal projection onto
![]() $\mathbb C\varphi $
, given
$\mathbb C\varphi $
, given
![]() $M\in \mathcal S^{\Lambda }_{N,k}$
, we abuse the notation and write
$M\in \mathcal S^{\Lambda }_{N,k}$
, we abuse the notation and write
![]() $\pi _M$
for
$\pi _M$
for
![]() $\pi _{\varphi _M}$
, so
$\pi _{\varphi _M}$
, so
![]() $\pi _{M} = \left ( \prod _{j\in M}\mathcal {N}_j \right ) P_+^{M^c}$
, and note that
$\pi _{M} = \left ( \prod _{j\in M}\mathcal {N}_j \right ) P_+^{M^c}$
, and note that
![]() $ \chi _N^\Lambda Q^\Lambda _{\le k}= \sum _{M\in \mathcal S_{N,k}^\Lambda } \pi _M. $
$ \chi _N^\Lambda Q^\Lambda _{\le k}= \sum _{M\in \mathcal S_{N,k}^\Lambda } \pi _M. $
Given
![]() $ A\subset \Lambda $
, we set
$ A\subset \Lambda $
, we set
![]() $\mathcal S^{\Lambda ,A}_{N,k}=\left \{ M\in \mathcal S^{\Lambda }_{N,k}: \ M\cap A\ne \emptyset \right \}$
, and note that
$\mathcal S^{\Lambda ,A}_{N,k}=\left \{ M\in \mathcal S^{\Lambda }_{N,k}: \ M\cap A\ne \emptyset \right \}$
, and note that
![]() $ \chi _N^\Lambda Q^\Lambda _{\le k} P_-^A= \sum _{M\in \mathcal S_{N,k}^{\Lambda ,A}} \pi _M. $
We set
$ \chi _N^\Lambda Q^\Lambda _{\le k} P_-^A= \sum _{M\in \mathcal S_{N,k}^{\Lambda ,A}} \pi _M. $
We set
Note that
![]() $\operatorname {\mathrm {diam}}_\Lambda (M)=N-1$
for
$\operatorname {\mathrm {diam}}_\Lambda (M)=N-1$
for
![]() $k=1$
and
$k=1$
and
![]() $\operatorname {\mathrm {diam}}_\Lambda (M)\ge N\ge 2$
for
$\operatorname {\mathrm {diam}}_\Lambda (M)\ge N\ge 2$
for
![]() $k\ge 2$
.
$k\ge 2$
.
If
![]() $ 8kN < \rho ^\Lambda (A,B)$
, we will use the following lemma.
$ 8kN < \rho ^\Lambda (A,B)$
, we will use the following lemma.
Lemma 3.8. Fix
![]() $k\ge 2$
. Let
$k\ge 2$
. Let
![]() $A\subset B\subset \Lambda $
be such that
$A\subset B\subset \Lambda $
be such that
![]() $8kN < \rho ^\Lambda (A,B)<\infty $
, and let
$8kN < \rho ^\Lambda (A,B)<\infty $
, and let
![]() $M\in \mathcal S^{\Lambda ,A}_{N,k}$
.
$M\in \mathcal S^{\Lambda ,A}_{N,k}$
.
-
1. Suppose
 $\gamma _A(M) < 4kN$
. Then setting
$\gamma _A(M) < 4kN$
. Then setting
 $Z=[A]^\Lambda _{6kN}$
, we have (3.64)
$Z=[A]^\Lambda _{6kN}$
, we have (3.64) $$ \begin{align}\begin{aligned} A \cup M\subset [Z]_{-1}\subset Z \subset [Z]_1\subset B; \;\rho^\Lambda(A\cup M,Z)\ge 2kN; \quad \rho^\Lambda(Z,B)\ge 2kN. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} A \cup M\subset [Z]_{-1}\subset Z \subset [Z]_1\subset B; \;\rho^\Lambda(A\cup M,Z)\ge 2kN; \quad \rho^\Lambda(Z,B)\ge 2kN. \end{aligned}\end{align} $$
-
2. Suppose
 $ \rho ^\Lambda (A,B)\le 2 \gamma _A(M)$
. Let
$ \rho ^\Lambda (A,B)\le 2 \gamma _A(M)$
. Let
 $ d_\rho := \left \lfloor \tfrac { \rho ^\Lambda (A,B)}{6k}\right \rfloor $
. Then there exists
$ d_\rho := \left \lfloor \tfrac { \rho ^\Lambda (A,B)}{6k}\right \rfloor $
. Then there exists
 $a \in \left \{ 1,2,\ldots , 3k-1 \right \}$
, such that, letting
$a \in \left \{ 1,2,\ldots , 3k-1 \right \}$
, such that, letting
 $K= [A]^\Lambda _{a d_\rho }$
, we have (3.65)Moreover, letting
$K= [A]^\Lambda _{a d_\rho }$
, we have (3.65)Moreover, letting $$ \begin{align}\begin{aligned} \rho^\Lambda \left( \partial^\Lambda K, \Lambda\setminus M \right) \ge d_\rho -1. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \rho^\Lambda \left( \partial^\Lambda K, \Lambda\setminus M \right) \ge d_\rho -1. \end{aligned}\end{align} $$
 $M_1= M\cap K$
and
$M_1= M\cap K$
and
 $M_2= M\cap K^c $
, we have
$M_2= M\cap K^c $
, we have
 $K\subset B$
and
$K\subset B$
and
 $M_{i}\neq \emptyset $
for
$M_{i}\neq \emptyset $
for
 $i=1,2$
.
$i=1,2$
.
-
3. Suppose
 $ 8kN< 2\gamma _A(M)< \rho ^\Lambda (A,B )$
. Let
$ 8kN< 2\gamma _A(M)< \rho ^\Lambda (A,B )$
. Let
 $ d_\gamma := \left \lfloor \frac { \gamma _A(M)}{3k}\right \rfloor $
. Then there exists
$ d_\gamma := \left \lfloor \frac { \gamma _A(M)}{3k}\right \rfloor $
. Then there exists
 $a \in \left \{ 1,2,\ldots , 3k-1 \right \}$
, such that, letting (3.66)we have
$a \in \left \{ 1,2,\ldots , 3k-1 \right \}$
, such that, letting (3.66)we have $$ \begin{align}\begin{aligned} K= [A]^\Lambda_{a d_\gamma}\cup\left( [A]^\Lambda_{\gamma_A(M)+d_\gamma}\setminus [A]^\Lambda_{a d_\gamma+1} \right), \end{aligned}\end{align} $$
(3.67)Moreover, letting
$$ \begin{align}\begin{aligned} K= [A]^\Lambda_{a d_\gamma}\cup\left( [A]^\Lambda_{\gamma_A(M)+d_\gamma}\setminus [A]^\Lambda_{a d_\gamma+1} \right), \end{aligned}\end{align} $$
(3.67)Moreover, letting $$ \begin{align}\begin{aligned} \rho^\Lambda \left( \partial^\Lambda K, \Lambda\setminus M \right) \ge d_\gamma -1. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \rho^\Lambda \left( \partial^\Lambda K, \Lambda\setminus M \right) \ge d_\gamma -1. \end{aligned}\end{align} $$
 $M_1= M\cap [A]^\Lambda _{j d_\gamma }$
and
$M_1= M\cap [A]^\Lambda _{j d_\gamma }$
and
 $M_2= M\cap [A]^\Lambda _{\gamma _A(M)}\setminus [A]^\Lambda _{j d_\gamma +1}$
, we have
$M_2= M\cap [A]^\Lambda _{\gamma _A(M)}\setminus [A]^\Lambda _{j d_\gamma +1}$
, we have
 $M_1\cup M_2=M\subset K\subset B$
and
$M_1\cup M_2=M\subset K\subset B$
and
 $M_{i}\neq \emptyset $
for
$M_{i}\neq \emptyset $
for
 $i=1,2$
.
$i=1,2$
.
Proof. Part (i) is obvious. To prove Parts (ii) and (iii), let
![]() $d=d_\rho $
in Part (ii), and
$d=d_\rho $
in Part (ii), and
![]() $d=d_\gamma $
in Part (ii); note that
$d=d_\gamma $
in Part (ii); note that
![]() $ d \ge N$
in both cases. We set
$ d \ge N$
in both cases. We set
![]() $Y_{a}=[A]^\Lambda _{{a} {d}}\setminus [A]^\Lambda _{({a}-1) {d}}\subset B$
for
$Y_{a}=[A]^\Lambda _{{a} {d}}\setminus [A]^\Lambda _{({a}-1) {d}}\subset B$
for
![]() ${a}=1,2,\ldots , 3k$
; note
${a}=1,2,\ldots , 3k$
; note
![]() $3k d\le \frac {\rho ^\Lambda (A,B)}2$
in both cases.
$3k d\le \frac {\rho ^\Lambda (A,B)}2$
in both cases.
The set M consists of s clusters where
![]() $2\le s \le k$
, so
$2\le s \le k$
, so
![]() $N\ge 2$
. Each cluster has length
$N\ge 2$
. Each cluster has length
![]() $\le N-1$
, so it can intersect at most two of the
$\le N-1$
, so it can intersect at most two of the
![]() $Y_{a}$
’s (as
$Y_{a}$
’s (as
![]() $ d \ge N$
); hence, M can intersect at most
$ d \ge N$
); hence, M can intersect at most
![]() $2k$
of the distinct
$2k$
of the distinct
![]() $Y_{a}$
’s. Thus, there exists
$Y_{a}$
’s. Thus, there exists
![]() ${a}_* \in \left \{ 1,2,\ldots , 3k-1 \right \}$
such that
${a}_* \in \left \{ 1,2,\ldots , 3k-1 \right \}$
such that
and
![]() $M_1= M\cap [A]^\Lambda _{{({a}_*-1)}d}\ne \emptyset $
since
$M_1= M\cap [A]^\Lambda _{{({a}_*-1)}d}\ne \emptyset $
since
![]() $A\cap M\neq \emptyset $
.
$A\cap M\neq \emptyset $
.
To prove Part (ii) with
![]() $d=d_\rho $
, set
$d=d_\rho $
, set
![]() $K= [A]^\Lambda _{{a}_* d_\rho }\subset B$
. Then
$K= [A]^\Lambda _{{a}_* d_\rho }\subset B$
. Then
![]() $M_1= M\cap K\ne \emptyset $
since
$M_1= M\cap K\ne \emptyset $
since
![]() $A\cap M\neq \emptyset $
, and
$A\cap M\neq \emptyset $
, and
![]() $M_2= M\cap (\Lambda \setminus K)\ne \emptyset $
as
$M_2= M\cap (\Lambda \setminus K)\ne \emptyset $
as
![]() $\rho ^\Lambda (A,B) \le 2\gamma _A(M)$
by hypothesis. Moreover, (3.65) holds due to (3.68).
$\rho ^\Lambda (A,B) \le 2\gamma _A(M)$
by hypothesis. Moreover, (3.65) holds due to (3.68).
To prove Part (iii) with
![]() $d=d_\gamma $
, let K be given in (3.66). Then
$d=d_\gamma $
, let K be given in (3.66). Then
![]() $M_1= M\cap K\ne \emptyset $
since
$M_1= M\cap K\ne \emptyset $
since
![]() $A\cap M\neq \emptyset $
, and
$A\cap M\neq \emptyset $
, and
![]() $M_2= M\cap (\Lambda \setminus K)\ne \emptyset $
as
$M_2= M\cap (\Lambda \setminus K)\ne \emptyset $
as
![]() $\rho ^\Lambda (A,B) \le 2\gamma _A(M)$
by hypothesis. Moreover, (3.65) holds due to (3.68).
$\rho ^\Lambda (A,B) \le 2\gamma _A(M)$
by hypothesis. Moreover, (3.65) holds due to (3.68).
Motivated by Lemma 3.8, given
![]() $A\subset B\subset \Lambda $
with
$A\subset B\subset \Lambda $
with
![]() $ 8kN< \rho ^\Lambda (A,B)<\infty $
, we decompose
$ 8kN< \rho ^\Lambda (A,B)<\infty $
, we decompose
![]() $\mathcal S^{\Lambda ,A}_{N,k}$
into three distinct groups:
$\mathcal S^{\Lambda ,A}_{N,k}$
into three distinct groups:
-
1. Small
 $\gamma _A(M)$
:
$\gamma _A(M)$
:
 $M\in \mathcal {G}_1^{\Lambda ,N}(A,B)$
if
$M\in \mathcal {G}_1^{\Lambda ,N}(A,B)$
if
 $2\gamma _A(M)\le 8kN < \rho ^\Lambda (A,B) $
.
$2\gamma _A(M)\le 8kN < \rho ^\Lambda (A,B) $
. -
2. Large
 $\gamma _A(M)$
:
$\gamma _A(M)$
:
 $M\in \mathcal {G}_2^{\Lambda ,N}(A,B)$
if
$M\in \mathcal {G}_2^{\Lambda ,N}(A,B)$
if
 $ 8kN< \rho ^\Lambda (A,B)\le 2 \gamma _A(M)$
.
$ 8kN< \rho ^\Lambda (A,B)\le 2 \gamma _A(M)$
. -
3. Intermediate
 $\gamma _A(M)$
:
$\gamma _A(M)$
:
 $M\in \mathcal {G}_3^{\Lambda ,N}(A,B)$
if
$M\in \mathcal {G}_3^{\Lambda ,N}(A,B)$
if
 $ 8kN< 2\gamma _A(M)< \rho ^\Lambda (A,B)$
.
$ 8kN< 2\gamma _A(M)< \rho ^\Lambda (A,B)$
.
Note that for
![]() $ 8kN< \rho ^\Lambda (A,B)<\infty $
, we have
$ 8kN< \rho ^\Lambda (A,B)<\infty $
, we have
 $$ \begin{align} \chi_N^\Lambda Q^\Lambda_{\le k} P_-^A= \sum_{1=1}^3 \pi_{ \mathcal{G}_i^{\Lambda,N}(A,B)}, \quad\text{where}\quad \pi_{ \mathcal{G}_i^{\Lambda,N}(A,B)},= \sum_{M\in \mathcal{G}_i^{\Lambda,N}(A,B)} \pi_M. \end{align} $$
$$ \begin{align} \chi_N^\Lambda Q^\Lambda_{\le k} P_-^A= \sum_{1=1}^3 \pi_{ \mathcal{G}_i^{\Lambda,N}(A,B)}, \quad\text{where}\quad \pi_{ \mathcal{G}_i^{\Lambda,N}(A,B)},= \sum_{M\in \mathcal{G}_i^{\Lambda,N}(A,B)} \pi_M. \end{align} $$
3.8 Decoupling revisited
We will need to estimate
![]() $\chi ^\Lambda _N Q^\Lambda _{\le k}P_-^AR_E^\Lambda P_+^{B}Q^\Lambda _{\le k}$
. If
$\chi ^\Lambda _N Q^\Lambda _{\le k}P_-^AR_E^\Lambda P_+^{B}Q^\Lambda _{\le k}$
. If
![]() $ 8kN\ge \rho ^\Lambda (A,B)$
, we use (3.49). If
$ 8kN\ge \rho ^\Lambda (A,B)$
, we use (3.49). If
![]() $ 8kN< \rho ^\Lambda (A,B)$
, we note that
$ 8kN< \rho ^\Lambda (A,B)$
, we note that
We will use different strategies for
![]() $M\in \mathcal {G}_i=\mathcal {G}_i^{\Lambda ,N}(A,B)$
,
$M\in \mathcal {G}_i=\mathcal {G}_i^{\Lambda ,N}(A,B)$
,
![]() $i=1,2,3$
.
$i=1,2,3$
.
If
![]() $M\in \mathcal {G}_1$
, we use the decoupling argument of Section 3.6, getting (3.62) with
$M\in \mathcal {G}_1$
, we use the decoupling argument of Section 3.6, getting (3.62) with
![]() $K=[A]^\Lambda _{8kN}$
. The estimation for the expression in the first parenthesis in (3.62) will be performed using directly the a priori estimate (3.48) and (3.64). (No energy reduction.) This yields exponential decay in
$K=[A]^\Lambda _{8kN}$
. The estimation for the expression in the first parenthesis in (3.62) will be performed using directly the a priori estimate (3.48) and (3.64). (No energy reduction.) This yields exponential decay in
![]() $\gamma _A(M)$
for this type of contributions, and the sub-harmonicity argument concludes the analysis.
$\gamma _A(M)$
for this type of contributions, and the sub-harmonicity argument concludes the analysis.
To handle
![]() $M\in \mathcal {G}_2$
, we consider
$M\in \mathcal {G}_2$
, we consider
![]() $K, M_1,M_2$
as in Lemma 3.8(ii), set
$K, M_1,M_2$
as in Lemma 3.8(ii), set
![]() $S=[\partial K]^\Lambda _{d_\gamma -1} $
, and note that
$S=[\partial K]^\Lambda _{d_\gamma -1} $
, and note that
Using
![]() $M_1 \subset B$
, we get
$M_1 \subset B$
, we get
The expression in parenthesis is estimated by reduction to lower energies
![]() $E'\in I_{\le k-1}$
, allowing the use of the induction hypothesis (in k) together with the estimate (3.65) to obtain exponential decay in
$E'\in I_{\le k-1}$
, allowing the use of the induction hypothesis (in k) together with the estimate (3.65) to obtain exponential decay in
![]() $\rho ^\Lambda (A,B)$
.
$\rho ^\Lambda (A,B)$
.
If
![]() $M\in \mathcal {G}_3$
, we use a decoupling based on Lemma 3.8(iii), we get exponential decay in
$M\in \mathcal {G}_3$
, we use a decoupling based on Lemma 3.8(iii), we get exponential decay in
![]() $\gamma _A(M)$
from the induction hypothesis (in k), and the sub-harmonicity argument concludes the analysis.
$\gamma _A(M)$
from the induction hypothesis (in k), and the sub-harmonicity argument concludes the analysis.
3.9 Reduction to lower energies
We first observe that
![]() $P_-^A R^{\Lambda }_{E}P_+^B=P_-^A \widehat R^{\Lambda }_{0,E}P_+^B$
decays exponentially in
$P_-^A R^{\Lambda }_{E}P_+^B=P_-^A \widehat R^{\Lambda }_{0,E}P_+^B$
decays exponentially in
![]() $\rho ^\Lambda (A,B)$
for
$\rho ^\Lambda (A,B)$
for
![]() $E\le \tfrac 34\left ( 1- \tfrac {1}{\Delta } \right )$
due to (3.23) with
$E\le \tfrac 34\left ( 1- \tfrac {1}{\Delta } \right )$
due to (3.23) with
![]() $k=0$
; that is, Theorem 2.4 holds for k=0. Suppose now that we already established (2.17) for all energies
$k=0$
; that is, Theorem 2.4 holds for k=0. Suppose now that we already established (2.17) for all energies
![]() $E\in I_{\le k-1}$
and we want to push the allowable energies to the interval
$E\in I_{\le k-1}$
and we want to push the allowable energies to the interval
![]() $I_{\le k}$
. The principal idea here is to observe that if
$I_{\le k}$
. The principal idea here is to observe that if
![]() $\emptyset \ne K \subsetneq \Lambda $
, then we have the nontrivial decoupling
$\emptyset \ne K \subsetneq \Lambda $
, then we have the nontrivial decoupling
![]() $H^{K,K^c}= H^{K} + H^{K^c}$
, and
$H^{K,K^c}= H^{K} + H^{K^c}$
, and
![]() $R_E^{K,K^c}$
can be decomposed as
$R_E^{K,K^c}$
can be decomposed as
 $$ \begin{align}\begin{aligned} R_E^{K,K^c} =\sum_{\nu\in \sigma (H^{K^c})} {R_{E-\nu}^{K}\otimes \pi_{\kappa_\nu}}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} R_E^{K,K^c} =\sum_{\nu\in \sigma (H^{K^c})} {R_{E-\nu}^{K}\otimes \pi_{\kappa_\nu}}, \end{aligned}\end{align} $$
where
![]() $\left \{ \kappa _\nu \right \}_{\nu \in \sigma (H^{K^c})}$
is an orthonormal basis for
$\left \{ \kappa _\nu \right \}_{\nu \in \sigma (H^{K^c})}$
is an orthonormal basis for
![]() $\mathcal {H}_{K^c}$
that diagonalizes
$\mathcal {H}_{K^c}$
that diagonalizes
![]() $H^{K^c}$
:
$H^{K^c}$
:
![]() $H^{K^c}\kappa _\nu =\nu \kappa _\nu $
. In particular, if
$H^{K^c}\kappa _\nu =\nu \kappa _\nu $
. In particular, if
![]() $K_1\subset K $
and
$K_1\subset K $
and
![]() $K_2\subset K^c$
, we deduce that
$K_2\subset K^c$
, we deduce that
 $$ \begin{align}\begin{aligned} P_-^{K_1}P_-^{K_2}R_E^{K,K^c} =\sum_{\nu\in \sigma (H^{K^c})\cap[1- \frac{1}{\Delta},\infty)} \left( P_-^{K_1}R_{E-\nu}^{K} \right)\otimes \left( P_-^{K_2}\pi_{\kappa_\nu} \right), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_-^{K_1}P_-^{K_2}R_E^{K,K^c} =\sum_{\nu\in \sigma (H^{K^c})\cap[1- \frac{1}{\Delta},\infty)} \left( P_-^{K_1}R_{E-\nu}^{K} \right)\otimes \left( P_-^{K_2}\pi_{\kappa_\nu} \right), \end{aligned}\end{align} $$
since
![]() $P_-^{K_2}\pi _{\kappa _0}=0$
, and we have
$P_-^{K_2}\pi _{\kappa _0}=0$
, and we have
![]() $\min _{\nu \in \sigma (H^{K^c})\setminus \left \{ 0 \right \}}\,\nu \ge 1- \frac {1}{\Delta }$
. This is exactly the type of setup we have in (3.71)–(3.72). It means that the factor
$\min _{\nu \in \sigma (H^{K^c})\setminus \left \{ 0 \right \}}\,\nu \ge 1- \frac {1}{\Delta }$
. This is exactly the type of setup we have in (3.71)–(3.72). It means that the factor
![]() $P_-^{K_1}P_-^{K_2}$
allows us effectively to lower the energy
$P_-^{K_1}P_-^{K_2}$
allows us effectively to lower the energy
![]() $E\in I_{\le k}$
to
$E\in I_{\le k}$
to
![]() $E-\nu \in I_{\le k-1}$
and therefore use the induction hypothesis to obtain exponential decay (we of course still need to control the summation over
$E-\nu \in I_{\le k-1}$
and therefore use the induction hypothesis to obtain exponential decay (we of course still need to control the summation over
![]() $\nu $
on the right-hand side of (3.74)).
$\nu $
on the right-hand side of (3.74)).
4 Proof of the main theorem
In this section, we prove Theorem 2.4. We fix
![]() $\Delta _0> 5$
and
$\Delta _0> 5$
and
![]() $\lambda _0>0$
, and assume
$\lambda _0>0$
, and assume
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
. As discussed in Remark 3.3, the argument can be modified for
$\lambda \ge \lambda _0$
. As discussed in Remark 3.3, the argument can be modified for
![]() $\Delta _0>1$
.
$\Delta _0>1$
.
The proof proceeds by induction on k. Theorem 2.4 holds for
![]() $k=0$
, since in this case, (2.17) follows from (3.23) with
$k=0$
, since in this case, (2.17) follows from (3.23) with
![]() $F_0=C_0$
,
$F_0=C_0$
,
![]() $\xi _0=0$
and
$\xi _0=0$
and
![]() $\theta _0=m_0$
as
$\theta _0=m_0$
as
![]() $P_-^A R_E^\Lambda = P_-^A R_{0,E}^\Lambda $
. Given
$P_-^A R_E^\Lambda = P_-^A R_{0,E}^\Lambda $
. Given
![]() $k\in \mathbb N$
, we assume the theorem holds for
$k\in \mathbb N$
, we assume the theorem holds for
![]() $k-1$
, and we will prove the theorem holds for k.
$k-1$
, and we will prove the theorem holds for k.
We now fix
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $\Lambda \subset \mathbb Z$
, finite and nonempty. We also fix
$\Lambda \subset \mathbb Z$
, finite and nonempty. We also fix
![]() $A\subset B \subset \Lambda $
, where A is a nonempty subset connected in
$A\subset B \subset \Lambda $
, where A is a nonempty subset connected in
![]() $\Lambda $
; it follows that
$\Lambda $
; it follows that
![]() $[A]^\Lambda _p$
is also connected in
$[A]^\Lambda _p$
is also connected in
![]() $\Lambda $
and
$\Lambda $
and
![]() $\left \lvert ]A[^\Lambda _{p} \right \rvert \le 2$
for all
$\left \lvert ]A[^\Lambda _{p} \right \rvert \le 2$
for all
![]() $p\in \mathbb Z$
.
$p\in \mathbb Z$
.
To derive the bound (2.17) from Lemma 3.6(i), we will estimate
![]() $\mathbb E \left ( \left \lVert F^\Lambda _{p,q}(E,A) \right \rVert _{HS}^s \right )$
for
$\mathbb E \left ( \left \lVert F^\Lambda _{p,q}(E,A) \right \rVert _{HS}^s \right )$
for
![]() $p,q= -\left \lvert A \right \rvert , -\left \lvert A \right \rvert +1,\ldots , \left \lvert \Lambda \right \rvert $
for
$p,q= -\left \lvert A \right \rvert , -\left \lvert A \right \rvert +1,\ldots , \left \lvert \Lambda \right \rvert $
for
![]() $E\in I_{\le k}$
, where
$E\in I_{\le k}$
, where
![]() $F^\Lambda _{p,q}(E,A)$
is given in (3.36). The estimate (3.33) gives the a priori bound (
$F^\Lambda _{p,q}(E,A)$
is given in (3.36). The estimate (3.33) gives the a priori bound (
![]() $F_{p,q}=F^\Lambda _{p,q}(E,A)$
)
$F_{p,q}=F^\Lambda _{p,q}(E,A)$
)
Since
![]() $F_{p,q}=F_{q,p}^*$
, we may assume
$F_{p,q}=F_{q,p}^*$
, we may assume
![]() $ p\le q$
. If
$ p\le q$
. If
![]() $p=q$
, we use (4.1); if
$p=q$
, we use (4.1); if
![]() $p<q$
, we note that
$p<q$
, we note that
 $$ \begin{align}\begin{aligned} \left\lVert F_{p,q} \right\rVert_{HS}&\le \left\lVert Q^\Lambda_{\le k}P_-^{ ]A[^{\Lambda}_p} R^{\Lambda}_{E} P_+^{[A]^{\Lambda}_q}Q^\Lambda_{\le k} \right\rVert_{HS} \le \sum_{j\in ]A[^{\Lambda}_p}\left\lVert Q^\Lambda_{\le k}\mathcal{N}_j R^{\Lambda}_{E} P_+^{[j]^{\Lambda}_{q-p-1}}Q^\Lambda_{\le k} \right\rVert_{HS}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert F_{p,q} \right\rVert_{HS}&\le \left\lVert Q^\Lambda_{\le k}P_-^{ ]A[^{\Lambda}_p} R^{\Lambda}_{E} P_+^{[A]^{\Lambda}_q}Q^\Lambda_{\le k} \right\rVert_{HS} \le \sum_{j\in ]A[^{\Lambda}_p}\left\lVert Q^\Lambda_{\le k}\mathcal{N}_j R^{\Lambda}_{E} P_+^{[j]^{\Lambda}_{q-p-1}}Q^\Lambda_{\le k} \right\rVert_{HS}, \end{aligned}\end{align} $$
where we used
![]() $[ ]A[^{\Lambda }_{p}]^{\Lambda }_{q-p-1}\subset [A]^{\Lambda }_q $
for
$[ ]A[^{\Lambda }_{p}]^{\Lambda }_{q-p-1}\subset [A]^{\Lambda }_q $
for
![]() $p<q$
.
$p<q$
.
For
![]() $r\in {\mathbb {N}}^0$
and
$r\in {\mathbb {N}}^0$
and
![]() $E\in I_{\le k}$
, we set
$E\in I_{\le k}$
, we set
and prove the following lemma.
Lemma 4.1. Let
![]() $k\in \mathbb N$
,
$k\in \mathbb N$
,
![]() $s\in (0,\frac 13)$
, and assume Theorem 2.4 holds for
$s\in (0,\frac 13)$
, and assume Theorem 2.4 holds for
![]() $k-1$
. Then there exist constants
$k-1$
. Then there exist constants
![]() $D_k,C_k, \zeta _k , m_k>0$
(depending on k,
$D_k,C_k, \zeta _k , m_k>0$
(depending on k,
![]() $\Delta _0$
,
$\Delta _0$
,
![]() $ \lambda _0$
and s), such that such that, for all
$ \lambda _0$
and s), such that such that, for all
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
with
$\lambda \ge \lambda _0$
with
![]() $\lambda \Delta ^2\ge D_k$
,
$\lambda \Delta ^2\ge D_k$
,
![]() $\Lambda \subset \mathbb Z$
finite, energy
$\Lambda \subset \mathbb Z$
finite, energy
![]() $E\in I_{\le k}$
, and
$E\in I_{\le k}$
, and
![]() $r\in {\mathbb {N}}^0$
, we have
$r\in {\mathbb {N}}^0$
, we have
To finish the proof of the theorem, we assume that
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
with
$\lambda \ge \lambda _0$
with
![]() $\lambda \Delta ^2\ge D_k$
as in the lemma. Then, since
$\lambda \Delta ^2\ge D_k$
as in the lemma. Then, since
![]() $\mathbb E \left ( \left \lVert F_{p,q} \right \rVert \right )_{HS}^s\le 2 f^\Lambda (k,E, \left \lvert q-p \right \rvert -1)$
for
$\mathbb E \left ( \left \lVert F_{p,q} \right \rVert \right )_{HS}^s\le 2 f^\Lambda (k,E, \left \lvert q-p \right \rvert -1)$
for
![]() $\left \lvert q-p \right \rvert \ge 1$
, and we have (4.1) for
$\left \lvert q-p \right \rvert \ge 1$
, and we have (4.1) for
![]() $q=p$
, we obtain
$q=p$
, we obtain
 $$ \begin{align}\begin{aligned} &\mathbb E\, \left( \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(p)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\left\lVert F_{p,q} \right\rVert \right)^s \le C_k \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-s m_k t}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &\mathbb E\, \left( \sum_{p=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_0(p)_+}\mathrm{e}^{-m_0\left( t-q-1 \right)_+}\left\lVert F_{p,q} \right\rVert \right)^s \le C_k \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-s m_k t}. \end{aligned}\end{align} $$
The estimate (2.17) now follows from (3.36) and (4.5) (recall (3.6)), so Theorem 2.4 holds for k.
To complete the proof of Theorem 2.4, we need to prove Lemma 4.1. To do so, we need the following lemma.
Lemma 4.2. Let
![]() $k\in \mathbb N$
,
$k\in \mathbb N$
,
![]() $s\in (0,\frac 13)$
, and assume Theorem 2.4 holds for
$s\in (0,\frac 13)$
, and assume Theorem 2.4 holds for
![]() $k-1$
. Then there exist constants
$k-1$
. Then there exist constants
![]() $C_k, \zeta _k , m_k>0$
(depending on k,
$C_k, \zeta _k , m_k>0$
(depending on k,
![]() $\Delta _0$
,
$\Delta _0$
,
![]() $ \lambda _0$
and s), such that, for all
$ \lambda _0$
and s), such that, for all
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
,
$\lambda \ge \lambda _0$
,
![]() $j \in \Lambda \subset \mathbb Z$
finite, energy
$j \in \Lambda \subset \mathbb Z$
finite, energy
![]() $E\in I_{\le k}$
,
$E\in I_{\le k}$
,
![]() $N\in \mathbb N$
, and
$N\in \mathbb N$
, and
![]() $r\in {\mathbb {N}}^0$
such that
$r\in {\mathbb {N}}^0$
such that
![]() $8kN < r$
, we have
$8kN < r$
, we have
 $$ \begin{align}\begin{aligned} G^\Lambda_N(r)&= \mathbb E\,\left( \left\lVert \chi_N^{\Lambda}Q_{\le k}^{\Lambda} \mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right)\\& \le C_k \left( \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-m_k r} + \mathrm{e}^{- m_k N} \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} f_N^\Lambda(p) \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} G^\Lambda_N(r)&= \mathbb E\,\left( \left\lVert \chi_N^{\Lambda}Q_{\le k}^{\Lambda} \mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right)\\& \le C_k \left( \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-m_k r} + \mathrm{e}^{- m_k N} \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} f_N^\Lambda(p) \right). \end{aligned}\end{align} $$
Proof. Let
![]() $k\in \mathbb N$
,
$k\in \mathbb N$
,
![]() $s\in (0,\frac 13)$
, and assume Theorem 2.4 holds for
$s\in (0,\frac 13)$
, and assume Theorem 2.4 holds for
![]() $k-1$
. Let
$k-1$
. Let
![]() $j \in \Lambda \subset \mathbb Z$
finite and
$j \in \Lambda \subset \mathbb Z$
finite and
![]() $E\in I_{\le k}$
,
$E\in I_{\le k}$
,
![]() $N\in \mathbb N$
, and
$N\in \mathbb N$
, and
![]() $r\in {\mathbb {N}}^0$
such that
$r\in {\mathbb {N}}^0$
such that
![]() $8kN < r$
. Let
$8kN < r$
. Let
![]() $G^\Lambda _N(r)$
be as in (4.6). It follows from (3.69), setting
$G^\Lambda _N(r)$
be as in (4.6). It follows from (3.69), setting
![]() $\mathcal {G}^N_i =\mathcal {G}_i^{\Lambda ,N}(\left \{ j \right \}, [j]^\Lambda _r)$
,
$\mathcal {G}^N_i =\mathcal {G}_i^{\Lambda ,N}(\left \{ j \right \}, [j]^\Lambda _r)$
,
![]() $i=1,2,3$
(see Section 3.7), that
$i=1,2,3$
(see Section 3.7), that
 $$ \begin{align}\begin{aligned} G^\Lambda_N(r)&\le \sum_{i=1}^3 G_i(r), \;\text{where}\; G_i(r)=G^{\Lambda,N}_i(r)= \mathbb E\left( \left\lVert \pi_{ \mathcal{G}^N_i }\mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} G^\Lambda_N(r)&\le \sum_{i=1}^3 G_i(r), \;\text{where}\; G_i(r)=G^{\Lambda,N}_i(r)= \mathbb E\left( \left\lVert \pi_{ \mathcal{G}^N_i }\mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right). \end{aligned}\end{align} $$
To estimate
![]() $G_1(r)$
, we use (3.62) with
$G_1(r)$
, we use (3.62) with
![]() $M= [j]_{4kN}^\Lambda $
and
$M= [j]_{4kN}^\Lambda $
and
![]() $K= [j]_{6kN}^\Lambda $
, (3.25) and (A.6), obtaining
$K= [j]_{6kN}^\Lambda $
, (3.25) and (A.6), obtaining
 $$ \begin{align}\begin{aligned} &G_1(r) \le C \left( \lambda \Delta^2 \right)^{-s} \,\mathbb E_K\left( \left\lVert Y \right\rVert_{HS}^s \right)\,\mathbb E_{\left( [K]_1^\Lambda \right)^c} \left( \left\lVert Z \right\rVert_{HS}^s \right);\\ & \quad Y:= \chi_N^{K} Q^K_{\le k}{P_+^{K\setminus M}R_E^{K}P_-^{\partial_{in}^{\Lambda} K}},\quad Z:=P_-^{\partial_{ex}^{\Lambda} [K]_1} R_E^{\left( [K]_1^\Lambda \right)^c}P_+^{[j]^\Lambda_r\cap\left( [K]_1^\Lambda \right)^c}Q^{\left( [K]_1^\Lambda \right)^c}_{\le k}\chi_N^{\left( [K]_1^\Lambda \right)^c}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &G_1(r) \le C \left( \lambda \Delta^2 \right)^{-s} \,\mathbb E_K\left( \left\lVert Y \right\rVert_{HS}^s \right)\,\mathbb E_{\left( [K]_1^\Lambda \right)^c} \left( \left\lVert Z \right\rVert_{HS}^s \right);\\ & \quad Y:= \chi_N^{K} Q^K_{\le k}{P_+^{K\setminus M}R_E^{K}P_-^{\partial_{in}^{\Lambda} K}},\quad Z:=P_-^{\partial_{ex}^{\Lambda} [K]_1} R_E^{\left( [K]_1^\Lambda \right)^c}P_+^{[j]^\Lambda_r\cap\left( [K]_1^\Lambda \right)^c}Q^{\left( [K]_1^\Lambda \right)^c}_{\le k}\chi_N^{\left( [K]_1^\Lambda \right)^c}. \end{aligned}\end{align} $$
To estimate
![]() $\mathbb E_K\left ( \left \lVert Y \right \rVert _{HS}^s \right )$
, note that
$\mathbb E_K\left ( \left \lVert Y \right \rVert _{HS}^s \right )$
, note that
 $$ \begin{align}\begin{aligned} \left\lVert Y \right\rVert_{HS} \le \sum_{u\in \partial_{in}^{\Lambda} K} {\left\lVert Y_u \right\rVert_{HS}}, \;\text{where}\; Y_u= \chi_N^{K} Q^K_{\le k}P_+^{K\setminus M}R_E^{K} \mathcal{N}_u, \;\text{and}\; \left\lvert \partial_{in}^{\Lambda} K \right\rvert\le 2. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert Y \right\rVert_{HS} \le \sum_{u\in \partial_{in}^{\Lambda} K} {\left\lVert Y_u \right\rVert_{HS}}, \;\text{where}\; Y_u= \chi_N^{K} Q^K_{\le k}P_+^{K\setminus M}R_E^{K} \mathcal{N}_u, \;\text{and}\; \left\lvert \partial_{in}^{\Lambda} K \right\rvert\le 2. \end{aligned}\end{align} $$
Using (3.37) and
![]() $\rho ^K(\partial _{in}^{\Lambda } K,K\setminus M) \ge 2kN$
, for
$\rho ^K(\partial _{in}^{\Lambda } K,K\setminus M) \ge 2kN$
, for
![]() $u\in \partial ^{\Lambda } _{in} K$
, we get
$u\in \partial ^{\Lambda } _{in} K$
, we get
 $$ \begin{align}\begin{aligned} \mathbb E_K\left( \left\lVert Y_u \right\rVert_{HS}^s \right)&\le C_k^s\left( \left\lvert K \right\rvert^{sk}\mathrm{e}^{-sm_0 2kN}+ \sum_{q=-1}^{\left\lvert K \right\rvert} \mathrm{e}^{-sm_0\left( q \right)_+} \mathbb E\left( \Big\|{\chi_N^{K} Q^K_{\le k}P_-^{]u[^K_{q}}R^K_{E}P_+^{K\setminus M} Q^K_{\le k}}^s_{HS}\Big\| \right) \right)\\ & \le C_{k,s}\left( \left\lvert K \right\rvert^{2sk+1} \mathrm{e}^{-sm_02kN}+ 2 \sum_{q=-1}^{2kN-1} \mathrm{e}^{-sm_0\left( q \right)_+} f_N^K(2kN-q-1) \right) \\ & \le C_{k,s} \mathrm{e}^{- m_{0,k}^\prime k N}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E_K\left( \left\lVert Y_u \right\rVert_{HS}^s \right)&\le C_k^s\left( \left\lvert K \right\rvert^{sk}\mathrm{e}^{-sm_0 2kN}+ \sum_{q=-1}^{\left\lvert K \right\rvert} \mathrm{e}^{-sm_0\left( q \right)_+} \mathbb E\left( \Big\|{\chi_N^{K} Q^K_{\le k}P_-^{]u[^K_{q}}R^K_{E}P_+^{K\setminus M} Q^K_{\le k}}^s_{HS}\Big\| \right) \right)\\ & \le C_{k,s}\left( \left\lvert K \right\rvert^{2sk+1} \mathrm{e}^{-sm_02kN}+ 2 \sum_{q=-1}^{2kN-1} \mathrm{e}^{-sm_0\left( q \right)_+} f_N^K(2kN-q-1) \right) \\ & \le C_{k,s} \mathrm{e}^{- m_{0,k}^\prime k N}, \end{aligned}\end{align} $$
where we used the a priori bounds (3.33) and (3.48).
Similarly,
 $$ \begin{align}\begin{aligned} \left\lVert Z \right\rVert_{HS}\le\sum_{u\in \partial_{ex}^{\Lambda} [K]_1} {\left\lVert Z_u \right\rVert_{HS}}, \;\text{where}\; Z_u= \mathcal{N}_u R_E^{\left( [K]_1^\Lambda \right)^c}P_+^{[j]^\Lambda_r\cap \left( [K]_1^\Lambda \right)^c}Q^{\left( [K]_1^\Lambda \right)^c}_{\le k}\chi_N^{\left( [K]_1^\Lambda \right)^c}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert Z \right\rVert_{HS}\le\sum_{u\in \partial_{ex}^{\Lambda} [K]_1} {\left\lVert Z_u \right\rVert_{HS}}, \;\text{where}\; Z_u= \mathcal{N}_u R_E^{\left( [K]_1^\Lambda \right)^c}P_+^{[j]^\Lambda_r\cap \left( [K]_1^\Lambda \right)^c}Q^{\left( [K]_1^\Lambda \right)^c}_{\le k}\chi_N^{\left( [K]_1^\Lambda \right)^c}, \end{aligned}\end{align} $$
and
![]() $ \left \lvert \partial _{ex}^{\Lambda } [K]_1 \right \rvert \le 2$
. Using (3.37), for
$ \left \lvert \partial _{ex}^{\Lambda } [K]_1 \right \rvert \le 2$
. Using (3.37), for
![]() $u\in \partial _{ex} [K]_1$
, we get
$u\in \partial _{ex} [K]_1$
, we get
 $$ \begin{align}\begin{aligned} &\mathbb E_{\left( [K]_1^\Lambda \right)^c}\left( \left\lVert Z_u \right\rVert_{HS}^s \right) \le C_k^s\left(\left\lvert \Lambda \right\rvert^{sk}\mathrm{e}^{-sm_0 (r-6kN-2)}+ \right. \\ & \quad \left. \sum_{q=-1}^{\left\lvert \Lambda \right\rvert} \mathrm{e}^{-sm_0\left( q \right)_+} \mathbb E\Big({\Big\|{\chi_N^{{\left( [K]_1^\Lambda \right)^c}} Q^{\left( [K]_1^\Lambda \right)^c}_{\le k} P_-^{]u[^{\left( [K]_1^\Lambda \right)^c}_{q}} R_E^{\left( [K]_1^\Lambda \right)^c} P_+^{[j]^\Lambda_r\cap \left( [K]_1^\Lambda \right)^c} Q^{\left( [K]_1^\Lambda \right)^c}_{\le k}}\Big\|^s_{HS}}\Big)\right)\\ & \le C_k^s\left( \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-sm_0 (r-6kN-2)}+ \sum_{q=-1}^{r-6kN-3} \mathrm{e}^{-sm_0\left( q \right)_+} f_N^\Lambda(r-6kN-q-3) \right)\\ & = C_k^s \left( \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-sm_0 (r-6kN-2)}+ \sum_{p=0}^{r-6kN-2} \mathrm{e}^{-sm_0\left( r-p-6kN -3 \right)_+} f_N^\Lambda(p) \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &\mathbb E_{\left( [K]_1^\Lambda \right)^c}\left( \left\lVert Z_u \right\rVert_{HS}^s \right) \le C_k^s\left(\left\lvert \Lambda \right\rvert^{sk}\mathrm{e}^{-sm_0 (r-6kN-2)}+ \right. \\ & \quad \left. \sum_{q=-1}^{\left\lvert \Lambda \right\rvert} \mathrm{e}^{-sm_0\left( q \right)_+} \mathbb E\Big({\Big\|{\chi_N^{{\left( [K]_1^\Lambda \right)^c}} Q^{\left( [K]_1^\Lambda \right)^c}_{\le k} P_-^{]u[^{\left( [K]_1^\Lambda \right)^c}_{q}} R_E^{\left( [K]_1^\Lambda \right)^c} P_+^{[j]^\Lambda_r\cap \left( [K]_1^\Lambda \right)^c} Q^{\left( [K]_1^\Lambda \right)^c}_{\le k}}\Big\|^s_{HS}}\Big)\right)\\ & \le C_k^s\left( \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-sm_0 (r-6kN-2)}+ \sum_{q=-1}^{r-6kN-3} \mathrm{e}^{-sm_0\left( q \right)_+} f_N^\Lambda(r-6kN-q-3) \right)\\ & = C_k^s \left( \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-sm_0 (r-6kN-2)}+ \sum_{p=0}^{r-6kN-2} \mathrm{e}^{-sm_0\left( r-p-6kN -3 \right)_+} f_N^\Lambda(p) \right). \end{aligned}\end{align} $$
Combining (4.8)–(4.12), we get
 $$ \begin{align}\begin{aligned} &G_1(r) \le C \left( \lambda \Delta^2 \right)^{-s} \mathrm{e}^{- m_k^\prime k N}\Big({ \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-m_k^\prime r}+ \sum_{p=0}^{r} \mathrm{e}^{-m_k^\prime \left( r-p \right)} f_N^\Lambda(p)}\Big), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &G_1(r) \le C \left( \lambda \Delta^2 \right)^{-s} \mathrm{e}^{- m_k^\prime k N}\Big({ \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-m_k^\prime r}+ \sum_{p=0}^{r} \mathrm{e}^{-m_k^\prime \left( r-p \right)} f_N^\Lambda(p)}\Big), \end{aligned}\end{align} $$
for an appropriate
![]() $m_k^\prime>0$
.
$m_k^\prime>0$
.
To estimate
![]() $G_2(r)$
, we note that it follows from Lemma 3.8(ii), letting
$G_2(r)$
, we note that it follows from Lemma 3.8(ii), letting
that
 $$ \begin{align}\begin{aligned} G_2(r) \le \sum_{a=1}^{3k-1} G^{\left(a\right)}_2(r), \quad G^{\left(a\right)}_2(r)= \mathbb E\left( \left\lVert \chi_N^{\Lambda} Q^\Lambda_{\le k}P_+^{S(a)}P_-^{K(a)}P_-^{(K(a))^c}\mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} G_2(r) \le \sum_{a=1}^{3k-1} G^{\left(a\right)}_2(r), \quad G^{\left(a\right)}_2(r)= \mathbb E\left( \left\lVert \chi_N^{\Lambda} Q^\Lambda_{\le k}P_+^{S(a)}P_-^{K(a)}P_-^{(K(a))^c}\mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right). \end{aligned}\end{align} $$
To estimate
![]() $ G^{\left (a\right )}_2(r)$
, we use (3.71) and (3.72), the Cauchy-Schwarz inequality and Hölder’s inequality (recall
$ G^{\left (a\right )}_2(r)$
, we use (3.71) and (3.72), the Cauchy-Schwarz inequality and Hölder’s inequality (recall
![]() $3s <1$
) to get (we mostly omit a from the notation)
$3s <1$
) to get (we mostly omit a from the notation)
 $$ \begin{align}\begin{aligned} G^{\left(a\right)}_2(r) &\le C \Delta^{-s} \left( \mathbb E \left\lVert Y \right\rVert^{2s} \right)^{1/2}\left( \mathbb E\left\lVert Z \right\rVert^{2s}_{HS} \right)^{1/2}\\ & \le C \Delta^{-s} \left( \mathbb E\left\lVert Y \right\rVert^{s} \right)^{1/4} \left( \mathbb E\left\lVert Y \right\rVert^{3s} \right)^{1/4}\left( \mathbb E\left\lVert Z \right\rVert^{2s}_{HS} \right)^{1/2} , \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} G^{\left(a\right)}_2(r) &\le C \Delta^{-s} \left( \mathbb E \left\lVert Y \right\rVert^{2s} \right)^{1/2}\left( \mathbb E\left\lVert Z \right\rVert^{2s}_{HS} \right)^{1/2}\\ & \le C \Delta^{-s} \left( \mathbb E\left\lVert Y \right\rVert^{s} \right)^{1/4} \left( \mathbb E\left\lVert Y \right\rVert^{3s} \right)^{1/4}\left( \mathbb E\left\lVert Z \right\rVert^{2s}_{HS} \right)^{1/2} , \end{aligned}\end{align} $$
where
It follows immediately from (3.38) that
where we used
![]() $\left \lvert \partial ^{\Lambda } K(a) \right \rvert \le 4$
since
$\left \lvert \partial ^{\Lambda } K(a) \right \rvert \le 4$
since
![]() $K(a)$
is connected, and hence, we have
$K(a)$
is connected, and hence, we have
To estimate
![]() $E\left \lVert Y \right \rVert ^{s}$
, we use ( the dependence on a is being ommitted)
$E\left \lVert Y \right \rVert ^{s}$
, we use ( the dependence on a is being ommitted)
We consider first the case
![]() $x\in \partial ^{\Lambda }_{in}K$
. Using (3.74), we can further decompose
$x\in \partial ^{\Lambda }_{in}K$
. Using (3.74), we can further decompose
![]() $Y_x$
as
$Y_x$
as
 $$ \begin{align}\begin{aligned} Y_x =\sum_{ \nu\in \sigma (H^{K^c})\cap [1- \frac{1}{\Delta},\infty)} Y_{x,\nu}, \quad Y_{x,\nu}= \chi_N^{\Lambda} Q^\Lambda_{\le k}P_+^{S}P_-^{K}P_-^{K^c}\mathcal{N}_j\left( R_{E-\nu}^{K}\otimes \pi_{\kappa_\nu} \right)\mathcal{N}_x. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} Y_x =\sum_{ \nu\in \sigma (H^{K^c})\cap [1- \frac{1}{\Delta},\infty)} Y_{x,\nu}, \quad Y_{x,\nu}= \chi_N^{\Lambda} Q^\Lambda_{\le k}P_+^{S}P_-^{K}P_-^{K^c}\mathcal{N}_j\left( R_{E-\nu}^{K}\otimes \pi_{\kappa_\nu} \right)\mathcal{N}_x. \end{aligned}\end{align} $$
Note that
 $$ \begin{align}\begin{aligned} \left\lVert Y_x \right\rVert=\max_\nu\left\lVert Y_{x,\nu} \right\rVert\le \sum_{ \nu\in \sigma (H^{K^c})\cap [1- \frac{1}{\Delta},k(1- \frac{1}{\Delta}))} \left\lVert Y_{x,\nu} \right\rVert+\max_{ \nu\in \sigma (H^{K^c})\cap [k(1- \frac{1}{\Delta}),\infty)} \left\lVert Y_{x,\nu} \right\rVert. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert Y_x \right\rVert=\max_\nu\left\lVert Y_{x,\nu} \right\rVert\le \sum_{ \nu\in \sigma (H^{K^c})\cap [1- \frac{1}{\Delta},k(1- \frac{1}{\Delta}))} \left\lVert Y_{x,\nu} \right\rVert+\max_{ \nu\in \sigma (H^{K^c})\cap [k(1- \frac{1}{\Delta}),\infty)} \left\lVert Y_{x,\nu} \right\rVert. \end{aligned}\end{align} $$
Clearly, we can bound
For
![]() $\nu \ge 1- \frac {1}{\Delta }$
, we have
$\nu \ge 1- \frac {1}{\Delta }$
, we have
![]() $E-\nu \in I_{\le k-1} $
for
$E-\nu \in I_{\le k-1} $
for
![]() $E\in I_{\le k}$
(recall (2.14)). For
$E\in I_{\le k}$
(recall (2.14)). For
![]() $\nu \in \sigma (H^{K^c})\cap [1- \frac {1}{\Delta },k(1- \frac {1}{\Delta })) $
, we use the induction hypothesis for Theorem 2.4 and the statistical independence of
$\nu \in \sigma (H^{K^c})\cap [1- \frac {1}{\Delta },k(1- \frac {1}{\Delta })) $
, we use the induction hypothesis for Theorem 2.4 and the statistical independence of
![]() $H^{K^c}$
and
$H^{K^c}$
and
![]() $\left \{ \omega _i \right \}_{i\in K}$
to conclude that
$\left \{ \omega _i \right \}_{i\in K}$
to conclude that
where we used (3.65).
For
![]() $\nu \in \sigma (H^{K^c})\cap [k(1- \frac {1}{\Delta }),\infty )$
,
$\nu \in \sigma (H^{K^c})\cap [k(1- \frac {1}{\Delta }),\infty )$
,
![]() $E-\nu \le \frac 34 \left ( 1- \tfrac {1}{\Delta } \right )$
, and in this case,
$E-\nu \le \frac 34 \left ( 1- \tfrac {1}{\Delta } \right )$
, and in this case,
so it follows from (3.23) with
![]() $k=0$
, using (3.65), that
$k=0$
, using (3.65), that
Using (4.22), (4.24), (4.26) and (3.27), we get
Similar considerations show that the estimate (4.27) holds also for
![]() $x\in \partial _{ex}^{\Lambda }K $
.
$x\in \partial _{ex}^{\Lambda }K $
.
Combining (4.20) and (4.27) and recalling
![]() $\left \lvert \partial ^{\Lambda } K \right \rvert \le 4$
, we get
$\left \lvert \partial ^{\Lambda } K \right \rvert \le 4$
, we get
Combining (4.19) and (4.28), we see that
It now follows from (4.15) and (4.29) that
To estimate
![]() $ G_3(r)$
, given
$ G_3(r)$
, given
![]() $4kN< \gamma < \frac r 2$
, we let
$4kN< \gamma < \frac r 2$
, we let
![]() $ d_\gamma := \left \lfloor \frac { \gamma }{3k}\right \rfloor $
. Given
$ d_\gamma := \left \lfloor \frac { \gamma }{3k}\right \rfloor $
. Given
![]() $a\in \left \{ 1,2,\ldots ,3k-1 \right \} $
, we let
$a\in \left \{ 1,2,\ldots ,3k-1 \right \} $
, we let
![]() $K(a,\gamma )$
be as in (3.66) with
$K(a,\gamma )$
be as in (3.66) with
![]() $A=\left \{ j \right \}$
, and let
$A=\left \{ j \right \}$
, and let
![]() $K_1(a,\gamma )=[j ]^\Lambda _{a d_\gamma }$
, the connected component of
$K_1(a,\gamma )=[j ]^\Lambda _{a d_\gamma }$
, the connected component of
![]() $K(a,\gamma )$
that contains j. We also set
$K(a,\gamma )$
that contains j. We also set
![]() $K_2(a,\gamma )=K(a,\gamma )\setminus K_1(a,\gamma )$
,
$K_2(a,\gamma )=K(a,\gamma )\setminus K_1(a,\gamma )$
,
![]() $S(a,\gamma )=[\partial ^\Lambda K(a,\gamma )]^\Lambda _{d_\gamma -1}$
, and
$S(a,\gamma )=[\partial ^\Lambda K(a,\gamma )]^\Lambda _{d_\gamma -1}$
, and
![]() $T(a,\gamma )=[j]^\Lambda _{\gamma _{\left \{ j \right \}}(M)}$
. It follows from Lemma 3.8(iii) that
$T(a,\gamma )=[j]^\Lambda _{\gamma _{\left \{ j \right \}}(M)}$
. It follows from Lemma 3.8(iii) that
for some
![]() $a\in \left \{ 1,2,\ldots ,3k-1 \right \}$
, and hence,
$a\in \left \{ 1,2,\ldots ,3k-1 \right \}$
, and hence,
 $$ \begin{align}\begin{aligned} G_3(r) &\le \sum_{\gamma=4kN+1}^{\left\lfloor \frac r 2\right \rfloor} \sum_{a=1}^{3k-1} G^{\left(a,\gamma\right)}_3(r), \quad\text{where}\quad \\ G^{\left(a,\gamma\right)}_3(r)& = \mathbb E\left( \left\lVert \chi_N^{\Lambda} Q^\Lambda_{\le k}P_+^{T(a,\gamma)}P_+^{S(a,\gamma)}P_-^{K_1(a,\gamma)}P_-^{K_2(a,\gamma)}\mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} G_3(r) &\le \sum_{\gamma=4kN+1}^{\left\lfloor \frac r 2\right \rfloor} \sum_{a=1}^{3k-1} G^{\left(a,\gamma\right)}_3(r), \quad\text{where}\quad \\ G^{\left(a,\gamma\right)}_3(r)& = \mathbb E\left( \left\lVert \chi_N^{\Lambda} Q^\Lambda_{\le k}P_+^{T(a,\gamma)}P_+^{S(a,\gamma)}P_-^{K_1(a,\gamma)}P_-^{K_2(a,\gamma)}\mathcal{N}_j R^{\Lambda}_E P_+^{[j]^\Lambda_r}Q_{\le k}^{\Lambda} \right\rVert_{HS}^s \right). \end{aligned}\end{align} $$
To estimate
![]() $G^{\left (a,\gamma \right )}_3(r)$
, we start with the following analogue of (4.8) (we mostly omit
$G^{\left (a,\gamma \right )}_3(r)$
, we start with the following analogue of (4.8) (we mostly omit
![]() $(a,\gamma )$
from the notation):
$(a,\gamma )$
from the notation):
 $$ \begin{align}\begin{aligned} &G^{\left(a,\gamma\right)}_3(r)\le C \left( \lambda \Delta^2 \right)^{-s} \,\mathbb E_K\left( \left\lVert Y \right\rVert^s \right)\,\mathbb E_{[K]_1^c} \left( \left\lVert Z \right\rVert_{HS}^s \right);\\ & \quad Y:= \chi_N^{K} Q^K_{\le k}P_+^{T\cap K}P_+^{S}P_-^{K_1}P_-^{K_2}R_E^{K}P_-^{\partial^\Lambda_{in} K},\\ & \quad Z:=P_-^{\partial_{ex}^\Lambda [K]_1} R_E^{\left( [K]_1^\Lambda \right)^c}P_+^{[j]^\Lambda_r\cap{\left( [K]_1^\Lambda \right)^c}}Q^{{\left( [K]_1^\Lambda \right)^c}}_{\le k}\chi_N^{{\left( [K]_1^\Lambda \right)^c}}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &G^{\left(a,\gamma\right)}_3(r)\le C \left( \lambda \Delta^2 \right)^{-s} \,\mathbb E_K\left( \left\lVert Y \right\rVert^s \right)\,\mathbb E_{[K]_1^c} \left( \left\lVert Z \right\rVert_{HS}^s \right);\\ & \quad Y:= \chi_N^{K} Q^K_{\le k}P_+^{T\cap K}P_+^{S}P_-^{K_1}P_-^{K_2}R_E^{K}P_-^{\partial^\Lambda_{in} K},\\ & \quad Z:=P_-^{\partial_{ex}^\Lambda [K]_1} R_E^{\left( [K]_1^\Lambda \right)^c}P_+^{[j]^\Lambda_r\cap{\left( [K]_1^\Lambda \right)^c}}Q^{{\left( [K]_1^\Lambda \right)^c}}_{\le k}\chi_N^{{\left( [K]_1^\Lambda \right)^c}}. \end{aligned}\end{align} $$
Proceeding exactly as in (4.11)–(4.12), we get
 $$ \begin{align}\begin{aligned} \mathbb E_{\left( [K]_1^\Lambda \right)^c}\left( \left\lVert Z \right\rVert_{HS}^s \right) \le C_k^s\Big({ \left\lvert \Lambda \right\rvert^{\xi_k} \mathrm{e}^{-sm_0 (r-\gamma -d_\gamma)}+ \sum_{p=0}^{r-(\gamma +d_\gamma)-2} \mathrm{e}^{-sm_0\left( r-p-(\gamma +d_\gamma) -3 \right)_+} f_N^\Lambda(p)}\Big). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E_{\left( [K]_1^\Lambda \right)^c}\left( \left\lVert Z \right\rVert_{HS}^s \right) \le C_k^s\Big({ \left\lvert \Lambda \right\rvert^{\xi_k} \mathrm{e}^{-sm_0 (r-\gamma -d_\gamma)}+ \sum_{p=0}^{r-(\gamma +d_\gamma)-2} \mathrm{e}^{-sm_0\left( r-p-(\gamma +d_\gamma) -3 \right)_+} f_N^\Lambda(p)}\Big). \end{aligned}\end{align} $$
We estimate
![]() $E\left \lVert Y \right \rVert ^{s}$
similarly to (4.20)–(4.28). We have
$E\left \lVert Y \right \rVert ^{s}$
similarly to (4.20)–(4.28). We have
We consider first the case
![]() $x=x_i\in \partial _{in}{\left ( [K]_1^\Lambda \right )^c}K_i$
,
$x=x_i\in \partial _{in}{\left ( [K]_1^\Lambda \right )^c}K_i$
,
![]() $i\in \left \{ 1,2 \right \}$
, and
$i\in \left \{ 1,2 \right \}$
, and
![]() $i'=\left \{ 1,2 \right \}\setminus \left \{ i \right \}$
. Using (3.74), we can further decompose
$i'=\left \{ 1,2 \right \}\setminus \left \{ i \right \}$
. Using (3.74), we can further decompose
![]() $Y_x$
as
$Y_x$
as
 $$ \begin{align}\begin{aligned} Y_{x_i} =\sum_{ \nu\in \sigma (H^{K_{i'}})\cap [1- \frac{1}{\Delta},\infty)} Y_{x_i,\nu}, \quad Y_{x_i,\nu}= P_+^{S} P_-^{K_{i'}} \left( R_{E-\nu}^{K_i}\otimes \pi_{\kappa_\nu} \right)\mathcal{N}_x. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} Y_{x_i} =\sum_{ \nu\in \sigma (H^{K_{i'}})\cap [1- \frac{1}{\Delta},\infty)} Y_{x_i,\nu}, \quad Y_{x_i,\nu}= P_+^{S} P_-^{K_{i'}} \left( R_{E-\nu}^{K_i}\otimes \pi_{\kappa_\nu} \right)\mathcal{N}_x. \end{aligned}\end{align} $$
Note that
 $$ \begin{align}\begin{aligned} \left\lVert Y_{x_i} \right\rVert=\max_\nu\left\lVert Y_{{x_i} ,\nu} \right\rVert\le \sum_{ \nu\in \sigma (H^{K_{i'}})\cap [1- \frac{1}{\Delta},k(1- \frac{1}{\Delta}))} \left\lVert Y_{{x_i} ,\nu} \right\rVert+\max_{ \nu\in \sigma (H^{K_{i'}})\cap [k(1- \frac{1}{\Delta}),\infty)} \left\lVert Y_{{x_i} ,\nu} \right\rVert. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\lVert Y_{x_i} \right\rVert=\max_\nu\left\lVert Y_{{x_i} ,\nu} \right\rVert\le \sum_{ \nu\in \sigma (H^{K_{i'}})\cap [1- \frac{1}{\Delta},k(1- \frac{1}{\Delta}))} \left\lVert Y_{{x_i} ,\nu} \right\rVert+\max_{ \nu\in \sigma (H^{K_{i'}})\cap [k(1- \frac{1}{\Delta}),\infty)} \left\lVert Y_{{x_i} ,\nu} \right\rVert. \end{aligned}\end{align} $$
Clearly, we can bound
For
![]() $\nu \ge 1- \frac {1}{\Delta }$
, we have
$\nu \ge 1- \frac {1}{\Delta }$
, we have
![]() $E-\nu \in I_{\le k-1} $
for
$E-\nu \in I_{\le k-1} $
for
![]() $E\in I_{\le k}$
(recall (2.14)). For
$E\in I_{\le k}$
(recall (2.14)). For
![]() $\nu \in \sigma (H^{K_{i'}})\cap [1- \frac {1}{\Delta },k(1- \frac {1}{\Delta })) $
, we use the induction hypothesis for Theorem 2.4 and the statistical independence of
$\nu \in \sigma (H^{K_{i'}})\cap [1- \frac {1}{\Delta },k(1- \frac {1}{\Delta })) $
, we use the induction hypothesis for Theorem 2.4 and the statistical independence of
![]() $H^{K_{i'}}$
and
$H^{K_{i'}}$
and
![]() $\left \{ \omega _i \right \}_{i\in K_i}$
to conclude that
$\left \{ \omega _i \right \}_{i\in K_i}$
to conclude that
For
![]() $\nu \in \sigma (H^{K_{i'}})\cap [k(1- \frac {1}{\Delta }),\infty )$
,
$\nu \in \sigma (H^{K_{i'}})\cap [k(1- \frac {1}{\Delta }),\infty )$
,
![]() $E-\nu \le \frac 34 \left ( 1- \tfrac {1}{\Delta } \right )$
, and in this case,
$E-\nu \le \frac 34 \left ( 1- \tfrac {1}{\Delta } \right )$
, and in this case,
so it follows from (3.23) with
![]() $k=0$
that
$k=0$
that
Using (4.37), (4.39), (4.40) and (3.27), we get
Combining (4.35) and (4.41) and recalling
![]() $\left \lvert \partial _{in}^\Lambda K_i \right \rvert \le 4$
, we get
$\left \lvert \partial _{in}^\Lambda K_i \right \rvert \le 4$
, we get
Combining (4.33), (4.34) and (4.42), we get
 $$ \begin{align}\begin{aligned} G^{\left(a,\gamma\right)}_3(r)\le C_k \left( \lambda \Delta^2 \right)^{-s}\mathrm{e}^{- \theta^\prime_{k-1} \gamma} \Big({ \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-s \theta^\prime_{k-1} r}+ \sum_{p=0}^{r } \mathrm{e}^{-s \theta^\prime_{k-1} \left( r-p \right)}f_N^\Lambda(p) }\Big). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} G^{\left(a,\gamma\right)}_3(r)\le C_k \left( \lambda \Delta^2 \right)^{-s}\mathrm{e}^{- \theta^\prime_{k-1} \gamma} \Big({ \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-s \theta^\prime_{k-1} r}+ \sum_{p=0}^{r } \mathrm{e}^{-s \theta^\prime_{k-1} \left( r-p \right)}f_N^\Lambda(p) }\Big). \end{aligned}\end{align} $$
It follows from (4.32) and (4.43) that
 $$ \begin{align}\begin{aligned} G_3(r) \le C_k \left( \lambda \Delta^2 \right)^{-s} \mathrm{e}^{-\widehat m N}\Big({ \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-s\theta^\prime_{k-1}r}+ \sum_{p=0}^{r} \mathrm{e}^{-s \theta^\prime_{k-1} \left( r-p \right)}f_N^\Lambda(p) }\Big). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} G_3(r) \le C_k \left( \lambda \Delta^2 \right)^{-s} \mathrm{e}^{-\widehat m N}\Big({ \left\lvert \Lambda \right\rvert^{2sk+2} \mathrm{e}^{-s\theta^\prime_{k-1}r}+ \sum_{p=0}^{r} \mathrm{e}^{-s \theta^\prime_{k-1} \left( r-p \right)}f_N^\Lambda(p) }\Big). \end{aligned}\end{align} $$
Putting together (4.7), (4.13), (4.30) and (4.44), we obtain (4.6).
We can now prove Lemma 4.1.
Proof of Lemma 4.1
For
![]() $\Lambda \subset \mathbb Z$
finite,
$\Lambda \subset \mathbb Z$
finite,
![]() $E\in I_{\le k}$
,
$E\in I_{\le k}$
,
![]() $N\in \mathbb N$
, and
$N\in \mathbb N$
, and
![]() $r\in {\mathbb {N}}^0$
, we set
$r\in {\mathbb {N}}^0$
, we set
Note that
![]() $f^\Lambda _N(r)$
is monotone increasing in
$f^\Lambda _N(r)$
is monotone increasing in
![]() $\Lambda $
, and it follows from (3.33) that
$\Lambda $
, and it follows from (3.33) that
Moreover, if
![]() $8kN \ge r$
, it follows from (3.49) that
$8kN \ge r$
, it follows from (3.49) that
If
![]() $8kN < r$
, we use Lemma 4.2. Since this lemma holds for arbitrary finite subsets of
$8kN < r$
, we use Lemma 4.2. Since this lemma holds for arbitrary finite subsets of
![]() $\mathbb Z$
, it follows from (4.6) that for
$\mathbb Z$
, it follows from (4.6) that for
![]() $8kN < r$
, we have
$8kN < r$
, we have
 $$ \begin{align} f_N^\Lambda(r) \le C_k \left( \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-m_k r} + \mathrm{e}^{- m_k N} \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} f_N^\Lambda(p) \right), \end{align} $$
$$ \begin{align} f_N^\Lambda(r) \le C_k \left( \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-m_k r} + \mathrm{e}^{- m_k N} \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} f_N^\Lambda(p) \right), \end{align} $$
for all
![]() $\Lambda \subset \mathbb Z$
finite. Combining with (4.47), we get (with possibly slightly different constants C,
$\Lambda \subset \mathbb Z$
finite. Combining with (4.47), we get (with possibly slightly different constants C,
![]() $m_k>0$
,
$m_k>0$
,
![]() $\zeta _k>0$
)
$\zeta _k>0$
)
 $$ \begin{align}\begin{aligned} f^\Lambda(r) \le \sum_{N=1} ^{\left\lvert \Lambda \right\rvert} f_N^\Lambda(r) \le C\left( \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-m_k r} + \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} f^\Lambda(r) \le \sum_{N=1} ^{\left\lvert \Lambda \right\rvert} f_N^\Lambda(r) \le C\left( \left\lvert \Lambda \right\rvert^{\zeta_k} \mathrm{e}^{-m_k r} + \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} \right). \end{aligned}\end{align} $$
The proof can now be completed by a standard subharmonicity argument. Let
![]() $h^\Lambda (r)= f^\Lambda (r) - 2C\left \lvert \Lambda \right \rvert ^{{\zeta _k}} \mathrm {e}^{-m_k \frac r2}$
, and take
$h^\Lambda (r)= f^\Lambda (r) - 2C\left \lvert \Lambda \right \rvert ^{{\zeta _k}} \mathrm {e}^{-m_k \frac r2}$
, and take
![]() $\Delta \ge \Delta _0$
and
$\Delta \ge \Delta _0$
and
![]() $\lambda \ge \lambda _0$
such that
$\lambda \ge \lambda _0$
such that
 $$ \begin{align}\begin{aligned} 2C \left( \lambda \Delta^2 \right)^{-s} \sum_{q=-\infty}^\infty \mathrm{e}^{-m_k \frac {\left\lvert q \right\rvert} 2}\le1. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} 2C \left( \lambda \Delta^2 \right)^{-s} \sum_{q=-\infty}^\infty \mathrm{e}^{-m_k \frac {\left\lvert q \right\rvert} 2}\le1. \end{aligned}\end{align} $$
Then (4.49) implies that
 $$ \begin{align}\begin{aligned} h^\Lambda(r) &\le C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \mathrm{e}^{-m_k r}- 2C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \mathrm{e}^{-m_k \frac r2}\\ & \qquad + C \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} \left( h^\Lambda(p)+ 2C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \mathrm{e}^{-m_k \frac p2} \right)\\ & \le C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \left( \mathrm{e}^{-m_k r}-\mathrm{e}^{-m_k \frac r2} \right)+C \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} h^\Lambda(p), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} h^\Lambda(r) &\le C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \mathrm{e}^{-m_k r}- 2C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \mathrm{e}^{-m_k \frac r2}\\ & \qquad + C \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} \left( h^\Lambda(p)+ 2C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \mathrm{e}^{-m_k \frac p2} \right)\\ & \le C\left\lvert \Lambda \right\rvert^{{\zeta_k}} \left( \mathrm{e}^{-m_k r}-\mathrm{e}^{-m_k \frac r2} \right)+C \left( \lambda \Delta^2 \right)^{-s} \sum_{p=0}^{r} \mathrm{e}^{-m_k \left( r-p \right)} h^\Lambda(p), \end{aligned}\end{align} $$
for all
![]() $r\in {\mathbb {N}}^0$
. In addition, it follows from (4.46) that
$r\in {\mathbb {N}}^0$
. In addition, it follows from (4.46) that
We claim that
![]() $R\le 0$
, which implies that (4.4) holds (with different constants), finishing the proof of Lemma 4.1. Indeed, suppose that
$R\le 0$
, which implies that (4.4) holds (with different constants), finishing the proof of Lemma 4.1. Indeed, suppose that
![]() $R>0$
. Then it follows from (4.51) and (4.50) that
$R>0$
. Then it follows from (4.51) and (4.50) that
 $$ \begin{align}\begin{aligned} R\le C \left( \lambda \Delta^2 \right)^{-s} \sup_{r\in{\mathbb{N}}^0}\left( \sum_{p=0}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_k\left\lvert r-p \right\rvert} \right) R \le C \left( \lambda \Delta^2 \right)^{-s} \left( \sum_{q=-\infty}^\infty \mathrm{e}^{-m_k\frac {\left\lvert q \right\rvert} 2} \right)R \le \tfrac 12 R, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} R\le C \left( \lambda \Delta^2 \right)^{-s} \sup_{r\in{\mathbb{N}}^0}\left( \sum_{p=0}^{\left\lvert \Lambda \right\rvert}\mathrm{e}^{-m_k\left\lvert r-p \right\rvert} \right) R \le C \left( \lambda \Delta^2 \right)^{-s} \left( \sum_{q=-\infty}^\infty \mathrm{e}^{-m_k\frac {\left\lvert q \right\rvert} 2} \right)R \le \tfrac 12 R, \end{aligned}\end{align} $$
a contradiction.
The proof of Theorem 2.4 is complete.
5 Quasi-locality in expectation
In this section, we prove Corollary 2.6. To do so, we first extract from Theorem 2.4 a probabilistic statement (cf. [Reference Elgart, Tautenhahn and Veselić20, Proposition 5.1] and [Reference Elgart, Klein and Stolz19, Lemma 7.2]).
We fix
![]() $k\in \mathbb N$
and let
$k\in \mathbb N$
and let
![]() $s, \theta _k, \xi _k$
be as in (2.17), slightly modified so (2.17) holds with
$s, \theta _k, \xi _k$
be as in (2.17), slightly modified so (2.17) holds with
![]() $\rho ^\Lambda (A,B)$
substituted for
$\rho ^\Lambda (A,B)$
substituted for
![]() $\operatorname {\mathrm {dist}}_\Lambda (A,B^c)$
(recall (3.6)).
$\operatorname {\mathrm {dist}}_\Lambda (A,B^c)$
(recall (3.6)).
We fix a finite subset
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathbb Z$
. Given
$\mathbb Z$
. Given
![]() $\emptyset \ne K\subset \Lambda $
, we let
$\emptyset \ne K\subset \Lambda $
, we let
![]() $H^{K^\prime }$
be the restriction of
$H^{K^\prime }$
be the restriction of
![]() $H^K$
to
$H^K$
to
![]() $\operatorname {\mathrm {Ran}} P_-^K=\operatorname {\mathrm {Ran}} \chi _{\mathbb N}(\mathcal {N}_K)$
,
$\operatorname {\mathrm {Ran}} P_-^K=\operatorname {\mathrm {Ran}} \chi _{\mathbb N}(\mathcal {N}_K)$
,
![]() $K^c=\Lambda \setminus K$
(we allow
$K^c=\Lambda \setminus K$
(we allow
![]() $K^c=\emptyset $
), and consider
$K^c=\emptyset $
), and consider
![]() $H^{{K^\prime ,K^c}} =H^{K^\prime }+ H^{K^c} $
,
$H^{{K^\prime ,K^c}} =H^{K^\prime }+ H^{K^c} $
,
![]() $ \Gamma ^{{K^\prime ,K^c}} =H^\Lambda -H^{{K^\prime ,K^c}} $
,
$ \Gamma ^{{K^\prime ,K^c}} =H^\Lambda -H^{{K^\prime ,K^c}} $
,
![]() $R_E^{{K^\prime ,K^c}} =(H^{{K^\prime ,K^c}} -E)^{-1}$
, operators on
$R_E^{{K^\prime ,K^c}} =(H^{{K^\prime ,K^c}} -E)^{-1}$
, operators on
![]() $ \operatorname {\mathrm {Ran}} P_-^K \oplus \mathcal {H}_{K^c}$
. Given an interval I and an operator H, we set
$ \operatorname {\mathrm {Ran}} P_-^K \oplus \mathcal {H}_{K^c}$
. Given an interval I and an operator H, we set
![]() $\sigma _I(H)=\sigma (H)\cap I$
.
$\sigma _I(H)=\sigma (H)\cap I$
.
We start by proving Wegner-like estimates for the XXZ model.
Lemma 5.1. Let
![]() $\emptyset \ne K\subset \Lambda $
.
$\emptyset \ne K\subset \Lambda $
.
-
1. Consider the open interval
 $I\subset I_k$
. Then (5.1)
$I\subset I_k$
. Then (5.1) $$ \begin{align}\begin{aligned} \mathbb P_K \left\{ \sigma_I(H^{{K^\prime,K^c}} ) \ne \emptyset \right\} \le C_k \lambda^{-1} \left\lvert I \right\rvert \left\lvert \Lambda \right\rvert^{2k+1}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb P_K \left\{ \sigma_I(H^{{K^\prime,K^c}} ) \ne \emptyset \right\} \le C_k \lambda^{-1} \left\lvert I \right\rvert \left\lvert \Lambda \right\rvert^{2k+1}. \end{aligned}\end{align} $$
-
2. Let
 $0< \delta < \frac 1 4{\left ( 1- \frac {1}{\Delta } \right )}$
. Then (recall (2.14)) (5.2)
$0< \delta < \frac 1 4{\left ( 1- \frac {1}{\Delta } \right )}$
. Then (recall (2.14)) (5.2) $$ \begin{align}\begin{aligned} \mathbb P\left\{ \operatorname{\mathrm{dist}} \left\{ \sigma_{\widehat I_k}(H^{{K^\prime,K^c} }), \sigma_{\widehat I_k} (H^{K^c}) \right\}<\delta \right\}\le C_k \lambda^{-1} \delta \left\lvert \Lambda \right\rvert^{4k+1}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb P\left\{ \operatorname{\mathrm{dist}} \left\{ \sigma_{\widehat I_k}(H^{{K^\prime,K^c} }), \sigma_{\widehat I_k} (H^{K^c}) \right\}<\delta \right\}\le C_k \lambda^{-1} \delta \left\lvert \Lambda \right\rvert^{4k+1}. \end{aligned}\end{align} $$
Proof. To prove Part (i), recall (3.27) (it applies to
![]() $H^{\left ( K^\prime ,K^c \right )} $
), and let
$H^{\left ( K^\prime ,K^c \right )} $
), and let
![]() $E_1 \le E_2 \le \ldots $
be the at most
$E_1 \le E_2 \le \ldots $
be the at most
![]() $Ck\left \lvert \Lambda \right \rvert ^{2k}$
eigenvalues of
$Ck\left \lvert \Lambda \right \rvert ^{2k}$
eigenvalues of
![]() $H^{{K^\prime ,K^c} }$
in
$H^{{K^\prime ,K^c} }$
in
![]() $\widehat I_{\le k}$
, counted with multiplicity, which we consider as functions of
$\widehat I_{\le k}$
, counted with multiplicity, which we consider as functions of
![]() $ \omega _{K}$
for fixed
$ \omega _{K}$
for fixed
![]() $\omega _{K^c}$
. Since
$\omega _{K^c}$
. Since
![]() $\mathcal {N}_K \ge 1$
, each
$\mathcal {N}_K \ge 1$
, each
![]() $E_n( \omega _{K})$
is a monotone function on
$E_n( \omega _{K})$
is a monotone function on
![]() $\mathbb R^{\left \lvert K \right \rvert }$
. Let
$\mathbb R^{\left \lvert K \right \rvert }$
. Let
![]() $e=(1,1,\ldots ,1)\in \mathbb R^{\left \lvert K \right \rvert }$
. We have
$e=(1,1,\ldots ,1)\in \mathbb R^{\left \lvert K \right \rvert }$
. We have
![]() $E_n(\omega _{K}+te) - E_n(\omega _{K}) \ge \lambda t$
for all
$E_n(\omega _{K}+te) - E_n(\omega _{K}) \ge \lambda t$
for all
![]() $t>0$
and all n by the min-max principle, so we can apply Stollmann’s Lemma [Reference Stollmann46] to get
$t>0$
and all n by the min-max principle, so we can apply Stollmann’s Lemma [Reference Stollmann46] to get
In view of (3.27), (5.1) follows using (5.3) for each one of the eigenvalues
![]() $E_n$
.
$E_n$
.
Part (ii) follows from Part (i) and (3.27) for
![]() $H^{K^c}$
, since the random variables
$H^{K^c}$
, since the random variables
![]() $\omega _{K}$
and
$\omega _{K}$
and
![]() $\omega _{K^c}$
are independent.
$\omega _{K^c}$
are independent.
Let
![]() $E\in \mathbb R$
,
$E\in \mathbb R$
,
![]() $m>0$
,
$m>0$
,
![]() $ r\in \mathbb N$
,
$ r\in \mathbb N$
,
![]() $\emptyset \ne K\subset \Lambda $
, and let
$\emptyset \ne K\subset \Lambda $
, and let
![]() $H^\sharp $
denote either
$H^\sharp $
denote either
![]() $H^K$
or
$H^K$
or
![]() $H^{\left ( K^\prime ,K^c \right )}$
. Then the operator
$H^{\left ( K^\prime ,K^c \right )}$
. Then the operator
![]() $H^{K^\sharp }$
is said to be
$H^{K^\sharp }$
is said to be
![]() $(m,E,r)$
-regular if
$(m,E,r)$
-regular if
 $$ \begin{align}\begin{aligned} &F^{K^\sharp}_E \le \mathrm{e}^{-mr} \quad\text{and}\quad \operatorname{\mathrm{dist}}(E,\sigma (H^{K^\sharp}))>\mathrm{e}^{-mr} ,\\ & \text{where}\quad F^{K^\sharp}_E= \max_{i\in K}F^{K^\sharp}_E(i) \quad\text{with}\quad F^{K^\sharp}_E (i)=\left\lVert \mathcal{N}_i R^{K^\sharp}_E P_+^{[i]_r^K} \right\rVert. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &F^{K^\sharp}_E \le \mathrm{e}^{-mr} \quad\text{and}\quad \operatorname{\mathrm{dist}}(E,\sigma (H^{K^\sharp}))>\mathrm{e}^{-mr} ,\\ & \text{where}\quad F^{K^\sharp}_E= \max_{i\in K}F^{K^\sharp}_E(i) \quad\text{with}\quad F^{K^\sharp}_E (i)=\left\lVert \mathcal{N}_i R^{K^\sharp}_E P_+^{[i]_r^K} \right\rVert. \end{aligned}\end{align} $$
In addition, consider the probabilistic event
Lemma 5.2. Let
![]() $\emptyset \ne K\subsetneq \Lambda $
, and let
$\emptyset \ne K\subsetneq \Lambda $
, and let
![]() $r\in \mathbb N$
,
$r\in \mathbb N$
,
![]() $r\ge \frac {18} {\theta _k}$
. Then
$r\ge \frac {18} {\theta _k}$
. Then
Proof. Let
![]() $\emptyset \ne K\subsetneq \Lambda $
,
$\emptyset \ne K\subsetneq \Lambda $
,
![]() $r\ge \tfrac {18} {{\theta _k}}$
, and set
$r\ge \tfrac {18} {{\theta _k}}$
, and set
![]() $m= \frac {{\theta _k}} 9$
, so
$m= \frac {{\theta _k}} 9$
, so
![]() $\mathrm {e}^{mr}\ge 4$
. Let S denote either the pair
$\mathrm {e}^{mr}\ge 4$
. Let S denote either the pair
![]() ${{K^\prime ,K^c}}$
or
${{K^\prime ,K^c}}$
or
![]() ${K^c}$
, and let
${K^c}$
, and let
![]() $S^\prime =K$
if
$S^\prime =K$
if
![]() $S={{K^\prime ,K^c}} $
, or
$S={{K^\prime ,K^c}} $
, or
![]() $S^\prime =K^c$
if
$S^\prime =K^c$
if
![]() $S= K^c$
. Consider the (random) energy sets
$S= K^c$
. Consider the (random) energy sets
and the event
Using (2.17), we get
 $$ \begin{align}\begin{aligned} \mathbb P\left\{ \mathcal{J}_S \right\} & \le \mathrm{e}^{5mr} \, \mathbb E \left\{ \left\lvert J_S \right\rvert \right\} \le \mathrm{e}^{5mr} \, \mathbb E \left\{ \int_{I_k} \mathrm{e}^{2s mr} \left( F^{S}_E \right)^s \ dE \right\}\\ & \le \mathrm{e}^{7 mr} \int_{I_k} \sum_{i \in S^\prime} \mathbb E\left\{ \left( F^{S}_E(i) \right)^s \right\}\ dE \le C_k \left\lvert \Lambda \right\rvert^{\xi_k+1} e^{-2mr}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb P\left\{ \mathcal{J}_S \right\} & \le \mathrm{e}^{5mr} \, \mathbb E \left\{ \left\lvert J_S \right\rvert \right\} \le \mathrm{e}^{5mr} \, \mathbb E \left\{ \int_{I_k} \mathrm{e}^{2s mr} \left( F^{S}_E \right)^s \ dE \right\}\\ & \le \mathrm{e}^{7 mr} \int_{I_k} \sum_{i \in S^\prime} \mathbb E\left\{ \left( F^{S}_E(i) \right)^s \right\}\ dE \le C_k \left\lvert \Lambda \right\rvert^{\xi_k+1} e^{-2mr}. \end{aligned}\end{align} $$
We now consider the (random) energy set
and claim that
![]() $D_S \subset Y_S$
on the complementary event
$D_S \subset Y_S$
on the complementary event
![]() $\mathcal {J}_S^c= \left \{ \left \lvert J_S \right \rvert \le e^{-5mr} \right \} $
.
$\mathcal {J}_S^c= \left \{ \left \lvert J_S \right \rvert \le e^{-5mr} \right \} $
.
To see this, suppose
![]() $\left \lvert J_S \right \rvert \le e^{-5mr}$
and
$\left \lvert J_S \right \rvert \le e^{-5mr}$
and
![]() $E\in D_S\setminus Y_S$
. Since
$E\in D_S\setminus Y_S$
. Since
![]() $E\in D_S$
, there exists
$E\in D_S$
, there exists
![]() $i\in S^\prime $
such that
$i\in S^\prime $
such that
![]() $F_E^S(i)> e^{-mr}$
. Let
$F_E^S(i)> e^{-mr}$
. Let
![]() $E^\prime \in I_k$
such that
$E^\prime \in I_k$
such that
![]() $\left \lvert E^\prime -E \right \rvert \le 2 e^{-5mr}$
. Using
$\left \lvert E^\prime -E \right \rvert \le 2 e^{-5mr}$
. Using
![]() $E \in Y_S$
, we get
$E \in Y_S$
, we get
![]() $\operatorname {\mathrm {dist}}(E^\prime , \sigma (H^S)> e^{-mr}- 2 e^{-5mr}\ge \frac 1 2 e^{-mr}$
. Thus, using the resolvent identity and
$\operatorname {\mathrm {dist}}(E^\prime , \sigma (H^S)> e^{-mr}- 2 e^{-5mr}\ge \frac 1 2 e^{-mr}$
. Thus, using the resolvent identity and
![]() $r\ge \frac {18} {\theta _k}$
, we have
$r\ge \frac {18} {\theta _k}$
, we have
It follows that
![]() $[E- 2 e^{-5mr}, E+ 2 e^{-5mr}]\cap I_k \subset J_S$
. Since
$[E- 2 e^{-5mr}, E+ 2 e^{-5mr}]\cap I_k \subset J_S$
. Since
![]() $\left \lvert I_k \right \rvert \ge 2 e^{-5mr}$
as
$\left \lvert I_k \right \rvert \ge 2 e^{-5mr}$
as
![]() $r\ge \frac {18} {\theta _k}$
, we conclude that
$r\ge \frac {18} {\theta _k}$
, we conclude that
![]() $\left \lvert J_S \right \rvert \ge 2 e^{-5mr}> e^{-5mr}$
, a contradiction.
$\left \lvert J_S \right \rvert \ge 2 e^{-5mr}> e^{-5mr}$
, a contradiction.
We proved that
![]() $\left \lvert J_S \right \rvert \le e^{-5mr} $
implies
$\left \lvert J_S \right \rvert \le e^{-5mr} $
implies
![]() $ D_S \subset Y_S$
, so
$ D_S \subset Y_S$
, so
![]() $\widehat Y_S= I_k\setminus Y_S\subset I_k\setminus D_S$
. In particular, outside the event
$\widehat Y_S= I_k\setminus Y_S\subset I_k\setminus D_S$
. In particular, outside the event
![]() $\mathcal {J}_S$
,
$\mathcal {J}_S$
,
![]() $E\in \widehat Y_S$
implies that
$E\in \widehat Y_S$
implies that
![]() $H^S$
is
$H^S$
is
![]() $(m,E,r)$
-regular.
$(m,E,r)$
-regular.
We now consider the event
 $$ \begin{align}\begin{aligned} \mathcal{E}_K&= \left\{ I_k\setminus(\widehat Y_{{K^\prime,K^c}} \cup \widehat Y_{K^c})\ne \emptyset \right\}= \left\{ I_k \cap Y_{{K^\prime,K^c}}\cap Y_{K^c}\ne \emptyset \right\} \\ & \subset \left\{ \operatorname{\mathrm{dist}} \left\{ \sigma_{\widehat I_k}(H^{{{K^\prime,K^c}} }), \sigma_{\widehat I_k} (H^{K^c}) \right\}\le 2 e^{-mr} \right\} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathcal{E}_K&= \left\{ I_k\setminus(\widehat Y_{{K^\prime,K^c}} \cup \widehat Y_{K^c})\ne \emptyset \right\}= \left\{ I_k \cap Y_{{K^\prime,K^c}}\cap Y_{K^c}\ne \emptyset \right\} \\ & \subset \left\{ \operatorname{\mathrm{dist}} \left\{ \sigma_{\widehat I_k}(H^{{{K^\prime,K^c}} }), \sigma_{\widehat I_k} (H^{K^c}) \right\}\le 2 e^{-mr} \right\} \end{aligned}\end{align} $$
and note that it follows from Lemma 5.1(ii) that
Since
and on the complementary event, we have
![]() $I_k= \widehat Y_{{K^\prime ,K^c}} \cup \widehat Y_{K^c}$
, so for
$I_k= \widehat Y_{{K^\prime ,K^c}} \cup \widehat Y_{K^c}$
, so for
![]() $E\in I_k$
, either
$E\in I_k$
, either
![]() $H^{{K^\prime ,K^c}}$
or
$H^{{K^\prime ,K^c}}$
or
![]() $H^{K^c}$
is
$H^{K^c}$
is
![]() $(m,E,r)$
-regular, the lemma is proved.
$(m,E,r)$
-regular, the lemma is proved.
Proof of Corollary 2.6
Let
![]() $A\subset B\subset \Lambda $
, A connected in
$A\subset B\subset \Lambda $
, A connected in
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $r=\rho ^\Lambda (A,B)$
, and recall
$r=\rho ^\Lambda (A,B)$
, and recall
![]() $\left \lVert P_-^{A}f(H^\Lambda ) P_+^{B} \right \rVert \le \left \lVert P_-^{A}f(H^\Lambda ) P_+^{[A]^\Lambda _r} \right \rVert $
.
$\left \lVert P_-^{A}f(H^\Lambda ) P_+^{B} \right \rVert \le \left \lVert P_-^{A}f(H^\Lambda ) P_+^{[A]^\Lambda _r} \right \rVert $
.
We set
 $$ \begin{align}\begin{aligned} \Theta^\Lambda(A,r)& =\sup_{\substack{f\in B(I_{\le k}):\\\|f\|_\infty\le1}}\left\lVert P_-^{A}f(H^\Lambda) P_+^{[A]^\Lambda_r} \right\rVert\le 1. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \Theta^\Lambda(A,r)& =\sup_{\substack{f\in B(I_{\le k}):\\\|f\|_\infty\le1}}\left\lVert P_-^{A}f(H^\Lambda) P_+^{[A]^\Lambda_r} \right\rVert\le 1. \end{aligned}\end{align} $$
To estimate
![]() $\mathbb E\left \{ \Theta ^\Lambda (A,r) \right \}$
, note that
$\mathbb E\left \{ \Theta ^\Lambda (A,r) \right \}$
, note that
 $$ \begin{align}\begin{aligned} \Theta^{\Lambda}(A,r) \le \sum_{E\in \sigma_{I_k}(H^{\Lambda})} \left\lVert {P_-^{A}} P_{\left\{ E \right\}}P_+^{[A]^\Lambda_r} \right\rVert, \quad\text{where}\quad P_{\left\{ E \right\}}= \chi_{\left\{ E \right\}}(H^\Lambda). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \Theta^{\Lambda}(A,r) \le \sum_{E\in \sigma_{I_k}(H^{\Lambda})} \left\lVert {P_-^{A}} P_{\left\{ E \right\}}P_+^{[A]^\Lambda_r} \right\rVert, \quad\text{where}\quad P_{\left\{ E \right\}}= \chi_{\left\{ E \right\}}(H^\Lambda). \end{aligned}\end{align} $$
The spectrum of
![]() $H^\Lambda $
is simple almost surely, as commented in [Reference Elgart, Klein and Stolz19, Section 3], so we assume this on what follows for simplicity. (Otherwise, we just need to label the eigenvalues taking into account multiplicity.) For
$H^\Lambda $
is simple almost surely, as commented in [Reference Elgart, Klein and Stolz19, Section 3], so we assume this on what follows for simplicity. (Otherwise, we just need to label the eigenvalues taking into account multiplicity.) For
![]() $E\in \sigma (H^\Lambda )$
, we let
$E\in \sigma (H^\Lambda )$
, we let
![]() $\phi _E$
denote the corresponding eigenfunction, and let
$\phi _E$
denote the corresponding eigenfunction, and let
![]() $N_E\in {\mathbb {N}}^0$
be given by
$N_E\in {\mathbb {N}}^0$
be given by
![]() $\mathcal {N}_\Lambda \phi _E= N_E \phi _E$
.
$\mathcal {N}_\Lambda \phi _E= N_E \phi _E$
.
For
![]() $E\in I_k$
, we have
$E\in I_k$
, we have
 $$ \begin{align}\begin{aligned} P_{\left\{ E \right\}}&=\widehat R^{\Lambda}_{k,E}\left( \widehat H^\Lambda_k-E \right)P_{\left\{ E \right\}}=\widehat R^{\Lambda}_{k,E}\left( \widehat H^\Lambda_k-H^\Lambda+(H^\Lambda -E) \right)P_{\left\{ E \right\}}\\&=k\left( 1- \tfrac{1}{\Delta} \right)\widehat R^{\Lambda}_{k,E}\,Q_{\le k}^{\Lambda}P_{\left\{ E \right\}}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_{\left\{ E \right\}}&=\widehat R^{\Lambda}_{k,E}\left( \widehat H^\Lambda_k-E \right)P_{\left\{ E \right\}}=\widehat R^{\Lambda}_{k,E}\left( \widehat H^\Lambda_k-H^\Lambda+(H^\Lambda -E) \right)P_{\left\{ E \right\}}\\&=k\left( 1- \tfrac{1}{\Delta} \right)\widehat R^{\Lambda}_{k,E}\,Q_{\le k}^{\Lambda}P_{\left\{ E \right\}}. \end{aligned}\end{align} $$
Let
![]() $r \ge R_k = 6k(\lceil \frac {18} {\theta _k} \rceil +2)$
. Using (A.7) and (3.23), we obtain
$r \ge R_k = 6k(\lceil \frac {18} {\theta _k} \rceil +2)$
. Using (A.7) and (3.23), we obtain
 $$ \begin{align}\begin{aligned} {\left\lVert {P_-^{A}}P_{\left\{ E \right\}} P_+^{[A]^\Lambda_r} \right\rVert}&=k \left( 1- \tfrac{1}{\Delta} \right) {\left\lVert {P_-^{A}}\widehat R^{\Lambda}_{k,E}\,Q_{\le k}^{\Lambda}P_{\left\{ E \right\}} P_+^{[A]^\Lambda_r} \right\rVert}\\ & =k \left( 1- \tfrac{1}{\Delta} \right) {\left\lVert {P_-^{A}}\widehat R^{\Lambda}_{k,E}P_-^{[A]_\infty^\Lambda}\,Q_{\le k}^{\Lambda}P_{\left\{ E \right\}} P_+^{[A]^\Lambda_r} \right\rVert} \\ &\le k { \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} } {\left\lVert {P_-^{A}}\widehat R^{\Lambda}_{k,E}P_+^{[A]^\Lambda_q} \right\rVert}{\left\lVert P_-^{]A[^\Lambda_q} Q_{\le k}^{\Lambda}P_{\left\{ E \right\}}P_+^{[A]^\Lambda_r} \right\rVert} \\ &\le C_0{ \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} } \mathrm{e}^{-m_0(q)_+}{\left\lVert P_-^{]A[^\Lambda_q} Q_{\le k}^{\Lambda}P_{\left\{ E \right\}}P_+^{[A]^\Lambda_r} \right\rVert} \\ &\le 2 C_0{ \sum_{q=-\left\lvert A \right\rvert}^{r-1 - R_k}} \mathrm{e}^{-m_0(q)_+} \sum_{u\in ]A[^\Lambda_q} {\left\lVert Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{r-q-1}} \right\rVert} + C_k\left\lvert \Lambda \right\rvert \mathrm{e}^{-m_0 r}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\left\lVert {P_-^{A}}P_{\left\{ E \right\}} P_+^{[A]^\Lambda_r} \right\rVert}&=k \left( 1- \tfrac{1}{\Delta} \right) {\left\lVert {P_-^{A}}\widehat R^{\Lambda}_{k,E}\,Q_{\le k}^{\Lambda}P_{\left\{ E \right\}} P_+^{[A]^\Lambda_r} \right\rVert}\\ & =k \left( 1- \tfrac{1}{\Delta} \right) {\left\lVert {P_-^{A}}\widehat R^{\Lambda}_{k,E}P_-^{[A]_\infty^\Lambda}\,Q_{\le k}^{\Lambda}P_{\left\{ E \right\}} P_+^{[A]^\Lambda_r} \right\rVert} \\ &\le k { \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} } {\left\lVert {P_-^{A}}\widehat R^{\Lambda}_{k,E}P_+^{[A]^\Lambda_q} \right\rVert}{\left\lVert P_-^{]A[^\Lambda_q} Q_{\le k}^{\Lambda}P_{\left\{ E \right\}}P_+^{[A]^\Lambda_r} \right\rVert} \\ &\le C_0{ \sum_{q=-\left\lvert A \right\rvert}^{\left\lvert \Lambda \right\rvert} } \mathrm{e}^{-m_0(q)_+}{\left\lVert P_-^{]A[^\Lambda_q} Q_{\le k}^{\Lambda}P_{\left\{ E \right\}}P_+^{[A]^\Lambda_r} \right\rVert} \\ &\le 2 C_0{ \sum_{q=-\left\lvert A \right\rvert}^{r-1 - R_k}} \mathrm{e}^{-m_0(q)_+} \sum_{u\in ]A[^\Lambda_q} {\left\lVert Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{r-q-1}} \right\rVert} + C_k\left\lvert \Lambda \right\rvert \mathrm{e}^{-m_0 r}. \end{aligned}\end{align} $$
Let
![]() $u\in \Lambda $
and
$u\in \Lambda $
and
![]() $p\ge R_k$
. If
$p\ge R_k$
. If
![]() $8kN_E \ge p$
, it follows from (3.53)–(3.55) that
$8kN_E \ge p$
, it follows from (3.53)–(3.55) that
 $$ \begin{align}\begin{aligned} &\left\lVert \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert\le \chi_{{{\mathcal B_k^{N_E}}}},\\ &\mathbb P_\Lambda \left( {\mathcal B_k^{N_E}} \right) \le C_k \left\lvert \Lambda \right\rvert^{2k}e^{- c_\mu {N_E}}\le C_k \left\lvert \Lambda \right\rvert^{2k}\mathrm{e}^{- \frac {c_\mu}{8k}p}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &\left\lVert \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert\le \chi_{{{\mathcal B_k^{N_E}}}},\\ &\mathbb P_\Lambda \left( {\mathcal B_k^{N_E}} \right) \le C_k \left\lvert \Lambda \right\rvert^{2k}e^{- c_\mu {N_E}}\le C_k \left\lvert \Lambda \right\rvert^{2k}\mathrm{e}^{- \frac {c_\mu}{8k}p}. \end{aligned}\end{align} $$
If
![]() $p> 8k{N_E}$
, we set (cf. (4.14))
$p> 8k{N_E}$
, we set (cf. (4.14))
 $$ \begin{align}\begin{aligned} K(0)&= [u]^\Lambda _{\frac {3p}4} \quad\text{and}\quad K(a)=[ u]^\Lambda_{a \left\lfloor \frac p {6k}\right \rfloor} \; \ \text{for}\; \ a=1,2,\ldots, 3k-1,\\ S(a)& =[\partial^\Lambda K(a)]^\Lambda_{\left\lfloor \frac p {6k}\right \rfloor-1} \quad\text{for}\quad a=0,1,\ldots, 3k-1. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} K(0)&= [u]^\Lambda _{\frac {3p}4} \quad\text{and}\quad K(a)=[ u]^\Lambda_{a \left\lfloor \frac p {6k}\right \rfloor} \; \ \text{for}\; \ a=1,2,\ldots, 3k-1,\\ S(a)& =[\partial^\Lambda K(a)]^\Lambda_{\left\lfloor \frac p {6k}\right \rfloor-1} \quad\text{for}\quad a=0,1,\ldots, 3k-1. \end{aligned}\end{align} $$
Using Lemma 3.8, we get
 $$ \begin{align}\begin{aligned} {\Big\|{ \chi^\Lambda_{N_E} Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}}\Big\|} \le \sum_{a=0}^{3k-1} {\Big\| \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_u Y(a) P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}\Big\|}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\Big\|{ \chi^\Lambda_{N_E} Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}}\Big\|} \le \sum_{a=0}^{3k-1} {\Big\| \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_u Y(a) P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}\Big\|}, \end{aligned}\end{align} $$
where
![]() $Y(0)=P_+^{ \Lambda \setminus [u]^\Lambda _{\frac p2} } $
and
$Y(0)=P_+^{ \Lambda \setminus [u]^\Lambda _{\frac p2} } $
and
![]() $Y(a)=P_+^{S(a)}P_-^{K(a)}P_-^{K^c(a)}$
for
$Y(a)=P_+^{S(a)}P_-^{K(a)}P_-^{K^c(a)}$
for
![]() $a>0$
.
$a>0$
.
We now consider the event (see (5.5))
 $$ \begin{align}\begin{aligned} & \mathcal{J}_k (u,p) =\bigcap_{a=0}^{3k-1} \mathcal{F}_{k}^\Lambda (K(a), {\widehat {\theta_k}} ,\widehat p), \;\text{where}\; \widehat {\theta_k}=\tfrac {{\theta_k}} 9\;\text{and}\;\widehat p= \left\lfloor \tfrac p {6k}\right \rfloor-1\ge \tfrac {18} {{\theta_k}} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} & \mathcal{J}_k (u,p) =\bigcap_{a=0}^{3k-1} \mathcal{F}_{k}^\Lambda (K(a), {\widehat {\theta_k}} ,\widehat p), \;\text{where}\; \widehat {\theta_k}=\tfrac {{\theta_k}} 9\;\text{and}\;\widehat p= \left\lfloor \tfrac p {6k}\right \rfloor-1\ge \tfrac {18} {{\theta_k}} \end{aligned}\end{align} $$
and note that it follows from Lemma 5.2 that
For
![]() $\omega \in \mathcal {J}_k (u,p) $
and
$\omega \in \mathcal {J}_k (u,p) $
and
![]() $a\in \left \{ 0,1,\ldots , 3k-1 \right \}$
, either
$a\in \left \{ 0,1,\ldots , 3k-1 \right \}$
, either
![]() $H^{\left ( K(a), K^c(a) \right ) }$
or
$H^{\left ( K(a), K^c(a) \right ) }$
or
![]() $H^{{K^c}(a)}$
is
$H^{{K^c}(a)}$
is
![]() $({\widehat {\theta _k}} ,E,\widehat p)$
-regular (
$({\widehat {\theta _k}} ,E,\widehat p)$
-regular (
![]() ${K^c}(a)=\left ( K(a) \right )^c$
). If
${K^c}(a)=\left ( K(a) \right )^c$
). If
![]() $H^{{K^c}(a)}$
is
$H^{{K^c}(a)}$
is
![]() $({\widehat {\theta _k}} ,E,\widehat p)$
-regular, we note that
$({\widehat {\theta _k}} ,E,\widehat p)$
-regular, we note that
 $$ \begin{align}\begin{aligned} P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} &=P_{\left\{ E \right\}}\left( H^{K(a)}+H^{{K^c}(a)}-E \right) R^{{K^c}(a)}_EP_+^{[u]^\Lambda_{p}}\\ & = -P_{\left\{ E \right\}}\Gamma^{\left( K(a),K^c(a) \right)}P_-^{\partial^\Lambda_{ex} K(a)}P_+^{K(a)} R^{{K^c}(a)}_EP_+^{[u]^\Lambda_{p}} , \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} &=P_{\left\{ E \right\}}\left( H^{K(a)}+H^{{K^c}(a)}-E \right) R^{{K^c}(a)}_EP_+^{[u]^\Lambda_{p}}\\ & = -P_{\left\{ E \right\}}\Gamma^{\left( K(a),K^c(a) \right)}P_-^{\partial^\Lambda_{ex} K(a)}P_+^{K(a)} R^{{K^c}(a)}_EP_+^{[u]^\Lambda_{p}} , \end{aligned}\end{align} $$
where we have used
![]() $R^{{K^c}(a)}_EP_+^{[u]^\Lambda _{p}}=P_+^{K(a)}R^{{K^c}(a)}_EP_+^{[u]^\Lambda _{p}}$
due to
$R^{{K^c}(a)}_EP_+^{[u]^\Lambda _{p}}=P_+^{K(a)}R^{{K^c}(a)}_EP_+^{[u]^\Lambda _{p}}$
due to
![]() $K(a)\subset [u]^\Lambda _{p}$
. We deduce that
$K(a)\subset [u]^\Lambda _{p}$
. We deduce that
 $$ \begin{align}\begin{aligned} {\left\lVert \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_u Y(a) P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert}\le \left\lVert P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert\le \tfrac 1 \Delta \left\lVert P_-^{\partial_{ex}^\Lambda K(a)} R^{{K^c}(a)}_EP_+^{[u]^\Lambda_{p}\cap ({K^c}(a))} \right\rVert\le \tfrac {2\mathrm{e}^{-\widehat {\theta_k}\widehat p}} \Delta , \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\left\lVert \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_u Y(a) P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert}\le \left\lVert P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert\le \tfrac 1 \Delta \left\lVert P_-^{\partial_{ex}^\Lambda K(a)} R^{{K^c}(a)}_EP_+^{[u]^\Lambda_{p}\cap ({K^c}(a))} \right\rVert\le \tfrac {2\mathrm{e}^{-\widehat {\theta_k}\widehat p}} \Delta , \end{aligned}\end{align} $$
using (A.3), (5.4) and the definition of
![]() $K(a)$
. If
$K(a)$
. If
![]() $H^{\left ( K(a),K^c(a) \right )}$
is
$H^{\left ( K(a),K^c(a) \right )}$
is
![]() $({\widehat {\theta _k}} ,E,\widehat p)$
-regular, we use
$({\widehat {\theta _k}} ,E,\widehat p)$
-regular, we use
 $$ \begin{align}\begin{aligned} \mathcal{N}_{u}P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} &=\mathcal{N}_{u}R^{\left( K(a),K^c(a) \right)}_E\left( H^{\left( K(a),K^c(a) \right)}-E \right)P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \\ &=-\mathcal{N}_{u}R^{\left( K(a),K^c(a) \right)}_E P_-^{\partial^\Lambda K(a)}\Gamma^{\left( K(a),K^c(a) \right)}P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathcal{N}_{u}P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} &=\mathcal{N}_{u}R^{\left( K(a),K^c(a) \right)}_E\left( H^{\left( K(a),K^c(a) \right)}-E \right)P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \\ &=-\mathcal{N}_{u}R^{\left( K(a),K^c(a) \right)}_E P_-^{\partial^\Lambda K(a)}\Gamma^{\left( K(a),K^c(a) \right)}P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}. \end{aligned}\end{align} $$
Thus,
 $$ \begin{align}\begin{aligned} {\left\lVert \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_u Y(a) P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert}&\le \left\lVert \mathcal{N}_{u} Y(a)P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert\le \tfrac 1 \Delta \left\lVert \mathcal{N}_{u} Y(a)R^{\left( K(a),K^c(a) \right)}_E P_-^{\partial^\Lambda K(a)} \right\rVert\\ &\le \tfrac 1 \Delta \left\lVert P_+^{S(a)}R^{\left( K(a),K^c(a) \right)}_E P_-^{\partial^\Lambda K(a)} \right\rVert\le \tfrac 2 \Delta \mathrm{e}^{-\widehat {\theta_k}\widehat p}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\left\lVert \chi_{N_E}^\Lambda Q_{\le k}^{\Lambda}\mathcal{N}_u Y(a) P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert}&\le \left\lVert \mathcal{N}_{u} Y(a)P_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert\le \tfrac 1 \Delta \left\lVert \mathcal{N}_{u} Y(a)R^{\left( K(a),K^c(a) \right)}_E P_-^{\partial^\Lambda K(a)} \right\rVert\\ &\le \tfrac 1 \Delta \left\lVert P_+^{S(a)}R^{\left( K(a),K^c(a) \right)}_E P_-^{\partial^\Lambda K(a)} \right\rVert\le \tfrac 2 \Delta \mathrm{e}^{-\widehat {\theta_k}\widehat p}, \end{aligned}\end{align} $$
using (A.3), (5.4) and the definition of
![]() $S(a)$
.
$S(a)$
.
Combining (5.21), (5.25) and (5.27), we conclude that for
![]() $p>8kN_E$
and
$p>8kN_E$
and
![]() $\omega \in \mathcal {J}_k (u,p) $
, we have
$\omega \in \mathcal {J}_k (u,p) $
, we have
 $$ \begin{align}\begin{aligned} {\left\lVert \chi^\Lambda_{N_E} Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert} \le \tfrac {12k} \Delta \mathrm{e}^{-\widehat {\theta_k}\widehat p}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\left\lVert \chi^\Lambda_{N_E} Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert} \le \tfrac {12k} \Delta \mathrm{e}^{-\widehat {\theta_k}\widehat p}. \end{aligned}\end{align} $$
Since
 $ {\left \lVert \chi ^\Lambda _{N_E} Q_{\le k}^{\Lambda }\mathcal {N}_uP_{\left \{ E \right \}}P_+^{[u]^\Lambda _{p}} \right \rVert } \le 1$
, it follows that for
$ {\left \lVert \chi ^\Lambda _{N_E} Q_{\le k}^{\Lambda }\mathcal {N}_uP_{\left \{ E \right \}}P_+^{[u]^\Lambda _{p}} \right \rVert } \le 1$
, it follows that for
![]() $p>8kN_E $
, we have
$p>8kN_E $
, we have
 $$ \begin{align}\begin{aligned} {\left\lVert \chi^\Lambda_{N_E} Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert} \le \tfrac {12k} \Delta \mathrm{e}^{-\widehat {\theta_k}\widehat p} + \chi_{ {\mathcal{J}_k (u,p)}^c}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\left\lVert \chi^\Lambda_{N_E} Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}} \right\rVert} \le \tfrac {12k} \Delta \mathrm{e}^{-\widehat {\theta_k}\widehat p} + \chi_{ {\mathcal{J}_k (u,p)}^c}. \end{aligned}\end{align} $$
It follows that for
![]() $u\in \Lambda $
and
$u\in \Lambda $
and
![]() $p\ge R_k$
, using (5.19), (5.29) and (3.27), we conclude that
$p\ge R_k$
, using (5.19), (5.29) and (3.27), we conclude that
 $$ \begin{align}\begin{aligned} \mathbb E \Big({ \sum_{E\in \sigma_{I_k}(H^{\Lambda})}\Big\|{ Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}} }\Big\|\Big) \le C_k \left\lvert \Lambda \right\rvert^{\xi^{\prime}_k}\mathrm{e}^{- \theta^\prime_k p}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbb E \Big({ \sum_{E\in \sigma_{I_k}(H^{\Lambda})}\Big\|{ Q_{\le k}^{\Lambda}\mathcal{N}_uP_{\left\{ E \right\}}P_+^{[u]^\Lambda_{p}}} }\Big\|\Big) \le C_k \left\lvert \Lambda \right\rvert^{\xi^{\prime}_k}\mathrm{e}^{- \theta^\prime_k p}. \end{aligned}\end{align} $$
Combining with (5.16), (5.18) and (3.27), we obtain
The estimate (5.31) holds for
![]() $r\ge R_k$
. Since
$r\ge R_k$
. Since
![]() $\mathbb E\left \{ \Theta ^\Lambda (A,r) \right \}\le 1$
for all
$\mathbb E\left \{ \Theta ^\Lambda (A,r) \right \}\le 1$
for all
![]() $r\ge 0$
, it holds for all
$r\ge 0$
, it holds for all
![]() $r\ge 0$
if the constant
$r\ge 0$
if the constant
![]() $C_k$
is replaced by the constant
$C_k$
is replaced by the constant
![]() $\widetilde C_k= C_k \mathrm {e}^{ {\theta _k^\prime } \widehat R_k}$
.
$\widetilde C_k= C_k \mathrm {e}^{ {\theta _k^\prime } \widehat R_k}$
.
A Useful identities
In this appendix, we list some useful identities. Their derivations are straightforward, so we leave out the proofs.
We fix
![]() $\Lambda \subset \mathbb Z$
finite,
$\Lambda \subset \mathbb Z$
finite,
-
○ For all
 $i,j\in \Lambda $
, we have (recall (2.15)) (A.1)
$i,j\in \Lambda $
, we have (recall (2.15)) (A.1) $$ \begin{align}\begin{aligned} P_-^{\left\{ i \right\}}&=\mathcal{N}_i, \\ P_-^{\left\{ i,j \right\}}&=\mathcal{N}_i +\mathcal{N}_j -\mathcal{N}_i \mathcal{N}_j= \mathcal{N}_i\left( 1-\mathcal{N}_j \right) + \mathcal{N}_j= P_+^{\left(\left\{ j \right\}\right)}\mathcal{N}_i+ \mathcal{N}_j. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_-^{\left\{ i \right\}}&=\mathcal{N}_i, \\ P_-^{\left\{ i,j \right\}}&=\mathcal{N}_i +\mathcal{N}_j -\mathcal{N}_i \mathcal{N}_j= \mathcal{N}_i\left( 1-\mathcal{N}_j \right) + \mathcal{N}_j= P_+^{\left(\left\{ j \right\}\right)}\mathcal{N}_i+ \mathcal{N}_j. \end{aligned}\end{align} $$
-
○ Consider the self-adjoint operator
 ${h}_{i,i+1}$
(recall (2.8)) on the four-dimensional Hilbert space
${h}_{i,i+1}$
(recall (2.8)) on the four-dimensional Hilbert space
 $\mathcal {H}_{\left \{ i,i+1 \right \}}=\mathbb C_i^2\otimes \mathbb C_{i+1}^2$
. An explicit calculation shows that
$\mathcal {H}_{\left \{ i,i+1 \right \}}=\mathbb C_i^2\otimes \mathbb C_{i+1}^2$
. An explicit calculation shows that
 ${h}_{i,i+1}$
has eigenvalues
${h}_{i,i+1}$
has eigenvalues
 $-1,0, \pm \frac 1 \Delta $
. It follows that if
$-1,0, \pm \frac 1 \Delta $
. It follows that if
 $\left \{ i,i+1 \right \}\subset \Lambda $
, we have (A.2)
$\left \{ i,i+1 \right \}\subset \Lambda $
, we have (A.2) $$ \begin{align} \left\lVert {h}_{i,i+1} \right\rVert=1 \quad\text{on}\quad \mathcal{H}_\Lambda. \end{align} $$
$$ \begin{align} \left\lVert {h}_{i,i+1} \right\rVert=1 \quad\text{on}\quad \mathcal{H}_\Lambda. \end{align} $$
-
○ The following identities hold on
 $\mathcal {H}_\Lambda $
for
$\mathcal {H}_\Lambda $
for
 $\left \{ i,i+1 \right \}\subset \Lambda $
: (A.3)In particular, the first identity above implies
$\left \{ i,i+1 \right \}\subset \Lambda $
: (A.3)In particular, the first identity above implies $$ \begin{align}\begin{aligned} &{h}_{i,i+1}P_+^{\left\{ i,i+1 \right\}}=P_+^{\left\{ i,i+1 \right\}}{h}_{i,i+1}=0,\\ &\left\lVert P_+^{\left\{ i \right\}}{h}_{i,i+1} \right\rVert=\left\lVert P_+^{\left\{ i+1 \right\}}{h}_{i,i+1} \right\rVert={ \tfrac 1{2\Delta}},\\ &P_+^{\left(\left\{ i \right\}\right)}{h}_{i,i+1}P_+^{\left(\left\{ i \right\}\right)}=P_+^{\left(\left\{ i+1 \right\}\right)}{h}_{i,i+1}P_+^{\left(\left\{ i+1 \right\}\right)}=0,\\ &{h}_{i,i+1} \mathcal{N}_i\mathcal{N}_{i+1} = \mathcal{N}_i\mathcal{N}_{i+1} {h}_{i,i+1}= \mathcal{N}_i\mathcal{N}_{i+1}{h}_{i,i+1} \mathcal{N}_i\mathcal{N}_{i+1}. \end{aligned}\end{align} $$
(A.4)
$$ \begin{align}\begin{aligned} &{h}_{i,i+1}P_+^{\left\{ i,i+1 \right\}}=P_+^{\left\{ i,i+1 \right\}}{h}_{i,i+1}=0,\\ &\left\lVert P_+^{\left\{ i \right\}}{h}_{i,i+1} \right\rVert=\left\lVert P_+^{\left\{ i+1 \right\}}{h}_{i,i+1} \right\rVert={ \tfrac 1{2\Delta}},\\ &P_+^{\left(\left\{ i \right\}\right)}{h}_{i,i+1}P_+^{\left(\left\{ i \right\}\right)}=P_+^{\left(\left\{ i+1 \right\}\right)}{h}_{i,i+1}P_+^{\left(\left\{ i+1 \right\}\right)}=0,\\ &{h}_{i,i+1} \mathcal{N}_i\mathcal{N}_{i+1} = \mathcal{N}_i\mathcal{N}_{i+1} {h}_{i,i+1}= \mathcal{N}_i\mathcal{N}_{i+1}{h}_{i,i+1} \mathcal{N}_i\mathcal{N}_{i+1}. \end{aligned}\end{align} $$
(A.4) $$ \begin{align} {h}_{i,i+1}= {h}_{i,i+1}P_-^{\left\{ i,i+1 \right\}}=P_-^{\left\{ i,i+1 \right\}}{h}_{i,i+1}=P_-^{\left\{ i,i+1 \right\}}{h}_{i,i+1}P_-^{\left\{ i,i+1 \right\}}. \end{align} $$
$$ \begin{align} {h}_{i,i+1}= {h}_{i,i+1}P_-^{\left\{ i,i+1 \right\}}=P_-^{\left\{ i,i+1 \right\}}{h}_{i,i+1}=P_-^{\left\{ i,i+1 \right\}}{h}_{i,i+1}P_-^{\left\{ i,i+1 \right\}}. \end{align} $$
-
○ Let
 $K\subset \Lambda $
, and recall (3.10). It follows from (A.4) that (A.5)If K is connected in
$K\subset \Lambda $
, and recall (3.10). It follows from (A.4) that (A.5)If K is connected in $$ \begin{align} \Gamma^K= P_-^{ \partial^\Lambda K} \Gamma^K P_-^{ \partial^\Lambda K}. \end{align} $$
$$ \begin{align} \Gamma^K= P_-^{ \partial^\Lambda K} \Gamma^K P_-^{ \partial^\Lambda K}. \end{align} $$
 $\Lambda $
, it follows from (A.5) that (A.6)
$\Lambda $
, it follows from (A.5) that (A.6) $$ \begin{align} \left\lVert P_+^{K} \Gamma^K \right\rVert\le \tfrac 1 \Delta \quad\text{and}\quad \left\lVert P_+^{K^c} \Gamma^K \right\rVert\le \tfrac 1 \Delta. \end{align} $$
$$ \begin{align} \left\lVert P_+^{K} \Gamma^K \right\rVert\le \tfrac 1 \Delta \quad\text{and}\quad \left\lVert P_+^{K^c} \Gamma^K \right\rVert\le \tfrac 1 \Delta. \end{align} $$
-
○ The following identities hold for any nonempty
 $M\subset \Lambda $
(recall (2.16)): (A.7)
$M\subset \Lambda $
(recall (2.16)): (A.7) $$ \begin{align}\begin{aligned} P_-^{[M]_\infty} P_+^M & = \sum_{q=0}^{\left\lvert \Lambda \right\rvert} P_+^{[M]^\Lambda_{q}}P_-^{]M[^\Lambda_q}= \sum_{q=0}^{\left\lvert \Lambda \right\rvert} P_+^{[M]^\Lambda_{q}} P_-^{{\partial_{ex}^\Lambda{[M]_{q}}}} ,\\ P_-^{ M}&= \sum_{q=-\left\lvert M \right\rvert}^{-1}P_+^{[M]^\Lambda_{q}} P_-^{]M[^\Lambda_q}=\sum_{q=-\left\lvert M \right\rvert}^{-1}P_+^{[M]^\Lambda_{q}} P_-^{{\partial_{in }^\Lambda{[M]_{q+1}}}} , \\P_-^{[M]^\Lambda_\infty} &= \sum_{q=-\left\lvert M \right\rvert}^{\left\lvert \Lambda \right\rvert}P_+^{[M]^\Lambda_{q}} P_-^{]M[^\Lambda_{q}}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_-^{[M]_\infty} P_+^M & = \sum_{q=0}^{\left\lvert \Lambda \right\rvert} P_+^{[M]^\Lambda_{q}}P_-^{]M[^\Lambda_q}= \sum_{q=0}^{\left\lvert \Lambda \right\rvert} P_+^{[M]^\Lambda_{q}} P_-^{{\partial_{ex}^\Lambda{[M]_{q}}}} ,\\ P_-^{ M}&= \sum_{q=-\left\lvert M \right\rvert}^{-1}P_+^{[M]^\Lambda_{q}} P_-^{]M[^\Lambda_q}=\sum_{q=-\left\lvert M \right\rvert}^{-1}P_+^{[M]^\Lambda_{q}} P_-^{{\partial_{in }^\Lambda{[M]_{q+1}}}} , \\P_-^{[M]^\Lambda_\infty} &= \sum_{q=-\left\lvert M \right\rvert}^{\left\lvert \Lambda \right\rvert}P_+^{[M]^\Lambda_{q}} P_-^{]M[^\Lambda_{q}}. \end{aligned}\end{align} $$
B Many-body quasi-locality
In this appendix, we prove (1.6). Recall we only consider finite subsets of
![]() $\mathbb Z$
. We fix
$\mathbb Z$
. We fix
![]() $\Lambda \subset \mathbb Z$
and consider the Hilbert space
$\Lambda \subset \mathbb Z$
and consider the Hilbert space
![]() $\mathcal {H}_\Lambda $
.
$\mathcal {H}_\Lambda $
.
Lemma B.1. Suppose that
![]() $H\in \mathcal A_{\Lambda }$
satisfies
$H\in \mathcal A_{\Lambda }$
satisfies
-
1. For all
 $K \subset {\Lambda } $
, we have
$K \subset {\Lambda } $
, we have
 $[P_-^{K},H]P_+^{[K]_1^{\Lambda }}=0$
.
$[P_-^{K},H]P_+^{[K]_1^{\Lambda }}=0$
. -
2. For all connected
 $K \subset {\Lambda } $
, we have
$K \subset {\Lambda } $
, we have
 $\left \lVert [P_-^{K},H] \right \rVert \le \gamma $
.
$\left \lVert [P_-^{K},H] \right \rVert \le \gamma $
.
Then for all
![]() $A\subset B\subset {\Lambda }$
, A connected in
$A\subset B\subset {\Lambda }$
, A connected in
![]() ${\Lambda }$
, we have
${\Lambda }$
, we have
Proof. We note that
![]() $[ A]^{\Lambda }_{s} \subset B$
for
$[ A]^{\Lambda }_{s} \subset B$
for
![]() $s=0,1,\ldots ,r-1$
. We have
$s=0,1,\ldots ,r-1$
. We have
 $$ \begin{align}\begin{aligned} P_-^{ A}\,e^{itH}\,P_+^{ B} =ie^{itH}\int_0^tK(s)\,P_+^{B}ds, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_-^{ A}\,e^{itH}\,P_+^{ B} =ie^{itH}\int_0^tK(s)\,P_+^{B}ds, \end{aligned}\end{align} $$
where
![]() $K(s)=e^{-isH}\,[P_-^{ A},H]\,e^{isH}$
. If
$K(s)=e^{-isH}\,[P_-^{ A},H]\,e^{isH}$
. If
![]() $r\ge 2$
, condition (i) of the Lemma yields
$r\ge 2$
, condition (i) of the Lemma yields
![]() $K(s)=e^{-isH}\,[P_-^{ A},H] P_-^{ [A]^{\Lambda }_1}\,e^{isH}$
. Proceeding recursively, we get
$K(s)=e^{-isH}\,[P_-^{ A},H] P_-^{ [A]^{\Lambda }_1}\,e^{isH}$
. Proceeding recursively, we get
 $$ \begin{align}\begin{aligned} P_-^{ A}\,e^{itH}\,P_+^{ B}&=i^{r}\int_0^t\int_0^{s_1}\ldots\int_0^{s_{r-1}}\prod_{j=1}^{r} K_{j-1}(s_j)ds_j \,P_+^{B},\\ K_j(s)&=e^{-isH}\,[P_-^{ [A]_j},H] \,e^{isH}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P_-^{ A}\,e^{itH}\,P_+^{ B}&=i^{r}\int_0^t\int_0^{s_1}\ldots\int_0^{s_{r-1}}\prod_{j=1}^{r} K_{j-1}(s_j)ds_j \,P_+^{B},\\ K_j(s)&=e^{-isH}\,[P_-^{ [A]_j},H] \,e^{isH}. \end{aligned}\end{align} $$
Using assumption (ii), we get
Lemma B.2. Let
![]() $f\in C_0^n$
(i.e., f is compactly supported and n times differentiable function on
$f\in C_0^n$
(i.e., f is compactly supported and n times differentiable function on
![]() $\mathbb R$
(with
$\mathbb R$
(with
![]() $n\ge 2$
)). Then for
$n\ge 2$
)). Then for
![]() $A,B,H$
as in Lemma B.1 and
$A,B,H$
as in Lemma B.1 and
![]() $r=\operatorname {\mathrm {dist}}_\Lambda \left ( A,B^c \right )$
, we have
$r=\operatorname {\mathrm {dist}}_\Lambda \left ( A,B^c \right )$
, we have
Proof. Let
![]() $\hat f$
denote the Fourier transform of f. Then we have
$\hat f$
denote the Fourier transform of f. Then we have
![]() $\left \lvert \hat f(t) \right \rvert \le C(f,n)\langle t\rangle ^{-n}$
for
$\left \lvert \hat f(t) \right \rvert \le C(f,n)\langle t\rangle ^{-n}$
for
![]() $t\in \mathbb R$
(we recall that
$t\in \mathbb R$
(we recall that
![]() $\langle t\rangle :=\sqrt {1+t^2}$
). We can bound
$\langle t\rangle :=\sqrt {1+t^2}$
). We can bound
where
![]() $\mathcal R:=[-R,R]$
, where
$\mathcal R:=[-R,R]$
, where
![]() $R>0$
will be chosen later.
$R>0$
will be chosen later.
We can bound the first integral on the right-hand side of (B.6) using (B.1) as
 $$ \begin{align}\begin{aligned} \int_{\mathcal R}\left\lVert P_-^A\ e^{itH}\, P_+^B \right\rVert\left\lvert \hat f(t) \right\rvert dt & \le C(f,n)\frac{\gamma^{r}}{r!}\int_{\mathcal R} \left\lvert t \right\rvert^r\langle t\rangle^{-n}dt\le C_n C(f,n)\frac{\gamma^{r}{R}^{1+(r-n)_+}}{r!}\\ & \le C'_n C(f,n)\left( \frac {\mathrm{e} \gamma }r \right)^r{R}^{1+(r-n)_+}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \int_{\mathcal R}\left\lVert P_-^A\ e^{itH}\, P_+^B \right\rVert\left\lvert \hat f(t) \right\rvert dt & \le C(f,n)\frac{\gamma^{r}}{r!}\int_{\mathcal R} \left\lvert t \right\rvert^r\langle t\rangle^{-n}dt\le C_n C(f,n)\frac{\gamma^{r}{R}^{1+(r-n)_+}}{r!}\\ & \le C'_n C(f,n)\left( \frac {\mathrm{e} \gamma }r \right)^r{R}^{1+(r-n)_+}, \end{aligned}\end{align} $$
where we used
![]() $r!\ge e^{1-r}r^r$
.
$r!\ge e^{1-r}r^r$
.
We can bound the second integral in (B.6) as
Choosing
![]() $R=\left ( \frac r{e\gamma } \right )^{\frac {r}{n+ (r-n)_+}}$
, we get (B.5).
$R=\left ( \frac r{e\gamma } \right )^{\frac {r}{n+ (r-n)_+}}$
, we get (B.5).
Competing interest
The authors have no competing interest to declare.
Funding statement
A.E. was supported in part by the NSF under grants DMS-1907435 and DMS-2307093 and by the Simons Fellowship in Mathematics Grant 522404.