1. INTRODUCTION
Moving charged particles can radiate energy by processes such as Synchrotron, coherent transition, and Cherenkov radiation (Jackson, Reference Jackson1999). Traditionally, charged particle beams have been employed to generate coherent radiation in the far ends of the electromagnetic spectrum, which are not accessible by bound-electron devices. Therefore, high-energy particle beams from traditional accelerators are employed to generate radiation by the above-mentioned processes. Meanwhile, advances in laser technology have opened up the possibility to miniaturize the accelerating structures and to accelerate the electrons to several GeVs and ions to sub-relativistic energies (Tajima & Dawson, Reference Tajima and Dawson1979; Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001). In return, laser–matter interaction and laser-based accelerator schemes were successfully tested to generate coherent radiation in the far ends of the electromagnetic spectrum (Murnane et al., Reference Murnane, Kapteyn, Rosen and Falcone1991; Hamster et al., Reference Hamster, Sullivan, Gordon, White and Falcone1993; Macklin et al., Reference Macklin, Kmetec and Gordon1993; Schlenvoigt et al., Reference Schlenvoigt, Haupt, Debus, Pfotenhauer, Schwoerer, Budde, Jackel, Rohwer, Gallacher, Brunetti, Shanks, Wiggins and Jaroszynski2008). Latest addition to these studies is the generation of gigawatt (GW) power radiation in the terahertz band of the electromagnetic spectrum by a compact laser-driven accelerator (Gopal et al., Reference Gopal, Singh, Herzer, Reinhard, Schmidt, Dillner, May, Meyer, Ziegler and Paulus2013b). Laser-driven ion accelerators extend the unique possibility to generate multiple high-power tunable terahertz pulses with variable time delay, which will enable pump–probe studies in materials, otherwise not feasible (Jones et al., Reference Jones, You and Bucksbaum1993; Back et al., Reference Back, Weller, Heidmann, Mauri, Guarisco, Garwin and Siegmann1998; Kampfrath et al., Reference Kampfrath, Tanaka and Neloson2013). In our earlier work, we showed that high-power broadband terahertz pulses are emitted by the transient sheath field which is also responsible for the acceleration of protons and ions during laser–solid interaction (Gopal et al., Reference Gopal, May, Herzer, Reinhard, Minardi, Schubert, Dillner, Pradarutti, Polz, Gaumnitz, Kaluza, Jaeckel, Riehemann, Ziegler, Gemuend, Meyer and Paulus2012, Reference Gopal, Herzer, Schmidt, Singh Reinhard, Ziegler, Broemmel, Karmakar, Gibbon, Dillner, May, Meyer and Paulus2013a).
Here we present the generation of secondary terahertz pulses using Smith–Purcell (SP) effect, by sending the charged particle beams from a laser-driven ion accelerator close to a periodic structure. To the best of our knowledge, this is the first experimental study of this kind with charged particles from the target normal sheath acceleration (TNSA) process. In Section 2, we present the principles of SP effect. Section 3 describes the experimental geometry and the terahertz and particle diagnostics. In Section 4, we discuss the experimental results and in Section 5, we conclude and discuss the future goals.
2. SP RADIATION
Radiation is emitted when a charged particle travels close to a periodic structure. The first experimental observation was reported by Smith and Purcell when they sent a beam of energetic electrons very close to a grating, generating visible light (Smith & Purcell, Reference Smith and Purcell1953). The periodic structure causes angular dispersion of the emitted wavelength with respect to the observation angle. For an observer at infinity and at a plane perpendicular to the grating, the emitted wavelength follows the dispersion relation:
where D g is the grating period, n is the diffraction order, β( = v/c) is the normalized particle velocity, and θ is the angle of observation in the x–z plane (see Fig. 1 for the definition of the coordinate system). Thus, the wavelength of the emitted radiation is defined by the grating period for a particle beam with defined energy. Therefore, by choosing the appropriate grating structure the wavelength of the emitted radiation can be tuned.

Fig. 1. Schematic representation of the experimental setup.
In the literature, one may find various theoretical models discussing the radiation process and estimating the spectral intensity (Karlovets & Potylitsyn, Reference Karlovets and Potylitsyn2006, and references therein). Among the existing theoretical treatments, the model which describes the emission due to the current induced on the grating surface by the particle beam, while passing close to the surface is mostly in agreement with the experimental results until now (Brownell et al., Reference Brownell, Walsh and Doucas1998; Doucas et al., Reference Doucas, Blackmore, Ottewell, Perry, Huggard, Castro-Camus, Johnston, Lloyd Hughes, Kimmitt, Redlich and van der Meer2006). According to this model, the energy emitted per solid angle by a single particle per grating period can be written as (Kube, Reference Kube2005)
 $$\eqalign{{\left( {\displaystyle{{dP} \over {d\Omega}}} \right)}_1 & = {\rm \alpha} \hbar c \displaystyle{{2{\rm \pi}} \over {D_{\rm g}}} \displaystyle{{n^2} \over {({\rm \beta}^{-1} - \cos {\rm \theta} )^3}} {\vert \overrightarrow R_n \vert}^2 \cr & \quad {e^{\left[ { - \displaystyle{b \over {h_{{\rm int}}}} \sqrt {1 + ({\rm \beta \gamma} \sin {\rm \theta} \cos {\rm \phi} )^2}} \right]}}}$$
$$\eqalign{{\left( {\displaystyle{{dP} \over {d\Omega}}} \right)}_1 & = {\rm \alpha} \hbar c \displaystyle{{2{\rm \pi}} \over {D_{\rm g}}} \displaystyle{{n^2} \over {({\rm \beta}^{-1} - \cos {\rm \theta} )^3}} {\vert \overrightarrow R_n \vert}^2 \cr & \quad {e^{\left[ { - \displaystyle{b \over {h_{{\rm int}}}} \sqrt {1 + ({\rm \beta \gamma} \sin {\rm \theta} \cos {\rm \phi} )^2}} \right]}}}$$
where α is the fine structure constant, ![]() $\hbar $ is the reduced Plank's constant, ϕ is the observation angle in the y–z plane, γ the Lorentz factor, and b the distance between the beam and the grating surface.
$\hbar $ is the reduced Plank's constant, ϕ is the observation angle in the y–z plane, γ the Lorentz factor, and b the distance between the beam and the grating surface. ![]() $\vert\overrightarrow R _n \vert$ is the radiation factor and it is the vector sum of the field contributions from each grating plane (Brownell & Doucas, Reference Brownell and Doucas2005). h int is the interaction length and is given by h int = λβγ/4π. To estimate the contribution due to a particle bunch, it is necessary to consider the distribution of the particles, and the emission can be coherently increased when the emitted wavelength is longer than the longitudinal extension of the particle bunch. The energy emitted per unit solid angle by N particles is given by
$\vert\overrightarrow R _n \vert$ is the radiation factor and it is the vector sum of the field contributions from each grating plane (Brownell & Doucas, Reference Brownell and Doucas2005). h int is the interaction length and is given by h int = λβγ/4π. To estimate the contribution due to a particle bunch, it is necessary to consider the distribution of the particles, and the emission can be coherently increased when the emitted wavelength is longer than the longitudinal extension of the particle bunch. The energy emitted per unit solid angle by N particles is given by
where S incoh is the incoherent integral, which is given by
where X is the particle density distribution in the x-direction. λe is the evanescent wavelength and is given by, 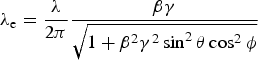 ${\rm \lambda} _{\rm e} = {{\rm \lambda} \over 2{\rm \pi}} {{\rm \beta} {\rm \gamma} \over \sqrt {1 + {\rm \beta} ^2 {\rm \gamma} ^2 \mathop {\sin} \nolimits^2 {\rm \theta} \mathop {\cos} \nolimits^2 {\rm \phi}} } $. S coh is the coherent integral which is proportional to the square modulus of the Fourier transform f(ω) of the longitudinal density profile of the bunch (Brownell & Doucas, Reference Brownell and Doucas2005). For bunch durations larger than the wavelength of the emitted radiation, the incoherent term in the above equation will dominate and the intensity of the emitted radiation will be the product of the particle number and the contribution due to a single particle. Otherwise, S coh will be the dominant term and the emission will be enhanced. That is (dP n/dΩ)N = (dP n/dΩ)1N 2S coh. Thus by choosing the optimum grating parameters, the longitudinal bunch profile can be directly estimated. In addition, the emission process has negligible influence on the particle trajectories compared with other secondary radiation generation processes. Thus, SP radiation is an ideal candidate to characterize the longitudinal bunch duration of the electron beams in accelerator facilities (Nguyen, Reference Nguyen1997; Mizuno et al., Reference Mizuno, Pae, Nozokido and Furuya1987; Doucas et al., Reference Doucas, Blackmore, Ottewell, Perry, Huggard, Castro-Camus, Johnston, Lloyd Hughes, Kimmitt, Redlich and van der Meer2006).
${\rm \lambda} _{\rm e} = {{\rm \lambda} \over 2{\rm \pi}} {{\rm \beta} {\rm \gamma} \over \sqrt {1 + {\rm \beta} ^2 {\rm \gamma} ^2 \mathop {\sin} \nolimits^2 {\rm \theta} \mathop {\cos} \nolimits^2 {\rm \phi}} } $. S coh is the coherent integral which is proportional to the square modulus of the Fourier transform f(ω) of the longitudinal density profile of the bunch (Brownell & Doucas, Reference Brownell and Doucas2005). For bunch durations larger than the wavelength of the emitted radiation, the incoherent term in the above equation will dominate and the intensity of the emitted radiation will be the product of the particle number and the contribution due to a single particle. Otherwise, S coh will be the dominant term and the emission will be enhanced. That is (dP n/dΩ)N = (dP n/dΩ)1N 2S coh. Thus by choosing the optimum grating parameters, the longitudinal bunch profile can be directly estimated. In addition, the emission process has negligible influence on the particle trajectories compared with other secondary radiation generation processes. Thus, SP radiation is an ideal candidate to characterize the longitudinal bunch duration of the electron beams in accelerator facilities (Nguyen, Reference Nguyen1997; Mizuno et al., Reference Mizuno, Pae, Nozokido and Furuya1987; Doucas et al., Reference Doucas, Blackmore, Ottewell, Perry, Huggard, Castro-Camus, Johnston, Lloyd Hughes, Kimmitt, Redlich and van der Meer2006).
3. EXPERIMENTAL SETUP
The experiments were carried out at the 40 TW JETI laser system at the Institute of Optics and Quantum Electronics. The multi-terawatt laser pulses (λ = 800 nm, τL = 30 fs, E l = 1 J) were tightly focused onto a 5 µm thick titanium foil placed inside the experimental vacuum chamber. The expected intensity on the target was above 1019 W/cm2. Proton and ion beams were generated and accelerated by the TNSA mechanism (Hatchett et al., Reference Hatchett, Brown, Cowan, Henry, Johnson, Key, Koch, Langdon, Lasinski, Lee, Mackinnon, Pennington, Perry, Phillips, Roth, Sangster, Singh, Snavely, Mark, Stoyer, Wilks and Yasuike2000; Maksimchuck et al., Reference Maksimchuck, Gu, Flippo, Umstadter and Bychenkov2000; Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000; Nemoto et al., Reference Nemoto, Maksimchuk, Banerjee, Flippo, Mourou, Umstadter and Bychenkov2001; Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001). A Thomson parabola spectrometer with a microchannel plate and a CCD camera as detector was employed to record single-shot spectra (Schwoerer et al., Reference Schwoerer, Pfotenhauer, Jaeckel, Amthor, Liesfeld, Ziegler, Sauerbrey, Ledingham and Esirkepov2006). To generate the SP radiation a metallic grating structure was mounted on a carousel attached to a remote-controlled kinematic stage and placed parallel to the proton beam path as shown in Figure 1. Roughly 12.5 mm long grating structures with periods 79 and 300 lines/mm and a blank metallic mirror were placed on three orthogonal faces of the carousel. Rotating the carousel by 90° the next grating surface is exposed to the beam. A variable aperture was placed along the beam path before the grating structure, so that only the highest energy particles at the center of the beam axis could reach the grating. The high-resolution kinematic stage allowed the precise alignment of the grating with respect to the particle beam and its alignment was cross-checked with the particle spectra recorded by the ion spectrometer. The grating was aligned in such a way that when it is moved in the plane perpendicular to the particle propagation direction, the proton, and ion spectra on the Thomson spectrometer was partially cut or blocked.
The SP radiation was collected using a 3 inch off-axis parabolic mirror placed at a distance equal to the focal length (f = 76.8 mm, thus subtending a solid angle of 0.773 sr) and relayed out of the experimental vacuum chamber through a silicon window onto a calibrated pyroelectric detector placed outside the target chamber. The silicon window and a spectral splitter (highly reflective for 800 nm) placed in front of the terahertz detector eliminated any laser frequency and its harmonics reaching the detector. Moreover, the detector was placed inside a Faraday cage and the cables were shielded to eliminate any interference due to electromagnetic noises generated during the laser–matter interaction.
4. RESULTS AND DISCUSSION
Initially, we recorded the proton and ion spectra without any grating placed inside the experimental chamber. A typical ion spectra obtained during this experimental campaign is shown in Figure 2. The maximum observed proton energy for this measurement was 1.7 MeV. In previous experiments (Gopal et al., Reference Gopal, Singh, Herzer, Reinhard, Schmidt, Dillner, May, Meyer, Ziegler and Paulus2013b), peak energies upto 4.7 MeV were generated. We believe this variation in the peak particle energy is due to the non-optimal performance of the laser during the experimental campaign. Since protons were the dominant ion species, we calculated the expected wavelength of the SP radiation using Eq. (1) as a function of the proton velocity and the observation angle.

Fig. 2. A typical ion spectra recorded with the Thomson parabola detector.
The result is plotted in Figure 3. Most of the radiation is emitted between the 194 and 300 μm, which is well within the wavelength range of our detector. A small shot to shot variation in the peak energy of the protons was observed, which only limited the spectral extent of the generated SP radiation, described by Eq. (1).
From both the particle spectra and the grating parameters, we calculated the expected radiation intensity using Eq. (3). The maximum energy of the radiation for the whole proton bunch for the entire grating length is estimated by taking into consideration the number of particles in each energy range. The results show a minimum value of 1.4 × 107 eV/sr. Taking into consideration the collection angle of our optical system the detected energy should be several picojoules.
Next, we compared these results with the space–time-averaged energy of the generated radiation recorded on the pyroelectric detector. We inserted the grating close to the particle propagation direction. The grating was moved close to the particle beam while simultaneously recording the particle spectra and the terahertz signal. The detectable minimum terahertz signal was recorded when the grating was placed at a position (1200 µm in Fig. 4) where the unobstructed particle spectra was also obtained. We next reduced the distance (b) between the grating and the beam and recorded the terahertz signal.

Fig. 4. Signal recorded by the pyroelectric detector with respect to the beam height from the grating.
The measured voltage was multiplied with the calibration factor of the detector and the transmission efficiency of the optical components in the beam path. The results are presented in Figure 4. Grating with 79 lines/mm generated maximum signal strength, leading to up to 0.26 μJ pulses. As the distance between the grating and the beam was reduced the signal increased exponentially. When the distance was further reduced (b < 640 μm) still some signal above the background level was detected. This could be due to the fact that the beam was physically interacting with the grating and generating diffraction or transition radiation from such an interaction (Jackson, Reference Jackson1999).
The signal recorded by the pyroelectric detector is much higher than the calculated value using the theoretical treatment based on the surface current model with the proton spectrum plotted in Figure 2. The discrepancy in the results obtained by the two methods can be attributed to many factors. Firstly, the opening aperture of the Thomson parabola (300 μm diameter) is much smaller than the aperture in front of the grating (2 mm). This indicates that the particle spectra recorded on the Thomson parabola spectrometer is smaller than the actual beam interacting with the grating, thereby significantly influencing the calculations based on the particle spectra. Another major factor could be the contribution from the co-propagating electrons and ions. Since the pyroelectric detector measures the time-integrated signal, the contributions from co-propagating particles cannot be distinguished. However, a contribution from co-moving electrons with energies higher than the trailing protons and ions (Mora, Reference Mora2003; Schreiber et al., Reference Schreiber, Bell, Gruener, Schramm, Geissler, Schnuerer, Ter-Avetisyan, Hegelich, Cobble, Brambrink, Fuchs, Audebert and Habs2006) should give rise to radiation in the visible or shorter wavelength regime for the grating used in the experiment. While the less energetic electrons with similar velocity range as that of the protons can generate radiation in the similar wavelength regime and this might have contributed to the measurements. Additionally, the other ion species accelerated along with the protons could also contribute to the cause. However, due to their low velocity this contribution is negligible compared with protons. One may be able to separate these contributions temporally by carrying out single-shot pump–probe studies based on the electro-optic technique or using a magnet to separate the charges before the grating structure.
Additionally, if there is any coherent radiation generation due to the interaction, then the power of the emitted radiation is proportional to N 2 (N being the particle number). However, in our case the particle beam with a Maxwellian distribution should be several tens of pico seconds long when it reaches the grating [assuming the bunch was initially 1.3τL, τL being the incident laser pulse duration (Schreiber et al., Reference Schreiber, Bell, Gruener, Schramm, Geissler, Schnuerer, Ter-Avetisyan, Hegelich, Cobble, Brambrink, Fuchs, Audebert and Habs2006)], thus requiring much larger grating periods to generate coherent radiation. On the other hand, if one assumes that the whole grating structure (L = 1.25 cm) was acting like a single grating period, one may also observe radiation. However, such a contribution can be neglected as the calculations show that the value (~ 10−18 J) is significantly small to make any influence on the measurements. Another factor could be the radiation arising from the background, such as self-generated terahertz radiation from the laser–matter interaction (Gopal et al., Reference Gopal, Herzer, Schmidt, Singh Reinhard, Ziegler, Broemmel, Karmakar, Gibbon, Dillner, May, Meyer and Paulus2013a). However, these contributing factors should not decay exponentially when the distance between the beam and the grating is increased. This argument is clearly supported by the measurements with the 300 lines/mm grating and the blank mirror. In both cases, the signals were below the background level. Should the contribution be due to the background radiation (i.e., radiation generated by the plasma), then these two measurements should have recorded signals too.
5. CONCLUSION AND FUTURE WORK
The first measurements of SP radiation using charged particles from a TNSA interaction show the generation of secondary terahertz radiation. The strength of the SP radiation decreases exponentially, when the distance between the grating and the beam is increased, a clear signature of the emission process. TNSA process generates electrons, protons, and ions; thus, the recorded signal might include contributions from various species. To distinguish the respective contributions, it is necessary to isolate the charges before the grating using a magnet. Additionally, non-collinear single-shot pump–probe studies based on the electro-optic technique could be employed to distinguish various contributions. Future studies will also focus on using the SP effect to estimate the longitudinal bunch duration of the proton and ion beam at the grating (Nguyen, Reference Nguyen1997; Doucas et al., Reference Doucas, Blackmore, Ottewell, Perry, Huggard, Castro-Camus, Johnston, Lloyd Hughes, Kimmitt, Redlich and van der Meer2006). The coherent and incoherent contributions can be identified by carrying out measurements with different grating periods (D g ≥ longitudinal bunch duration). Since the SP effect does not alter the beam trajectory, an online particle diagnostic can be developed using this scheme for potential applications (Busold et al., Reference Busold, Schumacher, Brabetz, Deppert, Kroll, Blazevic, Bagnoud and Roth2014). In addition to the self-generated terahertz radiation (Gopal et al., Reference Gopal, Herzer, Schmidt, Singh Reinhard, Ziegler, Broemmel, Karmakar, Gibbon, Dillner, May, Meyer and Paulus2013a), the possibility to generate temporally delayed energetic secondary terahertz pulses provide unique environments for pump–probe studies (Jones et al., Reference Jones, You and Bucksbaum1993; Back et al., Reference Back, Weller, Heidmann, Mauri, Guarisco, Garwin and Siegmann1998; Kampfrath et al., Reference Kampfrath, Tanaka and Neloson2013) and novel particle acceleration schemes (Mizuno et al., Reference Mizuno, Pae, Nozokido and Furuya1987).
ACKNOWLEDGEMENTS
This work was supported by the Deutsche Forschung Gemeinschaft (Project no.1998/ Go 3-1). The authors also thank B. Beleites, F. Ronneberger, and O. Jäckel for the technical support and fruitful discussions.



