1. Introduction
X-ray sources based on Compton scattering of a laser from a relativistic counter-propagating electron beam (e-beam) have recently drawn increasing interest due to several potential advantages over magnetostatic free electron lasers (FELs), such as compact size, low-cost operation, and reduced e-beam energy requirements. Recent work[Reference Karagodsky, Schieber and Schächter1] demonstrated that X-ray radiation emitted by relativistic electrons scattered by a counter-propagating laser pulse guided by an adequate Bragg structure (spontaneous emission) surpassed by about two orders of magnitude the intensity generated by a conventional free-space Gaussian-beam configuration, given the same e-beam and injected laser power in both configurations.
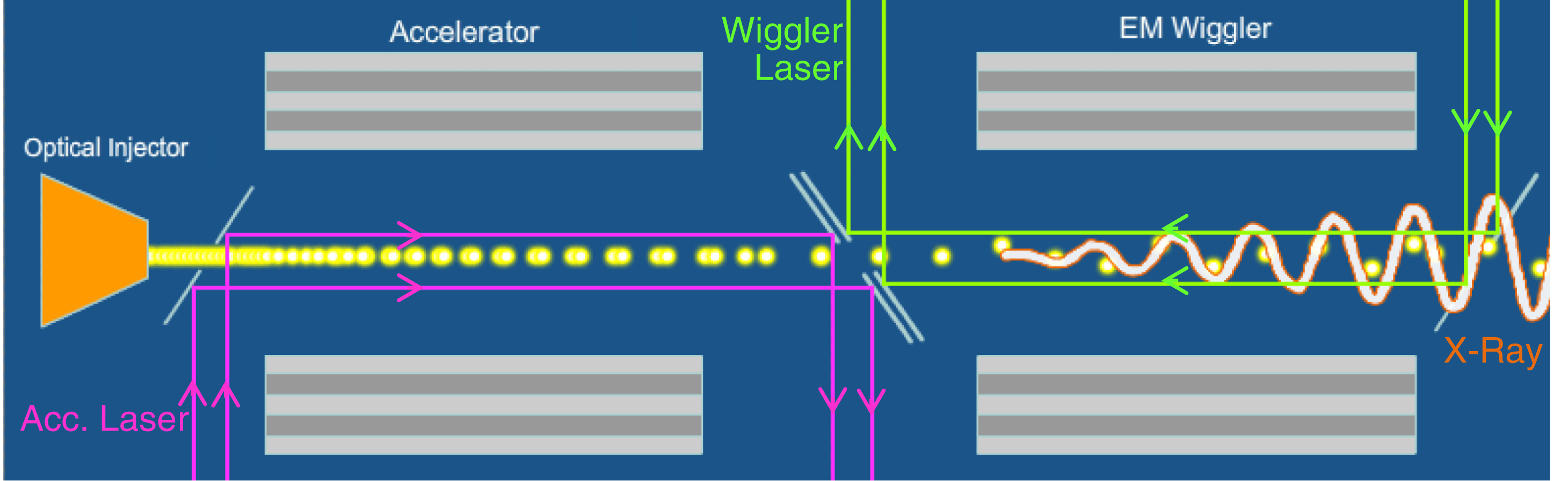
Figure 1. Schematic of an all-Bragg system. On the left, the Bragg accelerator supports a co-propagating ![]() $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{TM}_{01}$ mode which accelerates the e-beam. The latter is injected into another Bragg structure which supports a TEM mode (inside the vacuum core) counter-propagating to the electrons, which as a result generates X-ray radiation.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{TM}_{01}$ mode which accelerates the e-beam. The latter is injected into another Bragg structure which supports a TEM mode (inside the vacuum core) counter-propagating to the electrons, which as a result generates X-ray radiation.
Based on this configuration, we proposed a Bragg configuration based X-FEL operating in the collective regime. The full system consists of three main components (Figure 1): an optical injector bunches the electrons to the accelerator Bragg structure which supports a ![]() $\mathrm{TM}_{01}$ mode. The co-propagating laser which accelerates the electrons is dumped at the end. Next, the electrons are transported into a second Bragg waveguide. This structure supports a TEM laser mode in the vacuum core (TM mode at the Bragg layers) counter-propagating to the e-beam – the latter acts as an electromagnetic (EM) wiggler. The scattering of free electrons with a counter-propagating TEM-like laser mode generates X-ray radiation – inverse Compton scattering.
$\mathrm{TM}_{01}$ mode. The co-propagating laser which accelerates the electrons is dumped at the end. Next, the electrons are transported into a second Bragg waveguide. This structure supports a TEM laser mode in the vacuum core (TM mode at the Bragg layers) counter-propagating to the e-beam – the latter acts as an electromagnetic (EM) wiggler. The scattering of free electrons with a counter-propagating TEM-like laser mode generates X-ray radiation – inverse Compton scattering.
In this study we focus on the Bragg accelerator. Structure-based laser-driven linear accelerators have been the subject of intense investigation, primarily for use with relativistic particles, where obtaining high energies in compact geometries is desired.
To accelerate particles efficiently, EM waves must be guided or confined to the region in which the particles travel. An electric field component in the direction of desired acceleration is strictly necessary. Traditionally, EM waves have been confined to a vacuum channel surrounded by metallic structures. Field confinement can also be achieved through surrounding dielectric layers where reflections from different layers interfere constructively (Bragg reflection).
A planar Bragg waveguide[Reference Mizrahi and Schächter2] consists of dielectric layers surrounding a sub-wavelength vacuum region which is symmetrical relative to the central plane (Figure 2). The clearance is a vacuum region of width ![]() $2D_{\mathrm{int}}$, surrounding alternating periodic layers (
$2D_{\mathrm{int}}$, surrounding alternating periodic layers (![]() $\varepsilon _{2}=4$,
$\varepsilon _{2}=4$, ![]() $\varepsilon _{3}=2.1$).
$\varepsilon _{3}=2.1$).
The layers are made of two lossless dielectric materials; the first layer has a relative dielectric coefficient ![]() $\varepsilon _{1}$. For single-mode operation:
$\varepsilon _{1}$. For single-mode operation: ![]() $D_{\mathrm{int}} = 0.25 \lambda _{L} \to 0.55 \lambda _{L}$. For an optical accelerator having a vacuum core, the surrounding layers must have, at the operating wavelength, an effective dielectric coefficient smaller than unity, i.e.,
$D_{\mathrm{int}} = 0.25 \lambda _{L} \to 0.55 \lambda _{L}$. For an optical accelerator having a vacuum core, the surrounding layers must have, at the operating wavelength, an effective dielectric coefficient smaller than unity, i.e., ![]() $\varepsilon _{\mathrm{eff}} < 1$, thus creating the need for a Bragg structure with a matching layer[Reference Mizrahi and Schächter3].
$\varepsilon _{\mathrm{eff}} < 1$, thus creating the need for a Bragg structure with a matching layer[Reference Mizrahi and Schächter3].
The present study is organized as follows: A self-consistent solution for maximum gradient is presented in Section 2. In Section 3 we present the optimal charge of the e-beam injected into the acceleration module from a perspective of high efficiency. A charged-line moving in a planar Bragg acceleration structure generates a reaction field which, by virtue of linearity of Maxwell’s equations, is related through the so-called, wake coefficient. We show a detailed evaluation of the wake coefficient in Section 4 for a single bunch and in Section 5 for train of micro-bunches.

Figure 2. Planar Bragg waveguide with a vacuum region of width ![]() $2D_{\mathrm{int}}$.
$2D_{\mathrm{int}}$.
2. Accelerating gradient
For assessment of the accelerating gradient, we examine the maximum energy flux that can be sustained by the structure; typically, this occurs at the vacuum–dielectric interface, where ![]() $S_{z,\max } (D_{\mathrm{int}}^{+}) = \frac {1}{2} H_{y}^{\ast } (D_{\mathrm{int}}^{+}) E_{x}(D_{\mathrm{int}}^{+})$. The material is characterized by the fluence (
$S_{z,\max } (D_{\mathrm{int}}^{+}) = \frac {1}{2} H_{y}^{\ast } (D_{\mathrm{int}}^{+}) E_{x}(D_{\mathrm{int}}^{+})$. The material is characterized by the fluence (![]() $F$), which represents the energy per unit surface before breakdown occurs. Consequently, the threshold for a pulse of duration
$F$), which represents the energy per unit surface before breakdown occurs. Consequently, the threshold for a pulse of duration ![]() $\tau _{p}$ is determined by
$\tau _{p}$ is determined by
where ![]() $G_{0}$ is the accelerating field gradient,
$G_{0}$ is the accelerating field gradient, ![]() $\omega _{L}$ is the laser frequency and
$\omega _{L}$ is the laser frequency and ![]() $\eta _{0}$ is the vacuum impedance. We rely on the three EM field components of the accelerating mode in the vacuum region
$\eta _{0}$ is the vacuum impedance. We rely on the three EM field components of the accelerating mode in the vacuum region
 $$\begin{equation} \label {eq2} \begin{array}{r@{~}c@{~}l} E_{z} &=& \displaystyle G_{0} \exp \left (-j \frac {\omega _{L}}{c}z\right ), \\ E_{x} (x) &=& \displaystyle j \frac {\omega _{L}}{c}xG_{0} \exp \left (-j \frac {\omega _{L}}{c}z\right ),\\ H_{y} (x) &=& \displaystyle j \frac {\omega _{L}}{c} x \frac {G_{0}}{\eta _{0}} \exp \left (-j\frac {\omega _{L}}{c}z\right ). \end{array} \end{equation}$$
$$\begin{equation} \label {eq2} \begin{array}{r@{~}c@{~}l} E_{z} &=& \displaystyle G_{0} \exp \left (-j \frac {\omega _{L}}{c}z\right ), \\ E_{x} (x) &=& \displaystyle j \frac {\omega _{L}}{c}xG_{0} \exp \left (-j \frac {\omega _{L}}{c}z\right ),\\ H_{y} (x) &=& \displaystyle j \frac {\omega _{L}}{c} x \frac {G_{0}}{\eta _{0}} \exp \left (-j\frac {\omega _{L}}{c}z\right ). \end{array} \end{equation}$$Dielectric damage involves heating of conduction band electrons by the incident radiation and transfer of this energy to the lattice; damage occurs via conventional heat deposition. Thus, we consider the threshold fluence (energy/area) of the material, which, in turn, depends on the pulse duration. An empirical fluence threshold of fused silica has been published[Reference Stuart, Feit, Rubenchik, Shore and Perry4] by the LLNL group
 $$\begin{equation} \label {eq3} F \left (\frac {\mathrm {J}}{\mathrm {cm}^{2}}\right ) = \begin{cases} 1.44 \tau _{p}^{1/2} & \tau _{p}\ (\mbox {ps}) > 10\\ 2.51 \tau _{p}^{1/4} & 0.4 < \tau _{p}\ (\mbox {ps}) < 10 \\ 2 & \tau _{p}\ (\mbox {ps}) < 0.4. \end{cases} \end{equation}$$
$$\begin{equation} \label {eq3} F \left (\frac {\mathrm {J}}{\mathrm {cm}^{2}}\right ) = \begin{cases} 1.44 \tau _{p}^{1/2} & \tau _{p}\ (\mbox {ps}) > 10\\ 2.51 \tau _{p}^{1/4} & 0.4 < \tau _{p}\ (\mbox {ps}) < 10 \\ 2 & \tau _{p}\ (\mbox {ps}) < 0.4. \end{cases} \end{equation}$$It should be pointed out that the above empirical expression assumes a TEM mode impinging perpendicular to the dielectric surface, whereas in our case the energy flows in the parallel direction. It is assumed that since the electric field is vertical to the surface the probability of flash-over is reduced – therefore, adopting this criterion (Equation (3)) is an underestimate of the fluence our structure can sustain.

Figure 3. (a) Gradient versus clearance of the accelerator structure. Red line for a single bunch and green line for ![]() $M=10^{4}$. As the clearance is increased, the gradient drops. (b) Gradient versus number of micro-bunches in the train. Red line for
$M=10^{4}$. As the clearance is increased, the gradient drops. (b) Gradient versus number of micro-bunches in the train. Red line for ![]() $D_{\mathrm{int}}=0.25\lambda _{{L}}$; green line for
$D_{\mathrm{int}}=0.25\lambda _{{L}}$; green line for ![]() $D_{\mathrm{int}}=0.55\lambda _{{L}}$, multiplied by a factor (2.377) such that at
$D_{\mathrm{int}}=0.55\lambda _{{L}}$, multiplied by a factor (2.377) such that at ![]() $M=1$ both curves coincide for
$M=1$ both curves coincide for ![]() $G_{0}$ (
$G_{0}$ (![]() $D_{\mathrm{int}}=0.25\lambda _{{L}}$). There is a critical value at approximately
$D_{\mathrm{int}}=0.25\lambda _{{L}}$). There is a critical value at approximately ![]() $M=1000$.
$M=1000$.
In RF-based accelerators, the radiation wavelength is typically more than 10 cm in length, thus we may use ![]() $10^{10}$ electrons in a
$10^{10}$ electrons in a ![]() $100\ \mu \mathrm{m}$ bunch. Assuming similar dimensions in the transverse directions, we realize that the density of electrons is on the order of
$100\ \mu \mathrm{m}$ bunch. Assuming similar dimensions in the transverse directions, we realize that the density of electrons is on the order of ![]() $n\sim 10^{23}\ \mathrm{m}^{-3}$. If the density is kept the same in the optical regime, say
$n\sim 10^{23}\ \mathrm{m}^{-3}$. If the density is kept the same in the optical regime, say ![]() $\lambda _{L} \sim 1\ \mu \mathrm{m}$, the micro-bunch needs to be on the order of 30 nm long, 100 nm high and, assuming a sheet-beam about
$\lambda _{L} \sim 1\ \mu \mathrm{m}$, the micro-bunch needs to be on the order of 30 nm long, 100 nm high and, assuming a sheet-beam about ![]() $10\ \mu \mathrm{m}$ wide, then the number of electrons in one optical micro-bunch is 300. In spite of this clearly being a very rough estimate, in order to accelerate a significant number of electrons, and keep the electron density as in an RF machine, we need to use a multiple number of periods of the accelerating mode, thus the accelerated bunch is actually a train of micro-bunches.
$10\ \mu \mathrm{m}$ wide, then the number of electrons in one optical micro-bunch is 300. In spite of this clearly being a very rough estimate, in order to accelerate a significant number of electrons, and keep the electron density as in an RF machine, we need to use a multiple number of periods of the accelerating mode, thus the accelerated bunch is actually a train of micro-bunches.
Moreover, it is strictly necessary to use a pre-bunched beam at optical wavelengths before injection into the optical accelerator. Without the pre-bunching, the beam energy spread is too large to be useful. Energy modulation converted into a density modulation may also lead to increased efficiency in the accelerator. A configuration of modulator and chicane may be used as a pre-buncher injector to increase the number of electrons in the optimal phase of the accelerating laser. An efficient method for bunching the beam at optical wavelengths was suggested in[Reference Hemsing and Xiang5] and it was demonstrated that a pre-bunched beam at optical wavelengths indeed reduced the beam energy spread in laser accelerators[Reference Dunning, Hemsing, Hast, Raubenheimer, Weathersby, Xiang and Fu6]. We are in the process of analysing a novel injector that generates density-modulated beams at optical wavelengths, but this is beyond the scope of this study.
An assessment of the laser pulse duration requires one to take into consideration that the EM wave propagates at the group/energy velocity whereas the electrons propagate virtually at the speed of light in vacuum. For full overlap of the two pulses, the duration of the EM pulse is
where ![]() $L_{\mathrm{beam}} = (M-1) \lambda _{L}$ is the train length,
$L_{\mathrm{beam}} = (M-1) \lambda _{L}$ is the train length, ![]() $M$ represents the number of micro-bunches in the train, and
$M$ represents the number of micro-bunches in the train, and ![]() $\lambda _{L}$ is the laser wavelength in vacuum. The geometrical length of the structure is
$\lambda _{L}$ is the laser wavelength in vacuum. The geometrical length of the structure is ![]() $L_{\mathrm{geo}} = \gamma m_{e} c^{2}/eG_{0}$, where
$L_{\mathrm{geo}} = \gamma m_{e} c^{2}/eG_{0}$, where ![]() $\gamma = \sqrt{\lambda _{L} / 4\lambda _{r}}$ is the relativistic factor and is set by the resonance condition in an EM wiggler. As an example, for a laser wavelength of 1 micron and a radiation wavelength of X-rays
$\gamma = \sqrt{\lambda _{L} / 4\lambda _{r}}$ is the relativistic factor and is set by the resonance condition in an EM wiggler. As an example, for a laser wavelength of 1 micron and a radiation wavelength of X-rays ![]() $\lambda _{X} = 0.1\ \mathrm{nm}$ we get
$\lambda _{X} = 0.1\ \mathrm{nm}$ we get ![]() $\gamma \simeq 50$.
$\gamma \simeq 50$.
Due to the constraint imposed by the fluence and for the specified energy (![]() $\gamma \simeq 50$), the maximum accelerating gradient depends on two parameters: the clearance of the structure (
$\gamma \simeq 50$), the maximum accelerating gradient depends on two parameters: the clearance of the structure (![]() $D_{\mathrm{int}}$) and the number of micro-bunches in the train (
$D_{\mathrm{int}}$) and the number of micro-bunches in the train (![]() $M$). Note the interdependence between the various parameters requires a self-consistent solution: the laser field depends on the laser pulse duration, which in turn depends on the train’s total charge and the gradient itself.
$M$). Note the interdependence between the various parameters requires a self-consistent solution: the laser field depends on the laser pulse duration, which in turn depends on the train’s total charge and the gradient itself.
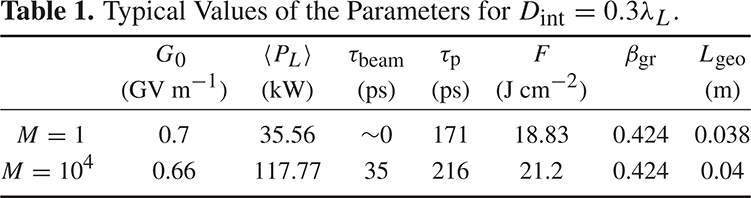
Table 1. Typical Values of the Parameters for ![]() $D_{\mathrm{int}} =0.3\lambda _{L}$.
$D_{\mathrm{int}} =0.3\lambda _{L}$.
A self-consistent solution is illustrated in Figure 3. For ![]() $M < 10^{3}$ micro-bunches, the gradient is virtually independent of
$M < 10^{3}$ micro-bunches, the gradient is virtually independent of ![]() $M$ (see Figure 3(b)). For larger values of
$M$ (see Figure 3(b)). For larger values of ![]() $M$ the gradient decreases for the same clearance. Figure 3(a) shows that it is advantageous to operate with the smallest possible vacuum tunnel – leading to a maximum gradient of less than 0.9 GV m
$M$ the gradient decreases for the same clearance. Figure 3(a) shows that it is advantageous to operate with the smallest possible vacuum tunnel – leading to a maximum gradient of less than 0.9 GV m![]() $^{-1}$. Further simulations show it is better to use a lower dielectric coefficient for the first layer, and in order to achieve a gradient of
$^{-1}$. Further simulations show it is better to use a lower dielectric coefficient for the first layer, and in order to achieve a gradient of ![]() $1\ {\rm GV}\ {\rm m}^{-1}$ we need to replace the silica with a material whose typical fluence is higher by a factor of 1.5 – assuming the pulse dependence is the same. Typical values of the parameters for
$1\ {\rm GV}\ {\rm m}^{-1}$ we need to replace the silica with a material whose typical fluence is higher by a factor of 1.5 – assuming the pulse dependence is the same. Typical values of the parameters for ![]() $D_{\mathrm{int}} = 0.3 \lambda _{{L}}$ are given in Table 1.
$D_{\mathrm{int}} = 0.3 \lambda _{{L}}$ are given in Table 1.
At this point it warrants making a comment regarding a more realistic scenario: The wake generated by the accelerated bunches tends to reduce the laser field – this is the well known beam-loading effect. Consequently, in the presence of the electrons, the field experienced by the structure is thus reduced accordingly for a given fluence, the applied gradient may be significantly higher. In the context of the fluence effect we consider the worst case scenario and ignore this process. Taking it into consideration, we estimate that the accelerating gradient will be enhanced.
3. Optimal charge
Given the accelerating gradient ![]() $G_{0}$, which is evaluated self-consistently, we now calculate the optimal number of electrons in a micro-bunch injected into the acceleration module. Optimum charge occurs for maximum efficiency of the acceleration process. We can interpret the reason for this optimum as follows: for a given accelerating gradient, if the accelerated charge is small, the energy transferred is negligibly small (zero). At the other extreme, when the charge is large, beam loading may suppress the effective accelerating gradient to zero; therefore, again, the transferred energy is minuscule. Between these two ‘zeros’ the function of energy transferred is expected to have a maximum.
$G_{0}$, which is evaluated self-consistently, we now calculate the optimal number of electrons in a micro-bunch injected into the acceleration module. Optimum charge occurs for maximum efficiency of the acceleration process. We can interpret the reason for this optimum as follows: for a given accelerating gradient, if the accelerated charge is small, the energy transferred is negligibly small (zero). At the other extreme, when the charge is large, beam loading may suppress the effective accelerating gradient to zero; therefore, again, the transferred energy is minuscule. Between these two ‘zeros’ the function of energy transferred is expected to have a maximum.
3.1. Single bunch
In the single bunch case (![]() $M=1)$, the efficiency of the acceleration process may be determined as
$M=1)$, the efficiency of the acceleration process may be determined as
where ![]() $q_{0} = G_{0}/\kappa $ is the charge for which the wake generated by the bunch balances the laser gradient – in other words, there is no net acceleration. The maximum value of efficiency, occurring for
$q_{0} = G_{0}/\kappa $ is the charge for which the wake generated by the bunch balances the laser gradient – in other words, there is no net acceleration. The maximum value of efficiency, occurring for ![]() $q_{\mathrm{opt}} = q_{0}/2$, is determined by the projection of the total deceleration, represented by
$q_{\mathrm{opt}} = q_{0}/2$, is determined by the projection of the total deceleration, represented by ![]() $\kappa $, on the fundamental mode, represented in turn by
$\kappa $, on the fundamental mode, represented in turn by ![]() $\kappa _{1}$ – explicitly,
$\kappa _{1}$ – explicitly, ![]() $\eta _{\max } = \kappa _{1} / \kappa \equiv W_{1}$;
$\eta _{\max } = \kappa _{1} / \kappa \equiv W_{1}$; ![]() $W_{1}$ is the weight function of the first mode[Reference Schächter, Byer and Siemann7]. The maximum efficiency is dependent on the clearance (Stupakov & Bane[Reference Bane and Stupakov8]):
$W_{1}$ is the weight function of the first mode[Reference Schächter, Byer and Siemann7]. The maximum efficiency is dependent on the clearance (Stupakov & Bane[Reference Bane and Stupakov8]):
where ![]() $\kappa $,
$\kappa $, ![]() $\beta _{gr}$, and
$\beta _{gr}$, and ![]() $Z_{\mathrm{int}}$ are dependent on the vacuum clearance[Reference Mizrahi and Schächter2]. In the case of a dielectric planar Bragg waveguide with a vacuum tunnel of
$Z_{\mathrm{int}}$ are dependent on the vacuum clearance[Reference Mizrahi and Schächter2]. In the case of a dielectric planar Bragg waveguide with a vacuum tunnel of ![]() $2D_{\mathrm{int}}$ along which a charged-line propagates, the wake coefficient associated with the decelerating field is
$2D_{\mathrm{int}}$ along which a charged-line propagates, the wake coefficient associated with the decelerating field is ![]() $\kappa = E^{({\rm dec})}/q = 1/(4\varepsilon _{0} D_{\mathrm{int}})$ (see Section 4).
$\kappa = E^{({\rm dec})}/q = 1/(4\varepsilon _{0} D_{\mathrm{int}})$ (see Section 4).

Figure 4. Maximum efficiency for a single bunch versus half clearance width (Equation (6)).
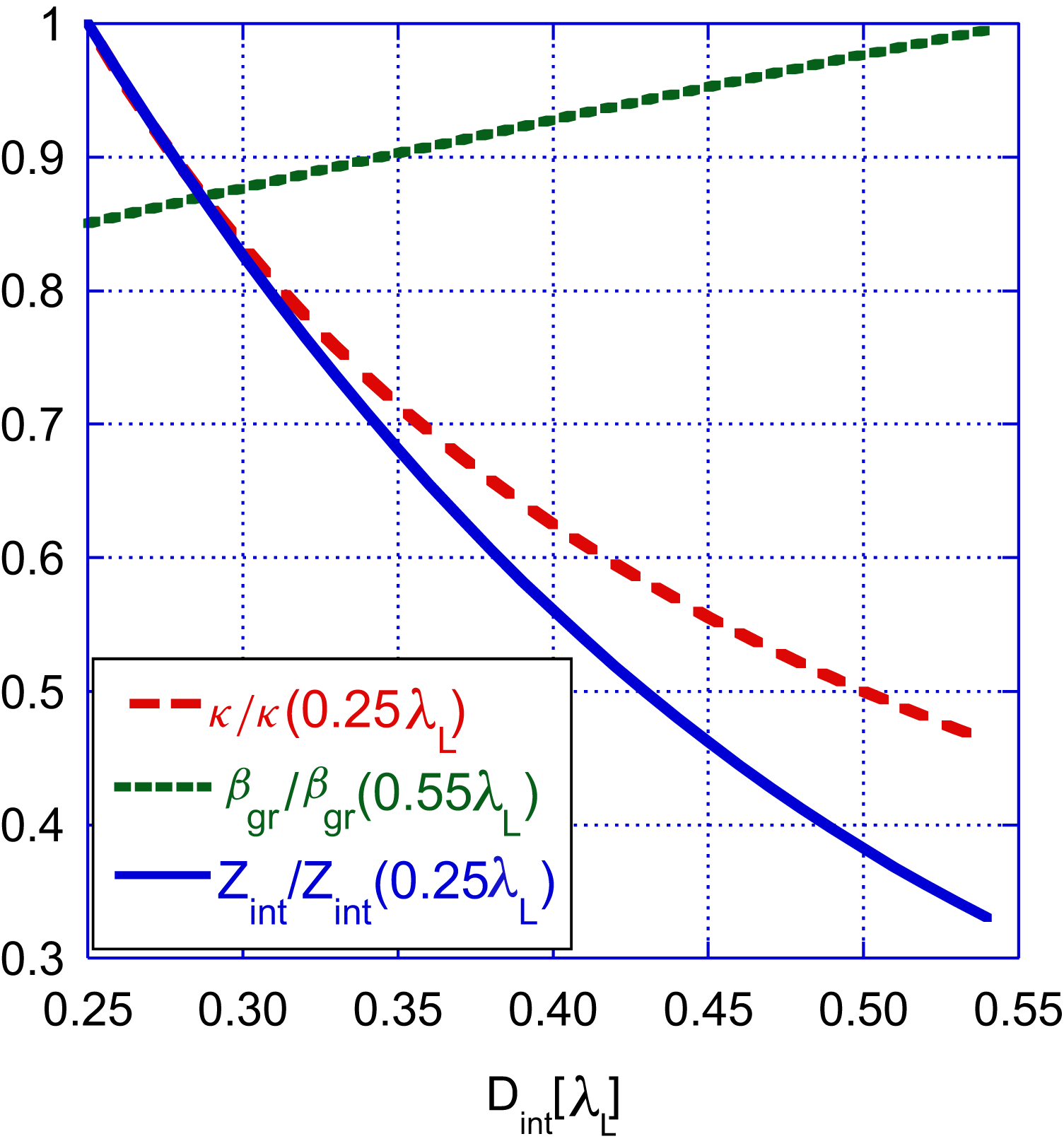
Figure 5. Wake coefficient, interaction impedance, and group velocity versus half clearance width. Each of the parameters is normalized to its maximum value.
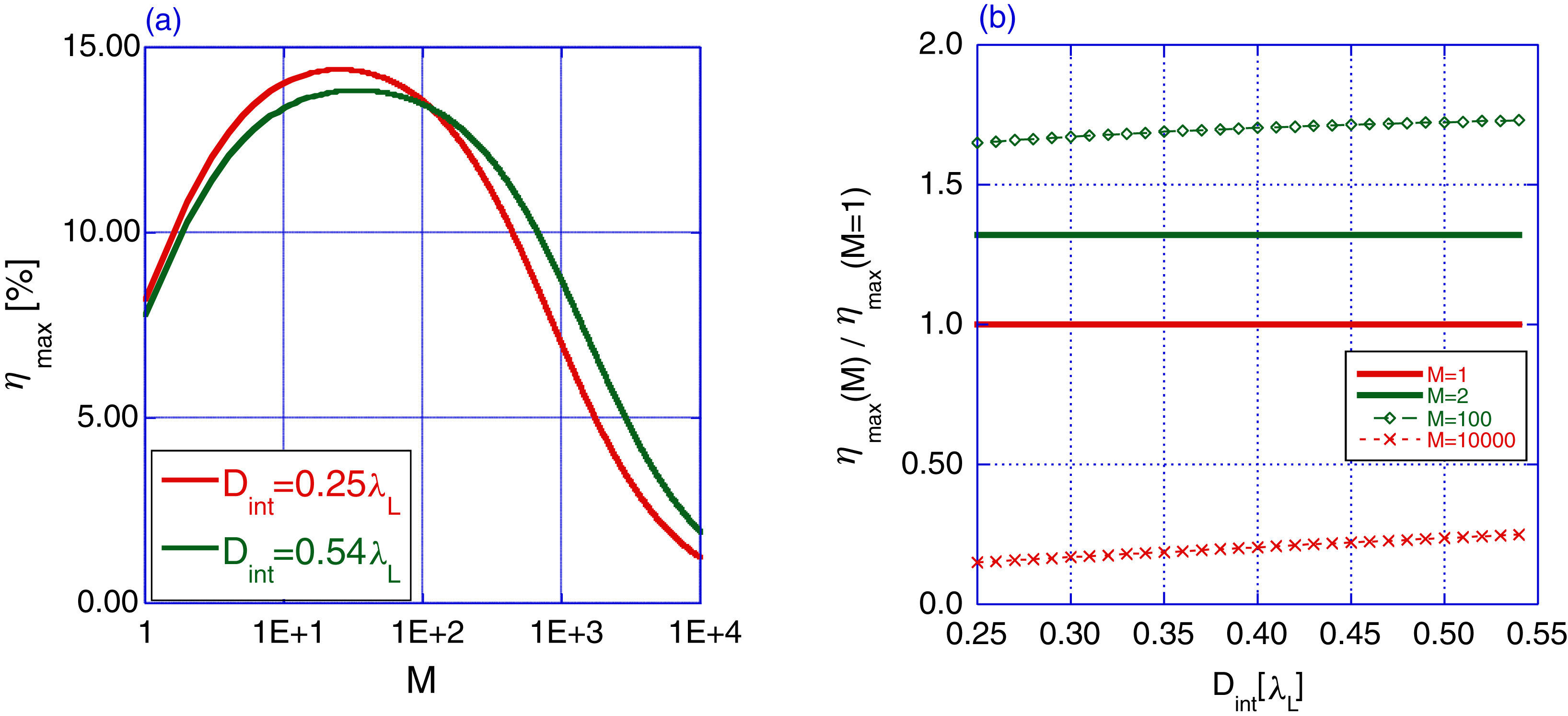
Figure 6. (a) Maximum efficiency versus number of micro-bunches in the train. Red line for ![]() $D_{\mathrm{int}} =0.25\lambda _{{L}}$ and green line for
$D_{\mathrm{int}} =0.25\lambda _{{L}}$ and green line for ![]() $D_{\mathrm{int}}=0.54\lambda _{{L}}$. The optimum value is 15% for
$D_{\mathrm{int}}=0.54\lambda _{{L}}$. The optimum value is 15% for ![]() $M=30$. (b) Maximum efficiency normalized to the single bunch case versus clearance of the accelerator structure. For each clearance there is an optimal value for
$M=30$. (b) Maximum efficiency normalized to the single bunch case versus clearance of the accelerator structure. For each clearance there is an optimal value for ![]() $M$.
$M$.
The maximum efficiency itself has an optimum at ![]() $D_{\mathrm{int}} = 0.35\lambda _{L}$ (Figure 4). The reason for this optimum is a combination of two facts: the wake coefficient and the interaction impedance drop as the clearance is widened, whereas the group velocity increases (Figure 5).
$D_{\mathrm{int}} = 0.35\lambda _{L}$ (Figure 4). The reason for this optimum is a combination of two facts: the wake coefficient and the interaction impedance drop as the clearance is widened, whereas the group velocity increases (Figure 5).
3.2. Train of micro-bunches
For the case of train of ![]() $M$ micro-bunches, the beam-loading causes different micro-bunches to experience different effective accelerating gradients. In order to eliminate this effect, the laser pulse must be tapered according to
$M$ micro-bunches, the beam-loading causes different micro-bunches to experience different effective accelerating gradients. In order to eliminate this effect, the laser pulse must be tapered according to
where ![]() $q_{\mathrm{mb}}$ is the charge in one micro-bunch; tacitly assuming that all micro-bunches are identical. It is assumed that for a sufficiently large number of
$q_{\mathrm{mb}}$ is the charge in one micro-bunch; tacitly assuming that all micro-bunches are identical. It is assumed that for a sufficiently large number of ![]() $M$ the weight function of the first mode is dominant, i.e.,
$M$ the weight function of the first mode is dominant, i.e., ![]() $\kappa _{1}\sim \kappa $.
$\kappa _{1}\sim \kappa $. ![]() $\kappa $ is the wake coefficient, which depends on the structure and number of accelerated micro-bunches. The wake coefficients for a single bunch and train of micro-bunches are different; however, since the laser is tapered, we consider the wake coefficient for a single bunch and a single discontinuity.
$\kappa $ is the wake coefficient, which depends on the structure and number of accelerated micro-bunches. The wake coefficients for a single bunch and train of micro-bunches are different; however, since the laser is tapered, we consider the wake coefficient for a single bunch and a single discontinuity.
The EM energy injected into the system may be readily calculated using
together with Equation (4). The efficiency in this case is given by
By neglecting the geometric length dependence on the charge, since it does not change significantly, the optimal charge is
Several facts are evident: (i) The maximum efficiency value depends on two parameters – the clearance and the number of micro-bunches in a train. Figure 6(a) illustrates the efficiency and its maximum. (ii) For the case of a single bunch (![]() $M=1$) we get
$M=1$) we get ![]() $\xi (M=1)=0.5$, and get the maximum efficiency which was calculated explicitly for a single bunch. (iii) Comparing to the latter case, the efficiency more than doubled for
$\xi (M=1)=0.5$, and get the maximum efficiency which was calculated explicitly for a single bunch. (iii) Comparing to the latter case, the efficiency more than doubled for ![]() $M\sim 50$. (iv) Figure 6(b) shows a weak dependence of the maximum efficiency on the vacuum clearance and a strong dependence on the number of micro-bunches.
$M\sim 50$. (iv) Figure 6(b) shows a weak dependence of the maximum efficiency on the vacuum clearance and a strong dependence on the number of micro-bunches.
Another perspective of the energy conversion efficiency is the total amount of charge accelerated and its distribution among the various numbers of micro-bunches. The number of electrons in a train as a function of the number of micro-bunches is almost constant ![]() ${\sim }1\times 10^{6}$. Thus, for larger values of
${\sim }1\times 10^{6}$. Thus, for larger values of ![]() $M$, the number of electrons in a micro-bunch drops. Figure 7 reveals a weak dependence of
$M$, the number of electrons in a micro-bunch drops. Figure 7 reveals a weak dependence of ![]() $q_{\mathrm{mb}}$ and
$q_{\mathrm{mb}}$ and ![]() $Mq_{\mathrm{mb}}$ on the vacuum clearance.
$Mq_{\mathrm{mb}}$ on the vacuum clearance.
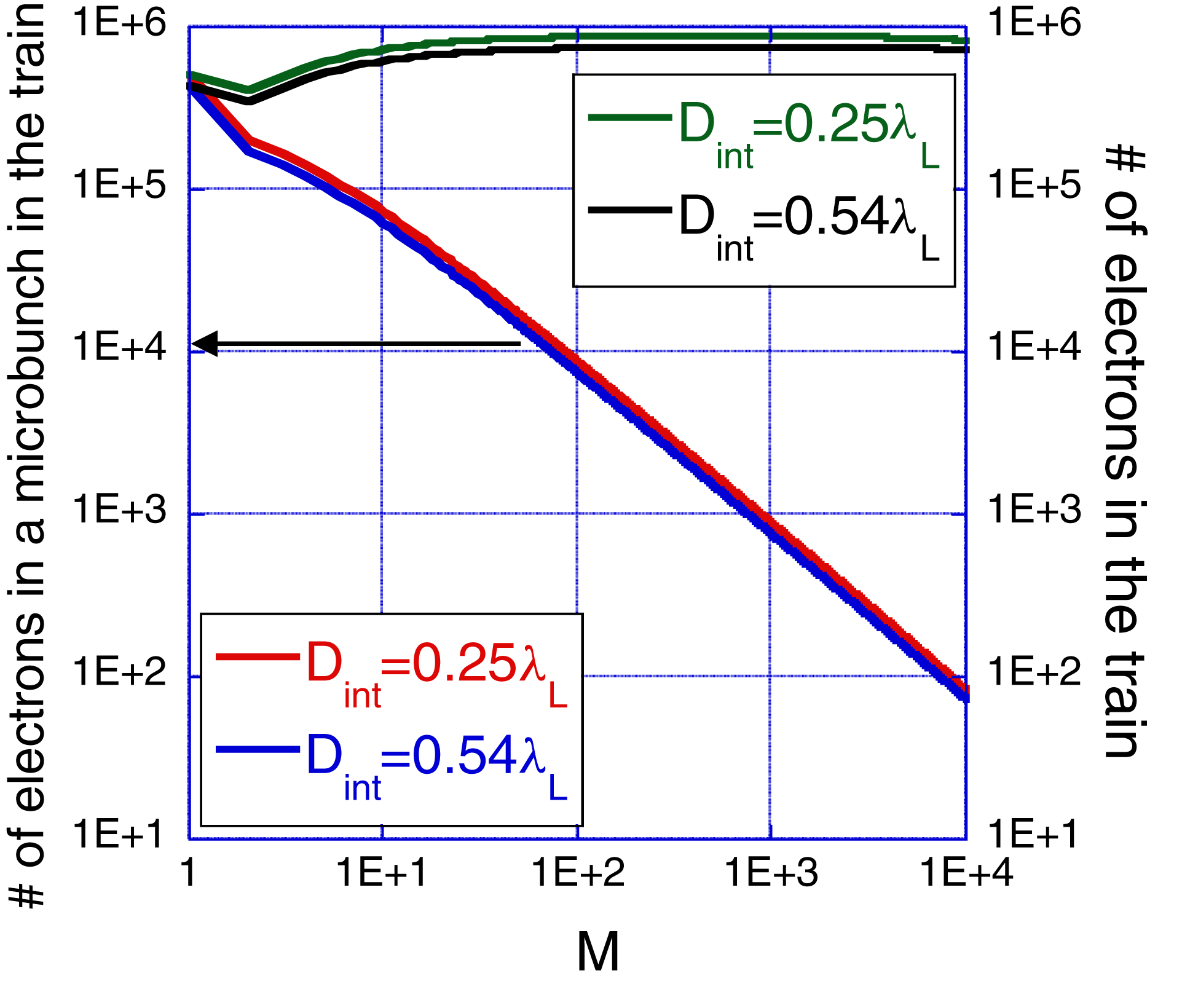
Figure 7. Number of electrons in a microbunch (left ![]() $y$-axis) and number of electrons in the train (right
$y$-axis) and number of electrons in the train (right ![]() $y$-axis) versus the number of micro-bunches for
$y$-axis) versus the number of micro-bunches for ![]() $D_{\mathrm{int}}=0.25 \lambda _{L}$,
$D_{\mathrm{int}}=0.25 \lambda _{L}$, ![]() $0.54 \lambda _{L}$.
$0.54 \lambda _{L}$.
The average power per unit length (![]() $\Delta _y$) of the tapered laser is given by
$\Delta _y$) of the tapered laser is given by
 $$\begin{eqnarray} \langle P_{L} \rangle &=& \frac {U_{\mathrm {EM}}}{\tau _{\mathrm {P}}} = \frac {1}{\tau _{\mathrm {P}}} \int _0^{\tau _{\mathrm {P}}}dtP_L (t) \\ &=& \Delta _{y} \frac {|\lambda _L|^2}{Z_{\mathrm {int}}} \left [G_{0}^{2} + \frac {\alpha ^{2}}{3} + \alpha G_{0} \right ], \label {eq11} \end{eqnarray}$$
$$\begin{eqnarray} \langle P_{L} \rangle &=& \frac {U_{\mathrm {EM}}}{\tau _{\mathrm {P}}} = \frac {1}{\tau _{\mathrm {P}}} \int _0^{\tau _{\mathrm {P}}}dtP_L (t) \\ &=& \Delta _{y} \frac {|\lambda _L|^2}{Z_{\mathrm {int}}} \left [G_{0}^{2} + \frac {\alpha ^{2}}{3} + \alpha G_{0} \right ], \label {eq11} \end{eqnarray}$$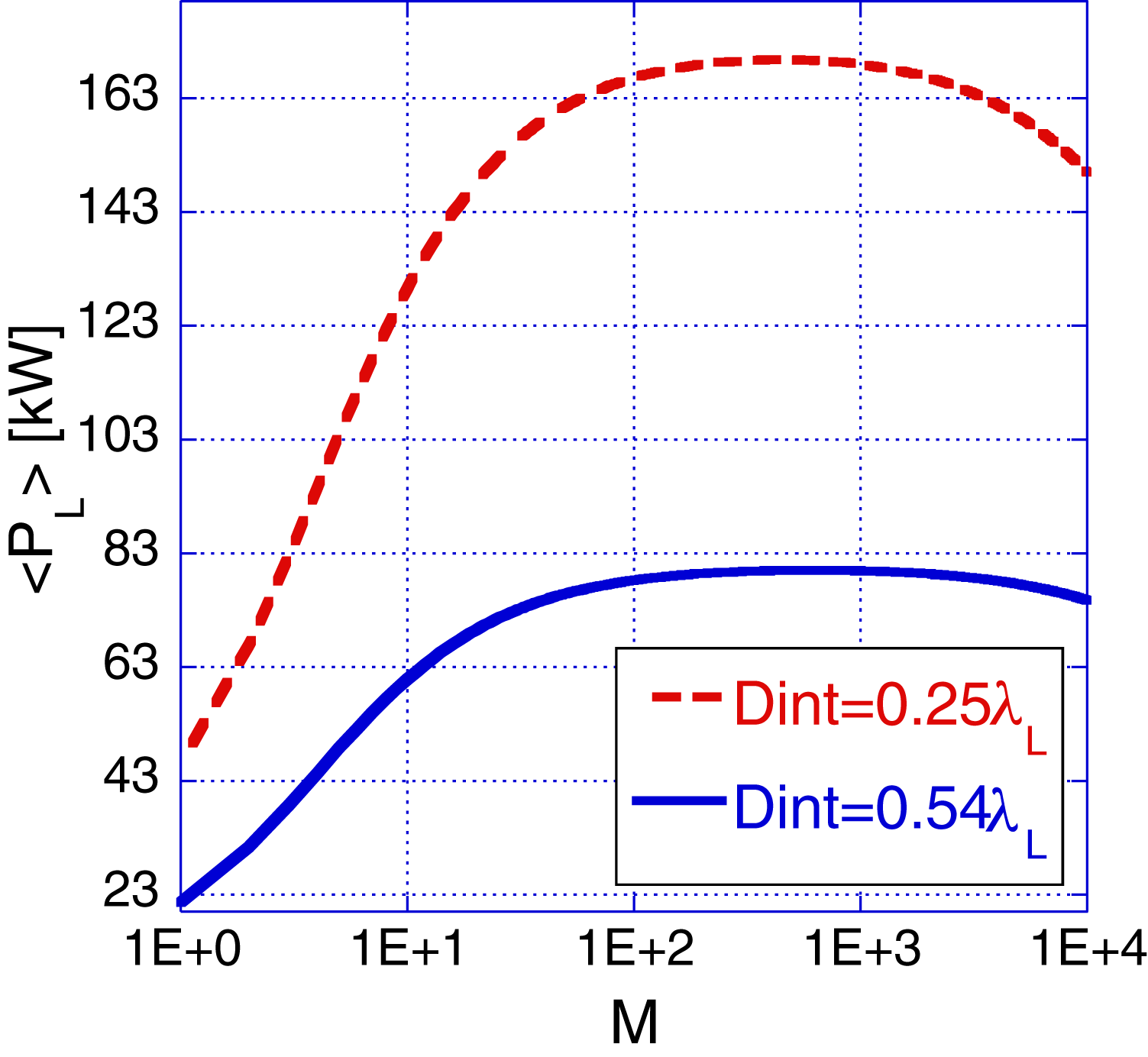
Figure 8. Average laser power for ![]() $D_{\mathrm{int}} = 0.25\lambda _{L}$,
$D_{\mathrm{int}} = 0.25\lambda _{L}$, ![]() $0.54\lambda _{L}$. Its maximum (170 kW) occurs for
$0.54\lambda _{L}$. Its maximum (170 kW) occurs for ![]() $D_{\mathrm{int}} = 0.25 \lambda _{L}$,
$D_{\mathrm{int}} = 0.25 \lambda _{L}$, ![]() $M=700$.
$M=700$.

Figure 9. Planar waveguide acceleration module with a vacuum region of width ![]() $2D_{\mathrm{int}}$. The e-beam is accelerated by a co-propagating
$2D_{\mathrm{int}}$. The e-beam is accelerated by a co-propagating ![]() $\mathrm{TM}_{01}$ laser mode. The macrobunch consists of a train of
$\mathrm{TM}_{01}$ laser mode. The macrobunch consists of a train of ![]() $M$ line charges, separated by a laser wavelength.
$M$ line charges, separated by a laser wavelength.
4. Wake coefficient – single bunch
In this section we determine and investigate the wake coefficient (![]() $\kappa $) for a single bunch (in the following section we repeat this for a train of micro-bunches). Both are essential for establishing the optimal charge in the micro-bunch and determining the beam loading effect.
$\kappa $) for a single bunch (in the following section we repeat this for a train of micro-bunches). Both are essential for establishing the optimal charge in the micro-bunch and determining the beam loading effect.
A laser pulse accelerates a point charge ![]() $q_{\mathrm{mb}}$ moving in a vacuum tunnel of planar Bragg acceleration structure and generates an EM wake (Cerenkov radiation). Associated with this wake there is a decelerating electric field which, by virtue of the linearity of Maxwell’s equations, is proportional to the charge, namely
$q_{\mathrm{mb}}$ moving in a vacuum tunnel of planar Bragg acceleration structure and generates an EM wake (Cerenkov radiation). Associated with this wake there is a decelerating electric field which, by virtue of the linearity of Maxwell’s equations, is proportional to the charge, namely ![]() $E_{\mathrm{dec}} =\kappa q$, where the wake coefficient
$E_{\mathrm{dec}} =\kappa q$, where the wake coefficient ![]() $\kappa $ depends on the structure.
$\kappa $ depends on the structure.
The vacuum–dielectric discontinuity generates a reflected wave that can affect the point charge. Any reflection occurring further away from the first discontinuity reaches the structure’s axis only after the point charge has passed–thus it may affect only trailing micro-bunches.
In the absence of reflections, the wake coefficient is determined by the structure (Appendix A) and given as
In the presence of reflections, for a single bunch, only the first discontinuity affects a line-charge. However, we demonstrate that quantitatively using a previously defined formulation[Reference Mizrahi and Schächter2]. The effective wake coefficient on the first bunch ![]() $(\bar{\tau }=0)$ is
$(\bar{\tau }=0)$ is
where the ![]() ${R}(\omega )$ is the reflection coefficient of the structure – including the effect of the first (matching) layer as well as the ‘Bragg layers’. Numerical evaluation of Equation (13) reveals that
${R}(\omega )$ is the reflection coefficient of the structure – including the effect of the first (matching) layer as well as the ‘Bragg layers’. Numerical evaluation of Equation (13) reveals that ![]() $\bar{\kappa } = \kappa $, with an error of less than 0.1% – i.e., the wake coefficient for a single bunch including reflections is almost equal to the wake coefficient with no reflections. In fact, it is possible to demonstrate analytically that since reflection reaches the axis behind the charged-line micro-bunch,
$\bar{\kappa } = \kappa $, with an error of less than 0.1% – i.e., the wake coefficient for a single bunch including reflections is almost equal to the wake coefficient with no reflections. In fact, it is possible to demonstrate analytically that since reflection reaches the axis behind the charged-line micro-bunch, ![]() $\bar{\kappa } = \kappa $.
$\bar{\kappa } = \kappa $.
5. Wake coefficient – train of bunches
In the case of a train of micro-bunches the field spatial distribution trailing the particle is strongly affected. The Bragg dielectric structure allows energy to escape from the structure through the layers, and the trailing bunches are less affected by the wake field – except eigenmodes of the structure.
For a train of ![]() $M$ micro-bunches, of length
$M$ micro-bunches, of length ![]() $L_{\mathrm{mb}}$ each, separated by one wavelength
$L_{\mathrm{mb}}$ each, separated by one wavelength ![]() $\lambda _{L}$ (Figure 9), the wake coefficient in the case of a train of micro-bunches is strongly dependent on the structure
$\lambda _{L}$ (Figure 9), the wake coefficient in the case of a train of micro-bunches is strongly dependent on the structure
where ![]() $\chi = 2\pi L_{\mathrm{mb}} / \lambda _L$ is the relative length of the micro-bunch and
$\chi = 2\pi L_{\mathrm{mb}} / \lambda _L$ is the relative length of the micro-bunch and ![]() $W(\bar{\omega }) \equiv \bigl [\frac {1-{ R}(\omega )}{1+{R}(\omega )} + j\bar{\omega } \bigr ]^{-1}$ are the weights[Reference Mizrahi and Schächter2].
$W(\bar{\omega }) \equiv \bigl [\frac {1-{ R}(\omega )}{1+{R}(\omega )} + j\bar{\omega } \bigr ]^{-1}$ are the weights[Reference Mizrahi and Schächter2].
Several observations are evident: ![]() $\tilde{\, \kappa }$ decays as
$\tilde{\, \kappa }$ decays as ![]() $1/M^{2}$ and the ‘sinc’ function acts as a low-pass filter (Figure 10); higher frequencies than the fundamental are suppressed (shorter wavelengths).
$1/M^{2}$ and the ‘sinc’ function acts as a low-pass filter (Figure 10); higher frequencies than the fundamental are suppressed (shorter wavelengths). ![]() $M$ has an effect on the non-fundamental modes, i.e.,
$M$ has an effect on the non-fundamental modes, i.e., ![]() $\tilde{\kappa }\simeq \kappa _{1}$.
$\tilde{\kappa }\simeq \kappa _{1}$. ![]() $\kappa _{1}$ is independent of the number of micro-bunches (
$\kappa _{1}$ is independent of the number of micro-bunches (![]() $M$) and thus remains the same. The projection of the wake on the fundamental mode (
$M$) and thus remains the same. The projection of the wake on the fundamental mode (![]() $W_{1}$-weight of the first mode) increases with the number of micro-bunches in the train (since higher frequencies are suppressed). Therefore, we should be able to enhance to some extent the efficiency for
$W_{1}$-weight of the first mode) increases with the number of micro-bunches in the train (since higher frequencies are suppressed). Therefore, we should be able to enhance to some extent the efficiency for ![]() $M\gg 1$, and increase the amount of charge accelerated.
$M\gg 1$, and increase the amount of charge accelerated.

Figure 10. Spectrum of the decelerating field multiplied by the ‘sinc’ function of the number of micro-bunches: ![]() $h(\omega ,M) = w(\omega ) \mathrm{sinc}^{2} (\pi \omega M/\omega _L)/\mathrm{sinc}^{2}(\pi \omega /\omega _L)$ on a log–log scale. Frequencies other than the fundamental are suppressed as the number of micro-bunches in the train increases.
$h(\omega ,M) = w(\omega ) \mathrm{sinc}^{2} (\pi \omega M/\omega _L)/\mathrm{sinc}^{2}(\pi \omega /\omega _L)$ on a log–log scale. Frequencies other than the fundamental are suppressed as the number of micro-bunches in the train increases.
Our simplified model allows all ![]() $n\cdot \omega _{L}$ harmonics, since the dielectric coefficient is independent of frequency. In practice, the dielectric function is frequency dependent and, as a result, the higher harmonics are also suppressed.
$n\cdot \omega _{L}$ harmonics, since the dielectric coefficient is independent of frequency. In practice, the dielectric function is frequency dependent and, as a result, the higher harmonics are also suppressed.
6. Conclusions
The maximum accelerating gradient is evaluated self-consistently based on the constraints imposed by the pulse duration and fluence. It depends on two parameters: the clearance of the structure (![]() $D_{\mathrm{int}}$) and the number of micro-bunches in the train (
$D_{\mathrm{int}}$) and the number of micro-bunches in the train (![]() $M$). In the worst case scenario, it may reach levels of
$M$). In the worst case scenario, it may reach levels of ![]() $1\ \mathrm{GV\ m}^{-1}$.
$1\ \mathrm{GV\ m}^{-1}$.
Optimum charge occurs for maximum efficiency of the acceleration process. For a train of micro-bunches, two constraints must be satisfied: the laser pulse duration must be longer than the macro bunch length and the laser’s envelope must be tapered to compensate for the beam loading, ensuring uniform gradient acceleration of all micro-bunches. The maximum efficiency has an optimal value (![]() ${\sim }15\%$) which depends on two parameters: a weak dependence on the vacuum clearance and a strong dependence on the number of micro-bunches.
${\sim }15\%$) which depends on two parameters: a weak dependence on the vacuum clearance and a strong dependence on the number of micro-bunches.
The optimal number of electrons to be accelerated is determined by the laser field and the maximum efficiency requirement. For ![]() $M=1000$, the number electrons in a micro-bunch is
$M=1000$, the number electrons in a micro-bunch is ![]() ${\sim }1150$, while the total number of electrons in the train is almost constant (
${\sim }1150$, while the total number of electrons in the train is almost constant (![]() ${\sim }10^{6}$). There is weak dependence of
${\sim }10^{6}$). There is weak dependence of ![]() $q_{\mathrm{mb}}$ and
$q_{\mathrm{mb}}$ and ![]() $Mq_{\mathrm{mb}}$ on the vacuum clearance.
$Mq_{\mathrm{mb}}$ on the vacuum clearance.
The optimal charge in the micro-bunch and the beam loading effect are also determined by the wake coefficient. The latter is a property of the structure and refers to the decelerating field. The maximum efficiency increases with the number of micro-bunches in the train since higher frequencies are suppressed.
Acknowledgements
This study was supported by the BiNational US–Israel Science Foundation and the Israel Ministry of Science.
We investigate the wake field, separating the wake into two components, as developed in Refs. [Reference Hemsing and Xiang5] and [Reference Schächter, Byer and Siemann7]. For the primary we consider a line charge, infinite in the ![]() $y$ direction, moving with a constant velocity
$y$ direction, moving with a constant velocity ![]() $v$ in the
$v$ in the ![]() $z$-direction inside the vacuum core of the planar Bragg acceleration. All field components are excited by the current density
$z$-direction inside the vacuum core of the planar Bragg acceleration. All field components are excited by the current density ![]() $J_{z} = - \bar{\lambda } v \delta (x) \delta (z-vt)$, where
$J_{z} = - \bar{\lambda } v \delta (x) \delta (z-vt)$, where ![]() $\bar{\lambda } = q / \Delta _{y}$ is the charge per unit length.
$\bar{\lambda } = q / \Delta _{y}$ is the charge per unit length.
The EM field is derived from the nonhomogeneous wave equation of the magnetic vector potential, subject to the Lorentz gauge ![]() $\nabla \cdot A +(\varepsilon /c^{2}) \partial _{t} \phi = 0$, thus
$\nabla \cdot A +(\varepsilon /c^{2}) \partial _{t} \phi = 0$, thus
On the one hand this primary field is generated by a charged-line in free space, whereas on the other hand the secondary field is the reaction to the presence of the surrounding structure. It is this secondary field which is responsible for the decelerating force which acts on the charged-line.
Using the time Fourier transform defined by ![]() $A_z(x, \tau = t-z/v) = \textstyle \int _{-\infty }^{+\infty } d\omega \ e^{j\omega \tau }A_z (x,\omega )$ and its corresponding source term
$A_z(x, \tau = t-z/v) = \textstyle \int _{-\infty }^{+\infty } d\omega \ e^{j\omega \tau }A_z (x,\omega )$ and its corresponding source term ![]() $J_z (x,\omega ) = \bar{\lambda } \delta (x)/2\pi $, Equation (A1) reads
$J_z (x,\omega ) = \bar{\lambda } \delta (x)/2\pi $, Equation (A1) reads
and the general solution has the form
 $$\begin{equation} \label {eq17} A_{z}^{(p)} (x,\omega ) = \begin{cases} a \exp \left (-\frac {|\omega |x}{c\beta \gamma }\right ) & x > 0 \\ b \exp \left (+\frac {|\omega |x}{c\beta \gamma }\right ) & x < 0. \end{cases} \end{equation}$$
$$\begin{equation} \label {eq17} A_{z}^{(p)} (x,\omega ) = \begin{cases} a \exp \left (-\frac {|\omega |x}{c\beta \gamma }\right ) & x > 0 \\ b \exp \left (+\frac {|\omega |x}{c\beta \gamma }\right ) & x < 0. \end{cases} \end{equation}$$ By integrating both sides of the equation ![]() $\partial _{x} A_z (0^+,\omega ) - \partial _x A_z (0^-,\omega ) = \mu _0 \bar{\lambda }/2\pi $, the constants are
$\partial _{x} A_z (0^+,\omega ) - \partial _x A_z (0^-,\omega ) = \mu _0 \bar{\lambda }/2\pi $, the constants are ![]() $a = b = -\mu _0 \bar{\lambda } c \beta \gamma /4\pi |\omega |$. Finally,the magnetic vector potential for the primary field is
$a = b = -\mu _0 \bar{\lambda } c \beta \gamma /4\pi |\omega |$. Finally,the magnetic vector potential for the primary field is
 $$\begin{eqnarray} A_{z}^{(p)} (x,z,t) &=& -\frac {\mu _0 \bar {\lambda }}{4\pi } \int _{-\infty }^{+\infty } d\omega \ \frac {\gamma v}{|\omega |} \\ && \times \, \exp \left [- j \frac {\omega }{v} (z - vt) - \frac {1}{v\gamma } |\omega x|\right ]. \qquad \label {eq18} \end{eqnarray}$$
$$\begin{eqnarray} A_{z}^{(p)} (x,z,t) &=& -\frac {\mu _0 \bar {\lambda }}{4\pi } \int _{-\infty }^{+\infty } d\omega \ \frac {\gamma v}{|\omega |} \\ && \times \, \exp \left [- j \frac {\omega }{v} (z - vt) - \frac {1}{v\gamma } |\omega x|\right ]. \qquad \label {eq18} \end{eqnarray}$$ $$\begin{eqnarray} A_{z}^{(s)} (x,\tau ) &=& - \frac {\mu _{0} \bar {\lambda }}{4\pi } \int _{-\infty }^{+\infty } d\omega \ \frac {\gamma v}{|\omega |} \exp (j\omega \tau ) \\ && \times \begin{cases} A_1 \exp [-\Gamma (x - D _{\mathrm {int}})] & x > D_{\mathrm {int}} \\ A_0 \cosh \left (\frac {|\omega |}{\gamma v}x \right ) & | x| < D_{\mathrm {int}} \\ A_2 \exp [\Gamma (x-D_{\mathrm {int}})] & x < - D_{\mathrm {int}}, \end{cases} \\ \label {eq19} \end{eqnarray}$$
$$\begin{eqnarray} A_{z}^{(s)} (x,\tau ) &=& - \frac {\mu _{0} \bar {\lambda }}{4\pi } \int _{-\infty }^{+\infty } d\omega \ \frac {\gamma v}{|\omega |} \exp (j\omega \tau ) \\ && \times \begin{cases} A_1 \exp [-\Gamma (x - D _{\mathrm {int}})] & x > D_{\mathrm {int}} \\ A_0 \cosh \left (\frac {|\omega |}{\gamma v}x \right ) & | x| < D_{\mathrm {int}} \\ A_2 \exp [\Gamma (x-D_{\mathrm {int}})] & x < - D_{\mathrm {int}}, \end{cases} \\ \label {eq19} \end{eqnarray}$$thus
or, explicitly,
 $$\begin{eqnarray} E_{z}^{(p)} &=& \frac {\mu _{0} \bar {\lambda }}{4\pi } \int _{-\infty }^{+\infty } d \omega \ \frac {j\omega \gamma v}{| \omega |} \left ({1-\frac {1}{\beta ^{2}}}\right ) \\ && \times \,\exp \left [{j\omega \tau - \frac {1}{v\gamma } | {\omega x}|} \right ] \\ E_{z}^{(s)} &=& \frac {\mu _{0}\bar {\lambda }}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {j\omega \gamma v}{| \omega |}\exp ({j\omega \tau })} \\ && \times \begin{cases} {\left ({1-\frac {1}{\varepsilon \beta ^{2}}} \right )A_{1} \exp \left [{-\Gamma ({x-D_{\mathrm {int}}})}\right ]} \\ \qquad {x>D_{\mathrm {int}}} \\ {\left ({1-\frac {1}{\beta ^{2}}}\right )A_{0} \cosh \left ({\frac {| \omega |}{\gamma v}x} \right )} \\ \qquad {| x |<D_{\mathrm {int}}}. \end{cases} \label {eq22} \end{eqnarray}$$
$$\begin{eqnarray} E_{z}^{(p)} &=& \frac {\mu _{0} \bar {\lambda }}{4\pi } \int _{-\infty }^{+\infty } d \omega \ \frac {j\omega \gamma v}{| \omega |} \left ({1-\frac {1}{\beta ^{2}}}\right ) \\ && \times \,\exp \left [{j\omega \tau - \frac {1}{v\gamma } | {\omega x}|} \right ] \\ E_{z}^{(s)} &=& \frac {\mu _{0}\bar {\lambda }}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {j\omega \gamma v}{| \omega |}\exp ({j\omega \tau })} \\ && \times \begin{cases} {\left ({1-\frac {1}{\varepsilon \beta ^{2}}} \right )A_{1} \exp \left [{-\Gamma ({x-D_{\mathrm {int}}})}\right ]} \\ \qquad {x>D_{\mathrm {int}}} \\ {\left ({1-\frac {1}{\beta ^{2}}}\right )A_{0} \cosh \left ({\frac {| \omega |}{\gamma v}x} \right )} \\ \qquad {| x |<D_{\mathrm {int}}}. \end{cases} \label {eq22} \end{eqnarray}$$ $$\begin{eqnarray} H_{y}^{(p )} &=& -\frac {\mu _{0} \bar {{\lambda }}}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {1}{\mu _{0} }\exp \left [{j\omega \tau -\frac {1}{v\gamma }| {\omega x}|} \right ]} \mathrm {sign} (x) \\ H_{y}^{(s )} &=& \frac {\mu _{0} \bar {{\lambda }}}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {1}{\mu _{0} }\exp ({j\omega \tau } )} \\ && \times \begin{cases} {-\gamma \sqrt {1-\beta ^{2}\varepsilon } A_{1} \exp \left [{-\Gamma ({x-D_{\mathrm {int}} } )} \right ]} \\ \qquad {x>D_{\mathrm {int}} } \\ {A_{0} \sinh \left ({\frac {\left | \omega \right |}{\gamma v}x} \right )} \quad {\left | x \right |<D_{\mathrm {int}}}. \end{cases} \label {eq23} \end{eqnarray}$$
$$\begin{eqnarray} H_{y}^{(p )} &=& -\frac {\mu _{0} \bar {{\lambda }}}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {1}{\mu _{0} }\exp \left [{j\omega \tau -\frac {1}{v\gamma }| {\omega x}|} \right ]} \mathrm {sign} (x) \\ H_{y}^{(s )} &=& \frac {\mu _{0} \bar {{\lambda }}}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {1}{\mu _{0} }\exp ({j\omega \tau } )} \\ && \times \begin{cases} {-\gamma \sqrt {1-\beta ^{2}\varepsilon } A_{1} \exp \left [{-\Gamma ({x-D_{\mathrm {int}} } )} \right ]} \\ \qquad {x>D_{\mathrm {int}} } \\ {A_{0} \sinh \left ({\frac {\left | \omega \right |}{\gamma v}x} \right )} \quad {\left | x \right |<D_{\mathrm {int}}}. \end{cases} \label {eq23} \end{eqnarray}$$ whereas the continuity of ![]() $H_{y}$ entails
$H_{y}$ entails ![]() $H_{y}^{(p)} ({x=D_{\mathrm{int}}^{-}}) + H_{y}^{(s)} ({x=D_{\mathrm{int}}^{-}} ) = H_{y}^{(s)} ({x=D_{\mathrm{int}}^{+}})$
$H_{y}^{(p)} ({x=D_{\mathrm{int}}^{-}}) + H_{y}^{(s)} ({x=D_{\mathrm{int}}^{-}} ) = H_{y}^{(s)} ({x=D_{\mathrm{int}}^{+}})$
 $$\begin{eqnarray} && -{\mathrm {exp}} \left ({-\frac {1}{v\gamma }| \omega |D_{\mathrm {int}} } \right ) + A_{0} \sinh \left ({\frac {| \omega |}{\gamma v}D_{\mathrm {int}} }\right ) \\ && \quad = -\gamma \sqrt {1-\beta ^{2}\varepsilon } A_{1}. \label {eq25} \end{eqnarray}$$
$$\begin{eqnarray} && -{\mathrm {exp}} \left ({-\frac {1}{v\gamma }| \omega |D_{\mathrm {int}} } \right ) + A_{0} \sinh \left ({\frac {| \omega |}{\gamma v}D_{\mathrm {int}} }\right ) \\ && \quad = -\gamma \sqrt {1-\beta ^{2}\varepsilon } A_{1}. \label {eq25} \end{eqnarray}$$ where ![]() $\Omega = - \sqrt{1-\beta ^{2}\varepsilon } /[{\gamma \varepsilon ({1-\beta ^{2}} )} ] = - \gamma \sqrt{1-\beta ^{2}\varepsilon _{{\kern 1pt}} } /\varepsilon $. Accordingly, the decelerating field is the secondary field acting on the charged particle in the vacuum core
$\Omega = - \sqrt{1-\beta ^{2}\varepsilon } /[{\gamma \varepsilon ({1-\beta ^{2}} )} ] = - \gamma \sqrt{1-\beta ^{2}\varepsilon _{{\kern 1pt}} } /\varepsilon $. Accordingly, the decelerating field is the secondary field acting on the charged particle in the vacuum core
 $$\begin{eqnarray} && E_{\mathrm {dec}} \triangleq E_{z}^{(s )} ({x=0,z=vt,t} ) \\ &&\quad = \frac {\mu _{0} \bar {{\lambda }}}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {j\omega \gamma v}{| \omega |}\left ({1-\frac {1}{\beta ^{2}}} \right )A_{0} } \\ &&\quad = -\frac {\mu _{0} \bar {{\lambda }}}{4\pi }2Re\left \{ {\int _0^{+\infty } {d\omega \ \frac {jv}{\gamma \beta ^{2}}\frac {2}{\frac {\rmOmega -1}{\rmOmega +1}\exp \bigl ({2\frac {| \omega |}{\gamma v}D_{\mathrm {int}} }\bigr )-1}} } \right \} \\ &&\quad = - \frac {\mu _{0} \bar {{\lambda }}}{4\pi }2Re\left \{ {\frac {2\gamma v}{2D_{\mathrm {int}} }\frac {jv}{\gamma \beta ^{2}}\ln \left ({\frac {1-\rmOmega }{2}} \right )} \right \}.\label {eq27} \end{eqnarray}$$
$$\begin{eqnarray} && E_{\mathrm {dec}} \triangleq E_{z}^{(s )} ({x=0,z=vt,t} ) \\ &&\quad = \frac {\mu _{0} \bar {{\lambda }}}{4\pi }\int _{-\infty }^{+\infty } {d\omega \ \frac {j\omega \gamma v}{| \omega |}\left ({1-\frac {1}{\beta ^{2}}} \right )A_{0} } \\ &&\quad = -\frac {\mu _{0} \bar {{\lambda }}}{4\pi }2Re\left \{ {\int _0^{+\infty } {d\omega \ \frac {jv}{\gamma \beta ^{2}}\frac {2}{\frac {\rmOmega -1}{\rmOmega +1}\exp \bigl ({2\frac {| \omega |}{\gamma v}D_{\mathrm {int}} }\bigr )-1}} } \right \} \\ &&\quad = - \frac {\mu _{0} \bar {{\lambda }}}{4\pi }2Re\left \{ {\frac {2\gamma v}{2D_{\mathrm {int}} }\frac {jv}{\gamma \beta ^{2}}\ln \left ({\frac {1-\rmOmega }{2}} \right )} \right \}.\label {eq27} \end{eqnarray}$$ $$\begin{eqnarray*} && \int _0^{+\infty } {d\omega \ \frac {1}{u_{1} \exp ({u_{2} | \omega |} )-1}} \\ && \quad = \frac {1}{u_{2} }\left . {\ln \left ({1-\frac {\exp ({-u_{2} | \omega |})}{u_{1} }} \right )} \right |_{0}^{\infty } \\ && \quad = \frac {1}{u_{2} }\ln \left ({\frac {u_{1} }{u_{1} -1}} \right ) \end{eqnarray*}$$
$$\begin{eqnarray*} && \int _0^{+\infty } {d\omega \ \frac {1}{u_{1} \exp ({u_{2} | \omega |} )-1}} \\ && \quad = \frac {1}{u_{2} }\left . {\ln \left ({1-\frac {\exp ({-u_{2} | \omega |})}{u_{1} }} \right )} \right |_{0}^{\infty } \\ && \quad = \frac {1}{u_{2} }\ln \left ({\frac {u_{1} }{u_{1} -1}} \right ) \end{eqnarray*}$$ With Taylor expansion for ![]() $x\to \infty \ln ({1+jx} )=-\ln ({1/x} )+j/x$, together with
$x\to \infty \ln ({1+jx} )=-\ln ({1/x} )+j/x$, together with ![]() $\ln ({-j\varsigma })=\ln (\varsigma )-j\pi /2$, the deceleration field is
$\ln ({-j\varsigma })=\ln (\varsigma )-j\pi /2$, the deceleration field is
 $$\begin{eqnarray} E_{\mathrm {dec}} &=& -\frac {\bar {{\lambda }}}{2\pi \varepsilon _{0}D_{\mathrm {int}}} \mathit {Re} \left \{ {j\ln \left ({1+j\gamma \sqrt {\frac {\varepsilon -1}{\varepsilon ^{2}}} } \right )} \right \} \\ \quad &\mathop {\simeq }^{\gamma \to \infty }& \frac {\bar {{\lambda }}}{2\pi \varepsilon _{0} D_{\mathrm {int}} }\frac {\pi }{2} \\ &=& \frac {\bar {{\lambda }}}{4\varepsilon _{0} D_{\mathrm {int}}}, \label {eq28} \end{eqnarray}$$
$$\begin{eqnarray} E_{\mathrm {dec}} &=& -\frac {\bar {{\lambda }}}{2\pi \varepsilon _{0}D_{\mathrm {int}}} \mathit {Re} \left \{ {j\ln \left ({1+j\gamma \sqrt {\frac {\varepsilon -1}{\varepsilon ^{2}}} } \right )} \right \} \\ \quad &\mathop {\simeq }^{\gamma \to \infty }& \frac {\bar {{\lambda }}}{2\pi \varepsilon _{0} D_{\mathrm {int}} }\frac {\pi }{2} \\ &=& \frac {\bar {{\lambda }}}{4\varepsilon _{0} D_{\mathrm {int}}}, \label {eq28} \end{eqnarray}$$












