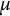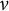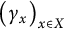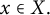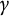1 Introduction
Let X and Y be Polish spaces equipped with Borel probability measures
![]() $\mu $
on X and
$\mu $
on X and
![]() $\nu $
on
$\nu $
on
![]() $Y.$
Recall that a measure is called continuous if
$Y.$
Recall that a measure is called continuous if
![]() $\mu \big (\{x\}\big )=0$
for all
$\mu \big (\{x\}\big )=0$
for all
![]() $x \in X.$
Let
$x \in X.$
Let
![]() $\Pi (\mu ,\nu )$
be the set of Borel probability measures on
$\Pi (\mu ,\nu )$
be the set of Borel probability measures on
![]() $X\times Y$
which have X-marginal
$X\times Y$
which have X-marginal
![]() $\mu $
and Y-marginal
$\mu $
and Y-marginal
![]() $\nu .$
Let
$\nu .$
Let
![]() $\gamma \in \Pi (\mu ,\nu ). $
In what follows, we say that
$\gamma \in \Pi (\mu ,\nu ). $
In what follows, we say that
![]() $\gamma \in \Pi (\mu ,\nu )$
is concentrated on a set S if the outer measure of its complement is zero, i.e.,
$\gamma \in \Pi (\mu ,\nu )$
is concentrated on a set S if the outer measure of its complement is zero, i.e.,
![]() $\gamma ^*(S^c)=0.$
The support of the measure
$\gamma ^*(S^c)=0.$
The support of the measure
![]() $\gamma $
is denoted by
$\gamma $
is denoted by
![]() $\mathrm{spt}(\gamma )$
and is the smallest closed set such that
$\mathrm{spt}(\gamma )$
and is the smallest closed set such that
![]() $\gamma $
is zero on its complement. We now define precisely some notation describing measures concentrated on several graphs.
$\gamma $
is zero on its complement. We now define precisely some notation describing measures concentrated on several graphs.
Definition 1.1 Let X and Y be Polish spaces with Borel probability measures
![]() $\mu $
on X and
$\mu $
on X and
![]() $\nu $
on
$\nu $
on
![]() $Y.$
Let
$Y.$
Let
![]() $k \in \mathbb {N}\cup \{\infty \}.$
We say that a measure
$k \in \mathbb {N}\cup \{\infty \}.$
We say that a measure
![]() $\gamma \in \Pi (\mu , \nu )$
is concentrated on the graphs of measurable maps
$\gamma \in \Pi (\mu , \nu )$
is concentrated on the graphs of measurable maps
![]() $\{G_i\}_{i=1}^k$
from X to Y, if there exists a sequence of measurable nonnegative functions
$\{G_i\}_{i=1}^k$
from X to Y, if there exists a sequence of measurable nonnegative functions
![]() $\{\alpha _i\}_{i=1}^k$
from X to
$\{\alpha _i\}_{i=1}^k$
from X to ![]() with
with
![]() $\sum _{i=1}^k \alpha _i(x)=1$
(
$\sum _{i=1}^k \alpha _i(x)=1$
(
![]() $\mu $
-almost surely) such that for each bounded continuous function
$\mu $
-almost surely) such that for each bounded continuous function ![]() ,
,
 $$\begin{align*}\int_{X \times Y} f(x,y)\, d \gamma= \sum_{i=1}^k\int_X \alpha_i(x) f(x,G_ix) \, d\mu. \end{align*}$$
$$\begin{align*}\int_{X \times Y} f(x,y)\, d \gamma= \sum_{i=1}^k\int_X \alpha_i(x) f(x,G_ix) \, d\mu. \end{align*}$$
In this case, we write
![]() $\gamma =\sum _{i=1}^k (Id \times G_i)_\#(\alpha _i \mu ).$
$\gamma =\sum _{i=1}^k (Id \times G_i)_\#(\alpha _i \mu ).$
Setting
![]() $\Gamma =\mathrm{spt}(\gamma ),$
for every
$\Gamma =\mathrm{spt}(\gamma ),$
for every
![]() $x \in X$
, we denote by
$x \in X$
, we denote by
![]() $\Gamma _x$
the x-section of
$\Gamma _x$
the x-section of
![]() $\Gamma $
, i.e.,
$\Gamma $
, i.e.,
Here is our main result in this paper.
Theorem 1.2 Let
![]() $\mu $
and
$\mu $
and
![]() $\nu $
be Borel probability measures on complete separable metric spaces X and Y, respectively. Assume that at least one of
$\nu $
be Borel probability measures on complete separable metric spaces X and Y, respectively. Assume that at least one of
![]() $\mu $
or
$\mu $
or
![]() $\nu $
is continuous. Let
$\nu $
is continuous. Let
![]() ${\gamma \in \Pi (\mu ,\nu )}$
and
${\gamma \in \Pi (\mu ,\nu )}$
and
![]() $\Gamma =\mathrm{spt}(\gamma ).$
The following assertions hold:
$\Gamma =\mathrm{spt}(\gamma ).$
The following assertions hold:
-
1. If there exists
 $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
 $\text {card} \big (\Gamma _x \big ) \leq m$
for
$\text {card} \big (\Gamma _x \big ) \leq m$
for
 $\mu $
-a.e.
$\mu $
-a.e.
 $x\in X,$
then there exists
$x\in X,$
then there exists
 $k\leq m$
and a sequence of Borel measurable maps
$k\leq m$
and a sequence of Borel measurable maps
 $\{G_i\}_{i=1}^k$
from X to Y such that the measure
$\{G_i\}_{i=1}^k$
from X to Y such that the measure
 $\gamma $
is concentrated on their graphs.
$\gamma $
is concentrated on their graphs. -
2. If
 $\text {card} \big (\Gamma _x \big )< \infty $
for
$\text {card} \big (\Gamma _x \big )< \infty $
for
 $\mu $
-a.e.
$\mu $
-a.e.
 $x\in X,$
then there exist
$x\in X,$
then there exist
 $k\in \mathbb {N}\cup \{\infty \}$
and a sequence of Borel measurable maps
$k\in \mathbb {N}\cup \{\infty \}$
and a sequence of Borel measurable maps
 $\{G_i\}^k_{i=1}$
from X to Y such that the measure
$\{G_i\}^k_{i=1}$
from X to Y such that the measure
 $\gamma $
is concentrated on their graphs.
$\gamma $
is concentrated on their graphs.
This theorem has direct applications in the theory of optimal transportation as it provides a precise description of the structure of optimal plans [Reference Ahmad, Kim and McCann1, Reference Levin6, Reference McCann and Rifford7, Reference Moameni and Rifford10–Reference Villani12]. Theorem 1.2 has a straightforward generalization to the multi-marginal case (see Corollary 2.9). We refer to [Reference Moameni and Pass9] for applications of this result in multi-marginal mass transportation. We also remark that a weaker version of Theorem 1.2 is proved implicitly in [Reference Moameni8]. The next section is devoted to the proof of the main theorem.
2 Preliminaries and the proof of Theorem 1.2
We shall need some important preliminaries from the theory of measures before proving Theorem 1.2. Let
![]() $(X, \mathcal {B}, \mu )$
be a finite, not necessarily complete measure space, and let
$(X, \mathcal {B}, \mu )$
be a finite, not necessarily complete measure space, and let
![]() $(Y, \Sigma )$
be a measurable space. The completion of
$(Y, \Sigma )$
be a measurable space. The completion of
![]() $\mathcal {B}$
with respect to
$\mathcal {B}$
with respect to
![]() $\mu $
is denoted by
$\mu $
is denoted by
![]() $\mathcal {B}_\mu .$
When necessary, we identify
$\mathcal {B}_\mu .$
When necessary, we identify
![]() $\mu $
with its completion on
$\mu $
with its completion on
![]() $\mathcal {B}_\mu .$
The push forward of the measure
$\mathcal {B}_\mu .$
The push forward of the measure
![]() $\mu $
by a map
$\mu $
by a map
![]() $T: (X, \mathcal {B}, \mu ) \to (Y, \Sigma )$
is denoted by
$T: (X, \mathcal {B}, \mu ) \to (Y, \Sigma )$
is denoted by
![]() $T_\# \mu ,$
i.e.,
$T_\# \mu ,$
i.e.,
Definition 2.1 Let
![]() $T: X \to Y$
be
$T: X \to Y$
be
![]() $(\mathcal {B}, \Sigma )$
-measurable, and let
$(\mathcal {B}, \Sigma )$
-measurable, and let
![]() $\nu $
be a positive measure on
$\nu $
be a positive measure on
![]() $\Sigma .$
We call a map
$\Sigma .$
We call a map
![]() $F: Y \to X$
a
$F: Y \to X$
a
![]() $(\Sigma _\nu ,\mathcal {B})$
-measurable section of T if F is
$(\Sigma _\nu ,\mathcal {B})$
-measurable section of T if F is
![]() $(\Sigma _\nu ,\mathcal {B})$
- measurable and
$(\Sigma _\nu ,\mathcal {B})$
- measurable and
![]() $T \circ F = \text {Id}_Y.$
$T \circ F = \text {Id}_Y.$
If X is a topological space we denote by
![]() $\mathcal {B}(X)$
the set of Borel sets on
$\mathcal {B}(X)$
the set of Borel sets on
![]() $X.$
The space of Borel probability measures on a topological space X is denoted by
$X.$
The space of Borel probability measures on a topological space X is denoted by
![]() $\mathcal {P}(X)$
. The following definition and proposition are essential in the sequel.
$\mathcal {P}(X)$
. The following definition and proposition are essential in the sequel.
Definition 2.2 Let X be a Polish space, let
![]() $T: X \to X$
be a surjective Borel measurable map, and let
$T: X \to X$
be a surjective Borel measurable map, and let
![]() $\mu $
be a positive finite measure on
$\mu $
be a positive finite measure on
![]() $\mathcal {B}(X).$
Denote by
$\mathcal {B}(X).$
Denote by
![]() $\mathcal {S}(T)$
the set of all measurable sections of T, i.e.,
$\mathcal {S}(T)$
the set of all measurable sections of T, i.e.,
Let
![]() $\mathcal {K} \subset \mathcal {S}(T).$
We say that a measurable function
$\mathcal {K} \subset \mathcal {S}(T).$
We say that a measurable function
![]() $F:\big (X, \mathcal {B}(X)_\mu \big ) \to \big (X,\mathcal {B}(X)\big )$
is generated by
$F:\big (X, \mathcal {B}(X)_\mu \big ) \to \big (X,\mathcal {B}(X)\big )$
is generated by
![]() $\mathcal {K}$
if there exist a sequence
$\mathcal {K}$
if there exist a sequence
![]() $\{F_i\}_{i=1}^\infty \subset \mathcal {K}$
such that
$\{F_i\}_{i=1}^\infty \subset \mathcal {K}$
such that
We also denote by
![]() $\mathcal {G}(\mathcal {K})$
the set of all functions generated by
$\mathcal {G}(\mathcal {K})$
the set of all functions generated by
![]() $\mathcal {K}.$
It is easily seen that
$\mathcal {K}.$
It is easily seen that
![]() $\mathcal {K} \subseteq \mathcal {G}(\mathcal {K})\subseteq \mathcal {S}(T).$
$\mathcal {K} \subseteq \mathcal {G}(\mathcal {K})\subseteq \mathcal {S}(T).$
Proposition 2.1 Let X be a Polish space, let
![]() $T: X \to X$
be a surjective Borel measurable map, and let
$T: X \to X$
be a surjective Borel measurable map, and let
![]() $\mu $
be a positive finite measure on
$\mu $
be a positive finite measure on
![]() $\mathcal {B}(X).$
Let
$\mathcal {B}(X).$
Let
![]() $\mathcal {K}$
be a nonempty subset of
$\mathcal {K}$
be a nonempty subset of
![]() $\mathcal {S}(T).$
Then, there exist
$\mathcal {S}(T).$
Then, there exist
![]() $ k \in \mathbb {N} \cup \{\infty \}$
and a sequence
$ k \in \mathbb {N} \cup \{\infty \}$
and a sequence
![]() $\{F_i\}_{i=1}^k \subset \mathcal {G}(\mathcal {K})$
such that the following assertions hold:
$\{F_i\}_{i=1}^k \subset \mathcal {G}(\mathcal {K})$
such that the following assertions hold:
-
1. For each
 $i\in \mathbb {N}$
with
$i\in \mathbb {N}$
with
 $i\leq k$
, we have
$i\leq k$
, we have
 $\mu (B_{i})>0,$
where
$\mu (B_{i})>0,$
where
 $\{B_i\}_{i=1}^k$
is defined recursively as follows:
$\{B_i\}_{i=1}^k$
is defined recursively as follows:  $$\begin{align*}B_1=X \quad and \quad B_{i+1}=\Big \{x \in B_i; \,\, F_{i+1}(x)\not\in \{F_1(x),\dots, F_i(x) \}\Big\}\quad \text{provided } k>1.\end{align*}$$
$$\begin{align*}B_1=X \quad and \quad B_{i+1}=\Big \{x \in B_i; \,\, F_{i+1}(x)\not\in \{F_1(x),\dots, F_i(x) \}\Big\}\quad \text{provided } k>1.\end{align*}$$
-
2. For all
 $F \in \mathcal {G}(\mathcal {K})$
, we have
$F \in \mathcal {G}(\mathcal {K})$
, we have  $$\begin{align*}\mu \Big(\big \{x \in B_{i+1}^c\,{\backslash}\, B^c_{i}; \, \, F(x) \not\in \{F_1(x),\dots, F_i(x) \}\big\} \Big)=0.\end{align*}$$
$$\begin{align*}\mu \Big(\big \{x \in B_{i+1}^c\,{\backslash}\, B^c_{i}; \, \, F(x) \not\in \{F_1(x),\dots, F_i(x) \}\big\} \Big)=0.\end{align*}$$
-
3. If
 $k\not =\infty $
, then for all
$k\not =\infty $
, then for all
 $F \in \mathcal {G}(\mathcal {K}),$
$F \in \mathcal {G}(\mathcal {K}),$
 $$\begin{align*}\mu \Big(\big \{x \in B_k; \, \, F(x) \not\in \{F_1(x),\dots, F_k(x) \}\big\} \Big)=0.\end{align*}$$
$$\begin{align*}\mu \Big(\big \{x \in B_k; \, \, F(x) \not\in \{F_1(x),\dots, F_k(x) \}\big\} \Big)=0.\end{align*}$$
Moreover, if either
![]() $k\not =\infty $
or,
$k\not =\infty $
or,
![]() $k=\infty $
and
$k=\infty $
and
![]() $\mu (\cap _{i=1}^\infty B_i)=0$
, then for every
$\mu (\cap _{i=1}^\infty B_i)=0$
, then for every
![]() $F \in \mathcal {G}(\mathcal {K}),$
the measure
$F \in \mathcal {G}(\mathcal {K}),$
the measure
![]() $\varrho _F=F_\#\mu $
is absolutely continuous with respect to the measure
$\varrho _F=F_\#\mu $
is absolutely continuous with respect to the measure
![]() $\sum _{i=1}^k \varrho _i $
, where
$\sum _{i=1}^k \varrho _i $
, where
![]() $\varrho _i={F_i}_\#\mu .$
$\varrho _i={F_i}_\#\mu .$
We refer to Proposition 3.1 in [Reference Moameni8] for the proof of Proposition 2.1.
The following result shows that every
![]() $(\Sigma _\nu ,\mathcal {B}(X))$
-measurable map has a
$(\Sigma _\nu ,\mathcal {B}(X))$
-measurable map has a
![]() $(\Sigma ,\mathcal {B}(X))$
-measurable representation (see [Reference Bogachev2, Corollary 6.7.6]). Recall that a Souslin space is the image of a Polish space under a continuous mapping.
$(\Sigma ,\mathcal {B}(X))$
-measurable representation (see [Reference Bogachev2, Corollary 6.7.6]). Recall that a Souslin space is the image of a Polish space under a continuous mapping.
Proposition 2.2 Let
![]() $\nu $
be a finite measure on a measurable space
$\nu $
be a finite measure on a measurable space
![]() $(Y, \Sigma )$
, let X be a Souslin space, and let
$(Y, \Sigma )$
, let X be a Souslin space, and let
![]() $F : Y\to X$
be a
$F : Y\to X$
be a
![]() $(\Sigma _\nu , \mathcal {B}(X))$
-measurable mapping. Then, there exists a mapping
$(\Sigma _\nu , \mathcal {B}(X))$
-measurable mapping. Then, there exists a mapping
![]() $G: Y \to X $
such that
$G: Y \to X $
such that
![]() $G = F$
$G = F$
![]() $\nu $
-a.e. and
$\nu $
-a.e. and
![]() $G^{-1}(B) \in \Sigma $
for all
$G^{-1}(B) \in \Sigma $
for all
![]() $ B \in \mathcal B(X).$
$ B \in \mathcal B(X).$
For a measurable map
![]() $T: (X, \mathcal {B}(X) ) \to (Y,\Sigma , \nu )$
denote by
$T: (X, \mathcal {B}(X) ) \to (Y,\Sigma , \nu )$
denote by
![]() $\mathcal {M}( T, \nu )$
the set of all measures
$\mathcal {M}( T, \nu )$
the set of all measures
![]() $\lambda $
on
$\lambda $
on
![]() $\mathcal {B} $
so that T pushes
$\mathcal {B} $
so that T pushes
![]() $\lambda $
forward to
$\lambda $
forward to
![]() $\nu ,$
i.e.,
$\nu ,$
i.e.,
Evidently,
![]() $\mathcal {M}( T, \nu )$
is a convex set. A measure
$\mathcal {M}( T, \nu )$
is a convex set. A measure
![]() $\lambda $
is an extreme point of
$\lambda $
is an extreme point of
![]() $\mathcal {M}( T, \nu )$
if the identity
$\mathcal {M}( T, \nu )$
if the identity
![]() $ \lambda = \theta \lambda _1+(1-\theta )\lambda _2$
with
$ \lambda = \theta \lambda _1+(1-\theta )\lambda _2$
with
![]() $\theta \in (0,1) $
and
$\theta \in (0,1) $
and
![]() $\lambda _1, \lambda _2 \in \mathcal {M}( T, \nu )$
imply that
$\lambda _1, \lambda _2 \in \mathcal {M}( T, \nu )$
imply that
![]() $ \lambda _1=\lambda _2$
. The set of extreme points of
$ \lambda _1=\lambda _2$
. The set of extreme points of
![]() $\mathcal {M}( T, \nu )$
is denoted by
$\mathcal {M}( T, \nu )$
is denoted by
![]() $\mathrm{ext}\,\mathcal {M}( T, \nu ).$
$\mathrm{ext}\,\mathcal {M}( T, \nu ).$
We recall the following result from [Reference Graf4] in which a characterization of the set
![]() $\mathrm{ext}\,\mathcal {M}( T, \nu )$
is given.
$\mathrm{ext}\,\mathcal {M}( T, \nu )$
is given.
Theorem 2.3 Let
![]() $(Y,\Sigma , \nu )$
be a probability space, let
$(Y,\Sigma , \nu )$
be a probability space, let
![]() $(X, \mathcal {B}(X))$
be a Hausdorff space with a Radon probability measure
$(X, \mathcal {B}(X))$
be a Hausdorff space with a Radon probability measure
![]() $\lambda $
, and let
$\lambda $
, and let
![]() $T : X\to Y$
be a
$T : X\to Y$
be a
![]() $(\mathcal {B}(X), \Sigma )$
-measurable mapping. Assume that T is surjective and
$(\mathcal {B}(X), \Sigma )$
-measurable mapping. Assume that T is surjective and
![]() $\Sigma $
is countably separated. The following conditions are equivalent:
$\Sigma $
is countably separated. The following conditions are equivalent:
-
(i)
 $\lambda $
is an extreme point of
$\lambda $
is an extreme point of
 $M(T, \nu )$
;
$M(T, \nu )$
; -
(ii) there exists a
 $(\Sigma _\nu ,\mathcal {B}(X))$
-measurable section
$(\Sigma _\nu ,\mathcal {B}(X))$
-measurable section
 $F : Y \to X$
of the mapping T with
$F : Y \to X$
of the mapping T with
 $\lambda = F_\# \nu $
.
$\lambda = F_\# \nu $
.
By making use of the Choquet theory in the setting of non-compact sets of measures [Reference von Weizsäcker and Winkler13], each
![]() $ \lambda \in M(T, \nu )$
can be represented as a Choquet-type integral over
$ \lambda \in M(T, \nu )$
can be represented as a Choquet-type integral over
![]() $ \mathrm{ext} \, M(T, \nu ).$
Denote by
$ \mathrm{ext} \, M(T, \nu ).$
Denote by
![]() $\Sigma _{ \mathrm{ext} \, M(T, \nu )}$
the
$\Sigma _{ \mathrm{ext} \, M(T, \nu )}$
the
![]() $\sigma $
-algebra over
$\sigma $
-algebra over
![]() $\mathrm{ext}\, M(T, \nu )$
generated by the functions
$\mathrm{ext}\, M(T, \nu )$
generated by the functions
![]() $\varrho \to \varrho (B)$
,
$\varrho \to \varrho (B)$
,
![]() $B \in \mathcal {B}(X).$
We have the following result (see [Reference Moameni8] for a proof).
$B \in \mathcal {B}(X).$
We have the following result (see [Reference Moameni8] for a proof).
Theorem 2.4 Let X and Y be complete separable metric spaces, and let
![]() $\nu $
be a probability measure on
$\nu $
be a probability measure on
![]() $\mathcal {B} (Y).$
Let
$\mathcal {B} (Y).$
Let
![]() $T:(X, \mathcal {B}(X)) \to (Y, \mathcal {B}(Y))$
be a surjective measurable mapping, and let
$T:(X, \mathcal {B}(X)) \to (Y, \mathcal {B}(Y))$
be a surjective measurable mapping, and let
![]() $\lambda \in M(T, \nu ).$
Then, there exists a probability measure
$\lambda \in M(T, \nu ).$
Then, there exists a probability measure
![]() $\xi $
on
$\xi $
on
![]() $\sum _{\mathrm{ext} \, M(T, \nu )}$
such that for each
$\sum _{\mathrm{ext} \, M(T, \nu )}$
such that for each
![]() $B \in \mathcal {B}(X)$
,
$B \in \mathcal {B}(X)$
,
We now recall the notion of isomorphisms for measures.
Definition 2.5 Assume that X and Y are topological spaces with Borel probability measures
![]() $\mu $
on X and
$\mu $
on X and
![]() $\nu $
on
$\nu $
on
![]() $Y.$
We say that
$Y.$
We say that
![]() $(X,B(X), \mu )$
is isomorphic to
$(X,B(X), \mu )$
is isomorphic to
![]() $(Y,B(Y ), \nu )$
if there exists a one-to-one map T of X onto Y such that for all
$(Y,B(Y ), \nu )$
if there exists a one-to-one map T of X onto Y such that for all
![]() $A \in B(X),$
we have
$A \in B(X),$
we have
![]() $T(A) \in B(Y)$
and
$T(A) \in B(Y)$
and
![]() $\mu (A) = \nu \big (T(A)\big ),$
and for all
$\mu (A) = \nu \big (T(A)\big ),$
and for all
![]() $B \in B(Y),$
we have
$B \in B(Y),$
we have
![]() $T^{-1}(B) \in B(X)$
and
$T^{-1}(B) \in B(X)$
and
![]() $\mu \big (T^{-1}(B)\big ) = \nu (B)$
.
$\mu \big (T^{-1}(B)\big ) = \nu (B)$
.
Here is the well-known measure isomorphism theorem (see Theorem 17.41 in [Reference Kechris5] for a proof).
Theorem 2.6 Let
![]() $\mu $
be a Borel probability measure on a Polish space X. If
$\mu $
be a Borel probability measure on a Polish space X. If
![]() $\mu $
is continuous, then
$\mu $
is continuous, then
![]() $(X,B(X), \mu )$
and
$(X,B(X), \mu )$
and
![]() $([0, 1], \lambda )$
, where
$([0, 1], \lambda )$
, where
![]() $\lambda $
is Lebesgue measure, are isomorphic.
$\lambda $
is Lebesgue measure, are isomorphic.
Lemma 2.7 Let
![]() $\gamma \in \Pi (\mu ,\nu ).$
If either
$\gamma \in \Pi (\mu ,\nu ).$
If either
![]() $\mu $
or
$\mu $
or
![]() $\nu $
is continuous, then so is
$\nu $
is continuous, then so is
![]() $\gamma .$
$\gamma .$
Proof Assume that
![]() $\mu $
is continuous. Take
$\mu $
is continuous. Take
![]() $(x,y)\in X \times Y.$
It follows that
$(x,y)\in X \times Y.$
It follows that
from which the desired result follows. The proof is similar if
![]() $\nu $
is continuous.
$\nu $
is continuous.
Proof of Theorem 1.2
We assume that
![]() $\mu $
is a continuous measure. It follows from Lemma 2.7 that
$\mu $
is a continuous measure. It follows from Lemma 2.7 that
![]() $\gamma $
is also continuous. It follows from Theorem 2.6 that the Borel measurable spaces
$\gamma $
is also continuous. It follows from Theorem 2.6 that the Borel measurable spaces
![]() $(X, \mathcal {B}(X), \mu )$
and
$(X, \mathcal {B}(X), \mu )$
and
![]() $(X \times Y, \mathcal {B}(X \times Y), \gamma )$
are isomorphic. Thus, there exists an isomorphism
$(X \times Y, \mathcal {B}(X \times Y), \gamma )$
are isomorphic. Thus, there exists an isomorphism
![]() $T=(T_1, T_2)$
from
$T=(T_1, T_2)$
from
![]() $(X, \mathcal {B}(X), \mu )$
onto
$(X, \mathcal {B}(X), \mu )$
onto
![]() $(X \times Y, \mathcal {B}(X \times Y), \gamma )$
. It can be easily deduced that
$(X \times Y, \mathcal {B}(X \times Y), \gamma )$
. It can be easily deduced that
![]() $T_1 : X\to X$
and
$T_1 : X\to X$
and
![]() $T_2: X \to Y$
are surjective maps and
$T_2: X \to Y$
are surjective maps and
Consider the convex set
and note that
![]() $\mu \in \mathcal {M}(T_1, \mu ).$
Since
$\mu \in \mathcal {M}(T_1, \mu ).$
Since
![]() $ \mu \in \mathcal {M}(T_1, \mu )$
, it follows from Theorem 2.4 that there exists a probability measure
$ \mu \in \mathcal {M}(T_1, \mu )$
, it follows from Theorem 2.4 that there exists a probability measure
![]() $\xi $
on
$\xi $
on
![]() $\sum _{\mathrm{ext} \, M(T_1, \mu )}$
such that for each
$\sum _{\mathrm{ext} \, M(T_1, \mu )}$
such that for each
![]() $B \in \mathcal {B}(X)$
,
$B \in \mathcal {B}(X)$
,
Since
![]() $\Gamma =\mathrm{spt}(\gamma ),$
it follows that
$\Gamma =\mathrm{spt}(\gamma ),$
it follows that
![]() $T^{-1}(\Gamma )$
is a measurable subset of X with
$T^{-1}(\Gamma )$
is a measurable subset of X with
![]() ${\mu \big (T^{-1}(\Gamma ) \big )=1.}$
Let
${\mu \big (T^{-1}(\Gamma ) \big )=1.}$
Let
![]() $A_\gamma \in \mathcal {B}(X)$
be the set such that
$A_\gamma \in \mathcal {B}(X)$
be the set such that
![]() $A_\gamma \subseteq T^{-1}(\Gamma )$
and for all
$A_\gamma \subseteq T^{-1}(\Gamma )$
and for all
![]() $ x \in A_\gamma $
, the cardinality of the set
$ x \in A_\gamma $
, the cardinality of the set
![]() $\Gamma _x$
does not exceed m. It follows from the assumption that
$\Gamma _x$
does not exceed m. It follows from the assumption that
![]() $\mu (A_\gamma )=1.$
Since
$\mu (A_\gamma )=1.$
Since
![]() $\mu (X\,{\backslash}\, A_\gamma )=0,$
it follows from (1) that
$\mu (X\,{\backslash}\, A_\gamma )=0,$
it follows from (1) that
and therefore there exists a
![]() $\xi $
-full measure subset
$\xi $
-full measure subset
![]() $K_\gamma $
of
$K_\gamma $
of
![]() $\mathrm{ext} \, M(T_1, \mu )$
such that
$\mathrm{ext} \, M(T_1, \mu )$
such that
![]() ${\varrho (X\,{\backslash}\, A_\gamma )=0}$
for all
${\varrho (X\,{\backslash}\, A_\gamma )=0}$
for all
![]() $\varrho \in K_\gamma .$
Let
$\varrho \in K_\gamma .$
Let
![]() $\mathcal {S}(T_1)$
be the set of all sections of
$\mathcal {S}(T_1)$
be the set of all sections of
![]() $T_1$
and define
$T_1$
and define
Let
![]() $\mathcal {G}(\mathcal {K})$
be the set of all measurable sections of
$\mathcal {G}(\mathcal {K})$
be the set of all measurable sections of
![]() $T_1$
generated by
$T_1$
generated by
![]() $\mathcal {K}$
as in Definition 2.2. By Proposition 2.1, there exists a sequence
$\mathcal {K}$
as in Definition 2.2. By Proposition 2.1, there exists a sequence
![]() $\{F_i\}_{i=1}^k \subset \mathcal {G}(\mathcal {K})$
with
$\{F_i\}_{i=1}^k \subset \mathcal {G}(\mathcal {K})$
with
![]() $ k \in \mathbb {N} \cup \{\infty \}$
satisfying assertions (1)–(3) in that proposition. Let
$ k \in \mathbb {N} \cup \{\infty \}$
satisfying assertions (1)–(3) in that proposition. Let
![]() $B_\gamma :=\cap _{i=1}^{k}F_i^{-1}(A_\gamma ),$
and for each
$B_\gamma :=\cap _{i=1}^{k}F_i^{-1}(A_\gamma ),$
and for each
![]() $k \in \mathbb {N}\cup \{\infty \}$
, define
$k \in \mathbb {N}\cup \{\infty \}$
, define

Let
![]() $\varrho _i:={F_i}_\# \mu $
for each
$\varrho _i:={F_i}_\# \mu $
for each
![]() $i \in \mathbb {N}_k.$
We shall now proceed with the proof in several steps.
$i \in \mathbb {N}_k.$
We shall now proceed with the proof in several steps.
Step I: In this step, we show that
![]() $\mu \big (B_\gamma \big )=1$
and
$\mu \big (B_\gamma \big )=1$
and
Note first that
![]() $\varrho _i(X\,{\backslash}\, A_\gamma )=0$
for each
$\varrho _i(X\,{\backslash}\, A_\gamma )=0$
for each
![]() $i \in \mathbb {N}_k$
. In fact, for a fixed
$i \in \mathbb {N}_k$
. In fact, for a fixed
![]() $i\in \mathbb {N}_k,$
since
$i\in \mathbb {N}_k,$
since
![]() ${F_i \in \mathcal {G}(\mathcal {K})}$
there exists a sequence
${F_i \in \mathcal {G}(\mathcal {K})}$
there exists a sequence
![]() $\{F_{\sigma _j}\}_{j=1}^{\infty } \subset \mathcal {K}$
such that
$\{F_{\sigma _j}\}_{j=1}^{\infty } \subset \mathcal {K}$
such that
![]() $X=\cup _{j=1}^{\infty }A_j$
, where
$X=\cup _{j=1}^{\infty }A_j$
, where
Let
![]() $\sigma _j \in K_{\gamma }$
be such that the map
$\sigma _j \in K_{\gamma }$
be such that the map
![]() $F_{\sigma _j}$
is a push-forward from
$F_{\sigma _j}$
is a push-forward from
![]() $\sigma _j$
to
$\sigma _j$
to
![]() $\mu .$
It follows that
$\mu .$
It follows that
 $$ \begin{align*} \varrho_i(X\,{\backslash}\, A_\gamma)=\mu\big (F_i^{-1}(X\,{\backslash}\, A_{\gamma})\big )&=\mu\big ((\cup_{j=1}^{\infty}A_j) \cap F_i^{-1}(X\,{\backslash}\, A_{\gamma})\big )\\ &\leq \sum_{j=1}^\infty \mu\big (A_j \cap F_i^{-1}(X\,{\backslash}\, A_{\gamma})\big )\\ &=\sum_{j=1}^\infty \mu\big (A_j \cap F_{\sigma_j}^{-1}(X\,{\backslash}\, A_{\gamma})\big )\\ &\leq \sum_{j=1}^\infty \mu\big ( F_{\sigma_j}^{-1}(X\,{\backslash}\, A_{\gamma})\big )=\sum_{j=1}^\infty \sigma_j(X\,{\backslash}\, A_{\gamma})=0. \end{align*} $$
$$ \begin{align*} \varrho_i(X\,{\backslash}\, A_\gamma)=\mu\big (F_i^{-1}(X\,{\backslash}\, A_{\gamma})\big )&=\mu\big ((\cup_{j=1}^{\infty}A_j) \cap F_i^{-1}(X\,{\backslash}\, A_{\gamma})\big )\\ &\leq \sum_{j=1}^\infty \mu\big (A_j \cap F_i^{-1}(X\,{\backslash}\, A_{\gamma})\big )\\ &=\sum_{j=1}^\infty \mu\big (A_j \cap F_{\sigma_j}^{-1}(X\,{\backslash}\, A_{\gamma})\big )\\ &\leq \sum_{j=1}^\infty \mu\big ( F_{\sigma_j}^{-1}(X\,{\backslash}\, A_{\gamma})\big )=\sum_{j=1}^\infty \sigma_j(X\,{\backslash}\, A_{\gamma})=0. \end{align*} $$
This proves that
![]() $\varrho _i(X\,{\backslash}\, A_\gamma )=0.$
Since
$\varrho _i(X\,{\backslash}\, A_\gamma )=0.$
Since
![]() $\varrho _i$
is a probability measure, we have that
$\varrho _i$
is a probability measure, we have that
![]() $\varrho _i(A_\gamma )=1$
for every
$\varrho _i(A_\gamma )=1$
for every
![]() $i \in \mathbb {N}_k.$
Therefore,
$i \in \mathbb {N}_k.$
Therefore,
![]() $\mu \big (F_i^{-1}(A_\gamma )\big )=\varrho _i(A_\gamma )=1$
. This implies that
$\mu \big (F_i^{-1}(A_\gamma )\big )=\varrho _i(A_\gamma )=1$
. This implies that
![]() $\mu (B_\gamma )=\mu \big (\cap _{i=1}^{k}F_i^{-1}(A_\gamma )\big )=1.$
We shall now prove that
$\mu (B_\gamma )=\mu \big (\cap _{i=1}^{k}F_i^{-1}(A_\gamma )\big )=1.$
We shall now prove that
Since for all
![]() $x \in A_\gamma $
, we have
$x \in A_\gamma $
, we have
![]() $T(x)=(T_1 x, T_2x) \in \Gamma $
, it follows that for each
$T(x)=(T_1 x, T_2x) \in \Gamma $
, it follows that for each
![]() $i \in \mathbb {N}_k,$
$i \in \mathbb {N}_k,$
from which together with
![]() $T_1 \circ F_i=Id_X$
one obtains
$T_1 \circ F_i=Id_X$
one obtains
Thus,
This completes the proof of Step I.
Step II: In this step, we assume that assumption (1) of the theorem holds. In this case, we show that
![]() $k \leq m.$
$k \leq m.$
To do this, let us assume that
![]() $k>m. $
It follows from Step I that
$k>m. $
It follows from Step I that
Note that by assertion
![]() $(1)$
in Proposition 2.1, we have
$(1)$
in Proposition 2.1, we have
![]() $\mu (B_{m+1})>0.$
Since
$\mu (B_{m+1})>0.$
Since
![]() $\mu (B_\gamma )=1$
and
$\mu (B_\gamma )=1$
and
![]() $\mu (B_{m+1})>0,$
it follows that
$\mu (B_{m+1})>0,$
it follows that
![]() $B_\gamma \cap B_{m+1}\not =\emptyset .$
Take
$B_\gamma \cap B_{m+1}\not =\emptyset .$
Take
![]() $x \in B_\gamma \cap B_{m+1}.$
We have that the cardinality of the set
$x \in B_\gamma \cap B_{m+1}.$
We have that the cardinality of the set
![]() $\Gamma _x$
is at most m. On the other hand, it follows from (4) that
$\Gamma _x$
is at most m. On the other hand, it follows from (4) that
![]() $T_2 \circ F_i(x) \in \Gamma _x$
for all
$T_2 \circ F_i(x) \in \Gamma _x$
for all
![]() $i \in \{1,2,\dots ,m+1\}.$
Thus, there exist
$i \in \{1,2,\dots ,m+1\}.$
Thus, there exist
![]() $i, j \in \{1,2,\dots ,m+1\}$
with
$i, j \in \{1,2,\dots ,m+1\}$
with
![]() $i <j$
such that
$i <j$
such that
![]() $T_2 \circ F_i(x)=T_2 \circ F_j(x).$
Since
$T_2 \circ F_i(x)=T_2 \circ F_j(x).$
Since
![]() $T_1 \circ F_i=T_1 \circ F_j=Id_X$
and the map
$T_1 \circ F_i=T_1 \circ F_j=Id_X$
and the map
![]() ${T=(T_1,T_2)}$
is injective, it follows that
${T=(T_1,T_2)}$
is injective, it follows that
![]() $F_{i}(x)=F_j(x).$
On the other hand,
$F_{i}(x)=F_j(x).$
On the other hand,
![]() ${x \in B_{m+1} \subseteq B_j}$
from which we have
${x \in B_{m+1} \subseteq B_j}$
from which we have
![]() $F_j(x)\not \in \{F_1(x),\dots ,F_{j-1}(x)\}.$
This leads to a contradiction and therefore
$F_j(x)\not \in \{F_1(x),\dots ,F_{j-1}(x)\}.$
This leads to a contradiction and therefore
![]() $k\leq m$
in this case.
$k\leq m$
in this case.
Step III: In this step, we assume that assumption (2) of the theorem holds. In this case, we prove that if
![]() $k=\infty $
, then
$k=\infty $
, then
![]() $\mu (\cap _{i=1}^\infty B_i)=0.$
$\mu (\cap _{i=1}^\infty B_i)=0.$
To prove this, let us assume that
![]() $ k=\infty $
and
$ k=\infty $
and
![]() $\mu (\cap _{i=1}^\infty B_i)>0.$
By Step I, we have that
$\mu (\cap _{i=1}^\infty B_i)>0.$
By Step I, we have that
![]() $\mu (B_\gamma )=1$
and
$\mu (B_\gamma )=1$
and
Take
![]() $x \in \big ( \cap _{i=1}^\infty B_i\big ) \cap B_\gamma. $
It follows from (5) that
$x \in \big ( \cap _{i=1}^\infty B_i\big ) \cap B_\gamma. $
It follows from (5) that
![]() $T_2 \circ F_i x \in \Gamma _x$
for each
$T_2 \circ F_i x \in \Gamma _x$
for each
![]() $i \in \mathbb {N}.$
On the other hand, by assumption, we have that
$i \in \mathbb {N}.$
On the other hand, by assumption, we have that
![]() $card(\Gamma _x)<\infty .$
Thus, there exist
$card(\Gamma _x)<\infty .$
Thus, there exist
![]() $i, j$
with
$i, j$
with
![]() $i <j$
such that
$i <j$
such that
![]() $T_2 \circ F_i(x)=T_2 \circ F_j(x).$
As in Step II, since
$T_2 \circ F_i(x)=T_2 \circ F_j(x).$
As in Step II, since
![]() $T_1 \circ F_i=T_1 \circ F_j=Id_X$
and the map
$T_1 \circ F_i=T_1 \circ F_j=Id_X$
and the map
![]() ${T=(T_1,T_2)}$
is injective, it follows that
${T=(T_1,T_2)}$
is injective, it follows that
![]() $F_{i}(x)=F_j(x).$
On the other hand,
$F_{i}(x)=F_j(x).$
On the other hand,
![]() $x \in \cap _{i=1}^\infty B_i \subseteq B_j$
from which we have
$x \in \cap _{i=1}^\infty B_i \subseteq B_j$
from which we have
![]() $F_j(x)\not \in \{F_1(x),\dots ,F_{j-1}(x)\}.$
This leads to a contradiction and Step III follows.
$F_j(x)\not \in \{F_1(x),\dots ,F_{j-1}(x)\}.$
This leads to a contradiction and Step III follows.
It now follows from Steps II and III that either
![]() $k\not =\infty $
or, if
$k\not =\infty $
or, if
![]() $k=\infty $
, then
$k=\infty $
, then
![]() ${\mu (\cap _{i=1}^\infty B_i)=0}$
. On the other hand, Proposition 2.1 yields that if either
${\mu (\cap _{i=1}^\infty B_i)=0}$
. On the other hand, Proposition 2.1 yields that if either
![]() $k\not =\infty $
or,
$k\not =\infty $
or,
![]() $k=\infty $
and
$k=\infty $
and
![]() $\mu (\cap _{i=1}^\infty B_i)=0$
, then for every
$\mu (\cap _{i=1}^\infty B_i)=0$
, then for every
![]() $F \in \mathcal {G}(\mathcal {K})$
, the measure
$F \in \mathcal {G}(\mathcal {K})$
, the measure
![]() $\varrho _F=F_\#\mu $
is absolutely continuous with respect to the measure
$\varrho _F=F_\#\mu $
is absolutely continuous with respect to the measure
![]() $\sum _{i=1}^k \varrho _i $
, where
$\sum _{i=1}^k \varrho _i $
, where
![]() $\varrho _i={F_i}_\#\mu $
for
$\varrho _i={F_i}_\#\mu $
for
![]() $i \in \mathbb {N}_k.$
This together with the representation
$i \in \mathbb {N}_k.$
This together with the representation
imply that
![]() $\mu $
is absolutely continuous with respect to
$\mu $
is absolutely continuous with respect to
![]() $\sum _{i=1}^k \varrho _i.$
It then follows that there exists a nonnegative measurable function
$\sum _{i=1}^k \varrho _i.$
It then follows that there exists a nonnegative measurable function ![]() such that
such that
 $$\begin{align*}\frac{d \mu}{d \big(\sum_{i=1}^k \varrho_i\big)}=\alpha. \end{align*}$$
$$\begin{align*}\frac{d \mu}{d \big(\sum_{i=1}^k \varrho_i\big)}=\alpha. \end{align*}$$
Define
![]() $\alpha _i=\alpha \circ F_i$
for
$\alpha _i=\alpha \circ F_i$
for
![]() $i\in \mathbb {N}_k.$
We show that
$i\in \mathbb {N}_k.$
We show that
![]() $ \sum _{i=1}^k\alpha _i(x)=1$
for
$ \sum _{i=1}^k\alpha _i(x)=1$
for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x \in X.$
In fact, for each
$x \in X.$
In fact, for each
![]() $B \in \mathcal {B}(X),$
we have
$B \in \mathcal {B}(X),$
we have
 $$ \begin{align*} \mu(B)&=\mu(T_1^{-1}(B))\\[5pt]&=\sum_{i=1}^k\int_{T_1^{-1}(B)} \alpha(x) \, d\varrho_i =\sum_{i=1}^k\int_{F_i^{-1}\circ T_1^{-1}(B)} \alpha(F_ix) \, d \mu =\sum_{i=1}^k\int_{B} \alpha_i(x) \, d \mu, \end{align*} $$
$$ \begin{align*} \mu(B)&=\mu(T_1^{-1}(B))\\[5pt]&=\sum_{i=1}^k\int_{T_1^{-1}(B)} \alpha(x) \, d\varrho_i =\sum_{i=1}^k\int_{F_i^{-1}\circ T_1^{-1}(B)} \alpha(F_ix) \, d \mu =\sum_{i=1}^k\int_{B} \alpha_i(x) \, d \mu, \end{align*} $$
from which we obtain
![]() $\mu (B)=\sum _{i=1}^k\int _{B} \alpha _i(x) \, d \mu .$
Since this holds for all
$\mu (B)=\sum _{i=1}^k\int _{B} \alpha _i(x) \, d \mu .$
Since this holds for all
![]() $B \in \mathcal {B}(X),$
we have
$B \in \mathcal {B}(X),$
we have
 $$\begin{align*}\sum_{i=1}^k\alpha_i(x)=1, \qquad \quad \mu-a.e. \end{align*}$$
$$\begin{align*}\sum_{i=1}^k\alpha_i(x)=1, \qquad \quad \mu-a.e. \end{align*}$$
It now follows from Proposition 2.2 that each
![]() $F_i$
is
$F_i$
is
![]() $\mu $
-a.e. equal to a
$\mu $
-a.e. equal to a
![]() $(\mathcal {B}(X),\mathcal {B}(X))$
-measurable function for which we still denote it by
$(\mathcal {B}(X),\mathcal {B}(X))$
-measurable function for which we still denote it by
![]() $F_i.$
For each
$F_i.$
For each
![]() $i \in \mathbb {N}_k,$
let
$i \in \mathbb {N}_k,$
let
![]() $G_i=T_2 \circ F_i.$
We now show that
$G_i=T_2 \circ F_i.$
We now show that
![]() $\gamma =\sum _{i=1}^k (\text {Id}\times G_i)_\# (\alpha _i \mu )$
. For each bounded continuous function
$\gamma =\sum _{i=1}^k (\text {Id}\times G_i)_\# (\alpha _i \mu )$
. For each bounded continuous function ![]() , it follows that
, it follows that
 $$ \begin{align*} \int_{X \times Y} f(x,y) \, d \gamma=\int_X f(T_1x,T_2x) \, d\mu&= \sum_{i=1}^k\int_X \alpha(x)f(T_1x,T_2x) \, d\varrho_i\\[5pt] &= \sum_{i=1}^k\int_X \alpha\big (F_i (x)\big ) f\big (T_1\circ F_i (x),T_2 \circ F_i (x) \big ) \, d\mu\\[5pt] &= \sum_{i=1}^k\int_X \alpha_i(x) f\big (x,G_i (x) \big ) \, d\mu. \end{align*} $$
$$ \begin{align*} \int_{X \times Y} f(x,y) \, d \gamma=\int_X f(T_1x,T_2x) \, d\mu&= \sum_{i=1}^k\int_X \alpha(x)f(T_1x,T_2x) \, d\varrho_i\\[5pt] &= \sum_{i=1}^k\int_X \alpha\big (F_i (x)\big ) f\big (T_1\circ F_i (x),T_2 \circ F_i (x) \big ) \, d\mu\\[5pt] &= \sum_{i=1}^k\int_X \alpha_i(x) f\big (x,G_i (x) \big ) \, d\mu. \end{align*} $$
Therefore,
 $$\begin{align*}\gamma =\sum_{i=1}^k (\text{Id}\times G_i)_\# (\alpha_i \mu).\\[-42pt]\end{align*}$$
$$\begin{align*}\gamma =\sum_{i=1}^k (\text{Id}\times G_i)_\# (\alpha_i \mu).\\[-42pt]\end{align*}$$
Remark 2.8 It follows from the last part of the proof of Theorem 1.2 that if
![]() ${G_i(x)=G_j(x)}$
for some
${G_i(x)=G_j(x)}$
for some
![]() $x\in X$
, then
$x\in X$
, then
![]() $\alpha _i(x)=\alpha _j(x)$
. In fact, let us assume that
$\alpha _i(x)=\alpha _j(x)$
. In fact, let us assume that
![]() $G_i(x)=G_j(x)$
for some
$G_i(x)=G_j(x)$
for some
![]() $x\in X.$
It implies that
$x\in X.$
It implies that
![]() $T_2\circ F_i(x)=T_2 \circ F_j(x).$
Since
$T_2\circ F_i(x)=T_2 \circ F_j(x).$
Since
![]() $T_1\circ F_i(x)=T_1 \circ F_j(x)=x$
and
$T_1\circ F_i(x)=T_1 \circ F_j(x)=x$
and
![]() $T=(T_1, T_2) $
is injective, we obtain that
$T=(T_1, T_2) $
is injective, we obtain that
![]() $F_i(x)=F_j(x).$
This yields that
$F_i(x)=F_j(x).$
This yields that
as claimed.
It is worth noting that Theorem 1.2 has a straight forward generalization to the multi-marginal case.
Corollary 2.9 Let
![]() $\mu _1,\dots ,\mu _n$
be Borel probability measures on complete separable metric spaces
$\mu _1,\dots ,\mu _n$
be Borel probability measures on complete separable metric spaces
![]() $X_1,\dots ,X_n$
respectively. Assume that
$X_1,\dots ,X_n$
respectively. Assume that
![]() $\mu _1$
is continuous. Let
$\mu _1$
is continuous. Let
![]() $\gamma $
be a probability measure on
$\gamma $
be a probability measure on
![]() $X_1 \times \cdots \times X_n$
with fixed marginal
$X_1 \times \cdots \times X_n$
with fixed marginal
![]() $\mu _i$
on
$\mu _i$
on
![]() $X_i,$
and let
$X_i,$
and let
![]() $\Gamma =\mathrm{spt}(\gamma ).$
The following assertions hold:
$\Gamma =\mathrm{spt}(\gamma ).$
The following assertions hold:
-
1. If there exists
 $m \in \mathbb {N}$
such that the cardinality of the set does not exceed m for
$m \in \mathbb {N}$
such that the cardinality of the set does not exceed m for $$\begin{align*}\Gamma_{x_1}:=\big \{(x_2,\dots,x_n)\in X_2\times\cdots\times X_n; \, \, (x_1,\dots,x_n)\in \Gamma \big \}\end{align*}$$
$$\begin{align*}\Gamma_{x_1}:=\big \{(x_2,\dots,x_n)\in X_2\times\cdots\times X_n; \, \, (x_1,\dots,x_n)\in \Gamma \big \}\end{align*}$$
 $\mu _1$
-a.e.
$\mu _1$
-a.e.
 $x_1\in X_1,$
then there exists
$x_1\in X_1,$
then there exists
 $k\leq m$
and a sequence of Borel measurable maps
$k\leq m$
and a sequence of Borel measurable maps
 $\{G_i\}_{i=1}^k$
from
$\{G_i\}_{i=1}^k$
from
 $X_1$
to
$X_1$
to
 $X_2 \times \cdots \times X_n$
such that the measure
$X_2 \times \cdots \times X_n$
such that the measure
 $\gamma $
is concentrated on their graphs.
$\gamma $
is concentrated on their graphs.
-
2. If
 $\text {card} \big (\Gamma _{x_1} \big )< \infty $
for
$\text {card} \big (\Gamma _{x_1} \big )< \infty $
for
 $\mu _1$
-a.e.
$\mu _1$
-a.e.
 $x_1\in X_1,$
then there exist
$x_1\in X_1,$
then there exist
 $k\in \mathbb {N}\cup \{\infty \}$
and a sequence of Borel measurable maps
$k\in \mathbb {N}\cup \{\infty \}$
and a sequence of Borel measurable maps
 $\{G_i\}^k_{i=1}$
from
$\{G_i\}^k_{i=1}$
from
 $X_1$
to
$X_1$
to
 $X_2\times \cdots \times X_n$
such that the measure
$X_2\times \cdots \times X_n$
such that the measure
 $\gamma $
is concentrated on their graphs.
$\gamma $
is concentrated on their graphs.
Proof Let
![]() $Y=X_2\times \cdots \times X_n$
and
$Y=X_2\times \cdots \times X_n$
and
![]() $\nu $
be the projection of
$\nu $
be the projection of
![]() $\gamma $
on
$\gamma $
on
![]() $Y.$
It follows that
$Y.$
It follows that
![]() ${\gamma \in \Pi (\mu _1, \nu ).}$
Since
${\gamma \in \Pi (\mu _1, \nu ).}$
Since
![]() $\mu _1$
is continuous the desired result follows from Theorem 1.2.
$\mu _1$
is continuous the desired result follows from Theorem 1.2.
3 Applications in optimal transportation
Here, we shall provide an application of Theorem 1.2. Let
![]() $\mathcal {T}$
be a
$\mathcal {T}$
be a
![]() $(2,3)$
-torus knot in
$(2,3)$
-torus knot in
![]() $\mathbb {R}^3$
(see Figure 1). Our goal is to describe the structure of optimal plans for the cost
$\mathbb {R}^3$
(see Figure 1). Our goal is to describe the structure of optimal plans for the cost ![]() given by
given by
Let
![]() $\mu $
and
$\mu $
and
![]() $\nu $
be two probability measures on
$\nu $
be two probability measures on
![]() $\mathcal {T}$
. Since the function c is bounded and continuous on
$\mathcal {T}$
. Since the function c is bounded and continuous on
![]() $\mathcal {T} \times \mathcal {T}$
it follows that the problem
$\mathcal {T} \times \mathcal {T}$
it follows that the problem
admits a solution. We have the following result.

Figure 1
![]() $(2, 3)$
-torus knot
$(2, 3)$
-torus knot
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Theorem 3.1 Assume that the nonatomic measure
![]() $\mu $
is absolutely continuous in each coordinate chart on
$\mu $
is absolutely continuous in each coordinate chart on
![]() $\mathcal {T}$
. Then any optimal plan of (6) is concentrated on the graphs of at most eight measurable maps.
$\mathcal {T}$
. Then any optimal plan of (6) is concentrated on the graphs of at most eight measurable maps.
Proof By standard results in the theory of optimal transportation, there exist measurable functions ![]() and
and ![]() with
with
such that for any optimal plan
![]() $\gamma $
of (6),
$\gamma $
of (6),
Since
![]() $\mathcal {T}$
is bounded, it follows from Lemma C.1 in [Reference Gangbo and McCann3] that
$\mathcal {T}$
is bounded, it follows from Lemma C.1 in [Reference Gangbo and McCann3] that
![]() ${\varphi }$
is locally Lipschitz on
${\varphi }$
is locally Lipschitz on
![]() $\mathcal {T}$
. Let
$\mathcal {T}$
. Let
![]() $M=\mathrm{Dom} (D {\varphi }).$
It follows from Rademacher’s theorem together with the absolute continuity of
$M=\mathrm{Dom} (D {\varphi }).$
It follows from Rademacher’s theorem together with the absolute continuity of
![]() $\mu $
that
$\mu $
that
![]() $\mu (M)=1.$
For
$\mu (M)=1.$
For
![]() $x_0 \in M$
, if there exist
$x_0 \in M$
, if there exist
![]() $y_0, y \in \mathcal {T}$
with
$y_0, y \in \mathcal {T}$
with
![]() $(x_0,y_0)$
and
$(x_0,y_0)$
and
![]() $ (x_0,y) \in \mathrm{spt}(\gamma ),$
then we must have
$ (x_0,y) \in \mathrm{spt}(\gamma ),$
then we must have
![]() $D_1c(x_0,y_0)=D_1c(x_0,y).$
Let
$D_1c(x_0,y_0)=D_1c(x_0,y).$
Let
![]() $\vec {N}(x_0)$
be the outward normal vector at
$\vec {N}(x_0)$
be the outward normal vector at
![]() $x_o.$
If
$x_o.$
If
then
![]() $y-y_0=\alpha \vec {N}(x_0) $
for some
$y-y_0=\alpha \vec {N}(x_0) $
for some ![]() This implies that
This implies that
![]() $y=y_0+ \alpha \vec {N}(x_0).$
The latter argument shows that all the points in the set
$y=y_0+ \alpha \vec {N}(x_0).$
The latter argument shows that all the points in the set
live on a straight line through
![]() $y_0$
and parallel to the normal vector
$y_0$
and parallel to the normal vector
![]() $\vec {N}(x_0).$
On the other hand, one can easily observe that any straight line can intersect the manifold
$\vec {N}(x_0).$
On the other hand, one can easily observe that any straight line can intersect the manifold
![]() $\mathcal {T}$
in at most eight points. This proves that
$\mathcal {T}$
in at most eight points. This proves that
![]() $\text {card} \big (\Gamma _x \big )\leq 8 $
is for
$\text {card} \big (\Gamma _x \big )\leq 8 $
is for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in \mathcal {T}$
where
$x\in \mathcal {T}$
where
![]() ${\Gamma _x=\big \{y \in \mathcal {T}; \, (x,y)\in \mathrm{spt} (\gamma )\big \}.}$
Therefore, by Theorem 1.2, there exist
${\Gamma _x=\big \{y \in \mathcal {T}; \, (x,y)\in \mathrm{spt} (\gamma )\big \}.}$
Therefore, by Theorem 1.2, there exist
![]() $k\in \{1,2,\dots ,8\}$
and a sequence of Borel measurable maps
$k\in \{1,2,\dots ,8\}$
and a sequence of Borel measurable maps
![]() $\{G_i\}^k_{i=1}$
from
$\{G_i\}^k_{i=1}$
from
![]() $\mathcal {T}$
to
$\mathcal {T}$
to
![]() $\mathcal {T}$
such that the measure
$\mathcal {T}$
such that the measure
![]() $\gamma $
is concentrated on their graphs.
$\gamma $
is concentrated on their graphs.
Data availability statement
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Competing interests
The author declares no competing financial interests or personal relationships that could have appeared to influence the work reported in this article.