Introduction
Single crystals of sea and NaCl ice have a characteristic cellular substructure consisting of evenly spaced ice platelets or cells separated by small-angle grain boundaries. Because ice exhibits only extremely limited solid solution with the salts in sea-water and because these ice platelets form regular protuberances on the ice—water interface during ice growth, the salt in sea ice is present as liquid inclusions trapped along these substructures. It is hardly surprising, therefore, that this cellular substructure is important in determining the mechanical properties of the resulting ice (Reference Weeks, Assur, Gold and WilliamsWeeks and Assur, 1968). Changes in the platelet size and geometry during freezing should also influence the total amount of brine trapped in the ice.
Laboratory measurements by Reference FrenchFrench (unpublished), Reference Assur and WeeksAssur and Weeks (1963, Reference Assur and Weeks1964), and Reference Rohatgi and AdamsRohatgi and Adams (1967 [b], Reference Rohatgi and Adams[c]) show that in several salt-water systems the plate width a 0 (the distance between the mid-points of the intercellular grooves measured parallel to the crystallographic c-axis) increases as the growth velocity of the ice decreases. Field measurements by Reference Weeks and HamiltonWeeks and Hamilton (1962) and Reference Tabata and OnoTabata and Ono (1962) show a systematic increase in the average plate width a 0 with increasing depth in a sheet of sea ice. These results are in agreement because when sea ice forms, increased ice thickness invariably means decreased growth velocity. Rohatgi and Adams also show that the plate width increases as the solute content of the freezing solution increases. These two parameters, growth velocity υ and solute concentration of the freezing solution C, are, therefore, the most obvious factors that influence a 0 . Only Assur and Weeks, and Rohatgi and Adams have examined the problem using unidirectional freezing which most closely approximates (natural) sea-ice growth conditions. Assur and Weeks’s experiments were, however, not designed to study the variation of plate width with the above parameters and their results only indicate that a general relationship does exist. Rohatgi and Adams’s experiments, on the other hand, were designed to freeze from the bottom up so that the problem of free convection, which occurs during the formation of natural sea ice, was not encountered.
Origin of the Substructure
Once a continuous skim of ice has formed across the upper surface of an aqueous NaCl solution, crystal growth due to purely thermal supercooling is no longer possible. The latent heat is extracted entirely through the ice sheet and the growth rate is determined by the temperature gradient in the sheet, its density, and effective thermal conductivity. Supercooling, if it exists, must be the result of the impurity build-up in the melt ahead of the interface. This phenomenon has been termed constitutional supercooling by metallurgists (Reference Ratter and ChalmersRatter and Chalmers, 1953). The critical growth conditions for the presence of constitutional supercooling under the conditions of no mixing in the liquid have been shown to occur (Reference TillerTiller and others, 1953) if

where G is the temperature gradient in the liquid at the freezing interface, υ is the growth velocity, m the liquidus slope, C 0 the initial concentration of NaCl in the solution, k 0 the equilibrium partition coefficient, and D the diffusion coefficient of the solute in the melt. This relation has been found to be in good agreement with experimental observations in metal systems (Reference WaltonWalton and others, 1955). When Equation (1) is applied to the freezing of both salt solutions and sea-water, it is found that even when optimum conditions for the maintenance of a planar interface occur (υ≈10−6cm/s, G≈1.0 deg/cm, and k 0 = 10−4) the ratio G/υ = 106. For this ratio constitutional supercooling should exist (Reference Weeks and CurrieWeeks, 1968, fig. 5) even for salinities representative of typical lake water (≈ 100 p.p.m or 0.1‰) much less the salt contents studied in this paper (1‰ and greater).
Although the existence of a constitutional supercooling layer ahead of the advancing solid-liquid interface is necessary for cell formation, it is not necessarily sufficient. In addition, there is considerable uncertainty in the preceding calculation as the result of possible variations in G. This difficulty can be avoided by calculating whether the growth conditions are such that the steep-walled cell boundary grooves associated with the entrapment of brine along plate boundaries are stable. The stability criterion for the formation of these grooves is (Reference TillerTiller, 1962)

where G s is the temperature gradient in the solid and C i is the composition of the liquid at the interface. If transfer in the liquid is by diffusion only, C i = C 0/k 0 and Equation (2) becomes similar to Equation (1) with G s substituted for G. Equation (2) is a more stringent criterion than (1) because for ice—solute systems G s ≫ G. Now if

(Reference Carslaw and JaegerCarslaw and Jaeger, 1959) where t is the time, ρ the density of the solid, L the latent heat of fusion, ΔT 0 the difference between the solid surface (i.e. cold plate-ice) temperature and the freezing temperature of the solution, λ the thickness of the solid, and λ the thermal conductivity of the solid, then

and

Therefore Equation (2) becomes

in which C 0 is the only parameter under the control of the experimenter. Substitution of numerical values in Equation (6) shows that for all NaCl concentrations used in this study, cell boundary grooves are stable if solute transfer in the liquid is by diffusion only. In actuality when ice freezes from the top down, the primary mechanism of solute transfer is free convection which causes C 1 to approach C 0. This explains the observations of Reference Weeks, Lofgren and AuraWeeks and Lofgren (1967) who recorded transitions from a non-planar to a planar interface during the freezing of 1‰ (unstirred) and 3‰ (stirred) NaCl solutions.
Once constitutional supercooling is established and a cell-boundary groove is stable, the planar ice—water interface breaks down into parallel rows of cellular projections within each grain (Reference Harrison, Tiller and KingeryHarrison and Tiller, 1963). Concentrated brine is accumulated in the grooves that develop between the rows of cells and is eventually trapped when adjacent cells develop lateral connections. The entrapped brine leaves a permanent record of the positions of the intercellular grooves. It is the distance between the mid-points of these intercellular grooves that is termed the plate width as used in this paper.
Previous Work
A rigorous solution of the simultaneous temperature and solute distribution ahead of a perturbed moving interface has proven to be quite difficult (Reference Mullins and SekerkaMullins and Sekerka, 1964) although it undoubtedly will be possible to treat this problem using a numerical approach similar to that discussed by Reference OldfieldOldfield and others (1967). In existing attempts to relate the width of cells to growth conditions theoretically, it has been necessary to make a number of simplifications. Two different types of model have been utilized. The first considers rejection of salt into the bulk liquid around the cell tips and was developed by Reference Bolling and TillerBolling and Tiller (1960). Although the final form of this analysis is approximate, it compactly indicates the various factors controlling a 0. The physical reasoning behind their relation is quite clear and will be outlined here. The exact solution to the steady-state solute distribution in the liquid ahead of an advancing cell cap is known to consist of both plane-wave and non-plane-wave terms. These non-plane-wave terms cause lateral diffusion and can be considered to extend some effective distance y into the liquid. Once lateral diffusion has started it continues until terminated by the advancing interface. The allowable time for diffusion is t = (y+y ⋆)/υ where y ⋆ is a function of interface shape. The distance x the solute can diffuse in this time is

where γ is the solid—liquid interfacial energy, ΔS is the entropy of fusion per unit volume, and G′0 is the effective temperature gradient at the tip of the cell which s a function of the plate shape. This relation indicates that a 0” increases with an increase in γ (observed in metal systems) and with an increase in C 0 (
where A is a constant, is 1 and
The alternate analysis currently available considers mass transport behind the macroscopic interface in a pool of liquid between two parallel dendritic plates. This theory was initially developed to analyze substructures in rapidly solidified alloys (Reference Brown and AdamsBrown and Adams, 1960) and has been modified and applied to the freezing of salt solutions by Reference FrenchFrench (unpublished) and Reference Rohatgi and AdamsRohatgi and Adams (1967[b], Reference Rohatgi and Adams[c]). In the interdendritic pool model, the liquid ahead of a freezing interface is assumed to be capable of sustaining some critical amount of constitutional supercooling. This amount is believed to depend on the type of solute and the average concentration of the solution. If for a given plate width the interface moves too rapidly, the solute build-up ahead of the interface will cause the constitutional supercooling to exceed this critical value. The interface morphology will then adjust itself by decreasing the plate width so that less solute will be rejected per unit area of interface. The final plate width is assumed to be that which sustains just the critical constitutional supercooling in the liquid. A convenient form in which to present the results of this theory is

where (df s/dt) is the lateral freezing rate, ΔT the supercooling, and the other parameters are as defined earlier. The terms on the right-hand side of Equation (9) can be considered approximately constant. Although this type of model may well apply to growth conditions under which the side branching of dendrites occurs behind the macroscopic interface, the present authors find it difficult to visualize how details of the freezing process in the intercellular grooves can effect the spacing of the cell tips at the advancing macroscopic interface. This is particularly true if changes in the value of a 0 are produced by divergent plate growth as reported by Reference Rohatgi and AdamsRohatgi and Adams (1967[c]). The effect of changes in the composition of the melt on ao is quite clear in the interdendritic pool model:
The only currently available measurements of changes in a 0 with changes in growth parameters during the unidirectional freezing of salt solutions are those of Reference Rohatgi and AdamsRohatgi and Adams (1967[b], Reference Rohatgi and Adams[c]). Their results clearly indicate that a 0 increases as a linear function of solute concentration. This is in general agreement with Equation (7) and in contradiction to Equation (9) unless, as suggested by Rohatgi (unpublished), the supercooling ΔT increases more rapidly than the concentration. Rohatgi and Adams also observed that a 0 consistently increased as a linear function of the distance x from the constant-temperature chill. Now if the value of a 0 is in some way related to the velocity of the macroscopic interface, h may be substituted for x giving
Because their experimental conditions ideally correspond to the case of parabolic ice growth with a constant surface temperature (Reference Rohatgi and AdamsRohatgi and Adams, 1967[a], figure 4), we may substitute for h from Equation (4) giving

where c 2 = (c 1λΔT 0)/(ρ L). This expresses a 0 in terms of the velocity of the macroscopic interface and allows Rohatgi and Adams’s results to be compared with Equation (7). The results of such a comparison are shown in Figure 1. The heavy line schematically represents the relation suggested by Bolling and Tiller (Equation (7)) which is transitional between the limiting cases of a 0 υ = const and

Fig. 1. Schematic comparison of the relations a0υ = constant and
Experimental Procedures
The apparatus used (Fig. 2) to attain unidirectional freezing consisted of a lucite tube 14 cm in diameter and 62 cm long. A copper cold plate was set on top of the tube in contact with the solution. Interface temperatures were measured by a thermistor imbedded in the cold plate at the interface. A coolant was then circulated through the cold plate at a specified temperature (usually either −20° or −70°C). The time at which the initial ice skim formed on the cold plate was noted as time zero. There was necessarily a time lag (on the average 3.6 h) before the specified cold-plate temperature was reached because of the initial rapid heat flow into the plate. Runs lasted 48 to 110 h during which time, ice thickness, temperature and conductivity cell readings were made. The runs are designated by a number followed by either the letter a or c. The number indicates the approximate starting salinity (‰) of the freezing solution and the letter the general temperature of the cold plate (a = –20°, c = –70°C).

Fig. 2. Schematic drawing of the freezing apparatus.
Salinity samples were taken immediately upon terminating a run. The samples, each representing 1 cm of vertical growth, were allowed to melt and the salinities determined with a conductivity bridge. The water salinities corresponding to the time of growth of each sample were then calculated using the relations given in Reference Weeks, Lofgren and AuraWeeks and Lofgren (1967). Thin sections were prepared in a cold room at −34°C by cutting precisely located slabs of ice perpendicular to the growth direction. The thin sections were then photographed and the average plate width a 0 was determined from measurements on the photographs. Figures 3 and 4 are typical thin-section photographs showing the change in a 0 in a given run. The growth velocity wasobtained by fitting for each freezing run a 4th degree polynomial to the graph of time against ice thickness measurements. Representative plots of ice thickness against time and the fitted least-squares curves are shown in Figure 5. This relation was then differentiated to obtain an estimate of υ at any position in that ice sheet. A complete tabulation of the results is contained in U.S. Cold Regions Research and Engineering Laboratory. Research Report 195 which can be obtained from the authors.

Fig. 3. Photomicrograph of thin section of NaCl ice showing substructure: Ron 3a, υ = 1.8×10−4cm s−1, distance from cold-plate 5.88 cm.

Fig. 4. Photomicrograph of thin section of NaCl ice showing substructure: Run 3a, υ = 2.39×10−5 cm s−1, distance from cold-plate 23.18 cm.

Fig. 5. Ice thickness versus elapsed time for some representative freezing runs.
Experimental Results
Figure 6 shows the experimental results plotted as
As Figure 6 clearly shows, the data do not fall on a straight line and n appears to be some smooth function of υ. As υ becomes large, n approaches a value of

or
suggests a convenient form for presenting these results within the range of the data. By trial we have found that when f(υ) is represented by


is surprisingly linear. The data and the least-squares fitted line are plotted in this form in Figure 7 (log A = −4.069, n 1 = – 0.093). The curve in Figure 6 shows Equation (15) plotted on a graph of


Fig. 7. Plot of
An interesting aspect of Figure 6 is the suggestion that at small growth velocities a 0 becomes relatively independent of υ. Some evidence in support of such a suggestion has been obtained from the study of thick perennial polar floes. Both Reference SchwarzacherSchwarzacher (1959) and A. Assur (personal communication) have noted that plate widths found in such sea ice are remarkably constant with an average value of approximately 1 mm. Although no detailed growth velocity measurements are available for this type of ice, a rough estimate may be obtained by noting that the ice grows ≈50 cm in a growing season of ≈10 months giving an average velocity ≈10−6 cm/sec. Such values do not contradict the results shown in Figure 6.
The obvious question posed by Figure 6 is: why does the value of n appear to approach zero at low values of υ instead of a value of 1 as predicted by Bolling and Tiller? The answer becomes apparent by examining the paths of individual freezing runs as shown on Figure 6.
Only four runs (1a, 5c, 30c and 100c) have average n values close to or greater than 0.5. Run 1a is in exact agreement with the predictions of Bolling and Tiller with n changing from
The effects of convection also appear in Figure 8 which is a plot of a 0 against the square root of the calculated water salinity from which each measured set of platelets grew. The lines represent constant growth velocities which were obtained by using Equation (15) to determine a 0 values for a fixed set of velocities for each individual run. In the S w range 1 to 100‰, the plate width decreases as the solute concentration increases. A minimum indicated by the dashed line occurs in the range 10 to 25% and appears to depend on the growth velocity. At S w values greater than 25‰ there is initially an increase in a0 and then a slight decrease. Although we currently do not understand the details of this complex pattern, a few observations can be made. The minimum in Figure 8 is clearly not the eutectic composition (233‰) and occurs close to the composition where the maximum density of the solution is at its freezing point (24.7‰). As the growth velocity increases, increased solute build-up would cause convection to start at lower bulk solute concentrations. This agrees with the observed decrease in the salinity of the minimum with an increase in υ. The behavior shown in Figure 8 is strikingly different from the results of Rohatgi and Adams (1967[c], fig. 14) who found a simple linear increase in a. of 0.06 mm as C increased from 0 to 100‰. In Figure 8 this effect appears to be masked by the variation in a 0 produced by convection. Further experimental studies are clearly needed.
It also should be remembered that overall interface morphology changes as a function of υ. At high growth velocities the shapes of the platelet or cell “caps” should, to a good approximation, be parabolic (Reference Bolling and TillerBolling and Tiller, 1961; Reference Harrison, Tiller and KingeryHarrison and Tiller, 1963). As the velocities become slower the cell caps become broader (Reference Bolling and TillerBolling and “Tiller, 1960) presumably becoming almost rectangular at very low growth rates. The transition between these different morphologies is apparently gradual (Reference WaltonWalton and others, 1955; Reference Plaskett and WinegardPlaskett and Winegard, 1960; Reference JamesJames, 1966). These changes will also presumably be part of any complete understanding of the variation in a 0 with growth parameters.
This study appears to have produced more problems than it has solved. During the formation of natural sea ice, convection occurs continuously. Therefore, it is imperative that its effect on the sea-ice substructure be taken into account. We feel that these results should also be of interest to metallurgists. Attention has recently been focused on the effect of convective processes in influencing the columnar-to-equiaxed transition during the solidification of ingots by the studies of Reference Cole and BollingCole and Bolling (1965, Reference Cole and Bolling1966, Reference Cole and Bolling1967[a], Reference Cole and Bolling[b]) and Reference ColeCole (1967). The present paper suggests the importance of similar convective processes in controlling the size of intracrystalline substructures during the solidification of metals.
Acknowledgements
We would like to thank W. F. Reeves for assisting us during the experimental phase of this study and Drs A. Assur, G. F. Bolling, J. B. Lyons, P. K. Rohatgi and W. A. Tiller for their advice.


 to 1 as
to 1 as 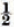 to approximately o as
to approximately o as 








