Quantifying Morphology and Diffusion Properties of Mesoporous Carbon From High-Fidelity 3D Reconstructions

Abstract

A reliable quantitative analysis in electron tomography, which depends on the segmentation of the three-dimensional reconstruction, is challenging because of constraints during tilt-series acquisition (missing wedge) and reconstruction artifacts introduced by reconstruction algorithms such as the Simultaneous Iterative Reconstruction Technique (SIRT) and Discrete Algebraic Reconstruction Technique (DART). We have carefully evaluated the fidelity of segmented reconstructions analyzing a disordered mesoporous carbon used as support in catalysis. Using experimental scanning transmission electron microscopy (STEM) tomography data as well as realistic phantoms, we have quantitatively analyzed the effect on the morphological description as well as on diffusion properties (based on a random-walk particle-tracking simulation) to understand the role of porosity in catalysis. The morphological description of the pore structure can be obtained reliably both using SIRT and DART reconstructions even in the presence of a limited missing wedge. However, the measured pore volume is sensitive to the threshold settings, which are difficult to define globally for SIRT reconstructions. This leads to noticeable variations of the diffusion coefficients in the case of SIRT reconstructions, whereas DART reconstructions resulted in more reliable data. In addition, the anisotropy of the determined diffusion properties was evaluated, which was significant in the presence of a limited missing wedge for SIRT and strongly reduced for DART.

Introduction

Mesoporous materials have attracted a lot of attention and are of great importance in many advanced applications due to their remarkable properties, such as high specific surface area, versatile pore structure, chemical inertness, and good mechanical stability (Ryoo et al., 2001; Taguchi & Schüth, 2005; Liang et al., 2008). In heterogeneous catalysis, various porous materials have been used as support for the active nanometer-sized particles (Taguchi & Schüth, 2005; Yang et al., 2011). All aspects of the performance of supported catalysts (activity, selectivity, and stability) are strongly influenced by the architecture of the porous support: (i) the mesopores (2–50 nm) and micropores (<2 nm) improve the stability of the catalyst (Zuiderveld, 1994; Taguchi & Schüth, 2005); (ii) the morphology of the macro- and mesopores (geometry and topology) controls mass transport during catalyst preparation, thus determining the distribution of the active centers (Ruthven & Post, 2001; Armatas et al., 2003; Gommes et al., 2009); (iii) the meso- and micropore morphology confines the diffusion of reactants and products thereby affecting selectivity and activity (Christensen et al., 2003; Olsbye et al., 2012; Wang et al., 2018).

Bulk techniques such as physisorption or small angle X-ray diffraction provide an average measure of the pore structure and pore volume. However, those techniques require assumptions on the pore shape and connectivity and are not sufficient for an accurate three-dimensional (3D) characterization of the structure of disordered porous materials. To fully understand the complex 3D structure of meso- and microporous materials and to evaluate how the local and average pore structure influences the catalyst properties, alternative techniques are needed. Electron tomography in combination with advanced analysis has been demonstrated to provide quantifiable 3D structural information at the nanoscale (Kübel et al., 2005; Bals et al., 2007; Friedrich et al., 2009; Midgley & Dunin-Borkowski, 2009). For example, SBA-15, an ordered mesoporous silica, has been investigated using electron tomography, which revealed the pore corrugation and its spatial correlation along the main channels (Gommes et al., 2009). Furthermore, the sensitive interrelationship between morphology and transport properties of SBA-15 has been highlighted recently (Reich et al., 2018). The pore-scale simulations of hindered diffusion within a 3D reconstruction of this material demonstrated that even a small amount of structural imperfections in the primary mesopore system has drastic consequences for the transport properties. Quantitative information about the pore network in Zeolite Y, including two types of blocked mesopores (closed and constricted mesopores), the tortuosity of the mesopores, and the size distribution has been obtained by electron tomography (Zečević et al., 2012). However, any quantitative analysis of electron tomograms critically depends on the fidelity of the segmentation, the assignment of each voxel to a specific feature or composition depending on the gray level and/or local neighborhood. In general, segmentation of tomographic data can be achieved by three approaches: manual segmentation, various types of image processing as well as advanced reconstruction algorithms that directly result in (partially) segmented reconstructions. Careful manual segmentation is typically considered as the reference for unknown objects. However, manual segmentation is very time-consuming, labor-intensive, and difficult to perform fully reproducible. During image processing the 3D volume is processed in order to reduce noise and to get well-separated image intensities to enable extraction of the features using global (Russ, 1992; Jähne, 2005; Vala & Baxi, 2013) or adaptive local (Niblack, 1985) thresholding. However, in practice, global thresholding typically over/underestimates some of the features in the 3D volume due to noise and, more critically, systematic reconstruction artifacts of the commonly used weighted back projection (WBP) or simultaneous iterative reconstruction technique (SIRT) (Norton, 1985; Kübel et al., 2010). More recently, advanced reconstruction algorithms have been proposed that make use of prior knowledge to improve the overall reconstruction quality and fidelity. The discrete algebraic reconstruction technique (DART) (Batenburg et al., 2009) includes a segmentation in the reconstruction process itself based on the prior knowledge that the overall sample can be represented by a few different materials, corresponding to a few grey levels in the 3D reconstruction. The DART algorithm starts from a simple thresholded reconstruction, where voxels close to a boundary are iteratively refined to achieve the best agreement between the re-projections from the current segmentation and the experimental projections (Batenburg et al., 2009). Thereby, the reconstruction directly produces a segmented 3D volume of the original object. As another alternative, total variation minimization (TVM) compressive sensing (CS) (Goris et al., 2012) assumes a sparse gradient of grey levels as normalization to improve the 3D reconstruction. The fidelity of the different approaches has been estimated by a number of groups for various materials and shapes (Batenburg & Sijbers, 2009; Biermans et al., 2010; Kübel et al., 2010; Saghi et al., 2011; Roelandts et al., 2012; Goris et al., 2013).

However, the effect of the limited fidelity of the segmented 3D reconstruction on the measured/calculated properties of the investigated material has not been addressed. Moreover, investigations providing quantitative information on the geometry and topology of disordered pore structures, or even relating this information to relevant transport properties (Müllner et al., 2016), are still very limited. In this work, we combine electron tomography with advanced image analysis to elucidate the 3D structure of a disordered mesoporous carbon, which is commonly used as support in heterogeneous catalysis. The fidelity of the segmented 3D object obtained from a SIRT reconstruction followed by image processing and with the DART algorithm is investigated using both experimental data and realistic phantoms for the material. The effect of the reconstruction approach on the pore morphology is discussed in terms of pore size, pore length, tortuosity, and connectivity. Most importantly, the effect of reconstruction variations on physical properties calculated from the support structure is evaluated, looking at obstructed diffusion as one of the critical properties of the mesoporous materials.

Materials and Methods

Mesoporous Carbon

Details of the mesoporous carbon synthesis have been published previously (Villa et al., 2015). The material has a specific surface area of 589 m²/g with an average pore diameter of 6.9 nm according to BET analysis.

Electron Tomography Data Acquisition

The dry mesoporous carbon powder was directly dispersed on 100 × 400 mesh carbon-coated copper grids (Quantifoil Micro Tools GmbH) with a support film thickness of 10–20 nm. The support film was labeled with Au colloidal particles (6.5 nm diameter). Electron tomography was performed using a Fischione 2020 tomography holder on a Titan 80–300 microscope (FEI Company) operated at 300 kV in STEM mode with a convergence angle of 10 mrad and a nominal beam diameter of 0.27 nm. ADF-STEM images (1,024 × 1,024 pixels, pixel size 0.32 nm) were acquired at a camera length of 195 mm with a high-angle annular dark-field (HAADF) detector within inner angle of 31 mrad using the Xplore3D software (FEI Company) over a tilt range of ±76° with a tilt increment of 2°. Alignment of the tilt series was performed in IMOD (Kremer et al., 1996) tracking 14 Au particles as fiducial markers, manually refining their position and enabling refinement of magnification and image rotation and grouping tilt-angles every three tilts without applying a distortion correction, to reach a mean residual alignment error of 0.44 pixels.

Reconstruction and Segmentation

The 3D reconstruction of the aligned tilt series was performed in Inspect3D Version 3.0 (FEI Company) using the simultaneous iterative reconstruction technique (SIRT) with 25 iterations. In the reconstructed volume, the y-axis is parallel to the tilt axis during data acquisition, the x-axis is perpendicular to the tilt axis, and the z-direction is parallel to the electron beam direction at 0° sample tilt. Several image processing steps were carried out on the reconstructed tomogram to segment the 3D volume. The goal of the image processing was to reduce noise and get well-separated image intensities to facilitate segmentation while preserving the sharp boundaries between components. The image processing was performed using plugins in the Fiji software package (Schindelin et al., 2012): (i) noise reduction of the image stack using the PureDenoise plugin (Luisier et al., 2010) and the anisotropic diffusion filter (Tschumperlé & Deriche, 2005); (ii) enhancement of local contrast using the CLAHE plugin (Zuiderveld, 1994); (iii) binarization by global thresholding. The generated binary 3D reconstruction volume (labeled as segmented-SIRT) was further separated into three parts: vacuum, pore, and carbon using the pore filling approach implemented in Amira 6.1.1 (FEI Company) to separate internal pores and vacuum around the mesoporous carbon particle; any contribution from the supporting carbon films has been ignored. The full image processing steps are illustrated in Figure 1. For comparison with the DART reconstruction, the aligned tilt series was reconstructed using the DART implementation of the TomoJ plugin (MessaoudiI et al., 2007) in Fiji (labeled as DART). The resulting tomogram has an edge length of the voxels of 0.32 nm.

Fig. 1. Illustration of the image processing steps after SIRT reconstruction for the mesoporous carbon.

Validation of Experimental Reconstruction and Segmentation

The segmented models based on the segmented-SIRT and the DART reconstruction were used to create tilt-series of 2D projections covering the angular range of ±90° in 2° steps. MATLAB was used to generate projections based on a simple linear integration of the intensities in the projection direction using nearest neighbor interpolation. The mean absolute error (MAE) (Sage & Unser, 2003) was used to estimate the difference between the experimental tilt-series and the re-projected segmented images, in which the gold markers within the experimental tilt-series images were removed by interpolating the image intensities in the corresponding areas using IMOD. For the MAE calculation, the complete tilt-series of projected images was scaled to cover the full 8-bit intensity range of 0–255 with the intensity of the vacuum regions set to 0.

Phantom Study

The DART reconstruction of the particle was used as a phantom to evaluate the fidelity of the reconstruction and segmentation approaches in more detail. For this, 3D reconstructions were performed using the re-projected tilt-series in the angular range of ±76° and ±90° with a tilt step of 2° created in MATLAB by rotating the original object using the function “imrotate”. Experimental error sources such as detection noise, scan errors or limited alignment quality were excluded in this phantom study as well as the supporting carbon film. The reconstruction and segmentation were done following the same procedure as before for the experimental data. The resulting reconstructions are labeled as Phantom.segmented-SIRT and Phantom.DART. For these phantom reconstructions, we can quantitatively compare the mesopore morphology and the diffusion simulations with the initial phantom in addition to evaluating any differences on a voxel level.

Morphological Characterization of the Pore Structure

Skeleton Analysis

In order to quantify the geometry and topology of the pore structure, the pore volume was analyzed using the skeletonization function in Amira 6.1 based on the segmented data. The skeletonization procedure reduces the pore space to a branch-node network (skeleton), as described in the literature (Fouard et al., 2006), while both the geometrical and topological information are preserved. The skeletonization procedure is illustrated in Supplementary Figure 1. In the process, the mean pore diameter of all individual pores was calculated as the average from the diameter along each skeleton. The pore length was obtained from summation of a number of voxels along the skeleton. The pore coordination number was determined by counting the number of individual branches connected to a common point. The skeletonized data were further analyzed by a home-written code in MATLAB to calculate the tortuosity of the pores. The average tortuosity of the pore structure was estimated by analyzing each individual branch of the derived skeleton. The tortuosity (τ) of an individual branch is defined as the pore length (d_l) divided by the Euclidean distance (d _eucl.) between pore entrance and exit points:

(1)$$\tau = d_l/d_{{\rm eucl}{\rm.}} $$

Chord Length Distribution (CLD) Analysis

The pore space within the segmented volume was analyzed using CLD analysis (Bruns & Tallarek, 2011; Stoeckel et al., 2014; Kroll et al., 2018). For each reconstruction 10⁷ chords were generated. These chords originate from randomly chosen points in the void space. From each point, 26 equispaced vectors were defined and the length of these vectors determined after they hit the solid phase. Chords that projected out of the image were discarded. The resulting chord length is the sum of the absolute lengths of any two opposing pairs of vectors. The histogram of the CLD was fitted with a k-gamma function (Aste & Di Matteo, 2008)

(2)$$f\lpar {l_c} \rpar = \displaystyle{{k^k} \over {{\rm \Gamma} \lpar k \rpar }}\displaystyle{{l_c^{k-1}} \over {\mu ^k}}{\rm exp}\left( {-k\displaystyle{{l_c} \over \mu}} \right)$$

where l _c is the chord length, Γ is the gamma function, μ is the first statistical moment of the distribution, and k is a second-moment parameter defined by the mean and the standard deviation σ as k = (μ ²/σ²). The values for μ and k obtained from the k-gamma fit to the CLD are quantitative measures for the average pore size and for the homogeneity of the pore volume distribution (Gille et al., 2002; Aste & Di Matteo, 2008; Hormann & Tallarek, 2013; Müllner et al., 2016).

Diffusion Simulations

Diffusion in the void space of cubic subdomains for each reconstruction was simulated by a random-walk particle-tracking technique (Delay et al., 2005). For that purpose, a large number (typically N = 10⁷) of passive, point-like tracers were randomly distributed in the reconstructed void space. At each time step Δt of the simulation, the random displacement Δr of every tracer due to the random diffusive motion was calculated as

(3)$$\Delta {\bi r} = {\bi \gamma} \sqrt {6D_{{\rm bulk}}\Delta t} $$

where D _bulk is the tracer diffusion coefficient in the open space and γ is a vector with random orientation in space and a length governed by a Gaussian distribution with zero mean and unity standard deviation. The value of Δt was adjusted such that the mean diffusive displacement did not exceed Δh/10 (where Δh = 0.32 nm is the voxel size of the reconstruction). To restrict diffusion to the void space, a multiple-rejection boundary condition was implemented at the solid—void interface: if at the current iteration a tracer crossed the solid—void interface, this displacement was rejected and recalculated until the tracer position was in the void space. At the external faces of the reconstructed domain, mirror boundary conditions were imposed, i.e. when a tracer hit an external face, it was mirror-reflected from that face. During the simulation, the displacements of every tracer along x-, y-, and z-direction were monitored, which allowed us to determine time-dependent diffusion coefficients along each direction j according to (Brenner, 1980)

(4)$$D_j\lpar t \rpar = \displaystyle{1 \over {2N}}\displaystyle{d \over {dt}}\mathop \sum \limits_{i = 1}^N \lsqb {\Delta r_{ij}\lpar t \rpar } \rsqb ^2$$

where j denotes the x, y, or z direction, and Δr _ij(t) is the accumulated displacement of the i^th tracer along direction j after time t. A decrease of D _j(t)/D _bulk with time (i.e., the number of iterations) from the initial value of 1 results from passive interactions of the tracers with the solid phase. At short times, only a small fraction of the tracers experiences geometric confinement during their random walk. At long times, the transient diffusion coefficients approach asymptotically the targeted effective (time-independent) values D _eff.

Results and Discussion

Quantitative Comparison of the Morphological Information Obtained From Experimental SIRT and DART Reconstructions

The ADF-STEM tilt-series (Supplementary Fig. 2) gives a first idea of the disordered pore structure of the investigated mesoporous carbon material. The overall particle on the support film and its internal mesopore structure are better revealed in the reconstructed slices (Fig. 2a), where their irregular shape and non-uniform size can be seen. In order to provide any quantitative 3D structural information, some kind of segmentation has to be performed after reconstruction. The resulting quantitative analysis strongly depends on the fidelity of the obtained segmentation.

Fig. 2. Typical (a–c) xy and (d–f) xz slices of the SIRT reconstruction (left), the segmented-SIRT (middle) and the DART reconstruction (right) (the areas highlighted by red cycles exhibit pore size variations and the blue regions indicate differences in connectivity of the pores in 2D).

Representative 2D slices of the SIRT reconstruction, the segmented-SIRT, and the DART reconstruction are shown in Figure 2. Most of the features visually detected in the SIRT reconstruction (Fig. 2a) are also present in the slices of the segmented-SIRT and the DART reconstruction (Figs. 2b/c). However, when looking closely at the highlighted regions (red and blue circles in Fig. 2), we found that the size and connectivity of some of the pores in the 2D slices is different in the two segmented results and does not necessarily fit to our visual interpretation of the SIRT reconstruction. As one measure for the fidelity of the segmented reconstructions we used the calculated re-projection tilt-series from the segmented-SIRT and DART reconstruction and compared it to the experimental tilt-series (Fig. 3). The mean absolute error (MAE) was calculated to estimate the difference between the experimental projections and the re-projections. The MAE values for the nine re-projection directions shown in Figure 3d are slightly larger for the segmented-SIRT reconstruction than for the DART reconstruction, but the differences are so small that it would be difficult to judge which reconstruction is better.

Fig. 3. Projected images at 0° for (a) experimental STEM tilt-series, (b) segmented-SIRT and (c) DART reconstructions. (d) MAE calculation for re-projected images from the segmented-SIRT (purple) and DART (blue) reconstructions at angles of −70°, −50°, −30°, −10°, 0°, 10°, 30°, 50°, and 70°.

The pore morphology of the segmented reconstructions was quantified by CLD and skeleton analysis. The Supplementary Figure 3 schematically shows the CLD analysis of the pore space and the resulting CLD for the segmented-SIRT and the DART reconstruction. The distribution of chords (Supplementary Fig. 3b) and the k-Gamma fitting of the CLD histograms (Table 1) indicate that the geometry and the homogeneity of the pore space are similar for the segmented-SIRT and the DART reconstruction. From the skeleton analysis, the important features related to the geometry and topology of the pore network such as pore size, pore length, tortuosity, and interconnectivity are summarized in Figure 4. The pore diameter distribution (Fig. 4a) shows that a higher percentage of pores with diameters below 4 nm are observed in the segmented SIRT reconstruction, thereby resulting in a smaller mean pore diameter (Table 1) compared to the DART reconstruction. Nevertheless, the pore length distribution (Fig. 4b) and the mean pore length are very similar in the two reconstructions, in agreement with the similar mean chord length determined from the CLD analysis. Furthermore, the branch tortuosity (Fig. 4c) and the coordination number of the branch-node network (Fig. 4d), two important parameters regarding topology, are also similar. This fits to the CLD results and indicates that the overall morphology of the two reconstructions is similar, independent of the reconstruction method (Table 1). However, the total pore volume of the two reconstructions differs noticeably (~25%). This pore volume difference should result in a significant difference in the MAE calculation if performed using a forward simulation of the STEM images with a fully quantified detection sensitivity (LeBeau et al., 2008). However, for the MAE calculations presented in Figure 3, the experimental tilt-series and the calculated projection intensities were both scaled to cover 8-bits, thereby compensating for most of the pore volume differences. This difference of the total pore volume is mainly caused by the difficulty to define a good global threshold for the SIRT reconstruction. Despite the local contrast enhancement, the average reconstructed intensity for the pore/solid varies noticeably in different parts of the particle, rendering a global segmentation difficult. More details on the effect of the segmentation threshold will be discussed with the phantom studies.

Fig. 4. (a) Pore size distribution, (b) pore length distribution, (c) pore tortuosity and (d) coordination number based on the segmented-SIRT and the DART reconstruction.

Table 1. Morphological descriptors for the pore structure of the segmented-SIRT and DART reconstructions.

Diffusion Simulations Based on Experimental Segmented-SIRT and DART Reconstructions

Transport properties of mesoporous materials are one of the critical aspects to understand activity and selectivity in catalysis (Ruthven & Post, 2001; Armatas et al., 2003; Gommes et al., 2009), as well as their efficiency as supports in chemical separation (Dullien, 1979; Brenner, 1980; D'Alessandro et al., 2010). To analyze diffusion properties for this particle, taking into account the experimental pore shape, we used a cubic domain with a size of up to 220 × 220 × 220 voxels to derive effective diffusion coefficients through direct pore-scale simulations (Fig. 5). With increasing domain size, the diffusion coefficients become almost stable, indicating that the domain is starting to approach a statistically representative volume considering the structural variations in the material. When comparing the segmented-SIRT and the DART reconstruction of exactly the same volume (Fig. 5c), we found that the normalized diffusion coefficient D _eff/D _bulk within the largest cubic domain from the DART reconstruction differs noticeably (~50%) from the segmented-SIRT reconstruction. Considering that the topology of both reconstructions is similar, this significant difference should be due to the larger pore volume (higher porosity) of the DART reconstruction. As the limited convergence of the SIRT reconstruction is known to introduce local and global intensity variations (Norton, 1985; Kübel et al., 2010) and as we experimentally noticed how difficult it is to define a global threshold even after image processing to enhance the local contrast, we assume that the DART reconstruction and thus the DART-based diffusion simulations are more accurate. However, this is difficult to verify from the experimentally available data. Moreover, we do not have a good experimental measure to judge the fidelity of the DART-based diffusion simulations.

Fig. 5. (a) Overall 3D morphology of the mesoporous carbon particle, (b) cubic substructure used for the diffusion simulations and (c) calculated effective diffusion coefficients normalized by the bulk diffusivity depending on the cube edge length for the segmented-SIRT and the DART reconstruction.

Fidelity of the 3D Reconstruction and Effect on Morphology and Diffusivity

To further evaluate the fidelity of the 3D reconstruction of mesoporous materials and to estimate the effect on the calculated properties of this material, we employed the DART reconstruction as a phantom to directly quantify differences between the SIRT and DART-based reconstructions obtained using the same procedures as for the experimental data, but ignoring the 15–18% intensity contribution of the supporting carbon film to the total image intensity. The phantom-based SIRT and DART reconstructions were carried out for tilt-angles ranges of ±76° and ±90° to further evaluate effects due to the missing wedge. As already discussed for the experimental data, defining the segmentation threshold is critical for evaluating the reconstructions, both for SIRT and for DART. We tested some common unbiased approaches to define a global threshold for segmentation such as the isodata-algorithm (Ridler & Calvard, 1978), the moment-preserving threshold (Tsai, 1985 and Otsu, 1979) and a representative slice of the corresponding segmented volume is shown in Supplementary Figure 4. However, there are significant differences (highlighted by red arrows) in all cases compared to the visual features in the slice of the initial SIRT reconstruction. Therefore, we were visually defining the best onset threshold for the segmentation of the SIRT reconstruction. For the DART reconstruction, we estimated the onset threshold from several regions based on the mean pore and carbon intensities, as is commonly done in the literature (Batenburg et al., 2009; Biermans et al., 2010). Afterwards, we varied the threshold by 10% and 20% to evaluate the sensitivity to the threshold settings. The resulting effect on the reconstructed pore volume is shown in Figure 6b. The pore volume determined from the segmented SIRT reconstruction is more sensitive to variations of the threshold compared to the DART reconstruction. This means that, experimentally, it is more difficult to reproducibly segment a SIRT reconstruction compared to a DART reconstruction in these mesoporous materials.

Fig. 6. (a) Intensity histogram of a 3D reconstruction showing two main peaks corresponding to pore (void) and carbon (solid); (b) effect of threshold on the reconstructed pore volume within Phantom.segmented-SIRT and the Phantom.DART reconstructions (the dashed line indicates the pore volume of the reference phantom).

For a more detailed analysis, we have evaluated representative 2D slices (Fig. 7) of the Phantom.segmented-SIRT and the Phantom.DART reconstructions (based on the onset threshold) and the corresponding surface rendering of the pores (Fig. 8). All four reconstructions show a high similarity with the original Phantom, exhibiting a very similar morphology. However, the size and 2D connectivity of some of the pores (highlighted areas in Figs. 7b–7e) are affected by the artifacts introduced during the reconstruction and segmentation process. To understand the differences between the segmented volumes better, the differences are highlighted, with red coloring indicating “missing” pixels/voxels and green representing “additional” pixels/voxels in the reconstructions compared to the reference phantom. With a good threshold, the missing and additional voxels in the pores are more or less balanced. The pore variations are mainly present in a few voxel-wide boundary regions of the pores. As is visually obvious, the Phantom.DART ±90° reconstruction exhibits the least variations with a lower number of “missing” and “additional” voxels compared to other reconstructions.

Fig. 7. Slices of the (a) DART phantom reference, (b) Phantom.segmented-SIRT ±76°, (c) Phantom.segmented-SIRT ±90°, (d) Phantom.DART ±76° and (e) Phantom.DART ±90° reconstructions with (f–i) the differences in the pore structures: the pixels of the red and green parts represent “missing” and “additional” voxels of the reconstructed pore compared to the phantom. (Areas highlighted by red circles exhibit pore size variations and the blue regions indicate differences in the connectivity of the pores.).

Fig. 8. 3D view of a selected pore: (a) reference, (b) Phantom.segmented-SIRT ±76°, (c) Phantom.segmented-SIRT ±90°, (d) Phantom.DART ±76° and (e) Phantom.DART ±90°. Differences are highlighted in red (missing voxels) and green (additional voxels).

To quantify the variations between these reconstructions and the reference phantom, the number of voxels differing (“missing” and “additional”) for each reconstruction are counted and compared to the total number of pore voxels both on a slice-by-slice basis (Fig. 9a) as well as for the overall volume. In addition, the structural similarity (SSIM) index (Wang and Bovik, 2004) is used to measure the similarity between reconstructed slices and the corresponding slices of the phantom (Fig. 9b). The Phantom.DART ±90° and Phantom.DART ±76° reconstructions show a lower pore variation in all investigated slices compared to the Phantom.segmented-SIRT reconstructions and the SSIM calculation also indicates that the Phantom.DART ±90° data has the highest structural similarity with the initial structure. This is confirmed by the overall differences in 3D in Table 2. The comparison further clearly shows the effect of the missing wedge. The fidelity of both the SIRT and the DART reconstructions obtained with a missing wedge of 28° is lower compared to the ones without missing wedge. However, in the case of the DART reconstruction, this difference is smaller and might partially be due to the reduced number of projections. The same trend can also be seen looking at the MAE calculations for this phantom study (Supplementary Fig. 5). All MAE values are well below 1%, which is significantly lower compared to the experimental counterpart, presumably mostly due to the missing noise in the phantom studies. Furthermore, slight structural changes, contamination, and the beam convergence might add to the higher MAE values for the experimental reconstructions.

Fig. 9. (a) Percentage of pore variation (the dashed lines indicate the average values of the pore variation in the 3D volume) and (b) SSIM calculated for slices distributed throughout the reconstructed volume for the four phantom reconstructions.

Table 2. Pore variation and SSIM calculation for the phantom segmented 3D reconstructions.

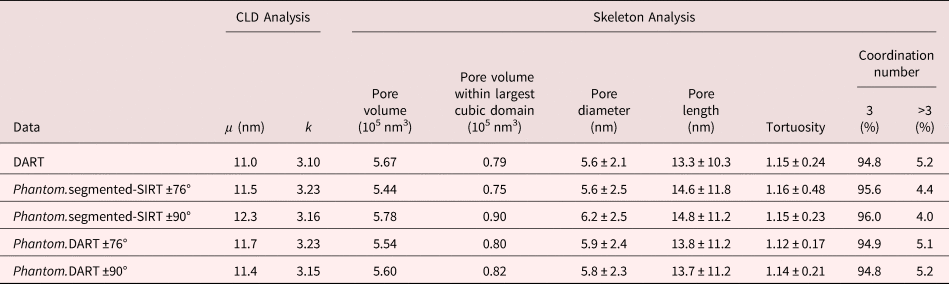
With the evaluation above, it is clear that the segmented 3D reconstructions are not perfect, but visually they nevertheless appear to be close to the original phantom structure. In order to analyze the effect of the differences on the morphology and diffusion properties, we analyzed the reconstructed phantom structures in comparison to the experimental data. The quantitative information on the pore morphology derived from CLD and skeleton analysis are summarized in Table 3. Overall, the morphological parameters are quite similar for all four reconstructions compared to the reference phantom. In particular, the topology of the constructed volume fits well based on the mean coordination number and the tortuosity. This fits the visual analysis of the pores (as in Fig. 8) and means that connectivity differences seen in individual slices of the 3D volume (Fig. 7) do not lead to a significant number of changes in the 3D pore connectivity. However, looking at the geometry-related parameters, such as pore length and width or the mean chord length μ as well as the total power volume, slightly stronger differences are noticeable. These parameters are most sensitive to slight threshold variations. In addition, the k values (as a measure of the homogeneity) are higher for both the segmented-SIRT and the DART reconstructions compared to the phantom reference, especially for the limited tilt range of ±76°. This indicates that the reconstruction process causes a smoothing of pore variations, especially if the reconstruction is affected by the missing wedge.

Table 3. Quantitative morphological information on the pore structure.

The diffusion behavior within the 3D pore volume of the phantom reconstructions has been simulated as before in the case of the experimental data (Fig. 10a) to compare the differences between the reconstruction algorithms and to evaluate the effect of the missing wedge. We found that the effective diffusion within the largest cubic domain of the Phantom.segmented-SIRT ±76° reconstruction is about 14% lower compared to the reference, while the value of Phantom.segmented-SIRT ±90° reconstruction is about 21% higher. This difference is partially due to the variations in the pore volume between the reconstructions, which is ~5% lower than in the reference for the Phantom.segmented-SIRT ±76° (in the volume used for the diffusion simulation), whereas the pore volume of the Phantom.segmented-SIRT ±90° is ~14% higher compared to the reference phantom. For the Phantom.DART reconstructions, the variation of the diffusion coefficients compared to the reference is significantly smaller. It is about 7% (Phantom.DART ±76°) and about 3% (Phantom.DART ±90°) higher than in the reference phantom. However, it should be noted that the corresponding pore volume of the Phantom.DART ±76° is almost the same as in the reference (1% higher), while the pore volume in the Phantom.DART ±90° reconstruction is 4% higher. This clearly shows that the pore volume is not the only factor affecting the variations in diffusion coefficients between the 3D reconstructions, but the slight morphological differences and potentially also necking between pores play a role. Another critical point is the effect of the missing wedge on the measured diffusion properties and, in particular, on the anisotropy of the determined diffusion properties that it causes. This was evaluated by separately analyzing the x-component (perpendicular to the tilt-axis and the electron beam direction), y-component (parallel to the tilt-axis) and z-component (parallel to the electron beam direction) of the diffusion coefficients (Figs. 10b, 10c and 10d). As the investigated volume is not necessarily fully isotropic, we did not compare the absolute diffusion coefficient components in the different directions but only the differences of each component relative to the reference phantom. In the case of the Phantom.segmented-SIRT ±76°, the diffusion in 3D is 14% lower compared to the reference, but the z-component of the diffusion is enhanced and almost the same as the diffusion in this direction in the reference. This is the expected result of the missing wedge, leading to a lower intensity for pore walls oriented perpendicular to the electron beam, thus enhancing the pore length/connectivity in z-direction. In addition, we noticed that the missing wedge has a significantly different effect on the x- and y-component of the diffusion coefficients. The x-component of the diffusion is 10% lower than the reference value and thus slightly enhanced compared to the difference in 3D. However, the y-component of the diffusion is strongly reduced; it is 56% lower than the reference.

Fig. 10. Effective diffusion coefficients normalized by the bulk diffusivity as a function of the simulation box size. (a) 3D, (b) x-component, (c) y-component and (d) z-component.

To better understand this anisotropy, we investigated the effect of the SIRT reconstruction from a series of projections of a 3D shell model covering a tilt-angle range of ±76° (Supplementary Fig. 6). As commonly considered, the missing wedge results in a significant reduction of the reconstructed intensities of the shell in z-direction, because this part of the shell has strong Fourier coefficients within the missing wedge (Supplementary Fig. 6a/b). However, the reconstruction also reveals a slight anisotropy for the central slice in x- and y-direction (Supplementary Fig. 6c). This leads to the highest reconstructed intensities for pore walls perpendicular to the y-direction, which is a bit higher than the intensities perpendicular to the x-direction and again higher than the intensities perpendicular to the z-direction (Supplementary Fig. 6d). In turn, the components of the effective diffusion coefficient should be inversely affected, which is exactly the trend we notice in our diffusion simulations based on the Phantom.segmented-SIRT ±76° reconstruction compared to the reference. For the Phantom.DART ±76° reconstruction, the anisotropy of the diffusion components is significantly reduced compared to the Phantom.segmented-SIRT ±76° reconstruction. This means that the DART reconstruction significantly reduces the missing wedge artifacts. However, a deeper analysis shows that we still see the same trend as for the SIRT reconstruction. The z-component is enhanced (13%) compared to the reference, the x-component and the y-component are almost the same. This residual anisotropy suggests that the DART reconstruction did not fully converge to suppress the missing wedge artifacts.

In the reconstruction based on the full tilt-angle range of ±90°, the Phantom.segmented-SIRT ±90° exhibits slightly higher normalized diffusion coefficients in the x- and z-direction compared to the y-direction. The SIRT reconstruction of a tilt-series of projections of a 3D shell model covering the full tilt-range of ±90° revealed that the intensity in x- and z-direction is lower compared to the y-direction (Supplementary Fig. 6e), which would lead to higher diffusion both in x- and z-direction, which is exactly what we observe in our diffusion simulations for the Phantom.segmented-SIRT ±90° reconstruction. This anisotropy of the SIRT reconstructions, even with the full ±90° tilt-angle range, is due to the discrete angular sampling during tilting (2° tilt step here), which can be considered as a set of mini missing wedges in the x–z plane, whereas the y-direction along the tilt-axis will not be affected. Also, in this case, the anisotropy of the diffusion components is again significantly reduced by the Phantom.DART ±90°, resulting in a just slightly higher component in the z-direction compared to the other two directions.

Conclusions

The morphological description and the diffusion properties of a disordered mesoporous carbon material have been quantified based on an electron tomographic reconstruction. The quantitative analysis strongly depends on the fidelity of the reconstruction and the segmentation, which are affected by pore size variations, the missing wedge during tomographic acquisition and the reconstruction approach. The morphological description of the pore structure in terms of simple geometric and topological parameters can be performed reliably based on both the SIRT and DART reconstruction even in the presence of a limited missing wedge. However, the measured pore size and length vary somewhat depending on the threshold used for segmentation, and in particular, for the SIRT reconstruction, it is difficult to reproducibly define a uniform global threshold. This has a noticeable effect on the measured pore volume, which differed by ~25% in our experimental SIRT and DART reconstructions. Since diffusion through a pore network depends essentially on porosity, i.e., on the void volume fraction, the simulated diffusion coefficients also differed significantly (by ~50%) between the experimental SIRT and the DART reconstruction.

In a phantom study based on the reconstructed mesoporous carbon, we analyzed the fidelity of the reconstruction and segmentation approach for disordered mesoporous materials in more detail. This revealed that the sensitivity of the pore volume to the threshold settings is higher for the SIRT reconstruction compared to the DART reconstruction, making it more difficult to define a good threshold and, thus, to reproducibly measure the pore volume based on a SIRT reconstruction. However, we found that the pore variations introduced in the reconstruction and segmentation process are mainly present in a few voxel-wide boundary regions of the pores, slightly altering the local size of the pore structure, but not significantly affecting the morphology. Due mainly to the differences in the pore volume, the simulated diffusion coefficients also varied for the different reconstructions. Nevertheless, in the case of the DART reconstruction, a reproducible simulation of the diffusion coefficient was possible.

Missing wedge artifacts result in a noticeable anisotropy of the measured x-, y- and z-components of the diffusion coefficient based on the SIRT reconstruction, with the highest coefficients in the z-direction and the lowest coefficient in the y-direction. This anisotropy is strongly reduced in the DART reconstruction, resulting in differences of only a few percents even in the presence of a limited missing wedge.

In summary, our studies indicate that a reproducible and reliable analysis of the pore structure of mesoporous materials is possible by electron tomography based on a DART reconstruction. It enables a reliable analysis of the effective diffusion properties, thereby providing input to the understanding of morphology—transport relationships, e.g. in heterogeneous catalysis.