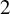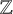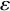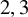1. Introduction
We work over a field k of prime characteristic
![]() $p>0$
. When running the Minimal Model Program (MMP for short) for klt projective varieties Z with canonical divisor
$p>0$
. When running the Minimal Model Program (MMP for short) for klt projective varieties Z with canonical divisor
![]() $K_Z$
not pseudo-effective, the outcomes are Mori fibre spaces (i.e., projective fibrations
$K_Z$
not pseudo-effective, the outcomes are Mori fibre spaces (i.e., projective fibrations
![]() $f \colon X \to B$
of relative Picard rank 1 where X has klt singularities,
$f \colon X \to B$
of relative Picard rank 1 where X has klt singularities,
![]() $\dim B < \dim X$
and the anti-canonical divisor
$\dim B < \dim X$
and the anti-canonical divisor
![]() $-K_X$
is f-ample). It is then natural to study the geometry of X in terms of the base B and the general fibre. In characteristic
$-K_X$
is f-ample). It is then natural to study the geometry of X in terms of the base B and the general fibre. In characteristic
![]() $p>0$
, the theorem on generic smoothness on general fibres does not always hold, and there are examples of Mori fibre spaces where the general fibre might fail to be normal or even reduced [Reference Mori and SaitoMS03]. In this case, it is natural to study the generic fibre
$p>0$
, the theorem on generic smoothness on general fibres does not always hold, and there are examples of Mori fibre spaces where the general fibre might fail to be normal or even reduced [Reference Mori and SaitoMS03]. In this case, it is natural to study the generic fibre
![]() $X_{k(B)}$
, which is a klt Fano variety defined over the fraction field
$X_{k(B)}$
, which is a klt Fano variety defined over the fraction field
![]() $k(B)$
, which is imperfect as soon as
$k(B)$
, which is imperfect as soon as
![]() $\dim (B) \geq 1$
.
$\dim (B) \geq 1$
.
Thanks to the recent development of the 3-dimensional MMP [Reference Hacon and XuHX15, Reference Cascini, Tanaka and XuCTX15, Reference Birkar and WaldronBW17, Reference Hacon and WitaszekHW22, Reference WaldronWal23], Mori fibre spaces are known to exist for 3-folds over fields of characteristic
![]() $p> 5$
. The next step in the classification problem consists in understanding the generic fibre of a 3-fold Mori fibre space. This work is motivated by the following general question:
$p> 5$
. The next step in the classification problem consists in understanding the generic fibre of a 3-fold Mori fibre space. This work is motivated by the following general question:
Question 1.1. Do the generic fibers of Mori fibre spaces form a bounded family? Can we give explicit bounds on their cohomological invariants?
The main invariant we are interested in is the irregularity of the generic fibre. Recall that the irregularity of
![]() $X_{k(B)}$
is defined as
$X_{k(B)}$
is defined as
![]() $h^1(X_{k(B)},\mathcal {O}_{X_{k(B)}}):=\dim _{k(B)} H^1(X_{k(B)}, \mathcal {O}_{X_{k(B)}})$
. The case of relative dimension 1 is easy to treat: regular Fano curves are conics, they have vanishing irregularity and they fail to be geometrically regular only in characteristic
$h^1(X_{k(B)},\mathcal {O}_{X_{k(B)}}):=\dim _{k(B)} H^1(X_{k(B)}, \mathcal {O}_{X_{k(B)}})$
. The case of relative dimension 1 is easy to treat: regular Fano curves are conics, they have vanishing irregularity and they fail to be geometrically regular only in characteristic
![]() $p=2$
. The case of relative dimension 2 (i.e., the geometry of del Pezzo surfaces over imperfect fields) has turned out to be more difficult to handle. There are two known series of examples of canonical del Pezzo surfaces with positive irregularity:
$p=2$
. The case of relative dimension 2 (i.e., the geometry of del Pezzo surfaces over imperfect fields) has turned out to be more difficult to handle. There are two known series of examples of canonical del Pezzo surfaces with positive irregularity:
-
1. In [Reference SchröerSch07], Schröer constructs a canonical del Pezzo surface X with a unique singular factorial point of type
 $A_1$
,
$A_1$
,
 $h^1(X, \mathcal {O}_X)=1, \rho (X)=1$
and
$h^1(X, \mathcal {O}_X)=1, \rho (X)=1$
and
 $K_X^2=1$
over an arbitrary imperfect field of characteristic 2.
$K_X^2=1$
over an arbitrary imperfect field of characteristic 2. -
2. In [Reference MaddockMad16], Maddock constructs regular del Pezzo surfaces
 $X_1$
and
$X_1$
and
 $X_2$
defined over an imperfect field of p-degree
$X_2$
defined over an imperfect field of p-degree
 $3$
(resp.
$3$
(resp.
 $4$
) with
$4$
) with
 $K_{X_d}^2 = d$
and
$K_{X_d}^2 = d$
and
 $h^1(X_d,\mathcal {O}_{X_d}) = 1$
. Moreover,
$h^1(X_d,\mathcal {O}_{X_d}) = 1$
. Moreover,
 $X_1$
is geometrically integral, and
$X_1$
is geometrically integral, and
 $X_2$
is not.
$X_2$
is not.
On the positive side, the recent works [Reference Patakfalvi and WaldronPW22, Reference Fanelli and SchröerFS20, Reference Ji and WaldronJW21, Reference Bernasconi and TanakaBT22] indicate that the pathological behaviour of del Pezzo fibrations is particular to small characteristics. In this article, we further restrict the possibilities for the irregularity of geometrically integral canonical del Pezzo surfaces defined over imperfect fields. Our first main result is the following:
Theorem 1.2. Let X be a geometrically integral normal locally complete intersection del Pezzo surface over a field k of characteristic p. If
![]() $h^1(X, \mathcal {O}_X) \neq 0$
, then k is an imperfect field,
$h^1(X, \mathcal {O}_X) \neq 0$
, then k is an imperfect field,
![]() $\rho (X)=1$
, and either
$\rho (X)=1$
, and either
-
1.
 $p=3$
,
$p=3$
,
 $h^1(X, \mathcal {O}_X)=2$
,
$h^1(X, \mathcal {O}_X)=2$
,
 $K_X^2 = 1$
, and X is not canonical, or
$K_X^2 = 1$
, and X is not canonical, or -
2.
 $p=2$
,
$p=2$
,
 $h^1(X, \mathcal {O}_X)=1$
, and
$h^1(X, \mathcal {O}_X)=1$
, and
 $K_X^2 \leq 2$
.
$K_X^2 \leq 2$
.
We note that our bound on the irregularity in the regular case is sharp, as Maddock’s example shows. In Proposition 4.11, we describe torsors over the regular wild del Pezzo surfaces in characteristic
![]() $p = 2$
. This is a first step towards a classification of wild regular del Pezzo surfaces. In particular, it may be useful for the construction of explicit examples in the style of Maddock. Note that the hypothesis on geometric integrality is automatically satisfied for normal del Pezzo surfaces appearing as generic fibres of 3-folds by [Reference SchröerSch10, Theorem 2.3].
$p = 2$
. This is a first step towards a classification of wild regular del Pezzo surfaces. In particular, it may be useful for the construction of explicit examples in the style of Maddock. Note that the hypothesis on geometric integrality is automatically satisfied for normal del Pezzo surfaces appearing as generic fibres of 3-folds by [Reference SchröerSch10, Theorem 2.3].
In the second part of this article, we prove boundedness results for del Pezzo surfaces over imperfect fields. The Borisov–Alexeev–Borisov (BAB) conjecture (see Conjecture 5.2) states that mildly singular (
![]() $\varepsilon $
-klt) Fano varieties of dimension d form a bounded family over
$\varepsilon $
-klt) Fano varieties of dimension d form a bounded family over
![]() $ {\mathrm {Spec}} \mathbb {Z}$
. While the conjecture has been proven over fields of characteristic 0 by Birkar [Reference BirkarBir21], it is still open over fields of characteristic p.
$ {\mathrm {Spec}} \mathbb {Z}$
. While the conjecture has been proven over fields of characteristic 0 by Birkar [Reference BirkarBir21], it is still open over fields of characteristic p.
More precisely, while the case of del Pezzo surfaces over perfect fields has been known for a long time (see [Reference AlexeevAle94, Reference Alexeev and MoriAM04] and [Reference Cascini, Tanaka and WitaszekCTW17, Lemma 3.1]), already the boundedness of
![]() $3$
-dimensional Fano varieties is open. In this direction, the BAB conjecture for generic fibres of Mori fibre spaces would be desirable. In [Reference TanakaTan24], Tanaka showed that geometrically integral regular del Pezzo surfaces form a bounded family. Using Theorem 1.2 and the results on the irregularity of klt del Pezzo surfaces of [Reference Bernasconi and TanakaBT22], we are able to prove various instances of the BAB conjecture, following the strategy of Alexeev–Mori [Reference Alexeev and MoriAM04]:
$3$
-dimensional Fano varieties is open. In this direction, the BAB conjecture for generic fibres of Mori fibre spaces would be desirable. In [Reference TanakaTan24], Tanaka showed that geometrically integral regular del Pezzo surfaces form a bounded family. Using Theorem 1.2 and the results on the irregularity of klt del Pezzo surfaces of [Reference Bernasconi and TanakaBT22], we are able to prove various instances of the BAB conjecture, following the strategy of Alexeev–Mori [Reference Alexeev and MoriAM04]:
Theorem 1.3. The following classes of del Pezzo surfaces are bounded over
![]() $ {\mathrm {Spec}} \mathbb {Z}$
:
$ {\mathrm {Spec}} \mathbb {Z}$
:
 $$ \begin{align*} \mathcal{X}_{\text{dP}, \text{can}} &= \left\{ X \mid X \text{ is a geometrically integral canonical del Pezzo surface}\right\}, \\ \mathcal{X}_{\text{dP}, \varepsilon}^{\text{tame}} &= \left\{ X \mid X \text{ is a geometrically integral tame } \varepsilon\text{-klt del Pezzo surface} \right\}, \text{ and} \\ \mathcal{X}_{\text{dP}, \varepsilon}^{>5} &= \left\{ X \mid X \text{ is an } \varepsilon\text{-klt del Pezzo surface s.t. char}(H^0(X, \mathcal{O}_X)) \neq 2, 3, 5 \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{X}_{\text{dP}, \text{can}} &= \left\{ X \mid X \text{ is a geometrically integral canonical del Pezzo surface}\right\}, \\ \mathcal{X}_{\text{dP}, \varepsilon}^{\text{tame}} &= \left\{ X \mid X \text{ is a geometrically integral tame } \varepsilon\text{-klt del Pezzo surface} \right\}, \text{ and} \\ \mathcal{X}_{\text{dP}, \varepsilon}^{>5} &= \left\{ X \mid X \text{ is an } \varepsilon\text{-klt del Pezzo surface s.t. char}(H^0(X, \mathcal{O}_X)) \neq 2, 3, 5 \right\}. \end{align*} $$
We briefly explain the organisation of the article. In section 2, we collect various results on geometry over imperfect fields and del Pezzo surfaces. In section 3, we generalise the main results of Tanaka [Reference TanakaTan24] to the canonical case. We use Ekedahl’s technique [Reference EkedahlEke88] on the construction of
![]() $\alpha $
-torsor to show an effective Kodaira vanishing theorem (Proposition 3.6) from which we deduce that
$\alpha $
-torsor to show an effective Kodaira vanishing theorem (Proposition 3.6) from which we deduce that
![]() $\omega _X^{-12}$
is very ample (Theorem 3.10). Starting from section 4, we specialise to the study of geometrically integral del Pezzo surfaces. We show that the Frobenius length of geometric non-normality (an invariant introduced by Tanaka [Reference TanakaTan21]) is at most 1 (Corollary 4.4) on normal Gorenstein del Pezzo surfaces, a result we use to find lower bounds on the dimension of the space of anti-pluricanonical sections. We combine these estimates together with Maddock’s bound [Reference MaddockMad16, Corollary 1.2.6] and a careful study of
$\omega _X^{-12}$
is very ample (Theorem 3.10). Starting from section 4, we specialise to the study of geometrically integral del Pezzo surfaces. We show that the Frobenius length of geometric non-normality (an invariant introduced by Tanaka [Reference TanakaTan21]) is at most 1 (Corollary 4.4) on normal Gorenstein del Pezzo surfaces, a result we use to find lower bounds on the dimension of the space of anti-pluricanonical sections. We combine these estimates together with Maddock’s bound [Reference MaddockMad16, Corollary 1.2.6] and a careful study of
![]() $\alpha $
-torsors to prove Theorem 1.2. In section 5, we apply our results to the BAB conjecture over arbitrary fields, and we prove Theorem 1.3.
$\alpha $
-torsors to prove Theorem 1.2. In section 5, we apply our results to the BAB conjecture over arbitrary fields, and we prove Theorem 1.3.
2. Preliminaries
2.1. Notations
-
1. Given a field k, we denote by
 $\overline {k}$
(resp.
$\overline {k}$
(resp.
 $k^{\text {sep}}$
) an algebraic (resp. separable) closure. We denote by
$k^{\text {sep}}$
) an algebraic (resp. separable) closure. We denote by
 $k^{1/p^{\infty }}$
the perfect closure of k.
$k^{1/p^{\infty }}$
the perfect closure of k. -
2. Given a field k, a scheme X is a k-variety if it is an integral separated scheme of finite type over k. If X has dimension 1 (resp. 2, 3), we say X is a curve (resp. surface, 3-fold).
-
3. Given a projective integral k-variety X, we let
 $d_X:=[H^0(X, \mathcal {O}_X):k]$
.
$d_X:=[H^0(X, \mathcal {O}_X):k]$
. -
4. Given an
 $\mathbb {F}_p$
-scheme X, we denote by
$\mathbb {F}_p$
-scheme X, we denote by
 $F \colon X \to X$
the absolute Frobenius morphism of X. We say X is F-finite if F is a finite morphism.
$F \colon X \to X$
the absolute Frobenius morphism of X. We say X is F-finite if F is a finite morphism. -
5. For an F-finite field k, its p-degree (or degree of imperfection) is defined as
 $ {\mathrm{p-deg}}(k):=\log _{p}[k:k^p]$
.
$ {\mathrm{p-deg}}(k):=\log _{p}[k:k^p]$
. -
6. We say
 $(X, \Delta )$
is a pair if X is a normal k-variety,
$(X, \Delta )$
is a pair if X is a normal k-variety,
 $\Delta $
is an effective
$\Delta $
is an effective
 $\mathbb {Q}$
-divisor with coefficients in
$\mathbb {Q}$
-divisor with coefficients in
 $[0, 1]$
and
$[0, 1]$
and
 $K_X+\Delta $
is a
$K_X+\Delta $
is a
 $\mathbb {Q}$
-Cartier divisor.
$\mathbb {Q}$
-Cartier divisor. -
7. For the definitions of the singularities of the MMP (as canonical, klt and log canonical), we refer to [Reference KollárKol13, Definition 2.8].
-
8. Given an integral scheme X with normalisation
 $\nu \colon Y \to X$
, we denote by
$\nu \colon Y \to X$
, we denote by
 $\mathcal {I} \subset \mathcal {O}_X$
the conductor ideal (i.e., the annihilator of the
$\mathcal {I} \subset \mathcal {O}_X$
the conductor ideal (i.e., the annihilator of the
 $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
 $\nu _*(\mathcal {O}_Y)/\mathcal {O}_X)$
). The corresponding closed subscheme
$\nu _*(\mathcal {O}_Y)/\mathcal {O}_X)$
). The corresponding closed subscheme
 $D \subset X$
is called the conductor scheme of
$D \subset X$
is called the conductor scheme of
 $\nu $
. Note that
$\nu $
. Note that
 $\mathcal {I}$
is also an ideal of
$\mathcal {I}$
is also an ideal of
 $\mathcal {O}_Y$
and the corresponding subscheme
$\mathcal {O}_Y$
and the corresponding subscheme
 $C \subset Y$
is called ramification locus of
$C \subset Y$
is called ramification locus of
 $\nu $
.
$\nu $
. -
9. A projective morphism
 $f \colon X \to Y$
of normal schemes is a contraction if
$f \colon X \to Y$
of normal schemes is a contraction if
 $f_*\mathcal {O}_X=\mathcal {O}_Y$
.
$f_*\mathcal {O}_X=\mathcal {O}_Y$
.
2.2. Geometric reducedness and normality
We collect well-known results on the geometry of algebraic varieties, especially surfaces, defined over imperfect fields that we need in this article.
Definition 2.1. A k-variety X is geometrically reduced (resp. geometrically normal, geometrically regular) if the base change
![]() $X_{\overline {k}}$
is reduced (resp. normal, regular).
$X_{\overline {k}}$
is reduced (resp. normal, regular).
We recall Tate’s base change formula for purely inseparable field extensions.
Theorem 2.2 [Reference Patakfalvi and WaldronPW22, Theorem 1.1]
Let X be a normal k-variety such that k is algebraically closed in
![]() $K(X)$
. Let Y be the normalisation of the reduced scheme
$K(X)$
. Let Y be the normalisation of the reduced scheme
![]() $(X \times _k \overline {k})_{ {\mathrm {red}}}$
together with the natural morphism
$(X \times _k \overline {k})_{ {\mathrm {red}}}$
together with the natural morphism
![]() $f \colon Y \to X$
. Then there exists an effective divisor
$f \colon Y \to X$
. Then there exists an effective divisor
![]() $C \geq 0$
such that
$C \geq 0$
such that
![]() $K_Y+(p-1)C=f^*K_X.$
If X is geometrically integral, then
$K_Y+(p-1)C=f^*K_X.$
If X is geometrically integral, then
![]() $(p-1)C$
can be chosen to be the ramification divisor of f.
$(p-1)C$
can be chosen to be the ramification divisor of f.
We start with the behaviour of geometric reducedeness under birational equivalence.
Lemma 2.3 [Reference Bernasconi and TanakaBT22, Lemma 2.2]
Let X and Y be two k-birational varieties. Then X is geometrically reduced over k if and only if Y is geometrically reduced over k.
Next, we note that geometric normality descends under birational contractions. For the definition of the
![]() $(S_n)$
-property, we refer to [Sta, Tag 033Q].
$(S_n)$
-property, we refer to [Sta, Tag 033Q].
Proposition 2.4. Let
![]() $\pi \colon X \to Y$
be a projective birational morphism of normal k-varieties. If X is geometrically normal, so is Y.
$\pi \colon X \to Y$
be a projective birational morphism of normal k-varieties. If X is geometrically normal, so is Y.
Proof. Recall that a variety X over k has the property
![]() $(S_n)$
if and only if
$(S_n)$
if and only if
![]() $X_{\overline {k}}$
also has, by faithfully flat descent. As Y is
$X_{\overline {k}}$
also has, by faithfully flat descent. As Y is
![]() $(S_2)$
, by Serre’s criterion [Sta, Tag 031S], Y is geometrically normal if and only if it is geometrically
$(S_2)$
, by Serre’s criterion [Sta, Tag 031S], Y is geometrically normal if and only if it is geometrically
![]() $(R_1)$
. Suppose by contradiction that there exists a codimension 1 point
$(R_1)$
. Suppose by contradiction that there exists a codimension 1 point
![]() $\eta \in Y$
such that the localisation
$\eta \in Y$
such that the localisation
![]() $\mathcal {O}_{Y, \eta }$
is not geometrically regular. As Y is normal,
$\mathcal {O}_{Y, \eta }$
is not geometrically regular. As Y is normal,
![]() $\pi $
is an isomorphism over codimension 1 points of Y, and thus, X is not geometrically
$\pi $
is an isomorphism over codimension 1 points of Y, and thus, X is not geometrically
![]() $(R_1)$
, reaching the contradiction.
$(R_1)$
, reaching the contradiction.
We discuss singularities of the MMP over imperfect fields.
Definition 2.5. Let
![]() $(X,\Delta )$
be a pair over k such that k is algebraically closed in
$(X,\Delta )$
be a pair over k such that k is algebraically closed in
![]() $K(X)$
. We say it is geometrically canonical (resp. klt, log canonical) if the base change
$K(X)$
. We say it is geometrically canonical (resp. klt, log canonical) if the base change
![]() $(X_{\overline {k}}, \Delta _{\overline {k}})$
is so.
$(X_{\overline {k}}, \Delta _{\overline {k}})$
is so.
In particular, note that geometrically log canonical implies geometrically normal. If X is geometrically canonical (resp. klt, lc), then X is also canonical (resp. klt, lc) by [Reference Bernasconi and TanakaBT22, Proposition 2.3]. We now specialise to the case of surfaces. Recall that the existence of resolution of singularities for excellent surfaces has been proven in [Reference LipmanLip78].
Proposition 2.6. Let X be the spectrum of a local excellent ring
![]() $(R,\mathfrak {m})$
with closed point x. If
$(R,\mathfrak {m})$
with closed point x. If
![]() $(X, \Delta )$
is a klt surface pair for some
$(X, \Delta )$
is a klt surface pair for some
![]() $\Delta \geq 0$
, then X has rational and
$\Delta \geq 0$
, then X has rational and
![]() $\mathbb {Q}$
-factorial singularities. Therefore, if two projective k-surfaces X and Y with klt singularies are k-birational, then
$\mathbb {Q}$
-factorial singularities. Therefore, if two projective k-surfaces X and Y with klt singularies are k-birational, then
![]() $H^i(X, \mathcal {O}_X) \simeq H^i(Y, \mathcal {O}_Y)$
for every
$H^i(X, \mathcal {O}_X) \simeq H^i(Y, \mathcal {O}_Y)$
for every
![]() $i \geq 0$
.
$i \geq 0$
.
Proof. Rationality of klt surface singularities follows from [Reference KollárKol13, Proposition 2.28], and
![]() $\mathbb {Q}$
-factoriality of rational singularities is proven in [Reference LipmanLip69, Proposition 17.1]. The last statement is obvious by considering a common resolution of X and Y.
$\mathbb {Q}$
-factoriality of rational singularities is proven in [Reference LipmanLip69, Proposition 17.1]. The last statement is obvious by considering a common resolution of X and Y.
Corollary 2.7. Let
![]() $(x \in X)$
be a Gorenstein normal surface singularity. Then X is canonical if and only if it is rational.
$(x \in X)$
be a Gorenstein normal surface singularity. Then X is canonical if and only if it is rational.
Proof. If X is canonical, then it is rational by Proposition 2.6. Suppose now that X is rational and let
![]() $f \colon Y \to X$
be a resolution of singularities. As X is Gorenstein and X has rational singularities, we have that
$f \colon Y \to X$
be a resolution of singularities. As X is Gorenstein and X has rational singularities, we have that
![]() $f_*\omega _Y = \omega _X$
by [Reference KollárKol13, Proposition 2.77], which in turn implies that X has canonical singularities by [Reference KollárKol13, Claim 2.3.1].
$f_*\omega _Y = \omega _X$
by [Reference KollárKol13, Proposition 2.77], which in turn implies that X has canonical singularities by [Reference KollárKol13, Claim 2.3.1].
2.3. Del Pezzo surfaces
In this subsection, we collect some terminology on del Pezzo surfaces and recall previously known results.
Definition 2.8. We say X is a Gorenstein (resp. canonical, regular) del Pezzo surface over k if X is a reduced k-projective Gorenstein (resp. canonical, regular) surface with
![]() $H^0(X, \mathcal {O}_X)=k$
and
$H^0(X, \mathcal {O}_X)=k$
and
![]() $\omega _X^{-1}$
is ample. We say X is a weak del Pezzo if
$\omega _X^{-1}$
is ample. We say X is a weak del Pezzo if
![]() $\omega _X^{-1}$
is big and nef.
$\omega _X^{-1}$
is big and nef.
We recall the classification of Gorenstein normal del Pezzo surfaces over algebraically closed fields:
Proposition 2.9 [Reference Hidaka and WatanabeHW81, Theorem 2.2]
Let X be a normal Gorenstein del Pezzo surface over an algebraically closed field k. Then one of the following holds:
-
1. X is a canonical del Pezzo surface and the explicit list is described in [Reference DolgachevDol12, Section 8], or
-
2. the minimal resolution
 $Z \to X$
is a ruled surface of the form
$Z \to X$
is a ruled surface of the form
 $\mathbb {P}_E(\mathcal {O}_E \oplus \mathcal {L})$
, where E is an elliptic curve and
$\mathbb {P}_E(\mathcal {O}_E \oplus \mathcal {L})$
, where E is an elliptic curve and
 $\deg \mathcal {L}<0$
. The surface X is obtained by contracting the negative section of Z.
$\deg \mathcal {L}<0$
. The surface X is obtained by contracting the negative section of Z.
In [Reference Bernasconi and TanakaBT22, Theorem 3.3], it is shown that canonical del Pezzo surfaces which are geometrically normal are geometrically canonical. We present a different proof of this result relying on Proposition 2.9 and the following observation:
Lemma 2.10. Let
![]() $(y \in Y)$
be a geometrically log canonical surface singularity over k. Suppose that Y has rational singularities. Then
$(y \in Y)$
be a geometrically log canonical surface singularity over k. Suppose that Y has rational singularities. Then
![]() $Y_{\overline {k}}$
has rational singularities.
$Y_{\overline {k}}$
has rational singularities.
Proof. We can suppose k is separably closed and Y is the spectrum of a local henselian ring
![]() $(R, \mathfrak {m})$
by the existence of resolution of singularities [Reference LipmanLip78]. Let
$(R, \mathfrak {m})$
by the existence of resolution of singularities [Reference LipmanLip78]. Let ![]() be the punctured spectrum. Since Y is rational, the group
be the punctured spectrum. Since Y is rational, the group
![]() $ {\mathrm {Pic}}(U)$
is finite by [Reference LipmanLip69, Proposition 17.1]. Therefore, also
$ {\mathrm {Pic}}(U)$
is finite by [Reference LipmanLip69, Proposition 17.1]. Therefore, also
![]() $X:=Y_{\overline {k}}$
is
$X:=Y_{\overline {k}}$
is
![]() $\mathbb {Q}$
-factorial by [Reference TanakaTan18a, Lemma 2.5], and thus,
$\mathbb {Q}$
-factorial by [Reference TanakaTan18a, Lemma 2.5], and thus,
![]() $ {\mathrm {Pic}}(U_{\overline {k}})$
is a torsion group. Let
$ {\mathrm {Pic}}(U_{\overline {k}})$
is a torsion group. Let
![]() $f \colon W \to X$
be the minimal resolution with exceptional divisor
$f \colon W \to X$
be the minimal resolution with exceptional divisor
![]() $E=\sum _{i=1}^n E_i$
. As defined in [Reference LipmanLip69],
$E=\sum _{i=1}^n E_i$
. As defined in [Reference LipmanLip69],
![]() $ {\mathrm {Pic}}^0(W)$
is the group of line bundles L on W such that
$ {\mathrm {Pic}}^0(W)$
is the group of line bundles L on W such that
![]() $L \cdot E_i=0$
for every i and there is an exact sequence of groups
$L \cdot E_i=0$
for every i and there is an exact sequence of groups
![]() $0 \to {\mathrm {Pic}}^0(W) \to {\mathrm {Pic}}(W) \to \bigoplus \mathbb {Z}[E_i] \to 0$
. By [Reference LipmanLip69, Proposition 14.4],
$0 \to {\mathrm {Pic}}^0(W) \to {\mathrm {Pic}}(W) \to \bigoplus \mathbb {Z}[E_i] \to 0$
. By [Reference LipmanLip69, Proposition 14.4],
![]() $ {\mathrm {Pic}}^0(W)$
embeds into
$ {\mathrm {Pic}}^0(W)$
embeds into
![]() $ {\mathrm {Pic}}(U_{\overline {k}})$
, and thus, we deduce it is a torsion group.
$ {\mathrm {Pic}}(U_{\overline {k}})$
, and thus, we deduce it is a torsion group.
Suppose now by contradiction that X is not rational. By the classification of log canonical singularities [Reference KollárKol13, Corollary 3.39], the exceptional divisor E is either an elliptic curve, a nodal curve or a circle of smooth rational curves. In the first case,
![]() $ {\mathrm {Pic}}^0(E)\simeq E(k)$
, while in the latter cases,
$ {\mathrm {Pic}}^0(E)\simeq E(k)$
, while in the latter cases,
![]() $ {\mathrm {Pic}}^0(E) \simeq k^*$
by [Reference Bosch, Lütkebohmert and RaynaudBLR90, Chapter 9.3, Corollary 11 and 12] and since
$ {\mathrm {Pic}}^0(E) \simeq k^*$
by [Reference Bosch, Lütkebohmert and RaynaudBLR90, Chapter 9.3, Corollary 11 and 12] and since
![]() $h^1(E,\mathcal {O}_E) = 1$
. By [Reference LipmanLip69, Lemma 14.3], the restriction map
$h^1(E,\mathcal {O}_E) = 1$
. By [Reference LipmanLip69, Lemma 14.3], the restriction map
![]() $ {\mathrm {Pic}}(W) \to {\mathrm {Pic}}(E)$
is surjective. Considering the exact sequence
$ {\mathrm {Pic}}(W) \to {\mathrm {Pic}}(E)$
is surjective. Considering the exact sequence
![]() $0 \to {\mathrm {Pic}}^0(E) \to {\mathrm {Pic}}(E) \to \mathbb {Z}^{n} \to 0$
, we can deduce that the map
$0 \to {\mathrm {Pic}}^0(E) \to {\mathrm {Pic}}(E) \to \mathbb {Z}^{n} \to 0$
, we can deduce that the map
![]() $ {\mathrm {Pic}}^0(W) \to {\mathrm {Pic}}^0(E) $
is surjective. This is a contradiction, as
$ {\mathrm {Pic}}^0(W) \to {\mathrm {Pic}}^0(E) $
is surjective. This is a contradiction, as
![]() $ {\mathrm {Pic}}^0(W)$
is torsion while
$ {\mathrm {Pic}}^0(W)$
is torsion while
![]() $k^*$
and
$k^*$
and
![]() $E(k)$
are not.
$E(k)$
are not.
Proposition 2.11. Let X be a canonical del Pezzo surface. If X is geometrically normal, then it is geometrically canonical.
Proof. By Proposition 2.9, X is geometrically log canonical. As X has rational singularities, X is geometrically rational by Lemma 2.10. As X is Gorenstein, we conclude that X is geometrically canonical by Corollary 2.7.
We now recall the results of Reid on the classification of non-normal Gorenstein del Pezzo surfaces [Reference ReidRei94]. We fix some notations we will use throughout the article (cf. subsection 2.1 for the terminology used).
Definition 2.12. Let X be a non-normal integral Gorenstein del Pezzo surface with normalisation
![]() $\nu \colon Y \to X$
. We say X is tame if
$\nu \colon Y \to X$
. We say X is tame if
![]() $H^1(X, \mathcal {O}_X)=0$
.
$H^1(X, \mathcal {O}_X)=0$
.
One can characterise tame del Pezzo surfaces in terms of the conductor.
Theorem 2.13. Let X be a non-normal integral Gorenstein del Pezzo surface over an algebraically closed field. Then the conductor
![]() $D \subset X$
is integral. Moreover,
$D \subset X$
is integral. Moreover,
-
1. X is tame if and only if
 $D \simeq \mathbb {P}^1$
;
$D \simeq \mathbb {P}^1$
; -
2.
 $(p-1)$
divides
$(p-1)$
divides
 $h^1( \mathcal {O}_X)$
.
$h^1( \mathcal {O}_X)$
.
Proof. The integrality of the conductor follows from [Reference ReidRei94, Lemma, page 718] for integral del Pezzo surfaces. Then, (1) follows from the proof of [Reference ReidRei94, Corollary 4.10], as D is irreducible. (2) is proved in [Reference ReidRei94, 4.11]
We will repeatedly use the following:
Lemma 2.14. Let
![]() $\pi \colon X \to Y$
be a proper birational morphism of k-surfaces. If X is a regular (resp. canonical) del Pezzo surface, then so is Y. If X is a regular (or canonical) weak del Pezzo surface, then also Y is a canonical weak del Pezzo surface.
$\pi \colon X \to Y$
be a proper birational morphism of k-surfaces. If X is a regular (resp. canonical) del Pezzo surface, then so is Y. If X is a regular (or canonical) weak del Pezzo surface, then also Y is a canonical weak del Pezzo surface.
Proof. We only prove the case where X is a regular weak del Pezzo surface, as the others are similar. As
![]() $-K_X$
is
$-K_X$
is
![]() $\pi $
-big and
$\pi $
-big and
![]() $\pi $
-nef, we conclude that Y has canonical singularities by the negativity lemma [Reference TanakaTan18b, Lemma 2.11]. As
$\pi $
-nef, we conclude that Y has canonical singularities by the negativity lemma [Reference TanakaTan18b, Lemma 2.11]. As
![]() $-K_Y=\pi _*(-K_X)$
, we conclude by projection formula that
$-K_Y=\pi _*(-K_X)$
, we conclude by projection formula that
![]() $-K_Y$
is big and nef.
$-K_Y$
is big and nef.
From the point of view of the MMP, it is natural to consider surfaces of del Pezzo type. For their basic properties, we refer to [Reference Bernasconi and TanakaBT22, Section 2.3].
Definition 2.15. We say X is a surface of del Pezzo type over k if X is a projective k-variety with
![]() $H^0(X, \mathcal {O}_X)=k$
and there exists
$H^0(X, \mathcal {O}_X)=k$
and there exists
![]() $\Delta \geq 0$
such that
$\Delta \geq 0$
such that
![]() $(X,\Delta )$
is a log del Pezzo pair (i.e.,
$(X,\Delta )$
is a log del Pezzo pair (i.e.,
![]() $(X,\Delta )$
klt and
$(X,\Delta )$
klt and
![]() $-(K_X+\Delta )$
is big and nef).
$-(K_X+\Delta )$
is big and nef).
The following describes the Picard scheme of del Pezzo surfaces.
Proposition 2.16. Let X be a surface of del Pezzo type. Then
![]() $ {\mathrm {Pic}}^0_{X/k}$
is a unipotent smooth commutative k-group scheme of finite type over k of dimension
$ {\mathrm {Pic}}^0_{X/k}$
is a unipotent smooth commutative k-group scheme of finite type over k of dimension
![]() $h^1(X, \mathcal {O}_X)$
.
$h^1(X, \mathcal {O}_X)$
.
Proof. By Serre duality, we have
![]() $H^2(X, \mathcal {O}_X)=H^0(X, \omega _X)=0$
, and therefore, by [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and VistoliFGI05, Corollary 9.4.18.3, Corollary 9.5.13 and Remark 9.5.15], the group scheme
$H^2(X, \mathcal {O}_X)=H^0(X, \omega _X)=0$
, and therefore, by [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and VistoliFGI05, Corollary 9.4.18.3, Corollary 9.5.13 and Remark 9.5.15], the group scheme
![]() $ {\mathrm {Pic}}^0_{X/k}$
is smooth of dimension
$ {\mathrm {Pic}}^0_{X/k}$
is smooth of dimension
![]() $h^1(\mathcal {O}_X)$
. We are left to show that
$h^1(\mathcal {O}_X)$
. We are left to show that
![]() $ {\mathrm {Pic}}^0_{X/k}$
is unipotent. For this, we can suppose k is separably closed. By [Reference Bernasconi and TanakaBT22, Theorem 1.3], there exists
$ {\mathrm {Pic}}^0_{X/k}$
is unipotent. For this, we can suppose k is separably closed. By [Reference Bernasconi and TanakaBT22, Theorem 1.3], there exists
![]() $n>0$
such that for every
$n>0$
such that for every
![]() $L \in {\mathrm {Pic}}^0(X)$
, we have
$L \in {\mathrm {Pic}}^0(X)$
, we have
![]() $L^{\otimes p^n} \simeq \mathcal {O}_X$
. In other words, multiplication by
$L^{\otimes p^n} \simeq \mathcal {O}_X$
. In other words, multiplication by
![]() $p^n$
on
$p^n$
on
![]() $ {\mathrm {Pic}}^0_{X/k}$
coincides with the zero homomorphism on k-rational points. By density of rational points [Reference PoonenPoo17, Proposition 3.5.70] and since
$ {\mathrm {Pic}}^0_{X/k}$
coincides with the zero homomorphism on k-rational points. By density of rational points [Reference PoonenPoo17, Proposition 3.5.70] and since
![]() $ {\mathrm {Pic}}^0_{X/k}$
is reduced, we conclude that taking
$ {\mathrm {Pic}}^0_{X/k}$
is reduced, we conclude that taking
![]() $p^n$
-powers on
$p^n$
-powers on
![]() $ {\mathrm {Pic}}^0_{X/k}$
coincides with the zero homomorphism as a morphism of schemes, and thus,
$ {\mathrm {Pic}}^0_{X/k}$
coincides with the zero homomorphism as a morphism of schemes, and thus,
![]() $ {\mathrm {Pic}}^0_{X/k}$
is unipotent.
$ {\mathrm {Pic}}^0_{X/k}$
is unipotent.
3. Bounds on the anticanonical volume and effective very ampleness
In this section, we prove bounds on the anticanonical volume and very ampleness statements for canonical del Pezzo surfaces over imperfect fields.
3.1. Bounding volumes
We start by bounding the volume of canonical del Pezzo surfaces in terms of their thickening exponent
![]() $\epsilon (X/k)$
(see [Reference TanakaTan24, Definition 7.4] and Definition 3.2 below). First, we need an explicit bound on the Cartier index of a klt surface singularity. For a
$\epsilon (X/k)$
(see [Reference TanakaTan24, Definition 7.4] and Definition 3.2 below). First, we need an explicit bound on the Cartier index of a klt surface singularity. For a
![]() $\mathbb {Q}$
-factorial variety X, we define its Cartier index to be the smallest integer
$\mathbb {Q}$
-factorial variety X, we define its Cartier index to be the smallest integer
![]() $n>0$
such that for every Weil divisor D in X, the Weil divisor
$n>0$
such that for every Weil divisor D in X, the Weil divisor
![]() $nD$
is Cartier.
$nD$
is Cartier.
Lemma 3.1. Let X be the spectrum of a local k-algebra
![]() $(R,\mathfrak {m})$
, and let x be the closed point corresponding to
$(R,\mathfrak {m})$
, and let x be the closed point corresponding to
![]() $\mathfrak {m}$
. Suppose
$\mathfrak {m}$
. Suppose
![]() $(X, \Delta )$
is a klt surface pair for some
$(X, \Delta )$
is a klt surface pair for some
![]() $\Delta \geq 0$
. Let
$\Delta \geq 0$
. Let
![]() $f \colon Y \to X$
be the minimal resolution of singularities, with exceptional divisor
$f \colon Y \to X$
be the minimal resolution of singularities, with exceptional divisor
![]() $E=\sum _{i=1}^n E_i$
. Let
$E=\sum _{i=1}^n E_i$
. Let
![]() $M=(E_i \cdot _k E_j)_{i,j=1}^n$
be the intersection matrix and let
$M=(E_i \cdot _k E_j)_{i,j=1}^n$
be the intersection matrix and let
![]() $d= \det (M)$
. Then there exists
$d= \det (M)$
. Then there exists
![]() $d_x$
such that
$d_x$
such that
![]() $d=d_x[k(x):k]$
and the Cartier index of X divides
$d=d_x[k(x):k]$
and the Cartier index of X divides
![]() $d_x$
.
$d_x$
.
Proof. Recall that X is rational and
![]() $\mathbb {Q}$
-factorial by Proposition 2.6. Let D be a Weil integral divisor on X, and write
$\mathbb {Q}$
-factorial by Proposition 2.6. Let D be a Weil integral divisor on X, and write
![]() $f^{*} D = f_*^{-1} D + \sum _{i=1}^n a_i E_i$
for some
$f^{*} D = f_*^{-1} D + \sum _{i=1}^n a_i E_i$
for some
![]() $a_i \in \mathbb {Q}$
.
$a_i \in \mathbb {Q}$
.
We claim it is sufficient to show
![]() $d_xa_i$
is integral. Indeed, then
$d_xa_i$
is integral. Indeed, then
![]() $f^{*} (d_xD)$
is an integral divisor on a regular surface, and thus,
$f^{*} (d_xD)$
is an integral divisor on a regular surface, and thus,
![]() $f^{*} (d_xD)$
is Cartier. If we write
$f^{*} (d_xD)$
is Cartier. If we write
![]() $K_Y+\Delta _Y=f^*(K_X+\Delta )$
, then
$K_Y+\Delta _Y=f^*(K_X+\Delta )$
, then
![]() $\Delta _Y$
is effective by the negativity lemma and
$\Delta _Y$
is effective by the negativity lemma and
![]() $(Y,\Delta _Y)$
is klt. As
$(Y,\Delta _Y)$
is klt. As
![]() $f^*(d_xD)-(K_Y+\Delta _Y)$
is f-nef and big, and
$f^*(d_xD)-(K_Y+\Delta _Y)$
is f-nef and big, and
![]() $f^*(d_xD)$
is f-trivial, there exists
$f^*(d_xD)$
is f-trivial, there exists
![]() $b_0>0$
such that for all
$b_0>0$
such that for all
![]() $b \geq b_0$
, we have that
$b \geq b_0$
, we have that
![]() $bf^*(d_xD)=f^*A_{b}$
for a Cartier divisor
$bf^*(d_xD)=f^*A_{b}$
for a Cartier divisor
![]() $A_b$
on X by the base point free theorem for excellent surfaces [Reference TanakaTan18b, Theorem 4.4]. Then
$A_b$
on X by the base point free theorem for excellent surfaces [Reference TanakaTan18b, Theorem 4.4]. Then
![]() $f^*(d_xD)=(b_0+1)f^*d_xD-b_0f^*d_xD=f^*(A_{b_0+1}-A_{b_0})$
, and thus,
$f^*(d_xD)=(b_0+1)f^*d_xD-b_0f^*d_xD=f^*(A_{b_0+1}-A_{b_0})$
, and thus,
![]() $d_xD$
is Cartier.
$d_xD$
is Cartier.
We denote by
![]() $(a_i)$
(resp.
$(a_i)$
(resp.
![]() $f_*^{-1} D \cdot E_j$
) the vector
$f_*^{-1} D \cdot E_j$
) the vector
![]() $(a_1, \dots , a_n)$
(resp.
$(a_1, \dots , a_n)$
(resp.
![]() $(f_*^{-1} D \cdot E_1, \dots , f_*^{-1} D \cdot E_n)$
). Given a closed point
$(f_*^{-1} D \cdot E_1, \dots , f_*^{-1} D \cdot E_n)$
). Given a closed point
![]() $x \in X$
, we denote by
$x \in X$
, we denote by
![]() $k(x)$
the residue field of X at x. By the projection formula,
$k(x)$
the residue field of X at x. By the projection formula,
where A is a matrix with integer coefficients. We have
![]() $(-f_*^{-1} D \cdot E_j) = \sum _j m_j [k(y_j):k]$
for some
$(-f_*^{-1} D \cdot E_j) = \sum _j m_j [k(y_j):k]$
for some
![]() $m_j \in \mathbb {Z}$
, where the
$m_j \in \mathbb {Z}$
, where the
![]() $y_j$
are the intersection points of
$y_j$
are the intersection points of
![]() $f_*^{-1}D$
with
$f_*^{-1}D$
with
![]() $E_j$
. As
$E_j$
. As
![]() $k(x) \subset k(y_j)$
, we conclude that
$k(x) \subset k(y_j)$
, we conclude that
![]() $[k(x):k]$
divides
$[k(x):k]$
divides
![]() $(f_*^{-1} D \cdot E_j)$
, thus showing
$(f_*^{-1} D \cdot E_j)$
, thus showing
![]() $d_x a_i$
is an integer.
$d_x a_i$
is an integer.
We bound the volume of canonical del Pezzo surfaces, generalising the regular case proven in [Reference TanakaTan24, Theorem 4.7].
Definition 3.2 [Reference TanakaTan21, Definition 5.1, Definition 7.4]
Let X be a normal variety over k such that k is algebraically closed in
![]() $K(X)$
. We define the Frobenius length of geometric non-normality
$K(X)$
. We define the Frobenius length of geometric non-normality
![]() $\ell _F(X/k)$
as
$\ell _F(X/k)$
as
Set R to be the local ring of
![]() $X \times _k k^{1/p^{\infty }}$
at the generic point. We define the thickening exponent
$X \times _k k^{1/p^{\infty }}$
at the generic point. We define the thickening exponent
![]() $\epsilon (X/k)$
as the non-negative integer such that
$\epsilon (X/k)$
as the non-negative integer such that
![]() $ {\mathrm {length}}_R R = p^{\epsilon (X/k)}$
$ {\mathrm {length}}_R R = p^{\epsilon (X/k)}$
For a discussion of the properties of
![]() $\ell _F(X/k)$
and
$\ell _F(X/k)$
and
![]() $\epsilon (X/k)$
, we refer the reader to [Reference TanakaTan21, Section 5, Section 7].
$\epsilon (X/k)$
, we refer the reader to [Reference TanakaTan21, Section 5, Section 7].
We fix some notation. For
![]() $d \geq 1$
, we denote the Hirzebruch surface
$d \geq 1$
, we denote the Hirzebruch surface
![]() $\mathbb {P}_{\mathbb {P}^1}(\mathcal {O}_{\mathbb {P}^1} \oplus \mathcal {O}_{\mathbb {P}^1}(-d))$
by
$\mathbb {P}_{\mathbb {P}^1}(\mathcal {O}_{\mathbb {P}^1} \oplus \mathcal {O}_{\mathbb {P}^1}(-d))$
by
![]() $\mathbb {F}_d$
, a closed rational fibre by F and the negative section by
$\mathbb {F}_d$
, a closed rational fibre by F and the negative section by
![]() $C_d$
. The contraction of
$C_d$
. The contraction of
![]() $C_d$
is the morphism
$C_d$
is the morphism
![]() $p \colon \mathbb {F}_d \to \mathbb {P}(1,1,d)$
, and we denote by
$p \colon \mathbb {F}_d \to \mathbb {P}(1,1,d)$
, and we denote by ![]() the generator of its class group. Recall that
the generator of its class group. Recall that
![]() $L \in |\mathcal {O}_{\mathbb {P}(1,1,d)}(1)|$
and that
$L \in |\mathcal {O}_{\mathbb {P}(1,1,d)}(1)|$
and that
![]() $L^2 =\frac {1}{d}$
.
$L^2 =\frac {1}{d}$
.
Lemma 3.3. The divisor class
![]() $nK_{\mathbb {P}(1,1,d)}$
is Cartier if and only if
$nK_{\mathbb {P}(1,1,d)}$
is Cartier if and only if
![]() $d \mid n(d+2).$
$d \mid n(d+2).$
Proof. As
![]() $K_{\mathbb {P}(1,1,d)} \sim (-d-2)L$
and the Cartier index of L is d, the lemma is immediate.
$K_{\mathbb {P}(1,1,d)} \sim (-d-2)L$
and the Cartier index of L is d, the lemma is immediate.
Proposition 3.4. Let X be a canonical del Pezzo surface. Then
-
1. if X is geometrically normal, then it is geometrically canonical and
 $K_X^2 \leq 9$
;
$K_X^2 \leq 9$
; -
2. if X is not geometrically normal, then
 $p\in \left \{2,3 \right \}$
and
$p\in \left \{2,3 \right \}$
and-
(a) if
 $p=3$
,
$p=3$
,
 $\ell _F(X/k)=1$
and
$\ell _F(X/k)=1$
and
 $K_X^2 \leq 12 \cdot 3^{\epsilon (X/k)}$
.
$K_X^2 \leq 12 \cdot 3^{\epsilon (X/k)}$
. -
(b) if
 $p=2$
,
$p=2$
,
 $\ell _F(X/k)\leq 2$
and
$\ell _F(X/k)\leq 2$
and
 $K_X^2 \leq 16 \cdot 2^{\epsilon (X/k)}$
.
$K_X^2 \leq 16 \cdot 2^{\epsilon (X/k)}$
.
-
Proof. We can assume k to be separably closed, and we will repeatedly use the fact that
![]() $\epsilon (X/k)$
is a k-birational invariant [Reference TanakaTan21, Proposition 7.10]. If X is geometrically normal, then we conclude by Proposition 2.11. So we suppose that X is not geometrically normal and
$\epsilon (X/k)$
is a k-birational invariant [Reference TanakaTan21, Proposition 7.10]. If X is geometrically normal, then we conclude by Proposition 2.11. So we suppose that X is not geometrically normal and
![]() $p =2,3$
by [Reference Bernasconi and TanakaBT22, Theorem 3.7.(1)]. The bounds on
$p =2,3$
by [Reference Bernasconi and TanakaBT22, Theorem 3.7.(1)]. The bounds on
![]() $\ell _F(X/k)$
are proven in [Reference Bernasconi and TanakaBT22, Theorem 3.7.(2)-(3)].
$\ell _F(X/k)$
are proven in [Reference Bernasconi and TanakaBT22, Theorem 3.7.(2)-(3)].
Let
![]() $Z \to X$
be the minimal resolution of X. As Z is a regular weak del Pezzo surface, by Lemma 2.14, a
$Z \to X$
be the minimal resolution of X. As Z is a regular weak del Pezzo surface, by Lemma 2.14, a
![]() $K_Z$
-MMP will end with a regular weak del Pezzo surface Y admitting a Mori fibre space
$K_Z$
-MMP will end with a regular weak del Pezzo surface Y admitting a Mori fibre space
![]() $f \colon Y \to B$
(i.e., f is a contraction where
$f \colon Y \to B$
(i.e., f is a contraction where
![]() $-K_Y$
is f-ample and
$-K_Y$
is f-ample and
![]() $\dim (B) \leq 1$
). Note that
$\dim (B) \leq 1$
). Note that
![]() $K_Y^2 \geq K_Z^2=K_X^2$
.
$K_Y^2 \geq K_Z^2=K_X^2$
.
If
![]() $B= {\mathrm {Spec}}(k)$
, then Y is a regular del Pezzo surface, and we conclude by [Reference TanakaTan24, Theorem 4.7]. If B is a curve, as Y is weak del Pezzo, the cone theorem [Reference TanakaTan18b, Theorem 2.14] implies that the Mori cone of Y is
$B= {\mathrm {Spec}}(k)$
, then Y is a regular del Pezzo surface, and we conclude by [Reference TanakaTan24, Theorem 4.7]. If B is a curve, as Y is weak del Pezzo, the cone theorem [Reference TanakaTan18b, Theorem 2.14] implies that the Mori cone of Y is
where F the class of a closed fibre of f and
![]() $\Gamma $
is the class of an integral curve with self-intersection
$\Gamma $
is the class of an integral curve with self-intersection
![]() $\Gamma ^2 \leq 0$
. If
$\Gamma ^2 \leq 0$
. If
![]() $K_Y \cdot _k \Gamma <0$
, then Y is a regular del Pezzo surface by Kleiman’s criterion, and we conclude again by [Reference TanakaTan24, Theorem 4.7].
$K_Y \cdot _k \Gamma <0$
, then Y is a regular del Pezzo surface by Kleiman’s criterion, and we conclude again by [Reference TanakaTan24, Theorem 4.7].
If
![]() $K_Y \cdot _k \Gamma =0$
, by the Hodge index theorem
$K_Y \cdot _k \Gamma =0$
, by the Hodge index theorem
![]() $\Gamma ^2<0$
and, if we denote
$\Gamma ^2<0$
and, if we denote
![]() $k_{\Gamma }=H^0(\Gamma , \mathcal {O}_{\Gamma })$
, by adjunction, the equality
$k_{\Gamma }=H^0(\Gamma , \mathcal {O}_{\Gamma })$
, by adjunction, the equality
![]() $\Gamma ^2=\deg _k \omega _{\Gamma /k}=-2[k_{\Gamma }:k]$
holds. Then there exists a birational contraction
$\Gamma ^2=\deg _k \omega _{\Gamma /k}=-2[k_{\Gamma }:k]$
holds. Then there exists a birational contraction
![]() $Y \to T$
where T is a canonical del Pezzo surface of Picard rank 1 with a unique singular point x and
$Y \to T$
where T is a canonical del Pezzo surface of Picard rank 1 with a unique singular point x and
![]() $K_T^2=K_Y^2$
. As
$K_T^2=K_Y^2$
. As
![]() $k_\Gamma =k(x)$
by [Reference KollárKol13, Corollary 10.10], we have
$k_\Gamma =k(x)$
by [Reference KollárKol13, Corollary 10.10], we have
![]() $\Gamma ^2=-2[k(x):k]$
, which implies that the Cartier index of T divides
$\Gamma ^2=-2[k(x):k]$
, which implies that the Cartier index of T divides
![]() $2$
by Lemma 3.1. If T is geometrically normal, it is geometrically canonical by [Reference Bernasconi and TanakaBT22, Theorem 3.7]. Moreover, as
$2$
by Lemma 3.1. If T is geometrically normal, it is geometrically canonical by [Reference Bernasconi and TanakaBT22, Theorem 3.7]. Moreover, as
![]() $T_{\overline {k}}$
has Picard rank 1 and a singular point, we conclude
$T_{\overline {k}}$
has Picard rank 1 and a singular point, we conclude
![]() $K_X^{2} \leq 8$
. If T is not geometrically normal and
$K_X^{2} \leq 8$
. If T is not geometrically normal and
![]() $g \colon V=(T \times _k \overline {k})_{ {\mathrm {red}}}^{ {\mathrm {norm}}} \to T$
is the normalised base change where
$g \colon V=(T \times _k \overline {k})_{ {\mathrm {red}}}^{ {\mathrm {norm}}} \to T$
is the normalised base change where
![]() $K_V+(p-1)C=g^*K_T$
, we deduce that
$K_V+(p-1)C=g^*K_T$
, we deduce that
![]() $2p^{\ell _F(T/k)} K_V$
is Cartier by [Reference TanakaTan21, Theorem 5.12]. By the classification of the normalised base changes of canonical del Pezzo surfaces with Picard rank 1 [Reference Patakfalvi and WaldronPW22, Theorem 4.1], the bounds on the Frobenius length [Reference Bernasconi and TanakaBT22, Theorem 3.7] and Lemma 3.3, we deduce the following:
$2p^{\ell _F(T/k)} K_V$
is Cartier by [Reference TanakaTan21, Theorem 5.12]. By the classification of the normalised base changes of canonical del Pezzo surfaces with Picard rank 1 [Reference Patakfalvi and WaldronPW22, Theorem 4.1], the bounds on the Frobenius length [Reference Bernasconi and TanakaBT22, Theorem 3.7] and Lemma 3.3, we deduce the following:
-
○ if
 $p=3$
, then
$p=3$
, then
 $6K_V$
is Cartier, and thus,
$6K_V$
is Cartier, and thus,
 $V \simeq \mathbb {P}(1,1,d)$
for
$V \simeq \mathbb {P}(1,1,d)$
for
 $d \in \left \{1, 2, 3, 4, 6, 12\right \}$
and
$d \in \left \{1, 2, 3, 4, 6, 12\right \}$
and
 $C =L$
;
$C =L$
; -
○ if
 $p=2$
, then
$p=2$
, then
 $8K_V$
is Cartier, and thus,
$8K_V$
is Cartier, and thus,
 $V \simeq \mathbb {P}(1,1,d)$
for
$V \simeq \mathbb {P}(1,1,d)$
for
 $d \in \left \{1, 2, 4, 8, 16\right \}$
and
$d \in \left \{1, 2, 4, 8, 16\right \}$
and
 $C=L$
or
$C=L$
or
 $2L$
by [Reference TanakaTan24, Proposition 4.1].
$2L$
by [Reference TanakaTan24, Proposition 4.1].
Using [Reference TanakaTan24, Lemma 4.5], we have
If
![]() $p=3$
, we have
$p=3$
, we have
![]() $V=\mathbb {P}(1,1,d)$
,
$V=\mathbb {P}(1,1,d)$
,
![]() $C=L$
, and thus,
$C=L$
, and thus,
![]() $K_T^2 \leq (dL)^2 \cdot 3^{\epsilon (X/k)}= d \cdot 3^{\epsilon (X/k)} \leq 12 \cdot 3^{\epsilon (X/k)} $
. Similarly, in the case where
$K_T^2 \leq (dL)^2 \cdot 3^{\epsilon (X/k)}= d \cdot 3^{\epsilon (X/k)} \leq 12 \cdot 3^{\epsilon (X/k)} $
. Similarly, in the case where
![]() $p=2$
, we obtain that
$p=2$
, we obtain that
![]() $K_T^2 \leq 16 \cdot 2^{\epsilon (X/k)}$
.
$K_T^2 \leq 16 \cdot 2^{\epsilon (X/k)}$
.
Using the bounds on the anticanonical volume, we can restrict the possibilities for the normalised base changes of non-normal canonical del Pezzo surfaces obtained in [Reference Patakfalvi and WaldronPW22, Theorem 4.1]. For the analogous result in the regular case, see [Reference TanakaTan24, Theorem 4.6].
Theorem 3.5. Let X be a canonical del Pezzo surface. Let
![]() $\nu \colon Y \to (X \times _k \overline k)_{ {\mathrm {red}}}$
be the normalisation morphism and let
$\nu \colon Y \to (X \times _k \overline k)_{ {\mathrm {red}}}$
be the normalisation morphism and let
![]() $f \colon Y \to X \times _k \overline k $
be the composite morphism.
$f \colon Y \to X \times _k \overline k $
be the composite morphism.
-
1. If X is geometrically normal, then it is geometrically canonical.
-
2. If
 $p \geq 5$
, then X is geometrically normal.
$p \geq 5$
, then X is geometrically normal. -
3. If
 $p=3$
and X is not geometrically normal, then
$p=3$
and X is not geometrically normal, then
 $\ell _{F}(X/k) = 1$
and
$\ell _{F}(X/k) = 1$
and
 $(Y, C)$
is isomorphic to
$(Y, C)$
is isomorphic to
 $(\mathbb {P}(1,1,d), L)$
for some
$(\mathbb {P}(1,1,d), L)$
for some
 $d \leq 12$
.
$d \leq 12$
. -
4. If
 $p=2$
and X is not geometrically normal, then
$p=2$
and X is not geometrically normal, then
 $\ell _{F}(X/k) \in \left \{1,2\right \}$
and
$\ell _{F}(X/k) \in \left \{1,2\right \}$
and
 $(Y,C)$
is isomorphic to one of the following:
$(Y,C)$
is isomorphic to one of the following:-
(a)
 $(\mathbb {P}^2,L)$
and
$(\mathbb {P}^2,L)$
and
 $\ell _F(X/k)=1$
;
$\ell _F(X/k)=1$
; -
(b)
 $(\mathbb {P}^2, C \in |2L|)$
;
$(\mathbb {P}^2, C \in |2L|)$
; -
(c)
 $(\mathbb {P}(1,1,d),2L)$
for
$(\mathbb {P}(1,1,d),2L)$
for
 $2 \leq d \leq 16$
.
$2 \leq d \leq 16$
. -
(d)
 $(\mathbb {P}^1 \times \mathbb {P}^1, C \in |F_1+F_2|)$
and
$(\mathbb {P}^1 \times \mathbb {P}^1, C \in |F_1+F_2|)$
and
 $\ell _F(X/k)=1$
;
$\ell _F(X/k)=1$
; -
(e)
 $(\mathbb {P}^1 \times \mathbb {P}^1, F_i)$
and
$(\mathbb {P}^1 \times \mathbb {P}^1, F_i)$
and
 $\ell _F(X/k)=1$
;
$\ell _F(X/k)=1$
; -
(f)
 $(\mathbb {F}_d, D \in |C_d+F|)$
, where
$(\mathbb {F}_d, D \in |C_d+F|)$
, where
 $C_d$
is the negative section and
$C_d$
is the negative section and
 $\ell _F(X/k)=1$
for
$\ell _F(X/k)=1$
for
 $1 \leq d \leq 14$
;
$1 \leq d \leq 14$
; -
(g)
 $(\mathbb {F}_d, C_d)$
and
$(\mathbb {F}_d, C_d)$
and
 $\ell _F(X/k)=1$
for
$\ell _F(X/k)=1$
for
 $1 \leq d \leq 12$
;
$1 \leq d \leq 12$
;
-
Proof. By Proposition 3.4, we are only left to prove the classification in (3) and (4). Suppose
![]() $p=3$
. The only possible normalised base change is
$p=3$
. The only possible normalised base change is
![]() $\mathbb {P}(1,1,d)$
by [Reference TanakaTan24, Proposition 4.1 and Remark 4.3]. However, by Proposition 3.4, we have
$\mathbb {P}(1,1,d)$
by [Reference TanakaTan24, Proposition 4.1 and Remark 4.3]. However, by Proposition 3.4, we have
![]() $K_X^2=p^{\epsilon (X/k)} d \leq 12 \cdot p^{\epsilon (X/k)} $
.
$K_X^2=p^{\epsilon (X/k)} d \leq 12 \cdot p^{\epsilon (X/k)} $
.
Suppose
![]() $p=2$
. The list of possibilities without the bounds on d is proved in [Reference TanakaTan24, Proposition 4.1]. It is now sufficient to note that in Case (4f),
$p=2$
. The list of possibilities without the bounds on d is proved in [Reference TanakaTan24, Proposition 4.1]. It is now sufficient to note that in Case (4f),
![]() $K_X^2=p^{\epsilon (X/k)}(d+2)$
; in Case (4g),
$K_X^2=p^{\epsilon (X/k)}(d+2)$
; in Case (4g),
![]() $K_X^2=p^{\epsilon (X/k)}(d+4)$
; and in Case (4c),
$K_X^2=p^{\epsilon (X/k)}(d+4)$
; and in Case (4c),
![]() $K_X^2=p^{\epsilon (X/k)}d$
. Using Proposition 3.4, we deduce the desired bounds on d.
$K_X^2=p^{\epsilon (X/k)}d$
. Using Proposition 3.4, we deduce the desired bounds on d.
3.2. Effective Kodaira vanishing and very ampleness on del Pezzo surfaces
In this section, we prove an effective version of the Kawamata–Viehweg vanishing theorem on canonical del Pezzo surfaces. From this, we deduce bounds on the effective global generation and very ampleness for the anti-pluricanonical linear systems.
We start by giving an effective version of [Reference Patakfalvi and WaldronPW22, Theorem 1.9] in the 2-dimensional case.
Proposition 3.6. Let X be a canonical del Pezzo surface and let A be a big and nef Cartier divisor on X. Then
-
1. if
 $p>3$
, then
$p>3$
, then
 $H^1(X, \mathcal {O}_X(-A))=0$
;
$H^1(X, \mathcal {O}_X(-A))=0$
; -
2. if
 $p=3$
, then
$p=3$
, then
 $H^1(X, \mathcal {O}_X(-dA))=0$
if
$H^1(X, \mathcal {O}_X(-dA))=0$
if
 $d \geq 2$
;
$d \geq 2$
; -
3. if
 $p=2$
, then
$p=2$
, then
 $H^1(X, \mathcal {O}_X(-dA))=0$
if
$H^1(X, \mathcal {O}_X(-dA))=0$
if
 $d \geq 4$
.
$d \geq 4$
.
If X is a normal Gorenstein del Pezzo surface, the same results hold if A is ample.
Proof. We let
![]() $\mathcal {A}_m=\mathcal {O}_X(mA)$
for
$\mathcal {A}_m=\mathcal {O}_X(mA)$
for
![]() $m \in \mathbb {Z}$
. We fix
$m \in \mathbb {Z}$
. We fix
![]() $d>0$
. We show that
$d>0$
. We show that
![]() $H^1(X, \mathcal {A}_{-dn})=0$
for n sufficiently large. If A is ample, we conclude by Serre duality and Serre vanishing. If A is only big and nef and X is a canonical del Pezzo surface, by the base point free theorem [Reference BernasconiBer21b, Proposition 2.1], there is a birational contraction
$H^1(X, \mathcal {A}_{-dn})=0$
for n sufficiently large. If A is ample, we conclude by Serre duality and Serre vanishing. If A is only big and nef and X is a canonical del Pezzo surface, by the base point free theorem [Reference BernasconiBer21b, Proposition 2.1], there is a birational contraction
![]() $\pi \colon X \to Y$
such that
$\pi \colon X \to Y$
such that
![]() $A=\pi ^*H$
, where H is an ample Cartier divisor and by Lemma 2.14, Y is a del Pezzo surface with canonical singularities. Thus, the singularities of Y are rational by Proposition 2.6, and the projection formula implies
$A=\pi ^*H$
, where H is an ample Cartier divisor and by Lemma 2.14, Y is a del Pezzo surface with canonical singularities. Thus, the singularities of Y are rational by Proposition 2.6, and the projection formula implies
![]() $H^1(X, \mathcal {A}_{-dn})=H^1(Y, \mathcal {H}_{-dn})$
. As Y is a normal, we can apply Serre duality to deduce
$H^1(X, \mathcal {A}_{-dn})=H^1(Y, \mathcal {H}_{-dn})$
. As Y is a normal, we can apply Serre duality to deduce
![]() $H^1(Y, \mathcal {H}_{-dn}) \simeq H^1(Y, \omega _X \otimes \mathcal {H}_{dn})$
, which vanishes for n large enough by Serre vanishing.
$H^1(Y, \mathcal {H}_{-dn}) \simeq H^1(Y, \omega _X \otimes \mathcal {H}_{dn})$
, which vanishes for n large enough by Serre vanishing.
Suppose
![]() $H^1(X,\mathcal {A}_{-d}) \neq 0$
. Without loss of generality by the previous paragraph, we can assume
$H^1(X,\mathcal {A}_{-d}) \neq 0$
. Without loss of generality by the previous paragraph, we can assume
![]() $F^*\colon H^1(X,\mathcal {A}_{-d}) \to H^1(X,\mathcal {A}_{-pd})$
has a nontrivial element
$F^*\colon H^1(X,\mathcal {A}_{-d}) \to H^1(X,\mathcal {A}_{-pd})$
has a nontrivial element
![]() $\zeta $
in the kernel
$\zeta $
in the kernel
![]() $H^1_{ {\mathrm {fppf}}}(X, \alpha _{\mathcal {A}_{-d}})$
. By [Reference Patakfalvi and WaldronPW22, Theorem 2.11], associated to
$H^1_{ {\mathrm {fppf}}}(X, \alpha _{\mathcal {A}_{-d}})$
. By [Reference Patakfalvi and WaldronPW22, Theorem 2.11], associated to
![]() $\zeta $
there exists a degree p purely inseparable morphism
$\zeta $
there exists a degree p purely inseparable morphism
![]() $\pi \colon Z \to X$
such that Z is an integral Gorenstein surface with
$\pi \colon Z \to X$
such that Z is an integral Gorenstein surface with
![]() $\omega _Z=\pi ^*(\omega _X(-(p-1)dA))$
. Let
$\omega _Z=\pi ^*(\omega _X(-(p-1)dA))$
. Let
![]() $\nu \colon Z^{ {\mathrm {norm}}} \to Z$
be the normalisation and let
$\nu \colon Z^{ {\mathrm {norm}}} \to Z$
be the normalisation and let
![]() $\mu \colon Y:=(Z^{ {\mathrm {norm}}} \times _k \overline {k})_{ {\mathrm {red}}}^{ {\mathrm {norm}}} \to Z^{ {\mathrm {norm}}}$
be the normalised base change to the algebraic closure. We denote by
$\mu \colon Y:=(Z^{ {\mathrm {norm}}} \times _k \overline {k})_{ {\mathrm {red}}}^{ {\mathrm {norm}}} \to Z^{ {\mathrm {norm}}}$
be the normalised base change to the algebraic closure. We denote by
![]() $\Gamma $
the divisorial part of the ramification locus. We have
$\Gamma $
the divisorial part of the ramification locus. We have
![]() $\mathcal {O}_{Z^{ {\mathrm {norm}}}}(K_{Z^{ {\mathrm {norm}}}}+\Gamma )=\nu ^*(\omega _Z)$
, and there exists an effective Weil divisor
$\mathcal {O}_{Z^{ {\mathrm {norm}}}}(K_{Z^{ {\mathrm {norm}}}}+\Gamma )=\nu ^*(\omega _Z)$
, and there exists an effective Weil divisor
![]() $D \geq 0$
such that
$D \geq 0$
such that
![]() $K_Y+(p-1)D = \mu ^*K_{Z^{ {\mathrm {norm}}}}$
by [Reference Patakfalvi and WaldronPW22, Theorem 1.1], and we conclude
$K_Y+(p-1)D = \mu ^*K_{Z^{ {\mathrm {norm}}}}$
by [Reference Patakfalvi and WaldronPW22, Theorem 1.1], and we conclude
where
![]() $f =\pi \circ \nu \circ \mu $
. Consider a general curve C on Y of genus
$f =\pi \circ \nu \circ \mu $
. Consider a general curve C on Y of genus
![]() $g \geq 1$
so that C is contained in the smooth locus of Y and
$g \geq 1$
so that C is contained in the smooth locus of Y and
![]() $C \cdot ((p-1)D+\mu ^*\Gamma ) \geq 0$
. Therefore,
$C \cdot ((p-1)D+\mu ^*\Gamma ) \geq 0$
. Therefore,
![]() $K_Y \cdot C<0$
, and the bend and break lemma [Reference KollárKol96, Chapter II, Theorem 5.8] shows that for every point
$K_Y \cdot C<0$
, and the bend and break lemma [Reference KollárKol96, Chapter II, Theorem 5.8] shows that for every point
![]() $x \in C$
, there exists a rational curve
$x \in C$
, there exists a rational curve
![]() $L_x$
such that
$L_x$
such that
as
![]() $-(K_Y+(p-1)D+\mu ^*\Gamma )$
is big and nef. Since
$-(K_Y+(p-1)D+\mu ^*\Gamma )$
is big and nef. Since
![]() $-K_X$
is ample, we infer the inequality
$-K_X$
is ample, we infer the inequality
As
![]() $A=\pi ^*H$
where H is an ample Cartier divisor and x is a general point on C, we have
$A=\pi ^*H$
where H is an ample Cartier divisor and x is a general point on C, we have
![]() $f^*A \cdot L_x \geq 1$
, and thus, we have
$f^*A \cdot L_x \geq 1$
, and thus, we have
![]() $(p-1)d \leq 3$
, which concludes the proof.
$(p-1)d \leq 3$
, which concludes the proof.
Lemma 3.7. Let X be a canonical del Pezzo surface such that X is not geometrically normal. Let A be a big and nef Cartier divisor on X. Then
-
1. if
 $p=3$
, then
$p=3$
, then
 $\mathcal {O}_X(3A)$
is globally generated;
$\mathcal {O}_X(3A)$
is globally generated; -
2. if
 $p=2$
and
$p=2$
and
 $\ell _F(X/k)=1$
, then
$\ell _F(X/k)=1$
, then
 $\mathcal {O}_X(2A)$
is globally generated;
$\mathcal {O}_X(2A)$
is globally generated; -
3. if
 $p=2$
and
$p=2$
and
 $\ell _F(X/k)=2$
, then
$\ell _F(X/k)=2$
, then
 $\mathcal {O}_X(4A)$
is globally generated.
$\mathcal {O}_X(4A)$
is globally generated.
Proof. The proof is the same as [Reference TanakaTan24, Theorem 3.5]. There is a factorisation of the iterated Frobenius morphism by [Reference TanakaTan21, Theorem 5.9]:
where
![]() $(X \times _k \overline {k})_{ {\mathrm {red}}}^{ {\mathrm {norm}}}$
is a toric variety by Theorem 3.5. Thus,
$(X \times _k \overline {k})_{ {\mathrm {red}}}^{ {\mathrm {norm}}}$
is a toric variety by Theorem 3.5. Thus,
![]() $\mu ^*A$
is globally generated and also
$\mu ^*A$
is globally generated and also
![]() $(F^\ell _F(X/k)_{X \times _k \overline {k}})^*A=A^{p^{\ell _F(X/k)}}.$
$(F^\ell _F(X/k)_{X \times _k \overline {k}})^*A=A^{p^{\ell _F(X/k)}}.$
We recall the following very ampleness criterion for line bundles. For the notion of Castelnuovo–Mumford regularity and its basic properties, we refer to [Reference LazarsfeldLaz04, Section 1.8].
Proposition 3.8 [Reference TanakaTan21, Lemma 11.2]
Let X be a geometrically irreducible k-projective variety of dimension n. Let
![]() $\mathcal {A}$
be a globally generated ample line bundle and suppose
$\mathcal {A}$
be a globally generated ample line bundle and suppose
![]() $\mathcal {L}$
is an ample line bundle which is
$\mathcal {L}$
is an ample line bundle which is
![]() $0$
-regular with respect to
$0$
-regular with respect to
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
![]() $\mathcal {A} \otimes \mathcal {L}$
is very ample.
$\mathcal {A} \otimes \mathcal {L}$
is very ample.
The following is a generalisation of [Reference TanakaTan24, Theorem 3.5] including the case of canonical del Pezzo surfaces.
Proposition 3.9. Let X be a canonical del Pezzo surface such that X is not geometrically normal. Then
-
1. if
 $p = 3$
, then
$p = 3$
, then
 $\omega _X^{ -9}$
is very ample;
$\omega _X^{ -9}$
is very ample; -
2. if
 $p=2$
and
$p=2$
and
 $\ell _F(X/k)=1$
, then
$\ell _F(X/k)=1$
, then
 $\omega _X^{ -7}$
is very ample;
$\omega _X^{ -7}$
is very ample; -
3. if
 $p=2$
and
$p=2$
and
 $\ell _F(X/k)=2$
, then
$\ell _F(X/k)=2$
, then
 $\omega _X^{ -12}$
is very ample.
$\omega _X^{ -12}$
is very ample.
Proof. By Lemma 3.7 and Proposition 3.8, it is sufficient to verify that for
![]() $p=3$
(resp.
$p=3$
(resp.
![]() $p=2, \ell _F(X/k)\,{=}\,1$
and
$p=2, \ell _F(X/k)\,{=}\,1$
and
![]() $p=2, \ell _F(X/k)=2$
), the line bundle
$p=2, \ell _F(X/k)=2$
), the line bundle
![]() $\omega _X^{ -6}$
(resp.
$\omega _X^{ -6}$
(resp.
![]() $\omega _X^{ -5}$
and
$\omega _X^{ -5}$
and
![]() $\omega _X^{ -8}$
) is
$\omega _X^{ -8}$
) is
![]() $0$
-regular with respect to
$0$
-regular with respect to
![]() $\omega _X^{ -3}$
(resp.
$\omega _X^{ -3}$
(resp.
![]() $\omega _X^{ -2}$
and
$\omega _X^{ -2}$
and
![]() $\omega _X^{ -4}$
) to show the statement. We prove only the case
$\omega _X^{ -4}$
) to show the statement. We prove only the case
![]() $p=2$
and
$p=2$
and
![]() $\ell _F(X/k)=2$
, as the others are analogous. In this case,
$\ell _F(X/k)=2$
, as the others are analogous. In this case,
![]() $H^1(X, \omega _X^{ -8} \otimes \omega _X^{ 4})=H^1(X, \omega _X^{ -4})=H^1(X, \omega _X^{ 5})=0$
by Proposition 3.6 and
$H^1(X, \omega _X^{ -8} \otimes \omega _X^{ 4})=H^1(X, \omega _X^{ -4})=H^1(X, \omega _X^{ 5})=0$
by Proposition 3.6 and
![]() $H^2(X, \mathcal {O}_X)=H^0(X, \omega _X)=0$
.
$H^2(X, \mathcal {O}_X)=H^0(X, \omega _X)=0$
.
We now show the effective statements on very ampleness for the pluri-anticanonical systems.
Theorem 3.10. Let X be a canonical del Pezzo surface. Then
![]() $\omega _X^{ -12}$
is very ample.
$\omega _X^{ -12}$
is very ample.
Proof. If X is geometrically normal, then it is geometrically canonical by Proposition 2.11 and
![]() $\omega _X^{\otimes -6}$
is very ample by [Reference Bernasconi and TanakaBT22, Proposition 2.14]. If X is not geometrically normal, we apply Proposition 3.9.
$\omega _X^{\otimes -6}$
is very ample by [Reference Bernasconi and TanakaBT22, Proposition 2.14]. If X is not geometrically normal, we apply Proposition 3.9.
4. Bounds on the irregularity
In this section, we study geometrically integral geometrically non-normal Gorenstein del Pezzo surfaces X. The additional condition on geometric integrality allows to find additional constraints on the normalised base changes to the algebraic closure and the irregularity of X.
4.1. A bound on
 $\gamma (X/k)$
for geometrically integral varieties
$\gamma (X/k)$
for geometrically integral varieties
Given a geometrically integral normal variety X over k, we relate the
![]() $\delta $
-invariant measuring the singularities in codimension 1 of
$\delta $
-invariant measuring the singularities in codimension 1 of
![]() $X_{\overline {k}}$
with the capacity of denormalising extensions
$X_{\overline {k}}$
with the capacity of denormalising extensions
![]() $\gamma (X/k)$
introduced by Tanaka [Reference TanakaTan21, Section 4].
$\gamma (X/k)$
introduced by Tanaka [Reference TanakaTan21, Section 4].
Definition 4.1. For an integral k-variety X with normalization
![]() $\nu \colon Y \to X$
with ramification
$\nu \colon Y \to X$
with ramification
![]() $C \subseteq Y$
and conductor
$C \subseteq Y$
and conductor
![]() $D \subseteq X$
, we define the
$D \subseteq X$
, we define the
![]() $\delta $
-invariant of X over k as
$\delta $
-invariant of X over k as
where
![]() $\eta $
runs over all generic points of irreducible components of D.
$\eta $
runs over all generic points of irreducible components of D.
Proposition 4.2. Let X be a geometrically integral normal variety over a field k. Then
Proof. The inequality
![]() $\ell _F(X/k) \leq \gamma (X/k)$
is shown in [Reference TanakaTan21, Proposition 8.7], so we are left to show
$\ell _F(X/k) \leq \gamma (X/k)$
is shown in [Reference TanakaTan21, Proposition 8.7], so we are left to show
![]() $\gamma (X/k) \leq \delta (X_{\bar {k}}/\bar {k})$
. As the statement can be checked on an open covering of X, we can assume that the conductor D of
$\gamma (X/k) \leq \delta (X_{\bar {k}}/\bar {k})$
. As the statement can be checked on an open covering of X, we can assume that the conductor D of
![]() $X_{\bar {k}}$
is irreducible, with generic point
$X_{\bar {k}}$
is irreducible, with generic point
![]() $\eta $
.
$\eta $
.
By definition of
![]() $\gamma (X/k)$
[Reference TanakaTan21, Definition 4.1], we can find a sequence of purely inseparable field extensions
$\gamma (X/k)$
[Reference TanakaTan21, Definition 4.1], we can find a sequence of purely inseparable field extensions ![]() such that, if we inductively define
such that, if we inductively define
![]() $X_0 := X$
and
$X_0 := X$
and
![]() $X_i := (X_{i-1,k_i})^{ {\mathrm {norm}}}$
, then
$X_i := (X_{i-1,k_i})^{ {\mathrm {norm}}}$
, then
![]() $X_{i,{k_{i+1}}}$
is not normal and there is no longer sequence of fields with this property. In particular,
$X_{i,{k_{i+1}}}$
is not normal and there is no longer sequence of fields with this property. In particular,
![]() $X_{\gamma (X/k)}$
is geometrically normal, and the normalization
$X_{\gamma (X/k)}$
is geometrically normal, and the normalization
![]() $\nu : Y \to X_{\bar {k}}$
of
$\nu : Y \to X_{\bar {k}}$
of
![]() $X_{\bar {k}}$
factors as
$X_{\bar {k}}$
factors as
Note that each
![]() $X_{i,{\bar {k}}}$
has the property
$X_{i,{\bar {k}}}$
has the property
![]() $(S_2)$
, being the base change of a normal variety along a field extension.
$(S_2)$
, being the base change of a normal variety along a field extension.
Now, after localizing at
![]() $\eta $
, the factorization of
$\eta $
, the factorization of
![]() $\nu $
corresponds to an ascending chain of subrings
$\nu $
corresponds to an ascending chain of subrings ![]() Each inclusion
Each inclusion
![]() $\mathcal {O}_{X_{i-1,{\bar {k}}},\eta } \subseteq \mathcal {O}_{X_{i,{\bar {k}}},\eta }$
is strict: otherwise,
$\mathcal {O}_{X_{i-1,{\bar {k}}},\eta } \subseteq \mathcal {O}_{X_{i,{\bar {k}}},\eta }$
is strict: otherwise,
![]() $\nu _i$
would be an isomorphism in codimension
$\nu _i$
would be an isomorphism in codimension
![]() $1$
, and hence so would be
$1$
, and hence so would be
![]() $X_i \to X_{i-1,k_i}$
. Since
$X_i \to X_{i-1,k_i}$
. Since
![]() $X_i$
is normal and
$X_i$
is normal and
![]() $X_{i-1,k_i}$
has property
$X_{i-1,k_i}$
has property
![]() $(S_2)$
, this would imply that
$(S_2)$
, this would imply that
![]() $X_{i-1,k_i}$
is normal as well, contradicting our choice of
$X_{i-1,k_i}$
is normal as well, contradicting our choice of
![]() $k_i$
.
$k_i$
.
By definition, we have isomorphisms of
![]() $(\mathcal {O}_{X_{\bar k},\eta })$
-modules
$(\mathcal {O}_{X_{\bar k},\eta })$
-modules
Note that both sides are annihilated by the conductor ideal
![]() $\mathcal {C}_{\eta }$
; hence, this is also an isomorphism of
$\mathcal {C}_{\eta }$
; hence, this is also an isomorphism of
![]() $(\mathcal {O}_{D,\eta })$
-modules. Therefore, by strictness of
$(\mathcal {O}_{D,\eta })$
-modules. Therefore, by strictness of
![]() $\mathcal {O}_{X_{i-1,{\bar {k}}},\eta } \subseteq \mathcal {O}_{X_{i,{\bar {k}}},\eta }$
for every
$\mathcal {O}_{X_{i-1,{\bar {k}}},\eta } \subseteq \mathcal {O}_{X_{i,{\bar {k}}},\eta }$
for every
![]() $i \leq \gamma (X/k)$
, we have
$i \leq \gamma (X/k)$
, we have
as claimed.
Proposition 4.3. Let X be a geometrically integral normal Gorenstein variety. Then,
![]() $\ell _F(X/k) \leq \gamma (X/k) \leq \delta (X_{\bar {k}}/{\bar k}) = \max _{\eta \in D} \mathrm {length}_{\mathcal {O}_{D,\eta }}(\mathcal {O}_{D, \eta })$
. In particular, if every component of D is reduced, then
$\ell _F(X/k) \leq \gamma (X/k) \leq \delta (X_{\bar {k}}/{\bar k}) = \max _{\eta \in D} \mathrm {length}_{\mathcal {O}_{D,\eta }}(\mathcal {O}_{D, \eta })$
. In particular, if every component of D is reduced, then
![]() $\ell _F(X/k) \leq 1.$
$\ell _F(X/k) \leq 1.$
Proof. By Proposition 4.2, we only have to show the last equality. Let
![]() $\eta $
be the generic point of an irreducible component of the conductor
$\eta $
be the generic point of an irreducible component of the conductor
![]() $D \subset X$
. The Gorenstein condition implies
$D \subset X$
. The Gorenstein condition implies
![]() $ {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{C, \eta }}=2 {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{D, \eta }}$
by [Reference Fanelli and SchröerFS20, Proposition A.2], which shows that
$ {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{C, \eta }}=2 {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{D, \eta }}$
by [Reference Fanelli and SchröerFS20, Proposition A.2], which shows that
![]() $\delta (X_{\overline {k}}/\overline {k})= \max _{\eta \in D} {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{D, \eta }}$
by [Sta, Tag 00IV], as claimed.
$\delta (X_{\overline {k}}/\overline {k})= \max _{\eta \in D} {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{D, \eta }}$
by [Sta, Tag 00IV], as claimed.
The last statement is immediate as
![]() $ {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{D, \eta }}=1$
if D is reduced.
$ {\mathrm {length}}_{\mathcal {O}_{D,\eta }}{\mathcal {O}_{D, \eta }}=1$
if D is reduced.
We can improve the bounds of [Reference Bernasconi and TanakaBT22] in the geometrically integral case.
Corollary 4.4. Let X be a geometrically integral normal Gorenstein del Pezzo surface. Then
![]() ${\ell _F(X/k) \leq 1.}$
Moreover, if L is a torsion line bundle, then
${\ell _F(X/k) \leq 1.}$
Moreover, if L is a torsion line bundle, then
![]() $L^{\otimes p} \cong \mathcal {O}_X$
. In particular,
$L^{\otimes p} \cong \mathcal {O}_X$
. In particular,
![]() $ {\mathrm {Pic}}^0_{X_{\bar {k}}/\bar {k}} \cong \mathbb {G}_{a,\bar {k}}^{h^1(X,\mathcal {O}_X)}$
.
$ {\mathrm {Pic}}^0_{X_{\bar {k}}/\bar {k}} \cong \mathbb {G}_{a,\bar {k}}^{h^1(X,\mathcal {O}_X)}$
.
Proof. By Theorem 2.13, the conductor D is reduced, and thus, we can apply Proposition 4.3 to conclude. The proof of the assertion on torsion line bundles follows as in [Reference Bernasconi and TanakaBT22, Theorem 4.1]. For the last statement, by Proposition 2.16, the Picard scheme
![]() $ {\mathrm {Pic}}^0_{X_{\bar {k}}/\bar {k}}$
is a smooth commutative unipotent algebraic group of dimension
$ {\mathrm {Pic}}^0_{X_{\bar {k}}/\bar {k}}$
is a smooth commutative unipotent algebraic group of dimension
![]() $h^1(X,\mathcal {O}_X)$
. As it is annihilated by p, we conclude by [Reference SerreSer88, Proposition VII.11].
$h^1(X,\mathcal {O}_X)$
. As it is annihilated by p, we conclude by [Reference SerreSer88, Proposition VII.11].
The previous analysis allows to obtain better estimates for the global generation than Proposition 3.9 in the geometrically integral canonical case.
Corollary 4.5. Let X be a geometrically integral canonical del Pezzo surface. Let A be a big and nef Cartier divisor on X and suppose X is not geometrically normal. Then
![]() $p \in \{2,3\}$
and the following hold:
$p \in \{2,3\}$
and the following hold:
-
1. If
 $p=3$
, then
$p=3$
, then
 $\mathcal {O}_X(3A)$
is globally generated and
$\mathcal {O}_X(3A)$
is globally generated and
 $\omega _X^{- 9}$
is very ample;
$\omega _X^{- 9}$
is very ample; -
2. If
 $p=2$
, then
$p=2$
, then
 $\mathcal {O}_X(2A)$
is globally generated and
$\mathcal {O}_X(2A)$
is globally generated and
 $\omega _X^{- 7}$
is very ample.
$\omega _X^{- 7}$
is very ample.
4.2. Anti-pluricanonical maps of non-normal del Pezzo surfaces
In this section, we assume k is algebraically closed. Let X be a non-normal integral Gorenstein del Pezzo surface with normalization
![]() $\nu \colon Y \to X$
with ramification
$\nu \colon Y \to X$
with ramification
![]() $C \subseteq Y$
and conductor
$C \subseteq Y$
and conductor
![]() $D \subseteq X$
. As Gorenstein del Pezzo surfaces have the property
$D \subseteq X$
. As Gorenstein del Pezzo surfaces have the property
![]() $(S_2)$
, by [Reference ReidRei94, Theorem, Section 2.6], there is an exact sequence
$(S_2)$
, by [Reference ReidRei94, Theorem, Section 2.6], there is an exact sequence
where
![]() $ {\mathrm {Res}}$
is the pushforward of the classical residue map
$ {\mathrm {Res}}$
is the pushforward of the classical residue map
![]() $\omega _Y(C) \to \omega _C$
(where we identify
$\omega _Y(C) \to \omega _C$
(where we identify
![]() $\omega _Y(C) \cong \nu ^* \omega _X$
and
$\omega _Y(C) \cong \nu ^* \omega _X$
and
![]() $\omega _Y(C)|_{C} \cong \omega _C$
by adjunction). The homomorphism
$\omega _Y(C)|_{C} \cong \omega _C$
by adjunction). The homomorphism
![]() $ {\mathrm {Tr}}$
is the trace map which, over the generic point
$ {\mathrm {Tr}}$
is the trace map which, over the generic point
![]() $\eta $
of D, is given by the
$\eta $
of D, is given by the
![]() $(\mathcal {O}_{D,\eta })$
-dual of the inclusion
$(\mathcal {O}_{D,\eta })$
-dual of the inclusion
![]() $\mathcal {O}_{D,\eta } \subseteq \nu _* \mathcal {O}_{C,\eta }$
by [Reference ReidRei94, Remark 2.9]. Tensoring with
$\mathcal {O}_{D,\eta } \subseteq \nu _* \mathcal {O}_{C,\eta }$
by [Reference ReidRei94, Remark 2.9]. Tensoring with
![]() $\omega _X^{-(n+1)}$
and applying the projection formula, we obtain
$\omega _X^{-(n+1)}$
and applying the projection formula, we obtain
As
![]() $\nu _* \nu ^* \omega _X^{-\otimes n}$
is canonically isomorphic to
$\nu _* \nu ^* \omega _X^{-\otimes n}$
is canonically isomorphic to
![]() $\nu _*(\omega _Y^{-\otimes n}(-nC))$
, taking global sections, we deduce the following:
$\nu _*(\omega _Y^{-\otimes n}(-nC))$
, taking global sections, we deduce the following:
Lemma 4.6. We have the following equality of subspaces of
![]() $H^0(Y,\omega _Y^{- n}(-nC))$
:
$H^0(Y,\omega _Y^{- n}(-nC))$
:
We now prove a useful lower bound on the dimension of the space of anti-pluricanonical sections on del Pezzo surfaces. It will be the main tool to bound the irregularity of del Pezzo surfaces.
Corollary 4.7. There is an inclusion of k-vector spaces:
Thus, if
![]() $\omega _X^{- n}$
is globally generated, then
$\omega _X^{- n}$
is globally generated, then
Proof. By the natural identifiation
![]() $\omega _Y(C)|_C \cong \omega _C$
given by adjunction, the space V is equal to the kernel of the homomorphism
$\omega _Y(C)|_C \cong \omega _C$
given by adjunction, the space V is equal to the kernel of the homomorphism
![]() $H^0( {\mathrm {Res}} \otimes \omega _X^{-n-1})$
; hence, it is contained in the kernel of
$H^0( {\mathrm {Res}} \otimes \omega _X^{-n-1})$
; hence, it is contained in the kernel of
![]() $H^0(( {\mathrm {Tr}} \circ {\mathrm {Res}}) \otimes \omega _X^{-n-1}) = \nu ^* H^0(X,\omega _X^{-n})$
by Lemma 4.6.
$H^0(( {\mathrm {Tr}} \circ {\mathrm {Res}}) \otimes \omega _X^{-n-1}) = \nu ^* H^0(X,\omega _X^{-n})$
by Lemma 4.6.
If
![]() $\omega _{X}^{-n}$
is globally generated, then the linear system
$\omega _{X}^{-n}$
is globally generated, then the linear system
![]() $|\nu ^* H^0(X,\omega _X^{-n})|$
has no base points on C. Since all sections in V vanish on C and
$|\nu ^* H^0(X,\omega _X^{-n})|$
has no base points on C. Since all sections in V vanish on C and
![]() $\omega _X^{-1}$
is ample, there are at least two more linearly independent sections of
$\omega _X^{-1}$
is ample, there are at least two more linearly independent sections of
![]() $\nu ^* H^0(X,\omega _X^{-n})$
that are nonzero when restricted to C, thus concluding the inequality.
$\nu ^* H^0(X,\omega _X^{-n})$
that are nonzero when restricted to C, thus concluding the inequality.
4.3. Irregularity of geometrically integral l.c.i. del Pezzo surfaces
We prove effective bounds on the values of the irregularity of locally complete intersection (lci) del Pezzo surfaces.
Proposition 4.8. Let X be a geometrically integral normal locally complete intersection del Pezzo surface over a field k of characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $\nu \colon Y \to X_{\bar {k}}$
be the normalization of
$\nu \colon Y \to X_{\bar {k}}$
be the normalization of
![]() $X_{\bar {k}}$
and let
$X_{\bar {k}}$
and let
![]() $C \subseteq Y$
be the ramification of
$C \subseteq Y$
be the ramification of
![]() $\nu $
. Then, one of the following holds:
$\nu $
. Then, one of the following holds:
-
1.
 $h^1(X,\omega _X^{ n}) = 0$
for all
$h^1(X,\omega _X^{ n}) = 0$
for all
 $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
. -
2.
 $p = 3$
,
$p = 3$
,
 $(Y,C) = (\mathbb {P}^2,2L)$
,
$(Y,C) = (\mathbb {P}^2,2L)$
,
 $h^1(X,\mathcal {O}_X) = 2$
, and
$h^1(X,\mathcal {O}_X) = 2$
, and
 $h^1(X,\omega _X^{ n}) = 0$
for all
$h^1(X,\omega _X^{ n}) = 0$
for all
 $n \geq 2$
.
$n \geq 2$
. -
3.
 $p = 2$
,
$p = 2$
,
 $(Y,C) = (\mathbb {P}^2,2L)$
,
$(Y,C) = (\mathbb {P}^2,2L)$
,
 $h^1(X,\mathcal {O}_X) = 1$
, and
$h^1(X,\mathcal {O}_X) = 1$
, and
 $h^1(X,\omega _X^{ n}) = 0$
for all
$h^1(X,\omega _X^{ n}) = 0$
for all
 $n \geq 2$
.
$n \geq 2$
. -
4.
 $p = 2$
,
$p = 2$
,
 $(Y,C) = (\mathbb {P}(1,1,2),2L)$
,
$(Y,C) = (\mathbb {P}(1,1,2),2L)$
,
 $h^1(X,\mathcal {O}_X) = 1$
, and
$h^1(X,\mathcal {O}_X) = 1$
, and
 $h^1(X,\omega _X^{ n}) = 0$
for all
$h^1(X,\omega _X^{ n}) = 0$
for all
 $n \geq 2$
.
$n \geq 2$
.
Proof. If X is geometrically normal, then X is geometrically canonical by Proposition 2.11. By Serre duality, it is sufficient to show that
![]() $h^1(X_{\overline {k}}, \omega _{X_{\overline {k}}}^{\otimes n})=0$
for
$h^1(X_{\overline {k}}, \omega _{X_{\overline {k}}}^{\otimes n})=0$
for
![]() $n> 0$
. This follows from [Reference BernasconiBer21a, Theorem 5.6.a]. If X is not geometrically normal and the ramification divisor contains a reduced component, then
$n> 0$
. This follows from [Reference BernasconiBer21a, Theorem 5.6.a]. If X is not geometrically normal and the ramification divisor contains a reduced component, then
![]() $X_{\overline {k}}$
is tame and
$X_{\overline {k}}$
is tame and
![]() $h^1(X,\omega _X^{\otimes n}) = 0$
for all
$h^1(X,\omega _X^{\otimes n}) = 0$
for all
![]() $n \in \mathbb {Z}$
by [Reference ReidRei94, Corollary 4.10]. Therefore, by [Reference Patakfalvi and WaldronPW22, Theorem 4.1], we may assume that
$n \in \mathbb {Z}$
by [Reference ReidRei94, Corollary 4.10]. Therefore, by [Reference Patakfalvi and WaldronPW22, Theorem 4.1], we may assume that
![]() $p \in \{2,3\}$
,
$p \in \{2,3\}$
,
![]() $h^1(X,\mathcal {O}_X)> 0$
and
$h^1(X,\mathcal {O}_X)> 0$
and
![]() $(Y,C) = (\mathbb {P}(1,1,d),2L)$
for some
$(Y,C) = (\mathbb {P}(1,1,d),2L)$
for some
![]() $d \geq 1$
where L is a line through the vertex of the cone.
$d \geq 1$
where L is a line through the vertex of the cone.
Choose weighted coordinates
![]() $x,y,z$
of degree
$x,y,z$
of degree
![]() $1,1,d$
on Y such that
$1,1,d$
on Y such that
![]() $L=\left \{x = 0 \right \}$
, hence
$L=\left \{x = 0 \right \}$
, hence
![]() ${2L=\left \{x^2=0 \right \}}$
in weighted coordinates. Let
${2L=\left \{x^2=0 \right \}}$
in weighted coordinates. Let
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $V_{n,d} \subseteq H^0(\mathbb {P}(1,1,d),\mathcal {O}(nd))$
be the subspace of sections vanishing along
$V_{n,d} \subseteq H^0(\mathbb {P}(1,1,d),\mathcal {O}(nd))$
be the subspace of sections vanishing along
![]() $2L$
. Then,
$2L$
. Then,
![]() $V_{n,d}$
consists of weighted homogeneous polynomials of the form
$V_{n,d}$
consists of weighted homogeneous polynomials of the form
![]() $x^2f_{nd-2}(x,y,z)$
; hence,
$x^2f_{nd-2}(x,y,z)$
; hence,
![]() $\dim V_{n,d} = \sum _{j=1}^{n} (jd - 1) = \frac {n^2 + n}{2}d - n.$
As
$\dim V_{n,d} = \sum _{j=1}^{n} (jd - 1) = \frac {n^2 + n}{2}d - n.$
As
![]() $\nu ^* \omega _{X_{\bar {k}}} \cong \mathcal {O}(-dL)$
, we have
$\nu ^* \omega _{X_{\bar {k}}} \cong \mathcal {O}(-dL)$
, we have
![]() $\nu ^* \omega _{X_{\bar {k}}}^{-n} \cong \mathcal {O}(ndL)$
. By Corollary 4.7, we have
$\nu ^* \omega _{X_{\bar {k}}}^{-n} \cong \mathcal {O}(ndL)$
. By Corollary 4.7, we have
 $$ \begin{align} h^0(X,\omega_X^{- n}) \geq \begin{cases} \frac{n^2 + n}{2}d - n. \\ \frac{n^2 + n}{2}d - n+2 \text{ if, additionally}, \omega_X^{-n} \text{ is globally generated.} \end{cases} \end{align} $$
$$ \begin{align} h^0(X,\omega_X^{- n}) \geq \begin{cases} \frac{n^2 + n}{2}d - n. \\ \frac{n^2 + n}{2}d - n+2 \text{ if, additionally}, \omega_X^{-n} \text{ is globally generated.} \end{cases} \end{align} $$
By the Riemann–Roch formula [Reference TanakaTan18b, Theorem 2.10], we have
Thus, if we assume
![]() $h^1(X, \omega _X^{- n})=0$
, we deduce from Equation (4.1) that
$h^1(X, \omega _X^{- n})=0$
, we deduce from Equation (4.1) that
 $$ \begin{align} h^1(X,\mathcal{O}_X) = 1 - h^0(X,\omega_X^{- n}) + \frac{n^2 + n}{2}d \leq \begin{cases} n + 1 \\ n - 1 \text{ if, additionally}, \omega_X^{- n} \text{is g.g. } \end{cases} \end{align} $$
$$ \begin{align} h^1(X,\mathcal{O}_X) = 1 - h^0(X,\omega_X^{- n}) + \frac{n^2 + n}{2}d \leq \begin{cases} n + 1 \\ n - 1 \text{ if, additionally}, \omega_X^{- n} \text{is g.g. } \end{cases} \end{align} $$
We also recall Maddock’s bound [Reference MaddockMad16, Corollary 1.2.6]: if
![]() $h^1(X,\omega _X^{ n}) \neq 0$
but
$h^1(X,\omega _X^{ n}) \neq 0$
but
![]() $h^1(X,\omega _X^{pn}) = 0$
, then
$h^1(X,\omega _X^{pn}) = 0$
, then
Now assume
![]() $p = 3$
. By Serre vanishing and
$p = 3$
. By Serre vanishing and
![]() $h^1(\mathcal {O}_X) \neq 0$
, there exists a largest
$h^1(\mathcal {O}_X) \neq 0$
, there exists a largest
![]() $N \geq 0$
such that
$N \geq 0$
such that
![]() $h^1(X,\omega _X^{- N}) = h^1(X,\omega _X^{ (N + 1)}) \neq 0$
. By (4.2) and (4.3), we have the following chain:
$h^1(X,\omega _X^{- N}) = h^1(X,\omega _X^{ (N + 1)}) \neq 0$
. By (4.2) and (4.3), we have the following chain:
Hence,
![]() $N = 0$
,
$N = 0$
,
![]() $d = 1$
, showing
$d = 1$
, showing
![]() $h^1(X, \mathcal {O}_X) \leq 2$
. Finally,
$h^1(X, \mathcal {O}_X) \leq 2$
. Finally,
![]() $h^1(X,\mathcal {O}_X) = 2$
by Theorem 2.13.
$h^1(X,\mathcal {O}_X) = 2$
by Theorem 2.13.
Now assume
![]() $p = 2$
. Then, the argument of the previous paragraph yields
$p = 2$
. Then, the argument of the previous paragraph yields
Hence,
![]() $N \leq 3$
. Therefore,
$N \leq 3$
. Therefore,
![]() $h^1(X,\omega _X^{- 4}) = 0$
, and, by Corollary 4.5,
$h^1(X,\omega _X^{- 4}) = 0$
, and, by Corollary 4.5,
![]() $\omega _X^{- 4}$
is globally generated, so
$\omega _X^{- 4}$
is globally generated, so
![]() $h^1(X,\mathcal {O}_X) \leq 3$
by (4.2). If
$h^1(X,\mathcal {O}_X) \leq 3$
by (4.2). If
![]() $h^1(X,\mathcal {O}_X) = 1$
, then
$h^1(X,\mathcal {O}_X) = 1$
, then
![]() $N = 0$
and
$N = 0$
and
![]() $d \in \{1,2\}$
by (4.4), and we get Cases (3) and (4).
$d \in \{1,2\}$
by (4.4), and we get Cases (3) and (4).
So, it remains to exclude the possibility
![]() $h^1(X,\mathcal {O}_X) \geq 2$
in characteristic
$h^1(X,\mathcal {O}_X) \geq 2$
in characteristic
![]() $p = 2$
. By Corollary 4.5,
$p = 2$
. By Corollary 4.5,
![]() $\omega _X^{- 2}$
is globally generated, so by (4.4), the inequality
$\omega _X^{- 2}$
is globally generated, so by (4.4), the inequality
![]() $h^1(X,\mathcal {O}_X) \geq 2$
implies
$h^1(X,\mathcal {O}_X) \geq 2$
implies
![]() $N = 2$
,
$N = 2$
,
![]() $d = 1$
, and
$d = 1$
, and
![]() $h^1(X,\mathcal {O}_X) = 3$
.
$h^1(X,\mathcal {O}_X) = 3$
.
Seeking a contradiction, assume that there exists an X with these invariants. Since
![]() $N = 2$
, we have
$N = 2$
, we have
![]() $H^1(X, \omega _X^{3}) \neq 0$
and
$H^1(X, \omega _X^{3}) \neq 0$
and
![]() $H^1(X, \omega _X^6)=0$
. Let
$H^1(X, \omega _X^6)=0$
. Let
![]() $Z \to X$
be a nontrivial
$Z \to X$
be a nontrivial
![]() $\alpha _{\omega _X^3}$
-torsor and let
$\alpha _{\omega _X^3}$
-torsor and let
![]() $k_Z:=H^0(Z, \mathcal {O}_Z)$
. Note that Z is an l.c.i. del Pezzo surface by [Reference MaddockMad16, Theorem 1.2.3], and by [Reference MaddockMad16, Equation (1.2.4)], we have
$k_Z:=H^0(Z, \mathcal {O}_Z)$
. Note that Z is an l.c.i. del Pezzo surface by [Reference MaddockMad16, Theorem 1.2.3], and by [Reference MaddockMad16, Equation (1.2.4)], we have
![]() $[k_Z :k] (1-h^1(Z, \mathcal {O}_Z)) = 2$
so that we have
$[k_Z :k] (1-h^1(Z, \mathcal {O}_Z)) = 2$
so that we have
![]() $[k_Z :k]=2$
and
$[k_Z :k]=2$
and
![]() $H^1(Z,\mathcal {O}_Z) = 0$
. By [Reference MaddockMad16, Equation (1.2.5)], we then conclude that
$H^1(Z,\mathcal {O}_Z) = 0$
. By [Reference MaddockMad16, Equation (1.2.5)], we then conclude that
![]() $K_Z^2=16$
. Now, we consider the following diagram:
$K_Z^2=16$
. Now, we consider the following diagram:

where
![]() $Z_{\bar {k}} = Z \times _{ {\mathrm {Spec}} k_Z} {\mathrm {Spec}} \bar {k}$
. Since f and
$Z_{\bar {k}} = Z \times _{ {\mathrm {Spec}} k_Z} {\mathrm {Spec}} \bar {k}$
. Since f and
![]() $X_{k_Z} \to X$
are finite of degree
$X_{k_Z} \to X$
are finite of degree
![]() $2$
, the morphism
$2$
, the morphism
![]() $\pi $
is finite and birational. In particular, Z, considered as a
$\pi $
is finite and birational. In particular, Z, considered as a
![]() $k_Z$
-scheme, is geometrically integral and the induced map
$k_Z$
-scheme, is geometrically integral and the induced map
![]() $(\pi _{\bar {k}})^{ {\mathrm {norm}}}$
of the normalisations is an isomorphism. As
$(\pi _{\bar {k}})^{ {\mathrm {norm}}}$
of the normalisations is an isomorphism. As
![]() $(X_{\bar {k}})^{ {\mathrm {norm}}} \cong \mathbb {P}^2$
,
$(X_{\bar {k}})^{ {\mathrm {norm}}} \cong \mathbb {P}^2$
,
![]() $16=K_Z^2 \leq K_{(Z_{\bar {k}})^{ {\mathrm {norm}}}}^2=9$
, reaching a contradiction.
$16=K_Z^2 \leq K_{(Z_{\bar {k}})^{ {\mathrm {norm}}}}^2=9$
, reaching a contradiction.
Corollary 4.9. Let X be a geometrically integral normal locally complete intersection del Pezzo surface over a field k of characteristic p. Let
![]() $\nu \colon Y \to X_{\bar {k}}$
be the normalization of
$\nu \colon Y \to X_{\bar {k}}$
be the normalization of
![]() $X_{\bar {k}}$
and let
$X_{\bar {k}}$
and let
![]() $C \subseteq Y$
be the ramification of
$C \subseteq Y$
be the ramification of
![]() $\nu $
. Then, one of the following holds:
$\nu $
. Then, one of the following holds:
-
1.
 $h^1(X,\mathcal {O}_X) = 0$
,
$h^1(X,\mathcal {O}_X) = 0$
,
 $K_X^2 \geq 3$
, and
$K_X^2 \geq 3$
, and
 $\omega _X^{-1}$
is very ample.
$\omega _X^{-1}$
is very ample. -
2.
 $h^1(X,\mathcal {O}_X) = 0$
,
$h^1(X,\mathcal {O}_X) = 0$
,
 $K_X^2 = 2$
, and
$K_X^2 = 2$
, and
 $\omega _X^{-2}$
is very ample.
$\omega _X^{-2}$
is very ample. -
3.
 $h^1(X,\mathcal {O}_X) = 0$
,
$h^1(X,\mathcal {O}_X) = 0$
,
 $K_X^2 = 1$
, and
$K_X^2 = 1$
, and
 $\omega _X^{-3}$
is very ample.
$\omega _X^{-3}$
is very ample. -
4.
 $h^1(X,\mathcal {O}_X) = 1$
,
$h^1(X,\mathcal {O}_X) = 1$
,
 $p=2$
,
$p=2$
,
 $(Y,C, K_X^2) \in \{(\mathbb {P}^2,2L, 1),(\mathbb {P}(1,1,2),2L,2)\}$
, and
$(Y,C, K_X^2) \in \{(\mathbb {P}^2,2L, 1),(\mathbb {P}(1,1,2),2L,2)\}$
, and
 $\omega _X^{-6}$
is very ample.
$\omega _X^{-6}$
is very ample. -
5.
 $h^1(X,\mathcal {O}_X) = 2$
,
$h^1(X,\mathcal {O}_X) = 2$
,
 $p=3$
,
$p=3$
,
 $(Y,C,K_X^2) = (\mathbb {P}^2,2L,1)$
, and
$(Y,C,K_X^2) = (\mathbb {P}^2,2L,1)$
, and
 $\omega _X^{-7}$
is very ample.
$\omega _X^{-7}$
is very ample.
Proof. Claims (1), (2) and (3) are a consequence of [Reference Bernasconi and TanakaBT22, Proposition 2.14] if X is geometrically normal, and hence geometrically canonical, and [Reference ReidRei94, Corollary 4.10] if X is not geometrically normal.
Let us prove Claim (4). By Proposition 4.8, we have
![]() $p=2$
and the desired classification of
$p=2$
and the desired classification of
![]() $(Y,C)$
. By Lemma 3.7,
$(Y,C)$
. By Lemma 3.7,
![]() $\omega _X^{-2}$
is globally generated. Using Proposition 4.8, it is easy to check that
$\omega _X^{-2}$
is globally generated. Using Proposition 4.8, it is easy to check that
![]() $\omega _X^{-4}$
is
$\omega _X^{-4}$
is
![]() $0$
-regular with respect to
$0$
-regular with respect to
![]() $\omega _X^{-2}$
. Claim (5) is proven similarly.
$\omega _X^{-2}$
. Claim (5) is proven similarly.
4.4. Refinements in the regular and canonical case
We show various refinements of the bounds of Proposition 4.8 in the case where we assume X to be a regular or canonical del Pezzo surface. We start with the case
![]() $p=3$
.
$p=3$
.
Proposition 4.10. Let X be a geometrically integral canonical del Pezzo surface over a field k of characteristic
![]() $p = 3$
. Then, X is tame.
$p = 3$
. Then, X is tame.
Proof. Without loss of generality, we may assume that k is separably closed.
First, assume that X is regular. Seeking a contradiction, we assume that
![]() $h^1(X, \mathcal {O}_X) \neq 0$
. Let
$h^1(X, \mathcal {O}_X) \neq 0$
. Let
![]() ${\nu \colon Y \to X_{\bar {k}}}$
be the normalisation of
${\nu \colon Y \to X_{\bar {k}}}$
be the normalisation of
![]() $X_{\bar {k}}$
and let
$X_{\bar {k}}$
and let
![]() $C \subseteq Y$
be the ramification of
$C \subseteq Y$
be the ramification of
![]() $\nu $
. By Proposition 4.8 and Serre duality, we know that
$\nu $
. By Proposition 4.8 and Serre duality, we know that
![]() $h^1(X,\mathcal {O}_X) = 2$
,
$h^1(X,\mathcal {O}_X) = 2$
,
![]() $K_X^2 = 1$
,
$K_X^2 = 1$
,
![]() $h^1(X,\omega _X^{-n}) = 0$
for
$h^1(X,\omega _X^{-n}) = 0$
for
![]() $n> 0$
, and
$n> 0$
, and
![]() $(Y,C) = (\mathbb {P}^2,2L)$
.
$(Y,C) = (\mathbb {P}^2,2L)$
.
First, we claim that
![]() $h^0(X,\omega _X^{-n} \otimes \mathcal {L}) = 0$
for all nontrivial torsion line bundles
$h^0(X,\omega _X^{-n} \otimes \mathcal {L}) = 0$
for all nontrivial torsion line bundles
![]() $\mathcal {L}$
and for
$\mathcal {L}$
and for
![]() $n \in \left \{0, 1\right \}$
. Since X is reduced, this holds if
$n \in \left \{0, 1\right \}$
. Since X is reduced, this holds if
![]() $n = 0$
. For the case
$n = 0$
. For the case
![]() $n=1$
, by the Riemann–Roch theorem, we have
$n=1$
, by the Riemann–Roch theorem, we have
so if
![]() $h^1(X,\omega _X^{-1} \otimes \mathcal {L}) \neq 0$
, then
$h^1(X,\omega _X^{-1} \otimes \mathcal {L}) \neq 0$
, then
![]() $h^1(X,\omega _X^{2} \otimes \mathcal {L}^{-1}) \neq 0$
by Serre duality. Since
$h^1(X,\omega _X^{2} \otimes \mathcal {L}^{-1}) \neq 0$
by Serre duality. Since
![]() $\omega _X^{6} \otimes \mathcal {L}^{-3} \cong \omega _X^{6}$
by Corollary 4.4 and
$\omega _X^{6} \otimes \mathcal {L}^{-3} \cong \omega _X^{6}$
by Corollary 4.4 and
![]() $h^1(X,\omega _X^{6}) = 0$
by Proposition 4.8, there exists a nontrivial
$h^1(X,\omega _X^{6}) = 0$
by Proposition 4.8, there exists a nontrivial
![]() $\alpha _{(\omega _X^{2} \otimes \mathcal {L}^{-1})}$
-torsor
$\alpha _{(\omega _X^{2} \otimes \mathcal {L}^{-1})}$
-torsor
![]() $Z \to X$
such that Z is an l.c.i. del Pezzo surface. Moreover, by [Reference MaddockMad16, Equation (1.2.5)], we have
$Z \to X$
such that Z is an l.c.i. del Pezzo surface. Moreover, by [Reference MaddockMad16, Equation (1.2.5)], we have
![]() $ 2^e(1-q_Z)= 10 $
for some integers
$ 2^e(1-q_Z)= 10 $
for some integers
![]() $0 \leq e \leq 1$
and
$0 \leq e \leq 1$
and
![]() $q_Z \geq 0$
, contradicting our assumption.
$q_Z \geq 0$
, contradicting our assumption.
By Riemann–Roch, we have
![]() $h^0(X,\omega _X^{-2}) = 2$
. Write
$h^0(X,\omega _X^{-2}) = 2$
. Write
where F is the fixed part and M is the movable part of the linear system. Since
![]() $M \neq 0$
, we have
$M \neq 0$
, we have
![]() $F \in |-nK_X + E|$
for some
$F \in |-nK_X + E|$
for some
![]() $0 \leq n \leq 1$
and a divisor E such that
$0 \leq n \leq 1$
and a divisor E such that
![]() $\mathcal {O}_X(E)$
is torsion. By the previous paragraph, we have
$\mathcal {O}_X(E)$
is torsion. By the previous paragraph, we have
![]() $h^0(X,\omega _X^{-n}(E)) = 0$
; hence,
$h^0(X,\omega _X^{-n}(E)) = 0$
; hence,
![]() $F = 0$
.
$F = 0$
.
Since the linear system
![]() $|-2K_X|$
does not have fixed components, its base locus Z is
$|-2K_X|$
does not have fixed components, its base locus Z is
![]() $0$
-dimensional, and we denote by A the ring of global section
$0$
-dimensional, and we denote by A the ring of global section
![]() $H^0(Z, \mathcal {O}_Z)$
. Since
$H^0(Z, \mathcal {O}_Z)$
. Since
![]() $(-2K_X)^2 = 4$
, we have
$(-2K_X)^2 = 4$
, we have
![]() $\mathrm {length}_k(A) = 4$
, so A is an Artinian k-algebra of length
$\mathrm {length}_k(A) = 4$
, so A is an Artinian k-algebra of length
![]() $4$
. As k is separably closed, we can write
$4$
. As k is separably closed, we can write
![]() $A = \prod _{i=1}^s A_i$
where each
$A = \prod _{i=1}^s A_i$
where each
![]() $A_i$
is a local Artinian k-algebra of dimension
$A_i$
is a local Artinian k-algebra of dimension
![]() $n_i$
over its residue field
$n_i$
over its residue field
![]() $k_i$
and
$k_i$
and
![]() $k_i$
is a purely inseparable extension of k. Since
$k_i$
is a purely inseparable extension of k. Since
 $$ \begin{align*}4 = \mathrm{length}_k(A) = \sum_{i=1}^s \mathrm{length}_k(A_i) = \sum_{i=1}^s n_i [k_i:k] \end{align*} $$
$$ \begin{align*}4 = \mathrm{length}_k(A) = \sum_{i=1}^s \mathrm{length}_k(A_i) = \sum_{i=1}^s n_i [k_i:k] \end{align*} $$
and
![]() $p = 3$
, we have
$p = 3$
, we have
![]() $k_i = k$
for at least one i. In other words, at least one of the base points of
$k_i = k$
for at least one i. In other words, at least one of the base points of
![]() $|-2K_X|$
is a k-rational point P.
$|-2K_X|$
is a k-rational point P.
If P is in the image of the conductor D under the natural map
![]() $X_{\bar {k}} \to X$
, then P lies in the non-smooth locus of
$X_{\bar {k}} \to X$
, then P lies in the non-smooth locus of
![]() $X \to {\mathrm {Spec}} k$
, so X cannot be regular at P by [Reference Fanelli and SchröerFS20, Corollary 2.6]. Hence, in this case, the proof is finished.
$X \to {\mathrm {Spec}} k$
, so X cannot be regular at P by [Reference Fanelli and SchröerFS20, Corollary 2.6]. Hence, in this case, the proof is finished.
So, seeking a contradiction, assume that P is not in the image of D. Let
![]() $P'$
be the unique preimage of P under the map
$P'$
be the unique preimage of P under the map
![]() $Y \to X_{\bar {k}} \to X$
. Since
$Y \to X_{\bar {k}} \to X$
. Since
![]() $\nu $
is an isomorphism around
$\nu $
is an isomorphism around
![]() $P'$
, the point
$P'$
, the point
![]() $P'$
lies in the base locus of
$P'$
lies in the base locus of
![]() $\nu ^* |-2K_{X_{\bar {k}}}|$
. By Corollary 4.7, we know that
$\nu ^* |-2K_{X_{\bar {k}}}|$
. By Corollary 4.7, we know that
![]() $C = 2L \in \nu ^* |-2K_{X_{\bar {k}}}|$
hence,
$C = 2L \in \nu ^* |-2K_{X_{\bar {k}}}|$
hence,
![]() $P' \in C$
, and thus, P is in the image of D under
$P' \in C$
, and thus, P is in the image of D under
![]() $X_{\bar {k}} \to X$
. This contradicts our choice of P.
$X_{\bar {k}} \to X$
. This contradicts our choice of P.
Finally, assume that X is canonical. By Proposition 2.6, we can replace X with its minimal resolution, which is a regular weak del Pezzo surface. By running a
![]() $K_X$
-MMP, we can suppose X is a weak del Pezzo surface admitting a Mori fibre space structure
$K_X$
-MMP, we can suppose X is a weak del Pezzo surface admitting a Mori fibre space structure
![]() $\pi \colon X \to B$
. If X is a regular del Pezzo surface, we conclude by the previous case. If B is a curve and X is a weak del Pezzo surface, then the generic fibre F is a regular conic. As
$\pi \colon X \to B$
. If X is a regular del Pezzo surface, we conclude by the previous case. If B is a curve and X is a weak del Pezzo surface, then the generic fibre F is a regular conic. As
![]() $p = 3$
, F is smooth by [Reference Bernasconi and TanakaBT22, Lemma 2.17], and thus,
$p = 3$
, F is smooth by [Reference Bernasconi and TanakaBT22, Lemma 2.17], and thus,
![]() $-K_B$
is ample by [Reference EjiriEji19, Corollary 4.10.c]. Therefore,
$-K_B$
is ample by [Reference EjiriEji19, Corollary 4.10.c]. Therefore,
![]() $H^1(B, \mathcal {O}_B)=0$
and, as
$H^1(B, \mathcal {O}_B)=0$
and, as
![]() $H^1(X, \mathcal {O}_X)=H^1(B, \mathcal {O}_B)=0$
by the relative Kawamata–Viehweg vanishing theorem [Reference TanakaTan18b, Theorem 4.2], we conclude.
$H^1(X, \mathcal {O}_X)=H^1(B, \mathcal {O}_B)=0$
by the relative Kawamata–Viehweg vanishing theorem [Reference TanakaTan18b, Theorem 4.2], we conclude.
In the following proposition, we describe the geometry of
![]() $\alpha _{\omega _X}$
-torsors over wild regular del Pezzo surfaces in characteristic
$\alpha _{\omega _X}$
-torsors over wild regular del Pezzo surfaces in characteristic
![]() $p = 2$
. The reader should compare this with the construction of the regular wild del Pezzo surfaces of degree
$p = 2$
. The reader should compare this with the construction of the regular wild del Pezzo surfaces of degree
![]() $1$
in [Reference MaddockMad16].
$1$
in [Reference MaddockMad16].
Proposition 4.11. Let X be a geometrically integral regular del Pezzo surface over a field k of characteristic
![]() $p = 2$
. Assume that
$p = 2$
. Assume that
![]() $h^1(X,\mathcal {O}_X) \neq 0$
. Then,
$h^1(X,\mathcal {O}_X) \neq 0$
. Then,
![]() $ {\mathrm {p-deg}}(k) \geq 2$
,
$ {\mathrm {p-deg}}(k) \geq 2$
,
![]() $K_X^2 \leq 2$
, and there exists an
$K_X^2 \leq 2$
, and there exists an
![]() $\alpha _{\omega _X}$
-torsor
$\alpha _{\omega _X}$
-torsor
![]() $Z \to X$
such that Z satisfies the following properties:
$Z \to X$
such that Z satisfies the following properties:
-
1. If
 $K_X^2 = 2$
, then
$K_X^2 = 2$
, then  is a purely inseparable extension of k of degree
is a purely inseparable extension of k of degree
 $2$
and Z is a twisted form of
$2$
and Z is a twisted form of
 $\mathbb {P}(1,1,2)$
over
$\mathbb {P}(1,1,2)$
over
 $k_Z$
.
$k_Z$
. -
2. If
 $K_X^2=1$
, then Z is a normal tame del Pezzo surface such that
$K_X^2=1$
, then Z is a normal tame del Pezzo surface such that
 $\epsilon (Z/k)=1$
,
$\epsilon (Z/k)=1$
,
 $K_Z^2=8$
and the normalised base change
$K_Z^2=8$
and the normalised base change
 $((Z_{\overline {k}})_{ {\mathrm {red}}}^{ {\mathrm {norm}}}, E)$
is
$((Z_{\overline {k}})_{ {\mathrm {red}}}^{ {\mathrm {norm}}}, E)$
is
 $(\mathbb {P}^2,L)$
.
$(\mathbb {P}^2,L)$
.
Proof. If X is not tame, then
![]() $\rho (X)=1$
by Proposition 4.8. If
$\rho (X)=1$
by Proposition 4.8. If
![]() $ {\mathrm {p-deg}}(k)=1$
, then X is geometrically canonical by [Reference Fanelli and SchröerFS20], contradicting
$ {\mathrm {p-deg}}(k)=1$
, then X is geometrically canonical by [Reference Fanelli and SchröerFS20], contradicting
![]() $h^1(X, \mathcal {O}_X) \neq 0$
.
$h^1(X, \mathcal {O}_X) \neq 0$
.
By Proposition 4.8, we have
![]() $h^1(X,\mathcal {O}_X) = h^1(X,\omega _X) = 1$
,
$h^1(X,\mathcal {O}_X) = h^1(X,\omega _X) = 1$
,
![]() $h^1(X,\omega _X^{n}) = 0$
for
$h^1(X,\omega _X^{n}) = 0$
for
![]() $n \geq 2$
, and
$n \geq 2$
, and
![]() $K_X^2 \in \{1,2\}$
. In particular, there exists a nontrivial
$K_X^2 \in \{1,2\}$
. In particular, there exists a nontrivial
![]() $\alpha _{\omega _X}$
-torsor
$\alpha _{\omega _X}$
-torsor
![]() $f \colon Z \to X$
. In the following, we treat the cases
$f \colon Z \to X$
. In the following, we treat the cases
![]() $K_X^2 = 2$
and
$K_X^2 = 2$
and
![]() $K_X^2 = 1$
separately. We set
$K_X^2 = 1$
separately. We set ![]() . Note that, by the same proof as for the second paragraph of the proof of Proposition 4.10, we have
. Note that, by the same proof as for the second paragraph of the proof of Proposition 4.10, we have
![]() $h^1(X,\omega _X^{n} \otimes \mathcal {L}) = 0$
for all torsion line bundles
$h^1(X,\omega _X^{n} \otimes \mathcal {L}) = 0$
for all torsion line bundles
![]() $\mathcal {L}$
and all
$\mathcal {L}$
and all
![]() $n \geq 2$
.
$n \geq 2$
.
Assume
![]() $K_X^2 = 2$
. In this case, by [Reference MaddockMad16, Equation (1.2.5)], we have
$K_X^2 = 2$
. In this case, by [Reference MaddockMad16, Equation (1.2.5)], we have
![]() $[k_Z:k] = 2$
,
$[k_Z:k] = 2$
,
![]() $h^1(Z,\mathcal {O}_Z) = 0$
, and
$h^1(Z,\mathcal {O}_Z) = 0$
, and
![]() $K_Z^2 = 8$
, where we compute the self-intersection over
$K_Z^2 = 8$
, where we compute the self-intersection over
![]() $k_Z$
. Now, consider the commutative diagram
$k_Z$
. Now, consider the commutative diagram

where
![]() $Z_{\bar {k}} = Z \times _{ {\mathrm {Spec}} k_Z} {\mathrm {Spec}} \bar {k}$
. As in the end of the proof of Proposition 4.8, the diagram shows that Z is geometrically integral when considered as a
$Z_{\bar {k}} = Z \times _{ {\mathrm {Spec}} k_Z} {\mathrm {Spec}} \bar {k}$
. As in the end of the proof of Proposition 4.8, the diagram shows that Z is geometrically integral when considered as a
![]() $k_Z$
-scheme and
$k_Z$
-scheme and
![]() $(\pi _{\bar {k}})^{ {\mathrm {norm}}}$
is an isomorphism; hence,
$(\pi _{\bar {k}})^{ {\mathrm {norm}}}$
is an isomorphism; hence,
![]() $(Z_{\bar {k}})^{ {\mathrm {norm}}} \cong (X_{\bar {k}})^{ {\mathrm {norm}}} \cong \mathbb {P}(1, 1, 2)$
by Proposition 4.8. In particular, we have
$(Z_{\bar {k}})^{ {\mathrm {norm}}} \cong (X_{\bar {k}})^{ {\mathrm {norm}}} \cong \mathbb {P}(1, 1, 2)$
by Proposition 4.8. In particular, we have
![]() $K_Z^2 = 8 = K^2_{(Z_{\bar {k}})^{ {\mathrm {norm}}}}$
, so Z is in fact geometrically normal. Therefore,
$K_Z^2 = 8 = K^2_{(Z_{\bar {k}})^{ {\mathrm {norm}}}}$
, so Z is in fact geometrically normal. Therefore,
![]() $Z_{\bar {k}} \cong \mathbb {P}(1,1,2)$
, so Z is a twisted form of
$Z_{\bar {k}} \cong \mathbb {P}(1,1,2)$
, so Z is a twisted form of
![]() $\mathbb {P}(1,1,2)$
over
$\mathbb {P}(1,1,2)$
over
![]() $k_Z$
.
$k_Z$
.
Assume
![]() $K_X^2=1$
. In this case, by [Reference MaddockMad16, Equation (1.2.5)], we have
$K_X^2=1$
. In this case, by [Reference MaddockMad16, Equation (1.2.5)], we have
![]() $k_Z = k$
and
$k_Z = k$
and
![]() $h^1(Z, \mathcal {O}_Z)=0$
. We first claim that Z is not geometrically reduced. Indeed, let
$h^1(Z, \mathcal {O}_Z)=0$
. We first claim that Z is not geometrically reduced. Indeed, let
![]() $\psi \colon \mathbb {P}^2 \to X$
be the normalised base change and consider the
$\psi \colon \mathbb {P}^2 \to X$
be the normalised base change and consider the
![]() $\alpha _{\psi ^*\omega _X}$
-torsor
$\alpha _{\psi ^*\omega _X}$
-torsor
![]() $T:=Z \times _{X} \mathbb {P}^2 \to \mathbb {P}^2$
obtained by base changing along
$T:=Z \times _{X} \mathbb {P}^2 \to \mathbb {P}^2$
obtained by base changing along
![]() $\psi $
. As
$\psi $
. As
![]() $\psi ^*\omega _X$
is anti-ample, considering the exact sequence
$\psi ^*\omega _X$
is anti-ample, considering the exact sequence
we have that
![]() $H^1_{{ {\mathrm {fppf}}}}(\mathbb {P}^2, \alpha _{\psi ^*\omega _X})=0$
, so that
$H^1_{{ {\mathrm {fppf}}}}(\mathbb {P}^2, \alpha _{\psi ^*\omega _X})=0$
, so that
![]() $T \to \mathbb {P}^2$
is a trivial torsor, and thus, T is not reduced. Since
$T \to \mathbb {P}^2$
is a trivial torsor, and thus, T is not reduced. Since
![]() $T \to Z_{\bar {k}}$
is generically an isomorphism, Z is not geometrically reduced.
$T \to Z_{\bar {k}}$
is generically an isomorphism, Z is not geometrically reduced.
Next, we claim that Z is normal. Suppose by contradiction it is not and let
![]() $\nu \colon Z^{ {\mathrm {norm}}} \to Z$
be the normalisation. In this case, as
$\nu \colon Z^{ {\mathrm {norm}}} \to Z$
be the normalisation. In this case, as
![]() $\nu $
is not an isomorphism, we have that
$\nu $
is not an isomorphism, we have that
![]() $K_{Z^{ {\mathrm {norm}}}}^2>8$
, where we calculate the self-intersection number over k. Let
$K_{Z^{ {\mathrm {norm}}}}^2>8$
, where we calculate the self-intersection number over k. Let
![]() $g \colon Z^{ {\mathrm {norm}}} \to X$
be the composition
$g \colon Z^{ {\mathrm {norm}}} \to X$
be the composition
![]() $f \circ \nu $
. As X is regular and
$f \circ \nu $
. As X is regular and
![]() $Z^{ {\mathrm {norm}}}$
is integral, by [Reference MaddockMad16, Proposition 2.2.1], there exists a line bundle
$Z^{ {\mathrm {norm}}}$
is integral, by [Reference MaddockMad16, Proposition 2.2.1], there exists a line bundle
![]() $\mathcal {M}$
numerically equivalent to
$\mathcal {M}$
numerically equivalent to
![]() $mK_X$
for some integer m such that g is a nontrivial
$mK_X$
for some integer m such that g is a nontrivial
![]() $\alpha _{\mathcal {M}}$
-torsor. In particular,
$\alpha _{\mathcal {M}}$
-torsor. In particular,
![]() $Z^{ {\mathrm {norm}}}$
is Gorenstein, and thus, as it is the normalization of a del Pezzo surface,
$Z^{ {\mathrm {norm}}}$
is Gorenstein, and thus, as it is the normalization of a del Pezzo surface,
![]() $Z^{ {\mathrm {norm}}}$
is also a del Pezzo surface. Therefore,
$Z^{ {\mathrm {norm}}}$
is also a del Pezzo surface. Therefore,
![]() $m \geq 0$
. We now distinguish two cases:
$m \geq 0$
. We now distinguish two cases:
-
1. if
 $H^0(Z^{ {\mathrm {norm}}}, \mathcal {O}_{Z^{ {\mathrm {norm}}}}) =k$
, by [Reference MaddockMad16, Equation (1.2.4)], we have
$H^0(Z^{ {\mathrm {norm}}}, \mathcal {O}_{Z^{ {\mathrm {norm}}}}) =k$
, by [Reference MaddockMad16, Equation (1.2.4)], we have
 $2(1+m)^2 = K_{Z^{ {\mathrm {norm}}}}^2>8$
, which implies that
$2(1+m)^2 = K_{Z^{ {\mathrm {norm}}}}^2>8$
, which implies that
 $m>1$
, contradicting Proposition 4.8;
$m>1$
, contradicting Proposition 4.8; -
2. if
 $[H^0(Z^{ {\mathrm {norm}}}, \mathcal {O}_{Z^{ {\mathrm {norm}}}}):k ]=2$
, we have that
$[H^0(Z^{ {\mathrm {norm}}}, \mathcal {O}_{Z^{ {\mathrm {norm}}}}):k ]=2$
, we have that
 $(1+m)^2=K_{Z^{ {\mathrm {norm}}}}^2>4$
, which also implies that
$(1+m)^2=K_{Z^{ {\mathrm {norm}}}}^2>4$
, which also implies that
 $m>1$
, contradicting Proposition 4.8 as well. Note that, here, we calculate the self-intersection
$m>1$
, contradicting Proposition 4.8 as well. Note that, here, we calculate the self-intersection
 $K_{Z^{ {\mathrm {norm}}}}^2$
over
$K_{Z^{ {\mathrm {norm}}}}^2$
over
 $H^0(Z^{ {\mathrm {norm}}}, \mathcal {O}_{Z^{ {\mathrm {norm}}}})$
.
$H^0(Z^{ {\mathrm {norm}}}, \mathcal {O}_{Z^{ {\mathrm {norm}}}})$
.
Thus, Z must be normal.
By [Reference KleimanKle66, Example 1], we have that
![]() $8=K_Z^2=2^{\epsilon (Z/k)}(K_{(Z_{\bar {k}})_{ {\mathrm {red}}}^{ {\mathrm {norm}}}} + E)^2 $
. Since Z is geometrically non-reduced, we have
$8=K_Z^2=2^{\epsilon (Z/k)}(K_{(Z_{\bar {k}})_{ {\mathrm {red}}}^{ {\mathrm {norm}}}} + E)^2 $
. Since Z is geometrically non-reduced, we have
![]() $\epsilon (Z/k) \geq 1$
, and since f is finite flat of degree
$\epsilon (Z/k) \geq 1$
, and since f is finite flat of degree
![]() $2$
and
$2$
and
![]() $\epsilon (X/k) = 0$
, we have
$\epsilon (X/k) = 0$
, we have
![]() $\epsilon (Z/k) \leq 1$
; hence,
$\epsilon (Z/k) \leq 1$
; hence,
![]() $\epsilon (Z/k) = 1$
. As Z is normal and Gorenstein, we can apply [Reference Patakfalvi and WaldronPW22, Theorem 4.1] to conclude that
$\epsilon (Z/k) = 1$
. As Z is normal and Gorenstein, we can apply [Reference Patakfalvi and WaldronPW22, Theorem 4.1] to conclude that
![]() $Z=\mathbb {P}^2$
and E is a line.
$Z=\mathbb {P}^2$
and E is a line.
5. On the BAB conjecture for surfaces over arbitrary fields
In this section, we prove boundedness results for del Pezzo surfaces over arbitrary fields.
We recall some terminology when discussing boundedness in birational geometry. For the following definition, we say that a scheme X is a projective variety if X is integral,
![]() $H^0(X, \mathcal {O}_X)$
is a field k and the natural morphism
$H^0(X, \mathcal {O}_X)$
is a field k and the natural morphism
![]() $\pi _X \colon X \to {\mathrm {Spec}}(k)$
is projective. We will always consider X as a k-variety via the natural morphism
$\pi _X \colon X \to {\mathrm {Spec}}(k)$
is projective. We will always consider X as a k-variety via the natural morphism
![]() $\pi _X$
.
$\pi _X$
.
Definition 5.1. We say that a class of projective varieties
![]() $\mathcal {X}$
is bounded (resp. birationally bounded) if there exists a projective flat morphism
$\mathcal {X}$
is bounded (resp. birationally bounded) if there exists a projective flat morphism
![]() $Y \to T$
of finite type
$Y \to T$
of finite type
![]() $\mathbb {Z}$
-schemes such that for every
$\mathbb {Z}$
-schemes such that for every
![]() $X \in \mathcal {X}$
with
$X \in \mathcal {X}$
with ![]() , there exists a morphism
, there exists a morphism
![]() $ {\mathrm {Spec}}(k) \to T$
and a k-isomorphism (resp. a k-birational map)
$ {\mathrm {Spec}}(k) \to T$
and a k-isomorphism (resp. a k-birational map)
![]() $X \to Y \times _V {\mathrm {Spec}}(k)$
.
$X \to Y \times _V {\mathrm {Spec}}(k)$
.
The Borisov–Alexeev–Borisov (BAB) conjecture states that mildly singular Fano varieties form a bounded family in every dimension.
Conjecture 5.2 (BAB)
For any rational number
![]() $\varepsilon>0$
, the class
$\varepsilon>0$
, the class
is bounded.
Remark 5.3. The presence of the
![]() $\varepsilon $
–klt hypothesis is necessary in the BAB conjecture, already in dimension 2. Indeed, Gorenstein del Pezzo surfaces with general log canonical singularities are not bounded as cones over elliptic curves of Proposition 2.9 show. Moreover, boundedness already fails for klt del Pezzo surfaces as the set of weighted projective planes
$\varepsilon $
–klt hypothesis is necessary in the BAB conjecture, already in dimension 2. Indeed, Gorenstein del Pezzo surfaces with general log canonical singularities are not bounded as cones over elliptic curves of Proposition 2.9 show. Moreover, boundedness already fails for klt del Pezzo surfaces as the set of weighted projective planes
![]() $\left \{\mathbb {P}(1,1,d)\right \}_{d \geq 1}$
shows.
$\left \{\mathbb {P}(1,1,d)\right \}_{d \geq 1}$
shows.
We discuss the BAB conjecture for surfaces defined over arbitrary fields. The result of [Reference AlexeevAle94, Reference Cascini, Tanaka and WitaszekCTW17] shows that the class of geometrically
![]() $\varepsilon $
-klt del Pezzo surfaces form a bounded family. However, the conjecture is still open for
$\varepsilon $
-klt del Pezzo surfaces form a bounded family. However, the conjecture is still open for
![]() $\varepsilon $
-klt del Pezzo surfaces defined over an imperfect field.
$\varepsilon $
-klt del Pezzo surfaces defined over an imperfect field.
In subsection 5.1, we settle the BAB conjecture for geometrically integral canonical del Pezzo surfaces. In the remaining two subsections, we discuss the general
![]() $\varepsilon $
-klt case. In subsection 5.2, we prove boundedness of the anticanonical volumes for
$\varepsilon $
-klt case. In subsection 5.2, we prove boundedness of the anticanonical volumes for
![]() $\varepsilon $
-klt del Pezzo surfaces over imperfect fields. This, together with a bound on the
$\varepsilon $
-klt del Pezzo surfaces over imperfect fields. This, together with a bound on the
![]() $\mathbb {Q}$
-Gorenstein index proven in subsection 5.3, implies the BAB Conjecture 5.2 for such surfaces in characteristic
$\mathbb {Q}$
-Gorenstein index proven in subsection 5.3, implies the BAB Conjecture 5.2 for such surfaces in characteristic
![]() $p>5$
(cf. Theorem 5.12).
$p>5$
(cf. Theorem 5.12).
5.1. Boundedness of geometrically integral canonical del Pezzo surfaces
In [Reference TanakaTan24], Tanaka proves boundedness for geometrically integral regular del Pezzo surfaces. As a consequence of our results in section 3 and section 4, we can extend Tanaka’s result to the canonical case.
Theorem 5.4. The class
is bounded.
Proof. As X is geometrically integral,
![]() $\epsilon (X/k)=0$
, and thus,
$\epsilon (X/k)=0$
, and thus,
![]() $K_X^2 \leq 16$
by Proposition 3.4. Since X is canonical,
$K_X^2 \leq 16$
by Proposition 3.4. Since X is canonical,
![]() $K_X$
is Cartier and
$K_X$
is Cartier and
![]() $K_X^2$
is an integer. By Proposition 4.8, Theorem 3.10 and Riemann–Roch, there exists an
$K_X^2$
is an integer. By Proposition 4.8, Theorem 3.10 and Riemann–Roch, there exists an
![]() $N> 0$
such that
$N> 0$
such that
![]() $\omega _X^{-12}$
embeds X into
$\omega _X^{-12}$
embeds X into
![]() $\mathbb {P}^n_k$
for some
$\mathbb {P}^n_k$
for some
![]() $n \leq N$
. Again by Proposition 4.8, and since
$n \leq N$
. Again by Proposition 4.8, and since
![]() $K_X^2 \leq 16$
, the possibilities for the Hilbert polynomial
$K_X^2 \leq 16$
, the possibilities for the Hilbert polynomial
![]() $\chi (X, \omega _X^{ -12})$
are finite. Therefore, all X arise via pullback from a universal family over a suitable finite union of Hilbert scheme of finite type over
$\chi (X, \omega _X^{ -12})$
are finite. Therefore, all X arise via pullback from a universal family over a suitable finite union of Hilbert scheme of finite type over
![]() $ {\mathrm {Spec}} \mathbb {Z}$
[Reference KollárKol96, Theorem 1.4].
$ {\mathrm {Spec}} \mathbb {Z}$
[Reference KollárKol96, Theorem 1.4].
5.2. Bounds on the volume of
 $\varepsilon $
-klt del Pezzo surfaces
$\varepsilon $
-klt del Pezzo surfaces
We prove an explicit bound for the volumes of
![]() $\varepsilon $
-klt del Pezzo surfaces, generalising the results of [Reference AlexeevAle94, Reference Alexeev and MoriAM04] to imperfect fields. To do so, we start with some elementary computations on surfaces of del Pezzo type admitting a Mori fibration onto a curve. Recall the definition of surfaces of del Pezzo type from Definition 2.15.
$\varepsilon $
-klt del Pezzo surfaces, generalising the results of [Reference AlexeevAle94, Reference Alexeev and MoriAM04] to imperfect fields. To do so, we start with some elementary computations on surfaces of del Pezzo type admitting a Mori fibration onto a curve. Recall the definition of surfaces of del Pezzo type from Definition 2.15.
Lemma 5.5. Let X be a regular surface of del Pezzo type. Let
![]() $\pi \colon X \to B$
be a Mori fibre space onto a regular curve and let
$\pi \colon X \to B$
be a Mori fibre space onto a regular curve and let
![]() $F_b=\pi ^*b$
, where b is a closed point of B. Then, there exists an integral curve
$F_b=\pi ^*b$
, where b is a closed point of B. Then, there exists an integral curve
![]() $\Gamma $
such that
$\Gamma $
such that
Moreover, setting ![]() and
and
![]() $m_{\Gamma } = [k(\Gamma ):k(B)]$
, there exists
$m_{\Gamma } = [k(\Gamma ):k(B)]$
, there exists
![]() $n \geq 0$
such that
$n \geq 0$
such that
and
 $$ \begin{align} K_X^2=\frac{d_\Gamma}{m_\Gamma^2} (8m_{\Gamma}+4n(1-m_{\Gamma})) \leq 8. \end{align} $$
$$ \begin{align} K_X^2=\frac{d_\Gamma}{m_\Gamma^2} (8m_{\Gamma}+4n(1-m_{\Gamma})) \leq 8. \end{align} $$
Proof. The existence of
![]() $\Gamma $
is a consequence of the cone theorem [Reference TanakaTan18b, Theorem 2.14], while Equation (5.1) is proved in [Reference Bernasconi and TanakaBT22, Lemmas 4.3, 4.6]. To prove Equation (5.2), we write
$\Gamma $
is a consequence of the cone theorem [Reference TanakaTan18b, Theorem 2.14], while Equation (5.1) is proved in [Reference Bernasconi and TanakaBT22, Lemmas 4.3, 4.6]. To prove Equation (5.2), we write
![]() $K_X \equiv xF_b+y\Gamma $
for some
$K_X \equiv xF_b+y\Gamma $
for some
![]() $x,y \in \mathbb {Q}$
. Set
$x,y \in \mathbb {Q}$
. Set
![]() $d_b = [k(b):k]$
. As
$d_b = [k(b):k]$
. As
![]() $K_X\cdot F_b=-2d_b$
, we conclude that
$K_X\cdot F_b=-2d_b$
, we conclude that
![]() $y=-\frac {2}{m_\Gamma }.$
Therefore,
$y=-\frac {2}{m_\Gamma }.$
Therefore,
which implies
 $$ \begin{align*}K_X \equiv \frac{d_\Gamma(m_\Gamma(n-2)-2n)}{m_\Gamma^2d_b} F_b - \frac{2}{m_\Gamma}\Gamma.\end{align*} $$
$$ \begin{align*}K_X \equiv \frac{d_\Gamma(m_\Gamma(n-2)-2n)}{m_\Gamma^2d_b} F_b - \frac{2}{m_\Gamma}\Gamma.\end{align*} $$
A straightforward computation with intersection numbers then shows Equation (5.2). Finally, as
![]() ${(1-m_\Gamma ) \leq 0}$
, we have
${(1-m_\Gamma ) \leq 0}$
, we have
![]() $K_X^2 \leq \frac {d_\Gamma }{m_\Gamma } 8$
and, as
$K_X^2 \leq \frac {d_\Gamma }{m_\Gamma } 8$
and, as
![]() $d_\Gamma \leq m_\Gamma ,$
we conclude.
$d_\Gamma \leq m_\Gamma ,$
we conclude.
We now prove bounds on the anticanonical volume of
![]() $\varepsilon $
-klt del Pezzo.
$\varepsilon $
-klt del Pezzo.
Theorem 5.6. Fix a rational number
![]() $\varepsilon>0$
. Then for every geometrically integral
$\varepsilon>0$
. Then for every geometrically integral
![]() $\varepsilon $
-klt del Pezzo surface X, we have
$\varepsilon $
-klt del Pezzo surface X, we have
 $$ \begin{align*}K_X^2 \leq \max \left\{ 9, 8+ 20\frac{(1-\varepsilon)^2}{\varepsilon} \right\}.\end{align*} $$
$$ \begin{align*}K_X^2 \leq \max \left\{ 9, 8+ 20\frac{(1-\varepsilon)^2}{\varepsilon} \right\}.\end{align*} $$
Proof. Let
![]() $f\colon Y \to X$
be the minimal resolution, and write
$f\colon Y \to X$
be the minimal resolution, and write
![]() $K_Y+\sum _i b_i E_i = f^*K_X$
. By the
$K_Y+\sum _i b_i E_i = f^*K_X$
. By the
![]() $\varepsilon $
-klt hypothesis and minimality of f, we have
$\varepsilon $
-klt hypothesis and minimality of f, we have
![]() $0 < b_i < 1-\varepsilon .$
We run a
$0 < b_i < 1-\varepsilon .$
We run a
![]() $K_Y$
-MMP which ends with
$K_Y$
-MMP which ends with
![]() $\psi \colon Y \to Z$
, where Z is a regular projective surface admitting a Mori fibre space structure
$\psi \colon Y \to Z$
, where Z is a regular projective surface admitting a Mori fibre space structure
![]() ${\pi \colon Z \to B}$
. Since
${\pi \colon Z \to B}$
. Since
![]() $-(K_Y+\sum _i b_i E_i)$
is big and nef, so is
$-(K_Y+\sum _i b_i E_i)$
is big and nef, so is
![]() $-(K_Z+\Delta _Z)$
, where
$-(K_Z+\Delta _Z)$
, where
![]() $\Delta _Z=\psi _* \left ( \sum b_i E_i \right )$
. Moreover,
$\Delta _Z=\psi _* \left ( \sum b_i E_i \right )$
. Moreover,
![]() ${K_X^2 = (K_Y+\sum _i b_i B_i)^2 \leq (K_Z+\Delta _Z)^2.}$
${K_X^2 = (K_Y+\sum _i b_i B_i)^2 \leq (K_Z+\Delta _Z)^2.}$
Suppose
![]() $\dim (B)=0$
. Then Z is a regular del Pezzo surface of Picard rank 1. As
$\dim (B)=0$
. Then Z is a regular del Pezzo surface of Picard rank 1. As
![]() $-(K_Z+\Delta _Z)$
is ample, there exists
$-(K_Z+\Delta _Z)$
is ample, there exists
![]() $0 \leq \lambda <1$
such that
$0 \leq \lambda <1$
such that
![]() $\Delta _Z \equiv - \lambda K_Z$
. Therefore, we deduce
$\Delta _Z \equiv - \lambda K_Z$
. Therefore, we deduce
![]() $(K_Z+\Delta _Z)^2=(1-\lambda )^2K_Z^2 \leq K_Z^2 \leq 9$
, where the last inequality follows by [Reference TanakaTan24, Theorem 1.2].
$(K_Z+\Delta _Z)^2=(1-\lambda )^2K_Z^2 \leq K_Z^2 \leq 9$
, where the last inequality follows by [Reference TanakaTan24, Theorem 1.2].
Suppose
![]() $\dim (B)=1$
. Let
$\dim (B)=1$
. Let
![]() $\Gamma $
be the extremal curve described in Lemma 5.5. We write
$\Gamma $
be the extremal curve described in Lemma 5.5. We write
![]() $\Delta _Z=\alpha \Gamma + G$
, where
$\Delta _Z=\alpha \Gamma + G$
, where
![]() $\text {Supp}(G)$
does not contain
$\text {Supp}(G)$
does not contain
![]() $\Gamma $
. Since the Picard rank of Z is
$\Gamma $
. Since the Picard rank of Z is
![]() $2$
, G is a
$2$
, G is a
![]() $\mathbb {Q}$
-Cartier nef divisor. As
$\mathbb {Q}$
-Cartier nef divisor. As
![]() $-(K_Z+\Delta _Z)$
and
$-(K_Z+\Delta _Z)$
and
![]() $-(K_Z+\alpha \Gamma )$
are big and nef classes, their intersection with G is non-positive, and thus, we have
$-(K_Z+\alpha \Gamma )$
are big and nef classes, their intersection with G is non-positive, and thus, we have
Therefore, it is sufficient to bound the volume of del Pezzo surface pairs
![]() $(Z, \alpha \Gamma )$
, where
$(Z, \alpha \Gamma )$
, where
![]() $Z \to B$
is a Mori fibre space onto a curve,
$Z \to B$
is a Mori fibre space onto a curve,
![]() $\Gamma $
is the extremal curve of Lemma 5.5 and
$\Gamma $
is the extremal curve of Lemma 5.5 and
![]() $0 \leq \alpha <1-\varepsilon $
. Note that
$0 \leq \alpha <1-\varepsilon $
. Note that
Claim 5.7. The self-intersection of
![]() $\Gamma $
is bounded:
$\Gamma $
is bounded:
Proof of Claim
By adjunction,
As
![]() $-(K_Z+\alpha \Gamma )$
is big and nef and
$-(K_Z+\alpha \Gamma )$
is big and nef and
![]() $1-\varepsilon> \alpha $
, we have
$1-\varepsilon> \alpha $
, we have
![]() $(K_Z+\alpha \Gamma )\cdot \Gamma +(1-\varepsilon -\alpha ) \Gamma ^2 \leq 0$
, and therefore, we deduce
$(K_Z+\alpha \Gamma )\cdot \Gamma +(1-\varepsilon -\alpha ) \Gamma ^2 \leq 0$
, and therefore, we deduce
![]() $2 d_\Gamma \geq \varepsilon d_\Gamma \cdot n$
.
$2 d_\Gamma \geq \varepsilon d_\Gamma \cdot n$
.
If
![]() $K_Z \cdot \Gamma \leq 0$
, then
$K_Z \cdot \Gamma \leq 0$
, then
![]() $(K_Z+\alpha \Gamma )^2 \leq K_Z^2 \leq 8$
by Lemma 5.5, and we are done. So, assume
$(K_Z+\alpha \Gamma )^2 \leq K_Z^2 \leq 8$
by Lemma 5.5, and we are done. So, assume
![]() $K_Z \cdot \Gamma>0$
, or, equivalently,
$K_Z \cdot \Gamma>0$
, or, equivalently,
![]() $n>2$
. In this case, we have
$n>2$
. In this case, we have
![]() $d_\Gamma \leq m_\Gamma \leq 5$
by [Reference Bernasconi and TanakaBT22, Proposition 4.7]. Therefore, by Equation (5.3) and Claim 5.7, we deduce the following series of inequalities:
$d_\Gamma \leq m_\Gamma \leq 5$
by [Reference Bernasconi and TanakaBT22, Proposition 4.7]. Therefore, by Equation (5.3) and Claim 5.7, we deduce the following series of inequalities:
 $$ \begin{align*} (K_Z+\alpha \Gamma)^2 & = K_Z^2+d_\Gamma \alpha \left( 2(n-2)-n\alpha \right) \\ & \leq K_Z^2+ 5 \alpha \left( 2n-4\right) \leq K_Z^2+ 5(1-\varepsilon)\left(\frac{4}{\varepsilon}-4\right) \\ & \leq 8+20 \frac{(1-\varepsilon)^2}{\varepsilon}.\\[-42pt] \end{align*} $$
$$ \begin{align*} (K_Z+\alpha \Gamma)^2 & = K_Z^2+d_\Gamma \alpha \left( 2(n-2)-n\alpha \right) \\ & \leq K_Z^2+ 5 \alpha \left( 2n-4\right) \leq K_Z^2+ 5(1-\varepsilon)\left(\frac{4}{\varepsilon}-4\right) \\ & \leq 8+20 \frac{(1-\varepsilon)^2}{\varepsilon}.\\[-42pt] \end{align*} $$
As a consequence, we can show a boundedness result for klt del Pezzo surfaces of bounded Gorenstein index in characteristic
![]() $p>5$
(cf. [Reference Hacon, McKernan and XuHMX14, Corollary 1.8] for the analogue in characteristic 0). In the following, we say that a klt del Pezzo surface is tame if
$p>5$
(cf. [Reference Hacon, McKernan and XuHMX14, Corollary 1.8] for the analogue in characteristic 0). In the following, we say that a klt del Pezzo surface is tame if
![]() $h^1(X,\mathcal {O}_X) = 0$
.
$h^1(X,\mathcal {O}_X) = 0$
.
Corollary 5.8. Let
![]() $n>0$
be an integer. Then, the classes
$n>0$
be an integer. Then, the classes
 $$ \begin{align*} \mathcal{X}_{\mathrm{dP}, n}^{\mathrm{tame}} &=& \left\{ X \mid X\ \mathrm{is\ a\ geometrically\ integral\ tame\ klt\ del\ Pezzo\ surface}\ \mathrm{s.t.}\ nK_X\ \mathrm{is\ Cartier} \right\},\ \mathrm{and} \\ \mathcal{X}_{\mathrm{dP}, n}^{>5} &=& \left\{ X \mid X\ \mathrm{is\ a\ klt\ del\ Pezzo surface}\ \mathrm{s.t.}\ nK_X\ \mathrm{is\ Cartier}\ \mathrm{and}\ \mathrm{char}(H^0(X, \mathcal{O}_X)) \neq 2,3, 5 \right\} \end{align*} $$
$$ \begin{align*} \mathcal{X}_{\mathrm{dP}, n}^{\mathrm{tame}} &=& \left\{ X \mid X\ \mathrm{is\ a\ geometrically\ integral\ tame\ klt\ del\ Pezzo\ surface}\ \mathrm{s.t.}\ nK_X\ \mathrm{is\ Cartier} \right\},\ \mathrm{and} \\ \mathcal{X}_{\mathrm{dP}, n}^{>5} &=& \left\{ X \mid X\ \mathrm{is\ a\ klt\ del\ Pezzo surface}\ \mathrm{s.t.}\ nK_X\ \mathrm{is\ Cartier}\ \mathrm{and}\ \mathrm{char}(H^0(X, \mathcal{O}_X)) \neq 2,3, 5 \right\} \end{align*} $$
are bounded.
Proof. By [Reference Bernasconi and TanakaBT22, Corollary 5.5] and [Reference Bernasconi and TanakaBT22, Theorem 5.7], klt del Pezzo surfaces in characteristic bigger than
![]() $5$
are geometrically integral and tame, so it suffices to show that
$5$
are geometrically integral and tame, so it suffices to show that
![]() $\mathcal {X}_{\text {dP}, n}^{\text {tame}}$
is bounded.
$\mathcal {X}_{\text {dP}, n}^{\text {tame}}$
is bounded.
So, let
![]() $X \in \mathcal {X}_{\text {dP}, n}^{\text {tame}}$
. As X is
$X \in \mathcal {X}_{\text {dP}, n}^{\text {tame}}$
. As X is
![]() $\left (\frac {1}{n} \right )$
-klt, Theorem 5.6 implies that
$\left (\frac {1}{n} \right )$
-klt, Theorem 5.6 implies that
![]() $K_X^2$
is bounded. As the Cartier index of
$K_X^2$
is bounded. As the Cartier index of
![]() $K_X$
is fixed, the set of volumes
$K_X$
is fixed, the set of volumes
![]() $\left \{K_X^2 \mid X \in \mathcal {X}_{\text {dP}, n}^{\text {tame}} \right \}$
is a finite set. As X has rational singularities by Proposition 2.6, we can apply Riemann–Roch to compute for all
$\left \{K_X^2 \mid X \in \mathcal {X}_{\text {dP}, n}^{\text {tame}} \right \}$
is a finite set. As X has rational singularities by Proposition 2.6, we can apply Riemann–Roch to compute for all
![]() $t \geq 1$
:
$t \geq 1$
:
As X is tame,
![]() $\chi (X, \mathcal {O}_X)=1$
, and therefore, there are only a finite number of possibilities for the Hilbert polynomials
$\chi (X, \mathcal {O}_X)=1$
, and therefore, there are only a finite number of possibilities for the Hilbert polynomials
![]() $P_n(t):=\chi (X, \mathcal {O}_X(-ntK_X))$
. Finally, we apply [Reference KollárKol85, Theorem 2.1.2] to conclude that
$P_n(t):=\chi (X, \mathcal {O}_X(-ntK_X))$
. Finally, we apply [Reference KollárKol85, Theorem 2.1.2] to conclude that
![]() $X_{\overline {K}}$
form a bounded family over
$X_{\overline {K}}$
form a bounded family over
![]() $ {\mathrm {Spec}}(\mathbb {Z}[1/30])$
. In particular, there exists
$ {\mathrm {Spec}}(\mathbb {Z}[1/30])$
. In particular, there exists
![]() $m:=m(n)$
such that
$m:=m(n)$
such that
![]() $-mnK_{X_{\overline {K}}}$
is very ample, and thus, by faithfully flat descent,
$-mnK_{X_{\overline {K}}}$
is very ample, and thus, by faithfully flat descent,
![]() $-mnK_{X}$
is very ample. Therefore, there exists
$-mnK_{X}$
is very ample. Therefore, there exists
![]() $N=N(n)>0$
such that
$N=N(n)>0$
such that
![]() $-mnK_{X}$
embeds X into some
$-mnK_{X}$
embeds X into some
![]() $\mathbb {P}^N$
with a finite number of possibilities for the Hilbert polynomial. This concludes that X belongs to a bounded family by a classical Hilbert scheme argument.
$\mathbb {P}^N$
with a finite number of possibilities for the Hilbert polynomial. This concludes that X belongs to a bounded family by a classical Hilbert scheme argument.
5.3. Bounds on the
 $\mathbb {Q}$
-Gorenstein index of
$\mathbb {Q}$
-Gorenstein index of
 $\varepsilon $
-klt del Pezzo surfaces
$\varepsilon $
-klt del Pezzo surfaces
After Corollary 5.8, to conclude the proof of boundedness of
![]() $\varepsilon $
-klt del Pezzo surfaces, we are only left to prove a bound on the Cartier index of
$\varepsilon $
-klt del Pezzo surfaces, we are only left to prove a bound on the Cartier index of
![]() $K_X$
depending only on
$K_X$
depending only on
![]() $\varepsilon $
. We start with the following result, which is well known over perfect fields.
$\varepsilon $
. We start with the following result, which is well known over perfect fields.
Lemma 5.9. Fix
![]() $ \varepsilon \in \mathbb {Q}_{>0}$
and
$ \varepsilon \in \mathbb {Q}_{>0}$
and
![]() $ n \in \mathbb {Z}_{>0}$
. Then, there exists
$ n \in \mathbb {Z}_{>0}$
. Then, there exists
![]() $N = N(\varepsilon ,n)$
such that for every
$N = N(\varepsilon ,n)$
such that for every
![]() $\varepsilon $
-klt surface X admitting a minimal resolution
$\varepsilon $
-klt surface X admitting a minimal resolution
![]() $f \colon Y \to X$
with
$f \colon Y \to X$
with
![]() $\rho (Y) \leq n$
, the divisor
$\rho (Y) \leq n$
, the divisor
![]() $NK_X$
is Cartier.
$NK_X$
is Cartier.
Proof. Without loss of generality, we assume that X is the spectrum of a local ring and that
![]() $\rho (Y) = n$
. Let
$\rho (Y) = n$
. Let
![]() $E= \sum _{i=1}^n E_i$
be the sum of the exceptional divisors of f, and write
$E= \sum _{i=1}^n E_i$
be the sum of the exceptional divisors of f, and write
![]() $K_Y + \sum _{i=1}^n b_i E_i =f^*K_X$
for some
$K_Y + \sum _{i=1}^n b_i E_i =f^*K_X$
for some
![]() $0 \leq b_i< 1-\varepsilon $
. By the base point free theorem [Reference TanakaTan18b, Theorem 4.2], it suffices to find an effective
$0 \leq b_i< 1-\varepsilon $
. By the base point free theorem [Reference TanakaTan18b, Theorem 4.2], it suffices to find an effective
![]() $N=N(\varepsilon ,n)$
such that
$N=N(\varepsilon ,n)$
such that
![]() $Nb_i$
is integral. For each i, we write
$Nb_i$
is integral. For each i, we write
![]() $E_i^2 = -d_{E_i} n_i$
for some integer
$E_i^2 = -d_{E_i} n_i$
for some integer
![]() $n_i>0$
, where
$n_i>0$
, where
![]() $d_{E_i} = [H^0(E_i,\mathcal {O}_{E_i}):k]$
. Moreover, for each
$d_{E_i} = [H^0(E_i,\mathcal {O}_{E_i}):k]$
. Moreover, for each
![]() $i \neq j$
, we write
$i \neq j$
, we write
![]() $E_i \cdot E_j = d_{E_j} n_{ij}$
for some
$E_i \cdot E_j = d_{E_j} n_{ij}$
for some
![]() $n_{ij}>0$
. The
$n_{ij}>0$
. The
![]() $b_i$
are determined by the following system of equations:
$b_i$
are determined by the following system of equations:
Since X is
![]() $\varepsilon $
-klt, we have
$\varepsilon $
-klt, we have
Indeed,
 $$ \begin{align*} \begin{split} 0 & =(K_Y+\sum b_iE_i) \cdot E_j \geq (K_Y+b_j E_j) \cdot E_j \\ & \geq -2d_{E_j} + (b_j-1) \cdot (-d_{E_j}n_j) \geq -2d_{E_j}+\varepsilon n_jd_{E_j}. \\ \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} 0 & =(K_Y+\sum b_iE_i) \cdot E_j \geq (K_Y+b_j E_j) \cdot E_j \\ & \geq -2d_{E_j} + (b_j-1) \cdot (-d_{E_j}n_j) \geq -2d_{E_j}+\varepsilon n_jd_{E_j}. \\ \end{split} \end{align*} $$
Moreover,
![]() $n_{ij}$
is bounded from above by [Reference KollárKol13, Corollary 3.31 and Section 3.41] and [Reference SatoSat23, Appendix A]. As the
$n_{ij}$
is bounded from above by [Reference KollárKol13, Corollary 3.31 and Section 3.41] and [Reference SatoSat23, Appendix A]. As the
![]() $n_i$
and
$n_i$
and
![]() $n_{ij}$
are integers, we only have a finite number of possibilities for the coefficients in Equation 5.4, so we conclude that there are only finitely many possibilities for the solutions
$n_{ij}$
are integers, we only have a finite number of possibilities for the coefficients in Equation 5.4, so we conclude that there are only finitely many possibilities for the solutions
![]() $b_i$
, thus showing the existence of a
$b_i$
, thus showing the existence of a
![]() $N(\varepsilon , n)$
for which
$N(\varepsilon , n)$
for which
![]() $Nb_i$
is integral.
$Nb_i$
is integral.
Lemma 5.10. Let X be a geometrically integral regular projective surface of del Pezzo type over k, and let
![]() $\pi \colon X \to B$
be a Mori fibre space. Let
$\pi \colon X \to B$
be a Mori fibre space. Let
![]() $\Delta =\sum b_i E_i$
be an effective
$\Delta =\sum b_i E_i$
be an effective
![]() $\mathbb {Q}$
-divisor such that
$\mathbb {Q}$
-divisor such that
![]() $(X,\Delta )$
is klt and
$(X,\Delta )$
is klt and
![]() $-(K_X+\Delta )$
is nef. Then
$-(K_X+\Delta )$
is nef. Then
-
1. if
 $\dim (B)=0$
, then
$\dim (B)=0$
, then
 $\sum b_i \leq 3$
;
$\sum b_i \leq 3$
; -
2. if
 $\dim (B)=1$
, then
$\dim (B)=1$
, then
 $\sum b_i \leq 4$
.
$\sum b_i \leq 4$
.
Proof. Suppose
![]() $\dim (B)=0$
. Let H be an ample Cartier divisor generating
$\dim (B)=0$
. Let H be an ample Cartier divisor generating
![]() $ {\mathrm {Num}}(X)$
, and let
$ {\mathrm {Num}}(X)$
, and let
![]() $d \geq 0$
such that
$d \geq 0$
such that
![]() $-K_X \equiv dH$
. As X is a regular del Pezzo surface, we have
$-K_X \equiv dH$
. As X is a regular del Pezzo surface, we have
![]() $K_X^2 \leq 9$
by [Reference TanakaTan24, Theorem 1.2], and therefore,
$K_X^2 \leq 9$
by [Reference TanakaTan24, Theorem 1.2], and therefore,
![]() $d \leq 3$
. Since X is regular, the
$d \leq 3$
. Since X is regular, the
![]() $B_i$
are Cartier divisors, and thus,
$B_i$
are Cartier divisors, and thus,
![]() $\sum b_i \leq 3$
.
$\sum b_i \leq 3$
.
Suppose
![]() $\dim (B)=1$
. Let
$\dim (B)=1$
. Let
![]() $F_b$
be a closed fibre of
$F_b$
be a closed fibre of
![]() $\pi $
and
$\pi $
and
![]() $\Gamma $
the curve given by Lemma 5.5. Set
$\Gamma $
the curve given by Lemma 5.5. Set ![]() . We write
. We write
![]() $\Delta =b_0\Gamma + \sum b_iE_i$
as a sum of pairwise distinct prime divisors. As
$\Delta =b_0\Gamma + \sum b_iE_i$
as a sum of pairwise distinct prime divisors. As
![]() $0 \geq (K_X+\Delta ) \cdot F_b$
, adjunction implies
$0 \geq (K_X+\Delta ) \cdot F_b$
, adjunction implies
As
![]() $K_X \cdot \Gamma =d_\Gamma (n-2)$
,
$K_X \cdot \Gamma =d_\Gamma (n-2)$
,
![]() $0 \geq (K_X+\Delta ) \cdot \Gamma $
, and
$0 \geq (K_X+\Delta ) \cdot \Gamma $
, and
![]() $b_0 \leq 1$
, adjunction implies
$b_0 \leq 1$
, adjunction implies
Summing the two equations and using that every curve on X intersects either
![]() $\Gamma $
or
$\Gamma $
or
![]() $F_b$
, we obtain
$F_b$
, we obtain
![]() $ 4 \geq \sum b_i, $
as desired.
$ 4 \geq \sum b_i, $
as desired.
Proposition 5.11. Let
![]() $\varepsilon>0$
. Then, there exists a constant
$\varepsilon>0$
. Then, there exists a constant
![]() $D(\varepsilon )$
such that for all geometrically integral
$D(\varepsilon )$
such that for all geometrically integral
![]() $\varepsilon $
-klt del Pezzo surfaces X, the minimal resolution
$\varepsilon $
-klt del Pezzo surfaces X, the minimal resolution
![]() $f \colon Y \to X$
satisfies
$f \colon Y \to X$
satisfies
![]() $\rho (Y) \leq D(\varepsilon ).$
$\rho (Y) \leq D(\varepsilon ).$
Proof. We can suppose k is separably closed. We follow the computations of [Reference Alexeev and MoriAM04, Theorem 1.8], verifying that the explicit classification of rational Mori fibre spaces over algebraically closed fields is not needed. Without loss of generality, we can suppose
![]() $\varepsilon < \frac {2}{3}$
. Since
$\varepsilon < \frac {2}{3}$
. Since
![]() $-K_X$
is ample, by Bertini’s theorem, we can choose
$-K_X$
is ample, by Bertini’s theorem, we can choose
![]() $H \sim _{\mathbb {Q}} -K_X$
to be an effective
$H \sim _{\mathbb {Q}} -K_X$
to be an effective
![]() $\mathbb {Q}$
-divisor whose support is regular and contained in the regular locus of X such that
$\mathbb {Q}$
-divisor whose support is regular and contained in the regular locus of X such that
![]() $(X,H)$
is
$(X,H)$
is
![]() $\varepsilon $
-klt. Let
$\varepsilon $
-klt. Let
![]() $f \colon Y \to X$
be the minimal resolution and write
$f \colon Y \to X$
be the minimal resolution and write
![]() $K_Y+\Gamma _Y = f^*(K_X+H) \sim _{\mathbb {Q}} 0$
, where
$K_Y+\Gamma _Y = f^*(K_X+H) \sim _{\mathbb {Q}} 0$
, where ![]() and
and
![]() $b_i < 1- \varepsilon $
by hypothesis. We run a
$b_i < 1- \varepsilon $
by hypothesis. We run a
![]() $K_Y$
-MMP which ends with
$K_Y$
-MMP which ends with
![]() $g \colon Y \to Z$
, where Z is a regular projective surface admitting a Mori fibre space structure
$g \colon Y \to Z$
, where Z is a regular projective surface admitting a Mori fibre space structure
![]() $\pi \colon Z \to B$
. We summarise the situation in the following diagram:
$\pi \colon Z \to B$
. We summarise the situation in the following diagram:

We fix the following notation:
-
○
 .
. -
○
 .
. -
○

-
○
 .
. -
○

Note that, by construction, g is a
![]() $(K_Y+\Delta _Y)$
-non-positive (resp.
$(K_Y+\Delta _Y)$
-non-positive (resp.
![]() $(K_Y+\Gamma _Y)$
-trivial) birational contraction and
$(K_Y+\Gamma _Y)$
-trivial) birational contraction and
![]() $(Z, \Delta _Z)$
(resp.
$(Z, \Delta _Z)$
(resp.
![]() $(Z, \Gamma _Z)$
) is a log del Pezzo pair (resp. Calabi–Yau pair) with
$(Z, \Gamma _Z)$
) is a log del Pezzo pair (resp. Calabi–Yau pair) with
![]() $\varepsilon $
-klt singularities.
$\varepsilon $
-klt singularities.
The morphism g is a composition of blow-ups of closed points on regular surfaces by [Sta, Tag 0C5R]. We can decompose g as
where
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
are proper birational morphisms between regular surfaces such that
$\varphi $
are proper birational morphisms between regular surfaces such that
-
1.
 $\varphi $
is a composition of blow-ups at closed points P such that
$\varphi $
is a composition of blow-ups at closed points P such that
 $\text {mult}_P(\widetilde {\Gamma _Z})$
has multiplicity at least
$\text {mult}_P(\widetilde {\Gamma _Z})$
has multiplicity at least
 $\nu :=\frac {\varepsilon }{2}$
, where
$\nu :=\frac {\varepsilon }{2}$
, where
 $\widetilde {\Gamma _Z}$
denotes the strict transform of
$\widetilde {\Gamma _Z}$
denotes the strict transform of
 $\Gamma _Z$
;
$\Gamma _Z$
; -
2.
 $\psi $
is a composition of blow-ups at closed points P, where
$\psi $
is a composition of blow-ups at closed points P, where
 $\text {mult}_P(\widetilde {\Gamma _Z})$
has multiplicity
$\text {mult}_P(\widetilde {\Gamma _Z})$
has multiplicity
 $< \nu $
.
$< \nu $
.
We first bound
![]() $\rho (W/Z)$
in terms of
$\rho (W/Z)$
in terms of
![]() $\varepsilon $
. On Y, as
$\varepsilon $
. On Y, as
![]() $f_*^{-1}H$
is big and nef, we can apply Equation (5.5) to obtain
$f_*^{-1}H$
is big and nef, we can apply Equation (5.5) to obtain
 $$ \begin{align} (g_*^{-1}\Gamma_Z)^2 \geq \sum_{i \in I} b_i^2 (g_*^{-1} E_{i,Z})^2 \geq \sum_{i \in I_Z} b_{i} (1-\varepsilon)\left(\frac{-2}{\varepsilon}\right). \end{align} $$
$$ \begin{align} (g_*^{-1}\Gamma_Z)^2 \geq \sum_{i \in I} b_i^2 (g_*^{-1} E_{i,Z})^2 \geq \sum_{i \in I_Z} b_{i} (1-\varepsilon)\left(\frac{-2}{\varepsilon}\right). \end{align} $$
If
![]() $\dim (B)=0$
(resp.
$\dim (B)=0$
(resp.
![]() $1$
), we have
$1$
), we have
![]() $\sum _{i \in I_Z} b_i \leq 4$
(resp.
$\sum _{i \in I_Z} b_i \leq 4$
(resp.
![]() $\leq 3$
) by Lemma 5.10, and thus,
$\leq 3$
) by Lemma 5.10, and thus,
 $$ \begin{align} (g_{*}^{-1}\Gamma_Z)^2 \geq \begin{cases} 6-\frac{6}{\varepsilon} \text{ if } \dim(B)=0 \\ 8-\frac{8}{\varepsilon} \text{ if } \dim(B)=1. \end{cases} \end{align} $$
$$ \begin{align} (g_{*}^{-1}\Gamma_Z)^2 \geq \begin{cases} 6-\frac{6}{\varepsilon} \text{ if } \dim(B)=0 \\ 8-\frac{8}{\varepsilon} \text{ if } \dim(B)=1. \end{cases} \end{align} $$
After each of the blow-ups in
![]() $\varphi $
, the self-intersection of
$\varphi $
, the self-intersection of
![]() $\widetilde {\Gamma _Z}$
decreases by at least
$\widetilde {\Gamma _Z}$
decreases by at least
![]() $\nu ^2$
, and we deduce that
$\nu ^2$
, and we deduce that
![]() $(g_*^{-1}\Gamma _Z)^2 \leq \Gamma _Z^2-\nu ^2 \rho (W/Z)$
. If
$(g_*^{-1}\Gamma _Z)^2 \leq \Gamma _Z^2-\nu ^2 \rho (W/Z)$
. If
![]() $\dim (B)=0$
(resp.
$\dim (B)=0$
(resp.
![]() $1$
), then
$1$
), then
![]() $\Gamma _Z^2=K_Z^2 \leq 9$
(resp.
$\Gamma _Z^2=K_Z^2 \leq 9$
(resp.
![]() $8$
) by [Reference TanakaTan24, Theorem 1.2] (resp. Lemma 5.5). Therefore,
$8$
) by [Reference TanakaTan24, Theorem 1.2] (resp. Lemma 5.5). Therefore,
![]() $ (g_*^{-1}\Gamma _Z)^2 \leq 9-\nu ^2 \rho (W/Z)$
(resp.
$ (g_*^{-1}\Gamma _Z)^2 \leq 9-\nu ^2 \rho (W/Z)$
(resp.
![]() $8-\nu ^2 \rho (W/Z)$
). Together with (5.9), we conclude
$8-\nu ^2 \rho (W/Z)$
). Together with (5.9), we conclude
 $$ \begin{align} \rho(W/Z) \leq \begin{cases} \frac{(3\varepsilon + 6)}{\varepsilon \nu^2} \text{if } \dim(B)=0; \\ \frac{8}{\varepsilon \nu^2} \text{ if } \dim(B)=1. \end{cases} \end{align} $$
$$ \begin{align} \rho(W/Z) \leq \begin{cases} \frac{(3\varepsilon + 6)}{\varepsilon \nu^2} \text{if } \dim(B)=0; \\ \frac{8}{\varepsilon \nu^2} \text{ if } \dim(B)=1. \end{cases} \end{align} $$
As we chose
![]() $\varepsilon < \frac {2}{3}$
, we have
$\varepsilon < \frac {2}{3}$
, we have
![]() $\frac {(3\varepsilon + 6)}{\varepsilon \nu ^2}< \frac {8}{\varepsilon \nu ^2} $
.
$\frac {(3\varepsilon + 6)}{\varepsilon \nu ^2}< \frac {8}{\varepsilon \nu ^2} $
.
We now prove a bound on
![]() $\rho (Y/W)$
depending only on
$\rho (Y/W)$
depending only on
![]() $\varepsilon $
. Let
$\varepsilon $
. Let
![]() $F=\sum _{i \in J} F_i$
be the sum of the exceptional divisors of
$F=\sum _{i \in J} F_i$
be the sum of the exceptional divisors of
![]() $\varphi $
and let
$\varphi $
and let
![]() $f_i:=\text {coeff}_{F_i}(\Gamma _W)$
, where
$f_i:=\text {coeff}_{F_i}(\Gamma _W)$
, where ![]() . As W and Z are regular surfaces,
. As W and Z are regular surfaces,
![]() $\text {Supp}(F)$
is an snc divisor. Let
$\text {Supp}(F)$
is an snc divisor. Let
![]() $\psi \colon Y \xrightarrow {s} T \xrightarrow {t} W$
be a factorisation of
$\psi \colon Y \xrightarrow {s} T \xrightarrow {t} W$
be a factorisation of
![]() $\psi $
, where t is a blow-up at a point P of W with exceptional divisor C. Write
$\psi $
, where t is a blow-up at a point P of W with exceptional divisor C. Write
We claim that P must lie on the intersection of two components
![]() $F_1$
and
$F_1$
and
![]() $F_2$
of F. For this, let
$F_2$
of F. For this, let ![]() . Then, since
. Then, since
![]() $\text {mult}_P(\widetilde {\Gamma }_Z) \leq \nu < \varepsilon $
and
$\text {mult}_P(\widetilde {\Gamma }_Z) \leq \nu < \varepsilon $
and
![]() $f_i < 1-\varepsilon $
, we have that
$f_i < 1-\varepsilon $
, we have that
Hence,
![]() $|J_F| \geq 2$
. Since
$|J_F| \geq 2$
. Since
![]() $\mathrm {Supp}(F)$
is an snc divisor, this implies
$\mathrm {Supp}(F)$
is an snc divisor, this implies
![]() $|J_F| = 2$
, as desired. This argument can be repeated for each blow-up
$|J_F| = 2$
, as desired. This argument can be repeated for each blow-up
![]() $T \to W$
factorising
$T \to W$
factorising
![]() $Y \to W$
.
$Y \to W$
.
As the number of nodes of F is bounded by
![]() $\rho (W/Z)-1$
, it remains to bound the number of times we are allowed to blow-up along a node to obtain a bound on
$\rho (W/Z)-1$
, it remains to bound the number of times we are allowed to blow-up along a node to obtain a bound on
![]() $\rho (Y/W)$
. This follows from a straightforward induction as in [Reference Alexeev and MoriAM04, Lemma 1.9]. An explicit computation shows that
$\rho (Y/W)$
. This follows from a straightforward induction as in [Reference Alexeev and MoriAM04, Lemma 1.9]. An explicit computation shows that
 $$ \begin{align*}\rho(Y)=\rho(Y/W)+\rho(W/Z)+\rho(Z) \leq \left(\frac{1}{(\varepsilon-\nu)^2}-1 \right) \cdot \left( \frac{8}{\varepsilon \nu^2} -1 \right) + \left( \frac{8}{\varepsilon \nu^2} \right) +2.\end{align*} $$
$$ \begin{align*}\rho(Y)=\rho(Y/W)+\rho(W/Z)+\rho(Z) \leq \left(\frac{1}{(\varepsilon-\nu)^2}-1 \right) \cdot \left( \frac{8}{\varepsilon \nu^2} -1 \right) + \left( \frac{8}{\varepsilon \nu^2} \right) +2.\end{align*} $$
As
![]() $\nu =\frac {\varepsilon }{2}$
, we deduce that
$\nu =\frac {\varepsilon }{2}$
, we deduce that
 $$ \begin{align*} \rho(Y) \leq \frac{128}{\varepsilon^5}+\left(3-\frac{4}{\varepsilon^2}\right) \leq \frac{128}{\varepsilon^5}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \rho(Y) \leq \frac{128}{\varepsilon^5}+\left(3-\frac{4}{\varepsilon^2}\right) \leq \frac{128}{\varepsilon^5}.\\[-42pt] \end{align*} $$
We now have all the ingredients to prove the BAB conjecture in dimension 2 and characteristic
![]() $p \neq 2, 3 $
and
$p \neq 2, 3 $
and
![]() $5$
.
$5$
.
Theorem 5.12. Let
![]() $\varepsilon>0$
be a rational number. Then, the classes
$\varepsilon>0$
be a rational number. Then, the classes
 $$ \begin{align*} \mathcal{X}_{\mathrm{dP}, \varepsilon}^{\mathrm{tame}} &= \left\{ X \mid X\ \mathrm{is\ a\ geometrically\ integral\ tame}\ \varepsilon\text{-}\mathrm{klt\ del\ Pezzo\ surface}\right\},\ \mathrm{and} \\ \mathcal{X}_{\mathrm{dP}, \varepsilon}^{>5} &= \left\{ X \mid X\ \mathrm{is\ an}\ \varepsilon\text{-}\mathrm{klt\ del\ Pezzo\ surface\ s.t.\ char}(H^0(X, \mathcal{O}_X)) \neq 2, 3, 5 \right\} \end{align*} $$
$$ \begin{align*} \mathcal{X}_{\mathrm{dP}, \varepsilon}^{\mathrm{tame}} &= \left\{ X \mid X\ \mathrm{is\ a\ geometrically\ integral\ tame}\ \varepsilon\text{-}\mathrm{klt\ del\ Pezzo\ surface}\right\},\ \mathrm{and} \\ \mathcal{X}_{\mathrm{dP}, \varepsilon}^{>5} &= \left\{ X \mid X\ \mathrm{is\ an}\ \varepsilon\text{-}\mathrm{klt\ del\ Pezzo\ surface\ s.t.\ char}(H^0(X, \mathcal{O}_X)) \neq 2, 3, 5 \right\} \end{align*} $$
are bounded.
Proof. By Lemma 5.9 and Proposition 5.11, there exists
![]() $n=n(\varepsilon )>0$
such that
$n=n(\varepsilon )>0$
such that
![]() $-nK_X$
is Cartier for all geometrically integral
$-nK_X$
is Cartier for all geometrically integral
![]() $\varepsilon $
-klt del Pezzo surfaces X. Hence, we can apply Corollary 5.8 to conclude that
$\varepsilon $
-klt del Pezzo surfaces X. Hence, we can apply Corollary 5.8 to conclude that
![]() $\mathcal {X}_{\text {dP}, \varepsilon }^{\text {tame}} $
and
$\mathcal {X}_{\text {dP}, \varepsilon }^{\text {tame}} $
and
![]() $\mathcal {X}_{\text {dP}, \varepsilon }^{>5}$
are bounded.
$\mathcal {X}_{\text {dP}, \varepsilon }^{>5}$
are bounded.
Remark 5.13. To prove the geometrically integral case of the BAB conjecture in characteristic
![]() $p \leq 5$
, the missing ingredient is a bound on the irregularity for
$p \leq 5$
, the missing ingredient is a bound on the irregularity for
![]() $\varepsilon $
-klt del Pezzo surface. While the canonical case (the characteristic
$\varepsilon $
-klt del Pezzo surface. While the canonical case (the characteristic
![]() $p>5$
klt case) has been treated in Theorem 1.2 (resp. [Reference Bernasconi and TanakaBT22, Theorem 5.7]), we are not able to prove a similar bound in the general case. Note that klt del Pezzo surfaces with
$p>5$
klt case) has been treated in Theorem 1.2 (resp. [Reference Bernasconi and TanakaBT22, Theorem 5.7]), we are not able to prove a similar bound in the general case. Note that klt del Pezzo surfaces with
![]() $h^1(X, \mathcal {O}_X)=1$
are constructed in [Reference TanakaTan20] over fields k of characteristic
$h^1(X, \mathcal {O}_X)=1$
are constructed in [Reference TanakaTan20] over fields k of characteristic
![]() $p=2, 3$
and
$p=2, 3$
and
![]() $ {\mathrm {p-deg}}(k)=1$
.
$ {\mathrm {p-deg}}(k)=1$
.
Acknowledgements
We would like to thank A. Fanelli, S. Filipazzi, J. Waldron and H. Tanaka for useful discussions on the topic of this article. This work started at EPFL and then continued at the University of Bonn during mutual visits. We would like to thank both universities for the support. Part of this work was written while the first author was visiting l’Université de Poitiers within the program ‘Chaire Aliénor’ of the Fédération MARGAUx: he would like to thank S. Boissière for the kind hospitality.
Competing interests
The authors have no competing interest to declare.
Ethical Standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.