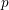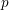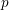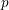1 Introduction
In the celebrated paper [Reference TateTat67], Tate studied the Galois cohomology of
![]() $p$
-adic fields and obtained the so-called Hodge–Tate decomposition of the Tate module of a
$p$
-adic fields and obtained the so-called Hodge–Tate decomposition of the Tate module of a
![]() $p$
-divisible group with good reduction. The paper has been influential in the developments of
$p$
-divisible group with good reduction. The paper has been influential in the developments of
![]() $p$
-adic Hodge theory, and one of the earliest progresses was done by Sen. In [Reference SenSen81], he attached to each
$p$
-adic Hodge theory, and one of the earliest progresses was done by Sen. In [Reference SenSen81], he attached to each
![]() $p$
-adic Galois representation of a
$p$
-adic Galois representation of a
![]() $p$
-adic field
$p$
-adic field
![]() $k$
a multiset of numbers that are algebraic over
$k$
a multiset of numbers that are algebraic over
![]() $k$
. These numbers are called generalized Hodge–Tate weights, and they serve as one of the basic invariants in
$k$
. These numbers are called generalized Hodge–Tate weights, and they serve as one of the basic invariants in
![]() $p$
-adic Hodge theory, especially for the study of Galois representations that may not be Hodge–Tate (e.g. Galois representations attached to finite slope overconvergent modular forms).
$p$
-adic Hodge theory, especially for the study of Galois representations that may not be Hodge–Tate (e.g. Galois representations attached to finite slope overconvergent modular forms).
In this paper, we study how generalized Hodge–Tate weights vary in a geometric family. To be precise, we consider an étale
![]() $\mathbb{Q}_{p}$
-local system on a rigid analytic varieties over
$\mathbb{Q}_{p}$
-local system on a rigid analytic varieties over
![]() $k$
and regard it as a family of Galois representations of residue fields of its classical points. Here is one of the main theorems of this paper.
$k$
and regard it as a family of Galois representations of residue fields of its classical points. Here is one of the main theorems of this paper.
Theorem 1.1 (Corollary 4.9).
Let
![]() $X$
be a geometrically connected smooth rigid analytic variety over
$X$
be a geometrically connected smooth rigid analytic variety over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X$
. Then the generalized Hodge–Tate weights of the
$X$
. Then the generalized Hodge–Tate weights of the
![]() $p$
-adic Galois representations
$p$
-adic Galois representations
![]() $\mathbb{L}_{\overline{x}}$
of
$\mathbb{L}_{\overline{x}}$
of
![]() $k(x)$
are constant on the set of classical points
$k(x)$
are constant on the set of classical points
![]() $x$
of
$x$
of
![]() $X$
.
$X$
.
The theorem gives one instance of the rigidity of a geometric family of Galois representations. It is worth noting that arithmetic families of Galois representations do not have such rigidity; consider a representation of the absolute Galois group of
![]() $k$
with coefficients in some
$k$
with coefficients in some
![]() $\mathbb{Q}_{p}$
-affinoid algebra. One can associate to each maximal ideal a Galois representation of
$\mathbb{Q}_{p}$
-affinoid algebra. One can associate to each maximal ideal a Galois representation of
![]() $k$
. In such a situation, the generalized Hodge–Tate weights vary over the maximal ideals.
$k$
. In such a situation, the generalized Hodge–Tate weights vary over the maximal ideals.
To explain ideas of the proof of Theorem 1.1 as well as other results of this paper, let us recall the work of Sen mentioned above. For each
![]() $p$
-adic Galois representation
$p$
-adic Galois representation
![]() $V$
of
$V$
of
![]() $k$
, we set
$k$
, we set
where
![]() $\mathbb{C}_{p}$
is the
$\mathbb{C}_{p}$
is the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $\overline{k}$
and
$\overline{k}$
and
![]() $k_{\infty }:=k(\unicode[STIX]{x1D707}_{p^{\infty }})$
is the cyclotomic extension of
$k_{\infty }:=k(\unicode[STIX]{x1D707}_{p^{\infty }})$
is the cyclotomic extension of
![]() $k$
. This is a vector space over the
$k$
. This is a vector space over the
![]() $p$
-adic completion
$p$
-adic completion
![]() $K$
of
$K$
of
![]() $k_{\infty }$
equipped with a continuous semilinear action of
$k_{\infty }$
equipped with a continuous semilinear action of
![]() $\operatorname{Gal}(k_{\infty }/k)$
and satisfies
$\operatorname{Gal}(k_{\infty }/k)$
and satisfies
![]() $\dim _{K}{\mathcal{H}}(V)=\dim _{\mathbb{Q}_{p}}V$
. Sen developed a theory of decompletion; he found a natural
$\dim _{K}{\mathcal{H}}(V)=\dim _{\mathbb{Q}_{p}}V$
. Sen developed a theory of decompletion; he found a natural
![]() $k_{\infty }$
-vector subspace
$k_{\infty }$
-vector subspace
![]() ${\mathcal{H}}(V)_{\text{fin}}\subset {\mathcal{H}}(V)$
that is stable under
${\mathcal{H}}(V)_{\text{fin}}\subset {\mathcal{H}}(V)$
that is stable under
![]() $\operatorname{Gal}(k_{\infty }/k)$
-action and satisfies
$\operatorname{Gal}(k_{\infty }/k)$
-action and satisfies
![]() ${\mathcal{H}}(V)_{\text{fin}}\otimes _{k_{\infty }}K={\mathcal{H}}(V)$
. He then defined a
${\mathcal{H}}(V)_{\text{fin}}\otimes _{k_{\infty }}K={\mathcal{H}}(V)$
. He then defined a
![]() $k_{\infty }$
-endomorphism
$k_{\infty }$
-endomorphism
![]() $\unicode[STIX]{x1D719}_{V}$
on
$\unicode[STIX]{x1D719}_{V}$
on
![]() ${\mathcal{H}}(V)_{\text{fin}}$
, called the Sen endomorphism of
${\mathcal{H}}(V)_{\text{fin}}$
, called the Sen endomorphism of
![]() $V$
, by considering the infinitesimal action of
$V$
, by considering the infinitesimal action of
![]() $\operatorname{Gal}(k_{\infty }/k)$
. The generalized Hodge–Tate weights are defined to be eigenvalues of
$\operatorname{Gal}(k_{\infty }/k)$
. The generalized Hodge–Tate weights are defined to be eigenvalues of
![]() $\unicode[STIX]{x1D719}_{V}$
.
$\unicode[STIX]{x1D719}_{V}$
.
Therefore, the first step toward Theorem 1.1 is to define generalizations of
![]() ${\mathcal{H}}(V)$
and
${\mathcal{H}}(V)$
and
![]() $\unicode[STIX]{x1D719}_{V}$
for each
$\unicode[STIX]{x1D719}_{V}$
for each
![]() $\mathbb{Q}_{p}$
-local system. For this, we use the
$\mathbb{Q}_{p}$
-local system. For this, we use the
![]() $p$
-adic Simpson correspondence by Liu and Zhu [Reference Liu and ZhuLZ17]; based on recent developments in relative
$p$
-adic Simpson correspondence by Liu and Zhu [Reference Liu and ZhuLZ17]; based on recent developments in relative
![]() $p$
-adic Hodge theory by Kedlaya–Liu and Scholze, Liu and Zhu associated to each
$p$
-adic Hodge theory by Kedlaya–Liu and Scholze, Liu and Zhu associated to each
![]() $\mathbb{Q}_{p}$
-local system
$\mathbb{Q}_{p}$
-local system
![]() $\mathbb{L}$
on
$\mathbb{L}$
on
![]() $X$
a vector bundle
$X$
a vector bundle
![]() ${\mathcal{H}}(\mathbb{L})$
of the same rank on
${\mathcal{H}}(\mathbb{L})$
of the same rank on
![]() $X_{K}$
equipped with a
$X_{K}$
equipped with a
![]() $\operatorname{Gal}(k_{\infty }/k)$
-action and a Higgs field, where
$\operatorname{Gal}(k_{\infty }/k)$
-action and a Higgs field, where
![]() $X_{K}$
is the base change of
$X_{K}$
is the base change of
![]() $X$
to
$X$
to
![]() $K$
. When
$K$
. When
![]() $X$
is a point and
$X$
is a point and
![]() $\mathbb{L}$
corresponds to
$\mathbb{L}$
corresponds to
![]() $V$
, this agrees with
$V$
, this agrees with
![]() ${\mathcal{H}}(V)$
as the notation suggests. Following Sen, we will define the arithmetic Sen endomorphism
${\mathcal{H}}(V)$
as the notation suggests. Following Sen, we will define the arithmetic Sen endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
of
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
of
![]() $\mathbb{L}$
by decompleting
$\mathbb{L}$
by decompleting
![]() ${\mathcal{H}}(\mathbb{L})$
and considering the infinitesimal action of
${\mathcal{H}}(\mathbb{L})$
and considering the infinitesimal action of
![]() $\operatorname{Gal}(k_{\infty }/k)$
. Then Theorem 1.1 is reduced to the following.
$\operatorname{Gal}(k_{\infty }/k)$
. Then Theorem 1.1 is reduced to the following.
Theorem 1.2 (Theorem 4.8).
The eigenvalues of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L},x}$
for
$\unicode[STIX]{x1D719}_{\mathbb{L},x}$
for
![]() $x\in X_{K}$
are algebraic over
$x\in X_{K}$
are algebraic over
![]() $k$
and constant on
$k$
and constant on
![]() $X_{K}$
.
$X_{K}$
.
Before discussing ideas of the proof, let us mention consequences of Theorem 1.2. Sen proved that a
![]() $p$
-adic Galois representation
$p$
-adic Galois representation
![]() $V$
is Hodge–Tate if and only if
$V$
is Hodge–Tate if and only if
![]() $\unicode[STIX]{x1D719}_{V}$
is semisimple with integer eigenvalues. In the same way, we use
$\unicode[STIX]{x1D719}_{V}$
is semisimple with integer eigenvalues. In the same way, we use
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
to study Hodge–Tate sheaves. We define a sheaf
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
to study Hodge–Tate sheaves. We define a sheaf
![]() $D_{\text{HT}}(\mathbb{L})$
on the étale site
$D_{\text{HT}}(\mathbb{L})$
on the étale site
![]() $X_{\acute{\text{e}}\text{t}}$
by
$X_{\acute{\text{e}}\text{t}}$
by
where
![]() ${\mathcal{O}}\mathbb{B}_{\text{HT}}$
is the Hodge–Tate period sheaf on the pro-étale site
${\mathcal{O}}\mathbb{B}_{\text{HT}}$
is the Hodge–Tate period sheaf on the pro-étale site
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
and
$X_{\text{pro}\acute{\text{e}}\text{t}}$
and
![]() $\unicode[STIX]{x1D708}:X_{\text{pro}\acute{\text{e}}\text{t}}\rightarrow X_{\acute{\text{e}}\text{t}}$
is the projection (see § 5). A
$\unicode[STIX]{x1D708}:X_{\text{pro}\acute{\text{e}}\text{t}}\rightarrow X_{\acute{\text{e}}\text{t}}$
is the projection (see § 5). A
![]() $\mathbb{Q}_{p}$
-local system
$\mathbb{Q}_{p}$
-local system
![]() $\mathbb{L}$
is called Hodge–Tate if
$\mathbb{L}$
is called Hodge–Tate if
![]() $D_{\text{HT}}(\mathbb{L})$
is a vector bundle on
$D_{\text{HT}}(\mathbb{L})$
is a vector bundle on
![]() $X$
of rank equal to
$X$
of rank equal to
![]() $\operatorname{rank}\mathbb{L}$
.
$\operatorname{rank}\mathbb{L}$
.
Theorem 1.3 (Theorem 5.5).
The following conditions are equivalent for a
![]() $\mathbb{Q}_{p}$
-local system
$\mathbb{Q}_{p}$
-local system
![]() $\mathbb{L}$
on
$\mathbb{L}$
on
![]() $X$
:
$X$
:
(i)
 $\mathbb{L}$
is Hodge–Tate;
$\mathbb{L}$
is Hodge–Tate;(ii)
 $\unicode[STIX]{x1D719}_{\mathbb{L}}$
is semisimple with integer eigenvalues.
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
is semisimple with integer eigenvalues.
The study of the Sen endomorphism for a geometric family was initiated by Brinon as a generalization of Sen’s theory to the case of non-perfect residue fields [Reference BrinonBri03]. Tsuji obtained Theorem 1.3 in the case of schemes with semistable reduction [Reference TsujiTsu11].
Using this characterization, we prove the following basic property of Hodge–Tate sheaves.
Theorem 1.4 (Theorem 5.10).
Let
![]() $f:X\rightarrow Y$
be a smooth proper morphism between smooth rigid analytic varieties over
$f:X\rightarrow Y$
be a smooth proper morphism between smooth rigid analytic varieties over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Z}_{p}$
-local system on
$\mathbb{Z}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Then if
$X_{\acute{\text{e}}\text{t}}$
. Then if
![]() $\mathbb{L}$
is a Hodge–Tate sheaf on
$\mathbb{L}$
is a Hodge–Tate sheaf on
![]() $X_{\acute{\text{e}}\text{t}}$
,
$X_{\acute{\text{e}}\text{t}}$
,
![]() $R^{i}f_{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
$R^{i}f_{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
![]() $Y_{\acute{\text{e}}\text{t}}$
.
$Y_{\acute{\text{e}}\text{t}}$
.
Hyodo introduced the notion of Hodge–Tate sheaves and proved Theorem 1.4 in the case of schemes [Reference HyodoHyo86]. Links between Hodge–Tate sheaves and the
![]() $p$
-adic Simpson correspondence can be seen in his work and were also studied by Abbes–Gros–Tsuji [Reference Abbes, Gros and TsujiAGT16] and Tsuji [Reference TsujiTsu18]. In fact, they undertook a systematic development of the
$p$
-adic Simpson correspondence can be seen in his work and were also studied by Abbes–Gros–Tsuji [Reference Abbes, Gros and TsujiAGT16] and Tsuji [Reference TsujiTsu18]. In fact, they undertook a systematic development of the
![]() $p$
-adic Simpson correspondence started by Faltings [Reference FaltingsFal05] and their focus is much broader than ours. Andreatta and Brinon also studied Higgs modules and Sen endomorphisms in a different setting [Reference Andreatta and BrinonAB10]. In these works, one is restricted to working with schemes or log schemes, whereas we work with rigid analytic varieties.
$p$
-adic Simpson correspondence started by Faltings [Reference FaltingsFal05] and their focus is much broader than ours. Andreatta and Brinon also studied Higgs modules and Sen endomorphisms in a different setting [Reference Andreatta and BrinonAB10]. In these works, one is restricted to working with schemes or log schemes, whereas we work with rigid analytic varieties.
We now turn to the proof of Theorem 1.2. The key idea to obtain such constancy is to describe
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
as the residue of a certain formal integrable connection. Such an idea occurs in the work [Reference Andreatta and BrinonAB10] of Andreatta and Brinon. Roughly speaking, they associated to
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
as the residue of a certain formal integrable connection. Such an idea occurs in the work [Reference Andreatta and BrinonAB10] of Andreatta and Brinon. Roughly speaking, they associated to
![]() $\mathbb{L}$
a formal connection over some pro-étale cover of
$\mathbb{L}$
a formal connection over some pro-étale cover of
![]() $X_{K}$
when
$X_{K}$
when
![]() $X$
is an affine scheme admitting invertible coordinates. In our case, we want to work over
$X$
is an affine scheme admitting invertible coordinates. In our case, we want to work over
![]() $X_{K}$
, and thus we use the geometric
$X_{K}$
, and thus we use the geometric
![]() $p$
-adic Riemann–Hilbert correspondence by Liu and Zhu [Reference Liu and ZhuLZ17] and Fontaine’s decompletion theory for the de Rham period ring
$p$
-adic Riemann–Hilbert correspondence by Liu and Zhu [Reference Liu and ZhuLZ17] and Fontaine’s decompletion theory for the de Rham period ring
![]() $B_{\text{dR}}(K)$
in the relative setting.
$B_{\text{dR}}(K)$
in the relative setting.
Liu and Zhu associated to each
![]() $\mathbb{Q}_{p}$
-local system
$\mathbb{Q}_{p}$
-local system
![]() $\mathbb{L}$
on
$\mathbb{L}$
on
![]() $X$
a locally free
$X$
a locally free
![]() ${\mathcal{O}}_{X}\,\hat{\otimes }\,B_{\text{dR}}(K)$
-module
${\mathcal{O}}_{X}\,\hat{\otimes }\,B_{\text{dR}}(K)$
-module
![]() ${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
equipped with a filtration, an integrable connection
${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
equipped with a filtration, an integrable connection
and a
![]() $\operatorname{Gal}(k_{\infty }/k)$
-action (see § 4.1 for the notation). To regard
$\operatorname{Gal}(k_{\infty }/k)$
-action (see § 4.1 for the notation). To regard
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
as a residue, we also need a connection in the arithmetic direction
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
as a residue, we also need a connection in the arithmetic direction
![]() $B_{\text{dR}}(K)$
. For this we use Fontaine’s decompletion theory [Reference FontaineFon04]; recall the natural inclusion
$B_{\text{dR}}(K)$
. For this we use Fontaine’s decompletion theory [Reference FontaineFon04]; recall the natural inclusion
![]() $k_{\infty }((t))\subset B_{\text{dR}}(K)$
where
$k_{\infty }((t))\subset B_{\text{dR}}(K)$
where
![]() $t$
is the
$t$
is the
![]() $p$
-adic analogue of the complex period
$p$
-adic analogue of the complex period
![]() $2\unicode[STIX]{x1D70B}i$
. Fontaine extended the work of Sen and developed a decompletion theory for
$2\unicode[STIX]{x1D70B}i$
. Fontaine extended the work of Sen and developed a decompletion theory for
![]() $B_{\text{dR}}(K)$
-representations of
$B_{\text{dR}}(K)$
-representations of
![]() $\operatorname{Gal}(k_{\infty }/k)$
. We generalize Fontaine’s decompletion theory to the relative setting, i.e. that for
$\operatorname{Gal}(k_{\infty }/k)$
. We generalize Fontaine’s decompletion theory to the relative setting, i.e. that for
![]() ${\mathcal{O}}_{X}\,\hat{\otimes }\,B_{\text{dR}}(K)$
-modules (Theorem 2.5 and Proposition 2.24), which yields an endomorphism
${\mathcal{O}}_{X}\,\hat{\otimes }\,B_{\text{dR}}(K)$
-modules (Theorem 2.5 and Proposition 2.24), which yields an endomorphism
![]() $\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L}}$
on
$\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L}}$
on
![]() ${\mathcal{R}}{\mathcal{H}}(\mathbb{L})_{\text{fin}}$
satisfying
${\mathcal{R}}{\mathcal{H}}(\mathbb{L})_{\text{fin}}$
satisfying
and
![]() $\operatorname{gr}^{0}\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L}}=\unicode[STIX]{x1D719}_{\mathbb{L}}$
. Informally, this means that we have an integrable connection
$\operatorname{gr}^{0}\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L}}=\unicode[STIX]{x1D719}_{\mathbb{L}}$
. Informally, this means that we have an integrable connection
over
![]() $X\,\hat{\otimes }\,B_{\text{dR}}(K)$
whose residue along
$X\,\hat{\otimes }\,B_{\text{dR}}(K)$
whose residue along
![]() $t=0$
coincides with the arithmetic Sen endomorphism
$t=0$
coincides with the arithmetic Sen endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
. We develop a theory of formal connections to analyze our connection and prove Theorem 1.2.
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
. We develop a theory of formal connections to analyze our connection and prove Theorem 1.2.
Finally, let us mention two more results in this paper. The first result is a rigidity of Hodge–Tate local systems of rank at most two.
Theorem 1.5 (Theorem 5.12).
Let
![]() $X$
be a geometrically connected smooth rigid analytic variety over
$X$
be a geometrically connected smooth rigid analytic variety over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Assume that
$X_{\acute{\text{e}}\text{t}}$
. Assume that
![]() $\operatorname{rank}\mathbb{L}$
is at most two. If
$\operatorname{rank}\mathbb{L}$
is at most two. If
![]() $\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation at a classical point
$\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation at a classical point
![]() $x\in X$
, then
$x\in X$
, then
![]() $\mathbb{L}$
is a Hodge–Tate sheaf. In particular,
$\mathbb{L}$
is a Hodge–Tate sheaf. In particular,
![]() $\mathbb{L}_{\overline{y}}$
is a Hodge–Tate representation at every classical point
$\mathbb{L}_{\overline{y}}$
is a Hodge–Tate representation at every classical point
![]() $y\in X$
.
$y\in X$
.
Liu and Zhu proved such a rigidity for de Rham local systems [Reference Liu and ZhuLZ17, Theorem 1.3]. We do not know whether a similar statement holds for Hodge–Tate local systems of higher rank.
The second result concerns the relative
![]() $p$
-adic monodromy conjecture for de Rham local systems; the conjecture states that a de Rham local system on
$p$
-adic monodromy conjecture for de Rham local systems; the conjecture states that a de Rham local system on
![]() $X$
becomes semistable at every classical point after a finite étale extension of
$X$
becomes semistable at every classical point after a finite étale extension of
![]() $X$
(cf. [Reference Kedlaya and LiuKL15, § 0.8], [Reference Liu and ZhuLZ17, Remark 1.4]). This is a relative version of the
$X$
(cf. [Reference Kedlaya and LiuKL15, § 0.8], [Reference Liu and ZhuLZ17, Remark 1.4]). This is a relative version of the
![]() $p$
-adic monodromy theorem proved by Berger [Reference BergerBer02], and it is a major open problem in relative
$p$
-adic monodromy theorem proved by Berger [Reference BergerBer02], and it is a major open problem in relative
![]() $p$
-adic Hodge theory. We work on the case of de Rham local systems with a single Hodge–Tate weight, in which case the result follows from a theorem of Sen (Theorem 5.13).
$p$
-adic Hodge theory. We work on the case of de Rham local systems with a single Hodge–Tate weight, in which case the result follows from a theorem of Sen (Theorem 5.13).
Theorem 1.6 (Theorem 5.15).
Let
![]() $X$
be a smooth rigid analytic variety over
$X$
be a smooth rigid analytic variety over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Z}_{p}$
-local system on
$\mathbb{Z}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Assume that
$X_{\acute{\text{e}}\text{t}}$
. Assume that
![]() $\mathbb{L}$
is a Hodge–Tate sheaf with a single Hodge–Tate weight. Then there exists a finite étale cover
$\mathbb{L}$
is a Hodge–Tate sheaf with a single Hodge–Tate weight. Then there exists a finite étale cover
![]() $f:Y\rightarrow X$
such that
$f:Y\rightarrow X$
such that
![]() $(f^{\ast }\mathbb{L})_{\overline{y}}$
is semistable at every classical point
$(f^{\ast }\mathbb{L})_{\overline{y}}$
is semistable at every classical point
![]() $y$
of
$y$
of
![]() $Y$
.
$Y$
.
This is the simplest case of the relative
![]() $p$
-adic monodromy conjecture. In [Reference ColmezCol08], Colmez gave a proof of the
$p$
-adic monodromy conjecture. In [Reference ColmezCol08], Colmez gave a proof of the
![]() $p$
-adic monodromy theorem for de Rham Galois representations using Sen’s theorem mentioned above. It is an interesting question whether one can adapt Colmez’s strategy to the relative setting using Theorem 1.6.
$p$
-adic monodromy theorem for de Rham Galois representations using Sen’s theorem mentioned above. It is an interesting question whether one can adapt Colmez’s strategy to the relative setting using Theorem 1.6.
The organization of the paper is as follows: § 2 presents Sen–Fontaine’s decompletion theory in the relative setting. In § 3, we review the
![]() $p$
-adic Simpson correspondence by Liu and Zhu, and define the arithmetic Sen endomorphism
$p$
-adic Simpson correspondence by Liu and Zhu, and define the arithmetic Sen endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
. Section 4 discusses a Fontaine-type decompletion for the geometric
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
. Section 4 discusses a Fontaine-type decompletion for the geometric
![]() $p$
-adic Riemann–Hilbert correspondence by Liu and Zhu, and develops a theory of formal connections. Combining them together we prove Theorem 1.1. Section 5 presents applications of the study of the arithmetic Sen endomorphism including basic properties of Hodge–Tate sheaves, a rigidity of Hodge–Tate sheaves, and the relative
$p$
-adic Riemann–Hilbert correspondence by Liu and Zhu, and develops a theory of formal connections. Combining them together we prove Theorem 1.1. Section 5 presents applications of the study of the arithmetic Sen endomorphism including basic properties of Hodge–Tate sheaves, a rigidity of Hodge–Tate sheaves, and the relative
![]() $p$
-adic monodromy conjecture.
$p$
-adic monodromy conjecture.
Conventions. We will use Huber’s adic spaces as our language for non-Archimedean analytic geometry. In particular, a rigid analytic variety over
![]() $\mathbb{Q}_{p}$
will refer to a quasi-separated adic space that is locally of finite type over
$\mathbb{Q}_{p}$
will refer to a quasi-separated adic space that is locally of finite type over
![]() $\operatorname{Spa}(\mathbb{Q}_{p},\mathbb{Z}_{p})$
. See [Reference HuberHub94, § 4], [Reference HuberHub96, 1.11.1].
$\operatorname{Spa}(\mathbb{Q}_{p},\mathbb{Z}_{p})$
. See [Reference HuberHub94, § 4], [Reference HuberHub96, 1.11.1].
We will use Scholze’s theory of perfectoid spaces and pro-étale site. For the pro-étale site, we will use the one introduced in [Reference ScholzeSch13, Reference ScholzeSch16].
2 Sen–Fontaine’s decompletion theory for an arithmetic family
2.1 Set-up
Let
![]() $k$
be a complete discrete valuation field of characteristic
$k$
be a complete discrete valuation field of characteristic
![]() $0$
with perfect residue field of characteristic
$0$
with perfect residue field of characteristic
![]() $p$
. We set
$p$
. We set
![]() $k_{m}:=k(\unicode[STIX]{x1D707}_{p^{m}})$
and
$k_{m}:=k(\unicode[STIX]{x1D707}_{p^{m}})$
and
![]() $k_{\infty }:=\mathop{\varinjlim }\nolimits_{m}k_{m}$
. Let
$k_{\infty }:=\mathop{\varinjlim }\nolimits_{m}k_{m}$
. Let
![]() $K$
denote the
$K$
denote the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $k_{\infty }$
. We set
$k_{\infty }$
. We set
![]() $\unicode[STIX]{x1D6E4}_{k}:=\operatorname{Gal}(k_{\infty }/k)$
. Then
$\unicode[STIX]{x1D6E4}_{k}:=\operatorname{Gal}(k_{\infty }/k)$
. Then
![]() $\unicode[STIX]{x1D6E4}_{k}$
is identified with an open subgroup of
$\unicode[STIX]{x1D6E4}_{k}$
is identified with an open subgroup of
![]() $\mathbb{Z}_{p}^{\times }$
via the cyclotomic character
$\mathbb{Z}_{p}^{\times }$
via the cyclotomic character
![]() $\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}_{k}\rightarrow \mathbb{Z}_{p}^{\times }$
and it acts continuously on
$\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}_{k}\rightarrow \mathbb{Z}_{p}^{\times }$
and it acts continuously on
![]() $K$
.
$K$
.
Let
![]() $L_{\text{dR}}^{+}$
(respectively
$L_{\text{dR}}^{+}$
(respectively
![]() $L_{\text{dR}}$
) denote the de Rham period ring
$L_{\text{dR}}$
) denote the de Rham period ring
![]() $B_{\text{dR}}^{+}(K)$
(respectively
$B_{\text{dR}}^{+}(K)$
(respectively
![]() $B_{\text{dR}}(K)$
) introduced by Fontaine. We fix a compatible sequence of
$B_{\text{dR}}(K)$
) introduced by Fontaine. We fix a compatible sequence of
![]() $p$
-power roots of unity
$p$
-power roots of unity
![]() $(\unicode[STIX]{x1D701}_{p^{n}})$
and set
$(\unicode[STIX]{x1D701}_{p^{n}})$
and set
![]() $t:=\log [\unicode[STIX]{x1D700}]$
where
$t:=\log [\unicode[STIX]{x1D700}]$
where
![]() $\unicode[STIX]{x1D700}=(1,\unicode[STIX]{x1D701}_{p},\unicode[STIX]{x1D701}_{p^{2}},\ldots )\in {\mathcal{O}}_{K^{\flat }}$
. Then
$\unicode[STIX]{x1D700}=(1,\unicode[STIX]{x1D701}_{p},\unicode[STIX]{x1D701}_{p^{2}},\ldots )\in {\mathcal{O}}_{K^{\flat }}$
. Then
![]() $\unicode[STIX]{x1D6E4}_{k}$
acts on
$\unicode[STIX]{x1D6E4}_{k}$
acts on
![]() $t$
via the cyclotomic character and the
$t$
via the cyclotomic character and the
![]() $\mathbb{Z}_{p}$
-submodule
$\mathbb{Z}_{p}$
-submodule
![]() $\mathbb{Z}_{p}t\subset L_{\text{dR}}^{+}$
does not depend on the choice of
$\mathbb{Z}_{p}t\subset L_{\text{dR}}^{+}$
does not depend on the choice of
![]() $(\unicode[STIX]{x1D701}_{p^{n}})$
. Note that
$(\unicode[STIX]{x1D701}_{p^{n}})$
. Note that
![]() $L_{\text{dR}}$
is a discrete valuation ring with residue field
$L_{\text{dR}}$
is a discrete valuation ring with residue field
![]() $K$
, fraction field
$K$
, fraction field
![]() $L_{\text{dR}}$
, and uniformizer
$L_{\text{dR}}$
, and uniformizer
![]() $t$
, and that
$t$
, and that
![]() $k_{\infty }[[t]]$
is embedded into
$k_{\infty }[[t]]$
is embedded into
![]() $L_{\text{dR}}^{+}$
.
$L_{\text{dR}}^{+}$
.
We now recall the Sen–Fontaine’s decompletion theory [Reference SenSen81, Theorem 3], [Reference FontaineFon04, Théorème 3.6].
Theorem 2.1. (i) (Sen) Let
![]() $V$
be a
$V$
be a
![]() $K$
-representation of
$K$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Denote by
$\unicode[STIX]{x1D6E4}_{k}$
. Denote by
![]() $V_{\text{fin}}$
the union of finite-dimensional
$V_{\text{fin}}$
the union of finite-dimensional
![]() $k$
-vector subspaces of
$k$
-vector subspaces of
![]() $V$
that are stable under the action of
$V$
that are stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then the natural map
$\unicode[STIX]{x1D6E4}_{k}$
. Then the natural map
is an isomorphism.
(ii) (Fontaine) Let
![]() $V$
be an
$V$
be an
![]() $L_{dR}^{+}$
-representation of
$L_{dR}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and set
$\unicode[STIX]{x1D6E4}_{k}$
and set
where
![]() $(V/t^{n}V)_{\text{fin}}$
is defined to be the union of finite-dimensional
$(V/t^{n}V)_{\text{fin}}$
is defined to be the union of finite-dimensional
![]() $k$
-vector subspaces of
$k$
-vector subspaces of
![]() $V/t^{n}V$
that are stable under the action of
$V/t^{n}V$
that are stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then the natural map
$\unicode[STIX]{x1D6E4}_{k}$
. Then the natural map
is an isomorphism.
Using this theorem, Sen defined the so-called Sen endomorphism
![]() $\unicode[STIX]{x1D719}_{V}$
on
$\unicode[STIX]{x1D719}_{V}$
on
![]() $V_{\infty }$
for a
$V_{\infty }$
for a
![]() $K$
-representation
$K$
-representation
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
(cf. [Reference SenSen81, Theorem 4]), and Fontaine defined a formal connection on
$\unicode[STIX]{x1D6E4}_{k}$
(cf. [Reference SenSen81, Theorem 4]), and Fontaine defined a formal connection on
![]() $V_{\text{fin}}$
for an
$V_{\text{fin}}$
for an
![]() $L_{\text{dR}}^{+}$
-representation
$L_{\text{dR}}^{+}$
-representation
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
(cf. [Reference FontaineFon04, Proposition 3.7]).
$\unicode[STIX]{x1D6E4}_{k}$
(cf. [Reference FontaineFon04, Proposition 3.7]).
We now turn to the relative setting. Let
![]() $A$
be a Tate
$A$
be a Tate
![]() $k$
-algebra that is reduced and topologically of finite type over
$k$
-algebra that is reduced and topologically of finite type over
![]() $k$
. It is equipped with the supremum norm and we use this norm when we regard
$k$
. It is equipped with the supremum norm and we use this norm when we regard
![]() $A$
as a Banach
$A$
as a Banach
![]() $k$
-algebra. We further assume that
$k$
-algebra. We further assume that
![]() $(A,A^{\circ })$
is smooth over
$(A,A^{\circ })$
is smooth over
![]() $(k,{\mathcal{O}}_{k})$
. We set
$(k,{\mathcal{O}}_{k})$
. We set
Here we use a slightly heavy notation
![]() $A_{k_{m}}$
to reserve
$A_{k_{m}}$
to reserve
![]() $A_{m}$
for a different ring in a later section. Since
$A_{m}$
for a different ring in a later section. Since
![]() $A$
,
$A$
,
![]() $k_{m}$
, and
$k_{m}$
, and
![]() $K$
are all complete Tate
$K$
are all complete Tate
![]() $k$
-algebras, the completed tensor product is well-defined (or one can use Banach
$k$
-algebras, the completed tensor product is well-defined (or one can use Banach
![]() $k$
-algebra structures). Note that
$k$
-algebra structures). Note that
![]() $A_{k_{m}}$
(respectively
$A_{k_{m}}$
(respectively
![]() $A_{K}$
) is a complete Tate
$A_{K}$
) is a complete Tate
![]() $k_{m}$
-algebra (respectively
$k_{m}$
-algebra (respectively
![]() $K$
-algebra), that
$K$
-algebra), that
![]() $A_{\infty }$
is a Tate
$A_{\infty }$
is a Tate
![]() $k_{\infty }$
-algebra and that
$k_{\infty }$
-algebra and that
![]() $A_{K}$
is the completion of
$A_{K}$
is the completion of
![]() $A_{\infty }$
.
$A_{\infty }$
.
We introduce the relative versions of
![]() $k_{\infty }[[t]]$
,
$k_{\infty }[[t]]$
,
![]() $L_{\text{dR}}^{+}$
, and
$L_{\text{dR}}^{+}$
, and
![]() $L_{\text{dR}}$
over
$L_{\text{dR}}$
over
![]() $A$
. We set
$A$
. We set
and equip
![]() $A_{\infty }[[t]]$
with the inverse limit topology of Tate
$A_{\infty }[[t]]$
with the inverse limit topology of Tate
![]() $k_{\infty }$
-algebras
$k_{\infty }$
-algebras
![]() $A_{\infty }[t]/(t^{n})$
. We also set
$A_{\infty }[t]/(t^{n})$
. We also set
and equip
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
with the inverse limit topology. We finally set
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
with the inverse limit topology. We finally set
and equip
![]() $A\,\hat{\otimes }\,L_{\text{dR}}$
with the inductive limit topology. Note that
$A\,\hat{\otimes }\,L_{\text{dR}}$
with the inductive limit topology. Note that
![]() $\unicode[STIX]{x1D6E4}_{k}$
acts continuously on these rings (cf. [Reference BellovinBel15, Appendix]).
$\unicode[STIX]{x1D6E4}_{k}$
acts continuously on these rings (cf. [Reference BellovinBel15, Appendix]).
Definition 2.2. In this paper, an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
is an
$\unicode[STIX]{x1D6E4}_{k}$
is an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-module
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-module
![]() $V$
that is isomorphic to either
$V$
that is isomorphic to either
![]() $(A\,\hat{\otimes }\,L_{\text{dR}}^{+})^{r}$
or
$(A\,\hat{\otimes }\,L_{\text{dR}}^{+})^{r}$
or
![]() $(A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n}))^{r}$
for some
$(A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n}))^{r}$
for some
![]() $r$
and
$r$
and
![]() $n$
, equipped with a continuous
$n$
, equipped with a continuous
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-semilinear action of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-semilinear action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. We denote the category of
$\unicode[STIX]{x1D6E4}_{k}$
. We denote the category of
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
![]() $\unicode[STIX]{x1D6E4}_{k}$
by
$\unicode[STIX]{x1D6E4}_{k}$
by
![]() $\text{Rep}_{\unicode[STIX]{x1D6E4}_{k}}(A\,\hat{\otimes }\,L_{\text{dR}}^{+})$
. An
$\text{Rep}_{\unicode[STIX]{x1D6E4}_{k}}(A\,\hat{\otimes }\,L_{\text{dR}}^{+})$
. An
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
that is annihilated by
$\unicode[STIX]{x1D6E4}_{k}$
that is annihilated by
![]() $t$
is also called an
$t$
is also called an
![]() $A_{K}$
-representation of
$A_{K}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.
If
![]() $V$
is isomorphic to either
$V$
is isomorphic to either
![]() $(A\,\hat{\otimes }\,L_{\text{dR}}^{+})^{r}$
or
$(A\,\hat{\otimes }\,L_{\text{dR}}^{+})^{r}$
or
![]() $(A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n}))^{r}$
then
$(A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n}))^{r}$
then
![]() $V$
admits a topology by taking a basis and the topology is independent of the choice of the basis. Thus the continuity condition of the action of
$V$
admits a topology by taking a basis and the topology is independent of the choice of the basis. Thus the continuity condition of the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
makes sense. Note that if
$\unicode[STIX]{x1D6E4}_{k}$
makes sense. Note that if
![]() $V$
is an
$V$
is an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, then so are
$\unicode[STIX]{x1D6E4}_{k}$
, then so are
![]() $t^{n}V$
and
$t^{n}V$
and
![]() $V/t^{n}V$
.
$V/t^{n}V$
.
We are going to discuss the relative version of Sen–Fontaine’s theory. Namely, we will work on
![]() $A_{K}$
-representations of
$A_{K}$
-representations of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and
$\unicode[STIX]{x1D6E4}_{k}$
and
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Note that Sen’s theory in the relative setting is established by Sen himself [Reference SenSen88, Reference SenSen93] and that Fontaine’s decompletion theory in the relative setting is established by Berger–Colmez and Bellovin for representations which come from
$\unicode[STIX]{x1D6E4}_{k}$
. Note that Sen’s theory in the relative setting is established by Sen himself [Reference SenSen88, Reference SenSen93] and that Fontaine’s decompletion theory in the relative setting is established by Berger–Colmez and Bellovin for representations which come from
![]() $A$
-representations of
$A$
-representations of
![]() $\operatorname{Gal}(\overline{k}/k)$
via the theory of
$\operatorname{Gal}(\overline{k}/k)$
via the theory of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules [Reference Berger and ColmezBC08, Reference BellovinBel15]. Since we need a Fontaine-type decompletion theory for arbitrary
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules [Reference Berger and ColmezBC08, Reference BellovinBel15]. Since we need a Fontaine-type decompletion theory for arbitrary
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, we give detailed arguments; we will discuss the decompletion theory in the next subsection, and define Sen’s endomorphism and Fontaine’s connection in § 2.3.
$\unicode[STIX]{x1D6E4}_{k}$
, we give detailed arguments; we will discuss the decompletion theory in the next subsection, and define Sen’s endomorphism and Fontaine’s connection in § 2.3.
We end this subsection with establishing basic properties of the rings we have introduced.
Proposition 2.3.
(i) For each
 $n\geqslant 1$
,
$n\geqslant 1$
,
 $A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
is Noetherian and faithfully flat over
$A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
is Noetherian and faithfully flat over
 $A_{\infty }[t]/(t^{n})$
.
$A_{\infty }[t]/(t^{n})$
.(ii)
 $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
is a
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
is a
 $t$
-adically complete flat
$t$
-adically complete flat
 $L_{\text{dR}}^{+}$
-algebra with
$L_{\text{dR}}^{+}$
-algebra with
 $(A\,\hat{\otimes }\,L_{\text{dR}}^{+})/(t^{n})=A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
.
$(A\,\hat{\otimes }\,L_{\text{dR}}^{+})/(t^{n})=A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
.
Proof. For (i), the first assertion is proved in [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 13.4]. We prove that
![]() $A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
is faithfully flat over
$A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
is faithfully flat over
![]() $A_{\infty }[t]/(t^{n})$
.
$A_{\infty }[t]/(t^{n})$
.
First we deal with the case
![]() $n=1$
, i.e. faithful flatness of
$n=1$
, i.e. faithful flatness of
![]() $A_{K}$
over
$A_{K}$
over
![]() $A_{\infty }$
. The proof is similar to that of [Reference Andreatta and BrinonAB10, Lemme 5.9]. Recall
$A_{\infty }$
. The proof is similar to that of [Reference Andreatta and BrinonAB10, Lemme 5.9]. Recall
![]() $A_{\infty }=\mathop{\varinjlim }\nolimits_{n}A_{k_{m}}$
. Since
$A_{\infty }=\mathop{\varinjlim }\nolimits_{n}A_{k_{m}}$
. Since
![]() $k_{m}$
and
$k_{m}$
and
![]() $K$
are both complete valuation fields,
$K$
are both complete valuation fields,
![]() $A_{K}=A_{k_{m}}\,\hat{\otimes }_{k_{m}}\,K$
is faithfully flat over
$A_{K}=A_{k_{m}}\,\hat{\otimes }_{k_{m}}\,K$
is faithfully flat over
![]() $A_{k_{m}}$
(e.g. use [Reference Bosch, Güntzer and RemmertBGR84, Proposition 2.1.7/8 and Theorem 2.8.2/2]).
$A_{k_{m}}$
(e.g. use [Reference Bosch, Güntzer and RemmertBGR84, Proposition 2.1.7/8 and Theorem 2.8.2/2]).
We prove that
![]() $A_{K}$
is flat over
$A_{K}$
is flat over
![]() $A_{\infty }$
. For this it suffices to show that for any finitely generated ideal
$A_{\infty }$
. For this it suffices to show that for any finitely generated ideal
![]() $I\subset A_{\infty }$
, the map
$I\subset A_{\infty }$
, the map
![]() $I\otimes _{A_{\infty }}A_{K}\rightarrow A_{K}$
is injective. Take such an ideal
$I\otimes _{A_{\infty }}A_{K}\rightarrow A_{K}$
is injective. Take such an ideal
![]() $I$
. As
$I$
. As
![]() $I$
is finitely generated, there exist a positive integer
$I$
is finitely generated, there exist a positive integer
![]() $m$
and a finitely generated ideal
$m$
and a finitely generated ideal
![]() $I_{m}\subset A_{k_{m}}$
such that
$I_{m}\subset A_{k_{m}}$
such that
![]() $I=\operatorname{Im}(I_{m}\,\otimes _{A_{k_{m}}}A_{\infty }\rightarrow A_{\infty })$
. Since
$I=\operatorname{Im}(I_{m}\,\otimes _{A_{k_{m}}}A_{\infty }\rightarrow A_{\infty })$
. Since
![]() $A_{K}$
is flat over
$A_{K}$
is flat over
![]() $A_{k_{m}}$
, the map
$A_{k_{m}}$
, the map
![]() $I_{m}\otimes _{A_{k_{m}}}A_{K}\rightarrow A_{K}$
is injective. On the other hand, this map factors as
$I_{m}\otimes _{A_{k_{m}}}A_{K}\rightarrow A_{K}$
is injective. On the other hand, this map factors as
![]() $I_{m}\otimes _{A_{k_{m}}}A_{K}\rightarrow I\otimes _{A_{\infty }}A_{K}\rightarrow A_{K}$
and the first map is surjective by the choice of
$I_{m}\otimes _{A_{k_{m}}}A_{K}\rightarrow I\otimes _{A_{\infty }}A_{K}\rightarrow A_{K}$
and the first map is surjective by the choice of
![]() $I_{m}$
. Hence the second map
$I_{m}$
. Hence the second map
![]() $I\otimes _{A_{\infty }}A_{K}\rightarrow A_{K}$
is injective.
$I\otimes _{A_{\infty }}A_{K}\rightarrow A_{K}$
is injective.
For faithful flatness, it remains to prove that the map
![]() $\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A_{\infty }$
is surjective. Assume the contrary and take a prime ideal
$\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A_{\infty }$
is surjective. Assume the contrary and take a prime ideal
![]() $\mathfrak{P}\in \operatorname{Spec}A_{\infty }$
that is not in the image of the map. Set
$\mathfrak{P}\in \operatorname{Spec}A_{\infty }$
that is not in the image of the map. Set
![]() $\mathfrak{p}=\mathfrak{P}\cap A\in \operatorname{Spec}A$
. Note that the prime ideals of
$\mathfrak{p}=\mathfrak{P}\cap A\in \operatorname{Spec}A$
. Note that the prime ideals of
![]() $A_{\infty }$
above
$A_{\infty }$
above
![]() $\mathfrak{p}$
are conjugate to each other by the action of
$\mathfrak{p}$
are conjugate to each other by the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. From this we see that no prime ideal of
$\unicode[STIX]{x1D6E4}_{k}$
. From this we see that no prime ideal of
![]() $A_{\infty }$
above
$A_{\infty }$
above
![]() $\mathfrak{p}$
is in the image of
$\mathfrak{p}$
is in the image of
![]() $\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A_{\infty }$
. Hence
$\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A_{\infty }$
. Hence
![]() $\mathfrak{p}$
does not lie in the image of
$\mathfrak{p}$
does not lie in the image of
![]() $\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A$
, which contradicts that
$\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A$
, which contradicts that
![]() $A_{K}$
is faithfully flat over
$A_{K}$
is faithfully flat over
![]() $A$
.
$A$
.
Next we deal with the general
![]() $n$
. By the local flatness criterion [Reference MatsumuraMat89, Theorem 22.3] applied to the nilpotent ideal
$n$
. By the local flatness criterion [Reference MatsumuraMat89, Theorem 22.3] applied to the nilpotent ideal
![]() $(t)\subset A_{\infty }[t]/(t^{n})$
, the flatness follows from the case
$(t)\subset A_{\infty }[t]/(t^{n})$
, the flatness follows from the case
![]() $n=1$
. Moreover, since
$n=1$
. Moreover, since
![]() $\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A_{\infty }$
is surjective, so is
$\operatorname{Spec}A_{K}\rightarrow \operatorname{Spec}A_{\infty }$
is surjective, so is
![]() $\operatorname{Spec}A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})\rightarrow \operatorname{Spec}A_{\infty }[t]/(t^{n})$
. Hence
$\operatorname{Spec}A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})\rightarrow \operatorname{Spec}A_{\infty }[t]/(t^{n})$
. Hence
![]() $A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
is faithfully flat over
$A\,\hat{\otimes }_{k}\,L_{\text{dR}}^{+}/(t^{n})$
is faithfully flat over
![]() $A_{\infty }[t]/(t^{n})$
.
$A_{\infty }[t]/(t^{n})$
.
Assertion (ii) is proved in [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 13.4]. Note that the proof of [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 13.4] works in our setting since we assume the smoothness of
![]() $A$
.◻
$A$
.◻
2.2 Sen–Fontaine’s decompletion theory in the relative setting
Definition 2.4. For an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, we define the subspace
$\unicode[STIX]{x1D6E4}_{k}$
, we define the subspace
![]() $V_{\text{fin}}$
as follows.
$V_{\text{fin}}$
as follows.
– If
 $V$
is annihilated by
$V$
is annihilated by
 $t^{n}$
for some
$t^{n}$
for some
 $n\geqslant 1$
, then
$n\geqslant 1$
, then
 $V_{\text{fin}}$
is defined to be the union of finitely generated
$V_{\text{fin}}$
is defined to be the union of finitely generated
 $A$
-submodules of
$A$
-submodules of
 $V$
that are stable under the action of
$V$
that are stable under the action of
 $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.– In general, define
 $$\begin{eqnarray}V_{\text{fin}}:=\mathop{\varprojlim }\nolimits_{n}(V/t^{n}V)_{\text{fin}}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\text{fin}}:=\mathop{\varprojlim }\nolimits_{n}(V/t^{n}V)_{\text{fin}}.\end{eqnarray}$$
If
![]() $V$
is killed by
$V$
is killed by
![]() $t^{n}$
, then
$t^{n}$
, then
![]() $V_{\text{fin}}$
is an
$V_{\text{fin}}$
is an
![]() $A_{\infty }[t]/(t^{n})$
-module. In general,
$A_{\infty }[t]/(t^{n})$
-module. In general,
![]() $V_{\text{fin}}$
is an
$V_{\text{fin}}$
is an
![]() $A_{\infty }[[t]]$
-module equipped with a semilinear action of
$A_{\infty }[[t]]$
-module equipped with a semilinear action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.
The following theorem is the main goal of this subsection.
Theorem 2.5. For an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
that is finite free of rank
$\unicode[STIX]{x1D6E4}_{k}$
that is finite free of rank
![]() $r$
over
$r$
over
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
, the
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
, the
![]() $A_{\infty }[[t]]$
-module
$A_{\infty }[[t]]$
-module
![]() $V_{\text{fin}}$
is finite free of rank
$V_{\text{fin}}$
is finite free of rank
![]() $r$
. Moreover, the natural map
$r$
. Moreover, the natural map
is an isomorphism, and
![]() $V_{\text{fin}}/t^{n}V_{\text{fin}}$
is isomorphic to
$V_{\text{fin}}/t^{n}V_{\text{fin}}$
is isomorphic to
![]() $(V/t^{n}V)_{\text{fin}}$
for each
$(V/t^{n}V)_{\text{fin}}$
for each
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
The key tool in the proof is the Sen method, which is axiomatized in [Reference Berger and ColmezBC08, § 3]. We review parts of the Tate–Sen conditions that are used in our proofs. For a thorough treatment, we refer the reader to [Reference Berger and ColmezBC08, § 3].
Consider Tate’s normalized trace map
On
![]() $k_{m+m^{\prime }}\subset K$
, this map is defined as
$k_{m+m^{\prime }}\subset K$
, this map is defined as
and it extends continuously to
![]() $R_{k,m}:K\rightarrow k_{m}$
. We denote the kernel
$R_{k,m}:K\rightarrow k_{m}$
. We denote the kernel
![]() $\operatorname{Ker}R_{k,m}$
by
$\operatorname{Ker}R_{k,m}$
by
![]() $X_{m}$
. The map
$X_{m}$
. The map
![]() $R_{k,m}$
extends
$R_{k,m}$
extends
![]() $A$
-linearly to the map
$A$
-linearly to the map
![]() $R_{A,m}:A_{K}\rightarrow A_{k_{m}}$
. Fix a real number
$R_{A,m}:A_{K}\rightarrow A_{k_{m}}$
. Fix a real number
![]() $c_{3}>1$
. By work of Tate and Sen [Reference Berger and ColmezBC08, Propositions 3.1.4 and 4.1.1],
$c_{3}>1$
. By work of Tate and Sen [Reference Berger and ColmezBC08, Propositions 3.1.4 and 4.1.1],
![]() $G_{0}=\unicode[STIX]{x1D6E4}_{k}$
,
$G_{0}=\unicode[STIX]{x1D6E4}_{k}$
,
![]() $\tilde{\unicode[STIX]{x1D6EC}}=A_{K}$
,
$\tilde{\unicode[STIX]{x1D6EC}}=A_{K}$
,
![]() $R_{m}$
, and the valuation
$R_{m}$
, and the valuation
![]() $\operatorname{val}$
on
$\operatorname{val}$
on
![]() $A_{K}$
satisfy the Tate–Sen axioms in [Reference Berger and ColmezBC08, § 3] for any fixed positive numbers
$A_{K}$
satisfy the Tate–Sen axioms in [Reference Berger and ColmezBC08, § 3] for any fixed positive numbers
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
.
$c_{2}$
.
In particular,
![]() $X_{A,m}:=A\,\hat{\otimes }_{k}\,X_{m}$
is the kernel of
$X_{A,m}:=A\,\hat{\otimes }_{k}\,X_{m}$
is the kernel of
![]() $R_{A,m}$
, and we have topological splitting
$R_{A,m}$
, and we have topological splitting
![]() $A_{K}=A_{k_{m}}\oplus X_{A,m}$
. For
$A_{K}=A_{k_{m}}\oplus X_{A,m}$
. For
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
, let
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
, let
![]() $m(\unicode[STIX]{x1D6FE})\in \mathbb{Z}$
be the valuation of
$m(\unicode[STIX]{x1D6FE})\in \mathbb{Z}$
be the valuation of
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})-1\in \mathbb{Z}_{p}$
. Then there exists a positive integer
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})-1\in \mathbb{Z}_{p}$
. Then there exists a positive integer
![]() $m(k)$
such that for each
$m(k)$
such that for each
![]() $m\geqslant m(k)$
and
$m\geqslant m(k)$
and
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
with
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
with
![]() $m(\unicode[STIX]{x1D6FE})\leqslant m$
,
$m(\unicode[STIX]{x1D6FE})\leqslant m$
,
![]() $\unicode[STIX]{x1D6FE}-1$
is invertible on
$\unicode[STIX]{x1D6FE}-1$
is invertible on
![]() $X_{A,m}$
and
$X_{A,m}$
and
for each
![]() $a\in A_{K}$
.
$a\in A_{K}$
.
Finally, for each matrix
![]() $U=(a_{ij})\in M_{r}(A_{K})$
, we set
$U=(a_{ij})\in M_{r}(A_{K})$
, we set
![]() $\operatorname{val}U:=\min _{i,j}\operatorname{val}a_{ij}$
.
$\operatorname{val}U:=\min _{i,j}\operatorname{val}a_{ij}$
.
Proposition 2.6. Each finitely generated
![]() $A$
-submodule of
$A$
-submodule of
![]() $A_{K}$
that is stable under the action of an open subgroup of
$A_{K}$
that is stable under the action of an open subgroup of
![]() $\unicode[STIX]{x1D6E4}_{k}$
is contained in
$\unicode[STIX]{x1D6E4}_{k}$
is contained in
![]() $A_{\infty }$
.
$A_{\infty }$
.
Proof. We follow the proof of [Reference SenSen81, Proposition 3]. By [Reference Berger and ColmezBC08, Corollaire 2.1.4], there exist complete discrete valuation fields
![]() $E_{1},\ldots ,E_{s}$
and an isometric embedding
$E_{1},\ldots ,E_{s}$
and an isometric embedding
![]() $A{\hookrightarrow}\prod _{i=1}^{s}E_{i}$
. Then extending the scalar yields an isometric embedding
$A{\hookrightarrow}\prod _{i=1}^{s}E_{i}$
. Then extending the scalar yields an isometric embedding
preserving the topological splittings.
Let
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
be an open subgroup of
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
be an open subgroup of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and
$\unicode[STIX]{x1D6E4}_{k}$
and
![]() $W$
a finitely generated
$W$
a finitely generated
![]() $A$
-submodule of
$A$
-submodule of
![]() $A_{K}$
that is stable under the action of
$A_{K}$
that is stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
. Let
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
. Let
![]() $W_{i}$
be the finite-dimensional
$W_{i}$
be the finite-dimensional
![]() $E_{i}$
-vector subspace of
$E_{i}$
-vector subspace of
![]() $E_{i}\,\hat{\otimes }_{k}\,K$
generated by the image of
$E_{i}\,\hat{\otimes }_{k}\,K$
generated by the image of
![]() $W$
under the map
$W$
under the map
![]() $A_{K}\rightarrow \prod _{i=1}^{s}E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
. To prove that
$A_{K}\rightarrow \prod _{i=1}^{s}E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
. To prove that
![]() $W$
is contained in
$W$
is contained in
![]() $A_{\infty }=\bigcup _{m}A_{k_{m}}$
, it suffices to prove that for each
$A_{\infty }=\bigcup _{m}A_{k_{m}}$
, it suffices to prove that for each
![]() $i$
, there exists a large integer
$i$
, there exists a large integer
![]() $m$
such that
$m$
such that
![]() $W_{i}$
is contained in
$W_{i}$
is contained in
![]() $E_{i}\,\hat{\otimes }_{k}\,k_{m}$
.
$E_{i}\,\hat{\otimes }_{k}\,k_{m}$
.
Replacing
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
by a smaller open subgroup if necessary, we may assume that there exists a topological generator
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
by a smaller open subgroup if necessary, we may assume that there exists a topological generator
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
. Replacing
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
. Replacing
![]() $E_{i}$
by a finite field extension, we may also assume that all the eigenvalues of the
$E_{i}$
by a finite field extension, we may also assume that all the eigenvalues of the
![]() $E_{i}$
-endomorphism
$E_{i}$
-endomorphism
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $W_{i}$
lie in
$W_{i}$
lie in
![]() $E_{i}$
.
$E_{i}$
.
Let
![]() $w\in W_{i}$
be an eigenvector for
$w\in W_{i}$
be an eigenvector for
![]() $\unicode[STIX]{x1D6FE}$
and let
$\unicode[STIX]{x1D6FE}$
and let
![]() $\unicode[STIX]{x1D706}_{i}\in E$
be its eigenvalue. Note that
$\unicode[STIX]{x1D706}_{i}\in E$
be its eigenvalue. Note that
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
acts continuously on
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
acts continuously on
![]() $W_{i}$
. When
$W_{i}$
. When
![]() $j$
goes to infinity,
$j$
goes to infinity,
![]() $\unicode[STIX]{x1D6FE}^{p^{j}}$
approaches
$\unicode[STIX]{x1D6FE}^{p^{j}}$
approaches
![]() $1$
and thus
$1$
and thus
![]() $\unicode[STIX]{x1D706}^{p^{j}}$
approaches
$\unicode[STIX]{x1D706}^{p^{j}}$
approaches
![]() $1$
. This implies that
$1$
. This implies that
![]() $\unicode[STIX]{x1D706}$
is a principal unit, i.e.
$\unicode[STIX]{x1D706}$
is a principal unit, i.e.
![]() $|\unicode[STIX]{x1D706}-1|_{E_{i}}<1$
.
$|\unicode[STIX]{x1D706}-1|_{E_{i}}<1$
.
Lemma 2.7. The eigenvalue
![]() $\unicode[STIX]{x1D706}$
is a
$\unicode[STIX]{x1D706}$
is a
![]() $p$
-power root of unity.
$p$
-power root of unity.
Proof. We follow the proof of [Reference TateTat67, Proposition 7(c)]. Assume the contrary. We will prove that
![]() $\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}:E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
is bijective, which would contradict that the non-zero element
$\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}:E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
is bijective, which would contradict that the non-zero element
![]() $w\in W_{i}\subset E_{i}\,\hat{\otimes }_{k}\,K$
satisfies
$w\in W_{i}\subset E_{i}\,\hat{\otimes }_{k}\,K$
satisfies
![]() $(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706})w=0$
.
$(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706})w=0$
.
Let
![]() $m$
be the integer such that
$m$
be the integer such that
![]() $k_{m}$
is the fixed subfield of
$k_{m}$
is the fixed subfield of
![]() $k_{\infty }$
by
$k_{\infty }$
by
![]() $\unicode[STIX]{x1D6FE}$
. Consider the map
$\unicode[STIX]{x1D6FE}$
. Consider the map
![]() $\unicode[STIX]{x1D6FE}-1:E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
. This map preserves the decomposition
$\unicode[STIX]{x1D6FE}-1:E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
. This map preserves the decomposition
![]() $E_{i}\,\hat{\otimes }_{k}\,K=E_{i}\,\hat{\otimes }_{k}\,k_{m}\oplus E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. Moreover, it is zero on
$E_{i}\,\hat{\otimes }_{k}\,K=E_{i}\,\hat{\otimes }_{k}\,k_{m}\oplus E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. Moreover, it is zero on
![]() $E_{i}\,\hat{\otimes }_{k}\,k_{m}$
and bijective on
$E_{i}\,\hat{\otimes }_{k}\,k_{m}$
and bijective on
![]() $E_{i}\,\hat{\otimes }_{k}\,X_{m}$
with continuous inverse. Denote the inverse by
$E_{i}\,\hat{\otimes }_{k}\,X_{m}$
with continuous inverse. Denote the inverse by
![]() $\unicode[STIX]{x1D70C}$
. Then
$\unicode[STIX]{x1D70C}$
. Then
![]() $\unicode[STIX]{x1D70C}$
is a bounded
$\unicode[STIX]{x1D70C}$
is a bounded
![]() $E_{i}\,\hat{\otimes }_{k}\,k_{m}$
-linear operator with operator norm at most
$E_{i}\,\hat{\otimes }_{k}\,k_{m}$
-linear operator with operator norm at most
![]() $p^{c_{3}}$
. Since
$p^{c_{3}}$
. Since
![]() $\unicode[STIX]{x1D706}\in E_{i}$
and
$\unicode[STIX]{x1D706}\in E_{i}$
and
![]() $\unicode[STIX]{x1D706}\neq 1$
, the map
$\unicode[STIX]{x1D706}\neq 1$
, the map
![]() $\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
is bijective on
$\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
is bijective on
![]() $E_{i}\,\hat{\otimes }_{k}\,k_{m}$
. So it suffices to prove that
$E_{i}\,\hat{\otimes }_{k}\,k_{m}$
. So it suffices to prove that
![]() $\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
is bijective on
$\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
is bijective on
![]() $E_{i}\,\hat{\otimes }_{k}\,X_{m}$
.
$E_{i}\,\hat{\otimes }_{k}\,X_{m}$
.
As operators on
![]() $E_{i}\,\hat{\otimes }_{k}\,X_{m}$
, we have
$E_{i}\,\hat{\otimes }_{k}\,X_{m}$
, we have
Thus if
![]() $|\unicode[STIX]{x1D706}-1|_{E_{i}}p^{c_{3}}<1$
, then
$|\unicode[STIX]{x1D706}-1|_{E_{i}}p^{c_{3}}<1$
, then
![]() $1-(\unicode[STIX]{x1D706}-1)\unicode[STIX]{x1D70C}$
has an inverse on
$1-(\unicode[STIX]{x1D706}-1)\unicode[STIX]{x1D70C}$
has an inverse on
![]() $E_{i}\,\hat{\otimes }_{k}\,X_{m}$
given by a geometric series, and hence
$E_{i}\,\hat{\otimes }_{k}\,X_{m}$
given by a geometric series, and hence
![]() $\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
admits a continuous inverse on
$\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
admits a continuous inverse on
![]() $E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. If
$E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. If
![]() $|\unicode[STIX]{x1D706}-1|_{E_{i}}p^{c_{3}}\geqslant 1$
, first take a large integer
$|\unicode[STIX]{x1D706}-1|_{E_{i}}p^{c_{3}}\geqslant 1$
, first take a large integer
![]() $j$
with
$j$
with
![]() $|\unicode[STIX]{x1D706}^{p^{j}}-1|_{E_{i}}p^{c_{3}}<1$
. Then we can prove that
$|\unicode[STIX]{x1D706}^{p^{j}}-1|_{E_{i}}p^{c_{3}}<1$
. Then we can prove that
![]() $\unicode[STIX]{x1D6FE}^{p^{j}}-\unicode[STIX]{x1D706}^{p^{j}}$
has a bounded inverse on
$\unicode[STIX]{x1D6FE}^{p^{j}}-\unicode[STIX]{x1D706}^{p^{j}}$
has a bounded inverse on
![]() $E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. Hence so does
$E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. Hence so does
![]() $\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
.◻
$\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D706}$
.◻
We continue the proof of the proposition. Since each eigenvalue of
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $W_{i}$
is a
$W_{i}$
is a
![]() $p$
-power root of unity, we replace
$p$
-power root of unity, we replace
![]() $\unicode[STIX]{x1D6FE}$
by a higher
$\unicode[STIX]{x1D6FE}$
by a higher
![]() $p$
-power and may assume that
$p$
-power and may assume that
![]() $\unicode[STIX]{x1D6FE}$
acts on
$\unicode[STIX]{x1D6FE}$
acts on
![]() $W_{i}$
unipotently. Thus
$W_{i}$
unipotently. Thus
![]() $\unicode[STIX]{x1D6FE}-1$
acts on
$\unicode[STIX]{x1D6FE}-1$
acts on
![]() $W_{i}$
nilpotently.
$W_{i}$
nilpotently.
Let
![]() $m$
be the integer such that
$m$
be the integer such that
![]() $k_{m}$
is the fixed subfield of
$k_{m}$
is the fixed subfield of
![]() $k_{\infty }$
by
$k_{\infty }$
by
![]() $\unicode[STIX]{x1D6FE}$
. Then the map
$\unicode[STIX]{x1D6FE}$
. Then the map
![]() $\unicode[STIX]{x1D6FE}-1:E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
is zero on
$\unicode[STIX]{x1D6FE}-1:E_{i}\,\hat{\otimes }_{k}\,K\rightarrow E_{i}\,\hat{\otimes }_{k}\,K$
is zero on
![]() $E_{i}\,\hat{\otimes }_{k}\,k_{m}$
and bijective on
$E_{i}\,\hat{\otimes }_{k}\,k_{m}$
and bijective on
![]() $E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. This implies that the nilpotent endomorphism
$E_{i}\,\hat{\otimes }_{k}\,X_{m}$
. This implies that the nilpotent endomorphism
![]() $\unicode[STIX]{x1D6FE}-1$
on
$\unicode[STIX]{x1D6FE}-1$
on
![]() $W_{i}$
is actually zero and thus
$W_{i}$
is actually zero and thus
![]() $W_{i}$
is contained in
$W_{i}$
is contained in
![]() $E_{i}\,\hat{\otimes }_{k}\,k_{m}$
.◻
$E_{i}\,\hat{\otimes }_{k}\,k_{m}$
.◻
Example 2.8. For the trivial
![]() $A_{K}$
-representation
$A_{K}$
-representation
![]() $V=A_{K}$
of
$V=A_{K}$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, we have
$\unicode[STIX]{x1D6E4}_{k}$
, we have
![]() $V_{\text{fin}}=A_{\infty }$
by Proposition 2.6.
$V_{\text{fin}}=A_{\infty }$
by Proposition 2.6.
The following theorem describes
![]() $V_{\text{fin}}$
for a general
$V_{\text{fin}}$
for a general
![]() $A_{K}$
-representation
$A_{K}$
-representation
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, and it was first proved by Sen [Reference SenSen88, Reference SenSen93].
$\unicode[STIX]{x1D6E4}_{k}$
, and it was first proved by Sen [Reference SenSen88, Reference SenSen93].
Theorem 2.9. For an
![]() $A_{K}$
-representation
$A_{K}$
-representation
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, the
$\unicode[STIX]{x1D6E4}_{k}$
, the
![]() $A_{\infty }$
-module
$A_{\infty }$
-module
![]() $V_{\text{fin}}$
is finite free. Moreover, the natural map
$V_{\text{fin}}$
is finite free. Moreover, the natural map
is an isomorphism.
Proof. First we prove the following lemma.
Lemma 2.10. There exist an
![]() $A_{K}$
-basis
$A_{K}$
-basis
![]() $v_{1},\ldots ,v_{r}\in V$
and a large positive integer
$v_{1},\ldots ,v_{r}\in V$
and a large positive integer
![]() $m$
such that the transformation matrix of
$m$
such that the transformation matrix of
![]() $\unicode[STIX]{x1D6FE}$
with respect to this basis has entries in
$\unicode[STIX]{x1D6FE}$
with respect to this basis has entries in
![]() $A_{k_{m}}$
for each
$A_{k_{m}}$
for each
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.
Proof. This follows from the Tate–Sen method for
![]() $\unicode[STIX]{x1D6E4}_{k}$
-representations in the relative setting. By [Reference ChenevierChe09, Lemme 3.18],
$\unicode[STIX]{x1D6E4}_{k}$
-representations in the relative setting. By [Reference ChenevierChe09, Lemme 3.18],
![]() $V$
has a
$V$
has a
![]() $\unicode[STIX]{x1D6E4}_{k}$
-stable
$\unicode[STIX]{x1D6E4}_{k}$
-stable
![]() $A_{K}^{\circ }$
-lattice. Note that [Reference ChenevierChe09, Lemme 3.18] only concerns reduced affinoid algebras over a finite extension of
$A_{K}^{\circ }$
-lattice. Note that [Reference ChenevierChe09, Lemme 3.18] only concerns reduced affinoid algebras over a finite extension of
![]() $\mathbb{Q}_{p}$
but the same proof works for
$\mathbb{Q}_{p}$
but the same proof works for
![]() $A_{K}$
since one can apply Raynaud’s theory to
$A_{K}$
since one can apply Raynaud’s theory to
![]() $A_{K}$
.
$A_{K}$
.
By [Reference Berger and ColmezBC08, Corollaire 3.2.4], there exist an
![]() $A_{K}$
-basis
$A_{K}$
-basis
![]() $v_{1},\ldots ,v_{r}\in V$
, a large positive integer
$v_{1},\ldots ,v_{r}\in V$
, a large positive integer
![]() $m$
, and an open subgroup
$m$
, and an open subgroup
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
of
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
such that the transformation matrix of
$\unicode[STIX]{x1D6E4}_{k}$
such that the transformation matrix of
![]() $\unicode[STIX]{x1D6FE}$
with respect to this basis has entries in
$\unicode[STIX]{x1D6FE}$
with respect to this basis has entries in
![]() $A_{k_{m}}$
for each
$A_{k_{m}}$
for each
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
. By shrinking
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
. By shrinking
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
if necessary, we may also assume that
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
if necessary, we may also assume that
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
acts trivially on
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
acts trivially on
![]() $A_{k_{m}}$
.
$A_{k_{m}}$
.
For each
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
, we denote by
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
, we denote by
![]() $U_{\unicode[STIX]{x1D6FE}}\in \operatorname{GL}_{r}(A_{K})$
the transformation matrix of
$U_{\unicode[STIX]{x1D6FE}}\in \operatorname{GL}_{r}(A_{K})$
the transformation matrix of
![]() $\unicode[STIX]{x1D6FE}$
with respect to
$\unicode[STIX]{x1D6FE}$
with respect to
![]() $v_{1},\ldots ,v_{r}$
. Note that
$v_{1},\ldots ,v_{r}$
. Note that
![]() $U_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FE}^{\prime }}=U_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FE}(U_{\unicode[STIX]{x1D6FE}^{\prime }})$
for
$U_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FE}^{\prime }}=U_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FE}(U_{\unicode[STIX]{x1D6FE}^{\prime }})$
for
![]() $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}$
.
Take a set
![]() $\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{s}\}$
of coset representatives of
$\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{s}\}$
of coset representatives of
![]() $\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }$
and let
$\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }$
and let
![]() $W$
be the finitely generated
$W$
be the finitely generated
![]() $A_{k_{m}}$
-submodule of
$A_{k_{m}}$
-submodule of
![]() $A_{K}$
generated by the entries of
$A_{K}$
generated by the entries of
![]() $U_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,U_{\unicode[STIX]{x1D6FE}_{s}}$
. Since
$U_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,U_{\unicode[STIX]{x1D6FE}_{s}}$
. Since
![]() $U_{\unicode[STIX]{x1D6FE}_{i}\unicode[STIX]{x1D6FE}^{\prime }}=U_{\unicode[STIX]{x1D6FE}_{i}}\unicode[STIX]{x1D6FE}_{i}(U_{\unicode[STIX]{x1D6FE}^{\prime }})$
and
$U_{\unicode[STIX]{x1D6FE}_{i}\unicode[STIX]{x1D6FE}^{\prime }}=U_{\unicode[STIX]{x1D6FE}_{i}}\unicode[STIX]{x1D6FE}_{i}(U_{\unicode[STIX]{x1D6FE}^{\prime }})$
and
![]() $\unicode[STIX]{x1D6FE}_{i}(U_{\unicode[STIX]{x1D6FE}^{\prime }})$
has entries in
$\unicode[STIX]{x1D6FE}_{i}(U_{\unicode[STIX]{x1D6FE}^{\prime }})$
has entries in
![]() $A_{k_{m}}$
for
$A_{k_{m}}$
for
![]() $\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
by our construction, it follows that
$\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
by our construction, it follows that
![]() $W$
is independent of the choice of the representatives
$W$
is independent of the choice of the representatives
![]() $\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{s}$
. Moreover, we have
$\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{s}$
. Moreover, we have
![]() $\unicode[STIX]{x1D6FE}^{\prime }(U_{\unicode[STIX]{x1D6FE}_{i}})=U_{\unicode[STIX]{x1D6FE}^{\prime }}^{-1}U_{\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}_{i}}$
for
$\unicode[STIX]{x1D6FE}^{\prime }(U_{\unicode[STIX]{x1D6FE}_{i}})=U_{\unicode[STIX]{x1D6FE}^{\prime }}^{-1}U_{\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}_{i}}$
for
![]() $\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
. From this we see that
$\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
. From this we see that
![]() $W$
is stable under the action of
$W$
is stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }$
.
$\unicode[STIX]{x1D6E4}_{k}^{\prime }$
.
Proposition 2.6 implies that
![]() $W\subset A_{\infty }$
, namely,
$W\subset A_{\infty }$
, namely,
![]() $U_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,U_{\unicode[STIX]{x1D6FE}_{s}}\in \operatorname{GL}_{r}(A_{\infty })$
. Thus if we increase
$U_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,U_{\unicode[STIX]{x1D6FE}_{s}}\in \operatorname{GL}_{r}(A_{\infty })$
. Thus if we increase
![]() $m$
so that
$m$
so that
![]() $U_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,U_{\unicode[STIX]{x1D6FE}_{s}}\in \operatorname{GL}_{r}(A_{k_{m}})$
, then
$U_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,U_{\unicode[STIX]{x1D6FE}_{s}}\in \operatorname{GL}_{r}(A_{k_{m}})$
, then
![]() $U_{\unicode[STIX]{x1D6FE}}\in \operatorname{GL}_{r}(A_{k_{m}})$
for any
$U_{\unicode[STIX]{x1D6FE}}\in \operatorname{GL}_{r}(A_{k_{m}})$
for any
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.◻
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.◻
We keep the notation in the proof of the lemma. From the lemma, we see that
![]() $\bigoplus _{i=1}^{r}A_{\infty }v_{i}\subset V_{\text{fin}}$
. So it suffices to prove that this is an equality.
$\bigoplus _{i=1}^{r}A_{\infty }v_{i}\subset V_{\text{fin}}$
. So it suffices to prove that this is an equality.
Take any
![]() $v\in V_{\text{fin}}$
. Let
$v\in V_{\text{fin}}$
. Let
![]() $W_{v}$
be the
$W_{v}$
be the
![]() $A_{k_{m}}$
-submodule of
$A_{k_{m}}$
-submodule of
![]() $A_{K}$
generated by the coordinates of
$A_{K}$
generated by the coordinates of
![]() $\unicode[STIX]{x1D6FE}v$
with respect to the basis
$\unicode[STIX]{x1D6FE}v$
with respect to the basis
![]() $v_{1},\ldots ,v_{r}$
where
$v_{1},\ldots ,v_{r}$
where
![]() $\unicode[STIX]{x1D6FE}$
runs over all elements of
$\unicode[STIX]{x1D6FE}$
runs over all elements of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Since
$\unicode[STIX]{x1D6E4}_{k}$
. Since
![]() $v\in V_{\text{fin}}$
, this is a finitely generated
$v\in V_{\text{fin}}$
, this is a finitely generated
![]() $A_{k_{m}}$
-module.
$A_{k_{m}}$
-module.
Write
![]() $v=\sum _{i=1}^{r}a_{i}v_{i}$
with
$v=\sum _{i=1}^{r}a_{i}v_{i}$
with
![]() $a_{i}\in A_{K}$
and denote the column vector of the
$a_{i}\in A_{K}$
and denote the column vector of the
![]() $a_{i}$
by
$a_{i}$
by
![]() $\vec{a}$
. Then it is easy to see that
$\vec{a}$
. Then it is easy to see that
![]() $W_{v}$
is generated by the entries of
$W_{v}$
is generated by the entries of
![]() $U_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FE}(\vec{a})$
(
$U_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FE}(\vec{a})$
(
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
). Since
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
). Since
![]() $U_{\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}}=U_{\unicode[STIX]{x1D6FE}^{\prime }}\unicode[STIX]{x1D6FE}^{\prime }(U_{\unicode[STIX]{x1D6FE}})$
for
$U_{\unicode[STIX]{x1D6FE}^{\prime }\unicode[STIX]{x1D6FE}}=U_{\unicode[STIX]{x1D6FE}^{\prime }}\unicode[STIX]{x1D6FE}^{\prime }(U_{\unicode[STIX]{x1D6FE}})$
for
![]() $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}$
, we compute
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime }\in \unicode[STIX]{x1D6E4}_{k}$
, we compute
From this we see that
![]() $W_{v}$
is stable under the action of
$W_{v}$
is stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.
By Proposition 2.6, we have
![]() $W_{v}\subset A_{\infty }$
. In particular,
$W_{v}\subset A_{\infty }$
. In particular,
![]() $a_{1},\ldots ,a_{r}\in A_{\infty }$
and thus
$a_{1},\ldots ,a_{r}\in A_{\infty }$
and thus
![]() $v\in \bigoplus _{i=1}^{r}A_{\infty }v_{i}$
.◻
$v\in \bigoplus _{i=1}^{r}A_{\infty }v_{i}$
.◻
Proposition 2.11. Let
![]() $V$
be an
$V$
be an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. If
$\unicode[STIX]{x1D6E4}_{k}$
. If
![]() $V$
is finite free of rank
$V$
is finite free of rank
![]() $r$
over
$r$
over
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
, then
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
, then
![]() $V_{\text{fin}}$
is finite free of rank
$V_{\text{fin}}$
is finite free of rank
![]() $r$
over
$r$
over
![]() $A_{\infty }[t]/(t^{n})$
. Moreover, the natural map
$A_{\infty }[t]/(t^{n})$
. Moreover, the natural map
is an isomorphism.
Proof. We prove this proposition by induction on
![]() $n$
. When
$n$
. When
![]() $n=1$
, this is Theorem 2.9. So we assume
$n=1$
, this is Theorem 2.9. So we assume
![]() $n>1$
.
$n>1$
.
Set
![]() $V^{\prime }:=t^{n-1}V$
and
$V^{\prime }:=t^{n-1}V$
and
![]() $V^{\prime \prime }:=V/V^{\prime }$
. They are
$V^{\prime \prime }:=V/V^{\prime }$
. They are
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representations of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and
$\unicode[STIX]{x1D6E4}_{k}$
and
![]() $V^{\prime \prime }$
is finite free of rank
$V^{\prime \prime }$
is finite free of rank
![]() $r$
over
$r$
over
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n-1})$
. By induction hypothesis,
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n-1})$
. By induction hypothesis,
![]() $V_{\text{fin}}^{\prime \prime }$
is finite free of rank
$V_{\text{fin}}^{\prime \prime }$
is finite free of rank
![]() $r$
over
$r$
over
![]() $A_{\infty }[t]/(t^{n-1})$
and
$A_{\infty }[t]/(t^{n-1})$
and
![]() $V_{\text{fin}}^{\prime \prime }\otimes _{A_{\infty }[t]/(t^{n-1})}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n-1})\cong V^{\prime \prime }$
.
$V_{\text{fin}}^{\prime \prime }\otimes _{A_{\infty }[t]/(t^{n-1})}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n-1})\cong V^{\prime \prime }$
.
Take lifts
![]() $v_{1},\ldots ,v_{r}$
of a basis of
$v_{1},\ldots ,v_{r}$
of a basis of
![]() $V_{\text{fin}}^{\prime \prime }$
to
$V_{\text{fin}}^{\prime \prime }$
to
![]() $V$
. Then
$V$
. Then
![]() $v_{1},\ldots ,v_{r}$
form an
$v_{1},\ldots ,v_{r}$
form an
![]() $A_{\infty }[t]/(t^{n})$
-basis of
$A_{\infty }[t]/(t^{n})$
-basis of
![]() $V$
. We will prove that after a suitable modification of
$V$
. We will prove that after a suitable modification of
![]() $v_{1},\ldots ,v_{r}$
the transformation matrix of
$v_{1},\ldots ,v_{r}$
the transformation matrix of
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $V$
with respect to the new basis has entries in
$V$
with respect to the new basis has entries in
![]() $A_{\infty }[t]/(t^{n})$
for every
$A_{\infty }[t]/(t^{n})$
for every
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.
Suppose that we are given an element
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. For each
$\unicode[STIX]{x1D6E4}_{k}$
. For each
![]() $1\leqslant j\leqslant r$
, write
$1\leqslant j\leqslant r$
, write
![]() $\unicode[STIX]{x1D6FE}v_{j}=\sum _{i=1}^{r}a_{ij}v_{i}$
with
$\unicode[STIX]{x1D6FE}v_{j}=\sum _{i=1}^{r}a_{ij}v_{i}$
with
![]() $a_{ij}\in A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
. Then the
$a_{ij}\in A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
. Then the
![]() $r\times r$
matrix
$r\times r$
matrix
![]() $T:=(a_{ij})$
is invertible since it is invertible modulo
$T:=(a_{ij})$
is invertible since it is invertible modulo
![]() $t^{n-1}$
. By the property of
$t^{n-1}$
. By the property of
![]() $V_{\text{fin}}^{\prime \prime }$
, we can write
$V_{\text{fin}}^{\prime \prime }$
, we can write
Set
![]() $U:=(a_{ij}^{0}\hspace{0.2em}{\rm mod}\hspace{0.2em}\,t)\in M_{r}(A_{\infty })$
. This is invertible. In fact,
$U:=(a_{ij}^{0}\hspace{0.2em}{\rm mod}\hspace{0.2em}\,t)\in M_{r}(A_{\infty })$
. This is invertible. In fact,
![]() $U$
is the transformation matrix of
$U$
is the transformation matrix of
![]() $\unicode[STIX]{x1D6FE}$
acting on
$\unicode[STIX]{x1D6FE}$
acting on
![]() $V/tV$
with respect to the basis
$V/tV$
with respect to the basis
![]() $(v_{i}\hspace{0.2em}{\rm mod}\hspace{0.2em}\,t)$
.
$(v_{i}\hspace{0.2em}{\rm mod}\hspace{0.2em}\,t)$
.
Since
![]() $\unicode[STIX]{x1D6E4}_{k}$
acts continuously on
$\unicode[STIX]{x1D6E4}_{k}$
acts continuously on
![]() $V/tV$
,
$V/tV$
,
![]() $\operatorname{val}(U-1)>c_{3}$
and
$\operatorname{val}(U-1)>c_{3}$
and
![]() $m(\unicode[STIX]{x1D6FE})>\max \{c_{3},m(k)\}$
for some
$m(\unicode[STIX]{x1D6FE})>\max \{c_{3},m(k)\}$
for some
![]() $\unicode[STIX]{x1D6FE}\neq 1$
close to
$\unicode[STIX]{x1D6FE}\neq 1$
close to
![]() $1$
. From now on, we fix such
$1$
. From now on, we fix such
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.
Claim 2.12. There exists an element in
![]() $\operatorname{GL}_{r}(A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n}))$
of the form
$\operatorname{GL}_{r}(A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n}))$
of the form
![]() $1+t^{n-1}M$
with
$1+t^{n-1}M$
with
![]() $M\in M_{r}(A_{K})$
such that the
$M\in M_{r}(A_{K})$
such that the
![]() $r\times r$
matrix
$r\times r$
matrix
lies in
![]() $\operatorname{GL}_{r}(A_{\infty }[t]/(t^{n}))$
.
$\operatorname{GL}_{r}(A_{\infty }[t]/(t^{n}))$
.
Proof. Noting that every element in
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
is annihilated by
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
is annihilated by
![]() $t^{n}$
, we compute
$t^{n}$
, we compute
 $$\begin{eqnarray}\displaystyle (1+t^{n-1}M)^{-1}T\unicode[STIX]{x1D6FE}(1+t^{n-1}M) & = & \displaystyle (1-t^{n-1}M)T(1+\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}t^{n-1}\unicode[STIX]{x1D6FE}(M))\nonumber\\ \displaystyle & = & \displaystyle T-t^{n-1}(MT-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}T\unicode[STIX]{x1D6FE}(M))\nonumber\\ \displaystyle & & \displaystyle -\,t^{2(n-1)}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}MT\unicode[STIX]{x1D6FE}(M)\nonumber\\ \displaystyle & = & \displaystyle T-t^{n-1}(MU-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}U\unicode[STIX]{x1D6FE}(M)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (1+t^{n-1}M)^{-1}T\unicode[STIX]{x1D6FE}(1+t^{n-1}M) & = & \displaystyle (1-t^{n-1}M)T(1+\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}t^{n-1}\unicode[STIX]{x1D6FE}(M))\nonumber\\ \displaystyle & = & \displaystyle T-t^{n-1}(MT-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}T\unicode[STIX]{x1D6FE}(M))\nonumber\\ \displaystyle & & \displaystyle -\,t^{2(n-1)}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}MT\unicode[STIX]{x1D6FE}(M)\nonumber\\ \displaystyle & = & \displaystyle T-t^{n-1}(MU-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{n-1}U\unicode[STIX]{x1D6FE}(M)).\nonumber\end{eqnarray}$$
Since
![]() $T=(a_{ij}^{0})+t^{n-1}(a_{ij}^{1})$
with
$T=(a_{ij}^{0})+t^{n-1}(a_{ij}^{1})$
with
![]() $(a_{ij}^{0})\in \operatorname{GL}_{r}(A_{\infty }[t]/(t^{n}))$
, it suffices to find
$(a_{ij}^{0})\in \operatorname{GL}_{r}(A_{\infty }[t]/(t^{n}))$
, it suffices to find
![]() $M\in M_{r}(A_{K})$
such that
$M\in M_{r}(A_{K})$
such that
We will apply Lemma 2.13 below to
![]() $U$
,
$U$
,
![]() $U^{\prime }=U^{-1}$
and
$U^{\prime }=U^{-1}$
and
![]() $s=n-1$
. Take
$s=n-1$
. Take
![]() $m\geqslant m(\unicode[STIX]{x1D6FE})$
large enough so that
$m\geqslant m(\unicode[STIX]{x1D6FE})$
large enough so that
![]() $U$
and
$U$
and
![]() $U^{-1}$
lie in
$U^{-1}$
lie in
![]() $\operatorname{GL}_{r}(A_{k_{m}})$
. Recall the normalized trace map
$\operatorname{GL}_{r}(A_{k_{m}})$
. Recall the normalized trace map
![]() $R_{A,m}:A_{K}\rightarrow A_{k_{m}}$
with kernel
$R_{A,m}:A_{K}\rightarrow A_{k_{m}}$
with kernel
![]() $X_{A,m}$
. Since
$X_{A,m}$
. Since
![]() $R_{A,m}$
is
$R_{A,m}$
is
![]() $A_{k_{m}}$
-linear, we see that
$A_{k_{m}}$
-linear, we see that
![]() $((1-R_{A,m})(a_{ij}^{1}))U^{-1}\in M_{r}(X_{A,m})$
. Therefore, by Lemma 2.13, there exists
$((1-R_{A,m})(a_{ij}^{1}))U^{-1}\in M_{r}(X_{A,m})$
. Therefore, by Lemma 2.13, there exists
![]() $M_{0}\in M_{r}(X_{A,m})$
such that
$M_{0}\in M_{r}(X_{A,m})$
such that
From this we have
and the matrix
![]() $1+t^{n-1}M_{0}$
satisfies the condition of the lemma.◻
$1+t^{n-1}M_{0}$
satisfies the condition of the lemma.◻
We continue the proof of the proposition. We replace the basis
![]() $v_{1},\ldots ,v_{r}$
by the one corresponding to the matrix
$v_{1},\ldots ,v_{r}$
by the one corresponding to the matrix
![]() $1+t^{n-1}M$
in the lemma. Then the transformation matrix of our fixed
$1+t^{n-1}M$
in the lemma. Then the transformation matrix of our fixed
![]() $\unicode[STIX]{x1D6FE}$
with respect to the new
$\unicode[STIX]{x1D6FE}$
with respect to the new
![]() $v_{1},\ldots ,v_{r}$
has entries in
$v_{1},\ldots ,v_{r}$
has entries in
![]() $A_{k_{m}}[t]/(t^{n})$
. Thus for each
$A_{k_{m}}[t]/(t^{n})$
. Thus for each
![]() $1\leqslant i\leqslant r$
, the
$1\leqslant i\leqslant r$
, the
![]() $\unicode[STIX]{x1D6FE}^{\mathbb{Z}_{p}}$
-orbit of
$\unicode[STIX]{x1D6FE}^{\mathbb{Z}_{p}}$
-orbit of
![]() $v_{i}$
is contained in a finitely generated
$v_{i}$
is contained in a finitely generated
![]() $A_{k_{m}}[t]/(t^{n})$
-submodule of
$A_{k_{m}}[t]/(t^{n})$
-submodule of
![]() $V$
that is stable under
$V$
that is stable under
![]() $\unicode[STIX]{x1D6FE}^{\mathbb{Z}_{p}}$
. Since
$\unicode[STIX]{x1D6FE}^{\mathbb{Z}_{p}}$
. Since
![]() $\unicode[STIX]{x1D6FE}^{\mathbb{Z}_{p}}$
is of finite index in
$\unicode[STIX]{x1D6FE}^{\mathbb{Z}_{p}}$
is of finite index in
![]() $\unicode[STIX]{x1D6E4}_{k}$
, the
$\unicode[STIX]{x1D6E4}_{k}$
, the
![]() $\unicode[STIX]{x1D6E4}_{k}$
-orbit of
$\unicode[STIX]{x1D6E4}_{k}$
-orbit of
![]() $v_{i}$
is also contained in a finitely generated
$v_{i}$
is also contained in a finitely generated
![]() $A_{k_{m}}[t]/(t^{n})$
-submodule of
$A_{k_{m}}[t]/(t^{n})$
-submodule of
![]() $V$
that is stable under
$V$
that is stable under
![]() $\unicode[STIX]{x1D6E4}_{k}$
. This means that
$\unicode[STIX]{x1D6E4}_{k}$
. This means that
![]() $v_{1},\ldots ,v_{r}\in V_{\text{fin}}$
. Hence
$v_{1},\ldots ,v_{r}\in V_{\text{fin}}$
. Hence
![]() $\bigoplus _{i=1}^{r}A_{\infty }[t]/(t^{n})v_{i}\subset V_{\text{fin}}$
.
$\bigoplus _{i=1}^{r}A_{\infty }[t]/(t^{n})v_{i}\subset V_{\text{fin}}$
.
It remains to prove that
![]() $\bigoplus _{i=1}^{r}A_{\infty }[t]/(t^{n})v_{i}=V_{\text{fin}}$
. Since
$\bigoplus _{i=1}^{r}A_{\infty }[t]/(t^{n})v_{i}=V_{\text{fin}}$
. Since
![]() $A_{\infty }[t]/(t^{n})\rightarrow A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
is faithfully flat and
$A_{\infty }[t]/(t^{n})\rightarrow A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
is faithfully flat and
![]() $V=\bigoplus _{i=1}^{r}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})v_{i}$
, it is enough to show that the natural map
$V=\bigoplus _{i=1}^{r}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})v_{i}$
, it is enough to show that the natural map
![]() $V_{\text{fin}}\otimes _{A_{\infty }[t]/(t^{n})}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})\rightarrow V$
is injective. Note that
$V_{\text{fin}}\otimes _{A_{\infty }[t]/(t^{n})}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})\rightarrow V$
is injective. Note that
![]() $V_{\text{fin}}\otimes _{A_{\infty }[t]/(t^{n})}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})=V_{\text{fin}}\otimes _{A_{\infty }[[t]]}A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
.
$V_{\text{fin}}\otimes _{A_{\infty }[t]/(t^{n})}A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})=V_{\text{fin}}\otimes _{A_{\infty }[[t]]}A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
.
Recall the exact sequence
![]() $0\rightarrow V^{\prime }\rightarrow V\rightarrow V^{\prime \prime }\rightarrow 0$
. From this we have an exact sequence
$0\rightarrow V^{\prime }\rightarrow V\rightarrow V^{\prime \prime }\rightarrow 0$
. From this we have an exact sequence
![]() $0\rightarrow V_{\text{fin}}^{\prime }\rightarrow V_{\text{fin}}\rightarrow V_{\text{fin}}^{\prime \prime }$
, and it yields the following commutative diagram with exact rows
$0\rightarrow V_{\text{fin}}^{\prime }\rightarrow V_{\text{fin}}\rightarrow V_{\text{fin}}^{\prime \prime }$
, and it yields the following commutative diagram with exact rows

where the tensor products in the first row are taken over
![]() $A_{\infty }[[t]]$
. By induction hypothesis, the first and the third vertical maps are isomorphisms. Hence the second vertical map is injective and this completes the proof.◻
$A_{\infty }[[t]]$
. By induction hypothesis, the first and the third vertical maps are isomorphisms. Hence the second vertical map is injective and this completes the proof.◻
The following lemma is used in the proof of Proposition 2.11.
Lemma 2.13. Let
![]() $s$
be a positive integer. Let
$s$
be a positive integer. Let
![]() $U,U^{\prime }$
be elements in
$U,U^{\prime }$
be elements in
![]() $M_{r}(A_{\infty })$
satisfying
$M_{r}(A_{\infty })$
satisfying
![]() $\operatorname{val}(U-1)>c_{3}$
and
$\operatorname{val}(U-1)>c_{3}$
and
![]() $\operatorname{val}(U^{\prime }-1)>c_{3}$
. Take a positive integer
$\operatorname{val}(U^{\prime }-1)>c_{3}$
. Take a positive integer
![]() $m$
such that
$m$
such that
![]() $m>\max \{m(k),c_{3}\}$
and
$m>\max \{m(k),c_{3}\}$
and
![]() $U,U^{\prime }\in M_{r}(A_{k_{m}})$
. Then for any
$U,U^{\prime }\in M_{r}(A_{k_{m}})$
. Then for any
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
with
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
with
![]() $c_{3}<m(\unicode[STIX]{x1D6FE})\leqslant m$
, the map
$c_{3}<m(\unicode[STIX]{x1D6FE})\leqslant m$
, the map
is bijective on the subset
![]() $M_{r}(X_{A,m})$
consisting of the
$M_{r}(X_{A,m})$
consisting of the
![]() $r\times r$
matrices with entries in the kernel
$r\times r$
matrices with entries in the kernel
![]() $X_{A,m}$
of
$X_{A,m}$
of
![]() $R_{A,m}:A_{K}\rightarrow A_{k_{m}}$
.
$R_{A,m}:A_{K}\rightarrow A_{k_{m}}$
.
Proof. The proof of [Reference Brinon and ConradBC09, Lemma 15.3.9] works in our setting. For the convenience of the reader, we reproduce their proof here.
We first check that
![]() $f$
restricts to an endomorphism on
$f$
restricts to an endomorphism on
![]() $M_{r}(X_{A,m})$
. This follows from the fact that the map
$M_{r}(X_{A,m})$
. This follows from the fact that the map
![]() $R_{A,m}$
is
$R_{A,m}$
is
![]() $A_{k_{m}}$
-linear and
$A_{k_{m}}$
-linear and
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant and thus
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant and thus
![]() $X_{A,m}$
is an
$X_{A,m}$
is an
![]() $A_{k_{m}}$
-module stable under the action of
$A_{k_{m}}$
-module stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.
We define a map
![]() $h:M_{r}(A_{K})\rightarrow M_{r}(A_{K})$
by
$h:M_{r}(A_{K})\rightarrow M_{r}(A_{K})$
by
Then the same argument as above shows that
![]() $h$
restricts to an endomorphism on
$h$
restricts to an endomorphism on
![]() $M_{r}(X_{A,m})$
. We also have
$M_{r}(X_{A,m})$
. We also have
![]() $f(M)=(1-\unicode[STIX]{x1D6FE})M+h(\unicode[STIX]{x1D6FE}M)$
.
$f(M)=(1-\unicode[STIX]{x1D6FE})M+h(\unicode[STIX]{x1D6FE}M)$
.
Recall that the map
![]() $1-\unicode[STIX]{x1D6FE}:M_{r}(X_{A,m})\rightarrow M_{r}(X_{A,m})$
admits a continuous inverse with operator norm at most
$1-\unicode[STIX]{x1D6FE}:M_{r}(X_{A,m})\rightarrow M_{r}(X_{A,m})$
admits a continuous inverse with operator norm at most
![]() $p^{c_{3}}$
. We denote this inverse by
$p^{c_{3}}$
. We denote this inverse by
![]() $\unicode[STIX]{x1D70C}$
. Since
$\unicode[STIX]{x1D70C}$
. Since
![]() $(f\circ \unicode[STIX]{x1D70C}-\operatorname{id})M=h(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70C}(M))$
, it suffices to prove that the operator norm of
$(f\circ \unicode[STIX]{x1D70C}-\operatorname{id})M=h(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70C}(M))$
, it suffices to prove that the operator norm of
![]() $h$
is less than
$h$
is less than
![]() $p^{-c_{3}}$
; this will imply that the operator norm of
$p^{-c_{3}}$
; this will imply that the operator norm of
![]() $h\circ \unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D70C}$
is less than
$h\circ \unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D70C}$
is less than
![]() $1$
. Thus
$1$
. Thus
![]() $f\circ \unicode[STIX]{x1D70C}$
admits a continuous inverse given by a geometric series and hence
$f\circ \unicode[STIX]{x1D70C}$
admits a continuous inverse given by a geometric series and hence
![]() $f$
is bijective on
$f$
is bijective on
![]() $M_{r}(X_{A,m})$
.
$M_{r}(X_{A,m})$
.
By the second expression of
![]() $h$
, we have
$h$
, we have
From this we have
where
![]() $\unicode[STIX]{x1D6FF}:=\min \{m(\unicode[STIX]{x1D6FE}),\operatorname{val}(U-1),\operatorname{val}(U^{\prime }-1)\}$
. Thus the operator norm of
$\unicode[STIX]{x1D6FF}:=\min \{m(\unicode[STIX]{x1D6FE}),\operatorname{val}(U-1),\operatorname{val}(U^{\prime }-1)\}$
. Thus the operator norm of
![]() $h$
is at most
$h$
is at most
![]() $p^{-\unicode[STIX]{x1D6FF}}$
. Since
$p^{-\unicode[STIX]{x1D6FF}}$
. Since
![]() $\unicode[STIX]{x1D6FF}>c_{3}$
by assumption, this completes the proof.◻
$\unicode[STIX]{x1D6FF}>c_{3}$
by assumption, this completes the proof.◻
Proof of Theorem 2.5.
For each
![]() $n\geqslant 1$
, put
$n\geqslant 1$
, put
![]() $V_{n}:=V/t^{n}V$
. This is an
$V_{n}:=V/t^{n}V$
. This is an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
that is finite free of rank
$\unicode[STIX]{x1D6E4}_{k}$
that is finite free of rank
![]() $r$
over
$r$
over
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
. Thus by Proposition 2.11,
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
. Thus by Proposition 2.11,
![]() $(V_{n})_{\text{fin}}$
is finite free of rank
$(V_{n})_{\text{fin}}$
is finite free of rank
![]() $r$
over
$r$
over
![]() $A_{\infty }[t]/(t^{n})$
, and
$A_{\infty }[t]/(t^{n})$
, and
![]() $(V_{n})_{\text{fin}}\otimes _{A_{\infty }[[t]]}(A\,\hat{\otimes }\,L_{\text{dR}}^{+})\rightarrow V_{n}$
is an isomorphism.
$(V_{n})_{\text{fin}}\otimes _{A_{\infty }[[t]]}(A\,\hat{\otimes }\,L_{\text{dR}}^{+})\rightarrow V_{n}$
is an isomorphism.
By definition, we have
![]() $V_{\text{fin}}=\mathop{\varprojlim }\nolimits_{n}(V_{n})_{\text{fin}}$
. Since the natural map
$V_{\text{fin}}=\mathop{\varprojlim }\nolimits_{n}(V_{n})_{\text{fin}}$
. Since the natural map
![]() $V_{n+1}\rightarrow V_{n}$
is surjective, so is the map
$V_{n+1}\rightarrow V_{n}$
is surjective, so is the map
![]() $(V_{n+1})_{\text{fin}}\rightarrow (V_{n})_{\text{fin}}$
by the faithfully flatness of
$(V_{n+1})_{\text{fin}}\rightarrow (V_{n})_{\text{fin}}$
by the faithfully flatness of
![]() $A_{\infty }[t]/(t^{n+1})\rightarrow A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n+1})$
. Thus lifting a basis of
$A_{\infty }[t]/(t^{n+1})\rightarrow A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n+1})$
. Thus lifting a basis of
![]() $(V_{n})_{\text{fin}}$
gives a basis of
$(V_{n})_{\text{fin}}$
gives a basis of
![]() $V_{\text{fin}}$
and we see that
$V_{\text{fin}}$
and we see that
![]() $V_{\text{fin}}$
is finite free of rank
$V_{\text{fin}}$
is finite free of rank
![]() $r$
over
$r$
over
![]() $A_{\infty }[[t]]$
. The remaining assertions also follow from this.◻
$A_{\infty }[[t]]$
. The remaining assertions also follow from this.◻
Proposition 2.14. For an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
that is finite free of rank
$\unicode[STIX]{x1D6E4}_{k}$
that is finite free of rank
![]() $r$
over
$r$
over
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
, the
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
, the
![]() $A_{\infty }[[t]]$
-module
$A_{\infty }[[t]]$
-module
![]() $V_{\text{fin}}$
is the union of finitely generated
$V_{\text{fin}}$
is the union of finitely generated
![]() $A_{\infty }[[t]]$
-submodules of
$A_{\infty }[[t]]$
-submodules of
![]() $V$
that are stable under the action of
$V$
that are stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. In particular, the natural inclusion
$\unicode[STIX]{x1D6E4}_{k}$
. In particular, the natural inclusion
is an isomorphism.
Proof. Let
![]() $V_{\text{fin}}^{\prime }$
denote the union of finitely generated
$V_{\text{fin}}^{\prime }$
denote the union of finitely generated
![]() $A_{\infty }[[t]]$
-submodules of
$A_{\infty }[[t]]$
-submodules of
![]() $V$
that are stable under the action of
$V$
that are stable under the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then
$\unicode[STIX]{x1D6E4}_{k}$
. Then
![]() $V_{\text{fin}}\subset V_{\text{fin}}^{\prime }$
by Theorem 2.5. So it remains to prove the opposite inclusion. For this it suffices to prove
$V_{\text{fin}}\subset V_{\text{fin}}^{\prime }$
by Theorem 2.5. So it remains to prove the opposite inclusion. For this it suffices to prove
![]() $V_{\text{fin}}^{\prime }/t^{n}V_{\text{fin}}^{\prime }\subset V_{\text{fin}}/t^{n}V_{\text{fin}}$
for each
$V_{\text{fin}}^{\prime }/t^{n}V_{\text{fin}}^{\prime }\subset V_{\text{fin}}/t^{n}V_{\text{fin}}$
for each
![]() $n\geqslant 1$
. Since
$n\geqslant 1$
. Since
![]() $V_{\text{fin}}/t^{n}V_{\text{fin}}=(V/t^{n}V)_{\text{fin}}$
by Theorem 2.5, the desired inclusion follows from the definition of
$V_{\text{fin}}/t^{n}V_{\text{fin}}=(V/t^{n}V)_{\text{fin}}$
by Theorem 2.5, the desired inclusion follows from the definition of
![]() $(V/t^{n}V)_{\text{fin}}$
noting
$(V/t^{n}V)_{\text{fin}}$
noting
![]() $A_{\infty }[t]/(t^{n})=\bigcup _{m}A_{k_{m}}[t]/(t^{n})$
. The second assertion follows from the first.◻
$A_{\infty }[t]/(t^{n})=\bigcup _{m}A_{k_{m}}[t]/(t^{n})$
. The second assertion follows from the first.◻
Example 2.15. For the trivial
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation
![]() $V=A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
of
$V=A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, we have
$\unicode[STIX]{x1D6E4}_{k}$
, we have
![]() $V_{\text{fin}}=A_{\infty }[[t]]$
.
$V_{\text{fin}}=A_{\infty }[[t]]$
.
Finally, we discuss topologies on
![]() $V_{\text{fin}}$
and the continuity of the action of
$V_{\text{fin}}$
and the continuity of the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.
Lemma 2.16. Let
![]() $W$
be a finite free
$W$
be a finite free
![]() $A_{\infty }[[t]]/(t^{n})$
-module equipped with an action of
$A_{\infty }[[t]]/(t^{n})$
-module equipped with an action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then
$\unicode[STIX]{x1D6E4}_{k}$
. Then
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action is continuous with respect to the topology on
$\unicode[STIX]{x1D6E4}_{k}$
-action is continuous with respect to the topology on
![]() $W$
induced from the product topology on
$W$
induced from the product topology on
![]() $A_{\infty }[[t]]/(t^{n})\cong A_{\infty }^{n}$
if and only if it is continuous with respect to the topology on
$A_{\infty }[[t]]/(t^{n})\cong A_{\infty }^{n}$
if and only if it is continuous with respect to the topology on
![]() $W$
induced from the subspace topology on
$W$
induced from the subspace topology on
![]() $A_{\infty }[[t]]/(t^{n})\subset A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
.
$A_{\infty }[[t]]/(t^{n})\subset A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
.
Proof. For each of the two topologies on
![]() $W$
, the continuity of
$W$
, the continuity of
![]() $\unicode[STIX]{x1D6E4}_{k}$
implies that there exist an
$\unicode[STIX]{x1D6E4}_{k}$
implies that there exist an
![]() $A_{\infty }[[t]]/(t^{n})$
-basis
$A_{\infty }[[t]]/(t^{n})$
-basis
![]() $w_{1},\ldots ,w_{r}$
of
$w_{1},\ldots ,w_{r}$
of
![]() $W$
and a large positive integer
$W$
and a large positive integer
![]() $m$
such that
$m$
such that
![]() $W_{m}:=\bigoplus _{i=1}^{r}A_{k_{m}}[[t]]/(t^{n})w_{i}$
is stable under
$W_{m}:=\bigoplus _{i=1}^{r}A_{k_{m}}[[t]]/(t^{n})w_{i}$
is stable under
![]() $\unicode[STIX]{x1D6E4}_{k}$
and its action on
$\unicode[STIX]{x1D6E4}_{k}$
and its action on
![]() $W_{m}$
is continuous with respect to the induced topology
$W_{m}$
is continuous with respect to the induced topology
![]() $W_{m}\subset W$
. Conversely, if the
$W_{m}\subset W$
. Conversely, if the
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action on
$\unicode[STIX]{x1D6E4}_{k}$
-action on
![]() $W_{m}$
is continuous with respect to the induced topology
$W_{m}$
is continuous with respect to the induced topology
![]() $W_{m}\subset W$
for such
$W_{m}\subset W$
for such
![]() $\unicode[STIX]{x1D6E4}_{k}$
-stable
$\unicode[STIX]{x1D6E4}_{k}$
-stable
![]() $A_{k_{m}}[[t]]/(t^{n})$
-submodule
$A_{k_{m}}[[t]]/(t^{n})$
-submodule
![]() $W_{m}$
with
$W_{m}$
with
![]() $W_{m}\otimes _{A_{k_{m}}[[t]]/(t^{n})}A_{\infty }[[t]]/(t^{n})=W$
, the
$W_{m}\otimes _{A_{k_{m}}[[t]]/(t^{n})}A_{\infty }[[t]]/(t^{n})=W$
, the
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action on
$\unicode[STIX]{x1D6E4}_{k}$
-action on
![]() $W$
is continuous.
$W$
is continuous.
The subspace topology on
![]() $A_{k_{m}}[[t]]/(t^{n})$
from
$A_{k_{m}}[[t]]/(t^{n})$
from
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
coincides with the product topology on
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
coincides with the product topology on
![]() $A_{k_{m}}[[t]]/(t^{n})\cong A_{k_{m}}^{n}$
. From this we find that the continuity conditions on the action of
$A_{k_{m}}[[t]]/(t^{n})\cong A_{k_{m}}^{n}$
. From this we find that the continuity conditions on the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
on
$\unicode[STIX]{x1D6E4}_{k}$
on
![]() $W_{m}$
with respect to the two topologies coincide. Hence the two continuity properties of the action of
$W_{m}$
with respect to the two topologies coincide. Hence the two continuity properties of the action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
on
$\unicode[STIX]{x1D6E4}_{k}$
on
![]() $W$
are equivalent.◻
$W$
are equivalent.◻
Definition 2.17. Let
![]() $V$
be an
$V$
be an
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.
– If
 $V$
is finite free over
$V$
is finite free over
 $A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
for some
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}/(t^{n})$
for some
 $n\geqslant 1$
, we equip
$n\geqslant 1$
, we equip
 $V_{\text{fin}}$
with the topology acquired from topologizing
$V_{\text{fin}}$
with the topology acquired from topologizing
 $A_{\infty }[[t]]/(t^{n})$
with the product topology of the
$A_{\infty }[[t]]/(t^{n})$
with the product topology of the
 $p$
-adic topology on
$p$
-adic topology on
 $A_{\infty }$
. Then
$A_{\infty }$
. Then
 $\unicode[STIX]{x1D6E4}_{k}$
acts continuously on
$\unicode[STIX]{x1D6E4}_{k}$
acts continuously on
 $V_{\text{fin}}$
by Lemma 2.16.
$V_{\text{fin}}$
by Lemma 2.16.– If
 $V$
is finite free over
$V$
is finite free over
 $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
, we equip
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
, we equip
 $V_{\text{fin}}$
with the inverse limit topology via
$V_{\text{fin}}$
with the inverse limit topology via
 $V_{\text{fin}}=\mathop{\varprojlim }\nolimits_{n}(V/t^{n}V)_{\text{fin}}$
. Then
$V_{\text{fin}}=\mathop{\varprojlim }\nolimits_{n}(V/t^{n}V)_{\text{fin}}$
. Then
 $\unicode[STIX]{x1D6E4}_{k}$
acts continuously on
$\unicode[STIX]{x1D6E4}_{k}$
acts continuously on
 $V_{\text{fin}}$
.
$V_{\text{fin}}$
.
Definition 2.18. An
![]() $A_{\infty }[[t]]$
-representation of
$A_{\infty }[[t]]$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
is an
$\unicode[STIX]{x1D6E4}_{k}$
is an
![]() $A_{\infty }[[t]]$
-module
$A_{\infty }[[t]]$
-module
![]() $W$
that is isomorphic to either
$W$
that is isomorphic to either
![]() $(A_{\infty }[[t]])^{r}$
or
$(A_{\infty }[[t]])^{r}$
or
![]() $(A_{\infty }[[t]]/(t^{n}))^{r}$
for some
$(A_{\infty }[[t]]/(t^{n}))^{r}$
for some
![]() $r$
and
$r$
and
![]() $n$
, equipped with a continuous
$n$
, equipped with a continuous
![]() $A_{\infty }[[t]]$
-semilinear action of
$A_{\infty }[[t]]$
-semilinear action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
(here the topology on
$\unicode[STIX]{x1D6E4}_{k}$
(here the topology on
![]() $W$
is acquired from the
$W$
is acquired from the
![]() $p$
-adic topology on
$p$
-adic topology on
![]() $A_{\infty }$
by considering the product topology and the inverse limit topology as before). We denote the category of
$A_{\infty }$
by considering the product topology and the inverse limit topology as before). We denote the category of
![]() $A_{\infty }[[t]]$
-representations of
$A_{\infty }[[t]]$
-representations of
![]() $\unicode[STIX]{x1D6E4}_{k}$
by
$\unicode[STIX]{x1D6E4}_{k}$
by
![]() $\text{Rep}_{\unicode[STIX]{x1D6E4}_{k}}(A_{\infty }[[t]])$
. An
$\text{Rep}_{\unicode[STIX]{x1D6E4}_{k}}(A_{\infty }[[t]])$
. An
![]() $A_{\infty }[[t]]$
-representation of
$A_{\infty }[[t]]$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
that is annihilated by
$\unicode[STIX]{x1D6E4}_{k}$
that is annihilated by
![]() $t$
is also called an
$t$
is also called an
![]() $A_{\infty }$
-representation of
$A_{\infty }$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6E4}_{k}$
.
Theorem 2.19. The decompletion functor
is an equivalence of categories. A quasi-inverse is given by
![]() $W\mapsto W\otimes _{A_{\infty }[[t]]}(A\,\hat{\otimes }\,L_{\text{dR}}^{+})$
.
$W\mapsto W\otimes _{A_{\infty }[[t]]}(A\,\hat{\otimes }\,L_{\text{dR}}^{+})$
.
2.3 Sen’s endomorphism and Fontaine’s connection in the relative setting
Proposition 2.20. Let
![]() $W$
be an
$W$
be an
![]() $A_{\infty }$
-representation of
$A_{\infty }$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then there exists a unique
$\unicode[STIX]{x1D6E4}_{k}$
. Then there exists a unique
![]() $A_{\infty }$
-linear map
$A_{\infty }$
-linear map
![]() $\unicode[STIX]{x1D719}_{W}:W\rightarrow W$
satisfying the following property: for any
$\unicode[STIX]{x1D719}_{W}:W\rightarrow W$
satisfying the following property: for any
![]() $w\in W$
, there exists an open subgroup
$w\in W$
, there exists an open subgroup
![]() $\unicode[STIX]{x1D6E4}_{k,w}$
of
$\unicode[STIX]{x1D6E4}_{k,w}$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
such that
$\unicode[STIX]{x1D6E4}_{k}$
such that
for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k,w}$
. Here
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k,w}$
. Here
![]() $\log$
(respectively
$\log$
(respectively
![]() $\exp$
) is the
$\exp$
) is the
![]() $p$
-adic logarithm (respectively exponential). Moreover,
$p$
-adic logarithm (respectively exponential). Moreover,
![]() $\unicode[STIX]{x1D719}_{W}$
is
$\unicode[STIX]{x1D719}_{W}$
is
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant and functorial with respect to
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant and functorial with respect to
![]() $W$
.
$W$
.
Remark 2.21. The proposition says that the endomorphism
![]() $\unicode[STIX]{x1D719}_{W}$
is computed as
$\unicode[STIX]{x1D719}_{W}$
is computed as
for
![]() $w\in W$
.
$w\in W$
.
Proof. This is standard; arguments in [Reference SenSen81, Theorem 4] also work in our setting. See also [Reference SenSen93, § 2], [Reference SenSen88, Proposition 4], [Reference FontaineFon04, Proposition 2.5], and [Reference Brinon and ConradBC09, § 15.1]. ◻
The following lemma is also proved by standard arguments.
Lemma 2.22. Let
![]() $W_{1}$
and
$W_{1}$
and
![]() $W_{2}$
be
$W_{2}$
be
![]() $A_{\infty }$
-representations of
$A_{\infty }$
-representations of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then we have the following equalities:
$\unicode[STIX]{x1D6E4}_{k}$
. Then we have the following equalities:
–
 $\unicode[STIX]{x1D719}_{W_{1}\oplus W_{2}}=\unicode[STIX]{x1D719}_{W_{1}}\oplus \unicode[STIX]{x1D719}_{W_{2}}$
on
$\unicode[STIX]{x1D719}_{W_{1}\oplus W_{2}}=\unicode[STIX]{x1D719}_{W_{1}}\oplus \unicode[STIX]{x1D719}_{W_{2}}$
on
 $W_{1}\oplus W_{2}$
;
$W_{1}\oplus W_{2}$
;–
 $\unicode[STIX]{x1D719}_{W_{1}\otimes W_{2}}=\unicode[STIX]{x1D719}_{W_{1}}\otimes \operatorname{id}_{W_{2}}+\operatorname{id}_{W_{1}}\otimes \,\unicode[STIX]{x1D719}_{W_{2}}$
on
$\unicode[STIX]{x1D719}_{W_{1}\otimes W_{2}}=\unicode[STIX]{x1D719}_{W_{1}}\otimes \operatorname{id}_{W_{2}}+\operatorname{id}_{W_{1}}\otimes \,\unicode[STIX]{x1D719}_{W_{2}}$
on
 $W_{1}\otimes W_{2}$
;
$W_{1}\otimes W_{2}$
;–
 $\unicode[STIX]{x1D719}_{\operatorname{Hom}(W_{1},W_{2})}(f)=\unicode[STIX]{x1D719}_{W_{2}}\circ f-f\circ \unicode[STIX]{x1D719}_{W_{1}}$
for
$\unicode[STIX]{x1D719}_{\operatorname{Hom}(W_{1},W_{2})}(f)=\unicode[STIX]{x1D719}_{W_{2}}\circ f-f\circ \unicode[STIX]{x1D719}_{W_{1}}$
for
 $f\in \operatorname{Hom}(W_{1},W_{2})$
.
$f\in \operatorname{Hom}(W_{1},W_{2})$
.
Definition 2.23. Let
![]() $V$
be an
$V$
be an
![]() $A_{K}$
-representation of
$A_{K}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. We denote by
$\unicode[STIX]{x1D6E4}_{k}$
. We denote by
![]() $\unicode[STIX]{x1D719}_{V}$
the
$\unicode[STIX]{x1D719}_{V}$
the
![]() $A_{K}$
-linear endomorphism
$A_{K}$
-linear endomorphism
![]() $\unicode[STIX]{x1D719}_{V_{\text{fin}}}\otimes \operatorname{id}_{A_{K}}$
on
$\unicode[STIX]{x1D719}_{V_{\text{fin}}}\otimes \operatorname{id}_{A_{K}}$
on
![]() $V=V_{\text{fin}}\otimes _{A_{\infty }}A_{K}$
.
$V=V_{\text{fin}}\otimes _{A_{\infty }}A_{K}$
.
Proposition 2.24. Let
![]() $W$
be an
$W$
be an
![]() $A_{\infty }[[t]]$
-representation of
$A_{\infty }[[t]]$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then there exists a unique
$\unicode[STIX]{x1D6E4}_{k}$
. Then there exists a unique
![]() $A_{\infty }$
-linear map
$A_{\infty }$
-linear map
![]() $\unicode[STIX]{x1D719}_{\text{dR},W}:W\rightarrow W$
satisfying the following property: for each
$\unicode[STIX]{x1D719}_{\text{dR},W}:W\rightarrow W$
satisfying the following property: for each
![]() $n\in \mathbb{N}$
and
$n\in \mathbb{N}$
and
![]() $w\in W$
, there exists an open subgroup
$w\in W$
, there exists an open subgroup
![]() $\unicode[STIX]{x1D6E4}_{k,n,w}$
of
$\unicode[STIX]{x1D6E4}_{k,n,w}$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
such that
$\unicode[STIX]{x1D6E4}_{k}$
such that
for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k,n,w}$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k,n,w}$
.
Proof. Note that
![]() $A_{\infty }[[t]]/(t^{n})$
is a finite free
$A_{\infty }[[t]]/(t^{n})$
is a finite free
![]() $A_{\infty }$
-module of rank
$A_{\infty }$
-module of rank
![]() $n$
and thus
$n$
and thus
![]() $W/t^{n}W$
can be regarded an
$W/t^{n}W$
can be regarded an
![]() $A_{\infty }$
-representation of
$A_{\infty }$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. So the proposition follows from Proposition 2.20.◻
$\unicode[STIX]{x1D6E4}_{k}$
. So the proposition follows from Proposition 2.20.◻
Definition 2.25. Set
![]() $A_{\infty }((t)):=A_{\infty }[[t]][t^{-1}]$
. We denote by
$A_{\infty }((t)):=A_{\infty }[[t]][t^{-1}]$
. We denote by
![]() $\unicode[STIX]{x2202}_{t}$
the
$\unicode[STIX]{x2202}_{t}$
the
![]() $A_{\infty }$
-linear endomorphism
$A_{\infty }$
-linear endomorphism
The restriction of
![]() $\unicode[STIX]{x2202}_{t}$
to
$\unicode[STIX]{x2202}_{t}$
to
![]() $A_{\infty }[[t]]$
is also denoted by
$A_{\infty }[[t]]$
is also denoted by
![]() $\unicode[STIX]{x2202}_{t}$
.
$\unicode[STIX]{x2202}_{t}$
.
Proposition 2.26. For an
![]() $A_{\infty }[[t]]$
-representation
$A_{\infty }[[t]]$
-representation
![]() $W$
of
$W$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
, the endomorphism
$\unicode[STIX]{x1D6E4}_{k}$
, the endomorphism
![]() $\unicode[STIX]{x1D719}_{\text{dR},W}:W\rightarrow W$
satisfies
$\unicode[STIX]{x1D719}_{\text{dR},W}:W\rightarrow W$
satisfies
for every
![]() $\unicode[STIX]{x1D6FC}\in A_{\infty }[[t]]$
and
$\unicode[STIX]{x1D6FC}\in A_{\infty }[[t]]$
and
![]() $w\in W$
.
$w\in W$
.
Proof. By the characterizing property of
![]() $\unicode[STIX]{x1D719}_{\text{dR},W}$
, we may assume that
$\unicode[STIX]{x1D719}_{\text{dR},W}$
, we may assume that
![]() $W$
is annihilated by some power of
$W$
is annihilated by some power of
![]() $t$
. In this case, it is enough to check the equality for
$t$
. In this case, it is enough to check the equality for
![]() $\unicode[STIX]{x1D6FC}=t^{j}$
by
$\unicode[STIX]{x1D6FC}=t^{j}$
by
![]() $A_{\infty }$
-linearity of
$A_{\infty }$
-linearity of
![]() $\unicode[STIX]{x1D719}_{\text{dR},W}$
. By induction on
$\unicode[STIX]{x1D719}_{\text{dR},W}$
. By induction on
![]() $j$
, we may further assume that
$j$
, we may further assume that
![]() $\unicode[STIX]{x1D6FC}=t$
.
$\unicode[STIX]{x1D6FC}=t$
.
So we need to show
![]() $\unicode[STIX]{x1D719}_{\text{dR},W}(tw)=tw+t\unicode[STIX]{x1D719}_{\text{dR},W}(w)$
. This follows from
$\unicode[STIX]{x1D719}_{\text{dR},W}(tw)=tw+t\unicode[STIX]{x1D719}_{\text{dR},W}(w)$
. This follows from
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\text{dR},W}(tw) & = & \displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow 1}\frac{\unicode[STIX]{x1D6FE}(tw)-tw}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & = & \displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow 1}\frac{\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})-1}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}t\unicode[STIX]{x1D6FE}(w)+t\lim _{\unicode[STIX]{x1D6FE}\rightarrow 1}\frac{\unicode[STIX]{x1D6FE}(w)-w}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & = & \displaystyle tw+t\unicode[STIX]{x1D719}_{\text{dR},W}(w).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\text{dR},W}(tw) & = & \displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow 1}\frac{\unicode[STIX]{x1D6FE}(tw)-tw}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & = & \displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow 1}\frac{\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})-1}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}t\unicode[STIX]{x1D6FE}(w)+t\lim _{\unicode[STIX]{x1D6FE}\rightarrow 1}\frac{\unicode[STIX]{x1D6FE}(w)-w}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & = & \displaystyle tw+t\unicode[STIX]{x1D719}_{\text{dR},W}(w).\Box \nonumber\end{eqnarray}$$
Lemma-Definition 2.27. Let
![]() $W$
be a finite free
$W$
be a finite free
![]() $A_{\infty }[[t]]$
-representation of
$A_{\infty }[[t]]$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. Then
$\unicode[STIX]{x1D6E4}_{k}$
. Then
![]() $W[t^{-1}]:=W\otimes _{A_{\infty }[[t]]}A_{\infty }((t))$
is a finite free
$W[t^{-1}]:=W\otimes _{A_{\infty }[[t]]}A_{\infty }((t))$
is a finite free
![]() $A_{\infty }((t))$
-module equipped with
$A_{\infty }((t))$
-module equipped with
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action and
$\unicode[STIX]{x1D6E4}_{k}$
-action and
![]() $\unicode[STIX]{x1D6E4}_{k}$
-stable decreasing filtration defined by
$\unicode[STIX]{x1D6E4}_{k}$
-stable decreasing filtration defined by
![]() $\operatorname{Fil}^{j}W[t^{-1}]:=t^{j}W$
. Moreover, the
$\operatorname{Fil}^{j}W[t^{-1}]:=t^{j}W$
. Moreover, the
![]() $A_{\infty }$
-linear endomorphism
$A_{\infty }$
-linear endomorphism
![]() $\unicode[STIX]{x1D719}_{\text{dR},W[t^{-1}]}:W[t^{-1}]\rightarrow W[t^{-1}]$
sending
$\unicode[STIX]{x1D719}_{\text{dR},W[t^{-1}]}:W[t^{-1}]\rightarrow W[t^{-1}]$
sending
![]() $w\in \operatorname{Fil}^{j}W[t^{-1}]$
to
$w\in \operatorname{Fil}^{j}W[t^{-1}]$
to
is well-defined and satisfies
![]() $\unicode[STIX]{x1D719}_{\text{dR},W[t^{-1}]}|_{W}=\unicode[STIX]{x1D719}_{\text{dR},W}$
.
$\unicode[STIX]{x1D719}_{\text{dR},W[t^{-1}]}|_{W}=\unicode[STIX]{x1D719}_{\text{dR},W}$
.
Proof. This follows from Proposition 2.26. ◻
Definition 2.28. Let
![]() $V$
be a finite free
$V$
be a finite free
![]() $A\,\hat{\otimes }\,L_{\text{dR}}$
-module equipped with
$A\,\hat{\otimes }\,L_{\text{dR}}$
-module equipped with
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action and
$\unicode[STIX]{x1D6E4}_{k}$
-action and
![]() $\unicode[STIX]{x1D6E4}_{k}$
-stable decreasing filtration
$\unicode[STIX]{x1D6E4}_{k}$
-stable decreasing filtration
![]() $\operatorname{Fil}^{j}V$
such that
$\operatorname{Fil}^{j}V$
such that
![]() $\operatorname{Fil}^{0}V$
is a finite free
$\operatorname{Fil}^{0}V$
is a finite free
![]() $A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
$A\,\hat{\otimes }\,L_{\text{dR}}^{+}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and
$\unicode[STIX]{x1D6E4}_{k}$
and
![]() $\operatorname{Fil}^{j}V=t^{j}\operatorname{Fil}^{0}V$
for all
$\operatorname{Fil}^{j}V=t^{j}\operatorname{Fil}^{0}V$
for all
![]() $j\in \mathbb{Z}$
. Define
$j\in \mathbb{Z}$
. Define
By Lemma-Definition 2.27,
![]() $V_{\text{fin}}$
is a finite free
$V_{\text{fin}}$
is a finite free
![]() $A_{\infty }((t))$
-module equipped with
$A_{\infty }((t))$
-module equipped with
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action,
$\unicode[STIX]{x1D6E4}_{k}$
-action,
![]() $\unicode[STIX]{x1D6E4}_{k}$
-stable decreasing filtration
$\unicode[STIX]{x1D6E4}_{k}$
-stable decreasing filtration
![]() $\operatorname{Fil}^{j}V_{\text{fin}}$
, and
$\operatorname{Fil}^{j}V_{\text{fin}}$
, and
![]() $\unicode[STIX]{x1D719}_{\text{dR},V_{\text{fin}}}$
. Since
$\unicode[STIX]{x1D719}_{\text{dR},V_{\text{fin}}}$
. Since
![]() $\unicode[STIX]{x1D719}_{\text{dR},V_{\text{fin}}}$
preserves the filtration, it defines an
$\unicode[STIX]{x1D719}_{\text{dR},V_{\text{fin}}}$
preserves the filtration, it defines an
![]() $A_{\infty }$
-linear endomorphism on
$A_{\infty }$
-linear endomorphism on
![]() $\operatorname{gr}^{0}V_{\text{fin}}$
, which we denote by
$\operatorname{gr}^{0}V_{\text{fin}}$
, which we denote by
![]() $\text{Res}_{\operatorname{Fil}^{0}V_{\text{fin}}}\unicode[STIX]{x1D719}_{\text{dR},V_{\text{fin}}}$
. It follows from the definition that
$\text{Res}_{\operatorname{Fil}^{0}V_{\text{fin}}}\unicode[STIX]{x1D719}_{\text{dR},V_{\text{fin}}}$
. It follows from the definition that
as endomorphisms on the finite free
![]() $A_{\infty }$
-module
$A_{\infty }$
-module
![]() $\operatorname{gr}^{0}(V_{\text{fin}})=(\operatorname{gr}^{0}V)_{\text{fin}}$
.
$\operatorname{gr}^{0}(V_{\text{fin}})=(\operatorname{gr}^{0}V)_{\text{fin}}$
.
3 The arithmetic Sen endomorphism of a
 $p$
-adic local system
$p$
-adic local system
From this section, we study relative
![]() $p$
-adic Hodge theory in geometric families. Let
$p$
-adic Hodge theory in geometric families. Let
![]() $k$
be a finite field extension of
$k$
be a finite field extension of
![]() $\mathbb{Q}_{p}$
and let
$\mathbb{Q}_{p}$
and let
![]() $X$
be an
$X$
be an
![]() $n$
-dimensional smooth rigid analytic variety over
$n$
-dimensional smooth rigid analytic variety over
![]() $\operatorname{Spa}(k,{\mathcal{O}}_{k})$
. Let
$\operatorname{Spa}(k,{\mathcal{O}}_{k})$
. Let
![]() $K$
be the
$K$
be the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $k_{\infty }:=\bigcup _{n}k(\unicode[STIX]{x1D707}_{p^{n}})$
and let
$k_{\infty }:=\bigcup _{n}k(\unicode[STIX]{x1D707}_{p^{n}})$
and let
![]() $X_{K}$
denote the base change of
$X_{K}$
denote the base change of
![]() $X$
to
$X$
to
![]() $\operatorname{Spa}(K,{\mathcal{O}}_{K})$
. We denote by
$\operatorname{Spa}(K,{\mathcal{O}}_{K})$
. We denote by
![]() $\unicode[STIX]{x1D6E4}_{k}$
the Galois group
$\unicode[STIX]{x1D6E4}_{k}$
the Galois group
![]() $\operatorname{Gal}(k_{\infty }/k)$
.
$\operatorname{Gal}(k_{\infty }/k)$
.
Based on the recent progresses on relative
![]() $p$
-adic Hodge theory [Reference Kedlaya and LiuKL15, Reference Kedlaya and LiuKL16, Reference ScholzeSch12, Reference ScholzeSch13], Liu and Zhu attached to an étale
$p$
-adic Hodge theory [Reference Kedlaya and LiuKL15, Reference Kedlaya and LiuKL16, Reference ScholzeSch12, Reference ScholzeSch13], Liu and Zhu attached to an étale
![]() $\mathbb{Q}_{p}$
-local system
$\mathbb{Q}_{p}$
-local system
![]() $\mathbb{L}$
a nilpotent Higgs bundle
$\mathbb{L}$
a nilpotent Higgs bundle
![]() ${\mathcal{H}}(\mathbb{L})$
on
${\mathcal{H}}(\mathbb{L})$
on
![]() $X_{K}$
equipped with
$X_{K}$
equipped with
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action [Reference Liu and ZhuLZ17]. Our goal is to define an endomorphism
$\unicode[STIX]{x1D6E4}_{k}$
-action [Reference Liu and ZhuLZ17]. Our goal is to define an endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
on
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
on
![]() ${\mathcal{H}}(\mathbb{L})$
by decompleting the
${\mathcal{H}}(\mathbb{L})$
by decompleting the
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action. The endomorphism
$\unicode[STIX]{x1D6E4}_{k}$
-action. The endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
, which we will call the arithmetic Sen endomorphism, is a natural generalization of the Sen endomorphism of a
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
, which we will call the arithmetic Sen endomorphism, is a natural generalization of the Sen endomorphism of a
![]() $p$
-adic Galois representation of
$p$
-adic Galois representation of
![]() $k$
.
$k$
.
3.1 Review of the
 $p$
-adic Simpson correspondence à la Liu and Zhu
$p$
-adic Simpson correspondence à la Liu and Zhu
First let us briefly recall the sites and sheaves that we use. Let
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
be the pro-étale site on
$X_{\text{pro}\acute{\text{e}}\text{t}}$
be the pro-étale site on
![]() $X$
in the sense of [Reference ScholzeSch13, Reference ScholzeSch16]. The pro-étale site is equipped with a natural projection to the étale site on
$X$
in the sense of [Reference ScholzeSch13, Reference ScholzeSch16]. The pro-étale site is equipped with a natural projection to the étale site on
![]() $X$
$X$
Let
![]() $\unicode[STIX]{x1D708}^{\prime }:X_{\text{pro}\acute{\text{e}}\text{t}}/X_{K}\rightarrow (X_{K})_{\acute{\text{e}}\text{t}}$
be the restriction of
$\unicode[STIX]{x1D708}^{\prime }:X_{\text{pro}\acute{\text{e}}\text{t}}/X_{K}\rightarrow (X_{K})_{\acute{\text{e}}\text{t}}$
be the restriction of
![]() $\unicode[STIX]{x1D708}$
and we identify
$\unicode[STIX]{x1D708}$
and we identify
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}/X_{K}$
with
$X_{\text{pro}\acute{\text{e}}\text{t}}/X_{K}$
with
![]() $(X_{K})_{\text{pro}\acute{\text{e}}\text{t}}$
(see a discussion before [Reference ScholzeSch13, Proposition 6.10]).
$(X_{K})_{\text{pro}\acute{\text{e}}\text{t}}$
(see a discussion before [Reference ScholzeSch13, Proposition 6.10]).
We denote by
![]() $\hat{\mathbb{Z}}_{p}$
(respectively
$\hat{\mathbb{Z}}_{p}$
(respectively
![]() $\hat{\mathbb{Q}}_{p}$
) the constant sheaf on
$\hat{\mathbb{Q}}_{p}$
) the constant sheaf on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
associated to
$X_{\text{pro}\acute{\text{e}}\text{t}}$
associated to
![]() $\mathbb{Z}_{p}$
(respectively
$\mathbb{Z}_{p}$
(respectively
![]() $\mathbb{Q}_{p}$
). For a
$\mathbb{Q}_{p}$
). For a
![]() $\mathbb{Z}_{p}$
-local system
$\mathbb{Z}_{p}$
-local system
![]() $\mathbb{L}$
(respectively
$\mathbb{L}$
(respectively
![]() $\mathbb{Q}_{p}$
-local system) on
$\mathbb{Q}_{p}$
-local system) on
![]() $X_{\acute{\text{e}}\text{t}}$
, let
$X_{\acute{\text{e}}\text{t}}$
, let
![]() $\hat{\mathbb{L}}$
denote the
$\hat{\mathbb{L}}$
denote the
![]() $\hat{\mathbb{Z}}_{p}$
-module (respectively
$\hat{\mathbb{Z}}_{p}$
-module (respectively
![]() $\hat{\mathbb{Q}}_{p}$
-module) on
$\hat{\mathbb{Q}}_{p}$
-module) on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
associated to
$X_{\text{pro}\acute{\text{e}}\text{t}}$
associated to
![]() $\mathbb{L}$
(see [Reference ScholzeSch13, § 8.2]).
$\mathbb{L}$
(see [Reference ScholzeSch13, § 8.2]).
We define sheaves on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
as follows. We set
$X_{\text{pro}\acute{\text{e}}\text{t}}$
as follows. We set
We also set
![]() $\unicode[STIX]{x1D6FA}_{X}^{1}=\unicode[STIX]{x1D708}^{\ast }\unicode[STIX]{x1D6FA}_{X_{\acute{\text{e}}\text{t}}}^{1}$
and we denote its
$\unicode[STIX]{x1D6FA}_{X}^{1}=\unicode[STIX]{x1D708}^{\ast }\unicode[STIX]{x1D6FA}_{X_{\acute{\text{e}}\text{t}}}^{1}$
and we denote its
![]() $i$
th exterior power by
$i$
th exterior power by
![]() $\unicode[STIX]{x1D6FA}_{X}^{i}$
. Moreover, Scholze introduced the de Rham period sheaves
$\unicode[STIX]{x1D6FA}_{X}^{i}$
. Moreover, Scholze introduced the de Rham period sheaves
![]() $\mathbb{B}_{\text{dR}}^{+}$
,
$\mathbb{B}_{\text{dR}}^{+}$
,
![]() $\mathbb{B}_{\text{dR}}$
,
$\mathbb{B}_{\text{dR}}$
,
![]() ${\mathcal{O}}\mathbb{B}_{\text{dR}}^{+}$
and
${\mathcal{O}}\mathbb{B}_{\text{dR}}^{+}$
and
![]() ${\mathcal{O}}\mathbb{B}_{\text{dR}}$
on
${\mathcal{O}}\mathbb{B}_{\text{dR}}$
on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
in [Reference ScholzeSch13, § 6] and [Reference ScholzeSch16]. The structural de Rham sheaf
$X_{\text{pro}\acute{\text{e}}\text{t}}$
in [Reference ScholzeSch13, § 6] and [Reference ScholzeSch16]. The structural de Rham sheaf
![]() ${\mathcal{O}}\mathbb{B}_{\text{dR}}$
has the following properties: it is a sheaf of
${\mathcal{O}}\mathbb{B}_{\text{dR}}$
has the following properties: it is a sheaf of
![]() ${\mathcal{O}}_{X}$
-algebras equipped with a decreasing filtration
${\mathcal{O}}_{X}$
-algebras equipped with a decreasing filtration
![]() $\operatorname{Fil}^{\bullet }{\mathcal{O}}\mathbb{B}_{\text{dR}}$
and an integrable connection
$\operatorname{Fil}^{\bullet }{\mathcal{O}}\mathbb{B}_{\text{dR}}$
and an integrable connection
satisfying the Griffiths transversality. Since
![]() $X$
is assumed to be smooth of dimension
$X$
is assumed to be smooth of dimension
![]() $n$
, this gives rise to the following exact sequence of sheaves on
$n$
, this gives rise to the following exact sequence of sheaves on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
:
$X_{\text{pro}\acute{\text{e}}\text{t}}$
:
Finally, we set
![]() ${\mathcal{O}}\mathbb{C}:=\operatorname{gr}^{0}{\mathcal{O}}\mathbb{B}_{\text{dR}}$
. Taking the associated graded connection of
${\mathcal{O}}\mathbb{C}:=\operatorname{gr}^{0}{\mathcal{O}}\mathbb{B}_{\text{dR}}$
. Taking the associated graded connection of
![]() $\unicode[STIX]{x1D6FB}$
on
$\unicode[STIX]{x1D6FB}$
on
![]() ${\mathcal{O}}\mathbb{B}_{\text{dR}}$
equips
${\mathcal{O}}\mathbb{B}_{\text{dR}}$
equips
![]() ${\mathcal{O}}\mathbb{C}$
with a Higgs field
${\mathcal{O}}\mathbb{C}$
with a Higgs field
where
![]() $(-1)$
stands for the
$(-1)$
stands for the
![]() $(-1)$
st Tate twist.
$(-1)$
st Tate twist.
We review the formulation of the
![]() $p$
-adic Simpson correspondence by Liu and Zhu. Let
$p$
-adic Simpson correspondence by Liu and Zhu. Let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
of rank
$X_{\acute{\text{e}}\text{t}}$
of rank
![]() $r$
. We define
$r$
. We define
Then Liu and Zhu proved the following theorem.
Theorem 3.1 (Rough form of [Reference Liu and ZhuLZ17, Theorem 2.1]).
![]() ${\mathcal{H}}(\mathbb{L})$
is a vector bundle on
${\mathcal{H}}(\mathbb{L})$
is a vector bundle on
![]() $X_{K}$
of rank
$X_{K}$
of rank
![]() $r$
equipped with a nilpotent Higgs field
$r$
equipped with a nilpotent Higgs field
![]() $\unicode[STIX]{x1D717}_{\mathbb{L}}$
and a semilinear action of
$\unicode[STIX]{x1D717}_{\mathbb{L}}$
and a semilinear action of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. The functor
$\unicode[STIX]{x1D6E4}_{k}$
. The functor
![]() ${\mathcal{H}}$
is a tensor functor from the category of
${\mathcal{H}}$
is a tensor functor from the category of
![]() $\mathbb{Q}_{p}$
-local systems on
$\mathbb{Q}_{p}$
-local systems on
![]() $X_{\acute{\text{e}}\text{t}}$
to the category of nilpotent Higgs bundles on
$X_{\acute{\text{e}}\text{t}}$
to the category of nilpotent Higgs bundles on
![]() $X_{K}$
. Moreover,
$X_{K}$
. Moreover,
![]() ${\mathcal{H}}$
is compatible with pullback and smooth proper pushforward.Footnote
1
${\mathcal{H}}$
is compatible with pullback and smooth proper pushforward.Footnote
1
Remark 3.2. For our purpose, we use the
![]() $p$
-adic Simpson correspondence formulated by Liu and Zhu as their output is a Higgs bundle over
$p$
-adic Simpson correspondence formulated by Liu and Zhu as their output is a Higgs bundle over
![]() $X_{K}$
with a
$X_{K}$
with a
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action. See [Reference FaltingsFal05] and [Reference Abbes, Gros and TsujiAGT16] for the
$\unicode[STIX]{x1D6E4}_{k}$
-action. See [Reference FaltingsFal05] and [Reference Abbes, Gros and TsujiAGT16] for the
![]() $p$
-adic Simpson correspondence by Faltings and Abbes–Gros–Tsuji in a more general setting, and see [Reference Andreatta and BrinonAB08, Reference Andreatta and BrinonAB10] for the one over a pro-étale cover of
$p$
-adic Simpson correspondence by Faltings and Abbes–Gros–Tsuji in a more general setting, and see [Reference Andreatta and BrinonAB08, Reference Andreatta and BrinonAB10] for the one over a pro-étale cover of
![]() $X_{K}$
by Andreatta and Brinon.
$X_{K}$
by Andreatta and Brinon.
To define the arithmetic Sen endomorphism on
![]() ${\mathcal{H}}(\mathbb{L})$
and discuss its properties, let us recall Liu and Zhu’s arguments in the proof of Theorem 3.1.
${\mathcal{H}}(\mathbb{L})$
and discuss its properties, let us recall Liu and Zhu’s arguments in the proof of Theorem 3.1.
We follow the notation on base changes of adic spaces and rings in [Reference Liu and ZhuLZ17]. We denote by
![]() $\mathbb{T}^{n}$
the
$\mathbb{T}^{n}$
the
![]() $n$
-dimensional rigid analytic torus
$n$
-dimensional rigid analytic torus
For
![]() $m\geqslant 0$
, we set
$m\geqslant 0$
, we set
We denote by
![]() $\tilde{\mathbb{T}}_{\infty }^{n}$
the affinoid perfectoid
$\tilde{\mathbb{T}}_{\infty }^{n}$
the affinoid perfectoid
![]() $\mathop{\varprojlim }\nolimits_{m}\mathbb{T}_{m}^{n}$
in
$\mathop{\varprojlim }\nolimits_{m}\mathbb{T}_{m}^{n}$
in
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
.
$X_{\text{pro}\acute{\text{e}}\text{t}}$
.
To study properties of
![]() ${\mathcal{H}}(\mathbb{L})$
, we introduce the following base
${\mathcal{H}}(\mathbb{L})$
, we introduce the following base
![]() ${\mathcal{B}}$
for
${\mathcal{B}}$
for
![]() $(X_{K})_{\acute{\text{e}}\text{t}}$
: objects of
$(X_{K})_{\acute{\text{e}}\text{t}}$
: objects of
![]() ${\mathcal{B}}$
are the étale maps to
${\mathcal{B}}$
are the étale maps to
![]() $X_{K}$
that are the base changes of standard étale morphisms
$X_{K}$
that are the base changes of standard étale morphisms
![]() $Y\rightarrow X_{k^{\prime }}$
defined over some finite extension
$Y\rightarrow X_{k^{\prime }}$
defined over some finite extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
in
$k$
in
![]() $K$
where
$K$
where
![]() $Y$
is affinoid admitting a toric chart after some finite extension of
$Y$
is affinoid admitting a toric chart after some finite extension of
![]() $k^{\prime }$
. Recall that an étale morphism between adic spaces is called standard étale if it is a composite of rational localizations and finite étale morphisms and that a toric chart means a standard étale morphism to
$k^{\prime }$
. Recall that an étale morphism between adic spaces is called standard étale if it is a composite of rational localizations and finite étale morphisms and that a toric chart means a standard étale morphism to
![]() $\mathbb{T}^{n}$
. Morphisms of
$\mathbb{T}^{n}$
. Morphisms of
![]() ${\mathcal{B}}$
are the base changes of étale morphisms over some finite extension of
${\mathcal{B}}$
are the base changes of étale morphisms over some finite extension of
![]() $k$
in
$k$
in
![]() $K$
. We equip
$K$
. We equip
![]() ${\mathcal{B}}$
with the induced topology from
${\mathcal{B}}$
with the induced topology from
![]() $(X_{K})_{\acute{\text{e}}\text{t}}$
. Then the associated topoi
$(X_{K})_{\acute{\text{e}}\text{t}}$
. Then the associated topoi
![]() $(X_{K})_{\acute{\text{e}}\text{t}}^{{\sim}}$
and
$(X_{K})_{\acute{\text{e}}\text{t}}^{{\sim}}$
and
![]() ${\mathcal{B}}^{{\sim}}$
are equivalent [Reference Liu and ZhuLZ17, Lemma 2.5].
${\mathcal{B}}^{{\sim}}$
are equivalent [Reference Liu and ZhuLZ17, Lemma 2.5].
When
![]() $Y=\operatorname{Spa}(B,B^{+})$
admits a toric chart over
$Y=\operatorname{Spa}(B,B^{+})$
admits a toric chart over
![]() $k$
, we use the following notation: we set
$k$
, we use the following notation: we set
Then
![]() ${\tilde{Y}}_{\infty }:=Y\times _{\mathbb{T}^{n}}\tilde{\mathbb{T}}_{\infty }^{n}$
is the affinoid perfectoid in
${\tilde{Y}}_{\infty }:=Y\times _{\mathbb{T}^{n}}\tilde{\mathbb{T}}_{\infty }^{n}$
is the affinoid perfectoid in
![]() $Y_{\text{pro}\acute{\text{e}}\text{t}}$
represented by the relative toric tower
$Y_{\text{pro}\acute{\text{e}}\text{t}}$
represented by the relative toric tower
![]() $(Y_{n})$
. We denote by
$(Y_{n})$
. We denote by
![]() $(\hat{B}_{\infty },\hat{B}_{\infty }^{+})$
the perfectoid affinoid completed direct limit of the affinoid rings
$(\hat{B}_{\infty },\hat{B}_{\infty }^{+})$
the perfectoid affinoid completed direct limit of the affinoid rings
![]() $(B_{m},B_{m}^{+})$
and set
$(B_{m},B_{m}^{+})$
and set
![]() ${\hat{Y}}_{\infty }:=\operatorname{Spa}(\hat{B}_{\infty },\hat{B}_{\infty }^{+})$
, the affinoid perfectoid space associated to
${\hat{Y}}_{\infty }:=\operatorname{Spa}(\hat{B}_{\infty },\hat{B}_{\infty }^{+})$
, the affinoid perfectoid space associated to
![]() $Y_{\infty }$
. We also set
$Y_{\infty }$
. We also set
![]() $B_{k_{m}}=B\otimes _{k}k_{m}$
as in § 2.1. When
$B_{k_{m}}=B\otimes _{k}k_{m}$
as in § 2.1. When
![]() $Y$
admits a toric chart over a finite extension of
$Y$
admits a toric chart over a finite extension of
![]() $k$
in
$k$
in
![]() $K$
, we similarly define these objects using the rigid analytic torus over the field.
$K$
, we similarly define these objects using the rigid analytic torus over the field.
Let
![]() $Y_{K,m}:=\operatorname{Spa}(B_{K,m},B_{K,m}^{+})$
be the base change of
$Y_{K,m}:=\operatorname{Spa}(B_{K,m},B_{K,m}^{+})$
be the base change of
![]() $Y_{m}$
from
$Y_{m}$
from
![]() $k_{m}$
to
$k_{m}$
to
![]() $K$
and let
$K$
and let
![]() ${\tilde{Y}}_{K,\infty }$
be the affinoid perfectoid represented by the toric tower
${\tilde{Y}}_{K,\infty }$
be the affinoid perfectoid represented by the toric tower
![]() $(Y_{K,m})$
. We denote the associated affinoid perfectoid space by
$(Y_{K,m})$
. We denote the associated affinoid perfectoid space by
![]() ${\hat{Y}}_{K,\infty }=\operatorname{Spa}(\hat{B}_{K,m},\hat{B}_{K,m}^{+})$
. The cover
${\hat{Y}}_{K,\infty }=\operatorname{Spa}(\hat{B}_{K,m},\hat{B}_{K,m}^{+})$
. The cover
![]() ${\tilde{Y}}_{K,\infty }/Y$
is Galois. We denote its Galois group by
${\tilde{Y}}_{K,\infty }/Y$
is Galois. We denote its Galois group by
![]() $\unicode[STIX]{x1D6E4}$
. Then
$\unicode[STIX]{x1D6E4}$
. Then
![]() $\unicode[STIX]{x1D6E4}$
fits into a splitting exact sequence
$\unicode[STIX]{x1D6E4}$
fits into a splitting exact sequence
To prove Theorem 3.1, Liu and Zhu gave a simple description of
for
![]() $(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}$
, which we recall now.
$(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}$
, which we recall now.
Proposition 3.3 [Reference Liu and ZhuLZ17, Proposition 2.8].
Put
![]() ${\mathcal{M}}=\hat{\mathbb{L}}\,\otimes _{\hat{\mathbb{Q}}_{p}}\hat{{\mathcal{O}}}_{X}$
. Then there exists a unique finite projective
${\mathcal{M}}=\hat{\mathbb{L}}\,\otimes _{\hat{\mathbb{Q}}_{p}}\hat{{\mathcal{O}}}_{X}$
. Then there exists a unique finite projective
![]() $B_{K}$
-submodule
$B_{K}$
-submodule
![]() $M_{K}(Y)$
of
$M_{K}(Y)$
of
![]() ${\mathcal{M}}({\tilde{Y}}_{K,\infty })$
, which is stable under
${\mathcal{M}}({\tilde{Y}}_{K,\infty })$
, which is stable under
![]() $\unicode[STIX]{x1D6E4}$
, such that
$\unicode[STIX]{x1D6E4}$
, such that
(i)
 $M_{K}(Y)\otimes _{B_{K}}\hat{B}_{K,\infty }={\mathcal{M}}({\tilde{Y}}_{K,\infty })$
, and
$M_{K}(Y)\otimes _{B_{K}}\hat{B}_{K,\infty }={\mathcal{M}}({\tilde{Y}}_{K,\infty })$
, and(ii) the
 $B_{K}$
-linear representation of
$B_{K}$
-linear representation of
 $\unicode[STIX]{x1D6E4}_{\text{geom}}$
on
$\unicode[STIX]{x1D6E4}_{\text{geom}}$
on
 $M_{K}(Y)$
is unipotent.
$M_{K}(Y)$
is unipotent.
In addition, the module
![]() $M_{K}(Y)$
has the following properties.
$M_{K}(Y)$
has the following properties.
(P1) There exist some positive integer
 $j_{0}$
and some finite projective
$j_{0}$
and some finite projective
 $B_{k_{j_{0}}}$
-submodule
$B_{k_{j_{0}}}$
-submodule
 $M(Y)$
of
$M(Y)$
of
 $M_{K}(Y)$
stable under
$M_{K}(Y)$
stable under
 $\unicode[STIX]{x1D6E4}$
such that
$\unicode[STIX]{x1D6E4}$
such that
 $M(Y)\otimes _{B_{k_{j_{0}}}}B_{K}=M_{K}(Y)$
. Moreover, the construction of
$M(Y)\otimes _{B_{k_{j_{0}}}}B_{K}=M_{K}(Y)$
. Moreover, the construction of
 $M(Y)$
is compatible with base change along standard étale morphisms.
$M(Y)$
is compatible with base change along standard étale morphisms.(P2) The natural map
is an isomorphism. $$\begin{eqnarray}M_{K}(Y)^{\unicode[STIX]{x1D6E4}_{\text{geom}}}\rightarrow {\mathcal{M}}({\tilde{Y}}_{K,\infty })^{\unicode[STIX]{x1D6E4}_{\text{geom}}}\end{eqnarray}$$
$$\begin{eqnarray}M_{K}(Y)^{\unicode[STIX]{x1D6E4}_{\text{geom}}}\rightarrow {\mathcal{M}}({\tilde{Y}}_{K,\infty })^{\unicode[STIX]{x1D6E4}_{\text{geom}}}\end{eqnarray}$$
Once this proposition is proved, we can describe
![]() ${\mathcal{H}}(\mathbb{L})(Y_{K})$
in terms of
${\mathcal{H}}(\mathbb{L})(Y_{K})$
in terms of
![]() $M_{K}(Y)$
as follows: the vanishing theorem on affinoid perfectoid spaces [Reference ScholzeSch12, Proposition 7.13] implies the degeneration of the Cartan–Leray spectral sequence to the Galois cover
$M_{K}(Y)$
as follows: the vanishing theorem on affinoid perfectoid spaces [Reference ScholzeSch12, Proposition 7.13] implies the degeneration of the Cartan–Leray spectral sequence to the Galois cover
![]() $\{{\tilde{Y}}_{K,\infty }\rightarrow Y_{K}\}$
with Galois group
$\{{\tilde{Y}}_{K,\infty }\rightarrow Y_{K}\}$
with Galois group
![]() $\unicode[STIX]{x1D6E4}_{\text{geom}}$
, and thus we have
$\unicode[STIX]{x1D6E4}_{\text{geom}}$
, and thus we have
Moreover, we know that
![]() ${\mathcal{O}}\mathbb{C}|_{{\tilde{Y}}_{K,\infty }}\cong (\hat{{\mathcal{O}}}_{X}|_{{\tilde{Y}}_{K,\infty }})[V_{1},\ldots ,V_{n}]$
, where
${\mathcal{O}}\mathbb{C}|_{{\tilde{Y}}_{K,\infty }}\cong (\hat{{\mathcal{O}}}_{X}|_{{\tilde{Y}}_{K,\infty }})[V_{1},\ldots ,V_{n}]$
, where
![]() $V_{i}=t^{-1}\log ([T_{i}^{\flat }]/T_{i})$
for a fixed compatible sequence of
$V_{i}=t^{-1}\log ([T_{i}^{\flat }]/T_{i})$
for a fixed compatible sequence of
![]() $p$
-power roots of the coordinate
$p$
-power roots of the coordinate
![]() $T_{i}^{\flat }=(T_{i},T_{i}^{1/p},\ldots )$
. It follows from these results and a simple argument on the direct limit of sheaves on
$T_{i}^{\flat }=(T_{i},T_{i}^{1/p},\ldots )$
. It follows from these results and a simple argument on the direct limit of sheaves on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
that the natural
$X_{\text{pro}\acute{\text{e}}\text{t}}$
that the natural
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant map
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant map
is an isomorphism. A simple computation shows that the map
![]() $M_{K}(Y)[V_{1},\ldots ,V_{n}]\rightarrow M_{K}(Y)$
sending
$M_{K}(Y)[V_{1},\ldots ,V_{n}]\rightarrow M_{K}(Y)$
sending
![]() $V_{i}$
to
$V_{i}$
to
![]() $0$
induces a
$0$
induces a
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant isomorphism
Thus we have a
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant isomorphism
The above discussion is summarized in the following commutative diagram.

Finally, we recall the Higgs field
![]() $\unicode[STIX]{x1D717}_{\mathbb{L}}$
. This is defined to be
$\unicode[STIX]{x1D717}_{\mathbb{L}}$
. This is defined to be
under the identification
![]() $\unicode[STIX]{x1D708}_{\ast }^{\prime }(\hat{\mathbb{L}}\otimes {\mathcal{O}}\mathbb{C}\otimes \unicode[STIX]{x1D6FA}_{X}^{1}(-1))\cong {\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/k}^{1}(-1)$
. Here
$\unicode[STIX]{x1D708}_{\ast }^{\prime }(\hat{\mathbb{L}}\otimes {\mathcal{O}}\mathbb{C}\otimes \unicode[STIX]{x1D6FA}_{X}^{1}(-1))\cong {\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/k}^{1}(-1)$
. Here
![]() ${\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/k}^{1}(-1)$
denotes the
${\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/k}^{1}(-1)$
denotes the
![]() ${\mathcal{O}}_{X_{K}}$
-module
${\mathcal{O}}_{X_{K}}$
-module
![]() ${\mathcal{H}}(\mathbb{L})\,\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X/k}^{1}(-1)={\mathcal{H}}(\mathbb{L})\,\otimes _{{\mathcal{O}}_{X_{K}}}\unicode[STIX]{x1D6FA}_{X_{K}/K}^{1}(-1)$
equipped with a natural
${\mathcal{H}}(\mathbb{L})\,\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X/k}^{1}(-1)={\mathcal{H}}(\mathbb{L})\,\otimes _{{\mathcal{O}}_{X_{K}}}\unicode[STIX]{x1D6FA}_{X_{K}/K}^{1}(-1)$
equipped with a natural
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action.
$\unicode[STIX]{x1D6E4}_{k}$
-action.
We have another description under the isomorphism
![]() ${\mathcal{H}}(\mathbb{L})(Y_{K})\cong M_{K}(Y)$
, which proves that
${\mathcal{H}}(\mathbb{L})(Y_{K})\cong M_{K}(Y)$
, which proves that
![]() $\unicode[STIX]{x1D717}_{\mathbb{L}}$
is nilpotent. Namely, let
$\unicode[STIX]{x1D717}_{\mathbb{L}}$
is nilpotent. Namely, let
![]() $\unicode[STIX]{x1D70C}_{\text{geom}}$
denote the action of
$\unicode[STIX]{x1D70C}_{\text{geom}}$
denote the action of
![]() $\unicode[STIX]{x1D6E4}_{\text{geom}}$
on
$\unicode[STIX]{x1D6E4}_{\text{geom}}$
on
![]() $M_{K}(Y)$
and let
$M_{K}(Y)$
and let
![]() $\unicode[STIX]{x1D712}_{i}:\unicode[STIX]{x1D6E4}_{\text{geom}}\cong \mathbb{Z}_{p}(1)^{n}\rightarrow \mathbb{Z}_{p}(1)$
denote the composite of the natural identification and projection to the
$\unicode[STIX]{x1D712}_{i}:\unicode[STIX]{x1D6E4}_{\text{geom}}\cong \mathbb{Z}_{p}(1)^{n}\rightarrow \mathbb{Z}_{p}(1)$
denote the composite of the natural identification and projection to the
![]() $i$
th component. We can take the logarithm of
$i$
th component. We can take the logarithm of
![]() $\unicode[STIX]{x1D70C}_{\text{geom}}$
on
$\unicode[STIX]{x1D70C}_{\text{geom}}$
on
![]() $M(Y)\subset M_{K}(Y)$
since the action is unipotent. Suppose the logarithm is written as
$M(Y)\subset M_{K}(Y)$
since the action is unipotent. Suppose the logarithm is written as
where
![]() $\unicode[STIX]{x1D717}_{i}\in \operatorname{End}(M(Y))$
. Then
$\unicode[STIX]{x1D717}_{i}\in \operatorname{End}(M(Y))$
. Then
![]() $\unicode[STIX]{x1D717}_{i}$
can be regarded as an endomorphism on
$\unicode[STIX]{x1D717}_{i}$
can be regarded as an endomorphism on
![]() $M_{K}(Y)$
by extension of scalars and we define
$M_{K}(Y)$
by extension of scalars and we define
We can check
![]() $\unicode[STIX]{x1D717}_{M_{K}(Y)}\wedge \unicode[STIX]{x1D717}_{M_{K}(Y)}=0$
and this defines a Higgs field on
$\unicode[STIX]{x1D717}_{M_{K}(Y)}\wedge \unicode[STIX]{x1D717}_{M_{K}(Y)}=0$
and this defines a Higgs field on
![]() $M_{K}(Y)$
. It turns out that
$M_{K}(Y)$
. It turns out that
![]() $\unicode[STIX]{x1D717}_{\mathbb{L}}(Y_{K})=\unicode[STIX]{x1D717}_{M_{K}(Y)}$
under the
$\unicode[STIX]{x1D717}_{\mathbb{L}}(Y_{K})=\unicode[STIX]{x1D717}_{M_{K}(Y)}$
under the
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant isomorphism
![]() ${\mathcal{H}}(\mathbb{L})(Y_{K})\cong M_{K}(Y)$
. See [Reference Liu and ZhuLZ17, § 2] for the detail.
${\mathcal{H}}(\mathbb{L})(Y_{K})\cong M_{K}(Y)$
. See [Reference Liu and ZhuLZ17, § 2] for the detail.
3.2 Definition and properties of the arithmetic Sen endomorphism
We will define the arithmetic Sen endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\in \operatorname{End}{\mathcal{H}}(\mathbb{L})$
. Let
$\unicode[STIX]{x1D719}_{\mathbb{L}}\in \operatorname{End}{\mathcal{H}}(\mathbb{L})$
. Let
![]() ${\mathcal{B}}_{\mathbb{L}}$
be the refinement of the base
${\mathcal{B}}_{\mathbb{L}}$
be the refinement of the base
![]() ${\mathcal{B}}$
for
${\mathcal{B}}$
for
![]() $(X_{K})_{\acute{\text{e}}\text{t}}$
whose objects consist of
$(X_{K})_{\acute{\text{e}}\text{t}}$
whose objects consist of
![]() $(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}$
such that
$(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}$
such that
![]() ${\mathcal{H}}(\mathbb{L})(Y_{K})$
is a finite free
${\mathcal{H}}(\mathbb{L})(Y_{K})$
is a finite free
![]() $B_{K}$
-module.
$B_{K}$
-module.
For
![]() $(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
,
$(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
,
![]() ${\mathcal{H}}(\mathbb{L})(Y_{K})$
is a
${\mathcal{H}}(\mathbb{L})(Y_{K})$
is a
![]() $B_{K}$
-representation of
$B_{K}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k^{\prime }}:=\operatorname{Gal}(K/k^{\prime })$
in the sense of Definition 2.2. Thus Proposition 2.20 and Definition 2.23 equip
$\unicode[STIX]{x1D6E4}_{k^{\prime }}:=\operatorname{Gal}(K/k^{\prime })$
in the sense of Definition 2.2. Thus Proposition 2.20 and Definition 2.23 equip
![]() ${\mathcal{H}}(\mathbb{L})(Y_{K})$
with the
${\mathcal{H}}(\mathbb{L})(Y_{K})$
with the
![]() $B_{K}$
-linear endomorphism
$B_{K}$
-linear endomorphism
Lemma-Definition 3.4. The assignment of endomorphisms
defines an endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
of the vector bundle
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
of the vector bundle
![]() ${\mathcal{H}}_{\mathbb{L}}$
on
${\mathcal{H}}_{\mathbb{L}}$
on
![]() $(X_{K})_{\acute{\text{e}}\text{t}}$
. We call
$(X_{K})_{\acute{\text{e}}\text{t}}$
. We call
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
the arithmetic Sen endomorphism of
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
the arithmetic Sen endomorphism of
![]() $\mathbb{L}$
.
$\mathbb{L}$
.
Proof. We need to check the compatibility of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L},Y_{K}}$
via the pullback
$\unicode[STIX]{x1D719}_{\mathbb{L},Y_{K}}$
via the pullback
![]() $Y_{K}^{\prime \prime }\rightarrow Y_{K}$
for
$Y_{K}^{\prime \prime }\rightarrow Y_{K}$
for
For this it suffices to prove that
as
![]() $B_{\infty }^{\prime \prime }$
-representation of
$B_{\infty }^{\prime \prime }$
-representation of
![]() $\operatorname{Gal}(k_{\infty }/k^{\prime \prime })$
, where
$\operatorname{Gal}(k_{\infty }/k^{\prime \prime })$
, where
![]() $B_{\infty }$
and
$B_{\infty }$
and
![]() $B_{\infty }^{\prime \prime }$
are defined as in § 2.1.
$B_{\infty }^{\prime \prime }$
are defined as in § 2.1.
Since
![]() ${\mathcal{H}}(\mathbb{L})$
is a vector bundle on
${\mathcal{H}}(\mathbb{L})$
is a vector bundle on
![]() $X_{K}$
, we have the natural isomorphisms
$X_{K}$
, we have the natural isomorphisms
On the other hand, we see from definition
![]() ${\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}\otimes _{B_{\infty }}B_{\infty }^{\prime \prime }\subset {\mathcal{H}}(\mathbb{L})(Y_{K}^{\prime \prime })_{\text{fin}}$
. Hence the lemma follows from the faithful flatness of
${\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}\otimes _{B_{\infty }}B_{\infty }^{\prime \prime }\subset {\mathcal{H}}(\mathbb{L})(Y_{K}^{\prime \prime })_{\text{fin}}$
. Hence the lemma follows from the faithful flatness of
![]() $B_{\infty }^{\prime \prime }\rightarrow B_{K}^{\prime \prime }$
.◻
$B_{\infty }^{\prime \prime }\rightarrow B_{K}^{\prime \prime }$
.◻
Proposition 3.5. The following diagram commutes.

In particular, the endomorphisms
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-i(\operatorname{id}\otimes \operatorname{id})$
on
$\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-i(\operatorname{id}\otimes \operatorname{id})$
on
![]() ${\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/k}^{i}(-i)$
give rise to an endomorphism on the complex of
${\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/k}^{i}(-i)$
give rise to an endomorphism on the complex of
![]() ${\mathcal{O}}_{X_{K}}$
-modules on
${\mathcal{O}}_{X_{K}}$
-modules on
![]() $X_{K}$
$X_{K}$
induced by the Higgs field.
Proof. It is enough to check the commutativity of the diagram evaluated at
![]() $Y_{K}$
for each
$Y_{K}$
for each
![]() $(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
. In this setting, we can use the identification
$(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
. In this setting, we can use the identification
So it suffices to show the commutativity of the following diagram.

Moreover, since
![]() $M(Y)\,\otimes _{B_{k_{j_{0}}}}B_{K}=M_{K}(Y)$
, we only need to check the commutativity on
$M(Y)\,\otimes _{B_{k_{j_{0}}}}B_{K}=M_{K}(Y)$
, we only need to check the commutativity on
![]() $M(Y)\subset M_{K}(Y)$
.
$M(Y)\subset M_{K}(Y)$
.
We use the notation in (3.1). Then we have
and
Thus we need to show that
![]() $[\unicode[STIX]{x1D719}_{M_{K}(Y)},\unicode[STIX]{x1D717}_{i}]=\unicode[STIX]{x1D717}_{i}$
for each
$[\unicode[STIX]{x1D719}_{M_{K}(Y)},\unicode[STIX]{x1D717}_{i}]=\unicode[STIX]{x1D717}_{i}$
for each
![]() $i$
. To see this, take a topological generator
$i$
. To see this, take a topological generator
![]() $\unicode[STIX]{x1D6FE}_{i}$
of the
$\unicode[STIX]{x1D6FE}_{i}$
of the
![]() $i$
th component of
$i$
th component of
![]() $\unicode[STIX]{x1D6E4}_{\text{geom}}\cong \mathbb{Z}_{p}(1)^{n}$
. Let
$\unicode[STIX]{x1D6E4}_{\text{geom}}\cong \mathbb{Z}_{p}(1)^{n}$
. Let
![]() $\unicode[STIX]{x1D70C}_{\text{geom}}$
denote the action of
$\unicode[STIX]{x1D70C}_{\text{geom}}$
denote the action of
![]() $\unicode[STIX]{x1D6E4}_{\text{geom}}$
on
$\unicode[STIX]{x1D6E4}_{\text{geom}}$
on
![]() $M_{K}(Y)$
and write
$M_{K}(Y)$
and write
![]() $\log \unicode[STIX]{x1D70C}_{\text{geom}}=\sum _{i=1}^{n}\unicode[STIX]{x1D717}_{i}\otimes \unicode[STIX]{x1D712}_{i}\otimes t^{-1}$
as before. Since
$\log \unicode[STIX]{x1D70C}_{\text{geom}}=\sum _{i=1}^{n}\unicode[STIX]{x1D717}_{i}\otimes \unicode[STIX]{x1D712}_{i}\otimes t^{-1}$
as before. Since
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FE}_{i}\unicode[STIX]{x1D6FE}^{-1}=\unicode[STIX]{x1D6FE}_{i}^{\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}$
for
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FE}_{i}\unicode[STIX]{x1D6FE}^{-1}=\unicode[STIX]{x1D6FE}_{i}^{\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}$
for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
, we have
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
, we have
Hence
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D717}_{i}=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D717}_{i}\unicode[STIX]{x1D6FE}$
for
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D717}_{i}=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D717}_{i}\unicode[STIX]{x1D6FE}$
for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
.
For
![]() $m\in M(Y)$
, we compute
$m\in M(Y)$
, we compute
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{M_{K}(Y)}\unicode[STIX]{x1D717}_{i}m & = & \displaystyle \lim _{j\rightarrow \infty }\frac{1}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\frac{\unicode[STIX]{x1D6FE}^{p^{j}}\unicode[STIX]{x1D717}_{i}m-\unicode[STIX]{x1D717}_{i}m}{p^{j}}\nonumber\\ \displaystyle & = & \displaystyle \lim _{j\rightarrow \infty }\frac{1}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\frac{(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{p^{j}}-1)\unicode[STIX]{x1D717}_{i}\unicode[STIX]{x1D6FE}^{p^{j}}m+\unicode[STIX]{x1D717}_{i}(\unicode[STIX]{x1D6FE}^{p^{j}}m-m)}{p^{j}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D717}_{i}m+\unicode[STIX]{x1D717}_{i}\unicode[STIX]{x1D719}_{M_{K}(Y)}m.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{M_{K}(Y)}\unicode[STIX]{x1D717}_{i}m & = & \displaystyle \lim _{j\rightarrow \infty }\frac{1}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\frac{\unicode[STIX]{x1D6FE}^{p^{j}}\unicode[STIX]{x1D717}_{i}m-\unicode[STIX]{x1D717}_{i}m}{p^{j}}\nonumber\\ \displaystyle & = & \displaystyle \lim _{j\rightarrow \infty }\frac{1}{\log \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})}\frac{(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})^{p^{j}}-1)\unicode[STIX]{x1D717}_{i}\unicode[STIX]{x1D6FE}^{p^{j}}m+\unicode[STIX]{x1D717}_{i}(\unicode[STIX]{x1D6FE}^{p^{j}}m-m)}{p^{j}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D717}_{i}m+\unicode[STIX]{x1D717}_{i}\unicode[STIX]{x1D719}_{M_{K}(Y)}m.\nonumber\end{eqnarray}$$
Hence
![]() $[\unicode[STIX]{x1D719}_{M_{K}(Y)},\unicode[STIX]{x1D717}_{i}]=\unicode[STIX]{x1D717}_{i}$
.◻
$[\unicode[STIX]{x1D719}_{M_{K}(Y)},\unicode[STIX]{x1D717}_{i}]=\unicode[STIX]{x1D717}_{i}$
.◻
Remark 3.6. Brinon generalized Sen’s theory to the case of
![]() $p$
-adic fields with imperfect residue fields in [Reference BrinonBri03]. Analogues of
$p$
-adic fields with imperfect residue fields in [Reference BrinonBri03]. Analogues of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
and
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
and
![]() $\unicode[STIX]{x1D717}_{i}$
have already appeared in his work.
$\unicode[STIX]{x1D717}_{i}$
have already appeared in his work.
We discuss properties of the arithmetic Sen endomorphism along the lines of Theorem 3.1 (i.e. [Reference Liu and ZhuLZ17, Theorem 2.1]).
Theorem 3.7. (i) There are canonical isomorphisms
and
(ii) Let
![]() $f:Y\rightarrow X$
be a morphism between smooth rigid analytic varieties over
$f:Y\rightarrow X$
be a morphism between smooth rigid analytic varieties over
![]() $k$
and
$k$
and
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Then there is a canonical isomorphism
$X_{\acute{\text{e}}\text{t}}$
. Then there is a canonical isomorphism
Proof. Part (i) follows from [Reference Liu and ZhuLZ17, Theorem 2.1(iv)] and Lemma 2.22. Part (ii) follows from [Reference Liu and ZhuLZ17, Theorem 2.1(iii)] and Proposition 2.20 (functoriality of
![]() $\unicode[STIX]{x1D719}_{W}$
).◻
$\unicode[STIX]{x1D719}_{W}$
).◻
By construction, we also have the following in the case of points.
Proposition 3.8. If
![]() $X$
is a point, then
$X$
is a point, then
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
coincides with the Sen endomorphism attached to the Galois representation
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
coincides with the Sen endomorphism attached to the Galois representation
![]() $\mathbb{L}$
.
$\mathbb{L}$
.
For pushforwards, we have the following theorem (the notation is explained after the statement).
Theorem 3.9. Let
![]() $f:X\rightarrow Y$
be a smooth proper morphism between smooth rigid analytic varieties over
$f:X\rightarrow Y$
be a smooth proper morphism between smooth rigid analytic varieties over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Z}_{p}$
-local system on
$\mathbb{Z}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Then we have
$X_{\acute{\text{e}}\text{t}}$
. Then we have
Moreover, under this isomorphism, we have
Let us explain the notation in the theorem. Recall the complex of
![]() ${\mathcal{O}}_{X_{K}}$
-modules
${\mathcal{O}}_{X_{K}}$
-modules
This has an
![]() ${\mathcal{O}}_{X_{K}}$
-linear endomorphism
${\mathcal{O}}_{X_{K}}$
-linear endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
by Proposition 3.5. The complex yields a complex of
$\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
by Proposition 3.5. The complex yields a complex of
![]() ${\mathcal{O}}_{X_{K}}$
-modules
${\mathcal{O}}_{X_{K}}$
-modules
by composing with the projection
![]() $\unicode[STIX]{x1D6FA}_{X/k}^{i}\rightarrow \unicode[STIX]{x1D6FA}_{X/Y}^{i}$
. The new complex has an induced
$\unicode[STIX]{x1D6FA}_{X/k}^{i}\rightarrow \unicode[STIX]{x1D6FA}_{X/Y}^{i}$
. The new complex has an induced
![]() ${\mathcal{O}}_{X_{K}}$
-linear endomorphism, which we still denote by
${\mathcal{O}}_{X_{K}}$
-linear endomorphism, which we still denote by
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
.
$\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
.
We denote by
![]() $f_{K}:X_{K}\rightarrow Y_{K}$
the base change of
$f_{K}:X_{K}\rightarrow Y_{K}$
the base change of
![]() $f$
. Then
$f$
. Then
![]() $R^{i}f_{\text{Higgs},\ast }$
is the
$R^{i}f_{\text{Higgs},\ast }$
is the
![]() $i$
th derived pushforward of the complex with the Higgs field. In particular,
$i$
th derived pushforward of the complex with the Higgs field. In particular,
![]() $R^{i}f_{\text{Higgs},\ast }({\mathcal{H}}(\mathbb{L})\,\otimes \,\unicode[STIX]{x1D6FA}_{X/Y}^{\bullet }(-\bullet ),\bar{\unicode[STIX]{x1D717}_{\mathbb{L}}})$
is the
$R^{i}f_{\text{Higgs},\ast }({\mathcal{H}}(\mathbb{L})\,\otimes \,\unicode[STIX]{x1D6FA}_{X/Y}^{\bullet }(-\bullet ),\bar{\unicode[STIX]{x1D717}_{\mathbb{L}}})$
is the
![]() ${\mathcal{O}}_{X_{K},\acute{\text{e}}\text{t}}$
-module
${\mathcal{O}}_{X_{K},\acute{\text{e}}\text{t}}$
-module
![]() $R^{i}f_{K,\acute{\text{e}}\text{t},\ast }({\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/Y}^{\bullet }(-\bullet ))$
together with a Higgs field.
$R^{i}f_{K,\acute{\text{e}}\text{t},\ast }({\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/Y}^{\bullet }(-\bullet ))$
together with a Higgs field.
Proof. The first part is [Reference Liu and ZhuLZ17, Theorem 2.1(v)] (see Theorem 3.1). Note that [Reference Liu and ZhuLZ17, Theorem 2.1(v)] has an additional assumption that
![]() $R^{i}f_{\ast }\mathbb{L}$
is a
$R^{i}f_{\ast }\mathbb{L}$
is a
![]() $\mathbb{Z}_{p}$
-local system on
$\mathbb{Z}_{p}$
-local system on
![]() $Y_{\acute{\text{e}}\text{t}}$
for every
$Y_{\acute{\text{e}}\text{t}}$
for every
![]() $i$
, but this is always the case; to see this, it suffices to check that
$i$
, but this is always the case; to see this, it suffices to check that
![]() $(R^{i}f_{\ast }\mathbb{L})|_{Y_{\hat{\overline{k}}},\acute{\text{e}}\text{t}}$
is a
$(R^{i}f_{\ast }\mathbb{L})|_{Y_{\hat{\overline{k}}},\acute{\text{e}}\text{t}}$
is a
![]() $\mathbb{Z}_{p}$
-local system, which follows from [Reference Scholze and WeinsteinSW18, Theorem 10.5.1]. So we will prove the statement on arithmetic Sen endomorphisms.
$\mathbb{Z}_{p}$
-local system, which follows from [Reference Scholze and WeinsteinSW18, Theorem 10.5.1]. So we will prove the statement on arithmetic Sen endomorphisms.
Since the statement is local on
![]() $Y$
, we may assume that
$Y$
, we may assume that
![]() $Y$
is an affinoid
$Y$
is an affinoid
![]() $\operatorname{Spa}(A,A^{+})$
and that
$\operatorname{Spa}(A,A^{+})$
and that
![]() ${\mathcal{H}}(R^{i}f_{\ast }\mathbb{L})$
is a globally free vector bundle on
${\mathcal{H}}(R^{i}f_{\ast }\mathbb{L})$
is a globally free vector bundle on
![]() $Y_{K}$
. So
$Y_{K}$
. So
![]() ${\mathcal{H}}(R^{i}f_{\ast }\mathbb{L})$
is associated to a finite free
${\mathcal{H}}(R^{i}f_{\ast }\mathbb{L})$
is associated to a finite free
![]() $A_{K}$
-module (say
$A_{K}$
-module (say
![]() $V$
). Then
$V$
). Then
![]() $V$
is an
$V$
is an
![]() $A_{K}$
-representation of
$A_{K}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and the endomorphism
$\unicode[STIX]{x1D6E4}_{k}$
and the endomorphism
![]() $\unicode[STIX]{x1D719}_{R^{i}f_{\ast }\mathbb{L}}$
is associated to
$\unicode[STIX]{x1D719}_{R^{i}f_{\ast }\mathbb{L}}$
is associated to
![]() $\unicode[STIX]{x1D719}_{V}$
.
$\unicode[STIX]{x1D719}_{V}$
.
Since
![]() $X$
is quasi-compact, there exists a finite affinoid open cover
$X$
is quasi-compact, there exists a finite affinoid open cover
![]() $X=\bigcup _{i\in I}U^{(i)}$
with
$X=\bigcup _{i\in I}U^{(i)}$
with
![]() $U^{(i)}=\operatorname{Spa}(B^{(i)},B^{(i),+})$
such that
$U^{(i)}=\operatorname{Spa}(B^{(i)},B^{(i),+})$
such that
![]() ${\mathcal{H}}(\mathbb{L})|_{U_{K}^{(i)}}$
is a globally finite free vector bundle for each
${\mathcal{H}}(\mathbb{L})|_{U_{K}^{(i)}}$
is a globally finite free vector bundle for each
![]() $i$
. So
$i$
. So
![]() ${\mathcal{H}}(\mathbb{L})|_{U_{K}^{(i)}}$
gives rise to a
${\mathcal{H}}(\mathbb{L})|_{U_{K}^{(i)}}$
gives rise to a
![]() $B_{K}^{(i)}$
-representation of
$B_{K}^{(i)}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and the latter is defined over
$\unicode[STIX]{x1D6E4}_{k}$
and the latter is defined over
![]() $B_{k_{m}}^{(i)}$
for a sufficiently large
$B_{k_{m}}^{(i)}$
for a sufficiently large
![]() $m$
(cf. the proof of Theorem 2.9). Since the same holds for
$m$
(cf. the proof of Theorem 2.9). Since the same holds for
![]() ${\mathcal{H}}(\mathbb{L})|_{U_{K}^{(i)}\cap U_{K}^{(j)}}$
, there exists a large integer
${\mathcal{H}}(\mathbb{L})|_{U_{K}^{(i)}\cap U_{K}^{(j)}}$
, there exists a large integer
![]() $m$
such that the complex of
$m$
such that the complex of
![]() ${\mathcal{O}}_{X_{K}}$
-modules
${\mathcal{O}}_{X_{K}}$
-modules
with the
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action and the endomorphism
$\unicode[STIX]{x1D6E4}_{k}$
-action and the endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
descends to a complex of
$\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
descends to a complex of
![]() ${\mathcal{O}}_{X_{k_{m}}}$
-modules
${\mathcal{O}}_{X_{k_{m}}}$
-modules
on
![]() $X_{k_{m}}$
equipped with
$X_{k_{m}}$
equipped with
![]() $\unicode[STIX]{x1D6E4}$
-action and an endomorphism
$\unicode[STIX]{x1D6E4}$
-action and an endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \,\operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
such that
$\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \,\operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
such that
![]() ${\mathcal{H}}(\mathbb{L})_{k_{m}}|_{U_{k_{m}}^{(i)}}$
is a globally finite free vector bundle for each
${\mathcal{H}}(\mathbb{L})_{k_{m}}|_{U_{k_{m}}^{(i)}}$
is a globally finite free vector bundle for each
![]() $i$
. We denote by
$i$
. We denote by
![]() ${\mathcal{F}}^{\bullet }$
the complex on
${\mathcal{F}}^{\bullet }$
the complex on
![]() $X_{k_{m}}$
and by
$X_{k_{m}}$
and by
![]() $\unicode[STIX]{x1D719}^{\bullet }$
the descended endomorphism.
$\unicode[STIX]{x1D719}^{\bullet }$
the descended endomorphism.
Let
![]() $f_{k_{m}}:X_{k_{m}}\rightarrow Y_{k_{m}}$
denote the base change of
$f_{k_{m}}:X_{k_{m}}\rightarrow Y_{k_{m}}$
denote the base change of
![]() $f$
. Set
$f$
. Set
Since
![]() $f_{k_{m}}$
is proper, this is a coherent
$f_{k_{m}}$
is proper, this is a coherent
![]() ${\mathcal{O}}_{Y_{k_{m}}}$
-module by Kiehl’s finiteness theorem.Footnote
2
We have
${\mathcal{O}}_{Y_{k_{m}}}$
-module by Kiehl’s finiteness theorem.Footnote
2
We have
and this is isomorphic to
![]() ${\mathcal{H}}(R^{i}f_{\ast }\mathbb{L})$
by the first assertion. Thus (after increasing
${\mathcal{H}}(R^{i}f_{\ast }\mathbb{L})$
by the first assertion. Thus (after increasing
![]() $m$
)
$m$
)
![]() ${\mathcal{H}}_{Y,k_{m}}$
is globally finite free and associated to a finite free
${\mathcal{H}}_{Y,k_{m}}$
is globally finite free and associated to a finite free
![]() $A_{k_{m}}$
-module (say
$A_{k_{m}}$
-module (say
![]() $V_{k_{m}}$
) with
$V_{k_{m}}$
) with
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action satisfying
$\unicode[STIX]{x1D6E4}_{k}$
-action satisfying
![]() $V_{k_{m}}\otimes _{A_{k_{m}}}A_{K}=V$
. By construction,
$V_{k_{m}}\otimes _{A_{k_{m}}}A_{K}=V$
. By construction,
![]() $V_{k_{m}}$
is contained in
$V_{k_{m}}$
is contained in
![]() $V_{\text{fin}}$
and the
$V_{\text{fin}}$
and the
![]() $A_{K}$
-linear endomorphism
$A_{K}$
-linear endomorphism
![]() $\unicode[STIX]{x1D719}_{V}$
on
$\unicode[STIX]{x1D719}_{V}$
on
![]() $V$
is uniquely characterized by the following property: for each
$V$
is uniquely characterized by the following property: for each
![]() $v\in V_{k_{m}}$
, there exists an open subgroup
$v\in V_{k_{m}}$
, there exists an open subgroup
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }\subset \unicode[STIX]{x1D6E4}_{k}$
such that
$\unicode[STIX]{x1D6E4}_{k}^{\prime }\subset \unicode[STIX]{x1D6E4}_{k}$
such that
for all
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
.
We will show that
![]() $R^{i}f_{K,\acute{\text{e}}\text{t},\ast }(\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id}))$
defines an
$R^{i}f_{K,\acute{\text{e}}\text{t},\ast }(\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id}))$
defines an
![]() $A_{K}$
-linear endomorphism on
$A_{K}$
-linear endomorphism on
![]() $V$
with the same property. To see this, we compute
$V$
with the same property. To see this, we compute
![]() $V_{k_{m}}$
via the Čech-to-derived functor spectral sequence. Note that
$V_{k_{m}}$
via the Čech-to-derived functor spectral sequence. Note that
by definition.
Let us briefly recall the Čech-to-derived functor spectral sequence. Set
![]() ${\mathcal{U}}:=\{U_{k_{m}}^{(i)}\}_{i\in I}$
. For
${\mathcal{U}}:=\{U_{k_{m}}^{(i)}\}_{i\in I}$
. For
![]() $i_{0},\ldots ,i_{a}\in I$
, we denote by
$i_{0},\ldots ,i_{a}\in I$
, we denote by
![]() $U_{k_{m}}^{(i_{0}\cdots i_{a})}$
the affinoid open
$U_{k_{m}}^{(i_{0}\cdots i_{a})}$
the affinoid open
![]() $U_{k_{m}}^{(i_{0})}\cap \cdots \cap U_{k_{m}}^{(i_{a})}$
. Consider the Čech double complex
$U_{k_{m}}^{(i_{0})}\cap \cdots \cap U_{k_{m}}^{(i_{a})}$
. Consider the Čech double complex
![]() ${\check{C}}^{\bullet }({\mathcal{U}},{\mathcal{F}}^{\bullet })$
associated to the complex
${\check{C}}^{\bullet }({\mathcal{U}},{\mathcal{F}}^{\bullet })$
associated to the complex
![]() ${\mathcal{F}}^{\bullet }$
; this is defined by
${\mathcal{F}}^{\bullet }$
; this is defined by
Let
![]() $\text{}\underline{H}^{b}$
be the
$\text{}\underline{H}^{b}$
be the
![]() $b$
th right derived functor of the forgetful functor from the category of abelian sheaves on
$b$
th right derived functor of the forgetful functor from the category of abelian sheaves on
![]() $X_{k_{m},\acute{\text{e}}\text{t}}$
to the category of abelian presheaves on
$X_{k_{m},\acute{\text{e}}\text{t}}$
to the category of abelian presheaves on
![]() $X_{k_{m},\acute{\text{e}}\text{t}}$
; for an abelian sheaf
$X_{k_{m},\acute{\text{e}}\text{t}}$
; for an abelian sheaf
![]() ${\mathcal{G}}$
,
${\mathcal{G}}$
,
![]() $\text{}\underline{H}^{b}({\mathcal{G}})$
associates to
$\text{}\underline{H}^{b}({\mathcal{G}})$
associates to
![]() $(U\rightarrow X_{k_{m}})$
the abelian group
$(U\rightarrow X_{k_{m}})$
the abelian group
![]() $H^{b}(U,{\mathcal{G}})$
. Then the Čech-to-derived functor spectral sequence is a spectral sequence with
$H^{b}(U,{\mathcal{G}})$
. Then the Čech-to-derived functor spectral sequence is a spectral sequence with
converging to
![]() $R^{a+b}\unicode[STIX]{x1D6E4}(X_{k_{m},\acute{\text{e}}\text{t}},{\mathcal{F}}^{\bullet })$
. Moreover, this is functorial in
$R^{a+b}\unicode[STIX]{x1D6E4}(X_{k_{m},\acute{\text{e}}\text{t}},{\mathcal{F}}^{\bullet })$
. Moreover, this is functorial in
![]() ${\mathcal{F}}^{\bullet }$
.
${\mathcal{F}}^{\bullet }$
.
In our case,
![]() ${\mathcal{F}}^{\bullet }$
consists of coherent
${\mathcal{F}}^{\bullet }$
consists of coherent
![]() ${\mathcal{O}}_{k_{m}}$
-modules and
${\mathcal{O}}_{k_{m}}$
-modules and
![]() $U_{k_{m}}^{(i_{0}\cdots i_{a})}$
are all affinoid. So
$U_{k_{m}}^{(i_{0}\cdots i_{a})}$
are all affinoid. So
![]() $\text{}\underline{H}^{b}({\mathcal{F}}^{c})(U_{k_{m}}^{(i_{0}\cdots i_{a})})=0$
for each
$\text{}\underline{H}^{b}({\mathcal{F}}^{c})(U_{k_{m}}^{(i_{0}\cdots i_{a})})=0$
for each
![]() $b>0$
and any
$b>0$
and any
![]() $a$
and
$a$
and
![]() $c$
by Kiehl’s theorem. Thus the spectral sequence yields an isomorphism
$c$
by Kiehl’s theorem. Thus the spectral sequence yields an isomorphism
Moreover, this isomorphism is
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant as the construction is functorial in
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant as the construction is functorial in
![]() ${\mathcal{F}}^{\bullet }$
.
${\mathcal{F}}^{\bullet }$
.
Let us unwind the definition of
![]() ${\check{C}}^{a}({\mathcal{U}},{\mathcal{F}}^{b})$
:
${\check{C}}^{a}({\mathcal{U}},{\mathcal{F}}^{b})$
:
Set
and
They have a natural
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action, and
$\unicode[STIX]{x1D6E4}_{k}$
-action, and
![]() $W_{k_{m}}^{(i_{0}\cdots i_{a}),b}$
is contained in
$W_{k_{m}}^{(i_{0}\cdots i_{a}),b}$
is contained in
![]() $(W^{(i_{0}\cdots i_{a}),b})_{\text{fin}}$
. In particular, the restriction of
$(W^{(i_{0}\cdots i_{a}),b})_{\text{fin}}$
. In particular, the restriction of
![]() $\unicode[STIX]{x1D719}_{W^{(i_{0}\cdots i_{a}),b}}$
to
$\unicode[STIX]{x1D719}_{W^{(i_{0}\cdots i_{a}),b}}$
to
![]() $W_{k_{m}}^{(i_{0}\cdots i_{a}),b}$
satisfies the following property: for each
$W_{k_{m}}^{(i_{0}\cdots i_{a}),b}$
satisfies the following property: for each
![]() $w\in W_{k_{m}}^{(i_{0}\cdots i_{a}),b}$
, there exists an open subgroup
$w\in W_{k_{m}}^{(i_{0}\cdots i_{a}),b}$
, there exists an open subgroup
![]() $\unicode[STIX]{x1D6E4}_{k}^{\prime }\subset \unicode[STIX]{x1D6E4}_{k}$
such that
$\unicode[STIX]{x1D6E4}_{k}^{\prime }\subset \unicode[STIX]{x1D6E4}_{k}$
such that
for all
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }$
.
It follows from our construction that under the isomorphism
![]() $H^{i}(\operatorname{Tot}({\check{C}}^{\bullet }({\mathcal{U}},{\mathcal{F}}^{\bullet })))\cong R^{i}\unicode[STIX]{x1D6E4}(X_{k_{m},\acute{\text{e}}\text{t}},{\mathcal{F}}^{\bullet })=V_{k_{m}}$
, the endomorphism
$H^{i}(\operatorname{Tot}({\check{C}}^{\bullet }({\mathcal{U}},{\mathcal{F}}^{\bullet })))\cong R^{i}\unicode[STIX]{x1D6E4}(X_{k_{m},\acute{\text{e}}\text{t}},{\mathcal{F}}^{\bullet })=V_{k_{m}}$
, the endomorphism
![]() $R^{i}f_{K,\acute{\text{e}}\text{t},\ast }(\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id}))|_{V_{k_{m}}}=R^{i}f_{k_{m},\acute{\text{e}}\text{t},\ast }\unicode[STIX]{x1D719}^{\bullet }$
corresponds to
$R^{i}f_{K,\acute{\text{e}}\text{t},\ast }(\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id}))|_{V_{k_{m}}}=R^{i}f_{k_{m},\acute{\text{e}}\text{t},\ast }\unicode[STIX]{x1D719}^{\bullet }$
corresponds to
Since differentials in the complex
![]() $\operatorname{Tot}({\check{C}}^{\bullet }({\mathcal{U}},{\mathcal{F}}^{\bullet }))$
are all
$\operatorname{Tot}({\check{C}}^{\bullet }({\mathcal{U}},{\mathcal{F}}^{\bullet }))$
are all
![]() $\unicode[STIX]{x1D6E4}_{k}$
-equivariant, we see that
$\unicode[STIX]{x1D6E4}_{k}$
-equivariant, we see that
![]() $H^{i}(\operatorname{Tot}(\prod _{i_{0},\ldots ,i_{a}\in I}\unicode[STIX]{x1D719}_{W^{(i_{0}\cdots i_{a}),b}}))$
satisfies the above-mentioned characterizing property of
$H^{i}(\operatorname{Tot}(\prod _{i_{0},\ldots ,i_{a}\in I}\unicode[STIX]{x1D719}_{W^{(i_{0}\cdots i_{a}),b}}))$
satisfies the above-mentioned characterizing property of
![]() $\unicode[STIX]{x1D719}_{V}$
. This completes the proof.◻
$\unicode[STIX]{x1D719}_{V}$
. This completes the proof.◻
4 Constancy of generalized Hodge–Tate weights
In this section, we prove the multiset of eigenvalues of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
is constant on
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
is constant on
![]() $X_{K}$
(Theorem 4.8). For this we give a description of
$X_{K}$
(Theorem 4.8). For this we give a description of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
as the residue of a formal connection in § 4.1. Then the constancy is proved by the theory of formal connections developed in § 4.2.
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
as the residue of a formal connection in § 4.1. Then the constancy is proved by the theory of formal connections developed in § 4.2.
4.1 The decompletion of the geometric Riemann–Hilbert correspondence
We review the geometric Riemann–Hilbert correspondence by Liu and Zhu and discuss its decompletion.
Keep the notation in § 3. Let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
of rank
$X_{\acute{\text{e}}\text{t}}$
of rank
![]() $r$
. Following [Reference Liu and ZhuLZ17], we define
$r$
. Following [Reference Liu and ZhuLZ17], we define
In order to state their theorem, let us recall a ringed space
![]() ${\mathcal{X}}$
introduced in [Reference Liu and ZhuLZ17, § 3.1]. Let
${\mathcal{X}}$
introduced in [Reference Liu and ZhuLZ17, § 3.1]. Let
![]() $L_{\text{dR}}^{+}$
denote the de Rham period ring
$L_{\text{dR}}^{+}$
denote the de Rham period ring
![]() $\mathbb{B}_{\text{dR}}^{+}(K,{\mathcal{O}}_{K})$
as before ([Reference Liu and ZhuLZ17] uses
$\mathbb{B}_{\text{dR}}^{+}(K,{\mathcal{O}}_{K})$
as before ([Reference Liu and ZhuLZ17] uses
![]() $B_{\text{dR}}^{+}$
but we prefer to use
$B_{\text{dR}}^{+}$
but we prefer to use
![]() $L_{\text{dR}}^{+}$
). Define a sheaf
$L_{\text{dR}}^{+}$
). Define a sheaf
![]() ${\mathcal{O}}_{X}\,\hat{\otimes }\,(L_{\text{dR}}^{+}/t^{i})$
on
${\mathcal{O}}_{X}\,\hat{\otimes }\,(L_{\text{dR}}^{+}/t^{i})$
on
![]() $X_{K,\acute{\text{e}}\text{t}}$
by assigning
$X_{K,\acute{\text{e}}\text{t}}$
by assigning
This defines a sheaf by the Tate acyclicity theorem. We also set
and
We denote the ringed space
![]() $(X_{K},{\mathcal{O}}_{X}\,\hat{\otimes }\,L_{\text{dR}})$
by
$(X_{K},{\mathcal{O}}_{X}\,\hat{\otimes }\,L_{\text{dR}})$
by
![]() ${\mathcal{X}}$
. We have a natural base change functor
${\mathcal{X}}$
. We have a natural base change functor
![]() ${\mathcal{E}}\mapsto {\mathcal{E}}\,\hat{\otimes }\,L_{\text{dR}}$
from the category of vector bundles on
${\mathcal{E}}\mapsto {\mathcal{E}}\,\hat{\otimes }\,L_{\text{dR}}$
from the category of vector bundles on
![]() $X$
to the category of vector bundles on
$X$
to the category of vector bundles on
![]() ${\mathcal{X}}$
. We set
${\mathcal{X}}$
. We set
Theorem 4.1 [Reference Liu and ZhuLZ17, Theorem 3.8].
(i)
 ${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
is a filtered vector bundle on
${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
is a filtered vector bundle on
 ${\mathcal{X}}$
of rank
${\mathcal{X}}$
of rank
 $r$
equipped with an integrable connection that satisfies the Griffiths transversality. Moreover,
$r$
equipped with an integrable connection that satisfies the Griffiths transversality. Moreover, $$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{\mathbb{L}}:{\mathcal{R}}{\mathcal{H}}(\mathbb{L})\longrightarrow {\mathcal{R}}{\mathcal{H}}(\mathbb{L})\otimes _{{\mathcal{O}}_{{\mathcal{X}}}}\unicode[STIX]{x1D6FA}_{{\mathcal{X}}/L_{\text{dR}}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{\mathbb{L}}:{\mathcal{R}}{\mathcal{H}}(\mathbb{L})\longrightarrow {\mathcal{R}}{\mathcal{H}}(\mathbb{L})\otimes _{{\mathcal{O}}_{{\mathcal{X}}}}\unicode[STIX]{x1D6FA}_{{\mathcal{X}}/L_{\text{dR}}}\end{eqnarray}$$
 $\operatorname{Gal}(K/k)$
acts on
$\operatorname{Gal}(K/k)$
acts on
 ${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
semilinearly, and the action preserves the filtration and commutes with
${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
semilinearly, and the action preserves the filtration and commutes with
 $\unicode[STIX]{x1D6FB}_{\mathbb{L}}$
.
$\unicode[STIX]{x1D6FB}_{\mathbb{L}}$
.(ii) There is a canonical isomorphism
 $$\begin{eqnarray}(\operatorname{gr}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L}),\operatorname{gr}^{0}(\unicode[STIX]{x1D6FB}_{\mathbb{ L}}))\cong ({\mathcal{H}}(\mathbb{L}),\unicode[STIX]{x1D717}_{\mathbb{L}}).\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{gr}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L}),\operatorname{gr}^{0}(\unicode[STIX]{x1D6FB}_{\mathbb{ L}}))\cong ({\mathcal{H}}(\mathbb{L}),\unicode[STIX]{x1D717}_{\mathbb{L}}).\end{eqnarray}$$
We want to consider a decompletion of
![]() ${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
. Here we only develop an ad hoc local theory that is sufficient for our purpose.
${\mathcal{R}}{\mathcal{H}}(\mathbb{L})$
. Here we only develop an ad hoc local theory that is sufficient for our purpose.
Take
![]() $(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
and consider
$(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
and consider
![]() $\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
. Since
$\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
. Since
![]() $\operatorname{gr}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
is a finite free
$\operatorname{gr}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
is a finite free
![]() $B_{K}$
-module by the definition of
$B_{K}$
-module by the definition of
![]() ${\mathcal{B}}_{\mathbb{L}}$
, the
${\mathcal{B}}_{\mathbb{L}}$
, the
![]() $B\,\hat{\otimes }_{k^{\prime }}\,L_{\text{dR}}^{+}$
-module
$B\,\hat{\otimes }_{k^{\prime }}\,L_{\text{dR}}^{+}$
-module
![]() $\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
is also finite free. Thus
$\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
is also finite free. Thus
![]() $\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
is a
$\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})$
is a
![]() $B\,\hat{\otimes }_{k^{\prime }}\,L_{\text{dR}}^{+}$
-representation of
$B\,\hat{\otimes }_{k^{\prime }}\,L_{\text{dR}}^{+}$
-representation of
![]() $\operatorname{Gal}(K/k^{\prime })$
, and
$\operatorname{Gal}(K/k^{\prime })$
, and
![]() ${\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})=(\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K}))[t^{-1}]$
.
${\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})=(\operatorname{Fil}^{0}{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K}))[t^{-1}]$
.
Definition 2.28 yields the
![]() $B_{\infty }((t))$
-module
$B_{\infty }((t))$
-module
![]() ${\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}$
and the
${\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}$
and the
![]() $B_{\infty }$
-linear endomorphism
$B_{\infty }$
-linear endomorphism
For simplicity, we denote
![]() $\unicode[STIX]{x1D719}_{\text{dR},{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}}$
by
$\unicode[STIX]{x1D719}_{\text{dR},{\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}}$
by
![]() $\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L},Y_{K}}$
. It satisfies
$\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L},Y_{K}}$
. It satisfies
for every
![]() $\unicode[STIX]{x1D6FC}\in B_{\infty }((t))$
and
$\unicode[STIX]{x1D6FC}\in B_{\infty }((t))$
and
![]() $m\in {\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}$
. Note that
$m\in {\mathcal{R}}{\mathcal{H}}(\mathbb{L})(Y_{K})_{\text{fin}}$
. Note that
![]() $\unicode[STIX]{x1D6FB}_{\mathbb{L}}$
is
$\unicode[STIX]{x1D6FB}_{\mathbb{L}}$
is
![]() $\operatorname{Gal}(K/k)$
-equivariant. Hence under the identification
$\operatorname{Gal}(K/k)$
-equivariant. Hence under the identification
we have
Proposition 4.2. The following diagram commutes.

Moreover, we have
Proof. The commutativity of the diagram follows from the fact that
![]() $\unicode[STIX]{x1D6FB}_{\mathbb{L}}$
is
$\unicode[STIX]{x1D6FB}_{\mathbb{L}}$
is
![]() $\operatorname{Gal}(K/k)$
-equivariant. The second assertion is a consequence of Theorem 4.1(ii) (cf. Definition 2.28).◻
$\operatorname{Gal}(K/k)$
-equivariant. The second assertion is a consequence of Theorem 4.1(ii) (cf. Definition 2.28).◻
Remark 4.3. In [Reference Andreatta and BrinonAB10], Andreatta and Brinon developed a Fontaine-type decompletion theory in the relative setting. Roughly speaking, they associated to a local system on
![]() $X$
a formal connection over the pro-étale cover
$X$
a formal connection over the pro-étale cover
![]() $\widetilde{X}_{K,\infty }$
over
$\widetilde{X}_{K,\infty }$
over
![]() $X_{K}$
when
$X_{K}$
when
![]() $X$
is an affine scheme admitting a toric chart.
$X$
is an affine scheme admitting a toric chart.
4.2 Theory of formal connections
To study
![]() $\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L},Y_{K}}$
in the previous subsection, we develop a theory of formal connections. We work on the following general setting: let
$\unicode[STIX]{x1D719}_{\text{dR},\mathbb{L},Y_{K}}$
in the previous subsection, we develop a theory of formal connections. We work on the following general setting: let
![]() $R$
be an integral domain of characteristic
$R$
be an integral domain of characteristic
![]() $0$
(e.g.
$0$
(e.g.
![]() $R=B_{\infty }$
in the previous subsection) and fix an algebraic closure of the fraction field of
$R=B_{\infty }$
in the previous subsection) and fix an algebraic closure of the fraction field of
![]() $R$
. Consider the ring of Laurent series
$R$
. Consider the ring of Laurent series
![]() $R((t))$
and define the
$R((t))$
and define the
![]() $R$
-linear derivation
$R$
-linear derivation
![]() $d_{0}:R((t))\rightarrow R((t))$
by
$d_{0}:R((t))\rightarrow R((t))$
by
Let
![]() $M$
be a finite free
$M$
be a finite free
![]() $R((t))$
-module of rank
$R((t))$
-module of rank
![]() $r$
and let
$r$
and let
![]() $D_{0}:M\rightarrow M$
be an
$D_{0}:M\rightarrow M$
be an
![]() $R$
-linear map which satisfies the Leibniz rule
$R$
-linear map which satisfies the Leibniz rule
Definition 4.4. A
![]() $tD_{0}$
-stable lattice of
$tD_{0}$
-stable lattice of
![]() $M$
is a finite free
$M$
is a finite free
![]() $R[[t]]$
-submodule
$R[[t]]$
-submodule
![]() $\unicode[STIX]{x1D6EC}$
of
$\unicode[STIX]{x1D6EC}$
of
![]() $M$
that satisfies
$M$
that satisfies
For a
![]() $tD_{0}$
-stable lattice
$tD_{0}$
-stable lattice
![]() $\unicode[STIX]{x1D6EC}$
of
$\unicode[STIX]{x1D6EC}$
of
![]() $M$
, we have
$M$
, we have
![]() $tD_{0}(t\unicode[STIX]{x1D6EC})\subset t\unicode[STIX]{x1D6EC}$
by the Leibniz rule. Thus
$tD_{0}(t\unicode[STIX]{x1D6EC})\subset t\unicode[STIX]{x1D6EC}$
by the Leibniz rule. Thus
![]() $tD_{0}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}$
induces an
$tD_{0}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}$
induces an
![]() $R$
-linear endomorphism on
$R$
-linear endomorphism on
![]() $\unicode[STIX]{x1D6EC}/t\unicode[STIX]{x1D6EC}$
. We denote this endomorphism by
$\unicode[STIX]{x1D6EC}/t\unicode[STIX]{x1D6EC}$
. We denote this endomorphism by
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
. Since
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
. Since
![]() $\unicode[STIX]{x1D6EC}/t\unicode[STIX]{x1D6EC}$
is a finite free
$\unicode[STIX]{x1D6EC}/t\unicode[STIX]{x1D6EC}$
is a finite free
![]() $R$
-module of rank
$R$
-module of rank
![]() $r$
, the endomorphism
$r$
, the endomorphism
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
has
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
has
![]() $r$
eigenvalues (counted with multiplicity) in the algebraic closure of the fraction field of
$r$
eigenvalues (counted with multiplicity) in the algebraic closure of the fraction field of
![]() $R$
.
$R$
.
The following is known for
![]() $tD_{0}$
-stable lattices.
$tD_{0}$
-stable lattices.
Theorem 4.5. Assume that
![]() $R$
is an algebraically closed field.
$R$
is an algebraically closed field.
(i) There exists a finite subset
 ${\mathcal{A}}$
of
${\mathcal{A}}$
of
 $R$
such that the submodule is a
$R$
such that the submodule is a $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}:=\bigoplus _{\unicode[STIX]{x1D6FC}\in {\mathcal{A}}}\operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{r}\otimes _{R}R[[t]]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}:=\bigoplus _{\unicode[STIX]{x1D6FC}\in {\mathcal{A}}}\operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{r}\otimes _{R}R[[t]]\end{eqnarray}$$
 $tD_{0}$
-stable lattice of
$tD_{0}$
-stable lattice of
 $M$
. In particular, the eigenvalues of
$M$
. In particular, the eigenvalues of
 $\text{Res}_{\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}}D_{0}$
lie in
$\text{Res}_{\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}}D_{0}$
lie in
 ${\mathcal{A}}$
.
${\mathcal{A}}$
.(ii) For any
 $tD_{0}$
-stable lattices
$tD_{0}$
-stable lattices
 $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
 $\unicode[STIX]{x1D6EC}^{\prime }$
of
$\unicode[STIX]{x1D6EC}^{\prime }$
of
 $M$
, the eigenvalues of
$M$
, the eigenvalues of
 $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
and those of
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
and those of
 $\text{Res}_{\unicode[STIX]{x1D6EC}^{\prime }}D_{0}$
differ by integers. Namely, for each eigenvalue
$\text{Res}_{\unicode[STIX]{x1D6EC}^{\prime }}D_{0}$
differ by integers. Namely, for each eigenvalue
 $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
 $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
, there exists an eigenvalue
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
, there exists an eigenvalue
 $\unicode[STIX]{x1D6FC}^{\prime }$
of
$\unicode[STIX]{x1D6FC}^{\prime }$
of
 $\text{Res}_{\unicode[STIX]{x1D6EC}^{\prime }}D_{0}$
such that
$\text{Res}_{\unicode[STIX]{x1D6EC}^{\prime }}D_{0}$
such that
 $\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }\in \mathbb{Z}$
.
$\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }\in \mathbb{Z}$
.
See [Reference Dwork, Gerotto and SullivanDGS94, III.8 and V. Lemma 2.4] and [Reference André and BaldassarriAB01, ch. 1, Proposition 3.2.2] for details.
We now turn to the following multivariable situation: Let
![]() $R$
be an integral domain of characteristic 0 as before. Suppose that
$R$
be an integral domain of characteristic 0 as before. Suppose that
![]() $R$
is equipped with pairwise commuting derivations
$R$
is equipped with pairwise commuting derivations
![]() $d_{1},\ldots ,d_{n}$
; this means that for each
$d_{1},\ldots ,d_{n}$
; this means that for each
![]() $i=1,\ldots ,n$
, the map
$i=1,\ldots ,n$
, the map
![]() $d_{i}:R\rightarrow R$
is additive and satisfies the Leibniz rule
$d_{i}:R\rightarrow R$
is additive and satisfies the Leibniz rule
and
![]() $d_{i}\circ d_{j}=d_{j}\circ d_{i}$
for each
$d_{i}\circ d_{j}=d_{j}\circ d_{i}$
for each
![]() $i$
and
$i$
and
![]() $j$
. Since
$j$
. Since
![]() $R$
is an integral domain of characteristic 0, the derivations
$R$
is an integral domain of characteristic 0, the derivations
![]() $d_{1},\ldots ,d_{n}$
extend uniquely over the algebraic closure of the fraction field of
$d_{1},\ldots ,d_{n}$
extend uniquely over the algebraic closure of the fraction field of
![]() $R$
.
$R$
.
For each
![]() $i=1,\ldots ,n$
, we extend
$i=1,\ldots ,n$
, we extend
![]() $d_{i}:R\rightarrow R$
to an additive map
$d_{i}:R\rightarrow R$
to an additive map
![]() $d_{i}:R((t))\rightarrow R((t))$
by
$d_{i}:R((t))\rightarrow R((t))$
by
Then endomorphisms
![]() $d_{0},d_{1},\ldots ,d_{n}$
on
$d_{0},d_{1},\ldots ,d_{n}$
on
![]() $R((t))$
commute with each other. Moreover,
$R((t))$
commute with each other. Moreover,
![]() $d_{1},\ldots ,d_{n}$
commute with
$d_{1},\ldots ,d_{n}$
commute with
![]() $td_{0}$
.
$td_{0}$
.
Let
![]() $M$
be a finite free
$M$
be a finite free
![]() $R((t))$
-module of rank
$R((t))$
-module of rank
![]() $r$
together with pairwise commuting additive endomorphisms
$r$
together with pairwise commuting additive endomorphisms
![]() $D_{0},D_{1},\ldots ,D_{n}:M\rightarrow M$
satisfying the Leibniz rule
$D_{0},D_{1},\ldots ,D_{n}:M\rightarrow M$
satisfying the Leibniz rule
Note that
![]() $D_{0}$
is
$D_{0}$
is
![]() $R$
-linear and
$R$
-linear and
![]() $D_{1},\ldots ,D_{n}$
commute with
$D_{1},\ldots ,D_{n}$
commute with
![]() $tD_{0}$
.
$tD_{0}$
.
The following proposition is the key to the constancy of generalized Hodge–Tate weights.
Proposition 4.6. With the notation as above, let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $tD_{0}$
-stable lattice of
$tD_{0}$
-stable lattice of
![]() $M$
. Then each eigenvalue
$M$
. Then each eigenvalue
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
in the algebraic closure of the fraction field of
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
in the algebraic closure of the fraction field of
![]() $R$
satisfies
$R$
satisfies
Proof. By extending scalars from
![]() $R$
to the algebraic closure of its fraction field, we may assume that
$R$
to the algebraic closure of its fraction field, we may assume that
![]() $R$
is an algebraically closed field. By Theorem 4.5(i), there exists a finite subset
$R$
is an algebraically closed field. By Theorem 4.5(i), there exists a finite subset
![]() ${\mathcal{A}}$
of
${\mathcal{A}}$
of
![]() $R$
such that the submodule
$R$
such that the submodule
is a
![]() $tD_{0}$
-stable lattice of
$tD_{0}$
-stable lattice of
![]() $M$
.
$M$
.
By Theorem 4.5(ii), the eigenvalues of
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
and those of
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
and those of
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}}D_{0}$
differ by integers. Since every integer
$\text{Res}_{\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}}D_{0}$
differ by integers. Since every integer
![]() $a$
satisfies
$a$
satisfies
![]() $d_{1}(a)=\cdots =d_{n}(a)=0$
, it suffices to treat the case where
$d_{1}(a)=\cdots =d_{n}(a)=0$
, it suffices to treat the case where
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
.
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
.
Lemma 4.7. The finite free
![]() $R[[t]]$
-submodule
$R[[t]]$
-submodule
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
is stable under
$\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
is stable under
![]() $D_{1},\ldots ,D_{n}$
.
$D_{1},\ldots ,D_{n}$
.
Note that Lemma 4.7 says that the connection
![]() $(\unicode[STIX]{x1D6EC}_{{\mathcal{A}}},D_{0},\ldots ,D_{n})$
is regular singular along
$(\unicode[STIX]{x1D6EC}_{{\mathcal{A}}},D_{0},\ldots ,D_{n})$
is regular singular along
![]() $t=0$
. In this case, Proposition 4.6 is easy to prove. In fact, this is an algebraic analogue of the following fact: let
$t=0$
. In this case, Proposition 4.6 is easy to prove. In fact, this is an algebraic analogue of the following fact: let
![]() $X$
be the complex affine space
$X$
be the complex affine space
![]() $\mathbb{A}_{\mathbb{C}}^{n+1}$
and
$\mathbb{A}_{\mathbb{C}}^{n+1}$
and
![]() $D$
the divisor
$D$
the divisor
![]() $\{0\}\times \mathbb{A}_{\mathbb{C}}^{n}$
. Consider a vector bundle
$\{0\}\times \mathbb{A}_{\mathbb{C}}^{n}$
. Consider a vector bundle
![]() $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
![]() $X$
and an integrable connection
$X$
and an integrable connection
![]() $\unicode[STIX]{x1D6FB}$
on
$\unicode[STIX]{x1D6FB}$
on
![]() $\unicode[STIX]{x1D6EC}|_{X\setminus D}$
that admits logarithmic poles along
$\unicode[STIX]{x1D6EC}|_{X\setminus D}$
that admits logarithmic poles along
![]() $D$
. Let
$D$
. Let
![]() $T$
be the monodromy transformation of
$T$
be the monodromy transformation of
![]() $(\unicode[STIX]{x1D6EC}|_{X\setminus D})^{\unicode[STIX]{x1D6FB}=0}$
defined by the positive generator of
$(\unicode[STIX]{x1D6EC}|_{X\setminus D})^{\unicode[STIX]{x1D6FB}=0}$
defined by the positive generator of
![]() $\unicode[STIX]{x1D70B}_{1}(X\setminus D)=\mathbb{Z}$
. Then
$\unicode[STIX]{x1D70B}_{1}(X\setminus D)=\mathbb{Z}$
. Then
![]() $T$
extends to an automorphism
$T$
extends to an automorphism
![]() $\widetilde{T}$
of
$\widetilde{T}$
of
![]() $\unicode[STIX]{x1D6EC}$
and satisfies
$\unicode[STIX]{x1D6EC}$
and satisfies
See [Reference DeligneDel70, Proposition 3.11].
Proof of Lemma 4.7.
This is [Reference André and BaldassarriAB01, Lemma 3.3.2]. For the convenience of the reader, we reproduce the proof here. Fix
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{A}}$
. It is enough to show that for each
$\unicode[STIX]{x1D6FC}\in {\mathcal{A}}$
. It is enough to show that for each
![]() $0\leqslant j\leqslant r$
,
$0\leqslant j\leqslant r$
,
We prove this inclusion by induction on
![]() $j$
. The assertion is trivial when
$j$
. The assertion is trivial when
![]() $j=0$
. Assume
$j=0$
. Assume
![]() $j>0$
and take
$j>0$
and take
![]() $m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
. Then
$m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
. Then
![]() $(tD_{0}-\unicode[STIX]{x1D6FC})m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j-1}$
, and thus
$(tD_{0}-\unicode[STIX]{x1D6FC})m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j-1}$
, and thus
![]() $D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
by the induction hypothesis. We need to show
$D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
by the induction hypothesis. We need to show
![]() $(tD_{0}-\unicode[STIX]{x1D6FC})^{j+1}D_{i}m=0$
. Since
$(tD_{0}-\unicode[STIX]{x1D6FC})^{j+1}D_{i}m=0$
. Since
![]() $D_{i}$
commutes with
$D_{i}$
commutes with
![]() $tD_{0}$
and satisfies
$tD_{0}$
and satisfies
![]() $D_{i}(\unicode[STIX]{x1D6FC}m)=\unicode[STIX]{x1D6FC}D_{i}(m)+d_{i}(\unicode[STIX]{x1D6FC})m$
, we have
$D_{i}(\unicode[STIX]{x1D6FC}m)=\unicode[STIX]{x1D6FC}D_{i}(m)+d_{i}(\unicode[STIX]{x1D6FC})m$
, we have
Therefore
 $$\begin{eqnarray}\displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j+1}D_{i}m & = & \displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j}(tD_{0}-\unicode[STIX]{x1D6FC})D_{i}m\nonumber\\ \displaystyle & = & \displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j}D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m+(tD_{0}-\unicode[STIX]{x1D6FC})^{j}d_{i}(\unicode[STIX]{x1D6FC})m\nonumber\\ \displaystyle & = & \displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j}D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m+d_{i}(\unicode[STIX]{x1D6FC})(tD_{0}-\unicode[STIX]{x1D6FC})^{j}m.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j+1}D_{i}m & = & \displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j}(tD_{0}-\unicode[STIX]{x1D6FC})D_{i}m\nonumber\\ \displaystyle & = & \displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j}D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m+(tD_{0}-\unicode[STIX]{x1D6FC})^{j}d_{i}(\unicode[STIX]{x1D6FC})m\nonumber\\ \displaystyle & = & \displaystyle (tD_{0}-\unicode[STIX]{x1D6FC})^{j}D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m+d_{i}(\unicode[STIX]{x1D6FC})(tD_{0}-\unicode[STIX]{x1D6FC})^{j}m.\nonumber\end{eqnarray}$$
For the third equality, note that
![]() $d_{i}(\unicode[STIX]{x1D6FC})\in R$
and
$d_{i}(\unicode[STIX]{x1D6FC})\in R$
and
![]() $D_{0}$
is
$D_{0}$
is
![]() $R$
-linear. Since
$R$
-linear. Since
![]() $D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
and
$D_{i}(tD_{0}-\unicode[STIX]{x1D6FC})m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
and
![]() $m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
, the last sum is zero.◻
$m\in \operatorname{Ker}(tD_{0}-\unicode[STIX]{x1D6FC})^{j}$
, the last sum is zero.◻
We continue the proof of Proposition 4.6. Fix an
![]() $R[[t]]$
-basis of
$R[[t]]$
-basis of
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
and identify
$\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
and identify
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
with
$\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}$
with
![]() $R[[t]]^{r}$
. Note that
$R[[t]]^{r}$
. Note that
![]() $R[[t]]^{r}$
has natural differentials
$R[[t]]^{r}$
has natural differentials
![]() $d_{0},d_{1},\ldots ,d_{n}:R[[t]]^{r}\rightarrow R[[t]]^{r}$
. Consider the map
$d_{0},d_{1},\ldots ,d_{n}:R[[t]]^{r}\rightarrow R[[t]]^{r}$
. Consider the map
This is
![]() $R[[t]]$
-linear. We denote the corresponding
$R[[t]]$
-linear. We denote the corresponding
![]() $r\times r$
matrix by
$r\times r$
matrix by
![]() $C_{0}\in M_{r}(R[[t]])$
.
$C_{0}\in M_{r}(R[[t]])$
.
Fix
![]() $1\leqslant i\leqslant n$
. By Lemma 4.7, the map
$1\leqslant i\leqslant n$
. By Lemma 4.7, the map
![]() $D_{i}$
gives an endomorphism on
$D_{i}$
gives an endomorphism on
![]() $R[[t]]^{r}$
that satisfies the Leibniz rule, and thus
$R[[t]]^{r}$
that satisfies the Leibniz rule, and thus
![]() $D_{i}-d_{i}$
is an
$D_{i}-d_{i}$
is an
![]() $R[[t]]$
-linear endomorphism on
$R[[t]]$
-linear endomorphism on
![]() $R[[t]]^{r}$
. We denote the corresponding
$R[[t]]^{r}$
. We denote the corresponding
![]() $r\times r$
matrix by
$r\times r$
matrix by
![]() $C_{i}\in M_{r}(R[[t]])$
.
$C_{i}\in M_{r}(R[[t]])$
.
We have
![]() $[tD_{0},D_{i}]=0$
and
$[tD_{0},D_{i}]=0$
and
![]() $[td_{0},d_{i}]=0$
in
$[td_{0},d_{i}]=0$
in
![]() $\operatorname{End}(R[[t]]^{r})$
. Plugging
$\operatorname{End}(R[[t]]^{r})$
. Plugging
![]() $tD_{0}=td_{0}+C_{0}$
and
$tD_{0}=td_{0}+C_{0}$
and
![]() $D_{i}=d_{i}+C_{i}$
into
$D_{i}=d_{i}+C_{i}$
into
![]() $[tD_{0},D_{i}]=0$
yields
$[tD_{0},D_{i}]=0$
yields
where
![]() $d_{0}$
and
$d_{0}$
and
![]() $d_{i}$
are derivatives acting on the matrices entrywise.
$d_{i}$
are derivatives acting on the matrices entrywise.
Consider the surjection
![]() $R[[t]]\rightarrow R$
evaluating
$R[[t]]\rightarrow R$
evaluating
![]() $t$
by 0. We denote the image of
$t$
by 0. We denote the image of
![]() $C_{0}$
(respectively
$C_{0}$
(respectively
![]() $C_{i}$
) in
$C_{i}$
) in
![]() $M_{r}(R)$
by
$M_{r}(R)$
by
![]() $\overline{C}_{0}$
(respectively
$\overline{C}_{0}$
(respectively
![]() $\overline{C}_{i}$
). By construction
$\overline{C}_{i}$
). By construction
![]() $\overline{C}_{0}$
is the matrix corresponding to
$\overline{C}_{0}$
is the matrix corresponding to
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}}D_{0}$
. Thus it suffices to show that each eigenvalue of
$\text{Res}_{\unicode[STIX]{x1D6EC}_{{\mathcal{A}}}}D_{0}$
. Thus it suffices to show that each eigenvalue of
![]() $\overline{C}_{0}$
is killed by
$\overline{C}_{0}$
is killed by
![]() $d_{i}$
. This is standard. Namely, by (4.1), we have
$d_{i}$
. This is standard. Namely, by (4.1), we have
This implies that
Similarly, for each
![]() $j\in \mathbb{N}$
,
$j\in \mathbb{N}$
,
In particular, we get
This implies that each eigenvalue of
![]() $\overline{C}_{0}$
is killed by
$\overline{C}_{0}$
is killed by
![]() $d_{i}$
.◻
$d_{i}$
.◻
4.3 Constancy of generalized Hodge–Tate weights
Here is the key theorem of this paper.
Theorem 4.8. Let
![]() $k$
be a finite extension of
$k$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $X$
be a smooth rigid analytic variety over
$X$
be a smooth rigid analytic variety over
![]() $k$
and
$k$
and
![]() $\mathbb{L}$
a
$\mathbb{L}$
a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Consider the arithmetic Sen endomorphism
$X_{\acute{\text{e}}\text{t}}$
. Consider the arithmetic Sen endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\in \operatorname{End}({\mathcal{H}}(\mathbb{L}))$
. Then eigenvalues of
$\unicode[STIX]{x1D719}_{\mathbb{L}}\in \operatorname{End}({\mathcal{H}}(\mathbb{L}))$
. Then eigenvalues of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L},x}\in \operatorname{End}({\mathcal{H}}(\mathbb{L})_{x})$
for
$\unicode[STIX]{x1D719}_{\mathbb{L},x}\in \operatorname{End}({\mathcal{H}}(\mathbb{L})_{x})$
for
![]() $x\in X_{K}$
are algebraic over
$x\in X_{K}$
are algebraic over
![]() $k$
and constant on each connected component of
$k$
and constant on each connected component of
![]() $X_{K}$
.
$X_{K}$
.
We call these eigenvalues generalized Hodge–Tate weights of
![]() $\mathbb{L}$
.
$\mathbb{L}$
.
Proof. Since
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
is an endomorphism on the vector bundle
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
is an endomorphism on the vector bundle
![]() ${\mathcal{H}}(\mathbb{L})$
on
${\mathcal{H}}(\mathbb{L})$
on
![]() $X_{K}$
, it suffices to prove the statement étale locally on
$X_{K}$
, it suffices to prove the statement étale locally on
![]() $X$
. Thus we may assume that
$X$
. Thus we may assume that
![]() $X$
is an affinoid
$X$
is an affinoid
![]() $\operatorname{Spa}(B,B^{+})$
which admits a toric chart
$\operatorname{Spa}(B,B^{+})$
which admits a toric chart
![]() $X_{k^{\prime }}\rightarrow \mathbb{T}_{k^{\prime }}^{n}$
over some finite extension
$X_{k^{\prime }}\rightarrow \mathbb{T}_{k^{\prime }}^{n}$
over some finite extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
in
$k$
in
![]() $K$
.
$K$
.
Take
![]() $(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
. We may assume that
$(Y=\operatorname{Spa}(B,B^{+})\rightarrow X_{k^{\prime }})\in {\mathcal{B}}_{\mathbb{L}}$
. We may assume that
![]() $B_{\infty }$
is connected, hence an integral domain. Note that
$B_{\infty }$
is connected, hence an integral domain. Note that
![]() $Y$
admits a toric chart
$Y$
admits a toric chart
after base change to a finite extension
![]() $k^{\prime \prime }$
of
$k^{\prime \prime }$
of
![]() $k^{\prime }$
in
$k^{\prime }$
in
![]() $K$
. Then the derivations
$K$
. Then the derivations
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{n}$
on
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{n}$
on
![]() $k^{\prime \prime }\langle T_{1}^{\pm },\ldots ,T_{n}^{\pm }\rangle$
extends over
$k^{\prime \prime }\langle T_{1}^{\pm },\ldots ,T_{n}^{\pm }\rangle$
extends over
![]() $B_{\infty }$
. We also denote the extensions by
$B_{\infty }$
. We also denote the extensions by
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{n}$
.
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{1},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}T_{n}$
.
We set
Consider the
![]() $R((t))$
-module
$R((t))$
-module
equipped with endomorphisms
By Proposition 4.2, they satisfy the assumptions in the previous subsection.
Consider the
![]() $R[[t]]$
-submodule of
$R[[t]]$
-submodule of
![]() $M$
$M$
Then
![]() $\unicode[STIX]{x1D6EC}$
is
$\unicode[STIX]{x1D6EC}$
is
![]() $tD_{0}$
-stable, and
$tD_{0}$
-stable, and
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
is
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
is
![]() $\unicode[STIX]{x1D719}_{\mathbb{L},Y_{K}}$
. Thus by Proposition 4.6, each eigenvalue
$\unicode[STIX]{x1D719}_{\mathbb{L},Y_{K}}$
. Thus by Proposition 4.6, each eigenvalue
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
in an algebraic closure
$\text{Res}_{\unicode[STIX]{x1D6EC}}D_{0}$
in an algebraic closure
![]() $L$
of
$L$
of
![]() $\operatorname{Frac}R$
satisfies
$\operatorname{Frac}R$
satisfies
On the other hand, we can check that
Therefore the eigenvalues of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L},Y_{K}}$
are algebraic over
$\unicode[STIX]{x1D719}_{\mathbb{L},Y_{K}}$
are algebraic over
![]() $k$
and constant on
$k$
and constant on
![]() $Y_{K}$
.◻
$Y_{K}$
.◻
Corollary 4.9. Let
![]() $k$
be a finite extension of
$k$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $X$
be a geometrically connected smooth rigid analytic variety over
$X$
be a geometrically connected smooth rigid analytic variety over
![]() $k$
and
$k$
and
![]() $\mathbb{L}$
a
$\mathbb{L}$
a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X$
. Then the multiset of generalized Hodge–Tate weights of the
$X$
. Then the multiset of generalized Hodge–Tate weights of the
![]() $p$
-adic representations
$p$
-adic representations
![]() $\mathbb{L}_{\overline{x}}$
of
$\mathbb{L}_{\overline{x}}$
of
![]() $\operatorname{Gal}(\overline{k(x)}/k(x))$
does not depend on the choice of a classical point
$\operatorname{Gal}(\overline{k(x)}/k(x))$
does not depend on the choice of a classical point
![]() $x$
of
$x$
of
![]() $X$
.
$X$
.
In particular, if
![]() $\mathbb{L}_{\overline{x}}$
is presque Hodge–Tate for one classical point
$\mathbb{L}_{\overline{x}}$
is presque Hodge–Tate for one classical point
![]() $x$
of
$x$
of
![]() $X$
(i.e. generalized Hodge–Tate weights are all integers),
$X$
(i.e. generalized Hodge–Tate weights are all integers),
![]() $\mathbb{L}_{\overline{y}}$
is presque Hodge–Tate for every classical point
$\mathbb{L}_{\overline{y}}$
is presque Hodge–Tate for every classical point
![]() $y$
of
$y$
of
![]() $X$
.
$X$
.
Proof. This follows from Theorem 4.8. ◻
5 Applications and related topics
We study properties of Hodge–Tate sheaves using the arithmetic Sen endomorphism. We keep the notation in § 3.
Consider the Hodge–Tate period sheaf on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
:
$X_{\text{pro}\acute{\text{e}}\text{t}}$
:
For a
![]() $\mathbb{Q}_{p}$
-local system
$\mathbb{Q}_{p}$
-local system
![]() $\mathbb{L}$
on
$\mathbb{L}$
on
![]() $X_{\acute{\text{e}}\text{t}}$
, we define a sheaf
$X_{\acute{\text{e}}\text{t}}$
, we define a sheaf
![]() $D_{\text{HT}}(\mathbb{L})$
on
$D_{\text{HT}}(\mathbb{L})$
on
![]() $X_{\acute{\text{e}}\text{t}}$
by
$X_{\acute{\text{e}}\text{t}}$
by
Proposition 5.1. The sheaf
![]() $D_{\text{HT}}(\mathbb{L})$
is a coherent
$D_{\text{HT}}(\mathbb{L})$
is a coherent
![]() ${\mathcal{O}}_{X_{\acute{\text{e}}\text{t}}}$
-module. Moreover, for every affinoid
${\mathcal{O}}_{X_{\acute{\text{e}}\text{t}}}$
-module. Moreover, for every affinoid
![]() $Y\in X_{\acute{\text{e}}\text{t}}$
,
$Y\in X_{\acute{\text{e}}\text{t}}$
,
Proof. This follows from the proof of [Reference Liu and ZhuLZ17, Theorem 3.9(i)]. ◻
Remark 5.2. In [Reference Kedlaya and LiuKL16, Theorem 8.6.2(a)], Kedlaya and Liu proved this statement for pseudocoherent modules over a pro-coherent analytic field.
We are going to study the relation between
![]() $D_{\text{HT}}(\mathbb{L})$
and
$D_{\text{HT}}(\mathbb{L})$
and
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\in \operatorname{End}{\mathcal{H}}(\mathbb{L})$
. For each
$\unicode[STIX]{x1D719}_{\mathbb{L}}\in \operatorname{End}{\mathcal{H}}(\mathbb{L})$
. For each
![]() $j\in \mathbb{Z}$
, we set
$j\in \mathbb{Z}$
, we set
This is a coherent
![]() ${\mathcal{O}}_{X_{K,\acute{\text{e}}\text{t}}}$
-module. We denote by
${\mathcal{O}}_{X_{K,\acute{\text{e}}\text{t}}}$
-module. We denote by
![]() $D_{\text{HT}}(\mathbb{L})|_{X_{K}}$
the coherent
$D_{\text{HT}}(\mathbb{L})|_{X_{K}}$
the coherent
![]() ${\mathcal{O}}_{X_{K},\acute{\text{e}}\text{t}}$
-module associated to the pullback of
${\mathcal{O}}_{X_{K},\acute{\text{e}}\text{t}}$
-module associated to the pullback of
![]() $D_{\text{HT}}(\mathbb{L})$
on
$D_{\text{HT}}(\mathbb{L})$
on
![]() $X$
to
$X$
to
![]() $X_{K}$
as coherent sheaves.
$X_{K}$
as coherent sheaves.
Proposition 5.3. Let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system of rank
$\mathbb{Q}_{p}$
-local system of rank
![]() $r$
on
$r$
on
![]() $X_{\acute{\text{e}}\text{t}}$
. Assume that
$X_{\acute{\text{e}}\text{t}}$
. Assume that
![]() $\mathbb{L}$
satisfies one of the following conditions:
$\mathbb{L}$
satisfies one of the following conditions:
(i)
 ${\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
is a vector bundle on
${\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
is a vector bundle on
 $X_{K,\acute{\text{e}}\text{t}}$
for each
$X_{K,\acute{\text{e}}\text{t}}$
for each
 $j\in \mathbb{Z}$
;
$j\in \mathbb{Z}$
;(ii)
 $D_{\text{HT}}(\mathbb{L})$
is a vector bundle of rank
$D_{\text{HT}}(\mathbb{L})$
is a vector bundle of rank
 $r$
on
$r$
on
 $X_{\acute{\text{e}}\text{t}}$
.
$X_{\acute{\text{e}}\text{t}}$
.
Then we have
Moreover, this is isomorphic to
![]() $\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
. In particular,
$\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
. In particular,
![]() $D_{\text{HT}}(\mathbb{L})$
is a vector bundle on
$D_{\text{HT}}(\mathbb{L})$
is a vector bundle on
![]() $X_{\acute{\text{e}}\text{t}}$
and
$X_{\acute{\text{e}}\text{t}}$
and
![]() $\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
is a vector bundle on
$\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
is a vector bundle on
![]() $X_{K,\acute{\text{e}}\text{t}}$
.
$X_{K,\acute{\text{e}}\text{t}}$
.
Proof. The statement is local. So it suffices to prove that for each affinoid
![]() $Y=\operatorname{Spa}(B,B^{+})\in X_{\acute{\text{e}}\text{t}}$
such that
$Y=\operatorname{Spa}(B,B^{+})\in X_{\acute{\text{e}}\text{t}}$
such that
![]() ${\mathcal{H}}(\mathbb{L})|_{Y_{K}}$
is associated to a finite free
${\mathcal{H}}(\mathbb{L})|_{Y_{K}}$
is associated to a finite free
![]() $B_{K}$
-module (say
$B_{K}$
-module (say
![]() $V$
), we have
$V$
), we have
Note
![]() $\unicode[STIX]{x1D6E4}(Y,D_{\text{HT}}(\mathbb{L}))=\bigoplus _{j\in \mathbb{Z}}(V(j))^{\unicode[STIX]{x1D6E4}_{k}}$
. Moreover, it follows from the Tate–Sen method [Reference Liu and ZhuLZ17, Lemma 3.10] that
$\unicode[STIX]{x1D6E4}(Y,D_{\text{HT}}(\mathbb{L}))=\bigoplus _{j\in \mathbb{Z}}(V(j))^{\unicode[STIX]{x1D6E4}_{k}}$
. Moreover, it follows from the Tate–Sen method [Reference Liu and ZhuLZ17, Lemma 3.10] that
Lemma 5.4.
(i)
 $(V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0})\otimes _{B_{\infty }}B_{K}\cong V^{\unicode[STIX]{x1D719}_{V}=0}$
.
$(V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0})\otimes _{B_{\infty }}B_{K}\cong V^{\unicode[STIX]{x1D719}_{V}=0}$
.(ii) The natural map
is injective. $$\begin{eqnarray}(V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}})\otimes _{B}B_{\infty }\rightarrow V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}\end{eqnarray}$$
$$\begin{eqnarray}(V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}})\otimes _{B}B_{\infty }\rightarrow V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}\end{eqnarray}$$
Proof. Part (i) follows from the flatness of
![]() $B_{\infty }\rightarrow B_{K}$
and
$B_{\infty }\rightarrow B_{K}$
and
![]() $V_{\text{fin}}\otimes _{B_{\infty }}B_{K}\cong V$
.
$V_{\text{fin}}\otimes _{B_{\infty }}B_{K}\cong V$
.
We prove part (ii). By the definition of
![]() $\unicode[STIX]{x1D719}_{V}$
, the natural map
$\unicode[STIX]{x1D719}_{V}$
, the natural map
factors through
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
. So we show that the above map is injective.
$V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
. So we show that the above map is injective.
We denote the total fraction ring of
![]() $B$
(respectively
$B$
(respectively
![]() $B_{\infty }$
) by
$B_{\infty }$
) by
![]() $\operatorname{Frac}B$
(respectively
$\operatorname{Frac}B$
(respectively
![]() $\operatorname{Frac}B_{\infty }$
). We first claim that the natural map
$\operatorname{Frac}B_{\infty }$
). We first claim that the natural map
is injective. To see this, note that
![]() $V_{\text{fin}}$
is a finite free
$V_{\text{fin}}$
is a finite free
![]() $B_{\infty }$
-module. Hence the composite
$B_{\infty }$
-module. Hence the composite
is injective, and thus so is the first map. Since the composite
coincides with the composite of injective maps
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\rightarrow V_{\text{fin}}$
and
$V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\rightarrow V_{\text{fin}}$
and
![]() $V_{\text{fin}}\rightarrow V_{\text{fin}}\otimes _{B}\operatorname{Frac}B$
, the map
$V_{\text{fin}}\rightarrow V_{\text{fin}}\otimes _{B}\operatorname{Frac}B$
, the map
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\rightarrow V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}\operatorname{Frac}B$
is also injective.
$V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\rightarrow V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}\operatorname{Frac}B$
is also injective.
By the above claim, it suffices to show the injectivity of the natural map
Now that
![]() $\operatorname{Frac}B$
and
$\operatorname{Frac}B$
and
![]() $\operatorname{Frac}B_{\infty }$
are products of fields, this follows from standard arguments; we may assume that
$\operatorname{Frac}B_{\infty }$
are products of fields, this follows from standard arguments; we may assume that
![]() $\operatorname{Frac}B$
is a field. Replacing
$\operatorname{Frac}B$
is a field. Replacing
![]() $k$
by an algebraic closure in
$k$
by an algebraic closure in
![]() $\operatorname{Frac}B$
, we may further assume that
$\operatorname{Frac}B$
, we may further assume that
![]() $\operatorname{Frac}B_{\infty }$
is also a field. Note that
$\operatorname{Frac}B_{\infty }$
is also a field. Note that
![]() $\operatorname{Frac}B_{\infty }=(\operatorname{Frac}B)\otimes _{k}k_{\infty }$
and thus
$\operatorname{Frac}B_{\infty }=(\operatorname{Frac}B)\otimes _{k}k_{\infty }$
and thus
![]() $(\operatorname{Frac}B_{\infty })^{\unicode[STIX]{x1D6E4}_{k}}=\operatorname{Frac}B$
.
$(\operatorname{Frac}B_{\infty })^{\unicode[STIX]{x1D6E4}_{k}}=\operatorname{Frac}B$
.
Assume the contrary. Let
![]() $a>0$
be the minimal positive integer such that there exist
$a>0$
be the minimal positive integer such that there exist
![]() $v_{1},\ldots ,v_{a}\in V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}\operatorname{Frac}B$
that are linearly independent over
$v_{1},\ldots ,v_{a}\in V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}\operatorname{Frac}B$
that are linearly independent over
![]() $\operatorname{Frac}B$
and non-zero
$\operatorname{Frac}B$
and non-zero
![]() $b_{1},\ldots ,b_{a}\in \operatorname{Frac}B_{\infty }$
satisfying
$b_{1},\ldots ,b_{a}\in \operatorname{Frac}B_{\infty }$
satisfying
![]() $b_{1}v_{1}+\cdots +b_{a}v_{a}=0$
. By replacing
$b_{1}v_{1}+\cdots +b_{a}v_{a}=0$
. By replacing
![]() $b_{i}$
by
$b_{i}$
by
![]() $b_{1}^{-1}b_{i}$
, we may further assume
$b_{1}^{-1}b_{i}$
, we may further assume
![]() $b_{1}=1$
. Take any
$b_{1}=1$
. Take any
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
. As
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
. As
![]() $v_{1},\ldots ,v_{a}\in V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}\operatorname{Frac}B$
, we have
$v_{1},\ldots ,v_{a}\in V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}\operatorname{Frac}B$
, we have
![]() $v_{1}+\unicode[STIX]{x1D6FE}(b_{2})v_{2}+\cdots +\unicode[STIX]{x1D6FE}(b_{a})v_{a}=0$
and thus
$v_{1}+\unicode[STIX]{x1D6FE}(b_{2})v_{2}+\cdots +\unicode[STIX]{x1D6FE}(b_{a})v_{a}=0$
and thus
![]() $(\unicode[STIX]{x1D6FE}(b_{2})-b_{2})v_{2}+\cdots +(\unicode[STIX]{x1D6FE}(b_{a})-b_{a})v_{a}=0$
. By the minimality, we have
$(\unicode[STIX]{x1D6FE}(b_{2})-b_{2})v_{2}+\cdots +(\unicode[STIX]{x1D6FE}(b_{a})-b_{a})v_{a}=0$
. By the minimality, we have
![]() $\unicode[STIX]{x1D6FE}(b_{i})=b_{i}$
for each
$\unicode[STIX]{x1D6FE}(b_{i})=b_{i}$
for each
![]() $2\leqslant i\leqslant a$
and
$2\leqslant i\leqslant a$
and
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
. Therefore we have
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
. Therefore we have
![]() $b_{i}\in \operatorname{Frac}B$
for all
$b_{i}\in \operatorname{Frac}B$
for all
![]() $i$
, which contradicts the linear independence of
$i$
, which contradicts the linear independence of
![]() $v_{1},\ldots ,v_{a}$
over
$v_{1},\ldots ,v_{a}$
over
![]() $\operatorname{Frac}B$
.◻
$\operatorname{Frac}B$
.◻
We continue the proof of Proposition 5.3. By Lemma 5.4 and discussions above, it is enough to show
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\,\otimes _{B}\,B_{\infty }\cong V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
assuming either condition (i) or (ii). In fact, the Tate twist of this isomorphism implies
$V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\,\otimes _{B}\,B_{\infty }\cong V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
assuming either condition (i) or (ii). In fact, the Tate twist of this isomorphism implies
![]() $(V(j))^{\unicode[STIX]{x1D6E4}_{k}}\,\hat{\otimes }_{B}\,B_{K}\cong (V(j))^{\unicode[STIX]{x1D719}_{V(j)}=0}$
, and a choice of a generator of
$(V(j))^{\unicode[STIX]{x1D6E4}_{k}}\,\hat{\otimes }_{B}\,B_{K}\cong (V(j))^{\unicode[STIX]{x1D719}_{V(j)}=0}$
, and a choice of a generator of
![]() ${\mathcal{O}}_{X_{K,\acute{\text{e}}\text{t}}}(j)$
yields
${\mathcal{O}}_{X_{K,\acute{\text{e}}\text{t}}}(j)$
yields
![]() ${\mathcal{H}}(\mathbb{L}(j))^{\unicode[STIX]{x1D719}_{\mathbb{L}(j)}=0}\cong {\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=-j}$
.
${\mathcal{H}}(\mathbb{L}(j))^{\unicode[STIX]{x1D719}_{\mathbb{L}(j)}=0}\cong {\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=-j}$
.
We show that condition (ii) implies condition (i). For each
![]() $j\in \mathbb{Z}$
, let
$j\in \mathbb{Z}$
, let
![]() $V_{\text{fin}}^{(j)}$
denote the generalized eigenspace of
$V_{\text{fin}}^{(j)}$
denote the generalized eigenspace of
![]() $\unicode[STIX]{x1D719}_{V}$
on
$\unicode[STIX]{x1D719}_{V}$
on
![]() $V_{\text{fin}}$
with eigenvalue
$V_{\text{fin}}$
with eigenvalue
![]() $j$
. By the constancy of
$j$
. By the constancy of
![]() $\unicode[STIX]{x1D719}_{V}$
,
$\unicode[STIX]{x1D719}_{V}$
,
![]() $V_{\text{fin}}^{(j)}$
is a direct summand of
$V_{\text{fin}}^{(j)}$
is a direct summand of
![]() $V_{\text{fin}}$
and thus a finite projective
$V_{\text{fin}}$
and thus a finite projective
![]() $B_{\infty }$
-module. By Lemma 5.4(ii), we have injective
$B_{\infty }$
-module. By Lemma 5.4(ii), we have injective
![]() $B_{\infty }$
-linear maps
$B_{\infty }$
-linear maps
for each
![]() $j\in \mathbb{Z}$
. From this we obtain
$j\in \mathbb{Z}$
. From this we obtain
Hence it follows from condition (ii) that
![]() $(V_{\text{fin}}(j))^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}B_{\infty }$
and
$(V_{\text{fin}}(j))^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}B_{\infty }$
and
![]() $V_{\text{fin}}^{(-j)}$
are finite projective
$V_{\text{fin}}^{(-j)}$
are finite projective
![]() $B_{\infty }$
-modules of the same rank. This implies
$B_{\infty }$
-modules of the same rank. This implies
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=-j}=V_{\text{fin}}^{(-j)}$
. So
$V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=-j}=V_{\text{fin}}^{(-j)}$
. So
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=-j}$
is a finite projective
$V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=-j}$
is a finite projective
![]() $B_{\infty }$
-module for every
$B_{\infty }$
-module for every
![]() $j\in \mathbb{Z}$
and thus
$j\in \mathbb{Z}$
and thus
![]() ${\mathcal{H}}(\mathbb{L})$
satisfies condition (i).
${\mathcal{H}}(\mathbb{L})$
satisfies condition (i).
From now on, we assume that
![]() ${\mathcal{H}}(\mathbb{L})$
satisfies condition (i). By condition (i) and Lemma 5.4(i),
${\mathcal{H}}(\mathbb{L})$
satisfies condition (i). By condition (i) and Lemma 5.4(i),
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
is finite projective over
$V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
is finite projective over
![]() $B_{\infty }$
. So shrinking
$B_{\infty }$
. So shrinking
![]() $Y$
if necessary, we may assume that
$Y$
if necessary, we may assume that
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
is finite free over
$V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
is finite free over
![]() $B_{\infty }$
. Note that we only concern the
$B_{\infty }$
. Note that we only concern the
![]() $B_{\infty }$
-representation
$B_{\infty }$
-representation
![]() $V_{\text{fin}}$
of
$V_{\text{fin}}$
of
![]() $\unicode[STIX]{x1D6E4}_{k}$
and we have
$\unicode[STIX]{x1D6E4}_{k}$
and we have
![]() $(V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0})^{\unicode[STIX]{x1D6E4}_{k}}=V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}$
. Thus replacing
$(V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0})^{\unicode[STIX]{x1D6E4}_{k}}=V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}$
. Thus replacing
![]() $V_{\text{fin}}$
by the subrepresentation
$V_{\text{fin}}$
by the subrepresentation
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
, we may further assume
$V_{\text{fin}}^{\unicode[STIX]{x1D719}_{V}=0}$
, we may further assume
![]() $\unicode[STIX]{x1D719}_{V}=0$
on
$\unicode[STIX]{x1D719}_{V}=0$
on
![]() $V_{\text{fin}}$
. Under this assumption, it remains to prove
$V_{\text{fin}}$
. Under this assumption, it remains to prove
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}B_{\infty }\cong V_{\text{fin}}$
.
$V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}\otimes _{B}B_{\infty }\cong V_{\text{fin}}$
.
Fix a
![]() $B_{\infty }$
-basis
$B_{\infty }$
-basis
![]() $v_{1},\ldots ,v_{r}$
of
$v_{1},\ldots ,v_{r}$
of
![]() $V_{\text{fin}}$
. Then there exists a large positive integer
$V_{\text{fin}}$
. Then there exists a large positive integer
![]() $m$
such that for each
$m$
such that for each
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
the matrix of
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}$
the matrix of
![]() $\unicode[STIX]{x1D6FE}$
with respect to
$\unicode[STIX]{x1D6FE}$
with respect to
![]() $(v_{i})$
has entries in
$(v_{i})$
has entries in
![]() $\operatorname{GL}_{r}(B_{k_{m}})$
. Since
$\operatorname{GL}_{r}(B_{k_{m}})$
. Since
![]() $\unicode[STIX]{x1D719}_{V}=0$
, by increasing
$\unicode[STIX]{x1D719}_{V}=0$
, by increasing
![]() $m$
if necessary, we may further assume that
$m$
if necessary, we may further assume that
![]() $\unicode[STIX]{x1D6FE}v_{i}=v_{i}$
for each
$\unicode[STIX]{x1D6FE}v_{i}=v_{i}$
for each
![]() $1\leqslant i\leqslant r$
and
$1\leqslant i\leqslant r$
and
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }:=\operatorname{Gal}(k_{\infty }/k_{m})\subset \unicode[STIX]{x1D6E4}_{k}$
. Set
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{k}^{\prime }:=\operatorname{Gal}(k_{\infty }/k_{m})\subset \unicode[STIX]{x1D6E4}_{k}$
. Set
![]() $V_{k_{m}}:=\bigoplus _{1\leqslant i\leqslant r}B_{k_{m}}v_{i}$
. This is a
$V_{k_{m}}:=\bigoplus _{1\leqslant i\leqslant r}B_{k_{m}}v_{i}$
. This is a
![]() $B_{k_{m}}$
-representation of
$B_{k_{m}}$
-representation of
![]() $\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }=\operatorname{Gal}(k_{m}/k)$
and satisfies
$\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }=\operatorname{Gal}(k_{m}/k)$
and satisfies
![]() $V_{\text{fin}}=V_{k_{m}}\otimes _{B_{k_{m}}}B_{\infty }$
.
$V_{\text{fin}}=V_{k_{m}}\otimes _{B_{k_{m}}}B_{\infty }$
.
It follows from [Reference Berger and ColmezBC08, Proposition 2.2.1] that
![]() $(V_{k_{m}})^{\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }}$
is a finite projective
$(V_{k_{m}})^{\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }}$
is a finite projective
![]() $B$
-module and that
$B$
-module and that
![]() $(V_{k_{m}})^{\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }}\otimes _{B}B_{k_{m}}\cong V_{k_{m}}$
. As
$(V_{k_{m}})^{\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }}\otimes _{B}B_{k_{m}}\cong V_{k_{m}}$
. As
![]() $V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}=(V_{k_{m}})^{\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }}$
, this yields
$V_{\text{fin}}^{\unicode[STIX]{x1D6E4}_{k}}=(V_{k_{m}})^{\unicode[STIX]{x1D6E4}_{k}/\unicode[STIX]{x1D6E4}_{k}^{\prime }}$
, this yields
Theorem 5.5. Let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system of rank
$\mathbb{Q}_{p}$
-local system of rank
![]() $r$
on
$r$
on
![]() $X_{\acute{\text{e}}\text{t}}$
. Then the following conditions are equivalent:
$X_{\acute{\text{e}}\text{t}}$
. Then the following conditions are equivalent:
(i)
 $D_{\text{HT}}(\mathbb{L})$
is a vector bundle of rank
$D_{\text{HT}}(\mathbb{L})$
is a vector bundle of rank
 $r$
on
$r$
on
 $X_{\acute{\text{e}}\text{t}}$
;
$X_{\acute{\text{e}}\text{t}}$
;(ii)
 $\unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}\mathbb{B}_{\text{HT}}\cong \hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}}$
;
$\unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}\mathbb{B}_{\text{HT}}\cong \hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}}$
;(iii)
 $\unicode[STIX]{x1D719}_{\mathbb{L}}$
is a semisimple endomorphism on
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
is a semisimple endomorphism on
 ${\mathcal{H}}(\mathbb{L})$
with integer eigenvalues;
${\mathcal{H}}(\mathbb{L})$
with integer eigenvalues;(iv) there exist integers
 $j_{1}<\cdots <j_{a}$
such that if we set
$j_{1}<\cdots <j_{a}$
such that if we set
 $F(s):=\prod _{1\leqslant i\leqslant a}(s-j_{i})\in \mathbb{Z}[s]$
, then as an endomorphism of
$F(s):=\prod _{1\leqslant i\leqslant a}(s-j_{i})\in \mathbb{Z}[s]$
, then as an endomorphism of $$\begin{eqnarray}F(\unicode[STIX]{x1D719}_{\mathbb{L}})=0\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D719}_{\mathbb{L}})=0\end{eqnarray}$$
 ${\mathcal{H}}(\mathbb{L})$
.
${\mathcal{H}}(\mathbb{L})$
.
Definition 5.6. A
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
is a Hodge–Tate sheaf if it satisfies the equivalent conditions in Theorem 5.5.
$X_{\acute{\text{e}}\text{t}}$
is a Hodge–Tate sheaf if it satisfies the equivalent conditions in Theorem 5.5.
Remark 5.7. Tsuji obtained Theorem 5.5 in the case of semistable schemes [Reference TsujiTsu11, Theorem 9.1]. He also gave a characterization of Hodge–Tate local systems in terms of restrictions to divisors. See [Reference TsujiTsu11, Theorem 9.1] for the detail.
Proof of Theorem 5.5.
The equivalence of (iii) and (iv) is clear, and (iii) implies (i) by Proposition 5.3. Conversely, assume condition (i). Thus
![]() $D_{\text{HT}}(\mathbb{L})|_{X_{K}}$
is a vector bundle of rank
$D_{\text{HT}}(\mathbb{L})|_{X_{K}}$
is a vector bundle of rank
![]() $r$
on
$r$
on
![]() $X_{K,\acute{\text{e}}\text{t}}$
. By Proposition 5.3, it is also isomorphic to
$X_{K,\acute{\text{e}}\text{t}}$
. By Proposition 5.3, it is also isomorphic to
![]() $\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
. Thus
$\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}$
. Thus
![]() $\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}={\mathcal{H}}(\mathbb{L})$
, and there exist integers
$\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j}={\mathcal{H}}(\mathbb{L})$
, and there exist integers
![]() $j_{1}<\cdots <j_{a}$
such that
$j_{1}<\cdots <j_{a}$
such that
![]() $\bigoplus _{1\leqslant i\leqslant a}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j_{i}}={\mathcal{H}}(\mathbb{L})$
. So
$\bigoplus _{1\leqslant i\leqslant a}{\mathcal{H}}(\mathbb{L})^{\unicode[STIX]{x1D719}_{\mathbb{L}}=j_{i}}={\mathcal{H}}(\mathbb{L})$
. So
![]() $F(s):=\prod _{1\leqslant i\leqslant a}(s-j_{i})$
satisfies
$F(s):=\prod _{1\leqslant i\leqslant a}(s-j_{i})$
satisfies
![]() $F(\unicode[STIX]{x1D719}_{\mathbb{L}})=0$
, which is condition (iv).
$F(\unicode[STIX]{x1D719}_{\mathbb{L}})=0$
, which is condition (iv).
Next we show that condition (iv) implies (ii). Obviously, there is a natural morphism
on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
and we will prove that this is an isomorphism. It is enough to check this on
$X_{\text{pro}\acute{\text{e}}\text{t}}$
and we will prove that this is an isomorphism. It is enough to check this on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}/X_{K}\cong X_{K,\text{pro}\acute{\text{e}}\text{t}}$
. Recall a canonical isomorphism in [Reference Liu and ZhuLZ17, Theorem 2.1(ii)]:
$X_{\text{pro}\acute{\text{e}}\text{t}}/X_{K}\cong X_{K,\text{pro}\acute{\text{e}}\text{t}}$
. Recall a canonical isomorphism in [Reference Liu and ZhuLZ17, Theorem 2.1(ii)]:
Then the restriction of the morphism (5.1) to
![]() $X_{K,\text{pro}\acute{\text{e}}\text{t}}$
is obtained as
$X_{K,\text{pro}\acute{\text{e}}\text{t}}$
is obtained as
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}} & \cong & \displaystyle \unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\otimes _{{\mathcal{O}}_{X_{K}}}{\mathcal{O}}\mathbb{B}_{\text{HT}}|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D708}^{\prime \ast }(D_{\text{HT}}(\mathbb{L})|_{X_{K}})\otimes _{{\mathcal{O}}_{X_{K}}}\biggl(\bigoplus _{j\in \mathbb{Z}}{\mathcal{O}}\mathbb{C}(j)\biggr)\biggr|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D708}^{\prime \ast }\biggl(D_{\text{HT}}(\mathbb{L})|_{X_{K}}\otimes \bigoplus _{j\in \mathbb{Z}}{\mathcal{O}}_{X_{K}}(j)\biggr)\otimes _{{\mathcal{O}}_{X_{K}}}{\mathcal{O}}\mathbb{C}|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \rightarrow & \displaystyle \unicode[STIX]{x1D708}^{\prime \ast }\biggl(\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})(j)\biggr)\otimes _{{\mathcal{O}}_{X_{K}}}{\mathcal{O}}\mathbb{C}|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \cong & \displaystyle \biggl(\bigoplus _{j\in \mathbb{Z}}\hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{C}(j)\biggr)\biggr|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\cong (\hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}} & \cong & \displaystyle \unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\otimes _{{\mathcal{O}}_{X_{K}}}{\mathcal{O}}\mathbb{B}_{\text{HT}}|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D708}^{\prime \ast }(D_{\text{HT}}(\mathbb{L})|_{X_{K}})\otimes _{{\mathcal{O}}_{X_{K}}}\biggl(\bigoplus _{j\in \mathbb{Z}}{\mathcal{O}}\mathbb{C}(j)\biggr)\biggr|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D708}^{\prime \ast }\biggl(D_{\text{HT}}(\mathbb{L})|_{X_{K}}\otimes \bigoplus _{j\in \mathbb{Z}}{\mathcal{O}}_{X_{K}}(j)\biggr)\otimes _{{\mathcal{O}}_{X_{K}}}{\mathcal{O}}\mathbb{C}|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \rightarrow & \displaystyle \unicode[STIX]{x1D708}^{\prime \ast }\biggl(\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L})(j)\biggr)\otimes _{{\mathcal{O}}_{X_{K}}}{\mathcal{O}}\mathbb{C}|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\nonumber\\ \displaystyle & \cong & \displaystyle \biggl(\bigoplus _{j\in \mathbb{Z}}\hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{C}(j)\biggr)\biggr|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\cong (\hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}.\nonumber\end{eqnarray}$$
This can be checked by considering affinoid perfectoids represented by the toric tower, and the verification is left to the reader. It follows from condition (iii) and Proposition 5.3 that
Hence
![]() $(\unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\cong (\hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}$
.
$(\unicode[STIX]{x1D708}^{\ast }D_{\text{HT}}(\mathbb{L})\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}\cong (\hat{\mathbb{L}}\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}}$
.
Finally we show that (ii) implies (i). By condition (ii), we have
On the other hand, it is easy to check
Since
![]() $\unicode[STIX]{x1D708}_{\ast }^{\prime }((\hat{\mathbb{L}}\,\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}})=\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L}(j))$
, we have
$\unicode[STIX]{x1D708}_{\ast }^{\prime }((\hat{\mathbb{L}}\,\otimes _{\hat{\mathbb{Q}}_{p}}{\mathcal{O}}\mathbb{B}_{\text{HT}})|_{X_{K,\text{pro}\acute{\text{e}}\text{t}}})=\bigoplus _{j\in \mathbb{Z}}{\mathcal{H}}(\mathbb{L}(j))$
, we have
In particular,
![]() $D_{\text{HT}}(\mathbb{L})|_{X_{K}}$
is a vector bundle on
$D_{\text{HT}}(\mathbb{L})|_{X_{K}}$
is a vector bundle on
![]() $X_{K,\acute{\text{e}}\text{t}}$
, and thus
$X_{K,\acute{\text{e}}\text{t}}$
, and thus
![]() $D_{\text{HT}}(\mathbb{L})$
is a vector bundle on
$D_{\text{HT}}(\mathbb{L})$
is a vector bundle on
![]() $X_{\acute{\text{e}}\text{t}}$
. Moreover, condition (ii) implies
$X_{\acute{\text{e}}\text{t}}$
. Moreover, condition (ii) implies
![]() $\operatorname{rank}D_{\text{HT}}(\mathbb{L})=r$
.◻
$\operatorname{rank}D_{\text{HT}}(\mathbb{L})=r$
.◻
Example 5.8. Suppose that there exists a Zariski dense subset
![]() $T\subset X$
consisting of classical rigid points with residue field finite over
$T\subset X$
consisting of classical rigid points with residue field finite over
![]() $k$
such that the restriction of
$k$
such that the restriction of
![]() $\mathbb{L}$
to each
$\mathbb{L}$
to each
![]() $x\in T$
defines a Hodge–Tate representation. Then
$x\in T$
defines a Hodge–Tate representation. Then
![]() $\mathbb{L}$
is a Hodge–Tate sheaf by Theorems 4.8 and 5.5(iii). See [Reference Kedlaya and LiuKL16, Theorem 8.6.6] for a generalization of this remark.
$\mathbb{L}$
is a Hodge–Tate sheaf by Theorems 4.8 and 5.5(iii). See [Reference Kedlaya and LiuKL16, Theorem 8.6.6] for a generalization of this remark.
Corollary 5.9.
(i) Hodge–Tate sheaves are stable under taking dual, tensor product, and subquotients.
(ii) Let
 $f:Y\rightarrow X$
be a morphism between smooth rigid analytic varieties over
$f:Y\rightarrow X$
be a morphism between smooth rigid analytic varieties over
 $k$
. If
$k$
. If
 $\mathbb{L}$
is a Hodge–Tate sheaf on
$\mathbb{L}$
is a Hodge–Tate sheaf on
 $X_{\acute{\text{e}}\text{t}}$
, then
$X_{\acute{\text{e}}\text{t}}$
, then
 $f^{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
$f^{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
 $Y_{\acute{\text{e}}\text{t}}$
.
$Y_{\acute{\text{e}}\text{t}}$
.
We next turn to the pushforward of Hodge–Tate sheaves.
Theorem 5.10. Let
![]() $f:X\rightarrow Y$
be a smooth proper morphism between smooth rigid analytic varieties over
$f:X\rightarrow Y$
be a smooth proper morphism between smooth rigid analytic varieties over
![]() $k$
of relative dimension
$k$
of relative dimension
![]() $m$
and let
$m$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Z}_{p}$
-local system on
$\mathbb{Z}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
.
$X_{\acute{\text{e}}\text{t}}$
.
(i) If
 $\unicode[STIX]{x1D6FC}\in \overline{k}$
is a generalized Hodge–Tate for
$\unicode[STIX]{x1D6FC}\in \overline{k}$
is a generalized Hodge–Tate for
 $R^{i}f_{\ast }\mathbb{L}$
, then
$R^{i}f_{\ast }\mathbb{L}$
, then
 $\unicode[STIX]{x1D6FC}$
is of the form
$\unicode[STIX]{x1D6FC}$
is of the form
 $\unicode[STIX]{x1D6FD}-j$
with a generalized Hodge–Tate weight
$\unicode[STIX]{x1D6FD}-j$
with a generalized Hodge–Tate weight
 $\unicode[STIX]{x1D6FD}$
of
$\unicode[STIX]{x1D6FD}$
of
 $\mathbb{L}$
and an integer
$\mathbb{L}$
and an integer
 $j\in [0,m]$
.
$j\in [0,m]$
.(ii) If
 $\mathbb{L}$
is a Hodge–Tate sheaf on
$\mathbb{L}$
is a Hodge–Tate sheaf on
 $X_{\acute{\text{e}}\text{t}}$
, then
$X_{\acute{\text{e}}\text{t}}$
, then
 $R^{i}f_{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
$R^{i}f_{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
 $Y_{\acute{\text{e}}\text{t}}$
.Footnote
3
$Y_{\acute{\text{e}}\text{t}}$
.Footnote
3
Remark 5.11. Theorem 5.10(ii) is proved by Hyodo [Reference HyodoHyo86, § 3, Corollary] when
![]() $f:X\rightarrow Y$
and
$f:X\rightarrow Y$
and
![]() $\mathbb{L}$
are analytifications of corresponding algebraic objects.
$\mathbb{L}$
are analytifications of corresponding algebraic objects.
Proof. Let
![]() $f_{K}:X_{K}\rightarrow Y_{K}$
denote the base change of
$f_{K}:X_{K}\rightarrow Y_{K}$
denote the base change of
![]() $f$
over
$f$
over
![]() $K$
.
$K$
.
Part (i) easily follows from Theorem 3.9. In fact, we have the isomorphism
and under this identification
![]() $\unicode[STIX]{x1D719}_{R^{i}f_{\ast }\mathbb{L}}$
corresponds to
$\unicode[STIX]{x1D719}_{R^{i}f_{\ast }\mathbb{L}}$
corresponds to
![]() $R^{i}f_{K,\acute{\text{e}}\text{t},\ast }(\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id}))$
. Consider the spectral sequence with
$R^{i}f_{K,\acute{\text{e}}\text{t},\ast }(\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id}))$
. Consider the spectral sequence with
converging to
![]() ${\mathcal{H}}(R^{a+b}f_{\ast }\mathbb{L})$
. Then the endomorphism
${\mathcal{H}}(R^{a+b}f_{\ast }\mathbb{L})$
. Then the endomorphism
![]() $R^{b}f_{K,\acute{\text{e}}\text{t},\ast }((\unicode[STIX]{x1D719}_{\mathbb{L}}-a)\otimes \operatorname{id})$
on
$R^{b}f_{K,\acute{\text{e}}\text{t},\ast }((\unicode[STIX]{x1D719}_{\mathbb{L}}-a)\otimes \operatorname{id})$
on
![]() $E_{1}^{a,b}$
converges to
$E_{1}^{a,b}$
converges to
![]() $\unicode[STIX]{x1D719}_{R^{a+b}f_{\ast }\mathbb{L}}$
, and this implies part (i).
$\unicode[STIX]{x1D719}_{R^{a+b}f_{\ast }\mathbb{L}}$
, and this implies part (i).
For part (ii), we need arguments similar to the proof of Theorem 3.9. We may assume that
![]() $Y$
is affinoid. Take a finite affinoid covering
$Y$
is affinoid. Take a finite affinoid covering
![]() ${\mathcal{U}}=\{U_{K}^{(i)}\}$
of
${\mathcal{U}}=\{U_{K}^{(i)}\}$
of
![]() $X_{K}$
. Let
$X_{K}$
. Let
![]() ${\mathcal{F}}^{\bullet }$
denote the complex of
${\mathcal{F}}^{\bullet }$
denote the complex of
![]() ${\mathcal{O}}_{X_{K}}$
-modules
${\mathcal{O}}_{X_{K}}$
-modules
on
![]() $X_{K}$
equipped with the natural
$X_{K}$
equipped with the natural
![]() $\unicode[STIX]{x1D6E4}_{k}$
-action and the endomorphism
$\unicode[STIX]{x1D6E4}_{k}$
-action and the endomorphism
![]() $\unicode[STIX]{x1D719}_{{\mathcal{F}}^{\bullet }}=\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
.
$\unicode[STIX]{x1D719}_{{\mathcal{F}}^{\bullet }}=\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-\bullet (\operatorname{id}\otimes \operatorname{id})$
.
Recall also the Čech-to-derived functor spectral sequence with
converging to
![]() $R^{a+b}\unicode[STIX]{x1D6E4}(X_{K,\acute{\text{e}}\text{t}},{\mathcal{F}}^{\bullet })$
. This spectral sequence degenerates at
$R^{a+b}\unicode[STIX]{x1D6E4}(X_{K,\acute{\text{e}}\text{t}},{\mathcal{F}}^{\bullet })$
. This spectral sequence degenerates at
![]() $E_{2}$
and yields
$E_{2}$
and yields
Note that both source and target in (5.2) have arithmetic Sen endomorphisms and they are compatible under the isomorphism.
Since
![]() $\mathbb{L}$
is a Hodge–Tate sheaf, there exist integers
$\mathbb{L}$
is a Hodge–Tate sheaf, there exist integers
![]() $j_{1}<\cdots <j_{a}$
such that
$j_{1}<\cdots <j_{a}$
such that
![]() $F(\unicode[STIX]{x1D719}_{\mathbb{L}})=0$
with
$F(\unicode[STIX]{x1D719}_{\mathbb{L}})=0$
with
![]() $F(s):=\prod _{1\leqslant i\leqslant a}(s-j_{i})$
. Set
$F(s):=\prod _{1\leqslant i\leqslant a}(s-j_{i})$
. Set
![]() $J:=\{j_{1}-m,j_{1}-m+1,\ldots ,j_{a}-1,j_{a}\}$
. This is a finite subset of
$J:=\{j_{1}-m,j_{1}-m+1,\ldots ,j_{a}-1,j_{a}\}$
. This is a finite subset of
![]() $\mathbb{Z}$
. We set
$\mathbb{Z}$
. We set
![]() $G(s):=\prod _{j\in J}(s-j)\in \mathbb{Z}[s]$
. For each
$G(s):=\prod _{j\in J}(s-j)\in \mathbb{Z}[s]$
. For each
![]() $0\leqslant j\leqslant m$
, the endomorphism
$0\leqslant j\leqslant m$
, the endomorphism
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-j(\operatorname{id}\otimes \operatorname{id})$
on
$\unicode[STIX]{x1D719}_{\mathbb{L}}\otimes \operatorname{id}-j(\operatorname{id}\otimes \operatorname{id})$
on
![]() ${\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/Y}^{j}(-j)$
satisfies
${\mathcal{H}}(\mathbb{L})\otimes \unicode[STIX]{x1D6FA}_{X/Y}^{j}(-j)$
satisfies
This implies
![]() $G(\unicode[STIX]{x1D719}_{{\mathcal{F}}^{\bullet }})=0$
, and thus
$G(\unicode[STIX]{x1D719}_{{\mathcal{F}}^{\bullet }})=0$
, and thus
![]() $G(\operatorname{Tot}({\check{C}}^{\bullet }({\mathcal{U}},\unicode[STIX]{x1D719}_{{\mathcal{F}}^{\bullet }})))=0$
. Therefore (5.2) yields
$G(\operatorname{Tot}({\check{C}}^{\bullet }({\mathcal{U}},\unicode[STIX]{x1D719}_{{\mathcal{F}}^{\bullet }})))=0$
. Therefore (5.2) yields
Hence
![]() $R^{i}f_{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
$R^{i}f_{\ast }\mathbb{L}$
is a Hodge–Tate sheaf on
![]() $Y_{\acute{\text{e}}\text{t}}$
.◻
$Y_{\acute{\text{e}}\text{t}}$
.◻
We now turn to a rigidity of Hodge–Tate representations. Let us first recall Liu and Zhu’s rigidity result for de Rham representations [Reference Liu and ZhuLZ17, Theorem 1.3]: let
![]() $X$
be a geometrically connected smooth rigid analytic variety over
$X$
be a geometrically connected smooth rigid analytic variety over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. If
$X_{\acute{\text{e}}\text{t}}$
. If
![]() $\mathbb{L}_{\overline{x}}$
is a de Rham representation at a classical point
$\mathbb{L}_{\overline{x}}$
is a de Rham representation at a classical point
![]() $x\in X$
, then
$x\in X$
, then
![]() $\mathbb{L}$
is a de Rham sheaf. In particular,
$\mathbb{L}$
is a de Rham sheaf. In particular,
![]() $\mathbb{L}_{\overline{y}}$
is a de Rham representation at every classical point
$\mathbb{L}_{\overline{y}}$
is a de Rham representation at every classical point
![]() $y\in X$
.
$y\in X$
.
The same result holds for Hodge–Tate local systems of rank at most two. We do not know whether this is true for Hodge–Tate local systems of higher rank.
Theorem 5.12. Let
![]() $k$
be a finite extension of
$k$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $X$
be a geometrically connected smooth rigid analytic variety over
$X$
be a geometrically connected smooth rigid analytic variety over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Q}_{p}$
-local system on
$\mathbb{Q}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Assume that
$X_{\acute{\text{e}}\text{t}}$
. Assume that
![]() $\operatorname{rank}\mathbb{L}$
is at most two. If
$\operatorname{rank}\mathbb{L}$
is at most two. If
![]() $\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation at a classical point
$\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation at a classical point
![]() $x\in X$
, then
$x\in X$
, then
![]() $\mathbb{L}$
is a Hodge–Tate sheaf. In particular,
$\mathbb{L}$
is a Hodge–Tate sheaf. In particular,
![]() $\mathbb{L}_{\overline{y}}$
is a Hodge–Tate representation at every classical point
$\mathbb{L}_{\overline{y}}$
is a Hodge–Tate representation at every classical point
![]() $y\in X.$
$y\in X.$
Before the proof, let us recall a remarkable theorem by Sen on Hodge–Tate representations of weight
![]() $0$
.
$0$
.
Theorem 5.13 [Reference SenSen81, § Corollary].
Let
![]() $k$
be a finite extension of
$k$
be a finite extension of
![]() $\mathbb{Q}_{p}$
and let
$\mathbb{Q}_{p}$
and let
![]() $\unicode[STIX]{x1D70C}:G_{k}\rightarrow \operatorname{GL}_{r}(\mathbb{Q}_{p})$
be a continuous representation of the absolute Galois group
$\unicode[STIX]{x1D70C}:G_{k}\rightarrow \operatorname{GL}_{r}(\mathbb{Q}_{p})$
be a continuous representation of the absolute Galois group
![]() $G_{k}$
of
$G_{k}$
of
![]() $k$
. Then
$k$
. Then
![]() $\unicode[STIX]{x1D70C}$
is a Hodge–Tate representation with all the Hodge–Tate weights zero if and only if
$\unicode[STIX]{x1D70C}$
is a Hodge–Tate representation with all the Hodge–Tate weights zero if and only if
![]() $\unicode[STIX]{x1D70C}$
is potentially unramified, i.e. the image of the inertia subgroup of
$\unicode[STIX]{x1D70C}$
is potentially unramified, i.e. the image of the inertia subgroup of
![]() $k$
is finite.
$k$
is finite.
Note that
![]() $\unicode[STIX]{x1D70C}$
being a Hodge–Tate representation with all the Hodge–Tate weights zero is equivalent to the Sen endomorphism of
$\unicode[STIX]{x1D70C}$
being a Hodge–Tate representation with all the Hodge–Tate weights zero is equivalent to the Sen endomorphism of
![]() $\unicode[STIX]{x1D70C}$
being zero. Since potentially unramified representations are de Rham and de Rham representations are stable under Tate twists, Theorem 5.13 implies that a Hodge–Tate representation with a single weight is necessarily de Rham.
$\unicode[STIX]{x1D70C}$
being zero. Since potentially unramified representations are de Rham and de Rham representations are stable under Tate twists, Theorem 5.13 implies that a Hodge–Tate representation with a single weight is necessarily de Rham.
Proof of Theorem 5.12.
We check condition (iii) in Theorem 5.5. By Theorem 4.8 and assumption, all the eigenvalues of
![]() $\unicode[STIX]{x1D719}_{\mathbb{L}}$
are integers. So the statement is obvious either when
$\unicode[STIX]{x1D719}_{\mathbb{L}}$
are integers. So the statement is obvious either when
![]() $\operatorname{rank}\mathbb{L}=1$
or when
$\operatorname{rank}\mathbb{L}=1$
or when
![]() $\operatorname{rank}\mathbb{L}=2$
and two eigenvalues are distinct integers.
$\operatorname{rank}\mathbb{L}=2$
and two eigenvalues are distinct integers.
Assume that
![]() $\operatorname{rank}\mathbb{L}=2$
and two eigenvalues are the same integer. Then
$\operatorname{rank}\mathbb{L}=2$
and two eigenvalues are the same integer. Then
![]() $\mathbb{L}_{\overline{x}}$
is de Rham by Theorem 5.13, and thus
$\mathbb{L}_{\overline{x}}$
is de Rham by Theorem 5.13, and thus
![]() $\mathbb{L}$
is de Rham by the above-mentioned rigidity theorem for de Rham representations by Liu and Zhu [Reference Liu and ZhuLZ17, Theorem 1.3]. In particular,
$\mathbb{L}$
is de Rham by the above-mentioned rigidity theorem for de Rham representations by Liu and Zhu [Reference Liu and ZhuLZ17, Theorem 1.3]. In particular,
![]() $\mathbb{L}$
is a Hodge–Tate sheaf.◻
$\mathbb{L}$
is a Hodge–Tate sheaf.◻
Remark 5.14. The proof shows that Theorem 5.12 holds for
![]() $\mathbb{L}$
of an arbitrary rank if one of the following conditions holds.
$\mathbb{L}$
of an arbitrary rank if one of the following conditions holds.
(i)
 $\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation with a single weight at a classical point
$\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation with a single weight at a classical point
 $x\in X$
.
$x\in X$
.(ii)
 $\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation with
$\mathbb{L}_{\overline{x}}$
is a Hodge–Tate representation with
 $\operatorname{rank}\mathbb{L}$
distinct weights at a classical point
$\operatorname{rank}\mathbb{L}$
distinct weights at a classical point
 $x\in X$
.
$x\in X$
.
We end with another application of Sen’s theorem in the relative setting.
Theorem 5.15. Let
![]() $k$
be a finite extension of
$k$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $X$
be a smooth rigid analytic variety over
$X$
be a smooth rigid analytic variety over
![]() $k$
and let
$k$
and let
![]() $\mathbb{L}$
be a
$\mathbb{L}$
be a
![]() $\mathbb{Z}_{p}$
-local system on
$\mathbb{Z}_{p}$
-local system on
![]() $X_{\acute{\text{e}}\text{t}}$
. Assume that
$X_{\acute{\text{e}}\text{t}}$
. Assume that
![]() $\mathbb{L}$
is a Hodge–Tate sheaf with a single Hodge–Tate weight. Then there exists a finite étale cover
$\mathbb{L}$
is a Hodge–Tate sheaf with a single Hodge–Tate weight. Then there exists a finite étale cover
![]() $f:Y\rightarrow X$
such that
$f:Y\rightarrow X$
such that
![]() $(f^{\ast }\mathbb{L})_{\overline{y}}$
is semistable at every classical point
$(f^{\ast }\mathbb{L})_{\overline{y}}$
is semistable at every classical point
![]() $y$
of
$y$
of
![]() $Y$
.
$Y$
.
Proof. Since semistable representations are stable under Tate twists, we may assume that
![]() $\mathbb{L}$
is a Hodge–Tate sheaf with all the weights zero. Let
$\mathbb{L}$
is a Hodge–Tate sheaf with all the weights zero. Let
![]() $\overline{\mathbb{L}}$
denote the
$\overline{\mathbb{L}}$
denote the
![]() $\mathbb{Z}/p^{2}$
-local system
$\mathbb{Z}/p^{2}$
-local system
![]() $\mathbb{L}/p^{2}\mathbb{L}$
on
$\mathbb{L}/p^{2}\mathbb{L}$
on
![]() $X_{\acute{\text{e}}\text{t}}$
. Then there exists a finite étale cover
$X_{\acute{\text{e}}\text{t}}$
. Then there exists a finite étale cover
![]() $f:Y\rightarrow X$
such that
$f:Y\rightarrow X$
such that
![]() $f^{\ast }\overline{\mathbb{L}}$
is trivial on
$f^{\ast }\overline{\mathbb{L}}$
is trivial on
![]() $Y_{\acute{\text{e}}\text{t}}$
. We will prove that this
$Y_{\acute{\text{e}}\text{t}}$
. We will prove that this
![]() $Y$
works.
$Y$
works.
Let
![]() $y$
be a classical point of
$y$
be a classical point of
![]() $Y$
. We denote by
$Y$
. We denote by
![]() $k^{\prime }$
the residue field of
$k^{\prime }$
the residue field of
![]() $y$
. Let
$y$
. Let
![]() $\unicode[STIX]{x1D70C}:G_{k^{\prime }}\rightarrow \operatorname{GL}(V)$
be the Galois representation of
$\unicode[STIX]{x1D70C}:G_{k^{\prime }}\rightarrow \operatorname{GL}(V)$
be the Galois representation of
![]() $k^{\prime }$
corresponding to the stalk
$k^{\prime }$
corresponding to the stalk
![]() $V:=(f^{\ast }\overline{\mathbb{L}})_{\overline{y}}$
at a geometric point
$V:=(f^{\ast }\overline{\mathbb{L}})_{\overline{y}}$
at a geometric point
![]() $\overline{y}$
above
$\overline{y}$
above
![]() $y$
. By assumption,
$y$
. By assumption,
![]() $\unicode[STIX]{x1D70C}$
is a Hodge–Tate representation with all the weights zero, and thus it is potentially unramified by Theorem 5.13. Hence if we denote the inertia group of
$\unicode[STIX]{x1D70C}$
is a Hodge–Tate representation with all the weights zero, and thus it is potentially unramified by Theorem 5.13. Hence if we denote the inertia group of
![]() $k^{\prime }$
by
$k^{\prime }$
by
![]() $I_{k^{\prime }}$
,
$I_{k^{\prime }}$
,
![]() $\unicode[STIX]{x1D70C}(I_{k^{\prime }})$
is finite.
$\unicode[STIX]{x1D70C}(I_{k^{\prime }})$
is finite.
By construction, the mod
![]() $p^{2}$
representation
$p^{2}$
representation
is trivial. On the other hand,
![]() $\operatorname{Ker}(\operatorname{GL}(V)\rightarrow \operatorname{GL}(V/p^{2}V))$
does not contain elements of finite order except the identity. Thus we see that
$\operatorname{Ker}(\operatorname{GL}(V)\rightarrow \operatorname{GL}(V/p^{2}V))$
does not contain elements of finite order except the identity. Thus we see that
![]() $\unicode[STIX]{x1D70C}(I_{k^{\prime }})$
is trivial and hence
$\unicode[STIX]{x1D70C}(I_{k^{\prime }})$
is trivial and hence
![]() $\unicode[STIX]{x1D70C}$
is an unramified representation. In particular,
$\unicode[STIX]{x1D70C}$
is an unramified representation. In particular,
![]() $\unicode[STIX]{x1D70C}$
is semistable.◻
$\unicode[STIX]{x1D70C}$
is semistable.◻
Remark 5.16. As mentioned in the introduction, it is an interesting question whether one can extend Colmez’s strategy [Reference ColmezCol08] to prove the relative
![]() $p$
-adic monodromy conjecture using Theorem 5.15.
$p$
-adic monodromy conjecture using Theorem 5.15.
Acknowledgements
The author thanks Mark Kisin for his constant encouragement and useful feedback. He also thanks Héctor Pastén and the referees for their helpful comments towards improving this paper.