1. Introduction
Sea ice interacts in a variety of ways with the climate system of the earth: for example, it reflects most of the incoming solar radiation and thereby influences the energy balance in polar regions; it expels salt into the underlying water and thereby influences the thermohaline structure and the circulation pattern of the world’s oceans; and it thermally insulates the atmosphere from the ocean, greatly reducing the heat flux between the two.
In order to model any of these processes realistically, the bulk salinity evolution of sea ice must be known, which determines both the salt flux into the underlying ocean and the distribution of the two main constituents of sea ice, namely freshwater-ice crystals and interstitial liquid salty brine. however, usually the evolution of the bulk salinity is not modelled explicitly. most sea-ice models prescribe a uniform bulk salinity that changes as a function of ice thickness (e.g. Reference Ebert and CurryEbert and curry, 1993) or a salinity profile that is independent of ice thickness (e.g. Reference Maykut and UntersteinerMaykut and untersteiner, 1971). notable exceptions are, for example, the model by Reference Cox and WeeksCox and weeks (1988), which simulates the bulk salinity evolution of first-year sea ice, mostly using empirical relationships derived from in situ laboratory measurements, and the two-dimensional model presented recently by Reference Oertling and WattsOertling and watts (2004) that is in principle capable of capturing the main features of the salinity evolution in young sea ice.
The one-dimensional (1-d) model that we present here is aimed at filling the gap in complexity that currently exists between the model by Reference Cox and WeeksCox and weeks (1988) and that by Reference Oertling and WattsOertling and watts (2004). our model simulates the solid-fraction and bulk-salinity evolution of sea ice and its interaction with the other components of the polar climate system on a single computational domain, including, for example, the direct interaction with melt ponds. it allows new insight into the physical processes governing the evolution of the bulk salinity of sea ice, with, however, the limitation that gravity drainage is currently not implemented into the model. it is expected that this limitation will be overcome in future work.
Our model is based on the enthalpy method, which is introduced in section 2. in section 3, the numerical model itself is described. we present comparisons of our model results with laboratory experiments and results from an idealized simulation of the evolution of arctic sea ice in section 4. finally, we discuss implications of this work in section 5.
2. The Enthalpy Method
Our sea-ice model is based on an enthalpy method, the basic concept of which we outline in this section. a model based on this method allows the representation of multiple internal phase boundaries, as occur in the context of sea ice during the formation and refreezing of surface melt ponds, for example. the drainage of these melt ponds and their impact on the bulk-salinity profile of sea ice can therefore be studied with greater ease than by using traditional sea-ice models based on front tracking.
Front-tracking models also have difficulties in representing the properties of sea ice close to the ice–ocean interface realistically. in such models, the ice-growth rate dh/dt is calculated from the stefan condition
Where ![]() is the mean density of sea ice at the interface, ΔQ is the imbalance in heat fluxes at the interface, and L is the latent heat of fusion for sea ice at the interface, which is proportional to the mass fraction of solid ice, δ
m, at the interface. often, δ
m at the interface is taken to be 0.9, based on an estimate by Reference UntersteinerUntersteiner (1964) resulting in L = 300 kj kg–1. however, it can be shown theoretically that the solid fraction at the ice–ocean interface must be zero during ice growth (Reference Chiareli, Huppert and WorsterChiareli and others, 1994; Reference NotzNotz, 2005). this is in accordance with laboratory and field measurements of the solid-fraction distribution in growing sea ice (Reference NotzNotz, 2005; Reference Notz, Wettlaufer and WorsterNotz and others, 2005) and implies that the latent heat that is exchanged directly at the interface must be zero during ice growth. latent heat is rather released by changes in the overall solid-fraction distribution within the sea ice. according to the stefan condition, the heat-flux imbalance at the interface then becomes zero and the classical front-tracking method cannot be used straightforwardly to model the solid-fraction field of sea ice.
is the mean density of sea ice at the interface, ΔQ is the imbalance in heat fluxes at the interface, and L is the latent heat of fusion for sea ice at the interface, which is proportional to the mass fraction of solid ice, δ
m, at the interface. often, δ
m at the interface is taken to be 0.9, based on an estimate by Reference UntersteinerUntersteiner (1964) resulting in L = 300 kj kg–1. however, it can be shown theoretically that the solid fraction at the ice–ocean interface must be zero during ice growth (Reference Chiareli, Huppert and WorsterChiareli and others, 1994; Reference NotzNotz, 2005). this is in accordance with laboratory and field measurements of the solid-fraction distribution in growing sea ice (Reference NotzNotz, 2005; Reference Notz, Wettlaufer and WorsterNotz and others, 2005) and implies that the latent heat that is exchanged directly at the interface must be zero during ice growth. latent heat is rather released by changes in the overall solid-fraction distribution within the sea ice. according to the stefan condition, the heat-flux imbalance at the interface then becomes zero and the classical front-tracking method cannot be used straightforwardly to model the solid-fraction field of sea ice.
These limitations can be overcome by using an enthalpy method, which is a well-established method for modelling the solidification of general multi-phase systems, of which sea ice is but an example (see Reference Alexiades and SolomonAlexiades and solomon (1993) for a general introduction and Reference Beckermann and WangBeckermann and wang (1995) for a review). the enthalpy-based sea-ice model that we present here consists of gridcells which keep a constant size and location throughout the model run. the main model variables are the salt and the enthalpy (heat) content of each gridcell, which can change by advection of brine and, for the latter, by heat conduction. from these two variables, the temperature and the solid fraction within a certain gridcell can unambiguously be determined a posteriori. they are linked to the heat content (enthalpy) H of a certain gridcell according to
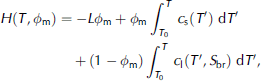
Where c is heat capacity, indices s and l denote the solid and liquid phases, respectively, S br(T) is the brine salinity, which is a function of temperature alone (Reference Cox and WeeksCox and weeks, 1986), and T 0 is a reference temperature. the first term on the righthand side, which is zero for all cells that are fully liquid, describes the latent-heat content of the cell, whereas the second and third terms describe the sensible heat content relative to the reference temperature T 0. the solid mass fraction is linked to the bulk salinity S bu according to
And by solving equations (1) and (2) for the two unknowns T and δ m the temperature and solid fraction within a certain gridcell can be determined.
If, for example, the formation of sea ice from open water is to be simulated, the model would be initialized with an energy and salt distribution to represent the open water. the energy content is given by the water temperature according to equation (1). by extracting energy from the uppermost gridcell, which is in contact with the cold atmosphere, its temperature decreases until at some point the freezing point is reached and ice starts to form, the solid fraction of which is given by equation (2). the bulk salinity of the ice will start to decrease as brine is lost into the underlying gridcells. by simply tracking the movement of the brine and its salt and energy content and allowing heat to be conducted from one gridcell to another, the evolution of the internal temperature and solid-fraction fields can be simulated. the ice–ocean interface is given as the lowest gridcell with a non-zero solid fraction, and the uppermost layer of the ocean and the sea ice are both simulated on the same grid. if, during summer, atmospheric heat and radiation fluxes increase the energy content of the uppermost gridcells sufficiently, the cells can become fully liquid again and a surface melt pond is automatically included into the model. its flushing leads to an increase of the brine flux within the remaining sea ice, and the interaction of melt ponds and the underlying sea ice can be simulated using existing model physics. this integrated approach is the main reason why the enthalpy method can be preferable to the classical front-tracking approach if the interior of sea ice and its interaction with the polar climate system is to be modelled realistically.
3. A 1-D Enthalpy Model of SEA ice
In the description of the numerical model in this section we concentrate on the enthalpy-method implementation of brine movement within the ice, because the general model layout is rather standard and described, for example, by Reference Alexiades and SolomonAlexiades and solomon (1993). additionally, a detailed model description is given by Reference NotzNotz (2005).
3.1. General model layout
The model variables are updated at each time-step by calculating the heat fluxes across the gridcell boundaries from the known temperature and solid-fraction fields at the previous time-step. these heat fluxes change the enthalpy content of the individual gridcells, which is also changed by the movement of brine as described in the following sections. from the known new enthalpy and bulk-salinity content of the gridcells, the new temperature and solid-fraction fields can be calculated from equations (1) and (2).
Our model consists of m gridcells, not necessarily equally sized. it is initialized with the bulk salinity and the energy content within each cell, where the latter is usually calculated for a given temperature from equation (1). we solve the heat equation explicitly and use a volume-fraction-weighted average of the heat conductivities of the solid ice and the liquid brine to calculate the heat that is conducted through a certain gridcell. hence, the heat conductivity is expressed as
(Reference Alexiades and SolomonAlexiades and solomon, 1993), where δ v is solid volume fraction and indices l and s refer to liquid and solid, respectively. especially at temperatures close to the bulk freezing point of the ice, this expression is preferable to the commonly used empirical expression by Reference UntersteinerUntersteiner (1964), which can result in negative heat conductivities (see Reference NotzNotz, 2005).
3.2. Implementation of moving brine
To account for enthalpy and salinity changes induced by the movement of brine, we introduce the vertical brine displacement δzi averaged over the full horizontal area of a gridcell i (and not only across the part of a gridcell that is liquid). the absolute enthalpy content of a gridcell, changes for a given δzi by
Here, Hl = clρlT is the enthalpy of the moving brine and j is either +1 or –1, depending on whether the flow through a cell is upward or downward.
Similarly, the absolute salt content Sabs = SbuΔz changes through import or export of salt with moving brine according to
These equations are generally valid and allow the simulation of all desalination processes that are based on the physical movement of brine, namely brine expulsion, gravity drainage and flushing (Reference UntersteinerUntersteiner, 1968). to implement these processes into the model, expressions are required that link them to the physical displacement of the brine. such expressions are derived next.
3.3. Brine expulsion
The density of ice is roughly 10% less than that of brine. this density change leads to a fluid flow whenever the solid fraction within a gridcell changes. it has been suggested that this fluid flow is the dominating cause of salt loss from very young sea ice and is referred to as brine expulsion (Reference UntersteinerUntersteiner, 1968; Reference Cox and WeeksCox and weeks, 1975, Reference Cox and Weeks1988). the velocity field U that is caused by brine expulsion is given by
As is readily derived using global mass conservation (Reference Worster, Davis, Huppert and MullerWorster, 1992). because in sea ice the temperature field is to a very good approximation horizontally homogeneous, brine expulsion is almost exclusively a 1-d process. the net displacement of brine from a certain gridcell within one time-step can hence be expressed as
Starting iteratively from i = 1 with δzi, 0 set to zero (no flux through top boundary). here Δzi is the size of the gridcell and δΦ v the change in solid fraction over one time-step. using this expression together with equations (4) and (5) allows the calculation of the change in enthalpy and salinity within a certain gridcell that is caused by brine expulsion.
3.4. Flushing
Modelling flushing as a 1-d process might be too simplistic an approach, because field measurements suggest a significant two-dimensionality of this process (Reference Eicken, Krouse, Kadko and PerovichEicken and others, 2002, Reference Eicken, Grenfell, Perovich, Richter-Menge and Frey2004). however, all net salt loss is due to vertical movement of brine, which is why a 1-d model can give a good estimate of the total salt loss caused by flushing. in addition, the 1-d model is helpful in understanding the interaction between the salinity field and the water percolating vertically through the ice. in our model, flushing is incorporated as follows.
Whenever the top gridcell(s) become fully liquid during a model run, it is assumed that a certain amount of flushing occurs at each consecutive time-step. the amount of downward displacement of the surface of the melt pond, Δz mp, is calculated from darcy’s law (e.g. Reference Eicken, Grenfell, Perovich, Richter-Menge and FreyEicken and others, 2004). for a known downward displacement of the pond’s surface, Δz mp, the downward displacement of the brine within each underlying gridcell is given by continuity as
Which combined with equations (4) and (5) allows us to calculate the change in enthalpy and salinity within a certain gridcell that is caused by flushing.
As far as the permeability of sea ice is concerned, for want of an expression valid for older ice we use
As found by Reference FreitagFreitag (1999) for young sea ice. since flushing is limited by the minimum permeability of the underlying ice, we use the maximum solid fraction of the modelled sea ice in the calculation of Π. permeabilities calculated in this way are comfortably within the range measured by Reference Eicken, Krouse, Kadko and PerovichEicken and others (2002) in arctic summer sea ice.
3.5. Salt entrapment at the ice–ocean interface
The loss of salt at the ice–ocean interface as described by an effective distribution coefficient is often assumed to be the most important factor for the determination of the bulk salinity of sea ice. however, Reference NotzNotz (2005) showed analytically, numerically and experimentally both in the laboratory and in the field that the salinity field at the ice–ocean interface is continuous while the ice is growing. hence, introducing an effective distribution coefficient based on ice-growth velocity is not warranted in the context of sea ice, and this process has not been implemented into the model presented here.
3.6. Gravity drainage
Having ruled out all other processes, it was shown by Reference NotzNotz (2005) that gravity drainage and flushing are the only processes that cause the bulk salinity of sea ice to be lower than that of sea water. hence, during winter all salt flux from sea ice into the underlying ocean is caused by gravity drainage. for a realistic simulation of the salinity evolution of sea ice, this process must therefore be included into a numerical model. however, currently our understanding of this important process is too limited to allow for its realistic implementation into our model. measurements and theoretical considerations by Reference Wettlaufer, Worster and HuppertWettlaufer and others (1997) and by Reference NotzNotz (2005) suggest that such an implementation will ultimately be based on a mush rayleigh number that determines both the onset and the strength of gravity drainage.
3.7. Atmospheric and oceanic fluxes
The coupling of the sea-ice model to atmospheric heat and radiation fluxes is carried out roughly in the same way as in classical sea-ice models and will therefore not be discussed here. it should, however, be noted that the depth of surface melt ponds is an integral part of our enthalpy model, which is why the implementation of complex albedo parameterization like that presented by Reference Curry, Schramm, Perovich and PintoCurry and others (2001) is more straightforward than in classical sea-ice models.
The implementation of oceanic heat fluxes at the ice–ocean interface differs from that in classical sea-ice models, because the interface lies within the model domain rather than at the lowermost boundary of the grid. to implement oceanic heat fluxes, we use an approach in which the heat-transfer coefficient in the water, K w, is adjusted at each time-step to match the oceanic heat flux Q oc. we solve the
Equation
For K w, where zf denotes the frontal gridcell, which is given by the lowermost gridcell with a non-zero solid fraction. the value of K w that is obtained in this way is then used as the heat-transfer coefficient for the evolution of the temperature field of the two gridcells f and f + 1. the temperature of all other gridcells in the ocean is kept at the far-field temperature. this approach gives excellent agreement between model results and analytical predictions.
4. Model Results
Sea ice is a multi-component, multi-phase porous medium and can hence be referred to as a mushy layer. for constant boundary conditions and without gravitational overturning, its evolution is therefore governed by the mushy-layer equations (Reference Worster, Davis, Huppert and MullerWorster, 1992, Reference Worster, Batchelor, Moffatt and Worster2000). by solving these equations it can be shown, for example, that for constant boundary conditions no salt is lost from sea ice through brine expulsion (Reference NotzNotz, 2005). however, no such analytic solution exists for varying boundary conditions, and the importance of brine expulsion can then only be examined numerically. therefore, in this section we present a comparison of model results with measurements from a laboratory experiment, in which an nacl solution was solidified with periodically varying boundary conditions. we also present results from a simulation of an annual cycle of sea-ice development, which illustrates, albeit highly idealized, the applicability of our model for the study of sea-ice–melt-pond interaction.
4.1. Comparison with a laboratory experiment
We have carried out a number of laboratory experiments in which a 34 ppt nacl solution was cooled from below to form artificial sea ice. because of the cooling from below, the resulting brine distribution of the forming ice is stable and gravity drainage does not occur (Reference Huppert and WorsterHuppert and worster, 1985). in this way, the salt loss caused by brine expulsion and by the rejection of salt at the interface can be quantified because these processes are both independent of gravity. the nacl solution was initially cooled to a temperature of –1˚c. the temperature of the cooling plate was then, at the start of the experiment, lowered to –5˚c and changed between –5˚c and –10˚c every 12 hours for 48 hours to test the impact of varying boundary conditions. the tank was kept airtight throughout the experiment, and by simultaneously measuring the water level in an attached expansion tube and the ice thickness it was possible to calculate the mean solid volume fraction δ v of the forming ice, as described by Reference Wettlaufer, Worster and HuppertWettlaufer and others (1997).
figure 1 shows a comparison of the measured and the modelled evolution of the mean solid volume fraction δ v of the forming ice. apart from the very early stages of the experiment, there is excellent agreement between model predictions and measurements, indicating that our model is able to predict the evolution of sea ice with the neglect of gravitational overturning to a very high degree of accuracy. the deviation in the initial stages of the experiment is caused by the fact that the calculation of the mass balance in these early stages with very thin ice is highly sensitive to the thickness of the ice, which is very difficult to determine precisely. the slight deviation towards the end of the two periods with a base temperature of –10˚c is caused by the neglect of the change in the tank volume in the calculation of δ v from the measurements.

Fig. 1. Comparison of the predicted (solid line) and measured (dots) evolution of the mean solid volume fraction δ v for an experiment in which a 34 ppt NaCl solution was cooled from below with a varying temperature T 0.
The numerically predicted profiles of the temperature, the solid volume fraction and the bulk salinity at various times of the experiment are shown in figure 2. throughout the whole simulation period, the mean bulk salinity remains constant, showing that no salt is rejected at the advancing interface and that brine expulsion does not lead to the loss of salt from sea ice, even for strongly varying boundary conditions. the latter is due to the fact that the ice-growth velocity at the interface is always larger than the velocity of the brine that is caused by brine expulsion.
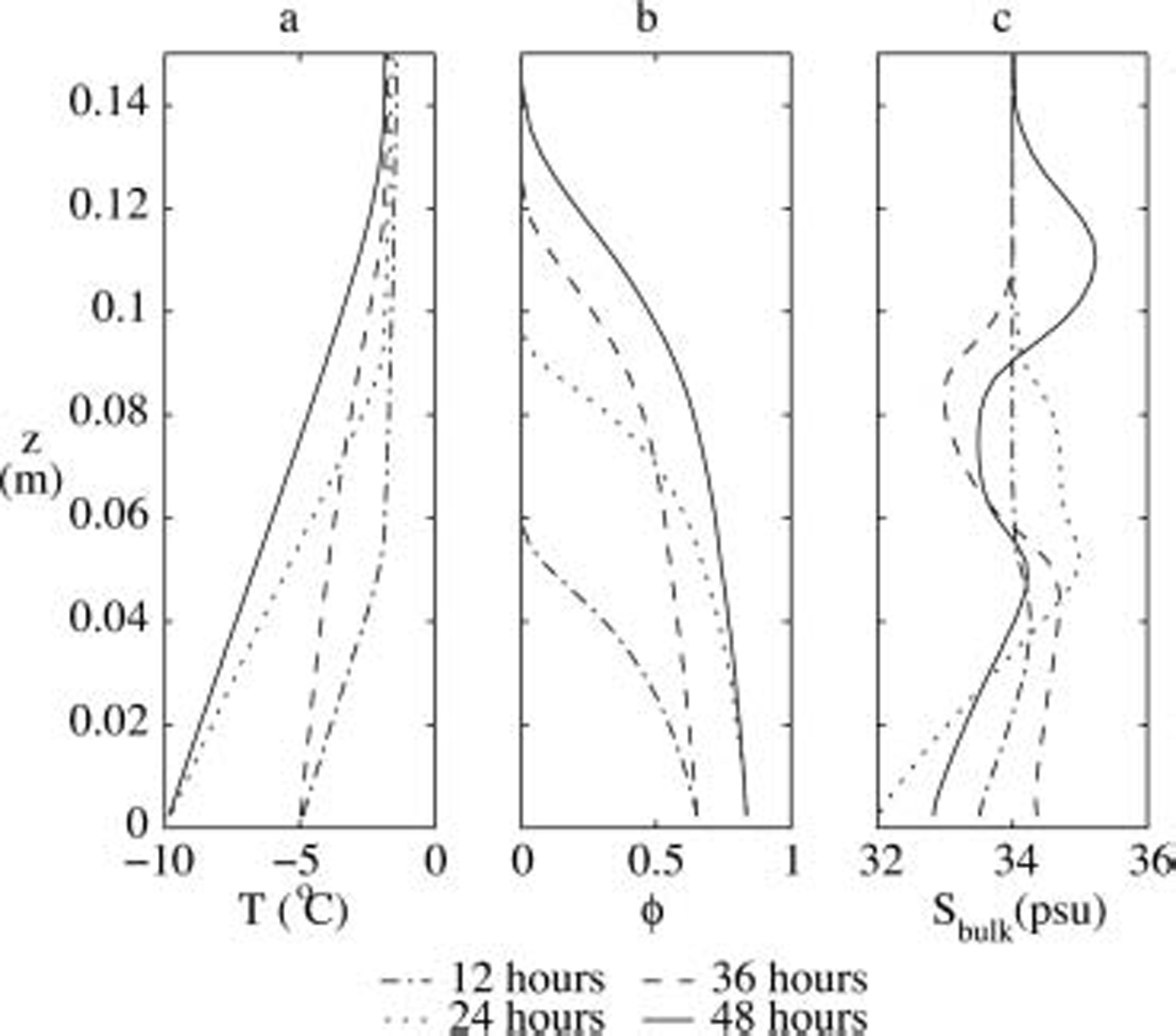
Fig. 2. Profiles of (a) temperature, (b) solid fraction and (c) bulk salinity as obtained from our numerical model for the same experiment as in Figure 1.
4.2. An annual cycle of sea-ice development
To test the functionality of our model for the simulation of sea-ice growth and decay, we set up a simple test case in which we modelled the development of sea ice throughout the course of 2 years. this test case was not meant to provide any quantitative results, but rather to show the applicability of an enthalpy-based model for the study of annual cycles of sea-ice development. for a quantitative study, gravity drainage and a more refined albedo and melt-pond parameterization, including a snow layer on top of the ice, must be added to the model, which will be the subject of future work. despite these limitations, the results that we outline here underline why future studies of the interaction between sea ice and melt ponds, for example, might profit from using the modelling approach described in this work.
The test case was set up as follows. the atmospheric fluxes were prescribed according to gaussian-peak fits to the data tabulated by Reference Maykut and UntersteinerMaykut and untersteiner (1971), whereas the albedo was prescribed according to a lorentzian-peak fit to data from the SHEBA (surface heat budget of the arctic ocean program) field campaign (Reference PerovichPerovich and others, 1999; for details of the fits see Reference NotzNotz, 2005). the amount of solar radiation penetrating through the surface layer of the ice was set to i 0 = 0.7. the extinction coefficient к was set to 4.67 m–1 for z < 0.05 m, to 2.0 m–1 for 0:05 ≤ z < 0:1m and to 1.4 m–1 for z ≥ 0:1m, as given by Reference Grenfell and MaykutGrenfell and maykut (1977). note that a constant value of к = 1.4 m–1 throughout the whole sea ice, which is used in some sea-ice models, halves the amount of solar radiation absorbed in the top 10cm of the ice.
Since gravity drainage is not incorporated into the model so far, the salinity of the forming ice was artificially reduced to 10% of the sea-water salinity of 34 psu and no flushing was allowed in this simple test case. the far-field ocean temperature was held at –1.8˚c, which is unrealistically cold during the summer months. the friction velocity used in the calculation of the ocean heat flux was set to a constant value of 0.01 ms–1. the model simulation was carried out for the course of 2 years, starting on 1 august.
figure 3 shows the development of the sea-ice cover and the surface temperature for this simple test case. the figure underlines one of the advantages of using a single-domain model for the simulation of sea ice: without any adjustment to the model physics, the formation of melt ponds on top of the ice and their refreezing at the onset of the winter are natural outcomes of the model run.

Fig. 3. Development of the sea-ice cover and the surface temperature for the idealized test case.
The distribution of the enthalpy, temperature and solid fraction on 1 april and 1 july of the first year of the model run are shown in figure 4. these dates were chosen as being representative of the conditions before and after the onset of summer melting. in july, the solid fraction, which in warm ice is closely linked to the inverse of the temperature profile, is very low directly underneath the melt pond, and very efficient flushing would occur at this stage. in a similar model run, which had flushing incorporated, this flushing led to the formation of an almost impermeable layer close to the ice–ocean interface. this layer formed because the temperature in the ice during summer is lowest at this interface, and the solid fraction there is highest for the assumed initially uniform salinity. the exchange of the existing brine with less saline brine from above decreases the salinity, which leads to a further increase in the solid fraction. this cycle continues, until the ice becomes almost impermeable at this layer and the flushing almost comes to a halt. this result indicates that flushing might be controlled by the properties of the ice close to the ice–ocean interface, rather than those close to the surface, as is usually assumed. however, the incorporation of snow and the subsequent formation of very fresh meltwater on top of the ice might change this picture.

Fig. 4. Vertical profiles of (a) the enthalpy, (b) the temperature and (c) the solid fraction on 1 April (gray crosses) and 1 July (black dots) of the first year of the test case described in this section.
One further model result worth mentioning is the jump in the solid fraction at the ice–ocean interface for the summer profile. such a jump is possible because the continuity of the solid-fraction field at the ice–ocean interface need only be fulfilled during periods of new ice formation, as is apparent in the april profiles shown in the figure.
5. Discussion
In this paper, we have presented a 1-d sea-ice model that allows the realistic simulation of the internal structure of sea ice and its interaction with the polar climate system. results obtained from this model are in excellent agreement with analytical predictions and laboratory experiments, without any free parameters to tune the model. this shows that the single-domain enthalpy method on which our model is based allows the direct and physically realistic simulation of a variety of different processes related to the development of sea ice. in such a model, energy is automatically conserved and no extra care needs to be taken in the treatment of phase changes at the ice surface, the importance of which was examined by Reference Bitz and LipscombBitz and lipscomb (1999) for example.
Currently, the main limitation of the model presented in this work is the missing implementation of gravity drainage, which was shown by Reference NotzNotz (2005) to be the only process that leads to any significant net salt loss from sea ice during winter. our understanding of this crucial desalination process is still too limited to allow for a physically based implementation into our model. further studies of the functioning of gravity drainage are therefore very desirable,
Which could include numerical simulations, for example with a two-dimensional enthalpy model similar to that presented by Reference Oertling and WattsOertling and watts (2004), and further laboratory and field experiments, for example with the instrument developed by Reference Notz, Wettlaufer and WorsterNotz and others (2005).
Both the 1-d model presented in this work and the two-dimensional model presented by Reference Oertling and WattsOertling and watts (2004) are currently computationally too expensive to be incorporated into a large-scale coupled climate model. however, they can help to reduce substantially the uncertainty associated with the parameterizations that are used for the representation of sea ice in climate models. currently, most of these parameterizations are derived from measurements that were carried out under today’s climate conditions and are not necessarily valid in a different climate. for example, with a predicted thinning of the global sea-ice cover, the impact of the sea–ice properties close to the ice–ocean interface becomes more important. as discussed above, the structure of sea ice in this lowest part is not realistically represented in current models. two-dimensional enthalpy-based single-domain models can be used to understand gravity drainage, for example, which can then be incorporated in a meaningful way into the 1-d model presented in this work. this 1-d model would then form a full, coupled thermodynamic–salinity model incorporating flushing, gravity drainage, melt ponds, radiative effects, ocean heat and salt flux, etc., and could be used for physically realistic sensitivity studies. the results from such studies can then be used to justify the choice of simple parameterizations of air–ice–sea interactions in large-scale models. we believe that in such a way future numerical studies of sea ice will profit from using an approach similar to that presented in this paper.
Acknowledgements
We thank p.v. bogorodsky and an anonymous referee for constructive and helpful comments. this work was made possible by support from the uk natural environment research council under grant ner/b/s/2002/00521 (d.n. and m.g.w.) and the studienstiftung des deutschen volkes (d.n.), which are both very gratefully acknowledged.






