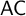1 Introduction
In Tachtsis [Reference Tachtsis17, Reference Tachtsis18], the research was centered around open problems which concerned the set-theoretic strength of statements on the existence of almost disjoint and maximal almost disjoint (MAD) families on any infinite set, such as “Every infinite set has an uncountable almost disjoint family”; “Every almost disjoint family in an infinite set X can be extended to a MAD family in X”; “No infinite MAD family in an infinite set has cardinality
![]() $\aleph _{0}$
” in mild extensions of
$\aleph _{0}$
” in mild extensions of
![]() $\mathsf {ZF}$
(Zermelo–Fraenkel set theory without the
$\mathsf {ZF}$
(Zermelo–Fraenkel set theory without the
![]() $\mathsf {AC}$
) and of
$\mathsf {AC}$
) and of
![]() $\mathsf {ZFA}$
(
$\mathsf {ZFA}$
(
![]() $\mathsf {ZF}$
with the Axiom of Extensionality modified in order to allow atoms), that is, in
$\mathsf {ZF}$
with the Axiom of Extensionality modified in order to allow atoms), that is, in
![]() $\mathsf {ZF} +$
Weak Choice and in
$\mathsf {ZF} +$
Weak Choice and in
![]() $\mathsf {ZFA} +$
Weak Choice.
$\mathsf {ZFA} +$
Weak Choice.
In the current paper, we investigate the open problem of the deductive strength of analogous statements in the realm of infinite-dimensional vector spaces and we determine their placement in the hierarchy of weak choice principles. Among other results, we will prove the following (complete definitions of notions and terms appearing in the following list, will be given in Section 2):
-
(1)
 $\mathsf {MC}^{\aleph _{0}}$
is equivalent to “For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
$\mathsf {MC}^{\aleph _{0}}$
is equivalent to “For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
 $\aleph _{0}$
.” (Theorem 4.1.)
$\aleph _{0}$
.” (Theorem 4.1.) -
(2) The statement “For every well orderable field F and every infinite-dimensional vector space V over F with a well orderable basis, no MAD2 family in V has cardinality
 $\aleph _{0}$
” is provable in
$\aleph _{0}$
” is provable in
 $\mathsf {ZF}$
. (Theorem 4.2.)
$\mathsf {ZF}$
. (Theorem 4.2.) -
(3)
 $\mathsf {AC}^{\aleph _{0}}$
implies “For every field F and every infinite-dimensional vector space V over F, there is an AD2 family in V of cardinality
$\mathsf {AC}^{\aleph _{0}}$
implies “For every field F and every infinite-dimensional vector space V over F, there is an AD2 family in V of cardinality
 $2^{\aleph _{0}}$
.” (Theorem 4.6.)
$2^{\aleph _{0}}$
.” (Theorem 4.6.) -
(4)
 $\mathsf {BPI}$
does not imply the statement “For every field F and every infinite-dimensional vector space V over F, there is an infinite AD1 family in V” in
$\mathsf {BPI}$
does not imply the statement “For every field F and every infinite-dimensional vector space V over F, there is an infinite AD1 family in V” in
 $\mathsf {ZF}$
. (Theorem 4.9.)
$\mathsf {ZF}$
. (Theorem 4.9.) -
(5) In
 $\mathsf {ZFA}$
,
$\mathsf {ZFA}$
,
 $\mathsf {MC}$
implies “In every infinite-dimensional vector space V over any field, every AD1 family of infinite-dimensional subspaces of V can be extended to a MAD1 family in V”. Hence, the latter statement does not imply
$\mathsf {MC}$
implies “In every infinite-dimensional vector space V over any field, every AD1 family of infinite-dimensional subspaces of V can be extended to a MAD1 family in V”. Hence, the latter statement does not imply
 $\mathsf {AC}$
in
$\mathsf {AC}$
in
 $\mathsf {ZFA}$
. (Theorem 4.10.)
$\mathsf {ZFA}$
. (Theorem 4.10.) -
(6)
 $\mathsf {AC^{LO}}$
does not imply “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” in
$\mathsf {AC^{LO}}$
does not imply “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” in
 $\mathsf {ZFA}$
. Hence, neither
$\mathsf {ZFA}$
. Hence, neither
 $\mathsf {LW}$
nor
$\mathsf {LW}$
nor
 $\mathsf {AC^{WO}}$
imply the above proposition in
$\mathsf {AC^{WO}}$
imply the above proposition in
 $\mathsf {ZFA}$
. Furthermore, the above proposition is not provable in
$\mathsf {ZFA}$
. Furthermore, the above proposition is not provable in
 $\mathsf {ZF}$
. (Theorem 4.11.)
$\mathsf {ZF}$
. (Theorem 4.11.) -
(7) For every uncountable regular cardinal
 $\aleph _{\alpha }$
, there exists a Fraenkel–Mostowski model
$\aleph _{\alpha }$
, there exists a Fraenkel–Mostowski model
 $\mathcal {N}_{\aleph _{\alpha }}$
such that for every infinite cardinal
$\mathcal {N}_{\aleph _{\alpha }}$
such that for every infinite cardinal
 $\lambda <\aleph _{\alpha }$
,
$\lambda <\aleph _{\alpha }$
,
 $\mathsf {DC}_{\lambda }$
is true in
$\mathsf {DC}_{\lambda }$
is true in
 $\mathcal {N}_{\aleph _{\alpha }}$
, but there exists an infinite-dimensional vector space over some field which has an AD1 family in
$\mathcal {N}_{\aleph _{\alpha }}$
, but there exists an infinite-dimensional vector space over some field which has an AD1 family in
 $\mathcal {N}_{\aleph _{\alpha }}$
that cannot be extended to a MAD1 family in
$\mathcal {N}_{\aleph _{\alpha }}$
that cannot be extended to a MAD1 family in
 $\mathcal {N}_{\aleph _{\alpha }}$
. The result is transferable to
$\mathcal {N}_{\aleph _{\alpha }}$
. The result is transferable to
 $\mathsf {ZF}$
. (Theorem 4.13.)
$\mathsf {ZF}$
. (Theorem 4.13.)
The only sources of relevant information in this area of research which are known to us are the papers of Kolman [Reference Kolman8] and Smythe [Reference Smythe14]. However, their perspective is fairly different from the one here. In particular, the above papers deal with the possible cardinality of infinite almost disjoint and MAD families in countably infinite-dimensional vector spaces over a countable (possibly finite) field and the definability of MAD families in such spaces in certain models of
![]() $\mathsf {ZF}+\neg \mathsf {AC}$
.
$\mathsf {ZF}+\neg \mathsf {AC}$
.
2 Notation, terminology, and known results
Notation 2.1. Let X be a set and also let F be a field.
If
![]() $f\in F^{X}$
, where
$f\in F^{X}$
, where
![]() $F^X$
is the set of all functions from X to F, then
$F^X$
is the set of all functions from X to F, then
![]() $\operatorname {\mathrm {{supp}}}(f)$
denotes the support of f, i.e.,
$\operatorname {\mathrm {{supp}}}(f)$
denotes the support of f, i.e.,
![]() $\operatorname {\mathrm {{supp}}}(f)=\{x\in X:f(x)\neq 0_{F}\}$
, where
$\operatorname {\mathrm {{supp}}}(f)=\{x\in X:f(x)\neq 0_{F}\}$
, where
![]() $0_{F}$
is the additive identity of F.
$0_{F}$
is the additive identity of F.
If
![]() $A\subseteq X$
, then the element
$A\subseteq X$
, then the element
![]() $\chi _{A}$
of
$\chi _{A}$
of
![]() $F^{X}$
denotes the characteristic function of A, i.e.,
$F^{X}$
denotes the characteristic function of A, i.e.,
![]() $\chi _{A}(x)=1_{F}$
if
$\chi _{A}(x)=1_{F}$
if
![]() $x\in A$
and
$x\in A$
and
![]() $\chi _{A}(x)=0_{F}$
if
$\chi _{A}(x)=0_{F}$
if
![]() $x\in X\setminus A$
, where
$x\in X\setminus A$
, where
![]() $1_{F}$
is the multiplicative identity of F.
$1_{F}$
is the multiplicative identity of F.
![]() $[X]^{<\omega }$
denotes the set of finite subsets of X and, for
$[X]^{<\omega }$
denotes the set of finite subsets of X and, for
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $[X]^{n}$
denotes the set of n-element subsets of X.
$[X]^{n}$
denotes the set of n-element subsets of X.
Definition 2.2. Let
![]() $(V,+,\cdot )$
be a vector space over a field F.
$(V,+,\cdot )$
be a vector space over a field F.
If
![]() $X\subseteq V$
, then
$X\subseteq V$
, then
![]() $\langle X\rangle $
denotes the linear span of X.
$\langle X\rangle $
denotes the linear span of X.
V is called finite-dimensional if V is finitely generated, i.e., if there exists a finite set
![]() $X\subseteq V$
such that
$X\subseteq V$
such that
![]() $V=\langle X\rangle $
. Otherwise, V is called infinite-dimensional.
$V=\langle X\rangle $
. Otherwise, V is called infinite-dimensional.
If
![]() $W_{1},\ldots ,W_{n}$
(where n is some positive integer) are subspaces of V, then the sum of the subspaces
$W_{1},\ldots ,W_{n}$
(where n is some positive integer) are subspaces of V, then the sum of the subspaces
![]() $W_i$
of V is the subspace of V,
$W_i$
of V is the subspace of V,
 $\sum \limits _{i=1}^{n}W_{i}=\bigg\{\sum \limits _{i=1}^{n}x_{i}:\forall i\in \{1,\ldots ,n\}(x_{i}\in W_{i})\bigg\}$
.
$\sum \limits _{i=1}^{n}W_{i}=\bigg\{\sum \limits _{i=1}^{n}x_{i}:\forall i\in \{1,\ldots ,n\}(x_{i}\in W_{i})\bigg\}$
.
As usual, ‘
![]() $W\leq V$
’ denotes that W is a vector subspace of V.
$W\leq V$
’ denotes that W is a vector subspace of V.
It is part of the folklore that, in
![]() $\mathsf {ZF}$
, every finite-dimensional vector space has a basis. However, it is a celebrated result of Blass [Reference Blass1] that, in
$\mathsf {ZF}$
, every finite-dimensional vector space has a basis. However, it is a celebrated result of Blass [Reference Blass1] that, in
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $\mathsf {AC}$
is equivalent to “For every field F, every vector space over F has a basis”. In particular, Blass showed that the latter algebraic statement implies the Axiom of Multiple Choice (
$\mathsf {AC}$
is equivalent to “For every field F, every vector space over F has a basis”. In particular, Blass showed that the latter algebraic statement implies the Axiom of Multiple Choice (
![]() $\mathsf {MC}$
), which is equivalent to
$\mathsf {MC}$
), which is equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZF}$
, but it is not equivalent to
$\mathsf {ZF}$
, but it is not equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZFA}$
(see [Reference Howard and Rubin3] [Reference Jech7, Theorems 9.1 and 9.2]).
$\mathsf {ZFA}$
(see [Reference Howard and Rubin3] [Reference Jech7, Theorems 9.1 and 9.2]).
Definition 2.3. Let X be an infinite set. A family
![]() $\mathcal {A}$
of infinite subsets of X is called almost disjoint in X if for all
$\mathcal {A}$
of infinite subsets of X is called almost disjoint in X if for all
![]() $A,B\in \mathcal {A}$
with
$A,B\in \mathcal {A}$
with
![]() $A\ne B$
,
$A\ne B$
,
![]() $A\cap B$
is finite. An almost disjoint family
$A\cap B$
is finite. An almost disjoint family
![]() $\mathcal {A}$
in X is called MAD in X if for every almost disjoint family
$\mathcal {A}$
in X is called MAD in X if for every almost disjoint family
![]() $\mathcal {B}$
in X with
$\mathcal {B}$
in X with
![]() $\mathcal {A}\subseteq \mathcal {B}$
,
$\mathcal {A}\subseteq \mathcal {B}$
,
![]() $\mathcal {A}=\mathcal {B}$
.
$\mathcal {A}=\mathcal {B}$
.
Definition 2.4. Let V be an infinite-dimensional vector space over a field F and let
![]() $\mathcal {A}$
be a family of infinite-dimensional vector subspaces of V.
$\mathcal {A}$
be a family of infinite-dimensional vector subspaces of V.
(1)
![]() $\mathcal {A}$
is called almost disjoint-1 in V (abbreviated by AD1) if for all
$\mathcal {A}$
is called almost disjoint-1 in V (abbreviated by AD1) if for all
![]() $U,W\in \mathcal {A}$
with
$U,W\in \mathcal {A}$
with
![]() $U\ne W$
,
$U\ne W$
,
![]() $U\cap W$
is finite-dimensional.
$U\cap W$
is finite-dimensional.
(2)
![]() $\mathcal {A}$
is called almost disjoint-2 in V (abbreviated by AD2) if for every (non-empty) finite subset
$\mathcal {A}$
is called almost disjoint-2 in V (abbreviated by AD2) if for every (non-empty) finite subset
![]() $\mathcal {B}\subset \mathcal {A}$
,
$\mathcal {B}\subset \mathcal {A}$
,
![]() $B\cap (\sum _{X\in \mathcal {B}\setminus \{B\}}X)$
is finite-dimensional for all
$B\cap (\sum _{X\in \mathcal {B}\setminus \{B\}}X)$
is finite-dimensional for all
![]() $B\in \mathcal {B}$
.
$B\in \mathcal {B}$
.
(3) Let
![]() $i\in \{1,2\}$
. If
$i\in \{1,2\}$
. If
![]() $\mathcal {A}$
is an ADi family in V, then
$\mathcal {A}$
is an ADi family in V, then
![]() $\mathcal {A}$
is called maximal almost disjoint MAD- i in V (abbreviated by MADi) if for every ADi family
$\mathcal {A}$
is called maximal almost disjoint MAD- i in V (abbreviated by MADi) if for every ADi family
![]() $\mathcal {B}$
in V with
$\mathcal {B}$
in V with
![]() $\mathcal {A}\subseteq \mathcal {B}$
,
$\mathcal {A}\subseteq \mathcal {B}$
,
![]() $\mathcal {A}=\mathcal {B}$
.
$\mathcal {A}=\mathcal {B}$
.
Remark 2.5. It is clear that AD2
![]() $\Rightarrow $
AD1. However, the converse may fail to be true. Indeed, let V be the infinite-dimensional vector space
$\Rightarrow $
AD1. However, the converse may fail to be true. Indeed, let V be the infinite-dimensional vector space
![]() $\mathbb {R}^{\omega }$
over
$\mathbb {R}^{\omega }$
over
![]() $\mathbb {R}$
(where addition and scalar multiplication are the usual coordinatewise operations). Consider the following infinite-dimensional subspaces of V:
$\mathbb {R}$
(where addition and scalar multiplication are the usual coordinatewise operations). Consider the following infinite-dimensional subspaces of V:
![]() $W_{1}=\langle \{\chi _{\{2n\}}:n\in \omega \}\rangle $
,
$W_{1}=\langle \{\chi _{\{2n\}}:n\in \omega \}\rangle $
,
![]() $W_{2}=\langle \{\chi _{\{2n+1\}}:n\in \omega \}\rangle $
, and
$W_{2}=\langle \{\chi _{\{2n+1\}}:n\in \omega \}\rangle $
, and
![]() $W_{3}=\langle \{\chi _{\{2n,2n+1\}}:n\in \omega \}\rangle $
. Then the family
$W_{3}=\langle \{\chi _{\{2n,2n+1\}}:n\in \omega \}\rangle $
. Then the family
![]() $\mathcal {A}=\{W_{1},W_{2},W_{3}\}$
is AD1 but not AD2.
$\mathcal {A}=\{W_{1},W_{2},W_{3}\}$
is AD1 but not AD2.
Definition 2.6. Let X be a set.
X is called denumerable if
![]() $|X|=\aleph _{0}$
, i.e., if there is a bijection
$|X|=\aleph _{0}$
, i.e., if there is a bijection
![]() $f:\omega \rightarrow X$
.
$f:\omega \rightarrow X$
.
X is called countable if X is either finite or denumerable.
X is called Dedekind-finite if
![]() $\aleph _{0}\not \leq |X|$
, i.e., if there is no one-to-one function
$\aleph _{0}\not \leq |X|$
, i.e., if there is no one-to-one function
![]() $f:\omega \rightarrow X$
. Otherwise, X is called Dedekind-infinite.
$f:\omega \rightarrow X$
. Otherwise, X is called Dedekind-infinite.
If X is infinite, then X is called amorphous if it cannot be written as a disjoint union of two infinite subsets.Footnote 1
Next, we list the set-theoretic principles that will be used in this paper.
Definition 2.7.
-
(1) The Axiom of Multiple Choice
 $\mathsf {MC}$
(Form 67 in [Reference Howard and Rubin3]): For every set X of non-empty sets there is a function F with domain X such that for all
$\mathsf {MC}$
(Form 67 in [Reference Howard and Rubin3]): For every set X of non-empty sets there is a function F with domain X such that for all
 $x\in X$
,
$x\in X$
,
 $F(x)$
is a non-empty finite subset of x. The function F is called a multiple choice function for X.
$F(x)$
is a non-empty finite subset of x. The function F is called a multiple choice function for X. -
(2) The Axiom of Countable Multiple Choice
 $\mathsf {MC}^{\aleph _{0}}$
(Form 126 in [Reference Howard and Rubin3]): Every denumerable family of non-empty sets has a multiple choice function.
$\mathsf {MC}^{\aleph _{0}}$
(Form 126 in [Reference Howard and Rubin3]): Every denumerable family of non-empty sets has a multiple choice function. -
(3)
 $\mathsf {AC^{LO}}$
(Form 202 in [Reference Howard and Rubin3]): Every linearly ordered family of non-empty sets has a choice function.
$\mathsf {AC^{LO}}$
(Form 202 in [Reference Howard and Rubin3]): Every linearly ordered family of non-empty sets has a choice function. -
(4)
 $\mathsf {AC^{WO}}$
(Form 40 in [Reference Howard and Rubin3]): Every well-ordered family of non-empty sets has a choice function.
$\mathsf {AC^{WO}}$
(Form 40 in [Reference Howard and Rubin3]): Every well-ordered family of non-empty sets has a choice function. -
(5) The Axiom of Countable Choice
 $\mathsf {AC}^{\aleph _{0}}$
(Form 8 in [Reference Howard and Rubin3]): Every denumerable family of non-empty sets has a choice function.
$\mathsf {AC}^{\aleph _{0}}$
(Form 8 in [Reference Howard and Rubin3]): Every denumerable family of non-empty sets has a choice function. -
(6)
 $\mathsf {LW}$
(Form 90 in [Reference Howard and Rubin3]): Every linearly ordered set can be well ordered.
$\mathsf {LW}$
(Form 90 in [Reference Howard and Rubin3]): Every linearly ordered set can be well ordered. -
(7) Let
 $\kappa $
be an infinite well-ordered cardinal number.
$\kappa $
be an infinite well-ordered cardinal number.
 $\mathsf {DC}_{\kappa }$
(Form 87(
$\mathsf {DC}_{\kappa }$
(Form 87(
 $\kappa $
) in [Reference Howard and Rubin3]): Let S be a non-empty set and let
$\kappa $
) in [Reference Howard and Rubin3]): Let S be a non-empty set and let
 $\mathrel R$
be a binary relation such that for every
$\mathrel R$
be a binary relation such that for every
 $\alpha <\kappa $
and every
$\alpha <\kappa $
and every
 $\alpha $
-sequence
$\alpha $
-sequence
 $s=(s_\xi )_{\xi <\alpha }$
of elements of S there exists
$s=(s_\xi )_{\xi <\alpha }$
of elements of S there exists
 $y\in S$
such that
$y\in S$
such that
 $s\mathrel R y$
. Then there is a function
$s\mathrel R y$
. Then there is a function
 $f:\kappa \to S$
such that for every
$f:\kappa \to S$
such that for every
 $\alpha <\kappa $
,
$\alpha <\kappa $
,
 $(f\upharpoonright \alpha )\mathrel R f(\alpha )$
.
$(f\upharpoonright \alpha )\mathrel R f(\alpha )$
.(Note that
 $\mathsf {DC}_{\aleph _0}$
is a reformulation of the Principle of Dependent Choices (
$\mathsf {DC}_{\aleph _0}$
is a reformulation of the Principle of Dependent Choices (
 $\mathsf {DC}$
) (Form 43 in [Reference Howard and Rubin3]).)
$\mathsf {DC}$
) (Form 43 in [Reference Howard and Rubin3]).) -
(8) The Boolean Prime Ideal Theorem
 $\mathsf {BPI}$
(Form 14 in [Reference Howard and Rubin3]): Every Boolean algebra has a prime ideal.
$\mathsf {BPI}$
(Form 14 in [Reference Howard and Rubin3]): Every Boolean algebra has a prime ideal. -
(9) Let
 $\kappa $
be an infinite well-ordered cardinal number.
$\kappa $
be an infinite well-ordered cardinal number. $\mathsf {MA}(\kappa )$
is the principle: if
$\mathsf {MA}(\kappa )$
is the principle: if
 $(P,\le )$
is a non-empty c.c.c. partial orderFootnote
2
and if
$(P,\le )$
is a non-empty c.c.c. partial orderFootnote
2
and if
 $\mathcal D$
is a family of
$\mathcal D$
is a family of
 $\le \kappa $
dense sets in P, then there is a filter F of P such that
$\le \kappa $
dense sets in P, then there is a filter F of P such that
 $F\cap D\ne \emptyset $
for all
$F\cap D\ne \emptyset $
for all
 $D\in \mathcal D$
. (Such a filter F of P is called a
$D\in \mathcal D$
. (Such a filter F of P is called a
 $\mathcal D$
-generic filter of P.)
$\mathcal D$
-generic filter of P.)For
 $\kappa =\aleph _0$
,
$\kappa =\aleph _0$
,
 $\mathsf {MA}(\aleph _0)$
is Form 339 in [Reference Howard and Rubin3].
$\mathsf {MA}(\aleph _0)$
is Form 339 in [Reference Howard and Rubin3].Martin’s Axiom
 $\mathsf {MA}$
:
$\mathsf {MA}$
:
 $\forall \kappa <2^{\aleph _0} (\mathsf {MA}(\kappa ))$
, where the parameter
$\forall \kappa <2^{\aleph _0} (\mathsf {MA}(\kappa ))$
, where the parameter
 $\kappa $
runs through the well-ordered cardinal numbers.
$\kappa $
runs through the well-ordered cardinal numbers.
Remark 2.8.
![]() $\mathsf {MC}^{\aleph _{0}}$
is equivalent to its partial version
$\mathsf {MC}^{\aleph _{0}}$
is equivalent to its partial version
![]() $\mathsf {PMC}^{\aleph _{0}}$
, i.e. the statement “Every denumerable family
$\mathsf {PMC}^{\aleph _{0}}$
, i.e. the statement “Every denumerable family
![]() $\mathcal {A}$
of non-empty sets has an infinite subfamily
$\mathcal {A}$
of non-empty sets has an infinite subfamily
![]() $\mathcal {B}$
with a multiple choice function” (a multiple choice function for an infinite subfamily of
$\mathcal {B}$
with a multiple choice function” (a multiple choice function for an infinite subfamily of
![]() $\mathcal {A}$
is called a partial multiple choice function for
$\mathcal {A}$
is called a partial multiple choice function for
![]() $\mathcal {A}$
); see [Reference Howard and Rubin3].
$\mathcal {A}$
); see [Reference Howard and Rubin3].
Both
![]() $\mathsf {AC^{LO}}$
and
$\mathsf {AC^{LO}}$
and
![]() $\mathsf {LW}$
are equivalent to
$\mathsf {LW}$
are equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZF}$
, but none of them are equivalent to
$\mathsf {ZF}$
, but none of them are equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZFA}$
(see [Reference Howard and Rubin3]). Furthermore, both
$\mathsf {ZFA}$
(see [Reference Howard and Rubin3]). Furthermore, both
![]() $\mathsf {LW}$
and
$\mathsf {LW}$
and
![]() $\mathsf {AC^{WO}}$
are strictly weaker than
$\mathsf {AC^{WO}}$
are strictly weaker than
![]() $\mathsf {AC^{LO}}$
in
$\mathsf {AC^{LO}}$
in
![]() $\mathsf {ZFA}$
, and
$\mathsf {ZFA}$
, and
![]() $\mathsf {AC^{WO}}$
is strictly weaker than
$\mathsf {AC^{WO}}$
is strictly weaker than
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZF}$
(see [Reference Howard and Rubin3]).
$\mathsf {ZF}$
(see [Reference Howard and Rubin3]).
For any infinite well-ordered cardinal number
![]() $\kappa $
,
$\kappa $
,
![]() $\mathsf {DC}_{\kappa }$
implies “Every family which has cardinality
$\mathsf {DC}_{\kappa }$
implies “Every family which has cardinality
![]() $\kappa $
and comprises non-empty sets, has a choice function.” Furthermore,
$\kappa $
and comprises non-empty sets, has a choice function.” Furthermore,
![]() $\forall \kappa (\mathsf {DC}_{\kappa })$
(where the parameter
$\forall \kappa (\mathsf {DC}_{\kappa })$
(where the parameter
![]() $\kappa $
runs through the infinite well-ordered cardinals) is equivalent to
$\kappa $
runs through the infinite well-ordered cardinals) is equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZFA}$
(see [Reference Jech7, Theorem 8.1((b),(c))]).
$\mathsf {ZFA}$
(see [Reference Jech7, Theorem 8.1((b),(c))]).
We also recall the following renowned results about almost disjoint and MAD families; for their proof, see (for example) Kunen [Reference Kunen9, Chapter II].
Theorem 2.9. The following hold:
(i)
![]() $(\mathsf {ZF})$
There is an almost disjoint family in
$(\mathsf {ZF})$
There is an almost disjoint family in
![]() $\omega $
of cardinality
$\omega $
of cardinality
![]() $2^{\aleph _{0}}$
.
$2^{\aleph _{0}}$
.
(ii) Assume
![]() $\mathsf {MA}(\kappa )$
for some well-ordered cardinal
$\mathsf {MA}(\kappa )$
for some well-ordered cardinal
![]() $\kappa $
with
$\kappa $
with
![]() ${\aleph _{0}\le \kappa <2^{\aleph _{0}}}$
. If
${\aleph _{0}\le \kappa <2^{\aleph _{0}}}$
. If
![]() $\mathcal {A}\subseteq \mathcal {P}(\omega )$
is an almost disjoint family with cardinality
$\mathcal {A}\subseteq \mathcal {P}(\omega )$
is an almost disjoint family with cardinality
![]() $\kappa $
, then
$\kappa $
, then
![]() $\mathcal {A}$
is not MAD. (The case where
$\mathcal {A}$
is not MAD. (The case where
![]() $\kappa =\aleph _{0}$
is provable in
$\kappa =\aleph _{0}$
is provable in
![]() $\mathsf {ZF}$
.)
$\mathsf {ZF}$
.)
(iii)
![]() $(\mathsf {ZFC})$
For every infinite set X, every almost disjoint family in X can be extended to a MAD family in X.
$(\mathsf {ZFC})$
For every infinite set X, every almost disjoint family in X can be extended to a MAD family in X.
3 Diagram of results
In Figure 1, we summarize main results of our paper. Some explanations about Figure 1 are in order:
-
(1) For use in Figure 1, we insert some notation here:
-
•
 $\mathsf {AD}1\hookrightarrow \mathsf {MAD}1$
: For every field F and every infinite-dimensional vector space V over F, every AD1 family of infinite-dimensional subspaces of V can be extended to a MAD1 family in V.
$\mathsf {AD}1\hookrightarrow \mathsf {MAD}1$
: For every field F and every infinite-dimensional vector space V over F, every AD1 family of infinite-dimensional subspaces of V can be extended to a MAD1 family in V. -
•
 $|\mathsf {MAD}2|\ne \aleph _{0}$
: For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
$|\mathsf {MAD}2|\ne \aleph _{0}$
: For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
 $\aleph _{0}$
.
$\aleph _{0}$
. -
•
 $|\mathsf {MAD}2|_{\mathsf {wvs}}\ne \aleph _{0}$
: For every well orderable field F and every infinite-dimensional vector space V over F with a well orderable basis, no MAD2 family in V has cardinality
$|\mathsf {MAD}2|_{\mathsf {wvs}}\ne \aleph _{0}$
: For every well orderable field F and every infinite-dimensional vector space V over F with a well orderable basis, no MAD2 family in V has cardinality
 $\aleph _{0}$
.
$\aleph _{0}$
. -
•
 $\forall V\exists \mathsf {AD}2(|\mathsf {AD}2|=2^{\aleph _{0}})$
: For every field F and every infinite-dimensional vector space V over F, there is an AD2 family in V of cardinality
$\forall V\exists \mathsf {AD}2(|\mathsf {AD}2|=2^{\aleph _{0}})$
: For every field F and every infinite-dimensional vector space V over F, there is an AD2 family in V of cardinality
 $2^{\aleph _{0}}$
.
$2^{\aleph _{0}}$
. -
•
 $\forall V\exists \mathsf {AD}1(|\mathsf {AD}1|=\infty )$
: For every field F and every infinite-dimensional vector space V over F, there is an infinite AD1 family in V.
$\forall V\exists \mathsf {AD}1(|\mathsf {AD}1|=\infty )$
: For every field F and every infinite-dimensional vector space V over F, there is an infinite AD1 family in V.
-
-
(2) Arrows or negated arrows without a label that refer to some result in the paper, represent implications or non-implications, respectively, that are “known” or “straightforward.” The reader is referred to Howard and Rubin [Reference Howard and Rubin3] for known results.
-
(3) A dashed arrow from
 $\mathsf {A}$
to
$\mathsf {A}$
to
 $\mathsf {B}$
which is labeled with ‘(
$\mathsf {B}$
which is labeled with ‘(
 $\mathsf {ZF}$
)’ (respectively, with ‘(
$\mathsf {ZF}$
)’ (respectively, with ‘(
 $\mathsf {ZFA}$
)’) means that
$\mathsf {ZFA}$
)’) means that
 $\mathsf {A}$
implies
$\mathsf {A}$
implies
 $\mathsf {B}$
, but the implication is not reversible in
$\mathsf {B}$
, but the implication is not reversible in
 $\mathsf {ZF}$
(respectively, in
$\mathsf {ZF}$
(respectively, in
 $\mathsf {ZFA}$
).
$\mathsf {ZFA}$
). -
(4) If proposition
 $\mathsf {A}$
is equivalent to proposition
$\mathsf {A}$
is equivalent to proposition
 $\mathsf {B}$
, then we use a thick left-right arrow between
$\mathsf {B}$
, then we use a thick left-right arrow between
 $\mathsf {A}$
and
$\mathsf {A}$
and
 $\mathsf {B}$
.
$\mathsf {B}$
.

Figure 1 Main results of the paper.
4 Main results
Our first result, Theorem 4.1, shows that the statement “For every field F and for every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
![]() $\aleph _{0}$
” is equivalent to a well-known weak choice principle, namely
$\aleph _{0}$
” is equivalent to a well-known weak choice principle, namely
![]() $\mathsf {MC}^{\aleph _{0}}$
.
$\mathsf {MC}^{\aleph _{0}}$
.
Theorem 4.1. The following statements are equivalent:
(i)
![]() $\mathsf {MC}^{\aleph _{0}}$
.
$\mathsf {MC}^{\aleph _{0}}$
.
(ii) For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
![]() $\aleph _{0}$
.
$\aleph _{0}$
.
Proof. (i)
![]() $\Rightarrow $
(ii) Let F be any field, and also let V be an infinite-dimensional vector space over F. Let
$\Rightarrow $
(ii) Let F be any field, and also let V be an infinite-dimensional vector space over F. Let
![]() $\mathcal {A}=\{W_{n}:n\in \omega \}$
be an AD2 family of infinite-dimensional subspaces of V with cardinality
$\mathcal {A}=\{W_{n}:n\in \omega \}$
be an AD2 family of infinite-dimensional subspaces of V with cardinality
![]() $\aleph _{0}$
(the mapping
$\aleph _{0}$
(the mapping
![]() $n\mapsto W_{n}$
is a bijection). Let
$n\mapsto W_{n}$
is a bijection). Let
![]() $U_{0}=W_{0}$
and for
$U_{0}=W_{0}$
and for
![]() $n\in \omega \setminus \{0\}$
, let
$n\in \omega \setminus \{0\}$
, let
Since
![]() $\mathcal {A}$
is AD2, it follows that for all
$\mathcal {A}$
is AD2, it follows that for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $U_{n}\ne \emptyset $
; in particular,
$U_{n}\ne \emptyset $
; in particular,
![]() $\langle U_{n}\rangle $
is an infinite-dimensional subspace of V for all
$\langle U_{n}\rangle $
is an infinite-dimensional subspace of V for all
![]() $n\in \omega $
. By
$n\in \omega $
. By
![]() $\mathsf {MC}^{\aleph _{0}}$
, let f be a multiple choice function for the denumerable, disjoint family
$\mathsf {MC}^{\aleph _{0}}$
, let f be a multiple choice function for the denumerable, disjoint family
![]() $\mathcal {B}=\{U_{n}:n\in \omega \}$
. Then
$\mathcal {B}=\{U_{n}:n\in \omega \}$
. Then
is an infinite-dimensional subspace of V since, for every
![]() $n\in \omega $
, any choice set for
$n\in \omega $
, any choice set for
![]() $\{U_{i}:i<n+1\}$
is a linearly independent subset of V with cardinality
$\{U_{i}:i<n+1\}$
is a linearly independent subset of V with cardinality
![]() $n+1$
(and hence Z has arbitrarily large finite linearly independent subsets).
$n+1$
(and hence Z has arbitrarily large finite linearly independent subsets).
Furthermore,
![]() $Z\not \in \mathcal {A}$
and
$Z\not \in \mathcal {A}$
and
![]() $\mathcal {A}\cup \{Z\}$
is AD2. Indeed, if
$\mathcal {A}\cup \{Z\}$
is AD2. Indeed, if
![]() $Z\in \mathcal {A}$
, then
$Z\in \mathcal {A}$
, then
![]() $Z=W_{n}$
for some
$Z=W_{n}$
for some
![]() $n\in \omega $
. But then, for any
$n\in \omega $
. But then, for any
![]() $u\in f(U_{n+1})\subseteq Z$
, we have
$u\in f(U_{n+1})\subseteq Z$
, we have
![]() $u\not \in W_{n}=Z$
, which is a contradiction.
$u\not \in W_{n}=Z$
, which is a contradiction.
For the second assertion, let
![]() $\{W_{n_{1}},W_{n_{2}},\ldots ,W_{n_{k}}\}\subset \mathcal {A}$
, where
$\{W_{n_{1}},W_{n_{2}},\ldots ,W_{n_{k}}\}\subset \mathcal {A}$
, where
![]() $n_{1}<n_{2}<\cdots <n_{k}$
. Fix
$n_{1}<n_{2}<\cdots <n_{k}$
. Fix
![]() $j\in \{1,\ldots ,k\}$
. Since
$j\in \{1,\ldots ,k\}$
. Since
![]() $f(U_{n})\subset W_{n}\setminus (W_{0}+\cdots +W_{n-1})$
for all
$f(U_{n})\subset W_{n}\setminus (W_{0}+\cdots +W_{n-1})$
for all
![]() $n\in \omega \setminus \{0\}$
, it follows that
$n\in \omega \setminus \{0\}$
, it follows that
 $$ \begin{align} W_{n_{j}}\cap\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right)+Z\right)=W_{n_{j}}\cap\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right)+ \left\langle \bigcup\{f(U_{i}):i\leq n_{k}\} \right\rangle \right). \end{align} $$
$$ \begin{align} W_{n_{j}}\cap\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right)+Z\right)=W_{n_{j}}\cap\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right)+ \left\langle \bigcup\{f(U_{i}):i\leq n_{k}\} \right\rangle \right). \end{align} $$
Let
(recall that
![]() $\mathcal {A}$
is AD2). Then it is not hard to verify that
$\mathcal {A}$
is AD2). Then it is not hard to verify that
 $$ \begin{align*}{W_{n_{j}}}{\cap}\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right){+} \left\langle \bigcup\{f(U_{i}):i\leq n_{k}\} \right\rangle \right) &\subseteq \Big\langle \{u_{1},u_{2},\ldots,u_{m}\} \\ & \cup \left(\bigcup\{f(U_{i}):i\leq n_{k}\}\right) \Big\rangle ,\end{align*} $$
$$ \begin{align*}{W_{n_{j}}}{\cap}\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right){+} \left\langle \bigcup\{f(U_{i}):i\leq n_{k}\} \right\rangle \right) &\subseteq \Big\langle \{u_{1},u_{2},\ldots,u_{m}\} \\ & \cup \left(\bigcup\{f(U_{i}):i\leq n_{k}\}\right) \Big\rangle ,\end{align*} $$
and thus, by Equation (1), we have
 $$ \begin{align*}W_{n_{j}}\cap\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right)+Z\right)\subseteq \left\langle \{u_{1},u_{2},\ldots,u_{m}\}\cup \left(\bigcup\{f(U_{i}):i\leq n_{k}\}\right) \right\rangle .\end{align*} $$
$$ \begin{align*}W_{n_{j}}\cap\left(\left(\sum_{n_{i}\ne n_{j}}W_{n_{i}}\right)+Z\right)\subseteq \left\langle \{u_{1},u_{2},\ldots,u_{m}\}\cup \left(\bigcup\{f(U_{i}):i\leq n_{k}\}\right) \right\rangle .\end{align*} $$
Therefore,
![]() $W_{n_{j}}\cap ((\sum _{n_{i}\ne n_{j}}W_{n_{i}})+Z)$
is finite-dimensional.
$W_{n_{j}}\cap ((\sum _{n_{i}\ne n_{j}}W_{n_{i}})+Z)$
is finite-dimensional.
On the other hand, it is easy to see that
 $$ \begin{align*}Z\cap\left(\sum_{j=1}^{k}W_{n_{j}}\right)\subseteq \left\langle \bigcup\{f(U_{j}):j\leq n_{k}\} \right\rangle ,\end{align*} $$
$$ \begin{align*}Z\cap\left(\sum_{j=1}^{k}W_{n_{j}}\right)\subseteq \left\langle \bigcup\{f(U_{j}):j\leq n_{k}\} \right\rangle ,\end{align*} $$
and hence
![]() $Z\cap (\sum _{j=1}^{k}W_{n_{j}})$
is finite-dimensional. We leave the details of the above observations to the interested reader. Thus
$Z\cap (\sum _{j=1}^{k}W_{n_{j}})$
is finite-dimensional. We leave the details of the above observations to the interested reader. Thus
![]() $\mathcal {A}\cup \{Z\}$
is an AD2 family in V which properly contains
$\mathcal {A}\cup \{Z\}$
is an AD2 family in V which properly contains
![]() $\mathcal {A}$
. Hence,
$\mathcal {A}$
. Hence,
![]() $\mathcal {A}$
is not MAD2.
$\mathcal {A}$
is not MAD2.
(ii)
![]() $\Rightarrow $
(i) Assume the hypothesis. Let
$\Rightarrow $
(i) Assume the hypothesis. Let
![]() $\mathcal {A}=\{A_{i}:i\in \omega \}$
be a denumerable family of non-empty sets. Without loss of generality, we assume that
$\mathcal {A}=\{A_{i}:i\in \omega \}$
be a denumerable family of non-empty sets. Without loss of generality, we assume that
![]() $\mathcal {A}$
is disjoint and that every member of
$\mathcal {A}$
is disjoint and that every member of
![]() $\mathcal {A}$
is infinite.
$\mathcal {A}$
is infinite.
Let
![]() $A=\bigcup \mathcal {A}$
and also let
$A=\bigcup \mathcal {A}$
and also let
i.e.,
![]() $V=\{f\in \mathbb {Z}_{2}^{A}:|f^{-1}(\{1\})|<\aleph _{0}\}$
. Then V with pointwise operations is an infinite-dimensional vector space over
$V=\{f\in \mathbb {Z}_{2}^{A}:|f^{-1}(\{1\})|<\aleph _{0}\}$
. Then V with pointwise operations is an infinite-dimensional vector space over
![]() $\mathbb {Z}_{2}$
(and note that
$\mathbb {Z}_{2}$
(and note that
![]() $\{\chi _{\{a\}}:a\in A\}$
is a basis for V).
$\{\chi _{\{a\}}:a\in A\}$
is a basis for V).
For each
![]() $i\in \omega $
we let
$i\in \omega $
we let
(so an element f of V is in
![]() $V_{i}$
if and only if
$V_{i}$
if and only if
![]() $\operatorname {\mathrm {{supp}}}(f)\subset A_{i}$
). It is clear that for every
$\operatorname {\mathrm {{supp}}}(f)\subset A_{i}$
). It is clear that for every
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $V_{i}$
is an infinite-dimensional vector subspace of V (and furthermore, note that
$V_{i}$
is an infinite-dimensional vector subspace of V (and furthermore, note that
![]() $\{\chi _{\{a\}}:a\in A_{i}\}$
is a basis for
$\{\chi _{\{a\}}:a\in A_{i}\}$
is a basis for
![]() $V_{i}$
). We let
$V_{i}$
). We let
![]() $\mathcal {V}$
is an AD2 family in V since, if J is a finite subset of
$\mathcal {V}$
is an AD2 family in V since, if J is a finite subset of
![]() $\omega $
(with at least two elements) and
$\omega $
(with at least two elements) and
![]() $i\in J$
, then
$i\in J$
, then
![]() $V_{i}\cap (\sum _{j\in J\setminus \{i\}}V_{j})=\{0\}$
. Furthermore,
$V_{i}\cap (\sum _{j\in J\setminus \{i\}}V_{j})=\{0\}$
. Furthermore,
![]() $|\mathcal {V}|=\aleph _{0}$
, and thus (by our hypothesis)
$|\mathcal {V}|=\aleph _{0}$
, and thus (by our hypothesis)
![]() $\mathcal {V}$
is not MAD2 in V. So there exists an infinite-dimensional subspace W of V such that
$\mathcal {V}$
is not MAD2 in V. So there exists an infinite-dimensional subspace W of V such that
![]() $W\not \in \mathcal {V}$
and
$W\not \in \mathcal {V}$
and
![]() $\mathcal {W}=\mathcal {V}\cup \{W\}$
is AD2 in V.
$\mathcal {W}=\mathcal {V}\cup \{W\}$
is AD2 in V.
Since the field of scalars (i.e.,
![]() $\mathbb {Z}_{2}$
) is finite and
$\mathbb {Z}_{2}$
) is finite and
![]() $\mathcal {W}$
is AD2, we have that
$\mathcal {W}$
is AD2, we have that
 $$ \begin{align} \forall J\in[\omega]^{<\omega}\left(|W\cap \left(\sum_{j\in J}V_{j}\right)|<\aleph_{0}\right). \end{align} $$
$$ \begin{align} \forall J\in[\omega]^{<\omega}\left(|W\cap \left(\sum_{j\in J}V_{j}\right)|<\aleph_{0}\right). \end{align} $$
By (2) and the fact that W is infinite-dimensional (and thus W is infinite), it follows that for every
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $W\nsubseteq \sum _{j\leq i}V_{j}$
, and thus there exists a strictly increasing sequence
$W\nsubseteq \sum _{j\leq i}V_{j}$
, and thus there exists a strictly increasing sequence
![]() $(n_{i})_{i\in \omega }$
of natural numbers and a sequence
$(n_{i})_{i\in \omega }$
of natural numbers and a sequence
![]() $(F_{n_{i}})_{i\in \omega }$
of finite sets which have the following two properties:
$(F_{n_{i}})_{i\in \omega }$
of finite sets which have the following two properties:
(a) for every
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $F_{n_{i}}\subseteq W\cap (\sum _{j\leq n_{i}}V_{j})$
and
$F_{n_{i}}\subseteq W\cap (\sum _{j\leq n_{i}}V_{j})$
and
(b) for every
![]() $i\in \omega $
and every
$i\in \omega $
and every
![]() $f\in F_{n_{i}}$
,
$f\in F_{n_{i}}$
,
![]() $\operatorname {\mathrm {{supp}}}(f\upharpoonright A_{n_{i}})\ne \emptyset $
.
$\operatorname {\mathrm {{supp}}}(f\upharpoonright A_{n_{i}})\ne \emptyset $
.
We define
Then h is a multiple choice function for the infinite subfamily
![]() $\{A_{n_{i}}:i\in \omega \}$
of
$\{A_{n_{i}}:i\in \omega \}$
of
![]() $\mathcal {A}$
(and hence h is a partial multiple choice function for
$\mathcal {A}$
(and hence h is a partial multiple choice function for
![]() $\mathcal {A}$
).
$\mathcal {A}$
).
The conclusion now follows from the fact that
![]() $\mathsf {MC}^{\aleph _{0}}$
is equivalent to
$\mathsf {MC}^{\aleph _{0}}$
is equivalent to
![]() $\mathsf {PMC}^{\aleph _{0}}$
(see Remark 2.8). This completes the proof of “(ii)
$\mathsf {PMC}^{\aleph _{0}}$
(see Remark 2.8). This completes the proof of “(ii)
![]() $\Rightarrow $
(i)” and of the theorem.⊣
$\Rightarrow $
(i)” and of the theorem.⊣
Next, following the ideas of the proof of “(i)
![]() $\Rightarrow $
(ii)” of Theorem 4.1, we establish the algebraic statement of Theorem 4.2 within
$\Rightarrow $
(ii)” of Theorem 4.1, we establish the algebraic statement of Theorem 4.2 within
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Theorem 4.2. The statement “For every well orderable field F and every infinite-dimensional vector space V over F with a well orderable basis, no MAD2 family in V has cardinality
![]() $\aleph _{0}$
” is provable in
$\aleph _{0}$
” is provable in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. Let V be an infinite-dimensional vector space over a well-ordered field
![]() $F=\{r_{\beta }:\beta <\lambda \}$
, having a well-ordered basis
$F=\{r_{\beta }:\beta <\lambda \}$
, having a well-ordered basis
![]() $B=\{b_{\alpha }:\alpha <\kappa \}$
, where
$B=\{b_{\alpha }:\alpha <\kappa \}$
, where
![]() $\lambda $
is a well-ordered cardinal number (possibly finite) and
$\lambda $
is a well-ordered cardinal number (possibly finite) and
![]() $\kappa $
is an infinite well-ordered cardinal number. Then
$\kappa $
is an infinite well-ordered cardinal number. Then
![]() $[F]^{<\omega }$
and
$[F]^{<\omega }$
and
![]() $[B]^{<\omega }$
are well orderable (recall that, in
$[B]^{<\omega }$
are well orderable (recall that, in
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $|[\mu ]^{<\omega }|=\mu $
for any infinite well-ordered cardinal
$|[\mu ]^{<\omega }|=\mu $
for any infinite well-ordered cardinal
![]() $\mu $
—see [Reference Levy11, Proposition 4.21(ii)]).
$\mu $
—see [Reference Levy11, Proposition 4.21(ii)]).
Let
![]() $\mathcal {A}=\{W_{n}:n\in \omega \}$
be an AD2 family of infinite-dimensional subspaces of V with cardinality
$\mathcal {A}=\{W_{n}:n\in \omega \}$
be an AD2 family of infinite-dimensional subspaces of V with cardinality
![]() $\aleph _{0}$
, and also let
$\aleph _{0}$
, and also let
![]() $U_{0}=W_{0}$
, and for
$U_{0}=W_{0}$
, and for
![]() $n\in \omega \setminus \{0\}$
,
$n\in \omega \setminus \{0\}$
,
![]() $U_{n}=W_{n}\setminus (W_{0}+\cdots +W_{n-1})$
.
$U_{n}=W_{n}\setminus (W_{0}+\cdots +W_{n-1})$
.
For every
![]() $n\in \omega $
, let
$n\in \omega $
, let
 $$ \begin{align*}J_{n}= \left\{\{b_{\alpha_{1}},\ldots,b_{\alpha_{k}}\}\in [B]^{<\omega}:\exists\{r_{\beta_{1}},\ldots,r_{\beta_{k}}\}\in [F]^{<\omega}\left(\sum_{j=1}^{k}r_{\beta_{j}}b_{\alpha_{j}}\in U_{n}\right)\right\}.\end{align*} $$
$$ \begin{align*}J_{n}= \left\{\{b_{\alpha_{1}},\ldots,b_{\alpha_{k}}\}\in [B]^{<\omega}:\exists\{r_{\beta_{1}},\ldots,r_{\beta_{k}}\}\in [F]^{<\omega}\left(\sum_{j=1}^{k}r_{\beta_{j}}b_{\alpha_{j}}\in U_{n}\right)\right\}.\end{align*} $$
Since
![]() $J_{n}$
is non-empty (for
$J_{n}$
is non-empty (for
![]() $U_{n}\ne \emptyset $
for all
$U_{n}\ne \emptyset $
for all
![]() $n\in \omega $
), and
$n\in \omega $
), and
![]() $[B]^{<\omega }$
and
$[B]^{<\omega }$
and
![]() $[F]^{<\omega }$
are well-ordered, we may pick the smallest
$[F]^{<\omega }$
are well-ordered, we may pick the smallest
![]() $\{b_{\alpha _{1}},\ldots ,b_{\alpha _{k}}\}\in J_{n}$
, and for this element of
$\{b_{\alpha _{1}},\ldots ,b_{\alpha _{k}}\}\in J_{n}$
, and for this element of
![]() $J_{n}$
, the smallest
$J_{n}$
, the smallest
![]() $\{r_{\beta _{1}},\ldots ,r_{\beta _{k}}\}\in [F]^{<\omega }$
(with respect to some prescribed well orderings of
$\{r_{\beta _{1}},\ldots ,r_{\beta _{k}}\}\in [F]^{<\omega }$
(with respect to some prescribed well orderings of
![]() $[B]^{<\omega }$
and
$[B]^{<\omega }$
and
![]() $[F]^{<\omega }$
) such that the vector
$[F]^{<\omega }$
) such that the vector
 $$ \begin{align*}u_{n}=\sum_{j=1}^{k}r_{\beta_{j}}b_{\alpha_{j}}\end{align*} $$
$$ \begin{align*}u_{n}=\sum_{j=1}^{k}r_{\beta_{j}}b_{\alpha_{j}}\end{align*} $$
is an element of
![]() $U_{n}$
. We may now follow the proof of “(i)
$U_{n}$
. We may now follow the proof of “(i)
![]() $\Rightarrow $
(ii)” of Theorem 4.1 in order to establish that
$\Rightarrow $
(ii)” of Theorem 4.1 in order to establish that
is an infinite-dimensional subspace of V such that
![]() $Z\not \in \mathcal {A}$
and
$Z\not \in \mathcal {A}$
and
![]() $\mathcal {A}\cup \{Z\}$
is AD2.⊣
$\mathcal {A}\cup \{Z\}$
is AD2.⊣
Remark 4.3. As the referee pointed out to us, Theorem 4.2 can be also proved by using an absoluteness argument. Indeed, we can encode the well-orderable field F, the well-orderable basis B, and the denumerable AD2 family
![]() $\mathcal {A}$
as a set of ordinals, E say. Then in
$\mathcal {A}$
as a set of ordinals, E say. Then in
![]() $L[E]$
(i.e., the class of all sets constructible from E), which is a model of
$L[E]$
(i.e., the class of all sets constructible from E), which is a model of
![]() $\mathsf {ZFC}$
(see Jech [Reference Jech6, Relative Constructibility and Theorem 13.22, p. 192]), we have that
$\mathsf {ZFC}$
(see Jech [Reference Jech6, Relative Constructibility and Theorem 13.22, p. 192]), we have that
![]() $\mathcal {A}$
is not maximal, and therefore not maximal in V either (and we recall here that if A is an arbitrary set and if M is an inner model of
$\mathcal {A}$
is not maximal, and therefore not maximal in V either (and we recall here that if A is an arbitrary set and if M is an inner model of
![]() $\mathsf {ZF}$
such that
$\mathsf {ZF}$
such that
![]() $A\cap M\in M$
, then
$A\cap M\in M$
, then
![]() $L[A]\subset M$
, see [Reference Jech6, Theorem 13.22]).
$L[A]\subset M$
, see [Reference Jech6, Theorem 13.22]).
While the algebraic statement of Theorem 4.2 requires no choice principles for its proof, substantial difficulty arises when one tries to prove the following related statements: “For every countable field F and every vector space V over F with a denumerable basis, no MADi family in V has cardinality
![]() $\kappa $
for any well-ordered cardinal number
$\kappa $
for any well-ordered cardinal number
![]() $\kappa $
with
$\kappa $
with
![]() $\aleph _{0}\le \kappa < 2^{\aleph _{0}}$
” (
$\aleph _{0}\le \kappa < 2^{\aleph _{0}}$
” (
![]() $i=1,2$
). Kolman [Reference Kolman8] and Smythe [Reference Smythe14], using a slight modification of Solovay’s partial order (see Kunen [Reference Kunen9, Definition 2.7, p. 55] for this partial order), established that Martin’s Axiom
$i=1,2$
). Kolman [Reference Kolman8] and Smythe [Reference Smythe14], using a slight modification of Solovay’s partial order (see Kunen [Reference Kunen9, Definition 2.7, p. 55] for this partial order), established that Martin’s Axiom
![]() $\mathsf {MA}$
implies the above statements for
$\mathsf {MA}$
implies the above statements for
![]() $i=2$
and
$i=2$
and
![]() $i=1$
, respectively. Furthermore, by employing
$i=1$
, respectively. Furthermore, by employing
![]() $\mathsf {AC}$
, they obtained that for every vector space V with a denumerable basis, every MADi (
$\mathsf {AC}$
, they obtained that for every vector space V with a denumerable basis, every MADi (
![]() $i=1,2$
) family in V has power
$i=1,2$
) family in V has power
![]() $2^{\aleph _{0}}$
.Footnote
3
We label the above two results as Theorem 4.4.
$2^{\aleph _{0}}$
.Footnote
3
We label the above two results as Theorem 4.4.
Theorem 4.4. [Reference Kolman8, Reference Smythe14] Let
![]() $\kappa $
be a well-ordered cardinal number with
$\kappa $
be a well-ordered cardinal number with
![]() $\aleph _{0}\le \kappa < 2^{\aleph _{0}}$
. Then, in
$\aleph _{0}\le \kappa < 2^{\aleph _{0}}$
. Then, in
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $\mathsf {MA}(\kappa )$
implies “For every countable field F and every vector space V over F with a denumerable basis, no MADi family (
$\mathsf {MA}(\kappa )$
implies “For every countable field F and every vector space V over F with a denumerable basis, no MADi family (
![]() $i=1,2$
) in V has cardinality
$i=1,2$
) in V has cardinality
![]() $\kappa $
.”
$\kappa $
.”
We would like to note here that it is an open problem whether or not the instance
![]() $\mathsf {MA}(\aleph _{0})$
of
$\mathsf {MA}(\aleph _{0})$
of
![]() $\mathsf {MA}$
implies either of
$\mathsf {MA}$
implies either of
![]() $\mathsf {AC}^{\aleph _{0}}$
and
$\mathsf {AC}^{\aleph _{0}}$
and
![]() $\mathsf {MC}^{\aleph _{0}}$
(and hence, by Theorem 4.1, it is unknown whether
$\mathsf {MC}^{\aleph _{0}}$
(and hence, by Theorem 4.1, it is unknown whether
![]() $\mathsf {MA}(\aleph _{0})$
implies “For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
$\mathsf {MA}(\aleph _{0})$
implies “For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
![]() $\aleph _{0}$
”).
$\aleph _{0}$
”).
It is also an open problem whether or not
![]() $\mathsf {AC}^{\aleph _{0}}$
implies
$\mathsf {AC}^{\aleph _{0}}$
implies
![]() $\mathsf {MA}(\aleph _{0})$
, whereas it has been established recently by Tachtsis [Reference Tachtsis15, Theorem 2.11] that
$\mathsf {MA}(\aleph _{0})$
, whereas it has been established recently by Tachtsis [Reference Tachtsis15, Theorem 2.11] that
![]() $\mathsf {ZFA}+\mathsf {MC}$
(and hence
$\mathsf {ZFA}+\mathsf {MC}$
(and hence
![]() $\mathsf {ZFA}+\mathsf {MC}^{\aleph _{0}}$
) cannot prove
$\mathsf {ZFA}+\mathsf {MC}^{\aleph _{0}}$
) cannot prove
![]() $\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras. (Further study on the relative strength of
$\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras. (Further study on the relative strength of
![]() $\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras has been conducted in [Reference Tachtsis19].)
$\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras has been conducted in [Reference Tachtsis19].)
By Theorem 4.1 and [Reference Tachtsis15, Theorem 2.11], we obtain the following corollary.
Corollary 4.5. The statement “For every field F and every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
![]() $\aleph _{0}$
” does not imply
$\aleph _{0}$
” does not imply
![]() $\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras in
$\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras in
![]() $\mathsf {ZFA}$
.
$\mathsf {ZFA}$
.
Theorem 4.6.
![]() $\mathsf {AC}^{\aleph _{0}}$
implies “For every field F and every infinite-dimensional vector space V over F, there is an AD2 family in V of cardinality
$\mathsf {AC}^{\aleph _{0}}$
implies “For every field F and every infinite-dimensional vector space V over F, there is an AD2 family in V of cardinality
![]() $2^{\aleph _{0}}$
.”
$2^{\aleph _{0}}$
.”
Proof. Assume the hypothesis. We will use the following lemma, which has been established by Howard and Tachtsis [Reference Howard and Tachtsis5]. For the reader’s convenience, and in the interest of making our paper self-contained, we include its proof here.⊣
Lemma 4.7.
![]() $\mathsf {AC}^{\aleph _0}$
implies “For every field F, every infinite-dimensional vector space V over F has a denumerable linearly independent subset.”
$\mathsf {AC}^{\aleph _0}$
implies “For every field F, every infinite-dimensional vector space V over F has a denumerable linearly independent subset.”
Proof. Let F be any field and let V be an infinite-dimensional vector space over F. For each
![]() $n\in \omega \setminus \{0\}$
, let
$n\in \omega \setminus \{0\}$
, let
Since V is infinite-dimensional, it follows that
![]() $A_n\ne \emptyset $
for all
$A_n\ne \emptyset $
for all
![]() $n\in \omega \setminus \{0\}$
. Let
$n\in \omega \setminus \{0\}$
. Let
![]() $\mathcal A=\{A_n:n\in \omega \setminus \{0\}\}$
and let, by
$\mathcal A=\{A_n:n\in \omega \setminus \{0\}\}$
and let, by
![]() $\mathsf {AC}^{\aleph _0}$
,
$\mathsf {AC}^{\aleph _0}$
,
![]() $f=\{(n,(v_0^{(n)},v_1^{(n)},\ldots ,v_n^{(n)})):n\in \omega \setminus \{0\}\}$
be a choice function for
$f=\{(n,(v_0^{(n)},v_1^{(n)},\ldots ,v_n^{(n)})):n\in \omega \setminus \{0\}\}$
be a choice function for
![]() $\mathcal A$
. Note that by definition of
$\mathcal A$
. Note that by definition of
![]() $A_n$
,
$A_n$
,
![]() $\operatorname {\mathrm {{ran}}}(f(n))$
is an
$\operatorname {\mathrm {{ran}}}(f(n))$
is an
![]() $(n+1)$
-sized set of linearly independent vectors of V.
$(n+1)$
-sized set of linearly independent vectors of V.
Let
![]() $A=\bigcup \{\operatorname {\mathrm {{ran}}}(f(n)):n\in \omega \setminus \{0\}\}$
. It is clear that A is denumerable. Furthermore, since A has finite sequences of linearly independent vectors of arbitrary finite length, we may construct via mathematical induction a denumerable linearly independent subset of V. Indeed, let
$A=\bigcup \{\operatorname {\mathrm {{ran}}}(f(n)):n\in \omega \setminus \{0\}\}$
. It is clear that A is denumerable. Furthermore, since A has finite sequences of linearly independent vectors of arbitrary finite length, we may construct via mathematical induction a denumerable linearly independent subset of V. Indeed, let
![]() $w_0=v_0^{(1)}$
. Then
$w_0=v_0^{(1)}$
. Then
![]() $w_0$
is linearly independent, since
$w_0$
is linearly independent, since
![]() $w_0\ne 0$
(see the definition of
$w_0\ne 0$
(see the definition of
![]() $A_n$
). Assume that for some
$A_n$
). Assume that for some
![]() $n\in \omega \setminus \{0\}$
we have chosen linearly independent vectors
$n\in \omega \setminus \{0\}$
we have chosen linearly independent vectors
![]() $w_0,w_1,\ldots ,w_n\in A$
. Since
$w_0,w_1,\ldots ,w_n\in A$
. Since
![]() $\dim (\langle w_0,w_1,\ldots ,w_n\rangle )= n+1$
and
$\dim (\langle w_0,w_1,\ldots ,w_n\rangle )= n+1$
and
![]() $\operatorname {\mathrm {{ran}}}(f(n+1))$
consists of
$\operatorname {\mathrm {{ran}}}(f(n+1))$
consists of
![]() $n+2$
linearly independent vectors, there exists
$n+2$
linearly independent vectors, there exists
![]() $v\in \operatorname {\mathrm {{ran}}}(f(n+1))\setminus \langle w_0,w_1,\ldots ,w_n\rangle $
. Let
$v\in \operatorname {\mathrm {{ran}}}(f(n+1))\setminus \langle w_0,w_1,\ldots ,w_n\rangle $
. Let
![]() $j_{n+1}=\min \{j:j< n+2$
and
$j_{n+1}=\min \{j:j< n+2$
and
![]() $v_j^{(n+1)}\in \operatorname {\mathrm {{ran}}}(f(n+1))\setminus \langle w_0,w_1,\ldots ,w_n\rangle \}$
. Put
$v_j^{(n+1)}\in \operatorname {\mathrm {{ran}}}(f(n+1))\setminus \langle w_0,w_1,\ldots ,w_n\rangle \}$
. Put
![]() $w_{n+1}=v_{j_{n+1}}^{(n+1)}$
. This completes the inductive step.
$w_{n+1}=v_{j_{n+1}}^{(n+1)}$
. This completes the inductive step.
From the above construction, we conclude that
![]() $\{w_n:n\in \omega \}$
is a denumerable linearly independent subset of V.⊣
$\{w_n:n\in \omega \}$
is a denumerable linearly independent subset of V.⊣
Now we turn to the proof of the theorem. Fix a field F and an infinite-dimensional vector space V over F. By Lemma 4.7, let
![]() $I=\{v_{n}:n\in \omega \}$
be a denumerable linearly independent subset of V (the mapping
$I=\{v_{n}:n\in \omega \}$
be a denumerable linearly independent subset of V (the mapping
![]() $n\mapsto v_{n}$
is a bijection). We also let
$n\mapsto v_{n}$
is a bijection). We also let
![]() $W=\langle I\rangle $
. Then W is an infinite-dimensional subspace of V (and I is a denumerable basis for W). By Theorem 2.9(i), let
$W=\langle I\rangle $
. Then W is an infinite-dimensional subspace of V (and I is a denumerable basis for W). By Theorem 2.9(i), let
![]() $\mathcal {A}$
be an almost disjoint family in
$\mathcal {A}$
be an almost disjoint family in
![]() $\omega $
of cardinality
$\omega $
of cardinality
![]() $2^{\aleph _{0}}$
. We let
$2^{\aleph _{0}}$
. We let
Then
![]() $\mathcal {W}=\{W_{X}:X\in \mathcal {A}\}$
is an AD2 family in V with cardinality
$\mathcal {W}=\{W_{X}:X\in \mathcal {A}\}$
is an AD2 family in V with cardinality
![]() $2^{\aleph _{0}}$
(since
$2^{\aleph _{0}}$
(since
![]() $|\mathcal {W}|=|\mathcal {A}|=2^{\aleph _{0}}$
). To see that
$|\mathcal {W}|=|\mathcal {A}|=2^{\aleph _{0}}$
). To see that
![]() $\mathcal {W}$
is AD2, note that if
$\mathcal {W}$
is AD2, note that if
![]() $\mathcal {C}$
is a finite subset of
$\mathcal {C}$
is a finite subset of
![]() $\mathcal {W}$
, then for every
$\mathcal {W}$
, then for every
![]() $C\in \mathcal {C}$
we have
$C\in \mathcal {C}$
we have
 $$ \begin{align*}C\kern-1pt\cap\kern-1pt \left(\kern-1pt\sum_{D\in\mathcal{C}\setminus\{C\}}D\kern-2pt\right)\kern-1.5pt\subseteq \left\langle \bigcup\{\kern-1pt\{v_{n}:n\in X\kern-1pt\cap\kern-1pt Y\}: X, Y\in\mathcal{A},\ X\ne Y, \text{and } W_{X},W_{Y}\in\mathcal{C}\}\kern-1pt \right\rangle .\end{align*} $$
$$ \begin{align*}C\kern-1pt\cap\kern-1pt \left(\kern-1pt\sum_{D\in\mathcal{C}\setminus\{C\}}D\kern-2pt\right)\kern-1.5pt\subseteq \left\langle \bigcup\{\kern-1pt\{v_{n}:n\in X\kern-1pt\cap\kern-1pt Y\}: X, Y\in\mathcal{A},\ X\ne Y, \text{and } W_{X},W_{Y}\in\mathcal{C}\}\kern-1pt \right\rangle .\end{align*} $$
Since the set
![]() $\bigcup \{\{v_{n}:n\in X\cap Y\}: X, Y\in \mathcal {A}, X\ne Y$
, and
$\bigcup \{\{v_{n}:n\in X\cap Y\}: X, Y\in \mathcal {A}, X\ne Y$
, and
![]() $W_{X},W_{Y}\in \mathcal {C}\}$
is finite (for
$W_{X},W_{Y}\in \mathcal {C}\}$
is finite (for
![]() $\mathcal {C}$
is finite and
$\mathcal {C}$
is finite and
![]() $\mathcal {A}$
is almost disjoint in
$\mathcal {A}$
is almost disjoint in
![]() $\omega $
), we conclude that
$\omega $
), we conclude that
![]() $C\cap (\sum _{D\in \mathcal {C}\setminus \{C\}}D)$
is finite-dimensional.⊣
$C\cap (\sum _{D\in \mathcal {C}\setminus \{C\}}D)$
is finite-dimensional.⊣
Tachtsis [Reference Tachtsis16] established that “For every field F, every infinite-dimensional vector space V over F has an infinite linearly independent subset” (which is formally weaker than “For every field F, every infinite-dimensional vector space V over F has a denumerable linearly independent subset”) implies
![]() $\mathsf {MC}^{\aleph _{0}}$
. This, together with Theorem 4.1, gives us the following result.
$\mathsf {MC}^{\aleph _{0}}$
. This, together with Theorem 4.1, gives us the following result.
Theorem 4.8. “For every field F, every infinite-dimensional vector space V over F has an infinite linearly independent subset” implies “For every field F and for every infinite-dimensional vector space V over F, no MAD2 family in V has cardinality
![]() $\aleph _{0}$
.”
$\aleph _{0}$
.”
Läuchli [Reference Läuchli10] proved that it is relatively consistent with
![]() $\mathsf {ZFA}$
that there is an infinite-dimensional vector space V over
$\mathsf {ZFA}$
that there is an infinite-dimensional vector space V over
![]() $\mathbb {Q}$
(the set of rational numbers) which has no basis, but every proper subspace of V is finite-dimensional. The latter result can be transferred to
$\mathbb {Q}$
(the set of rational numbers) which has no basis, but every proper subspace of V is finite-dimensional. The latter result can be transferred to
![]() $\mathsf {ZF}$
via the Jech–Sochor First Embedding Theorem (see [Reference Jech7, Theorem 6.1 and Problem 1 (p. 94)]). Therefore, the statement “Every infinite-dimensional vector space has an infinite AD1 family” is not provable in
$\mathsf {ZF}$
via the Jech–Sochor First Embedding Theorem (see [Reference Jech7, Theorem 6.1 and Problem 1 (p. 94)]). Therefore, the statement “Every infinite-dimensional vector space has an infinite AD1 family” is not provable in
![]() $\mathsf {ZF}$
, and thus neither is “Every infinite-dimensional vector space has an infinite AD2 family” provable in
$\mathsf {ZF}$
, and thus neither is “Every infinite-dimensional vector space has an infinite AD2 family” provable in
![]() $\mathsf {ZF}$
(recall that AD2
$\mathsf {ZF}$
(recall that AD2
![]() $\Rightarrow $
AD1).
$\Rightarrow $
AD1).
In the next theorem, we provide a substantial strengthening of the latter result by showing that
![]() $\mathsf {ZF}+\mathsf {BPI}$
cannot prove “Every infinite-dimensional vector space has an infinite AD1 family” (and thus
$\mathsf {ZF}+\mathsf {BPI}$
cannot prove “Every infinite-dimensional vector space has an infinite AD1 family” (and thus
![]() $\mathsf {ZF}+\mathsf {BPI}$
can neither prove “Every infinite-dimensional vector space has an infinite AD2 family”).
$\mathsf {ZF}+\mathsf {BPI}$
can neither prove “Every infinite-dimensional vector space has an infinite AD2 family”).
Theorem 4.9. The statement “Every infinite-dimensional vector space has an infinite AD1 family” is not provable in
![]() $\mathsf {ZF}+\mathsf {BPI}$
.
$\mathsf {ZF}+\mathsf {BPI}$
.
Proof. We will first establish the independence of the above statement from
![]() $\mathsf {BPI}$
in
$\mathsf {BPI}$
in
![]() $\mathsf {ZFA}$
and then we will transfer the result to
$\mathsf {ZFA}$
and then we will transfer the result to
![]() $\mathsf {ZF}$
by using a suitable transfer theorem of Pincus [Reference Pincus13].
$\mathsf {ZF}$
by using a suitable transfer theorem of Pincus [Reference Pincus13].
We consider the Mostowski Linearly Ordered Model of
![]() $\mathsf {ZFA}$
, which is labeled as ‘Model
$\mathsf {ZFA}$
, which is labeled as ‘Model
![]() $\mathcal {N}3$
’ in Howard–Rubin [Reference Howard and Rubin3]: The set A of atoms is denumerable and is equipped with an ordering
$\mathcal {N}3$
’ in Howard–Rubin [Reference Howard and Rubin3]: The set A of atoms is denumerable and is equipped with an ordering
![]() $\leq $
chosen so that
$\leq $
chosen so that
![]() $(A,\le )$
is order-isomorphic to the set
$(A,\le )$
is order-isomorphic to the set
![]() $\mathbb {Q}$
of rational numbers with the usual ordering; G is the group of all order automorphisms of
$\mathbb {Q}$
of rational numbers with the usual ordering; G is the group of all order automorphisms of
![]() $(A,\le )$
; and
$(A,\le )$
; and
![]() $\mathcal {F}$
is the finite support (normal) filter on G, i.e.,
$\mathcal {F}$
is the finite support (normal) filter on G, i.e.,
![]() $\mathcal {F}$
is the filter on G which is generated by the subgroups
$\mathcal {F}$
is the filter on G which is generated by the subgroups
![]() $\operatorname {\mathrm {{fix}}}_{G}(E)=\{\phi \in G:\forall e\in E(\phi (e)=e)\}$
,
$\operatorname {\mathrm {{fix}}}_{G}(E)=\{\phi \in G:\forall e\in E(\phi (e)=e)\}$
,
![]() $E\in [A]^{<\omega }$
.
$E\in [A]^{<\omega }$
.
![]() $\mathcal {N}3$
is the permutation model determined by A, G and
$\mathcal {N}3$
is the permutation model determined by A, G and
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Let us recall that every
![]() $x\in \mathcal {N}3$
has a least (finite) support, which we shall denote by
$x\in \mathcal {N}3$
has a least (finite) support, which we shall denote by
![]() $E_{x}$
(see Jech [Reference Jech7, Lemma 4.5]). Furthermore, it is a renowned result of Halpern [Reference Halpern2] that
$E_{x}$
(see Jech [Reference Jech7, Lemma 4.5]). Furthermore, it is a renowned result of Halpern [Reference Halpern2] that
![]() $\mathsf {BPI}$
is true in the model
$\mathsf {BPI}$
is true in the model
![]() $\mathcal {N}3$
. Thus we only need to show that there exists an infinite-dimensional vector space in
$\mathcal {N}3$
. Thus we only need to show that there exists an infinite-dimensional vector space in
![]() $\mathcal {N}3$
which has no infinite AD1 family in
$\mathcal {N}3$
which has no infinite AD1 family in
![]() $\mathcal {N}3$
.
$\mathcal {N}3$
.
To this end, we consider the set
equipped with pointwise operations of addition and multiplication with scalars from
![]() $\mathbb {Z}_{2}$
. Then
$\mathbb {Z}_{2}$
. Then
![]() $(V,+,\cdot )$
is an infinite-dimensional vector space over
$(V,+,\cdot )$
is an infinite-dimensional vector space over
![]() $\mathbb {Z}_{2}$
, and
$\mathbb {Z}_{2}$
, and
![]() $(V,+,\cdot )\in \mathcal {N}3$
since, for every
$(V,+,\cdot )\in \mathcal {N}3$
since, for every
![]() $\phi \in G$
,
$\phi \in G$
,
![]() $\phi ((V,+,\cdot ))=(V,+,\cdot )$
.
$\phi ((V,+,\cdot ))=(V,+,\cdot )$
.
We assert that V has no infinite AD1 family in
![]() $\mathcal {N}3$
. Assume not, and let
$\mathcal {N}3$
. Assume not, and let
![]() $\mathcal {W}\in \mathcal {N}3$
be an infinite AD1 family of infinite-dimensional subspaces of V. Let
$\mathcal {W}\in \mathcal {N}3$
be an infinite AD1 family of infinite-dimensional subspaces of V. Let
![]() $E=\{e_{1},e_{2},\ldots ,e_{n}\}\subset A$
, where
$E=\{e_{1},e_{2},\ldots ,e_{n}\}\subset A$
, where
![]() $e_{1}<e_{2}<\cdots <e_{n}$
, be a finite support of
$e_{1}<e_{2}<\cdots <e_{n}$
, be a finite support of
![]() $\mathcal {W}$
. Then E determines
$\mathcal {W}$
. Then E determines
![]() $n+1$
pairwise disjoint, open intervals in the ordering of A, namely
$n+1$
pairwise disjoint, open intervals in the ordering of A, namely
![]() $(-\infty ,e_{1})$
,
$(-\infty ,e_{1})$
,
![]() $(e_{i},e_{i+1})$
(
$(e_{i},e_{i+1})$
(
![]() $1\leq i<n$
),
$1\leq i<n$
),
![]() $(e_{n},+\infty )$
. Let
$(e_{n},+\infty )$
. Let
A couple of observations are in order:
-
(a) Since
 $\mathcal {W}$
is AD1 and the field of scalars (i.e.
$\mathcal {W}$
is AD1 and the field of scalars (i.e.
 $\mathbb {Z}_{2}$
) is finite,
$\mathbb {Z}_{2}$
) is finite,
 $\mathcal {W}$
is almost disjoint in V in the sense of Definition 2.3, i.e., for every
$\mathcal {W}$
is almost disjoint in V in the sense of Definition 2.3, i.e., for every
 $W,W'\in \mathcal {W}$
, if
$W,W'\in \mathcal {W}$
, if
 $W\ne W'$
then
$W\ne W'$
then
 $W\cap W'$
is finite.
$W\cap W'$
is finite. -
(b) Since
 $\mathcal {W}$
is infinite and
$\mathcal {W}$
is infinite and
 $\mathcal {Z}\cup \{E\}$
is a finite partition of A, a straightforward pigeonhole-type argument yields that there exist distinct
$\mathcal {Z}\cup \{E\}$
is a finite partition of A, a straightforward pigeonhole-type argument yields that there exist distinct
 $W,W'\in \mathcal {W}$
and an
$W,W'\in \mathcal {W}$
and an
 $I\in \mathcal {Z}$
such that: (3)
$I\in \mathcal {Z}$
such that: (3) $$ \begin{align} \forall X\in\{W,W'\}(\{I\cap\operatorname{\mathrm{{supp}}}(f):f\in X\} \text{ is infinite}). \end{align} $$
$$ \begin{align} \forall X\in\{W,W'\}(\{I\cap\operatorname{\mathrm{{supp}}}(f):f\in X\} \text{ is infinite}). \end{align} $$
Fix
![]() $W,W'\in \mathcal {W}$
and
$W,W'\in \mathcal {W}$
and
![]() $I\in \mathcal {Z}$
as in (b). Since (by (b))
$I\in \mathcal {Z}$
as in (b). Since (by (b))
![]() $W\neq W'$
, (a) yields that
$W\neq W'$
, (a) yields that
![]() $W\cap W'$
is finite. This, together with (3) and the fact that
$W\cap W'$
is finite. This, together with (3) and the fact that
![]() $E_{W}\cup E_{W'}$
is finite, readily implies that there exist distinct
$E_{W}\cup E_{W'}$
is finite, readily implies that there exist distinct
![]() $f_{W}\in W$
,
$f_{W}\in W$
,
![]() $f_{W'}\in W'$
such that
$f_{W'}\in W'$
such that
![]() $(I\cap \operatorname {\mathrm {{supp}}}(f_{W}))\setminus E_{W}\ne \emptyset $
and
$(I\cap \operatorname {\mathrm {{supp}}}(f_{W}))\setminus E_{W}\ne \emptyset $
and
![]() $(I\cap \operatorname {\mathrm {{supp}}}(f_{W'}))\setminus E_{W'}\ne \emptyset $
.
$(I\cap \operatorname {\mathrm {{supp}}}(f_{W'}))\setminus E_{W'}\ne \emptyset $
.
Let
![]() $z=\min ((I\cap \operatorname {\mathrm {{supp}}}(f_{W}))\setminus E_{W})$
and also let
$z=\min ((I\cap \operatorname {\mathrm {{supp}}}(f_{W}))\setminus E_{W})$
and also let
![]() $z'\in I\setminus E_{W}$
such that
$z'\in I\setminus E_{W}$
such that
![]() $z'<z$
and
$z'<z$
and
![]() $(z',z)\cap E_{W}=\emptyset $
. Construct a
$(z',z)\cap E_{W}=\emptyset $
. Construct a
![]() $\phi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
so that
$\phi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
so that
![]() $\phi (z)=z'$
and
$\phi (z)=z'$
and
![]() $f_{W},\phi (f_{W})$
agree on
$f_{W},\phi (f_{W})$
agree on
![]() $A\setminus \{z',z\}$
. Since
$A\setminus \{z',z\}$
. Since
![]() $E_{W}$
is a support of W and
$E_{W}$
is a support of W and
![]() $\phi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
, we have
$\phi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
, we have
![]() $\phi (W)=W$
. Thus
$\phi (W)=W$
. Thus
![]() $\phi (f_{W})\in \phi (W)=W$
, and since W is a subspace of V, we have
$\phi (f_{W})\in \phi (W)=W$
, and since W is a subspace of V, we have
![]() $f_{W}+\phi (f_{W})\in W$
. Furthermore, it is clear that
$f_{W}+\phi (f_{W})\in W$
. Furthermore, it is clear that
![]() $\operatorname {\mathrm {{supp}}}(f_{W}+\phi (f_{W}))=\{z',z\}\subset I\setminus E_{W}$
.
$\operatorname {\mathrm {{supp}}}(f_{W}+\phi (f_{W}))=\{z',z\}\subset I\setminus E_{W}$
.
Using
![]() $f_{W}+\phi (f_{W})$
and suitable elements of
$f_{W}+\phi (f_{W})$
and suitable elements of
![]() $\operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
, it is not hard to verify that there exist infinitely many
$\operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
, it is not hard to verify that there exist infinitely many
![]() $g_{W}\in W$
such that
$g_{W}\in W$
such that
![]() $\operatorname {\mathrm {{supp}}}(g_{W})\in [I\setminus E_{W}]^{2}$
and
$\operatorname {\mathrm {{supp}}}(g_{W})\in [I\setminus E_{W}]^{2}$
and
![]() $\max (\operatorname {\mathrm {{supp}}}(g_{W}))<z'$
, and infinitely many
$\max (\operatorname {\mathrm {{supp}}}(g_{W}))<z'$
, and infinitely many
![]() $h_{W}\in W$
such that
$h_{W}\in W$
such that
![]() $\operatorname {\mathrm {{supp}}}(h_{W})\in [I\setminus E_{W}]^{2}$
and
$\operatorname {\mathrm {{supp}}}(h_{W})\in [I\setminus E_{W}]^{2}$
and
![]() $z<\min (\operatorname {\mathrm {{supp}}}(h_{W}))$
. In particular, for every
$z<\min (\operatorname {\mathrm {{supp}}}(h_{W}))$
. In particular, for every
![]() $a,b\in I\setminus E_{W}$
such that
$a,b\in I\setminus E_{W}$
such that
![]() $a<b<z'$
and
$a<b<z'$
and
![]() $(a,z')\cap E_{W}=\emptyset $
, we may consider a
$(a,z')\cap E_{W}=\emptyset $
, we may consider a
![]() $\pi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
such that
$\pi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
such that
![]() $\operatorname {\mathrm {{supp}}}(\pi (f_{W}+\phi (f_{W})))=\{a,b\}$
. Letting
$\operatorname {\mathrm {{supp}}}(\pi (f_{W}+\phi (f_{W})))=\{a,b\}$
. Letting
![]() $g_{W}=\pi (f_{W}+\phi (f_{W}))$
, we have
$g_{W}=\pi (f_{W}+\phi (f_{W}))$
, we have
![]() $g_W\in W$
(for
$g_W\in W$
(for
![]() $f_{W}+\phi (f_{W})\in W$
,
$f_{W}+\phi (f_{W})\in W$
,
![]() $\pi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
and
$\pi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W})$
and
![]() $E_{W}$
is a support of W),
$E_{W}$
is a support of W),
![]() $\operatorname {\mathrm {{supp}}}(g_{W})=\{a,b\}\in [I\setminus E_{W}]^{2}$
and
$\operatorname {\mathrm {{supp}}}(g_{W})=\{a,b\}\in [I\setminus E_{W}]^{2}$
and
![]() $\max (\operatorname {\mathrm {{supp}}}(g_{W}))=b<z'$
. We may work in a similar manner for the
$\max (\operatorname {\mathrm {{supp}}}(g_{W}))=b<z'$
. We may work in a similar manner for the
![]() $h_{W}$
’s, and thus we leave this to the interested reader. By the above considerations, we have:
$h_{W}$
’s, and thus we leave this to the interested reader. By the above considerations, we have:
As with
![]() $f_{W}$
, we may let
$f_{W}$
, we may let
![]() $t=\min ((I\cap \operatorname {\mathrm {{supp}}}(f_{W'}))\setminus E_{W'})$
,
$t=\min ((I\cap \operatorname {\mathrm {{supp}}}(f_{W'}))\setminus E_{W'})$
,
![]() $t'\in I\setminus E_{W'}$
such that
$t'\in I\setminus E_{W'}$
such that
![]() $t'<t$
and
$t'<t$
and
![]() $(t',t)\cap E_{W'}=\emptyset $
, and a
$(t',t)\cap E_{W'}=\emptyset $
, and a
![]() $\psi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W'})$
such that
$\psi \in \operatorname {\mathrm {{fix}}}_{G}(E\cup E_{W'})$
such that
![]() $f_{W'}+\psi (f_{W'})\in W'$
and
$f_{W'}+\psi (f_{W'})\in W'$
and
![]() $\operatorname {\mathrm {{supp}}}(f_{W'}+\psi (f_{W'}))=\{t',t\}\subset I\setminus E_{W'}$
. Furthermore, similarly to the arguments of the previous paragraph, we may conclude that there exist infinitely many
$\operatorname {\mathrm {{supp}}}(f_{W'}+\psi (f_{W'}))=\{t',t\}\subset I\setminus E_{W'}$
. Furthermore, similarly to the arguments of the previous paragraph, we may conclude that there exist infinitely many
![]() $g_{W'}\in W'$
such that
$g_{W'}\in W'$
such that
![]() $\operatorname {\mathrm {{supp}}}(g_{W'})\in [I\setminus E_{W'}]^{2}$
and
$\operatorname {\mathrm {{supp}}}(g_{W'})\in [I\setminus E_{W'}]^{2}$
and
![]() $\max (\operatorname {\mathrm {{supp}}}(g_{W'}))<t'$
, and infinitely many
$\max (\operatorname {\mathrm {{supp}}}(g_{W'}))<t'$
, and infinitely many
![]() $h_{W'}\in W'$
such that
$h_{W'}\in W'$
such that
![]() $\operatorname {\mathrm {{supp}}}(h_{W'})\in [I\setminus E_{W'}]^{2}$
and
$\operatorname {\mathrm {{supp}}}(h_{W'})\in [I\setminus E_{W'}]^{2}$
and
![]() $t<\min (\operatorname {\mathrm {{supp}}}(h_{W'}))$
. Hence, we have:
$t<\min (\operatorname {\mathrm {{supp}}}(h_{W'}))$
. Hence, we have:
Since
![]() $W\cap W'$
is finite and the sets of functions
$W\cap W'$
is finite and the sets of functions
![]() $h_{W}$
and of
$h_{W}$
and of
![]() $h_{W'}$
are infinite subsets of W and
$h_{W'}$
are infinite subsets of W and
![]() $W'$
, respectively, we may pick an
$W'$
, respectively, we may pick an
![]() $h_{W}\in W\setminus W'$
and an
$h_{W}\in W\setminus W'$
and an
![]() $h_{W'}\in W'\setminus W$
(and thus
$h_{W'}\in W'\setminus W$
(and thus
![]() $h_{W}\neq h_{W'}$
).
$h_{W}\neq h_{W'}$
).
There are the following cases:
-
(i)
 $\min (\operatorname {\mathrm {{supp}}}(h_{W}))\leq \min (\operatorname {\mathrm {{supp}}}(h_{W'}))$
.Footnote
4
In view of (4), we may construct an
$\min (\operatorname {\mathrm {{supp}}}(h_{W}))\leq \min (\operatorname {\mathrm {{supp}}}(h_{W'}))$
.Footnote
4
In view of (4), we may construct an
 $\eta \in \operatorname {\mathrm {{fix}}}_{G}(E)$
such that
$\eta \in \operatorname {\mathrm {{fix}}}_{G}(E)$
such that
 $\eta (h_{W})=h_{W'}$
and
$\eta (h_{W})=h_{W'}$
and
 $\eta $
fixes each of the elements
$\eta $
fixes each of the elements
 $g_{W}$
of W, which are infinitely many. Since
$g_{W}$
of W, which are infinitely many. Since
 $h_{W'}=\eta (h_{W})\in \eta (W)$
and
$h_{W'}=\eta (h_{W})\in \eta (W)$
and
 $h_{W'}\not \in W$
, we obtain that
$h_{W'}\not \in W$
, we obtain that
 $\eta (W)\neq W$
. Furthermore, as
$\eta (W)\neq W$
. Furthermore, as
 $W\in \mathcal {W}$
, E is a support of
$W\in \mathcal {W}$
, E is a support of
 $\mathcal {W}$
and
$\mathcal {W}$
and
 $\eta \in \operatorname {\mathrm {{fix}}}_{G}(E)$
, we have
$\eta \in \operatorname {\mathrm {{fix}}}_{G}(E)$
, we have
 $\eta (W)\in \eta (\mathcal {W})=\mathcal {W}$
. Since
$\eta (W)\in \eta (\mathcal {W})=\mathcal {W}$
. Since
 $\eta $
fixes an infinite subset of W pointwise, namely the set of the functions
$\eta $
fixes an infinite subset of W pointwise, namely the set of the functions
 $g_{W}$
, we deduce that
$g_{W}$
, we deduce that
 $\eta (W)\cap W$
is infinite. But this contradicts the fact that
$\eta (W)\cap W$
is infinite. But this contradicts the fact that
 $\mathcal {W}$
is almost disjoint in V.
$\mathcal {W}$
is almost disjoint in V. -
(ii)
 $\min (\operatorname {\mathrm {{supp}}}(h_{W'}))<\min (\operatorname {\mathrm {{supp}}}(h_{W}))$
. In view of (5), we may construct a
$\min (\operatorname {\mathrm {{supp}}}(h_{W'}))<\min (\operatorname {\mathrm {{supp}}}(h_{W}))$
. In view of (5), we may construct a
 $\sigma \in \operatorname {\mathrm {{fix}}}_{G}(E)$
such that
$\sigma \in \operatorname {\mathrm {{fix}}}_{G}(E)$
such that
 $\sigma (h_{W'})=h_{W}$
and
$\sigma (h_{W'})=h_{W}$
and
 $\sigma $
fixes each of the elements
$\sigma $
fixes each of the elements
 $g_{W'}$
of
$g_{W'}$
of
 $W'$
, which are infinitely many. Working similarly to (i), we infer that
$W'$
, which are infinitely many. Working similarly to (i), we infer that
 $\sigma (W')\neq W'$
,
$\sigma (W')\neq W'$
,
 $\sigma (W')\in \mathcal {W}$
, and
$\sigma (W')\in \mathcal {W}$
, and
 $\sigma (W')\cap W'$
is infinite; thus contradicting
$\sigma (W')\cap W'$
is infinite; thus contradicting
 $\mathcal {W}$
’s being almost disjoint in V.
$\mathcal {W}$
’s being almost disjoint in V.
By the above arguments, we conclude that the vector space V has no infinite AD1 family in the model
![]() $\mathcal {N}3$
, as asserted.
$\mathcal {N}3$
, as asserted.
Now, we refer the reader to Pincus [Reference Pincus12] or [Reference Pincus13] (or to Howard–Rubin [Reference Howard and Rubin3, Note 103, pp. 284–285]) for the definition of the terms “boundable statement” and “injectively boundable statement.” To transfer the above result to
![]() $\mathsf {ZF}$
, we will apply the following transfer theorem of Pincus (see [Reference Pincus13, Theorem 4 and note added in proof]): “If a conjunction of injectively boundable statements and
$\mathsf {ZF}$
, we will apply the following transfer theorem of Pincus (see [Reference Pincus13, Theorem 4 and note added in proof]): “If a conjunction of injectively boundable statements and
![]() $\mathsf {BPI}$
has a Fraenkel–Mostowski model, then it also has a
$\mathsf {BPI}$
has a Fraenkel–Mostowski model, then it also has a
![]() $\mathsf {ZF}$
-model.”
$\mathsf {ZF}$
-model.”
It is easy to see that
![]() $\Psi =$
“There exists an infinite-dimensional vector space which has no infinite AD1 family” is a boundable statement, and thus
$\Psi =$
“There exists an infinite-dimensional vector space which has no infinite AD1 family” is a boundable statement, and thus
![]() $\Psi $
is injectively boundable (boundable statements are (up to equivalence) injectively boundable, see Pincus [Reference Pincus12, p. 722]). Letting
$\Psi $
is injectively boundable (boundable statements are (up to equivalence) injectively boundable, see Pincus [Reference Pincus12, p. 722]). Letting
![]() $\Phi =\mathsf {BPI}\wedge \Psi $
, we have that
$\Phi =\mathsf {BPI}\wedge \Psi $
, we have that
![]() $\Phi $
satisfies the hypotheses of [Reference Pincus13, Theorem 4] stated above, and thus
$\Phi $
satisfies the hypotheses of [Reference Pincus13, Theorem 4] stated above, and thus
![]() $\Phi $
has a
$\Phi $
has a
![]() $\mathsf {ZF}$
-model. This completes the proof of the theorem.⊣
$\mathsf {ZF}$
-model. This completes the proof of the theorem.⊣
Theorem 4.10.
![]() $(\mathsf {ZFA})\ \mathsf {MC}$
implies “For every field F and for every infinite-dimensional vector space V over F, every AD1 family of infinite-dimensional subspaces of V can be extended to a MAD1 family in V.” Hence, the latter statement does not imply
$(\mathsf {ZFA})\ \mathsf {MC}$
implies “For every field F and for every infinite-dimensional vector space V over F, every AD1 family of infinite-dimensional subspaces of V can be extended to a MAD1 family in V.” Hence, the latter statement does not imply
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZFA}$
.
$\mathsf {ZFA}$
.
Proof. Assume the hypothesis. Let V be an infinite-dimensional vector space over a field F, and let
![]() $\mathcal {A}$
be an AD1 family in V. Assume that
$\mathcal {A}$
be an AD1 family in V. Assume that
![]() $\mathcal {A}$
is not MAD1 (otherwise, there is nothing to show). By
$\mathcal {A}$
is not MAD1 (otherwise, there is nothing to show). By
![]() $\mathsf {MC}$
, let f be a multiple choice function for
$\mathsf {MC}$
, let f be a multiple choice function for
![]() $\wp (\wp (V))\setminus \{\emptyset \}$
.
$\wp (\wp (V))\setminus \{\emptyset \}$
.
By transfinite recursion, we will construct a MAD1 family in V which contains
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
Since
![]() $\mathcal {A}$
is not maximal,
$\mathcal {A}$
is not maximal,
![]() $\mathcal {R}_{0}\neq \emptyset $
. We let
$\mathcal {R}_{0}\neq \emptyset $
. We let
and
The family
![]() $\mathcal {A}_{0}$
has the following properties:
$\mathcal {A}_{0}$
has the following properties:
(a)
![]() $\mathcal {A}\subsetneq \mathcal {A}_{0}$
. Indeed, pick any element T of
$\mathcal {A}\subsetneq \mathcal {A}_{0}$
. Indeed, pick any element T of
![]() $\mathcal {T}_{0}$
. Then
$\mathcal {T}_{0}$
. Then
![]() $T=\bigcap \mathcal {U}$
for some
$T=\bigcap \mathcal {U}$
for some
![]() $\mathcal {U}\in \mathcal {S}_{0}$
. We assert that
$\mathcal {U}\in \mathcal {S}_{0}$
. We assert that
![]() $T\not \in \mathcal {A}$
. If not (i.e., if
$T\not \in \mathcal {A}$
. If not (i.e., if
![]() $T\in \mathcal {A}$
), then we choose any element Z of
$T\in \mathcal {A}$
), then we choose any element Z of
![]() $\mathcal {U}$
. Since
$\mathcal {U}$
. Since
![]() $Z\in \mathcal {R}_{0}$
(for
$Z\in \mathcal {R}_{0}$
(for
![]() $Z\in f(\mathcal {R}_{0})\subseteq \mathcal {R}_{0}$
), we have that
$Z\in f(\mathcal {R}_{0})\subseteq \mathcal {R}_{0}$
), we have that
![]() $\mathcal {A}\cup \{Z\}$
is AD1. However,
$\mathcal {A}\cup \{Z\}$
is AD1. However,
![]() $T\cap Z=(\bigcap \mathcal {U})\cap Z=\bigcap \mathcal {U}$
(for
$T\cap Z=(\bigcap \mathcal {U})\cap Z=\bigcap \mathcal {U}$
(for
![]() $Z\in \mathcal {U}$
). Since
$Z\in \mathcal {U}$
). Since
![]() $\bigcap \mathcal {U}$
is infinite-dimensional, we have obtained a contradiction to the fact that
$\bigcap \mathcal {U}$
is infinite-dimensional, we have obtained a contradiction to the fact that
![]() $\mathcal {A}\cup \{Z\}$
is AD1. Therefore,
$\mathcal {A}\cup \{Z\}$
is AD1. Therefore,
![]() $T\in \mathcal {A}_{0}\setminus \mathcal {A}$
, and thus
$T\in \mathcal {A}_{0}\setminus \mathcal {A}$
, and thus
![]() $\mathcal {A}\subsetneq \mathcal {A}_{0}$
.
$\mathcal {A}\subsetneq \mathcal {A}_{0}$
.
(b)
![]() $\mathcal {A}_{0}$
is AD1. Let
$\mathcal {A}_{0}$
is AD1. Let
![]() $U,W\in \mathcal {A}_{0}$
with
$U,W\in \mathcal {A}_{0}$
with
![]() $U\ne W$
. There are the following cases:
$U\ne W$
. There are the following cases:
(b1)
![]() $U,W\in \mathcal {A}$
. Then
$U,W\in \mathcal {A}$
. Then
![]() $U\cap W$
is finite-dimensional since
$U\cap W$
is finite-dimensional since
![]() $\mathcal {A}$
is AD1.
$\mathcal {A}$
is AD1.
(b2)
![]() $U,W\in \mathcal {T}_{0}$
. Then
$U,W\in \mathcal {T}_{0}$
. Then
![]() $U=\bigcap \mathcal {U}$
and
$U=\bigcap \mathcal {U}$
and
![]() $W=\bigcap \mathcal {U}'$
for some
$W=\bigcap \mathcal {U}'$
for some
![]() $\mathcal {U},\mathcal {U}'\in \mathcal {S}_{0}$
. Since
$\mathcal {U},\mathcal {U}'\in \mathcal {S}_{0}$
. Since
![]() $U\neq W$
, we have
$U\neq W$
, we have
![]() $\mathcal {U}\neq \mathcal {U}'$
so
$\mathcal {U}\neq \mathcal {U}'$
so
![]() $\mathcal {U}\not \subseteq \mathcal {U}'$
and
$\mathcal {U}\not \subseteq \mathcal {U}'$
and
![]() $\mathcal {U}'\not \subseteq \mathcal {U}$
, for
$\mathcal {U}'\not \subseteq \mathcal {U}$
, for
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {U}'$
are maximal subsets of
$\mathcal {U}'$
are maximal subsets of
![]() $f(\mathcal {R}_{0})$
such that
$f(\mathcal {R}_{0})$
such that
![]() $\bigcap \mathcal {U}$
and
$\bigcap \mathcal {U}$
and
![]() $\bigcap \mathcal {U}'$
are infinite-dimensional. It follows that
$\bigcap \mathcal {U}'$
are infinite-dimensional. It follows that
![]() $\mathcal {U},\mathcal {U}'\subsetneq \mathcal {U}\cup \mathcal {U}'$
, so
$\mathcal {U},\mathcal {U}'\subsetneq \mathcal {U}\cup \mathcal {U}'$
, so
![]() $\bigcap (\mathcal {U}\cup \mathcal {U}')=(\bigcap \mathcal {U})\cap (\bigcap \mathcal {U}')=U\cap W$
is finite-dimensional.
$\bigcap (\mathcal {U}\cup \mathcal {U}')=(\bigcap \mathcal {U})\cap (\bigcap \mathcal {U}')=U\cap W$
is finite-dimensional.
(b3)
![]() $U\in \mathcal {A}$
,
$U\in \mathcal {A}$
,
![]() $W\in \mathcal {T}_{0}$
. There exists
$W\in \mathcal {T}_{0}$
. There exists
![]() $\mathcal {U}\in \mathcal {S}_{0}$
such that
$\mathcal {U}\in \mathcal {S}_{0}$
such that
![]() $W=\bigcap \mathcal {U}$
. Pick any element Z of
$W=\bigcap \mathcal {U}$
. Pick any element Z of
![]() $\mathcal {U}$
. Then
$\mathcal {U}$
. Then
![]() $U\cap Z$
is finite-dimensional, for
$U\cap Z$
is finite-dimensional, for
![]() $U\in \mathcal {A}$
and
$U\in \mathcal {A}$
and
![]() $\mathcal {A}\cup \{Z\}$
is AD1. Since
$\mathcal {A}\cup \{Z\}$
is AD1. Since
![]() $U\cap W\subseteq U\cap Z$
, we have that
$U\cap W\subseteq U\cap Z$
, we have that
![]() $U\cap W$
is finite-dimensional.
$U\cap W$
is finite-dimensional.
(b4)
![]() $U\in \mathcal {T}_{0}$
,
$U\in \mathcal {T}_{0}$
,
![]() $W\in \mathcal {A}$
. Similarly to (b3), we conclude that
$W\in \mathcal {A}$
. Similarly to (b3), we conclude that
![]() $U\cap W$
is finite-dimensional.
$U\cap W$
is finite-dimensional.
Hence,
![]() $\mathcal {A}_{0}$
is AD1.
$\mathcal {A}_{0}$
is AD1.
We assume that for some ordinal number
![]() $\alpha $
we have constructed an
$\alpha $
we have constructed an
![]() $\subseteq $
-increasing sequence
$\subseteq $
-increasing sequence
![]() $(\mathcal {A}_{\beta })_{\beta <\alpha }$
of AD1 families in V such that
$(\mathcal {A}_{\beta })_{\beta <\alpha }$
of AD1 families in V such that
![]() $\mathcal {A}\subsetneq \mathcal {A}_{0}$
. Let
$\mathcal {A}\subsetneq \mathcal {A}_{0}$
. Let
and also let
Since
![]() $(\mathcal {A}_{\beta })_{\beta <\alpha }$
is a chain of AD1 families,
$(\mathcal {A}_{\beta })_{\beta <\alpha }$
is a chain of AD1 families,
![]() $\mathcal {B}_{\alpha }$
is AD1. If
$\mathcal {B}_{\alpha }$
is AD1. If
![]() $\mathcal {R}_{\alpha }=\emptyset $
, then
$\mathcal {R}_{\alpha }=\emptyset $
, then
![]() $\mathcal {B}_{\alpha }$
is a MAD1 family in V which contains
$\mathcal {B}_{\alpha }$
is a MAD1 family in V which contains
![]() $\mathcal {A}$
, and we are done. Otherwise, (that is, if
$\mathcal {A}$
, and we are done. Otherwise, (that is, if
![]() $\mathcal {R}_{\alpha }\ne \emptyset $
), we define
$\mathcal {R}_{\alpha }\ne \emptyset $
), we define
 $$ \begin{align*}\mathcal{A}_{\alpha}=\mathcal{B}_{\alpha}\cup & \Big\{\bigcap\mathcal{U}:\mathcal{U}\text{ is a}\ \subseteq\text{-maximal subset of}\ f(\mathcal{R}_{\alpha})\ \text{such that}\\ & \quad \bigcap\mathcal{U}\ \text{is infinite-dimensional}\Big\}. \end{align*} $$
$$ \begin{align*}\mathcal{A}_{\alpha}=\mathcal{B}_{\alpha}\cup & \Big\{\bigcap\mathcal{U}:\mathcal{U}\text{ is a}\ \subseteq\text{-maximal subset of}\ f(\mathcal{R}_{\alpha})\ \text{such that}\\ & \quad \bigcap\mathcal{U}\ \text{is infinite-dimensional}\Big\}. \end{align*} $$
Since
![]() $\mathsf {Ord}$
(i.e., the class of all ordinal numbers) is a proper class, the recursion must terminate at some ordinal stage. By the above construction, the ending of the recursion yields a MAD1 family in V which contains
$\mathsf {Ord}$
(i.e., the class of all ordinal numbers) is a proper class, the recursion must terminate at some ordinal stage. By the above construction, the ending of the recursion yields a MAD1 family in V which contains
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
The second assertion of the theorem follows from the first and the fact that
![]() $\mathsf {MC}$
does not imply
$\mathsf {MC}$
does not imply
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZFA}$
(see [Reference Jech7, Theorem 9.2(i)]). This completes the proof of the theorem.⊣
$\mathsf {ZFA}$
(see [Reference Jech7, Theorem 9.2(i)]). This completes the proof of the theorem.⊣
In the next theorem, we show that
![]() $\mathsf {AC^{LO}}$
does not imply “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” in
$\mathsf {AC^{LO}}$
does not imply “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” in
![]() $\mathsf {ZFA}$
. Hence, neither
$\mathsf {ZFA}$
. Hence, neither
![]() $\mathsf {LW}$
nor
$\mathsf {LW}$
nor
![]() $\mathsf {AC^{WO}}$
imply the above algebraic proposition in
$\mathsf {AC^{WO}}$
imply the above algebraic proposition in
![]() $\mathsf {ZFA}$
(see also Remark 2.8). We also recall here that
$\mathsf {ZFA}$
(see also Remark 2.8). We also recall here that
![]() $\mathsf {AC^{LO}}$
(and hence
$\mathsf {AC^{LO}}$
(and hence
![]() $\mathsf {LW}$
) is equivalent to
$\mathsf {LW}$
) is equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Thus Theorem 4.11, on the one hand, justifies that the above proposition cannot be proved from the
![]() $\mathsf {ZF}$
axioms alone, and on the other hand, it indicates that this proposition is actually a strong axiom. The latter fact is also suggested by the forthcoming Theorem 4.13.
$\mathsf {ZF}$
axioms alone, and on the other hand, it indicates that this proposition is actually a strong axiom. The latter fact is also suggested by the forthcoming Theorem 4.13.
Theorem 4.11.
![]() $\mathsf {AC^{LO}}$
does not imply “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” in
$\mathsf {AC^{LO}}$
does not imply “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” in
![]() $\mathsf {ZFA}$
. Hence, neither
$\mathsf {ZFA}$
. Hence, neither
![]() $\mathsf {LW}$
nor
$\mathsf {LW}$
nor
![]() $\mathsf {AC^{WO}}$
imply the above proposition in
$\mathsf {AC^{WO}}$
imply the above proposition in
![]() $\mathsf {ZFA}$
. Furthermore, the above proposition is not provable in
$\mathsf {ZFA}$
. Furthermore, the above proposition is not provable in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. We will use a permutation model which was constructed by Howard and Tachtsis [Reference Howard and Tachtsis4], and whose description is as follows: We start with a model M of
![]() $\mathsf {ZFA}$
+
$\mathsf {ZFA}$
+
![]() $\mathsf {AC}$
with an
$\mathsf {AC}$
with an
![]() $\aleph _1$
-sized set A of atoms, which is a disjoint, denumerable union of
$\aleph _1$
-sized set A of atoms, which is a disjoint, denumerable union of
![]() $\aleph _1$
-sized sets so that
$\aleph _1$
-sized sets so that
Let G be the group of all permutations of A, which fix
![]() $A_i$
for all
$A_i$
for all
![]() $i\in \omega $
. Note that any element of G also fixes the bijection
$i\in \omega $
. Note that any element of G also fixes the bijection
![]() $i\mapsto A_{i}$
, and hence fixes the ordered partition
$i\mapsto A_{i}$
, and hence fixes the ordered partition
![]() $(A_{i})_{i\in \omega }$
of A. (And also note that for every
$(A_{i})_{i\in \omega }$
of A. (And also note that for every
![]() $i\in \omega $
and every permutation
$i\in \omega $
and every permutation
![]() $\phi $
of A (not necessarily in G),
$\phi $
of A (not necessarily in G),
![]() $\phi (i)=i$
since the natural numbers are pure sets (i.e., their transitive closure contains no atoms) and pure sets are fixed by any permutation of A.) Let
$\phi (i)=i$
since the natural numbers are pure sets (i.e., their transitive closure contains no atoms) and pure sets are fixed by any permutation of A.) Let
![]() $\mathcal {F}$
be the (normal) filter of subgroups of G generated by the subgroups
$\mathcal {F}$
be the (normal) filter of subgroups of G generated by the subgroups
![]() $\operatorname {\mathrm {{fix}}}_G(E)$
, where
$\operatorname {\mathrm {{fix}}}_G(E)$
, where
![]() $E\subset A$
and
$E\subset A$
and
![]() $|E|<\aleph _1$
. Let
$|E|<\aleph _1$
. Let
![]() $\mathcal {N}$
be the Fraenkel–Mostowski model determined by M, G and
$\mathcal {N}$
be the Fraenkel–Mostowski model determined by M, G and
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
In [Reference Howard and Tachtsis4, proof B of Theorem 2], it was shown that each of
![]() $\mathsf {LW}$
and
$\mathsf {LW}$
and
![]() $\mathsf {AC^{LO}}$
(and hence
$\mathsf {AC^{LO}}$
(and hence
![]() $\mathsf {AC^{WO}}$
) are true in
$\mathsf {AC^{WO}}$
) are true in
![]() $\mathcal {N}$
. Therefore, it suffices to show that in
$\mathcal {N}$
. Therefore, it suffices to show that in
![]() $\mathcal {N}$
, there exists an infinite-dimensional vector space over some field which has an AD1 family in
$\mathcal {N}$
, there exists an infinite-dimensional vector space over some field which has an AD1 family in
![]() $\mathcal {N}$
that cannot be extended to a MAD1 family in
$\mathcal {N}$
that cannot be extended to a MAD1 family in
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
To this end, we consider the following infinite-dimensional vector space V over
![]() $\mathbb {Z}_{2}$
,
$\mathbb {Z}_{2}$
,
where V is equipped with pointwise operations. Then
![]() $(V,+,\cdot )\in \mathcal {N}$
(for
$(V,+,\cdot )\in \mathcal {N}$
(for
![]() $(V,+,\cdot )$
is fixed by every permutation of A in G). For each
$(V,+,\cdot )$
is fixed by every permutation of A in G). For each
![]() $n\in \omega $
, consider the infinite-dimensional vector subspace of V,
$n\in \omega $
, consider the infinite-dimensional vector subspace of V,
Let
![]() $\mathcal {V}$
is an AD1 family in V which belongs to the model
$\mathcal {V}$
is an AD1 family in V which belongs to the model
![]() $\mathcal {N}$
(any element of G fixes
$\mathcal {N}$
(any element of G fixes
![]() $\mathcal {V}$
pointwise, so
$\mathcal {V}$
pointwise, so
![]() $\mathcal {V}$
is also denumerable in
$\mathcal {V}$
is also denumerable in
![]() $\mathcal {N}$
).
$\mathcal {N}$
).
![]() $\mathcal {V}$
is not MAD1 in
$\mathcal {V}$
is not MAD1 in
![]() $\mathcal {N}$
. Indeed, let H be a choice function for
$\mathcal {N}$
. Indeed, let H be a choice function for
![]() $\mathcal {A}=\{A_{n}:n\in \omega \}$
. (Note that by definition of the filter
$\mathcal {A}=\{A_{n}:n\in \omega \}$
. (Note that by definition of the filter
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\operatorname {\mathrm {{ran}}}(H)$
is a support of (every element of) H, and hence
$\operatorname {\mathrm {{ran}}}(H)$
is a support of (every element of) H, and hence
![]() $H\in \mathcal {N}$
.) Let
$H\in \mathcal {N}$
.) Let
![]() $W={\langle }\{F_{n}:n\in \omega \}{\rangle }$
, where for
$W={\langle }\{F_{n}:n\in \omega \}{\rangle }$
, where for
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $F_{n}\upharpoonright A_{m}=0$
(the zero function) for
$F_{n}\upharpoonright A_{m}=0$
(the zero function) for
![]() $m\in \omega \setminus \{n\}$
, and
$m\in \omega \setminus \{n\}$
, and
![]() $F_{n}\upharpoonright A_{n}=\chi _{\{H(n)\}}$
. Then W is an infinite-dimensional subspace of V such that
$F_{n}\upharpoonright A_{n}=\chi _{\{H(n)\}}$
. Then W is an infinite-dimensional subspace of V such that
![]() $W\not \in \mathcal {V}$
and
$W\not \in \mathcal {V}$
and
![]() $\mathcal {V}\cup \{W\}$
is AD1 in
$\mathcal {V}\cup \{W\}$
is AD1 in
![]() $\mathcal {N}$
.⊣
$\mathcal {N}$
.⊣
Claim 4.12. There is no MAD1 family in
![]() $\mathcal {N}$
containing
$\mathcal {N}$
containing
![]() $\mathcal {V}$
.
$\mathcal {V}$
.
Proof. We prove the claim by contradiction. Let
![]() $\mathcal {M}$
be a MAD1 family in
$\mathcal {M}$
be a MAD1 family in
![]() $\mathcal {N}$
which contains
$\mathcal {N}$
which contains
![]() $\mathcal {V}$
(and thus, by the observations in the previous paragraph,
$\mathcal {V}$
(and thus, by the observations in the previous paragraph,
![]() $\mathcal {V}\subsetneq \mathcal {M}$
), and also let
$\mathcal {V}\subsetneq \mathcal {M}$
), and also let
![]() $E\subset A$
be a support of
$E\subset A$
be a support of
![]() $\mathcal {M}$
. We assert the following:
$\mathcal {M}$
. We assert the following:
If not, then there exist
![]() $Z\in \mathcal {M}\setminus \mathcal {V}$
,
$Z\in \mathcal {M}\setminus \mathcal {V}$
,
![]() $f\in Z$
,
$f\in Z$
,
![]() $n\in \omega $
, and
$n\in \omega $
, and
![]() $a\in \operatorname {\mathrm {{supp}}}(f\upharpoonright A_{n})\setminus (E\cap A_{n})$
.
$a\in \operatorname {\mathrm {{supp}}}(f\upharpoonright A_{n})\setminus (E\cap A_{n})$
.
Since
![]() $Z\cap V_{n}$
is finite-dimensional (actually,
$Z\cap V_{n}$
is finite-dimensional (actually,
![]() $Z\cap V_{n}$
is finite since it is a finite-dimensional space over
$Z\cap V_{n}$
is finite since it is a finite-dimensional space over
![]() $\mathbb {Z}_{2}$
) and any support of Z meets
$\mathbb {Z}_{2}$
) and any support of Z meets
![]() $A_n$
in a countable set, there exists
$A_n$
in a countable set, there exists
![]() $b\in A_{n}\setminus \{a\}$
such that for every
$b\in A_{n}\setminus \{a\}$
such that for every
![]() $g\in Z$
,
$g\in Z$
,
![]() $b\not \in \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n})$
. If not, i.e., if for every
$b\not \in \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n})$
. If not, i.e., if for every
![]() $b\in A_{n}\setminus \{a\}$
there exists
$b\in A_{n}\setminus \{a\}$
there exists
![]() $g\in Z$
with
$g\in Z$
with
![]() $b\in \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n})$
, then let
$b\in \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n})$
, then let
![]() $E_{Z}$
be a support of Z. (So
$E_{Z}$
be a support of Z. (So
![]() $E_{Z}\cap A_{n}$
is countable.) Fix
$E_{Z}\cap A_{n}$
is countable.) Fix
![]() $c\in R$
, where
$c\in R$
, where
![]() $R=A_{n}\setminus [(\operatorname {\mathrm {{supp}}}({f\upharpoonright A_{n}})\cup E\cup E_{Z}]$
, and let
$R=A_{n}\setminus [(\operatorname {\mathrm {{supp}}}({f\upharpoonright A_{n}})\cup E\cup E_{Z}]$
, and let
![]() $g\in Z$
such that
$g\in Z$
such that
![]() $c\in \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n})$
. For every
$c\in \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n})$
. For every
![]() $r\in R\setminus (\{c\}\cup \operatorname {\mathrm {{supp}}}(g)\})$
, let
$r\in R\setminus (\{c\}\cup \operatorname {\mathrm {{supp}}}(g)\})$
, let
![]() $\phi _{r}=(c,r)$
(i.e.,
$\phi _{r}=(c,r)$
(i.e.,
![]() $\phi _{r}$
interchanges the atoms c and r and leaves all the other atoms of A fixed). Then
$\phi _{r}$
interchanges the atoms c and r and leaves all the other atoms of A fixed). Then
![]() $S=\{\phi _{r}(g):r\in R\setminus (\{c\}\cup \operatorname {\mathrm {{supp}}}(g)\})\}$
is an infinite, linearly independent subset of Z (since
$S=\{\phi _{r}(g):r\in R\setminus (\{c\}\cup \operatorname {\mathrm {{supp}}}(g)\})\}$
is an infinite, linearly independent subset of Z (since
![]() $\phi _r\in \operatorname {\mathrm {{fix}}}_{G}(E_Z)$
and
$\phi _r\in \operatorname {\mathrm {{fix}}}_{G}(E_Z)$
and
![]() $g\in Z$
), and thus
$g\in Z$
), and thus
![]() $\{\sum _{x\in F}x:F\in [S]^{<\omega }\}$
is an infinite, linearly independent subset of
$\{\sum _{x\in F}x:F\in [S]^{<\omega }\}$
is an infinite, linearly independent subset of
![]() $Z\cap V_{n}$
. But this contradicts
$Z\cap V_{n}$
. But this contradicts
![]() $Z\cap V_{n}$
’s being finite-dimensional.
$Z\cap V_{n}$
’s being finite-dimensional.
Let
![]() $\pi =(a,b)$
, where (by the above argument)
$\pi =(a,b)$
, where (by the above argument)
![]() $b\in A_{n}\setminus (\{a\}\cup \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n}))$
for all
$b\in A_{n}\setminus (\{a\}\cup \operatorname {\mathrm {{supp}}}(g\upharpoonright A_{n}))$
for all
![]() $g\in Z$
. Then
$g\in Z$
. Then
![]() $\pi \in \operatorname {\mathrm {{fix}}}_{G}(E)$
, and hence
$\pi \in \operatorname {\mathrm {{fix}}}_{G}(E)$
, and hence
![]() $\pi (\mathcal {M})=\mathcal {M}$
. Thus
$\pi (\mathcal {M})=\mathcal {M}$
. Thus
![]() $\pi (Z)\in \mathcal {M}$
(and also
$\pi (Z)\in \mathcal {M}$
(and also
![]() $\pi (Z)\not \in \mathcal {V}$
), and furthermore,
$\pi (Z)\not \in \mathcal {V}$
), and furthermore,
![]() $\pi (Z)\ne Z$
(for
$\pi (Z)\ne Z$
(for
![]() $\pi (f)\in \pi (Z)\setminus Z$
, since
$\pi (f)\in \pi (Z)\setminus Z$
, since
![]() $f\in Z$
and
$f\in Z$
and
![]() $b\in \operatorname {\mathrm {{supp}}}(\pi (f)\upharpoonright A_{n})$
).
$b\in \operatorname {\mathrm {{supp}}}(\pi (f)\upharpoonright A_{n})$
).
Since Z is not included in any finite sum of the
![]() $V_{i}$
’s, and
$V_{i}$
’s, and
![]() $Z\cap V_{i}$
is finite-dimensional for all
$Z\cap V_{i}$
is finite-dimensional for all
![]() $i\in \omega $
, it is not hard to verify that
$i\in \omega $
, it is not hard to verify that
![]() $\pi (Z)\cap Z$
contains an infinite linearly independent subset. But this contradicts the fact that
$\pi (Z)\cap Z$
contains an infinite linearly independent subset. But this contradicts the fact that
![]() $\mathcal {M}$
is AD1. Thus (6) is true as asserted.
$\mathcal {M}$
is AD1. Thus (6) is true as asserted.
On the basis of (6), and working similarly to the argument that
![]() $\mathcal {V}$
is not MAD1 in
$\mathcal {V}$
is not MAD1 in
![]() $\mathcal {N}$
, we may show that neither
$\mathcal {N}$
, we may show that neither
![]() $\mathcal {M}$
is MAD1 in
$\mathcal {M}$
is MAD1 in
![]() $\mathcal {N}$
. But this contradicts our assumption on
$\mathcal {N}$
. But this contradicts our assumption on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Thus the AD1 family
![]() $\mathcal {V}$
cannot be extended to a MAD1 family in the model
$\mathcal {V}$
cannot be extended to a MAD1 family in the model
![]() $\mathcal {N}$
, finishing the proof of the claim.⊣
$\mathcal {N}$
, finishing the proof of the claim.⊣
For the last assertion of the theorem (i.e., nonprovability of the algebraic statement in
![]() $\mathsf {ZF}$
), note that since the negation of “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” is a boundable statement, and has a
$\mathsf {ZF}$
), note that since the negation of “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” is a boundable statement, and has a
![]() $\mathsf {ZFA}$
-model, it follows from the Jech–Sochor First Embedding Theorem (see [Reference Jech7, Theorem 6.1 and Problem 1 (p. 94)]) that it has a (symmetric)
$\mathsf {ZFA}$
-model, it follows from the Jech–Sochor First Embedding Theorem (see [Reference Jech7, Theorem 6.1 and Problem 1 (p. 94)]) that it has a (symmetric)
![]() $\mathsf {ZF}$
-model. This completes the proof of the theorem.⊣
$\mathsf {ZF}$
-model. This completes the proof of the theorem.⊣
We note that the model
![]() $\mathcal {N}$
of the proof of Theorem 4.11 is actually an element of a class of permutation models. Indeed, for any uncountable regular cardinal
$\mathcal {N}$
of the proof of Theorem 4.11 is actually an element of a class of permutation models. Indeed, for any uncountable regular cardinal
![]() $\aleph _{\alpha }$
, we may construct a Fraenkel–Mostowski model
$\aleph _{\alpha }$
, we may construct a Fraenkel–Mostowski model
![]() $\mathcal {N}_{\aleph _{\alpha }}$
by taking: (a) an
$\mathcal {N}_{\aleph _{\alpha }}$
by taking: (a) an
![]() $\aleph _{\alpha }$
-sized set A of atoms, which is a disjoint, denumerable union of
$\aleph _{\alpha }$
-sized set A of atoms, which is a disjoint, denumerable union of
![]() $\aleph _\alpha $
-sized sets so that
$\aleph _\alpha $
-sized sets so that
![]() $A=\bigcup \{A_i:i\in \omega \}$
,
$A=\bigcup \{A_i:i\in \omega \}$
,
![]() $|A_{i}|=\aleph _{\alpha }$
; (b) G to be the group of all permutations of A, which fix
$|A_{i}|=\aleph _{\alpha }$
; (b) G to be the group of all permutations of A, which fix
![]() $A_i$
for all
$A_i$
for all
![]() $i\in \omega $
; and (c)
$i\in \omega $
; and (c)
![]() $\mathcal {F}$
to be the (normal) filter of subgroups of G generated by the subgroups
$\mathcal {F}$
to be the (normal) filter of subgroups of G generated by the subgroups
![]() $\operatorname {\mathrm {{fix}}}_G(E)$
, where
$\operatorname {\mathrm {{fix}}}_G(E)$
, where
![]() $E\subset A$
and
$E\subset A$
and
![]() $|E|<\aleph _\alpha $
.
$|E|<\aleph _\alpha $
.
Now, in each of the models
![]() $\mathcal {N}_{\aleph _{\alpha }}$
,
$\mathcal {N}_{\aleph _{\alpha }}$
,
![]() $\mathsf {DC}_{\lambda }$
is true for every infinite cardinal
$\mathsf {DC}_{\lambda }$
is true for every infinite cardinal
![]() $\lambda <\aleph _{\alpha }$
(see also [Reference Jech7, Lemma 8.4, p. 123]), and in much the same way as the proof of Theorem 4.11, the statement “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” is false in
$\lambda <\aleph _{\alpha }$
(see also [Reference Jech7, Lemma 8.4, p. 123]), and in much the same way as the proof of Theorem 4.11, the statement “In every infinite-dimensional vector space V, every AD1 family in V can be extended to a MAD1 family” is false in
![]() $\mathcal {N}_{\aleph _{\alpha }}$
. Furthermore, by applying the following transfer theorem of Pincus (see [Reference Pincus13, Theorem 4]): “For every ordinal
$\mathcal {N}_{\aleph _{\alpha }}$
. Furthermore, by applying the following transfer theorem of Pincus (see [Reference Pincus13, Theorem 4]): “For every ordinal
![]() $\eta $
, if
$\eta $
, if
![]() $\Phi $
is a conjunction of injectively boundable statements and “
$\Phi $
is a conjunction of injectively boundable statements and “
![]() $\forall \xi <\eta (\mathsf {DC}_{\xi })$
” and
$\forall \xi <\eta (\mathsf {DC}_{\xi })$
” and
![]() $\Phi $
has a Fraenkel–Mostowski model, then
$\Phi $
has a Fraenkel–Mostowski model, then
![]() $\Phi $
has a
$\Phi $
has a
![]() $\mathsf {ZF}$
-model,” the above
$\mathsf {ZF}$
-model,” the above
![]() $\mathsf {ZFA}$
-independence result can be transferred to
$\mathsf {ZFA}$
-independence result can be transferred to
![]() $\mathsf {ZF}$
. Hence, we obtain the following theorem.
$\mathsf {ZF}$
. Hence, we obtain the following theorem.
Theorem 4.13. For every uncountable regular cardinal
![]() $\aleph _{\alpha }$
, there exists a Fraenkel–Mostowski model
$\aleph _{\alpha }$
, there exists a Fraenkel–Mostowski model
![]() $\mathcal {N}_{\aleph _{\alpha }}$
such that for every infinite cardinal
$\mathcal {N}_{\aleph _{\alpha }}$
such that for every infinite cardinal
![]() $\lambda <\aleph _{\alpha }$
,
$\lambda <\aleph _{\alpha }$
,
![]() $\mathsf {DC}_{\lambda }$
is true in
$\mathsf {DC}_{\lambda }$
is true in
![]() $\mathcal {N}_{\aleph _{\alpha }}$
, but there exists an infinite-dimensional vector space over some field which has an AD1 family in
$\mathcal {N}_{\aleph _{\alpha }}$
, but there exists an infinite-dimensional vector space over some field which has an AD1 family in
![]() $\mathcal {N}_{\aleph _{\alpha }}$
that cannot be extended to a MAD1 family in
$\mathcal {N}_{\aleph _{\alpha }}$
that cannot be extended to a MAD1 family in
![]() $\mathcal {N}_{\aleph _{\alpha }}$
. The result is transferable to
$\mathcal {N}_{\aleph _{\alpha }}$
. The result is transferable to
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
5 Concluding remarks and open questions
As the referee pointed out, the vector space
![]() $V=\{f\in \mathbb {Z}_{2}^{A}:|\operatorname {\mathrm {{supp}}}(f)|<\aleph _{0}\}$
(for some infinite set A), which is used in the majority of the proofs, is essentially the same as
$V=\{f\in \mathbb {Z}_{2}^{A}:|\operatorname {\mathrm {{supp}}}(f)|<\aleph _{0}\}$
(for some infinite set A), which is used in the majority of the proofs, is essentially the same as
![]() $[A]^{<\omega }$
equipped with the symmetric difference as addition. (Note also that
$[A]^{<\omega }$
equipped with the symmetric difference as addition. (Note also that
![]() $F:V\rightarrow [A]^{<\omega }$
defined by
$F:V\rightarrow [A]^{<\omega }$
defined by
![]() $F(f)=\operatorname {\mathrm {{supp}}}(f)$
is a bijection.) So, an almost disjoint (either AD1 or AD2) family in V can be viewed as an almost disjoint family in
$F(f)=\operatorname {\mathrm {{supp}}}(f)$
is a bijection.) So, an almost disjoint (either AD1 or AD2) family in V can be viewed as an almost disjoint family in
![]() $[A]^{<\omega }$
(in the sense of Definition 2.3), and thus one may also adopt this approach in order to carry out the arguments in the proofs of certain results, for example, of Theorem 4.9.
$[A]^{<\omega }$
(in the sense of Definition 2.3), and thus one may also adopt this approach in order to carry out the arguments in the proofs of certain results, for example, of Theorem 4.9.
It is thus natural and interesting to investigate the possibility of extracting some combinatorial property that bridges the linear-algebraic approach with the set-approach in the realm of almost disjointness. To provide further incentive towards this direction, let us recall in view of the above discussion and the characterization of
![]() $\mathsf {MC}^{\aleph _{0}}$
given by Theorem 4.1, our result of [Reference Tachtsis17, Theorem 7] that
$\mathsf {MC}^{\aleph _{0}}$
given by Theorem 4.1, our result of [Reference Tachtsis17, Theorem 7] that
![]() $\mathsf {MC}^{\aleph _{0}}$
is also equivalent to the statement “For every infinite set X, no infinite MAD family in X has cardinality
$\mathsf {MC}^{\aleph _{0}}$
is also equivalent to the statement “For every infinite set X, no infinite MAD family in X has cardinality
![]() $\aleph _{0}$
”—see also open question (6) in the subsequent list and [Reference Tachtsis18].
$\aleph _{0}$
”—see also open question (6) in the subsequent list and [Reference Tachtsis18].
-
(1) Is
 $\mathsf {MC}^{\aleph _{0}}$
equivalent to “For every infinite-dimensional vector space V over any field, no MAD1 family in V has cardinality
$\mathsf {MC}^{\aleph _{0}}$
equivalent to “For every infinite-dimensional vector space V over any field, no MAD1 family in V has cardinality
 $\aleph _{0}$
”?
$\aleph _{0}$
”? -
(2) What is the status of “For every infinite-dimensional vector space V with a well orderable basis, no MADi family in V has cardinality
 $\aleph _{0}$
” (
$\aleph _{0}$
” (
 $i=1,2$
)?
$i=1,2$
)? -
(3) What weak choice principles are implied by “For every countable field F and every vector space V over F with a denumerable basis, no MADi (
 $i=1,2$
) family in V has cardinality
$i=1,2$
) family in V has cardinality
 $\kappa $
, for any well-ordered cardinal number
$\kappa $
, for any well-ordered cardinal number
 $\kappa $
with
$\kappa $
with
 $\aleph _{0}\le \kappa < 2^{\aleph _{0}}$
”?
$\aleph _{0}\le \kappa < 2^{\aleph _{0}}$
”? -
(4) Does
 $\mathsf {MC}$
imply “AD2 families in infinite-dimensional vector spaces can be extended to MAD2 families”?
$\mathsf {MC}$
imply “AD2 families in infinite-dimensional vector spaces can be extended to MAD2 families”? -
(5) Is there a model of
 $\mathsf {ZFA}$
, or of
$\mathsf {ZFA}$
, or of
 $\mathsf {ZF}$
, in which “AD1 families in infinite-dimensional vector spaces can be extended to MAD1 families” is true, but
$\mathsf {ZF}$
, in which “AD1 families in infinite-dimensional vector spaces can be extended to MAD1 families” is true, but
 $\mathsf {MC}$
is false?
$\mathsf {MC}$
is false? -
(6) For
 $i\in \{1,2\}$
, does
$i\in \{1,2\}$
, does
 $\mathsf {BPI}$
imply “Every ADi family in an infinite-dimensional vector space V can be extended to a MADi family in V”?
$\mathsf {BPI}$
imply “Every ADi family in an infinite-dimensional vector space V can be extended to a MADi family in V”? -
(7) Is the statement “Every infinite-dimensional vector space has an infinite AD1 family” false in the Basic Cohen Model of
 $\mathsf {ZF}+\mathsf {BPI}$
? (For the latter model, see Howard and Rubin [Reference Howard and Rubin3, Model
$\mathsf {ZF}+\mathsf {BPI}$
? (For the latter model, see Howard and Rubin [Reference Howard and Rubin3, Model
 $\mathbf{\mathcal{M}}1$
, p. 146] or Jech [Reference Jech7, Section 5.3].)
$\mathbf{\mathcal{M}}1$
, p. 146] or Jech [Reference Jech7, Section 5.3].)
Acknowledgements
We are grateful to the anonymous referee for carefully reading our paper and for several comments and suggestions which improved the quality and the exposition of the paper. We are especially thankful to the referee for giving us further motivation that resulted in establishing Theorem 4.9, which answers his/her corresponding (open until now) question posed to us and which is a considerable strengthening of a former version of the theorem. The open questions (6) and (7) in the above list were also suggested to us by the referee.