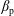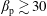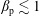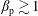1 Introduction
In the mid-twentieth century several authors published hydrodynamic models of the solar wind that imposed a fixed temperature at the coronal base and took thermal conduction to be the only heating mechanism (e.g. Parker Reference Parker1958, Reference Parker1965; Hartle & Sturrock Reference Hartle and Sturrock1968; Durney Reference Durney1972). These models were unable to explain the high proton temperatures and fast-solar-wind speeds observed at a heliocentric distance
![]() $r$
of 1 astronomical unit (au) for realistic values of the coronal temperature and density, indicating that the fast solar wind is heated primarily by some mechanism other than thermal conduction. Parker (Reference Parker1965) and Coleman (Reference Coleman1968) proposed that Alfvén waves (AWs) and AW turbulence provide this additional heating. Support for this suggestion can be found in the many spacecraft observations of AW-like turbulence in the solar wind (see Belcher Reference Belcher1971; Tu & Marsch Reference Tu and Marsch1995; Bale et al.
Reference Bale, Kellogg, Mozer, Horbury and Reme2005), remote observations of AW-like fluctuations in the solar corona (see De Pontieu et al.
Reference De Pontieu, McIntosh, Carlsson, Hansteen, Tarbell, Schrijver, Title, Shine, Tsuneta and Katsukawa2007; Tomczyk et al.
Reference Tomczyk, McIntosh, Keil, Judge, Schad, Seeley and Edmondson2007) and the agreement between AW-driven solar-wind models and solar-wind temperature, density and flow-speed profiles (Cranmer, van Ballegooijen & Edgar Reference Cranmer, van Ballegooijen and Edgar2007; Verdini et al.
Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2010; Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011; van der Holst et al.
Reference van der Holst, Sokolov, Meng, Jin, Manchester, Tóth and Gombosi2014).
$r$
of 1 astronomical unit (au) for realistic values of the coronal temperature and density, indicating that the fast solar wind is heated primarily by some mechanism other than thermal conduction. Parker (Reference Parker1965) and Coleman (Reference Coleman1968) proposed that Alfvén waves (AWs) and AW turbulence provide this additional heating. Support for this suggestion can be found in the many spacecraft observations of AW-like turbulence in the solar wind (see Belcher Reference Belcher1971; Tu & Marsch Reference Tu and Marsch1995; Bale et al.
Reference Bale, Kellogg, Mozer, Horbury and Reme2005), remote observations of AW-like fluctuations in the solar corona (see De Pontieu et al.
Reference De Pontieu, McIntosh, Carlsson, Hansteen, Tarbell, Schrijver, Title, Shine, Tsuneta and Katsukawa2007; Tomczyk et al.
Reference Tomczyk, McIntosh, Keil, Judge, Schad, Seeley and Edmondson2007) and the agreement between AW-driven solar-wind models and solar-wind temperature, density and flow-speed profiles (Cranmer, van Ballegooijen & Edgar Reference Cranmer, van Ballegooijen and Edgar2007; Verdini et al.
Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2010; Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011; van der Holst et al.
Reference van der Holst, Sokolov, Meng, Jin, Manchester, Tóth and Gombosi2014).
AWs oscillate at a frequency
![]() $\unicode[STIX]{x1D714}=k_{\Vert }v_{\text{A}}$
, where
$\unicode[STIX]{x1D714}=k_{\Vert }v_{\text{A}}$
, where
![]() $k_{\Vert }$
(
$k_{\Vert }$
(
![]() $k_{\bot }$
) is the component of the wave vector
$k_{\bot }$
) is the component of the wave vector
![]() $\boldsymbol{k}$
parallel (perpendicular) to the background magnetic field,
$\boldsymbol{k}$
parallel (perpendicular) to the background magnetic field,
![]() $\boldsymbol{B}_{0}$
,
$\boldsymbol{B}_{0}$
,
![]() $v_{\text{A}}=B_{0}/\sqrt{4\unicode[STIX]{x03C0}n_{\text{p}}m}$
is the Alfvén speed,
$v_{\text{A}}=B_{0}/\sqrt{4\unicode[STIX]{x03C0}n_{\text{p}}m}$
is the Alfvén speed,
![]() $n_{\text{p}}$
is the proton number density and
$n_{\text{p}}$
is the proton number density and
![]() $m$
is the proton mass.Footnote
1
In AW turbulence, interactions between counter-propagating AWs cause AW energy to cascade from larger to smaller scales. This energy cascade is anisotropic, in the sense that the small-scale AW ‘eddies’, or wave packets, generated by the cascade vary much more rapidly perpendicular to the magnetic field than along the magnetic field (e.g. Shebalin, Matthaeus & Montgomery Reference Shebalin, Matthaeus and Montgomery1983; Goldreich & Sridhar Reference Goldreich and Sridhar1995; Cho & Vishniac Reference Cho and Vishniac2000; Horbury, Forman & Oughton Reference Horbury, Forman and Oughton2008; Podesta Reference Podesta2013; Chen Reference Chen2016). As a consequence, within the inertial range (scales larger than the thermal-proton gyroradius
$m$
is the proton mass.Footnote
1
In AW turbulence, interactions between counter-propagating AWs cause AW energy to cascade from larger to smaller scales. This energy cascade is anisotropic, in the sense that the small-scale AW ‘eddies’, or wave packets, generated by the cascade vary much more rapidly perpendicular to the magnetic field than along the magnetic field (e.g. Shebalin, Matthaeus & Montgomery Reference Shebalin, Matthaeus and Montgomery1983; Goldreich & Sridhar Reference Goldreich and Sridhar1995; Cho & Vishniac Reference Cho and Vishniac2000; Horbury, Forman & Oughton Reference Horbury, Forman and Oughton2008; Podesta Reference Podesta2013; Chen Reference Chen2016). As a consequence, within the inertial range (scales larger than the thermal-proton gyroradius
![]() $\unicode[STIX]{x1D70C}_{\text{th}}$
and smaller than the outer scale or driving scale),
$\unicode[STIX]{x1D70C}_{\text{th}}$
and smaller than the outer scale or driving scale),
![]() $\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D6FA}$
, where
$\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D6FA}$
, where
![]() $\unicode[STIX]{x1D6FA}$
is the proton cyclotron frequency. At
$\unicode[STIX]{x1D6FA}$
is the proton cyclotron frequency. At
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
, the AW cascade transitions to a kinetic-Alfvén-wave (KAW) cascade (Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009).
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
, the AW cascade transitions to a kinetic-Alfvén-wave (KAW) cascade (Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009).
Studies of the dissipation of low-frequency (
![]() $\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D6FA}$
), anisotropic, AW/KAW turbulence based on linear wave damping (e.g. Quataert Reference Quataert1998; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008) conclude that AW/KAW turbulence leads mostly to parallel heating of the particles (i.e. heating that increases the speed of the thermal motions along
$\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D6FA}$
), anisotropic, AW/KAW turbulence based on linear wave damping (e.g. Quataert Reference Quataert1998; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008) conclude that AW/KAW turbulence leads mostly to parallel heating of the particles (i.e. heating that increases the speed of the thermal motions along
![]() $\boldsymbol{B}$
). On the other hand, perpendicular ion heating is the dominant form of heating in the near-Sun solar wind (Esser et al.
Reference Esser, Fineschi, Dobrzycka, Habbal, Edgar, Raymond, Kohl and Guhathakurta1999; Marsch Reference Marsch2006; Cranmer et al.
Reference Cranmer, Matthaeus, Breech and Kasper2009; Hellinger et al.
Reference Hellinger, Trávníček, Štverák, Matteini and Velli2013). This discrepancy suggests that AW/KAW turbulence in the solar wind dissipates via some nonlinear mechanism (e.g. Dmitruk, Matthaeus & Seenu Reference Dmitruk, Matthaeus and Seenu2004; Markovskii et al.
Reference Markovskii, Vasquez, Smith and Hollweg2006; Lehe, Parrish & Quataert Reference Lehe, Parrish and Quataert2009; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Servidio et al.
Reference Servidio, Greco, Matthaeus, Osman and Dmitruk2011; Lynn et al.
Reference Lynn, Parrish, Quataert and Chandran2012; Xia et al.
Reference Xia, Perez, Chandran and Quataert2013; Kawazura, Barnes & Schekochihin Reference Kawazura, Barnes and Schekochihin2018). This suggestion is supported by studies that find a correlation between ion temperatures and fluctuation amplitudes in solar-wind measurements and numerical simulations (e.g. Wu et al.
Reference Wu, Wan, Matthaeus, Shay and Swisdak2013; Grošelj et al.
Reference Grošelj, Cerri, Bañón Navarro, Willmott, Told, Loureiro, Califano and Jenko2017; Hughes et al.
Reference Hughes, Gary, Wang and Parashar2017; Vech, Klein & Kasper Reference Vech, Klein and Kasper2018).
$\boldsymbol{B}$
). On the other hand, perpendicular ion heating is the dominant form of heating in the near-Sun solar wind (Esser et al.
Reference Esser, Fineschi, Dobrzycka, Habbal, Edgar, Raymond, Kohl and Guhathakurta1999; Marsch Reference Marsch2006; Cranmer et al.
Reference Cranmer, Matthaeus, Breech and Kasper2009; Hellinger et al.
Reference Hellinger, Trávníček, Štverák, Matteini and Velli2013). This discrepancy suggests that AW/KAW turbulence in the solar wind dissipates via some nonlinear mechanism (e.g. Dmitruk, Matthaeus & Seenu Reference Dmitruk, Matthaeus and Seenu2004; Markovskii et al.
Reference Markovskii, Vasquez, Smith and Hollweg2006; Lehe, Parrish & Quataert Reference Lehe, Parrish and Quataert2009; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Servidio et al.
Reference Servidio, Greco, Matthaeus, Osman and Dmitruk2011; Lynn et al.
Reference Lynn, Parrish, Quataert and Chandran2012; Xia et al.
Reference Xia, Perez, Chandran and Quataert2013; Kawazura, Barnes & Schekochihin Reference Kawazura, Barnes and Schekochihin2018). This suggestion is supported by studies that find a correlation between ion temperatures and fluctuation amplitudes in solar-wind measurements and numerical simulations (e.g. Wu et al.
Reference Wu, Wan, Matthaeus, Shay and Swisdak2013; Grošelj et al.
Reference Grošelj, Cerri, Bañón Navarro, Willmott, Told, Loureiro, Califano and Jenko2017; Hughes et al.
Reference Hughes, Gary, Wang and Parashar2017; Vech, Klein & Kasper Reference Vech, Klein and Kasper2018).
In this paper, we consider one such nonlinear mechanism: stochastic heating. In stochastic proton heating, AW/KAW fluctuations at the proton gyroscale have sufficiently large amplitudes that they disrupt the normally smooth cyclotron motion of the protons, leading to non-conservation of the first adiabatic invariant, the magnetic moment (McChesney, Stern & Bellan Reference McChesney, Stern and Bellan1987; Chen, Lin & White Reference Chen, Lin and White2001a
; Johnson & Cheng Reference Johnson and Cheng2001; Chaston et al.
Reference Chaston, Bonnell, Carlson, McFadden, Ergun, Strangeway and Lund2004a
; Fiksel et al.
Reference Fiksel, Almagri, Chapman, Mirnov, Ren, Sarff and Terry2009; Xia et al.
Reference Xia, Perez, Chandran and Quataert2013). Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) used phenomenological arguments to derive an analytical formula for the stochastic-heating rate at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
, where
$\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
, where
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
is the ratio of the proton pressure to the magnetic pressure (see (2.3)). In § 2 we use phenomenological arguments to obtain an analytic formula for the proton-stochastic-heating rate in low-frequency AW/KAW turbulence when
$\unicode[STIX]{x1D6FD}_{\text{p}}$
is the ratio of the proton pressure to the magnetic pressure (see (2.3)). In § 2 we use phenomenological arguments to obtain an analytic formula for the proton-stochastic-heating rate in low-frequency AW/KAW turbulence when
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1$
–30. We limit our analysis to
$\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1$
–30. We limit our analysis to
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 30$
, since KAWs become non-propagating at
$\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 30$
, since KAWs become non-propagating at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
at larger
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
at larger
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
values (see appendix A and Hellinger & Matsumoto (Reference Hellinger and Matsumoto2000), Kawazura et al. (Reference Kawazura, Barnes and Schekochihin2018), Kunz et al. (Reference Kunz, Abel, Klein and Schekochihin2018)). In § 3 we present results from simulations of test particles interacting with a spectrum of randomly phased AWs/KAWs, which we use to test our analytic formula for the stochastic-heating rate. Throughout this paper, we focus on perpendicular proton heating rather than parallel proton heating. Stochastic heating can in principle to the parallel proton heating that results from linear damping of AW/KAW turbulence at
$\unicode[STIX]{x1D6FD}_{\text{p}}$
values (see appendix A and Hellinger & Matsumoto (Reference Hellinger and Matsumoto2000), Kawazura et al. (Reference Kawazura, Barnes and Schekochihin2018), Kunz et al. (Reference Kunz, Abel, Klein and Schekochihin2018)). In § 3 we present results from simulations of test particles interacting with a spectrum of randomly phased AWs/KAWs, which we use to test our analytic formula for the stochastic-heating rate. Throughout this paper, we focus on perpendicular proton heating rather than parallel proton heating. Stochastic heating can in principle to the parallel proton heating that results from linear damping of AW/KAW turbulence at
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}\gtrsim 1$
, but we leave a discussion of this possibility to future work.
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}\gtrsim 1$
, but we leave a discussion of this possibility to future work.
2 Stochastic proton heating by AW/KAW turbulence at the proton gyroscale
A proton interacting with a uniform background magnetic field
![]() $\boldsymbol{B}_{0}$
and fluctuating electric and magnetic fields
$\boldsymbol{B}_{0}$
and fluctuating electric and magnetic fields
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{E}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{E}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
undergoes nearly periodic motion in the plane perpendicular to
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
undergoes nearly periodic motion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
if
$\boldsymbol{B}_{0}$
if
![]() $\unicode[STIX]{x1D6FF}E$
and
$\unicode[STIX]{x1D6FF}E$
and
![]() $\unicode[STIX]{x1D6FF}B$
are sufficiently small or
$\unicode[STIX]{x1D6FF}B$
are sufficiently small or
![]() $L/\unicode[STIX]{x1D70C}$
is sufficiently large, where
$L/\unicode[STIX]{x1D70C}$
is sufficiently large, where
![]() $L$
is the characteristic length scale of
$L$
is the characteristic length scale of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{E}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{E}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
,
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
,
![]() $\unicode[STIX]{x1D70C}=v_{\bot }/\unicode[STIX]{x1D6FA}$
is the proton’s gyroradius,
$\unicode[STIX]{x1D70C}=v_{\bot }/\unicode[STIX]{x1D6FA}$
is the proton’s gyroradius,
![]() $\boldsymbol{v}_{\bot }$
is the component of the proton’s velocity
$\boldsymbol{v}_{\bot }$
is the component of the proton’s velocity
![]() $\boldsymbol{v}$
perpendicular to the magnetic field,
$\boldsymbol{v}$
perpendicular to the magnetic field,
![]() $\unicode[STIX]{x1D6FA}=qB_{0}/mc$
is the proton gyrofrequency,
$\unicode[STIX]{x1D6FA}=qB_{0}/mc$
is the proton gyrofrequency,
![]() $m$
and
$m$
and
![]() $q$
are the proton mass and charge and
$q$
are the proton mass and charge and
![]() $c$
is the speed of light. When (i) the proton’s motion in the plane perpendicular to
$c$
is the speed of light. When (i) the proton’s motion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
is nearly periodic and (ii)
$\boldsymbol{B}_{0}$
is nearly periodic and (ii)
![]() $\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D70F}\gg 1$
, where
$\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D70F}\gg 1$
, where
![]() $\unicode[STIX]{x1D70F}$
is the characteristic time scale of
$\unicode[STIX]{x1D70F}$
is the characteristic time scale of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{E}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{E}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
, the proton’s magnetic moment
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
, the proton’s magnetic moment
![]() $\unicode[STIX]{x1D707}=mv_{\bot }^{2}/2B_{0}$
is almost exactly conserved (Kruskal Reference Kruskal1962).
$\unicode[STIX]{x1D707}=mv_{\bot }^{2}/2B_{0}$
is almost exactly conserved (Kruskal Reference Kruskal1962).
Perpendicular heating of protons (by which we mean a secular increase in the average value of
![]() $\unicode[STIX]{x1D707}$
) requires that one of the above two conditions for
$\unicode[STIX]{x1D707}$
) requires that one of the above two conditions for
![]() $\unicode[STIX]{x1D707}$
conservation be violated. For example, Alfvén/ion-cyclotron waves can cause perpendicular proton heating via a cyclotron resonance if
$\unicode[STIX]{x1D707}$
conservation be violated. For example, Alfvén/ion-cyclotron waves can cause perpendicular proton heating via a cyclotron resonance if
![]() $\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D70F}\sim 1$
(Hollweg & Isenberg Reference Hollweg and Isenberg2002). Alternatively, low-frequency AW/KAW fluctuations can cause perpendicular proton heating if their amplitudes at
$\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D70F}\sim 1$
(Hollweg & Isenberg Reference Hollweg and Isenberg2002). Alternatively, low-frequency AW/KAW fluctuations can cause perpendicular proton heating if their amplitudes at
![]() $k_{\bot }\unicode[STIX]{x1D70C}\sim 1$
are sufficiently large that the proton motion in the plane perpendicular to
$k_{\bot }\unicode[STIX]{x1D70C}\sim 1$
are sufficiently large that the proton motion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
becomes disordered or ‘stochastic’ (McChesney et al.
Reference McChesney, Stern and Bellan1987; Johnson & Cheng Reference Johnson and Cheng2001; Chen, Lin & White Reference Chen, Lin and White2001b
; Chaston et al.
Reference Chaston, Bonnell, Carlson, McFadden, Ergun, Strangeway and Lund2004b
; Fiksel et al.
Reference Fiksel, Almagri, Chapman, Mirnov, Ren, Sarff and Terry2009).
$\boldsymbol{B}_{0}$
becomes disordered or ‘stochastic’ (McChesney et al.
Reference McChesney, Stern and Bellan1987; Johnson & Cheng Reference Johnson and Cheng2001; Chen, Lin & White Reference Chen, Lin and White2001b
; Chaston et al.
Reference Chaston, Bonnell, Carlson, McFadden, Ergun, Strangeway and Lund2004b
; Fiksel et al.
Reference Fiksel, Almagri, Chapman, Mirnov, Ren, Sarff and Terry2009).
We focus on this second type of heating, stochastic heating, and on ‘thermal’ protons, for which
where
![]() $w_{\bot }=\sqrt{2k_{\text{B}}T_{\bot \text{p}}/m}$
and
$w_{\bot }=\sqrt{2k_{\text{B}}T_{\bot \text{p}}/m}$
and
![]() $w_{\Vert }=\sqrt{2k_{\text{B}}T_{\Vert \text{p}}/m}$
are the perpendicular and parallel thermal speeds,
$w_{\Vert }=\sqrt{2k_{\text{B}}T_{\Vert \text{p}}/m}$
are the perpendicular and parallel thermal speeds,
![]() $T_{\bot \text{p}}$
and
$T_{\bot \text{p}}$
and
![]() $T_{\Vert \text{p}}$
are the perpendicular and parallel proton temperatures,
$T_{\Vert \text{p}}$
are the perpendicular and parallel proton temperatures,
![]() $k_{\text{B}}$
is Boltzmann’s constant and
$k_{\text{B}}$
is Boltzmann’s constant and
![]() $\unicode[STIX]{x1D70C}_{\text{th}}=w_{\bot }/\unicode[STIX]{x1D6FA}$
is the thermal-proton gyroradius. We restrict our attention to the contribution to the stochastic-heating rate from turbulent AW/KAW fluctuations with
$\unicode[STIX]{x1D70C}_{\text{th}}=w_{\bot }/\unicode[STIX]{x1D6FA}$
is the thermal-proton gyroradius. We restrict our attention to the contribution to the stochastic-heating rate from turbulent AW/KAW fluctuations with
where
![]() $\unicode[STIX]{x1D706}$
is the length scale of the fluctuations measured perpendicular to the background magnetic field, and to
$\unicode[STIX]{x1D706}$
is the length scale of the fluctuations measured perpendicular to the background magnetic field, and to
where
As mentioned above and discussed further in appendix A, KAWs at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
become non-propagating at significantly larger values of
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
become non-propagating at significantly larger values of
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
(see also Hellinger & Matsumoto Reference Hellinger and Matsumoto2000; Kawazura et al.
Reference Kawazura, Barnes and Schekochihin2018; Kunz et al.
Reference Kunz, Abel, Klein and Schekochihin2018). For simplicity, we assume that
$\unicode[STIX]{x1D6FD}_{\text{p}}$
(see also Hellinger & Matsumoto Reference Hellinger and Matsumoto2000; Kawazura et al.
Reference Kawazura, Barnes and Schekochihin2018; Kunz et al.
Reference Kunz, Abel, Klein and Schekochihin2018). For simplicity, we assume that
which implies that
and that
![]() $T_{\text{e}}\sim T_{\text{p}}$
, where
$T_{\text{e}}\sim T_{\text{p}}$
, where
![]() $T_{\text{e}}$
is the electron temperature. We also assume that
$T_{\text{e}}$
is the electron temperature. We also assume that
where
![]() $\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
is the root-mean-square (r.m.s.) amplitude of the magnetic fluctuations with
$\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
is the root-mean-square (r.m.s.) amplitude of the magnetic fluctuations with
![]() $\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D70C}_{\text{th}}$
, and that the fluctuations are in critical balance (Goldreich & Sridhar Reference Goldreich and Sridhar1995), which implies that
$\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D70C}_{\text{th}}$
, and that the fluctuations are in critical balance (Goldreich & Sridhar Reference Goldreich and Sridhar1995), which implies that
where
![]() $l$
is the correlation length of the gyroscale AW/KAW fluctuations measured parallel to the background magnetic field, and
$l$
is the correlation length of the gyroscale AW/KAW fluctuations measured parallel to the background magnetic field, and
![]() $\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
is the r.m.s. amplitude of the
$\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
is the r.m.s. amplitude of the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity of the AW/KAW fluctuations with
$\boldsymbol{E}\times \boldsymbol{B}$
velocity of the AW/KAW fluctuations with
![]() $\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D70C}_{\text{th}}$
. Since the linear and nonlinear time scales are comparable in the critical-balance model, we take the ratios of the amplitudes of different fluctuating variables to be comparable to the ratios that arise for linear AW/KAWs at
$\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D70C}_{\text{th}}$
. Since the linear and nonlinear time scales are comparable in the critical-balance model, we take the ratios of the amplitudes of different fluctuating variables to be comparable to the ratios that arise for linear AW/KAWs at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
, which, given (2.2) and (2.3), implies that
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
, which, given (2.2) and (2.3), implies that
where
![]() $\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}$
and
$\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}$
and
![]() $\unicode[STIX]{x1D6FF}B_{\bot \unicode[STIX]{x1D70C}}$
are, respectively, the r.m.s. amplitudes of the components of the fluctuating magnetic field parallel and perpendicular to
$\unicode[STIX]{x1D6FF}B_{\bot \unicode[STIX]{x1D70C}}$
are, respectively, the r.m.s. amplitudes of the components of the fluctuating magnetic field parallel and perpendicular to
![]() $\boldsymbol{B}_{0}$
(TenBarge et al.
Reference TenBarge, Podesta, Klein and Howes2012). Equations (2.2) through (2.9) imply that
$\boldsymbol{B}_{0}$
(TenBarge et al.
Reference TenBarge, Podesta, Klein and Howes2012). Equations (2.2) through (2.9) imply that
2.1 Stochastic motion perpendicular to the magnetic field
To understand how gyroscale AW/KAW fluctuations modify a proton’s motion, we cannot use the adiabatic approximation (Northrop Reference Northrop1963), which assumes
![]() $\unicode[STIX]{x1D706}\gg \unicode[STIX]{x1D70C}$
. Nevertheless, we can still define an effective guiding centre
$\unicode[STIX]{x1D706}\gg \unicode[STIX]{x1D70C}$
. Nevertheless, we can still define an effective guiding centre
where
![]() $\hat{\boldsymbol{b}}=\boldsymbol{B}/B$
. This effective guiding centre is always a distance
$\hat{\boldsymbol{b}}=\boldsymbol{B}/B$
. This effective guiding centre is always a distance
![]() $\unicode[STIX]{x1D70C}$
from the particle’s position
$\unicode[STIX]{x1D70C}$
from the particle’s position
![]() $\boldsymbol{r}$
and is, at any given time, the location about which the particle attempts to gyrate under the influence of the Lorentz force. We find it useful to focus on
$\boldsymbol{r}$
and is, at any given time, the location about which the particle attempts to gyrate under the influence of the Lorentz force. We find it useful to focus on
![]() $\boldsymbol{R}$
rather than
$\boldsymbol{R}$
rather than
![]() $\boldsymbol{r}$
because the motion of
$\boldsymbol{r}$
because the motion of
![]() $\boldsymbol{R}$
largely excludes the high-frequency cyclotron motion of the proton. Upon taking the time derivative of (2.11) and making use of the relations
$\boldsymbol{R}$
largely excludes the high-frequency cyclotron motion of the proton. Upon taking the time derivative of (2.11) and making use of the relations
![]() $\text{d}\boldsymbol{r}/\text{d}t=\boldsymbol{v}$
and
$\text{d}\boldsymbol{r}/\text{d}t=\boldsymbol{v}$
and
![]() $\text{d}\boldsymbol{v}/\text{d}t=(q/m)(\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}/c)$
, we obtain
$\text{d}\boldsymbol{v}/\text{d}t=(q/m)(\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}/c)$
, we obtain
where
![]() $v_{\Vert }=\boldsymbol{v}\boldsymbol{\cdot }\hat{\boldsymbol{b}}$
. The perpendicular component of
$v_{\Vert }=\boldsymbol{v}\boldsymbol{\cdot }\hat{\boldsymbol{b}}$
. The perpendicular component of
![]() $\text{d}\boldsymbol{R}/\text{d}t$
,
$\text{d}\boldsymbol{R}/\text{d}t$
,
can be found by substituting the right-hand side of (2.12) into the right-hand side of (2.13), which yields
We now estimate each term on the right-hand side of (2.14). Since we are considering only gyroscale fluctuations,Footnote 2 the first term on the right-hand side of (2.14) satisfies the relation
To estimate the second and third terms on the right-hand side of (2.14), we take
which is satisfied by the majority of particles. The time derivative of the field strength along the particle’s trajectory is
As outlined above, our assumption of critical balance implies that
![]() $\unicode[STIX]{x1D706}\ll l$
and
$\unicode[STIX]{x1D706}\ll l$
and
![]() $\unicode[STIX]{x1D714}\ll v_{\bot }/\unicode[STIX]{x1D70C}\sim w_{\bot }/\unicode[STIX]{x1D70C}_{\text{th}}$
. The second term on the right-hand side of (2.17) is thus much larger than either the first or third terms, and
$\unicode[STIX]{x1D714}\ll v_{\bot }/\unicode[STIX]{x1D70C}\sim w_{\bot }/\unicode[STIX]{x1D70C}_{\text{th}}$
. The second term on the right-hand side of (2.17) is thus much larger than either the first or third terms, and
The second term on the right-hand side of (2.14) thus satisfies
which is larger than the first term on the right-hand side of (2.14) by a factor of
![]() ${\sim}\unicode[STIX]{x1D6FD}_{\text{p}}^{1/2}$
, given (2.6) and (2.9).
${\sim}\unicode[STIX]{x1D6FD}_{\text{p}}^{1/2}$
, given (2.6) and (2.9).
For the moment, we assume that the second term on the right-hand side of (2.14) is the dominant term; we discuss the third term in more detail below. If the second term is dominant, then
During a single cyclotron period
![]() $2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FA}$
, a proton passes through an order-unity number of uncorrelated gyroscale AW/KAW eddies, and the values of
$2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FA}$
, a proton passes through an order-unity number of uncorrelated gyroscale AW/KAW eddies, and the values of
![]() $(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }$
within different gyroscale eddies are uncorrelated. If
$(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }$
within different gyroscale eddies are uncorrelated. If
![]() $(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }$
is small compared to
$(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }$
is small compared to
![]() $w_{\bot }$
, then a proton undergoes nearly circular gyromotion. However, if
$w_{\bot }$
, then a proton undergoes nearly circular gyromotion. However, if
![]() $|(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }|$
is a significant fraction of
$|(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }|$
is a significant fraction of
![]() $w_{\bot }$
, then a proton and its guiding centre will move in an essentially unpredictable way, and the proton’s orbit will become stochastic rather than quasi-periodic. Given (2.9),
$w_{\bot }$
, then a proton and its guiding centre will move in an essentially unpredictable way, and the proton’s orbit will become stochastic rather than quasi-periodic. Given (2.9),
![]() $|(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }|$
is a significant fraction of
$|(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }|$
is a significant fraction of
![]() $w_{\bot }$
if the stochasticity parameter
$w_{\bot }$
if the stochasticity parameter
is a significant fraction of unity.
We illustrate how the value of
![]() $\unicode[STIX]{x1D6FF}$
affects a proton’s motion in figure 1. We compute the particle trajectories shown in this figure by numerically integrating the equations of motion for protons interacting with randomly phased AWs and KAWs. We present the details of our numerical method and more extensive numerical results in § 3. In the numerical calculation shown in figure 1(a),
$\unicode[STIX]{x1D6FF}$
affects a proton’s motion in figure 1. We compute the particle trajectories shown in this figure by numerically integrating the equations of motion for protons interacting with randomly phased AWs and KAWs. We present the details of our numerical method and more extensive numerical results in § 3. In the numerical calculation shown in figure 1(a),
![]() $\unicode[STIX]{x1D6FF}=0.03$
, and the proton’s motion in the plane perpendicular to
$\unicode[STIX]{x1D6FF}=0.03$
, and the proton’s motion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
is quasi-periodic. In the numerical calculation shown in figure 1(b),
$\boldsymbol{B}_{0}$
is quasi-periodic. In the numerical calculation shown in figure 1(b),
![]() $\unicode[STIX]{x1D6FF}=0.15$
, and the proton trajectory is more disordered or random.
$\unicode[STIX]{x1D6FF}=0.15$
, and the proton trajectory is more disordered or random.

Figure 1. Trajectories of test-particle protons interacting with a spectrum of randomly phased AWs and KAWs for different values of the stochasticity parameter
![]() $\unicode[STIX]{x1D6FF}$
defined in (2.21).
$\unicode[STIX]{x1D6FF}$
defined in (2.21).
We now consider the third term on the right-hand side of (2.14). The instantaneous value of this term is comparable to the instantaneous value of the second term given (2.9) and (2.16), but the third term is less effective at causing guiding-centre displacements over time for the following reason. Because of (2.7), the time
![]() $t_{\Vert }$
required for
$t_{\Vert }$
required for
![]() $v_{\Vert }$
to change by a factor of order unity is
$v_{\Vert }$
to change by a factor of order unity is
![]() $\gg \unicode[STIX]{x1D6FA}^{-1}$
. If we integrate the third term on the right-hand side of (2.14) from
$\gg \unicode[STIX]{x1D6FA}^{-1}$
. If we integrate the third term on the right-hand side of (2.14) from
![]() $t=0$
to
$t=0$
to
![]() $t=t_{\text{f}}$
, where
$t=t_{\text{f}}$
, where
![]() $\unicode[STIX]{x1D6FA}^{-1}\ll t_{\text{f}}\ll t_{\Vert }$
, we can treat
$\unicode[STIX]{x1D6FA}^{-1}\ll t_{\text{f}}\ll t_{\Vert }$
, we can treat
![]() $v_{\Vert }$
as approximately constant in (2.14), obtaining
$v_{\Vert }$
as approximately constant in (2.14), obtaining
to leading order in
![]() $\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}/B_{0}$
, where
$\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}/B_{0}$
, where
![]() $\unicode[STIX]{x1D6FA}_{0}=qB_{0}/mc$
and
$\unicode[STIX]{x1D6FA}_{0}=qB_{0}/mc$
and
![]() $\unicode[STIX]{x0394}\hat{\boldsymbol{b}}=\hat{\boldsymbol{b}}(t_{\text{f}})-\hat{\boldsymbol{b}}(0)$
is the change in
$\unicode[STIX]{x0394}\hat{\boldsymbol{b}}=\hat{\boldsymbol{b}}(t_{\text{f}})-\hat{\boldsymbol{b}}(0)$
is the change in
![]() $\hat{\boldsymbol{b}}$
. There is, however, no secular change in the value of
$\hat{\boldsymbol{b}}$
. There is, however, no secular change in the value of
![]() $\hat{\boldsymbol{b}}$
at the proton’s location; the magnetic-field unit vector merely undergoes small-amplitude fluctuations about the direction of the background magnetic field. Thus, over time, the guiding-centre displacements caused by the third term on the right-hand side of (2.14) are largely reversible and tend to cancel out. The third term is thus less effective than the second term at making proton orbits stochastic.
$\hat{\boldsymbol{b}}$
at the proton’s location; the magnetic-field unit vector merely undergoes small-amplitude fluctuations about the direction of the background magnetic field. Thus, over time, the guiding-centre displacements caused by the third term on the right-hand side of (2.14) are largely reversible and tend to cancel out. The third term is thus less effective than the second term at making proton orbits stochastic.
When the stochasticity parameter
![]() $\unicode[STIX]{x1D6FF}$
defined in (2.21) exceeds some threshold, the motion of a thermal proton’s guiding centre in the plane perpendicular to
$\unicode[STIX]{x1D6FF}$
defined in (2.21) exceeds some threshold, the motion of a thermal proton’s guiding centre in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
is reasonably approximated by a random walk. To estimate the time step of this random walk, we begin by defining the cyclotron average of
$\boldsymbol{B}_{0}$
is reasonably approximated by a random walk. To estimate the time step of this random walk, we begin by defining the cyclotron average of
![]() $(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }$
,
$(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }$
,
As stated above, during a single cyclotron period, a proton’s motion projected onto the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
carries the proton through an order-unity number of uncorrelated gyroscale AW/KAW ‘eddies’. For simplicity, we take the amplitude and direction of each vector term on the right-hand side of (2.14) to be approximately constant within any single gyroscale eddy and the values of these vector terms within different eddies to be uncorrelated. This makes
$\boldsymbol{B}_{0}$
carries the proton through an order-unity number of uncorrelated gyroscale AW/KAW ‘eddies’. For simplicity, we take the amplitude and direction of each vector term on the right-hand side of (2.14) to be approximately constant within any single gyroscale eddy and the values of these vector terms within different eddies to be uncorrelated. This makes
![]() $\boldsymbol{v}_{R}$
approximately equal to the average of some order-unity number of uncorrelated vectors of comparable magnitude. The amplitude of this average is comparable to the instantaneous value of
$\boldsymbol{v}_{R}$
approximately equal to the average of some order-unity number of uncorrelated vectors of comparable magnitude. The amplitude of this average is comparable to the instantaneous value of
![]() $|(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }|$
. Thus, given (2.6), (2.9), and (2.20),
$|(\text{d}\boldsymbol{R}/\text{d}t)_{\bot }|$
. Thus, given (2.6), (2.9), and (2.20),
Because we are considering the effects of just the gyroscale AW/KAW eddies,
![]() $\boldsymbol{v}_{R}$
decorrelates after the proton’s guiding centre has moved a distance
$\boldsymbol{v}_{R}$
decorrelates after the proton’s guiding centre has moved a distance
![]() ${\sim}\unicode[STIX]{x1D70C}_{\text{th}}$
in the plane perpendicular to
${\sim}\unicode[STIX]{x1D70C}_{\text{th}}$
in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
, which takes a time
$\boldsymbol{B}_{0}$
, which takes a time
Thermal protons thus undergo spatial diffusion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
with a spatial diffusion coefficient
$\boldsymbol{B}_{0}$
with a spatial diffusion coefficient
Given (2.8), (2.16) and (2.24),
The time required for a particle to wander a distance
![]() ${\sim}\unicode[STIX]{x1D70C}_{\text{th}}$
perpendicular to the background magnetic field is thus comparable to the time required for the particle to traverse the parallel dimension of a gyroscale AW/KAW eddy.
${\sim}\unicode[STIX]{x1D70C}_{\text{th}}$
perpendicular to the background magnetic field is thus comparable to the time required for the particle to traverse the parallel dimension of a gyroscale AW/KAW eddy.
2.2 Energy diffusion and heating
The total energy of a proton is given by its Hamiltonian,
where
![]() $\unicode[STIX]{x1D6F7}$
is the electrostatic potential,
$\unicode[STIX]{x1D6F7}$
is the electrostatic potential,
![]() $\boldsymbol{p}$
is the canonical momentum and
$\boldsymbol{p}$
is the canonical momentum and
![]() $\boldsymbol{A}$
is the vector potential. From Hamilton’s equations,
$\boldsymbol{A}$
is the vector potential. From Hamilton’s equations,
where
![]() $\boldsymbol{v}=m^{-1}(\boldsymbol{p}-q\boldsymbol{A}/c)$
is the velocity, and the electric field is
$\boldsymbol{v}=m^{-1}(\boldsymbol{p}-q\boldsymbol{A}/c)$
is the velocity, and the electric field is
![]() $\boldsymbol{E}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}-c^{-1}\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t$
. The second term on the right-hand side of (2.29) is
$\boldsymbol{E}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}-c^{-1}\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t$
. The second term on the right-hand side of (2.29) is
![]() $q\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{E}_{\text{s}}$
, where
$q\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{E}_{\text{s}}$
, where
![]() $\boldsymbol{E}_{\text{s}}=-c^{-1}\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t$
is the solenoidal component of the electric field. Equation (46) of Hollweg (Reference Hollweg1999) gives the ratio of
$\boldsymbol{E}_{\text{s}}=-c^{-1}\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t$
is the solenoidal component of the electric field. Equation (46) of Hollweg (Reference Hollweg1999) gives the ratio of
![]() $E_{\text{s}}$
to the magnitude of the irrotational component of the electric field
$E_{\text{s}}$
to the magnitude of the irrotational component of the electric field
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}|$
for AWs/KAWs with
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}|$
for AWs/KAWs with
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\lesssim 1$
,Footnote
3
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\lesssim 1$
,Footnote
3
In their treatment of stochastic heating at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
, Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) neglected the second term on the right-hand side of (2.29), because this term makes a small contribution to the heating rate when
$\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
, Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) neglected the second term on the right-hand side of (2.29), because this term makes a small contribution to the heating rate when
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
is small. Here we focus on the effects of
$\unicode[STIX]{x1D6FD}_{\text{p}}$
is small. Here we focus on the effects of
![]() $\boldsymbol{E}_{\text{s}}$
and make the approximation that
$\boldsymbol{E}_{\text{s}}$
and make the approximation that
We show in appendix B that the irrotational part of the electric field contributes less to the heating rate than does the solenoidal part when
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
.
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
.
As a proton undergoes spatial diffusion in the plane perpendicular to the background magnetic field, the electromagnetic field at its location resulting from gyroscale AW/KAW fluctuations decorrelates on the time scale
![]() $\unicode[STIX]{x0394}t$
given in (2.27). Within each time interval of length
$\unicode[STIX]{x0394}t$
given in (2.27). Within each time interval of length
![]() ${\sim}\unicode[STIX]{x0394}t$
, the proton energy changes by an amount
${\sim}\unicode[STIX]{x0394}t$
, the proton energy changes by an amount
![]() $\unicode[STIX]{x1D6FF}H$
(which can be positive or negative), and the values of
$\unicode[STIX]{x1D6FF}H$
(which can be positive or negative), and the values of
![]() $\unicode[STIX]{x1D6FF}H$
are uncorrelated within successive time intervals of length
$\unicode[STIX]{x1D6FF}H$
are uncorrelated within successive time intervals of length
![]() $\unicode[STIX]{x0394}t$
. As a consequence, the proton undergoes energy diffusion.
$\unicode[STIX]{x0394}t$
. As a consequence, the proton undergoes energy diffusion.
To estimate the r.m.s. value of
![]() $\unicode[STIX]{x1D6FF}H$
, which we denote
$\unicode[STIX]{x1D6FF}H$
, which we denote
![]() $\unicode[STIX]{x0394}H$
, we adopt a simple model of a proton’s motion, in which the proton’s complicated trajectory is replaced by a repeating two-step process. In the first step, the proton undergoes circular cyclotron motion in the plane perpendicular to
$\unicode[STIX]{x0394}H$
, we adopt a simple model of a proton’s motion, in which the proton’s complicated trajectory is replaced by a repeating two-step process. In the first step, the proton undergoes circular cyclotron motion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
for a time
$\boldsymbol{B}_{0}$
for a time
![]() $\unicode[STIX]{x0394}t$
. In the second step, the proton is instantly translated a distance
$\unicode[STIX]{x0394}t$
. In the second step, the proton is instantly translated a distance
![]() $\unicode[STIX]{x1D70C}_{\text{th}}$
in some random direction perpendicular to
$\unicode[STIX]{x1D70C}_{\text{th}}$
in some random direction perpendicular to
![]() $\boldsymbol{B}_{0}$
.Footnote
4
$\boldsymbol{B}_{0}$
.Footnote
4
In this simple model, a proton undergoes
![]() $N\sim \unicode[STIX]{x1D6FA}\unicode[STIX]{x0394}t\sim (v_{\bot }/\unicode[STIX]{x1D70C}_{\text{th}})\times (l/v_{\Vert })\sim l/\unicode[STIX]{x1D70C}_{\text{th}}\gg 1$
circular gyrations in the plane perpendicular to
$N\sim \unicode[STIX]{x1D6FA}\unicode[STIX]{x0394}t\sim (v_{\bot }/\unicode[STIX]{x1D70C}_{\text{th}})\times (l/v_{\Vert })\sim l/\unicode[STIX]{x1D70C}_{\text{th}}\gg 1$
circular gyrations in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
during a time
$\boldsymbol{B}_{0}$
during a time
![]() $\unicode[STIX]{x0394}t$
. Integrating (2.31) for a time
$\unicode[STIX]{x0394}t$
. Integrating (2.31) for a time
![]() $\unicode[STIX]{x0394}t$
, we obtain
$\unicode[STIX]{x0394}t$
, we obtain
where
![]() $\boldsymbol{r}(t)$
is the proton’s position at time
$\boldsymbol{r}(t)$
is the proton’s position at time
![]() $t$
. Since
$t$
. Since
![]() $\unicode[STIX]{x0394}t\sim \unicode[STIX]{x1D6FD}_{\text{p}}^{-1/2}\unicode[STIX]{x1D70C}_{\text{th}}/\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
, when
$\unicode[STIX]{x0394}t\sim \unicode[STIX]{x1D6FD}_{\text{p}}^{-1/2}\unicode[STIX]{x1D70C}_{\text{th}}/\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
, when
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
, the time
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
, the time
![]() $\unicode[STIX]{x0394}t$
for a particle to diffuse across one set of gyroscale eddies is shorter than or comparable to the linear or nonlinear time scale
$\unicode[STIX]{x0394}t$
for a particle to diffuse across one set of gyroscale eddies is shorter than or comparable to the linear or nonlinear time scale
![]() $\unicode[STIX]{x1D70C}_{\text{th}}/\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
of those eddies. We thus approximate the right-hand side of (2.32) by setting
$\unicode[STIX]{x1D70C}_{\text{th}}/\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
of those eddies. We thus approximate the right-hand side of (2.32) by setting
![]() $\boldsymbol{E}_{\text{s}}(\boldsymbol{r}(t),t)=\boldsymbol{E}_{\text{s}}(\boldsymbol{r}(t),0)$
and rewrite (2.32) as
$\boldsymbol{E}_{\text{s}}(\boldsymbol{r}(t),t)=\boldsymbol{E}_{\text{s}}(\boldsymbol{r}(t),0)$
and rewrite (2.32) as
where the line integral is along the proton’s path during one complete circular gyration in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
, the surface integral is over the circular surface
$\boldsymbol{B}_{0}$
, the surface integral is over the circular surface
![]() $S$
of radius
$S$
of radius
![]() $\unicode[STIX]{x1D70C}_{\text{th}}$
enclosed by the gyration, and we have used Faraday’s law
$\unicode[STIX]{x1D70C}_{\text{th}}$
enclosed by the gyration, and we have used Faraday’s law
![]() $\unicode[STIX]{x1D735}\times \boldsymbol{E}=(-1/c)\unicode[STIX]{x2202}\boldsymbol{B}/\unicode[STIX]{x2202}t$
. The surface
$\unicode[STIX]{x1D735}\times \boldsymbol{E}=(-1/c)\unicode[STIX]{x2202}\boldsymbol{B}/\unicode[STIX]{x2202}t$
. The surface
![]() $S$
is perpendicular to
$S$
is perpendicular to
![]() $\boldsymbol{B}_{0}$
, and
$\boldsymbol{B}_{0}$
, and
![]() $\text{d}\boldsymbol{S}$
is anti-parallel to
$\text{d}\boldsymbol{S}$
is anti-parallel to
![]() $\boldsymbol{B}_{0}$
(anti-parallel rather than parallel since
$\boldsymbol{B}_{0}$
(anti-parallel rather than parallel since
![]() $q>0$
). The r.m.s. value of
$q>0$
). The r.m.s. value of
![]() $\unicode[STIX]{x1D6FF}H$
thus satisfies the order-of-magnitude relation
$\unicode[STIX]{x1D6FF}H$
thus satisfies the order-of-magnitude relation
where
is the nonlinear frequency of the gyroscale fluctuations. Upon setting
![]() $q/c=\unicode[STIX]{x1D6FA}m/B$
,
$q/c=\unicode[STIX]{x1D6FA}m/B$
,
![]() $N=\unicode[STIX]{x1D6FA}\unicode[STIX]{x0394}t$
and
$N=\unicode[STIX]{x1D6FA}\unicode[STIX]{x0394}t$
and
![]() $\unicode[STIX]{x1D70C}_{\text{th}}^{2}=w_{\bot }^{2}/\unicode[STIX]{x1D6FA}^{2}$
in (2.34), we obtain
$\unicode[STIX]{x1D70C}_{\text{th}}^{2}=w_{\bot }^{2}/\unicode[STIX]{x1D6FA}^{2}$
in (2.34), we obtain
Although we are in the process of estimating the rate at which
![]() $\unicode[STIX]{x1D707}$
changes over long times, our estimate of
$\unicode[STIX]{x1D707}$
changes over long times, our estimate of
![]() $\unicode[STIX]{x0394}H$
is comparable to the value that would follow from
$\unicode[STIX]{x0394}H$
is comparable to the value that would follow from
![]() $\unicode[STIX]{x1D707}$
conservation:
$\unicode[STIX]{x1D707}$
conservation:
![]() $\unicode[STIX]{x0394}H\sim \unicode[STIX]{x1D707}\unicode[STIX]{x0394}B\sim (mw_{\bot }^{2}/B)\unicode[STIX]{x1D714}_{\text{eff}}\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\unicode[STIX]{x0394}t$
, where
$\unicode[STIX]{x0394}H\sim \unicode[STIX]{x1D707}\unicode[STIX]{x0394}B\sim (mw_{\bot }^{2}/B)\unicode[STIX]{x1D714}_{\text{eff}}\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\unicode[STIX]{x0394}t$
, where
![]() $\unicode[STIX]{x0394}B\sim \unicode[STIX]{x1D714}_{\text{eff}}\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\unicode[STIX]{x0394}t$
is the r.m.s. amplitude of the change in the magnetic flux through the proton’s Larmor orbit, divided by
$\unicode[STIX]{x0394}B\sim \unicode[STIX]{x1D714}_{\text{eff}}\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\unicode[STIX]{x0394}t$
is the r.m.s. amplitude of the change in the magnetic flux through the proton’s Larmor orbit, divided by
![]() $\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}^{2}$
, during the time
$\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}^{2}$
, during the time
![]() $\unicode[STIX]{x0394}t$
in which the proton is (in our simple two-step model of proton motion) undergoing continuous, circular, cyclotron motion. This correspondence highlights an alternative interpretation of the stochastic-heating process at
$\unicode[STIX]{x0394}t$
in which the proton is (in our simple two-step model of proton motion) undergoing continuous, circular, cyclotron motion. This correspondence highlights an alternative interpretation of the stochastic-heating process at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
. In the guiding-centre approximation, when
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
. In the guiding-centre approximation, when
![]() $v_{\bot }^{2}$
increases by some factor because of
$v_{\bot }^{2}$
increases by some factor because of
![]() $\boldsymbol{E}_{\text{s}}$
, the field strength at the particle’s guiding centre increases by approximately the same factor, essentially because of Faraday’s law. This proportionality underlies
$\boldsymbol{E}_{\text{s}}$
, the field strength at the particle’s guiding centre increases by approximately the same factor, essentially because of Faraday’s law. This proportionality underlies
![]() $\unicode[STIX]{x1D707}$
conservation. In stochastic heating, the same proportionality is approximately satisfied during a single time interval
$\unicode[STIX]{x1D707}$
conservation. In stochastic heating, the same proportionality is approximately satisfied during a single time interval
![]() $\unicode[STIX]{x0394}t$
, but the proton is then stochastically transported to a neighbouring set of gyroscale eddies, in which the field strength is not correlated with the field strength at the proton’s original location. The proton thus ‘forgets’ about what happened to the field strength at its original location and gets to keep the energy that it gained without ‘paying the price’ of residing in a higher-field-strength location. In this way, spatial diffusion perpendicular to
$\unicode[STIX]{x0394}t$
, but the proton is then stochastically transported to a neighbouring set of gyroscale eddies, in which the field strength is not correlated with the field strength at the proton’s original location. The proton thus ‘forgets’ about what happened to the field strength at its original location and gets to keep the energy that it gained without ‘paying the price’ of residing in a higher-field-strength location. In this way, spatial diffusion perpendicular to
![]() $\boldsymbol{B}$
breaks the connection between changes to
$\boldsymbol{B}$
breaks the connection between changes to
![]() $v_{\bot }^{2}$
and changes to
$v_{\bot }^{2}$
and changes to
![]() $B$
that arises in the
$B$
that arises in the
![]() $\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D706}\rightarrow 0$
limit.
$\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D706}\rightarrow 0$
limit.
In our simple model, the energy gained by a proton is in the form of perpendicular kinetic energy,
because we neglect the parallel motion of protons. (We do not preclude the possibility of parallel stochastic heating, but we do not consider it further here.) The perpendicular-kinetic-energy diffusion coefficient
![]() $D_{K}$
is thus
$D_{K}$
is thus
![]() ${\sim}\unicode[STIX]{x0394}H^{2}/\unicode[STIX]{x0394}t$
, or
${\sim}\unicode[STIX]{x0394}H^{2}/\unicode[STIX]{x0394}t$
, or
where we have used (2.27) to estimate
![]() $\unicode[STIX]{x0394}t$
and (2.9) to set
$\unicode[STIX]{x0394}t$
and (2.9) to set
![]() $\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\sim \unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
. A single proton undergoing a random walk in energy can gain or lose energy with equal probability during a time
$\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\sim \unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
. A single proton undergoing a random walk in energy can gain or lose energy with equal probability during a time
![]() $\unicode[STIX]{x0394}t$
. However, if a large number of thermal protons (e.g. with an initially Maxwellian distribution) undergo energy diffusion, then on average more protons will gain energy than lose energy, leading to proton heating. The heating time scale
$\unicode[STIX]{x0394}t$
. However, if a large number of thermal protons (e.g. with an initially Maxwellian distribution) undergo energy diffusion, then on average more protons will gain energy than lose energy, leading to proton heating. The heating time scale
![]() $\unicode[STIX]{x1D70F}_{\text{h}}$
is the characteristic time for the perpendicular kinetic energy of a thermal proton to double,
$\unicode[STIX]{x1D70F}_{\text{h}}$
is the characteristic time for the perpendicular kinetic energy of a thermal proton to double,
![]() $\unicode[STIX]{x1D70F}_{\text{h}}\sim (mw_{\bot }^{2})^{2}/D_{K}$
, and the perpendicular-heating rate per unit mass is
$\unicode[STIX]{x1D70F}_{\text{h}}\sim (mw_{\bot }^{2})^{2}/D_{K}$
, and the perpendicular-heating rate per unit mass is
![]() $Q_{\bot }\sim K_{\bot }/(m\unicode[STIX]{x1D70F}_{\text{h}})\sim D_{K}/(mK_{\bot })$
, or,
$Q_{\bot }\sim K_{\bot }/(m\unicode[STIX]{x1D70F}_{\text{h}})\sim D_{K}/(mK_{\bot })$
, or,
To account for the uncertainties introduced by our numerous order-of-magnitude estimates, we multiply the right-hand side of (2.39) by an as-yet-unknown dimensionless constant
![]() $\unicode[STIX]{x1D70E}_{1}$
. As
$\unicode[STIX]{x1D70E}_{1}$
. As
![]() $\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}\rightarrow 0$
,
$\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}\rightarrow 0$
,
![]() $\text{d}\unicode[STIX]{x1D707}/\text{d}t$
decreases faster than any power of
$\text{d}\unicode[STIX]{x1D707}/\text{d}t$
decreases faster than any power of
![]() $\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
(Kruskal Reference Kruskal1962). To account for this ‘exponential’
$\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
(Kruskal Reference Kruskal1962). To account for this ‘exponential’
![]() $\unicode[STIX]{x1D707}$
conservation in the small-
$\unicode[STIX]{x1D707}$
conservation in the small-
![]() $\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
limit, we follow Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) by multiplying the right-hand side of (2.39) by the factor
$\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
limit, we follow Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) by multiplying the right-hand side of (2.39) by the factor
![]() $\exp (-\unicode[STIX]{x1D70E}_{2}/\unicode[STIX]{x1D6FF})$
,
$\exp (-\unicode[STIX]{x1D70E}_{2}/\unicode[STIX]{x1D6FF})$
,
where
![]() $\unicode[STIX]{x1D70E}_{2}$
is another as-yet-unknown dimensionless constant, and
$\unicode[STIX]{x1D70E}_{2}$
is another as-yet-unknown dimensionless constant, and
![]() $\unicode[STIX]{x1D6FF}$
is defined in (2.21).
$\unicode[STIX]{x1D6FF}$
is defined in (2.21).
For comparison, the stochastic-heating rate per unit mass found by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) when
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
is
$\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
is
where
and the dimensionless constants
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
serve the same purpose as those in (2.40). As discussed by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) for the case of
$c_{2}$
serve the same purpose as those in (2.40). As discussed by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) for the case of
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
, we expect the constants
$c_{2}$
, we expect the constants
![]() $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
to depend on the nature of the fluctuations. For example, at fixed
$\unicode[STIX]{x1D70E}_{2}$
to depend on the nature of the fluctuations. For example, at fixed
![]() $\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
, we expect stronger heating rates (i.e. larger
$\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
, we expect stronger heating rates (i.e. larger
![]() $\unicode[STIX]{x1D70E}_{1}$
and/or smaller
$\unicode[STIX]{x1D70E}_{1}$
and/or smaller
![]() $\unicode[STIX]{x1D70E}_{2}$
) from intermittent turbulence than from randomly phased waves (Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Xia et al.
Reference Xia, Perez, Chandran and Quataert2013; Mallet et al.
Reference Mallet, Klein, Chandran, Groselj, Hoppock, Bowen, Salem and Bale2018), because, in intermittent turbulence, most of the heating takes place near coherent structures in which the fluctuations are unusually strong and in which the proton orbits are more stochastic than on average.
$\unicode[STIX]{x1D70E}_{2}$
) from intermittent turbulence than from randomly phased waves (Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Xia et al.
Reference Xia, Perez, Chandran and Quataert2013; Mallet et al.
Reference Mallet, Klein, Chandran, Groselj, Hoppock, Bowen, Salem and Bale2018), because, in intermittent turbulence, most of the heating takes place near coherent structures in which the fluctuations are unusually strong and in which the proton orbits are more stochastic than on average.
2.3 Orbit stochasticity from parallel motion
In § 2.1, we focused on proton motion perpendicular to
![]() $\boldsymbol{B}$
. However, motion along the magnetic field can also produce stochastic motion in the plane perpendicular to
$\boldsymbol{B}$
. However, motion along the magnetic field can also produce stochastic motion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
(see, e.g. Hauff et al.
Reference Hauff, Jenko, Shalchi and Schlickeiser2010). In particular, the perpendicular magnetic fluctuations at the scale of a proton’s gyroradius perturb the direction of
$\boldsymbol{B}_{0}$
(see, e.g. Hauff et al.
Reference Hauff, Jenko, Shalchi and Schlickeiser2010). In particular, the perpendicular magnetic fluctuations at the scale of a proton’s gyroradius perturb the direction of
![]() $\hat{\boldsymbol{b}}$
. These perturbations, when fed into the first term on the right-hand side of (2.12),
$\hat{\boldsymbol{b}}$
. These perturbations, when fed into the first term on the right-hand side of (2.12),
![]() $v_{\Vert }\hat{\boldsymbol{b}}$
, cause the proton’s guiding centre
$v_{\Vert }\hat{\boldsymbol{b}}$
, cause the proton’s guiding centre
![]() $\boldsymbol{R}$
to acquire a velocity perpendicular to
$\boldsymbol{R}$
to acquire a velocity perpendicular to
![]() $\boldsymbol{B}_{0}$
of
$\boldsymbol{B}_{0}$
of
where
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot \unicode[STIX]{x1D70C}}$
is the component of
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\bot \unicode[STIX]{x1D70C}}$
is the component of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
(from gyroscale fluctuations) perpendicular to
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
(from gyroscale fluctuations) perpendicular to
![]() $\boldsymbol{B}_{0}$
at the proton’s location. The value of
$\boldsymbol{B}_{0}$
at the proton’s location. The value of
![]() $\boldsymbol{u}_{\bot }$
varies in an incoherent manner in time, with a correlation time
$\boldsymbol{u}_{\bot }$
varies in an incoherent manner in time, with a correlation time
![]() ${\sim}\unicode[STIX]{x1D6FA}^{-1}$
. If
${\sim}\unicode[STIX]{x1D6FA}^{-1}$
. If
![]() $u_{\bot }$
is a significant fraction of
$u_{\bot }$
is a significant fraction of
![]() $v_{\bot }$
, then
$v_{\bot }$
, then
![]() $\boldsymbol{u}_{\bot }$
will cause a proton’s orbit in the plane perpendicular to
$\boldsymbol{u}_{\bot }$
will cause a proton’s orbit in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
to become stochastic. This leads to an alternative high-
$\boldsymbol{B}_{0}$
to become stochastic. This leads to an alternative high-
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
stochasticity parameter,
$\unicode[STIX]{x1D6FD}_{\text{p}}$
stochasticity parameter,
As
![]() $\tilde{\unicode[STIX]{x1D6FF}}$
increases towards unity, proton orbits become stochastic. For thermal protons with
$\tilde{\unicode[STIX]{x1D6FF}}$
increases towards unity, proton orbits become stochastic. For thermal protons with
![]() $v_{\bot }\sim v_{\Vert }$
and
$v_{\bot }\sim v_{\Vert }$
and
![]() $\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}_{\text{th}}$
,
$\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}_{\text{th}}$
,
![]() $\tilde{\unicode[STIX]{x1D6FF}}$
is equivalent to
$\tilde{\unicode[STIX]{x1D6FF}}$
is equivalent to
![]() $\unicode[STIX]{x1D6FF}$
in (2.21), which was based upon the parallel magnetic-field fluctuation
$\unicode[STIX]{x1D6FF}$
in (2.21), which was based upon the parallel magnetic-field fluctuation
![]() $\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}$
(even though we set
$\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}$
(even though we set
![]() $\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\sim \unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
in (2.21))). The contribution of parallel motion to orbit stochasticity thus does not change our conclusions about the rate at which thermal protons are heated stochastically. However, the contribution of parallel motion to orbit stochasticity should be taken into account when considering the ability of stochastic heating to produce superthermal tails, because in AW turbulence the perpendicular (parallel) magnetic fluctuation at perpendicular scale
$\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D70C}}\sim \unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
in (2.21))). The contribution of parallel motion to orbit stochasticity thus does not change our conclusions about the rate at which thermal protons are heated stochastically. However, the contribution of parallel motion to orbit stochasticity should be taken into account when considering the ability of stochastic heating to produce superthermal tails, because in AW turbulence the perpendicular (parallel) magnetic fluctuation at perpendicular scale
![]() $\unicode[STIX]{x1D706}$
, denoted
$\unicode[STIX]{x1D706}$
, denoted
![]() $\unicode[STIX]{x1D6FF}B_{\bot \unicode[STIX]{x1D706}}$
(
$\unicode[STIX]{x1D6FF}B_{\bot \unicode[STIX]{x1D706}}$
(
![]() $\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D706}}$
), is an increasing (decreasing) function of
$\unicode[STIX]{x1D6FF}B_{\Vert \unicode[STIX]{x1D706}}$
), is an increasing (decreasing) function of
![]() $\unicode[STIX]{x1D706}$
when
$\unicode[STIX]{x1D706}$
when
![]() $\unicode[STIX]{x1D706}$
is in the inertial range. Orbit stochasticity through the interaction between parallel motion and
$\unicode[STIX]{x1D706}$
is in the inertial range. Orbit stochasticity through the interaction between parallel motion and
![]() $\unicode[STIX]{x1D6FF}B_{\bot \unicode[STIX]{x1D70C}}$
could thus contribute to the development of superthermal tails when
$\unicode[STIX]{x1D6FF}B_{\bot \unicode[STIX]{x1D70C}}$
could thus contribute to the development of superthermal tails when
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
. An investigation of superthermal tails, however, lies beyond the scope of this paper.
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
. An investigation of superthermal tails, however, lies beyond the scope of this paper.
3 Numerical test-particle calculations
To test the phenomenological theory developed in § 2, we numerically track test-particle protons interacting with a spectrum of low-frequency randomly phased AWs and KAWs. The initial particle positions are random and uniformly distributed within a cubical region of volume
![]() $(100d_{\text{p}})^{3}$
, where
$(100d_{\text{p}})^{3}$
, where
![]() $d_{\text{p}}=v_{\text{A}}/\unicode[STIX]{x1D6FA}$
is the proton inertial length. The initial velocity distribution is an isotropic Maxwellian with proton temperature
$d_{\text{p}}=v_{\text{A}}/\unicode[STIX]{x1D6FA}$
is the proton inertial length. The initial velocity distribution is an isotropic Maxwellian with proton temperature
![]() $T_{\text{p}}$
. To trace each particle, we solve the equations of motion,
$T_{\text{p}}$
. To trace each particle, we solve the equations of motion,
using the Boris method (Boris Reference Boris1970) with a time step of
![]() $0.01\unicode[STIX]{x1D6FA}^{-1}$
.
$0.01\unicode[STIX]{x1D6FA}^{-1}$
.
3.1 Randomly phased waves
The code used to implement the AW/KAW spectrum is similar to the code used by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). The magnetic field is
![]() $\boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
, where
$\boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
, where
![]() $B_{0}$
is constant. We take
$B_{0}$
is constant. We take
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
to be the sum of the electric and magnetic fields of waves at each of 81 different wave vectors, with two waves of equal amplitude at each wave vector, one with
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
to be the sum of the electric and magnetic fields of waves at each of 81 different wave vectors, with two waves of equal amplitude at each wave vector, one with
![]() $\unicode[STIX]{x1D714}/k_{z}<0$
and the other with
$\unicode[STIX]{x1D714}/k_{z}<0$
and the other with
![]() $\unicode[STIX]{x1D714}/k_{z}>0$
.Footnote
5
The initial phase of each wave is randomly chosen.
$\unicode[STIX]{x1D714}/k_{z}>0$
.Footnote
5
The initial phase of each wave is randomly chosen.
The 81 wave vectors correspond to nine evenly spaced values of the azimuthal angle in
![]() $\boldsymbol{k}$
space (in cylindrical coordinates aligned with
$\boldsymbol{k}$
space (in cylindrical coordinates aligned with
![]() $\boldsymbol{B}_{0}$
) at each of nine specific values of
$\boldsymbol{B}_{0}$
) at each of nine specific values of
![]() $k_{\bot i}:i\in [0,\ldots ,8]$
. The values of
$k_{\bot i}:i\in [0,\ldots ,8]$
. The values of
![]() $k_{\bot i}$
are evenly spaced in
$k_{\bot i}$
are evenly spaced in
![]() $\ln (k_{\bot })$
-space, with
$\ln (k_{\bot })$
-space, with
![]() $\ln (k_{\bot i}\unicode[STIX]{x1D70C}_{\text{th}})=-4/3+i/3$
. The middle three cells, in which
$\ln (k_{\bot i}\unicode[STIX]{x1D70C}_{\text{th}})=-4/3+i/3$
. The middle three cells, in which
![]() $i=3,4$
and
$i=3,4$
and
![]() $5$
, have a combined width of unity in
$5$
, have a combined width of unity in
![]() $\ln (k_{\bot })$
-space, centred at precisely
$\ln (k_{\bot })$
-space, centred at precisely
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
. We computationally evaluate
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
. We computationally evaluate
![]() $\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
and
$\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
and
![]() $\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
via the r.m.s. values of the
$\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
via the r.m.s. values of the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity and
$\boldsymbol{E}\times \boldsymbol{B}$
velocity and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
that result from the waves in just these middle three cells.
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
that result from the waves in just these middle three cells.
There is one value of
![]() $k_{\Vert }\equiv |k_{z}|$
at each
$k_{\Vert }\equiv |k_{z}|$
at each
![]() $k_{\bot i}$
, denoted
$k_{\bot i}$
, denoted
![]() $k_{\Vert i}$
. We determine
$k_{\Vert i}$
. We determine
![]() $k_{\Vert 4}$
by setting the linear frequency at
$k_{\Vert 4}$
by setting the linear frequency at
![]() $k_{\Vert 4}$
equal to
$k_{\Vert 4}$
equal to
![]() $k_{\bot 4}\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
. At other values of
$k_{\bot 4}\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
. At other values of
![]() $k_{\bot }$
, we set
$k_{\bot }$
, we set
 $$\begin{eqnarray}\frac{k_{\Vert i}}{k_{\Vert 4}}=\left\{\begin{array}{@{}l@{}}\displaystyle \left(\frac{k_{\bot i}}{k_{\bot 4}}\right)^{2/3}:0\leqslant i<4\quad \\ \displaystyle \left(\frac{k_{\bot i}}{k_{\bot 4}}\right)^{1/3}:4<i\leqslant 8.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\frac{k_{\Vert i}}{k_{\Vert 4}}=\left\{\begin{array}{@{}l@{}}\displaystyle \left(\frac{k_{\bot i}}{k_{\bot 4}}\right)^{2/3}:0\leqslant i<4\quad \\ \displaystyle \left(\frac{k_{\bot i}}{k_{\bot 4}}\right)^{1/3}:4<i\leqslant 8.\quad \end{array}\right.\end{eqnarray}$$
The exponents
![]() $2/3$
and
$2/3$
and
![]() $1/3$
in (3.2) are chosen to match the scalings in the critical-balance models of Goldreich & Sridhar (Reference Goldreich and Sridhar1995) and Cho & Lazarian (Reference Cho and Lazarian2004), respectively. We take the individual wave magnetic-field amplitudes to be proportional to
$1/3$
in (3.2) are chosen to match the scalings in the critical-balance models of Goldreich & Sridhar (Reference Goldreich and Sridhar1995) and Cho & Lazarian (Reference Cho and Lazarian2004), respectively. We take the individual wave magnetic-field amplitudes to be proportional to
![]() $k_{\bot }^{-1/3}$
and
$k_{\bot }^{-1/3}$
and
![]() $k_{\bot }^{-2/3}$
for
$k_{\bot }^{-2/3}$
for
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}<1$
and
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}<1$
and
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}>1$
, respectively, in order to match the same two critical-balance models. (All the waves at the same value of
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}>1$
, respectively, in order to match the same two critical-balance models. (All the waves at the same value of
![]() $k_{\bot i}$
have the same amplitudes.) We determine the wave frequency and relative amplitudes of the different components of the fluctuating electric and magnetic fields using Hollweg’s (Reference Hollweg1999) two-fluid analysis of linear KAWs, setting
$k_{\bot i}$
have the same amplitudes.) We determine the wave frequency and relative amplitudes of the different components of the fluctuating electric and magnetic fields using Hollweg’s (Reference Hollweg1999) two-fluid analysis of linear KAWs, setting
where
![]() $T_{\text{e}}$
and
$T_{\text{e}}$
and
![]() $T_{\text{p}}$
are the (isotropic) electron and proton temperatures. We do not expect the particular choices in (3.3) to have a large effect on our results, but choose those values to facilitate a direct comparison to the previous numerical results of Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). Since we take
$T_{\text{p}}$
are the (isotropic) electron and proton temperatures. We do not expect the particular choices in (3.3) to have a large effect on our results, but choose those values to facilitate a direct comparison to the previous numerical results of Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). Since we take
![]() $T_{\bot \text{p}}=T_{\Vert \text{p}}$
, we set
$T_{\bot \text{p}}=T_{\Vert \text{p}}$
, we set
3.2 A note on the electric field
Following Lehe et al. (Reference Lehe, Parrish and Quataert2009), we correct the electric field because the magnetic field (including its fluctuations, i.e.
![]() $\boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
) in the simulation is not orientated along the
$\boldsymbol{B}=B_{0}\hat{\boldsymbol{z}}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
) in the simulation is not orientated along the
![]() $z$
-axis. The simulation, however, equates the parallel and perpendicular components of the electric field to the parallel and perpendicular components of the wave electric field that would arise if the magnetic field were aligned exactly on the
$z$
-axis. The simulation, however, equates the parallel and perpendicular components of the electric field to the parallel and perpendicular components of the wave electric field that would arise if the magnetic field were aligned exactly on the
![]() $z$
-axis. The result is a numerical addition of perpendicular electric-field terms to the parallel electric field, which, in turn, causes non-physical parallel heating. This may be seen in figure 2 of Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). To fix this, we replace the sum of the individual wave electric fields described in § 3.1, which we denote
$z$
-axis. The result is a numerical addition of perpendicular electric-field terms to the parallel electric field, which, in turn, causes non-physical parallel heating. This may be seen in figure 2 of Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). To fix this, we replace the sum of the individual wave electric fields described in § 3.1, which we denote
![]() $\boldsymbol{E}_{\text{wave}}$
, with the modified electric field
$\boldsymbol{E}_{\text{wave}}$
, with the modified electric field
![]() $\boldsymbol{E}=\boldsymbol{E}_{\text{wave}}+\hat{\boldsymbol{b}}(\hat{\boldsymbol{z}}\boldsymbol{\cdot }\boldsymbol{E}_{\text{wave}}-\hat{\boldsymbol{b}}\boldsymbol{\cdot }\boldsymbol{E}_{\text{wave}})$
.
$\boldsymbol{E}=\boldsymbol{E}_{\text{wave}}+\hat{\boldsymbol{b}}(\hat{\boldsymbol{z}}\boldsymbol{\cdot }\boldsymbol{E}_{\text{wave}}-\hat{\boldsymbol{b}}\boldsymbol{\cdot }\boldsymbol{E}_{\text{wave}})$
.
3.3 Perpendicular heating
We perform numerical test-particle calculations at five different values of
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
, in particular
$\unicode[STIX]{x1D6FD}_{\text{p}}$
, in particular
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=\{0.006,0.01,0.1,1,10\}$
. For each
$\unicode[STIX]{x1D6FD}_{\text{p}}=\{0.006,0.01,0.1,1,10\}$
. For each
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
value, we carry out test-particle calculations for five different values of
$\unicode[STIX]{x1D6FD}_{\text{p}}$
value, we carry out test-particle calculations for five different values of
![]() $\unicode[STIX]{x1D6FF}$
(or, equivalently, five different values of
$\unicode[STIX]{x1D6FF}$
(or, equivalently, five different values of
![]() $\unicode[STIX]{x1D700}$
). Each calculation returns the values of
$\unicode[STIX]{x1D700}$
). Each calculation returns the values of
![]() $\langle v_{\bot }^{2}\rangle$
and
$\langle v_{\bot }^{2}\rangle$
and
![]() $\langle v_{\Vert }^{2}\rangle$
as functions of time. We show two examples in figure 2. The slope of the best-fit line for each
$\langle v_{\Vert }^{2}\rangle$
as functions of time. We show two examples in figure 2. The slope of the best-fit line for each
![]() $\langle v_{\bot }^{2}(t)\rangle$
curve determines the perpendicular-heating rate per unit mass
$\langle v_{\bot }^{2}(t)\rangle$
curve determines the perpendicular-heating rate per unit mass
![]() $Q_{\bot }=(1/2)(\text{d}/\text{d}t)\langle v_{\bot }^{2}\rangle$
, where
$Q_{\bot }=(1/2)(\text{d}/\text{d}t)\langle v_{\bot }^{2}\rangle$
, where
![]() $\langle \,\cdots \,\rangle$
indicates an average over the
$\langle \,\cdots \,\rangle$
indicates an average over the
![]() $10^{4}$
or
$10^{4}$
or
![]() $10^{5}$
particles in the simulation. (We use more particles in simulations with smaller
$10^{5}$
particles in the simulation. (We use more particles in simulations with smaller
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $\unicode[STIX]{x1D6FF}$
because the heating rates are smaller in these simulations, and the extra particles increase the signal-to-noise ratio.) We fit the
$\unicode[STIX]{x1D6FF}$
because the heating rates are smaller in these simulations, and the extra particles increase the signal-to-noise ratio.) We fit the
![]() $\langle v_{\bot }^{2}(t)\rangle$
curves during the time interval
$\langle v_{\bot }^{2}(t)\rangle$
curves during the time interval
![]() $(t_{\text{i}},t_{\text{f}})$
, where
$(t_{\text{i}},t_{\text{f}})$
, where
![]() $t_{\text{i}}=20\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FA}$
and
$t_{\text{i}}=20\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FA}$
and
![]() $t_{\text{f}}$
is the smaller of the following two values:
$t_{\text{f}}$
is the smaller of the following two values:
![]() $10^{4}\unicode[STIX]{x1D6FA}^{-1}$
and the time required for
$10^{4}\unicode[STIX]{x1D6FA}^{-1}$
and the time required for
![]() $\langle v_{\bot }^{2}\rangle$
to increase by
$\langle v_{\bot }^{2}\rangle$
to increase by
![]() $\simeq 30\,\%$
. We do not include the first ten cyclotron periods when calculating
$\simeq 30\,\%$
. We do not include the first ten cyclotron periods when calculating
![]() $Q_{\bot }$
, because it takes the particles a few cyclotron periods to adjust to the presence of the waves, during which time there is typically strong transient heating. (As figure 2 shows, the test particles undergo parallel heating as well as perpendicular heating, as was found previously by Xia et al. (Reference Xia, Perez, Chandran and Quataert2013) in simulations of test particles interacting with reduced magnetohydrodynamic turbulence at
$Q_{\bot }$
, because it takes the particles a few cyclotron periods to adjust to the presence of the waves, during which time there is typically strong transient heating. (As figure 2 shows, the test particles undergo parallel heating as well as perpendicular heating, as was found previously by Xia et al. (Reference Xia, Perez, Chandran and Quataert2013) in simulations of test particles interacting with reduced magnetohydrodynamic turbulence at
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=1$
.)
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=1$
.)

Figure 2. The mean square velocity perpendicular to
![]() $\boldsymbol{B}_{0}$
,
$\boldsymbol{B}_{0}$
,
![]() $\langle v_{\bot }^{2}\rangle$
, as a function of time in two test-particle calculations, each of which tracks
$\langle v_{\bot }^{2}\rangle$
, as a function of time in two test-particle calculations, each of which tracks
![]() $10^{5}$
protons. The value of the stochasticity parameter
$10^{5}$
protons. The value of the stochasticity parameter
![]() $\unicode[STIX]{x1D6FF}$
(defined in (2.21)) is 0.15 in both calculations.
$\unicode[STIX]{x1D6FF}$
(defined in (2.21)) is 0.15 in both calculations.
The perpendicular-heating rates in our test-particle calculations are shown in figure 3. The solid-line curves in (a,c) on the left correspond to (2.41), with
These values are very similar to the values
![]() $c_{1}=0.75$
and
$c_{1}=0.75$
and
![]() $c_{2}=0.34$
obtained by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) at
$c_{2}=0.34$
obtained by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010) at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=0.006$
. The solid-line curves in (b,d) on the right correspond to (2.40) with
$\unicode[STIX]{x1D6FD}_{\text{p}}=0.006$
. The solid-line curves in (b,d) on the right correspond to (2.40) with
The agreement between our numerical results and (2.40) suggests that the approximations used to derive this equation are reasonable.

Figure 3. Numerical results for the perpendicular-heating rate per unit mass,
![]() $Q_{\bot }$
, for protons interacting with randomly phased AWs and KAWs. (a)
$Q_{\bot }$
, for protons interacting with randomly phased AWs and KAWs. (a)
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}<1$
, and
$\unicode[STIX]{x1D6FD}_{\text{p}}<1$
, and
![]() $Q_{\bot }$
normalized by
$Q_{\bot }$
normalized by
![]() $\unicode[STIX]{x1D6FA}v_{\text{A}}^{2}$
. (b)
$\unicode[STIX]{x1D6FA}v_{\text{A}}^{2}$
. (b)
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\geqslant 1$
and
$\unicode[STIX]{x1D6FD}_{\text{p}}\geqslant 1$
and
![]() $Q_{\bot }$
normalized by
$Q_{\bot }$
normalized by
![]() $\unicode[STIX]{x1D6FA}v_{\text{A}}^{2}$
. (c)
$\unicode[STIX]{x1D6FA}v_{\text{A}}^{2}$
. (c)
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}<1$
and
$\unicode[STIX]{x1D6FD}_{\text{p}}<1$
and
![]() $Q_{\bot }$
normalized by
$Q_{\bot }$
normalized by
![]() $\unicode[STIX]{x1D6FA}w^{2}$
, where
$\unicode[STIX]{x1D6FA}w^{2}$
, where
![]() $w$
is the proton thermal speed defined in (3.4); the numerical results for all three
$w$
is the proton thermal speed defined in (3.4); the numerical results for all three
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
values (0.006, 0.01, and 0.1) are within the bars shown. (d)
$\unicode[STIX]{x1D6FD}_{\text{p}}$
values (0.006, 0.01, and 0.1) are within the bars shown. (d)
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\geqslant 1$
and
$\unicode[STIX]{x1D6FD}_{\text{p}}\geqslant 1$
and
![]() $Q_{\bot }$
normalized by
$Q_{\bot }$
normalized by
![]() $\unicode[STIX]{x1D6FA}w^{2}$
. In (a,c) the solid lines are plots of (2.41) for the best-fit values of
$\unicode[STIX]{x1D6FA}w^{2}$
. In (a,c) the solid lines are plots of (2.41) for the best-fit values of
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
given in (3.5). In (b,d) the solid lines are plots of (2.40) for the best-fit values of
$c_{2}$
given in (3.5). In (b,d) the solid lines are plots of (2.40) for the best-fit values of
![]() $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
in (3.6).
$\unicode[STIX]{x1D70E}_{2}$
in (3.6).
Figure 3(c) shows that at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}<1$
,
$\unicode[STIX]{x1D6FD}_{\text{p}}<1$
,
![]() $Q_{\bot }/(\unicode[STIX]{x1D6FA}w^{2})$
is a function of
$Q_{\bot }/(\unicode[STIX]{x1D6FA}w^{2})$
is a function of
![]() $\unicode[STIX]{x1D700}$
alone, consistent with the fact that (2.41) can be rewritten in the form
$\unicode[STIX]{x1D700}$
alone, consistent with the fact that (2.41) can be rewritten in the form
Figure 3(b) shows that at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\geqslant 1$
,
$\unicode[STIX]{x1D6FD}_{\text{p}}\geqslant 1$
,
![]() $Q_{\bot }/(\unicode[STIX]{x1D6FA}v_{\text{A}}^{2})$
is a function of
$Q_{\bot }/(\unicode[STIX]{x1D6FA}v_{\text{A}}^{2})$
is a function of
![]() $\unicode[STIX]{x1D6FF}$
alone, consistent with the fact that (2.40) can be rewritten as
$\unicode[STIX]{x1D6FF}$
alone, consistent with the fact that (2.40) can be rewritten as
We note that in our model of randomly phased KAWs (Chandran et al. Reference Chandran, Li, Rogers, Quataert and Germaschewski2010),
and thus
As a consequence, if we adopt the best-fit values of
![]() $\unicode[STIX]{x1D70E}_{1}$
,
$\unicode[STIX]{x1D70E}_{1}$
,
![]() $\unicode[STIX]{x1D70E}_{2}$
,
$\unicode[STIX]{x1D70E}_{2}$
,
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
, then the value of
$c_{2}$
, then the value of
![]() $Q_{\bot }$
at
$Q_{\bot }$
at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=1$
in (2.40), which matches our test-particle calculations quite well, exceeds the value that would follow from (2.41) at
$\unicode[STIX]{x1D6FD}_{\text{p}}=1$
in (2.40), which matches our test-particle calculations quite well, exceeds the value that would follow from (2.41) at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=1$
. A similar phenomenon was found by Xia et al. (Reference Xia, Perez, Chandran and Quataert2013) in numerical simulations of test particles interacting with strong reduced magnetohydrodynamic turbulence.
$\unicode[STIX]{x1D6FD}_{\text{p}}=1$
. A similar phenomenon was found by Xia et al. (Reference Xia, Perez, Chandran and Quataert2013) in numerical simulations of test particles interacting with strong reduced magnetohydrodynamic turbulence.
To obtain a fitting formula that can be used to model stochastic heating at large
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
, small
$\unicode[STIX]{x1D6FD}_{\text{p}}$
, small
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
and
$\unicode[STIX]{x1D6FD}_{\text{p}}$
and
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\simeq 1$
, we use (3.4) and (3.10) to rewrite the low-
$\unicode[STIX]{x1D6FD}_{\text{p}}\simeq 1$
, we use (3.4) and (3.10) to rewrite the low-
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
heating rate in (3.7) in terms of
$\unicode[STIX]{x1D6FD}_{\text{p}}$
heating rate in (3.7) in terms of
![]() $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
![]() $v_{\text{A}}$
. We then add the low-
$v_{\text{A}}$
. We then add the low-
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
heating rate to the high-
$\unicode[STIX]{x1D6FD}_{\text{p}}$
heating rate to the high-
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
heating rate in (3.8), obtaining
$\unicode[STIX]{x1D6FD}_{\text{p}}$
heating rate in (3.8), obtaining
The first term on the right-hand side dominates at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
in part because
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
in part because
![]() $\unicode[STIX]{x1D70E}_{1}\simeq 6.5c_{1}$
. The second term on the right-hand side dominates at
$\unicode[STIX]{x1D70E}_{1}\simeq 6.5c_{1}$
. The second term on the right-hand side dominates at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\ll 1$
. Figure 4 shows that (3.11) is consistent with our numerical results. This figure also illustrates how, at fixed
$\unicode[STIX]{x1D6FD}_{\text{p}}\ll 1$
. Figure 4 shows that (3.11) is consistent with our numerical results. This figure also illustrates how, at fixed
![]() $\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}/B_{0}$
, the stochastic-heating rate increases as
$\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}/B_{0}$
, the stochastic-heating rate increases as
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
decreases.
$\unicode[STIX]{x1D6FD}_{\text{p}}$
decreases.
As mentioned above, stochastic heating becomes more effective as the fluctuations become more intermittent (Xia et al.
Reference Xia, Perez, Chandran and Quataert2013; Mallet et al.
Reference Mallet, Klein, Chandran, Groselj, Hoppock, Bowen, Salem and Bale2018). The randomly phased waves in our test-particle simulations are not intermittent, but gyroscale fluctuations in space and astrophysical plasmas generally are (see, e.g. Mangeney et al.
Reference Mangeney, Salem, Veltri, Cecconi and Warmbein2001; Carbone et al.
Reference Carbone, Bruno, Sorriso-Valvo and Lepreti2004; Salem et al.
Reference Salem, Mangeney, Bale and Veltri2009; Chandran, Schekochihin & Mallet Reference Chandran, Schekochihin and Mallet2015; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2015). Further work is needed to determine how the best-fit constants in (3.5) and (3.6) depend upon the degree of intermittency at the proton gyroradius scale. Until this dependency is determined, some caution should be exercised when applying (3.11) to space and astrophysical plasmas. For reference, Bourouaine & Chandran (Reference Bourouaine and Chandran2013) found that lowering
![]() $c_{2}$
to
$c_{2}$
to
![]() $\simeq 0.2$
led the heating rate in (2.41) to be consistent with the proton-heating rate and fluctuation amplitudes inferred from measurements of the fast solar wind from the Helios spacecraft at
$\simeq 0.2$
led the heating rate in (2.41) to be consistent with the proton-heating rate and fluctuation amplitudes inferred from measurements of the fast solar wind from the Helios spacecraft at
![]() $r=0.3\text{ au}$
. However, if
$r=0.3\text{ au}$
. However, if
![]() $c_{2}=0.33$
, then the heating rate in (2.41) is too weak to explain the proton heating seen in the Helios measurements.
$c_{2}=0.33$
, then the heating rate in (2.41) is too weak to explain the proton heating seen in the Helios measurements.

Figure 4. The data points reproduce the numerical results from figure 3 for
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=0.01,0.1,1.0$
and 10. The dotted, long-dashed, solid and short-dashed lines plot (3.11) for, respectively,
$\unicode[STIX]{x1D6FD}_{\text{p}}=0.01,0.1,1.0$
and 10. The dotted, long-dashed, solid and short-dashed lines plot (3.11) for, respectively,
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=0.01$
,
$\unicode[STIX]{x1D6FD}_{\text{p}}=0.01$
,
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=0.1$
,
$\unicode[STIX]{x1D6FD}_{\text{p}}=0.1$
,
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=1$
and
$\unicode[STIX]{x1D6FD}_{\text{p}}=1$
and
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}=10$
. The solid and short-dashed lines are difficult to distinguish because they are nearly on top of each other.
$\unicode[STIX]{x1D6FD}_{\text{p}}=10$
. The solid and short-dashed lines are difficult to distinguish because they are nearly on top of each other.
4 Summary
In this paper we use phenomenological arguments to derive an analytic formula for the rate at which thermal protons are stochastically heated by AW/KAW turbulence at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
. We focus on
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
. We focus on
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1-30$
. Smaller values of
$\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1-30$
. Smaller values of
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
were considered by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). At larger values of
$\unicode[STIX]{x1D6FD}_{\text{p}}$
were considered by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). At larger values of
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
, KAWs at
$\unicode[STIX]{x1D6FD}_{\text{p}}$
, KAWs at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
become non-propagating, and some of the scalings we have assumed do not apply. At
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
become non-propagating, and some of the scalings we have assumed do not apply. At
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1-30$
, the motion of a proton’s effective guiding centre is dominated by the interaction between the proton and gyroscale fluctuations in the magnetic field, whose amplitude is denoted
$\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1-30$
, the motion of a proton’s effective guiding centre is dominated by the interaction between the proton and gyroscale fluctuations in the magnetic field, whose amplitude is denoted
![]() $\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
. As
$\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}$
. As
![]() $\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}/B_{0}$
increases from infinitesimal values towards unity, the proton motion in the plane perpendicular to
$\unicode[STIX]{x1D6FF}B_{\unicode[STIX]{x1D70C}}/B_{0}$
increases from infinitesimal values towards unity, the proton motion in the plane perpendicular to
![]() $\boldsymbol{B}_{0}$
becomes random (stochastic), leading to spatial diffusion, and this spatial diffusion breaks the strong correlation between changes in a proton’s perpendicular kinetic energy and the magnetic-field strength at the proton’s location that normally gives rise to magnetic-moment conservation. The interaction between the proton and the electric field then becomes a Markov process that causes the proton to diffuse in energy. This energy diffusion leads to heating. At
$\boldsymbol{B}_{0}$
becomes random (stochastic), leading to spatial diffusion, and this spatial diffusion breaks the strong correlation between changes in a proton’s perpendicular kinetic energy and the magnetic-field strength at the proton’s location that normally gives rise to magnetic-moment conservation. The interaction between the proton and the electric field then becomes a Markov process that causes the proton to diffuse in energy. This energy diffusion leads to heating. At
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1{-}30$
, it is the solenoidal component of the electric field that dominates the heating.
$\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1{-}30$
, it is the solenoidal component of the electric field that dominates the heating.
The analytic formula that we derive for the stochastic heating rate
![]() $Q_{\bot }$
contains two dimensionless constants,
$Q_{\bot }$
contains two dimensionless constants,
![]() $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
, whose values depend upon the nature of the AW/KAW fluctuations with which the proton interacts (e.g. randomly phased waves or intermittent turbulence). We numerically track test particles interacting with randomly phased AWs and KAWs and find that our analytic formula for
$\unicode[STIX]{x1D70E}_{2}$
, whose values depend upon the nature of the AW/KAW fluctuations with which the proton interacts (e.g. randomly phased waves or intermittent turbulence). We numerically track test particles interacting with randomly phased AWs and KAWs and find that our analytic formula for
![]() $Q_{\bot }$
agrees well with the heating rate of these test particles for the choices
$Q_{\bot }$
agrees well with the heating rate of these test particles for the choices
![]() $\unicode[STIX]{x1D70E}_{1}=5.0$
and
$\unicode[STIX]{x1D70E}_{1}=5.0$
and
![]() $\unicode[STIX]{x1D70E}_{2}=0.21$
. We note that previous work has shown that for fixed r.m.s. amplitudes of the gyroscale fluctuations, stochastic heating is more effective when protons interact with intermittent turbulence than when protons interact with randomly phased waves (Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Xia et al.
Reference Xia, Perez, Chandran and Quataert2013; Mallet et al.
Reference Mallet, Klein, Chandran, Groselj, Hoppock, Bowen, Salem and Bale2018). The reason for this is that in intermittent turbulence, most of the heating occurs near coherent structures, in which the fluctuation amplitudes are larger than average and in which the particle orbits are more stochastic than on average.
$\unicode[STIX]{x1D70E}_{2}=0.21$
. We note that previous work has shown that for fixed r.m.s. amplitudes of the gyroscale fluctuations, stochastic heating is more effective when protons interact with intermittent turbulence than when protons interact with randomly phased waves (Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Xia et al.
Reference Xia, Perez, Chandran and Quataert2013; Mallet et al.
Reference Mallet, Klein, Chandran, Groselj, Hoppock, Bowen, Salem and Bale2018). The reason for this is that in intermittent turbulence, most of the heating occurs near coherent structures, in which the fluctuation amplitudes are larger than average and in which the particle orbits are more stochastic than on average.
Our work leaves a number of interesting questions unanswered. Two such questions are how the energy-diffusion coefficient depends on energy at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1-30$
and how the proton distribution function evolves in the presence of stochastic heating. (For a discussion of the low-
$\unicode[STIX]{x1D6FD}_{\text{p}}\sim 1-30$
and how the proton distribution function evolves in the presence of stochastic heating. (For a discussion of the low-
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
case, see Klein & Chandran (Reference Klein and Chandran2016).) We also have not addressed the question of how stochastic heating changes as
$\unicode[STIX]{x1D6FD}_{\text{p}}$
case, see Klein & Chandran (Reference Klein and Chandran2016).) We also have not addressed the question of how stochastic heating changes as
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
is increased to values
$\unicode[STIX]{x1D6FD}_{\text{p}}$
is increased to values
![]() ${\gtrsim}30$
and KAWs at
${\gtrsim}30$
and KAWs at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
become non-propagating, or how the stochastic-heating rate for minor ions depends upon minor-ion mass, charge and average flow speed along
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
become non-propagating, or how the stochastic-heating rate for minor ions depends upon minor-ion mass, charge and average flow speed along
![]() $\boldsymbol{B}_{0}$
in the proton frame. (For a discussion of the low-
$\boldsymbol{B}_{0}$
in the proton frame. (For a discussion of the low-
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
case, see Chandran et al. (Reference Chandran, Verscharen, Quataert, Kasper, Isenberg and Bourouaine2013).) Previous studies have compared observationally inferred heating rates in the solar wind with the low-
$\unicode[STIX]{x1D6FD}_{\text{p}}$
case, see Chandran et al. (Reference Chandran, Verscharen, Quataert, Kasper, Isenberg and Bourouaine2013).) Previous studies have compared observationally inferred heating rates in the solar wind with the low-
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}$
stochastic-heating rate in (2.41) derived by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010), finding quantitative agreement at
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}$
stochastic-heating rate in (2.41) derived by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010), finding quantitative agreement at
![]() $r=0.3\text{ au}$
assuming
$r=0.3\text{ au}$
assuming
![]() $c_{2}\simeq 0.2$
(Bourouaine & Chandran Reference Bourouaine and Chandran2013) and qualitative agreement at
$c_{2}\simeq 0.2$
(Bourouaine & Chandran Reference Bourouaine and Chandran2013) and qualitative agreement at
![]() $r=1\text{ au}$
(Vech, Klein & Kasper Reference Vech, Klein and Kasper2017). However, it is not yet clear whether the stochastic-heating rate in (2.40) agrees with solar-wind measurements in the large-
$r=1\text{ au}$
(Vech, Klein & Kasper Reference Vech, Klein and Kasper2017). However, it is not yet clear whether the stochastic-heating rate in (2.40) agrees with solar-wind measurements in the large-
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}$
regime. In addition, stochastic heating at
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}$
regime. In addition, stochastic heating at
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}\gtrsim 1$
could trigger temperature-anisotropy instabilities, which could in turn modify the rate(s) of perpendicular (and parallel) proton heating. Future investigations of these questions will be important for determining more accurately the role of stochastic heating in space and astrophysical plasmas.
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}\gtrsim 1$
could trigger temperature-anisotropy instabilities, which could in turn modify the rate(s) of perpendicular (and parallel) proton heating. Future investigations of these questions will be important for determining more accurately the role of stochastic heating in space and astrophysical plasmas.
Acknowledgements
We thank L. Arzamasskiy, Y. Kawazura, M. Kunz, E. Quataert and A. Schekochihin for valuable discussions. This work was supported in part by NASA grants NNX15AI80, NNX16AG81G, NNS16AM23G, NNX17AI18G, and NNN06AA01C and NSF grant PHY-1500041. D.V. acknowledges the support of STFC Ernest Rutherford Fellowship ST/P003826/1.
Appendix A. Non-propagation of KAWs at
 $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
at high
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}\sim 1$
at high
 $\unicode[STIX]{x1D6FD}_{\text{p}}$
$\unicode[STIX]{x1D6FD}_{\text{p}}$
In figure 5, we compare the AW/KAW dispersion relation from the two-fluid model of Hollweg (Reference Hollweg1999) and the PLUME hot-plasma-dispersion-relation solver (Klein & Howes Reference Klein and Howes2015) for
![]() $T_{\text{e}}/T_{\text{p}}=0.5$
and
$T_{\text{e}}/T_{\text{p}}=0.5$
and
![]() $v_{\text{A}}/c=0.003$
and for various values of
$v_{\text{A}}/c=0.003$
and for various values of
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
. The PLUME results shown here assume that
$\unicode[STIX]{x1D6FD}_{\text{p}}$
. The PLUME results shown here assume that
![]() $k_{\Vert }\unicode[STIX]{x1D70C}_{\text{th}}=0.001$
and that the proton and electron distributions are Maxwellian. The two-fluid dispersion relation agrees reasonably well with the more accurate PLUME results at
$k_{\Vert }\unicode[STIX]{x1D70C}_{\text{th}}=0.001$
and that the proton and electron distributions are Maxwellian. The two-fluid dispersion relation agrees reasonably well with the more accurate PLUME results at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
. However, at
$\unicode[STIX]{x1D6FD}_{\text{p}}\lesssim 1$
. However, at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
, the PLUME results deviate from the two-fluid theory because of ion damping, which becomes stronger as
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
, the PLUME results deviate from the two-fluid theory because of ion damping, which becomes stronger as
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
increases (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008; Kunz et al.
Reference Kunz, Abel, Klein and Schekochihin2018). Starting at
$\unicode[STIX]{x1D6FD}_{\text{p}}$
increases (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008; Kunz et al.
Reference Kunz, Abel, Klein and Schekochihin2018). Starting at
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\simeq 30$
(for
$\unicode[STIX]{x1D6FD}_{\text{p}}\simeq 30$
(for
![]() $T_{\text{e}}/T_{\text{p}}=0.5$
,
$T_{\text{e}}/T_{\text{p}}=0.5$
,
![]() $v_{\text{A}}/c=0.003$
and
$v_{\text{A}}/c=0.003$
and
![]() $k_{\Vert }\unicode[STIX]{x1D70C}_{\text{p}}=0.001$
), the real part (but not the imaginary part) of the KAW frequency at
$k_{\Vert }\unicode[STIX]{x1D70C}_{\text{p}}=0.001$
), the real part (but not the imaginary part) of the KAW frequency at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
vanishes (i.e. KAWs become damped, non-propagating modes). For larger
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}=1$
vanishes (i.e. KAWs become damped, non-propagating modes). For larger
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
values, KAWs are non-propagating throughout an interval of
$\unicode[STIX]{x1D6FD}_{\text{p}}$
values, KAWs are non-propagating throughout an interval of
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}$
values centred on unity that broadens to both larger and smaller values as
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}$
values centred on unity that broadens to both larger and smaller values as
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
increases (Kawazura et al.
Reference Kawazura, Barnes and Schekochihin2018).
$\unicode[STIX]{x1D6FD}_{\text{p}}$
increases (Kawazura et al.
Reference Kawazura, Barnes and Schekochihin2018).

Figure 5. The KAW dispersion relation from Hollweg’s (Reference Hollweg1999) two-fluid model (solid lines) and the PLUME hot-plasma-dispersion-relation solver (Klein & Howes Reference Klein and Howes2015) (dotted lines) for
![]() $T_{\text{e}}/T_{\text{p}}=0.5$
and
$T_{\text{e}}/T_{\text{p}}=0.5$
and
![]() $v_{\text{A}}/c=0.003$
for various powers of
$v_{\text{A}}/c=0.003$
for various powers of
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}$
.
$\unicode[STIX]{x1D6FD}_{\text{p}}$
.
Appendix B. Stochastic heating by the electrostatic potential at
 $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
In § 2 we considered the r.m.s. change to a thermal proton’s energy
![]() $\unicode[STIX]{x0394}H$
resulting from the solenoidal component of the electric field
$\unicode[STIX]{x0394}H$
resulting from the solenoidal component of the electric field
![]() $\boldsymbol{E}_{\text{s}}$
during the particle residence time
$\boldsymbol{E}_{\text{s}}$
during the particle residence time
![]() $\unicode[STIX]{x0394}t$
within one set of gyroscale eddies. We also evaluated the contribution of
$\unicode[STIX]{x0394}t$
within one set of gyroscale eddies. We also evaluated the contribution of
![]() $\boldsymbol{E}_{\text{s}}$
to the stochastic heating rate
$\boldsymbol{E}_{\text{s}}$
to the stochastic heating rate
![]() $Q_{\bot }$
. Here, we show that the contribution to
$Q_{\bot }$
. Here, we show that the contribution to
![]() $Q_{\bot }$
from
$Q_{\bot }$
from
![]() $\boldsymbol{E}_{\text{s}}$
is larger than the contribution from the electrostatic potential
$\boldsymbol{E}_{\text{s}}$
is larger than the contribution from the electrostatic potential
![]() $\unicode[STIX]{x1D6F7}$
when
$\unicode[STIX]{x1D6F7}$
when
![]() $\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
.
$\unicode[STIX]{x1D6FD}_{\text{p}}\gtrsim 1$
.
We assume that the r.m.s. amplitude of the potential part of the electric field at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}$
is comparable to the r.m.s. amplitude of the total gyroscale electric-field fluctuation,
$k_{\bot }\unicode[STIX]{x1D70C}_{\text{th}}$
is comparable to the r.m.s. amplitude of the total gyroscale electric-field fluctuation,
![]() $\unicode[STIX]{x1D6FF}E_{\unicode[STIX]{x1D70C}}$
, which in turn is
$\unicode[STIX]{x1D6FF}E_{\unicode[STIX]{x1D70C}}$
, which in turn is
![]() ${\sim}\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}B_{0}/c$
. As discussed by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010), the contribution of the time-varying electrostatic potential to
${\sim}\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}B_{0}/c$
. As discussed by Chandran et al. (Reference Chandran, Li, Rogers, Quataert and Germaschewski2010), the contribution of the time-varying electrostatic potential to
![]() $\unicode[STIX]{x0394}H$
is
$\unicode[STIX]{x0394}H$
is
where
![]() $\unicode[STIX]{x1D714}_{\text{eff}}=\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}/\unicode[STIX]{x1D70C}_{\text{th}}$
(see (2.35)), and
$\unicode[STIX]{x1D714}_{\text{eff}}=\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}/\unicode[STIX]{x1D70C}_{\text{th}}$
(see (2.35)), and
Since (2.27) gives
![]() $\unicode[STIX]{x0394}t\sim \unicode[STIX]{x1D6FD}_{\text{p}}^{-1/2}\unicode[STIX]{x1D70C}_{\text{th}}/\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
,
$\unicode[STIX]{x0394}t\sim \unicode[STIX]{x1D6FD}_{\text{p}}^{-1/2}\unicode[STIX]{x1D70C}_{\text{th}}/\unicode[STIX]{x1D6FF}v_{\unicode[STIX]{x1D70C}}$
,
Combining (B 1) through (B 3), we obtain
and
which is a factor of
![]() ${\sim}\unicode[STIX]{x1D6FD}_{\text{p}}^{-1}$
smaller than the estimate of
${\sim}\unicode[STIX]{x1D6FD}_{\text{p}}^{-1}$
smaller than the estimate of
![]() $Q_{\bot }$
in (2.39).
$Q_{\bot }$
in (2.39).