Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T06:48:41.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Bootstrap current and parallel ion velocity in imperfectly optimized stellarators

Part of: Focus on Fusion

Published online by Cambridge University Press:  13 January 2020

Peter J. Catto Open the ORCID record for Peter J. Catto [Opens in a new window]  and
Per Helander Open the ORCID record for Per Helander [Opens in a new window]
Peter J. Catto*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Per Helander
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17491 Greifswald, Germany
*
†Email address for correspondence: catto@psfc.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A novel derivation of the parallel ion velocity, and the bootstrap and Pfirsch–Schlüter currents in an imperfectly optimized (that is, almost omnigenous) stellarator magnetic field, 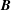$\boldsymbol{B}$, is presented that somewhat more generally recovers expressions completely consistent with previous analytic results. However, it is also shown that, when the conventional radially local form of the drift kinetic equation is employed, the flow velocity and the bootstrap current acquire a spurious contribution proportional to 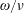$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708}$, where $\unicode[STIX]{x1D714}$ denotes the 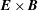$\boldsymbol{E}\times \boldsymbol{B}$ rotation frequency (due to the radial electric field 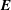$\boldsymbol{E}$) and $\unicode[STIX]{x1D708}$ the collision frequency. This contribution is particularly large in the 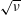$\sqrt{\unicode[STIX]{x1D708}}$ regime and at smaller collisionalities, where 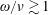$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708}\gtrsim 1$, and is presumably present in most numerical calculations, but it disappears if a more accurate drift kinetic equation is used.

Keywords

fusion plasmaplasma confinementplasma flows
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 1 , February 2020 , 905860105
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, F., Almagri, A., Anderson, D., Matthews, P., Talmadge, J. & Shohet, J. 1995 The helically symmetric experiment, (HSX) goals, design and status. Fusion Technol. 27, 273–277.CrossRefGoogle Scholar
Beidler, C. D., Allmaier, K., Isaev, M. Y., Kasilov, S. V., Kernbichler, W., Leitold, G. O., Maaßberg, H., Mikkelsen, D. R., Murakami, S., Schmidt, M. et al. 2011 Benchmarking of the mono-energetic transport coefficients – results from the international collaboration on neoclassical transport in stellarators (ICNTS). Nucl. Fusion 51 (7), 076001.CrossRefGoogle Scholar
Beidler, C. D. & D’haeseleer, W. D. 1995 A general solution of the ripple-averaged kinetic equation (GSRAKE). Plasma Phys. Control. Fusion 37, 463–490.CrossRefGoogle Scholar
Beidler, C. D., Grieger, G., Hermegger, F., Hameyer, E., Kisslinger, J., Lotz, W., Maassberg, H., Merkel, P., Nührenberg, J., Rau, F. et al. 1990 Physics and engineering design for Wendelstein VII-X. Fusion Technol. 17, 148–168.CrossRefGoogle Scholar
Boozer, A. H. 1981 Plasma equilibrium with rational magnetic surfaces. Phys. Fluids 24, 1999–2003.CrossRefGoogle Scholar
Boozer, A. H. 1995 Quasi-helical symmetry in stellarators. Plasma Phys. Control. Fusion 37, A103–A117.CrossRefGoogle Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2017 The effect of tangential drifts on neoclassical transport in stellarators close to omnigeneity. Plasma Phys. Control. Fusion 59, 055014.CrossRefGoogle Scholar
Cary, J. R. & Shasharina, S. G. 1997a Omnigenity and quasihelicity in helical plasma confinement systems. Phys. Plasmas 4, 3323–3333.CrossRefGoogle Scholar
Cary, J. R. & Shasharina, S. G. 1997b Helical plasma confinement devices with good confinement properties. Phys. Rev. Lett. 78, 674–677.CrossRefGoogle Scholar
Catto, P. J. 2019 Collisional alpha transport in a weakly non-quasisymmetric stellarator magnetic field. J. Plasmas Physics 85, 905850213; corrigendum 85, 945850501.Google Scholar
Catto, P. J., Hastie, R. J., Hutchinson, I. H. & Helander, P. 2001 Effect of the inductive electric field on ion flow in tokamaks. Phys. Plasmas 8, 3334–3341.CrossRefGoogle Scholar
Connor, J. W., Grimm, R. C., Hastie, R. J. & Keeping, P. M. 1973 The conductivity of a toroidal plasma. Nucl. Fusion 13, 211–214.CrossRefGoogle Scholar
Galeev, A. A., Sagdeev, R. Z., Furth, H. P. & Rosenbluth, M. N. 1969 Plasma diffusion in a toroidal stellarator. Phys. Rev. Lett. 22, 511–514.CrossRefGoogle Scholar
Garren, D. A. & Boozer, A. H. 1991 Existence of quasihelically symmetric stellarators. Phys. Fluids B 3, 2822–2834.CrossRefGoogle Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2007 Table of Integrals, Series, and Products, 7th edn, pp. 93–94. Elsevier/Academic.Google Scholar
Grieger, G., Lotz, W., Merkel, P., Nührenberg, J., Sapper, J., Strumberger, E., Wobig, H., Burhenn, V., Erckmannn, V. et al. & the W7-X Team 1992 Physics optimization of stellarators. Phys. Fluids B 4, 2081–2091.CrossRefGoogle Scholar
Hazeltine, R. D. 1973 Recursive derivation of the drift-kinetic equation. Plasma Phys. 15, 77–80.CrossRefGoogle Scholar
Helander, P. 2014 The theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77, 087001.CrossRefGoogle ScholarPubMed
Helander, P., Geiger, J. & Maaßberg, H. 2011 On the bootstrap current in stellarators and tokamaks. Phys. Plasmas 18, 092505.CrossRefGoogle Scholar
Helander, P. & Nührenberg, J. 2009 Bootstrap current and neoclassical transport in quasi-isodynamic stellarators. Plasma Phys. Control. Fusion 51, 055004.CrossRefGoogle Scholar
Helander, P., Parra, F. I. & Newton, S. L. 2017 Stellarator bootstrap current and plasma flow velocity at low collisionality. J. Plasma Phys. 83, 905830206.CrossRefGoogle Scholar
Helander, P. & Sigmar, D. J. 2002 Collisional Transport in Magnetized Plasmas. pp. 191–195 and 206–207. Cambridge University Press.Google Scholar
Henneberg, S. A., Drevlak, M., Nührenberg, C., Beidler, C. D., Turkin, Y., Loizu, J. & Helander, P. 2019 Properties of a new quasi-axisymmetric configuration. Nucl. Fusion 59, 026014.CrossRefGoogle Scholar
Ho, D. D.-M. & Kulsrud, R. M. 1987 Neoclassical transport in stellarators. Phys. Fluids 30, 442–461.CrossRefGoogle Scholar
Kagan, G. & Catto, P. J. 2010 Neoclassical ion heat flux and poloidal flow in a tokamak pedestal. Plasma Phys. Control. Fusion 52, 055004.CrossRefGoogle Scholar
Kernbichler, W., Kasilov, S. V., Kapper, G., Martitsch, A. F., Nemov, V. V., Albert, C. & Heyn, M. F. 2016 Solution of drift kinetic equation in stellarators and tokamaks with broken symmetry using the code NEO-2. Plasma Phys. Control. Fusion 58, 104001.CrossRefGoogle Scholar
Landreman, M. & Catto, P. J. 2012 Omnigenity as generalized quasisymmetry. Phys. Plasmas 19, 056103.CrossRefGoogle Scholar
Landreman, M. & Sengupta, W. 2018 Direct construction of optimized stellarator shapes. Part 1. Theory in cylindrical coordinates. J. Plasma Phys. 84, 905840616.CrossRefGoogle Scholar
Landreman, M., Sengupta, W. & Plunk, G. G. 2019 Direct construction of optimized stellarator shapes. Part 2. Numerical quasisymmetric solutions. J. Plasma Phys. 85, 905850103.CrossRefGoogle Scholar
Landreman, M., Smith, H. M., Mollen, A. & Helander, P. 2014 Comparison of particle trajectories and collision operators for collisional transport in nonaxisymmetric plasmas. Phys. Plasmas 21, 042503.CrossRefGoogle Scholar
Matsuoka, S., Satake, S., Kanno, R. & Sugama, H. 2015 Effects of magnetic drift tangential to magnetic surfaces on neoclassical transport in non-axisymmetric plasmas. Phys. Plasmas 22, 072511.CrossRefGoogle Scholar
Nührenberg, J. 2010 Development of quasi-isodynamic stellarators. Plasma Phys. Control. Fusion 52, 124003.CrossRefGoogle Scholar
Nührenberg, J. & Zille, R. 1988 Quasi-helically symmetric toroidal stellarators. Phys. Lett. A 129, 113–117.CrossRefGoogle Scholar
Plunk, G. G. & Helander, P. 2018 Quasi-axisymmetric equilibria: weakly non-axisymmetric case in a vacuum. J. Plasma Phys. 84, 905840205.CrossRefGoogle Scholar
Rosenbluth, M. N., Hazeltine, R. D. & Hinton, F. L. 1972 Plasma transport in toroidal confinement systems. Phys. Fluids 15, 116–140 (see appendix A).CrossRefGoogle Scholar
Shaing, K. C. 2015 Superbanana and superbanana plateau transport in finite aspect ratio tokamaks with broken symmetry. J. Plasma Phys. 81, 905810203.CrossRefGoogle Scholar
Shaing, K. C., Carreras, B. A., Dominguez, N., Lynch, V. E. & Tolliver, J. S. 1989 Bootstrap current control in stellarators. Phys. Fluids B 1, 1663–1670.CrossRefGoogle Scholar
Simakov, A. N. & Catto, P. J. 2005 Drift kinetic equation exact through second order in gyro-radius expansion. Phys. Plasmas 12, 012105.CrossRefGoogle Scholar
Simakov, A. N. & Helander, P. 2009 Neoclassical momentum transport in a collisional stellarator and a rippled tokamak. Phys. Plasmas 16, 042503.CrossRefGoogle Scholar