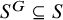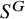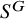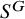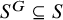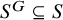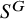1 Introduction
The classical invariant rings that we study here are determinantal rings, rings defined by Pfaffians of alternating matrices, symmetric determinantal rings and the Plücker coordinate rings of Grassmannians. Over a field of characteristic zero, these are all invariant rings for classical groups as in Weyl [Reference WeylWe]; by [Reference IgusaIg, Reference De Concini and ProcesiDP, Reference HashimotoHa], these are also invariant rings for the corresponding classical groups over an infinite field of positive characteristic. The embedding
![]() $S^G\subseteq S$
, for S a polynomial ring and G a classical group, is the natural embedding of the title. We describe these in turn, for K a field of arbitrary characteristic.
$S^G\subseteq S$
, for S a polynomial ring and G a classical group, is the natural embedding of the title. We describe these in turn, for K a field of arbitrary characteristic.
-
(a) Let Y and Z be
 $m\times t$
and
$m\times t$
and
 $t\times n$
matrices of indeterminates, respectively. Set S to be the polynomial ring
$t\times n$
matrices of indeterminates, respectively. Set S to be the polynomial ring
 $K[Y,Z]$
, and take R to be the K-subalgebra generated by the entries of the product matrix
$K[Y,Z]$
, and take R to be the K-subalgebra generated by the entries of the product matrix
 $YZ$
. Then R is isomorphic to the determinantal ring
$YZ$
. Then R is isomorphic to the determinantal ring
 $K[X]/I_{t+1}(X)$
, where X is an
$K[X]/I_{t+1}(X)$
, where X is an
 $m\times n$
matrix of indeterminates, and
$m\times n$
matrix of indeterminates, and
 $I_{t+1}(X)$
is the ideal generated by its size
$I_{t+1}(X)$
is the ideal generated by its size
 $t+1$
minors. The general linear group
$t+1$
minors. The general linear group
 $\operatorname {GL}_t(K)$
acts K-linearly on S via where
$\operatorname {GL}_t(K)$
acts K-linearly on S via where $$\begin{align*}M\colon\begin{cases} Y & \longmapsto YM^{-1}\\ Z & \longmapsto MZ\end{cases}, \end{align*}$$
$$\begin{align*}M\colon\begin{cases} Y & \longmapsto YM^{-1}\\ Z & \longmapsto MZ\end{cases}, \end{align*}$$
 $M\in \operatorname {GL}_t(K)$
. When the field K is infinite, R is precisely the ring of invariants; see [Reference De Concini and ProcesiDP, §3] or [Reference HashimotoHa, Theorem 4.1].
$M\in \operatorname {GL}_t(K)$
. When the field K is infinite, R is precisely the ring of invariants; see [Reference De Concini and ProcesiDP, §3] or [Reference HashimotoHa, Theorem 4.1].
-
(b) Let Y be a
 $2t\times n$
matrix of indeterminates, and set
$2t\times n$
matrix of indeterminates, and set
 . Let (1.0.1)be the size
. Let (1.0.1)be the size
 $2t$
standard symplectic block matrix, where
$2t$
standard symplectic block matrix, where
 is the size t identity matrix. The K-algebra
is the size t identity matrix. The K-algebra
 is isomorphic to
is isomorphic to
 $K[X]/\operatorname {Pf}_{2t+2}(X)$
, where X is an
$K[X]/\operatorname {Pf}_{2t+2}(X)$
, where X is an
 $n\times n$
alternating matrix of indeterminates, and
$n\times n$
alternating matrix of indeterminates, and
 $\operatorname {Pf}_{2t+2}(X)$
the ideal generated by its principal size
$\operatorname {Pf}_{2t+2}(X)$
the ideal generated by its principal size
 $2t+2$
Pfaffians; see §6. The symplectic group acts K-linearly on S, where
$2t+2$
Pfaffians; see §6. The symplectic group acts K-linearly on S, where
 $$\begin{align*}M\colon Y\longmapsto MY\qquad\text{ for }\ M\in\operatorname{Sp}_{2t}(K). \end{align*}$$
$$\begin{align*}M\colon Y\longmapsto MY\qquad\text{ for }\ M\in\operatorname{Sp}_{2t}(K). \end{align*}$$
It is readily seen that
 $Y^{\operatorname {tr}}\Omega Y\longmapsto Y^{\operatorname {tr}} M^{\operatorname {tr}}\Omega MY=Y^{\operatorname {tr}}\Omega Y$
for
$Y^{\operatorname {tr}}\Omega Y\longmapsto Y^{\operatorname {tr}} M^{\operatorname {tr}}\Omega MY=Y^{\operatorname {tr}}\Omega Y$
for
 $M\in \operatorname {Sp}_{2t}(K)$
, so the entries of the matrix
$M\in \operatorname {Sp}_{2t}(K)$
, so the entries of the matrix
 $Y^{\operatorname {tr}}\Omega Y$
are invariant under the action; when K is infinite, the invariant ring is precisely the ring R; see [Reference De Concini and ProcesiDP, §6] or [Reference HashimotoHa, Theorem 5.1].
$Y^{\operatorname {tr}}\Omega Y$
are invariant under the action; when K is infinite, the invariant ring is precisely the ring R; see [Reference De Concini and ProcesiDP, §6] or [Reference HashimotoHa, Theorem 5.1]. -
(c) Let Y be a
 $d\times n$
matrix of indeterminates. Set
$d\times n$
matrix of indeterminates. Set
 , and let R be the K-subalgebra generated by the entries of
, and let R be the K-subalgebra generated by the entries of
 $Y^{\operatorname {tr}} Y$
. Then R is isomorphic to
$Y^{\operatorname {tr}} Y$
. Then R is isomorphic to
 $K[X]/I_{d+1}(X)$
, for X an
$K[X]/I_{d+1}(X)$
, for X an
 $n\times n$
symmetric matrix of indeterminates. The orthogonal group acts K-linearly on S via
$n\times n$
symmetric matrix of indeterminates. The orthogonal group acts K-linearly on S via
 $$\begin{align*}M\colon Y\longmapsto MY\qquad\text{ for }\ M\in\operatorname{O}_d(K). \end{align*}$$
$$\begin{align*}M\colon Y\longmapsto MY\qquad\text{ for }\ M\in\operatorname{O}_d(K). \end{align*}$$
Note that
 $Y^{\operatorname {tr}} Y\longmapsto Y^{\operatorname {tr}} M^{\operatorname {tr}} MY=Y^{\operatorname {tr}} Y$
for
$Y^{\operatorname {tr}} Y\longmapsto Y^{\operatorname {tr}} M^{\operatorname {tr}} MY=Y^{\operatorname {tr}} Y$
for
 $M\in \operatorname {O}_d(K)$
, so the entries of
$M\in \operatorname {O}_d(K)$
, so the entries of
 $Y^{\operatorname {tr}} Y$
are invariant under the action; when the field K is infinite of characteristic other than two, the invariant ring is precisely the subring R, as proved in [Reference De Concini and ProcesiDP, §5]. When K is infinite of characteristic two, as proved in [Reference RichmanRi, §5], the invariant ring has the additional generators
$Y^{\operatorname {tr}} Y$
are invariant under the action; when the field K is infinite of characteristic other than two, the invariant ring is precisely the subring R, as proved in [Reference De Concini and ProcesiDP, §5]. When K is infinite of characteristic two, as proved in [Reference RichmanRi, §5], the invariant ring has the additional generators  $$\begin{align*}y_{1j}+\dots+y_{dj}\qquad\text{ where }1\leqslant j\leqslant n. \end{align*}$$
$$\begin{align*}y_{1j}+\dots+y_{dj}\qquad\text{ where }1\leqslant j\leqslant n. \end{align*}$$
-
(d) Let Y be a
 $d\times n$
matrix of indeterminates over K, where
$d\times n$
matrix of indeterminates over K, where
 $d\leqslant n$
, and set
$d\leqslant n$
, and set
 . Let where
. Let where
 $\{\Delta \}$
is the set of size d minors of Y. Then R is the Plücker coordinate ring of the Grassmannian of d-dimensional subspaces of an n-dimensional vector space. The special linear group
$\{\Delta \}$
is the set of size d minors of Y. Then R is the Plücker coordinate ring of the Grassmannian of d-dimensional subspaces of an n-dimensional vector space. The special linear group
 $\operatorname {SL}_d(K)$
acts K-linearly on S where
$\operatorname {SL}_d(K)$
acts K-linearly on S where  $$\begin{align*}M\colon Y\longmapsto MY\qquad\text{ for }\ M\in\operatorname{SL}_d(K). \end{align*}$$
$$\begin{align*}M\colon Y\longmapsto MY\qquad\text{ for }\ M\in\operatorname{SL}_d(K). \end{align*}$$
Each size d minor of Y is fixed under the group action; when K is an infinite field, the invariant ring is precisely R, as proved in [Reference IgusaIg] or [Reference De Concini and ProcesiDP, §3].
If K has characteristic zero, the groups
![]() $\operatorname {GL}_t(K)$
,
$\operatorname {GL}_t(K)$
,
![]() $\operatorname {Sp}_{2t}(K)$
,
$\operatorname {Sp}_{2t}(K)$
,
![]() $\operatorname {O}_d(K)$
and
$\operatorname {O}_d(K)$
and
![]() $\operatorname {SL}_d(K)$
are linearly reductive; it follows that, in each case, the invariant ring R is a direct summand of S as an R-module, equivalently that
$\operatorname {SL}_d(K)$
are linearly reductive; it follows that, in each case, the invariant ring R is a direct summand of S as an R-module, equivalently that
![]() $R\subseteq S$
is pure. See §2 for the equivalence. This then implies a wealth of strong properties for R; see [Reference BoutotBo, Reference Hochster and HunekeHH1, Reference Hochster and RobertsHR, Reference KempfKe3]. Over fields of positive characteristic, these invariant rings maintain favorable properties such as the Cohen–Macaulay property and F-regularity (see [Reference Hochster and HunekeHH2, Theorem 7.14]), though the groups are typically not linearly reductive. Indeed, in positive characteristic, each of the classical groups above admits a representation for which the invariant ring is not Cohen–Macaulay [Reference KohlsKo]. It is natural to ask if the embeddings (a)–(d) are pure when K has positive characteristic. We prove:
$R\subseteq S$
is pure. See §2 for the equivalence. This then implies a wealth of strong properties for R; see [Reference BoutotBo, Reference Hochster and HunekeHH1, Reference Hochster and RobertsHR, Reference KempfKe3]. Over fields of positive characteristic, these invariant rings maintain favorable properties such as the Cohen–Macaulay property and F-regularity (see [Reference Hochster and HunekeHH2, Theorem 7.14]), though the groups are typically not linearly reductive. Indeed, in positive characteristic, each of the classical groups above admits a representation for which the invariant ring is not Cohen–Macaulay [Reference KohlsKo]. It is natural to ask if the embeddings (a)–(d) are pure when K has positive characteristic. We prove:
Theorem 1.1. Let K be a field of characteristic
![]() $p>0$
. Fix positive integers
$p>0$
. Fix positive integers
![]() $d,m,n$
and t, and let
$d,m,n$
and t, and let
![]() $R\subseteq S$
denote one of the following inclusions:
$R\subseteq S$
denote one of the following inclusions:
-
(a)
 $K[YZ] \subseteq K[Y,Z]$
, where Y and Z are
$K[YZ] \subseteq K[Y,Z]$
, where Y and Z are
 $m\times t$
and
$m\times t$
and
 $t\times n$
matrices of indeterminates;
$t\times n$
matrices of indeterminates; -
(b)
 $K[Y^{\operatorname {tr}} \Omega Y] \subseteq K[Y]$
, where Y is a
$K[Y^{\operatorname {tr}} \Omega Y] \subseteq K[Y]$
, where Y is a
 $2t \times n$
matrix of indeterminates;
$2t \times n$
matrix of indeterminates; -
(c)
 $K[Y^{\operatorname {tr}} Y] \subseteq K[Y]$
, where Y is a
$K[Y^{\operatorname {tr}} Y] \subseteq K[Y]$
, where Y is a
 $d \times n$
matrix of indeterminates;
$d \times n$
matrix of indeterminates; -
(d)
 $K[\{ \Delta \} ] \subseteq K[Y]$
, where Y is a
$K[\{ \Delta \} ] \subseteq K[Y]$
, where Y is a
 $d \times n$
matrix of indeterminates with
$d \times n$
matrix of indeterminates with
 $d\leqslant n$
.
$d\leqslant n$
.
Then
![]() $R\subseteq S$
is pure if and only if, in the respective cases,
$R\subseteq S$
is pure if and only if, in the respective cases,
-
(a)
 $t=1$
or
$t=1$
or
 $\min \{m,n\} \leqslant t$
;
$\min \{m,n\} \leqslant t$
; -
(b)
 $n\leqslant t+1$
;
$n\leqslant t+1$
; -
(c)
 $d=1$
;
$d=1$
;
 $d=2$
and p is odd;
$d=2$
and p is odd;
 $p=2$
and
$p=2$
and
 $n \leqslant (d+1)/2$
; or p is odd and
$n \leqslant (d+1)/2$
; or p is odd and
 $n\leqslant (d+2)/2$
;
$n\leqslant (d+2)/2$
; -
(d)
 $d=1$
or
$d=1$
or
 $d=n$
.
$d=n$
.
Suppose the field K in Theorem 1.1 is infinite; in case (c) assume also that the characteristic of K is odd. In this setting, the ring R is the invariant ring
![]() $S^G$
for an action of a classical group G on S, as recorded earlier. It is notable that whenever
$S^G$
for an action of a classical group G on S, as recorded earlier. It is notable that whenever
![]() $S^G\subseteq S$
is pure, either the invariant ring
$S^G\subseteq S$
is pure, either the invariant ring
![]() $S^G$
is regular or the group G is linearly reductive.
$S^G$
is regular or the group G is linearly reductive.
In (a),
![]() $S^G$
is regular if
$S^G$
is regular if
![]() $\min \{m,n\} \leqslant t$
, while if
$\min \{m,n\} \leqslant t$
, while if
![]() $t=1$
, then
$t=1$
, then
![]() $\operatorname {GL}_1(K)$
is the torus
$\operatorname {GL}_1(K)$
is the torus
![]() $K^\times $
, which is linearly reductive. For (b),
$K^\times $
, which is linearly reductive. For (b),
![]() $S^G$
is regular if
$S^G$
is regular if
![]() $n\leqslant 2t+1$
, though
$n\leqslant 2t+1$
, though
![]() $S^G\subseteq S$
is pure in the more restrictive range
$S^G\subseteq S$
is pure in the more restrictive range
![]() $n\leqslant t+1$
. In case (c), the orthogonal group
$n\leqslant t+1$
. In case (c), the orthogonal group
![]() $\operatorname {O}_d(K)$
is linearly reductive if
$\operatorname {O}_d(K)$
is linearly reductive if
![]() $d=1$
and also if
$d=1$
and also if
![]() $d=2$
and p is odd, as discussed in the proof of Theorem 7.14. The ring
$d=2$
and p is odd, as discussed in the proof of Theorem 7.14. The ring
![]() $S^G$
is regular if
$S^G$
is regular if
![]() $n\leqslant d$
, though
$n\leqslant d$
, though
![]() $S^G\subseteq S$
is pure in a smaller range and one that depends on the characteristic. Lastly, in (d),
$S^G\subseteq S$
is pure in a smaller range and one that depends on the characteristic. Lastly, in (d),
![]() $S^G$
is regular precisely if d equals
$S^G$
is regular precisely if d equals
![]() $1$
,
$1$
,
![]() $n-1$
, or n.
$n-1$
, or n.
The cases (a)–(d) of Theorem 1.1 are proven as Theorems 4.2, 6.9, 7.14 and 3.1, respectively. In each case, this involves investigating the nullcone of the action of G on S, namely the ring
![]() $S/\mathfrak {m}_{S^G}S$
, where
$S/\mathfrak {m}_{S^G}S$
, where
![]() $\mathfrak {m}_{S^G}$
is the homogeneous maximal ideal of the invariant ring
$\mathfrak {m}_{S^G}$
is the homogeneous maximal ideal of the invariant ring
![]() $S^G$
(or, more generally, the ring
$S^G$
(or, more generally, the ring
![]() $S/\mathfrak {m}_RS$
). The study of nullcones goes back at least to Hilbert’s proof of the finite generation of invariant rings [Reference HilbertHi]; more recent work includes [Reference HesselinkHe, Reference Kraft and SchwarzKS, Reference Kraft and WallachKW, Reference SchwarzSc]. Specifically, Kraft and Schwartz determine, for classical invariant rings of characteristic zero, precisely when the nullcone is reduced or a domain [Reference Kraft and SchwarzKS, Theorem 9.1]. Our paper includes the corresponding results in the positive characteristic case.
$S/\mathfrak {m}_RS$
). The study of nullcones goes back at least to Hilbert’s proof of the finite generation of invariant rings [Reference HilbertHi]; more recent work includes [Reference HesselinkHe, Reference Kraft and SchwarzKS, Reference Kraft and WallachKW, Reference SchwarzSc]. Specifically, Kraft and Schwartz determine, for classical invariant rings of characteristic zero, precisely when the nullcone is reduced or a domain [Reference Kraft and SchwarzKS, Theorem 9.1]. Our paper includes the corresponding results in the positive characteristic case.
The easiest to settle is the
![]() $\operatorname {SL}_n(K)$
case: The invariant ring is the homogeneous coordinate ring for the Plücker embedding of a Grassmannian variety, and the nullcone is a determinantal ring, hence Cohen–Macaulay by Hochster–Eagon [Reference HesselinkHE]. More work is needed in the other cases. For the
$\operatorname {SL}_n(K)$
case: The invariant ring is the homogeneous coordinate ring for the Plücker embedding of a Grassmannian variety, and the nullcone is a determinantal ring, hence Cohen–Macaulay by Hochster–Eagon [Reference HesselinkHE]. More work is needed in the other cases. For the
![]() $\operatorname {GL}_n(K)$
action, the invariant rings are generic determinantal rings, but the nullcone typically fails to be Cohen–Macaulay or even equidimensional. We use the theory of varieties of complexes as introduced by Buchsbaum–Eisenbud [Reference Buchsbaum and EisenbudBE] and expanded by Kempf [Reference KempfKe1], De Concini–Strickland [Reference De Concini and StricklandDS] and Huneke [Reference HunekeHu]. We settle the purity question by examining the irreducible components and their intersections.
$\operatorname {GL}_n(K)$
action, the invariant rings are generic determinantal rings, but the nullcone typically fails to be Cohen–Macaulay or even equidimensional. We use the theory of varieties of complexes as introduced by Buchsbaum–Eisenbud [Reference Buchsbaum and EisenbudBE] and expanded by Kempf [Reference KempfKe1], De Concini–Strickland [Reference De Concini and StricklandDS] and Huneke [Reference HunekeHu]. We settle the purity question by examining the irreducible components and their intersections.
In the symplectic group
![]() $\operatorname {Sp}_{2n}(K)$
case, the invariant rings are defined by the principal Pfaffians of fixed size of an alternating matrix of indeterminates. It is worth mention that there is much amongst our results that is new even in the case of characteristic zero: for example, for the
$\operatorname {Sp}_{2n}(K)$
case, the invariant rings are defined by the principal Pfaffians of fixed size of an alternating matrix of indeterminates. It is worth mention that there is much amongst our results that is new even in the case of characteristic zero: for example, for the
![]() $\operatorname {Sp}_{2n}(\mathbb {C})$
case, Kraft and Schwarz [Reference Kraft and SchwarzKS, Theorem 9.1.3] prove that the nullcone is irreducible and normal. We prove that it is, in addition, Cohen–Macaulay.
$\operatorname {Sp}_{2n}(\mathbb {C})$
case, Kraft and Schwarz [Reference Kraft and SchwarzKS, Theorem 9.1.3] prove that the nullcone is irreducible and normal. We prove that it is, in addition, Cohen–Macaulay.
Theorem 1.2. Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K, where t and n are positive integers. Set
$2t\times n$
matrix of indeterminates over a field K, where t and n are positive integers. Set
![]() , and take
, and take
![]() $\mathfrak {P}$
to be the ideal generated by the entries of the matrix
$\mathfrak {P}$
to be the ideal generated by the entries of the matrix
![]() $Y^{\operatorname {tr}}\Omega Y$
, where
$Y^{\operatorname {tr}}\Omega Y$
, where
![]() $\Omega $
is the size
$\Omega $
is the size
![]() $2t$
standard symplectic matrix as displayed in equation (1.0.1).
$2t$
standard symplectic matrix as displayed in equation (1.0.1).
Then
![]() $\mathfrak {P}$
is a prime ideal, and the ring
$\mathfrak {P}$
is a prime ideal, and the ring
![]() $S/\mathfrak {P}$
is Cohen–Macaulay.
$S/\mathfrak {P}$
is Cohen–Macaulay.
The situation is more complicated in the case of the orthogonal group
![]() $\operatorname {O}_d(K)$
; the characteristic zero case of parts (1a) and (1b) of the following is [Reference Kraft and SchwarzKS, Theorem 9.1.4]:
$\operatorname {O}_d(K)$
; the characteristic zero case of parts (1a) and (1b) of the following is [Reference Kraft and SchwarzKS, Theorem 9.1.4]:
Theorem 1.3. Let Y be a
![]() $d\times n$
matrix of indeterminates over a field K, where d and n are positive integers. Set
$d\times n$
matrix of indeterminates over a field K, where d and n are positive integers. Set
![]() , and take
, and take
![]() $\mathfrak {A}$
to be the ideal generated by the entries of
$\mathfrak {A}$
to be the ideal generated by the entries of
![]() $Y^{\operatorname {tr}} Y$
.
$Y^{\operatorname {tr}} Y$
.
-
(1) Suppose K has characteristic other than
 $2$
. Then:
$2$
. Then:-
(a) The ideal
 $\mathfrak {A}$
is radical if and only if
$\mathfrak {A}$
is radical if and only if
 $2n\leqslant d$
.
$2n\leqslant d$
. -
(b) If K contains a primitive fourth root of unity, then
 $\mathfrak {A}$
is prime if and only if
$\mathfrak {A}$
is prime if and only if
 $2n<d$
.
$2n<d$
. -
(c) If d is odd, or if
 $2n<d$
, then
$2n<d$
, then
 $S/\operatorname {rad}\,\mathfrak {A}$
is a Cohen–Macaulay integral domain.
$S/\operatorname {rad}\,\mathfrak {A}$
is a Cohen–Macaulay integral domain. -
(d) Suppose d is even,
 $2n\geqslant d$
and K contains a primitive fourth root of unity. Then
$2n\geqslant d$
and K contains a primitive fourth root of unity. Then
 $\mathfrak {A}$
has minimal primes
$\mathfrak {A}$
has minimal primes
 $\mathfrak {P}$
and
$\mathfrak {P}$
and
 $\mathfrak {Q}$
(see Definition 7.7) and the rings
$\mathfrak {Q}$
(see Definition 7.7) and the rings
 $K[Y]/\mathfrak {P}$
and
$K[Y]/\mathfrak {P}$
and
 $K[Y]/\mathfrak {Q}$
are Cohen–Macaulay.
$K[Y]/\mathfrak {Q}$
are Cohen–Macaulay.
-
-
(2) Suppose K has characteristic two. Then
 $\mathfrak {A}$
is not radical; however,
$\mathfrak {A}$
is not radical; however,
 $S/\operatorname {rad}\,\mathfrak {A}$
is a Cohen–Macaulay integral domain.
$S/\operatorname {rad}\,\mathfrak {A}$
is a Cohen–Macaulay integral domain.
Theorem 1.2 is part of Theorem 6.8, while Theorem 1.3 is covered by Theorems 7.2, 7.12 and 7.13. It is worth emphasizing that, in all cases (a)–(d) of Theorem 1.1, the minimal primes of
![]() $\mathfrak {m}_{S^G}S$
—the defining ideal of the nullcone—are perfect ideals, that is, they define Cohen–Macaulay rings. This supports the maxim, ‘Perfection is often hunted for and usually found in generic situations’ (Bruns [Reference BrunsBr2]). A key technique used to establish the perfection is that of principal radical systems, introduced by Hochster–Eagon in their study of determinantal rings [Reference HesselinkHE]. This is reviewed in §5.
$\mathfrak {m}_{S^G}S$
—the defining ideal of the nullcone—are perfect ideals, that is, they define Cohen–Macaulay rings. This supports the maxim, ‘Perfection is often hunted for and usually found in generic situations’ (Bruns [Reference BrunsBr2]). A key technique used to establish the perfection is that of principal radical systems, introduced by Hochster–Eagon in their study of determinantal rings [Reference HesselinkHE]. This is reviewed in §5.
Theorem 1.3 is related to work on Lovász–Saks–Schrijver ideals. Given a simple graph G on a vertex set
![]() $\{1,\dots ,n\}$
, an integer d and a field K, let Y be an
$\{1,\dots ,n\}$
, an integer d and a field K, let Y be an
![]() $n\times d$
matrix of indeterminates over K. The Lovász–Saks–Schrijver ideal
$n\times d$
matrix of indeterminates over K. The Lovász–Saks–Schrijver ideal
![]() $L^K_G(d)$
is the ideal of
$L^K_G(d)$
is the ideal of
![]() $K[Y]$
generated by the entries of
$K[Y]$
generated by the entries of
![]() $YY^{\operatorname {tr}}$
in the positions
$YY^{\operatorname {tr}}$
in the positions
![]() $(i,j)$
that are edges of G. In [Reference Herzog, Macchia, Madani and WelkerHMSW] and [Reference Conca and WelkerCW], the conditions that the ideal
$(i,j)$
that are edges of G. In [Reference Herzog, Macchia, Madani and WelkerHMSW] and [Reference Conca and WelkerCW], the conditions that the ideal
![]() $L^K_G(d)$
is radical, prime or a complete intersection are related to various conditions on G and d. Notably, the restriction to simple graphs ensures that the ideals
$L^K_G(d)$
is radical, prime or a complete intersection are related to various conditions on G and d. Notably, the restriction to simple graphs ensures that the ideals
![]() $L^K_G(d)$
are generated by elements whose initial terms are square-free, allowing for Gröbner degeneration techniques. It is easy to see that the ideal
$L^K_G(d)$
are generated by elements whose initial terms are square-free, allowing for Gröbner degeneration techniques. It is easy to see that the ideal
![]() $\mathfrak {A}$
from Theorem 1.3 has no square-free initial ideal.
$\mathfrak {A}$
from Theorem 1.3 has no square-free initial ideal.
Let V be a commutative ring, and let R denote either a Pfaffian ring
![]() $V[X]/\operatorname {Pf}_{2t+2}(X)$
or a determinantal or symmetric determinantal ring
$V[X]/\operatorname {Pf}_{2t+2}(X)$
or a determinantal or symmetric determinantal ring
![]() $V[X]/I_{t+1}(X)$
. While Theorem 1.1 addresses the purity of the natural embedding
$V[X]/I_{t+1}(X)$
. While Theorem 1.1 addresses the purity of the natural embedding
![]() $R\subseteq S$
when V is a field of positive characteristic, it remains unresolved whether R is a pure subring of some polynomial ring over V. However, when V is the ring of integers or the ring of p-adic integers, the following theorem addresses embeddings in arbitrary polynomial rings over V.
$R\subseteq S$
when V is a field of positive characteristic, it remains unresolved whether R is a pure subring of some polynomial ring over V. However, when V is the ring of integers or the ring of p-adic integers, the following theorem addresses embeddings in arbitrary polynomial rings over V.
Theorem 1.4 [Reference Jeffries and SinghJS, Theorem 9.1].
Let V denote either the ring of integers
![]() $\mathbb {Z}$
or a ring of p-adic integers
$\mathbb {Z}$
or a ring of p-adic integers
![]() $\widehat {\mathbb {Z}_{(p)}}$
. Let
$\widehat {\mathbb {Z}_{(p)}}$
. Let
![]() $d,m,n$
and t be positive integers.
$d,m,n$
and t be positive integers.
-
(a) Let
 , where X is an
, where X is an
 $m\times n$
matrix of indeterminates. Then R is a pure subring of a polynomial ring over V if and only
$m\times n$
matrix of indeterminates. Then R is a pure subring of a polynomial ring over V if and only
 $t=1$
or
$t=1$
or
 $\min \{m,n\}\leqslant t$
.
$\min \{m,n\}\leqslant t$
. -
(b) Let
 , where X is an
, where X is an
 $n\times n$
alternating matrix of indeterminates. Then R is a pure subring of a polynomial ring over V if and only if
$n\times n$
alternating matrix of indeterminates. Then R is a pure subring of a polynomial ring over V if and only if
 $n\leqslant 2t+1$
, that is, if and only if R is itself a polynomial ring over V.
$n\leqslant 2t+1$
, that is, if and only if R is itself a polynomial ring over V. -
(c) Let
 , where X is a symmetric
, where X is a symmetric
 $n\times n$
matrix of indeterminates. Then R is a pure subring of a polynomial ring over V if and only if
$n\times n$
matrix of indeterminates. Then R is a pure subring of a polynomial ring over V if and only if
 $n\leqslant d$
, or
$n\leqslant d$
, or
 $d=1$
, or
$d=1$
, or
 $d=2$
and
$d=2$
and
 $V=\widehat {\mathbb {Z}_{(p)}}$
for p an odd prime.
$V=\widehat {\mathbb {Z}_{(p)}}$
for p an odd prime.
The formulation of the theorem in [Reference Jeffries and SinghJS] is in terms of direct summands rather than pure subrings, but the notions are equivalent when V above is a ring of p-adic integers, from which the remaining assertions follow. Specifically, conditions (1) and (2) in Theorem 2.1 remain equivalent when
![]() $R_0=S_0$
is, more generally, a complete local ring. The proof in this case uses [Reference Bruns and HerzogBH, Theorem 3.6.17].
$R_0=S_0$
is, more generally, a complete local ring. The proof in this case uses [Reference Bruns and HerzogBH, Theorem 3.6.17].
Notation
For commutative rings
![]() $R\subseteq S$
and M a matrix with entries from S, we use
$R\subseteq S$
and M a matrix with entries from S, we use
![]() $R[M]$
to denote the R-algebra generated by the entries of M, and
$R[M]$
to denote the R-algebra generated by the entries of M, and
![]() $(M)$
or
$(M)$
or
![]() $(M)S$
to denote the ideal of S generated by the entries of M. For a product matrix
$(M)S$
to denote the ideal of S generated by the entries of M. For a product matrix
![]() $MN$
, one has
$MN$
, one has
![]() $(MN)\subseteq (M)$
, so if N is invertible, then
$(MN)\subseteq (M)$
, so if N is invertible, then
![]() $(MN)=(M)$
.
$(MN)=(M)$
.
We use
![]() for the identity matrix, or
for the identity matrix, or
![]() if the size needs to be specified. For a matrix M, we use
if the size needs to be specified. For a matrix M, we use
![]() $M|_s$
to denote the submatrix consisting of the first s columns of M. This should not be confused with the notation
$M|_s$
to denote the submatrix consisting of the first s columns of M. This should not be confused with the notation
![]() $M_{\alpha |\beta }$
—used only in §7.3—for the submatrix with rows indexed by
$M_{\alpha |\beta }$
—used only in §7.3—for the submatrix with rows indexed by
![]() $\alpha $
and columns indexed by
$\alpha $
and columns indexed by
![]() $\beta $
.
$\beta $
.
2 Pure, split and solid extensions
A ring homomorphism
![]() $R\longrightarrow S$
is pure if
$R\longrightarrow S$
is pure if
![]() $R\otimes _RM \longrightarrow S\otimes _RM$
is injective for each R-module M. It is readily seen that if R is a direct summand of S as an R-module, that is, if the inclusion
$R\otimes _RM \longrightarrow S\otimes _RM$
is injective for each R-module M. It is readily seen that if R is a direct summand of S as an R-module, that is, if the inclusion
![]() $R\longrightarrow S$
is split in the category of R-modules, then
$R\longrightarrow S$
is split in the category of R-modules, then
![]() $R\longrightarrow S$
is pure.
$R\longrightarrow S$
is pure.
A related notion is that of a solid algebra: Let R be an integral domain. Following [Reference HochsterHo2], an R-algebra S is solid if
![]() $\operatorname {Hom}_R(S,R)$
is nonzero. If R is a direct summand of S as an R-module, it follows that S is a solid R-algebra. More generally, we have:
$\operatorname {Hom}_R(S,R)$
is nonzero. If R is a direct summand of S as an R-module, it follows that S is a solid R-algebra. More generally, we have:
Theorem 2.1 (cf. [Reference HochsterHo2, Corollary 2.4]).
Let
![]() $R\longrightarrow S$
be a degree-preserving inclusion of
$R\longrightarrow S$
be a degree-preserving inclusion of
![]() $\mathbb {N}$
-graded normal rings that are finitely generated over a field
$\mathbb {N}$
-graded normal rings that are finitely generated over a field
![]() $R_0=S_0$
. Set
$R_0=S_0$
. Set
![]() $\mathfrak {m}_R$
to be the homogeneous maximal ideal of R, and set
$\mathfrak {m}_R$
to be the homogeneous maximal ideal of R, and set
![]() . Let
. Let
![]() $E_R$
denote the injective hull of
$E_R$
denote the injective hull of
![]() $R/\mathfrak {m}_R$
in the category of graded R-modules. Consider the following statements:
$R/\mathfrak {m}_R$
in the category of graded R-modules. Consider the following statements:
-
(1) The ring R is a direct summand of S as an R-module.
-
(2) The map
 $R\longrightarrow S$
is pure.
$R\longrightarrow S$
is pure. -
(3) The induced map
 $R\otimes _RE_R\longrightarrow S\otimes _RE_R$
is injective.
$R\otimes _RE_R\longrightarrow S\otimes _RE_R$
is injective. -
(4) The local cohomology module
 $H^d_{\mathfrak {m}_R}(S)$
is nonzero.
$H^d_{\mathfrak {m}_R}(S)$
is nonzero. -
(5) The R-algebra S is solid.
Then (1), (2) and (3) are equivalent, and imply the equivalent conditions (4) and (5). If R is a polynomial ring over a field of positive characteristic, then (1)–(5) are equivalent.
Since it is an issue that will come up often, we take this opportunity to clarify a point regarding (4): As S is an R-module, so is the local cohomology
![]() $H^d_{\mathfrak {m}_R}(S)$
. This is the same R-module as considering the S-module
$H^d_{\mathfrak {m}_R}(S)$
. This is the same R-module as considering the S-module
![]() $H^d_{\mathfrak {m}_R S}(S)$
and restricting scalars.
$H^d_{\mathfrak {m}_R S}(S)$
and restricting scalars.
Proof. The implications (1)
![]() $\implies $
(2)
$\implies $
(2)
![]() $\implies $
(3) are clear; for (3)
$\implies $
(3) are clear; for (3)
![]() $\implies $
(1), applying the graded dual
$\implies $
(1), applying the graded dual
![]() $\operatorname {Hom}_R(-,E_R)$
yields the surjection
$\operatorname {Hom}_R(-,E_R)$
yields the surjection

where the bottom map is simply
![]() $\varphi \longmapsto \varphi (1)$
.
$\varphi \longmapsto \varphi (1)$
.
The equivalence of (4) and (5) is the graded version of [Reference HochsterHo2, Corollary 2.4]; the proof there is readily modified using instead a homogeneous Noether normalization and duality in the graded setting.
For (2)
![]() $\implies $
(4), note that the induced map
$\implies $
(4), note that the induced map
is injective, where the second equality holds by the right exactness of
![]() $H^d_{\mathfrak {m}_R}(-)$
.
$H^d_{\mathfrak {m}_R}(-)$
.
Lastly, suppose R is the polynomial ring
![]() $K[x_1,\dots ,x_d]$
, where K is a field of positive characteristic p, and that (4) holds. The local cohomology module
$K[x_1,\dots ,x_d]$
, where K is a field of positive characteristic p, and that (4) holds. The local cohomology module
![]() $H^d_{\mathfrak {m}_R}(R)$
agrees with
$H^d_{\mathfrak {m}_R}(R)$
agrees with
![]() $E_R$
up to a grading shift, so to show that (3) holds, it suffices to verify that the map (2.1.1) is injective. Computing
$E_R$
up to a grading shift, so to show that (3) holds, it suffices to verify that the map (2.1.1) is injective. Computing
![]() $H^d_{\mathfrak {m}_R}(R)$
using a Čech complex on
$H^d_{\mathfrak {m}_R}(R)$
using a Čech complex on
![]() $x_1,\dots ,x_d$
, its socle is spanned by the cohomology class
$x_1,\dots ,x_d$
, its socle is spanned by the cohomology class

so one need only verify that the image of
![]() $\eta $
in
$\eta $
in
![]() $H^d_{\mathfrak {m}_R}(S)$
is nonzero. Indeed, if this image were zero, then applying the Frobenius map iteratively, the elements
$H^d_{\mathfrak {m}_R}(S)$
is nonzero. Indeed, if this image were zero, then applying the Frobenius map iteratively, the elements

would be zero for each integer
![]() $e\geqslant 1$
. But these generate
$e\geqslant 1$
. But these generate
![]() $H^d_{\mathfrak {m}_R}(S)$
as an S-module.
$H^d_{\mathfrak {m}_R}(S)$
as an S-module.
The equivalence of the conditions in Theorem 2.1 may fail when R is a polynomial ring over a field of characteristic zero, as we see next.
Example 2.2. Set R to be the polynomial ring
![]() $\mathbb {Q}[x_1,x_2,x_3]$
, and S to be the hypersurface
$\mathbb {Q}[x_1,x_2,x_3]$
, and S to be the hypersurface
 $$\begin{align*}\mathbb{Q}[x_1,x_2,x_3,y_1,y_2,y_3]/\big((x_1x_2x_3)^2-\sum_{i=1}^3y_ix_i^3\big). \end{align*}$$
$$\begin{align*}\mathbb{Q}[x_1,x_2,x_3,y_1,y_2,y_3]/\big((x_1x_2x_3)^2-\sum_{i=1}^3y_ix_i^3\big). \end{align*}$$
Consider the grading with
![]() $\deg x_i=1$
and
$\deg x_i=1$
and
![]() $\deg y_i=3$
for each i. A difficult computation of Roberts [Reference RobertsRo] shows that
$\deg y_i=3$
for each i. A difficult computation of Roberts [Reference RobertsRo] shows that
![]() $H^3_{(x_1,x_2,x_3)}(S)$
is nonzero, that is, the inclusion
$H^3_{(x_1,x_2,x_3)}(S)$
is nonzero, that is, the inclusion
![]() $R\longrightarrow S$
satisfies condition (4) in Theorem 2.1. However, it does not satisfy (1) since
$R\longrightarrow S$
satisfies condition (4) in Theorem 2.1. However, it does not satisfy (1) since
![]() $(x_1x_2x_3)^2$
is an element of the ideal
$(x_1x_2x_3)^2$
is an element of the ideal
![]() $(x_1^3,\ x_2^3,\ x_3^3)S$
though not of
$(x_1^3,\ x_2^3,\ x_3^3)S$
though not of
![]() $(x_1^3,\ x_2^3,\ x_3^3)R$
.
$(x_1^3,\ x_2^3,\ x_3^3)R$
.
Even when
![]() $R\longrightarrow S$
is an inclusion of polynomial rings over a field K, the purity may be quite subtle; for example, it may depend on the characteristic of K. Let Y be a
$R\longrightarrow S$
is an inclusion of polynomial rings over a field K, the purity may be quite subtle; for example, it may depend on the characteristic of K. Let Y be a
![]() $2\times 3$
matrix of indeterminates over a field K, and set
$2\times 3$
matrix of indeterminates over a field K, and set
![]() . Let R be the K-algebra generated by the size
. Let R be the K-algebra generated by the size
![]() $2$
minors of Y. Since the minors are algebraically independent over K in this case, the ring R is a polynomial ring. The inclusion
$2$
minors of Y. Since the minors are algebraically independent over K in this case, the ring R is a polynomial ring. The inclusion
![]() $R\longrightarrow S$
is pure precisely when K has characteristic zero; this is a special case of the result of the next section, a key ingredient being the vanishing theorem of Peskine–Szpiro, recorded below in the graded setting.
$R\longrightarrow S$
is pure precisely when K has characteristic zero; this is a special case of the result of the next section, a key ingredient being the vanishing theorem of Peskine–Szpiro, recorded below in the graded setting.
Theorem 2.3 [Reference Peskine and SzpiroPS, Proposition III.4.1].
Let S be a polynomial ring over a field of positive characteristic. If
![]() $\mathfrak {a}$
is a homogeneous ideal such that
$\mathfrak {a}$
is a homogeneous ideal such that
![]() $S/\mathfrak {a}$
is Cohen–Macaulay, then
$S/\mathfrak {a}$
is Cohen–Macaulay, then
3 Plücker embeddings of Grassmannians
The first case of Theorem 1.1 that we address is (d), namely the case of the special linear group. This ends up being the easiest by far, the nullcones here being the well-studied determinantal rings.
Fix integers
![]() $1\leqslant d\leqslant n$
. Let Y be a
$1\leqslant d\leqslant n$
. Let Y be a
![]() $d\times n$
matrix of indeterminates over a field K, and set
$d\times n$
matrix of indeterminates over a field K, and set
![]() . Let R denote the K-algebra generated by the size d minors of Y. Then R is the homogeneous coordinate ring, under the Plücker embedding, of the Grassmannian
. Let R denote the K-algebra generated by the size d minors of Y. Then R is the homogeneous coordinate ring, under the Plücker embedding, of the Grassmannian
![]() $G(d,n)$
of d-dimensional subspaces of an n-dimensional vector space. The ring R is regular when d equals
$G(d,n)$
of d-dimensional subspaces of an n-dimensional vector space. The ring R is regular when d equals
![]() $1$
,
$1$
,
![]() $n-1$
or n; in other cases, the relations between the size d minors are quadratic—these are the Plücker relations, [Reference Hodge and PedoeHP, Chapter VII, §6]. The ring R is a Gorenstein unique factorization domain, [Reference HochsterHo1, Reference LaksovLa, Reference MusiliMu], of dimension
$n-1$
or n; in other cases, the relations between the size d minors are quadratic—these are the Plücker relations, [Reference Hodge and PedoeHP, Chapter VII, §6]. The ring R is a Gorenstein unique factorization domain, [Reference HochsterHo1, Reference LaksovLa, Reference MusiliMu], of dimension
![]() $d(n-d)+1$
.
$d(n-d)+1$
.
Consider the K-linear action of the special linear group
![]() $\operatorname {SL}_d(K)$
on S, where
$\operatorname {SL}_d(K)$
on S, where
It is readily seen that the size d minors of Y are fixed by the group action; when the field K is infinite, the invariant ring is precisely the subring R, see [Reference IgusaIg] or [Reference De Concini and ProcesiDP, §3]. If K is a field of characteristic zero, then the group
![]() $\operatorname {SL}_d(K)$
is linearly reductive, and it follows that the invariant ring R is a direct summand of S as an R-module. In particular, the inclusion
$\operatorname {SL}_d(K)$
is linearly reductive, and it follows that the invariant ring R is a direct summand of S as an R-module. In particular, the inclusion
![]() $R\subseteq S$
is pure when K has characteristic zero. In the case of positive characteristic, we have:
$R\subseteq S$
is pure when K has characteristic zero. In the case of positive characteristic, we have:
Theorem 3.1. Let K be a field of positive characteristic. Let Y be a
![]() $d\times n$
matrix of indeterminates where
$d\times n$
matrix of indeterminates where
![]() $1\leqslant d\leqslant n$
, and set
$1\leqslant d\leqslant n$
, and set
![]() . Let R be the K-algebra generated by the size d minors of Y. Then the inclusion
. Let R be the K-algebra generated by the size d minors of Y. Then the inclusion
![]() $R\subseteq S$
is pure if and only if
$R\subseteq S$
is pure if and only if
![]() $d=1$
or
$d=1$
or
![]() $d=n$
.
$d=n$
.
Proof. Set
![]() $\mathfrak {m}_R$
to be the homogeneous maximal ideal of R. Since the ring R has dimension
$\mathfrak {m}_R$
to be the homogeneous maximal ideal of R. Since the ring R has dimension
![]() $d(n-d)+1$
, if the inclusion
$d(n-d)+1$
, if the inclusion
![]() $R\subseteq S$
is pure, then
$R\subseteq S$
is pure, then
![]() $H^{d(n-d)+1}_{\mathfrak {m}_R}(S)$
must be nonzero by Theorem 2.1. But
$H^{d(n-d)+1}_{\mathfrak {m}_R}(S)$
must be nonzero by Theorem 2.1. But
![]() $\mathfrak {m}_{R}S$
equals the determinantal ideal
$\mathfrak {m}_{R}S$
equals the determinantal ideal
![]() $I_d(Y)$
, which has height
$I_d(Y)$
, which has height
![]() $n-d+1$
, and defines a Cohen–Macaulay ring
$n-d+1$
, and defines a Cohen–Macaulay ring
![]() $K[Y]/I_d(Y)$
; see [Reference Eagon and NorthcottEN] or [Reference HesselinkHE]. But then Theorem 2.3 implies that
$K[Y]/I_d(Y)$
; see [Reference Eagon and NorthcottEN] or [Reference HesselinkHE]. But then Theorem 2.3 implies that
so
![]() $d=1$
or
$d=1$
or
![]() $d=n$
.
$d=n$
.
Conversely, if
![]() $d=1$
or
$d=1$
or
![]() $d=n$
, then R is a polynomial ring and
$d=n$
, then R is a polynomial ring and
![]() $\operatorname {ht}(\mathfrak {m}_{R}S)=\dim R$
, so the module
$\operatorname {ht}(\mathfrak {m}_{R}S)=\dim R$
, so the module
![]() $H^{d(n-d)+1}_{\mathfrak {m}_R}(S)$
is nonzero; hence, the inclusion
$H^{d(n-d)+1}_{\mathfrak {m}_R}(S)$
is nonzero; hence, the inclusion
![]() $R\subseteq S$
is pure by Theorem 2.1.
$R\subseteq S$
is pure by Theorem 2.1.
Note that when
![]() $d=n-1$
in Theorem 3.1, the ring R is regular but
$d=n-1$
in Theorem 3.1, the ring R is regular but
![]() $R\subseteq S$
is not pure. The argument above serves as the template for the other cases of Theorem 1.1, namely we proceed by studying the expansion of the homogeneous maximal ideal
$R\subseteq S$
is not pure. The argument above serves as the template for the other cases of Theorem 1.1, namely we proceed by studying the expansion of the homogeneous maximal ideal
![]() $\mathfrak {m}_R$
of the subring R to the ambient polynomial ring S and analyze the local cohomology obstruction
$\mathfrak {m}_R$
of the subring R to the ambient polynomial ring S and analyze the local cohomology obstruction
![]() $H^{\dim R}_{\mathfrak {m}_R}(S)$
. In the remaining cases, the ideal
$H^{\dim R}_{\mathfrak {m}_R}(S)$
. In the remaining cases, the ideal
![]() $\mathfrak {m}_RS$
may be more subtle: In the case of determinantal rings treated next, the ideal
$\mathfrak {m}_RS$
may be more subtle: In the case of determinantal rings treated next, the ideal
![]() $\mathfrak {m}_RS$
is typically not equidimensional.
$\mathfrak {m}_RS$
is typically not equidimensional.
4 Generic determinantal rings
Let K be a field, and let Y and Z be
![]() $m\times t$
and
$m\times t$
and
![]() $t\times n$
matrices of indeterminates, respectively. Set
$t\times n$
matrices of indeterminates, respectively. Set
![]() , and take R to be the K-subalgebra of S generated by the entries of the product matrix
, and take R to be the K-subalgebra of S generated by the entries of the product matrix
![]() $YZ$
. Then R is isomorphic to the determinantal ring
$YZ$
. Then R is isomorphic to the determinantal ring
![]() $K[X]/I_{t+1}(X)$
, where X is an
$K[X]/I_{t+1}(X)$
, where X is an
![]() $m\times n$
matrix of indeterminates, and
$m\times n$
matrix of indeterminates, and
![]() $I_{t+1}(X)$
is the ideal generated by its size
$I_{t+1}(X)$
is the ideal generated by its size
![]() $t+1$
minors. The ring R is Cohen–Macaulay by [Reference HesselinkHE]; it is regular precisely if
$t+1$
minors. The ring R is Cohen–Macaulay by [Reference HesselinkHE]; it is regular precisely if
![]() $\min \{m,n\} \leqslant t$
since this corresponds to
$\min \{m,n\} \leqslant t$
since this corresponds to
![]() $I_{t+1}(X)=0$
. Outside of the regular case, the ring R has dimension
$I_{t+1}(X)=0$
. Outside of the regular case, the ring R has dimension
![]() $mt+nt-t^2$
, class group
$mt+nt-t^2$
, class group
![]() $\mathbb {Z}$
by Bruns [Reference BrunsBr1] and is Gorenstein precisely if m equals n by Svanes [Reference SvanesSv].
$\mathbb {Z}$
by Bruns [Reference BrunsBr1] and is Gorenstein precisely if m equals n by Svanes [Reference SvanesSv].
The general linear group
![]() $\operatorname {GL}_t(K)$
acts K-linearly on S via
$\operatorname {GL}_t(K)$
acts K-linearly on S via
 $$\begin{align*}M\colon\begin{cases} Y & \longmapsto YM^{-1}\\ Z & \longmapsto MZ,\end{cases} \end{align*}$$
$$\begin{align*}M\colon\begin{cases} Y & \longmapsto YM^{-1}\\ Z & \longmapsto MZ,\end{cases} \end{align*}$$
where
![]() $M\in \operatorname {GL}_t(K)$
. When K is infinite, the ring R is precisely the ring of invariants for this action; see [Reference De Concini and ProcesiDP, §3] or [Reference HashimotoHa, Theorem 4.1]. If, moreover, the field K has characteristic zero, then
$M\in \operatorname {GL}_t(K)$
. When K is infinite, the ring R is precisely the ring of invariants for this action; see [Reference De Concini and ProcesiDP, §3] or [Reference HashimotoHa, Theorem 4.1]. If, moreover, the field K has characteristic zero, then
![]() $\operatorname {GL}_t(K)$
is linearly reductive, so the ring extension
$\operatorname {GL}_t(K)$
is linearly reductive, so the ring extension
![]() $R\longrightarrow S$
is pure.
$R\longrightarrow S$
is pure.
4.1 Irreducible components of the nullcone
A complex of K-vector spaces
can be regarded as a point in affine space using the entries of the matrices
![]() $M_k$
. Setting
$M_k$
. Setting
![]() $r_k$
to be the rank of
$r_k$
to be the rank of
![]() $M_k$
, the matrices satisfy the rank conditions
$M_k$
, the matrices satisfy the rank conditions
![]() $r_1\leqslant b_0$
, and
$r_1\leqslant b_0$
, and
![]() $r_h\leqslant b_h$
, and
$r_h\leqslant b_h$
, and
Given sequences
![]() $(b_0,\dots ,b_h)$
and
$(b_0,\dots ,b_h)$
and
![]() $(r_1,\dots ,r_h)$
satisfying these rank conditions, consider matrices of indeterminates
$(r_1,\dots ,r_h)$
satisfying these rank conditions, consider matrices of indeterminates
![]() $X_k$
of size
$X_k$
of size
![]() $b_{k-1}\times b_k$
for
$b_{k-1}\times b_k$
for
![]() $1\leqslant k\leqslant h$
. The corresponding variety of complexes is the algebraic set defined by the vanishing of the entries of the matrices
$1\leqslant k\leqslant h$
. The corresponding variety of complexes is the algebraic set defined by the vanishing of the entries of the matrices
![]() $X_kX_{k+1}$
and the determinantal ideals
$X_kX_{k+1}$
and the determinantal ideals
![]() $I_{r_k+1}(X_k)$
. When K has characteristic zero, these varieties were shown to be Cohen–Macaulay and normal, with rational singularities, by Kempf [Reference KempfKe1] using [Reference KempfKe2]. The Cohen–Macaulay property is proved in arbitrary characteristic by Huneke [Reference HunekeHu, Theorem 6.2] using principal radical systems, and by De Concini–Strickland [Reference De Concini and StricklandDS, Theorem 2.7] using Hodge algebra methods; however, as pointed out by Tchernev [Reference TchernevTc, Example 9.2], the Hodge algebra structure of [Reference De Concini and StricklandDS] is not correct, though the assertions can be obtained instead using Gröbner bases as in [Reference TchernevTc]. See also [Reference Musili and SeshadriMS] and the discussion in the proof of [Reference Conca and WelkerCW, Theorem 8.6]. The normality is [Reference HunekeHu, Theorem 7.1].
$I_{r_k+1}(X_k)$
. When K has characteristic zero, these varieties were shown to be Cohen–Macaulay and normal, with rational singularities, by Kempf [Reference KempfKe1] using [Reference KempfKe2]. The Cohen–Macaulay property is proved in arbitrary characteristic by Huneke [Reference HunekeHu, Theorem 6.2] using principal radical systems, and by De Concini–Strickland [Reference De Concini and StricklandDS, Theorem 2.7] using Hodge algebra methods; however, as pointed out by Tchernev [Reference TchernevTc, Example 9.2], the Hodge algebra structure of [Reference De Concini and StricklandDS] is not correct, though the assertions can be obtained instead using Gröbner bases as in [Reference TchernevTc]. See also [Reference Musili and SeshadriMS] and the discussion in the proof of [Reference Conca and WelkerCW, Theorem 8.6]. The normality is [Reference HunekeHu, Theorem 7.1].
Returning to our setting where Y and Z are
![]() $m\times t$
and
$m\times t$
and
![]() $t\times n$
matrices of indeterminates, and
$t\times n$
matrices of indeterminates, and
![]() $S=K[Y,Z]$
, one has
$S=K[Y,Z]$
, one has
![]() $h=2$
and the complex at hand is
$h=2$
and the complex at hand is
The papers above give:
Theorem 4.1 [Reference De Concini and StricklandDS, Reference HunekeHu, Reference KempfKe1, Reference Musili and SeshadriMS, Reference TchernevTc].
Let K be a field. Fix positive integers
![]() $m,n$
and t, and set
$m,n$
and t, and set
, where Y and Z are, respectively,
![]() $m\times t$
and
$m\times t$
and
![]() $t\times n$
matrices of indeterminates. For nonnegative integers
$t\times n$
matrices of indeterminates. For nonnegative integers
![]() $i,j$
with
$i,j$
with
![]() $i+j\leqslant t$
, set
$i+j\leqslant t$
, set
where
![]() $(YZ)S$
is the ideal generated by the entries of the matrix
$(YZ)S$
is the ideal generated by the entries of the matrix
![]() $YZ$
. Then:
$YZ$
. Then:
-
(1) For each
 $i,j$
, the ring
$i,j$
, the ring
 $S/\mathfrak {p}_{i,j}$
is a Cohen–Macaulay normal domain.
$S/\mathfrak {p}_{i,j}$
is a Cohen–Macaulay normal domain. -
(2) If
 $i\leqslant m$
and
$i\leqslant m$
and
 $j\leqslant n$
, then
$j\leqslant n$
, then
 $\operatorname {ht}(\mathfrak {p}_{i,j}) = (m-i)(t-i) + (n-j)(t-j) + ij$
.
$\operatorname {ht}(\mathfrak {p}_{i,j}) = (m-i)(t-i) + (n-j)(t-j) + ij$
. -
(3) The radical of
 $(YZ)S$
is the intersection of the prime ideals
$(YZ)S$
is the intersection of the prime ideals
 $\mathfrak {p}_{i,j}$
with
$\mathfrak {p}_{i,j}$
with
 $i+j=t$
.
$i+j=t$
.
It is perhaps amusing to note that varieties of complexes with
![]() $h=1$
give us determinantal rings, their Cohen–Macaulay property being used in the
$h=1$
give us determinantal rings, their Cohen–Macaulay property being used in the
![]() $\operatorname {SL}_d(K)$
case of Theorem 1.1.
$\operatorname {SL}_d(K)$
case of Theorem 1.1.
4.2 The purity of the embedding
We next settle the
![]() $\operatorname {GL}_t(K)$
case of Theorem 1.1.
$\operatorname {GL}_t(K)$
case of Theorem 1.1.
Theorem 4.2. Let K be a field of positive characteristic. Fix positive integers
![]() $m,n,t$
and consider the inclusion
$m,n,t$
and consider the inclusion
![]() $\varphi \colon K[YZ]\longrightarrow K[Y,Z]$
, where Y and Z are, respectively,
$\varphi \colon K[YZ]\longrightarrow K[Y,Z]$
, where Y and Z are, respectively,
![]() $m\times t$
and
$m\times t$
and
![]() $t\times n$
matrices of indeterminates. Then
$t\times n$
matrices of indeterminates. Then
![]() $\varphi $
is pure if and only if
$\varphi $
is pure if and only if
![]() $t=1$
, or
$t=1$
, or
![]() $m\leqslant t$
, or
$m\leqslant t$
, or
![]() $n\leqslant t$
.
$n\leqslant t$
.
Proof. We claim that if the inclusion
![]() $\varphi \colon K[YZ]\longrightarrow K[Y,Z]$
is pure for a fixed triple of positive integers
$\varphi \colon K[YZ]\longrightarrow K[Y,Z]$
is pure for a fixed triple of positive integers
![]() $(m,n,t)$
, then purity holds as well for the inclusion of the K-algebras corresponding to a triple
$(m,n,t)$
, then purity holds as well for the inclusion of the K-algebras corresponding to a triple
![]() $(m',n',t)$
with
$(m',n',t)$
with
![]() $m'\leqslant m$
and
$m'\leqslant m$
and
![]() $n'\leqslant n$
.
$n'\leqslant n$
.
To see this, set
![]() $Y'$
to be the matrix consisting of the first
$Y'$
to be the matrix consisting of the first
![]() $m'$
rows of Y, and
$m'$
rows of Y, and
![]() $Z'$
to be the matrix consisting of the first
$Z'$
to be the matrix consisting of the first
![]() $n'$
columns of Z, and consider the
$n'$
columns of Z, and consider the
![]() $\mathbb {N}$
-grading on
$\mathbb {N}$
-grading on
![]() $K[Y,Z]$
where the indeterminates from the submatrices
$K[Y,Z]$
where the indeterminates from the submatrices
![]() $Y'$
and
$Y'$
and
![]() $Z'$
have degree
$Z'$
have degree
![]() $0$
, as does K, while the remaining indeterminates have degree
$0$
, as does K, while the remaining indeterminates have degree
![]() $1$
so that
$1$
so that
![]() ${K[Y,Z]}_0\ =\ K[Y',Z']$
. Then
${K[Y,Z]}_0\ =\ K[Y',Z']$
. Then
so
![]() $K[Y'Z']$
is a pure subring of
$K[Y'Z']$
is a pure subring of
![]() $K[YZ]$
. Since we are assuming
$K[YZ]$
. Since we are assuming
![]() $K[YZ]\longrightarrow K[Y,Z]$
is pure, it follows that the composition
$K[YZ]\longrightarrow K[Y,Z]$
is pure, it follows that the composition
is pure as well, but then so is
![]() $K[Y'Z']\subseteq K[Y',Z']$
. This proves the claim; similar reduction arguments will be used for other matrix families later in the paper.
$K[Y'Z']\subseteq K[Y',Z']$
. This proves the claim; similar reduction arguments will be used for other matrix families later in the paper.
Set
and
. We next prove that
![]() $\varphi $
is pure in the cases claimed in the theorem. When
$\varphi $
is pure in the cases claimed in the theorem. When
![]() $t=1$
, the ring R coincides with the Segre product of the polynomial rings
$t=1$
, the ring R coincides with the Segre product of the polynomial rings
![]() $K[Y]$
and
$K[Y]$
and
![]() $K[Z]$
, which is a pure subring of S. For the case
$K[Z]$
, which is a pure subring of S. For the case
![]() $m\leqslant t$
, in light of the reduction step, it suffices to establish the purity when
$m\leqslant t$
, in light of the reduction step, it suffices to establish the purity when
![]() $m=t$
and
$m=t$
and
![]() $n\geqslant t$
. In this case, the ring R has dimension
$n\geqslant t$
. In this case, the ring R has dimension
![]() $mn$
, specifically the matrix entries
$mn$
, specifically the matrix entries
are algebraically independent over K and hence form a homogeneous system of parameters for R. By Theorem 2.1, it suffices to show that
![]() $H^{mn}_{\mathfrak {m}_R}(S)$
is nonzero; we show that
$H^{mn}_{\mathfrak {m}_R}(S)$
is nonzero; we show that
 $$\begin{align*}\left[\frac{1}{\prod x_{ij}}\right]\ \in\ H^{mn}_{\mathfrak{m}_R}(S) \end{align*}$$
$$\begin{align*}\left[\frac{1}{\prod x_{ij}}\right]\ \in\ H^{mn}_{\mathfrak{m}_R}(S) \end{align*}$$
is a nonzero element, equivalently that for each
![]() $k\geqslant 1$
, one has
$k\geqslant 1$
, one has
It is enough to show the above after specializing the entries of Y to the
![]() $t\times t$
identity matrix. This specialization maps
$t\times t$
identity matrix. This specialization maps
![]() $YZ$
to Z, with the image of S being the polynomial ring
$YZ$
to Z, with the image of S being the polynomial ring
![]() $K[Z]$
. The above display then takes the form
$K[Z]$
. The above display then takes the form
which is immediately seen to hold. The case
![]() $n\leqslant t$
is much the same.
$n\leqslant t$
is much the same.
Next, suppose
![]() $t\geqslant 2$
. It remains to prove that
$t\geqslant 2$
. It remains to prove that
![]() $\varphi \colon K[YZ]\longrightarrow K[Y,Z]$
is not pure if
$\varphi \colon K[YZ]\longrightarrow K[Y,Z]$
is not pure if
![]() $m>t$
and
$m>t$
and
![]() $n>t$
. By the reduction step at the beginning of the proof, it suffices to show that
$n>t$
. By the reduction step at the beginning of the proof, it suffices to show that
![]() $\varphi $
is not pure in the case
$\varphi $
is not pure in the case
![]() $m=t+1=n$
. In this case, the ring
$m=t+1=n$
. In this case, the ring
![]() $R=K[YZ]$
is a hypersurface of dimension
$R=K[YZ]$
is a hypersurface of dimension
![]() $t^2+2t$
, so it suffices by Theorem 2.1 to show that the local cohomology module
$t^2+2t$
, so it suffices by Theorem 2.1 to show that the local cohomology module
is zero, where
![]() $\mathfrak {m}_R$
is the homogeneous maximal ideal of R. The minimal primes of the ideal
$\mathfrak {m}_R$
is the homogeneous maximal ideal of R. The minimal primes of the ideal
![]() $\mathfrak {m}_RS$
are described by Theorem 4.1; in the notation of that theorem, these are the primes
$\mathfrak {m}_RS$
are described by Theorem 4.1; in the notation of that theorem, these are the primes
![]() $\mathfrak {p}_{0,t},\ \mathfrak {p}_{1,t-1},\ \dots ,\ \mathfrak {p}_{t,0}$
. With
$\mathfrak {p}_{0,t},\ \mathfrak {p}_{1,t-1},\ \dots ,\ \mathfrak {p}_{t,0}$
. With
![]() $\operatorname {cd}$
denoting the cohomological dimension, we shall prove that for each integer k with
$\operatorname {cd}$
denoting the cohomological dimension, we shall prove that for each integer k with
![]() $0\leqslant k\leqslant t$
, one has
$0\leqslant k\leqslant t$
, one has
from which it follows that
![]() $\operatorname {cd}(\mathfrak {m}_RS)\leqslant t^2+t+1$
; since
$\operatorname {cd}(\mathfrak {m}_RS)\leqslant t^2+t+1$
; since
![]() $t\geqslant 2$
, one has
$t\geqslant 2$
, one has
![]() $t^2+t+1<t^2+2t$
.
$t^2+t+1<t^2+2t$
.
We first claim that
 $$ \begin{align} \operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right)\ &\leqslant\ \max\left\{\operatorname{cd}(\mathfrak{p}_{0,t}),\ \operatorname{cd}(\mathfrak{p}_{1,t-1}),\ \dots,\ \operatorname{cd}(\mathfrak{p}_{k,t-k}),\right. \notag \\&\quad \left. \operatorname{cd}(\mathfrak{p}_{0,t-1})-1,\ \operatorname{cd}(\mathfrak{p}_{1,t-2})-1,\ \dots,\ \operatorname{cd}(\mathfrak{p}_{k-1,t-k})-1\right\}. \end{align} $$
$$ \begin{align} \operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right)\ &\leqslant\ \max\left\{\operatorname{cd}(\mathfrak{p}_{0,t}),\ \operatorname{cd}(\mathfrak{p}_{1,t-1}),\ \dots,\ \operatorname{cd}(\mathfrak{p}_{k,t-k}),\right. \notag \\&\quad \left. \operatorname{cd}(\mathfrak{p}_{0,t-1})-1,\ \operatorname{cd}(\mathfrak{p}_{1,t-2})-1,\ \dots,\ \operatorname{cd}(\mathfrak{p}_{k-1,t-k})-1\right\}. \end{align} $$
Quite generally, for ideals
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {b}$
of S, the Mayer–Vietoris sequence
$\mathfrak {b}$
of S, the Mayer–Vietoris sequence
shows that
Using this for the ideals
and
, one has
 $$ \begin{align*} &\operatorname{cd}\left([\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}]\cap\mathfrak{p}_{k+1,t-k-1}\right)\ \leqslant\ \max\left\{\operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right),\right. \\&\qquad\quad\qquad\qquad\qquad\qquad\left. \operatorname{cd}(\mathfrak{p}_{k+1,t-k-1}),\\operatorname{cd}\left([\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}]+\mathfrak{p}_{k+1,t-k-1}\right)-1\right\}. \end{align*} $$
$$ \begin{align*} &\operatorname{cd}\left([\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}]\cap\mathfrak{p}_{k+1,t-k-1}\right)\ \leqslant\ \max\left\{\operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right),\right. \\&\qquad\quad\qquad\qquad\qquad\qquad\left. \operatorname{cd}(\mathfrak{p}_{k+1,t-k-1}),\\operatorname{cd}\left([\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}]+\mathfrak{p}_{k+1,t-k-1}\right)-1\right\}. \end{align*} $$
Up to taking radicals, the ideal
coincides with
 $$ \begin{align*} (\mathfrak{p}_{0,t}+\mathfrak{p}_{k+1,t-k-1})\cap(\mathfrak{p}_{1,t-1}+\mathfrak{p}_{k+1,t-k-1}) &\cap\dots\cap(\mathfrak{p}_{k,t-k}+\mathfrak{p}_{k+1,t-k-1})\\ &\quad \ =\ \mathfrak{p}_{0,t-k-1}\cap\mathfrak{p}_{1,t-k-1}\cap\dots\cap\mathfrak{p}_{k,t-k-1}\ =\ \mathfrak{p}_{k,t-k-1}, \end{align*} $$
$$ \begin{align*} (\mathfrak{p}_{0,t}+\mathfrak{p}_{k+1,t-k-1})\cap(\mathfrak{p}_{1,t-1}+\mathfrak{p}_{k+1,t-k-1}) &\cap\dots\cap(\mathfrak{p}_{k,t-k}+\mathfrak{p}_{k+1,t-k-1})\\ &\quad \ =\ \mathfrak{p}_{0,t-k-1}\cap\mathfrak{p}_{1,t-k-1}\cap\dots\cap\mathfrak{p}_{k,t-k-1}\ =\ \mathfrak{p}_{k,t-k-1}, \end{align*} $$
since
![]() $\mathfrak {p}_{i_1,j_1}+\mathfrak {p}_{i_2,j_2}=\mathfrak {p}_{i,j}$
for
$\mathfrak {p}_{i_1,j_1}+\mathfrak {p}_{i_2,j_2}=\mathfrak {p}_{i,j}$
for
and
. It follows that
 $$ \begin{align*} &\operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k+1,t-k-1}\right)\\&\qquad\qquad\qquad\qquad \leqslant\ \max\left\{\operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right),\ \operatorname{cd}(\mathfrak{p}_{k+1,t-k-1}),\ \operatorname{cd}(\mathfrak{p}_{k,t-k-1})-1\right\}. \end{align*} $$
$$ \begin{align*} &\operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k+1,t-k-1}\right)\\&\qquad\qquad\qquad\qquad \leqslant\ \max\left\{\operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right),\ \operatorname{cd}(\mathfrak{p}_{k+1,t-k-1}),\ \operatorname{cd}(\mathfrak{p}_{k,t-k-1})-1\right\}. \end{align*} $$
Using this inductively, one obtains the inequality (4.2.2).
Since the rings
![]() $S/\mathfrak {p}_{i,j}$
are Cohen–Macaulay for
$S/\mathfrak {p}_{i,j}$
are Cohen–Macaulay for
![]() $i+j\leqslant t$
, Theorem 2.3 implies that
$i+j\leqslant t$
, Theorem 2.3 implies that
![]() $\operatorname {cd}(\mathfrak {p}_{i,j}) = \operatorname {ht}(\mathfrak {p}_{i,j})$
. Consequently, the inequality (4.2.2) gives
$\operatorname {cd}(\mathfrak {p}_{i,j}) = \operatorname {ht}(\mathfrak {p}_{i,j})$
. Consequently, the inequality (4.2.2) gives
 $$ \begin{align*} \operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right)\ \leqslant\ \max &\left\{\operatorname{ht}(\mathfrak{p}_{0,t}),\ \operatorname{ht}(\mathfrak{p}_{1,t-1}),\ \dots,\ \operatorname{ht}(\mathfrak{p}_{k,t-k}),\right. \\&\quad \left. \operatorname{ht}(\mathfrak{p}_{0,t-1})-1,\ \operatorname{ht}(\mathfrak{p}_{1,t-2})-1,\ \dots,\ \operatorname{ht}(\mathfrak{p}_{k-1,t-k})-1\right\}. \end{align*} $$
$$ \begin{align*} \operatorname{cd}\left(\mathfrak{p}_{0,t}\cap\mathfrak{p}_{1,t-1}\cap\dots\cap\mathfrak{p}_{k,t-k}\right)\ \leqslant\ \max &\left\{\operatorname{ht}(\mathfrak{p}_{0,t}),\ \operatorname{ht}(\mathfrak{p}_{1,t-1}),\ \dots,\ \operatorname{ht}(\mathfrak{p}_{k,t-k}),\right. \\&\quad \left. \operatorname{ht}(\mathfrak{p}_{0,t-1})-1,\ \operatorname{ht}(\mathfrak{p}_{1,t-2})-1,\ \dots,\ \operatorname{ht}(\mathfrak{p}_{k-1,t-k})-1\right\}. \end{align*} $$
Using the formula for
![]() $\operatorname {ht}(\mathfrak {p}_{i,j})$
from Theorem 4.1, it is readily verified that for each fixed integer
$\operatorname {ht}(\mathfrak {p}_{i,j})$
from Theorem 4.1, it is readily verified that for each fixed integer
![]() $\ell $
with
$\ell $
with
![]() $0\leqslant \ell \leqslant t$
, one has
$0\leqslant \ell \leqslant t$
, one has
which then yields the inequality (4.2.1).
5 Principal radical systems
Our approach to Theorems 1.2 and 1.3 is via the technique of principal radical systems, developed by Hochster and Eagon in [Reference HesselinkHE]. This is a method used to prove that a given homogeneous ideal in a polynomial ring is prime and defines a Cohen–Macaulay ring, by constructing a finite family of radical ideals that contains the ideal of interest and inductively prove primality and the Cohen–Macaulay property for select ideals in the family — the desired properties are first proved for larger ideals in the family. The power of the technique was first demonstrated in proving that generic determinantal rings are Cohen–Macaulay, a result that we used in the proof of Theorem 3.1. It was also used in Huneke’s proof [Reference HunekeHu] of Theorem 4.1. Kutz [Reference KutzKu] used principal radical systems to prove that symmetric determinantal rings are Cohen–Macaulay, while the corresponding result for Pfaffians is due to Kleppe–Laksov [Reference Kleppe and LaksovKL] and independently Marinov [Reference MarinovMa1, Reference MarinovMa2]. The technique uses the following lemma from [Reference HesselinkHE, Section 5]; the proof, being brief, is included for the convenience of the reader.
Lemma 5.1. Let S be an
![]() $\mathbb {N}$
-graded ring, finitely generated over a field
$\mathbb {N}$
-graded ring, finitely generated over a field
![]() $S_0$
. Let I be a homogeneous ideal, and P a homogenous prime ideal such that
$S_0$
. Let I be a homogeneous ideal, and P a homogenous prime ideal such that
![]() $I\subseteq P$
. Suppose there exists a homogeneous element x of positive degree such that
$I\subseteq P$
. Suppose there exists a homogeneous element x of positive degree such that
![]() $x\notin P$
and
$x\notin P$
and
![]() $I+xS$
is a radical ideal.
$I+xS$
is a radical ideal.
-
(1) If
 $xP\subseteq I$
, then I is radical.
$xP\subseteq I$
, then I is radical. -
(2) If
 $\operatorname {rad}\, I=P$
, then
$\operatorname {rad}\, I=P$
, then
 $I=P$
.
$I=P$
.
Proof. (1) Let u be a homogeneous element in the radical of I. Then,
![]() $u = i+xs$
for homogeneous elements i in I and s in S. Then,
$u = i+xs$
for homogeneous elements i in I and s in S. Then,
![]() $xs = u-i$
lies in the radical of I and therefore in P. Since x does not belong to P, the element s must. But then
$xs = u-i$
lies in the radical of I and therefore in P. Since x does not belong to P, the element s must. But then
![]() $xs$
is an element of
$xs$
is an element of
![]() $xP\subseteq I$
, so
$xP\subseteq I$
, so
![]() $u=i+xs$
belongs to I.
$u=i+xs$
belongs to I.
(2) Replacing S by
![]() $S/I$
, it suffices to prove that S is a domain; the prime ideal P is now the nilradical of S. Let u be a homogeneous element in P. Since
$S/I$
, it suffices to prove that S is a domain; the prime ideal P is now the nilradical of S. Let u be a homogeneous element in P. Since
![]() $S/xS$
is reduced,
$S/xS$
is reduced,
![]() $u=xv$
for some
$u=xv$
for some
![]() $v\in S$
. But
$v\in S$
. But
![]() $xv$
lies in the prime ideal P and x does not, so
$xv$
lies in the prime ideal P and x does not, so
![]() $v\in P$
. Thus,
$v\in P$
. Thus,
![]() $P=xP$
which, by the graded version of Nakayama’s lemma, implies that P is zero.
$P=xP$
which, by the graded version of Nakayama’s lemma, implies that P is zero.
We will also need the following elementary lemma for inductively proving the Cohen–Macaulay property along a principal radical system.
Lemma 5.2. Let S be an
![]() $\mathbb {N}$
-graded ring, finitely generated over a field
$\mathbb {N}$
-graded ring, finitely generated over a field
![]() $S_0$
. Let
$S_0$
. Let
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
be ideals such that
$Q_2$
be ideals such that
![]() $S/Q_1$
and
$S/Q_1$
and
![]() $S/Q_2$
are Cohen–Macaulay rings of equal dimension, say d, and such that
$S/Q_2$
are Cohen–Macaulay rings of equal dimension, say d, and such that
![]() $S/(Q_1+Q_2)$
is Cohen–Macaulay of dimension
$S/(Q_1+Q_2)$
is Cohen–Macaulay of dimension
![]() $d-1$
. Then the ring
$d-1$
. Then the ring
![]() $S/(Q_1\cap Q_2)$
is Cohen–Macaulay of dimension d.
$S/(Q_1\cap Q_2)$
is Cohen–Macaulay of dimension d.
Proof. One has an exact sequence of the form
The result follows from the local cohomology exact sequence obtained by applying the functor
![]() $H^{\bullet }_{\mathfrak {m}}(-)$
, where
$H^{\bullet }_{\mathfrak {m}}(-)$
, where
![]() $\mathfrak {m}$
is the homogeneous maximal ideal of S.
$\mathfrak {m}$
is the homogeneous maximal ideal of S.
The following result will be used in order to employ Lemma 5.1.
Lemma 5.3. Let M be a matrix with entries from a commutative ring. Fix an integer
![]() $c>0$
, and set
$c>0$
, and set
![]() $M|_c$
to be the submatrix consisting of the first c columns of M. Then, for each integer b with
$M|_c$
to be the submatrix consisting of the first c columns of M. Then, for each integer b with
![]() $b>c$
, one has
$b>c$
, one has
Proof. Working modulo the ideal
![]() $I_{k+1}(M)+(m_{11},\ m_{12},\ \dots ,\ m_{1c})$
, we reuse the notation M and
$I_{k+1}(M)+(m_{11},\ m_{12},\ \dots ,\ m_{1c})$
, we reuse the notation M and
![]() $m_{ij}$
in the quotient ring and show that
$m_{ij}$
in the quotient ring and show that
![]() $m_{1b}$
annihilates the ideal
$m_{1b}$
annihilates the ideal
![]() $I_k(M|_c)$
. If c is less than k, then
$I_k(M|_c)$
. If c is less than k, then
![]() $I_k(M|_c)=0$
. Assume
$I_k(M|_c)=0$
. Assume
![]() $c\geqslant k$
, and fix b and a
$c\geqslant k$
, and fix b and a
![]() $k \times k$
minor of
$k \times k$
minor of
![]() $M|_c$
. If the minor involves the first row of M, it clearly vanishes. Therefore, we may assume that the minor involves k rows other than the first row. Consider the
$M|_c$
. If the minor involves the first row of M, it clearly vanishes. Therefore, we may assume that the minor involves k rows other than the first row. Consider the
![]() $(k+1) \times (k+1)$
submatrix of M that involves, additionally, the first row and the b-th column of M. This matrix has determinant zero, so the result follows.
$(k+1) \times (k+1)$
submatrix of M that involves, additionally, the first row and the b-th column of M. This matrix has determinant zero, so the result follows.
6 Pfaffian rings
Let t be a positive integer, and X a
![]() $2t \times 2t$
alternating matrix. The Pfaffian of X is
$2t \times 2t$
alternating matrix. The Pfaffian of X is
where the sum is taken over permutations of
![]() $\{1,2,\dots ,2t\}$
that satisfy
$\{1,2,\dots ,2t\}$
that satisfy
It is readily seen that
![]() $(\operatorname {pf} X)^2=\det X$
.
$(\operatorname {pf} X)^2=\det X$
.
For an alternating matrix X with entries from a commutative ring, we use
![]() $\operatorname {Pf}_{2t}(X)$
to denote the ideal generated by the Pfaffians of the size
$\operatorname {Pf}_{2t}(X)$
to denote the ideal generated by the Pfaffians of the size
![]() $2t$
principal submatrices of X.
$2t$
principal submatrices of X.
Suppose X is an
![]() $n\times n$
alternating matrix of indeterminates over a field K. In this case, the ring
$n\times n$
alternating matrix of indeterminates over a field K. In this case, the ring
![]() $K[X]/\operatorname {Pf}_{2t+2}(X)$
is a Gorenstein unique factorization domain of dimension
$K[X]/\operatorname {Pf}_{2t+2}(X)$
is a Gorenstein unique factorization domain of dimension
 $$\begin{align*}\binom{n}{2} - \binom{n-2t}{2}, \end{align*}$$
$$\begin{align*}\binom{n}{2} - \binom{n-2t}{2}, \end{align*}$$
with the convention that
![]() $\binom {i}{j}=0$
if
$\binom {i}{j}=0$
if
![]() $i<j$
. The ring
$i<j$
. The ring
![]() $K[X]/\operatorname {Pf}_{2t+2}(X)$
is regular precisely if
$K[X]/\operatorname {Pf}_{2t+2}(X)$
is regular precisely if
![]() $n\leqslant 2t+1$
, for then
$n\leqslant 2t+1$
, for then
![]() $\operatorname {Pf}_{2t+2}(X)=0$
. The Cohen–Macaulay property is due to [Reference Kleppe and LaksovKL] and [Reference MarinovMa1, Reference MarinovMa2]; the rings are unique factorization domains by [Reference AvramovAv], hence Gorenstein.
$\operatorname {Pf}_{2t+2}(X)=0$
. The Cohen–Macaulay property is due to [Reference Kleppe and LaksovKL] and [Reference MarinovMa1, Reference MarinovMa2]; the rings are unique factorization domains by [Reference AvramovAv], hence Gorenstein.
The ideal
![]() $\operatorname {Pf}_4(X)$
is generated by the elements
$\operatorname {Pf}_4(X)$
is generated by the elements
These are precisely the Plücker relations for the Grassmannian
![]() $G(2,n)$
, and
$G(2,n)$
, and
![]() $K[X]/\operatorname {Pf}_4(X)$
is isomorphic to the homogeneous coordinate ring for
$K[X]/\operatorname {Pf}_4(X)$
is isomorphic to the homogeneous coordinate ring for
![]() $G(2,n)$
from §3.
$G(2,n)$
from §3.
Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K. Set
$2t\times n$
matrix of indeterminates over a field K. Set
![]() , and let
, and let
![]() $\Omega $
be the size
$\Omega $
be the size
![]() $2t$
standard symplectic block matrix (1.0.1). Then
$2t$
standard symplectic block matrix (1.0.1). Then
![]() $Y^{\operatorname {tr}}\Omega Y$
is an alternating matrix of rank
$Y^{\operatorname {tr}}\Omega Y$
is an alternating matrix of rank
![]() $\min \{2t,n\}$
. For X an
$\min \{2t,n\}$
. For X an
![]() $n \times n$
alternating matrix of indeterminates, the entrywise map
$n \times n$
alternating matrix of indeterminates, the entrywise map
induces a K-algebra isomorphism between
![]() $K[X]/\operatorname {Pf}_{2t+2}(X)$
and the subring
$K[X]/\operatorname {Pf}_{2t+2}(X)$
and the subring
![]() of S. Our goal in this section is to determine when the inclusion
of S. Our goal in this section is to determine when the inclusion
![]() $\varphi \colon R\longrightarrow S$
is pure. The symplectic group
$\varphi \colon R\longrightarrow S$
is pure. The symplectic group
![]() $\operatorname {Sp}_{2t}(K)$
acts K-linearly on S, where
$\operatorname {Sp}_{2t}(K)$
acts K-linearly on S, where
Since
![]() $M^{\operatorname {tr}}\Omega M=\Omega $
for
$M^{\operatorname {tr}}\Omega M=\Omega $
for
![]() $M\in \operatorname {Sp}_{2t}(K)$
, it follows that the entries of
$M\in \operatorname {Sp}_{2t}(K)$
, it follows that the entries of
![]() $Y^{\operatorname {tr}}\Omega Y$
are fixed by the group action; when the field K is infinite, the invariant ring is precisely the subring R; see [Reference De Concini and ProcesiDP, §6] or [Reference HashimotoHa, Theorem 5.1]. When the field K has characteristic zero, the group
$Y^{\operatorname {tr}}\Omega Y$
are fixed by the group action; when the field K is infinite, the invariant ring is precisely the subring R; see [Reference De Concini and ProcesiDP, §6] or [Reference HashimotoHa, Theorem 5.1]. When the field K has characteristic zero, the group
![]() $\operatorname {Sp}_{2t}(K)$
is linearly reductive and it follows that the invariant ring R is a direct summand of S as an R-module; hence,
$\operatorname {Sp}_{2t}(K)$
is linearly reductive and it follows that the invariant ring R is a direct summand of S as an R-module; hence,
![]() $\varphi \colon R\longrightarrow S$
is pure when K has characteristic zero.
$\varphi \colon R\longrightarrow S$
is pure when K has characteristic zero.
6.1 Symplectic forms and preliminaries
Let K be a field and V the vector space
![]() $K^{2t}$
with the standard basis. Then
$K^{2t}$
with the standard basis. Then
![]() $\Omega $
determines the bilinear form
$\Omega $
determines the bilinear form
![]() $B\colon V\times V\longrightarrow K$
given by
$B\colon V\times V\longrightarrow K$
given by
Note that B is nondegenerate and alternating, that is,
![]() $B(v,v)=0$
for all
$B(v,v)=0$
for all
![]() $v\in V$
; in other words, B is a symplectic form on V. One has
$v\in V$
; in other words, B is a symplectic form on V. One has
The matrix for B with respect to the chosen basis is
![]() $\Omega $
, while a change of basis results in a matrix of the form
$\Omega $
, while a change of basis results in a matrix of the form
![]() $C^{\operatorname {tr}}\Omega C$
. In view of this, matrices M and N are cogredient if there exists an invertible matrix C such that
$C^{\operatorname {tr}}\Omega C$
. In view of this, matrices M and N are cogredient if there exists an invertible matrix C such that
A vector subspace W of V is isotropic if
![]() $B(w_1,w_2)=0$
for all
$B(w_1,w_2)=0$
for all
![]() $w_i\in W$
, equivalently if
$w_i\in W$
, equivalently if
![]() $W\subseteq W^\perp $
. Since B is nondegenerate, for any subspace W one has
$W\subseteq W^\perp $
. Since B is nondegenerate, for any subspace W one has
Hence, an isotropic subspace of V has rank at most t. Any isotropic subspace of V is contained in one that has maximal rank, which is a Lagrangian subspace.
Lemma 6.1. Let K be a field. Consider the vector space
![]() $K^{2t}$
equipped with a symplectic form. Let L be a nonzero linear functional on
$K^{2t}$
equipped with a symplectic form. Let L be a nonzero linear functional on
![]() $K^{2t}$
, and let
$K^{2t}$
, and let
be isotropic subspaces of
![]() $K^{2t}$
with
$K^{2t}$
with
![]() $\operatorname {rank} V_j\leqslant j$
for each j, with
$\operatorname {rank} V_j\leqslant j$
for each j, with
![]() $m\leqslant t$
. Let k be an integer with
$m\leqslant t$
. Let k be an integer with
![]() $1\leqslant k\leqslant m$
.
$1\leqslant k\leqslant m$
.
Suppose L vanishes on
![]() $V_k$
. Then there exist isotropic subspaces
$V_k$
. Then there exist isotropic subspaces
such that, for each j, one has
![]() $V_j\subseteq W_j$
and
$V_j\subseteq W_j$
and
![]() $\operatorname {rank} W_j=j$
, and L vanishes on
$\operatorname {rank} W_j=j$
, and L vanishes on
![]() $W_k$
.
$W_k$
.
Proof. It suffices to consider the case where
![]() $m=t$
. Denote the symplectic form by B, and set
$m=t$
. Denote the symplectic form by B, and set
![]() , a codimension one subspace. We construct the subspaces
, a codimension one subspace. We construct the subspaces
![]() $W_j$
by reverse induction on j. If
$W_j$
by reverse induction on j. If
![]() $V_t$
has dimension t, simply choose
$V_t$
has dimension t, simply choose
![]() $W_t$
to be
$W_t$
to be
![]() $V_t$
itself. If
$V_t$
itself. If
![]() $V_t$
has dimension less than t, then
$V_t$
has dimension less than t, then
![]() $\dim (V_t^\perp )>t$
, so
$\dim (V_t^\perp )>t$
, so
![]() $\dim (V_t^\perp \cap H) \geqslant t$
.
$\dim (V_t^\perp \cap H) \geqslant t$
.
If
![]() $k<t$
, take
$k<t$
, take
![]() $W_t$
to be a Lagrangian subspace of
$W_t$
to be a Lagrangian subspace of
![]() $K^{2t}$
containing
$K^{2t}$
containing
![]() $V_t$
. If
$V_t$
. If
![]() $k=t$
, since
$k=t$
, since
![]() ${V_t\subset H}$
, there exists a nonzero vector
${V_t\subset H}$
, there exists a nonzero vector
![]() $x\in (V_t^\perp \cap H) \smallsetminus V$
. Then
$x\in (V_t^\perp \cap H) \smallsetminus V$
. Then
Continuing in this manner, we can extend
![]() $V_t$
to a Lagrangian subspace of
$V_t$
to a Lagrangian subspace of
![]() $K^{2t}$
on which L vanishes.
$K^{2t}$
on which L vanishes.
Assume that the vector spaces
![]() $W_{j+1}, W_{j+2}, \dots , W_t$
have been constructed satisfying the required conditions. There are two cases: If j is different from k, simply choose
$W_{j+1}, W_{j+2}, \dots , W_t$
have been constructed satisfying the required conditions. There are two cases: If j is different from k, simply choose
![]() $W_j$
of dimension j such that
$W_j$
of dimension j such that
![]() $V_j \subseteq W_j \subseteq W_{j+1}$
. This can be done since
$V_j \subseteq W_j \subseteq W_{j+1}$
. This can be done since
![]() $V_j$
has dimension at most j and
$V_j$
has dimension at most j and
![]() $W_{j+1}$
has dimension
$W_{j+1}$
has dimension
![]() $j+1$
. If j equals k, choose
$j+1$
. If j equals k, choose
![]() $W_k$
of dimension k such that
$W_k$
of dimension k such that
![]() ${V_k \subseteq W_k \subseteq H \cap W_{k+1}}$
; this can indeed be done since
${V_k \subseteq W_k \subseteq H \cap W_{k+1}}$
; this can indeed be done since
![]() $V_k$
has dimension at most k, and
$V_k$
has dimension at most k, and
![]() $H \cap W_{k+1}$
has dimension at least
$H \cap W_{k+1}$
has dimension at least
Finally, since any subspace of an isotropic subspace is isotropic, we are done.
Let M be a size
![]() $2t\times n$
matrix over K, satisfying
$2t\times n$
matrix over K, satisfying
![]() $M^{\operatorname {tr}}\Omega M = 0$
. Then the columns of M span an isotropic subspace, so
$M^{\operatorname {tr}}\Omega M = 0$
. Then the columns of M span an isotropic subspace, so
![]() $\operatorname {rank} M \leqslant t$
, that is,
$\operatorname {rank} M \leqslant t$
, that is,
![]() $I_{t+1}(M)=0$
. By the Nullstellensatz, if Y is a size
$I_{t+1}(M)=0$
. By the Nullstellensatz, if Y is a size
![]() $2t\times n$
matrix of indeterminates over an algebraically closed field K, then
$2t\times n$
matrix of indeterminates over an algebraically closed field K, then
where
![]() $(Y^{\operatorname {tr}}\Omega Y)$
is the ideal of
$(Y^{\operatorname {tr}}\Omega Y)$
is the ideal of
![]() $K[Y]$
generated by the entries of the matrix
$K[Y]$
generated by the entries of the matrix
![]() $Y^{\operatorname {tr}}\Omega Y$
. We strengthen this next.
$Y^{\operatorname {tr}}\Omega Y$
. We strengthen this next.
Lemma 6.2. Let Y be a size
![]() $2t\times n$
matrix of indeterminates over a field K. Then, in the polynomial ring
$2t\times n$
matrix of indeterminates over a field K. Then, in the polynomial ring
![]() $K[Y]$
, one has
$K[Y]$
, one has
Proof. If
![]() $n\leqslant t$
, there is nothing to prove. If
$n\leqslant t$
, there is nothing to prove. If
![]() $Y'$
is a truncation of Y obtained by deleting certain columns, then the alternating matrix
$Y'$
is a truncation of Y obtained by deleting certain columns, then the alternating matrix
![]() $Y^{\prime \operatorname {tr}}\Omega Y'$
is a truncation of the alternating matrix
$Y^{\prime \operatorname {tr}}\Omega Y'$
is a truncation of the alternating matrix
![]() $Y^{\operatorname {tr}}\Omega Y$
obtained by deleting the corresponding columns and rows; thus, it suffices to prove the lemma when Y is size
$Y^{\operatorname {tr}}\Omega Y$
obtained by deleting the corresponding columns and rows; thus, it suffices to prove the lemma when Y is size
![]() $2t\times (t+1)$
.
$2t\times (t+1)$
.
Next, note that any size
![]() $t+1$
minor of Y equals the determinants of a matrix of the form
$t+1$
minor of Y equals the determinants of a matrix of the form
![]() $Y\# Z$
, where Z is a suitable size
$Y\# Z$
, where Z is a suitable size
![]() $2t\times (t-1)$
matrix with entries
$2t\times (t-1)$
matrix with entries
![]() $0$
and
$0$
and
![]() $1$
, and
$1$
, and
![]() $\#$
denotes the concatenation of matrices; for example, for the upper size
$\#$
denotes the concatenation of matrices; for example, for the upper size
![]() $t+1$
minor, one may take Z to be the block matrix
$t+1$
minor, one may take Z to be the block matrix
![]() .
.
Thus, it suffices to prove that for all matrices Z of size
![]() $2t\times (t-1)$
, one has
$2t\times (t-1)$
, one has
Since
![]() $\det (Y\# Z)=\operatorname {pf}((Y\# Z)^{\operatorname {tr}}\Omega (Y\# Z))$
, it suffices to prove that
$\det (Y\# Z)=\operatorname {pf}((Y\# Z)^{\operatorname {tr}}\Omega (Y\# Z))$
, it suffices to prove that
But
![]() $(Y\# Z)^{\operatorname {tr}}\Omega (Y\# Z)$
is a size
$(Y\# Z)^{\operatorname {tr}}\Omega (Y\# Z)$
is a size
![]() $2t$
alternating matrix, and
$2t$
alternating matrix, and
![]() $Y^{\operatorname {tr}}\Omega Y$
its upper-left size
$Y^{\operatorname {tr}}\Omega Y$
its upper-left size
![]() $t+1$
submatrix. Working modulo the entries of
$t+1$
submatrix. Working modulo the entries of
![]() $Y^{\operatorname {tr}}\Omega Y$
, it suffices to check that the Pfaffian of a size
$Y^{\operatorname {tr}}\Omega Y$
, it suffices to check that the Pfaffian of a size
![]() $2t$
alternating matrix of the form
$2t$
alternating matrix of the form
 $$\begin{align*}\begin{pmatrix} 0 & A\\ -A^{\operatorname{tr}} & B \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0 & A\\ -A^{\operatorname{tr}} & B \end{pmatrix} \end{align*}$$
is zero, where A and B are size
![]() $t\times t$
, and the first column of A is zero. This is immediate, as the determinant of such a matrix is zero.
$t\times t$
, and the first column of A is zero. This is immediate, as the determinant of such a matrix is zero.
When
![]() $t=1$
in Lemma 6.2, one has the equality
$t=1$
in Lemma 6.2, one has the equality
![]() $I_{t+1}(Y)=(Y^{\operatorname {tr}}\Omega Y)$
, as we will see in the following discussion.
$I_{t+1}(Y)=(Y^{\operatorname {tr}}\Omega Y)$
, as we will see in the following discussion.
6.2 Secant varieties of Grassmannians
Let Y be a size
![]() $2t\times n$
matrix of indeterminates over a field K. Set
$2t\times n$
matrix of indeterminates over a field K. Set
![]() $\mathfrak {P}$
to be the ideal generated by the entries of
$\mathfrak {P}$
to be the ideal generated by the entries of
![]() $Y^{\operatorname {tr}}\Omega Y$
. While we will prove later that
$Y^{\operatorname {tr}}\Omega Y$
. While we will prove later that
![]() $\mathfrak {P}$
is prime and defines a Cohen–Macaulay ring, it is worth mentioning that when
$\mathfrak {P}$
is prime and defines a Cohen–Macaulay ring, it is worth mentioning that when
![]() $t=1$
one has
$t=1$
one has

that is,
![]() $Y^{\operatorname {tr}}\Omega Y$
is an alternating matrix where, for
$Y^{\operatorname {tr}}\Omega Y$
is an alternating matrix where, for
![]() $i<j$
, the matrix entry
$i<j$
, the matrix entry
![]() $(Y^{\operatorname {tr}}\Omega Y)_{ij}$
is
$(Y^{\operatorname {tr}}\Omega Y)_{ij}$
is
It follows that
![]() $\mathfrak {P}$
coincides with the determinantal ideal
$\mathfrak {P}$
coincides with the determinantal ideal
![]() $I_2(Y)$
that has height
$I_2(Y)$
that has height
![]() $n-1$
, and defines a Cohen–Macaulay ring
$n-1$
, and defines a Cohen–Macaulay ring
![]() $K[Y]/\mathfrak {P}$
. The ring
$K[Y]/\mathfrak {P}$
. The ring
![]() $K[Y^{\operatorname {tr}}\Omega Y]$
is the homogeneous coordinate ring of the Grassmannian
$K[Y^{\operatorname {tr}}\Omega Y]$
is the homogeneous coordinate ring of the Grassmannian
![]() $G(2,n)$
under the Plücker embedding in
$G(2,n)$
under the Plücker embedding in
![]() $\mathbb {P}^{\binom {n}{2}-1}$
.
$\mathbb {P}^{\binom {n}{2}-1}$
.
More generally, for
![]() $t\geqslant 1$
, the ring
$t\geqslant 1$
, the ring
![]() $K[Y^{\operatorname {tr}}\Omega Y]$
is the homogeneous coordinate ring of the order
$K[Y^{\operatorname {tr}}\Omega Y]$
is the homogeneous coordinate ring of the order
![]() $t-1$
secant variety
$t-1$
secant variety
![]() $G(2,n)^{t-1}$
, which is the closure of the union of linear spaces spanned by t points of
$G(2,n)^{t-1}$
, which is the closure of the union of linear spaces spanned by t points of
![]() $G(2,n)$
: For
$G(2,n)$
: For
![]() $1\leqslant i<j\leqslant n$
, the alternating matrix
$1\leqslant i<j\leqslant n$
, the alternating matrix
![]() $Y^{\operatorname {tr}}\Omega Y$
has
$Y^{\operatorname {tr}}\Omega Y$
has
![]() $ij$
-th entry
$ij$
-th entry
![]() $B(v_i,v_j)$
, where
$B(v_i,v_j)$
, where
![]() $v_i$
and
$v_i$
and
![]() $v_j$
are the i-th and j-th columns of Y, and B is the symplectic form (6.0.1); specifically,
$v_j$
are the i-th and j-th columns of Y, and B is the symplectic form (6.0.1); specifically,
In particular,
 $$\begin{align*}\dim G(2,n)^{t-1}\ =\ \binom{n}{2} - \binom{n-2t}{2}-1. \end{align*}$$
$$\begin{align*}\dim G(2,n)^{t-1}\ =\ \binom{n}{2} - \binom{n-2t}{2}-1. \end{align*}$$
Recall that for an irreducible closed projective variety X of dimension d in
![]() $\mathbb {P}^N$
, the expected dimension of the order s secant variety
$\mathbb {P}^N$
, the expected dimension of the order s secant variety
![]() $X^s$
is
$X^s$
is
![]() $\min \{N,\ ds+d+s\}$
; when
$\min \{N,\ ds+d+s\}$
; when
![]() $\dim X^s$
is less than the expected dimension,
$\dim X^s$
is less than the expected dimension,
![]() $X^s$
is defective. Using the formula above, it is readily seen that
$X^s$
is defective. Using the formula above, it is readily seen that
![]() $G(2,n)^{t-1}$
is defective precisely if
$G(2,n)^{t-1}$
is defective precisely if
![]() $t\geqslant 2$
and
$t\geqslant 2$
and
![]() $n\geqslant 2t+2$
, confer [Reference Catalisano, Geramita and GimiglianoCGG, Theorem 2.1]. The dimension and the defining equations of secant varieties of other Grassmannians are largely unknown.
$n\geqslant 2t+2$
, confer [Reference Catalisano, Geramita and GimiglianoCGG, Theorem 2.1]. The dimension and the defining equations of secant varieties of other Grassmannians are largely unknown.
6.3 The complete intersection property
The ideal
![]() $\mathfrak {P}$
has
$\mathfrak {P}$
has
![]() $\binom {n}{2}$
minimal generators corresponding to the upper triangular entries of the alternating matrix
$\binom {n}{2}$
minimal generators corresponding to the upper triangular entries of the alternating matrix
![]() $Y^{\operatorname {tr}}\Omega Y$
. We next prove that in the case
$Y^{\operatorname {tr}}\Omega Y$
. We next prove that in the case
![]() $n\leqslant t+1$
, these generators form a regular sequence, in other words, that
$n\leqslant t+1$
, these generators form a regular sequence, in other words, that
![]() $K[Y]/\mathfrak {P}$
is a complete intersection ring.
$K[Y]/\mathfrak {P}$
is a complete intersection ring.
Theorem 6.3. Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K, where
$2t\times n$
matrix of indeterminates over a field K, where
![]() $n\leqslant t+1$
. Set
$n\leqslant t+1$
. Set
![]() and
and
![]() . Then
. Then
![]() $S/\mathfrak {P}$
is a complete intersection ring.
$S/\mathfrak {P}$
is a complete intersection ring.
Proof. It suffices to prove that
![]() $K[Y]/\mathfrak {P}$
is a complete intersection ring after specializing the entries of the rows indexed
$K[Y]/\mathfrak {P}$
is a complete intersection ring after specializing the entries of the rows indexed
to zero since this leaves the number of defining equations unchanged. We may hence assume that the matrix Y has
![]() $2t-2(t+1-n)=2n-2$
rows, that is, Y is size
$2t-2(t+1-n)=2n-2$
rows, that is, Y is size
![]() $2(n-1)\times n$
, equivalently, size
$2(n-1)\times n$
, equivalently, size
![]() $2t\times (t+1)$
. Next, specialize the entries of Y to the corresponding entries of the matrix
$2t\times (t+1)$
. Next, specialize the entries of Y to the corresponding entries of the matrix

This entails killing
 $$\begin{align*}\binom{t+1}{2}+t(t+1)\ =\ 2t(t+1) -\binom{t+1}{2} \end{align*}$$
$$\begin{align*}\binom{t+1}{2}+t(t+1)\ =\ 2t(t+1) -\binom{t+1}{2} \end{align*}$$
linear forms in
![]() $K[Y]$
. As
$K[Y]$
. As
![]() $K[\overline {Y}]/(\overline {Y}^{\operatorname {tr}}\Omega \overline {Y})$
is Artinian,
$K[\overline {Y}]/(\overline {Y}^{\operatorname {tr}}\Omega \overline {Y})$
is Artinian,
![]() $K[Y]/\mathfrak {P}$
is a complete intersection ring.
$K[Y]/\mathfrak {P}$
is a complete intersection ring.
Corollary 6.4. Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K, where
$2t\times n$
matrix of indeterminates over a field K, where
![]() $n\leqslant t$
. Set
$n\leqslant t$
. Set
![]() and
and
![]() . Let
. Let
![]() $\mathfrak {a}$
be an ideal generated by k distinct entries from rows
$\mathfrak {a}$
be an ideal generated by k distinct entries from rows
![]() $1$
and
$1$
and
![]() $t+1$
of the matrix Y. Then
$t+1$
of the matrix Y. Then
 $$\begin{align*}\dim S/(\mathfrak{P}+\mathfrak{a})\ =\ 2nt-\binom{n}{2}-k, \end{align*}$$
$$\begin{align*}\dim S/(\mathfrak{P}+\mathfrak{a})\ =\ 2nt-\binom{n}{2}-k, \end{align*}$$
so, in particular,
![]() $S/(\mathfrak {P}+\mathfrak {a})$
is a complete intersection ring.
$S/(\mathfrak {P}+\mathfrak {a})$
is a complete intersection ring.
Proof. As seen in the previous proof, the generators of the ideal
![]() $\mathfrak {a}$
form part of a system of parameters for the ring
$\mathfrak {a}$
form part of a system of parameters for the ring
![]() $S/\mathfrak {P}$
.
$S/\mathfrak {P}$
.
The following lemma will be used to prove the irreducibility of certain algebraic sets of the form
![]() $V(\mathfrak {P}+\mathfrak {a})$
in Proposition 6.6.
$V(\mathfrak {P}+\mathfrak {a})$
in Proposition 6.6.
Lemma 6.5. Let Y be a
![]() $2t\times t$
matrix of indeterminates over a field K. Set
$2t\times t$
matrix of indeterminates over a field K. Set
and
Let
![]() $\Delta $
be the upper
$\Delta $
be the upper
![]() $t \times t$
minor of Y. Then
$t \times t$
minor of Y. Then
![]() $\Delta $
is a nonzerodivisor on
$\Delta $
is a nonzerodivisor on
![]() $S/I$
.
$S/I$
.
Proof. It suffices to consider the case where the field K is algebraically closed. Since
![]() $S/I$
is a complete intersection ring by the corollary above, we need to show that
$S/I$
is a complete intersection ring by the corollary above, we need to show that
![]() $\Delta $
does not belong to any minimal prime of the ideal I.
$\Delta $
does not belong to any minimal prime of the ideal I.
Let G be the subgroup of
![]() $\operatorname {Sp}_{2t}(K)$
consisting of matrices
$\operatorname {Sp}_{2t}(K)$
consisting of matrices
![]() with
with
 $$ \begin{align*} m_{11} &= 1 = m_{t+1,t+1} \\ m_{1i} &= 0 = m_{i1} \qquad \text{for}\ i\neq 1\\ m_{t+1,i} &= 0 = m_{i,t+1} \quad \text{for} \ i\neq t+1. \end{align*} $$
$$ \begin{align*} m_{11} &= 1 = m_{t+1,t+1} \\ m_{1i} &= 0 = m_{i1} \qquad \text{for}\ i\neq 1\\ m_{t+1,i} &= 0 = m_{i,t+1} \quad \text{for} \ i\neq t+1. \end{align*} $$
Deleting rows and columns
![]() $1$
and
$1$
and
![]() $t+1$
shows that G is isomorphic to
$t+1$
shows that G is isomorphic to
![]() $\operatorname {Sp}_{2t-2}(K)$
and is hence a connected algebraic group. The action of G on S via
$\operatorname {Sp}_{2t-2}(K)$
and is hence a connected algebraic group. The action of G on S via
![]() $M\colon Y\longmapsto MY$
induces an action on
$M\colon Y\longmapsto MY$
induces an action on
![]() $S/I$
and thus on the (necessarily finite) set of minimal primes of
$S/I$
and thus on the (necessarily finite) set of minimal primes of
![]() $S/I$
. Since G is connected the action must be trivial, that is, G stabilizes each minimal prime of I.
$S/I$
. Since G is connected the action must be trivial, that is, G stabilizes each minimal prime of I.
Suppose a minimal prime P of I contains
![]() $\Delta $
. Using the fact that G stabilizes P, we shall first show that P contains each maximal minor of Y that involves the first row. Since row
$\Delta $
. Using the fact that G stabilizes P, we shall first show that P contains each maximal minor of Y that involves the first row. Since row
![]() $t+1$
of Y is contained in I, hence in P, we need only consider maximal minors of Y that involve the first row and not row
$t+1$
of Y is contained in I, hence in P, we need only consider maximal minors of Y that involve the first row and not row
![]() $t+1$
. We use
$t+1$
. We use
![]() to denote the image of
to denote the image of
![]() $\Delta $
under an element M of G.
$\Delta $
under an element M of G.
Let
![]() $\alpha $
be a size t subset of the row indices
$\alpha $
be a size t subset of the row indices
![]() $\{1,\dots ,2t\}$
such that
$\{1,\dots ,2t\}$
such that
![]() $1\in \alpha $
and
$1\in \alpha $
and
![]() $t+1\notin \alpha $
. We use
$t+1\notin \alpha $
. We use
![]() $Y_{\alpha }$
for the square submatrix with rows
$Y_{\alpha }$
for the square submatrix with rows
![]() $\alpha $
, and set
$\alpha $
, and set
![]() $\ell (\alpha )$
to be the number of indices
$\ell (\alpha )$
to be the number of indices
![]() $a\in \alpha $
such that
$a\in \alpha $
such that
![]() $a\leqslant t$
and
$a\leqslant t$
and
![]() $a+t\in \alpha $
. The proof that
$a+t\in \alpha $
. The proof that
![]() $\det (Y_{\alpha })\in P$
is by induction on
$\det (Y_{\alpha })\in P$
is by induction on
![]() $\ell (\alpha )$
.
$\ell (\alpha )$
.
For the case
![]() $\ell (\alpha )=0$
, proceed by induction on the number w of
$\ell (\alpha )=0$
, proceed by induction on the number w of
![]() $a\in \alpha $
with
$a\in \alpha $
with
![]() $a>t$
. When
$a>t$
. When
![]() $w=0$
, one has
$w=0$
, one has
![]() $\det (Y_{\alpha })=\Delta $
, which is an element of P. For the inductive step, consider the
$\det (Y_{\alpha })=\Delta $
, which is an element of P. For the inductive step, consider the
![]() $2t\times 2t$
matrix M with
$2t\times 2t$
matrix M with

Observe that
![]() $M\in G$
, and that the matrix
$M\in G$
, and that the matrix
![]() $MY$
is obtained from Y by the row operations where row
$MY$
is obtained from Y by the row operations where row
![]() $i+t$
is added to row i whenever
$i+t$
is added to row i whenever
![]() $i\leqslant t$
and
$i\leqslant t$
and
![]() $i+t\in \alpha $
. It follows that
$i+t\in \alpha $
. It follows that
is the determinant of the
![]() $t\times t$
matrix whose i-th row is the sum of rows i and
$t\times t$
matrix whose i-th row is the sum of rows i and
![]() $i+t$
of Y if
$i+t$
of Y if
![]() $i\leqslant t$
and
$i\leqslant t$
and
![]() $i+t\in \alpha $
, and is row i of Y otherwise. By the linearity of determinants along a row,
$i+t\in \alpha $
, and is row i of Y otherwise. By the linearity of determinants along a row,
is the sum of
![]() $t\times t$
minors of Y, each of which is indexed by a set of rows
$t\times t$
minors of Y, each of which is indexed by a set of rows
![]() $\beta $
with
$\beta $
with
![]() $\ell (\beta )=0$
. One of these is
$\ell (\beta )=0$
. One of these is
![]() $\det (Y_{\alpha })$
, while the others have fewer indices greater than t. Using
$\det (Y_{\alpha })$
, while the others have fewer indices greater than t. Using
and the inductive hypothesis, it follows that
![]() $\det (Y_{\alpha })\in P$
, settling the case
$\det (Y_{\alpha })\in P$
, settling the case
![]() $\ell (\alpha )=0$
.
$\ell (\alpha )=0$
.
Next, fix
![]() $\alpha $
with
$\alpha $
with
![]() $\ell (\alpha )>0$
. Let
$\ell (\alpha )>0$
. Let
![]() $i,j\in \{1,\dots ,t\}$
be such that
$i,j\in \{1,\dots ,t\}$
be such that
![]() $i, i+t\in \alpha $
and
$i, i+t\in \alpha $
and
![]() $j,j+t\notin \alpha $
; such a j exists by cardinality reasons. Let
$j,j+t\notin \alpha $
; such a j exists by cardinality reasons. Let
![]() $\alpha ' = \alpha \smallsetminus \{i,i+t\}$
. Observe that each of
$\alpha ' = \alpha \smallsetminus \{i,i+t\}$
. Observe that each of
is strictly less than
![]() $\ell (\alpha )$
. Let M be the
$\ell (\alpha )$
. Let M be the
![]() $2t \times 2t$
matrix with
$2t \times 2t$
matrix with

Note that
![]() $M\in G$
, and that the matrix
$M\in G$
, and that the matrix
![]() $MY$
is obtained from Y by row operations where the
$MY$
is obtained from Y by row operations where the
![]() $(j+t)$
-th row is added to the i-th row, and the
$(j+t)$
-th row is added to the i-th row, and the
![]() $(i+t)$
-th row is added to the j-th row. Hence, up to choices of signs,
$(i+t)$
-th row is added to the j-th row. Hence, up to choices of signs,
is the sum of
By the inductive hypothesis,
![]() $\det (Y_{\alpha '\cup \{i,j\}})$
and
$\det (Y_{\alpha '\cup \{i,j\}})$
and
![]() $\det (Y_{\alpha '\cup \{i+t,j+t\}}$
are elements of the prime P, as is
$\det (Y_{\alpha '\cup \{i+t,j+t\}}$
are elements of the prime P, as is
![]() $\det (Y_{\alpha '\cup \{i,j\}})$
and hence
$\det (Y_{\alpha '\cup \{i,j\}})$
and hence
. It follows that, with a sign choice, one of
is an element of P. We claim that there exists a Plücker relation in
![]() $K[Y]$
of the form
$K[Y]$
of the form
 $$ \begin{align} \det(Y_{\alpha'\cup\{i,i+t\}}) \det(Y_{\alpha'\cup\{j,j+t\}}) \ \pm\ \det(Y_{\alpha'\cup\{i,j\}}) &\det(Y_{\alpha'\cup\{i+t,j+t\}}) \notag \\ &\ \ \pm\ \det(Y_{\alpha'\cup\{i,j+t\}}) \det(Y_{\alpha'\cup\{i+t,j\}})\ =\ 0. \end{align} $$
$$ \begin{align} \det(Y_{\alpha'\cup\{i,i+t\}}) \det(Y_{\alpha'\cup\{j,j+t\}}) \ \pm\ \det(Y_{\alpha'\cup\{i,j\}}) &\det(Y_{\alpha'\cup\{i+t,j+t\}}) \notag \\ &\ \ \pm\ \det(Y_{\alpha'\cup\{i,j+t\}}) \det(Y_{\alpha'\cup\{i+t,j\}})\ =\ 0. \end{align} $$
This may be verified, for example, by passing to a dense open subset of matrices where the rows
![]() $\alpha '\cup \{i,i+t\}$
form a basis for
$\alpha '\cup \{i,i+t\}$
form a basis for
![]() $K^t$
, and multiplying on the right by an invertible matrix so as reduce to the case where these rows are the standard basis for
$K^t$
, and multiplying on the right by an invertible matrix so as reduce to the case where these rows are the standard basis for
![]() $K^t$
. The equality is now readily checked.
$K^t$
. The equality is now readily checked.
Since the other terms in (6.5.2) belong to P by the induction hypothesis, one obtains
Combining (6.5.1) and (6.5.3), bearing in mind that P is prime, it follows that
completing the proof that P contains each
![]() $t\times t$
minor of Y that involves the first row.
$t\times t$
minor of Y that involves the first row.
If P contains
![]() $y_{11}$
, Corollary 6.4 gives a contradiction. It follows that the prime ideal P must contain each size
$y_{11}$
, Corollary 6.4 gives a contradiction. It follows that the prime ideal P must contain each size
![]() $t-1$
minor of the last
$t-1$
minor of the last
![]() $t-1$
columns of Y.
$t-1$
columns of Y.
Let
![]() $Y'$
be the
$Y'$
be the
![]() $2(t-1)\times t$
submatrix obtained by deleting rows
$2(t-1)\times t$
submatrix obtained by deleting rows
![]() $1$
and
$1$
and
![]() $t+1$
of Y, and
$t+1$
of Y, and
![]() $\Omega '$
be the size
$\Omega '$
be the size
![]() $2t-2$
standard symplectic block matrix. Set
$2t-2$
standard symplectic block matrix. Set
![]() $I'$
to be the ideal of
$I'$
to be the ideal of
![]() $K[Y']$
generated by the entries of
$K[Y']$
generated by the entries of
![]() $Y^{\prime \operatorname {tr}}\Omega 'Y'$
along with the size
$Y^{\prime \operatorname {tr}}\Omega 'Y'$
along with the size
![]() $t-1$
minors of the last
$t-1$
minors of the last
![]() $t-1$
columns of
$t-1$
columns of
![]() $Y'$
. On an open dense subset of
$Y'$
. On an open dense subset of
![]() $V(I')$
, the last column belongs to the span of colums
$V(I')$
, the last column belongs to the span of colums
![]() $2,3,\dots ,t-1$
. Since the dimension of the Pfaffian nullcone corresponding to a
$2,3,\dots ,t-1$
. Since the dimension of the Pfaffian nullcone corresponding to a
![]() $2(t-1)\times (t-1)$
matrix is
$2(t-1)\times (t-1)$
matrix is
 $$\begin{align*}2(t-1)^2-\binom{t-1}{2} \end{align*}$$
$$\begin{align*}2(t-1)^2-\binom{t-1}{2} \end{align*}$$
by Corollary 6.4, it follows that
 $$\begin{align*}\dim V(I')\ \leqslant\ 2(t-1)^2-\binom{t-1}{2}+(t-2). \end{align*}$$
$$\begin{align*}\dim V(I')\ \leqslant\ 2(t-1)^2-\binom{t-1}{2}+(t-2). \end{align*}$$
Accounting for the matrix entry
![]() $y_{11}$
, this implies
$y_{11}$
, this implies
 $$\begin{align*}\dim V(P)\ \leqslant\ 2(t-1)^2-\binom{t-1}{2}+(t-2)+1\ =\ 2t^2-\binom{t}{2}-2t. \end{align*}$$
$$\begin{align*}\dim V(P)\ \leqslant\ 2(t-1)^2-\binom{t-1}{2}+(t-2)+1\ =\ 2t^2-\binom{t}{2}-2t. \end{align*}$$
But then
 $$\begin{align*}\dim V(P)\ <\ \dim V(I)\ =\ 2t^2-\binom{t}{2}-(2t-1), \end{align*}$$
$$\begin{align*}\dim V(P)\ <\ \dim V(I)\ =\ 2t^2-\binom{t}{2}-(2t-1), \end{align*}$$
where the equality uses, again, Corollary 6.4. This is not possible since P is a minimal prime of I.
The following proposition serves as a building block in the proof of Theorem 6.7; the primality of
![]() $I_a$
or
$I_a$
or
![]() $I^{\prime }_a$
does not follow immediately from the proof here, in view of the initial reduction step, though it will be obtained later as part of Theorem 6.7.
$I^{\prime }_a$
does not follow immediately from the proof here, in view of the initial reduction step, though it will be obtained later as part of Theorem 6.7.
Proposition 6.6. Let Y be a
![]() $2t\times n$
matrix of indeterminates over an algebraically closed field K, where
$2t\times n$
matrix of indeterminates over an algebraically closed field K, where
![]() $n\leqslant t$
. Set
$n\leqslant t$
. Set
and
. For a with
![]() $0\leqslant a\leqslant n-1$
, set
$0\leqslant a\leqslant n-1$
, set
Then the algebraic sets
![]() $V(I_a)$
and
$V(I_a)$
and
![]() $V(I^{\prime }_a)$
are irreducible.
$V(I^{\prime }_a)$
are irreducible.
Proof. Since the projection map onto the first n columns provides a surjection of algebraic sets, it suffices to prove each result in the case
![]() $n=t$
. Let
$n=t$
. Let
![]() $\Delta $
be the upper
$\Delta $
be the upper
![]() $t\times t$
minor of Y.
$t\times t$
minor of Y.
We first consider
![]() $I_a$
. In this case, Corollary 6.4 and Lemma 6.5—after permuting columns—show that
$I_a$
. In this case, Corollary 6.4 and Lemma 6.5—after permuting columns—show that
![]() $\Delta $
is a nonzerodivisor modulo
$\Delta $
is a nonzerodivisor modulo
![]() $I_a$
. Write Y as
$I_a$
. Write Y as
where
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
are size
$Y_2$
are size
![]() $t\times t$
. Since
$t\times t$
. Since
![]() $Y_1$
is invertible over the ring
$Y_1$
is invertible over the ring
![]() $S_{\Delta }$
, one has
$S_{\Delta }$
, one has
![]() $S_{\Delta }=K[Y_1,\ Z]_{\Delta }$
, where the entries of
$S_{\Delta }=K[Y_1,\ Z]_{\Delta }$
, where the entries of
![]() $Y_1$
and
$Y_1$
and
are algebraically independent over K. Note that

so the ideal
![]() $(Y^{\operatorname {tr}}\Omega Y)S_{\Delta }$
is generated by the entries of
$(Y^{\operatorname {tr}}\Omega Y)S_{\Delta }$
is generated by the entries of

It follows that
Since
![]() $I_a S_{\Delta }$
is generated by linear forms belonging to the polynomial ring
$I_a S_{\Delta }$
is generated by linear forms belonging to the polynomial ring
![]() $K[Y_1,\ Z]$
, it is a prime ideal of
$K[Y_1,\ Z]$
, it is a prime ideal of
![]() $S_{\Delta }$
; as
$S_{\Delta }$
; as
![]() $\Delta $
is a nonzerodivisor modulo
$\Delta $
is a nonzerodivisor modulo
![]() $I_a$
, there is a bijection between the minimal primes of
$I_a$
, there is a bijection between the minimal primes of
![]() $I_a$
and those of
$I_a$
and those of
![]() $I_a S_{\Delta }$
. It follows that
$I_a S_{\Delta }$
. It follows that
![]() $I_a$
has a unique minimal prime, so
$I_a$
has a unique minimal prime, so
![]() $V(I_a)$
is irreducible.
$V(I_a)$
is irreducible.
In the case of
![]() $I^{\prime }_a$
, working again with
$I^{\prime }_a$
, working again with
![]() $n=t$
, the ring
$n=t$
, the ring
![]() $S/I^{\prime }_a$
is a polynomial extension of
$S/I^{\prime }_a$
is a polynomial extension of
where
![]() $Y'$
is the
$Y'$
is the
![]() $(2t-2)\times t$
matrix of indeterminates obtained by deleting rows
$(2t-2)\times t$
matrix of indeterminates obtained by deleting rows
![]() $1$
and
$1$
and
![]() $t+1$
of Y, and
$t+1$
of Y, and
, and
![]() $\Omega '$
is the size
$\Omega '$
is the size
![]() $2t-2$
standard symplectic block matrix. It suffices to prove that the ring
$2t-2$
standard symplectic block matrix. It suffices to prove that the ring
![]() $S'/(Y^{\prime \operatorname {tr}}\Omega ' Y')$
has a unique minimal prime. Let
$S'/(Y^{\prime \operatorname {tr}}\Omega ' Y')$
has a unique minimal prime. Let
![]() $\Delta '$
be the upper left size
$\Delta '$
be the upper left size
![]() $t-1$
minor of
$t-1$
minor of
![]() $Y'$
. Lemma 6.5 implies that
$Y'$
. Lemma 6.5 implies that
![]() $\Delta '$
is a nonzerodivisor on
$\Delta '$
is a nonzerodivisor on
![]() $S'/(Y^{\prime \operatorname {tr}}\Omega ' Y')$
. Writing the matrix
$S'/(Y^{\prime \operatorname {tr}}\Omega ' Y')$
. Writing the matrix
![]() $Y'$
as
$Y'$
as
 $$\begin{align*}Y'\ =\ \begin{pmatrix}Y_1 & W_1\\ Y_2 & W_2\end{pmatrix}, \end{align*}$$
$$\begin{align*}Y'\ =\ \begin{pmatrix}Y_1 & W_1\\ Y_2 & W_2\end{pmatrix}, \end{align*}$$
where
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
are square matrices of size
$Y_2$
are square matrices of size
![]() $t-1$
, one has
$t-1$
, one has

The entries of
![]() $Y_1$
,
$Y_1$
,
![]() $W_1$
,
$W_1$
,
and
are algebraically independent over K, and
![]() $S^{\prime }_{\Delta '}$
may be viewed as
$S^{\prime }_{\Delta '}$
may be viewed as
![]() $K[Y_1,\ W_1,\ Z_1,\ Z_2]_{\Delta '}$
. Since
$K[Y_1,\ W_1,\ Z_1,\ Z_2]_{\Delta '}$
. Since

it follows that
and is hence a domain. In particular, it has a unique minimal prime.
6.4 Nullcones of Pfaffian rings are Cohen–Macaulay
We now set up the principal radical system needed to study the nullcones of Pfaffian rings. Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K, and set
$2t\times n$
matrix of indeterminates over a field K, and set
![]() $\mathfrak {P}$
to be the ideal generated by the entries of the matrix
$\mathfrak {P}$
to be the ideal generated by the entries of the matrix
![]() $Y^{\operatorname {tr}}\Omega Y$
. Let
$Y^{\operatorname {tr}}\Omega Y$
. Let
be a sequence of integers with
![]() $0\leqslant s_k\leqslant n$
for each k, and
$0\leqslant s_k\leqslant n$
for each k, and
![]() $s_m=n$
. Set
$s_m=n$
. Set
where
![]() $I_{k+1}\big (Y|_{s_k}\big )$
denotes the ideal generated by the size
$I_{k+1}\big (Y|_{s_k}\big )$
denotes the ideal generated by the size
![]() $k+1$
minors of the submatrix consisting of the first
$k+1$
minors of the submatrix consisting of the first
![]() $s_k$
columns of Y.
$s_k$
columns of Y.
In studying
![]() $K[Y]/I_{\sigma }$
, there is little loss of generality in assuming
$K[Y]/I_{\sigma }$
, there is little loss of generality in assuming
![]() $s_0=0$
since one may replace Y by a smaller matrix. In light of Lemma 6.2, one may also stipulate
$s_0=0$
since one may replace Y by a smaller matrix. In light of Lemma 6.2, one may also stipulate
![]() $m\leqslant t$
. Note that for positive integers j and k, one has
$m\leqslant t$
. Note that for positive integers j and k, one has
so one may restrict to
![]() $\sigma $
where the entries are strictly increasing. We say
$\sigma $
where the entries are strictly increasing. We say
![]() $\sigma $
is standard if
$\sigma $
is standard if
The ideal
![]() $\mathfrak {P}$
indeed equals
$\mathfrak {P}$
indeed equals
![]() $I_{\sigma }$
for a choice of
$I_{\sigma }$
for a choice of
![]() $\sigma $
that is standard: Take
$\sigma $
that is standard: Take
 $$\begin{align*}\sigma=\begin{cases} (0,1,2,\dots,n-1,n) & \text{ if }\ n\leqslant t,\\ (0,1,2,\dots,t-1,n) & \text{ if }\ n>t.\\ \end{cases} \end{align*}$$
$$\begin{align*}\sigma=\begin{cases} (0,1,2,\dots,n-1,n) & \text{ if }\ n\leqslant t,\\ (0,1,2,\dots,t-1,n) & \text{ if }\ n>t.\\ \end{cases} \end{align*}$$
For integers a with
![]() $0\leqslant a\leqslant n$
, set
$0\leqslant a\leqslant n$
, set
Note that if
is standard,
![]() $m=t$
and
$m=t$
and
![]() $s_{m-1}<a<s_m$
, then
$s_{m-1}<a<s_m$
, then
since rows
![]() $1$
and
$1$
and
![]() $t+1$
of
$t+1$
of
![]() $Y|_a$
are zero modulo
$Y|_a$
are zero modulo
![]() $J^{\prime }_a$
, so Lemma 6.2 gives
$J^{\prime }_a$
, so Lemma 6.2 gives
With this notation, we prove:
Theorem 6.7. Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K, and set
$2t\times n$
matrix of indeterminates over a field K, and set
![]() . Let
. Let
![]() be a sequence of integers with
be a sequence of integers with
![]() $0\leqslant s_k\leqslant n$
for each k, and
$0\leqslant s_k\leqslant n$
for each k, and
![]() $s_m=n$
. Let a be an integer with
$s_m=n$
. Let a be an integer with
![]() $0\leqslant a\leqslant n$
. Then:
$0\leqslant a\leqslant n$
. Then:
-
(1) If
 $\sigma $
is standard, then the algebraic sets
$\sigma $
is standard, then the algebraic sets
 $V(I_{\sigma }+J_{s_k})$
and
$V(I_{\sigma }+J_{s_k})$
and
 $V(I_{\sigma }+J^{\prime }_{s_k})$
are irreducible for each k with
$V(I_{\sigma }+J^{\prime }_{s_k})$
are irreducible for each k with
 $0\leqslant k\leqslant m$
.
$0\leqslant k\leqslant m$
. -
(2) The ideals
 $I_{\sigma }+J_a$
and
$I_{\sigma }+J_a$
and
 $I_{\sigma }+J^{\prime }_a$
are radical. If
$I_{\sigma }+J^{\prime }_a$
are radical. If
 $\sigma $
is standard, then the ideals
$\sigma $
is standard, then the ideals
 $I_{\sigma }+J_{s_k}$
and
$I_{\sigma }+J_{s_k}$
and
 $I_{\sigma }+J^{\prime }_{s_k}$
are prime for each k with
$I_{\sigma }+J^{\prime }_{s_k}$
are prime for each k with
 $0\leqslant k\leqslant m$
.
$0\leqslant k\leqslant m$
. -
(3) Suppose
 $\sigma $
is standard. If
$\sigma $
is standard. If
 $a=s_k$
for some k with
$a=s_k$
for some k with
 $0\leqslant k\leqslant m$
, then
$0\leqslant k\leqslant m$
, then
 $S/(I_{\sigma }+J_a)$
is a Cohen–Macaulay integral domain of dimension If
$S/(I_{\sigma }+J_a)$
is a Cohen–Macaulay integral domain of dimension If $$\begin{align*}m(2t+n-m)-k-\sum_{j=1}^{m-1}s_j. \end{align*}$$
$$\begin{align*}m(2t+n-m)-k-\sum_{j=1}^{m-1}s_j. \end{align*}$$
 $a=s_k$
for some k with
$a=s_k$
for some k with
 $0\leqslant k\leqslant m-1$
, then
$0\leqslant k\leqslant m-1$
, then
 $S/(I_{\sigma }+J^{\prime }_a)$
is a Cohen–Macaulay integral domain of dimension
$S/(I_{\sigma }+J^{\prime }_a)$
is a Cohen–Macaulay integral domain of dimension  $$\begin{align*}m(2t+n-m-1)-k-\sum_{j=1}^{m-1}s_j. \end{align*}$$
$$\begin{align*}m(2t+n-m-1)-k-\sum_{j=1}^{m-1}s_j. \end{align*}$$
Proof. It suffices to prove the assertions when K is algebraically closed; we indeed work under this assumption. We begin by proving (1) for the algebraic set
![]() $V(I_{\sigma }+J_{s_k})$
. Consider matrices B of size
$V(I_{\sigma }+J_{s_k})$
. Consider matrices B of size
![]() $2t\times m$
for which the columns span an isotropic subspace, and the first k entries of the first row are zero. Since
$2t\times m$
for which the columns span an isotropic subspace, and the first k entries of the first row are zero. Since
![]() $m\leqslant t$
, Proposition 6.6 implies that the matrices B are the points of an irreducible algebraic set that we denote
$m\leqslant t$
, Proposition 6.6 implies that the matrices B are the points of an irreducible algebraic set that we denote
![]() $\mathbb {V}_0$
.
$\mathbb {V}_0$
.
For
![]() $1\leqslant j\leqslant m$
, let
$1\leqslant j\leqslant m$
, let
![]() $C_j$
be a matrix of size
$C_j$
be a matrix of size
![]() $j\times (s_j-s_{j-1})$
, and set A to be the matrix
$j\times (s_j-s_{j-1})$
, and set A to be the matrix
where
![]() $\#$
denotes the concatenation of matrices. It is readily seen that A is an element of the algebraic set
$\#$
denotes the concatenation of matrices. It is readily seen that A is an element of the algebraic set
![]() $V(I_{\sigma }+J_{s_k})$
. The matrices
$V(I_{\sigma }+J_{s_k})$
. The matrices
![]() $C_1,\dots ,C_m$
may be regarded as the points of an affine space
$C_1,\dots ,C_m$
may be regarded as the points of an affine space
![]() $\mathbb {V}_1$
of dimension
$\mathbb {V}_1$
of dimension
 $$\begin{align*}\sum_{j=1}^m j(s_j-s_{j-1}), \end{align*}$$
$$\begin{align*}\sum_{j=1}^m j(s_j-s_{j-1}), \end{align*}$$
so that the construction (6.7.1) gives a map
Since the image of an irreducible algebraic set is irreducible, it suffices to verify that this map is surjective.
Let A be a matrix in the algebraic set
![]() $V(I_{\sigma }+J_{s_k})$
. For
$V(I_{\sigma }+J_{s_k})$
. For
![]() $1\leqslant j\leqslant m$
, let
$1\leqslant j\leqslant m$
, let
![]() $V_j$
denote the span of the columns of the truncated matrix
$V_j$
denote the span of the columns of the truncated matrix
![]() $A|_{s_j}$
. Consider the symplectic form (6.0.1) on
$A|_{s_j}$
. Consider the symplectic form (6.0.1) on
![]() $K^{2t}$
and the linear functional L that is projection to the first coordinate. By Lemma 6.1, there exist isotropic subspaces
$K^{2t}$
and the linear functional L that is projection to the first coordinate. By Lemma 6.1, there exist isotropic subspaces
such that
![]() $V_j\subseteq W_j$
for each j, and
$V_j\subseteq W_j$
for each j, and
![]() $W_j$
has rank j. Consider a size
$W_j$
has rank j. Consider a size
![]() $2t\times m$
matrix B such that
$2t\times m$
matrix B such that
![]() $B|_j$
spans
$B|_j$
spans
![]() $W_j$
for each j. Then the columns of
$W_j$
for each j. Then the columns of
![]() $A|_{s_j}$
belong to the column span of
$A|_{s_j}$
belong to the column span of
![]() $B|_j$
for each j, so there exist matrices
$B|_j$
for each j, so there exist matrices
![]() $C_j$
using which A may be obtained as in (6.7.1).
$C_j$
using which A may be obtained as in (6.7.1).
The proof that
![]() $V(I_{\sigma }+J^{\prime }_{s_k})$
is irreducible is similar: We consider instead matrices B of size
$V(I_{\sigma }+J^{\prime }_{s_k})$
is irreducible is similar: We consider instead matrices B of size
![]() $2t\times m$
, where the columns span an isotropic subspace, and for which the first row is zero, and the first k entries of row
$2t\times m$
, where the columns span an isotropic subspace, and for which the first row is zero, and the first k entries of row
![]() $t+1$
are zero. Proposition 6.6 implies that such matrices B are the points of an irreducible algebraic set. The linear functional used when applying Lemma 6.1 is now projection to the
$t+1$
are zero. Proposition 6.6 implies that such matrices B are the points of an irreducible algebraic set. The linear functional used when applying Lemma 6.1 is now projection to the
![]() $t+1$
coordinate.
$t+1$
coordinate.
The proof of (2) is via induction, assuming the result for matrices Y of smaller size, as well as for larger ideals in the family, and applying Lemma 5.1. Set I to be either
![]() $I_{\sigma }+J_a$
or
$I_{\sigma }+J_a$
or
![]() $I_{\sigma }+J^{\prime }_a$
. In the latter case, assume that
$I_{\sigma }+J^{\prime }_a$
. In the latter case, assume that
![]() $a<n$
since otherwise
$a<n$
since otherwise
![]() $K[Y]/(I_{\sigma }+J^{\prime }_a)$
arises from the smaller matrix obtained by deleting rows
$K[Y]/(I_{\sigma }+J^{\prime }_a)$
arises from the smaller matrix obtained by deleting rows
![]() $1$
and
$1$
and
![]() $t+1$
of Y. To apply Lemma 5.1, choose
$t+1$
of Y. To apply Lemma 5.1, choose

Specializing x to
![]() $1$
and each other entry to
$1$
and each other entry to
![]() $0$
, we obtain a matrix in
$0$
, we obtain a matrix in
![]() $V(I)\smallsetminus V(I+xS)$
, from which it follows that
$V(I)\smallsetminus V(I+xS)$
, from which it follows that
![]() $I+xS$
is a larger ideal in the family, and hence radical by the inductive hypothesis. If
$I+xS$
is a larger ideal in the family, and hence radical by the inductive hypothesis. If
![]() $a=s_k$
for some k, then
$a=s_k$
for some k, then
is prime by (1); since
![]() $x\notin P$
, Lemma 5.1 implies that
$x\notin P$
, Lemma 5.1 implies that
![]() $I=P$
, so I is prime.
$I=P$
, so I is prime.
In the remaining cases, there exists an integer k with
![]() $s_k<a<s_{k+1}$
and the element x is either
$s_k<a<s_{k+1}$
and the element x is either
![]() $y_{1,a+1}$
or
$y_{1,a+1}$
or
![]() $y_{t+1,a+1}$
. Set
$y_{t+1,a+1}$
. Set
and take P to be the prime ideal
![]() $I_{\sigma '}+J_a$
or
$I_{\sigma '}+J_a$
or
![]() $I_{\sigma '}+J^{\prime }_a$
in the respective cases; if
$I_{\sigma '}+J^{\prime }_a$
in the respective cases; if
![]() $k=0$
, then
$k=0$
, then
is not standard, but the primality follows nonetheless from the case of a matrix of size
![]() $2t\times (n-a)$
. The specialization used earlier shows that
$2t\times (n-a)$
. The specialization used earlier shows that
![]() $x\notin P$
. Using Lemma 5.3, one has
$x\notin P$
. Using Lemma 5.3, one has
and
so
![]() $xP\subseteq I$
in either case. It follows that I is radical by Lemma 5.1.
$xP\subseteq I$
in either case. It follows that I is radical by Lemma 5.1.
For (3), let V denote the algebraic set
![]() $V(I_{\sigma }+J_a)$
or
$V(I_{\sigma }+J_a)$
or
![]() $V(I_{\sigma }+J^{\prime }_a)$
. We first compute the dimension of V. In each case, V has an open subset U in which each matrix has the property that the submatrix consisting of the columns indexed
$V(I_{\sigma }+J^{\prime }_a)$
. We first compute the dimension of V. In each case, V has an open subset U in which each matrix has the property that the submatrix consisting of the columns indexed
has rank exactly m. Note that
![]() $m\leqslant t$
and that
$m\leqslant t$
and that
![]() $m\leqslant n$
. This open set U is nonempty, hence dense, for it contains the matrix in which the columns indexed (6.7.2) are, respectively, the standard basis vectors
$m\leqslant n$
. This open set U is nonempty, hence dense, for it contains the matrix in which the columns indexed (6.7.2) are, respectively, the standard basis vectors
and all other columns are zero. The order of the standard basis vectors above accounts for the possibility that V may be
![]() $V(I_{\sigma }+J^{\prime }_{n-1})$
, though it cannot be
$V(I_{\sigma }+J^{\prime }_{n-1})$
, though it cannot be
![]() $V(I_{\sigma }+J^{\prime }_n)$
, given our hypotheses. It suffices to compute the dimension of U.
$V(I_{\sigma }+J^{\prime }_n)$
, given our hypotheses. It suffices to compute the dimension of U.
Given a matrix A in the open set U, let B denote the
![]() $2t \times m$
submatrix consisting of the columns indexed (6.7.2). For each j with
$2t \times m$
submatrix consisting of the columns indexed (6.7.2). For each j with
![]() $1\leqslant j\leqslant m$
, the submatrix
$1\leqslant j\leqslant m$
, the submatrix
![]() $D_j$
of A consisting of the columns indexed
$D_j$
of A consisting of the columns indexed
![]() $s_{j-1}+1,\dots ,s_j$
can be uniquely written as a linear combination of the columns of
$s_{j-1}+1,\dots ,s_j$
can be uniquely written as a linear combination of the columns of
![]() $B|_j$
. The coefficients needed comprise the columns of a size
$B|_j$
. The coefficients needed comprise the columns of a size
![]() $j\times (s_j-s_{j-1})$
matrix that we denote
$j\times (s_j-s_{j-1})$
matrix that we denote
![]() $C_j$
. The first column of
$C_j$
. The first column of
![]() $C_j$
is
$C_j$
is
while the other
![]() $j(s_j-s_{j-1}-1)$
entries are arbitrary scalars. In the case
$j(s_j-s_{j-1}-1)$
entries are arbitrary scalars. In the case
![]() $V(I_{\sigma }+J_a)$
, the matrices B vary in a space of dimension
$V(I_{\sigma }+J_a)$
, the matrices B vary in a space of dimension
 $$\begin{align*}2mt-\binom{m}{2}-k \end{align*}$$
$$\begin{align*}2mt-\binom{m}{2}-k \end{align*}$$
by Corollary 6.4, and it follows that U has dimension
 $$ \begin{align*} 2mt-\binom{m}{2}-k+1(s_1-s_0-1)+2(s_2-s_1-1)+\dots+m &(s_m-s_{m-1}-1) \\ &\qquad\quad =\ m(2t+n-m)-k-\sum_{j=1}^{m-1}s_j. \end{align*} $$
$$ \begin{align*} 2mt-\binom{m}{2}-k+1(s_1-s_0-1)+2(s_2-s_1-1)+\dots+m &(s_m-s_{m-1}-1) \\ &\qquad\quad =\ m(2t+n-m)-k-\sum_{j=1}^{m-1}s_j. \end{align*} $$
The dimension count for
![]() $V(I_{\sigma }+J^{\prime }_a)$
is similar, bearing in mind that in this case the matrices B vary in a space of dimension
$V(I_{\sigma }+J^{\prime }_a)$
is similar, bearing in mind that in this case the matrices B vary in a space of dimension
 $$\begin{align*}2mt-\binom{m}{2}-m-k. \end{align*}$$
$$\begin{align*}2mt-\binom{m}{2}-m-k. \end{align*}$$
The proof of the Cohen–Macaulay property is again via induction, assuming the result for matrices Y of smaller size, as well as for larger ideals in the family. Consider a prime of the form
![]() $I_{\sigma }+J_{s_k}$
, where
$I_{\sigma }+J_{s_k}$
, where
![]() $k\leqslant m-1$
. Since
$k\leqslant m-1$
. Since
![]() $y_{1,s_k+1}$
is a nonzerodivisor on
$y_{1,s_k+1}$
is a nonzerodivisor on
![]() $S/(I_{\sigma }+J_{s_k})$
, it suffices to prove that
$S/(I_{\sigma }+J_{s_k})$
, it suffices to prove that
is Cohen–Macaulay. If
![]() $s_k+1=s_{k+1}$
, then this is immediate from the inductive hypothesis. Else,
$s_k+1=s_{k+1}$
, then this is immediate from the inductive hypothesis. Else,
![]() $s_k+1<s_{k+1}$
, and we claim that
$s_k+1<s_{k+1}$
, and we claim that
![]() $I_{\sigma }+J_{s_k+1}$
has minimal primes
$I_{\sigma }+J_{s_k+1}$
has minimal primes
where
if
![]() $k=0$
, then
$k=0$
, then
![]() $\sigma '=(1,s_1,\dots ,s_m)$
is not standard, but
$\sigma '=(1,s_1,\dots ,s_m)$
is not standard, but
![]() $Q_2$
is prime by the case of a matrix of size
$Q_2$
is prime by the case of a matrix of size
![]() $2t\times (n-1)$
, and the dimension of
$2t\times (n-1)$
, and the dimension of
![]() $S/Q_2$
is readily computed. Since
$S/Q_2$
is readily computed. Since
![]() $I_{\sigma }+J_{s_k+1}$
is radical and contained in each
$I_{\sigma }+J_{s_k+1}$
is radical and contained in each
![]() $Q_i$
, it suffices to verify that
$Q_i$
, it suffices to verify that
This is straightforward since
for each b with
![]() $b\leqslant s_{k+1}$
by Lemma 5.3. By the inductive hypothesis, each
$b\leqslant s_{k+1}$
by Lemma 5.3. By the inductive hypothesis, each
![]() $Q_i$
is prime, defining a Cohen–Macaulay ring
$Q_i$
is prime, defining a Cohen–Macaulay ring
![]() $S/Q_i$
. Moreover,
$S/Q_i$
. Moreover,
is prime, and Lemma 5.2 applies since
 $$\begin{align*}\dim S/Q_1\ =\ \dim S/Q_2\ =\ m(2t+n-m)-k-1-\sum_{j=1}^{m-1}s_j\ =\ \dim S/(Q_1+Q_2)+1. \end{align*}$$
$$\begin{align*}\dim S/Q_1\ =\ \dim S/Q_2\ =\ m(2t+n-m)-k-1-\sum_{j=1}^{m-1}s_j\ =\ \dim S/(Q_1+Q_2)+1. \end{align*}$$
This concludes the argument that
is Cohen–Macaulay. The proof for a prime ideal of the form
![]() $I_{\sigma }+J^{\prime }_{s_k}$
, with
$I_{\sigma }+J^{\prime }_{s_k}$
, with
![]() $k\leqslant m-1$
, is similar.
$k\leqslant m-1$
, is similar.
The remaining case is a prime of the form
![]() $I_{\sigma }+J_n$
, where it suffices to prove that
$I_{\sigma }+J_n$
, where it suffices to prove that
is Cohen–Macaulay. This follows from the inductive hypothesis if
![]() $s_1=1$
. If
$s_1=1$
. If
![]() $s_1>1$
, we claim that
$s_1>1$
, we claim that
![]() $I_{\sigma }+J^{\prime }_1$
has minimal primes
$I_{\sigma }+J^{\prime }_1$
has minimal primes
For this, it suffices to verify that
![]() $Q_1Q_2\subseteq I_{\sigma }+J^{\prime }_1$
, which follows using
$Q_1Q_2\subseteq I_{\sigma }+J^{\prime }_1$
, which follows using
![]() $I_2(Y|_{s_1})\subseteq I_{\sigma }$
. Note that
$I_2(Y|_{s_1})\subseteq I_{\sigma }$
. Note that
![]() $S/Q_2$
and
$S/Q_2$
and
![]() $S/(Q_1+Q_2)$
are Cohen–Macaulay using the case of a smaller matrix, namely the matrix with the first column of Y deleted. Since
$S/(Q_1+Q_2)$
are Cohen–Macaulay using the case of a smaller matrix, namely the matrix with the first column of Y deleted. Since
 $$\begin{align*}\dim S/Q_1\ =\ \dim S/Q_2\ =\ m(2t+n-m-1)-1-\sum_{j=1}^{m-1}s_j\ =\ \dim S/(Q_1+Q_2)+1, \end{align*}$$
$$\begin{align*}\dim S/Q_1\ =\ \dim S/Q_2\ =\ m(2t+n-m-1)-1-\sum_{j=1}^{m-1}s_j\ =\ \dim S/(Q_1+Q_2)+1, \end{align*}$$
Lemma 5.2 allows us to conclude that
is Cohen–Macaulay.
We single out the main case of the previous theorem.
Theorem 6.8. Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K, where t and n are positive integers. Set
$2t\times n$
matrix of indeterminates over a field K, where t and n are positive integers. Set
![]() and
and
![]() , that is,
, that is,
![]() $\mathfrak {P}$
is the ideal generated by the entries of the matrix
$\mathfrak {P}$
is the ideal generated by the entries of the matrix
![]() $Y^{\operatorname {tr}}\Omega Y$
. Then
$Y^{\operatorname {tr}}\Omega Y$
. Then
![]() $S/\mathfrak {P}$
is a Cohen–Macaulay integral domain, and
$S/\mathfrak {P}$
is a Cohen–Macaulay integral domain, and
 $$\begin{align*}\dim S/\mathfrak{P}=\begin{cases} 2nt -\displaystyle{\binom{n}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t.\\ \end{cases} \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{P}=\begin{cases} 2nt -\displaystyle{\binom{n}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t.\\ \end{cases} \end{align*}$$
Proof. The formulae for the dimension coincide when n equals t or
![]() $t+1$
.
$t+1$
.
If
![]() $n\leqslant t$
, take
$n\leqslant t$
, take
![]() $\sigma =(0,1,2,\dots ,n-1,n)$
in Theorem 6.7.3, to obtain
$\sigma =(0,1,2,\dots ,n-1,n)$
in Theorem 6.7.3, to obtain
 $$\begin{align*}\dim S/\mathfrak{P}\ =\ n(2t+n-n)-(1+2+\dots+(n-1))\ =\ 2nt -\displaystyle{\binom{n}{2}}, \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{P}\ =\ n(2t+n-n)-(1+2+\dots+(n-1))\ =\ 2nt -\displaystyle{\binom{n}{2}}, \end{align*}$$
while if
![]() $n>t$
, take
$n>t$
, take
![]() $\sigma =(0,1,2,\dots ,t-1,n)$
, in which case the theorem gives
$\sigma =(0,1,2,\dots ,t-1,n)$
, in which case the theorem gives
 $$\begin{align*}\dim S/\mathfrak{P}\ =\ t(2t+n-t)-(1+2+\dots+t-1)\ =\ nt+\binom{t+1}{2}, \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{P}\ =\ t(2t+n-t)-(1+2+\dots+t-1)\ =\ nt+\binom{t+1}{2}, \end{align*}$$
completing the proof.
6.5 The purity of the embedding
Using this, we settle the
![]() $\operatorname {Sp}_{2t}(K)$
case of Theorem 1.1.
$\operatorname {Sp}_{2t}(K)$
case of Theorem 1.1.
Theorem 6.9. Let K be a field of positive characteristic. Fix positive integers n and t, and consider the inclusion
![]() $\varphi \colon K[Y^{\operatorname {tr}}\Omega Y]\longrightarrow K[Y]$
, where Y is a size
$\varphi \colon K[Y^{\operatorname {tr}}\Omega Y]\longrightarrow K[Y]$
, where Y is a size
![]() $2t\times n$
matrix of indeterminates. Then
$2t\times n$
matrix of indeterminates. Then
![]() $\varphi $
is pure if and only if
$\varphi $
is pure if and only if
![]() $n\leqslant t+1$
.
$n\leqslant t+1$
.
Proof. We claim that if the inclusion
![]() $\varphi \colon K[Y^{\operatorname {tr}}\Omega Y]\longrightarrow K[Y]$
is pure for fixed
$\varphi \colon K[Y^{\operatorname {tr}}\Omega Y]\longrightarrow K[Y]$
is pure for fixed
![]() $(n,t)$
, then purity holds as well for the inclusion of the K-algebras corresponding to
$(n,t)$
, then purity holds as well for the inclusion of the K-algebras corresponding to
![]() $(n',t)$
with
$(n',t)$
with
![]() $n'\leqslant n$
.
$n'\leqslant n$
.
Set
![]() , that is,
, that is,
![]() $Y'$
is the submatrix consisting of the first
$Y'$
is the submatrix consisting of the first
![]() $n'$
columns of Y. Consider the
$n'$
columns of Y. Consider the
![]() $\mathbb {N}$
-grading on
$\mathbb {N}$
-grading on
![]() $K[Y]$
, where the indeterminates from
$K[Y]$
, where the indeterminates from
![]() $Y'$
have degree
$Y'$
have degree
![]() $0$
, as does K, while the remaining indeterminates have degree
$0$
, as does K, while the remaining indeterminates have degree
![]() $1$
. Then
$1$
. Then
so
![]() $K[Y^{\prime \operatorname {tr}}\Omega Y']$
is a pure subring of
$K[Y^{\prime \operatorname {tr}}\Omega Y']$
is a pure subring of
![]() $K[Y]$
. It follows that the composition
$K[Y]$
. It follows that the composition
is pure as well, but then so is
![]() $K[Y^{\prime \operatorname {tr}}\Omega Y']\subseteq K[Y']$
.
$K[Y^{\prime \operatorname {tr}}\Omega Y']\subseteq K[Y']$
.
Set
![]() and
and
![]() . We next prove that
. We next prove that
![]() $\varphi $
is pure in the case
$\varphi $
is pure in the case
![]() $n=t+1$
. In this case, the ring R is regular, with the upper triangular entries of
$n=t+1$
. In this case, the ring R is regular, with the upper triangular entries of
![]() $Y^{\operatorname {tr}}\Omega Y$
forming a regular homogeneous system of parameters for R. As
$Y^{\operatorname {tr}}\Omega Y$
forming a regular homogeneous system of parameters for R. As
![]() $\dim R=\binom {n}{2}$
, it suffices by Theorem 2.1 to verify that the local cohomology module
$\dim R=\binom {n}{2}$
, it suffices by Theorem 2.1 to verify that the local cohomology module
is nonzero, where
![]() $\mathfrak {m}_R$
is the homogeneous maximal ideal of R. This is immediate from Theorem 6.8, which implies that
$\mathfrak {m}_R$
is the homogeneous maximal ideal of R. This is immediate from Theorem 6.8, which implies that
![]() $\mathfrak {m}_RS$
is an ideal of height
$\mathfrak {m}_RS$
is an ideal of height
![]() $\binom {n}{2}$
.
$\binom {n}{2}$
.
It remains to prove that
![]() $\varphi \colon R\longrightarrow S$
is not pure if
$\varphi \colon R\longrightarrow S$
is not pure if
![]() $n\geqslant t+2$
. By the reduction step, this comes down to the case
$n\geqslant t+2$
. By the reduction step, this comes down to the case
![]() $n=t+2$
. In this case, the ring
$n=t+2$
. In this case, the ring
![]() $R=K[Y^{\operatorname {tr}}\Omega Y]$
is again regular, of dimension
$R=K[Y^{\operatorname {tr}}\Omega Y]$
is again regular, of dimension
![]() $\binom {n}{2}$
, so by Theorem 2.1 it suffices to verify the vanishing of
$\binom {n}{2}$
, so by Theorem 2.1 it suffices to verify the vanishing of
![]() $H^{\binom {n}{2}}_{\mathfrak {m}_R}(S)$
. This follows from Theorem 6.8, which implies that
$H^{\binom {n}{2}}_{\mathfrak {m}_R}(S)$
. This follows from Theorem 6.8, which implies that
![]() $\mathfrak {m}_RS$
is an ideal of height
$\mathfrak {m}_RS$
is an ideal of height
 $$\begin{align*}\binom{n}{2}-1, \end{align*}$$
$$\begin{align*}\binom{n}{2}-1, \end{align*}$$
defining a Cohen–Macaulay ring
![]() $S/\mathfrak {m}_RS$
.
$S/\mathfrak {m}_RS$
.
7 Symmetric determinantal rings
Let X be an
![]() $n\times n$
symmetric matrix of indeterminates over a field K. For d a positive integer, the ring
$n\times n$
symmetric matrix of indeterminates over a field K. For d a positive integer, the ring
![]() $K[X]/I_{d+1}(X)$
is a Cohen–Macaulay normal domain of dimension
$K[X]/I_{d+1}(X)$
is a Cohen–Macaulay normal domain of dimension
 $$\begin{align*}\binom{n+1}{2} - \binom{n+1-d}{2}, \end{align*}$$
$$\begin{align*}\binom{n+1}{2} - \binom{n+1-d}{2}, \end{align*}$$
with the convention that
![]() $\binom {i}{j}=0$
if
$\binom {i}{j}=0$
if
![]() $i<j$
. The Cohen–Macaulay property is due to Kutz [Reference KutzKu]. The ring
$i<j$
. The Cohen–Macaulay property is due to Kutz [Reference KutzKu]. The ring
![]() $K[X]/I_{d+1}(X)$
is regular precisely if
$K[X]/I_{d+1}(X)$
is regular precisely if
![]() $n\leqslant d$
. When that is not the case, it has class group
$n\leqslant d$
. When that is not the case, it has class group
![]() $\mathbb {Z}/2$
, and is Gorenstein precisely if
$\mathbb {Z}/2$
, and is Gorenstein precisely if
![]() $n\equiv d + 1 {\,\operatorname {mod}\,} 2$
, [Reference GotoGo1, Reference GotoGo2].
$n\equiv d + 1 {\,\operatorname {mod}\,} 2$
, [Reference GotoGo1, Reference GotoGo2].
Let Y be a
![]() $d\times n$
matrix of indeterminates over a field K, and set
$d\times n$
matrix of indeterminates over a field K, and set
![]() . For X as above, the entrywise map of matrices
. For X as above, the entrywise map of matrices
induces a K-algebra isomorphism between
![]() $K[X]/I_{d+1}(X)$
and the subring
$K[X]/I_{d+1}(X)$
and the subring
![]() of S. Our goal in this section is to determine when the inclusion
of S. Our goal in this section is to determine when the inclusion
![]() $\varphi \colon R\longrightarrow S$
is pure. The orthogonal group
$\varphi \colon R\longrightarrow S$
is pure. The orthogonal group
![]() $\operatorname {O}_d(K)$
acts K-linearly on S via
$\operatorname {O}_d(K)$
acts K-linearly on S via
Since
![]() $M^{\operatorname {tr}} M$
equals the identity matrix for
$M^{\operatorname {tr}} M$
equals the identity matrix for
![]() $M\in \operatorname {O}_d(K)$
, the entries of
$M\in \operatorname {O}_d(K)$
, the entries of
![]() $Y^{\operatorname {tr}} Y$
are fixed by the group action. When the field K is infinite, of characteristic other than two, the invariant ring is precisely the subring R, see [Reference De Concini and ProcesiDP, §5]. When K is an infinite field of characteristic two, the invariant ring is
$Y^{\operatorname {tr}} Y$
are fixed by the group action. When the field K is infinite, of characteristic other than two, the invariant ring is precisely the subring R, see [Reference De Concini and ProcesiDP, §5]. When K is an infinite field of characteristic two, the invariant ring is
 $$\begin{align*}K[Y^{\operatorname{tr}} Y,\ \sum_{i=1}^d y_{ij}\ |\ 1\leqslant j\leqslant n], \end{align*}$$
$$\begin{align*}K[Y^{\operatorname{tr}} Y,\ \sum_{i=1}^d y_{ij}\ |\ 1\leqslant j\leqslant n], \end{align*}$$
as proved by Richman [Reference RichmanRi, §5]. This corrects an error in [Reference De Concini and ProcesiDP, pp. 353–354]. A presentation for the invariant ring in this case is provided by [Reference RichmanRi, Proposition 23].
If K has characteristic zero, then
![]() $\operatorname {O}_d(K)$
is linearly reductive, and it follows that the invariant ring R is a direct summand of S as an R-module; specifically,
$\operatorname {O}_d(K)$
is linearly reductive, and it follows that the invariant ring R is a direct summand of S as an R-module; specifically,
![]() $\varphi \colon R\longrightarrow S$
is pure when K has characteristic zero.
$\varphi \colon R\longrightarrow S$
is pure when K has characteristic zero.
7.1 The complete intersection property
We work out the analogue of Theorem 6.3 in the symmetric case. The ideal
![]() $(Y^{\operatorname {tr}} Y)$
has
$(Y^{\operatorname {tr}} Y)$
has
 $$\begin{align*}\binom{n+1}{2} \end{align*}$$
$$\begin{align*}\binom{n+1}{2} \end{align*}$$
minimal generators, coming from the distinct entries of the symmetric matrix
![]() $Y^{\operatorname {tr}} Y$
. We next prove that in the case
$Y^{\operatorname {tr}} Y$
. We next prove that in the case
![]() $n\leqslant (d+1)/2$
, these generators form a regular sequence, in other words, that
$n\leqslant (d+1)/2$
, these generators form a regular sequence, in other words, that
![]() $K[Y]/(Y^{\operatorname {tr}} Y)$
is a complete intersection ring. More generally:
$K[Y]/(Y^{\operatorname {tr}} Y)$
is a complete intersection ring. More generally:
Theorem 7.1. Let Y be a
![]() $d\times n$
matrix of indeterminates over a field K, where d and n are positive integers with
$d\times n$
matrix of indeterminates over a field K, where d and n are positive integers with
![]() $n\leqslant (d+1)/2$
. For
$n\leqslant (d+1)/2$
. For
![]() $k<n$
, let
$k<n$
, let
![]() $\mathfrak {a}$
be an ideal generated by k distinct entries from the first row. Then
$\mathfrak {a}$
be an ideal generated by k distinct entries from the first row. Then
 $$\begin{align*}\dim K[Y]/((Y^{\operatorname{tr}} Y)+\mathfrak{a})\ =\ dn-\binom{n+1}{2}-k, \end{align*}$$
$$\begin{align*}\dim K[Y]/((Y^{\operatorname{tr}} Y)+\mathfrak{a})\ =\ dn-\binom{n+1}{2}-k, \end{align*}$$
so, in particular,
![]() $K[Y]/((Y^{\operatorname {tr}} Y)+\mathfrak {a})$
is a complete intersection ring.
$K[Y]/((Y^{\operatorname {tr}} Y)+\mathfrak {a})$
is a complete intersection ring.
Proof. It suffices to prove the assertion after specializing the entries of the last
![]() $d-2n+1$
rows to zero. We may hence assume that
$d-2n+1$
rows to zero. We may hence assume that
![]() $n=(d+1)/2$
, that is, Y is size
$n=(d+1)/2$
, that is, Y is size
![]() $(2n-1)\times n$
.
$(2n-1)\times n$
.
First, suppose
![]() $k=0$
. Specialize the entries of Y to the corresponding entries of the matrix
$k=0$
. Specialize the entries of Y to the corresponding entries of the matrix

A routine—albeit tedious—count shows that this specialization entails killing
linear forms in
![]() $K[Y]$
. The ideal
$K[Y]$
. The ideal
![]() $(Y^{\operatorname {tr}} Y)$
has
$(Y^{\operatorname {tr}} Y)$
has
![]() $\binom {n+1}{2}$
minimal generators; since
$\binom {n+1}{2}$
minimal generators; since
 $$\begin{align*}\dim K[Y]\ =\ (2n-1)n\ =\ \binom{n+1}{2} + \frac{3}{2}n(n-1), \end{align*}$$
$$\begin{align*}\dim K[Y]\ =\ (2n-1)n\ =\ \binom{n+1}{2} + \frac{3}{2}n(n-1), \end{align*}$$
it suffices to verify that
has dimension zero. The
![]() $(1,n)$
entry of the matrix
$(1,n)$
entry of the matrix
![]() $\overline {Y}^{\operatorname {tr}}\overline {Y}$
is
$\overline {Y}^{\operatorname {tr}}\overline {Y}$
is
![]() $y_{n1}^2$
. Modulo
$y_{n1}^2$
. Modulo
![]() $y_{n1}$
, the
$y_{n1}$
, the
![]() $(2,n)$
entry is
$(2,n)$
entry is
![]() $y_{n+1,2}^2$
. Proceeding in this order, examining the last column of
$y_{n+1,2}^2$
. Proceeding in this order, examining the last column of
![]() $\overline {Y}^{\operatorname {tr}}\overline {Y}$
, we see that
$\overline {Y}^{\operatorname {tr}}\overline {Y}$
, we see that
are nilpotent in
![]() $K[\overline {Y}]/(\overline {Y}^{\operatorname {tr}}\overline {Y})$
. Modulo these elements, the last column and the last two rows of
$K[\overline {Y}]/(\overline {Y}^{\operatorname {tr}}\overline {Y})$
. Modulo these elements, the last column and the last two rows of
![]() $\overline {Y}$
are zero; proceed inductively.
$\overline {Y}$
are zero; proceed inductively.
Since the displayed specialization
![]() $\overline {Y}$
entails killing
$\overline {Y}$
entails killing
![]() $n-1$
entries from the first row, the case
$n-1$
entries from the first row, the case
![]() $0<k<n$
follows as well.
$0<k<n$
follows as well.
7.2 Nullcones of symmetric determinantal rings in characteristic two
Let Y be a matrix of indeterminates of size
![]() $d\times n$
, over a field K of characteristic two. The diagonal entries of the product matrix
$d\times n$
, over a field K of characteristic two. The diagonal entries of the product matrix
![]() $Y^{\operatorname {tr}} Y$
are
$Y^{\operatorname {tr}} Y$
are
Working in the ring
, the ideal
agrees with
![]() $(Y^{\operatorname {tr}} Y)S$
up to radical. We prove next that
$(Y^{\operatorname {tr}} Y)S$
up to radical. We prove next that
![]() $\mathfrak {S}$
is a prime ideal, defining a Cohen–Macaulay ring.
$\mathfrak {S}$
is a prime ideal, defining a Cohen–Macaulay ring.
Theorem 7.2. Let Y be a
![]() $d\times n$
matrix of indeterminates over a field K of characteristic two. Set
$d\times n$
matrix of indeterminates over a field K of characteristic two. Set
![]() and let
and let
![]() $\mathfrak {S}$
be as above. Write d as
$\mathfrak {S}$
be as above. Write d as
![]() $2t+1$
or
$2t+1$
or
![]() $2t+2$
, where t is a nonnegative integer. Then
$2t+2$
, where t is a nonnegative integer. Then
![]() $S/\mathfrak {S}$
is a Cohen–Macaulay integral domain, and
$S/\mathfrak {S}$
is a Cohen–Macaulay integral domain, and
 $$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} nd -\displaystyle{\binom{n+1}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if } d=2t+1 \text{ and }\ n\geqslant t,\\ n(t+1)+\displaystyle{\binom{t+1}{2}}& \text{if } d=2t+2 \text{ and }\ n\geqslant t. \end{cases} \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} nd -\displaystyle{\binom{n+1}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if } d=2t+1 \text{ and }\ n\geqslant t,\\ n(t+1)+\displaystyle{\binom{t+1}{2}}& \text{if } d=2t+2 \text{ and }\ n\geqslant t. \end{cases} \end{align*}$$
Proof. Let
![]() $\widetilde {Y}$
denote the upper
$\widetilde {Y}$
denote the upper
![]() $(d-1)\times n$
submatrix of Y. In the ring
$(d-1)\times n$
submatrix of Y. In the ring
![]() $S/\mathfrak {S}$
, one has
$S/\mathfrak {S}$
, one has
for each i, so
![]() $S/\mathfrak {S}$
is a homomorphic image of
$S/\mathfrak {S}$
is a homomorphic image of
![]() $K[\widetilde {Y}]$
. Making the substitutions using the equation displayed above, one sees that
$K[\widetilde {Y}]$
. Making the substitutions using the equation displayed above, one sees that
where
![]() $\Psi $
is the
$\Psi $
is the
![]() $(d-1)\times (d-1)$
alternating matrix
$(d-1)\times (d-1)$
alternating matrix
 $$\begin{align*}\Psi\ =\ \begin{pmatrix} 0 & 1 & 1 & \ldots & 1\\ 1 & 0 & 1 & \ldots & 1\\ 1 & 1 & 0 & & 1\\ \vdots & \vdots & & \ddots & \\ 1 & 1 & 1 & & 0 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\Psi\ =\ \begin{pmatrix} 0 & 1 & 1 & \ldots & 1\\ 1 & 0 & 1 & \ldots & 1\\ 1 & 1 & 0 & & 1\\ \vdots & \vdots & & \ddots & \\ 1 & 1 & 1 & & 0 \end{pmatrix}. \end{align*}$$
It is readily checked that
![]() $\Psi $
is invertible if
$\Psi $
is invertible if
![]() $d-1$
is even and that it has rank
$d-1$
is even and that it has rank
![]() $d-2$
otherwise. Since alternating matrices of the same size are cogredient as in (6.0.2) precisely if they have the same rank, if
$d-2$
otherwise. Since alternating matrices of the same size are cogredient as in (6.0.2) precisely if they have the same rank, if
![]() $d-1$
is even, then
$d-1$
is even, then
![]() $\Psi $
is cogredient to the standard symplectic block matrix
$\Psi $
is cogredient to the standard symplectic block matrix
![]() $\Omega $
, whereas, if
$\Omega $
, whereas, if
![]() $d-1$
is odd, then
$d-1$
is odd, then
![]() $\Psi $
is cogredient to
$\Psi $
is cogredient to
 $$\begin{align*}\begin{pmatrix} \Omega & 0\\ 0 & 0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} \Omega & 0\\ 0 & 0 \end{pmatrix}, \end{align*}$$
where
![]() $\Omega $
is size
$\Omega $
is size
![]() $d-2$
. This largely reduces the proof to an application of Theorem 6.8:
$d-2$
. This largely reduces the proof to an application of Theorem 6.8:
If
![]() $d=2t+1$
, the ring
$d=2t+1$
, the ring
![]() $S/\mathfrak {S}$
is isomorphic to
$S/\mathfrak {S}$
is isomorphic to
![]() $K[Z]/(Z^{\operatorname {tr}}\Omega Z)$
, where Z is a
$K[Z]/(Z^{\operatorname {tr}}\Omega Z)$
, where Z is a
![]() $2t\times n$
matrix of indeterminates. It follows that
$2t\times n$
matrix of indeterminates. It follows that
![]() $S/\mathfrak {S}$
is a Cohen–Macaulay integral domain, with
$S/\mathfrak {S}$
is a Cohen–Macaulay integral domain, with
 $$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} 2nt -\displaystyle{\binom{n}{2}} \ =\ nd -\displaystyle{\binom{n+1}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t. \end{cases} \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} 2nt -\displaystyle{\binom{n}{2}} \ =\ nd -\displaystyle{\binom{n+1}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t. \end{cases} \end{align*}$$
If
![]() $d=2t+2$
, then
$d=2t+2$
, then
![]() $S/\mathfrak {S}$
is isomorphic to a polynomial ring in n indeterminates over the ring
$S/\mathfrak {S}$
is isomorphic to a polynomial ring in n indeterminates over the ring
![]() $K[Z]/(Z^{\operatorname {tr}}\Omega Z)$
, where Z is a matrix of indeterminates of size
$K[Z]/(Z^{\operatorname {tr}}\Omega Z)$
, where Z is a matrix of indeterminates of size
![]() $2t\times n$
. It follows that
$2t\times n$
. It follows that
![]() $S/\mathfrak {S}$
is again a Cohen–Macaulay integral domain and that
$S/\mathfrak {S}$
is again a Cohen–Macaulay integral domain and that
 $$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} n+2nt-\displaystyle{\binom{n}{2}}\ =\ nd -\displaystyle{\binom{n+1}{2}}& \text{if }\ n\leqslant t+1,\\ n+nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t, \end{cases} \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} n+2nt-\displaystyle{\binom{n}{2}}\ =\ nd -\displaystyle{\binom{n+1}{2}}& \text{if }\ n\leqslant t+1,\\ n+nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t, \end{cases} \end{align*}$$
which completes the proof.
7.3 Nullcones of symmetric determinantal rings in characteristic other than two
Throughout this section, K will denote a field of characteristic other than two. We study the nullcone
![]() $K[Y]/(Y^{\operatorname {tr}} Y)$
, where Y is a matrix of indeterminates of size
$K[Y]/(Y^{\operatorname {tr}} Y)$
, where Y is a matrix of indeterminates of size
![]() $d\times n$
.
$d\times n$
.
Let V be the vector space
![]() $K^d$
with the standard basis. Let
$K^d$
with the standard basis. Let
![]() $B\colon V\times V\longrightarrow K$
be the symmetric bilinear form given by
$B\colon V\times V\longrightarrow K$
be the symmetric bilinear form given by
A subspace W of V is isotropic if
![]() $B(w_1,w_2)=0$
for all
$B(w_1,w_2)=0$
for all
![]() $w_i\in W$
. Since B is nondegenerate, an isotropic subspace W has rank at most
$w_i\in W$
. Since B is nondegenerate, an isotropic subspace W has rank at most
![]() $d/2$
, where V has rank d.
$d/2$
, where V has rank d.
Let M be a size
![]() $d\times n$
matrix over K with
$d\times n$
matrix over K with
![]() $M^{\operatorname {tr}} M = 0$
. Then the columns of M span an isotropic subspace, so
$M^{\operatorname {tr}} M = 0$
. Then the columns of M span an isotropic subspace, so
![]() $\operatorname {rank} M \leqslant d/2$
. Setting
$\operatorname {rank} M \leqslant d/2$
. Setting
, it follows that
![]() $I_{t+1}(M)=0$
. If K is algebraically closed, the Nullstellensatz implies that
$I_{t+1}(M)=0$
. If K is algebraically closed, the Nullstellensatz implies that
in the polynomial ring
![]() $K[Y]$
. In view of this, set
$K[Y]$
. In view of this, set
When the size of Y needs to be referenced, we use the notation
![]() $\mathfrak {S}_{d\times n}$
. When d is odd, we shall prove that the ideal
$\mathfrak {S}_{d\times n}$
. When d is odd, we shall prove that the ideal
![]() $\mathfrak {S}$
is prime and defines a Cohen–Macaulay ring
$\mathfrak {S}$
is prime and defines a Cohen–Macaulay ring
![]() $K[Y]/\mathfrak {S}$
. When d is even with
$K[Y]/\mathfrak {S}$
. When d is even with
![]() $d\leqslant 2n$
, it turns out that
$d\leqslant 2n$
, it turns out that
![]() $\mathfrak {S}$
has minimal primes
$\mathfrak {S}$
has minimal primes
![]() $\mathfrak {P}$
and
$\mathfrak {P}$
and
![]() $\mathfrak {Q}$
(see Definition 7.7) with the rings
$\mathfrak {Q}$
(see Definition 7.7) with the rings
![]() $K[Y]/\mathfrak {P}$
and
$K[Y]/\mathfrak {P}$
and
![]() $K[Y]/\mathfrak {Q}$
being Cohen–Macaulay. All of this will be proved using principal radical systems.
$K[Y]/\mathfrak {Q}$
being Cohen–Macaulay. All of this will be proved using principal radical systems.
The proof of the following is much the same as that of Lemma 6.1.
Lemma 7.3. Let K be a field. Consider the vector space
![]() $K^d$
equipped with a nondegenerate symmetric bilinear form. Let L be a nonzero linear functional on
$K^d$
equipped with a nondegenerate symmetric bilinear form. Let L be a nonzero linear functional on
![]() $K^d$
, and let
$K^d$
, and let
be isotropic subspaces of
![]() $K^d$
with
$K^d$
with
![]() $\operatorname {rank} V_j\leqslant j$
for each j, where
$\operatorname {rank} V_j\leqslant j$
for each j, where
![]() $m\leqslant \lfloor d/2\rfloor $
.
$m\leqslant \lfloor d/2\rfloor $
.
Suppose L vanishes on
![]() $V_k$
for some k. Then there exist isotropic subspaces
$V_k$
for some k. Then there exist isotropic subspaces
such that, for each j, one has
![]() $V_j\subseteq W_j$
and
$V_j\subseteq W_j$
and
![]() $\operatorname {rank} W_j=j$
, and L vanishes on
$\operatorname {rank} W_j=j$
, and L vanishes on
![]() $W_k$
.
$W_k$
.
Remark 7.4. Let K be an algebraically closed field of characteristic other than two. The orthogonal group
![]() $\operatorname {O}_n(K)$
is the group of
$\operatorname {O}_n(K)$
is the group of
![]() $n\times n$
matrices M over K with
$n\times n$
matrices M over K with
![]() . It follows that
. It follows that
![]() $\operatorname {O}_n(K)$
is an algebraic group; it has two connected components, the special orthogonal group
$\operatorname {O}_n(K)$
is an algebraic group; it has two connected components, the special orthogonal group
![]() $\operatorname {SO}_n(K)$
consisting of elements with determinant
$\operatorname {SO}_n(K)$
consisting of elements with determinant
![]() $1$
and its complement consisting of orthogonal matrices of determinant
$1$
and its complement consisting of orthogonal matrices of determinant
![]() $-1$
.
$-1$
.
Let W be an
![]() $n\times n$
matrix of indeterminates over K, in which case
$n\times n$
matrix of indeterminates over K, in which case
![]() $\operatorname {O}_n(K)$
may be viewed as the algebraic set
$\operatorname {O}_n(K)$
may be viewed as the algebraic set
![]() . The ideal
. The ideal
![]() is radical in
is radical in
![]() $K[W]$
, minimally generated by
$K[W]$
, minimally generated by
![]() $\binom {n+1}{2}$
polynomials that form a regular sequence; see, for example, [Reference ProcesiPr, page 238]. Since
$\binom {n+1}{2}$
polynomials that form a regular sequence; see, for example, [Reference ProcesiPr, page 238]. Since
![]() $\operatorname {O}_n(K)$
is nonsingular, being an algebraic group, each irreducible component is nonsingular. By Serre’s criterion,
$\operatorname {O}_n(K)$
is nonsingular, being an algebraic group, each irreducible component is nonsingular. By Serre’s criterion,
![]() is a normal ring; it is a product of normal domains corresponding to the two connected components.
is a normal ring; it is a product of normal domains corresponding to the two connected components.
For an integer k with
![]() $k<n$
, let
$k<n$
, let
denote the submatrix consisting of the first k columns of W. A minimal generating set for the ideal
extends to one for the ideal
, so
is also a normal complete intersection ring. The map
given by truncating columns is surjective since each matrix in
can be extended to one in
![]() $\operatorname {SO}_n(K)$
. Since
$\operatorname {SO}_n(K)$
. Since
![]() $\operatorname {SO}_n(K)$
is irreducible, so is its image. It follows that
$\operatorname {SO}_n(K)$
is irreducible, so is its image. It follows that
is a normal domain.
Definition 7.5. Let
![]() $\alpha $
be a subset of
$\alpha $
be a subset of
![]() $\{1,\dots ,n\}$
, and
$\{1,\dots ,n\}$
, and
![]() $\alpha ^{\mathrm {c}}$
its complement. Set
$\alpha ^{\mathrm {c}}$
its complement. Set
![]() $\operatorname {sgn}(\alpha )$
to be the sign of the permutation that sends the n-tuple
$\operatorname {sgn}(\alpha )$
to be the sign of the permutation that sends the n-tuple
![]() $(1,\dots ,n)$
to the n-tuple
$(1,\dots ,n)$
to the n-tuple
![]() $(\alpha ,\alpha ^{\mathrm {c}})$
, where the entries of each of
$(\alpha ,\alpha ^{\mathrm {c}})$
, where the entries of each of
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{\mathrm {c}}$
are in ascending order.
$\alpha ^{\mathrm {c}}$
are in ascending order.
For a matrix M, a subset
![]() $\alpha $
of the row indices, and a subset
$\alpha $
of the row indices, and a subset
![]() $\beta $
of the column indices, set
$\beta $
of the column indices, set
![]() $M_{\alpha |\beta }$
to be the submatrix with rows
$M_{\alpha |\beta }$
to be the submatrix with rows
![]() $\alpha $
and columns
$\alpha $
and columns
![]() $\beta $
. The following lemma appears to be well known, but we include a proof based on [Reference JagyJa].
$\beta $
. The following lemma appears to be well known, but we include a proof based on [Reference JagyJa].
Lemma 7.6. Let
![]() $Q\in \operatorname {O}_n(K)$
. Let
$Q\in \operatorname {O}_n(K)$
. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be subsets of
$\beta $
be subsets of
![]() $\{1,\dots ,n\}$
of cardinality k, where
$\{1,\dots ,n\}$
of cardinality k, where
![]() $1\leqslant k \leqslant n-1$
. Then
$1\leqslant k \leqslant n-1$
. Then
Proof. First, consider the case
![]() $\alpha =\{1,\dots ,k\}=\beta $
. Let
$\alpha =\{1,\dots ,k\}=\beta $
. Let
 $$\begin{align*}Q\ =\ \begin{pmatrix} A & B\\ C & D \end{pmatrix}, \end{align*}$$
$$\begin{align*}Q\ =\ \begin{pmatrix} A & B\\ C & D \end{pmatrix}, \end{align*}$$
where A is a square matrix of size k, and D is a square matrix of size
![]() $n-k$
. Then
$n-k$
. Then

using which one has

Taking determinants gives
which is precisely the assertion of the lemma in this case.
For arbitrary
![]() $\alpha ,\beta $
, permute the rows of Q by sending the rows indexed
$\alpha ,\beta $
, permute the rows of Q by sending the rows indexed
![]() $(\alpha ,\alpha ^{\mathrm {c}})$
to the rows indexed
$(\alpha ,\alpha ^{\mathrm {c}})$
to the rows indexed
![]() $(1,\dots ,n)$
, and the columns indexed
$(1,\dots ,n)$
, and the columns indexed
![]() $(\beta ,\beta ^{\mathrm {c}})$
to the columns indexed
$(\beta ,\beta ^{\mathrm {c}})$
to the columns indexed
![]() $(1,\dots ,n)$
. This yields an orthogonal matrix with determinant
$(1,\dots ,n)$
. This yields an orthogonal matrix with determinant
![]() $\operatorname {sgn}(\alpha )\operatorname {sgn}(\beta )\det (Q)$
. The result now follows from the previous case.
$\operatorname {sgn}(\alpha )\operatorname {sgn}(\beta )\det (Q)$
. The result now follows from the previous case.
Definition 7.7. Let Y be a
![]() $2t \times n$
matrix of indeterminates over a field K of characteristic other than two, where
$2t \times n$
matrix of indeterminates over a field K of characteristic other than two, where
![]() $t\leqslant n$
. Assume that K contains an element i with
$t\leqslant n$
. Assume that K contains an element i with
![]() $i^2=-1$
.
$i^2=-1$
.
Set
![]() $\mathfrak {P}$
to be the ideal of
$\mathfrak {P}$
to be the ideal of
![]() $K[Y]$
generated by
$K[Y]$
generated by
![]() $\mathfrak {S}$
and the polynomials
$\mathfrak {S}$
and the polynomials
for all subsets
![]() $\alpha \subseteq \{1,\dots ,2t\}$
and
$\alpha \subseteq \{1,\dots ,2t\}$
and
![]() $\beta \subseteq \{1,\dots ,n\}$
of size t.
$\beta \subseteq \{1,\dots ,n\}$
of size t.
Similarly, set
![]() $\mathfrak {Q}$
to be the ideal generated by
$\mathfrak {Q}$
to be the ideal generated by
![]() $\mathfrak {S}$
and the polynomials
$\mathfrak {S}$
and the polynomials
for all
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
as before. We use
$\beta $
as before. We use
![]() $\mathfrak {P}_{2t\times n}$
and
$\mathfrak {P}_{2t\times n}$
and
![]() $\mathfrak {Q}_{2t\times n}$
when the size of Y needs clarification.
$\mathfrak {Q}_{2t\times n}$
when the size of Y needs clarification.
It is readily seen that
in
![]() $K[Y]$
, and that setting
$K[Y]$
, and that setting
![]() one has
one has
Lemma 7.8. Suppose M and Q are
![]() $n\times n$
matrices over a field K, where
$n\times n$
matrices over a field K, where
![]() $Q\in \operatorname {O}_n(K)$
. Let
$Q\in \operatorname {O}_n(K)$
. Let
![]() $\alpha $
be a size n subset of
$\alpha $
be a size n subset of
![]() $\{1,\dots ,2n\}$
, and
$\{1,\dots ,2n\}$
, and
![]() $\alpha ^{\mathrm {c}}$
its complement. Then
$\alpha ^{\mathrm {c}}$
its complement. Then
 $$\begin{align*}\det\left[\begin{pmatrix} M \\ -iQM \end{pmatrix}_{\alpha}\right]\ =\ i^n \operatorname{sgn}(\alpha)(\det Q)\det\left[\begin{pmatrix} M \\ -iQM \end{pmatrix}_{\alpha^{\mathrm{c}}}\right], \end{align*}$$
$$\begin{align*}\det\left[\begin{pmatrix} M \\ -iQM \end{pmatrix}_{\alpha}\right]\ =\ i^n \operatorname{sgn}(\alpha)(\det Q)\det\left[\begin{pmatrix} M \\ -iQM \end{pmatrix}_{\alpha^{\mathrm{c}}}\right], \end{align*}$$
where
![]() $(\phantom {M})_{\alpha }$
denotes the submatrix with rows
$(\phantom {M})_{\alpha }$
denotes the submatrix with rows
![]() $\alpha $
, and
$\alpha $
, and
![]() $\operatorname {sgn}(\alpha )$
is as in Definition 7.5.
$\operatorname {sgn}(\alpha )$
is as in Definition 7.5.
Proof. Using
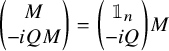
, it suffices to prove the result when M is the identity matrix. First, consider the case
and write

where
 $Q=\begin {pmatrix}A & B\\C & D\end {pmatrix}$
for square matrices A and D of size k and
$Q=\begin {pmatrix}A & B\\C & D\end {pmatrix}$
for square matrices A and D of size k and
![]() $n-k$
respectively. Then
$n-k$
respectively. Then

and

The required verification is now
which follows since
![]() $\operatorname {sgn}(\alpha )=(-1)^{n(n-k)}$
and
$\operatorname {sgn}(\alpha )=(-1)^{n(n-k)}$
and
![]() $\det Q\det D=\det A$
by Lemma 7.6.
$\det Q\det D=\det A$
by Lemma 7.6.
For an arbitrary
![]() $\alpha $
, permute rows and columns, keeping track of sign changes, so as to reduce to the case settled above.
$\alpha $
, permute rows and columns, keeping track of sign changes, so as to reduce to the case settled above.
The following proposition is the analogue of Proposition 6.6 in the symmetric case:
Proposition 7.9. Let d and n be positive integers with
![]() $n\leqslant d/2$
. Let Y be a
$n\leqslant d/2$
. Let Y be a
![]() $d\times n$
matrix of indeterminates over an algebraically closed field K of characteristic other than two. For a an integer with
$d\times n$
matrix of indeterminates over an algebraically closed field K of characteristic other than two. For a an integer with
![]() $0\leqslant a \leqslant n$
, set
$0\leqslant a \leqslant n$
, set
and
, where
.
-
(1) If
 $n<d/2$
and
$n<d/2$
and
 $a<n$
, then
$a<n$
, then
 $V(I)$
is irreducible.
$V(I)$
is irreducible. -
(2) If
 $n=d/2$
and
$n=d/2$
and
 $a<n$
, then
$a<n$
, then
 $V(I)$
has irreducible components
$V(I)$
has irreducible components
 $V(\mathfrak {P}+J_a)$
,
$V(\mathfrak {P}+J_a)$
,
 $V(\mathfrak {Q}+J_a)$
.
$V(\mathfrak {Q}+J_a)$
.
Proof. Let
![]() $\Delta $
be the upper
$\Delta $
be the upper
![]() $n\times n$
minor of Y. We claim that
$n\times n$
minor of Y. We claim that
![]() $\Delta $
is a nonzerodivisor on
$\Delta $
is a nonzerodivisor on
![]() $S/I$
. Since
$S/I$
. Since
![]() $S/I$
is a complete intersection ring by Theorem 7.1, it suffices to show that
$S/I$
is a complete intersection ring by Theorem 7.1, it suffices to show that
![]() $\Delta $
does not belong to any minimal prime of I.
$\Delta $
does not belong to any minimal prime of I.
Let G be a copy of
![]() $\operatorname {SO}_{d-1}(K)$
, embedded in
$\operatorname {SO}_{d-1}(K)$
, embedded in
![]() $\operatorname {SO}_d(K)$
as
$\operatorname {SO}_d(K)$
as
 $$\begin{align*}\begin{pmatrix} 1 & 0\\ 0 & Q \end{pmatrix}, \qquad\text{ for }\ Q\in\operatorname{SO}_{d-1}(K). \end{align*}$$
$$\begin{align*}\begin{pmatrix} 1 & 0\\ 0 & Q \end{pmatrix}, \qquad\text{ for }\ Q\in\operatorname{SO}_{d-1}(K). \end{align*}$$
The action of G on S with
![]() $M\colon Y\longmapsto MY$
induces an action on
$M\colon Y\longmapsto MY$
induces an action on
![]() $S/I$
, and hence on the set of minimal primes of
$S/I$
, and hence on the set of minimal primes of
![]() $S/I$
. Since G is connected, this action must be trivial, that is, G stabilizes each minimal prime of
$S/I$
. Since G is connected, this action must be trivial, that is, G stabilizes each minimal prime of
![]() $S/I$
.
$S/I$
.
Up to sign changes, rows of Y other than the first row may be permuted using an element of G. It follows that under the action of G on S, each maximal minor of Y that involves the first row is in the orbit of
![]() $\Delta $
, so any minimal prime of I containing
$\Delta $
, so any minimal prime of I containing
![]() $\Delta $
also contains each maximal minor involving the first row. Said otherwise, if
$\Delta $
also contains each maximal minor involving the first row. Said otherwise, if
![]() $\Delta $
vanishes on an irreducible component of
$\Delta $
vanishes on an irreducible component of
![]() $V(I)$
, then so does each such minor.
$V(I)$
, then so does each such minor.
For a
![]() $d\times n$
matrix over K, if each maximal minor that involves the first row is zero, and some other maximal minor is nonzero, then the first row must be zero. Hence if
$d\times n$
matrix over K, if each maximal minor that involves the first row is zero, and some other maximal minor is nonzero, then the first row must be zero. Hence if
![]() $\Delta $
vanishes on some irreducible component of
$\Delta $
vanishes on some irreducible component of
![]() $V(I)$
, then either
$V(I)$
, then either
![]() $J_n$
or
$J_n$
or
![]() $I_n(Y)$
vanishes on that component. In other words, any minimal prime of I containing
$I_n(Y)$
vanishes on that component. In other words, any minimal prime of I containing
![]() $\Delta $
must contain either
$\Delta $
must contain either
![]() $J_n$
or each maximal minor of Y. Since
$J_n$
or each maximal minor of Y. Since
![]() $a<n$
, one has
$a<n$
, one has
 $$\begin{align*}\dim V(I)\ =\ dn-\binom{n+1}{2}-a\>\ \dim V(I + J_n)\ =\ (d-1)n-\binom{n+1}{2}, \end{align*}$$
$$\begin{align*}\dim V(I)\ =\ dn-\binom{n+1}{2}-a\>\ \dim V(I + J_n)\ =\ (d-1)n-\binom{n+1}{2}, \end{align*}$$
so no minimal prime of I contains
![]() $J_n$
. It follows that any minimal prime of I that contains
$J_n$
. It follows that any minimal prime of I that contains
![]() $\Delta $
also contains
$\Delta $
also contains
![]() $I_n(Y)$
.
$I_n(Y)$
.
Let
![]() $Y'$
be the submatrix consisting of the first
$Y'$
be the submatrix consisting of the first
![]() $n-1$
columns of Y, and consider the ideal
$n-1$
columns of Y, and consider the ideal
of
![]() $K[Y']$
. Viewing a point of
$K[Y']$
. Viewing a point of
![]() $V(I')$
as columns
$V(I')$
as columns
![]() $(v_1,\dots ,v_{n-1})$
, the image of the map
$(v_1,\dots ,v_{n-1})$
, the image of the map
 $$\begin{align*}V(I') \times K^{n-1}\qquad\qquad\ &\longrightarrow\ V(I+I_n(Y))\\ ((v_1,\dots,v_{n-1})\ \,,\ (c_1,\dots,c_{n-1}))\ &\longmapsto\ (v_1,\dots,v_{n-1},\sum c_iv_i) \end{align*}$$
$$\begin{align*}V(I') \times K^{n-1}\qquad\qquad\ &\longrightarrow\ V(I+I_n(Y))\\ ((v_1,\dots,v_{n-1})\ \,,\ (c_1,\dots,c_{n-1}))\ &\longmapsto\ (v_1,\dots,v_{n-1},\sum c_iv_i) \end{align*}$$
includes the open subset of
![]() $V(I+I_n(Y))$
where the first
$V(I+I_n(Y))$
where the first
![]() $n-1$
columns are linearly independent. Hence,
$n-1$
columns are linearly independent. Hence,
 $$\begin{align*}\dim V(I+I_n(Y))\ \leqslant\ \dim V(I')+(n-1)\ =\ d(n-1)-\binom{n}{2} - a +(n-1)\ <\ \dim V(I). \end{align*}$$
$$\begin{align*}\dim V(I+I_n(Y))\ \leqslant\ \dim V(I')+(n-1)\ =\ d(n-1)-\binom{n}{2} - a +(n-1)\ <\ \dim V(I). \end{align*}$$
It follows that a minimal prime of I cannot contain
![]() $I_n(Y)$
and hence that
$I_n(Y)$
and hence that
![]() $\Delta $
is not in any minimal prime of I. The completes the proof that
$\Delta $
is not in any minimal prime of I. The completes the proof that
![]() $\Delta $
is a nonzerodivisor on
$\Delta $
is a nonzerodivisor on
![]() $S/I$
. In light of this, there is a bijection between the minimal primes of
$S/I$
. In light of this, there is a bijection between the minimal primes of
![]() $S/I$
and those of
$S/I$
and those of
![]() $S_{\Delta }/I$
.
$S_{\Delta }/I$
.
Write the matrix Y as
![]() $\begin {pmatrix}Y_1\\ Y_2\end {pmatrix}$
, where
$\begin {pmatrix}Y_1\\ Y_2\end {pmatrix}$
, where
![]() $Y_1$
is the upper
$Y_1$
is the upper
![]() $n\times n$
submatrix so that
$n\times n$
submatrix so that
![]() $\Delta =\det Y_1$
. Since
$\Delta =\det Y_1$
. Since
![]() $Y_1$
is an invertible matrix over
$Y_1$
is an invertible matrix over
![]() $S_{\Delta }$
, one has
$S_{\Delta }$
, one has
so the entries of
![]() $Y_2Y_1^{-1}$
, and hence of
$Y_2Y_1^{-1}$
, and hence of
, are algebraically independent over the fraction field of
![]() $K[Y_1]$
. Since
$K[Y_1]$
. Since

the ideal
![]() $(Y^{\operatorname {tr}} Y)S_{\Delta }$
agrees with the ideal generated by the entries of
$(Y^{\operatorname {tr}} Y)S_{\Delta }$
agrees with the ideal generated by the entries of

that is,
. As
![]() $J_a$
is generated by indeterminates from the matrix
$J_a$
is generated by indeterminates from the matrix
![]() $Y_1$
, the minimal primes of
$Y_1$
, the minimal primes of
![]() $S_{\Delta }/I$
correspond to those of
$S_{\Delta }/I$
correspond to those of
, and it suffices to prove the theorem in the case
![]() $a=0$
.
$a=0$
.
If
![]() $n<d/2$
, one has
$n<d/2$
, one has
![]() $n<d-n$
, so
$n<d-n$
, so
![]() is a domain by Remark 7.4, completing the proof of (1). When
is a domain by Remark 7.4, completing the proof of (1). When
![]() $n=d/2$
, the matrix Z is
$n=d/2$
, the matrix Z is
![]() $n\times n$
, so
$n\times n$
, so
![]() $V(Y^{\operatorname {tr}} Y)$
has two irreducible components corresponding to the two components of
$V(Y^{\operatorname {tr}} Y)$
has two irreducible components corresponding to the two components of
![]() , though it remains to verify that these are precisely
, though it remains to verify that these are precisely
![]() $V(\mathfrak {P})$
and
$V(\mathfrak {P})$
and
![]() $V(\mathfrak {Q})$
.
$V(\mathfrak {Q})$
.
The homomorphism
with
![]() $Y_2\longmapsto -iZY_1$
kills
$Y_2\longmapsto -iZY_1$
kills
![]() $(Y^{\operatorname {tr}} Y)$
, giving a homomorphism
$(Y^{\operatorname {tr}} Y)$
, giving a homomorphism
that is an isomorphism upon inverting
![]() $\Delta $
. Since
$\Delta $
. Since
![]() $\Delta $
is nonzerodivisor in
$\Delta $
is nonzerodivisor in
![]() $K[Y]/(Y^{\operatorname {tr}} Y)$
, the ideal
$K[Y]/(Y^{\operatorname {tr}} Y)$
, the ideal
![]() $(Y^{\operatorname {tr}} Y)$
is radical. The homomorphism above gives a map
$(Y^{\operatorname {tr}} Y)$
is radical. The homomorphism above gives a map
 $$ \begin{align*} \mathbb{A}^{\!n^2} \times \operatorname{O}_n(K)\ &\longrightarrow \ \ V(Y^{\operatorname{tr}} Y)\\ (A \ \,,\, Q)\kern-1pt\qquad &\longmapsto \ \begin{pmatrix}A\\ -iQA\end{pmatrix}. \end{align*} $$
$$ \begin{align*} \mathbb{A}^{\!n^2} \times \operatorname{O}_n(K)\ &\longrightarrow \ \ V(Y^{\operatorname{tr}} Y)\\ (A \ \,,\, Q)\kern-1pt\qquad &\longmapsto \ \begin{pmatrix}A\\ -iQA\end{pmatrix}. \end{align*} $$
Using Lemma 7.8, the matrix
 $\begin {pmatrix}A\\ -iQA\end {pmatrix}$
lies in the algebraic set
$\begin {pmatrix}A\\ -iQA\end {pmatrix}$
lies in the algebraic set
![]() $V(\mathfrak {P})$
if
$V(\mathfrak {P})$
if
![]() $Q\in \operatorname {SO}_n(K)$
, and in the algebraic set
$Q\in \operatorname {SO}_n(K)$
, and in the algebraic set
![]() $V(\mathfrak {Q})$
otherwise. Hence, the map displayed above restricts to maps
$V(\mathfrak {Q})$
otherwise. Hence, the map displayed above restricts to maps
Since
![]() $V(\mathfrak {P})\cup V(\mathfrak {Q})$
contains
$V(\mathfrak {P})\cup V(\mathfrak {Q})$
contains
![]() $V(Y^{\operatorname {tr}} Y)\smallsetminus V(\Delta )$
, we have
$V(Y^{\operatorname {tr}} Y)\smallsetminus V(\Delta )$
, we have
Using again that
![]() $\Delta $
is nonzerodivisor in
$\Delta $
is nonzerodivisor in
![]() $K[Y]/(Y^{\operatorname {tr}} Y)$
, it follows that
$K[Y]/(Y^{\operatorname {tr}} Y)$
, it follows that
![]() $\mathfrak {P}\cap \mathfrak {Q}=(Y^{\operatorname {tr}} Y)$
.
$\mathfrak {P}\cap \mathfrak {Q}=(Y^{\operatorname {tr}} Y)$
.
Corollary 7.10. Let Y be a
![]() $2t\times n$
matrix of indeterminates over an algebraically closed field of characteristic other than two. Then the algebraic set
$2t\times n$
matrix of indeterminates over an algebraically closed field of characteristic other than two. Then the algebraic set
![]() $V(Y^{\operatorname {tr}} Y)$
equals
$V(Y^{\operatorname {tr}} Y)$
equals
![]() $V(\mathfrak {P})\cup V(\mathfrak {Q})$
.
$V(\mathfrak {P})\cup V(\mathfrak {Q})$
.
Proof. One containment is immediate as the ideals
![]() $\mathfrak {P}$
and
$\mathfrak {P}$
and
![]() $\mathfrak {Q}$
contain
$\mathfrak {Q}$
contain
![]() $(Y^{\operatorname {tr}} Y)$
. Let M be a matrix in
$(Y^{\operatorname {tr}} Y)$
. Let M be a matrix in
![]() $V(Y^{\operatorname {tr}} Y)$
. If M has rank less than t, then it belongs to each of
$V(Y^{\operatorname {tr}} Y)$
. If M has rank less than t, then it belongs to each of
![]() $V(\mathfrak {P})$
and
$V(\mathfrak {P})$
and
![]() $V(\mathfrak {Q})$
. In the remaining case, M has rank exactly t; assume without loss of generality that the first t columns of M are linearly independent. Then the
$V(\mathfrak {Q})$
. In the remaining case, M has rank exactly t; assume without loss of generality that the first t columns of M are linearly independent. Then the
![]() $2t\times t$
submatrix
$2t\times t$
submatrix
![]() $M|_t$
belongs to
$M|_t$
belongs to
![]() $V(\mathfrak {P}|_t)$
or
$V(\mathfrak {P}|_t)$
or
![]() $V(\mathfrak {Q}|_t)$
by Proposition 7.9. Since the remaining columns of M are linear combinations of the columns of
$V(\mathfrak {Q}|_t)$
by Proposition 7.9. Since the remaining columns of M are linear combinations of the columns of
![]() $M|_t$
, it follows that M belongs to
$M|_t$
, it follows that M belongs to
![]() $V(\mathfrak {P})$
or
$V(\mathfrak {P})$
or
![]() $V(\mathfrak {Q})$
.
$V(\mathfrak {Q})$
.
We now set up the principal radical system needed to study the ideals
![]() $\mathfrak {P}$
,
$\mathfrak {P}$
,
![]() $\mathfrak {Q}$
and
$\mathfrak {Q}$
and
![]() $\mathfrak {S}$
. Let Y be a
$\mathfrak {S}$
. Let Y be a
![]() $d\times n$
matrix of indeterminates over K; recall that
$d\times n$
matrix of indeterminates over K; recall that
where
. Let
be a sequence of integers with
![]() $0\leqslant s_k\leqslant n$
for each k, and
$0\leqslant s_k\leqslant n$
for each k, and
![]() $s_m=n$
. Set
$s_m=n$
. Set
where, as earlier,
![]() $I_{k+1}\big (Y|_{s_k}\big )$
denotes the ideal generated by the size
$I_{k+1}\big (Y|_{s_k}\big )$
denotes the ideal generated by the size
![]() $k+1$
minors of the submatrix consisting of the first
$k+1$
minors of the submatrix consisting of the first
![]() $s_k$
columns of Y. If
$s_k$
columns of Y. If
![]() $d=2t$
, set
$d=2t$
, set
and
Note that if
![]() $m<t$
, then both
$m<t$
, then both
![]() $I^{\prime }_{\sigma }$
and
$I^{\prime }_{\sigma }$
and
![]() $I^{\prime \prime }_{\sigma }$
contain
$I^{\prime \prime }_{\sigma }$
contain
![]() $I_t(Y)$
, and hence equal
$I_t(Y)$
, and hence equal
![]() $I_{\sigma }$
.
$I_{\sigma }$
.
We say
![]() $\sigma $
is standard if
$\sigma $
is standard if
For integers a with
![]() $0\leqslant a\leqslant n$
, set
$0\leqslant a\leqslant n$
, set
Suppose
is standard,
![]() $d=2t$
,
$d=2t$
,
![]() $m=t$
and
$m=t$
and
![]() $s_{m-1}<a<s_m$
. Define
$s_{m-1}<a<s_m$
. Define
We claim that
For the first equality, it suffices to verify that
which holds by equation (7.7.2) since the first row of
![]() $Y|_a$
is zero modulo
$Y|_a$
is zero modulo
![]() $J_a$
. The second is similar.
$J_a$
. The second is similar.
With the notation as above, we prove:
Theorem 7.11. Let Y be a
![]() $d\times n$
matrix of indeterminates over an algebraically closed field K of characteristic other than two, and set
$d\times n$
matrix of indeterminates over an algebraically closed field K of characteristic other than two, and set
![]() . Let
. Let
![]() be a sequence of integers with
be a sequence of integers with
![]() $0\leqslant s_k\leqslant n$
for each k and
$0\leqslant s_k\leqslant n$
for each k and
![]() $s_m=n$
. Fix a with
$s_m=n$
. Fix a with
![]() $0\leqslant a\leqslant n$
.
$0\leqslant a\leqslant n$
.
-
(1) Suppose
 $\sigma $
is standard and
$\sigma $
is standard and
 $a=s_k$
, where
$a=s_k$
, where
 $0\leqslant k\leqslant m-1$
. If d is odd, then
$0\leqslant k\leqslant m-1$
. If d is odd, then
 $V(I_{\sigma } + J_a)$
is irreducible; if d is even, then
$V(I_{\sigma } + J_a)$
is irreducible; if d is even, then
 $V(I^{\prime }_{\sigma } + J_a)$
and
$V(I^{\prime }_{\sigma } + J_a)$
and
 $V(I^{\prime \prime }_{\sigma } + J_a)$
are irreducible.
$V(I^{\prime \prime }_{\sigma } + J_a)$
are irreducible. -
(2) The ideal
 $I_{\sigma }+J_a$
is radical. If d is even, the ideals
$I_{\sigma }+J_a$
is radical. If d is even, the ideals
 $I^{\prime }_{\sigma }+J_a$
and
$I^{\prime }_{\sigma }+J_a$
and
 $I^{\prime \prime }_{\sigma }+J_a$
are radical.
$I^{\prime \prime }_{\sigma }+J_a$
are radical. -
(3) Suppose
 $\sigma $
is standard and
$\sigma $
is standard and
 $a=s_k$
, where
$a=s_k$
, where
 $0\leqslant k\leqslant m-1$
. If d is odd, then
$0\leqslant k\leqslant m-1$
. If d is odd, then
 $I_{\sigma }+J_a$
defines a Cohen–Macaulay integral domain. If d is even,
$I_{\sigma }+J_a$
defines a Cohen–Macaulay integral domain. If d is even,
 $I^{\prime }_{\sigma } + J_a$
and
$I^{\prime }_{\sigma } + J_a$
and
 $I^{\prime \prime }_{\sigma } + J_a$
both define Cohen–Macaulay integral domains. In each case, the domain has dimension
$I^{\prime \prime }_{\sigma } + J_a$
both define Cohen–Macaulay integral domains. In each case, the domain has dimension  $$\begin{align*}m(d+n-m-1)-k-\sum_{j=1}^{m-1}s_j. \end{align*}$$
$$\begin{align*}m(d+n-m-1)-k-\sum_{j=1}^{m-1}s_j. \end{align*}$$
Proof. Let
![]() $\mathbb {V}$
denote one of the algebraic sets
$\mathbb {V}$
denote one of the algebraic sets
![]() $V(I_{\sigma }+J_{s_k})$
or
$V(I_{\sigma }+J_{s_k})$
or
![]() $V(I^{\prime }_{\sigma }+J_{s_k})$
or
$V(I^{\prime }_{\sigma }+J_{s_k})$
or
![]() $V(I^{\prime \prime }_{\sigma }+J_{s_k})$
under the hypotheses of (1). We first prove that
$V(I^{\prime \prime }_{\sigma }+J_{s_k})$
under the hypotheses of (1). We first prove that
![]() $\mathbb {V}$
is irreducible. Take
$\mathbb {V}$
is irreducible. Take
![]() $\mathbb {V}_0$
to be the set of
$\mathbb {V}_0$
to be the set of
![]() $d\times m$
matrices lying in either
$d\times m$
matrices lying in either
![]() $V(\mathfrak {S}_{d\times m})$
or
$V(\mathfrak {S}_{d\times m})$
or
![]() $V(\mathfrak {P}_{d\times m})$
or
$V(\mathfrak {P}_{d\times m})$
or
![]() $V(\mathfrak {Q}_{d\times m})$
, in the respective cases, with the additional condition that the first k entries of the first row are
$V(\mathfrak {Q}_{d\times m})$
, in the respective cases, with the additional condition that the first k entries of the first row are
![]() $0$
. Note that
$0$
. Note that
![]() $m\leqslant d/2$
and
$m\leqslant d/2$
and
![]() $k<m$
, so
$k<m$
, so
![]() $\mathbb {V}_0$
is irreducible by Proposition 7.9.
$\mathbb {V}_0$
is irreducible by Proposition 7.9.
Let B be an element of
![]() $\mathbb {V}_0$
. For
$\mathbb {V}_0$
. For
![]() $1\leqslant j\leqslant m$
, let
$1\leqslant j\leqslant m$
, let
![]() $C_j$
be a matrix of size
$C_j$
be a matrix of size
![]() $j\times (s_j-s_{j-1})$
and set A to be the matrix
$j\times (s_j-s_{j-1})$
and set A to be the matrix
where
![]() $\#$
denotes concatenation. It is readily seen that A is an element of the algebraic set
$\#$
denotes concatenation. It is readily seen that A is an element of the algebraic set
![]() $\mathbb {V}$
. The matrices
$\mathbb {V}$
. The matrices
![]() $C_1,\dots ,C_m$
may be regarded as the points of an affine space
$C_1,\dots ,C_m$
may be regarded as the points of an affine space
![]() $\mathbb {V}_1$
of dimension
$\mathbb {V}_1$
of dimension
 $$\begin{align*}\sum_{j=1}^m j(s_j-s_{j-1}) \end{align*}$$
$$\begin{align*}\sum_{j=1}^m j(s_j-s_{j-1}) \end{align*}$$
so that the construction (7.11.1) gives a map
![]() $\mathbb {V}_0\times \mathbb {V}_1\longrightarrow \mathbb {V}$
. Since the image of an irreducible algebraic set is irreducible, it suffices to verify that this map is surjective.
$\mathbb {V}_0\times \mathbb {V}_1\longrightarrow \mathbb {V}$
. Since the image of an irreducible algebraic set is irreducible, it suffices to verify that this map is surjective.
Let A be a matrix in the algebraic set
![]() $\mathbb {V}$
. For
$\mathbb {V}$
. For
![]() $1\leqslant j\leqslant m$
, let
$1\leqslant j\leqslant m$
, let
![]() $V_j$
denote the span of the columns of the truncated matrix
$V_j$
denote the span of the columns of the truncated matrix
![]() $A|_{s_j}$
. Consider the linear functional L that is projection to the first coordinate, and the symmetric bilinear form is as defined in (7.2.1). By Lemma 7.3, there exist isotropic subspaces
$A|_{s_j}$
. Consider the linear functional L that is projection to the first coordinate, and the symmetric bilinear form is as defined in (7.2.1). By Lemma 7.3, there exist isotropic subspaces
such that
![]() $V_j\subseteq W_j$
for each j, and
$V_j\subseteq W_j$
for each j, and
![]() $W_j$
has rank j. Consider a size
$W_j$
has rank j. Consider a size
![]() $d\times m$
matrix B such that
$d\times m$
matrix B such that
![]() $B|_j$
spans
$B|_j$
spans
![]() $W_j$
for each j. Then the columns of
$W_j$
for each j. Then the columns of
![]() $A|_{s_j}$
belong to the column span of
$A|_{s_j}$
belong to the column span of
![]() $B|_j$
for each j, so there exist matrices
$B|_j$
for each j, so there exist matrices
![]() $C_j$
using which A may be obtained as in (7.11.1). This concludes the proof of (1).
$C_j$
using which A may be obtained as in (7.11.1). This concludes the proof of (1).
Set
![]() $I^*_{\sigma }$
to be one of
$I^*_{\sigma }$
to be one of
![]() $I_{\sigma }, I^{\prime }_{\sigma }, I^{\prime \prime }_{\sigma }$
and
$I_{\sigma }, I^{\prime }_{\sigma }, I^{\prime \prime }_{\sigma }$
and
![]() . To show I is radical or prime, we assume the result for matrices Y of smaller size, as well as for larger ideals in the family, and apply Lemma 5.1. The three families are interlaced in the inductive process, since
. To show I is radical or prime, we assume the result for matrices Y of smaller size, as well as for larger ideals in the family, and apply Lemma 5.1. The three families are interlaced in the inductive process, since
using equation (7.7.2), and Corollary 7.10 gives
Assume
![]() $a<n$
, since otherwise
$a<n$
, since otherwise
![]() $K[Y]/I$
effectively involves a matrix of size
$K[Y]/I$
effectively involves a matrix of size
![]() $(d-1)\times n$
. In applying Lemma 5.1, set
$(d-1)\times n$
. In applying Lemma 5.1, set
Specializing Y such that
![]() $y_{1,a+1}\longmapsto 1$
, and
$y_{1,a+1}\longmapsto 1$
, and
![]() $y_{2,a+1}\longmapsto \pm i$
, and every other entry maps to
$y_{2,a+1}\longmapsto \pm i$
, and every other entry maps to
![]() $0$
, we obtain a matrix in
$0$
, we obtain a matrix in
![]() $V(I)\smallsetminus V(I+xS)$
. The choice of sign in
$V(I)\smallsetminus V(I+xS)$
. The choice of sign in
![]() $\pm i$
is relevant when
$\pm i$
is relevant when
![]() $d=2$
and depends on whether I contains
$d=2$
and depends on whether I contains
![]() $\mathfrak {P}$
or
$\mathfrak {P}$
or
![]() $\mathfrak {Q}$
. It follows that
$\mathfrak {Q}$
. It follows that
![]() $I+xS$
is a strictly larger ideal: In particular, for
$I+xS$
is a strictly larger ideal: In particular, for
![]() $a<n-1$
we have
$a<n-1$
we have
and for
![]() $a=n-1$
we have
$a=n-1$
we have
![]() $I+xS = I^*_{\sigma } + J_n$
, which effectively puts us in the case of a smaller matrix. Hence, in each case,
$I+xS = I^*_{\sigma } + J_n$
, which effectively puts us in the case of a smaller matrix. Hence, in each case,
![]() $I+xS$
is radical by the inductive hypothesis. If a is as in (1), the ideal
$I+xS$
is radical by the inductive hypothesis. If a is as in (1), the ideal
is prime. Since
![]() $x\notin P$
, Lemma 5.1 implies that
$x\notin P$
, Lemma 5.1 implies that
![]() $I=P$
, and hence that I is prime. Else, there exists an integer k with
$I=P$
, and hence that I is prime. Else, there exists an integer k with
![]() $s_k<a<s_{k+1}$
. Set
$s_k<a<s_{k+1}$
. Set
and take P to be the prime
![]() $I^*_{\sigma '}+J_a$
; if
$I^*_{\sigma '}+J_a$
; if
![]() $k=0$
, then
$k=0$
, then
![]() $\sigma '=(a,s_1,\dots ,s_m)$
is not standard, but the primality still holds from the case of a smaller matrix. The specialization used earlier shows that
$\sigma '=(a,s_1,\dots ,s_m)$
is not standard, but the primality still holds from the case of a smaller matrix. The specialization used earlier shows that
![]() $x\notin P$
. To conclude that I is radical by Lemma 5.1, it remains to verify that
$x\notin P$
. To conclude that I is radical by Lemma 5.1, it remains to verify that
![]() $xP\subseteq I$
. For this, note that
$xP\subseteq I$
. For this, note that
where the first inclusion is using Lemma 5.3.
For a as in (3), we next compute the dimension of the algebraic set
![]() . Consider the open subset U of
. Consider the open subset U of
![]() $\mathbb {V}$
in which each matrix has the property that the submatrix consisting of the columns indexed
$\mathbb {V}$
in which each matrix has the property that the submatrix consisting of the columns indexed
has rank exactly m. This open set U is nonempty hence dense, for it contains the matrix in which the columns indexed (7.11.2) are the first m columns of the matrix
 $$\begin{align*}\begin{pmatrix} 0 & 0 & \ldots & 0\\ 1 & 0 & \ldots & 0\\ i & 0 & \ldots & 0\\ 0 & 1 & & 0\\ 0 & i & & 0\\ \vdots & & & \\ 0 & 0 & & 1\\ 0 & 0 & & i \end{pmatrix} \quad\text{ or }\quad \begin{pmatrix} 0 & 0 & \ldots & 0 & 1\\ 0 & 0 & \ldots & 0 & i\\ 1 & 0 & \ldots & 0 & 0\\ i & 0 & \ldots & 0 & 0\\ 0 & 1 & & 0 & 0\\ 0 & i & & 0 & 0\\ \vdots & & & & \vdots\\ 0 & 0 & & 1 & 0\\ 0 & 0 & & i & 0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0 & 0 & \ldots & 0\\ 1 & 0 & \ldots & 0\\ i & 0 & \ldots & 0\\ 0 & 1 & & 0\\ 0 & i & & 0\\ \vdots & & & \\ 0 & 0 & & 1\\ 0 & 0 & & i \end{pmatrix} \quad\text{ or }\quad \begin{pmatrix} 0 & 0 & \ldots & 0 & 1\\ 0 & 0 & \ldots & 0 & i\\ 1 & 0 & \ldots & 0 & 0\\ i & 0 & \ldots & 0 & 0\\ 0 & 1 & & 0 & 0\\ 0 & i & & 0 & 0\\ \vdots & & & & \vdots\\ 0 & 0 & & 1 & 0\\ 0 & 0 & & i & 0 \end{pmatrix}, \end{align*}$$
depending on whether d is odd or even, respectively, and the remaining columns are zero.
It suffices to compute the dimension of U. Given a matrix A in the U, let B denote the
![]() $d\times m$
submatrix consisting of the columns indexed (7.11.2). For each j with
$d\times m$
submatrix consisting of the columns indexed (7.11.2). For each j with
![]() $1\leqslant j\leqslant m$
, the submatrix
$1\leqslant j\leqslant m$
, the submatrix
![]() $D_j$
of A consisting of the columns indexed
$D_j$
of A consisting of the columns indexed
![]() $s_{j-1}+1,\dots ,s_j$
can be uniquely written as a linear combination of the columns of
$s_{j-1}+1,\dots ,s_j$
can be uniquely written as a linear combination of the columns of
![]() $B|_j$
. The coefficients needed comprise the columns of a size
$B|_j$
. The coefficients needed comprise the columns of a size
![]() $j\times (s_j-s_{j-1})$
matrix that we denote
$j\times (s_j-s_{j-1})$
matrix that we denote
![]() $C_j$
. The first column of
$C_j$
. The first column of
![]() $C_j$
is
$C_j$
is
while the other
![]() $j(s_j-s_{j-1}-1)$
entries are arbitrary scalars. By Proposition 7.9, the matrices B vary in a space of dimension
$j(s_j-s_{j-1}-1)$
entries are arbitrary scalars. By Proposition 7.9, the matrices B vary in a space of dimension
 $$\begin{align*}dm-\binom{m+1}{2}-k, \end{align*}$$
$$\begin{align*}dm-\binom{m+1}{2}-k, \end{align*}$$
so U has dimension
 $$ \begin{align*} dm -\binom{m+1}{2}-k+1(s_1-s_0-1)+2(s_2-s_1-1)+\dots+m &(s_m-s_{m-1}-1) \\ &\quad =\ m(d+n-m-1)-k-\sum_{j=1}^{m-1}s_j. \end{align*} $$
$$ \begin{align*} dm -\binom{m+1}{2}-k+1(s_1-s_0-1)+2(s_2-s_1-1)+\dots+m &(s_m-s_{m-1}-1) \\ &\quad =\ m(d+n-m-1)-k-\sum_{j=1}^{m-1}s_j. \end{align*} $$
It follows that
![]() $V(I_{\sigma }+J_a)$
has the dimension as claimed. When d is even,
$V(I_{\sigma }+J_a)$
has the dimension as claimed. When d is even,
![]() $V(I^{\prime }_{\sigma } + J_a)$
and
$V(I^{\prime }_{\sigma } + J_a)$
and
![]() $V(I^{\prime \prime }_{\sigma } + J_a)$
also have the dimension displayed above.
$V(I^{\prime \prime }_{\sigma } + J_a)$
also have the dimension displayed above.
The proof of the Cohen–Macaulay property is again via induction, assuming the result for smaller matrices and for larger ideals in the family. Consider first a prime ideal of the form
![]() $I_{\sigma }+J_a$
, where
$I_{\sigma }+J_a$
, where
![]() , and d is odd. Since the element
, and d is odd. Since the element
![]() $y_{1,a+1}$
is a nonzerodivisor on
$y_{1,a+1}$
is a nonzerodivisor on
![]() $S/(I_{\sigma }+J_a)$
, it suffices to verify that
$S/(I_{\sigma }+J_a)$
, it suffices to verify that
is a Cohen–Macaulay ring. The proof of this, for d odd, is split into five cases:
Case (i): Suppose
![]() $k\leqslant m-2$
. If
$k\leqslant m-2$
. If
![]() $a+1=s_{k+1}$
, then
$a+1=s_{k+1}$
, then
![]() $S/(I_{\sigma }+J_{a+1})$
is Cohen–Macaulay by the inductive hypothesis. If
$S/(I_{\sigma }+J_{a+1})$
is Cohen–Macaulay by the inductive hypothesis. If
![]() $a+1<s_{k+1}$
, we claim that
$a+1<s_{k+1}$
, we claim that
![]() $I_{\sigma }+J_{a+1}$
is the intersection of the prime ideals
$I_{\sigma }+J_{a+1}$
is the intersection of the prime ideals
where
. If
![]() $k=0$
, then
$k=0$
, then
![]() $Q_2$
is prime by the case of a matrix of size
$Q_2$
is prime by the case of a matrix of size
![]() $d\times (n-1)$
. Since
$d\times (n-1)$
. Since
![]() $I_{\sigma }+J_{a+1}$
is radical and contained in each
$I_{\sigma }+J_{a+1}$
is radical and contained in each
![]() $Q_i$
, it suffices to verify that
$Q_i$
, it suffices to verify that
which comes down to
This is straightforward, since for each b with
![]() $b\leqslant s_{k+1}$
, one has
$b\leqslant s_{k+1}$
, one has
using Lemma 5.3. By the inductive hypothesis, each prime
![]() $Q_i$
defines a Cohen–Macaulay ring
$Q_i$
defines a Cohen–Macaulay ring
![]() $S/Q_i$
. Moreover,
$S/Q_i$
. Moreover,
is prime, and Lemma 5.2 applies since
 $$\begin{align*}\dim S/Q_1\ =\ \dim S/Q_2\ =\ m(d+n-m-1)-k-1-\sum_{j=1}^{m-1}s_j\ =\ \dim S/(Q_1+Q_2)+1. \end{align*}$$
$$\begin{align*}\dim S/Q_1\ =\ \dim S/Q_2\ =\ m(d+n-m-1)-k-1-\sum_{j=1}^{m-1}s_j\ =\ \dim S/(Q_1+Q_2)+1. \end{align*}$$
It follows that
is Cohen–Macaulay.
Case (ii): Next suppose
![]() $k=m-1$
, and
$k=m-1$
, and
![]() $m<\lfloor d/2\rfloor $
and
$m<\lfloor d/2\rfloor $
and
![]() $a+1=n$
. Set
$a+1=n$
. Set
![]() , and let
, and let
![]() $Y'$
denote the lower
$Y'$
denote the lower
![]() $2t\times n$
submatrix of Y. Since
$2t\times n$
submatrix of Y. Since
![]() $I_{\sigma }$
contains the ideal
$I_{\sigma }$
contains the ideal
![]() $I_{m+1}(Y)$
and hence
$I_{m+1}(Y)$
and hence
![]() $I_{t}(Y)$
, it follows that
$I_{t}(Y)$
, it follows that
![]() $I_{\sigma } + J_n$
contains
$I_{\sigma } + J_n$
contains
![]() $\mathfrak {P}_{2t\times n}(Y')$
and
$\mathfrak {P}_{2t\times n}(Y')$
and
![]() $\mathfrak {Q}_{2t\times n}(Y')$
by (7.7.1). But then
$\mathfrak {Q}_{2t\times n}(Y')$
by (7.7.1). But then
which is Cohen–Macaulay by the case of a smaller matrix.
Case (iii): Suppose
![]() $k=m-1$
, and
$k=m-1$
, and
![]() $m<\lfloor d/2\rfloor $
, and
$m<\lfloor d/2\rfloor $
, and
![]() $a+1<n$
. Then
$a+1<n$
. Then
![]() $I_{\sigma }+J_{a+1}$
is the intersection of the prime ideals
$I_{\sigma }+J_{a+1}$
is the intersection of the prime ideals
where
. The ring
![]() $S/Q_1$
is Cohen–Macaulay by the case of a smaller matrix, and the proof proceeds along the lines of Case (i).
$S/Q_1$
is Cohen–Macaulay by the case of a smaller matrix, and the proof proceeds along the lines of Case (i).
Case (iv): Suppose
![]() $k=m-1$
, and
$k=m-1$
, and
![]() $m=\lfloor d/2\rfloor $
, and
$m=\lfloor d/2\rfloor $
, and
![]() $a+1=n$
. Then
$a+1=n$
. Then
is the intersection of the prime ideals
where
and
, with
![]() $Y'$
the lower
$Y'$
the lower
![]() $2m\times n$
submatrix of Y. The rings
$2m\times n$
submatrix of Y. The rings
![]() $S/Q_1$
and
$S/Q_1$
and
![]() $S/Q_2$
are Cohen–Macaulay by the inductive hypothesis, of dimension
$S/Q_2$
are Cohen–Macaulay by the inductive hypothesis, of dimension
 $$\begin{align*}m(m+n-1)-\sum_{j=1}^{m-1}s_j. \end{align*}$$
$$\begin{align*}m(m+n-1)-\sum_{j=1}^{m-1}s_j. \end{align*}$$
Moreover,
where
, so
![]() $S/(Q_1+Q_2)$
is Cohen–Macaulay of dimension
$S/(Q_1+Q_2)$
is Cohen–Macaulay of dimension
 $$\begin{align*}(m-1)(m+n)-\sum_{j=1}^{m-2}s_j. \end{align*}$$
$$\begin{align*}(m-1)(m+n)-\sum_{j=1}^{m-2}s_j. \end{align*}$$
But then
so Lemma 5.2 implies that
![]() $S/(Q_1\cap Q_2)$
is Cohen–Macaulay.
$S/(Q_1\cap Q_2)$
is Cohen–Macaulay.
Case (v): Lastly, suppose
![]() $k=m-1$
, and
$k=m-1$
, and
![]() $m=\lfloor d/2\rfloor $
, and
$m=\lfloor d/2\rfloor $
, and
![]() $a+1<n$
. We claim that the ideal
$a+1<n$
. We claim that the ideal
![]() $I_{\sigma }+J_{a+1}$
is the intersection of three prime ideals
$I_{\sigma }+J_{a+1}$
is the intersection of three prime ideals
where
and
, with
![]() $Y'$
the lower
$Y'$
the lower
![]() $2m\times n$
submatrix of Y, and
$2m\times n$
submatrix of Y, and
Since
![]() $Q_1\cap Q_2=I_{\sigma }+J_n$
and
$Q_1\cap Q_2=I_{\sigma }+J_n$
and
![]() $I_{\sigma }+J_{a+1}$
is radical, it suffices to verify that
$I_{\sigma }+J_{a+1}$
is radical, it suffices to verify that
which is a now-routine application of Lemma 5.3.
Towards proving that
![]() $S/(Q_1\cap Q_2\cap Q_3)$
is Cohen–Macaulay, first note that
$S/(Q_1\cap Q_2\cap Q_3)$
is Cohen–Macaulay, first note that
so the dimension formula proved earlier gives
Lemma 5.2 implies that
![]() $S/(Q_1\cap Q_3)$
is Cohen–Macaulay. Next, we claim that
$S/(Q_1\cap Q_3)$
is Cohen–Macaulay. Next, we claim that
Assuming the claim, one has
so Lemma 5.2 shows that
![]() $S/(Q_1\cap Q_2\cap Q_3)$
is Cohen–Macaulay.
$S/(Q_1\cap Q_2\cap Q_3)$
is Cohen–Macaulay.
The verification of the claim reduces immediately to
which, in turn reduces to
Since the ideals on the right contain
![]() $J_{a+1}$
, it suffices to show that
$J_{a+1}$
, it suffices to show that
But
and
This concludes the proof that
![]() $S/(I_{\sigma }+J_a)$
is Cohen–Macaulay for
$S/(I_{\sigma }+J_a)$
is Cohen–Macaulay for
![]() $\sigma $
standard,
$\sigma $
standard,
![]() $a=s_k<n$
, and d odd. When d is even, the proof that the rings
$a=s_k<n$
, and d odd. When d is even, the proof that the rings
![]() $S/(I^{\prime }_{\sigma }+J_a)$
and
$S/(I^{\prime }_{\sigma }+J_a)$
and
![]() $S/(I^{\prime \prime }_{\sigma }+J_a)$
are Cohen–Macaulay resembles the proof in Case (i); one does not have to separately consider the cases where
$S/(I^{\prime \prime }_{\sigma }+J_a)$
are Cohen–Macaulay resembles the proof in Case (i); one does not have to separately consider the cases where
![]() $k=m-1$
.
$k=m-1$
.
We record the main consequences of Theorem 7.11.
Theorem 7.12. Let Y be a
![]() $(2t+1)\times n$
matrix of indeterminates over a field K of characteristic other than two. Set
$(2t+1)\times n$
matrix of indeterminates over a field K of characteristic other than two. Set
and
Then
![]() $S/\mathfrak {S}$
is a Cohen–Macaulay integral domain, with
$S/\mathfrak {S}$
is a Cohen–Macaulay integral domain, with
 $$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} 2nt -\displaystyle{\binom{n}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t. \end{cases} \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}=\begin{cases} 2nt -\displaystyle{\binom{n}{2}}& \text{if }\ n\leqslant t+1,\\ nt+\displaystyle{\binom{t+1}{2}}& \text{if }\ n\geqslant t. \end{cases} \end{align*}$$
Proof. If
![]() $n\leqslant t$
, take
$n\leqslant t$
, take
![]() $\sigma =(0,1,2,\dots ,n-1,n)$
in Theorem 7.12, so
$\sigma =(0,1,2,\dots ,n-1,n)$
in Theorem 7.12, so
![]() $m=n$
and
$m=n$
and
 $$\begin{align*}\dim S/\mathfrak{S}=n((2t+1)+n-n-1)-(1+2+\dots+(n-1))\ =\ 2nt -\displaystyle{\binom{n}{2}}. \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}=n((2t+1)+n-n-1)-(1+2+\dots+(n-1))\ =\ 2nt -\displaystyle{\binom{n}{2}}. \end{align*}$$
If
![]() $n>t$
, take
$n>t$
, take
![]() $\sigma =(0,1,2,\dots ,t-1,n)$
, in which case
$\sigma =(0,1,2,\dots ,t-1,n)$
, in which case
![]() $m=t$
, and the theorem gives
$m=t$
, and the theorem gives
 $$\begin{align*}\dim S/\mathfrak{S}=t((2t+1)+n-t-1)-(1+2+\dots+(t-1))\ =\ nt+\binom{t+1}{2}.\\[-42pt] \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}=t((2t+1)+n-t-1)-(1+2+\dots+(t-1))\ =\ nt+\binom{t+1}{2}.\\[-42pt] \end{align*}$$
In the case of a symmetric bilinear form of even rank, that is, when the number of rows of Y is even, we have the following theorem. Note that if
![]() $n\leqslant t-1$
, then
$n\leqslant t-1$
, then
![]() $\mathfrak {P}=\mathfrak {S}=\mathfrak {Q}$
.
$\mathfrak {P}=\mathfrak {S}=\mathfrak {Q}$
.
Theorem 7.13. Let Y be a
![]() $2t\times n$
matrix of indeterminates over a field K of characteristic other than two. Set
$2t\times n$
matrix of indeterminates over a field K of characteristic other than two. Set
![]() and
and
![]() , and let
, and let
![]() $\mathfrak {P}$
and
$\mathfrak {P}$
and
![]() $\mathfrak {Q}$
be as in Definition 7.7.
$\mathfrak {Q}$
be as in Definition 7.7.
If
![]() $n\leqslant t-1$
, then
$n\leqslant t-1$
, then
![]() $\mathfrak {P}=\mathfrak {S}=\mathfrak {Q}$
, and
$\mathfrak {P}=\mathfrak {S}=\mathfrak {Q}$
, and
![]() $S/\mathfrak {S}$
is a Cohen–Macaulay integral domain with
$S/\mathfrak {S}$
is a Cohen–Macaulay integral domain with
 $$\begin{align*}\dim S/\mathfrak{S}\ =\ 2nt -\displaystyle{\binom{n+1}{2}}. \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}\ =\ 2nt -\displaystyle{\binom{n+1}{2}}. \end{align*}$$
If
![]() $n\geqslant t$
, then
$n\geqslant t$
, then
![]() $S/\mathfrak {P}$
,
$S/\mathfrak {P}$
,
![]() $S/\mathfrak {Q}$
, and
$S/\mathfrak {Q}$
, and
![]() $S/(\mathfrak {P}+\mathfrak {Q})$
are Cohen–Macaulay integral domains with
$S/(\mathfrak {P}+\mathfrak {Q})$
are Cohen–Macaulay integral domains with
 $$\begin{align*}\dim S/\mathfrak{P}\ =\ nt+\displaystyle{\binom{t}{2}}\ =\ \dim S/\mathfrak{Q}, \quad\text{ and }\quad \dim S/(\mathfrak{P}+\mathfrak{Q})\ =\ nt-n-1+\displaystyle{\binom{t+1}{2}}. \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{P}\ =\ nt+\displaystyle{\binom{t}{2}}\ =\ \dim S/\mathfrak{Q}, \quad\text{ and }\quad \dim S/(\mathfrak{P}+\mathfrak{Q})\ =\ nt-n-1+\displaystyle{\binom{t+1}{2}}. \end{align*}$$
Proof. If
![]() $n\leqslant t-1$
, take
$n\leqslant t-1$
, take
![]() $\sigma =(0,1,2,\dots ,n-1,n)$
in Theorem 7.11, so
$\sigma =(0,1,2,\dots ,n-1,n)$
in Theorem 7.11, so
![]() $m=n$
and
$m=n$
and
 $$\begin{align*}\dim S/\mathfrak{S}=n(2t+n-n-1)-(1+2+\dots+(n-1))\ =\ 2nt -\displaystyle{\binom{n+1}{2}}. \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{S}=n(2t+n-n-1)-(1+2+\dots+(n-1))\ =\ 2nt -\displaystyle{\binom{n+1}{2}}. \end{align*}$$
If
![]() $n\geqslant t$
, take
$n\geqslant t$
, take
![]() $\sigma =(0,1,2,\dots ,t-1,n)$
, in which case
$\sigma =(0,1,2,\dots ,t-1,n)$
, in which case
![]() $m=t$
, and
$m=t$
, and
 $$\begin{align*}\dim S/\mathfrak{P}=t(2t+n-t-1)-(1+2+\dots+(t-1))\ =\ nt+\binom{t}{2}. \end{align*}$$
$$\begin{align*}\dim S/\mathfrak{P}=t(2t+n-t-1)-(1+2+\dots+(t-1))\ =\ nt+\binom{t}{2}. \end{align*}$$
The case of
![]() $S/\mathfrak {Q}$
is similar. Next, note that
$S/\mathfrak {Q}$
is similar. Next, note that
and that, if
![]() $n\geqslant t$
, taking
$n\geqslant t$
, taking
![]() $\sigma =(0,1,2,\dots ,t-2,n)$
in Theorem 7.11 gives
$\sigma =(0,1,2,\dots ,t-2,n)$
in Theorem 7.11 gives
 $$ \begin{align*} \dim S/(\mathfrak{P}+\mathfrak{Q})\ =\ (t-1)(2t+n-(t-1)-1)-(1+2+\dots+(t-2)) \ =\ nt-n-1+\displaystyle{\binom{t+1}{2}}, \end{align*} $$
$$ \begin{align*} \dim S/(\mathfrak{P}+\mathfrak{Q})\ =\ (t-1)(2t+n-(t-1)-1)-(1+2+\dots+(t-2)) \ =\ nt-n-1+\displaystyle{\binom{t+1}{2}}, \end{align*} $$
which completes the proof.
7.4 The purity of the embedding
Finally, we are in a position to settle the
![]() $\operatorname {O}_d(K)$
case of Theorem 1.1.
$\operatorname {O}_d(K)$
case of Theorem 1.1.
Theorem 7.14. Let K be a field of positive characteristic p. Fix positive integers d and n, and consider the inclusion
![]() $\varphi \colon K[Y^{\operatorname {tr}} Y]\longrightarrow K[Y]$
, where Y is a size
$\varphi \colon K[Y^{\operatorname {tr}} Y]\longrightarrow K[Y]$
, where Y is a size
![]() $d\times n$
matrix of indeterminates. Then
$d\times n$
matrix of indeterminates. Then
![]() $\varphi $
is pure if and only if
$\varphi $
is pure if and only if
-
(1)
 $d=1$
, or
$d=1$
, or -
(2)
 $d=2$
and p is odd, or
$d=2$
and p is odd, or -
(3)
 $p=2$
and
$p=2$
and
 $n\leqslant (d+1)/2$
, or
$n\leqslant (d+1)/2$
, or -
(4) p is odd and
 $n\leqslant (d+2)/2$
.
$n\leqslant (d+2)/2$
.
Proof. As with the other matrix families, if
![]() $\varphi \colon K[Y^{\operatorname {tr}} Y]\longrightarrow K[Y]$
is pure for fixed
$\varphi \colon K[Y^{\operatorname {tr}} Y]\longrightarrow K[Y]$
is pure for fixed
![]() $(n,d)$
, then purity holds as well for the inclusion of the K-algebras corresponding to
$(n,d)$
, then purity holds as well for the inclusion of the K-algebras corresponding to
![]() $(n',d)$
with
$(n',d)$
with
![]() $n'\leqslant n$
. Set
$n'\leqslant n$
. Set
![]() and
and
![]() , and note that
, and note that
![]() $\mathfrak {m}_RS=(Y^{\operatorname {tr}} Y)S$
.
$\mathfrak {m}_RS=(Y^{\operatorname {tr}} Y)S$
.
When
![]() $d=1$
, the ring R coincides with the Veronese subring
$d=1$
, the ring R coincides with the Veronese subring
![]() $S^{(2)}$
and is hence a pure subring of S.
$S^{(2)}$
and is hence a pure subring of S.
Next, consider the case where
![]() $d=2$
and p is odd. In proving the purity, one may enlarge K so as to assume that it is algebraically closed. The special orthogonal group
$d=2$
and p is odd. In proving the purity, one may enlarge K so as to assume that it is algebraically closed. The special orthogonal group
![]() $\operatorname {SO}_2(K)$
is then isomorphic to the torus
$\operatorname {SO}_2(K)$
is then isomorphic to the torus
![]() $K^\times $
, so
$K^\times $
, so
![]() $\operatorname {O}_2(K)$
is the extension of
$\operatorname {O}_2(K)$
is the extension of
![]() $\mathbb {Z}/2$
by a torus, hence linearly reductive; see also [Reference Jeffries and SinghJS, Remark 8.2]. It follows that purity holds in case (2).
$\mathbb {Z}/2$
by a torus, hence linearly reductive; see also [Reference Jeffries and SinghJS, Remark 8.2]. It follows that purity holds in case (2).
When
![]() $n\leqslant (d+1)/2$
, Theorem 7.1 implies that the ideal
$n\leqslant (d+1)/2$
, Theorem 7.1 implies that the ideal
![]() $\mathfrak {m}_RS$
is generated by a regular sequence of length
$\mathfrak {m}_RS$
is generated by a regular sequence of length
![]() $\binom {n+1}{2}$
. Since this is also the dimension of R, it follows that
$\binom {n+1}{2}$
. Since this is also the dimension of R, it follows that
![]() $\varphi $
is pure.
$\varphi $
is pure.
If
![]() $p=2$
, suppose first that d is odd, say
$p=2$
, suppose first that d is odd, say
![]() $d=2t+1$
. We need to verify that
$d=2t+1$
. We need to verify that
![]() $\varphi $
is not pure if
$\varphi $
is not pure if
![]() $n=t+2$
. This follows from Theorem 7.2 since
$n=t+2$
. This follows from Theorem 7.2 since
![]() $S/(\operatorname {rad}\,\mathfrak {m}_RS)$
is Cohen–Macaulay and
$S/(\operatorname {rad}\,\mathfrak {m}_RS)$
is Cohen–Macaulay and
 $$ \begin{align} \dim R - \operatorname{ht}\mathfrak{m}_RS\ =\ \binom{n+1}{2}-\left[dn-nt-\binom{t+1}{2}\right]\ =\ 1. \end{align} $$
$$ \begin{align} \dim R - \operatorname{ht}\mathfrak{m}_RS\ =\ \binom{n+1}{2}-\left[dn-nt-\binom{t+1}{2}\right]\ =\ 1. \end{align} $$
Similarly, when
![]() $d=2t+2$
, it suffices to verify that
$d=2t+2$
, it suffices to verify that
![]() $\varphi $
is not pure in the case
$\varphi $
is not pure in the case
![]() $n=t+2$
. Theorem 7.2 implies that
$n=t+2$
. Theorem 7.2 implies that
![]() $S/\!\operatorname {rad}\,\mathfrak {m}_RS$
is Cohen–Macaulay and that
$S/\!\operatorname {rad}\,\mathfrak {m}_RS$
is Cohen–Macaulay and that
 $$\begin{align*}\dim R - \operatorname{ht}\mathfrak{m}_RS\ =\ \binom{n+1}{2}-\left[dn-n(t+1)-\binom{t+1}{2}\right]\ =\ 1, \end{align*}$$
$$\begin{align*}\dim R - \operatorname{ht}\mathfrak{m}_RS\ =\ \binom{n+1}{2}-\left[dn-n(t+1)-\binom{t+1}{2}\right]\ =\ 1, \end{align*}$$
which completes the case
![]() $p=2$
. Specifically, the argument above is valid in the case
$p=2$
. Specifically, the argument above is valid in the case
![]() $d=2$
, where one has
$d=2$
, where one has
![]() $t=0$
.
$t=0$
.
In the remaining cases, p is an odd prime, and d is at least
![]() $3$
. When
$3$
. When
![]() $d=2t+1$
, we need to check that
$d=2t+1$
, we need to check that
![]() $\varphi $
is not pure in the case
$\varphi $
is not pure in the case
![]() $n=t+2$
. This is much the same as equation (7.14.1), with Theorem 7.12 providing the needful.
$n=t+2$
. This is much the same as equation (7.14.1), with Theorem 7.12 providing the needful.
Suppose
![]() $d=2t$
and
$d=2t$
and
![]() $t\geqslant 2$
. It suffices to verify that
$t\geqslant 2$
. It suffices to verify that
![]() $\varphi $
is pure in the case
$\varphi $
is pure in the case
![]() $n=t+1$
, and that it is not pure in the case
$n=t+1$
, and that it is not pure in the case
![]() $n=t+2$
. In either case, the ring R is regular, with
$n=t+2$
. In either case, the ring R is regular, with
![]() $\dim R=\binom {n+1}{2}$
, so the critical local cohomology module is
$\dim R=\binom {n+1}{2}$
, so the critical local cohomology module is
By Theorem 7.13, the ideals
![]() $\mathfrak {P}$
,
$\mathfrak {P}$
,
![]() $\mathfrak {Q}$
and
$\mathfrak {Q}$
and
![]() $\mathfrak {P}+\mathfrak {Q}$
, define Cohen–Macaulay rings, and
$\mathfrak {P}+\mathfrak {Q}$
, define Cohen–Macaulay rings, and
 $$\begin{align*}\operatorname{ht}\mathfrak{P} = nt-\binom{t}{2} = \operatorname{ht}\mathfrak{Q} \quad\text{ and }\quad \operatorname{ht}(\mathfrak{P} + \mathfrak{Q}) = nt+n+1-\binom{t+1}{2}. \end{align*}$$
$$\begin{align*}\operatorname{ht}\mathfrak{P} = nt-\binom{t}{2} = \operatorname{ht}\mathfrak{Q} \quad\text{ and }\quad \operatorname{ht}(\mathfrak{P} + \mathfrak{Q}) = nt+n+1-\binom{t+1}{2}. \end{align*}$$
When
![]() $n=t+1$
, the Mayer–Vietoris sequence
$n=t+1$
, the Mayer–Vietoris sequence
shows that
![]() $H^{\binom {n+1}{2}}_{\mathfrak {P}\cap \mathfrak {Q}}(S)$
is nonzero since the middle term is nonzero and the term to the right vanishes. When
$H^{\binom {n+1}{2}}_{\mathfrak {P}\cap \mathfrak {Q}}(S)$
is nonzero since the middle term is nonzero and the term to the right vanishes. When
![]() $n=t+2$
, the vanishing of
$n=t+2$
, the vanishing of
![]() $H^{\binom {n+1}{2}}_{\mathfrak {P}\cap \mathfrak {Q}}(S)$
follows from the vanishing of the outer terms in the exact sequence
$H^{\binom {n+1}{2}}_{\mathfrak {P}\cap \mathfrak {Q}}(S)$
follows from the vanishing of the outer terms in the exact sequence
In the case that the field K has characteristic two, it is also reasonable to ask when the inclusion
![]() $K[Y^{\operatorname {tr}} Y,\ \sum _i y_{ij}\ |\ 1\leqslant j\leqslant n] \subseteq K[Y]$
is pure; we record the answer.
$K[Y^{\operatorname {tr}} Y,\ \sum _i y_{ij}\ |\ 1\leqslant j\leqslant n] \subseteq K[Y]$
is pure; we record the answer.
Theorem 7.15. Let K be a field of characteristic two. Fix positive integers d and n, and consider a
![]() $d\times n$
matrix of indeterminates Y. Then the inclusion
$d\times n$
matrix of indeterminates Y. Then the inclusion
is pure if and only if
![]() $d=1$
or
$d=1$
or
![]() $n\leqslant (d+1)/2$
.
$n\leqslant (d+1)/2$
.
Proof. The ring
![]() is an integral extension of the symmetric determinantal ring
is an integral extension of the symmetric determinantal ring
![]() $K[Y^{\operatorname {tr}} Y]$
, and hence has the same dimension as
$K[Y^{\operatorname {tr}} Y]$
, and hence has the same dimension as
![]() $K[Y^{\operatorname {tr}} Y]$
. Also, when
$K[Y^{\operatorname {tr}} Y]$
. Also, when
![]() $K[Y^{\operatorname {tr}} Y]$
is regular, so is R. Set
$K[Y^{\operatorname {tr}} Y]$
is regular, so is R. Set
![]() . By Theorem 7.2, the ideal
. By Theorem 7.2, the ideal
defines a Cohen–Macaulay ring
![]() $S/\mathfrak {m}_RS$
.
$S/\mathfrak {m}_RS$
.
If
![]() $d=1$
, then
$d=1$
, then
![]() $R=S$
. Assume
$R=S$
. Assume
![]() $d\geqslant 2$
, and express d as
$d\geqslant 2$
, and express d as
![]() $2t+1$
or
$2t+1$
or
![]() $2t+2$
, for t an integer. Using the reduction as in the proof of Theorem 7.14, it suffices to verify that
$2t+2$
, for t an integer. Using the reduction as in the proof of Theorem 7.14, it suffices to verify that
![]() $R\subseteq S$
is pure in the case
$R\subseteq S$
is pure in the case
![]() $n=t+1$
and that it is not pure in the case
$n=t+1$
and that it is not pure in the case
![]() $n=t+2$
. In either case, the ring R is regular with
$n=t+2$
. In either case, the ring R is regular with
![]() $\dim R=\binom {n+1}{2}$
, and the critical local cohomology module is
$\dim R=\binom {n+1}{2}$
, and the critical local cohomology module is
![]() $H^{\dim R}_{\mathfrak {m}_RS}(S)$
. Using Theorem 7.2, this module is nonzero in the case
$H^{\dim R}_{\mathfrak {m}_RS}(S)$
. Using Theorem 7.2, this module is nonzero in the case
![]() $n=t+1$
since
$n=t+1$
since
![]() $\operatorname {ht}\mathfrak {m}_RS=\binom {n+1}{2}$
, whereas, if
$\operatorname {ht}\mathfrak {m}_RS=\binom {n+1}{2}$
, whereas, if
![]() $n=t+2$
, then
$n=t+2$
, then
 $$\begin{align*}\dim R - \operatorname{ht}\mathfrak{m}_RS\ =\ \binom{n+1}{2}-\left[n(t+1)-\binom{t+1}{2}\right]\ =\ 1, \end{align*}$$
$$\begin{align*}\dim R - \operatorname{ht}\mathfrak{m}_RS\ =\ \binom{n+1}{2}-\left[n(t+1)-\binom{t+1}{2}\right]\ =\ 1, \end{align*}$$
so
![]() $H^{\dim R}_{\mathfrak {m}_RS}(S)=0$
.
$H^{\dim R}_{\mathfrak {m}_RS}(S)=0$
.
Acknowledgements
Several of the results were verified using the computer algebra systems Macaulay2 [Reference Grayson and StillmanGS] and Magma [Reference Bosma, Cannon and PlayoustBCP]. The use of these is gratefully acknowledged. We are also indebted to the referee for a careful reading of the manuscript, and for helpful comments.
Competing interest
The authors have no competing interest to declare.
Funding statement
Hochster was supported by NSF grants DMS 1902116 and DMS 2200501, Jeffries by NSF CAREER Award DMS 2044833 and Pandey and Singh by NSF grants DMS 1801285 and DMS 2101671.