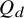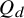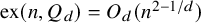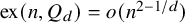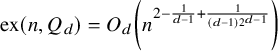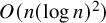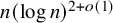1. Introduction
For a graph H and positive integer n, the Turán number (or extremal number)
![]() $\mathrm {ex}(n,H)$
is the maximum possible number of edges in an n-vertex graph which does not contain H as a subgraph. By a result of Turán [Reference Turán29], the exact value of this function is known when H is a complete graph. More generally, the function is well understood for graphs with chromatic number at least 3 by the celebrated Erdős–Stone–Simonovits theorem [Reference Erdős and Stone15, Reference Erdős and Simonovits13] which states that
$\mathrm {ex}(n,H)$
is the maximum possible number of edges in an n-vertex graph which does not contain H as a subgraph. By a result of Turán [Reference Turán29], the exact value of this function is known when H is a complete graph. More generally, the function is well understood for graphs with chromatic number at least 3 by the celebrated Erdős–Stone–Simonovits theorem [Reference Erdős and Stone15, Reference Erdős and Simonovits13] which states that
 $$ \begin{align*}\mathrm{ex}(n,H)=\left(1-\frac{1}{\chi(H)-1}+o(1)\right)\binom{n}{2}.\end{align*} $$
$$ \begin{align*}\mathrm{ex}(n,H)=\left(1-\frac{1}{\chi(H)-1}+o(1)\right)\binom{n}{2}.\end{align*} $$
However, for bipartite graphs H, the known bounds are much less accurate. It is known that for any bipartite graph H there is some
![]() $\varepsilon =\varepsilon (H)>0$
such that
$\varepsilon =\varepsilon (H)>0$
such that
![]() $\mathrm {ex}(n,H)=O(n^{2-\varepsilon })$
and it is conjectured that in fact there is some
$\mathrm {ex}(n,H)=O(n^{2-\varepsilon })$
and it is conjectured that in fact there is some
![]() $\alpha =\alpha (H)$
such that
$\alpha =\alpha (H)$
such that
![]() $\mathrm {ex}(n,H)=\Theta (n^{\alpha })$
. However, this is not known even for some very simple graphs such as the complete bipartite graph
$\mathrm {ex}(n,H)=\Theta (n^{\alpha })$
. However, this is not known even for some very simple graphs such as the complete bipartite graph
![]() $K_{4,4}$
, the even cycle
$K_{4,4}$
, the even cycle
![]() $C_8$
and the three-dimensional cube
$C_8$
and the three-dimensional cube
![]() $Q_3$
. In 1964, Erdős [Reference Erdős10] wrote that Turán had proposed the study of the extremal number of the five platonic solids (to be more precise, that of the graph of these polyhedra). The graph of the tetrahedron is
$Q_3$
. In 1964, Erdős [Reference Erdős10] wrote that Turán had proposed the study of the extremal number of the five platonic solids (to be more precise, that of the graph of these polyhedra). The graph of the tetrahedron is
![]() $K_4$
, so its extremal number is known by Turán’s theorem. Erdős and Simonovits determined the Turán number of the octahedron [Reference Erdős and Simonovits12], and Simonovits determined the extremal number of the dodecahedron [Reference Simonovits25] and the icosahedron [Reference Simonovits24]. However, the case of the cube is much more difficult as, unlike the other solids, its graph is bipartite.
$K_4$
, so its extremal number is known by Turán’s theorem. Erdős and Simonovits determined the Turán number of the octahedron [Reference Erdős and Simonovits12], and Simonovits determined the extremal number of the dodecahedron [Reference Simonovits25] and the icosahedron [Reference Simonovits24]. However, the case of the cube is much more difficult as, unlike the other solids, its graph is bipartite.
In the same paper from 1964, Erdős [Reference Erdős10] also mentions the problem of determining the Turán number of higher-dimensional cubes. The d-dimensional cube
![]() $Q_d$
is the graph whose vertex set is
$Q_d$
is the graph whose vertex set is
![]() $\{0,1\}^d$
and in which two vertices are joined by an edge if they differ in exactly one coordinate. In 1969, Erdős and Simonovits [Reference Erdős and Simonovits11] proved that
$\{0,1\}^d$
and in which two vertices are joined by an edge if they differ in exactly one coordinate. In 1969, Erdős and Simonovits [Reference Erdős and Simonovits11] proved that
![]() $\mathrm {ex}(n,Q_3)=O(n^{8/5})$
which is still the best known upper bound for this problem. The best known lower bound is
$\mathrm {ex}(n,Q_3)=O(n^{8/5})$
which is still the best known upper bound for this problem. The best known lower bound is
![]() $\mathrm {ex}(n,Q_3)=\Omega (n^{3/2})$
and follows from the observation that
$\mathrm {ex}(n,Q_3)=\Omega (n^{3/2})$
and follows from the observation that
![]() $Q_3$
contains a
$Q_3$
contains a
![]() $4$
-cycle. Any improvement on these long-standing bounds would be considered a major breakthrough.
$4$
-cycle. Any improvement on these long-standing bounds would be considered a major breakthrough.
The high-dimensional case seems to be even more challenging. It can be derived from a result of Füredi [Reference Füredi16] that if H is a bipartite graph with maximum degree at most d on one side, then
![]() $\mathrm {ex}(n,H)=O(n^{2-1/d})$
. Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov2] gave another proof of this estimate as one of the first applications of the celebrated dependent random choice method. Clearly, this implies in particular that
$\mathrm {ex}(n,H)=O(n^{2-1/d})$
. Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov2] gave another proof of this estimate as one of the first applications of the celebrated dependent random choice method. Clearly, this implies in particular that
![]() $\mathrm {ex}(n,Q_d)=O(n^{2-1/d})$
. A few years ago, Conlon and Lee made the following beautiful conjecture.
$\mathrm {ex}(n,Q_d)=O(n^{2-1/d})$
. A few years ago, Conlon and Lee made the following beautiful conjecture.
Conjecture 1.1 (Conlon–Lee [Reference Conlon and Lee7]).
Let H be a
![]() $K_{d,d}$
-free bipartite graph with maximum degree at most d on one side. Then
$K_{d,d}$
-free bipartite graph with maximum degree at most d on one side. Then
holds for some
![]() $\varepsilon =\varepsilon (H)>0$
.
$\varepsilon =\varepsilon (H)>0$
.
While Conjecture 1.1 is wide open, there are a few partial results towards it. Conlon and Lee [Reference Conlon and Lee7] proved the conjecture in the special case
![]() $d=2$
. Conlon, Janzer and Lee [Reference Conlon, Janzer and Lee5] showed that if H is a
$d=2$
. Conlon, Janzer and Lee [Reference Conlon, Janzer and Lee5] showed that if H is a
![]() $K_{2,2}$
-free bipartite graph with maximum degree d on one side, then
$K_{2,2}$
-free bipartite graph with maximum degree d on one side, then
![]() $\mathrm {ex}(n,H)=o(n^{2-1/d})$
. This was improved by Sudakov and Tomon who proved the following.
$\mathrm {ex}(n,H)=o(n^{2-1/d})$
. This was improved by Sudakov and Tomon who proved the following.
Theorem 1.2 (Sudakov–Tomon [Reference Sudakov and Tomon26]).
Let H be a
![]() $K_{d,d}$
-free bipartite graph with maximum degree at most d on one side. Then
$K_{d,d}$
-free bipartite graph with maximum degree at most d on one side. Then
Since for
![]() $d\geq 3$
,
$d\geq 3$
,
![]() $Q_d$
does not contain
$Q_d$
does not contain
![]() $K_{d,d}$
as a subgraph, Theorem 1.2 implies that
$K_{d,d}$
as a subgraph, Theorem 1.2 implies that
![]() $\mathrm {ex}(n,Q_d)=o(n^{2-1/d})$
. Liu asked the following question.
$\mathrm {ex}(n,Q_d)=o(n^{2-1/d})$
. Liu asked the following question.
Question 1.3 (Liu [Reference Liu23]).
Let
![]() $d\geq 3$
be an integer. Is it true that there exists some
$d\geq 3$
be an integer. Is it true that there exists some
![]() $\varepsilon =\varepsilon (d)>0$
such that
$\varepsilon =\varepsilon (d)>0$
such that
We answer this question affirmatively by proving the first power-improvement over the dependent random choice bound.
Theorem 1.4. For any integer
![]() $d\geq 3$
,
$d\geq 3$
,
 $$ \begin{align*}\mathrm{ex}(n,Q_d)=O_d\left(n^{2-\frac{1}{d-1}+\frac{1}{(d-1)2^{d-1}}}\right).\end{align*} $$
$$ \begin{align*}\mathrm{ex}(n,Q_d)=O_d\left(n^{2-\frac{1}{d-1}+\frac{1}{(d-1)2^{d-1}}}\right).\end{align*} $$
As a side note, we remark that an improvement for the Ramsey number of the hypercube was obtained very recently by Tikhomirov [Reference Tikhomirov27]. He showed that there is a positive constant c such that
![]() $r(Q_n)=O(2^{2n-cn})$
. This improved the previous best bound,
$r(Q_n)=O(2^{2n-cn})$
. This improved the previous best bound,
![]() $r(Q_n)=O(2^{2n})$
, proved by Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov4] which had been established using the dependent random choice method. In fact, in both of these results, the proofs show that the denser of the two colours contains
$r(Q_n)=O(2^{2n})$
, proved by Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov4] which had been established using the dependent random choice method. In fact, in both of these results, the proofs show that the denser of the two colours contains
![]() $Q_n$
. Our result can be viewed as an analogue of Tikhomirov’s result for the related Turán problem (the difference being that our forbidden hypercube has constant size, but the host graph is much sparser). However, we point out that our methods are completely different from Tikhomirov’s.
$Q_n$
. Our result can be viewed as an analogue of Tikhomirov’s result for the related Turán problem (the difference being that our forbidden hypercube has constant size, but the host graph is much sparser). However, we point out that our methods are completely different from Tikhomirov’s.
In 1984, about 15 years after their proof of the bound
![]() $\mathrm {ex}(n,Q_3)=O(n^{8/5})$
, Erdős and Simonovits [Reference Erdős and Simonovits14] showed that in fact any n-vertex graph with more than
$\mathrm {ex}(n,Q_3)=O(n^{8/5})$
, Erdős and Simonovits [Reference Erdős and Simonovits14] showed that in fact any n-vertex graph with more than
![]() $Cn^{8/5}$
edges has not just one, but at least as many copies (up to a constant factor) of
$Cn^{8/5}$
edges has not just one, but at least as many copies (up to a constant factor) of
![]() $Q_3$
as a random graph with the same edge density. This phenomenon is called supersaturation. We are able to get an analogous result for higher dimensions. We note that the previous proofs using dependent random choice or Theorem 1.2 did not give a supersaturation result even at those higher densities.
$Q_3$
as a random graph with the same edge density. This phenomenon is called supersaturation. We are able to get an analogous result for higher dimensions. We note that the previous proofs using dependent random choice or Theorem 1.2 did not give a supersaturation result even at those higher densities.
Theorem 1.5. For any integer
![]() $d\geq 3$
, there are positive constants
$d\geq 3$
, there are positive constants
![]() $c=c(d)$
and
$c=c(d)$
and
![]() $C=C(d)$
such that any n-vertex graph with edge density
$C=C(d)$
such that any n-vertex graph with edge density
![]() $p\geq Cn^{-\frac {1}{d-1}+\frac {1}{(d-1)2^{d-1}}}$
has at least
$p\geq Cn^{-\frac {1}{d-1}+\frac {1}{(d-1)2^{d-1}}}$
has at least
![]() $cn^{2^d}p^{d2^{d-1}}$
copies of
$cn^{2^d}p^{d2^{d-1}}$
copies of
![]() $Q_d$
.
$Q_d$
.
Here and below, we say that an n-vertex graph G has edge density p if it has
![]() $pn^2/2$
edges.
$pn^2/2$
edges.
Our methods can also be applied to prove Conjecture 1.1 for a larger class of graphs. We will discuss the precise description of all graphs for which the technique is applicable in the next section. For now, we just highlight another family of graphs (known as the bipartite Kneser graphs) for which we can verify Conjecture 1.1.
Definition 1.6. For
![]() $1\leq \ell <k/2$
, the bipartite Kneser graph
$1\leq \ell <k/2$
, the bipartite Kneser graph
![]() $H_{\ell ,k}$
is the bipartite graph whose parts are
$H_{\ell ,k}$
is the bipartite graph whose parts are
![]() $[k]^{(\ell )}$
and
$[k]^{(\ell )}$
and
![]() $[k]^{(k-\ell )}$
and in which
$[k]^{(k-\ell )}$
and in which
![]() $S\in [k]^{(\ell )}$
and
$S\in [k]^{(\ell )}$
and
![]() $T\in [k]^{(k-\ell )}$
are joined by an edge if
$T\in [k]^{(k-\ell )}$
are joined by an edge if
![]() $S\subset T$
. Note that
$S\subset T$
. Note that
![]() $H_{\ell ,k}$
is a regular graph.
$H_{\ell ,k}$
is a regular graph.
In the above definition and in what follows,
![]() $[k]^{(\ell )}$
stands for the family of subsets of size
$[k]^{(\ell )}$
stands for the family of subsets of size
![]() $\ell $
in
$\ell $
in
![]() $[k]$
.
$[k]$
.
Theorem 1.7. Let d be the degree of the vertices in
![]() $H_{\ell ,k}$
. Then there is some
$H_{\ell ,k}$
. Then there is some
![]() $\varepsilon =\varepsilon (\ell ,k)>0$
such that
$\varepsilon =\varepsilon (\ell ,k)>0$
such that
![]() $\mathrm {ex}(n,H_{\ell ,k})=O(n^{2-1/d-\varepsilon })$
.
$\mathrm {ex}(n,H_{\ell ,k})=O(n^{2-1/d-\varepsilon })$
.
We remark that with the same argument we could also prove a supersaturation result for
![]() $H_{\ell ,k}$
.
$H_{\ell ,k}$
.
1.1. Rainbow cycles
We will also use our methods to improve the best known upper bound for finding rainbow cycles. The study of rainbow Turán problems was initiated by Keevash, Mubayi, Sudakov and Verstraëte [Reference Keevash, Mubayi, Sudakov and Verstraëte20]. They asked how many edges one can have in a properly edge-coloured n-vertex graph without containing a rainbow cycle (i.e., a cycle in which all edges have a different colour). Let us write
![]() $f(n)$
for this number. They observed that if the edges of a hypercube are coloured according to the ‘direction’ of the edge, then the resulting properly edge-coloured graph does not have a rainbow cycle (and in fact every colour that appears in a given cycle must appear at least twice in it). Hence,
$f(n)$
for this number. They observed that if the edges of a hypercube are coloured according to the ‘direction’ of the edge, then the resulting properly edge-coloured graph does not have a rainbow cycle (and in fact every colour that appears in a given cycle must appear at least twice in it). Hence,
![]() $f(n)=\Omega (n\log n)$
. The first nontrivial upper bound was obtained by Das, Lee and Sudakov [Reference Das, Lee and Sudakov9], who showed that for any
$f(n)=\Omega (n\log n)$
. The first nontrivial upper bound was obtained by Das, Lee and Sudakov [Reference Das, Lee and Sudakov9], who showed that for any
![]() $\gamma>0$
and sufficiently large n, we have
$\gamma>0$
and sufficiently large n, we have
![]() $f(n)\leq n\exp ((\log n)^{1/2+\gamma })$
. Janzer [Reference Janzer18] proved that
$f(n)\leq n\exp ((\log n)^{1/2+\gamma })$
. Janzer [Reference Janzer18] proved that
![]() $f(n)=O(n(\log n)^4)$
. The current best bound is due to Tomon [Reference Tomon28] who showed that
$f(n)=O(n(\log n)^4)$
. The current best bound is due to Tomon [Reference Tomon28] who showed that
![]() $f(n)\leq n(\log n)^{2+o(1)}$
. We improve this further as follows.
$f(n)\leq n(\log n)^{2+o(1)}$
. We improve this further as follows.
Theorem 1.8. If n is sufficiently large, then any properly edge-coloured n-vertex graph with at least
![]() $8n(\log n)^2$
edges contains a rainbow cycle.
$8n(\log n)^2$
edges contains a rainbow cycle.
Keevash, Mubayi, Sudakov and Verstraëte [Reference Keevash, Mubayi, Sudakov and Verstraëte20] also proved that if G is a properly edge-coloured n-vertex graph with at least
![]() $n\log _2(n+3)-2n$
edges, then for some k it contains a cycle of length k which has more than
$n\log _2(n+3)-2n$
edges, then for some k it contains a cycle of length k which has more than
![]() $k/2$
different colours. Because of the hypercube construction, this is tight up to a constant factor. We significantly strengthen this result by finding a cycle which is almost rainbow.
$k/2$
different colours. Because of the hypercube construction, this is tight up to a constant factor. We significantly strengthen this result by finding a cycle which is almost rainbow.
Theorem 1.9. If n is sufficiently large,
![]() $0<\varepsilon <1/2$
and G is a properly edge-coloured n-vertex graph with at least
$0<\varepsilon <1/2$
and G is a properly edge-coloured n-vertex graph with at least
![]() $\frac {4}{\varepsilon }n\log n$
edges, then for some k it contains a cycle of length k with more than
$\frac {4}{\varepsilon }n\log n$
edges, then for some k it contains a cycle of length k with more than
![]() $(1-\varepsilon )k$
different colours.
$(1-\varepsilon )k$
different colours.
The rest of this paper is organized as follows. In the next section, we prove our results on ordinary Turán numbers and supersaturation. In Section 3, we prove our results on rainbow and almost rainbow cycles. We finish the paper with some concluding remarks in Section 4.
2. Ordinary Turán numbers
2.1. Illustration of our method and some preliminaries
In this subsection, we illustrate our method on the example of the three-dimensional cube and prove the following result (which is of course slightly weaker than the result of Erdős and Simonovits [Reference Erdős and Simonovits14] that obtains the same conclusion for graphs with edge density
![]() $p\geq Cn^{-2/5}$
).
$p\geq Cn^{-2/5}$
).
Proposition 2.1. There are positive constants c and C such that any n-vertex graph with edge density
![]() $p\geq Cn^{-3/8}$
contains at least
$p\geq Cn^{-3/8}$
contains at least
![]() $cn^8p^{12}$
copies of
$cn^8p^{12}$
copies of
![]() $Q_3$
.
$Q_3$
.
Given graphs H and G, a homomorphism from H to G is a map
![]() $V(H)\rightarrow V(G)$
which sends edges to edges. Often we call such a map a homomorphic copy of H in G. We write
$V(H)\rightarrow V(G)$
which sends edges to edges. Often we call such a map a homomorphic copy of H in G. We write
![]() $\hom (H,G)$
for the number of homomorphisms from H to G.
$\hom (H,G)$
for the number of homomorphisms from H to G.
The proof of Proposition 2.1 is via an inequality between the number of certain homomorphic copies of
![]() $Q_3$
in G. More precisely, we show that if a positive proportion of the homomorphic copies of
$Q_3$
in G. More precisely, we show that if a positive proportion of the homomorphic copies of
![]() $Q_3$
in G are not injective, then a positive proportion of the homomorphisms are actually very far from being injective: Namely, all four vertices in one part of the bipartition of
$Q_3$
in G are not injective, then a positive proportion of the homomorphisms are actually very far from being injective: Namely, all four vertices in one part of the bipartition of
![]() $Q_3$
are mapped to the same vertex. However, the latter is the same as a homomorphic copy of a star with four edges in G, and we can easily bound the number of such copies from above by
$Q_3$
are mapped to the same vertex. However, the latter is the same as a homomorphic copy of a star with four edges in G, and we can easily bound the number of such copies from above by
![]() $n\Delta (G)^4$
. Hence, as long as the number of homomorphic copies of
$n\Delta (G)^4$
. Hence, as long as the number of homomorphic copies of
![]() $Q_3$
in G is much bigger than
$Q_3$
in G is much bigger than
![]() $n\Delta (G)^4$
, it follows that most homomorphisms from
$n\Delta (G)^4$
, it follows that most homomorphisms from
![]() $Q_3$
to G are injective (i.e., genuine labelled copies of
$Q_3$
to G are injective (i.e., genuine labelled copies of
![]() $Q_3$
). It is well known that
$Q_3$
). It is well known that
![]() $Q_3$
satisfies Sidorenko’s conjecture; therefore, if G has edge density p, then it contains
$Q_3$
satisfies Sidorenko’s conjecture; therefore, if G has edge density p, then it contains
![]() $\Omega (n^8p^{12})$
homomorphic copies of
$\Omega (n^8p^{12})$
homomorphic copies of
![]() $Q_3$
. Now, if G has maximum degree
$Q_3$
. Now, if G has maximum degree
![]() $O(pn)$
(which can be assumed by standard reduction results), then we require
$O(pn)$
(which can be assumed by standard reduction results), then we require
![]() $n^8p^{12}\gg n(pn)^4$
, which is
$n^8p^{12}\gg n(pn)^4$
, which is
![]() $p\gg n^{-3/8}$
. This means that an n-vertex graph with edge density
$p\gg n^{-3/8}$
. This means that an n-vertex graph with edge density
![]() $\gg n^{-3/8}$
contains the desired number of copies of
$\gg n^{-3/8}$
contains the desired number of copies of
![]() $Q_3$
.
$Q_3$
.
Let us prove the promised inequalities between the number of various homomorphisms
![]() $Q_3\rightarrow G$
. For graphs H, G and a set
$Q_3\rightarrow G$
. For graphs H, G and a set
![]() $R\subset V(H)$
, let us write
$R\subset V(H)$
, let us write
![]() $\hom (H,G;R)$
for the number of graph homomorphisms
$\hom (H,G;R)$
for the number of graph homomorphisms
![]() $V(H)\rightarrow V(G)$
with the property that all vertices in R are mapped to the same vertex in G. Identify
$V(H)\rightarrow V(G)$
with the property that all vertices in R are mapped to the same vertex in G. Identify
![]() $V(Q_3)$
with
$V(Q_3)$
with
![]() $\{0,1\}^3=\{000,001,\dots ,111\}$
(and see Figure 1). The key inequalities are as follows.
$\{0,1\}^3=\{000,001,\dots ,111\}$
(and see Figure 1). The key inequalities are as follows.

Figure 1 The cube.
Lemma 2.2. For any graph G, we have
Furthermore,
Proof. Let us start with the first inequality. Let
![]() $f:Q_3[\{000,001,110,111\}]\rightarrow G$
be a homomorphism. Let
$f:Q_3[\{000,001,110,111\}]\rightarrow G$
be a homomorphism. Let
![]() $\alpha _f$
be the number of maps
$\alpha _f$
be the number of maps
![]() $g:\{010,011\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
$g:\{010,011\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
![]() $Q_3[\{000,001,110,111,010,011\}]$
to G. Note that by the symmetry of
$Q_3[\{000,001,110,111,010,011\}]$
to G. Note that by the symmetry of
![]() $Q_3$
this is the same as the number of maps
$Q_3$
this is the same as the number of maps
![]() $h:\{100,101\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
$h:\{100,101\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
![]() $Q_3[\{000,001,110,111,100,101\}]$
to G.
$Q_3[\{000,001,110,111,100,101\}]$
to G.
Let
![]() $\beta _f$
be the number of maps
$\beta _f$
be the number of maps
![]() $g:\{010,011\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
$g:\{010,011\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
![]() $Q_3[\{000,001,110,111,010,011\}]$
to G, and in addition
$Q_3[\{000,001,110,111,010,011\}]$
to G, and in addition
![]() $g(011)=f(000)$
. Note that by the symmetry of
$g(011)=f(000)$
. Note that by the symmetry of
![]() $Q_3$
this is the same as the number of maps
$Q_3$
this is the same as the number of maps
![]() $h:\{100,101\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
$h:\{100,101\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
![]() $Q_3[\{000,001,110,111,100,101\}]$
to G, and in addition
$Q_3[\{000,001,110,111,100,101\}]$
to G, and in addition
![]() $h(101)=f(000)$
.
$h(101)=f(000)$
.
Now, note that
 $$ \begin{align*}\hom(Q_3,G;\{000,011\})=\sum_{f} \alpha_f \beta_f,\end{align*} $$
$$ \begin{align*}\hom(Q_3,G;\{000,011\})=\sum_{f} \alpha_f \beta_f,\end{align*} $$
where the summation is over all homomorphisms
![]() $f:Q_3[\{000,001,110,111\}]\rightarrow G$
. Indeed,
$f:Q_3[\{000,001,110,111\}]\rightarrow G$
. Indeed,
![]() $\alpha _f \beta _f$
is the number of suitable homomorphisms
$\alpha _f \beta _f$
is the number of suitable homomorphisms
![]() $\theta $
extending f since there are
$\theta $
extending f since there are
![]() $\alpha _f$
ways to choose
$\alpha _f$
ways to choose
![]() $\theta |_{\{100,101\}}$
, there are
$\theta |_{\{100,101\}}$
, there are
![]() $\beta _f$
ways to choose
$\beta _f$
ways to choose
![]() $\theta |_{\{010,011\}}$
, and any such pair is suitable because there are no edges between
$\theta |_{\{010,011\}}$
, and any such pair is suitable because there are no edges between
![]() $\{100,101\}$
and
$\{100,101\}$
and
![]() $\{010,011\}$
. Similarly,
$\{010,011\}$
. Similarly,
 $$ \begin{align*}\hom(Q_3,G;\{000,011,101\})=\sum_{f} \beta_f^2\end{align*} $$
$$ \begin{align*}\hom(Q_3,G;\{000,011,101\})=\sum_{f} \beta_f^2\end{align*} $$
and
 $$ \begin{align*}\hom(Q_3,G)= \sum_{f} \alpha_f^2.\end{align*} $$
$$ \begin{align*}\hom(Q_3,G)= \sum_{f} \alpha_f^2.\end{align*} $$
The required inequality follows from the Cauchy–Schwarz inequality.
Let us now prove the second inequality. Let
![]() $f:Q_3[\{010,011,100,101\}]\rightarrow G$
be a homomorphism such that
$f:Q_3[\{010,011,100,101\}]\rightarrow G$
be a homomorphism such that
![]() $f(101)=f(011)$
. Let
$f(101)=f(011)$
. Let
![]() $\alpha _f$
be the number of maps
$\alpha _f$
be the number of maps
![]() $g:\{000,001\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
$g:\{000,001\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
![]() $Q_3[\{010,011,100,101,000,001\}]$
to G. Note that by the symmetry of
$Q_3[\{010,011,100,101,000,001\}]$
to G. Note that by the symmetry of
![]() $Q_3$
this is the same as the number of maps
$Q_3$
this is the same as the number of maps
![]() $h:\{110,111\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
$h:\{110,111\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
![]() $Q_3[\{010,011,100,101,110,111\}]$
to G.
$Q_3[\{010,011,100,101,110,111\}]$
to G.
Let
![]() $\beta _f$
be the number of maps
$\beta _f$
be the number of maps
![]() $g:\{000,001\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
$g:\{000,001\}\rightarrow V(G)$
such that f and g together induce a homomorphism from
![]() $Q_3[\{010,011,100,101,000,001\}]$
to G, and in addition
$Q_3[\{010,011,100,101,000,001\}]$
to G, and in addition
![]() $g(000)=f(011)=f(101)$
. Note that by the symmetry of
$g(000)=f(011)=f(101)$
. Note that by the symmetry of
![]() $Q_3$
this is the same as the number of maps
$Q_3$
this is the same as the number of maps
![]() $h:\{110,111\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
$h:\{110,111\}\rightarrow V(G)$
such that f and h together induce a homomorphism from
![]() $Q_3[\{010,011,100,101,110,111\}]$
to G, and in addition
$Q_3[\{010,011,100,101,110,111\}]$
to G, and in addition
![]() $h(110)=f(011)=f(101)$
.
$h(110)=f(011)=f(101)$
.
Now, note that
 $$ \begin{align*}\hom(Q_3,G;\{000,011,101\})=\sum_{f} \alpha_f \beta_f,\end{align*} $$
$$ \begin{align*}\hom(Q_3,G;\{000,011,101\})=\sum_{f} \alpha_f \beta_f,\end{align*} $$
where the summation is over all homomorphisms
![]() $f:Q_3[\{010,011,100,101\}]\rightarrow G$
such that
$f:Q_3[\{010,011,100,101\}]\rightarrow G$
such that
![]() $f(101)=f(011)$
. Indeed,
$f(101)=f(011)$
. Indeed,
![]() $\alpha _f \beta _f$
is the number of suitable homomorphisms extending f. Similarly,
$\alpha _f \beta _f$
is the number of suitable homomorphisms extending f. Similarly,
 $$ \begin{align*}\hom(Q_3,G;\{000,011,101,110\})=\sum_{f} \beta_f^2\end{align*} $$
$$ \begin{align*}\hom(Q_3,G;\{000,011,101,110\})=\sum_{f} \beta_f^2\end{align*} $$
and
 $$ \begin{align*}\hom(Q_3,G)\geq \sum_{f} \alpha_f^2.\end{align*} $$
$$ \begin{align*}\hom(Q_3,G)\geq \sum_{f} \alpha_f^2.\end{align*} $$
The required inequality follows from the Cauchy–Schwarz inequality.
It is straightforward to combine the two inequalities in Lemma 2.2 to conclude the following.
Corollary 2.3. For any graph G, we have
 $$ \begin{align*}\hom(Q_3,G;\{000,011,101,110\})\geq \frac{\hom(Q_3,G;\{000,011\})^4}{\hom(Q_3,G)^3}.\end{align*} $$
$$ \begin{align*}\hom(Q_3,G;\{000,011,101,110\})\geq \frac{\hom(Q_3,G;\{000,011\})^4}{\hom(Q_3,G)^3}.\end{align*} $$
We say that a graph G is K-almost regular if
![]() $\Delta (G)\leq K\delta (G)$
. We are now in a position to prove Proposition 2.1 for the special case of bipartite almost regular graphs.
$\Delta (G)\leq K\delta (G)$
. We are now in a position to prove Proposition 2.1 for the special case of bipartite almost regular graphs.
Proposition 2.4. For any
![]() $K>0$
, there are positive constants
$K>0$
, there are positive constants
![]() $c=c(K)$
and
$c=c(K)$
and
![]() $C=C(K)$
such that any bipartite K-almost regular n-vertex graph with edge density
$C=C(K)$
such that any bipartite K-almost regular n-vertex graph with edge density
![]() $p\geq Cn^{-3/8}$
contains at least
$p\geq Cn^{-3/8}$
contains at least
![]() $cn^8p^{12}$
copies of
$cn^8p^{12}$
copies of
![]() $Q_3$
.
$Q_3$
.
As we have mentioned, the proof uses the fact that
![]() $Q_3$
satisfies Sidorenko’s conjecture. Sidorenko’s conjecture states that for every bipartite graph H and n-vertex graph G with edge density p, we have
$Q_3$
satisfies Sidorenko’s conjecture. Sidorenko’s conjecture states that for every bipartite graph H and n-vertex graph G with edge density p, we have
![]() $\hom (H,G)\geq n^{v(H)}p^{e(H)}$
. We say that a graph H satisfies Sidorenko’s conjecture if this inequality holds for every G. Hatami proved that
$\hom (H,G)\geq n^{v(H)}p^{e(H)}$
. We say that a graph H satisfies Sidorenko’s conjecture if this inequality holds for every G. Hatami proved that
![]() $Q_d$
satisfies Sidorenko’s conjecture for every d.
$Q_d$
satisfies Sidorenko’s conjecture for every d.
Lemma 2.5 (Hatami [Reference Hatami17]).
Let d be a positive integer. Then any n-vertex graph G with edge density p satisfies
![]() $\hom (Q_d,G)\geq n^{2^d}p^{d2^{d-1}}$
.
$\hom (Q_d,G)\geq n^{2^d}p^{d2^{d-1}}$
.
Proof of Proposition 2.4.
Let C be sufficiently large, and let G be a bipartite K-almost regular n-vertex graph with edge density
![]() $p\geq Cn^{-3/8}$
.
$p\geq Cn^{-3/8}$
.
Assume, for the sake of contradiction, that
![]() $\hom (Q_3,G;\{000,011\})\geq \frac {1}{24}\hom (Q_3,G)$
. Then Corollary 2.3 implies that
$\hom (Q_3,G;\{000,011\})\geq \frac {1}{24}\hom (Q_3,G)$
. Then Corollary 2.3 implies that
On the other hand, observe that
so, using Lemma 2.5, we have
It follows that
![]() $p\leq (24^4 K^4 )^{1/8} n^{-3/8}$
, which contradicts
$p\leq (24^4 K^4 )^{1/8} n^{-3/8}$
, which contradicts
![]() $p\geq Cn^{-3/8}$
provided that C is sufficiently large.
$p\geq Cn^{-3/8}$
provided that C is sufficiently large.
Hence, we have
![]() $\hom (Q_3,G;\{000,011\})< \frac {1}{24}\hom (Q_3,G)$
. It follows by symmetry that for any
$\hom (Q_3,G;\{000,011\})< \frac {1}{24}\hom (Q_3,G)$
. It follows by symmetry that for any
![]() $u,v\in V(Q_3)$
of distance two,
$u,v\in V(Q_3)$
of distance two,
![]() $\hom (Q_3,G;\{u,v\})<\frac {1}{24}\hom (Q_3,G)$
. Since G is bipartite, the total number of noninjective homomorphic copies of
$\hom (Q_3,G;\{u,v\})<\frac {1}{24}\hom (Q_3,G)$
. Since G is bipartite, the total number of noninjective homomorphic copies of
![]() $Q_3$
in G is at most
$Q_3$
in G is at most
![]() $\sum \hom (Q_3,G;\{u,v\})$
, where the summation is over all u and v of distance two in
$\sum \hom (Q_3,G;\{u,v\})$
, where the summation is over all u and v of distance two in
![]() $Q_3$
. By the above inequality, this sum is less than
$Q_3$
. By the above inequality, this sum is less than
![]() $12\cdot \frac {1}{24}\hom (Q_3,G)=\hom (Q_3,G)/2$
. Hence, there are at least
$12\cdot \frac {1}{24}\hom (Q_3,G)=\hom (Q_3,G)/2$
. Hence, there are at least
![]() $\hom (Q_3,G)/2$
injective homomorphic copies of
$\hom (Q_3,G)/2$
injective homomorphic copies of
![]() $Q_3$
in G. Proposition 2.4 now follows by another application of Lemma 2.5.
$Q_3$
in G. Proposition 2.4 now follows by another application of Lemma 2.5.
In order to deduce Proposition 2.1 from Proposition 2.4, we can use a regularization lemma of Jiang and Yepremyan. We remark that the first result of this kind was established by Erdős and Simonovits [Reference Erdős and Simonovits11] in order to bound the Turán number of the (three-dimensional) cube. Roughly speaking, they showed that in bipartite Turán problems, it suffices to consider almost regular host graphs. Jiang and Yepremyan extended this to supersaturation problems. While their result applies for general linear hypergraphs, we will only need it in the special case of graphs.
Lemma 2.6 (Jiang–Yepremyan [Reference Jiang and Yepremyan19, Theorem 3.3]).
Let
![]() $0<\alpha <1$
be a real number. Let H be a graph with
$0<\alpha <1$
be a real number. Let H be a graph with
![]() $e(H)\geq v(H)$
. There exists a real number
$e(H)\geq v(H)$
. There exists a real number
![]() $K=K(\alpha ,H)\geq 1$
such that the following holds. Suppose that there are positive constants c and C (possibly depending on H) such that for each n, every n-vertex, K-almost regular bipartite graph G with edge density
$K=K(\alpha ,H)\geq 1$
such that the following holds. Suppose that there are positive constants c and C (possibly depending on H) such that for each n, every n-vertex, K-almost regular bipartite graph G with edge density
![]() $p\geq Cn^{-\alpha }$
has at least
$p\geq Cn^{-\alpha }$
has at least
![]() $cn^{v(H)}p^{e(H)}$
copies of H. Then there exist positive constants
$cn^{v(H)}p^{e(H)}$
copies of H. Then there exist positive constants
![]() $c'$
and
$c'$
and
![]() $C'$
(possibly depending on H) such that for each n, every n-vertex bipartite graph G with edge density
$C'$
(possibly depending on H) such that for each n, every n-vertex bipartite graph G with edge density
![]() $p\geq C'n^{-\alpha }$
has at least
$p\geq C'n^{-\alpha }$
has at least
![]() $c'n^{v(H)}p^{e(H)}$
copies of H.
$c'n^{v(H)}p^{e(H)}$
copies of H.
It is straightforward to deduce Proposition 2.1 from Proposition 2.4 using this lemma. We will give the details in the next subsection (in a more general setting).
2.2. Our main general result
In this subsection, we present our main technical results. We remark that our method resembles that of Conlon and Lee from [Reference Conlon and Lee6] where they prove Sidorenko’s conjecture for a certain class of graphs.
Given a graph automorphism
![]() $\phi :V(H)\rightarrow V(H)$
, we write
$\phi :V(H)\rightarrow V(H)$
, we write
![]() $F_{\phi }=\{v\in V(H): \phi (v)=v\}$
.
$F_{\phi }=\{v\in V(H): \phi (v)=v\}$
.
Definition 2.7. Let H be a connected bipartite graph. We say that vertex sets
![]() $A,B\subset V(H)$
and a graph automorphism
$A,B\subset V(H)$
and a graph automorphism
![]() $\phi :V(H)\rightarrow V(H)$
form a symmetric triple if
$\phi :V(H)\rightarrow V(H)$
form a symmetric triple if
![]() $\phi =\phi ^{-1}$
; A, B and
$\phi =\phi ^{-1}$
; A, B and
![]() $F_{\phi }$
partition
$F_{\phi }$
partition
![]() $V(H)$
;
$V(H)$
;
![]() $F_{\phi }$
separates A and B and
$F_{\phi }$
separates A and B and
![]() $\phi (A)=B$
.
$\phi (A)=B$
.
Given a further subset
![]() $R\subset V(H)$
, we say that R is intersecting for a symmetric triple
$R\subset V(H)$
, we say that R is intersecting for a symmetric triple
![]() $(A,B,\phi )$
if all vertices of R are in the same part of the bipartition of H, and R intersects both
$(A,B,\phi )$
if all vertices of R are in the same part of the bipartition of H, and R intersects both
![]() $A\cup F_{\phi }$
and
$A\cup F_{\phi }$
and
![]() $B\cup F_{\phi }$
.
$B\cup F_{\phi }$
.
Example 2.8. Let H be the three-dimensional cube, as depicted on Figure 2. Let
![]() $\phi $
be the automorphism which swaps the first digit with the second digit, that is, which maps
$\phi $
be the automorphism which swaps the first digit with the second digit, that is, which maps
![]() $abc$
to
$abc$
to
![]() $bac$
. Let
$bac$
. Let
![]() $A=\{100,101\}$
, and let
$A=\{100,101\}$
, and let
![]() $B=\{010,011\}$
. Then
$B=\{010,011\}$
. Then
![]() $(A,B,\phi )$
is a symmetric triple. Moreover, if
$(A,B,\phi )$
is a symmetric triple. Moreover, if
![]() $R=\{000,011\}$
, then R is intersecting for
$R=\{000,011\}$
, then R is intersecting for
![]() $(A,B,\phi )$
.
$(A,B,\phi )$
.

Figure 2 A symmetric triple
![]() $(A,B,\phi )$
.
$(A,B,\phi )$
.
Definition 2.9. Let H be a connected bipartite graph, let
![]() $(A,B,\phi )$
be a symmetric triple and let
$(A,B,\phi )$
be a symmetric triple and let
![]() $R\subset V(H)$
. Then
$R\subset V(H)$
. Then
Informally, we keep all members of R that are in
![]() $A\cup F_{\phi }$
but replace
$A\cup F_{\phi }$
but replace
![]() $R\cap B$
by
$R\cap B$
by
![]() $\phi (R\cap A)$
.
$\phi (R\cap A)$
.
Remark 2.10. If
![]() $(A,B,\phi )$
is a symmetric triple, then so is
$(A,B,\phi )$
is a symmetric triple, then so is
![]() $(B,A,\phi )$
, and if R is intersecting for
$(B,A,\phi )$
, and if R is intersecting for
![]() $(A,B,\phi )$
, then it is intersecting also for
$(A,B,\phi )$
, then it is intersecting also for
![]() $(B,A,\phi )$
. Moreover, in this case
$(B,A,\phi )$
. Moreover, in this case
![]() $\psi _{A,B,\phi }(R)\neq \emptyset $
. Also, note that all vertices in
$\psi _{A,B,\phi }(R)\neq \emptyset $
. Also, note that all vertices in
![]() $\psi _{A,B,\phi }(R)$
are in the same part of the bipartition of H as R.
$\psi _{A,B,\phi }(R)$
are in the same part of the bipartition of H as R.
We can now state the main technical lemma, which generalizes the inequalities from Lemma 2.2.
Lemma 2.11. Let H be a connected bipartite graph, let
![]() $(A,B,\phi )$
be a symmetric triple and let R be an intersecting set for
$(A,B,\phi )$
be a symmetric triple and let R be an intersecting set for
![]() $(A,B,\phi )$
. Then, for any graph G, we have
$(A,B,\phi )$
. Then, for any graph G, we have
In particular, for any graph G,
Proof. Let
![]() $v\in V(G)$
and let
$v\in V(G)$
and let
![]() $f:H[F_{\phi }]\rightarrow G$
be a homomorphism which maps each vertex in
$f:H[F_{\phi }]\rightarrow G$
be a homomorphism which maps each vertex in
![]() $R\cap F_{\phi }$
to v. Let
$R\cap F_{\phi }$
to v. Let
![]() $\alpha _{v,f}$
be the number of maps
$\alpha _{v,f}$
be the number of maps
![]() $g:A\rightarrow V(G)$
such that f and g together induce a homomorphism from
$g:A\rightarrow V(G)$
such that f and g together induce a homomorphism from
![]() $H[A\cup F_{\phi }]$
to G and which maps each vertex in
$H[A\cup F_{\phi }]$
to G and which maps each vertex in
![]() $R\cap A$
to v. Finally, let
$R\cap A$
to v. Finally, let
![]() $\beta _{v,f}$
be the number of maps
$\beta _{v,f}$
be the number of maps
![]() $h:B\rightarrow V(G)$
such that f and h together induce a homomorphism from
$h:B\rightarrow V(G)$
such that f and h together induce a homomorphism from
![]() $H[B\cup F_{\phi }]$
to G and which map each vertex in
$H[B\cup F_{\phi }]$
to G and which map each vertex in
![]() $R\cap B$
to v.
$R\cap B$
to v.
Note that the number of homomorphisms
![]() $\theta :H\rightarrow G$
which extend f and which map R to v is precisely
$\theta :H\rightarrow G$
which extend f and which map R to v is precisely
![]() $\alpha _{v,f}\beta _{v,f}$
. Indeed, there are
$\alpha _{v,f}\beta _{v,f}$
. Indeed, there are
![]() $\alpha _{v,f}$
ways to chose
$\alpha _{v,f}$
ways to chose
![]() $\theta |_A$
, there are
$\theta |_A$
, there are
![]() $\beta _{v,f}$
ways to choose
$\beta _{v,f}$
ways to choose
![]() $\theta |_B$
and since there are no edges in H between A and B, any pair gives a suitable choice. Hence,
$\theta |_B$
and since there are no edges in H between A and B, any pair gives a suitable choice. Hence,
 $$ \begin{align*}\hom(H,G;R)=\sum_{v,f} \alpha_{v,f}\beta_{v,f},\end{align*} $$
$$ \begin{align*}\hom(H,G;R)=\sum_{v,f} \alpha_{v,f}\beta_{v,f},\end{align*} $$
where the summation is over all v and f as above. Observe that, by the properties of a symmetric triple, ![]() is a bijection (with inverse
is a bijection (with inverse ![]() ) between
) between
-
○ maps
 $h:B\rightarrow V(G)$
with the property that f and h together induce a homomorphism from
$h:B\rightarrow V(G)$
with the property that f and h together induce a homomorphism from
 $H[B\cup F_{\phi }]$
to G and which map
$H[B\cup F_{\phi }]$
to G and which map
 $\phi (R\cap A)$
to v and
$\phi (R\cap A)$
to v and -
○ maps
 $g:A\rightarrow V(G)$
with the property that f and g together induce a homomorphism from
$g:A\rightarrow V(G)$
with the property that f and g together induce a homomorphism from
 $H[A\cup F_{\phi }]$
to G and which map
$H[A\cup F_{\phi }]$
to G and which map
 $R\cap A$
to v.
$R\cap A$
to v.
(Indeed, if f and h together induce a homomorphism from
![]() $H[B\cup F_{\phi }]$
to G, then
$H[B\cup F_{\phi }]$
to G, then
![]() $f\circ \phi $
and
$f\circ \phi $
and
![]() $h\circ \phi $
together induce a homomorphism from
$h\circ \phi $
together induce a homomorphism from
![]() $H[\phi ^{-1}(B\cup F_{\phi })]=H[A\cup F_{\phi }]$
to G, but
$H[\phi ^{-1}(B\cup F_{\phi })]=H[A\cup F_{\phi }]$
to G, but
![]() $f\circ \phi =f$
on
$f\circ \phi =f$
on
![]() $F_{\phi }$
.)
$F_{\phi }$
.)
Therefore, the number of maps
![]() $h:B\rightarrow V(G)$
with the property that f and h together induce a homomorphism from
$h:B\rightarrow V(G)$
with the property that f and h together induce a homomorphism from
![]() $H[B\cup F_{\phi }]$
to G and which map
$H[B\cup F_{\phi }]$
to G and which map
![]() $\phi (R\cap A)$
to v is precisely
$\phi (R\cap A)$
to v is precisely
![]() $\alpha _{v,f}$
. Hence, using that
$\alpha _{v,f}$
. Hence, using that
![]() $\psi _{A,B,\phi }(R)\neq \emptyset $
, we have
$\psi _{A,B,\phi }(R)\neq \emptyset $
, we have
 $$ \begin{align*}\hom(H,G;\psi_{A,B,\phi}(R))=\sum_{v,f} \alpha_{v,f}^2,\end{align*} $$
$$ \begin{align*}\hom(H,G;\psi_{A,B,\phi}(R))=\sum_{v,f} \alpha_{v,f}^2,\end{align*} $$
where the summation is over all pairs
![]() $v,f$
as above. Similarly, we obtain
$v,f$
as above. Similarly, we obtain
 $$ \begin{align*}\hom(H,G;\psi_{B,A,\phi}(R))=\sum_{v,f} \beta_{v,f}^2\end{align*} $$
$$ \begin{align*}\hom(H,G;\psi_{B,A,\phi}(R))=\sum_{v,f} \beta_{v,f}^2\end{align*} $$
and we are done by the Cauchy–Schwarz inequality.
We can now describe the main condition that a graph H needs to satisfy in order for our method to apply.
Definition 2.12. Let H be a connected bipartite graph with parts
![]() $X_1$
and
$X_1$
and
![]() $X_2$
. We say that H is reflective if the following holds. Let
$X_2$
. We say that H is reflective if the following holds. Let
![]() $R\subset X_i$
be a set of size two for some
$R\subset X_i$
be a set of size two for some
![]() $i\in \{1,2\}$
. Then there exists a sequence of symmetric triples
$i\in \{1,2\}$
. Then there exists a sequence of symmetric triples
![]() $(A_j,B_j,\phi _j)$
for
$(A_j,B_j,\phi _j)$
for
![]() $j=0,1,\dots ,m-1$
and intersecting sets
$j=0,1,\dots ,m-1$
and intersecting sets
![]() $R_j$
for
$R_j$
for
![]() $(A_j,B_j,\phi _j)$
such that
$(A_j,B_j,\phi _j)$
such that
![]() $R_0=R$
,
$R_0=R$
,
![]() $R_m=X_i$
and
$R_m=X_i$
and
![]() $R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
$R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
![]() $0\leq j\leq m-1$
.
$0\leq j\leq m-1$
.
Remark 2.13. Observe that if R is intersecting for a symmetric triple
![]() $(A,B,\phi )$
and
$(A,B,\phi )$
and
![]() $S\supset R$
, then S is also intersecting for
$S\supset R$
, then S is also intersecting for
![]() $(A,B,\phi )$
and
$(A,B,\phi )$
and
![]() $\psi _{A,B,\phi }(S)\supset \psi _{A,B,\phi }(R)$
. Hence, H is reflective if for each
$\psi _{A,B,\phi }(S)\supset \psi _{A,B,\phi }(R)$
. Hence, H is reflective if for each
![]() $R\subset X_i$
of size two for some
$R\subset X_i$
of size two for some
![]() $i\in \{1,2\}$
, there exists a sequence of symmetric triples
$i\in \{1,2\}$
, there exists a sequence of symmetric triples
![]() $(A_j,B_j,\phi _j)$
for
$(A_j,B_j,\phi _j)$
for
![]() $j=0,1,\dots ,m-1$
and intersecting sets
$j=0,1,\dots ,m-1$
and intersecting sets
![]() $R_j$
for
$R_j$
for
![]() $(A_j,B_j,\phi _j)$
such that
$(A_j,B_j,\phi _j)$
such that
![]() $R_0=R$
,
$R_0=R$
,
![]() $R_m=X_i$
and
$R_m=X_i$
and
![]() $R_{j+1}\subset \psi _{A_j,B_j,\phi _j}(R_j)$
for all
$R_{j+1}\subset \psi _{A_j,B_j,\phi _j}(R_j)$
for all
![]() $0\leq j\leq m-1$
.
$0\leq j\leq m-1$
.
The following lemma generalizes Corollary 2.3.
Lemma 2.14. Let H be a reflective connected bipartite graph, and let
![]() $R\subset X$
be a set of size two, where X is one of the parts of H. Then there is a positive integer s such that for every graph G, we have
$R\subset X$
be a set of size two, where X is one of the parts of H. Then there is a positive integer s such that for every graph G, we have
Proof. Since H is reflective, we can choose a sequence of symmetric triples
![]() $(A_j,B_j,\phi _j)$
for
$(A_j,B_j,\phi _j)$
for
![]() $j=0, 1,\dots ,m-1$
and intersecting sets
$j=0, 1,\dots ,m-1$
and intersecting sets
![]() $R_j$
for
$R_j$
for
![]() $(A_j,B_j,\phi _j)$
such that
$(A_j,B_j,\phi _j)$
such that
![]() $R_0=R$
,
$R_0=R$
,
![]() $R_m=X$
and
$R_m=X$
and
![]() $R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
$R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
![]() $0\leq j\leq m-1$
. By Lemma 2.11, we have
$0\leq j\leq m-1$
. By Lemma 2.11, we have
for each
![]() $0\leq j\leq m-1$
. It is easy to see that this implies that
$0\leq j\leq m-1$
. It is easy to see that this implies that
 $$ \begin{align*}\hom(H,G;X)=\hom(H,G;R_m)\geq \frac{\hom(H,G;R_0)^{2^m}}{\hom(H,G)^{2^m-1}}=\frac{\hom(H,G;R)^{2^m}}{\hom(H,G)^{2^m-1}},\end{align*} $$
$$ \begin{align*}\hom(H,G;X)=\hom(H,G;R_m)\geq \frac{\hom(H,G;R_0)^{2^m}}{\hom(H,G)^{2^m-1}}=\frac{\hom(H,G;R)^{2^m}}{\hom(H,G)^{2^m-1}},\end{align*} $$
so we may take
![]() $s=2^m$
.
$s=2^m$
.
The next proposition is our main result restricted to almost regular bipartite host graphs.
Proposition 2.15. Let H be a reflective connected bipartite graph which satisfies Sidorenko’s conjecture. Let
![]() $K\geq 1$
be a real number. Then there are positive constants
$K\geq 1$
be a real number. Then there are positive constants
![]() $c=c(H)$
and
$c=c(H)$
and
![]() $C=C(H,K)$
such that if G is a K-almost regular bipartite n-vertex graph with edge density p satisfying
$C=C(H,K)$
such that if G is a K-almost regular bipartite n-vertex graph with edge density p satisfying
![]() $n^{v(H)}p^{e(H)}\geq Cn(pn)^t$
, where t is the size of the larger part in the bipartition of H, then G contains at least
$n^{v(H)}p^{e(H)}\geq Cn(pn)^t$
, where t is the size of the larger part in the bipartition of H, then G contains at least
![]() $cn^{v(H)}p^{e(H)}$
copies of H.
$cn^{v(H)}p^{e(H)}$
copies of H.
Proof. Let
![]() $c=c(H)$
be a sufficiently small positive real, and let
$c=c(H)$
be a sufficiently small positive real, and let
![]() $C=C(H,K)$
be sufficiently large. Let G be a K-almost regular bipartite n-vertex graph with edge density p satisfying
$C=C(H,K)$
be sufficiently large. Let G be a K-almost regular bipartite n-vertex graph with edge density p satisfying
![]() $n^{v(H)}p^{e(H)}\geq Cn(pn)^t$
, where t is the size of the larger part in the bipartition of H. Since H satisfies Sidorenko’s conjecture, we have
$n^{v(H)}p^{e(H)}\geq Cn(pn)^t$
, where t is the size of the larger part in the bipartition of H. Since H satisfies Sidorenko’s conjecture, we have
![]() $\hom (H,G)\geq n^{v(H)}p^{e(H)}$
.
$\hom (H,G)\geq n^{v(H)}p^{e(H)}$
.
Claim. For every
![]() $R\subset V(H)$
of size two, we have
$R\subset V(H)$
of size two, we have
Proof of Claim. Suppose, for the sake of contradiction, that
In particular, there is a homomorphism
![]() $H\rightarrow G$
which maps the two elements of R to the same vertex. Hence, as G is bipartite, the two elements of R are in the same part of the bipartition of H. Let X be this part. By Lemma 2.14, we have
$H\rightarrow G$
which maps the two elements of R to the same vertex. Hence, as G is bipartite, the two elements of R are in the same part of the bipartition of H. Let X be this part. By Lemma 2.14, we have
for some positive integer s that only depends on H. Since
![]() $\hom (H,G;X)\leq n\Delta (G)^{v(H)-|X|}\leq n(Kpn)^{v(H)-|X|}\leq n(Kpn)^t$
and
$\hom (H,G;X)\leq n\Delta (G)^{v(H)-|X|}\leq n(Kpn)^{v(H)-|X|}\leq n(Kpn)^t$
and
![]() $\hom (H,G)\geq n^{v(H)}p^{e(H)}$
, Equation (2.1) implies that
$\hom (H,G)\geq n^{v(H)}p^{e(H)}$
, Equation (2.1) implies that
However, this contradicts the assumption that
![]() $n^{v(H)}p^{e(H)}\geq Cn(pn)^t$
and that C is sufficiently large. This completes the proof of the claim.
$n^{v(H)}p^{e(H)}\geq Cn(pn)^t$
and that C is sufficiently large. This completes the proof of the claim.
Now, note that the number of noninjective homomorphisms
![]() $H\rightarrow G$
is at most
$H\rightarrow G$
is at most
![]() $\sum _R \hom (H,G;R)$
, where the summation is over all
$\sum _R \hom (H,G;R)$
, where the summation is over all
![]() $R\subset V(H)$
of size two. By the claim, this sum is at most
$R\subset V(H)$
of size two. By the claim, this sum is at most
![]() $\binom {v(H)}{2}\cdot \frac {\hom (H,G)}{v(H)^2}\leq \frac {1}{2}\hom (H,G)$
. Hence, there are at least
$\binom {v(H)}{2}\cdot \frac {\hom (H,G)}{v(H)^2}\leq \frac {1}{2}\hom (H,G)$
. Hence, there are at least
![]() $\frac {1}{2}\hom (H,G)$
injective homomorphisms
$\frac {1}{2}\hom (H,G)$
injective homomorphisms
![]() $H\rightarrow G$
, which implies that there are at least
$H\rightarrow G$
, which implies that there are at least
![]() $c\hom (H,G)\geq cn^{v(H)}p^{e(H)}$
copies of H in G, provided that c is sufficiently small.
$c\hom (H,G)\geq cn^{v(H)}p^{e(H)}$
copies of H in G, provided that c is sufficiently small.
We are now in a position to state and prove our main result, which follows easily from Proposition 2.15 and Lemma 2.6.
Theorem 2.16. Let H be a reflective connected bipartite graph which satisfies Sidorenko’s conjecture and which is not a tree. Then there are positive constants
![]() $c=c(H)$
and
$c=c(H)$
and
![]() $C=C(H)$
such that if G is an n-vertex graph with edge density
$C=C(H)$
such that if G is an n-vertex graph with edge density
![]() $p\geq Cn^{-\frac {v(H)-t-1}{e(H)-t}}$
, where t is the size of the larger part in the bipartition of H, then G contains at least
$p\geq Cn^{-\frac {v(H)-t-1}{e(H)-t}}$
, where t is the size of the larger part in the bipartition of H, then G contains at least
![]() $cn^{v(H)}p^{e(H)}$
copies of H.
$cn^{v(H)}p^{e(H)}$
copies of H.
Proof. Let
![]() $\alpha =\frac {v(H)-t-1}{e(H)-t}$
. Let
$\alpha =\frac {v(H)-t-1}{e(H)-t}$
. Let
![]() $K=K(\alpha ,H)$
be the constant provided by Lemma 2.6. By Proposition 2.15, there are positive constants
$K=K(\alpha ,H)$
be the constant provided by Lemma 2.6. By Proposition 2.15, there are positive constants
![]() $c'=c'(H)$
and
$c'=c'(H)$
and
![]() $C"=C"(H)$
such that if G is a K-almost regular bipartite n-vertex graph with edge density p satisfying
$C"=C"(H)$
such that if G is a K-almost regular bipartite n-vertex graph with edge density p satisfying
![]() $n^{v(H)}p^{e(H)}\geq C"n(pn)^t$
, then G has at least
$n^{v(H)}p^{e(H)}\geq C"n(pn)^t$
, then G has at least
![]() $c'n^{v(H)}p^{e(H)}$
copies of H. Now, note that there is some
$c'n^{v(H)}p^{e(H)}$
copies of H. Now, note that there is some
![]() $C'=C'(H)$
such that if
$C'=C'(H)$
such that if
![]() $p\geq C'n^{-\alpha }$
, then
$p\geq C'n^{-\alpha }$
, then
![]() $n^{v(H)}p^{e(H)}\geq C"n(pn)^t$
holds. Hence, any K-almost regular bipartite n-vertex graph G with edge density
$n^{v(H)}p^{e(H)}\geq C"n(pn)^t$
holds. Hence, any K-almost regular bipartite n-vertex graph G with edge density
![]() $p\geq C'n^{-\alpha }$
contains at least
$p\geq C'n^{-\alpha }$
contains at least
![]() $c'n^{v(H)}p^{e(H)}$
copies of H. It follows by Lemma 2.6 that there are positive constants
$c'n^{v(H)}p^{e(H)}$
copies of H. It follows by Lemma 2.6 that there are positive constants
![]() $c=c(H)$
and
$c=c(H)$
and
![]() $C=C(H)$
such that if G is a bipartite n-vertex graph with edge density
$C=C(H)$
such that if G is a bipartite n-vertex graph with edge density
![]() $p\geq Cn^{-\alpha }$
, then G contains at least
$p\geq Cn^{-\alpha }$
, then G contains at least
![]() $cn^{v(H)}p^{e(H)}$
copies of H. This proves the theorem for all bipartite host graphs G. The general case follows easily by noting that any graph G has a bipartite subgraph with at least half of the edges of G.
$cn^{v(H)}p^{e(H)}$
copies of H. This proves the theorem for all bipartite host graphs G. The general case follows easily by noting that any graph G has a bipartite subgraph with at least half of the edges of G.
We also state a simple corollary of our main result.
Theorem 2.17. Let H be a d-regular, reflective, connected bipartite graph which satisfies Sidorenko’s conjecture and which is not
![]() $K_{d,d}$
. Then there is some
$K_{d,d}$
. Then there is some
![]() $\varepsilon =\varepsilon (H)>0$
such that
$\varepsilon =\varepsilon (H)>0$
such that
![]() $\mathrm {ex}(n,H)=O(n^{2-1/d-\varepsilon })$
.
$\mathrm {ex}(n,H)=O(n^{2-1/d-\varepsilon })$
.
Proof. By Theorem 2.16, there are positive constants
![]() $c=c(H)$
and
$c=c(H)$
and
![]() $C=C(H)$
such that if G is an n-vertex graph with edge density
$C=C(H)$
such that if G is an n-vertex graph with edge density
![]() $p\geq Cn^{-\frac {v(H)-t-1}{e(H)-t}}$
, where t is the size of the larger part in the bipartition of H, then G contains at least
$p\geq Cn^{-\frac {v(H)-t-1}{e(H)-t}}$
, where t is the size of the larger part in the bipartition of H, then G contains at least
![]() $cn^{v(H)}p^{e(H)}$
copies of H. This implies that
$cn^{v(H)}p^{e(H)}$
copies of H. This implies that
Since H is d-regular, we have
![]() $t=v(H)/2$
and
$t=v(H)/2$
and
![]() $e(H)=dv(H)/2$
, so
$e(H)=dv(H)/2$
, so
where the last inequality follows from
![]() $v(H)/2>d$
(which is true since H is d-regular and
$v(H)/2>d$
(which is true since H is d-regular and
![]() $H\neq K_{d,d}$
). This completes the proof.
$H\neq K_{d,d}$
). This completes the proof.
2.3. Hypercubes
In this subsection, we show that any hypercube is reflective and use this to deduce Theorem 1.5.
Lemma 2.18. For any
![]() $d\geq 3$
, the hypercube
$d\geq 3$
, the hypercube
![]() $Q_d$
is reflective.
$Q_d$
is reflective.
Proof. Identify
![]() $Q_d$
with
$Q_d$
with
![]() $\{0,1\}^d$
. Let
$\{0,1\}^d$
. Let
![]() $Q_d(0)=\{\textbf {x}\in Q_d: \sum _i x_i\equiv 0 \mod 2\}$
. By the symmetry of the cube, it suffices to prove that for any
$Q_d(0)=\{\textbf {x}\in Q_d: \sum _i x_i\equiv 0 \mod 2\}$
. By the symmetry of the cube, it suffices to prove that for any
![]() $R\subset Q_d(0)$
of size two, there exists a sequence of symmetric triples
$R\subset Q_d(0)$
of size two, there exists a sequence of symmetric triples
![]() $(A_j,B_j,\phi _j)$
for
$(A_j,B_j,\phi _j)$
for
![]() $j=0,\dots ,m-1$
and intersecting sets
$j=0,\dots ,m-1$
and intersecting sets
![]() $R_j$
for
$R_j$
for
![]() $(A_j,B_j,\phi _j)$
such that
$(A_j,B_j,\phi _j)$
such that
![]() $R_0=R$
,
$R_0=R$
,
![]() $R_m=Q_d(0)$
and
$R_m=Q_d(0)$
and
![]() $R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
$R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
![]() $0\leq j\leq m-1$
.
$0\leq j\leq m-1$
.
First, we prove this in the special case where the two vertices of R has distance two in
![]() $Q_d$
. By the symmetry of the cube, we may assume that
$Q_d$
. By the symmetry of the cube, we may assume that
![]() $R=\{(0,0,0,\dots ,0),(1,1,0,\dots ,0)\}$
.
$R=\{(0,0,0,\dots ,0),(1,1,0,\dots ,0)\}$
.
For every
![]() $0\leq k\leq d$
, let
$0\leq k\leq d$
, let
Also, for
![]() $1\leq k\leq d-1$
, let
$1\leq k\leq d-1$
, let
Observe that
![]() $R=S_2$
and that
$R=S_2$
and that
![]() $Q_d(0)=S_d$
.
$Q_d(0)=S_d$
.
Claim. For every
![]() $2\leq k\leq d-1$
, there is a symmetric triple
$2\leq k\leq d-1$
, there is a symmetric triple
![]() $(A,B,\phi )$
such that
$(A,B,\phi )$
such that
![]() $S_k$
is intersecting for
$S_k$
is intersecting for
![]() $(A,B,\phi )$
and
$(A,B,\phi )$
and
![]() $T_{k}=\psi _{A,B,\phi }(S_k)$
. Also, there is a symmetric triple
$T_{k}=\psi _{A,B,\phi }(S_k)$
. Also, there is a symmetric triple
![]() $(A',B',\phi ')$
such that
$(A',B',\phi ')$
such that
![]() $T_{k}$
is intersecting for
$T_{k}$
is intersecting for
![]() $(A',B',\phi ')$
and
$(A',B',\phi ')$
and
![]() $S_{k+1}=\psi _{A',B',\phi '}(T_{k})$
.
$S_{k+1}=\psi _{A',B',\phi '}(T_{k})$
.
Proof of Claim. We start with the first assertion. Let
![]() $\phi $
be the automorphism of
$\phi $
be the automorphism of
![]() $Q_d$
which swaps the kth and the
$Q_d$
which swaps the kth and the
![]() $(k+1)$
th coordinate of each element in
$(k+1)$
th coordinate of each element in
![]() $Q_d$
. Let
$Q_d$
. Let
![]() $A=\{\textbf {x}\in Q_d: x_k=1, x_{k+1}=0\}$
and let
$A=\{\textbf {x}\in Q_d: x_k=1, x_{k+1}=0\}$
and let
![]() $B=\{\textbf {x}\in Q_d: x_k=0, x_{k+1}=1\}$
. Clearly,
$B=\{\textbf {x}\in Q_d: x_k=0, x_{k+1}=1\}$
. Clearly,
![]() $\phi ^{-1}=\phi $
; A, B and
$\phi ^{-1}=\phi $
; A, B and
![]() $F_{\phi }$
partition
$F_{\phi }$
partition
![]() $Q_d$
;
$Q_d$
;
![]() $F_{\phi }$
separates A and B and
$F_{\phi }$
separates A and B and
![]() $\phi (A)=B$
. Moreover,
$\phi (A)=B$
. Moreover,
![]() $S_k$
is intersecting for
$S_k$
is intersecting for
![]() $(A,B,\phi )$
since
$(A,B,\phi )$
since
![]() $(0,0,\dots ,0)\in S_k\cap F_{\phi }$
. Recall that
$(0,0,\dots ,0)\in S_k\cap F_{\phi }$
. Recall that
![]() $\psi _{A,B,\phi }(S_k)=(S_k\cap (A\cup F_{\phi }))\cup \phi (S_k\cap A)$
. Hence,
$\psi _{A,B,\phi }(S_k)=(S_k\cap (A\cup F_{\phi }))\cup \phi (S_k\cap A)$
. Hence,
 $$ \begin{align*} \psi_{A,B,\phi}(S_k) &=(S_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})\neq (0,1)\})\cup \phi(S_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})=(1,0)\}) \\ &=S_k\cup \phi(S_k\cap \{\textbf{x}\in Q_d: x_k=1\}) \\ &=T_{k}. \end{align*} $$
$$ \begin{align*} \psi_{A,B,\phi}(S_k) &=(S_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})\neq (0,1)\})\cup \phi(S_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})=(1,0)\}) \\ &=S_k\cup \phi(S_k\cap \{\textbf{x}\in Q_d: x_k=1\}) \\ &=T_{k}. \end{align*} $$
For the second assertion, let
![]() $\phi '$
be the automorphism of
$\phi '$
be the automorphism of
![]() $Q_d$
defined by
$Q_d$
defined by
Let
![]() $A'=\{\textbf {x}\in Q_d: x_k=0, x_{k+1}=0\}$
, and let
$A'=\{\textbf {x}\in Q_d: x_k=0, x_{k+1}=0\}$
, and let
![]() $B'=\{\textbf {x}\in Q_d: x_k=1, x_{k+1}=1\}$
. Clearly,
$B'=\{\textbf {x}\in Q_d: x_k=1, x_{k+1}=1\}$
. Clearly,
![]() $(\phi ')^{-1}=\phi '$
;
$(\phi ')^{-1}=\phi '$
;
![]() $A'$
,
$A'$
,
![]() $B'$
and
$B'$
and
![]() $F_{\phi '}$
partition
$F_{\phi '}$
partition
![]() $Q_d$
;
$Q_d$
;
![]() $F_{\phi '}$
separates
$F_{\phi '}$
separates
![]() $A'$
and
$A'$
and
![]() $B'$
and
$B'$
and
![]() $\phi '(A')=B'$
. Moreover,
$\phi '(A')=B'$
. Moreover,
![]() $T_{k}$
is intersecting for
$T_{k}$
is intersecting for
![]() $(A',B',\phi ')$
since
$(A',B',\phi ')$
since
![]() $T_k\cap F_{\phi '}$
contains the vector whose only nonzero coordinates are the first and the kth coordinate. Finally,
$T_k\cap F_{\phi '}$
contains the vector whose only nonzero coordinates are the first and the kth coordinate. Finally,
 $$ \begin{align*} \psi_{A',B',\phi'}(T_k) &=(T_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})\neq (1,1)\})\cup \phi'(T_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})=(0,0)\}) \\ &=T_k\cup \phi'(T_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})=(0,0)\}) \\ &=S_{k+1}, \end{align*} $$
$$ \begin{align*} \psi_{A',B',\phi'}(T_k) &=(T_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})\neq (1,1)\})\cup \phi'(T_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})=(0,0)\}) \\ &=T_k\cup \phi'(T_k\cap \{\textbf{x}\in Q_d: (x_k,x_{k+1})=(0,0)\}) \\ &=S_{k+1}, \end{align*} $$
which completes the proof of the claim.
The claim implies that whenever
![]() $R\subset Q_d(0)$
consists of two elements of distance two in
$R\subset Q_d(0)$
consists of two elements of distance two in
![]() $Q_d$
, there exists a sequence of symmetric triples
$Q_d$
, there exists a sequence of symmetric triples
![]() $(A_j,B_j,\phi _j)$
for
$(A_j,B_j,\phi _j)$
for
![]() $j=0,\dots ,m-1$
and intersecting sets
$j=0,\dots ,m-1$
and intersecting sets
![]() $R_j$
for
$R_j$
for
![]() $(A_j,B_j,\phi _j)$
such that
$(A_j,B_j,\phi _j)$
such that
![]() $R_0=R$
,
$R_0=R$
,
![]() $R_m=Q_d(0)$
and
$R_m=Q_d(0)$
and
![]() $R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
$R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
![]() $0\leq j\leq m-1$
. It is therefore sufficient (by Remark 2.13) to prove that if
$0\leq j\leq m-1$
. It is therefore sufficient (by Remark 2.13) to prove that if
![]() $P\subset Q_d(0)$
has size two, then there is a symmetric triple
$P\subset Q_d(0)$
has size two, then there is a symmetric triple
![]() $(A,B,\phi )$
such that P is intersecting for
$(A,B,\phi )$
such that P is intersecting for
![]() $(A,B,\phi )$
and
$(A,B,\phi )$
and
![]() $\psi _{A,B,\phi }(P)$
contains two elements of distance two. Let
$\psi _{A,B,\phi }(P)$
contains two elements of distance two. Let
![]() $P=\{u,v\}$
. We consider two cases.
$P=\{u,v\}$
. We consider two cases.
Case 1. u and v are not antipodal points of
![]() $Q_d$
. Without loss of generality, we may assume that
$Q_d$
. Without loss of generality, we may assume that
![]() $u=(0,0,\dots ,0)$
(so
$u=(0,0,\dots ,0)$
(so
![]() $v\neq (1,1,\dots ,1)$
by assumption). In particular, there exist some
$v\neq (1,1,\dots ,1)$
by assumption). In particular, there exist some
![]() $1\leq i<j\leq d$
such that
$1\leq i<j\leq d$
such that
![]() $v_i\neq v_j$
. Let
$v_i\neq v_j$
. Let
![]() $\phi $
be the automorphism of
$\phi $
be the automorphism of
![]() $Q_d$
which swaps the ith and the jth coordinate. Let
$Q_d$
which swaps the ith and the jth coordinate. Let
![]() $A=\{\textbf {x}\in Q_d: x_i=v_i, x_j=v_j\}$
, and let
$A=\{\textbf {x}\in Q_d: x_i=v_i, x_j=v_j\}$
, and let
![]() $B=\{\textbf {x}\in Q_d: x_i=1-v_i, x_j=1-v_j\}$
. Note that
$B=\{\textbf {x}\in Q_d: x_i=1-v_i, x_j=1-v_j\}$
. Note that
![]() $(A,B,\phi )$
is a symmetric triple and
$(A,B,\phi )$
is a symmetric triple and
![]() $u\in F_{\phi }$
, so P is intersecting for
$u\in F_{\phi }$
, so P is intersecting for
![]() $(A,B,\phi )$
. Now,
$(A,B,\phi )$
. Now,
![]() $\psi _{A,B,\phi }(P)$
contains both v and
$\psi _{A,B,\phi }(P)$
contains both v and
![]() $\phi (v)$
, so it contains two elements of distance two in
$\phi (v)$
, so it contains two elements of distance two in
![]() $Q_d$
.
$Q_d$
.
Case 2. u and v are antipodal in
![]() $Q_d$
. Without loss of generality,
$Q_d$
. Without loss of generality,
![]() $u=(0,0,\dots ,0)$
and
$u=(0,0,\dots ,0)$
and
![]() $v=(1,1,\dots ,1)$
. Let
$v=(1,1,\dots ,1)$
. Let
![]() $\phi $
be the automorphism of
$\phi $
be the automorphism of
![]() $Q_d$
which maps
$Q_d$
which maps
![]() $(x_1,x_2,x_3,\dots ,x_d)$
to
$(x_1,x_2,x_3,\dots ,x_d)$
to
![]() $(1-x_2,1-x_1,x_3,\dots ,x_d)$
. Let
$(1-x_2,1-x_1,x_3,\dots ,x_d)$
. Let
![]() $A=\{\textbf {x}\in Q_d: x_1=0, x_2=0\}$
, and let
$A=\{\textbf {x}\in Q_d: x_1=0, x_2=0\}$
, and let
![]() $B=\{\textbf {x}\in Q_d: x_1=1, x_2=1\}$
. Then
$B=\{\textbf {x}\in Q_d: x_1=1, x_2=1\}$
. Then
![]() $(A,B,\phi )$
is a symmetric triple and
$(A,B,\phi )$
is a symmetric triple and
![]() $u\in A$
,
$u\in A$
,
![]() $v\in B$
, so P is intersecting for
$v\in B$
, so P is intersecting for
![]() $(A,B,\phi )$
. Now,
$(A,B,\phi )$
. Now,
![]() $\psi _{A,B,\phi }(P)$
contains both u and
$\psi _{A,B,\phi }(P)$
contains both u and
![]() $\phi (u)$
, so it contains two elements of distance two in
$\phi (u)$
, so it contains two elements of distance two in
![]() $Q_d$
.
$Q_d$
.
We can now easily deduce Theorem 1.5.
Proof of Theorem 1.5.
Let
![]() $d\geq 3$
be an integer. By Lemma 2.18,
$d\geq 3$
be an integer. By Lemma 2.18,
![]() $Q_d$
is reflective. By Lemma 2.5, it satisfies Sidorenko’s conjecture. Hence, by Theorem 2.16, there are positive constants
$Q_d$
is reflective. By Lemma 2.5, it satisfies Sidorenko’s conjecture. Hence, by Theorem 2.16, there are positive constants
![]() $c=c(d)$
and
$c=c(d)$
and
![]() $C=C(d)$
such that if G is an n-vertex graph with edge density
$C=C(d)$
such that if G is an n-vertex graph with edge density
![]() $p\geq Cn^{-\frac {v(Q_d)-t-1}{e(Q_d)-t}}$
, where t is the size of a part of the bipartition of
$p\geq Cn^{-\frac {v(Q_d)-t-1}{e(Q_d)-t}}$
, where t is the size of a part of the bipartition of
![]() $Q_d$
, then G contains at least
$Q_d$
, then G contains at least
![]() $cn^{v(Q_d)}p^{e(Q_d)}$
copies of
$cn^{v(Q_d)}p^{e(Q_d)}$
copies of
![]() $Q_d$
. The result follows by noting that
$Q_d$
. The result follows by noting that
![]() $v(Q_d)=2^d$
,
$v(Q_d)=2^d$
,
![]() $e(Q_d)=d2^{d-1}$
and
$e(Q_d)=d2^{d-1}$
and
![]() $t=2^{d-1}$
.
$t=2^{d-1}$
.
2.4. Bipartite Kneser graphs
In this subsection, we prove that bipartite Kneser graphs (see Definition 1.6) are reflective and use this to deduce Theorem 1.7.
Lemma 2.19. For any
![]() $1\leq \ell <k/2$
, the graph
$1\leq \ell <k/2$
, the graph
![]() $H_{\ell ,k}$
from Definition 1.6 is reflective.
$H_{\ell ,k}$
from Definition 1.6 is reflective.
Proof. By the symmetry of the two parts of
![]() $H_{\ell ,k}$
, it suffices to prove that if
$H_{\ell ,k}$
, it suffices to prove that if
![]() $R\subset [k]^{(\ell )}$
is a set of size two, then there exists a sequence of symmetric triples
$R\subset [k]^{(\ell )}$
is a set of size two, then there exists a sequence of symmetric triples
![]() $(A_j,B_j,\phi _j)$
for
$(A_j,B_j,\phi _j)$
for
![]() $j=0,1,\dots ,m-1$
and intersecting sets
$j=0,1,\dots ,m-1$
and intersecting sets
![]() $R_j$
for
$R_j$
for
![]() $(A_j,B_j,\phi _j)$
such that
$(A_j,B_j,\phi _j)$
such that
![]() $R_0=R$
,
$R_0=R$
,
![]() $R_m=[k]^{(\ell )}$
and
$R_m=[k]^{(\ell )}$
and
![]() $R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
$R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
![]() $0\leq j\leq m-1$
.
$0\leq j\leq m-1$
.
We first prove this for sets of the form
![]() $R=\{S,T\}$
, where
$R=\{S,T\}$
, where
![]() $|S\Delta T|=1$
. Without loss of generality, we may assume that
$|S\Delta T|=1$
. Without loss of generality, we may assume that
![]() $S=[\ell ]$
and
$S=[\ell ]$
and
![]() $T=[\ell -1]\cup \{\ell +1\}$
.
$T=[\ell -1]\cup \{\ell +1\}$
.
For each
![]() $1\leq i<j\leq k$
, let
$1\leq i<j\leq k$
, let
and let
Let
![]() $\varphi _{i,j}$
be the automorphism of
$\varphi _{i,j}$
be the automorphism of
![]() $H_{\ell ,k}$
that swaps i and j, that is, which is defined as
$H_{\ell ,k}$
that swaps i and j, that is, which is defined as
 $$ \begin{align*}\varphi_{i,j}(P)= \begin{cases} (P\cup \{j\})\setminus \{i\} \text{ if } P\in C_{i,j} \\ (P\cup \{i\})\setminus \{j\} \text{ if } P\in D_{i,j} \\ P \text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\varphi_{i,j}(P)= \begin{cases} (P\cup \{j\})\setminus \{i\} \text{ if } P\in C_{i,j} \\ (P\cup \{i\})\setminus \{j\} \text{ if } P\in D_{i,j} \\ P \text{ otherwise.} \end{cases} \end{align*} $$
Note that
![]() $(C_{i,j},D_{i,j},\varphi _{i,j})$
is a symmetric triple. Define the following sequence:
$(C_{i,j},D_{i,j},\varphi _{i,j})$
is a symmetric triple. Define the following sequence:
![]() $\phi _0=\varphi _{\ell ,\ell +1}$
,
$\phi _0=\varphi _{\ell ,\ell +1}$
,
![]() $\phi _1=\varphi _{\ell ,\ell +2}$
, …,
$\phi _1=\varphi _{\ell ,\ell +2}$
, …,
![]() $\phi _{k-\ell -1}=\varphi _{\ell ,k}$
,
$\phi _{k-\ell -1}=\varphi _{\ell ,k}$
,
![]() $\phi _{k-\ell }=\varphi _{\ell -1,\ell }$
,
$\phi _{k-\ell }=\varphi _{\ell -1,\ell }$
,
![]() $\phi _{k-\ell +1}=\varphi _{\ell -1,\ell +1}$
, …,
$\phi _{k-\ell +1}=\varphi _{\ell -1,\ell +1}$
, …,
![]() $\phi _{2k-2\ell }=\varphi _{\ell -1,k}$
,
$\phi _{2k-2\ell }=\varphi _{\ell -1,k}$
,
![]() $\phi _{2k-2\ell +1}=\varphi _{\ell -2,\ell -1}$
,
$\phi _{2k-2\ell +1}=\varphi _{\ell -2,\ell -1}$
,
![]() $\phi _{2k-2\ell +2}=\varphi _{\ell -2,\ell }$
, …,
$\phi _{2k-2\ell +2}=\varphi _{\ell -2,\ell }$
, …,
![]() $\phi _{\binom {k}{2}-\binom {k-\ell }{2}-2}=\varphi _{1,k-1}$
,
$\phi _{\binom {k}{2}-\binom {k-\ell }{2}-2}=\varphi _{1,k-1}$
,
![]() $\phi _{\binom {k}{2}-\binom {k-\ell }{2}-1}=\varphi _{1,k}$
. Similarly, for
$\phi _{\binom {k}{2}-\binom {k-\ell }{2}-1}=\varphi _{1,k}$
. Similarly, for
![]() $0\leq t\leq \binom {k}{2}-\binom {k-\ell }{2}-1$
, let
$0\leq t\leq \binom {k}{2}-\binom {k-\ell }{2}-1$
, let
![]() $A_t=C_{i,j}$
and
$A_t=C_{i,j}$
and
![]() $B_t=D_{i,j}$
for those
$B_t=D_{i,j}$
for those
![]() $i,j$
with
$i,j$
with
![]() $\phi _t=\varphi _{i,j}$
.
$\phi _t=\varphi _{i,j}$
.
Now, for all
![]() $0\leq t\leq \binom {k}{2}-\binom {k-\ell }{2}-1$
, let
$0\leq t\leq \binom {k}{2}-\binom {k-\ell }{2}-1$
, let
![]() $R_{t+1}=\psi _{A_t,B_t,\phi _t}(R_t)$
.
$R_{t+1}=\psi _{A_t,B_t,\phi _t}(R_t)$
.
Claim. Let
![]() $0\leq t\leq \binom {k}{2}-\binom {k-\ell }{2}-1$
. Assume that
$0\leq t\leq \binom {k}{2}-\binom {k-\ell }{2}-1$
. Assume that
![]() $\phi _t=\varphi _{i,j}$
. Then
$\phi _t=\varphi _{i,j}$
. Then
Proof of Claim. We use induction on t. For
![]() $t=0$
, note that
$t=0$
, note that
![]() $(i,j)=(\ell ,\ell +1)$
and
$(i,j)=(\ell ,\ell +1)$
and
Assume now that we have already proved that for some t with
![]() $\phi _t=\varphi _{i,j}$
, we have
$\phi _t=\varphi _{i,j}$
, we have
There are two cases. The first case is where
![]() $j=k$
. Then
$j=k$
. Then
![]() $\phi _{t+1}=\varphi _{i-1,i}$
. Let
$\phi _{t+1}=\varphi _{i-1,i}$
. Let
![]() $P\in [k]^{(\ell )}$
satisfy
$P\in [k]^{(\ell )}$
satisfy
![]() $P\supset [i-2]$
and
$P\supset [i-2]$
and
![]() $P\cap \{i-1,i\}\neq \emptyset $
.
$P\cap \{i-1,i\}\neq \emptyset $
.
If
![]() $P\in D_{i-1,i}=B_{t+1}$
, then
$P\in D_{i-1,i}=B_{t+1}$
, then
![]() $\varphi _{i-1,i}(P)\supset [i-1]$
, so
$\varphi _{i-1,i}(P)\supset [i-1]$
, so
![]() $\varphi _{i-1,i}(P)\in R_{t+1}$
. Also,
$\varphi _{i-1,i}(P)\in R_{t+1}$
. Also,
![]() $\varphi _{i-1,i}(P)\in C_{i-1,i}=A_{t+1}$
, so
$\varphi _{i-1,i}(P)\in C_{i-1,i}=A_{t+1}$
, so
![]() $\varphi _{i-1,i}(P)\in R_{t+1}\cap A_{t+1}$
, which implies that
$\varphi _{i-1,i}(P)\in R_{t+1}\cap A_{t+1}$
, which implies that
![]() $P\in \varphi _{i-1,i}(R_{t+1}\cap A_{t+1})$
as
$P\in \varphi _{i-1,i}(R_{t+1}\cap A_{t+1})$
as
![]() $\varphi _{i-1,i}$
is an involution.
$\varphi _{i-1,i}$
is an involution.
Else (i.e., if
![]() $P\not \in D_{i-1,i}$
)
$P\not \in D_{i-1,i}$
)
![]() $P\supset [i-1]$
, so
$P\supset [i-1]$
, so
![]() $P\in R_{t+1}\cap (A_{t+1}\cup F_{\phi _{t+1}})$
. Hence, in both cases,
$P\in R_{t+1}\cap (A_{t+1}\cup F_{\phi _{t+1}})$
. Hence, in both cases,
![]() $P\in \psi _{A_{t+1},B_{t+1},\phi _{t+1}}(R_{t+1})=R_{t+2}$
. Thus,
$P\in \psi _{A_{t+1},B_{t+1},\phi _{t+1}}(R_{t+1})=R_{t+2}$
. Thus,
completing the induction step.
The second case is where
![]() $j\neq k$
. Then
$j\neq k$
. Then
![]() $\phi _{t+1}=\varphi _{i,j+1}$
. Let
$\phi _{t+1}=\varphi _{i,j+1}$
. Let
![]() $P\in [k]^{(\ell )}$
satisfy
$P\in [k]^{(\ell )}$
satisfy
![]() $P\supset [i-1]$
and
$P\supset [i-1]$
and
![]() $P\cap \{i,i+1,\dots ,j+1\}\neq \emptyset $
. If
$P\cap \{i,i+1,\dots ,j+1\}\neq \emptyset $
. If
![]() $P\in D_{i,j+1}=B_{t+1}$
, then
$P\in D_{i,j+1}=B_{t+1}$
, then
![]() $\varphi _{i,j+1}(P)\supset [i]$
, so
$\varphi _{i,j+1}(P)\supset [i]$
, so
![]() $\varphi _{i,j+1}(P)\in R_{t+1}$
. Else,
$\varphi _{i,j+1}(P)\in R_{t+1}$
. Else,
![]() $P\cap \{i,i+1,\dots ,j\}\neq \emptyset $
, so
$P\cap \{i,i+1,\dots ,j\}\neq \emptyset $
, so
![]() $P\in R_{t+1}$
. Hence, in both cases,
$P\in R_{t+1}$
. Hence, in both cases,
![]() $P\in \psi _{A_{t+1},B_{t+1},\phi _{t+1}}(R_{t+1})=R_{t+2}$
. Thus,
$P\in \psi _{A_{t+1},B_{t+1},\phi _{t+1}}(R_{t+1})=R_{t+2}$
. Thus,
completing the induction step and the proof of the claim.
By the claim, for
![]() $m=\binom {k}{2}-\binom {k-\ell }{2}$
, we have
$m=\binom {k}{2}-\binom {k-\ell }{2}$
, we have
![]() $R_m=[k]^{(\ell )}$
, so it remains to show that for each t,
$R_m=[k]^{(\ell )}$
, so it remains to show that for each t,
![]() $R_t$
is intersecting for
$R_t$
is intersecting for
![]() $(A_t,B_t,\phi _t)$
. This is clear for
$(A_t,B_t,\phi _t)$
. This is clear for
![]() $t=0$
, so let
$t=0$
, so let
![]() $t>0$
. Let
$t>0$
. Let
![]() $\phi _t=\varphi _{i,j}$
. Again, we consider two cases. If
$\phi _t=\varphi _{i,j}$
. Again, we consider two cases. If
![]() $i=\ell $
, then
$i=\ell $
, then
![]() $j\geq \ell +2$
and
$j\geq \ell +2$
and
![]() $\phi _{t-1}=\varphi _{\ell ,j-1}$
, so by the claim we have
$\phi _{t-1}=\varphi _{\ell ,j-1}$
, so by the claim we have
Hence,
![]() $[\ell -1]\cup \{\ell +1\}\in R_t$
, so
$[\ell -1]\cup \{\ell +1\}\in R_t$
, so
![]() $R_t\cap F_{\phi _t}\neq \emptyset $
. In particular,
$R_t\cap F_{\phi _t}\neq \emptyset $
. In particular,
![]() $R_t$
is intersecting for
$R_t$
is intersecting for
![]() $(A_t,B_t,\phi _t)$
. The other case is
$(A_t,B_t,\phi _t)$
. The other case is
![]() $i<\ell $
. In this case, either
$i<\ell $
. In this case, either
![]() $\phi _{t-1}=\varphi _{i',j'}$
for some
$\phi _{t-1}=\varphi _{i',j'}$
for some
![]() $i'<\ell $
, or
$i'<\ell $
, or
![]() $\phi _{t-1}=\varphi _{\ell ,k}$
. Either way, the claim implies that
$\phi _{t-1}=\varphi _{\ell ,k}$
. Either way, the claim implies that
Hence,
![]() $R_t$
has an element which contains both i and j, so
$R_t$
has an element which contains both i and j, so
![]() $R_t\cap F_{\phi _t}\neq \emptyset $
. In particular,
$R_t\cap F_{\phi _t}\neq \emptyset $
. In particular,
![]() $R_t$
is intersecting for
$R_t$
is intersecting for
![]() $(A_t,B_t,\phi _t)$
.
$(A_t,B_t,\phi _t)$
.
We have proved that if
![]() $R\subset [k]^{(\ell )}$
consists of two sets differing by one element, then there exists a sequence of symmetric triples
$R\subset [k]^{(\ell )}$
consists of two sets differing by one element, then there exists a sequence of symmetric triples
![]() $(A_j,B_j,\phi _j)$
for
$(A_j,B_j,\phi _j)$
for
![]() $j=0,1,\dots ,m-1$
and intersecting sets
$j=0,1,\dots ,m-1$
and intersecting sets
![]() $R_j$
for
$R_j$
for
![]() $(A_j,B_j,\phi _j)$
such that
$(A_j,B_j,\phi _j)$
such that
![]() $R_0=R$
,
$R_0=R$
,
![]() $R_m=[k]^{(\ell )}$
and
$R_m=[k]^{(\ell )}$
and
![]() $R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
$R_{j+1}=\psi _{A_j,B_j,\phi _j}(R_j)$
for all
![]() $0\leq j\leq m-1$
. To complete the proof, it suffices to prove that for any
$0\leq j\leq m-1$
. To complete the proof, it suffices to prove that for any
![]() $R\subset [k]^{(\ell )}$
of size two, there is a symmetric triple
$R\subset [k]^{(\ell )}$
of size two, there is a symmetric triple
![]() $(A,B,\phi )$
such that R is intersecting for
$(A,B,\phi )$
such that R is intersecting for
![]() $(A,B,\phi )$
and
$(A,B,\phi )$
and
![]() $\psi _{A,B,\phi }(R)$
contains two sets which differ by one element. Let
$\psi _{A,B,\phi }(R)$
contains two sets which differ by one element. Let
![]() $R=\{S,T\}$
. Let
$R=\{S,T\}$
. Let
![]() $i\in S\setminus T$
, and let
$i\in S\setminus T$
, and let
![]() $j\in [k]\setminus (S\cup T)$
(which exists since
$j\in [k]\setminus (S\cup T)$
(which exists since
![]() $|S\cup T|\leq 2\ell <k$
). Without loss of generality, let us assume that
$|S\cup T|\leq 2\ell <k$
). Without loss of generality, let us assume that
![]() $i<j$
. Now, let
$i<j$
. Now, let
![]() $\phi =\varphi _{i,j}$
,
$\phi =\varphi _{i,j}$
,
![]() $A=C_{i,j}$
and
$A=C_{i,j}$
and
![]() $B=D_{i,j}$
. Then
$B=D_{i,j}$
. Then
![]() $T\in F_{\phi }$
, so R is intersecting for
$T\in F_{\phi }$
, so R is intersecting for
![]() $(A,B,\phi )$
. Moreover,
$(A,B,\phi )$
. Moreover,
![]() $\psi _{A,B,\phi }(R)$
contains both S and
$\psi _{A,B,\phi }(R)$
contains both S and
![]() $\varphi _{i,j}(S)$
, so it contains two sets which differ by one element. This completes the proof.
$\varphi _{i,j}(S)$
, so it contains two sets which differ by one element. This completes the proof.
The other condition that we need to check for our Theorem 2.17 to apply is that
![]() $H_{\ell ,k}$
satisfies Sidorenko’s conjecture. This was proved by Conlon and Lee [Reference Conlon and Lee6, Theorem 1.1].
$H_{\ell ,k}$
satisfies Sidorenko’s conjecture. This was proved by Conlon and Lee [Reference Conlon and Lee6, Theorem 1.1].
Lemma 2.20 (Conlon–Lee [Reference Conlon and Lee6]).
For any
![]() $1\leq \ell <k/2$
, the graph
$1\leq \ell <k/2$
, the graph
![]() $H_{\ell ,k}$
from Definition 1.6 satisfies Sidorenko’s conjecture.
$H_{\ell ,k}$
from Definition 1.6 satisfies Sidorenko’s conjecture.
Notice that Theorem 1.7 follows from Theorem 2.17, Lemma 2.19 and Lemma 2.20.
3. Rainbow Turán number of cycles
In this section, we prove Theorems 1.8 and 1.9. As before, we establish certain inequalities between various homomorphism counts. However, we can no longer assume freely that the host graph is almost regular because it is too sparse for the regularization method to work. Instead, we introduce weights for our cycles and count these weighted homomorphic cycles.
Definition 3.1. Let k be a positive integer and let G be a graph. The weight of an edge
![]() $uv$
is defined to be
$uv$
is defined to be
Now, the weight of a walk
![]() $P=(u_0,u_1,\dots ,u_k)$
is defined to be the product of the weights of the edges in it, that is,
$P=(u_0,u_1,\dots ,u_k)$
is defined to be the product of the weights of the edges in it, that is,
 $$ \begin{align*}w(P)=\frac{1}{d_G(u_0)^{1/2}d_G(u_k)^{1/2}\prod_{i=1}^{k-1} d_G(u_i)}.\end{align*} $$
$$ \begin{align*}w(P)=\frac{1}{d_G(u_0)^{1/2}d_G(u_k)^{1/2}\prod_{i=1}^{k-1} d_G(u_i)}.\end{align*} $$
Similarly, the weight of a homomorphic cycle
![]() $C=(u_0,u_1,\dots ,u_{2k-1})$
is
$C=(u_0,u_1,\dots ,u_{2k-1})$
is
 $$ \begin{align*}w(C)=\frac{1}{\prod_{i=0}^{2k-1} d_G(u_i)}.\end{align*} $$
$$ \begin{align*}w(C)=\frac{1}{\prod_{i=0}^{2k-1} d_G(u_i)}.\end{align*} $$
Finally, let
![]() $h_{2k}$
be the sum of the weights of all homomorphic cycles of length
$h_{2k}$
be the sum of the weights of all homomorphic cycles of length
![]() $2k$
in G (here, a homomorphic cycle of length
$2k$
in G (here, a homomorphic cycle of length
![]() $2$
is just an edge with labelled endpoints).
$2$
is just an edge with labelled endpoints).
The next lemma can be viewed as a weighted variant of Sidorenko’s conjecture for even cycles.
Lemma 3.2. For any graph G and any positive integer k, we have
![]() $h_{2k}\geq 1$
.
$h_{2k}\geq 1$
.
Proof. Let A be the matrix whose rows and columns are labelled by
![]() $V(G)$
and which has entries
$V(G)$
and which has entries
 $$ \begin{align*}A_{u,v}= \begin{cases} w(uv)=\frac{1}{d_G(u)^{1/2}d_G(v)^{1/2}} &\text{ if } uv\in E(G) \\ 0 &\text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}A_{u,v}= \begin{cases} w(uv)=\frac{1}{d_G(u)^{1/2}d_G(v)^{1/2}} &\text{ if } uv\in E(G) \\ 0 &\text{ otherwise.} \end{cases} \end{align*} $$
Observe that
![]() $h_{2k}=\mathrm {tr}(A^{2k})$
. Let
$h_{2k}=\mathrm {tr}(A^{2k})$
. Let
![]() $\textbf {x}\in \mathbb {R}^{V(G)}$
be the vector with
$\textbf {x}\in \mathbb {R}^{V(G)}$
be the vector with
![]() $\textbf {x}_u=d_G(u)^{1/2}$
. Then
$\textbf {x}_u=d_G(u)^{1/2}$
. Then
 $$ \begin{align*}(A\textbf{x})_u=\sum_{v\in V(G)} A_{uv}\textbf{x}_v=\sum_{v\in N_G(u)} \frac{1}{d_G(u)^{1/2}d_G(v)^{1/2}}d_G(v)^{1/2}=d_G(u)^{1/2}.\end{align*} $$
$$ \begin{align*}(A\textbf{x})_u=\sum_{v\in V(G)} A_{uv}\textbf{x}_v=\sum_{v\in N_G(u)} \frac{1}{d_G(u)^{1/2}d_G(v)^{1/2}}d_G(v)^{1/2}=d_G(u)^{1/2}.\end{align*} $$
Hence,
![]() $A\textbf {x}=\textbf {x}$
, so
$A\textbf {x}=\textbf {x}$
, so
![]() $1$
is an eigenvalue of A. Writing
$1$
is an eigenvalue of A. Writing
![]() $\lambda _1,\dots ,\lambda _n$
for the eigenvalues of A (which are real numbers since A is a symmetric matrix), we obtain
$\lambda _1,\dots ,\lambda _n$
for the eigenvalues of A (which are real numbers since A is a symmetric matrix), we obtain
![]() $\mathrm {tr}(A^{2k})=\sum _{i=1}^n \lambda _i^{2k}\geq 1$
, completing the proof.
$\mathrm {tr}(A^{2k})=\sum _{i=1}^n \lambda _i^{2k}\geq 1$
, completing the proof.
An interpretation of Lemma 3.2 is that if we choose a vertex uniformly at random in an n-vertex graph and start a random walk (choosing each neighbour with the same probability), then the probability of ending up at the starting vertex after
![]() $2k$
steps is at least
$2k$
steps is at least
![]() $1/n$
. Results from which this follows already exist in the literature on random walks (see, e.g., Proposition 10.25 in [Reference Levin and Peres22]), but since our proof is very short, we included it for the sake of completeness. There is another related result in [Reference Alon and Spencer3] (see the “Probabilistic lens: Random walks”). There it is shown, using the Cauchy–Schwarz inequality, that under the extra assumption that the graph is vertex-transitive, for any two vertices u and v, the probability that a random walk of length
$1/n$
. Results from which this follows already exist in the literature on random walks (see, e.g., Proposition 10.25 in [Reference Levin and Peres22]), but since our proof is very short, we included it for the sake of completeness. There is another related result in [Reference Alon and Spencer3] (see the “Probabilistic lens: Random walks”). There it is shown, using the Cauchy–Schwarz inequality, that under the extra assumption that the graph is vertex-transitive, for any two vertices u and v, the probability that a random walk of length
![]() $2k$
starting from u ends at u is at least as large as the probability that it ends at v.
$2k$
starting from u ends at u is at least as large as the probability that it ends at v.
In what follows, indices are considered modulo
![]() $2k$
, for example,
$2k$
, for example,
![]() $u_{2k}=u_0$
.
$u_{2k}=u_0$
.
Definition 3.3. Given a graph G with an edge-colouring
![]() $c:E(G)\rightarrow \mathcal {C}$
and positive integers
$c:E(G)\rightarrow \mathcal {C}$
and positive integers
![]() $i,j,k$
, let
$i,j,k$
, let
![]() $h_{2k}(i,j)$
be the sum of the weights of homomorphic
$h_{2k}(i,j)$
be the sum of the weights of homomorphic
![]() $2k$
-cycles
$2k$
-cycles
![]() $(u_0,u_1,\dots ,u_{2k-1})$
with
$(u_0,u_1,\dots ,u_{2k-1})$
with
![]() $c(u_{i-1}u_i)=c(u_{j-1}u_j)$
.
$c(u_{i-1}u_i)=c(u_{j-1}u_j)$
.
The key lemma is as follows.
Lemma 3.4. For any
![]() $1\leq \ell \leq k$
, we have
$1\leq \ell \leq k$
, we have
![]() $h_{2k}(\ell ,2k)^2\leq h_{2k}(1,2k)h_{2k}(\ell ,2k+1-\ell )$
.
$h_{2k}(\ell ,2k)^2\leq h_{2k}(1,2k)h_{2k}(\ell ,2k+1-\ell )$
.
Proof. For any
![]() $u_0,u_k\in V(G)$
and
$u_0,u_k\in V(G)$
and
![]() $R\in \mathcal {C}$
, let
$R\in \mathcal {C}$
, let
![]() $\alpha (u_0,u_k,R)$
be the sum of the weights of all walks
$\alpha (u_0,u_k,R)$
be the sum of the weights of all walks
![]() $(u_0,u_1,\dots ,u_k)$
in G with
$(u_0,u_1,\dots ,u_k)$
in G with
![]() $c(u_{\ell -1},u_{\ell })=R$
. Moreover, let
$c(u_{\ell -1},u_{\ell })=R$
. Moreover, let
![]() $\beta (u_0,u_k,R)$
be the sum of the weights of all walks
$\beta (u_0,u_k,R)$
be the sum of the weights of all walks
![]() $(u_0,u_1,\dots ,u_k)$
in G with
$(u_0,u_1,\dots ,u_k)$
in G with
![]() $c(u_0,u_1)=R$
. Note that
$c(u_0,u_1)=R$
. Note that
 $$ \begin{align*}h_{2k}(\ell,2k)&=\sum_{u_0,u_k\in V(G), R\in \mathcal{C}} \alpha(u_0,u_k,R)\beta(u_0,u_k,R),\\h_{2k}(1,2k)&=\sum_{u_0,u_k\in V(G), R\in \mathcal{C}} \beta(u_0,u_k,R)^2 \end{align*} $$
$$ \begin{align*}h_{2k}(\ell,2k)&=\sum_{u_0,u_k\in V(G), R\in \mathcal{C}} \alpha(u_0,u_k,R)\beta(u_0,u_k,R),\\h_{2k}(1,2k)&=\sum_{u_0,u_k\in V(G), R\in \mathcal{C}} \beta(u_0,u_k,R)^2 \end{align*} $$
and
 $$ \begin{align*}h_{2k}(\ell,2k+1-\ell)=\sum_{u_0,u_k\in V(G), R\in \mathcal{C}} \alpha(u_0,u_k,R)^2.\end{align*} $$
$$ \begin{align*}h_{2k}(\ell,2k+1-\ell)=\sum_{u_0,u_k\in V(G), R\in \mathcal{C}} \alpha(u_0,u_k,R)^2.\end{align*} $$
Hence, the statement of the lemma follows from the Cauchy–Schwarz inequality.
Lemma 3.5. We have
![]() $h_{2k}(1,2k)=\max _{1\leq i<j\leq 2k} h_{2k}(i,j)$
.
$h_{2k}(1,2k)=\max _{1\leq i<j\leq 2k} h_{2k}(i,j)$
.
Proof. Choose
![]() $1\leq i'<j'\leq 2k$
such that
$1\leq i'<j'\leq 2k$
such that
![]() $h_{2k}(i',j')=\max _{1\leq i<j\leq 2k} h_{2k}(i,j)$
. Trivially, we have
$h_{2k}(i',j')=\max _{1\leq i<j\leq 2k} h_{2k}(i,j)$
. Trivially, we have
![]() $h_{2k}(i',j')=h_{2k}(i'+t,j'+t)$
for every positive integer t (here, as before, indices are considered modulo
$h_{2k}(i',j')=h_{2k}(i'+t,j'+t)$
for every positive integer t (here, as before, indices are considered modulo
![]() $2k$
). Hence, there is some
$2k$
). Hence, there is some
![]() $1\leq \ell \leq k$
such that
$1\leq \ell \leq k$
such that
![]() $h_{2k}(\ell ,2k)=h_{2k}(i',j')=\max _{1\leq i<j\leq 2k} h_{2k}(i,j)$
.
$h_{2k}(\ell ,2k)=h_{2k}(i',j')=\max _{1\leq i<j\leq 2k} h_{2k}(i,j)$
.
Now, by Lemma 3.4, we have
Hence,
as desired.
Lemma 3.6. For any properly edge-coloured graph G with
![]() $\delta (G)>0$
and integer
$\delta (G)>0$
and integer
![]() $k\geq 2$
, we have
$k\geq 2$
, we have
Proof. Let
![]() $C=(u_0,u_1,\dots ,u_{2k-1})$
be a homomorphic
$C=(u_0,u_1,\dots ,u_{2k-1})$
be a homomorphic
![]() $2k$
-cycle in G with the property that
$2k$
-cycle in G with the property that
![]() $c(u_0 u_1)=c(u_{2k-1} u_0)$
. Since c is a proper colouring, we have
$c(u_0 u_1)=c(u_{2k-1} u_0)$
. Since c is a proper colouring, we have
![]() $u_1=u_{2k-1}$
. This means that
$u_1=u_{2k-1}$
. This means that
![]() $C'=(u_1,u_2,\dots ,u_{2k-2})$
is a homomorphic
$C'=(u_1,u_2,\dots ,u_{2k-2})$
is a homomorphic
![]() $(2k-2)$
-cycle. Note that
$(2k-2)$
-cycle. Note that
![]() $w(C)=\frac {w(C')}{d_G(u_0)d_G(u_1)}\leq \frac {w(C')}{\delta (G)d_G(u_1)}$
. Furthermore, any homomorphic
$w(C)=\frac {w(C')}{d_G(u_0)d_G(u_1)}\leq \frac {w(C')}{\delta (G)d_G(u_1)}$
. Furthermore, any homomorphic
![]() $(2k-2)$
-cycle
$(2k-2)$
-cycle
![]() $(u_1,\dots ,u_{2k-1})$
arises as
$(u_1,\dots ,u_{2k-1})$
arises as
![]() $C'$
for precisely
$C'$
for precisely
![]() $d_G(u_1)$
choices of C. The desired inequality follows.
$d_G(u_1)$
choices of C. The desired inequality follows.
Lemma 3.7. Let G be a properly edge-coloured graph with
![]() $\delta (G)>0$
, and let
$\delta (G)>0$
, and let
![]() $k\geq 2$
be an integer. If G has no rainbow cycle, then
$k\geq 2$
be an integer. If G has no rainbow cycle, then
![]() $h_{2k}\leq \frac {2k^2}{\delta (G)} h_{2k-2}$
.
$h_{2k}\leq \frac {2k^2}{\delta (G)} h_{2k-2}$
.
Proof. Since G has no rainbow cycle, we have
 $$ \begin{align*}h_{2k}\leq \sum_{1\leq i<j\leq 2k} h_{2k}(i,j).\end{align*} $$
$$ \begin{align*}h_{2k}\leq \sum_{1\leq i<j\leq 2k} h_{2k}(i,j).\end{align*} $$
Using Lemmas 3.5 and 3.6, we have
 $$ \begin{align*}\sum_{1\leq i<j\leq 2k} h_{2k}(i,j)\leq \binom{2k}{2}h_{2k}(1,2k)\leq \binom{2k}{2}\frac{h_{2k-2}}{\delta(G)},\end{align*} $$
$$ \begin{align*}\sum_{1\leq i<j\leq 2k} h_{2k}(i,j)\leq \binom{2k}{2}h_{2k}(1,2k)\leq \binom{2k}{2}\frac{h_{2k-2}}{\delta(G)},\end{align*} $$
which implies that the desired inequality.
Corollary 3.8. Let G be an n-vertex properly edge-coloured graph with
![]() $\delta (G)>0$
, and let
$\delta (G)>0$
, and let
![]() $k\geq 2$
be an integer. If G has no rainbow cycle, then
$k\geq 2$
be an integer. If G has no rainbow cycle, then
![]() $h_{2k}\leq (\frac {2k^2}{\delta (G)})^k n$
.
$h_{2k}\leq (\frac {2k^2}{\delta (G)})^k n$
.
Proof. By repeated applications of Lemma 3.7, we obtain
![]() $h_{2k}\leq \frac {2^{k-1}(k!)^2}{\delta (G)^{k-1}}h_2$
. Furthermore,
$h_{2k}\leq \frac {2^{k-1}(k!)^2}{\delta (G)^{k-1}}h_2$
. Furthermore,
 $$ \begin{align*}h_2=\sum_{u,v\in V(G): uv\in E(G)} \frac{1}{d_G(u)d_G(v)}\leq \frac{1}{\delta(G)}\sum_{u,v\in V(G): uv\in E(G)} \frac{1}{d_G(u)}=\frac{1}{\delta(G)}\sum_{u\in V(G)} 1=\frac{n}{\delta(G)},\end{align*} $$
$$ \begin{align*}h_2=\sum_{u,v\in V(G): uv\in E(G)} \frac{1}{d_G(u)d_G(v)}\leq \frac{1}{\delta(G)}\sum_{u,v\in V(G): uv\in E(G)} \frac{1}{d_G(u)}=\frac{1}{\delta(G)}\sum_{u\in V(G)} 1=\frac{n}{\delta(G)},\end{align*} $$
which implies the result.
Proof of Theorem 1.8.
Let n be sufficiently large, and let G be a properly edge-coloured n-vertex graph with at least
![]() $8n(\log n)^2$
edges. Then G has a nonempty subgraph
$8n(\log n)^2$
edges. Then G has a nonempty subgraph
![]() $G'$
with
$G'$
with
![]() $\delta (G')\geq 8(\log n)^2$
.
$\delta (G')\geq 8(\log n)^2$
.
Assume, for contradiction that
![]() $G'$
has no rainbow cycle. Let
$G'$
has no rainbow cycle. Let
![]() $k=\lceil \log n\rceil $
. Writing
$k=\lceil \log n\rceil $
. Writing
![]() $h_{2k}$
for the total weight of the homomorphic
$h_{2k}$
for the total weight of the homomorphic
![]() $2k$
-cycles in
$2k$
-cycles in
![]() $G'$
(rather than G), Lemma 3.2 and Corollary 3.8 imply that
$G'$
(rather than G), Lemma 3.2 and Corollary 3.8 imply that
 $$ \begin{align*}1\leq h_{2k}\leq \left(\frac{2k^2}{\delta(G')}\right)^k |V(G')|\leq \left(\frac{2k^2}{\delta(G')}\right)^k n\leq 3^{-k}n<1,\end{align*} $$
$$ \begin{align*}1\leq h_{2k}\leq \left(\frac{2k^2}{\delta(G')}\right)^k |V(G')|\leq \left(\frac{2k^2}{\delta(G')}\right)^k n\leq 3^{-k}n<1,\end{align*} $$
which is a contradiction.
It remains to prove Theorem 1.9. The proof uses suitable variants of Lemma 3.7 and Corollary 3.8. For these variants, we will need the following simple lemma.
Lemma 3.9. Let
![]() $0<\varepsilon <1/2$
and let G be an edge-coloured graph in which for every k, every cycle of length k has at most
$0<\varepsilon <1/2$
and let G be an edge-coloured graph in which for every k, every cycle of length k has at most
![]() $(1-\varepsilon )k$
different colours. Then for every k, every homomorphic k-cycle has at most
$(1-\varepsilon )k$
different colours. Then for every k, every homomorphic k-cycle has at most
![]() $(1-\varepsilon )k$
different colours.
$(1-\varepsilon )k$
different colours.
Proof. We prove by induction on k that every homomorphic k-cycle has at most
![]() $(1-\varepsilon )k$
different colours. The statement is clear for
$(1-\varepsilon )k$
different colours. The statement is clear for
![]() $k=2$
since a homomorphic
$k=2$
since a homomorphic
![]() $2$
-cycle has only one colour. Now, let
$2$
-cycle has only one colour. Now, let
![]() $k>2$
and let C be a homomorphic cycle of length k in G. If C is a genuine cycle, then it follows from the assumptions that it has at most
$k>2$
and let C be a homomorphic cycle of length k in G. If C is a genuine cycle, then it follows from the assumptions that it has at most
![]() $(1-\varepsilon )k$
different colours. Else, we can write C as the concatenation of nontrivial homomorphic cycles
$(1-\varepsilon )k$
different colours. Else, we can write C as the concatenation of nontrivial homomorphic cycles
![]() $C_1$
and
$C_1$
and
![]() $C_2$
. Writing
$C_2$
. Writing
![]() $\ell $
and
$\ell $
and
![]() $k-\ell $
for the length of these homomorphic cycles, the induction hypothesis implies that
$k-\ell $
for the length of these homomorphic cycles, the induction hypothesis implies that
![]() $C_1$
has at most
$C_1$
has at most
![]() $(1-\varepsilon )\ell $
different colours and
$(1-\varepsilon )\ell $
different colours and
![]() $C_2$
has at most
$C_2$
has at most
![]() $(1-\varepsilon )(k-\ell )$
different colours. It follows that C has at most
$(1-\varepsilon )(k-\ell )$
different colours. It follows that C has at most
![]() $(1-\varepsilon )k$
different colours, completing the induction step.
$(1-\varepsilon )k$
different colours, completing the induction step.
We can now state and prove the variant of Lemma 3.7.
Lemma 3.10. Let G be a properly edge-coloured graph with
![]() $\delta (G)>0$
, let
$\delta (G)>0$
, let
![]() $0<\varepsilon <1/2$
and let
$0<\varepsilon <1/2$
and let
![]() $k\geq 2$
be an integer. If for every
$k\geq 2$
be an integer. If for every
![]() $\ell $
, G has no cycle of length
$\ell $
, G has no cycle of length
![]() $\ell $
with more than
$\ell $
with more than
![]() $(1-\varepsilon )\ell $
different colours, then
$(1-\varepsilon )\ell $
different colours, then
![]() $h_{2k}\leq \frac {k}{\varepsilon \delta (G)} h_{2k-2}$
.
$h_{2k}\leq \frac {k}{\varepsilon \delta (G)} h_{2k-2}$
.
Proof. By Lemma 3.9, every homomorphic cycle of length
![]() $2k$
has at most
$2k$
has at most
![]() $(1-\varepsilon )2k$
different colours. Hence, any such cycle ‘contributes’ to
$(1-\varepsilon )2k$
different colours. Hence, any such cycle ‘contributes’ to
![]() $h_{2k}(i,j)$
for at least
$h_{2k}(i,j)$
for at least
![]() $\varepsilon \cdot 2k$
pairs
$\varepsilon \cdot 2k$
pairs
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leq i<j\leq 2k$
. Thus,
$1\leq i<j\leq 2k$
. Thus,
 $$ \begin{align*}2\varepsilon k h_{2k}\leq \sum_{1\leq i<j\leq 2k} h_{2k}(i,j).\end{align*} $$
$$ \begin{align*}2\varepsilon k h_{2k}\leq \sum_{1\leq i<j\leq 2k} h_{2k}(i,j).\end{align*} $$
The variant of Corollary 3.8 is as follows.
Corollary 3.11. Let G be an n-vertex properly edge-coloured graph with
![]() $\delta (G)>0$
, let
$\delta (G)>0$
, let
![]() $0<\varepsilon <1/2$
and let
$0<\varepsilon <1/2$
and let
![]() $k\geq 2$
be an integer. If for every
$k\geq 2$
be an integer. If for every
![]() $\ell $
, G has no cycle of length
$\ell $
, G has no cycle of length
![]() $\ell $
with more than
$\ell $
with more than
![]() $(1-\varepsilon )\ell $
different colours, then
$(1-\varepsilon )\ell $
different colours, then
![]() $h_{2k}\leq (\frac {k}{\varepsilon \delta (G)})^k n$
.
$h_{2k}\leq (\frac {k}{\varepsilon \delta (G)})^k n$
.
Proof. By repeated applications of Lemma 3.10, we obtain
![]() $h_{2k}\leq \frac {k!}{(\varepsilon \delta (G))^{k-1}}h_2$
. As we have seen in the proof of Corollary 3.8,
$h_{2k}\leq \frac {k!}{(\varepsilon \delta (G))^{k-1}}h_2$
. As we have seen in the proof of Corollary 3.8,
![]() $h_2\leq \frac {n}{\delta (G)}$
, which implies the result.
$h_2\leq \frac {n}{\delta (G)}$
, which implies the result.
Proof of Theorem 1.9.
Let n be sufficiently large, let
![]() $0<\varepsilon <1/2$
and let G be a properly edge-coloured n-vertex graph with at least
$0<\varepsilon <1/2$
and let G be a properly edge-coloured n-vertex graph with at least
![]() $\frac {4}{\varepsilon }n\log n$
edges. Then G has a nonempty subgraph
$\frac {4}{\varepsilon }n\log n$
edges. Then G has a nonempty subgraph
![]() $G'$
with
$G'$
with
![]() $\delta (G')\geq \frac {4}{\varepsilon }\log n$
.
$\delta (G')\geq \frac {4}{\varepsilon }\log n$
.
Assume, for contradiction, that for every
![]() $\ell $
,
$\ell $
,
![]() $G'$
has no cycle of length
$G'$
has no cycle of length
![]() $\ell $
with more than
$\ell $
with more than
![]() $(1-\varepsilon )\ell $
different colours. Let
$(1-\varepsilon )\ell $
different colours. Let
![]() $k=\lceil \log n\rceil $
. Writing
$k=\lceil \log n\rceil $
. Writing
![]() $h_{2k}$
for the total weight of the homomorphic
$h_{2k}$
for the total weight of the homomorphic
![]() $2k$
-cycles in
$2k$
-cycles in
![]() $G'$
(rather than G), Lemma 3.2 and Corollary 3.11 imply that
$G'$
(rather than G), Lemma 3.2 and Corollary 3.11 imply that
 $$ \begin{align*}1\leq h_{2k}\leq \left(\frac{k}{\varepsilon\delta(G')}\right)^k |V(G')|\leq \left(\frac{k}{\varepsilon\delta(G')}\right)^k n\leq 3^{-k}n<1,\end{align*} $$
$$ \begin{align*}1\leq h_{2k}\leq \left(\frac{k}{\varepsilon\delta(G')}\right)^k |V(G')|\leq \left(\frac{k}{\varepsilon\delta(G')}\right)^k n\leq 3^{-k}n<1,\end{align*} $$
which is a contradiction.
4. Concluding remarks
In this paper, we proved the first power improvement over the dependent random choice bound for
![]() $\mathrm {ex}(n,Q_d)$
. When d is a power of two, such an improvement can be deduced from known results. Conlon and Lee [Reference Conlon and Lee7, Theorem 6.2] showed that their Conjecture 1.1 holds for subdivisions of d-partite d-uniform hypergraphs. Here, for a hypergraph
$\mathrm {ex}(n,Q_d)$
. When d is a power of two, such an improvement can be deduced from known results. Conlon and Lee [Reference Conlon and Lee7, Theorem 6.2] showed that their Conjecture 1.1 holds for subdivisions of d-partite d-uniform hypergraphs. Here, for a hypergraph
![]() $\mathcal {H}$
, the subdivision of
$\mathcal {H}$
, the subdivision of
![]() $\mathcal {H}$
is the bipartite graph whose parts are
$\mathcal {H}$
is the bipartite graph whose parts are
![]() $V(\mathcal {H})$
and
$V(\mathcal {H})$
and
![]() $E(\mathcal {H})$
and in which
$E(\mathcal {H})$
and in which
![]() $v\in V(\mathcal {H})$
is adjacent to
$v\in V(\mathcal {H})$
is adjacent to
![]() $e\in E(\mathcal {H})$
if
$e\in E(\mathcal {H})$
if
![]() $v\in e$
. It is not hard to see that
$v\in e$
. It is not hard to see that
![]() $Q_d$
is a subdivision of a d-partite d-uniform hypergraph if and only if d is a power of two. However, even for these values of d, the
$Q_d$
is a subdivision of a d-partite d-uniform hypergraph if and only if d is a power of two. However, even for these values of d, the
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $\mathrm {ex}(n,Q_d)=O(n^{2-1/d-\varepsilon })$
coming from their result is smaller than exponential in
$\mathrm {ex}(n,Q_d)=O(n^{2-1/d-\varepsilon })$
coming from their result is smaller than exponential in
![]() $-d$
, so much smaller than the one obtained in this paper. We remark that for a general value of d, the best known lower bound is
$-d$
, so much smaller than the one obtained in this paper. We remark that for a general value of d, the best known lower bound is
![]() $\mathrm {ex}(n,Q_d)=\Omega \Big (n^{2-\frac {2^d-2}{d2^{d-1}-1}}\Big )\geq \Omega (n^{2-2/d})$
, coming from the probabilistic deletion method.
$\mathrm {ex}(n,Q_d)=\Omega \Big (n^{2-\frac {2^d-2}{d2^{d-1}-1}}\Big )\geq \Omega (n^{2-2/d})$
, coming from the probabilistic deletion method.
We have already mentioned that our method resembles that of another paper of Conlon and Lee [Reference Conlon and Lee6] in which they prove Sidorenko’s conjecture for a certain class of graphs. The class of graphs their method applies to is similar to our ‘reflective’ graphs (see our Definition 2.12): Their graphs are also required to have many symmetric triples (see our Definition 2.7), and it is needed that a certain reflection sequence, similar to the one in our Definition 2.12, on the set of edges eventually covers the entire edge set. However, the two sequences are slightly different (theirs runs on edges and ours runs on vertices) and it is not true that every graph for which their proof verifies Sidorenko’s conjecture is reflective: For example, the
![]() $2$
-blowup of an even cycle of length at least six is not reflective, but their proof applies to it. Nevertheless, the similarity is close enough for it to make sense to look for further reflective graphs in their class of examples; indeed, this is how we chose the graphs from Definition 1.6. In this paper, we have decided not to pursue this direction further.
$2$
-blowup of an even cycle of length at least six is not reflective, but their proof applies to it. Nevertheless, the similarity is close enough for it to make sense to look for further reflective graphs in their class of examples; indeed, this is how we chose the graphs from Definition 1.6. In this paper, we have decided not to pursue this direction further.
It is worth mentioning that, building on Conlon and Lee’s work [Reference Conlon and Lee6], Coregliano [Reference Coregliano8] proved Sidorenko’s conjecture for a family of graphs extending the family considered by Conlon and Lee, by studying a sequence of reflections on vertices, similarly to our paper. However, the crucial condition in our Definition 2.7 that R intersects both
![]() $A\cup F_{\phi }$
and
$A\cup F_{\phi }$
and
![]() $B\cup F_{\phi }$
means that the family of graphs for which his result applies to and the family of our reflective graphs are not identical.
$B\cup F_{\phi }$
means that the family of graphs for which his result applies to and the family of our reflective graphs are not identical.
Note added.
After this paper was written, we learnt that Kim, Lee, Liu and Tran [Reference Kim, Lee, Liu and Tran21] independently showed that an n-vertex properly edge-coloured graph with at least
![]() $Cn(\log n)^2$
edges has a rainbow cycle (i.e., our Theorem 1.8). For regular graphs their proof is similar to ours, but they use a different approach to deal with degree irregularities.
$Cn(\log n)^2$
edges has a rainbow cycle (i.e., our Theorem 1.8). For regular graphs their proof is similar to ours, but they use a different approach to deal with degree irregularities.
Ten months after posting our paper, Alon, Bucić, Sauermann, Zakharov and Zamir [Reference Alon, Bucić, Sauermann, Zakharov and Zamir1] obtained an improved bound
![]() $O(n\log n\cdot \log \log n)$
for this problem.
$O(n\log n\cdot \log \log n)$
for this problem.
Acknowledgements
The first author is grateful to Cosmin Pohoata for bringing reference [Reference Liu23] to his attention and for useful discussions. We are also grateful to Noga Alon, Zach Hunter and the two referees for helpful comments.
Competing interests
The authors have no competing interest to declare.
Financial support
The research of the first author was supported by an ETH Zürich Postdoctoral Fellowship (grant number 20-1 FEL-35). The research of the second author was supported in part by an SNSF grant (grant number 200021_196965).