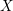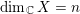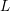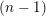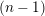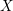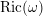1 Introduction
One of the most fundamental topics in algebraic geometry is the characterizing ampleness of line bundles by using numerical and cohomological vanishing theorems. The theorem of Cartan–Serre–Grothendieck is a milestone in this direction. The following statements are equivalent:
(i)
 $L$
is an ample line bundle over a projective manifold
$L$
is an ample line bundle over a projective manifold
 $X$
;
$X$
;(ii) for every coherent sheaf
 ${\mathcal{F}}$
on
${\mathcal{F}}$
on
 $X$
, there exists a positive integer
$X$
, there exists a positive integer
 $m_{0}=m_{0}(X,{\mathcal{F}},L)$
such that for all
$m_{0}=m_{0}(X,{\mathcal{F}},L)$
such that for all $$\begin{eqnarray}H^{i}(X,{\mathcal{F}}\otimes L^{\otimes m})=0\end{eqnarray}$$
$$\begin{eqnarray}H^{i}(X,{\mathcal{F}}\otimes L^{\otimes m})=0\end{eqnarray}$$
 $i>0$
and all
$i>0$
and all
 $m\geqslant m_{0}$
.
$m\geqslant m_{0}$
.
On complex projective manifolds, ampleness is also equivalent to the existence of a smooth metric with positive curvature, thanks to the celebrated Kodaira embedding theorem.
In [Reference Andreotti and GrauertAG62], Andreotti and Grauert considered the case of line bundles with curvature of mixed signature. Now it is formulated into the following definition.
Definition 1.1. Let
![]() $L$
be a holomorphic line bundle over a compact complex manifold
$L$
be a holomorphic line bundle over a compact complex manifold
![]() $X$
with
$X$
with
![]() $\dim _{\mathbb{C}}X=n$
.
$\dim _{\mathbb{C}}X=n$
.
(i)
 $L$
is called
$L$
is called
 $q$
-positive, if there exists a smooth Hermitian metric
$q$
-positive, if there exists a smooth Hermitian metric
 $h$
on
$h$
on
 $L$
such that the Chern curvature
$L$
such that the Chern curvature
 $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
has at least
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
has at least
 $(n-q)$
positive eigenvalues at every point on
$(n-q)$
positive eigenvalues at every point on
 $X$
.
$X$
.(ii)
 $L$
is called
$L$
is called
 $q$
-ample, if for any coherent sheaf
$q$
-ample, if for any coherent sheaf
 ${\mathcal{F}}$
on
${\mathcal{F}}$
on
 $X$
there exists a positive integer
$X$
there exists a positive integer
 $m_{0}=m_{0}(X,L,{\mathcal{F}})>0$
such that (1)
$m_{0}=m_{0}(X,L,{\mathcal{F}})>0$
such that (1) $$\begin{eqnarray}H^{i}(X,{\mathcal{F}}\otimes L^{m})=0\quad \text{for}~i>q,~m\geqslant m_{0}.\end{eqnarray}$$
$$\begin{eqnarray}H^{i}(X,{\mathcal{F}}\otimes L^{m})=0\quad \text{for}~i>q,~m\geqslant m_{0}.\end{eqnarray}$$
It is obvious that
![]() $L$
is
$L$
is
![]() $0$
-positive if and only if
$0$
-positive if and only if
![]() $L$
is positive, and
$L$
is positive, and
![]() $L$
is
$L$
is
![]() $0$
-ample if and only if
$0$
-ample if and only if
![]() $L$
is ample. Hence the
$L$
is ample. Hence the
![]() $0$
-positivity and
$0$
-positivity and
![]() $0$
-ampleness are equivalent. In [Reference Andreotti and GrauertAG62, Theorem 14], Andreotti and Grauert proved the following fundamental theorem (see also [Reference Demailly, Peternell and SchneiderDPS96, Proposition 2.1]).
$0$
-ampleness are equivalent. In [Reference Andreotti and GrauertAG62, Theorem 14], Andreotti and Grauert proved the following fundamental theorem (see also [Reference Demailly, Peternell and SchneiderDPS96, Proposition 2.1]).
Theorem 1.2 (Andreotti–Grauert).
A
![]() $q$
-positive line bundle is
$q$
-positive line bundle is
![]() $q$
-ample.
$q$
-ample.
Historically, the Andreotti–Grauert theorem is the first result on the relationship between (partially) positive line bundles and the cohomological vanishing theorems. In the pioneer work [Reference Demailly, Peternell and SchneiderDPS96], Demailly, Peternell and Schneider systematically investigated partial vanishing theorems and proposed the following problem on the converse to the Andreotti–Grauert theorem.
Problem 1.3. On a projective manifold, if a line bundle is
![]() $q$
-ample, is it
$q$
-ample, is it
![]() $q$
-positive?
$q$
-positive?
This is a long-standing open problem. The key difficulty arises from constructing a precise metric according to the formal partial vanishing theorem (1). Recently, there has been some progress on this problem, mainly contributed by Demailly, Totaro, Ottem, Küronya, Matsumura, Brown and so on (see [Reference DemaillyDem11, Reference TotaroTot13, Reference MatsumuraMat13, Reference OttemOtt12, Reference BrownBro12, Reference KüronyaKür13, Reference Greb and KüronyaGK15] and also the references therein). Totaro proved in [Reference TotaroTot13] that the notion of
![]() $q$
-ampleness is equivalent to others previously studied in [Reference Demailly, Peternell and SchneiderDPS96]. As a result, the
$q$
-ampleness is equivalent to others previously studied in [Reference Demailly, Peternell and SchneiderDPS96]. As a result, the
![]() $q$
-ampleness of a line bundle depends only on its numerical class, and the cone of such bundles is open. In particular, Totaro established that the
$q$
-ampleness of a line bundle depends only on its numerical class, and the cone of such bundles is open. In particular, Totaro established that the
![]() $(n-1)$
-ample cone of an
$(n-1)$
-ample cone of an
![]() $n$
-dimensional projective manifold
$n$
-dimensional projective manifold
![]() $X$
is equal to the negative of the complement of the pseudo-effective cone of
$X$
is equal to the negative of the complement of the pseudo-effective cone of
![]() $X$
(see also Corollary 1.6). In dimension two, Demailly proved in [Reference DemaillyDem11] an asymptotic version of this converse to the Andreotti–Grauert theorem using tools related to the holomorphic Morse inequality and asymptotic cohomology; subsequently, Matsumura obtained in [Reference MatsumuraMat13, Theorem 1.3] a positive answer to the question for projective surfaces. However, there exist higher-dimensional counter-examples to the converse Andreotti–Grauert problem in the range
$X$
(see also Corollary 1.6). In dimension two, Demailly proved in [Reference DemaillyDem11] an asymptotic version of this converse to the Andreotti–Grauert theorem using tools related to the holomorphic Morse inequality and asymptotic cohomology; subsequently, Matsumura obtained in [Reference MatsumuraMat13, Theorem 1.3] a positive answer to the question for projective surfaces. However, there exist higher-dimensional counter-examples to the converse Andreotti–Grauert problem in the range
![]() $(\dim X)/2\,-\,1<q<\dim X\,-\,2$
, constructed by Ottem [Reference OttemOtt12, Theorem 10.3]. Our main result in this paper is a partial converse to the Andreotti–Grauert theorem on smooth projective manifolds.
$(\dim X)/2\,-\,1<q<\dim X\,-\,2$
, constructed by Ottem [Reference OttemOtt12, Theorem 10.3]. Our main result in this paper is a partial converse to the Andreotti–Grauert theorem on smooth projective manifolds.
Theorem 1.4. Let
![]() $L$
be a line bundle over a smooth projective manifold
$L$
be a line bundle over a smooth projective manifold
![]() $X$
with
$X$
with
![]() $\dim _{\mathbb{C}}X=n$
. If
$\dim _{\mathbb{C}}X=n$
. If
![]() $L$
is
$L$
is
![]() $(n-1)$
-ample, then it is
$(n-1)$
-ample, then it is
![]() $(n-1)$
-positive.
$(n-1)$
-positive.
In particular, when
![]() $\dim _{\mathbb{C}}X=2$
, the converse Andreotti–Grauert problem 1.3 is true (see also [Reference MatsumuraMat13, Theorem 1.3]). Actually, Theorem 1.4 is a straightforward application of the following result on general compact complex manifolds.
$\dim _{\mathbb{C}}X=2$
, the converse Andreotti–Grauert problem 1.3 is true (see also [Reference MatsumuraMat13, Theorem 1.3]). Actually, Theorem 1.4 is a straightforward application of the following result on general compact complex manifolds.
Theorem 1.5. Let
![]() $X$
be a compact complex manifold with
$X$
be a compact complex manifold with
![]() $\dim _{\mathbb{C}}X=n$
. Then the following statements are equivalent:
$\dim _{\mathbb{C}}X=n$
. Then the following statements are equivalent:
(i)
 $L$
is
$L$
is
 $(n-1)$
-positive;
$(n-1)$
-positive;(ii) the dual line bundle
 $L^{-1}$
is not pseudo-effective.
$L^{-1}$
is not pseudo-effective.
Note that, Theorem 1.5 is also valid if we replace the line bundle
![]() $L$
by a Bott–Chern class
$L$
by a Bott–Chern class
![]() $\unicode[STIX]{x1D6FC}\in H_{\text{BC}}^{1,1}(X)$
(see Theorem 4.2). The key ingredients in the proof of Theorem 1.5 rely on several results in our previous paper [Reference YangYan17] on geometric characterizations of pseudo-effective line bundles (respectively Bott–Chern classes). As an application of Theorems 1.4, 1.5 and 1.2, one has the following.
$\unicode[STIX]{x1D6FC}\in H_{\text{BC}}^{1,1}(X)$
(see Theorem 4.2). The key ingredients in the proof of Theorem 1.5 rely on several results in our previous paper [Reference YangYan17] on geometric characterizations of pseudo-effective line bundles (respectively Bott–Chern classes). As an application of Theorems 1.4, 1.5 and 1.2, one has the following.
Corollary 1.6. On a projective manifold
![]() $X$
of complex dimension
$X$
of complex dimension
![]() $n$
, the following are equivalent:
$n$
, the following are equivalent:
(i)
 $L$
is
$L$
is
 $(n-1)$
-ample;
$(n-1)$
-ample;(ii)
 $L$
is
$L$
is
 $(n-1)$
-positive;
$(n-1)$
-positive;(iii)
 $L^{-1}$
is not pseudo-effective.
$L^{-1}$
is not pseudo-effective.
Note that the equivalence of
![]() $(1)$
and
$(1)$
and
![]() $(3)$
is also obtained in [Reference Demailly, Peternell and SchneiderDPS96, Proposition 2.5], [Reference TotaroTot13, Theorem 9.1] and [Reference MatsumuraMat13, Lemma 2.4] by different methods in one direction.
$(3)$
is also obtained in [Reference Demailly, Peternell and SchneiderDPS96, Proposition 2.5], [Reference TotaroTot13, Theorem 9.1] and [Reference MatsumuraMat13, Lemma 2.4] by different methods in one direction.
According to Ottem’s counter-examples in [Reference OttemOtt12, Theorem 10.3], for
![]() $(\dim X)/2-1<q<\dim X-2$
, the
$(\dim X)/2-1<q<\dim X-2$
, the
![]() $q$
-ampleness cannot imply the
$q$
-ampleness cannot imply the
![]() $q$
-positivity. On the contrary, by Theorem 1.4, we obtain the following.
$q$
-positivity. On the contrary, by Theorem 1.4, we obtain the following.
Proposition 1.7. Let
![]() $X$
be a smooth projective manifold with
$X$
be a smooth projective manifold with
![]() $\dim _{\mathbb{C}}X=n$
. Suppose
$\dim _{\mathbb{C}}X=n$
. Suppose
![]() $L$
is
$L$
is
![]() $q$
-ample, then the restriction of
$q$
-ample, then the restriction of
![]() $L$
to every codimension-
$L$
to every codimension-
![]() $(n-q-1)$
smooth submanifold
$(n-q-1)$
smooth submanifold
![]() $Y$
is
$Y$
is
![]() $q$
-positive.
$q$
-positive.
In particular, we have the following.
Corollary 1.8. Let
![]() $X$
be a smooth projective manifold with
$X$
be a smooth projective manifold with
![]() $\dim _{\mathbb{C}}X=n$
. If
$\dim _{\mathbb{C}}X=n$
. If
![]() $L$
is
$L$
is
![]() $(n\,-\,2)$
-ample, then the restriction of
$(n\,-\,2)$
-ample, then the restriction of
![]() $L$
to every codimension-
$L$
to every codimension-
![]() $1$
smooth submanifold is
$1$
smooth submanifold is
![]() $(n-2)$
-positive.
$(n-2)$
-positive.
On the other hand, by using the classical result of [Reference Boucksom, Demailly, Paun and PeternellBDPP13], one obtains the following.
Corollary 1.9. On a projective manifold
![]() $X$
of complex dimension
$X$
of complex dimension
![]() $n$
, the following are equivalent:
$n$
, the following are equivalent:
(i)
 $X$
is uniruled;
$X$
is uniruled;(ii)
 $K_{X}^{-1}$
is
$K_{X}^{-1}$
is
 $(n-1)$
-positive, i.e. there exists a Hermitian metric
$(n-1)$
-positive, i.e. there exists a Hermitian metric
 $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
 $X$
such that its Ricci curvature
$X$
such that its Ricci curvature
 $\text{Ric}(\unicode[STIX]{x1D714})$
has at least one positive eigenvalue everywhere;
$\text{Ric}(\unicode[STIX]{x1D714})$
has at least one positive eigenvalue everywhere;(iii)
 $K_{X}$
is not pseudo-effective;
$K_{X}$
is not pseudo-effective;(iv)
 $K_{X}^{-1}$
is
$K_{X}^{-1}$
is
 $(n-1)$
-ample.
$(n-1)$
-ample.
2 Partially positive line bundles on compact complex manifolds
In this section, we deal with two different notions on
![]() $q$
-positive line bundles over compact complex manifolds.
$q$
-positive line bundles over compact complex manifolds.
Definition 2.1. Let X be a compact complex manifold and
![]() $L$
be a holomorphic line bundle over
$L$
be a holomorphic line bundle over
![]() $X$
.
$X$
.
(i)
 $L$
is called
$L$
is called
 $q$
-positive, if there exists a smooth Hermitian metric
$q$
-positive, if there exists a smooth Hermitian metric
 $h$
on
$h$
on
 $L$
and a smooth Hermitian metric
$L$
and a smooth Hermitian metric
 $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
 $X$
such that the Chern curvature
$X$
such that the Chern curvature
 $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
has at least
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
has at least
 $(n-q)$
positive eigenvalues at any point on
$(n-q)$
positive eigenvalues at any point on
 $X$
(with respect to
$X$
(with respect to
 $\unicode[STIX]{x1D714}$
).
$\unicode[STIX]{x1D714}$
).(ii)
 $L$
is called uniformly
$L$
is called uniformly
 $q$
-positive, if there exists a Hermitian metric
$q$
-positive, if there exists a Hermitian metric
 $h$
on
$h$
on
 $L$
and a smooth Hermitian metric
$L$
and a smooth Hermitian metric
 $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
 $X$
such that the summation of any distinct
$X$
such that the summation of any distinct
 $(q+1)$
eigenvalues (counting multiplicity) of the Chern curvature
$(q+1)$
eigenvalues (counting multiplicity) of the Chern curvature
 $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
is positive at any point of
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
is positive at any point of
 $X$
(with respect to
$X$
(with respect to
 $\unicode[STIX]{x1D714}$
).
$\unicode[STIX]{x1D714}$
).
The following result is obtained by changing the metric on the complex manifold and the background idea dates back to [Reference Andreotti and VesentiniAV65, §5].
Proposition 2.2. The following statements are equivalent:
(i)
 $L$
is
$L$
is
 $q$
-positive;
$q$
-positive;(ii)
 $L$
is uniformly
$L$
is uniformly
 $q$
-positive.
$q$
-positive.
Proof.
![]() $(2)\Longrightarrow (1)$
. Let
$(2)\Longrightarrow (1)$
. Let
![]() $\unicode[STIX]{x1D714}$
be a Hermitian metric on
$\unicode[STIX]{x1D714}$
be a Hermitian metric on
![]() $X$
and
$X$
and
![]() $h$
be a smooth Hermitian metric on
$h$
be a smooth Hermitian metric on
![]() $L$
such that
$L$
such that
![]() $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
is uniformly
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
is uniformly
![]() $q$
-positive. Let
$q$
-positive. Let
![]() $\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{n}$
be the eigenvalues of
$\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{n}$
be the eigenvalues of
![]() $R^{(L,h)}$
with respect to
$R^{(L,h)}$
with respect to
![]() $\unicode[STIX]{x1D714}$
over some coordinate chart. We have
$\unicode[STIX]{x1D714}$
over some coordinate chart. We have
![]() $\unicode[STIX]{x1D706}_{n-q}>0$
. Otherwise, the summation of
$\unicode[STIX]{x1D706}_{n-q}>0$
. Otherwise, the summation of
![]() $q+1$
eigenvalues
$q+1$
eigenvalues
![]() $\unicode[STIX]{x1D706}_{n-q}+\unicode[STIX]{x1D706}_{n-q+1}+\cdots +\unicode[STIX]{x1D706}_{n}\leqslant 0$
.
$\unicode[STIX]{x1D706}_{n-q}+\unicode[STIX]{x1D706}_{n-q+1}+\cdots +\unicode[STIX]{x1D706}_{n}\leqslant 0$
.
![]() $(1)\Longrightarrow (2)$
. We assume that there exists a smooth Hermitian metric
$(1)\Longrightarrow (2)$
. We assume that there exists a smooth Hermitian metric
![]() $h$
on
$h$
on
![]() $L$
such that the curvature
$L$
such that the curvature
![]() $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
has at least
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
has at least
![]() $(n-q)$
positive eigenvalues at each point
$(n-q)$
positive eigenvalues at each point
![]() $p\in X$
. Let
$p\in X$
. Let
![]() $\unicode[STIX]{x1D714}_{0}$
be a fixed Hermitian metric on
$\unicode[STIX]{x1D714}_{0}$
be a fixed Hermitian metric on
![]() $X$
. For simplicity, we denote by
$X$
. For simplicity, we denote by
![]() $R$
and
$R$
and
![]() $\unicode[STIX]{x1D6FA}$
the local matrix representations of the matrices
$\unicode[STIX]{x1D6FA}$
the local matrix representations of the matrices
![]() $R^{(L,h)}$
and
$R^{(L,h)}$
and
![]() $\unicode[STIX]{x1D714}_{0}$
respectively, in some local holomorphic frames of
$\unicode[STIX]{x1D714}_{0}$
respectively, in some local holomorphic frames of
![]() $X$
. Let
$X$
. Let
be the eigenvalues of
![]() $R^{(L,h)}$
with respect to
$R^{(L,h)}$
with respect to
![]() $\unicode[STIX]{x1D714}_{0}$
. It is obvious that
$\unicode[STIX]{x1D714}_{0}$
. It is obvious that
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}$
are eigenvalues of the matrix
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}$
are eigenvalues of the matrix
![]() $R\unicode[STIX]{x1D6FA}^{-1}$
. Note that
$R\unicode[STIX]{x1D6FA}^{-1}$
. Note that
![]() $R\unicode[STIX]{x1D6FA}^{-1}$
represents a tensor in
$R\unicode[STIX]{x1D6FA}^{-1}$
represents a tensor in
![]() $\unicode[STIX]{x1D6E4}(X,\text{End}(T^{1,0}X))$
, and so the eigenvalues
$\unicode[STIX]{x1D6E4}(X,\text{End}(T^{1,0}X))$
, and so the eigenvalues
![]() $\unicode[STIX]{x1D706}_{i}$
are independent of the choice of coordinates. Since
$\unicode[STIX]{x1D706}_{i}$
are independent of the choice of coordinates. Since
![]() $\unicode[STIX]{x1D706}_{n-q}$
is a continuous function, we set
$\unicode[STIX]{x1D706}_{n-q}$
is a continuous function, we set
![]() $\unicode[STIX]{x1D706}_{0}$
is a positive number since
$\unicode[STIX]{x1D706}_{0}$
is a positive number since
![]() $L$
is
$L$
is
![]() $q$
-positive and
$q$
-positive and
![]() $X$
is compact. We define a new Hermitian metric
$X$
is compact. We define a new Hermitian metric
![]() $\unicode[STIX]{x1D714}$
over
$\unicode[STIX]{x1D714}$
over
![]() $X$
with local matrix representation
$X$
with local matrix representation
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
by the following formula
$\widetilde{\unicode[STIX]{x1D6FA}}$
by the following formula
Note that the matrix
![]() $\widetilde{\unicode[STIX]{x1D6FA}}^{-1}$
is positive definite. Indeed, the eigenvalues of the matrix
$\widetilde{\unicode[STIX]{x1D6FA}}^{-1}$
is positive definite. Indeed, the eigenvalues of the matrix
![]() $\operatorname{Id}+\sum _{k=1}^{\infty }(\unicode[STIX]{x1D706}_{0}^{k}(R\unicode[STIX]{x1D6FA}^{-1})^{k}/(k+1)!)$
are given by
$\operatorname{Id}+\sum _{k=1}^{\infty }(\unicode[STIX]{x1D706}_{0}^{k}(R\unicode[STIX]{x1D6FA}^{-1})^{k}/(k+1)!)$
are given by
It is not hard to see that the Hermitian metric
![]() $\unicode[STIX]{x1D714}$
is globally well-defined on
$\unicode[STIX]{x1D714}$
is globally well-defined on
![]() $X$
. Let
$X$
. Let
![]() $\unicode[STIX]{x1D705}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D705}_{n}$
be the eigenvalues of
$\unicode[STIX]{x1D705}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D705}_{n}$
be the eigenvalues of
![]() $R^{(L,h)}$
with respect to the new metric
$R^{(L,h)}$
with respect to the new metric
![]() $\unicode[STIX]{x1D714}$
, i.e. they are the eigenvalues of
$\unicode[STIX]{x1D714}$
, i.e. they are the eigenvalues of
![]() $R\widetilde{\unicode[STIX]{x1D6FA}}^{-1}$
. Note also that
$R\widetilde{\unicode[STIX]{x1D6FA}}^{-1}$
. Note also that
A straightforward computation shows
For any summation of
![]() $(q+1)$
(distinct) eigenvalues of
$(q+1)$
(distinct) eigenvalues of
![]() $R^{(L,h)}$
with respect to the new metric
$R^{(L,h)}$
with respect to the new metric
![]() $\unicode[STIX]{x1D714}$
, we have the inequality
$\unicode[STIX]{x1D714}$
, we have the inequality
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\ell =1}^{q+1}\unicode[STIX]{x1D705}_{i_{\ell }} & {\geqslant} & \displaystyle \unicode[STIX]{x1D705}_{n-q}+\cdots +\unicode[STIX]{x1D705}_{n}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \unicode[STIX]{x1D705}_{n-q}+q\unicode[STIX]{x1D705}_{n}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \unicode[STIX]{x1D706}_{0}^{-1}(e^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n-q}}+qe^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n}}-(q+1))\nonumber\\ \displaystyle & {>} & \displaystyle \unicode[STIX]{x1D706}_{0}^{-1}(e^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n-q}}-(q+1))>0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\ell =1}^{q+1}\unicode[STIX]{x1D705}_{i_{\ell }} & {\geqslant} & \displaystyle \unicode[STIX]{x1D705}_{n-q}+\cdots +\unicode[STIX]{x1D705}_{n}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \unicode[STIX]{x1D705}_{n-q}+q\unicode[STIX]{x1D705}_{n}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \unicode[STIX]{x1D706}_{0}^{-1}(e^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n-q}}+qe^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n}}-(q+1))\nonumber\\ \displaystyle & {>} & \displaystyle \unicode[STIX]{x1D706}_{0}^{-1}(e^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n-q}}-(q+1))>0\nonumber\end{eqnarray}$$
since
![]() $e^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n-q}}=e^{\log (n+1)(\unicode[STIX]{x1D706}_{n-q}/\text{inf}_{X}\,\unicode[STIX]{x1D706}_{n-q})}\geqslant n+1$
by (2).
$e^{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{n-q}}=e^{\log (n+1)(\unicode[STIX]{x1D706}_{n-q}/\text{inf}_{X}\,\unicode[STIX]{x1D706}_{n-q})}\geqslant n+1$
by (2).
The following special case of Proposition 2.2 is of particular interest in complex geometry.
Corollary 2.3. The following statements are equivalent:
(i)
 $L$
is
$L$
is
 $(n-1)$
-positive;
$(n-1)$
-positive;(ii) there exists a smooth Hermitian metric
 $h$
on
$h$
on
 $L$
and a Hermitian metric
$L$
and a Hermitian metric
 $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
 $X$
such that the function (4)
$X$
such that the function (4) $$\begin{eqnarray}\text{tr}_{\unicode[STIX]{x1D714}}(-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h)>0.\end{eqnarray}$$
$$\begin{eqnarray}\text{tr}_{\unicode[STIX]{x1D714}}(-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h)>0.\end{eqnarray}$$
Remark 2.4. The function
![]() $\text{tr}_{\unicode[STIX]{x1D714}}(-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h)$
is globally defined on
$\text{tr}_{\unicode[STIX]{x1D714}}(-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h)$
is globally defined on
![]() $X$
and it is independent of the choice of coordinates. It is also called the scalar curvature of the Chern curvature
$X$
and it is independent of the choice of coordinates. It is also called the scalar curvature of the Chern curvature
![]() $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
with respect to the Hermitian metric
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
with respect to the Hermitian metric
![]() $\unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D714}$
.
3 The pseudo-effective line bundles on compact complex manifolds
A line bundle
![]() $L$
on a compact complex manifold
$L$
on a compact complex manifold
![]() $X$
is called pseudo-effective if there exists a (possibly) singular Hermitian metric
$X$
is called pseudo-effective if there exists a (possibly) singular Hermitian metric
![]() $h$
on
$h$
on
![]() $L$
such that its Chern curvature
$L$
such that its Chern curvature
![]() $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h\geqslant 0$
in the sense of current. In order to describe pseudo-effective line bundles in a differential geometric setting, we introduce the Bott–Chern cohomology on
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h\geqslant 0$
in the sense of current. In order to describe pseudo-effective line bundles in a differential geometric setting, we introduce the Bott–Chern cohomology on
![]() $X$
:
$X$
:
Let
![]() $\text{Pic}(X)$
be the set of holomorphic line bundles over
$\text{Pic}(X)$
be the set of holomorphic line bundles over
![]() $X$
. As similar as the first Chern class map
$X$
. As similar as the first Chern class map
![]() $c_{1}:\text{Pic}(X)\rightarrow H_{\overline{\unicode[STIX]{x2202}}}^{1,1}(X)$
, there is a first Bott–Chern class map
$c_{1}:\text{Pic}(X)\rightarrow H_{\overline{\unicode[STIX]{x2202}}}^{1,1}(X)$
, there is a first Bott–Chern class map
Given any holomorphic line bundle
![]() $L\rightarrow X$
and any Hermitian metric
$L\rightarrow X$
and any Hermitian metric
![]() $h$
on
$h$
on
![]() $L$
, we define
$L$
, we define
![]() $c_{1}^{\text{BC}}(L)$
to be the class of its curvature form
$c_{1}^{\text{BC}}(L)$
to be the class of its curvature form
![]() $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
in
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
in
![]() $H_{\text{BC}}^{1,1}(X)$
(modulo a constant
$H_{\text{BC}}^{1,1}(X)$
(modulo a constant
![]() $2\unicode[STIX]{x1D70B}$
). A Hermitian metric
$2\unicode[STIX]{x1D70B}$
). A Hermitian metric
![]() $\unicode[STIX]{x1D714}$
is called a Gauduchon metric if
$\unicode[STIX]{x1D714}$
is called a Gauduchon metric if
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D714}^{n-1}=0$
where
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D714}^{n-1}=0$
where
![]() $\dim _{\mathbb{C}}X=n$
. It is proved by Gauduchon [Reference GauduchonGau77a] that, in the conformal class of each Hermitian metric, there exists a unique Gauduchon metric (up to constant scaling).
$\dim _{\mathbb{C}}X=n$
. It is proved by Gauduchon [Reference GauduchonGau77a] that, in the conformal class of each Hermitian metric, there exists a unique Gauduchon metric (up to constant scaling).
Proposition 3.1. The following statements are equivalent:
(i)
 $L$
is pseudo-effective;
$L$
is pseudo-effective;(ii) for any Gauduchon metric
 $\unicode[STIX]{x1D714}_{\text{G}}$
on
$\unicode[STIX]{x1D714}_{\text{G}}$
on
 $X$
, one has (6)
$X$
, one has (6) $$\begin{eqnarray}\int _{X}c_{1}^{\text{BC}}(L)\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1}\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}c_{1}^{\text{BC}}(L)\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1}\geqslant 0.\end{eqnarray}$$
Proof. The proof is essentially contained in [Reference YangYan17, Theorem 1.1] or [Reference YangYan17, Theorem 3.4] which relies on Lamari’s positivity criterion [Reference LamariLam99] and an observation of Michelsohn [Reference MichelsohnMic82]. For readers’ convenience, we include a proof here.
![]() $(1)\Longrightarrow (2)$
. Suppose
$(1)\Longrightarrow (2)$
. Suppose
![]() $L$
is pseudo-effective, it is well-known that there exist a smooth Hermitian metric
$L$
is pseudo-effective, it is well-known that there exist a smooth Hermitian metric
![]() $h$
on
$h$
on
![]() $L$
and a real valued function
$L$
and a real valued function
![]() $\unicode[STIX]{x1D711}\in \mathscr{L}^{1}(X,\mathbb{R})$
such that
$\unicode[STIX]{x1D711}\in \mathscr{L}^{1}(X,\mathbb{R})$
such that
in the sense of current where
![]() $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
. Then for any smooth Gauduchon metric
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
. Then for any smooth Gauduchon metric
![]() $\unicode[STIX]{x1D714}_{\text{G}}$
, we have
$\unicode[STIX]{x1D714}_{\text{G}}$
, we have
 $$\begin{eqnarray}\displaystyle \mathscr{\int }_{X}c_{1}^{\text{BC}}(L)\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1} & = & \displaystyle \int _{X}R^{(L,h)}\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle (R^{(L,h)}+\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711},\unicode[STIX]{x1D714}_{\text{G}}^{n-1})\geqslant 0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{\int }_{X}c_{1}^{\text{BC}}(L)\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1} & = & \displaystyle \int _{X}R^{(L,h)}\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle (R^{(L,h)}+\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711},\unicode[STIX]{x1D714}_{\text{G}}^{n-1})\geqslant 0\nonumber\end{eqnarray}$$
since
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D714}_{G}^{n-1}=0$
and
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D714}_{G}^{n-1}=0$
and
![]() $R^{(L,h)}+\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}\geqslant 0$
in the sense of current.
$R^{(L,h)}+\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}\geqslant 0$
in the sense of current.
![]() $(2)\Longrightarrow (1)$
. We define several sets:
$(2)\Longrightarrow (1)$
. We define several sets:
–
 $\mathscr{E}$
is the set of real
$\mathscr{E}$
is the set of real
 $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-closed
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-closed
 $(n-1,n-1)$
forms on
$(n-1,n-1)$
forms on
 $X$
;
$X$
;–
 $\mathscr{V}$
is the set of real positive
$\mathscr{V}$
is the set of real positive
 $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-closed
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-closed
 $(n-1,n-1)$
forms on
$(n-1,n-1)$
forms on
 $X$
;
$X$
;–
 $\mathscr{G}=\{\unicode[STIX]{x1D714}^{n-1}\mid \unicode[STIX]{x1D714}~\text{is a Gauduchon metric}\}$
.
$\mathscr{G}=\{\unicode[STIX]{x1D714}^{n-1}\mid \unicode[STIX]{x1D714}~\text{is a Gauduchon metric}\}$
.
In [Reference MichelsohnMic82, pp. 279–280], Michelsohn observed that
![]() $\mathscr{V}=\mathscr{G}$
. Let
$\mathscr{V}=\mathscr{G}$
. Let
![]() $\mathscr{W}$
be the space of smooth Gauduchon metrics on
$\mathscr{W}$
be the space of smooth Gauduchon metrics on
![]() $X$
. We also define
$X$
. We also define
![]() $\mathscr{F}:\mathscr{W}\rightarrow \mathbb{R}$
by
$\mathscr{F}:\mathscr{W}\rightarrow \mathbb{R}$
by
Hence, by the assumption of
![]() $(2)$
, we have
$(2)$
, we have
![]() $\mathscr{F}(\unicode[STIX]{x1D714})\geqslant 0$
for every
$\mathscr{F}(\unicode[STIX]{x1D714})\geqslant 0$
for every
![]() $\unicode[STIX]{x1D714}\in \mathscr{W}$
. Fix an arbitrary smooth Hermitian metric
$\unicode[STIX]{x1D714}\in \mathscr{W}$
. Fix an arbitrary smooth Hermitian metric
![]() $h$
on
$h$
on
![]() $L$
. Since
$L$
. Since
![]() $\mathscr{V}=\mathscr{G}$
, for any
$\mathscr{V}=\mathscr{G}$
, for any
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-closed positive
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-closed positive
![]() $(n-1,n-1)$
form
$(n-1,n-1)$
form
![]() $\unicode[STIX]{x1D713}\in \mathscr{V}$
, there exists a smooth Gauduchon metric
$\unicode[STIX]{x1D713}\in \mathscr{V}$
, there exists a smooth Gauduchon metric
![]() $\unicode[STIX]{x1D714}$
such that
$\unicode[STIX]{x1D714}$
such that
![]() $\unicode[STIX]{x1D714}^{n-1}=\unicode[STIX]{x1D713}$
. Hence
$\unicode[STIX]{x1D714}^{n-1}=\unicode[STIX]{x1D713}$
. Hence
That means, as a functional on
![]() $\mathscr{V}$
,
$\mathscr{V}$
,
![]() $R^{(L,h)}$
is non-negative. Note that
$R^{(L,h)}$
is non-negative. Note that
![]() $\mathscr{V}$
is a hyperplane in
$\mathscr{V}$
is a hyperplane in
![]() $\mathscr{E}$
. As proved in [Reference LamariLam99, Lemma 3.3], by Hahn-Banach theorem,
$\mathscr{E}$
. As proved in [Reference LamariLam99, Lemma 3.3], by Hahn-Banach theorem,
![]() $c_{1}^{\text{BC}}(L)$
is pseudo-effective, and there exists a locally integrable function
$c_{1}^{\text{BC}}(L)$
is pseudo-effective, and there exists a locally integrable function
![]() $\unicode[STIX]{x1D711}\in \mathscr{L}^{1}(X,\mathbb{R})$
such that
$\unicode[STIX]{x1D711}\in \mathscr{L}^{1}(X,\mathbb{R})$
such that
in the sense of current. That means,
![]() $L$
is pseudo-effective.
$L$
is pseudo-effective.
Of course, Proposition 3.1 has the following variant.
Proposition 3.2. The following statements are equivalent:
(i) the dual line bundle
 $L^{-1}$
is not pseudo-effective;
$L^{-1}$
is not pseudo-effective;(ii) there exists a Gauduchon metric
 $\unicode[STIX]{x1D714}_{\text{G}}$
such that
$\unicode[STIX]{x1D714}_{\text{G}}$
such that  $$\begin{eqnarray}\int _{X}c_{1}^{\text{BC}}(L)\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1}>0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}c_{1}^{\text{BC}}(L)\wedge \unicode[STIX]{x1D714}_{\text{G}}^{n-1}>0.\end{eqnarray}$$
4 The proofs of Theorems 1.4 and 1.5
In this section, we prove Theorems 1.4, 1.5 and Proposition 1.7.
The proof of Theorem 1.5.
![]() $(1)\Longrightarrow (2)$
. By Corollary 2.3, there exist a smooth Hermitian metric
$(1)\Longrightarrow (2)$
. By Corollary 2.3, there exist a smooth Hermitian metric
![]() $h$
on
$h$
on
![]() $L$
and a Hermitian metric
$L$
and a Hermitian metric
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() $X$
such that the function
$X$
such that the function
Let
![]() $\unicode[STIX]{x1D714}_{\text{G}}=e^{f}\unicode[STIX]{x1D714}$
be a Gauduchon metric in the conformal class of
$\unicode[STIX]{x1D714}_{\text{G}}=e^{f}\unicode[STIX]{x1D714}$
be a Gauduchon metric in the conformal class of
![]() $\unicode[STIX]{x1D714}$
[Reference GauduchonGau77b], then by (8), we obtain
$\unicode[STIX]{x1D714}$
[Reference GauduchonGau77b], then by (8), we obtain
where
![]() $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
. In particular, we have
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
. In particular, we have
By Proposition 3.2, the dual line bundle
![]() $L^{-1}$
is not pseudo-effective.
$L^{-1}$
is not pseudo-effective.
![]() $(2)\Longrightarrow (1)$
. If
$(2)\Longrightarrow (1)$
. If
![]() $L^{-1}$
is not pseudo-effective, by Proposition 3.2, there exists a Gauduchon metric
$L^{-1}$
is not pseudo-effective, by Proposition 3.2, there exists a Gauduchon metric
![]() $\unicode[STIX]{x1D714}_{\text{G}}$
such that
$\unicode[STIX]{x1D714}_{\text{G}}$
such that
We shall use Gauduchon’s conformal trick ([Reference GauduchonGau77a, Reference GauduchonGau84], see also [Reference YangYan16, Reference YangYan17]) to construct a smooth Hermitian metric
![]() $h$
on
$h$
on
![]() $L$
such that
$L$
such that
![]() $\text{tr}_{\unicode[STIX]{x1D714}_{\text{G}}}(-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h)>0$
. Hence, by Corollary 2.3,
$\text{tr}_{\unicode[STIX]{x1D714}_{\text{G}}}(-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h)>0$
. Hence, by Corollary 2.3,
![]() $L$
is
$L$
is
![]() $(n-1)$
-positive.
$(n-1)$
-positive.
Fix a smooth Hermitian metric
![]() $h_{0}$
on
$h_{0}$
on
![]() $L$
. Let
$L$
. Let
be the Chern curvature of
![]() $(L,h_{0})$
. It is easy to see that
$(L,h_{0})$
. It is easy to see that
Since
![]() $\unicode[STIX]{x1D714}_{\text{G}}$
is Gauduchon, i.e.
$\unicode[STIX]{x1D714}_{\text{G}}$
is Gauduchon, i.e.
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D714}_{\text{G}}^{n-1}=0$
and the integration
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D714}_{\text{G}}^{n-1}=0$
and the integration
the equation
has a solution
![]() $f\in C^{\infty }(X)$
which is well-known (e.g. [Reference GauduchonGau77a] or [Reference Chu, Tosatti and WeinkoveCTW16, Theorem 2.2]). Let
$f\in C^{\infty }(X)$
which is well-known (e.g. [Reference GauduchonGau77a] or [Reference Chu, Tosatti and WeinkoveCTW16, Theorem 2.2]). Let
![]() $h=e^{f}\cdot h_{0}$
be a smooth Hermitian metric on
$h=e^{f}\cdot h_{0}$
be a smooth Hermitian metric on
![]() $L$
. The Hermitian line bundle
$L$
. The Hermitian line bundle
![]() $(L,h)$
has Chern curvature
$(L,h)$
has Chern curvature
The scalar curvature of
![]() $R^{(L,h)}$
with respect to
$R^{(L,h)}$
with respect to
![]() $\unicode[STIX]{x1D714}_{\text{G}}$
is
$\unicode[STIX]{x1D714}_{\text{G}}$
is
The proof of Theorem 1.5 is completed. ◻
By Corollary 2.3, Proposition 3.2 and Theorem 1.5, we obtain the following.
Theorem 4.1. Let
![]() $L$
be a line bundle over a compact complex manifold
$L$
be a line bundle over a compact complex manifold
![]() $X$
with
$X$
with
![]() $\dim _{\mathbb{C}}X=n$
. The following statements are equivalent:
$\dim _{\mathbb{C}}X=n$
. The following statements are equivalent:
(i) the dual line bundle
 $L^{-1}$
is not pseudo-effective;
$L^{-1}$
is not pseudo-effective;(ii) there exists a smooth Gauduchon metric
 $\unicode[STIX]{x1D714}_{\text{G}}$
on
$\unicode[STIX]{x1D714}_{\text{G}}$
on
 $X$
such that
$X$
such that  $$\begin{eqnarray}\int _{X}c_{1}^{\text{BC}}(L)\cdot \unicode[STIX]{x1D714}_{\text{G}}^{n-1}>0;\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}c_{1}^{\text{BC}}(L)\cdot \unicode[STIX]{x1D714}_{\text{G}}^{n-1}>0;\end{eqnarray}$$
(iii) there exist a smooth Hermitian metric
 $h$
on
$h$
on
 $L$
and a Hermitan metric
$L$
and a Hermitan metric
 $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
 $X$
such that the scalar curvature of the Chern curvature
$X$
such that the scalar curvature of the Chern curvature
 $R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
with respect to
$R^{(L,h)}=-\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log h$
with respect to
 $\unicode[STIX]{x1D714}$
is positive, i.e.
$\unicode[STIX]{x1D714}$
is positive, i.e.  $$\begin{eqnarray}s=\text{tr}_{\unicode[STIX]{x1D714}}R^{(L,h)}>0;\end{eqnarray}$$
$$\begin{eqnarray}s=\text{tr}_{\unicode[STIX]{x1D714}}R^{(L,h)}>0;\end{eqnarray}$$
(iv)
 $L$
is
$L$
is
 $(n-1)$
-positive.
$(n-1)$
-positive.
It is easy to see that Theorem 4.1 has the following version on Bott–Chern classes.
Theorem 4.2. Let
![]() $X$
be a compact complex manifold
$X$
be a compact complex manifold
![]() $X$
with
$X$
with
![]() $\dim _{\mathbb{C}}X=n$
and
$\dim _{\mathbb{C}}X=n$
and
![]() $[\unicode[STIX]{x1D6FC}]\in H_{\text{BC}}^{1,1}(X)$
. The following statements are equivalent:
$[\unicode[STIX]{x1D6FC}]\in H_{\text{BC}}^{1,1}(X)$
. The following statements are equivalent:
(i) the class
 $-[\unicode[STIX]{x1D6FC}]_{\text{BC}}$
is not pseudo-effective;
$-[\unicode[STIX]{x1D6FC}]_{\text{BC}}$
is not pseudo-effective;(ii) there exists a smooth Gauduchon metric
 $\unicode[STIX]{x1D714}_{\text{G}}$
on
$\unicode[STIX]{x1D714}_{\text{G}}$
on
 $X$
such that
$X$
such that  $$\begin{eqnarray}\int _{X}[\unicode[STIX]{x1D6FC}]_{\text{BC}}\cdot \unicode[STIX]{x1D714}_{\text{G}}^{n-1}>0;\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}[\unicode[STIX]{x1D6FC}]_{\text{BC}}\cdot \unicode[STIX]{x1D714}_{\text{G}}^{n-1}>0;\end{eqnarray}$$
(iii) there exist a smooth
 $(1,1)$
form
$(1,1)$
form
 $\unicode[STIX]{x1D712}\in [\unicode[STIX]{x1D6FC}]_{\text{BC}}$
and a Hermitian metric
$\unicode[STIX]{x1D712}\in [\unicode[STIX]{x1D6FC}]_{\text{BC}}$
and a Hermitian metric
 $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
 $X$
such that
$X$
such that  $$\begin{eqnarray}\text{tr}_{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D712}>0;\end{eqnarray}$$
$$\begin{eqnarray}\text{tr}_{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D712}>0;\end{eqnarray}$$
(iv)
 $[\unicode[STIX]{x1D6FC}]_{\text{BC}}$
is
$[\unicode[STIX]{x1D6FC}]_{\text{BC}}$
is
 $(n-1)$
-positive.
$(n-1)$
-positive.
Now we are ready to prove our main theorem.
The proof of Theorem 1.4.
The proof follows from Theorem 1.5 and a simple argument by the Serre duality.
Since
![]() $L$
is
$L$
is
![]() $(n\,-\,1)$
-ample, by Definition 1.1, for any ample line bundle
$(n\,-\,1)$
-ample, by Definition 1.1, for any ample line bundle
![]() $A$
, there exists a positive number
$A$
, there exists a positive number
![]() $m_{0}=m_{0}(K_{X}\otimes A^{-1})$
such that when
$m_{0}=m_{0}(K_{X}\otimes A^{-1})$
such that when
![]() $m>m_{0}$
, we have
$m>m_{0}$
, we have
which is also equivalent to
by the Serre duality.
We argue by contradiction, i.e. suppose
![]() $L$
is
$L$
is
![]() $(n-1)$
-ample, but
$(n-1)$
-ample, but
![]() $L$
is not
$L$
is not
![]() $(n-1)$
-positive. In this case, by Theorem 1.5, we know the dual line bundle
$(n-1)$
-positive. In this case, by Theorem 1.5, we know the dual line bundle
![]() $L^{-1}$
must be pseudo-effective. For the pseudo-effective line bundle
$L^{-1}$
must be pseudo-effective. For the pseudo-effective line bundle
![]() $L^{-1}$
, it is well-known that, there exists an ample line bundle
$L^{-1}$
, it is well-known that, there exists an ample line bundle
![]() $A$
on
$A$
on
![]() $X$
such that for every positive integer
$X$
such that for every positive integer
![]() $m$
$m$
This contradicts with (12).
For readers’ convenience, we present a sketched analytical proof of (13) following [Reference Demailly, Peternell and SchneiderDPS96, Proposition 1.5]. Indeed, for a fixed very ample line bundle
![]() $H$
, we choose an ample line bundle
$H$
, we choose an ample line bundle
![]() $A$
such that
$A$
such that
![]() $A\otimes K_{X}^{-1}\otimes H^{-n}$
is also ample. Hence, there exists a positive rational number
$A\otimes K_{X}^{-1}\otimes H^{-n}$
is also ample. Hence, there exists a positive rational number
![]() $\unicode[STIX]{x1D700}_{0}$
, such that for all
$\unicode[STIX]{x1D700}_{0}$
, such that for all
![]() $m\geqslant 0$
and rational number
$m\geqslant 0$
and rational number
![]() $\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D700}_{0})$
,
$\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D700}_{0})$
,
lies in the interior of the effective cone of
![]() $X$
. It implies that
$X$
. It implies that
![]() $L^{-m}\otimes A\otimes K_{X}^{-1}\otimes H^{-(n+\unicode[STIX]{x1D700})}$
is linearly equivalent to an effective
$L^{-m}\otimes A\otimes K_{X}^{-1}\otimes H^{-(n+\unicode[STIX]{x1D700})}$
is linearly equivalent to an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $D$
plus a numerically trivial line bundle
$D$
plus a numerically trivial line bundle
![]() $T$
. Hence
$T$
. Hence
Now, fix a point
![]() $x_{0}\notin D$
. Let
$x_{0}\notin D$
. Let
![]() $\{s_{j}\}\subset H^{0}(X,H)$
be a basis such that all
$\{s_{j}\}\subset H^{0}(X,H)$
be a basis such that all
![]() $s_{j}$
vanish at point
$s_{j}$
vanish at point
![]() $x_{0}$
. Fix a local holomorphic basis
$x_{0}$
. Fix a local holomorphic basis
![]() $e_{H}$
of
$e_{H}$
of
![]() $H$
and write
$H$
and write
![]() $s_{j}=h_{j}e_{H}$
. Then
$s_{j}=h_{j}e_{H}$
. Then
is a singular Hermitian metric on
![]() $H^{n}$
with semi-positive curvature in the sense of current. Moreover, the weight function of
$H^{n}$
with semi-positive curvature in the sense of current. Moreover, the weight function of
![]() $h$
is not integrable at point
$h$
is not integrable at point
![]() $x_{0}$
and the Lelong number of the curvature current is
$x_{0}$
and the Lelong number of the curvature current is
![]() ${\geqslant}n$
. On the other hand, we can put a singular metric
${\geqslant}n$
. On the other hand, we can put a singular metric
![]() $h_{\unicode[STIX]{x1D700}}$
on
$h_{\unicode[STIX]{x1D700}}$
on
![]() $H^{\unicode[STIX]{x1D700}}\otimes D\otimes T$
such that the curvature current of
$H^{\unicode[STIX]{x1D700}}\otimes D\otimes T$
such that the curvature current of
![]() $h_{\unicode[STIX]{x1D700}}$
equals
$h_{\unicode[STIX]{x1D700}}$
equals
![]() $\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}+[D]$
where
$\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}+[D]$
where
![]() $\unicode[STIX]{x1D714}$
is a Kähler form in
$\unicode[STIX]{x1D714}$
is a Kähler form in
![]() $c_{1}(H)$
and
$c_{1}(H)$
and
![]() $[D]$
is the current of integration over
$[D]$
is the current of integration over
![]() $D$
. Since
$D$
. Since
![]() $x_{0}\notin D$
, the weight function of the singular metric
$x_{0}\notin D$
, the weight function of the singular metric
![]() $hh_{\unicode[STIX]{x1D700}}$
on
$hh_{\unicode[STIX]{x1D700}}$
on
![]() $H^{(n+\unicode[STIX]{x1D700})}\otimes D\otimes T$
has isolated singularity at point
$H^{(n+\unicode[STIX]{x1D700})}\otimes D\otimes T$
has isolated singularity at point
![]() $x_{0}$
. Moreover,
$x_{0}$
. Moreover,
in the sense of current and the weight function of
![]() $hh_{\unicode[STIX]{x1D700}}$
has Lelong number
$hh_{\unicode[STIX]{x1D700}}$
has Lelong number
![]() ${\geqslant}n$
at point
${\geqslant}n$
at point
![]() $x_{0}$
. By Hörmander’s
$x_{0}$
. By Hörmander’s
![]() $L^{2}$
existence theorem (e.g. [Reference Demailly, Hulek, Peternell, Schneider and SchreyerDem92, Corollary 3.3]), we know
$L^{2}$
existence theorem (e.g. [Reference Demailly, Hulek, Peternell, Schneider and SchreyerDem92, Corollary 3.3]), we know
By (14), we obtain (13). The proof of Theorem 1.4 is completed. ◻
The proof of Proposition 1.7.
Let
![]() $f:Y\rightarrow X$
be the inclusion map. Using the projection formula and the Leray spectral sequence, one has
$f:Y\rightarrow X$
be the inclusion map. Using the projection formula and the Leray spectral sequence, one has
Hence, if
![]() $L\rightarrow X$
is
$L\rightarrow X$
is
![]() $q$
-ample,
$q$
-ample,
![]() $f^{\ast }L\rightarrow Y$
is also
$f^{\ast }L\rightarrow Y$
is also
![]() $q$
-ample. On the other hand, since
$q$
-ample. On the other hand, since
![]() $\dim _{\mathbb{C}}Y=q+1$
and by Theorem 1.4, the
$\dim _{\mathbb{C}}Y=q+1$
and by Theorem 1.4, the
![]() $q$
-ample line bundle
$q$
-ample line bundle
![]() $L|_{Y}$
is
$L|_{Y}$
is
![]() $q$
-positive.◻
$q$
-positive.◻
Acknowledgements
I am very grateful to Professor Kefeng Liu for his support, encouragement and stimulating discussions over many years. I would also like to thank Professors Junyan Cao, J.-P. Demailly, S. Matsumura, Yum-Tong Siu, Junchao Shentu, Xiaotao Sun, Valentino Tosatti, Jian Xiao and Xiangyu Zhou for some useful suggestions. The author would also like to thank the anonymous referees whose comments and suggestions helped improve and clarify the paper. This work was partially supported by China’s Recruitment Program of Global Experts and NSFC 11688101.