Introduction
The glaciers of Alaska and northwest Canada are significant contributors to current sea-level rise (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002, Reference Arendt2013; Reference Meier and DyurgerovMeier and Dyurgerov, 2002; Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010; Reference GardnerGardner and others, 2013), but determining the magnitude of their recent contribution is a complex problem (Reference ArendtArendt, 2011). The Gravity Recovery and Climate Experiment (GRACE) provides frequent measurements of mass change (e.g. Reference ArendtArendt and others, 2013; Reference GardnerGardner and others, 2013), but separating out the various contributors to that mass change can be difficult, requiring models of terrestrial water storage and glacial isostatic adjustment that have relatively large associated uncertainties (e.g. Reference ArendtArendt and others, 2013). The spatial resolution of GRACE is also low, making it difficult to identify the contribution of individual glaciers to the overall mass change of an icefield, which can be significant (e.g. Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013).
Previous studies have differenced pairs of digital elevation models (DEMs) to provide regional estimates of mass change for all the Alaskan icefields (e.g. Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010). Here we update those works with recent observations through 2013 to produce an estimate of mass change at the Juneau Icefield (JIF), using a technique that produces ![]() incorporating all available Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and Shuttle Radar Topography Mission (SRTM) (C-band) elevation data (e.g. Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013).
incorporating all available Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and Shuttle Radar Topography Mission (SRTM) (C-band) elevation data (e.g. Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013).
The JIF is a 3830 km2 (Reference McGeeMcGee and others, 2007) temperate icefield in southeast Alaska and British Columbia (Fig. 1) and is the fifth-largest icefield in the Western Hemisphere (Reference Sprenke, Miller, McGee, Adema and LangSprenke and others, 1999).

Fig. 1. Gulf of Alaska region, containing the Juneau Icefield, Stikine Icefield and Glacier Bay. These three icefields have a total area of ~14 500 km2. Glacier outlines are from GLIMS.
The icefields of southeast Alaska as a whole are losing a large amount of mass (e.g. Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference ArendtArendt and others, 2013), which is likely linked to an average temperature rise of 1.3–2.0˚C in this region from 1948 to 2010 (Reference Stafford, Wendler and CurtisStafford and others, 2000; Reference Rasmussen and ConwayRasmussen and Conway, 2004; Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference Johnson, Larsen, Murphy, Arendt and ZirnheldJohnson and others, 2013; Trussel and others, 2013).
We focus on the JIF to examine if mass changes there are due to changes in ice dynamics or are directly related to the climatic warming, and compare the average thinning rate and mass change rate of the JIF with rates elsewhere in Alaska. The Juneau Icefield Research Program (JIRP) has been collecting data on the JIF since 1946 (e.g. Reference Pelto and MillerPelto and Miller, 1990), which provides excellent ground-truth data against which to compare both mass loss and velocity measurements. Global Land Ice Measurements from Space (GLIMS) provides the glacier outlines used in this study, based on imagery from 2001 to 2006.
We have developed an automated processing chain (e.g. Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a, Reference Willis, Melkonian, Pritchard and Ramageb; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013) that provides a reliable, high-resolution map of surface elevation change rates ![]() by applying a weighted linear regression to a time series of stacked ASTER DEMs and the SRTM DEM on a pixel-by-pixel basis. We reduce our overall uncertainty on volume changes (
by applying a weighted linear regression to a time series of stacked ASTER DEMs and the SRTM DEM on a pixel-by-pixel basis. We reduce our overall uncertainty on volume changes (![]() multiplied by area) by incorporating multiple DEMs. ASTER DEMs can be somewhat unreliable in the accumulation zone of an icefield due to low contrast, variable cloud and snow cover. We alleviate this by stacking multiple DEMs and constraining our linear regression to filter out spurious elevations from DEM errors.
multiplied by area) by incorporating multiple DEMs. ASTER DEMs can be somewhat unreliable in the accumulation zone of an icefield due to low contrast, variable cloud and snow cover. We alleviate this by stacking multiple DEMs and constraining our linear regression to filter out spurious elevations from DEM errors.
A separate automated processing chain uses pixel-tracking to estimate velocities from ASTER optical image pairs and Advanced Land Observing Satellite (ALOS) synthetic aperture radar (SAR) image pairs, with additional velocities obtained by applying the surface parallel-flow assumption to two 1 day European Remote-sensing Satellite (ERS) interferograms. We produce a synoptic map of glacier speeds over many of the outlet glaciers on the JIF with these velocities. Most velocity pairs have an uncertainty of about ±0.1 to ±0.2 m d–1, which makes detection of changes in speed of less than ~15% difficult, given the relatively low speeds of outlet glaciers on the JIF (e.g. when compared with Patagonia (Reference Willis, Melkonian, Pritchard and RamageWillis and others, 2012b; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013)). These speed variations could be easily measured by GPS, but our method, although it has lower precision, provides much better spatial sampling, with ASTER, in particular, expanding coverage in the ablation zone (where GPS measurements are more sparse).
After providing a synoptic overview of ![]() and speeds for the whole icefield we focus on two glaciers, Taku and Mendenhall. Depth profiles available at both glaciers are combined with our
and speeds for the whole icefield we focus on two glaciers, Taku and Mendenhall. Depth profiles available at both glaciers are combined with our ![]() and velocities to estimate flux over different time periods in order to look for changes at both glaciers and determine the calving contribution to mass loss at Mendenhall Glacier.
and velocities to estimate flux over different time periods in order to look for changes at both glaciers and determine the calving contribution to mass loss at Mendenhall Glacier.
The 60 km long Taku Glacier is the largest on the JIF, covering 775 km2. Taku Glacier has been advancing since 1850 (Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009). It continues to advance due to the long history of positive mass balance (e.g. Reference Pelto and MillerPelto and Miller, 1990; Reference Post and MotykaPost and Motyka, 1995; Reference PeltoPelto and others, 2008, Reference Pelto, Kavanaugh and McNeil2013), and ASTER imagery shows the front advancing from 2002 to 2009 to 2010, with roughly 100–200 m of total advance from 2002 to 2010.
Mendenhall Glacier is ~22 km long and covers ~96 km2 (Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Reference MolniaMolnia, 2007). It is historically land-terminating, but much of the front now ends in a proglacial lake (Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Reference MolniaMolnia, 2007). Its close proximity to Juneau, Alaska, has made it the subject of many previous studies (e.g. Reference LawrenceLawrence, 1950; Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Reference Boyce, Motyka and TrufferBoyce and others, 2007; Reference MolniaMolnia, 2007). We compare our results with Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) and Reference Boyce, Motyka and TrufferBoyce and others (2007) to detect any change in the area-averaged mass balance and pattern of ![]() , as well as any change in the calving flux.
, as well as any change in the calving flux.
We also follow previous studies (e.g. Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others, 2008) in examining snowfall and temperature data from the Juneau International Airport station. We compare changes in these climate factors to differences in the area-averaged mass balance and pattern of ![]() between our results and previous studies
between our results and previous studies
Methods
Elevation change rates
We begin processing by horizontally and vertically co-registering 75 ASTER DEMs (Fig. 2) to the SRTM DEM (acquired 11–22 February 2000; Reference Rasmussen and ConwayRabus and others, 2003).

Fig. 2. Dates of the 75 ASTER DEMs incorporated into ![]() .
.
Horizontal co-registration is performed using ROI_PAC (Repeat Orbit Interferometry PACkage) (Reference Rosen, Hensley, Peltzer and SimonsRosen and others, 2004) tools that find and apply an affine transformation between hillshades of the ASTER and SRTM DEMs. Subsequent ![]() processing steps are detailed in Reference Willis, Melkonian, Pritchard and RiveraWillis and others (2012a) and Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others (2013) and are only briefly described below. Each individual ASTER DEM is assigned a 1σ uncertainty defined as the standard deviation of the bedrock elevation differences between it and the SRTM DEM. The standard deviation of stable ground elevation differences with a reference DEM is a common measure of the uncertainty associated with ASTER DEM elevations (Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others, 2005; Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a). We typically find the standard deviation of off-ice elevation differences between ASTER DEMs and the SRTM DEM to be 8–20 m, similar to the uncertainty found for ASTER DEMs by other studies (Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others, 2005; Reference San and SüzenSan and Süzen, 2005; Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a). We compare internal bedrock elevations from laser altimetry acquired over Taku Glacier on 10 September 2011 with the closest cloud-free ASTER DEM in time, acquired on 7 June 2010. After adjusting for the geoid we find a mean difference of –0.33 m and standard deviation of 5.8 m from 1848 points, which compares well with the uncertainty of 8.1 m we assign to this DEM based on bedrock elevation differences with the SRTM DEM. The SRTM is assigned a 1 uncertainty of 5 m (Reference Carabajal and HardingCarabajal and Harding, 2005; Reference RodríguezRodríguez and others, 2005).
processing steps are detailed in Reference Willis, Melkonian, Pritchard and RiveraWillis and others (2012a) and Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others (2013) and are only briefly described below. Each individual ASTER DEM is assigned a 1σ uncertainty defined as the standard deviation of the bedrock elevation differences between it and the SRTM DEM. The standard deviation of stable ground elevation differences with a reference DEM is a common measure of the uncertainty associated with ASTER DEM elevations (Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others, 2005; Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a). We typically find the standard deviation of off-ice elevation differences between ASTER DEMs and the SRTM DEM to be 8–20 m, similar to the uncertainty found for ASTER DEMs by other studies (Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others, 2005; Reference San and SüzenSan and Süzen, 2005; Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a). We compare internal bedrock elevations from laser altimetry acquired over Taku Glacier on 10 September 2011 with the closest cloud-free ASTER DEM in time, acquired on 7 June 2010. After adjusting for the geoid we find a mean difference of –0.33 m and standard deviation of 5.8 m from 1848 points, which compares well with the uncertainty of 8.1 m we assign to this DEM based on bedrock elevation differences with the SRTM DEM. The SRTM is assigned a 1 uncertainty of 5 m (Reference Carabajal and HardingCarabajal and Harding, 2005; Reference RodríguezRodríguez and others, 2005).
C-band penetration into snow and ice (Reference Rignot, Echelmeyer and KrabillRignot and others, 2001) is taken into account for the SRTM DEM by comparing C-band SRTM elevations after applying a curvature adjustment to X-band SRTM (Reference Rasmussen and ConwayRabus and others, 2003) elevations over the JIF, a technique developed by Reference Gardelle, Berthier and ArnaudGardelle and others (2012) and used by Reference Willis, Melkonian, Pritchard and RiveraWillis and others (2012a) and Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others (2013). ASTER DEMs are derived from stereo-optical imagery, so there is no penetration. X-band penetration should be small relative to C-band (e.g. Reference Rignot, Echelmeyer and KrabillRignot and others, 2001; Reference Gardelle, Berthier and ArnaudGardelle and others, 2012), and both X-band and C-band were acquired at the same time by the SRTM, a necessary condition for assessing penetration on glaciers that are changing elevation. Figure 3 shows the difference between X-band (99.95% coverage over the JIF) and C-band elevations over ice before and after the curvature adjustment, which only has a small influence. We calculate and apply a linear least-squares fit to the differences between X- and C-band elevations from 700 to 1650 m because the elevations up to 650 m show little evidence of penetration and the area above 1650 m is too small to be confident in the results there. The linear fit gives 0.3 m of additional penetration per 100 m increase in elevation. Above 1650 m we assume 3 m of penetration. Overall, this results in a mean penetration of 2.2 m, compared with 1.4–3.4 m of penetration found by Reference Gardelle, Berthier, Arnaud and Ka¨a¨bGardelle and others (2013) in the Himalaya and 2 m of penetration in Patagonia found by Reference Willis, Melkonian, Pritchard and RiveraWillis and others (2012a).

Fig. 3. SRTM X-band minus C-band elevations, before and after curvature correction based on off-ice pixels. ‘Adjusted’ refers to the curvature correction used to correct for the bias due to DEMs of different resolutions. The trend shown by the black line from 700 to 1650 m elevation is added to our SRTM elevations to account for C-band penetration. For elevations above 1650 m, 3 m of penetration is assumed. Error bars indicate the standard deviation of elevation differences for selected 50 m bins.
We apply a weighted linear regression at each individual pixel of the icefield, adjusting for the SRTM C-band penetration. Each DEM is weighted by the inverse of its associated uncertainty. We exclude elevations from the regression that deviate by more than +4.4/–10 m a–1 (in the ablation zone) or +4.4/–5 m a–1 (in the accumulation zone) from the first elevation in the time series, which is the SRTM DEM for >99% of our results. The radar-derived SRTM DEM is not influenced by clouds and shadows present in the optically derived ASTER DEMs, so using the SRTM as a reference surface mitigates the influence of bad ASTER elevations on our overall results. Accumulation and ablation zones are determined using the SRTM DEM according to the equilibrium-line altitude (ELA) for the individual glacier basins that comprise the JIF.
The maximum allowed positive deviation of +4.4 m a–1 is based on estimates of accumulation rates at Juneau of 4 ~m w.e. a–1 (Reference Pelto and MillerPelto and Miller, 1990; Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003). The maximum allowed negative deviation of –10 m a–1 is a conservative approximation of the maximum thinning of ~8ma–1 measured at the front of Mendenhall Glacier by Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003). We do not expect significant areas with thinning greater than 10 m a–1 based on the ![]() gradient we observe below the ELA. Given that thickening is less than precipitation in m w.e. a–1, our overall volume change rates should be considered a minimum volume loss rate.
gradient we observe below the ELA. Given that thickening is less than precipitation in m w.e. a–1, our overall volume change rates should be considered a minimum volume loss rate.
About 2% of the icefield has gaps in coverage because too few elevations remain in the stack after filtering. These gaps are filled with the median ![]() value of pixels within 1 km to avoid the influence of extremely high or low
value of pixels within 1 km to avoid the influence of extremely high or low ![]() . We prefer this method to interpolation, because these gaps are often due to cloud cover or DEM errors, so the edges of the gaps have extreme values.
. We prefer this method to interpolation, because these gaps are often due to cloud cover or DEM errors, so the edges of the gaps have extreme values.
The volume change rate ![]() at each pixel is the
at each pixel is the ![]() for the pixel multiplied by the area of the pixel (30 m ×30 m, or 900 m2). Summing together the
for the pixel multiplied by the area of the pixel (30 m ×30 m, or 900 m2). Summing together the ![]() of every pixel yields a
of every pixel yields a ![]() for the entire icefield. We account for erosion of soft sediments caused by the advance of Taku Glacier (Reference Motyka, Truffer, Kruiger and BuckiMotyka and others, 2006) by adding +2 ±1ma –1 to our
for the entire icefield. We account for erosion of soft sediments caused by the advance of Taku Glacier (Reference Motyka, Truffer, Kruiger and BuckiMotyka and others, 2006) by adding +2 ±1ma –1 to our ![]() from Profile 1 (see Fig. 5) to the terminus of Taku. A mass change rate (
from Profile 1 (see Fig. 5) to the terminus of Taku. A mass change rate (![]() ) estimate is calculated from
) estimate is calculated from ![]() by assuming mass change has the density of glacier ice in the ablation zone, ~900 kg m –1 (e.g. Reference McGeeMcGee, 1995; Reference Rignot, Rivera and CasassaRignot and others, 2003; Reference Berthier, Arnaud, Baratoux, Vincent and RémyBerthier and others, 2004, Reference Berthier, Schiefer, Clarke, Menounos and Rémy2010; Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009), and assigning a density of 700 kg m−3 to mass change in the accumulation zone (e.g. Reference ZempZemp and others, 2010; Reference GardnerGardner and others, 2013). Dividing the mass change rate for a particular region, basin or sub-basin (e.g. accumulation or ablation zone) by its area produces an area-averaged mass balance (m w.e. a–1).
by assuming mass change has the density of glacier ice in the ablation zone, ~900 kg m –1 (e.g. Reference McGeeMcGee, 1995; Reference Rignot, Rivera and CasassaRignot and others, 2003; Reference Berthier, Arnaud, Baratoux, Vincent and RémyBerthier and others, 2004, Reference Berthier, Schiefer, Clarke, Menounos and Rémy2010; Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009), and assigning a density of 700 kg m−3 to mass change in the accumulation zone (e.g. Reference ZempZemp and others, 2010; Reference GardnerGardner and others, 2013). Dividing the mass change rate for a particular region, basin or sub-basin (e.g. accumulation or ablation zone) by its area produces an area-averaged mass balance (m w.e. a–1).
Mass change rate – uncertainties
Sources of uncertainty for our measurements are the uncertainty on the elevations incoporated into the regression, uncertainty on the ELA, the effect of varying the maximum deviation allowed from the first elevation, different density scenarios, and uncertainty of the penetration depth of the C-band SRTM DEM. These are covered in turn below.
The uncertainty associated with the ![]() for each pixel is calculated from the model covariance matrix (e.g. Reference Aster, Borchers and ThurburAster and others, 2005), which accounts for the uncertainties on the elevations incorporated into the regression. The 95% confidence interval for the volume change rate uncertainty is calculated using the formula
for each pixel is calculated from the model covariance matrix (e.g. Reference Aster, Borchers and ThurburAster and others, 2005), which accounts for the uncertainties on the elevations incorporated into the regression. The 95% confidence interval for the volume change rate uncertainty is calculated using the formula ![]() (e.g. Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a). U is the total ‘volume’ of uncertainty, calculated by taking the uncertainty at each pixel, multiplying it by the area of the pixel (to determine a ‘volume’ of uncertainty for that pixel) and then adding together ‘volume’ of uncertainty for each pixel where
(e.g. Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a). U is the total ‘volume’ of uncertainty, calculated by taking the uncertainty at each pixel, multiplying it by the area of the pixel (to determine a ‘volume’ of uncertainty for that pixel) and then adding together ‘volume’ of uncertainty for each pixel where ![]() is calculated. N is the number of independent pixels (e.g. Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a), which we determine by dividing the total area by the area over which off-ice
is calculated. N is the number of independent pixels (e.g. Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a), which we determine by dividing the total area by the area over which off-ice ![]() are correlated (e.g. Reference Rolstad, Haug and DenbyRolstad and others, 2009). We estimate the scale at which the
are correlated (e.g. Reference Rolstad, Haug and DenbyRolstad and others, 2009). We estimate the scale at which the ![]() are independent by finding the area at which the variance of the off-ice
are independent by finding the area at which the variance of the off-ice ![]() begins to ‘flatten’ (for details of the method see Reference Rolstad, Haug and DenbyRolstad and others, 2009; Reference Willis, Melkonian, Pritchard and RamageWillis and others, 2012b), which we estimate to be 810 m ×810 m (see Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a, Reference Willis, Melkonian, Pritchard and Ramageb; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013, for examples). The total contribution from the uncertainty of individual elevations is ~0.05 Gt a–1.
begins to ‘flatten’ (for details of the method see Reference Rolstad, Haug and DenbyRolstad and others, 2009; Reference Willis, Melkonian, Pritchard and RamageWillis and others, 2012b), which we estimate to be 810 m ×810 m (see Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a, Reference Willis, Melkonian, Pritchard and Ramageb; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013, for examples). The total contribution from the uncertainty of individual elevations is ~0.05 Gt a–1.
We use ELAs of 925, 1100 and 1050 m for Taku, Menden-hall and Lemon Creek glaciers, respectively (Reference PeltoPelto, 2000; Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Reference Boyce, Motyka and TrufferBoyce and others, 2007; Reference PeltoPelto and others, 2008). A regional ELA of 1000 m (e.g. Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007) is used for the rest of the icefield. The choice of ELA determines the accumulation and ablation zone for each glacier basin, which affects our mass change rate in two ways. First, it determines the percentage of the ![]() calculated using +4.4/–10 m a−1 versus +4.4/–5 m a−1 allowed deviation from the first elevation. Second, it determines the percentage of the
calculated using +4.4/–10 m a−1 versus +4.4/–5 m a−1 allowed deviation from the first elevation. Second, it determines the percentage of the ![]() for which a density of 700 kg m –3 vs 900 kg m –3 is assumed. We assume an ELA uncertainty of ±200 m, and difference the mass change rates at the upper and lower bounds. This difference (0.18 Gt a–1) is taken as the uncertainty due to ELA for our mass change rate.
for which a density of 700 kg m –3 vs 900 kg m –3 is assumed. We assume an ELA uncertainty of ±200 m, and difference the mass change rates at the upper and lower bounds. This difference (0.18 Gt a–1) is taken as the uncertainty due to ELA for our mass change rate.
The deviation allowed from the first elevation in the time series has a large impact on the mass loss rate (e.g. Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013). The unsymmetric cut-off (+4.4/–5 m a−1 in the accumulation zone, +4.4/–10 m a–1 in the ablation zone) may bias our results towards thinning, but an unsymmetric cut-off is more physically justified than a symmetric cut-off (Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013). One year of accumulated precipitation undergoes densification into firn and eventually ice, so +4.4 m a–1 is chosen as a reasonable upper limit on the maximum thickening expected over the large areas covered in this study. We note that a point measurement may yield a ![]() higher than +4.4 m a –1 but we would not expect a single point to be representative of sustained thickening rates over many hundreds of square kilometers. Figure 4 highlights the importance of applying this cut-off, showing that cloud-influenced elevations would seriously degrade the quality of our regression for each pixel. Tests using a higher positive cut-off produced discontinuous and incoherent ‘splotches’ of extreme positive
higher than +4.4 m a –1 but we would not expect a single point to be representative of sustained thickening rates over many hundreds of square kilometers. Figure 4 highlights the importance of applying this cut-off, showing that cloud-influenced elevations would seriously degrade the quality of our regression for each pixel. Tests using a higher positive cut-off produced discontinuous and incoherent ‘splotches’ of extreme positive ![]() that are unrealistic.
that are unrealistic.

Fig. 4. Elevation values and ![]() for randomly selected pixels over Field Glacier. The leftmost elevation in each graph is the SRTM elevation at that pixel. Blue lines indicate the
for randomly selected pixels over Field Glacier. The leftmost elevation in each graph is the SRTM elevation at that pixel. Blue lines indicate the ![]() calculated for each pixel. Elevation points bolded red are excluded from
calculated for each pixel. Elevation points bolded red are excluded from ![]() calculation. The bottom right panel shows the
calculation. The bottom right panel shows the ![]() map (location in Fig. 5), with numbered circles indicating the location corresponding to each graph.
map (location in Fig. 5), with numbered circles indicating the location corresponding to each graph.
To assess the uncertainty due to the choice of maximum deviation allowed, we find the mode of the distribution of elevation differences between all ASTER DEMs and the SRTM DEM, normalized by dividing by the time interval between each ASTER DEM and the SRTM DEM (Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013). The mode is not affected by the choice of allowed deviation, and so is an independent measure to which we can compare our regression-derived rates. We are not suggesting the mode rate represents the best estimate of the average ![]() . It is, rather, approximately what the rate would be if the distribution were Gaussian around the peak
. It is, rather, approximately what the rate would be if the distribution were Gaussian around the peak ![]() . The ‘mode rate’ is –0.10 m w.e. a –1. We incorporate the difference between the mode rate and our regression rate (0.08 Gt a –1) that results from using the same density and penetration assumptions as our regression rate to our uncertainties to fully account for any possible bias.
. The ‘mode rate’ is –0.10 m w.e. a –1. We incorporate the difference between the mode rate and our regression rate (0.08 Gt a –1) that results from using the same density and penetration assumptions as our regression rate to our uncertainties to fully account for any possible bias.
We assume volume change in the ablation zone is at a density of 900 kg m –3 (e.g. Reference McGeeMcGee, 1995; Reference Rignot, Rivera and CasassaRignot and others, 2003; Reference Berthier, Arnaud, Baratoux, Vincent and RémyBerthier and others, 2004, 2009; Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009) and volume change in the accumulation zone has a density of 700 kg m –3 (e.g. Reference ZempZemp and others, 2010; Reference GardnerGardner and others, 2013). However, the density of the lost material is likely variable. We take the difference between the mass change rate obtained using our density scenario and the rate produced by assuming all mass change is at a density of 900 kg m –3 as the uncertainty due to density (0.13 Gt a−1), similar to Reference Ka¨a¨b, Berthier, Nuth, Gardelle and ArnaudKa¨a¨b and others (2012).
The penetration depth of the C-band SRTM into snow and ice is an additional source of uncertainty. Reference Rignot, Echelmeyer and KrabillRignot and others (2001) cited uncertainties of ±2 m for C-band penetration on temperate ice in Alaska; we take 0 m penetration (the minimum possible penetration) and 4 m penetration to be end-member cases and examine the effect on our mass change rate. Assuming 0 m penetration depth reduces the mass loss rate by +0.38 Gt a–1, assuming 4 m of penetration increases the mass loss rate by –0.38 Gt a–1. We therefore add 0.38 Gt a –1 to our uncertainties to account for penetration depth uncertainty. Our consideration of the penetration depth uncertainty is conservative, as we have already tried to correct for the penetration effect.
Taking the square root of the sum of the squared uncertainties gives us an overall uncertainty of 0.46 Gt a–1 (equivalent to an area-averaged mass balance of 0.12 m w.e. a –1). Uncertainties beyond the uncertainty from the regression itself are added as an average rate to the uncertainties for individual glacier basins in Table 1.
Table 1. Mass change rates and average mass balances for selected outlet glaciers on the JIF

Velocities
ASTER (optical)
Feature- or pixel-tracking has been used to track glacier speeds at numerous locations (e.g. Reference Scambos, Dutkiewicz, Wilson and BindschadlerScambos and others, 1992; Reference Stearns and HamiltonStearns and Hamilton, 2005; Reference Howat, Joughin, Fahnestock, Smith and ScambosHowat and others, 2008b; Reference Willis, Melkonian, Pritchard and RamageWillis and others, 2012b).
To prepare the images we first use NASA’s Automatic Co-Registration and Orthorectification Package (AROP) (Reference Gao, Masek and WolfeGao and others, 2009) to co-register ASTER level 1B images to a Landsat reference image and orthorectify them using the SRTM DEM (Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a). We then produce sub-pixel offsets using the ‘ampcor’ normalized amplitude cross-correlation routine from ROI_PAC (Reference Rosen, Hensley, Peltzer and SimonsRosen and others, 2004; Reference Willis, Melkonian, Pritchard and RamageWillis and others, 2012b). We produce offset measurements every 120 m (8 pixels) using a reference window (matrix used to calculate the cross-correlation coefficient) of 480 m ˟ 480 m (32 ˟32 pixels) (Reference Willis, Melkonian, Pritchard and RiveraWillis and others, 2012a; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013). We experimented with offset samplings of <120 m (which increases computation time), but this did not increase our effective resolution or fill gaps in our spatial coverage.
The results are post-filtered by excluding offsets with a signal-to-noise ratio (SNR, which is the peak cross-correlation coefficient divided by the average cross-correlation coefficient) below a manually selected threshold. The threshold is determined by finding the maximum SNR that does not exclude coherent glacier velocities. An elevation- dependent correction (determined from ‘bedrock’ velocities) is applied to the speeds to correct for the elevation-dependent bias due to imprecise co-registration/orthorectification (Reference Ahn and HowatAhn and Howat, 2011). Applying an elevation-dependent correction significantly improves the contrast between bedrock offsets and glacier offsets (e.g. Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013).
Each ASTER pair covers multiple glacier basins. One or both of the images in a pair may be cloudy over some basins. We esimate the uncertainty for each pair from motion on ice-adjacent ‘bedrock’ (Reference Willis, Melkonian, Pritchard and RamageWillis and others, 2012b; Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013), which should be zero. Ice-adjacent ‘bedrock’ is defined as non-water, off-ice area within 5 km of a glacier, excluding the closest 600 m (5 pixels) to ensure glacier motion does not contaminate the ‘bedrock’. We calculate ice-adjacent bedrock speeds for each basin within the results from an individual image pair. We clip the ice-adjacent bedrock speeds within each basin at the mean plus or minus two standard deviations, then iteratively recalculate the mean and standard deviation to provide an estimate of uncertainty due to poor co-registration and DEM errors. We take the basin with the minimum mean plus one standard deviation of ice-adjacent bedrock speeds to be representative of well-correlated bedrock for the pair and assign this as the pair’s overall uncertainty. We feel this is justified, as the textured, low surface slopes of the glaciers usually display much more coherent, slowly spatially varying motions than the steeper bedrock.
Velocity uncertainty from pixel-tracking is well described in the literature (e.g. Reference Scherler, Leprince and StreckerScherler and others, 2008; Reference Ahn and HowatAhn and Howat, 2011). Using the techniques suggested by other studies and further developed in our previously published material (outlined above), we estimate velocity uncertainties to be around 0.1–0.2 m d –1. The magnitude of our uncertainty is higher than that of some other studies (e.g. Reference Scherler, Leprince and StreckerScherler and others, 2008) that have also applied pixel-tracking to ASTER imagery to estimate glacier velocities. Reference Scherler, Leprince and StreckerScherler and others (2008) took the mean and standard deviation of off-ice, or ‘stable ground’ motion as a measure of uncertainty, with ‘stable ground’ being defined by them as all displacements from –10 m to +10 m. We apply the method of Reference Scherler, Leprince and StreckerScherler and others (2008) to one of our ASTER image pairs (4 October 2004 to 8 May 2005) to compare with the uncertainty obtained using our method. Our method yields an uncertainty of ±0.09 m d–1, while the method of Reference Scherler, Leprince and StreckerScherler and others (2008) provides an uncertainty of ±0.03 m d−1. Consistently lower uncertainties would be expected using the method of Reference Scherler, Leprince and StreckerScherler and others (2008), because cutting off displacements at 10 m is generally a more severe restriction than our 2 clipping of adjacent off-ice displacements. However, they noted that removing glacier displacements using glacier outlines, which is part of our method, would be preferable to assuming all displacements from –10 m to +10 m are stable ground. We therefore consider our approach to be a reasonable and conservative estimate of the uncertainty for coherent motion, i.e. motion that has a high SNR and is spatially consistent with neighboring motions.
ALOS (radar)
We use L-band SAR pixel-tracking (e.g. Reference RignotRignot, 2008; Reference Strozzi, Kouraev, Wiesmann, Sharov and WernerStrozzi and others, 2008; Reference Rignot, Mouginot and ScheuchlRignot and others, 2011; Reference Burgess, Forster and LarsenBurgess and others, 2013) from five 46 day, ascending ALOS pairs to produce ice velocities for the Juneau Icefield. The ALOS SAR images have an initial pixel resolution of 3.3m (azimuth) by 8.3 m (range). The offsets have an effective resolution of approximately 150 m (azimuth) by 200 m (range), based on the step size of 50 pixels (azimuth) by 25 pixels (range). SAR images cover a broader area than the optical images and are not limited by cloud cover, providing velocities at many glaciers with no ASTER observations. SAR pixel-tracking also performs well in the snow-covered, high-altitude accumulation zone where optical images lack trackable features.
Raw ALOS SAR data are processed using ROI_PAC, and offsets are produced by ‘ampcor’. The results are SNR-filtered and run through the elevation-dependent correction routine. The SNR threshold we use for ALOS is less than ASTER; it depends on various aspects of the processing (chip size, sensor type) and is adjusted so that coherent areas of offset over glaciers are not excluded. ALOS interferometry does not yield much velocity information due to the relatively large motions, long separation between scenes, and changing surface characteristics.
Parallel flow (ERS)
We use ROI_PAC to process 1 day SAR image pairs taken by ERS to provide additional velocity measurements over the southern part of the JIF, including Taku Glacier. An ascending track interferogram from 28 to 29 October 1995 and a descending track interferogram from 29 to 30 October 1995 are unwrapped at a resolution of 41 m × 46 m, then georeferenced and down-sampled to a resolution of 300 m × 300 m. The interferograms are unwrapped using the branch-cut method (Reference Goldstein and WernerGoldstein and others, 1988) and power spectrum filter (Reference Goldstein and WernerGoldstein and Werner, 1998). Combining the results of these two unwrapped interferograms and applying the surface parallel-flow assumption – that all motion is parallel to the surface gradient of the glacier, obtained from the SRTM DEM – yields east–west and north–south velocities. Reference Joughin, Kwok and FahnestockJoughin and others (1998) provided the equations used to convert the unwrapped interferograms to velocities.
GPS
Transverse and longitudinal profiles of velocities and elevations on the JIF have been collected using rapid-static and real-time kinematic GPS surveying from 1993 through 2007 (e.g. Reference McGeeMcGee, 1995; Reference LangLang, 1997; Reference McGeeMcGee and others, 2007) and made available on the web (http://www.crevassezone.org). Several profiles are surveyed at least once per year to monitor year-to-year elevation change, and ~1000 stakes have been surveyed twice in a given year (within 7–14 days) to measure velocities (Reference McGeeMcGee and others, 2007; Reference McGeeMcGee, 2009). These surveys are always performed during July and August (Reference McGeeMcGee and others, 2007; Reference McGeeMcGee, 2009). The GPS displacements are estimated to have horizontal and vertical accuracy of 1 and 5 cm, respectively (Reference McGeeMcGee, 1995; Reference McGeeMcGee and others, 2007).
Flux
Ice thickness profiles available for Mendenhall and Taku Glaciers, combined with our velocities, ![]() and DEMs, enable us to produce flux estimates. We calculate flux at Mendenhall Glacier primarily to estimate the calving flux and thus the dynamic contribution to mass loss. Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) used radio-echo sounding (RES) to determine ice thicknesses for several transects on Mendenhall Glacier. Combining these with GPS velocity measurements, they were able to estimate the calving flux as a percentage of the average volume loss for Mendenhall Glacier.
and DEMs, enable us to produce flux estimates. We calculate flux at Mendenhall Glacier primarily to estimate the calving flux and thus the dynamic contribution to mass loss. Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) used radio-echo sounding (RES) to determine ice thicknesses for several transects on Mendenhall Glacier. Combining these with GPS velocity measurements, they were able to estimate the calving flux as a percentage of the average volume loss for Mendenhall Glacier.
We find the location of their transects from Figures 2 and 4 in Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003). Gridding the cross sections shown in Figure 5 of Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) and applying a ninth-order polynomial fit yields a close approximation of their RES depth results.

Fig. 5. Elevation change rates from ASTER DEMs and the SRTM DEM for the Juneau Icefield (2000 through 2009–13), with notable glaciers indicated by arrows. There is a strong thinning signal at the front of most outlet glaciers, with the exception of Taku Glacier. Black lines indicate glacier boundaries as defined by GLIMS. Box surrounding Field Glacier indicates location of ![]() map in Figure 4. The red line shows the ELA for Taku Glacier (925 m). Green lines show the location of Profiles 1 and 4 on Taku Glacier
map in Figure 4. The red line shows the ELA for Taku Glacier (925 m). Green lines show the location of Profiles 1 and 4 on Taku Glacier
We update the ice thicknesses from our polynomial fit by applying our ![]() over the appropriate time period. We then use our ALOS-derived velocities from 2007 to 2011 (only ALOS produced good results over Mendenhall Glacier) to obtain flux estimates for gates e and g from Figure 5 of Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003).
over the appropriate time period. We then use our ALOS-derived velocities from 2007 to 2011 (only ALOS produced good results over Mendenhall Glacier) to obtain flux estimates for gates e and g from Figure 5 of Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003).
We move flux gate g north by 300 m to ensure that we are not profiling a portion of Mendenhall that has already calved off. Linear interpolation between the maximum depths of gates e and g (~3 km apart) yields an increase in maximum depth of 30% 300 m north of gate g. We therefore increase the depths at gate g by 30% to account for the applied northward shift. Further details of our method for calculating flux are given in Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others (2013).
Reference PeltoPelto and others (2008) used seismic methods to determine ice depth at tranverse ‘Profile 4’ in the accumulation zone of Taku Glacier (green line in Fig. 5). We calculate flux at Profile 4 using their ice depths with the ALOS pairs spanning 2007–11 and the ERS parallel-flow velocities from 1995 using the same methods detailed above.
We provide two estimates for all fluxes. The first is an upper constraint assuming sliding only, with the vertically integrated flow velocity equal to the surface velocity. The second is a lower constraint assuming no sliding, where the vertically integrated flow velocity is 80% of the surface velocity (e.g. Reference Burgess, Forster and LarsenBurgess and others, 2013).
Results
Elevation change rates
Figure 5 shows ![]() for the JIF. The period covered by the
for the JIF. The period covered by the ![]() results is 2000–13 for ~40% of the area of the JIF, 2000–10 for ~45%, and 2000–09 for the remainder (located in the northwest). Every major outlet glacier except Taku is thinning. Taku Glacier stands out, with thickening at the front and a mix of thickening and thinning elsewhere. Volume change rates are broken down for selected glaciers in Table 1. We estimate a total mass change rate of –0.50 ±0.46 Gt a−1 from our
results is 2000–13 for ~40% of the area of the JIF, 2000–10 for ~45%, and 2000–09 for the remainder (located in the northwest). Every major outlet glacier except Taku is thinning. Taku Glacier stands out, with thickening at the front and a mix of thickening and thinning elsewhere. Volume change rates are broken down for selected glaciers in Table 1. We estimate a total mass change rate of –0.50 ±0.46 Gt a−1 from our ![]() (Fig. 5), equivalent to an area-averaged mass balance for the JIF of –0.13 ±0.12 m w.e. a–1. Excluding Taku Glacier yields an area-averaged mass balance of –0.31 0.17 m w.e. a –1 for the remainder of the JIF, more than twice the thinning rate with Taku Glacier included.
(Fig. 5), equivalent to an area-averaged mass balance for the JIF of –0.13 ±0.12 m w.e. a–1. Excluding Taku Glacier yields an area-averaged mass balance of –0.31 0.17 m w.e. a –1 for the remainder of the JIF, more than twice the thinning rate with Taku Glacier included.
Taku Glacier
Taku Glacier has an area-averaged mass balance of +0.44 ±0.15 m w.e. a–1 for 2000–10, and its continued advance corroborates the positive ![]() we find at its front. It contributes +0.34 ±0.12 Gt a –1 to the total mass change rate for the JIF.
we find at its front. It contributes +0.34 ±0.12 Gt a –1 to the total mass change rate for the JIF.
Mendenhall Glacier
We find an area-averaged mass balance of –0.48 ±0.19 m we. a−1 for Mendenhall Glacier from 2000 to 2013. Peak thinning rates of 9 m a−1 are observed between 2000 and 2013 near the calving front of Mendenhall Glacier. These rates are comparable to the 1995–2000 thinning rate of 9ma–1 in the terminus region produced by differencing center-line airborne laser profiles in 1995, 1999 and 2000 (Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003).
Velocities
Figure 6 shows a blended velocity map for the entire icefield made from 48 ASTER pairs, 5 ALOS pairs and ERS parallel-flow velocities spanning 28–30 October 1995. The pixel at each point is a filtered average of the speeds at that point. Optical pixel-tracking yields the most coherent and extensive offsets in the ablation zone, where trackable features such as crevasses are exposed. Radar pixel-tracking and interferometry yields good velocities in the accumulation zone, complementing the ASTER offsets found in the ablation zones.

Fig. 6. Speeds for the Juneau Icefield, a filtered average of 48 ASTER pairs with dates from August 2001 to June 2010, 5 ALOS pairs with dates from January 2008 to February 2011, and ERS-derived parallel-flow speeds from October 1995. Gray triangles indicate the location of GPS velocities shown in Figure 7. Red lines show the location of the profiles in Figure 9. Yellow lines show the location of the flux gates.
Maximum speeds at the icefield of 1.4 ±0.1 m d –1 occur along the center line of Taku Glacier 8 km up-glacier from the front. Overall, speeds at Taku Glacier are in close agreement with previous surveys (e.g. Reference McGeeMcGee and others, 2007; Reference PeltoPelto and others, 2008; Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009). Our study finds a speed of ~0.9 m d –1 just below the ELA of Taku Glacier (Fig. 7), which is identical to that found by Reference PeltoPelto and others (2008) (Fig. 8, point 14) in 2001 and 2004, indicating no acceleration has taken place since that time.

Fig. 7. GPS, ASTER and ERS parallel-flow speeds along the trunk of Taku Glacier (location shown in Fig. 6 as gray triangles). Uncertainties are . The GPS speeds are systematically higher, likely a seasonal effect due to the fact that they were measured in late July.

Fig. 8. Total winter (October–April) snowfall (cm) in blue, and average summer (June–August) temperature (8C) in red, for study periods spanning 1948–2013, shown as deviations from the 1970– 2000 averages (horizontal black line). Data are from the Juneau International Airport station.
Even though our velocity results are temporally sparse, we find no significant interannual changes in velocity at the ±10% level between 1995 and 2011. ERS provides a velocity map over much of the icefield in 1995, with ASTER and ALOS giving us velocities over different parts of the icefield at different times from 2001 to 2011. We have enough temporal resolution to detect small seasonal variations in the speed at the front of Taku Glacier, which are compared to the results of Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others (2009) in the discussion. There we also compare velocities from optical and radar pixel-tracking with GPS velocities measured by the JIRP to test the accuracy of our measurements and search for evidence of acceleration.
Discussion
Elevation change rates
Juneau Icefield versus other icefields
The JIF is closer to being in a state of mass balance (–0.13 ±0.12 m w.e. a –1) than any other Alaskan icefield. GRACE mass loss estimates for glacierized Alaska given by Reference GardnerGardner and others (2013) (for 2003–09, area 87 100 km2) and Reference ArendtArendt and others (2013) (for 2003–10, area 82 505 km2) are equivalent to area-averaged mass balances of –0.61 ±0.21 and –0.79 ±0.13 m w.e. a –1, respectively.The longer-term mass balances for Alaska in general, and southeast Alaska in particular, are also more negative than for the JIF. Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) found an area-averaged mass balance of –0.48 0.10 m w.e. a –1 for Alaskan glaciers from 1962 to 2006 (area 87 862 km2), and Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) found an area-averaged mass balance of –1.03 ±0.27 m w.e. a –1 from 1948/1961/1982/1987 to 2000 for glaciers in southeast Alaska (area 14 580 km2).
Comparison with DEM-differencing results for the Juneau Icefield
Comparison of our results with those of Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) and Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) suggests the possibility that the thinning rate has slowed at the JIF over the last 10 years compared to earlier years. Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) estimated an area-averaged mass balance between 1964 and 2006 of –0.48 0.±14 m w.e. a –1 for the JIF (personal communication from E. Berthier, 2013). This is more negative than our average (–0.13 0.12 m w.e. a –1). Part of the difference is due to the lack of coverage over Taku Glacier (a large positive contributor) in Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010). Removing Taku Glacier from our results produces an area-averaged mass balance of –0.31 0.17 m w.e. a –1.While this is still more positive than the area-averaged mass balance found by Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010), the difference is of the same magnitud as the uncertainties.
Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) estimated an area-averaged mass balance of –0.62 m w.e. a–1 for the JIF from 1948/1982/1987 to 2000. Their estimate includes Taku Glacier, meaning its mass balance is significantly more negative than our estimate and likely more negative than that of Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010), who again lack the positive contribution of Taku Glacier.
Spatially, the difference between our ![]() and those of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) and Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) appears to be concentrated at higher elevations (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007, Fig. 7; Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010, supplemental figure S1g), which would be expected if the difference is driven by accumulation. We discuss this in more depth below, where we examine the connections between decadal-scale climate variability and thinning at the JIF.
and those of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) and Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) appears to be concentrated at higher elevations (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007, Fig. 7; Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010, supplemental figure S1g), which would be expected if the difference is driven by accumulation. We discuss this in more depth below, where we examine the connections between decadal-scale climate variability and thinning at the JIF.
Taku Glacier
We find an area-averaged mass balance of 0.44 ±0.15 m w.e. a–1 for Taku Glacier from 2000 to 2010. We compare this rate with those from other studies below, highlighting the decadal-scale variability of mass balance at Taku Glacier, and note the possible effect of differences in the spatial extent of measurements between studies.
Reference Pelto, Kavanaugh and McNeilPelto and others (2013) used surface mass-balance measurements collected by JIRP from 1946 to 2011 to estimate the average mass balance for Taku Glacier, with surface mass balance defined as the ‘difference between the net snow accumulation and net ablation over one hydro-logic year’. They found a 1946–88 area-averaged mass balance of ~0.4 m w.e. a−1. Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) differenced DEMs over a somewhat longer time period, 1948–2000, and found an area-averaged mass balance of ~0.4 m w.e. a –1. Both of these are close to our more recent, 2000–10 area-averaged mass balance.
The 1988–2006 results of Reference PeltoPelto and others (2008) show a shift to mass loss at Taku Glacier, with an area-averaged mass balance of –0.14 m a–1. The anomalously large snowfalls at the JIF in late 2006 and early 2007 (e.g. Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others, 2008) noted above, which are not included in the measurements of Pelto and others (2008), account for a small part of the difference between our area-averaged mass balance and their 1988–2006 rate. These years are included in the surface mass-balance results of Reference Pelto, Kavanaugh and McNeilPelto and others (2013), who found a 2000–10 mass balance of –0.04 m a –1 for Taku Glacier, more positive than the 1988–2006 rate but still more negative than our rate of 0.44 0.15 m w.e. a –1.
A significant part of the difference is therefore due to factors other than the different time periods covered. This is also evident from calculating the average mass balance using the data in Reference Pelto, Kavanaugh and McNeilPelto and others (2013) for the study period of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007). Tabulating the mass-balance estimates of Reference Pelto, Kavanaugh and McNeilPelto and others (2013) for 1948–2000 yields an area-averaged mass balance of 0.26 m w.e. a−1, somewhat less than Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007).
Reference Pelto, Kavanaugh and McNeilPelto and others (2013) did not have any surface massbalance measurements in the ablation zone, where we find overall thickening, which may account for part of the difference between their rate and the rates found by our study and Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007). Reference Pelto, Kavanaugh and McNeilPelto and others (2013) acknowledge this as ‘the principal (source of) error’ in their mass-balance record. The lowspatial density of surface massbalance measurements is another acknowledged source of error (Reference PeltoPelto and others, 2008, Reference Pelto, Kavanaugh and McNeil2013). However, we do not peculate in what direction this would bias their results.
Mendenhall Glacier
Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) found mass loss rates from 1948 to 1995 and 1995 to 1999 at Mendenhall Glacier that are two to three times our 2000–13 area-averaged mass balance of –0.48±0.19m w.e. a−1. They estimated an area-averaged mass balance of −0.86±0.10 m w.e. a−1 from 1948 to 1995 (by differencing a 1948 topographic map with a 1995 airborne laser profile) and –1.29±0.03 m w.e. a−1 from 1995 to 1999 (repeat airborne laser profiles). In 1999–2000 they found a dramatic, positive shift to an areaaveraged mass balance of +0.85 ±0.11 m w.e. a –1. Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) attributed this to the anomalously cool and wet summer of 2000. The positive mass balance in 2000, along with high snowfall in late 2006 and early 2007, likely contributes to the more positive average mass balance we observe for Mendenhall from 2000 to 2013.
The surface mass-balance data available during our study period are sparse, but yield a more positive average mass balance than the preceding time periods given in Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003). Reference Boyce, Motyka and TrufferBoyce and others (2007) extended the results of Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003), estimating surface mass balances for 2003, 2004 and 2005 of –1.8, –1.2 and –0.9 m w.e. a –1, respectively. The average mass balance obtained by adding the values in Reference Boyce, Motyka and TrufferBoyce and others (2007) for 2000, 2003, 2004 and 2005 is –0.63 ±0.15 m w.e. a –1 assuming independent, annual uncertainties on mass balance of 0.3 m w.e. a–1). Nevertheless, the effect of a positive balance year on the average surface mass balance is significant, and the high snowfall mentioned above for 2006–07 would have a similar effect to 2000 on the average ![]() for Mendenhall Glacier.
for Mendenhall Glacier.
We spatially isolate the difference between our average ![]() and the rates of Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) by separating out our ‘lower glacier’
and the rates of Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) by separating out our ‘lower glacier’ ![]() using the SRTM DEM (<800 m a.s.l.; Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003). Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) measured a lower glacier thinning rate of 1 m a–1 between 1948 and 1982 and twice that between 1982 and 2000 (measured by differencing the 2000 center-line airborne laser profile with a center-line profile taken from 1982 topographic data). Our lower glacier thinning rate for 2000– 13 is 2.2 ± 0.3 m a –1. This is approximately the same as the 1982–2000 rate found by Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003), therefore the difference between our 2000–13
using the SRTM DEM (<800 m a.s.l.; Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003). Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) measured a lower glacier thinning rate of 1 m a–1 between 1948 and 1982 and twice that between 1982 and 2000 (measured by differencing the 2000 center-line airborne laser profile with a center-line profile taken from 1982 topographic data). Our lower glacier thinning rate for 2000– 13 is 2.2 ± 0.3 m a –1. This is approximately the same as the 1982–2000 rate found by Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003), therefore the difference between our 2000–13 ![]() and their 1982–2000 rate is concentrated at higher elevations.
and their 1982–2000 rate is concentrated at higher elevations.
Comparison of climate changes to thinning
We examine snowfall and summer temperature data from the Juneau International Airport station (provided on the US National Oceanic and Atmospheric Administration website, http://www.arh.noaa.gov/cliMap/akClimate.php) to determine if there is an association between changes in these climate variables and the various estimates of mass balance/![]() for the JIF given above. Figure 8 shows the tabulation of these data into average yearly snowfall (October–April) and average summer (June–August) temperature for study periods spanning 1948–2013 relative to 1970–2000 averages. The periods 1948–1982/2000 have the highest snowfall and lowest summer temperatures, 1982/1987–2000 and 1995– 99 have the lowest snowfall and highest summer temperatures, and 2000–2009/2010/2013 are intermediate, close to the 1970–2000 averages.
for the JIF given above. Figure 8 shows the tabulation of these data into average yearly snowfall (October–April) and average summer (June–August) temperature for study periods spanning 1948–2013 relative to 1970–2000 averages. The periods 1948–1982/2000 have the highest snowfall and lowest summer temperatures, 1982/1987–2000 and 1995– 99 have the lowest snowfall and highest summer temperatures, and 2000–2009/2010/2013 are intermediate, close to the 1970–2000 averages.
These trends are reflected in the average ELA of Taku Glacier, which we tabulate from data provided in Reference Pelto, Kavanaugh and McNeilPelto and others (2013). Taku’s average ELA is 917 m for 1948–82, 931 m for 1948–2000, 958 m for 1982–2000, 999 m for 1987–2000, 1089 m for 1995–99, and 949–959 m for 2000– 2009/2011. The higher thinning rates observed at Menden-hall from 1995 to 1999 by Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) are also consistent with temperature data that show this study period has the highest average summer temperature.
Higher average summer temperatures and lower average snowfall from 1982/1987–2000 versus 1948–2000 and 2000–2009/2010/2013 are likely also a factor in the higher thinning rates found by Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007). Comparing Figure 2 and Figure 7a of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007), there is a clear jump in thinning rates for the JIF at the transition from the 1948 DEM to the 1982/1987 DEMs. Taku Glacier is largely covered by the 1948 DEM in their study, and they find an average ![]() similar to ours (~0.4 m w.e. a−1).Llewellyn Glacier, covered by the 1987 and 1982 DEMs, is a clear example of the higher thinning rates they obtained using those more recent DEMs. We find an area-averaged mass balance for Llewellyn Glacier that is close to 0 (see Table 1), whereas Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) estimated a
similar to ours (~0.4 m w.e. a−1).Llewellyn Glacier, covered by the 1987 and 1982 DEMs, is a clear example of the higher thinning rates they obtained using those more recent DEMs. We find an area-averaged mass balance for Llewellyn Glacier that is close to 0 (see Table 1), whereas Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) estimated a ![]() of roughly –0.7 km3 a−1, equivalent to an area-averaged mass balance of –1.3 to –1.4 m w.e. a–1. The difference in
of roughly –0.7 km3 a−1, equivalent to an area-averaged mass balance of –1.3 to –1.4 m w.e. a–1. The difference in ![]() appears to be concentrated almost exclusively at higher elevations, where they found higher thinning than at the front of Llewellyn Glacier.
appears to be concentrated almost exclusively at higher elevations, where they found higher thinning than at the front of Llewellyn Glacier.
We examine the accumulation-area ratio (AAR) at Llewellyn Glacier and its sensitivity to the ELA in order to see if it is consistent with the lack of thinning that we observe at higher elevations. Figure 9 illustrates the effect of changing the ELA on the AAR for the six largest glaciers on the JIF (including Llewellyn), as well as Mendenhall Glacier. Only 1.5% of Llewellyn’s area is below 800 m, compared with 10–20% for the other glaciers. Assuming the ELA we use in our study (1000 m, also the average ELA used by Larsen and others 2007), the AAR of Llewellyn Glacier is 0.96, the highest of any of the six largest glaciers on the JIF. None of the others have an AAR above 0.9. Raising the ELA to 1400 m only decreases the AAR of Llewellyn Glacier to 0.82, the highest AAR assuming a 1400 m ELA of any of the glaciers shown in Figure 9. This suggests that rising temperatures would have a smaller impact at Llewellyn Glacier than at the other large glaciers on the JIF. Lower average snowfall from 1982/1987 to 2000 may therefore be a larger factor in high-elevation thinning at Llewellyn over that period relative to other glaciers.

Fig. 9. AAR vs elevation for the six largest glaciers on the JIF and Mendenhall Glacier. The green dots show AAR at the ELA we use, the blue dots show the AAR at 800 m, and the red dots show the AAR at 1400 m. Elevations are from the SRTM DEM.
A high AAR, relative insensitivity of AAR to ELA changes, and higher average snowfall and lower average summer temperatures from 2000 to 2009/2010/2013 versus 1982/1987–2000 are all consistent with the lower thinning rates we find at the higher elevations of Llewellyn Glacier compared with Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007).
Velocities
Here we compare ice velocities from ASTER/ALOS pixel-tracking and ERS parallel flow to GPS velocities observed by the JIRP for the purposes of validation and comparison. Regular, repeat GPS surveys of JIRP stake networks show speeds at the JIF were quite stable from 1993 to 2006 (Reference McGeeMcGee and others, 2007), and, although pixel-tracking is an established technique, significant deviation from GPS velocities might suggest error or bias in our results, depending on the magnitude and pattern of the deviation. The GPS speeds farthest down-glacier on Taku are the only GPS speeds we can compare with our ASTER results. The comparison shows seasonal speed variations that have previously been reported by Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others (1995) and Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others (2009).
At the front of Taku Glacier we are able to compare ASTER results with pixel-tracking results from aerial photography (Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009), both of which show seasonal speed differences. The purpose of this comparison is to demonstrate the ability of our ASTER results to discern previously documented dynamic behavior at Taku Glacier and extend the period over which that behavior has been observed with data from 2004/05, 2009 and 2009/10.
We combine ice thicknesses along selected profiles from Taku and Mendenhall Glaciers (Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Reference PeltoPelto and others, 2008) with our ![]() and velocity results to estimate flux. Reference McGeeMcGee and others (2007) documented a velocity increase (maximum 7% increase) in 2007 at four profiles on Taku Glacier and suggested that this may ‘contribute to the further advancement of the Taku Glacier’. We calculate flux using velocities from four ALOS pairs spanning 2007–11 at the transverse Profile 4 (green line in Fig. 5), one of the profiles where Reference McGeeMcGee and others (2007) found a speed increase in 2007, to determine whether we can detect a significant change in flux. We also calculate flux using ERS parallel-flow velocities from 1995, providing a point of comparison.
and velocity results to estimate flux. Reference McGeeMcGee and others (2007) documented a velocity increase (maximum 7% increase) in 2007 at four profiles on Taku Glacier and suggested that this may ‘contribute to the further advancement of the Taku Glacier’. We calculate flux using velocities from four ALOS pairs spanning 2007–11 at the transverse Profile 4 (green line in Fig. 5), one of the profiles where Reference McGeeMcGee and others (2007) found a speed increase in 2007, to determine whether we can detect a significant change in flux. We also calculate flux using ERS parallel-flow velocities from 1995, providing a point of comparison.
Depth profile g from Motyka and others (2002, Fig. 5) at the front of Mendenhall Glacier allows us to estimate the calving flux using the same four ALOS pairs spanning 2007–11. From these fluxes we obtain the dynamic contribution to mass loss at Mendenhall Glacier.
ASTER vs GPS speeds
Several observations of velocity using surveyed stakes and GPS spanning 1950–2006 were made at Taku Glacier along transverse Profile 4, near the equilibrium line (Reference McGeeMcGee and others, 2007; Reference PeltoPelto and others, 2008). No significant interannual variations in flow were observed despite changes to the mass balance of the glacier (Reference McGeeMcGee and others, 2007; Reference PeltoPelto and others, 2008). Pelto and others (2008) speculated that the velocity stability is due to the great thickness of Taku Glacier, which is up to 1500 m deep (Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others, 1995). This thickness produces a high basal shear stress that limits basal sliding, which is more likely to be temporally variable (Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others, 1995)). Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others, 1995) and Reference PeltoPelto and others (2008) therefore concluded that motion of Taku Glacier is likely primarily due to internal deformation. However, seasonal speed variations, which are generally the result of changes in sliding (Reference PeltoPelto and others, 2008), are observed at Taku Glacier (Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others, 1995); Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009). This suggests that sliding is a non-negligible component of motion at Taku Glacier, at least in the ablation zone.
Most of the JIRP GPS measurements were made in areas that are covered with snow for long periods during the year (Reference McGeeMcGee, 2009). The low-contrast snow cover makes acquiring reliable ASTER motions difficult. An exception is the JIRP ‘Longitudinal A’ profile, which runs down the center line of Taku Glacier and extends far enough into the ablation zone to overlap with reliable ASTER-derived speeds. Figure 7 compares GPS speeds from 20 to 23 July 2001 with ASTER speeds from image pairs covering October 2004 to May 2005, March 2009 to July 2009, and August 2009 to June 2010 and the 1995 ERS speeds (discussed below). Figure 6 shows the location of the points in Figure 7 as gray triangles.
The GPS speeds are consistently ~0.1 m d 1 higher than the ASTER speeds. This is likely a seasonal effect, such as that observed by Reference Nolan, Motyka, Echelmeyer and TrabantNolan and others (1995) at their ‘Goat Ridge’ transect and Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others (2009) further down-glacier at the terminus. The GPS speeds shown in Figure 7 are from a short period (3 days) in late July, whereas the ASTER speeds are months-long averages and are from different years. The velocity stability noted above at Profile 4 is significantly up-glacier from these points, which lie along the trunk of Taku Glacier, well into the ablation zone.
Although the GPS has lower uncertainties, the ASTER results are more extensive, helping to fill in areas missed by GPS, such as the 14 km gap in GPS speeds for Taku Glacier between the lower end of the Longitudinal A profile and the terminus (Reference McGeeMcGee, 2009). ASTER and GPS speeds are complementary, as most ASTER measurements are in the ablation zone and most GPS measurements are in the accumulation zone. GPS speeds steadily increase down the Longitudinal A profile to a maximum of 1.14 m d–1 at the point furthest down-glacier (Reference McGeeMcGee, 2009), ~10 km from the terminus. ASTER-derived speeds exhibit a maximum along the trunk of Taku Glacier in the bend north of Hole-in-the-Wall Glacier, below the maximum GPS speed of the Longitudinal A profile. Both the March 2009 to July 2009 and May 2010 to June 2010 pairs show this area of maximum speed, and decorrelation over the same area in the October 2004 to May 2005 pair could be due to relatively faster motion there.
Parallel-flow velocities, ALOS pixel-tracking vs GPS
The parallel-flow assumption applied to ERS interferometry extends our temporal coverage of speeds at Taku Glacier back to late October 1995, providing further information on the long-term variability in speeds at Taku Glacier. We check the velocities this produces against GPS velocities measured by the JIRP. The mean difference is 0.08 m d–1, with a standard deviation of 0.08 m d–1. Figure 10 gives a visual comparison of the GPS and parallel-flow velocities in map view. Figure 11 shows a one-to-one plot of GPS vs ERS velocities as gray triangles, and GPS vs ALOS velocities as red circles.

Fig. 10. Map of parallel-flow speeds calculated from one ascending and one descending ERS interferogram (from 28 October 1995 to 29 October 1995 and 29 October 1995 to 30 October 1995, respectively) and GPS velocities (red arrows) from JIRP. White arrows indicate ERS velocity at GPS points.

Fig. 11. One-to-one plot of GPS speeds (x –axis) vs ALOS (red circles) and ERS (gray triangles) speeds (y –axis). Dates are year/month.
The agreement between GPS and ALOS/ERS results illustrates the advantage of using radar to obtain reliable velocities in the accumulation zone, as this is where most GPS velocity measurements are made. ERS parallel-flow velocities are a better match with GPS in the accumulation zone than ALOS pixel-tracking. The time separation of the ALOS pairs leads to decorrelation, reducing the quality of velocities obtained in the accumulation zone. Interferometric synthetic aperture radar (InSAR)-derived velocities are an order of magnitude better than pixel-tracking for a given time separation (e.g. Reference Fialko, Simons and AgnewFialko and others, 2001), so the 1 day ERS InSAR can provide reliable results even over slower-moving areas.
Figure 7 shows the ERS speeds as well as ASTER and GPS for the lowest eight points of Longitudinal Profile A on Taku Glacier. The ERS speeds match the ASTER speeds, and are also consistently ~0.1 m d−1 lower than the GPS speeds, again demonstrating the seasonality of speeds in the ablation zone of Taku Glacier, in contrast to the relative stability at Profile 4 near the ELA. The quality of the match between the ERS and GPS velocities and the match between ERS and ASTER speeds shown in Figure 7 corroborates the ASTER results, as ERS and ASTER are from two different data sources using two different techniques.
Interannual speed changes
We find no interannual acceleration at any of the outlet glaciers on the JIF. Figure 12 shows the lack of significant speed changes at Taku, Gilkey, Llewellyn, Meade and Field glaciers. At Taku Glacier, ASTER speeds from October 2004 to May 2005 closely match ALOS speeds from 2009 to 2011 along the first 6 km of the profile. The profiles at Meade Glacier show no interannual speed change from 2004 to 2009, although summer pairs from 2004 and 2009 indicate a possible seasonal effect. At Llewellyn Glacier there is a possible ‘shift’ in the speed profile from 1995 to 2004 by ~1 km, although with the large relative uncertainties this is not clear. The 1995, 2005 and 2009/2010 profiles all show a consistent top speed of 0.7–0.8 m d−1. Speeds at Field Glacier are consistent, with the exception of small stretches of some high-uncertainty pairs, and no interannual or seasonal variations are discernible. For Gilkey Glacier, all pairs have low speeds at the front; the ALOS pairs from 2007– 08 and 2009–10 match the ASTER pair from June 2004 to August 2004. These are higher than the ASTER speeds from August 2004 to April 2005, and August 2009 to May 2010, starting at ~3.5 km along the profile, indicating possible seasonal variations in speeds at Gilkey. There is, however, no evidence of interannual acceleration, as ASTER and ALOS speeds separated by 5 years closely match. The absence of acceleration outside our uncertainties (~±0.1 m d−1) indicates that the thinning observed at the front of Gilkey, Meade, Field and Llewellyn glaciers is not dynamic, and is instead primarily due to increasing ablation caused by rising temperatures in the region (Reference Stafford, Wendler and CurtisStafford and others, 2000).

Fig. 12. Longitudinal profile of speeds from velocity pairs covering Taku (a), Meade (b), Llewellyn (c), Field (d) and Gilkey (e) glaciers, starting at the front. Dates are year/month.
Taku Glacier – seasonal speed changes
Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others (2009) used GPS and repeat aerial photography to examine daily, seasonal and interannual speed changes at the terminus of Taku Glacier. Seasonal speed changes there are related to changing basal conditions (Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2009). Figure 13 shows the SNR-filtered speeds from three ASTER image pairs, a ‘summer’ pair (March to July 2009), ‘non-summer’ pair (October 2004 to May 2005) and a ‘year-round’ average (August 2009 to June 2010). Tracks 1–3 are approximately in the same place as the tracks used by Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others (2009). Figure 14 shows speeds from three ASTER pairs along these tracks.

Fig. 13. Speeds from ASTER image pairs October 2004 to May 2005 (a), March 2009 to July 2009 (b) and August 2009 to June 2010 (c). The bottom left image shows the ablation zone of Taku Glacier and the location of images (a), (b) and (c). Speeds are higher in (b), which is the ‘summer’ pair.

Fig. 14. Speeds along tracks 1, 2 and 3 (see Fig. 13) for ASTER image pairs October 2004 to May 2005 (red), March 2009 to July 2009 (blue) and August 2009 to June 2010 (green). Uncertainties (μ ± σ) represented as gray bars. All speeds increase with distance from the front, ranging from about 0.05 to 0.7 m d−1. ‘Summer’ speeds (March 2009 to July 2009) are higher than speeds for the other pairs, especially for track 3 (the southwestern track).
The ASTER speeds are approximately the same as Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others (2009), increasing from 0.1 m d−1 near the front to 0.7 m d−1 about 2000–2500 m upstream. Speeds from the ‘summer’ (blue) pair are 0.2–0.3 m d−1 higher along track 3 than the non-summer and year-round speeds at distances >2000 m from the front. This result matches the findings of Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others (2009).
Summer temperatures are higher, leading to increased surface melting. Melt, in turn, may percolate to the glacier bed, increasing the pressure of the basal water system and reducing basal friction (Reference Iken and BindschadlerIken and Bindschadler, 1986) or altering the configuration of the subglacial drainage (Reference Howat, Tulaczyk, Waddington and BjörnssonHowat and others, 2008c). Reduced basal friction can lead to an increase in speed, accounting for higher summer speeds at the front of Taku Glacier. This has been suggested as a mechanism for velocity variations on Glaciar Soler, Northern Patagonia Icefield, by Reference Yamaguchi, Naruse, Matsumoto and OhnoYamaguchi and others (2003), who observed that higher speeds were associated with a higher liquid water input (either from increased melt or rainwater) and postulated that this reached the bed, reducing friction and increasing basal sliding (Reference Iken and BindschadlerIken and Bindschadler, 1986). Reduced basal friction from increased meltwater input to the base also leads to higher summer speeds at Mendenhall Glacier (Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003) and causes seasonal velocity variation at many other temperate glaciers (e.g. Reference Yamaguchi, Naruse, Matsumoto and OhnoYamaguchi and others, 2003; Reference Truffer, Motyka, Hekkers, Howat and KingTruffer and others, 2005; Reference Howat, Tulaczyk, Waddington and BjörnssonHowat and others, 2008c; Reference PeltoPelto and others, 2008; Reference SugiyamaSugiyama and others, 2011). This effect is less significant further up-glacier around the ELA (e.g. Profile 4), where greater thickness might contribute to higher basal friction and more stable velocities (Reference PeltoPelto and others, 2008).
Taku Glacier – flux
Table 2 gives the flux results at transverse Profile 4 on Taku Glacier for the ALOS pairs spanning 2007–11 and the ERS velocities from 1995. There is no significant variation in the flux between the ALOS pairs, which varies from (0.32–0.40) ±0.16 to (0.36–0.45) ±0.17 km3 a−1 from 2007 to 2011, although the ERS flux from 1995 is somewhat greater at (0.51–0.64) 0.16 km3 a−1 due to the higher velocities measured. Reference PeltoPelto and others (2008) use GPS velocities to measure a mean flux of 0.53 km3 a−1 from 1996 to 2004, varying by 0.02 km3 a−1. This value lies within the uncertainty for all of our flux estimates, indicating a stability in the flux at Profile 4 from 1995 to 2011. The precision of the remote-sensing-based techniques is not as great as GPS, but the consistency of the ALOS measurements suggests that the flux is indeed relatively stable.
Table 2. Taku Glacier: flux (km3 a−1) at Profile 4. Lower and upper constraints given, assuming vertically integrated flow velocity is 80% of surface velocity and 100% of surface velocity, respectively

Mendenhall Glacier – flux
Table 3 shows the fluxes at gates e and g (with g shifted 300 m north for our study) from Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) for the four ALOS pairs from 2007 to 2011. Our estimates do not show a significant change in flux as the glacier continues to thin and retreat. Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) do not give a value for flux at these gates; however, they do list a value of 0.08 km3 a−1 for the ‘flux gate’ (Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Fig. 5d).
Table 3. Mendenhall Glacier: flux (km3 a−1) at gates e and g. Lower and upper constraints given, assuming vertically integrated flow velocity is 80% of surface velocity and 100% of surface velocity

We take the flux at gate g to approximate calving flux, as the transect is very close to the glacier front. We shift this gate 300 m to the north to avoid profiling a section of Mendenhall Glacier that has already calved off by the time the ALOS imagery was acquired. With this in mind, we find that calving constitutes approximately 2.5 ±2% to 5 ±4% of total volume loss at Mendenhall Glacier, roughly the same as the 6% estimated by Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) and about the same as Reference Boyce, Motyka and TrufferBoyce and others (2007), who found that calving flux was ‘about 2.6% of ice lost by surface melting between 2002 and 2005’. This is significantly less than the percentage of mass loss due to calving at tidewater-cycle glaciers such as Marinelli Glacier on the Cordillera Darwin Icefield, Chile, where ~70% of the mass loss is from calving (Reference Melkonian, Willis, Pritchard, Rivera, Bown and BernsteinMelkonian and others, 2013), and is evidence that mass loss at Mendenhall Glacier continues to be primarily due to warming-induced thinning (e.g. Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003).
Flux at other glaciers on the JIF
All major outlet glaciers show a similar pattern and magnitude of velocities to those of Mendenhall, with higher speeds up-glacier and low front speeds (~0.1 m d−1). Meade, Gilkey and many other glaciers on the JIF are lake-terminating, and tend to have much lower calving rates than tidewater-calving glaciers for equivalent depths (Reference Van der VeenVan der Veen, 2002). Low terminus speeds also suggest low calving rates (Reference Van der VeenVan der Veen, 2002), although without thickness measurements we cannot measure the calving flux to determine its magnitude relative to the overall mass change rate. There are certainly rapidly thinning lacustrine glaciers, but many of the most rapidly thinning (e.g. Glaciar Upsala, Southern Patagonia Icefield) calve into deep lakes and show a different pattern of glacier speeds, with speed rapidly increasing to a maximum at the front (e.g. Reference Skvarca, Raup and AngelisSkvarca and others, 2003; Reference Sakakibara, Sugiyama, Sawagaki, Marinsek and SkvarcaSakakibara and others, 2013). Back-of-the-envelope calculations show that the calving front of Meade and Gilkey Glaciers would have to be 300–500 m thick at the current front width and speed for the calving flux to account for even 10% of the current mass loss rate. Tabular icebergs indicate retreat driven by buoyancy-induced calving as the glacier recedes into deeper waters. Measuring the area loss at the front of Gilkey and Field Glaciers from ASTER imagery and assuming an average thickness of 100 m for ice lost yields a volume loss rate from retreat that is approximately 10% and 25% of the![]() volume loss rate for those glaciers, respectively. Even an average depth of 100 m for the ice lost at the front seems too high for these glaciers; again, without measurements of the ice depth we cannot be certain. Overall, the lack of acceleration and low front speeds show that the
volume loss rate for those glaciers, respectively. Even an average depth of 100 m for the ice lost at the front seems too high for these glaciers; again, without measurements of the ice depth we cannot be certain. Overall, the lack of acceleration and low front speeds show that the ![]() pattern (e.g. the areas of maximum thinning behind the front of these glaciers) is primarily due to melting.
pattern (e.g. the areas of maximum thinning behind the front of these glaciers) is primarily due to melting.
Conclusion
We have produced a complete, high spatial resolution map of surface elevation change and a high spatial resolution map of outlet glacier speeds for the JIF. Thinning is prevalent at lower elevations, with only one major glacier, Taku, thickening. None of the glaciers we examined are accelerating (within uncertainty), therefore ice dynamics cannot be the cause of the observed thinning. The principal cause of mass loss must be a regional increase in melting due to rising temperatures (Reference Stafford, Wendler and CurtisStafford and others, 2000). The JIF has a significantly more positive area-averaged mass balance (–0.13 ± 0.12 m w.e. a−1) than Alaska in general (–0.79 ± 0.13 m w.e. a−1) (Reference ArendtArendt, 2013). Some of the larger mass loss rates at other Alaskan icefields are likely the result of tidewater glacier retreat.
We estimate a lower overall average thinning rate for the JIF than studies covering earlier time periods, particularly those that look at rates between 1980 and 2000 (e.g. Reference Motyka, Neel, Connor and EchelmeyerMotyka and others, 2003; Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007). While the long-term trend in the region is increasing temperatures, climate data from the Juneau International Airport station indicate that 1980–2000 had higher average summer temperatures and lower average snowfall than 2000–2009/2010/2013. These climate factors likely contributed to greater thinning during that period.
We find that Taku Glacier gained volume in both the ablation and accumulation zones from 2000 to 2010. The average ![]() and
and ![]() for Taku Glacier are close to those found by Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) from DEM differencing for the period 1948–2000. The thickening we find in the ablation zone is consistent with the continued advance of Taku Glacier, observable in ASTER imagery. Volume flux measurements above the ELA from late 2007 to early 2011 and from a 2 day period in 1995 do not show significant interannual change and are not significantly different from the flux Reference PeltoPelto and others (2008) found from 1996 to 2004.
for Taku Glacier are close to those found by Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) from DEM differencing for the period 1948–2000. The thickening we find in the ablation zone is consistent with the continued advance of Taku Glacier, observable in ASTER imagery. Volume flux measurements above the ELA from late 2007 to early 2011 and from a 2 day period in 1995 do not show significant interannual change and are not significantly different from the flux Reference PeltoPelto and others (2008) found from 1996 to 2004.
Mendenhall Glacier has a peak thinning rate of 9 m a–1 and a lower glacier thinning rate of 2.2 0.3 m a –1 from 2000 to 2013. Our lower glacier and peak thinning rates are the same as Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) found for 1982–2000, but our overall thinning rate is lower than Reference Motyka, Neel, Connor and EchelmeyerMotyka and others (2003) because we find substantially less thinning in the accumulation zone. Climate factors mentioned above likely account for part of the difference in ![]() at higher elevations. Volume flux does not vary significantly from late 2007 to early 2011, and flux measurements at the front reveal that calving is a small portion of the total volume loss at Mendenhall.
at higher elevations. Volume flux does not vary significantly from late 2007 to early 2011, and flux measurements at the front reveal that calving is a small portion of the total volume loss at Mendenhall.
Acknowledgements
Matthew E. Pritchard, Andrew K. Melkonian and Michael J. Willis were supported by US National Science Foundation grant EAR-0955547. We thank undergraduates Sasha Bernstein (supported by the Rawlings Cornell Presidential Research Scholar program) and Grace DiCinti (a NASA/New York Space Grant summer intern) for helping to develop this project. ASTER data were provided by the Land Processes Distributed Active Archive Center. We thank T. Schwartz for starting this project while a Cornell graduate student, and S. Leprince for helpful comments.


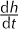 at the Juneau Icefield (JIF), southeastern Alaska, in order to quantify its contribution to sea-level rise between 2000 and 2009/2013. We also produce the first high-resolution map of ice speeds at the JIF, which we use to constrain flux and look for acceleration. We calculate
at the Juneau Icefield (JIF), southeastern Alaska, in order to quantify its contribution to sea-level rise between 2000 and 2009/2013. We also produce the first high-resolution map of ice speeds at the JIF, which we use to constrain flux and look for acceleration. We calculate 
















