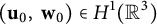1 Introduction and main results
In 1965, Eringen [Reference Eringen11] first introduced the micropolar equations in order to model micropolar fluids. Micropolar fluids are fluids with microstructure. They belong to a class of fluids with nonsymmetric stress tensor (called polar fluids) and include, as a special case, the classical fluids modeled by the Navier–Stokes equations (see, e.g., [Reference Cowin4, Reference Erdogan10, Reference Eringen12, Reference Lukaszewicz21]). The system of the micropolar equations is a significant generalization of the Navier–Stokes equations covering many more phenomena such as fluids consisting of particles suspended in a viscous medium (see, e.g., [Reference Lukaszewicz21, Reference Popel, Regirer and Usick23, Reference Stokes24]). The micropolar equations have been extensively studied and applied by many engineers and physicists.
The 3D micropolar equations can be stated as
 $$ \begin{align} \left\{ \begin{array}{l} \partial_t \mathbf{u} +\mathbf{u}\cdot\nabla\mathbf{u}+\nabla\pi=(\nu+\kappa)\Delta\mathbf{u}+2\kappa\nabla\times\mathbf{w},\\[6pt] \partial_t \mathbf{w} +\mathbf{u}\cdot\nabla\mathbf{w}+4\kappa\mathbf{w}=\gamma\Delta\mathbf{w}+\mu\nabla\nabla\cdot\mathbf{w}+2\kappa\nabla\times\mathbf{u},\\[6pt] \nabla\cdot\mathbf{u}=0.\\ \end{array} \right.\end{align} $$
$$ \begin{align} \left\{ \begin{array}{l} \partial_t \mathbf{u} +\mathbf{u}\cdot\nabla\mathbf{u}+\nabla\pi=(\nu+\kappa)\Delta\mathbf{u}+2\kappa\nabla\times\mathbf{w},\\[6pt] \partial_t \mathbf{w} +\mathbf{u}\cdot\nabla\mathbf{w}+4\kappa\mathbf{w}=\gamma\Delta\mathbf{w}+\mu\nabla\nabla\cdot\mathbf{w}+2\kappa\nabla\times\mathbf{u},\\[6pt] \nabla\cdot\mathbf{u}=0.\\ \end{array} \right.\end{align} $$
Here,
![]() $\mathbf {u}=\mathbf {u}(x,t)\in \mathbb {R}^3$
denotes the fluid velocity,
$\mathbf {u}=\mathbf {u}(x,t)\in \mathbb {R}^3$
denotes the fluid velocity,
![]() $\mathbf {w}=\mathbf {w}(x,t)\in \mathbb {R}^3$
the field of microrotation representing the angular velocity of the rotation of the fluid particles,
$\mathbf {w}=\mathbf {w}(x,t)\in \mathbb {R}^3$
the field of microrotation representing the angular velocity of the rotation of the fluid particles,
![]() $\pi (x,t)$
the scalar pressure, and the positive parameter
$\pi (x,t)$
the scalar pressure, and the positive parameter
![]() $\nu $
denotes the kinematic viscosity,
$\nu $
denotes the kinematic viscosity,
![]() $\kappa $
the microrotation viscosity, and
$\kappa $
the microrotation viscosity, and
![]() $\gamma , \mu $
the angular viscosities.
$\gamma , \mu $
the angular viscosities.
The micropolar equations are not only important in physics, but also mathematically significant. The well-posedness problem on the micropolar and closely related equations, such as the magneto-micropolar equations, have been extensively investigated (see, e.g., [Reference Chen and Miao2, Reference Dong and Chen6, Reference Ferreira and Precioso13, Reference Galdi and Rionero15, Reference Lukaszewicz19–Reference Lukaszewicz21, Reference Yamaguchi29, Reference Yamazaki30, Reference Yuan33, Reference Yuan34]). For the initial boundary-value problem, Galdi and Rionero [Reference Galdi and Rionero15] obtained the weak solution. Lukaszewicz [Reference Lukaszewicz19] established the global existence of weak solutions with sufficiently regular initial data. The existence and uniqueness of strong solutions to the micropolar equations either local for large data or global for small data are considered in [Reference Chen and Miao2, Reference Ferreira and Villamizar-Roa14, Reference Lukaszewicz20, Reference Yamaguchi29] and the references therein. However, whether or not the smooth solutions of micropolar equations (1.1) can develop finite-time singularities remains open. Generally speaking, the global regularity problem for the micropolar equations is easier than that for the corresponding incompressible magnetohydrodynamic equations and harder than that for the corresponding incompressible Boussinesq equations. The global existence of weak solutions and strong solutions with initial data small for 3D micropolar equations were obtained in [Reference Galdi and Rionero15, Reference Lukaszewicz21].
In the 2D case, the global well-posedness problem on the 2D micropolar equations with full dissipation can be obtained similarly as that for the 2D Navier–Stokes equations (see, e.g., [Reference Constantin and Foias3, Reference Doering and Gibbon5, Reference Dong, Li and Wu7, Reference Majda and Bertozzi22, Reference Temam26]). Recently, a lot of works are focused on the 2D micropolar equations with partial dissipation (see, e.g., [Reference Dong, Wu, Xu and Ye8, Reference Dong and Zhang9, Reference Xue28]). We will apologize for not addressing exhaustive reference in this paper.
When
![]() $\mathbf {w}=0$
and
$\mathbf {w}=0$
and
![]() $\kappa =0$
, the system (1.1) is reduced to the 3D incompressible Navier–Stokes equations.
$\kappa =0$
, the system (1.1) is reduced to the 3D incompressible Navier–Stokes equations.
 $$ \begin{align} \left\{ \begin{array}{l} \partial_t \mathbf{u} +\mathbf{u}\cdot\nabla\mathbf{u}+\nabla\pi=\nu\Delta\mathbf{u}, \ \ x\in\mathbb{R}^3,\ t>0,\\[6pt] \nabla\cdot\mathbf{u}=0.\\ \end{array} \right.\end{align} $$
$$ \begin{align} \left\{ \begin{array}{l} \partial_t \mathbf{u} +\mathbf{u}\cdot\nabla\mathbf{u}+\nabla\pi=\nu\Delta\mathbf{u}, \ \ x\in\mathbb{R}^3,\ t>0,\\[6pt] \nabla\cdot\mathbf{u}=0.\\ \end{array} \right.\end{align} $$
Whether or not the classical solutions of the 3D incompressible Navier–Stokes equations (1.2) can develop finite-time singularities remains an outstanding open problem. The Millennium prize problem is supercritical in the sense that the standard Laplacian dissipation in (1.2) may not provide sufficient regularization. Some works (see, e.g., [Reference Katz and Pavlovic16, Reference Lions18]) proved that the following generalized Navier–Stokes equations
 $$ \begin{align} \left\{ \begin{array}{l} \partial_t \mathbf{u} +\mathbf{u}\cdot\nabla\mathbf{u}+\nabla\pi=-\nu(-\Delta)^\alpha\mathbf{u}, \ \ x\in\mathbb{R}^3,\ t>0,\\[6pt] \nabla\cdot\mathbf{u}=0\\ \end{array} \right.\end{align} $$
$$ \begin{align} \left\{ \begin{array}{l} \partial_t \mathbf{u} +\mathbf{u}\cdot\nabla\mathbf{u}+\nabla\pi=-\nu(-\Delta)^\alpha\mathbf{u}, \ \ x\in\mathbb{R}^3,\ t>0,\\[6pt] \nabla\cdot\mathbf{u}=0\\ \end{array} \right.\end{align} $$
has a unique global-in-time solution with
![]() $\alpha \geq \frac 54$
and any smooth initial data
$\alpha \geq \frac 54$
and any smooth initial data
![]() $\mathbf {u}_0$
which has finite energy. The following reference [Reference Wu27] is also relevant on the generalized Navier–Stokes equations. It gives a very simple proof on the global well-posedness for
$\mathbf {u}_0$
which has finite energy. The following reference [Reference Wu27] is also relevant on the generalized Navier–Stokes equations. It gives a very simple proof on the global well-posedness for
![]() $\alpha \geq \frac 54$
. Here, the fractional Laplacian operator
$\alpha \geq \frac 54$
. Here, the fractional Laplacian operator
![]() $(-\Delta )^\alpha $
is defined via the Fourier transform
$(-\Delta )^\alpha $
is defined via the Fourier transform
However, some scholars devoted to consider whether or not the global existence and regularity can be constructed for any
![]() $\alpha <\frac 54$
. Tao [Reference Tao25] obtained the global regularity for the system which just replace the operator
$\alpha <\frac 54$
. Tao [Reference Tao25] obtained the global regularity for the system which just replace the operator
![]() $(-\Delta )^\alpha $
by
$(-\Delta )^\alpha $
by
 $\frac {(-\Delta )^{\frac 54}}{\sqrt {\log (2-\Delta )}}$
in (1.3). Replacing the operator
$\frac {(-\Delta )^{\frac 54}}{\sqrt {\log (2-\Delta )}}$
in (1.3). Replacing the operator
![]() $\sqrt {\log (2-\Delta )}$
by
$\sqrt {\log (2-\Delta )}$
by
![]() $\log (2-\Delta )$
, Barbato, Morandin, and Romito [Reference Barbato, Morandin and Romito1] improved those result. All of these results imply that it is extremely difficult to reduce
$\log (2-\Delta )$
, Barbato, Morandin, and Romito [Reference Barbato, Morandin and Romito1] improved those result. All of these results imply that it is extremely difficult to reduce
![]() $\alpha $
lower than
$\alpha $
lower than
![]() $\frac 54$
. For the system (1.3),
$\frac 54$
. For the system (1.3),
![]() $\alpha =\frac 54$
may be thought as the critical index of the natural energy functional. More precisely, if we assume
$\alpha =\frac 54$
may be thought as the critical index of the natural energy functional. More precisely, if we assume
and inserting
![]() $\mathbf {u}_\lambda (x,t)=\lambda ^{2\alpha -1}\mathbf {u}(\lambda x,\ \lambda ^{2\alpha }t)$
into the above equation to obtain
$\mathbf {u}_\lambda (x,t)=\lambda ^{2\alpha -1}\mathbf {u}(\lambda x,\ \lambda ^{2\alpha }t)$
into the above equation to obtain
and the natural energy functional is invariant just when
![]() $\alpha =\frac 54$
.
$\alpha =\frac 54$
.
Very recently, Yang, Jiu, and Wu [Reference Yang, Jiu and Wu31] studied the global regularity problem on 3D Navier–Stokes equations with partial hyperdissipation. They obtained the global existence and uniqueness of strong solutions.
In this paper, we consider the 3D incompressible micropolar equations with hyperdissipation as follows:
 $$ \begin{align} \kern1pc\left\{ \begin{array}{l} \partial_t u_1 +\mathbf{u}\cdot\nabla u_1=-\partial_1\pi-(\nu+\kappa)\Lambda_{2}^{\frac52}u_1-(\nu+\kappa)\Lambda_{3}^{\frac52}u_1+2\kappa\varepsilon_{1jk}\partial_j\text{w}_k,\\[6pt] \partial_t u_2 +\mathbf{u}\cdot\nabla u_2=-\partial_2\pi-(\nu+\kappa)\Lambda_{1}^{\frac52}u_2-(\nu+\kappa)\Lambda_{3}^{\frac52}u_2+2\kappa\varepsilon_{2jk}\partial_j\text{w}_k,\\[6pt] \partial_t u_3 +\mathbf{u}\cdot\nabla u_3=-\partial_3\pi-(\nu+\kappa)\Lambda_{1}^{\frac52}u_3-(\nu+\kappa)\Lambda_{2}^{\frac52}u_3+2\kappa\varepsilon_{3jk}\partial_j\text{w}_k,\\[6pt] \partial_t\text{w}_1 +\mathbf{u}\cdot\nabla\text{w}_1+4\kappa\text{w}_1=-\gamma\Lambda_{2}^{\frac52}\text{w}_1-\gamma\Lambda_{3}^{\frac52}\text{w}_1 +\mu\partial_1(\nabla\cdot\mathbf{w})+2\kappa\varepsilon_{1jk}\partial_ju_k,\\[6pt] \partial_t\text{w}_2 +\mathbf{u}\cdot\nabla\text{w}_2+4\kappa\text{w}_2=-\gamma\Lambda_{1}^{\frac52}\text{w}_2-\gamma\Lambda_{3}^{\frac52}\text{w}_2 +\mu\partial_2(\nabla\cdot\mathbf{w})+2\kappa\varepsilon_{2jk}\partial_ju_k,\\[6pt] \partial_t\text{w}_3 +\mathbf{u}\cdot\nabla\text{w}_3+4\kappa\text{w}_3=-\gamma\Lambda_{1}^{\frac52}\text{w}_3-\gamma\Lambda_{2}^{\frac52}\text{w}_3 +\mu\partial_3(\nabla\cdot\mathbf{w})+2\kappa\varepsilon_{3jk}\partial_ju_k,\\[6pt] \nabla\cdot\mathbf{u}=0,\ \mathbf{u}(x,0)=\mathbf{u}_0(x),\ \mathbf{w}(x,0)=\mathbf{w}_0(x).\\ \end{array} \right.\end{align} $$
$$ \begin{align} \kern1pc\left\{ \begin{array}{l} \partial_t u_1 +\mathbf{u}\cdot\nabla u_1=-\partial_1\pi-(\nu+\kappa)\Lambda_{2}^{\frac52}u_1-(\nu+\kappa)\Lambda_{3}^{\frac52}u_1+2\kappa\varepsilon_{1jk}\partial_j\text{w}_k,\\[6pt] \partial_t u_2 +\mathbf{u}\cdot\nabla u_2=-\partial_2\pi-(\nu+\kappa)\Lambda_{1}^{\frac52}u_2-(\nu+\kappa)\Lambda_{3}^{\frac52}u_2+2\kappa\varepsilon_{2jk}\partial_j\text{w}_k,\\[6pt] \partial_t u_3 +\mathbf{u}\cdot\nabla u_3=-\partial_3\pi-(\nu+\kappa)\Lambda_{1}^{\frac52}u_3-(\nu+\kappa)\Lambda_{2}^{\frac52}u_3+2\kappa\varepsilon_{3jk}\partial_j\text{w}_k,\\[6pt] \partial_t\text{w}_1 +\mathbf{u}\cdot\nabla\text{w}_1+4\kappa\text{w}_1=-\gamma\Lambda_{2}^{\frac52}\text{w}_1-\gamma\Lambda_{3}^{\frac52}\text{w}_1 +\mu\partial_1(\nabla\cdot\mathbf{w})+2\kappa\varepsilon_{1jk}\partial_ju_k,\\[6pt] \partial_t\text{w}_2 +\mathbf{u}\cdot\nabla\text{w}_2+4\kappa\text{w}_2=-\gamma\Lambda_{1}^{\frac52}\text{w}_2-\gamma\Lambda_{3}^{\frac52}\text{w}_2 +\mu\partial_2(\nabla\cdot\mathbf{w})+2\kappa\varepsilon_{2jk}\partial_ju_k,\\[6pt] \partial_t\text{w}_3 +\mathbf{u}\cdot\nabla\text{w}_3+4\kappa\text{w}_3=-\gamma\Lambda_{1}^{\frac52}\text{w}_3-\gamma\Lambda_{2}^{\frac52}\text{w}_3 +\mu\partial_3(\nabla\cdot\mathbf{w})+2\kappa\varepsilon_{3jk}\partial_ju_k,\\[6pt] \nabla\cdot\mathbf{u}=0,\ \mathbf{u}(x,0)=\mathbf{u}_0(x),\ \mathbf{w}(x,0)=\mathbf{w}_0(x).\\ \end{array} \right.\end{align} $$
Here,
![]() $\mathbf {u}=(u_1,\ u_2,\ u_3)$
denotes the velocity field and
$\mathbf {u}=(u_1,\ u_2,\ u_3)$
denotes the velocity field and
![]() $\mathbf {w}=(\text {w}_1,\ \text {w}_2,\ \text {w}_3)$
the microrotation field.
$\mathbf {w}=(\text {w}_1,\ \text {w}_2,\ \text {w}_3)$
the microrotation field.
![]() $\varepsilon _{ijk}, (i,j,k)\in \{1,2,3 \}$
is Levi-Civita alternating tensor defined as follows:
$\varepsilon _{ijk}, (i,j,k)\in \{1,2,3 \}$
is Levi-Civita alternating tensor defined as follows:
 $$ \begin{align} \varepsilon_{ijk}=\left\{ \begin{array}{l} 1,\ \ \text {if}\ (i, j,k)\ \text {is an even permutation},\\[6pt] -1,\ \ \text{if}\ (i, j,k)\ \text {is an odd permutation},\\[6pt] 0,\ \ \text {otherwise}.\\ \end{array} \right.\end{align} $$
$$ \begin{align} \varepsilon_{ijk}=\left\{ \begin{array}{l} 1,\ \ \text {if}\ (i, j,k)\ \text {is an even permutation},\\[6pt] -1,\ \ \text{if}\ (i, j,k)\ \text {is an odd permutation},\\[6pt] 0,\ \ \text {otherwise}.\\ \end{array} \right.\end{align} $$
Here ,
![]() $\Lambda _k^\alpha $
with
$\Lambda _k^\alpha $
with
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $k=1,2,3$
denote the directional fractional operators defined via the Fourier transform
$k=1,2,3$
denote the directional fractional operators defined via the Fourier transform
where
![]() $\xi =(\xi _1,\ \xi _2,\ \xi _3)$
and
$\xi =(\xi _1,\ \xi _2,\ \xi _3)$
and
![]() $\Lambda =(-\Delta )^{\frac 12}$
denotes the Zygmund operator.
$\Lambda =(-\Delta )^{\frac 12}$
denotes the Zygmund operator.
The main results of this paper are stated as follows.
Theorem 1.1 Assume
![]() $(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$
. Then, system (
1.4
) has a global strong solution
$(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$
. Then, system (
1.4
) has a global strong solution
![]() $(\mathbf {u},\ \mathbf {w})$
satisfying
$(\mathbf {u},\ \mathbf {w})$
satisfying
 $$ \begin{align} \begin{aligned} &(\mathbf{u},\ \mathbf{w})\in L^\infty(0,\infty;\ H^1), \\[3pt] &\Lambda_2^{\frac54}u_1,\ \Lambda_3^{\frac54}u_1,\ \Lambda_2^{\frac54}\nabla u_1,\ \Lambda_3^{\frac54}\nabla u_1\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}u_2,\ \Lambda_3^{\frac54}u_2,\ \Lambda_1^{\frac54}\nabla u_2,\ \Lambda_3^{\frac54}\nabla u_2\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}u_3,\ \Lambda_2^{\frac54}u_3,\ \Lambda_1^{\frac54}\nabla u_3,\ \Lambda_2^{\frac54}\nabla u_3\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_2^{\frac54}\text{w}_1,\ \Lambda_3^{\frac54}\text{w}_1,\ \Lambda_2^{\frac54}\nabla \text{w}_1,\ \Lambda_3^{\frac54}\nabla\text{w}_1\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}\text{w}_2,\ \Lambda_3^{\frac54}\text{w}_2,\ \Lambda_1^{\frac54}\nabla \text{w}_2,\ \Lambda_3^{\frac54}\nabla \text{w}_2\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}\text{w}_3,\ \Lambda_2^{\frac54}\text{w}_3,\ \Lambda_1^{\frac54}\nabla \text{w}_3,\ \Lambda_2^{\frac54}\nabla \text{w}_3\in L^2(0,\infty;\ L^2).\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &(\mathbf{u},\ \mathbf{w})\in L^\infty(0,\infty;\ H^1), \\[3pt] &\Lambda_2^{\frac54}u_1,\ \Lambda_3^{\frac54}u_1,\ \Lambda_2^{\frac54}\nabla u_1,\ \Lambda_3^{\frac54}\nabla u_1\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}u_2,\ \Lambda_3^{\frac54}u_2,\ \Lambda_1^{\frac54}\nabla u_2,\ \Lambda_3^{\frac54}\nabla u_2\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}u_3,\ \Lambda_2^{\frac54}u_3,\ \Lambda_1^{\frac54}\nabla u_3,\ \Lambda_2^{\frac54}\nabla u_3\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_2^{\frac54}\text{w}_1,\ \Lambda_3^{\frac54}\text{w}_1,\ \Lambda_2^{\frac54}\nabla \text{w}_1,\ \Lambda_3^{\frac54}\nabla\text{w}_1\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}\text{w}_2,\ \Lambda_3^{\frac54}\text{w}_2,\ \Lambda_1^{\frac54}\nabla \text{w}_2,\ \Lambda_3^{\frac54}\nabla \text{w}_2\in L^2(0,\infty;\ L^2),\\[3pt] &\Lambda_1^{\frac54}\text{w}_3,\ \Lambda_2^{\frac54}\text{w}_3,\ \Lambda_1^{\frac54}\nabla \text{w}_3,\ \Lambda_2^{\frac54}\nabla \text{w}_3\in L^2(0,\infty;\ L^2).\\ \end{aligned} \end{align} $$
The bound of
![]() $(\mathbf {u},\ \mathbf {w})$
in (
1.6
) is uniform in time.
$(\mathbf {u},\ \mathbf {w})$
in (
1.6
) is uniform in time.
Remark 1.1 Due to the symmetric, one can easily check the similar results as Theorem 1.1 holds for the cases that if
![]() $(u_1,\ \text {w}_1)$
are only lack of the hyperdissipation in the
$(u_1,\ \text {w}_1)$
are only lack of the hyperdissipation in the
![]() $x_2$
direction,
$x_2$
direction,
![]() $(u_2,\ \text {w}_2)$
are only lack of the hyperdissipation in the
$(u_2,\ \text {w}_2)$
are only lack of the hyperdissipation in the
![]() $x_3$
direction and
$x_3$
direction and
![]() $(u_3,\ \text {w}_3)$
are only lack of the hyperdissipation in the
$(u_3,\ \text {w}_3)$
are only lack of the hyperdissipation in the
![]() $x_1$
direction or
$x_1$
direction or
![]() $(u_1,\ \text {w}_1)$
are only lack of the hyperdissipation in the
$(u_1,\ \text {w}_1)$
are only lack of the hyperdissipation in the
![]() $x_3$
direction,
$x_3$
direction,
![]() $(u_2,\ \text {w}_2)$
are only lack of the hyperdissipation in the
$(u_2,\ \text {w}_2)$
are only lack of the hyperdissipation in the
![]() $x_1$
direction and
$x_1$
direction and
![]() $(u_3,\ \text {w}_3)$
are only lack of the hyperdissipation in the
$(u_3,\ \text {w}_3)$
are only lack of the hyperdissipation in the
![]() $x_2$
direction.
$x_2$
direction.
The rest of this paper is arranged as follows: Some notation and preliminaries will be given in Section 2. In Section 3, we will prove our main results. The proof of Theorem 1.1 will be divided into three stages. First, we will show the
![]() $L^2$
-bound of
$L^2$
-bound of
![]() $(\mathbf {u},\ \mathbf {w})$
. Second, we will obtain the
$(\mathbf {u},\ \mathbf {w})$
. Second, we will obtain the
![]() $L^2$
-bound of
$L^2$
-bound of
![]() $(\nabla \mathbf {u},\ \nabla \mathbf {w})$
, and then we establish the global a priori bound for
$(\nabla \mathbf {u},\ \nabla \mathbf {w})$
, and then we establish the global a priori bound for
![]() $(\mathbf {u},\ \mathbf {w})$
in
$(\mathbf {u},\ \mathbf {w})$
in
![]() $H^1$
. This section is the main parts of the proof of Theorem 1.1. There are a lot of triple product terms bounded by using divergence-free condition, Sobolev’s inequalities, Minkowski’s inequality, and so forth. Finally, we will prove the uniqueness.
$H^1$
. This section is the main parts of the proof of Theorem 1.1. There are a lot of triple product terms bounded by using divergence-free condition, Sobolev’s inequalities, Minkowski’s inequality, and so forth. Finally, we will prove the uniqueness.
2 Notation and preliminaries
For simplicity, some notations will be introduced before we prove our main results, which are used throughout this paper. We denote
 $$ \begin{align*} &\|f\|_{L^2(\mathbb{R}^3)}=\|f\|_2,\ \frac{\partial f}{\partial x_i}=\partial_i f,\\[6pt] &\|\Lambda_i^{\frac54}f_k\|_{L^2(\mathbb{R}^3)}+\|\Lambda_j^{\frac54}f_k\|_{L^2(\mathbb{R}^3)}\triangleq\|(\Lambda_i^{\frac54},\ \Lambda_j^{\frac54})f_k\|_2\ \ (i,j,k)\in \{1,2,3 \},\\[6pt] &\|\partial_if_k\|_{L^2(\mathbb{R}^3)}+\|\partial_jf_k\|_{L^2(\mathbb{R}^3)}\triangleq\|(\partial_i,\ \partial_j)f_k\|_2\ \ (i,j,k)\in \{1,2,3 \},\\[6pt] &\int f dxdydz=\iiint_{\mathbb{R}^3}f dxdydz, \end{align*} $$
$$ \begin{align*} &\|f\|_{L^2(\mathbb{R}^3)}=\|f\|_2,\ \frac{\partial f}{\partial x_i}=\partial_i f,\\[6pt] &\|\Lambda_i^{\frac54}f_k\|_{L^2(\mathbb{R}^3)}+\|\Lambda_j^{\frac54}f_k\|_{L^2(\mathbb{R}^3)}\triangleq\|(\Lambda_i^{\frac54},\ \Lambda_j^{\frac54})f_k\|_2\ \ (i,j,k)\in \{1,2,3 \},\\[6pt] &\|\partial_if_k\|_{L^2(\mathbb{R}^3)}+\|\partial_jf_k\|_{L^2(\mathbb{R}^3)}\triangleq\|(\partial_i,\ \partial_j)f_k\|_2\ \ (i,j,k)\in \{1,2,3 \},\\[6pt] &\int f dxdydz=\iiint_{\mathbb{R}^3}f dxdydz, \end{align*} $$
and
We denote the one-dimensional
![]() $L^2$
-norm with respect to
$L^2$
-norm with respect to
![]() $x_i$
by
$x_i$
by
![]() $\|f\|_{L_{x_i}^{2}} (i=1,2,3)$
and
$\|f\|_{L_{x_i}^{2}} (i=1,2,3)$
and
![]() $\|f\|_{L_{x_ix_j}^{2}} (i,j\in \{1,2,3\})$
denote the two-dimensional
$\|f\|_{L_{x_ix_j}^{2}} (i,j\in \{1,2,3\})$
denote the two-dimensional
![]() $L^2$
-norm with respect to
$L^2$
-norm with respect to
![]() $x_i$
and
$x_i$
and
![]() $x_j$
. In addition, we denote
$x_j$
. In addition, we denote
The following lemma is Minkowski’s inequality (see, e.g., [Reference Lieb and Loss17]), which will be useful.
Lemma 2.1 Assume that
![]() $f=f(x,y)$
with
$f=f(x,y)$
with
![]() $(x,y)\in (\mathbb {R}^m\times \mathbb {R}^n)$
is a measurable function. Let
$(x,y)\in (\mathbb {R}^m\times \mathbb {R}^n)$
is a measurable function. Let
![]() $1\leq q\leq p\leq \infty $
. Then,
$1\leq q\leq p\leq \infty $
. Then,
The next lemma is the Sobolev embedding inequality, which will be used frequently in this paper (see [Reference Yang, Jiu and Wu32]).
Lemma 2.2 Assume that
![]() $2\leq p\leq \infty $
and
$2\leq p\leq \infty $
and
 $s>d\left(\frac 12-\frac 1p\right)$
. Then, there exists a constant
$s>d\left(\frac 12-\frac 1p\right)$
. Then, there exists a constant
![]() $C=C(d, p, s)$
such that, for any d-dimensional functions
$C=C(d, p, s)$
such that, for any d-dimensional functions
![]() $f\in H^s(\mathbb {R}^d)$
,
$f\in H^s(\mathbb {R}^d)$
,
In particular, when
![]() $p\neq \infty $
, (
2.2
) also holds for
$p\neq \infty $
, (
2.2
) also holds for
 $s=d\left(\frac 12-\frac 1p\right)$
.
$s=d\left(\frac 12-\frac 1p\right)$
.
The following is the Hölder-type inequality, which will be useful as well.
Lemma 2.3 Assume that
![]() $f_1,\ f_2\geq 0$
and
$f_1,\ f_2\geq 0$
and
![]() $f_1,\ f_2\in L^p$
. Assume that
$f_1,\ f_2\in L^p$
. Assume that
![]() $s_1,\ s_2\in [0,1]$
and
$s_1,\ s_2\in [0,1]$
and
![]() $s_1+s_2=1$
. Assume that
$s_1+s_2=1$
. Assume that
![]() $1\leq p\leq \infty $
, then
$1\leq p\leq \infty $
, then
3 Global regularity for the strong solution to the 3D incompressible micropolar fluid flows
In this section, we will prove Theorem 1.1. Theorem 1.1 is proved through three stages. The first step is to establish the
![]() $L^2$
-estimate of
$L^2$
-estimate of
![]() $(\mathbf {u},\mathbf {w})$
. Second, we will obtain the
$(\mathbf {u},\mathbf {w})$
. Second, we will obtain the
![]() $H^1$
-bound for
$H^1$
-bound for
![]() $(\mathbf {u},\mathbf {w})$
. Finally, we will achieve the uniqueness of
$(\mathbf {u},\mathbf {w})$
. Finally, we will achieve the uniqueness of
![]() $(\mathbf {u},\mathbf {w})$
.
$(\mathbf {u},\mathbf {w})$
.
Step 1. Global
![]() $L^2$
-bound.
$L^2$
-bound.
Proposition 3.1 Suppose that
![]() $(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$
. Then, system (
1.4
) has a global solution
$(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$
. Then, system (
1.4
) has a global solution
![]() $(\mathbf {u},\mathbf {w})$
satisfying
$(\mathbf {u},\mathbf {w})$
satisfying
 $$ \begin{align} &\|\mathbf{u},\ \mathbf{w}\|_2^2+4\kappa\|\mathbf{w}\|_2^2+\mu\|\text{div}\mathbf{w}\|_2^2 +(\nu+\kappa) \nonumber \\ & \quad \times \int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2 \,dt \nonumber\\ & \quad +\gamma\int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2 \,dt\leq C,\end{align} $$
$$ \begin{align} &\|\mathbf{u},\ \mathbf{w}\|_2^2+4\kappa\|\mathbf{w}\|_2^2+\mu\|\text{div}\mathbf{w}\|_2^2 +(\nu+\kappa) \nonumber \\ & \quad \times \int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2 \,dt \nonumber\\ & \quad +\gamma\int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2 \,dt\leq C,\end{align} $$
for any
![]() $T>0$
, where
$T>0$
, where
![]() $C>0$
is a constant, depending on
$C>0$
is a constant, depending on
![]() $\|\mathbf {u}_0,\mathbf {w}_0\|_2^2$
.
$\|\mathbf {u}_0,\mathbf {w}_0\|_2^2$
.
Proof Multiplying equations (1.4)
![]() $_1$
, (1.4)
$_1$
, (1.4)
![]() $_2$
, (1.4)
$_2$
, (1.4)
![]() $_3$
, (1.4)
$_3$
, (1.4)
![]() $_4$
, (1.4)
$_4$
, (1.4)
![]() $_5$
, and (1.4)
$_5$
, and (1.4)
![]() $_6$
by
$_6$
by
![]() $u_1,\ u_2,\ u_3,\ \text {w}_1,\ \text {w}_2$
, and
$u_1,\ u_2,\ u_3,\ \text {w}_1,\ \text {w}_2$
, and
![]() $\text {w}_3$
, respectively, and taking the
$\text {w}_3$
, respectively, and taking the
![]() $L^2$
-inner product, integrating by parts, using the divergence-free condition
$L^2$
-inner product, integrating by parts, using the divergence-free condition
![]() $\nabla \cdot \mathbf {u}=0$
and adding them together, yield that
$\nabla \cdot \mathbf {u}=0$
and adding them together, yield that
 $$ \begin{align}&\frac12\frac{d}{dt}\|\mathbf{u},\ \mathbf{w}\|_2^2+4\kappa\|\mathbf{w}\|_2^2+\mu\|\text{div}\mathbf{w}\|_2^2\nonumber\\ & \quad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2 \nonumber\\ & \quad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2 =4\kappa\int\nabla\times\mathbf{w}\cdot\mathbf{u}dxdydz.\nonumber\\ \end{align} $$
$$ \begin{align}&\frac12\frac{d}{dt}\|\mathbf{u},\ \mathbf{w}\|_2^2+4\kappa\|\mathbf{w}\|_2^2+\mu\|\text{div}\mathbf{w}\|_2^2\nonumber\\ & \quad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2 \nonumber\\ & \quad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2 =4\kappa\int\nabla\times\mathbf{w}\cdot\mathbf{u}dxdydz.\nonumber\\ \end{align} $$
The right-hand side of (3.2) can be estimated as
 $$ \begin{align*}4\kappa\int\nabla\times\mathbf{w}\cdot\mathbf{u}dxdydz&=4\kappa\int(\varepsilon_{1jk}\partial_j\text{w}_ku_1 +\varepsilon_{2jk}\partial_j\text{w}_ku_2+\varepsilon_{3jk}\partial_j\text{w}_ku_3)dxdydz\\ & =I_1+I_2+I_3.\end{align*} $$
$$ \begin{align*}4\kappa\int\nabla\times\mathbf{w}\cdot\mathbf{u}dxdydz&=4\kappa\int(\varepsilon_{1jk}\partial_j\text{w}_ku_1 +\varepsilon_{2jk}\partial_j\text{w}_ku_2+\varepsilon_{3jk}\partial_j\text{w}_ku_3)dxdydz\\ & =I_1+I_2+I_3.\end{align*} $$
To begin with the term
![]() $I_1$
, applying Lemmas 2.2 and 2.3, we obtain
$I_1$
, applying Lemmas 2.2 and 2.3, we obtain
 $$ \begin{align} I_1&=4\kappa\int (\partial_2\text{w}_3-\partial_3\text{w}_2)u_1\, dxdydz \nonumber\\&\leq C\|u_1\|_2(\|\partial_2\text{w}_3\|_2+\|\partial_3\text{w}_2)\|_2\nonumber\\&\leq C\|u_1\|_2(\|\text{w}_3\|_2^{\frac15}\|\Lambda_2^{\frac54}\text{w}_3\|_2^{\frac45} +\|\text{w}_2\|_2^{\frac15}\|\Lambda_3^{\frac54}\text{w}_2\|_2^{\frac45})\nonumber\\&\leq\varepsilon\|\Lambda_3^{\frac54}\text{w}_2,\ \Lambda_2^{\frac54}\text{w}_3\|_2^2 +C_\varepsilon\|u_1\|_2^2. \end{align} $$
$$ \begin{align} I_1&=4\kappa\int (\partial_2\text{w}_3-\partial_3\text{w}_2)u_1\, dxdydz \nonumber\\&\leq C\|u_1\|_2(\|\partial_2\text{w}_3\|_2+\|\partial_3\text{w}_2)\|_2\nonumber\\&\leq C\|u_1\|_2(\|\text{w}_3\|_2^{\frac15}\|\Lambda_2^{\frac54}\text{w}_3\|_2^{\frac45} +\|\text{w}_2\|_2^{\frac15}\|\Lambda_3^{\frac54}\text{w}_2\|_2^{\frac45})\nonumber\\&\leq\varepsilon\|\Lambda_3^{\frac54}\text{w}_2,\ \Lambda_2^{\frac54}\text{w}_3\|_2^2 +C_\varepsilon\|u_1\|_2^2. \end{align} $$
Similarly,
 $$ \begin{align} I_2&=4\kappa\int (\partial_3\text{w}_1-\partial_1\text{w}_3)u_2\, dxdydz\nonumber\\&\leq C\|u_2\|_2(\|\text{w}_1\|_2^{\frac15}\|\Lambda_3^{\frac54}\text{w}_1\|_2^{\frac45}+\|\text{w}_3\|_2^{\frac15}\|\Lambda_1^{\frac54}\text{w}_3\|_2^{\frac45} )\nonumber\\&\leq\varepsilon\|\Lambda_3^{\frac54}\text{w}_1,\ \Lambda_1^{\frac54}\text{w}_3\|_2^2 +C_\varepsilon\|u_2\|_2^2, \end{align} $$
$$ \begin{align} I_2&=4\kappa\int (\partial_3\text{w}_1-\partial_1\text{w}_3)u_2\, dxdydz\nonumber\\&\leq C\|u_2\|_2(\|\text{w}_1\|_2^{\frac15}\|\Lambda_3^{\frac54}\text{w}_1\|_2^{\frac45}+\|\text{w}_3\|_2^{\frac15}\|\Lambda_1^{\frac54}\text{w}_3\|_2^{\frac45} )\nonumber\\&\leq\varepsilon\|\Lambda_3^{\frac54}\text{w}_1,\ \Lambda_1^{\frac54}\text{w}_3\|_2^2 +C_\varepsilon\|u_2\|_2^2, \end{align} $$
and
Inserting the above inequalities (3.3)–(3.5) into (3.2), choosing
![]() $\varepsilon $
small enough, and integrating from
$\varepsilon $
small enough, and integrating from
![]() $0$
to
$0$
to
![]() $T>0$
yield the desired estimate (3.1).
$T>0$
yield the desired estimate (3.1).
Step 2. Global
![]() $H^1$
-bound.
$H^1$
-bound.
The goal of this section is to establish the global
![]() $L^2$
-estimate of
$L^2$
-estimate of
![]() $(\nabla \mathbf {u},\ \nabla \mathbf {w})$
. The process of this section is more complex.
$(\nabla \mathbf {u},\ \nabla \mathbf {w})$
. The process of this section is more complex.
Proposition 3.2 Suppose that
![]() $(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$
. Then, system (
1.4
) has a global solution
$(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$
. Then, system (
1.4
) has a global solution
![]() $(\mathbf {u},\mathbf {w})$
satisfying
$(\mathbf {u},\mathbf {w})$
satisfying
 $$ \begin{align} &\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2+4\kappa\|\nabla\mathbf{w}\|_2^2+\mu\|\nabla\text{div}\mathbf{w}\|_2^2\nonumber\\&\quad +(\nu+\kappa)\int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2 \,dt\nonumber\\&\quad +\gamma\int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2 \,dt\leq C,\end{align} $$
$$ \begin{align} &\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2+4\kappa\|\nabla\mathbf{w}\|_2^2+\mu\|\nabla\text{div}\mathbf{w}\|_2^2\nonumber\\&\quad +(\nu+\kappa)\int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2 \,dt\nonumber\\&\quad +\gamma\int^T_0\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2 \,dt\leq C,\end{align} $$
for any
![]() $T>0$
, where
$T>0$
, where
![]() $C>0$
is a constant, depending on
$C>0$
is a constant, depending on
![]() $\|\mathbf {u}_0,\mathbf {w}_0\|_{H^1(\mathbb {R}^3)}^2$
.
$\|\mathbf {u}_0,\mathbf {w}_0\|_{H^1(\mathbb {R}^3)}^2$
.
Proof In order to obtain the global
![]() $H^1$
-bound, we apply the operator
$H^1$
-bound, we apply the operator
![]() $\nabla $
to system (1.4), and taking the inner product by the resulting equations with
$\nabla $
to system (1.4), and taking the inner product by the resulting equations with
![]() $\nabla \mathbf {u}$
and
$\nabla \mathbf {u}$
and
![]() $\nabla \mathbf {w}$
, respectively, integrating by parts, we obtain
$\nabla \mathbf {w}$
, respectively, integrating by parts, we obtain
 $$ \begin{align}&\frac12\frac{d}{dt}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2+4\kappa\|\nabla\mathbf{w}\|_2^2+\mu\|\nabla\text{div}\mathbf{w}\|_2^2\nonumber\\ & \qquad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\ & \qquad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2 \nonumber\\ & \quad =-\int\nabla(\mathbf{u}\cdot\nabla\mathbf{u})\cdot\nabla\mathbf{u}\, dxdydz -\int\nabla(\mathbf{u}\cdot\nabla\mathbf{w})\cdot\nabla\mathbf{w}\, dxdydz\nonumber\\ & \qquad +4\kappa\int\nabla\nabla\times\mathbf{u}\cdot\nabla\mathbf{w}\, dxdydz\nonumber\\ & \quad =J_1+J_2+J_3.\end{align} $$
$$ \begin{align}&\frac12\frac{d}{dt}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2+4\kappa\|\nabla\mathbf{w}\|_2^2+\mu\|\nabla\text{div}\mathbf{w}\|_2^2\nonumber\\ & \qquad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\ & \qquad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2 \nonumber\\ & \quad =-\int\nabla(\mathbf{u}\cdot\nabla\mathbf{u})\cdot\nabla\mathbf{u}\, dxdydz -\int\nabla(\mathbf{u}\cdot\nabla\mathbf{w})\cdot\nabla\mathbf{w}\, dxdydz\nonumber\\ & \qquad +4\kappa\int\nabla\nabla\times\mathbf{u}\cdot\nabla\mathbf{w}\, dxdydz\nonumber\\ & \quad =J_1+J_2+J_3.\end{align} $$
Due to the divergence-free condition
![]() $\nabla \cdot \mathbf {u}=0$
, integrating by parts, we can rewrite
$\nabla \cdot \mathbf {u}=0$
, integrating by parts, we can rewrite
![]() $J_1$
and
$J_1$
and
![]() $J_2$
as follows:
$J_2$
as follows:
and
To start with the term
![]() $J_1$
, similar to [Reference Yang, Jiu and Wu32], we consider the first nine terms in
$J_1$
, similar to [Reference Yang, Jiu and Wu32], we consider the first nine terms in
![]() $J_1$
denoted by
$J_1$
denoted by
![]() $J_{11}$
. The remaining terms in
$J_{11}$
. The remaining terms in
![]() $J_1$
can be handled similar to
$J_1$
can be handled similar to
![]() $J_{11}$
.
$J_{11}$
.
 $$ \begin{align}J_{11}&=-\int((\partial_1u_1)^3+\partial_1u_1\partial_1u_2\partial_2u_1+\partial_1u_1\partial_1u_3\partial_3u_1\nonumber\\ & \quad +(\partial_2u_1)^2\partial_1u_1+(\partial_2u_1)^2\partial_2u_2+\partial_2u_1\partial_2u_3\partial_3u_1\nonumber\\ & \quad +(\partial_3u_1)^2\partial_1u_1+\partial_3u_1\partial_3u_2\partial_2u_1+(\partial_3u_1)^2\partial_3u_3)\ dxdydz\nonumber\\ &=\sum_{m=1}^9J_{11m}.\end{align} $$
$$ \begin{align}J_{11}&=-\int((\partial_1u_1)^3+\partial_1u_1\partial_1u_2\partial_2u_1+\partial_1u_1\partial_1u_3\partial_3u_1\nonumber\\ & \quad +(\partial_2u_1)^2\partial_1u_1+(\partial_2u_1)^2\partial_2u_2+\partial_2u_1\partial_2u_3\partial_3u_1\nonumber\\ & \quad +(\partial_3u_1)^2\partial_1u_1+\partial_3u_1\partial_3u_2\partial_2u_1+(\partial_3u_1)^2\partial_3u_3)\ dxdydz\nonumber\\ &=\sum_{m=1}^9J_{11m}.\end{align} $$
For the term
![]() $J_{111}$
, integrating by parts and applying Lemmas 2.2 and 2.3, using the divergence-free condition
$J_{111}$
, integrating by parts and applying Lemmas 2.2 and 2.3, using the divergence-free condition
![]() $\nabla \cdot \mathbf {u}=0$
, one has
$\nabla \cdot \mathbf {u}=0$
, one has
 $$ \begin{align} J_{111}=&-\int((\partial_1u_1)^3\ dxdydz=2\int u_1\partial_{11}u_1\partial_1u_1\ dxdydz\nonumber\\ &\leq C\|\partial_{11}u_1\|_{L^4_{x_1}L^2_{x_2x_3}}\|\partial_1u_1\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|u_1\|_{L^2_{x_1x_2}L^{\infty}_{x_3}}\nonumber\\ &\leq\|\Lambda_1^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac54}u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}} \|u_1\|_2^{\frac35}\|\Lambda_3^{\frac54}u_1\|_2^{\frac25}\nonumber\\ &\leq\varepsilon\|\Lambda_1^{\frac54}\partial_1u_1\|_2^2+C_\varepsilon\|u_1\|_2^{\frac65}\|\Lambda_3^{\frac54}u_1\|_2^{\frac45} \|\Lambda_1^{\frac54}u_1\|_2\|\Lambda_1^{\frac54}\Lambda_2u_1\|_2\nonumber\\ &\leq\varepsilon(\|\Lambda_1^{\frac54}\partial_1u_1\|_2^2+\|\Lambda_1^{\frac54}\Lambda_2u_1\|_2) +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2(\|u_1\|_2^{\frac89}\|\Lambda_1^{\frac54}\partial_1u_1\|_2^{\frac{10}{9}})\nonumber\\ &\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ \Lambda_2^{\frac54}\partial_1u_1\|_2^2+C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2. \end{align} $$
$$ \begin{align} J_{111}=&-\int((\partial_1u_1)^3\ dxdydz=2\int u_1\partial_{11}u_1\partial_1u_1\ dxdydz\nonumber\\ &\leq C\|\partial_{11}u_1\|_{L^4_{x_1}L^2_{x_2x_3}}\|\partial_1u_1\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|u_1\|_{L^2_{x_1x_2}L^{\infty}_{x_3}}\nonumber\\ &\leq\|\Lambda_1^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac54}u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}} \|u_1\|_2^{\frac35}\|\Lambda_3^{\frac54}u_1\|_2^{\frac25}\nonumber\\ &\leq\varepsilon\|\Lambda_1^{\frac54}\partial_1u_1\|_2^2+C_\varepsilon\|u_1\|_2^{\frac65}\|\Lambda_3^{\frac54}u_1\|_2^{\frac45} \|\Lambda_1^{\frac54}u_1\|_2\|\Lambda_1^{\frac54}\Lambda_2u_1\|_2\nonumber\\ &\leq\varepsilon(\|\Lambda_1^{\frac54}\partial_1u_1\|_2^2+\|\Lambda_1^{\frac54}\Lambda_2u_1\|_2) +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2(\|u_1\|_2^{\frac89}\|\Lambda_1^{\frac54}\partial_1u_1\|_2^{\frac{10}{9}})\nonumber\\ &\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ \Lambda_2^{\frac54}\partial_1u_1\|_2^2+C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2. \end{align} $$
Similarly,
 $$ \begin{align*} J_{112}&=-\!\int\!\partial_1u_1\partial_1u_2\partial_2u_1\ dxdydz =\!\int\! u_1\partial_{12}u_1\partial_1u_2\ dxdydz+\!\int\! u_1\partial_{12}u_2\partial_1u_1\ dxdydz\\&=J_{1121}+J_{1122}. \end{align*} $$
$$ \begin{align*} J_{112}&=-\!\int\!\partial_1u_1\partial_1u_2\partial_2u_1\ dxdydz =\!\int\! u_1\partial_{12}u_1\partial_1u_2\ dxdydz+\!\int\! u_1\partial_{12}u_2\partial_1u_1\ dxdydz\\&=J_{1121}+J_{1122}. \end{align*} $$
Using Lemmas 2.1 and 2.3, we can bound the term
![]() $J_{1121}$
as follows:
$J_{1121}$
as follows:
 $$ \begin{align*} |J_{1121}|&\leq C\|\partial_{12}u_1\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_1u_2\|_{L^4_{x_1}L^2_{x_2}L^{\infty}_{x_3}} \|u_1\|_{L^4_{x_1x_2}L^{2}_{x_3}}\\ &\leq C\|\Lambda_2^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac54}u_2\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_2\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\partial_1u_1,\ \partial_2u_1\|_2^{\frac12}\\ &\leq\varepsilon(\|\Lambda_2^{\frac54}\partial_1u_1\|_2^2+\|\Lambda_1^{\frac54}\partial_3u_2\|_2^2) +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^2\|\nabla\mathbf{u}\|_2^2 \end{align*} $$
$$ \begin{align*} |J_{1121}|&\leq C\|\partial_{12}u_1\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_1u_2\|_{L^4_{x_1}L^2_{x_2}L^{\infty}_{x_3}} \|u_1\|_{L^4_{x_1x_2}L^{2}_{x_3}}\\ &\leq C\|\Lambda_2^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac54}u_2\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_2\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\partial_1u_1,\ \partial_2u_1\|_2^{\frac12}\\ &\leq\varepsilon(\|\Lambda_2^{\frac54}\partial_1u_1\|_2^2+\|\Lambda_1^{\frac54}\partial_3u_2\|_2^2) +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^2\|\nabla\mathbf{u}\|_2^2 \end{align*} $$
and
 $$ \begin{align*} |J_{1122}|&\leq C\|\partial_{12}u_2\|_{L^4_{x_1}L^2_{x_2x_3}}\|\partial_1u_1\|_{L^4_{x_1}L^2_{x_2}L^{\infty}_{x_3}} \|u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}}\\ &\leq C\|\Lambda_1^{\frac54}\partial_2u_2\|_2\|\Lambda_1^{\frac54}u_1\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_1\|_2^{\frac35}\|\Lambda_2{}^{\frac54}u_1\|_2^{\frac25}\\ &\leq\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2\|_2^2+C_\varepsilon\|u_1\|_2^{\frac65}\|\Lambda_2{}^{\frac54}u_1\|_2^{\frac45} \|\Lambda_1^{\frac54}u_1\|_2\|\Lambda_1^{\frac54}\Lambda_3u_1\|_2\\ &\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_1u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2. \end{align*} $$
$$ \begin{align*} |J_{1122}|&\leq C\|\partial_{12}u_2\|_{L^4_{x_1}L^2_{x_2x_3}}\|\partial_1u_1\|_{L^4_{x_1}L^2_{x_2}L^{\infty}_{x_3}} \|u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}}\\ &\leq C\|\Lambda_1^{\frac54}\partial_2u_2\|_2\|\Lambda_1^{\frac54}u_1\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_1\|_2^{\frac35}\|\Lambda_2{}^{\frac54}u_1\|_2^{\frac25}\\ &\leq\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2\|_2^2+C_\varepsilon\|u_1\|_2^{\frac65}\|\Lambda_2{}^{\frac54}u_1\|_2^{\frac45} \|\Lambda_1^{\frac54}u_1\|_2\|\Lambda_1^{\frac54}\Lambda_3u_1\|_2\\ &\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_1u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2. \end{align*} $$
Combining the above two estimates, we obtain
 $$ \begin{align} |J_{112}|&\leq 4\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
$$ \begin{align} |J_{112}|&\leq 4\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
Next, we will bound the term
![]() $J_{113}$
, and integrating by parts, we find that
$J_{113}$
, and integrating by parts, we find that
 $$ \begin{align*} J_{113}&=-\!\int\!\partial_1u_1\partial_1u_3\partial_3u_1\ dxdydz =\!\int\! u_1\partial_{13}u_1\partial_1u_3\ dxdydz+\!\int\! u_1\partial_{13}u_3\partial_1u_1\ dxdydz\\&=J_{1131}+J_{1132}. \end{align*} $$
$$ \begin{align*} J_{113}&=-\!\int\!\partial_1u_1\partial_1u_3\partial_3u_1\ dxdydz =\!\int\! u_1\partial_{13}u_1\partial_1u_3\ dxdydz+\!\int\! u_1\partial_{13}u_3\partial_1u_1\ dxdydz\\&=J_{1131}+J_{1132}. \end{align*} $$
Similar to
![]() $J_{1121}$
, one has
$J_{1121}$
, one has
 $$ \begin{align*} |J_{1131}|&\leq C\|\partial_{13}u_1\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_1u_3\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|u_1\|_{L^4_{x_1x_3}L^{2}_{x_3}}\\ &\leq C\|\Lambda_3^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac54}u_3\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_3\|_2^{\frac12} \|u_1\|_2^{\frac12}\|(\partial_1,\ \partial_3)u_1\|_2^{\frac12}\\ &\leq\varepsilon\|\Lambda_3^{\frac54}\partial_1u_1,\ \Lambda_1^{\frac54}\partial_3u_3\|_2^2 +C_\varepsilon\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_3\|_2^2)^2\|\nabla u_1\|_2^2. \end{align*} $$
$$ \begin{align*} |J_{1131}|&\leq C\|\partial_{13}u_1\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_1u_3\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|u_1\|_{L^4_{x_1x_3}L^{2}_{x_3}}\\ &\leq C\|\Lambda_3^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac54}u_3\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_3\|_2^{\frac12} \|u_1\|_2^{\frac12}\|(\partial_1,\ \partial_3)u_1\|_2^{\frac12}\\ &\leq\varepsilon\|\Lambda_3^{\frac54}\partial_1u_1,\ \Lambda_1^{\frac54}\partial_3u_3\|_2^2 +C_\varepsilon\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_3\|_2^2)^2\|\nabla u_1\|_2^2. \end{align*} $$
Applying the similar method to
![]() $J_{1122}$
, we have
$J_{1122}$
, we have
 $$ \begin{align*} |J_{1132}|&\leq C\|\partial_{13}u_3\|_{L^4_{x_1}L^2_{x_2x_3}}\|\partial_1u_2\|_{L^4_{x_1}L^2_{x_2}L^{\infty}_{x_3}} \|u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}}\\ &\leq C\|\Lambda_1^{\frac54}\partial_3u_3\|_2\|\Lambda_1^{\frac54}u_1\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_1\|_2^{\frac35}\|\Lambda_2^{\frac54}u_1\|_2^{\frac25}\\ &\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_1u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2. \end{align*} $$
$$ \begin{align*} |J_{1132}|&\leq C\|\partial_{13}u_3\|_{L^4_{x_1}L^2_{x_2x_3}}\|\partial_1u_2\|_{L^4_{x_1}L^2_{x_2}L^{\infty}_{x_3}} \|u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}}\\ &\leq C\|\Lambda_1^{\frac54}\partial_3u_3\|_2\|\Lambda_1^{\frac54}u_1\|_2^{\frac12}\|\Lambda_1^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_1\|_2^{\frac35}\|\Lambda_2^{\frac54}u_1\|_2^{\frac25}\\ &\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_1u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2. \end{align*} $$
Therefore,
 $$ \begin{align} |J_{113}|&\leq 6\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
$$ \begin{align} |J_{113}|&\leq 6\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^{\frac92}\|u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_1^{\frac54}u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
Integrating by parts and invoking the divergence-free condition
![]() $\nabla \cdot \mathbf {u}=0$
, one has
$\nabla \cdot \mathbf {u}=0$
, one has
 $$ \begin{align} J_{114}+J_{115}&=-\int(\partial_2u_1)^2(\partial_1u_1+\partial_2u_2)\ dxdydz\nonumber\\&=\int(\partial_2u_1)^2\partial_3u_3\ dxdydz=-2\int u_3\partial_{23}u_1\partial_2u_1\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_1\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_2u_1\|_{L^4_{x_2}L^2_{x_1}L^{\infty}_{x_3}} \|u_3\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_3u_1\|_2\|\Lambda_2^{\frac54}u_1\|_2^{\frac12}\|\Lambda_2^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_3\|_2^{\frac12}\|\Lambda_1u_3\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|\Lambda_2^{\frac54}\partial_3u_1\|_2^2+C_\varepsilon(\|u_3\|_2^2+ \|\Lambda_2^{\frac54}u_1\|_2^2)^2\|\partial_1u_3\|_2^2. \end{align} $$
$$ \begin{align} J_{114}+J_{115}&=-\int(\partial_2u_1)^2(\partial_1u_1+\partial_2u_2)\ dxdydz\nonumber\\&=\int(\partial_2u_1)^2\partial_3u_3\ dxdydz=-2\int u_3\partial_{23}u_1\partial_2u_1\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_1\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_2u_1\|_{L^4_{x_2}L^2_{x_1}L^{\infty}_{x_3}} \|u_3\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_3u_1\|_2\|\Lambda_2^{\frac54}u_1\|_2^{\frac12}\|\Lambda_2^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_3\|_2^{\frac12}\|\Lambda_1u_3\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|\Lambda_2^{\frac54}\partial_3u_1\|_2^2+C_\varepsilon(\|u_3\|_2^2+ \|\Lambda_2^{\frac54}u_1\|_2^2)^2\|\partial_1u_3\|_2^2. \end{align} $$
To bound the term
![]() $J_{116}$
, integrating by parts, one yields that
$J_{116}$
, integrating by parts, one yields that
 $$ \begin{align*} J_{116}&=\int u_1\partial_{23}u_3\partial_2u_1\ dxdydz+\int u_1\partial_{23}u_1\partial_2u_3\ dxdydz\\&=J_{1161}+J_{1162}. \end{align*} $$
$$ \begin{align*} J_{116}&=\int u_1\partial_{23}u_3\partial_2u_1\ dxdydz+\int u_1\partial_{23}u_1\partial_2u_3\ dxdydz\\&=J_{1161}+J_{1162}. \end{align*} $$
Applying the similar method to
![]() $J_{1131}$
, one can easily find that
$J_{1131}$
, one can easily find that
 $$ \begin{align*} |J_{1161}|&\leq C\|\partial_{23}u_3\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_2u_1\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_1\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\\ &\leq C\|\Lambda_2^{\frac54}\partial_3u_3\|_2\|\Lambda_2^{\frac54}u_1\|_2^{\frac12}\|\Lambda_2^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\Lambda_1u_1\|_2^{\frac12}\\ &\leq\varepsilon\|\Lambda_2^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_3u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^2\|\nabla u_1\|_2^2 \end{align*} $$
$$ \begin{align*} |J_{1161}|&\leq C\|\partial_{23}u_3\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_2u_1\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_1\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\\ &\leq C\|\Lambda_2^{\frac54}\partial_3u_3\|_2\|\Lambda_2^{\frac54}u_1\|_2^{\frac12}\|\Lambda_2^{\frac54}\Lambda_3u_1\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\Lambda_1u_1\|_2^{\frac12}\\ &\leq\varepsilon\|\Lambda_2^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_3u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^2\|\nabla u_1\|_2^2 \end{align*} $$
Moreover,
 $$ \begin{align*} |J_{1162}|&\leq C\|\partial_{23}u_1\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_2u_3\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_1\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\\ &\leq\varepsilon\|\Lambda_2^{\frac54}\partial_3u_1,\ \Lambda_2^{\frac54}\partial_3u_3\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_3\|_2^2)^2\|\nabla u_1\|_2^2. \end{align*} $$
$$ \begin{align*} |J_{1162}|&\leq C\|\partial_{23}u_1\|_{L^4_{x_2}L^2_{x_1x_3}}\|\partial_2u_3\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_1\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\\ &\leq\varepsilon\|\Lambda_2^{\frac54}\partial_3u_1,\ \Lambda_2^{\frac54}\partial_3u_3\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_3\|_2^2)^2\|\nabla u_1\|_2^2. \end{align*} $$
Furthermore,
 $$ \begin{align} |J_{116}|&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\ & \quad +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2+\|\Lambda_2^{\frac54}u_3\|_2^2)^2\|\nabla u_1\|_2^2.\end{align} $$
$$ \begin{align} |J_{116}|&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\ & \quad +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2+\|\Lambda_2^{\frac54}u_3\|_2^2)^2\|\nabla u_1\|_2^2.\end{align} $$
Due to the divergence-free condition
![]() $\nabla \cdot \mathbf {u}=0$
, we will rewrite the last three terms as follows:
$\nabla \cdot \mathbf {u}=0$
, we will rewrite the last three terms as follows:
Integrating by parts, the term
![]() $J_{117}$
can be bounded as
$J_{117}$
can be bounded as
 $$ \begin{align} J_{117}&=\int u_1\partial_{23}u_1\partial_3u_2\ dxdydz+\int u_1\partial_{23}u_2\partial_3u_1\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_1\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_3u_2\|_{L^4_{x_3}L^{\infty}_{x_1}L^2_{x_2}} \|u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}}\nonumber\\&\quad +C\|\partial_{23}u_2\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_3u_1\|_{L^4_{x_3}L^{\infty}_{x_2}L^2_{x_1}} \|u_1\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\nonumber\\&\leq C\|\Lambda_3^{\frac54}\partial_2u_1\|_2\|\Lambda_3^{\frac54}u_2\|_2^{\frac12}\|\Lambda_3^{\frac54}\Lambda_1u_2\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\Lambda_2u_1\|_2^{\frac12}\nonumber\\&\quad +C\|\Lambda_3^{\frac54}\partial_2u_2\|_2\|\Lambda_3^{\frac54}u_1\|_2^{\frac12}\|\Lambda_3^{\frac54}\Lambda_2u_2\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\Lambda_1u_1\|_2^{\frac12}\nonumber\\&\leq2\varepsilon\|\Lambda_3^{\frac54}\nabla u_2,\ \Lambda_3^{\frac54}\nabla u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2 +\|\Lambda_3^{\frac54}u_2\|_2^2)^2\|\nabla u_1\|_2^2. \end{align} $$
$$ \begin{align} J_{117}&=\int u_1\partial_{23}u_1\partial_3u_2\ dxdydz+\int u_1\partial_{23}u_2\partial_3u_1\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_1\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_3u_2\|_{L^4_{x_3}L^{\infty}_{x_1}L^2_{x_2}} \|u_1\|_{L^2_{x_1x_3}L^{\infty}_{x_2}}\nonumber\\&\quad +C\|\partial_{23}u_2\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_3u_1\|_{L^4_{x_3}L^{\infty}_{x_2}L^2_{x_1}} \|u_1\|_{L^2_{x_2x_3}L^{\infty}_{x_1}}\nonumber\\&\leq C\|\Lambda_3^{\frac54}\partial_2u_1\|_2\|\Lambda_3^{\frac54}u_2\|_2^{\frac12}\|\Lambda_3^{\frac54}\Lambda_1u_2\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\Lambda_2u_1\|_2^{\frac12}\nonumber\\&\quad +C\|\Lambda_3^{\frac54}\partial_2u_2\|_2\|\Lambda_3^{\frac54}u_1\|_2^{\frac12}\|\Lambda_3^{\frac54}\Lambda_2u_2\|_2^{\frac12} \|u_1\|_2^{\frac12}\|\Lambda_1u_1\|_2^{\frac12}\nonumber\\&\leq2\varepsilon\|\Lambda_3^{\frac54}\nabla u_2,\ \Lambda_3^{\frac54}\nabla u_1\|_2^2 +C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2 +\|\Lambda_3^{\frac54}u_2\|_2^2)^2\|\nabla u_1\|_2^2. \end{align} $$
Similarly,
 $$ \begin{align}J_{118}&=-2\int u_2\partial_{23}u_1\partial_3u_1\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_1\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_3u_1\|_{L^4_{x_3}L^{\infty}_{x_2}L^2_{x_1}} \|u_2\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq C\|\Lambda_3^{\frac54}\partial_2u_1\|_2\|\Lambda_3^{\frac54}u_1\|_2^{\frac12}\|\Lambda_3^{\frac54}\Lambda_2u_1\|_2^{\frac12} \|u_2\|_2^{\frac12}\|\Lambda_1u_2\|_2^{\frac12}\nonumber\\&\leq2\varepsilon\|\Lambda_3^{\frac54}\nabla u_1\|_2^2 +C_\varepsilon(\|u_2\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2\|\nabla u_2\|_2^2.\end{align} $$
$$ \begin{align}J_{118}&=-2\int u_2\partial_{23}u_1\partial_3u_1\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_1\|_{L^4_{x_3}L^2_{x_1x_2}}\|\partial_3u_1\|_{L^4_{x_3}L^{\infty}_{x_2}L^2_{x_1}} \|u_2\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq C\|\Lambda_3^{\frac54}\partial_2u_1\|_2\|\Lambda_3^{\frac54}u_1\|_2^{\frac12}\|\Lambda_3^{\frac54}\Lambda_2u_1\|_2^{\frac12} \|u_2\|_2^{\frac12}\|\Lambda_1u_2\|_2^{\frac12}\nonumber\\&\leq2\varepsilon\|\Lambda_3^{\frac54}\nabla u_1\|_2^2 +C_\varepsilon(\|u_2\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2\|\nabla u_2\|_2^2.\end{align} $$
Inserting the bounds (3.9)–(3.15) into equation (3.8), we obtain
 $$ \begin{align} |J_{11}|&\leq 24\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54}, \Lambda_3^{\frac54})u_1\|_2^2)^{\frac92}\|\mathbf{u}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
$$ \begin{align} |J_{11}|&\leq 24\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54}, \Lambda_3^{\frac54})u_1\|_2^2)^{\frac92}\|\mathbf{u}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
Next, we will bound the second nine terms of
![]() $J_1$
denoted by
$J_1$
denoted by
![]() $J_{12}$
. We write it explicitly,
$J_{12}$
. We write it explicitly,
 $$ \begin{align} J_{12}&=-\int(\partial_1u_1(\partial_1u_2)^2+(\partial_1u_2)^2\partial_2u_2 +\partial_1u_3\partial_3u_2\partial_1u_2\nonumber\\&\quad +\partial_2u_1\partial_1u_2\partial_2u_2+(\partial_2u_2)^3+\partial_2u_3\partial_3u_2\partial_2u_2\nonumber\\&\quad +\partial_3u_1\partial_1u_2\partial_3u_2+\partial_3u_2\partial_2u_2\partial_3u_2+\partial_3u_3(\partial_3u_2)^2)\ dxdydz\nonumber\\&=\sum_{l=1}^9J_{12l}.\end{align} $$
$$ \begin{align} J_{12}&=-\int(\partial_1u_1(\partial_1u_2)^2+(\partial_1u_2)^2\partial_2u_2 +\partial_1u_3\partial_3u_2\partial_1u_2\nonumber\\&\quad +\partial_2u_1\partial_1u_2\partial_2u_2+(\partial_2u_2)^3+\partial_2u_3\partial_3u_2\partial_2u_2\nonumber\\&\quad +\partial_3u_1\partial_1u_2\partial_3u_2+\partial_3u_2\partial_2u_2\partial_3u_2+\partial_3u_3(\partial_3u_2)^2)\ dxdydz\nonumber\\&=\sum_{l=1}^9J_{12l}.\end{align} $$
Most terms in (3.17) can be bounded similarly as
![]() $J_{11}$
, we just estimate one of the most difficult terms, such as
$J_{11}$
, we just estimate one of the most difficult terms, such as
![]() $J_{125}$
, integrating by parts, yields
$J_{125}$
, integrating by parts, yields
 $$ \begin{align} J_{125}&=-\int(\partial_2u_2)^3\ dxdydz=2\int u_2\partial_2u_2\partial_{22}u_2\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_2\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2u_2\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_2\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_2u_2\|_2\|\Lambda_2^{\frac54}u_2\|_2^{\frac12} \|\Lambda_2^{\frac54}\Lambda_3u_2\|_2^{\frac12}\|u_2\|_2^{\frac35}\|\Lambda_1^{\frac54}u_2\|_2^{\frac25}\nonumber\\&\leq 4\varepsilon\|\Lambda_2^{\frac54}\partial_1u_1,\ \Lambda_2^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_2u_2\|_2^2 +C_\varepsilon(\|u_2\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^{\frac92}\|u_2\|_2^2. \end{align} $$
$$ \begin{align} J_{125}&=-\int(\partial_2u_2)^3\ dxdydz=2\int u_2\partial_2u_2\partial_{22}u_2\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_2\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2u_2\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_2\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_2u_2\|_2\|\Lambda_2^{\frac54}u_2\|_2^{\frac12} \|\Lambda_2^{\frac54}\Lambda_3u_2\|_2^{\frac12}\|u_2\|_2^{\frac35}\|\Lambda_1^{\frac54}u_2\|_2^{\frac25}\nonumber\\&\leq 4\varepsilon\|\Lambda_2^{\frac54}\partial_1u_1,\ \Lambda_2^{\frac54}\partial_3u_3,\ \Lambda_3^{\frac54}\partial_2u_2\|_2^2 +C_\varepsilon(\|u_2\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^{\frac92}\|u_2\|_2^2. \end{align} $$
Furthermore, one can easily check that
 $$ \begin{align} |J_{12}|&\leq 24\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54}, \Lambda_3^{\frac54})u_2\|_2^2)^{\frac92}\|\mathbf{u}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
$$ \begin{align} |J_{12}|&\leq 24\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54}, \Lambda_3^{\frac54})u_2\|_2^2)^{\frac92}\|\mathbf{u}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2. \end{align} $$
Similarly,
 $$ \begin{align} |J_{13}|&\leq 24\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54}, \Lambda_2^{\frac54})u_3\|_2^2)^{\frac92}\|\mathbf{u}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2.\end{align} $$
$$ \begin{align} |J_{13}|&\leq 24\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54}, \Lambda_2^{\frac54})u_3\|_2^2)^{\frac92}\|\mathbf{u}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\mathbf{u},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2)^2\|\nabla\mathbf{u}\|_2^2.\end{align} $$
Next, we will bound the term
![]() $J_2$
. Similar to
$J_2$
. Similar to
![]() $J_1$
, we consider the first nine terms in
$J_1$
, we consider the first nine terms in
![]() $J_2$
denoted by
$J_2$
denoted by
![]() $J_{21}$
, firstly.
$J_{21}$
, firstly.
 $$ \begin{align}J_{21}&=-\int(\partial_1u_1(\partial_1\text{w}_1)^2+\partial_1u_2\partial_1\text{w}_1\partial_2\text{w}_1 +\partial_1u_3\partial_3\text{w}_1\partial_1\text{w}_1\nonumber\\&\quad +\partial_2u_1\partial_1\text{w}_1\partial_2\text{w}_1+(\partial_2\text{w}_1)^2\partial_2u_2+\partial_2u_3\partial_3\text{w}_1\partial_2\text{w}_1\nonumber\\&\quad +\partial_3u_1\partial_1\text{w}_1\partial_3\text{w}_1+\partial_3u_2\partial_2\text{w}_1\partial_3\text{w}_1+\partial_3u_3(\partial_3\text{w}_1)^2)\ dxdydz\nonumber\\&=\sum_{n=1}^9J_{21n}.\end{align} $$
$$ \begin{align}J_{21}&=-\int(\partial_1u_1(\partial_1\text{w}_1)^2+\partial_1u_2\partial_1\text{w}_1\partial_2\text{w}_1 +\partial_1u_3\partial_3\text{w}_1\partial_1\text{w}_1\nonumber\\&\quad +\partial_2u_1\partial_1\text{w}_1\partial_2\text{w}_1+(\partial_2\text{w}_1)^2\partial_2u_2+\partial_2u_3\partial_3\text{w}_1\partial_2\text{w}_1\nonumber\\&\quad +\partial_3u_1\partial_1\text{w}_1\partial_3\text{w}_1+\partial_3u_2\partial_2\text{w}_1\partial_3\text{w}_1+\partial_3u_3(\partial_3\text{w}_1)^2)\ dxdydz\nonumber\\&=\sum_{n=1}^9J_{21n}.\end{align} $$
To start with term
![]() $J_{211}$
, we rewrite it as follows:
$J_{211}$
, we rewrite it as follows:
 $$ \begin{align} J_{211}&=-\int\partial_1u_1(\partial_1\text{w}_1)^2\ dxdydz=-\int\partial_1u_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\partial_1\text{w}_1\ dxdydz\nonumber\\&\quad -\int(\partial_1u_1\text{div}\mathbf{w}\partial_1\text{w}_1-\partial_1u_1\partial_2\text{w}_2\partial_1\text{w}_1-\partial_1u_1\partial_3\text{w}_3\partial_1\text{w}_1)\ dxdydz\nonumber\\&=J_{2111}+J_{2112}+J_{2113}.\nonumber\\ \end{align} $$
$$ \begin{align} J_{211}&=-\int\partial_1u_1(\partial_1\text{w}_1)^2\ dxdydz=-\int\partial_1u_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\partial_1\text{w}_1\ dxdydz\nonumber\\&\quad -\int(\partial_1u_1\text{div}\mathbf{w}\partial_1\text{w}_1-\partial_1u_1\partial_2\text{w}_2\partial_1\text{w}_1-\partial_1u_1\partial_3\text{w}_3\partial_1\text{w}_1)\ dxdydz\nonumber\\&=J_{2111}+J_{2112}+J_{2113}.\nonumber\\ \end{align} $$
Applying Lemmas 2.2 and 2.3, we can bound the term
![]() $J_{2111}$
as follows:
$J_{2111}$
as follows:
 $$ \begin{align} J_{2111}&=-\int\partial_1u_1\text{div}\mathbf{w}\partial_1\text{w}_1 \ dxdydz\nonumber\\&\leq C\|\text{div}\mathbf{w}\|_2 \|\partial_1u_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\partial_1\text{w}_1\|_{L^2_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq C\|\text{div}\mathbf{w}\|_2\|\Lambda_2^{\frac14}\partial_1u_1\|_2^{\frac12}\|\Lambda_2^{\frac14}\Lambda_1\partial_1u_1\|_2^{\frac12} \|\Lambda_2^{\frac14}\partial_1\text{w}_1\|_2^{\frac12}\|\Lambda_2^{\frac14}\Lambda_3\partial_1\text{w}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_1u_1,\ \Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1\text{w}_1\|_2^2 +C_\varepsilon\|\text{div}\mathbf{w}\|_2^{\frac52}\|\partial_1u_1,\ \partial_1\text{w}_1\|_2^2.\nonumber\\ \end{align} $$
$$ \begin{align} J_{2111}&=-\int\partial_1u_1\text{div}\mathbf{w}\partial_1\text{w}_1 \ dxdydz\nonumber\\&\leq C\|\text{div}\mathbf{w}\|_2 \|\partial_1u_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\partial_1\text{w}_1\|_{L^2_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq C\|\text{div}\mathbf{w}\|_2\|\Lambda_2^{\frac14}\partial_1u_1\|_2^{\frac12}\|\Lambda_2^{\frac14}\Lambda_1\partial_1u_1\|_2^{\frac12} \|\Lambda_2^{\frac14}\partial_1\text{w}_1\|_2^{\frac12}\|\Lambda_2^{\frac14}\Lambda_3\partial_1\text{w}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_1u_1,\ \Lambda_1^{\frac54}\partial_2u_2,\ \Lambda_1^{\frac54}\partial_3u_3,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1\text{w}_1\|_2^2 +C_\varepsilon\|\text{div}\mathbf{w}\|_2^{\frac52}\|\partial_1u_1,\ \partial_1\text{w}_1\|_2^2.\nonumber\\ \end{align} $$
Integrating by parts, by Lemmas 2.1 and 2.2,
![]() $J_{2112}$
can be bounded as
$J_{2112}$
can be bounded as
 $$ \begin{align} J_{2112}&=\int\partial_1u_1\partial_2\text{w}_2\partial_1\text{w}_1 \ dxdydz=-\int \text{w}_1\partial_{11}u_1\partial_2\text{w}_2\ dxdydz\nonumber\\& \quad -\int \text{w}_1\partial_{12}\text{w}_2\partial_1u_1\ dxdydz\nonumber\\&\leq C\|\partial_{11}u_1\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_2\text{w}_2\|_{L^4_{x_1}L^{\infty}_{x_3}L^2_{x_2}} \|\text{w}_1\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\nonumber\\&\quad +C\|\partial_{12}\text{w}_2\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_1u_1\|_{L^4_{x_1}L^{\infty}_{x_3}L^2_{x_2}} \|\text{w}_1\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\nonumber\\&\leq C\|\Lambda_1^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac14}\partial_2\text{w}_2\|_2^{\frac12} \|\Lambda_1^{\frac14}\Lambda_3\partial_2\text{w}_2\|_2^{\frac12}\|\text{w}_1\|_2^{\frac35}\|\Lambda_2^{\frac54}\text{w}_1\|_2^{\frac25}\nonumber\\&\quad +C\|\Lambda_1^{\frac54}\partial_2\text{w}_2\|_2\|\Lambda_1^{\frac14}\partial_1u_1\|_2^{\frac12} \|\Lambda_1^{\frac14}\Lambda_3\partial_1u_1\|_2^{\frac12}\|\text{w}_1\|_2^{\frac35}\|\Lambda_2^{\frac54}\text{w}_1\|_2^{\frac25}\nonumber\\&\leq 2\varepsilon\|\Lambda_1^{\frac54}\partial_2 u_2,\ \Lambda_1^{\frac54}\partial_3 u_3,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_2 \|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{w}_1\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2)^{\frac52}\|\partial_1u_1,\ \partial_2\text{w}_2\|_2^2. \end{align} $$
$$ \begin{align} J_{2112}&=\int\partial_1u_1\partial_2\text{w}_2\partial_1\text{w}_1 \ dxdydz=-\int \text{w}_1\partial_{11}u_1\partial_2\text{w}_2\ dxdydz\nonumber\\& \quad -\int \text{w}_1\partial_{12}\text{w}_2\partial_1u_1\ dxdydz\nonumber\\&\leq C\|\partial_{11}u_1\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_2\text{w}_2\|_{L^4_{x_1}L^{\infty}_{x_3}L^2_{x_2}} \|\text{w}_1\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\nonumber\\&\quad +C\|\partial_{12}\text{w}_2\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_1u_1\|_{L^4_{x_1}L^{\infty}_{x_3}L^2_{x_2}} \|\text{w}_1\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\nonumber\\&\leq C\|\Lambda_1^{\frac54}\partial_1u_1\|_2\|\Lambda_1^{\frac14}\partial_2\text{w}_2\|_2^{\frac12} \|\Lambda_1^{\frac14}\Lambda_3\partial_2\text{w}_2\|_2^{\frac12}\|\text{w}_1\|_2^{\frac35}\|\Lambda_2^{\frac54}\text{w}_1\|_2^{\frac25}\nonumber\\&\quad +C\|\Lambda_1^{\frac54}\partial_2\text{w}_2\|_2\|\Lambda_1^{\frac14}\partial_1u_1\|_2^{\frac12} \|\Lambda_1^{\frac14}\Lambda_3\partial_1u_1\|_2^{\frac12}\|\text{w}_1\|_2^{\frac35}\|\Lambda_2^{\frac54}\text{w}_1\|_2^{\frac25}\nonumber\\&\leq 2\varepsilon\|\Lambda_1^{\frac54}\partial_2 u_2,\ \Lambda_1^{\frac54}\partial_3 u_3,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_2 \|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{w}_1\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2)^{\frac52}\|\partial_1u_1,\ \partial_2\text{w}_2\|_2^2. \end{align} $$
Similarly, one can easily check that
![]() $J_{2113}$
satisfies
$J_{2113}$
satisfies
 $$ \begin{align} J_{2113}&=\int\partial_1u_1\partial_3\text{w}_3\partial_1\text{w}_1 \ dxdydz=-\int \text{w}_1\partial_{11}u_1\partial_3\text{w}_3\ dxdydz\nonumber\\& \quad -\int \text{w}_1\partial_{13}\text{w}_3\partial_1u_1\ dxdydz\nonumber\\&\leq C\|\partial_{11}u_1\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_3\text{w}_3\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\quad+C\|\partial_{13}\text{w}_3\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_1u_1\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\leq 2\varepsilon\|\Lambda_1^{\frac54}\partial_2 u_2,\ \Lambda_1^{\frac54}\partial_3 u_3,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\partial_3\text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{w}_1\|_2^2+\|\Lambda_3^{\frac54}\text{w}_1\|_2^2)^{\frac52}\|\partial_1u_1,\ \partial_3\text{w}_3\|_2^2. \end{align} $$
$$ \begin{align} J_{2113}&=\int\partial_1u_1\partial_3\text{w}_3\partial_1\text{w}_1 \ dxdydz=-\int \text{w}_1\partial_{11}u_1\partial_3\text{w}_3\ dxdydz\nonumber\\& \quad -\int \text{w}_1\partial_{13}\text{w}_3\partial_1u_1\ dxdydz\nonumber\\&\leq C\|\partial_{11}u_1\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_3\text{w}_3\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\quad+C\|\partial_{13}\text{w}_3\|_{L^4_{x_1}L^2_{x_2x_3}} \|\partial_1u_1\|_{L^4_{x_1}L^{\infty}_{x_2}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\leq 2\varepsilon\|\Lambda_1^{\frac54}\partial_2 u_2,\ \Lambda_1^{\frac54}\partial_3 u_3,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\partial_3\text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{w}_1\|_2^2+\|\Lambda_3^{\frac54}\text{w}_1\|_2^2)^{\frac52}\|\partial_1u_1,\ \partial_3\text{w}_3\|_2^2. \end{align} $$
Inserting the estimates (3.23)–(3.25) into (3.22), we obtain
 $$ \begin{align} |J_{211}&|\leq 6\varepsilon\| \Lambda_2^{\frac54}\nabla u_1,\ \Lambda_1^{\frac54}\partial_2 u_2,\ \Lambda_1^{\frac54}\partial_3 u_3,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\nonumber\\& \quad\qquad \times (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align} $$
$$ \begin{align} |J_{211}&|\leq 6\varepsilon\| \Lambda_2^{\frac54}\nabla u_1,\ \Lambda_1^{\frac54}\partial_2 u_2,\ \Lambda_1^{\frac54}\partial_3 u_3,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\nonumber\\& \quad\qquad \times (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align} $$
Next, we will bound
![]() $J_{212}$
. Integrating by parts, using Lemmas 2.1 and 2.2, we have
$J_{212}$
. Integrating by parts, using Lemmas 2.1 and 2.2, we have
 $$ \begin{align} J_{212}&=-\int \partial_1u_2\partial_1\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int u_2\partial_{12}\text{w}_1\partial_1\text{w}_1\ dxdydz+\int u_2\partial_{11}\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=J_{2121}+J_{2122}. \end{align} $$
$$ \begin{align} J_{212}&=-\int \partial_1u_2\partial_1\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int u_2\partial_{12}\text{w}_1\partial_1\text{w}_1\ dxdydz+\int u_2\partial_{11}\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=J_{2121}+J_{2122}. \end{align} $$
Employing Lemmas 2.1 and 2.2 yields
 $$ \begin{align} J_{2121}&=\int u_2\partial_{12}\text{w}_1\partial_1\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{12}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_1\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_2\|_{L^{2}_{x_2}L^{\infty}_{x_1}L^2_{x_3}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_1\text{w}_1\|_2\|\Lambda_2^{\frac14}\partial_1\text{w}_1\|_2^{\frac12} \|\Lambda_2^{\frac14}\Lambda_3\partial_1\text{w}_1\|_2^{\frac12}\|u_2\|_2^{\frac35}\|\Lambda_1^{\frac54}u_2\|_2^{\frac25}\nonumber\\&\leq 4\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^{\frac52}\|\partial_1\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} J_{2121}&=\int u_2\partial_{12}\text{w}_1\partial_1\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{12}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_1\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|u_2\|_{L^{2}_{x_2}L^{\infty}_{x_1}L^2_{x_3}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_1\text{w}_1\|_2\|\Lambda_2^{\frac14}\partial_1\text{w}_1\|_2^{\frac12} \|\Lambda_2^{\frac14}\Lambda_3\partial_1\text{w}_1\|_2^{\frac12}\|u_2\|_2^{\frac35}\|\Lambda_1^{\frac54}u_2\|_2^{\frac25}\nonumber\\&\leq 4\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|\Lambda_1^{\frac54}u_2\|_2^2)^{\frac52}\|\partial_1\text{w}_1\|_2^2. \end{align} $$
For the term
![]() $J_{2122}$
, we rewrite it as follows:
$J_{2122}$
, we rewrite it as follows:
 $$ \begin{align} J_{2122}&=\int u_2\partial_{11}\text{w}_1\partial_2\text{w}_1\ dxdydz=\int u_2\partial_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int (u_2\partial_1\text{div}\mathbf{w}\partial_2\text{w}_1-u_2\partial_{12}\text{w}_2\partial_2\text{w}_1 -u_2\partial_{13}\text{w}_3\partial_2\text{w}_1)\ dxdydz\nonumber\\&=J_{21221}+J_{21222}+J_{21223}. \end{align} $$
$$ \begin{align} J_{2122}&=\int u_2\partial_{11}\text{w}_1\partial_2\text{w}_1\ dxdydz=\int u_2\partial_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int (u_2\partial_1\text{div}\mathbf{w}\partial_2\text{w}_1-u_2\partial_{12}\text{w}_2\partial_2\text{w}_1 -u_2\partial_{13}\text{w}_3\partial_2\text{w}_1)\ dxdydz\nonumber\\&=J_{21221}+J_{21222}+J_{21223}. \end{align} $$
Now, we will estimate
![]() $J_{21221}$
, and one can easily find that
$J_{21221}$
, and one can easily find that
 $$ \begin{align} J_{21221}&=\int u_2\partial_1\text{div}\mathbf{w}\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_1\text{div}\mathbf{w}\|_2\|\partial_2\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_2\|_{L^{\infty}_{x_1}L^2_{x_2}L^4_{x_3}}\nonumber\\&\leq C\|\partial_1\text{div}\mathbf{w}\|_2\|\Lambda_3^{\frac14}\partial_2\text{w}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\partial_1\text{w}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}u_2\|_2^{\frac12}\|\Lambda_3^{\frac14}\Lambda_1u_2\|_2^{\frac12}\nonumber\\&\leq 4\varepsilon\|\partial_1\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2\|_2^2)^{\frac52}\|\partial_2\text{w}_1\|_2^2.\end{align} $$
$$ \begin{align} J_{21221}&=\int u_2\partial_1\text{div}\mathbf{w}\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_1\text{div}\mathbf{w}\|_2\|\partial_2\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_2\|_{L^{\infty}_{x_1}L^2_{x_2}L^4_{x_3}}\nonumber\\&\leq C\|\partial_1\text{div}\mathbf{w}\|_2\|\Lambda_3^{\frac14}\partial_2\text{w}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\partial_1\text{w}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}u_2\|_2^{\frac12}\|\Lambda_3^{\frac14}\Lambda_1u_2\|_2^{\frac12}\nonumber\\&\leq 4\varepsilon\|\partial_1\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2\|_2^2)^{\frac52}\|\partial_2\text{w}_1\|_2^2.\end{align} $$
Similar to
![]() $J_{2121}$
, one can estimate
$J_{2121}$
, one can estimate
![]() $J_{21222}$
as follows:
$J_{21222}$
as follows:
 $$ \begin{align} J_{21222}&=\int u_2\partial_{12}\text{w}_2\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{12}\text{w}_2\|_{L^{4}_{x_1}L^2_{x_2x_3}}\|\partial_2\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_2\|_{L^{2}_{x_2}L^4_{x_1x_3}}\nonumber\\&\leq C\|\Lambda_1^{\frac54}\partial_2\text{w}_2\|_2\|\Lambda_3^{\frac14}\partial_2\text{w}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\partial_2\text{w}_1\|_2^{\frac12} \|u_2\|_2^{\frac12}\|(\partial_1,\ \partial_3)u_2\|_2^{\frac12}\nonumber\\&\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2\text{w}_2,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|(\partial_1,\ \partial_3)u_2\|_2^2.\nonumber\\ \end{align} $$
$$ \begin{align} J_{21222}&=\int u_2\partial_{12}\text{w}_2\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{12}\text{w}_2\|_{L^{4}_{x_1}L^2_{x_2x_3}}\|\partial_2\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_2\|_{L^{2}_{x_2}L^4_{x_1x_3}}\nonumber\\&\leq C\|\Lambda_1^{\frac54}\partial_2\text{w}_2\|_2\|\Lambda_3^{\frac14}\partial_2\text{w}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\partial_2\text{w}_1\|_2^{\frac12} \|u_2\|_2^{\frac12}\|(\partial_1,\ \partial_3)u_2\|_2^{\frac12}\nonumber\\&\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_2\text{w}_2,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|(\partial_1,\ \partial_3)u_2\|_2^2.\nonumber\\ \end{align} $$
Similarly,
 $$ \begin{align} J_{21223}&=\int u_2\partial_{13}\text{w}_3\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{13}\text{w}_3\|_{L^{4}_{x_1}L^2_{x_2x_3}}\|\partial_2\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_2\|_{L^{2}_{x_2}L^4_{x_1x_3}}\nonumber\\&\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_3\text{w}_3,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^2\|(\partial_1,\ \partial_3)u_2\|_2^2.\nonumber\\ \end{align} $$
$$ \begin{align} J_{21223}&=\int u_2\partial_{13}\text{w}_3\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{13}\text{w}_3\|_{L^{4}_{x_1}L^2_{x_2x_3}}\|\partial_2\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_2\|_{L^{2}_{x_2}L^4_{x_1x_3}}\nonumber\\&\leq 4\varepsilon\|\Lambda_1^{\frac54}\partial_3\text{w}_3,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^2\|(\partial_1,\ \partial_3)u_2\|_2^2.\nonumber\\ \end{align} $$
Combining the inequalities (3.28) and (3.30)–(3.32) with (3.27), one has
 $$ \begin{align} |J_{212}|&\leq 16\varepsilon\| \nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align} $$
$$ \begin{align} |J_{212}|&\leq 16\varepsilon\| \nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align} $$
For the term
![]() $J_{213}$
, using the similar method to
$J_{213}$
, using the similar method to
![]() $J_{212}$
, one can easily check that
$J_{212}$
, one can easily check that
 $$ \begin{align} |J_{213}|&\leq 16\varepsilon\| \nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align} $$
$$ \begin{align} |J_{213}|&\leq 16\varepsilon\| \nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\mathbf{u}\|_2^2+\|(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align} $$
Next, we will estimate the term
![]() $J_{214}$
. Integrating by parts, one has
$J_{214}$
. Integrating by parts, one has
 $$ \begin{align} J_{214}&=-\int \partial_2u_1\partial_1\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{22}u_1\partial_1\text{w}_1\ dxdydz+\int \text{w}_1\partial_{12}\text{w}_1\partial_2u_1\ dxdydz\nonumber\\&=J_{2141}+J_{2142}. \end{align} $$
$$ \begin{align} J_{214}&=-\int \partial_2u_1\partial_1\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{22}u_1\partial_1\text{w}_1\ dxdydz+\int \text{w}_1\partial_{12}\text{w}_1\partial_2u_1\ dxdydz\nonumber\\&=J_{2141}+J_{2142}. \end{align} $$
First, we can bound the second term
![]() $J_{2142}$
as
$J_{2142}$
as
 $$ \begin{align} J_{2142}&=\int \text{w}_1\partial_{12}\text{w}_1\partial_2u_1\ dxdydz\nonumber\\&\leq C\|\partial_{12}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2u_1\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|\text{w}_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_1\text{w}_1\|_2\|\Lambda_2^{\frac54}u_1\|_2^{\frac12} \|\Lambda_2^{\frac54}\Lambda_3u_1\|_2^{\frac12}\|\text{w}_1\|_2^{\frac12}\|\Lambda_1\text{w}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_3u_1,\ \Lambda_2^{\frac54}\partial_1\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^2\|\partial_1\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} J_{2142}&=\int \text{w}_1\partial_{12}\text{w}_1\partial_2u_1\ dxdydz\nonumber\\&\leq C\|\partial_{12}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2u_1\|_{L^4_{x_2}L^{\infty}_{x_3}L^2_{x_1}} \|\text{w}_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_1\text{w}_1\|_2\|\Lambda_2^{\frac54}u_1\|_2^{\frac12} \|\Lambda_2^{\frac54}\Lambda_3u_1\|_2^{\frac12}\|\text{w}_1\|_2^{\frac12}\|\Lambda_1\text{w}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_3u_1,\ \Lambda_2^{\frac54}\partial_1\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54}u_1\|_2^2)^2\|\partial_1\text{w}_1\|_2^2. \end{align} $$
Now, we return to estimate the term
![]() $J_{2141}$
. Similar to
$J_{2141}$
. Similar to
![]() $J_{2122}$
, we rewrite it as
$J_{2122}$
, we rewrite it as
 $$ \begin{align} J_{2141}&=\int \text{w}_1\partial_{22}u_1\partial_1\text{w}_1\ dxdydz=\int \text{w}_1\partial_{22}u_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\ dxdydz\nonumber\\&=\int (\text{w}_1\partial_{22}u_1\text{div}\mathbf{w}-\text{w}_1\partial_{22}u_1\partial_2\text{w}_2 -\text{w}_1\partial_{22}u_1\partial_3\text{w}_3)\ dxdydz\nonumber\\&=J_{21411}+J_{21412}+J_{21413}. \end{align} $$
$$ \begin{align} J_{2141}&=\int \text{w}_1\partial_{22}u_1\partial_1\text{w}_1\ dxdydz=\int \text{w}_1\partial_{22}u_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\ dxdydz\nonumber\\&=\int (\text{w}_1\partial_{22}u_1\text{div}\mathbf{w}-\text{w}_1\partial_{22}u_1\partial_2\text{w}_2 -\text{w}_1\partial_{22}u_1\partial_3\text{w}_3)\ dxdydz\nonumber\\&=J_{21411}+J_{21412}+J_{21413}. \end{align} $$
Applying Lemmas 2.1–2.3, we have
 $$ \begin{align} J_{21411}&=\int \text{w}_1\partial_{22}u_1\text{div}\mathbf{w}\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_1\|_{L^4_{x_2}L^{2}_{x_1x_3}}\|\text{div}\mathbf{w}\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1}L^4_{x_2}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_2u_1\|_2\|\text{div}\mathbf{w}\|_2^{\frac12} \|\Lambda_1\text{div}\mathbf{w}\|_2^{\frac12} \|\Lambda_2^{\frac14}\text{w}_1\|_2^{\frac12}\|\Lambda_2^{\frac14}\Lambda_3\text{w}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|\partial_1\text{div}\mathbf{w},\ \Lambda_2^{\frac54}\partial_2u_1\|_2^2 +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\partial_2\text{w}_1\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} J_{21411}&=\int \text{w}_1\partial_{22}u_1\text{div}\mathbf{w}\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_1\|_{L^4_{x_2}L^{2}_{x_1x_3}}\|\text{div}\mathbf{w}\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1}L^4_{x_2}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_2u_1\|_2\|\text{div}\mathbf{w}\|_2^{\frac12} \|\Lambda_1\text{div}\mathbf{w}\|_2^{\frac12} \|\Lambda_2^{\frac14}\text{w}_1\|_2^{\frac12}\|\Lambda_2^{\frac14}\Lambda_3\text{w}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|\partial_1\text{div}\mathbf{w},\ \Lambda_2^{\frac54}\partial_2u_1\|_2^2 +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\partial_2\text{w}_1\|_2^2\nonumber\\& \quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
Similarly,
 $$ \begin{align} J_{21412}&=\int \text{w}_1\partial_{22}u_1\partial_2\text{w}_2\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_1\|_{L^{4}_{x_2}L^2_{x_1x_3}}\|\partial_2\text{w}_2\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_2u_1,\ \Lambda_1^{\frac54}\partial_2\text{w}_2\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_2\text{w}_2\|_2^2 \end{align} $$
$$ \begin{align} J_{21412}&=\int \text{w}_1\partial_{22}u_1\partial_2\text{w}_2\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_1\|_{L^{4}_{x_2}L^2_{x_1x_3}}\|\partial_2\text{w}_2\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_2u_1,\ \Lambda_1^{\frac54}\partial_2\text{w}_2\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_2\text{w}_2\|_2^2 \end{align} $$
and
 $$ \begin{align} J_{21413}&=\int \text{w}_1\partial_{22}u_1\partial_3\text{w}_3\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_1\|_{L^{4}_{x_2}L^2_{x_1x_3}}\|\partial_3\text{w}_3\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_2u_1,\ \Lambda_1^{\frac54}\partial_3\text{w}_3\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_3\text{w}_3\|_2^2.\end{align} $$
$$ \begin{align} J_{21413}&=\int \text{w}_1\partial_{22}u_1\partial_3\text{w}_3\ dxdydz\nonumber\\&\leq C\|\partial_{22}u_1\|_{L^{4}_{x_2}L^2_{x_1x_3}}\|\partial_3\text{w}_3\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_2^{\frac54}\partial_2u_1,\ \Lambda_1^{\frac54}\partial_3\text{w}_3\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_3\text{w}_3\|_2^2.\end{align} $$
Furthermore, inserting the inequalities (3.38)–(3.40) into (3.37), we obtain
 $$ \begin{align} |J_{214}|&\leq 16\varepsilon\|\nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2 u_1,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ \Lambda_1^{\frac54}\partial_2 \text{w}_2,\ \Lambda_1^{\frac54}\partial_3 \text{w}_3\|_2^2\nonumber\\&\quad +C_\varepsilon((\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54})u_1\|_2^2)^2+(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2+\|\text{div}\mathbf{w}\|_2^2)^{\frac52}\nonumber\\&\quad +(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} |J_{214}|&\leq 16\varepsilon\|\nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_2 u_1,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ \Lambda_1^{\frac54}\partial_2 \text{w}_2,\ \Lambda_1^{\frac54}\partial_3 \text{w}_3\|_2^2\nonumber\\&\quad +C_\varepsilon((\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54})u_1\|_2^2)^2+(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2+\|\text{div}\mathbf{w}\|_2^2)^{\frac52}\nonumber\\&\quad +(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
Integrating by parts, the term
![]() $J_{215}$
can be estimated as
$J_{215}$
can be estimated as
 $$ \begin{align} J_{215}&=-\int (\partial_2\text{w}_1)^2\partial_2u_2\ dxdydz=2\int u_2\partial_{22}\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{22}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|u_2\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_2\text{w}_1\|_2\|\Lambda_2^{\frac54}\text{w}_1\|_2^{\frac12} \|\Lambda_2^{\frac54}\Lambda_1\text{w}_1\|_2^{\frac12}\|u_2\|_2^{\frac12}\|\Lambda_3u_2\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|\Lambda_2^{\frac54}\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2)^2\|\partial_3u_2\|_2^2. \end{align} $$
$$ \begin{align} J_{215}&=-\int (\partial_2\text{w}_1)^2\partial_2u_2\ dxdydz=2\int u_2\partial_{22}\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{22}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|u_2\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\leq C\|\Lambda_2^{\frac54}\partial_2\text{w}_1\|_2\|\Lambda_2^{\frac54}\text{w}_1\|_2^{\frac12} \|\Lambda_2^{\frac54}\Lambda_1\text{w}_1\|_2^{\frac12}\|u_2\|_2^{\frac12}\|\Lambda_3u_2\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|\Lambda_2^{\frac54}\partial_2\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{u}\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2)^2\|\partial_3u_2\|_2^2. \end{align} $$
Similarly,
 $$ \begin{align} J_{216}&=-\int\partial_2u_3\partial_3\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{23}u_3\partial_2\text{w}_1\ dxdydz+\int \text{w}_1\partial_{23}\text{w}_1\partial_2u_3\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_3\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\quad +C\|\partial_{23}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2u_3\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\leq 2\varepsilon\|\Lambda_2^{\frac54}\nabla u_3,\ \Lambda_2^{\frac54}\nabla\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2)^2\|\partial_3\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} J_{216}&=-\int\partial_2u_3\partial_3\text{w}_1\partial_2\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{23}u_3\partial_2\text{w}_1\ dxdydz+\int \text{w}_1\partial_{23}\text{w}_1\partial_2u_3\ dxdydz\nonumber\\&\leq C\|\partial_{23}u_3\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\quad +C\|\partial_{23}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_2u_3\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\text{w}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}}\nonumber\\&\leq 2\varepsilon\|\Lambda_2^{\frac54}\nabla u_3,\ \Lambda_2^{\frac54}\nabla\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2)^2\|\partial_3\text{w}_1\|_2^2. \end{align} $$
Employing the similar method to
![]() $J_{214}$
, we can bound the term
$J_{214}$
, we can bound the term
![]() $J_{217}$
as
$J_{217}$
as
 $$ \begin{align} J_{217}&=-\int \partial_3u_1\partial_1\text{w}_1\partial_3\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{33}u_1\partial_1\text{w}_1\ dxdydz+\int \text{w}_1\partial_{13}\text{w}_1\partial_3u_1\ dxdydz\nonumber\\&=J_{2171}+J_{2172}. \end{align} $$
$$ \begin{align} J_{217}&=-\int \partial_3u_1\partial_1\text{w}_1\partial_3\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{33}u_1\partial_1\text{w}_1\ dxdydz+\int \text{w}_1\partial_{13}\text{w}_1\partial_3u_1\ dxdydz\nonumber\\&=J_{2171}+J_{2172}. \end{align} $$
Furthermore, we will estimate the second term
![]() $J_{2172}$
first as follows:
$J_{2172}$
first as follows:
 $$ \begin{align} J_{2172}&=\int \text{w}_1\partial_{13}\text{w}_1\partial_3u_1\ dxdydz\nonumber\\&\leq C\|\partial_{13}\text{w}_1\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_3u_1\|_{L^4_{x_3}L^{\infty}_{x_2}L^2_{x_1}} \|\text{w}_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_3^{\frac54}\partial_2u_1,\ \Lambda_3^{\frac54}\partial_1\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2\|\partial_1\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} J_{2172}&=\int \text{w}_1\partial_{13}\text{w}_1\partial_3u_1\ dxdydz\nonumber\\&\leq C\|\partial_{13}\text{w}_1\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_3u_1\|_{L^4_{x_3}L^{\infty}_{x_2}L^2_{x_1}} \|\text{w}_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_3^{\frac54}\partial_2u_1,\ \Lambda_3^{\frac54}\partial_1\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2\|\partial_1\text{w}_1\|_2^2. \end{align} $$
Now, we return to estimate the term
![]() $J_{2171}$
. Similar to
$J_{2171}$
. Similar to
![]() $J_{2122}$
, we rewrite it as
$J_{2122}$
, we rewrite it as
 $$ \begin{align}\kern2.5pc J_{2171}&=\int \text{w}_1\partial_{33}u_1\partial_1\text{w}_1\ dxdydz=\int \text{w}_1\partial_{33}u_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\ dxdydz\nonumber\\&=\int (\text{w}_1\partial_{33}u_1\text{div}\mathbf{w}-\text{w}_1\partial_{33}u_1\partial_2\text{w}_2 -\text{w}_1\partial_{33}u_1\partial_3\text{w}_3)\ dxdydz\nonumber\\&=J_{21711}+J_{21712}+J_{21713}. \end{align} $$
$$ \begin{align}\kern2.5pc J_{2171}&=\int \text{w}_1\partial_{33}u_1\partial_1\text{w}_1\ dxdydz=\int \text{w}_1\partial_{33}u_1(\text{div}\mathbf{w}-\partial_2\text{w}_2-\partial_3\text{w}_3)\ dxdydz\nonumber\\&=\int (\text{w}_1\partial_{33}u_1\text{div}\mathbf{w}-\text{w}_1\partial_{33}u_1\partial_2\text{w}_2 -\text{w}_1\partial_{33}u_1\partial_3\text{w}_3)\ dxdydz\nonumber\\&=J_{21711}+J_{21712}+J_{21713}. \end{align} $$
Applying Lemmas 2.1–2.3, we have
 $$ \begin{align}\kern2.5pc J_{21711}&=\int \text{w}_1\partial_{33}u_1\text{div}\mathbf{w}\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_1\|_{L^4_{x_3}L^{2}_{x_1x_2}}\|\text{div}\mathbf{w}\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\text{w}_1\|_{L^{\infty}_{x_2}L^2_{x_1}L^4_{x_3}}\nonumber\\&\leq \varepsilon\|\partial_1\text{div}\mathbf{w},\ \Lambda_3^{\frac54}\partial_3u_1\|_2^2 +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\partial_2\text{w}_1\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align}\kern2.5pc J_{21711}&=\int \text{w}_1\partial_{33}u_1\text{div}\mathbf{w}\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_1\|_{L^4_{x_3}L^{2}_{x_1x_2}}\|\text{div}\mathbf{w}\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\text{w}_1\|_{L^{\infty}_{x_2}L^2_{x_1}L^4_{x_3}}\nonumber\\&\leq \varepsilon\|\partial_1\text{div}\mathbf{w},\ \Lambda_3^{\frac54}\partial_3u_1\|_2^2 +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\partial_2\text{w}_1\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
Similarly,
 $$ \begin{align} J_{21712}&=\int \text{w}_1\partial_{33}u_1\partial_2\text{w}_2\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_1\|_{L^{4}_{x_2}L^2_{x_1x_3}}\|\partial_2\text{w}_2\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_3^{\frac54}\partial_3u_1,\ \Lambda_1^{\frac54}\partial_2\text{w}_2\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_2\text{w}_2\|_2^2 \end{align} $$
$$ \begin{align} J_{21712}&=\int \text{w}_1\partial_{33}u_1\partial_2\text{w}_2\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_1\|_{L^{4}_{x_2}L^2_{x_1x_3}}\|\partial_2\text{w}_2\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2}L^{\infty}_{x_3}}\nonumber\\&\leq \varepsilon\|\Lambda_3^{\frac54}\partial_3u_1,\ \Lambda_1^{\frac54}\partial_2\text{w}_2\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_2\text{w}_2\|_2^2 \end{align} $$
and
 $$ \begin{align} J_{21713}&=\int \text{w}_1\partial_{33}u_1\partial_3\text{w}_3\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_1\|_{L^{4}_{x_3}L^2_{x_1x_2}}\|\partial_3\text{w}_3\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_3}L^{\infty}_{x_2}}\nonumber\\&\leq \varepsilon\|\Lambda_3^{\frac54}\partial_3u_1,\ \Lambda_1^{\frac54}\partial_3\text{w}_3\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_3\text{w}_3\|_2^2. \end{align} $$
$$ \begin{align} J_{21713}&=\int \text{w}_1\partial_{33}u_1\partial_3\text{w}_3\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_1\|_{L^{4}_{x_3}L^2_{x_1x_2}}\|\partial_3\text{w}_3\|_{L^2_{x_2x_3}L^{\infty}_{x_1}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_3}L^{\infty}_{x_2}}\nonumber\\&\leq \varepsilon\|\Lambda_3^{\frac54}\partial_3u_1,\ \Lambda_1^{\frac54}\partial_3\text{w}_3\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53}\|\partial_3\text{w}_3\|_2^2. \end{align} $$
Furthermore, inserting the inequalities (3.47)–(3.49) and (3.45) into (3.44), we obtain
 $$ \begin{align} |J_{217}|&\leq 16\varepsilon\|\nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ \Lambda_1^{\frac54}\partial_2 \text{w}_2,\ \Lambda_1^{\frac54}\partial_3 \text{w}_3\|_2^2\nonumber\\&\quad +C_\varepsilon((\|\mathbf{w}\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2 +(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2+\|\text{div}\mathbf{w}\|_2^2)^{\frac52}\nonumber\\&\quad +(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} |J_{217}|&\leq 16\varepsilon\|\nabla\text{div}\mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ \Lambda_1^{\frac54}\partial_2 \text{w}_2,\ \Lambda_1^{\frac54}\partial_3 \text{w}_3\|_2^2\nonumber\\&\quad +C_\varepsilon((\|\mathbf{w}\|_2^2+\|\Lambda_3^{\frac54}u_1\|_2^2)^2 +(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2+\|\text{div}\mathbf{w}\|_2^2)^{\frac52}\nonumber\\&\quad +(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\text{w}_1\|_2^2. \end{align} $$
Integrating by parts, one can dominate
![]() $J_{218}$
as
$J_{218}$
as
 $$ \begin{align} J_{218}&=-\int\partial_3u_2\partial_2\text{w}_1\partial_3\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{33}u_2\partial_2\text{w}_1\ dxdydz+\int \text{w}_1\partial_{23}\text{w}_1\partial_3u_2\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_2\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_2\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2x_3}}\nonumber\\&\quad +C\|\partial_{23}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_3u_2\|_{L^4_{x_3}L^{\infty}_{x_1}L^2_{x_2}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2x_3}}\nonumber\\&\leq 2\varepsilon\|\Lambda_3^{\frac54}\nabla u_2,\ \Lambda_2^{\frac54}\nabla\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2 +\|\Lambda_3^{\frac54}u_2\|_2^2)^2\|\nabla\text{w}_1\|_2^2. \end{align} $$
$$ \begin{align} J_{218}&=-\int\partial_3u_2\partial_2\text{w}_1\partial_3\text{w}_1\ dxdydz\nonumber\\&=\int \text{w}_1\partial_{33}u_2\partial_2\text{w}_1\ dxdydz+\int \text{w}_1\partial_{23}\text{w}_1\partial_3u_2\ dxdydz\nonumber\\&\leq C\|\partial_{33}u_2\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_2\text{w}_1\|_{L^4_{x_2}L^{\infty}_{x_1}L^2_{x_3}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2x_3}}\nonumber\\&\quad +C\|\partial_{23}\text{w}_1\|_{L^4_{x_2}L^2_{x_1x_3}} \|\partial_3u_2\|_{L^4_{x_3}L^{\infty}_{x_1}L^2_{x_2}} \|\text{w}_1\|_{L^{2}_{x_1}L^4_{x_2x_3}}\nonumber\\&\leq 2\varepsilon\|\Lambda_3^{\frac54}\nabla u_2,\ \Lambda_2^{\frac54}\nabla\text{w}_1\|_2^2 +C_\varepsilon(\|\mathbf{w}\|_2^2+\|\Lambda_2^{\frac54}\text{w}_1\|_2^2 +\|\Lambda_3^{\frac54}u_2\|_2^2)^2\|\nabla\text{w}_1\|_2^2. \end{align} $$
Finally, we will estimate the term
![]() $J_{219}$
, and applying the divergence-free condition
$J_{219}$
, and applying the divergence-free condition
![]() $\nabla \cdot \mathbf {u}=0$
and integrating by parts, we obtain
$\nabla \cdot \mathbf {u}=0$
and integrating by parts, we obtain
 $$ \begin{align} J_{219}&=-\int\partial_3u_3(\partial_3\text{w}_1)^2\ dxdydz\nonumber\\&=\int\partial_1u_1(\partial_3\text{w}_1)^2\ dxdydz+\int\partial_2u_2(\partial_3\text{w}_1)^2\ dxdydz\nonumber\\&=-2\int u_1\partial_{13}\text{w}_1\partial_3\text{w}_1\ dxdydz-2\int u_2\partial_{23}\text{w}_1\partial_3\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{13}\text{w}_1\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_3\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\quad + C\|\partial_{23}\text{w}_1\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_3\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq 4\varepsilon\|\Lambda_3^{\frac54}\nabla\text{w}_1\|_2^2+ C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}\text{w}_1\|_2^2)^2\|\partial_1u_1\|_2^2. \end{align} $$
$$ \begin{align} J_{219}&=-\int\partial_3u_3(\partial_3\text{w}_1)^2\ dxdydz\nonumber\\&=\int\partial_1u_1(\partial_3\text{w}_1)^2\ dxdydz+\int\partial_2u_2(\partial_3\text{w}_1)^2\ dxdydz\nonumber\\&=-2\int u_1\partial_{13}\text{w}_1\partial_3\text{w}_1\ dxdydz-2\int u_2\partial_{23}\text{w}_1\partial_3\text{w}_1\ dxdydz\nonumber\\&\leq C\|\partial_{13}\text{w}_1\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_3\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\quad + C\|\partial_{23}\text{w}_1\|_{L^4_{x_3}L^2_{x_1x_2}} \|\partial_3\text{w}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^4_{x_3}} \|u_1\|_{L^{\infty}_{x_1}L^2_{x_2x_3}}\nonumber\\&\leq 4\varepsilon\|\Lambda_3^{\frac54}\nabla\text{w}_1\|_2^2+ C_\varepsilon(\|u_1\|_2^2+\|\Lambda_3^{\frac54}\text{w}_1\|_2^2)^2\|\partial_1u_1\|_2^2. \end{align} $$
Combining the estimates (3.26), (3.33), (3.34), (3.41)–(3.43), and (3.50)–(3.52), we obtain
 $$ \begin{align} |J_{21}|&\leq 80\varepsilon(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3,\ \nabla\text{div}\mathbf{w}\|_2^2)\nonumber\\&\quad +C_\varepsilon((\|\mathbf{u},\ \mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^2\nonumber\\&\quad +(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}+(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\mathbf{w}\|_2^2.\nonumber\\ \end{align} $$
$$ \begin{align} |J_{21}|&\leq 80\varepsilon(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3,\ \nabla\text{div}\mathbf{w}\|_2^2)\nonumber\\&\quad +C_\varepsilon((\|\mathbf{u},\ \mathbf{w},\ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^2\nonumber\\&\quad +(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}+(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\&\quad +C_\varepsilon(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\|\mathbf{w}\|_2^2.\nonumber\\ \end{align} $$
The remaining terms in
![]() $J_2$
can be handled similar to
$J_2$
can be handled similar to
![]() $J_{21}$
. We omit it here. Next, we will estimate the term
$J_{21}$
. We omit it here. Next, we will estimate the term
![]() $J_3$
:
$J_3$
:
 $$ \begin{align} J_3&=4\kappa\int\nabla\nabla\times\mathbf{u}\cdot\nabla\mathbf{w}\, dxdydz=4\kappa\int\nabla(\partial_2u_3-\partial_3u_2)\nabla\text{w}_1\, dxdydz\nonumber\\&\quad +4\kappa\int\nabla(\partial_3u_1-\partial_1u_3)\nabla\text{w}_2\, dxdydz +4\kappa\int\nabla(\partial_1u_2-\partial_2u_1)\nabla\text{w}_3\, dxdydz\nonumber\\&=J_{31}+J_{32}+J_{33}.\nonumber\\ \end{align} $$
$$ \begin{align} J_3&=4\kappa\int\nabla\nabla\times\mathbf{u}\cdot\nabla\mathbf{w}\, dxdydz=4\kappa\int\nabla(\partial_2u_3-\partial_3u_2)\nabla\text{w}_1\, dxdydz\nonumber\\&\quad +4\kappa\int\nabla(\partial_3u_1-\partial_1u_3)\nabla\text{w}_2\, dxdydz +4\kappa\int\nabla(\partial_1u_2-\partial_2u_1)\nabla\text{w}_3\, dxdydz\nonumber\\&=J_{31}+J_{32}+J_{33}.\nonumber\\ \end{align} $$
To start with
![]() $J_{31}$
, we write it explicitly:
$J_{31}$
, we write it explicitly:
 $$ \begin{align*} J_{31}&=4\kappa\int\nabla(\partial_2u_3-\partial_3u_2)\nabla\text{w}_1\, dxdydz\\&\leq\|\nabla u_3\|_2^{\frac15}\|\Lambda_2^{\frac54}\nabla u_3\|_2^{\frac45}\|\nabla\text{w}_1\|_2+\|\nabla u_2\|_2^{\frac15}\|\Lambda_3^{\frac54}\nabla u_2\|_2^{\frac45}\|\nabla\text{w}_1\|_2\\&\leq\varepsilon\|\Lambda_2^{\frac54}\nabla u_3,\ \Lambda_3^{\frac54}\nabla u_2\|_2^2+C_\varepsilon\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align*} $$
$$ \begin{align*} J_{31}&=4\kappa\int\nabla(\partial_2u_3-\partial_3u_2)\nabla\text{w}_1\, dxdydz\\&\leq\|\nabla u_3\|_2^{\frac15}\|\Lambda_2^{\frac54}\nabla u_3\|_2^{\frac45}\|\nabla\text{w}_1\|_2+\|\nabla u_2\|_2^{\frac15}\|\Lambda_3^{\frac54}\nabla u_2\|_2^{\frac45}\|\nabla\text{w}_1\|_2\\&\leq\varepsilon\|\Lambda_2^{\frac54}\nabla u_3,\ \Lambda_3^{\frac54}\nabla u_2\|_2^2+C_\varepsilon\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2. \end{align*} $$
Similarly, one can easily check that
Furthermore,
Inserting the estimates of
![]() $J_{31}$
,
$J_{31}$
,
![]() $J_{32}$
, and
$J_{32}$
, and
![]() $J_{33}$
into (3.31), we obtain
$J_{33}$
into (3.31), we obtain
Combining the estimates (3.16), (3.19), (3.20), (3.53), and (3.55), choosing
![]() $\varepsilon $
small enough, we have
$\varepsilon $
small enough, we have
 $$ \begin{align}&\frac{d}{dt}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2+4\kappa\|\nabla\mathbf{w}\|_2^2+\mu\|\nabla\text{div}\mathbf{w}\|_2^2\nonumber\\& \quad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\& \quad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2 \nonumber\\& \quad \leq C_\varepsilon((\|\mathbf{u},\ \mathbf{w},\ \text{div}\mathbf{w}, \ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2\nonumber\\& \quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^2+(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\nonumber\\& \quad +(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\& \quad +((\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54}, \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54}, \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54}, \Lambda_2^{\frac54})u_3\|_2^2)^{\frac92}\nonumber\\& \quad +(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^{\frac52})\|\mathbf{u},\ \mathbf{w}\|_2^2.\nonumber\\ \end{align} $$
$$ \begin{align}&\frac{d}{dt}\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2+4\kappa\|\nabla\mathbf{w}\|_2^2+\mu\|\nabla\text{div}\mathbf{w}\|_2^2\nonumber\\& \quad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla u_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla u_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla u_3\|_2^2\nonumber\\& \quad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla \text{w}_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla \text{w}_3\|_2^2 \nonumber\\& \quad \leq C_\varepsilon((\|\mathbf{u},\ \mathbf{w},\ \text{div}\mathbf{w}, \ (\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})u_3\|_2^2\nonumber\\& \quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^2+(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1\|_2^2)^{\frac52}\nonumber\\& \quad +(\|\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^{\frac53})\|\nabla\mathbf{u},\ \nabla\mathbf{w}\|_2^2\nonumber\\& \quad +((\|\mathbf{u}\|_2^2+\|(\Lambda_2^{\frac54}, \Lambda_3^{\frac54})u_1,\ (\Lambda_1^{\frac54}, \Lambda_3^{\frac54})u_2,\ (\Lambda_1^{\frac54}, \Lambda_2^{\frac54})u_3\|_2^2)^{\frac92}\nonumber\\& \quad +(\|\text{div}\mathbf{w}\|_2^2+\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\text{w}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\text{w}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\text{w}_3\|_2^2)^{\frac52})\|\mathbf{u},\ \mathbf{w}\|_2^2.\nonumber\\ \end{align} $$
Applying Gronwall’s inequality, integrating from
![]() $0$
to T, we complete the proof of Proposition 3.2.
$0$
to T, we complete the proof of Proposition 3.2.
Step 3. Uniqueness
This section we will prove the uniqueness.
Proposition 3.3 Assume that the initial
![]() $(\mathbf {u}_0, \mathbf {w}_0)$
satisfies the conditions stated in Theorem 1.1. Suppose that
$(\mathbf {u}_0, \mathbf {w}_0)$
satisfies the conditions stated in Theorem 1.1. Suppose that
![]() $(\mathbf {u}^{(1)},\ \mathbf {w}^{(1)})$
and
$(\mathbf {u}^{(1)},\ \mathbf {w}^{(1)})$
and
![]() $(\mathbf {u}^{(2)},\ \mathbf {w}^{(2)})$
are two solutions to the system (
1.4
), then
$(\mathbf {u}^{(2)},\ \mathbf {w}^{(2)})$
are two solutions to the system (
1.4
), then
![]() $(\mathbf {u}^{(1)},\ \mathbf {w}^{(1)})=(\mathbf {u}^{(2)},\ \mathbf {w}^{(2)})$
.
$(\mathbf {u}^{(1)},\ \mathbf {w}^{(1)})=(\mathbf {u}^{(2)},\ \mathbf {w}^{(2)})$
.
Proof Denoting by
![]() $\pi ^{(1)}$
and
$\pi ^{(1)}$
and
![]() $\pi ^{(2)}$
the associated pressures, then the differences
$\pi ^{(2)}$
the associated pressures, then the differences
satisfy
 $$ \begin{align} \left\{ \begin{array}{l} \partial_t \tilde{u}_1 +\mathbf{u}^{(1)}\cdot\nabla\tilde{u}_1+\tilde{\mathbf{u}}\cdot\nabla u^{(2)}_1=-\partial_1\tilde{\pi}-(\nu+\kappa)\Lambda_2^{\frac52}\tilde{u}_1-(\nu+\kappa)\Lambda_3^{\frac52}\tilde{u}_1 +2\kappa\varepsilon_{1jk}\partial_j\tilde{\text{w}}_k,\\[6pt]\partial_t \tilde{u}_2 +\mathbf{u}^{(1)}\cdot\nabla\tilde{u}_2+\tilde{\mathbf{u}}\cdot\nabla u^{(2)}_2=-\partial_2\tilde{\pi}-(\nu+\kappa)\Lambda_1^{\frac52}\tilde{u}_2-(\nu+\kappa)\Lambda_3^{\frac52}\tilde{u}_2 +2\kappa\varepsilon_{2jk}\partial_j\tilde{\text{w}}_k,\\[6pt]\partial_t \tilde{u}_3 +\mathbf{u}^{(1)}\cdot\nabla\tilde{u}_3+\tilde{\mathbf{u}}\cdot\nabla u^{(2)}_3=-\partial_3\tilde{\pi}-(\nu+\kappa)\Lambda_1^{\frac52}\tilde{u}_3-(\nu+\kappa)\Lambda_2^{\frac52}\tilde{u}_3 +2\kappa\varepsilon_{3jk}\partial_j\tilde{\text{w}}_k,\\[6pt]\partial_t \tilde{\text{w}}_1 +\mathbf{u}^{(1)}\cdot\nabla\tilde{\text{w}}_1+\tilde{\mathbf{u}}\cdot\nabla \text{w}_1^{(2)}+4\kappa\tilde{\text{w}}_1=-\gamma\Lambda_2^{\frac52}\tilde{\text{w}}_1 -\gamma\Lambda_3^{\frac52}\tilde{\text{w}}_1 +\mu\partial_1(\nabla\cdot\tilde{\mathbf{w}})+2\kappa\varepsilon_{1jk}\partial_j\tilde{u}_k,\\[6pt]\partial_t \tilde{\text{w}}_2 +\mathbf{u}^{(1)}\cdot\nabla\tilde{\text{w}}_2+\tilde{\mathbf{u}}\cdot\nabla \text{w}_2^{(2)}+4\kappa\tilde{\text{w}}_2=-\gamma\Lambda_1^{\frac52}\tilde{\text{w}}_2 -\gamma\Lambda_3^{\frac52}\tilde{\text{w}}_2 +\mu\partial_2(\nabla\cdot\tilde{\mathbf{w}})+2\kappa\varepsilon_{2jk}\partial_j\tilde{u}_k,\\[6pt]\partial_t \tilde{\text{w}}_3 +\mathbf{u}^{(1)}\cdot\nabla\tilde{\text{w}}_3+\tilde{\mathbf{u}}\cdot\nabla \text{w}_3^{(2)}+4\kappa\tilde{\text{w}}_3=-\gamma\Lambda_1^{\frac52}\tilde{\text{w}}_3 -\gamma\Lambda_2^{\frac52}\tilde{\text{w}}_3 +\mu\partial_3(\nabla\cdot\tilde{\mathbf{w}})+2\kappa\varepsilon_{3jk}\partial_j\tilde{u}_k,\\[6pt]\nabla\cdot\tilde{\mathbf{u}}=0,\ \ \ \ \ \ \\\tilde{\mathbf{u}}(x,0)=0,\ \tilde{\mathbf{w}}(x,0)=0.\\ \end{array} \right.\end{align} $$
$$ \begin{align} \left\{ \begin{array}{l} \partial_t \tilde{u}_1 +\mathbf{u}^{(1)}\cdot\nabla\tilde{u}_1+\tilde{\mathbf{u}}\cdot\nabla u^{(2)}_1=-\partial_1\tilde{\pi}-(\nu+\kappa)\Lambda_2^{\frac52}\tilde{u}_1-(\nu+\kappa)\Lambda_3^{\frac52}\tilde{u}_1 +2\kappa\varepsilon_{1jk}\partial_j\tilde{\text{w}}_k,\\[6pt]\partial_t \tilde{u}_2 +\mathbf{u}^{(1)}\cdot\nabla\tilde{u}_2+\tilde{\mathbf{u}}\cdot\nabla u^{(2)}_2=-\partial_2\tilde{\pi}-(\nu+\kappa)\Lambda_1^{\frac52}\tilde{u}_2-(\nu+\kappa)\Lambda_3^{\frac52}\tilde{u}_2 +2\kappa\varepsilon_{2jk}\partial_j\tilde{\text{w}}_k,\\[6pt]\partial_t \tilde{u}_3 +\mathbf{u}^{(1)}\cdot\nabla\tilde{u}_3+\tilde{\mathbf{u}}\cdot\nabla u^{(2)}_3=-\partial_3\tilde{\pi}-(\nu+\kappa)\Lambda_1^{\frac52}\tilde{u}_3-(\nu+\kappa)\Lambda_2^{\frac52}\tilde{u}_3 +2\kappa\varepsilon_{3jk}\partial_j\tilde{\text{w}}_k,\\[6pt]\partial_t \tilde{\text{w}}_1 +\mathbf{u}^{(1)}\cdot\nabla\tilde{\text{w}}_1+\tilde{\mathbf{u}}\cdot\nabla \text{w}_1^{(2)}+4\kappa\tilde{\text{w}}_1=-\gamma\Lambda_2^{\frac52}\tilde{\text{w}}_1 -\gamma\Lambda_3^{\frac52}\tilde{\text{w}}_1 +\mu\partial_1(\nabla\cdot\tilde{\mathbf{w}})+2\kappa\varepsilon_{1jk}\partial_j\tilde{u}_k,\\[6pt]\partial_t \tilde{\text{w}}_2 +\mathbf{u}^{(1)}\cdot\nabla\tilde{\text{w}}_2+\tilde{\mathbf{u}}\cdot\nabla \text{w}_2^{(2)}+4\kappa\tilde{\text{w}}_2=-\gamma\Lambda_1^{\frac52}\tilde{\text{w}}_2 -\gamma\Lambda_3^{\frac52}\tilde{\text{w}}_2 +\mu\partial_2(\nabla\cdot\tilde{\mathbf{w}})+2\kappa\varepsilon_{2jk}\partial_j\tilde{u}_k,\\[6pt]\partial_t \tilde{\text{w}}_3 +\mathbf{u}^{(1)}\cdot\nabla\tilde{\text{w}}_3+\tilde{\mathbf{u}}\cdot\nabla \text{w}_3^{(2)}+4\kappa\tilde{\text{w}}_3=-\gamma\Lambda_1^{\frac52}\tilde{\text{w}}_3 -\gamma\Lambda_2^{\frac52}\tilde{\text{w}}_3 +\mu\partial_3(\nabla\cdot\tilde{\mathbf{w}})+2\kappa\varepsilon_{3jk}\partial_j\tilde{u}_k,\\[6pt]\nabla\cdot\tilde{\mathbf{u}}=0,\ \ \ \ \ \ \\\tilde{\mathbf{u}}(x,0)=0,\ \tilde{\mathbf{w}}(x,0)=0.\\ \end{array} \right.\end{align} $$
Multiplying equations (3.57)
![]() $_1$
, (3.57)
$_1$
, (3.57)
![]() $_2$
, (3.57)
$_2$
, (3.57)
![]() $_3$
, (3.57)
$_3$
, (3.57)
![]() $_4$
, (3.57)
$_4$
, (3.57)
![]() $_5$
, and (3.57)
$_5$
, and (3.57)
![]() $_6$
with
$_6$
with
![]() $\tilde {u}_1$
,
$\tilde {u}_1$
,
![]() $\tilde {u}_2$
,
$\tilde {u}_2$
,
![]() $\tilde {u}_3$
,
$\tilde {u}_3$
,
![]() $\tilde {\text {w}}_1$
,
$\tilde {\text {w}}_1$
,
![]() $\tilde {\text {w}}_2$
, and
$\tilde {\text {w}}_2$
, and
![]() $\tilde {\text {w}}_3$
, respectively, integrating by parts, summing the results together, yields
$\tilde {\text {w}}_3$
, respectively, integrating by parts, summing the results together, yields
 $$ \begin{align}&\frac12\frac{d}{dt}\|\tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2+4\kappa\|\tilde{\mathbf{w}}\|_2^2+\mu\|\text{div}\tilde{\mathbf{w}}\|_2^2\nonumber\\& \qquad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2\nonumber\\&\qquad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\text{w}}_3\|_2^2 \nonumber\\&\quad =-\int\tilde{\mathbf{u}}\cdot\nabla\mathbf{u}^{(2)}\tilde{\mathbf{u}}\, dxdydz -\int\tilde{\mathbf{u}}\cdot\nabla\mathbf{w}^{(2)}\tilde{\mathbf{w}}\, dxdydz+4\kappa\int\nabla\times\tilde{\mathbf{w}}\cdot\tilde{\mathbf{u}}dxdydz\nonumber\\&\quad =K_1+K_2+K_3.\nonumber\\ \end{align} $$
$$ \begin{align}&\frac12\frac{d}{dt}\|\tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2+4\kappa\|\tilde{\mathbf{w}}\|_2^2+\mu\|\text{div}\tilde{\mathbf{w}}\|_2^2\nonumber\\& \qquad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2\nonumber\\&\qquad +\gamma\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\text{w}}_3\|_2^2 \nonumber\\&\quad =-\int\tilde{\mathbf{u}}\cdot\nabla\mathbf{u}^{(2)}\tilde{\mathbf{u}}\, dxdydz -\int\tilde{\mathbf{u}}\cdot\nabla\mathbf{w}^{(2)}\tilde{\mathbf{w}}\, dxdydz+4\kappa\int\nabla\times\tilde{\mathbf{w}}\cdot\tilde{\mathbf{u}}dxdydz\nonumber\\&\quad =K_1+K_2+K_3.\nonumber\\ \end{align} $$
To start with
![]() $K_1$
, we write it explicitly:
$K_1$
, we write it explicitly:
 $$ \begin{align} K_1&=-\int\tilde{\mathbf{u}}\cdot\nabla\mathbf{u}^{(2)}\tilde{\mathbf{u}}\, dxdydz=-\int(\tilde{u}_1\partial_1u^{(2)}_1\tilde{u}_1+\tilde{u}_1\partial_1u^{(2)}_2\tilde{u}_2 +\tilde{u}_1\partial_1u^{(2)}_3\tilde{u}_3\nonumber\\&\quad +\tilde{u}_2\partial_2u^{(2)}_1\tilde{u}_1+\tilde{u}_2\partial_2u^{(2)}_2\tilde{u}_2 +\tilde{u}_2\partial_2u^{(2)}_3\tilde{u}_3\nonumber\\&\quad +\tilde{u}_3\partial_3u^{(2)}_1\tilde{u}_1+\tilde{u}_3\partial_3u^{(2)}_2\tilde{u}_2 +\tilde{u}_3\partial_3u^{(2)}_1\tilde{u}_3)\, dxdydz\nonumber\\&=\sum_{i=1}^9K_{1i}. \end{align} $$
$$ \begin{align} K_1&=-\int\tilde{\mathbf{u}}\cdot\nabla\mathbf{u}^{(2)}\tilde{\mathbf{u}}\, dxdydz=-\int(\tilde{u}_1\partial_1u^{(2)}_1\tilde{u}_1+\tilde{u}_1\partial_1u^{(2)}_2\tilde{u}_2 +\tilde{u}_1\partial_1u^{(2)}_3\tilde{u}_3\nonumber\\&\quad +\tilde{u}_2\partial_2u^{(2)}_1\tilde{u}_1+\tilde{u}_2\partial_2u^{(2)}_2\tilde{u}_2 +\tilde{u}_2\partial_2u^{(2)}_3\tilde{u}_3\nonumber\\&\quad +\tilde{u}_3\partial_3u^{(2)}_1\tilde{u}_1+\tilde{u}_3\partial_3u^{(2)}_2\tilde{u}_2 +\tilde{u}_3\partial_3u^{(2)}_1\tilde{u}_3)\, dxdydz\nonumber\\&=\sum_{i=1}^9K_{1i}. \end{align} $$
Applying the divergence-free condition
![]() $\nabla \cdot \mathbf {\tilde {u}}=0$
, by Lemmas 2.1–2.3, we can bound
$\nabla \cdot \mathbf {\tilde {u}}=0$
, by Lemmas 2.1–2.3, we can bound
![]() $K_{11}$
as follows:
$K_{11}$
as follows:
 $$ \begin{align} K_{11}&=-\int \tilde{u}_1\partial_1u^{(2)}_1\tilde{u}_1\ dxdydz\nonumber\\&\leq C\|\partial_1u^{(2)}_1\|_{L^\infty_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|^2_{L^2_{x_1}L^4_{x_2x_3}}\nonumber\\&\leq C\|\partial_1u^{(2)}_1\|_2^{\frac35}\|\Lambda_1^{\frac54}\partial_1u^{(2)}_1\|_2^{\frac25} \|\Lambda_2^{\frac14}\tilde{u}_1\|_2^{\frac32}\|\Lambda_2^{\frac14}\Lambda_3\tilde{u}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1\|_2^2 +C_\varepsilon(\|\partial_1u_1^{(2)}\|_2^2+\|\Lambda_1^{\frac54}\partial_2u_2^{(2)},\ \Lambda_1^{\frac54}\partial_3u_3^{(2)}\|_2^2)^{\frac56}\|\tilde{u}_1\|_2^2 .\end{align} $$
$$ \begin{align} K_{11}&=-\int \tilde{u}_1\partial_1u^{(2)}_1\tilde{u}_1\ dxdydz\nonumber\\&\leq C\|\partial_1u^{(2)}_1\|_{L^\infty_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|^2_{L^2_{x_1}L^4_{x_2x_3}}\nonumber\\&\leq C\|\partial_1u^{(2)}_1\|_2^{\frac35}\|\Lambda_1^{\frac54}\partial_1u^{(2)}_1\|_2^{\frac25} \|\Lambda_2^{\frac14}\tilde{u}_1\|_2^{\frac32}\|\Lambda_2^{\frac14}\Lambda_3\tilde{u}_1\|_2^{\frac12}\nonumber\\&\leq \varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1\|_2^2 +C_\varepsilon(\|\partial_1u_1^{(2)}\|_2^2+\|\Lambda_1^{\frac54}\partial_2u_2^{(2)},\ \Lambda_1^{\frac54}\partial_3u_3^{(2)}\|_2^2)^{\frac56}\|\tilde{u}_1\|_2^2 .\end{align} $$
Using the similar method to
![]() $K_{11}$
, the term
$K_{11}$
, the term
![]() $K_{12}$
can be estimated as
$K_{12}$
can be estimated as
 $$ \begin{align} K_{12}&=-\int \tilde{u}_1\partial_1u^{(2)}_2\tilde{u}_2\ dxdydz\nonumber\\&\leq C\|\partial_1u^{(2)}_2\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^{4}_{x_3}} \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_1}L^{4}_{x_3}}\nonumber\\&\leq C\|\partial_1u^{(2)}_2\|_2\|\Lambda_3^{\frac14}\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\tilde{u}_2\|_2^{\frac12}\|\Lambda_3^{\frac14}\Lambda_1\tilde{u}_2\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2\|_2^2 +C_\varepsilon\|\partial_1u_2^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_2\|_2^2 .\end{align} $$
$$ \begin{align} K_{12}&=-\int \tilde{u}_1\partial_1u^{(2)}_2\tilde{u}_2\ dxdydz\nonumber\\&\leq C\|\partial_1u^{(2)}_2\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^{4}_{x_3}} \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_1}L^{4}_{x_3}}\nonumber\\&\leq C\|\partial_1u^{(2)}_2\|_2\|\Lambda_3^{\frac14}\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\tilde{u}_2\|_2^{\frac12}\|\Lambda_3^{\frac14}\Lambda_1\tilde{u}_2\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2\|_2^2 +C_\varepsilon\|\partial_1u_2^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_2\|_2^2 .\end{align} $$
Similarly,
 $$ \begin{align} K_{13}&=-\int \tilde{u}_1\partial_1u^{(2)}_3\tilde{u}_3\ dxdydz\nonumber\\&\leq C\|\partial_1u^{(2)}_3\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_3}L^{4}_{x_2}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_1}L^{4}_{x_2}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_1u_3^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_3\|_2^2 .\end{align} $$
$$ \begin{align} K_{13}&=-\int \tilde{u}_1\partial_1u^{(2)}_3\tilde{u}_3\ dxdydz\nonumber\\&\leq C\|\partial_1u^{(2)}_3\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_3}L^{4}_{x_2}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_1}L^{4}_{x_2}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_1u_3^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_3\|_2^2 .\end{align} $$
Furthermore,
 $$ \begin{align} K_{14}&=-\int \tilde{u}_2\partial_2u^{(2)}_1\tilde{u}_1\ dxdydz\nonumber\\&\leq C\|\partial_2u^{(2)}_1\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^{4}_{x_3}} \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_1}L^{4}_{x_3}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2\|_2^2 +C_\varepsilon\|\partial_2u_1^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_2\|_2^2 .\end{align} $$
$$ \begin{align} K_{14}&=-\int \tilde{u}_2\partial_2u^{(2)}_1\tilde{u}_1\ dxdydz\nonumber\\&\leq C\|\partial_2u^{(2)}_1\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_2}L^{4}_{x_3}} \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_1}L^{4}_{x_3}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2\|_2^2 +C_\varepsilon\|\partial_2u_1^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_2\|_2^2 .\end{align} $$
For the term
![]() $K_{15}$
, applying the similar method to
$K_{15}$
, applying the similar method to
![]() $K_{11}$
, we find that
$K_{11}$
, we find that
 $$ \begin{align} K_{15}&=-\int \tilde{u}_2\partial_2u^{(2)}_2\tilde{u}_2\ dxdydz\nonumber\\&\leq C\|\partial_2u^{(2)}_2\|_{L^\infty_{x_2}L^2_{x_1x_3}} \|\tilde{u}_2\|^2_{L^2_{x_2}L^4_{x_1x_3}}\nonumber\\&\leq \varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2\|_2^2 +C_\varepsilon(\|\partial_2u_2^{(2)}\|_2^2+\|\Lambda_2^{\frac54}\partial_1u_1^{(2)},\ \Lambda_2^{\frac54}\partial_3u_3^{(2)}\|_2^2)^{\frac56}\|\tilde{u}_2\|_2^2 .\end{align} $$
$$ \begin{align} K_{15}&=-\int \tilde{u}_2\partial_2u^{(2)}_2\tilde{u}_2\ dxdydz\nonumber\\&\leq C\|\partial_2u^{(2)}_2\|_{L^\infty_{x_2}L^2_{x_1x_3}} \|\tilde{u}_2\|^2_{L^2_{x_2}L^4_{x_1x_3}}\nonumber\\&\leq \varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2\|_2^2 +C_\varepsilon(\|\partial_2u_2^{(2)}\|_2^2+\|\Lambda_2^{\frac54}\partial_1u_1^{(2)},\ \Lambda_2^{\frac54}\partial_3u_3^{(2)}\|_2^2)^{\frac56}\|\tilde{u}_2\|_2^2 .\end{align} $$
Similar to
![]() $K_{12}$
, we can easily bound the terms
$K_{12}$
, we can easily bound the terms
![]() $K_{16}$
,
$K_{16}$
,
![]() $K_{17}$
, and
$K_{17}$
, and
![]() $K_{18}$
as
$K_{18}$
as
 $$ \begin{align} K_{16}&=-\int \tilde{u}_2\partial_2u^{(2)}_3\tilde{u}_3\ dxdydz\nonumber\\&\leq C\|\partial_2u^{(2)}_3\|_2 \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_3}L^{4}_{x_1}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_2}L^{4}_{x_1}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_2u_3^{(2)}\|_2^{\frac52}\|\tilde{u}_2,\ \tilde{u}_3\|_2^2 ,\end{align} $$
$$ \begin{align} K_{16}&=-\int \tilde{u}_2\partial_2u^{(2)}_3\tilde{u}_3\ dxdydz\nonumber\\&\leq C\|\partial_2u^{(2)}_3\|_2 \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_3}L^{4}_{x_1}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_2}L^{4}_{x_1}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_2u_3^{(2)}\|_2^{\frac52}\|\tilde{u}_2,\ \tilde{u}_3\|_2^2 ,\end{align} $$
 $$ \begin{align} K_{17}&=-\int \tilde{u}_3\partial_3u^{(2)}_1\tilde{u}_1\ dxdydz\nonumber\\&\leq C\|\partial_3u^{(2)}_1\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_3}L^{4}_{x_2}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_1}L^{4}_{x_2}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_3u_1^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_3\|_2^2 ,\end{align} $$
$$ \begin{align} K_{17}&=-\int \tilde{u}_3\partial_3u^{(2)}_1\tilde{u}_1\ dxdydz\nonumber\\&\leq C\|\partial_3u^{(2)}_1\|_2 \|\tilde{u}_1\|_{L^2_{x_1}L^{\infty}_{x_3}L^{4}_{x_2}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_1}L^{4}_{x_2}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_3u_1^{(2)}\|_2^{\frac52}\|\tilde{u}_1,\ \tilde{u}_3\|_2^2 ,\end{align} $$
and
 $$ \begin{align} K_{18}&=-\int \tilde{u}_3\partial_3u^{(2)}_2\tilde{u}_2\ dxdydz\nonumber\\&\leq C\|\partial_3u^{(2)}_2\|_2 \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_3}L^{4}_{x_1}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_2}L^{4}_{x_1}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_3u_2^{(2)}\|_2^{\frac52}\|\tilde{u}_2,\ \tilde{u}_3\|_2^2 .\end{align} $$
$$ \begin{align} K_{18}&=-\int \tilde{u}_3\partial_3u^{(2)}_2\tilde{u}_2\ dxdydz\nonumber\\&\leq C\|\partial_3u^{(2)}_2\|_2 \|\tilde{u}_2\|_{L^2_{x_2}L^{\infty}_{x_3}L^{4}_{x_1}} \|\tilde{u}_3\|_{L^2_{x_3}L^{\infty}_{x_2}L^{4}_{x_1}}\nonumber\\&\leq 2\varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon\|\partial_3u_2^{(2)}\|_2^{\frac52}\|\tilde{u}_2,\ \tilde{u}_3\|_2^2 .\end{align} $$
Finally, we will estimate the term
![]() $K_{19}$
. Using the similar method to
$K_{19}$
. Using the similar method to
![]() $K_{11}$
, we obtain
$K_{11}$
, we obtain
 $$ \begin{align} K_{19}&=-\int \tilde{u}_3\partial_3u^{(2)}_3\tilde{u}_3\ dxdydz\nonumber\\&\leq C\|\partial_3u^{(2)}_3\|_{L^\infty_{x_3}L^2_{x_1x_2}} \|\tilde{u}_3\|^2_{L^2_{x_3}L^4_{x_1x_2}}\nonumber\\&\leq \varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon(\|\partial_3u_3^{(2)}\|_2^2+\|\Lambda_3^{\frac54}\partial_1u_1^{(2)},\ \Lambda_3^{\frac54}\partial_2u_2^{(2)}\|_2^2)^{\frac56}\|\tilde{u}_3\|_2^2 .\end{align} $$
$$ \begin{align} K_{19}&=-\int \tilde{u}_3\partial_3u^{(2)}_3\tilde{u}_3\ dxdydz\nonumber\\&\leq C\|\partial_3u^{(2)}_3\|_{L^\infty_{x_3}L^2_{x_1x_2}} \|\tilde{u}_3\|^2_{L^2_{x_3}L^4_{x_1x_2}}\nonumber\\&\leq \varepsilon\|(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon(\|\partial_3u_3^{(2)}\|_2^2+\|\Lambda_3^{\frac54}\partial_1u_1^{(2)},\ \Lambda_3^{\frac54}\partial_2u_2^{(2)}\|_2^2)^{\frac56}\|\tilde{u}_3\|_2^2 .\end{align} $$
Inserting the above bounds (3.37)–(3.45) into equation (3.36) yields
 $$ \begin{align} |K_1|&\leq 18\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon(\|\nabla\mathbf{u}^{(2)}\|_2^{\frac52}\nonumber\\&\quad +(\|\partial_1u_1^{(2)},\ \partial_2u_2^{(2)},\ \partial_3u_3^{(2)}\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1u_1^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\partial_2u_2^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\partial_3u_3^{(2)}\|_2^2)^{\frac56}\|\tilde{\mathbf{u}}\|_2^2 .\end{align} $$
$$ \begin{align} |K_1|&\leq 18\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +C_\varepsilon(\|\nabla\mathbf{u}^{(2)}\|_2^{\frac52}\nonumber\\&\quad +(\|\partial_1u_1^{(2)},\ \partial_2u_2^{(2)},\ \partial_3u_3^{(2)}\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1u_1^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\partial_2u_2^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\partial_3u_3^{(2)}\|_2^2)^{\frac56}\|\tilde{\mathbf{u}}\|_2^2 .\end{align} $$
Next, we will estimate
![]() $K_2$
, and we write it in terms of components:
$K_2$
, and we write it in terms of components:
 $$ \begin{align*}K_2=-\int\tilde{u}_i \partial_i\text{w}^{(2)}_{j}\tilde{\text{w}}_{j}\ dxdydz=\sum_{k=1}^9K_{2k}.\end{align*} $$
$$ \begin{align*}K_2=-\int\tilde{u}_i \partial_i\text{w}^{(2)}_{j}\tilde{\text{w}}_{j}\ dxdydz=\sum_{k=1}^9K_{2k}.\end{align*} $$
To start with
![]() $K_{21}$
, we rewrite it as follows:
$K_{21}$
, we rewrite it as follows:
 $$ \begin{align*} K_{21}&=-\int\tilde{u}_1 \partial_1\text{w}^{(2)}_{1}\tilde{\text{w}}_{1}\ dxdydz =-\int\tilde{u}_1 (\text{div}\text{w}^{(2)}-\partial_2\text{w}^{(2)}_2-\partial_3\text{w}^{(2)}_3)\tilde{\text{w}}_{1}\ dxdydz\\&=K_{211}+K_{212}+K_{213}. \end{align*} $$
$$ \begin{align*} K_{21}&=-\int\tilde{u}_1 \partial_1\text{w}^{(2)}_{1}\tilde{\text{w}}_{1}\ dxdydz =-\int\tilde{u}_1 (\text{div}\text{w}^{(2)}-\partial_2\text{w}^{(2)}_2-\partial_3\text{w}^{(2)}_3)\tilde{\text{w}}_{1}\ dxdydz\\&=K_{211}+K_{212}+K_{213}. \end{align*} $$
Using Lemmas 2.1–2.3, we can estimate
![]() $K_{211}$
as
$K_{211}$
as
 $$ \begin{align*} K_{211}&=-\int\tilde{u}_1\text{div}\text{w}^{(2)}\tilde{\text{w}}_{1}\ dxdydz\\&\leq C\|\text{div}\text{w}^{(2)}\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}} \|\tilde{\text{w}}_{1}\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\\&\leq C\|\text{div}\text{w}^{(2)}\|_2^{\frac12}\|\Lambda_1\text{div}\text{w}^{(2)}\|_2^{\frac12} \|\tilde{u}_1\|_2^{\frac35}\|\Lambda_3^{\frac54}\tilde{u}_1\|_2^{\frac25} \|\tilde{\text{w}}_{1}\|_2^{\frac35}\|\Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^{\frac25}\\&\leq \varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2 +C_\varepsilon((\|\text{div}\text{w}^{(2)}\|_2^2+\|\nabla\text{div}\text{w}^{(2)}\|_2^2)^{\frac53}+1)\|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2. \end{align*} $$
$$ \begin{align*} K_{211}&=-\int\tilde{u}_1\text{div}\text{w}^{(2)}\tilde{\text{w}}_{1}\ dxdydz\\&\leq C\|\text{div}\text{w}^{(2)}\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}} \|\tilde{\text{w}}_{1}\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\\&\leq C\|\text{div}\text{w}^{(2)}\|_2^{\frac12}\|\Lambda_1\text{div}\text{w}^{(2)}\|_2^{\frac12} \|\tilde{u}_1\|_2^{\frac35}\|\Lambda_3^{\frac54}\tilde{u}_1\|_2^{\frac25} \|\tilde{\text{w}}_{1}\|_2^{\frac35}\|\Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^{\frac25}\\&\leq \varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2 +C_\varepsilon((\|\text{div}\text{w}^{(2)}\|_2^2+\|\nabla\text{div}\text{w}^{(2)}\|_2^2)^{\frac53}+1)\|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2. \end{align*} $$
Similarly,
 $$ \begin{align*} K_{212}&=\int\tilde{u}_1\partial_2\text{w}^{(2)}_2\tilde{\text{w}}_{1}\ dxdydz\\&\leq C\|\partial_2\text{w}^{(2)}_2\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}} \|\tilde{\text{w}}_{1}\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\\&\leq \varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2 +C_\varepsilon((\|\partial_2\text{w}^{(2)}_2\|_2^2+\|\Lambda_1^{\frac54}\partial_2\text{w}^{(2)}_2\|_2^2)^{\frac53}+1)\|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2 \end{align*} $$
$$ \begin{align*} K_{212}&=\int\tilde{u}_1\partial_2\text{w}^{(2)}_2\tilde{\text{w}}_{1}\ dxdydz\\&\leq C\|\partial_2\text{w}^{(2)}_2\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}} \|\tilde{\text{w}}_{1}\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\\&\leq \varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2 +C_\varepsilon((\|\partial_2\text{w}^{(2)}_2\|_2^2+\|\Lambda_1^{\frac54}\partial_2\text{w}^{(2)}_2\|_2^2)^{\frac53}+1)\|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2 \end{align*} $$
and
 $$ \begin{align*} K_{213}&=\int\tilde{u}_1\partial_3\text{w}^{(2)}_3\tilde{\text{w}}_{1}\ dxdydz\\&\leq C\|\partial_3\text{w}^{(2)}_3\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}} \|\tilde{\text{w}}_{1}\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\\&\leq \varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2 +C_\varepsilon((\|\partial_3\text{w}^{(2)}_3\|_2^2+\|\Lambda_1^{\frac54}\partial_3\text{w}^{(2)}_3\|_2^2)^{\frac53}+1)\|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2, \end{align*} $$
$$ \begin{align*} K_{213}&=\int\tilde{u}_1\partial_3\text{w}^{(2)}_3\tilde{\text{w}}_{1}\ dxdydz\\&\leq C\|\partial_3\text{w}^{(2)}_3\|_{L^{\infty}_{x_1}L^2_{x_2x_3}} \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1x_2}} \|\tilde{\text{w}}_{1}\|_{L^{\infty}_{x_2}L^2_{x_1x_3}}\\&\leq \varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2 +C_\varepsilon((\|\partial_3\text{w}^{(2)}_3\|_2^2+\|\Lambda_1^{\frac54}\partial_3\text{w}^{(2)}_3\|_2^2)^{\frac53}+1)\|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2, \end{align*} $$
Combining the estimates of
![]() $K_{211}$
–
$K_{211}$
–
![]() $ K_{213}$
, we obtain
$ K_{213}$
, we obtain
 $$ \begin{align} |K_{21}|&\leq 3\varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2+C_\varepsilon((\|\text{div}\text{w}^{(2)}\|_2^2+\|\nabla\text{div}\text{w}^{(2)}\|_2^2)^{\frac53}\nonumber\\&\quad +(\|\partial_2\text{w}^{(2)}_2\|_2^2+\|\Lambda_1^{\frac54}\partial_2\text{w}^{(2)}_2\|_2^2)^{\frac53}\nonumber\\&\quad +(\|\partial_3\text{w}^{(2)}_3\|_2^2+\|\Lambda_1^{\frac54}\partial_3\text{w}^{(2)}_3\|_2^2)^{\frac53}+1) \|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2.\end{align} $$
$$ \begin{align} |K_{21}|&\leq 3\varepsilon\|\Lambda_3^{\frac54}\tilde{u}_1,\ \Lambda_2^{\frac54}\tilde{\text{w}}_{1}\|_2^2+C_\varepsilon((\|\text{div}\text{w}^{(2)}\|_2^2+\|\nabla\text{div}\text{w}^{(2)}\|_2^2)^{\frac53}\nonumber\\&\quad +(\|\partial_2\text{w}^{(2)}_2\|_2^2+\|\Lambda_1^{\frac54}\partial_2\text{w}^{(2)}_2\|_2^2)^{\frac53}\nonumber\\&\quad +(\|\partial_3\text{w}^{(2)}_3\|_2^2+\|\Lambda_1^{\frac54}\partial_3\text{w}^{(2)}_3\|_2^2)^{\frac53}+1) \|\tilde{u}_1,\ \tilde{\text{w}}_{1}\|_2^2.\end{align} $$
Similar to
![]() $K_{12}$
,
$K_{12}$
,
![]() $K_{22}$
can be bounded as
$K_{22}$
can be bounded as
 $$ \begin{align} K_{22}&=-\int\tilde{u}_1 \partial_1\text{w}^{(2)}_{2}\tilde{\text{w}}_{2}\ dxdydz\nonumber\\&\leq C\|\partial_1\text{w}^{(2)}_{2}\|_2 \|\tilde{u}_1\|_{L^{\infty}_{x_2}L^2_{x_1}L^4_{x_3}} \|\tilde{\text{w}}_{2}\|_{L^{\infty}_{x_1}L^2_{x_2}L^4_{x_3}}\nonumber\\&\leq C \|\partial_1\text{w}^{(2)}_{2}\|_2\|\Lambda_3^{\frac14}\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\tilde{\text{w}}_{2}\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_1\tilde{\text{w}}_{2}\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_{2}\|_2^2 +C_\varepsilon\|\partial_1\text{w}^{(2)}_{2}\|_2^{\frac52} \|\tilde{u}_1,\ \tilde{\text{w}}_{2}\|_2^2.\end{align} $$
$$ \begin{align} K_{22}&=-\int\tilde{u}_1 \partial_1\text{w}^{(2)}_{2}\tilde{\text{w}}_{2}\ dxdydz\nonumber\\&\leq C\|\partial_1\text{w}^{(2)}_{2}\|_2 \|\tilde{u}_1\|_{L^{\infty}_{x_2}L^2_{x_1}L^4_{x_3}} \|\tilde{\text{w}}_{2}\|_{L^{\infty}_{x_1}L^2_{x_2}L^4_{x_3}}\nonumber\\&\leq C \|\partial_1\text{w}^{(2)}_{2}\|_2\|\Lambda_3^{\frac14}\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_2\tilde{u}_1\|_2^{\frac12} \|\Lambda_3^{\frac14}\tilde{\text{w}}_{2}\|_2^{\frac12} \|\Lambda_3^{\frac14}\Lambda_1\tilde{\text{w}}_{2}\|_2^{\frac12}\nonumber\\&\leq 2\varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_{2}\|_2^2 +C_\varepsilon\|\partial_1\text{w}^{(2)}_{2}\|_2^{\frac52} \|\tilde{u}_1,\ \tilde{\text{w}}_{2}\|_2^2.\end{align} $$
Furthermore,
 $$ \begin{align} K_{23}&=-\int\tilde{u}_1 \partial_1\text{w}^{(2)}_{3}\tilde{\text{w}}_{3}\ dxdydz\nonumber\\&\leq C\|\partial_1\text{w}^{(2)}_{3}\|_2 \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1}L^4_{x_2}} \|\tilde{\text{w}}_{3}\|_{L^{\infty}_{x_1}L^2_{x_3}L^4_{x_2}}\nonumber\\&\leq \varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\text{w}}_{3}\|_2^2 +C_\varepsilon\|\partial_1\text{w}^{(2)}_{2}\|_2^{\frac52} \|\tilde{u}_1,\ \tilde{\text{w}}_{3}\|_2^2.\end{align} $$
$$ \begin{align} K_{23}&=-\int\tilde{u}_1 \partial_1\text{w}^{(2)}_{3}\tilde{\text{w}}_{3}\ dxdydz\nonumber\\&\leq C\|\partial_1\text{w}^{(2)}_{3}\|_2 \|\tilde{u}_1\|_{L^{\infty}_{x_3}L^2_{x_1}L^4_{x_2}} \|\tilde{\text{w}}_{3}\|_{L^{\infty}_{x_1}L^2_{x_3}L^4_{x_2}}\nonumber\\&\leq \varepsilon\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\text{w}}_{3}\|_2^2 +C_\varepsilon\|\partial_1\text{w}^{(2)}_{2}\|_2^{\frac52} \|\tilde{u}_1,\ \tilde{\text{w}}_{3}\|_2^2.\end{align} $$
The other terms in
![]() $K_2$
can be bounded as
$K_2$
can be bounded as
![]() $K_{21}$
–
$K_{21}$
–
![]() $ K_{23}$
. We omit it here. Furthermore, one can easily check that
$ K_{23}$
. We omit it here. Furthermore, one can easily check that
 $$ \begin{align} |K_2|&\leq 18\varepsilon(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\mathbf{w}}\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\text{w}}_3\|_2^2)\nonumber\\&\quad +C_\varepsilon((\|\nabla\mathbf{w}^{(2)}\|_2^2+\|\text{div}\mathbf{w}^{(2)}\|_2^2+\|\nabla\text{div}\mathbf{w}^{(2)}\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla\tilde{\text{w}}_3\|_2^2)^{\frac53}\nonumber\\&\quad +\|\nabla\mathbf{w}^{(2)}\|_2^{\frac52}+1)\|\tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2.\end{align} $$
$$ \begin{align} |K_2|&\leq 18\varepsilon(\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\mathbf{w}}\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\text{w}}_3\|_2^2)\nonumber\\&\quad +C_\varepsilon((\|\nabla\mathbf{w}^{(2)}\|_2^2+\|\text{div}\mathbf{w}^{(2)}\|_2^2+\|\nabla\text{div}\mathbf{w}^{(2)}\|_2^2\nonumber\\&\quad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla\tilde{\text{w}}_3\|_2^2)^{\frac53}\nonumber\\&\quad +\|\nabla\mathbf{w}^{(2)}\|_2^{\frac52}+1)\|\tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2.\end{align} $$
Finally, we will bound the term
![]() $K_3$
. Applying the similar methods to (3.3)–(3.5), one can easily check that
$K_3$
. Applying the similar methods to (3.3)–(3.5), one can easily check that
Inserting the estimates of (3.69), (3.73), and (3.74) into (3.58), and choosing
![]() $\varepsilon $
small enough, we have
$\varepsilon $
small enough, we have
 $$ \begin{align}&\frac{d}{dt}\|\tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2+4\kappa\|\tilde{\mathbf{w}}\|_2^2+\mu\|\text{div}\tilde{\mathbf{w}}\|_2^2\nonumber\\&\qquad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +\gamma\|(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\mathbf{w}}\|_2^2 \nonumber\\&\quad \leq C_\varepsilon(\|\nabla\mathbf{u}^{(2)}\|_2^{\frac52}+(\|\partial_1u_1^{(2)},\ \partial_2u_2^{(2)},\ \partial_3u_3^{(2)}\|_2^2\nonumber\\&\qquad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1u_1^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\partial_2u_2^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\partial_3u_3^{(2)}\|_2^2)^{\frac56}\nonumber\\&\qquad +(\|\nabla\mathbf{w}^{(2)}\|_2^2+\|\text{div}\mathbf{w}^{(2)}\|_2^2+\|\nabla\text{div}\mathbf{w}^{(2)}\|_2^2\nonumber\\&\qquad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla\tilde{\text{w}}_3\|_2^2)^{\frac53}\nonumber\\&\qquad +\|\nabla\mathbf{w}^{(2)}\|_2^{\frac52}+1)\|\ \tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2.\nonumber\\[-16pt] \end{align} $$
$$ \begin{align}&\frac{d}{dt}\|\tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2+4\kappa\|\tilde{\mathbf{w}}\|_2^2+\mu\|\text{div}\tilde{\mathbf{w}}\|_2^2\nonumber\\&\qquad +(\nu+\kappa)\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_1,(\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\tilde{u}_2,(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{u}_3\|_2^2 +\gamma\|(\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\tilde{\mathbf{w}}\|_2^2 \nonumber\\&\quad \leq C_\varepsilon(\|\nabla\mathbf{u}^{(2)}\|_2^{\frac52}+(\|\partial_1u_1^{(2)},\ \partial_2u_2^{(2)},\ \partial_3u_3^{(2)}\|_2^2\nonumber\\&\qquad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\partial_1u_1^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\partial_2u_2^{(2)},\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\partial_3u_3^{(2)}\|_2^2)^{\frac56}\nonumber\\&\qquad +(\|\nabla\mathbf{w}^{(2)}\|_2^2+\|\text{div}\mathbf{w}^{(2)}\|_2^2+\|\nabla\text{div}\mathbf{w}^{(2)}\|_2^2\nonumber\\&\qquad +\|(\Lambda_2^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_1,\ (\Lambda_1^{\frac54},\ \Lambda_3^{\frac54})\nabla\tilde{\text{w}}_2,\ (\Lambda_1^{\frac54},\ \Lambda_2^{\frac54})\nabla\tilde{\text{w}}_3\|_2^2)^{\frac53}\nonumber\\&\qquad +\|\nabla\mathbf{w}^{(2)}\|_2^{\frac52}+1)\|\ \tilde{\mathbf{u}},\ \tilde{\mathbf{w}}\|_2^2.\nonumber\\[-16pt] \end{align} $$
Applying Gronwall’s inequality and the previous estimates, we obtain
![]() $(\tilde {\mathbf {u}},\ \tilde {\mathbf {w}})\equiv 0$
. Then, we complete the proof of Proposition 3.3. Furthermore, combining Propositions 3.1–3.3, we complete the proof of Theorem 1.1.
$(\tilde {\mathbf {u}},\ \tilde {\mathbf {w}})\equiv 0$
. Then, we complete the proof of Proposition 3.3. Furthermore, combining Propositions 3.1–3.3, we complete the proof of Theorem 1.1.
Acknowledgment
The author would like to thank the editors for the excellent handling of our manuscript and to express our thanks to the anonymous reviewers for the constructive and valuable suggestions to update our manuscript.