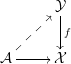1 Introduction
1.1 Main result
In this paper we answer the following question, posed by Gross. Consider two logarithmically smooth complex projective varieties
![]() $X$
and
$X$
and
![]() $Y$
and a logarithmic modification
$Y$
and a logarithmic modification
![]() $h:Y\rightarrow X$
between them. How are the logarithmic Gromov–Witten invariants of
$h:Y\rightarrow X$
between them. How are the logarithmic Gromov–Witten invariants of
![]() $X$
and
$X$
and
![]() $Y$
related? We show in Theorem 1.1.1 that the canonical morphism
$Y$
related? We show in Theorem 1.1.1 that the canonical morphism
![]() $\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
between the associated spaces of logarithmic stable maps is virtually birational, and, as a consequence, the Gromov–Witten theories with primary insertions coming from
$\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
between the associated spaces of logarithmic stable maps is virtually birational, and, as a consequence, the Gromov–Witten theories with primary insertions coming from
![]() $X$
coincide (see Corollary 1.3.1).
$X$
coincide (see Corollary 1.3.1).
If
![]() $X$
is a proper logarithmic scheme, there is a logarithmic algebraic stack
$X$
is a proper logarithmic scheme, there is a logarithmic algebraic stack
![]() $\overline{{\mathcal{M}}}(X)$
parameterizing stable logarithmic maps from logarithmic curves into
$\overline{{\mathcal{M}}}(X)$
parameterizing stable logarithmic maps from logarithmic curves into
![]() $X$
[Reference Gross and SiebertGS13, Reference ChenChe14, Reference Abramovich and ChenAC14, Reference WiseWis16]. When
$X$
[Reference Gross and SiebertGS13, Reference ChenChe14, Reference Abramovich and ChenAC14, Reference WiseWis16]. When
![]() $X$
is also logarithmically smooth, the underlying algebraic stack of
$X$
is also logarithmically smooth, the underlying algebraic stack of
![]() $\overline{{\mathcal{M}}}(X)$
has a virtual fundamental class
$\overline{{\mathcal{M}}}(X)$
has a virtual fundamental class
![]() $[\overline{{\mathcal{M}}}(X)]^{\text{vir}}$
that can be used to define Gromov–Witten invariants.
$[\overline{{\mathcal{M}}}(X)]^{\text{vir}}$
that can be used to define Gromov–Witten invariants.
A logarithmic modification is a proper, birational, logarithmically étale morphism
![]() $Y\rightarrow X$
. By [Reference Abramovich, Marcus and WiseAMW14, Theorem B.6], a logarithmic modification
$Y\rightarrow X$
. By [Reference Abramovich, Marcus and WiseAMW14, Theorem B.6], a logarithmic modification
![]() $Y\rightarrow X$
induces a morphism
$Y\rightarrow X$
induces a morphism
![]() $\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
.
$\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
.
Theorem 1.1.1. Let
![]() $h:Y\rightarrow X$
be a logarithmic modification of logarithmically smooth schemes inducing a projection
$h:Y\rightarrow X$
be a logarithmic modification of logarithmically smooth schemes inducing a projection
![]() $\unicode[STIX]{x1D70B}:\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
. Then
$\unicode[STIX]{x1D70B}:\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
. Then
We will work throughout this paper in the language of logarithmic schemes. Following Ogus, we refer to the underlying scheme of a logarithmic scheme
![]() $X$
by decoration with an underline:
$X$
by decoration with an underline:
![]() $\text{}\underline{X}$
.
$\text{}\underline{X}$
.
1.2 Toroidal structures and logarithmic structures
We summarize the relationship between toroidal embeddings and logarithmic structures, giving a brief summary of the basic definitions. For an authentic introduction we refer the reader to [Reference KatoKat89] or to [Reference Abramovich, Chen, Gillam, Huang, Olsson, Satriano and SunACG+13].
Logarithmic structures are a recent addition to algebraic geometry and Gromov–Witten theory, but logarithmically smooth varieties and logarithmic modifications between them have a concrete classical description in terms of toroidal embeddings and toroidal modifications.
A toroidal embedding is an open subset
![]() $\text{}\underline{U}\subset \text{}\underline{X}$
such that, if
$\text{}\underline{U}\subset \text{}\underline{X}$
such that, if
![]() $\widehat{\text{}\underline{X}}=\operatorname{Spec}\widehat{{\mathcal{O}}}_{X,x}$
is the formal completion of
$\widehat{\text{}\underline{X}}=\operatorname{Spec}\widehat{{\mathcal{O}}}_{X,x}$
is the formal completion of
![]() $\text{}\underline{X}$
at any closed point
$\text{}\underline{X}$
at any closed point
![]() $x$
, and
$x$
, and
![]() $\widehat{\text{}\underline{U}}$
is the preimage of
$\widehat{\text{}\underline{U}}$
is the preimage of
![]() $\text{}\underline{U}$
in
$\text{}\underline{U}$
in
![]() $\widehat{\text{}\underline{X}}$
, then the pair
$\widehat{\text{}\underline{X}}$
, then the pair
![]() $(\widehat{X},\widehat{\text{}\underline{U}})$
is isomorphic to
$(\widehat{X},\widehat{\text{}\underline{U}})$
is isomorphic to
![]() $(\widehat{V},\widehat{T})$
, where
$(\widehat{V},\widehat{T})$
, where
![]() $\widehat{V}$
and
$\widehat{V}$
and
![]() $\widehat{T}$
are constructed in the same way at a point
$\widehat{T}$
are constructed in the same way at a point
![]() $v$
of a toric variety
$v$
of a toric variety
![]() $V$
with dense torus orbit
$V$
with dense torus orbit
![]() $T$
; in other words, there is an isomorphism
$T$
; in other words, there is an isomorphism
![]() $\widehat{{\mathcal{O}}}_{X,x}\rightarrow \widehat{{\mathcal{O}}}_{V,v}$
carrying
$\widehat{{\mathcal{O}}}_{X,x}\rightarrow \widehat{{\mathcal{O}}}_{V,v}$
carrying
![]() ${\mathcal{I}}_{X\smallsetminus U}\widehat{{\mathcal{O}}}_{X,x}$
to
${\mathcal{I}}_{X\smallsetminus U}\widehat{{\mathcal{O}}}_{X,x}$
to
![]() ${\mathcal{I}}_{V\smallsetminus T}\widehat{{\mathcal{O}}}_{V,v}$
as in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, Definition II.1.1]. The toric variety
${\mathcal{I}}_{V\smallsetminus T}\widehat{{\mathcal{O}}}_{V,v}$
as in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, Definition II.1.1]. The toric variety
![]() $V$
may depend on the choice of point in
$V$
may depend on the choice of point in
![]() $X$
where we perform the completion. Informally, a toroidal variety
$X$
where we perform the completion. Informally, a toroidal variety
![]() $\text{}\underline{X}$
locally looks formally, and therefore also étale locally, like a toric variety. Similarly, a dominant morphism
$\text{}\underline{X}$
locally looks formally, and therefore also étale locally, like a toric variety. Similarly, a dominant morphism
![]() $\text{}\underline{Y}\rightarrow \text{}\underline{X}$
of varieties with toroidal structures
$\text{}\underline{Y}\rightarrow \text{}\underline{X}$
of varieties with toroidal structures
![]() $\text{}\underline{U}_{Y}\subset \text{}\underline{Y},~\text{}\underline{U}_{X}\subset \text{}\underline{X}$
is toroidal if it locally looks like a torus equivariant morphism of toric varieties. This notion of toroidal morphisms was introduced in [Reference Abramovich and KaruAK00, Definition 1.3], but the birational case was already present in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, Definition II.2.1, Theorem II.2.1*, Definition II.2.3]. We note that sometimes one indicates the toroidal structure on
$\text{}\underline{U}_{Y}\subset \text{}\underline{Y},~\text{}\underline{U}_{X}\subset \text{}\underline{X}$
is toroidal if it locally looks like a torus equivariant morphism of toric varieties. This notion of toroidal morphisms was introduced in [Reference Abramovich and KaruAK00, Definition 1.3], but the birational case was already present in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, Definition II.2.1, Theorem II.2.1*, Definition II.2.3]. We note that sometimes one indicates the toroidal structure on
![]() $\text{}\underline{X}$
by specifying the divisor
$\text{}\underline{X}$
by specifying the divisor
![]() $\text{}\underline{D}_{X}:=\text{}\underline{X}\setminus \text{}\underline{U}$
instead of
$\text{}\underline{D}_{X}:=\text{}\underline{X}\setminus \text{}\underline{U}$
instead of
![]() $\text{}\underline{U}$
.
$\text{}\underline{U}$
.
A logarithmic structure on a scheme
![]() $\text{}\underline{X}$
is an étale sheaf of monoids
$\text{}\underline{X}$
is an étale sheaf of monoids
![]() $M_{X}$
and a homomorphism
$M_{X}$
and a homomorphism
![]() $\unicode[STIX]{x1D700}:M_{X}\rightarrow {\mathcal{O}}_{\text{}\underline{X}}$
, with
$\unicode[STIX]{x1D700}:M_{X}\rightarrow {\mathcal{O}}_{\text{}\underline{X}}$
, with
![]() ${\mathcal{O}}_{\text{}\underline{X}}$
given its multiplicative monoidal structure, such that every unit of
${\mathcal{O}}_{\text{}\underline{X}}$
given its multiplicative monoidal structure, such that every unit of
![]() ${\mathcal{O}}_{\text{}\underline{X}}$
is the image of a unique element of
${\mathcal{O}}_{\text{}\underline{X}}$
is the image of a unique element of
![]() $M_{X}$
. The triple
$M_{X}$
. The triple
![]() $X=(\text{}\underline{X},M_{X},\unicode[STIX]{x1D700})$
is called a logarithmic scheme.
$X=(\text{}\underline{X},M_{X},\unicode[STIX]{x1D700})$
is called a logarithmic scheme.
If
![]() $i:\text{}\underline{U}\subset \text{}\underline{X}$
is an open subset then
$i:\text{}\underline{U}\subset \text{}\underline{X}$
is an open subset then
![]() $M_{X}={\mathcal{O}}_{\text{}\underline{X}}\times _{i_{\ast }{\mathcal{O}}_{\text{}\underline{U}}}i_{\ast }{\mathcal{O}}_{\text{}\underline{U}}^{\ast }$
(the fiber product taken as sheaves in the étale topology) along with the projection to
$M_{X}={\mathcal{O}}_{\text{}\underline{X}}\times _{i_{\ast }{\mathcal{O}}_{\text{}\underline{U}}}i_{\ast }{\mathcal{O}}_{\text{}\underline{U}}^{\ast }$
(the fiber product taken as sheaves in the étale topology) along with the projection to
![]() ${\mathcal{O}}_{\text{}\underline{X}}$
gives a logarithmic structure on
${\mathcal{O}}_{\text{}\underline{X}}$
gives a logarithmic structure on
![]() $\text{}\underline{X}$
. Concretely, the local sections of
$\text{}\underline{X}$
. Concretely, the local sections of
![]() $M_{X}$
are the sections of
$M_{X}$
are the sections of
![]() ${\mathcal{O}}_{\text{}\underline{X}}$
that become invertible when restricted to
${\mathcal{O}}_{\text{}\underline{X}}$
that become invertible when restricted to
![]() $\text{}\underline{U}$
. When
$\text{}\underline{U}$
. When
![]() $\text{}\underline{U}\subset \text{}\underline{X}$
is a toroidal embedding, the logarithmic scheme
$\text{}\underline{U}\subset \text{}\underline{X}$
is a toroidal embedding, the logarithmic scheme
![]() $X$
just constructed is fine, saturated, and logarithmically smooth and
$X$
just constructed is fine, saturated, and logarithmically smooth and
![]() $\text{}\underline{U}$
can be recovered as the open subset of
$\text{}\underline{U}$
can be recovered as the open subset of
![]() $\text{}\underline{X}$
on which the map
$\text{}\underline{X}$
on which the map
![]() $\unicode[STIX]{x1D700}:M_{X}\rightarrow {\mathcal{O}}_{\text{}\underline{X}}$
is an isomorphism onto
$\unicode[STIX]{x1D700}:M_{X}\rightarrow {\mathcal{O}}_{\text{}\underline{X}}$
is an isomorphism onto
![]() ${\mathcal{O}}_{\text{}\underline{X}}^{\ast }$
.
${\mathcal{O}}_{\text{}\underline{X}}^{\ast }$
.
A morphism of logarithmic schemes
![]() $f:Y\rightarrow X$
consists of a morphism of the underlying schemes
$f:Y\rightarrow X$
consists of a morphism of the underlying schemes
![]() $\text{}\underline{Y}\rightarrow \text{}\underline{X}$
, for which we use the same symbol
$\text{}\underline{Y}\rightarrow \text{}\underline{X}$
, for which we use the same symbol
![]() $f$
, and a morphism of étale sheaves of monoids
$f$
, and a morphism of étale sheaves of monoids
![]() $f^{-1}M_{X}\rightarrow M_{Y}$
such that the diagram
$f^{-1}M_{X}\rightarrow M_{Y}$
such that the diagram

commutes. It can be seen easily from the definition that a morphism of toroidal varieties
![]() $(\text{}\underline{Y},\text{}\underline{V})\rightarrow (\text{}\underline{X},\text{}\underline{U})$
(in which
$(\text{}\underline{Y},\text{}\underline{V})\rightarrow (\text{}\underline{X},\text{}\underline{U})$
(in which
![]() $\text{}\underline{V}$
maps to
$\text{}\underline{V}$
maps to
![]() $\text{}\underline{U}$
) induces a morphism of logarithmic schemes. Moreover, a toroidal morphism
$\text{}\underline{U}$
) induces a morphism of logarithmic schemes. Moreover, a toroidal morphism
![]() $(\text{}\underline{Y},\text{}\underline{V})\rightarrow (\text{}\underline{X},\text{}\underline{U})$
such that
$(\text{}\underline{Y},\text{}\underline{V})\rightarrow (\text{}\underline{X},\text{}\underline{U})$
such that
![]() $\text{}\underline{V}\rightarrow \text{}\underline{U}$
is étale or smooth induces a morphism of logarithmic schemes
$\text{}\underline{V}\rightarrow \text{}\underline{U}$
is étale or smooth induces a morphism of logarithmic schemes
![]() $Y\rightarrow X$
that has the same property, logarithmically, by [Reference KatoKat89, Proposition (3.4)].
$Y\rightarrow X$
that has the same property, logarithmically, by [Reference KatoKat89, Proposition (3.4)].
1.3 Implication for logarithmic Gromov–Witten invariants
If
![]() $X$
is a projective logarithmic scheme,
$X$
is a projective logarithmic scheme,
![]() $\overline{{\mathcal{M}}}(X)$
decomposes as a disjoint union of open and closed substacks
$\overline{{\mathcal{M}}}(X)$
decomposes as a disjoint union of open and closed substacks
![]() $\overline{{\mathcal{M}}}_{\unicode[STIX]{x1D6E4}}(X)$
, each of finite type with a projective coarse moduli space, indexed by combinatorial data
$\overline{{\mathcal{M}}}_{\unicode[STIX]{x1D6E4}}(X)$
, each of finite type with a projective coarse moduli space, indexed by combinatorial data
![]() $\unicode[STIX]{x1D6E4}$
. This was proved with additional technical hypotheses in [Reference Gross and SiebertGS13, Reference Abramovich and ChenAC14], but those restrictions were eliminated, using some of the methods developed in this paper, in [Reference Abramovich, Chen, Marcus and WiseACMW17]. Associated to each datum
$\unicode[STIX]{x1D6E4}$
. This was proved with additional technical hypotheses in [Reference Gross and SiebertGS13, Reference Abramovich and ChenAC14], but those restrictions were eliminated, using some of the methods developed in this paper, in [Reference Abramovich, Chen, Marcus and WiseACMW17]. Associated to each datum
![]() $\unicode[STIX]{x1D6E4}$
one has logarithmic Gromov–Witten invariants of
$\unicode[STIX]{x1D6E4}$
one has logarithmic Gromov–Witten invariants of
![]() $X$
, as defined in [Reference Gross and SiebertGS13, Reference Abramovich and ChenAC14].
$X$
, as defined in [Reference Gross and SiebertGS13, Reference Abramovich and ChenAC14].
Corollary 1.3.1. Let
![]() $Y\rightarrow X$
be a logarithmic modification of logarithmically smooth schemes. Then the logarithmic Gromov–Witten invariants of
$Y\rightarrow X$
be a logarithmic modification of logarithmically smooth schemes. Then the logarithmic Gromov–Witten invariants of
![]() $X$
and
$X$
and
![]() $Y$
with primary insertions coming from
$Y$
with primary insertions coming from
![]() $X$
coincide: given numerical data
$X$
coincide: given numerical data
![]() $\unicode[STIX]{x1D6E4}_{X}$
on
$\unicode[STIX]{x1D6E4}_{X}$
on
![]() $X$
, there is a unique choice of numerical data
$X$
, there is a unique choice of numerical data
![]() $\unicode[STIX]{x1D6E4}_{Y}$
with
$\unicode[STIX]{x1D6E4}_{Y}$
with
![]() $h_{\ast }\unicode[STIX]{x1D6E4}_{Y}=\unicode[STIX]{x1D6E4}_{X}$
, such that
$h_{\ast }\unicode[STIX]{x1D6E4}_{Y}=\unicode[STIX]{x1D6E4}_{X}$
, such that
and for all other choices
![]() $\unicode[STIX]{x1D6E4}_{Y}^{\prime }$
with
$\unicode[STIX]{x1D6E4}_{Y}^{\prime }$
with
![]() $h_{\ast }\unicode[STIX]{x1D6E4}_{Y}^{\prime }=\unicode[STIX]{x1D6E4}_{X}$
the invariants vanish.
$h_{\ast }\unicode[STIX]{x1D6E4}_{Y}^{\prime }=\unicode[STIX]{x1D6E4}_{X}$
the invariants vanish.
We stress that our result applies only for toroidal morphisms. Suppose
![]() $X=\mathbf{P}^{2}$
with its toric structure. Our result applies when
$X=\mathbf{P}^{2}$
with its toric structure. Our result applies when
![]() $Y$
is the toric blowing up of
$Y$
is the toric blowing up of
![]() $X$
at a torus fixed point, such as the origin. It does not apply if
$X$
at a torus fixed point, such as the origin. It does not apply if
![]() $Y$
is the non-toric blowing up of
$Y$
is the non-toric blowing up of
![]() $X$
at any point which is not fixed by the torus.
$X$
at any point which is not fixed by the torus.
On the one hand, this result is to be expected: consider the case of a toroidal degeneration
![]() $\unicode[STIX]{x1D70B}:X\rightarrow B$
, where
$\unicode[STIX]{x1D70B}:X\rightarrow B$
, where
![]() $B$
is a curve with toroidal divisor
$B$
is a curve with toroidal divisor
![]() $D_{B}=\{b_{0}\}\in B$
and
$D_{B}=\{b_{0}\}\in B$
and
![]() $D_{X}=\unicode[STIX]{x1D70B}^{-1}D_{B}$
. Suppose given a birational modification
$D_{X}=\unicode[STIX]{x1D70B}^{-1}D_{B}$
. Suppose given a birational modification
![]() $Y\rightarrow X$
such that
$Y\rightarrow X$
such that
![]() $Y\rightarrow B$
is also toroidal. This implies that over a general point
$Y\rightarrow B$
is also toroidal. This implies that over a general point
![]() $b\neq b_{0}$
of
$b\neq b_{0}$
of
![]() $B$
we have
$B$
we have
![]() $Y_{b}=X_{b}$
, so they have identical Gromov–Witten invariants. This implies that the most important Gromov–Witten invariants of
$Y_{b}=X_{b}$
, so they have identical Gromov–Witten invariants. This implies that the most important Gromov–Witten invariants of
![]() $X$
and
$X$
and
![]() $Y$
, namely those with fiberwise curve classes and global insertions, automatically coincide, whether or not the morphism
$Y$
, namely those with fiberwise curve classes and global insertions, automatically coincide, whether or not the morphism
![]() $Y\rightarrow X$
is toroidal.
$Y\rightarrow X$
is toroidal.
On the other hand, this result may be somewhat surprising. There are curve classes on
![]() $Y$
which are not present on
$Y$
which are not present on
![]() $X$
, for instance an exceptional curve
$X$
, for instance an exceptional curve
![]() $E$
. The corollary says in particular that all logarithmic Gromov–Witten invariants on
$E$
. The corollary says in particular that all logarithmic Gromov–Witten invariants on
![]() $Y$
with curve class
$Y$
with curve class
![]() $dE$
vanish. In fact in this case the moduli spaces
$dE$
vanish. In fact in this case the moduli spaces
![]() $\overline{{\mathcal{M}}}_{\unicode[STIX]{x1D6E4}_{Y}^{\prime }}(Y)$
are empty, in dramatic contrast to conventional Gromov–Witten invariants.
$\overline{{\mathcal{M}}}_{\unicode[STIX]{x1D6E4}_{Y}^{\prime }}(Y)$
are empty, in dramatic contrast to conventional Gromov–Witten invariants.
1.4 Gromov–Witten invariants and birational invariance
Algebraic Gromov–Witten invariants are virtual curve counts on a complex projective variety
![]() $X$
, thus are biregular invariants. The formalism of virtual fundamental class shows that they are automatically deformation invariant: if
$X$
, thus are biregular invariants. The formalism of virtual fundamental class shows that they are automatically deformation invariant: if
![]() $X$
appears as a fiber of a smooth family, then its invariants coincide with the invariants of other smooth fibers. This property is fundamental in Gromov–Witten theory.
$X$
appears as a fiber of a smooth family, then its invariants coincide with the invariants of other smooth fibers. This property is fundamental in Gromov–Witten theory.
By contrast, the behavior of Gromov–Witten invariants under a birational transformation
![]() $Y\rightarrow X$
is generally subtle. Many have studied this subtlety and found that good behavior can be obtained in special situations. Here is a non-exhaustive list:
$Y\rightarrow X$
is generally subtle. Many have studied this subtlety and found that good behavior can be obtained in special situations. Here is a non-exhaustive list:
-
(a) Gathmann [Reference GathmannGat01, Theorem 2.1] provided a procedure for calculating the behavior of genus-0 invariants under point blowing up;
-
(b) Hu [Reference HuHu00, Theorem 1.2] showed the birational invariance of Gromov–Witten numbers of genus less than or equal to
 $1$
under blowing up a point or a smooth curve, as well as arbitrary genus invariants when
$1$
under blowing up a point or a smooth curve, as well as arbitrary genus invariants when
 $\dim X\leqslant 3$
;
$\dim X\leqslant 3$
; -
(c) Lai [Reference LaiLai09, Theorem 1.4] showed the birational invariance in genus 0 if
 $Y\rightarrow X$
is the blowing up of a smooth subvariety
$Y\rightarrow X$
is the blowing up of a smooth subvariety
 $Z$
with convex normal bundle with enough sections, or if
$Z$
with convex normal bundle with enough sections, or if
 $Z$
contains no images of
$Z$
contains no images of
 $\mathbf{P}^{1}$
;
$\mathbf{P}^{1}$
; -
(d) Manolache [Reference ManolacheMan12, Proposition 5.14] showed birational invariance in genus 0 if
 $Z$
is the transversal intersection of
$Z$
is the transversal intersection of
 $X$
with a smooth subvariety of an ambient homogeneous space.
$X$
with a smooth subvariety of an ambient homogeneous space.
A number of authors, including Maulik and Pandharipande [Reference Maulik and PandharipandeMP06] and Hu, Li, and Ruan [Reference Hu, Li and RuanHLR08], considered the behavior of invariants under blowing up using the degeneration formula.
Theorem 1.1.1 shows that logarithmic Gromov–Witten invariants are well suited to questions of birational invariance. It would be interesting to understand how Gromov–Witten invariants with primary and descendant insertions from
![]() $Y$
behave. It would also be interesting to obtain comparison mechanisms between logarithmic and usual invariants similar to the results of [Reference Maulik and PandharipandeMP06]. Such a mechanism should allow a comparison of Gromov–Witten invariants of
$Y$
behave. It would also be interesting to obtain comparison mechanisms between logarithmic and usual invariants similar to the results of [Reference Maulik and PandharipandeMP06]. Such a mechanism should allow a comparison of Gromov–Witten invariants of
![]() $X$
and
$X$
and
![]() $Y$
even if
$Y$
even if
![]() $Y\rightarrow X$
is not a toroidal morphism.
$Y\rightarrow X$
is not a toroidal morphism.
1.5 Artin fans
Let
![]() $\mathsf{Log}$
denote the stack of logarithmic structures introduced in [Reference OlssonOls03]. As explained in that work, a logarithmic variety
$\mathsf{Log}$
denote the stack of logarithmic structures introduced in [Reference OlssonOls03]. As explained in that work, a logarithmic variety
![]() $X$
is logarithmically smooth if and only if the associated map
$X$
is logarithmically smooth if and only if the associated map
![]() $\text{}\underline{X}\rightarrow \mathsf{Log}$
is smooth. As we show in § 2 below, this map factors as
$\text{}\underline{X}\rightarrow \mathsf{Log}$
is smooth. As we show in § 2 below, this map factors as
![]() $\text{}\underline{X}\rightarrow \text{}\underline{{\mathcal{X}}}\rightarrow \mathsf{Log}$
where
$\text{}\underline{X}\rightarrow \text{}\underline{{\mathcal{X}}}\rightarrow \mathsf{Log}$
where
![]() $X\rightarrow {\mathcal{X}}$
is a strict smooth map and
$X\rightarrow {\mathcal{X}}$
is a strict smooth map and
![]() ${\mathcal{X}}$
is a ‘locally toric stack’, meaning it has an étale cover by finitely many stacks of the form
${\mathcal{X}}$
is a ‘locally toric stack’, meaning it has an étale cover by finitely many stacks of the form
![]() $[V/T]$
, where
$[V/T]$
, where
![]() $V$
is a toric variety and
$V$
is a toric variety and
![]() $T$
its dense torus. The stack
$T$
its dense torus. The stack
![]() ${\mathcal{X}}$
is logarithmically étale over a point. We show in Corollary 2.6.7 that the map
${\mathcal{X}}$
is logarithmically étale over a point. We show in Corollary 2.6.7 that the map
![]() $Y\rightarrow X$
is obtained as the pullback of a toric modification
$Y\rightarrow X$
is obtained as the pullback of a toric modification
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
. In the local picture, this means that
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
. In the local picture, this means that
![]() $V^{\prime }={\mathcal{Y}}\times _{{\mathcal{X}}}V$
is a toric variety for the same torus
$V^{\prime }={\mathcal{Y}}\times _{{\mathcal{X}}}V$
is a toric variety for the same torus
![]() $T$
.
$T$
.
We intended to name the stack
![]() ${\mathcal{X}}$
the ‘Olsson fan of
${\mathcal{X}}$
the ‘Olsson fan of
![]() $X$
’; however, the name ‘Artin fan of
$X$
’; however, the name ‘Artin fan of
![]() $X$
’ seems to have stuck, and we will use it here.
$X$
’ seems to have stuck, and we will use it here.
The construction of
![]() ${\mathcal{X}}$
has its origin in unpublished notes on gluing Gromov–Witten invariants by Chen and by Gross. Those notes showed that a solid treatment of Artin fans would require a significant amount of pain. Having endured it, we hope we have managed to hide this pain and present in this paper a pleasant theory.
${\mathcal{X}}$
has its origin in unpublished notes on gluing Gromov–Witten invariants by Chen and by Gross. Those notes showed that a solid treatment of Artin fans would require a significant amount of pain. Having endured it, we hope we have managed to hide this pain and present in this paper a pleasant theory.
A precursor of Artin fans in a special case was given in [Reference Abramovich, Cadman, Fantechi and WiseACFW13]. (A further generalization of our treatment here, allowing arbitrarily singular logarithmic schemes, is given in [Reference Abramovich, Chen, Marcus and WiseACMW17, § 3.1].) Since then Artin fans have taken on a life of their own: Ulirsch [Reference UlirschUli15] shows that the Berkovich analytification
![]() ${\mathcal{X}}^{\beth }$
of the Artin fan of
${\mathcal{X}}^{\beth }$
of the Artin fan of
![]() $X$
provides an analytic structure on the tropicalization of
$X$
provides an analytic structure on the tropicalization of
![]() $X$
. Ranganathan [Reference RanganathanRan17a] shows that superabundance of tropical geometry is explained by obstructions to lifting curves from
$X$
. Ranganathan [Reference RanganathanRan17a] shows that superabundance of tropical geometry is explained by obstructions to lifting curves from
![]() ${\mathcal{X}}$
to
${\mathcal{X}}$
to
![]() $X$
. In [Reference RanganathanRan17b] Ranganathan uses Artin fans as a tool in giving a toroidal description of the space of logarithmic stable maps of genus 0 in the toric case.
$X$
. In [Reference RanganathanRan17b] Ranganathan uses Artin fans as a tool in giving a toroidal description of the space of logarithmic stable maps of genus 0 in the toric case.
1.6 Outline of proof
The structure of the proof is very similar to that of the main theorem in [Reference Abramovich, Marcus and WiseAMW14].
In § 3 we construct moduli stacks of pre-stable logarithmic maps
![]() $\mathfrak{M}({\mathcal{Y}})$
and
$\mathfrak{M}({\mathcal{Y}})$
and
![]() $\mathfrak{M}({\mathcal{X}})$
with maps
$\mathfrak{M}({\mathcal{X}})$
with maps
![]() $\unicode[STIX]{x1D713}_{X}:\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
and
$\unicode[STIX]{x1D713}_{X}:\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
and
![]() $\unicode[STIX]{x1D713}_{Y}:\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}})$
constructed in § 4. We show the following proposition.
$\unicode[STIX]{x1D713}_{Y}:\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}})$
constructed in § 4. We show the following proposition.
Proposition 1.6.1 (See Propositions 3.1 and 3.2).
The stacks
![]() $\mathfrak{M}({\mathcal{Y}})$
and
$\mathfrak{M}({\mathcal{Y}})$
and
![]() $\mathfrak{M}({\mathcal{X}})$
are algebraic and are logarithmically smooth.
$\mathfrak{M}({\mathcal{X}})$
are algebraic and are logarithmically smooth.
In order to compare the moduli spaces we construct another stack
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
in § 3, as well as morphisms
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
in § 3, as well as morphisms
![]() $\unicode[STIX]{x1D713}_{Y}^{\prime }:\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
and
$\unicode[STIX]{x1D713}_{Y}^{\prime }:\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
and
![]() $\unicode[STIX]{x1D6FC}:\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
in § 4, such that
$\unicode[STIX]{x1D6FC}:\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
in § 4, such that
![]() $\unicode[STIX]{x1D713}_{Y}=\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D713}_{Y}^{\prime }$
. We show the following proposition.
$\unicode[STIX]{x1D713}_{Y}=\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D713}_{Y}^{\prime }$
. We show the following proposition.
Proposition 1.6.2 (See Corollary 3.5, Lemma 4.1, and § 5.1).
The stack
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is algebraic and the morphism
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is algebraic and the morphism
![]() $\unicode[STIX]{x1D6FC}$
is étale and strict.
$\unicode[STIX]{x1D6FC}$
is étale and strict.
We construct
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
with a morphism
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
with a morphism
![]() $\mathfrak{M}(h):\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{X}})$
. We obtain a diagram
$\mathfrak{M}(h):\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{X}})$
. We obtain a diagram

and prove the following propositions.
Proposition 1.6.4 (See Proposition 5.2.1).
The morphism
![]() $\mathfrak{M}(h)$
is of pure degree 1.
$\mathfrak{M}(h)$
is of pure degree 1.
We construct obstruction theories
![]() ${\mathcal{E}}_{X}$
relative to
${\mathcal{E}}_{X}$
relative to
![]() $\unicode[STIX]{x1D713}_{X}$
and
$\unicode[STIX]{x1D713}_{X}$
and
![]() ${\mathcal{E}}_{Y}$
relative to
${\mathcal{E}}_{Y}$
relative to
![]() $\unicode[STIX]{x1D713}_{Y}$
and prove the following proposition.
$\unicode[STIX]{x1D713}_{Y}$
and prove the following proposition.
Proposition 1.6.5 (See Proposition 6.3.1).
We have
and
![]() $\overline{{\mathcal{M}}}(h)^{\ast }{\mathcal{E}}_{X}={\mathcal{E}}_{Y}$
.
$\overline{{\mathcal{M}}}(h)^{\ast }{\mathcal{E}}_{X}={\mathcal{E}}_{Y}$
.
Theorem 1.1.1 then follows from Costello’s result [Reference CostelloCos06, Theorem 5.0.1]; see also [Reference ManolacheMan12, Proposition 5.29] and [Reference LaiLai09, Proposition 3.15].
1.7 Conventions
We work over an algebraically closed field
![]() $k$
of characteristic zero. With one exception (in Proposition 2.6.2) all logarithmic structures in this paper are fine and saturated.
$k$
of characteristic zero. With one exception (in Proposition 2.6.2) all logarithmic structures in this paper are fine and saturated.
2 Construction of
 ${\mathcal{X}}$
and
${\mathcal{X}}$
and
 ${\mathcal{Y}}$
${\mathcal{Y}}$
We construct Artin fans only for logarithmically smooth logarithmic schemes. A more general construction appears in [Reference Abramovich, Chen, Marcus and WiseACMW17]. The general case is also treated in [Reference UlirschUli17], where it is connected to Kato fans, polyhedral complexes and Berkovich analytic spaces.
We construct the stack
![]() ${\mathcal{X}}$
as a universal object depending on
${\mathcal{X}}$
as a universal object depending on
![]() $X$
. First, there is a canonical morphism
$X$
. First, there is a canonical morphism
![]() $X\rightarrow \mathsf{Log}$
; its image is an open substack of
$X\rightarrow \mathsf{Log}$
; its image is an open substack of
![]() $\mathsf{Log}$
, but it is too coarse an object because different strata of
$\mathsf{Log}$
, but it is too coarse an object because different strata of
![]() $X$
can map to the same point of
$X$
can map to the same point of
![]() $\mathsf{Log}$
. The idea is to correct this deficiency in a universal way. We then construct
$\mathsf{Log}$
. The idea is to correct this deficiency in a universal way. We then construct
![]() ${\mathcal{Y}}$
by repeating the same construction, this time working relative to
${\mathcal{Y}}$
by repeating the same construction, this time working relative to
![]() $\mathsf{Log}({\mathcal{X}})$
.
$\mathsf{Log}({\mathcal{X}})$
.
2.1 Connected components of the fibers of a smooth morphism
Let
![]() $f:X\rightarrow Y$
be a smooth, quasicompact morphism of schemes. Let
$f:X\rightarrow Y$
be a smooth, quasicompact morphism of schemes. Let
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
be the étale
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
be the étale
![]() $Y$
-space defined in [Reference Laumon and Moret-BaillyLM00, § (6.8)]. A point of
$Y$
-space defined in [Reference Laumon and Moret-BaillyLM00, § (6.8)]. A point of
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
lying above a geometric point
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
lying above a geometric point
![]() $y$
of
$y$
of
![]() $Y$
corresponds to a connected component of the fiber
$Y$
corresponds to a connected component of the fiber
![]() $X_{y}$
. We will generalize the construction of
$X_{y}$
. We will generalize the construction of
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
to a smooth, quasicompact morphism of algebraic stacks.
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
to a smooth, quasicompact morphism of algebraic stacks.
Remark 2.1.1. This section is closely related to, and overlaps somewhat with, [Reference WiseWis16, § 4.1]. As in loc. cit., one could eliminate the smoothness requirement and replace it with local finite presentation, flatness, and reduced geometric fibers, but that generality is not necessary here.
Proposition 2.1.2. Let
![]() $X\rightarrow Y$
be a smooth morphism of schemes. Then
$X\rightarrow Y$
be a smooth morphism of schemes. Then
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
is the initial factorization of
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
is the initial factorization of
![]() $X\rightarrow Y$
through an étale
$X\rightarrow Y$
through an étale
![]() $Y$
-space.
$Y$
-space.
Proof. It will be sufficient to show that for any other such factorization
![]() $X\rightarrow Z\rightarrow Y$
, there is an inclusion
$X\rightarrow Z\rightarrow Y$
, there is an inclusion
![]() $X\times _{\unicode[STIX]{x1D70B}_{0}(X/Y)}X\subset X\times _{Z}X$
as open subschemes of
$X\times _{\unicode[STIX]{x1D70B}_{0}(X/Y)}X\subset X\times _{Z}X$
as open subschemes of
![]() $X\times _{Y}X$
. For this it is sufficient to show there is an inclusion on the level of points. Since everything in sight commutes with base change in
$X\times _{Y}X$
. For this it is sufficient to show there is an inclusion on the level of points. Since everything in sight commutes with base change in
![]() $Y$
, we may assume
$Y$
, we may assume
![]() $Y$
is the spectrum of a separably closed field. In this case, the inclusion reduces to the well-known universal property of
$Y$
is the spectrum of a separably closed field. In this case, the inclusion reduces to the well-known universal property of
![]() $\unicode[STIX]{x1D70B}_{0}(X)=\unicode[STIX]{x1D70B}_{0}(X/Y)$
.◻
$\unicode[STIX]{x1D70B}_{0}(X)=\unicode[STIX]{x1D70B}_{0}(X/Y)$
.◻
As the formation of
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
commutes with base change in
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
commutes with base change in
![]() $Y$
, the definition extends to a smooth, quasicompact morphism
$Y$
, the definition extends to a smooth, quasicompact morphism
![]() $f:X\rightarrow Y$
that is representable by schemes. We show it can be extended to an arbitrary morphism of algebraic stacks.
$f:X\rightarrow Y$
that is representable by schemes. We show it can be extended to an arbitrary morphism of algebraic stacks.
First, let
![]() $f:X\rightarrow Y$
be a smooth morphism from an algebraic stack to a scheme
$f:X\rightarrow Y$
be a smooth morphism from an algebraic stack to a scheme
![]() $Y$
. Regard
$Y$
. Regard
![]() $\unicode[STIX]{x1D6F7}:X^{\prime }\mapsto \unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y)$
as a functor from the category of smooth
$\unicode[STIX]{x1D6F7}:X^{\prime }\mapsto \unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y)$
as a functor from the category of smooth
![]() $X$
-schemes to the category of étale
$X$
-schemes to the category of étale
![]() $Y$
-spaces. By the universal property of
$Y$
-spaces. By the universal property of
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
, this functor respects colimits where defined. Therefore it can be extended to the category of all smooth
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
, this functor respects colimits where defined. Therefore it can be extended to the category of all smooth
![]() $X$
-spaces, and in particular to
$X$
-spaces, and in particular to
![]() $X$
, by the following formula:
$X$
, by the following formula:
Note that the colimit is taken in the category of étale
![]() $Y$
-spaces, which is equivalent to the category of étale sheaves on the small étale site of
$Y$
-spaces, which is equivalent to the category of étale sheaves on the small étale site of
![]() $Y$
[Reference MilneMil80, Theorem V.1.5]. Since colimits of étale sheaves exist, so does the colimit defining
$Y$
[Reference MilneMil80, Theorem V.1.5]. Since colimits of étale sheaves exist, so does the colimit defining
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
, and it is automatically étale over
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
, and it is automatically étale over
![]() $Y$
.
$Y$
.
Corollary 2.1.3. The conclusion of Proposition 2.1.2 is valid for smooth morphisms from algebraic stacks to schemes.
Proof. Suppose that
![]() $X\rightarrow Y^{\prime }\rightarrow Y$
is a factorization of
$X\rightarrow Y^{\prime }\rightarrow Y$
is a factorization of
![]() $X\rightarrow Y$
through an étale
$X\rightarrow Y$
through an étale
![]() $Y$
-scheme
$Y$
-scheme
![]() $Y^{\prime }$
. Then for each smooth
$Y^{\prime }$
. Then for each smooth
![]() $X^{\prime }$
over
$X^{\prime }$
over
![]() $X$
, we obtain a factorization
$X$
, we obtain a factorization
![]() $X^{\prime }\rightarrow Y^{\prime }\rightarrow Y$
of the map
$X^{\prime }\rightarrow Y^{\prime }\rightarrow Y$
of the map
![]() $X^{\prime }\rightarrow Y$
. By the universal property of
$X^{\prime }\rightarrow Y$
. By the universal property of
![]() $\unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y)$
, this factors uniquely as
$\unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y)$
, this factors uniquely as
The universal property of the colimit used to define
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
now gives the required map
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
now gives the required map
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)\rightarrow Y^{\prime }$
.◻
$\unicode[STIX]{x1D70B}_{0}(X/Y)\rightarrow Y^{\prime }$
.◻
Proposition 2.1.4. Let
![]() $X\rightarrow Y$
be a smooth morphism of an algebraic stack to a scheme. The formation of the étale
$X\rightarrow Y$
be a smooth morphism of an algebraic stack to a scheme. The formation of the étale
![]() $Y$
-space
$Y$
-space
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
commutes with base change in
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
commutes with base change in
![]() $Y$
.
$Y$
.
Proof. Let
![]() $Y^{\prime }\rightarrow Y$
be a morphism of schemes and let
$Y^{\prime }\rightarrow Y$
be a morphism of schemes and let
![]() $X^{\prime }$
be the base change of
$X^{\prime }$
be the base change of
![]() $X$
. Choose a presentation of
$X$
. Choose a presentation of
![]() $X$
as a colimit of smooth
$X$
as a colimit of smooth
![]() $X$
-schemes
$X$
-schemes
![]() $X_{i}$
. Let
$X_{i}$
. Let
![]() $X_{i}^{\prime }=X_{i}\times _{Y}Y^{\prime }$
. Then
$X_{i}^{\prime }=X_{i}\times _{Y}Y^{\prime }$
. Then
![]() $X^{\prime }=X\times _{Y}Y^{\prime }$
is the colimit of the smooth
$X^{\prime }=X\times _{Y}Y^{\prime }$
is the colimit of the smooth
![]() $X^{\prime }$
-schemes
$X^{\prime }$
-schemes
![]() $X_{i}^{\prime }$
and so
$X_{i}^{\prime }$
and so
using the commutation of
![]() $\unicode[STIX]{x1D70B}_{0}$
with base change for schemes and the fact that colimits of sheaves commute with pullback.◻
$\unicode[STIX]{x1D70B}_{0}$
with base change for schemes and the fact that colimits of sheaves commute with pullback.◻
The proposition allows us to extend the definition of
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
to an arbitrary smooth morphism of algebraic stacks. Let
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
to an arbitrary smooth morphism of algebraic stacks. Let
![]() $Y^{\prime }\rightarrow Y$
be a smooth cover by a scheme and put
$Y^{\prime }\rightarrow Y$
be a smooth cover by a scheme and put
![]() $X^{\prime }=X\times _{Y}Y^{\prime }$
. Then
$X^{\prime }=X\times _{Y}Y^{\prime }$
. Then
![]() $\unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y^{\prime })$
is an étale
$\unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y^{\prime })$
is an étale
![]() $Y^{\prime }$
-space, and this construction is functorial in the
$Y^{\prime }$
-space, and this construction is functorial in the
![]() $Y$
-scheme
$Y$
-scheme
![]() $Y^{\prime }$
. Therefore
$Y^{\prime }$
. Therefore
![]() $\unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y^{\prime })$
descends to an étale
$\unicode[STIX]{x1D70B}_{0}(X^{\prime }/Y^{\prime })$
descends to an étale
![]() $Y$
-space
$Y$
-space
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
.
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
.
Proposition 2.1.5. The map
![]() $X\rightarrow \unicode[STIX]{x1D70B}_{0}(X/Y)$
has connected fibers.
$X\rightarrow \unicode[STIX]{x1D70B}_{0}(X/Y)$
has connected fibers.
Proof. Since the formation of
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)$
commutes with base change in
$\unicode[STIX]{x1D70B}_{0}(X/Y)$
commutes with base change in
![]() $Y$
, it is sufficient to treat the case where
$Y$
, it is sufficient to treat the case where
![]() $Y$
is the spectrum of an algebraically closed field. In that case
$Y$
is the spectrum of an algebraically closed field. In that case
![]() $\unicode[STIX]{x1D70B}_{0}(X/Y)=\unicode[STIX]{x1D70B}_{0}(X)$
and the assertion is immediate from the definition of
$\unicode[STIX]{x1D70B}_{0}(X/Y)=\unicode[STIX]{x1D70B}_{0}(X)$
and the assertion is immediate from the definition of
![]() $\unicode[STIX]{x1D70B}_{0}$
.◻
$\unicode[STIX]{x1D70B}_{0}$
.◻
2.2 Artin cones
Suppose that
![]() $\unicode[STIX]{x1D70E}$
is a fine, saturated, sharp monoid. For a logarithmic scheme
$\unicode[STIX]{x1D70E}$
is a fine, saturated, sharp monoid. For a logarithmic scheme
![]() $(X,M_{X})$
, define a contravariant functor
$(X,M_{X})$
, define a contravariant functor
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
from logarithmic schemes to sets:
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
from logarithmic schemes to sets:
When
![]() $\unicode[STIX]{x1D70E}=\mathbf{N}$
is the monoid of natural numbers, we write
$\unicode[STIX]{x1D70E}=\mathbf{N}$
is the monoid of natural numbers, we write
![]() ${\mathcal{A}}={\mathcal{A}}_{\mathbf{N}}$
.
${\mathcal{A}}={\mathcal{A}}_{\mathbf{N}}$
.
We record two key results of Olsson (recall that, by convention, all logarithmic structures are fine and saturated in this paper).
Proposition 2.2.1.
-
(i) The functor
 ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is representable by the logarithmic stack
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is representable by the logarithmic stack
 $[V/T]$
where
$[V/T]$
where
 $V$
is the toric variety associated to
$V$
is the toric variety associated to
 $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
 $T$
is its dense torus [Reference OlssonOls03, Proposition 5.17].
$T$
is its dense torus [Reference OlssonOls03, Proposition 5.17]. -
(ii) The stacks
 ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, with their natural maps to
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, with their natural maps to
 $\mathsf{Log}$
, form a representable étale cover [Reference OlssonOls07, Corollary 5.25 and Remark 5.26].
$\mathsf{Log}$
, form a representable étale cover [Reference OlssonOls07, Corollary 5.25 and Remark 5.26].
Lemma 2.2.2. The stabilizer group of a logarithmic structure over a field is the semidirect product of a finite group and a torus. In particular, it is affine.
Proof. Let
![]() $k$
be a field and let
$k$
be a field and let
![]() $M$
be a logarithmic structure over
$M$
be a logarithmic structure over
![]() $k$
. The automorphisms of
$k$
. The automorphisms of
![]() $M$
are the semidirect product of the automorphism group of the characteristic monoid
$M$
are the semidirect product of the automorphism group of the characteristic monoid
![]() $\overline{M}$
and the torus
$\overline{M}$
and the torus
![]() $\operatorname{Hom}(\overline{M}^{\text{gp}},\mathbf{G}_{m})$
.◻
$\operatorname{Hom}(\overline{M}^{\text{gp}},\mathbf{G}_{m})$
.◻
Definition 2.2.3. A logarithmic algebraic stack isomorphic to
![]() $[V/T]$
, where
$[V/T]$
, where
![]() $V$
is a toric variety and
$V$
is a toric variety and
![]() $T$
is its torus, is called an Artin cone.
$T$
is its torus, is called an Artin cone.
2.2.1 Maps of Artin cones
Observe that we have
![]() $\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},\overline{M}_{{\mathcal{A}}_{\unicode[STIX]{x1D70E}}})=\unicode[STIX]{x1D70E}^{\vee }$
, so that
$\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},\overline{M}_{{\mathcal{A}}_{\unicode[STIX]{x1D70E}}})=\unicode[STIX]{x1D70E}^{\vee }$
, so that
for any fine, saturated, sharp monoids
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70F}$
. In particular,
$\unicode[STIX]{x1D70F}$
. In particular,
![]() $\operatorname{Hom}({\mathcal{A}},{\mathcal{A}}_{\unicode[STIX]{x1D70E}})=\unicode[STIX]{x1D70E}$
and
$\operatorname{Hom}({\mathcal{A}},{\mathcal{A}}_{\unicode[STIX]{x1D70E}})=\unicode[STIX]{x1D70E}$
and
![]() $\operatorname{Hom}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},{\mathcal{A}})=\unicode[STIX]{x1D70E}^{\vee }$
.
$\operatorname{Hom}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},{\mathcal{A}})=\unicode[STIX]{x1D70E}^{\vee }$
.
Definition 2.2.4. We call a coherent logarithmic scheme
![]() $X$
atomic if its logarithmic structure has Zariski charts, there is a unique stratum in its stratification by the isomorphism type of the stalks of its characteristic monoid that is closed and connected, and the restriction of the characteristic monoid to the closed stratum is a constant sheaf.
$X$
atomic if its logarithmic structure has Zariski charts, there is a unique stratum in its stratification by the isomorphism type of the stalks of its characteristic monoid that is closed and connected, and the restriction of the characteristic monoid to the closed stratum is a constant sheaf.
Lemma 2.2.5.
-
(i) Every coherent logarithmic scheme whose strata are locally connected (in particular, every logarithmically smooth logarithmic scheme) has an étale cover by atomic logarithmic schemes.
-
(ii) If
 $X$
is an atomic logarithmic scheme and
$X$
is an atomic logarithmic scheme and
 $x$
is a point of the closed stratum of
$x$
is a point of the closed stratum of
 $X$
then
$X$
then
 $\unicode[STIX]{x1D6E4}(X,\overline{M}_{X})\rightarrow \overline{M}_{X,x}$
is an isomorphism.
$\unicode[STIX]{x1D6E4}(X,\overline{M}_{X})\rightarrow \overline{M}_{X,x}$
is an isomorphism.
Proof. For every geometric point
![]() $x$
of
$x$
of
![]() $X$
, there is an étale neighborhood
$X$
, there is an étale neighborhood
![]() $U$
of
$U$
of
![]() $x$
such that
$x$
such that
![]() $M_{X}$
has a chart by
$M_{X}$
has a chart by
![]() $\overline{M}_{X,x}$
, lifting the identity map on
$\overline{M}_{X,x}$
, lifting the identity map on
![]() $\overline{M}_{X,x}$
. The first assertion is local on
$\overline{M}_{X,x}$
. The first assertion is local on
![]() $X$
, so we can assume this is in fact a global chart. Removing all components of the closed strata other than the one containing
$X$
, so we can assume this is in fact a global chart. Removing all components of the closed strata other than the one containing
![]() $x$
, we can assume that the closed stratum is connected. The global chart then gives a trivialization of
$x$
, we can assume that the closed stratum is connected. The global chart then gives a trivialization of
![]() $\overline{M}_{X}$
over the closed stratum.
$\overline{M}_{X}$
over the closed stratum.
For the second claim, observe simply that to give a section of
![]() $\overline{M}_{X}$
, we must give a section over each stratum in a way that is compatible with generization. But every stratum is a generization of the closed stratum, so every section of
$\overline{M}_{X}$
, we must give a section over each stratum in a way that is compatible with generization. But every stratum is a generization of the closed stratum, so every section of
![]() $\overline{M}_{X}$
over the closed stratum extends to a global section. But
$\overline{M}_{X}$
over the closed stratum extends to a global section. But
![]() $\overline{M}_{X}$
has no monodromy on the closed stratum, so the sections of
$\overline{M}_{X}$
has no monodromy on the closed stratum, so the sections of
![]() $\overline{M}_{X}$
on the closed stratum are the same as the sections at any point.◻
$\overline{M}_{X}$
on the closed stratum are the same as the sections at any point.◻
Proposition 2.2.6. An étale sheaf on
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is constructible with respect to the stratification of
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is constructible with respect to the stratification of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
associated to its finitely many points, and is constant on each stratum.
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
associated to its finitely many points, and is constant on each stratum.
Proof. Write
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}=[V/T]$
, and stratify
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}=[V/T]$
, and stratify
![]() $V=\coprod V_{i}$
, with orbits
$V=\coprod V_{i}$
, with orbits
![]() $V_{i}\simeq T/T_{i}$
. Then
$V_{i}\simeq T/T_{i}$
. Then
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is stratified as
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is stratified as
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}=\coprod [V_{i}/T]=\coprod \text{B}T_{i}$
. Since we are working over an algebraically closed field
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}=\coprod [V_{i}/T]=\coprod \text{B}T_{i}$
. Since we are working over an algebraically closed field
![]() $k$
we have
$k$
we have
![]() $T_{i}\simeq \mathbf{G}_{m}^{r}$
, so each stratum of
$T_{i}\simeq \mathbf{G}_{m}^{r}$
, so each stratum of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is isomorphic to
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is isomorphic to
![]() $\text{B}\mathbf{G}_{m}^{r}$
for some
$\text{B}\mathbf{G}_{m}^{r}$
for some
![]() $r$
. It thus suffices to show that all étale covers of
$r$
. It thus suffices to show that all étale covers of
![]() $\text{B}\mathbf{G}_{m}^{r}$
split. Indeed, an étale cover of
$\text{B}\mathbf{G}_{m}^{r}$
split. Indeed, an étale cover of
![]() $\text{B}\mathbf{G}_{m}^{r}$
corresponds to a
$\text{B}\mathbf{G}_{m}^{r}$
corresponds to a
![]() $\mathbf{G}_{m}^{r}$
-equivariant étale cover
$\mathbf{G}_{m}^{r}$
-equivariant étale cover
![]() ${\mathcal{W}}\rightarrow \operatorname{Spec}k$
. This is a scheme of the form
${\mathcal{W}}\rightarrow \operatorname{Spec}k$
. This is a scheme of the form
![]() ${\mathcal{W}}=\coprod _{W}\operatorname{Spec}k$
with
${\mathcal{W}}=\coprod _{W}\operatorname{Spec}k$
with
![]() $W$
a finite set. Since
$W$
a finite set. Since
![]() $\mathbf{G}_{m}^{r}$
is connected it acts trivially on
$\mathbf{G}_{m}^{r}$
is connected it acts trivially on
![]() $W$
, hence any
$W$
, hence any
![]() $w\in W$
provides an equivariant splitting
$w\in W$
provides an equivariant splitting
![]() $\operatorname{Spec}k\rightarrow {\mathcal{W}}$
.◻
$\operatorname{Spec}k\rightarrow {\mathcal{W}}$
.◻
Corollary 2.2.7. Let
![]() $F_{\unicode[STIX]{x1D70E}}$
be the set of faces of
$F_{\unicode[STIX]{x1D70E}}$
be the set of faces of
![]() $\unicode[STIX]{x1D70E}$
, partially ordered by inclusion. Then the category of étale sheaves on
$\unicode[STIX]{x1D70E}$
, partially ordered by inclusion. Then the category of étale sheaves on
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
may be identified with the category of presheaves on
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
may be identified with the category of presheaves on
![]() $F_{\unicode[STIX]{x1D70E}}$
.
$F_{\unicode[STIX]{x1D70E}}$
.
Proof. We may identify the elements of
![]() $F_{\unicode[STIX]{x1D70E}}$
with the strata of
$F_{\unicode[STIX]{x1D70E}}$
with the strata of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Under this identification, inclusion of faces corresponds to specialization. We now apply the standard description of sheaves that are constructible with respect to a fixed stratification (see [Reference Artin, Grothendieck and VerdierSGA4, Théorème 9.5.4] for the case of two strata; the general case is an immediate induction). ◻
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Under this identification, inclusion of faces corresponds to specialization. We now apply the standard description of sheaves that are constructible with respect to a fixed stratification (see [Reference Artin, Grothendieck and VerdierSGA4, Théorème 9.5.4] for the case of two strata; the general case is an immediate induction). ◻
Corollary 2.2.8. Let
![]() $z$
be the unique closed point of
$z$
be the unique closed point of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. If
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. If
![]() ${\mathcal{Y}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is étale and representable then the restriction map
${\mathcal{Y}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is étale and representable then the restriction map
is a bijection.
Proof. Under the identification from the last corollary,
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
itself corresponds to the presheaf with constant value a singleton. Therefore
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
itself corresponds to the presheaf with constant value a singleton. Therefore
![]() $\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},{\mathcal{Y}})$
is determined by its value on the initial object of the category
$\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\unicode[STIX]{x1D70E}},{\mathcal{Y}})$
is determined by its value on the initial object of the category
![]() $F_{\unicode[STIX]{x1D70E}}$
, which corresponds to the closed stratum of
$F_{\unicode[STIX]{x1D70E}}$
, which corresponds to the closed stratum of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
.◻
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
.◻
2.3 Artin fans
Lemma 2.3.1. If
![]() ${\mathcal{X}}$
is an algebraic stack that is representable and étale over
${\mathcal{X}}$
is an algebraic stack that is representable and étale over
![]() $\mathsf{Log}$
then
$\mathsf{Log}$
then
![]() ${\mathcal{X}}$
has a strict étale cover by Artin cones.
${\mathcal{X}}$
has a strict étale cover by Artin cones.
Proof. Let
![]() $x$
be a point of
$x$
be a point of
![]() ${\mathcal{X}}$
. By Proposition 2.2.1 there exist an Artin cone
${\mathcal{X}}$
. By Proposition 2.2.1 there exist an Artin cone
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
and a map
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
and a map
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow \mathsf{Log}$
that takes the closed point
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow \mathsf{Log}$
that takes the closed point
![]() $z$
of
$z$
of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
to the image of
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
to the image of
![]() $x$
. Let
$x$
. Let
![]() ${\mathcal{Y}}$
be the base change of
${\mathcal{Y}}$
be the base change of
![]() ${\mathcal{X}}\rightarrow \mathsf{Log}$
to
${\mathcal{X}}\rightarrow \mathsf{Log}$
to
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Then
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Then
![]() ${\mathcal{Y}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is étale and representable and contains a point
${\mathcal{Y}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is étale and representable and contains a point
![]() $y$
of
$y$
of
![]() ${\mathcal{Y}}$
lying over
${\mathcal{Y}}$
lying over
![]() $x$
in
$x$
in
![]() ${\mathcal{X}}$
and over
${\mathcal{X}}$
and over
![]() $z$
in
$z$
in
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. By Corollary 2.2.8, there is a section of
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. By Corollary 2.2.8, there is a section of
![]() ${\mathcal{Y}}$
over
${\mathcal{Y}}$
over
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
passing through
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
passing through
![]() $y$
. The image of this section in
$y$
. The image of this section in
![]() ${\mathcal{X}}$
is an étale map whose image contains
${\mathcal{X}}$
is an étale map whose image contains
![]() $x$
. Therefore
$x$
. Therefore
![]() ${\mathcal{X}}$
has a strict étale cover by Artin cones.◻
${\mathcal{X}}$
has a strict étale cover by Artin cones.◻
Definition 2.3.2.
-
(i) We will say that a logarithmic algebraic stack is an Artin fan if it has a strict, representable, étale cover by Artin cones.
-
(ii) Let
 $X$
be a logarithmically smooth logarithmic scheme. Then the tautological map
$X$
be a logarithmically smooth logarithmic scheme. Then the tautological map
 $X\rightarrow \mathsf{Log}$
is smooth. Let
$X\rightarrow \mathsf{Log}$
is smooth. Let
 ${\mathcal{X}}=\unicode[STIX]{x1D70B}_{0}(X/\mathsf{Log})$
. We call
${\mathcal{X}}=\unicode[STIX]{x1D70B}_{0}(X/\mathsf{Log})$
. We call
 ${\mathcal{X}}$
the Artin fan of
${\mathcal{X}}$
the Artin fan of
 $X$
.
$X$
.
Remark 2.3.3. Since Artin cones are étale over
![]() $\mathsf{Log}$
, so are Artin fans. As Artin cones are representable by algebraic spaces over
$\mathsf{Log}$
, so are Artin fans. As Artin cones are representable by algebraic spaces over
![]() $\mathsf{Log}$
, every strict étale morphism from an Artin cone to an Artin fan is representable by algebraic spaces. In fact, it follows from this observation and Proposition 2.3.11, below, that all morphisms from Artin cones to Artin fans are representable by algebraic spaces.
$\mathsf{Log}$
, every strict étale morphism from an Artin cone to an Artin fan is representable by algebraic spaces. In fact, it follows from this observation and Proposition 2.3.11, below, that all morphisms from Artin cones to Artin fans are representable by algebraic spaces.
Remark 2.3.4. The Artin fan of a logarithmic scheme
![]() ${\mathcal{X}}$
is representable over
${\mathcal{X}}$
is representable over
![]() $\mathsf{Log}$
so by Lemma 2.3.1, it is an Artin fan in the sense of the first part of the definition.
$\mathsf{Log}$
so by Lemma 2.3.1, it is an Artin fan in the sense of the first part of the definition.
Remark 2.3.5. In [Reference Abramovich, Chen, Marcus and WiseACMW17] we give a more general construction of Artin fans for logarithmic schemes that are not necessarily logarithmically smooth. While these satisfy the same universal property as the Artin fans introduced here, the Artin fan of a general logarithmic scheme
![]() $X$
cannot be interpreted in general as
$X$
cannot be interpreted in general as
![]() $\unicode[STIX]{x1D70B}_{0}(X/\mathsf{Log})$
. In fact, the morphism from
$\unicode[STIX]{x1D70B}_{0}(X/\mathsf{Log})$
. In fact, the morphism from
![]() $X$
to its Artin fan need not even be surjective.
$X$
to its Artin fan need not even be surjective.
Lemma 2.3.6. Let
![]() ${\mathcal{X}}$
be a connected Artin fan. Then
${\mathcal{X}}$
be a connected Artin fan. Then
![]() ${\mathcal{X}}$
has a unique open point, up to isomorphism.
${\mathcal{X}}$
has a unique open point, up to isomorphism.
Proof. As
![]() ${\mathcal{X}}$
is connected, any two open points can be linked by a chain of generizations and specializations. If
${\mathcal{X}}$
is connected, any two open points can be linked by a chain of generizations and specializations. If
![]() $u$
and
$u$
and
![]() $v$
are open points of
$v$
are open points of
![]() ${\mathcal{X}}$
with a common specialization
${\mathcal{X}}$
with a common specialization
![]() $z$
, then the images of
$z$
, then the images of
![]() $u$
and
$u$
and
![]() $v$
in
$v$
in
![]() $\mathsf{Log}$
would be open points with a common specialization. But
$\mathsf{Log}$
would be open points with a common specialization. But
![]() ${\mathcal{X}}\rightarrow \mathsf{Log}$
is étale, and
${\mathcal{X}}\rightarrow \mathsf{Log}$
is étale, and
![]() $\mathsf{Log}$
has a unique open point, so
$\mathsf{Log}$
has a unique open point, so
![]() $u$
and
$u$
and
![]() $v$
have the same image in
$v$
have the same image in
![]() $\mathsf{Log}$
. Generizations lift uniquely under étale maps, so this implies
$\mathsf{Log}$
. Generizations lift uniquely under étale maps, so this implies
![]() $u=v$
.◻
$u=v$
.◻
The Artin fan of an atomic (Definition 2.2.4) logarithmically smooth scheme is an Artin cone.
Lemma 2.3.7. Let
![]() $X$
be an atomic logarithmically smooth logarithmic scheme and let
$X$
be an atomic logarithmically smooth logarithmic scheme and let
![]() ${\mathcal{X}}$
be its Artin fan. The natural map
${\mathcal{X}}$
be its Artin fan. The natural map
![]() ${\mathcal{X}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D6E4}(X,\overline{M})^{\vee }}$
is an isomorphism.
${\mathcal{X}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D6E4}(X,\overline{M})^{\vee }}$
is an isomorphism.
Proof. Let
![]() ${\mathcal{Y}}={\mathcal{A}}_{\unicode[STIX]{x1D6E4}(X,\overline{M})^{\vee }}$
. The map
${\mathcal{Y}}={\mathcal{A}}_{\unicode[STIX]{x1D6E4}(X,\overline{M})^{\vee }}$
. The map
![]() $X\rightarrow {\mathcal{Y}}$
factors uniquely through
$X\rightarrow {\mathcal{Y}}$
factors uniquely through
![]() ${\mathcal{X}}$
by the universal property of
${\mathcal{X}}$
by the universal property of
![]() ${\mathcal{X}}$
. The fibers of the map
${\mathcal{X}}$
. The fibers of the map
![]() $X\rightarrow {\mathcal{X}}$
are precisely the connected components of the stratification of
$X\rightarrow {\mathcal{X}}$
are precisely the connected components of the stratification of
![]() $X$
by isomorphism type of the characteristic monoid. The closed stratum of
$X$
by isomorphism type of the characteristic monoid. The closed stratum of
![]() $X$
is connected by assumption, so
$X$
is connected by assumption, so
![]() ${\mathcal{X}}$
has a unique closed point. This maps to the unique closed point of
${\mathcal{X}}$
has a unique closed point. This maps to the unique closed point of
![]() ${\mathcal{Y}}$
. Therefore, by Corollary 2.2.8, there is a unique section of
${\mathcal{Y}}$
. Therefore, by Corollary 2.2.8, there is a unique section of
![]() ${\mathcal{X}}$
over
${\mathcal{X}}$
over
![]() ${\mathcal{Y}}$
. Let
${\mathcal{Y}}$
. Let
![]() ${\mathcal{X}}^{\prime }$
be the image of this section. This is an open substack of
${\mathcal{X}}^{\prime }$
be the image of this section. This is an open substack of
![]() ${\mathcal{X}}$
containing the closed point so its preimage in
${\mathcal{X}}$
containing the closed point so its preimage in
![]() $X$
is an open subscheme containing the closed stratum. This means the preimage is all of
$X$
is an open subscheme containing the closed stratum. This means the preimage is all of
![]() $X$
, and as
$X$
, and as
![]() $X\rightarrow {\mathcal{X}}$
is surjective, this means the section
$X\rightarrow {\mathcal{X}}$
is surjective, this means the section
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is surjective, and is therefore an isomorphism.◻
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is surjective, and is therefore an isomorphism.◻
Lemma 2.3.8.
-
(i) An Artin fan is quasicompact if and only if it has finitely many points.
-
(ii) An Artin fan that is representable over
 $\mathsf{Log}$
is quasiseparated.
$\mathsf{Log}$
is quasiseparated.
Proof. It is immediate that an Artin fan with finitely many points is quasicompact. Conversely, a quasicompact Artin fan has an étale cover by finitely many Artin cones, and an Artin cone has only finitely many points. This proves the first assertion.
Now suppose that
![]() ${\mathcal{X}}$
is an Artin fan whose canonical projection to
${\mathcal{X}}$
is an Artin fan whose canonical projection to
![]() $\mathsf{Log}$
is representable. We wish to show that the diagonal of
$\mathsf{Log}$
is representable. We wish to show that the diagonal of
![]() ${\mathcal{X}}$
is quasicompact. This is a local assertion on
${\mathcal{X}}$
is quasicompact. This is a local assertion on
![]() ${\mathcal{X}}\times {\mathcal{X}}$
, and
${\mathcal{X}}\times {\mathcal{X}}$
, and
![]() ${\mathcal{X}}$
has an étale cover by Artin cones, so it is sufficient to show that
${\mathcal{X}}$
has an étale cover by Artin cones, so it is sufficient to show that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is quasicompact when
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is quasicompact when
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
and
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
and
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
are étale over
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
are étale over
![]() ${\mathcal{X}}$
. We note that
${\mathcal{X}}$
. We note that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is quasiseparated since it can be presented as
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is quasiseparated since it can be presented as
![]() $[V/T]$
where
$[V/T]$
where
![]() $V$
is a toric variety and
$V$
is a toric variety and
![]() $T$
is its dense torus. Therefore it suffices to demonstrate that
$T$
is its dense torus. Therefore it suffices to demonstrate that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is quasicompact.
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is quasicompact.
We argue that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times _{\mathsf{Log}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
has finitely many points. Indeed, the fiber over a geometric point of
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\times _{\mathsf{Log}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
has finitely many points. Indeed, the fiber over a geometric point of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
, of which there are only finitely many, corresponds to the fiber of
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
, of which there are only finitely many, corresponds to the fiber of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
over a geometric point of
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
over a geometric point of
![]() $\mathsf{Log}$
. But if
$\mathsf{Log}$
. But if
![]() $s$
is the spectrum of an algebraically closed field, a morphism
$s$
is the spectrum of an algebraically closed field, a morphism
![]() $s\rightarrow \mathsf{Log}$
is a logarithmic structure
$s\rightarrow \mathsf{Log}$
is a logarithmic structure
![]() $M_{s}$
on
$M_{s}$
on
![]() $s$
, and the lifts to
$s$
, and the lifts to
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
correspond to homomorphisms
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
correspond to homomorphisms
![]() $\unicode[STIX]{x1D70E}^{\vee }\rightarrow \overline{M}_{s}$
that can be lifted to charts. These are in bijection with isomorphisms between
$\unicode[STIX]{x1D70E}^{\vee }\rightarrow \overline{M}_{s}$
that can be lifted to charts. These are in bijection with isomorphisms between
![]() $\overline{M}_{s}$
and
$\overline{M}_{s}$
and
![]() $\unicode[STIX]{x1D70C}^{\vee }$
for a face
$\unicode[STIX]{x1D70C}^{\vee }$
for a face
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\unicode[STIX]{x1D70E}$
, and there are only finitely many of these.◻
$\unicode[STIX]{x1D70E}$
, and there are only finitely many of these.◻
Corollary 2.3.9. The Artin fan of a quasicompact, logarithmically smooth logarithmic scheme is quasicompact and quasiseparated.
Proof. If
![]() ${\mathcal{X}}$
is the Artin fan of a quasicompact, logarithmically smooth logarithmic scheme
${\mathcal{X}}$
is the Artin fan of a quasicompact, logarithmically smooth logarithmic scheme
![]() $X$
then
$X$
then
![]() $X\rightarrow {\mathcal{X}}$
is surjective, so
$X\rightarrow {\mathcal{X}}$
is surjective, so
![]() ${\mathcal{X}}$
is quasicompact. By definition,
${\mathcal{X}}$
is quasicompact. By definition,
![]() ${\mathcal{X}}$
is representable over
${\mathcal{X}}$
is representable over
![]() $\mathsf{Log}$
, so it is quasiseparated as well.◻
$\mathsf{Log}$
, so it is quasiseparated as well.◻
Remark 2.3.10. It is not true that every algebraic stack that is strict and étale over
![]() $\mathsf{Log}$
has an étale cover by Artin cones. For example, let
$\mathsf{Log}$
has an étale cover by Artin cones. For example, let
![]() $\mathbf{G}_{m}$
act on
$\mathbf{G}_{m}$
act on
![]() $\mathbf{A}^{1}$
by
$\mathbf{A}^{1}$
by
![]() $t.x=t^{2}x$
. The quotient
$t.x=t^{2}x$
. The quotient
![]() ${\mathcal{Y}}$
is étale over
${\mathcal{Y}}$
is étale over
![]() $\mathsf{Log}$
when given its natural logarithmic structure. The map
$\mathsf{Log}$
when given its natural logarithmic structure. The map
![]() ${\mathcal{Y}}\rightarrow \mathsf{Log}$
factors through
${\mathcal{Y}}\rightarrow \mathsf{Log}$
factors through
![]() ${\mathcal{X}}:={\mathcal{A}}$
, the Artin fan of
${\mathcal{X}}:={\mathcal{A}}$
, the Artin fan of
![]() ${\mathcal{Y}}$
, as a
${\mathcal{Y}}$
, as a
![]() $\unicode[STIX]{x1D707}_{2}$
-gerbe. This gerbe is non-trivial because it is the stack of square roots of the tautological bundle on
$\unicode[STIX]{x1D707}_{2}$
-gerbe. This gerbe is non-trivial because it is the stack of square roots of the tautological bundle on
![]() ${\mathcal{X}}$
, and
${\mathcal{X}}$
, and
![]() $\operatorname{Pic}({\mathcal{X}})=\mathbf{Z}$
. Therefore it has no section.
$\operatorname{Pic}({\mathcal{X}})=\mathbf{Z}$
. Therefore it has no section.
On the other hand, if
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{Y}}$
were a strict étale map whose image contains the closed point then
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{Y}}$
were a strict étale map whose image contains the closed point then
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
would be a strict étale cover. But the only strict étale cover of
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
would be a strict étale cover. But the only strict étale cover of
![]() ${\mathcal{A}}$
by an Artin cone is the identity, so if
${\mathcal{A}}$
by an Artin cone is the identity, so if
![]() ${\mathcal{Y}}$
had a cover by an Artin cone, the cover would be a section of
${\mathcal{Y}}$
had a cover by an Artin cone, the cover would be a section of
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
, and we have just seen there is no such section.
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
, and we have just seen there is no such section.
Proposition 2.3.11. Let
![]() ${\mathcal{X}}$
be an Artin fan and let
${\mathcal{X}}$
be an Artin fan and let
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
be a morphism of Artin fans. Then there is an initial example of a strict étale map
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
be a morphism of Artin fans. Then there is an initial example of a strict étale map
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{X}}$
and a factorization of the morphism
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{X}}$
and a factorization of the morphism
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
through a morphism
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
through a morphism
![]() $u:{\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
.
$u:{\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
.
Proof. Pick a strict, étale map
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{X}}$
whose image contains the image of the closed point of
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{X}}$
whose image contains the image of the closed point of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Pulling back to
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Pulling back to
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, we get an étale cover
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, we get an étale cover
![]() ${\mathcal{Y}}$
of
${\mathcal{Y}}$
of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, which necessarily has a section by extending any section over the closed point. We can then replace
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, which necessarily has a section by extending any section over the closed point. We can then replace
![]() $\unicode[STIX]{x1D70F}$
with its smallest face that contains the image of
$\unicode[STIX]{x1D70F}$
with its smallest face that contains the image of
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Now we argue that the factorization is initial. Suppose that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}$
is another factorization. Then we obtain a commutative square of solid arrows:
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}$
is another factorization. Then we obtain a commutative square of solid arrows:

We seek a dashed arrow completing the diagram. As the closed point of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
maps to the closed point of
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
maps to the closed point of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
by assumption, the strict map
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
by assumption, the strict map
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}$
covers the image of
${\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}$
covers the image of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
. Therefore
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
. Therefore
![]() $\unicode[STIX]{x1D71B}:{\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is an étale cover with a given section
$\unicode[STIX]{x1D71B}:{\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is an étale cover with a given section
![]() $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D6FE},u)$
over
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D6FE},u)$
over
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
.
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
.
Note that the composite morphism
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}\rightarrow \mathsf{Log}$
is the tautological morphism, which is representable (Lemma 2.2.1). Hence
${\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}\rightarrow \mathsf{Log}$
is the tautological morphism, which is representable (Lemma 2.2.1). Hence
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}$
is necessarily representable.
${\mathcal{A}}_{\unicode[STIX]{x1D70F}^{\prime }}\rightarrow {\mathcal{X}}$
is necessarily representable.
The closed point
![]() $p_{\unicode[STIX]{x1D70E}}\in {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
maps to the closed point
$p_{\unicode[STIX]{x1D70E}}\in {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
maps to the closed point
![]() $u(p_{\unicode[STIX]{x1D70E}})=p_{\unicode[STIX]{x1D70F}}\in {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
. It follows that the point
$u(p_{\unicode[STIX]{x1D70E}})=p_{\unicode[STIX]{x1D70F}}\in {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
. It follows that the point
![]() $\unicode[STIX]{x1D709}(p_{\unicode[STIX]{x1D70E}})$
lies over
$\unicode[STIX]{x1D709}(p_{\unicode[STIX]{x1D70E}})$
lies over
![]() $p_{\unicode[STIX]{x1D70F}}$
, hence by Corollary 2.2.8 there is a unique section
$p_{\unicode[STIX]{x1D70F}}$
, hence by Corollary 2.2.8 there is a unique section
![]() $\unicode[STIX]{x1D70D}=(\unicode[STIX]{x1D719},\text{id})$
of
$\unicode[STIX]{x1D70D}=(\unicode[STIX]{x1D719},\text{id})$
of
![]() $\unicode[STIX]{x1D71B}$
sending
$\unicode[STIX]{x1D71B}$
sending
![]() $p_{\unicode[STIX]{x1D70F}}\mapsto \unicode[STIX]{x1D709}(p_{\unicode[STIX]{x1D70E}})$
. Moreover, the pullback
$p_{\unicode[STIX]{x1D70F}}\mapsto \unicode[STIX]{x1D709}(p_{\unicode[STIX]{x1D70E}})$
. Moreover, the pullback
![]() $\unicode[STIX]{x1D70D}\circ u$
of
$\unicode[STIX]{x1D70D}\circ u$
of
![]() $\unicode[STIX]{x1D70D}$
to
$\unicode[STIX]{x1D70D}$
to
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is determined by its restriction to
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is determined by its restriction to
![]() $p_{\unicode[STIX]{x1D70E}}$
, and thus coincides with
$p_{\unicode[STIX]{x1D70E}}$
, and thus coincides with
![]() $\unicode[STIX]{x1D709}$
. Therefore
$\unicode[STIX]{x1D709}$
. Therefore
![]() $\unicode[STIX]{x1D719}$
extends
$\unicode[STIX]{x1D719}$
extends
![]() $\unicode[STIX]{x1D6FE}$
, as needed.◻
$\unicode[STIX]{x1D6FE}$
, as needed.◻
Corollary 2.3.12. Let
![]() ${\mathcal{Y}}$
be an Artin fan,
${\mathcal{Y}}$
be an Artin fan,
![]() $\unicode[STIX]{x1D719}:{\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
a strict étale map and
$\unicode[STIX]{x1D719}:{\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
a strict étale map and
![]() $b:{\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
its barycenter. Then
$b:{\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
its barycenter. Then
![]() $\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719})=\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719}b)$
.
$\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719})=\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719}b)$
.
Proof. We have

In the first equality, we identify
![]() $\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719})$
as the set of dashed arrows making the triangle 2-commute. For the second equality, we observe that every automorphism of
$\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719})$
as the set of dashed arrows making the triangle 2-commute. For the second equality, we observe that every automorphism of
![]() $\unicode[STIX]{x1D70F}$
commutes with the inclusion of the barycenter. The third equality is Proposition 2.3.11. And the fourth equality is the identification of
$\unicode[STIX]{x1D70F}$
commutes with the inclusion of the barycenter. The third equality is Proposition 2.3.11. And the fourth equality is the identification of
![]() $\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719}b)$
with the set of 2-commutative squares as implied by the diagram.◻
$\operatorname{Aut}_{{\mathcal{Y}}}(\unicode[STIX]{x1D719}b)$
with the set of 2-commutative squares as implied by the diagram.◻
Example 2.3.13. Consider the open substack
![]() ${\mathcal{Y}}$
of
${\mathcal{Y}}$
of
![]() $\mathsf{Log}$
parameterizing those logarithmic structures that admit charts by
$\mathsf{Log}$
parameterizing those logarithmic structures that admit charts by
![]() $\mathbf{N}^{2}$
. This is the Artin fan of the Whitney umbrella [Reference Abramovich, Chen, Marcus, Ulirsch, Wise, Baker and PayneACMUW, § 4.6.2]. For any pair of natural numbers
$\mathbf{N}^{2}$
. This is the Artin fan of the Whitney umbrella [Reference Abramovich, Chen, Marcus, Ulirsch, Wise, Baker and PayneACMUW, § 4.6.2]. For any pair of natural numbers
![]() $(a,b)$
we have a map
$(a,b)$
we have a map
![]() $\mathbf{N}^{2}\rightarrow \mathbf{N}$
. Viewing
$\mathbf{N}^{2}\rightarrow \mathbf{N}$
. Viewing
![]() $\mathbf{N}$
as the set of global sections of the characteristic monoid of
$\mathbf{N}$
as the set of global sections of the characteristic monoid of
![]() ${\mathcal{A}}$
, this induces a logarithmic structure
${\mathcal{A}}$
, this induces a logarithmic structure
![]() $M(a,b)$
on
$M(a,b)$
on
![]() ${\mathcal{A}}$
with a chart by
${\mathcal{A}}$
with a chart by
![]() $\mathbf{N}^{2}$
.
$\mathbf{N}^{2}$
.
If
![]() $a=b=0$
then the
$a=b=0$
then the
![]() ${\mathcal{A}}\rightarrow {\mathcal{Y}}$
factors through the open point. If one of
${\mathcal{A}}\rightarrow {\mathcal{Y}}$
factors through the open point. If one of
![]() $a$
or
$a$
or
![]() $b$
is zero but the other is not then
$b$
is zero but the other is not then
![]() ${\mathcal{A}}\rightarrow {\mathcal{Y}}$
is strict, hence is its own initial factorization. If
${\mathcal{A}}\rightarrow {\mathcal{Y}}$
is strict, hence is its own initial factorization. If
![]() $a\neq b$
and neither is zero then we have two factorizations
$a\neq b$
and neither is zero then we have two factorizations
![]() ${\mathcal{A}}\rightarrow {\mathcal{A}}^{2}$
corresponding to the two maps
${\mathcal{A}}\rightarrow {\mathcal{A}}^{2}$
corresponding to the two maps
![]() $(a,b),(b,a):\mathbf{N}^{2}\rightarrow \mathbf{N}$
. There is a unique isomorphism
$(a,b),(b,a):\mathbf{N}^{2}\rightarrow \mathbf{N}$
. There is a unique isomorphism
![]() $\unicode[STIX]{x1D6FE}:{\mathcal{A}}^{2}\rightarrow {\mathcal{A}}^{2}$
(induced from the automorphism
$\unicode[STIX]{x1D6FE}:{\mathcal{A}}^{2}\rightarrow {\mathcal{A}}^{2}$
(induced from the automorphism
![]() $\mathbf{N}^{2}\rightarrow \mathbf{N}^{2}$
sending
$\mathbf{N}^{2}\rightarrow \mathbf{N}^{2}$
sending
![]() $(x,y)$
to
$(x,y)$
to
![]() $(y,x)$
) making the diagram
$(y,x)$
) making the diagram

commute.
The final case is where
![]() $a=b\neq 0$
. In this case we have a single map
$a=b\neq 0$
. In this case we have a single map
![]() ${\mathcal{A}}\xrightarrow[{}]{(a,a)}{\mathcal{A}}^{2}$
inducing
${\mathcal{A}}\xrightarrow[{}]{(a,a)}{\mathcal{A}}^{2}$
inducing
![]() $M(a,a)$
by pullback. However, a commutative square of solid lines
$M(a,a)$
by pullback. However, a commutative square of solid lines

involves the specification of an isomorphism between
![]() $M(a,a)$
and itself, commuting with the map to
$M(a,a)$
and itself, commuting with the map to
![]() $\mathbf{N}$
. There are two choices of this isomorphism, the identity and the map that exchanges the generators. Each of these is induced from a unique dashed arrow making the diagram commute.
$\mathbf{N}$
. There are two choices of this isomorphism, the identity and the map that exchanges the generators. Each of these is induced from a unique dashed arrow making the diagram commute.
2.4 Proper morphisms of Artin fans
We note that the formation of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is functorial in
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is functorial in
![]() $\unicode[STIX]{x1D70E}$
. In particular, if
$\unicode[STIX]{x1D70E}$
. In particular, if
![]() $\unicode[STIX]{x1D70E}$
is a face of
$\unicode[STIX]{x1D70E}$
is a face of
![]() $\unicode[STIX]{x1D70F}$
then
$\unicode[STIX]{x1D70F}$
then
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is an open embedding. If
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is an open embedding. If
![]() $\unicode[STIX]{x1D6F4}$
is a fan then we can define
$\unicode[STIX]{x1D6F4}$
is a fan then we can define
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D6F4}}$
by gluing the
${\mathcal{A}}_{\unicode[STIX]{x1D6F4}}$
by gluing the
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
associated to the
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
associated to the
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
along their common faces. If
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
along their common faces. If
![]() $V$
is the toric variety associated to
$V$
is the toric variety associated to
![]() $\unicode[STIX]{x1D6F4}$
then
$\unicode[STIX]{x1D6F4}$
then
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D6F4}}\simeq [V/T]$
where
${\mathcal{A}}_{\unicode[STIX]{x1D6F4}}\simeq [V/T]$
where
![]() $T$
is the dense torus of
$T$
is the dense torus of
![]() $V$
.
$V$
.
We observe that
![]() $\operatorname{Hom}({\mathcal{A}},{\mathcal{A}}_{\unicode[STIX]{x1D6F4}})=|\unicode[STIX]{x1D6F4}|$
, where, by definition,
$\operatorname{Hom}({\mathcal{A}},{\mathcal{A}}_{\unicode[STIX]{x1D6F4}})=|\unicode[STIX]{x1D6F4}|$
, where, by definition,
![]() $|\unicode[STIX]{x1D6F4}|=\bigcup _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D70E}$
.
$|\unicode[STIX]{x1D6F4}|=\bigcup _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D70E}$
.
If a fan
![]() $\unicode[STIX]{x1D6F4}$
is a subdivision of
$\unicode[STIX]{x1D6F4}$
is a subdivision of
![]() $\unicode[STIX]{x1D70F}$
then we call the map
$\unicode[STIX]{x1D70F}$
then we call the map
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D6F4}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
a subdivision. If
${\mathcal{A}}_{\unicode[STIX]{x1D6F4}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
a subdivision. If
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is a morphism of Artin fans such that
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is a morphism of Artin fans such that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\times _{{\mathcal{X}}}{\mathcal{Y}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is a subdivision for every strict logarithmic map
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\times _{{\mathcal{X}}}{\mathcal{Y}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
is a subdivision for every strict logarithmic map
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{X}}$
then we call
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{X}}$
then we call
![]() ${\mathcal{Y}}$
a subdivision of
${\mathcal{Y}}$
a subdivision of
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
Theorem 2.4.1. Let
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
be a representable morphism of connected Artin fans. The following are equivalent:
$f:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
be a representable morphism of connected Artin fans. The following are equivalent:
-
(i)
 $f$
is proper;
$f$
is proper; -
(ii) for any strict logarithmic map
 ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
, the map
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
, the map
 ${\mathcal{Y}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is proper;
${\mathcal{Y}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is proper; -
(iii) for any strict logarithmic map
 ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
, the map
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
, the map
 ${\mathcal{Y}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is a subdivision;
${\mathcal{Y}}\times _{{\mathcal{X}}}{\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is a subdivision; -
(iv)
 $f$
is a subdivision;
$f$
is a subdivision; -
(v) every map
 ${\mathcal{A}}\rightarrow {\mathcal{X}}$
lifts uniquely along
${\mathcal{A}}\rightarrow {\mathcal{X}}$
lifts uniquely along
 $f$
: any commutative diagram of logarithmic morphisms(2)admits a unique completion by a dashed arrow.
$f$
: any commutative diagram of logarithmic morphisms(2)admits a unique completion by a dashed arrow.
Proof. Item (iii) is the definition of subdivision, hence equivalent to (iv). The equivalence of (i) and (ii) follows by étale descent from the fact that the strict logarithmic maps
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
form an étale cover.
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
form an étale cover.
For the equivalence of (ii) and (iii), it is sufficient to assume
![]() ${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Present
${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Present
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
as
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
as
![]() $[V/T]$
, where
$[V/T]$
, where
![]() $V$
is a toric variety and
$V$
is a toric variety and
![]() $T$
is its dense torus. Pulling back via
$T$
is its dense torus. Pulling back via
![]() $V\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, we obtain a map
$V\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, we obtain a map
![]() $W\rightarrow V$
whose properness is equivalent to that of
$W\rightarrow V$
whose properness is equivalent to that of
![]() ${\mathcal{Y}}$
over
${\mathcal{Y}}$
over
![]() ${\mathcal{X}}$
, as well as an action of
${\mathcal{X}}$
, as well as an action of
![]() $T$
on
$T$
on
![]() $W$
whose quotient is
$W$
whose quotient is
![]() ${\mathcal{Y}}$
. But
${\mathcal{Y}}$
. But
![]() ${\mathcal{Y}}$
has a unique open point by Lemma 2.3.6, which corresponds to a dense orbit of
${\mathcal{Y}}$
has a unique open point by Lemma 2.3.6, which corresponds to a dense orbit of
![]() $T$
. Therefore
$T$
. Therefore
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is proper if and only if
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is proper if and only if
![]() $W\rightarrow V$
is a proper morphism of toric varieties with the same dense torus. By [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, § I.2, Theorem 8] or [Reference FultonFul93, § 2.4, Proposition] this is equivalent to the condition that the fan of
$W\rightarrow V$
is a proper morphism of toric varieties with the same dense torus. By [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, § I.2, Theorem 8] or [Reference FultonFul93, § 2.4, Proposition] this is equivalent to the condition that the fan of
![]() $W$
subdivides
$W$
subdivides
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
We check that (iii) implies (v). As any map
![]() ${\mathcal{A}}\rightarrow {\mathcal{X}}$
factors through some strict
${\mathcal{A}}\rightarrow {\mathcal{X}}$
factors through some strict
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
(see Proposition 2.3.11), it is sufficient to assume that
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}\rightarrow {\mathcal{X}}$
(see Proposition 2.3.11), it is sufficient to assume that
![]() ${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. We can thus assume
${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. We can thus assume
![]() ${\mathcal{Y}}={\mathcal{A}}_{\unicode[STIX]{x1D6F4}}$
for some subdivision
${\mathcal{Y}}={\mathcal{A}}_{\unicode[STIX]{x1D6F4}}$
for some subdivision
![]() $\unicode[STIX]{x1D6F4}$
of
$\unicode[STIX]{x1D6F4}$
of
![]() $\unicode[STIX]{x1D70E}$
. Consider a diagram of solid lines, (2). A lift completing the upper triangle in (2) amounts to giving a map
$\unicode[STIX]{x1D70E}$
. Consider a diagram of solid lines, (2). A lift completing the upper triangle in (2) amounts to giving a map
![]() ${\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D6F4}}$
, which, as we observed above, is equivalent to giving a point of
${\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D6F4}}$
, which, as we observed above, is equivalent to giving a point of
![]() $|\unicode[STIX]{x1D6F4}|$
. But
$|\unicode[STIX]{x1D6F4}|$
. But
![]() $|\unicode[STIX]{x1D6F4}|\rightarrow |\unicode[STIX]{x1D70E}|$
is a bijection, by definition of a subdivision, so there is a unique such completion making the triangle commute.
$|\unicode[STIX]{x1D6F4}|\rightarrow |\unicode[STIX]{x1D70E}|$
is a bijection, by definition of a subdivision, so there is a unique such completion making the triangle commute.
Now we show that (v) implies (iii). Suppose that
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
satisfies the lifting criterion of (v). We assume without loss of generality that
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
satisfies the lifting criterion of (v). We assume without loss of generality that
![]() ${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Let
${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. Let
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
be a strict map. We argue that the map
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
be a strict map. We argue that the map
![]() $\unicode[STIX]{x1D70F}\rightarrow \unicode[STIX]{x1D70E}$
induced from the composition
$\unicode[STIX]{x1D70F}\rightarrow \unicode[STIX]{x1D70E}$
induced from the composition
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}\rightarrow {\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is an injection. Let
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}\rightarrow {\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
is an injection. Let
![]() $\unicode[STIX]{x1D70F}^{\circ }$
denote the interior of
$\unicode[STIX]{x1D70F}^{\circ }$
denote the interior of
![]() $\unicode[STIX]{x1D70F}$
, viewed as the set
$\unicode[STIX]{x1D70F}$
, viewed as the set
![]() $N_{\unicode[STIX]{x1D70E}}\cap \unicode[STIX]{x1D70E}_{\mathbb{R}}$
of lattice points of a rational polyhedral cone
$N_{\unicode[STIX]{x1D70E}}\cap \unicode[STIX]{x1D70E}_{\mathbb{R}}$
of lattice points of a rational polyhedral cone
![]() $\unicode[STIX]{x1D70E}_{\mathbb{R}}$
. It is sufficient to show that
$\unicode[STIX]{x1D70E}_{\mathbb{R}}$
. It is sufficient to show that
![]() $\unicode[STIX]{x1D70F}^{\circ }\rightarrow \unicode[STIX]{x1D70E}$
is injective. Suppose that
$\unicode[STIX]{x1D70F}^{\circ }\rightarrow \unicode[STIX]{x1D70E}$
is injective. Suppose that
![]() $t,u\in \unicode[STIX]{x1D70F}^{\circ }$
have the same image in
$t,u\in \unicode[STIX]{x1D70F}^{\circ }$
have the same image in
![]() $\unicode[STIX]{x1D70E}$
. These correspond to maps
$\unicode[STIX]{x1D70E}$
. These correspond to maps
![]() $t,u:{\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
with the same image in
$t,u:{\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
with the same image in
![]() ${\mathcal{X}}$
. But
${\mathcal{X}}$
. But
![]() $\operatorname{Hom}({\mathcal{A}},{\mathcal{Y}})\rightarrow \operatorname{Hom}({\mathcal{A}},{\mathcal{X}})$
is a bijection, so
$\operatorname{Hom}({\mathcal{A}},{\mathcal{Y}})\rightarrow \operatorname{Hom}({\mathcal{A}},{\mathcal{X}})$
is a bijection, so
![]() $t$
and
$t$
and
![]() $u$
induce the same map
$u$
induce the same map
![]() ${\mathcal{A}}\rightarrow {\mathcal{Y}}$
. In other words, we have a commutative square of solid arrows:
${\mathcal{A}}\rightarrow {\mathcal{Y}}$
. In other words, we have a commutative square of solid arrows:

But
![]() $t$
and
$t$
and
![]() $u$
are interior points of
$u$
are interior points of
![]() $\unicode[STIX]{x1D70F}$
, so
$\unicode[STIX]{x1D70F}$
, so
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
is the minimal strict factorization of either of the compositions
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
is the minimal strict factorization of either of the compositions
so that Proposition 2.3.11 implies there is a unique automorphism of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
over
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
over
![]() ${\mathcal{Y}}$
sending
${\mathcal{Y}}$
sending
![]() $u$
to
$u$
to
![]() $t$
(the dashed arrow in the diagram). By Corollary 2.3.12,
$t$
(the dashed arrow in the diagram). By Corollary 2.3.12,
where
![]() $b$
denotes the barycenter of
$b$
denotes the barycenter of
![]() $\unicode[STIX]{x1D70F}$
and the corresponding map
$\unicode[STIX]{x1D70F}$
and the corresponding map
![]() ${\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
. But
${\mathcal{A}}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70F}}$
. But
![]() $\operatorname{Aut}_{{\mathcal{Y}}}(b)$
injects into
$\operatorname{Aut}_{{\mathcal{Y}}}(b)$
injects into
![]() $\operatorname{Aut}_{{\mathcal{X}}}(b)$
, because
$\operatorname{Aut}_{{\mathcal{X}}}(b)$
, because
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
was assumed to be representable. Therefore this automorphism is the identity and
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
was assumed to be representable. Therefore this automorphism is the identity and
![]() $t=u$
.
$t=u$
.
We conclude that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
is injective. As it is also strict, it is an open embedding and
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
is injective. As it is also strict, it is an open embedding and
![]() $\unicode[STIX]{x1D70F}\subset \unicode[STIX]{x1D70E}$
is a subcone. A strict family of maps
$\unicode[STIX]{x1D70F}\subset \unicode[STIX]{x1D70E}$
is a subcone. A strict family of maps
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
therefore corresponds to a family of subcones
${\mathcal{A}}_{\unicode[STIX]{x1D70F}}\rightarrow {\mathcal{Y}}$
therefore corresponds to a family of subcones
![]() $\unicode[STIX]{x1D70F}\subset \unicode[STIX]{x1D70E}$
. Each lattice point of
$\unicode[STIX]{x1D70F}\subset \unicode[STIX]{x1D70E}$
. Each lattice point of
![]() $\unicode[STIX]{x1D70E}$
must be contained in at least one
$\unicode[STIX]{x1D70E}$
must be contained in at least one
![]() $\unicode[STIX]{x1D70F}$
. By Proposition 2.3.11, there is a minimal such cone, up to inclusion of faces. It follows, therefore, that
$\unicode[STIX]{x1D70F}$
. By Proposition 2.3.11, there is a minimal such cone, up to inclusion of faces. It follows, therefore, that
![]() ${\mathcal{Y}}$
is representable by a subdivision of
${\mathcal{Y}}$
is representable by a subdivision of
![]() $\unicode[STIX]{x1D70E}$
.◻
$\unicode[STIX]{x1D70E}$
.◻
2.5 A substitute for functoriality
By construction the map
![]() $X\rightarrow {\mathcal{X}}$
is strict if we give
$X\rightarrow {\mathcal{X}}$
is strict if we give
![]() ${\mathcal{X}}$
the logarithmic structure associated to the map
${\mathcal{X}}$
the logarithmic structure associated to the map
![]() ${\mathcal{X}}\rightarrow \mathsf{Log}$
. The universal property characterizing
${\mathcal{X}}\rightarrow \mathsf{Log}$
. The universal property characterizing
![]() ${\mathcal{X}}$
implies that
${\mathcal{X}}$
implies that
![]() ${\mathcal{X}}$
, and the map
${\mathcal{X}}$
, and the map
![]() $X\rightarrow {\mathcal{X}}$
, are functorial in
$X\rightarrow {\mathcal{X}}$
, are functorial in
![]() $X$
with respect to strict morphisms. The same functoriality does not hold for arbitrary morphisms (see [Reference Abramovich, Chen, Marcus, Ulirsch, Wise, Baker and PayneACMUW, § 5.4.1]) and we do not know in what generality Artin fans should be functorial. We demonstrate a weaker sort of functoriality below.
$X$
with respect to strict morphisms. The same functoriality does not hold for arbitrary morphisms (see [Reference Abramovich, Chen, Marcus, Ulirsch, Wise, Baker and PayneACMUW, § 5.4.1]) and we do not know in what generality Artin fans should be functorial. We demonstrate a weaker sort of functoriality below.
Suppose that
![]() $Y\rightarrow X$
is a logarithmically smooth morphism of logarithmically smooth schemes. Let
$Y\rightarrow X$
is a logarithmically smooth morphism of logarithmically smooth schemes. Let
![]() ${\mathcal{X}}$
be the Artin fan of
${\mathcal{X}}$
be the Artin fan of
![]() $X$
. Then the morphism of logarithmic algebraic stacks
$X$
. Then the morphism of logarithmic algebraic stacks
![]() $Y\rightarrow {\mathcal{X}}$
corresponds to a smooth morphism of algebraic stacks
$Y\rightarrow {\mathcal{X}}$
corresponds to a smooth morphism of algebraic stacks
![]() $Y\rightarrow \mathsf{Log}({\mathcal{X}})$
. Let
$Y\rightarrow \mathsf{Log}({\mathcal{X}})$
. Let
![]() ${\mathcal{Y}}=\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
. Then by composition we have a map from
${\mathcal{Y}}=\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
. Then by composition we have a map from
![]() ${\mathcal{Y}}$
to
${\mathcal{Y}}$
to
![]() ${\mathcal{X}}$
:
${\mathcal{X}}$
:
We verify below that
![]() ${\mathcal{Y}}$
is an Artin fan. First, note that there is a map
${\mathcal{Y}}$
is an Artin fan. First, note that there is a map
![]() $\mathsf{Log}({\mathcal{X}})\rightarrow \mathsf{Log}$
, defined by taking a scheme
$\mathsf{Log}({\mathcal{X}})\rightarrow \mathsf{Log}$
, defined by taking a scheme
![]() $S$
with logarithmic structure
$S$
with logarithmic structure
![]() $M_{S}$
and morphism
$M_{S}$
and morphism
![]() $(S,M_{S})\rightarrow {\mathcal{X}}$
and forgetting the map.
$(S,M_{S})\rightarrow {\mathcal{X}}$
and forgetting the map.
Lemma 2.5.1. For any Artin cone
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, the map
${\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, the map
![]() $\mathsf{Log}({\mathcal{A}}_{\unicode[STIX]{x1D70E}})\rightarrow \mathsf{Log}$
is strict and étale.
$\mathsf{Log}({\mathcal{A}}_{\unicode[STIX]{x1D70E}})\rightarrow \mathsf{Log}$
is strict and étale.
Proof. Strictness is immediate from the definitions of the logarithmic structures. The fiber of
![]() $\mathsf{Log}({\mathcal{X}})\rightarrow \mathsf{Log}$
over
$\mathsf{Log}({\mathcal{X}})\rightarrow \mathsf{Log}$
over
![]() $(S,M_{S})$
is the space of logarithmic maps
$(S,M_{S})$
is the space of logarithmic maps
![]() $(S,M_{S})\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, which may be identified with
$(S,M_{S})\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
, which may be identified with
![]() $\operatorname{Hom}(\unicode[STIX]{x1D70E}^{\vee },\unicode[STIX]{x1D6E4}(S,\overline{M}_{S}))$
. Since
$\operatorname{Hom}(\unicode[STIX]{x1D70E}^{\vee },\unicode[STIX]{x1D6E4}(S,\overline{M}_{S}))$
. Since
![]() $\overline{M}_{S}$
is a constructible étale sheaf, these maps may be identified with the sections of the espace étalé of the étale sheaf
$\overline{M}_{S}$
is a constructible étale sheaf, these maps may be identified with the sections of the espace étalé of the étale sheaf
![]() $\text{}\underline{\operatorname{Hom}}(\unicode[STIX]{x1D70E}^{\vee },\unicode[STIX]{x1D6E4}(S,\overline{M}_{S}))$
on
$\text{}\underline{\operatorname{Hom}}(\unicode[STIX]{x1D70E}^{\vee },\unicode[STIX]{x1D6E4}(S,\overline{M}_{S}))$
on
![]() $S$
.◻
$S$
.◻
Corollary 2.5.2. Suppose
![]() $Y$
is logarithmically smooth over an Artin cone
$Y$
is logarithmically smooth over an Artin cone
![]() ${\mathcal{X}}$
. Then
${\mathcal{X}}$
. Then
![]() $\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))\simeq \unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log})$
.
$\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))\simeq \unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log})$
.
Proof. Since
![]() $\mathsf{Log}({\mathcal{X}})$
is strict and étale over
$\mathsf{Log}({\mathcal{X}})$
is strict and étale over
![]() $\mathsf{Log}$
, these stacks have the same universal property.◻
$\mathsf{Log}$
, these stacks have the same universal property.◻
Corollary 2.5.3. Let
![]() ${\mathcal{X}}$
be an Artin fan and
${\mathcal{X}}$
be an Artin fan and
![]() $Y\rightarrow {\mathcal{X}}$
a logarithmically smooth morphism. Then
$Y\rightarrow {\mathcal{X}}$
a logarithmically smooth morphism. Then
![]() $\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
is an Artin fan.
$\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
is an Artin fan.
Proof. Let
![]() ${\mathcal{Y}}=\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
. We must show that
${\mathcal{Y}}=\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
. We must show that
![]() ${\mathcal{Y}}$
has a strict étale cover by Artin cones. Since
${\mathcal{Y}}$
has a strict étale cover by Artin cones. Since
![]() ${\mathcal{X}}$
has a strict, étale cover by Artin cones, and
${\mathcal{X}}$
has a strict, étale cover by Artin cones, and
![]() $\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
commutes with base change in
$\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
commutes with base change in
![]() ${\mathcal{X}}$
, we may assume that
${\mathcal{X}}$
, we may assume that
![]() ${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. In this case, it follows from the previous corollary.◻
${\mathcal{X}}={\mathcal{A}}_{\unicode[STIX]{x1D70E}}$
. In this case, it follows from the previous corollary.◻
Definition 2.5.4. Let
![]() $Y\rightarrow X$
be a logarithmically smooth morphism and let
$Y\rightarrow X$
be a logarithmically smooth morphism and let
![]() ${\mathcal{X}}$
be the Artin fan of
${\mathcal{X}}$
be the Artin fan of
![]() $X$
. We call
$X$
. We call
![]() $\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
the relative Artin fan of
$\unicode[STIX]{x1D70B}_{0}(Y/\mathsf{Log}({\mathcal{X}}))$
the relative Artin fan of
![]() $Y$
over
$Y$
over
![]() $X$
.
$X$
.
We record the following lemma for later reference.
Lemma 2.5.5. Let
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
be the morphism of Artin fans associated to a logarithmically smooth morphism of logarithmically smooth logarithmic schemes. Then
$f:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
be the morphism of Artin fans associated to a logarithmically smooth morphism of logarithmically smooth logarithmic schemes. Then
![]() $f$
is quasiseparated, locally of finite presentation, and its fibers over field-valued points have affine stabilizers.
$f$
is quasiseparated, locally of finite presentation, and its fibers over field-valued points have affine stabilizers.
Proof. We note that all of these properties are étale local in
![]() ${\mathcal{X}}$
. We can therefore assume that
${\mathcal{X}}$
. We can therefore assume that
![]() ${\mathcal{X}}$
is an Artin cone and therefore that
${\mathcal{X}}$
is an Artin cone and therefore that
![]() ${\mathcal{Y}}$
is the Artin fan of a logarithmically smooth logarithmic scheme. Then
${\mathcal{Y}}$
is the Artin fan of a logarithmically smooth logarithmic scheme. Then
![]() ${\mathcal{Y}}$
is quasiseparated by Corollary 2.3.9 and it is locally of finite presentation because it has an étale cover by Artin cones by Definition 2.3.2. In this case,
${\mathcal{Y}}$
is quasiseparated by Corollary 2.3.9 and it is locally of finite presentation because it has an étale cover by Artin cones by Definition 2.3.2. In this case,
![]() ${\mathcal{Y}}$
is representable over
${\mathcal{Y}}$
is representable over
![]() $\mathsf{Log}$
, so if
$\mathsf{Log}$
, so if
![]() $k$
is a field, the stabilizer group of
$k$
is a field, the stabilizer group of
![]() $y\in {\mathcal{Y}}(k)$
is a closed subgroup of the automorphism group of the image of
$y\in {\mathcal{Y}}(k)$
is a closed subgroup of the automorphism group of the image of
![]() $y$
in
$y$
in
![]() $\mathsf{Log}$
. The kernel of the map
$\mathsf{Log}$
. The kernel of the map
![]() $\operatorname{Aut}_{{\mathcal{Y}}}(y)\rightarrow \operatorname{Aut}_{{\mathcal{X}}}(f(y))$
is a closed subgroup of this finite group, hence is affine.◻
$\operatorname{Aut}_{{\mathcal{Y}}}(y)\rightarrow \operatorname{Aut}_{{\mathcal{X}}}(f(y))$
is a closed subgroup of this finite group, hence is affine.◻
2.6 Modifications
We will only consider logarithmic modifications of logarithmically smooth logarithmic schemes here, so we are content to define logarithmic modifications only in that generality. Kato has given a more general definition in [Reference KatoKat99, Definition 3.14].Footnote 1
Definition 2.6.1. A logarithmic modification of a logarithmically smooth logarithmic scheme
![]() $X$
is a proper, representable, birational, logarithmically étale morphism
$X$
is a proper, representable, birational, logarithmically étale morphism
![]() $Y\rightarrow X$
.
$Y\rightarrow X$
.
The main purpose of this section is to prove Corollary 2.6.7, which says that all logarithmic modifications are deduced by base change from modifications of Artin fans. The proof is by reduction, via logarithmic base change, to the case of a logarithmic modification of a logarithmic scheme whose logarithmic structure is the one associated to a smooth Cartier divisor. As all logarithmic modifications of such logarithmic schemes are isomorphisms, the result is trivial in this case.
We frequently make use in this section of logarithmic changes of base. Consistent with our assumption that all logarithmic structures are integral and saturated, these fiber products will all be taken in the category of integral, saturated logarithmic schemes. In order to emphasize this, we refer to ‘fine and saturated logarithmic base change’ in the sequel. Notably, the underlying scheme of a fine and saturated fiber product of logarithmic schemes need not coincide with the fiber product of the underlying schemes in the diagram, unless at least one of the morphisms in the diagram is strict (or, more generally, saturated).
Proposition 2.6.2. Let
![]() $p:Y\rightarrow X$
be a proper morphism of logarithmic schemes and
$p:Y\rightarrow X$
be a proper morphism of logarithmic schemes and
![]() $X^{\prime }\rightarrow X$
an arbitrary morphism of logarithmic schemes. Then the map
$X^{\prime }\rightarrow X$
an arbitrary morphism of logarithmic schemes. Then the map
![]() $p^{\prime }:Y^{\prime }\rightarrow X^{\prime }$
deduced from
$p^{\prime }:Y^{\prime }\rightarrow X^{\prime }$
deduced from
![]() $p$
by fine and saturated logarithmic base change is also proper.
$p$
by fine and saturated logarithmic base change is also proper.
We thank the referee for the following proof, which is significantly simpler than our original argument.
Proof. Consider the scheme-theoretic base change
![]() $\text{}\underline{Z}^{\prime }:=\text{}\underline{X}^{\prime }\times _{\text{}\underline{X}}\text{}\underline{Y}$
and the natural morphism
$\text{}\underline{Z}^{\prime }:=\text{}\underline{X}^{\prime }\times _{\text{}\underline{X}}\text{}\underline{Y}$
and the natural morphism
![]() $\text{}\underline{Y}^{\prime }\rightarrow \text{}\underline{Z}^{\prime }$
. Since properness of morphisms of schemes is stable under base change we have that
$\text{}\underline{Y}^{\prime }\rightarrow \text{}\underline{Z}^{\prime }$
. Since properness of morphisms of schemes is stable under base change we have that
![]() $\text{}\underline{Z}^{\prime }\rightarrow \text{}\underline{X}^{\prime }$
is proper. It is shown in [Reference OgusOgu17, III, Corollary 2.1.6] that
$\text{}\underline{Z}^{\prime }\rightarrow \text{}\underline{X}^{\prime }$
is proper. It is shown in [Reference OgusOgu17, III, Corollary 2.1.6] that
![]() $\text{}\underline{Y}^{\prime }\rightarrow \text{}\underline{Z}^{\prime }$
is finite, hence proper. Therefore
$\text{}\underline{Y}^{\prime }\rightarrow \text{}\underline{Z}^{\prime }$
is finite, hence proper. Therefore
![]() $\text{}\underline{Y}^{\prime }\rightarrow \text{}\underline{X}^{\prime }$
is proper, as required.◻
$\text{}\underline{Y}^{\prime }\rightarrow \text{}\underline{X}^{\prime }$
is proper, as required.◻
Corollary 2.6.3. Suppose that
![]() $X^{\prime }\rightarrow X$
is a morphism of logarithmically smooth logarithmic schemes and
$X^{\prime }\rightarrow X$
is a morphism of logarithmically smooth logarithmic schemes and
![]() $Y\rightarrow X$
is a logarithmic modification. Let
$Y\rightarrow X$
is a logarithmic modification. Let
![]() $Y^{\prime }\rightarrow X^{\prime }$
be the morphism deduced by fine and saturated base change. Then
$Y^{\prime }\rightarrow X^{\prime }$
be the morphism deduced by fine and saturated base change. Then
![]() $Y^{\prime }$
is a logarithmic modification of
$Y^{\prime }$
is a logarithmic modification of
![]() $X^{\prime }$
.
$X^{\prime }$
.
Proof. The schemes
![]() $X,X^{\prime },Y$
and
$X,X^{\prime },Y$
and
![]() $Y^{\prime }$
are logarithmically smooth, hence the loci
$Y^{\prime }$
are logarithmically smooth, hence the loci
![]() $U_{X},U_{X^{\prime }},U_{Y}$
and
$U_{X},U_{X^{\prime }},U_{Y}$
and
![]() $U_{Y^{\prime }}$
where the logarithmic structure is trivial are dense. The morphism
$U_{Y^{\prime }}$
where the logarithmic structure is trivial are dense. The morphism
![]() $U_{Y}\rightarrow U_{X}$
is an isomorphism, and
$U_{Y}\rightarrow U_{X}$
is an isomorphism, and
![]() $U_{X^{\prime }}$
maps to
$U_{X^{\prime }}$
maps to
![]() $U_{X}$
, hence the pullback
$U_{X}$
, hence the pullback
![]() $U_{Y^{\prime }}\rightarrow U_{X^{\prime }}$
is an isomorphism. It follows that
$U_{Y^{\prime }}\rightarrow U_{X^{\prime }}$
is an isomorphism. It follows that
![]() $Y^{\prime }\rightarrow X^{\prime }$
is birational, and, by Proposition 2.6.2, it is proper. The morphism
$Y^{\prime }\rightarrow X^{\prime }$
is birational, and, by Proposition 2.6.2, it is proper. The morphism
![]() $Y^{\prime }\rightarrow X^{\prime }$
is logarithmically étale by base change, hence it is a logarithmic modification, as required.◻
$Y^{\prime }\rightarrow X^{\prime }$
is logarithmically étale by base change, hence it is a logarithmic modification, as required.◻
Proposition 2.6.4. Suppose that
![]() $X$
is logarithmically smooth with the logarithmic structure associated to a smooth Cartier divisor. Then
$X$
is logarithmically smooth with the logarithmic structure associated to a smooth Cartier divisor. Then
![]() $X$
has no non-trivial logarithmic modifications.
$X$
has no non-trivial logarithmic modifications.
Proof. Let
![]() $Y\rightarrow X$
be a logarithmic modification with
$Y\rightarrow X$
be a logarithmic modification with
![]() $X$
as in the statement of the proposition. We may work locally in
$X$
as in the statement of the proposition. We may work locally in
![]() $X$
and therefore we may assume that there is a strict map
$X$
and therefore we may assume that there is a strict map
![]() $X\rightarrow \mathbf{A}^{1}$
, where
$X\rightarrow \mathbf{A}^{1}$
, where
![]() $\mathbf{A}^{1}$
is given its standard toric logarithmic structure. By Kato’s criterion [Reference KatoKat89, (3.5.2)],
$\mathbf{A}^{1}$
is given its standard toric logarithmic structure. By Kato’s criterion [Reference KatoKat89, (3.5.2)],
![]() $Y$
is étale over
$Y$
is étale over
![]() $Z\times _{\mathbf{A}^{1}}X$
for some toric map
$Z\times _{\mathbf{A}^{1}}X$
for some toric map
![]() $Z\rightarrow \mathbf{A}^{1}$
with
$Z\rightarrow \mathbf{A}^{1}$
with
![]() $\dim Z=1$
. All such
$\dim Z=1$
. All such
![]() $Z$
are quasifinite over
$Z$
are quasifinite over
![]() $\mathbf{A}^{1}$
, so
$\mathbf{A}^{1}$
, so
![]() $Y$
must be quasifinite over
$Y$
must be quasifinite over
![]() $X$
. On the other hand,
$X$
. On the other hand,
![]() $Y\rightarrow X$
is proper and birational. It is therefore an isomorphism, by Zariski’s main theorem.◻
$Y\rightarrow X$
is proper and birational. It is therefore an isomorphism, by Zariski’s main theorem.◻
Corollary 2.6.5. Suppose that
![]() $Y$
is a logarithmic modification of a logarithmic scheme
$Y$
is a logarithmic modification of a logarithmic scheme
![]() $X$
and
$X$
and
![]() $X^{\prime }$
is logarithmically smooth with logarithmic structure associated to a smooth Cartier divisor in
$X^{\prime }$
is logarithmically smooth with logarithmic structure associated to a smooth Cartier divisor in
![]() $X$
. For any logarithmic morphism
$X$
. For any logarithmic morphism
![]() $X^{\prime }\rightarrow X$
the
$X^{\prime }\rightarrow X$
the
![]() $X^{\prime }$
-scheme
$X^{\prime }$
-scheme
![]() $Y^{\prime }$
deduced from
$Y^{\prime }$
deduced from
![]() $Y$
by fine and saturated logarithmic base change is isomorphic to
$Y$
by fine and saturated logarithmic base change is isomorphic to
![]() $X^{\prime }$
.
$X^{\prime }$
.
Corollary 2.6.6. Let
![]() $Y\rightarrow X$
be a logarithmically étale modification with
$Y\rightarrow X$
be a logarithmically étale modification with
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
the associated morphism of Artin fans. Then the map
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
the associated morphism of Artin fans. Then the map
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is proper.
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is proper.
Proof. Recall that by Theorem 2.4.1, a representable morphism of Artin fans
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is proper if and only if it has the right lifting property with respect to the inclusion of the open point in
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is proper if and only if it has the right lifting property with respect to the inclusion of the open point in
![]() ${\mathcal{A}}$
. For a given instance of diagram (2), we may verify the existence of a lift after changing base via the given map
${\mathcal{A}}$
. For a given instance of diagram (2), we may verify the existence of a lift after changing base via the given map
![]() ${\mathcal{A}}\rightarrow {\mathcal{X}}$
. Set
${\mathcal{A}}\rightarrow {\mathcal{X}}$
. Set
![]() ${\mathcal{X}}^{\prime }={\mathcal{A}}$
and write
${\mathcal{X}}^{\prime }={\mathcal{A}}$
and write
![]() $X^{\prime }$
,
$X^{\prime }$
,
![]() $Y^{\prime }$
, and
$Y^{\prime }$
, and
![]() ${\mathcal{Y}}^{\prime }$
for the logarithmic algebraic spaces and stack obtained by fine and saturated base change from
${\mathcal{Y}}^{\prime }$
for the logarithmic algebraic spaces and stack obtained by fine and saturated base change from
![]() $X$
,
$X$
,
![]() $Y$
, and
$Y$
, and
![]() ${\mathcal{Y}}$
, respectively. We will conclude by showing that
${\mathcal{Y}}$
, respectively. We will conclude by showing that
![]() ${\mathcal{Y}}^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
is an isomorphism.
${\mathcal{Y}}^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
is an isomorphism.
As
![]() $X\rightarrow {\mathcal{X}}$
is strict, the fine and saturated pullback respects underlying schemes:
$X\rightarrow {\mathcal{X}}$
is strict, the fine and saturated pullback respects underlying schemes:
![]() $\text{}\underline{X}^{\prime }=\text{}\underline{X}\times _{\text{}\underline{{\mathcal{X}}}}\text{}\underline{{\mathcal{X}}}^{\prime }$
. Therefore
$\text{}\underline{X}^{\prime }=\text{}\underline{X}\times _{\text{}\underline{{\mathcal{X}}}}\text{}\underline{{\mathcal{X}}}^{\prime }$
. Therefore
![]() $X^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
is smooth and surjective with connected geometric fibers. In particular,
$X^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
is smooth and surjective with connected geometric fibers. In particular,
![]() ${\mathcal{X}}^{\prime }$
is the Artin fan of
${\mathcal{X}}^{\prime }$
is the Artin fan of
![]() $X^{\prime }$
. For the same reasons,
$X^{\prime }$
. For the same reasons,
![]() ${\mathcal{Y}}^{\prime }$
is the relative Artin fan for
${\mathcal{Y}}^{\prime }$
is the relative Artin fan for
![]() $Y^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
.
$Y^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
.
We have
![]() $Y^{\prime }=Y\times _{X}X^{\prime }$
, so Corollary 2.6.3 implies that
$Y^{\prime }=Y\times _{X}X^{\prime }$
, so Corollary 2.6.3 implies that
![]() $Y^{\prime }\rightarrow X^{\prime }$
is a logarithmic modification. But
$Y^{\prime }\rightarrow X^{\prime }$
is a logarithmic modification. But
![]() $X^{\prime }$
is smooth over
$X^{\prime }$
is smooth over
![]() ${\mathcal{X}}^{\prime }={\mathcal{A}}$
, so the logarithmic structure on
${\mathcal{X}}^{\prime }={\mathcal{A}}$
, so the logarithmic structure on
![]() $X^{\prime }$
is the one associated to a smooth Cartier divisor (namely, the pullback of the distinguished divisor of
$X^{\prime }$
is the one associated to a smooth Cartier divisor (namely, the pullback of the distinguished divisor of
![]() ${\mathcal{A}}$
). Therefore, by Corollary 2.6.5, the map
${\mathcal{A}}$
). Therefore, by Corollary 2.6.5, the map
![]() $Y^{\prime }\rightarrow X^{\prime }$
is an isomorphism. Thus the universal property of the relative Artin fan implies
$Y^{\prime }\rightarrow X^{\prime }$
is an isomorphism. Thus the universal property of the relative Artin fan implies
![]() ${\mathcal{Y}}^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
is an isomorphism as well.◻
${\mathcal{Y}}^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
is an isomorphism as well.◻
Corollary 2.6.7. If
![]() $Y\rightarrow X$
is a logarithmically étale modification then
$Y\rightarrow X$
is a logarithmically étale modification then
![]() $Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is an isomorphism.
$Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is an isomorphism.
Proof. First of all,
![]() ${\mathcal{Y}}\times _{{\mathcal{X}}}X$
is a modification of
${\mathcal{Y}}\times _{{\mathcal{X}}}X$
is a modification of
![]() $X$
, so
$X$
, so
![]() $Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is a modification. On the other hand,
$Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is a modification. On the other hand,
![]() $Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is strict and both
$Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is strict and both
![]() $Y$
and
$Y$
and
![]() ${\mathcal{Y}}\times _{{\mathcal{X}}}X$
are logarithmically étale over
${\mathcal{Y}}\times _{{\mathcal{X}}}X$
are logarithmically étale over
![]() $X$
, so
$X$
, so
![]() $Y$
is étale over
$Y$
is étale over
![]() ${\mathcal{Y}}\times _{{\mathcal{X}}}X$
. Thus
${\mathcal{Y}}\times _{{\mathcal{X}}}X$
. Thus
![]() $Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is étale, proper, and birational, hence an isomorphism by Zariski’s main theorem.◻
$Y\rightarrow {\mathcal{Y}}\times _{{\mathcal{X}}}X$
is étale, proper, and birational, hence an isomorphism by Zariski’s main theorem.◻
3 Algebraicity
Let
![]() $S$
be a logarithmic scheme and let
$S$
be a logarithmic scheme and let
![]() ${\mathcal{X}}$
be an algebraic stack over
${\mathcal{X}}$
be an algebraic stack over
![]() $S$
, equipped with a logarithmic structure. We write
$S$
, equipped with a logarithmic structure. We write
![]() $\mathfrak{M}({\mathcal{X}}/S)$
for the stack whose
$\mathfrak{M}({\mathcal{X}}/S)$
for the stack whose
![]() $T$
-points are commutative diagrams
$T$
-points are commutative diagrams

in which
![]() $C\rightarrow T$
is a family of pre-stable logarithmic curves. We write
$C\rightarrow T$
is a family of pre-stable logarithmic curves. We write
![]() $\mathfrak{M}({\mathcal{X}})$
for
$\mathfrak{M}({\mathcal{X}})$
for
![]() $\mathfrak{M}({\mathcal{X}}/S)$
when
$\mathfrak{M}({\mathcal{X}}/S)$
when
![]() $S$
is a point and we write
$S$
is a point and we write
![]() $\mathfrak{M}$
for
$\mathfrak{M}$
for
![]() $\mathfrak{M}({\mathcal{X}}/S)$
when both
$\mathfrak{M}({\mathcal{X}}/S)$
when both
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() $S$
are points.
$S$
are points.
Proposition 3.1. If
![]() ${\mathcal{X}}$
is a quasicompact, quasiseparated Artin fan (for example, if
${\mathcal{X}}$
is a quasicompact, quasiseparated Artin fan (for example, if
![]() ${\mathcal{X}}$
is the Artin fan of a quasicompact, quasiseparated, logarithmically smooth logarithmic scheme, or the relative Artin fan of a logarithmically smooth morphism of logarithmically smooth, quasicompact, quasiseparated logarithmic schemes), then
${\mathcal{X}}$
is the Artin fan of a quasicompact, quasiseparated, logarithmically smooth logarithmic scheme, or the relative Artin fan of a logarithmically smooth morphism of logarithmically smooth, quasicompact, quasiseparated logarithmic schemes), then
![]() $\mathfrak{M}({\mathcal{X}})$
is represented by an algebraic stack with a logarithmic structure.
$\mathfrak{M}({\mathcal{X}})$
is represented by an algebraic stack with a logarithmic structure.
Proof. In view of Lemma 2.5.5, this is immediate from [Reference WiseWis16, Corollary 1.1.1]. ◻
We remark that the underlying stack
![]() $\mathfrak{M}({\mathcal{X}})$
represents pre-stable maps with minimal logarithmic structure.
$\mathfrak{M}({\mathcal{X}})$
represents pre-stable maps with minimal logarithmic structure.
Proposition 3.2. Let
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be a logarithmically étale
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be a logarithmically étale
![]() $S$
-morphism of logarithmic algebraic stacks that are locally of finite presentation over
$S$
-morphism of logarithmic algebraic stacks that are locally of finite presentation over
![]() $S$
. Assume that
$S$
. Assume that
![]() $\mathfrak{M}({\mathcal{Y}}/S)$
and
$\mathfrak{M}({\mathcal{Y}}/S)$
and
![]() $\mathfrak{M}({\mathcal{X}}/S)$
are representable by algebraic stacks with logarithmic structures. Then
$\mathfrak{M}({\mathcal{X}}/S)$
are representable by algebraic stacks with logarithmic structures. Then
![]() $\mathfrak{M}({\mathcal{Y}}/S)\rightarrow \mathfrak{M}({\mathcal{X}}/S)$
is logarithmically étale.
$\mathfrak{M}({\mathcal{Y}}/S)\rightarrow \mathfrak{M}({\mathcal{X}}/S)$
is logarithmically étale.
Proof. First we verify that
![]() $\mathfrak{M}({\mathcal{X}}/S)$
is locally of finite presentation. We must show that, for any cofiltered system of affine
$\mathfrak{M}({\mathcal{X}}/S)$
is locally of finite presentation. We must show that, for any cofiltered system of affine
![]() $S$
-schemes
$S$
-schemes
![]() $T_{i}$
with limit
$T_{i}$
with limit
![]() $T$
, the morphism
$T$
, the morphism
is an equivalence. An object of
![]() $\mathfrak{M}({\mathcal{X}}/S)(T)$
is a logarithmic curve
$\mathfrak{M}({\mathcal{X}}/S)(T)$
is a logarithmic curve
![]() $C$
over
$C$
over
![]() $T$
and a
$T$
and a
![]() $T$
-morphism
$T$
-morphism
![]() $C\rightarrow {\mathcal{X}}$
. Since the stack of logarithmic curves is locally of finite presentation,
$C\rightarrow {\mathcal{X}}$
. Since the stack of logarithmic curves is locally of finite presentation,
![]() $C$
is induced from a logarithmic curve
$C$
is induced from a logarithmic curve
![]() $C_{i}$
over some
$C_{i}$
over some
![]() $T_{i}$
, uniquely up to unique isomorphism and enlargement of
$T_{i}$
, uniquely up to unique isomorphism and enlargement of
![]() $i$
. As
$i$
. As
![]() ${\mathcal{X}}$
is locally of finite presentation, the map
${\mathcal{X}}$
is locally of finite presentation, the map
![]() $C\rightarrow {\mathcal{X}}$
is induced from
$C\rightarrow {\mathcal{X}}$
is induced from
![]() $C_{i}\rightarrow {\mathcal{X}}$
for some, possibly larger, value of
$C_{i}\rightarrow {\mathcal{X}}$
for some, possibly larger, value of
![]() $i$
, again uniquely up to unique isomorphism and further enlargement of
$i$
, again uniquely up to unique isomorphism and further enlargement of
![]() $i$
. This proves that
$i$
. This proves that
![]() $\mathfrak{M}({\mathcal{X}}/S)$
(and likewise
$\mathfrak{M}({\mathcal{X}}/S)$
(and likewise
![]() $\mathfrak{M}({\mathcal{Y}}/S)$
) is locally of finite presentation.
$\mathfrak{M}({\mathcal{Y}}/S)$
) is locally of finite presentation.
To prove that
![]() $\mathfrak{M}({\mathcal{Y}}/S)\rightarrow \mathfrak{M}({\mathcal{X}}/S)$
is logarithmically étale, it remains to verify the infinitesimal lifting property. Consider a strict infinitesimal extension
$\mathfrak{M}({\mathcal{Y}}/S)\rightarrow \mathfrak{M}({\mathcal{X}}/S)$
is logarithmically étale, it remains to verify the infinitesimal lifting property. Consider a strict infinitesimal extension
![]() $T\subset T^{\prime }$
and a lifting problem:
$T\subset T^{\prime }$
and a lifting problem:

We must show that this diagram has a unique lift.
This corresponds to a lifting problem

in which
![]() $C\rightarrow {\mathcal{Y}}$
and
$C\rightarrow {\mathcal{Y}}$
and
![]() $C^{\prime }\rightarrow {\mathcal{X}}$
are, respectively, the families of maps over
$C^{\prime }\rightarrow {\mathcal{X}}$
are, respectively, the families of maps over
![]() $T$
and
$T$
and
![]() $T^{\prime }$
classified by the diagram (3). As
$T^{\prime }$
classified by the diagram (3). As
![]() $C\subset C^{\prime }$
is a strict infinitesimal extension, this diagram has a unique lift.◻
$C\subset C^{\prime }$
is a strict infinitesimal extension, this diagram has a unique lift.◻
Remark 3.3. If
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
has logarithmically quasifinite diagonal then the conclusion of the proposition is valid, even without the assumption that
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
has logarithmically quasifinite diagonal then the conclusion of the proposition is valid, even without the assumption that
![]() $\mathfrak{M}({\mathcal{Y}}/S)$
and
$\mathfrak{M}({\mathcal{Y}}/S)$
and
![]() $\mathfrak{M}({\mathcal{X}}/S)$
be algebraic, in the sense that
$\mathfrak{M}({\mathcal{X}}/S)$
be algebraic, in the sense that
![]() $\mathfrak{M}({\mathcal{Y}}/S)\rightarrow \mathfrak{M}({\mathcal{X}}/S)$
is representable by étale morphisms of algebraic stacks. As we do not need the additional generality, and the proof is more involved, we have omitted it.
$\mathfrak{M}({\mathcal{Y}}/S)\rightarrow \mathfrak{M}({\mathcal{X}}/S)$
is representable by étale morphisms of algebraic stacks. As we do not need the additional generality, and the proof is more involved, we have omitted it.
Proof of Proposition 1.6.1.
By Proposition 3.1, the stack
![]() $\mathfrak{M}({\mathcal{X}})$
is algebraic. Since
$\mathfrak{M}({\mathcal{X}})$
is algebraic. Since
![]() ${\mathcal{X}}\rightarrow \operatorname{Spec}k$
is logarithmically étale, Proposition 3.2 implies that the morphism
${\mathcal{X}}\rightarrow \operatorname{Spec}k$
is logarithmically étale, Proposition 3.2 implies that the morphism
![]() $\mathfrak{M}({\mathcal{X}})\rightarrow \mathfrak{M}$
to the stack of pre-stable curves is logarithmically étale. As
$\mathfrak{M}({\mathcal{X}})\rightarrow \mathfrak{M}$
to the stack of pre-stable curves is logarithmically étale. As
![]() $\mathfrak{M}$
is logarithmically smooth,
$\mathfrak{M}$
is logarithmically smooth,
![]() $\mathfrak{M}({\mathcal{X}})$
is logarithmically smooth as well, as needed.◻
$\mathfrak{M}({\mathcal{X}})$
is logarithmically smooth as well, as needed.◻
Our arguments require another stack
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, the moduli space whose objects over a logarithmic scheme
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, the moduli space whose objects over a logarithmic scheme
![]() $T$
are diagrams
$T$
are diagrams
in which
![]() $C$
and
$C$
and
![]() $\overline{C}$
are pre-stable logarithmic curves; arrows over a logarithmic morphism
$\overline{C}$
are pre-stable logarithmic curves; arrows over a logarithmic morphism
![]() $T^{\prime }\rightarrow T$
are given by fiber diagrams. We write
$T^{\prime }\rightarrow T$
are given by fiber diagrams. We write
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
for the open substack of
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
for the open substack of
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
where:
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
where:
-
(a) the automorphism group of (4) relative to its image
 $\overline{C}\rightarrow {\mathcal{X}}$
in
$\overline{C}\rightarrow {\mathcal{X}}$
in
 $\mathfrak{M}({\mathcal{X}})$
is finite; and
$\mathfrak{M}({\mathcal{X}})$
is finite; and -
(b) the stabilization of the map
 $C\rightarrow \overline{C}$
is an isomorphism (that is, it is a contraction of unstable rational components).
$C\rightarrow \overline{C}$
is an isomorphism (that is, it is a contraction of unstable rational components).
Proposition 3.4. Let
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be the morphism of Artin fans associated to a logarithmically smooth morphism of logarithmic schemes. Then the morphism from
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be the morphism of Artin fans associated to a logarithmically smooth morphism of logarithmic schemes. Then the morphism from
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
to
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
to
![]() $\mathfrak{M}({\mathcal{X}})$
is representable by algebraic stacks.
$\mathfrak{M}({\mathcal{X}})$
is representable by algebraic stacks.
Proof. Working relative to
![]() $\mathfrak{M}({\mathcal{X}})$
, we may assume that a diagram
$\mathfrak{M}({\mathcal{X}})$
, we may assume that a diagram

is given. Then we are to prove that the stack of all logarithmically commutative diagrams

where the bottom left square is cartesian, is algebraic. We may identify this as the space of pre-stable logarithmic maps
![]() $\mathfrak{M}({\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}/S)$
. But by Lemma 2.5.5, the map
$\mathfrak{M}({\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}/S)$
. But by Lemma 2.5.5, the map
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is locally of finite presentation, quasiseparated, and has affine stabilizers, so the same applies to
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is locally of finite presentation, quasiseparated, and has affine stabilizers, so the same applies to
![]() ${\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}\rightarrow \overline{C}_{0}$
by base change; as
${\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}\rightarrow \overline{C}_{0}$
by base change; as
![]() $\overline{C}_{0}$
is a family of pre-stable curves, we conclude that
$\overline{C}_{0}$
is a family of pre-stable curves, we conclude that
![]() ${\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}$
is also locally of finite presentation, quasiseparated, and has affine stabilizers. We may therefore apply [Reference WiseWis16, Corollary 1.1.1], from which it follows that
${\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}$
is also locally of finite presentation, quasiseparated, and has affine stabilizers. We may therefore apply [Reference WiseWis16, Corollary 1.1.1], from which it follows that
![]() $\mathfrak{M}({\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}/S)$
is algebraic.◻
$\mathfrak{M}({\mathcal{Y}}\times _{{\mathcal{X}}}\overline{C}_{0}/S)$
is algebraic.◻
Corollary 3.5. Let
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be a logarithmic morphism between Artin fans. Then the stack
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be a logarithmic morphism between Artin fans. Then the stack
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is algebraic.
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is algebraic.
Proof. By Proposition 3.1, we know that
![]() $\mathfrak{M}({\mathcal{X}})$
is algebraic. By Proposition 3.4, we deduce that
$\mathfrak{M}({\mathcal{X}})$
is algebraic. By Proposition 3.4, we deduce that
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is relatively algebraic over
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is relatively algebraic over
![]() $\mathfrak{M}({\mathcal{X}})$
, hence is algebraic. But the stability condition defining
$\mathfrak{M}({\mathcal{X}})$
, hence is algebraic. But the stability condition defining
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
inside
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
inside
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is open, so it now follows that
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is open, so it now follows that
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is algebraic.◻
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is algebraic.◻
This gives the algebraicity statement of Proposition 1.6.2.
4 The cartesian diagram
Let
![]() $Y\rightarrow X$
be a logarithmic modification of proper logarithmic schemes. Section 2 provides us a cartesian diagram of logarithmic stacks
$Y\rightarrow X$
be a logarithmic modification of proper logarithmic schemes. Section 2 provides us a cartesian diagram of logarithmic stacks

in which:
-
(a)
 ${\mathcal{X}}$
and
${\mathcal{X}}$
and
 ${\mathcal{Y}}$
are Artin fans;
${\mathcal{Y}}$
are Artin fans; -
(b) the vertical arrows are strict, smooth, and surjective; and
-
(c)
 $X$
and
$X$
and
 $Y$
are proper logarithmic schemes.
$Y$
are proper logarithmic schemes.
We consider the diagram

with the following definitions:
-
(a)
 $\overline{{\mathcal{M}}}(X)$
and
$\overline{{\mathcal{M}}}(X)$
and
 $\overline{{\mathcal{M}}}(Y)$
are, respectively, the moduli stacks of stable logarithmic maps into
$\overline{{\mathcal{M}}}(Y)$
are, respectively, the moduli stacks of stable logarithmic maps into
 $X$
and
$X$
and
 $Y$
;
$Y$
; -
(b)
 $\mathfrak{M}({\mathcal{X}})$
is the moduli space of pre-stable logarithmic maps into
$\mathfrak{M}({\mathcal{X}})$
is the moduli space of pre-stable logarithmic maps into
 ${\mathcal{X}}$
; and
${\mathcal{X}}$
; and -
(c)
 $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is the moduli space of diagrams (4) described in § 3 above, with the relative stability condition described there.
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is the moduli space of diagrams (4) described in § 3 above, with the relative stability condition described there.
The map
![]() $\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
is defined by composition of
$\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
is defined by composition of
![]() $C\rightarrow X$
with
$C\rightarrow X$
with
![]() $X\rightarrow {\mathcal{X}}$
. The map
$X\rightarrow {\mathcal{X}}$
. The map
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{X}})$
is obtained by sending a diagram (4) to the map
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{X}})$
is obtained by sending a diagram (4) to the map
![]() $\overline{C}\rightarrow {\mathcal{X}}$
. The map
$\overline{C}\rightarrow {\mathcal{X}}$
. The map
![]() $\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
is defined using [Reference Abramovich, Marcus and WiseAMW14, B.6]: an object
$\overline{{\mathcal{M}}}(Y)\rightarrow \overline{{\mathcal{M}}}(X)$
is defined using [Reference Abramovich, Marcus and WiseAMW14, B.6]: an object
![]() $C\rightarrow Y$
of
$C\rightarrow Y$
of
![]() $\overline{{\mathcal{M}}}(Y)$
induces a stable map
$\overline{{\mathcal{M}}}(Y)$
induces a stable map
![]() $\overline{C}\rightarrow X$
by stabilization of the composition
$\overline{C}\rightarrow X$
by stabilization of the composition
![]() $C\rightarrow Y\rightarrow X$
; it comes along with a commutative diagram
$C\rightarrow Y\rightarrow X$
; it comes along with a commutative diagram

Since
![]() $Y=X\times _{{\mathcal{X}}}{\mathcal{Y}}$
, this extends uniquely to
$Y=X\times _{{\mathcal{X}}}{\mathcal{Y}}$
, this extends uniquely to

This gives us the map
![]() $\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. We argue that it takes values in
$\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. We argue that it takes values in
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. Suppose that
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. Suppose that
![]() $C\rightarrow Y$
is an object of
$C\rightarrow Y$
is an object of
![]() $\overline{{\mathcal{M}}}(Y)$
, let
$\overline{{\mathcal{M}}}(Y)$
, let
![]() $H$
be the automorphism group of its image in
$H$
be the automorphism group of its image in
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, and let
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, and let
![]() $H^{\prime }$
be the subgroup of
$H^{\prime }$
be the subgroup of
![]() $H$
fixing
$H$
fixing
![]() $\overline{C}\rightarrow {\mathcal{X}}$
. Let
$\overline{C}\rightarrow {\mathcal{X}}$
. Let
![]() $G$
be the automorphism group of
$G$
be the automorphism group of
![]() $C\rightarrow Y$
and let
$C\rightarrow Y$
and let
![]() $G^{\prime }$
be the subgroup fixing
$G^{\prime }$
be the subgroup fixing
![]() $\overline{C}\rightarrow X$
. By the universal property of fiber products,
$\overline{C}\rightarrow X$
. By the universal property of fiber products,
![]() $G^{\prime }$
and
$G^{\prime }$
and
![]() $H^{\prime }$
are isomorphic; as
$H^{\prime }$
are isomorphic; as
![]() $G$
is finite, so is
$G$
is finite, so is
![]() $G^{\prime }$
, and therefore so is
$G^{\prime }$
, and therefore so is
![]() $H^{\prime }$
. Thus
$H^{\prime }$
. Thus
![]() $\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
takes values in
$\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
takes values in
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, as claimed.
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, as claimed.
Lemma 4.1. The maps
-
(i)
 $\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
,
$\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
, -
(ii)
 $\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, and
$\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, and -
(iii)
 $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
are strict.
Proof. For the map
![]() $\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
we consider an
$\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
we consider an
![]() $S$
-point
$S$
-point
![]() $f:C\rightarrow X$
of
$f:C\rightarrow X$
of
![]() $\overline{{\mathcal{M}}}(X)$
. Let
$\overline{{\mathcal{M}}}(X)$
. Let
![]() $g:C\rightarrow {\mathcal{X}}$
be the induced
$g:C\rightarrow {\mathcal{X}}$
be the induced
![]() $S$
-point of
$S$
-point of
![]() $\mathfrak{M}({\mathcal{X}})$
. The minimality condition defining the logarithmic structures of
$\mathfrak{M}({\mathcal{X}})$
. The minimality condition defining the logarithmic structures of
![]() $\overline{{\mathcal{M}}}(X)$
and
$\overline{{\mathcal{M}}}(X)$
and
![]() $\mathfrak{M}({\mathcal{X}})$
depend, respectively, only on the morphisms of logarithmic structures
$\mathfrak{M}({\mathcal{X}})$
depend, respectively, only on the morphisms of logarithmic structures
![]() $f^{\ast }M_{X}\rightarrow M_{C}$
and
$f^{\ast }M_{X}\rightarrow M_{C}$
and
![]() $g^{\ast }M_{{\mathcal{X}}}\rightarrow M_{C}$
on
$g^{\ast }M_{{\mathcal{X}}}\rightarrow M_{C}$
on
![]() $C$
. As
$C$
. As
![]() $X\rightarrow {\mathcal{X}}$
is strict, these data coincide.
$X\rightarrow {\mathcal{X}}$
is strict, these data coincide.
For the map
![]() $\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, first note that
$\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, first note that
![]() $\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}})$
is strict by the previous paragraph. It is therefore sufficient to show that
$\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}({\mathcal{Y}})$
is strict by the previous paragraph. It is therefore sufficient to show that
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
is strict. The definition of minimality for
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
is strict. The definition of minimality for
![]() $\mathfrak{M}({\mathcal{Y}})$
at an
$\mathfrak{M}({\mathcal{Y}})$
at an
![]() $S$
-point
$S$
-point
![]() $f:C\rightarrow {\mathcal{Y}}$
depends, as above, on the morphism
$f:C\rightarrow {\mathcal{Y}}$
depends, as above, on the morphism
![]() $f^{\ast }M_{{\mathcal{Y}}}\rightarrow M_{C}$
. The definition of minimality for
$f^{\ast }M_{{\mathcal{Y}}}\rightarrow M_{C}$
. The definition of minimality for
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
at an
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
at an
![]() $S$
-point
$S$
-point

depends on the maps
![]() $f^{\ast }M_{{\mathcal{Y}}}\rightarrow M_{C}$
and
$f^{\ast }M_{{\mathcal{Y}}}\rightarrow M_{C}$
and
![]() $g^{\ast }M_{{\mathcal{X}}}\rightarrow M_{\overline{C}}$
. However, the latter of these may be constructed from the former as the composition
$g^{\ast }M_{{\mathcal{X}}}\rightarrow M_{\overline{C}}$
. However, the latter of these may be constructed from the former as the composition
taking into account the isomorphism
![]() $\unicode[STIX]{x1D70F}_{\ast }M_{C}\simeq M_{\overline{C}}$
of [Reference Abramovich, Marcus and WiseAMW14, Theorem B.6]. Therefore the minimality conditions depend on the same data, so they yield the same logarithmic structures.◻
$\unicode[STIX]{x1D70F}_{\ast }M_{C}\simeq M_{\overline{C}}$
of [Reference Abramovich, Marcus and WiseAMW14, Theorem B.6]. Therefore the minimality conditions depend on the same data, so they yield the same logarithmic structures.◻
Proof of Proposition 1.6.3.
We verify that diagram (6) is logarithmically cartesian. As its vertical arrows are strict by Lemma 4.1, this will imply that the underlying diagram of algebraic stacks is cartesian as well.
Suppose that we are given maps
![]() $S\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
and
$S\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
and
![]() $S\rightarrow \overline{{\mathcal{M}}}(X)$
along with an isomorphism between the induced maps
$S\rightarrow \overline{{\mathcal{M}}}(X)$
along with an isomorphism between the induced maps
![]() $S\rightarrow \mathfrak{M}({\mathcal{X}})$
. These data correspond to a diagram of solid lines
$S\rightarrow \mathfrak{M}({\mathcal{X}})$
. These data correspond to a diagram of solid lines

of logarithmic algebraic stacks over
![]() $S$
. We obtain a map
$S$
. We obtain a map
![]() $C\rightarrow Y_{S}$
completing the commutative diagram by the universal property of the fiber product.
$C\rightarrow Y_{S}$
completing the commutative diagram by the universal property of the fiber product.
It remains to verify that
![]() $C\rightarrow Y_{S}$
is stable. Fixing diagram (7), we let
$C\rightarrow Y_{S}$
is stable. Fixing diagram (7), we let
![]() $H$
denote the automorphism group of the induced object of
$H$
denote the automorphism group of the induced object of
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. We let
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. We let
![]() $H^{\prime \prime }$
be the automorphism group of the induced object
$H^{\prime \prime }$
be the automorphism group of the induced object
![]() $\overline{C}\rightarrow {\mathcal{X}}_{S}$
of
$\overline{C}\rightarrow {\mathcal{X}}_{S}$
of
![]() $\mathfrak{M}({\mathcal{X}})$
and we take
$\mathfrak{M}({\mathcal{X}})$
and we take
![]() $H^{\prime }$
to be the kernel of
$H^{\prime }$
to be the kernel of
![]() $H\rightarrow H^{\prime \prime }$
, that is, the subgroup of
$H\rightarrow H^{\prime \prime }$
, that is, the subgroup of
![]() $H$
fixing
$H$
fixing
![]() $\overline{C}\rightarrow {\mathcal{X}}_{S}$
. We define
$\overline{C}\rightarrow {\mathcal{X}}_{S}$
. We define
![]() $G$
to be the automorphism group of the left-hand square in diagram (7), thought of as an object of
$G$
to be the automorphism group of the left-hand square in diagram (7), thought of as an object of
![]() $\mathfrak{M}(Y\rightarrow X)$
as in diagram (4). We take
$\mathfrak{M}(Y\rightarrow X)$
as in diagram (4). We take
![]() $G^{\prime \prime }$
to be the automorphism group of
$G^{\prime \prime }$
to be the automorphism group of
![]() $\overline{C}\rightarrow X_{S}$
as an object of
$\overline{C}\rightarrow X_{S}$
as an object of
![]() $\mathfrak{M}(X)$
, and we take
$\mathfrak{M}(X)$
, and we take
![]() $G^{\prime }$
to be the kernel of
$G^{\prime }$
to be the kernel of
![]() $G\rightarrow G^{\prime \prime }$
. Then
$G\rightarrow G^{\prime \prime }$
. Then
![]() $G^{\prime \prime }$
is finite, because
$G^{\prime \prime }$
is finite, because
![]() $\overline{C}\rightarrow X_{S}$
is in
$\overline{C}\rightarrow X_{S}$
is in
![]() $\overline{{\mathcal{M}}}(X)$
by hypothesis, and
$\overline{{\mathcal{M}}}(X)$
by hypothesis, and
![]() $H^{\prime }$
is finite, because the outer square of (7) is in
$H^{\prime }$
is finite, because the outer square of (7) is in
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, by hypothesis. But
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, by hypothesis. But
![]() $H^{\prime }\simeq G^{\prime }$
by the universal property of the fiber product, so we conclude that
$H^{\prime }\simeq G^{\prime }$
by the universal property of the fiber product, so we conclude that
![]() $G$
is finite.
$G$
is finite.
Now,
![]() $\overline{C}\rightarrow X_{S}$
is stable, it must be the stabilization of
$\overline{C}\rightarrow X_{S}$
is stable, it must be the stabilization of
![]() $C\rightarrow X_{S}$
. In particular, it is determined functorially from
$C\rightarrow X_{S}$
. In particular, it is determined functorially from
![]() $C\rightarrow Y_{S}$
, so that the automorphism group of the object of
$C\rightarrow Y_{S}$
, so that the automorphism group of the object of
![]() $\mathfrak{M}(Y\rightarrow X)$
induced from (7) coincides with the automorphism group of
$\mathfrak{M}(Y\rightarrow X)$
induced from (7) coincides with the automorphism group of
![]() $C\rightarrow Y_{S}$
as an object of
$C\rightarrow Y_{S}$
as an object of
![]() $\mathfrak{M}(Y)$
. Thus
$\mathfrak{M}(Y)$
. Thus
![]() $C\rightarrow Y_{S}$
has finite automorphism group and lies therefore in
$C\rightarrow Y_{S}$
has finite automorphism group and lies therefore in
![]() $\overline{{\mathcal{M}}}(Y)$
.◻
$\overline{{\mathcal{M}}}(Y)$
.◻
5 The universal logarithmic modification
Let
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be the morphism of Artin fans associated to
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
be the morphism of Artin fans associated to
![]() $Y\rightarrow X$
constructed in § 2.5. We obtain a correspondence
$Y\rightarrow X$
constructed in § 2.5. We obtain a correspondence

where
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is the moduli space of minimal logarithmic diagrams (4) constructed in § 3.
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is the moduli space of minimal logarithmic diagrams (4) constructed in § 3.
5.1 The arrow
 $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
: proof of Proposition 1.6.2
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
: proof of Proposition 1.6.2
Algebraicity was shown in Corollary 3.5 and strictness was shown in Lemma 4.1. All that is left is to show that
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is logarithmically étale over
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
is logarithmically étale over
![]() $\mathfrak{M}({\mathcal{Y}})$
. A logarithmic infinitesimal lifting problem
$\mathfrak{M}({\mathcal{Y}})$
. A logarithmic infinitesimal lifting problem

corresponds to a logarithmic extension problem

Now,
![]() $C\rightarrow \overline{C}$
is a contraction of unstable components so we may apply [Reference Abramovich, Marcus and WiseAMW14, Appendix B] to obtain
$C\rightarrow \overline{C}$
is a contraction of unstable components so we may apply [Reference Abramovich, Marcus and WiseAMW14, Appendix B] to obtain
![]() $\overline{C}^{\prime }$
uniquely. All that is left is to produce the map
$\overline{C}^{\prime }$
uniquely. All that is left is to produce the map
![]() $\overline{C}^{\prime }\rightarrow {\mathcal{X}}$
and show it is unique. This follows from the lemmas below.
$\overline{C}^{\prime }\rightarrow {\mathcal{X}}$
and show it is unique. This follows from the lemmas below.
Lemma 5.1.1.
![]() $\overline{C}^{\prime }$
is the pushout of the maps
$\overline{C}^{\prime }$
is the pushout of the maps
![]() $C\rightarrow \overline{C}$
and
$C\rightarrow \overline{C}$
and
![]() $C\rightarrow C^{\prime }$
in the category of logarithmic schemes.
$C\rightarrow C^{\prime }$
in the category of logarithmic schemes.
Proof. As
![]() $C\rightarrow C^{\prime }$
and
$C\rightarrow C^{\prime }$
and
![]() $\overline{C}\rightarrow \overline{C}^{\prime }$
are homeomorphisms, the underlying topological space of
$\overline{C}\rightarrow \overline{C}^{\prime }$
are homeomorphisms, the underlying topological space of
![]() $\overline{C}^{\prime }$
is the pushout of the maps underlying
$\overline{C}^{\prime }$
is the pushout of the maps underlying
![]() $C\rightarrow \overline{C}$
and
$C\rightarrow \overline{C}$
and
![]() $C\rightarrow C^{\prime }$
. As in [Reference Abramovich, Marcus and WiseAMW14, Lemma B.1] the structure sheaf of
$C\rightarrow C^{\prime }$
. As in [Reference Abramovich, Marcus and WiseAMW14, Lemma B.1] the structure sheaf of
![]() $\overline{C}^{\prime }$
is the pushforward of the structure sheaf of
$\overline{C}^{\prime }$
is the pushforward of the structure sheaf of
![]() $C^{\prime }$
, hence
$C^{\prime }$
, hence
![]() $\overline{C}^{\prime }$
is the pushout of underlying schemes. Also the logarithmic structure on
$\overline{C}^{\prime }$
is the pushout of underlying schemes. Also the logarithmic structure on
![]() $\overline{C}^{\prime }$
is constructed as the pushforward of the logarithmic structure on
$\overline{C}^{\prime }$
is constructed as the pushforward of the logarithmic structure on
![]() $C^{\prime }$
. This implies the result.◻
$C^{\prime }$
. This implies the result.◻
Lemma 5.1.2.
![]() $\overline{C}^{\prime }$
is the pushout of the maps
$\overline{C}^{\prime }$
is the pushout of the maps
![]() $C\rightarrow \overline{C}$
and
$C\rightarrow \overline{C}$
and
![]() $C\rightarrow C^{\prime }$
in the 2-category of logarithmic stacks.
$C\rightarrow C^{\prime }$
in the 2-category of logarithmic stacks.
Proof. The construction of
![]() $\overline{C}^{\prime }$
is local in the étale topology of
$\overline{C}^{\prime }$
is local in the étale topology of
![]() $\overline{C}$
, so we may work étale locally in
$\overline{C}$
, so we may work étale locally in
![]() $\overline{C}$
. We may therefore assume that given maps
$\overline{C}$
. We may therefore assume that given maps
![]() $\overline{C}\rightarrow {\mathcal{X}}$
and
$\overline{C}\rightarrow {\mathcal{X}}$
and
![]() $C^{\prime }\rightarrow {\mathcal{X}}$
factor through a smooth, strict chart
$C^{\prime }\rightarrow {\mathcal{X}}$
factor through a smooth, strict chart
![]() $X\rightarrow {\mathcal{X}}$
. But then these maps extend uniquely in a compatible way to
$X\rightarrow {\mathcal{X}}$
. But then these maps extend uniquely in a compatible way to
![]() $\overline{C}^{\prime }\rightarrow X$
by the previous lemma. The uniqueness of this extension guarantees that the induced map
$\overline{C}^{\prime }\rightarrow X$
by the previous lemma. The uniqueness of this extension guarantees that the induced map
![]() $\overline{C}^{\prime }\rightarrow {\mathcal{X}}$
is independent of the chart and therefore descends.◻
$\overline{C}^{\prime }\rightarrow {\mathcal{X}}$
is independent of the chart and therefore descends.◻
5.2 Birationality: proof of Proposition 1.6.4
Proposition 5.2.1. Suppose that
![]() ${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is a logarithmic modification of Artin fans. Then the maps
${\mathcal{Y}}\rightarrow {\mathcal{X}}$
is a logarithmic modification of Artin fans. Then the maps
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{X}})$
and
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{X}})$
and
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
are birational.
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
are birational.
Proof. All of the stacks
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
,
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
,
![]() $\mathfrak{M}({\mathcal{X}})$
, and
$\mathfrak{M}({\mathcal{X}})$
, and
![]() $\mathfrak{M}({\mathcal{Y}})$
are logarithmically smooth. Therefore they have dense open substacks where their logarithmic structures are trivial. We show that these dense open substacks are all isomorphic to one another by the given maps.
$\mathfrak{M}({\mathcal{Y}})$
are logarithmically smooth. Therefore they have dense open substacks where their logarithmic structures are trivial. We show that these dense open substacks are all isomorphic to one another by the given maps.
Consider an
![]() $S$
-point of
$S$
-point of
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, where
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, where
![]() $S$
has the trivial logarithmic structure. We have a commutative diagram
$S$
has the trivial logarithmic structure. We have a commutative diagram

with both
![]() $C$
and
$C$
and
![]() $\overline{C}$
logarithmically smooth. This implies first that the underlying curves of
$\overline{C}$
logarithmically smooth. This implies first that the underlying curves of
![]() $C$
and
$C$
and
![]() $\overline{C}$
are smooth, and second that the map of schemes underlying
$\overline{C}$
are smooth, and second that the map of schemes underlying
![]() $C\rightarrow \overline{C}$
is a branched cover. But the stabilization of
$C\rightarrow \overline{C}$
is a branched cover. But the stabilization of
![]() $C\rightarrow \overline{C}$
must also be an isomorphism, so its degree must be
$C\rightarrow \overline{C}$
must also be an isomorphism, so its degree must be
![]() $1$
and therefore
$1$
and therefore
![]() $C\rightarrow \overline{C}$
is an isomorphism. This proves that
$C\rightarrow \overline{C}$
is an isomorphism. This proves that
![]() $\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
is an isomorphism over the loci with trivial logarithmic structures.
$\mathfrak{M}({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
is an isomorphism over the loci with trivial logarithmic structures.
Now consider an
![]() $S$
-point
$S$
-point
![]() $\overline{C}\rightarrow {\mathcal{X}}$
of
$\overline{C}\rightarrow {\mathcal{X}}$
of
![]() $\mathfrak{M}({\mathcal{X}})$
, where
$\mathfrak{M}({\mathcal{X}})$
, where
![]() $S$
is still assumed to have trivial logarithmic structure, so the underlying curve of
$S$
is still assumed to have trivial logarithmic structure, so the underlying curve of
![]() $\overline{C}$
is smooth. Consider the fine and saturated base change
$\overline{C}$
is smooth. Consider the fine and saturated base change
![]() $C=\overline{C}\times _{{\mathcal{X}}}{\mathcal{Y}}$
. The fibers of
$C=\overline{C}\times _{{\mathcal{X}}}{\mathcal{Y}}$
. The fibers of
![]() $\overline{C}$
over
$\overline{C}$
over
![]() $S$
are logarithmically smooth and the logarithmic structure of each is associated to a smooth Cartier divisor. Therefore
$S$
are logarithmically smooth and the logarithmic structure of each is associated to a smooth Cartier divisor. Therefore
![]() $C=\overline{C}$
by Corollary 2.6.5. This immediately yields a section of
$C=\overline{C}$
by Corollary 2.6.5. This immediately yields a section of
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
over the locus where the logarithmic structure is trivial. It remains only to verify that if (8) is an
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
over the locus where the logarithmic structure is trivial. It remains only to verify that if (8) is an
![]() $S$
-point of
$S$
-point of
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
then
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
then
![]() $C=\overline{C}\times _{{\mathcal{X}}}{\mathcal{Y}}$
. However, this follows from the fact that
$C=\overline{C}\times _{{\mathcal{X}}}{\mathcal{Y}}$
. However, this follows from the fact that
![]() $C\rightarrow \overline{C}$
is an isomorphism, as we saw above.◻
$C\rightarrow \overline{C}$
is an isomorphism, as we saw above.◻
6 Obstruction theories
6.1 The arrow
 $\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
$\overline{{\mathcal{M}}}(X)\rightarrow \mathfrak{M}({\mathcal{X}})$
First we show that the natural obstruction theory for
![]() $\overline{{\mathcal{M}}}(X)$
over
$\overline{{\mathcal{M}}}(X)$
over
![]() $\mathfrak{M}({\mathcal{X}})$
agrees with the one over
$\mathfrak{M}({\mathcal{X}})$
agrees with the one over
![]() $\mathsf{Log}(\mathfrak{M})$
defined in [Reference Abramovich and ChenAC14, Reference ChenChe14, Reference Gross and SiebertGS13]. Let
$\mathsf{Log}(\mathfrak{M})$
defined in [Reference Abramovich and ChenAC14, Reference ChenChe14, Reference Gross and SiebertGS13]. Let
![]() $S\subset S^{\prime }$
be a strict square-zero extension over
$S\subset S^{\prime }$
be a strict square-zero extension over
![]() $\mathfrak{M}({\mathcal{X}})$
with ideal
$\mathfrak{M}({\mathcal{X}})$
with ideal
![]() $J$
and assume given an
$J$
and assume given an
![]() $S$
-point of
$S$
-point of
![]() $\overline{{\mathcal{M}}}(X)$
. We have a diagram of solid lines
$\overline{{\mathcal{M}}}(X)$
. We have a diagram of solid lines

Note that because
![]() ${\mathcal{X}}$
is étale over
${\mathcal{X}}$
is étale over
![]() $\mathsf{Log}$
, lifts of this diagram are precisely the same as lifts of the diagram
$\mathsf{Log}$
, lifts of this diagram are precisely the same as lifts of the diagram

Since
![]() $X$
is smooth over
$X$
is smooth over
![]() ${\mathcal{X}}$
, the logarithmic lifts of either of these diagrams form a torsor on
${\mathcal{X}}$
, the logarithmic lifts of either of these diagrams form a torsor on
![]() $C$
under the sheaf of abelian groups
$C$
under the sheaf of abelian groups
![]() $f^{\ast }T_{X/{\mathcal{X}}}\otimes J=f^{\ast }T_{X}^{\log }\otimes J$
. Therefore if we define
$f^{\ast }T_{X/{\mathcal{X}}}\otimes J=f^{\ast }T_{X}^{\log }\otimes J$
. Therefore if we define
![]() ${\mathcal{E}}(J)$
to be the stack on
${\mathcal{E}}(J)$
to be the stack on
![]() $S$
of
$S$
of
![]() $f^{\ast }T_{X}^{\log }\otimes J$
-torsors on
$f^{\ast }T_{X}^{\log }\otimes J$
-torsors on
![]() $C$
we obtain an obstruction theory in the sense of [Reference WiseWis11] for
$C$
we obtain an obstruction theory in the sense of [Reference WiseWis11] for
![]() $\overline{{\mathcal{M}}}(X)$
over
$\overline{{\mathcal{M}}}(X)$
over
![]() $\mathfrak{M}({\mathcal{X}})$
or over
$\mathfrak{M}({\mathcal{X}})$
or over
![]() $\mathsf{Log}(\mathfrak{M})$
. The latter of these is the one defined in [Reference Abramovich and ChenAC14, Reference ChenChe14, Reference Gross and SiebertGS13].
$\mathsf{Log}(\mathfrak{M})$
. The latter of these is the one defined in [Reference Abramovich and ChenAC14, Reference ChenChe14, Reference Gross and SiebertGS13].
6.2 The arrow
 $\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
$\overline{{\mathcal{M}}}(Y)\rightarrow \mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
A similar argument will apply to give the obstruction theory for
![]() $\overline{{\mathcal{M}}}(Y)$
over
$\overline{{\mathcal{M}}}(Y)$
over
![]() $\mathfrak{M}({\mathcal{Y}})$
. Since
$\mathfrak{M}({\mathcal{Y}})$
. Since
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
is étale this also serves as an obstruction theory over
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})\rightarrow \mathfrak{M}({\mathcal{Y}})$
is étale this also serves as an obstruction theory over
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. Explicitly, a lifting problem
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
. Explicitly, a lifting problem

corresponds to the lifting problem

As before, the lifts form a torsor under
![]() $g^{\ast }T_{Y/{\mathcal{Y}}}\otimes J=g^{\ast }T_{Y}^{\log }\otimes J$
. Taking
$g^{\ast }T_{Y/{\mathcal{Y}}}\otimes J=g^{\ast }T_{Y}^{\log }\otimes J$
. Taking
![]() ${\mathcal{E}}^{\prime }(J)$
to be the stack on
${\mathcal{E}}^{\prime }(J)$
to be the stack on
![]() $S$
parameterizing torsors on
$S$
parameterizing torsors on
![]() $C$
under
$C$
under
![]() $g^{\ast }T_{Y}^{\log }\otimes J$
therefore gives a perfect relative obstruction theory.
$g^{\ast }T_{Y}^{\log }\otimes J$
therefore gives a perfect relative obstruction theory.
We now demonstrate that the obstruction for
![]() $\overline{{\mathcal{M}}}(X)$
considered in § 6.1 pulls back to the same obstruction theory for
$\overline{{\mathcal{M}}}(X)$
considered in § 6.1 pulls back to the same obstruction theory for
![]() $\overline{{\mathcal{M}}}(Y)$
over
$\overline{{\mathcal{M}}}(Y)$
over
![]() $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
.
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
.
Recall that
![]() ${\mathcal{E}}(J)$
was defined in § 6.1 to be the stack of
${\mathcal{E}}(J)$
was defined in § 6.1 to be the stack of
![]() $f^{\ast }T_{X}^{\log }\otimes J$
-torsors on
$f^{\ast }T_{X}^{\log }\otimes J$
-torsors on
![]() $\overline{C}$
and the obstruction was the torsor of lifts of the diagram below:
$\overline{C}$
and the obstruction was the torsor of lifts of the diagram below:

To identify
![]() ${\mathcal{E}}(J)$
with
${\mathcal{E}}(J)$
with
![]() ${\mathcal{E}}^{\prime }(J)$
we note that because
${\mathcal{E}}^{\prime }(J)$
we note that because
![]() $C\rightarrow \overline{C}$
is a contraction of chains of rational curves and
$C\rightarrow \overline{C}$
is a contraction of chains of rational curves and
![]() $Y\rightarrow X$
logarithmically étale,
$Y\rightarrow X$
logarithmically étale,
so that
![]() $g^{\ast }T_{Y}^{\log }\otimes J$
-torsors on
$g^{\ast }T_{Y}^{\log }\otimes J$
-torsors on
![]() $C$
may be identified with
$C$
may be identified with
![]() $f^{\ast }T_{X}^{\log }\otimes J$
-torsors on
$f^{\ast }T_{X}^{\log }\otimes J$
-torsors on
![]() $\overline{C}$
by pullback. Moreover, the compatibility of the lifting problems
$\overline{C}$
by pullback. Moreover, the compatibility of the lifting problems

ensures that the torsors of lifts of (10) and (11) are identified. This shows that the obstruction theories coincide.
6.3 Conclusion
We have therefore proved the following precise restatement of Proposition 1.6.5.
Proposition 6.3.1. Let
![]() ${\mathcal{E}}$
denote the perfect relative obstruction theory for
${\mathcal{E}}$
denote the perfect relative obstruction theory for
![]() $\overline{{\mathcal{M}}}(X)$
over
$\overline{{\mathcal{M}}}(X)$
over
![]() $\mathsf{Log}(\mathfrak{M})$
and let
$\mathsf{Log}(\mathfrak{M})$
and let
![]() ${\mathcal{E}}^{\prime }$
denote the perfect relative obstruction theory for
${\mathcal{E}}^{\prime }$
denote the perfect relative obstruction theory for
![]() $\overline{{\mathcal{M}}}(Y)$
over
$\overline{{\mathcal{M}}}(Y)$
over
![]() $\mathsf{Log}(\mathfrak{M})$
. Then:
$\mathsf{Log}(\mathfrak{M})$
. Then:
-
(a)
 ${\mathcal{E}}$
is also a perfect relative obstruction theory for
${\mathcal{E}}$
is also a perfect relative obstruction theory for
 $\overline{{\mathcal{M}}}(X)$
over
$\overline{{\mathcal{M}}}(X)$
over
 $\mathfrak{M}({\mathcal{X}})$
, and in particular
$\mathfrak{M}({\mathcal{X}})$
, and in particular
 $[\overline{{\mathcal{M}}}(X)]^{\text{vir}}=(\unicode[STIX]{x1D713}_{X})_{{\mathcal{E}}}^{!}[\mathfrak{M}({\mathcal{X}})]$
;
$[\overline{{\mathcal{M}}}(X)]^{\text{vir}}=(\unicode[STIX]{x1D713}_{X})_{{\mathcal{E}}}^{!}[\mathfrak{M}({\mathcal{X}})]$
; -
(b)
 ${\mathcal{E}}^{\prime }$
is also a perfect relative obstruction theory for
${\mathcal{E}}^{\prime }$
is also a perfect relative obstruction theory for
 $\overline{{\mathcal{M}}}(Y)$
over
$\overline{{\mathcal{M}}}(Y)$
over
 $\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, and in particular
$\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})$
, and in particular
 $[\overline{{\mathcal{M}}}(Y)]^{\text{vir}}=(\unicode[STIX]{x1D713}_{Y}^{\prime })_{{\mathcal{E}}^{\prime }}^{!}[\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})]$
;
$[\overline{{\mathcal{M}}}(Y)]^{\text{vir}}=(\unicode[STIX]{x1D713}_{Y}^{\prime })_{{\mathcal{E}}^{\prime }}^{!}[\mathfrak{M}^{\prime }({\mathcal{Y}}\rightarrow {\mathcal{X}})]$
; -
(c)
 $\overline{{\mathcal{M}}}(h)^{\ast }{\mathcal{E}}={\mathcal{E}}^{\prime }$
.
$\overline{{\mathcal{M}}}(h)^{\ast }{\mathcal{E}}={\mathcal{E}}^{\prime }$
.
We may now combine Propositions 5.2.1 and 6.3.1 with Costello’s theorem [Reference CostelloCos06, Theorem 5.0.1] to deduce
![]() $\overline{{\mathcal{M}}}(h)_{\ast }[\overline{{\mathcal{M}}}(Y)]^{\text{vir}}=[\overline{{\mathcal{M}}}(X)]^{\text{vir}}$
.
$\overline{{\mathcal{M}}}(h)_{\ast }[\overline{{\mathcal{M}}}(Y)]^{\text{vir}}=[\overline{{\mathcal{M}}}(X)]^{\text{vir}}$
.
Acknowledgements
We thank Mark Gross, who asked the question and offered several suggestions, and Steffen Marcus, with whom some of the techniques used here were developed in [Reference Abramovich, Marcus and WiseAMW14]. Special thanks are due to Jim Bryan, who pointed out that understanding primary and descendant insertions from
![]() $Y$
would require additional work. We are very grateful as well to Zhi Jin, Martin Ulirsch, and the anonymous referee for their careful reading, comments, questions, and suggestions.
$Y$
would require additional work. We are very grateful as well to Zhi Jin, Martin Ulirsch, and the anonymous referee for their careful reading, comments, questions, and suggestions.