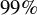1 Introduction
As an advanced accelerator method, laser wakefield accelerators (LWFAs)[ Reference Tajima and Dawson 1 , Reference Esarey, Schroeder and Leemans 2 ] have been developing steadily both theoretically and experimentally in recent decades[ Reference Gonsalves, Nakamura, Daniels, Benedetti, Pieronek, de Raadt, Steinke, Bin, Bulanov, van Tilborg, Geddes, Schroeder, Tóth, Esarey, Swanson, Fan-Chiang, Bagdasarov, Bobrova, Gasilov, Korn, Sasorov and Leemans 3 – Reference Leemans, Nagler, Gonsalves, Tóth, Nakamura, Geddes, Esarey, Schroeder and Hooker 13 ] owing to rapidly advancing laser technology, especially chirped-pulse amplification[ Reference Mourou and Umstadter 14 ]. A variety of mechanisms have been proposed to control the electron beams properties, such as energy spectra[ Reference Gonsalves, Nakamura, Daniels, Benedetti, Pieronek, de Raadt, Steinke, Bin, Bulanov, van Tilborg, Geddes, Schroeder, Tóth, Esarey, Swanson, Fan-Chiang, Bagdasarov, Bobrova, Gasilov, Korn, Sasorov and Leemans 3 – Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa, Tsai, Pai, Quevedo, Dyer, Gaul, Martinez, Bernstein, Borger, Spinks, Donovan, Khudik, Shvets, Ditmire and Downer 7 ], controllability[ Reference Cho, Pathak, Kim and Nam 8 ], stability[ Reference Osterhoff, Popp, Major, Marx, Rowlands-Rees, Fuchs, Geissler, Hörlein, Hidding, Becker, Peralta, Schramm, Grüner, Habs, Krausz, Hooker and Karsch 9 , Reference Buck, Wenz, Xu, Khrennikov, Schmid, Heigoldt, Mikhailova, Geissler, Shen, Krausz, Karsch and Veisz 10 ], beam emittance[ Reference Brunetti, Shanks, Manahan, Islam, Ersfeld, Anania, Cipiccia, Issac, Raj, Vieux, Welsh, Wiggins and Jaroszynski 11 , Reference Weingartner, Raith, Popp, Chou, Wenz, Khrennikov, Heigoldt, Maier, Kajumba, Fuchs, Zeitler, Krausz, Karsch and Grüner 12 ] and beam energy[ Reference Leemans, Nagler, Gonsalves, Tóth, Nakamura, Geddes, Esarey, Schroeder and Hooker 13 ], which are comparable with those from conventional particle accelerators. Many efforts have been made with controllable injection mechanisms to improve the electron beam quality, such as density-transition injection[ Reference Bulanov, Naumova, Pegoraro and Sakai 15 , Reference Wang, Zeng, Li, Wang, Lu and Gao 16 ], ionization-induced injection[ Reference Pak, Marsh, Martins, Lu, Mori and Joshi 17 ] or colliding-pulse injection[ Reference Esarey, Hubbard, Leemans, Ting and Sprangle 18 ]. However, the control of electron beam polarization has not been investigated thoroughly.
Spin-polarized electron beams have been widely used in material science[
Reference Schultz and Lynn
19
], particle and nuclear physics[
Reference Glashausser
20
–
Reference Shiltsev and Zimmermann
23
]. Such beams are generally produced by radiative polarization due to the Sokolov–Ternov effect in conventional accelerators[
Reference Sokolov and Ternov
24
,
Reference Mane, Shatunov and Yokoya
25
], that is, storage rings, which takes around a few hours in polarization build-up. In contrast, the acceleration process can be accomplished within a few picoseconds in a plasma accelerator. In
![]() $2017$
, a pre-polarized gas plasma was produced through laser-induced photo-dissociation in an experiment[
Reference Sofikitis, Glodic, Koumarianou, Jiang, Bougas, Samartzis, Andreev and Rakitzis
26
]. Later, Wen et al.
[
Reference Wen, Tamburini and Keitel
27
] proposed to generate high-current polarized electron beams with
$2017$
, a pre-polarized gas plasma was produced through laser-induced photo-dissociation in an experiment[
Reference Sofikitis, Glodic, Koumarianou, Jiang, Bougas, Samartzis, Andreev and Rakitzis
26
]. Later, Wen et al.
[
Reference Wen, Tamburini and Keitel
27
] proposed to generate high-current polarized electron beams with
![]() $90.6\%$
spin polarization through an LWFA based on the density-transition injection mechanism. The study of Nie et al.
[
Reference Nie, Li, Morales, Patchkovskii, Smirnova, An, Nambu, Matteo, Marsh, Tsung, Mori and Joshi
28
,
Reference Nie, Li, Morales, Patchkovskii, Smirnova, An, Zhang, Wu, Nambu, Matteo, Marsh, Tsung, Mori and Joshi
29
] showed that an electron beam with up to approximately 56% polarization could be obtained using the ionization-induced injection mechanism. More recently, the effect of bubble geometry on the polarization of self-injection electrons has been studied. It was found that the deviation from a perfect spherical symmetry severely degrades the polarization of electron beams during the transverse injection[
Reference Fan, Liu, Li, Qu, Yu, Kong, Weng, Chen, Büscher, Gibbon, Kawata and Sheng
30
]. Recently, Gong et al.
[
Reference Gong, Quin, Bohlen, Keitel, Põder and Tamburini
31
,
Reference Bohlen, Gong, Quin, Tamburini and Põder
32
] proposed that the colliding-pulse injection scheme enables the production of quasi-monoenergetic electron beams in excess of
$90.6\%$
spin polarization through an LWFA based on the density-transition injection mechanism. The study of Nie et al.
[
Reference Nie, Li, Morales, Patchkovskii, Smirnova, An, Nambu, Matteo, Marsh, Tsung, Mori and Joshi
28
,
Reference Nie, Li, Morales, Patchkovskii, Smirnova, An, Zhang, Wu, Nambu, Matteo, Marsh, Tsung, Mori and Joshi
29
] showed that an electron beam with up to approximately 56% polarization could be obtained using the ionization-induced injection mechanism. More recently, the effect of bubble geometry on the polarization of self-injection electrons has been studied. It was found that the deviation from a perfect spherical symmetry severely degrades the polarization of electron beams during the transverse injection[
Reference Fan, Liu, Li, Qu, Yu, Kong, Weng, Chen, Büscher, Gibbon, Kawata and Sheng
30
]. Recently, Gong et al.
[
Reference Gong, Quin, Bohlen, Keitel, Põder and Tamburini
31
,
Reference Bohlen, Gong, Quin, Tamburini and Põder
32
] proposed that the colliding-pulse injection scheme enables the production of quasi-monoenergetic electron beams in excess of
![]() $80\%$
polarization and tens of pC charge with commercial
$80\%$
polarization and tens of pC charge with commercial
![]() $10$
TW laser systems in a pre-polarized plasma. Furthermore, Sun et al.
[
Reference Sun, Zhao, Wan, Salamin and Li
33
] proposed to generate attosecond electron bunches with polarization of approximately 90% through using a radially polarized laser interacted with a pre-polarized plasma. Moreover, energetic spin-polarization electron beams can also be produced by a vortex Laguerre–Gaussian laser[
Reference Wu, Ji, Geng, Yu, Wang, Feng, Guo, Wang, Qin, Yan, Zhang, Thomas, Hützen, Büscher, Rakitzis, Pukhov, Shen and Li
34
] or beam-driven wakefield acceleration[
Reference Wu, Ji, Geng, Yu, Wang, Feng, Guo, Wang, Qin, Yan, Zhang, Thomas, Hützen, Pukhov, Büscher, Shen and Li
35
].
$10$
TW laser systems in a pre-polarized plasma. Furthermore, Sun et al.
[
Reference Sun, Zhao, Wan, Salamin and Li
33
] proposed to generate attosecond electron bunches with polarization of approximately 90% through using a radially polarized laser interacted with a pre-polarized plasma. Moreover, energetic spin-polarization electron beams can also be produced by a vortex Laguerre–Gaussian laser[
Reference Wu, Ji, Geng, Yu, Wang, Feng, Guo, Wang, Qin, Yan, Zhang, Thomas, Hützen, Büscher, Rakitzis, Pukhov, Shen and Li
34
] or beam-driven wakefield acceleration[
Reference Wu, Ji, Geng, Yu, Wang, Feng, Guo, Wang, Qin, Yan, Zhang, Thomas, Hützen, Pukhov, Büscher, Shen and Li
35
].
While these injection mechanisms have been investigated to control the polarization on LWFA electron beams[
Reference Wen, Tamburini and Keitel
27
–
Reference Sun, Zhao, Wan, Salamin and Li
33
], a self-injection mechanism with relatively simple setup still needs to be analyzed thoroughly. There are two self-injection schemes, transverse and longitudinal, as demonstrated in Ref. [Reference Corde, Thaury, Lifschitz, Lambert, Phuoc, Davoine, Lehe, Douillet, Rousse and Malka36]. The transverse injection mainly happens in the
![]() $3$
D nonlinear bubble regime. The accelerated electrons initially stay away from the laser axis, move in the bubble sheath, arrive at the tail of bubble and are injected in wakefield[
Reference Corde, Thaury, Lifschitz, Lambert, Phuoc, Davoine, Lehe, Douillet, Rousse and Malka
36
–
Reference Kalmykov, Beck, Yi, Khudik, Downer, Lefebvre, Shadwick and Umstadter
40
]. However, the trajectories of the accelerated electrons in the longitudinal injection scheme are different, which mainly takes place in the quasi-1D regime of the wakefield[
Reference Li, Sheng, Liu, Meyer-ter-Vehn, Mori, Lu and Zhang
41
]. The electrons are initially located at the front of the laser pulse slip backward along the laser axis after interacting with the laser. Once reaching the tail of wakefield, the electrons are injected and finally accelerated by the wakefield[
Reference Li, Sheng, Liu, Meyer-ter-Vehn, Mori, Lu and Zhang
41
,
Reference Weikum, Li, Assmann, Sheng and Jaroszynski
42
].
$3$
D nonlinear bubble regime. The accelerated electrons initially stay away from the laser axis, move in the bubble sheath, arrive at the tail of bubble and are injected in wakefield[
Reference Corde, Thaury, Lifschitz, Lambert, Phuoc, Davoine, Lehe, Douillet, Rousse and Malka
36
–
Reference Kalmykov, Beck, Yi, Khudik, Downer, Lefebvre, Shadwick and Umstadter
40
]. However, the trajectories of the accelerated electrons in the longitudinal injection scheme are different, which mainly takes place in the quasi-1D regime of the wakefield[
Reference Li, Sheng, Liu, Meyer-ter-Vehn, Mori, Lu and Zhang
41
]. The electrons are initially located at the front of the laser pulse slip backward along the laser axis after interacting with the laser. Once reaching the tail of wakefield, the electrons are injected and finally accelerated by the wakefield[
Reference Li, Sheng, Liu, Meyer-ter-Vehn, Mori, Lu and Zhang
41
,
Reference Weikum, Li, Assmann, Sheng and Jaroszynski
42
].
Previous studies[ Reference Wen, Tamburini and Keitel 27 – Reference Sun, Zhao, Wan, Salamin and Li 33 ] have shown that the properties of the electron beams depend on the electron injection mechanism. The electron polarization mainly changes during the injection process. In this paper, we study the polarization of the electron beam for the longitudinal injection scheme in a fully pre-polarized plasma with an up-ramp-plateau density profile. The longitudinal scheme is found to be more beneficial in generating high-spin polarization electron beams as compared to the transverse case. Our work is divided into three sections. Section 2 introduces the simulation setup with a brief description of the longitudinal injection scheme. In Section 3, we present numerical results and a discussion. The conclusions can be found in Section 4.
2 Simulation method
In this study, 2D particle-in-cell (PIC) simulations were performed with a modified version of the EPOCH code[
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers
43
], which includes the spin evolution module based on the Thomas–Bargmann–Michel–Telegdi (TBMT)[
Reference Mane, Shatunov and Yokoya
25
,
Reference Thomas
44
] equation via the Boris pusher method[
Reference Li, Gibbon, Hützen, Büscher, Weng, Chen and Sheng
45
]. The electron spin is regarded as a quasi-classical quantity with a vector
![]() $\boldsymbol{s}$
, which has an absolute value of
$\boldsymbol{s}$
, which has an absolute value of
![]() $1$
and a direction calculated from the TBMT equation
$1$
and a direction calculated from the TBMT equation
![]() $\mathrm{d}\boldsymbol{s}/\mathrm{d}t=\boldsymbol{\varOmega} \times \boldsymbol{s}$
with the following:
$\mathrm{d}\boldsymbol{s}/\mathrm{d}t=\boldsymbol{\varOmega} \times \boldsymbol{s}$
with the following:
 $$\begin{align}\boldsymbol{\varOmega} =\frac{e}{m_{\mathrm{e}}}\left[\left({a}_{\mathrm{e}}+\frac{1}{\gamma}\right)\boldsymbol{B}-\frac{{\boldsymbol{a}}_{\boldsymbol{e}}\gamma }{\gamma +1}\boldsymbol{v}\cdot \boldsymbol{B}\frac{\boldsymbol{v}}{c^2}-\left({a}_{\mathrm{e}}+\frac{1}{\gamma +1}\right)\frac{\boldsymbol{v}}{c^2}\times \boldsymbol{E}\right],\end{align}$$
$$\begin{align}\boldsymbol{\varOmega} =\frac{e}{m_{\mathrm{e}}}\left[\left({a}_{\mathrm{e}}+\frac{1}{\gamma}\right)\boldsymbol{B}-\frac{{\boldsymbol{a}}_{\boldsymbol{e}}\gamma }{\gamma +1}\boldsymbol{v}\cdot \boldsymbol{B}\frac{\boldsymbol{v}}{c^2}-\left({a}_{\mathrm{e}}+\frac{1}{\gamma +1}\right)\frac{\boldsymbol{v}}{c^2}\times \boldsymbol{E}\right],\end{align}$$
where
![]() ${m}_{\mathrm{e}}$
,
${m}_{\mathrm{e}}$
,
![]() $e$
and
$e$
and
![]() ${a}_{\mathrm{e}}\approx 1.16\times {10}^{-3}$
are the electron mass, charge and dimensionless anomalous magnetic moment, respectively,
${a}_{\mathrm{e}}\approx 1.16\times {10}^{-3}$
are the electron mass, charge and dimensionless anomalous magnetic moment, respectively,
![]() $\gamma$
is the Lorentz factor of the electron,
$\gamma$
is the Lorentz factor of the electron,
![]() $c$
is the light speed in vacuum,
$c$
is the light speed in vacuum,
![]() $\boldsymbol{B}$
is the magnetic field and
$\boldsymbol{B}$
is the magnetic field and
![]() $\boldsymbol{E}$
is the electric field in the laboratory frame. The effects of the radiation reaction, Stern–Gerlach effect and Sokolov–Ternov effect, can be ignored during the study of LWFAs, based on the work of Thomas et al.
[
Reference Thomas, Hützen, Lehrach, Pukhov, Ji, Wu, Geng and Büscher
46
].
$\boldsymbol{E}$
is the electric field in the laboratory frame. The effects of the radiation reaction, Stern–Gerlach effect and Sokolov–Ternov effect, can be ignored during the study of LWFAs, based on the work of Thomas et al.
[
Reference Thomas, Hützen, Lehrach, Pukhov, Ji, Wu, Geng and Büscher
46
].
In the simulation, the laser propagates in the
![]() $x$
-direction with linear polarization and a Gaussian envelope in the
$x$
-direction with linear polarization and a Gaussian envelope in the
![]() $y$
-direction:
$y$
-direction:
 $$\begin{align}E=\frac{E_0{w}_0}{w(x)}\exp \left[-\frac{y^2+{z}^2}{w{(x)}^2}-\frac{{\left(t-\tau \right)}^2}{{\left(0.5\tau \right)}^2}\right]\cos \left(\varphi \right),\end{align}$$
$$\begin{align}E=\frac{E_0{w}_0}{w(x)}\exp \left[-\frac{y^2+{z}^2}{w{(x)}^2}-\frac{{\left(t-\tau \right)}^2}{{\left(0.5\tau \right)}^2}\right]\cos \left(\varphi \right),\end{align}$$
with the laser wavelength
![]() $\lambda =800\ \mathrm{nm}$
, the initial laser waist
$\lambda =800\ \mathrm{nm}$
, the initial laser waist
![]() ${w}_0=20\lambda$
,
${w}_0=20\lambda$
,
![]() $w(x)={w}_0{\left[1+{\left(x-{x}_0\right)}^2/{z}_{\mathrm{R}}^2\right]}^{0.5}$
,
$w(x)={w}_0{\left[1+{\left(x-{x}_0\right)}^2/{z}_{\mathrm{R}}^2\right]}^{0.5}$
,
![]() ${z}_{\mathrm{R}}=\pi {w}_0^2/\lambda$
, the pulse duration
${z}_{\mathrm{R}}=\pi {w}_0^2/\lambda$
, the pulse duration
![]() $\tau =17\ \mathrm{fs}$
and the normalized laser amplitude
$\tau =17\ \mathrm{fs}$
and the normalized laser amplitude
![]() ${a}_0={eE}_0/{m}_{\mathrm{e}}\omega c=6$
, corresponding to a peak intensity of
${a}_0={eE}_0/{m}_{\mathrm{e}}\omega c=6$
, corresponding to a peak intensity of
![]() ${I}_0=7.71\times {10}^{19}\ \mathrm{W}/{\mathrm{cm}}^2$
. The phase is
${I}_0=7.71\times {10}^{19}\ \mathrm{W}/{\mathrm{cm}}^2$
. The phase is
![]() $\varphi = kx-\omega t+\phi (x)+k\left({y}^2+{z}^2\right)/2R(x)$
, where
$\varphi = kx-\omega t+\phi (x)+k\left({y}^2+{z}^2\right)/2R(x)$
, where
![]() $R(x)=x\left[1+{\left({z}_{\mathrm{R}}/x\right)}^2\right]$
and
$R(x)=x\left[1+{\left({z}_{\mathrm{R}}/x\right)}^2\right]$
and
![]() ${\phi (x)=\arctan \left(x/{z}_{\mathrm{R}}\right)}$
are the radius of curvature of the beam’s wavefronts and the Gouy phase at
${\phi (x)=\arctan \left(x/{z}_{\mathrm{R}}\right)}$
are the radius of curvature of the beam’s wavefronts and the Gouy phase at
![]() $x$
, respectively. The simulation box is
$x$
, respectively. The simulation box is
![]() $200\lambda (x)\times 120\lambda (y)$
with resolution
$200\lambda (x)\times 120\lambda (y)$
with resolution
![]() $\mathrm{d}x=0.02\lambda$
and
$\mathrm{d}x=0.02\lambda$
and
![]() $\mathrm{d}y=0.08\lambda$
. Open boundary conditions are used in each direction and there are four pseudo-particles per cell for each particle species.
$\mathrm{d}y=0.08\lambda$
. Open boundary conditions are used in each direction and there are four pseudo-particles per cell for each particle species.
The initial longitudinal profile of the pre-polarized plasma is an up-ramp followed by a plateau with constant density
![]() ${n}_0=0.04{n}_{\mathrm{c}}$
, as shown in Figure 1(a), marked with a yellow dashed line. Such a density profile makes longitudinal electron injection possible, as first introduced in Ref. [Reference Li, Sheng, Liu, Meyer-ter-Vehn, Mori, Lu and Zhang41]. Here, the length of the up-ramp transition is
${n}_0=0.04{n}_{\mathrm{c}}$
, as shown in Figure 1(a), marked with a yellow dashed line. Such a density profile makes longitudinal electron injection possible, as first introduced in Ref. [Reference Li, Sheng, Liu, Meyer-ter-Vehn, Mori, Lu and Zhang41]. Here, the length of the up-ramp transition is
![]() ${L}_1=45\lambda$
and the laser pulse is focused on the left-hand edge of the plasma target at
${L}_1=45\lambda$
and the laser pulse is focused on the left-hand edge of the plasma target at
![]() ${x}_0=30\lambda$
. The pre-polarized plasma could be realized by using the ultra-violet polarization method[
Reference Sofikitis, Glodic, Koumarianou, Jiang, Bougas, Samartzis, Andreev and Rakitzis
26
]. For simplicity, the initial polarization rate of the plasma is assumed as
${x}_0=30\lambda$
. The pre-polarized plasma could be realized by using the ultra-violet polarization method[
Reference Sofikitis, Glodic, Koumarianou, Jiang, Bougas, Samartzis, Andreev and Rakitzis
26
]. For simplicity, the initial polarization rate of the plasma is assumed as
![]() $100\%$
, where we are interested in the evolution of the polarization during the electron self-injection scheme. The net polarization of a particle beam is defined as
$100\%$
, where we are interested in the evolution of the polarization during the electron self-injection scheme. The net polarization of a particle beam is defined as
![]() ${P=\sqrt{{\left\langle {s}_x\right\rangle}^2+{\langle {s}_y\rangle}^2+{\left\langle {s}_z\right\rangle}^2}}$
, where
${P=\sqrt{{\left\langle {s}_x\right\rangle}^2+{\langle {s}_y\rangle}^2+{\left\langle {s}_z\right\rangle}^2}}$
, where
![]() ${s}_i$
is the component of spin polarization in each direction and
${s}_i$
is the component of spin polarization in each direction and
![]() $\left\langle {s}_i\right\rangle$
is the corresponding average value.
$\left\langle {s}_i\right\rangle$
is the corresponding average value.

Figure 1 (a) Schematic representation of the initially pre-polarized plasma. The longitudinal profile of the electron density is marked by the yellow dashed line, including an up-ramp from
![]() $0$
to
$0$
to
![]() ${n}_0$
with length
${n}_0$
with length
![]() ${L}_1$
and a plateau with
${L}_1$
and a plateau with
![]() ${n}_0$
. The initial polarization direction is aligned along the
${n}_0$
. The initial polarization direction is aligned along the
![]() $x$
-direction, as denoted by the arrows. The laser is focused at the left-hand boundary of the plasma
$x$
-direction, as denoted by the arrows. The laser is focused at the left-hand boundary of the plasma
![]() $\left({x}_0=30\lambda \right)$
. For the case of longitudinal injection (Case A), (b)–(d) show the density distribution of electron longitudinal polarization
$\left({x}_0=30\lambda \right)$
. For the case of longitudinal injection (Case A), (b)–(d) show the density distribution of electron longitudinal polarization
![]() $\left({n}_{\left\langle {s}_x\right\rangle}\right)$
at three different times, that is,
$\left({n}_{\left\langle {s}_x\right\rangle}\right)$
at three different times, that is,
![]() ${n}_{\left\langle {s}_x\right\rangle }$
is the product of electron density (normalized by
${n}_{\left\langle {s}_x\right\rangle }$
is the product of electron density (normalized by
![]() ${n}_0)$
and the average of polarization in the
${n}_0)$
and the average of polarization in the
![]() $x$
-direction
$x$
-direction
![]() $\left(\left\langle {s}_x\right\rangle \right)$
per cell. Here,
$\left(\left\langle {s}_x\right\rangle \right)$
per cell. Here,
![]() ${a}_0=6$
,
${a}_0=6$
,
![]() $\tau =17\ \mathrm{fs}$
,
$\tau =17\ \mathrm{fs}$
,
![]() ${w}_0=20\lambda$
,
${w}_0=20\lambda$
,
![]() ${n}_0=0.04{n}_{\mathrm{c}}$
and
${n}_0=0.04{n}_{\mathrm{c}}$
and
![]() ${L}_1=45\lambda$
. For the case of transverse injection (Case B), (e)–(g) present the corresponding distributions of
${L}_1=45\lambda$
. For the case of transverse injection (Case B), (e)–(g) present the corresponding distributions of
![]() ${n}_{\left\langle {s}_x\right\rangle }$
at different times, where
${n}_{\left\langle {s}_x\right\rangle }$
at different times, where
![]() ${w}_0=10\lambda$
,
${w}_0=10\lambda$
,
![]() ${n}_0=0.01{n}_{\mathrm{c}}$
,
${n}_0=0.01{n}_{\mathrm{c}}$
,
![]() ${L}_1=10\lambda$
and the other parameters are the same as in Case A. The electrons with kinetic energy
${L}_1=10\lambda$
and the other parameters are the same as in Case A. The electrons with kinetic energy
![]() ${E}_{\mathrm{k}}>13\ \mathrm{MeV}$
in Case A (or
${E}_{\mathrm{k}}>13\ \mathrm{MeV}$
in Case A (or
![]() ${E}_{\mathrm{k}}>30\ \mathrm{MeV}$
in Case B) are chosen as the accelerated electrons, which are marked by a green box in (d) and (g), respectively.
${E}_{\mathrm{k}}>30\ \mathrm{MeV}$
in Case B) are chosen as the accelerated electrons, which are marked by a green box in (d) and (g), respectively.
3 Results and discussion
Generally, the profile of the wakefield depends on the parameters of the laser and plasma, which inevitably causes the variation of the self-injection scheme, further leading to different evolution of spin polarization during the self-injection process. When the laser spot size is larger than the plasma wavelength (Case A), the wakefield is a quasi-1D regime, as shown in Figure 1(b). At this time, the wakefield propagates in the up-ramp density. When the wakefield reaches the uniform density regime
![]() $\left(x=75\lambda \right)$
, several electrons located at the tail of the wakefield
$\left(x=75\lambda \right)$
, several electrons located at the tail of the wakefield
![]() $\left(x=88\lambda \right)$
, can be captured and accelerated due to the breaking-wave effect, as presented in Figure 1(c). After that, owing to the effect of laser self-focusing, the laser intensity increases, the wakefield develops into a 3D nonlinear bubble regime and the electrons are accelerated continually, as revealed in Figure 1(d). On the other hand, when the laser spot size is equal to the plasma wavelength and the laser intensity
$\left(x=88\lambda \right)$
, can be captured and accelerated due to the breaking-wave effect, as presented in Figure 1(c). After that, owing to the effect of laser self-focusing, the laser intensity increases, the wakefield develops into a 3D nonlinear bubble regime and the electrons are accelerated continually, as revealed in Figure 1(d). On the other hand, when the laser spot size is equal to the plasma wavelength and the laser intensity
![]() ${a}_0$
is larger than 4, that is, Case B, the bubble regime can be formed directly as the laser propagates into the plasma. In order to avoid the electron at the left-hand boundary being injected into the bubble, an up-ramp density with a short length is also used, as shown in Figure 1(f). Different from the case of longitudinal injection, the bubble regime is a 3D nonlinear regime initially and the corresponding phase velocity slows down. As the bubble geometry changes following the laser evolution, several electrons can be injected into the bubble and achieve acceleration, as shown in Figure 1(g).
${a}_0$
is larger than 4, that is, Case B, the bubble regime can be formed directly as the laser propagates into the plasma. In order to avoid the electron at the left-hand boundary being injected into the bubble, an up-ramp density with a short length is also used, as shown in Figure 1(f). Different from the case of longitudinal injection, the bubble regime is a 3D nonlinear regime initially and the corresponding phase velocity slows down. As the bubble geometry changes following the laser evolution, several electrons can be injected into the bubble and achieve acceleration, as shown in Figure 1(g).
Not surprisingly, the distribution of the electron polarization is different in the two cases and the influence of the laser on the electron polarization cannot be ignored. In the quasi-1D regime (Case A), the values of
![]() ${s}_x$
for injection electrons mostly are positive, as plotted in Figure 1(c). Meanwhile, in the bubble regime (Case B), the values of
${s}_x$
for injection electrons mostly are positive, as plotted in Figure 1(c). Meanwhile, in the bubble regime (Case B), the values of
![]() ${s}_x$
about the electrons located at the sheath are negative, as revealed in Figure 1(f). For further analysis, the accelerated electrons are chosen to analyze the evolution of polarization, as marked in the green region in Figures 1(d) and 1(g), respectively. For Case A,
${s}_x$
about the electrons located at the sheath are negative, as revealed in Figure 1(f). For further analysis, the accelerated electrons are chosen to analyze the evolution of polarization, as marked in the green region in Figures 1(d) and 1(g), respectively. For Case A,
![]() $6056$
electrons are chosen with a polarization
$6056$
electrons are chosen with a polarization
![]() ${P=0.99}$
. For Case B, there are
${P=0.99}$
. For Case B, there are
![]() $32,078$
electrons chosen with a polarization
$32,078$
electrons chosen with a polarization
![]() $P=0.18$
. Moreover, as presented in Figure 1(d), another bunch of electrons
$P=0.18$
. Moreover, as presented in Figure 1(d), another bunch of electrons
![]() $\left(x\simeq 150\lambda \right)$
was injected in the wakefield owing to the nonlinear evolution of the laser pulse and bubble, which has been analyzed in the work of Kalmykov et al.
[
Reference Kalmykov, Yi, Khudik and Shvets
39
,
Reference Kalmykov, Beck, Yi, Khudik, Downer, Lefebvre, Shadwick and Umstadter
40
]. The trajectories of these electrons are similar to those in the case of transverse injection (Case B). Their polarization is nearly 0.8, which is lower than that of the first bunch of electrons; this will be discussed in this paper.
$\left(x\simeq 150\lambda \right)$
was injected in the wakefield owing to the nonlinear evolution of the laser pulse and bubble, which has been analyzed in the work of Kalmykov et al.
[
Reference Kalmykov, Yi, Khudik and Shvets
39
,
Reference Kalmykov, Beck, Yi, Khudik, Downer, Lefebvre, Shadwick and Umstadter
40
]. The trajectories of these electrons are similar to those in the case of transverse injection (Case B). Their polarization is nearly 0.8, which is lower than that of the first bunch of electrons; this will be discussed in this paper.

Figure 2 The history of particle properties,
![]() $\left\langle {s}_x\right\rangle$
(a),
$\left\langle {s}_x\right\rangle$
(a),
![]() $\langle {s}_y\rangle$
(b) and the average kinetic energy
$\langle {s}_y\rangle$
(b) and the average kinetic energy
![]() $\left\langle {E}_{\mathrm{k}}\right\rangle$
(c) about accelerated electrons in the case of the longitudinal scheme. The distribution of
$\left\langle {E}_{\mathrm{k}}\right\rangle$
(c) about accelerated electrons in the case of the longitudinal scheme. The distribution of
![]() ${s}_x$
(or
${s}_x$
(or
![]() ${s}_y$
) in the x-direction is shown in the insert of (a) (or (b)). (d)–(f) The corresponding quantities in the case of the transverse scheme. The accelerated electrons are marked in the Figures 1(d) and 1(g), respectively.
${s}_y$
) in the x-direction is shown in the insert of (a) (or (b)). (d)–(f) The corresponding quantities in the case of the transverse scheme. The accelerated electrons are marked in the Figures 1(d) and 1(g), respectively.
The histories of
![]() $\left\langle {s}_x\right\rangle$
,
$\left\langle {s}_x\right\rangle$
,
![]() $\langle {s}_y\rangle$
and the average energy
$\langle {s}_y\rangle$
and the average energy
![]() $\left\langle {E}_{\mathrm{k}}\right\rangle$
for these two cases are plotted in Figure 2. As presented in Figures 2(a)–2(c), the evolution of the polarization for the longitudinal injection can be divided into three stages. (i) Here,
$\left\langle {E}_{\mathrm{k}}\right\rangle$
for these two cases are plotted in Figure 2. As presented in Figures 2(a)–2(c), the evolution of the polarization for the longitudinal injection can be divided into three stages. (i) Here,
![]() $t<{t}_{\mathrm{I}}=198\ \mathrm{fs}$
, with the electron fixed. (ii) Here,
$t<{t}_{\mathrm{I}}=198\ \mathrm{fs}$
, with the electron fixed. (ii) Here,
![]() ${t}_{\mathrm{I}}<t<{t}_{\mathrm{II}}=234\ \mathrm{fs}$
, where the value of
${t}_{\mathrm{I}}<t<{t}_{\mathrm{II}}=234\ \mathrm{fs}$
, where the value of
![]() $\left\langle {s}_x\right\rangle$
decreases firstly and then returns nearly to the initial value during a short time, which is nearly the duration of the laser
$\left\langle {s}_x\right\rangle$
decreases firstly and then returns nearly to the initial value during a short time, which is nearly the duration of the laser
![]() $\left(\sim 36\ \mathrm{fs}\right)$
. As presented in the insert of Figure 2(a), the distribution of
$\left(\sim 36\ \mathrm{fs}\right)$
. As presented in the insert of Figure 2(a), the distribution of
![]() ${s}_x$
shows that the laser can affect the electron spin directly at
${s}_x$
shows that the laser can affect the electron spin directly at
![]() $216\ \mathrm{fs}$
. The oscillation period is nearly
$216\ \mathrm{fs}$
. The oscillation period is nearly
![]() $0.5\lambda$
for
$0.5\lambda$
for
![]() $\left\langle {s}_x\right\rangle$
and
$\left\langle {s}_x\right\rangle$
and
![]() $1\lambda$
for
$1\lambda$
for
![]() $\langle {s}_y\rangle$
, which means that the electron spin is affected by the laser field directly. Meanwhile, the average energy increases firstly and then decreases. (iii) Here,
$\langle {s}_y\rangle$
, which means that the electron spin is affected by the laser field directly. Meanwhile, the average energy increases firstly and then decreases. (iii) Here,
![]() $t>{t}_{\mathrm{II}}$
, where the value of
$t>{t}_{\mathrm{II}}$
, where the value of
![]() $\left\langle {s}_x\right\rangle$
does not change significantly. The value of
$\left\langle {s}_x\right\rangle$
does not change significantly. The value of
![]() $\langle {s}_y\rangle$
is nearly 0 owing to the azimuthal symmetry of the wakefield. At this stage, the electron energy increases with time, which means the electrons are continuously accelerated in the wakefield.
$\langle {s}_y\rangle$
is nearly 0 owing to the azimuthal symmetry of the wakefield. At this stage, the electron energy increases with time, which means the electrons are continuously accelerated in the wakefield.
For the case of the transverse injection scheme (Case B), as analyzed in Ref. [Reference Fan, Liu, Li, Qu, Yu, Kong, Weng, Chen, Büscher, Gibbon, Kawata and Sheng30], the evolution of polarization can be divided into four stages. (i) Here,
![]() $t<{t}_{\mathrm{I}}$
, where the electrons do not feel the wakefield. (ii) Here,
$t<{t}_{\mathrm{I}}$
, where the electrons do not feel the wakefield. (ii) Here,
![]() ${t}_{\mathrm{I}}<t<{t}_{\mathrm{II}}$
, where the electrons are located on the bubble shell. Further,
${t}_{\mathrm{I}}<t<{t}_{\mathrm{II}}$
, where the electrons are located on the bubble shell. Further,
![]() $\left\langle {s}_x\right\rangle$
decreases and
$\left\langle {s}_x\right\rangle$
decreases and
![]() $\langle {s}_y\rangle$
oscillates in the laser field and stays at nearly
$\langle {s}_y\rangle$
oscillates in the laser field and stays at nearly
![]() $0$
due to the azimuthal symmetry of the bubble field, as shown in Figure 2(d). (iii) Here,
$0$
due to the azimuthal symmetry of the bubble field, as shown in Figure 2(d). (iii) Here,
![]() ${t}_{\mathrm{II}}<t<{t}_{\mathrm{III}}$
, where the electrons reach the tail of the bubble and
${t}_{\mathrm{II}}<t<{t}_{\mathrm{III}}$
, where the electrons reach the tail of the bubble and
![]() $\left\langle {s}_x\right\rangle$
increases, as revealed in Figure 2(d). (iv) Here,
$\left\langle {s}_x\right\rangle$
increases, as revealed in Figure 2(d). (iv) Here,
![]() $t>{t}_{\mathrm{III}}$
, where the electrons are captured in the bubble and their spin precession slows down.
$t>{t}_{\mathrm{III}}$
, where the electrons are captured in the bubble and their spin precession slows down.
The electron spin evolution during the transverse injection has been studied through single particle dynamics in the work of Fan et al.
[
Reference Fan, Liu, Li, Qu, Yu, Kong, Weng, Chen, Büscher, Gibbon, Kawata and Sheng
30
]. It is found that the electron spin is mainly affected by the magnetic field of the bubble during the second stage and affected by the electric field of the bubble in the third stage. In the fourth stage, the electron moves along with the laser axis, so its spin does not change obviously. For the longitudinal injection, a typical accelerated electron is also analyzed, as shown in Figure 3. The trajectory of the electron in the wakefield coordinate system between 195 and
![]() $235\ \mathrm{fs}$
is presented in Figure 3(a). At
$235\ \mathrm{fs}$
is presented in Figure 3(a). At
![]() $195\ \mathrm{fs}$
, the electron is located at the head of the wakefield, and then it slips backward. When reaching the tail of the wakefield, it is captured. Although it vibrates in the transverse direction, the transverse position does not change obviously in the wakefield.
$195\ \mathrm{fs}$
, the electron is located at the head of the wakefield, and then it slips backward. When reaching the tail of the wakefield, it is captured. Although it vibrates in the transverse direction, the transverse position does not change obviously in the wakefield.

Figure 3 (a) Trajectory of a typical tracked electron for the longitudinal self-injection scheme (Case A) at the wakefield frame, where
![]() ${v}_{\mathrm{b}}$
is the phase velocity of the wakefield calculated using the plateau density. The electron is initially located at the front of the wakefield. (b) The history of
${v}_{\mathrm{b}}$
is the phase velocity of the wakefield calculated using the plateau density. The electron is initially located at the front of the wakefield. (b) The history of
![]() ${s}_x$
(blue solid line) and
${s}_x$
(blue solid line) and
![]() ${s}_y$
(red dashed line) for the tracked electron. (c) The evolution of the spin direction
${s}_y$
(red dashed line) for the tracked electron. (c) The evolution of the spin direction
![]() $\left(\theta =\mathrm{arctan}\left({s}_y/{s}_x\right)\right)$
with time. (d) The evolution of
$\left(\theta =\mathrm{arctan}\left({s}_y/{s}_x\right)\right)$
with time. (d) The evolution of
![]() ${\boldsymbol{\varOmega}}_z$
(green solid line), the term
${\boldsymbol{\varOmega}}_z$
(green solid line), the term
![]() ${\boldsymbol{\varOmega}}_{B_z}$
(blue dashed line) and the term
${\boldsymbol{\varOmega}}_{B_z}$
(blue dashed line) and the term
![]() ${\boldsymbol{\varOmega}}_{v_x{E}_y}$
(magenta dashed line) of
${\boldsymbol{\varOmega}}_{v_x{E}_y}$
(magenta dashed line) of
![]() ${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
(black solid line) caused by
${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
(black solid line) caused by
![]() ${v}_x{E}_y$
, and the term
${v}_x{E}_y$
, and the term
![]() ${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
(red solid line) of
${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
(red solid line) of
![]() ${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
caused by
${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
caused by
![]() $-{v}_y{E}_x$
for the tracked electron.
$-{v}_y{E}_x$
for the tracked electron.
Moreover, the evolutions of
![]() ${s}_x$
and
${s}_x$
and
![]() ${s}_y$
are plotted in Figure 3(b). Based on the TBMT equation, the electron spin precesses in the XY plane with the laser field. Its spin changes rapidly in the laser field and the
${s}_y$
are plotted in Figure 3(b). Based on the TBMT equation, the electron spin precesses in the XY plane with the laser field. Its spin changes rapidly in the laser field and the
![]() ${s}_x$
returns to its initial value at each cycle. The amplitude of oscillation coincides with the laser intensity, and the profile of
${s}_x$
returns to its initial value at each cycle. The amplitude of oscillation coincides with the laser intensity, and the profile of
![]() ${s}_x$
is similar to the laser duration. However, the period of oscillation increases firstly and then decreases. If we defined the spin angle
${s}_x$
is similar to the laser duration. However, the period of oscillation increases firstly and then decreases. If we defined the spin angle
![]() ${\theta =\mathrm{arctan}\left({s}_y/{s}_x\right)}$
, the quiver of electron spin is presented more clearly in Figure 3(c). The electron spin oscillates around the x-direction in the laser field and it causes the oscillation period of
${\theta =\mathrm{arctan}\left({s}_y/{s}_x\right)}$
, the quiver of electron spin is presented more clearly in Figure 3(c). The electron spin oscillates around the x-direction in the laser field and it causes the oscillation period of
![]() ${s}_y$
to be twice as that of
${s}_y$
to be twice as that of
![]() ${s}_x$
. In addition, the period of oscillation decreases with time.
${s}_x$
. In addition, the period of oscillation decreases with time.
In order to investigate the dynamics of the electron spin, the contribution of the electromagnetic field to the precession frequency
![]() $\boldsymbol{\varOmega}$
is analyzed in detail. Equation (1) can be rewritten as
$\boldsymbol{\varOmega}$
is analyzed in detail. Equation (1) can be rewritten as
![]() $\boldsymbol{\varOmega} ={\boldsymbol{\varOmega}}_{\mathrm{a}}+{\boldsymbol{\varOmega}}_{\mathrm{T}}$
, where the following applies:
$\boldsymbol{\varOmega} ={\boldsymbol{\varOmega}}_{\mathrm{a}}+{\boldsymbol{\varOmega}}_{\mathrm{T}}$
, where the following applies:
 $$\begin{align}{\boldsymbol{\varOmega}}_{\mathrm{a}}={a}_{\mathrm{e}}\frac{e}{m_{\mathrm{e}}}\left(\boldsymbol{B}-\frac{\gamma }{\gamma +1}\boldsymbol{v}\cdot \boldsymbol{B}\frac{\boldsymbol{v}}{c^2}-\frac{\boldsymbol{v}}{c^2}\times \boldsymbol{E}\right),\end{align}$$
$$\begin{align}{\boldsymbol{\varOmega}}_{\mathrm{a}}={a}_{\mathrm{e}}\frac{e}{m_{\mathrm{e}}}\left(\boldsymbol{B}-\frac{\gamma }{\gamma +1}\boldsymbol{v}\cdot \boldsymbol{B}\frac{\boldsymbol{v}}{c^2}-\frac{\boldsymbol{v}}{c^2}\times \boldsymbol{E}\right),\end{align}$$
and
 $$\begin{align}{\boldsymbol{\varOmega}}_{\mathrm{T}}=\frac{e}{m_{\mathrm{e}}}\left(\frac{1}{\gamma}\boldsymbol{B}-\frac{1}{\gamma +1}\frac{\boldsymbol{v}}{c^2}\times \boldsymbol{E}\right).\end{align}$$
$$\begin{align}{\boldsymbol{\varOmega}}_{\mathrm{T}}=\frac{e}{m_{\mathrm{e}}}\left(\frac{1}{\gamma}\boldsymbol{B}-\frac{1}{\gamma +1}\frac{\boldsymbol{v}}{c^2}\times \boldsymbol{E}\right).\end{align}$$
Considering
![]() ${a}_{\mathrm{e}}\approx 1.16\times {10}^{-3}$
for electrons, the value of
${a}_{\mathrm{e}}\approx 1.16\times {10}^{-3}$
for electrons, the value of
![]() ${\boldsymbol{\varOmega}}_{\mathrm{a}}$
is much smaller than
${\boldsymbol{\varOmega}}_{\mathrm{a}}$
is much smaller than
![]() ${\boldsymbol{\varOmega}}_{\mathrm{T}}$
at the initial stage of acceleration, that is,
${\boldsymbol{\varOmega}}_{\mathrm{T}}$
at the initial stage of acceleration, that is,
![]() ${a}_{\mathrm{e}}\ll 1/\gamma$
. With the increase of electron energy, the contribution of
${a}_{\mathrm{e}}\ll 1/\gamma$
. With the increase of electron energy, the contribution of
![]() ${\boldsymbol{\varOmega}}_{\mathrm{a}}$
gradually increases and cannot be ignored, especially when
${\boldsymbol{\varOmega}}_{\mathrm{a}}$
gradually increases and cannot be ignored, especially when
![]() $\gamma \simeq 1/{a}_{\mathrm{e}}\simeq 862$
. As presented in Figure 2(c), the electron energy is smaller than 10 MeV during the process of injection. Therefore, the contribution of
$\gamma \simeq 1/{a}_{\mathrm{e}}\simeq 862$
. As presented in Figure 2(c), the electron energy is smaller than 10 MeV during the process of injection. Therefore, the contribution of
![]() ${\boldsymbol{\varOmega}}_{\mathrm{a}}$
can be ignored and
${\boldsymbol{\varOmega}}_{\mathrm{a}}$
can be ignored and
![]() $\boldsymbol{\varOmega} \simeq {\boldsymbol{\varOmega}}_{\mathrm{T}}$
can be used in the next analysis.
$\boldsymbol{\varOmega} \simeq {\boldsymbol{\varOmega}}_{\mathrm{T}}$
can be used in the next analysis.
As shown in Figure 3(c), the electron precesses in the XY plane, which is caused by the part of
![]() ${\boldsymbol{\varOmega}}_z$
. It can be divided into three terms,
${\boldsymbol{\varOmega}}_z$
. It can be divided into three terms,
![]() ${\boldsymbol{\varOmega}}_{B_z}$
,
${\boldsymbol{\varOmega}}_{B_z}$
,
![]() ${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
and
${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
and
![]() ${\boldsymbol{\varOmega}}_{v_x{E}_y}$
. Figure 3(d) presents the history of
${\boldsymbol{\varOmega}}_{v_x{E}_y}$
. Figure 3(d) presents the history of
![]() ${\boldsymbol{\varOmega}}_z$
, and the contributions of the three different terms have been compared. It is found that the contribution of
${\boldsymbol{\varOmega}}_z$
, and the contributions of the three different terms have been compared. It is found that the contribution of
![]() ${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
can be ignored because the motion of electrons is nearly along the laser axis, where
${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
can be ignored because the motion of electrons is nearly along the laser axis, where
![]() ${E}_x$
is nearly zero. The contribution of
${E}_x$
is nearly zero. The contribution of
![]() ${\boldsymbol{\varOmega}}_{v_x{E}_y}$
is comparable with
${\boldsymbol{\varOmega}}_{v_x{E}_y}$
is comparable with
![]() ${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
. Following with time, the contribution of
${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
. Following with time, the contribution of
![]() ${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
increases firstly and then decreases, which is consistent with the evolution of electron velocity. More importantly, the net contribution of
${\boldsymbol{\varOmega}}_{\boldsymbol{v}\times \boldsymbol{E}}$
increases firstly and then decreases, which is consistent with the evolution of electron velocity. More importantly, the net contribution of
![]() ${\boldsymbol{\varOmega}}_z$
is nearly zero at one cycle, such that the effect of the laser field on electron spin can be ignored.
${\boldsymbol{\varOmega}}_z$
is nearly zero at one cycle, such that the effect of the laser field on electron spin can be ignored.

Figure 4 (a) The green dots denote the positions of the chosen accelerated electrons, which are marked in Figure 1(d). The magnetic field
![]() ${B}_z$
at the laser axis is presented as a black solid line. (b) The spectra of
${B}_z$
at the laser axis is presented as a black solid line. (b) The spectra of
![]() ${s}_x$
(black line) and the longitudinal position
${s}_x$
(black line) and the longitudinal position
![]() $x$
(magenta line) for the accelerated electrons at
$x$
(magenta line) for the accelerated electrons at
![]() $330\ \mathrm{fs}$
. (c) The profiles of
$330\ \mathrm{fs}$
. (c) The profiles of
![]() ${E}_y$
(red line) and
${E}_y$
(red line) and
![]() ${E}_x$
(blue line) at the laser axis. (d) The spectra of the longitudinal velocity
${E}_x$
(blue line) at the laser axis. (d) The spectra of the longitudinal velocity
![]() ${v}_x$
(red line) and transverse velocity
${v}_x$
(red line) and transverse velocity
![]() ${v}_y$
(blue line).
${v}_y$
(blue line).
As revealed in Figure 2(a), in the third stage, the electron spin does not change obviously. The distribution of the magnetic field at
![]() $330$
fs is shown in Figure 4(a). The accelerated electrons are denoted as green dots and they are located at the tail of the wakefield. The spectrum of
$330$
fs is shown in Figure 4(a). The accelerated electrons are denoted as green dots and they are located at the tail of the wakefield. The spectrum of
![]() ${s}_x$
indicates that the spin does not change obviously compared with the initial value, as presented in Figure 4(b), which means that the effect of the wakefield can be ignored. Furthermore, the width of the accelerated electron beam is
${s}_x$
indicates that the spin does not change obviously compared with the initial value, as presented in Figure 4(b), which means that the effect of the wakefield can be ignored. Furthermore, the width of the accelerated electron beam is
![]() $0.039\lambda$
(or
$0.039\lambda$
(or
![]() $103.20$
as), where the full width at half maximum (FWHM) of the energy spectrum was used. The distribution of the electromagnetic field at the laser axis is presented in Figure 4(c) and the spectra of
$103.20$
as), where the full width at half maximum (FWHM) of the energy spectrum was used. The distribution of the electromagnetic field at the laser axis is presented in Figure 4(c) and the spectra of
![]() ${v}_x$
and
${v}_x$
and
![]() ${v}_y$
are plotted in Figure 4(d). At the tail of the wakefield,
${v}_y$
are plotted in Figure 4(d). At the tail of the wakefield,
![]() ${B}_z$
and
${B}_z$
and
![]() ${E}_y$
are nearly zero. Then their contribution to
${E}_y$
are nearly zero. Then their contribution to
![]() ${\boldsymbol{\varOmega}}_z$
can be ignored. Because of the small
${\boldsymbol{\varOmega}}_z$
can be ignored. Because of the small
![]() ${v}_y$
, the contribution of
${v}_y$
, the contribution of
![]() ${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
can also be ignored, which is an essential difference compared with transverse injection. In the case of longitudinal injection, due to the motion of electrons close to the laser axis, the electron spin is affected by the laser field only. Since the laser field cannot depolarize the electrons, it is advantageous to obtain a polarized electron beam with a high energy in LWFAs. Finally, a nearly
${\boldsymbol{\varOmega}}_{-{v}_y{E}_x}$
can also be ignored, which is an essential difference compared with transverse injection. In the case of longitudinal injection, due to the motion of electrons close to the laser axis, the electron spin is affected by the laser field only. Since the laser field cannot depolarize the electrons, it is advantageous to obtain a polarized electron beam with a high energy in LWFAs. Finally, a nearly
![]() $115\ \mathrm{as}$
electron beam with
$115\ \mathrm{as}$
electron beam with
![]() $99\%$
polarization and average kinetic energy of
$99\%$
polarization and average kinetic energy of
![]() $64\ \mathrm{MeV}$
is obtained at
$64\ \mathrm{MeV}$
is obtained at
![]() $400\ \mathrm{fs}$
.
$400\ \mathrm{fs}$
.
In this work, the spin dynamics of injection electrons and the related physical mechanism have been briefly addressed based on a series of 2D simulations. Since the evolutions of the laser pulse and bubble regime are 3D nonlinear phenomena, it is necessary to use 3D simulation to analyze more accurately the characteristics of the electron beam, such as electron charge and transverse emittance[ Reference Kalmykov, Beck, Yi, Khudik, Downer, Lefebvre, Shadwick and Umstadter 40 , Reference Tsung, Lu, Tzoufras, Mori, Joshi, Vieira, Silva and Fonseca 47 ].The polarization of electron beams could also be influenced by other effects, that is, beam loading and laser polarization. Besides, a plasma with 100% of the initial polarization rate was assumed since the state of pre-polarization has not been measured in the experiment. The polarization of the acceleration electron could be smaller than the result of simulation, even using the longitudinal injection mechanism. The details will be studied in our future work.
4 Summary
We have studied the generation of an electron beam, including its polarization properties in the bubble regime of an LWFA. By using a series of 2D PIC simulations, it is found that the depolarization process depends on the self-injection scheme. Compared with transverse self-injection, longitudinal self-injection is more suitable to generate an electron beam with higher polarization. The accelerated electrons move around the laser axis in the case of longitudinal injection. It causes the motion and the spin of the electrons to oscillate in the laser field, and the net influence of the laser field can be ignored. The contribution of the bubble field to the spin precession is also negligible, since the transverse electromagnetic field and the transverse velocity of the electrons are both very small. Ultimately, an attosecond electron beam with polarization of
![]() $99\%$
is obtained in the simulation. Our work helps to generate a polarized electron beam using the longitudinal self-injection scheme in a pre-polarized plasma and guide future experiments for producing ultra-short electron beams with high polarization.
$99\%$
is obtained in the simulation. Our work helps to generate a polarized electron beam using the longitudinal self-injection scheme in a pre-polarized plasma and guide future experiments for producing ultra-short electron beams with high polarization.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 11804348, 11775056, 11975154 and 11991074) and the Science Challenge Project (No. TZ2018005). X. F. Li was also supported by the Shanghai Pujiang Program (No. 23PJ1414600). The work of M. Büscher was carried out in the framework of the Jülich Short-Pulse Particle and Radiation Center[ Reference Büscher, Adam, Tusche, Hützen, Wiemann, Chen and Schneider 48 ] and was supported by the Accelerator Technology Helmholtz Infrastructure consortium ATHENA.