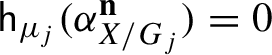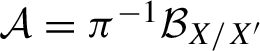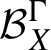1 Introduction and main results
The map
![]() $T_p:x \mapsto px$
on
$T_p:x \mapsto px$
on
![]() $\mathbb {T}=\mathbb {R}/\mathbb {Z}$
has many closed invariant sets and many invariant measures. Furstenberg initiated the study of jointly invariant sets in his seminal paper [Reference Furstenberg14]. A set
$\mathbb {T}=\mathbb {R}/\mathbb {Z}$
has many closed invariant sets and many invariant measures. Furstenberg initiated the study of jointly invariant sets in his seminal paper [Reference Furstenberg14]. A set
![]() $A \subseteq \mathbb {T}$
is called jointly invariant under
$A \subseteq \mathbb {T}$
is called jointly invariant under
![]() $T_p$
and
$T_p$
and
![]() $T_q$
if
$T_q$
if
![]() $T_p (A)\subseteq A$
and
$T_p (A)\subseteq A$
and
![]() ${T_q(A)\subseteq A}$
. Furstenberg proved that if p and q are multiplicatively independent integers, then any closed jointly invariant set is either finite or all of
${T_q(A)\subseteq A}$
. Furstenberg proved that if p and q are multiplicatively independent integers, then any closed jointly invariant set is either finite or all of
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
Furstenberg also raised the question concerning what are the jointly invariant measures, that is, which probability measures
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {T}$
satisfy
$\mathbb {T}$
satisfy
![]() $(T_p)_*\mu =(T_q)_*\mu =\mu $
. The obvious ones are the Lebesgue measure, atomic measures supported on finite invariant sets, and (non-ergodic) convex combinations of these.
$(T_p)_*\mu =(T_q)_*\mu =\mu $
. The obvious ones are the Lebesgue measure, atomic measures supported on finite invariant sets, and (non-ergodic) convex combinations of these.
In the following, a solenoid X is a compact, connected, abelian group whose Pontryagin dual
![]() $\widehat {X}$
can be embedded into a finite-dimensional vector space over
$\widehat {X}$
can be embedded into a finite-dimensional vector space over
![]() $\mathbb Q$
. The simplest example is a finite-dimensional torus. A
$\mathbb Q$
. The simplest example is a finite-dimensional torus. A
![]() $\mathbb {Z}^{d}$
-action
$\mathbb {Z}^{d}$
-action
![]() $\alpha $
by automorphisms of a solenoid X is called irreducible if there is no proper infinite closed subgroup which is invariant under
$\alpha $
by automorphisms of a solenoid X is called irreducible if there is no proper infinite closed subgroup which is invariant under
![]() $\alpha $
, and totally irreducible if there is no finite index subgroup
$\alpha $
, and totally irreducible if there is no finite index subgroup
![]() $\Lambda \subseteq \mathbb {Z}^{d}$
and no proper infinite closed subgroup
$\Lambda \subseteq \mathbb {Z}^{d}$
and no proper infinite closed subgroup
![]() $Y \subseteq X$
which is invariant under the induced action
$Y \subseteq X$
which is invariant under the induced action
![]() $\alpha _\Lambda $
. A
$\alpha _\Lambda $
. A
![]() $\mathbb {Z}^{d}$
-action is virtually cyclic if there exists
$\mathbb {Z}^{d}$
-action is virtually cyclic if there exists
![]() $\mathbf {n} \in \mathbb {Z}^{d}$
such that for every element
$\mathbf {n} \in \mathbb {Z}^{d}$
such that for every element
![]() $\mathbf {m} \in \Lambda $
of a finite index subgroup
$\mathbf {m} \in \Lambda $
of a finite index subgroup
![]() $\Lambda \subseteq \mathbb {Z}^{d}$
, there exists some
$\Lambda \subseteq \mathbb {Z}^{d}$
, there exists some
![]() $k \in \mathbb {Z}$
with
$k \in \mathbb {Z}$
with
![]() ${\alpha ^{\mathbf {m}}}=\alpha ^{k\mathbf {n}}$
.
${\alpha ^{\mathbf {m}}}=\alpha ^{k\mathbf {n}}$
.
We briefly summarize the history of this problem. The topological generalization of Furstenberg’s result to higher dimensions was given by Berend [Reference Berend1, Reference Berend2]: An action on a torus or solenoid has no proper, infinite, closed, and invariant subsets if and only if it is totally irreducible, not virtually cyclic, and contains a hyperbolic element.
The first partial result for the measure problem on
![]() $\mathbb {T}$
was given by Lyons [Reference Lyons31] under a strong additional assumption. Rudolph [Reference Rudolph34] weakened this assumption considerably, and proved the following theorem.
$\mathbb {T}$
was given by Lyons [Reference Lyons31] under a strong additional assumption. Rudolph [Reference Rudolph34] weakened this assumption considerably, and proved the following theorem.
Theorem 1.1. [Reference Rudolph34, Theorem 4.9]
Let
![]() $p, q \geq 2$
be relatively prime positive integers, and let
$p, q \geq 2$
be relatively prime positive integers, and let
![]() $\mu $
be a
$\mu $
be a
![]() $T_p$
,
$T_p$
,
![]() $T_q$
-invariant, and ergodic measure on
$T_q$
-invariant, and ergodic measure on
![]() $\mathbb {T}$
. Then either
$\mathbb {T}$
. Then either
![]() $\mu =m_{\mathbb {T}}$
is the Lebesgue measure on
$\mu =m_{\mathbb {T}}$
is the Lebesgue measure on
![]() $\mathbb {T}$
, or the entropy of
$\mathbb {T}$
, or the entropy of
![]() $T_p$
and
$T_p$
and
![]() $T_q$
is zero.
$T_q$
is zero.
Johnson [Reference Johnson17] lifted the relative primality assumption, by showing it is enough to assume that p and q are multiplicatively independent. Feldman [Reference Feldman13], Parry [Reference Parry33], and Host [Reference Host15] have found different proofs of this theorem, but positive entropy remains a crucial assumption.
Anatole Katok and Spatzier [Reference Katok and Spatzier22, Reference Katok and Spatzier23] obtained the first analogous results for actions on higher dimensional tori and homogeneous spaces. However, their method required either an additional ergodicity assumption on the measure (satisfied for example if every one parameter subgroup of the suspension acts ergodically), or that the action is totally non-symplectic (TNS). A careful and readable account of these results has been written by Kalinin and Anatole Katok [Reference Kalinin and Katok18], which also fixed some minor inaccuracies. The following theorem (already proven in the announcement [Reference Einsiedler and Lindenstrauss7]) gives a full generalization of the result of Rudolph and Johnson to actions on higher-dimensional solenoids.
Theorem 1.2. [Reference Einsiedler and Lindenstrauss7, Theorem 1.1]
Let
![]() $\alpha $
be a totally irreducible, not virtually cyclic
$\alpha $
be a totally irreducible, not virtually cyclic
![]() $\mathbb {Z}^{d}$
-action by automorphisms of a solenoid X. Let
$\mathbb {Z}^{d}$
-action by automorphisms of a solenoid X. Let
![]() $\mu $
be an
$\mu $
be an
![]() $\alpha $
-invariant and ergodic probability measure. Then either
$\alpha $
-invariant and ergodic probability measure. Then either
![]() $\mu =m_X$
is the Haar measure of X, or the entropy
$\mu =m_X$
is the Haar measure of X, or the entropy
![]() ${\sf h}_\mu (\alpha ^{\mathbf {n}})=0$
vanishes for all
${\sf h}_\mu (\alpha ^{\mathbf {n}})=0$
vanishes for all
![]() $\mathbf {n} \in \mathbb {Z}^{d}$
.
$\mathbf {n} \in \mathbb {Z}^{d}$
.
1.1 The general positive entropy measure rigidity theorem
Without total irreducibility, the Haar measure of the group is no longer the only measure with positive entropy. Thus our main theorem below is (necessarily) longer in its formulation than Theorem 1.2. It strengthens e.g. [Reference Kalinin and Katok18, Theorem 3.1] which has a similar conclusion but stronger assumptions.
Theorem 1.3. (Positive entropy rigidity theorem)
Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $\mathbb {Z}^{d}$
-action (
$\mathbb {Z}^{d}$
-action (
![]() $d \geq 2$
) by automorphisms of a solenoid X. Suppose
$d \geq 2$
) by automorphisms of a solenoid X. Suppose
![]() $\alpha $
has no virtually cyclic factors, and let
$\alpha $
has no virtually cyclic factors, and let
![]() $\mu $
be an
$\mu $
be an
![]() $\alpha $
-invariant and ergodic probability measure on X. Then there exists a subgroup
$\alpha $
-invariant and ergodic probability measure on X. Then there exists a subgroup
![]() $\Lambda \subseteq \mathbb {Z}^{d}$
of finite index and a decomposition
$\Lambda \subseteq \mathbb {Z}^{d}$
of finite index and a decomposition
![]() $\mu =({1}/{J})(\mu _1+\cdots +\mu _J)$
of
$\mu =({1}/{J})(\mu _1+\cdots +\mu _J)$
of
![]() $\mu $
into mutually singular measures with the following properties for every
$\mu $
into mutually singular measures with the following properties for every
![]() $j=1,\ldots ,J$
.
$j=1,\ldots ,J$
.
-
(1) The measure
 $\mu _j$
is
$\mu _j$
is
 $\alpha _\Lambda $
-ergodic, where
$\alpha _\Lambda $
-ergodic, where
 $\alpha _\Lambda $
is the restriction of
$\alpha _\Lambda $
is the restriction of
 $\alpha $
to
$\alpha $
to
 $\Lambda $
.
$\Lambda $
. -
(2) There exists an
 $\alpha _\Lambda $
-invariant closed subgroup
$\alpha _\Lambda $
-invariant closed subgroup
 $G_j$
such that
$G_j$
such that
 $\mu _j$
is invariant under translation with elements in
$\mu _j$
is invariant under translation with elements in
 $G_j$
, that is,
$G_j$
, that is,
 $\mu _j(B)=\mu _j(B+g)$
for all
$\mu _j(B)=\mu _j(B+g)$
for all
 $g \in G_j$
and every measurable set
$g \in G_j$
and every measurable set
 $B\subseteq X$
.
$B\subseteq X$
. -
(3) For
 $\mathbf {n} \in \mathbb {Z}^{d}$
,
$\mathbf {n} \in \mathbb {Z}^{d}$
,
 $\alpha ^{\mathbf {n}}_*\mu _j=\mu _k$
for some
$\alpha ^{\mathbf {n}}_*\mu _j=\mu _k$
for some
 $k\in \{1,\ldots ,J\}$
and
$k\in \{1,\ldots ,J\}$
and
 $\alpha ^{\mathbf {n}}(G_j)=G_k$
.
$\alpha ^{\mathbf {n}}(G_j)=G_k$
. -
(4) The measure
 $\mu _j$
induces a measure on the factor
$\mu _j$
induces a measure on the factor
 $X/G_j$
with
$X/G_j$
with
 ${\sf h}_{\mu _j}(\alpha ^{\mathbf {n}}_{X/G_j})=0$
for any
${\sf h}_{\mu _j}(\alpha ^{\mathbf {n}}_{X/G_j})=0$
for any
 $\mathbf {n} \in \Lambda $
. (Here
$\mathbf {n} \in \Lambda $
. (Here
 $\alpha _{X/G_j}$
denotes the action induced on
$\alpha _{X/G_j}$
denotes the action induced on
 $X/G_j$
.)
$X/G_j$
.)
We remark that in the topological category, there is a big gap between our understanding of the totally irreducible case and the general case of
![]() $\mathbb {Z} ^ d$
-actions by automorphisms on a solenoid. In the totally irreducible case, Berend [Reference Berend2] gave an if-and-only-if condition for a
$\mathbb {Z} ^ d$
-actions by automorphisms on a solenoid. In the totally irreducible case, Berend [Reference Berend2] gave an if-and-only-if condition for a
![]() $\mathbb {Z} ^ d$
-action to have the property that every orbit is either finite or dense, and the same methods could be pushed further to give a complete classification of closed invariant subsets for a totally irreducible
$\mathbb {Z} ^ d$
-action to have the property that every orbit is either finite or dense, and the same methods could be pushed further to give a complete classification of closed invariant subsets for a totally irreducible
![]() $\mathbb {Z} ^ d$
-action on the solenoid; for
$\mathbb {Z} ^ d$
-action on the solenoid; for
![]() $\mathbb {Z} ^ d$
-action on tori, this is due to Z. Wang [Reference Wang36, Theorem 1.10], and his proof certainly works also for solenoids though this does not seem to have been written (a special case, with a very nice application, can be found in Manner’s paper [Reference Manners32]). In the non-irreducible case, orbit closures and closed invariant sets are much less understood. We refer to [Reference Lindenstrauss and Wang30] by Z. Wang and the second named author for some results in this direction and additional details.
$\mathbb {Z} ^ d$
-action on tori, this is due to Z. Wang [Reference Wang36, Theorem 1.10], and his proof certainly works also for solenoids though this does not seem to have been written (a special case, with a very nice application, can be found in Manner’s paper [Reference Manners32]). In the non-irreducible case, orbit closures and closed invariant sets are much less understood. We refer to [Reference Lindenstrauss and Wang30] by Z. Wang and the second named author for some results in this direction and additional details.
The proofs of Theorem 1.2 and Theorem 1.3 follow the outline of Rudolph’s proof of Theorem 1.1. One of the main ingredients there was the observation that
![]() ${\sf h}_\mu (T_p)/ \log p = {\sf h}_\mu (T_q)/\log q$
(and a relativized version of this equality). This follows from the particularly simple geometry of this system where both
${\sf h}_\mu (T_p)/ \log p = {\sf h}_\mu (T_q)/\log q$
(and a relativized version of this equality). This follows from the particularly simple geometry of this system where both
![]() $T_p$
and
$T_p$
and
![]() $T_q$
expand the one-dimensional space
$T_q$
expand the one-dimensional space
![]() $\mathbb {T}$
with fixed factors. There is no simple geometrical reason why such an equality should be true for more complicated
$\mathbb {T}$
with fixed factors. There is no simple geometrical reason why such an equality should be true for more complicated
![]() $\mathbb {Z} ^ d$
-actions on solenoids, and indeed is easily seen to fail in the reducible case. However, somewhat surprisingly, such an equality is true for irreducible
$\mathbb {Z} ^ d$
-actions on solenoids, and indeed is easily seen to fail in the reducible case. However, somewhat surprisingly, such an equality is true for irreducible
![]() $\mathbb {Z} ^ d$
-actions, even though this is true for subtler reasons (see Theorem 7.1 below).
$\mathbb {Z} ^ d$
-actions, even though this is true for subtler reasons (see Theorem 7.1 below).
In the following two subsections we also apply Theorem 1.3 to obtain new information about the measurable structure, with respect to the Haar measure, of algebraic
![]() $\mathbb {Z}^{d}$
-actions on tori and solenoids.
$\mathbb {Z}^{d}$
-actions on tori and solenoids.
1.2 Characterization of disjointness
Let
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
be two measure-preserving
$\alpha _2$
be two measure-preserving
![]() $\mathbb {Z}^{d}$
-actions on the probability spaces
$\mathbb {Z}^{d}$
-actions on the probability spaces
![]() $(X_1,\mathcal {B}_{X_1},\mu _1)$
and
$(X_1,\mathcal {B}_{X_1},\mu _1)$
and
![]() $(X_2,\mathcal {B}_{X_2},\mu _2)$
. A joining between
$(X_2,\mathcal {B}_{X_2},\mu _2)$
. A joining between
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
is an
$\alpha _2$
is an
![]() $\alpha _1\times \alpha _2$
-invariant probability measure
$\alpha _1\times \alpha _2$
-invariant probability measure
![]() $\nu $
on
$\nu $
on
![]() $X_1\times X_2$
, which projects to
$X_1\times X_2$
, which projects to
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
under the projection maps
$\mu _2$
under the projection maps
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
. In other words we require
$\pi _2$
. In other words we require
![]() $\nu (\alpha _1^{\mathbf {n}}\times \alpha _2^{\mathbf {n}}(C))=\nu (C)$
for
$\nu (\alpha _1^{\mathbf {n}}\times \alpha _2^{\mathbf {n}}(C))=\nu (C)$
for
![]() $\mathbf {n}\in \mathbb {Z}^d$
and
$\mathbf {n}\in \mathbb {Z}^d$
and
![]() $C\in \mathcal {B}_{X_1\times X_2}$
,
$C\in \mathcal {B}_{X_1\times X_2}$
,
![]() $\nu (A\times X_2)=\mu _1(A)$
for
$\nu (A\times X_2)=\mu _1(A)$
for
![]() $A\in \mathcal {B}_{X_1}$
, and also
$A\in \mathcal {B}_{X_1}$
, and also
![]() $\nu (X_1\times B)=\mu _2(B)$
for
$\nu (X_1\times B)=\mu _2(B)$
for
![]() $B\in \mathcal {B}_{X_2}$
. The product measure
$B\in \mathcal {B}_{X_2}$
. The product measure
![]() $\mu _1\times \mu _2$
is always a joining, called the trivial joining. If the trivial joining is the only joining, the two actions are disjoint. This implies that the two actions are measurably non-isomorphic. In fact if they are disjoint, there is no non-trivial common factor of the two systems, see for instance §9 where we recall the construction of the relatively independent joining over a common factor.
$\mu _1\times \mu _2$
is always a joining, called the trivial joining. If the trivial joining is the only joining, the two actions are disjoint. This implies that the two actions are measurably non-isomorphic. In fact if they are disjoint, there is no non-trivial common factor of the two systems, see for instance §9 where we recall the construction of the relatively independent joining over a common factor.
Let now
![]() $\alpha _j$
be measure preserving
$\alpha _j$
be measure preserving
![]() $\mathbb {Z}^{d}$
-actions on
$\mathbb {Z}^{d}$
-actions on
![]() $(X_j,\mathcal {B}_{X_j},\mu _j)$
for
$(X_j,\mathcal {B}_{X_j},\mu _j)$
for
![]() $j=1,\ldots ,r$
. A joining between
$j=1,\ldots ,r$
. A joining between
![]() $\alpha _j$
for
$\alpha _j$
for
![]() $j=1,\ldots ,r$
is a measure
$j=1,\ldots ,r$
is a measure
![]() $\nu $
on
$\nu $
on
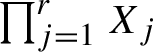 $\prod _{j=1}^rX_j$
which projects to
$\prod _{j=1}^rX_j$
which projects to
![]() $\mu _j$
under the coordinate projections
$\mu _j$
under the coordinate projections
![]() $\pi _j$
for
$\pi _j$
for
![]() $j=1,\ldots ,r$
, and is invariant under the
$j=1,\ldots ,r$
, and is invariant under the
![]() $\mathbb {Z}^{d}$
-action
$\mathbb {Z}^{d}$
-action
![]() $\alpha _1\times \cdots \times \alpha _r$
. The product measure is the trivial joining, and the
$\alpha _1\times \cdots \times \alpha _r$
. The product measure is the trivial joining, and the
![]() $\mathbb {Z}^{d}$
-actions are mutually disjoint if the trivial joining is the only joining.
$\mathbb {Z}^{d}$
-actions are mutually disjoint if the trivial joining is the only joining.
Suppose now
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are actions by automorphisms on solenoids
$\alpha _2$
are actions by automorphisms on solenoids
![]() $X_1$
and
$X_1$
and
![]() $X_2$
, respectively. We will classify disjointness with respect to the Haar measures
$X_2$
, respectively. We will classify disjointness with respect to the Haar measures
![]() $m_{X_j}$
on the group
$m_{X_j}$
on the group
![]() $X_j$
for
$X_j$
for
![]() $j=1,2$
. If
$j=1,2$
. If
![]() $\varphi :X_1\rightarrow X_2$
is a continuous surjective homomorphism and satisfies
$\varphi :X_1\rightarrow X_2$
is a continuous surjective homomorphism and satisfies
![]() $\alpha _2^{\mathbf {n}}\circ \varphi =\varphi \circ \alpha _1^{\mathbf {n}}$
for all
$\alpha _2^{\mathbf {n}}\circ \varphi =\varphi \circ \alpha _1^{\mathbf {n}}$
for all
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
, we say
$\mathbf {n}\in \mathbb {Z}^{d}$
, we say
![]() $\varphi $
is an algebraic factor map. If
$\varphi $
is an algebraic factor map. If
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are both finite-to-one factors of each other by algebraic factor maps, we say they are algebraically weakly isomorphic. Equivalently,
$\alpha _2$
are both finite-to-one factors of each other by algebraic factor maps, we say they are algebraically weakly isomorphic. Equivalently,
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are algebraically weakly isomorphic if they have a common finite-to-one algebraic factor.
$\alpha _2$
are algebraically weakly isomorphic if they have a common finite-to-one algebraic factor.
The following generalizes a theorem of Kalinin and Anatole Katok [Reference Kalinin and Katok19, Theorem 3.1] and of Kalinin and Spatzier [Reference Kalinin and Spatzier20, Theorem 4.7], where the main difference is that we do not assume that the actions are totally non-symplectic or hyperbolic.
Corollary 1.4. (Classification of disjointness)
If
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are totally irreducible and not virtually cyclic, then they are not disjoint (with respect to the Haar measures) if and only if there exists a finite index subgroup
$\alpha _2$
are totally irreducible and not virtually cyclic, then they are not disjoint (with respect to the Haar measures) if and only if there exists a finite index subgroup
![]() $\Lambda \subseteq \mathbb {Z}^{d}$
for which
$\Lambda \subseteq \mathbb {Z}^{d}$
for which
![]() $\alpha _{1,\Lambda }$
and
$\alpha _{1,\Lambda }$
and
![]() $\alpha _{2,\Lambda }$
are algebraically weakly isomorphic.
$\alpha _{2,\Lambda }$
are algebraically weakly isomorphic.
More generally, let
![]() $\alpha _j$
be
$\alpha _j$
be
![]() $\mathbb {Z}^{d}$
-actions on solenoids (not necessarily irreducible) without virtually cyclic factors for
$\mathbb {Z}^{d}$
-actions on solenoids (not necessarily irreducible) without virtually cyclic factors for
![]() $j=1,\ldots ,r$
. Then they are not mutually disjoint if and only if there exist indices
$j=1,\ldots ,r$
. Then they are not mutually disjoint if and only if there exist indices
![]() $i, j\in \{1,\ldots ,r\}$
with
$i, j\in \{1,\ldots ,r\}$
with
![]() $i\neq j$
, a finite index subgroup
$i\neq j$
, a finite index subgroup
![]() $\Lambda \subseteq \mathbb {Z}^{d}$
, and a non-trivial
$\Lambda \subseteq \mathbb {Z}^{d}$
, and a non-trivial
![]() $\Lambda $
-action
$\Lambda $
-action
![]() $\beta $
on a solenoid Y which is an algebraic factor of
$\beta $
on a solenoid Y which is an algebraic factor of
![]() $\alpha _{i,\Lambda }$
and
$\alpha _{i,\Lambda }$
and
![]() $\alpha _{j,\Lambda }$
.
$\alpha _{j,\Lambda }$
.
1.3 Algebraicity of factors
Anatole Katok, Svetlana Katok, and Schmidt [Reference Katok, Katok and Schmidt21, Theorem 5.6] studied measurable factor maps between
![]() $\mathbb {Z}^{d}$
-actions by automorphisms of tori. Our second application gives an extension of this by characterizing the structure of measurable factors (or equivalently invariant
$\mathbb {Z}^{d}$
-actions by automorphisms of tori. Our second application gives an extension of this by characterizing the structure of measurable factors (or equivalently invariant
![]() $\sigma $
-algebras). We start by giving two algebraic constructions that give invariant
$\sigma $
-algebras). We start by giving two algebraic constructions that give invariant
![]() $\sigma $
-algebras.
$\sigma $
-algebras.
-
• If
 $X^{\prime }\subseteq X $
is a closed
$X^{\prime }\subseteq X $
is a closed
 $\alpha $
-invariant subgroup and
$\alpha $
-invariant subgroup and
 $\pi :X\rightarrow X/X^{\prime } $
denotes the canonical projection map, then the preimage
$\pi :X\rightarrow X/X^{\prime } $
denotes the canonical projection map, then the preimage
 $\mathcal {A}=\pi ^{-1}\mathcal {B}_{X/X^{\prime }}$
of the Borel
$\mathcal {A}=\pi ^{-1}\mathcal {B}_{X/X^{\prime }}$
of the Borel
 $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal {B}_{X/X^{\prime }} $
of
$\mathcal {B}_{X/X^{\prime }} $
of
 $X/X^{\prime }$
is
$X/X^{\prime }$
is
 $\alpha $
-invariant.
$\alpha $
-invariant. -
• If
 $\Gamma $
is a finite group of affine automorphisms that is normalized by
$\Gamma $
is a finite group of affine automorphisms that is normalized by
 $\alpha $
, then the
$\alpha $
, then the
 $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal {B}_X^\Gamma $
of
$\mathcal {B}_X^\Gamma $
of
 $\Gamma $
-invariant Borel subsets of X is
$\Gamma $
-invariant Borel subsets of X is
 $\alpha $
-invariant.
$\alpha $
-invariant.
Corollary 1.5. (Algebraicity of measurable factors)
Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $\mathbb {Z}^{d}$
-action by automorphisms of the solenoid X without virtually cyclic factors, and let
$\mathbb {Z}^{d}$
-action by automorphisms of the solenoid X without virtually cyclic factors, and let
![]() $\mathcal {A}\subseteq \mathcal {B}_X$
be an invariant
$\mathcal {A}\subseteq \mathcal {B}_X$
be an invariant
![]() $\sigma $
-algebra. Then there exists a closed
$\sigma $
-algebra. Then there exists a closed
![]() $\alpha $
-invariant subgroup
$\alpha $
-invariant subgroup
![]() $X^{\prime }\subseteq X$
and a finite group
$X^{\prime }\subseteq X$
and a finite group
![]() $\Gamma $
of affine automorphisms of
$\Gamma $
of affine automorphisms of
![]() $X/X^{\prime }$
that is normalized by the action
$X/X^{\prime }$
that is normalized by the action
![]() $\alpha _{X/X^{\prime }}$
induced by
$\alpha _{X/X^{\prime }}$
induced by
![]() $\alpha $
on
$\alpha $
on
![]() $X/X^{\prime }$
such that
$X/X^{\prime }$
such that
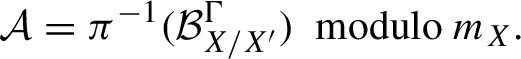 $$ \begin{align*} \mathcal{A}=\pi^{-1}(\mathcal{B}_{X/X^{\prime}}^\Gamma)\ \operatorname{modulo}m_X. \end{align*} $$
$$ \begin{align*} \mathcal{A}=\pi^{-1}(\mathcal{B}_{X/X^{\prime}}^\Gamma)\ \operatorname{modulo}m_X. \end{align*} $$
In other words, the corollary states that every measurable factor of
![]() $\alpha $
arises by a combination of the two algebraic constructions given above.
$\alpha $
arises by a combination of the two algebraic constructions given above.
In the irreducible case, the theorem gives that every non-trivial measurable factor of
![]() $\alpha $
is a quotient of X by the action of a finite affine group. The simplest examples of such groups are finite translation groups. However, more complicated examples are also possible; for example, let
$\alpha $
is a quotient of X by the action of a finite affine group. The simplest examples of such groups are finite translation groups. However, more complicated examples are also possible; for example, let
![]() $w \in X$
be any
$w \in X$
be any
![]() $\alpha $
-fixed point. Then the action of
$\alpha $
-fixed point. Then the action of
![]() $G=\{ \operatorname {Id},-\operatorname {Id}+w \}$
on X commutes with
$G=\{ \operatorname {Id},-\operatorname {Id}+w \}$
on X commutes with
![]() $\alpha $
.
$\alpha $
.
The proof of Corollary 1.5 uses the relatively independent joining of the Haar measure with itself over the factor
![]() $\mathcal {A}$
, which gives an invariant measure on
$\mathcal {A}$
, which gives an invariant measure on
![]() $X \times X$
analyzable by Theorem 1.3. This is similar to the proof of isomorphism rigidity in [Reference Katok, Katok and Schmidt21], which followed a suggestion by Thouvenot.
$X \times X$
analyzable by Theorem 1.3. This is similar to the proof of isomorphism rigidity in [Reference Katok, Katok and Schmidt21], which followed a suggestion by Thouvenot.
We will discuss further corollaries towards factors in §9.
1.4 Remarks and acknowledgements
The results of this paper were obtained in 2002 and announced in [Reference Einsiedler and Lindenstrauss7]; indeed this was the first result we worked on together. Since then, there was always another newer result that we wanted to write, and we never seemed to have the time to finally write down the general case of the results announced in [Reference Einsiedler and Lindenstrauss7]. One important ingredient in this work is the product structure for coarse Lyapunov foliations developed around that time by Anatole Katok and the first author.
The ideas behind the proof of Theorem 1.3 were used by Z. Wang to prove his strong measure classification result for invariant measures on nilmanifolds [Reference Wang37]. Actions by automorphisms on nilmanifolds generalize actions on tori which are covered by the results of this paper; solenoids are more general than tori, but more importantly, in that paper, Z. Wang does not allow for zero entropy factors, as we do here. Hence the results of this paper are (to the best of our knowledge) ‘new’ in the sense that they have not appeared in print before. We thank Z. Wang for encouraging us to write down the complete proof of [Reference Einsiedler and Lindenstrauss7] and for his willingness to help us do so. We also would like to thank the anonymous referee and Manuel Luethi for their comments.
2 Actions on adelic solenoids
2.1 Adeles, local and global fields
We review some basic facts and definitions regarding local fields, global fields, and the adeles. A general reference to these topics is Weil’s classical book [Reference Weil38, Chs. I–IV]; note that Weil calls what is now commonly referred to as global fields
![]() $\mathbb A$
-fields. Throughout this paper, the term local field will denote a locally compact field of characteristic zero; these include
$\mathbb A$
-fields. Throughout this paper, the term local field will denote a locally compact field of characteristic zero; these include
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\mathbb {C}$
as well as finite extensions of the field of p-adic numbers
$\mathbb {C}$
as well as finite extensions of the field of p-adic numbers
![]() $\mathbb Q_p$
. (The terminology of global and local fields was introduced to incorporate both the positive and zero characteristic cases on an equal footing, but dynamically there are rather fundamental differences (see e.g. [Reference Einsiedler3, Reference Kitchens and Schmidt24]) and we restrict ourselves in this paper to the zero characteristic case.) Let
$\mathbb Q_p$
. (The terminology of global and local fields was introduced to incorporate both the positive and zero characteristic cases on an equal footing, but dynamically there are rather fundamental differences (see e.g. [Reference Einsiedler3, Reference Kitchens and Schmidt24]) and we restrict ourselves in this paper to the zero characteristic case.) Let
![]() $\mathbb {K}$
be a local field and let
$\mathbb {K}$
be a local field and let
![]() be the Haar measure on
be the Haar measure on
![]() $\mathbb {K}$
. We define
$\mathbb {K}$
. We define
![]() $\delta (\mathbb {K})$
as the degree of the field extension
$\delta (\mathbb {K})$
as the degree of the field extension
![]() $\mathbb {K}$
over the closure of
$\mathbb {K}$
over the closure of
![]() $\mathbb Q$
in
$\mathbb Q$
in
![]() $\mathbb {K}$
, which can be isomorphic to either
$\mathbb {K}$
, which can be isomorphic to either
![]() $\mathbb {R}$
if
$\mathbb {R}$
if
![]() $\mathbb {K}$
is Archimedean or
$\mathbb {K}$
is Archimedean or
![]() $\mathbb Q_p$
for some prime p otherwise (to make the notation more consistent, we will also write
$\mathbb Q_p$
for some prime p otherwise (to make the notation more consistent, we will also write
![]() $\mathbb Q_\infty $
for
$\mathbb Q_\infty $
for
![]() $\mathbb {R}$
). Local fields come equipped with an absolute value
$\mathbb {R}$
). Local fields come equipped with an absolute value
![]() $|\cdot |_{\mathbb {K}}$
, which we will always normalize to coincide with the usual absolute value on
$|\cdot |_{\mathbb {K}}$
, which we will always normalize to coincide with the usual absolute value on
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb Q_p$
. We note that in any of these cases we have
$\mathbb Q_p$
. We note that in any of these cases we have
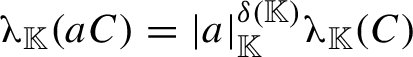
for any measurable set
![]() $C \subseteq \mathbb {K}$
.
$C \subseteq \mathbb {K}$
.
We recall that a global field
![]() $\mathbb {K}$
is a finite field extension of
$\mathbb {K}$
is a finite field extension of
![]() $\mathbb Q$
. We will denote the completions of
$\mathbb Q$
. We will denote the completions of
![]() $\mathbb {K}$
by
$\mathbb {K}$
by
![]() $\mathbb {K}_\sigma $
, where
$\mathbb {K}_\sigma $
, where
![]() $\sigma $
stands for the (Archimedean or non-Archimedean) place—that is, an equivalence class of absolute values. We choose the representative to coincide with either
$\sigma $
stands for the (Archimedean or non-Archimedean) place—that is, an equivalence class of absolute values. We choose the representative to coincide with either
![]() ${ | {\cdot } |}_\infty $
of
${ | {\cdot } |}_\infty $
of
![]() ${ | {\cdot } |}_p$
on
${ | {\cdot } |}_p$
on
![]() $\mathbb Q$
. We recall that
$\mathbb Q$
. We recall that
![]() $\mathbb {K}_\sigma $
is a local field and will use the abbreviation
$\mathbb {K}_\sigma $
is a local field and will use the abbreviation
![]() ${ | {\cdot } |}_\sigma ={ | {\cdot } |}_{\mathbb {K}_\sigma }$
for the norms satisfying (2.1) on
${ | {\cdot } |}_\sigma ={ | {\cdot } |}_{\mathbb {K}_\sigma }$
for the norms satisfying (2.1) on
![]() $\mathbb {K}_\sigma $
. If
$\mathbb {K}_\sigma $
. If
![]() ${ | {\cdot } |}_\sigma $
coincides with
${ | {\cdot } |}_\sigma $
coincides with
![]() ${ | {\cdot } |}_p$
on
${ | {\cdot } |}_p$
on
![]() $\mathbb Q$
, then we say that
$\mathbb Q$
, then we say that
![]() $\sigma $
lies over p; if
$\sigma $
lies over p; if
![]() ${ | {\cdot } |}_\sigma $
is Archimedean, we say that
${ | {\cdot } |}_\sigma $
is Archimedean, we say that
![]() $ \sigma $
is an infinite place of
$ \sigma $
is an infinite place of
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
For a global field
![]() $\mathbb {K}$
, the ring of adeles
$\mathbb {K}$
, the ring of adeles
![]() $\mathbb A_{\mathbb {K}}$
over
$\mathbb A_{\mathbb {K}}$
over
![]() $\mathbb {K}$
is defined as the restricted direct product of all completions of
$\mathbb {K}$
is defined as the restricted direct product of all completions of
![]() $\mathbb {K}$
with respect to the maximal compact subrings for all non-Archimedean completions. In other words,
$\mathbb {K}$
with respect to the maximal compact subrings for all non-Archimedean completions. In other words,
![]() $(t_\sigma )_\sigma \in \mathbb A_{\mathbb {K}}$
if
$(t_\sigma )_\sigma \in \mathbb A_{\mathbb {K}}$
if
![]() $t_\sigma \in \mathbb {K}_\sigma $
for all places
$t_\sigma \in \mathbb {K}_\sigma $
for all places
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {K}$
and, except for finitely many
$\mathbb {K}$
and, except for finitely many
![]() $\sigma $
(an exceptional set that is assumed to include all infinite places), we have that in fact
$\sigma $
(an exceptional set that is assumed to include all infinite places), we have that in fact
![]() $t_\sigma $
lies in the maximal compact subring
$t_\sigma $
lies in the maximal compact subring
![]() $\mathcal {O}_{\mathbb {K},\sigma } < \mathbb {K}_\sigma $
. In the special case
$\mathcal {O}_{\mathbb {K},\sigma } < \mathbb {K}_\sigma $
. In the special case
![]() $\mathbb {K}=\mathbb Q$
, this takes the form
$\mathbb {K}=\mathbb Q$
, this takes the form
 $$ \begin{align*} \mathbb A=\textstyle{\mathbb{R}\times\prod_p^{\prime}\mathbb Q_p}=\mathbb{R}\times\bigcup_S(\prod_{p\in S}\mathbb Q_p\times\prod_{p\notin S}\mathbb{Z}_p), \end{align*} $$
$$ \begin{align*} \mathbb A=\textstyle{\mathbb{R}\times\prod_p^{\prime}\mathbb Q_p}=\mathbb{R}\times\bigcup_S(\prod_{p\in S}\mathbb Q_p\times\prod_{p\notin S}\mathbb{Z}_p), \end{align*} $$
where the union runs over all finite subsets S of the primes. The general case of the ring of adeles
![]() $\mathbb A_{\mathbb {K}}$
over a global field
$\mathbb A_{\mathbb {K}}$
over a global field
![]() $\mathbb {K}$
is defined similarly, but can also be obtained via
$\mathbb {K}$
is defined similarly, but can also be obtained via
We shall identify
![]() $\mathbb {K}_\sigma $
with the corresponding subring in
$\mathbb {K}_\sigma $
with the corresponding subring in
![]() $\mathbb A_{\mathbb {K}}$
. Using a basis of
$\mathbb A_{\mathbb {K}}$
. Using a basis of
![]() $\mathbb {K}$
over
$\mathbb {K}$
over
![]() $\mathbb Q$
, we obtain an additive group isomorphism (indeed, an isomorphism of vector spaces over
$\mathbb Q$
, we obtain an additive group isomorphism (indeed, an isomorphism of vector spaces over
![]() $\mathbb Q$
)
$\mathbb Q$
)
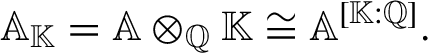 $$ \begin{align} \mathbb A_{\mathbb{K}}=\mathbb A\otimes_{\mathbb Q}\mathbb{K}\cong \mathbb A^{[\mathbb{K}:\mathbb Q]}. \end{align} $$
$$ \begin{align} \mathbb A_{\mathbb{K}}=\mathbb A\otimes_{\mathbb Q}\mathbb{K}\cong \mathbb A^{[\mathbb{K}:\mathbb Q]}. \end{align} $$
We recall moreover that
![]() $\mathbb Q$
diagonally embedded into
$\mathbb Q$
diagonally embedded into
![]() $\mathbb A$
is discrete and cocompact and that the Pontryagin dual
$\mathbb A$
is discrete and cocompact and that the Pontryagin dual
![]() $\widehat {\mathbb A}$
of
$\widehat {\mathbb A}$
of
![]() $\mathbb A$
can be identified with
$\mathbb A$
can be identified with
![]() $\mathbb A$
itself. Finally the isomorphism between
$\mathbb A$
itself. Finally the isomorphism between
![]() $\widehat {\mathbb A}$
and
$\widehat {\mathbb A}$
and
![]() $\mathbb A$
can be chosen so that the annihilator of
$\mathbb A$
can be chosen so that the annihilator of
![]() $\mathbb Q$
is
$\mathbb Q$
is
![]() $\mathbb Q$
itself, which implies that the Pontryagin dual of
$\mathbb Q$
itself, which implies that the Pontryagin dual of
![]() $\mathbb Q$
can be identified with
$\mathbb Q$
can be identified with
![]() $\mathbb A/\mathbb Q$
. This extends similarly to global fields, see e.g. [Reference Weil38, pp. 64–69].
$\mathbb A/\mathbb Q$
. This extends similarly to global fields, see e.g. [Reference Weil38, pp. 64–69].
2.2 Adelic actions
For us, the adelic setup gives a concrete language to discuss actions on general solenoids. We note however that for automorphisms on tori, it suffices to consider all Archimedean places of
![]() $\mathbb {K}$
and for irreducible actions, it would suffice to consider only finitely many places (see also [Reference Einsiedler and Lindenstrauss7] for the latter).
$\mathbb {K}$
and for irreducible actions, it would suffice to consider only finitely many places (see also [Reference Einsiedler and Lindenstrauss7] for the latter).
Indeed, let us fix a dimension
![]() $m\geq 1$
, a rank
$m\geq 1$
, a rank
![]() $d\geq 1$
, and d commuting matrices
$d\geq 1$
, and d commuting matrices
![]() $A_1,\ldots ,A_d\in \operatorname {GL}_m(\mathbb Q)$
. We use them to define a linear representation
$A_1,\ldots ,A_d\in \operatorname {GL}_m(\mathbb Q)$
. We use them to define a linear representation
![]() $\widetilde {\alpha }$
of
$\widetilde {\alpha }$
of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb Q^m$
. Using the matrices in the same way as within vector spaces, this extends to an action of
$\mathbb Q^m$
. Using the matrices in the same way as within vector spaces, this extends to an action of
![]() $\mathbb {Z}^d$
by group automorphisms on
$\mathbb {Z}^d$
by group automorphisms on
![]() $\mathbb A^m$
, which we will also denote by
$\mathbb A^m$
, which we will also denote by
![]() $\widetilde {\alpha }$
. Finally, we take the quotient by the discrete cocompact invariant subgroup
$\widetilde {\alpha }$
. Finally, we take the quotient by the discrete cocompact invariant subgroup
![]() $\mathbb Q^m$
and obtain an action
$\mathbb Q^m$
and obtain an action
![]() $\alpha $
of
$\alpha $
of
![]() $\mathbb {Z}^d$
by automorphisms on the solenoid
$\mathbb {Z}^d$
by automorphisms on the solenoid
We will refer to
![]() $X_m$
as an adelic solenoid and to this action as the adelic action on
$X_m$
as an adelic solenoid and to this action as the adelic action on
![]() $X_m$
defined by the matrices (or equivalently the linear maps)
$X_m$
defined by the matrices (or equivalently the linear maps)
![]() $A_1,\ldots ,A_d$
.
$A_1,\ldots ,A_d$
.
Since every group automorphism of
![]() $\mathbb Q^m$
is in fact
$\mathbb Q^m$
is in fact
![]() $\mathbb Q$
-linear and defined by an invertible matrix in
$\mathbb Q$
-linear and defined by an invertible matrix in
![]() $\operatorname {GL}_m(\mathbb Q)$
, it follows from Pontryagin duality that every action of
$\operatorname {GL}_m(\mathbb Q)$
, it follows from Pontryagin duality that every action of
![]() $\mathbb {Z}^d$
by automorphisms on
$\mathbb {Z}^d$
by automorphisms on
![]() $X_m$
can be defined this way. We will explain this step in a more general form in §4.1.
$X_m$
can be defined this way. We will explain this step in a more general form in §4.1.
We say that a closed subgroup
![]() $Y<X_m$
of an adelic solenoid
$Y<X_m$
of an adelic solenoid
![]() $X_m=\widehat {\mathbb Q}^m$
is adelic if it is a linear subspace over
$X_m=\widehat {\mathbb Q}^m$
is adelic if it is a linear subspace over
![]() $\mathbb Q$
(that is,
$\mathbb Q$
(that is,
![]() $\mathbb Q Y\subseteq Y$
). Since this notion will be useful for us, we wish to study it briefly in the following lemma.
$\mathbb Q Y\subseteq Y$
). Since this notion will be useful for us, we wish to study it briefly in the following lemma.
Lemma 2.1. Let
![]() $m\geq 1$
and let
$m\geq 1$
and let
![]() $Y\leq X_m$
be a closed subgroup. Then the following conditions are equivalent:
$Y\leq X_m$
be a closed subgroup. Then the following conditions are equivalent:
-
(1)
 $Y\leq X_m$
is an adelic subgroup;
$Y\leq X_m$
is an adelic subgroup; -
(2) the annihilator
 $Y^\perp \leq \mathbb Q^m$
is a
$Y^\perp \leq \mathbb Q^m$
is a
 $\mathbb Q$
-linear subspace;
$\mathbb Q$
-linear subspace; -
(3) there exists a
 $\mathbb Q$
-linear subspace
$\mathbb Q$
-linear subspace
 $V\leq \mathbb Q^m$
so that Y is the image of
$V\leq \mathbb Q^m$
so that Y is the image of
 $\mathbb A\otimes _{\mathbb Q} V\leq \mathbb A^m$
modulo
$\mathbb A\otimes _{\mathbb Q} V\leq \mathbb A^m$
modulo
 $\mathbb Q^m$
.
$\mathbb Q^m$
.
Proof The equivalence of (1) and (2) follows from Pontryagin duality. Indeed
![]() $aY=Y$
for
$aY=Y$
for
![]() $a\in \mathbb {Z}\setminus \{0\}$
(and then also
$a\in \mathbb {Z}\setminus \{0\}$
(and then also
![]() $a\in \mathbb Q\setminus \{0\}$
) is equivalent to
$a\in \mathbb Q\setminus \{0\}$
) is equivalent to
![]() $a(Y^\perp )=Y^\perp $
(since
$a(Y^\perp )=Y^\perp $
(since
![]() $(aY)^\perp =a^{-1}Y^\perp $
).
$(aY)^\perp =a^{-1}Y^\perp $
).
Suppose now
![]() $V<\mathbb Q^m$
is a linear subspace as in (3). Then
$V<\mathbb Q^m$
is a linear subspace as in (3). Then
![]() $\mathbb A\otimes _{\mathbb Q} V$
is clearly invariant under
$\mathbb A\otimes _{\mathbb Q} V$
is clearly invariant under
![]() $\mathbb Q$
and hence defines modulo
$\mathbb Q$
and hence defines modulo
![]() $\mathbb Q^m$
, an adelic subgroup.
$\mathbb Q^m$
, an adelic subgroup.
Finally assume that Y is adelic as in (1) (and equivalently (2)). Let
![]() $W=Y^\perp <\mathbb Q^m$
so that W is a linear subspace and
$W=Y^\perp <\mathbb Q^m$
so that W is a linear subspace and
![]() $Y=W^\perp $
by Pontryagin duality. By [Reference Weil38, Ch. IV], there exists a character
$Y=W^\perp $
by Pontryagin duality. By [Reference Weil38, Ch. IV], there exists a character
![]() $\chi _0\in \widehat {\mathbb A}$
so that the isomorphism
$\chi _0\in \widehat {\mathbb A}$
so that the isomorphism
![]() $\widehat {\mathbb A}\cong \mathbb A$
is induced by the definition
$\widehat {\mathbb A}\cong \mathbb A$
is induced by the definition
![]() $\langle a,b\rangle =\chi _0(ab)$
for all
$\langle a,b\rangle =\chi _0(ab)$
for all
![]() $a,b\in \mathbb A$
and with this isomorphism, we have
$a,b\in \mathbb A$
and with this isomorphism, we have
![]() $\mathbb Q^\perp =\mathbb Q$
. Moreover, this also gives
$\mathbb Q^\perp =\mathbb Q$
. Moreover, this also gives
![]() $\widehat {\mathbb A^m}\cong \mathbb A^m$
using the pairing
$\widehat {\mathbb A^m}\cong \mathbb A^m$
using the pairing
for all
![]() $(a_1,\ldots ,a_m),(b_1,\ldots ,b_m)\in \mathbb A^m$
. Since
$(a_1,\ldots ,a_m),(b_1,\ldots ,b_m)\in \mathbb A^m$
. Since
![]() $W<\mathbb Q^m$
is a linear subspace, we may apply a linear isomorphism
$W<\mathbb Q^m$
is a linear subspace, we may apply a linear isomorphism
![]() $A\in \operatorname {GL}_m(\mathbb Q)$
so that
$A\in \operatorname {GL}_m(\mathbb Q)$
so that
![]() $W_1=A(W)$
is precisely the span of the first k standard basis vectors. Applying the inverse of the dual (transpose) linear automorphism to Y, this shows that
$W_1=A(W)$
is precisely the span of the first k standard basis vectors. Applying the inverse of the dual (transpose) linear automorphism to Y, this shows that
![]() $Y_1=(A^t)^{-1}(Y)$
satisfies that
$Y_1=(A^t)^{-1}(Y)$
satisfies that
 $Y_1^\perp =W_1$
. Now let
$Y_1^\perp =W_1$
. Now let
![]() $(a_1,\ldots ,a_m)\in Y_1$
. Hence we have
$(a_1,\ldots ,a_m)\in Y_1$
. Hence we have
![]() $\chi _0(a_jb)=1$
for all
$\chi _0(a_jb)=1$
for all
![]() $b\in \mathbb Q$
and
$b\in \mathbb Q$
and
![]() $j=1,\ldots ,k$
. However, this gives by the properties of
$j=1,\ldots ,k$
. However, this gives by the properties of
![]() $\chi _0$
that
$\chi _0$
that
![]() $a_j\in \mathbb Q$
for
$a_j\in \mathbb Q$
for
![]() $j=1,\ldots ,k$
. It follows that
$j=1,\ldots ,k$
. It follows that
![]() $Y_1=\mathbb Q^m+\mathbb A\otimes _{\mathbb Q} V_1$
, where
$Y_1=\mathbb Q^m+\mathbb A\otimes _{\mathbb Q} V_1$
, where
![]() $V_1$
is the linear hull of the last
$V_1$
is the linear hull of the last
![]() $m-k$
basis vectors. Applying
$m-k$
basis vectors. Applying
![]() $A^t$
to this claim gives the description of Y as in (3).
$A^t$
to this claim gives the description of Y as in (3).
2.3 Irreducible adelic actions
We say that an adelic action on
![]() $X_m$
is
$X_m$
is
![]() $\mathbb A$
-irreducible if the associated linear representation of
$\mathbb A$
-irreducible if the associated linear representation of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb Q^m$
is irreducible over
$\mathbb Q^m$
is irreducible over
![]() $\mathbb Q$
, that is, if there does not exist a rational nontrivial proper invariant subspace. Note however that
$\mathbb Q$
, that is, if there does not exist a rational nontrivial proper invariant subspace. Note however that
![]() $\mathbb A$
-irreduciblity does not coincide with the notion of irreducibility defined on p. 5. In fact, an adelic action is never irreducible but it will be convenient to study
$\mathbb A$
-irreduciblity does not coincide with the notion of irreducibility defined on p. 5. In fact, an adelic action is never irreducible but it will be convenient to study
![]() $\mathbb A$
-irreducible adelic actions as basic building blocks of other adelic actions.
$\mathbb A$
-irreducible adelic actions as basic building blocks of other adelic actions.
We note that given a global field
![]() $\mathbb {K}$
and
$\mathbb {K}$
and
![]() $d\geq 1$
elements
$d\geq 1$
elements
![]() $\zeta _1,\ldots ,\zeta _d\in \mathbb {K}$
, we may consider multiplication by these elements as a
$\zeta _1,\ldots ,\zeta _d\in \mathbb {K}$
, we may consider multiplication by these elements as a
![]() $\mathbb Q$
-linear map on the vector space
$\mathbb Q$
-linear map on the vector space
![]() $\mathbb {K}$
over
$\mathbb {K}$
over
![]() $\mathbb Q$
to define an adelic action of
$\mathbb Q$
to define an adelic action of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb A_{\mathbb {K}}/\mathbb {K}$
. Using a fixed basis of
$\mathbb A_{\mathbb {K}}/\mathbb {K}$
. Using a fixed basis of
![]() $\mathbb {K}$
over
$\mathbb {K}$
over
![]() $\mathbb Q$
, we may identify
$\mathbb Q$
, we may identify
![]() $\mathbb {K}$
with
$\mathbb {K}$
with
![]() $\mathbb Q^m$
and multiplication by
$\mathbb Q^m$
and multiplication by
![]() $\zeta _1,\ldots ,\zeta _d$
with certain matrices
$\zeta _1,\ldots ,\zeta _d$
with certain matrices
![]() $A_1,\ldots ,A_d$
. In this way, our discussions of §2.2 also apply to the multiplication maps by
$A_1,\ldots ,A_d$
. In this way, our discussions of §2.2 also apply to the multiplication maps by
![]() $\zeta _1,\ldots ,\zeta _d$
on
$\zeta _1,\ldots ,\zeta _d$
on
![]() $\mathbb {K}$
. The point of the following proposition is that every
$\mathbb {K}$
. The point of the following proposition is that every
![]() $\mathbb A$
-irreducible action of
$\mathbb A$
-irreducible action of
![]() $\mathbb {Z}^d$
arises in this way from a global number field and d of its elements.
$\mathbb {Z}^d$
arises in this way from a global number field and d of its elements.
Proposition 2.2. (Diagonalization of
 $\mathbb A$
-irreducible action)
$\mathbb A$
-irreducible action)
Let
![]() $m,d\geq 1$
and let
$m,d\geq 1$
and let
![]() $\alpha $
be an
$\alpha $
be an
![]() $\mathbb A$
-irreducible adelic action of
$\mathbb A$
-irreducible adelic action of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $X_m=(\mathbb A/\mathbb Q)^m$
. Then there exists a global field
$X_m=(\mathbb A/\mathbb Q)^m$
. Then there exists a global field
![]() $\mathbb {K}$
of degree m over
$\mathbb {K}$
of degree m over
![]() $\mathbb Q$
and d non-zero elements
$\mathbb Q$
and d non-zero elements
![]() $\zeta _1,\ldots ,\zeta _d\in \mathbb {K}^\times $
so that
$\zeta _1,\ldots ,\zeta _d\in \mathbb {K}^\times $
so that
![]() $\alpha $
is isomorphic to the action on
$\alpha $
is isomorphic to the action on
![]() $\mathbb A_{\mathbb {K}}/\mathbb {K}$
generated by the maps
$\mathbb A_{\mathbb {K}}/\mathbb {K}$
generated by the maps
![]() $a\in \mathbb {K}\mapsto \zeta _j a\in \mathbb {K}$
for
$a\in \mathbb {K}\mapsto \zeta _j a\in \mathbb {K}$
for
![]() $j=1,\ldots ,d$
. More explicitly, this action on
$j=1,\ldots ,d$
. More explicitly, this action on
![]() $\mathbb A_{\mathbb {K}}/\mathbb {K}$
(which as an additive topological group is isomorphic to
$\mathbb A_{\mathbb {K}}/\mathbb {K}$
(which as an additive topological group is isomorphic to
![]() $X_m$
) can be given as follows:
$X_m$
) can be given as follows:
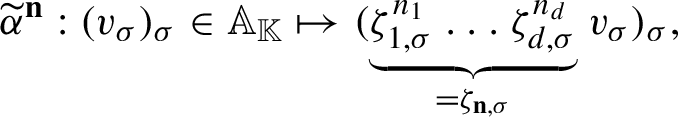 $$ \begin{align*} \widetilde{\alpha}^{\mathbf{n}}: (v_\sigma)_\sigma\in\mathbb A_{\mathbb{K}}\mapsto (\underbrace{\zeta_{1,\sigma}^{n_1}\ldots \zeta_{d,\sigma}^{n_d}}_{=\zeta_{\mathbf{n},\sigma}}v_\sigma)_\sigma, \end{align*} $$
$$ \begin{align*} \widetilde{\alpha}^{\mathbf{n}}: (v_\sigma)_\sigma\in\mathbb A_{\mathbb{K}}\mapsto (\underbrace{\zeta_{1,\sigma}^{n_1}\ldots \zeta_{d,\sigma}^{n_d}}_{=\zeta_{\mathbf{n},\sigma}}v_\sigma)_\sigma, \end{align*} $$
where
![]() $\zeta _{1,\sigma },\ldots ,\zeta _{d,\sigma }\in \mathbb {K}_\sigma $
and
$\zeta _{1,\sigma },\ldots ,\zeta _{d,\sigma }\in \mathbb {K}_\sigma $
and
![]() $\zeta _{\mathbf {n},\sigma }$
denote the image of
$\zeta _{\mathbf {n},\sigma }$
denote the image of
![]() $\zeta _1,\ldots ,\zeta _d$
respectively of
$\zeta _1,\ldots ,\zeta _d$
respectively of
![]() $\zeta _{\mathbf {n}}=\zeta _1^{n_1}\ldots \zeta _d^{n_d}$
in the completion
$\zeta _{\mathbf {n}}=\zeta _1^{n_1}\ldots \zeta _d^{n_d}$
in the completion
![]() $\mathbb {K}_\sigma $
.
$\mathbb {K}_\sigma $
.
Proof Let
![]() $\zeta _j=\widetilde {\alpha }^{\mathbf {e}_j}\in \operatorname {GL}_m(\mathbb Q)$
for
$\zeta _j=\widetilde {\alpha }^{\mathbf {e}_j}\in \operatorname {GL}_m(\mathbb Q)$
for
![]() $j=1,\ldots ,d$
be the matrices that define the action
$j=1,\ldots ,d$
be the matrices that define the action
![]() $\widetilde {\alpha }$
on
$\widetilde {\alpha }$
on
![]() $\mathbb Q^m$
and
$\mathbb Q^m$
and
![]() $\mathbb A^m$
associated to
$\mathbb A^m$
associated to
![]() $\alpha $
.
$\alpha $
.
We define
![]() $\mathbb {K}=\mathbb Q[\zeta _1,\ldots ,\zeta _d]\subseteq \operatorname {GL}_m(\mathbb Q)$
to be the ring of polynomial expressions f in the matrices
$\mathbb {K}=\mathbb Q[\zeta _1,\ldots ,\zeta _d]\subseteq \operatorname {GL}_m(\mathbb Q)$
to be the ring of polynomial expressions f in the matrices
![]() $\zeta _1,\ldots ,\zeta _d$
and with rational coefficients. We note that Lemma 2.1 implies that
$\zeta _1,\ldots ,\zeta _d$
and with rational coefficients. We note that Lemma 2.1 implies that
![]() $\mathbb Q^m$
has no proper rational subspaces invariant under
$\mathbb Q^m$
has no proper rational subspaces invariant under
![]() $\mathbb {K}$
. Since
$\mathbb {K}$
. Since
![]() $\zeta _1,\ldots ,\zeta _d$
commute, it follows that any such polynomial expression
$\zeta _1,\ldots ,\zeta _d$
commute, it follows that any such polynomial expression
![]() $f\in \mathbb {K}$
is either zero or is invertible (as an element of
$f\in \mathbb {K}$
is either zero or is invertible (as an element of
![]() $\operatorname {GL}_m(\mathbb Q)$
). In particular, we have that
$\operatorname {GL}_m(\mathbb Q)$
). In particular, we have that
![]() $\mathbb {K}$
is an integral domain. As it is also a finite dimensional algebra over
$\mathbb {K}$
is an integral domain. As it is also a finite dimensional algebra over
![]() $\mathbb Q$
, it follows that
$\mathbb Q$
, it follows that
![]() $\mathbb {K}$
is field extension of
$\mathbb {K}$
is field extension of
![]() $\mathbb Q$
. Once more because
$\mathbb Q$
. Once more because
![]() $\mathbb Q^m$
has no proper invariant subspaces, it also follows that
$\mathbb Q^m$
has no proper invariant subspaces, it also follows that
![]() $\varphi : a\in \mathbb {K}\mapsto a(\mathbf {e}_1)\in \mathbb Q^m$
must be surjective. By definition the kernel
$\varphi : a\in \mathbb {K}\mapsto a(\mathbf {e}_1)\in \mathbb Q^m$
must be surjective. By definition the kernel
![]() $\ker (\varphi )$
is an ideal, which implies that
$\ker (\varphi )$
is an ideal, which implies that
![]() $\varphi $
is injective since
$\varphi $
is injective since
![]() $\mathbb {K}$
is a field. It follows that
$\mathbb {K}$
is a field. It follows that
![]() $\varphi $
is a linear isomorphism.
$\varphi $
is a linear isomorphism.
To summarize, we have found a global field
![]() $\mathbb {K}$
and elements
$\mathbb {K}$
and elements
![]() $\zeta _1,\ldots ,\zeta _d\in \mathbb {K}^\times $
so that up to a linear isomorphism our linear representation
$\zeta _1,\ldots ,\zeta _d\in \mathbb {K}^\times $
so that up to a linear isomorphism our linear representation
![]() $\widetilde {\alpha }^{\mathbf {n}}$
on
$\widetilde {\alpha }^{\mathbf {n}}$
on
![]() $\mathbb Q^m$
is defined for every
$\mathbb Q^m$
is defined for every
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
by multiplication by
$\mathbf {n}\in \mathbb {Z}^{d}$
by multiplication by
![]() $\zeta _{\mathbf {n}}=\zeta _1^{n_1}\ldots \zeta _d^{n_d}$
on the vector space
$\zeta _{\mathbf {n}}=\zeta _1^{n_1}\ldots \zeta _d^{n_d}$
on the vector space
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
To obtain the adelic action, we tensorize with
![]() $\mathbb A$
. On one hand, for the action on
$\mathbb A$
. On one hand, for the action on
![]() $\mathbb Q^m$
this gives the action of
$\mathbb Q^m$
this gives the action of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb A^m$
we started with. On the other hand, we may tensorize the linear isomorphism between
$\mathbb A^m$
we started with. On the other hand, we may tensorize the linear isomorphism between
![]() $\mathbb Q^m$
and
$\mathbb Q^m$
and
![]() $\mathbb {K}$
with
$\mathbb {K}$
with
![]() $\mathbb A$
to obtain the group isomorphism
$\mathbb A$
to obtain the group isomorphism
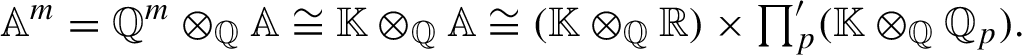 $$ \begin{align*} \mathbb A^m=\mathbb Q^m\otimes_{\mathbb Q}\mathbb A\cong\mathbb{K}\otimes_{\mathbb Q}\mathbb A\cong (\mathbb{K}\otimes_{\mathbb Q}\mathbb{R})\times\textstyle{\prod^{\prime}_p(\mathbb{K}\otimes_{\mathbb Q}\mathbb Q_p)}. \end{align*} $$
$$ \begin{align*} \mathbb A^m=\mathbb Q^m\otimes_{\mathbb Q}\mathbb A\cong\mathbb{K}\otimes_{\mathbb Q}\mathbb A\cong (\mathbb{K}\otimes_{\mathbb Q}\mathbb{R})\times\textstyle{\prod^{\prime}_p(\mathbb{K}\otimes_{\mathbb Q}\mathbb Q_p)}. \end{align*} $$
Now notice that we can identify
![]() $\mathbb {K}$
with the quotient
$\mathbb {K}$
with the quotient
![]() $\mathbb Q[x]/(p(x))$
for some irreducible polynomial
$\mathbb Q[x]/(p(x))$
for some irreducible polynomial
![]() $p(x)\in \mathbb Q[x]$
, which implies that
$p(x)\in \mathbb Q[x]$
, which implies that
![]() $\mathbb {K}\otimes \mathbb {R}$
is isomorphic
$\mathbb {K}\otimes \mathbb {R}$
is isomorphic
![]() $\mathbb {R}[x]/(p(x))$
. Since the irreducible factors of
$\mathbb {R}[x]/(p(x))$
. Since the irreducible factors of
![]() $p(x)\in \mathbb {R}[x]$
correspond precisely to the roots of
$p(x)\in \mathbb {R}[x]$
correspond precisely to the roots of
![]() $p(x)$
(all appearing with multiplicity one) and hence also to the Galois embeddings of
$p(x)$
(all appearing with multiplicity one) and hence also to the Galois embeddings of
![]() $\mathbb {K}$
into
$\mathbb {K}$
into
![]() $\mathbb {C}$
, it follows that
$\mathbb {C}$
, it follows that
![]() $\mathbb {K}\otimes \mathbb {R}$
is as a ring isomorphic to
$\mathbb {K}\otimes \mathbb {R}$
is as a ring isomorphic to
 $\prod _{\sigma |\infty }\mathbb {K}_\sigma $
, where the product runs over all places of
$\prod _{\sigma |\infty }\mathbb {K}_\sigma $
, where the product runs over all places of
![]() $\mathbb {K}$
lying above
$\mathbb {K}$
lying above
![]() $\infty $
, that is, over all Archimedean completions of
$\infty $
, that is, over all Archimedean completions of
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
This argument applies similarly for the tensor product with
![]() $\mathbb Q_p$
so that
$\mathbb Q_p$
so that
![]() $\mathbb {K}\otimes _{\mathbb Q}\mathbb Q_p$
is isomorphic as a ring to the product
$\mathbb {K}\otimes _{\mathbb Q}\mathbb Q_p$
is isomorphic as a ring to the product
 $\prod _{\sigma |p}\mathbb {K}_\sigma $
and
$\prod _{\sigma |p}\mathbb {K}_\sigma $
and
![]() $\sigma $
denotes here all places of
$\sigma $
denotes here all places of
![]() $\mathbb {K}$
above p, see also [Reference Weil38, p. 56]. Applying this argument at all places of
$\mathbb {K}$
above p, see also [Reference Weil38, p. 56]. Applying this argument at all places of
![]() $\mathbb Q$
, we obtain that
$\mathbb Q$
, we obtain that
![]() $\mathbb A^m$
is isomorphic to
$\mathbb A^m$
is isomorphic to
![]() $\mathbb A_{\mathbb {K}}$
.
$\mathbb A_{\mathbb {K}}$
.
Application of
![]() $\widetilde {\alpha }^{\mathbf {e}_j}$
corresponds under this isomorphism from
$\widetilde {\alpha }^{\mathbf {e}_j}$
corresponds under this isomorphism from
![]() $\mathbb A^m$
to
$\mathbb A^m$
to
![]() $\mathbb A_{\mathbb {K}}=\prod _{\sigma }^{\prime }\mathbb {K}_\sigma $
to multiplication by the image of
$\mathbb A_{\mathbb {K}}=\prod _{\sigma }^{\prime }\mathbb {K}_\sigma $
to multiplication by the image of
![]() $\zeta _j$
in the factor
$\zeta _j$
in the factor
![]() $\mathbb {K}_\sigma $
for every place
$\mathbb {K}_\sigma $
for every place
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {K}$
. This gives the proposition.
$\mathbb {K}$
. This gives the proposition.
Let us write
![]() $\delta (\sigma )=\delta (\mathbb {K}_\sigma )\in \mathbb {N}$
for any place
$\delta (\sigma )=\delta (\mathbb {K}_\sigma )\in \mathbb {N}$
for any place
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {K}$
. The following product formula is a crucial ingredient in our proof.
$\mathbb {K}$
. The following product formula is a crucial ingredient in our proof.
Proposition 2.3. (Product formula)
Let
![]() $\alpha $
be an
$\alpha $
be an
![]() $\mathbb A$
-irreducible adelic
$\mathbb A$
-irreducible adelic
![]() $\mathbb {Z}^{d}$
-action as in Proposition 2.2. Then we have
$\mathbb {Z}^{d}$
-action as in Proposition 2.2. Then we have
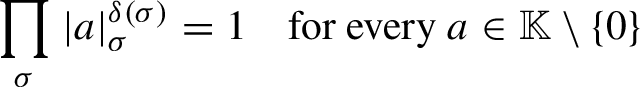 $$ \begin{align} \prod_{\sigma}|a|_{\sigma}^{\delta(\sigma)}= 1\quad\mbox{for every }a \in \mathbb{K}\setminus\{0\} \end{align} $$
$$ \begin{align} \prod_{\sigma}|a|_{\sigma}^{\delta(\sigma)}= 1\quad\mbox{for every }a \in \mathbb{K}\setminus\{0\} \end{align} $$
and this applies in particular to
![]() $a=\zeta _{\mathbf {n}}$
for every
$a=\zeta _{\mathbf {n}}$
for every
![]() $\mathbf {n}\in \mathbb {Z}^d$
.
$\mathbf {n}\in \mathbb {Z}^d$
.
We note that one way to obtain this result is precisely to interpret the product as the modular character for the automorphism defined by multiplication by a on the compact group
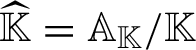 $\widehat {\mathbb {K}}=\mathbb A_{\mathbb {K}}/\mathbb {K}$
(cf. (2.1)). We refer to [Reference Weil38, p. 75] for a proof along these lines.
$\widehat {\mathbb {K}}=\mathbb A_{\mathbb {K}}/\mathbb {K}$
(cf. (2.1)). We refer to [Reference Weil38, p. 75] for a proof along these lines.
2.4 A filtration by
 $\mathbb A$
-irreducible adelic actions
$\mathbb A$
-irreducible adelic actions
The following lemma reveals an advantage of adelic actions by connecting structural questions concerning
![]() $\alpha $
to linear algebra on the dual.
$\alpha $
to linear algebra on the dual.
Lemma 2.4. (Decomposition into
 $\mathbb A$
-irreducible factors)
$\mathbb A$
-irreducible factors)
Let
![]() $m,d\geq 1$
and let
$m,d\geq 1$
and let
![]() $\alpha $
be an adelic
$\alpha $
be an adelic
![]() $\mathbb {Z}^d$
-action on
$\mathbb {Z}^d$
-action on
![]() $X_m$
. Then there exist closed
$X_m$
. Then there exist closed
![]() $\alpha $
-invariant adelic subgroups
$\alpha $
-invariant adelic subgroups
such that the action induced by
![]() $\alpha $
on
$\alpha $
on
![]() $Y_{j}/Y_{j-1}$
is an
$Y_{j}/Y_{j-1}$
is an
![]() $\mathbb A$
-irreducible adelic
$\mathbb A$
-irreducible adelic
![]() $\mathbb {Z}^d$
-action for all
$\mathbb {Z}^d$
-action for all
![]() $j=1,\ldots ,r$
.
$j=1,\ldots ,r$
.
We will refer to the
![]() $\mathbb A$
-irreducible adelic actions appearing in Lemma 2.4 as the
$\mathbb A$
-irreducible adelic actions appearing in Lemma 2.4 as the
![]() $\mathbb A$
-irreducible factors associated to
$\mathbb A$
-irreducible factors associated to
![]() $\alpha $
.
$\alpha $
.
Proof By Pontryagin duality, we may consider instead of
![]() $\alpha $
the linear representation
$\alpha $
the linear representation
![]() $\widehat {\alpha }$
on
$\widehat {\alpha }$
on
![]() $\mathbb Q^m$
. Let
$\mathbb Q^m$
. Let
![]() $V_1\subseteq \mathbb Q^m$
be a non-trivial subspace that is invariant under
$V_1\subseteq \mathbb Q^m$
be a non-trivial subspace that is invariant under
![]() $\widehat {\alpha }$
and of minimal dimension. Note that this implies that the restriction of
$\widehat {\alpha }$
and of minimal dimension. Note that this implies that the restriction of
![]() $\widehat {\alpha }$
to
$\widehat {\alpha }$
to
![]() $V_1$
is irreducible over
$V_1$
is irreducible over
![]() $\mathbb Q$
. If
$\mathbb Q$
. If
![]() $V_1\neq \mathbb Q^m$
, we let
$V_1\neq \mathbb Q^m$
, we let
![]() $V_2$
be a subspace that is invariant under
$V_2$
be a subspace that is invariant under
![]() $\widehat {\alpha }$
, strictly contains
$\widehat {\alpha }$
, strictly contains
![]() $V_1$
and is among these of minimal dimension. Once more this implies that
$V_1$
and is among these of minimal dimension. Once more this implies that
![]() $V_2/V_1$
is irreducible over
$V_2/V_1$
is irreducible over
![]() $\mathbb Q$
(for the representation induced by
$\mathbb Q$
(for the representation induced by
![]() $\widehat {\alpha }$
).
$\widehat {\alpha }$
).
Continuing like this, we obtain a partial flag
consisting of
![]() $\widehat {\alpha }$
-invariant subspaces so that
$\widehat {\alpha }$
-invariant subspaces so that
![]() $V_{j}/V_{j-1}$
is irreducible over
$V_{j}/V_{j-1}$
is irreducible over
![]() $\mathbb Q$
. Applying Pontryagin duality (and reversing the indexing), this gives the lemma.
$\mathbb Q$
. Applying Pontryagin duality (and reversing the indexing), this gives the lemma.
3 Leafwise measures, invariant foliations, and entropy
We briefly recall the main properties of leafwise measures. These have been introduced in the context of higher rank rigidity theorems (under the name of conditional measures for foliations) by Anatole Katok and Spatzier in [Reference Katok and Spatzier22] and have since become an essential tool for all of the theorems in the area. Implicitly leafwise measures appear already in the proof of Rudolph’s Theorem in [Reference Rudolph34]. A general reference for this section is [Reference Einsiedler and Lindenstrauss10, §§6 and 7].
3.1 Leafwise measures
Given a quotient
![]() $X=G/\Gamma $
of a locally compact abelian group G by a lattice
$X=G/\Gamma $
of a locally compact abelian group G by a lattice
![]() $\Gamma <G$
and a closed subgroup
$\Gamma <G$
and a closed subgroup
![]() $V<G$
with
$V<G$
with
![]() $V\cap \Gamma =\{0\}$
, we consider the foliation of X into V-orbits. Let
$V\cap \Gamma =\{0\}$
, we consider the foliation of X into V-orbits. Let
![]() $\pi _X$
denote the natural projection
$\pi _X$
denote the natural projection
![]() $G\to X$
. As we will reduce our main theorem to the adelic case (Theorem 4.1), we consider the case that G is
$G\to X$
. As we will reduce our main theorem to the adelic case (Theorem 4.1), we consider the case that G is
![]() $\mathbb A^m$
(though everything we say below is equally valid for
$\mathbb A^m$
(though everything we say below is equally valid for
![]() $G=\mathbb {R}^m$
, or a finite product of local fields). We note that the metric on
$G=\mathbb {R}^m$
, or a finite product of local fields). We note that the metric on
![]() $\mathbb A^m$
is chosen so that the balls
$\mathbb A^m$
is chosen so that the balls
![]() $B_r^V=B_r(0)\cap V$
have compact closures for all
$B_r^V=B_r(0)\cap V$
have compact closures for all
![]() $r>0$
.
$r>0$
.
For our purposes, it will be important to work with an extension of X—a product
![]() $\widetilde {X}=X\times \Omega $
of X with an arbitrary compact metric space
$\widetilde {X}=X\times \Omega $
of X with an arbitrary compact metric space
![]() $\Omega $
. We let V act on
$\Omega $
. We let V act on
![]() $\widetilde {X}$
by translation on the first coordinate and trivially on the second coordinate, obtaining in this way a foliation of
$\widetilde {X}$
by translation on the first coordinate and trivially on the second coordinate, obtaining in this way a foliation of
![]() $\widetilde {X}$
into V orbits. This foliation of
$\widetilde {X}$
into V orbits. This foliation of
![]() $\widetilde X$
into V-orbits does not admit in general a Borel cross-section, and typically one cannot find a countably generated
$\widetilde X$
into V-orbits does not admit in general a Borel cross-section, and typically one cannot find a countably generated
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $\widetilde X$
whose atoms coincide with almost every (a.e.) V-orbits. Given a probability measure
$\widetilde X$
whose atoms coincide with almost every (a.e.) V-orbits. Given a probability measure
![]() $\mu $
on
$\mu $
on
![]() $\widetilde X$
, the foliation into V-orbits gives rise to a system of leafwise measures on
$\widetilde X$
, the foliation into V-orbits gives rise to a system of leafwise measures on
![]() $\widetilde X$
: a Borel measurable map
$\widetilde X$
: a Borel measurable map
![]() $ x \mapsto \mu _ x ^ V$
from a subset of full measure
$ x \mapsto \mu _ x ^ V$
from a subset of full measure
![]() $\widetilde X ^{\prime } \subset \widetilde X$
to locally finite (possibly infinite) measures on V. We say that a leafwise measure
$\widetilde X ^{\prime } \subset \widetilde X$
to locally finite (possibly infinite) measures on V. We say that a leafwise measure
![]() $\mu _x^V$
is trivial if it is a multiple of the Dirac measure at the identity; we say that the system of leafwise measures is trivial if it is trivial at a.e. point. We also note that almost surely
$\mu _x^V$
is trivial if it is a multiple of the Dirac measure at the identity; we say that the system of leafwise measures is trivial if it is trivial at a.e. point. We also note that almost surely
![]() $0$
belongs to the support of
$0$
belongs to the support of
![]() $\mu _x^V$
.
$\mu _x^V$
.
The system of leafwise measure satisfies the following compatibility condition: for any
![]() $v\in V$
and
$v\in V$
and
![]() $x \in \widetilde {X}^{\prime }$
so that
$x \in \widetilde {X}^{\prime }$
so that
![]() $x+v$
is also in
$x+v$
is also in
![]() ${\widetilde {X}}^{\prime }$
${\widetilde {X}}^{\prime }$
 $$ \begin{align} (\mu_{x+v}^V+v)\propto\mu_x^V. \end{align} $$
$$ \begin{align} (\mu_{x+v}^V+v)\propto\mu_x^V. \end{align} $$
Here and in the following, we write
![]() $\nu \propto \nu ^{\prime }$
for two measures
$\nu \propto \nu ^{\prime }$
for two measures
![]() $\nu ,\nu ^{\prime }$
if there exists
$\nu ,\nu ^{\prime }$
if there exists
![]() $c>0$
with
$c>0$
with
![]() $\nu =c\nu ^{\prime }$
.
$\nu =c\nu ^{\prime }$
.
One way to characterize the leafwise measures is through the notion of subordinate
![]() $\sigma $
-algebras:
$\sigma $
-algebras:
Definition 3.1. (Subordinate
 $\sigma $
-algebras)
$\sigma $
-algebras)
A
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A}$
of Borel subsets of
$\mathcal {A}$
of Borel subsets of
![]() $\widetilde X$
is subordinate to V if
$\widetilde X$
is subordinate to V if
![]() $\mathcal {A}$
is countably generated, for every
$\mathcal {A}$
is countably generated, for every
![]() $x \in \widetilde X$
the atom
$x \in \widetilde X$
the atom
![]() $[x]_{\mathcal {A}}$
of x with respect to
$[x]_{\mathcal {A}}$
of x with respect to
![]() $\mathcal {A}$
is contained in the leaf
$\mathcal {A}$
is contained in the leaf
![]() $x+V$
, and for a.e. x
$x+V$
, and for a.e. x
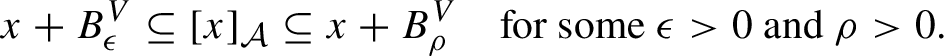 $$ \begin{align*} x+B_\epsilon^V\subseteq [x]_{\mathcal{A}}\subseteq x+B_\rho^V\quad\mbox{for some } \epsilon>0\mbox{ and }\rho>0. \end{align*} $$
$$ \begin{align*} x+B_\epsilon^V\subseteq [x]_{\mathcal{A}}\subseteq x+B_\rho^V\quad\mbox{for some } \epsilon>0\mbox{ and }\rho>0. \end{align*} $$
For these x, we define the shape
![]() $S_x$
of the atom
$S_x$
of the atom
![]() $[x]_{\mathcal {A}}$
(from the point of view of x) as the subset of V satisfying
$[x]_{\mathcal {A}}$
(from the point of view of x) as the subset of V satisfying
![]() $x+S_x=[x]_{\mathcal {A}}$
.
$x+S_x=[x]_{\mathcal {A}}$
.
Let
![]() $\mathcal {A}$
be a countably generated
$\mathcal {A}$
be a countably generated
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $\widetilde {X}$
that is subordinate to V. Then the leafwise measures for
$\widetilde {X}$
that is subordinate to V. Then the leafwise measures for
![]() $\mu $
with respect to V and the conditional measures of
$\mu $
with respect to V and the conditional measures of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\mathcal {A}$
satisfy that for a.e.
$\mathcal {A}$
satisfy that for a.e.
![]() $x\in \widetilde {X}$
, the conditional measure
$x\in \widetilde {X}$
, the conditional measure
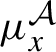 $\mu _x^{\mathcal {A}}$
at x with respect to
$\mu _x^{\mathcal {A}}$
at x with respect to
![]() $\mathcal {A}$
equals the normalized push forward
$\mathcal {A}$
equals the normalized push forward
![]() $x+(\mu _x^V|_{S_x})$
of the restriction
$x+(\mu _x^V|_{S_x})$
of the restriction
![]() $\mu _x^V|_{S_x}$
under the addition map
$\mu _x^V|_{S_x}$
under the addition map
![]() $v \mapsto x+v$
from
$v \mapsto x+v$
from
![]() $V \to \widetilde X$
.
$V \to \widetilde X$
.
A slightly subtler but important feature of the system of leafwise measures is that while they may be (and typically are) infinite measures, they have certain a priori restrictions on how fast they grow: There exists a concrete function
![]() $f_V$
on V (only depending on V) that is integrable with respect to
$f_V$
on V (only depending on V) that is integrable with respect to
![]() $\mu _x^V$
for every x in a set of full measure (that we may as well assume already contains the conull set
$\mu _x^V$
for every x in a set of full measure (that we may as well assume already contains the conull set
![]() $\widetilde {X}^{\prime }$
), see [Reference Einsiedler and Lindenstrauss10, Theorem 6.30]. In fact,
$\widetilde {X}^{\prime }$
), see [Reference Einsiedler and Lindenstrauss10, Theorem 6.30]. In fact,
![]() $f_V$
can be chosen with very mild (polynomial-like) decay properties.
$f_V$
can be chosen with very mild (polynomial-like) decay properties.
In particular, if
![]() $x \in {\widetilde {X}}^{\prime }$
and
$x \in {\widetilde {X}}^{\prime }$
and
![]() $v \in V$
satisfies
$v \in V$
satisfies
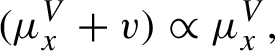 $$ \begin{align} (\mu_x^V+v)\propto\mu_x^V, \end{align} $$
$$ \begin{align} (\mu_x^V+v)\propto\mu_x^V, \end{align} $$
this in fact implies the formally stronger conclusion that
![]() $\mu _x^V$
is translation invariant by the same v, that is,
$\mu _x^V$
is translation invariant by the same v, that is,
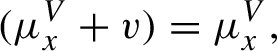 $$ \begin{align} (\mu_x^V+v)=\mu_x^V, \end{align} $$
$$ \begin{align} (\mu_x^V+v)=\mu_x^V, \end{align} $$
for otherwise
![]() $\mu _x^V$
would have exponential growth, which would contradict the polynomial-like growth condition. Finally we recall the following proposition.
$\mu _x^V$
would have exponential growth, which would contradict the polynomial-like growth condition. Finally we recall the following proposition.
Proposition 3.2. (Leafwise measures supported on subgroups [Reference Einsiedler and Lindenstrauss9, Lemma 3.2], [Reference Lindenstrauss28, §3])
Let
![]() $X=G/\Gamma $
and let
$X=G/\Gamma $
and let
![]() $W <V <G$
be closed subgroups. Let
$W <V <G$
be closed subgroups. Let
![]() $\mu $
be a probability measure on X. Suppose that for
$\mu $
be a probability measure on X. Suppose that for
![]() $\mu $
-a.e. x, the measure
$\mu $
-a.e. x, the measure
![]() $\mu _x^V$
is supported on W. Then, identifying locally finite measures on W with locally finite measures on V supported on W in the obvious way, we have that for
$\mu _x^V$
is supported on W. Then, identifying locally finite measures on W with locally finite measures on V supported on W in the obvious way, we have that for
![]() $\mu $
-a.e. x,
$\mu $
-a.e. x,
![]() $\mu _x^W \propto \mu _x^V$
.
$\mu _x^W \propto \mu _x^V$
.
3.2 Entropy and leafwise measures
Suppose now
![]() $T:G\to G$
is a group automorphism preserving
$T:G\to G$
is a group automorphism preserving
![]() $\Gamma $
and V. Recall that we have restricted ourselves without loss of generality to the case where X is the Pontryagin dual to an m-dimensional vector space L over
$\Gamma $
and V. Recall that we have restricted ourselves without loss of generality to the case where X is the Pontryagin dual to an m-dimensional vector space L over
![]() $\mathbb Q $
. Fixing a choice of basis in L, we can restrict our attention to the case of
$\mathbb Q $
. Fixing a choice of basis in L, we can restrict our attention to the case of
![]() $G=\mathbb A^m$
,
$G=\mathbb A^m$
,
![]() $\Gamma =\mathbb Q^m$
, and hence the automorphism T is defined by a rational matrix
$\Gamma =\mathbb Q^m$
, and hence the automorphism T is defined by a rational matrix
![]() $\mathbf T \in \operatorname {GL}_m(\mathbb Q)$
. We note however that some of the definitions below, e.g. the ‘sufficiently fine’ condition in (3.7), depend on the choice of basis used to give the isomorphism
$\mathbf T \in \operatorname {GL}_m(\mathbb Q)$
. We note however that some of the definitions below, e.g. the ‘sufficiently fine’ condition in (3.7), depend on the choice of basis used to give the isomorphism
![]() $L\cong \mathbb Q^m$
(which induces an isomorphism
$L\cong \mathbb Q^m$
(which induces an isomorphism
![]() $\Gamma \cong \mathbb Q^m$
).
$\Gamma \cong \mathbb Q^m$
).
We denote the resulting automorphism of
![]() $X=G/\Gamma $
also by T, and consider an extension
$X=G/\Gamma $
also by T, and consider an extension
![]() $\widetilde {T}=T\times T_\Omega :\widetilde {X}\to \widetilde {X}$
with
$\widetilde {T}=T\times T_\Omega :\widetilde {X}\to \widetilde {X}$
with
![]() $T_\Omega :\Omega \to \Omega $
measurable. Furthermore, suppose the probability measure
$T_\Omega :\Omega \to \Omega $
measurable. Furthermore, suppose the probability measure
![]() $\mu $
on
$\mu $
on
![]() $\widetilde {X}$
is invariant under
$\widetilde {X}$
is invariant under
![]() $\widetilde {T}$
. Then the characterizing properties of the leafwise measures
$\widetilde {T}$
. Then the characterizing properties of the leafwise measures
![]() $\mu _x^V$
imply the equivariance formula
$\mu _x^V$
imply the equivariance formula
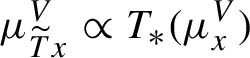 $$ \begin{align} \mu_{\widetilde{T}x}^V\propto T_*(\mu_x^V) \end{align} $$
$$ \begin{align} \mu_{\widetilde{T}x}^V\propto T_*(\mu_x^V) \end{align} $$
for a.e.
![]() $x\in {\widetilde {X}}^{\prime }$
, see e.g. [Reference Einsiedler and Lindenstrauss10, Lemma 7.16].
$x\in {\widetilde {X}}^{\prime }$
, see e.g. [Reference Einsiedler and Lindenstrauss10, Lemma 7.16].
We say that a closed subgroup
![]() $V<\mathbb A^m$
is S-linear where S is a finite set of places of
$V<\mathbb A^m$
is S-linear where S is a finite set of places of
![]() $\mathbb Q$
(that is, a set of prime numbers or infinity) if for each
$\mathbb Q$
(that is, a set of prime numbers or infinity) if for each
![]() $\sigma \in S$
there is a subspace
$\sigma \in S$
there is a subspace
![]() $V_\sigma <\mathbb Q_\sigma ^m$
so that V is the direct product of the
$V_\sigma <\mathbb Q_\sigma ^m$
so that V is the direct product of the
![]() $V_\sigma $
for
$V_\sigma $
for
![]() $\sigma \in S$
. Below we will frequently use the stable horospherical subgroup
$\sigma \in S$
. Below we will frequently use the stable horospherical subgroup
for T and the unstable horospherical subgroup
 $U_T^+=U_{T^{-1}}^-$
. If
$U_T^+=U_{T^{-1}}^-$
. If
then the horospherical subgroups
![]() $U_T^-$
and
$U_T^-$
and
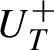 $U_T^+$
are S-linear for this S.
$U_T^+$
are S-linear for this S.
3.3 Increasing subordinate
 $\sigma $
-algebras and entropy
$\sigma $
-algebras and entropy
We continue with the notation of §3.2. We say that a countably generated
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A}$
on
$\mathcal {A}$
on
![]() $\widetilde {X}$
is increasing with respect to
$\widetilde {X}$
is increasing with respect to
![]() $\widetilde T$
if
$\widetilde T$
if
![]() $\mathcal {A} \subseteq \widetilde T\mathcal {A}$
(modulo
$\mathcal {A} \subseteq \widetilde T\mathcal {A}$
(modulo
![]() $\mu $
), that is, the atom
$\mu $
), that is, the atom
 $[\widetilde T x]_{\mathcal {A}}$
almost surely (a.s.) contains
$[\widetilde T x]_{\mathcal {A}}$
almost surely (a.s.) contains
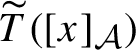 $\widetilde T ([x]_{\mathcal {A}})$
.
$\widetilde T ([x]_{\mathcal {A}})$
.
Let
![]() $\mathcal {P}$
be a finite partition of
$\mathcal {P}$
be a finite partition of
![]() $\widetilde X$
, which we identify with the corresponding finite algebra of sets. For any
$\widetilde X$
, which we identify with the corresponding finite algebra of sets. For any
![]() $\epsilon> 0$
, let
$\epsilon> 0$
, let
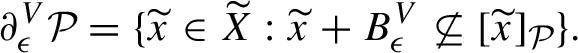 $$ \begin{align*} \partial ^ V _ \epsilon \mathcal{P} = \{ \widetilde x \in \widetilde X: \widetilde x + B _ \epsilon ^ V \not \subseteq [\widetilde x] _{\mathcal{P}} \}. \end{align*} $$
$$ \begin{align*} \partial ^ V _ \epsilon \mathcal{P} = \{ \widetilde x \in \widetilde X: \widetilde x + B _ \epsilon ^ V \not \subseteq [\widetilde x] _{\mathcal{P}} \}. \end{align*} $$
The following lemma follows quickly from monotonicity of the function
![]() $r\in [0,\infty )\mapsto \mu (B_r(x))$
for
$r\in [0,\infty )\mapsto \mu (B_r(x))$
for
![]() $x\in \widetilde {X}$
(and its almost sure differentiability) together with compactness of
$x\in \widetilde {X}$
(and its almost sure differentiability) together with compactness of
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
Lemma 3.3. [Reference Einsiedler and Lindenstrauss10, Lemma 7.27]
For any probability measure
![]() $\widetilde \mu $
on
$\widetilde \mu $
on
![]() $\widetilde X$
, there exists a finite partition
$\widetilde X$
, there exists a finite partition
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $ \widetilde X$
into arbitrarily small sets such that for some fixed C and for every
$ \widetilde X$
into arbitrarily small sets such that for some fixed C and for every
![]() $\epsilon>0$
$\epsilon>0$
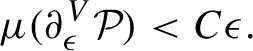 $$ \begin{align} \mu(\partial _ \epsilon ^ V\mathcal{P})<C \epsilon. \end{align} $$
$$ \begin{align} \mu(\partial _ \epsilon ^ V\mathcal{P})<C \epsilon. \end{align} $$
For more details, see [Reference Einsiedler and Lindenstrauss10, §7]. A partition
![]() $\mathcal {P}$
satisfying the conclusion of the above lemma will be said to have thin boundaries. We will assume throughout that any finite partition
$\mathcal {P}$
satisfying the conclusion of the above lemma will be said to have thin boundaries. We will assume throughout that any finite partition
![]() $\mathcal {P} $
of X we will consider below is sufficiently fine in the sense that
$\mathcal {P} $
of X we will consider below is sufficiently fine in the sense that
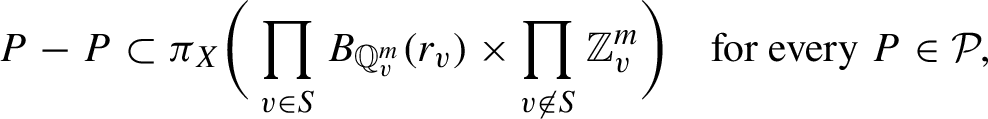 $$ \begin{align} P-P \subset \pi_X \bigg(\prod_ {v \in S} B _ {\mathbb Q _ v ^ m} (r _ v) \times \prod_ {v \not \in S} \mathbb{Z} _ v ^ m \bigg) \quad\text{for every}\ P \in \mathcal{P} ,\end{align} $$
$$ \begin{align} P-P \subset \pi_X \bigg(\prod_ {v \in S} B _ {\mathbb Q _ v ^ m} (r _ v) \times \prod_ {v \not \in S} \mathbb{Z} _ v ^ m \bigg) \quad\text{for every}\ P \in \mathcal{P} ,\end{align} $$
with
![]() $r _ v = 0.1 \max ({ \| {\mathbf T} \|}_v,{ \| {\mathbf T^{-1}} \|}_v)^{-1}$
(with respect to the operator norm on
$r _ v = 0.1 \max ({ \| {\mathbf T} \|}_v,{ \| {\mathbf T^{-1}} \|}_v)^{-1}$
(with respect to the operator norm on
![]() $\operatorname {GL} (\mathbb Q _ v)$
).
$\operatorname {GL} (\mathbb Q _ v)$
).
For any
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $-\infty \leq k_0<k_1 \leq \infty $
set
$-\infty \leq k_0<k_1 \leq \infty $
set
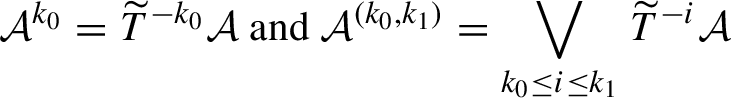 $$ \begin{align*} \mathcal{A}^{k_0}=\widetilde T^{{-k_0}}\mathcal{A}\mbox{ and }\mathcal{A}^{(k_0,k_1)}=\bigvee_{k_0 \leq i \leq k_ 1} \widetilde T^{{-i}}\mathcal{A} \end{align*} $$
$$ \begin{align*} \mathcal{A}^{k_0}=\widetilde T^{{-k_0}}\mathcal{A}\mbox{ and }\mathcal{A}^{(k_0,k_1)}=\bigvee_{k_0 \leq i \leq k_ 1} \widetilde T^{{-i}}\mathcal{A} \end{align*} $$
(for
![]() $k_0$
or
$k_0$
or
![]() $k_1 = \pm \infty $
strict inequality instead of
$k_1 = \pm \infty $
strict inequality instead of
![]() $\leq $
should be used).
$\leq $
should be used).
An easy Borel–Cantelli argument gives that if
![]() $\mathcal P$
is a sufficiently fine finite partition of X with small boundaries in the sense of (3.6) and (3.7), then
$\mathcal P$
is a sufficiently fine finite partition of X with small boundaries in the sense of (3.6) and (3.7), then
is a countably generated
![]() $\sigma $
-algebra satisfying one of the two conditions required by Definition 3.1 for
$\sigma $
-algebra satisfying one of the two conditions required by Definition 3.1 for
![]() $V = U _ T ^ -$
, namely for a.e. x it holds that there is an
$V = U _ T ^ -$
, namely for a.e. x it holds that there is an
![]() $\epsilon> 0$
so that
$\epsilon> 0$
so that
 $x + B _ {U _ T ^ -} (\epsilon ) \subset [x]_{\mathcal {P}}$
. (With a bit more care, using a countable partition
$x + B _ {U _ T ^ -} (\epsilon ) \subset [x]_{\mathcal {P}}$
. (With a bit more care, using a countable partition
![]() $\mathcal {P}$
with finite entropy, one can get that
$\mathcal {P}$
with finite entropy, one can get that
![]() $\mathcal {P} ^ {({0,\infty })}$
is actually
$\mathcal {P} ^ {({0,\infty })}$
is actually
![]() $U _ T ^ -$
-subordinate; we achieve a similar goal by a cruder approach below.)
$U _ T ^ -$
-subordinate; we achieve a similar goal by a cruder approach below.)
A modified version of this increasing
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {P} ^ {(0,{\infty })}$
can be used to construct for any S-linear T-normalized subgroup
$\mathcal {P} ^ {(0,{\infty })}$
can be used to construct for any S-linear T-normalized subgroup
![]() $V<U_T^-$
of
$V<U_T^-$
of
![]() $\mathbb A^m$
an increasing V subordinate
$\mathbb A^m$
an increasing V subordinate
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {C} _ V$
on
$\mathcal {C} _ V$
on
![]() $\widetilde {X}=X\times \Omega $
so that moreover
$\widetilde {X}=X\times \Omega $
so that moreover
![]() $ \mathcal {C} _ V = \tilde T ^{-1} \mathcal {C} _ V \vee \mathcal P$
. Indeed, first we construct starting from a (sufficiently fine, with small boundaries) finite partition
$ \mathcal {C} _ V = \tilde T ^{-1} \mathcal {C} _ V \vee \mathcal P$
. Indeed, first we construct starting from a (sufficiently fine, with small boundaries) finite partition
![]() $\mathcal P$
on X a
$\mathcal P$
on X a
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {P} _V$
on
$\mathcal {P} _V$
on
![]() $\widetilde {X}$
as follows: for each
$\widetilde {X}$
as follows: for each
![]() $P \in \mathcal {P}$
, lift it to a subset
$P \in \mathcal {P}$
, lift it to a subset
![]() $\widetilde P \subset \mathbb A ^ m$
contained in a translate of
$\widetilde P \subset \mathbb A ^ m$
contained in a translate of
 $\prod _ {v \in S} B _ {\mathbb Q _ v ^ m} (r _ v) \times \prod _ {v \not \in S} \mathbb {Z} _ v ^ m$
(up to translation by an element of
$\prod _ {v \in S} B _ {\mathbb Q _ v ^ m} (r _ v) \times \prod _ {v \not \in S} \mathbb {Z} _ v ^ m$
(up to translation by an element of
![]() $\mathbb Q ^ m$
, this lift is uniquely defined). Now take the countably generated
$\mathbb Q ^ m$
, this lift is uniquely defined). Now take the countably generated
![]() $\sigma $
-ring
$\sigma $
-ring
![]() $\widetilde { \mathcal {Q}} _ P$
of subsets C of
$\widetilde { \mathcal {Q}} _ P$
of subsets C of
![]() $\widetilde P$
with the property that if
$\widetilde P$
with the property that if
![]() $x \in C$
then
$x \in C$
then
![]() $(x +V) \cap \widetilde P \subseteq C$
. Since
$(x +V) \cap \widetilde P \subseteq C$
. Since
![]() $\pi _ X$
is a bijection from
$\pi _ X$
is a bijection from
![]() $\widetilde P$
to P, the image
$\widetilde P$
to P, the image
![]() $\mathcal {Q} _ P$
of
$\mathcal {Q} _ P$
of
![]() $ \widetilde {\mathcal {Q}} _ P$
in X is a countably generated
$ \widetilde {\mathcal {Q}} _ P$
in X is a countably generated
![]() $\sigma $
-ring, and now we define
$\sigma $
-ring, and now we define
![]() $\mathcal {P} _ V$
to be the
$\mathcal {P} _ V$
to be the
![]() $\sigma $
-algebra of subsets of X generated by the
$\sigma $
-algebra of subsets of X generated by the
![]() $\sigma $
-rings
$\sigma $
-rings
![]() $\mathcal {Q} _ P\times \mathcal {B}_\Omega $
for all
$\mathcal {Q} _ P\times \mathcal {B}_\Omega $
for all
![]() $P \in \mathcal P$
. Then
$P \in \mathcal P$
. Then
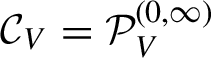 $\mathcal {C}_V=\mathcal {P} _ V ^ {({0,\infty })}$
is a T-increasing, countably generated
$\mathcal {C}_V=\mathcal {P} _ V ^ {({0,\infty })}$
is a T-increasing, countably generated
![]() $\sigma $
-algebra subordinate to V satisfying
$\sigma $
-algebra subordinate to V satisfying
![]() $\mathcal {C}_V= \widetilde T^{-1} \mathcal {C}_V \vee \mathcal {P}$
. Note also that by the way
$\mathcal {C}_V= \widetilde T^{-1} \mathcal {C}_V \vee \mathcal {P}$
. Note also that by the way
![]() $\mathcal {C} _ V$
is defined, there is a fixed
$\mathcal {C} _ V$
is defined, there is a fixed
![]() $\rho> 0$
so that
$\rho> 0$
so that
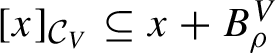 $[x] _ {\mathcal C _ V} \subseteq x + B _ \rho ^ V$
for all
$[x] _ {\mathcal C _ V} \subseteq x + B _ \rho ^ V$
for all
![]() $x \in \widetilde {X}$
. For more details, the reader is referred again to [Reference Einsiedler and Lindenstrauss10, §7].
$x \in \widetilde {X}$
. For more details, the reader is referred again to [Reference Einsiedler and Lindenstrauss10, §7].
For
![]() $V\leq U^-_T$
as above and
$V\leq U^-_T$
as above and
![]() $\mathcal {C}_V$
as above, we define the entropy contribution of V to be
$\mathcal {C}_V$
as above, we define the entropy contribution of V to be
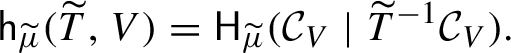 $$ \begin{align} {\sf h}_{\widetilde \mu}(\widetilde T,V)={\sf H}_{\widetilde \mu}(\mathcal{C}_V\mid \widetilde T^{-1}\mathcal{C}_V). \end{align} $$
$$ \begin{align} {\sf h}_{\widetilde \mu}(\widetilde T,V)={\sf H}_{\widetilde \mu}(\mathcal{C}_V\mid \widetilde T^{-1}\mathcal{C}_V). \end{align} $$
We also need the conditional form of this definition: if
![]() $\mathcal Y$
is a
$\mathcal Y$
is a
![]() $\widetilde T$
-invariant
$\widetilde T$
-invariant
![]() $\sigma $
-algebra, then the entropy contribution of V conditional on
$\sigma $
-algebra, then the entropy contribution of V conditional on
![]() $\mathcal Y$
is defined to be
$\mathcal Y$
is defined to be
 $$\begin{align} h _ {\widetilde \mu} (\widetilde T, V \mid \mathcal Y) = H _ {\widetilde \mu} (\mathcal C _ V \mid {\widetilde T} ^{-1} \mathcal C _ V \vee \mathcal Y), \end{align}$$
$$\begin{align} h _ {\widetilde \mu} (\widetilde T, V \mid \mathcal Y) = H _ {\widetilde \mu} (\mathcal C _ V \mid {\widetilde T} ^{-1} \mathcal C _ V \vee \mathcal Y), \end{align}$$
where, as usual, we will identify a factor Y of
![]() $\widetilde X$
with the corresponding
$\widetilde X$
with the corresponding
![]() $\widetilde T$
-invariant
$\widetilde T$
-invariant
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal Y$
of subsets of
$\mathcal Y$
of subsets of
![]() $\widetilde X$
. Formally the conditional entropy contribution is included in the previous case, replacing
$\widetilde X$
. Formally the conditional entropy contribution is included in the previous case, replacing
![]() $\Omega $
by
$\Omega $
by
![]() $\Omega \times Y$
, but notationally it will be useful to allow additional explicit conditioning. The following propositions shows that—as implied by the notation—
$\Omega \times Y$
, but notationally it will be useful to allow additional explicit conditioning. The following propositions shows that—as implied by the notation—
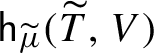 ${\sf h}_{\widetilde \mu }(\widetilde T,V)$
does not depend on the choice of
${\sf h}_{\widetilde \mu }(\widetilde T,V)$
does not depend on the choice of
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {C}_V$
.
$\mathcal {C}_V$
.
Proposition 3.4. Let
![]() $V\leq U^-_T$
be an S-linear subgroup normalized by T, and let
$V\leq U^-_T$
be an S-linear subgroup normalized by T, and let
![]() $\mathcal {C}_V$
be as above. Then
$\mathcal {C}_V$
be as above. Then
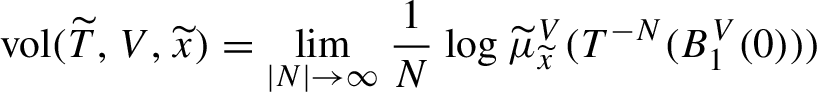 $$ \begin{align} \operatorname{vol}(\widetilde T,V,\widetilde x)=\lim_{|N| \rightarrow \infty}\frac{1}{N} \log{\widetilde \mu}_{\widetilde x}^V(T^{-N}(B_1^V(0))) \end{align} $$
$$ \begin{align} \operatorname{vol}(\widetilde T,V,\widetilde x)=\lim_{|N| \rightarrow \infty}\frac{1}{N} \log{\widetilde \mu}_{\widetilde x}^V(T^{-N}(B_1^V(0))) \end{align} $$
exists almost everywhere and
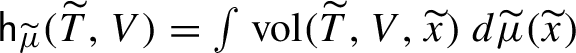 ${\sf h}_{\widetilde \mu }(\widetilde T,V)=\int \operatorname {vol}(\widetilde T,V,\widetilde x)\,{d}{\widetilde \mu }(\widetilde x)$
. Moreover, outside a set of
${\sf h}_{\widetilde \mu }(\widetilde T,V)=\int \operatorname {vol}(\widetilde T,V,\widetilde x)\,{d}{\widetilde \mu }(\widetilde x)$
. Moreover, outside a set of
![]() $\widetilde \mu $
-measure zero,
$\widetilde \mu $
-measure zero,
![]() $\operatorname {vol}(\widetilde T,V,x)=0$
if and only if
$\operatorname {vol}(\widetilde T,V,x)=0$
if and only if
![]() $\widetilde \mu _{x}^V$
is trivial. Furthermore,
$\widetilde \mu _{x}^V$
is trivial. Furthermore,
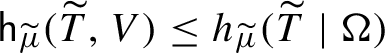 ${\sf h}_{\widetilde \mu }(\widetilde T,V) \leq h_{\widetilde \mu }(\widetilde T \mid \Omega )$
, with equality holding for
${\sf h}_{\widetilde \mu }(\widetilde T,V) \leq h_{\widetilde \mu }(\widetilde T \mid \Omega )$
, with equality holding for
![]() $V=U_T^-$
. In particular,
$V=U_T^-$
. In particular,
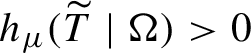 $h_\mu (\widetilde T\mid \Omega )>0$
if and only if
$h_\mu (\widetilde T\mid \Omega )>0$
if and only if
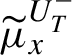 $\widetilde \mu _x^{U_T^-}$
is not almost everywhere trivial.
$\widetilde \mu _x^{U_T^-}$
is not almost everywhere trivial.
By the remark above, this proposition also covers the case of entropy contributions conditional on a factor. This proposition is essentially well known, and is e.g. heavily used by Ledrappier and Young in [Reference Ledrappier and Young25, Reference Ledrappier and Young26] (though we are using a version of these results relative to the factor
![]() $\Omega $
of
$\Omega $
of
![]() $\widetilde {X}$
). For proof, we refer the reader to [Reference Einsiedler and Lindenstrauss10, §7] where an exposition in the spirit of this paper can be found. (In [Reference Einsiedler and Lindenstrauss10, §7]. It is assumed that the acting group acts in a semisimple way on the leaves, which does not necessarily hold in our case as we are explicitly allowing actions with non-trivial Jordan form. However, the arguments of [Reference Einsiedler and Lindenstrauss10, §7] can be easily modified to handle this situation; we leave the details to the readers.)
$\widetilde {X}$
). For proof, we refer the reader to [Reference Einsiedler and Lindenstrauss10, §7] where an exposition in the spirit of this paper can be found. (In [Reference Einsiedler and Lindenstrauss10, §7]. It is assumed that the acting group acts in a semisimple way on the leaves, which does not necessarily hold in our case as we are explicitly allowing actions with non-trivial Jordan form. However, the arguments of [Reference Einsiedler and Lindenstrauss10, §7] can be easily modified to handle this situation; we leave the details to the readers.)
Assuming that
![]() $\mu $
is invariant and ergodic under a
$\mu $
is invariant and ergodic under a
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $\widetilde {\alpha }$
with
$\widetilde {\alpha }$
with
![]() $\widetilde T=\widetilde \alpha ^{\mathbf {n}}$
for some
$\widetilde T=\widetilde \alpha ^{\mathbf {n}}$
for some
![]() $\mathbf {n}\in \mathbb {Z}^d$
, the value of the limit in (3.9) defines an invariant function for
$\mathbf {n}\in \mathbb {Z}^d$
, the value of the limit in (3.9) defines an invariant function for
![]() $\widetilde \alpha $
, hence is almost everywhere constant, and so equals
$\widetilde \alpha $
, hence is almost everywhere constant, and so equals
 $h_\mu (\widetilde T, V\mid \Omega )$
for a.e.
$h_\mu (\widetilde T, V\mid \Omega )$
for a.e.
![]() $x\in \widetilde {X}$
. In particular, assuming
$x\in \widetilde {X}$
. In particular, assuming
![]() $\widetilde \alpha $
is ergodic, the following three statements are equivalent: (i)
$\widetilde \alpha $
is ergodic, the following three statements are equivalent: (i)
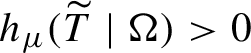 $h_\mu (\widetilde T\mid \Omega )>0$
; (ii)
$h_\mu (\widetilde T\mid \Omega )>0$
; (ii)
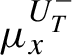 $\mu _x^{U_T^-}$
is non-trivial almost everywhere; (iii)
$\mu _x^{U_T^-}$
is non-trivial almost everywhere; (iii)
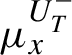 $\mu _x^{U_T^-}$
is non-trivial on a set of positive measure.
$\mu _x^{U_T^-}$
is non-trivial on a set of positive measure.
The entropy contributions for
 $V < U^+_T$
(also denoted
$V < U^+_T$
(also denoted
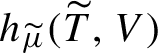 $ h _ {\widetilde \mu } (\widetilde T, V )$
) are defined similarly, and satisfy that
$ h _ {\widetilde \mu } (\widetilde T, V )$
) are defined similarly, and satisfy that
 $$ \begin{align*} h _ {\widetilde \mu} (\widetilde T, V ) = h _ {\widetilde \mu} (\widetilde T^{-1}, V ).\end{align*} $$
$$ \begin{align*} h _ {\widetilde \mu} (\widetilde T, V ) = h _ {\widetilde \mu} (\widetilde T^{-1}, V ).\end{align*} $$
Let
![]() $0 \to L _ 1 \to L \to K \to 0$
be an exact sequence of finite dimensional vector space over
$0 \to L _ 1 \to L \to K \to 0$
be an exact sequence of finite dimensional vector space over
![]() $\mathbb Q$
and let
$\mathbb Q$
and let
![]() $0 \to Y \to X \to X _ 1 \to 0$
be the corresponding dual exact sequence of adelic solenoids. Let
$0 \to Y \to X \to X _ 1 \to 0$
be the corresponding dual exact sequence of adelic solenoids. Let
![]() $T : X \to X$
be the dual map to a linear map in
$T : X \to X$
be the dual map to a linear map in
![]() $\operatorname {GL} (L)$
fixing
$\operatorname {GL} (L)$
fixing
![]() $L _ 1$
. Then T also induces a map
$L _ 1$
. Then T also induces a map
![]() $T _ 1: X _ 1 \to X _ 1$
. Let
$T _ 1: X _ 1 \to X _ 1$
. Let
![]() $V _ {Y, \mathbb A} < \mathbb A ^ m $
be the rational subspace projecting modulo
$V _ {Y, \mathbb A} < \mathbb A ^ m $
be the rational subspace projecting modulo
![]() $\mathbb Q ^ m$
to Y. Let
$\mathbb Q ^ m$
to Y. Let
![]() $T _ \Omega : \Omega \to \Omega $
be a continuous map on the compact metric space
$T _ \Omega : \Omega \to \Omega $
be a continuous map on the compact metric space
![]() $\Omega $
, and denote
$\Omega $
, and denote
![]() $\widetilde X = X \times \Omega $
,
$\widetilde X = X \times \Omega $
,
![]() $\widetilde T = T \times T _ \Omega $
,
$\widetilde T = T \times T _ \Omega $
,
![]() $\widetilde X _ 1 = X _ 1 \times \Omega $
, etc. We let
$\widetilde X _ 1 = X _ 1 \times \Omega $
, etc. We let
![]() $\pi $
denote both the projection from
$\pi $
denote both the projection from
![]() $\mathbb A^m \to \mathbb A^m/V _ {Y, \mathbb A}$
as well as the corresponding projection
$\mathbb A^m \to \mathbb A^m/V _ {Y, \mathbb A}$
as well as the corresponding projection
![]() $X \to X_1$
.
$X \to X_1$
.
Proposition 3.5. (Entropy contribution of factor and fiber, cf. [Reference Einsiedler and Lindenstrauss11, Proposition 6.4] or [Reference Einsiedler and Lindenstrauss8, Proposition 3.1])
With the notation above, let
![]() $\widetilde \mu $
be a
$\widetilde \mu $
be a
![]() $\widetilde T$
-invariant measure on X, let V be a S-linear subgroup of
$\widetilde T$
-invariant measure on X, let V be a S-linear subgroup of
![]() $U _ T ^ - <\mathbb A^m$
, and let
$U _ T ^ - <\mathbb A^m$
, and let
![]() $V_1$
be a S-linear subgroup of
$V_1$
be a S-linear subgroup of
![]() $U _ {T _ 1}^{-}<\mathbb A^m/V _ {Y, \mathbb A} $
so that
$U _ {T _ 1}^{-}<\mathbb A^m/V _ {Y, \mathbb A} $
so that
![]() $V \leq \pi ^{-1}(V_1)$
. Let
$V \leq \pi ^{-1}(V_1)$
. Let
![]() $\widetilde \mu _ 1 = \pi _ {*} \widetilde \mu $
. Then
$\widetilde \mu _ 1 = \pi _ {*} \widetilde \mu $
. Then
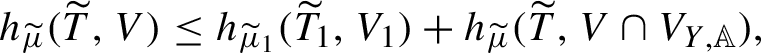 $$ \begin{align} h _ {\widetilde \mu} (\widetilde T, V) \leq h _ {\widetilde \mu _ 1} (\widetilde T _ 1, V _ 1) + h _ {\widetilde \mu} (\widetilde T, V \cap V _ {Y, \mathbb A}) ,\end{align} $$
$$ \begin{align} h _ {\widetilde \mu} (\widetilde T, V) \leq h _ {\widetilde \mu _ 1} (\widetilde T _ 1, V _ 1) + h _ {\widetilde \mu} (\widetilde T, V \cap V _ {Y, \mathbb A}) ,\end{align} $$
with equality holding for
![]() $V=U_T^-$
and
$V=U_T^-$
and
![]() $V_1=U_{T _ 1} ^{-}$
.
$V_1=U_{T _ 1} ^{-}$
.
Proof See [Reference Einsiedler and Lindenstrauss11, Proposition 6.4] (while the setting is a bit different, the proof there works verbatim also in our setting).
Note that by definition,
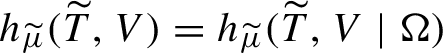 $h _ {\widetilde \mu } (\widetilde T, V) = h _ {\widetilde \mu } (\widetilde T, V\mid \Omega )$
and similarly for the other terms in (3.10).
$h _ {\widetilde \mu } (\widetilde T, V) = h _ {\widetilde \mu } (\widetilde T, V\mid \Omega )$
and similarly for the other terms in (3.10).
4 An adelic version of the positive entropy theorem
We show in this section that it suffices to prove the following more special version of Theorem 1.3.
Theorem 4.1. (Adelic theorem)
Let
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $d\geq 2$
, and let
$d\geq 2$
, and let
![]() $\alpha $
be an adelic
$\alpha $
be an adelic
![]() $\mathbb {Z}^d$
-action on
$\mathbb {Z}^d$
-action on
![]() $X_m$
without virtually cyclic factors. We suppose furthermore that the action satisfies that every adelic subgroup of
$X_m$
without virtually cyclic factors. We suppose furthermore that the action satisfies that every adelic subgroup of
![]() $X_m$
that is invariant under the restriction of
$X_m$
that is invariant under the restriction of
![]() $\alpha $
to a finite index subgroup of
$\alpha $
to a finite index subgroup of
![]() $\mathbb {Z}^d$
is actually invariant under
$\mathbb {Z}^d$
is actually invariant under
![]() $\mathbb {Z}^d$
. Let
$\mathbb {Z}^d$
. Let
![]() $\mu $
be an
$\mu $
be an
![]() $\alpha $
-invariant and ergodic probability measure on
$\alpha $
-invariant and ergodic probability measure on
![]() $X_m$
. Then there exists an adelic subgroup
$X_m$
. Then there exists an adelic subgroup
![]() $G<X_m$
so that
$G<X_m$
so that
![]() $\mu $
is invariant under translation by elements of G and
$\mu $
is invariant under translation by elements of G and
 $h_\mu (\alpha _{X/G}^{\mathbf {n}})=0$
for all
$h_\mu (\alpha _{X/G}^{\mathbf {n}})=0$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
.
$\mathbf {n}\in \mathbb {Z}^d$
.
We note that the reader interested in the heart of the argument may skip most of this section, which is dedicated to the reduction of Theorem 1.3 to Theorem 4.1, and should instead continue with §4.4.
4.1 Extension to adelic action
Suppose that
![]() $\alpha $
is a
$\alpha $
is a
![]() $\mathbb {Z}^d$
-action by automorphisms on a solenoid X as in Theorem 1.3. By definition, this means that the Pontryagin dual
$\mathbb {Z}^d$
-action by automorphisms on a solenoid X as in Theorem 1.3. By definition, this means that the Pontryagin dual
![]() $\widehat {X}$
is isomorphic to a subgroup
$\widehat {X}$
is isomorphic to a subgroup
![]() $V\subseteq \mathbb Q^m$
for some
$V\subseteq \mathbb Q^m$
for some
![]() $m\in \mathbb {N}$
. We may assume that m is minimal, that
$m\in \mathbb {N}$
. We may assume that m is minimal, that
![]() $\widehat {X}=V$
, and by applying some linear automorphism if necessary, we may also assume that the standard basis vectors of
$\widehat {X}=V$
, and by applying some linear automorphism if necessary, we may also assume that the standard basis vectors of
![]() $\mathbb Q^m$
belong to V. By Pontryagin duality, we also have that X is isomorphic to the quotient of
$\mathbb Q^m$
belong to V. By Pontryagin duality, we also have that X is isomorphic to the quotient of
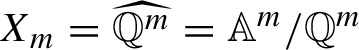 $X_m=\widehat {\mathbb Q^m}=\mathbb A^m/\mathbb Q^m$
modulo the annihilator
$X_m=\widehat {\mathbb Q^m}=\mathbb A^m/\mathbb Q^m$
modulo the annihilator
![]() $K=V^\perp <X_m$
of V.
$K=V^\perp <X_m$
of V.
Moreover, for every
![]() $\mathbf {n}\in \mathbb {Z}^d$
the dual
$\mathbf {n}\in \mathbb {Z}^d$
the dual
![]() $\widehat {\alpha }^{\mathbf {n}}$
of the automorphism
$\widehat {\alpha }^{\mathbf {n}}$
of the automorphism
![]() $\alpha ^{\mathbf {n}}$
is an automorphism of
$\alpha ^{\mathbf {n}}$
is an automorphism of
![]() $V\subseteq \mathbb Q^m$
. Using the standard basis of
$V\subseteq \mathbb Q^m$
. Using the standard basis of
![]() $\mathbb Q^m$
(contained in V by the above assumption), we can represent this dual automorphism by a rational matrix and extend it to linear automorphism of
$\mathbb Q^m$
(contained in V by the above assumption), we can represent this dual automorphism by a rational matrix and extend it to linear automorphism of
![]() $\mathbb Q^m$
(since
$\mathbb Q^m$
(since
![]() $V\otimes _{\mathbb Q}\mathbb Q$
can be identified with
$V\otimes _{\mathbb Q}\mathbb Q$
can be identified with
![]() $\mathbb Q^m$
). This shows that the dual action extends to a linear representation of
$\mathbb Q^m$
). This shows that the dual action extends to a linear representation of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb Q^m$
.
$\mathbb Q^m$
.
We take the transpose of this representation (that is, of each of the matrices defining
![]() $\widehat {\alpha }^{\mathbf {e}_j}$
for
$\widehat {\alpha }^{\mathbf {e}_j}$
for
![]() $j=1,\ldots ,d$
) to define an action
$j=1,\ldots ,d$
) to define an action
![]() $\widetilde {\alpha }$
of
$\widetilde {\alpha }$
of
![]() $\mathbb {Z}^d$
by automorphisms on
$\mathbb {Z}^d$
by automorphisms on
![]() $\mathbb Q^m$
and
$\mathbb Q^m$
and
![]() $\mathbb A^m$
. As discussed in §2.2, this defines an adelic action of
$\mathbb A^m$
. As discussed in §2.2, this defines an adelic action of
![]() $\mathbb {Z}^d$
by automorphisms of
$\mathbb {Z}^d$
by automorphisms of
![]() $X_m=\mathbb A^m/\mathbb Q^m$
. Moreover, since
$X_m=\mathbb A^m/\mathbb Q^m$
. Moreover, since
![]() $V\subseteq \mathbb Q^m$
is invariant under
$V\subseteq \mathbb Q^m$
is invariant under
![]() $\widehat {\alpha }$
, the annihilator
$\widehat {\alpha }$
, the annihilator
![]() $K=V^\perp $
is a closed invariant subgroup for
$K=V^\perp $
is a closed invariant subgroup for
![]() $\widetilde {\alpha }$
and the induced action on
$\widetilde {\alpha }$
and the induced action on
![]() $X_m/K$
is isomorphic to the original action on X.
$X_m/K$
is isomorphic to the original action on X.
Extending the above discussion, the following lemma allows us to switch our attention to the setting of an adelic
![]() $\mathbb {Z}^d$
-action
$\mathbb {Z}^d$
-action
![]() $\alpha $
on
$\alpha $
on
![]() $X_m$
for some
$X_m$
for some
![]() $m\in \mathbb {N}$
.
$m\in \mathbb {N}$
.
Lemma 4.2. Suppose Theorem 1.3 holds for adelic actions, then it also holds for all actions of
![]() $\mathbb {Z}^d$
by automorphisms on solenoids.
$\mathbb {Z}^d$
by automorphisms on solenoids.
Proof Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $\mathbb {Z}^d$
-action by automorphisms on a solenoid X and let
$\mathbb {Z}^d$
-action by automorphisms on a solenoid X and let
![]() $\mu $
be an
$\mu $
be an
![]() $\alpha $
-invariant and ergodic probability measure on X. Applying the above discussion, we can construct an adelic action (again denoted by
$\alpha $
-invariant and ergodic probability measure on X. Applying the above discussion, we can construct an adelic action (again denoted by
![]() $\alpha $
) on
$\alpha $
) on
![]() $X_m$
for some
$X_m$
for some
![]() $m\geq 1$
and an invariant compact subgroup K such that the action on
$m\geq 1$
and an invariant compact subgroup K such that the action on
![]() $X_m/K$
is isomorphic to the original action.
$X_m/K$
is isomorphic to the original action.
Next, we can define a probability measure
![]() $\mu _K$
on
$\mu _K$
on
![]() $X_m$
that is invariant under K and modulo K equals
$X_m$
that is invariant under K and modulo K equals
![]() $\mu $
. This describes
$\mu $
. This describes
![]() $\mu _K$
uniquely. By invariance of K under
$\mu _K$
uniquely. By invariance of K under
![]() $\alpha $
and uniqueness, this measure is also
$\alpha $
and uniqueness, this measure is also
![]() $\alpha $
-invariant. If it is not ergodic with respect to
$\alpha $
-invariant. If it is not ergodic with respect to
![]() $\alpha $
, we may consider an ergodic component
$\alpha $
, we may consider an ergodic component
![]() $\tilde {\mu }$
of
$\tilde {\mu }$
of
![]() $\mu _K$
. Due to ergodicity of
$\mu _K$
. Due to ergodicity of
![]() $\mu $
, almost surely the ergodic components will project to
$\mu $
, almost surely the ergodic components will project to
![]() $\mu $
. Let
$\mu $
. Let
![]() $\tilde \mu $
be one such ergodic component.
$\tilde \mu $
be one such ergodic component.
By our assumption (in Lemma 4.2), we know that Theorem 1.3 already holds for
![]() $\tilde \mu $
. In other words, there exists a finite index subgroup
$\tilde \mu $
. In other words, there exists a finite index subgroup
![]() $\Lambda <\mathbb {Z}^d$
and a decomposition
$\Lambda <\mathbb {Z}^d$
and a decomposition
![]() $\tilde \mu =(1/J)(\tilde \mu _1+\cdots +\tilde \mu _J)$
of
$\tilde \mu =(1/J)(\tilde \mu _1+\cdots +\tilde \mu _J)$
of
![]() $\tilde \mu $
into
$\tilde \mu $
into
![]() $\alpha _\Lambda $
-invariant and ergodic probability measures, and there exist closed
$\alpha _\Lambda $
-invariant and ergodic probability measures, and there exist closed
![]() $\alpha _\Lambda $
-invariant subgroup
$\alpha _\Lambda $
-invariant subgroup
![]() $G_j<X_m$
so that
$G_j<X_m$
so that
![]() $\tilde \mu _j$
is invariant under translation by elements of
$\tilde \mu _j$
is invariant under translation by elements of
![]() $G_j$
for
$G_j$
for
![]() $j=1,\ldots ,J$
. Moreover, the entropy of
$j=1,\ldots ,J$
. Moreover, the entropy of
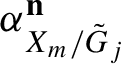 $\alpha ^{\mathbf {n}}_{X_m/\tilde G_j}$
with
$\alpha ^{\mathbf {n}}_{X_m/\tilde G_j}$
with
![]() $\mathbf {n}\in \Lambda $
with respect to
$\mathbf {n}\in \Lambda $
with respect to
![]() $\tilde \mu _j$
vanishes for all
$\tilde \mu _j$
vanishes for all
![]() $j=1,\ldots ,J$
. Taking the quotient of
$j=1,\ldots ,J$
. Taking the quotient of
![]() $X_m$
by the invariant subgroup K, all of these statements become the corresponding statements for the push forwards
$X_m$
by the invariant subgroup K, all of these statements become the corresponding statements for the push forwards
![]() $\mu _j$
of
$\mu _j$
of
![]() $\tilde \mu _j$
under the quotient map
$\tilde \mu _j$
under the quotient map
![]() $X_m\rightarrow X_m/K\cong X$
. We also note that the
$X_m\rightarrow X_m/K\cong X$
. We also note that the
![]() $\alpha _\Lambda $
-ergodic components of
$\alpha _\Lambda $
-ergodic components of
![]() $\mu $
are either equal or singular to each other. Hence, if
$\mu $
are either equal or singular to each other. Hence, if
![]() $\mu _j$
equals
$\mu _j$
equals
![]() $\mu _k$
for some
$\mu _k$
for some
![]() $j\neq k$
, we may simply collect equal terms and would again obtain a decomposition into mutually singular measures (of necessary equal weight due to ergodicity with respect to
$j\neq k$
, we may simply collect equal terms and would again obtain a decomposition into mutually singular measures (of necessary equal weight due to ergodicity with respect to
![]() $\alpha $
). Together, we obtain the conclusions of Theorem 1.3 for the original measure
$\alpha $
). Together, we obtain the conclusions of Theorem 1.3 for the original measure
![]() $\mu $
. This gives the lemma.
$\mu $
. This gives the lemma.
4.2 Choosing a good finite index subgroup
 $\Lambda <\mathbb {Z}^d$
$\Lambda <\mathbb {Z}^d$
Lemma 4.3. Let
![]() $m,d\geq 1$
and let
$m,d\geq 1$
and let
![]() $\alpha $
be an adelic
$\alpha $
be an adelic
![]() $\mathbb {Z}^d$
-action on
$\mathbb {Z}^d$
-action on
![]() $X_m$
. Then there exists a finite index subgroup
$X_m$
. Then there exists a finite index subgroup
![]() $\Lambda <\mathbb {Z}^d$
with the following property: applying Lemma 2.4 to the restriction
$\Lambda <\mathbb {Z}^d$
with the following property: applying Lemma 2.4 to the restriction
![]() $\alpha _\Lambda $
of
$\alpha _\Lambda $
of
![]() $\alpha $
to
$\alpha $
to
![]() $\Lambda $
, we obtain finitely many
$\Lambda $
, we obtain finitely many
![]() $\mathbb A$
-irreducible adelic actions. Then each one of them remains
$\mathbb A$
-irreducible adelic actions. Then each one of them remains
![]() $\mathbb A$
-irreducible if we restrict
$\mathbb A$
-irreducible if we restrict
![]() $\alpha _\Lambda $
further to a finite index subgroup
$\alpha _\Lambda $
further to a finite index subgroup
![]() $\Lambda ^{\prime }<\Lambda $
. Moreover,
$\Lambda ^{\prime }<\Lambda $
. Moreover,
![]() $\Lambda $
may be chosen so that an adelic subgroup
$\Lambda $
may be chosen so that an adelic subgroup
![]() $Y<X$
is invariant under
$Y<X$
is invariant under
![]() $\alpha _\Lambda $
if and only if it is invariant under
$\alpha _\Lambda $
if and only if it is invariant under
![]() $\alpha _{\Lambda ^{\prime }}$
for a finite index subgroup
$\alpha _{\Lambda ^{\prime }}$
for a finite index subgroup
![]() $\Lambda ^{\prime }<\Lambda $
.
$\Lambda ^{\prime }<\Lambda $
.
For the proof of the lemma and some of the following arguments, we first recall the Jordan decomposition. Given a matrix
![]() $A\in \operatorname {GL}_m(\mathbb Q)$
, there exist matrices
$A\in \operatorname {GL}_m(\mathbb Q)$
, there exist matrices
![]() $D,U\in \operatorname {GL}_m(\mathbb Q)$
so that
$D,U\in \operatorname {GL}_m(\mathbb Q)$
so that
![]() $A=DU=UD$
, D is semisimple (that is, is diagonalizable over
$A=DU=UD$
, D is semisimple (that is, is diagonalizable over
![]() $\overline {\mathbb Q}$
), and U is unipotent (that is, has only
$\overline {\mathbb Q}$
), and U is unipotent (that is, has only
![]() $1$
as eigenvalue). This decomposition is unique and if A commutes with a matrix B, then D and U as above also commute with B. Moreover, a subspace
$1$
as eigenvalue). This decomposition is unique and if A commutes with a matrix B, then D and U as above also commute with B. Moreover, a subspace
![]() $V<\mathbb Q$
is invariant under A if and only if V is invariant under both D and U.
$V<\mathbb Q$
is invariant under A if and only if V is invariant under both D and U.
By applying this to each of the matrices
![]() $\alpha ^{\mathbf {e}_i}$
for
$\alpha ^{\mathbf {e}_i}$
for
![]() $i=1,\ldots ,d$
, we obtain two representations of
$i=1,\ldots ,d$
, we obtain two representations of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb Q^m$
: the first representation
$\mathbb Q^m$
: the first representation
![]() $\alpha _{\mathrm {diag}}$
is semisimple, and the second
$\alpha _{\mathrm {diag}}$
is semisimple, and the second
![]() $\alpha _{\mathrm {uni}}$
is by unipotent matrices, the two representations commute, and we have
$\alpha _{\mathrm {uni}}$
is by unipotent matrices, the two representations commute, and we have
 $\alpha ^{\mathbf {n}}=\alpha _{\mathrm {diag}}^{\mathbf {n}}\alpha _{\mathrm {uni}}^{\mathbf {n}}$
for all
$\alpha ^{\mathbf {n}}=\alpha _{\mathrm {diag}}^{\mathbf {n}}\alpha _{\mathrm {uni}}^{\mathbf {n}}$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
.
$\mathbf {n}\in \mathbb {Z}^d$
.
Proof Proof of Lemma 4.3
We first consider an
![]() $\mathbb A$
-irreducible action
$\mathbb A$
-irreducible action
![]() $\alpha $
. As the proof of Lemma 2.2 shows,
$\alpha $
. As the proof of Lemma 2.2 shows,
![]() $\alpha $
corresponds in this case to a global field
$\alpha $
corresponds in this case to a global field
![]() $\mathbb {K}$
generated by d elements
$\mathbb {K}$
generated by d elements
![]() $\zeta _1,\ldots ,\zeta _d$
(obtained directly from the matrix representations of
$\zeta _1,\ldots ,\zeta _d$
(obtained directly from the matrix representations of
![]() $\widetilde \alpha ^{\mathbf {e}_j}$
). Restricting the action to a finite index subgroup results in replacing
$\widetilde \alpha ^{\mathbf {e}_j}$
). Restricting the action to a finite index subgroup results in replacing
![]() $\zeta _1,\ldots ,\zeta _d$
by d monomial expressions
$\zeta _1,\ldots ,\zeta _d$
by d monomial expressions
![]() $\xi _1,\ldots ,\xi _d$
(corresponding to a basis of
$\xi _1,\ldots ,\xi _d$
(corresponding to a basis of
![]() $\Lambda <\mathbb {Z}^d$
) in the numbers
$\Lambda <\mathbb {Z}^d$
) in the numbers
![]() $\zeta _1,\ldots ,\zeta _d$
. This in turn may result in
$\zeta _1,\ldots ,\zeta _d$
. This in turn may result in
![]() $\xi _1,\ldots ,\xi _d$
generating instead of
$\xi _1,\ldots ,\xi _d$
generating instead of
![]() $\mathbb {K}$
a subfield
$\mathbb {K}$
a subfield
![]() $\mathbb {L}$
of
$\mathbb {L}$
of
![]() $\mathbb {K}$
. In this case, the
$\mathbb {K}$
. In this case, the
![]() $\mathbb A$
-irreducible representation of
$\mathbb A$
-irreducible representation of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb {K}$
obtained in the proof of Lemma 2.2 becomes, when restricted to
$\mathbb {K}$
obtained in the proof of Lemma 2.2 becomes, when restricted to
![]() $\Lambda $
, isomorphic to a direct sum of
$\Lambda $
, isomorphic to a direct sum of
![]() $[\mathbb {K}:\mathbb {L}]$
many copies of the
$[\mathbb {K}:\mathbb {L}]$
many copies of the
![]() $\mathbb A$
-irreducible representation defined by multiplication by
$\mathbb A$
-irreducible representation defined by multiplication by
![]() $\xi _1,\ldots ,\xi _d$
on
$\xi _1,\ldots ,\xi _d$
on
![]() $\mathbb {L}$
. If this indeed happens, we may choose
$\mathbb {L}$
. If this indeed happens, we may choose
![]() $\Lambda $
so that
$\Lambda $
so that
![]() $\mathbb {L}$
is minimal in dimension. Hence for any finite index subgroup
$\mathbb {L}$
is minimal in dimension. Hence for any finite index subgroup
![]() $\Lambda ^{\prime }<\Lambda $
, the monomial expressions in the variables
$\Lambda ^{\prime }<\Lambda $
, the monomial expressions in the variables
![]() $\xi _1,\ldots ,\xi _d$
corresponding to a basis of
$\xi _1,\ldots ,\xi _d$
corresponding to a basis of
![]() $\Lambda ^{\prime }$
will still generate the same field
$\Lambda ^{\prime }$
will still generate the same field
![]() $\mathbb {L}$
and so the
$\mathbb {L}$
and so the
![]() $[\mathbb {K}:\mathbb {L}]$
many
$[\mathbb {K}:\mathbb {L}]$
many
![]() $\mathbb A$
-irreducible representations for the restriction to
$\mathbb A$
-irreducible representations for the restriction to
![]() $\Lambda $
will remain irreducible for the restriction to
$\Lambda $
will remain irreducible for the restriction to
![]() $\Lambda ^{\prime }$
. This proves the first part of the lemma in the
$\Lambda ^{\prime }$
. This proves the first part of the lemma in the
![]() $\mathbb A$
-irreducible case.
$\mathbb A$
-irreducible case.
Let now
![]() $\alpha $
be a general adelic action. Let
$\alpha $
be a general adelic action. Let
be as in Lemma 2.4, equation (2.5), with the action induced by
![]() $\widehat \alpha $
on
$\widehat \alpha $
on
![]() $V_i/V_{i-1}$
irreducible over
$V_i/V_{i-1}$
irreducible over
![]() $\mathbb Q$
, and let
$\mathbb Q$
, and let
![]() $\mathbb {K}_i$
be the corresponding finite extension of
$\mathbb {K}_i$
be the corresponding finite extension of
![]() $\mathbb Q$
as in Proposition 2.2 for
$\mathbb Q$
as in Proposition 2.2 for
![]() $V_i/V_{i-1}$
(or more precisely, for the dual adelic solenoid) for
$V_i/V_{i-1}$
(or more precisely, for the dual adelic solenoid) for
![]() $i=1,\ldots ,r$
. Applying the above discussion on each irreducible quotient by passing to a finite index subgroup
$i=1,\ldots ,r$
. Applying the above discussion on each irreducible quotient by passing to a finite index subgroup
![]() $\Lambda < \mathbb {Z}^d$
, we may assume that these quotients remain irreducible even if we pass to a further finite index subgroup of
$\Lambda < \mathbb {Z}^d$
, we may assume that these quotients remain irreducible even if we pass to a further finite index subgroup of
![]() $\Lambda $
, establishing the first part of the lemma.
$\Lambda $
, establishing the first part of the lemma.
Now let M be the least common multiple of the orders of the (finitely many) roots of unity in some finite degree Galois extension of
![]() $\mathbb Q$
containing the fields
$\mathbb Q$
containing the fields
![]() $\mathbb {K}_1,\ldots ,\mathbb {K}_r$
. We claim that if
$\mathbb {K}_1,\ldots ,\mathbb {K}_r$
. We claim that if
![]() $\Lambda _1 = M \Lambda $
and if
$\Lambda _1 = M \Lambda $
and if
![]() $V < \mathbb Q ^ m $
is invariant under
$V < \mathbb Q ^ m $
is invariant under
![]() $\widehat {\alpha }(\Lambda ^{\prime })$
for some
$\widehat {\alpha }(\Lambda ^{\prime })$
for some
![]() $\Lambda ^{\prime } < \Lambda _1$
, then V is invariant under
$\Lambda ^{\prime } < \Lambda _1$
, then V is invariant under
![]() $\widehat {\alpha } (\Lambda _ 1)$
.
$\widehat {\alpha } (\Lambda _ 1)$
.
Indeed, as discussed above, for any
![]() $\Lambda ^{\prime } \leq \mathbb {Z} ^ d$
, the space
$\Lambda ^{\prime } \leq \mathbb {Z} ^ d$
, the space
![]() $V=Y^\perp $
is
$V=Y^\perp $
is
![]() $\widehat {\alpha } (\Lambda ^{\prime })$
-invariant if and only if it is invariant under both
$\widehat {\alpha } (\Lambda ^{\prime })$
-invariant if and only if it is invariant under both
![]() $\widehat {\alpha }_{\mathrm {diag}} (\Lambda ^{\prime }) $
and
$\widehat {\alpha }_{\mathrm {diag}} (\Lambda ^{\prime }) $
and
![]() $\widehat {\alpha }_{\mathrm {uni}} (\Lambda ^{\prime })$
.
$\widehat {\alpha }_{\mathrm {uni}} (\Lambda ^{\prime })$
.
Since the map
![]() $\mathbf n \mapsto \widehat {\alpha }_{\mathrm {uni}} (\mathbf n)$
is polynomial, and since any finite index subgroup of
$\mathbf n \mapsto \widehat {\alpha }_{\mathrm {uni}} (\mathbf n)$
is polynomial, and since any finite index subgroup of
![]() $\mathbb {Z} ^ d$
is Zariski dense in affine d-dimensional space, a space V is
$\mathbb {Z} ^ d$
is Zariski dense in affine d-dimensional space, a space V is
![]() $\widehat {\alpha }_{\mathrm {uni}} (\Lambda ^{\prime })$
-invariant if and only if it is
$\widehat {\alpha }_{\mathrm {uni}} (\Lambda ^{\prime })$
-invariant if and only if it is
![]() $\widehat {\alpha }_{\mathrm {uni}} (\mathbb {Z} ^ d)$
-invariant (hence in particular
$\widehat {\alpha }_{\mathrm {uni}} (\mathbb {Z} ^ d)$
-invariant (hence in particular
![]() $\widehat {\alpha }_{\mathrm {uni}} (\Lambda _1)$
-invariant).
$\widehat {\alpha }_{\mathrm {uni}} (\Lambda _1)$
-invariant).
Suppose V is
![]() $\widehat {\alpha }_{\mathrm {diag}} (\Lambda ^{\prime }) $
-invariant but not
$\widehat {\alpha }_{\mathrm {diag}} (\Lambda ^{\prime }) $
-invariant but not
![]() $\widehat {\alpha }_{\mathrm {diag}} (\Lambda _1) $
-invariant. Let
$\widehat {\alpha }_{\mathrm {diag}} (\Lambda _1) $
-invariant. Let
![]() $\mathbf n = M \mathbf n ^{\prime } \in \Lambda _ 1$
so that
$\mathbf n = M \mathbf n ^{\prime } \in \Lambda _ 1$
so that
![]() $\widehat {\alpha }_{\mathrm {diag}} (\mathbf n)$
does not fix V. Since
$\widehat {\alpha }_{\mathrm {diag}} (\mathbf n)$
does not fix V. Since
![]() $\widehat {\alpha }_{\mathrm {diag}} (\Lambda ^{\prime }) $
leaves V invariant, it follows that there is some
$\widehat {\alpha }_{\mathrm {diag}} (\Lambda ^{\prime }) $
leaves V invariant, it follows that there is some
![]() $k \in \mathbb {N}$
so that
$k \in \mathbb {N}$
so that
![]() $\widehat {\alpha }_{\mathrm {diag}} (k\mathbf n) $
leaves V invariant.
$\widehat {\alpha }_{\mathrm {diag}} (k\mathbf n) $
leaves V invariant.
By Proposition 2.2, for every i, the action induced by
![]() $\alpha (\mathbf n ^{\prime })$
on each
$\alpha (\mathbf n ^{\prime })$
on each
![]() $V_i/V_{i-1}$
can be identified with multiplication by some
$V_i/V_{i-1}$
can be identified with multiplication by some
![]() $\xi \in \mathbb {K}_i$
on
$\xi \in \mathbb {K}_i$
on
![]() $\mathbb {K}_i$
. If
$\mathbb {K}_i$
. If
![]() $\widehat {\alpha }_{\mathrm {diag}} (\mathbf n)=\widehat {\alpha }_{\mathrm {diag}} (\mathbf n^{\prime })^M$
does not fix V but
$\widehat {\alpha }_{\mathrm {diag}} (\mathbf n)=\widehat {\alpha }_{\mathrm {diag}} (\mathbf n^{\prime })^M$
does not fix V but
![]() $\widehat {\alpha }_{\mathrm {diag}} (k \mathbf n)$
does, this implies that there is a j and
$\widehat {\alpha }_{\mathrm {diag}} (k \mathbf n)$
does, this implies that there is a j and
![]() $\xi ^{\prime }\in \mathbb {K}_j$
as well as embeddings
$\xi ^{\prime }\in \mathbb {K}_j$
as well as embeddings
![]() $\sigma ,\sigma ^{\prime }$
of
$\sigma ,\sigma ^{\prime }$
of
![]() $\mathbb {K}_i$
and
$\mathbb {K}_i$
and
![]() $\mathbb {K}_j$
into
$\mathbb {K}_j$
into
![]() $\mathbb {C}$
so that
$\mathbb {C}$
so that
![]() $\sigma (\xi )^ M \neq \sigma ^{\prime }(\xi ^{\prime }) ^ M$
but
$\sigma (\xi )^ M \neq \sigma ^{\prime }(\xi ^{\prime }) ^ M$
but
![]() $\sigma (\xi ) ^ {k M} = \sigma (\xi ^{\prime }) ^ {k M}$
. Then
$\sigma (\xi ) ^ {k M} = \sigma (\xi ^{\prime }) ^ {k M}$
. Then
![]() $\sigma (\xi ) \sigma ^{\prime } (\xi ^{\prime }) ^{-1}$
is an element of the compositum of
$\sigma (\xi ) \sigma ^{\prime } (\xi ^{\prime }) ^{-1}$
is an element of the compositum of
![]() $\sigma (\mathbb {K}_i)$
,
$\sigma (\mathbb {K}_i)$
,
![]() $\sigma ^{\prime }(\mathbb {K}_j)$
that is a root of unity of order not dividing M—a contradiction.
$\sigma ^{\prime }(\mathbb {K}_j)$
that is a root of unity of order not dividing M—a contradiction.
In particular, Lemma 4.3 shows that it is possible to restrict any adelic action to a finite index subgroup so that each of the
![]() $\mathbb A$
-irreducible adelic actions associated to its restriction are in fact totally
$\mathbb A$
-irreducible adelic actions associated to its restriction are in fact totally
![]() $\mathbb A$
-irreducible.
$\mathbb A$
-irreducible.
4.3 Reduction to Theorem 4.1
Using the above preparations, we are now ready to explain the following reduction step.
Proof Proof of Theorem 1.3 assuming Theorem 4.1
By Lemma 4.2 it suffices to consider adelic actions for the proof of Theorem 1.3. So let
![]() $d\geq 2$
, let
$d\geq 2$
, let
![]() $\alpha $
be an adelic
$\alpha $
be an adelic
![]() $\mathbb {Z}^d$
-action without virtually cyclic factors, and let
$\mathbb {Z}^d$
-action without virtually cyclic factors, and let
![]() $\mu $
be an
$\mu $
be an
![]() $\alpha $
-invariant and ergodic probability measure.
$\alpha $
-invariant and ergodic probability measure.
By Lemma 4.3 there exists a finite index subgroup
![]() $\Lambda <\mathbb {Z}^d$
so that the restriction of
$\Lambda <\mathbb {Z}^d$
so that the restriction of
![]() $\alpha $
to
$\alpha $
to
![]() $\Lambda $
satisfies the assumptions to Theorem 4.1. Note however, that the measure
$\Lambda $
satisfies the assumptions to Theorem 4.1. Note however, that the measure
![]() $\mu $
might not be ergodic with respect to
$\mu $
might not be ergodic with respect to
![]() $\alpha _\Lambda $
. Hence we may have to apply the ergodic decomposition. Since
$\alpha _\Lambda $
. Hence we may have to apply the ergodic decomposition. Since
![]() $\Lambda $
has finite index in
$\Lambda $
has finite index in
![]() $\mathbb {Z}^d$
, this ergodic decomposition simply takes the form
$\mathbb {Z}^d$
, this ergodic decomposition simply takes the form
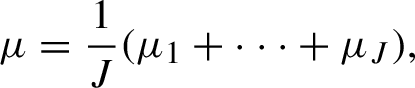 $$ \begin{align*} \mu=\frac1J(\mu_1+\cdots+\mu_J), \end{align*} $$
$$ \begin{align*} \mu=\frac1J(\mu_1+\cdots+\mu_J), \end{align*} $$
where the probability measures
![]() $\mu _j$
are
$\mu _j$
are
![]() $\alpha _\Lambda $
-invariant and ergodic for
$\alpha _\Lambda $
-invariant and ergodic for
![]() $j=1,\ldots ,J$
. Since
$j=1,\ldots ,J$
. Since
![]() $\mu $
is invariant under the full action
$\mu $
is invariant under the full action
![]() $\alpha $
, we also have that for every
$\alpha $
, we also have that for every
![]() $\mathbf {n}\in \mathbb {Z}^d$
and every index
$\mathbf {n}\in \mathbb {Z}^d$
and every index
![]() $j\in \{1,\ldots ,J\}$
there exists an index k with
$j\in \{1,\ldots ,J\}$
there exists an index k with
![]() $\alpha ^{\mathbf {n}}_*\mu _j=\mu _k$
. Since ergodic measure are either equal or singular to each other, we may also assume that the measure
$\alpha ^{\mathbf {n}}_*\mu _j=\mu _k$
. Since ergodic measure are either equal or singular to each other, we may also assume that the measure
![]() $\mu _1,\ldots ,\mu _J$
are mutually singular to each other. By ergodicity of
$\mu _1,\ldots ,\mu _J$
are mutually singular to each other. By ergodicity of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\alpha $
, we also have that for every pair of indices
$\alpha $
, we also have that for every pair of indices
![]() $j,k$
there exists some
$j,k$
there exists some
![]() $\mathbf {n}\in \mathbb {Z}^d$
so that
$\mathbf {n}\in \mathbb {Z}^d$
so that
![]() $\alpha ^{\mathbf {n}}\mu _j=\mu _k$
.
$\alpha ^{\mathbf {n}}\mu _j=\mu _k$
.
We now apply Theorem 4.1 to
![]() $\mu _1$
and the restriction
$\mu _1$
and the restriction
![]() $\alpha _\Lambda $
. Therefore there exists a closed subgroup
$\alpha _\Lambda $
. Therefore there exists a closed subgroup
![]() $G_1<X_m$
so that
$G_1<X_m$
so that
![]() $\mu _1$
is invariant under translation by elements in
$\mu _1$
is invariant under translation by elements in
![]() $G_1$
and for any
$G_1$
and for any
![]() $\mathbf {n}\in \Lambda $
, we have
$\mathbf {n}\in \Lambda $
, we have
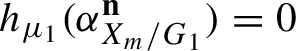 $h_{\mu _1}(\alpha ^{\mathbf {n}}_{X_m/G_1})=0$
. Applying the above transitivity claim we obtain the theorem.
$h_{\mu _1}(\alpha ^{\mathbf {n}}_{X_m/G_1})=0$
. Applying the above transitivity claim we obtain the theorem.
4.4 Standing assumptions for the proof of Theorem 4.1
Since we have shown that Theorem 4.1 implies Theorem 1.3, our aim for the the next sections is to show the former. Hence we will assume that
![]() $\alpha $
is an adelic
$\alpha $
is an adelic
![]() $\mathbb {Z}^d$
-action on
$\mathbb {Z}^d$
-action on
![]() $X_m$
satisfying the assumptions of Theorem 4.1. Furthermore we assume that
$X_m$
satisfying the assumptions of Theorem 4.1. Furthermore we assume that
![]() $\mu $
is an
$\mu $
is an
![]() $\alpha $
-invariant and ergodic probability measure.
$\alpha $
-invariant and ergodic probability measure.
Suppose that
![]() $\mu $
is translation invariant under an adelic subgroup
$\mu $
is translation invariant under an adelic subgroup
![]() $Y<X_m$
, then by invariance of
$Y<X_m$
, then by invariance of
![]() $\mu $
under
$\mu $
under
![]() $\alpha $
, it is also translation invariant under
$\alpha $
, it is also translation invariant under
![]() $\alpha ^{\mathbf {n}}(Y)$
. Taking the closed subgroup generated by these, it follows that there exists a maximal adelic subgroup
$\alpha ^{\mathbf {n}}(Y)$
. Taking the closed subgroup generated by these, it follows that there exists a maximal adelic subgroup
![]() $Y<X_m$
so that
$Y<X_m$
so that
![]() $\mu $
is invariant under translation by elements of Y and, moreover, that Y is
$\mu $
is invariant under translation by elements of Y and, moreover, that Y is
![]() $\alpha $
-invariant. We may replace
$\alpha $
-invariant. We may replace
![]() $X_m$
by
$X_m$
by
![]() $X_m/Y$
for this maximal
$X_m/Y$
for this maximal
![]() $\alpha $
-invariant adelic subgroup Y and consider the push forward of
$\alpha $
-invariant adelic subgroup Y and consider the push forward of
![]() $\mu $
under the canonical projection map
$\mu $
under the canonical projection map
![]() $X_m\rightarrow X_m/Y$
. If this new measure has zero entropy, Theorem 4.1 already holds for this action. Hence we may and will assume for the proof of Theorem 4.1 that:
$X_m\rightarrow X_m/Y$
. If this new measure has zero entropy, Theorem 4.1 already holds for this action. Hence we may and will assume for the proof of Theorem 4.1 that:
-
(i)
 $\mu $
is not invariant under any adelic subgroup; and
$\mu $
is not invariant under any adelic subgroup; and -
(ii) there exists some
 $\mathbf {n}\in \mathbb {Z}^d$
so that
$\mathbf {n}\in \mathbb {Z}^d$
so that
 $h_\mu (\alpha ^{\mathbf {n}})>0$
.
$h_\mu (\alpha ^{\mathbf {n}})>0$
.
Our aim is to derive a contradiction from these assumptions.
To be able to apply the method introduced in [Reference Einsiedler and Lindenstrauss7] (relying on arithmetic properties of
![]() $\mathbb A$
-irreducible actions), we start by applying Lemma 2.4 to the adelic action
$\mathbb A$
-irreducible actions), we start by applying Lemma 2.4 to the adelic action
![]() $\alpha $
on
$\alpha $
on
![]() $X_m$
. We now think of the chain of invariant subgroups as defining a chain of factor maps,
$X_m$
. We now think of the chain of invariant subgroups as defining a chain of factor maps,
 $$ \begin{align*} X=X_{(0)}=X_m&\rightarrow X_{(1)}=X/Y_1\rightarrow\cdots\\ &\rightarrow X_{(j)}=X/Y_{j}\rightarrow X_{(j+1)}=X/Y_{j+1}\rightarrow\cdots \rightarrow X_{(r)}=\{0\}. \end{align*} $$
$$ \begin{align*} X=X_{(0)}=X_m&\rightarrow X_{(1)}=X/Y_1\rightarrow\cdots\\ &\rightarrow X_{(j)}=X/Y_{j}\rightarrow X_{(j+1)}=X/Y_{j+1}\rightarrow\cdots \rightarrow X_{(r)}=\{0\}. \end{align*} $$
Applying the Rokhlin entropy addition formula inductively to these factors, we have
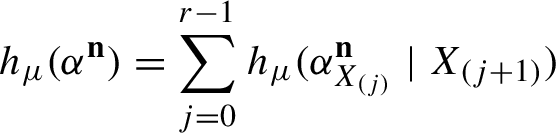 $$ \begin{align*} h_\mu(\alpha^{\mathbf{n}})=\sum_{j=0}^{r-1}h_\mu(\alpha^{\mathbf{n}}_{X_{(j)}}\mid X_{(j+1)}) \end{align*} $$
$$ \begin{align*} h_\mu(\alpha^{\mathbf{n}})=\sum_{j=0}^{r-1}h_\mu(\alpha^{\mathbf{n}}_{X_{(j)}}\mid X_{(j+1)}) \end{align*} $$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
, where we write
$\mathbf {n}\in \mathbb {Z}^d$
, where we write
![]() $\mu $
for the invariant measure on all of the factors, write
$\mu $
for the invariant measure on all of the factors, write
 $\alpha ^{\mathbf {n}}_{X_{(j)}}$
for the induced action on the factor
$\alpha ^{\mathbf {n}}_{X_{(j)}}$
for the induced action on the factor
![]() $X_{(j)}$
, and write
$X_{(j)}$
, and write
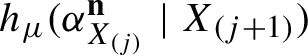 $h_\mu (\alpha ^{\mathbf {n}}_{X_{(j)}}\mid X_{(j+1)})$
for the conditional entropy of
$h_\mu (\alpha ^{\mathbf {n}}_{X_{(j)}}\mid X_{(j+1)})$
for the conditional entropy of
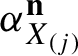 $\alpha ^{\mathbf {n}}_{X_{(j)}}$
conditioned on the next factor
$\alpha ^{\mathbf {n}}_{X_{(j)}}$
conditioned on the next factor
![]() $X_{(j+1)}$
.
$X_{(j+1)}$
.
By assumption (ii) above, there exists some
![]() $\mathbf {n}\in \mathbb {Z}^d$
so that
$\mathbf {n}\in \mathbb {Z}^d$
so that
![]() $h_\mu (\alpha ^{\mathbf {n}})>0$
. Hence, we may choose the minimal
$h_\mu (\alpha ^{\mathbf {n}})>0$
. Hence, we may choose the minimal
![]() $s\in \{0,\ldots ,r-1\}$
so that
$s\in \{0,\ldots ,r-1\}$
so that
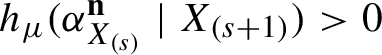 $h_\mu (\alpha ^{\mathbf {n}}_{X_{(s)}}\mid X_{(s+1)})>0$
for some
$h_\mu (\alpha ^{\mathbf {n}}_{X_{(s)}}\mid X_{(s+1)})>0$
for some
![]() $\mathbf {n}\in \mathbb {Z}^d$
. We define
$\mathbf {n}\in \mathbb {Z}^d$
. We define
![]() $Y_{\mathrm {base}}=Y_{s+1}$
,
$Y_{\mathrm {base}}=Y_{s+1}$
,
![]() $X_{\mathrm {base}}=X_{(s+1)}$
, and will always consider conditional entropy over the factor
$X_{\mathrm {base}}=X_{(s+1)}$
, and will always consider conditional entropy over the factor
![]() $X_{\mathrm {base}}$
. We also define
$X_{\mathrm {base}}$
. We also define
![]() $Y_{\mathrm {pos}}=Y_s$
(contained in
$Y_{\mathrm {pos}}=Y_s$
(contained in
![]() $Y_{\mathrm {base}}$
) and
$Y_{\mathrm {base}}$
) and
![]() $X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
(which factors on
$X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
(which factors on
![]() $X_{\mathrm {base}}$
). In this sense, the factor
$X_{\mathrm {base}}$
). In this sense, the factor
![]() $X_{{\mathrm {pos}}}$
will be important for us as it is a ‘positive entropy extension’ of
$X_{{\mathrm {pos}}}$
will be important for us as it is a ‘positive entropy extension’ of
![]() $X_{\mathrm {base}}$
and at the same time, an ‘adelic extension with
$X_{\mathrm {base}}$
and at the same time, an ‘adelic extension with
![]() $\mathbb A$
-irreducible fibers’. In fact by choice of s, there exists some
$\mathbb A$
-irreducible fibers’. In fact by choice of s, there exists some
![]() $\mathbf {n}\in \mathbb {Z}^d$
so that
$\mathbf {n}\in \mathbb {Z}^d$
so that
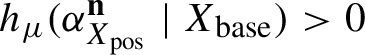 $h_\mu (\alpha ^{\mathbf {n}}_{X_{{\mathrm {pos}}}}\mid X_{\mathrm {base}})>0$
, we have
$h_\mu (\alpha ^{\mathbf {n}}_{X_{{\mathrm {pos}}}}\mid X_{\mathrm {base}})>0$
, we have
![]() $X_{{\mathrm {pos}}}=X/Y_{{\mathrm {pos}}}$
,
$X_{{\mathrm {pos}}}=X/Y_{{\mathrm {pos}}}$
,
![]() $X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
, and that the action induced on the fibers
$X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
, and that the action induced on the fibers
![]() $Y_{{\mathrm {irred}}}=Y_{\mathrm {base}}/Y_{{\mathrm {pos}}}$
is (totally)
$Y_{{\mathrm {irred}}}=Y_{\mathrm {base}}/Y_{{\mathrm {pos}}}$
is (totally)
![]() $\mathbb A$
-irreducible. Finally, as we have chosen s minimally, the original system X is a zero entropy extension of
$\mathbb A$
-irreducible. Finally, as we have chosen s minimally, the original system X is a zero entropy extension of
![]() $X_{{\mathrm {pos}}}$
in the sense that
$X_{{\mathrm {pos}}}$
in the sense that
![]() ${\sf h}_\mu (\alpha ^{\mathbf {n}}\mid X_{{\mathrm {pos}}})=0$
for all
${\sf h}_\mu (\alpha ^{\mathbf {n}}\mid X_{{\mathrm {pos}}})=0$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
.
$\mathbf {n}\in \mathbb {Z}^d$
.
To summarize the factor maps,
describe the original action as a zero-entropy extension of
![]() $X_{{\mathrm {pos}}}=X/Y_{\mathrm {pos}}$
, and
$X_{{\mathrm {pos}}}=X/Y_{\mathrm {pos}}$
, and
![]() $X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
as the quotient of
$X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
as the quotient of
![]() $X_{{\mathrm {pos}}}$
by an
$X_{{\mathrm {pos}}}$
by an
![]() $\alpha $
-invariant
$\alpha $
-invariant
![]() $\mathbb A$
-irreducible adelic subgroup
$\mathbb A$
-irreducible adelic subgroup
![]() $Y_{{\mathrm {irred}}} < X_{{\mathrm {pos}}}$
so that
$Y_{{\mathrm {irred}}} < X_{{\mathrm {pos}}}$
so that
![]() $X_{{\mathrm {pos}}}$
is a positive entropy extension over
$X_{{\mathrm {pos}}}$
is a positive entropy extension over
![]() $X_{\mathrm {base}}$
. More precisely,
$X_{\mathrm {base}}$
. More precisely,
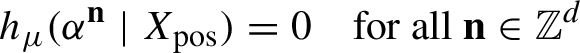 $$ \begin{align*} h_\mu(\alpha^{\mathbf n} \mid X_{{\mathrm{pos}}})=0 \quad\text{for all}\ \mathbf{n}\in\mathbb{Z}^d \end{align*} $$
$$ \begin{align*} h_\mu(\alpha^{\mathbf n} \mid X_{{\mathrm{pos}}})=0 \quad\text{for all}\ \mathbf{n}\in\mathbb{Z}^d \end{align*} $$
but
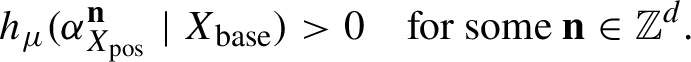 $$ \begin{align*} h_\mu(\alpha^{\mathbf n}_{X _{{\mathrm{pos}}}}\mid X_{\mathrm{base}})>0 \quad\text{for some}\ \mathbf{n} \in \mathbb{Z}^d. \end{align*} $$
$$ \begin{align*} h_\mu(\alpha^{\mathbf n}_{X _{{\mathrm{pos}}}}\mid X_{\mathrm{base}})>0 \quad\text{for some}\ \mathbf{n} \in \mathbb{Z}^d. \end{align*} $$
To the exact sequence
![]() $0 \to Y _{{\mathrm {irred}}} \to X _{{\mathrm {pos}}} \to X _{\mathrm {base}} \to 0$
, there is attached an exact sequence of
$0 \to Y _{{\mathrm {irred}}} \to X _{{\mathrm {pos}}} \to X _{\mathrm {base}} \to 0$
, there is attached an exact sequence of
![]() $\mathbb Q$
-vector spaces
$\mathbb Q$
-vector spaces
![]() $0 \to L _{\mathrm {base}}\to L _{{\mathrm {pos}}} \to L _{{\mathrm {irred}}} \to 0$
where
$0 \to L _{\mathrm {base}}\to L _{{\mathrm {pos}}} \to L _{{\mathrm {irred}}} \to 0$
where
 $L_{\mathrm {base}}=\widehat {X_{\mathrm {base}}}$
,
$L_{\mathrm {base}}=\widehat {X_{\mathrm {base}}}$
,
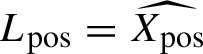 $L_{{\mathrm {pos}}}=\widehat {X_{{\mathrm {pos}}}}$
, and
$L_{{\mathrm {pos}}}=\widehat {X_{{\mathrm {pos}}}}$
, and
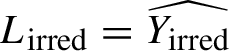 $L _{{\mathrm {irred}}}=\widehat {Y_{{\mathrm {irred}}}}$
can be identified as
$L _{{\mathrm {irred}}}=\widehat {Y_{{\mathrm {irred}}}}$
can be identified as
![]() $\mathbb Q$
-vector space with a number field
$\mathbb Q$
-vector space with a number field
![]() $\mathbb {K}$
. Viewing
$\mathbb {K}$
. Viewing
![]() $X _{{\mathrm {pos}}}$
as a quotient of
$X _{{\mathrm {pos}}}$
as a quotient of
![]() $\mathbb A ^{m_1}$
amounts to choosing a
$\mathbb A ^{m_1}$
amounts to choosing a
![]() $\mathbb Q$
-basis
$\mathbb Q$
-basis
![]() $v _ 1, \ldots , v _ {m_1}$
for the vector space
$v _ 1, \ldots , v _ {m_1}$
for the vector space
![]() $L_{\mathrm {pos}}^*$
.
$L_{\mathrm {pos}}^*$
.
Identifying
![]() $\mathbb {K}$
as a
$\mathbb {K}$
as a
![]() $\mathbb Q$
-vector space with its dual using the trace form, we have an embedding
$\mathbb Q$
-vector space with its dual using the trace form, we have an embedding
![]() $\mathbb {K} \to L _{{\mathrm {pos}}} ^{*}$
, and we will always choose our
$\mathbb {K} \to L _{{\mathrm {pos}}} ^{*}$
, and we will always choose our
![]() $\mathbb Q$
-basis so that
$\mathbb Q$
-basis so that
![]() $v _ 1, \ldots , v _ {[\mathbb {K}: \mathbb Q]}$
will be a basis for
$v _ 1, \ldots , v _ {[\mathbb {K}: \mathbb Q]}$
will be a basis for
![]() $\mathbb {K} < L ^{*} _{{\mathrm {pos}}}$
.
$\mathbb {K} < L ^{*} _{{\mathrm {pos}}}$
.
5 A bound on the entropy contribution
In this section, we prove the following theorem.
Theorem 5.1. (Cf. [Reference Einsiedler and Lindenstrauss7, Theorem 4.1])
Let
![]() $m, d \geq 1$
, and let
$m, d \geq 1$
, and let
![]() $\alpha $
be a
$\alpha $
be a
![]() $\mathbb {Z} ^ d$
-action on an adelic solenoid
$\mathbb {Z} ^ d$
-action on an adelic solenoid
![]() $X = \mathbb A ^ m / \mathbb Q ^ m$
. We also let
$X = \mathbb A ^ m / \mathbb Q ^ m$
. We also let
![]() $\alpha $
denote the corresponding action on
$\alpha $
denote the corresponding action on
![]() $\mathbb A ^ m$
. Let
$\mathbb A ^ m$
. Let
![]() ${Y _{{\mathrm {irred}}} \leq X}$
be an
${Y _{{\mathrm {irred}}} \leq X}$
be an
![]() $\alpha $
-invariant
$\alpha $
-invariant
![]() $\mathbb A$
-irreducible adelic subspace, and set
$\mathbb A$
-irreducible adelic subspace, and set
![]() $X _{\mathrm {base}} = X / Y _{{\mathrm {irred}}}$
. Let
$X _{\mathrm {base}} = X / Y _{{\mathrm {irred}}}$
. Let
![]() $\alpha _ \Omega $
be a
$\alpha _ \Omega $
be a
![]() $\mathbb {Z} ^ d$
-action on a compact metric space
$\mathbb {Z} ^ d$
-action on a compact metric space
![]() $\Omega $
,
$\Omega $
,
![]() $\widetilde \alpha = \alpha \times \alpha _ \Omega $
, and let
$\widetilde \alpha = \alpha \times \alpha _ \Omega $
, and let
![]() $\widetilde \mu $
be a
$\widetilde \mu $
be a
![]() $\widetilde \alpha $
-invariant measure on
$\widetilde \alpha $
-invariant measure on
![]() $\widetilde X = X \times \Omega $
. Fix
$\widetilde X = X \times \Omega $
. Fix
![]() $\mathbf n \in \mathbb {Z} ^ d$
, and let
$\mathbf n \in \mathbb {Z} ^ d$
, and let
![]() $V < U ^ - _ {\mathbf n} < \mathbb A ^ m$
be a closed
$V < U ^ - _ {\mathbf n} < \mathbb A ^ m$
be a closed
![]() $\alpha $
-invariant subspace. Let
$\alpha $
-invariant subspace. Let
![]() $V _ {{\mathrm {irred}}, \mathbb A} < \mathbb A ^ m$
be the rational subspace projecting modulo
$V _ {{\mathrm {irred}}, \mathbb A} < \mathbb A ^ m$
be the rational subspace projecting modulo
![]() $\mathbb Q ^ m$
to
$\mathbb Q ^ m$
to
![]() $Y _{{\mathrm {irred}}}$
. Then
$Y _{{\mathrm {irred}}}$
. Then
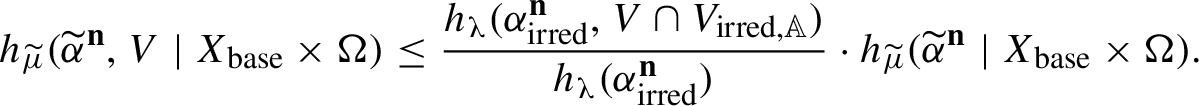
Notice that this estimate is sharp for a product measure
![]() with
with
![]() $\unicode{x3bb} $
being the Haar measure on X. Our treatment here follows closely in content (if not in notation) that of [Reference Einsiedler and Lindenstrauss7, §4]. A special case of this theorem appeared in [Reference Lindenstrauss27, Theorem 2.4].
$\unicode{x3bb} $
being the Haar measure on X. Our treatment here follows closely in content (if not in notation) that of [Reference Einsiedler and Lindenstrauss7, §4]. A special case of this theorem appeared in [Reference Lindenstrauss27, Theorem 2.4].
Proof We first note that
Indeed, if
![]() $\pi : X \to X _{\mathrm {base}}$
is the natural projection, then for any
$\pi : X \to X _{\mathrm {base}}$
is the natural projection, then for any
![]() $x \in X$
, we have that
$x \in X$
, we have that
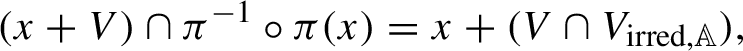 $$ \begin{align*} (x + V) \cap \pi ^{-1} \circ \pi (x) = x + (V \cap V _ {{\mathrm{irred}}, \mathbb A} ) ,\end{align*} $$
$$ \begin{align*} (x + V) \cap \pi ^{-1} \circ \pi (x) = x + (V \cap V _ {{\mathrm{irred}}, \mathbb A} ) ,\end{align*} $$
hence if
![]() $\mathcal {C} _ V$
is a decreasing V-subordinate
$\mathcal {C} _ V$
is a decreasing V-subordinate
![]() $\sigma $
-algebra of subsets of X, then
$\sigma $
-algebra of subsets of X, then
![]() $\mathcal {C} _ V \vee \mathcal {B} _{\mathrm {base}}$
is a decreasing
$\mathcal {C} _ V \vee \mathcal {B} _{\mathrm {base}}$
is a decreasing
![]() $\sigma $
-algebra subordinate to
$\sigma $
-algebra subordinate to
![]() $V \cap V _ {{\mathrm {irred}}, \mathbb A}$
(with
$V \cap V _ {{\mathrm {irred}}, \mathbb A}$
(with
![]() $\mathcal {B} _{\mathrm {base}}$
denoting the
$\mathcal {B} _{\mathrm {base}}$
denoting the
![]() $\sigma $
algebra of Borel subsets of
$\sigma $
algebra of Borel subsets of
![]() $X _{\mathrm {base}}$
, or more precisely the image under
$X _{\mathrm {base}}$
, or more precisely the image under
![]() $\pi ^{-1}$
of this
$\pi ^{-1}$
of this
![]() $\sigma $
-algebra in X). Therefore applying (3.8
′) twice, once for the V-subordinate
$\sigma $
-algebra in X). Therefore applying (3.8
′) twice, once for the V-subordinate
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {C} _ V$
and once for the
$\mathcal {C} _ V$
and once for the
![]() $V \cap V _ {{\mathrm {irred}}, \mathbb A}$
-subordinate
$V \cap V _ {{\mathrm {irred}}, \mathbb A}$
-subordinate
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {C} _ V \vee \mathcal B _{\mathrm {base}}$
, we get
$\mathcal {C} _ V \vee \mathcal B _{\mathrm {base}}$
, we get
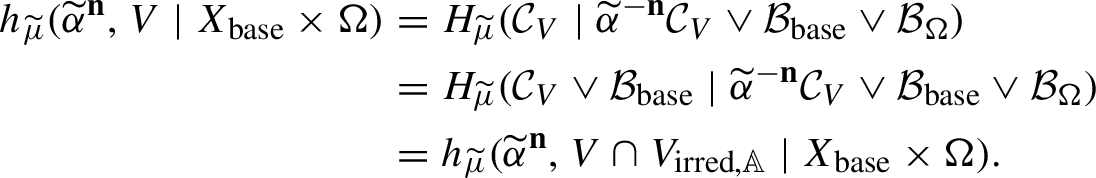 $$ \begin{align*} h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}}, V \mid X _{\mathrm{base}} \times \Omega)& = H _ {\widetilde \mu} (\mathcal{C} _ V \mid \widetilde \alpha ^ {- \mathbf{n}} \mathcal{C} _ V \vee \mathcal B _ {{\mathrm{base}}} \vee \mathcal B _ {\Omega}) \\ & = H _ {\widetilde \mu} (\mathcal{C} _ V \vee \mathcal{B} _ {{\mathrm{base}}} \mid \widetilde \alpha ^ {- \mathbf{n}} \mathcal{C} _ V \vee \mathcal B _ {\mathrm{base}} \vee \mathcal B _ {\Omega}) \\ & = h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}}, V \cap V _ {{\mathrm{irred}}, \mathbb A} \mid X _{\mathrm{base}} \times \Omega) .\end{align*} $$
$$ \begin{align*} h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}}, V \mid X _{\mathrm{base}} \times \Omega)& = H _ {\widetilde \mu} (\mathcal{C} _ V \mid \widetilde \alpha ^ {- \mathbf{n}} \mathcal{C} _ V \vee \mathcal B _ {{\mathrm{base}}} \vee \mathcal B _ {\Omega}) \\ & = H _ {\widetilde \mu} (\mathcal{C} _ V \vee \mathcal{B} _ {{\mathrm{base}}} \mid \widetilde \alpha ^ {- \mathbf{n}} \mathcal{C} _ V \vee \mathcal B _ {\mathrm{base}} \vee \mathcal B _ {\Omega}) \\ & = h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}}, V \cap V _ {{\mathrm{irred}}, \mathbb A} \mid X _{\mathrm{base}} \times \Omega) .\end{align*} $$
Since the right-hand side of (5.1) depends only on
![]() $V \cap V _ {{\mathrm {irred}}, \mathbb A}$
, we may (and will, for the remainder of the proof) assume that
$V \cap V _ {{\mathrm {irred}}, \mathbb A}$
, we may (and will, for the remainder of the proof) assume that
![]() $V \leq U_{\mathbf {n}}^- \cap V _ {{\mathrm {irred}}, \mathbb A}$
. We may also assume V is a proper subgroup of
$V \leq U_{\mathbf {n}}^- \cap V _ {{\mathrm {irred}}, \mathbb A}$
. We may also assume V is a proper subgroup of
![]() $U_{\mathbf {n}}^- \cap V _ {{\mathrm {irred}}, \mathbb A}$
since for
$U_{\mathbf {n}}^- \cap V _ {{\mathrm {irred}}, \mathbb A}$
since for
![]() $V=U_{\mathbf {n}}^- \cap V _ {{\mathrm {irred}}, \mathbb A}$
by first applying the above discussion and then using the second part of Proposition 3.4 twice,
$V=U_{\mathbf {n}}^- \cap V _ {{\mathrm {irred}}, \mathbb A}$
by first applying the above discussion and then using the second part of Proposition 3.4 twice,
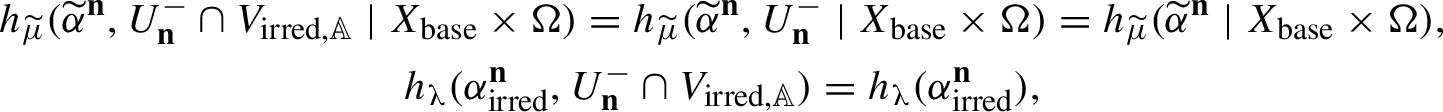 $$ \begin{gather*} h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}},U_{\mathbf{n}}^- \cap V _ {{\mathrm{irred}}, \mathbb A}\mid X _{\mathrm{base}} \times \Omega) = h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}},U_{\mathbf{n}}^- \mid X _{\mathrm{base}} \times \Omega) = h _ {\widetilde \mu} (\widetilde \alpha ^ {\mathbf n} \mid X _{\mathrm{base}} \times \Omega), \\ {h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, U_{\mathbf{n}}^- \cap V _{{\mathrm{irred}},\mathbb A}) }={ h _ \unicode{x3bb} (\alpha ^ {\mathbf n} _{{\mathrm{irred}}})} , \end{gather*} $$
$$ \begin{gather*} h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}},U_{\mathbf{n}}^- \cap V _ {{\mathrm{irred}}, \mathbb A}\mid X _{\mathrm{base}} \times \Omega) = h _ {\widetilde \mu} (\widetilde \alpha ^{\mathbf{n}},U_{\mathbf{n}}^- \mid X _{\mathrm{base}} \times \Omega) = h _ {\widetilde \mu} (\widetilde \alpha ^ {\mathbf n} \mid X _{\mathrm{base}} \times \Omega), \\ {h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, U_{\mathbf{n}}^- \cap V _{{\mathrm{irred}},\mathbb A}) }={ h _ \unicode{x3bb} (\alpha ^ {\mathbf n} _{{\mathrm{irred}}})} , \end{gather*} $$
establishing (5.1) in this case.
Let the rank of
![]() $V _ {{\mathrm {irred}}, \mathbb A}$
as a free
$V _ {{\mathrm {irred}}, \mathbb A}$
as a free
![]() $\mathbb A$
-module be k. Since
$\mathbb A$
-module be k. Since
![]() $Y _{{\mathrm {irred}}}$
is
$Y _{{\mathrm {irred}}}$
is
![]() $\alpha $
-invariant and
$\alpha $
-invariant and
![]() $\mathbb A$
-irreducible, by Proposition 2.2, there is a global field
$\mathbb A$
-irreducible, by Proposition 2.2, there is a global field
![]() $ \mathbb {K}$
with
$ \mathbb {K}$
with
![]() $[\mathbb {K}: \mathbb Q] = k$
, an injective homomorphism of
$[\mathbb {K}: \mathbb Q] = k$
, an injective homomorphism of
![]() $\mathbb Q$
-vector spaces
$\mathbb Q$
-vector spaces
![]() $\phi :\mathbb {K} \to \mathbb Q ^ m$
, and d non-zero elements
$\phi :\mathbb {K} \to \mathbb Q ^ m$
, and d non-zero elements
![]() $\zeta _ 1, \ldots , \zeta _ d \in \mathbb {K} ^ \times $
so that
$\zeta _ 1, \ldots , \zeta _ d \in \mathbb {K} ^ \times $
so that
![]() $\mathbb A \otimes \phi (\mathbb {K}) = V _ {{\mathrm {irred}}, \mathbb A}$
and so that for any
$\mathbb A \otimes \phi (\mathbb {K}) = V _ {{\mathrm {irred}}, \mathbb A}$
and so that for any
![]() $\mathbf {n} = (n _ 1, \ldots , n _ d)$
and
$\mathbf {n} = (n _ 1, \ldots , n _ d)$
and
![]() $\xi \in \mathbb A _ {\mathbb {K}} = \mathbb A \otimes \mathbb {K}$
$\xi \in \mathbb A _ {\mathbb {K}} = \mathbb A \otimes \mathbb {K}$
with
![]() $\phi _{\mathbb A}$
the isomorphism of
$\phi _{\mathbb A}$
the isomorphism of
![]() $\mathbb A$
-modules
$\mathbb A$
-modules
![]() $ \mathbb A_ {\mathbb {K}} \to V _ {{\mathrm {irred}}, \mathbb A}$
induced from
$ \mathbb A_ {\mathbb {K}} \to V _ {{\mathrm {irred}}, \mathbb A}$
induced from
![]() $\phi $
.
$\phi $
.
Fix
![]() $\mathbf {n} \in \mathbb {Z} ^ d$
. Then
$\mathbf {n} \in \mathbb {Z} ^ d$
. Then
![]() $U ^ - _ {\mathbf {n}} $
is S-linear for a finite set S of places of
$U ^ - _ {\mathbf {n}} $
is S-linear for a finite set S of places of
![]() $\mathbb Q$
(including
$\mathbb Q$
(including
![]() $\infty $
) as in (3.5). Let
$\infty $
) as in (3.5). Let
![]() $S_{\mathbb {K}}$
be the (finite) set of places of
$S_{\mathbb {K}}$
be the (finite) set of places of
![]() $\mathbb {K}$
lying over the places S of
$\mathbb {K}$
lying over the places S of
![]() $\mathbb Q$
. The
$\mathbb Q$
. The
![]() $\mathbb A$
-irreducibility of the action of
$\mathbb A$
-irreducibility of the action of
![]() $\alpha $
on
$\alpha $
on
![]() $Y _{{\mathrm {irred}}} \cong \mathbb A _ {\mathbb {K}} / \mathbb {K}$
implies that every
$Y _{{\mathrm {irred}}} \cong \mathbb A _ {\mathbb {K}} / \mathbb {K}$
implies that every
![]() $\alpha $
-invariant subspace
$\alpha $
-invariant subspace
![]() $V \leq V _ {{\mathrm {irred}}, \mathbb A} \cap U ^ - _ {\mathbf {n}}$
has the form
$V \leq V _ {{\mathrm {irred}}, \mathbb A} \cap U ^ - _ {\mathbf {n}}$
has the form
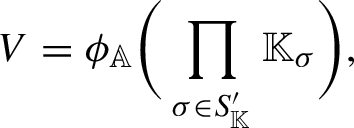 $$ \begin{align} V = \phi _{\mathbb A} \bigg(\prod_ {\sigma\in S ^{\prime} _ {\mathbb{K}}} \mathbb{K} _ \sigma \bigg), \end{align} $$
$$ \begin{align} V = \phi _{\mathbb A} \bigg(\prod_ {\sigma\in S ^{\prime} _ {\mathbb{K}}} \mathbb{K} _ \sigma \bigg), \end{align} $$
with
![]() $S ^{\prime } _ {\mathbb {K}} \subseteq S_{\mathbb {K}}$
. Similarly,
$S ^{\prime } _ {\mathbb {K}} \subseteq S_{\mathbb {K}}$
. Similarly,
 $$ \begin{align*} V _ {{\mathrm{irred}}, \mathbb A} \cap U ^ - _ {\mathbf{n}} = \phi _{\mathbb A} \bigg (\prod_ {\sigma\in S ^- _ {\mathbb{K}}} \mathbb{K} _ \sigma \bigg), \end{align*} $$
$$ \begin{align*} V _ {{\mathrm{irred}}, \mathbb A} \cap U ^ - _ {\mathbf{n}} = \phi _{\mathbb A} \bigg (\prod_ {\sigma\in S ^- _ {\mathbb{K}}} \mathbb{K} _ \sigma \bigg), \end{align*} $$
with
![]() $S ^ - _ {\mathbb {K}} \subseteq S_{\mathbb {K}}$
a finite set of places of
$S ^ - _ {\mathbb {K}} \subseteq S_{\mathbb {K}}$
a finite set of places of
![]() $\mathbb {K}$
with
$\mathbb {K}$
with
![]() $S^{\prime }_{\mathbb {K}} \subset S ^- _ {\mathbb {K}}$
. It follows from the relation between entropy contribution and leafwise measures in Proposition 3.4 that
$S^{\prime }_{\mathbb {K}} \subset S ^- _ {\mathbb {K}}$
. It follows from the relation between entropy contribution and leafwise measures in Proposition 3.4 that
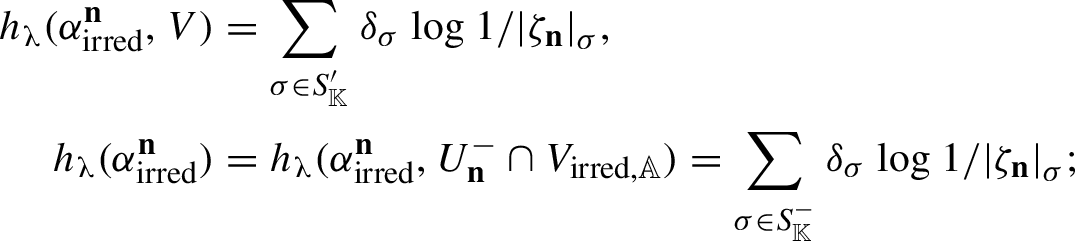 $$ \begin{align*} h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, V) & = \sum_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \delta _ \sigma \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma, \\ h _ \unicode{x3bb} (\alpha ^ {\mathbf n} _{{\mathrm{irred}}})& = h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, U_{\mathbf{n}}^- \cap V _ {{\mathrm{irred}}, \mathbb A}) = \sum _{\sigma \in S ^ - _ {\mathbb{K}}} \delta _ \sigma \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma; \end{align*} $$
$$ \begin{align*} h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, V) & = \sum_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \delta _ \sigma \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma, \\ h _ \unicode{x3bb} (\alpha ^ {\mathbf n} _{{\mathrm{irred}}})& = h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, U_{\mathbf{n}}^- \cap V _ {{\mathrm{irred}}, \mathbb A}) = \sum _{\sigma \in S ^ - _ {\mathbb{K}}} \delta _ \sigma \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma; \end{align*} $$
note that by definition of
![]() $U_{\mathbf {n}}^-$
and
$U_{\mathbf {n}}^-$
and
![]() $\zeta _{\mathbf {n}}$
, we have that
$\zeta _{\mathbf {n}}$
, we have that
![]() ${ | {\zeta _{\mathbf {n}}} |} _ \sigma < 1$
for every
${ | {\zeta _{\mathbf {n}}} |} _ \sigma < 1$
for every
![]() $\sigma \in S ^ - _ {\mathbb {K}}$
. Let
$\sigma \in S ^ - _ {\mathbb {K}}$
. Let
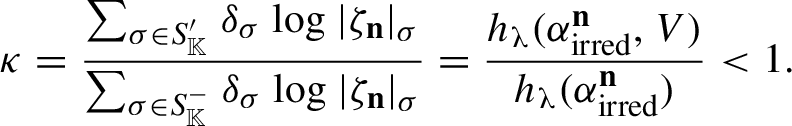 $$ \begin{align*} \kappa= \frac {\sum_ {\sigma \in S ^{\prime}_{\mathbb{K}}} \delta _ \sigma \log { | {\zeta_{\mathbf{n}}} |} _ \sigma}{ \sum_ {\sigma \in S_{\mathbb{K}}^-} \delta _ \sigma \log { | {\zeta_{\mathbf{n}}} |} _ \sigma} = \frac {h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, V ) }{ h _ \unicode{x3bb} (\alpha ^ {\mathbf n} _{{\mathrm{irred}}})} <1. \end{align*} $$
$$ \begin{align*} \kappa= \frac {\sum_ {\sigma \in S ^{\prime}_{\mathbb{K}}} \delta _ \sigma \log { | {\zeta_{\mathbf{n}}} |} _ \sigma}{ \sum_ {\sigma \in S_{\mathbb{K}}^-} \delta _ \sigma \log { | {\zeta_{\mathbf{n}}} |} _ \sigma} = \frac {h _ \unicode{x3bb} (\alpha _{{\mathrm{irred}}} ^ {\mathbf n}, V ) }{ h _ \unicode{x3bb} (\alpha ^ {\mathbf n} _{{\mathrm{irred}}})} <1. \end{align*} $$
Let
![]() $\mathcal {P}$
be a sufficiently fine finite partition with small boundaries of X, as in (3.6) and (3.7) (indeed, we will take it to be even finer), let
$\mathcal {P}$
be a sufficiently fine finite partition with small boundaries of X, as in (3.6) and (3.7) (indeed, we will take it to be even finer), let
![]() $\mathcal {P}_V$
be a corresponding
$\mathcal {P}_V$
be a corresponding
![]() $\sigma $
-algebra of subsets of
$\sigma $
-algebra of subsets of
![]() $X \times \Omega $
as in p. 50, and let
$X \times \Omega $
as in p. 50, and let
 $\mathcal {C}_V = \bigcup _{i\geq 0} \widetilde \alpha ^{-i\mathbf {n}}\mathcal {P}_V$
be as in §3.3. Then
$\mathcal {C}_V = \bigcup _{i\geq 0} \widetilde \alpha ^{-i\mathbf {n}}\mathcal {P}_V$
be as in §3.3. Then
![]() $\mathcal {C}_V$
and
$\mathcal {C}_V$
and
![]() $\mathcal {P}_V$
are both subordinate to V, and
$\mathcal {P}_V$
are both subordinate to V, and
![]() $\mathcal {C}_V$
is in addition decreasing with respect to
$\mathcal {C}_V$
is in addition decreasing with respect to
![]() $\widetilde \alpha ^{\mathbf {n}}$
. Moreover,
$\widetilde \alpha ^{\mathbf {n}}$
. Moreover,
Setting
![]() $\widetilde T = \widetilde \alpha ^{\mathbf n}$
, it follows from (5.3) that for any
$\widetilde T = \widetilde \alpha ^{\mathbf n}$
, it follows from (5.3) that for any
![]() $j\in \mathbb {N}$
,
$j\in \mathbb {N}$
,
 $$ \begin{align*}\mathcal{C} _ V = \mathcal{P} ^ {(0, j-1)} \vee \mathcal{C} _ V ^ j,\end{align*} $$
$$ \begin{align*}\mathcal{C} _ V = \mathcal{P} ^ {(0, j-1)} \vee \mathcal{C} _ V ^ j,\end{align*} $$
where we recall that
 $\mathcal {C} _ V ^ j = \widetilde T ^ {- j} \mathcal {C} _ V$
and
$\mathcal {C} _ V ^ j = \widetilde T ^ {- j} \mathcal {C} _ V$
and
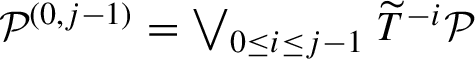 $\mathcal {P} ^ {(0, j -1)} = \bigvee _ {0 \leq i \leq j -1} \widetilde T ^ {- i} \mathcal {P}$
. The key point in the proof of Theorem 5.1 is that for
$\mathcal {P} ^ {(0, j -1)} = \bigvee _ {0 \leq i \leq j -1} \widetilde T ^ {- i} \mathcal {P}$
. The key point in the proof of Theorem 5.1 is that for
![]() $\ell =\lceil \kappa j \rceil $
, the atoms of
$\ell =\lceil \kappa j \rceil $
, the atoms of
 $\mathcal {P} ^ {(0, \ell )} \vee \mathcal {C} _ V ^ j$
are already very close to being equal to the atoms of
$\mathcal {P} ^ {(0, \ell )} \vee \mathcal {C} _ V ^ j$
are already very close to being equal to the atoms of
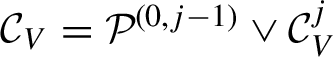 $\mathcal {C} _ V = \mathcal {P} ^ {(0, j-1)} \vee \mathcal {C} _ V ^ j$
(recall that
$\mathcal {C} _ V = \mathcal {P} ^ {(0, j-1)} \vee \mathcal {C} _ V ^ j$
(recall that
![]() $\kappa <1$
). In some simple cases (e.g. that considered in [Reference Lindenstrauss27]), these
$\kappa <1$
). In some simple cases (e.g. that considered in [Reference Lindenstrauss27]), these
![]() $\sigma $
-algebras literally coincide, though in general there may be a small disparity. What we now proceed to show (cf. [Reference Einsiedler and Lindenstrauss7, Lemma 4.2]) is that there is a set
$\sigma $
-algebras literally coincide, though in general there may be a small disparity. What we now proceed to show (cf. [Reference Einsiedler and Lindenstrauss7, Lemma 4.2]) is that there is a set
![]() $X_j$
with
$X_j$
with
![]() $\mu (X \setminus X_j ) \leq \exp (- c j)$
for appropriate
$\mu (X \setminus X_j ) \leq \exp (- c j)$
for appropriate
![]() $c> 0$
so that
$c> 0$
so that
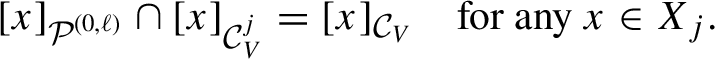 $$ \begin{align} [x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} = [x] _ {\mathcal{C} _ V} \quad \text{for any}\ x \in X _ j .\end{align} $$
$$ \begin{align} [x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} = [x] _ {\mathcal{C} _ V} \quad \text{for any}\ x \in X _ j .\end{align} $$
Since
![]() $\mathcal {C} _ V ^ j$
is V-subordinate for V as in (5.2), there is some
$\mathcal {C} _ V ^ j$
is V-subordinate for V as in (5.2), there is some
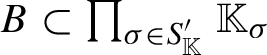 $B \subset \prod _ {\sigma \in S ^{\prime } _ {\mathbb {K}}} \mathbb {K} _ \sigma $
(depending on x and j) so that
$B \subset \prod _ {\sigma \in S ^{\prime } _ {\mathbb {K}}} \mathbb {K} _ \sigma $
(depending on x and j) so that
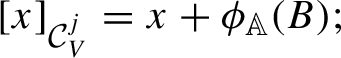 $$ \begin{align*} [x] _ {\mathcal{C} _ V ^ j} = x + \phi _{\mathbb A} (B); \end{align*} $$
$$ \begin{align*} [x] _ {\mathcal{C} _ V ^ j} = x + \phi _{\mathbb A} (B); \end{align*} $$
moreover for any
![]() $\eta> 0$
, by choosing
$\eta> 0$
, by choosing
![]() $\mathcal {P}$
sufficiently fine depending on
$\mathcal {P}$
sufficiently fine depending on
![]() $\eta $
, one can ensure that
$\eta $
, one can ensure that
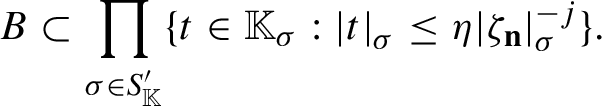 $$ \begin{align*} B \subset \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta { | {\zeta _{\mathbf{n}}} |}_\sigma ^ {-j} \} .\end{align*} $$
$$ \begin{align*} B \subset \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta { | {\zeta _{\mathbf{n}}} |}_\sigma ^ {-j} \} .\end{align*} $$
Notice that
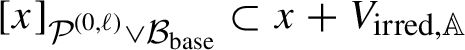 $[x] _ {\mathcal {P} ^ {(0, \ell )} \vee \mathcal B _{\mathrm {base}}} \subset x + V _ {{\mathrm {irred}}, \mathbb A}$
, hence there is some
$[x] _ {\mathcal {P} ^ {(0, \ell )} \vee \mathcal B _{\mathrm {base}}} \subset x + V _ {{\mathrm {irred}}, \mathbb A}$
, hence there is some
![]() $D \subset \mathbb A _ {\mathbb {K}}$
so that
$D \subset \mathbb A _ {\mathbb {K}}$
so that
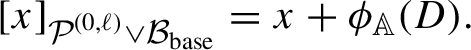 $$ \begin{align*} [x] _ {\mathcal{P} ^ {(0, \ell)} \vee \mathcal B _{\mathrm{base}}} = x + \phi _{\mathbb A} (D) .\end{align*} $$
$$ \begin{align*} [x] _ {\mathcal{P} ^ {(0, \ell)} \vee \mathcal B _{\mathrm{base}}} = x + \phi _{\mathbb A} (D) .\end{align*} $$
If the partition
![]() $\mathcal {P}$
was chosen to be sufficiently fine (again, depending on the parameter
$\mathcal {P}$
was chosen to be sufficiently fine (again, depending on the parameter
![]() $\eta> 0$
introduced above), we may assume that
$\eta> 0$
introduced above), we may assume that
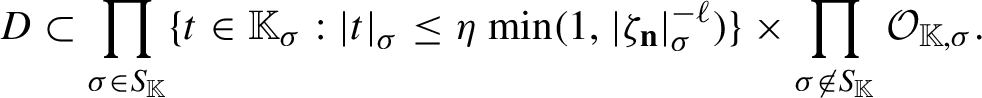 $$ \begin{align*} D \subset \prod_ {\sigma \in S _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta \min(1,{ | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {- \ell}) \} \times \prod_ {\sigma \not \in S _ {\mathbb{K}}} \mathcal{O} _ {\mathbb{K}, \sigma} .\end{align*} $$
$$ \begin{align*} D \subset \prod_ {\sigma \in S _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta \min(1,{ | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {- \ell}) \} \times \prod_ {\sigma \not \in S _ {\mathbb{K}}} \mathcal{O} _ {\mathbb{K}, \sigma} .\end{align*} $$
Note that
![]() ${ | {\zeta _{\mathbf {n}}} |} _ \sigma <1$
for every
${ | {\zeta _{\mathbf {n}}} |} _ \sigma <1$
for every
![]() $\sigma \in S^{\prime }_{\mathbb {K}}$
but may be
$\sigma \in S^{\prime }_{\mathbb {K}}$
but may be
![]() $<1$
,
$<1$
,
![]() $=1$
, or
$=1$
, or
![]() $>1$
for
$>1$
for
![]() $\sigma \in S_{\mathbb {K}}$
; however by choice of S (hence of
$\sigma \in S_{\mathbb {K}}$
; however by choice of S (hence of
![]() $S_{\mathbb {K}}$
),
$S_{\mathbb {K}}$
),
![]() ${ | {\zeta _{\mathbf {n}}} |} _ \sigma =1$
for
${ | {\zeta _{\mathbf {n}}} |} _ \sigma =1$
for
![]() $\sigma \not \in S_{\mathbb {K}}$
. Since
$\sigma \not \in S_{\mathbb {K}}$
. Since
![]() $ \mathbb Q ^ m \cap V _ {{\mathrm {irred}}, \mathbb A} = \phi _{\mathbb A} (\mathbb {K}) $
, and using the fact that
$ \mathbb Q ^ m \cap V _ {{\mathrm {irred}}, \mathbb A} = \phi _{\mathbb A} (\mathbb {K}) $
, and using the fact that
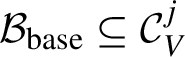 $\mathcal B _{\mathrm {base}} \subseteq \mathcal {C} _ V^j$
(modulo
$\mathcal B _{\mathrm {base}} \subseteq \mathcal {C} _ V^j$
(modulo
![]() $\widetilde \mu $
), we see that
$\widetilde \mu $
), we see that
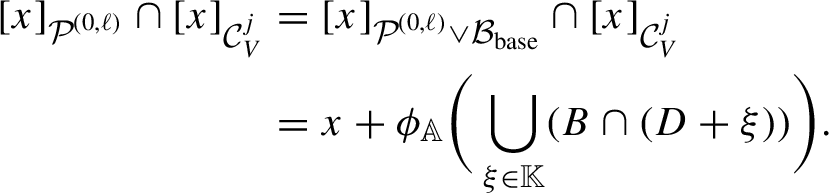 $$ \begin{align*} [x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} &= [x]_{\mathcal{P} ^ {(0, \ell)}\vee\mathcal{B}_{\mathrm{base}}} \cap [x]_{\mathcal{C} _ V ^ j} \\ &= x + \phi_{\mathbb A} \bigg(\bigcup_{\xi\in\mathbb{K}}(B\cap(D+\xi))\bigg). \end{align*} $$
$$ \begin{align*} [x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} &= [x]_{\mathcal{P} ^ {(0, \ell)}\vee\mathcal{B}_{\mathrm{base}}} \cap [x]_{\mathcal{C} _ V ^ j} \\ &= x + \phi_{\mathbb A} \bigg(\bigcup_{\xi\in\mathbb{K}}(B\cap(D+\xi))\bigg). \end{align*} $$
However, if
![]() $B \cap (D + \xi ) \neq \emptyset $
, that is
$B \cap (D + \xi ) \neq \emptyset $
, that is
![]() $\xi \in B - D$
, then
$\xi \in B - D$
, then
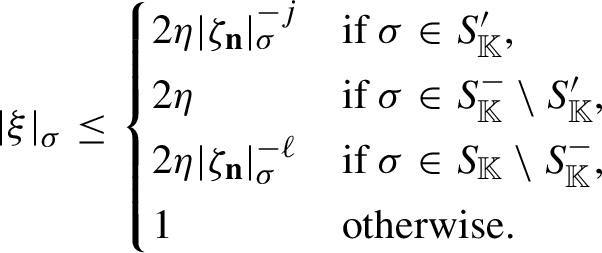 $$ \begin{align*} { | {\xi} |} _ \sigma \leq\begin{cases} 2 \eta { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {- j}& \text{if}\ \sigma \in S ^{\prime} _ {\mathbb{K}}, \\ 2 \eta & \text{if}\ \sigma \in S ^-_ {\mathbb{K}} \setminus S ^{\prime} _ {\mathbb{K}}, \\ 2 \eta { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {- \ell} & \text{if}\ \sigma \in S _ {\mathbb{K}} \setminus S ^- _{\mathbb{K}}, \\ 1& \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} { | {\xi} |} _ \sigma \leq\begin{cases} 2 \eta { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {- j}& \text{if}\ \sigma \in S ^{\prime} _ {\mathbb{K}}, \\ 2 \eta & \text{if}\ \sigma \in S ^-_ {\mathbb{K}} \setminus S ^{\prime} _ {\mathbb{K}}, \\ 2 \eta { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {- \ell} & \text{if}\ \sigma \in S _ {\mathbb{K}} \setminus S ^- _{\mathbb{K}}, \\ 1& \text{otherwise.} \end{cases} \end{align*} $$
By Proposition 2.3, if moreover
![]() $\xi \in \mathbb {K} ^ \times $
and
$\xi \in \mathbb {K} ^ \times $
and
![]() $\eta $
was chosen small enough (
$\eta $
was chosen small enough (
![]() $<1/2$
),
$<1/2$
),
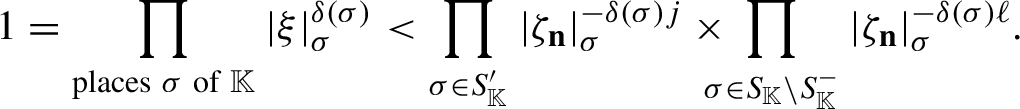 $$ \begin{align} 1 = \prod_ {\text{places}\ \sigma\ \text{of}\ \mathbb{K}} { | {\xi} |} _ \sigma ^{\delta(\sigma)} < \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {-\delta(\sigma)j} \times \!\!\!\prod_ {\sigma \in S _ {\mathbb{K}} \setminus S ^ - _ {\mathbb{K}}} { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {-\delta(\sigma)\ell} .\end{align} $$
$$ \begin{align} 1 = \prod_ {\text{places}\ \sigma\ \text{of}\ \mathbb{K}} { | {\xi} |} _ \sigma ^{\delta(\sigma)} < \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {-\delta(\sigma)j} \times \!\!\!\prod_ {\sigma \in S _ {\mathbb{K}} \setminus S ^ - _ {\mathbb{K}}} { | {\zeta _{\mathbf{n}}} |} _ \sigma ^ {-\delta(\sigma)\ell} .\end{align} $$
Applying Proposition 2.3 to
![]() $\zeta _{\mathbf {n}}$
,
$\zeta _{\mathbf {n}}$
,
 $$ \begin{align*} 1=\prod_ {\text{places}\ \sigma\ \text{of}\ \mathbb{K}} { | { \zeta_{\mathbf{n}}} |} _ \sigma ^{\delta(\sigma)} = \prod_ {\sigma \in S ^ - _ {\mathbb{K}}} { | { \zeta_{\mathbf{n}}} |} _ \sigma ^{\delta(\sigma)} \times \prod_ {\sigma \in S _ {\mathbb{K}} \setminus S ^ - _ {\mathbb{K}}} { | { \zeta_{\mathbf{n}}} |} _ \sigma ^{\delta(\sigma)}, \end{align*} $$
$$ \begin{align*} 1=\prod_ {\text{places}\ \sigma\ \text{of}\ \mathbb{K}} { | { \zeta_{\mathbf{n}}} |} _ \sigma ^{\delta(\sigma)} = \prod_ {\sigma \in S ^ - _ {\mathbb{K}}} { | { \zeta_{\mathbf{n}}} |} _ \sigma ^{\delta(\sigma)} \times \prod_ {\sigma \in S _ {\mathbb{K}} \setminus S ^ - _ {\mathbb{K}}} { | { \zeta_{\mathbf{n}}} |} _ \sigma ^{\delta(\sigma)}, \end{align*} $$
hence
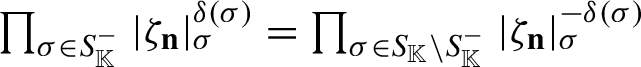 $\prod _ {\sigma \in S ^ - _ {\mathbb {K}}} { | { \zeta _{\mathbf {n}}} |} _ \sigma ^{\delta (\sigma )} = \prod _ {\sigma \in S _ {\mathbb {K}} \setminus S ^ - _ {\mathbb {K}}} { | { \zeta _{\mathbf {n}}} |} _ \sigma ^{-\delta (\sigma )}$
. Thus (5.5) implies
$\prod _ {\sigma \in S ^ - _ {\mathbb {K}}} { | { \zeta _{\mathbf {n}}} |} _ \sigma ^{\delta (\sigma )} = \prod _ {\sigma \in S _ {\mathbb {K}} \setminus S ^ - _ {\mathbb {K}}} { | { \zeta _{\mathbf {n}}} |} _ \sigma ^{-\delta (\sigma )}$
. Thus (5.5) implies
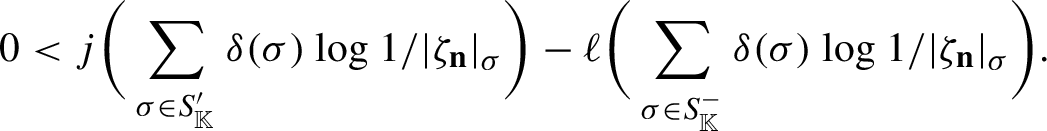 $$ \begin{align*} 0 < j \bigg (\sum_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \delta (\sigma) \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma \bigg) - \ell \bigg (\sum_ {\sigma \in S ^- _ {\mathbb{K}}} \delta (\sigma) \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma \bigg) .\end{align*} $$
$$ \begin{align*} 0 < j \bigg (\sum_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \delta (\sigma) \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma \bigg) - \ell \bigg (\sum_ {\sigma \in S ^- _ {\mathbb{K}}} \delta (\sigma) \log 1/{ | {\zeta _{\mathbf{n}}} |} _ \sigma \bigg) .\end{align*} $$
But this contradicts the definition of
![]() $\kappa $
and
$\kappa $
and
![]() $\ell \geq \kappa j$
.
$\ell \geq \kappa j$
.
Thus we obtain the important conclusion that if
![]() $\ell =\lceil \kappa j \rceil $
,
$\ell =\lceil \kappa j \rceil $
,
 $$ \begin{align*} [x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} = x + \phi _{\mathbb A} (B ^{\prime}), \end{align*} $$
$$ \begin{align*} [x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} = x + \phi _{\mathbb A} (B ^{\prime}), \end{align*} $$
where
 $$ \begin{align*} B ^{\prime} = B \cap D \subset \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta \} .\end{align*} $$
$$ \begin{align*} B ^{\prime} = B \cap D \subset \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta \} .\end{align*} $$
It follows that
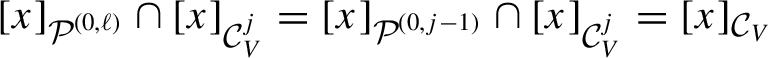 $$ \begin{align*}[x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} = [x]_{\mathcal{P} ^ {(0, j-1)}} \cap [x]_{\mathcal{C} _ V ^ j} = [x] _ {\mathcal{C} _ V}\end{align*} $$
$$ \begin{align*}[x]_{\mathcal{P} ^ {(0, \ell)}} \cap [x]_{\mathcal{C} _ V ^ j} = [x]_{\mathcal{P} ^ {(0, j-1)}} \cap [x]_{\mathcal{C} _ V ^ j} = [x] _ {\mathcal{C} _ V}\end{align*} $$
unless there is a
![]() $\ell < \ell ^{\prime } < j$
so that
$\ell < \ell ^{\prime } < j$
so that
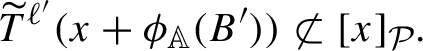 $$ \begin{align*} \widetilde T ^ {\ell ^{\prime}} (x+ \phi _{\mathbb A} (B ^{\prime})) \not\subset [x]_{\mathcal {P}} .\end{align*} $$
$$ \begin{align*} \widetilde T ^ {\ell ^{\prime}} (x+ \phi _{\mathbb A} (B ^{\prime})) \not\subset [x]_{\mathcal {P}} .\end{align*} $$
If
![]() $s = \max _ {\sigma \in S ^{\prime } _ {\mathbb {K}}} { | {\zeta _{\mathbf {n}}} |} _ \sigma < 1$
, then
$s = \max _ {\sigma \in S ^{\prime } _ {\mathbb {K}}} { | {\zeta _{\mathbf {n}}} |} _ \sigma < 1$
, then
![]() $\widetilde T ^ {\ell ^{\prime }} (x+ \phi _{\mathbb A} (B ^{\prime })) = \widetilde T ^ {\ell ^{\prime }} (x)+ \phi _{\mathbb A} (B ^{\prime \prime })$
, where
$\widetilde T ^ {\ell ^{\prime }} (x+ \phi _{\mathbb A} (B ^{\prime })) = \widetilde T ^ {\ell ^{\prime }} (x)+ \phi _{\mathbb A} (B ^{\prime \prime })$
, where
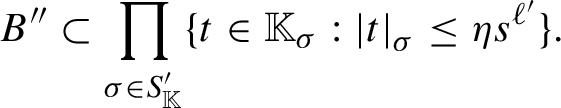 $$ \begin{align*} B ^{\prime\prime} \subset \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta s^{\ell^{\prime}} \}. \end{align*} $$
$$ \begin{align*} B ^{\prime\prime} \subset \prod_ {\sigma \in S ^{\prime} _ {\mathbb{K}}} \{ t \in \mathbb{K} _ \sigma: { | {t} |} _ \sigma \leq \eta s^{\ell^{\prime}} \}. \end{align*} $$
By (3.6), the set of such x has
![]() $\widetilde \mu $
measure which decays exponentially in
$\widetilde \mu $
measure which decays exponentially in
![]() $\ell ^{\prime }$
, hence in j, establishing (5.4).
$\ell ^{\prime }$
, hence in j, establishing (5.4).
Once (5.4) has been established, establishing (5.1) is easy. Indeed, if
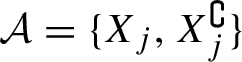 $\mathcal {A} = \{ X _ j, X _ j^ \complement \}$
for
$\mathcal {A} = \{ X _ j, X _ j^ \complement \}$
for
![]() $X _ j$
, as in (5.4), then for j large and
$X _ j$
, as in (5.4), then for j large and
![]() $\ell =\lceil \kappa j \rceil $
,
$\ell =\lceil \kappa j \rceil $
,
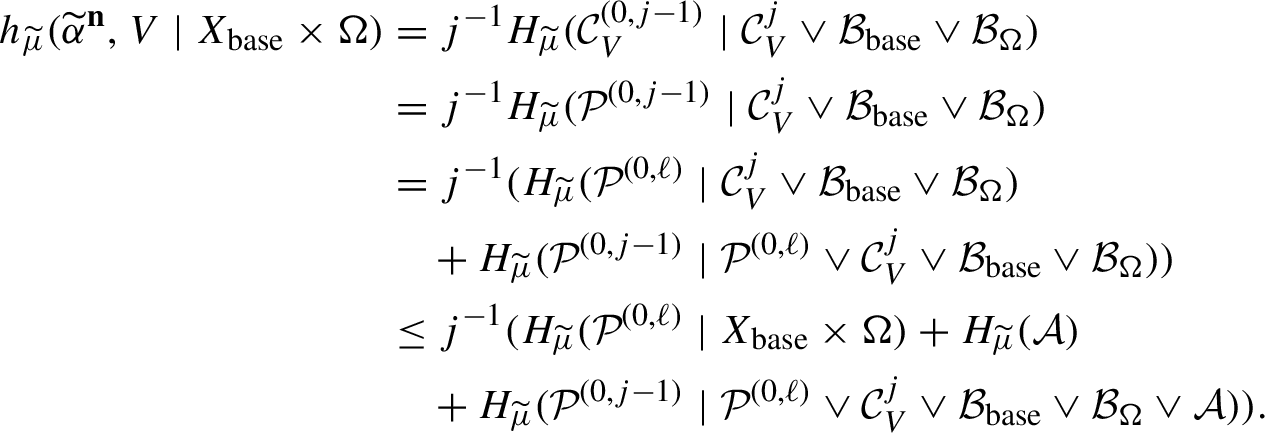 $$ \begin{align} h _ {\widetilde \mu} (\widetilde \alpha ^ {\mathbf n}, V \mid X _{\mathrm{base}} \times \Omega) & = j^{-1} H _ {\widetilde \mu} (\mathcal{C}_V^{(0,j-1)} \mid \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) \notag\\ & = j^{-1} H _ {\widetilde \mu} (\mathcal{P}^{(0,j-1)} \mid \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega ) \notag\\ & = j^{-1} (H _ {\widetilde \mu} (\mathcal{P}^{(0,\ell)} \mid \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega ) \notag\\ &\quad+H _ {\widetilde \mu} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega ) )\notag\\ & \leq j^{-1} (H _ {\widetilde \mu} (\mathcal{P}^{(0,\ell)}\mid X_{\mathrm{base}} \times \Omega) + H_{\widetilde\mu}(\mathcal{A}) \notag\\ &\quad+H _ {\widetilde \mu} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega \vee \mathcal{A} ) ). \end{align} $$
$$ \begin{align} h _ {\widetilde \mu} (\widetilde \alpha ^ {\mathbf n}, V \mid X _{\mathrm{base}} \times \Omega) & = j^{-1} H _ {\widetilde \mu} (\mathcal{C}_V^{(0,j-1)} \mid \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) \notag\\ & = j^{-1} H _ {\widetilde \mu} (\mathcal{P}^{(0,j-1)} \mid \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega ) \notag\\ & = j^{-1} (H _ {\widetilde \mu} (\mathcal{P}^{(0,\ell)} \mid \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega ) \notag\\ &\quad+H _ {\widetilde \mu} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega ) )\notag\\ & \leq j^{-1} (H _ {\widetilde \mu} (\mathcal{P}^{(0,\ell)}\mid X_{\mathrm{base}} \times \Omega) + H_{\widetilde\mu}(\mathcal{A}) \notag\\ &\quad+H _ {\widetilde \mu} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega \vee \mathcal{A} ) ). \end{align} $$
By definition,
 $$ \begin{align*} H _ {\widetilde \mu} &(\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega \vee \mathcal{A} ) \\ &=\widetilde \mu (X _ j) H _ {\widetilde \mu | X_j} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) \\ &\quad+ \widetilde \mu (X _ j ^\complement) H _ {\widetilde \mu | X_j ^\complement} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) .\end{align*} $$
$$ \begin{align*} H _ {\widetilde \mu} &(\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega \vee \mathcal{A} ) \\ &=\widetilde \mu (X _ j) H _ {\widetilde \mu | X_j} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) \\ &\quad+ \widetilde \mu (X _ j ^\complement) H _ {\widetilde \mu | X_j ^\complement} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) .\end{align*} $$
On
![]() $X_j$
, the atom
$X_j$
, the atom
 $[x]_{\mathcal {P}^{(0,j-1)}} \cap [x]_{\mathcal {C}_V^j} = [x]_{\mathcal {P}^{(0,\ell )}} \cap [x]_{\mathcal {C}_V^j}$
by (5.4), hence
$[x]_{\mathcal {P}^{(0,j-1)}} \cap [x]_{\mathcal {C}_V^j} = [x]_{\mathcal {P}^{(0,\ell )}} \cap [x]_{\mathcal {C}_V^j}$
by (5.4), hence
 $$ \begin{align*} H _ {\widetilde \mu | X_j} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) =0. \end{align*} $$
$$ \begin{align*} H _ {\widetilde \mu | X_j} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) =0. \end{align*} $$
On
![]() $X _ j ^\complement $
, we use the trivial bound
$X _ j ^\complement $
, we use the trivial bound
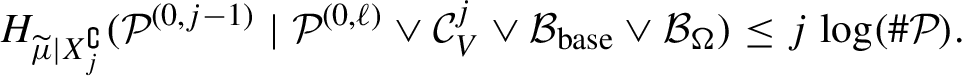 $$ \begin{align*} H _ {\widetilde \mu | X_j ^\complement} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) \leq j \log (\#\mathcal{P}). \end{align*} $$
$$ \begin{align*} H _ {\widetilde \mu | X_j ^\complement} (\mathcal{P}^{(0,j-1)} \mid \mathcal{P}^{(0,\ell)}\vee \mathcal{C}_V^j \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal{B}_\Omega) \leq j \log (\#\mathcal{P}). \end{align*} $$
Plugging these back in (5.6) and using
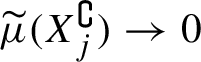 $\widetilde \mu (X_j^\complement )\to 0$
as
$\widetilde \mu (X_j^\complement )\to 0$
as
![]() $j \to \infty $
, we see that
$j \to \infty $
, we see that
establishing (5.1).
6 Coarse Lyapunov subgroups and the product structure
A crucial property of the leafwise measures for our argument is their product structure for the coarse Lyapunov subgroups as obtained by the first named author and Anatole Katok [Reference Einsiedler and Katok5] (see also [Reference Einsiedler and Katok4, Reference Lindenstrauss28]). For an introduction of the product structure, we also recommend [Reference Einsiedler and Lindenstrauss10, §8]. However, all of these papers assumed that the
![]() $\mathbb {Z}^d$
-action under consideration is semisimple. In our case we do not make this assumption, so our action is given by
$\mathbb {Z}^d$
-action under consideration is semisimple. In our case we do not make this assumption, so our action is given by
![]() $\alpha =\alpha _{\mathrm {diag}}\alpha _{\mathrm {uni}}$
, with both
$\alpha =\alpha _{\mathrm {diag}}\alpha _{\mathrm {uni}}$
, with both
![]() $\alpha _{\mathrm {diag}}$
and
$\alpha _{\mathrm {diag}}$
and
![]() $\alpha _{\mathrm {uni}}$
defined over
$\alpha _{\mathrm {uni}}$
defined over
![]() $\mathbb Q$
, that is, these can be thought of as homomorphisms from
$\mathbb Q$
, that is, these can be thought of as homomorphisms from
![]() $\mathbb {Z}^{d}$
to
$\mathbb {Z}^{d}$
to
![]() $\operatorname {GL}_m(\mathbb Q)$
; cf. p. 17. The purpose of this section is to recall the relevant notions and overcome the problems arising from the lack of semi-simplicity in the cases of interest.
$\operatorname {GL}_m(\mathbb Q)$
; cf. p. 17. The purpose of this section is to recall the relevant notions and overcome the problems arising from the lack of semi-simplicity in the cases of interest.
6.1 Lyapunov subgroups over
 $\mathbb Q_\sigma $
$\mathbb Q_\sigma $
Fix
![]() $\sigma $
a place of
$\sigma $
a place of
![]() $\mathbb Q$
, that is, either
$\mathbb Q$
, that is, either
![]() $\sigma =\infty $
or
$\sigma =\infty $
or
![]() $\sigma =p$
a prime. We consider the linear maps
$\sigma =p$
a prime. We consider the linear maps
![]() $\alpha ^{\mathbf {n}}$
for
$\alpha ^{\mathbf {n}}$
for
![]() $\mathbf {n}\in \mathbb {Z}^d$
on
$\mathbf {n}\in \mathbb {Z}^d$
on
![]() $\mathbb Q_\sigma ^m$
and are mostly interested in the asymptotic behavior of its elements with respect to the norm defined by
$\mathbb Q_\sigma ^m$
and are mostly interested in the asymptotic behavior of its elements with respect to the norm defined by
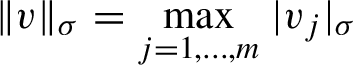 $$ \begin{align*} \|v\|_\sigma=\max_{j=1,\ldots,m}|v_j|_\sigma \end{align*} $$
$$ \begin{align*} \|v\|_\sigma=\max_{j=1,\ldots,m}|v_j|_\sigma \end{align*} $$
for all
![]() $v\in \mathbb Q_\sigma ^m$
. We will also consider this behavior restricted to an
$v\in \mathbb Q_\sigma ^m$
. We will also consider this behavior restricted to an
![]() $\alpha $
-invariant
$\alpha $
-invariant
![]() $\mathbb Q_\sigma $
-linear subspace V (even when not explicitly stated, V will always be assumed to be
$\mathbb Q_\sigma $
-linear subspace V (even when not explicitly stated, V will always be assumed to be
![]() $\alpha $
-invariant). For this, we will initially ignore
$\alpha $
-invariant). For this, we will initially ignore
![]() $\alpha _{\mathrm {uni}}$
(with polynomial behavior) and focus on
$\alpha _{\mathrm {uni}}$
(with polynomial behavior) and focus on
![]() $\alpha _{\mathrm {diag}}$
(with exponential behavior).
$\alpha _{\mathrm {diag}}$
(with exponential behavior).
Since
![]() $\alpha _{\mathrm {diag}}$
is semisimple,
$\alpha _{\mathrm {diag}}$
is semisimple,
![]() $\mathbb Q^m_\sigma $
(as well as any
$\mathbb Q^m_\sigma $
(as well as any
![]() $\alpha $
-invariant subspace V) is a direct sum of
$\alpha $
-invariant subspace V) is a direct sum of
![]() $\mathbb Q_\sigma $
-irreducible linear subspaces. On each of these irreducible subspaces, the action of
$\mathbb Q_\sigma $
-irreducible linear subspaces. On each of these irreducible subspaces, the action of
![]() $\alpha _{\mathrm {diag}}$
is isomorphic to the action defined by multiplication by d elements
$\alpha _{\mathrm {diag}}$
is isomorphic to the action defined by multiplication by d elements
![]() $\zeta _1,\ldots ,\zeta _d\in \mathbb {K}$
on a local field
$\zeta _1,\ldots ,\zeta _d\in \mathbb {K}$
on a local field
![]() $\mathbb {K}$
(similar to the discussion in the proof of Proposition 2.2). Recall that we extend the the norm on
$\mathbb {K}$
(similar to the discussion in the proof of Proposition 2.2). Recall that we extend the the norm on
![]() $\mathbb Q_\sigma $
to
$\mathbb Q_\sigma $
to
![]() $\mathbb {K}$
; this extended norm is denoted by
$\mathbb {K}$
; this extended norm is denoted by
![]() $|\cdot |_\sigma $
. We refer to the linear functional
$|\cdot |_\sigma $
. We refer to the linear functional
![]() $\chi :\mathbb {Z}^d\to \mathbb {R}$
given by
$\chi :\mathbb {Z}^d\to \mathbb {R}$
given by
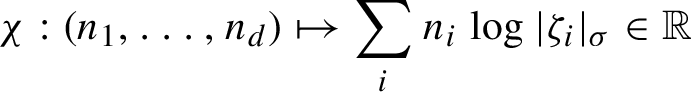 $$ \begin{align*} \chi : (n_1,\ldots,n_d)\mapsto \sum_i n_i\log|\zeta_i|_\sigma\in\mathbb{R} \end{align*} $$
$$ \begin{align*} \chi : (n_1,\ldots,n_d)\mapsto \sum_i n_i\log|\zeta_i|_\sigma\in\mathbb{R} \end{align*} $$
as the Lyapunov weight associated with the invariant subspace
![]() $\mathbb {K}$
, and denote the pairing of a functional
$\mathbb {K}$
, and denote the pairing of a functional
![]() $\chi $
and a vector
$\chi $
and a vector
![]() $\mathbf {n} \in \mathbb {Z}^d$
(or
$\mathbf {n} \in \mathbb {Z}^d$
(or
![]() $\mathbb {R}^d$
) by
$\mathbb {R}^d$
) by
![]() $\chi \cdot \mathbf {n}$
. We note that for a vector v in this subspace, we have
$\chi \cdot \mathbf {n}$
. We note that for a vector v in this subspace, we have
 $$ \begin{align} \|\alpha_{\mathrm{diag}}^{\mathbf{n}} v\|_\sigma\asymp e^{\chi\cdot \mathbf{n}}\|v\|_\sigma \end{align} $$
$$ \begin{align} \|\alpha_{\mathrm{diag}}^{\mathbf{n}} v\|_\sigma\asymp e^{\chi\cdot \mathbf{n}}\|v\|_\sigma \end{align} $$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
, where we write
$\mathbf {n}\in \mathbb {Z}^d$
, where we write
![]() $\asymp $
to indicate that we can bound each of the two terms by a multiple of the other. Here the implicit constants only depend on the action and not on the vector v or on
$\asymp $
to indicate that we can bound each of the two terms by a multiple of the other. Here the implicit constants only depend on the action and not on the vector v or on
![]() $\mathbf {n}$
. We will call
$\mathbf {n}$
. We will call
![]() $\mathbb {K}$
an
$\mathbb {K}$
an
![]() $\mathbb Q_\sigma $
-irreducible eigenspace (for
$\mathbb Q_\sigma $
-irreducible eigenspace (for
![]() $\alpha _{\mathrm {diag}}$
) with Lyapunov weight
$\alpha _{\mathrm {diag}}$
) with Lyapunov weight
![]() $\chi $
.
$\chi $
.
It follows that
![]() $\mathbb Q_\sigma ^m$
(respectively V) is isomorphic to a finite direct product of local fields
$\mathbb Q_\sigma ^m$
(respectively V) is isomorphic to a finite direct product of local fields
![]() $\mathbb {K}$
extending
$\mathbb {K}$
extending
![]() $\mathbb Q_\sigma $
so that the linear maps
$\mathbb Q_\sigma $
so that the linear maps
 $\alpha _{\mathrm {diag}}^{\mathbf {e}_1},\ldots ,\alpha _{\mathrm {diag}}^{\mathbf {e}_d}$
are written in diagonal form using this isomorphism. Moreover, we obtain in this way finitely many Lyapunov weights arising from the action on
$\alpha _{\mathrm {diag}}^{\mathbf {e}_1},\ldots ,\alpha _{\mathrm {diag}}^{\mathbf {e}_d}$
are written in diagonal form using this isomorphism. Moreover, we obtain in this way finitely many Lyapunov weights arising from the action on
![]() $\mathbb Q_\sigma ^m$
. Note however that these Lyapunov weights are all functionals into
$\mathbb Q_\sigma ^m$
. Note however that these Lyapunov weights are all functionals into
![]() $\mathbb {R}$
(independent of the place
$\mathbb {R}$
(independent of the place
![]() $\sigma $
).
$\sigma $
).
6.2 Coarse Lyapunov weights and subgroups
We now apply the above for each place
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb Q$
. Let S be a finite set of places containing
$\mathbb Q$
. Let S be a finite set of places containing
![]() $\infty $
so that
$\infty $
so that
 $\alpha _{\mathrm {diag}}^{\mathbf {e}_1},\ldots ,\alpha _{\mathrm {diag}}^{\mathbf {e}_d}$
all belong to
$\alpha _{\mathrm {diag}}^{\mathbf {e}_1},\ldots ,\alpha _{\mathrm {diag}}^{\mathbf {e}_d}$
all belong to
![]() $\operatorname {GL}_m(\mathbb {Z}_\sigma )$
for
$\operatorname {GL}_m(\mathbb {Z}_\sigma )$
for
![]() $\sigma \notin S$
. For
$\sigma \notin S$
. For
![]() $\sigma \notin S$
, the only Lyapunov weight for the action of
$\sigma \notin S$
, the only Lyapunov weight for the action of
![]() $\alpha _{\mathrm {diag}}$
on
$\alpha _{\mathrm {diag}}$
on
![]() $\mathbb Q_\sigma $
is the zero weight. Hence by varying
$\mathbb Q_\sigma $
is the zero weight. Hence by varying
![]() $\sigma $
over all places of
$\sigma $
over all places of
![]() $\mathbb Q$
, we only obtain finitely many non-zero Lyapunov weights.
$\mathbb Q$
, we only obtain finitely many non-zero Lyapunov weights.
We say that two non-zero Lyapunov weights
![]() $\chi ,\chi ^{\prime }$
(possibly arising from different places of
$\chi ,\chi ^{\prime }$
(possibly arising from different places of
![]() $\mathbb Q$
) are equivalent if there exists some
$\mathbb Q$
) are equivalent if there exists some
![]() $t>0$
so that
$t>0$
so that
![]() $\chi ^{\prime }=t\chi $
. We will denote the equivalence class of a non-zero Laypunov weight
$\chi ^{\prime }=t\chi $
. We will denote the equivalence class of a non-zero Laypunov weight
![]() $\chi $
by
$\chi $
by
![]() $[\chi ]$
and will refer to
$[\chi ]$
and will refer to
![]() $[\chi ]$
as a coarse Lyapunov weight.
$[\chi ]$
as a coarse Lyapunov weight.
For a coarse Lyapunov weight
![]() $[\chi ]$
, we define the coarse Lyapunov subgroup
$[\chi ]$
, we define the coarse Lyapunov subgroup
![]() $W^{[\chi ]}$
to be the S-linear subspace defined as the subgroup generated by all irreducible eigenspaces with Lyapunov weight
$W^{[\chi ]}$
to be the S-linear subspace defined as the subgroup generated by all irreducible eigenspaces with Lyapunov weight
![]() $\chi ^{\prime }$
equivalent to
$\chi ^{\prime }$
equivalent to
![]() $\chi $
. Alternatively, we can use (6.1) to see that the coarse Lyapunov subgroup could also be defined as an intersection of stable horospherical subgroups for
$\chi $
. Alternatively, we can use (6.1) to see that the coarse Lyapunov subgroup could also be defined as an intersection of stable horospherical subgroups for
![]() $\alpha _{\mathrm {diag}}$
, namely
$\alpha _{\mathrm {diag}}$
, namely
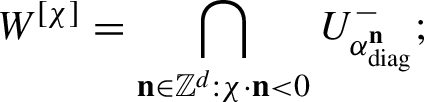 $$ \begin{align*} W^{[\chi]}=\bigcap_{\mathbf{n}\in\mathbb{Z}^d: \chi\cdot\mathbf{n}<0}U^-_{\alpha_{\mathrm{diag}}^{\mathbf{n}}}; \end{align*} $$
$$ \begin{align*} W^{[\chi]}=\bigcap_{\mathbf{n}\in\mathbb{Z}^d: \chi\cdot\mathbf{n}<0}U^-_{\alpha_{\mathrm{diag}}^{\mathbf{n}}}; \end{align*} $$
this relation to the horospherical subgroups is the reason for the dynamical importance of the coarse Lyapunov subgroups.
Because of the polynomial nature of
![]() $\alpha _{\mathrm {uni}}$
, we have that
$\alpha _{\mathrm {uni}}$
, we have that
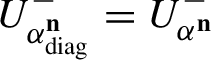 $U^-_{\alpha _{\mathrm {diag}}^{\mathbf {n}}}=U^-_{\alpha ^{\mathbf {n}}}$
for all
$U^-_{\alpha _{\mathrm {diag}}^{\mathbf {n}}}=U^-_{\alpha ^{\mathbf {n}}}$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
and hence
$\mathbf {n}\in \mathbb {Z}^d$
and hence
![]() $W^{[\chi ]}$
can be defined directly in terms of the action
$W^{[\chi ]}$
can be defined directly in terms of the action
![]() $\alpha $
by
$\alpha $
by
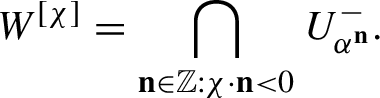 $$ \begin{align*} W^{[\chi]}=\bigcap_{\mathbf{n}\in\mathbb{Z}: \chi\cdot \mathbf{n}<0}U^-_{\alpha^{\mathbf{n}}}. \end{align*} $$
$$ \begin{align*} W^{[\chi]}=\bigcap_{\mathbf{n}\in\mathbb{Z}: \chi\cdot \mathbf{n}<0}U^-_{\alpha^{\mathbf{n}}}. \end{align*} $$
In particular,
![]() $W^{[\chi ]}$
is invariant under
$W^{[\chi ]}$
is invariant under
![]() $\alpha ^{\mathbf {n}}$
for all
$\alpha ^{\mathbf {n}}$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
.
$\mathbf {n}\in \mathbb {Z}^d$
.
Conversely, any stable horospherical group is a product of coarse Lyapunov subgroups: indeed, for any
![]() $\mathbf {n}\in \mathbb {Z}^d$
, we have
$\mathbf {n}\in \mathbb {Z}^d$
, we have
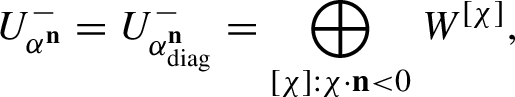 $$ \begin{align} U^-_{\alpha^{\mathbf{n}}}=U^-_{\alpha_{\mathrm{diag}}^{\mathbf{n}}}=\bigoplus_{[\chi]: \chi\cdot\mathbf{n}<0}W^{[\chi]}, \end{align} $$
$$ \begin{align} U^-_{\alpha^{\mathbf{n}}}=U^-_{\alpha_{\mathrm{diag}}^{\mathbf{n}}}=\bigoplus_{[\chi]: \chi\cdot\mathbf{n}<0}W^{[\chi]}, \end{align} $$
where the direct sum runs over all the coarse Lyapunov subspaces
![]() $W^{[\chi ]}$
satisfying that
$W^{[\chi ]}$
satisfying that
![]() $\chi \cdot \mathbf {n}<0$
.
$\chi \cdot \mathbf {n}<0$
.
Given an
![]() $\alpha $
-invariant S-linear subgroup
$\alpha $
-invariant S-linear subgroup
![]() $V<U^-_{\alpha ^{\mathbf {n}}}$
, we define
$V<U^-_{\alpha ^{\mathbf {n}}}$
, we define
![]() $V^{[\chi ]}=V\cap W^{[\chi ]}$
for any non-zero coarse Lyapunov weight
$V^{[\chi ]}=V\cap W^{[\chi ]}$
for any non-zero coarse Lyapunov weight
![]() $[\chi ]$
. These also satisfy that V is the direct sum of
$[\chi ]$
. These also satisfy that V is the direct sum of
![]() $V^{[\chi ]}$
for all
$V^{[\chi ]}$
for all
![]() $[\chi ]$
with
$[\chi ]$
with
![]() $\chi \cdot \mathbf {n}<0$
.
$\chi \cdot \mathbf {n}<0$
.
6.3 Product structure of leafwise measures
Recall that we assume that
![]() $\mu $
is as in Theorem 4.1. Let
$\mu $
is as in Theorem 4.1. Let
![]() $\Omega $
be an arbitrary compact metric space as in §3.1 equipped with an action of
$\Omega $
be an arbitrary compact metric space as in §3.1 equipped with an action of
![]() $\mathbb {Z}^{d}$
, let
$\mathbb {Z}^{d}$
, let
![]() $\widetilde {X}=X\times \Omega $
, and consider an invariant probability measure
$\widetilde {X}=X\times \Omega $
, and consider an invariant probability measure
![]() $\widetilde {\mu }$
on
$\widetilde {\mu }$
on
![]() $\widetilde {X}$
projecting to
$\widetilde {X}$
projecting to
![]() $\mu $
.
$\mu $
.
Theorem 6.1. (Entropy and product structure)
Let
![]() $X \to X_{\mathrm {pos}}\to X_{\mathrm {base}}$
with
$X \to X_{\mathrm {pos}}\to X_{\mathrm {base}}$
with
![]() $X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
and
$X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
and
![]() $X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
be as in (4.1) and let
$X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
be as in (4.1) and let
![]() $V_{\mathrm {base},\mathbb A}<\mathbb A^m$
be the rational
$V_{\mathrm {base},\mathbb A}<\mathbb A^m$
be the rational
![]() $\alpha $
-invariant subspace so that
$\alpha $
-invariant subspace so that
![]() $Y_{\mathrm {base}}$
is the image of
$Y_{\mathrm {base}}$
is the image of
![]() $V_{\mathrm {base},\mathbb A}$
modulo
$V_{\mathrm {base},\mathbb A}$
modulo
![]() $\mathbb Q^m$
. Let
$\mathbb Q^m$
. Let
![]() $\mathbf {n}_0\in \mathbb {Z}^{d}$
. Then the leafwise measure on
$\mathbf {n}_0\in \mathbb {Z}^{d}$
. Then the leafwise measure on
![]() $\widetilde {X}$
for
$\widetilde {X}$
for
is, up to proportionality, the product of the leafwise measures for its coarse Lyapunov subgroups
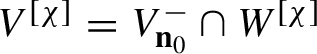 $V^{[\chi ]}=V^-_{\mathbf {n}_0}\cap W^{[\chi ]}$
, that is,
$V^{[\chi ]}=V^-_{\mathbf {n}_0}\cap W^{[\chi ]}$
, that is,
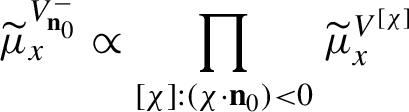 $$ \begin{align*} {\widetilde{\mu}}_x^{V^-_{\mathbf{n}_0}}\propto\prod_{[\chi]: (\chi\cdot\mathbf{n}_0)<0}{\widetilde{\mu}}_x^{V^{[\chi]}} \end{align*} $$
$$ \begin{align*} {\widetilde{\mu}}_x^{V^-_{\mathbf{n}_0}}\propto\prod_{[\chi]: (\chi\cdot\mathbf{n}_0)<0}{\widetilde{\mu}}_x^{V^{[\chi]}} \end{align*} $$
for a.e.
![]() $x\in \widetilde {X}$
. In particular, the relative entropy of
$x\in \widetilde {X}$
. In particular, the relative entropy of
![]() $\alpha ^{\mathbf {n}_0}$
conditional on the factor
$\alpha ^{\mathbf {n}_0}$
conditional on the factor
![]() $X_{\mathrm {base}}\times \Omega $
is equal to the sum of the entropy contributions of these coarse Lyapunov subgroups, that is,
$X_{\mathrm {base}}\times \Omega $
is equal to the sum of the entropy contributions of these coarse Lyapunov subgroups, that is,
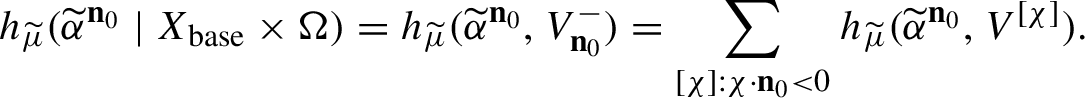 $$ \begin{align} h_{\widetilde{\mu}}(\widetilde{\alpha}^{\mathbf{n}_0}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\widetilde{\alpha}^{\mathbf{n}_0},V^-_{{\mathbf{n}_0}}) =\sum_{[\chi]: \chi\cdot\mathbf{n}_0<0}h_{\widetilde{\mu}}(\widetilde{\alpha}^{\mathbf{n}_0},V^{[\chi]}). \end{align} $$
$$ \begin{align} h_{\widetilde{\mu}}(\widetilde{\alpha}^{\mathbf{n}_0}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\widetilde{\alpha}^{\mathbf{n}_0},V^-_{{\mathbf{n}_0}}) =\sum_{[\chi]: \chi\cdot\mathbf{n}_0<0}h_{\widetilde{\mu}}(\widetilde{\alpha}^{\mathbf{n}_0},V^{[\chi]}). \end{align} $$
We note that our proof relies on the assumption that X is a zero entropy extension of
![]() $X_{\mathrm {pos}}$
, and does not extend the product structure to other cases with Jordan blocks. In fact our setup is used to show that Jordan blocks of
$X_{\mathrm {pos}}$
, and does not extend the product structure to other cases with Jordan blocks. In fact our setup is used to show that Jordan blocks of
![]() $\alpha ^{\mathbf {n}}$
cannot appear within the subspace
$\alpha ^{\mathbf {n}}$
cannot appear within the subspace
![]() $V^{[\chi ]}\cap \mathbb {R}^m$
and for ‘
$V^{[\chi ]}\cap \mathbb {R}^m$
and for ‘
![]() $\mathbf {n}$
in the kernel of
$\mathbf {n}$
in the kernel of
![]() $\chi $
’ (in the sense described below). Moreover, in the non-Archimedean parts of
$\chi $
’ (in the sense described below). Moreover, in the non-Archimedean parts of
![]() $V_{\mathbf {n}_0}^-$
, we use a different argument.
$V_{\mathbf {n}_0}^-$
, we use a different argument.
For any
![]() $\alpha $
-invariant S-linear subgroup V, we let
$\alpha $
-invariant S-linear subgroup V, we let
![]() $P<V$
be the minimal S-linear
$P<V$
be the minimal S-linear
![]() $\alpha $
-invariant subspace so that
$\alpha $
-invariant subspace so that
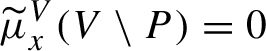 $$ \begin{align*} {\widetilde{\mu}}_x^{V}(V\setminus P)=0 \end{align*} $$
$$ \begin{align*} {\widetilde{\mu}}_x^{V}(V\setminus P)=0 \end{align*} $$
for a.e.
![]() $x\in \widetilde {X}$
. We will refer to P as the supporting subgroup of V. We note that
$x\in \widetilde {X}$
. We will refer to P as the supporting subgroup of V. We note that
![]() $\mu _x^V=\mu _x^P$
a.s. and if
$\mu _x^V=\mu _x^P$
a.s. and if
![]() $W<P$
is another S-linear
$W<P$
is another S-linear
![]() $\alpha $
-invariant subspace with
$\alpha $
-invariant subspace with
![]() $W\neq P$
, then
$W\neq P$
, then
![]() $\mu _x^V(W)=0$
a.s. This follows from [Reference Einsiedler and Lindenstrauss11, Lemma 5.2] (as we restrict here to
$\mu _x^V(W)=0$
a.s. This follows from [Reference Einsiedler and Lindenstrauss11, Lemma 5.2] (as we restrict here to
![]() $\alpha $
-invariant subspaces the assumption of class
$\alpha $
-invariant subspaces the assumption of class
![]() $\mathcal {A}^{\prime }$
can easily be avoided in the proof of that lemma).
$\mathcal {A}^{\prime }$
can easily be avoided in the proof of that lemma).
We say that
![]() $[\chi ]$
is an exposed coarse Lyapunov weight for an
$[\chi ]$
is an exposed coarse Lyapunov weight for an
![]() $\alpha $
-invariant S-linear subgroup
$\alpha $
-invariant S-linear subgroup
![]() $V<U^-_{\alpha ^{\mathbf {n}}}$
if
$V<U^-_{\alpha ^{\mathbf {n}}}$
if
![]() $V^{[\chi ]}$
is non-trivial,
$V^{[\chi ]}$
is non-trivial,
![]() $V=V^{[\chi ]}+V^{\prime }$
for a sum
$V=V^{[\chi ]}+V^{\prime }$
for a sum
![]() $V^{\prime }$
of coarse Lyapunov subgroups, and there exists some
$V^{\prime }$
of coarse Lyapunov subgroups, and there exists some
![]() $\mathbf {n}^{\prime }\in \mathbb {R}^d$
with
$\mathbf {n}^{\prime }\in \mathbb {R}^d$
with
![]() $\chi \cdot \mathbf {n}^{\prime }=0$
and
$\chi \cdot \mathbf {n}^{\prime }=0$
and
![]() $\chi ^{\prime }\cdot \mathbf {n}^{\prime }<0$
for all Lyapunov weights
$\chi ^{\prime }\cdot \mathbf {n}^{\prime }<0$
for all Lyapunov weights
![]() $\chi ^{\prime }$
of
$\chi ^{\prime }$
of
![]() $V^{\prime }$
.
$V^{\prime }$
.
We also recall that
![]() $\alpha _{\mathrm {uni}}^{\mathbf {n}}$
is a polynomial map from
$\alpha _{\mathrm {uni}}^{\mathbf {n}}$
is a polynomial map from
![]() $\mathbb {Z}^d \to \operatorname {GL}_m(\mathbb Q)$
and so extends to a homomorphism from
$\mathbb {Z}^d \to \operatorname {GL}_m(\mathbb Q)$
and so extends to a homomorphism from
![]() $\mathbb {R}^d$
to
$\mathbb {R}^d$
to
![]() $\operatorname {GL}_m(\mathbb {R})$
that will also be denoted by
$\operatorname {GL}_m(\mathbb {R})$
that will also be denoted by
![]() $\alpha _{\mathrm {uni}}$
.
$\alpha _{\mathrm {uni}}$
.
6.4 No shearing and proving the product structure
The following lemma stands in stark contrast to the non-Archimedean case, where
![]() $\alpha _{\mathrm {uni}}$
takes values in a compact group.
$\alpha _{\mathrm {uni}}$
takes values in a compact group.
Lemma 6.2. (Existence of logarithmic sequence for real Jordan blocks)
Let
![]() $\alpha $
be a representation of
$\alpha $
be a representation of
![]() $\mathbb {Z}^d$
on a real vector space P. Suppose that
$\mathbb {Z}^d$
on a real vector space P. Suppose that
![]() $\chi $
is a non-zero Lyapunov weight for
$\chi $
is a non-zero Lyapunov weight for
![]() $\alpha $
and that all other Lyapunov weights are equivalent to
$\alpha $
and that all other Lyapunov weights are equivalent to
![]() $\chi $
. Suppose that
$\chi $
. Suppose that
![]() $\alpha _{\mathrm {uni}}^{\mathbf {m}}$
is non-trivial for some
$\alpha _{\mathrm {uni}}^{\mathbf {m}}$
is non-trivial for some
![]() $\mathbf {m}\in \mathbb {R}^d$
with
$\mathbf {m}\in \mathbb {R}^d$
with
![]() $\chi \cdot \mathbf {m}=0$
. Then there exists a sequence
$\chi \cdot \mathbf {m}=0$
. Then there exists a sequence
![]() $\mathbf {n}_k\in \mathbb {Z}^d$
so that
$\mathbf {n}_k\in \mathbb {Z}^d$
so that
![]() $\alpha ^{\mathbf {n}_k}\in \operatorname {End}(P)$
converges to a non-zero non-invertible linear map
$\alpha ^{\mathbf {n}_k}\in \operatorname {End}(P)$
converges to a non-zero non-invertible linear map
![]() $L\in \operatorname {End}(P)$
.
$L\in \operatorname {End}(P)$
.
We will refer to the sequence
![]() $\mathbf {n}_k$
as a logarithmic sequence for P since it can be defined using the logarithm map in easy special cases.
$\mathbf {n}_k$
as a logarithmic sequence for P since it can be defined using the logarithm map in easy special cases.
Proof Proof of Lemma 6.2
Let
![]() $\alpha _{|\cdot |}$
be the representation of
$\alpha _{|\cdot |}$
be the representation of
![]() $\mathbb {Z}^d$
on P, which has every eigenvector of
$\mathbb {Z}^d$
on P, which has every eigenvector of
![]() $\alpha _{\mathrm {diag}}$
with eigenvalue
$\alpha _{\mathrm {diag}}$
with eigenvalue
![]() $\unicode{x3bb} $
also as eigenvector but with eigenvalue
$\unicode{x3bb} $
also as eigenvector but with eigenvalue
![]() $|\unicode{x3bb} |$
. Note that
$|\unicode{x3bb} |$
. Note that
![]() $\alpha _{|\cdot |}$
extends continuously to all
$\alpha _{|\cdot |}$
extends continuously to all
![]() $\mathbf {n}\in \mathbb {R}^d$
. Moreover for
$\mathbf {n}\in \mathbb {R}^d$
. Moreover for
![]() $\mathbf {n}\in \mathbb {Z}^d$
, the map
$\mathbf {n}\in \mathbb {Z}^d$
, the map
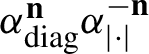 $\alpha ^{\mathbf {n}}_{\mathrm {diag}}\alpha _{|\cdot |}^{-\mathbf {n}}$
belongs to a fixed compact subgroup of
$\alpha ^{\mathbf {n}}_{\mathrm {diag}}\alpha _{|\cdot |}^{-\mathbf {n}}$
belongs to a fixed compact subgroup of
![]() $\operatorname {GL}(P)$
. Using nearest integer vectors, we see that it suffices to construct a sequence
$\operatorname {GL}(P)$
. Using nearest integer vectors, we see that it suffices to construct a sequence
![]() $\mathbf {n}_k\in \mathbb {R}^d$
so that
$\mathbf {n}_k\in \mathbb {R}^d$
so that
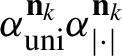 $\alpha _{\mathrm {uni}}^{\mathbf {n}_k}\alpha _{|\cdot |}^{\mathbf {n}_k}$
converges to a non-zero non-invertible linear map L.
$\alpha _{\mathrm {uni}}^{\mathbf {n}_k}\alpha _{|\cdot |}^{\mathbf {n}_k}$
converges to a non-zero non-invertible linear map L.
For this, we apply our assumption and pick a direction
![]() $\mathbf {m}\in \mathbb {R}^d$
with
$\mathbf {m}\in \mathbb {R}^d$
with
![]() $\chi \cdot \mathbf {m}=0$
so that
$\chi \cdot \mathbf {m}=0$
so that
![]() $\alpha ^{\mathbf {m}}_{\mathrm {uni}}$
is non-trivial. Also let
$\alpha ^{\mathbf {m}}_{\mathrm {uni}}$
is non-trivial. Also let
![]() $\mathbf {n}_-\in \mathbb {R}^d$
with
$\mathbf {n}_-\in \mathbb {R}^d$
with
![]() $\chi \cdot \mathbf {n}_-<0$
. As a non-zero real polynomial,
$\chi \cdot \mathbf {n}_-<0$
. As a non-zero real polynomial,
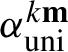 $\alpha _{\mathrm {uni}}^{k\mathbf {m}}$
diverges as
$\alpha _{\mathrm {uni}}^{k\mathbf {m}}$
diverges as
![]() $k\to \infty $
and
$k\to \infty $
and
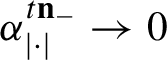 $\alpha _{|\cdot |}^{t \mathbf {n}_-}\to 0$
as
$\alpha _{|\cdot |}^{t \mathbf {n}_-}\to 0$
as
![]() $t\to \infty $
. Also note that
$t\to \infty $
. Also note that
 $\alpha _{|\cdot |}^{t \mathbf {n}_-}\to 0$
converges exponentially fast, while
$\alpha _{|\cdot |}^{t \mathbf {n}_-}\to 0$
converges exponentially fast, while
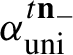 $\alpha _{\mathrm {uni}}^{t\mathbf {n}_-}$
can only diverge polynomially fast as
$\alpha _{\mathrm {uni}}^{t\mathbf {n}_-}$
can only diverge polynomially fast as
![]() $t\to \infty $
.
$t\to \infty $
.
This shows that for each sufficiently large
![]() $k\in \mathbb {N}$
, we can define
$k\in \mathbb {N}$
, we can define
![]() $\mathbf {n}_k=k \mathbf {m}+t_k \mathbf {n}_-$
, where
$\mathbf {n}_k=k \mathbf {m}+t_k \mathbf {n}_-$
, where
![]() $t_k>0$
is chosen (using the intermediate value theorem) minimally so that the Hilbert–Schmidt norms satisfy
$t_k>0$
is chosen (using the intermediate value theorem) minimally so that the Hilbert–Schmidt norms satisfy
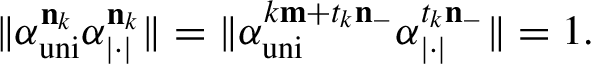 $$ \begin{align*} \|\alpha_{\mathrm{uni}}^{\mathbf{n}_k}\alpha_{|\cdot|}^{\mathbf{n}_k}\| =\|\alpha_{\mathrm{uni}}^{k\mathbf{m}+t_k\mathbf{n}_-}\alpha_{|\cdot|}^{t_k \mathbf{n}_-}\|=1. \end{align*} $$
$$ \begin{align*} \|\alpha_{\mathrm{uni}}^{\mathbf{n}_k}\alpha_{|\cdot|}^{\mathbf{n}_k}\| =\|\alpha_{\mathrm{uni}}^{k\mathbf{m}+t_k\mathbf{n}_-}\alpha_{|\cdot|}^{t_k \mathbf{n}_-}\|=1. \end{align*} $$
Since
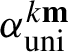 $\alpha _{\mathrm {uni}}^{k\mathbf {m}}$
diverges as
$\alpha _{\mathrm {uni}}^{k\mathbf {m}}$
diverges as
![]() $k\to \infty $
, we see that also
$k\to \infty $
, we see that also
![]() $t_k\to \infty $
. If now
$t_k\to \infty $
. If now
![]() $v\in P$
is a common eigenvector for
$v\in P$
is a common eigenvector for
![]() $\alpha $
, then
$\alpha $
, then
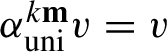 $\alpha _{\mathrm {uni}}^{k\mathbf {m}}v=v$
, and so
$\alpha _{\mathrm {uni}}^{k\mathbf {m}}v=v$
, and so
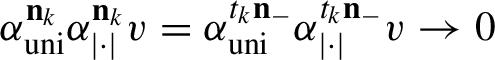 $$ \begin{align*} \alpha_{\mathrm{uni}}^{\mathbf{n}_k}\alpha_{|\cdot|}^{\mathbf{n}_k}v =\alpha_{\mathrm{uni}}^{t_k\mathbf{n}_-}\alpha_{|\cdot|}^{t_k \mathbf{n}_-}v\to 0 \end{align*} $$
$$ \begin{align*} \alpha_{\mathrm{uni}}^{\mathbf{n}_k}\alpha_{|\cdot|}^{\mathbf{n}_k}v =\alpha_{\mathrm{uni}}^{t_k\mathbf{n}_-}\alpha_{|\cdot|}^{t_k \mathbf{n}_-}v\to 0 \end{align*} $$
as
![]() $k\to \infty $
(since
$k\to \infty $
(since
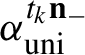 $\alpha _{\mathrm {uni}}^{t_k\mathbf {n}_-}$
is polynomial and
$\alpha _{\mathrm {uni}}^{t_k\mathbf {n}_-}$
is polynomial and
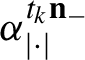 $\alpha _{|\cdot |}^{t_k \mathbf {n}_-}$
contracts P at exponential rate).
$\alpha _{|\cdot |}^{t_k \mathbf {n}_-}$
contracts P at exponential rate).
From this and the compactness of the unit ball in finite dimensions, it follows that there exists a converging subsequence of
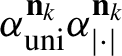 $\alpha _{\mathrm {uni}}^{\mathbf {n}_k}\alpha _{|\cdot |}^{\mathbf {n}_k}$
whose limit is non-zero and non-invertible. As indicated at the beginning of the proof, a subsequence of the integer vectors closest to
$\alpha _{\mathrm {uni}}^{\mathbf {n}_k}\alpha _{|\cdot |}^{\mathbf {n}_k}$
whose limit is non-zero and non-invertible. As indicated at the beginning of the proof, a subsequence of the integer vectors closest to
![]() $\mathbf {n}_k\in \mathbb {R}^d$
will satisfy the conclusions of the lemma.
$\mathbf {n}_k\in \mathbb {R}^d$
will satisfy the conclusions of the lemma.
We need the following upgrade to the above concerning exposed coarse Lyapunov weights.
Lemma 6.3. (Properties of logarithmic sequence for adelic action)
Let
![]() $\alpha $
be a linear representation of
$\alpha $
be a linear representation of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $\mathbb Q^m$
defining an adelic action on
$\mathbb Q^m$
defining an adelic action on
![]() $X_m$
. Let
$X_m$
. Let
![]() $\mathbf {n}_-\in \mathbb {Z}^d\setminus \{0\}$
and
$\mathbf {n}_-\in \mathbb {Z}^d\setminus \{0\}$
and
![]() $V<U^-_{\alpha ^{\mathbf {n}_-}}$
be an S-linear subspace. Let
$V<U^-_{\alpha ^{\mathbf {n}_-}}$
be an S-linear subspace. Let
![]() $[\chi ]$
be an exposed coarse Lyapunov weight
$[\chi ]$
be an exposed coarse Lyapunov weight
![]() $[\chi ]$
of V. Suppose that there exists some
$[\chi ]$
of V. Suppose that there exists some
![]() $\mathbf {m}\in \mathbb {R}^d$
with
$\mathbf {m}\in \mathbb {R}^d$
with
![]() $\chi \cdot \mathbf {m}=0$
so that
$\chi \cdot \mathbf {m}=0$
so that
![]() $(\alpha _{\mathrm {uni}}|_{V\cap \mathbb {R}^m})^{\mathbf {m}}$
is non-trivial. Then there exists a sequence
$(\alpha _{\mathrm {uni}}|_{V\cap \mathbb {R}^m})^{\mathbf {m}}$
is non-trivial. Then there exists a sequence
![]() $\mathbf {n}_k\in \mathbb {Z}^d$
so that
$\mathbf {n}_k\in \mathbb {Z}^d$
so that
![]() $(\alpha |_V)^{\mathbf {n}_k}$
converges (uniformly within compact subsets) to a non-zero map
$(\alpha |_V)^{\mathbf {n}_k}$
converges (uniformly within compact subsets) to a non-zero map
![]() $L\in \operatorname {End}(V)$
that vanishes on all non-Archimedean subspaces, vanishes on all coarse Lyapunov subgroups
$L\in \operatorname {End}(V)$
that vanishes on all non-Archimedean subspaces, vanishes on all coarse Lyapunov subgroups
![]() $V^{[\chi ^{\prime }]}$
with
$V^{[\chi ^{\prime }]}$
with
![]() $[\chi ^{\prime }]\neq [\chi ]$
, and whose restriction to
$[\chi ^{\prime }]\neq [\chi ]$
, and whose restriction to
![]() $V^{[\chi ]}\cap \mathbb {R}^m$
is non-invertible.
$V^{[\chi ]}\cap \mathbb {R}^m$
is non-invertible.
Proof This actually follows by the same argument as Lemma 6.2 after choosing
![]() $\mathbf {m}\in \mathbb {R}^d$
correctly. Indeed, we first note that the kernel of the homomorphism
$\mathbf {m}\in \mathbb {R}^d$
correctly. Indeed, we first note that the kernel of the homomorphism
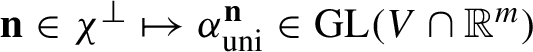 $\mathbf {n}\in \chi ^\perp \mapsto \alpha _{\mathrm {uni}}^{\mathbf {n}}\in \operatorname {GL}(V\cap \mathbb {R}^m)$
is a proper subspace
$\mathbf {n}\in \chi ^\perp \mapsto \alpha _{\mathrm {uni}}^{\mathbf {n}}\in \operatorname {GL}(V\cap \mathbb {R}^m)$
is a proper subspace
![]() $K<\chi ^\perp $
, and hence our first constraint on
$K<\chi ^\perp $
, and hence our first constraint on
![]() $\mathbf {m}$
is simply
$\mathbf {m}$
is simply
![]() $\mathbf {m}\in \chi ^\perp \setminus K$
.
$\mathbf {m}\in \chi ^\perp \setminus K$
.
By definition,
![]() $[\chi ]$
is an exposed coarse Lyapunov weight for V if there exists some
$[\chi ]$
is an exposed coarse Lyapunov weight for V if there exists some
![]() $\mathbf {m}\in \chi ^\perp $
with
$\mathbf {m}\in \chi ^\perp $
with
![]() $\chi ^{\prime }\cdot \mathbf {m}<0$
for all Lyapunov weights
$\chi ^{\prime }\cdot \mathbf {m}<0$
for all Lyapunov weights
![]() $\chi ^{\prime }$
of V inequivalent to
$\chi ^{\prime }$
of V inequivalent to
![]() $\chi $
. The latter condition is clearly satisfied by all elements of an open subset of
$\chi $
. The latter condition is clearly satisfied by all elements of an open subset of
![]() $\chi ^\perp $
. Hence we can find
$\chi ^\perp $
. Hence we can find
![]() $\mathbf {m}\in \chi ^\perp \setminus K$
with
$\mathbf {m}\in \chi ^\perp \setminus K$
with
![]() $\mathbf {m}\cdot \chi ^{\prime }<0$
for all Lyapunov weights
$\mathbf {m}\cdot \chi ^{\prime }<0$
for all Lyapunov weights
![]() $\chi ^{\prime }$
of V inequivalent to
$\chi ^{\prime }$
of V inequivalent to
![]() $\chi $
.
$\chi $
.
Using this
![]() $\mathbf {m}$
together with
$\mathbf {m}$
together with
![]() $\mathbf {n}_-$
, as in the assumptions of the lemma, we now go again through the construction in the proof of Lemma 6.2. Let
$\mathbf {n}_-$
, as in the assumptions of the lemma, we now go again through the construction in the proof of Lemma 6.2. Let
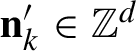 $\mathbf {n}_k^{\prime }\in \mathbb {Z}^d$
be a nearest integer approximation of
$\mathbf {n}_k^{\prime }\in \mathbb {Z}^d$
be a nearest integer approximation of
![]() $k\mathbf {m}$
and let
$k\mathbf {m}$
and let
![]() $\mathbf {n}_k$
be the nearest integer approximation of
$\mathbf {n}_k$
be the nearest integer approximation of
![]() $k\mathbf {m}+t_k\mathbf {n}_-$
. For all non-Archimedean subspaces
$k\mathbf {m}+t_k\mathbf {n}_-$
. For all non-Archimedean subspaces
![]() $V_\sigma $
, we note that
$V_\sigma $
, we note that
![]() $\alpha _{\mathrm {uni}}(\mathbb {Z}^d)|_{V_\sigma }$
has compact closure. Hence the restriction
$\alpha _{\mathrm {uni}}(\mathbb {Z}^d)|_{V_\sigma }$
has compact closure. Hence the restriction
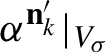 $\alpha ^{\mathbf {n}_k^{\prime }}|_{V_\sigma }$
belongs to a compact subset of
$\alpha ^{\mathbf {n}_k^{\prime }}|_{V_\sigma }$
belongs to a compact subset of
![]() $\operatorname {Hom}(V_\sigma )$
, which implies together with
$\operatorname {Hom}(V_\sigma )$
, which implies together with
![]() $\mathbf {n}_-$
contracting V and
$\mathbf {n}_-$
contracting V and
![]() $t_k\to \infty $
that the restriction
$t_k\to \infty $
that the restriction
![]() $\alpha ^{\mathbf {n}_k}|_{V_\sigma }$
converges to zero. Similarly, our choice of
$\alpha ^{\mathbf {n}_k}|_{V_\sigma }$
converges to zero. Similarly, our choice of
![]() $\mathbf {m}$
implies that for a coarse Lyapunov weight
$\mathbf {m}$
implies that for a coarse Lyapunov weight
![]() $[\chi ^{\prime }]\neq [\chi ]$
, both
$[\chi ^{\prime }]\neq [\chi ]$
, both
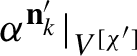 $\alpha ^{\mathbf {n}_k^{\prime }}|_{V^{[\chi ^{\prime }]}}$
and
$\alpha ^{\mathbf {n}_k^{\prime }}|_{V^{[\chi ^{\prime }]}}$
and
![]() $\alpha ^{\mathbf {n}_k}|_{V^{[\chi ^{\prime }]}}$
converge to the trivial map. Finally our proof of Lemma 6.2 ensures the claimed properties of the limit map
$\alpha ^{\mathbf {n}_k}|_{V^{[\chi ^{\prime }]}}$
converge to the trivial map. Finally our proof of Lemma 6.2 ensures the claimed properties of the limit map
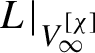 $L|_{V_\infty ^{[\chi ]}}$
.
$L|_{V_\infty ^{[\chi ]}}$
.
We will now combine the above with the setup of §4.4 to prove a restriction concerning the supporting subgroups (cf. §6.3).
Proposition 6.4. (No shearing on supporting subgroup)
Let P be the supporting subgroup of
![]() $V^-_{\mathbf {n}_0}=V_{\mathrm {base},\mathbb A}\cap U^-_{\alpha ^{\mathbf {n}_0}}$
(with
$V^-_{\mathbf {n}_0}=V_{\mathrm {base},\mathbb A}\cap U^-_{\alpha ^{\mathbf {n}_0}}$
(with
![]() $V_{\mathrm {base},\mathbb A}$
as defined in Theorem 6.1). Let
$V_{\mathrm {base},\mathbb A}$
as defined in Theorem 6.1). Let
![]() $\chi $
be an exposed Lyapunov weight of P. Then
$\chi $
be an exposed Lyapunov weight of P. Then
![]() $(\alpha _{\mathrm {uni}}|_{P^{[\chi ]}\cap \mathbb {R}^m})^{\mathbf {n}}$
is trivial for all
$(\alpha _{\mathrm {uni}}|_{P^{[\chi ]}\cap \mathbb {R}^m})^{\mathbf {n}}$
is trivial for all
![]() $\mathbf {n}\in \mathbb {R}^d$
with
$\mathbf {n}\in \mathbb {R}^d$
with
![]() $\chi \cdot \mathbf {n}=0$
.
$\chi \cdot \mathbf {n}=0$
.
Here we identified
![]() $\mathbb {R}^m$
with the corresponding subgroup of
$\mathbb {R}^m$
with the corresponding subgroup of
![]() $\mathbb A^m$
, and hence
$\mathbb A^m$
, and hence
![]() $P^{[\chi ]}\cap \mathbb {R}^m$
is the maximal real subspace of the supporting subgroup P.
$P^{[\chi ]}\cap \mathbb {R}^m$
is the maximal real subspace of the supporting subgroup P.
Proof We suppose in contradiction that
![]() $(\alpha _{\mathrm {uni}}|_{P^{[\chi ]}\cap \mathbb {R}^m})^{\mathbf {m}}$
is non-trivial for some
$(\alpha _{\mathrm {uni}}|_{P^{[\chi ]}\cap \mathbb {R}^m})^{\mathbf {m}}$
is non-trivial for some
![]() $\mathbf {m}\in \mathbb {R}^d$
with
$\mathbf {m}\in \mathbb {R}^d$
with
![]() $\chi \cdot \mathbf {m}=0$
. Applying Lemma 6.3, we find a logarithmic sequence
$\chi \cdot \mathbf {m}=0$
. Applying Lemma 6.3, we find a logarithmic sequence
![]() $\mathbf {n}_k$
and the limit
$\mathbf {n}_k$
and the limit
![]() $L\in \operatorname {End}(P)$
of
$L\in \operatorname {End}(P)$
of
![]() $(\alpha |_P)^{\mathbf {n}_k}$
.
$(\alpha |_P)^{\mathbf {n}_k}$
.
Recall that
![]() $Y_{\mathrm {base}}<X$
is the adelic subgroup so that
$Y_{\mathrm {base}}<X$
is the adelic subgroup so that
![]() $X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
, and that
$X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
, and that
![]() $V_{\mathrm {base},\mathbb A}$
is the rational subspace of
$V_{\mathrm {base},\mathbb A}$
is the rational subspace of
![]() $\mathbb A^m$
so that
$\mathbb A^m$
so that
![]() $Y_{\mathrm {base}}$
is the image of
$Y_{\mathrm {base}}$
is the image of
![]() $V_{\mathrm {base},\mathbb A}$
modulo
$V_{\mathrm {base},\mathbb A}$
modulo
![]() $\mathbb Q^m$
. Recall also that
$\mathbb Q^m$
. Recall also that
![]() $Y_{\mathrm {pos}}<Y_{\mathrm {base}}$
is the adelic subgroup so that
$Y_{\mathrm {pos}}<Y_{\mathrm {base}}$
is the adelic subgroup so that
![]() $X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
, and let
$X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
, and let
![]() $V_{{\mathrm {pos}},\mathbb A}<V_{\mathrm {base},\mathbb A}$
be the rational subspace so that
$V_{{\mathrm {pos}},\mathbb A}<V_{\mathrm {base},\mathbb A}$
be the rational subspace so that
![]() $Y_{\mathrm {pos}}$
is the image of
$Y_{\mathrm {pos}}$
is the image of
![]() $V_{{\mathrm {pos}},\mathbb A}$
modulo
$V_{{\mathrm {pos}},\mathbb A}$
modulo
![]() $\mathbb Q^m$
.
$\mathbb Q^m$
.
By construction we have that the action on
![]() $Y_{\mathrm {base}}/Y_{\mathrm {pos}}$
is
$Y_{\mathrm {base}}/Y_{\mathrm {pos}}$
is
![]() $\mathbb A$
-irreducible, or equivalently that the linear representation of
$\mathbb A$
-irreducible, or equivalently that the linear representation of
![]() $\mathbb {Z}^d$
on
$\mathbb {Z}^d$
on
![]() $V_{\mathrm {base},\mathbb A}/V_{{\mathrm {pos}},\mathbb A}$
(defined over
$V_{\mathrm {base},\mathbb A}/V_{{\mathrm {pos}},\mathbb A}$
(defined over
![]() $\mathbb Q$
) is irreducible over
$\mathbb Q$
) is irreducible over
![]() $\mathbb Q$
. In particular, this representation is semisimple. Unfolding the definitions and restricting to
$\mathbb Q$
. In particular, this representation is semisimple. Unfolding the definitions and restricting to
![]() $P^{[\chi ]}\cap \mathbb {R}^m$
, it follows that for any
$P^{[\chi ]}\cap \mathbb {R}^m$
, it follows that for any
![]() $v \in P^{[\chi ]}\cap \mathbb {R}^m$
,
$v \in P^{[\chi ]}\cap \mathbb {R}^m$
,
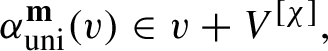 $$ \begin{align*} \alpha_{\mathrm{uni}}^{\mathbf{m}} (v) \in v + V^{[\chi]}, \end{align*} $$
$$ \begin{align*} \alpha_{\mathrm{uni}}^{\mathbf{m}} (v) \in v + V^{[\chi]}, \end{align*} $$
where
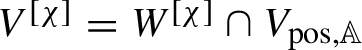 $V^{[\chi ]}=W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}$
. Combining this information with the construction of the logarithmic sequence and its limit L, it follows that
$V^{[\chi ]}=W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}$
. Combining this information with the construction of the logarithmic sequence and its limit L, it follows that
Next recall from (4.1) that X is a zero entropy extension over
![]() $X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
, that is,
$X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
, that is,
![]() $h_{\widetilde {\mu }}(\alpha ^{\mathbf {n}}\mid X_{\mathrm {pos}}\times \Omega )\leq h_\mu (\alpha ^n\mid X_{\mathrm {pos}})=0$
for all
$h_{\widetilde {\mu }}(\alpha ^{\mathbf {n}}\mid X_{\mathrm {pos}}\times \Omega )\leq h_\mu (\alpha ^n\mid X_{\mathrm {pos}})=0$
for all
![]() $\mathbf {n}\in \mathbb {Z}^d$
. This implies by the relationship between the leafwise measures and entropy that the leafwise measures
$\mathbf {n}\in \mathbb {Z}^d$
. This implies by the relationship between the leafwise measures and entropy that the leafwise measures
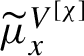 $\widetilde {\mu }_x^{V^{[\chi ]}}$
must be trivial almost everywhere—indeed otherwise there would be a positive entropy contribution for the relative entropy over the factor
$\widetilde {\mu }_x^{V^{[\chi ]}}$
must be trivial almost everywhere—indeed otherwise there would be a positive entropy contribution for the relative entropy over the factor
![]() $X_{\mathrm {pos}}\times \Omega $
. By the compatibility property (3.1), it follows that there exists a set
$X_{\mathrm {pos}}\times \Omega $
. By the compatibility property (3.1), it follows that there exists a set
![]() $X^{\prime }\subseteq \widetilde {X}=X\times \Omega $
of full measure so that
$X^{\prime }\subseteq \widetilde {X}=X\times \Omega $
of full measure so that
![]() $x,\ x+w\in X^{\prime }$
for some
$x,\ x+w\in X^{\prime }$
for some
![]() $w\in V^{[\chi ]}$
implies
$w\in V^{[\chi ]}$
implies
![]() $w=0$
. Using regularity of the Borel probability measure, we choose some compact
$w=0$
. Using regularity of the Borel probability measure, we choose some compact
![]() $K\subseteq X^{\prime }$
of measure
$K\subseteq X^{\prime }$
of measure
![]() ${\widetilde {\mu }}(K)>0.99$
.
${\widetilde {\mu }}(K)>0.99$
.
Our aim in the proof is to use the logarithmic sequence
![]() $\mathbf {n}_k$
and the limit L to derive a contradiction to the properties of K. For this, let
$\mathbf {n}_k$
and the limit L to derive a contradiction to the properties of K. For this, let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $\sigma $
-algebra that is subordinate to P. We define
$\sigma $
-algebra that is subordinate to P. We define
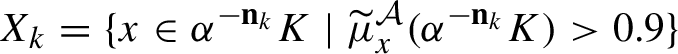 $$ \begin{align*} X_k=\{x\in \alpha^{-\mathbf{n}_k}K\mid {\widetilde{\mu}}_x^{\mathcal{A}}(\alpha^{-\mathbf{n}_k}K)>0.9\} \end{align*} $$
$$ \begin{align*} X_k=\{x\in \alpha^{-\mathbf{n}_k}K\mid {\widetilde{\mu}}_x^{\mathcal{A}}(\alpha^{-\mathbf{n}_k}K)>0.9\} \end{align*} $$
and note that
![]() ${\widetilde {\mu }}(X_k)>0.89$
. By the Lemma of Fatou (applied for the probability measure
${\widetilde {\mu }}(X_k)>0.89$
. By the Lemma of Fatou (applied for the probability measure
![]() ${\widetilde {\mu }}$
), it follows that
${\widetilde {\mu }}$
), it follows that
Hence there exists some
![]() $x_0$
and some subsequence
$x_0$
and some subsequence
![]() $\mathbf {n}_k^{\prime }$
of
$\mathbf {n}_k^{\prime }$
of
![]() $\mathbf {n}_k$
so that
$\mathbf {n}_k$
so that
![]() $\alpha ^{\mathbf {n}_k^{\prime }}x_0\in K$
and
$\alpha ^{\mathbf {n}_k^{\prime }}x_0\in K$
and
 ${\widetilde {\mu }}_{x_0}^{\mathcal {A}}(\alpha ^{-\mathbf {n}_k^{\prime }}K)>0.9$
. Applying Lemma of Fatou again—but this time for the probability measure
${\widetilde {\mu }}_{x_0}^{\mathcal {A}}(\alpha ^{-\mathbf {n}_k^{\prime }}K)>0.9$
. Applying Lemma of Fatou again—but this time for the probability measure
 ${\widetilde {\mu }}_{x_0}^{\mathcal {A}}$
—we obtain
${\widetilde {\mu }}_{x_0}^{\mathcal {A}}$
—we obtain
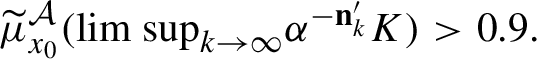 $$ \begin{align} {\widetilde{\mu}}_{x_0}^{\mathcal{A}}(\textstyle{\limsup_{k\to\infty}} \alpha^{-\mathbf{n}_k^{\prime}}K)>0.9. \end{align} $$
$$ \begin{align} {\widetilde{\mu}}_{x_0}^{\mathcal{A}}(\textstyle{\limsup_{k\to\infty}} \alpha^{-\mathbf{n}_k^{\prime}}K)>0.9. \end{align} $$
Also recall that P is the supporting subgroup of
![]() $V_{\mathbf {n}_0}^-$
and that
$V_{\mathbf {n}_0}^-$
and that
![]() $\ker L<P$
is a proper S-linear
$\ker L<P$
is a proper S-linear
![]() $\alpha $
-invariant subgroup. Using [Reference Einsiedler and Lindenstrauss11, Lemma 5.2] (cf. p. 112 above) this implies that
$\alpha $
-invariant subgroup. Using [Reference Einsiedler and Lindenstrauss11, Lemma 5.2] (cf. p. 112 above) this implies that
![]() ${\widetilde {\mu }}_x^P(\ker L)=0$
, which in turns implies
${\widetilde {\mu }}_x^P(\ker L)=0$
, which in turns implies
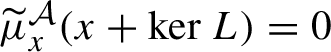 ${\widetilde {\mu }}_x^{\mathcal {A}}(x+\ker L)=0$
a.s. We may assume that our
${\widetilde {\mu }}_x^{\mathcal {A}}(x+\ker L)=0$
a.s. We may assume that our
![]() $x_0$
constructed above has this property. Hence there exists some
$x_0$
constructed above has this property. Hence there exists some
![]() $x_1\in [x_0]_{\mathcal {A}}\setminus (x_0+\ker L)$
and another subsequence
$x_1\in [x_0]_{\mathcal {A}}\setminus (x_0+\ker L)$
and another subsequence
![]() $\mathbf {n}_k^{\prime \prime }$
of
$\mathbf {n}_k^{\prime \prime }$
of
![]() $\mathbf {n}_k^{\prime }$
so that
$\mathbf {n}_k^{\prime }$
so that
![]() $\alpha ^{\mathbf {n}_k^{\prime \prime }}x_1\in K$
.
$\alpha ^{\mathbf {n}_k^{\prime \prime }}x_1\in K$
.
To summarize, we have found a subsequence
![]() $\mathbf {n}_k^{\prime \prime }$
of the logarithmic sequence
$\mathbf {n}_k^{\prime \prime }$
of the logarithmic sequence
![]() $\mathbf {n}_k$
, some
$\mathbf {n}_k$
, some
![]() $x_0\in X$
, and some
$x_0\in X$
, and some
![]() $x_1=x_0+v\in [x]_{\mathcal {A}}$
with
$x_1=x_0+v\in [x]_{\mathcal {A}}$
with
![]() $v\in P\setminus \ker L$
so that
$v\in P\setminus \ker L$
so that
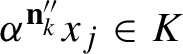 $\alpha ^{\mathbf {n}_k^{\prime \prime }}x_j\in K$
for
$\alpha ^{\mathbf {n}_k^{\prime \prime }}x_j\in K$
for
![]() $j=0,1$
. Using compactness of K, we can find yet another subsequence of
$j=0,1$
. Using compactness of K, we can find yet another subsequence of
![]() $\mathbf {n}_k^{\prime \prime }$
so that
$\mathbf {n}_k^{\prime \prime }$
so that
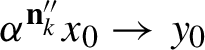 $\alpha ^{\mathbf {n}_k^{\prime \prime }}x_0 \to y_0$
and
$\alpha ^{\mathbf {n}_k^{\prime \prime }}x_0 \to y_0$
and
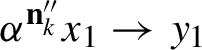 $\alpha ^{\mathbf {n}_k^{\prime \prime }}x_1 \to y_1$
with
$\alpha ^{\mathbf {n}_k^{\prime \prime }}x_1 \to y_1$
with
![]() $y_0,y_1\in K$
. Moreover, since
$y_0,y_1\in K$
. Moreover, since
![]() $\alpha ^{\mathbf {n}_k}v\rightarrow Lv$
as
$\alpha ^{\mathbf {n}_k}v\rightarrow Lv$
as
![]() $k\to \infty $
, we also have
$k\to \infty $
, we also have
![]() $y_1=y_0+Lv$
with
$y_1=y_0+Lv$
with
![]() $Lv\in V^{[\chi ]}\setminus \{0\}$
by the properties of L. However, this contradicts the properties of
$Lv\in V^{[\chi ]}\setminus \{0\}$
by the properties of L. However, this contradicts the properties of
![]() $K\subset X^{\prime }$
and so concludes the proof.
$K\subset X^{\prime }$
and so concludes the proof.
Proof Proof of Theorem 6.1
In view of Proposition 6.4, the product structure of the leafwise measure follows from [Reference Einsiedler and Katok4, Theorem 8.2] (or more precisely its proof).
For this, we first recall that if
![]() $P<V_{\mathbf {n}_0}^-$
is the corresponding supporting subgroup, then by Proposition 3.2, the leafwise measure
$P<V_{\mathbf {n}_0}^-$
is the corresponding supporting subgroup, then by Proposition 3.2, the leafwise measure
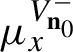 $\mu _x^{V_{\smash {\mathbf {n}_0}}^-}$
coincides with
$\mu _x^{V_{\smash {\mathbf {n}_0}}^-}$
coincides with
![]() $\mu _x^{P}$
for
$\mu _x^{P}$
for
![]() $\mu $
-a.e. x. Next we recall that by Proposition 6.4, we have for any non-trivial coarse Lyapunov weight
$\mu $
-a.e. x. Next we recall that by Proposition 6.4, we have for any non-trivial coarse Lyapunov weight
![]() $[\chi ]$
that
$[\chi ]$
that
![]() $\alpha _{\mathrm {uni}}^{\mathbf {m}}|_{P^{[\chi ]}\cap \mathbb {R}^m}$
is trivial for any
$\alpha _{\mathrm {uni}}^{\mathbf {m}}|_{P^{[\chi ]}\cap \mathbb {R}^m}$
is trivial for any
![]() $\mathbf {m} \in \ker \chi $
. We also note that
$\mathbf {m} \in \ker \chi $
. We also note that
![]() $\alpha _{\mathrm {uni}}(\mathbb {Z}^{d})$
restricted to the p-adic subspaces
$\alpha _{\mathrm {uni}}(\mathbb {Z}^{d})$
restricted to the p-adic subspaces
 $P^{[\chi ]}\cap \mathbb Q_p^m$
of the coarse Lyapunov subspace
$P^{[\chi ]}\cap \mathbb Q_p^m$
of the coarse Lyapunov subspace
![]() $P^{[\chi ]}$
has compact closure in
$P^{[\chi ]}$
has compact closure in
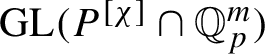 $\operatorname {GL}(P^{[\chi ]}\cap \mathbb Q_p^m)$
. Hence we may assume that the metric on
$\operatorname {GL}(P^{[\chi ]}\cap \mathbb Q_p^m)$
. Hence we may assume that the metric on
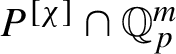 $P^{[\chi ]}\cap \mathbb Q_p^m$
is invariant under
$P^{[\chi ]}\cap \mathbb Q_p^m$
is invariant under
![]() $\alpha _{\mathrm {uni}}(\mathbb {Z}^d)$
. With these two observations, the inductive argument for [Reference Einsiedler and Katok4, Theorem 8.2] applies and proves the product structure for
$\alpha _{\mathrm {uni}}(\mathbb {Z}^d)$
. With these two observations, the inductive argument for [Reference Einsiedler and Katok4, Theorem 8.2] applies and proves the product structure for
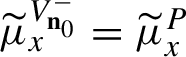 ${\widetilde {\mu }}_x^{V_{\smash {\mathbf {n}_0}}^-}={\widetilde {\mu }}_x^P$
.
${\widetilde {\mu }}_x^{V_{\smash {\mathbf {n}_0}}^-}={\widetilde {\mu }}_x^P$
.
The product structure implies now quite directly using (3.9) that the entropy contribution for
![]() $V_{\mathbf {n}_0}^-$
equals the sum of the entropy contributions of its coarse Lyapunov subgroups
$V_{\mathbf {n}_0}^-$
equals the sum of the entropy contributions of its coarse Lyapunov subgroups
![]() $V^{[\chi ]}$
, hence the second equality in (6.3).
$V^{[\chi ]}$
, hence the second equality in (6.3).
The first equality in (6.3), that is, the fact that
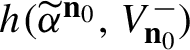 $h(\widetilde \alpha ^{\mathbf {n}_0},V^-_{\mathbf {n}_0})$
equals the conditional entropy of
$h(\widetilde \alpha ^{\mathbf {n}_0},V^-_{\mathbf {n}_0})$
equals the conditional entropy of
![]() $\widetilde \alpha ^{\mathbf {n}_0}$
over the factor
$\widetilde \alpha ^{\mathbf {n}_0}$
over the factor
![]() $X_{\mathrm {base}}\times \Omega $
follows e.g. from the proof of [Reference Einsiedler and Lindenstrauss10, Theorem 7.6]. Indeed by conditioning the calculation there on the factor
$X_{\mathrm {base}}\times \Omega $
follows e.g. from the proof of [Reference Einsiedler and Lindenstrauss10, Theorem 7.6]. Indeed by conditioning the calculation there on the factor
![]() $X_{\mathrm {base}}\times \Omega $
, the leafwise measure on the full stable horospherical is automatically supported on
$X_{\mathrm {base}}\times \Omega $
, the leafwise measure on the full stable horospherical is automatically supported on
![]() $V^-_{\mathbf {n}_0}$
, since a displacement by some element of the stable horospherical not belonging to
$V^-_{\mathbf {n}_0}$
, since a displacement by some element of the stable horospherical not belonging to
![]() $V_{\mathrm {base},\mathbb A}$
would change the point within
$V_{\mathrm {base},\mathbb A}$
would change the point within
![]() $X_{\mathrm {base}}$
.
$X_{\mathrm {base}}$
.
7 Proof of Theorem 4.1
7.1 Rigidity of the entropy function
In the following, we will again consider entropy contributions for various coarse Lyapunov subgroups with varying definitions of the second factor
![]() $\Omega $
in the framework of §3. Consistent with our notation so far, we will use e.g.
$\Omega $
in the framework of §3. Consistent with our notation so far, we will use e.g.
![]() $h_{\widetilde {\mu }}(\widetilde \alpha ^{\mathbf {n}},W^{[\chi ]}\mid X_{\mathrm {base}}\times \Omega )$
for the entropy contribution of a coarse Lyapunov subgroup
$h_{\widetilde {\mu }}(\widetilde \alpha ^{\mathbf {n}},W^{[\chi ]}\mid X_{\mathrm {base}}\times \Omega )$
for the entropy contribution of a coarse Lyapunov subgroup
![]() $W^{[\chi ]}$
on
$W^{[\chi ]}$
on
![]() $X\times \Omega $
and similarly for other factors and foliations.
$X\times \Omega $
and similarly for other factors and foliations.
We now establish the following identity regarding the relation between the entropies of individual elements of the action. This identity is central to our approach.
Theorem 7.1. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $\mathbb {Z}^{d}$
-action on
$\mathbb {Z}^{d}$
-action on
![]() $X=X_m$
without cyclic factors as in Theorem 4.1. Let
$X=X_m$
without cyclic factors as in Theorem 4.1. Let
![]() $\mu $
be an
$\mu $
be an
![]() $\alpha $
-invariant probability measure, let
$\alpha $
-invariant probability measure, let
![]() $X_{\mathrm {pos}},\ X_{\mathrm {base}},\ Y_{\mathrm {irred}}$
be as (4.1), and denote the Haar measure on
$X_{\mathrm {pos}},\ X_{\mathrm {base}},\ Y_{\mathrm {irred}}$
be as (4.1), and denote the Haar measure on
![]() $Y_{\mathrm {irred}}$
by
$Y_{\mathrm {irred}}$
by
![]() $\unicode{x3bb} $
. Moreover, let
$\unicode{x3bb} $
. Moreover, let
![]() $\Omega $
be a compact metric space equipped with an action of
$\Omega $
be a compact metric space equipped with an action of
![]() $\mathbb {Z}^{d}$
, let
$\mathbb {Z}^{d}$
, let
![]() $\widetilde {\alpha }$
be the corresponding
$\widetilde {\alpha }$
be the corresponding
![]() $\mathbb {Z}^{d}$
-action on
$\mathbb {Z}^{d}$
-action on
![]() $X\times \Omega $
, and let
$X\times \Omega $
, and let
![]() $\widetilde {\mu }$
be an invariant measure on
$\widetilde {\mu }$
be an invariant measure on
![]() $X\times \Omega $
projecting to
$X\times \Omega $
projecting to
![]() $\mu $
. Then there exists a constant
$\mu $
. Then there exists a constant
![]() $\kappa _{\widetilde {\mu },\Omega }>0$
with
$\kappa _{\widetilde {\mu },\Omega }>0$
with
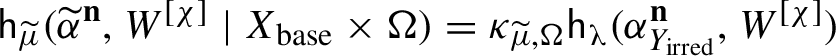 $$ \begin{align} \text{h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =\kappa_{\widetilde{\mu},\Omega}\text{h}_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}}, W^{[\chi]}) \end{align} $$
$$ \begin{align} \text{h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =\kappa_{\widetilde{\mu},\Omega}\text{h}_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}}, W^{[\chi]}) \end{align} $$
for every
![]() $\mathbf {n} \in \mathbb {Z}^{d}$
.
$\mathbf {n} \in \mathbb {Z}^{d}$
.
We recall that we use
![]() $\unicode{x3bb} $
to denote the Haar measure on the appropriate adelic quotient (that should hopefully be clear from the context; e.g. in (7.1),
$\unicode{x3bb} $
to denote the Haar measure on the appropriate adelic quotient (that should hopefully be clear from the context; e.g. in (7.1),
![]() $\unicode{x3bb} $
is the Haar measure on
$\unicode{x3bb} $
is the Haar measure on
![]() $Y_{\mathrm {irred}}$
). While the proof of Theorem 7.1 is much more complicated than in the case considered by Rudolph, this theorem plays a similar role in our proof as [Reference Rudolph34, Theorem 3.7] did in Rudolph’s proof in [Reference Rudolph34].
$Y_{\mathrm {irred}}$
). While the proof of Theorem 7.1 is much more complicated than in the case considered by Rudolph, this theorem plays a similar role in our proof as [Reference Rudolph34, Theorem 3.7] did in Rudolph’s proof in [Reference Rudolph34].
As a first step towards the theorem, we consider just one coarse Lyapunov subgroup. Note that unlike Theorem 7.1, which uses in an essential way the irreducibility of
![]() $Y _{{\mathrm {irred}}}$
, the next lemma only uses the fact that
$Y _{{\mathrm {irred}}}$
, the next lemma only uses the fact that
![]() $W ^ {[\chi ]}$
is a coarse Lyapunov group.
$W ^ {[\chi ]}$
is a coarse Lyapunov group.
Lemma 7.2. Using the same notation as in Theorem 7.1, let
![]() $[\chi ]$
be a coarse Lyapunov weight for
$[\chi ]$
be a coarse Lyapunov weight for
![]() $Y_{\mathrm {irred}}$
. Then there exists some
$Y_{\mathrm {irred}}$
. Then there exists some
![]() $\kappa _{\widetilde {\mu },\Omega ,[\chi ]} \geq 0$
with
$\kappa _{\widetilde {\mu },\Omega ,[\chi ]} \geq 0$
with
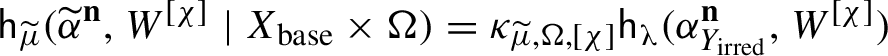 $$ \begin{align*} \text{h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =\kappa_{\widetilde{\mu},\Omega,[\chi]}\text{h}_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}}, W^{[\chi]}) \end{align*} $$
$$ \begin{align*} \text{h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =\kappa_{\widetilde{\mu},\Omega,[\chi]}\text{h}_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}}, W^{[\chi]}) \end{align*} $$
for every
![]() $\mathbf {n} \in \mathbb {Z}^{d}$
.
$\mathbf {n} \in \mathbb {Z}^{d}$
.
Proof We first note that for
![]() $\mathbf n\in \mathbb {Z}^{d}$
with
$\mathbf n\in \mathbb {Z}^{d}$
with
![]() $\chi \cdot \mathbf {n}<0$
and
$\chi \cdot \mathbf {n}<0$
and
![]() $k\in \mathbb {N}$
, Proposition 3.4 implies
$k\in \mathbb {N}$
, Proposition 3.4 implies
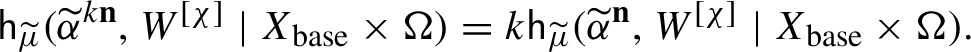 $$ \begin{align} {h}_{\widetilde\mu}(\widetilde\alpha^{k\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =k {h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega). \end{align} $$
$$ \begin{align} {h}_{\widetilde\mu}(\widetilde\alpha^{k\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =k {h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega). \end{align} $$
Moreover, since
![]() $W^{[\chi ]}$
is a coarse Lyapunov subgroup, for all
$W^{[\chi ]}$
is a coarse Lyapunov subgroup, for all
![]() $\mathbf {n},\mathbf {m}\in \mathbb {Z}^{d}$
with
$\mathbf {n},\mathbf {m}\in \mathbb {Z}^{d}$
with
![]() $\chi \cdot \mathbf {n} < \chi \cdot \mathbf {m}<0$
, we have that
$\chi \cdot \mathbf {n} < \chi \cdot \mathbf {m}<0$
, we have that
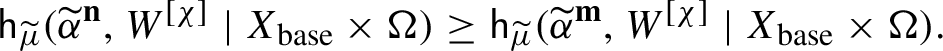 $$ \begin{align*} {h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) \geq {h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{m}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega). \end{align*} $$
$$ \begin{align*} {h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) \geq {h}_{\widetilde\mu}(\widetilde\alpha^{\mathbf{m}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega). \end{align*} $$
In conjunction with (7.2), this implies elementarily that there is a constant
![]() $c\geq 0$
depending only on
$c\geq 0$
depending only on
![]() $\tilde \mu $
,
$\tilde \mu $
,
![]() $W^{[\chi ]}$
, and
$W^{[\chi ]}$
, and
![]() $\alpha $
so that
$\alpha $
so that
![]() ${\sf h}_{\widetilde \mu }(\widetilde \alpha ^{\mathbf {n}}, W^{[\chi ]})=c |\chi \cdot \mathbf {n}|$
for all
${\sf h}_{\widetilde \mu }(\widetilde \alpha ^{\mathbf {n}}, W^{[\chi ]})=c |\chi \cdot \mathbf {n}|$
for all
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
.
$\mathbf {n}\in \mathbb {Z}^{d}$
.
Next notice that for similar reasons
![]() $\text{h}_{\unicode{x3bb} }(\alpha ^{\mathbf {n}}, W^{[\chi ]})$
is given by a similar formula for a constant
$\text{h}_{\unicode{x3bb} }(\alpha ^{\mathbf {n}}, W^{[\chi ]})$
is given by a similar formula for a constant
![]() $c_{\unicode{x3bb} }\geq 0$
. As
$c_{\unicode{x3bb} }\geq 0$
. As
![]() $[\chi ]$
is assumed to be a coarse Lyapunov weight for
$[\chi ]$
is assumed to be a coarse Lyapunov weight for
![]() $Y_{\mathrm {irred}}$
, we have
$Y_{\mathrm {irred}}$
, we have
![]() $c_{\unicode{x3bb} }>0$
and obtain the lemma with
$c_{\unicode{x3bb} }>0$
and obtain the lemma with
![]() $\kappa _{\widetilde {\mu },\Omega ,[\chi ]}=c/c_{\unicode{x3bb} }$
.
$\kappa _{\widetilde {\mu },\Omega ,[\chi ]}=c/c_{\unicode{x3bb} }$
.
Lemma 7.3. We again use the notation in Theorem 7.1. For any coarse Lyapunov weight
![]() $[\chi ]$
of X, we have
$[\chi ]$
of X, we have
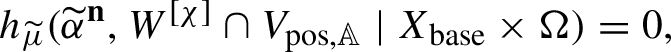 $$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega)=0, \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega)=0, \end{align*} $$
where
![]() $V_{{\mathrm {pos}},\mathbb A}<\mathbb A^m$
is the rationally defined subspace so that
$V_{{\mathrm {pos}},\mathbb A}<\mathbb A^m$
is the rationally defined subspace so that
![]() $Y_{\mathrm {pos}}$
is the image of
$Y_{\mathrm {pos}}$
is the image of
![]() $V_{{\mathrm {pos}},\mathbb A}$
modulo
$V_{{\mathrm {pos}},\mathbb A}$
modulo
![]() $\mathbb Q^m$
. Moreover, if
$\mathbb Q^m$
. Moreover, if
![]() $[\chi ]$
is not a coarse Lyapunov weight for
$[\chi ]$
is not a coarse Lyapunov weight for
![]() $Y_{\mathrm {irred}}$
, then
$Y_{\mathrm {irred}}$
, then
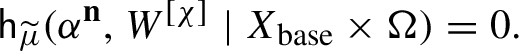 $$ \begin{align*} {\sf h}_{\widetilde\mu}(\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)=0. \end{align*} $$
$$ \begin{align*} {\sf h}_{\widetilde\mu}(\alpha^{\mathbf{n}}, W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)=0. \end{align*} $$
Proof We claim for the entropy contributions for
 $W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}$
that
$W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}$
that
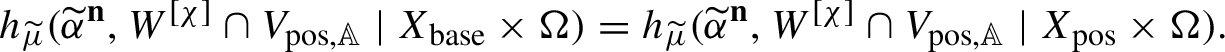 $$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) = h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{pos}}\times\Omega). \end{align} $$
$$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) = h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{pos}}\times\Omega). \end{align} $$
To see this, recall that
![]() $Y_{\mathrm {pos}}<Y_{\mathrm {base}}$
, and correspondingly
$Y_{\mathrm {pos}}<Y_{\mathrm {base}}$
, and correspondingly
![]() $X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
is a factor of
$X_{\mathrm {base}}=X/Y_{\mathrm {base}}$
is a factor of
![]() $X_{\mathrm {pos}}=X/Y_{{\mathrm {pos}}}$
. By (3.8
′), the conditional entropy contribution
$X_{\mathrm {pos}}=X/Y_{{\mathrm {pos}}}$
. By (3.8
′), the conditional entropy contribution
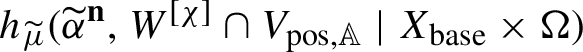 $$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) \end{align*} $$
is given by
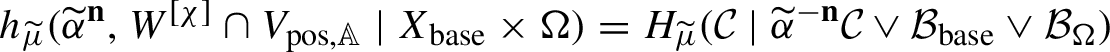 $$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) = H _ {\widetilde \mu} (\mathcal{C} \mid \widetilde\alpha^{-\mathbf{n}} \mathcal{C} \vee \mathcal{B} _ {{\mathrm{base}}} \vee \mathcal B _ {\Omega}) \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) = H _ {\widetilde \mu} (\mathcal{C} \mid \widetilde\alpha^{-\mathbf{n}} \mathcal{C} \vee \mathcal{B} _ {{\mathrm{base}}} \vee \mathcal B _ {\Omega}) \end{align*} $$
for
![]() $\mathcal C$
a
$\mathcal C$
a
 ${W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}}$
-subordinate
${W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}}$
-subordinate
![]() $\sigma $
-algebra for
$\sigma $
-algebra for
![]() $X\times \Omega $
(and
$X\times \Omega $
(and
![]() $\mathcal {B} _ {{\mathrm {base}}}$
and
$\mathcal {B} _ {{\mathrm {base}}}$
and
![]() $\mathcal B _ {\Omega }$
the
$\mathcal B _ {\Omega }$
the
![]() $\sigma $
-algebras of Borel measurable sets on
$\sigma $
-algebras of Borel measurable sets on
![]() $X_{\mathrm {base}}$
and
$X_{\mathrm {base}}$
and
![]() $\Omega $
, respectively). However, since each atom of
$\Omega $
, respectively). However, since each atom of
![]() $\mathcal C$
is contained in a single orbit of
$\mathcal C$
is contained in a single orbit of
![]() $Y_{\mathrm {pos}}$
, its image under the projection from X to
$Y_{\mathrm {pos}}$
, its image under the projection from X to
![]() $X _{{\mathrm {pos}}} = X / Y _{{\mathrm {pos}}}$
consists of a single point, so modulo
$X _{{\mathrm {pos}}} = X / Y _{{\mathrm {pos}}}$
consists of a single point, so modulo
![]() $\widetilde \mu $
,
$\widetilde \mu $
,
(with
![]() $\mathcal {B}_{\mathrm {pos}}$
the Borel
$\mathcal {B}_{\mathrm {pos}}$
the Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $X_{\mathrm {pos}}$
). It follows that
$X_{\mathrm {pos}}$
). It follows that
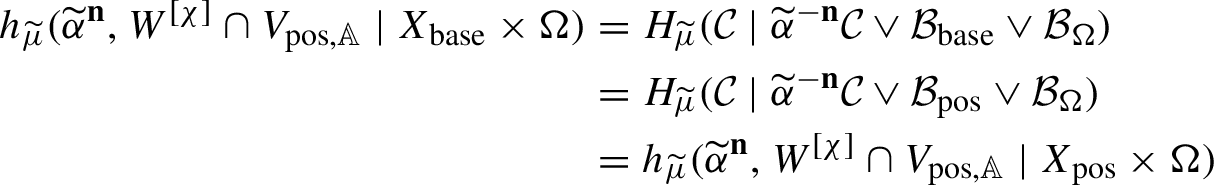 $$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) &= H _ {\widetilde \mu} (\mathcal{C} \mid \widetilde\alpha^{-\mathbf{n}} \mathcal{C} \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal B _ {\Omega}) \\ &=H _ {\widetilde \mu} (\mathcal{C} \mid \widetilde\alpha^{-\mathbf{n}} \mathcal{C} \vee \mathcal{B} _ {\mathrm{pos}} \vee \mathcal B _ {\Omega})\\ &=h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{pos}}\times\Omega) \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) &= H _ {\widetilde \mu} (\mathcal{C} \mid \widetilde\alpha^{-\mathbf{n}} \mathcal{C} \vee \mathcal{B} _{\mathrm{base}} \vee \mathcal B _ {\Omega}) \\ &=H _ {\widetilde \mu} (\mathcal{C} \mid \widetilde\alpha^{-\mathbf{n}} \mathcal{C} \vee \mathcal{B} _ {\mathrm{pos}} \vee \mathcal B _ {\Omega})\\ &=h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{pos}}\times\Omega) \end{align*} $$
as claimed.
Using (7.3) and the relation between entropy contributions and entropy in Proposition 3.4, we now obtain
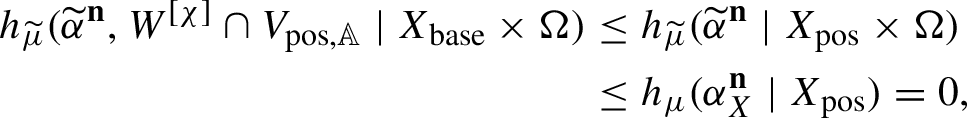 $$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) &\leq h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{pos}}\times\Omega) \\ &\leq h_{\mu}(\alpha_{X}^{\mathbf{n}}\mid X_{\mathrm{pos}})=0, \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega) &\leq h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{pos}}\times\Omega) \\ &\leq h_{\mu}(\alpha_{X}^{\mathbf{n}}\mid X_{\mathrm{pos}})=0, \end{align*} $$
where the last inequality follows from the choice of
![]() $X _{{\mathrm {pos}}}$
in §4.4.
$X _{{\mathrm {pos}}}$
in §4.4.
So suppose now that
![]() $[\chi ]$
is not a coarse Lyapunov weight for
$[\chi ]$
is not a coarse Lyapunov weight for
![]() $Y_{\mathrm {irred}}$
. Let
$Y_{\mathrm {irred}}$
. Let
![]() $V_{\mathrm {base},\mathbb A}<\mathbb A^m$
be the rational subspace corresponding to
$V_{\mathrm {base},\mathbb A}<\mathbb A^m$
be the rational subspace corresponding to
![]() $Y_{\mathrm {base}}$
. Since we consider entropy contribution conditional on
$Y_{\mathrm {base}}$
. Since we consider entropy contribution conditional on
![]() $X_{\mathrm {base}}\times \Omega $
, we may use the above argument again and replace the coarse Lyapunov subgroup
$X_{\mathrm {base}}\times \Omega $
, we may use the above argument again and replace the coarse Lyapunov subgroup
![]() $W^{[\chi ]}$
with intersection
$W^{[\chi ]}$
with intersection
![]() $W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}$
. However, since
$W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}$
. However, since
![]() $[\chi ]$
is not a coarse Lyapunov weight for
$[\chi ]$
is not a coarse Lyapunov weight for
![]() $Y_{\mathrm {irred}}=Y_{\mathrm {base}}/Y_{\mathrm {pos}}$
, it follows that
$Y_{\mathrm {irred}}=Y_{\mathrm {base}}/Y_{\mathrm {pos}}$
, it follows that
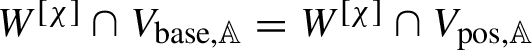 $W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}=W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}$
. Now the first part of the lemma implies that the entropy contribution vanishes. Since the entropy contribution for the Haar measure
$W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}=W^{[\chi ]}\cap V_{{\mathrm {pos}},\mathbb A}$
. Now the first part of the lemma implies that the entropy contribution vanishes. Since the entropy contribution for the Haar measure
![]() $\unicode{x3bb} $
on
$\unicode{x3bb} $
on
![]() $Y_{\mathrm {irred}}$
vanishes too, this proves the lemma.
$Y_{\mathrm {irred}}$
vanishes too, this proves the lemma.
Proof Proof of Theorem 7.1
By the Abromov–Rokhlin entropy addition formula, we have
 $$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{pos}}\times\Omega)+ h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega) \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{pos}}\times\Omega)+ h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega) \end{align*} $$
for all
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
. However, by properties of
$\mathbf {n}\in \mathbb {Z}^{d}$
. However, by properties of
![]() $X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
in (4.1), we have
$X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
in (4.1), we have
Therefore,
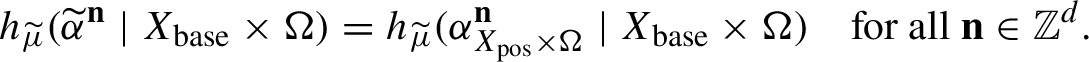 $$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega)\quad\text{for all}\ \mathbf{n}\in\mathbb{Z}^{d}. \end{align} $$
$$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}}\mid X_{\mathrm{base}}\times\Omega)\quad\text{for all}\ \mathbf{n}\in\mathbb{Z}^{d}. \end{align} $$
We claim that the entropy contributions for all coarse Lyapunov subgroups
![]() $W^{[\chi ]}$
satisfy a similar equation, namely
$W^{[\chi ]}$
satisfy a similar equation, namely
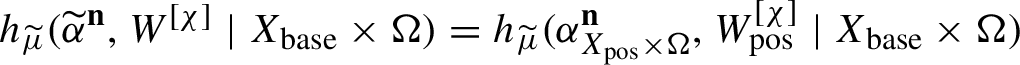 $$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) \end{align} $$
$$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)= h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) \end{align} $$
for all
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
with
$\mathbf {n}\in \mathbb {Z}^{d}$
with
![]() $\chi \cdot \mathbf {n}<0$
, where
$\chi \cdot \mathbf {n}<0$
, where
![]() $W^{[\chi ]}$
and
$W^{[\chi ]}$
and
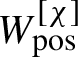 $W_{\mathrm {pos}}^{[\chi ]}$
denote the coarse Lyapunov subgroups for X and
$W_{\mathrm {pos}}^{[\chi ]}$
denote the coarse Lyapunov subgroups for X and
![]() $X_{\mathrm {pos}}$
, respectively. Applying Proposition 3.5 to
$X_{\mathrm {pos}}$
, respectively. Applying Proposition 3.5 to
![]() $W^{[\chi ]}$
and
$W^{[\chi ]}$
and
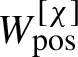 $W_{\mathrm {pos}}^{[\chi ]}$
(and with
$W_{\mathrm {pos}}^{[\chi ]}$
(and with
![]() $X_{\mathrm {base}}\times \Omega $
playing the role of
$X_{\mathrm {base}}\times \Omega $
playing the role of
![]() $\Omega $
in Proposition 3.5), we conclude that
$\Omega $
in Proposition 3.5), we conclude that
 $$ \begin{align*} & h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}}\times \Omega)\leq h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times \Omega) \\ &\quad+ h_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times \Omega) \end{align*} $$
$$ \begin{align*} & h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}}\times \Omega)\leq h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times \Omega) \\ &\quad+ h_{\widetilde\mu}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times \Omega) \end{align*} $$
with
![]() $V_{{\mathrm {pos}},\mathbb A} < \mathbb A^m$
as in Lemma 7.3. By Lemma 7.3,
$V_{{\mathrm {pos}},\mathbb A} < \mathbb A^m$
as in Lemma 7.3. By Lemma 7.3,
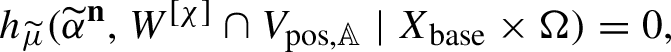 $$ \begin{align*}h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega)=0,\end{align*} $$
$$ \begin{align*}h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}}, W^{[\chi]}\cap V_{{\mathrm{pos}},\mathbb A}\mid X_{\mathrm{base}}\times\Omega)=0,\end{align*} $$
hence
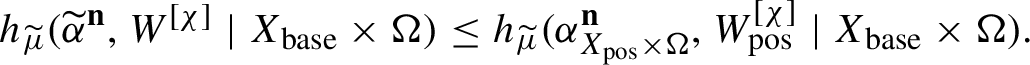 $$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)\leq h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega). \end{align} $$
$$ \begin{align} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)\leq h_{\widetilde{\mu}}(\alpha_{X_{\mathrm{pos}}\times\Omega}^{\mathbf{n}},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega). \end{align} $$
Now fix some
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
and take the sum over all coarse Lyapunov weights
$\mathbf {n}\in \mathbb {Z}^{d}$
and take the sum over all coarse Lyapunov weights
![]() $[\chi ]$
with
$[\chi ]$
with
![]() $(\chi \cdot \mathbf {n})<0$
. By the second claim in Theorem 6.1 (applied both to X and to
$(\chi \cdot \mathbf {n})<0$
. By the second claim in Theorem 6.1 (applied both to X and to
![]() $X_{\mathrm {pos}}$
), this leads to an inequality between the two terms in (7.5). However, since in (7.5) equality holds, equality for the entropy contributions in (7.7) must hold as well. Varying
$X_{\mathrm {pos}}$
), this leads to an inequality between the two terms in (7.5). However, since in (7.5) equality holds, equality for the entropy contributions in (7.7) must hold as well. Varying
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
gives (7.6) for all coarse Lyapunov weights
$\mathbf {n}\in \mathbb {Z}^{d}$
gives (7.6) for all coarse Lyapunov weights
![]() $[\chi ]$
.
$[\chi ]$
.
Next we are going to combine Theorem 5.1 and Theorem 6.1. By Theorem 5.1,
 $$ \begin{align} h_{\tilde{\mu}}(\alpha^{\mathbf{n}}_{X_{\mathrm{pos}}\times\Omega},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)\leq \frac{h_{\tilde{\mu}}(\alpha^{\mathbf{n}}|X_{\mathrm{base}}\times\Omega)}{h_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}})} h_{\unicode{x3bb}}(\alpha^{\mathbf{n}}_{Y_{\mathrm{irred}}},W_{Y_{\mathrm{irred}}}^{[\chi]}). \end{align} $$
$$ \begin{align} h_{\tilde{\mu}}(\alpha^{\mathbf{n}}_{X_{\mathrm{pos}}\times\Omega},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)\leq \frac{h_{\tilde{\mu}}(\alpha^{\mathbf{n}}|X_{\mathrm{base}}\times\Omega)}{h_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}})} h_{\unicode{x3bb}}(\alpha^{\mathbf{n}}_{Y_{\mathrm{irred}}},W_{Y_{\mathrm{irred}}}^{[\chi]}). \end{align} $$
Set
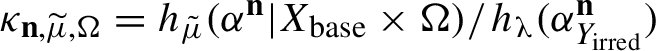 $\kappa _{\mathbf {n},\widetilde {\mu },\Omega } = h_{\tilde {\mu }}(\alpha ^{\mathbf {n}}|X_{\mathrm {base}}\times \Omega )/h_\unicode{x3bb} (\alpha _{Y_{\mathrm {irred}}}^{\mathbf {n}})$
; note that it does not depend on the coarse Lyapunov weight
$\kappa _{\mathbf {n},\widetilde {\mu },\Omega } = h_{\tilde {\mu }}(\alpha ^{\mathbf {n}}|X_{\mathrm {base}}\times \Omega )/h_\unicode{x3bb} (\alpha _{Y_{\mathrm {irred}}}^{\mathbf {n}})$
; note that it does not depend on the coarse Lyapunov weight
![]() $[\chi ]$
. Taking the sum over all coarse Lyapunov weights
$[\chi ]$
. Taking the sum over all coarse Lyapunov weights
![]() $[\chi ]$
with
$[\chi ]$
with
![]() $\chi \cdot \mathbf {n}<0$
gives, by (6.3) of Theorem 6.1 on the left-hand side, the conditional entropy
$\chi \cdot \mathbf {n}<0$
gives, by (6.3) of Theorem 6.1 on the left-hand side, the conditional entropy
![]() $h_{\tilde {\mu }}(\alpha ^{\mathbf {n}}|X_{\mathrm {base}}\times \Omega )$
and on the right-hand side, we obtain
$h_{\tilde {\mu }}(\alpha ^{\mathbf {n}}|X_{\mathrm {base}}\times \Omega )$
and on the right-hand side, we obtain
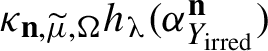 $ \kappa _{\mathbf {n},\widetilde {\mu },\Omega }h_\unicode{x3bb} (\alpha _{Y_{\mathrm {irred}}}^{\mathbf {n}})$
, which in view of the definition of
$ \kappa _{\mathbf {n},\widetilde {\mu },\Omega }h_\unicode{x3bb} (\alpha _{Y_{\mathrm {irred}}}^{\mathbf {n}})$
, which in view of the definition of
![]() $\kappa _{\mathbf {n},\widetilde {\mu },\Omega }$
also equals
$\kappa _{\mathbf {n},\widetilde {\mu },\Omega }$
also equals
![]() $ h_{\tilde {\mu }}(\alpha ^{\mathbf {n}}|X_{\mathrm {base}}\times \Omega )$
. This shows that in fact
$ h_{\tilde {\mu }}(\alpha ^{\mathbf {n}}|X_{\mathrm {base}}\times \Omega )$
. This shows that in fact
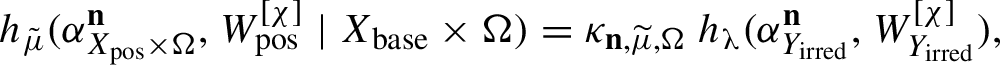 $$\begin{align} h_{\tilde{\mu}}(\alpha^{\mathbf{n}}_{X_{\mathrm{pos}}\times\Omega},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)=\kappa_{\mathbf{n},\widetilde{\mu},\Omega}\, h_{\unicode{x3bb}}(\alpha^{\mathbf{n}}_{Y_{\mathrm{irred}}},W_{Y_{\mathrm{irred}}}^{[\chi]}), \end{align}$$
$$\begin{align} h_{\tilde{\mu}}(\alpha^{\mathbf{n}}_{X_{\mathrm{pos}}\times\Omega},W_{\mathrm{pos}}^{[\chi]}\mid X_{\mathrm{base}}\times\Omega)=\kappa_{\mathbf{n},\widetilde{\mu},\Omega}\, h_{\unicode{x3bb}}(\alpha^{\mathbf{n}}_{Y_{\mathrm{irred}}},W_{Y_{\mathrm{irred}}}^{[\chi]}), \end{align}$$
for all coarse Lyapunov weights
![]() $[\chi ]$
with
$[\chi ]$
with
![]() $\chi \cdot \mathbf {n}<0$
.
$\chi \cdot \mathbf {n}<0$
.
We now choose
![]() $\mathbf {n}_0$
so that
$\mathbf {n}_0$
so that
![]() $\chi \cdot \mathbf {n}_0\neq 0$
for all coarse Lyapunov weights
$\chi \cdot \mathbf {n}_0\neq 0$
for all coarse Lyapunov weights
![]() $[\chi ]$
. Since
$[\chi ]$
. Since
equation (7.8 ′), together with (7.6), implies that
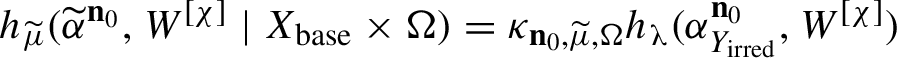 $$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}_0},W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =\kappa_{\mathbf{n}_0,\widetilde{\mu},\Omega} h_{\unicode{x3bb}}(\alpha^{\mathbf{n}_0}_{Y_{\mathrm{irred}}},W^{[\chi]}) \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\widetilde\alpha^{\mathbf{n}_0},W^{[\chi]}\mid X_{\mathrm{base}}\times\Omega) =\kappa_{\mathbf{n}_0,\widetilde{\mu},\Omega} h_{\unicode{x3bb}}(\alpha^{\mathbf{n}_0}_{Y_{\mathrm{irred}}},W^{[\chi]}) \end{align*} $$
for all coarse Lyapunov weights
![]() $[\chi ]$
. It follows that the constants appearing in Lemma 7.2, which may depend on
$[\chi ]$
. It follows that the constants appearing in Lemma 7.2, which may depend on
![]() $[\chi ]$
but not on
$[\chi ]$
but not on
![]() $\mathbf {n}_0$
, agree with
$\mathbf {n}_0$
, agree with
![]() $\kappa _{\mathbf {n}_0,\widetilde {\mu },\Omega }$
, which may depend on
$\kappa _{\mathbf {n}_0,\widetilde {\mu },\Omega }$
, which may depend on
![]() $\mathbf {n}_0$
but not on
$\mathbf {n}_0$
but not on
![]() $[\chi ]$
. This gives the theorem.
$[\chi ]$
. This gives the theorem.
7.2 Rigidity of the entropy function implies invariance
We are now ready to prove Theorem 4.1. As before, we work with the setup explained in §4.4, specifically (4.1):
![]() $X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
is a factor of X so that
$X_{\mathrm {pos}}=X/Y_{\mathrm {pos}}$
is a factor of X so that
![]() $h_\mu (\alpha ^{\mathbf {n}}|X_{\mathrm {pos}})=0$
for all
$h_\mu (\alpha ^{\mathbf {n}}|X_{\mathrm {pos}})=0$
for all
![]() $\mathbf {n} \in \mathbb {Z}^d$
,
$\mathbf {n} \in \mathbb {Z}^d$
,
![]() $Y_{\mathrm {irred}}$
is an
$Y_{\mathrm {irred}}$
is an
![]() $\alpha $
-invariant
$\alpha $
-invariant
![]() $\mathbb A$
-irreducible subgroup of
$\mathbb A$
-irreducible subgroup of
![]() $X_{\mathrm {pos}}$
, and
$X_{\mathrm {pos}}$
, and
![]() $X_{\mathrm {base}}=X/Y_{\mathrm {base}}=X_{\mathrm {pos}}/Y_{\mathrm {irred}}$
satisfies that for some
$X_{\mathrm {base}}=X/Y_{\mathrm {base}}=X_{\mathrm {pos}}/Y_{\mathrm {irred}}$
satisfies that for some
![]() $\mathbf {n}\in \mathbb {Z}^d$
we have that
$\mathbf {n}\in \mathbb {Z}^d$
we have that
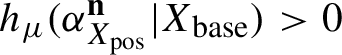 $h_\mu (\alpha ^{\mathbf {n}}_{X_{\mathrm {pos}}}|X_{\mathrm {base}})>0$
.
$h_\mu (\alpha ^{\mathbf {n}}_{X_{\mathrm {pos}}}|X_{\mathrm {base}})>0$
.
Applying Theorem 7.1 with
![]() $\Omega $
being the trivial factor, we obtain a constant
$\Omega $
being the trivial factor, we obtain a constant
![]() $\kappa _\mu>0$
so that
$\kappa _\mu>0$
so that
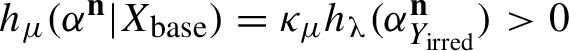 $h_\mu (\alpha ^{\mathbf {n}}|X_{\mathrm {base}})=\kappa _\mu h_\unicode{x3bb} (\alpha _{Y_{\mathrm {irred}}}^{\mathbf {n}})>0$
for all
$h_\mu (\alpha ^{\mathbf {n}}|X_{\mathrm {base}})=\kappa _\mu h_\unicode{x3bb} (\alpha _{Y_{\mathrm {irred}}}^{\mathbf {n}})>0$
for all
![]() $\mathbf {n} \in \mathbb {Z}^d$
.
$\mathbf {n} \in \mathbb {Z}^d$
.
Next we choose a coarse Lyapunov weight
![]() $[\chi ]$
of
$[\chi ]$
of
![]() $Y_{\mathrm {irred}}$
and consider it as a coarse Lyapunov weight for X. Let
$Y_{\mathrm {irred}}$
and consider it as a coarse Lyapunov weight for X. Let
![]() $V_{\mathrm {base},\mathbb A}<\mathbb A^m$
be the rational
$V_{\mathrm {base},\mathbb A}<\mathbb A^m$
be the rational
![]() $\alpha $
-invariant subspace so that
$\alpha $
-invariant subspace so that
![]() $Y_{\mathrm {base}}$
is the image of
$Y_{\mathrm {base}}$
is the image of
![]() $V_{\mathrm {base},\mathbb A}$
modulo
$V_{\mathrm {base},\mathbb A}$
modulo
![]() $\mathbb Q$
. We also set
$\mathbb Q$
. We also set
![]() $W=W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}$
. Let
$W=W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}$
. Let
![]() $f _ W$
be a positive function on W, which is integrable with respect to
$f _ W$
be a positive function on W, which is integrable with respect to
![]() $\mu _ x ^ W$
for every x in a set of full measure as in §3.1. We take
$\mu _ x ^ W$
for every x in a set of full measure as in §3.1. We take
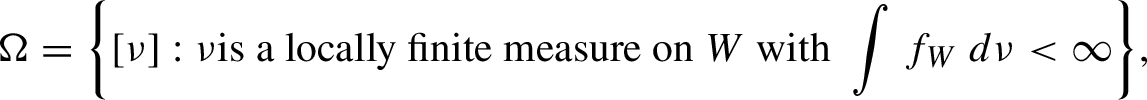 $$ \begin{align*} \Omega = \bigg\{ [\nu]: \nu \text{is a locally finite measure on}\ W\ \text{with}\ \int f _ W \,d \nu < \infty \bigg\}, \end{align*} $$
$$ \begin{align*} \Omega = \bigg\{ [\nu]: \nu \text{is a locally finite measure on}\ W\ \text{with}\ \int f _ W \,d \nu < \infty \bigg\}, \end{align*} $$
where
![]() $[\nu ]$
denotes the equivalence class of
$[\nu ]$
denotes the equivalence class of
![]() $\nu $
in the space of locally finite measures with respect to proportionality. One can equip
$\nu $
in the space of locally finite measures with respect to proportionality. One can equip
![]() $\Omega $
with the structure of a compact metric space in a standard way. The map (defined for a.e.
$\Omega $
with the structure of a compact metric space in a standard way. The map (defined for a.e.
![]() $x \in X$
) that takes
$x \in X$
) that takes
![]() $x \in X$
and maps it to the proportionality class of its leafwise measure
$x \in X$
and maps it to the proportionality class of its leafwise measure
![]() $[\mu _x^W]$
is, by (3.4), a factor map of the
$[\mu _x^W]$
is, by (3.4), a factor map of the
![]() $\mathbb {Z} ^ d$
-action
$\mathbb {Z} ^ d$
-action
![]() $\alpha $
on X to the action of
$\alpha $
on X to the action of
![]() $\mathbb {Z} ^ d$
on elements of
$\mathbb {Z} ^ d$
on elements of
![]() $\Omega $
by pushforward with respect to the linear action corresponding to
$\Omega $
by pushforward with respect to the linear action corresponding to
![]() $\alpha $
on W. Taking the product of
$\alpha $
on W. Taking the product of
![]() $\Omega $
with
$\Omega $
with
![]() $X_{\mathrm {base}}$
, we get a factor of X and we apply Theorem 7.1 once more over this factor
$X_{\mathrm {base}}$
, we get a factor of X and we apply Theorem 7.1 once more over this factor
![]() $X_{\mathrm {base}} \times \Omega $
to obtain a constant
$X_{\mathrm {base}} \times \Omega $
to obtain a constant
![]() $\kappa _{\widetilde {\mu },\Omega }\geq 0$
so that
$\kappa _{\widetilde {\mu },\Omega }\geq 0$
so that
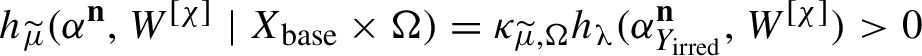 $$ \begin{align} h_{\widetilde{\mu}}(\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}} \times\Omega)= \kappa_{\widetilde{\mu},\Omega}h_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}},W^{[\chi]})>0 \end{align} $$
$$ \begin{align} h_{\widetilde{\mu}}(\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}} \times\Omega)= \kappa_{\widetilde{\mu},\Omega}h_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}},W^{[\chi]})>0 \end{align} $$
for all coarse Lyapunov weights
![]() $[\chi ]$
and
$[\chi ]$
and
![]() $\mathbf {n} \in \mathbb {Z}^d$
.
$\mathbf {n} \in \mathbb {Z}^d$
.
Lemma 7.4.
![]() $Y_{\mathrm {irred}}$
has at least two linearly independent Lyapunov weights.
$Y_{\mathrm {irred}}$
has at least two linearly independent Lyapunov weights.
Proof Since
![]() $Y_{\mathrm {irred}}$
is irreducible, we may apply Proposition 2.2 and describe the action on
$Y_{\mathrm {irred}}$
is irreducible, we may apply Proposition 2.2 and describe the action on
![]() $Y_{\mathrm {irred}}$
using a global field
$Y_{\mathrm {irred}}$
using a global field
![]() $\mathbb {K}$
and its elements. Also recall that the eigenspaces for
$\mathbb {K}$
and its elements. Also recall that the eigenspaces for
![]() $Y_{\mathrm {irred}}$
correspond to the completions of
$Y_{\mathrm {irred}}$
correspond to the completions of
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
Suppose in contradiction that
![]() $\alpha $
has no two linearly independent Lyapunov weights. Then every non-zero Lyapunov weight must be a multiple of
$\alpha $
has no two linearly independent Lyapunov weights. Then every non-zero Lyapunov weight must be a multiple of
![]() $\chi $
. We now define the hyperplane
$\chi $
. We now define the hyperplane
![]() $H<\mathbb {R}^d$
as the kernel of
$H<\mathbb {R}^d$
as the kernel of
![]() $\chi $
. Suppose
$\chi $
. Suppose
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
is close to H, that is, satisfies
$\mathbf {n}\in \mathbb {Z}^{d}$
is close to H, that is, satisfies
![]() $\chi ^{\prime }\cdot \mathbf {n}\in (-\epsilon ,\epsilon )$
for all Lyapunov weights
$\chi ^{\prime }\cdot \mathbf {n}\in (-\epsilon ,\epsilon )$
for all Lyapunov weights
![]() $\chi ^{\prime }$
of
$\chi ^{\prime }$
of
![]() $Y_{\mathrm {irred}}$
and some
$Y_{\mathrm {irred}}$
and some
![]() $\epsilon>0$
to be determined later. For the algebraic number
$\epsilon>0$
to be determined later. For the algebraic number
![]() $\zeta _{\mathbf {n}}$
corresponding to
$\zeta _{\mathbf {n}}$
corresponding to
![]() $\mathbf {n}$
, this becomes the inequality
$\mathbf {n}$
, this becomes the inequality
for all places
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {K}$
(and
$\mathbb {K}$
(and
![]() $|\zeta _{\mathbf {n}}|_\sigma =1$
for places
$|\zeta _{\mathbf {n}}|_\sigma =1$
for places
![]() $\sigma $
lying over finite primes p not in S, with S as in (3.5). However, for small enough
$\sigma $
lying over finite primes p not in S, with S as in (3.5). However, for small enough
![]() $\epsilon>0$
, it follows from (7.10) applied to all finite places that
$\epsilon>0$
, it follows from (7.10) applied to all finite places that
![]() $\zeta _{\mathbf {n}}$
must be an algebraic unit. Applying (7.10) also to all infinite places, we get that this unit satisfies that all its real and complex embeddings have absolute value close to one. It follows from Dirichlet’s unit theorem that
$\zeta _{\mathbf {n}}$
must be an algebraic unit. Applying (7.10) also to all infinite places, we get that this unit satisfies that all its real and complex embeddings have absolute value close to one. It follows from Dirichlet’s unit theorem that
![]() $\zeta $
must be a root of unity and
$\zeta $
must be a root of unity and
![]() $\mathbf {n}\in H$
. However, this implies that the action of
$\mathbf {n}\in H$
. However, this implies that the action of
![]() $\alpha (\mathbb {Z}^d)$
on
$\alpha (\mathbb {Z}^d)$
on
![]() $Y_{\mathrm {irred}}$
is virtually cyclic. By the Jordan decomposition over
$Y_{\mathrm {irred}}$
is virtually cyclic. By the Jordan decomposition over
![]() $\mathbb Q$
, X has a factor isomorphic to
$\mathbb Q$
, X has a factor isomorphic to
![]() $Y_{\mathrm {irred}}$
; the fact that
$Y_{\mathrm {irred}}$
; the fact that
![]() $\alpha (\mathbb {Z}^d)$
on
$\alpha (\mathbb {Z}^d)$
on
![]() $Y_{\mathrm {irred}}$
is virtually cyclic now contradicts our standing assumption that X has no virtually cyclic factors.
$Y_{\mathrm {irred}}$
is virtually cyclic now contradicts our standing assumption that X has no virtually cyclic factors.
Proposition 7.5. In fact,
![]() $\kappa _{\widetilde {\mu },\Omega }=\kappa _\mu $
(hence
$\kappa _{\widetilde {\mu },\Omega }=\kappa _\mu $
(hence
![]() $\kappa _{\widetilde {\mu },\Omega }>0$
).
$\kappa _{\widetilde {\mu },\Omega }>0$
).
Proof Let
![]() $\chi ^{\prime }$
be a Lyapunov weight of
$\chi ^{\prime }$
be a Lyapunov weight of
![]() $Y_{\mathrm {irred}}$
that is linearly independent to
$Y_{\mathrm {irred}}$
that is linearly independent to
![]() $\chi $
. The existence of
$\chi $
. The existence of
![]() $\chi ^{\prime }$
follows from Lemma 7.4. Choose some
$\chi ^{\prime }$
follows from Lemma 7.4. Choose some
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
so that
$\mathbf {n}\in \mathbb {Z}^{d}$
so that
![]() $\chi \cdot \mathbf {n}<0$
and
$\chi \cdot \mathbf {n}<0$
and
![]() $\chi ^{\prime }\cdot \mathbf {n}<0$
. The product structure of the leafwise measures in Theorem 6.1 (see also [Reference Einsiedler and Lindenstrauss10, Corollary 8.6]) now implies that for a set
$\chi ^{\prime }\cdot \mathbf {n}<0$
. The product structure of the leafwise measures in Theorem 6.1 (see also [Reference Einsiedler and Lindenstrauss10, Corollary 8.6]) now implies that for a set
![]() $X^{\prime }\subset X$
of full measure, we have the following property: for any
$X^{\prime }\subset X$
of full measure, we have the following property: for any
![]() $x\in X^{\prime }$
and any
$x\in X^{\prime }$
and any
![]() $w^{\prime }\in W^{[\chi ^{\prime }]}$
with
$w^{\prime }\in W^{[\chi ^{\prime }]}$
with
![]() $x+w^{\prime }\in X^{\prime }$
, we have
$x+w^{\prime }\in X^{\prime }$
, we have
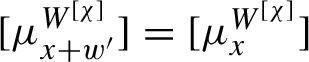 $ [\mu _{x+w^{\prime }}^{W^{[\chi ]}} ]= [\mu _{x}^{W^{[\chi ]}} ]$
. For a
$ [\mu _{x+w^{\prime }}^{W^{[\chi ]}} ]= [\mu _{x}^{W^{[\chi ]}} ]$
. For a
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A}$
subordinate to
$\mathcal {A}$
subordinate to
![]() $W^{[\chi ^{\prime }]}$
, this means that, on the complement of a null set, all points in a given atom of
$W^{[\chi ^{\prime }]}$
, this means that, on the complement of a null set, all points in a given atom of
![]() $\mathcal {A}$
are contained in the same fiber of the factor map from X to
$\mathcal {A}$
are contained in the same fiber of the factor map from X to
![]() $\Omega $
. In other words, the map
$\Omega $
. In other words, the map
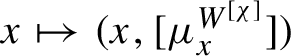 $x \mapsto (x, [\mu _x^{W^{[\chi ]}} ] )$
from X to
$x \mapsto (x, [\mu _x^{W^{[\chi ]}} ] )$
from X to
![]() $X\times \Omega $
maps
$X\times \Omega $
maps
![]() $\sigma $
-algebras subordinate to
$\sigma $
-algebras subordinate to
![]() $W^{[\chi ^{\prime }]}$
on X to
$W^{[\chi ^{\prime }]}$
on X to
![]() $\sigma $
-algebras subordinate to
$\sigma $
-algebras subordinate to
![]() $W^{[\chi ^{\prime }]}$
on
$W^{[\chi ^{\prime }]}$
on
![]() $X\times \Omega $
. From this it follows that the leafwise measures for X and for
$X\times \Omega $
. From this it follows that the leafwise measures for X and for
![]() $X\times \Omega $
with respect to the subgroup
$X\times \Omega $
with respect to the subgroup
![]() $W^{[\chi ^{\prime }]}$
agree. In particular, we have
$W^{[\chi ^{\prime }]}$
agree. In particular, we have
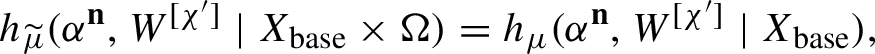 $$ \begin{align*} h_{\widetilde\mu}(\alpha^{\mathbf{n}},W^{[\chi^{\prime}]}\mid X_{\mathrm{base}}\times\Omega) = h_\mu(\alpha^{\mathbf{n}}, W^{[\chi^{\prime}]}\mid X_{\mathrm{base}}), \end{align*} $$
$$ \begin{align*} h_{\widetilde\mu}(\alpha^{\mathbf{n}},W^{[\chi^{\prime}]}\mid X_{\mathrm{base}}\times\Omega) = h_\mu(\alpha^{\mathbf{n}}, W^{[\chi^{\prime}]}\mid X_{\mathrm{base}}), \end{align*} $$
which together with Theorem 7.1 proves the proposition.
We continue working under the assumptions stated at the beginning of §7.2.
Corollary 7.6. For any subset
![]() $X^{\prime \prime }\subset X$
of full measure, there exist
$X^{\prime \prime }\subset X$
of full measure, there exist
![]() $x\in X^{\prime \prime }$
and a non-zero
$x\in X^{\prime \prime }$
and a non-zero
![]() $v\in W$
with
$v\in W$
with
![]() $x+v\in X^{\prime \prime }$
and
$x+v\in X^{\prime \prime }$
and
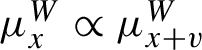 $\mu _x^{W}\propto \mu _{x+v}^{W}$
.
$\mu _x^{W}\propto \mu _{x+v}^{W}$
.
Proof By Proposition 7.5, we have
![]() $\kappa _{\widetilde {\mu },\Omega }>0$
. We now apply this to the coarse Lyapunov weight
$\kappa _{\widetilde {\mu },\Omega }>0$
. We now apply this to the coarse Lyapunov weight
![]() $[\chi ]$
and the subgroup
$[\chi ]$
and the subgroup
![]() $W=W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}$
that was used to define the factor
$W=W^{[\chi ]}\cap V_{\mathrm {base},\mathbb A}$
that was used to define the factor
![]() $\Omega $
. Choose
$\Omega $
. Choose
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
with
$\mathbf {n}\in \mathbb {Z}^{d}$
with
![]() $\chi \cdot \mathbf {n}<0$
. It now follows from the definition of
$\chi \cdot \mathbf {n}<0$
. It now follows from the definition of
![]() $\kappa _{\widetilde {\mu },\Omega }$
in Theorem 7.1 that
$\kappa _{\widetilde {\mu },\Omega }$
in Theorem 7.1 that
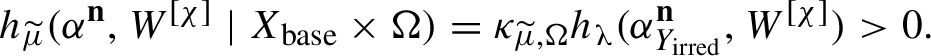 $$ \begin{align*} h_{\widetilde{\mu}}(\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}} \times\Omega)= \kappa_{\widetilde{\mu},\Omega}h_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}},W^{[\chi]})>0. \end{align*} $$
$$ \begin{align*} h_{\widetilde{\mu}}(\alpha^{\mathbf{n}},W^{[\chi]}\mid X_{\mathrm{base}} \times\Omega)= \kappa_{\widetilde{\mu},\Omega}h_\unicode{x3bb}(\alpha_{Y_{\mathrm{irred}}}^{\mathbf{n}},W^{[\chi]})>0. \end{align*} $$
We also note that
![]() $h_{\widetilde {\mu }}(\alpha ^{\mathbf {n}},W\mid X_{\mathrm {base}} \times \Omega )=h_{\widetilde {\mu }}(\alpha ^{\mathbf {n}},W^{[\chi ]}\mid X_{\mathrm {base}} \times \Omega )$
(c.f. e.g. the first lines in the proof of Theorem 5.1). We note that positive entropy contribution, as in (3.9), shows in particular that the leafwise measure
$h_{\widetilde {\mu }}(\alpha ^{\mathbf {n}},W\mid X_{\mathrm {base}} \times \Omega )=h_{\widetilde {\mu }}(\alpha ^{\mathbf {n}},W^{[\chi ]}\mid X_{\mathrm {base}} \times \Omega )$
(c.f. e.g. the first lines in the proof of Theorem 5.1). We note that positive entropy contribution, as in (3.9), shows in particular that the leafwise measure
![]() $\widetilde \mu _x^W$
gives zero mass to
$\widetilde \mu _x^W$
gives zero mass to
![]() $0\in W$
.
$0\in W$
.
By the characterizing properties of leafwise measures in terms of W-subordinate
![]() $\sigma $
-algebras, the fact that the leafwise measure
$\sigma $
-algebras, the fact that the leafwise measure
![]() $\widetilde \mu _x^W$
gives zero mass to
$\widetilde \mu _x^W$
gives zero mass to
![]() $0\in W$
implies that for any subset
$0\in W$
implies that for any subset
![]() $X^{\prime \prime }\subset \widetilde {X}$
of full measure for
$X^{\prime \prime }\subset \widetilde {X}$
of full measure for
![]() $\widetilde {\mu }$
,
$\widetilde {\mu }$
,
Since the action of W on
![]() $\widetilde {X}=X\times \Omega $
was defined to be trivial on
$\widetilde {X}=X\times \Omega $
was defined to be trivial on
![]() $\Omega $
and
$\Omega $
and
![]() $\widetilde {\mu }$
was defined as the push forward of
$\widetilde {\mu }$
was defined as the push forward of
![]() $\mu $
under the map
$\mu $
under the map
![]() $x\mapsto (x,[\mu _x^W])$
, (7.11) translates to the following statement: for every subset
$x\mapsto (x,[\mu _x^W])$
, (7.11) translates to the following statement: for every subset
![]() $X^{\prime \prime }\subset X$
of full measure for
$X^{\prime \prime }\subset X$
of full measure for
![]() $\mu $
, there exists
$\mu $
, there exists
![]() $x\in X^{\prime \prime }$
and
$x\in X^{\prime \prime }$
and
![]() $v\in W\setminus \{0\}$
with
$v\in W\setminus \{0\}$
with
![]() $x+v\in X^{\prime \prime }$
and
$x+v\in X^{\prime \prime }$
and
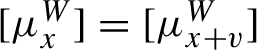 $[\mu _x^W]=[\mu _{x+v}^W]$
. However, this is precisely the claim in the corollary.
$[\mu _x^W]=[\mu _{x+v}^W]$
. However, this is precisely the claim in the corollary.
Proof Proof of Theorem 4.1
We first show how the statement in Corollary 7.6 implies invariance of
![]() $\mu $
under translation by all elements of a non-trivial adelic subgroup. We note that by (3.1), the claim in Corollary 7.6 amounts to saying that for any set
$\mu $
under translation by all elements of a non-trivial adelic subgroup. We note that by (3.1), the claim in Corollary 7.6 amounts to saying that for any set
![]() $X^{\prime \prime }\subseteq X^{\prime }$
of full measure, there exists some
$X^{\prime \prime }\subseteq X^{\prime }$
of full measure, there exists some
![]() $x\in X^{\prime \prime }$
and
$x\in X^{\prime \prime }$
and
![]() $v\in W\setminus \{0\}$
with
$v\in W\setminus \{0\}$
with
![]() $\mu _x^W+v\propto \mu _x^W$
. Moreover, by our discussion concerning (3.2)–(3.3), there exists
$\mu _x^W+v\propto \mu _x^W$
. Moreover, by our discussion concerning (3.2)–(3.3), there exists
![]() $X^{\prime \prime }$
of full measure so that for any
$X^{\prime \prime }$
of full measure so that for any
![]() $x\in X^{\prime \prime }$
, there is some
$x\in X^{\prime \prime }$
, there is some
![]() $v\in W$
with
$v\in W$
with
![]() $\mu _x^W+v=\mu _{x}^W$
(see also [Reference Einsiedler and Katok4, Lemma 5.10]). Hence Corollary 7.6 implies that for all
$\mu _x^W+v=\mu _{x}^W$
(see also [Reference Einsiedler and Katok4, Lemma 5.10]). Hence Corollary 7.6 implies that for all
![]() $x\in X^{\prime \prime }$
, the closed subgroup
$x\in X^{\prime \prime }$
, the closed subgroup
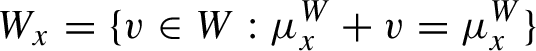 $$ \begin{align*} W_x=\{v\in W: \mu_x^W+v=\mu_{x}^W\} \end{align*} $$
$$ \begin{align*} W_x=\{v\in W: \mu_x^W+v=\mu_{x}^W\} \end{align*} $$
is non-trivial. We define
![]() $\widetilde {W}_x$
as the maximal S-linear subgroup of
$\widetilde {W}_x$
as the maximal S-linear subgroup of
![]() $W_x$
. We will show below (using the equivariance formula (3.4) and Poincarè recurrence) that a.s.
$W_x$
. We will show below (using the equivariance formula (3.4) and Poincarè recurrence) that a.s.
![]() $\widetilde {W}_x$
is non-trivial. In fact, [Reference Einsiedler and Katok4, Proposition 6.2] shows that
$\widetilde {W}_x$
is non-trivial. In fact, [Reference Einsiedler and Katok4, Proposition 6.2] shows that
![]() $W_x=\widetilde {W}_x$
is itself S-linear, at least if the action is semisimple.
$W_x=\widetilde {W}_x$
is itself S-linear, at least if the action is semisimple.
We define the dimension
![]() $D_x$
of
$D_x$
of
![]() $\widetilde {W}_x$
as the sum of the dimensions of the maximal subspaces over
$\widetilde {W}_x$
as the sum of the dimensions of the maximal subspaces over
![]() $\mathbb Q_\sigma $
contained in
$\mathbb Q_\sigma $
contained in
![]() $\widetilde {W}_x$
for all
$\widetilde {W}_x$
for all
![]() $\sigma \in S$
. Even though
$\sigma \in S$
. Even though
![]() $\widetilde {W}_x$
may not be normalized by
$\widetilde {W}_x$
may not be normalized by
![]() $\alpha $
, the equivariance formula (3.4) implies that both
$\alpha $
, the equivariance formula (3.4) implies that both
![]() $W_x$
and
$W_x$
and
![]() $\widetilde {W}_x$
are equivariant for the action. Hence the dimension of
$\widetilde {W}_x$
are equivariant for the action. Hence the dimension of
![]() $\widetilde {W}_x$
is invariant under
$\widetilde {W}_x$
is invariant under
![]() $\alpha $
. Therefore,
$\alpha $
. Therefore,
![]() $D_x$
is constant (say equal to D) for a.e. x.
$D_x$
is constant (say equal to D) for a.e. x.
We claim that Corollary 7.6 implies a.s. that
![]() $\widetilde {W}_x$
is non-trivial, or equivalently that
$\widetilde {W}_x$
is non-trivial, or equivalently that
![]() $D_x \geq 1$
a.s. For this, we apply Luzin’s theorem and let
$D_x \geq 1$
a.s. For this, we apply Luzin’s theorem and let
![]() $K\subset X^{\prime }$
be a compact subset of measure close to
$K\subset X^{\prime }$
be a compact subset of measure close to
![]() $1$
, on which all almost sure properties of the leafwise measures hold, and on which the map
$1$
, on which all almost sure properties of the leafwise measures hold, and on which the map
![]() $x\in K\mapsto \mu _x^W$
is continuous. To obtain the almost sure conclusion, we apply the following argument for an increasing sequence of such Luzin sets that cover almost all of the space.
$x\in K\mapsto \mu _x^W$
is continuous. To obtain the almost sure conclusion, we apply the following argument for an increasing sequence of such Luzin sets that cover almost all of the space.
By Poincaré recurrence, we see that for a.e.
![]() $x\in K$
, there exists two increasing sequences
$x\in K$
, there exists two increasing sequences
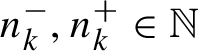 $n^-_k,n^+_k\in \mathbb {N}$
with
$n^-_k,n^+_k\in \mathbb {N}$
with
 $T^{-n^-_k}x, T^{n^+_k}x\in K$
converging to x as
$T^{-n^-_k}x, T^{n^+_k}x\in K$
converging to x as
![]() $k\to \infty $
. Suppose now
$k\to \infty $
. Suppose now
![]() ${v\in W_x\setminus \{0\}}$
for one such x so that
${v\in W_x\setminus \{0\}}$
for one such x so that
![]() $\mu _x^W+v=\mu _x^W$
. If v has a non-trivial real component, we are going to use the sequence
$\mu _x^W+v=\mu _x^W$
. If v has a non-trivial real component, we are going to use the sequence
![]() $n^+_k$
. Indeed applying (3.4) for these powers, we see that the leafwise measure at
$n^+_k$
. Indeed applying (3.4) for these powers, we see that the leafwise measure at
![]() $T^{n^+_k}x$
has translation invariance under
$T^{n^+_k}x$
has translation invariance under
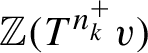 $\mathbb {Z} (T^{n^+_k}v)$
. Note that
$\mathbb {Z} (T^{n^+_k}v)$
. Note that
![]() $T^{n^+_k}v$
converges to
$T^{n^+_k}v$
converges to
![]() $0$
as
$0$
as
![]() $k\to \infty $
. However, since the unit ball in
$k\to \infty $
. However, since the unit ball in
![]() $\mathbb {R}^m$
is compact, we may choose a subsequence and assume in addition that the direction of
$\mathbb {R}^m$
is compact, we may choose a subsequence and assume in addition that the direction of
![]() $T^{n^+_k}v$
converges in projective space to
$T^{n^+_k}v$
converges in projective space to
![]() $\mathbb {R} \widetilde {v}$
for some
$\mathbb {R} \widetilde {v}$
for some
![]() $\widetilde {v}\neq 0$
. Note that this implies that the subgroups
$\widetilde {v}\neq 0$
. Note that this implies that the subgroups
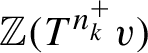 $\mathbb {Z} (T^{n^+_k}v)$
converge in the Chabauty topology to
$\mathbb {Z} (T^{n^+_k}v)$
converge in the Chabauty topology to
![]() $\mathbb {R}\widetilde {v}$
. Combined with continuity of the leafwise measures restricted to K, this now implies that
$\mathbb {R}\widetilde {v}$
. Combined with continuity of the leafwise measures restricted to K, this now implies that
![]() $\mu _x^W$
is invariant under translation by
$\mu _x^W$
is invariant under translation by
![]() $\mathbb {R}\widetilde {v}$
, which implies
$\mathbb {R}\widetilde {v}$
, which implies
![]() $\widetilde {v}\in \widetilde {W}_x$
and
$\widetilde {v}\in \widetilde {W}_x$
and
![]() $D_x\geq 1$
as desired.
$D_x\geq 1$
as desired.
So suppose now v has trivial real component and let us write
![]() $v_p$
for the p-adic component of v for all
$v_p$
for the p-adic component of v for all
![]() $p\in S$
. In this case, the invariance of
$p\in S$
. In this case, the invariance of
![]() $\mu _x^W$
under
$\mu _x^W$
under
![]() $\mathbb {Z} v$
implies invariance under
$\mathbb {Z} v$
implies invariance under
![]() $\overline {\mathbb {Z} v}$
, which by the Chinese Remainder Theorem is the product of the compact subgroups
$\overline {\mathbb {Z} v}$
, which by the Chinese Remainder Theorem is the product of the compact subgroups
![]() $\mathbb {Z}_p v_p$
for all primes
$\mathbb {Z}_p v_p$
for all primes
![]() $p\in S$
. To obtain a non-trivial S-linear subgroup, we fix a prime
$p\in S$
. To obtain a non-trivial S-linear subgroup, we fix a prime
![]() $p\in S$
with
$p\in S$
with
![]() $v_p\neq 0$
and we are going to use the sequence
$v_p\neq 0$
and we are going to use the sequence
![]() $n^-_k$
. Indeed, as above,
$n^-_k$
. Indeed, as above,
![]() $T^{-n^-_k}x\in K$
has invariance under
$T^{-n^-_k}x\in K$
has invariance under
 $\mathbb {Z}_p T^{-n^-_k}v_p$
, where
$\mathbb {Z}_p T^{-n^-_k}v_p$
, where
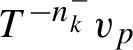 $T^{-n^-_k}v_p$
diverges to infinity but projectively converges to some
$T^{-n^-_k}v_p$
diverges to infinity but projectively converges to some
![]() $\mathbb Q_p \widetilde {v}$
. By continuity of the leafwise measures on K, this again implies
$\mathbb Q_p \widetilde {v}$
. By continuity of the leafwise measures on K, this again implies
![]() $\widetilde {v}\in \widetilde {W}_x$
and
$\widetilde {v}\in \widetilde {W}_x$
and
![]() $D_x\geq 1$
as desired.
$D_x\geq 1$
as desired.
We define the (measurable) factor map as
from X to the space
![]() $\mathcal F$
of closed subgroups of W in the Chabauty topology. We also decompose
$\mathcal F$
of closed subgroups of W in the Chabauty topology. We also decompose
![]() $\mu $
over
$\mu $
over
![]() $\phi $
, that is, we consider the conditional measures
$\phi $
, that is, we consider the conditional measures
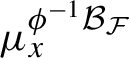 $\mu _x^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
. By the compatibility condition (3.1) and the definition of
$\mu _x^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
. By the compatibility condition (3.1) and the definition of
![]() $\widetilde {W}_x$
, we have
$\widetilde {W}_x$
, we have
![]() $\phi (x)=\phi (x+v)$
whenever
$\phi (x)=\phi (x+v)$
whenever
![]() $v\in W$
and both
$v\in W$
and both
![]() $x,x+v$
belong to
$x,x+v$
belong to
![]() $X^{\prime \prime }$
. In particular, this shows for a W-subordinate
$X^{\prime \prime }$
. In particular, this shows for a W-subordinate
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal A$
that
$\mathcal A$
that
![]() $\mathcal A$
contains
$\mathcal A$
contains
![]() $\phi ^{-1}\mathcal {B}_{\mathcal {F}}$
modulo null sets. Hence, after fixing a choice of the conditional measures
$\phi ^{-1}\mathcal {B}_{\mathcal {F}}$
modulo null sets. Hence, after fixing a choice of the conditional measures
 $\mu _x^{\mathcal {A}}$
, we have that the (doubly) conditional measure
$\mu _x^{\mathcal {A}}$
, we have that the (doubly) conditional measure
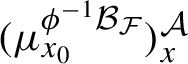 $(\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}})^{\mathcal A}_{x}$
agrees with
$(\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}})^{\mathcal A}_{x}$
agrees with
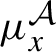 $\mu _x^{\mathcal {A}}$
for
$\mu _x^{\mathcal {A}}$
for
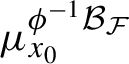 $\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e. x and
$\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e. x and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x_0$
. This in turn implies for the leafwise measures of
$x_0$
. This in turn implies for the leafwise measures of
![]() $\mu $
and
$\mu $
and
 $\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
with respect to W by the characterizing properties that
$\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
with respect to W by the characterizing properties that
 $$ \begin{align} (\mu_{x_0}^{\phi^{-1}\mathcal{B}_{\mathcal{F}}})_x^W=\mu_x^W \end{align} $$
$$ \begin{align} (\mu_{x_0}^{\phi^{-1}\mathcal{B}_{\mathcal{F}}})_x^W=\mu_x^W \end{align} $$
for
 $\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e. x and for
$\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e. x and for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x_0$
.
$x_0$
.
Fix some
![]() $x_0$
. Then essentially by definition of the factor
$x_0$
. Then essentially by definition of the factor
![]() $\phi $
, we have that
$\phi $
, we have that
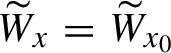 $\widetilde W_x=\widetilde W_{x_0}$
for
$\widetilde W_x=\widetilde W_{x_0}$
for
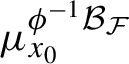 $\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e. x. In other words, by definition of
$\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e. x. In other words, by definition of
![]() $\widetilde W_x$
and (7.12), we have that for
$\widetilde W_x$
and (7.12), we have that for
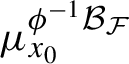 $\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e x, the leafwise measures
$\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
-a.e x, the leafwise measures
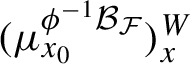 $(\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}})_x^W$
are invariant under the group
$(\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}})_x^W$
are invariant under the group
 $\widetilde W_{x_0}$
, hence by the standard properties of leafwise measures that
$\widetilde W_{x_0}$
, hence by the standard properties of leafwise measures that
 $\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
is itself invariant under the action of
$\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
is itself invariant under the action of
 $\widetilde {W}_{x_0}$
by translations. Note that, as far as we know at this point, the group
$\widetilde {W}_{x_0}$
by translations. Note that, as far as we know at this point, the group
![]() $\widetilde {W}_x$
may depend on x, and hence we have not established the invariance of
$\widetilde {W}_x$
may depend on x, and hence we have not established the invariance of
![]() $\mu $
itself under any translations yet.
$\mu $
itself under any translations yet.
As
![]() $X=\mathbb A^m/\mathbb Q^m$
is an abelian group and
$X=\mathbb A^m/\mathbb Q^m$
is an abelian group and
![]() $\mathbb Q^m$
acts trivially, this implies that
$\mathbb Q^m$
acts trivially, this implies that
 $\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
is in fact invariant under the closure
$\mu _{x_0}^{\phi ^{-1}\mathcal {B}_{\mathcal {F}}}$
is in fact invariant under the closure
![]() $G_x$
of
$G_x$
of
 $\widetilde {W}_{x_0}+\mathbb Q^m$
in X. Since
$\widetilde {W}_{x_0}+\mathbb Q^m$
in X. Since
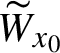 $\widetilde {W}_{x_0}$
, as an S-linear subgroup, is invariant under multiplication by
$\widetilde {W}_{x_0}$
, as an S-linear subgroup, is invariant under multiplication by
![]() $\mathbb Q$
, we have that its annihilator
$\mathbb Q$
, we have that its annihilator
![]() $G_x^\perp $
in the Pontryagin dual
$G_x^\perp $
in the Pontryagin dual
![]() $\mathbb Q^m$
to X is a vector space over
$\mathbb Q^m$
to X is a vector space over
![]() $\mathbb Q$
. Hence
$\mathbb Q$
. Hence
![]() $G_x$
is an adelic subgroup of X.
$G_x$
is an adelic subgroup of X.
The equivariance formula (3.4) implies a similar equivariance formula for
![]() $W_x$
, for
$W_x$
, for
![]() $\widetilde {W}_x$
, and hence also for
$\widetilde {W}_x$
, and hence also for
![]() $G_x$
. In other words,
$G_x$
. In other words,
![]() $x\mapsto G_x$
is a (measurable) factor map for
$x\mapsto G_x$
is a (measurable) factor map for
![]() $\alpha $
with values in the countable set of all adelic subspaces of
$\alpha $
with values in the countable set of all adelic subspaces of
![]() $X_m$
. Hence there exists an adelic subspace G so that
$X_m$
. Hence there exists an adelic subspace G so that
![]() $G_x=G$
on a set of positive measure. By Poincaré recurrence, we may conclude that there is a finite index subgroup
$G_x=G$
on a set of positive measure. By Poincaré recurrence, we may conclude that there is a finite index subgroup
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathbb {Z}^d$
so that
$\mathbb {Z}^d$
so that
![]() $\alpha (\Lambda )$
normalizes G. However, the assumption in Theorem 4.1 now implies that G is actually normalized by
$\alpha (\Lambda )$
normalizes G. However, the assumption in Theorem 4.1 now implies that G is actually normalized by
![]() $\mathbb {Z}^d$
. Ergodicity under
$\mathbb {Z}^d$
. Ergodicity under
![]() $\alpha $
now implies that
$\alpha $
now implies that
![]() $G_x=G$
a.s. Therefore,
$G_x=G$
a.s. Therefore,
![]() $\mu $
is invariant under G.
$\mu $
is invariant under G.
8 Disjointness
We will deduce in this section the rigidity of joinings and in particular prove Corollary 1.4. We say a measure on a solenoid X is homogeneous if it is the Y-invariant measure on a coset
![]() $Y+y$
of a closed subgroup
$Y+y$
of a closed subgroup
![]() $Y<X$
.
$Y<X$
.
Proposition 8.1. Let
![]() $d,r\geq 2$
and let
$d,r\geq 2$
and let
![]() $\alpha _i$
be
$\alpha _i$
be
![]() $\mathbb {Z}^{d}$
-actions on solenoids
$\mathbb {Z}^{d}$
-actions on solenoids
![]() $X_i$
(equipped with Haar measure
$X_i$
(equipped with Haar measure
![]() $\unicode{x3bb} _{X_i}$
) with no virtually cyclic factors for
$\unicode{x3bb} _{X_i}$
) with no virtually cyclic factors for
![]() $i=1,\ldots ,r$
. Suppose there exists a non-trivial joining
$i=1,\ldots ,r$
. Suppose there exists a non-trivial joining
![]() $\mu $
between
$\mu $
between
![]() $\alpha _i$
for
$\alpha _i$
for
![]() $i=1,\ldots ,r$
. Then there exists a finite index subgroup
$i=1,\ldots ,r$
. Then there exists a finite index subgroup
![]() $\Lambda \subseteq \mathbb {Z}^d$
such that there exists also a homogeneous non-trivial joining
$\Lambda \subseteq \mathbb {Z}^d$
such that there exists also a homogeneous non-trivial joining
![]() $\unicode{x3bb} _G$
between
$\unicode{x3bb} _G$
between
![]() $\alpha _{i,\Lambda }$
for
$\alpha _{i,\Lambda }$
for
![]() $i=1,\ldots ,r$
. In fact, the subgroup G can be chosen to be any of the groups in the conclusion of Theorem 1.3 when applied to an ergodic component of the positive entropy measure
$i=1,\ldots ,r$
. In fact, the subgroup G can be chosen to be any of the groups in the conclusion of Theorem 1.3 when applied to an ergodic component of the positive entropy measure
![]() $\mu $
on
$\mu $
on
![]() $X_1\times \cdots \times X_r$
.
$X_1\times \cdots \times X_r$
.
Proof Let
![]() $X=X_1\times \cdots \times X_r$
and
$X=X_1\times \cdots \times X_r$
and
![]() $\alpha =\alpha _1\times \cdots \times \alpha _r$
be the product group and action, and let
$\alpha =\alpha _1\times \cdots \times \alpha _r$
be the product group and action, and let
![]() $\mu $
be a non-trivial joining. Without loss of generality, we can assume
$\mu $
be a non-trivial joining. Without loss of generality, we can assume
![]() $\mu $
is
$\mu $
is
![]() $\alpha $
-ergodic (since a.e. ergodic component of a joining is again a joining). We apply Theorem 1.3 and obtain a finite index subgroup
$\alpha $
-ergodic (since a.e. ergodic component of a joining is again a joining). We apply Theorem 1.3 and obtain a finite index subgroup
![]() $\Lambda \subset \mathbb {Z}^{d}$
and an
$\Lambda \subset \mathbb {Z}^{d}$
and an
![]() $\alpha _\Lambda $
-invariant closed subgroup
$\alpha _\Lambda $
-invariant closed subgroup
![]() $G=G_1\subset X$
. We claim that the Haar measure of G is an homogeneous non-trivial joining for the
$G=G_1\subset X$
. We claim that the Haar measure of G is an homogeneous non-trivial joining for the
![]() $\Lambda $
-action.
$\Lambda $
-action.
To see this, let
![]() $\mu _j$
for
$\mu _j$
for
![]() $j=1,\ldots ,J$
be as in Theorem 1.3 and let
$j=1,\ldots ,J$
be as in Theorem 1.3 and let
![]() $\pi _i:X\rightarrow X_i$
for
$\pi _i:X\rightarrow X_i$
for
![]() $i=1,\ldots ,r$
be the coordinate projection map. First notice that the Haar measure of G cannot be the trivial joining. If it were, it would follow that
$i=1,\ldots ,r$
be the coordinate projection map. First notice that the Haar measure of G cannot be the trivial joining. If it were, it would follow that
![]() $G=X$
,
$G=X$
,
![]() $\mu _1=\unicode{x3bb} _X$
,
$\mu _1=\unicode{x3bb} _X$
,
![]() $\mu _j=(\alpha ^{\mathbf {n}})_*\mu _1=\unicode{x3bb} _X$
for all j and some
$\mu _j=(\alpha ^{\mathbf {n}})_*\mu _1=\unicode{x3bb} _X$
for all j and some
![]() $\mathbf {n}$
(that depends on j), and so
$\mathbf {n}$
(that depends on j), and so
![]() $\mu =\unicode{x3bb} _X$
would be the trivial joining. To show the claim, we only need to prove that
$\mu =\unicode{x3bb} _X$
would be the trivial joining. To show the claim, we only need to prove that
![]() $\pi _i(G)=X_j$
for
$\pi _i(G)=X_j$
for
![]() $i=1,\ldots ,r$
.
$i=1,\ldots ,r$
.
Fix some i. Clearly
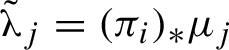 defines a measure on
defines a measure on
![]() $X_i$
that is invariant under
$X_i$
that is invariant under
![]() $\alpha _{i,\Lambda }$
. By assumption,
$\alpha _{i,\Lambda }$
. By assumption,
![]() . Note that
. Note that
![]() $\alpha _{i,\Lambda }$
acts ergodically on
$\alpha _{i,\Lambda }$
acts ergodically on
![]() $X_i$
with respect to
$X_i$
with respect to
![]() $\unicode{x3bb} _{X_i}$
by the assumption that there are no virtually cyclic factors. Therefore,
$\unicode{x3bb} _{X_i}$
by the assumption that there are no virtually cyclic factors. Therefore,
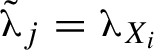 for all j, in other words,
for all j, in other words,
![]() $\mu _1$
is a joining. Consider now the group
$\mu _1$
is a joining. Consider now the group
![]() $Y=X_i/\pi _i(G)\cong X/(G+\ker \pi _i)$
endowed with the measure
$Y=X_i/\pi _i(G)\cong X/(G+\ker \pi _i)$
endowed with the measure
![]() $\nu $
induced by
$\nu $
induced by
![]() $\mu _1$
. However, by the above, the projection of
$\mu _1$
. However, by the above, the projection of
![]() $\mu _1$
to
$\mu _1$
to
![]() $X_i$
is
$X_i$
is
![]() $\unicode{x3bb} _{X_i}$
, and so
$\unicode{x3bb} _{X_i}$
, and so
![]() $\nu =\unicode{x3bb} _Y$
. Since Y is a factor of
$\nu =\unicode{x3bb} _Y$
. Since Y is a factor of
![]() $X/G$
, the entropy (with respect to
$X/G$
, the entropy (with respect to
![]() $\nu $
) of every element on Y of the action must vanish. However, the action on
$\nu $
) of every element on Y of the action must vanish. However, the action on
![]() $X_i$
contains elements with completely positive entropy. Therefore,
$X_i$
contains elements with completely positive entropy. Therefore,
![]() $Y=\{0\}$
and
$Y=\{0\}$
and
![]() $\pi _j(G)=X_i$
for all i.
$\pi _j(G)=X_i$
for all i.
Proof Proof of Corollary 1.4, simpler case
Assume first that
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are totally irreducible not virtually cyclic actions and let
$\alpha _2$
are totally irreducible not virtually cyclic actions and let
![]() $\alpha =\alpha _1\times \alpha _2$
. Suppose
$\alpha =\alpha _1\times \alpha _2$
. Suppose
![]() $\alpha _{1,\Lambda }$
and
$\alpha _{1,\Lambda }$
and
![]() $\alpha _{2,\Lambda }$
are algebraically weakly isomorphic for some finite index subgroup
$\alpha _{2,\Lambda }$
are algebraically weakly isomorphic for some finite index subgroup
![]() $\Lambda \subset \mathbb {Z}^{d}$
. So there exists a finite-to-one algebraic factor map
$\Lambda \subset \mathbb {Z}^{d}$
. So there exists a finite-to-one algebraic factor map
![]() $\varphi :X_1\rightarrow X_2$
for the two subactions. Clearly, the graph G of
$\varphi :X_1\rightarrow X_2$
for the two subactions. Clearly, the graph G of
![]() $\varphi $
is
$\varphi $
is
![]() $\alpha _\Lambda $
-invariant and so is its Haar measure
$\alpha _\Lambda $
-invariant and so is its Haar measure
![]() $\unicode{x3bb} _G$
. The average
$\unicode{x3bb} _G$
. The average
![]() $\mu $
over the elements
$\mu $
over the elements
![]() $\alpha ^{\mathbf {n}}_{*}{\unicode{x3bb} _G}$
in the (finite) orbit of
$\alpha ^{\mathbf {n}}_{*}{\unicode{x3bb} _G}$
in the (finite) orbit of
![]() $\unicode{x3bb} _G$
under the action of
$\unicode{x3bb} _G$
under the action of
![]() $\alpha $
defines a non-trivial joining between
$\alpha $
defines a non-trivial joining between
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
.
$\alpha _2$
.
Let
![]() $\mu $
be a joining between
$\mu $
be a joining between
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
. We have to show that either
$\alpha _2$
. We have to show that either
![]() $\mu =\unicode{x3bb} _{X_1}\times \unicode{x3bb} _{X_2}$
is the trivial joining, or find a finite index subgroup
$\mu =\unicode{x3bb} _{X_1}\times \unicode{x3bb} _{X_2}$
is the trivial joining, or find a finite index subgroup
![]() $\Lambda \subset \mathbb {Z}^{d}$
such that
$\Lambda \subset \mathbb {Z}^{d}$
such that
![]() $\alpha _{1,\Lambda }$
and
$\alpha _{1,\Lambda }$
and
![]() $\alpha _{2,\Lambda }$
are algebraically weakly isomorphic. Assume that
$\alpha _{2,\Lambda }$
are algebraically weakly isomorphic. Assume that
![]() $\mu $
is not the trivial joining, then there exists a finite index subgroup
$\mu $
is not the trivial joining, then there exists a finite index subgroup
![]() $\Lambda $
and a homogeneous non-trivial joining
$\Lambda $
and a homogeneous non-trivial joining
![]() $\unicode{x3bb} _G$
between
$\unicode{x3bb} _G$
between
![]() $\alpha _{1,\Lambda }$
and
$\alpha _{1,\Lambda }$
and
![]() $\alpha _{2,\Lambda }$
by Proposition 8.1. Here
$\alpha _{2,\Lambda }$
by Proposition 8.1. Here
![]() $G\subset X$
is a proper closed subgroup with
$G\subset X$
is a proper closed subgroup with
![]() $\pi _1(G)=X_1$
and
$\pi _1(G)=X_1$
and
![]() $\pi _2(G)=X_2$
.
$\pi _2(G)=X_2$
.
Next we study the factors
![]() $X^{\prime }_1=X_1/\{x_1:(x_1,0)\in G\}$
and
$X^{\prime }_1=X_1/\{x_1:(x_1,0)\in G\}$
and
![]() $X^{\prime }_2=X_2/\{x_2:(0,x_2)\in G\}$
. Suppose
$X^{\prime }_2=X_2/\{x_2:(0,x_2)\in G\}$
. Suppose
![]() $X^{\prime }_1$
is trivial, then
$X^{\prime }_1$
is trivial, then
![]() $X_1\times \{0\}\subset G$
and
$X_1\times \{0\}\subset G$
and
![]() $\pi _2(G)=X_2$
implies that
$\pi _2(G)=X_2$
implies that
![]() $G=X_1\times X_2$
, a contradiction to G being proper.
$G=X_1\times X_2$
, a contradiction to G being proper.
So assume now
![]() $X^{\prime }_1$
and
$X^{\prime }_1$
and
![]() $X^{\prime }_2$
are non-trivial, and let
$X^{\prime }_2$
are non-trivial, and let
![]() $G^{\prime }\subset X^{\prime }_1\times X^{\prime }_2$
be the subgroup defined by G. Then
$G^{\prime }\subset X^{\prime }_1\times X^{\prime }_2$
be the subgroup defined by G. Then
![]() $G^{\prime }\cap (X^{\prime }_1\times \{0\})=G^{\prime }\cap (\{0\}\times X^{\prime }_2)=\{0\}$
, so
$G^{\prime }\cap (X^{\prime }_1\times \{0\})=G^{\prime }\cap (\{0\}\times X^{\prime }_2)=\{0\}$
, so
![]() $G^{\prime }$
is the graph of an isomorphism between
$G^{\prime }$
is the graph of an isomorphism between
![]() $X_1^{\prime }$
and
$X_1^{\prime }$
and
![]() $X_2^{\prime }$
. Since
$X_2^{\prime }$
. Since
![]() $G^{\prime }$
is closed, compactness shows the isomorphism is continuous. Since all of the above are invariant subgroups, it follows that
$G^{\prime }$
is closed, compactness shows the isomorphism is continuous. Since all of the above are invariant subgroups, it follows that
![]() $\alpha _{1,\Lambda }$
and
$\alpha _{1,\Lambda }$
and
![]() $\alpha _{2,\Lambda }$
have a common non-trivial factor
$\alpha _{2,\Lambda }$
have a common non-trivial factor
![]() $X_1^{\prime }\cong X_2^{\prime }$
. By assumption
$X_1^{\prime }\cong X_2^{\prime }$
. By assumption
![]() $\alpha _{1,\Lambda }$
and
$\alpha _{1,\Lambda }$
and
![]() $\alpha _{2,\Lambda }$
are irreducible, so the kernel of the above factor maps must be finite. Let N be the order of the kernel, then multiplication by N defines a factor map
$\alpha _{2,\Lambda }$
are irreducible, so the kernel of the above factor maps must be finite. Let N be the order of the kernel, then multiplication by N defines a factor map
![]() $ \psi _N$
from
$ \psi _N$
from
![]() $X_1$
to
$X_1$
to
![]() $X_1$
that can be extended to a factor map
$X_1$
that can be extended to a factor map
![]() $ \psi _N$
from
$ \psi _N$
from
![]() $X_1^{\prime }$
to
$X_1^{\prime }$
to
![]() $X_1$
, that is, the two actions on
$X_1$
, that is, the two actions on
![]() $X_1$
and
$X_1$
and
![]() $X_1^{\prime }$
are weakly algebraically isomorphic.
$X_1^{\prime }$
are weakly algebraically isomorphic.
Proof Proof of Corollary 1.4, general case
Let
![]() $X=\prod _{=1}^r X_j$
and
$X=\prod _{=1}^r X_j$
and
![]() $\alpha =\alpha _1\times \cdots \times \alpha _r$
be the product group and action. Suppose
$\alpha =\alpha _1\times \cdots \times \alpha _r$
be the product group and action. Suppose
![]() $j\neq k\in \{1,\ldots ,r\}$
and
$j\neq k\in \{1,\ldots ,r\}$
and
![]() $\alpha _{j,\Lambda }$
and
$\alpha _{j,\Lambda }$
and
![]() $\alpha _{k,\Lambda }$
have a common non-trivial factor
$\alpha _{k,\Lambda }$
have a common non-trivial factor
![]() $\beta $
on a solenoid Y, where
$\beta $
on a solenoid Y, where
![]() $\Lambda \subset \mathbb {Z}^{d}$
is a finite index subgroup. Let
$\Lambda \subset \mathbb {Z}^{d}$
is a finite index subgroup. Let
![]() $\varphi _j:X_j\rightarrow Y$
and
$\varphi _j:X_j\rightarrow Y$
and
![]() $\varphi _k:X_k\rightarrow Y$
be the corresponding group homomorphisms. Then
$\varphi _k:X_k\rightarrow Y$
be the corresponding group homomorphisms. Then
![]() $G=\{x\in X:\varphi _j(x_j)=\varphi _k(x_k)\}$
is a non-trivial closed
$G=\{x\in X:\varphi _j(x_j)=\varphi _k(x_k)\}$
is a non-trivial closed
![]() $\alpha _\Lambda $
-invariant subgroup of X such that
$\alpha _\Lambda $
-invariant subgroup of X such that
![]() $\pi _i(G)=X_i$
for
$\pi _i(G)=X_i$
for
![]() $i=1,\ldots ,r$
. The Haar measure
$i=1,\ldots ,r$
. The Haar measure
![]() $\unicode{x3bb} _G$
on G has finite orbit under
$\unicode{x3bb} _G$
on G has finite orbit under
![]() $\alpha $
, and the average
$\alpha $
, and the average
![]() $\mu $
over the elements in the (finite) orbit of
$\mu $
over the elements in the (finite) orbit of
![]() $\unicode{x3bb} _G$
is a non-trivial joining.
$\unicode{x3bb} _G$
is a non-trivial joining.
Suppose now that
![]() $\mu $
is a non-trivial joining between
$\mu $
is a non-trivial joining between
![]() $\alpha _i$
for
$\alpha _i$
for
![]() $i=1,\ldots ,r$
, and apply Proposition 8.1. We obtain a finite index subgroup
$i=1,\ldots ,r$
, and apply Proposition 8.1. We obtain a finite index subgroup
![]() $\Lambda \subset \mathbb {Z}^{d}$
and an
$\Lambda \subset \mathbb {Z}^{d}$
and an
![]() $\alpha _\Lambda $
-invariant proper closed subgroup
$\alpha _\Lambda $
-invariant proper closed subgroup
![]() $G< X$
that satisfies
$G< X$
that satisfies
![]() $\pi _i(G)=X_i$
for
$\pi _i(G)=X_i$
for
![]() $i=1,\ldots ,r$
.
$i=1,\ldots ,r$
.
Next we factor
![]() $X_i$
by the subgroup
$X_i$
by the subgroup
to get
![]() $X_i^{\prime }=X_i/H_i$
for
$X_i^{\prime }=X_i/H_i$
for
![]() $i=1,\ldots ,r$
and the factor
$i=1,\ldots ,r$
and the factor
![]() $X^{\prime }=\prod _iX_i^{\prime }$
of X. If
$X^{\prime }=\prod _iX_i^{\prime }$
of X. If
![]() $X^{\prime }=\{0\}$
, then
$X^{\prime }=\{0\}$
, then
![]() $G=X$
which contradicts G being a proper subgroup.
$G=X$
which contradicts G being a proper subgroup.
So assume that
![]() $X^{\prime }$
is non-trivial, and therefore infinite. Let
$X^{\prime }$
is non-trivial, and therefore infinite. Let
![]() $G^{\prime }< X^{\prime }$
be the image of G. Clearly
$G^{\prime }< X^{\prime }$
be the image of G. Clearly
![]() $\pi _i(G^{\prime })=X_i^{\prime }$
for
$\pi _i(G^{\prime })=X_i^{\prime }$
for
![]() $i=1,\ldots ,r$
. Let i be minimal such that
$i=1,\ldots ,r$
. Let i be minimal such that
![]() $H=G^{\prime }\cap Z_i$
is infinite, where
$H=G^{\prime }\cap Z_i$
is infinite, where
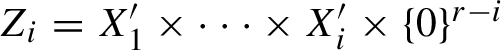 $Z_i=X_1^{\prime }\times \cdots \times X_i^{\prime }\times \{0\}^{r-i}$
. Then the kernel
$Z_i=X_1^{\prime }\times \cdots \times X_i^{\prime }\times \{0\}^{r-i}$
. Then the kernel
![]() $\{x\in H:x_i=0\}$
of
$\{x\in H:x_i=0\}$
of
![]() $\pi _i|_{H}$
is finite, and so
$\pi _i|_{H}$
is finite, and so
![]() $\pi _i(H)$
is an infinite closed
$\pi _i(H)$
is an infinite closed
![]() $\alpha _\Lambda $
-invariant subgroup of
$\alpha _\Lambda $
-invariant subgroup of
![]() $X_i^{\prime }$
. Let
$X_i^{\prime }$
. Let
![]() $\beta $
be an irreducible component of
$\beta $
be an irreducible component of
![]() $\alpha _\Lambda |_H$
. Since
$\alpha _\Lambda |_H$
. Since
![]() $\pi _i|_H$
is finite-to-one,
$\pi _i|_H$
is finite-to-one,
![]() $\beta $
is also an irreducible component of
$\beta $
is also an irreducible component of
![]() $\alpha _{i,\Lambda }|_{\pi _i(H)}$
. Since an irreducible component of a subgroup is also an irreducible component of the whole group, we see that
$\alpha _{i,\Lambda }|_{\pi _i(H)}$
. Since an irreducible component of a subgroup is also an irreducible component of the whole group, we see that
![]() $\alpha _{\Lambda }|_H$
and
$\alpha _{\Lambda }|_H$
and
![]() $\alpha _{i,\Lambda }$
share
$\alpha _{i,\Lambda }$
share
![]() $\beta $
as an irreducible component. By construction of
$\beta $
as an irreducible component. By construction of
![]() $X^{\prime }$
, we have
$X^{\prime }$
, we have
![]() $\{z\in H: z_k=0$
for all
$\{z\in H: z_k=0$
for all
![]() $k\neq i\}=\{0\}$
. Therefore H is isomorphic to a subgroup of
$k\neq i\}=\{0\}$
. Therefore H is isomorphic to a subgroup of
![]() $X_1^{\prime }\times \cdots \times X_{i-1}^{\prime }$
. We conclude that there exists
$X_1^{\prime }\times \cdots \times X_{i-1}^{\prime }$
. We conclude that there exists
![]() $j<i$
such that
$j<i$
such that
![]() $\alpha _{i,\Lambda }$
and
$\alpha _{i,\Lambda }$
and
![]() $\alpha _{j,\Lambda }$
have
$\alpha _{j,\Lambda }$
have
![]() $\beta $
as a common factor.
$\beta $
as a common factor.
9 Invariant
 $\sigma $
-algebras and measurable factors
$\sigma $
-algebras and measurable factors
In addition to the characterization of factors stated in Corollary 1.5, we prove in this section a generalization of the isomorphism rigidity [Reference Katok, Katok and Schmidt21] for higher rank actions. Indeed we characterize when two actions by automorphisms of solenoids have a common measurable factor.
Suppose
![]() $\alpha _1,\alpha _2 $
are
$\alpha _1,\alpha _2 $
are
![]() $\mathbb {Z}^{d} $
-actions by automorphisms of the solenoids
$\mathbb {Z}^{d} $
-actions by automorphisms of the solenoids
![]() $X_1$
and
$X_1$
and
![]() $X_2$
. Let
$X_2$
. Let
![]() $\Gamma _1$
respectively
$\Gamma _1$
respectively
![]() $\Gamma _2$
be finite groups of affine automorphisms of
$\Gamma _2$
be finite groups of affine automorphisms of
![]() $X_1$
and
$X_1$
and
![]() $X_2$
that are normalized by the respective actions. We say that the two factors of
$X_2$
that are normalized by the respective actions. We say that the two factors of
![]() $X_1 $
and
$X_1 $
and
![]() $X_2 $
arising from
$X_2 $
arising from
![]() $\Gamma _1$
respectively
$\Gamma _1$
respectively
![]() $\Gamma _2$
are isomorphic if there exists an affine isomorphism
$\Gamma _2$
are isomorphic if there exists an affine isomorphism
![]() $\Phi :X_1\rightarrow X_2$
such that
$\Phi :X_1\rightarrow X_2$
such that
![]() $\Phi \circ \alpha _1^{\mathbf {n}}\circ \Gamma _1=\alpha _2^{\mathbf {n}}\circ \Gamma _2\circ \Phi $
for all
$\Phi \circ \alpha _1^{\mathbf {n}}\circ \Gamma _1=\alpha _2^{\mathbf {n}}\circ \Gamma _2\circ \Phi $
for all
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
.
$\mathbf {n}\in \mathbb {Z}^{d}$
.
We claim that this is essentially the only way common measurable factors of higher rank actions on solenoids can arise.
Corollary 9.1. (Classification of common factors)
Let
![]() $d\geq 2$
and let
$d\geq 2$
and let
![]() $\alpha _1,\alpha _2$
be
$\alpha _1,\alpha _2$
be
![]() $\mathbb {Z}^{d} $
-actions by automorphisms of the solenoids
$\mathbb {Z}^{d} $
-actions by automorphisms of the solenoids
![]() $X_1$
and
$X_1$
and
![]() $X_2$
without virtually cyclic factors. Suppose
$X_2$
without virtually cyclic factors. Suppose
![]() $\alpha _1 $
and
$\alpha _1 $
and
![]() $\alpha _2$
have a common measurable factor. Then there exist closed invariant subgroups
$\alpha _2$
have a common measurable factor. Then there exist closed invariant subgroups
![]() $X^{\prime }_1\subseteq X_1$
and
$X^{\prime }_1\subseteq X_1$
and
![]() $X_2^{\prime }\subseteq X_2$
, finite groups
$X_2^{\prime }\subseteq X_2$
, finite groups
![]() $\Gamma _1$
of affine automorphisms of
$\Gamma _1$
of affine automorphisms of
![]() $X_1/X_1^{\prime }$
and
$X_1/X_1^{\prime }$
and
![]() $\Gamma _2$
of affine automorphisms of
$\Gamma _2$
of affine automorphisms of
![]() $X_2/X_2^{\prime }$
that are normalized by the corresponding actions such that this common measurable factor can be described alternatively as the factor of
$X_2/X_2^{\prime }$
that are normalized by the corresponding actions such that this common measurable factor can be described alternatively as the factor of
![]() $X_1/X_1^{\prime }$
by the orbit equivalence relation of
$X_1/X_1^{\prime }$
by the orbit equivalence relation of
![]() $\Gamma _1$
, or similarly using
$\Gamma _1$
, or similarly using
![]() $X_2/X_2^{\prime }$
and
$X_2/X_2^{\prime }$
and
![]() $\Gamma _2$
. Moreover, the isomorphism between these two realizations of the factor is algebraic in the following sense: there exists an affine isomorphism
$\Gamma _2$
. Moreover, the isomorphism between these two realizations of the factor is algebraic in the following sense: there exists an affine isomorphism
![]() $\Phi :X_1/X_1^{\prime }\rightarrow X_2/X_2^{\prime }$
such that
$\Phi :X_1/X_1^{\prime }\rightarrow X_2/X_2^{\prime }$
such that
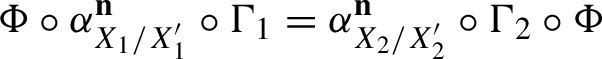 $$ \begin{align} \Phi\circ\alpha^{\mathbf{n}}_{X_1/X_1^{\prime}}\circ\Gamma_1= \alpha^{\mathbf{n}}_{X_2/X_2^{\prime}}\circ\Gamma_2\circ\Phi \end{align} $$
$$ \begin{align} \Phi\circ\alpha^{\mathbf{n}}_{X_1/X_1^{\prime}}\circ\Gamma_1= \alpha^{\mathbf{n}}_{X_2/X_2^{\prime}}\circ\Gamma_2\circ\Phi \end{align} $$
for all
![]() $\mathbf {n}\in \mathbb {Z}^{d}$
.
$\mathbf {n}\in \mathbb {Z}^{d}$
.
Note that we have more rigidity for the factors than we had for joinings in Corollary 1.4. In particular, there is no need to consider finite index subactions in order to classify when two
![]() $\mathbb {Z}^{d}$
actions on tori have a common factor; we illustrate this point with the following example.
$\mathbb {Z}^{d}$
actions on tori have a common factor; we illustrate this point with the following example.
Example 9.2. Let
![]() $\alpha _1 $
be the
$\alpha _1 $
be the
![]() $\mathbb {Z}^2$
-action by automorphisms of the solenoid
$\mathbb {Z}^2$
-action by automorphisms of the solenoid
![]() $X_1$
dual to
$X_1$
dual to
![]() ${\mathbb {Z}[1/2,1/3]}$
generated by multiplication by
${\mathbb {Z}[1/2,1/3]}$
generated by multiplication by
![]() $2$
and by
$2$
and by
![]() $3$
on
$3$
on
![]() $X_1$
(i.e. the
$X_1$
(i.e. the
![]() $\alpha _1$
action on
$\alpha _1$
action on
![]() $X_1$
is the invertible extension of the
$X_1$
is the invertible extension of the
![]() $\times 2, \times 3$
action on
$\times 2, \times 3$
action on
![]() $\mathbb {T}$
). We define a
$\mathbb {T}$
). We define a
![]() $\mathbb {Z}^2$
-action
$\mathbb {Z}^2$
-action
![]() $\alpha _2 $
on
$\alpha _2 $
on
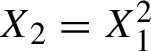 $X_2=X_1^2 $
by
$X_2=X_1^2 $
by
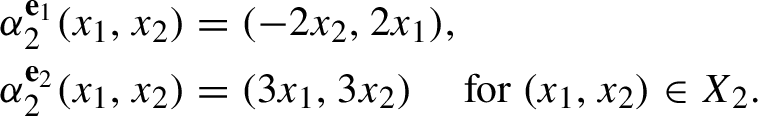 $$ \begin{align*} \alpha_2^{\mathbf{e}_1}(x_1,x_2)&=(-2x_2,2x_1),\\ \alpha_2^{\mathbf{e}_2}(x_1,x_2)&=(3x_1,3x_2)\quad\mbox{ for }(x_1,x_2)\in X_2. \end{align*} $$
$$ \begin{align*} \alpha_2^{\mathbf{e}_1}(x_1,x_2)&=(-2x_2,2x_1),\\ \alpha_2^{\mathbf{e}_2}(x_1,x_2)&=(3x_1,3x_2)\quad\mbox{ for }(x_1,x_2)\in X_2. \end{align*} $$
Then
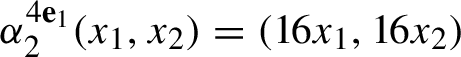 $\alpha _2^{4\mathbf {e}_1}(x_1,x_2)=(16x_1,16x_2)$
for
$\alpha _2^{4\mathbf {e}_1}(x_1,x_2)=(16x_1,16x_2)$
for
![]() $(x_1,x_2)\in X_2$
and so the restriction
$(x_1,x_2)\in X_2$
and so the restriction
![]() $\alpha _{2,\Lambda }$
of
$\alpha _{2,\Lambda }$
of
![]() $\alpha _2$
to
$\alpha _2$
to
![]() $\Lambda =(4\mathbb {Z})\times \mathbb {Z}$
is identical to the action
$\Lambda =(4\mathbb {Z})\times \mathbb {Z}$
is identical to the action
![]() $\alpha _{1,\Lambda }\times \alpha _{1,\Lambda }$
on
$\alpha _{1,\Lambda }\times \alpha _{1,\Lambda }$
on
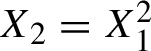 $X_2=X_1^2$
. By Theorem 1.4
$X_2=X_1^2$
. By Theorem 1.4
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2 $
are not disjoint. In fact, let
$\alpha _2 $
are not disjoint. In fact, let
Then
![]() $\pi _1(Z)=X_1$
and
$\pi _1(Z)=X_1$
and
![]() $\pi _2(Z)=X_2$
. Therefore, the Haar measure
$\pi _2(Z)=X_2$
. Therefore, the Haar measure
![]() $m_Z$
of Z satisfies
$m_Z$
of Z satisfies
![]() $(\pi _1)_*m_Z=m_{X_1}$
and
$(\pi _1)_*m_Z=m_{X_1}$
and
![]() $(\pi _2)_*m_Z=m_{X_2}$
. Since Z is only invariant under
$(\pi _2)_*m_Z=m_{X_2}$
. Since Z is only invariant under
![]() $(\alpha _1\times \alpha _2)_\Lambda $
,
$(\alpha _1\times \alpha _2)_\Lambda $
,
![]() $m_Z$
is not a joining. However, it is easy to check that
$m_Z$
is not a joining. However, it is easy to check that
 $\mu =\tfrac {1}{4}\sum _{j=0}^3(\alpha _1\times \alpha _2)^{j\mathbf {e}_1}m_Z$
is a non-trivial joining between
$\mu =\tfrac {1}{4}\sum _{j=0}^3(\alpha _1\times \alpha _2)^{j\mathbf {e}_1}m_Z$
is a non-trivial joining between
![]() $\alpha _1 $
and
$\alpha _1 $
and
![]() $\alpha _2 $
.
$\alpha _2 $
.
We note that
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are both irreducible actions. Suppose now that
$\alpha _2$
are both irreducible actions. Suppose now that
![]() $\alpha _1 $
and
$\alpha _1 $
and
![]() $\alpha _2 $
have a common measurable factor. By Corollary 9.1, there exist closed invariant subgroups
$\alpha _2 $
have a common measurable factor. By Corollary 9.1, there exist closed invariant subgroups
![]() $X^{\prime }_1\subseteq X_1$
and
$X^{\prime }_1\subseteq X_1$
and
![]() $X_2^{\prime }\subseteq X_2$
such that
$X_2^{\prime }\subseteq X_2$
such that
![]() $X_1/X^{\prime }_1$
and
$X_1/X^{\prime }_1$
and
![]() $X_2/X_2^{\prime }$
are isomorphic as groups. By irreducibility,
$X_2/X_2^{\prime }$
are isomorphic as groups. By irreducibility,
![]() $X^{\prime }_1$
and
$X^{\prime }_1$
and
![]() $X_2^{\prime }$
are either finite or everything. However, if
$X_2^{\prime }$
are either finite or everything. However, if
![]() $X^{\prime }_1$
and
$X^{\prime }_1$
and
![]() $X_2^{\prime }$
are finite, then
$X_2^{\prime }$
are finite, then
![]() $X_1/X_1^{\prime }$
is still one-dimensional while
$X_1/X_1^{\prime }$
is still one-dimensional while
![]() $X_2/X_2^{\prime }$
is still two-dimensional, and so these groups cannot be isomorphic. Therefore,
$X_2/X_2^{\prime }$
is still two-dimensional, and so these groups cannot be isomorphic. Therefore,
![]() $X^{\prime }_1=X_1$
,
$X^{\prime }_1=X_1$
,
![]() $X_2^{\prime }=X_2$
, and the common measurable factor has to be the trivial factor.
$X_2^{\prime }=X_2$
, and the common measurable factor has to be the trivial factor.
Before we start with the proofs of Corollary 1.5 and Corollary 9.1, we recall some basic facts about conditional measures and the construction of the relatively independent joining.
9.1 The relatively independent joining
Let
![]() $\alpha _1,\alpha _2,\beta $
be
$\alpha _1,\alpha _2,\beta $
be
![]() $\mathbb {Z}^{d}$
-actions on the standard Borel probability spaces
$\mathbb {Z}^{d}$
-actions on the standard Borel probability spaces
![]() $(X_1,\mathcal {B}_1,m_1)$
,
$(X_1,\mathcal {B}_1,m_1)$
,
![]() $(X_2,\mathcal {B}_2,m_2)$
, and
$(X_2,\mathcal {B}_2,m_2)$
, and
![]() $(Y,\mathcal {B}_Y,\rho )$
, respectively, and let
$(Y,\mathcal {B}_Y,\rho )$
, respectively, and let
![]() $ \psi _1:X_1\rightarrow Y$
and
$ \psi _1:X_1\rightarrow Y$
and
![]() $ \psi _2:X_2\rightarrow Y$
be factor maps. Then
$ \psi _2:X_2\rightarrow Y$
be factor maps. Then
 $\mathcal {A}_1= \psi _1^{-1}\mathcal {B}_Y$
and
$\mathcal {A}_1= \psi _1^{-1}\mathcal {B}_Y$
and
 $\mathcal {A}_2= \psi _2^{-1}\mathcal {B}_Y$
are invariant
$\mathcal {A}_2= \psi _2^{-1}\mathcal {B}_Y$
are invariant
![]() $\sigma $
-algebras with conditional measures
$\sigma $
-algebras with conditional measures
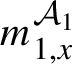 $m_{1,x}^{\mathcal {A}_1}$
for
$m_{1,x}^{\mathcal {A}_1}$
for
![]() $x\in X_1$
and
$x\in X_1$
and
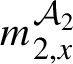 $m_{2,x}^{\mathcal {A}_2}$
for
$m_{2,x}^{\mathcal {A}_2}$
for
![]() $x\in X_2$
. By the basic properties of conditional measures, there is some null set
$x\in X_2$
. By the basic properties of conditional measures, there is some null set
![]() $N_1 \subset X_1$
so that
$N_1 \subset X_1$
so that
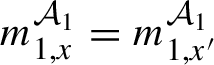 $m_{1,x}^{\mathcal {A}_1}=m_{1,x^{\prime }}^{\mathcal {A}_1}$
for every
$m_{1,x}^{\mathcal {A}_1}=m_{1,x^{\prime }}^{\mathcal {A}_1}$
for every
![]() $x,x^{\prime }\in X_1\setminus N_1$
with
$x,x^{\prime }\in X_1\setminus N_1$
with
![]() $ \psi _1(x)= \psi _1(x^{\prime })$
, and so we can remove a nullset from
$ \psi _1(x)= \psi _1(x^{\prime })$
, and so we can remove a nullset from
![]() $X_1$
and
$X_1$
and
![]() $ Y $
and define
$ Y $
and define
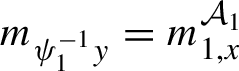 $m_{ \psi ^{-1}_1y}=m_{1,x}^{\mathcal {A}_1} $
for
$m_{ \psi ^{-1}_1y}=m_{1,x}^{\mathcal {A}_1} $
for
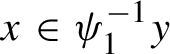 $x\in \psi ^{-1}_1y$
. We do this similarly for
$x\in \psi ^{-1}_1y$
. We do this similarly for
![]() $\mathcal {A}_2$
to define
$\mathcal {A}_2$
to define
![]() $m_{ \psi ^{-1}_2y} $
. The relatively independent joining
$m_{ \psi ^{-1}_2y} $
. The relatively independent joining
![]() $m_1\times _{(Y,\rho )}m_2$
of
$m_1\times _{(Y,\rho )}m_2$
of
![]() $m_1 $
and
$m_1 $
and
![]() $m_2 $
over the common factor
$m_2 $
over the common factor
![]() $(Y,\rho )$
is defined by
$(Y,\rho )$
is defined by
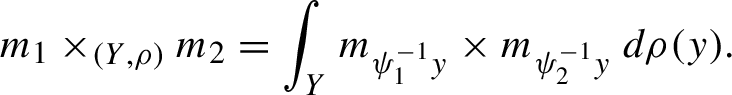 $$ \begin{align} m_1\times_{(Y,\rho)}m_2= \int_Y m_{ \psi^{-1}_1y}\times m_{ \psi^{-1}_2y}\,d\rho(y). \end{align} $$
$$ \begin{align} m_1\times_{(Y,\rho)}m_2= \int_Y m_{ \psi^{-1}_1y}\times m_{ \psi^{-1}_2y}\,d\rho(y). \end{align} $$
It is well known (and easy to verify directly) that
![]() $m_1\times _{(Y,\rho )}m_2 $
projects to
$m_1\times _{(Y,\rho )}m_2 $
projects to
![]() $m_1$
on
$m_1$
on
![]() $X_1$
and to
$X_1$
and to
![]() $m_2$
on
$m_2$
on
![]() $X_2$
and that
$X_2$
and that
![]() $m_1\times _{(Y,\rho )}m_2 $
is invariant under
$m_1\times _{(Y,\rho )}m_2 $
is invariant under
![]() $\alpha _1\times \alpha _2$
(hence is a joining between
$\alpha _1\times \alpha _2$
(hence is a joining between
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2 $
). Furthermore, the relatively independent joining
$\alpha _2 $
). Furthermore, the relatively independent joining
![]() $ m_1\times _{(Y,\rho )}m_2$
gives full measure to the set
$ m_1\times _{(Y,\rho )}m_2$
gives full measure to the set
and moreover
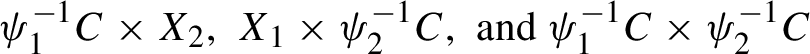 $$ \begin{align*} \psi_1^{-1}C\times X_2,\ X_1\times \psi_2^{-1}C,\mbox{ and } \psi_1^{-1}C\times \psi_2^{-1}C \end{align*} $$
$$ \begin{align*} \psi_1^{-1}C\times X_2,\ X_1\times \psi_2^{-1}C,\mbox{ and } \psi_1^{-1}C\times \psi_2^{-1}C \end{align*} $$
are equal up to a
![]() $m_1\times _{(Y,\rho )}m_2$
-nullset for any
$m_1\times _{(Y,\rho )}m_2$
-nullset for any
![]() $C\in \mathcal {B}_Y$
.
$C\in \mathcal {B}_Y$
.
9.2 Proofs of Corollary 1.5 and Corollary 9.1
Let
![]() $\alpha _1,\alpha _2, X_1, X_2$
be as in Corollary 9.1, and suppose the
$\alpha _1,\alpha _2, X_1, X_2$
be as in Corollary 9.1, and suppose the
![]() $\mathbb {Z}^{d}$
-action
$\mathbb {Z}^{d}$
-action
![]() $\beta $
on
$\beta $
on
![]() $(Y,\mathcal {B}_Y,\rho )$
is a common factor of
$(Y,\mathcal {B}_Y,\rho )$
is a common factor of
![]() $\alpha _1 $
and
$\alpha _1 $
and
![]() $\alpha _2$
. Let
$\alpha _2$
. Let
![]() $ \psi _1$
and
$ \psi _1$
and
![]() $ \psi _2$
be the corresponding factor maps,
$ \psi _2$
be the corresponding factor maps,
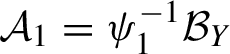 $\mathcal {A}_1= \psi _1^{-1}\mathcal {B}_Y$
and
$\mathcal {A}_1= \psi _1^{-1}\mathcal {B}_Y$
and
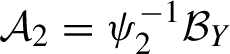 $\mathcal {A}_2= \psi _2^{-1}\mathcal {B}_Y$
the corresponding invariant
$\mathcal {A}_2= \psi _2^{-1}\mathcal {B}_Y$
the corresponding invariant
![]() $\sigma $
-algebras, and let
$\sigma $
-algebras, and let
![]() $\nu =\unicode{x3bb} _{X_1}{\times _{(Y,\rho )}}\unicode{x3bb} _{X_2}$
be the relatively independent joining.
$\nu =\unicode{x3bb} _{X_1}{\times _{(Y,\rho )}}\unicode{x3bb} _{X_2}$
be the relatively independent joining.
The main idea for the proof is to use Theorem 1.3 to study
![]() $\nu $
. In the following example, we see how the algebraic construction of the factor is encoded in the relatively independent joining, and that the latter does not have to be ergodic.
$\nu $
. In the following example, we see how the algebraic construction of the factor is encoded in the relatively independent joining, and that the latter does not have to be ergodic.
Example 9.3. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $\mathbb {Z}^{d}$
-action on a solenoid
$\mathbb {Z}^{d}$
-action on a solenoid
![]() $X $
, and let
$X $
, and let
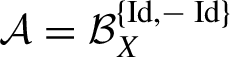 $\mathcal {A}=\mathcal {B}_X^{\{\operatorname {Id},-\operatorname {Id}\}}$
be the
$\mathcal {A}=\mathcal {B}_X^{\{\operatorname {Id},-\operatorname {Id}\}}$
be the
![]() $\alpha $
-invariant
$\alpha $
-invariant
![]() $\sigma $
-algebra of measurable subsets A satisfying
$\sigma $
-algebra of measurable subsets A satisfying
![]() $A=-A$
. Then the relatively independent joining
$A=-A$
. Then the relatively independent joining
![]() $\nu =\unicode{x3bb} _X{\times _{\mathcal {A}}} \unicode{x3bb} _X$
of
$\nu =\unicode{x3bb} _X{\times _{\mathcal {A}}} \unicode{x3bb} _X$
of
![]() $\unicode{x3bb} _X$
over the factor described by
$\unicode{x3bb} _X$
over the factor described by
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
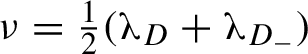 $\nu =\tfrac {1}{2}(\unicode{x3bb} _D+\unicode{x3bb} _{D_-})$
, where
$\nu =\tfrac {1}{2}(\unicode{x3bb} _D+\unicode{x3bb} _{D_-})$
, where
![]() $D=\{(x,x):x\in X\}$
and
$D=\{(x,x):x\in X\}$
and
![]() $D_-=\{(x,-x):x\in X\}$
. The ergodic components of
$D_-=\{(x,-x):x\in X\}$
. The ergodic components of
![]() $\nu $
are
$\nu $
are
![]() $\unicode{x3bb} _D$
and
$\unicode{x3bb} _D$
and
![]() $\unicode{x3bb} _{D_-}$
.
$\unicode{x3bb} _{D_-}$
.
This example shows that for the relatively independent joining over a factor, we have to take ergodic components in order to apply Theorem 1.3. However, in general, we also have to take ergodic components as in Theorem 1.3 with respect to a finite index subgroup to obtain measures invariant under translation by elements of certain subgroups.
Lemma 9.4. The set
is a closed
![]() $\alpha $
-invariant subgroup of
$\alpha $
-invariant subgroup of
![]() $X_1$
. Furthermore,
$X_1$
. Furthermore,
![]() $ \psi _1$
descends (on the complement of a nullset) to a well-defined factor map from
$ \psi _1$
descends (on the complement of a nullset) to a well-defined factor map from
![]() $X_1/X_1^{\prime }$
to Y.
$X_1/X_1^{\prime }$
to Y.
Proof Since
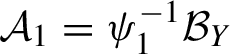 $\mathcal {A}_1= \psi _1^{-1}\mathcal {B}_Y$
is countably generated, it is easily seen that
$\mathcal {A}_1= \psi _1^{-1}\mathcal {B}_Y$
is countably generated, it is easily seen that
Furthermore, it is well known that
![]() $\unicode{x3bb} _{X_1}(A\vartriangle (A+x^{\prime }))$
depends continuously on
$\unicode{x3bb} _{X_1}(A\vartriangle (A+x^{\prime }))$
depends continuously on
![]() $x^{\prime }\in X$
for any
$x^{\prime }\in X$
for any
![]() $A\in \mathcal {B}_{X_1}$
. From this, it follows that
$A\in \mathcal {B}_{X_1}$
. From this, it follows that
![]() $X_1^{\prime }$
is a closed subgroup. Moreover,
$X_1^{\prime }$
is a closed subgroup. Moreover,
![]() $X_1^{\prime }$
is
$X_1^{\prime }$
is
![]() $\alpha _1$
-invariant since
$\alpha _1$
-invariant since
![]() $\mathcal {A}_1$
is invariant (equivalently, since
$\mathcal {A}_1$
is invariant (equivalently, since
![]() $ \psi _1$
is a factor map).
$ \psi _1$
is a factor map).
Note that
![]() $ \psi _1(t)= \psi _1(t+x^{\prime })$
for
$ \psi _1(t)= \psi _1(t+x^{\prime })$
for
![]() $\unicode{x3bb} _{X_1}\times \unicode{x3bb} _{X_1^{\prime }}$
-a.e.
$\unicode{x3bb} _{X_1}\times \unicode{x3bb} _{X_1^{\prime }}$
-a.e.
![]() $(t,x^{\prime })\in X_1\times X_1^{\prime }$
by definition of
$(t,x^{\prime })\in X_1\times X_1^{\prime }$
by definition of
![]() $X_1^{\prime }$
and Fubini’s theorem. Therefore, for
$X_1^{\prime }$
and Fubini’s theorem. Therefore, for
![]() $ \unicode{x3bb} _{X_1}$
-a.e.
$ \unicode{x3bb} _{X_1}$
-a.e.
![]() $t\in X_1$
, we know that
$t\in X_1$
, we know that
![]() $ \psi _1(t)= \psi _1(t+x^{\prime })$
for
$ \psi _1(t)= \psi _1(t+x^{\prime })$
for
![]() $ \unicode{x3bb} _{X_1^{\prime }}$
-a.e.
$ \unicode{x3bb} _{X_1^{\prime }}$
-a.e.
![]() $x^{\prime }\in X_1^{\prime }$
. Therefore,
$x^{\prime }\in X_1^{\prime }$
. Therefore,
![]() $ \psi _1(t)$
is (outside some nullset) independent of the representative
$ \psi _1(t)$
is (outside some nullset) independent of the representative
![]() $t\in X_1$
of the coset
$t\in X_1$
of the coset
![]() $t+X_1^{\prime }$
, which implies the second part of the lemma.
$t+X_1^{\prime }$
, which implies the second part of the lemma.
By Lemma 9.4, we can replace
![]() $X_1$
by
$X_1$
by
![]() $X_1/X_1^{\prime }$
and similarly
$X_1/X_1^{\prime }$
and similarly
![]() $X_2$
by
$X_2$
by
![]() $X_2/X_2^{\prime }$
for the remainder of the proof. Hence we assume that
$X_2/X_2^{\prime }$
for the remainder of the proof. Hence we assume that
and similarly for
![]() $X_2$
, and will show the existence of finite groups
$X_2$
, and will show the existence of finite groups
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
of affine automorphisms of
$\Gamma _2$
of affine automorphisms of
![]() $X_1$
and
$X_1$
and
![]() $X_2$
, and the existence of the affine isomorphism
$X_2$
, and the existence of the affine isomorphism
![]() $\Phi :X_1\rightarrow X_2$
satisfying (9.1).
$\Phi :X_1\rightarrow X_2$
satisfying (9.1).
Since Theorem 1.3 assumes ergodicity, we need to study the ergodic components of the relatively independent joining. The following easy consequence of the definition of the ergodic decomposition gives all the properties we will need for the ergodic components.
Lemma 9.5. Almost every ergodic component
![]() $\mu $
of the relatively independent joining
$\mu $
of the relatively independent joining
![]() $\nu $
of
$\nu $
of
![]() $X_1$
and
$X_1$
and
![]() $X_2$
over Y is still a joining between
$X_2$
over Y is still a joining between
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
that satisfies
$\alpha _2$
that satisfies
![]() $\mu (D_Y)=1$
, where
$\mu (D_Y)=1$
, where
![]() $D_Y$
is defined as in (9.3).
$D_Y$
is defined as in (9.3).
In the next lemma, we analyze what translation invariance for a measure
![]() $\mu $
as above tells us about the factor maps.
$\mu $
as above tells us about the factor maps.
Lemma 9.6. Let
![]() $\mu $
be a measure on
$\mu $
be a measure on
![]() $X_1\times X_2 $
that projects to the Haar measure
$X_1\times X_2 $
that projects to the Haar measure
![]() $ \unicode{x3bb} _{X_1}$
respectively
$ \unicode{x3bb} _{X_1}$
respectively
![]() $ \unicode{x3bb} _{X_2}$
and satisfies
$ \unicode{x3bb} _{X_2}$
and satisfies
![]() $\mu (D_Y)=1$
where
$\mu (D_Y)=1$
where
![]() $D_Y$
is defined in (9.3). Suppose
$D_Y$
is defined in (9.3). Suppose
![]() $\mu $
is translation invariant under elements of
$\mu $
is translation invariant under elements of
![]() $G\subset X_1\times X_2 $
and that G projects surjectively to
$G\subset X_1\times X_2 $
and that G projects surjectively to
![]() $X_1$
and
$X_1$
and
![]() $X_2$
. Then G is the graph of a group isomorphism
$X_2$
. Then G is the graph of a group isomorphism
![]() $\phi :X_1\rightarrow X_2$
. Moreover, there exists some
$\phi :X_1\rightarrow X_2$
. Moreover, there exists some
![]() $w_\phi \in X_2$
such that the affine isomorphism
$w_\phi \in X_2$
such that the affine isomorphism
![]() $\Phi (x)=\phi (x)+w_\phi $
satisfies
$\Phi (x)=\phi (x)+w_\phi $
satisfies
and that
![]() $\mu $
is the Haar measure of the graph of
$\mu $
is the Haar measure of the graph of
![]() $\Phi $
. The element
$\Phi $
. The element
![]() $w_\phi \in X_2$
is uniquely determined by
$w_\phi \in X_2$
is uniquely determined by
![]() $\phi $
and (9.5).
$\phi $
and (9.5).
Proof Suppose
![]() $(x^{\prime },0)\in G$
,
$(x^{\prime },0)\in G$
,
![]() $C\in \mathcal {B}_Y$
, and
$C\in \mathcal {B}_Y$
, and
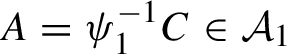 $A= \psi _1^{-1}C\in \mathcal {A}_1$
. Then
$A= \psi _1^{-1}C\in \mathcal {A}_1$
. Then
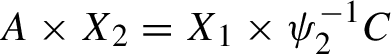 $A\times X_2= X_1\times \psi _2^{-1}C$
(modulo
$A\times X_2= X_1\times \psi _2^{-1}C$
(modulo
![]() $\mu $
) and
$\mu $
) and
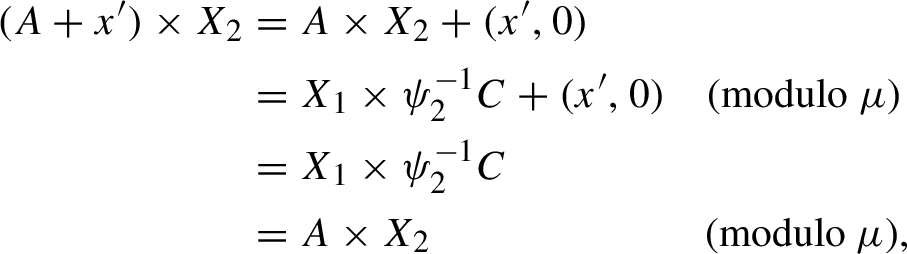 $$ \begin{align*} (A+x^{\prime})\times X_2&=A\times X_2+(x^{\prime},0)\\ &=X_1\times \psi_2^{-1}C+(x^{\prime},0)\quad\text{(modulo}\ \mu\text{)}\\ &=X_1\times \psi_2^{-1}C\\ &=A\times X_2\qquad\qquad\qquad\,{\kern0.7pt}\text{ (modulo}\ \mu\text{)}, \end{align*} $$
$$ \begin{align*} (A+x^{\prime})\times X_2&=A\times X_2+(x^{\prime},0)\\ &=X_1\times \psi_2^{-1}C+(x^{\prime},0)\quad\text{(modulo}\ \mu\text{)}\\ &=X_1\times \psi_2^{-1}C\\ &=A\times X_2\qquad\qquad\qquad\,{\kern0.7pt}\text{ (modulo}\ \mu\text{)}, \end{align*} $$
where we used invariance of
![]() $\mu $
under translation by
$\mu $
under translation by
![]() $(x^{\prime },0)$
in the transition from the first to the second line. It follows that
$(x^{\prime },0)$
in the transition from the first to the second line. It follows that
for any
![]() $A \in \mathcal {A}_1$
and so
$A \in \mathcal {A}_1$
and so
![]() $x^{\prime }\in X_1^{\prime }$
. Therefore,
$x^{\prime }\in X_1^{\prime }$
. Therefore,
![]() $x^{\prime }=0$
by assumption (9.4). The same holds for elements of the form
$x^{\prime }=0$
by assumption (9.4). The same holds for elements of the form
![]() $(0,x^{\prime })\in G$
. Together with our assumption that G projects onto
$(0,x^{\prime })\in G$
. Together with our assumption that G projects onto
![]() $X_1$
and onto
$X_1$
and onto
![]() $X_2$
, this implies that G is the graph of a group isomorphisms
$X_2$
, this implies that G is the graph of a group isomorphisms
![]() $\phi :X_1\rightarrow X_2$
.
$\phi :X_1\rightarrow X_2$
.
We show next that
![]() $w_\phi $
is uniquely determined. So suppose
$w_\phi $
is uniquely determined. So suppose
![]() $w,w^{\prime }\in X_2$
are such that (9.5) holds independently of whether
$w,w^{\prime }\in X_2$
are such that (9.5) holds independently of whether
![]() $\Phi $
is defined using w or using
$\Phi $
is defined using w or using
![]() $w^{\prime }$
. Let
$w^{\prime }$
. Let
![]() $v=\phi ^{-1}(w-w^{\prime })$
. Then
$v=\phi ^{-1}(w-w^{\prime })$
. Then
for
![]() $ \unicode{x3bb} _{X_1}$
-a.e.
$ \unicode{x3bb} _{X_1}$
-a.e.
![]() $x\in X$
. Therefore,
$x\in X$
. Therefore,
![]() $v\in X_1=\{0\}$
(by (9.4) again) and
$v\in X_1=\{0\}$
(by (9.4) again) and
![]() $w=w^{\prime }$
.
$w=w^{\prime }$
.
It remains to show the existence of
![]() $w_\phi $
and that
$w_\phi $
and that
![]() $\mu $
is the Haar measure of the graph of
$\mu $
is the Haar measure of the graph of
![]() $\Phi $
. Since
$\Phi $
. Since
![]() $\mu $
is invariant under translation by elements of G and since
$\mu $
is invariant under translation by elements of G and since
![]() $\mu (D_Y)=1$
, it follows that
$\mu (D_Y)=1$
, it follows that
In other words, we know for
![]() $\mu \times \unicode{x3bb} _{X_1}$
-a.e.
$\mu \times \unicode{x3bb} _{X_1}$
-a.e.
![]() $((z_1,z_2),x)\in (X_1\times X_2)\times X_1$
that
$((z_1,z_2),x)\in (X_1\times X_2)\times X_1$
that
![]() $(z_1,z_2)+(x,\phi (x))\in D_Y$
. By Fubini’s theorem, this shows for
$(z_1,z_2)+(x,\phi (x))\in D_Y$
. By Fubini’s theorem, this shows for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $(z_1,z_2)\in X_1\times X_2$
that
$(z_1,z_2)\in X_1\times X_2$
that
However, by definition of
![]() $D_Y$
, this is equivalent to
$D_Y$
, this is equivalent to
We define
![]() $w=z_2-\phi (z_1)$
, then (9.5) follows for
$w=z_2-\phi (z_1)$
, then (9.5) follows for
![]() $\Phi (x)=\phi (x)+w$
. However, by uniqueness
$\Phi (x)=\phi (x)+w$
. However, by uniqueness
![]() $w=w_\phi $
is independent of
$w=w_\phi $
is independent of
![]() $(z_1,z_2)$
. Therefore,
$(z_1,z_2)$
. Therefore,
![]() $z_2=\phi (z_1)+w_\phi $
and
$z_2=\phi (z_1)+w_\phi $
and
![]() $(z_1,z_2)$
belong to the graph of
$(z_1,z_2)$
belong to the graph of
![]() $\Phi (x)=\phi (x)+w_\phi $
. This holds for
$\Phi (x)=\phi (x)+w_\phi $
. This holds for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $(z_1,z_2)$
, and together with invariance of
$(z_1,z_2)$
, and together with invariance of
![]() $\mu $
under translation by elements of G, it follows that
$\mu $
under translation by elements of G, it follows that
![]() $\mu $
is the Haar measure of the graph of
$\mu $
is the Haar measure of the graph of
![]() $\Phi $
.
$\Phi $
.
Finally, we can describe the structure of the relatively independent joining.
Lemma 9.7. The relatively independent joining is a convex combination
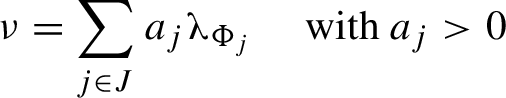
of at most countably many Haar measures
![]() $\unicode{x3bb} _{\Phi _j}$
on graphs of affine isomorphisms
$\unicode{x3bb} _{\Phi _j}$
on graphs of affine isomorphisms
![]() $\Phi _j$
that satisfy (9.5).
$\Phi _j$
that satisfy (9.5).
Proof Let
![]() $\mu $
be an ergodic component of
$\mu $
be an ergodic component of
![]() $\nu $
as in Lemma 9.5. By Theorem 1.3, there exist
$\nu $
as in Lemma 9.5. By Theorem 1.3, there exist
![]() $\mu _1,\ldots ,\mu_{M}$
and
$\mu _1,\ldots ,\mu_{M}$
and
![]() $G_1,\ldots ,G_M$
, such that
$G_1,\ldots ,G_M$
, such that
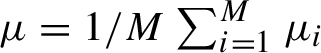 $\mu ={1}/{M}\sum _{i=1}^M \mu _i$
and
$\mu ={1}/{M}\sum _{i=1}^M \mu _i$
and
![]() $\mu _i$
is invariant under translation by elements of
$\mu _i$
is invariant under translation by elements of
![]() $G_i$
. By Proposition 8.1, each
$G_i$
. By Proposition 8.1, each
![]() $G_i$
projects surjectively to
$G_i$
projects surjectively to
![]() $X_1$
and
$X_1$
and
![]() $X_2$
. Therefore, Lemma 9.6 shows that
$X_2$
. Therefore, Lemma 9.6 shows that
![]() $\mu _i$
is the Haar measure
$\mu _i$
is the Haar measure
![]() $ \unicode{x3bb} _{\Phi }$
of the graph of an affine isomorphism
$ \unicode{x3bb} _{\Phi }$
of the graph of an affine isomorphism
![]() $\Phi (x)=\phi (x)+w_\phi $
that satisfies (9.5).
$\Phi (x)=\phi (x)+w_\phi $
that satisfies (9.5).
We claim that there are at most countably many group isomorphisms
![]() $\phi :X_1\rightarrow X_2$
. Since
$\phi :X_1\rightarrow X_2$
. Since
![]() $\phi $
uniquely determines
$\phi $
uniquely determines
![]() $w_\phi $
,
$w_\phi $
,
![]() $\Phi $
,
$\Phi $
,
![]() $\mu _i$
, and by ergodicity also
$\mu _i$
, and by ergodicity also
![]() $\mu $
, the above claim implies that there are at most countably many ergodic components
$\mu $
, the above claim implies that there are at most countably many ergodic components
![]() $\mu $
, each of which is a convex combinations of Haar measures.
$\mu $
, each of which is a convex combinations of Haar measures.
To prove the claim, it is enough to notice that every
![]() $\phi $
as above is uniquely determined by its dual
$\phi $
as above is uniquely determined by its dual
![]() $\hat \phi :\hat X_2 \rightarrow \hat X_1$
that is the restriction of a
$\hat \phi :\hat X_2 \rightarrow \hat X_1$
that is the restriction of a
![]() $\mathbb Q$
-linear map from
$\mathbb Q$
-linear map from
![]() $\mathbb Q^{n_2}\supseteq \hat X_2$
to
$\mathbb Q^{n_2}\supseteq \hat X_2$
to
![]() ${\mathbb Q^{n_1}\supseteq \hat X_1}$
.
${\mathbb Q^{n_1}\supseteq \hat X_1}$
.
Proof Proof of Corollary 1.5
It is well known that every invariant
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A} $
can be realized as
$\mathcal {A} $
can be realized as
![]() $ \psi ^{-1}\mathcal {B}_Y$
for some factor map
$ \psi ^{-1}\mathcal {B}_Y$
for some factor map
![]() $ \psi :X\rightarrow Y$
and some
$ \psi :X\rightarrow Y$
and some
![]() $\mathbb {Z}^{d}$
-action on a standard Borel probability space
$\mathbb {Z}^{d}$
-action on a standard Borel probability space
![]() $(Y,\mathcal {B}_Y,\rho )$
. Recall that by Lemma 9.4, we may assume that (9.4) holds.
$(Y,\mathcal {B}_Y,\rho )$
. Recall that by Lemma 9.4, we may assume that (9.4) holds.
Let
![]() $\nu $
be the relatively independent joining of
$\nu $
be the relatively independent joining of
![]() $\unicode{x3bb} _X$
and
$\unicode{x3bb} _X$
and
![]() $\unicode{x3bb} _X$
over
$\unicode{x3bb} _X$
over
![]() $(Y,\rho )$
. Let
$(Y,\rho )$
. Let
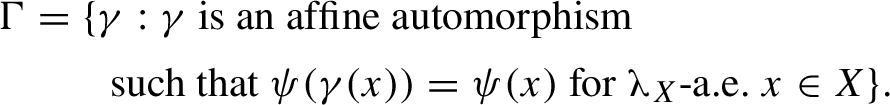
Then
![]() $\Gamma $
is a group normalized by
$\Gamma $
is a group normalized by
![]() $\alpha $
that is at most countable (see proof of Lemma 9.7) and satisfies
$\alpha $
that is at most countable (see proof of Lemma 9.7) and satisfies
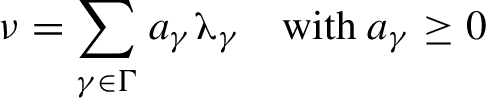
by Lemma 9.7. From the construction (9.2) of the relatively independent joining, it follows that the conditional measures of
![]() $\nu $
with respect to the
$\nu $
with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {C}=\mathcal {B}_X\times \{\emptyset ,X\}$
are
$\mathcal {C}=\mathcal {B}_X\times \{\emptyset ,X\}$
are

However, from the above decomposition of
![]() $\nu $
, it is also easy to calculate the conditional measures of
$\nu $
, it is also easy to calculate the conditional measures of
![]() $\nu $
with respect to
$\nu $
with respect to
![]() $\mathcal {C}$
, which shows that
$\mathcal {C}$
, which shows that
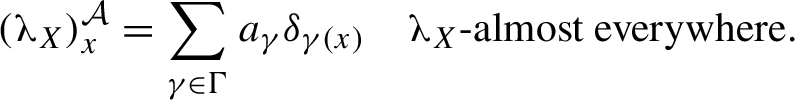
Since every
![]() $\gamma _0\in \Gamma $
preserves
$\gamma _0\in \Gamma $
preserves
![]() $ \unicode{x3bb} _X$
and
$ \unicode{x3bb} _X$
and
![]() $\mathcal {A}$
, it follows that
$\mathcal {A}$
, it follows that
 $(\unicode{x3bb} _{X})_{\gamma _0 x}^{\mathcal {A}}=(\gamma _0)_*(\unicode{x3bb} _{X})_x^{\mathcal {A}}$
almost everywhere, and hence
$(\unicode{x3bb} _{X})_{\gamma _0 x}^{\mathcal {A}}=(\gamma _0)_*(\unicode{x3bb} _{X})_x^{\mathcal {A}}$
almost everywhere, and hence
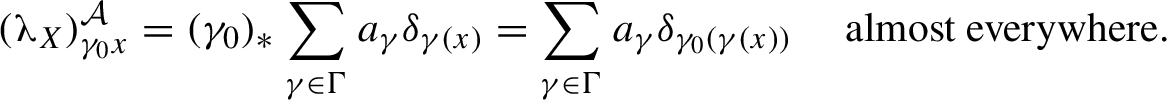
However, by definition
![]() $\gamma _0$
also preserves a.e. atom of
$\gamma _0$
also preserves a.e. atom of
![]() $\mathcal {A}$
and so
$\mathcal {A}$
and so
 $(\unicode{x3bb} _{X})_{\gamma _0 x}^{\mathcal {A}}=(\unicode{x3bb} _{X})_x^{\mathcal {A}}$
almost everywhere, hence
$(\unicode{x3bb} _{X})_{\gamma _0 x}^{\mathcal {A}}=(\unicode{x3bb} _{X})_x^{\mathcal {A}}$
almost everywhere, hence
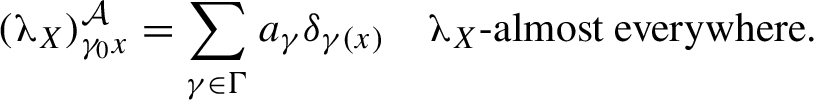
By comparing the above two displayed formulæ we conclude that
![]() $\Gamma $
is finite, and all the coefficients
$\Gamma $
is finite, and all the coefficients
![]() $a_{\gamma _0}$
are equal to each other, that is to say
$a_{\gamma _0}$
are equal to each other, that is to say
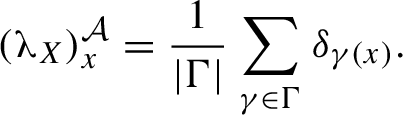
Since the conditional measures determine the
![]() $\sigma $
-algebra (modulo
$\sigma $
-algebra (modulo
![]() $ \unicode{x3bb} _X$
), the corollary follows.
$ \unicode{x3bb} _X$
), the corollary follows.
Proof Proof of Corollary 9.1
We already constructed
![]() $X_1^{\prime }$
and
$X_1^{\prime }$
and
![]() $X_2^{\prime } $
in Lemma 9.4. Applying Corollary 1.5, we find
$X_2^{\prime } $
in Lemma 9.4. Applying Corollary 1.5, we find
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2 $
. Finally, let
$\Gamma _2 $
. Finally, let
![]() $\Phi :X_1\rightarrow X_2$
be an affine isomorphism as in (9.5) that exists by Lemma 9.7. Then
$\Phi :X_1\rightarrow X_2$
be an affine isomorphism as in (9.5) that exists by Lemma 9.7. Then
![]() $\Phi ^{-1}\circ \gamma _2\circ \Phi $
belongs to
$\Phi ^{-1}\circ \gamma _2\circ \Phi $
belongs to
![]() $\Gamma _1$
(defined as in (9.6)) for any
$\Gamma _1$
(defined as in (9.6)) for any
![]() $\gamma _2\in \Gamma _2$
. By symmetry,
$\gamma _2\in \Gamma _2$
. By symmetry,
![]() $\Gamma _2\circ \Phi =\Phi \circ \Gamma _1$
which concludes the proof.
$\Gamma _2\circ \Phi =\Phi \circ \Gamma _1$
which concludes the proof.
Acknowledgements
M.E. acknowledges the support by SNF (grant no. 200020-178958) E.L. was supported by ERC 2020 grant HomDyn (grant no. 833423). Both authors thank the Hausdorff Research Institute for Mathematics at the Universität Bonn for its hospitality during the trimester program ‘Dynamics: Topology and Numbers’.