1. Introduction
Cold-room analyses of ice specimens extracted from cores drilled through polar ice disclose a dependence of the mechanical properties of polycrystalline ice upon the geometrical arrangement of the crystallites relative to one another (Reference Jacka and BuddJacka and Budd, 1989). This arrangement changes with the position in the borehole and is responsible for the induced anisotropy manifested in the ice of polar ice sheets. Other effects, such as the content of dust and other impurities, also play a role but are today thought to be less significant than 20 years ago.
The flow law of polycrystalline ice must account for this variability; the restriction to Glen’s isotropic flow law for ice fails to account for these effects. The problem is that in an ice specimen consisting of a large (ideally infinite) number of crystallites, the mechanical behaviour responds to interactions between neighbouring crystallites that determine the (macro) behaviour of the polycrystalline ice. Constructing such a macroscopic description from the detailed material science and thermodynamics of the microscopic properties and processes, called homogenization, is complex, and here we focus on a simplified treatment.
One important idealization in an attempt to describe a polycrystalline material is to suppose that a representative volume element (the specimen) contains an infinite number of crystallites which can be distinguished by their lattice orientation. To do this in a simplified way, we introduce at each point an additional two-dimensional space, the orientational space S2, defined as the surface of a unit sphere (cf. Reference Abraham, Marsden and RatiuAbraham and others, 1988). Each point of the surface of such a sphere represents a particular c-axis orientation and is denoted by a single radial unit vector ni, called orientation vector. A field of c axes is defined within every crystallite, in such a manner that, if ϱ(xi,t) denotes the mass density field of the ice composite (i.e. the mass of ice per unit volume), then ϱ* (xi,t,nj) d2 n defines the part of that field which at time t and position xi has the c axis oriented towards nj within the solid angle d2 n of the spherical surface S 2. In other words, ϱ* describes a kind of orientational distribution of crystalline mass. As a consequence, integration of ϱ* (xi , t, nj) over the entire unit sphere S 2 yields the density of ice ϱ(xi,t), i.e.
Here and in the following, ‘*’ denotes quantities that have a dependence upon nj .
Equation (1) is an example of how the homogenization from the micro- to the macroscale is executed for a given microstructure. An evolution equation is needed which describes how ϱ* (xi , t, nj changes with space and time.
Let vi be the translational velocity (with the incompressibility condition ∂vi/∂xi = 0 already taken into account), and ![]() a recrystallization production term (the fraction of the mass of the polycrystal that the crystallites with a given c-axis orientation ni
lose or gain from the other crystallites during grain boundary migration), to be prescribed by a constitutive relation. Then, the balance equation of mass can be expressed, as proposed by Reference Faria, Kremer and HutterFaria and others (2003), by
a recrystallization production term (the fraction of the mass of the polycrystal that the crystallites with a given c-axis orientation ni
lose or gain from the other crystallites during grain boundary migration), to be prescribed by a constitutive relation. Then, the balance equation of mass can be expressed, as proposed by Reference Faria, Kremer and HutterFaria and others (2003), by
where![]() is the rate of change of orientations (also called orientational velocity or transition rate) and
is the rate of change of orientations (also called orientational velocity or transition rate) and
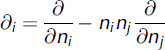
is the orientational gradient operator, which in spherical coordinates can be expressed as the usual (spatial) gradient operator on a sphere of fixed unit radius. Integration of Equation (2) over all orientations gives
which is simply an expression of the conservation of mass within the polycrystal.
2. Grain Boundary Migration and Nucleation
One of the main processes that is considered to influence the interaction of the crystallites at the microscale is the motion of the grain boundaries. Grain growth occurs when a large portion of the boundary of the grain is moving. The migration of the grain boundary is associated with the transfer of mass from one ice crystallite to its neighbour, and this corresponds to the recrystallization production term![]() and to a change in the distribution of the orientation of the crystallites. In the example shown in Figure 1, we have a simple mathematical interpretation, namely
and to a change in the distribution of the orientation of the crystallites. In the example shown in Figure 1, we have a simple mathematical interpretation, namely
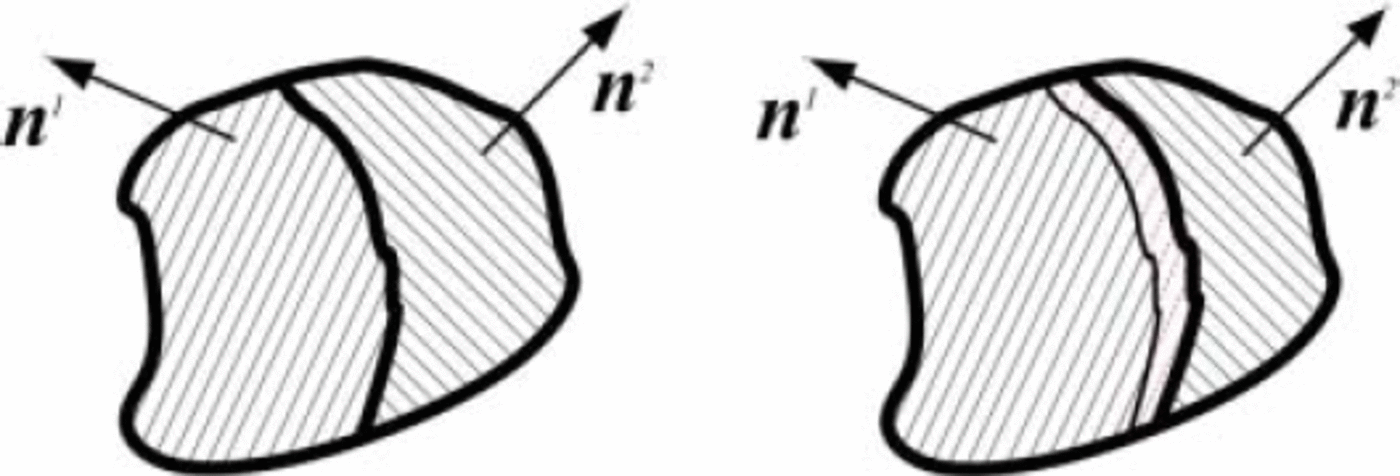
Fig. 1. Schematic two-dimensional illustration of grain boundary migration. The boundary between grains ‘1’ and ‘2’ migrates so that grain ‘1’ grows while grain ‘2’ shrinks. The parallel thin lines represent the basal planes of the two grains. Where boundary passes, the dislocation density decreases to almost zero. Basal planes represented by thin dashed lines indicate that the dislocation density in that region is very low.
Of different nature is the creation of new crystallites which generally occurs at large depths where the temperature is ≈263 K. Here, a small portion of the boundary of a grain bulges and starts to migrate uncontrollably in all directions, leaving behind it a large region of almost vanishing dislocation density. This crystal growth, also called recrystallization, can also be modelled by the specific mass production![]() appearing in Equation (2); even in this case some grains (e.g. grain ‘1’ in Fig. 1 which may have been created by nucleation) are enlarged and other grains (e.g. grain ‘2’ in Fig. 1) are shrunk. Besides, the mass of the entire polycrystal does not change and the loss and the gain of mass of the single crystallites are linked by Equation (4). Equation (4), originally assumed for an infinite number of crystallites, can also be applied to the example with only two crystallites shown in Figure 1 as follows:
appearing in Equation (2); even in this case some grains (e.g. grain ‘1’ in Fig. 1 which may have been created by nucleation) are enlarged and other grains (e.g. grain ‘2’ in Fig. 1) are shrunk. Besides, the mass of the entire polycrystal does not change and the loss and the gain of mass of the single crystallites are linked by Equation (4). Equation (4), originally assumed for an infinite number of crystallites, can also be applied to the example with only two crystallites shown in Figure 1 as follows:
Another important microscopic process to be analyzed in the next section is polygonization and its relation with grain growth.
3. Polygonization and Grain Growth
The stress distribution and the deformation in a polycrystal give rise to micromechanical processes influencing the macro behaviour of a polycrystalline ice specimen. Both stress and strain (rate) are generally inhomogeneously distributed across a specimen. A non-uniform stress distribution gives rise to bending of crystallites within the specimen and, if the stress inhomogeneity is sufficiently strong, to breaking and splitting into new crystals with new orientations. This process is called polygonization. Generally, when one moves down in an ice core the cross-sectional area of the crystallites grows more or less linearly and then stagnates, i.e. stops growing. Analyses of the ice core at Byrd Station, Antarctica, below 400m depth (Reference Alley, Gow and MeeseAlley and others, 1995) have shown that the stagnation is due to the breaking of the crystallites, i.e. to polygonization. This is a process that changes the lattice orientations in the sense that one part of the crystallite rotates in one direction and the other part rotates in another direction. Whereas grain boundary migration and nucleation correspond to discontinuous changes in the c-axis orientation of a given portion of mass of the polycrystal (consequently being described by the production term ![]() as in Equation (5)), the rotation and polygonization of the crystallites give rise to continuous changes of c-axis orientations and they are therefore described by the transition rate
as in Equation (5)), the rotation and polygonization of the crystallites give rise to continuous changes of c-axis orientations and they are therefore described by the transition rate ![]()
Bending is produced through couples acting on the grain. When a grain (see, e.g., Fig. 2a) is slightly bent, we can roughly imagine that the crystallite has something like ‘two c-axes very close to each other’, say ![]() (Fig. 2b). These three unit vectors
(Fig. 2b). These three unit vectors ![]() build a plane called plane of bending (in Fig. 2a, this plane is simply the plane of the figure). If the crystallite suffers further bending, then the c axes in the ‘two close orientations’
build a plane called plane of bending (in Fig. 2a, this plane is simply the plane of the figure). If the crystallite suffers further bending, then the c axes in the ‘two close orientations’ ![]() should rotate in different directions or at least with different transition
should rotate in different directions or at least with different transition ![]() rates, i.e. this implies that
rates, i.e. this implies that ![]() should not be a constant function of nj and the bending is proportional to the variation of the transition rate
should not be a constant function of nj and the bending is proportional to the variation of the transition rate ![]() with the orientation nj . Obviously, in this simple situation we know that the vector denoting the bending moment must be orthogonal to the bending plane. If we denote the intensity of this bending moment by
with the orientation nj . Obviously, in this simple situation we know that the vector denoting the bending moment must be orthogonal to the bending plane. If we denote the intensity of this bending moment by ![]() and introduce a unit vector
and introduce a unit vector ![]() which is orthogonal to ni and lies in the bending plane, then we immediately conclude that the bending couple required to bend (and eventually polygonize) the crystallite is given by
which is orthogonal to ni and lies in the bending plane, then we immediately conclude that the bending couple required to bend (and eventually polygonize) the crystallite is given by
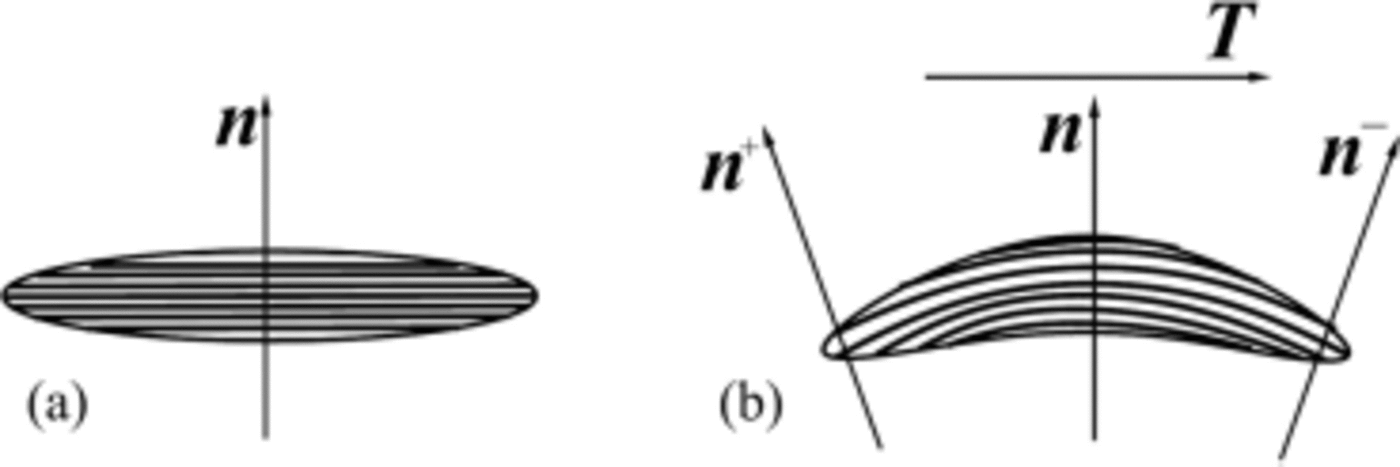
Fig. 2. (a) A single crystal is represented with its basal plane by parallel lines and with its c axis given by the orientation ni
. (b) The crystal is then subjected to a bending moment![]() orthogonal to the plane of the picture, and the bent crystal is represented by the ‘two close orientations’
orthogonal to the plane of the picture, and the bent crystal is represented by the ‘two close orientations’ ![]() orthogonal to the end cross-sections of the bent crystal. To be further bent, the transition rates of the ‘two close orientations’
orthogonal to the end cross-sections of the bent crystal. To be further bent, the transition rates of the ‘two close orientations’ ![]() have to be different:
have to be different: ![]() Furthermore, we denote with
Furthermore, we denote with ![]() a unit vector that is orthogonal to ni
and lies in the bending plane.
a unit vector that is orthogonal to ni
and lies in the bending plane.
where εijk are the components of the permutation tensor.
Besides, it is evident that grain-size D (the characteristic length of the grains) and polygonization are strictly correlated. While a rigorous theory would treat D as an independent variable with the same status as nj , we have not considered this complexity. Instead we treat D, a mean grain-size averaged over all orientations, as a dependent (internal) variable governed by an evolution equation, for which we propose, following Reference JackaJacka and Li (1994):
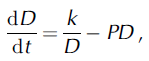
where k and P are constitutive quantities to be determined by experiments. They have the physical interpretation of grain boundary migration rate and of polygonization rate, respectively. The first term on the righthand side of Equation (8) accounts for the usual representation of normal grain growth, and the second term is proportional to the mean size of the crystallites: it is intuitively clear that the larger a grain is, the greater the possibility of its breaking. The simple evolution equation (8) is suitable to simulate the first 1200m grain-size profile of the Byrd ice core once k and P are properly identified: an easy way to do this is to fix the value of the steady-state grain-size (e.g. ![]() )Setting
)Setting ![]() this steady-state value is reached for all values of the non-dimensional factor g (see Fig. 3). Note that P and
this steady-state value is reached for all values of the non-dimensional factor g (see Fig. 3). Note that P and ![]() must be connected, since they are associated with the same phenomenon, but this has not been considered here. It is a future goal of the theory to find this relation, that will give us the possibility to measure
must be connected, since they are associated with the same phenomenon, but this has not been considered here. It is a future goal of the theory to find this relation, that will give us the possibility to measure ![]() from the grain-size profile of an ice core.
from the grain-size profile of an ice core.

Fig. 3. The curves based on Equation (8) fit well the experimental data given for the grain-size of the ice core at Byrd Station. The values k = gk̂ and P = g p̂ with k̂ = 9 mm2ka–1 and p̂ = 0.3ka–1 guarantee that they all reach the same steady state D eq = 6.3mm for each value of the non-dimensional factor g. The figure gives us the physical interpretation of this non-dimensional factor: the velocity in which the grain-size D reaches the steady state D eq.
4. Modelling of Polygonization in a Continuum Theory
In section 3, we introduced the bending couple of polygonization ![]() and concluded that the splitting of a crystallite into two was described by the variation of the transition rate
and concluded that the splitting of a crystallite into two was described by the variation of the transition rate ![]() with the orientation nj . In this section, we discuss how to incorporate these concepts in a continuum theory for ice sheets.
with the orientation nj . In this section, we discuss how to incorporate these concepts in a continuum theory for ice sheets.
Generally, in a continuum theory one assumes that material regions of a body interact with the environment and with each other through volume and surface actions. In Antarctica, the most important volume actions are the gravity acceleration gi , the solar radiation r and the external supply of entropy s. On the other hand, typical surface actions are represented by the Cauchy stress tensor tij and the fluxes of heat qi and entropy ϕi. However, none of these actions can describe polygonization, since the bending couples of polygonization arise from inhomogeneities in internal stresses, which vanish when averaged over a large number of crystallites. This happens owing to the conservation of angular momentum of the polycrystal.
A simple way of overcoming this problem is to ‘dissect’ the polycrystal into many components by considering it a mixture of c-axis orientations, or in other words, a mixture with continuous diversity. In this manner, the bending couples resulting from the interactions of the different ‘constituents’ of this ‘mixture’ can be identified, since each constituent behaves as an open thermomechanical system. Mathematically, this means that there exists an interaction couple ![]() describing the resultant couple on the crystallites with c axes in the nj direction imposed by all the other grains of the aggregate. Unfortunately, this description is not accurate enough, since sub-grain (i.e. very low-angle) interactions are conspicuously different from high-angle interactions. Therefore, it is convenient to split
describing the resultant couple on the crystallites with c axes in the nj direction imposed by all the other grains of the aggregate. Unfortunately, this description is not accurate enough, since sub-grain (i.e. very low-angle) interactions are conspicuously different from high-angle interactions. Therefore, it is convenient to split ![]() into a sum of a high-angle interaction couple
into a sum of a high-angle interaction couple ![]() and a sub-grain interaction couple
and a sub-grain interaction couple ![]() Notice that interactions between crystallites with very close orientations (in particular sub-grains and bent grains) is just what we want to include in a continuum theory, as far as polygonization is concerned. Therefore, from now on we confine our attention to
Notice that interactions between crystallites with very close orientations (in particular sub-grains and bent grains) is just what we want to include in a continuum theory, as far as polygonization is concerned. Therefore, from now on we confine our attention to ![]()
Since the sub-grain couple ![]() describes solely low-angle interactions, that is, those between the material with orientation ni and the mass oriented in its close orientational neighbourhood, we can regard
describes solely low-angle interactions, that is, those between the material with orientation ni and the mass oriented in its close orientational neighbourhood, we can regard ![]() as a kind of ‘contact’ interaction but ‘contact’ in a mathematical sense, i.e., ‘contact’ across a hyper-surface in the orientational space S
2 (see, e.g., the two orientations
as a kind of ‘contact’ interaction but ‘contact’ in a mathematical sense, i.e., ‘contact’ across a hyper-surface in the orientational space S
2 (see, e.g., the two orientations ![]() in Fig. 4b). Of course, a hyper-surface in a two-dimensional space like S
2 is just a curve, whose normal vector (tangent to the spherical surface of S
2) is denoted by
in Fig. 4b). Of course, a hyper-surface in a two-dimensional space like S
2 is just a curve, whose normal vector (tangent to the spherical surface of S
2) is denoted by ![]() (Fig. 4b).
(Fig. 4b).
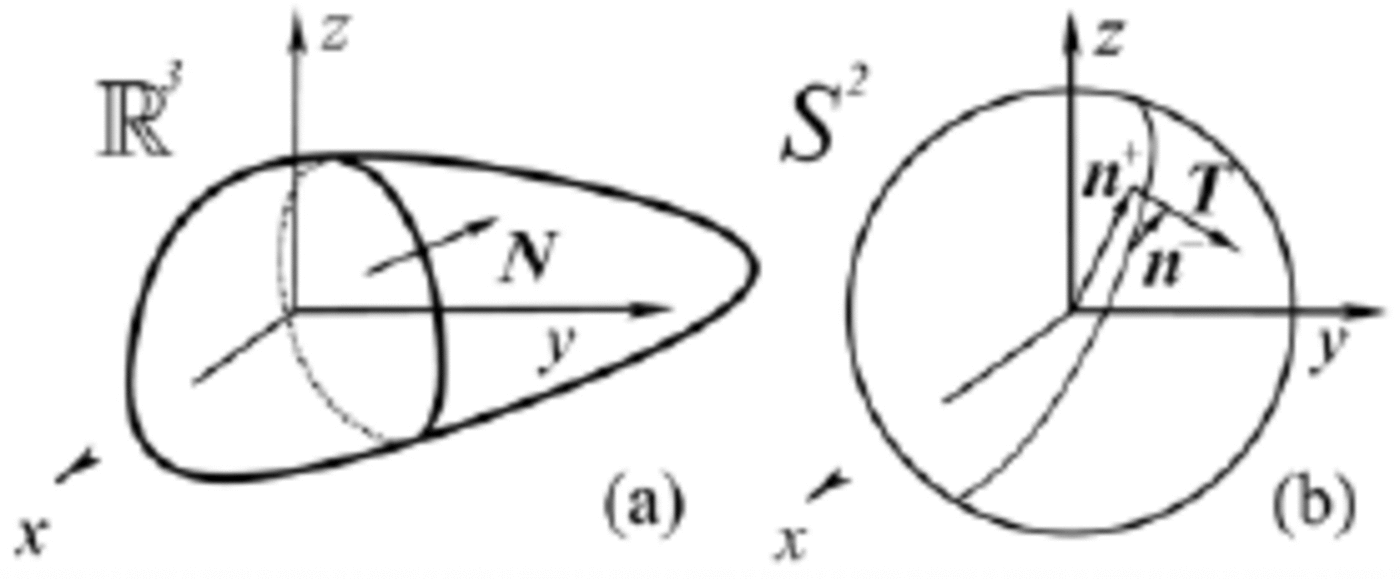
Fig. 4. (a) The contact interactions in the usual three-dimensional space act on the usual surfaces in R3. (b) The contact interactions in the orientational space act on hyper-surfaces in S
2, i.e. on curves that lie on the unit sphere S
2. Here we also show how to represent the ‘two close orientations’ ![]() and the unit vector
and the unit vector ![]() of Figure 2 on the unit sphere S
2.
of Figure 2 on the unit sphere S
2.
Because of the Cauchy theorem (see, e.g., Reference Truesdell, Toupin and FlüggeTruesdell and Toupin, 1960), the ‘contact’ interaction ![]() must be linearly dependent on the normal vector of the respective (hyper-) surface. In other words, there holds the relation
must be linearly dependent on the normal vector of the respective (hyper-) surface. In other words, there holds the relation
The tensor ![]() is the orientational couple stress. It is a fundamental constitutive quantity in the theory of mixtures with continuous diversity (cf. Reference FariaFaria, 2001; Reference Faria, Kremer and HutterFaria and others, 2003), and from the results of section 3 we are now able to prescribe an explicit constitutive representation for it. In section 3 we saw that polygonization is promoted by the bending moment
is the orientational couple stress. It is a fundamental constitutive quantity in the theory of mixtures with continuous diversity (cf. Reference FariaFaria, 2001; Reference Faria, Kremer and HutterFaria and others, 2003), and from the results of section 3 we are now able to prescribe an explicit constitutive representation for it. In section 3 we saw that polygonization is promoted by the bending moment ![]() which generates new c-axis orientations in close proximity. Evidently, such a bending is necessarily associated with the interaction of grains and sub-grains with close c-axis orientations, which, according to the discussion above, is mathematically described in a continuum theory by the interaction couple
which generates new c-axis orientations in close proximity. Evidently, such a bending is necessarily associated with the interaction of grains and sub-grains with close c-axis orientations, which, according to the discussion above, is mathematically described in a continuum theory by the interaction couple ![]() Consequently, by combining Equations (7) and (9) we finally find
Consequently, by combining Equations (7) and (9) we finally find
which is a suitable constitutive representation for ![]() Thus, we have found a clear physical interpretation of the couple stress tensor
Thus, we have found a clear physical interpretation of the couple stress tensor ![]() of the theory of mixtures with continuous diversity: it represents the bending moment associated with polygonization. A constitutive theory for polycrystalline ice should be consistent with Equation (10); in other words, it should yield a representation for
of the theory of mixtures with continuous diversity: it represents the bending moment associated with polygonization. A constitutive theory for polycrystalline ice should be consistent with Equation (10); in other words, it should yield a representation for ![]() which includes the righthand side of Equation (10) as its principal term.
which includes the righthand side of Equation (10) as its principal term.
Finally, we remark that the flux of c axes across the above-mentioned hyper-surface in S
2 with normal vector ![]() is described solely by the scalar product
is described solely by the scalar product ![]() When this product has the same value for all orientations, only a rigid lattice rotation is occurring along the hyper-surface; on the other hand, when this scalar product varies with ni , bending of crystallites might be taking place. Therefore, we conclude that the orientational divergence of
When this product has the same value for all orientations, only a rigid lattice rotation is occurring along the hyper-surface; on the other hand, when this scalar product varies with ni , bending of crystallites might be taking place. Therefore, we conclude that the orientational divergence of ![]() found in the balance equation of mass (Equation (2)) cannot vanish during polygonization.
found in the balance equation of mass (Equation (2)) cannot vanish during polygonization.
5. Conclusions
We have presented a simple continuum model for polygonization including an evolution equation for grain-size. The agreement with the experimental data from the first 1200 m of the the Byrd ice core is obtained only because of a good choice of parameters. A major feature is the demonstration that this microscopic process can be incorporated into a macroscopic model using simple idealization.






